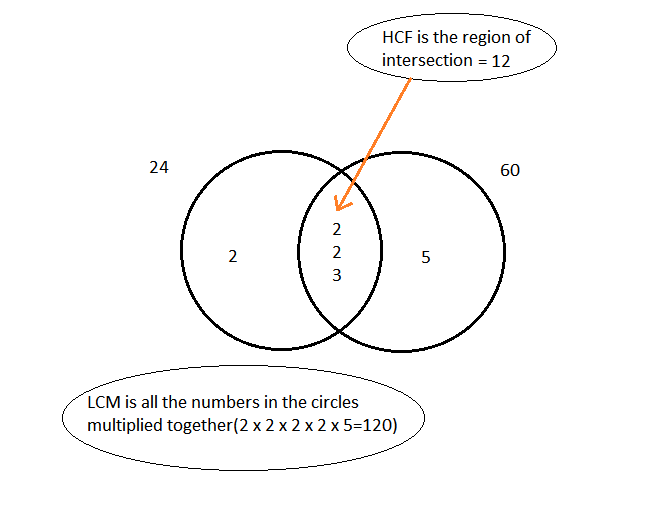What is GCF?

The Greatest Common Factor (also known as GCF, also called greatest common divisor or DCD, also known as highest common factor or HCF) for a pair or set of integers is the largest number that is a factor of each.

Example 1: Find the greatest common factor of 18 and 27 using the listing the factors method.

Solution:

The common factors of 18 and 27 are 1,3, and 9. Among these numbers, 9 is the greatest (largest) number. Thus, the GCF of 18 and 27 is 9. This is written as: \(\operatorname{GCF}(18,27)=9\).

Following are the three methods for finding the greatest common factor of two numbers:

• Listing out common factors: In this method, we list the factors of two or more numbers and find the common factors from the list. Then we select the greatest among all the common factors.
• Prime factorization: In this method, we use a factor tree to find the prime factorization of numbers and list out the common prime factors of the numbers. Then the product of all the common prime factors results in the greatest common factor.
• Division method: Division is a method of grouping objects in equal groups, whereas for large numbers we follow long division, which breaks down a division problem into a series of easier steps. 

GCF by Listing Factors

In this method by marking the common factors, we can choose the greatest one amongst all of them. Let’s look at the example given below:

Example 2: What is the GCF of 30 and 42?

Solution:

• Step 1: List out the factors of each number.
• Step 2: Mark all the common factors.
• Step 3: 6 is the common factor and the greatest one.

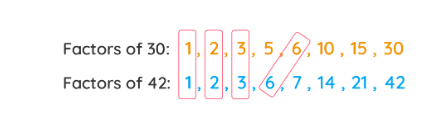
Therefore, GCF of 30 and 42=6 as 6 is the highest number among the common factors (1, 2, 3, and 6).

Finding the greatest common factor by listing factors may be difficult if the numbers are bigger. In such cases, we use the prime factorization method.

GCF by Prime Factorization

Prime factorization is a way of expressing a number as a product of its prime factors, starting from the smallest prime factor of that number. Let’s look at the example given below:

Example 3: What is the GCF of 60 and 90?

Solution:

• Step 1 – Represent the numbers in the prime factored form.
• Step 2 – GCF is the product of the factors that are common to each of the given numbers.

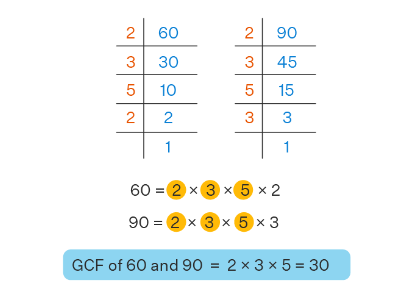
Factors that are common to 60 and 90 are 2, 3, and 5 and their product is 30. Thus, GCF \((60,90)=2^1 \times 3^1 \times 5^1=30\).

Further Explanation:

Factors of 60: List of positive integer factors of 60 that divides 60 without a remainder.
\(1,2,3,4,5,6,10,12,15,20,30\)

Factors of 90: List of positive integer factors of 90 that divides 60 without a remainder.
\(1,2,3,5,6,9,10,15,18,30,45\)

Final Step: Biggest Common Factor Number
We found the factors and prime factorization of 60 and 90. The biggest common factor number (which is 30) is the GCF number. So the greatest common factor 60 and 90 is 30.

GCF by Division Method (two numbers)

Division is a method of grouping objects in equal groups, whereas for large numbers we follow long division, which breaks down a division problem into a series of easier steps. The greatest common factor (GCF) of a set of whole numbers is the largest positive integer that divides all the given numbers, without leaving any remainder. Let’s look at the example given below:

Example 4: Find the GCF of 198 and 360 using the division method.

Solution:

Among the given two numbers, 360 is the larger number and 198 is the smaller number.

• Step 1: Divide the larger number by the smaller number using long division.
• Step 2: If the remainder is 0, then the divisor is the GCF. If the remainder is not 0, then make the remainder of the above step as the divisor and the divisor of the above step as the dividend and perform long division again.
• Step 3: If the remainder is 0, then the divisor of the last division is the GCF. If the remainder is not 0, then we have to repeat step 2 until we get the remainder 0.

Therefore, the GCF of the given two numbers is the divisor of the last division. In this case, the divisor of the last division is 18. Therefore, the GCF of 198 and 360 is 18. This method is the most appropriate method for finding GCF of large numbers.

GCF by Division Method (three numbers)

Let us see how to use the division method to find the greatest common factor of three numbers. In order to find the GCF of three numbers by long division, the following steps are to be followed:

• Step 1: First, we will find the GCF of two of the numbers.
• Step 2: Next, we will find the GCF of the third number and the GCF of the first two numbers.

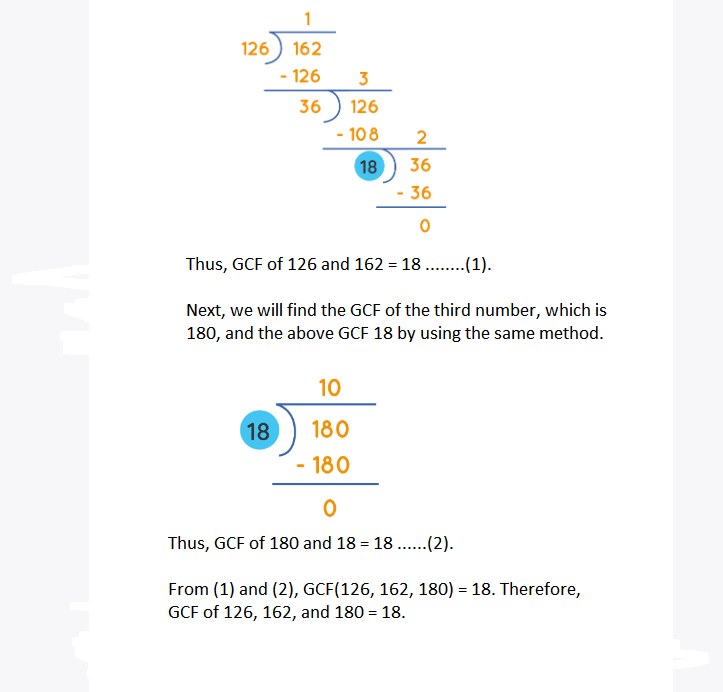
Example 5:  Find the GCF of 126, 162, and 180.

Solution:

First, we will find the GCF of the two numbers 126 and 162. [You can choose any two numbers out of the given three numbers]

Example 6: Find the GCF of 6, 12, and 36 by using the listing factors method.

Solution:

The given numbers are 6, 12, and 36. We will find the factors of each of these numbers. Then, circle the common factors.

Factors of \(6 = 1, 2, 3, 6\)
Factors of \(12 = 1, 2, 3, 4, 6, 12\)
Factors of \(36 = 1, 2, 3, 4, 6, 9,12,18,36\)

In this example, 1, 2, 3, and 6 are all common factors of 6, 12, and 36. Out of all these common factors, 6 is the greatest, and hence, GCF(6,12,36) = 6.

Example 7: Find the GCF of 168, 252, and 288 by the prime factorization method.

Solution:

The given numbers are 168, 252, and 288. We will find the prime factorization of each of these numbers.

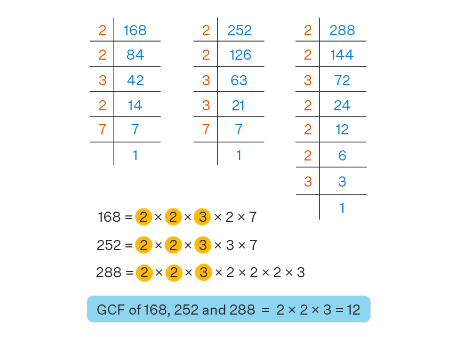
Thus, GCF \((168,252,288)=2 \times 2 \times 3=2^2 \times 3^1\). The GCF of these three numbers will be the product of the common prime factors of all three numbers. Thus, GCF of 168,252 and \(288=2^2 \times 3^1=\) 12.

Example 8:  Find the GCF of 9000 and 980 using the division method.

Solution:

Among the given numbers, 9000 is the largest, and 980 is the smallest. We will divide the larger number by the smaller number. Next, we will make the remainder as the divisor and the last divisor as the dividend and divide again. We will repeat this process until the remainder is 0.

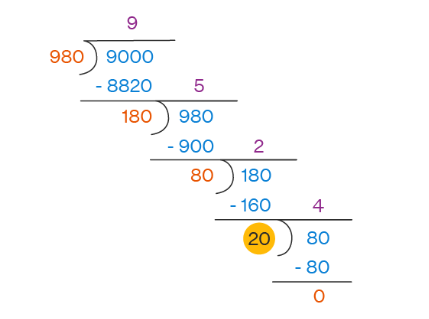
Therefore, the GCF of 9000 and 980 is 20.

What is LCM?

The Least Common Multiple (also known as LCM) is the smallest positive multiple that is common to a pair or set of numbers. A multiple is a value we get when we multiply a number by another number. Like 4 is a multiple of 2, as we multiply 2 by 2, we get 4.

Example 9: Find the least common multiple of 4 and 5. 

Solution:

Multiples of 4 are \(4,8,12,16,20,24,28,32,36,40,44, \ldots\)
Multiples of 5 are \(5,10,15,20,25,30,35,40,45,50,55, \ldots\)
The common multiples have been encircled below:

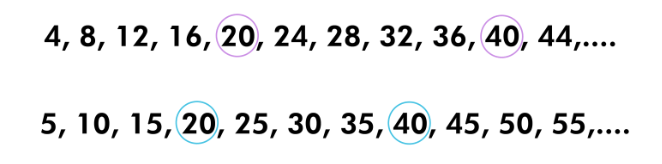
The common multiples of 4 and 5 are 20, 40, and so on. The least of these common multiples is 20. Hence the LCM of 4 and 5 is 20.

How to Find LCM?

LCM of numbers can be calculated using various methods. There are 3 methods to find the least common multiple of two numbers.

• LCM by Listing Method: In this method, we list the multiples of two or more numbers and find out the common multiples from the list. Then, the least among all common multiples is the least common multiple.
• LCM by Prime Factorization Method: In this method, we use the factor tree to find the prime factorization of the numbers. List each different factor where it appears the greatest number of times and multiply them to get the least common multiple.
• LCM using Division Method: In order to find the LCM by division method, we divide the numbers by a common prime number, and these prime factors are used to calculate the LCM of those numbers. 

LCM by Listing Method

We can find out the common multiples of two or more numbers by listing their multiples. Out of these common multiples, the least common multiple is considered and the LCM of two given numbers can thus be calculated. To calculate the LCM of the two numbers X and Y by the listing method, we use the steps given below:

• Step 1: List the first few multiples of X and Y.
• Step 2: Mark the common multiples from the multiples of both numbers.
• Step 3: Select the smallest common multiple. That lowest common multiple is the LCM of the two numbers.

Example 10: Find the LCM of 10 and 12.

Solution:

To calculate the LCM of 10 and 12 by listing out the common multiples, we can follow the given below steps:

• Step 1: List a few multiples of 10 (10, 20, 30, 40, 50, 60, 70, . . . ) and 12 (12, 24, 36, 48, 60, 72, . . . . )
• Step 2: The common multiples from the multiples of 10 and 12 are 60, 120, . . .
• Step 3: The smallest common multiple of 10 and 12 is 60.

Therefore the least common multiple of 10 and 12 = 60.

LCM by Prime Factorization Method

To calculate the LCM of two numbers using the prime factorization method, we use the steps given below:

• Step 1: Find the prime factors of the given numbers by repeated division method.
• Step 2: Write the numbers in their exponent form. Find the product of only those prime factors that have the highest power.
• Step 3: The product of these factors with the highest powers is the LCM of the given numbers.

Let us learn this method using the example given below.

Example 11: Find the least common multiple (LCM) of 60 and 90 using prime factorization.

Solution:

Let us find the LCM of 60 and 90 using the prime factorization method.

Step 1: The prime factorization of 60 and 90 are: \(60=2 \times 2 \times 3 \times 5\) and \(90=2 \times 3 \times 3 \times 5\)
Step 2: If we write these prime factors in their exponent form it will be expressed as, \(60=2^2 \times 3^1 \times 5^1\) and \(90=2^1 \times 3^2 \times 5^1\)
Step 3: Now, we will find the product of only those factors that have the highest powers among these. This will be, \(2^2 \times 3^2 \times 5^1=4 \times 9 \times 5\) \(=180\)
Therefore, LCM of 60 and \(90=180\).

Example 12: Find LCM of 12 and 18 by prime factorization method.

Solution:

Prime factorization of 12 and 18 is \((2 \times 2 \times 3)=2^2 \times 3^1\) and \((2 \times 3 \times 3)=2^1\) \(\times 3^2\) respectively.
LCM of 12 and 18 can be obtained by multiplying prime factors raised to their respective highest power, i.e. \(2^2 \times 3^2=36\).
Hence, the LCM of 12 and 18 by prime factorization is 36.

LCM by Division Method

In order to find the LCM by division method, we divide the numbers by a common prime number, and these prime factors are used to calculate the LCM of those numbers. Let us understand this method using the steps given below:

• Step 1: Find a prime number that is a factor of at least one of the given numbers. Write this prime number on the left of the given numbers.
• Step 2: If the prime number in step 1 is a factor of the number, then divide the number by the prime and write the quotient below it. If the prime number in step 1 is not a factor of the number, then write the number in the row below as it is. Continue the steps until 1 is left in the last row.

Let us learn this method using the example given below.

Example 13: Find the least common multiple (LCM) of 6 and 15 using the division method.

Solution:

Let us find the least common multiple (LCM) of 6 and 15 using the division method using the steps given below.

• Step 1: 2 is the smallest prime number and it is a factor of 6. Write 2 on the left of the two numbers. For each number in the right column, continue finding out prime numbers which are their factors.
• Step 2: 2 divides 6 but it is not a factor of 15, so we write the number 15 in the row below as it is. Continue the steps until 1 is left in the last row. Then, we divide 3 and 15 by 3. This gives us 1 and 3. Now, again we write 5 on the left side and we finally get 1, 1 as the quotient in the last row.
• Step 3: Then we multiply these numbers on the left. The LCM is the product of all these prime numbers LCM of 6 and 15 is, 2 × 3 × 5 = 30.

Note: Though we have three methods to find the least common multiple, the division method is the most common and easy method that we use. 

LCM Formula 

If \(a\) and \(b\) are the two integers then the formula for their least common multiple is given as:
\(
\operatorname{LCM}(a, b)=(a \times b) / H C F(a, b)
\)

Example 14: Find L.C.M. of 10 and 20.

Solution:

We know, for given two integers \(a\) and \(b\),
L.C.M. \((a, b)=(a \times b) / \operatorname{GCD}(a, b)\)
Therefore, L.C.M. \((10,20)=\left(10 \times 20\right) / \operatorname{HCF}(10,20)\)
The greatest common divisor for 10 and 20 is 10.
Thus, L.C.M. \((10,20)=200 / \operatorname{HCF}(10)\)
L.C.M. \((10,20)=20\)

LCM Formula for Fractions

The formula to find the LCM of fractions is given by:

L.C.M. = L.C.M Of Numerator/H.C.F Of Denominator

Example 15: Find LCM of 5/8,1/6.

Solution:

In the given fractions LCM of Numerators means LCM of 5,1.
Least Common Multiple of Numerators i.e. LCM of 5,1 is 5.

HCF of Denominators means HCF of 8,6 as per the given fractions.
HCF of 8,6 is 2 as it is the largest common factor for these numbers.
The formula to find the LCM of fractions is given by:

L.C.M. = L.C.M Of Numerator/H.C.F Of Denominator

\(
\operatorname{LCM}(5 / 8,1 / 6)=5 / 2
\)

Relationship Between LCM and HCF

\(
\operatorname{LCM}(a, b) \times \operatorname{HCF}(a, b)=a \times b
\)
or, Product of the two numbers \(=\) LCM of the numbers \(\times\) HCF of the numbers

Example 16: If HCF of two numbers,12 and 30, is 6. Then find their LCM. 

Solution:

\(\operatorname{LCM}(a, b)=a \times b / \operatorname{HCF}(a, b)\) [By the formula]
Therefore,
\(
\begin{aligned}
& \operatorname{LCM}(12,30)=(12 \times 30) / 6 \quad \text { [given] } \\
& \operatorname{LCM}(12,30)=60
\end{aligned}
\)

Difference Between LCM and HCF

LCM	HCF
The least common multiple of two or more numbers is the smallest number among all common multiples of the given numbers.	The highest common factor of two or more numbers is the highest number among all the common factors of the given numbers.
LCM of two or more prime numbers is always the product of those numbers.	HCF of two or more prime numbers is 1 always.
LCM of two or more numbers is always greater than or equal to each of the numbers.	HCF of two or more numbers is always less than or equal to each of the numbers.

Example 17: What is the smallest number when divided by the digits 5, 7, 9, and 12 gives the same remainder of 3 in every case?

Solution:

To find the least common multiple of the divisors and add the remainder.
LCM (5, 7, 9, 12) = 1260
The required number = 1260 + 3 = 1263

Example 18: What is the greatest 4-digit number that is divisible by exactly by 15, 21, and 28?

Solution:

The greatest 4-digit number is 9999.
LCM (15, 21, 28) = 420
Divide 9999 by 420, 339 is the remainder.
The required number is 9999 – 339 = 9660.

Example 19: Find the LCM 4,6 and 12.

Solution:

First, write the common multiples of all three numbers.
Common Multiples of 4 : 4,8,12,16,20,24,28,…..
Common Multiples of 6: 6,12,18,24,30,36,42…..
Common Multiples of 12: 12,24,36,48,60,72,….
From the above-given multiples of 4, 6, and 12, you can see, 12 is the smallest common multiple.
Therefore, LCM. of 4, 6, and 12 is 12.

Example 20:  The traffic policemen at 3 varied positions on the ground blow a whistle succeeding every 42 seconds, 60 seconds, and 78 seconds respectively. If all of them blow at the same time at 9:30 hours, find the time interval at which they whistle again together.

Solution:

The time interval at which they whistle again together = least common multiple of the separate whistleblowing pattern.
LCM \((42, 60, 78) = 2 \times 3 \times 7 \times 10 \times 13 = 5460\)
The policemen will blow the whistle again at the same time interval after 5460 seconds.
On conversion into hours and minutes, it is 1 hour 31 minutes.
In terms of time, it is 11:01:00 hours.

Example 21:  What is the greatest number when divided by the numbers 6, 7, and 8 leaves behind a remainder number 3, however when divided by the number 9 has no remainder.

Solution:

LCM (6, 7, 8) = 168
The number is of arrangement 168n + 3.
168n + 3 must be divisible by the number 9.
The given number is divisible by the number 9 when the total of its digits is a multiple of the number 9.
When n = 1, the number is 168 + 3 = 171, and the total of the digits is number 9.
The required number is 171.

Example 22: 2 digits are in the ratio 2:3. The product of the least common multiple and highest common factors is 294, what are the numbers?

Solution:

Assume the ratio that is common to be \(n\).
Let the numbers \(2 {n}\) and \(3 {n}\).
Product of assumed numbers = product of least common multiple and highest common factor
\(
\begin{aligned}
& \Rightarrow 2 n \times 3 n=294 \\
& \Rightarrow n^2=49 \\
& \Rightarrow n=7
\end{aligned}
\)
The numbers are \(2 n=2 \times 7=14\) and \(3 n=3 \times 7=21\).
The required numbers are 14 and 21.

Example 23: Sam writes a poem every 2 days and Annie writes a poem every 3 days. Today both Annie and Sam are writing poems. After how many days do they write a poem together again?

Solution:

You are given the number of days Sam and Annie take to write a poem. The LCM of the number of days will give us the time when they will write together again from this day. So, let’s find the LCM of 2 and 3.
Multiples of 2 are 2, 4, 6, 8, 10, 12, 14, 16, 18, 20.
Multiples of 3 are 3, 6, 9, 12, 15, 18, 21, 24, 27, 30.
The common multiples of 2 and 3 are 6,12 and 18. The least of these common factor is 6
so, the LCM of 2 and 3 is 6.
Hence, Sam and Annie will write together again on the 6th day from the current day.

Example 24: A merchant has 120 liters and 180 liters of two kinds of oil. He wants to sell the oil by filling the two kinds in tins of equal volumes. Find the greatest volume of such a tin.

Solution:

The given two quantities 120 and 180 can be divided by 10, 20,… exactly. That is, both kinds of oils can be sold in tins of equal volume of 10, 20,… liters. But, the target of the question is, the volume of oil filled in tins must be greatest.
So, we have to find the largest number which exactly divides 120 and 180. That is the highest common factor (HCF) of (120, 180).
HCF (120, 180) = 60 liters
The 1st kind 120 liters is sold in 2 tins of volume 60 liters in each tin.
The 2nd kind 180 liters is sold in 3 tins of volume 60 liters in each tin.
Hence, the greatest volume of the tin is 60 liters.

Example 25: Find the least number of square tiles by which the floor of a room of dimensions 16.58 m and 8.32 m can be covered completely.

Solution:

We require the least number of square tiles. So, each tile must be of maximum dimension.
To get the maximum dimension of the tile, we have to find the largest number which exactly divides 16.58 and 8.32. That is the highest common factor (HCF) of (16.58, 8.32).
To convert meters into centimeters, we have to multiply by 100.
16.58 ⋅ 100 = 1658 cm
8.32 ⋅ 100 = 832 cm
HCF (1658, 832) = 2 cm
Hence the side of the square tile is 2 cm.
Required no. of tiles:
\(
\begin{gathered}
=(\text { Area of the floor }) /(\text { Area of a square tile }) \\
=(1658 \cdot 832) /(2 \cdot 2) \\
=344,864
\end{gathered}
\)
Hence, the least number of square tiles required is 344,864.

Example 26: A wine seller had three types of wine. 403 liters of 1st kind, 434 liters of 2nd kind and 465 liters of 3rd kind. Find the least possible number of casks of equal size in which different types of wine can be filled without mixing.

Solution:

For the least possible number of casks of equal size, the size of each cask must be of the greatest volume.
To get the greatest volume of each cask, we have to find the largest number which exactly divides 403, 434 and 465. That is the highest common factor (HCF) of (403, 434, 465).
HCF (403, 434, 465) = 31 liters
Each cask must be of the volume 31 liters.
Required number casks:
= 403/31 + 434/31 + 465/31
= 13 + 14 + 15
= 42
Hence, the least possible number of casks of equal size required is 42.

Example 27: Six bells commence tolling together and toll at intervals of 2, 4, 6, 8 10, and 12 seconds respectively. In 30 minutes, how many times do they toll together? (excluding the one at the start)

Solution:

For example, let the two bells toll after every 3 and 4 seconds respectively.
Then the first bell tolls after every 3, 6, 9,12 seconds…
Like this, the second bell tolls after every 4, 8, 12 seconds…
So, if the two bell toll together now, again they will toll together after 12 seconds. This 12 is the least common multiple (LCM) of 3 and 4.
The same thing happened in our problem. To find the time, when they will all toll together, we have to find the LCM of (2, 4, 8, 6, 10, 12).
LCM (2, 4, 8, 6, 10, 12) is 120
That is, 120 seconds or 2 minutes.
So, after every two minutes, all the bell will toll together.
For example, in 10 minutes, they toll together :
10/2 = 5 times
That is, after 2, 4, 6, 8, 10 minutes. It does not include the one at the start.
Similarly, in 30 minutes, they toll together :
= 30/2
= 15 times (excluding one at the start).

Example 28: Find the least number of soldiers in a regiment such that they stand in rows of 15, 20, 25 and form a perfect square.

Solution:

To answer this question, we have to find the least number which is exactly divisible by the given numbers 15, 20 and 25. That is the least common multiple of (15, 20, 25).
LCM (15, 20, 25) = 300
So, we need 300 soldiers such that they stand in rows of 15, 20 , 25.
But, it has to form a perfect square (as per the question).
To form a perfect square, we have to multiply 300 by some number such that it has to be a perfect square.
To make 300 as perfect square, we have to multiply 300 by 3.
Then, it is 900 which is a perfect square.
Hence, the least number of soldiers required is 900.

Example 29: Sam is preparing dinner plates. He has 12 pieces of chicken and 16 rolls. If he wants to make all the plates identical without any food left over, what is the greatest number of plates Sam can prepare?

Solution:

To make all the plates identical and find the greatest number of plates, we have to find the greatest number which can divide 12 and 16 exactly.
That is nothing but H.C.F. of 12 and 16.
H.C.F of (12, 16) = 4
That is, 12 pieces of chicken would be served in 4 plates at the rate of 3 pieces per plate.
And 16 rolls would be served in 4 plates at the rate of 4 rolls per plate.
In this way, each of the 4 plates would have 3 pieces of chicken and 4 rolls. And all 4 plates would be identical.
Hence, the greatest number of plates Sam can prepare is 4.

Example 30: The drama club meets in the school auditorium every 2 days, and the choir meets there every 5 days. If the groups are both meeting in the auditorium today, then how many days from now will they next have to share the auditorium?

Solution:

If the drama club meets today, again they will meet after 2, 4, 6, 8, 10, 12…. days.
Like this, if the choir meets today, again they will meet after 5, 10, 15, 20 …. days.
From the explanation above, If both drama club and choir meet in the auditorium today, again, they will meet after 10 days.
And also, 10 is the L.C.M of (2, 5).
Hence, both groups will share the auditorium after ten days.

Example 31: John is printing orange and green forms. He notices that 3 orange forms fit on a page, and 5 green forms fit on a page. If John wants to print the exact same number of orange and green forms, what is the minimum number of each form that he could print?

Solution:

The condition of the question is, the number of orange forms taken must be equal to the number of green forms taken.
Let us assume that he takes 10 orange and 10 green forms.
10 green forms can be fit exactly on 2 pages at 5 forms/page. But,10 orange forms can’t fit exactly on any number of pages.
Because 3 orange forms can fit exactly on a page. In 10 orange forms, 9 forms can be fit exactly on 3 pages and 1 form will be remaining.
To get the number of forms in orange and green which can fit exactly on some number of pages, we have to find L.C.M of (3,5). That is 15.
15 orange forms can be fit exactly on 5 pages at 3 forms/page.
15 green forms can be fit exactly on 3 pages at 5 forms/page.
Hence, the smallest number of each form that could be printed is 15.

Example 32: Lily has collected 8 U.S. stamps and 12 international stamps. She wants to display them in identical groups of U.S. and international stamps, with no stamps left over. What is the greatest number of groups Lily can display them in?

Solution:

To make all the groups identical and find the greatest number of groups, we have to find the greatest number which can divide 8 and 12 exactly.
That is nothing but H.C.F. of 8 and 12.
H.C.F of (8, 12) = 4
That is, 8 U.S stamps can be displayed in 4 groups at 2 stamps/group.
And 12 international stamps can be displayed in 4 groups at 3 stamps/group.
In this way, each of the 4 groups would have 2 U.S. stamps and 3 international stamps. And all 4 groups would be identical.
Hence, the greatest number of groups that can be made is 4

Example 33: Abraham has two pieces of wire, one 6 feet long and the other 12 feet long. If he wants to cut them up to produce many pieces of wire that are all of the same length, with no wire left over, what is the greatest length, in feet, that he can make them?

Solution:

When the two wires are cut into small pieces, each piece must of the same length, and also it has to be the possible greatest length.
6 feet wire can be cut into pieces of (2, 2, 2) or (3, 3)
12 feet wire can be cut into pieces of (2, 2, 2, 2, 2, 2 ) or (3, 3, 3, 3)
The length of each small piece must be of the possible greatest length.
To find the possible greatest length, we have to find the greatest number which can divide both 6 and 12. That is H.C.F of (6, 12).
H.C.F of (6, 12) = 6.
Hence, the greatest length of each small piece will be 6 ft.
(That is, 6 feet of wire is not cut into small pieces and it is kept as it is. Only the 12 feet wire is cut into 2 pieces at the length of 6 feet/piece)

HCF and LCM using Venn Diagrams

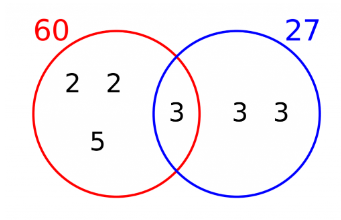
For large numbers, the easiest way to find the HCF and LCM is to use Venn diagrams. For example, let us Find the HCF and LCM of $60$ and $27$.

Step 1: We first need the prime factorization of both numbers, in which we would use factor trees. However, we already have the prime factorization of $60$, which is

\(
60=2 \times 2 \times 3 \times 5=2^2 \times 3 \times 5 \text { and } 27=3 \times 3 \times 3=3^3
\)

Step 2: Now, we draw a Venn diagram where one circle is for prime factors of $60$ and one circle is for prime factors of $27$.

Step 3: Looking at the list of factors, if one is shared by both numbers, then we will put it in the intersection and remove it from both lists (3 is shared and is removed from the list).

\(
60=2 \times 2  \times 5 \text { and } 27= 3 \times 3
\)

Step 4: Any factors that are not shared, we put them in their respective circles.

Step 5: To find the HCF, we multiply the numbers in the intersection (these are the factors that are common between both numbers). Here there is only one number, so HCF $=3$

Step 6: To find the LCM, we multiply all of the numbers in the Venn diagram together. So

LCM $=2\times 2\times 5\times 3\times 3\times 3$

Example 34: Find the HCF and LCM of 24 and 60. 

Solution:

Here is the shortcut to find HCF and LCM of 24 and 60.
That is, using a Venn diagram.
The Venn diagram shown below clearly illustrates, how to find HCF and LCM of 24 and 60 easily.
The following steps will be useful to find HCF and lcm using Venn diagram.
Step 1:
We have to decompose the given numbers into prime factors.
In the example shown above, we have the two numbers 24 and 60.
24 = 2 x 2 x 2 x 3
60 = 2 x 2 x 3 x 5
Step 2:
Now, we have to draw two circles as shown above. The first one is for 24 and the second one is for 60.
Step 3:
In the prime factors of 24 and 60, strike out the common factor (which is found in both 24 and 60) and write that one in the common region (intersection part) of two circles.
Step 4:
If we find a prime factor that is in 24 but not in 60, strike out that one and it has to be written in the circle of 24 (not in the common region).
If we find a prime factor that is in 60 but not in 24, strike out that one and it has to be written in the circle of 60 (not in the common region).
This process has to be continued until all the prime factors of both 24 and 60 are struck out.
Step 5:
Once all the prime factors of both 24 and 60 are struck out, we have to do the following work to get HCF and LCM.
HCF = Multiply the prime factors which are found in the common region (Intersection part).
So, the HCF of 24 and 60 is
= 2 x 2 x 3
= 12
LCM = Multiply all the prime factors which are found in the two circles (Including the prime factors in the common region)
So, the LCM of 24 and 60 is
= 2 x 2 x 2 x 3 x 5
= 120