Free Body Diagram Concept & its Application in Problem Solving
Free-body diagrams are diagrams used to show the relative magnitude and direction of all forces acting upon an object in a given situation. In a free-body vector diagram the size of the arrow in a free-body diagram reflects the magnitude of the force while the direction of the arrow denotes the direction in which the force acts. An example of a free-body diagram is shown at the right.
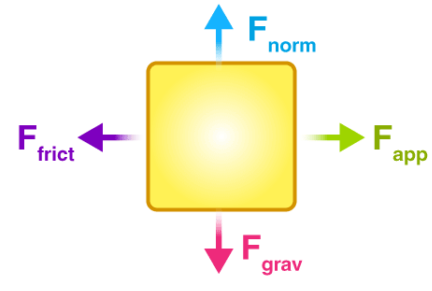
The free-body diagram above depicts four forces acting upon the object. Objects do not necessarily always have four forces acting upon them. There will be cases in which the number of forces depicted by a free-body diagram will be one, two, or three. There is no hard and fast rule about the number of forces that must be drawn in a free-body diagram. The only rule for drawing free-body diagrams is to depict all the forces that exist for that object in the given situation. Thus, to construct free body diagrams, it is extremely important to know the various types of forces.
Types of Forces
A force is a push or pull acting upon an object as a result of its interaction with another object. they are divided into contact and non-contact forces.
Contact Forces
- Frictional Force
- Tension Force
- Normal Force
- Air Resistance Force
- Applied Force
- Spring Force
Action-at-a-Distance Forces
- Gravitational Force
- Electrical Force
- Magnetic Force
Applied Force \(\mathrm{F}_{\mathrm{app}}\): An applied force is a force that is applied to an object by a person or another object. If a person is pushing a desk across the room, then there is an applied force acting upon the object. The applied force is the force exerted on the desk by the person.
Gravity Force (also known as weight) \(\mathrm{F}_{\text {grav }}\): The force of gravity is the force with which the earth, moon, or other massively large object attracts another object towards itself. By definition, this is the weight of the object. All objects upon earth experience a force of gravity that is directed “downward” towards the center of the earth. The force of gravity on earth is always equal to the weight of the object as found by the equation:
\(
\begin{gathered}
\text { Fgrav }=\mathrm{m} \times \mathrm{~g} \\
\text { where } \mathrm{g}=9.8 \mathrm{~N} / \mathrm{kg} \text { (on Earth) } \\
\text { and } \mathrm{m}=\text { mass (in } \mathrm{kg} \text { ) }
\end{gathered}
\)

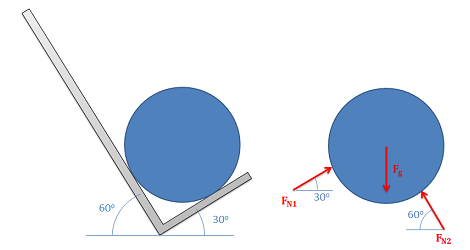
Normal Force or Reaction force \(\mathrm{F}_{\text {norm }}\): The normal force is the support force exerted upon an object that is in contact with another stable object. For example, if a book is resting upon a surface, then the surface is exerting an upward force upon the book in order to support the weight of the book. On occasions, a normal force is exerted horizontally between two objects that are in contact with each other. For instance, if a person leans against a wall, the wall pushes horizontally on the person.
Normal forces always act perpendicular to the surfaces in contact. The barrel in the hand truck shown on the left has a normal force at each contact point.
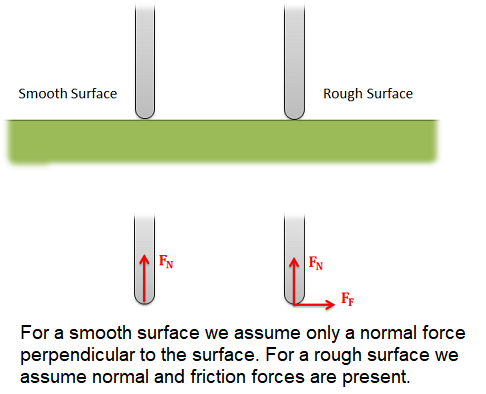
Friction Force \(F_{\text {frict }}\): The friction force is the force exerted by a surface as an object moves across it or makes an effort to move across it. There are at least two types of friction force – sliding and static friction. Though it is not always the case, the friction force often opposes the motion of an object. For example, if a book slides across the surface of a desk, then the desk exerts a friction force in the opposite direction of its motion. Friction results from the two surfaces being pressed together closely, causing intermolecular attractive forces between molecules of different surfaces. As such, friction depends upon the nature of the two surfaces and upon the degree to which they are pressed together. The maximum amount of friction force that a surface can exert upon an object can be calculated using the formula below:
\(
F_{\text {frict }}=\mu \times F_{\text {norm }}
\)
- For smooth surfaces we assume that there is no friction force.
- For rough surfaces we assume that the bodies will not slide relative to one another, no matter what. In this case, the friction force is always just large enough to prevent this sliding.
Air resistance Force \(\mathrm{F}_{\text {air }}\): The air resistance is a special type of frictional force that acts upon objects as they travel through the air. The force of air resistance is often observed to oppose the motion of an object. This force will frequently be neglected due to its negligible magnitude (and due to the fact that it is mathematically difficult to predict its value). It is most noticeable for objects that travel at high speeds (e.g., a skydiver or a downhill skier) or for objects with large surface areas.
Tension Force \(F_{\text {tens }}\): The tension force is the force that is transmitted through a string, rope, cable or wire when it is pulled tight by forces acting from opposite ends. The tension force is directed along the length of the wire and pulls equally on the objects on the opposite ends of the wire.
Cables, wires or ropes attached to the body will exert a tension force on the body in the direction of the cable. These forces will always pull on the body, as ropes, cables and other flexible tethers cannot be used for pushing.

Spring Force \(\mathrm{F}_{\text {spring }}\): The spring force is the force exerted by a compressed or stretched spring upon any object that is attached to it. An object that compresses or stretches a spring is always acted upon by a force that restores the object to its rest or equilibrium position. For most springs (specifically, for those that are said to obey “Hooke’s Law”), the magnitude of the force is directly proportional to the amount of stretch or compression of the spring.
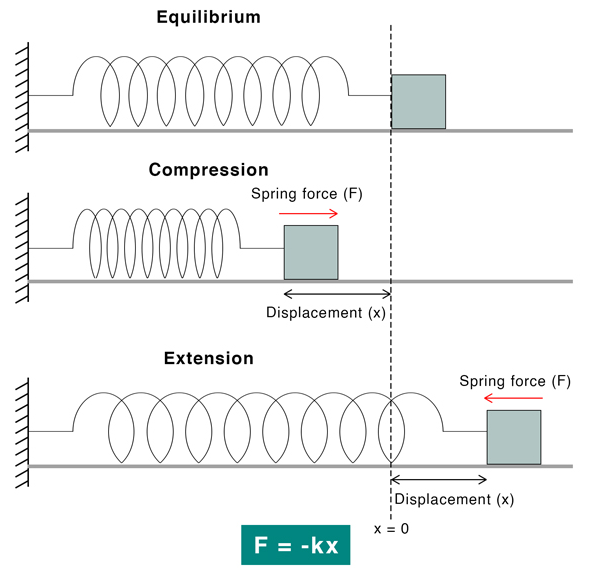
The spring force can be quantified using Hooke’s law. According to this law, when a spring stresses or compresses, the restoring force \(F\) is proportional to the displacement \(x\).
\(F \propto x\)
Spring Force Formula: \(F=-k x\) (k is a spring constant)
The negative sign is because the force is opposite to the displacement, that is, the force displaces the spring from its equilibrium position. This equation applies to both compression and extension of spring.
The magnitude of the spring constant is given by,
\(
k=F / X
\)
Suppose \(F=1 \mathrm{~N}\) and \(x=1 \mathrm{~m}\), then
\(
k=1 \mathrm{~N} / 1 \mathrm{~m}=1 \mathrm{~N} / \mathrm{m}
\)
The spring constant is defined as the force required to displace the spring by one meter. It has a unit of Newton per meter \((\mathrm{N} / \mathrm{m})\) and a dimension given by \(\mathrm{MT}^{-2}\).
How to Make a Free Body Diagram (FBD)?
In this section, we will explain the step-by-step procedure of drawing a free body diagram: You can draw a free-body diagram of an object following these 3 steps:
- Sketch what is happening
- Determine the forces that act on the object
- Draw the object in isolation with the forces that act on it
Example 1: A box is pushed up an incline with friction which makes an angle of \(20^{\circ}\) with the horizontal. Let’s draw the free-body diagram of the box.
Answer: Step-1: The first step is to sketch what is happening:
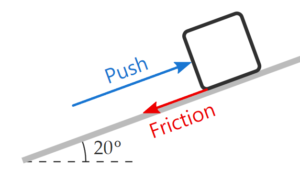
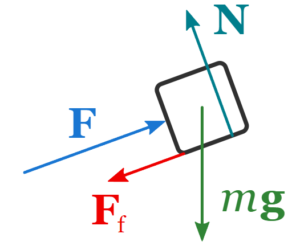
Step-2: The next step is to look at the sketch, and enumerate all the forces to which the box is subject:
- the upward push, \(\mathbf{F}\)
- the force of friction, \(\mathbf{F}_{\mathrm{f}}\)
- the normal force, \(\mathbf{N}\)
- and the force of gravity, \(m \mathbf{g}\)
Step-3: The final step is to draw the box with the 4 forces that act on it:
Example 2: (a) A book is at rest on a tabletop. Diagram the forces acting on the book
(b) A gymnast holding onto a bar, is suspended motionless in mid-air. The bar is supported by two ropes that attach to the ceiling. Diagram the forces acting on the combination of gymnast and bar.
(c) An egg is free-falling from a nest in a tree. Neglect air resistance. Diagram the forces acting on the egg as it is falling.
(d) A flying squirrel is gliding (no wing flaps) from a tree to the ground at constant velocity. Consider air resistance. Diagram the forces acting on the squirrel.
(e) A rightward force is applied to a book in order to move it across a desk with a rightward acceleration. Consider frictional forces. Neglect air resistance. Diagram the forces acting on the book.
(f) A rightward force is applied to a book in order to move it across a desk at constant velocity. Consider frictional forces. Neglect air resistance. Diagram the forces acting on the book.
(g) A college student rests a backpack upon his shoulder. The pack is suspended motionless by one strap from one shoulder. Diagram the vertical forces acting on the backpack.
(h) A skydiver is descending with a constant velocity. Consider air resistance. Diagram the forces acting upon the skydiver.
(i) A force is applied to the right to drag a sled across loosely packed snow with a rightward acceleration. Neglect air resistance. Diagram the forces acting upon the sled.
(j) A football is moving upwards towards its peak after having been booted by the punter. Neglect air resistance. Diagram the forces acting upon the football as it rises upward towards its peak.
(k) A car is coasting to the right and slowing down. Neglect air resistance. Diagram the forces acting upon the car.
Answer: FBD for each question drawn in the figure below.

Example 3: Draw the free-body diagram of the box when it is pulled parallel to the horizontal surface.
Answer:
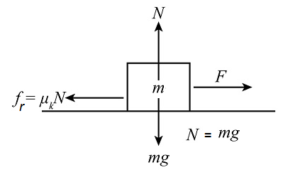
From the above figure, on balancing the forces, we get:
\(
\begin{aligned}
f_r & =F \\
\mu_k N & =F \quad(\therefore N=m g) \\
\mu_k m g & =F
\end{aligned}
\)
Example 4: Draw the free-body diagram of the box when it is pulled by a force at \(\theta=37^{\circ}\) above the horizontal surface.
Answer:
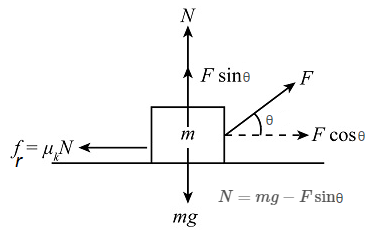
From the above figure, on balancing all the forces, we get:
\(
\begin{aligned}
f_r & =F \cos \theta=F \cos 37^{\circ} \\
\mu_k N & =F \cos \theta=F \cos 37^{\circ} \quad\left(\therefore N=m g-F \sin \theta=m g-F \sin 37^{\circ}\right) \\
\mu_k\left(m g-F \sin \theta\right) & =F \cos \theta \\
\mu_k\left(m g-F \sin 37^{\circ}\right) & =F \cos 37^{\circ}
\end{aligned}
\)
Example 5: Draw the free-body diagram of the box when it is pulled by a force at \(\theta\) above the horizontal surface.
Answer:
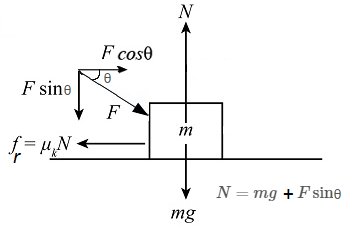
From the above figure, on balancing all the forces, we get:
\(
\begin{aligned}
f_r & =F \cos \theta \\
\mu_k N & =F \cos \theta \quad\left(\therefore N=m g+F \sin \theta\right) \\
\mu_k\left(m g+F \sin \theta\right) & =F \cos \theta \\
\end{aligned}
\)
Example 6: Draw the free body diagram of a body with mass \(m\) sliding down on an inclined plane.
Answer:
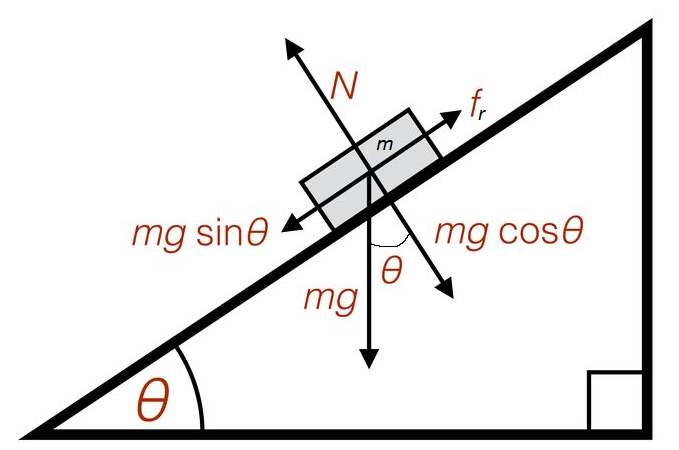
From the above figure, on balancing all the forces, we get:
\(N=m g \cos \theta\)
\(f_r=m g \sin \theta\)
Example 7: Draw the free body diagram of a body with mass \(m\) sliding down on an inclined plane shown below.
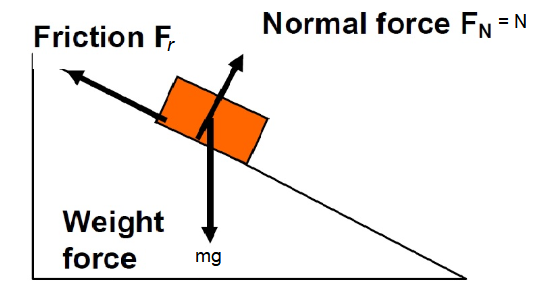
Answer: Weight Force acting on a block resolved into its components: Perpendicular and parallel to the incline. Remember that the normal force \(F_N\) is equal and opposite to the force exerted by the object on the plane \(m g \cos \theta\) (perpendicular to plane) otherwise it would fall through the plane, and \(m g \sin \theta\) (parallel to plane) forcing the object down the plane if no friction occurs.
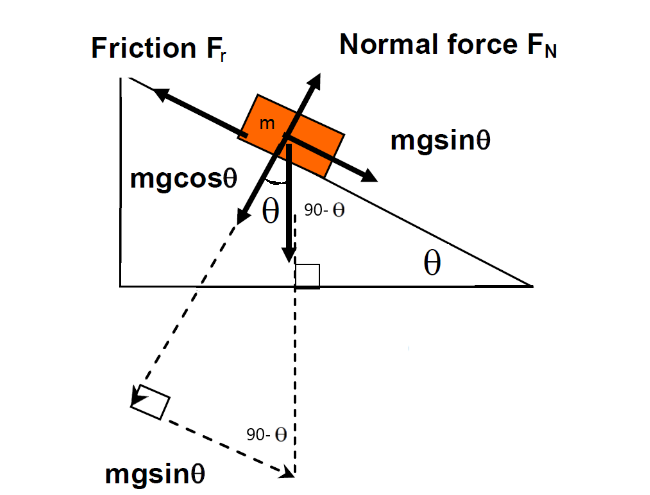
Note that with the above diagrams:
- Weight \(=m g\); acts through the centre of mass.
- Normal force \(F_N\) is always at right angles to the surface.
- Friction acts to oppose sliding motion (eg, if the mass were being dragged downhill, friction would act uphill)
- The weight force is resolved into 2 components:
- perpendicular to plane, and
- parallel to the plane.
- The resultant force \(\Sigma F\) down the slope is given by \(\Sigma F=m g \sin \theta-F_r\) where \(F_r\) is friction
- The resultant force \(\Sigma F\) perpendicular to the slope is zero (because it sits on the slope), hence: \(m g \cos \theta=F_N\)
Example 8: A toy car of mass \(50 \mathrm{~g}\) travels down a smooth incline at 30 degrees to the horizontal. Calculate:
(a) The net force acting on the car as it rolls down the slope, and
(b) The force of the incline on the car as it travels down the slope.
Friction may be ignored in this case.
\(
\text { Gravity }=9.8 \mathrm{~ms}^{-2} \text {. }
\)
Answer: Forces parallel to Slope:
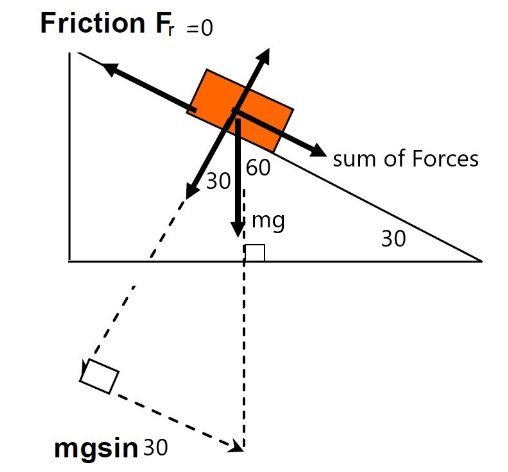
Note the angles: If slope is 30 degrees then \(90-30=60\) degrees in top corner then again \(90-60=30\) degrees from normal to vertical force so we would use \(m g \sin 30\) down the slope as the sum of all forces.
(a) As \(m g \sin \theta\) is the component of the force parallel to the slope then “sum of all forces” \(=\Sigma F\) :
\(
\begin{aligned}
\Sigma F & =m a \\
& =m g \sin \theta-F_r \\
& =m g \sin \theta-0 \\
& =m g \sin \theta
\end{aligned}
\)
Where \(m g \sin \theta\) is the component of the force parallel to the slope.
Note: the surface is friction-less (smooth) ie. \(F_r=0\), therefore the only force allowing the car to roll down the incline is the component of the gravitational force ‘ \(m g \sin \theta\) ‘.
\(
\begin{aligned}
\Sigma F & =m g \sin \theta \\
& =m \times g \times \sin \theta \\
& =50 \times 10^{-3} \times 9.8 \times \sin 30 \\
& =0.25 N
\end{aligned}
\)
Note: grams have been converted into kilograms
Forces perpendicular to slope:
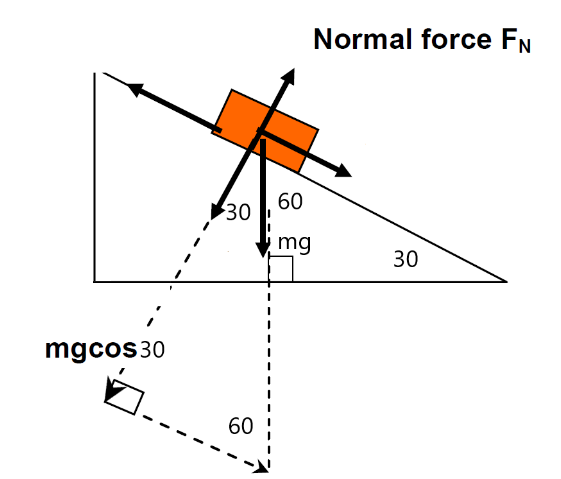
Also note the angles: If slope is 30 degrees then \(90-30=60\) degrees in top corner then again \(90-60=30\) degrees from normal to vertical force so we use \(m g \cos 30\) perpendicular to the slope as the normal force.
(b) The force of the incline on the car is a force that acts perpendicular to the slope, ie. the normal force \(F_N\) is equal to \(m g \cos \theta\)
\(
\begin{aligned}
F_N & =m g \cos \theta \\
& =m \times g \times \cos \theta \\
& =50 \times 10^{-3} \times 9.8 \times \cos 30 \\
& =0.43 N
\end{aligned}
\)
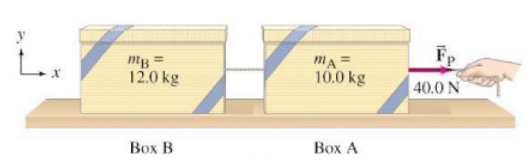
Example 9: Two boxes connected by a cord. Two boxes, A and B, are connected by a lightweight cord and are resting on a smooth (frictionless) table. The boxes have masses of \(12.0 \mathrm{~kg}\) and \(10.0 \mathrm{~kg}\). A horizontal force \(F_{\mathrm{P}}\) of \(40.0 \mathrm{~N}\) is applied to the \(10.0\mathrm{~kg}\) box, as shown in below. Find (a) the acceleration of each box, and
(b) the tension in the cord connecting the boxes.
Answer: We streamline our approach by not listing each step. We have two boxes so we need to draw a free-body diagram for each box. To draw them correctly, we must consider the forces on each box by itself, so that Newton’s second law can be applied to each. The person exerts a force \(F_{\mathrm{P}}\) on box A. Box A exerts a force \(F_{\mathrm{T}}\) on the connecting cord, and the cord exerts an opposite but equal magnitude force \(F_{\mathrm{T}}\) back on box A (Newton’s third law). These two horizontal forces on box A are shown in Fig.b, along with the force of gravity \(m_{\mathrm{A}} \overrightarrow{\mathbf{g}}\) downward and the normal force \(\overrightarrow{\mathbf{F}}_{\mathrm{AN}}\) exerted upward by the table. The cord is light, so we neglect its mass. The tension at each end of the cord is thus the same. Hence the cord exerts a force \(F_{\mathrm{T}}\) on the second box. Figure c shows the forces on box B, which are \(\overrightarrow{\mathbf{F}}_{\mathrm{T}}, m_{\mathrm{B}} \overrightarrow{\mathbf{g}}\), and the normal force \(\overrightarrow{\mathbf{F}}_{\mathrm{BN}}\). There will be only horizontal motion. We take the positive \(x\) axis to the right.
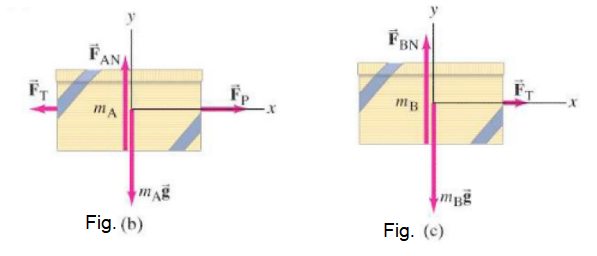
(a) We apply \(\Sigma F_x=m a_x\) to box A:
\(
\Sigma F_x=F_{\mathrm{P}}-F_{\mathrm{T}}=m_{\mathrm{A}} a_{\mathrm{A}} \quad \text { [box A] }
\)
For box B, the only horizontal force is \(F_{\mathrm{T}}\), so
\(
\Sigma F_x=F_{\mathrm{T}}=m_{\mathrm{B}} a_{\mathrm{B}} \quad \text { [box B] }
\)
The boxes are connected, and if the cord remains taut and doesn’t stretch, then the two boxes will have the same acceleration \(a\). Thus \(a_{\mathrm{A}}=a_{\mathrm{B}}=a\). We are given \(m_{\mathrm{A}}=10.0 \mathrm{~kg}\) and \(m_{\mathrm{B}}=12.0 \mathrm{~kg}\). We can add the two equations above to eliminate an unknown \(\left(F_{\mathrm{T}}\right)\) and obtain
\(
\left(m_{\mathrm{A}}+m_{\mathrm{B}}\right) a=F_{\mathrm{P}}-F_{\mathrm{T}}+F_{\mathrm{T}}=F_{\mathrm{P}}
\)
or
\(
a=\frac{F_{\mathrm{P}}}{m_{\mathrm{A}}+m_{\mathrm{B}}}=\frac{40.0 \mathrm{~N}}{22.0 \mathrm{~kg}}=1.82 \mathrm{~m} / \mathrm{s}^2 .
\)
Motion of bodies in contact
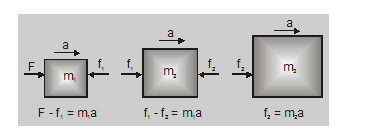
When the force \(F\) acts on the body with mass \(m_1\) as shown in fig. 1 and 1(a)
When two bodies of masses \(m_1\) and \(m_2\) are kept on the frictionless surface and a force \(\mathrm{F}\) is applied on one body, then the force with which one body presses the other at the point of contact is called force of contact. These two bodies will move with same acceleration a
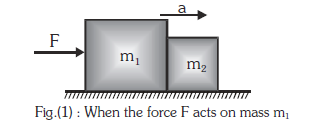
(i) When the force \(\mathrm{F}\) acts on the body with mass \(\mathrm{m}_1\) as shown in figure (1) : \(\mathrm{F}=\left(\mathrm{m}_1+\mathrm{m}_2\right) \mathrm{a}\)
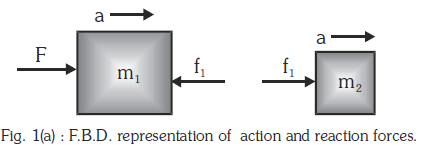
If the force exerted by \(\mathrm{m}_2\) on \(\mathrm{m}_1\) is \(\mathrm{f}_1\) (force of contact) then for body \(\mathrm{m}_1:\left(\mathrm{F}-\mathrm{f}_1\right)=\mathrm{m}_1 \mathrm{a}\)
\(
\begin{aligned}
&\mathrm{f}_1=\mathrm{F}-m_1 a\\
&=\left(m_1+m_2\right) a-m_1 a=m_2 a
\end{aligned}
\)
For body \(\mathrm{m}_2\) :
\(
\mathrm{f}_1=\mathrm{m}_2 \mathrm{a}
\)
\(\Rightarrow \text { action of } \mathrm{m}_1 \text { on } \mathrm{m}_2: \mathrm{f}_1=\frac{\mathrm{m}_2 \mathrm{~F}}{\mathrm{~m}_1+\mathrm{m}_2}\)
When the force \(\mathrm{F}\) acts on the body with mass \(m_2\) as shown in fig. 2 and 2(a)
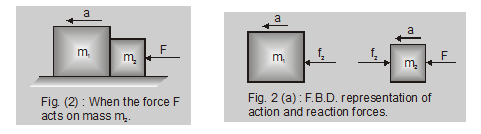
\(
\mathrm{F}=\left(\mathrm{m}_1+\mathrm{m}_2\right) \mathrm{a}
\)
for body with mass \(m_2\)
\(
\mathrm{F}-\mathrm{f}_2=\mathrm{m}_2 \mathrm{a}
\)
\(
\begin{aligned}
& \mathrm{f}_2=\mathrm{F}-\mathrm{m}_2 \mathrm{a} \\
& =\left(m_1+m_2\right) a-m_2 a=m_1 a
\end{aligned}
\)
or action of \(\mathrm{m}_2\) on \(\mathrm{m}_1\)
\(
\mathrm{f}_2=\frac{\mathrm{m}_1 \mathrm{~F}}{\mathrm{~m}_1+\mathrm{m}_2}
\)
Three bodies of masses \(\mathrm{m}_1, \mathrm{~m}_2\) and \(\mathrm{m}_3\) placed one after another and in contact
Let us now consider three bodies of masses \(\mathrm{m}_1, \mathrm{~m}_2\) and \(\mathrm{m}_3\) placed one after another and in contact with each other. Suppose a force \(\mathrm{F}\) is applied horizontally on mass \(\mathrm{m}_1\)
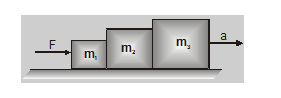
\(
\mathrm{F}-\mathrm{f}_1=\mathrm{m}_1 \mathrm{a}
\)
\(
f_1-f_2=m_2 a
\)
\(
\mathrm{f}_2=\mathrm{m}_3 \mathrm{a}
\)
Here \(\mathrm{F}=\left(\mathrm{m}_1+\mathrm{m}_2+\mathrm{m}_3\right) \mathrm{a}\)
\(
a=\frac{F}{\left(m_1+m_2+m_3\right)}
\)
\(\mathrm{f}_1=\frac{\left(\mathrm{m}_2+\mathrm{m}_3\right) \mathrm{F}}{\left(\mathrm{m}_1+\mathrm{m}_2+\mathrm{m}_3\right)}\) (action on both \(\mathrm{m}_2\) and \(\mathrm{m}_3\) )
and \(f_2=\frac{m_3 F}{\left(m_1+m_2+m_3\right)} \text { (action on } \mathrm{m}_3 \text { alone) }\)
when the force \(\mathrm{F}\) is applied on \(m_3\), then
\(\mathrm{f}_1=\frac{\mathrm{m}_1 \mathrm{~F}}{\left(\mathrm{~m}_1+\mathrm{m}_2+\mathrm{m}_3\right)} \text { (action on } \mathrm{m}_1 \text { alone) }\)
and \(f_2=\frac{\left(m_1+m_2\right) F}{\left(m_1+m_2+m_3\right)} \text { (action on } \mathrm{m}_1 \text { and } \mathrm{m}_2 \text { ) }\)
Free Body Diagram of a Pulley System
A single fixed pulley changes the direction of force only and in general, an ideal pulley assumed to be massless and frictionless. A pulley has three arm during its motion.
- Central arm is known as main arm.
- Handing two arm are known as side arm.
- Main arm is fixed while side arms are free to move. In this case net force acting on ideal pulley will always be zero. Because \(F=m a\), for ideal pulley \(m=0\) and hence \(F=0\)
- If the tension in the two side string is equal to \(T\), the tension in the main string will be equal to \(2 T\).
- Say, if \(m_2>m_1\), Since the length of the string is fixed, so if \(m_2\) comes down by a distance \(x, m_1\) will go up by \(x\) only. Therefore, acceleration of both the blocks are equal in magnitude and opposite direction.
Note: If \(a\) comes out positive then assumed direction of \(a\) is correct. If \(a\) comes out negative, then actual direction is opposite to the direction assumed.
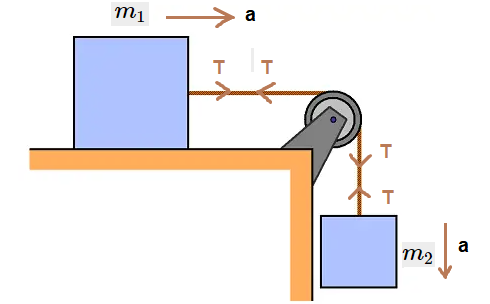
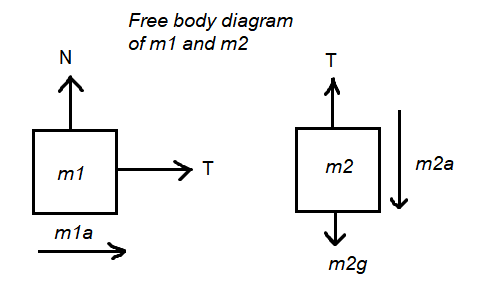
From free body diagram we get,
For mass \(m_1\) :
\(
T=m_1 a
\)
For mass \(m_2\) :
\(
m_2 g-T=m_2 a
\)
From these two equation we get,
\(
\text { Acceleration: } a=\frac{m_2}{\left(m_1+m_2\right)} g
\)
Tension of the string \(T=\frac{m_1 m_2}{\left(m_1+m_2\right)} g\)
Tension or thrust on pulley
\(
P=\sqrt{T^2+T^2}=\sqrt{2} T
\)
Inclined Pulley
Case-I: Two masses are suspended over a pulley on a friction-less inclined plane as shown below in the figure. The mass \(m_2\) descends with an acceleration \(a\). The mass \(m_1\) is on inclined plane:
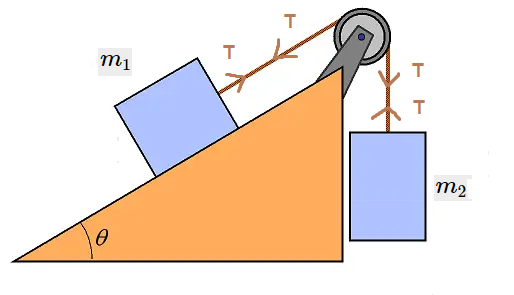
The free body diagram of the block with mass \(m_1\) and \(m_2\) are shown below.
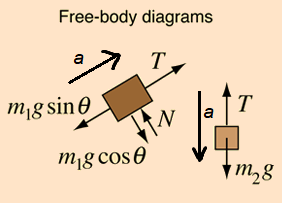
From free body diagram we get,
For mass \(m_1\) :
\(
T-m_1 g \sin \theta=m_1 a
\)
For mass \(m_2\) :
\(
m_2 g-T=m_2 a
\)
From these equation we get,
Acceleration \(a=\frac{\left(m_2-m_1 \sin \theta\right)}{\left(m_1+m_2\right)} g\)
and,
Tension of the string \(T=\frac{m_1 m_2(1+\sin \theta)}{\left(m_1+m_2\right)} g\)
Example 10: A body of mass \(5 \mathrm{~kg}\) rests on a smooth plane inclined at an angle of \(35^{\circ}\) to the horizontal. It is connected by a light inextensible string passing over a smooth pulley fixed at the top of the plane, to another body of mass \(19 \mathrm{~kg}\) hanging freely vertically below the pulley. Given that the acceleration due to gravity \(g=9.8 \mathrm{~m} / \mathrm{s}^2\), determine the acceleration of the system.
Answer: The following figure shows the forces acting on the bodies and what the forces on the \(5 \mathrm{~kg}\) mass body due to its weight and the normal reaction on it sum to.
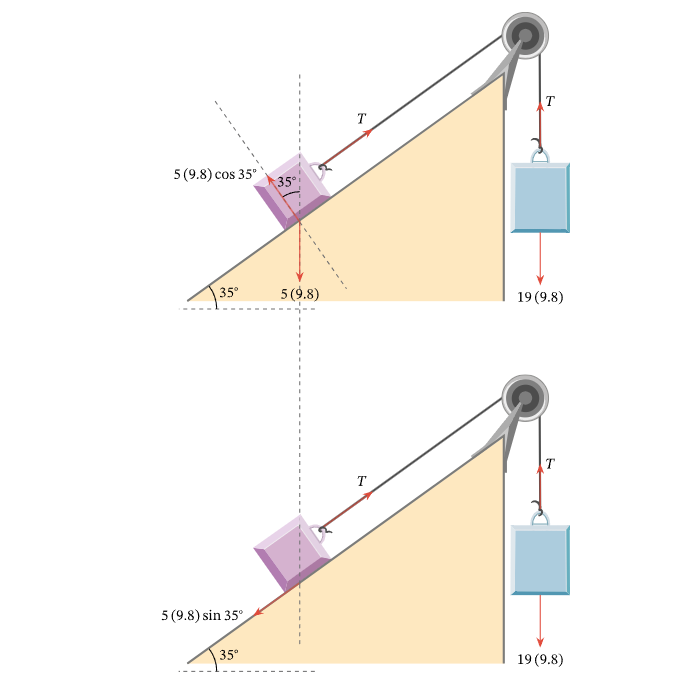
The accelerations of both bodies are equal. The acceleration of the \(19 \mathrm{~kg}\) mass body is given by
\(
a=\frac{\left(m_2 g\right)-T}{m_2}=\frac{19(9.8)-T}{19}=\frac{186.2-T}{19}
\)
\(
19 a=186.2-T \dots(1)
\)
The net force on the supported body can be expressed as
\(
F=T-\left(m_1 g \sin \theta\right)=T-\left(5(9.8) \sin 35^{\circ}\right)
\)
Force \(F\) can also be expressed as
\(
F=5 a
\)
Hence, we have
\(
5 a=T-\left(49 \sin 35^{\circ}\right) \dots(2)
\)
We now have two equations, (1) and (2), that can be added to give
\(
19 a+5 a=186.2-T+T-\left(49 \sin 35^{\circ}\right)
\)
This simplifies to
\(
\begin{aligned}
24 a & =186.2-\left(49 \sin \left(35^{\circ}\right)\right) \\
a & =\frac{186.2-\left(49 \sin \left(35^{\circ}\right)\right)}{24} .
\end{aligned}
\)
To two decimal places, this is \(6.59 \mathrm{~m} / \mathrm{s}^2\).
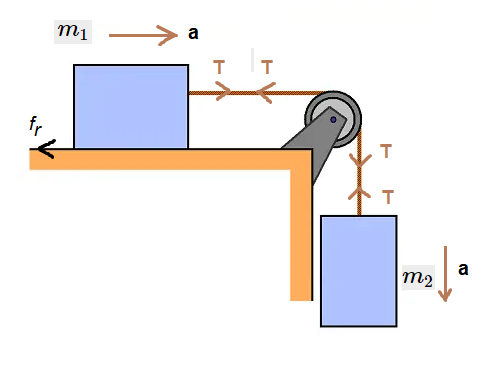
Case-II: When a body A of mass \(m_1\) rests on a horizontal surface with co-efficient of friction \(\mu\) between body and the table. Let a string passing over a pulley connect \(m_1\) with a body B of mass \(m_2\) as shown in below:
Free body diagram is shown below
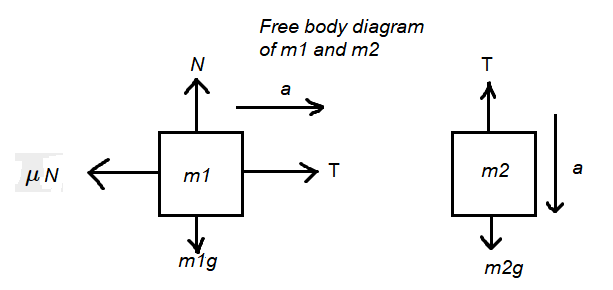
From free body diagram we get,
For mass \(m_1\) :
\(N=m_1 g\) and \(T-\mu N=m_1 a\)
or, \(T-\mu m_1 g=m_1 a\)
For mass \(m_2\) : \(m_2 g-T=m_2 a\)
From these two equation,
Acceleration \(a=\frac{\left(m_2-\mu m_1\right)}{\left(m_1+m_2\right)} g\)
and tension of the string \(T=\frac{m_1 m_2(1+\mu)}{\left(m_1+m_2\right)} g\)
Case-III: Two masses are suspended over a pulley on a inclined plane with coefficient of friction between the surface and the body is \(\mu\) as shown in figure below. The mass \(m_2\) descends with an acceleration \(a\). The mass \(m_1\) is on inclined plane:
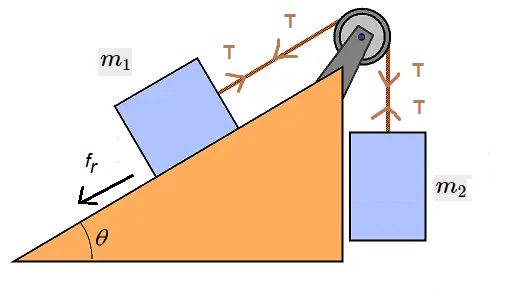
Free body diagram is shown below:
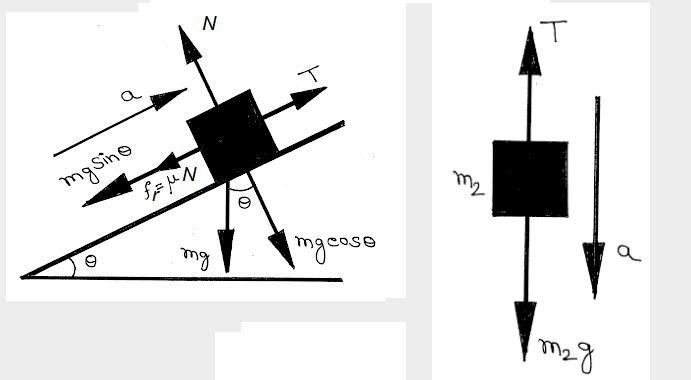
From free body diagram we get,
For mass \(m_1\) :
\(
N=m_1 g \cos \theta \text { and, } T-\mu N-m_1 g \sin \theta=m_1 a
\)
For mass \(m_2\) :
\(
m_2 g-T=m_2 a
\)
From these two equation we get,
Acceleration \(a=\frac{\left[m_2-m_1(\sin \theta+\mu \cos \theta)\right]}{\left(m_1+m_2\right)} g\) and,
Tension of the string \(T=\frac{m_1 m_2(1+\sin \theta+\mu \cos \theta)}{\left(m_1+m_2\right)} g\)
Case-IV: Two body \(\mathrm{A}\) and \(\mathrm{B}\) of masses \(m_1\) and \(m_2\) are connected by a string passing over a friction-less pulley such that \(m_2>m_1\) :
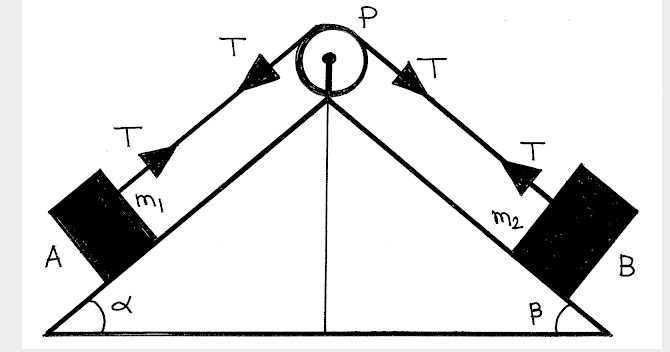
Free body diagram is shown below:
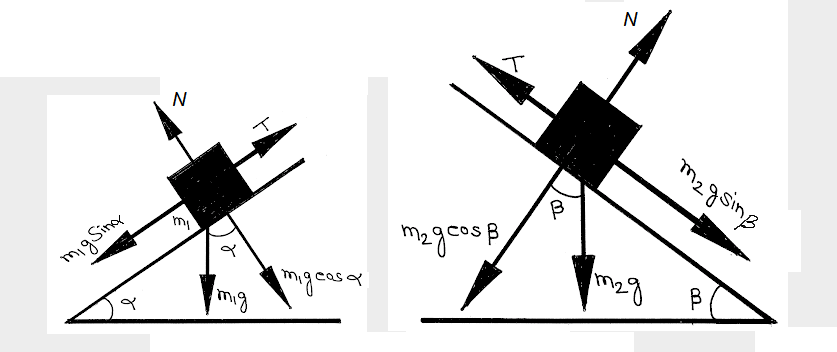
From free body diagram we get,
For mass \(m_1\) :
\(
T-m_1 g \sin \alpha=m_1 a
\)
For mass \(m_2\) :
\(
m_2 g \sin \beta-T=m_2 a
\)
From these two equation we get,
Acceleration \(a=\frac{\left(m_2 \sin \beta-m_1 \sin \alpha\right)}{\left(m_1+m_2\right)} g\) and,
Tension of the string \(T=\frac{m_1 m_2(\sin \alpha+\sin \beta)}{\left(m_1+m_2\right)} g\)
Case-V: The mass \(M\) is connected to \(m_1\) and \(m_2\) via string passing over alight pulleys. Let \(m_1>m_2\). Obviously \(m_1\) moves down an acceleration \(a\). The block on the horizontal table moves towards right with acceleration \(a:\)
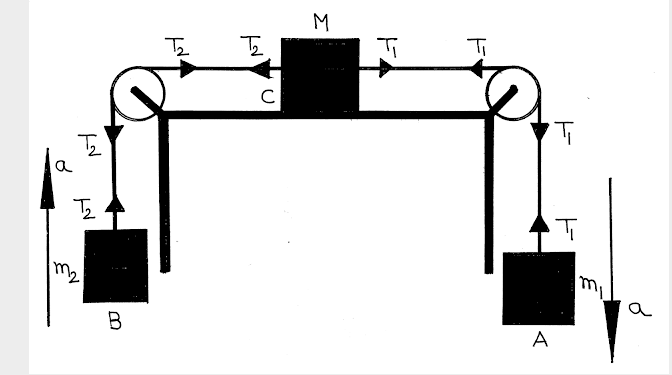
Free body Diagram is shown below:
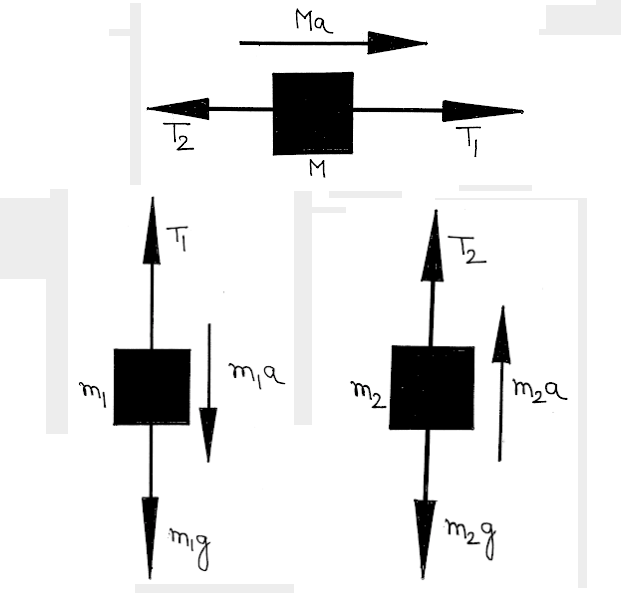
From free body Diagram we get,
For mass \(m_1\) :
\(
m_1 g-T_1=m_1 a
\)
For mass \(m_2\) :
\(
T_2-m_2 g=m_2 a
\)
For mass \(M\) :
\(
T_1-T_2=M a
\)
From these equation we get,
Acceleration \(a=\frac{\left(m_1-m_2\right)}{\left(m_1+m_2+M\right)} g\) and,
Tension of the string \(T_1=\frac{m_1\left(2 m_2+M\right)}{\left(m_1+m_2+M\right)} g\) and,
Tension of the string \(T_2=\frac{m_2\left(2 m_1+M\right)}{\left(m_1+m_2+M\right)} g\)
Case-VI: Two body of masses \(m_1\) and \(m_2\) are connected by a string passing over a friction-less pulley such that \(m_1>m_2\) :
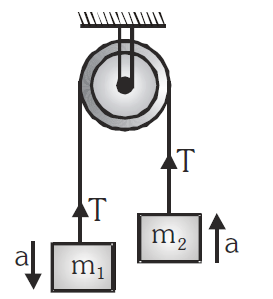
Now, we should be able to write the balancing forces acting on the body without drawing FBD.
Let \(\mathrm{m}_1>\mathrm{m}_2\) now for mass \(\mathrm{m}_1\):\(\mathrm{~m}_1 \mathrm{~g}-\mathrm{T}=\mathrm{m}_1 \mathrm{a}\)
for mass \(\mathrm{m}_2\):\(\mathrm{~T}-\mathrm{m}_2 \mathrm{~g}=\mathrm{m}_2 \mathrm{a}\)
\(
\text { Acceleration }=\mathrm{a}=\frac{\left(\mathrm{m}_1-\mathrm{m}_2\right)}{\left(\mathrm{m}_1+\mathrm{m}_2\right)} \mathrm{g}=\frac{\text { net pulling force }}{\text { total mass to be pulled }}
\)
\(
\text { Tension }=\mathrm{T}=\frac{2 \mathrm{~m}_1 \mathrm{~m}_2}{\left(\mathrm{~m}_1+\mathrm{m}_2\right)} \mathrm{g}=\frac{2 \times \text { Product of masses }}{\text { Sum of two masses }} \mathrm{g}
\)
Reaction at the suspension of pulley :
\(
\mathrm{R}=2 \mathrm{~T}=\frac{4 \mathrm{~m}_1 \mathrm{~m}_2 \mathrm{~g}}{\left(\mathrm{~m}_1+\mathrm{m}_2\right)}
\)
Case-VII: Blocks Hanging from multiple Pulleys
Pulleys (assume ideal pulley) get especially interesting in situations like the following example, where at least one of the pulleys is able to move. The two blocks remain at rest in the system of ropes and pulleys shown in the diagram. Given this information, can you conclude how the two masses compare?
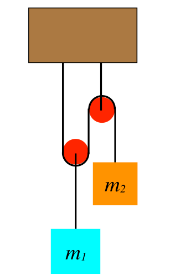
Lets draw the FBD

[We have taken the liberty of defining coordinate systems in our FBDs – up is the \(+y\)-direction for both – which we will need shortly.]
One might ask why there are two tension force vectors drawn for the pulley. The simplest answer is to consider what you would feel if you cut the rope on both sides of the pulley and held one end in each hand. Clearly you would feel both ends of the rope pulling down. Therefore by Newton’s third law, both ends of the rope are pulling up on the pulley. With the pulley massless and frictionless, these two tension forces must also be equal, which explains why they are labeled the same. Note that the tension vector on the block is also labeled with the same variable name. This is because it is the same rope, and our assumption of massless, frictionless pulleys ensures that everywhere that we measure the tension for a single piece of rope, it will be the same.
Another curious aspect of this FBD is the weight label of the left pulley. Technically, that force is acting on the block, and the block is pulling on the pulley. The pull on the pulley by the block happens to equal the weight of the block in this case, and the pulley has no weight of its own, so we are justified in taking this little shortcut. Another way to justify it is to treat the block + pulley as a single system, and the gravity force on the system is the force vector shown.
The next step in our analysis is to sum the forces for each object and apply Newton’s second law, which in this case involves zero acceleration. In taking the sum of forces, we have to take care to correctly use our coordinate system:
\(\left.\begin{array}{l}
0=a_1=\frac{F_{\text {net } 1}}{m_1}=\frac{2 T-m_1 g}{m_1} \quad \Rightarrow \quad T=\frac{m_1 g}{2} \\
0=a_2=\frac{F_{\text {net } 2}}{m_2}=\frac{T-m_2 g}{m_2} \Rightarrow T=m_2 g
\end{array}\right\} \Rightarrow m_1=2 m_2
\)
Notice that the light weight \(m_2\) holds up the heavier one because the placement of the pulley allows us to use the tension from the same rope twice on the heavier mass. This trick can actually be repeated as many times as we like (the pulley can have multiple tracks in it), and this enables us to lift very heavy weights with very little force. This invention is called a block and tackle. They are used for sailing ships (the heavy sails and boom can be pulled tighter), lifting engine blocks, and many other applications.
Example 11: The heights of the two blocks in the diagram below differ by \(36 \mathrm{~cm}\). When they are released from rest, the higher block falls while the lower block rises. One of the blocks has a mass that is three times the mass of the other block, the pulleys are massless and frictionless, and the string doesn’t stretch.
(a). Which is the heavier block? Explain.
(b). Find the distance that the lower block rises when the two blocks are aligned.
(c). Find the time it takes for the two blocks to be aligned.
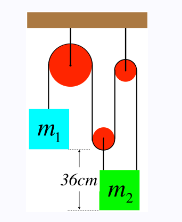
Answer: (a). The tension exerted by the string threaded through the pulleys is the same everywhere, so there is three times as much tension force acting up on the lower block as there is up on the higher one. If the lower block was three times heavier than the higher block, then the system would be balanced, and neither mass could be accelerating. [You should try doing the math of part (c) with the masses the other way, and demonstrate for yourself that it the acceleration would have to be zero.] Given that the system is accelerating, it must be the higher block with the greater mass.
(b). As the top block pulls the string down on one side of the large pulley, the same amount of string that is gained on the left side of the pulley is lost from the right side. The string on the right side of the large pulley is divided between the three segments holding up the other block. Therefore the lower block moves up one third as far as the higher block moves down. If the lower block rises a distance \(y\), then the higher block drops a distance \(3 y\), and since they reach the same height, the sum of those changes is \(36 \mathrm{~cm}\), which means the lower block rises a distance of \(y=9 \mathrm{~cm}\).
(c). To find the the time it takes them to align, we need to use their accelerations. We know their relative accelerations already: The lower block accelerates at one third the rate of the higher block. We’ll therefore call the higher block’s acceleration ” \(3 a\),” making the lower block’s acceleration equal to a. But we need Newton’s laws in order to go any further. FBD of the two systems involved look like this:
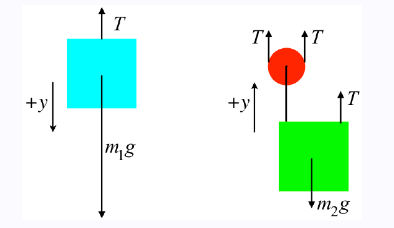
The higher mass is three times the lower mass, so we will call \(m_2\) simply ” \(m\),” which makes \(m_1\) equal to \(3 m\). Plugging everything into Newton’s second law for both FBDs gives these equations:
\(
\left.\begin{array}{lll}
a_1=\frac{F_{\text {net } 1}}{m_1} & \Rightarrow & 3 a=\frac{-T+3 m g}{3 m} \\
a_2=\frac{F_{\text {net } 2}}{m_2} & \Rightarrow & a=\frac{3 T-m g}{m}
\end{array}\right\} \Rightarrow a=\frac{2}{7} g
\)
With the acceleration of the lower block, the distance it travels, and the fact that it starts from rest, we can compute the time it takes to make the trip:
\(
y=v_o t+\frac{1}{2} a t^2 \Rightarrow t=\sqrt{\frac{7 y}{g}}=0.25 s
\)
Example 12: The system depicted in Figure below shows two blocks that remain at rest which are attached by a massless string over a massless, frictionless pulley, The plane is inclined at an angle theta up from the horizontal, and its surface is rough (i.e. not frictionless). The mass of the hanging block is given, as is the angle of incline and the coefficient of static friction. From these quantities, determine the minimum possible value of the mass of the block on the plane.
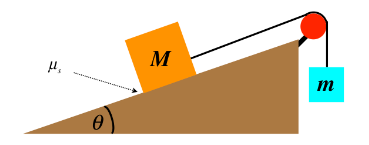
Answer: Starting (as always) with a FBD (including a coordinate system) for each block, we have:

Let’s take a moment to comment on the direction of the static friction force. Recall that a static friction force merely reacts to the “attempted” motion of the object along the surface. In this case, if the block was “trying” to slide down the plane, then the static friction force must be up the plane. Here it is drawn pointing down the plane, which means the other forces present must be such that they would accelerate it up the plane… How do we know this is the case? The answer lies in the statement of the question: We are looking for the minimum mass for the block on the plane. Imagine putting in a block whose mass balances the system. if a small mass is added to or subtracted from the block, the system may still remain at rest, as the static friction keeps the balance. If we add too much mass to that block, the static friction will reach its limit and the block will begin sliding down, while if we take away too much mass, it will slide up the plane. The static friction will oppose the intended motion, so for the minimum mass, the static friction force must point down the plane.
Breaking the vectors into components in our chosen coordinate systems and applying Newton’s second law (for zero acceleration) gives:
Block on plane :
\(x\)-direction forces \(: 0=a_x=\frac{f-T+M g \sin \theta}{M}\)
\(y-\) direction forces : \(0=a_y=\frac{N-M g \cos \theta}{M}\)
Hanging block: \(\quad y\)-direction forces : \(0=a_y=\frac{T-m g}{m}\)
Next, apply the constraint that relates the maximum static friction force (which occurs when the minimum mass is on the plane) and the normal force:
\(
\left.f \leq \mu_S N \Rightarrow \text { (maximum } f \text { for minimum } M\right) \Rightarrow f=\mu_S N
\)
The rest is algebra with four simultaneous equations, the result of which is:
\(
M_{\text {min }}=\frac{m}{\mu_S \cos \theta+\sin \theta}
\)
We should now check to see if this answer makes sense. If the angle theta is \(90^{\circ}\), then both masses are hanging, and there is not friction force (because there is no normal force). For the system not to accelerate, the two masses must be equal. Plugging in \(\theta=90^{\circ}\) indeed results in \(M=m\). The \(\theta=0^{\circ}\) case (a horizontal surface, where the normal force equals the weight of the block on the surface) will require that the friction force equals the weight of the hanging block. That is, we must have \(m g=f=\mu_S N=\mu_S M g \Rightarrow m=\mu_S M\), which is what we get when we plug in zero for \(\theta\).
Example 13: A rope is fastened to a \(50.0 \mathrm{~kg}\) block in two places and passes through a system of two pulleys, as shown in the diagram below. The block rests on a rough (coefficient of static friction is 0.400) horizontal surface. The bigger pulley is then pulled upward with gradually increasing force. Both pulleys are massless and frictionless, and the rope is also massless. The smaller pulley is fastened to the floor and the both pulleys are positioned such that the rope is perpendicular to the floor on one end and parallel to it on the other. When the pull force reaches a certain magnitude, the block just barely begins to slide to the right. Compute the magnitude of this pull force.
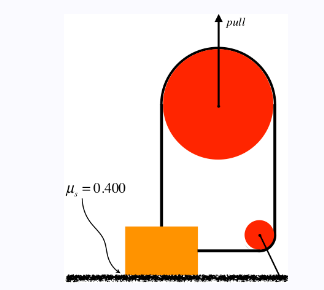
Answer:This problem is a good example of the importance of following the prescription listed above. Start with the free-body diagrams and coordinate systems. The FBD of the smaller pulley will yield us nothing useful, so there are just two FBDs to draw. Note that the tension on the side of the block comes from the same rope as the tension on the top of the block, so they are equal:
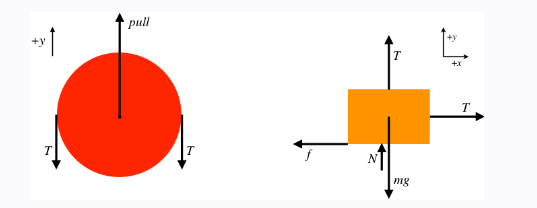
The block is not accelerating at all (nor is the pulley), so the sum of the forces in each of the \(x\) and \(y\) directions comes out to zero.
Block : \(\quad x\)-direction forces : \(0=T-f\)
\(y\)-direction forces : \(0=T+N-m g\)
Pulley: \(y\)-direction forces : \(0=\) pull \(-2 T\)
If we have to pull “just hard enough” to get the block moving, then this occurs when the horizontal pull equals the maximum static friction force, which gives us a constraint equation:
\(
f=\mu_S N
\)
Note that the block will have to start sliding before it starts rising, because rising requires than the normal force equals zero, and it will slide when the static friction force is small-but-non-zero. Now solve the equations simultaneously to get:
\(
\text { pull }=280 N
\)