Formulas of Logarithm and its Application in problem solving
There are a few of the formulas of logarithm given below:
- The logarithm of the number \(n\) to the base ‘ \(a\) ‘ is the exponent indicating the power to which the base ‘\(a\)‘ must be raised to obtain the number \(n\). This number is designated as \(\log _{ a } n\).
- \(\log _a n= x\), read as \(\log\) of \(n\) to the base \(a \Leftrightarrow a ^{ x }= n\), If \(a =10\) then we write \(\log n\) or \(\log _{10} n\) and if \(a =e\) we write \(\ln n\) or \(\log _e n\) (Natural log), \(\text { Necessary conditions : } n >0 ; a >0 ; a \neq 1\)
- \(\log _a(x . y)=\log _a x+\log _a y ; x, y>0\)
- \(\log _a\left(\frac{x}{y}\right)=\log _a x-\log _a y ; x, y>0\)
- \(\log _b\left(x^p\right)=p \log _b(x); x>0\)
- \(\log _{ a ^q} x=\frac{1}{ q } \log _{ a } x ; \quad x >0\)
- \(\log _{ a } x=\frac{1}{\log _x a} ; x>0, x \neq 1\)
- \(\log _a x=\log _b x / \log _b a ; x >0, a , b >0, b \neq 1, a \neq 1\)
- \(\log _{ a } b \cdot \log _{ b } c \cdot \log _{ c } d =\log _{ a } d ; a , b , c , d >0, \neq 1\)
- \(a^{\log _a x}=x ; a>0, a \neq 1\)
- \(a^{\log _b c}=c^{\log _b a} ; a, b, c>0 ; b \neq 1\)
- \(\log _{a^q} x^p=\frac{p}{q} \log _a x\)
- \(
\log _a x<\log _a y \Leftrightarrow\left[\begin{array}{llc}
x<y & \text { if } & a>1 \\
x>y & \text { if } & 0<a<1
\end{array}\right.
\) - \(\log _a x=\log _a y \Rightarrow x=y ; x, y>0 ; a>0, a \neq 1\)
- \(e^{\ln a^x}=a^x\)
- \({mlog}_a(x)+{nlog}_a(y)=\log _a\left(x^m y^n\right)\)
- \(\log _a(m+n)=\log _a m+\log _a\left(1+\frac{n}{m}\right)\)
- \(\log _a(m-n)=\log _a m+\log _a\left(1-\frac{n}{m}\right)\)
- \(\log _a a=1\)
- \(\log _{1 / a} a=-1\)
- \(\log _a 1=0\)
- \(\log _{10} 2=0.3010 ; \log _{10} 3=0.4771 ; \ell n 2=0.693, \ell n 10=2.303\)
- \(\text { If } a >1 \text { then } \log _{ a } x < p \Rightarrow 0< x < a ^{ p }\)
- \(\text { If } a>1 \text { then } \log _a x>p \Rightarrow x>a^p\)
- \(\text { If } 0< a <1 \text { then } \log _{ a } x < p \Rightarrow x > a ^{ p }\)
- \(\text { If } 0< a <1 \text { then } \log _{ a } x > p \Rightarrow 0< x < a ^{ p }\)
- If \(a_x=n\), then \(x=\log _a n\), where \(n>0, a>0\) and \(a \neq 1\).
- Exponential function is always positive.
- \(\log _a 0= \pm \infty\)
- \(\log _a \infty=\infty\)
- \(\log _a b \times \log _b a=1\)
- \(\log _a b \times \log _b c \times \log _c d \times \log _d a=1\)
- \(\log _a b \times \log _b c \times \log _c d \times \ldots \times \log _d a=1\)
- \(\log _{a^\alpha} b=\frac{1}{\alpha} \log _a b\)
- \(\log _{a^\alpha}\left(b^\beta\right)=\frac{\beta}{\alpha} \log _a b\)
Example 1: \(y=\log _{10}(x)\). Find \(\frac{d y}{d x}\).
Solution:
\(
y=\log _{10} x
\)
We know, \(\log _a b=\frac{\log _c b}{\log _c a}\)
\(
y=\frac{\log _e x}{\log _e 10}
\)
\(
y=\frac{1}{\log _e 10} \log _e x
\)
\(
\frac{d y}{d x}=\frac{1}{\log _e 10} \quad \frac{1}{x}
\)
\(
\frac{d y}{d x}=\frac{1}{x \log _e 10}
\)
Example 2: \(\text { Evaluate the given expression: } \log _2 8+\log _2 4 \text {. }\)
Solution:
Here, we will apply the rule,
\(
\begin{aligned}
& \log _2 8+\log _2 4=\log _2(8 \times 4) \\
& =\log _2 32
\end{aligned}
\)
Now, rewrite 32 in the exponential form to get the value of its exponent.
\(
32=2^5
\)
So, we have, \(\log _2 32=\log _2 2^5=5 \log _2 2=5 \times 1=5\)
Hence, the required answer is 5.
Example 3: \(\text { Find the value of } x \text { where, } 2 \log x=4 \log 3\)
Solution:
Given, \(2 \log x=4 \log 3\)
Here, you have to divide each side by the number 2 .
\(
\begin{aligned}
& \Rightarrow \log x=\frac{4 \log 3}{2} \\
& \Rightarrow \log x=2 \log 3 \\
& \Rightarrow \log x=\log 3^2 \\
& \Rightarrow \log x=\log 9
\end{aligned}
\)
Hence, \(x=9\).
Example 4: \(\text { Calculate } \log x+\log (x-1)=\log (3 x+12)\)
Solution:
Given, \(\log x+\log (x-1)=\log (3 x+12)\)
\(
\Rightarrow \log [x(x-1)]=\log (3 x+12)
\)
Now, you have to drop the logarithms to get:
\(
\Rightarrow[x(x-1)]=(3 x+12)
\)
Here, you have to use the distributive property to remove the brackets.
\(
\begin{aligned}
& \Rightarrow x^2-x=3 x+12 \\
& \Rightarrow x^2-x-3 x-12=0 \\
& \Rightarrow x^2-4 x-12=0 \\
& \Rightarrow(x-6)(x+2)=0 \\
& \Rightarrow x=-2, x=6
\end{aligned}
\)
The logarithm is not defined for negative real numbers. Hence, the required answer is \(x=6\).
Example 5: \(\text { Solve for } x \text { if } \log (x-1)+\log (x+1)=\log _2 1\)
Solution:
We have \(\log (x-1)+\log (x+1)=\log _2 1\)
\(
\begin{aligned}
& \log (x-1)+\log (x+1)=0 \\
& \log [(x-1)(x+1)]=0
\end{aligned}
\)
Now, we know that \(\log 1=0\)
\(
(x-1)(x+1)=1
\)
This becomes \(x^2-1=1\)
\(
x^2=2
\)
\(x=\pm \sqrt{2}\)
Thus, we know that log of the negative number is not defined.
Hence, the required answer is \(x=\sqrt{2}\).
Steps for Solving Logarithmic Equations Containing Only Logarithms
- Step 1: Determine if the problem contains only logarithms. If so, go to Step 2. If not, stop and use the Steps for Solving Logarithmic Equations Containing Terms without Logarithms.
- Step 2: Use the properties of logarithms to simplify the problem if needed. If the problem has more than one logarithm on either side of the equal sign then the problem can be simplified.
- Step 3: Rewrite the problem without the logarithms.
- Step 4: Simplify the problem.
- Step 5: Solve for x .
- Step 6: Check your answer(s). Remember we cannot take the logarithm of a negative number, so we need to make sure that when we plug our answer(s) back into the original equation we get a positive number. Otherwise, we must drop that answer(s).
Example 6: Solve the equation \(\log _3(7 x+3)=\log _3(5 x+9)\).
Solution: \(\log _3(7 x+3)=\log _3(5 x+9)\)
Since the problem has only two logarithms on opposite sides of the equal sign, the problem can be solved by dropping the logarithms.So, we drop the logarithms on both sides and we get
\(7 x+3=5 x+9\)
Solving we get \(x=3\)
Check the answer; this is an acceptable answer because we get a positive number when it is plugged back in.
Therefore, the solution to the problem \(\log _3(7 x+3)=\log _3(5 x+9)\) is \(x=3\).
Example 7: Solve \(\log _7(x-2)+\log _7(x+3)=\log _7 14\)
Solution: Let’s drop the logarithms on both side.
\(
(x-2)(x+3)=14
\)
Solving the equation we get
\(
\begin{aligned}
& x^2-x-6=14 \\
& x^2-x-20=0 \\
& (x+4)(x-5)=0 \\
& x=-4 \text { or } x=5 \\
& x=5
\end{aligned}
\)
Check the answers, only one answer is acceptable because the other answer produces a negative number when it is plugged back in.
Therefore, the solution to the problem \(\log _7(x-2)+\log _7(x+3)=\log _7 14\) is \(x=5\).
Steps for Solving Logarithmic Equations Containing Terms without Logarithms
- Step 1: Determine if the problem contains only logarithms. If so, stop and use Steps for Solving Logarithmic Equations Containing Only Logarithms. If not, go to Step 2.
- Step 2: Use the properties of logarithms to simplify the problem if needed. If the problem has more than one logarithm on either side of the equal sign then the problem can be simplified.
- Step 3: Rewrite the problem in exponential form.
- Step 4: Simplify the problem.
- Step 5: Solve for x .
- Step 6: Check your answer(s). Remember we cannot take the logarithm of a negative number, so we need to make sure that when we plug our answer(s) back into the original equation we get a positive number. Otherwise, we must drop that answer(s).
Example 8: Solve the problem \(\log _2(5 x+7)=5\)
Solution:
\(
\begin{aligned}
& 5 x+7=2^5 \\
& 5 x+7=32 \\
& x=5 \\
& x=5
\end{aligned}
\)
Therefore, the solution to the problem \(\log _2(5 x+7)=5\) is \(x=5\).
Example 9: \(\text { solve } \ln (4 x-1)=3\)
Solution:
\(
\begin{aligned}
& \ln (4 x-1)=3 \\
& 4 x-1=e^3 \\
& 4 x-1 \approx 20.085537 \\
& x \approx 5.271384 \\
& x \approx 5.271384
\end{aligned}
\)
Therefore, the solution to the problem \(\ln (4 x-1)=3\) is \(x \approx 5.271384\).
Example 10: Solve \(\log _3(9 x+2)=4\)
Solution:
\(
\begin{aligned}
& \log _3(9 x+2)=4 \\
& \log _3(9 x+2)=4 \\
& 9 x+2=3^4 \\
& 9 x+2=81 \\
& x=\frac{79}{9} \\
& x=\frac{79}{9}
\end{aligned}
\)
Therefore, the solution to the problem \(\log _3(9 x+2)=4\) is \(x=\frac{79}{9}\).
Example 11: Solve \(\log _4 x+\log _4(x-12)=3\)
Solution:
\(
\begin{aligned}
& \log _4 x+\log _4(x-12)=3 \\
& \log _4(x(x-12))=3 \\
& x(x-12)=4^3 \\
& x^2-12 x=64 \\
& x^2-12 x-64=0 \\
& (x+4)(x-16)=0 \\
& x=-4 \text { or } x=16 \\
& x=16
\end{aligned}
\)
Therefore, the solution to the problem \(\log _4 x+\log _4(x-12)=3\) is \(x=16\).
Example 12: Solve \(\log _4(2 x +1)=\log _4( x +2)-\log _4 3\)
Solution:
\(
\begin{aligned}
& \log _4(2 x+1)=\log _4(x+2)-\log _4 3 \\
& \log _4(2 x+1)=\log _4\left(\frac{x+2}{3}\right) \\
& 2 x+1=\frac{x+2}{3} \\
& 3(2 x+1)=x+2 \\
& 6 x+3=x+2 \\
& x=-\frac{1}{5}
\end{aligned}
\)
No Solution.
Therefore, the problem \(\log _4(2 x +1)=\log _4( x +2)-\log _4 3\) has no solution.
Example 13: Solve \(\log (5 x-11)=2\)
Solution:
\(
\begin{aligned}
& \log (5 x-11)=2 \\
& \log (5 x-11)=2 \\
& 5 x-2=10^2 \quad \text {For common logarithms the base is 10.} \\
& 5 x-2=100 \\
& x=\frac{102}{5} \\
& x=\frac{102}{5}
\end{aligned}
\)
Therefore, the solution to the problem \(\log (5 x-11)=2\) is \(x=\frac{102}{5}\).
Example 14: Solve \(\log _2(x+1)-\log _2(x-4)=3\)
Solution:
\(
\begin{aligned}
& \log _2(x+1)-\log _2(x-4)=3 \\
& \log _2\left(\frac{x+1}{x-4}\right)=3 \\
& \frac{x+1}{x-4}=2^3 \\
& \frac{x+1}{x-4}=8 \\
& x+1=8(x-4) \\
& x+1=8 x-32 \\
& x=\frac{33}{7} \\
& x=\frac{33}{7}
\end{aligned}
\)
Therefore, the solution to the problem \(\log _2(x+1)-\log _2(x-4)=3\) is \(x=\frac{33}{7}\).
Example 15: Solve \(\log _6(x+4)+\log _6(x-2)=\log _6(4 x)\)
Solution:
\(
\begin{aligned}
& \log _6(x+4)+\log _6(x-2)=\log _6(4 x) \\
& \log _6((x+4)(x-2))=\log _6(4 x) \\
& (x+4)(x-2)=4 x \\
& x^2+2 x-8=4 x \\
& x^2-2 x-8=0 \\
& (x+2)(x-4)=0 \\
& x=-2 \text { or } x=4 \\
& x=4
\end{aligned}
\)
Check the answers, only one answer is acceptable because the other answer produces a negative number when it is plugged back in.
Therefore, the solution to the problem \(\log _6(x+4)+\log _6(x-2)=\log _6(4 x)\) is \(x=4\).
Example 16: If \(\frac{1}{\log _3 \pi}+\frac{1}{\log _4 \pi}>x\) then \(x\) be
(a) 3 (b) 2 (c) \(\pi\) (d) None of these
Solution:
\(
\text { If } \frac{1}{\log _3 \pi}+\frac{1}{\log _4 \pi}>x
\)
\(
\begin{gathered}
\log _\pi 3+\log _\pi 4>x; \quad \log _a x=\frac{1}{\log _x a} \\
\log _\pi(3 \times 4)>x \\
\log _\pi 12>x \\
x<\log _\pi 12 \\
x<2.171
\end{gathered}
\)
So \(x\) will be 2.
Alternate:
\(
\begin{aligned}
\frac{1}{\log _3 \pi}+\frac{1}{\log _4 \pi} & =\log _\pi 3+\log _\pi 4 \\
& =\log _\pi(3 \times 4) \\
& =\log _\pi(12)>\log _\pi\left(\pi^2\right)=2
\end{aligned}
\)
Hence, the value of \(x\) is 2 .
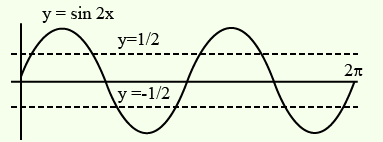
Example 17: The number of distinct solutions of the equation \(\log _{1 / 2}|\sin x|=2-\log _{1 / 2}\) \(|\cos x|\) in the interval \([0,2 \pi]\), is ____.
Solution:
\(
\begin{aligned}
& \log _{1 / 2}|\sin x|=2-\log _{1 / 2}|\cos x|: x \in[0.2 \pi] \\
& \Rightarrow \quad \log _{1 / 2}|\sin x|+\log _{1 / 2}|\cos x|=2 \\
& \Rightarrow \quad \log _{1 / 2}(|\sin x \cos x|)=2 \\
& \Rightarrow|\sin x \cos x|=\frac{1}{4} \Rightarrow|\sin 2 x|=\frac{1}{2} \\
\therefore \sin 2 x= \pm \frac{1}{2}
\end{aligned}
\)
\(\therefore\) We have 8 solutions for \(x \in[0,2 \pi]\)
Example 18: The value of \((0.16)^{\log _{2.5}\left(\frac{1}{3}+\frac{1}{3^2}+\cdots \infty\right)}\) is ____.
Solution:
\(
\begin{aligned}
& \frac{1}{3}+\frac{1}{3^2}+\frac{1}{3^3}+\ldots \infty \\
& =\frac{1 / 3}{1-1 / 3} \\
& =\frac{1}{2}
\end{aligned}
\)
\(
\begin{aligned}
& (0.16)^{\log _{2.5}\left(\frac{1}{3}+\frac{1}{3^2}+\frac{1}{3^3}+\ldots \infty\right)} \\
& =\left[(0.4)^2\right]^{\log _{\frac{5}{2}} \frac{1}{2}} \\
& =(0.4)^{\log _{\frac{5}{2}} \frac{1}{4}} \\
& =\left(\frac{1}{4}\right)^{\log _{\frac{5}{2}} \frac{2}{5}}\left(\because a^{\log _b c}=c^{\log _b a}\right) \\
& =(4)^{-\log _{\frac{5}{2}} \frac{2}{5}} \\
& =(4)^{\log _{\frac{2}{5}} \frac{2}{5}} \\
& =4
\end{aligned}
\)
Example 19: If
\(x=\log _{2 a}\left(\frac{b c d}{2}\right), y=\log _{3 b}\left(\frac{a c d}{3}\right), z=\log _{4 c}\left(\frac{a b d}{4}\right)\) and \(w\) \(=\log _{5 d}\left(\frac{a b c}{5}\right)\) and \(\frac{1}{x+1}+\frac{1}{y+1}+\frac{1}{z+1}+\frac{1}{w+1}=\log _{a b c d} N+1\), then value of \(\frac{N}{40}\) is
(a) 40 (b) 80 (c) 120 (d) 160
Solution:
\(
\begin{aligned}
& x=\log _{2 a}\left(\frac{b c d}{2}\right) \\
& \Rightarrow x+1=\log _{2 a}\left(\frac{2 a b c d}{2}\right)=\log _{2 a}(a b c d) \\
& \therefore \frac{1}{x+1}=\log _{a b c d} 2 a
\end{aligned}
\)
Similarly,
\(
\frac{1}{y+1}=\log _{a b c d} 3 b, \frac{1}{z+1}=\log _{a b c d} 4 c
\)
and
\(
\begin{aligned}
& \frac{1}{w+1}=\log _{a b c d} 5 d \\
& \therefore \frac{1}{x+1}+\frac{1}{y+1}+\frac{1}{z+1}+\frac{1}{w+1}=\log _{a b c d}(2 a \cdot 3 b \cdot 4 c \cdot 5 d) \\
& =\log _{a b c d}(120 a b c d) \\
& =\log _{a b c d} 120+1 \\
& =\log _{a b c d} N+1 \\
& \text { [given] }
\end{aligned}
\)
Comparing, we get \(N =120\)
Example 20: Let \(\left(x_0, y_0\right)\) be the solution of the following equations:
\(
(2 x)^{\ln 2}=(3 y)^{\ln 3} \text {, }
\)
\(3^{\ln x}=2^{\ln y}\), then \(x_0\) is
(a) \(1 / 6\)
(b) \(1 / 3\)
(c) \(1 / 2\)
(d) 6
Solution:
\(
\begin{aligned}
& \text { Given }(2 x)^{\ln 2}=(3 y)^{\ln 3} \\
& \Rightarrow \ln 2(\ln 2 x)=\ln 3(\ln 3 y) \\
& \Rightarrow \ln 2 \ln 2 x=\ln 3(\ln 3+\ln y) . .(i)
\end{aligned}
\)
\(
\begin{aligned}
& \text { Also, } 3^{\ln x}=2^{\ln y} \\
& \Rightarrow \ln x \ln 3=\ln y \ln 2 \\
& \Rightarrow \ln y=(\ln x . \ln 3) / \ln 2 . .(i i)
\end{aligned}
\)
Substitute (ii) in (i)
\(
\begin{aligned}
& \Rightarrow \ln 2(\ln 2 x)=\ln 3(\ln 3+(\ln x \cdot \ln 3) / \ln 2) \\
& \Rightarrow(\ln 2)^2(\ln 2 x)=\ln 3(\ln 3 \ln 2+\ln x \cdot \ln 3) \\
& \Rightarrow(\ln 2)^2(\ln 2 x)=(\ln 3)^2(\ln 2+\ln x) \\
& \Rightarrow(\ln 2)^2(\ln 2 x)=(\ln 3)^2 \ln 2 x \\
& \Rightarrow\left[(\ln 2)^2-(\ln 3)^2\right] \ln 2 x=0 \\
& \Rightarrow \ln 2 x=0 \\
& \Rightarrow 2 x=1 \\
& \Rightarrow x=1 / 2
\end{aligned}
\)
Example 21: If the sum of the first 20 terms of the series
\(
\log _{7^{1 / 2}} x+\log _{7^{1 / 3}} x+\log _{7^{1 / 4}} x+\ldots
\)
is 460 , then \(x\) is equal to:
(a) \(7^{1 / 2}\)
(b) \(7^2\)
(c) \(e^2\)
(d) \(7^{46 / 21}\)
Solution:
\(
\begin{aligned}
& \log _{\left(7^{1 / 2}\right)} x+\log _{\left(7^{1 / 3}\right)} x+\log _{\left(7^{1 / 4}\right)} x+\ldots \ldots \ldots \ldots 20 \text { terms } \\
& \quad=\frac{1}{\frac{1}{2}} \log _7 x+\frac{1}{\frac{1}{3}} \log _7 x+\frac{1}{\frac{1}{4}} \log _7 x+\ldots \ldots \ldots \ldots 20 \text { terms }
\end{aligned}
\)
\(
\left[By \quad \log _{a^n} b^m=\frac{m}{n} \cdot \log _a b\right]
\)
\(
\begin{aligned}
& =2 \log _7 x+3 \log _7 x+4 \log _7 x+\ldots \ldots \ldots \ldots .20 \text { terms } \\
& =\log _7 x(2+3+4+\ldots \ldots \ldots .20 \text { terms })
\end{aligned}
\)
Here, \(2+3+4+\ldots\).are in AP where, \(a=2, d=1\), and \(n=20\) \(\Rightarrow(2+3+4+\ldots \ldots \ldots .20\) terms \()=S_{20}\)
\(
\begin{aligned}
S_{20} & =\frac{20}{2}[2(2)+19(1)] \quad\left[B y S_n=\frac{n}{2}[2 a+(n-1) d]\right] \\
& =10(23) \\
& =230
\end{aligned}
\)
\(
\begin{aligned}
& \log _7 x(2+3+4+\ldots \ldots \ldots .20 \text { terms })=\log _7 x(230) \\
& \Rightarrow \quad 460=\log _7 x(230) \quad \text { (given) } \\
& \Rightarrow \quad 2=\log _7 x \\
& \Rightarrow \quad x=7^2 \\
&
\end{aligned}
\)
Example 22: Logarithm of
\(
32 \sqrt[5]{4}
\)
to the base \(2 \sqrt{ } 2\) is
(a) 3.6
(b) 5
(c) 4
(d) None of the above
Solution:
\(
\begin{aligned}
& 32 \sqrt[5]{4}= 2^5 \times 2^{\frac{2}{5}} \\
&=2^{\frac{27}{5}} \\
& 2 \sqrt{2}= 2^{\frac{3}{2}}
\end{aligned}
\)
Now,
\(
\begin{aligned}
\log _{2 \frac{3}{2}} \frac{27}{5}= & \frac{27}{5} \log _{2 \frac{3}{2}} 2 \\
& =\left(\frac{27}{5}\right)\left(\frac{2}{3}\right) \log _2 2 \\
& =\frac{18}{5} \\
& =3.6
\end{aligned}
\)
\(
\left[\because \log _{b^n} a=\frac{1}{n} \log _b a, \log _b a^n=n \log _b a\right]
\)
Example 23: If \(\log _7 2=m\), then \(\log _{49} 28\) is equal to
(a) \(2(1+2 m)\)
(b) \((1+2 m) / 2\)
(c) \(2 /(1+2 m)\)
(d) \(1+m\)
Solution:
\(\begin{aligned}
& \text { Given } \log _7 2= m \\
& \log _{49} 28=\log _{7^2} 28 \\
& =(1 / 2) \log _7 28 \\
& =(1 / 2)\left[\log _7(4 \times 7)\right] \\
& \left.=(1 / 2)\left[\log _7 4+\log _7 7\right)\right] \\
& \left.=(1 / 2)\left[\log _7 2^2+1\right)\right] \\
& \left.=(1 / 2)\left[2 \log _7 2+1\right)\right] \\
& =(1 / 2)[2 m+1)]
\end{aligned}
\)
Example 24: The value of \(\log _3 4 \log _4 5 \log _5 6 \log _6 7 \log _7 8 \log _8 9\) is
(a) 1
(b) 2
(c) 3
(d) 4
Solution: We know \(\log _b a=\log a / \log b\)
So \(\log _3 4 \log _4 5 \log _5 6 \log _6 7 \log _7 8 \log _8 9=(\log 4 / \log 3) \times(\log 5 / \log 4) \times(\log 6 / \log[latex] 5) \)\times[/latex]
\(
\begin{aligned}
& (\log 7 / \log 6) \times(\log 8 / \log 7) \times(\log 9 / \log 8) \\
& =\log 9 / \log 3 \\
& =\log 3^2 / \log 3 \\
& =2 \log 3 / \log 3 \\
& =2
\end{aligned}
\)
Example 25: If \(a^2+4 b^2=12 a b\), then \(\log (a+2 b)\) is
(a) \(1 / 2(4 \log 2+\log a+\log b)\)
(b) 0
(c) \((\log 2+\log a+\log b)\)
(d) \((4 \log 2+\log a-\log b)\)
Solution: Given, \(a ^2+4 b^2=12 ab\)
Adding 4 ab on both sides, we get
\(
\begin{aligned}
& a^2+4 b^2+4 a b=16 a b \\
& \Rightarrow(a+2 b)^2=16 a b
\end{aligned}
\)
Taking log on both sides,
\(
\begin{aligned}
& \log (a+2 b)^2=\log (16 a b) \\
& 2 \log (a+2 b)=\log 16+\log a+\log b \\
& 2 \log (a+2 b)=\log 2^4+\log a+\log b \\
& 2 \log (a+2 b)=4 \log 2+\log a+\log b \\
& \log (a+2 b)=1 / 2(4 \log 2+\log a+\log b)
\end{aligned}
\)
Example 26: The value of
\(
(0.05)^{\log _{\sqrt{2}}(0.1+0.01+0.001+\ldots)}
\)
(a) 81
(b) \(1 / 81\)
(c) 20
(d) \(1 / 20\)
Solution:
\(
\begin{aligned}
& 0.1+0.01+0.0001+\ldots . \Rightarrow \text { G.P } \\
& =(0.1)(1-0.1); \quad S_{\infty}=-\frac{a}{1-r} \\
& =\frac{0.1}{0.9}=\frac{1}{9}
\end{aligned}
\)
\(
\begin{aligned}
& \log _{\sqrt{20}}(1 / 9)=\log _{20^{1 / 2}}(1 / 9) \\
& =2 \log _{20}(1 / 9) \\
& =2 \log _{20}\left(9^{-1}\right) \\
& =-2 \log _{20} 9
\end{aligned}
\)
\(
\begin{aligned}
& (0.05)^{-2 \log _{20} 9}=\left(0.05^{-1}\right)^{2 \log _{20} 9} \\
& =(20)^{2 \log _{20} 9} \\
& \text { (since } 0.05=1 / 20) \\
& =(20)^{\log _{20} 9^2} \\
& =(20)^{\log _{20} 81} \\
& =81^{\log _{20} 20} \\
& =81
\end{aligned}
\)
Example 27: If \(a, b, c\) are distinct positive numbers, each different from 1 , such that \(\left[\log _b a \log _c a\right.\) \(\left.-\log _a a\right]+\left[\log _a b \log _c b-\log _b b\right]+\left[\log _a c \log _b c-\log _c c\right]=0\), then \(a b c=\)
(a) 1
(b) 2
(c) 3
(d) 4
Solution:
\(
\begin{aligned}
& \text { We use the property } \log _n m=\log m / \log n \\
& \text { Given }\left[\log _b a \log _c a-\log _a a\right]+\left[\log _a b \log _c b-\log _b b\right]+\left[\log _a c \log _b c-\log _c c\right]=0 \\
& \Rightarrow[(\log a / \log b)(\log a / \log c)-1]+[(\log b / \log a)(\log b / \log c)-1]+[(\log c / \log a) \\
& (\log c / \log b)-1]=0 \\
& \Rightarrow\left[(\log a)^2 / \log b \log c\right]+\left[(\log b)^2 / \log a \log c\right]+\left[(\log c)^2 / \log a \log b\right]=3
\end{aligned}
\)
Multiply both sides by \(\log\) a \(\log b \log c\)
\(
\begin{aligned}
& \Rightarrow(\log a)^3+(\log b)^3+(\log c)^3=3 \log a \log b \log c \\
& \Rightarrow \log a+\log b+\log c=0\left(\text { Use } x^3+y^3+z^3=3 x y z, \text { then } x+y+z=0\right) \\
& \Rightarrow \log (a b c)=0 \\
& \Rightarrow a b c=1
\end{aligned}
\)
Example 28: If \(a, b\), and \(c\) are consecutive positive integers and \(\log (1+a c)=2 k\), then the value of \(k\) is
(a) \(\log a\)
(b) \(\log b\)
(c) 2
(d) 1
Answer: Let \(a=n-1, b=n, c=n+1\), where \(n>1\).
\(
\begin{aligned}
& \text { Given } \log (1+a c)=2 k \\
& \Rightarrow \log (1+(n-1)(n+1))=2 k \\
& \Rightarrow \log \left(1+n^2-1\right)=2 k \\
& \Rightarrow \log n^2=2 k \\
& \Rightarrow 2 \log n=2 k \\
& \Rightarrow \log n=k \\
& \Rightarrow \log b=k
\end{aligned}
\)
Example 29: If \(\log _3 x+\log _3 y=2+\log _3 2\) and \(\log _3(x+y)=2\), then
(a) \(x=1, y=8\)
(b) \(x=8, y=1\)
(c) \(x=3, y=6\)
(d) \(x=9, y=3\)
Answer:
\(
\begin{aligned}
& \text { Given } \log _3 x+\log _3 y=2+\log _3 2 \\
& \Rightarrow \log _3 x y=\log _3 3^2+\log _3 2 \\
& \Rightarrow \log _3 x y=\log _3 9+\log _3 2 \\
& \left.\Rightarrow \log _3 x y=\log _3 18 \text { (since } \log a+\log b=\log a b\right) \\
& \Rightarrow x y=18 \ldots(i) \\
& \log _3(x+y)=2 \\
& \Rightarrow x+y=3^2 \\
& \Rightarrow x+y=9 \ldots(i i)
\end{aligned}
\)
Solving (i) and (ii), we get,
\(
x=3, y=6
\)