Differential Calculus : \(\frac{d y}{d x}\) As Rate Measurer

Consider two quantities \(y\) and \(x\) interrelated in such a way that for each value of \(x\) there is one and only one value of \(y\). The figure below represents the graph of \(y\) versus \(x\). The value of \(y\) at a particular \(x\) is obtained by the height of the ordinate at that \(x\). Let \(x\) be changed by a small amount \(\Delta x\), and the corresponding change in \(y\) be \(\Delta y\).

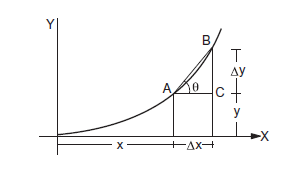
We can define the “rate of change” of \(y\) with respect to \(x\) in the following way. When \(x\) changes by \(\Delta x, y\) changes by \(\Delta y\) so that the rate of change seems to be equal to \(\frac{\Delta y}{\Delta x}\).

If \(A\) be the point \((x, y)\) and \(B\) be the point \((x+\Delta x, y+\Delta y)\), the rate \(\frac{\Delta y}{\Delta x}\) equals the slope of the line \(A B\). We have
\(
\frac{\Delta y}{\Delta x}=\frac{B C}{A C}=\tan \theta .
\)

However, this cannot be the precise definition of the rate. Because the rate also varies between the points \(A\) and \(B\). The curve is steeper at \(B\) than at \(A\). Thus, to know the rate of change of \(y\) at a particular value of \(x\), say at \(A\), we have to take \(\Delta x\) very small. However small we take \(\Delta x\), as long as it is not zero the rate may vary within that small part of the curve.

However, if we go on drawing the point \(B\) closer to \(A\) and every time calculate \(\frac{\Delta y}{\Delta x}=\tan \theta\), we shall see that as \(\Delta x\) is made smaller and smaller the slope \(\tan \theta\) of the line \(A B\) approaches the slope of the tangent at \(A\). This slope of the tangent at \(A\) thus gives the rate of change of \(y\) with respect to \(x\) at \(A\). This rate is denoted by \(\frac{d y}{d x}\). Thus,
\(
\frac{d y}{d x}=\lim _{\Delta x \rightarrow 0} \frac{\Delta y}{\Delta x} .
\)

For small changes \(\Delta x\) we can approximately write
\(
\Delta y=\frac{d y}{d x} \Delta x .
\)

Note that if the function \(y\) increases with an increase in \(x\) at a point, \(\frac{d y}{d x}\) is positive there, because both \(\Delta y\) and \(\Delta x\) are positive. If the function \(y\) decreases with an increase in \(x, \Delta y\) is negative when \(\Delta x\) is positive. Then \(\frac{\Delta y}{\Delta x}\) and hence \(\frac{d y}{d x}\) is negative.

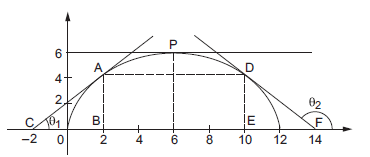
Example 1: From the curve given in the figure below find \(\frac{d y}{d x}\) at \(x=2\), 6 and 10.

Solution: 

The tangent to the curve at \(x=2\) is \(A C\). Its slope is \(\tan \theta_1=\frac{A B}{B C}=\frac{5}{4}\).
Thus, \(\quad \frac{d y}{d x}=\frac{5}{4}\) at \(x=2\).
The tangent to the curve at \(x=6\) is parallel to the \(X\)-axis. Thus, \(\quad \frac{d y}{d x}=\tan \theta=0\) at \(x=6\).

The tangent to the curve at \(x=10\) is \(D F\). Its slope is
\(
\tan \theta_2=\frac{D E}{E F}=-\frac{5}{4} .
\)
Thus, \(\quad \frac{d y}{d x}=-\frac{5}{4}\) at \(x=10\).

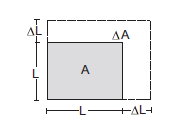
Example 2: Find \(\lim _{\Delta L \rightarrow 0} \frac{\Delta A}{\Delta L}\) for the figure shown below.

Solution:

The area \(A\) of a square of length \(L\) is \(A=L^2\).
If we change \(L\) to \(L+\Delta L\), the area will change from \(A\) to \(A+\triangle A\) (as shown in the figure).
\(
\begin{aligned}
A+\Delta A &=(L+\Delta L)^2 \\
&=L^2+2 L \Delta L+(\Delta L)^2 \\
\text { or, } & \Delta A =2 L(\Delta L)+(\Delta L)^2 \\
\text { or, } & \frac{\Delta A}{\Delta L}=2 L+\Delta L .
\end{aligned}
\)
Now if \(\Delta L\) is made smaller and smaller, \(2 L+\Delta L\) will approach \(2 L\).
Thus, \(\quad \frac{d A}{d L}=\lim _{\Delta L \rightarrow 0} \frac{\Delta A}{\Delta L}=2 L\).

Derivative of some common functions

\(
\begin{array}{|l|c|l|c|}
\hline {y} & \frac{d y}{d x} & y & \frac{d y}{d x} \\
\hline x^n & n x^{n-1} & \sec x & \sec x \tan x \\
\sin x & \cos x & \operatorname{cosec} x & -\operatorname{cosec} x \cot x \\
\cos x & -\sin x & \ln x & \frac{1}{x} \\
\tan x & \sec ^2 x & e^x & e^x \\
\cot x & -\operatorname{cosec}^2 x & & \\
\hline
\end{array}
\)

Besides, there are certain rules for finding the derivatives of composite functions.
(a) \(\frac{d}{d x}(c y)=c \frac{d y}{d x}\), ( \(c\) is a constant)
(b) \(\frac{d}{d x}(u+v)=\frac{d u}{d x}+\frac{d v}{d x}\)
(c) \(\frac{d}{d x}(u v)=u \frac{d v}{d x}+v \frac{d u}{d x}\)
(d) \(\frac{d}{d x}\left(\frac{u}{v}\right)=\frac{v \frac{d u}{d x}-u \frac{d v}{d x}}{v^2}\)
(e) \(\frac{d y}{d x}=\frac{d y}{d u} \cdot \frac{d u}{d x}\)
With these rules and the table shown above derivatives of almost all the functions of practical interest may be evaluated.

Example 3: Find \(\frac{d y}{d x}\) if \(y=e^x \sin x\)

Solution: \(y=e^x \sin x\).
\(
\begin{aligned}
\frac{d y}{d x} &=\frac{d}{d x}\left(e^x \sin x\right)=e^x \frac{d}{d x}(\sin x)+\sin x \frac{d}{d x}\left(e^x\right) \\
&=e^x \cos x+e^x \sin x=e^x(\cos x+\sin x)
\end{aligned}
\)