Definition
Sometimes, a numerical expression may involve multiplication, division or rational powers of large numbers. For such calculations, logarithms are very useful. They help us in making difficult calculations easy. In Chemistry, logarithm values are required in solving problems of chemical kinetics, thermodynamics, electrochemistry, etc. We shall first introduce this concept, and discuss the laws, which will have to be followed in working with logarithms, and then apply this technique to a number of problems to show how it makes difficult calculations simple.
We know that
\(
2^3=8,3^2=9,5^3=125,7^0=1
\)
In general, for a positive real number \(a\), and a rational number \(m\), let \(a^m=b\), where \(b\) is a real number. In other words
the \(\mathrm{m}^{\text {th }}\) power of base \(a\) is \(b\).
Another way of stating the same fact is logarithm of \(b\) to base \(a\) is \(\mathrm{m}\).
If for a positive real number \(a, a \neq 1\)
\(a^m=b\)
we say that \(m\) is the logarithm of \(b\) to the base \(a\).
We write this as \(\log _a b=m\),
“log” being the abbreviation of the word “logarithm”.
Thus, for example we have
\begin{array}{ll}
\log _2 8=3, & \text { Since } 2^3=8 \\
\log _3 9=2, & \text { Since } 3^2=9 \\
\log _5 125=3, & \text { Since } 5^3=125 \\
\log _7 1=0, & \text { Since } 7^0=1
\end{array}
\)
Definition:
\(
b^x=a \\
\log _b a=x
\)
Here, the right side of the arrow is read to be a logarithm of \(a\) to the base \(b\) is equal to \(x\).
Here,
- \(a\) and \(b\) are considered as the two positive real numbers.
- \(x\) is the real number.
- \(a\) which is inside the \(\log\), is known as the argument.
- \(b\), which is at the bottom of the \(\log\), is known as the base.
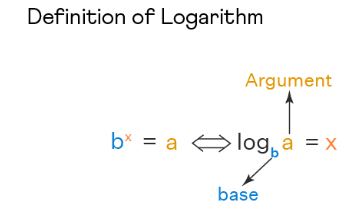
The above equation has two things to understand (from the symbol \(\Leftrightarrow\) ):
- \(b^x=a \Rightarrow \log _b a=x\). This is called “exponential to log form“
- \(\log _b a=x \Rightarrow b^x=a\). This is called “log to exponential form“
Here is a table to understand the conversions from one form to the other form
\(\begin{array}{|l|l|}
\hline \text { Exponential Form } & \text { Logarithmic Form } \\
\hline 2^5=32 & \log _2 32=5 \\
\hline 6^2=36 & \log _6 36=2 \\
\hline 3^{-2}=1 / 9 & \log _3(1 / 9)=-2 \\
\hline e^2=7.389 & \log _e 7.389=2 \\
\hline 10^3=1000 & \log _{10} 1000=3 \\
\hline
\end{array}
\)
\(
\log_b(y)=x
\)
is another way of specifying the relationship:
\(
b^x=y
\)
Let’s plug in some numbers to make this more clear. We will do base- 10 , so \(b =10\).
\(
\log_{10}(100)=2
\)
The base-10 logarithm of 100 is 2 because:
\(
10^ 2=100
\)
It’s basically asking how many b’s do I need to multiply together to get y. To get 100, I just need to multiply two 10’s together. This is actually a really nice way of dealing with multiplicative sequences.
For example, to figure out the magnitude of the number 50 ! (i.e., \(50 \times \cdots \times 1\) ), we proceed to calculate its logarithm, yielding that:
\(
\log (50!) \approx 64.483
\)
Natural Log and Common Log
Observe the last two rows of the above table. They have \(\log _e\) and \(\log _{10}\).
These two logs have specific importance and specific names in logarithms.
- \(\log _e\) is called the natural log
- \(\log _{10}\) is called the common log
Let us study more about each of these.
Natural Logarithm
Natural logarithm is nothing but log with base e. That is, a natural log means \(\log _{ e }\). But it is not usually represented as \(\log _{ e }\). Instead, it is represented as \(\ln\). i.e.,
- \(\log _e=\ln\)
Examples:
- \(e^x=2 \Rightarrow \log _e 2=x\) (or) \(\ln 2=x\).
- \(e ^{ x }=7 \Rightarrow \log _e 7=x\) (or) \(\ln 7=x\).
Common Logarithm
Common logarithm is nothing but log with base 10. That is, a common log means \(\log _{10}\). But usually, writing “log” is sufficient instead of writing \(\log _{10}\). i.e.,
- \(\log _{10}=\log\) i.e., if there is no base for a log it means that its \(\log _{10}\). In other words, it is a common logarithm.
Examples:
- \(10^2=100 \Rightarrow \log _{10} 100=2\) (or) \(\log 100=2\)
- \(10^{-2}=0.01 \Rightarrow \log _{10} 0.01=-2\) (or) \(\log 0.01=-2\)
Observe that we have not written 10 as the base in these examples, because that’s obvious.
\(\log 1\)
The value of \(\log 1\) irrespective of the base is 0 . Because from the properties of exponents, we know that, \(a^0=1\), for any ‘ \(a\) ‘. Converting this into \(\log\) form, \(\log _a 1=0\), for any ‘a’. Obviously, when \(a=10, \log _{10} 1=0\) (or) simply \(\log 1=0\).
When we extend this to the natural logarithm, we have, since \(e^0=1 \Rightarrow \ln 1\) \(=0\).
\(\log _{ a } a\)
Since \(a^1=a\), for any ‘ \(a\) ‘, converting this equation into log form, \(\log _a a=1\). Thus, the logarithm of any number to the same base is always 1 .
For example:
- \(\log _2 2=1\)
- \(\log _3 3=1\)
- \(\log 10=1\)
- \(\operatorname{In} e=1\)
Natural Log is About Time
The natural \(\log\) is the inverse of \(e^x\), a fancy term for opposite. Speaking of fancy, the Latin name is logarithmus naturali, giving the abbreviation \(\ln\).
Now what does this inverse or opposite stuff mean?
- \(e^x\) lets us plug in time and get growth.
- \(\ln (x)\) lets us plug in growth and get the time it would take.
For example:
- \(e^3\) is 20.08. After 3 units of time, we end up with 20.08 times what we started with.
- \(\ln (20.08)\) is about 3. If we want growth of 20.08 , we’d wait 3 units of time (again, assuming a \(100 \%\) continuous growth rate).
The natural log gives us the time needed to hit our desired growth.
What is \(\ln (1)\) ? Intuitively, the question is: How long do I wait to get 1 x my current amount?
You’re already at 1 x your current amount! It doesn’t take any time to grow from 1 to 1 .
- \(\ln (1)=0\)
Ok, how about a fractional value? How long to get \(1 / 2\) my current amount? Assuming you are growing continuously at \(100 \%\), we know that \(\ln (2)\) is the amount of time to double. If we reverse it (i.e., take the negative time) we’d have half of our current value.
- \(\ln (.5)=-\ln (2)=-.693\)
Makes sense, right? If we go backwards . 693 units (negative seconds, let’s say) we’d have half our current amount. In general, you can flip the fraction and take the negative: \(\ln (1 / 3)=-\ln (3)=-1.09\). This means if we go back 1.09 units of time, we’d have a third of what we have now.
Ok, how about the natural log of a negative number? How much time does it take to “grow” your bacteria colony from 1 to -3 ?
It’s impossible! You can’t have a “negative” amount of bacteria, can you? At most you can have zero, but there’s no way to have a negative amount of the little critters. Negative bacteria just doesn’t make sense.
- \(\ln (\) negative number \()=\) undefined
Undefined just means “there is no amount of time you can wait” to get a negative amount.