A Definite Integral has actual values to calculate between (they are put at the bottom and top of the “\(\int\)“) sign:

The definite integral is denoted by \(\int_a^b f(x) d x\), where \(a\) is the lower limit of the integral and \(b\) is the upper limit of the integral.

The definite integral of the function \(f(x)\) from \(x=a\) to \(x=b\) can be interpreted as the signed area under the curve of \(f(x)\) from \(x=a\) to \(x=b\); a visual representation of this integral is given in the diagram.

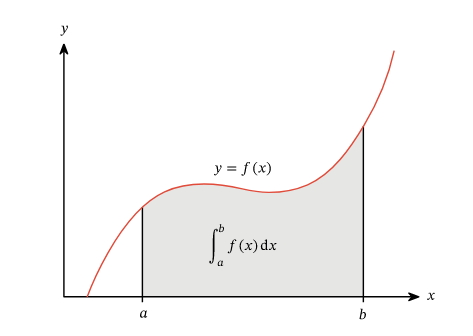
How are definite integrals defined?

Before we give the precise definition, we note that we can estimate the area under the curve for some function \(y=f(x)\), bounded by \(x=a\) and \(x=b\), by first splitting up the interval \([a, b]\) into \(n\) subintervals of equal width, \(\left[x_{i-1}, x_i\right]\) for \(i=1, \ldots, n\), as shown in the diagram.

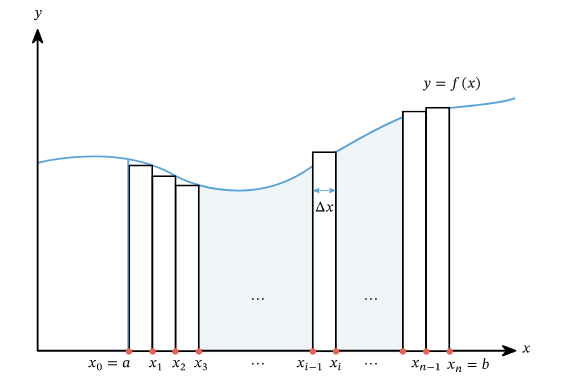
This gives \(n\) rectangles of equal width, \(\Delta x\), where the height of each rectangle is given by the value of the function at each point, \(f\left(x_i\right)\), from the right endpoint of each subinterval. The area of each rectangle is the product of this height and width, \(f\left(x_i\right) \Delta x\). We can estimate the area under the curve of \(f(x)\) by summing the areas of each rectangle as
\(
\begin{aligned}
\text { area } & \approx f\left(x_1\right) \Delta x+\cdots+f\left(x_n\right) \Delta x \\
&=\sum_{i=1}^n f\left(x_i\right) \Delta x
\end{aligned}
\)
This is also known as the right Riemann sum. As the number of rectangles \(n\) gets larger and the width \(\Delta x\) gets smaller, this estimate will get closer to the true area under the curve. In fact, the definite integral, which gives the exact area under the curve, is defined by taking the limit of this sum as the number of rectangles approaches infinity.

Definition of Definite Integral

Given a function \(f(x)\) that is continuous on the interval \([a, b]\) we divide the interval into \(n\) subintervals of equal width, \(\Delta x\), and from each interval choose a point, \(x_i^*\). Then the definite integral of \(f(x)\) from \(a\) to \(b\) is

\(
\int_a^b f(x) d x=\lim _{n \rightarrow \infty} \sum_{i=1}^n f\left(x_i^*\right) \Delta x
\)

The definite integral is evaluated in the following two ways:

(i) The definite integral as the limit of the sum
(ii) \(\int_a^b f(x) d x=\mathrm{F}(b)-\mathrm{F}(a)\), if \(\mathrm{F}\) is an antiderivative of \(f(x)\).

Note: In order to calculate integrals, we now see that it’s important to be able to find antiderivatives of functions. An antiderivative of a function \(f(x)\) is a function whose derivative is equal to \(f(x)\). That is, if \(F^{\prime}(x)=f(x)\), then \(F(x)\) is an antiderivative of \(f(x)\).

Importantly, antiderivatives are not unique. A given function can have many antiderivatives. For instance, the following functions are all antiderivatives of \(x^2\):
\(
\frac{x^3}{3}, \quad \frac{x^3}{3}+1, \quad \frac{x^3}{3}-42, \quad \frac{x^3}{3}+\pi
\)

(i) The definite integral as the limit of the sum

The definite integral \(\int_a^b f(x) d x\) is the area bounded by the curve \(y=f(x)\), the ordinates \(x=a, x=b\) and the \(x\)-axis and given by
\(
\int_a^b f(x) d x=(b-a) \lim _{n \rightarrow \infty} \frac{1}{n}[f(a)+f(a+h)+\ldots f(a+(n-1) h)]
\)

\(
\int_a^b f(x) d x=\lim _{h \rightarrow 0} h[f(a)+f(a+h)+\ldots+f(a+(n-1) h)]
\)

where \(h=\frac{b-a}{n} \rightarrow 0\) as \(n \rightarrow \infty\)

Example 1: \(\text { Evaluate } \int_{-1}^2(7 x-5) d x \text { as a limit of sums. }\)

Solution: Here \(a=-1, b=2\), and \(h=\frac{2+1}{n}\), i.e, \(n h=3\) and \(f(x)=7 x-5\).
Now, we have
\(
\int_{-1}^2(7 x-5) d x=\lim _{h \rightarrow 0} h[f(-1)+f(-1+h)+f(-1+2 h)+\ldots+f(-1+(n-1) h)]
\)
Note that
\(
f(-1)=-7-5=-12
\)
\(
f(-1+h)=-7+7 h-5=-12+7 h
\)
\(f(-1+(n-1) h)=7(n-1) h-12 .\)
Therefore,
\(
\begin{aligned}
&\int_{-1}^2(7 x-5) d x=\lim _{h \rightarrow 0} h[(-12)+(7 h-12)+(14 h-12)+\ldots+(7(n-1) h-12)] \\
&=\lim _{h \rightarrow 0} h[7 h[1+2+\ldots+(n-1)]-12 n]
\end{aligned}
\)
\(
\begin{aligned}
&=\lim _{h \rightarrow 0} h\left[7 h \frac{(n-1) n}{2}-.12 n\right]=\lim _{h \rightarrow 0}\left[\frac{7}{2}(n h)(n h-h)-12 n h\right] \\
&=\frac{7}{2}(3)(3-0)-12 \times 3=\frac{7 \times 9}{2}-36=\frac{-9}{2} .
\end{aligned}
\)

(ii) if \(\mathrm{F}\) is an antiderivative of \(f(x)\).

Let \(f\) be a real-valued function on a closed interval \([a, b]\) and \(\mathrm{F}\) an antiderivative of \(f(x)\) in \([a, b]\):

\(
\mathrm{F}^{\prime}(x)=f(x) .
\)

If \(f\) is integrable on \([a, b]\), then

\(
\begin{aligned}
\int_a^b f(x) \mathrm{d} t &=[\mathrm{F}(x)]_a^b \\
&=\mathrm{F}(b)-\mathrm{F}(a)
\end{aligned}
\)

Example 2: Evaluate the integral: \(\int_2^3 \mathrm{y}^2 \mathrm{dy}\)

Solution:

Let \(\mathrm{I}=\int_2^3 \mathrm{y}^2 \mathrm{dy}\)
As we know,
\(\int y^2 d y=y^3 / 3=\mathrm{F}(y)\)
Therefore, by second fundamental calculus theorem, we know; \(\mathrm{I}=\mathrm{F}(3)-\mathrm{F}(2)=27 / 3-8 / 3=19 / 3\)

Fundamental Theorem of Calculus

(i) Area function: The function \(\mathrm{A}(x)\) denotes the area function and is given by \(\mathrm{A}(x)=\int_a^x f(x) d x\)

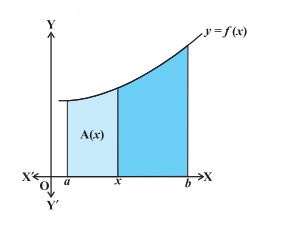
By definition, \(\int_a^b f(x) d x\) is the area of the region bounded by the curve \(y=f(x)\), the \(x\)-axis and the coordinates ‘ \(x=a\) ‘ and ‘ \(x=b\) ‘. If ‘ \(x\) ‘ is a point in \([a, b]\), then \(\int_a x f(x)\) \(\mathrm{dx}\) represents the area of the shaded region \(\{\mathrm{A}(\mathrm{x})\}\) in the figure above. This helps us define the two basic fundamental theorems of calculus described below.

Example 3: Find the area under the graph shown below between \(x=1\) and \(x=4\).

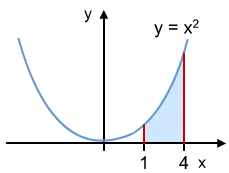
Solution: To find area we have to integrate the function between \(x=1\) and \(x=4\). This is written as:
\(\int_1^4 x^2 d x\)

To evaluate this we integrate and then substitute in the limits, subtracting the value of the lower limit from the value of the higher limit.
\(\int_1^4 x^2 d x=\left[\frac{x^3}{3}\right]_1^4=\left[\frac{4^3}{3}\right]-\left[\frac{1^3}{3}\right]=21\) square units.

(ii) First Fundamental Theorem of integral Calculus

The First Fundamental Theorem of calculus shows that integration and differentiation are inverse operations. Let \(f\) be a continuous function on the closed interval \([a, b]\) and let \(\mathrm{F}(x)\) be the area function and can be written as

\(F(x)=\int_a^x f(x) d x\)

Then \(\mathrm{F}^{\prime}(x)=f(x)\) for all \(x \in[a, b]\).

The First Fundamental Theorem of Calculus formula explains why \(F(x)\) is called the antiderivative function of \(f\) on \([a, b]\). Taking the derivative of \(F(x)=\int_a^x f(x) d x\) gives back the original function \(f(x)\).

We can write the theorem as follows: \(F^{\prime}(x)=\frac{d}{d x} \int_a^x f(x) d x=f(x)\)

This theorem guarantees that any continuous function has an antiderivative function.

Example 4:

\(\text { Let } g(x)=\int_2^x\left(5^x+7\right) d x \text {. Find } g^{\prime}(x)\)

Solution:

Note that \(5^x+7\) is continuous. Let \(f(x)=5^x+7\). Then, by the First Fundamental Theorem of Calculus, we know that
\(
\begin{gathered}
F^{\prime}(x)=\frac{d}{d x} \int_a^x f(x) d x=f(x) \\
g^{\prime}(x)=\frac{d}{d x} \int_2^x\left(5^x+7\right) d x=5^x+7
\end{gathered}
\)
Thus \(g^{\prime}(x)=5^x+7\)

(iii) Second Fundamental Theorem of Integral Calculus

The Second Fundamental Theorem of Calculus clarifies the relationship between the integral and the antiderivative function. It is also referred to as the Fundamental Theorem of Integral Calculus.

Let \(f\) be continuous function defined on the closed interval \([a, b]\) and \(\mathrm{F}\) be an antiderivative of \(f\).
\(
\int_a^b f(x) d x=[\mathrm{F}(x)]_a^b=\mathrm{F}(b)-\mathrm{F}(a) .
\)

Example 5: Evaluate \(\int_2^3\left(x^2+1\right) d x, \text { which is the area under the parabola } x^2+1 \text { between } 2 \text { and } 3 .\)

Solution: 

Let’s find just antiderivative, \(F(x)\), of the given function, and do the subtraction, \(F(b)-\) \(F(a)\). The simplest antiderivative to use is the one where \(C=0\). So, here’s how you use the theorem to find the area under the parabola from 2 to \(3 .\)
\(F(x)=\frac{1}{3} x^3+x\) is an antiderivative of \(x^2+1\).
So, by the theorem, \(\int_2^3\left(x^2+1\right) d x=F(3)-F(2)\); \(F(3)-F(2)\) can be written as \(\left[\frac{1}{3} x^3+x\right]_2^3\)
Thus we have
\(
\begin{aligned}
\int_2^3\left(x^2+1\right) d x &=\left[\frac{1}{3} x^3+x\right]_2^3 \\
&=\frac{1}{3} \cdot 3^3+3-\left(\frac{1}{3} \cdot 2^3+2\right) \\
&=12-4 \frac{2}{3} \\
&=7 \frac{1}{3}
\end{aligned}
\)

Example 6: What is \(\int_1^2 2 x d x\)

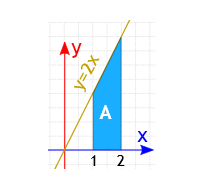
Solution:

Using the Rules of Integration we find that \(\int 2 x d x=x^2+C\)
Now calculate that at 1 , and 2 :
– At \(x=1: \int 2 x d x=1^2+C\)
– At \(x=2: \int 2 x d x=2^2+C\)
Subtract:
\(
\begin{aligned}
&\left(2^2+C\right)-\left(1^2+C\right) \\
&2^2+C-1^2-C \\
&4-1+C-C=3
\end{aligned}
\)

Answer is
\(
\int_1^2 2 x d x=3
\)
Check: with such a simple shape, let’s also try calculating the area by geometry:
\(
A=\frac{2+4}{2} \times 1=3
\)
Yes, it does have an area of \(3 .\)

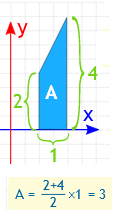
Using direct integration method we have

\(
\begin{aligned}
\int_1^2 2 x d x &=\left[x^2\right]_1^2 \\
&=2^2-1^2 \\
&=3
\end{aligned}
\)

Example 7: The Definite Integral, from \(0.5\) to \(1.0\), of \(\cos (\mathbf{x}) \mathrm{dx}\) :
\(
\int_{0.5}^1 \cos (x) d x
\)

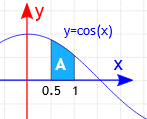
Solution: The Indefinite Integral is: \(\int \cos (x) d x=\sin (x)+C\)
We can ignore C for definite integrals (as we saw above) and we get:
\(
\begin{aligned}
\int_{0.5}^1 \cos (x) d x &=[\sin (x)]_{0.5}^1 \\
&=\sin (1)-\sin (0.5) \\
&=0.841 \ldots-0.479 \ldots \\
&=0.362 \ldots
\end{aligned}
\)

Indefinite Integral

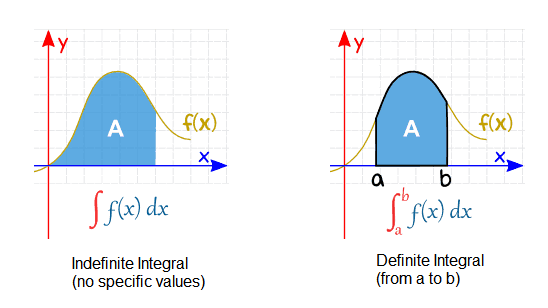
Indefinite integral is the integration of a function without any limits. Integration is the reverse process of differentiation and is referred to as the antiderivative of the function. Indefinite Integrals are the integrals that can be calculated by the reverse process of differentiation and are referred to as the antiderivatives of functions. The figure below shows the Indefinite integral vs definite integral. A Definite Integral has start and end values: in other words, there is an interval [a, b], whereas an indefinite integral has no start and end values.

Let \(\frac{d}{d x} \mathrm{~F}(x)=f(x)\). Then, we write \(\int f(x) d x=\mathrm{F}(x)+\mathrm{C}\). These integrals are called indefinite integrals or general integrals, \(\mathrm{C}\) is called a constant of integration. All these integrals differ by a constant.

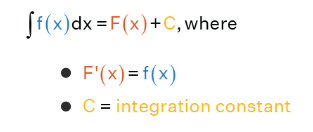
Example 8: Find the indefinite integral of \(x^{2 / 3}\).

Solution: By the power rule of integrals,
\(
\begin{aligned}
&\int x^{2 / 3} d x=x^{2 / 3+1} /(2 / 3+1)+C \\
&=x^{5 / 3} /(5 / 3)+C \\
&=3 x^{5 / 3} / 5+C
\end{aligned}
\)

Example 9: Find the indefinite integral of \(\tan ^2 x\).

Solution: We need to find the integral of \(\tan ^2 x\).
\(
\begin{aligned}
&\int \tan ^2 x d x=\int\left(\sec ^2 x-1\right) d x \\
&=\int \sec ^2 x d x-\int 1 d x \\
&=\tan x-x+C
\end{aligned}
\)