Course Overview

FORCE

A push or pull that one object exerts on another. It is defined as an agency (a push or pull) which changes or tends to change the state of rest or of uniform motion or the direction of motion of a body.

Balanced and Unbalanced Forces

When balanced forces are applied to an object, there will be no net effective force acting on the object. Balanced forces do not cause a change in motion.

Unbalanced forces acting on an object change its speed and/or direction of motion. It moves in the direction of the force with the highest magnitude.

Net force (Resultant Force)

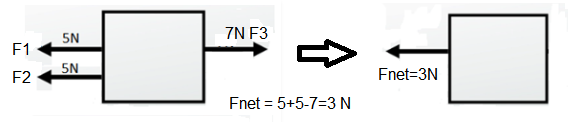
When multiple forces act on a body, they can be resolved into one component known as the net force acting on the object. For Example:

If \(\mathrm{N}\) is the number of forces acting on a body, the net force formula is given by,
\(
\mathrm{F}_{\mathrm{Net}}=\mathrm{F}_1+\mathrm{F}_2+\mathrm{F}_3 \ldots+\mathrm{FN}
\)
Where,
\(\mathrm{F}_1, \mathrm{~F}_2, \mathrm{~F}_3 \ldots \mathrm{FN}\) is the force acting on a body.

Forces in nature

There are four fundamental forces in nature :

• Gravitational force
• Electromagnetic force
• Strong nuclear force
• Weak force

Types of forces on macroscopic objects

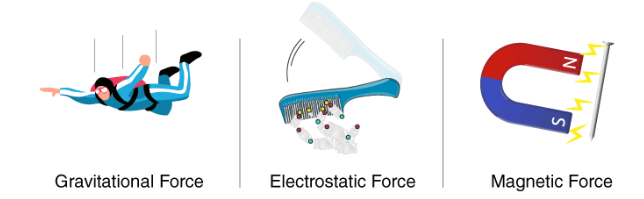
Field Forces or Range Forces (non-Contact Forces): These are the forces in which contact between two objects is not necessary. Examples are

1. Gravitational force between two bodies.
2. Electrostatic force between two charges.
3. Magnetic force between two objects.

Contact Forces : Contact forces exist only as long as the objects are touching each other. Examples are

1. Normal force.
2. Frictional force

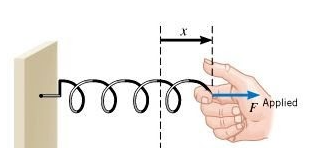
Attachment to Another Body : Tension \((\mathrm{T})\) in a string and spring force \((\mathrm{F}=\mathrm{kx})\) comes in this group.

Unit of Force

• In the centimeter gram second system of unit (CGS unit) force is expressed in dyne.
• In the standard international system of unit (SI unit) it is expressed in Newton (N).

Resolution of force into different components

If the force applied, imparts acceleration \(a\) to a body, then its components in \(X, Y\) and \(Z\)-axis are \(a=a_x \hat{\mathbf{i}}+a_y \hat{\mathbf{j}}+a_z \hat{\mathbf{k}}\). Components of force will be \(F_x, F_y\) and \(F_z\)
As, \(F=m a\)
\(
\Rightarrow \quad F_x \hat{\mathbf{i}}+F_y \hat{\mathbf{j}}+F_z \hat{\mathbf{k}}=m\left(a_x \hat{\mathbf{i}}+a_y \hat{\mathbf{j}}+a_z \hat{\mathbf{k}}\right)
\)
Thus,
\(
\begin{array}{l}
F_x=m a_x=m \frac{d v_x}{d t}=m \frac{d^2 x}{d t^2}=\frac{d p_x}{d t} \\
F_y=m a_y=m \frac{d v_y}{d t}=m \frac{d^2 y}{d t^2}=\frac{d p_y}{d t}
\end{array}
\)
\(
F_z=m a_z=m \frac{d v_z}{d t}=m \frac{d^2 z}{d t^2}=\frac{d p_z}{d t}
\)
The component form of Newton’s second law tells that if the applied force makes some angle with the velocity of the body, it changes the component of velocity along the direction of force. The component of velocity normal to the force remains unchanged.

Example: A force of \(100 \mathrm{~N}\) acts in the direction as shown in figure on a block of mass \(10 \mathrm{~kg}\) resting on a smooth horizontal table. The speed acquired by the block after it has .moved a distance of \(10 \mathrm{~m}\), will be
\(
\left(\mathrm{g}=10 \mathrm{~m} / \mathrm{sec}^2\right)
\)

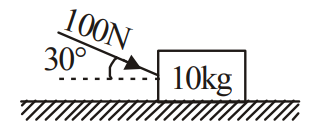
Answer:

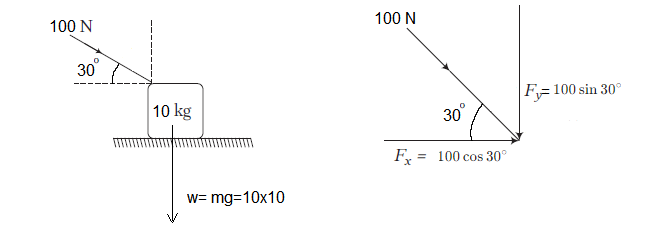
The force of \(100 \mathrm{~N}\) has
Horizontal component of the force \(=100 \cos 30^{\circ}=50 \sqrt{3} \mathrm{~N}\) and
Vertical component of the force \(=100 \sin 30^{\circ}=50 \mathrm{~N}\)
Since the block is always in contact with the table, the net vertical force(Resultant)
\(
\mathrm{F_r}=\mathrm{mg}+\mathrm{F} \sin \theta=(10 \times 10+50) \mathrm{N}=150 \mathrm{~N}
\)
\(
\text { Work }=\text { Force } \mathbf{x} \text { Displacement }
\)
When the block moves along the table, work is done by the horizontal component of the force. Since the distance moves is \(10 \mathrm{~m}\), the work done is
\(50 \sqrt{3} \times 10=500 \sqrt{3}\) Joule.
If \(v\) is the speed acquired by the block, the work done must be equal to the kinetic energy of the block. Therefore, we have
\(500 \sqrt{3}=\frac{1}{2} \times 10 \times {v}^2 \Rightarrow {v}^2=100 \sqrt{3} \Rightarrow \mathrm{v}=13.17 \mathrm{~m} / \mathrm{sec}\)

Newton’s First Law (Law of Inertia)

An object at rest will stay at rest, forever, as long as nothing pushes or pulls on it. An object in motion will stay in motion, travelling in a straight line, forever until a net external unbalanced force applied on it to change that state.

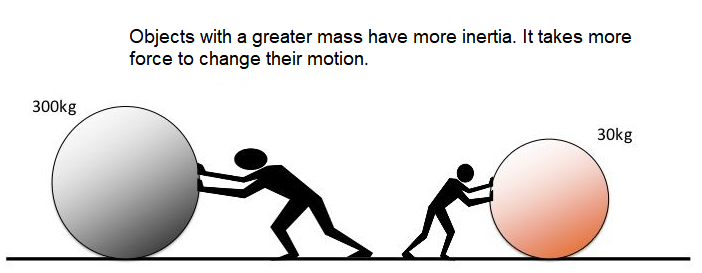
Inertia

Inertia is the property of the body due to which body opposes the change of it’s state. Inertia of a body is measured by mass of the body.

inertia \(\propto\) mass

Basically, all objects have a tendency to resist the change in the state of motion or rest. This tendency is called inertia. All bodies do not have the same inertia. Inertia depends on the mass of a body. Mass of an object is the measure of its inertia.

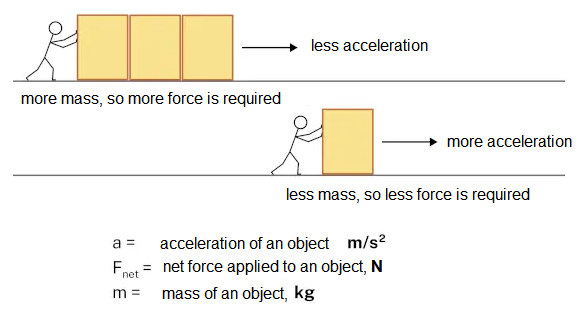
Newton’s Second Law

The acceleration of an object as produced by a net force is directly proportional to the magnitude of the net force, in the same direction as the net force, and inversely proportional to the mass of the object.

This statement is expressed in equation form as,
\(
a=\frac{F_{\text {net }}}{m}
\)
The above equation can be rearranged to a familiar form as
\(
F=m a
\)
Since force is a vector, Newton’s second law can be written as
\(
\vec{F}=m \vec{a}
\)

Units of Force

• In SI system, absolute unit of force is newton.
  One newton is defined as that much force which produces an acceleration of \(1 \mathrm{~ms}^{-2}\) in a body of mass \(1 \mathrm{~kg}\).
  \(
  \begin{array}{l}
  1 \mathrm{~N}=1 \mathrm{~kg} \times 1 \mathrm{~ms}^{-2} \\
  1 \mathrm{~N}=1 \mathrm{~kg} \mathrm{~ms}^{-2}
  \end{array}
  \)
• In CGS system, absolute unit of force is dyne.
  One dyne is that much of force which produces an acceleration of \(1 \mathrm{~cms}^{-2}\) in a body of mass \(1 \mathrm{~g}\).
  \(
  \begin{array}{l}
  1 \text { dyne }=1 \mathrm{~g} \times 1 \mathrm{cms}^{-2} \\
  1 \text { dyne }=1 \mathrm{~g} \mathrm{cms}^{-2}
  \end{array}
  \)
• In MKS system, gravitational unit of force is kilogram weight ( \(\mathrm{kg}-\mathrm{wt})\). One \(\mathrm{kg}\)-wt is that much of force which produces an acceleration of \(9.80 \mathrm{~ms}^{-2}\) in a body of mass 1 kg. It is also known as kilogram-force (kgf).
  \(
  1 \mathrm{~kg}-\mathrm{wt}=1 \mathrm{kgf}=9.8 \mathrm{~N}
  \)
• In CGS system, gravitational unit of force is gram weight ( \(\mathrm{g-}\mathrm{wt})\) or gram force (gf). It is defined as that force which produces an acceleration of \(980 \mathrm{~cms}^{-2}\) in a body of mass \(1 \mathrm{~g}\).
  \(
  1 \mathrm{~g-}\mathrm{wt}=1 \mathrm{gf}=980 \mathrm{~g} \mathrm{~cm} \mathrm{~s}^{-2} \text { or } 1 \mathrm{~gf}=980 \text { dyne }
  \)
  
  The equation shows that the direction of the total acceleration vector points in the same direction as the net force vector.

Let \(\mathbf{F}\) be external force applied on the body in the direction of motion of the body for time interval \(\Delta t\), then the velocity of a body of mass \(m\) changes from \(\mathbf{v}\) to \(\mathbf{v}+\Delta \mathbf{v}\), i.e. change in momentum, \(\Delta \mathbf{p}=m \Delta \mathbf{v}\).
According to Newton’s second law,
\(
\mathbf{F} \propto \frac{\Delta \mathbf{p}}{\Delta t} \text { or } \mathbf{F}=k \frac{\Delta \mathbf{p}}{\Delta t}
\)
where, \(k\) is a constant of proportionality.
If limit \(\Delta t \rightarrow 0\), then the term \(\frac{\Delta \mathbf{p}}{\Delta t}\) becomes the derivative \(\frac{d \mathbf{p}}{d t}\). Thus, \(\mathbf{F}=k \frac{d \mathbf{p}}{d t}\)

Note: The slope of momentum-time graph is equal to force on the particle.

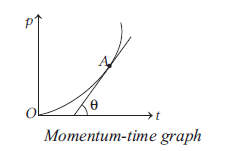
At point \(A, F=\frac{d p}{d t}=\) slope \(=\tan \theta\)
This graph depicts the motion of a body on which increasing force is acting.

Balanced Forces

• \(a=0 \mathrm{~m} \mathrm{~s}^{-2}\)
• Object at rest \(\left(v=0 \mathrm{~m} \mathrm{~s}^{-1}\right)\)
• Object Stays at rest.

Unbalanced Forces

• There is an acceleration.
• The acceleration depends directly upon the net force.
• The acceleration depends inversely upon the mass of the object.

Example 1: If there is a block of mass \(2 \mathrm{~kg}\), and a force of \(30 \mathrm{~N}\) is acting on it in the positive \(\mathrm{x}\) direction, and a force of \(40 \mathrm{~N}\) in the negative \(\mathrm{x}\)-direction, then what would be its acceleration?

Answer: 

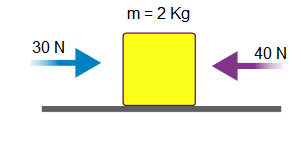
We first have to calculate the net force acting on it to calculate its acceleration.
\(
\begin{aligned}
& F_{n e t}=30 N-40 N=-10 N \\
& \text { Mass }=2 \mathrm{~kg}
\end{aligned}
\)

\(a=\frac{F_{\text {net }}}{m}\)
\(
\text { Acceleration }=\frac{-10 \mathrm{~N}}{2 \mathrm{~kg}}=-5 \mathrm{~m} / \mathrm{s}^2
\)

The negative acceleration indicates that the block is slowing and its acceleration vector is moving in an opposite direction directed opposite to the direction of motion.

Example 2: How much horizontal net force is required to accelerate a \(2000 \mathrm{~kg}\) car at \(4 \mathrm{~m} / \mathrm{s}^2\)?

Answer: Newton’s 2nd Law relates an object’s mass, the net force on it, and its acceleration:
Therefore, we can find the force as follows:
\(
\mathrm{F}_{\mathrm{net}}=\mathrm{ma}
\)
Substituting the values, we get
\(
2000 \mathrm{~kg} \times 4 \mathrm{~m} / \mathrm{s}^2=8000 \mathrm{~N}
\)
Therefore, the horizontal net force is required to accelerate a \(2000 \mathrm{~kg}\) car at \(4 \mathrm{~m} / \mathrm{s}^{2}\) is \(8000 \mathrm{~N}\).

Newton’s Third Law of Motion

Newton’s third law of motion states that to every action, there is an equal and opposite reaction. If a body \(A\) exerts a force \(\vec{F}\) on another body \(B\) then \(B\) exerts a force \(-\vec{F}\) on \(A\). i.e., for every action, there is equal and opposite reaction.

From Newton’s 3rd law, it can be analysed that we cannot produce a single isolated force in nature. Thus, forces occur in equal and opposite pairs. Whenever object \(A\) exerts a force on object \(B\), object \(B\) must also exert a force on object \(A\). The two forces are equal in magnitude and opposite in direction.

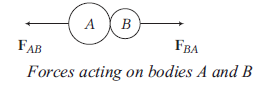
As shown in figure, if \(\mathrm{F}_{B A}\) is the force exerted by body \(A\) on \(B\) and \(\mathbf{F}_{A B}\) is the force exerted by \(B\) on \(A\), then according to Newton’s third law,
\(
\mathrm{F}_{A B}=-\mathrm{F}_{B A}
\)
Force on \(A\) by \(B=-\) Force on \(B\) by \(A\)

Important features of Newton’s 3rd law of motion

• Newton’s third law of motion is applicable irrespective of the nature of the forces: The forces of action and reaction may be mechanical, gravitational, electric or of any other nature.
• Action and reaction always act on two different bodies: If they act on the same body, the resultant force would be zero and there could never be accelerated motion.
• The force of action and reaction cannot cancel each other: This is because action and reaction, though equal and opposite forces always act on different bodies and so cannot cancel each other.
• No action can occur in the absence of a reaction: In a tug of war, one team can pull the rope only if the other team is pulling the other end of the rope; no force can be exerted, if the other end is free. One team exerts the force of action and the other team provides the force of reaction.

What Is a Frame of Reference?

We have learned about velocity, acceleration, and displacement. But all these quantities need a frame of reference from which they are measured. In physics, a frame of reference consists of an abstract coordinate system and the set of physical reference points that uniquely fix the coordinate system and standardize measurements within that frame.

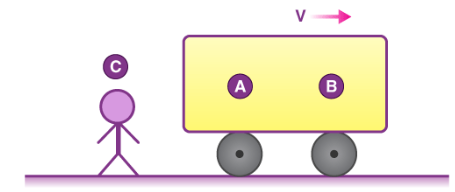
If we ask A what velocity of B is, he will say it is at rest. But if we ask the same question to C, he will say B is moving with a velocity V in the positive X direction. So we can see before specifying the velocity we have to specify in which frame we are or in simple terms, we need to define a frame of reference.

Types of Frame of Reference

Once we have chosen our reference they can be of two types:

• Inertial Frame of Reference
• Non-inertial Frame of Reference

Inertial Frame of Reference
An inertial frame of reference is a frame where Newton’s law holds true. That means if no external force is acting on a body it will stay at rest or remain in uniform motion. Suppose a body is kept on the surface of the earth, for a person on earth it is at rest while for a person on the moon it is in motion so which is my inertial frame here? Actually, the term inertial frame is relative i.e. first we assume a reference frame to be the inertial frame of reference. So a more general definition of an inertial frame would be: Inertial frame is at rest or moves with constant velocity with respect to my assumed inertial reference frame.

A reference frame which is either at rest or in uniform motion along the straight line. A non-accelerating frame of reference is called an inertial frame of reference. All the fundamental laws of physics have been formulated in respect of inertial frame of reference.
Non-inertial Frame of Reference
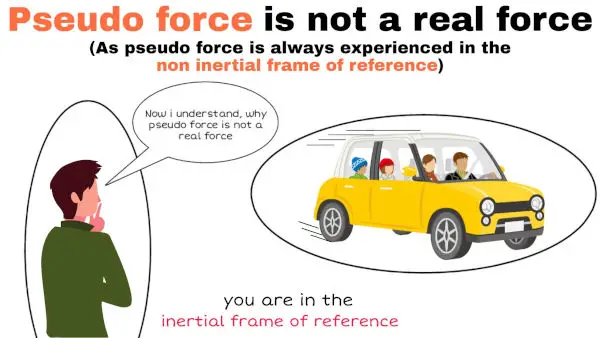
Now we can define a non-inertial frame as a frame that is accelerated with respect to the assumed inertial frame of reference. Newton’s law will not hold true in these frames. So in the above example if I assume earth to be an inertial reference frame the moon becomes a non-inertial reference frame as it is in accelerated motion with respect to earth. But if we want to make Newton’s law hold here we need to take some mysterious forces also known as pseudo forces.

An accelerating frame of reference is called a non-inertial frame of reference. Newton’s laws of motion are not directly applicable in such frames, before application we must add pseudo force.

Few examples are shown below:

A frame of reference, also referred to as a reference frame, is a conceptual framework used to establish a coordinate system and a set of reference points. Its purpose is to provide a standardized means of measuring and describing the position, velocity, and other characteristics of objects within that frame. By defining a coordinate system and reference points, a frame of reference facilitates the consistent and accurate comparison and analysis of physical phenomena from a particular perspective.

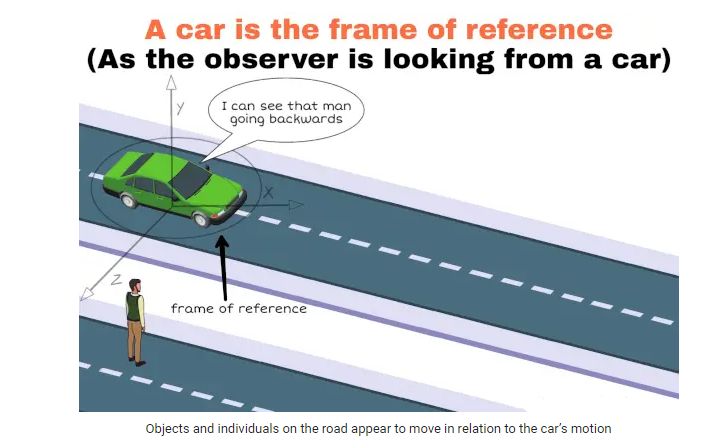
When driving a car, an individual may notice that a pedestrian walking on the road appears to be moving in the opposite direction. This perception is influenced by the frame of reference chosen, which is the car itself. From the perspective of the car, stationary objects and individuals on the road may seem to be in motion relative to the car’s own movement. This observation highlights the importance of considering the frame of reference when interpreting the motion of objects in relation to one’s own position and movement.

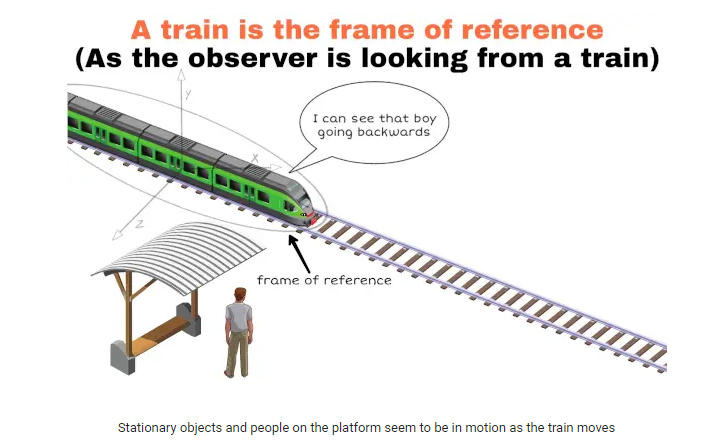
Imagine a train in motion, with an individual seated inside and observing the surroundings. From their vantage point, they will observe that the objects in the surrounding area, as well as the people on the platform, appear to be in motion. This observation is a consequence of the frame of reference they have chosen, which is the moving train itself. As the person inside the train moves along with it, they perceive the stationary objects on the platform as moving relative to their frame of reference.

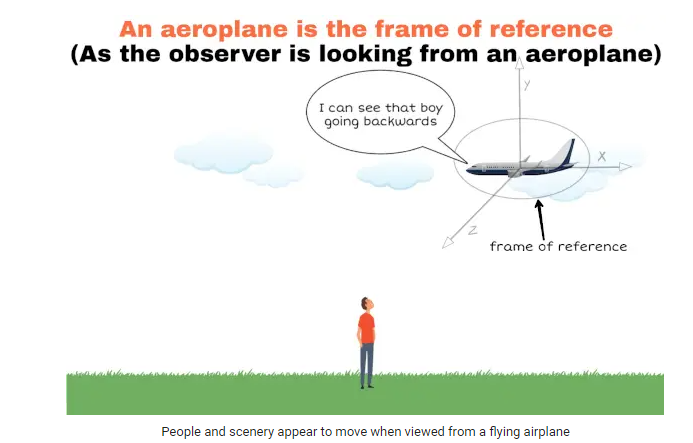
During an airplane takeoff, passengers may notice that the scenery outside seems to quickly move away from them. This happens because their frame of reference is the inside of the moving airplane. As the plane gains speed on the runway and lifts off the ground, the objects on the ground appear to move farther away from their perspective. This perception is a result of the relative motion between the airplane and the stationary objects on the ground, illustrating the influence of the chosen frame of reference on how we perceive motion during an airplane takeoff.

Pseudo Force

Pseudo, the word means false. Therefore, pseudo force is a false or an imaginary force. Pseudo force is a force that does not actually exist, but it appears to be present when the frame of reference is accelerating. It is also known as a fictitious force, inertial force, or d’Alembert force. It means that in the frame of every accelerating body, a pseudo force appears to be acting on all the objects contained in the frame. The direction of the pseudo force is always opposite to the direction of acceleration of the frame. The acceleration with which the objects in the frame appear to be moving is the same as that of the acceleration with which the object moves. The magnitude of the pseudo force is equal to the product of the mass of the object and the acceleration of the frame. The frame that is not accelerating is known as the inertial frame, whereas the frame that is accelerating is known as the non-inertial frame. Few examples are given below:

Case-I: Accelerating Bus

Case-II: A person watching a moving car

Case-III: Lift (Accelerating Upward)

When we descend in a lift, a tremendous force pulls our body higher. Due to this illusion force, things outside the moving lift appear to be going at the same rate as the lift but in the opposite direction. The pseudo force, a fictitious force, is the force that causes something to happen. When an elevator is moving with an acceleration, it becomes a non-inertial frame of reference. We find it difficult to apply Newton’s laws of motion for a non-inertial frame of reference when the observer is a part of that reference. 

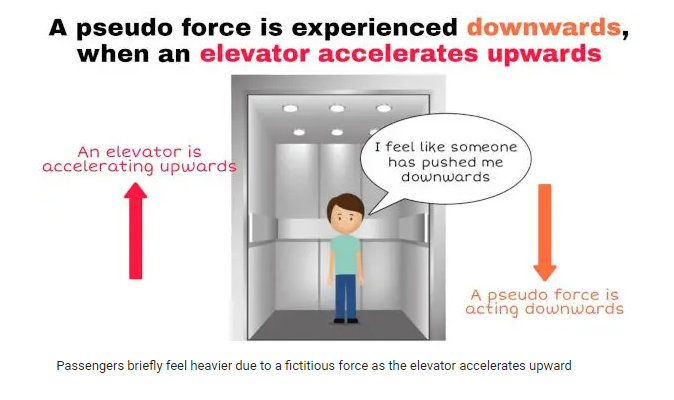
When an elevator accelerates upward, passengers inside may briefly feel a sensation of increased weight. This happens because, from their perspective inside the elevator, it appears as if a fictitious force is acting, making gravity seem stronger. In reality, gravity remains the only real force acting on passengers, constantly pulling them downward. However, when the elevator accelerates upward, passengers find themselves in a reference frame that is also undergoing acceleration. This creates the perception of an additional, or ‘fictitious,’ force pushing them downward, resulting in the feeling of greater weight. This change in apparent weight is due to the elevator’s upward acceleration, which alters how passengers perceive the effects of gravity.

Case-IV: Car speeding up

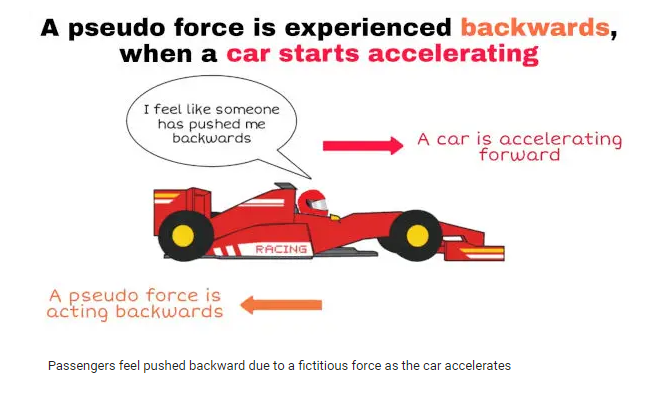
When a car accelerates, an observer inside the vehicle may sense a backward force, as if an invisible hand pushes them into their seat. This sensation results from fictitious force, specifically the ‘inertial’ or ‘pseudo’ force. No external force pushes the passenger; it’s the car’s acceleration itself. According to Newton’s first law of motion, objects stay at rest or move straight unless acted upon by an external force. As the car accelerates, the passenger tends to stay still due to their inertia. The apparent backward force arises as the car ‘drags’ the passenger along. This illustrates how fictitious forces help us understand motion in accelerating frames, despite no real external forces.

Formula

Pseudo force formula: \(F_p=-\) ma
where,
\(F_p=\) pseudo force acting on an object
\(\mathrm{m}\) = mass of an object
\(\mathrm{a}=\) acceleration of an object’s frame of reference
\((-)\) sign indicates that pseudo force is acting in the opposite direction to the acceleration of an object’s frame of reference.

Pseudo Force Calculation with Railroad Cart example-1:

Consider a situation in which one person is standing on a railroad cart and another is standing on the ground near the railway track. When the cart begins to move forward, the observer on the ground notices the vehicle moving but notices no movement in the rocks surrounding him. The guy standing on the railroad cart, on the other hand, perceives the rock on the ground as moving at the same rate as the railroad cart, which seems to be stationary to him. The rocks move backward without applying any force, according to the person standing on the cart. The rocks appear to be shifting due to the cart’s movement. A force seems to be acting on the rocks in the frame, pulling them backward. The pseudo force is the name given to this fake power.

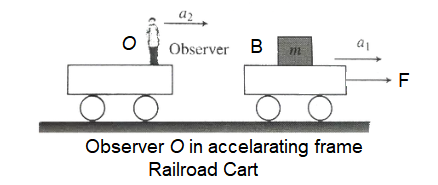
Let us assume that, a block \(B\) is moving on a cart when a constant force \(\vec{F}\) is applied on it, as shown in the figure, \(\vec{a_1}=\vec{F} / m\) is acceleration of the block having mass \(m\).
If this block \((B)\) is observed by an observer \((O)\) standing on frame which is accelerating with acceleration \(\vec{a}_2\), then acceleration of block w.r.t. observer,
\(
\vec{a}_{B / O}=\vec{a}_B-\vec{a}_O=\vec{a_1}-\vec{a}_2
\)
Force on the block as observed by the observer \(\vec{F}_{B / O}=m\left(\vec{a_1}-\vec{a}_2\right)=m \vec{a_1}-m \vec{a_2}\) or \(\vec{F}_{B / O}=\vec{F}+\vec{F}_{\text {pseudo }}\)
So, \(\vec{F}_{\text {pseudo }}=-m \vec{a}_2\)
If an object of mass \(m\) is observed from a non-inertial reference frame having acceleration, then pseudo force will be \(\vec{F}_{\text {pseudo }}=-m \vec{a}_2\)
For non-inertial frame, \(\vec{F}_{\text {ext }}+\vec{F}_{\text {pseudo }}=m \vec{a_1}\), where \(\vec{a_1}\) is the acceleration of the object with respect to the frame and \(F_{\text {ext }}\) is the external force.

Note: When we draw the free body diagram of a mass, with respect to an inertial frame of reference we apply only the real forces (forces which are actually acting on the mass). But when the free body diagram is drawn from a noninertial frame of reference a pseudo force (in addition to all real forces) has to be applied to make the equation \(\overrightarrow{\mathrm{F}}=\mathrm{m} \overrightarrow{\mathrm{a}}\) to be valid in this frame also.
\(\sum \overrightarrow{\mathrm{F}}_{\text {real }}+\overrightarrow{\mathrm{F}}_{\mathrm{pseudo}}=\mathrm{m}\overrightarrow{\mathrm{a}}\) (where \(\overrightarrow{\mathrm{a}}\) is acceleration of object in non inertial reference frame) & \(\overrightarrow{\mathrm{F}}_{\mathrm{pseudo}}=-\mathrm{m} \overrightarrow{\mathrm{a}}_{\mathrm{0}}\) (where \(\overrightarrow{\mathrm{a}}_0\) is acceleration of non inertial reference frame).

Momentum

Momentum of a body is the quantity of motion possessed by a moving body. It is measured as the product of mass and velocity of a body. It is represented by \(p\).
i.e. Momentum \((p)=\) Mass \((m) \times\) Velocity \((v)\)
SI unit of momentum is \(\mathrm{kg}\mathrm{-ms}^{-1}\) and CGS unit of momentum is \(\mathrm{g}-\mathrm{cms}^{-1}\).
The dimensional formula of momentum is \(\left[\mathrm{MLT}^{-1}\right]\). It is a vector quantity.

Impulse

When a large force acts on a body for very small time, then product of the average of total force for that small time period and the time period itself is called impulse.
\(
\text { Impulse }=\text { Average force } \times \text { Time }
\)

\(
I=F \Delta t \quad \text { or } \quad \mathbf{I}=\int_{t_1}^{t_2} \mathbf{F} d t
\)

It is a vector quantity and its direction is same as that of force. Dimensional formula of impulse is same as that of momentum, i.e. \(\left[\mathrm{MLT}^{-1}\right]\).
SI unit of impulse is \(\mathrm{N}\)-s or \(\mathrm{kg} \mathrm{ms}^{-1}\) and CGS unit of it is \(\mathrm{g}-\mathrm{cms}^{-1}\).

• Impulse = Change in momentum
• The integral of a force over a certain period of time.
• The value of the force is needed in order for it to be calculated.
• Takes into account the effects of both the force acting on the system and the duration of time for which it acts.

Example: A batsman hits back a ball of mass \(0.4 \mathrm{~kg}\) straight in the direction of the bowler without changing its initial speed of \(15 \mathrm{~ms}^{-1}\). Calculate the impulse imparted to the ball in N-s.

Answer: Impulse imparted on a ball:
\(
\begin{array}{l}
I=m \Delta v \\
I=m\left(v_2-v_1\right) \\
I=0.4 \times(15-(-15)) \\
=0.4 \times 2 \times 15=12 \mathrm{~N}-\mathrm{s}
\end{array}
\)

Example: A golfer hits a ball of mass \(45 \mathrm{~g}\) at a speed of \(40 \mathrm{~m} / \mathrm{s}\). The golf club is in contact with the ball for \(3 \mathrm{~s}\). Compute the average force applied by the club on the ball?

Answer:

\(
\begin{array}{l}
\mathrm{m}(\text { Mass })=0.045 \mathrm{~kg}, \\
{v}_i (\text { Initial Velocity })=0, \\
{v}_f(\text { Final Velocity })=40 \mathrm{~m} / \mathrm{s}, \\
\text { Impulse force } \mathrm{F}=\mathrm{ma}= m \frac{v_f-v_i}{t} =0.045 \times \frac{40}{0.003} =600 \mathrm{~N}
\end{array}
\)

Relation between momentum and impulse

Suppose \(\mathbf{F}\) is the value of force during impact at any time and \(p\) is the momentum of the body at that time, then according to Newton’s IInd law of motion,
\(
\mathbf{F}=\frac{d \mathbf{p}}{d t} \text { or } \mathbf{F} \cdot d t=d \mathbf{p} \dots(i)
\)
Suppose that the impact lasts for a small time \(t\) and during this time, the momentum of the body changes from \(p_1\) to \(p_2\). Then, integrating the above equation, we get
\(
\int_0^t \mathbf{F} d t=\int_{p_1}^{p_2} d \mathbf{p}=|\mathbf{p}|_{p_1}^{p_2} \Rightarrow \underbrace{\int_0^t \mathbf{F} d t}_{\text {Impulse }}=p_2-p_1
\)
From this equation, we found that impulse is equal to change in momentum of the body.
Also, if \(\mathbf{F}_{\mathrm{av}}\) is the average force (constant) during the impact, then
Impulse, \(\mathbf{I}=\int_0^t \mathbf{F}_{\mathrm{av}} d t=\mathbf{F}_{\mathrm{av}} \int_0^t d t=\mathbf{p}_2-\mathbf{p}_1\)
or \(\quad \mathbf{I}=\mathbf{F}_{\mathrm{av}} \cdot t=\mathbf{p}_2-\mathbf{p}_1=\Delta p\)
Thus, impulse is also equal to total change in momentum.
This is known as impulse-momentum theorem.

Calculation of impulse: graphical method

Case-I: When applied force is constant, then the graph, between this force and the time of application of this force is a straight line parallel to time axis.

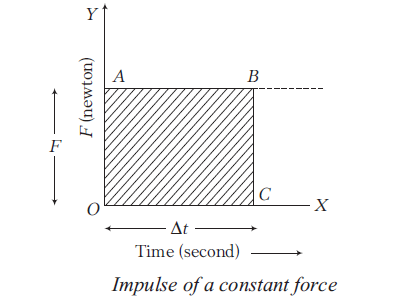
Here, impulse is given by the area covered by the graph.
i.e. \(I=F \times \Delta t\)
where, \(F=O A, \Delta t=O C\)
\(\therefore \quad I=O A \times O C=\) Area of rectangle \(O A B C\).

Case-II: When applied force is variable for the time of application \((\Delta t)\), then graph between force and time will be a curve as given in the figure below

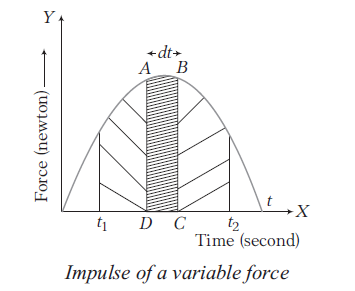
Here,
\(
\begin{aligned}
\text { impulse } & =\text { force } \times \text { time } \\
& =F \times d t \\
& =\text { Area of shaded region }
\end{aligned}
\)
Total impulse for the force applied during period from \(t_1\) to \(t_2\)
\(
\begin{array}{l}
=\int_{t_1}^{t_2} F \cdot d t \\
=\text { Area under } F \text { – } t \text { curve from } t_1 \text { to } t_2
\end{array}
\)
Total impulse for the force applied
\(=\) Area covered between the curve and time-axis

Conservation of Linear Momentum

The total momentum of an isolated system (a system having no external force acting on it) of constant mass remains constant or conserved and does not change with time. This is known as law of conservation of momentum. If the momentum of two particles system of masses \(m_1\) and \(m_2\) are \(p_1\) and \(p_2\) respectively, then the net momentum of whole system is given by
\(
p=p_1+p_2=\text { constant }
\)
This principle is a consequence of Newton’s second and third law of motion.

Conservation of linear momentum for a system of two or more particles

Force applied on particle 1 by particle 2 is \(F_{12}\) and force applied on particle 2 by particle 1 is \(F_{21}\) and their respective momentum are \(p_1\) and \(p_2\).
From Newton’s IInd law,
\(
\mathbf{F}_{12}=\frac{d p_1}{d t} \text { and } \mathbf{F}_{21}=\frac{d p_2}{d t}
\)
From Newton’s 3rd law,
\(
\mathbf{F}_{12}=-\mathbf{F}_{21} \Rightarrow \frac{d \mathbf{p}_1}{d t}=-\frac{d \mathbf{p}_2}{d t}
\)
\(
\text { or } \frac{d \mathbf{p}_1}{d t}+\frac{d \mathbf{p}_2}{d t}=0 \Rightarrow \frac{d}{d t}\left(\mathbf{p}_1+\mathbf{p}_2\right)=0
\)
Thus, \(\mathbf{p}_1+\mathbf{p}_2=\text { constant }\)
For \(n\) number of particles,
\(
\mathbf{p}_1+\mathbf{p}_2+\mathbf{p}_3+\ldots+\mathbf{p}_n=\text { constant }
\)

Conservation of linear momentum for the collision of two bodies

Case-I: Head-on collision (collision in a straight line) Two bodies of masses \(m_1\) and \(m_2\) collide on frictionless surface moving in the same direction with respective velocities \(u_1\) and \(u_2\). After collision, both the bodies separate with a variation in their velocities, i.e. \(v_1\) and \(v_2\), respectively.

Initial momentum (before collision),
\(
p_{1(\text { initial) }}=m_1 \mathbf{u}_1, p_{2 \text { (initial) }}=m_2 \mathbf{u}_2
\)
Final momentum (after collision),
\(
p_{1(\text { final })}=m_1 \mathbf{v}_1, \quad p_{2(\text { final })}=m_2 \mathbf{v}_2
\)

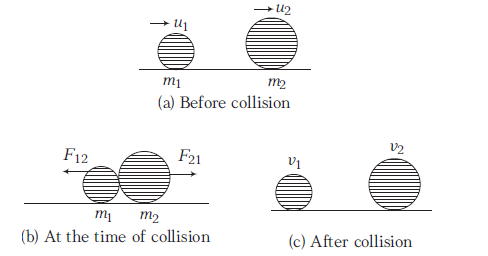
During collision, particle 1 exerts a force \(F_{21}\) on particle 2 and simultaneously particle 2 exerts a force \(F_{12}\) on particle 1.
\(
\begin{aligned}
\mathrm{F}_{12} & =\text { rate of change of momentum of particle } 1 \\
& =\frac{m_1 v_1-m_1 u_1}{t}=\frac{m_1\left(v_1-u_1\right)}{t}
\end{aligned}
\)

Similarly, \(\mathrm{F}_{21}=\) rate of change of momentum of particle 2
\(
=\frac{m_2 v_2-m_2 u_2}{t}=\frac{m_2\left(v_2-u_2\right)}{t}
\)

According to Newton’s 3rd law of motion,
\(
\begin{array}{l}
\mathrm{F}_{12}=-\mathrm{F}_{21} \\
\Rightarrow \quad \frac{m_1\left(v_1-u_1\right)}{t}=-\frac{m_2\left(v_2-u_2\right)}{t} \\
\text { or } \quad m_1 u_1+m_2 u_2=m_1 v_1+m_2 v_2 \\
\end{array}
\)
i.e. Total momentum before collision remains same as total momentum after collision.

Case-II: Oblique collision (collision of ball with wall) A ball of mass \(m\) strikes a wall with velocity \(u\) at an angle \(\theta\) from the normal of wall and rebounds with the same speed in time \(t\).
Here, initial momentum of the particle,
\(
\mathbf{p}_i=m u \cos \theta \hat{\mathbf{i}}-m u \sin \theta \hat{\mathbf{j}}
\)
Final momentum of the particle,
\(
\mathrm{p}_f=-m u \cos \theta \hat{\mathbf{i}}-m u \sin \theta \hat{\mathbf{j}}
\)

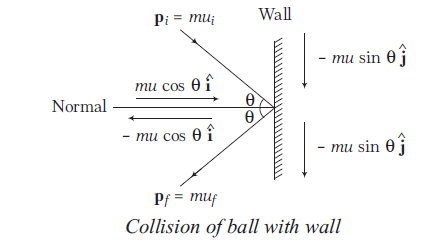
Now, change in momentum, \(\Delta \mathbf{p}=\mathbf{p}_f-\mathbf{p}_i\)
\(
\begin{array}{l}
=-m u \cos \theta \hat{\mathbf{i}}-m u \sin \theta \hat{\mathbf{j}}-m u \cos \theta \hat{\mathbf{i}}+m u \sin \theta \hat{\mathbf{j}} \\
=-2 m u \cos \theta \hat{\mathbf{i}}
\end{array}
\)
It means that momentum changes only along the normal to the wall but not along the wall. This is so because force is acting on the ball only normal to the wall (this force is reaction force of wall) and no force acts parallel to the wall.
\(
|\Delta \mathbf{p}|=2 m u \cos \theta
\)
Force,
\(
\begin{aligned}
\mathbf{F} & =\frac{\Delta \mathbf{p}}{\Delta t}=\frac{-2 m u \cos \theta}{t} \hat{\mathbf{i}} \\
|\mathbf{F}| & =\frac{2 m u \cos \theta}{t}
\end{aligned}
\)
There are two possible cases

Case-I: If \(\theta=0^{\circ}\), means ball is thrown perpendicular to the wall, then \(\Delta \mathbf{p}=-2 m u \cos 0^{\circ} \hat{\mathbf{i}}\)
\(
\begin{array}{ll}
\Rightarrow & \Delta \mathbf{p}=-2 m u \hat{\mathbf{i}} \\
\therefore & \mathbf{F}=\frac{\Delta \mathbf{p}}{\Delta t}=\frac{-2 m u}{t} \hat{\mathbf{i}}
\end{array}
\)

Case-II: If \(\theta\) is the angle measured from the wall, then
\(
\begin{aligned}
\Delta \mathbf{p} & =-2 m u \sin \theta \hat{\mathbf{i}} \Rightarrow|\Delta \mathbf{p}|=2 m u \sin \theta \\
\mathbf{F} & =\frac{-2 m u \sin \theta}{t} \hat{\mathbf{i}} \Rightarrow|\mathbf{F}|=\frac{2 m u \sin \theta}{t}
\end{aligned}
\)

Newton’s 3rd law can be derived from principle of conservation of linear momentum

If two particles of masses \(m_1\) and \(m_2\) are moving under action of their mutually interacting forces with each other, such that no external force acts on the system. Then, momentum of system remains constant.

\(
\begin{array}{l}
\text { i.e. } \quad \Delta \mathbf{p}_1+\Delta \mathbf{p}_2=0 \Rightarrow \Delta \mathbf{p}_1=-\Delta \mathbf{p}_2 \Rightarrow \frac{\Delta \mathbf{p}_1}{\Delta t}=-\frac{\Delta \mathbf{p}_2}{\Delta t} \\
\Rightarrow \quad \mathbf{F}_{12}=-\mathbf{F}_{21} \\
\end{array}
\)
\(
\text { Force on } \text { 1st due to } 2 \mathrm{nd}=- \text { Force on } \text { 2nd due to } \text {1st }
\)

Example: An explosion blows a rock into three parts. Two pieces go off at right angles to each other; 1.0 kg piece with a velocity of 12 m/s and other 2.0 kg piece with a velocity 8 m/s. If the third piece flies off with a velocity 40 m/s, compute the mass of third piece.

Answer: When an explosion breaks a rock, by the law of conservation of momentum, initial momentum is zero and for the three pieces,

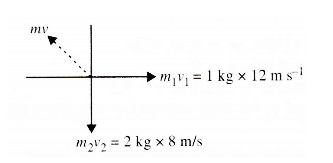
When an explosion breaks a rock, by the law of conservation Total momentum of the two pieces \(1 \mathrm{~kg}\) and \(2 \mathrm{~kg}\)
\(
=\sqrt{12^2+16^2}=20 \mathrm{~kg} \mathrm{~ms}^{-1} \text {. }
\)
The third piece has the same momentum and in the direction opposite to the resultant of these two momenta.
Momentum of the third piece
\(
=20 \mathrm{~kg} \mathrm{~ms}^{-1}
\)
Velocity \(=40 \mathrm{~ms}^{-1}\)
\(\therefore \quad\) Mass of the \(3^{\text {rd }}\) piece
\(
=\frac{m v}{v}=\frac{20}{40}=0.5 \mathrm{~kg}
\)

Friction

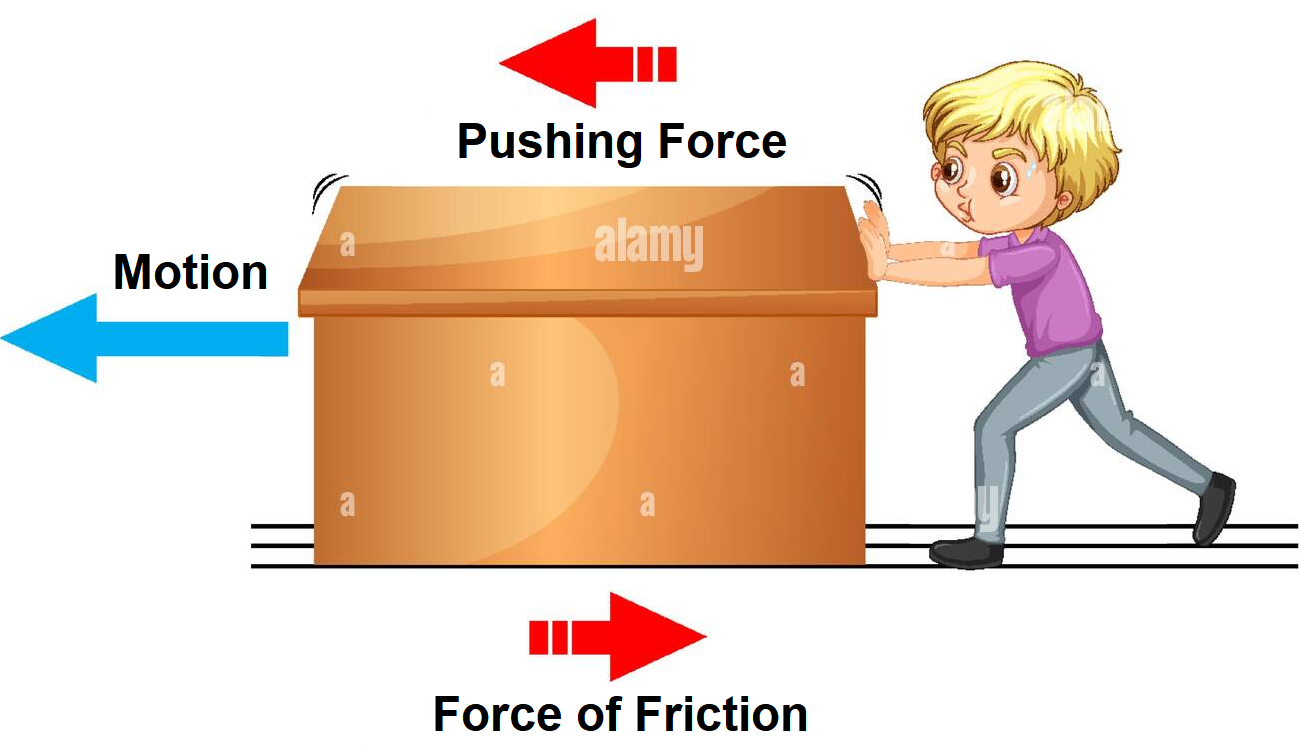
• Whenever a body tends to move over another body’s surface, an opposing force, called force of friction acts (Friction is the force of two surfaces in contact).
• Friction is a contact force that opposes relative motion.
• This force acts tangentially to the interface of two bodies.
• No friction exists till an external force is applied.

The Formula for Calculating Friction

The friction force, denoted as \(F_f\) can be calculated using the following formula:

\(F_f=\mu \cdot N\)
Where:
\(\mu\) represents the coefficient of friction
\(N\) represents the normal force acting on the object.

There are three types of frictional force :

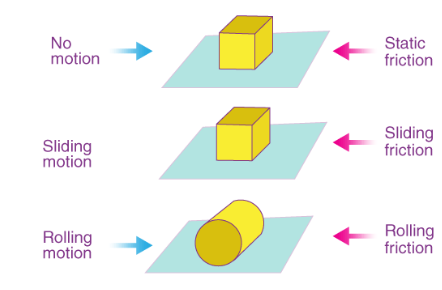
• Static friction (No relative motion between objects)
• Kinetic friction (There is relative motion between objects)
• Rolling friction (When an object is rolled on a surface)

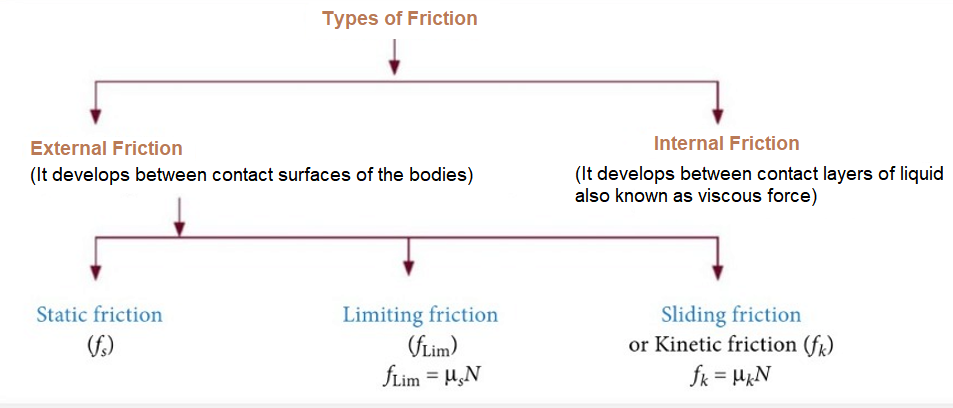
Static Friction

Static friction is a force that keeps an object at rest. Static friction definition can be written as the friction experienced when individuals try to move a stationary object on a surface, without actually triggering any relative motion between the body and the surface on which it is on.

It can be explained as the force of friction which precisely balances the applied force for the duration of the stationary state of the body. The static frictional force is self-regulating, i.e. static friction will at all times be equivalent and opposite to the force applied.

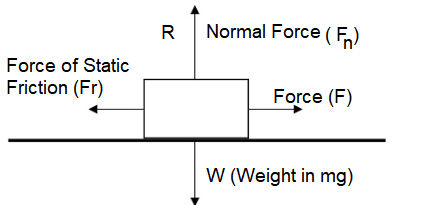
\(R\) is the reaction force (known as normal force \(F_n\)) because of the weight \(W\). The external force is \(F\), and \(F_r\) is the friction. \(F=-F_r\) when no motion takes place.

The coefficient of static friction is denoted as \(\mu_{\mathrm{s}}\). The maximum force of static friction is given as the product of the coefficient of static friction and normal force and force of static friction is less than or equal to the product of the coefficient of static friction and normal force. It is given as:
\(
\mathrm{F}_{\mathrm{s}} \max =\mu_{\mathrm{s}} N \text { and } \mathrm{F}_{\mathrm{s}} \leq \mu_{\mathrm{s}} N
\)
Where,
\(\mathrm{F}_{\mathrm{s}}\) is the force of static friction
\(\mu_{\mathrm{s}}\) is the coefficient of static friction
\(N\) is the normal force
\(\mathrm{F}_{\mathrm{s}} \mathrm{max}\) is the maximum force of static friction

Limiting Friction

The maximum friction force that can be developed at the contact surface, when body is just on the point of moving Is called limiting force of friction.
Maximum value of static friction is called limiting friction i.e., \(f_{\operatorname{Lim}}=\mu_s N\)
Where:
\(\mu_s\) represents the coefficient of limiting friction
\(N\) represents the normal force acting on the object.

Sliding Friction

Sliding friction is defined as the resistance that is created between any two objects when they are sliding against each other. The coefficient of sliding friction is denoted as \(\mu_{\mathrm{s}}\). The force of sliding friction is defined as the product of the coefficient of sliding friction and the normal force. It is given as:
\(
F_s=\mu_s \cdot N
\)

Kinetic Friction

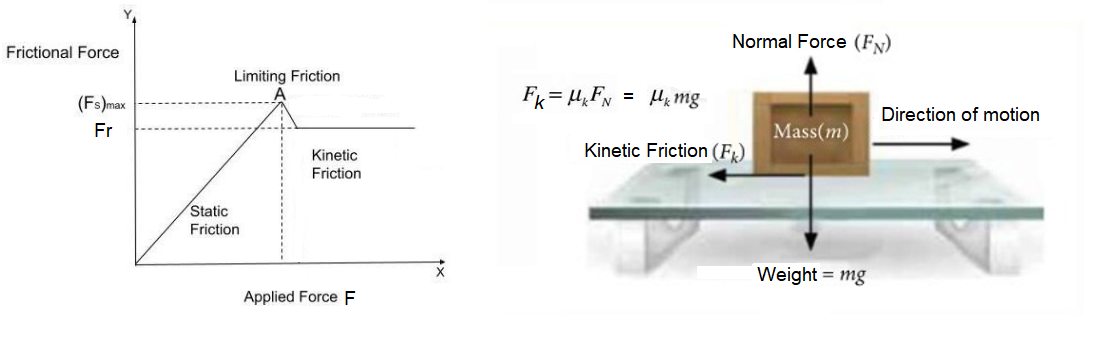
If the body is in motion, the friction opposing its motion is called dynamic or kinetic friction. This is always slightly less than the limiting friction.
Its numerical value is \(f_k=\mu_k N\).

Angle of Friction

Angle of friction \((\lambda)\) : The angle which the resultant of the force of limiting friction \(f\) and normal reaction \(N\) makes with the direction of normal reaction \(N\).

\(
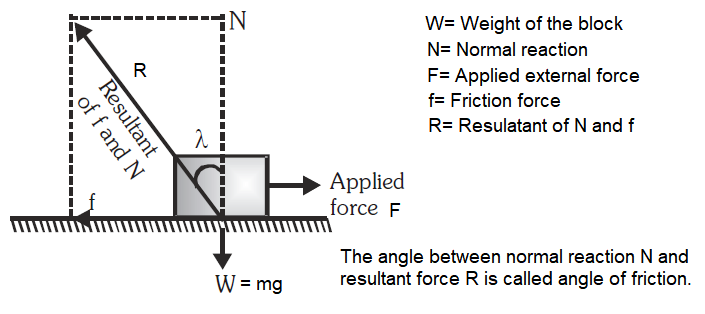
\tan \lambda=\frac{f}{N}=\mu \text { or, } \quad \lambda=\tan ^{-1} \mu
\)

Angle of repose or angle of sliding : It is defined as the maximum angle of inclination of a plane with the horizontal at which a body placed on it just begins to sliding down.

\(
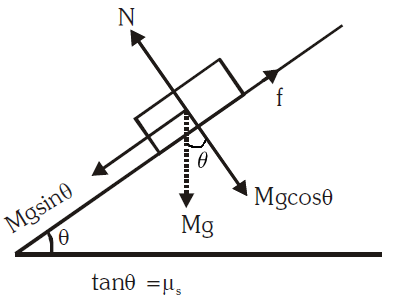
f=M g \sin \theta \text { and } N=M g \cos \theta
\)

Rolling Friction

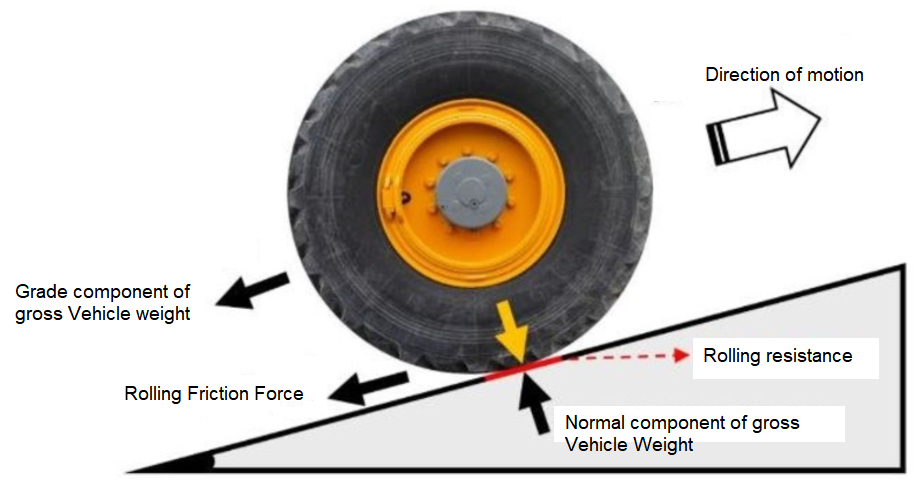
In rolling friction, there is just one point of contact between the body and the plane at every instant and this point is at rest with respect to the plane. There are three laws of rolling friction:

• With the increase in smoothness, the force of rolling friction decreases.
• Rolling friction is expressed as a product of load and constant to the fractional power.
  \(
  \mathrm{F}=\mathrm{kL}{ }^{\mathrm{n}}
  \)
• Rolling friction force is directly proportional to load and inversely proportional to the radius of curvature.
  \(
  F=\mu \times \frac{W}{r}
  \)

Coefficient of Rolling Friction is the ratio of the force of rolling friction to the total weight of the object.
In empirical terms, the coefficient of rolling resistance can be expressed as:
\(
F_r=\mu_r W
\)
where,
\(F_r\) is the resistive force of rolling resistance
\(\mu_{\mathrm{r}}\) is the coefficient of rolling resistance
\(\mathrm{W}\) is the weight of the rolling body

Lami’s theorem

It states that, “if three forces acting on a particle are in equilibrium, then each force is proportional to the sine of the angle between the other two forces.”
If an object \(O\) is in equilibrium under three concurrent coplanar forces \(\mathbf{F}_1, \mathbf{F}_2\) and \(\mathbf{F}_3\) as shown in figure below.

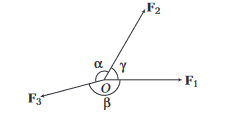
Then,
\(
\frac{F_1}{\sin \alpha}=\frac{F_2}{\sin \beta}=\frac{F_3}{\sin \gamma}
\)

If more than three forces are given in the problem, then solve the problem by using component approach. If three forces are in equilibrium, then the resultant of two forces is equal and opposite to the third.

\(
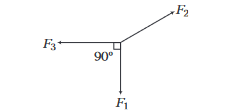
F_2=\sqrt{F_1^2+F_3^2}
\)

Example:  An iron block of mass 30 kg is hanging from the two supports, A and B, as shown in the diagram. Determine the tensions in both ropes. \(\text { (Take } \mathrm{g}=10 \mathrm{~m} / \mathrm{s} 2 \text { ) }\)

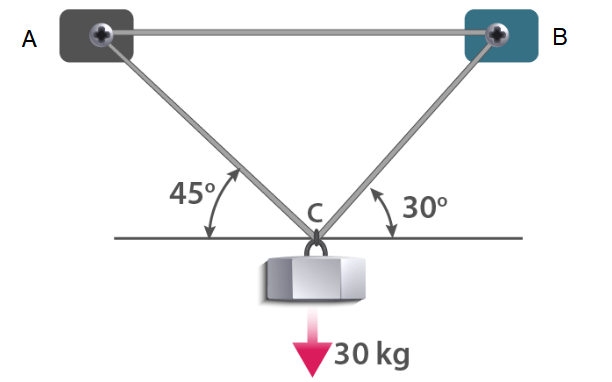
Answer:

Given : Mass m=30 kg
Force due to gravity on the bell \(=30 \times 10=300 \mathrm{~N}\)
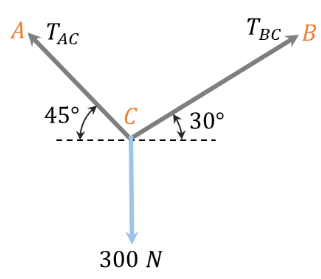
Now, drawing the free body diagram of the given situation taking bell at point \(\mathrm{C}\),
Using lami’s theorem
\(
\frac{A}{\sin \alpha}=\frac{B}{\sin \beta}=\frac{C}{\sin \gamma}
\)
Putting the values from diagram
\(
\frac{T_{A C}}{\sin (90+30)}=\frac{T_{B C}}{\sin (90+45)}=\frac{300}{\sin (180-30-45)}
\)
Taking first and third term,
\(
\begin{aligned}
\frac{T_{A C}}{\sin (90+30)} & =\frac{300}{\sin (180-30-45)} \\
T_{A C} & =268.97 \mathrm{~N}
\end{aligned}
\)
Taking the second and third term, Hence, the tensions in Strings are \(268.97 \mathrm{~N}\) and \(219.61 \mathrm{~N}\).

Example: Two persons A and B are drawing a bucket of water from a well using two ropes as shown in figure. In a given situation if person A is applying 30 N force. Find the Weight of the bucket.?

Answer: Given : \(F_A=30 \mathrm{~N}\)
Let the weight of water bucket \(=\mathrm{W}\)
Using lami’s theorem
\(
\frac{A}{\sin \alpha}=\frac{B}{\sin \beta}=\frac{C}{\sin \gamma}
\)
Putting the values from diagram
\(
\frac{F_A}{\sin (90+45)}=\frac{F_B}{\sin (90+30)}=\frac{W}{\sin (105)}
\)
Taking first and third term,
\(
\begin{aligned}
\frac{30 N}{\sin (90+30)} & =\frac{W}{\sin (180-30-45)} \\
W & =33.46 N
\end{aligned}
\)
Hence, the Weight of the bucket is \(33.46 \mathrm{~N}\).