Casework and Probability

Sometimes probability problems involve solving problems for multiple cases. Most of the problems so far could be done either by computing the probability of compound events or by counting favorable and total outcomes.

Example 1: A fair coin is tossed five times. What is the probability of flipping at least two heads?

Solution:

Calculating 2,3,4, or 5 heads, there are \(2^5=32\) possible outcomes, with \({ }^5 C_5=1\) plus \({ }^5 C_4=5\) plus \({ }^5 C_3=10\) plus \({ }^5 C_2=10\) or \(1+5+10+10\) ways out of \(32=26 / 32\) or \(13 / 16\).

Example 2: A fair coin is tossed 3 times. What is the probability of at least two consecutive heads?

Solution:

There are \(2^3=8\) ways to flip the coins, in order. There are two ways to get exactly two consecutive heads: HHT and THH. There is only one way to get three consecutive heads: \(\mathrm{HHH}\). Therefore, the probability of flipping at least two consecutive heads is \(\frac{3}{8}\).

Example 3: Oleg rolls a standard die three times. What is the probability that the third roll is greater than the sum of the first two rolls?

Solution:

We know that there are \(6^3=216\) possible outcomes for three rolls of a standard die. Now we must count the number of ways in which the third roll would be greater than the sum of the first two.
Remember to keep organized:
If the last roll is a six, the first two rolls could be: \((1,1)(1,2)(1,3)(1,4)(2,1)(2,2)(2,3)(3,1)(3,2)(4,1)\) If the last roll is a five, the first two rolls could be: \((1,1)(1,2)(1,3)(2,1)(2,2)(3,1)\) If the last roll is a four we have: \((1,1)(1,2)(2,1)\) And for three we have: \((1,1)\)
This gives us a total of 20 out of 216 rolls, or \(\frac{5}{54}\).

Example 4: The numbers 1 through 9 are placed in a bag. Juan selects three numbers from the bag at random and without replacement. What is the probability that the three numbers Juan picks are consecutive integers?

Solution:

There are \({ }^9 C_3=84\) ways to choose 3 digits from a set of 9. Of these 84 ways, there are 7 sets of consecutive integers(starting with 1-2-3 and ending with 7-8-9) 7/84=1/12.

Example 5: Without looking Jenny randomly selects two socks from a drawer containing four blue, three white, and five black socks, none of which are paired up. what is the probability that she chooses two socks of the same color?

Solution:

We can add the probability of choosing two blue, two white or two black socks, since they are mutually exclusive possible outcomes.
The total number of socks is \(4+3+5=12\)
The probability of choosing two blue socks is:
\(
\frac{4}{12} \times \frac{3}{11}=\frac{1}{11}
\)
The probability of choosing two white socks is:
\(
\frac{3}{12} \times \frac{2}{11}=\frac{1}{22}
\)
The probability of choosing two black socks is:
\(
\frac{5}{12} \times \frac{4}{11}=\frac{5}{33}
\)
In each case, the probability that the first sock is a particular colour is the number of socks of that colour divided by the total number (12) of socks. Once one sock of that colour has been removed, the probability of the second sock being the same colour is the number of socks remaining of that colour divided by the remaining total (11) number of socks in the drawer.
So the probability of choosing any pair with matching colour is:
\(
\frac{1}{11}+\frac{1}{22}+\frac{5}{33}=\frac{6}{66}+\frac{3}{66}+\frac{10}{66}=\frac{19}{66}
\)

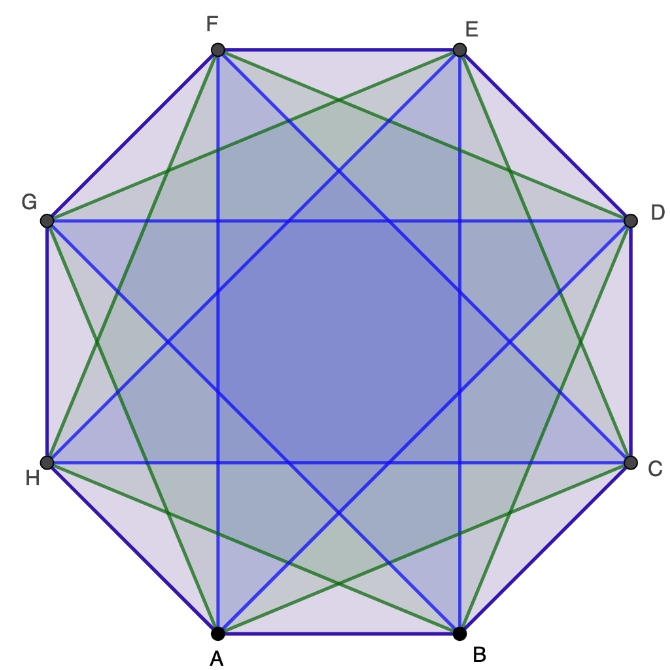
Example 6: Four of the vertices of a regular octagon are selected at random and connected to form a quadrilateral. What is the probability that the quadrilateral will be a rectangle?

Solution:

In an octagon, there are 8 vertices, Out of which 4 vertices are chosen.
There are \({ }^8 C_4=70\) ways to select 4 of the 8 vertices.
Only 6 of these combinations form rectangles as shown below, making the probability 6/70=3/35.

Example 7: Three of the vertices of a regular heptagon are connected to form a triangle. What is the probability that the triangle formed is isosceles?

Solution:

There are \({ }^7 C_3=35\) ways to connect three of the vertices to form a triangle. We can use any vertex of the heptagon as the apex angle for three different isosceles triangles for a total of 21 possible isosceles triangles (out of 35). This makes the probability 21/35=3/5.

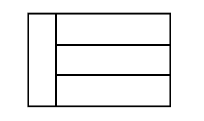
Example 8: An organization is choosing colors for the stripes on its flag. The flag has three horizontal stripes and a vertical stripe as shown. The color of each of the four stripes is selected at random from the colors red, white, and black. What is the probability that no two stripes of the same color share an edge?

Solution:

The total number of ways colors can be chosen for the flag is \(3^4=81\) (4 stripes can each be one of the three colors). Now let’s find out how many ways we can choose colors where no two same-colored stripes share an edge. Start by choosing any of the 3 colors for the vertical stripe. Once we choose a color for this stripe, none of the other stripes can be the same color. We can pick one of the 2 remaining colors for the middle horizontal stripe. The remaining stripes must both be the remaining color. This gives us only 3!=6 ways that no two same-colored stripes can share an edge. So, the probability = 6/81 = 2/27.

Example 9: Three numbers are selected at random and without replacement from a bag containing each of the numbers 1 through 9. What is the probability that all three share a common factor greater than 1?

Solution:

There are \({ }^9 C_3=84\) combinations of 3 numbers. Only 2 common factors greater than 1 are possible: 2 and 3. There are 4 even numbers, and \({ }^4 C_3=4\) possible sets of 3 even numbers. There is one set of three numbers that have 3 as a common factor {3, 6, 9}. This means that there are 5 out of 84 combinations of 3 numbers that share a common factor greater than 1: 5/84 is the probability of selecting one of these sets. 

Example 10: Each of the four faces of a cube is painted either white or black with equal probability. What is the probability that no two black faces share an edge?

Solution:

A cube has 6 faces. With 6 faces and two choices of color for each face, there are \(2^6=64\) ways to paint the faces of the cube. Of these 64 ways, there is 1 way to paint every face white, there are six ways to paint one face black, and three ways to paint two faces black so that no two black faces share an edge(front/back, left/right, or top/bottom). This makes 10 out of 64 ways or a probability of 5/32.