9.5 Geometric Progression (G.P.)

Geometric Sequence or Geometric Progression (GP)

A geometric progression is a sequence, if the ratio of any term and its just preceding term is constant throughout. This constant quantity is called the common ratio and is generally denoted by ‘ \(r\) ‘.
\(\quad \quad \quad \quad Or\)

A geometric progression (GP) is a sequence of numbers, whose first term is non-zero and each of the term is obtained by multiplying its just preceding term by a constant quantity. This constant quantity is called common ratio of the GP.

Let us consider the following sequences:
(i) \(2,4,8,16, \ldots\),
(ii) \(\frac{1}{9}, \frac{-1}{27}, \frac{1}{81}, \frac{-1}{243}\)
(iii) \(.01, .0001, .000001, \ldots\)

In each of these sequences, how their terms progress? We note that each term, except the first progresses in a definite order.
In (i), we have \(a_1=2, \frac{a_2}{a_1}=2, \frac{a_3}{a_2}=2, \frac{a_4}{a_3}=2\) and so on.
In (ii), we observe, \(a_1=\frac{1}{9}, \frac{a_2}{a_1}=\frac{1}{3}, \frac{a_3}{a_2}=\frac{1}{3}, \frac{a_4}{a_3}=\frac{1}{3}\) and so on.

Similarly, state how do the terms in (iii) progress? It is observed that in each case, every term except the first term bears a constant ratio to the term immediately preceding it. In (i), this constant ratio is 2 ; in (ii), it is \(-\frac{1}{3}\) and in (iii), the constant ratio is 0.01 . Such sequences are called geometric sequence or geometric progression abbreviated as G.P.
A sequence \(a_1, a_2, a_3, \ldots, a_n, \ldots\) is called geometric progression, if each term is non-zero and \(\frac{a_{k+1}}{a_k}=r\) (constant), for \(k \geq 1\).

By letting \(a_1=a\), we obtain a geometric progression, \(a, a r, a r^2, a r^3, \ldots\), where \(a\) is called the first term and \(r\) is called the common ratio of the G.P. Common ratio in geometric progression (i), (ii) and (iii) above are \(2,-\frac{1}{3}\) and 0.01 , respectively.

As in case of arithmetic progression, the problem of finding the \(n^{\text {th }}\) term or sum of \(n\) terms of a geometric progression containing a large number of terms would be difficult without the use of the formulae which we shall develop in the next Section. We shall use the following notations with these formulae:
\(
\begin{aligned}
& a=\text { the first term, } r=\text { the common ratio, } l=\text { the last term, } \\
& n=\text { the numbers of terms, } \\
& S _n=\text { the sum of first } n \text { terms. }
\end{aligned}
\)

Important Results

1. In a GP, neither \(a=0\) nor \(r=0\).
2. In a GP, no term can be equal to ‘ 0 ‘.
3. If in a GP, the terms are alternatively positive and negative, then its common ratio is always negative.
4. If we multiply the common ratio with any term of GP, we get the next following term and if we divide any term by the common ratio, we get the preceding term.
5. The common ratio of GP may be positive, negative or imaginary.
6. If common ratio of GP is equal to unity, then GP is known as Constant GP.
7. If common ratio of \(GP\) is imaginary or real, then \(GP\) is known as Imaginary GP.
8. Increasing and Decreasing GP
   For a GP to be increasing or decreasing \(r>0\). If \(r<0\), terms of GP are alternatively positive and negative and so neither increasing nor decreasing.
   \(
   \begin{array}{ccccc}
   \hline a & a>0 & a>0 & a<0 & a<0 \\
   \hline r & 0<r<1 & r>1 & r>1 & 0<r<1 \\
   \hline \text { Result } & \text { Decreasing } & \text { Increasing } & \text { Decreasing } & \text { Increasing } \\
   \hline
   \end{array}
   \)

Example 1: (i) \(1,2,4,8,16, \ldots\)
(ii) \(9,3,1, \frac{1}{3}, \frac{1}{9}, \ldots\)
(iii) \(-2,-6,-18, \ldots\)
(iv) \(-8,-4,-2,-1,-\frac{1}{2}, \ldots\)
(v) \(5,-10,20, \ldots\)
(vi) \(5,5,5,5, \ldots\)
(vii) \(1,1+i, 2 i,-2+2 i, \ldots ; i=\sqrt{-1}\)

Solution: (i) Here, \(a=1\) and \(r=\frac{2}{1}=\frac{4}{2}=\frac{8}{4}=\frac{16}{8}=\ldots=2\) i.e. \(a=1\) and \(r=2\) Increasing GP \((a>0, r>1)\)

(ii) Here, \(a=9\)
and \(r=\frac{3}{9}=\frac{1}{3}=\frac{\frac{1}{3}}{1}=\frac{\frac{1}{9}}{\frac{1}{3}}=\ldots=\frac{1}{3}\) i.e. \(a=9, r=\frac{1}{3}\)
Decreasing GP \((a>0,0<r<1)\)

(iii) Here, \(a=-2\)
and \(\quad r=\frac{-6}{-2}=\frac{-18}{-6}=\ldots=3\)
i.e. \(a=-2 r=3\)
Decreasing GP \((a<0, r>1)\)

(iv) Here, \(a=-8\)
and \(\quad r=\frac{-4}{-8}=\frac{-2}{-4}=\frac{-1}{-2}=\frac{-\frac{1}{2}}{-1}=\ldots .=\frac{1}{2}\)
i.e. \(\quad a=-8 r=\frac{1}{2}\)
Increasing GP \((a<0,0<r<1)\)

(v) Here, \(a=5\) and \(r=\frac{-10}{5}=\frac{20}{-10}=\ldots=-2\) i.e., \(a=5, r=-2\) Neither increasing nor decreasing \((r<0)\)

(vi) Here, \(a=5\) and \(r=\frac{5}{5}=\frac{5}{5}=\frac{5}{5}=\ldots=1\) i.e., \(a=5, r=1\) Constant GP \((r=1)\)

(vii) Here, \(a=1\) and \(\quad r=\frac{1+i}{1}=\frac{2 i}{1+i}=\frac{-2+2 i}{2 i}=\ldots\).
\(
\begin{aligned}
& =(1+i)=\frac{2 i(1-i)}{(1+i)(1-i)}=\frac{(-1+i) i}{i^2}=\ldots \\
& =(1+i)=(i+1)=(1+i)=\ldots
\end{aligned}
\)
i.e., \(\quad a=1, r=1+i\)
Imaginary GP \((r=\) imaginary \()\)

Example 2: Show that the sequence \(<t_n>\) defined by \(t_n=\frac{2^{2 n-1}}{3}\) for all values of \(n \in N\) is a GP. Also, find its common ratio.

Solution: We have, \(t_n=\frac{2^{2 n-1}}{3}\)
On replacing \(n\) by \(n-1\), we get
\(
t_{n-1}=\frac{2^{2 n-3}}{3} \Rightarrow \frac{t_n}{t_{n-1}}=\frac{\frac{2^{2 n-1}}{3}}{\frac{2^{2 n-3}}{3}}=2^2=4
\)
Clearly, \(\frac{t_n}{t_{n-1}}\) is independent of \(n\) and is equal to 4 . So, the given sequence is a GP with common ratio 4.

Example 3: Show that the sequence \(<t_n>\) defined by \(t_n=2 \cdot 3^n+1\) is not \(a\) GP.

Solution: We have, \(t_n=2 \cdot 3^n+1\)
On replacing \(n\) by \((n-1)\) in \(t_n\), we get
\(
\begin{aligned}
& t_{n-1}=2 \cdot 3^{n-1}+1 \\
& \Rightarrow \quad t_{n-1}=\frac{\left(2 \cdot 3^n+3\right)}{3} \\
& \therefore \quad \frac{t_n}{t_{n-1}}=\frac{\left(2 \cdot 3^n+1\right)}{\frac{\left(2 \cdot 3^n+3\right)}{3}}=\frac{3\left(2 \cdot 3^n+1\right)}{\left(2 \cdot 3^n+3\right)} \\
&
\end{aligned}
\)
Clearly, \(\frac{t_n}{t_{n-1}}\) is not independent of \(n\) and is therefore not constant. So, the given sequence is not a GP.

General term of a G.P.

Let us consider a G.P. with first non-zero term ‘ \(a\) ‘ and common ratio ‘ \(r\) ‘. Write a few terms of it. The second term is obtained by multiplying \(a\) by \(r\), thus \(a_2=a r\). Similarly, third term is obtained by multiplying \(a_2\) by \(r\). Thus, \(a_3=a_2 r=a r^2\), and so on.
We write below these and few more terms.
\(1^{\text {st }}\) term \(=a_1=a=a r^{1-1}, 2^{\text {nd }}\) term \(=a_2=a r=a r^{2-1}, 3^{\text {rd }}\) term \(=a_3=a r^2=a r^{3-1}\)
\(4^{\text {th }}\) term \(=a_4=a r^3=a r^{4-1}, 5^{\text {th }}\) term \(=a_5=a r^4=a r^{5-1}\)
Do you see a pattern? What will be \(16^{\text {th }}\) term?
\(
a_{16}=a r^{16-1}=a r^{15}
\)
Therefore, the pattern suggests that the \(n^{\text {th }}\) term of a G.P. is given by \(a_n=a r^{n-1}\).
Thus, \(a\), G.P. can be written as \(a, a r, a r^2, a r^3, \ldots a r^{n-1} ; a, a r, a r^2, \ldots, a r^{n-1} \ldots ;\) according as G.P. is finite or infinite, respectively.
The series \(a+a r+a r^2+\ldots+a r^{n-1}\) or \(a+a r+a r^2+\ldots+a r^{n-1}+\ldots\) are called finite or infinite geometric series, respectively.

(i) \(n\)th Term of a GP from Beginning

1st term from beginning \(=a_1=a=a r^{1-1}\)
2nd term from beginning \(=a_2=a r=a r^{2-1}\)
3rd term from beginning \(=a_3=a r^2=a r^{3-1}\)
\(n\)th term from beginning \(=a_n=a r^{n-1}, \forall n \in N\)
Hence, \(n\)th term of a GP from beginning
\(
a_n=a r^{n-1}=l \text { [last term] }
\)

(ii) \(n\)th Term of a GP from End

1st term from end \(=a_1^{\prime}=l=\frac{l}{r^{1-1}}\)
2nd term from end \(=a_2^{\prime}=\frac{l}{r}=\frac{l}{r^{2-1}}\)
3rd term from end \(=a^{\prime}{ }_3=\frac{l}{r^2}=\frac{l}{r^{3-1}}\)
\(\quad \vdots \quad \vdots \quad \vdots \quad \vdots\)
\(n\)th term from end \(=a^{\prime}{ }_n=\frac{l}{r^{n-1}}, \forall n \in N\)
Hence, \(n\)th term of a GP from end
\(
=a_n^{\prime}=\frac{l}{r^{n-1}}=a \text { [first term] }
\)
Now, it is clear that \(a_k \times a_k^{\prime}=a r^{k-1} \times \frac{l}{r^{k-1}}=a \times l\)
or \(a_k \times a_k^{\prime}=a \times l, \forall 1 \leq k \leq n\)
i.e. in a finite GP of \(n\) terms, the product of the \(k\) th term from the beginning and the \(k\) th term form the end is independent of \(k\) and equals the product of the first and last terms.

Remark

• nth term is also called the general term.
• If last term of GP be \(a_n\) and CR is \(r\), then terms of GP from end are \(a_n, \frac{a_n}{r}, \frac{a_n}{r^2}, \ldots\)
• If in a GP, the terms are altematively positive and negative, then its common ratio is always negative.
• If \(a\) and \(l\) represent first and last term of a GP respectively, then common ratio of \(GP =r=\left(\frac{l}{a}\right)^{\frac{1}{n-1}}\)
• If \(a_n, a_{n+1}, a_{n+2}\) are three consecutive terms of a GP, then
  \(
  \frac{a_{n+1}}{a_n}=\frac{a_{n+2}}{a_{n+1}} \Rightarrow a_{n+1}^2=a_n a_{n+2}
  \)
  In particular, if \(a, b, c\) are in GP, then \(\frac{b}{a}=\frac{c}{b} \Rightarrow b^2=a c\) On squaring, \(\frac{b^2}{a^2}=\frac{c^2}{b^2}\) Hence, \(a^2, b^2, c^2\) are also in GP.

Example 4: If first term of a GP is \(a\), third term is \(b\) and \((n+1)\) th term is \(c\). The \((2 n+1)\) th term of a GP is
(a) \(c \sqrt{\frac{b}{a}}\)
(b) \(\frac{b c}{a}\)
(c) \(a b c\)
(d) \(\frac{c^2}{a}\)

Solution: Let common ratio \(=r\)
\(
\therefore \quad b=a r^2 \Rightarrow r=\sqrt{\frac{b}{a}}
\)
Also,
\(
\begin{aligned}
& c=a r^n \Rightarrow r^n=\frac{c}{a} \\
& \therefore \quad t_{2 n+1}=a r^{2 n}=a\left(r^n\right)^2=a\left(\frac{c}{a}\right)^2=\frac{c^2}{a} \\
&
\end{aligned}
\)
Hence, (d) is the correct answer.

Example 5: The \((m+n)\) th and \((m-n)\) th terms of a GP are \(p\) and \(q\), respectively. Then, the \(m\) th term of the GP is
(a) \(p\left(\frac{q}{p}\right)^{\frac{m}{2 n}}\)
(b) \(\sqrt{p q}\)
(c) \(\sqrt{\frac{p}{q}}\)
(d) None of these

Solution: Let \(a\) be the first term and \(r\) be the common ratio, then
\(
\begin{aligned}
& t_{m+n}=p \Rightarrow a r^{m+n-1}=p \dots(i)\\
& t_{m-n}=q \Rightarrow a r^{m-n-1}=q \dots(ii)
\end{aligned}
\)
From Eqs. (i) and (ii), we get
\(
\begin{aligned}
& \text { ar }{ }^{m+n-1} \times a r^{m-n-1}=p \times q \\
& \Rightarrow \quad a^2 r^{2 m-2}=p q \Rightarrow a r^{m-1}=\sqrt{p q} \\
& \Rightarrow \quad t_m=\sqrt{p q} \\
&
\end{aligned}
\)
Hence, (b) is the correct answer.

Example 6: If \(\sin \theta, \sqrt{2}(\sin \theta+1), 6 \sin \theta+6\) are in GP, then the fifth term is
(a) 81
(b) \(81 \sqrt{2}\)
(c) 162
(d) \(162 \sqrt{2}\)

Solution:

\(
\begin{aligned}
& {[\sqrt{2}(\sin \theta+1)]^2=\sin \theta(6 \sin \theta+6)} \\
& \Rightarrow[(\sin \theta+1) 2(\sin \theta+1)-6 \sin \theta]=0
\end{aligned}
\)
We get, \(\quad \sin \theta=-1, \frac{1}{2}\)
\(
\therefore \quad \sin \theta=\frac{1}{2} \quad[\sin \theta=-1 \text { is not possible] }
\)
then first term \(=a=\sin \theta=\frac{1}{2}\) and common ratio
\(
\begin{aligned}
& =r=\frac{\sqrt{2}\left(\frac{1}{2}+1\right)}{\left(\frac{1}{2}\right)}=3 \sqrt{2} \\
\therefore \quad t_5 & =a r^4=\frac{1}{2}(3 \sqrt{2})^4=162
\end{aligned}
\)
Hence, (c) is the correct answer.

Example 7: The 1025th term in the sequence 1, 22, \(4444,88888888, \ldots\) is
(a) \(2^9\)
(b) \(2^{10}\)
(c) \(2^{11}\)
(d) \(2^{12}\)

Solution: The number of digits in each term of the sequence are \(1,\) \(2,4,8, \ldots\). which are in GP. Let 1025 th term is \(2^n\).
Then,
\(
\begin{aligned}
& 1+2+4+8+\ldots+2^{n-1}<1025 \leq 1+2+4+8+\ldots+2^n \\
& \Rightarrow \quad \frac{(2-1)\left(1+2+2^2+2^3+\ldots+2^{n-1}\right)}{(2-1)}<1025 \\
& \leq \frac{(2-1)\left(1+2+2^2+2^3+\ldots+2^n\right)}{(2-1)} \\
& \Rightarrow \quad 2^n-1<1025 \leq 2^{n+1}-1 \Rightarrow 2^n<1026 \leq 2^{n+1} \\
& \text { or } \quad 2^{n+1} \geq 1026>1024 \\
& \Rightarrow \quad 2^{n+1}>2^{10} \Rightarrow n+1>10 \\
& \therefore \quad n>9 \quad \therefore n=10 \text { [which is always satisfy Eq. (i)] } \\
&
\end{aligned}
\)
Hence, (b) is the correct answer.

Example 8: If \(a, b, c\) are real numbers such that \(3\left(a^2+b^2+c^2+1\right)=2(a+b+c+a b+b c+c a)\), then \(a, b, c\) are in
(a) AP only
(b) GP only
(c) GP and AP
(d) None of these

Solution:

\(
\begin{aligned}
& \text { Given, } 3\left(a^2+b^2+c^2+1\right)=2(a+b+c+a b+b c+c a) \\
& \Rightarrow \quad 2\left(a^2+b^2+c^2-a b-b c-c a\right)+ \\
& \quad\left(a^2+b^2+c^2-2 a-2 b-2 c+3\right)
\end{aligned}
\)
\(
\begin{array}{r}
\Rightarrow\left\{(a-b)^2+(b-c)^2+(c-a)^2\right\}+ \\
\left\{(a-1)^2+(b-1)^2+(c-1)^2\right\}=0
\end{array}
\)
\(
\begin{aligned}
& \Rightarrow a-b=b-c=c-a=0 \text { and } a-1=b-1=c-1=0 \\
& \Rightarrow \quad a=b=c=1 \\
& \Rightarrow a, b, c \text { are in GP and AP. }
\end{aligned}
\)
Hence, (c) is the correct answer.

Sum to \(n\) terms of \(a\) G.P.

Let the first term of a G.P. be \(a\) and the common ratio be \(r\). Let us denote by \(S _n\) the sum to first \(n\) terms of G.P. Then
\(
S _n=a+a r+a r^2+\ldots+a r^{n-1} \dots(1)
\)
Case 1: If \(r=1\), we have \(S _n=a+a+a+\ldots+a(n\) terms \()=n a\)
Case 2: If \(r \neq 1\), multiplying (1) by \(r\), we have
\(
r S _n=a r+a r^2+a r^3+\ldots+a r^n \dots(2)
\)
Subtracting (2) from (1), we get \((1-r) S _n=a-a r^n=a\left(1-r^n\right)\)
This gives \(\quad S _n=\frac{a\left(r^n-1\right)}{r-1}\)

Remarks

• If \(r=1\), the above formulae cannot be used. But, then the GP reduces to \(a, a, a, \ldots\)
  \(\therefore \quad S_n=a+a+a+\ldots n\) times \(=n a\)
• \(S_n=\frac{a\left(1-r^n\right)}{(1-r)} \text { when } r<1,\)
• \(S_n=\frac{a\left(r^n-1\right)}{(r-1)} \text {, }\) when \(r>1\)

Infinite GP Sum Formulas

If \(a\) be the first term, \(r\) be the common ratio of a GP, then
\(
S_n=\frac{a\left(1-r^n\right)}{(1-r)}=\frac{a}{(1-r)}-\frac{a r^n}{(1-r)}
\)
Let \(-1<r<1\) i.e. \(|r|<1\), then \(\lim _{n \rightarrow \infty} r^n \rightarrow 0\)
Let \(S_{\infty}\) denote the sum to infinity of the GP, then
\(S_{\infty}=\frac{a}{(1-r)},\) where \(-1<r<1\) or \(|r|<1\)
\(
S_{\infty}=\infty,|r| \geq 1
\)

Example 9: Find the \(10^{\text {th }}\) and \(n^{\text {th }}\) terms of the G.P. \(5,25,125, \ldots\).

Solution: Here \(a=5\) and \(r=5\). Thus, \(a_{10}=5(5)^{10-1}=5(5)^9=5^{10}\) and \(\quad a_n=a r^{n-1}=5(5)^{n-1}=5^n\).

Example 10: Which term of the G.P., \(2,8,32, \ldots\) up to \(n\) terms is 131072 ?

Solution: Let 131072 be the \(n^{\text {th }}\) term of the given G.P. Here \(a=2\) and \(r=4\).
Therefore \(\quad 131072=a_n=2(4)^{n-1}\) or \(\quad 65536=4^{n-1}\)
This gives \(\quad 4^8=4^{n-1}\).
So that \(n-1=8\), i.e., \(n=9\). Hence, 131072 is the \(9^{\text {th }}\) term of the G.P.

Example 11: In a G.P., the \(3^{\text {rd }}\) term is 24 and the \(6^{\text {th }}\) term is 192 . Find the \(10^{\text {th }}\) term.

Solution: Here, \(a_3=a r^2=24 \dots(1)\)
and \(\quad a_6=a r^5=192 \dots(2)\)
Dividing (2) by (1), we get \(r=2\). Substituting \(r=2\) in (1), we get \(a=6\).
Hence \(a_{10}=6(2)^9=3072\).

Example 12: Find the sum of first \(n\) terms and the sum of first 5 terms of the geometric series \(1+\frac{2}{3}+\frac{4}{9}+\ldots\)

Solution: Here \(a=1\) and \(r=\frac{2}{3}\). Therefore
\(
S _n=\frac{a\left(1-r^n\right)}{1-r}=\frac{\left[1-\left(\frac{2}{3}\right)^n\right]}{1-\frac{2}{3}}=3\left[1-\left(\frac{2}{3}\right)^n\right]
\)
In particular, \(\quad S _5=3\left[1-\left(\frac{2}{3}\right)^5\right]=3 \times \frac{211}{243}=\frac{211}{81}\).

Example 13: How many terms of the G.P. \(3, \frac{3}{2}, \frac{3}{4}, \ldots\) are needed to give the \(\operatorname{sum} \frac{3069}{512} ?\)

Solution: Let \(n\) be the number of terms needed. Given that \(a=3, r=\frac{1}{2}\) and \(S _n=\frac{3069}{512}\)
Since
\(
S _n=\frac{a\left(1-r^n\right)}{1-r}
\)
\(
\frac{3069}{512}=\frac{3\left(1-\frac{1}{2^n}\right)}{1-\frac{1}{2}}=6\left(1-\frac{1}{2^n}\right)
\)
\(
\begin{aligned}
\frac{3069}{3072} & =1-\frac{1}{2^n} \\
\frac{1}{2^n} & =1-\frac{3069}{3072}=\frac{3}{3072}=\frac{1}{1024} \\
2^n & =1024=2^{10}, \text { which gives } n=10 .
\end{aligned}
\)

Example 14: The sum of first three terms of a G.P. is \(\frac{13}{12}\) and their product is -1 . Find the common ratio and the terms.

Solution: Let \(\frac{a}{r}, a, a r\) be the first three terms of the G.P. Then
\(
\frac{a}{r}+a r+a=\frac{13}{12} \dots(1)
\)
and \(\left(\frac{a}{r}\right)(a)(a r)=-1 \dots(2)\)
From (2), we get \(a^3=-1\), i.e., \(a=-1\) (considering only real roots)
Substituting \(a=-1\) in (1), we have
\(
-\frac{1}{r}-1-r=\frac{13}{12} \text { or } 12 r^2+25 r+12=0 \text {. }
\)
This is a quadratic in \(r\), solving, we get \(r=-\frac{3}{4}\) or \(-\frac{4}{3}\).
Thus, the three terms of G.P. are \(: \frac{4}{3},-1, \frac{3}{4}\) for \(r=\frac{-3}{4}\) and \(\frac{3}{4},-1, \frac{4}{3}\) for \(r=\frac{-4}{3}\).

Example 15: Find the sum of the sequence \(7,77,777,7777, \ldots\) to \(n\) terms.

Solution: This is not a G.P., however, we can relate it to a G.P. by writing the terms as \(S _n=7+77+777+7777+\ldots\) to \(n\) terms
\(
\begin{aligned}
& =\frac{7}{9}[9+99+999+9999+\ldots \text { to } n \text { term }] \\
& =\frac{7}{9}\left[(10-1)+\left(10^2-1\right)+\left(10^3-1\right)+\left(10^4-1\right)+\ldots n \text { terms }\right] \\
& =\frac{7}{9}\left[\left(10+10^2+10^3+\ldots n \text { terms }\right)-(1+1+1+\ldots n \text { terms })\right] \\
& =\frac{7}{9}\left[\frac{10\left(10^n-1\right)}{10-1}-n\right]=\frac{7}{9}\left[\frac{10\left(10^n-1\right)}{9}-n\right] .
\end{aligned}
\)

Example 16: A person has 2 parents, 4 grandparents, 8 great grandparents, and so on. Find the number of his ancestors during the ten generations preceding his own.

Solution: Here \(a=2, r=2\) and \(n=10\)
Using the sum formula \(S _n=\frac{a\left(r^n-1\right)}{r-1}\)
We have
\(
S _{10}=2\left(2^{10}-1\right)=2046
\)
Hence, the number of ancestors preceding the person is 2046.

Geometric Mean (G.M.)

The geometric mean of two positive numbers \(a\) and \(b\) is the number \(\sqrt{a b}\). Therefore, the geometric mean of 2 and 8 is 4 . We observe that the three numbers \(2,4,8\) are consecutive terms of a G.P. This leads to a generalisation of the concept of geometric means of two numbers.
Given any two positive numbers \(a\) and \(b\), we can insert as many numbers as we like between them to make the resulting sequence in a G.P.
Let \(G _1, G _2, \ldots, G _n\) be \(n\) numbers between positive numbers \(a\) and \(b\) such that \(a, G _1, G _2, G _3, \ldots, G _n, b\) is a G.P. Thus, \(b\) being the \((n+2)^{\text {th }}\) term, we have
\(
b=a r^{n+1}, \quad \text { or } \quad r=\left(\frac{b}{a}\right)^{\frac{1}{n+1}} \text {. }
\)
Hence \(G _1=a r=a\left(\frac{b}{a}\right)^{\frac{1}{n+1}}, G _2=a r^2=a\left(\frac{b}{a}\right)^{\frac{2}{n+1}}, G _3=a r^3=a\left(\frac{b}{a}\right)^{\frac{3}{n+1}}\),
\(
G _n=a r^n=a\left(\frac{b}{a}\right)^{\frac{n}{n+1}}
\)

Example 17: Insert three numbers between 1 and 256 so that the resulting sequence is a G.P.

Solution: Let \(G _1, G _2, G _3\) be three numbers between 1 and 256 such that
\(
1, G _1, G _2, G _3, 256 \text { is a G.P. }
\)
Therefore \(\quad 256=r^4\) giving \(r= \pm 4\) (Taking real roots only)
For \(r=4\), we have \(G _1=a r=4, G _2=a r^2=16, G _3=a r^3=64\)
Similarly, for \(r=-4\), numbers are \(-4,16\) and -64.
Hence, we can insert \(4,16,64\) between 1 and 256 so that the resulting sequences are in G.P.

Recurring Decimal

Recurring decimal is a very good example of an infinite geometric series and its value can be obtained by means of infinite geometric series as follows

Let \(P\) denotes the figure which do not recur and suppose them \(p\) in number, \(Q\) denotes the recurring period consisting of \(q\) figures. Let \(R\) denotes the value of the recurring decimal.
\(
\begin{aligned}
& \text { Then, } \quad R=0 \cdot P Q Q Q \ldots \\
& \therefore \quad 10^P \times R=P \cdot Q Q Q \ldots \\
&
\end{aligned}
\)
and
\(
10^{p+q} \times R=P Q \cdot Q Q Q \ldots
\)
\(\therefore\) Therefore, by subtraction \(R=\frac{P Q-P}{\left(10^{p+q}-10^p\right)}\).

• Corollary I: If \(R=0 \cdot Q Q Q \ldots\)
  Then, \(R=\frac{Q}{10^q-1}\) (when \(Q\) denote the recurring period consisting of \(q\) figures)
  For example, If \(R={0.}\dot{3}\), then \(R=\frac{3}{10^1-1}=\frac{1}{3}\)
• Corollary II: The value of recurring decimal is always rational number.

Example 18: Find the value of \(0.32\dot{5}\dot{8}\).

Solution: Let \(\quad R=0.32\dot{5}\dot{8}\)
\(
\Rightarrow \quad R=0.3258585858 \ldots(i)
\)
Here, number of figures which are not recurring is 2 and number of figures which are recurring is also 2.
Then,
\(
\begin{aligned}
100 R & =32.58585858 \ldots (ii)\\
10000 R & =3258.58585858 \ldots (iii)
\end{aligned}
\)
On subtracting Eq. (ii) from Eq. (iii), we get
\(
\begin{aligned}
9900 R & =3226 \\
R & =\frac{3226}{9900} \\
R & =\frac{1613}{4950}
\end{aligned}
\)

Shortcut Methods for Recurring Decimals

• The numerator of the vulgar fraction is obtained by subtracting the non-recurring figure from the given figure.
• The denominator consists of as many 9’s as there are recurring figure and as many zero as there are non-recurring figure.
  For example,
  • \(0.36 \dot{5} \dot{4}=\frac{3654-36}{9900}=\frac{3618}{9900}\)
  • \(1.3 \dot{2} \dot{7}=1+0.3 \dot{2} \dot{7}=1+\frac{327-3}{990}=\frac{1314}{990}\)
  • \(0. \dot{3}=\frac{3-0}{9}=\frac{1}{3}\)

Example 19: Find the sum upto \(n\) terms of the series \(a+a a+a a a+a a a a+\ldots, \forall a \in N\) and \(1 \leq a \leq 9\).

Solution: Let \(S=a+a a+a a a+a a a a+\ldots\) upto \(n\) terms
\(
\begin{aligned}
& =a(1+11+111+1111+\ldots \text { upto } n \text { terms }) \\
& =\frac{a}{9}(9+99+999+9999+\ldots \text { upto } n \text { terms })
\end{aligned}
\)
\(=\frac{a}{9}\left\{\left(10^1-1\right)+\left(10^2-1\right)+\left(10^3-1\right)+\left(10^4-1\right)+\ldots\right.\) upto \(n\) terms
\(=\frac{a}{8}\left\{\left(10+10^2+10^3+\ldots\right.\right.\) upto \(n\) terms \()-(1+1+1+\ldots n \text { times })\}\)
\(
=\frac{a}{9}\left\{\frac{10\left(10^n-1\right)}{10-1}-n\right\}=\frac{a}{9}\left\{\frac{10}{9}\left(10^n-1\right)-n\right\} \text { [Remember] }
\)

In Particular
(i) For \(a=1,1+11+111+\ldots=\frac{1}{9}\left\{\frac{10}{9}\left(10^n-1\right)-n\right\}\)
(ii) For \(a=2,2+22+222+\ldots=\frac{2}{9}\left\{\frac{10}{9}\left(10^n-1\right)-n\right\}\)
(iii) For \(a=3,3+33+333+\ldots=\frac{3}{9}\left\{\frac{10}{9}\left(10^n-1\right)-n\right\}\)
(iv) For \(a=4,4+44+444+\ldots=\frac{4}{9}\left\{\frac{10}{9}\left(10^n-1\right)-n\right\}\)
(v) For \(a=5,5+55+555+\ldots=\frac{5}{9}\left\{\frac{10}{9}\left(10^n-1\right)-n\right\}\)
(vi) For \(a=6,6+66+666+\ldots=\frac{6}{9}\left\{\frac{10}{9}\left(10^n-1\right)-n\right\}\)
(vii) For \(a=7,7+77+777+\ldots=\frac{7}{9}\left\{\frac{10}{9}\left(10^n-1\right)-n\right\}\)
(viii) For \(a=8,8+88+888+\ldots=\frac{8}{9}\left\{\frac{10}{9}\left(10^n-1\right)-n\right\}\)
(ix) For \(a=9,9+99+999+\ldots=\frac{9}{9}\left\{\frac{10}{9}\left(10^n-1\right)-n\right\}\)

Example 20: Find the sum upto \(n\) terms of the series \(0 . b+0 . b b+0 . b b b+0 . b b b b+\ldots, \forall b \in N\) and \(1 \leq b \leq 9\).

Solution:

\(
\begin{aligned}
\text { Let } S & =0 . b+0 . b b+0 . b b b+0 . b b b b+\ldots \text { upto } n \text { terms } \\
& =b(0.1+0.11+0.111+0.1111+\ldots \text { upto } n \text { terms }) \\
& =\frac{b}{9}(0.9+0.99+0.999+0.9999+\ldots \text { upto } n \text { terms })
\end{aligned}
\)
\(=\frac{b}{9}\{(1-0.1)+(1-0.01)+(1-0.001)+(1-0.0001)+\ldots \text { upto }\) \(n[latex] terms [latex]\}\)
\(=\frac{b}{9}\{(1+1+1+1+\ldots\) upto \(n\) times \() -(0.1+0.01+0.001+0.0001+\ldots \text { upto } n \text { terms })\}\)
\(
\begin{aligned}
& =\frac{b}{9}\left\{n-\left(\frac{1}{10}+\frac{1}{10^2}+\frac{1}{10^3}+\frac{1}{10^4}+\ldots \text { upto } n \text { terms }\right)\right\} \\
& =\frac{b}{9}\left\{n-\frac{\frac{1}{10}\left(1-\left(\frac{1}{10}\right)^n\right)}{1-\frac{1}{10}}\right\}=\frac{b}{9}\left\{n-\frac{1}{9}\left[1-\left(\frac{1}{10}\right)^n\right]\right\} \text { [Remember] }
\end{aligned}
\)

In Particular

(i) For \(b=1\),
\(
0.1+0.11+0.111+\ldots=\frac{1}{9}\left\{n-\frac{1}{9}\left[1-\left(\frac{1}{10}\right)^n\right]\right\}
\)
(ii) For \(b=2\),
\(
0.2+0.22+0.222+\ldots=\frac{2}{9}\left\{n-\frac{1}{9}\left[1-\left(\frac{1}{10}\right)^n\right]\right\}
\)
(iii) For \(b=3\),
\(
0.3+0.33+0.333+\ldots=\frac{3}{9}\left\{n-\frac{1}{9}\left[1-\left(\frac{1}{10}\right)^n\right]\right\}
\)
(iv) For \(b=4\),
\(
0.4+0.44+0.444+\ldots=\frac{4}{9}\left\{n-\frac{1}{9}\left[1-\left(\frac{1}{10}\right)^n\right]\right\}
\)
(v) For \(b=5\),
\(
0.5+0.55+0.555+\ldots=\frac{5}{9}\left\{n-\frac{1}{9}\left[1-\left(\frac{1}{10}\right)^n\right]\right\}
\)
(vi) For \(b=6\),
\(
0.6+0.66+0.666+\ldots=\frac{6}{9}\left\{n-\frac{1}{9}\left[1-\left(\frac{1}{10}\right)^n\right]\right\}
\)
(vii) For \(b=7\),
\(
0.7+0.77+0.777+\ldots=\frac{7}{9}\left\{n-\frac{1}{9}\left[1-\left(\frac{1}{10}\right)^n\right]\right\}
\)
(viii) For \(b=8\),
\(
0.8+0.88+0.888+\ldots=\frac{8}{9}\left\{n-\frac{1}{9}\left[1-\left(\frac{1}{10}\right)^n\right]\right\}
\)
(ix) For \(b=9\),
\(
0.9+0.99+0.999+\ldots=\frac{9}{9}\left\{n-\frac{1}{9}\left[1-\left(\frac{1}{10}\right)^n\right]\right\}
\)

Example 21: If \(N\), the set of natural numbers is partitioned into groups \(S_1=\{1\}, S_2=\{2,3\}\), \(S_3=\{4,5,6,7\}, S_4=\{8,9,10,11,12,13,14,15\}, \ldots\), then find the sum of the numbers in \(S_{50}\).

Solution: The number of terms in the groups are \(1,2,2^2, 2^3, \ldots\)
\(\therefore\) The number of terms in the 50 th group \(=2^{50-1}=2^{49}\)
\(\because\) The first term of 1 st group \(=1=2^0=2^{1-1}\)
The first term of 2 nd group \(=2=2^1=2^{2-1}\)
The first term of 3 rd group \(=4=2^2=2^{3-1}\)
The first term of 50 th group \(=2^{50-1}=2^{49}\)
\(
\begin{aligned}
\therefore S_{50} & =\frac{2^{49}}{2}\left\{2 \times 2^{49}+\left(2^{49}-1\right) \times 1\right\} \\
& =2^{48}\left(2^{50}+2^{49}-1\right) \\
& =2^{48}\left[2^{49}(2+1)-1\right]=2^{48}\left(3 \cdot 2^{49}-1\right)
\end{aligned}
\)

Example 22: If \(S_n=1+\frac{1}{2}+\frac{1}{2^2}+\ldots+\frac{1}{2^{n-1}}\), then calculate the least value of \(n\) such that \(2-S_n<\frac{1}{100}\).

Solution:

\(
\text { Given, } S_n=1+\frac{1}{2}+\frac{1}{2^2}+\ldots+\frac{1}{2^{n-1}}=\frac{1 \cdot\left[1-\left(\frac{1}{2}\right)^n\right]}{\left(1-\frac{1}{2}\right)}
\)
\(
\begin{aligned}
& S_n= 2-\frac{1}{2^{n-1}} \\
& 2-S_n= \frac{1}{2^{n-1}}<\frac{1}{100} \quad\left[\because 2-S_n<\frac{1}{100}\right] \\
& 2^{n-1}>100>2^6 \\
& 2^{n-1}>2^6 \\
& n-1>6 \Rightarrow n>7
\end{aligned}
\)
Hence, the least value of \(n\) is 8.

Example 23: If \(x=1+a+a^2+a^3+\ldots+\infty\) and \(y=1+b+b^2+b^3+\ldots+\infty\) show that \(1+a b+a^2 b^2+a^3 b^3+\ldots+\infty=\frac{x y}{x+y-1}\), where \(0<a<1\) and \(0<b<1\).

Solution:

\(
\begin{aligned}
& \text { Given, } x=1+a+a^2+a^3+\ldots+\infty=\frac{1}{1-a} \\
& \Rightarrow \quad x-a x=1 \\
& \therefore \quad a=\left(\frac{x-1}{x}\right) \dots(i) \\
&
\end{aligned}
\)
and \(\quad y=1+b+b^2+b^3+\ldots+\infty\)
Similarly, \(\quad b=\left(\frac{y-1}{y}\right) \dots(ii)\)
Since, \(\quad 0<a<1,0<b<1\)
\(
\therefore \quad 0<a b<1
\)
Now, \(1+a b+a^2 b^2+a^3 b^3+\ldots+\infty=\frac{1}{1-a b}\)
\(
\begin{aligned}
& =\frac{1}{1-\left(\frac{x-1}{x}\right)\left(\frac{y-1}{y}\right)} \quad \text { [from Eqs. (i) and (ii)] } \\
& =\frac{x y}{x y-x y+x+y-1}
\end{aligned}
\)
Hence, \(1+a b+a^2 b^2+a^3 b^3+\ldots+\infty=\frac{x y}{x+y-1}\)

Properties of Geometric Progression

1. If \(a_1, a_2, a_3, \ldots\) are in GP with common ratio \(r\), then \(a_1 k, a_2 k, a_3 k, \ldots\) and \(\frac{a_1}{k}, \frac{a_2}{k}, \frac{a_3}{k}, \ldots\) are also in GP \((k \neq 0)\) with common ratio \(r\).
2. If \(a_1, a_2, a_3, \ldots\) are in GP with common ratio \(r\), then \(a_1 \pm k, a_2 \pm k, a_3 \pm k, \ldots\) are not in GP \((k \neq 0)\).
3. If \(a_1, a_2, a_3, \ldots\) are in GP with common ratio \(r\), then (i) \(\frac{1}{a_1}, \frac{1}{a_2}, \frac{1}{a_3}, \ldots\) are also in GP with common ratio \(\frac{1}{r}\).
   (ii) \(a_1^n, a_2^n, a_3^n, \ldots\) are also in GP with common ratio \(r^n\) and \(n \in Q\).
   (iii) \(\log a_1, \log a_2, \log a_3, \ldots\) are in \(\operatorname{AP}\left(a_i>0, \forall i\right)\) In this case, the converse also holds good.
4. If \(a_1, a_2, a_3, \ldots\) and \(b_1, b_2, b_3, \ldots\) are two GP’s with common ratios \(r_1\) and \(r_2\), respectively. Then, (i) \(a_1 b_1, a_2 b_2, a_3 b_3, \ldots\) and \(\frac{a_1}{b_1}, \frac{a_2}{b_2}, \frac{a_3}{b_3}, \ldots\) are also in GP with common ratios \(r_1 r_2\) and \(\frac{r_1}{r_2}\), respectively.
   (ii) \(a_1 \pm b_1, a_2 \pm b_2, a_3 \pm b_3, \ldots\) are not in GP.
5. If \(a_1, a_2, a_3, \ldots, a_{n-2}, a_{n-1}, a_n\) are in GP. Then,
   (i) \(a_1 a_n=a_2 a_{n-1}=a_3 a_{n-2}=\ldots\)
   (ii) \(a_r=\sqrt{a_{r-k} a_{r+k}}, \forall k, 0 \leq k \leq n-r\)
   (iii) \(\frac{a_2}{a_1}=\frac{a_3}{a_2}=\frac{a_4}{a_3}=\ldots=\frac{a_n}{a_{n-1}}\)
   \(\Rightarrow \quad a_2^2=a_3 a_1, a_3^2=a_2 a_4, \ldots\)
   Also, \(\quad a_2=a_1 r, a_3=a_1 r^2\),
   \(
   a_4=a_1 r^3, \ldots, a_n=a_1 r^{n-1}
   \)
   where, \(r\) is the common ratio of GP.
6. If three numbers in GP whose product is given are to be taken as \(\frac{a}{r}, a\), ar and if five numbers in GP whose product is given are to be taken as \(\frac{a}{r^2}, \frac{a}{r}, a, a r, a r^2\), etc.
   In general If \((2 m+1)\) numbers in GP whose product is given are to be taken as ( \(m \in N\) )
   \(
   \frac{a}{r^m}, \frac{a}{r^{m-1}}, \ldots, \frac{a}{r}, a, a r, \ldots, a r^{m-1}, a r^m
   \)

Remark

• Product of three numbers \(=a^3\)
  Product of five numbers \(=a^5\)
  \(\vdots \quad \vdots \quad \vdots \quad \vdots \quad \vdots\)
  Product of \((2 m+1)\) numbers \(=a^{2 m+1}\)
• From given conditions, find two equations in \(a\) and \(r\) and then solve them. Now, the numbers in GP can be obtained.

1. If four numbers in GP whose product is given are to be taken as \(\frac{a}{r^3}, \frac{a}{r}, a r, a r^3\) and if six numbers in GP whose product is given are to be taken as \(\frac{a}{r^5}, \frac{a}{r^3}, \frac{a}{r}, a r, a r^3, a r^5\), etc.
   In general If \((2 m)\) numbers in GP whose product is given are to be taken as \((m \in N)\)
   \([latex]
   \frac{a}{r^{2 m-1}}, \frac{a}{r^{2 m-3}}, \ldots, \frac{a}{r^3}, \frac{a}{r}, a r, a r^3, \ldots, a r^{2 m-3}, a r^{2 m-1}
   \)

Remark

• Product of four numbers \(=a^4\)
  Product of six numbers \(=a^6\)
  \(\vdots \quad \vdots \quad \vdots \quad \vdots \quad \vdots\)
  Product of \((2 m)\) numbers \(=a^{2 m}\)
• From given conditions, find two equations in \(a\) and \(r\) and then solve them. Now, the numbers in GP can be obtained.

Example 24: If \(S_1, S_2, S_3, \ldots, S_p\) are the sum of infinite geometric series whose first terms are \(1,2,3\), \(\ldots, p\) and whose common ratios are \(\frac{1}{2}, \frac{1}{3}, \frac{1}{4}, \ldots, \frac{1}{p+1}\) respectively, prove that
\(
S_1+S_2+S_3+\ldots+S_p=\frac{p(p+3)}{2}
\)

Solution:

\(
\begin{aligned}
S_p & =\frac{p}{1-\frac{1}{p+1}}=(p+1) \\
S_1 & =2, S_2=3, S_3=4, \ldots \\
\text { LHS } & =S_1+S_2+S_3+\ldots+S_p \\
& =2+3+4+\ldots+(p+1)=\frac{p}{2}(2+p+1) \\
& =\frac{p(p+3)}{2}=\text { RHS }
\end{aligned}
\)

Example 25: Let \(x_1\) and \(x_2\) be the roots of the equation \(x^2-3 x+A=0\) and let \(x_3\) and \(x_4\) be the roots of the equation \(x^2-12 x+B=0\). It is known that the numbers \(x_1, x_2, x_3, x_4\) (in that order) form an increasing GP. Find \(A\) and \(B\).

Solution: \(\because x_1, x_2, x_3, x_4\) are in GP.
Let \(\quad x_2=x_1 r, x_3=x_1 r^2, x_4=x_1 r^3\)
[here, product of \(x_1, x_2, x_3, x_4\) are not given]
Given, \(x_1+x_2=3, x_1 x_2=A\)
\(
\Rightarrow \quad x_1(1+r)=3, x_1^2 r=A \dots(i)
\)
and \(\quad x_3+x_4=12, x_3 x_4=B\)
\(
\Rightarrow x_1 r^2(1+r)=12, x_1^2 r^5=B \dots(ii)
\)
From Eqs. (i) and (ii),
\(r^2=4 \Rightarrow r=2\) [for increasing GP]
From Eq. (i), \(x_1=1\)
Now, \(A=x_1^2 r=1^2 \cdot 2=2\) [from Eq. (i)]
\(\text { and } B=x_1^2 r^5=1^2 \cdot 2^5=32 \)[from Eq. (ii)]

Example 26: Suppose \(a, b, c\) are in \(A P\) and \(a^2, b^2, c^2\) are in GP, if \(a>b>c\) and \(a+b+c=\frac{3}{2}\), then find the values of \(a\) and \(c\).

Solution: Since, \(a, b, c\) are in \(AP\) and sum of \(a, b, c\) is given.
Let
\(a=b-D, c=b+D\) \([D<0][\because a>b>c]\)
and given \(\quad a+b+c=\frac{3}{2}\)
\(
\begin{array}{rlrl}
\Rightarrow & b-D+b+b+D & =\frac{3}{2} \\
& \therefore & b & =\frac{1}{2}
\end{array}
\)
Then, \(a=\frac{1}{2}-D\) and \(c=\frac{1}{2}+D\)
Also, given \(a^2, b^2, c^2\) are in GP, then \(\left(b^2\right)^2=a^2 c^2\)
\(
\begin{array}{ll}
\Rightarrow & \pm b^2=a c \Rightarrow \pm \frac{1}{4}=\frac{1}{4}-D^2 \\
\Rightarrow & D^2=\frac{1}{4} \pm \frac{1}{4}=\frac{1}{2} [\because D \neq 0]
\end{array}
\)
\(
\therefore \quad D= \pm \frac{1}{\sqrt{2}} \Rightarrow D=-\frac{1}{\sqrt{2}} \quad[\because D<0]
\)
Hence, \(a=\frac{1}{2}+\frac{1}{\sqrt{2}}\) and \(c=\frac{1}{2}-\frac{1}{\sqrt{2}}\)

Example 27: If the continued product of three numbers in GP is 216 and the sum of their products in pairs is 156 , then find the sum of three numbers.

Solution: Here, product of numbers in GP is given.
\(\therefore\) Let the three numbers be \(\frac{a}{r}, a, a r\).
Then,
\(
\begin{aligned}
\frac{a}{r} \cdot a \cdot a r & =216 \\
a^3 & =216 \\
a & =6
\end{aligned}
\)
Sum of the products in pairs \(=156\)
\(
\Rightarrow \quad \frac{a}{r} \cdot a+a \cdot a r+a r \cdot \frac{a}{r}=156
\)
\(
\begin{aligned}
& a^2\left(\frac{1}{r}+r+1\right)=156 \Rightarrow 36\left(\frac{1+r^2+r}{r}\right)=156 \\
& 3\left(\frac{1+r+r^2}{r}\right)=13 \Rightarrow 3 r^2-10 r+3=0 \\
& (3 r-1)(r-3)=0 \Rightarrow r=\frac{1}{3} \text { or } r=3
\end{aligned}
\)
Putting the values of \(a\) and \(r\), the required numbers are 18, 6,2 or \(2,6,18\). Hence, the sum of numbers is 26.

Example 28: Find a three-digit number whose consecutive digits form a GP. If we subtract 792 from this number, we get a number consisting of the same digits written in the reverse order. Now, if we increase the second digit of the required number by 2 , then the resulting digits will form an AP.

Solution: Let the three digits be \(a, a r, a r^2\), then according to hypothesis
\(
\begin{aligned}
100 a+10 a r+a r^2-792 & =100 a r^2+10 a r+a \\
\Rightarrow \quad 99 a\left(1-r^2\right) & =792
\end{aligned}
\)
\(
a(1+r)(1-r)=8 \dots(i)
\)
and \(a, a r+2, a r^2\) are in AP.
Then,
\(
\begin{aligned}
& 2(a r+2)=a+a r^2 \\
& \Rightarrow \quad a\left(r^2-2 r+1\right)=4 \Rightarrow a(r-1)^2=4 \dots(ii) \\
&
\end{aligned}
\)
On dividing Eq. (i) by Eq. (ii), we get
\(
\frac{r+1}{r-1}=-2 \Rightarrow r=\frac{1}{3}
\)
From Eq. (ii), \(a=9\)
Thus, digits are \(9,3,1\) and so the required number is 931.

Use of GP in Solving Practical Problems

In this part, we will see how the formulae relating to GP can be made use of in solving practical problems.

Example 29: Dipesh writes letters to four of his friends. He asks each of them to copy the letter and mail to four different persons with the request that they continue the chain similarly. Assuming that the chain is not broken and that it costs 25 paise to mail one letter, find the total money spent on postage till the 8 th set of letters is mailed.

Solution: Number of letters in the 1st set \(=4\) (These are letters sent by Dipesh)
Number of letters in the 2 nd set \(=4+4+4+4=16\)
Number of letters in the 3rd set
\(
=4+4+4+\ldots+16 \text { terms }=64
\)
\(\vdots \quad \vdots \quad \vdots \quad \vdots \quad \vdots\)
The number of letters sent in the 1st set, 2nd set, 3rd set, … are respectively \(4,16,64, \ldots\) which is a GP with \(a=4\),
\(
r=\frac{16}{4}=\frac{64}{16}=4
\)
\(\therefore\) Total number of letters in all the first 8 sets
\(
=\frac{4\left(4^8-1\right)}{4-1}=87380
\)
\(\therefore\) Total money spent on letters \(=87380 \times \frac{25}{100}=₹ 21845\)

Example 30: An insect starts from a point and travels in a straight path \(1 mm\) in the first second and half of the distance covered in the previous second in the succeeding second. In how much time would it reach a point \(3 mm\) away from its starting point.

Solution: Distance covered by the insect in the 1 st second \(=1 mm\)
Distance covered by it in the 2nd second \(=1 \times \frac{1}{2}=\frac{1}{2} mm\)
Distance covered by it in the \(3 rd\) second \(=\frac{1}{2} \times \frac{1}{2}=\frac{1}{4} mm\)
\(\vdots \quad \vdots \quad \vdots \quad \vdots \quad \vdots\)
The distance covered by the insect in 1st second, 2nd second, 3rd second, … are respectively \(1, \frac{1}{2}, \frac{1}{4}, \ldots\), which are
in GP with \(a=1, r=\frac{1}{2}\). Let time taken by the insect in covering \(3 mm\) be \(n\) seconds.
\(\therefore 1+\frac{1}{2}+\frac{1}{4}+\ldots+n\) terms \(=3\)
\(\Rightarrow \quad \frac{1 \cdot\left[1-\left(\frac{1}{2}\right)^n\right]}{1-\frac{1}{2}}=3\)
\(\Rightarrow \quad 1-\left(\frac{1}{2}\right)^n=\frac{3}{2}\)
\(\Rightarrow \quad\left(\frac{1}{2}\right)^n=-\frac{1}{2}\)
\(\Rightarrow \quad 2^n=-2\)
which is impossible because \(2^n>0\)
\(\therefore\) Our supposition is wrong.
\(\therefore\) There is no \(n \in N\), for which the insect could never \(3 mm\) in \(n\) seconds.
Hence, it will never to able to cover \(3 mm\).

Remark

The maximum distance that the insect could cover is \(2 mm\).
i.e., \(1+\frac{1}{2}+\frac{1}{4}+\ldots=\frac{1}{1-\frac{1}{2}}=2\)

Example 31: The pollution in a normal atmosphere is less than \(0.01 \%\). Due to leakage of a gas from a factory, the pollution is increased to \(20 \%\). If every day \(80 \%\) of the pollution is neutralised, in how many days the atmosphere will be normal?

Solution: Let the pollution on 1 st day \(=20\)
The pollution on 2 nd day \(=20 \times 20 \%=20(0.20)\)
The pollution on 3rd day \(=20(0.20)^2\)
\(\vdots \quad \vdots \quad \vdots \quad \vdots \quad \vdots\)
Let in \(n\) days the atmosphere will be normal
\(
\begin{aligned}
& \therefore \quad 20(0.20)^{n-1}<0.01 \\
& \Rightarrow \quad\left(\frac{2}{10}\right)^{n-1}<\frac{1}{2000} \\
&
\end{aligned}
\)
Taking logarithm on base 10 , we get
\(
(n-1)(\log 2-\log 10)<\log 1-\log 2000
\)
\(
\begin{aligned}
&(n-1)(0.3010-1)<0-(0.3010+3) \\
& n-1>\frac{3.3010}{0.6990} \\
& n>5.722
\end{aligned}
\)
Hence, the atmosphere will be normal in 6 days.

Examples on Application of (Progression in Geometrical Figures)

Example 32: A square is drawn by joining the mid-points of the sides of a given square. A third square is drawn inside the second square in the same way and this process continues indefinitely. If a side of the first square is \(16 cm\), then determine the sum of the areas of all the squares.

Solution: Let \(a\) be the side length of square, then

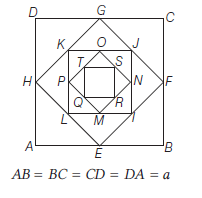
\(\because E, F, G, H\) are the mid-points of \(A B, B C, C D\) and \(D A\), respectively.
\(\therefore \quad E F=F G=G H=H E=\frac{a}{\sqrt{2}}\)
and \(I, J , K, L\) are the mid-points of \(E F, F G, G H\) and \(H E\), respectively.
\(
\therefore \quad I J = J K =K L=L I=\frac{a}{2}
\)
Similarly, \(\quad M N=N O=O P=P M=\frac{a}{2 \sqrt{2}}\) and
\(
Q R=R S=S T=T Q=\frac{a}{4}, \ldots
\)
\(
\begin{aligned}
& S=\text { Sum of areas } \\
& \quad=A B C D+E F G H+I J K L+M N O P+Q R S T+\ldots
\end{aligned}
\)
\(
\begin{aligned}
& =a^2+\left(\frac{a}{\sqrt{2}}\right)^2+\left(\frac{a}{2}\right)^2+\left(\frac{a}{2 \sqrt{2}}\right)^2+\ldots \\
& =a^2\left(1+\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\ldots\right)
\end{aligned}
\)
\(
=a^2\left(\frac{1}{1-\frac{1}{2}}\right)=2 a^2=2(16)^2 \quad[\because a=16 cm ]
\)
\(
=512 sq~ cm
\)

Example 33: One side of an equilateral triangle is 24 \(cm\). The mid-points of its sides are joined to form another triangle whose mid-points, in turn, are joined to form still another triangle. This process continues, indefinitely. Find the sum of the perimeters of all the triangles.

Solution: Let \(a\) be the side length of equilateral triangle, then
\(
A B=B C=C A=a
\)

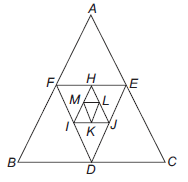
\(\because D, E, F\) are the mid-points of \(B C, C A\) and \(A B\), respectively.
\(
\therefore \quad E F=F D=D E=\frac{a}{2}
\)
and \(H, I, J\) are the mid-points of \(E F, F D\) and \(D E\), respectively.
\(
\therefore \quad I J = J H =H I=\frac{a}{4}
\)
Similarly,
\(
K L=M L=K M=\frac{a}{8}, \ldots
\)
\(
\begin{aligned}
P & =\text { Sum of perimeters }=3\left(a+\frac{a}{2}+\frac{a}{4}+\frac{a}{8}+\ldots\right) \\
& =3\left(\frac{a}{1-\frac{1}{2}}\right)=6 a=6 \times 24=144 cm \quad[\because a=24 cm ]
\end{aligned}
\)

Example 34: Let \(S_1, S_2, \ldots\) be squares such that for each \(n \geq 1\), the length of a side of \(S_n\) equals the length of a diagonal of \(S_{n+1}\). If the length of a side of \(S_1\) is \(10 cm\) and the area of \(S_n\) less than \(1 sq~ cm\). Then, find the value of \(n\).

Solution: We have, length of a side of \(S_n=\) length of diagonal of \(S_{n+1}\)
Length of a side of \(S_n=\sqrt{2}\) (length of a side of \(S_{n+1}\) )
\(\frac{\text { Length of a side of } S_{n+1}}{\text { Length of a side of } S_n}=\frac{1}{\sqrt{2}}\), for all \(n \geq 1\)
Sides of \(S_1, S_2, S_3, \ldots\) form a GP with common ratio \(\frac{1}{\sqrt{2}}\) and first term 10 .
\(
\begin{aligned}
& \therefore \quad \text { Side of } S_n=10\left(\frac{1}{\sqrt{2}}\right)^{n-1}=\frac{10}{2^{\frac{(n-1)}{2}}} \\
& \Rightarrow \text { Area of } S_n=(\text { Side })^2=\frac{100}{2^{n-1}}
\end{aligned}
\)
Now, given area of \(S_n<1\)
\(
\begin{array}{lc}
\Rightarrow & \frac{100}{2^{n-1}}<1 \Rightarrow 2^{n-1}>100>2^6 \\
\Rightarrow & 2^{n-1}>2^6 \Rightarrow n-1>6 \\
\therefore & n>7 \text { or } n \geq 8
\end{array}
\)

Example 35: The line \(x+y=1\) meets \(X\)-axis at \(A\) and \(Y\)-axis at \(B, P\) is the mid-point of \(A B, P_1\) is the foot of perpendicular from \(P\) to \(O A, M_1\) is that of \(P_1\) from \(O P\); \(P_2\) is that of \(M_1\) from \(O A, M_2\) is that of \(P_2\) from \(O P ; P_3\) is that of \(M_2\) from \(O A\) and so on. If \(P_n\) denotes the \(n\)th foot of the perpendicular on \(O A\), then find \(O P_n\).

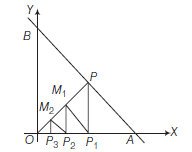
Solution: We have,
\(
\begin{aligned}
\left(O M_{n-1}\right)^2 & =\left(O P_n\right)^2+\left(P_n M_{n-1}\right)^2 \\
& =\left(O P_n\right)^2+\left(O P_n\right)^2=2\left(O P_n\right)^2=2 \alpha_n^2 \text { [say] }
\end{aligned}
\)
Also, \(\left(O P_{n-1}\right)^2=\left(O M_{n-1}\right)^2+\left(P_{n-1} M_{n-1}\right)^2\)
\(
\begin{aligned}
& \Rightarrow \quad \alpha_{n-1}^2=2 \alpha_n^2+\frac{1}{2} \alpha_{n-1}^2 \Rightarrow \alpha_n^2=\frac{1}{4} \alpha_{n-1}^2 \\
& \Rightarrow \quad \alpha_n=\frac{1}{2} \alpha_{n-1} \\
& \Rightarrow \quad O P_n=\alpha_n=\frac{1}{2} \alpha_{n-1}=\frac{1}{2^2} \alpha_{n-2}=\ldots=\frac{1}{2^n} \\
& \therefore \quad O P_n=\left(\frac{1}{2}\right)^n \\
&
\end{aligned}
\)