7.5 Entrance Corner

Factorial

The continued product of first \(n\) natural numbers is called the ” \(n\) factorial” and is denoted by \(n!\) i.e.
\(
n!=1 \times 2 \times 3 \times 4 \times \ldots \times(n-1) \times n
\)
For example,
\(
\begin{aligned}
& 5!=1 \times 2 \times 3 \times 4 \times 5 \text { and so on. } \\
& n!=(n-1)!n \text { for all } n \in N .
\end{aligned}
\)

Q1. If \(a_n=n(n!)\), then \(\sum_{r=1}^{100} a_r\) is equal to
(a) 101 !
(b) \(100!-1\)
(c) \(101!-1\)
(d) \(101!+1\)

Solution: (c) We have,
\(
\begin{aligned}
\sum_{r=1}^{100} a_r & =\sum_{r=1}^{100} r(r!)=\sum_{r=1}^{100}\{(r+1)-1\} r! \\
\Rightarrow \quad \sum_{r=1}^{100} a_r & =\sum_{r=1}^{100}\{(r+1)!-r!\} \\
\Rightarrow \quad \sum_{r=1}^{100} a_r & =(2!-1!)+(3!-2!)+(4!-3!)+\ldots .+(101!-100!) \\
\Rightarrow \quad \sum_{r=1}^{100} a_r & =101!-1
\end{aligned}
\)

Q2. If \(a_n=\frac{n}{(n+1)!}\), then \(\sum_{n=1}^{50} a_n\) is equal to
(a) \(\frac{50!-1}{50!}\)
(b) \(\frac{51!-1}{51!}\)
(c) \(\frac{1}{2(n-1)!}\)
(d) none of these

Solution: (b)
\(
\begin{aligned}
a_n & =\frac{n}{(n+1)!} \\
\Rightarrow \quad a_n & =\frac{(n+1)-1}{(n+1)!}
\end{aligned}
\)
\(
\begin{aligned}
& \Rightarrow \quad a_n=\frac{1}{n!}-\frac{1}{(n+1)!} \\
& \therefore \quad \sum_{n=1}^{50} a_n=\sum_{n=1}^{50}\left\{\frac{1}{n!}-\frac{1}{(n+1)!}\right\} \\
& \Rightarrow \quad \sum_{n=1}^{50} a_n=\left(\frac{1}{1!}-\frac{1}{2!}\right)+\left(\frac{1}{2!}-\frac{1}{3!}\right)+\left(\frac{1}{3!}-\frac{1}{4!}\right)+\ldots+\left(\frac{1}{50!}-\frac{1}{51!}\right) \\
& \Rightarrow \quad \sum_{n=1}^{50} a_n=1-\frac{1}{51!}=\frac{51!-1}{51!}
\end{aligned}
\)

Q3. If \(n!, 3 \times n!\) and \((n+1)!\) are in G.P., then \(n!, 5 \times n!\) and \((n+1)!\) are in
(a) A.P.
(b) G.P.
(c) H.P.
(d) none of these

Solution: (a) It is given that \(n!, 3 \times n!\) and \((n+1)!\) are in G.P.
\(
\begin{aligned}
& \therefore \quad(3 \times n!)^2=n!\times(n+1)! \\
& \Rightarrow \quad 9 \times(n!)^2=n!\times(n+1) n! \\
& \Rightarrow \quad 9=n+1 \\
& \Rightarrow \quad n=8 \\
& \therefore \quad n!=8!, 5 \times n!=5 \times 8!\text { and }(n+1)!=9!
\end{aligned}
\)
We observe that
\(
\begin{aligned}
2(5 \times n!) & =10 \times 8!=(9+1) \times 8!=9 \times 8!+8! \\
\Rightarrow \quad 2(5 \times n!) & =9!+8!=n!+(n+1)!
\end{aligned}
\)
Hence, \(n!, 5 \times n!\) and \((n+1)!\) are in A.P.

Q4. Sum of the series \(\sum_{r=1}^n\left(r^2+1\right) r!\), is
(a) \((n+1)\) !
(b) \((n+2)!-1\)
(c) \(n(n+1)\) !
(d) none of these

Solution: (c) We have,
\(
\begin{aligned}
& \sum_{r=1}^n\left(r^2+1\right) r! \\
& =\sum_{r=1}^n\{(r+2)(r+1)-3(r+1)+2\} r! \\
& =\sum_{r=1}^n\{(r+2)!-3(r+1)!+2 r!\} \\
& =\sum_{r=1}^n\{(r+2)!-(r+1)!\}-2 \sum_{r=1}^n\{(r+1)!-r!\} \\
& =(n+2)!-2!-2\{(n+1)!-1\}=n(n+1)!
\end{aligned}
\)

Exponent of Prime \(p\) in Factorial \(n\)

Let \(p\) be a prime number and \(n\) be a positive integer.
Let \(E_p(n)\) denote the exponent of the prime \(p\) in the positive integer \(n\). Then,
\(
E_p(n!)=\left[\frac{n}{p}\right]+\left[\frac{n}{p^2}\right]+\left[\frac{n}{p^3}\right]+\ldots+\left[\frac{n}{p^s}\right],
\)
where \(s\) is the largest positive integer such that \(p^s \leq n<p^{s+1}\)

Q5. The exponent of 3 in 100! is
(a) 47
(b) 48
(c) 49
(d) 46

Solution: (b) Let \(E_p(n)\) denote the exponent of \(p\) in \(n\). Then,
\(
E_p(n!)=\left[\frac{n}{p}\right]+\left[\frac{n}{p^2}\right]+\ldots+\left[\frac{n}{p^s}\right],
\)
where \(s\) is the largest positive integer such that \(p^s \leq n<p^s\) + 1
Here, \(n=100, p=3\)
\(
\begin{aligned}
& \because \quad 3^4<100<3^5 \\
& \therefore \quad s=4
\end{aligned}
\)
So,
\(
\begin{aligned}
E_3(100!) & =\left[\frac{100}{3}\right]+\left[\frac{100}{3^2}\right]+\left[\frac{100}{3^3}\right]+\left[\frac{100}{3^4}\right] \\
& =33+11+3+1=48
\end{aligned}
\)
Hence, the exponent of 3 in \(100!\) is 48.

Note: The exponent of 3 in 100! means the largest possible power, say \(3^r\), that divides 100! evenly. This value is the number of times 3 appears as a factor in the prime factorization of 100!.
100 ! is the product of all integers from 1 to \(100(1 \times 2 \times 3 \times \ldots \times 100)\).
The exponent represents the total count of the prime factor ‘ 3 ‘ within this entire product.
The actual value of this exponent is 48.
The calculation uses Legendre’s formula, which sums the integer parts of 100 divided by increasing powers of \(3(100 / 3+100 / 9+100 / 27+100 / 81)\).

Some Useful Symbols

If \(n\) is a natural number and \(r\) is a positive integer satisfying \(0 \leq r \leq n\), then the natural number \(\frac{n!}{(n-r)!}\) is denoted by the symbol \({ }^n P_r\) or, \(P(n, r)\).
i.e., \(\quad{ }^n P_r=P(n, r)=\frac{n!}{(n-r)!}\)
For example,
\(
{ }^5 P_2=P(5,2)=\frac{5!}{(5-2)!}=\frac{5!}{3!}=\frac{5 \times 4 \times 3!}{3!}=120
\)
Clearly, \({ }^n P_r=P(n, r)=\frac{n!}{(n-r)!}=n(n-1)(n-2) \ldots(n-(r-1))\)
Note: Dividing \(n!\) by \((n-r)!\) cancels out the terms from \((n-r)\) down to 1, leaving only the desired product from \(n\) down to \(n-r+1\).
Also, \({ }^n P_0=\frac{n!}{(n-0)!}=\frac{n!}{n!}=1 \text { and, }{ }^n P_n=\frac{n!}{(n-n)!}=\frac{n!}{0!}=n!\)

If \(n\) is \(a\) natural number and \(r\) is a positive integer satisfying \(0 \leq r \leq n\), then the natural number \(\frac{n!}{(n-r)!r!}\) is denoted by the symbol \({ }^n C_r\) or, \(C(n, r)\). Thus,
\(
{ }^n C_r=C(n, r)=\frac{n!}{(n-r)!r!}
\)

For example,
\(
{ }^7 C_5=C(7,5)=\frac{7!}{(7-5)!5!}=\frac{7!}{2!5!}=\frac{7 \times 6 \times 5!}{2!\times 5!}=21,
\)
Clearly,
\(
\begin{aligned}
{ }^n C_r & =\frac{n!}{(n-r)!r!} \\
\text { or, }{ }^n C_r & =\frac{n(n-1)(n-2) \ldots(n-(r-1))(n-r)!}{(n-r)!r!} \\
\text { or, }{ }^n C_r & =\frac{n(n-1)(n-2) \ldots(n-(r-1))}{r!} \\
\therefore \quad{ }^n C_0 & =1, n C_1=n,{ }^n C_2=\frac{n(n-1)}{2!},{ }^n C_3=\frac{n(n-1)(n-2)}{3!} \text { and so on. }
\end{aligned}
\)
Also, \({ }^n C_r=\frac{{ }^n P_r}{r!} \text { or, }{ }^n P_r={ }^n C_r \times r!\)

Property 1: \({ }^n C_r={ }^n C_{n-r}\), for \(0 \leq r \leq n\).

Proof: The formula for \({ }^n C_r\) is \({ }^n C_r=\frac{n!}{r!(n-r)!}\).
Substitute \((n-r)\) in place of \(r\) in the formula for \({ }^n C_{n-r}\) :
\(
{ }^n C_{n-r}=\frac{n!}{(n-r)!(n-(n-r))!} .
\)
Simplify the denominator:
\(
{ }^n C_{n-r}=\frac{n!}{(n-r)!(n-n+r)!}=\frac{n!}{(n-r)!r!}={ }^n C_r
\)

Remark: The above property can be restated as follows:
If \(x\) and \(y\) are non-negative integers such that \({ }^n C_x={ }^n C_y\), then \(x=y\) or, \(x+y=n\).

Proof: The binomial coefficient \({ }^n C_r\) is defined as \(\frac{n!}{r!(n-r)!}\). We are given that \({ }^n C_x={ }^n C_y\). Expanding both sides of the equation using the definition, we get:
\(
\frac{n!}{x!(n-x)!}=\frac{n!}{y!(n-y)!}
\)
We can cancel the common term \(n!\) from both sides and rearrange the equation to yield:
\(
\begin{aligned}
& \frac{1}{x!(n-x)!}=\frac{1}{y!(n-y)!} \\
& y!(n-y)!=x!(n-x)!
\end{aligned}
\)
The equation \(y!(n-y)!=x!(n-x)!\) has two primary solutions for non-negative integers \(\boldsymbol{x} \boldsymbol{,} \boldsymbol{y}\).
First, if \(x=y\), the equation holds true trivially, as both sides become identical. Second, we know from the fundamental symmetry property of binomial coefficients that \({ }^n C_r={ }^n C_{n-r}\). This identity arises directly from the definition:
\(
{ }^n C_{n-r}=\frac{n!}{(n-r)!(n-(n-r))!}=\frac{n!}{(n-r)!r!}={ }^n C_r
\)
Since \({ }^n C_x={ }^n C_y\) and \({ }^n C_y={ }^n C_{n-y}\), it implies \({ }^n C_x={ }^n C_{n-y}\). This equality holds if \(\boldsymbol{x}=\boldsymbol{n}-\boldsymbol{y}\), which can be rearranged to \({x}+{y}={n}\).

Q6. If \({ }^{15} C_{3 r}={ }^{15} C_{r+3}\), then \(r\) is equal to
(a) 5
(b) 4
(c) 3
(d) 2

Solution: (c) We have,
\(
{ }^{15} C_{3 r}={ }^{15} C_{r+3} \Rightarrow 3 r+r+3=15=r=3
\)

Q7. The number of positive integers satisfying the inequality \({ }^{n+1} C_{n-2}-{ }^{n+1} C_{n-1} \leq 100\), is
(a) 9
(b) 8
(c) 5
(d) none of these

Solution: (b) We have,
\(
\begin{aligned}
& { }^{n+1} C_{n-2}-{ }^{n+1} C_{n-1} \leq 100 \\
\Rightarrow \quad & { }^{n+1} C_3-{ }^{n+1} C_2 \leq 100 \left[\because{ }^n C_r={ }^n C_{n-r}\right]
\end{aligned}
\)
\(
\begin{aligned}
&\begin{array}{ll}
\Rightarrow & \frac{(n+1) n(n-1)}{6}-\frac{(n+1) n}{2} \leq 100 \\
\Rightarrow & (n+1) n(n-1)-3 n(n+1) \leq 600 \\
\Rightarrow & (n+1)(n)(n-4) \leq 600
\end{array}\\
&\text { The values of } n \text { satisfying this inequality are } 2,3,4,5,6,7,8,9 \text {. }
\end{aligned}
\)

Property 2: Let \(n\) and \(r\) be non-negative integers such that \(r \leq n\). Then, \({ }^n C_r+{ }^n C_{r-1}={ }^{n+1} C_r\)‘

Proof:
\(
\begin{aligned}
&{ }^n C_r=\frac{n!}{r!(n-r)!}, \quad{ }^n C_{r-1}=\frac{n!}{(r-1)!(n-r+1)!} .\\
&{ }^n C_r+{ }^n C_{r-1}=\frac{n!}{r!(n-r)!}+\frac{n!}{(r-1)!(n-r+1)!}
\end{aligned}
\)
Rewrite the second term to get a common denominator:
\(
\frac{n!}{r!(n-r)!}+\frac{n!\cdot r}{r!(n-r+1)!} .
\)
Factor:
\(
=\frac{n!}{r!(n-r)!}\left(1+\frac{r}{n-r+1}\right)=\frac{n!}{r!(n-r)!} \cdot \frac{n+1}{n-r+1} .
\)
Simplify:
\(
=\frac{(n+1)!}{r!(n+1-r)!}={ }^{n+1} C_r .
\)

Q8. For \(2 \leq r \leq n,\binom{n}{r}+2\binom{n}{r-1}+\binom{n}{r-2}=\)
(a) \(\binom{n+1}{r-1}\)
(b) \(2\binom{n+1}{r+1}\)
(c) \(\binom{n+2}{r}\)
(d) \(2\binom{n+2}{r}\)

Solution: (c) We have,
\(
\begin{aligned}
& \binom{n}{r}+2\binom{n}{r-1}+\binom{n}{r-2} \\
& =\left\{\binom{n}{r}+\binom{n}{r-1}\right\}+\left\{\binom{n}{r-1}+\binom{n}{r-2}\right\} \\
& =\binom{n+1}{r}+\binom{n+1}{r-1} \quad\left[\because\binom{k}{r}+\binom{k}{r-1}=\binom{k+1}{r}\right] \\
& =\binom{n+2}{r}
\end{aligned}
\)

Q9. The value of \({ }^{50} C_4+\sum_{r=1}^6 { }^{56-r} C_3\), is
(a) \({ }^{56} \mathrm{C}_4\)
(b) \({ }^{56} \mathrm{C}_3\)
(c) \({ }^{55} C_3\)
(d) \({ }^{55} \mathrm{C}_4\)

Solution: (a) We have,
\(
\begin{aligned}
& { }^{50} C_4+\sum_{r=1}^6{ }^{56-r} C_3 \\
& ={ }^{50} C_4+\left({ }^{55} C_3+{ }^{54} C_3+{ }^{53} C_3+{ }^{52} C_3+{ }^{51} C_3+{ }^{50} C_3\right) \\
& =\left({ }^{50} C_3+{ }^{50} C_4\right)+{ }^{51} C_3+{ }^{52} C_3+{ }^{53} C_3+{ }^{54} C_3+{ }^{55} C_3 \\
& =\left({ }^{51} C_4+{ }^{51} C_3\right)+{ }^{52} C_3+{ }^{53} C_3+{ }^{54} C_3+{ }^{55} C_3 \\
& =\left({ }^{52} C_4+{ }^{52} C_3\right)+{ }^{53} C_3+{ }^{54} C_3+{ }^{55} C_3 \\
& =\left({ }^{53} C_4+{ }^{53} C_3\right)+{ }^{54} C_3+{ }^{55} C_3 \\
& =\left({ }^{54} C_4+{ }^{54} C_3\right)+{ }^{55} C_3={ }^{55} C_4+{ }^{55} C_3={ }^{56} C_4
\end{aligned}
\)

Property 3: Let \(n\) and \(r\) be non-negative integers such that \(1 \leq r \leq n\). Then, \({ }^n C_r=\frac{n}{r} \cdot{ }^{n-1} C_{r-1}\)

Proof: To prove the identity \(\binom{n}{r}=\frac{n}{r} \cdot\binom{n-1}{r-1}\), expand the binomial coefficients using the factorial definition \(\binom{a}{b}=\frac{a!}{b!(a-b)!}\) :
Start with the right-hand side (RHS) of the equation:
\(
\frac{n}{r} \cdot{ }^{n-1} C_{r-1}=\frac{n}{r} \cdot \frac{(n-1)!}{(r-1)!(n-1-(r-1))!}
\)
Simplify the denominator inside the factorial expression:
\(
\frac{n}{r} \cdot \frac{(n-1)!}{(r-1)!(n-r)!}
\)
Combine the terms to form \(n!\) in the numerator \((n \cdot(n-1)!=n!)\) and \(r!\) in the denominator \((r \cdot(r-1)!=r!)\) :
\(
\frac{n \cdot(n-1)!}{r \cdot(r-1)!\cdot(n-r)!}=\frac{n!}{r!(n-r)!}
\)
The resulting expression is the definition of the left-hand side (LHS), \({ }^n C_r\) :
\(
\frac{n!}{r!(n-r)!}={ }^n C_r
\)
Therefore, the identity is proven:
\(
{ }^n C_r=\frac{n}{r} \cdot{ }^{n-1} C_{r-1}
\)

Remark: This property is very useful to find the value of ” \(C_r\) For example,
\(
\begin{aligned}
{ }^{10} C_3 & =\frac{10}{3} \times{ }^9 C_2=\frac{10}{3} \times \frac{9}{2} \times{ }^8 C_1=\frac{10}{3} \times \frac{9}{2} \times \frac{8}{1} \times{ }^7 C_0 \\
& =\frac{10}{3} \times \frac{9}{2} \times \frac{8}{1} \times 1=120
\end{aligned}
\)

Property 4: If \(1 \leq r \leq n\), then
\(
n \cdot{ }^{n-1} C_{r-1}=(n-r+1) { }^n C_{r-1}
\)

Proof: \({ }^{n-1} C_{r-1}=\frac{(n-1)!}{(r-1)!(n-r)!}\)
Multiply by \(n\) :
\(
n \cdot{ }^{n-1} C_{r-1}=n \cdot \frac{(n-1)!}{(r-1)!(n-r)!}=\frac{n!}{(r-1)!(n-r)!}
\)
Now compute:
\(
{ }^n C_{r-1}=\frac{n!}{(r-1)!(n-r+1)!}
\)
Multiply by \((n-r+1)\) :
\(
(n-r+1)^n C_{r-1}=(n-r+1) \cdot \frac{n!}{(r-1)!(n-r+1)!}
\)
Simplify the factor:
\(
(n-r+1) \cdot \frac{1}{(n-r+1)!}=\frac{1}{(n-r)!}
\)
So: \((n-r+1)^n C_{r-1}=\frac{n!}{(r-1)!(n-r)!}\)
And this is exactly equal to the earlier expression for \(n \cdot{ }^{n-1} C_{r-1}\).
Thus: \(n \cdot{ }^{n-1} C_{r-1}=(n-r+1)^n C_{r-1}\)

For example, \(n=5, r=3\)
Compute each side.
Left-hand side:
\(
n \cdot{ }^{n-1} C_{r-1}=5 \cdot{ }^4 C_2=5 \cdot 6=30 .
\)
Right-hand side:
\(
(n-r+1)^n C_{r-1}=(5-3+1)^5 C_2=3 \cdot 10=30 .
\)
So both sides match:
\(
30=30 \text {. }
\)

Intuitive Explanation (Combinatorial)
Both sides count the number of ways to:
“Choose an \((r-1)\)-subset, then mark one of the remaining elements appropriately.”
Left side:
Choose \(r-1\) elements from \(n-1\)
Then choose the remaining 1 element from all \(n\)
Right side:
Choose \(r-1\) elements from all \(n\)
Then choose 1 element from the remaining \((n-r+1)\)
Since both describe the same counting process, they are equal.

Property 5: If \(n\) is even, then the greatest value of \({ }^n C_r(0 \leq r \leq n)\) is \({ }^n C_{n / 2}\).

Proof: Consider the ratio of successive binomial coefficients:
\(
\frac{{ }^n C_{r+1}}{{ }^n C_r}=\frac{n-r}{r+1} .
\)
We analyze whether this fraction is greater than 1 , equal to 1 , or less than 1.
When is the sequence increasing?
\(
\begin{aligned}
& \frac{{ }^n C_{r+1}}{{ }^n C_r}>1 \\
& \frac{n-r}{r+1}>1 \\
& n-r>r+1 \\
& n-1>2 r \\
& r<\frac{n-1}{2} .
\end{aligned}
\)
So the binomial coefficients increase as long as:
\(
r<\frac{n-1}{2} .
\)
When is the sequence decreasing?
\(
\begin{gathered}
\frac{{ }^n C_{r+1}}{{ }^n C_r}<1 \\
n-r<r+1 \\
n+1<2 r \\
r>\frac{n+1}{2} .
\end{gathered}
\)
Thus binomial coefficients decrease for:
\(
r>\frac{n+1}{2} .
\)
What happens at the midpoint when \(n\) is even?
If \(n\) is even, write:
\(
n=2 k .
\)
Then the midpoint is:
\(
r=\frac{n}{2}=k .
\)
Now check the ratio at \(r=k-1\) :
\(
\frac{{ }^n C_k}{{ }^n C_{k-1}}=\frac{n-(k-1)}{k}=\frac{k+1}{k}>1 .
\)
And at \(r=k\) :
\(
\frac{{ }^n C_{k+1}}{{ }^n C_k}=\frac{n-k}{k+1}=\frac{k}{k+1}<1 .
\)
So the sequence increases up to \(r=k\) and decreases after \(r=k\).
Thus the maximum occurs exactly at:
\(
r=k=\frac{n}{2} .
\)
Therefore,
If \(n\) is even, the greatest binomial coefficient is \({ }^n C_{n / 2}\).

Intuitive Explanation

Because Pascal’s triangle is symmetric:
\(
{ }^n C_r={ }^n C_{n-r},
\)
the binomial coefficients form a symmetric “hill shape”.
When \(n\) is even, the peak of this hill is at the center:
\(
r=\frac{n}{2}
\)
When \(n\) is odd, the two middle values are equal peaks.

For example, \(n=4\)
Compute all binomial coefficients:
\(
{ }^4 C_0=1,{ }^4 C_1=4,{ }^4 C_2=6,{ }^4 C_3=4,{ }^4 C_4=1 .
\)
The largest value is:
\(
{ }^4 C_2=6 .
\)
And indeed:
\(
n / 2=4 / 2=2 .
\)

Property 6: If \(n\) is odd, then the greatest value of \(C_r(0 \leq r \leq n)\) is
\(
{ }^n C_{\frac{n+1}{2}} \text { or, }{ }^n C_{\frac{n-1}{2}}
\)

Proof: Let \(n=2 k+1\) (since \(n\) is odd).
Then the central binomial coefficients are:
one at \(r=k=\frac{n-1}{2}\),
the next at \(r=k+1=\frac{n+1}{2}\).
And we have symmetry:
\(
{ }^n C_r={ }^n C_{n-r} .
\)
Since:
\(
n-\frac{n-1}{2}=\frac{n+1}{2},
\)
the two central coefficients are equal.
Monotonicity argument
Consider:
\(
\frac{{ }^n C_{r+1}}{{ }^n C_r}=\frac{n-r}{r+1} .
\)
The sequence increases while:
\(
\frac{n-r}{r+1}>1 \Longleftrightarrow r<\frac{n-1}{2} .
\)
It decreases while:
\(
\frac{n-r}{r+1}<1 \Longleftrightarrow r>\frac{n+1}{2} .
\)
Thus:
The coefficients increase up to \(r=\frac{n-1}{2}\)
and decrease after \(r=\frac{n+1}{2}\)
So the two consecutive middle terms are both maximum and equal:
\(
{ }^n C_{\frac{n-1}{2}}={ }^n C_{\frac{n+1}{2}}
\)
If \(n\) is odd:
\(
\text { max } { }^n C_r={ }^n C_{\frac{n-1}{2}}={ }^n C_{\frac{n+1}{2}} .
\)

For Example, \(n=5\)
List all binomial coefficients:
\(
{ }^5 C_0=1,{ }^5 C_1=5,{ }^5 C_2=10,{ }^5 C_3=10,{ }^5 C_4=5,{ }^5 C_5=1 .
\)
The largest values are:
\(
{ }^5 C_2=10 \text { and }{ }^5 C_3=10
\)
And indeed:
\(
\frac{5-1}{2}=2, \quad \frac{5+1}{2}=3 .
\)

Fundamental Principle of Counting

Multiplication rule:

If there are two jobs such that one of them can be completed in \(m\) ways, and when it has been completed in any one of these \(m\) ways, second job can be completed in \(n\) ways; then the two jobs in succession can be completed in \(m \times n\) ways.

Q10. In a class there are 10 boys and 8 girls. The teacher wants to select a boy and a girl to represent the class in a function. The number of ways in which the teacher can make the selection is
(a) 18
(b) 80
(c) \(10^8\)
(d) \(8^{10}\)

Solution: (b) Here, the teacher is to perform two jobs:
(i) selecting a boy among 10 boys, and,
(ii) selecting a girl among 8 girls.
The first of these can be performed in 10 ways and the second in 8 ways. Therefore, by the fundamental principle of multiplication, the required number of ways is \(10 \times 8=80\).

Remark: If three operations can be separately performed in \(m, n\) and \(p\) ways, respectively, then the three operations together can be performed in \(m \times n \times p\) ways. Similar result holds for any number of operations.

Addition Rule:

If there are two jobs such that they can be performed independently in \(m\) and \(n\) ways respectively, then either of the two jobs can be performed in \((m+n)\) ways.

Q11. In a class there are 10 boys and 8 girls. The teacher wants to select either a boy or a girl to represent the class in a function. In how many ways the teacher can make this selection ?
(a) 18
(b) 80
(c) \(8^{10}\)
(d) \(10^8\)

Solution: (a) Here, the teacher is to perform either of the following two jobs :
(i) selecting a boy among 10 boys. or,
(ii) selecting a girl among 8 girls.
The first of these can be performed in 10 ways and the second in 8 ways. Therefore, by fundamental principle of addition either of the two jobs can be performed in \((10+8)=18\) ways. Hence, the teacher can make the selection of either a boy or a girl in 18 ways.

Q12. Five persons entered the lift cabin on the ground floor of an 8-floor house. Suppose each of them can leave the cabin independently at any floor beginning with the first. The total number of ways in which each of the five persons can leave the cabin at any one of the 7-floor is
(a) \(5^7\)
(b) 2520
(c) \(7^5\)
(d) 35

Solution: (c) Suppose \(A_1, A_2, A_3, A_4, A_5\) are five persons. \(A_1\) can leave the cabin at any of the seven floors. So, \(A_1\) can leave the cabin in 7 ways. Similarly, each of \(A_2, A_3, A_4, A_5\) can leave the cabin in 7 ways. Thus, the total number of ways in which each of the five persons can leave the cabin at any of the seven floors is \(7 \times 7 \times 7 \times 7 \times 7=7^5\).

Q13. The number of ways in which \(n\) distinct balls can be put into three boxes, is
(a) \(3 n\)
(b) \(n^3\)
(c) \(3^{\prime \prime}\)
(d) \(n+3\)

Solution: (c) Here, the job of putting \(n\) different balls in three boxes is divided into \(n\) sub-jobs as given below :
\(J_1\) : Putting first ball in one of the three boxes.
\(J_2\) : Putting second ball in one of the three boxes.
⋮
\(J_n\) : Putting \(n\)th ball in one of the three boxes.
We observe that each sub-job can be completed in three ways. So, by the fundamental principle of counting the total number of ways of putting \(n\) balls in three different boxes is
\(
\underset{n \text {-times }}{3 \times 3 \times 3 \times \ldots \times 3}=3^n
\)

Q14. The number of ways in which \(n\) distinct balls can be put into three boxes so that no two boxes remain empty, is
(a) \(3^n\)
(b) \(3^n-1\)
(c) \(3^n-2\)
(d) \(3^n-3\)

Solution: (d) In the above example, we have seen that \(n\) distinct balls can be put into three boxes in \(3^n\) ways. Out of these \(3^n\) ways, there are three ways
(i) When all balls are put in first box
(ii) When all balls are put in second box
(iii) When all balls are put in third box.
Thus, there are \(3^n-3\) ways in which no two of the three boxes are empty.

Q15. There are 10 true-false questions in an examination. The number of ways in which these questions can be answered, is
(a) 240
(b) 20
(c) 1024
(d) 100

Solution: (c) Each question can be answered in two ways. So, total number of ways of answering 10 questions is
\(
2 \times 2 \times 2 \times \ldots \times 2(10 \text { times })=2^{10}=1024
\)

Q16. For a set of five trueffalse questions, no student has written all correct answers, and no two students have given the same sequence of answers. What is the maximum number of students in the class, for this to be possible ?
(a) 9
(b) 32
(c) 31
(d) 24

Solution: (c) Since a true/false type question can be answered in 2 ways either by marking it true or false. So, there are 2 ways of answering each of the 5 questions. So,
Total number of different sequences of answers
\(
=2 \times 2 \times 2 \times 2 \times 2=2^5=32 .
\)
Out of these 32 sequences of answers there is only one sequence of answering all the five questions correctly. But, no student has written all the correct answers and different students have given different sequences of answers. So,
Maximum number of students in the class
\(=\) Number of sequences except one sequence in which all answers are correct
\(
=32-1=31
\)

Q17. Four die are rolled. The number of ways in which at least one die shows 3, is
(a) 625
(b) 671
(c) 1296
(d) 1256

Solution: (b) Since each dice can result in 6 ways. So, the total number of possible outcomes is \(6 \times 6 \times 6 \times 6=6^4\).
If 3 does not occur on any die, then each die can result in 5 ways.
∴ Total number of outcomes in which no die shows 3
\(
=5 \times 5 \times 5 \times 5=5^4
\)
Total number of possible outcomes in which at least one die shows 3 = Total number of possible outcomes -Number of outcomes in which no die shows 3
\(
=6^4-5^4=671 .
\)

Q18. A sequence is a ternary sequence, if it contains digits 0,1 and 2 . The total number of ternary sequences of length 9 which either begin with 210 or end with 210 , is
(a) 1458
(b) 1431
(c) 729
(d) 707

Solution: (b) Since each digit in a ternary sequence of length 9 can be filled in 3 ways. Therefore, the number of nine-digit ternary sequence beginning with 210 is \(3^6\) and the number of nine-digit ternary sequence ending with 210 is also \(3^6\). The number of ternary sequence of 9 digits which begin and end with 210 is \(3^3\).
Thus, the total number of sequences which either begin with 210 or end with 210 is
\(
3^6+3^6-3^3=729+729-27=1431
\)

Q19. The number of ways in which \(n\) distinct objects can be put into two identical boxes so that no box remains empty, is
(a) \(2^n-1\)
(b) \(2^n-2\)
(c) \(2^{n-1}-1\)
(d) none of these

Solution: (c) Let us first label the boxes \(B_1\) and \(B_2\). Now, each object can be put either in \(B_1\) or in \(B_2\). So, there are two ways to deal with each of the \(n\) objects. Consequently, \(n\) objects can be dealt with \(2^n\) ways. Out of these \(2^n\) ways, there are two ways (i) when all objects are put in box \(B_1\) (ii) when all objects are put in box \(B_2\). Thus, there are \(2^n-2\) ways in which neither box is empty. If we now remove the labels from the boxes so that they become identical, this number must be divided by 2 to get the required number of ways.
Hence, the required number of ways \(=\frac{1}{2}\left(2^n-2\right)=2^{n-1}-1\).

Q20. A gentleman has 6 friends to invite. In how many ways can he send invitation cards to them, if he has three servants to carry the cards ?
(a) \(3^6\)
(b) \(6^3\)
(c) 18
(d) none of these

Solution: (a) Since a card can be sent by any one of the three servants, so the number of ways of sending the invitation card to the first friend \(=3\). Similarly, invitation cards can be sent to each of the six friends in 3 ways.
\(\therefore \quad\) Required number of ways \(=3 \times 3 \times 3 \times 3 \times 3 \times 3=3^6\)

Q21. There are unlimited number of identical balls of four different colours. How many arrangements of at most 8 balls in a row can be made by using them ?
(a) 21845
(b) 87380
(c) 262140
(d) none of these

Solution: (b) Since there are balls of four different colours. Therefore,
Number of arrangements of one ball \(=4\)
Number of arrangements of two balls \(=4 \times 4=4^2\)
Number of arrangements of three balls \(=4 \times 4 \times 4=4^3\) etc.
∴ Required number of arrangements
\(
\begin{aligned}
& =4+4^2+4^3+\ldots+4^8 \\
& =4\left(\frac{4^8-1}{4-1}\right)=\frac{4}{3}\left(4^8-1\right)=87380
\end{aligned}
\)

Q22. A rectangle with sides of lengths \((2 n-1)\) and \((2 m-1)\) units is divided into squares of unit length. The number of rectangles which can be formed with sides of odd length, is [IIT (S) 2005]
(a) \(m^2 n^2\)
(b) \(m n(m+1)(n+1)\)
(c) \(4^{m+n-1}\)
(d) none of these

Solution: (a) Clearly,
Number of horizontal rectangles of 1 unit length \(=(2 m-1)\)
Number of horizontal rectangles of 3 unit length \(=(2 m-3)\)
Number of horizontal rectangles of 5 unit length \(=(2 m-5)\)
Similarly,
Number of rectangles of ( \(2 m-1\) ) unit length \(=1\)
∴ Total number of horizontal rectangles of odd length
\(
=(2 m-1)+(2 m-3)+\ldots+3+1=m^2
\)

Similarly,
Total number vertical rectangles of odd length \(=n^2\)
∴ Total number of rectangles \(=m^2 \times n^2\)

Q23. Find the number of different signals that can be generated by arranging at least 2 flags in order (one below the other) on a vertical staff, if five different flags are available.

Solution: Step 1: Calculate arrangements for exactly 2 flags
The number of different signals using exactly 2 flags from 5 different flags is a permutation \(P(5,2)\).
\(
P(5,2)=\frac{5!}{(5-2)!}=\frac{5!}{3!}=5 \times 4=20
\)
Step 2: Calculate arrangements for exactly 3 flags
The number of different signals using exactly 3 flags from 5 different flags is a permutation \(P(5,3)\).
\(
P(5,3)=\frac{5!}{(5-3)!}=\frac{5!}{2!}=5 \times 4 \times 3=60
\)
Step 3: Calculate arrangements for exactly 4 flags
The number of different signals using exactly 4 flags from 5 different flags is a permutation \(P(5,4)\).
\(
P(5,4)=\frac{5!}{(5-4)!}=\frac{5!}{1!}=5 \times 4 \times 3 \times 2=120
\)
Step 4: Calculate arrangements for exactly 5 flags
The number of different signals using exactly 5 flags from 5 different flags is a permutation \(P(5,5)\).
\(
P(5,5)=\frac{5!}{(5-5)!}=\frac{5!}{0!}=5 \times 4 \times 3 \times 2 \times 1=120
\)
Step 5: Sum the arrangements
The total number of signals is the sum of signals generated in each case (at least 2 flags).
\(
\text { Total Signals }=20+60+120+120=320
\)

Q24. Poor Dolly’s T.V. has only 4 channels; all of them quite boring, hence it is not surprising that she desires to switch (change) channel after every one minute. Then find the number of ways in which she can change the channels so that she is back to her original channel for the first time after 4 minutes.

Solution: Let there be 4 channels \(C_1 C_2 C_3\) and \(C_4\) at \(\mathrm{t}=0\) minute she is watching channel 1
∴ after \(1^{\text {st }}\) minute she has 3 choices to switch the channel ( \(C_2, C_3, C_4\) )
after \(2^{\text {nd }}\) minute she has 2 choices to switch the channel after \(3^{\text {rd }}\) minute she has 2 choices to switch the channel but after the \(4^{\text {th }}\) minute she has only 1 choice to switch the channel i.e. \(C_1\)
∴ Total number of ways \(=3 \times 2 \times 2=12\)

Q25. There are ‘ \(n\) ‘ locks and ‘ \(n\) ‘ matching keys. If all the locks and keys are to be perfectly matched, find the maximum number of trials required to open a lock.

Solution: The maximum number of trials needed for the first key is \(n\). For second key, it will be \(n-1\).
Now, for the \(r^{\text {th }}\) key, the maximum number of trials needed is \(n-r+1\). Thus, the required answer is
\(
n+(n-1)+\cdots+1=\frac{n(n+1)}{2}
\)

Q26: Three dice are rolled. Find the number of possible outcomes in which at least one dice shows 5 .

Solution: When a dice is rolled, there are six possible outcomes. So; the total number of outcomes when three dice are rolled is \(6 \times 6 \times 6=6^3\).
Now, the number of possible outcomes in which at least one dice shows 5 is as follows.
Total number of possible outcomes – Number of possible outcomes in which 5 does not appear on any dice \(=6^3-5^3 =91\)

Q27: Find the number of distinct rational numbers \(x\) such that \(0<x<1\) and \(x=p / q\), where \(p, q \in\{1,2,3\), 4, 5, 6}.

Solution: As \(0<x<1\), we have \(p<q\).
\(
\begin{array}{|l|l|}
\hline p & q \\
\hline 1 & 2,3,4,5,6 \\
\hline 2 & 3,4,5,6 \\
\hline 3 & 4,5,6 \\
\hline 4 & 5,6 \\
\hline 5 & 6 \\
\hline
\end{array}
\)
Thus, the number of rational numbers is \(5+4+3+2+1=15\).
When \(p\) and \(q\) have a common factor, we get some rational numbers, which are not different from those already counted. Here, there are four such numbers: \(2 / 4,2 / 6,3 / 6,4 / 6\).
Therefore, the required number of rational numbers is \(15-4=11\).

Q28: Find the total number of integer ‘ \(n\) ‘ such that \(2 \leq n \leq 2000\) and H.C.F. of \(n\) and 36 is 1.

Solution: \(36=2^2 \times 3^2\)
If H.C.F. of integer ‘ \(n\) ‘ and 36 is 1, then \(n\) should not be divisible by 2 or 3.
Let us first find the numbers that are divisible by 2 or 3 .
The number of integers in the range [ 2,2000 ] that are divisible by 2 is \(1000(2,4,6, \ldots, 1998,2000)\).
The number of integers in the range [2,2000] that are divisible by 3 is \(666(3,6,9, \ldots, 1995,1998)\).
The number of integers in the range [2,2000] that are divisible by 6 is \(333(6,12,18, \ldots, 1992,1998)\).
Total number of integers divisible by 2 or 3 is \(1000+666-33=1333\).
Thus, the total number of integers that are divisible by neither 2 nor 3 is \(1999-1333=666\).

Q29: Find the number of diagonals in the polygon of \(n\) sides.

Solution: For diagonal, we have to select any two vertices. The first vertex can be selected in \(n\) ways. Let \(A_1\) be chosen as first vertex. Now, diagonal cannot be formed if any of \(A_2\) and \(A_n\) is chosen. Hence, for \(A_1\) another vertex can be selected in \(n-3\) ways from remaining \(n-3\) vertices.

Again, by principle of counting, the number of ways two vertices can be selected is \(n(n-3)\).
Now, when \(A_1\) is chosen as the first vertex, sometimes \(A_4\) is chosen as the second vertex.
Similarly, when \(A_4\) is chosen as the first vertex, sometimes \(A_1\) is chosen as the second vertex.
Hence, each pair is selected twice. Therefore, the total number of diagonals is \(n(n-3) / 2\).

Permutations

A permutation is an ordered arrangement of items in a specific sequence, where changing the position of elements creates a new permutation (e.g., ABC is different from ACB). It signifies arrangements where order matters, unlike combinations where it doesn’t.

Case-1: Number of Permutations of \({n}\) Different Things Taken \(r\) at a Time:
\(P_r=n!/(n-r)!\)

Case-2: Number of Permutations of \({n}\) Different Things Taken All at a Time
\({ }^n P_n=n!\)

Q30: Seven athletes are participating in a race. In how many ways can the first three athletes win the prizes?

Solution: It is equivalent to filling 3 places (as prizes) with 7 persons The number of permutations of 7 objects taken three at a time is
\(
{ }^7 P_3=7 \times 6 \times 5=210
\)

Q31: How many different signals can be given using any number of flags from 5 flags of different colours?

Solution: The signals can be made by using one or more flags at a time.
The total number of signals when \(r\) flags are used at a time from 5 flags is equal to the number of arrangements of 5 , taking \(r\) at a time, i.e., \({ }^5 P_r\).
Since \(r\) can take the values \(1,2,3,4,5\), hence, by the fundamental principle of addition, the total number of signals is
\(
\begin{aligned}
{ }^5 P_1+{ }^5 P_2+{ }^5 P_3+{ }^5 P_4+{ }^5 P_5= & 5+(5 \times 4)+(5 \times 4 \times 3)+(5 \times 4 \times 3 \times 2) \\
& +(5 \times 4 \times 3 \times 2 \times 1) \\
= & 5+20+60+120+120 \\
= & 325
\end{aligned}
\)

Q32: How many 4-letter words, with or without meaning, can be formed out of the letters in the word ‘LOGARITHMS’, if repetition of letters is not allowed?

Solution: There are 10 letters in the word ‘LOGARITHMS’. So, the number of 4-letter words is equal to number of arrangements of 10 letters, taken 4 at a time, i.e., \({ }^{10} P_4=5040\).

Q33: Eleven animals of a circus have to be placed in eleven cages (one in each cage). If 4 of the cages are too small for 6 of the animals, then find the number of the ways of caging all the animals.

Solution: Let the 6 animals be placed in 7 of larger cages. This can be done in \({ }^7 P_6\) ways. In each of these ways, one larger cage is left vacant. The remaining five animals can be placed in the remaining five cages in 5 ! ways. Hence, by the fundamental theorem, the required number of ways is \({ }^7 P_6 \times 5!=604800\).

Case-3: Number of Permutations of \(\boldsymbol{n}\) Things Taken All Together When the Things Are Not All Different

To find the number of permutations of things taken all at a time when \(p\) of them are similar and are of one type, \(q\) of them are similar and are of second type, \(r\) of them are similar and are of third type and rest are all different.
\(
\therefore x=\frac{n!}{p!q!r!}
\)

Q34: How many words can be formed with the letters of the word ‘MATHEMATICS’ by rearranging them.

Solution: Since there are 2 M ‘s, 2 A ‘s and 2 T ‘s, the required number of ways is \(11!/(2!2!2!)\).

Q35: Find the total number of nine-digit numbers that can be formed using the digits \(2,2,3,3,5,5,8,8\), 8 so that the odd digit occupy the even places.

Solution: Odd digits \(3,3,5,5\) occupy four even places in \(4!/(2!2!) =6\) ways. Rest five digits \(2,2,8,8,8\) occupy rest five places in \(5!/(2!3!)=10\) ways. Hence, total number of ways is \(6 \times 10=60\).

Q36: Find the number of permutation of all the letters of the word “MATHEMATICS” which starts with consonants only.

Solution: (M M), (A A), (T T), H, E, I, C, S
Words starting with \(M\) or \(A\) or \(T\) are \(\frac{10!}{2!2!}\)
Words starting with H, E, I, C, S are \(\frac{10!}{2!2!2!}\)
Hence number of words are
\(
3 \frac{10!}{2!2!}+5 \frac{10!}{2!2!2!}=\frac{10!}{2!2!}\left(3+\frac{5}{2}\right)=\frac{11!}{8}
\)

Q37: There are six periods in each working day of a school. Find the number of ways in which 5 subjects can be arranged if each subject is allotted at least one period and no period remains vacant.

Solution: Let the five subjects are \(a, b, c, d, e\).
Since number of subjects are less than the number of periods, any one of the five subjects will occur twice.
If subject ‘ \(a\) ‘ occur twice ( \(a, a, b, c, d, e\) ), then six subjects can be arranged in \(\frac{6!}{2!}\) ways.
Similar number of ways when subject \(b, c, d\) and \(e\) occur twice.
Hence total number of ways are \(5 \times \frac{6!}{2!}=1800\)

Case-4: Number of Permutations of \(\boldsymbol{n}\) Different Things Taken \(r\) at a Time When Each Thing Can Be Repeated Any Number of Times

By multiplication rule of fundamental principle of counting, number of ways in which first, second, third, \(\ldots, r^{\text {th }}\) places can together be filled up is \(n \times n \times n \times \cdots r\) times \(=n^r\).

Q38: How many 4-digit numbers can be formed by using the digits \(1,2,3,4,5,6,7\) if at least one digit is repeated.

Solution: The numbers that can be formed when repetition of digits is allowed are \(7^4\).
The numbers that can be formed when all the digits are distinct or when repetition is not allowed are \({ }^7 P_4\).
Therefore, the numbers that can be formed when at least one digit is repeated are \(7^4-{ }^7 P_4\).

Q39: Find the total number of permutations of \(n\) different things taken not more than \(r\) at a time, when each thing may be repeated any number of times.

Solution: Here, we have to arrange \(p\) things out of \(n, 1 \leq p \leq r\), and repetition is allowed. When \(p=1\), the number of permutations is \(n\). When \(p=2\), the number of permutations is \(n \times n=n^2\).
(Since repetition is allowed, first thing can be taken in \(n\) ways and the second thing can also be taken in \(n\) ways.)
When \(p=3\), the number of permutations is \(n \times n \times n=n^3\). When \(p=r\), the number of permutations is \(n \times n \times n \cdots r\) times \(=n^{r}\).
Hence, total number of permutations is
\(
n+n^2+n^3+\cdots+n^r=\frac{n\left(n^r-1\right)}{(n-1)} \quad \text { [sum of G.P.] }
\)

Case-5: Permutations Under Restrictions:

(i) When Particular Objects Are Never Together (Gap Method)

Q40: Number of ways in which 5 girls and 5 boys can be arranged in a row if no two boys are together.

Solution: In the question, there is no condition for arranging the girls. Now, 5 girls can be arranged in \(5!\) ways.
\(
\times G \times G \times G \times G \times G \times
\)
When girls are arranged, six gaps are generated as shown above with ‘ \(x\) ‘.
Now, boys must occupy the places with ‘ \(x\) ‘ marked so that no two boys are together.
Therefore, five boys can be arranged in these six gaps in \({ }^6 P_5\) ways.
Hence, total number of arrangement is \(5!\times{ }^6 P_5\).

(ii) When Particular Objects Are Always Together

Q41: If the best and the worst papers never appear together, find in how many ways six examination papers can be arranged.

Solution: If the best and worst papers appear always together, the number of ways is \(5!\times 2\). Therefore, required number of ways is as follows.
Total number of ways without any restrictions – number of ways when best and worst paper are together \(=6!-5!\times 2 =480\).

Q42: Find the number of arrangements of the letters of the word ‘SALOON’, if the two O’s do not come together.

Solution: The total number of arrangements is \(6!/ 2!=360\). The number of ways in which O’s come together is \(5!=120\). Hence, the required number of ways is \(360-120=240\).

Q43: Find the number of seven letter words that can be formed by using the letters of the word SUCCESS so that the two C are together but no two S are together.

Solution: Considering CC as single object, U, CC, E can be arranged in 3 ! ways
\(
\times \mathrm{U} \times \mathrm{CC} \times \mathrm{E} \times
\)
Now the three S are to be placed in the four available places (X)
Hence required no. of ways \(=3!\cdot{ }^4 \mathrm{C}_3=24\).

Q44: There are six teachers. Out of them two are primary teachers, two are middle teachers and two secondary teaches. They are to stand in a row, so as the primary teaches, middle teaches and secondary teaches are always in a set. Find the number of ways in which they can do so.

Solution: There are 2 primary teachers. They can stand in a row in \(2!=2\) ways
There are 2 middle teachers. They can stand in a row in 2! \(=2\) ways.
There are 2 secondary teachers. They can stand in a row in \(2!=2\) ways.
These three sets can be arranged In themselves in \(=3!=6\) ways
Hence the required number of ways \(=2 \times 2 \times 2 \times 6=48\)

Q45: There are 2 identical white balls, 3 identical red balls and \(\mathbf{4}\) green balls of different shades. Find the number of ways in which they can be arranged in a row so that at least one ball is separated from the balls of the same colour.

Solution: Total number of arrangements without any restrictions \(= \frac{9!}{2!3!}\)
Now number of ways when balls of the same color are together \(=3!4!\)
Now required number of ways
= Total number of arrangements – number of ways when balls of the same colour are together
\(=\frac{9!}{2!3!}-3!4!=6(7!-4!)\)

Q46: Find the number of ways in which 6 boys and 6 girls can be seated in a row so that
(i) all the girls sit together and all the boys sit together,
(ii) all the girls are never together.

Solution:

(i) Considering boys and girls as two units, the number of permutations is \(2!\times 6!\times 6!=2 \times(6!)^2\).
(ii) The total arrangements where all girls are not together is as follows: Total arrangement without any restrictions – arrangement when all girls are together \(=(12)!-7!6!\).

Combinations

A combination is a selection of items from a larger set where the order of selection does not matter. For example, choosing apples and pears for a fruit salad is the same as choosing pears and apples.
In mathematics, the number of combinations of choosing \(r\) items from a total of \(n\) distinct items is calculated using the formula:
\(
C(n, r)=\frac{n!}{r!(n-r)!}
\)
where \(n!\) (\(n\) factorial) is the product of all positive integers up to \(n\). Combinations are a fundamental concept in probability and statistics.

Case-1: Number of Combinations of \({n}\) Different Things Taking \(r\) at a Time ( \(r<n\) )
\(
{ }^n C_r=\frac{n!}{r!(n-r)!}
\)

Proof:
The number of permutations of \(n\) different items taken \(r\) at a time is given by the formula:
\(
{ }^n P_r=\frac{n!}{(n-r)!}
\)
A permutation can be thought of as a two-step process: first, choosing a group of \({r}\) items (a combination), and second, arranging those \({r}\) items in a specific order.
The number of ways to choose \(r\) items from \(n\) (combinations) is \({ }^n C_r\).
The number of ways to arrange the chosen \(r\) items is \(r\) ! (the factorial of \(r\) ).
By the fundamental counting principle, the total number of permutations is the product of the number of combinations and the number of ways to arrange the chosen items:
\(
{ }^n P_r={ }^n C_r \times r!
\)
To find the formula for \({ }^n C_r\), rearrange the equation:
\(
{ }^n C_r=\frac{{ }^n P_r}{r!}
\)
Substitute the formula for \({ }^n P_r\) into this equation:
\(
{ }^n C_r=\frac{n!/(n-r)!}{r!}
\)
Simplify the expression to get the final combination formula:
\(
{ }^n C_r=\frac{n!}{r!(n-r)!}
\)

Properties of \({ }^n C_r\)

• \({ }^n C_r={ }^n C_{n-r}\)
• If \({ }^n C_x={ }^n C_y\), then either \(x=y\) or \(x+y=n\).
• \({ }^n C_r+{ }^n C_{r-1}={ }^{n+1} C_r\)
• \(r^n C_r=n^{n-1} C_{r-1}\)
• \(\frac{{ }^n C_r}{r+1}=\frac{{ }^{n+1} C_{r+1}}{n+1}\)
• \(\frac{{ }^n C_r}{{ }^n C_{r-1}}=\frac{n-r+1}{r}\)
• Maximum value of \({ }^n C_r\)
  We can Observe that in the list of \({ }^6 C_0,{ }^6 C_1,{ }^6 C_2,{ }^6 C_3,{ }^6 C_4,{ }^6 C_5\), and \({ }^6 C_6\), the maximum value is \({ }^6 C_3\).
  Also, in the list of \({ }^7 C_0,{ }^7 C_1,{ }^7 C_2,{ }^7 C_3,{ }^7 C_4,{ }^7 C_5,{ }^7 C_6\), and \({ }^7 C_7\), the maximum value is \({ }^7 C_3\) or \({ }^7 C_4\).
  In general, when \(n\) is even, maximum value of \({ }^n C_r\) is \({ }^n C_{n / 2}\) and when \(n\) is odd, maximum value of \({ }^n C_r\) is \({ }^n C_{(n-1) / 2}\) or \({ }^n C_{(n+1) / 2}\).
• The product of \(k\) consecutive positive integers is divisible by \(k!\)
• \({ }^n C_r\) is divisible by \(n\) only if \(n\) is a prime number \((1 \leq r \leq n-1)\)
  For example, \({ }^6 C_2\) is not divisible by 6 , but \({ }^7 C_4\) is divisible by 7.

Case-2: Restricted Combinations

(i) Number of Combinations of \(n\) Different Things Taken \(r\) at a Time when \(p\) Particular Things Are Always Included

Already \(p\) things are selected. The remaining \(r-p\) things from the remaining \(n-p\) things can be selected in \({ }^{n-p} C_{r-p}\) ways.

(ii) Number of Combinations of \(n\) Different Things Taken \(r\) at a Time when p Particular Things Are Always to Be Excluded

Since \(p\) particular things are always to be excluded, therefore, we have to select \(r\) things out of remaining \(n-p\) different things. This can be done in \({ }^{n-p} C_r\) ways.

Q47: If \({ }^n C_r=84,{ }^n C_{r-1}=36\) and \({ }^n C_{r+1}=126\), then find the value of \({n}\).

Solution: Step 1: Formulate the first equation
Using the ratio of consecutive combinations \(\frac{{ }^n C_r}{{ }^n C_{r-1}}=\frac{n-r+1}{r}\), we can write the equation:
\(
\frac{84}{36}=\frac{n-r+1}{r}
\)
Simplifying the fraction gives \(\frac{7}{3}\), leading to the equation \(7 r=3(n-r+1)\), which simplifies to \(10 r-3 n=3\).
Step 2: Formulate the second equation
Using the ratio of consecutive combinations \(\frac{{ }^n C_{r+1}}{{ }^n C_r}=\frac{n-r}{r+1}\), we can write the equation:
\(
\frac{126}{84}=\frac{n-r}{r+1}
\)
Simplifying the fraction gives \(\frac{3}{2}\), leading to the equation \(3(r+1)=2(n-r)\), which simplifies to \(5 r-2 n=-3\).
Step 3: Solve the system of equations
We have a system of two linear equations:
\(10 r-3 n=3 \dots(1)\)
\(5 r-2 n=-3 \dots(2)\)
Multiplying the second equation by 2 gives \(10 r-4 n=-6\). Subtracting this from the first equation \((10 r-3 n)-(10 r-4 n)=3-(-6)\) yields \(n=9\).
Substituting \(n=9\) into \(5 r-2 n=-3\) gives \(5 r-18=-3\), so \(5 r=15\), meaning \(r=3\).
The value of \({n}\) is 9.

Q48: If \({ }^n \boldsymbol{C}_8={ }^n \boldsymbol{C}_6\), then find \({ }^n \boldsymbol{C}_2\).

Solution: If \({ }^n C_x={ }^n C_y\) and \(x \neq y\), then \(x+y=n\). Hence,
\(
\begin{aligned}
& { }^n C_8={ }^n C_6 \\
\Rightarrow \quad & n=(8+6)=14
\end{aligned}
\)
Now,
\(
{ }^n C_2={ }^{14} C_2=\frac{14 \times 13}{2}=91
\)

Q49: If \({ }^{15} C_{3 r} : { }^{15} C_{r+1}=11: 3\), find the value of ‘ \(r\) ‘.

Solution: \({ }^{15} C_{3 r} : { }^{15} C_{r+1}=11: 3\)
Clearly, ‘ \(r\) ‘ can be \(0,1,2,3,4,5\) but possibilities of \(r=0\) or 5 are clearly ruled out (as \({ }^{15} C_0={ }^{15} C_{15}=1\) ).
For \(r=1\),
\(
\begin{aligned}
& { }^{15} C_{3 r}={ }^{15} C_3=\frac{15 \times 14 \times 13}{6} \text { and }{ }^{15} C_{r+1}={ }^{15} C_2=\frac{15 \times 14}{2} \\
& { }^{15} C_{3 r} : { }^{15} C_{r+1}=13: 3
\end{aligned}
\)
\(
\begin{aligned}
&\text { For } r=2 \text {, }\\
&\begin{aligned}
& { }^{15} C_{3 r}={ }^{15} C_6=\frac{15 \times 14 \times 13 \times 12 \times 11 \times 10}{6 \times 5 \times 4 \times 3 \times 2 \times 1} \\
& { }^{15} C_{r+1}={ }^{15} C_3=\frac{15 \times 14 \times 13}{6} \\
\therefore \quad & { }^{15} C_{3 r} : { }^{15} C_{r+1} \neq 11: 3
\end{aligned}
\end{aligned}
\)
For \(r=3\),
\(
{ }^{15} C_{3 r}={ }^{15} C_9=\frac{15 \times 14 \times 13 \times 12 \times 11 \times 10}{6 \times 5 \times 4 \times 3 \times 2 \times 1}
\)
\(
\begin{aligned}
& { }^{15} C_{r+1}={ }^{15} C_4=\frac{15 \times 14 \times 13 \times 12}{4 \times 3 \times 2 \times 1} \\
\therefore & { }^{15} C_{3 r} : { }^{15} C_{r+1}=11: 3
\end{aligned}
\)
For \(r=4\),
\(
{ }^{15} C_{3 r}={ }^{15} C_{12}={ }^{15} C_3=\frac{15 \times 14 \times 13}{3 \times 2 \times 1}
\)
\(
\begin{aligned}
&\begin{aligned}
& { }^{15} C_{r+1}={ }^{15} C_5=\frac{15 \times 14 \times 13 \times 12 \times 11}{5 \times 4 \times 3 \times 2 \times 1} \\
\therefore & { }^{15} C_{3 r} : { }^{15} C_{r+1}=5: 33
\end{aligned}\\
&\text { Thus, } r=3 \text {. }
\end{aligned}
\)

Q50: Twenty-eight games were played in a football tournament with each team playing once against each other. How many teams were there?

Solution: Let the number of teams be \(n\). Then number of matches to be played is \({ }^n C_2=28\).
\(
\begin{array}{ll}
\therefore & \frac{n(n-1)}{2}=28 \\
\Rightarrow & n^2-n-56=0 \\
\Rightarrow & (n-8)(n+7)=0 \\
\Rightarrow & n=8 \text { as } n \neq-7
\end{array}
\)

Q51: In a network of railways, a small island has 15 stations. Find the number of different types of tickets to be printed for each class, if every stations must have tickets for other stations.

Solution: For each pair of stations, two different types of tickets are required.
Now, the number of selections of 2 stations from 15 stations \(={ }^{15} \mathrm{C}_2\).
∴ Required number of types of tickets \(=2{ }^{15} \mathrm{C}_2=2 \frac{15!}{2!3!} =15 \times 14=210\).

Q52: In a certain algebraical exercise book there are 4 examples on arithmetical progressions, 5 examples on permutation and combination and 6 examples on binomial theorem. Find the number of ways a teacher can select for his pupils at least one but not more than 2 examples from each of these sets.

Solution: Number of ways teacher can select examples from arithmetic progression \(=\left({ }^4 C_1+{ }^4 C_2\right)\)
Number of ways teacher can select examples from permutation and combinations \(=\left({ }^5 C_1+{ }^5 C_2\right)\)
Number of ways teacher can select examples from binomial theorem \(=\left({ }^6 C_1+{ }^6 C_2\right)\)
Hence total number of ways \(=\left({ }^4 C_1+{ }^4 C_2\right)\left({ }^5 C_1+{ }^5 C_2\right)\left({ }^6 C_1+\right. { }^6 C_2\) )

Q53: A person tries to form as many different parties as he can, out of his 20 friends. Each party should consist of the same number. How many friends should be invited at a time? In how many of these parties would the same friends be found?

Solution: Let the person invite \(r\) number of friends at a time. Then, the number of parties is \({ }^{20} C\), which is maximum when \(r=10\).
If a particular friend will be found in \(x\) parties, then \(x\) is the number of combinations out of 20 in which this particular friend must be included. Therefore, we have to select 9 more from 19 remaining friends. Hence, \(x={ }^{19} C_9\).

Q54: In how many of the permutations of \(n\) things taken \(r\) at a time will three given things occur?

Solution: According to the condition of the problem, we have to select \(r-3\) things from remaining \(n-3\) things and permute these \(r\) things. So the number of permutations is
\(
{ }^{(n-3)} C_{(r-3)} r!=\frac{(n-3)!r!}{(r-3)!(n-r)!}
\)

Q55: Out of 10 consonants and 4 vowels, how many words can be formed each containing 3 consonants and 2 vowels?

Solution: The number of ways of selection of three consonants from 10 is \({ }^{10} C_3\). The number of ways of selection of two vowels from 4 is \({ }^4 C_2\). Permutation of these 5 letters (all distinct) is 5 ! Therefore, number of words that can be formed is \({ }^{10} C_3 \times{ }^{+} C_2 \times 5\) ! \(=86400\).

Q56: Find the maximum number of points of intersection of \(\mathbf{6}\) circles.

Solution: Two circles intersect maximum at two distinct points. Now, two circles can be selected in \({ }^6 C_2\) ways. Again, each selection of two circles gives two points of intersection. Therefore, the total number of points of intersection is \({ }^6 C_2 \times 2=30\).

Q57: There are 10 points on a plane of which no three points are collinear. If lines are formed joining these points, find the maximum points of intersection of these lines.

Solution: Two points are required to form a line. Then, the number of lines is equal to the number of ways two points are selected, i.e., \({ }^{10} C_2=45\).
Now, two lines intersect at one point. Hence, the number of points of intersection of lines is \({ }^{45} C_2\).

Q58: There are 10 points on a plane of which 5 points are collinear. Also, no three of the remaining 5 points are collinear. Then find (i) the number of straight lines joining these points; (ii) the number of triangles formed joining these points.

Solution: (i) Line is formed joining two points. Hence, number of lines is \({ }^{10} \boldsymbol{C}_2\). But joining any points from 5 collinear points gives the same line. Again, 2 points are selected from 5 in \({ }^5 C_2\) ways or lines joining collinear points is taken \({ }^5 C_2(=10)\) times. Then the number of straight lines \(={ }^{10} C_2-10+1=36\).
(ii) For a triangle, three non-collinear points are required. Three points can be selected in \({ }^{10} C_3\) ways. Now, the selection of three points from 5 collinear points does not form triangle. Hence, number of triangles is \({ }^{10} C_3-{ }^5 C_3\).

Q59: Find the total number of rectangles on the normal chessboard.

Solution: To form a rectangle on a chessboard two vertical lines and two horizontal lines should be selected. There are 9 vertical lines and 9 horizontal lines found on the chessboard. Selection of 2 vertical and 2 horizontal lines can be done in \({ }^9 C_2 \times{ }^9 C_2\) ways, which is equivalent to the number of rectangles.

Q60: A box contains 5 different red and 6 different white balls. In how many ways can 6 balls be selected so that there are at least two balls of each colour?

Solution: The selection of 6 balls, consisting of at least two balls of each colour from 5 red and 6 white balls, can be made in the following ways:
\(
\begin{array}{|l|l|l|}
\hline \text { Red balls(5) } & \text { White balls(6) } & \text { Number of ways } \\
\hline 2 & 4 & { }^5 C_2 \times{ }^6 C_4=150 \\
\hline 3 & 3 & { }^5 C_3 \times{ }^6 C_3=200 \\
\hline 4 & 2 & { }^5 C_4 \times{ }^6 C_2=75 \\
\hline & \text { Total } & 425 \\
\hline
\end{array}
\)

Q61: In a plane, there are 5 straight lines which will pass through a given point, 6 others which all pass through another given point and 7 others which all pass through a third given point. Supposing no three lines intersect at any point and no two are parallel, find the number of triangles formed by the intersection of the straight line.

Solution: Let 5 straight lines be passing through \(A, 6\) passing through \(B\) and 7 passing through \(C\). In all, there are 18 straight lines. To find the number of triangles equivalent, we have to find the number of selection of 3 lines from these 18 lines, keeping in mind that selection of 3 lines from the lines passing through \(A\), \(B\) or \(C\) will not give any triangle.
Hence, the required number of triangles is \({ }^{18} C_3-\left({ }^5 C_3+{ }^6 C_3\right. \left.+{ }^7 C_3\right)=751\).

Q62: A regular polygon of 10 sides is constructed. In how many ways can 3 vertices be selected so that no two vertices are consecutive?

Solution: The required number of selections is given as The number of selections without restriction (the number of selections when 3 vertices are consecutive) – (the number of selections when 2 vertices are consecutive).

Now, the number of selections of 3 vertices without restriction is \({ }^{10} C_3\).
The number of selections of 3 consecutive vertices is 10 (by observation: \(A_1 A_2 A_3, A_2 A_3 A_4, \ldots, A_{10} A_1 A_2\) ).
The number of selections when two vertices are consecutive is \(10 \times{ }^6 C_1\).
(After selecting two consecutive vertices in 10 ways, the third can be selected from 6 vertices.)
Therefore, the required number of selections is
\(
{ }^{10} C_3-10-10 \times{ }^6 C_1=\frac{10 \times 9 \times 8}{6}-10-60=120-70=50
\)

Q63: At an election, a voter may vote for any number of candidates, not greater than the number to be elected. There are 10 candidates and 4 are to be elected. If a voter votes for at least one candidate, then the number of ways in which he can vote, is [AIEEE 2006]
(a) 5040
(b) 6210
(c) 385
(d) 1110

Solution: (c) The number of ways in which a voter can vote is
\(
{ }^{10} \mathrm{C}_1+{ }^{10} \mathrm{C}_2+{ }^{10} \mathrm{C}_3+{ }^{10} \mathrm{C}_4=10+45+120+210=385
\)

Explanation: The voter may choose any subset of the 10 candidates, of size 1 to 4.
So the number of possible ways to vote is:
\(
\binom{10}{1}+\binom{10}{2}+\binom{10}{3}+\binom{10}{4}
\)
Compute:
\(\binom{10}{1}=10\)
\(\binom{10}{2}=45\)
\(\binom{10}{3}=120\)
\(\binom{10}{4}=210\)
Sum: \(10+45+120+210=385\)

Q64: The set \(S=\{1,2,3, \ldots, 12\}\) is to be partitioned into three sets \(A, B, C\) of equal size. Thus, \(A \cup B \cup C=S, A \cap B=B \cap C=A \cap C=\phi\). The number of ways to partition \(S\) is [AIEEE 2007]
(a) \(\frac{12!}{(4!)^3}\)
(b) \(\frac{12!}{(3!)^4}\)
(c) \(\frac{12!}{3!(4!)^3}\)
(d) \(\frac{12!}{3!(3!)^4}\)

Solution: (a) The number of ways of partitioning \(S\) into three disjoint sets is same as the number of ways of distributing 12 distinct items to three persons each getting same number of items.
\(
\text { ∴ Required number of ways }={ }^{12} C_4 \times{ }^8 C_4 \times{ }^4 C_4=\frac{12!}{(4!)^3}
\)

Explanation: Determine the number of ways to select elements for each set.
The number of ways to choose 4 elements for set \(A\) from 12 elements is given by the combination formula:
\(
\binom{12}{4}
\)
Select elements for set B.
After selecting 4 elements for set \(A\), there are 8 elements left. The number of ways to choose 4 elements for set \(B\) from these 8 elements is:
\(
\binom{8}{4}
\)
Select elements for set C.
Finally, the remaining 4 elements will automatically form set \(C\). The number of ways to choose 4 elements from these 4 is:
\(
\binom{4}{4}=1
\)
Calculate the total number of partitions.
The total number of ways to partition the set \(S\) into sets \(A, B\), and \(C\) is the product of the combinations calculated in the previous steps:
\(
\text { Total partitions }=\binom{12}{4} \times\binom{ 8}{4} \times\binom{ 4}{4}
\)
Express in factorial form.
Using the relationship between combinations and factorials, we can express the total partitions as:
\(
\text { Total partitions }=\frac{12!}{4!\cdot 8!} \times \frac{8!}{4!\cdot 4!} \times \frac{4!}{4!\cdot 0!}
\)
Simplifying this gives:
\(
=\frac{12!}{(4!)^3}
\)

Q65: From 6 different novels and 3 different dictionaries, 4 novels and 1 dictionary are to be selected and arranged in a row on a shelf so that the dictionary is always in the middle. Then, the number of such arrangements, is [AIEEE 2009]
(a) less than 500
(b) at least 500 but less than 750
(c) at least 750 but less than 1000
(d) at least 1000

Solution: (d) Out of 6 novels, 4 novels can be selected in \({ }^6 \mathrm{C}_4\) ways and 1 dictionary can be chosen out of 3 dictionaries in \({ }^3 C_1\) ways. Since 1 dictionary is to be fixed in the middle and a pair of novels on its either side. This can be done in \({ }^4 \mathrm{C}_2 \times 21 \times 21\) ways.
\(\therefore \quad\) Required number of arrangements
\(
={ }^6 C_4 \times{ }^3 C_1 \times{ }^4 C_2 \times 2!\times 2!=1080
\)

Explanation: Step 1: Select the books
First, the required number of novels and dictionaries must be selected from the available options.
The number of ways to select 4 novels from 6 different novels is given by the combination formula \(C(n, k)=\frac{n!}{k!(n-k)!}\).
\(
C(6,4)=\frac{6!}{4!2!}=15
\)
The number of ways to select 1 dictionary from 3 different dictionaries is:
\(
C(3,1)=\frac{3!}{1!2!}=3
\)
The total number of ways to select the set of 4 novels and 1 dictionary is \(15 \times 3=45\)
Step 2: Arrange the selected books with the dictionary in the middle
The selected 5 books are to be arranged in a row of 5 positions such that the dictionary is always in the middle position. The middle position is fixed for the selected dictionary.
The remaining 4 positions can be filled by the 4 selected novels. The number of permutations for 4 distinct novels in 4 distinct positions is \(P(4,4)=4!\).
\(
4!=4 \times 3 \times 2 \times 1=24
\)
Step 3: Calculate total arrangements
The total number of arrangements is the product of the number of ways to select the books and the number of ways to arrange them in the specified manner.
Total arrangements \(=(\) Ways to select \() \times(\) Ways to arrange \()=45 \times 24=1080\).

Q66: If all the letters of the word ‘AGAIN’ be arranged as in a dictionary, then the fiftieth word is
(a) NAAGI
(b) NAAIG
(c) NIAAG
(d) NAIAG

Solution: (b) In dictionary the words at each stage are arranged in alphabetical order. Starting with the letter A, and arranging the other four letters GAIN, we obtain \(4!=24\) words.
Thus, there are 24 words which start with A . These are the first 24 words.
Then, starting with G, and arranging the other four letters A, A, \(\mathrm{I}, \mathrm{N}\) in different ways, we obtain \(\frac{4!}{2!}=\frac{24}{2}=12\) words.
Thus, there are 12 words, which start with G.
Now, we start with I. The remaining 4 letters A, G, A, N can be arranged in \(\frac{4!}{2!}=12\) ways. So, there are 12 words, which start with I. Thus, we have so far constructed 48 words. The 49th word is NAAGI and hence the 50th word is NAAIG.

Q67: If the letters of the word ‘SACHIN’ are arranged in all possible ways and these words are written out as in a dictionary, then the word SACHIN appears at serial number [AIEEE 2005]
(a) 602
(b) 603
(c) 600
(d) 601

Solution: (d) In a dictionary the words at each stage are arranged in alphabetical order. We must therefore consider the words beginning with A, C, H, I, N, S in order. A will occur at first place as often as there are ways of arranging the remaining 5 letters all at a time i.e. A will occur at first place \(5!\) times.
Thus,
Number of words starting with \(\mathrm{A}=5!\)
Similarly,
Number of words starting with \(\mathrm{C}=5!\)
Number of words starting with \(\mathrm{H}=5\) !
Number of words starting with \(\mathrm{I}=5\) !
Number of words starting with \(\mathrm{N}=5\) !
SACHIN appears in the list of words beginning with S.
Clearly, it is the first word in the list of words beginning with S.
So, SACHIN appears at serial number
\(
(5!+5!+5!+5!+5!+1)=601
\)

Q68: The letters of the word COCHIN are permuted and all the permutations are arranged in an alphabetical order as in an English dictionary. The number of words that appear before the word COCHIN, is [IIT 2007]
(a) 360
(b) 192
(c) 96
(d) 48

Solution: (c) The number of words starting with \(\mathrm{CC}=4\) !
The number of words starting with \(\mathrm{CH}=4\) !
The number of words starting with \(\mathrm{CI}=4\) !
The number of words starting with \(\mathrm{CN}=4!\).
COCHIN is the first word in the list of words beginning with CO.
∴ Number of words that appear before the word COCHIN \(=96\)

Circular Permutations

The number of circular permutations of \(n\) distinct objects is \((n-1)\) !

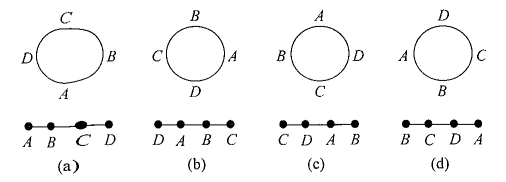
Let us consider that persons \(A, B, C, D\) are sitting around a round table. If all of them ( \(A, B, C, D\) ) are shifted at one place in anticlockwise order, then we will get Fig(b) from Fig(a). Now, if we shift \(A, B, C, D\) in anticlockwise order, we will get Fig(c). Again, if we shift them we will get Fig(d); and in the next time, Fig(a).

Thus, we see that if 4 persons are sitting at a round table, they can be shifted four times and the four different arrangements thus obtained will be the same, because anticlockwise order of \(A, B, C, D\) does not change.

But if \(A, B, C, D\) are sitting in a row and they are shifted in such an order that the last occupies the place of first, then the four arrangements will be different.

Thus, if there are 4 things, then for each circular arrangement number of linear arrangements is 4.

Similarly, if \(n\) different things are arranged along a circle, for each circular arrangement number of linear arrangements is \(n\).
Thus, each circular permutation gives \(n\) linear permutations. But, there are \(x\) circular permutations.
So, total number of linear permutations is \(x n\).
But, the number of linear permutations of \(n\) distinct objects is \(n!\).
\(
\therefore \quad x n=n!\Rightarrow x=\frac{n!}{n}=(n-1)!
\)

Note:

• In the above theorem anticlockwise and clockwise order of arrangements are considered as distinct permutations.
• Number of linear arrangements \(=n \times\) Number of circular arrangements.

Explanation:
Linear vs. Circular: In a linear arrangement (a row), an arrangement like (A, B, C) is different from (B, C, A) because they have distinct starting points. There are \(n!\) linear permutations for \(n\) objects.
Rotational Equivalence: In a circular arrangement (a round table), there is no distinct start or end point. Rotating an arrangement, e.g., (A, B, C) in a circle, yields ( \(\mathrm{B}, \mathrm{C}, \mathrm{A}\) ) and ( \(\mathrm{C}, \mathrm{A}, \mathrm{B}\) ), which are all considered the same single arrangement because the relative positions of the objects to each other haven’t changed.
Fixing a Position: To avoid counting these \(n\) identical rotations as separate permutations, we fix one object in place. This object acts as a reference point, effectively turning the circular problem into a linear one with \(n-1\) remaining spots.
Calculation: The remaining \(n-1\) objects can be arranged in the remaining positions in \((n-1)!\) ways.

For example, 3 People around a table:
\(n=3\).
Number of circular permutations \(=(3-1)!=2!=2\).
If the people are A, B, and C, the only two distinct arrangements are (A, B, C) and (A, C, B) (assuming clockwise and counter-clockwise are different). Any rotation of these two unique arrangements is the same as one of the originals.

Clockwise and Anticlockwise Arrangements

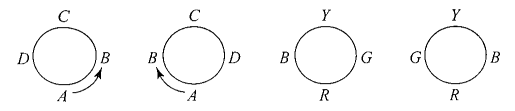
Let the four persons \(A, B, C, D\) sit at a round table in anticlockwise as well as clockwise directions. These two arrangements are different. But if four flowers \(R\) (red), \(G\) (green), \(Y\) (yellow) and \(B\) (blue) be arranged to form a garland in anticlockwise and in clockwise order, then the two arrangements are same because if we see the garland from one side the four flowers \(R, G, Y, B\) will appear in anticlockwise direction and if seen from the other side the four flowers will appear in the clockwise direction. Here, the two arrangements will be considered as one arrangement because the order of flowers is not changing rather only the side of observation is changing. Here, two permutations will be counted as one.
Therefore, when clockwise and anticlockwise arrangements are not different, i.e., when observation can be made from both sides, the number of circular arrangements of \(n\) different things is \((n-1)!/ 2\).

Q69: Five boys and 5 girls sit alternately around a round table. In how many ways can this be done?

Solution: 

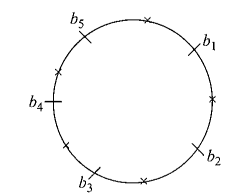
Five boys can be arranged in a circle in 4 ! ways.
After that girls can be arranged in the five gaps shown as ‘ \(\times\) ‘ in \(5!\) ways. Hence, total number of ways is \(4!\times 5!=2880\).

Explanation: Step 1 – Fix rotation
In circular arrangements, we fix one person to eliminate rotational symmetry.
Fix one boy in his seat.
Step 2 – Arrange the remaining boys
There are 4 remaining boy-slots between the girls’ seats.
They can be arranged in:
\(
4!=24 \text { ways }
\)
Step 3 – Arrange the girls
There are \(\mathbf{5}\) girl-slots alternating with the boys’ seats.
The \(\mathbf{5}\) girls can be arranged in:
\(
5!=120 \text { ways }
\)
Total number of alternating circular seatings
\(
4!\cdot 5!=24 \times 120=2880
\)

Q70: A round-table conference is to be held among 20 delegates belonging from 20 different countries. In how many ways can they be seated if two particular delegates are (i) always to sit together; (ii) never to sit together.

Solution: (i) Let the two particular delegates who wish to sit together be treated as one delegate. So we have 19 delegates who can be arranged on a round table in ( \(19-1\) )!, i.e., 18 ! ways.
After this, the two particular delegates can be permuted between themselves in \(2!=2\) ways. Hence, by product rule, number of required arrangements is \(2 \times(18)\) !.
(ii) The total number of arrangements of 20 delegates on a round table is 19 !.
Hence, the number of arrangements in which the two particular delegates never sit together is \(19!-2 \times 18!=18!(19-2) =17 \times 18!\).

Q71: A person invites a group of 10 friends at
dinner and sits
(i) 5 on a round table and 5 more on another round table,
(ii) 4 on one round table and 6 on the other round table.
Find the number of ways in each case in which he can arrange the guests.

Solution: (i) The number of ways of selection of 5 friends for first table is \({ }^{10} C_5\). Remaining 5 friends are left for second table.
The total number of permutations of 5 guests on each table is \(4!\). Hence, the total number of arrangements is \({ }^{10} C_5 \times 4!\times 4\) ! \(=10!/(5!\times 5!) 4!\times 4!=10!/ 25\).
(ii) The number of ways of selection of 6 guests is \({ }^{10} C_6\). The number of ways of permutations of 6 guests on round table is \(5!\). The number of permutation of 4 guests on round table is \(3!\).
Therefore, total number of arrangements is
\(
{ }^{10} C_6 \times 5!3!=\frac{(10)!}{6!\times 4!} 5!3!=\frac{(10)!}{24}
\)

Q72: Find the number of ways in which 10 different diamonds can be arranged to make a necklace.

Solution: Since diamonds do not have natural order of left and right so clockwise and anticlockwise arrangements are taken as identical. Therefore, the number of arrangements of 10 different diamonds to make a necklace is \(1 / 2 \times 9=181440\).

Q73: Six persons \(A, B, C, D, E, F\) are to be seated at a circular table. In how many ways can this be done if \(A\) should have either \(B\) or \(C\) on his right and \(B\) must always have either \(C\) or \(D\) on his right.

Solution: Let the seat occupied by \(A\) be numbered as 1 and the remaining 5 seats be numbered as \(2,3,4,5,6\) in anticlockwise direction. There arise two cases:
Case I: \(B\) is on right of \(A\), i.e., at number 2.
Then, seat number 3 can be occupied by \(C\) or \(D\) in \({ }^2 C_1\) ways and remaining 3 persons can have remaining 3 seats in 3 ! ways. Hence, the number of arrangements in this case is \(2 \times 6=12\).
Case II: \(C\) is on the right of \(A\), i.e., at number 2.
Then, \(B\) can occupy any seat from number 3 or 4 or 5. Then, \(D\) must be on the right of \(B\), so we are left with two persons and 2 seats, which can be occupied in 2 ! ways. Hence, the number of arrangements in this case is \({ }^3 C_1 \times 2!=6\). These cases are exclusive. So by sum rule total number of arrangements is \(12+6 =18\).

Q74: Find the number of ways in which six persons can be seated at a round table, so that all shall not have the same neighbours in any two arrangements.

Solution: In this case, anticlockwise and clockwise arrangements are the same.
Hence, the number of ways of arrangements is \(5!/ 2=60\).

Q75: persons were invited for a party. The number of ways they and the host be seated at a circular table if two particular persons sit on either side of the host, is
(a) 18 !
(b) \(18!\times 2!\)
(c) \(\frac{18!}{2!}\)
(d) 19 !

Solution: (b) Let \(P_1, P_2\) be two particular persons and \(H\) be the host. These two particular persons can be seated on either side of the host in the following two ways:
(i) \(P_1 H P_2\) and,
(ii) \(P_2 H P_1\).
Consider the two particular persons and the host as one person, we have 19 persons in all. These 19 persons can be seated round a circular table in \((19-1)!=18!\) ways. But, two particular persons can be seated on either side of the host in 2 ways. So, the number of ways of seating 21 persons at a circular table with two particular persons on either side of the host is \(18!\times 2\).

Q76: There are 20 persons among whom are two brothers. The number of ways in which we can arrange them around a circle so that there is exactly one person between the two brothers, is
(a) 18 !
(b) \(17!\times 2!\)
(c) \(18!\times 2!\)
(d) 20 !

Solution: (c) Let \(B_1\) and \(B_2\) be two brothers among 20 persons and let \(M\) be a person. Clearly, person \(M\) can be chosen from 18 persons (excluding \(B_1\) and \(B_2\) ) in 18 ways. Considering the two brothers \(B_1\) and \(B_2\) and person \(M\) as one person, we have 18 persons in all. These 18 persons can be arranged around a circle in \((18-1)!=17\) ! ways.
But, \(B_1\) and \(B_2\) can be arranged among themselves in 2! ways ( \(B_1 M B_2\) and \(B_2 M B_1\) ).
∴ Total number of ways \(=18 \times 17!\times 2!=2!\times 18!\).

Selection of One or More Objects

Case-I: Selection from different items

Theorem 1: The number of ways of selecting one or more items from a group of \(n\) distinct items is \(2^n-1\).

Proof: Out of \(n\) items, 1 item can be selected in \({ }^n C_1\) ways; 2 items can be selected in \({ }^n C_2\) ways; three items can be selected in \({ }^n C_3\) ways and so on.
Hence, the required number of ways
\(
\begin{aligned}
& ={ }^n C_1+{ }^n C_2+{ }^n C_3+\ldots+{ }^n C_n \\
& =\left({ }^n C_0+{ }^n C_1+{ }^n C_2+\ldots+{ }^n C_n\right)-{ }^n C_0=2^n-1
\end{aligned}
\)

Q77: A man has 6 friends, in how many ways may he invite one or more of them to dinner ?
(a) 64
(b) 65
(c) 63
(d) \(6!\)

Solution: (c) The man has to select some or all of his 6 friends. So, required number of ways \(=2^6-1=63\).

Case-II: Selection from Identical Objects

(i) The number of ways of selecting \(r\) items out of \(n\) identical items is 1.
Reason: If the items are identical, then choosing any \(r\)-subset is indistinguishable from any other. There is only one possible selection: “the set of \(r\) identical objects.”

Q78: How many ways can you select 4 balls from a pile of 10 identical balls?

Solution: All balls are identical, so selecting any 4 looks the same. Thus: 1

(ii) The total number of ways of selecting zero or more i.e. at least one item from a group of \(n\) identical items is \((n+1)\).
Reason: Possible numbers of items you may choose are:
\(
0,1,2, \ldots, n
\)
That is \(n+1\) possibilities.
Since each selection of a given size looks the same (objects identical), there are \(n+1\) selections.

Q79: From 5 identical pens, how many selections can you make if you may choose 0 to 5 pens?

Solution: Possible selections are choosing:
\(
0,1,2,3,4 \text {, or } 5 \text { pens }
\)
Number of possibilities:
\(
5+1=6
\)

(iii) The total number of selections of some or all out of \(p+q+r\) items where \(p\) are alike of one kind, \(q\) are alike of second kind and rest are alike of third kind is \([(p+1)(q+1)(r+1)]-1\).
Reason: From each group:
First kind: choose 0 to \(p\) items \(\rightarrow(p+1)\) choices
Second kind: choose 0 to \(q\) items \(\rightarrow(q+1)\) choices
Third kind: choose 0 to \(r\) items \(\rightarrow(r+1)\) choices
Total selections (including selecting none from all groups):
\(
(p+1)(q+1)(r+1)
\)
But we want some or all, i.e., exclude the empty selection:
\(
(p+1)(q+1)(r+1)-1
\)

Q80: A basket contains:
2 identical apples
5 identical bananas
4 identical mangoes
How many selections of some or all fruits are possible?

Solution: Choices:
Apples: \(2+1=3\)
Bananas: \(5+1=6\)
Mangoes: \(4+1=5\)
Total with empty selection:
\(
3 \cdot 6 \cdot 5=90
\)
Exclude empty set:
\(
90-1=89
\)

Case-III: Selection of Identical and Distinct Objects

Theorem 2: The total number of ways of selecting one or more items from \(p\) identical items of one kind; \(q\) identical items of second kind; \(r\) identical items of third kind and \(n\) different items is
\(
(p+1)(q+1)(r+1) 2^n-1
\)

Proof: Since we may select \(0,1,2,3, \ldots p\) items from \(p\) identical items, therefore \(p\) identical items may be dealt with in \((p+1)\) ways.
Similarly, \(q\) identical items may be dealt with in ( \(q+1\) ) ways and
\(r\) identical items in ( \(r+1\) ) ways.
Now, each of the \(n\) distinct items can be disposed of in two ways, either by selecting it or by rejecing it (so each has 2 possibilities). Therefore, the total number of ways of dealing with all the items is
\(
(p+1)(q+1)(r+1) \times 2^n
\)
But, this number also includes a case in which none of the items is taken (Exclude the empty selection), therefore the required number of ways of selecting at least one item is \((p+1)(q+1)(r+1) 2^n-1\).

Q81: A collection contains:
\(p=2\) identical red balls
\(q=3\) identical blue balls
\(r=1\) identical green ball
\(n=2\) distinct toys (say a car and a doll)
How many ways can you select one or more items?

Solution: Step 1: Selections from identical items
Red balls (2 identical)
Choose 0,1 , or \(2 \rightarrow 2+1=3\) choices
Blue balls (3 identical)
Choose \(0,1,2\), or \(3 \rightarrow 3+1=4\) choices
Green balls (1 identical)
Choose 0 or \(1 \rightarrow 1+1=2\) choices
So total choices from identical items:
\(
(2+1)(3+1)(1+1)=3 \cdot 4 \cdot 2=24
\)
Step 2: Selections from the two distinct toys
Each toy can be selected or not:
Car: 2 choices (select / not select)
Doll: 2 choices (select / not select)
Thus: Total choices from distinct items.
\(
2^2=4
\)
Step 3: Combine both
Independent selections, so multiply:
\(
24 \times 4=96
\)
This includes the empty selection.
Step 4: Exclude empty selection
Subtract 1:
\(
96-1=95
\)
So there are 95 ways to select one or more items from this mixed group.

Note: This example exactly demonstrates how the formula works:
\(
(p+1)(q+1)(r+1) 2^n-1
\)
Matches:
\(
(2+1)(3+1)(1+1) 2^2-1=3 \cdot 4 \cdot 2 \cdot 4-1=96-1=95 .
\)

Q82: The total number of proper factors of 7875 is
(a) 23
(b) 24
(c) 22
(d) 21

Solution: (c) We have,
\(
7875=3^2 \times 5^3 \times 7^1
\)
The total number of ways of selecting some or all out of two 3’s, three 5’s and one 7’s is
\(
(2+1)(3+1)(1+1)-1=23
\)
But, this includes the given number itself.
\(\therefore \quad\) Number of proper factors \(=\mathbf{2 2}\).

Q83: The number of factors (excluding 1 and the expression itself) of the product of \(a^7 b^4 c^3\) def, where \(a, b, c, d, e\), fare all prime numbers, is
(a) 1279
(b) 1278
(c) 1280
(d) 1277

Solution: (b) The total number of factors of the product \(a^7 b^4 c^3\) def is equal to the number of ways of selecting at least one from seven \(a\) ‘s, four \(b\) ‘s, three \(c\) ‘s, one \(d\) ‘s, one e’s and one f ‘s. The number of such ways is
\(
(7+1)(4+1)(3+1)(2)(2)(2)-1=1279
\)
But, this includes the given product.
\(\therefore \quad\) Required number of factors \(=1279-1=1278\)

Number of Divisors of \({N}\)

Case I: To find the number of divisors of an integer \({N}\), use its prime factorization.
Number of Divisors Formula:
Let
\(
N=p_1^{\alpha_1} p_2^{\alpha_2} p_3^{\alpha_3} \cdots p_k^{\alpha_k}
\)
be the prime factorization of \(N\), where each \(p_i\) is a prime and each exponent \(\alpha_i \geq 1\).
Then the number of positive divisors of \(N\) is:
\(
d(N)=\left(\alpha_1+1\right)\left(\alpha_2+1\right) \cdots\left(\alpha_k+1\right)
\)

Q84: Let’s compute the number of divisors of 360.

Solution: Step 1: Prime Factorization
\(
360=2^3 \cdot 3^2 \cdot 5^1
\)
Step 2: Apply Divisor Formula
If
\(
N=p_1^{\alpha_1} p_2^{\alpha_2} \cdots p_k^{\alpha_k},
\)
then
\(
d(N)=\left(\alpha_1+1\right)\left(\alpha_2+1\right) \cdots\left(\alpha_k+1\right) .
\)
So for 360:
exponent of \(2: 3 \Rightarrow 3+1=4\)
exponent of \(3: 2 \Rightarrow 2+1=3\)
exponent of 5: \(1 \Rightarrow 1+1=2\)
\(
d(360)=4 \times 3 \times 2=24.
\)

Case-II: If
\(
N=p_1^{\alpha_1} p_2^{\alpha_2} \cdots p_k^{\alpha_k}
\)
then the number of divisors of \(N\) is equal to the number of ways of selecting zero or more objects from each of the following groups of identical objects:
\(\left(p_1, p_1, \ldots, p_1\right)-\alpha_1\) identical objects
\(\left(p_2, p_2, \ldots, p_2\right)-\alpha_2\) identical objects
…
\(\left(p_k, p_k, \ldots, p_k\right)-\alpha_k\) identical objects
From the \(i\)-th group, you may select:
\(0,1,2, \ldots, \alpha_i\) objects
giving \(\alpha_i+1\) choices.
Thus, the total number of ways of selecting objects (one choice from each group) is:
\(
\left(\alpha_1+1\right)\left(\alpha_2+1\right) \cdots\left(\alpha_k+1\right)
\)
Each selection corresponds to a unique divisor of \(N\).
This count includes:
Selecting zero objects from all groups → the divisor 1,
Selecting all objects from all groups → the divisor \(N\).

Q85: Let’s compute the number of divisors of 860.

Solution: Let’s take
\(
840=2^3 \cdot 3^1 \cdot 5^1 \cdot 7^1
\)
So we have the following groups of identical prime objects:
Group 1: \((2,2,2) \rightarrow \alpha_1=3\)
Group 2: \((3) \rightarrow \alpha_2=1\)
Group 3: \((5) \rightarrow \alpha_3=1\)
Group 4: \((7) \rightarrow \alpha_4=1\)
Group 1: Three 2’s
Options: select
0, 1, 2, or 3 twos → 4 choices
This corresponds to exponents of \(2^e\) for \(e=0,1,2,3\).
Group 2: One 3
Options: select 0 or 1 three \(\boldsymbol{\rightarrow} 2\) choices (exponents: \(3^0, 3^1\) )
Group 3: One 5
Options:
0 or 1 five \(\boldsymbol{\rightarrow} 2\) choices
Group 4: One 7
Options:
0 or 1 seven \(\rightarrow 2\) choices
Total number of divisors
Multiply all choices:
\(
\begin{aligned}
d(840)= & (3+1)(1+1)(1+1)(1+1) \\
= & 4 \cdot 2 \cdot 2 \cdot 2=32
\end{aligned}
\)
Thus, 840 has 32 divisors.

Note:
All the divisors excluding 1 and \(N\) are called proper divisors.

• Also number of divisors of \(N\) can been seen as number of different terms in the expansion of
  \(
  \begin{aligned}
  \left(p_1^0+{p}_1^1+p_1^2 \cdots+p_1^{\alpha_1}\right) \times\left(p_2^0+p_2^1+\right. & \left.p_2^2+\cdots+p_2^{\alpha_2}\right) \times \cdots \\
  & \times\left(1+p_k+p_k^2+\cdots+p_k^{\alpha_k}\right)
  \end{aligned}
  \)
  Hence, sum of the divisors of \(N\) is
  \(
  \begin{aligned}
  & \left(1+p_1+p_1^2+\cdots+p_1^{\alpha 1}\right)\left(1+p_2+p_2^2+\cdots+p_2^{\alpha 2}\right) \cdots \\
  & \left(1+p_k+p_k^2+\cdots+p_k^{\alpha k}\right) \\
  & =\frac{p_1^{\alpha_1+1}-1}{p_1-1} \frac{p_2^{\alpha_2+1}-1}{p_2-1} \cdots \frac{p_k^{\alpha_k+1}-1}{p_k-1}
  \end{aligned}
  \)
• The number of ways of putting \(N\) as a product of two natural numbers is ( \(1 / 2)\left(\alpha_1+1\right)\left(\alpha_2+1\right) \cdots\left(\alpha_k+1\right)\) if \(N\) is not a perfect square.
  If \(N\) is a perfect square, then this is ( \(1 / 2\) ) \(\left[\left(\alpha_1+1\right)\left(\alpha_2+1\right) \ldots\right.\)
  \(
  \left.\left(\alpha_k+1\right)+1\right]
  \)

Q86: The number of even divisors of 10800 is
(a) 12
(b) 24
(c) 36
(d) 48

Solution: (d) We have,
\(
n=10800=2^4 \times 3^3 \times 5^2
\)
A divisor of 10800 will be of the form:
\(
2^a \cdot 3^b \cdot 5^c
\)
where:
\(0 \leq a \leq 4\)
\(0 \leq b \leq 3\)
\(0 \leq c \leq 2\)
A number is even iff it contains at least one factor of 2.
So:
\(
a \neq 0 \quad \Rightarrow \quad a=1,2,3,4 .
\)
That gives 4 choices for \(a\).
For \(b\) and \(c\), there is no restriction:
\(b=0,1,2,3 \rightarrow 4\) choices
\(c=0,1,2 \rightarrow 3\) choices
Total number of even divisors
\(
=4 \times 4 \times 3 =48.
\)

Q87. The number of divisors of 10800 which are divisible by 15 is
(a) 10
(b) 20
(c) 15
(d) 30

Solution: (d) We have, \(n=10800=2^4 \times 3^3 \times 5^2\).
A divisor of \(n\) will be a multiple of 15, if it contains at least one 3 out of three 3’s and at least one 5 out of two 5’s.
Hence, the number of divisors which are multiples of 15 is equal to \((4+1)(3)(2)=30\).

Q88. If \(r, s, t\) are prime numbers and \(p, q\) are the positive integers such that LCM of \(p, q\) is \(r^2 t^4 s^2\), then the number of ordered pair \((p, q)\) is [IIT 2006]
(a) 252
(b) 254
(c) 225
(d) 224

Solution: (d) Given
\(
\operatorname{LCM}(p, q)=r^2 s^2 t^4
\)
where \(r, s, t\) are primes.
Let
\(
p=r^{a_1} s^{a_2} t^{a_3}, \quad q=r^{b_1} s^{b_2} t^{b_3}
\)
where all exponents are non-negative integers.
The condition
\(
\operatorname{LCM}(p, q)=r^2 s^2 t^4
\)
means
\(
\max \left(a_1, b_1\right)=2, \quad \max \left(a_2, b_2\right)=2, \quad \max \left(a_3, b_3\right)=4 \text {. }
\)
We must count the number of ordered pairs ( \(p, q\) ), i.e., the number of exponent pairs that satisfy these conditions.
For a prime with exponent \(n\) in the LCM, the pair ( \(a, b\) ) must satisfy
\(0 \leq a, b \leq n\)
\(\max (a, b)=n\)
Total number of pairs:
\(
(n+1)^2-n^2=2 n+1 .
\)
(This removes the \(n^2\) pairs where both exponents are < \(n\).)
Count for each prime
For \(r^2: n=2\)
Number of pairs:
\(
2 n+1=2 \cdot 2+1=5
\)
For \(s^2: n=2\)
Number of pairs:
\(
2 n+1=2 \cdot 2+1=5
\)
For \(t^4: n=4\)
Number of pairs:
\(
2 n+1=2 \cdot 4+1=9
\)
Total number of ordered pairs ( \(p, q\) )
\(
5 \times 5 \times 9=225 .
\)

Q89. There are \(p\) copies each of \(n\) different books. Find the number of ways in which a non-empty selection can be made from them.

Solution: Number of selections of any number of copies of a book is \(p+1\) (because copies of the same book are identical things). Similar is the case for each book. Therefore, total number of selections is \((p+1)^n\).
But this includes a selection, which is empty, i.e., zero copy of each book. Excluding this, the required number of non-empty selections is \((p+1)^n-1\).

Q90. A person is permitted to select at least one and at most \(n\) coins from a collection of \((2 n+1)\) distinct coins. If the total number of ways in which he can select coins is \(\mathbf{2 5 5}\), find the value of \(\boldsymbol{n}\).

Solution: We have,
\(
{ }^{2 n+1} C_1+{ }^{2 n+1} C_2+\cdots+{ }^{2 n+1} C_n=255 \dots(1)
\)
Also the sum of binomial coefficients is
\(
\begin{aligned}
& { }^{2 n+1} C_0+{ }^{2 n+1} C_1+\cdots+{ }^{2 n+1} C_n+{ }^{2 n+1} C_{n+1}+\cdots+{ }^{2 n+1} C_{2 n+1} \\
& =(1+1)^{2 n+1}=2^{2 n+1} \\
\Rightarrow & { }^{2 n+1} C_0+2\left({ }^{2 n+1} C_1+{ }^{2 n+1} C_2+\cdots+{ }^{2 n+1} C_n\right)+{ }^{2 n+1} C_{2 n+1}=2^{2 n+1} \\
\Rightarrow & 1+2(255)+1=2^{2 n+1} \\
\Rightarrow & 1+255=2^{2 n} \\
\Rightarrow & 2^{2 n}=2^8 \Rightarrow n=4
\end{aligned}
\)

Q91. Nishi has 5 coins each of the different denomination. Find the number different sums of money she can form.

Solution: Number of different sums of money she can form is equal to number of ways she select one or more coins
∴ Required no. of ways \(={ }^5 C_1+{ }^5 C_2+{ }^5 C_3+{ }^5 C_4+{ }^5 C_5=2^5 -1=31\).

Q92. Find the number of groups that can be made from 5 different green balls, 4 different blue balls and 3 different red balls, if at least 1 green and 1 blue ball is to be included.

Solution: At least, one green ball can be selected out of 5 green balls in \(2^5-1\), i.e., in 31 ways.
Similarly, at least one blue ball can be selected from 4 blue balls in \(2^4-1=15\) ways. And at least one red or no red ball can be selected in \(2^3=8\) ways.
Hence, the required number of ways is \(31 \times 15 \times 8=3720\).

Q93. There are 3 books of mathematics, 4 of science, and 5 of literature. How many different collections can be made such that each collection consists of
(i) one book of each subject,
(ii) at least one book of each subject,
(iii) at least one book of literature.

Solution: (i) \({ }^3 C_1 \times{ }^4 C_1 \times{ }^5 C_1=3 \times 4 \times 5=60\)
(ii) \(\left(2^3-1\right)\left(2^4-1\right)\left(2^5-1\right)=7 \times 15 \times 31=3255\)
(iii) \(\left(2^5-1\right) \times 2^7=31 \times 128=3968\)

Q94. Find the total number of proper factors of the number 35700. Also find
(i) sum of all these factors,
(ii) sum of the odd proper divisors,
(iii) the number of proper divisors divisible by 10 and the sum of these divisors.

Solution: \(35700=5^2 \times 2^2 \times 3^1 \times 7^1 \times 17^1\)
The total number of factors is equal to the total number of selections from \((5,5),(2,2),(3),(7)\) and (17), which is given by \(3 \times 3 \times 2 \times 2 \times 2=72\).
These include 1 and 35700. Therefore, the number of proper divisors (excluding 1 and 35700 ) is \(72-2=70\)
Sum of all these factors (proper) is
\(
\begin{aligned}
& \left(5^0+5^1+5^2\right)\left(2^0+2^1+2^2\right)\left(3^0+3^1\right)\left(7^0+7^1\right)\left(17^0+17^1\right) \\
& \quad-1-35700 \\
& =31 \times 7 \times 4 \times 8 \times 18-1-35700=89291
\end{aligned}
\)
Now, the sum of odd proper divisors is
\(
\begin{aligned}
& \left(5^0+5^1+5^2\right)\left(3^0+3^1\right)\left(7^0+7^1\right)\left(17^0+17^1\right)-1 \\
& =31 \times 4 \times 8 \times 18-1=17856-1=17855
\end{aligned}
\)
(Here, 2 as a factor and 1 as a divisor or are to be excluded.)
The number of proper divisors divisible by 10 is equal to number of selections from (5, 5), (2, 2), (3), (7), (17) consisting of at least one 5 and at least one 2 and 35700 is to be excluded and is given by \(2 \times 2 \times 2 \times 2 \times 2-1=31\).
Sum of these divisors is
\(
\begin{aligned}
& \left(5^1+5^2\right)\left(2^1+2^2\right)\left(3^0+3^1\right)\left(7^0+7^1\right)\left(17^0+17^1\right)-35700 \\
& =30 \times 6 \times 4 \times 8 \times 18-35700=67980
\end{aligned}
\)

Q95. Find the number of ways in which the number 94864 can be resolved as a product of two factors.

Solution: \(94864=2^4 \times 7^2 \times 11^2\)
Hence, the number of ways is
\(
\frac{1}{2}[(4+1)(2+1)(2+1)+1]=23
\)

Q96. Find the number of divisors of the number \(\mathrm{N}=2^3 \cdot 3^5 \cdot 5^7 \cdot 7^9\) which are perfect square.

Solution: Since the divisor is perfect square each prime factor must occur even number of times.
2 can be taken in 2 ways ( \(2^{\circ}\) or \(2^2\) )
3 can be taken in 3 ways ( \(3^0\) or \(3^2\) or \(3^4\) )
Similarly 5 can be taken in 4 ways ( \(5^0\) or \(5^2\) or \(5^4\) or \(5^6\) )
and 7 can be taken in 5 ways ( \(7^0\) or \(7^2\) or \(7^4\) or \(7^6\) or \(7^8\) )
hence total divisors which are perfect squares
\(
=2 \cdot 3 \cdot 4 \cdot 5=120
\)

Q97. Find the number of ways in which the number 300300 can be split into 2 factors which are relatively prime.

Solution: \(300300=2^2 3^1 5^2 7^1 11^1 13^1\)
Now we have to make factors which are relative prime.
\(\Rightarrow 2^2, 3^1, 5^2, 7^1, 11^1, 13^1\) should behave as single identities.
So no. of divisors \((1+1)(1+1)(1+1)(1+1)(1+1)(1+1)\)
\(
=2^6=64
\)
No. of ways of splitting into 2 factors \(=\frac{64}{2}=32\)

Division of Objects into Groups

Case-I: Division into groups of Unequal Size

Theorem 1: Number of ways in which \((m+n)\) distinct items can be divided into two unequal groups containing \(m\) and \(n\) items is
\(
\frac{(m+n)!}{m!n!}
\)

Proof: The number of ways in which ( \(m+n\) ) items are divided into two groups containing \(m\) and \(n\) items is same as the number of combinations of ( \(m+n\) ) things taken \(m\) at a time.
Thus, the required number \(={ }^{m+n} C_m=\frac{(m+n)!}{m!n!}\)

Remark 1: The number of ways in which \((m+n+p)\) items can be divided into unequal groups containing \(m, n, p\) items, is
\(
{ }^{m+n+p} C_m \cdot{ }^{n+p} C_n=\frac{(m+n+p)!}{m!n!p!}
\)

Remark 2: The number of ways to distribute \((m+n+p)\) items among 3 persons in the groups containing \(m, n\) and \(p\) items is
\(
(\text { No. of ways to divide }) \times(\text { No. of groups })!=\frac{(m+n+p)!}{m!n!p!} \times 3!
\)

Case-II: Division into groups of Equal Size

The number of ways in which \(m n\) different objects can be divided equally into \(m\) groups, each containing \(n\) objects and the order of the groups is not important, is
\(
\left(\frac{(m n)!}{(n!)^m}\right) \frac{1}{m!}
\)
The number of ways in which \(m n\) different items can be divided equally into \(m\) groups, each containing \(n\) objects and the order of groups is important, is
\(
\left(\frac{(m n)!}{(n!)^m} \times \frac{1}{m!}\right) m!=\frac{(m n)!}{(n!)^m}
\)

Q98. The number of ways in which a pack of 52 cards can be divided equally into four groups, is
(a) \(\frac{52!}{(13!)^4}\)
(b) \(\frac{52!}{(13!)^4 4!}\)
(c) \(\frac{52!}{(13!)^4 \times 4}\)
(d) \(\frac{52!}{13!\times 4!}\)

Solution: (b) Step 1: Divide the deck into four groups of 13 cards
First, choose 13 cards for the first group:
\(
\binom{52}{13}=\frac{52!}{13!\cdot 39!}
\)
Next, choose 13 cards for the second group from the remaining 39 cards:
\(
\binom{39}{13}=\frac{39!}{13!\cdot 26!}
\)
Then, \(\mathbf{1 3}\) cards for the third group from the remaining 26 cards:
\(
\binom{26}{13}=\frac{26!}{13!\cdot 13!}
\)
The last 13 cards automatically form the fourth group.
Step 2: Multiply all choices
\(
\binom{52}{13} \cdot\binom{39}{13} \cdot\binom{26}{13} \cdot 1=\frac{52!}{(13!)^4}
\)
Step 3: Divide by \(\mathbf{4} \boldsymbol{!}\) to remove identical groups
Since the four groups are indistinguishable (order does not matter), divide by \(4!\) :
\(
\text { Number of ways }=\frac{52!}{(13!)^4 \cdot 4!}
\)

Q99. In how many ways can a pack of 52 cards be divided into 4 sets, three of them having 17 cards each and the fourth just one card?
(a) \(\frac{52!}{(17!)^3 3!}\)
(b) \(\frac{52!}{(17!)^3}\)
(c) \(\frac{52!}{51!(17!)^3}\)
(d) \(\frac{52!}{51!}\)

Solution: (a) Step 1: Separate the single card
Choose 1 card out of 52 for the singleton set:
\(
\binom{52}{1}=52=\frac{52!}{51!\cdot 1!}
\)
Remaining 51 cards will form the three sets of 17 cards each.
Step 2: Divide 51 cards into 3 groups of 17 cards
Number of ways to divide 51 cards into 3 indistinguishable groups of 17:
\(
\frac{51!}{(17!)^3 \cdot 3!}
\)
Here, 3 ! accounts for the fact that the three 17 -card groups are indistinguishable.
Step 3: Multiply the choices
\(
\text { Total ways }=\binom{52}{1} \cdot \frac{51!}{(17!)^3 \cdot 3!}=\frac{52!}{(17!)^3 \cdot 3!}
\)

Divisions of Identical Objects into Groups (Distribution of \(n\) Identical Objects in \(r\) Different Boxes if Empty Boxes Are Allowed)

The total number of ways of dividing \(n\) identical items among \(r\) persons, each one of whom, can receive 0, 1, 2, or more items \((\leq n)\) is \(\frac{(n+r-1)!}{n!(r-1)!}={ }^{n+r-1} C_{r-1}\)

Q100. The total number of ways in which 30 mangoes can be distributed among 5 persons is
(a) \({ }^{30} \mathrm{C}_5\)
(b) \(30^5\)
(c) \(5^{30}\)
(d) \({ }^{34} \mathrm{C}_4\)

Solution: (d) Required number of ways is same as the number of ways of dividing 30 identical items among 5 persons i.e., \(\quad{ }^{30+5-1} C_{5-1}={ }^{34} C_4\)

Number of Non-Negative Integral Solutions of the Equation \(x_1+x_2+\cdots+x_r=n\)

This is equivalent to the number of ways of distributing \(n\) identical objects into \(r\) different boxes if empty boxes are allowed which is \({ }^{n+r-1} C_{r-1}={ }^{n+r-1} C_n\).

Number of Positive Integral Solutions of the Equation \(x_1+x_2+\cdots+x_r=n\)

This is equivalent to the number of ways of distributing \(n\) identical objects into \(r\) different boxes if empty boxes are not allowed which is \({ }^{n-1} C_{r-1}\).

Q101. The number of ways of distributing 5 identical balls into three boxes so that no box is empty (each box being large enough to accommodate all balls), is
(a) \(3^5\)
(b) \(5^3\)
(c) 15
(d) 6

Solution: (d) The required number of ways is the number of ways of distributing 5 items among 3 persons so that a person receives at least one item \(={ }^{5-1} C_{3-1}={ }^4 C_2=6\).

Q102. Find the number of non-negative integral solutions of the equations \(\boldsymbol{x}+\boldsymbol{y}+\boldsymbol{z}=\mathbf{1 0}\).

Solution: Here, the number of solutions is equivalent to the number of ways. Ten identical objects are distributed in 3 distinct boxes if empty boxes are allowed, which is \({ }^{10+3-1} C_3={ }^{12} C_3\).

Q103. Find the number of positive integral solutions of the equations \(x+y+z=12\).

Solution: Here, the number of solutions is equivalent to number of ways. Twelve identical objects are distributed in 3 distinct boxes if empty boxes are not allowed, which is \({ }^{12-1} C_{3-1}={ }^{11} C_2 =55\).

Q104. Find the number of non-negative integral solutions of the equation \(x+y+z+2 w=20\).

Solution: Let \(w=0\). Then, the equation reduces to \(x+y+z=20\). Number of non-negative integral solutions is \({ }^{20+4-1} C_{4-1}={ }^{23} C_3\). If \(w=1\), then the equation reduces to \(x+y+z=18\). Number of non-negative integral solutions is \({ }^{18+4-1} C_{4-1}={ }^{21} C_3\).
Similarly, we have \(w=2,3, \ldots, 10\).
Therefore, the total number of solutions is \({ }^{23} C_3+{ }^{21} C_3+{ }^{19} C_3 +\cdots+{ }^5 C_3+{ }^3 C_3\).
Therefore, the total number of solutions is \({ }^{23} C_3+{ }^{21} C_3+{ }^{19} C_3 +\cdots+{ }^5 C_3+{ }^3 C_3\).

Q105. Find the total number of positive integral solutions for \((x, y, z)\) such that \(x y z=24\). Also find out the total number of integral solutions.

Solution: \(24=2^3 \times 3\)
Now, consider three boxes \(x, y, z. 3\) can be put in any of the three boxes.
Also, \(2,2,2\) can be distributed in the three boxes in \({ }^{3+3-1} C_{3-1} ={ }^5 C_2\) ways. Hence, the total number of positive integral solutions is equal to the number of distributions which is given by \(3 \times{ }^5 C_2=30\).
Note: If any box remains empty, say \(x\), than \(x=1\). To find integral solutions where negative integers are also allowed.
Any two of the factors in each factorization may be negative. Therefore, the number of ways to associate negative sign in each case is \({ }^3 C_2=3\). Hence, the total number of integral solutions is \(30+3 \times 30=120\).

Q106: Find the number of distinct throws which can be thrown with \(n\) six-faced normal dice, which are indistinguishable among themselves.

Solution: Step 1: Identify the problem type in combinatorics
This problem is a classic example of combinations with repetition because the order of the dice faces does not matter (indistinguishable dice), and a face value can appear multiple times. We are selecting \(n\) items (dice results) from 6 possible categories (faces 1 through 6).
Step 2: Apply the combinations with repetition formula
The number of combinations with repetition of choosing \(k\) items from \(m\) types is given by the stars and bars formula: \(\binom{k+m-1}{k}\) or equivalently \(\binom{k+m-1}{m-1}\).
In this specific scenario:
Number of types \((m)=6\) (the faces of the die)
Number of items chosen ( \(k\) or \(n\) ) \(=n\) (the number of dice thrown)
Substituting these values into the formula gives:
\(
C(n, 6)_{\text {with repetition }}=\binom{n+6-1}{6-1}=\binom{n+5}{5}
\)
or equivalently:
\(
C(n, 6)_{\text {with repetition }}=\binom{n+6-1}{n}=\binom{n+5}{n}
\)
The number of distinct throws is given by the formula \(\binom{\mathbf{n}+\mathbf{5}}{\mathbf{5}}\) (or equivalently \(\binom{\mathbf{n}+\mathbf{5}}{\mathbf{n}}\) ), which can also be expanded algebraically as \(\frac{(\mathbf{n}+\mathbf{5})!}{\mathbf{5}!\mathbf{n}!}\).

Multinomial Theorem

The total number of ways of dividing \(n\) identical objects into \(r\) groups, if blank groups are allowed, is \({ }^{n+r-1} C_{r-1}\).

Proof: Consider \(r\) brackets corresponding to \(r\) persons. In each bracket, take an expression given by \(x^0+x^1+x^2+\ldots+x^n\). Here, the various powers of \(x\) viz; \(0,1,2, \ldots, n\) correspond to the number of items each person can have in the distribution.
Since the total number of items is \(n\). So, the required number of ways is the coefficient of \(x n\) in the product
\(
\begin{array}{r}
\left(x^0+x^1+x^2+\ldots+x^n\right)\left(x^0+x^1+\ldots+x^n\right) \ldots \ldots \ldots \ldots \\
\ldots \ldots \ldots \ldots\left(x^0+x^1+x^2+\ldots+x^n\right) \\
(r-\text { brackets })
\end{array}
\)
Thus, the required number of ways
\(
\begin{aligned}
& =\text { Coeff of } x^n\left(x^0+x^1+x^2 \ldots+x^n\right)^r \\
& =\text { Coefficient of } x^n \text { in }\left(\frac{1-x^{n+1}}{1-x}\right)^r
\end{aligned}
\)
\(
\begin{aligned}
& =\text { Coefficient of } x^n \text { in }\left(1-x^{n+1}\right)^r(1-x)^{-r} \\
& =\text { Coefficient of } x^n \text { in }(1-x)^{-r} \\
& =\frac{(r+1)(r+2)(r+3) \ldots(r+n-1)}{1 \cdot 2 \cdot 3 \ldots r}={ }^{n+r-1} C_{r-1}
\end{aligned}
\)

Note: If there are \(l\) objects of one kind, \(m\) objects of second kind, \(n\) objects of third kind and so on, then the number of ways of choosing \(r\) objects out of these objects is the coefficient of \(x^r\) in the expansion of \(\left(1+x+x^2+x^3+\cdots+x^l\right) \times\left(1+x+x^2+\cdots\right. \left.+x^m\right) \times\left(1+x+x^2+\cdots+x^n\right)\).
Further, if one object of each kind is to be included, then the number of ways of choosing \(r\) objects out of these objects is the coefficient of \(x^r\) in the expansion of:
\(\left(x+x^2+x^3+\cdots+x^{l}\right) \times\left(x+x^2+x^3+\cdots+x^{m}\right) \times\left(x+x^2+x^3+\cdots+x^n\right)\)

For example 1 (distributing identical objects), How many ways can 7 identical objects be distributed to 3 people, allowing empty groups?
Step 1: Write the generating functions
Each person can receive:
\(
0,1,2, \ldots, 7 \quad \Rightarrow \quad 1+x+x^2+\cdots+x^7 .
\)
Total generating function:
\(
\left(1+x+x^2+\cdots+x^7\right)^3 .
\)
We need the coefficient of \(x^7\).
Step 2: Use the formula
Since empty groups are allowed, use:
\(
\binom{n+r-1}{r-1}=\binom{7+3-1}{3-1}=\binom{9}{2}=36 .
\)

For example 2, (Distributing identical objects, non-empty groups)
Distribute 10 identical objects to 4 people, each must get at least 1.
Let \(x_i \geq 1\).
Use substitution: \(x_i=y_i+1\), where \(y_i \geq 0\).
\(
y_1+y_2+y_3+y_4=10-4=6 .
\)
Now use stars and bars:
\(
\binom{6+4-1}{4-1}=\binom{9}{3}=84 .
\)
Answer \(=84\) ways
Generating function interpretation:
Each person has
\(
x+x^2+x^3+\cdots
\)
so total generating function is:
\(
\left(x+x^2+x^3+\cdots\right)^4=x^4(1-x)^{-4}
\)
Coefficient of \(x^{10}\) equals coefficient of \(x^6\) in \((1-x)^{-4}\) :
\(
\binom{6+4-1}{4-1}=\binom{9}{3}
\)

Q107: In how many ways can 20 identical toys be distributed among 4 children so that each one gets at least 3 toys ?
(a) \({ }^{11} \mathrm{C}_2\)
(b) \({ }^{12} C_3\)
(c) \({ }^{11} C_3\)
(d) \({ }^{12} \mathrm{C}_4\)

Solution: Step 1: Define the problem in mathematical terms
Let \(x_1, x_2, x_3, x_4\) be the number of toys each of the four children receives, respectively. Since the toys are identical, we are looking for the number of nonnegative integer solutions to the equation:
\(
x_1+x_2+x_3+x_4=20
\)
The condition that each child receives at least 3 toys imposes the constraints \(x_i \geq 3\) for \(i=1,2,3,4\).
Step 2: Adjust variables for constraints
To handle the minimum toy constraint, we introduce new variables \(y_i\) where \(x_i=y_i+3\) . This ensures that \(x_i \geq 3\) whenever \(y_i \geq 0\). Substituting this into the original equation, we get:
\(
\begin{gathered}
\left(y_1+3\right)+\left(y_2+3\right)+\left(y_3+3\right)+\left(y_4+3\right)=20 \\
y_1+y_2+y_3+y_4+12=20 \\
y_1+y_2+y_3+y_4=8
\end{gathered}
\)
The problem is now reduced to finding the number of non-negative integer solutions to
\(
y_1+y_2+y_3+y_4=8
\)
Step 3: Apply the stars and bars formula
The number of non-negative integer solutions to an equation of the form \(y_1+y_2+\ldots+y_k=n\) is given by the stars and bars formula:
\(
\binom{n+k-1}{k-1}=\binom{n+k-1}{n}
\)
Here, \(n=8\) (the sum) and \(k=4\) (number of variables).
The number of ways is:
\(
\binom{8+4-1}{4-1}=\binom{11}{3}
\)

Q108. The total number of non-negative integral solutions of \(x_1+x_2+x_3+x_4=100\), is
(a) \({ }^{100} \mathrm{C}_3\)
(b) \({ }^{99} \mathrm{C}_3\)
(c) \({ }^{100} \mathrm{C}_4\)
(d) \({ }^{99} \mathrm{C}_4\)

Solution: (a) Total number of non-negative integral solutions of the given equation is same as the number of ways of distributing 100 items among 4 persons such that each person can receive any number of items.
Hence, total number of solutions \(={ }^{100+4-1} C_{4-1}={ }^{103} C_3\).

Q109. The total number of integral solutions of the equation \(x+y+z+t=29\) where \(x \geq 1, y \geq 2, z \geq 3\) and \(t \geq 0\), is
(a) \({ }^{26} \mathrm{C}_4\)
(b) \({ }^{26} \mathrm{C}_3\)
(c) \({ }^{22} \mathrm{C}_3\)
(d) \({ }^{29} \mathrm{C}_3\)

Solution: (b) Step 1: Transform variables to non-negative constraints
We are given the equation \(x+y+z+t=29\) with constraints \(x \geq 1, y \geq 2, z \geq 3, t \geq 0\). To use the standard stars and bars formula for non-negative integers, we introduce new variables \(x^{\prime}, y^{\prime}, z^{\prime}, t^{\prime}\) such that they are all \(\geq 0\) :
\(
\begin{gathered}
x=x^{\prime}+1 \\
y=y^{\prime}+2 \\
z=z^{\prime}+3 \\
t=t^{\prime}
\end{gathered}
\)
Step 2: Substitute into the original equation
Substituting these expressions into the original equation, we get:
\(
\begin{gathered}
\left(x^{\prime}+1\right)+\left(y^{\prime}+2\right)+\left(z^{\prime}+3\right)+t^{\prime}=29 \\
x^{\prime}+y^{\prime}+z^{\prime}+t^{\prime}+6=29 \\
x^{\prime}+y^{\prime}+z^{\prime}+t^{\prime}=23
\end{gathered}
\)
Step 3: Apply the stars and bars formula
The problem is now reduced to finding the number of non-negative integer solutions to \(x^{\prime}+y^{\prime}+z^{\prime}+t^{\prime}=23\). This can be solved using the stars and bars formula, which states that the number of non-negative integer solutions to \(x_1+\ldots+x_n=k\) is given by the binomial coefficient \(\binom{k+n-1}{n-1}\).
Here, we have \(n=4\) variables and a sum \(k=23\).
The number of solutions is:
\(
\binom{23+4-1}{4-1}=\binom{26}{3}
\)

Q110. 4 Total number of integral solutions of the system of equations \(x_1+x_2+x_3+x_4+x_5=20\) and \(x_1+x_2+x_3=5\) when \(x_k \geq 0\), is
(a) 335
(b) 336
(c) 338
(d) 340

Solution: (b) We have,
\(
x_1+x_2+x_3+x_4+x_5=20
\)
and, \(x_1+x_2+x_3=5\)
These two equations reduce to
\(
\begin{gathered}
x_4+x_5=15 \dots(i) \\
\text { and, } x_1+x_2+x_3=5 \dots(ii)
\end{gathered}
\)
Since corresponding to each solution of (i) there are solutions of equation (ii). So, total number of solutions of the given system of equations
\(
\begin{aligned}
& =\text { No. of solutions of (i) × No. of solutions of (ii) } \\
& ={ }^{15+2-1} C_{2-1} \times{ }^{5+3-1} C_{3-1}={ }^{16} C_1 \times{ }^7 C_2=336
\end{aligned}
\)

Principle of Inclusion and Exclusion

\(
\begin{aligned}
&\text { In the above Venn’s diagram, we get }\\
&\begin{aligned}
& n(A \cup B)=n(A)+n(B)-n(A \cap B) \\
& n\left(A_1^{\prime} \cap A_2^{\prime}\right)=n(U)-n(A \cup B)
\end{aligned}
\end{aligned}
\)

In the above Venn’s diagram, we get
\(
\begin{gathered}
n(A \cup B \cup C)=n(A)+n(B)+n(C)-n(A \cap B)-n(B \cap C) \\
-n(A \cap C)+n(A \cap B \cap C) \\
n\left(A_1^{\prime} \cap A_2^{\prime} \cap A_3^{\prime}\right)=n(U)-n(A \cup B \cup C)
\end{gathered}
\)
In general, we have
\(
\begin{aligned}
&\text { For } n \text { sets } A_1, A_2, \ldots, A_n \text { : }\\
&\begin{aligned}
n\left(A_1 \cup A_2 \cup \cdots \cup A_n\right)= & \sum_i n\left(A_i\right) \\
& -\sum_{i<j} n\left(A_i \cap A_j\right) \\
& +\sum_{i<j<k} n\left(A_i \cap A_j \cap A_k\right) \\
& -\sum_{i<j<k<\ell} n\left(A_i \cap A_j \cap A_k \cap A_{\ell}\right) \\
& \pm \cdots \\
& +(-1)^{n-1} n\left(A_1 \cap A_2 \cap \cdots \cap A_n\right) .
\end{aligned}
\end{aligned}
\)

Q111.Find the numbers of positive integers from 1 to 1000 , which are divisible by at least 2,3 or 5.

Solution: We want:
\(
n\left(A_2 \cup A_3 \cup A_5\right)
\)
where:
\({A}_2\) : numbers divisible by 2
\(A_3\) : numbers divisible by 3
\(A_5\) : numbers divisible by 5
Step 1: Count numbers divisible by each
\(
\begin{aligned}
& n\left(A_2\right)=\left\lfloor\frac{1000}{2}\right\rfloor=500 \\
& n\left(A_3\right)=\left\lfloor\frac{1000}{3}\right\rfloor=333 \\
& n\left(A_5\right)=\left\lfloor\frac{1000}{5}\right\rfloor=200
\end{aligned}
\)
Step 2: Count numbers divisible by pairwise intersections
Use LCMs:
\(A_2 \cap A_3\) : divisible by \(\operatorname{lcm}(2,3)=6\)
\(A_3 \cap A_5\) : divisible by \(\operatorname{lcm}(3,5)=15\)
\(A_2 \cap A_5\) : divisible by \(\operatorname{lcm}(2,5)=10\)
Thus:
\(
\begin{aligned}
& n\left(A_2 \cap A_3\right)=\left\lfloor\frac{1000}{6}\right\rfloor=166 \\
& n\left(A_3 \cap A_5\right)=\left\lfloor\frac{1000}{15}\right\rfloor=66 \\
& n\left(A_2 \cap A_5\right)=\left\lfloor\frac{1000}{10}\right\rfloor=100
\end{aligned}
\)
Step 3: Count numbers divisible by all three
\(
\begin{gathered}
\operatorname{lcm}(2,3,5)=30 \\
n\left(A_2 \cap A_3 \cap A_5\right)=\left\lfloor\frac{1000}{30}\right\rfloor=33
\end{gathered}
\)
Step 4: Apply Inclusion-Exclusion
\(
\begin{aligned}
n\left(A_2 \cup A_3 \cup A_5\right)= & 500+333+200 \\
& -(166+66+100) \\
& +33 \\
= 734 .
\end{aligned}
\)
Final Answers
Numbers divisible by at least one of 2,3, or 5: 734
Numbers not divisible by 2,3, or 5:
\(
1000-734=266
\)

Q112. Find the number of ways in which two Americans, two British, one Chinese, one Dutch and one Egyptian can sit on a round table so that persons of the same nationality are separated.

Solution: Two Americans ( \(\mathrm{A}_1, \mathrm{~A}_2\) ), two British ( \(\mathrm{B}_1, \mathrm{~B}_2\) ), one Chinese ( C ), one Dutch ( D ), and one Egyptian ( E ) sit around a round table.
Persons of the same nationality must be separated (i.e., \(\mathrm{A}_1\) and \(\mathrm{A}_2\) not adjacent, \(\mathrm{B}_1\) and \(\mathrm{B}_2\) not adjacent).
Step 1: Total circular arrangements
For \(n\) people around a round table, total arrangements:
\(
(7-1)!=6!=720
\)
Step 2: Count arrangements where Americans sit together (event A)
If \(\mathrm{A}_1\) and \(\mathrm{A}_2\) sit together, treat them as one block.
Block + other 5 people ⇒ 6 units around a circle.
Circular permutations:
\(
(6-1)!=5!=120
\)
Inside the block, \(\mathrm{A}_1\) and \(\mathrm{A}_2\) can switch:
\(
2!=2
\)
Total:
\(
n(A)=5!\cdot 2!=120 \cdot 2=240
\)
Step 3: Count arrangements where British sit together (event \(\boldsymbol{B}\) )
Exactly the same logic:
\(
n(B)=240
\)
Step 4: Count arrangements where both Americans and British are together (event \(A \cap B\) )
Now we have two blocks:
Block \(\left[\mathrm{A}_1 \mathrm{~A}_2\right]\)
Block \(\left[\mathrm{B}_1 \mathrm{~B}_2\right]\)
Plus 3 individuals (C, D, E)
Total units = 2 blocks + 3 individuals = 5 units around a circle.
Circular permutations:
\(
(5-1)!=4!=24
\)
Internal arrangements:
A block can arrange internally in \(2!\) ways
B block can arrange internally in 2 ! ways
Total:
\(
n(A \cap B)=4!\cdot 2!\cdot 2!=24 \cdot 4=96
\)
Step 5: Use Inclusion-Exclusion
\(
\begin{gathered}
n(A \cup B)=n(A)+n(B)-n(A \cap B) \\
=240+240-96=384 .
\end{gathered}
\)
This is the number of arrangements where at least one nationality sits together.
Step 6: Required count
People of same nationality must be separated, i.e., neither A-block nor B-block occurs.
So we need the complement:
\(
n(\bar{A} \cap \bar{B})=6!-n(A \cup B)=720-384=336.
\)

Q113. Find the number of \(\mathbf{n}\)-digit numbers using digits
\(
\{2,3,4,5,6,7\}
\)
that contain both 2 and 7 , and do not use digits \(0,1,8,9\).

Solution: Step 1: Define the sample space
Allowed digits:
\(
2,3,4,5,6,7 \text { (6 digits) }
\)
So total possible \(n\)-digit numbers:
\(
n(S)=6^n .
\)
Step 2: Define “bad” events
Let:
A: numbers that do NOT contain 2
B: numbers that do NOT contain 7
We want numbers that contain both 2 and 7 , i.e.:
\(
\bar{A} \cap \bar{B} .
\)
Using inclusion-exclusion:
\(
n(\bar{A} \cap \bar{B})=6^n-n(A)-n(B)+n(A \cap B)
\)
Step 3: Count forbidden cases
Case A: numbers without 2
Allowed digits:
\(
3,4,5,6,7 \text { (5 digits) }
\)
So:
\(
n(A)=5^n .
\)
Case B: numbers without 7
Allowed digits:
\(
2,3,4,5,6 \text { (5 digits) }
\)
So:
\(
n(B)=5^n \text {. }
\)
Case \(\mathrm{A} \cap \mathrm{B}\) : numbers without 2 and without 7
Allowed digits:
\(
3,4,5,6 \text { (4 digits) }
\)
So:
\(
n(A \cap B)=4^n .
\)
STEP 4: Use Inclusion-Exclusion
We want numbers that contain both 2 and 7:
\(
6^n-5^n-5^n+4^n .
\)

Derangement

There are \(n\) letters and \(n\) corresponding envelopes. The number of ways in which letters can be placed in the envelopes (one letter in each envelope) so that no letter is placed in correct envelope is
\(
D(n)=n!\left[1-\frac{1}{1!}+\frac{1}{2!}+\cdots+\frac{(-1)^n}{n!}\right]
\)

Q114. There are four balls of different colours and four boxes of colours same as those of the balls. Find the number of ways in which the balls, one in each box, could be placed in such a way that a ball does not go to box of its own colour.

Solution: Number of derangements in such problems is given by
\(
n!\left\{1-\frac{1}{1!}+\frac{1}{2!}-\frac{1}{3!}+\frac{1}{4!}-\cdots+(-1)^n \frac{1}{n!}\right\}
\)
Hence, the required number of derangements is
\(
4!\left\{\frac{1}{2!}-\frac{1}{3!}+\frac{1}{4!}\right\}=12-4+1=9
\)

Distribution of \(n\) Distinct Objects into \(r\) Distinct Boxes if in Each Box at Least One Object is Placed

The number of ways in which \(n\) distinct objects can be distributed among \(r\) persons if each gets at least one object is
\(
\begin{aligned}
& r^n-{ }^r C_1(r-1)^n+{ }^r C_2(r-2) r^n-{ }^r C_3(r-3)^n+\cdots+(-1)^{r-1} \\
& { }^r C_{r-1} 1
\end{aligned}
\)

Q116. Find the number of ways in which 5 distinct balls can be distributed in three different boxes if no box remains empty.

Solution: By above formula, the number of ways is \(3^5-{ }^3 C_1 \times(3-1)^5+{ }^3 C_2(3-2)^5=243-96+3=150\).

Q117. If \(n(A)=5\) and \(n(B)=3\), then find the number of onto functions from \(A\) to \(B\).

Solution: We know that in onto function, each image must be assigned at least one pre-image.
This is equivalent to number of ways in which 5 different objects (pre-images) can be distributed in 3 different boxes (images) if no box remains empty. The total number is given by \(3^5-{ }^3 C_1(3-1)^5+{ }^3 C_2(3-2)^5=243-96+3=150\).