Combinations correspond to the selection of things from a given set of things. Here we do not intend to arrange things. We intend to select them. We denote the number of unique \(r\)-selections or combinations out of a group of \(n\) objects by \({ }^n C_r\).

Combination without repetition

Combinations are selections made by taking some or all of a number of objects, irrespective of their arrangements. The number combinations of \(n\) different things taken \(r\) at a time, denoted by \({ }^n C_r\) and it is given by (no repetition, order doesn’t matter),

\(
C(n, r)={ }^n C_r=\left(\begin{array}{l}
n \\
r
\end{array}\right)=\frac{n !}{r !(n-r) !}
\)

Example 1: Out of a group of 5 people, a pair needs to be formed. Calculate the number of possible combinations.

Solution: 

\(
{ }^5 \mathrm{C}_2=\frac{5 !}{2 !(5-2) !}=\frac{5 !}{2 ! 3 !}=\frac{120}{2 \times 6}=10
\)

Example 2: Find the number of 4-letter combinations which can be made from the letters of the word DRIVEN.

Solution:

\(
{ }^6 \mathrm{C}_4=\frac{6 !}{4 !(6-4) !}=\frac{6 !}{4 ! 2 !}=\frac{720}{24 \times 2}=15
\)

Combination with repetition

\(
\frac{(r+n-1) !}{r !(n-1) !}
\)
where \({n}\) is the number of things to choose from, and we choose \({r}\) of them repetition allowed, order doesn’t matter.

Example 3: Assume there are five flavors of ice cream: banana, chocolate, lemon, strawberry, and vanilla. We can have three scoops. How many variations will there be?

Solution:Let’s use letters for the flavors: \(\{b, c, l, s, v\}\). Example selections include

• \(\{c, c, c\}\) (3 scoops of chocolate)
• \(\{b, l, v\}\) (one each of banana, lemon and vanilla)
• \(\{b, v, v\}\) (one of banana, two of vanilla)

In this case, there are \({n}={5}\) things to choose from, we choose \({r}={3}\) of them, order does not matter, and we can repeat.

\(
\frac{(3+5-1) !}{3 !(5-1) !}=\frac{7 !}{3 ! 4 !}=\frac{5040}{6 \times 24}=35
\)
There are 35 ways of having 3 scoops from five flavors of ice cream.

Example 4:  A committee of 3 persons is to be constituted from a group of 2 men and 3 women. In how many ways can this be done? How many of these committees would consist of 1 man and 2 women?

Solution: Here, the order does not matter. Therefore, we need to count combinations. There will be as many committees as there are combinations of 5 different persons taken 3 at a time. Hence, the required number of ways \(={ }^5 \mathrm{C}_3=\frac{5 !}{3 ! 2 !}=\frac{4 \times 5}{2}=10\).
Now, 1 man can be selected from 2 men in \({ }^2 C_1\) ways and 2 women can be selected from 3 women in \({ }^3 \mathrm{C}_2\) ways. Therefore, the required number of committees

\(
={ }^2 \mathrm{C}_1 \times{ }^3 \mathrm{C}_2=\frac{2 !}{1 ! 1 !} \times \frac{3 !}{2 ! 1 !}=6
\)

Example 5: What is the number of ways of choosing 4 cards from a pack of 52 playing cards? In how many of these
(i) four cards are of the same suit,
(ii) four cards belong to four different suits,
(iii) are face cards,
(iv) two are red cards and two are black cards,
(v) cards are of the same colour?

Solution:

There will be as many ways of choosing 4 cards from 52 cards as there are combinations of 52 different things, taken 4 at a time. Therefore
The required number of ways \(={ }^{52} \mathrm{C}_4=\frac{52 !}{4 ! 48 !}=\frac{49 \times 50 \times 51 \times 52}{2 \times 3 \times 4}\) \(=270725\)

(i) There are four suits: diamond, club, spade, heart and there are 13 cards of each suit. Therefore, there are \({ }^{13} \mathrm{C}_4\) ways of choosing 4 diamonds. Similarly, there are \({ }^{13} \mathrm{C}_4\) ways of choosing 4 clubs, \({ }^{13} \mathrm{C}_4\) ways of choosing 4 spades and \({ }^{13} \mathrm{C}_4\) ways of choosing 4 hearts. Therefore
The required number of ways \(={ }^{13} \mathrm{C}_4+{ }^{13} \mathrm{C}_4+{ }^{13} \mathrm{C}_4+{ }^{13} \mathrm{C}_4\).
\(
=4 \times \frac{13 !}{4 ! 9 !}=2860
\)

(ii) There are 13 cards in each suit.
Therefore, there are \({ }^{13} \mathrm{C}_1\) ways of choosing 1 card from 13 cards of diamond, \({ }^{13} \mathrm{C}_1\) ways of choosing 1 card from 13 cards of hearts, \({ }^{13} \mathrm{C}_1\) ways of choosing 1 card from 13 cards of clubs, \({ }^{13} \mathrm{C}_1\) ways of choosing 1 card from 13 cards of spades. Hence, by multiplication principle, the required number of ways
\(
={ }^{13} C_1 \times{ }^{13} C_1 \times{ }^{13} C_1 \times{ }^{13} C_1=13^4
\)

(iii) There are 12 face cards and 4 are to be selected out of these 12 cards. This can be done in \({ }^{12} \mathrm{C}_4\) ways. Therefore, the required number of ways \(=\frac{12 !}{4 ! 8 !}=495\).

(iv) There are 26 red cards and 26 black cards. Therefore, the required number of
\(
\begin{aligned}
\text { ways }={ }^{26} \mathrm{C}_2 & \times{ }^{26} \mathrm{C}_2 \\
&=\left(\frac{26 !}{2 ! 24 !}\right)^2=(325)^2=105625
\end{aligned}
\)

(v) 4 red cards can be selected out of 26 red cards in \({ }^{26} \mathrm{C}_4\) ways. 4 black cards can be selected out of 26 black cards in \({ }^{26} \mathrm{C}_4\) ways.
Therefore, the required number of ways \(={ }^{26} \mathrm{C}_4+{ }^{26} \mathrm{C}_4\)
\(
=2 \times \frac{26 !}{4 ! 22 !}=29900
\)

Important points about combinations

• The number of ways of selecting \(n\) objects out of \(n\) objects is(\(r=n\)):
  \(
  { }^n C_n=\frac{n !}{n !(n-n) !}=\frac{n !}{n ! 0 !}=1
  \)
• The number of ways of selecting 0 objects out of \(n\) objects is:
  \(
  { }^n C_0=\frac{n !}{0 !(n-0) !}=\frac{n !}{0 ! n !}=1
  \)
• The number of ways of selecting 1 object out of \(n\) objects is:
  \(
  { }^n C_1=\frac{n !}{1 !(n-1) !}=\frac{n \times(n-1) !}{(n-1) !}=n
  \)
• \(
  { }^n \mathrm{C}_{n-r}=\frac{n !}{(n-r) !(n-(n-r)) !}=\frac{n !}{(n-r) ! r !}={ }^n \mathrm{C}_r
  \)
  \(
  \text { i.e., selecting } r \text { objects out of } n \text { objects is same as rejecting }(n-r) \text { objects. }
  \)
• \(
  { }^n \mathrm{C}_a={ }^n \mathrm{C}_b \Rightarrow a=b \text { or } a=n-b \text {, i.e., } n=a+b
  \)
• \(
  { }^n \mathrm{C}_r+{ }^n \mathrm{C}_{r-1}={ }^{n+1} \mathrm{C}_r
  \)
• \(
  { }^n C_0+{ }^n C_1+{ }^n C_2+\ldots \ldots \ldots+{ }^n C_n=2^n
  \)
• \(
  { }^n C_0^2+{ }^n C_1^2+{ }^n C_2^2+\ldots \ldots \ldots+{ }^n C_n^2={ }^{2 n} C_n
  \)
• The relationship between permutation and combination for \(r\) things taken from \(n\) things.
  \(
  { }^n P_r=r ! \times{ }^n C_r
  \)

Example 6: The number of zeros at the end of 70 ! is
(a) 16
(b) 5
(c) 7
(d) 70

Solution: (a) To find the number of trailing zeros in the factorial of a number, we need to determine how many times 10 is a factor in the prime factorization of that factorial. Since \(10=2 \times 5\), the number of factors of 10 is limited by the number of factors of 5 , as there are always more factors of 2.
Step 2: Apply Legendre’s formula
The number of factors of a prime number \(p\) in \(n!\) can be calculated using Legendre’s formula:
\(
\sum_{k=1}^{\infty}\left\lfloor\frac{n}{p^k}\right\rfloor
\)
where \(n=70\) and \(p=5 .\lfloor x\rfloor\) represents the floor function (the largest integer less than or equal to \(x\) ).
Step 3: Calculate the result
We sum the floor of the divisions by successive powers of 5 :
First term: \([70 / 5]=\lfloor 14\rfloor=14\)
Second term: \(\left\lfloor 70 / 5^2\right\rfloor=\lfloor 70 / 25\rfloor=\lfloor 2.8\rfloor=2\)
Third term: \(\left\lfloor 70 / 5^3\right\rfloor=\lfloor 70 / 125\rfloor=\lfloor 0.56\rfloor=0\)
The series stops when the term becomes 0. The total number of factors of 5 is the sum of these values:
\(
\left\lfloor\frac{70}{5}\right\rfloor+\left\lfloor\frac{70}{25}\right\rfloor+\left\lfloor\frac{70}{125}\right\rfloor=14+2=16
\).

Example 7: How many different 9 digit numbers can be formed from the number 223355888 by rearranging its digits so that the odd digits occupy even positions?
(a) 16
(b) 36
(c) 60
(d) 180

Solution: (c) Digits: 223355888
Odd digits → 3,3,5,5 (four odd digits)
Even digits \(\boldsymbol{\rightarrow} \mathbf{2 , 2 , 8 , 8 , 8}\) (five even digits)
We need odd digits in even positions of a 9-digit number.

Step 1: Even positions = 2,4,6,8 (4 positions)
Place the odd digits \(\{3,3,5,5\}\).
Number of distinct permutations:
\(
\frac{4!}{2!2!}=6
\)
Step 2: Odd positions = 1,3,5,7,9 (5 positions)
Place the even digits \(\{2,2,8,8,8\}\).
Number of distinct permutations:
\(
\frac{5!}{2!3!}=10
\)
Total number of valid 9-digit numbers
\(
6 \times 10=60
\)

Example 8: Six boys and six girls sit along a line alternately in \(x\) ways; and along a circle (again alternatively in \(y\) ways), then
(a) \(x=y\)
(b) \(y=12 x\)
(c) \(x=10 y\)
(d) \(x=12 y\)

Solution: (d) Step 1: Along a line (x ways)
For alternating seating along a line:
1. The line can start with either a boy or a girl \(\rightarrow 2\) choices.
2. Arrange the 6 boys \(\rightarrow 6!\) ways
3. Arrange the \(\mathbf{6}\) girls \(\rightarrow \mathbf{6}\) ! ways
\(
x=2 \times 6!\times 6!
\)
Step 2: Along a circle (y ways)
For a circle, rotations are considered identical, so we fix one seat to avoid counting rotations:
1. Fix one boy at a seat. Now seating is uniquely defined in a circle.
2. Remaining 5 boys can be arranged in 5 ! ways
3. The \(\mathbf{6}\) girls can be arranged in 6 ! ways
\(
y=5!\times 6!
\)
Step 3: Relation between \(\mathbf{x}\) and \(\mathbf{y}\)
\(
x=2 \cdot 6!\cdot 6!=2 \cdot 6 \cdot 5!\cdot 6!=12 \cdot(5!\cdot 6!)=12 y
\)

Example 9: In how many ways can a pack of 52 cards be divided equally among four players? In how many ways can you divide these cards in four sets, three of them having 17 cards each and the fourth one just one card? (IIT-JEE, 1979)

Solution: Step 1: Divide 52 cards equally among four players
The problem involves distributing 52 distinct cards into four distinct (labeled) groups (players) of 13 cards each. This is a partitioning problem solved using the multinomial coefficient.
The number of ways to choose 13 cards for the first player is \(\binom{52}{13}\). The number of ways to choose 13 from the remaining 39 for the second is \(\binom{39}{13}\), and so on.
The total number of ways is calculated as:
\(
\frac{52!}{13!(52-13)!} \times \frac{39!}{13!(39-13)!} \times \frac{26!}{13!(26-13)!} \times \frac{13!}{13!(13-13)!}
\)
Which simplifies to the multinomial coefficient formula:
\(
\frac{52!}{13!13!13!13!}=\frac{52!}{(13!)^4}
\)
Step 2: Divide cards into four sets (three of 17, one of 1)
The problem requires dividing 52 distinct cards into four sets with sizes 17, 17, 17, and 1. Here, the sets themselves are indistinguishable.
First, calculate the number of ways to form labeled groups using the multinomial coefficient:
\(
\frac{52!}{17!17!17!1!}
\)
Since three of the groups have the same size (17 cards), they are interchangeable if we treat them as unlabeled “sets”. To correct for overcounting the permutations of these three identical-sized sets ( \(3!\) permutations), we divide the result by \(3!\).
The total number of ways is:
\(
\frac{52!}{17!17!17!1!\times 3!}=\frac{52!}{(17!)^3 1!3!}
\)
The number of ways to divide a pack of 52 cards equally among four players is \(\frac{\mathbf{5 2 !}}{(\mathbf{1 3 !})^4}\). The number of ways to divide these cards into four sets, three having 17 cards each and the fourth one just one card, is \(\frac{52!}{(17!)^3 3!}\).

Example 10: Six \(X\) s have to be placed in the squares of figure below in such a way that each row contains at least one \(X\). In how many different ways can this be done?

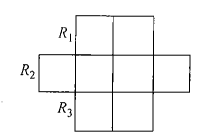
Solution:

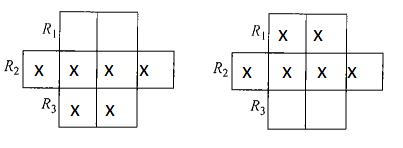
In the given figure there are 8 squares and we have to place 6 X’s this can be done in \({ }^8 C_6=.{ }^8 C_2=\frac{8 \cdot 7}{1 \cdot 2}=28\) ways
But these include the possibility that either headed row or lowest row may not have any X. these two possibilities are to be excluded.
∴ Required number of ways \(=28-2=26\)

Example 11: Five balls of different colours are to be placed in the boxes of different size. Each box can hold all five. In how many different ways can we place the balls so that no box remains empty? (IIT-JEE, 1981)

Solution: Case-by-Case Partitioning
Case 1: Distribution (3 balls, 1 ball, 1 ball)
Choose 3 balls out of \(5:\binom{5}{3}=10\) ways.
Choose 1 ball from the remaining 2: \(\binom{2}{1}=2\) ways.
Choose 1 ball from the last 1 : \(\binom{1}{1}=1\) way.
Assign these groups to the 3 different boxes (say A, B, C). The box with 3 balls can be A, B, or C ( 3 choices). The other two get one ball each ( \(2!\) ways to assign them). So \(10 \times 2 \times 1 \times 3=60\) ways. (Or \(\binom{5}{3}\binom{2}{1}\binom{1}{1} \times 3!/ 2!=10 \times 2 \times 1 \times 3=60\) ways).
Case 2: Distribution (2 balls, 2 balls, 1 ball)
Choose 2 balls from 5 : \(\binom{5}{2}=10\) ways.
Choose 2 balls from the remaining \(3:\binom{3}{2}=3\) ways.
Choose 1 ball from the last 1 : \(\binom{1}{1}=1\) way.
Assign these groups. The box with 1 ball can be A, B, or C ( 3 choices). The other two boxes get the pairs ( 1 way to assign them). So \(10 \times 3 \times 1 \times 3=90\) ways. (Or \(\binom{5}{2}\binom{3}{2}\binom{1}{1} \times 3!/ 2!=10 \times 3 \times 1 \times 3=90\) ways \()\).
Total Ways: \(60+90=150\) ways.

Example 12: \(m\) men and \(n\) women are to be seated in a row so that no two women sit together. If \(m>n\), then show that the number of ways in which they can be seated is \(m!(m+1)!/(m-n+1)!\). (IIT-JEE, 1983)

Solution: Step 1: Arrange the men
First, we arrange the \(m\) men in a row. The number of ways to arrange \(m\) distinct men is the number of permutations of \(m\) items, which is \(m!\).
Step 2: Identify spaces for the women
When the \(m\) men are seated, there are \(m+1\) potential spaces where the women can be placed such that no two women sit next to each other. These spaces are before the first man, between any two consecutive men, and after the last man.
Step 3: Select and arrange the women in the spaces
We must choose \(n\) distinct spaces out of the \(m+1\) available spaces and arrange the \(n\) women in those chosen spaces. The number of ways to select \(n\) spaces from \(m+1\) is given by the binomial coefficient \(\binom{m+1}{n}\). The number of ways to arrange \(n\) women in these \(n\) specific spaces is \(n!\).
The number of ways to choose and arrange the women is \(P(m+1, n)=\frac{(m+1)!}{(m+1-n)!}\)
Step 4: Calculate the total number of arrangements
By the multiplication principle, the total number of ways to seat both the men and women is the product of the ways to seat the men and the ways to place the women:
\(
\text { Total Ways }=m!\times \frac{(m+1)!}{(m+1-n)!}
\)
Step 5: Simplify the expression
Simplifying the expression gives the desired formula.
Total Ways \(=\frac{m!(m+1)!}{(m-n+1)!}\)

Example 13: Seven relatives of a man comprises four ladies and three gentlemen; his wife has also seven relatives-three of them are ladies and four gentlemen. In how many ways can they invite 3 ladies and 3 gentlemen at a dinner party so that there are three man’s relatives and three wife’s relatives? (IIT-JEE, 1985)

Solution: Given:
Man’s relatives: 4 ladies (L1, L2, L3, L4), 3 gentlemen (G1, G2, G3)
Wife’s relatives: 3 ladies (L5, L6, L7), 4 gentlemen (G4, G5, G6, G7)
We want to invite 3 ladies and 3 gentlemen, with 3 from man’s side and 3 from wife’s side.
Step 1: Split men and women in terms of sides
We have to pick:
3 ladies in total
3 gentlemen in total
And we must have 3 relatives from the man’s side and 3 from the wife’s side.
Since there are \(3+3=6\) guests, we need to decide how many men and women from each side.
Step 1a: Represent the situation
Let’s denote:
Man’s relatives invited: \(x\) ladies and \(3-x\) gentlemen
Wife’s relatives invited: \(3-x\) ladies and \(3-(3-x)=x\) gentlemen
Because total ladies \(=3\), total gentlemen \(=3\), total from each side \(=3\).
\(x=0,1,2,3\) possible number of ladies from man’s side.
Step 2: Count each case
Case 1: 0 ladies from man’s side
\(
\text { Man’s side: } 0 \text { ladies, } 3 \text { gentlemen → choose } 3 \text { from } 3 \text { men } \rightarrow\binom{3}{3}=1
\)
\(
\text { Wife’s side: } 3 \text { ladies (total 3-0=3), } 0 \text { gentlemen } \text { → } \text { choose } 3 \text { from } 3 \text { ladies } \rightarrow\binom{3}{3}=1
\)
Ways for this case: \(1 \cdot 1=1\)
Case 2: 1 lady from man’s side
Man’s side: 1 lady from \(4 \rightarrow\binom{4}{1}=4\)
Man’s side: 2 gentlemen from \(3 \rightarrow\binom{3}{2}=3\)
Wife’s side: 2 ladies from \(3 \rightarrow\binom{3}{2}=3\)
Wife’s side: 1 gentleman from \(4 \rightarrow\binom{4}{1}=4\)
Ways for this case: \(4 \cdot 3 \cdot 3 \cdot 4=144\)
Case 3: 2 ladies from man’s side
Man’s side: 2 ladies from \(4 \rightarrow\binom{4}{2}=6\)
Man’s side: 1 gentleman from \(3 \rightarrow\binom{3}{1}=3\)
Wife’s side: 1 lady from \(3 \rightarrow\binom{3}{1}=3\)
Wife’s side: 2 gentlemen from \(4 \rightarrow\binom{4}{2}=6\)
Ways for this case: \(6 \cdot 3 \cdot 3 \cdot 6=324\)
Case 4: \(\mathbf{3}\) ladies from man’s side
Man’s side: 3 ladies from \(4 \rightarrow\binom{4}{3}=4\)
Man’s side: 0 gentlemen \(\rightarrow\binom{3}{0}=1\)
Wife’s side: 0 ladies \(\rightarrow\binom{3}{0}=1\)
Wife’s side: 3 gentlemen from \(4 \rightarrow\binom{4}{3}=4\)
Ways for this case: \(4 \cdot 1 \cdot 1 \cdot 4=16\)
Step 3: Total ways
\(
1+144+324+16=485
\)

Example 14: A box contains two white balls, three black balls and four red balls. In how many ways can three balls be drawn from the box if at least one black ball is to be included in the draw?
(IIT-JEE, 1986)

Solution: Given:
White balls = 2
Black balls \(=3\)
Red balls \(=4\)
Total balls \(=2+3+4=9\)
We want to draw 3 balls with at least one black ball.
Step 1: Total ways without restriction
\(
\binom{9}{3}=84
\)
Step 2: Subtract the cases with no black balls
Balls that are not black: white + red \(=2+4=6\)
Ways to choose 3 balls with no black: \(\binom{6}{3}=20\)
Step 3: Ways with at least one black ball
\(
\text { Required ways }=\binom{9}{3}-\binom{6}{3}=84-20=64
\)

Example 15: A number of 18 guests have to be seated, half on each side of a long table. Four particular guests desire to sit on one particular side and three others on the other side. Determine the number of ways in which the sitting arrangements can be made. (IIT-JEE, 1991)

Solution: Step 1: Determine the number of guests and seating capacity per side
There are 18 guests in total, to be seated with half on each side of a long table. This means there are 18/2 = 9 seats available on each of the two sides.
Step 2: Account for guests with specific side preferences
Four particular guests want to sit on one specific side (let’s call it Side A), and three others want to sit on the other side (Side B).
Remaining seats on Side A: \(9-4=5\) seats.
Remaining seats on Side B: \(9-3=6\) seats.
Remaining guests without a pre-assigned side: \(18-4-3=11\) guests.
Step 3: Select and place the remaining guests
We need to select 5 guests from the remaining 11 to fill the remaining seats on Side A. This can be done in \(\binom{11}{5}\) ways.
\(
\binom{11}{5}=\frac{11!}{5!(11-5)!}=\frac{11!}{5!6!}=462
\)
The remaining \(11-5=6\) guests automatically fill the remaining 6 seats on Side B.
Step 4: Arrange guests on both sides
After the guests for each side are determined, the 9 guests on Side A can be arranged in 9 ! ways among the 9 seats. Similarly, the 9 guests on Side B can be arranged in 9 ! ways among the 9 seats.
Step 5: Calculate the total number of arrangements
The total number of ways the sitting arrangements can be made is the product of the number of ways to select the guests and the number of ways to arrange them on each side:
\(
\text { Total Ways }=\binom{11}{5} \times 9!\times 9!
\)

Example 16: A committee of 12 is to be formed from nine women and eight men. In how many ways can this be done if at least five women have to be included in a committee? In how many of these committees (IIT-JEE, 1994)
a. the women hold majority?
b. the men hold majority?

Solution: A committee of 12 is to be formed from 9 women and 8 men with minimum 5 women. Then we have following selection ways.
\(
\begin{array}{|l|l|l|}
\hline \text { Women (9) } & \text { Men (8) } & \text { Number of ways of selecting } \\
\hline 5 & 7 & { }^9 C_5 \times{ }^8 C_7=1008=s_1 \\
\hline 6 & 6 & { }^9 C_6 \times{ }^8 C_6=2352=s_2 \\
\hline 7 & 5 & { }^9 C_7 \times{ }^8 C_5=2016=s_3 \\
\hline 8 & 4 & { }^9 C_8 \times{ }^8 C_4=630=s_4 \\
\hline 9 & 3 & { }^9 C_9 \times{ }^8 C_3=56=s_3 \\
\hline & \text { Total } & 6062 \\
\hline
\end{array}
\)

a. Number of committee when women are in majority is \(s_3+s_4 +s_5=2702\).
b. Number of committee when men are in majority is \(s_1=1008\).

Alternate: Given:
Women \(=9\)
Men = 8
Committee size = 12
Condition: at least 5 women
We are asked:
a) Number of committees where women hold majority ( \(\geq 7\) women)
b) Number of committees where men hold majority (< 6 women, but at least 5 women? we’ll clarify)
Step 1: Total committees with at least 5 women
Committee size \(=12\), so possible number of women in committee:
\(
5,6,7,8,9 \quad(\text { since women } \geq 5, \text { total women } \leq 9)
\)
Corresponding men: 12 – women → \(7,6,5,4,3\)
Step 1a: Number of ways for each case
Women = 5: choose 5 women from \(9 \rightarrow\binom{9}{5}=126\)
Men \(=7 \rightarrow\) choose 7 men from \(8 \rightarrow\binom{8}{7}=8\)
Total \(=126 \cdot 8=1008\)
Women \(=6\) : choose 6 women \(\rightarrow\binom{9}{6}=84\)
Men = \(6 \rightarrow\) choose 6 men \(\rightarrow\binom{8}{6}=28\)
Total \(=84 \cdot 28=2352\)
Women = 7: choose 7 women \(\rightarrow\binom{9}{7}=36\)
Men \(=5 \rightarrow\) choose 5 men \(\rightarrow\binom{8}{5}=56\)
Total \(=36 \cdot 56=2016\)
Women = 8: choose 8 women \(\rightarrow\binom{9}{8}=9\)
Men = \(4 \rightarrow\) choose 4 men \(\rightarrow\binom{8}{4}=70\)
Total \(=9 \cdot 70=630\)
Women = 9: choose 9 women \(\rightarrow\binom{9}{9}=1\)
Men = \(3 \rightarrow\) choose 3 men \(\rightarrow\binom{8}{3}=56\)
Total \(=1 \cdot 56=56\)
Step 1b: Total number of committees with \(\mathbf{~} \mathbf{5}\) women
\(
1008+2352+2016+630+56=6062
\)
Step 2: Committees where women hold majority
Committee of \(12 \rightarrow\) majority \(=\geq 7\) women
So, women = 7,8,9
From Step 1a:
\(
2016+630+56=2702
\)
(a): 2702
Step 3: Committees where men hold majority
Committee of \(12 \rightarrow\) men majority \(=\geq 7\) men \(\rightarrow\) women \(\leq 5\)
But we have at least \(\mathbf{5}\) women restriction → women \(=\mathbf{5}\) only
From Step 1a (women = 5): 1008
(b): 1008
Summary of Answers
Total committees with \(\mathbf{\geq 5}\) women: 6062
Women majority: 2702
Men majority: 1008.

Example 17: The sides \(A B, B C\) and \(C A\) of a triangle \(A B C\) have 3, 4 and 5 interior points, respectively on them. The number of triangles that can be constructed using these interior points as vertices is ____. (IIT-JEE, 1984)

Solution: We have total \(3+4+5=12\) points. So, number of \(\Delta s\) that can be formed using 12 such points is given by
Total number of ways of selecting three point – Number of ways three collinear points are selected
\(
\begin{aligned}
& ={ }^{12} C_3-{ }^3 C_3-{ }^4 C_3-{ }^5 C_3 \\
& =\frac{12 \times 11 \times 10}{6}-1-4-\frac{5 \times 4}{2 \times 1} \\
& =220-15=205
\end{aligned}
\)

Example 18: The total number of ways in which six ‘ + ‘ and four ‘ – ‘ signs can be arranged in a line such that no two ‘-‘ signs occur together is ____. (IIT-JEE, 1988)

Solution: Given:
Signs: 6 ‘+’ and 4 ‘-‘
Condition: no two ‘-‘ are together
Find: total number of arrangements.
Step 1: Arrange ‘+’ signs first
Place the 6 ‘+’ signs in a line:
\(
++++++
\)
This creates 7 “gaps” where a ‘-‘ can be placed:
gaps: before the first ‘+’, between ‘+’ signs, after the last ‘+’
\(
-+-+-+-+-+-+-
\)
There are 7 gaps in total.
Step 2: Place ‘-‘ signs
We have 4 ‘-‘ signs
To avoid two ‘-‘ together, we can place at most one ‘-‘ in each gap
Number of ways to choose 4 gaps out of 7: \(\binom{7}{4}=35\)
Within the selected gaps, the ‘-‘ signs are identical, so no further arrangement needed.
Step 3: Total arrangements: 35.

Example 19: There are four balls of different colours and four boxes of colours same as those of the balls. The number of ways in which the balls, one each in a box, could be placed such that a ball does not go to a box of its own colour is ____. (IIT-JEE, 1992)

Solution: We know that number of derangements of \(n\) objects is
\(
n!\left[1-\frac{1}{1!}+\frac{1}{2!}-\frac{1}{3!}+\frac{1}{4!}-\cdots+\frac{1}{n!}\right]
\)
Therefore, number of ways of putting all the 4 balls into boxes of different colour is
\(
\begin{aligned}
4!\left[1-\frac{1}{1!}+\frac{1}{2!}-\frac{1}{3!}+\frac{1}{4!}\right] & =4!\left(\frac{1}{2}-\frac{1}{6}+\frac{1}{24}\right) \\
& =24\left(\frac{12-4+1}{24}\right) \\
& =9
\end{aligned}
\)

Example 20: Eight chairs are numbered 1 to 8 . Two women and three men wish to occupy one chair each. First, the women choose the chairs from amongst the chairs marked 1 to 4, and then the men select the chairs from amongst the remaining. The number of possible arrangements is (IIT-JEE, 1982)
a. \({ }^6 C_3 \times{ }^{4} C_2\)
b. \({ }^4 P_2 \times{ }^4 P_3\)
c. \({ }^4 C_2+{ }^4 P_3\)
d. none of these

Solution: Two women can choose two chairs out of \(1,2,3,4\) in \({ }^4 C_2\) ways, and can arrange among themselves in 2 ! ways. Three men can choose 3 chairs out of 6 remaining chairs in \({ }^6 C_3\) ways and can arrange themselves in 3 ! ways.
Therefore, total number of possible arrangements is \({ }^4 C_2 \times 2!\times{ }^6 C_3 \times 3!={ }^4 P_2 \times{ }^6 P_3\).