The fundamental counting principle is a rule to count all the possible ways for an event to happen or the total number of possible outcomes in a situation.

It states that when there are \(m\) ways to do one thing, and \(n\) ways to do another thing, then the number of ways to do both the things can be obtained by taking their product. 

This is expressed as \(m \times n\). Let’s look at a few examples.

In fact, the problems of the types shown in the examples below are solved by applying the following principle known as the fundamental principle of counting, or, simply, the multiplication principle, which states that

“If an event can occur in \(m\) different ways, following which another event can occur in \(n\) different ways, then the total number of occurrence of the events in the given order is \(m \times n\).”

Example 1: Sam has 2 shirts and 2 pants of different colors in his closet. The colors of the shirts are pink and black, while the colors of the pants are black and white. He wore one of the combinations, which were a pink shirt and a white pant. What do you think are the other possible combinations he could try?

Solution: He could wear any of the following 3 combinations apart from the one which is worn by him. This means using the 2 shirts and 2 pants, he could dress up in 4 different ways.

Shirt                 Pant
Pink                 Black
Pink                 White
Black                Black
Black                White 

If we apply the fundamental counting principle, we get to know that he can wear either a pink shirt or a black shirt. Similarly, he can either wear a white skirt or a black skirt. Hence, he can wear his shirts in 2 ways and pants in 2 ways. To get the total number of combinations possible, we take the product of ‘the number of ways in which he can wear his shirt’ with ‘the number of ways he can wear his pant’. Hence, the number of combinations are represented as 2 x 2 = 4. This shows that the sample space is 4.

Note: Sample space is referred to as the collection of all possible outcomes in any random experiment.

Example 2: Vincent has 2 bananas, 3 apples, and 3 oranges in a basket. In how many different ways can he consume the fruits in the basket?

Solution: Applying the above rules, we know that the total number of ways in which he can consume the fruits in the basket is: \(2 \times 3 \times 3=18\).

Hence, he has 18 different ways to consume the fruits. This tells us that 18 is the sample space in this case.

Example 3: There are 6 children in a classroom and 6 benches for them to sit on. The class teacher makes them sit at a different place every month. In how many ways can she make them sit in the classroom?

Solution: There are 6 children and 6 benches for them to sit on.
Hence, their teacher will apply the fundamental counting principle to find the number of ways in which she can make them sit.
The number of ways in which she can make the children sit in the classroom is \(6 \times 6=36\).

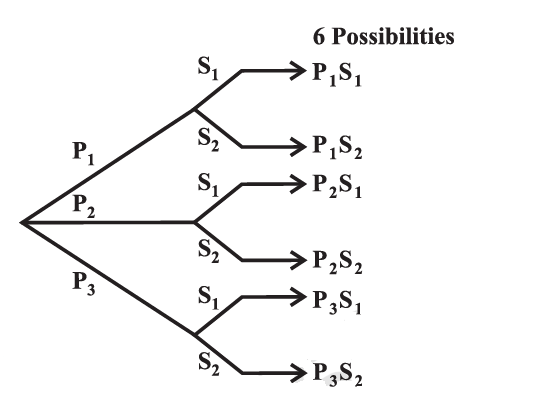
Example 4: Mohan has 3 pants and 2 shirts. How many different pairs of a pant and a shirt, can he dress up with?

Solution: There are 3 ways in which a pant can be chosen because there are 3 pants available. Similarly, a shirt can be chosen in 2 ways. For every choice of a pant, there are 2 choices of a shirt. Therefore, there are 3 × 2 = 6 pairs of a pant and a shirt.

Let us name the three pants as \(\mathrm{P}_1, \mathrm{P}_2, \mathrm{P}_3\) and the two shirts as \(\mathrm{S}_1, \mathrm{~S}_2\). Then, these six possibilities can be illustrated in the Figure below.

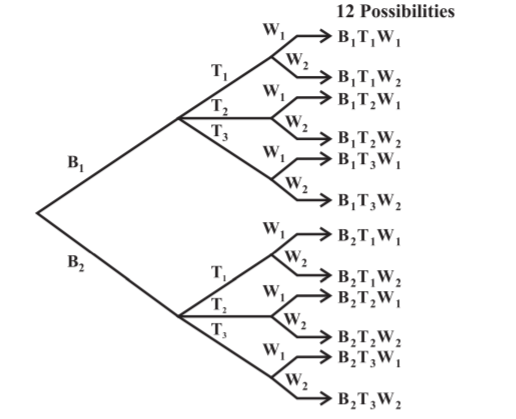
Example 5: Sabnam has 2 school bags, 3 tiffin boxes, and 2 water bottles. In how many ways can she carry these items (choosing one each)?

Solution:

• A school bag can be chosen in 2 different ways.
• After a school bag is chosen, a tiffin box can be chosen in 3 different ways.
• Hence, there are 2 × 3 = 6 pairs of school bag and a tiffin box.
• For each of these pairs, a water bottle can be chosen in 2 different ways.
• Hence, there are 6 × 2 = 12 different ways in which, Sabnam can carry these items to school.

If we name the 2 school bags as \(B_1, B_2\), the three tiffin boxes as \(T_1, T_2, T_3\) and the two water bottles as \(\mathrm{W}_1, \mathrm{~W}_2\), these possibilities can be illustrated in the Figure below.

Note: The above principle can be generalised for any finite number of events. For example, for 3 events, the principle is as follows:
‘If an event can occur in \(m\) different ways, following which another event can occur in \(n\) different ways, following which a third event can occur in \(p\) different ways, then the total number of occurrence to “the events in the given order is \(m \times n \times p\).”

Example 6: Find the number of 4-letter words, with or without meaning, which can be formed out of the letters of the word ROSE, where the repetition of the letters is not allowed.

Solution: There are as many words as there are ways of filling in 4 vacant places by the 4 letters, keeping in mind that the repetition is not allowed.

• The first place can be filled in 4 different ways by anyone of the 4 letters R, O, S, E.
• Following which, the second place can be filled in by anyone of the remaining 3 letters in 3 different ways.
• Following which the third place can be filled in 2 different ways.
• Following which, the fourth place can be filled in 1 way.
• Thus, the number of ways in which the 4 places can be filled, by the multiplication principle, is 4 × 3 × 2 × 1 = 24. Hence, the required number of words is 24.

Example 7: Given 4 flags of different colours, how many different signals can be generated, if a signal requires the use of 2 flags one below the other?

Solution: There will be as many signals as there are ways of filling in 2 vacant places in succession by the 4 flags of different colours. The upper vacant place can be filled in 4 different ways by anyone of the 4 flags; following which, the lower vacant place can be filled in 3 different ways by any one of the remaining 3 different flags. Hence, by the multiplication principle, the required number of signals = 4 × 3 = 12.

Example 8: How many 2-digit even numbers can be formed from the digits 1, 2, 3, 4, and 5 if the digits can be repeated?

Solution: There will be as many ways as there are ways of filling 2 vacant places in succession by the five given digits. Here, in this case, we start filling in unit’s place, because the options for this place are 2 and 4 only and this can be done in 2 ways; following which the ten’s place can be filled by any of the 5 digits in 5 different ways as the digits can be repeated. Therefore, by the multiplication principle, the required number of two digits even numbers is 2 × 5, i.e., 10.

Example 9: Find the number of different signals that can be generated by arranging at least 2 flags in order (one below the other) on a vertical staff, if five different flags are available.

Solution: A signal can consist of either 2 flags, 3 flags, 4 flags, or 5 flags. Now, let us count the possible number of signals consisting of 2 flags, 3 flags, 4 flags, and 5 flags separately and then add the respective numbers.
There will be as many 2 flag signals as there are ways of filling in 2 vacant places in succession by the 5 flags available. By the Multiplication rule, the number of ways is 5 × 4 = 20.
Similarly, there will be as many 3 flag signals as there are ways of filling in 3 vacant places in succession by the 5 flags. The number of ways is 5 × 4 × 3 = 60.
Continuing the same way, we find that
The number of 4 flag signals = 5 × 4 × 3 × 2 = 120
and the number of 5 flag signals = 5 × 4 × 3 × 2 × 1 = 120
Therefore, the required no of signals = 20 + 60 + 120 + 120 = 320.

Fundamental Principle of Addition

If two jobs can be performed independently in \(m\) and \(n\) ways respectively, then either of the two jobs can be performed in \((m+n)\) ways.

Example 10: There are 11 boys and 9 girls in each class. The teacher wants to choose a student to represent the class at an event. In how many ways can the teacher make this decision?

Solution: The teacher must choose one of the following two tasks:

• Selecting a boy from a group of 11, or
• Selecting a girl from a group of 9.

The first of them can be done in 11 different ways, while the second can be done in 9 different ways. As a result, either of the two can be done in \((11+9)=20\) different ways. Hence, the teacher has 20 options for selecting a class representative.

Example 11: How many words can be made from the letters in the word ‘MOTEL’ if all of the letters are used simultaneously (no letters are repeated)?

Solution: We know that 5 letters must be arranged in 5 places.

• The first spot can be filled in 5 different ways, using any of the five letters \(M, O, T, E, L\).
• There are four letters left, and any of them can be used to fill the second spot.
• Hence, the first two spots can be filled in \(5 \times 4\) different ways.
• There are three letters left, and one of them can go in third place.
• There are now two letters left, and one of them can be placed in the fourth position.
• Lastly, one letter remains, that must go into the fifth place.
  As a result, the total number of options to fill five spaces is \(=5 \times 4 \times 3 \times 2 \times 1=120\)

Example 12: How many 4-letter code words are possible using the first 10 letters of the English alphabet if
(i) No letter can be repeated
(ii) letters can be repeated

Solution: (i) The first letter of the code can be chosen in 10 ways, the second letter can be chosen in 9 ways, the third letter can be chosen in 8 ways, and the fourth letter can be chosen in 7 ways.
Total number of 4 letter code words \(=10 \times 9 \times 8 \times 7=5040\)

Hence, 5040 four-lettered codes can be formed using the first 10 letters of the English alphabet, if no letter is repeated.

(ii) The first letter of the code can be chosen in 10 different ways. Since the letters can be repeated, there are 10 possibilities for each of the other letters in the code.
Total number of 4 letter code words \(=10 \times 10 \times 10 \times 10=10000\)

Example 13: How many numbers lying between 100 and 1000 can be formed with the digits \(0,1,2,3,4,5\) if the repetition of digits is not allowed?

Solution: The numbers lying between 100 and 1000 consist of 3 digits. There are 6 different digits with which three places have to be filled. Repetition of digits is not allowed.
As 3-digit numbers are required, the hundred’s place is non-zero. So, it can be filled up in 5 ways. The ten’s place can be filled in 5 ways with any one of the remaining 5 digits as repetition is not allowed. Similarly, the unit’s place can be filled up in 4 ways.
By the fundamental principle of counting, the required number of numbers lying between 100 and \(1000=5 \times 5 \times 4=100\).

Example 14: How many ways can 2 prizes (in Science and Maths) be awarded to 15 students?

Solution: Number of students \(=15\)
Number of ways of awarding the prize in Science \(=15\)
Number of ways of awarding the prize in Maths \(=15\)
\(\therefore\) Number of ways of awarding 2 prizes (in Science and Maths) \(=15 \times 15=225\).

Example 15: Find the number of positive integers between 6000 and 7000 which are divisible by 5, provided that no digit is to be repeated.

Solution: The thousand’s place has to be filled up by the digit 6, so there is only one way to fill. As the numbers are divisible by 5, the unit’s place must be filled up either by 5 or 0. Thus, there are only 2 ways to fill the unit’s place.
Now, the hundred’s place can be filled up in 8 ways by any of the remaining 8 digits because two digits have already been used at thousand’s place and unit’s place.
Similarly, the ten’s place can be filled up in 7 ways.
\(\therefore\) The number of positive integers \(=1 \times 8 \times 7 \times 2=112\)

Summary

There are two fundamental principles of counting: the multiplication principle of counting and the addition principle of counting. According to the multiplication principle of counting, if there are \(n\) jobs \(J_1, J_2, \ldots J_n\) such that job \(J_i\) can be performed independently in \(m_i\) ways; \(i=1,2, \ldots, n\). Then the total number of ways in which all the jobs can be performed is \(m_1 \times m_2 \times m_3 \times \ldots \times m_n\).

And, according to the addition principle of counting, If \(E_1, E_2, \ldots E_k\) be disjoint events with \(n_1, n_2, \ldots n_k\) possible outcomes, respectively. Then the total number of outcomes for the event ” \(E_1\) or \(E_2\) or….or \(E_k\) ” is \(n_1+n_2+\cdots+n_k\).

Note: Disjoint events are two events that cannot happen at the same time. In other words, they are mutually exclusive. This means that if Event A happens, then Event B cannot happen, and vice versa.