Permutation: The re-arranging of the elements in an ordered set is called the process of permutation. The word “permutation” also refers to the act or process of replacing the linear order of an ordered set.

Combination: The process of selecting items from a collection where the order of selection does not matter is known as a combination, or the different groups or selections of several things taking some or all of them at a time are called combinations.

What’s the Difference?

In English, we use the word “combination” loosely, without thinking if the order of things is important. In other words:

“My fruit salad is a combination of apples, grapes, and bananas” We don’t care what order the fruits are in, they could also be “bananas, grapes, and apples” or “grapes, apples, and bananas”, it’s the same fruit salad.

“The combination to the safe is 472”. Now we do care about the order. “724” won’t work, nor will “247”. It has to be exactly 4-7-2.

So, in Mathematics we use more precise language:

• When the order doesn’t matter, it is a Combination.
• When the order does matter it is a Permutation.
  So, we should really call this a “Permutation Lock”!
  In other words: A Permutation is an ordered Combination.

In both combinations and permutations, we have two cases

Case-1: Repetition allowed

Case-2: Repetition not allowed

Example 1: How many 3-digit numbers can you make using the digits 1, 2, and 3 without repetitions?

Solution:

We can solve this problem in different way.

Method-1: Listing all possible numbers using a tree diagram.

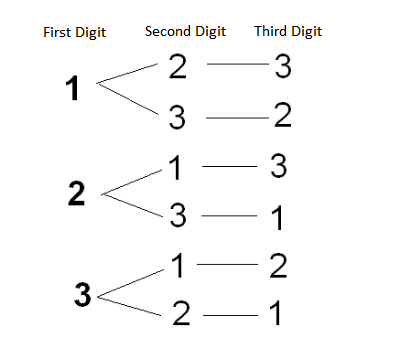
From the above tree diagram, it is clear we can make 6 numbers using 3 digits and without repetitions of the digits.

Method-2: Counting

By looking at the tree diagram, we have 3 choices for the first digit, 2 choices for the second digit, and 1 choice for the third digit. Using the counting principle, we can say:

The total number of 3-digit numbers is given by 3 x 2 x 1 = 6

There is a special notation for the product 3 × 2 × 1 = 3! and it is read 3 factorial. In general n! is read n factorial which is explained below. 

Note: Remember that 0! = 1.

Example 2: How many different words can we make using the letters A, B, E, and L?

Solution: We have 4 choices for the first letter, 3 choices for the second letter, 2 choices for the third letter, and 1 choice for the fourth letter. Hence the number of words is given by 4 x 3 x 2 x 1 = 4! = 24.

Permutations

Example 3: How many 2-digit numbers can you make using the digits 1, 2, 3, and 4 without repeating the digits?

Solution: This time we want to use 2 digits at a time to make 2-digit numbers.
For the first digit, we have 4 choices (1, 2, 3, and 4) and for the second digit, we have 3 choices (4 – 1 used already). Using the counting principle, the number of 2-digit numbers that we can make using 4 digits is given by 4 x 3 = 12.

The above problem is that of arranging 2 digits out of 4 in a specific order. This is also called permutating. The most important idea in permutations is that order is important. When you use the digits 3 and 4 to make a number, the numbers 34 and 43 are different hence the order of the digits 3 and 4 is important.

Combinations

Example 4: How many lines can you draw using 3 non-collinear (not in a single line) points A, B, and C on a plane?

Solution:

You need two points to draw a line. The order is not important. Line AB is the same as line BA. The problem is to select 2 points out of 3 to draw different lines. If we proceed as we did with permutations, we get the following pairs of points to draw lines.
AB , AC
BA , BC
CA , CB
There is a problem: line AB is the same as line BA, same for lines AC and CA and BC and CB.
The lines are AB, BC, and AC ; 3 lines only.
So, in fact, we can draw 3 lines and not 6 and that’s because in this problem the order of the points A, B, and C is not important.

Factorial Notations

Before going to different formulas of permutation and combination, one should know about factorial notation. The continued product of first \(n\) natural numbers is called the factorial of \(n\). It is denoted by \(n\) ! and is defined as
\(
\begin{aligned}
&n !=1.2 .3 \ldots \ldots(n-2)(n-1) n \\
&=n(n-1)(n-2) \ldots \ldots 3.2 .1 \\
&=n \times(n-1) ! \\
&=n \times(n-1) \times(n-2) ! \ldots \ldots \ldots
\end{aligned}
\)