In the previous Section, you have learnt how to solve linear inequality in one or two variables graphically. We will now illustrate the method for solving a system of linear inequalities in two variables graphically through some examples.

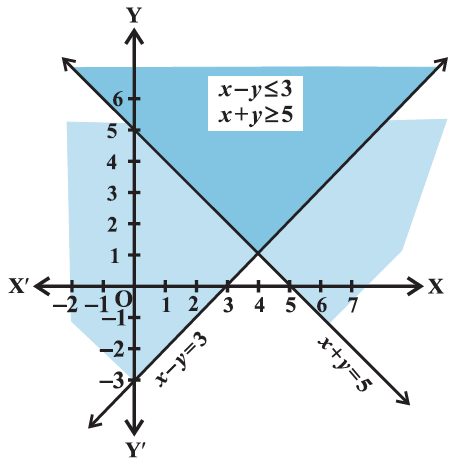
Example 1: Solve the following system of linear inequalities graphically.
\(
\begin{aligned}
& x+y \geq 5 \dots(1)\\
& x-y \leq 3 \dots(2)
\end{aligned}
\)

Solution:

The graph of linear equation \(x+y=5\) is drawn in Figure below.
We note that the solution of inequality (1) is represented by the shaded region above the line \(x+y=5\), including the points on the line.

On the same set of axes, we draw the graph of the equation \(x-y=3\) as shown in Figure below. Then we note that inequality (2) represents the shaded region above the line
\(x-y=3\), including the points on the line. Clearly, the double-shaded region, common to the above two shaded regions is the required solution region of the given system of inequalities.

Example 2: Solve the following system of inequalities graphically
\(
\begin{aligned}
& 5 x+4 y \leq 40 \dots(1)\\
& x \geq 2 \dots(2)\\
& y \geq 3 \dots(3)
\end{aligned}
\)

Solution:

We first draw the graph of the line \(5 x+4 y=40, x=2 \text { and } y=3\)

Then we note that the inequality (1) represents shaded region below the line \(5 x+4 y=40\) and inequality (2) represents the shaded region right of line \(x=2\) but inequality (3) represents the shaded region above the line \(y=3\). Hence, the shaded region (Figure below) including all the points on the lines are also the solution of the given system of the linear inequalities.

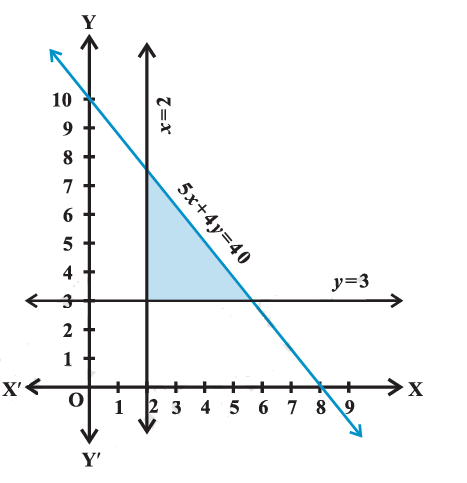
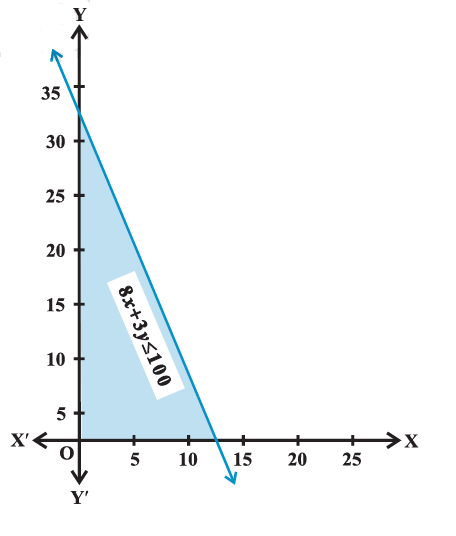
Example 3: Solve the following system of inequalities

\(
\begin{aligned}
& 8 x+3 y \leq 100 \dots(1) \\
& x \geq 0 \dots(2)\\
& y \geq 0 \dots(3)
\end{aligned}
\)

Solution:

We draw the graph of the line
\(
8 x+3 y=100
\)
The inequality \(8 x+3 y \leq 100\) represents the shaded region below the line, including the points on the line \(8 x+3 y=100\) (Figure below).
Since \(x \geq 0, y \geq 0\), every point in the shaded region in the first quadrant, including the points on the line and the axes, represents the solution of the given system of inequalities.

In many practical situations involving the system of inequalities the variable \(x\) and \(y\) often represent quantities that cannot have negative values, for example, the number of units produced, the number of articles purchased, the number of hours worked, etc. Clearly, in such cases, \(x \geq 0, y \geq 0\), and the solution region lies only in the first quadrant.

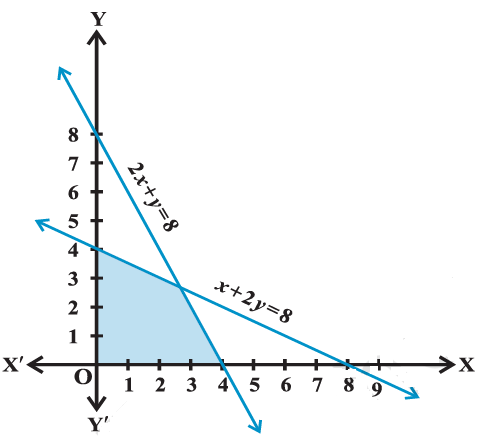
Example 4: Solve the following system of inequalities graphically

\(
\begin{aligned}
& x+2 y \leq 8 \\
& 2 x+y \leq 8 \\
& x \geq 0 \\
& y \geq 0
\end{aligned}
\)

Solution:

We draw the graphs of the lines \(x+2 y=8\) and \(2 x+y=8\). The inequality (1) and (2) represent the region below the two lines, including the point on the respective lines. Since \(x \geq 0, y \geq 0\), every point in the shaded region in the first quadrant represents a solution of the given system of inequalities (Figure below).

Important Points to Remember

A statement involving the symbols ‘ \(>\) ‘, ‘ \(<\) ‘, ‘ \(\geq\) ‘, ‘ \(\leq\) ‘ is called an inequality. For example \(5>3, x \leq 4, x+y \geq 9\).

• Inequalities which do not involve variables are called numerical inequalities. For example \(3<8,5 \geq 2\).
• Inequalities which involve variables are called literal inequalities. For example, \(x>3, y \leq 5, x-y \geq 0\).
• An inequality may contain more than one variable and it can be linear, quadratic or cubic etc. For example, \(3 x-2<0\) is a linear inequality in one variable, \(2 x+3 y \geq 4\) is a linear inequality in two variables and \(x^2+3 x+2<0\) is a quadratic inequality in one variable.
• Inequalities involving the symbol ‘ \(>\) ‘ or ‘ \(<\) ‘ are called strict inequalities. For example, \(3 x-y>5, x<3\).
• Inequalities involving the symbol ‘ \(\geq\) ‘ or ‘ \(\leq\) ‘ are called slack inequalities. For example, \(3 x-y \geq 5, x \leq 5\)

Solution of an inequality

(i) The value(s) of the variable(s) which makes the inequality a true statement is called its solutions. The set of all solutions of an inequality is called the solution set of the inequality. For example, \(x-1 \geq 0\), has infinite number of solutions as all real values greater than or equal to one make it a true statement. The inequality \(x^2+1<0\) has no solution in \(\mathbf{R}\) as no real value of \(x\) makes it a true statement.

To solve an inequality we can

(i) Add (or subtract) the same quantity to (from) both sides without changing the sign of inequality.
(ii) Multiply (or divide) both sides by the same positive quantity without changing the sign of inequality. However, if both sides of inequality are multiplied (or divided) by the same negative quantity the sign of inequality is reversed, i.e., ‘ \(>\) ‘ changes into ‘ \(<\) ‘ and vice versa.

Two important results
(a) If \(a, b \in \mathbf{R}\) and \(b \neq 0\), then

(i) \(a b>0\) or \(\frac{a}{b}>0 \Rightarrow a\) and \(b\) are of the same sign.

(ii) \(a b<0\) or \(\frac{a}{b}<0 \Rightarrow a\) and \(b\) are of opposite sign.

(b) If \(a\) is any positive real number, i.e., \(a>0\), then

(i) \(|x|<a \Leftrightarrow-a<x<a\)
\(|x| \leq a \Leftrightarrow-a \leq x \leq a\)

(ii) \(|x|>a \Leftrightarrow x<-a\) or \(x>a\)
\(|x| \geq a \Leftrightarrow x \leq-a\) or \(x \geq a\)