Linear Inequalities Rules

To solve a given linear inequation means to find the value or values of the variable used in it. Thus, to solve the inequation \(3 x+5>8\) means to find the variable \(x\) and to solve the inequation \(8-5 y<3\) means to find the variable \(y\) and so on. Thus, we state the following rules for solving an inequality:

• Rule 1: Equal numbers may be added to (or subtracted from) both sides of an inequality without affecting the sign of inequality.
• Rule 2: Both sides of an inequality can be multiplied (or divided) by the same positive number. But when both sides are multiplied or divided by a negative number, then the sign of inequality is reversed.

Example 1: Solve \(30 x<200\) when
(i) \(x\) is a natural number,
(ii) \(x\) is an integer.

Solution: We are given \(30 x<200\)
or \(\quad \frac{30 x}{30}<\frac{200}{30}\) (Rule 2), i.e., \(x<20 / 3\).
(i) When \(x\) is a natural number, in this case, the following values of \(x\) make the statement true.
\(1,2,3,4,5,6\)
The solution set of the inequality is \(\{1,2,3,4,5,6\}\).
(ii) When \(x\) is an integer, the solutions of the given inequality are
\(
\ldots,-3,-2,-1,0,1,2,3,4,5,6
\)
The solution set of the inequality is \(\{\ldots,-3,-2,-1,0,1,2,3,4,5,6\}\)

Example 2: Solve \(5 x-3<3 x+1\) when
(i) \(x\) is an integer,
(ii) \(x\) is a real number.

Solution: We have, \(5 x-3<3 x+1\)
or \(5 x-3+3<3 x+1+3\) (Rule 1)
or \(5 x<3 x+4\)
or \(5 x-3 x<3 x+4-3 x\) (Rule 1)
or \(2 x<4\)
or \(x<2\) (Rule 2)

(i) When \(x\) is an integer, the solutions of the given inequality are \(x \in\{\ldots, -3,-2,-1,0,1\}\)

(ii) When \(x\) is a real number, the solutions of the inequality are given by \(x<2\), i.e., all real numbers \(x\) which are less than 2 . Therefore, the solution set of the inequality is \(x \in(-\infty, 2)\).

Example 3: Solve \(4 x+3<6 x+7\)

Solution: We have, \(\quad 4 x+3<6 x+7\)
or \(4 x-6 x<6 x+4-6 x\)
or \(-2 x<4 \quad\) or \(x>-2\)
i.e., all the real numbers which are greater than \(-2\), are the solutions of the given inequality. Hence, the solution set is \((-2, \infty)\).

Example 4: Solve \(\frac{5-2 x}{3} \leq \frac{x}{6}-5\).

Solution: We have
\(
\frac{5-2 x}{3} \leq \frac{x}{6}-5
\)
or
\(
2(5-2 x) \leq x-30 \text {. }
\)
or \(10-4 x \leq x-30\)
or
\(
-5 x \leq-40 \text {, i.e., } x \geq 8
\)
Thus, all real numbers \(x\) which are greater than or equal to 8 are the solutions of the given inequality, i.e., \(x \in[8, \infty)\).

Graphing Linear Inequalities – One Variable

Example 5: Solve \(4 x>-3 x+21\)

Solution: 
\(
4 x+3 x>21 \Rightarrow 7 x>21 \Rightarrow x>3
\)
The graphical representation of the solutions are given in the Figure below.

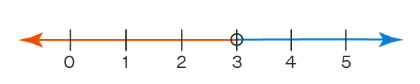
Any point lying on the blue part of the number line will satisfy this inequality. Note that in this case, we have drawn a hollow dot at point 3. This is to indicate that 3 is not a part of the solution set (this is because the given inequality has a strict inequality). As per the solution obtained, the blue part of the number line satisfies the inequality.

Example 6: Solve \(\frac{3 x-4}{2} \geq \frac{x+1}{4}-1\). Show the graph of the solutions on the number line.

Solution: We have
\(
\begin{aligned}
& \frac{3 x-4}{2} \geq \frac{x+1}{4}-1 \\
& \frac{3 x-4}{2} \geq \frac{x-3}{4} \\
& 2(3 x-4) \geq(x-3)
\end{aligned}
\)
\(
\begin{array}{ll}
\text { or } & 6 x-8 \geq x-3 \\
\text { or } & 5 x \geq 5 \text { or } x \geq 1
\end{array}
\)
The graphical representation of solutions is given in the Figure below (the blue arrow).

Example 7: The marks obtained by a student of Class XI in the first and second terminal examination are 62 and 48, respectively. Find the minimum marks he should get in the annual examination to have an average of at least 60 marks.

Solution: Let \(x\) be the marks obtained by the student in the annual examination. Then
\(
\frac{62+48+x}{3} \geq 60
\)
or \(\quad 110+x \geq 180\)
or \(\quad x \geq 70\)
Thus, the student must obtain a minimum of 70 marks to get an average of at least 60 marks.

Example 8: Find all pairs of consecutive odd natural numbers, both of which are larger than 10 , such that their sum is less than 40.

Solution Let \(x\) be the smaller of the two consecutive odd natural number so that the other one is \(x+2\). Then, we should have
\(x>10 \dots(1)\)
and \(x+(x+2)<40 \dots(2)\)
Solving (2), we get
\(
2 x+2<40
\)
i.e., \(x<19 \dots(3)\)
From (1) and (3), we get
\(
10<x<19
\)
Since \(x\) is an odd number, \(x\) can take the values \(11,13,15\), and 17. So, the required possible pairs will be
\(
(11,13),(13,15),(15,17),(17,19)
\)