5.2 Complex Numbers

Any number of the form \(a+i b\), where \(a\) and \(b\) are real numbers, is defined to be a complex number. We often use Z for a complex number.

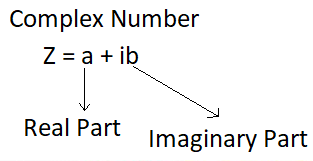
In the above complex number equation, z becomes:

1. Purely real if b =0; therefore z = a.
2. Purely Imaginary if a = 0; therefore z = ib (Imaginary numbers are the numbers when squared it gives the negative result; for example \( \mathrm{i} = \sqrt{-1}\); \(\mathrm{i}^2 \text { is }-1]\))
3. complex number if \((a \neq 0, b \neq 0)\)

Examples:

Real Numbers Examples : \(3,8,-2,0,9,13\)
Imaginary Numbers Examples: 3i, 7i, -2i, 8i, \(\sqrt{i}\)
Complex Numbers Examples: \(3+7 \mathrm{i}, 7- 6 \mathrm{i}, 0+20 \mathrm{i}=20 \mathrm{i}, 2+\mathrm{i}\).

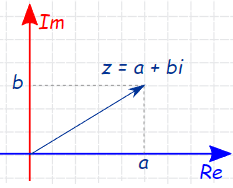
In a complex plane (complex number Z as a vector) it looks like this:

What are Real Numbers?

Any number which is present in a number system such as zero, positive, negative, integer, rational, irrational, fractions, etc. are real numbers. It is represented as \(\operatorname{Re}()\). For example: \(12,-25,0,1 / 3,2.6\), etc., are all real numbers.

What are Imaginary Numbers?

The numbers which are not real are imaginary numbers. When we square an imaginary number, it gives a negative result. It is represented as \(\operatorname{Im}()\). Example: \(\sqrt{-2}\), \(\sqrt{-5}\), \(\sqrt{-13}\) are all imaginary numbers.

The complex numbers were introduced to solve the equation \(x^2+1=0\). The roots of the equation are of form \(x=\) \(\pm \sqrt{-1}\) and no real roots exist. Thus, with the introduction of complex numbers, we have Imaginary roots. We denote \(\sqrt{-1}\) with the symbol ‘i’, which denotes lota (Imaginary number).

For the complex number \(z=a+i b, a\) is called the real part, denoted by \(\operatorname{Re} (z)\) and \(b\) is called the imaginary part denoted by \(\operatorname{Im} (z)\) of the complex number \(z\). For example, if \(z=2+i 5\), then \(\operatorname{Re} (z)=2\) and \(\operatorname{Im} (z)=5\).

Two complex numbers \(z_1=a+i b\) and \(z_2=c+i d\) are equal if \(a=c\) and \(b=d\).

Graphical representation

The graph below shows the representation of complex numbers along the axes. Here we can see, the \(x\)-axis represents real part, and \(y\) represents the imaginary part.

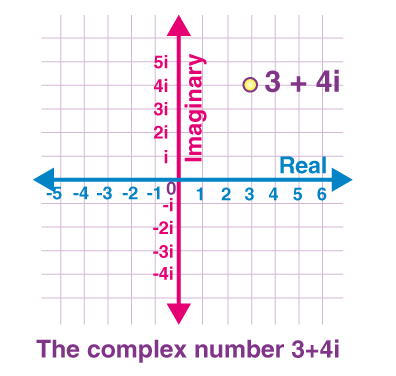
\(\text { Let us plot a graph of complex number } 3+4 i  \text {as shown below}\)

Is Zero(0) a complex Number?

As we know, 0 is a real number. And real numbers are part of complex numbers. Therefore, 0 is also a complex number and can be represented as \(0+0 i\). 0 can be considered purely real and purely imaginary.

Example 1: \(\sin ^{-1}\left(\frac{z-1}{i}\right)\), where \(z\) is non-real, can be the
angle of a triangle if angle of a triangle, if
(a) \(\operatorname{Re}(z)=1, \operatorname{Im}(z)=2\)
(b) \(\operatorname{Re}(z)=1,-1 \leq \operatorname{Im}(z) \leq 1\)
(c) \(\operatorname{Re}(z)+\operatorname{Im}(z)=0\)
(d) none of these

Solution: Let \(z=x+i y\). Then,
\(
\frac{z-1}{i}=\frac{(x-1)+i y}{i}=y-(x-1) i
\)
This will be real, if \(x-1=0\) i.e. \(x=1\) Also,
\(
-1 \leq \frac{z-1}{i} \leq 1 \Rightarrow-1 \leq y \leq 1
\)
Thus. \(\operatorname{Re}(z)=1\) and \(-1 \leq \operatorname{Im}(z) \leq 1\).

Example 2: If sum of square of roots of the equation \(x^2+(p+i q) x+3 i=0\) is 8 then find the value of \(p\) and \(q\), where \(p\) and \(q\) are real.

Solution: Let the roots are \(\alpha, \beta\)
We have \(\alpha+\beta=-(p+i q) ; \alpha \beta=3 \mathrm{i}\)
Given: \(\alpha^2+\beta^2=8\)
\(
\begin{aligned}
& \Rightarrow \quad(\alpha+\beta)^2-2 \alpha \beta=8 \\
& \Rightarrow \quad(p+i q)^2-6 i=8 \\
& \Rightarrow \quad p^2-q^2+i(2 p q-6)=8 \\
& \Rightarrow \quad p^2-q^2=8 \text { and } p q=3 \\
& \Rightarrow \quad p=3 \text { and } q=1 \text { or } p=-3 \text { and } q=-1
\end{aligned}
\)

Example 3: If \(z=x+i y, z^{1 / 3}=a-i b\) and \(x / a-y / b=k\left(a^2-b^2\right)\), then find the value of \(\boldsymbol{k}\).

Solution: \(\quad(x+i y)^{1 / 3}=a-i b\)
\(
\begin{aligned}
\Rightarrow & x+i y=(a-i b)^3 \\
& =\left(a^3-3 a b^2\right)+i\left(b^3-3 a^2 b\right) \\
\Rightarrow & x=a^3-3 a b^2, y=b^3-3 a^2 b \\
\Rightarrow & \frac{x}{a}=a^2-3 b^2 \text { and } \frac{y}{b}=b^2-3 a^2 \\
\Rightarrow & \frac{x}{a}-\frac{y}{b}=a^2-3 b^2-b^2+3 a^2=4\left(a^2-b^2\right) \\
\therefore & k=4
\end{aligned}
\)

Example 4: Let \(z\) be a complex number satisfying the equation \(z^2-(3+i) z+m+2 i=0\), where \(m \in R\). Suppose the equation has a real root. Then find the non-real root.

Solution: Let \(\alpha\) be the real root. Then,
\(
\begin{aligned}
& \alpha^2-(3+i) \alpha+m+2 i=0 \\
\Rightarrow & \left(\alpha^2-3 \alpha+m\right)+i(2-\alpha)=0 \\
\Rightarrow & \alpha=2 \Rightarrow 4-6+m=0 \Rightarrow m=2
\end{aligned}
\)
Product of the roots is \(2(1+i)\) with one root as 2. Hence the non-real root is \(1+i\).

Explanation: Step 1: Substitute Real Root and Separate Components
Assume the equation has a real root, \(x\). Substitute \(z=x\) into the equation and separate the real and imaginary parts to form a system of equations.
\(
\begin{gathered}
x^2-(3+i) x+m+2 i=0 \\
\left(x^2-3 x+m\right)+i(-x+2)=0
\end{gathered}
\)
Step 2: Solve for the Real Root and Parameter \(\mathbf{m}\)
Set both the real and imaginary parts to zero to find the value of the real root \(x\) and the parameter \(m\).
For the imaginary part: \(-x+2=0 \Longrightarrow x=2\).
For the real part: \(x^2-3 x+m=0\).
Substitute \(x=2:(2)^2-3(2)+m=0 \Longrightarrow 4-6+m=0 \Longrightarrow m=2\).
The real root is 2, and the value of \(m\) is 2.
Step 3: Find the Non-Real Root
Use the sum of roots formula for a quadratic equation \(a z^2+b z+c=0\), which states that the sum of the roots \(z_1+z_2=-\frac{b}{a}\).
The equation is \(z^2-(3+i) z+2+2 i=0\).
The real root \(z_1=2\).
\(
\begin{gathered}
z_1+z_2=-(-(3+i)) / 1=3+i \\
2+z_2=3+i \\
z_2=3+i-2 \\
z_2=1+i
\end{gathered}
\)