3.8 NCERT Exercise Q & A

Exercise 3.1

Q1. Find the radian measures corresponding to the following degree measures:
(i) \(25^{\circ}\)
(ii) \(-47^{\circ} 30^{\prime}\)
(iii) \(240^{\circ}\)
(iv) \(520^{\circ}\)

Answer: We know that \(180^{\circ}=\pi\) radian Therefore,
(i)
\(
\begin{aligned}
25^{\circ}=\frac{\pi}{180} \times & 25 \text { radian } \\
& =\frac{5 \pi}{36} \text { radian }
\end{aligned}
\)

(ii)
\(
\begin{aligned}
-47^{\circ} 30^{\prime}= & -\left(47 \frac{1}{2}\right)^{\circ}=-\left(\frac{95}{2}\right)^{\circ} \\
-\left(\frac{95}{2}\right)^{\circ}= & \frac{\pi}{180} \times-\left(\frac{95}{2}\right) {\text {radian }} \\
& =-\frac{19 \pi}{72} \text { radian }
\end{aligned}
\)

(iii)
\(
\begin{aligned}
245^{\circ}=\frac{\pi}{180} & \times 240 \text { radian } \\
& =\frac{3 \pi}{4} \text { radian }
\end{aligned}
\)

(iv)
\(
\begin{aligned}
520^{\circ}=\frac{\pi}{180} & \times 520 \text { radian } \\
& =\frac{26 \pi}{9} \text { radian }
\end{aligned}
\)

Q2. Find the degree measures corresponding to the following radian measures (Use \(\pi=\frac{22}{7}\) ).
(i) \(\frac{11}{16}\)
(ii) -4
(iii) \(\frac{5 \pi}{3}\)
(iv) \(\frac{7 \pi}{6}\)

Answer: We know that \(180^{\circ}=\pi\) radian Therefore,
(i) \(\frac{11}{16}\) radian \(=\frac{180^{\circ}}{\pi} \times \frac{11}{16}\)
\(
\begin{aligned}
& =180 \times \frac{7}{22} \times \frac{11}{16} \mathrm{deg} \\
& =\frac{315}{8} \mathrm{deg} \\
& =39 \frac{3}{8} \mathrm{deg} \\
& =39 \mathrm{deg}+\frac{3}{8} \times 60 \mathrm{~min} \left[\because 1^{\circ}=60^{\prime}\right] \\
& =39 \mathrm{deg}+22 \frac{1}{2} \mathrm{~min} \\
& =39 \mathrm{deg}+22 \mathrm{~min}+\frac{60}{2} \mathrm{sec} \left[\because 1^{\prime}=60^{\prime \prime}\right] \\
& =39^{\circ} 22^{\prime} 30^{\prime \prime}
\end{aligned}
\)

(ii)
\(
\begin{aligned}
-4 \text { radian } & =\frac{180^{\circ}}{\pi} \times(-4) \\
& =180 \times \frac{7}{22} \times(-4) \mathrm{deg} \\
& =-\frac{2520}{11} \mathrm{deg} \\
& =-229 \frac{1}{11} \mathrm{deg} \\
& =-229 \mathrm{deg}+\frac{60}{11} \mathrm{~min} \left[\because 1^{\circ}=60^{\prime}\right] \\
& =-22 \mathrm{deg}+5 \frac{5}{11} \mathrm{~min} \\
& =-22 \mathrm{deg}+5 \mathrm{~min}+\frac{5}{11} \times 60 \mathrm{sec} \left[\because 1^{\prime}=60^n\right] \\
& =-22^{\circ} 5^{\prime} 27^{\prime \prime}
\end{aligned}
\)

(iii)
\(
\begin{aligned}
\frac{5 \pi}{3} \text { radian } & =\frac{180^{\circ}}{\pi} \times \frac{5 \pi}{3} \\
& =300^{\circ}
\end{aligned}
\)

(iv) \(\frac{7 \pi}{6}\) radian \(=\frac{180^{\circ}}{\pi} \times \frac{7 \pi}{6}=210^{\circ}\)

Q3. A wheel makes 360 revolutions in one minute. Through how many radians does it turn in one second?

Answer: A wheel makes 360 revolutions in 1 minute (60 seconds)
Therefore, the Number of revolutions made by the wheel in 1 second \(=\frac{360}{60}=6\)
In one complete revolution, the wheel turns an angle of \(2 \pi\) radians
Hence, in 6 complete revolutions, it will turn an angle of \(6 \times 2 \pi=12 \pi\) radians
Thus, in one second, the wheel turns an angle of \(12 \pi\) radians.

Q4. Find the degree measure of the angle subtended at the centre of a circle of radius 100 cm by an arc of length \(22 \mathrm{~cm} .\left(\right.\) Use \(\left.\pi=\frac{22}{7}\right)\)

Answer: As we know that if in a circle of radius \(r\), an arc of length \(l\) subtends an angle of \(\theta\) radians,
Then \(l=r \theta\)
Therefore, \(\theta=\frac{l}{r}\) radian
\(
\begin{aligned}
\theta & =\frac{22 \mathrm{~cm}}{100 \mathrm{~cm}} \text { radian } \\
\theta & =\frac{11}{50} \times \frac{180}{\pi} \mathrm{deg} \\
& =\frac{11}{50} \times 180 \times \frac{7}{22} \mathrm{deg} \\
& =\frac{63}{5} \mathrm{deg} \\
& =12 \frac{3}{5} \mathrm{deg} \\
& =12 \mathrm{deg}+\frac{3}{5} \times 60 \mathrm{~min} \left[\because 1^{\circ}=60^{\prime}\right] \\
& =12^{\circ} 36^{\prime}
\end{aligned}
\)
Thus, the required angle is \(12^{\circ} 36^{\prime}\)

Q5. In a circle of diameter 40 cm, the length of a chord is 20 cm. Find the length of the minor arc of the chord.

Answer: Diameter of the circle \(=40 \mathrm{~cm}\)
Therefore, Radius of the circle \(r=\frac{40 \mathrm{~cm}}{2}=20 \mathrm{~cm}\)
Let \(A B\) be a chord of length 20 cm of the circle.
\(
\begin{aligned}
& \text { In } \triangle A O B \\
& A B=20 \mathrm{~cm} \\
& O A=O B=r=20 \mathrm{~cm}
\end{aligned}
\)

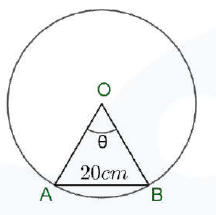
Hence, \(\triangle A O B\) is an equilateral triangle
Thus, \(\theta=60^{\circ}\) or \(\theta=\frac{\pi}{3}\) radian
As we know that if in a circle of radius \(r\), an arc of length \(l\) subtends an angle of \(\theta\) radians, Then \(l=r \theta\)
Therefore, \(l=r \theta\)
\(
\begin{aligned}
&\begin{aligned}
A B & =20 \mathrm{~cm} \times \frac{\pi}{3} \\
& =\frac{20 \pi}{3} \mathrm{~cm}
\end{aligned}\\
&\text { Hence, the length of the minor arc of the chord is } \frac{20 \pi}{3} \mathrm{~cm} \text {. }
\end{aligned}
\)

Q6. If in two circles, arcs of the same length subtend angles \(60^{\circ}\) and \(75^{\circ}\) at the centre, find the ratio of their radii.

Answer: Let the radii of the two circles be \(r\) and \(R\).
Let an arc of length \(l\) subtend an angle of \(60^{\circ}\) at the centre of the circle of radius \(r\), and \(75^{\circ}\) at the centre of the circle of radius \(R\).
Now, \(60^{\circ}=\frac{\pi}{3} \text { radian and } 75^{\circ}=\frac{5 \pi}{12} \text { radian }\)
As we know that if in a circle of radius \(r\), an arc of length \(l\) subtends an angle of \(\theta\) radians, Then \(l=r \theta\)
Therefore,
\(
\begin{aligned}
l & =r \times \frac{\pi}{3} \\
& =\frac{\pi r}{3}
\end{aligned}
\)
and
\(
\begin{aligned}
l & =R \times \frac{5 \pi}{12} \\
& =\frac{5 \pi R}{12}
\end{aligned}
\)
Thus,
\(
\begin{aligned}
& \frac{\pi r}{3}=\frac{5 \pi R}{12} \\
& \frac{r}{R}=\frac{5}{4} \\
& r: R=5: 4
\end{aligned}
\)
Hence, the ratio of their radii is \(5: 4\).

Q7. Find the angle in radian through which a pendulum swings if its length is 75 cm and the tip describes an arc of length
(i) 10 cm
(ii) 15 cm
(iii) 21 cm

Answer: As we know that if in a circle of radius \(r\), an arc of length \(l\) subtends an angle of \(\theta\) radians, Then \(l=r \theta\)
(i) Radius, \(r=75 \mathrm{~cm}\) and length of the arc, \(l=10 \mathrm{~cm}\)
\(
\begin{aligned}
\theta & =\frac{l}{r} \\
& =\frac{10 \mathrm{~cm}}{75 \mathrm{~cm}} \\
& =\frac{2}{15}
\end{aligned}
\)
Thus, \(\theta=\frac{2}{15}\) radian

(ii) Radius, \(r=75 \mathrm{~cm}\) and length of the arc, \(l=15 \mathrm{~cm}\)
\(
\begin{aligned}
\theta & =\frac{l}{r} \\
& =\frac{15 \mathrm{~cm}}{75 \mathrm{~cm}} \\
& =\frac{1}{5}
\end{aligned}
\)
Thus, \(\theta=\frac{1}{5}\) radian

(iii) Radius, \(r=75 \mathrm{~cm}\) and length of the arc, \(l=21 \mathrm{~cm}\)
\(
\begin{aligned}
\theta & =\frac{l}{r} \\
& =\frac{21 \mathrm{~cm}}{75 \mathrm{~cm}} \\
& =\frac{7}{25}
\end{aligned}
\)
Thus, \(\theta=\frac{7}{25}\) radian

Exercise 3.2

Find the values of the other five trigonometric functions in Exercises Q1 to Q5.

Q1. \(\cos x=-\frac{1}{2}, x\) lies in third quadrant.

Answer: As we know that
\(
\begin{aligned}
\sec x & =\frac{1}{\cos x} \\
& =\frac{1}{\left(-\frac{1}{2}\right)} \\
& =-2
\end{aligned}
\)
Now, \(\sin ^2 x+\cos ^2 x=1\)
\(
\begin{aligned}
\sin ^2 x & =1-\cos ^2 x \\
\sin x & = \pm \sqrt{1-\cos ^2 x} \\
& = \pm \sqrt{1-\left(-\frac{1}{2}\right)^2} \\
& = \pm \sqrt{1-\frac{1}{4}}
\end{aligned}
\)
\(
\begin{aligned}
& = \pm \sqrt{\frac{3}{4}} \\
& = \pm \frac{\sqrt{3}}{2}
\end{aligned}
\)
Since, \(x\) lies in the third quadrant, the value of \(\sin x\) will be negative.
Therefore,
\(
\sin x=-\frac{\sqrt{3}}{2}
\)
Now,
\(
\begin{aligned}
\operatorname{cosec} x & =\frac{1}{\sin x} \\
& =\frac{1}{\left(-\frac{\sqrt{3}}{2}\right)} \\
& =-\frac{2}{\sqrt{3}}
\end{aligned}
\)
Now,
\(
\begin{aligned}
&\begin{aligned}
\tan x & =\frac{\sin x}{\cos x} \\
& =\frac{\left(-\frac{1}{2}\right)}{\left(-\frac{\sqrt{3}}{2}\right)} \\
& =\sqrt{3}
\end{aligned}\\
&\text { Now, }\\
&\begin{aligned}
\cot x & =\frac{1}{\tan x} \\
& =\frac{1}{\sqrt{3}}
\end{aligned}
\end{aligned}
\)
\(
\text { Hence, } \sin x=-\frac{\sqrt{3}}{2}, \operatorname{cosec} x=-\frac{2}{\sqrt{3}}, \sec x=-2, \tan x=\sqrt{3} \text {, and } \cot x=\frac{1}{\sqrt{3}}
\)

Q2. \(\sin x=\frac{3}{5}, x\) lies in second quadrant.

Answer: As we know that
\(
\begin{aligned}
\operatorname{cosec} x & =\frac{1}{\sin x} \\
& =\frac{1}{\left(\frac{3}{5}\right)} \\
& =\frac{5}{3}
\end{aligned}
\)
Now, \(\sin ^2 x+\cos ^2 x=1\)
\(
\begin{aligned}
\cos ^2 x & =1-\sin ^2 x \\
\cos x & = \pm \sqrt{1-\sin ^2 x} \\
& = \pm \sqrt{1-\left(\frac{3}{5}\right)^2} \\
& = \pm \sqrt{1-\frac{9}{25}} \\
& = \pm \sqrt{\frac{16}{25}} \\
& = \pm \frac{4}{5}
\end{aligned}
\)
Since, \(x\) lies in the second quadrant, the value of \(\cos x\) will be negative. Therefore,
\(
\cos x=-\frac{4}{5}
\)
Now,
\(
\begin{aligned}
\sec x & =\frac{1}{\cos x} \\
& =\frac{1}{\left(-\frac{4}{5}\right)} \\
& =-\frac{5}{4}
\end{aligned}
\)
Now,
\(
\begin{aligned}
\tan x & =\frac{\sin x}{\cos x} \\
& =\frac{\left(\frac{3}{5}\right)}{\left(-\frac{4}{5}\right)} \\
& =-\frac{3}{4}
\end{aligned}
\)
Now,
\(
\begin{aligned}
\cot x & =\frac{1}{\tan x} \\
& =\frac{1}{\left(-\frac{3}{4}\right)} \\
& =-\frac{4}{3}
\end{aligned}
\)
Hence, \(\operatorname{cosec} x=\frac{5}{3}, \quad \cos x=-\frac{4}{5}, \quad \sec x=-\frac{5}{4}, \quad \tan x=-\frac{3}{4}, \text { and } \cot x=-\frac{4}{3}\)

Q3. \(\cot x=\frac{3}{4}, x\) lies in third quadrant.

Answer: As we know that
\(
\begin{aligned}
\tan x & =\frac{1}{\cot x} \\
& =\frac{1}{\left(\frac{3}{4}\right)} \\
& =\frac{4}{3}
\end{aligned}
\)
Now, \(1+\tan ^2 x=\sec ^2 x\)
\(
\begin{aligned}
\sec x & = \pm \sqrt{1+\tan ^2 x} \\
& = \pm \sqrt{1+\left(\frac{4}{3}\right)^2} \\
& = \pm \sqrt{1+\frac{16}{9}} \\
& = \pm \sqrt{\frac{25}{9}} \\
& = \pm \frac{5}{3}
\end{aligned}
\)
Since, \(x\) lies in the third quadrant, the value of \(\sec x\) will be negative. Therefore,
\(
\sec x=-\frac{5}{3}
\)
Now,
\(
\begin{aligned}
\cos x & =\frac{1}{\sec x} \\
& =\frac{1}{\left(-\frac{5}{3}\right)} \\
& =-\frac{3}{5}
\end{aligned}
\)
Now,
\(
\begin{aligned}
\tan x & =\frac{\sin x}{\cos x} \\
\sin x & =\tan x \cos x \\
& =\left(\frac{4}{3}\right) \times\left(-\frac{3}{5}\right) \\
& =-\frac{4}{5}
\end{aligned}
\)
Now,
\(
\begin{aligned}
\operatorname{cosec} x & =\frac{1}{\sin x} \\
& =\frac{1}{\left(-\frac{4}{5}\right)} \\
& =-\frac{5}{4}
\end{aligned}
\)
Hence, \(\sin x=-\frac{4}{5}, \quad \operatorname{cosec} x=-\frac{5}{4}, \quad \cos x=-\frac{3}{5}, \quad \sec x=-\frac{5}{3}, \text { and } \tan x=\frac{4}{3}\)

Q4. \(\sec x=\frac{13}{5}, x\) lies in fourth quadrant.

Answer: As we know that
\(
\begin{aligned}
\cos x & =\frac{1}{\sec x} \\
& =\frac{1}{\left(\frac{13}{5}\right)} \\
& =\frac{5}{13}
\end{aligned}
\)
Now, \(\sin ^2 x+\cos ^2 x=1\)
\(
\begin{aligned}
\sin ^2 x & =1-\cos ^2 x \\
\sin x & = \pm \sqrt{1-\cos ^2 x} \\
& = \pm \sqrt{1-\left(\frac{5}{13}\right)^2} \\
& = \pm \sqrt{1-\frac{25}{169}} \\
& = \pm \sqrt{\frac{144}{169}} \\
& = \pm \frac{12}{13}
\end{aligned}
\)
Since, \(x\) lies in the fourth quadrant, the value of \(\sin x\) will be negative.
Therefore,
\(
\sin x=-\frac{12}{13}
\)
Now,
\(
\begin{aligned}
\operatorname{cosec} x & =\frac{1}{\sin x} \\
& =\frac{1}{\left(-\frac{12}{13}\right)} \\
& =-\frac{13}{12}
\end{aligned}
\)
Now,
\(
\begin{aligned}
\tan x & =\frac{\sin x}{\cos x} \\
& =\frac{\left(-\frac{12}{13}\right)}{\left(\frac{5}{13}\right)} \\
& =-\frac{12}{5}
\end{aligned}
\)
Now,
\(
\begin{aligned}
\cot x & =\frac{1}{\tan x} \\
& =\frac{1}{\left(-\frac{12}{5}\right)} \\
& =-\frac{5}{12}
\end{aligned}
\)
Hence, \(\sin x=-\frac{12}{13}, \quad \operatorname{cosec} x=-\frac{13}{12}, \quad \cos x=\frac{5}{13}, \quad \tan x=-\frac{12}{5}\), and \(\cot x=-\frac{5}{12}\)

Q5. \(\tan x=-\frac{5}{12}, x\) lies in second quadrant.

Answer: As we know that
\(
\begin{aligned}
\cot x & =\frac{1}{\tan x} \\
& =\frac{1}{\left(-\frac{5}{12}\right)} \\
& =-\frac{12}{5}
\end{aligned}
\)
Now, \(1+\tan ^2 x=\sec ^2 x\)
\(
\begin{aligned}
\sec x & = \pm \sqrt{1+\tan ^2 x} \\
& = \pm \sqrt{1+\left(-\frac{5}{12}\right)^2} \\
& = \pm \sqrt{1+\frac{25}{144}} \\
& = \pm \sqrt{\frac{169}{144}} \\
& = \pm \frac{13}{12}
\end{aligned}
\)
Since, \(x\) lies in the second quadrant, the value of \(\sec x\) will be negative. Therefore,
\(
\sec x=-\frac{13}{12}
\)
Now,
\(
\begin{aligned}
\cos x & =\frac{1}{\sec x} \\
& =\frac{1}{\left(-\frac{13}{12}\right)} \\
& =-\frac{12}{13}
\end{aligned}
\)
Now,
\(
\begin{aligned}
\tan x & =\frac{\sin x}{\cos x} \\
\sin x & =\tan x \cos x \\
& =\left(-\frac{5}{12}\right) \times\left(-\frac{12}{13}\right) \\
& =\frac{5}{13}
\end{aligned}
\)
Now,
\(
\begin{aligned}
\operatorname{cosec} x & =\frac{1}{\sin x} \\
& =\frac{1}{\left(\frac{5}{13}\right)} \\
& =\frac{13}{5}
\end{aligned}
\)
Hence, \(\sin x=\frac{5}{13}, \operatorname{cosec} x=\frac{13}{5}, \cos x=-\frac{12}{13}, \sec x=-\frac{13}{12}\), and \(\cot x=-\frac{12}{5}\)

Find the values of the trigonometric functions in Exercises Q6 to Q10.

Q6. \(\sin 765^{\circ}\)

Answer: It is known that the value of \(\sin x\) repeat after an interval of 2 n or \(360^{\circ}\).
Therefore,
\(
\begin{aligned}
\sin 765^{\circ} & =\sin \left(2 \times 360^{\circ}+45^{\circ}\right) \\
& =\sin 45^{\circ} \\
& =\frac{1}{\sqrt{2}}
\end{aligned}
\)

Q7. \(\operatorname{cosec}\left(-1410^{\circ}\right)\)

Answer: It is known that the value of \(\sin x\) repeat after an interval of 2 n or \(360^{\circ}\). Therefore,
\(
\begin{aligned}
\operatorname{cosec}\left(-1410^{\circ}\right) & =\operatorname{cosec}\left(4 \times 360^{\circ}-1410^{\circ}\right) \\
& =\operatorname{cosec}\left(1440^{\circ}-1410^{\circ}\right) \\
& =\operatorname{cosec} 30^{\circ} \\
& =2
\end{aligned}
\)

Q8. \(\tan \frac{19 \pi}{3}\)

Answer: It is known that the value of \(\tan x\) repeat after an interval of n or \(180^{\circ}\).
Therefore,
\(
\begin{aligned}
\tan \frac{19 \pi}{3} & =\tan 6 \frac{1}{3} \pi \\
& =\tan \left(6 \pi+\frac{1}{3} \pi\right) \\
& =\tan \frac{\pi}{3} \\
& =\tan 60^{\circ} \\
& =\sqrt{3}
\end{aligned}
\)

Q9. \(\sin \left(-\frac{11 \pi}{3}\right)\)

Answer: It is known that the value of \(\sin x\) repeat after an interval of 2 n or \(360^{\circ}\).
Therefore,
\(
\begin{aligned}
\sin \left(-\frac{11 \pi}{3}\right) & =\sin \left(2 \times 2 \pi-\frac{11 \pi}{3}\right) \\
& =\sin \frac{\pi}{3} \\
& =\sin 60^{\circ} \\
& =\frac{\sqrt{3}}{2}
\end{aligned}
\)

Q10. \(\cot \left(-\frac{15 \pi}{4}\right)\)

Answer: It is known that the value of \(\cos x\) repeat after an interval of n or \(180^{\circ}\). Therefore,
\(
\begin{aligned}
\cot \left(-\frac{15 \pi}{4}\right) & =\cot \left(4 \pi-\frac{15 \pi}{4}\right) \\
& =\cot \frac{\pi}{4} \\
& =\cot 45^{\circ} \\
& =1
\end{aligned}
\)

Exercise 3.3

Q1. \(\sin ^2 \frac{\pi}{6}+\cos ^2 \frac{\pi}{3}-\tan ^2 \frac{\pi}{4}=-\frac{1}{2}\)

Answer:
\(
\begin{aligned}
\text { LHS } & =\sin ^2 \frac{\pi}{6}+\cos ^2 \frac{\pi}{3}-\tan ^2 \frac{\pi}{4} \\
& =\left(\frac{1}{2}\right)^2+\left(\frac{1}{2}\right)^2-(1)^2 \\
& =\frac{1}{4}+\frac{1}{4}-1 \\
& =\frac{1+1-4}{4} \\
& =\frac{-2}{4} \\
& =-\frac{1}{2}=\text { RHS }
\end{aligned}
\)

Q2. \(2 \sin ^2 \frac{\pi}{6}+\operatorname{cosec}^2 \frac{7 \pi}{6} \cos ^2 \frac{\pi}{3}=\frac{3}{2}\)

Answer:
\(
\begin{aligned}
\text { LHS } & =2 \sin ^2 \frac{\pi}{6}+\operatorname{cosec}^2 \frac{7 \pi}{6} \cos ^2 \frac{\pi}{3} \\
& =2\left(\frac{1}{2}\right)^2+\operatorname{cosec}^2\left(\pi+\frac{\pi}{6}\right) \times\left(\frac{1}{2}\right)^2 \\
& =2 \times \frac{1}{4}+\left(-\operatorname{cosec} \frac{\pi}{6}\right)^2 \times \frac{1}{4} \\
& =\frac{1}{2}+(-2)^2 \times \frac{1}{4} \\
& =\frac{1}{2}+1 \\
& =\frac{1+2}{2} \\
& =\frac{3}{2}=\text { RHS }
\end{aligned}
\)

Q3. \(\cot ^2 \frac{\pi}{6}+\operatorname{cosec}^2 \frac{5 \pi}{6}+3 \tan ^2 \frac{\pi}{6}=6\)

Answer:
\(
\begin{aligned}
L H S & =\cot ^2 \frac{\pi}{6}+\operatorname{cosec} \frac{5 \pi}{6}+3 \tan ^2 \frac{\pi}{6} \\
& =(\sqrt{3})^2+\operatorname{cosec}\left(\pi-\frac{\pi}{6}\right)+3\left(\frac{1}{\sqrt{3}}\right)^2 \\
& =3+\operatorname{cosec} \frac{\pi}{6}+3 \times \frac{1}{3} \\
& =3+2+1 \\
& =6=\text { RHS }
\end{aligned}
\)

Q4. \(2 \sin ^2 \frac{3 \pi}{4}+2 \cos ^2 \frac{\pi}{4}+2 \sec ^2 \frac{\pi}{3}=10\)

Answer:
\(
\begin{aligned}
L H S & =2 \sin ^2 \frac{3 \pi}{4}+2 \cos ^2 \frac{\pi}{4}+2 \sec ^2 \frac{\pi}{3} \\
& =2 \sin ^2\left(\pi-\frac{\pi}{4}\right)+2 \times\left(\frac{1}{\sqrt{2}}\right)^2+2 \times(2)^2 \\
& =2 \sin ^2 \frac{\pi}{4}+2 \times \frac{1}{2}+2 \times 4 \\
& =2 \times\left(\frac{1}{\sqrt{2}}\right)^2+1+8 \\
& =1+9 \\
& =10=\text { RHS }
\end{aligned}
\)

Q5. Find the value of:
(i) \(\sin 75^{\circ}\)
(ii) \(\tan 15^{\circ}\)

Answer: (i) \(\quad \sin 75^{\circ}\)
\(
\begin{aligned}
\sin 75^{\circ} & =\sin \left(45^{\circ}+30^{\circ}\right) \\
& =\sin 45^{\circ} \cos 30^{\circ}+\cos 45^{\circ} \sin 30^{\circ} [\because \sin (x+y)=\sin x \cos y+\cos x \sin y] \\
& =\left(\frac{1}{\sqrt{2}}\right) \times\left(\frac{\sqrt{3}}{2}\right)+\left(\frac{1}{\sqrt{2}}\right) \times\left(\frac{1}{2}\right) \\
& =\frac{\sqrt{3}}{2 \sqrt{2}}+\frac{1}{2 \sqrt{2}} \\
& =\frac{\sqrt{3}+1}{2 \sqrt{2}}
\end{aligned}
\)

(ii) \(\tan 15^{\circ}\)
\(
\begin{aligned}
\tan 15^{\circ} & =\tan \left(45^{\circ}-30^{\circ}\right) \\
& =\frac{\tan 45^{\circ}-\tan 30^{\circ}}{1+\tan 45^{\circ} \tan 30^{\circ}} \left[\because \tan (x-y)=\frac{\tan x-\tan y}{1+\tan x \tan y}\right] \\
& =\frac{1-\frac{1}{\sqrt{3}}}{1+1 \times \frac{1}{\sqrt{3}}} \\
& =\frac{\frac{\sqrt{3}-1}{\sqrt{3}}}{\frac{\sqrt{3}+1}{\sqrt{3}}} \\
& =\frac{\sqrt{3}-1}{\sqrt{3}+1} \\
& =\frac{\sqrt{3}-1}{\sqrt{3}+1} \times \frac{\sqrt{3}-1}{\sqrt{3}-1} \\
& =\frac{(\sqrt{3}-1)^2}{3-1} \\
& =\frac{3+1-2 \sqrt{3}}{2} \\
& =\frac{2(2-\sqrt{3})}{2} \\
& =2-\sqrt{3}
\end{aligned}
\)

Prove the following

Q6. \(\cos \left(\frac{\pi}{4}-x\right) \cos \left(\frac{\pi}{4}-y\right)-\sin \left(\frac{\pi}{4}-x\right) \sin \left(\frac{\pi}{4}-y\right)=\sin (x+y)\)

Answer:
\(
\begin{aligned}
\text { LHS } & =\cos \left(\frac{\pi}{4}-x\right) \cos \left(\frac{\pi}{4}-y\right)-\sin \left(\frac{\pi}{4}-x\right) \sin \left(\frac{\pi}{4}-y\right) \\
& =\frac{1}{2}\left[2 \cos \left(\frac{\pi}{4}-x\right) \cos \left(\frac{\pi}{4}-y\right)\right]+\frac{1}{2}\left[-2 \sin \left(\frac{\pi}{4}-x\right) \sin \left(\frac{\pi}{4}-y\right)\right] \\
& =\left(\frac{1}{2}\left[\cos \left\{\left(\frac{\pi}{4}-x\right)+\left(\frac{\pi}{4}-y\right)\right\}+\cos \left\{\left(\frac{\pi}{4}-x\right)-\left(\frac{\pi}{4}-y\right)\right\}\right]\right. \\
& \left.\quad+\frac{1}{2}\left[\cos \left\{\left(\frac{\pi}{4}-x\right)+\left(\frac{\pi}{4}-y\right)\right\}-\cos \left\{\left(\frac{\pi}{4}-x\right)-\left(\frac{\pi}{4}-y\right)\right\}\right]\right)
\end{aligned}
\)
\(
\left[\begin{array}{l}
\because 2 \cos A \cos B=\cos (A+B)+\cos (A-B) \\
-2 \sin A \sin B=\cos (A+B)-\cos (A-B)
\end{array}\right]
\)
\(
\begin{aligned}
& =\sin (x+y)=\text { RHS } \\
& =\left(\begin{array}{r}
\frac{1}{2}\left[\cos \left\{\frac{\pi}{4}-x+\frac{\pi}{4}-y\right\}+\cos \left\{\frac{\pi}{4}-x-\frac{\pi}{4}+y\right\}\right] \\
+\frac{1}{2}\left[\cos \left\{\frac{\pi}{4}-x+\frac{\pi}{4}-y\right\}-\cos \left\{\frac{\pi}{4}-x-\frac{\pi}{4}+y\right\}\right]
\end{array}\right. \\
& =\frac{1}{2}\left[\cos \left\{\frac{\pi}{2}-(x+y)\right\}+\cos \{-(x-y)\}+\cos \left\{\frac{\pi}{2}-(x+y)\right\}-\cos \{-(x-y)\}\right] \\
& =\frac{1}{2}\left[2 \cos \left\{\frac{\pi}{2}-(x+y)\right\}\right]
\end{aligned}
\)
\(
\begin{aligned}
& =\sin (x+y) \quad\left[\because \cos \left(\frac{\pi}{2}-A\right)=\sin A\right] \\
& =\text { RHS }
\end{aligned}
\)

Q7. \(\frac{\tan \left(\frac{\pi}{4}+x\right)}{\tan \left(\frac{\pi}{4}-x\right)}=\left(\frac{1+\tan x}{1-\tan x}\right)^2\)

Answer:
\(
\begin{aligned}
\text { LHS } & =\frac{\tan \left(\frac{\pi}{4}+x\right)}{\tan \left(\frac{\pi}{4}-x\right)} \\
& =\frac{\left(\frac{\tan \frac{\pi}{4}+\tan x}{1-\tan \frac{\pi}{4} \tan x}\right)}{\left(\frac{\tan \frac{\pi}{4}-\tan x}{1+\tan \frac{\pi}{4} \tan x}\right)} \left[\begin{array}{l}
\because \tan (A+B)=\frac{\tan A+\tan B}{1-\tan A \tan B} \\
\& \tan (A-B)=\frac{\tan A-\tan B}{1+\tan A \tan B}
\end{array}\right] \\
& =\frac{\left(\frac{1+\tan x}{1-\tan x}\right)}{\left(\frac{1-\tan x}{1+\tan x}\right)} \\
& =\left(\frac{1+\tan x}{1-\tan x}\right) \times\left(\frac{1+\tan x}{1-\tan x}\right) \\
& =\left(\frac{1+\tan x}{1-\tan x}\right)^2 \\
& =\text { RHS }
\end{aligned}
\)

Q8. \(\frac{\cos (\pi+x) \cos (-x)}{\sin (\pi-x) \cos \left(\frac{\pi}{2}+x\right)}=\cot ^2 x\)

Answer:
\(
\begin{aligned}
\text { LHS } & =\frac{\cos (\pi+x) \cos (-x)}{\sin (\pi-x) \cos \left(\frac{\pi}{2}+x\right)} \\
& =\frac{(-\cos x) \times(\cos x)}{(\sin x) \times(-\sin x)} \left[\begin{array}{l}
\because \cos (\pi+x)=-\cos x \\
\Rightarrow \cos (-x)=\cos x \\
\Rightarrow \cos \left(\frac{\pi}{2}+x\right)=-\sin x \\
\Rightarrow \sin (\pi-x)=\sin x
\end{array}\right] \\
& =\frac{-\cos ^2 x}{-\sin ^2 x} \\
& =\left(\frac{\cos x}{\sin x}\right)^2 \\
& =\cot ^2 x \left[\because \cot x=\frac{\cos x}{\sin x}\right] \\
& =\text { RHS }
\end{aligned}
\)

Q9. \(\cos \left(\frac{3 \pi}{2}+x\right) \cos (2 \pi+x)\left[\cot \left(\frac{3 \pi}{2}-x\right)+\cot (2 \pi+x)\right]=1\)

Answer:
\(
\begin{aligned}
L H S & =\cos \left(\frac{3 \pi}{2}+x\right) \cos (2 \pi+x)\left[\cot \left(\frac{3 \pi}{2}-x\right)+\cot (2 \pi+x)\right] \\
& =\cos \left\{\pi+\left(\frac{\pi}{2}+x\right)\right\} \cos x\left[\cot \left\{\pi+\left(\frac{\pi}{2}-x\right)\right\}+\cot x\right] \left[\begin{array}{l}
\because \cos (2 n \pi+\theta)=\cos \theta \\
\Rightarrow \cot (2 n \pi+\theta)=\cot \theta
\end{array}\right] \\
& =-\cos \left(\frac{\pi}{2}+x\right) \cos x\left[\cot \left(\frac{\pi}{2}-x\right)+\cot x\right] \left[\begin{array}{l}
\because \cos (\pi+\theta)=-\cos \theta \\
\Rightarrow \cot (\pi+\theta)=\cot \theta
\end{array}\right] \\
& =-(-\sin x) \cos x[\tan x+\cot x] \left[\begin{array}{l}
\because \cos \left(\frac{\pi}{2}+\theta\right)=-\sin \theta \\
\Rightarrow \cot (2 n \pi+\theta)=\cos \theta
\end{array}\right] \\
& =\sin x \cos x\left[\frac{\sin x}{\cos x}+\frac{\cos x}{\sin x}\right] \\
& =\sin ^2 x+\cos ^2 x \\
& =1 \\
& =\text { RHS }
\end{aligned}
\)

Q10. \(\sin (n+1) x \sin (n+2) x+\cos (n+1) x \cos (n+2) x=\cos x\)

Answer:
\(
\begin{aligned}
\text { LHS } & =\sin (n+1) x \sin (n+2) x+\cos (n+1) x \cos (n+2) x \\
& =\cos (n+2) x \cdot \cos (n+1) x+\sin (n+2) x \cdot \sin (n+1) x \\
& =\cos \{(n+2) x-(n+1) x\} [\because \cos (A-B)=\cos A \cos B+\sin A \sin B] \\
& =\cos \{n+2-n-1\} x \\
& =\cos x \\
& =\text { RHS }
\end{aligned}
\)

Q11. \(\cos \left(\frac{3 \pi}{4}+x\right)-\cos \left(\frac{3 \pi}{4}-x\right)=-\sqrt{2} \sin x\)

Answer:
\(
\begin{aligned}
\text { LHS } & =\cos \left(\frac{3 \pi}{4}+x\right)-\cos \left(\frac{3 \pi}{4}-x\right) \\
& =-2 \sin \left(\frac{\left(\frac{3 \pi}{4}+x\right)+\left(\frac{3 \pi}{4}-x\right)}{2}\right) \sin \left(\frac{\left(\frac{3 \pi}{4}+x\right)-\left(\frac{3 \pi}{4}-x\right)}{2}\right)
\end{aligned}
\)
\(
\left[\because \cos A-\cos B=-2 \sin \left(\frac{A+B}{2}\right) \sin \left(\frac{A-B}{2}\right)\right]
\)
\(
\begin{aligned}
& =-2 \sin \left(\frac{\frac{3 \pi}{4}+x+\frac{3 \pi}{4}-x}{2}\right) \sin \left(\frac{\frac{3 \pi}{4}+x-\frac{3 \pi}{4}+x}{2}\right) \\
& =-2 \sin \left(\frac{3 \pi}{4}\right) \sin \left(\frac{2 x}{2}\right) \\
& =-2 \sin \left(\pi-\frac{\pi}{4}\right) \sin x \\
& =-2 \sin \frac{\pi}{4} \sin x \\
& =-2 \times \frac{1}{\sqrt{2}} \times \sin x \\
& =-\sqrt{2} \sin x \\
& =\text { RHS }
\end{aligned} \quad[\because \sin (\pi-\theta)=\sin \theta]
\)

Q12. \(\sin ^2 6 x-\sin ^2 4 x=\sin 2 x \sin 10 x\)

Answer:
\(
\begin{aligned}
L H S & =\sin ^2 6 x-\sin ^2 4 x \\
& =(\sin 6 x+\sin 4 x)(\sin 6 x-\sin 4 x) \\
& =\left[2 \sin \left(\frac{6 x+4 x}{2}\right) \cos \left(\frac{6 x-4 x}{2}\right)\right] \times\left[2 \cos \left(\frac{6 x+4 x}{2}\right) \sin \left(\frac{6 x-4 x}{2}\right)\right]
\end{aligned}
\)
\(
\left[\begin{array}{l}
\because \sin A+\sin B=2 \sin \left(\frac{A+B}{2}\right) \cos \left(\frac{A-B}{2}\right) \\
\& \sin A-\sin B=2 \cos \left(\frac{A+B}{2}\right) \sin \left(\frac{A-B}{2}\right)
\end{array}\right]
\)
\(
\begin{aligned}
& =[2 \sin 5 x \cos x] \times[2 \cos 5 x \sin x] \\
& =[2 \sin 5 x \cos 5 x] \times[2 \sin x \cos x] \\
& =[\sin (5 x+5 x)+\sin (5 x-5 x)] \times[\sin (x+x)+\sin (x-x)]
\end{aligned}
\)
\(
[\because \quad 2 \sin A \cos B=\sin (A+B)+\sin (A-B)]
\)
\(
\begin{aligned}
& =[\sin 10 x+\sin 0] \times[\sin 2 x+\sin 0] \\
& =[\sin 10 x+0] \times[\sin 2 x+0] \\
& =\sin 2 x \sin 10 x \\
& =\text { RHS }
\end{aligned}
\)

Q13. \(\cos ^2 2 x-\cos ^2 6 x=\sin 4 x \sin 8 x\)

Answer:
\(
\begin{aligned}
\text { LHS } & =\cos ^2 2 x-\cos ^2 6 x \\
& =(\cos 2 x+\cos 6 x)(\cos 2 x-\cos 6 x) \quad\left[\because a^2-b^2=(a+b)(a-b)\right] \\
& =\left[2 \cos \left(\frac{2 x+6 x}{2}\right) \cos \left(\frac{2 x-6 x}{2}\right)\right] \times\left[-2 \sin \left(\frac{2 x+6 x}{2}\right) \sin \left(\frac{2 x-6 x}{2}\right)\right]
\end{aligned}
\)
\(
\left[\begin{array}{l}
\because \cos A+\cos B=2 \cos \left(\frac{A+B}{2}\right) \cos \left(\frac{A-B}{2}\right) \\
\& \cos A-\cos B=-2 \sin \left(\frac{A+B}{2}\right) \sin \left(\frac{A-B}{2}\right)
\end{array}\right]
\)
\(
\begin{aligned}
& =[2 \cos 4 x \cos (-2 x)] \times[-2 \sin 4 x \sin (-2 x)] \\
& =[2 \cos 4 x \cos 2 x] \times[-2 \sin 4 x(-\sin 2 x)]
\end{aligned}
\)
\(
\left[\begin{array}{l}
\because \cos (-\theta)=\cos \theta \\
\& \sin (-\theta)=-\sin \theta
\end{array}\right]
\)
\(
\begin{aligned}
& =[2 \cos 4 x \cos 2 x] \times[2 \sin 4 x \sin 2 x] \\
& =[2 \cos 4 x \sin 4 x] \times[2 \cos 2 x \sin 2 x] \\
& =[\sin (4 x+4 x)-\sin (4 x-4 x)] \times[\sin (2 x+2 x)-\sin (2 x-2 x)] [\because 2 \cos A \sin B=\sin (A+B)-\sin (A-B)]
\end{aligned}
\)
\(
\begin{aligned}
& =[\sin 8 x-\sin 0] \times[\sin 4 x-\sin 0] \\
& =[\sin 8 x-0] \times[\sin 4 x-0] \\
& =\sin 4 x \sin 8 x \\
& =\text { RHS }
\end{aligned}
\)

Q14. \(\sin 2 x+2 \sin 4 x+\sin 6 x=4 \cos ^2 x \sin 4 x\)

Answer:
\(
\begin{aligned}
L H S & =\sin 2 x+2 \sin 4 x+\sin 6 x \\
& =[\sin 2 x+\sin 6 x]+2 \sin 4 x \\
& =\left[2 \sin \left(\frac{2 x+6 x}{2}\right) \cos \left(\frac{2 x-6 x}{2}\right)\right]+2 \sin 4 x \left[\because \sin A+\sin B=2 \sin \left(\frac{A+B}{2}\right) \cos \left(\frac{A-B}{2}\right)\right]
\end{aligned}
\)
\(
\begin{aligned}
& =[2 \sin 4 x \cos (-2 x)]+2 \sin 4 x \\
& =2 \sin 4 x \cos 2 x+2 \sin 4 x \\
& =2 \sin 4 x(\cos 2 x+1) \\
& =2 \sin 4 x\left(2 \cos ^2 x-1+1\right) \\
& =2 \sin 4 x\left(2 \cos ^2 x\right) \left[\because \cos 2 x=2 \cos ^2 x-1\right] \\
& =4 \cos ^2 x \sin 4 x \\
& =\text { RHS }
\end{aligned}
\)

Q15. \(\cot 4 x(\sin 5 x+\sin 3 x)=\cot x(\sin 5 x-\sin 3 x)\)

Answer:
\(
\begin{aligned}
L H S & =\cot 4 x(\sin 5 x+\sin 3 x) \\
& =\cot 4 x\left[2 \sin \left(\frac{5 x+3 x}{2}\right) \cos \left(\frac{5 x-3 x}{2}\right)\right] \left[\because \sin A+\sin B=2 \sin \left(\frac{A+B}{2}\right) \cos \left(\frac{A-B}{2}\right)\right]
\end{aligned}
\)
\(
=\frac{\cos 4 x}{\sin 4 x}[2 \sin 4 x \cos x] \left[\because \cos 2 x=2 \cos ^2 x-1\right]
\)
\(
\begin{aligned}
& =2 \cos 4 x \cos x \\
& =2 \cos 4 x \cos x \times \frac{\sin x}{\sin x} \\
& =\frac{\cos x}{\sin x} \times[2 \cos 4 x \sin x] \\
& =\cot x[\sin (4 x+x)-\sin (4 x-x)] [\because 2 \cos A \sin B=\sin (A+B)-\sin (A-B)] \\
& =\cot x(\sin 5 x-\sin 3 x) \\
& =\text { RHS }
\end{aligned}
\)

Q16. \(\frac{\cos 9 x-\cos 5 x}{\sin 17 x-\sin 3 x}=-\frac{\sin 2 x}{\cos 10 x}\)

Answer:
\(
\begin{aligned}
\text { LHS } & =\frac{\cos 9 x-\cos 5 x}{\sin 17 x-\sin 3 x} \\
& =\frac{\left[-2 \sin \left(\frac{9 x+5 x}{2}\right) \sin \left(\frac{9 x-5 x}{2}\right)\right]}{\left[2 \cos \left(\frac{17 x+3 x}{2}\right) \sin \left(\frac{17 x-3 x}{2}\right)\right]} \left[\begin{array}{l}
\because \cos A-\cos B=-2 \sin \left(\frac{A+B}{2}\right) \sin \left(\frac{A-B}{2}\right) \\
\& \sin A-\sin B=2 \cos \left(\frac{A+B}{2}\right) \sin \left(\frac{A-B}{2}\right)
\end{array}\right] \\
& =\frac{[-2 \sin 7 x \sin 2 x]}{[2 \cos 10 x \sin 7 x]} \\
& =-\frac{\sin 2 x}{\cos 10 x} \\
& =\text { RHS }
\end{aligned}
\)

Q17. \(\frac{\sin 5 x+\sin 3 x}{\cos 5 x+\cos 3 x}=\tan 4 x\)

Answer:
\(
\begin{aligned}
L H S & =\frac{\sin 5 x+\sin 3 x}{\cos 5 x+\cos 3 x} \\
& =\frac{\left[2 \sin \left(\frac{5 x+3 x}{2}\right) \cos \left(\frac{5 x-3 x}{2}\right)\right]}{\left[2 \cos \left(\frac{5 x+3 x}{2}\right) \cos \left(\frac{5 x-3 x}{2}\right)\right]} \left[\begin{array}{l}
\because \sin A+\sin B=2 \sin \left(\frac{A+B}{2}\right) \cos \left(\frac{A-B}{2}\right) \\
\& \cos A+\cos B=2 \cos \left(\frac{A+B}{2}\right) \cos \left(\frac{A-B}{2}\right)
\end{array}\right] \\
& =\frac{\sin 4 x}{\cos 4 x} \\
& =\tan 4 x \\
& =\text { RHS }
\end{aligned}
\)

Q18. \(\frac{\sin x-\sin y}{\cos x+\cos y}=\tan \frac{x-y}{2}\)

Answer:
\(
\begin{aligned}
L H S & =\frac{\sin x-\sin y}{\cos x+\cos y} \\
& =\frac{\left[2 \cos \left(\frac{x+y}{2}\right) \sin \left(\frac{x-y}{2}\right)\right]}{\left[2 \cos \left(\frac{x+y}{2}\right) \cos \left(\frac{x-y}{2}\right)\right]} \left[\begin{array}{l}
\because \sin A-\sin B=2 \cos \left(\frac{A+B}{2}\right) \sin \left(\frac{A-B}{2}\right) \\
\& \cos A+\cos B=2 \cos \left(\frac{A+B}{2}\right) \cos \left(\frac{A-B}{2}\right)
\end{array}\right] \\
& =\frac{\sin \left(\frac{x-y}{2}\right)}{\cos \left(\frac{x-y}{2}\right)} \\
& =\tan \frac{x-y}{2} \\
& =R H S
\end{aligned}
\)

Q19. \(\frac{\sin x+\sin 3 x}{\cos x+\cos 3 x}=\tan 2 x\)

Answer:
\(
\begin{aligned}
\text { LHS } & =\frac{\sin x+\sin 3 x}{\cos x+\cos 3 x} \\
& =\frac{\left[2 \sin \left(\frac{x+3 x}{2}\right) \cos \left(\frac{x-3 x}{2}\right)\right]}{\left[2 \cos \left(\frac{x+3 x}{2}\right) \cos \left(\frac{x-3 x}{2}\right)\right]} \left[\begin{array}{l}
\because \sin A+\sin B=2 \sin \left(\frac{A+B}{2}\right) \cos \left(\frac{A-B}{2}\right) \\
\& \cos A+\cos B=2 \cos \left(\frac{A+B}{2}\right) \cos \left(\frac{A-B}{2}\right)
\end{array}\right] \\
& =\frac{\sin 2 x}{\cos 2 x} \\
& =\tan 2 x \\
& =\text { RHS }
\end{aligned}
\)

Q20. \(\frac{\sin x-\sin 3 x}{\sin ^2 x-\cos ^2 x}=2 \sin x\)

Answer:
\(
\begin{aligned}
\text { LHS } & =\frac{\sin x-\sin 3 x}{\sin ^2 x-\cos ^2 x} \\
& =\frac{\left[2 \cos \left(\frac{x+3 x}{2}\right) \sin \left(\frac{x-3 x}{2}\right)\right]}{-\left[\cos ^2 x-\sin ^2 x\right]} \left[\begin{array}{l}
\because \sin A-\sin B=2 \cos \left(\frac{A+B}{2}\right) \sin \left(\frac{A-B}{2}\right) \\
\& \cos A+\cos B=2 \cos \left(\frac{A+B}{2}\right) \cos \left(\frac{A-B}{2}\right)
\end{array}\right] \\
& =\frac{2 \cos 2 x \sin (-x)}{-\cos 2 x} \\
& =2 \sin x \\
& =\text { RHS }
\end{aligned}
\)

Q21. \(\frac{\cos 4 x+\cos 3 x+\cos 2 x}{\sin 4 x+\sin 3 x+\sin 2 x}=\cot 3 x\)

Answer:
\(
\begin{aligned}
\text { LHS } & =\frac{\cos 4 x+\cos 3 x+\cos 2 x}{\sin 4 x+\sin 3 x+\sin 2 x} \\
& =\frac{[\cos 4 x+\cos 2 x]+\cos 3 x}{[\sin 4 x+\sin 2 x]+\sin 3 x} \\
& =\frac{\left[2 \cos \left(\frac{4 x+2 x}{2}\right) \cos \left(\frac{4 x-2 x}{2}\right)\right]+\cos 3 x}{\left[2 \sin \left(\frac{4 x+2 x}{2}\right) \cos \left(\frac{4 x-2 x}{2}\right)\right]+\sin 3 x} \left[\begin{array}{l}
\because \cos A+\cos B=2 \cos \left(\frac{A+B}{2}\right) \cos \left(\frac{A-B}{2}\right) \\
\& \sin A+\sin B=2 \sin \left(\frac{A+B}{2}\right) \cos \left(\frac{A-B}{2}\right)
\end{array}\right]
\end{aligned}
\)
\(
\begin{aligned}
& =\frac{2 \cos 3 x \cos x+\cos 3 x}{2 \sin 3 x \cos x+\sin 3 x} \\
& =\frac{\cos 3 x(2 \cos x+1)}{\sin 3 x(2 \cos x+1)} \\
& =\frac{\cos 3 x}{\sin 3 x} \\
& =\cot 3 x \\
& =\text { RHS }
\end{aligned}
\)

Q22. \(\cot x \cot 2 x-\cot 2 x \cot 3 x-\cot 3 x \cot x=1\)

Answer:
\(
\begin{aligned}
L H S & =\cot x \cot 2 x-\cot 2 x \cot 3 x-\cot 3 x \cot x \\
& =\cot x \cot 2 x-\cot 3 x(\cot 2 x+\cot x) \\
& =\cot x \cot 2 x-\cot (2 x+x)(\cot 2 x+\cot x) \\
& =\cot x \cot 2 x-\left[\frac{\cot 2 x \cot x-1}{\cot 2 x+\cot x}\right](\cot 2 x+\cot x) \left[\because \cot (A+B)=\frac{\cot A \cot B-1}{\cot A+\cot B}\right] \\
& =\cot x \cot 2 x-[\cot 2 x \cot x-1] \\
& =\cot x \cot 2 x-\cot x \cot 2 x+1 \\
& =1 \\
& =\text { RHS }
\end{aligned}
\)

Q23. \(\tan 4 x=\frac{4 \tan x\left(1-\tan ^2 x\right)}{1-6 \tan ^2 x+\tan ^4 x}\)

Answer:
\(
\begin{aligned}
L H S & =\tan 4 x \\
& =\tan 2(2 x) \\
& =\frac{2 \tan 2 x}{1-\tan ^2 2 x} \left[\because \tan 2 A=\frac{2 \tan A}{1-\tan ^2 A}\right] \\
& =\frac{2\left(\frac{2 \tan x}{1-\tan ^2 x}\right)}{1-\left(\frac{2 \tan ^2 x}{1-\tan ^2 x}\right)^2} \left[\because \tan 2 A=\frac{2 \tan A}{1-\tan ^2 A}\right] \\
& =\frac{\left(\frac{4 \tan x}{1-\tan ^2 x}\right)}{1-\left(\frac{4 \tan ^2 x}{1+\tan ^4 x-2 \tan ^2 x}\right)} \left[\because(a-b)^2=a^2+b^2-2 a b\right]
\end{aligned}
\)
\(
\begin{aligned}
& =\frac{\left(\frac{4 \tan x}{1-\tan ^2 x}\right)}{\left(\frac{1+\tan ^4 x-2 \tan ^2 x-4 \tan ^2 x}{1+\tan ^4 x-2 \tan ^2 x}\right)} \\
& =\left(\frac{4 \tan x}{1-\tan ^2 x}\right) \times\left(\frac{1+\tan ^4 x-2 \tan ^2 x}{1+\tan ^4 x-6 \tan ^2 x}\right) \\
& =\frac{4 \tan x\left(1-\tan ^2 x\right)^2}{\left(1-\tan ^2 x\right)\left(1+\tan ^4 x-6 \tan ^2 x\right)} \left[\because a^2+b^2-2 a b=(a-b)^2\right] \\
& =\frac{4 \tan x\left(1-\tan ^2 x\right)}{1-6 \tan ^2 x+\tan ^4 x} \\
& =\text { RHS }
\end{aligned}
\)

Q24. \(\cos 4 x=1-8 \sin ^2 x \cos ^2 x\)

Answer:
\(
\begin{aligned}
L H S & =\cos 4 x \\
& =\cos 2(2 x) \\
& =1-2 \sin ^2 2 x \left[\because \cos 2 A=1-2 \sin ^2 x\right] \\
& =1-2(2 \sin x \cos x)^2 [\because \sin 2 A=2 \sin x \cos x] \\
& =1-2\left(4 \sin ^2 x \cos ^2 x\right) \\
& =1-8 \sin ^2 x \cos ^2 x \\
& =\text { RHS }
\end{aligned}
\)

Q25. \(\cos 6 x=32 \cos ^6 x-48 \cos ^4 x+18 \cos ^2 x-1\)

Answer:
\(
\begin{aligned}
L H S & =\cos 6 x \\
& =\cos 3(2 x) \\
& =4 \cos ^3 2 x-3 \cos 2 x \left[\because \cos 3 A=4 \cos ^3 x-3 \cos x\right] \\
& =4\left(2 \cos ^2 x-1\right)^3-3\left(2 \cos ^2 x-1\right) \left[\because \cos 2 A=2 \cos ^2 x-1\right] \\
& =4\left(8 \cos ^6 x-1-12 \cos ^4 x+6 \cos ^2 x\right)-6 \cos ^2 x+3 \left[\because(a-b)^3=a^3-b^3-3 a^2 b+3 a b^2\right]\\
& =32 \cos ^6 x-4-48 \cos ^4 x+24 \cos ^2 x-6 \cos ^2 x+3 \\
& =32 \cos ^6 x-48 \cos ^4 x+18 \cos ^2 x-1 \\
& =\text { RHS }
\end{aligned}
\)

Exercise 3.4

Find the principal and general solutions of the following equations:

Q1. \(\tan x=\sqrt{3}\)

Answer: It is given that \(\boldsymbol{\operatorname { t a n }} x=\sqrt{3}\)
We know that \(\tan \frac{\pi}{3}=\sqrt{3}\) and
\(
\begin{aligned}
\tan \frac{4 \pi}{3} & =\tan \left(\pi+\frac{\pi}{3}\right) \\
& =\tan \frac{\pi}{3} \\
& =\sqrt{3}
\end{aligned}
\)
Hence the principal solutions are \(x=\frac{\pi}{3}\) and \(\frac{4 \pi}{3}\).
Now,
\(
\tan x=\tan \frac{\pi}{3}
\)
Therefore, \(x=n \pi+\frac{\pi}{3}\), where \(n \in Z\).
Hence the general solution is \(x=n \pi+\frac{\pi}{3}\), where \(n \in Z\).

Q2. \(\sec x=2\)

Answer: It is given that \(\sec x=2\)
We know that \(\sec \frac{\pi}{3}=2\) and
\(
\begin{aligned}
\sec \frac{5 \pi}{3} & =\sec \left(2 \pi-\frac{\pi}{3}\right) \\
& =\sec \frac{\pi}{3} \\
& =\sqrt{3}
\end{aligned}
\)
Hence the principal solutions are \(x=\frac{\pi}{3}\) and \(\frac{5 \pi}{3}\).
Now,
\(
\begin{aligned}
& \sec x=\sec \frac{\pi}{3} \\
& \cos x=\cos \frac{\pi}{3}
\end{aligned}
\)
Therefore, \(x=2 n \pi \pm \frac{\pi}{3}\), where \(n \in Z\).
Hence the general solution is \(x=2 n \pi \pm \frac{\pi}{3}\), where \(n \in Z\).

Q3. \(\cot x=-\sqrt{3}\)

Answer: It is given that \(\cot x=-\sqrt{3}\)
We know that \(\cot \frac{\pi}{6}=\sqrt{3}\)
Therefore,
\(
\begin{aligned}
\cot \left(\pi-\frac{\pi}{6}\right) & =-\cot \frac{\pi}{6} \\
\cot \left(\frac{5 \pi}{6}\right) & =-\sqrt{3}
\end{aligned}
\)
and
\(
\begin{aligned}
\cot \left(2 \pi-\frac{\pi}{6}\right) & =-\cot \frac{\pi}{6} \\
\cot \left(\frac{11 \pi}{6}\right) & =-\sqrt{3}
\end{aligned}
\)
Hence the principal solutions are \(x=\frac{5 \pi}{6}\) and \(\frac{11 \pi}{6}\).
Now,
\(
\begin{aligned}
& \cot x=\cot \left(\frac{5 \pi}{6}\right) \\
& \tan x=\tan \left(\frac{5 \pi}{6}\right)
\end{aligned}
\)
Therefore, \(x=n \pi+\frac{5 \pi}{6}\), where \(n \in Z\).
Hence the general solution is \(x=n \pi+\frac{5 \pi}{6}\), where \(n \in Z\).

Q4. \(\operatorname{cosec} x=-2\)

Answer: It is given that \(\operatorname{cosec} x=-2\)
We know that \(\operatorname{cosec} \frac{\pi}{6}=2\) and Therefore,
\(
\begin{aligned}
\operatorname{cosec}\left(\pi+\frac{\pi}{6}\right) & =-\operatorname{cosec} \frac{\pi}{6} \\
\operatorname{cosec}\left(\frac{7 \pi}{6}\right) & =-2
\end{aligned}
\)
and
\(
\begin{aligned}
\operatorname{cosec}\left(2 \pi-\frac{\pi}{6}\right) & =-\operatorname{cosec} \frac{\pi}{6} \\
\operatorname{cosec}\left(\frac{11 \pi}{6}\right) & =-2
\end{aligned}
\)
Hence the principal solutions are \(x=\frac{7 \pi}{6}\) and \(\frac{11 \pi}{6}\).
Now,
\(
\begin{aligned}
\operatorname{cosec} x & =\operatorname{cosec} \frac{7 \pi}{6} \\
\sin x & =\sin \frac{7 \pi}{6}
\end{aligned}
\)
Therefore, \(x=n \pi+(-1)^n \frac{7 \pi}{6}\), where \(n \in Z\).
Hence the general solution is \(x=n \pi+(-1)^n \frac{7 \pi}{6}\), where \(n \in Z\).

Find the general solution for each of the following equations:

Q5. \(\cos 4 x=\cos 2 x\)

Answer:
\(
\begin{aligned}
&\begin{aligned}
& \cos 4 x-\cos 2 x=0 \\
& -2 \sin \left(\frac{4 x+2 x}{2}\right) \sin \left(\frac{4 x-2 x}{2}\right)=0 \left[\because \cos A-\cos B=-2 \sin \left(\frac{A+B}{2}\right) \sin \left(\frac{A-B}{2}\right)\right] \\
& \sin 3 x \sin x=0 \\
& \sin 3 x=0 \quad \text { or } \quad \sin x=0 \\
& 3 x=n \pi \quad \text { or } \quad x=n \pi \quad \text { where } n \in Z \\
& x=\frac{n \pi}{3} \quad \text { or } \quad x=n \pi
\end{aligned}\\
&\text { Therefore, } x=\frac{n \pi}{3} \text { or } n \pi \text {, where } n \in Z
\end{aligned}
\)

Q6. \(\cos 3 x+\cos x-\cos 2 x=0\)

Answer:
\(
\begin{aligned}
& \cos 3 x+\cos x-\cos 2 x=0 \\
& 2 \cos \left(\frac{3 x+x}{2}\right) \cos \left(\frac{3 x-x}{2}\right)-\cos 2 x=0 \left[\because \cos A+\cos B=2 \cos \left(\frac{A+B}{2}\right) \cos \left(\frac{A-B}{2}\right)\right] \\
& 2 \cos 2 x \cos x-\cos 2 x=0 \\
& \cos 2 x(2 \cos x-1)=0 \\
& \cos 2 x=0 \\
& 2 x=(2 n+1) \frac{\pi}{2} \quad \text { or } \quad 2 \cos x-1=0 \\
& x=(2 n+1) \frac{\pi}{4} \quad \text { or } \quad \cos x=\frac{1}{2} \text { or } \quad x=2 n \pi \pm \frac{\pi}{3}
\end{aligned}
\)
Therefore, \(x=(2 n+1) \frac{\pi}{4}\) or \(\left(2 n \pi \pm \frac{\pi}{3}\right)\), where \(n \in Z\)

Q7. \(\sin 2 x+\cos x=0\)

Answer:
\(
\begin{aligned}
& \sin 2 x+\cos x=0 \\
& 2 \sin x \cos x+\cos x=0 \\
& \cos x(2 \sin x+1)=0
\end{aligned} \quad[\because \sin 2 x=2 \sin x \cos x]
\)
Now,
\(
\cos x=0 \quad \text { or } \quad 2 \sin x+1=0
\)
Therefore, \(\cos x=0\)
\(
x=(2 n+1) \frac{\pi}{2} \quad n \in Z
\)
Or,
\(
\begin{aligned}
& 2 \sin x+1=0 \\
& \begin{aligned}
\sin x & =-\frac{1}{2} \\
& =-\sin \frac{\pi}{6} \\
& =\sin \left(\pi+\frac{\pi}{6}\right)
\end{aligned} \\
& \sin x=\sin \frac{7 \pi}{6} \\
& x=n \pi+(-1)^n \frac{7 \pi}{6} \quad n \in Z
\end{aligned}
\)
Therefore, \(x=(2 n+1) \frac{\pi}{2}\) or \(n \pi+(-1)^n \frac{7 \pi}{6}\), where \(n \in Z\)

Q8. \(\sec ^2 2 x=1-\tan 2 x\)

Answer:
\(
\begin{aligned}
&\begin{aligned}
& \sec ^2 2 x=1-\tan 2 x \\
& 1-\tan ^2 2 x=1-\tan 2 x \\
& \tan ^2 2 x-\tan 2 x=0 \\
& \tan 2 x(\tan 2 x-1)=0
\end{aligned}\\
&\text { Now, }\\
&\tan 2 x=0 \quad \text { or } \quad \tan 2 x-1=0
\end{aligned}
\)
\(
\begin{aligned}
&\text { Therefore, }\\
&\begin{aligned}
\tan 2 x & =0 \\
2 x & =n \pi n \in Z \\
x & =\frac{n \pi}{2}
\end{aligned}
\end{aligned}
\)
Or,
\(
\begin{aligned}
\tan 2 x-1 & =0 \\
\tan 2 x & =1 \\
& =-\tan \frac{\pi}{4} \\
& =\tan \left(\pi-\frac{\pi}{4}\right) \\
& =\tan \frac{3 \pi}{4} \\
2 x & =n \pi+\frac{3 \pi}{4} \quad n \in Z \\
x & =\frac{n \pi}{2}+\frac{3 \pi}{8}
\end{aligned}
\)
Therefore, \(x=\frac{n \pi}{2}\) or \(\left(\frac{n \pi}{2}+\frac{3 \pi}{8}\right)\), where \(n \in Z\)

Q9. \(\sin x+\sin 3 x+\sin 5 x=0\)

Answer:
\(
\begin{aligned}
& \sin x+\sin 3 x+\sin 5 x=0 \\
& 2 \sin \left(\frac{5 x+x}{2}\right) \cos \left(\frac{5 x-x}{2}\right)+\sin 3 x=0 \left[\because \sin A+\sin B=2 \sin \left(\frac{A+B}{2}\right) \cos \left(\frac{A-B}{2}\right)\right] \\
& 2 \sin 3 x \cos 2 x+\sin 3 x=0 \\
& \sin 3 x(2 \cos 2 x+1)=0
\end{aligned}
\)
Now,
\(
\sin 3 x=0 \quad \text { or } \quad 2 \cos 2 x+1=0
\)
Therefore,
\(
\begin{aligned}
\sin 3 x & =0 \\
3 x & =n \pi \\
x & =\frac{n \pi}{3}
\end{aligned}
\)
Or,
\(
\begin{aligned}
2 \cos 2 x+1 & =0 \\
\cos 2 x & =-\frac{1}{2} \\
& =-\cos \frac{\pi}{3} \\
& =\cos \left(\pi-\frac{\pi}{3}\right) \\
& =\cos \frac{2 \pi}{3} \\
2 x & =2 n \pi \pm \frac{2 \pi}{3} \quad n \in Z \\
x & =n \pi \pm \frac{\pi}{3}
\end{aligned}
\)
Therefore, \(x=\frac{n \pi}{3}\) or \(\left(n \pi \pm \frac{\pi}{3}\right)\), where \(n \in Z\)

MISCELLANEOUS EXERCISES

Q1. \(2 \cos \frac{\pi}{13} \cos \frac{9 \pi}{13}+\cos \frac{3 \pi}{13}+\cos \frac{5 \pi}{13}=0\)

Answer:
\(
\begin{aligned}
L H S & =2 \cos \frac{\pi}{13} \cos \frac{9 \pi}{13}+\cos \frac{3 \pi}{13}+\cos \frac{5 \pi}{13} \\
& =2 \cos \frac{\pi}{13} \cos \frac{9 \pi}{13}+2 \cos \left(\frac{\frac{3 \pi}{13}+\frac{5 \pi}{13}}{2}\right) \cos \left(\frac{\frac{3 \pi}{13}-\frac{5 \pi}{13}}{2}\right) \left[\because \cos A+\cos B=2 \cos \left(\frac{A+B}{2}\right) \cos \left(\frac{A-B}{2}\right)\right]
\end{aligned}
\)
\(
\begin{aligned}
& =2 \cos \frac{\pi}{13} \cos \frac{9 \pi}{13}+2 \cos \frac{4 \pi}{13} \cos \left(-\frac{\pi}{13}\right) \\
& =2 \cos \frac{\pi}{13} \cos \frac{9 \pi}{13}+2 \cos \frac{4 \pi}{13} \cos \frac{\pi}{13} \\
& =2 \cos \frac{\pi}{13}\left[\cos \frac{9 \pi}{13}+\cos \frac{4 \pi}{13}\right] \\
& =2 \cos \frac{\pi}{13}\left[2 \cos \left(\frac{\frac{9 \pi}{13}+\frac{4 \pi}{13}}{2}\right) \cos \left(\frac{\frac{9 \pi}{13}-\frac{4 \pi}{13}}{2}\right)\right] \left[\because \cos A+\cos B=2 \cos \left(\frac{A+B}{2}\right) \cos \left(\frac{A-B}{2}\right)\right]
\end{aligned}
\)
\(
\begin{aligned}
& =2 \cos \frac{\pi}{13}\left[2 \cos \frac{\pi}{2} \cos \frac{5 \pi}{26}\right] \\
& =2 \cos \frac{\pi}{13} \times 2 \times 0 \times \cos \frac{5 \pi}{26} \left[\because \cos \frac{\pi}{2}=0\right] \\
& =0 \\
& =\text { RHS }
\end{aligned}
\)

Q2. \((\sin 3 x+\sin x) \sin x+(\cos 3 x-\cos x) \cos x=0\)

Answer:
\(
\begin{aligned}
L H S & =(\sin 3 x+\sin x) \sin x+(\cos 3 x-\cos x) \cos x \\
& =\sin 3 x \sin x+\sin ^2 x+\cos 3 x \cos x-\cos ^2 x \\
& =\cos 3 x \cos x+\sin 3 x \sin x-\left(\cos ^2 x-\sin ^2 x\right) \left[\begin{array}{l}
\because \cos (A-B)=\cos A \cos B+\sin A \sin B \\
\& \cos 2 A=\cos ^2 A-\sin ^2 A
\end{array}\right]
\end{aligned}
\)
\(
\begin{aligned}
& =\cos (3 x-x)-\cos 2 x \\
& =\cos 2 x-\cos 2 x \\
& =0 \\
& =\text { RHS }
\end{aligned}
\)

Q3. \((\cos x+\cos y)^2+(\sin x-\sin y)^2=4 \cos ^2 \frac{x+y}{2}\)

Answer:
\(
\begin{aligned}
L H S & =(\cos x+\cos y)^2+(\sin x-\sin y)^2 \\
& =\cos ^2 x+\cos ^2 y+2 \cos x \cos y+\sin ^2 x+\sin ^2 y-2 \sin x \sin y \left[\begin{array}{l}
\because(a+b)^2=a^2+b^2+2 a b \\
\&(a-b)^2=a^2+b^2-2 a b
\end{array}\right]
\end{aligned}
\)
\(
=\left(\cos ^2 x+\sin ^2 x\right)+\left(\cos ^2 y+\sin ^2 y\right)+2(\cos x \cos y-\sin x \sin y)
\)
\(
=1+1+2 \cos (x+y) \quad\left[\begin{array}{l}
\because\left(\cos ^2 A+\sin ^2 A\right)=1 \\
\& \cos (A+B)=\cos A \cos B-\sin A \sin B
\end{array}\right]
\)
\(
\begin{aligned}
& =2+2 \cos (x+y) \\
& =2\left[1+\cos 2\left(\frac{x+y}{2}\right)\right] \\
& =2\left[1+2 \cos ^2\left(\frac{x+y}{2}\right)-1\right] \quad\left[\because \cos 2 A=2 \cos ^2 A-1\right] \\
& =4 \cos ^2 \frac{x+y}{2} \\
& =\text { RHS }
\end{aligned}
\)

Q4. \((\cos x-\cos y)^2+(\sin x-\sin y)^2=4 \sin ^2 \frac{x-y}{2}\)

Answer:
\(
\begin{aligned}
L H S & =(\cos x-\cos y)^2+(\sin x-\sin y)^2 \\
& =\cos ^2 x+\cos ^2 y-2 \cos x \cos y+\sin ^2 x+\sin ^2 y-2 \sin x \sin y \left[\begin{array}{l}
\because(a+b)^2=a^2+b^2+2 a b \\
\&(a-b)^2=a^2+b^2-2 a b
\end{array}\right] \\
& =\left(\cos ^2 x+\sin ^2 x\right)+\left(\cos ^2 y+\sin ^2 y\right)-2(\cos x \cos y+\sin x \sin y)
\end{aligned}
\)
\(
\begin{aligned}
& =1+1-2 \cos (x-y) \left[\begin{array}{l}
\because\left(\cos ^2 A+\sin ^2 A\right)=1 \\
\& \cos (A-B)=\cos A \cos B+\sin A \sin B
\end{array}\right] \\
& =2-2 \cos (x-y) \\
& =2\left[1-\cos 2\left(\frac{x-y}{2}\right)\right] \\
& =2\left[1-\left\{1-2 \sin ^2\left(\frac{x-y}{2}\right)\right\}\right] \\
& =2\left[1-1+2 \sin ^2\left(\frac{x-y}{2}\right)\right] \\
& =4 \sin ^2 \frac{x-y}{2} \\
& =\text { RHS }
\end{aligned}
\)

Q5. \(\sin x+\sin 3 x+\sin 5 x+\sin 7 x=4 \cos x \cos 2 x \sin 4 x\)

Answer:
\(
\begin{aligned}
L H S & =\sin x+\sin 3 x+\sin 5 x+\sin 7 x \\
& =(\sin 5 x+\sin x)+(\sin 7 x+\sin 3 x) \\
& =\left[2 \sin \left(\frac{5 x+x}{2}\right) \cos \left(\frac{5 x-x}{2}\right)\right]+\left[2 \sin \left(\frac{7 x+3 x}{2}\right) \cos \left(\frac{7 x-3 x}{2}\right)\right] \left[\because \sin A+\sin B=2 \sin \left(\frac{A+B}{2}\right) \cos \left(\frac{A-B}{2}\right)\right]
\end{aligned}
\)
\(
\begin{aligned}
& =2 \sin 3 x \cos 2 x+2 \sin 5 x \cos 2 x \\
& =2 \cos 2 x(\sin 5 x+\sin 3 x) \\
& =2 \cos 2 x\left[2 \sin \left(\frac{5 x+3 x}{2}\right) \cos \left(\frac{5 x-3 x}{2}\right)\right] \left[\because \sin A+\sin B=2 \sin \left(\frac{A+B}{2}\right) \cos \left(\frac{A-B}{2}\right)\right] \\
& =2 \cos 2 x[2 \sin 4 x \cos x] \\
& =4 \cos x \cos 2 x \sin 4 x \\
& =\text { RHS }
\end{aligned}
\)

Q6. \(\frac{(\sin 7 x+\sin 5 x)+(\sin 9 x+\sin 3 x)}{(\cos 7 x+\cos 5 x)+(\cos 9 x+\cos 3 x)}=\tan 6 x\)

Answer:
\(
\begin{aligned}
L H S & =\frac{(\sin 7 x+\sin 5 x)+(\sin 9 x+\sin 3 x)}{(\cos 7 x+\cos 5 x)+(\cos 9 x+\cos 3 x)} \\
& =\frac{2 \sin \left(\frac{7 x+5 x}{2}\right) \cos \left(\frac{7 x-5 x}{2}\right)+2 \sin \left(\frac{9 x+3 x}{2}\right) \cos \left(\frac{9 x-3 x}{2}\right)}{2 \cos \left(\frac{7 x+5 x}{2}\right) \cos \left(\frac{7 x-5 x}{2}\right)+2 \cos \left(\frac{9 x+3 x}{2}\right) \cos \left(\frac{9 x-3 x}{2}\right)} \left[\begin{array}{l}
\because \sin A+\sin B=2 \sin \left(\frac{A+B}{2}\right) \cos \left(\frac{A-B}{2}\right) \\
\& \cos A+\cos B=2 \cos \left(\frac{A+B}{2}\right) \cos \left(\frac{A-B}{2}\right)
\end{array}\right]
\end{aligned}
\)
\(
\begin{aligned}
& =\frac{2 \sin 6 x \cos x+2 \sin 6 x \cos 3 x}{2 \cos 6 x \cos x+2 \cos 6 x \cos 3 x} \\
& =\frac{2 \sin 6 x(\cos x+\cos 3 x)}{2 \cos 6 x(\cos x+\cos 3 x)} \\
& =\frac{\sin 6 x}{\cos 6 x} \\
& =\tan 6 x \\
& =\text { RHS }
\end{aligned}
\)

Q7. \(\sin 3 x+\sin 2 x-\sin x=4 \sin x \cos \frac{x}{2} \cos \frac{3 x}{2}\)

Answer:
\(
\begin{aligned}
L H S & =\sin 3 x+\sin 2 x-\sin x \\
& =\sin 3 x+(\sin 2 x-\sin x) \\
& =\sin 2\left(\frac{3 x}{2}\right)+\left[2 \cos \left(\frac{2 x+x}{2}\right) \sin \left(\frac{2 x-x}{2}\right)\right] \left[\because \sin A-\sin B=2 \cos \left(\frac{A+B}{2}\right) \sin \left(\frac{A-B}{2}\right)\right] \\
& =2 \sin \frac{3 x}{2} \cos \frac{3 x}{2}+2 \cos \frac{3 x}{2} \sin \frac{x}{2} [\because \sin 2 A=2 \sin A \cos A] \\
& =2 \cos \frac{3 x}{2}\left(\sin \frac{3 x}{2}+\sin \frac{x}{2}\right) \\
& =2 \cos \frac{3 x}{2}\left[2 \sin \left(\frac{\frac{3 x}{2}+\frac{x}{2}}{2}\right) \cos \left(\frac{\frac{3 x}{2}-\frac{x}{2}}{2}\right)\right] \left[\because \sin A+\sin B=2 \sin \left(\frac{A+B}{2}\right) \cos \left(\frac{A-B}{2}\right)\right] \\
& =2 \cos \frac{3 x}{2}\left[2 \sin x \cos \frac{x}{2}\right] \\
& =4 \sin x \cos \frac{x}{2} \cos \frac{3 x}{2} \\
& =\text { RHS }
\end{aligned}
\)

Find \(\sin \frac{x}{2}, \cos \frac{x}{2}\) and \(\tan \frac{x}{2}\) in each of the following:

Q8. \(\tan x=-\frac{4}{3}, x\) in quadrant II.

Answer: Since \(x\) lies in quadrant II
\(
\frac{\pi}{2}<x<\pi
\)
Therefore,
\(
\frac{\pi}{4}<\frac{x}{2}<\frac{\pi}{2}
\)
Hence, \(\sin \frac{x}{2}, \cos \frac{x}{2}\) and \(\tan \frac{x}{2}\) lie in quadrant \(I\) and all are positive.
It is given that \(\tan x=-\frac{4}{3}\)
\(
\begin{aligned}
\sec ^2 x & =1+\tan ^2 x \\
& =1+\left(-\frac{4}{3}\right)^2 \\
& =1+\frac{16}{9} \\
& =\frac{25}{9} \\
\sec x & = \pm \sqrt{\frac{25}{9}} \\
\frac{1}{\cos x} & = \pm \frac{5}{3} \\
\cos x & = \pm \frac{3}{5}
\end{aligned}
\)
\(
\begin{aligned}
&\text { As } x \text { is in quadrant II, } \cos x \text { is negative. }\\
&\begin{aligned}
\cos x & =-\frac{3}{5} \\
\cos 2\left(\frac{x}{2}\right) & =-\frac{3}{5} \\
2 \cos ^2 \frac{x}{2}-1 & =-\frac{3}{5} \\
2 \cos ^2 \frac{x}{2} & =1-\frac{3}{5} \\
\cos ^2 \frac{x}{2} & =\frac{2}{5} \times \frac{1}{2} \\
\cos ^2 \frac{x}{2} & =\frac{1}{5} \\
\cos \frac{x}{2} & = \pm \sqrt{\frac{1}{5}}
\end{aligned}
\end{aligned}
\)
Since, \(\cos \frac{x}{2}\) lies in quadrant I and positive, \(\cos \frac{x}{2}=\frac{1}{\sqrt{5}}\)
Now,
\(
\begin{aligned}
\sin ^2 \frac{x}{2} & =1-\cos ^2 \frac{x}{2} \quad\left[\because \sin ^2 A+\cos ^2 A=1\right] \\
& =1-\left(\frac{1}{\sqrt{5}}\right)^2 \\
& =1-\frac{1}{5} \\
& =\frac{4}{5} \\
\sin \frac{x}{2} & = \pm \sqrt{\frac{4}{5}} \\
\sin \frac{x}{2} & = \pm \frac{2}{\sqrt{5}}
\end{aligned}
\)
Since, \(\sin \frac{x}{2}\) lies in quadrant I and positive, \(\sin \frac{x}{2}=\frac{2}{\sqrt{5}}\)
Now,
\(
\begin{aligned}
\tan \frac{x}{2} & =\frac{\sin \frac{x}{2}}{\cos \frac{x}{2}} \\
& =\frac{\left(\frac{2}{\sqrt{5}}\right)}{\left(\frac{1}{\sqrt{5}}\right)} \\
& =\frac{2}{\sqrt{5}} \times \frac{\sqrt{5}}{1} \\
& =2
\end{aligned}
\)
Therefore, \(\sin \frac{x}{2}=\frac{2}{\sqrt{5}}, \quad \cos \frac{x}{2}=\frac{1}{\sqrt{5}}\) and \(\tan \frac{x}{2}=2\).

Q9. \(\cos x=-\frac{1}{3}, x\) in quadrant III.

Answer: Since \(x\) lies in quadrant III
\(
\pi<x<\frac{3 \pi}{2}
\)
Therefore,
\(
\frac{\pi}{2}<\frac{x}{2}<\frac{3 \pi}{4}
\)
Hence, \({ }^{\cos \frac{x}{2}}\) and \(\tan \frac{x}{2}\) are negative while \(\sin \frac{x}{2}\) is positive as all lie in quadrant II.
It is given that \(\cos x=-\frac{1}{3}\)
\(
\begin{aligned}
\cos 2\left(\frac{x}{2}\right) & =-\frac{1}{3} \\
2 \cos ^2 \frac{x}{2}-1 & =-\frac{1}{3} \\
2 \cos ^2 \frac{x}{2} & =1-\frac{1}{3} \\
\cos ^2 \frac{x}{2} & =\frac{2}{3} \times \frac{1}{2} \\
\cos ^2 \frac{x}{2} & =\frac{1}{3} \\
\cos \frac{x}{2} & = \pm \sqrt{\frac{1}{3}}
\end{aligned}
\)
Since, \(\cos \frac{x}{2}\) is negative
So,
\(
\begin{aligned}
\cos \frac{x}{2} & =-\frac{1}{\sqrt{3}} \\
& =-\frac{1}{\sqrt{3}} \times \frac{\sqrt{3}}{\sqrt{3}} \\
& =-\frac{\sqrt{3}}{3}
\end{aligned}
\)
Now,
\(
\begin{aligned}
\sin ^2 \frac{x}{2} & =1-\cos ^2 \frac{x}{2} \quad\left[\because \sin ^2 A+\cos ^2 A=1\right] \\
& =1-\left(-\frac{\sqrt{3}}{3}\right)^2 \\
& =1-\frac{1}{3} \\
& =\frac{2}{3}
\end{aligned}
\)
\(
\sin \frac{x}{2}= \pm \sqrt{\frac{2}{3}}
\)
Since, \(\sin \frac{x}{2}\) positive, So,
\(
\begin{aligned}
&\begin{aligned}
\sin \frac{x}{2} & =\sqrt{\frac{2}{3}} \\
& =\frac{\sqrt{2}}{\sqrt{3}} \times \frac{\sqrt{3}}{\sqrt{3}} \\
& =\frac{\sqrt{6}}{3}
\end{aligned}\\
&\text { Now, }\\
&\begin{aligned}
\tan \frac{x}{2} & =\frac{\sin \frac{x}{2}}{\cos \frac{x}{2}} \\
& =\frac{\frac{\sqrt{6}}{3}}{\left(-\frac{\sqrt{3}}{3}\right)} \\
& =\frac{\sqrt{6}}{3} \times\left(-\frac{3}{\sqrt{3}}\right) \\
& =-\sqrt{2}
\end{aligned}
\end{aligned}
\)
Therefore, \(\sin \frac{x}{2}=\frac{\sqrt{6}}{3}, \cos \frac{x}{2}=-\frac{\sqrt{3}}{3}\) and \(\tan \frac{x}{2}=-\sqrt{2}\).

Q10. \(\sin x=\frac{1}{4}, x\) in quadrant II.

Answer:
Since \(x\) lies in quadrant II
\(
\frac{\pi}{2}<x<\pi
\)
Therefore,
\(
\frac{\pi}{4}<\frac{x}{2}<\frac{\pi}{2}
\)
Hence, \(\sin \frac{x}{2}, \cos \frac{x}{2}\) and \(\tan \frac{x}{2}\) lie in quadrant \(I\) and all are positive.
It is given that \(\sin x=\frac{1}{4}\)
Therefore,
\(
\begin{aligned}
\cos ^2 x & =1-\sin ^2 x \left[\because \sin ^2 A+\cos ^2 A=1\right] \\
& =1-\left(\frac{1}{4}\right)^2 \\
& =1-\frac{1}{16} \\
& =\frac{15}{16} \\
\cos x & = \pm \sqrt{\frac{15}{16}}
\end{aligned}
\)
Since, \(\cos x\) lies in quadrant II and negative
So,
\(
\begin{aligned}
\cos x & =-\sqrt{\frac{15}{16}} \\
\cos 2\left(\frac{x}{2}\right) & =-\frac{\sqrt{15}}{4} \\
2 \cos ^2 \frac{x}{2}-1 & =-\frac{\sqrt{15}}{4} \\
2 \cos ^2 \frac{x}{2} & =1-\frac{\sqrt{15}}{4} \\
2 \cos ^2 \frac{x}{2} & =\frac{4-\sqrt{15}}{4} \\
\cos ^2 \frac{x}{2} & =\frac{4-\sqrt{15}}{8} \\
\cos \frac{x}{2} & = \pm \sqrt{\frac{4-\sqrt{15}}{8}}
\end{aligned}
\)
Since, \(\cos \frac{x}{2}\) lies in quadrant I and is positive.
So,
\(
\begin{aligned}
\cos \frac{x}{2} & =\sqrt{\frac{4-\sqrt{15}}{8}} \\
& =\sqrt{\frac{4-\sqrt{15}}{8} \times \frac{2}{2}} \\
& =\frac{\sqrt{8-2 \sqrt{15}}}{4}
\end{aligned}
\)
Now,
\(
\begin{aligned}
\sin ^2 \frac{x}{2} & =1-\cos ^2 \frac{x}{2} \left[\because \sin ^2 A+\cos ^2 A=1\right] \\
& =1-\left(\frac{\sqrt{8-2 \sqrt{15}}}{4}\right)^2 \\
& =1-\frac{8-2 \sqrt{15}}{16} \\
& =\frac{16-8+2 \sqrt{15}}{16} \\
& =\frac{8+2 \sqrt{15}}{16} \\
\sin \frac{x}{2} & = \pm \sqrt{\frac{8+2 \sqrt{15}}{16}}
\end{aligned}
\)
Since, \(\sin \frac{x}{2}\) positive,
So,
\(
\sin \frac{x}{2}=\frac{\sqrt{8+2 \sqrt{15}}}{4}
\)
Now,
\(
\begin{aligned}
\tan \frac{x}{2} & =\frac{\sin \frac{x}{2}}{\cos \frac{x}{2}} \\
& =\frac{\left(\frac{\sqrt{8+2 \sqrt{15}}}{4}\right)}{\left(\frac{\sqrt{8-2 \sqrt{15}}}{4}\right)} \\
& =\left(\frac{\sqrt{8+2 \sqrt{15}}}{4}\right) \times\left(\frac{4}{\sqrt{8-2 \sqrt{15}}}\right) \\
& =\sqrt{\frac{2(4+\sqrt{15})}{2(4-\sqrt{15})}} \\
& =\sqrt{\frac{4+\sqrt{15}}{4-\sqrt{15}} \times \frac{4+\sqrt{15}}{4+\sqrt{15}}} \\
& =\sqrt{\frac{(4+\sqrt{15})^2}{16-15}} \\
& =4+\sqrt{15}
\end{aligned}
\)
Therefore, \(\sin \frac{x}{2}=\frac{\sqrt{8+2 \sqrt{15}}}{4}, \cos \frac{x}{2}=\frac{\sqrt{8-2 \sqrt{15}}}{4}\) and \(\tan \frac{x}{2}=4+\sqrt{15}\).