3.7 Entrance Corner: Trigonometric Equations

TRIGONOMETRIC EQUATIONS

An equation involving one or more trigonometrical ratios of unknown angle is called a trigonometric equation, e.g., \(\cos ^2 x-4 \sin x=1\). It is to be noted that a trigonometrical identity is satisfied for every value of the unknown angle, whereas a trigonometric equation is satisfied only for some values (finite or infinite in number) of unknown angle, e.g., \(\sin ^2 x+\cos ^2 x=1\) is a trigonometrical identity as it is satisfied for every value of \(x \in R\).

Solution or Root of a Trigonometric Equation

The value of an unknown angle which satisfies the given trigonometric equation is called a solution or root of the equation. For example, \(2 \sin \theta=1\), clearly \(\theta=30^{\circ}\) and \(\theta=150^{\circ}\) satisfies the equation; therefore, \(30^{\circ}\) and \(150^{\circ}\) are solutions of the equation \(2 \sin \theta=1\) between \(0^{\circ}\) and \(360^{\circ}\).

Principal Solution of a Trigonometric Equation

The solutions of a trigonometric equation lie in the interval \([0,2 \pi)\). For example, \(\sin \theta=1 / 2\), then the two values of \(\theta\) between 0 and \(2 \pi\) are \(\pi / 6\) and \(5 \pi / 6\). Thus, \(\pi / 6\) and \(5 \pi / 6\) are the principal solutions of equation \(\sin \theta=1 / 2\).

General Solution of a Trigonometric Equation

It is known that trigonometric ratios are periodic functions. In fact, \(\sin x, \cos x, \sec x\) and \(\operatorname{cosec} x\) are periodic functions with a period \(2 \pi\), and \(\tan x\) and \(\cot x\) are periodic functions with a period \(\pi\). Therefore, solutions of trigonometric equations can be generalized with the help of the period of trigonometric functions. The solution consisting of all possible solutions of a trigonometric equation is called its general solution.

Clearly, general solution of a trigonometric equation will involve integral \(n \in Z\). The general solution of a trigonometric equation is also called a ‘solution’.

Here set of all integers is denoted by \(Z . n \in Z\) means \(n=0, \pm 1, \pm 2, \ldots\). For example, the general solution of the equation \(\cos \theta=1\) is \(\theta=2 n \pi\).

Some Important General Solutions of Equations

\(
\begin{array}{|l|l|}
\hline \text { Equation } & \text { Solution } \\
\hline \cos \theta=0 & \theta=(2 n+1) \frac{\pi}{2}, n \in Z \\
\hline \tan \theta=0 & \theta=n \pi, n \in Z \\
\hline \sin \theta=1 & \theta=(4 n+1) \frac{\pi}{2}, n \in Z \\
\hline \sin \theta=-1 & \theta=(4 n-1) \frac{\pi}{2}, n \in Z \\
\hline \cos \theta=1 & \theta=2 n \pi, n \in Z \\
\hline \cos \theta=-1 & \theta=(2 n+1) \pi, n \in Z \\
\hline \cot \theta=0 & \theta=(2 n+1) \frac{\pi}{2}, n \in Z \\
\hline
\end{array}
\)

Points to Remember

• While solving a trigonometric equation, squaring the equation at any step should be avoided as far as possible. If squaring is necessary, check the solution for extraneous values. Also see Example 3.1 for explanation.
• Never cancel terms containing unknown terms on the two sides which are in product. It may cause the loss of a genuine solution.
• The answer should not contain such values of angles which make any of the terms undefined or infinite. Also see Example 3.2 for explanation.
• Domain should not change while simplifying the equation. If it changes, necessary corrections must be made.
• Check that the denominator is not zero at any stage while solving the equations.

Example 3.1: Solve the equation \(\sin x+\cos x=1\).

Solution: Square both sides of the equation.
If we square we have \((\sin x+\cos x)^2=1\)
\(
\begin{aligned}
& \Rightarrow 1+\sin 2 x=1 \\
& \Rightarrow \sin 2 x=0 \\
& \Rightarrow 2 x=n \pi, n \in Z \\
& \Rightarrow x=n \pi / 2, n \in Z
\end{aligned}
\)
But for \(n=2,6,10, \ldots\)
\(\sin x+\cos =-1\) which contradicts the given equation.
Also for \(x=3,7,11, \ldots\)
\(
\sin x+\cos x=-1
\)
Hence, the solution is \(x=2 n \pi\) or \(x=(4 n+1) \frac{\pi}{2}\).(sinx+cosx)2=12sin2x+2sinxcosx+cos2x=1$$\begin{array}{rl}& (\sin x+\cos x{)}^2=1^2\\ & {\sin }^{2}x+2\sin x\cos x+{\cos }^{2}x\mathrm{}\end{array}$$

Example 3.2: Solve \(\frac{\tan 3 x-\tan 2 x}{1+\tan 3 x \tan 2 x}=1\).

Solution: \(\tan (3 x-2 x)=\tan x=1\)
Therefore, \(x=n \pi+(\pi / 4)\) but this values does not define \(\tan 2 x\). Hence, there is no solution.

Explanation: The tangent subtraction identity is \(\tan (A-B)=\frac{\tan A-\tan B}{1+\tan A \tan B}\).
The general solution for \(\tan \theta=1\) is \(\theta=n \pi+\frac{\pi}{4}\), where \(n\) is an integer.
The left side of the equation matches the form of \(\tan (A-B)\).
Let \(A=3 x\) and \(B=2 x\).
The equation becomes \(\tan (3 x-2 x)=1\).
This simplifies to \(\tan x=1\).
The general solution for \(\tan x=1\) is \(x=n \pi+\frac{\pi}{4}\).
Here, \(n\) represents any integer, i.e., \(n \in \mathbb{Z}\).
Next, we need to check the validity of this solution in the context of the original equation. Specifically, we must ensure that \(\tan (2 x)\) is defined for our solution.
Substituting \(x=n \pi+\frac{\pi}{4}\) into \(2 x\) :
\(
2 x=2\left(n \pi+\frac{\pi}{4}\right)=2 n \pi+\frac{\pi}{2}
\)
The tangent function is undefined for odd multiples of \(\frac{\pi}{2}\). Since \(2 n \pi+\frac{\pi}{2}\) is indeed an odd multiple of \(\frac{\pi}{2}\) for any integer \(n, \tan (2 x)\) is undefined.

Example 3.3: Find the values of \(\theta\) which satisfy \(r \sin \theta=3\) and \(r=4(1+\sin \theta), 0 \leq \theta \leq 2 \pi\).

Solution:
\(
\begin{aligned}
&0 \leq \theta \leq 2 \pi\\
&\text { Eliminating } r \text {, we have } 4 \sin ^2 \theta+4 \sin \theta-3=0\\
&\Rightarrow \sin \theta=\frac{1}{2},-\frac{3}{2} \text { (not possible) } \quad \Rightarrow \quad \theta=\frac{\pi}{6}, \pi-\frac{\pi}{6}=\frac{5 \pi}{6}
\end{aligned}
\)0≤θ≤2π Eliminating r, we have 4sin2θ+4sinθ−3=0⇒sinθ=12,−32 (not possible) ⇒θ=π6,π−π6=5π6$$\begin{array}{rl}& 0\le \theta \le 2\pi \\ & \text{ Eliminating }r\text{, we have }4{\sin }^2\theta +4\sin \theta -3=0\\ & \Rightarrow \sin \theta =\frac{1}{2},-\frac{3}{2}\text{ (not possible) }\Rightarrow \theta =\frac{\pi }{6},\pi -\frac{\pi }{6}=\frac{5}{}\end{array}$$

Example 3.4: Solve \(16^{\sin ^2 x}+16^{\cos ^2 x}=10,0 \leq x<2 \pi\).

Solution: \(16^{\sin ^2 x}+16^{1-\sin ^2 x}=10 \dots(i)\)
If \(16^{\sin ^2 x}=t\), then \(t+\frac{16}{t}=10\)
Then Eq. (i) becomes
\(
\begin{aligned}
&\text { Then Eq. (i) becomes }\\
&\begin{aligned}
& \Rightarrow \quad t^2-10 t+16=0 \\
& \Rightarrow \quad t=2,8 \\
& \Rightarrow \quad 16^{\sin ^2 x}=16^{1 / 4} \text { or } 16^{3 / 4} \\
& \Rightarrow \quad \sin x= \pm \frac{1}{2}, \pm \frac{\sqrt{3}}{2}
\end{aligned}
\end{aligned}
\)
\(
\begin{aligned}
& \text { Now } \sin x=\frac{1}{2}, \text { then } x=\frac{\pi}{6}, \frac{5 \pi}{6} \\
& \sin x=-\frac{1}{2}, \text { then } x=\frac{7 \pi}{6} \text { or } \frac{11 \pi}{6} \\
& \sin x=\frac{\sqrt{3}}{2} \quad \Rightarrow \quad x=\frac{\pi}{3}, \frac{2 \pi}{3} \\
& \sin x=-\frac{\sqrt{3}}{2} \quad \Rightarrow \quad x=\frac{4 \pi}{3}, \frac{5 \pi}{3}
\end{aligned}
\)
Hence, there will be eight solutions in all.

Example 3.5: Find general value of \(\theta\) which satisfies both \(\sin \theta=-1 / 2\) and \(\tan \theta=1 / \sqrt{3}\), simultaneously.

Solution: Here \(\sin \theta<0\) and \(\tan \theta>0\), then \({\theta}\) lies in the third quadrant.
Now \(\sin \theta=-\frac{1}{2} \quad \Rightarrow \quad \theta=\pi+\frac{\pi}{6}=\frac{7 \pi}{6}\)
Generalizing, we have \(\theta=2 n \pi+\frac{7 \pi}{6}, n \in Z\).

Explanation: You are finding the general value of \(\theta\) that simultaneously satisfies \(\sin \theta=-\frac{1}{2}\) and \(\tan \theta=\frac{1}{\sqrt{3}}\).
The equation \(\sin \theta=-\frac{1}{2}\) is given.
The equation \(\tan \theta=\frac{1}{\sqrt{3}}\) is given.
How to Solve?
Find the angles satisfying each equation separately, then identify the common general solution.
Step 1: Find the general solution for \(\sin \theta=-\frac{1}{2}\).
The reference angle for \(\sin \theta=\frac{1}{2}\) is \(\frac{\pi}{6}\).
Since \(\sin \theta\) is negative, \(\theta\) lies in Quadrant III or IV.
In Quadrant III: \(\theta=\pi+\frac{\pi}{6}=\frac{7 \pi}{6}\).
In Quadrant IV: \(\theta=2 \pi-\frac{\pi}{6}=\frac{11 \pi}{6}\).
The general solutions are \(\theta=2 n \pi+\frac{7 \pi}{6}\) or \(\theta=2 n \pi+\frac{11 \pi}{6}\), where \(n \in \mathbb{Z}\).
Step 2: Find the general solution for \(\tan \theta=\frac{1}{\sqrt{3}}\).
The reference angle for \(\tan \theta=\frac{1}{\sqrt{3}}\) is \(\frac{\pi}{6}\).
Since \(\tan \theta\) is positive, \(\theta\) lies in Quadrant I or III.
In Quadrant I: \(\theta=\frac{\pi}{6}\).
In Quadrant III: \(\theta=\pi+\frac{\pi}{6}=\frac{7 \pi}{6}\).
The general solution is \(\theta=n \pi+\frac{\pi}{6}\), where \(n \in \mathbb{Z}\).
Step 3: Find the common general solution.
Compare the solutions from Step 1 and Step 2.
The common angle is \(\frac{7 \pi}{6}\).
The general value satisfying both conditions is \(\theta=2 n \pi+\frac{7 \pi}{6}\), where \(n \in \mathbb{Z}\).
The general value of \(\theta\) satisfying both equations is \(\theta=2 n \pi+\frac{7 \pi}{6}\), where \(n \in \mathbb{Z}\).

Example 3.6: If \(\sin A=\sin B\) and \(\cos A=\cos B\), then find the value of \(A\) in terms of \(B\).

Solution:
\(
\begin{aligned}
&\begin{aligned}
& \sin A-\sin B=0 \text { and } \cos A-\cos B=0 \\
& \Rightarrow 2 \sin \frac{A-B}{2} \cos \frac{A+B}{2}=0 \text { and } 2 \sin \frac{A+B}{2} \sin \frac{B-A}{2}=0
\end{aligned}\\
&\text { We observe that the common factor gives } \sin \frac{A-B}{2}=0\\
&\begin{aligned}
& \Rightarrow \frac{A-B}{2}=n \pi, n \in Z \\
& \Rightarrow A-B=2 n \pi, n \in Z \\
& \Rightarrow A=2 n \pi+B, n \in Z
\end{aligned}
\end{aligned}
\)

Example 3.7: Find the number of solutions of \(\sin ^2 x-\sin x-1=0\) in \(|-2 \pi, 2 \pi|\).

Solution:
\(
\begin{aligned}
&\begin{aligned}
\sin ^2 x-\sin x-1=0 & \\
\Rightarrow \quad \sin x & =\frac{1 \pm \sqrt{5}}{2} \\
& =\frac{1-\sqrt{5}}{2}\left[\sin x=\frac{1+\sqrt{5}}{2}>1 \text { not possible }\right]
\end{aligned}\\
&\Rightarrow x \text { can attain two values in }[0,2 \pi] \text { and two more values in }[-2 \pi, 0) \text {. Thus, there are four solutions. }
\end{aligned}
\)

Example 3.8: Find the number of solutions of the equation \(e^{\sin x}-e^{-\sin x}-4=0\).

Solution:
\(
\begin{aligned}
& \text { Put } e^{\sin x}=t \Rightarrow t^2-4 t-1=0 \\
& \Rightarrow t=e^{\sin x}=2 \pm \sqrt{5}
\end{aligned}
\)
Now \(\sin x \in[-1,1]\)
\(
\Rightarrow e^{\sin x} \in\left[e^{-1}, e^1\right] \text { and } 2 \pm \sqrt{5} \notin\left[e^{-1}, e^1\right]
\)
Hence, there does not exist any solution. Put esinx=t⇒t2−4t−1=0⇒t=esinx=2±5–√$$\begin{array}{rl}& \text{ Put }{e}^{\sin x}=t\Rightarrow t^2-4t-1=0\\ & \Rightarrow t=e^{\sin x}=2\pm \sqrt{\mathrm{}}\end{array}$$

Example 3.9: If the equation \(a \sin x+\cos 2 x=2 a-7\) possesses a solution, then find the values of \(a\).

Solution: The given equation can be written as \(a \sin x+\left(1-2 \sin ^2 x\right)=2 a-7\)
\(
\begin{aligned}
& \Rightarrow \quad 2 \sin ^2 x-a \sin x+2 a-8=0 \\
& \Rightarrow \quad \sin x=\frac{a \pm \sqrt{a^2-8(2 a-8)}}{4}=\frac{a \pm(a-8)}{4} \\
& \quad=(a-4) / 2
\end{aligned} \quad(\because \sin x=2 \text { is not possible })
\)
Equation has solution if \(-1 \leq(a-4) / 2 \leq 1\)
\(
\begin{aligned}
& \Rightarrow \quad-2 \leq(a-4) \leq 2 \\
& \Rightarrow \quad 2 \leq a \leq 6
\end{aligned}
\)

Example 3.10: Solve \(\sin ^2 \theta-\cos \theta=\frac{1}{4}, 0 \leq \theta \leq 2 \pi\).

Solution:
\(
\sin ^2 \theta-\cos \theta=\frac{1}{4}
\)
Use the identity \(\sin ^2 \theta=1-\cos ^2 \theta\).
Substitute into the given equation: \(1-\cos ^2 \theta-\cos \theta=\frac{1}{4}\).
\(
4 \cos ^2 \theta+4 \cos \theta-3=0
\)
Let \(x=\cos \theta\), so \(4 x^2+4 x-3=0\).
Use the quadratic formula \(x=\frac{-b \pm \sqrt{b^2-4 a c}}{2 a}\).
Substitute values: \(x=\frac{-4 \pm \sqrt{4^2-4(4)(-3)}}{2(4)}\).
Calculate the discriminant: \(\sqrt{16+48}=\sqrt{64}=8\).
Find the values for \(x\) : \(x=\frac{-4 \pm 8}{8}\).
This gives two solutions: \(x_1=\frac{-4+8}{8}=\frac{4}{8}=\frac{1}{2}\) and \(x_2=\frac{-4-8}{8}=\frac{-12}{8}=-\frac{3}{2}\).
Since \(\cos \theta=x\), we have \(\cos \theta=\frac{1}{2}\) or \(\cos \theta=-\frac{3}{2}\).
The range of \(\cos \theta\) is \([-1,1]\), so \(\cos \theta=-\frac{3}{2}\) has no solution.
For \(\cos \theta=\frac{1}{2}\) in the interval \([0,2 \pi]\), the solutions are \(\theta=\frac{\pi}{3}\) and \(\theta=\frac{5 \pi}{3}\).
The solutions for \(\theta\) in the given interval are \(\frac{\pi}{3}\) and \(\frac{5 \pi}{3}\).$$\begin{array}{rl}& {\sin }^{2}x=1-{\cos }^{2}x\\ & \text{ The range of }\cos x\text{ is }[-1,1]\text{. }\end{array}$$

Example 3.11: Solve \(\sin 3 \theta-\sin \theta=4 \cos ^2 \theta-2\).

Solution: The equation is \(\sin 3 \theta-\sin \theta=4 \cos ^2 \theta-2\).
\(
\sin 3 \theta-\sin \theta=2 \cos \left(\frac{3 \theta+\theta}{2}\right) \sin \left(\frac{3 \theta-\theta}{2}\right) =2 \cos (2 \theta) \sin (\theta) .
\)
\(
4 \cos ^2 \theta-2=2\left(2 \cos ^2 \theta-1\right) =2 \cos (2 \theta) \cos 2 \theta=2 \cos ^2 \theta-1
\)
\(
2 \cos (2 \theta) \sin (\theta)=2 \cos (2 \theta)
\)
\(
2 \cos (2 \theta) \sin (\theta)-2 \cos (2 \theta)=0
\)
\(
2 \cos (2 \theta)(\sin (\theta)-1)=0
\)
Case 1: \(2 \cos (2 \theta)=0 \Longrightarrow \cos (2 \theta)=0\)
The general solution for \(\cos x=0\) is \(x=\frac{(2 n+1) \pi}{2}\) for integer \(n\).
So, \(2 \theta=\frac{(2 n+1) \pi}{2}\).
Thus, \(\theta=\frac{(2 n+1) \pi}{4}\).
Case 2: \(\sin (\theta)-1=0 \Longrightarrow \sin (\theta)=1\)
The general solution for \(\sin x=1\) is \(x=\frac{\pi}{2}+2 n \pi\) for integer \(n\).
Thus, \(\theta=\frac{\pi}{2}+2 n \pi\).
The general solutions for \(\theta\) are \(\theta=\frac{(2 n+1) \pi}{4}\) or \(\theta=\frac{\pi}{2}+2 n \pi\), where \(n\) is an integer.

GENERAL SOLUTION OF SOME STANDARD EQUATIONS

General Solution of the Equation \(\sin \theta=\sin \alpha\).
\(
\begin{aligned}
& \text { Given, } \sin \theta=\sin \alpha \quad \Rightarrow \sin \theta-\sin \alpha=0 \\
& \Rightarrow \quad 2 \cos \frac{\theta+\alpha}{2} \sin \frac{\theta-\alpha}{2}=0 \\
& \Rightarrow \quad \cos \frac{\theta+\alpha}{2}=0 \text { or } \sin \frac{\theta-\alpha}{2}=0
\end{aligned}
\)
\(
\begin{aligned}
& \Rightarrow \quad \frac{\theta+\alpha}{2}=(2 m+1) \frac{\pi}{2}, \frac{\theta-\alpha}{2}=m \pi, m \in Z \\
& \Rightarrow \quad \theta=(2 m+1) \pi-\alpha \text { or } \theta=2 m \pi+\alpha, m \in Z \dots(i) \\
& \Rightarrow \quad \theta=(2 m+1) \pi+(-1)^{2 m+1} \alpha, m \in Z \\
& \text { or } \quad \theta=2 m \pi+(-1)^{2 m} \alpha, m \in Z \dots(ii)
\end{aligned}
\)
Combining Eqs. (i) and (ii), we have \(\theta=n \pi+(-1)^n \alpha, n \in Z\)

Note: For the general solution of the equation \(\sin \theta=k\), where \(-1 \leq k \leq 1\). We have \(\sin \theta=\sin \left(\sin ^{-1} k\right)\) \(\Rightarrow \theta=n \pi+(-1)^n \cdot\left(\sin ^{-1} k\right), n \in Z\).

Example 12: Solve \(2 \cos ^2 \theta+3 \sin \theta=0\).

Solution: We have \(2 \cos ^2 \theta+3 \sin \theta=0\)
\(
\begin{aligned}
&\begin{aligned}
\Rightarrow & 2\left(1-\sin ^2 \theta\right)+3 \sin \theta=0 \\
\Rightarrow & 2 \sin ^2 \theta-3 \sin \theta-2=0 \\
\Rightarrow & (\sin \theta-2)(2 \sin \theta+1)=0 \\
\Rightarrow & 2 \sin \theta+1=0 & [\because \sin \theta \neq 2] \\
\Rightarrow & \sin \theta=-\frac{1}{2}=\sin \left(\frac{-\pi}{6}\right) \\
\Rightarrow & \theta=n \pi+(-\mathrm{i})^n\left(\frac{-\pi}{6}\right), n \in Z \\
& =n \pi+(-1)^{n+1} \frac{\pi}{6}, n \in Z
\end{aligned}\\
\end{aligned}
\)

Example 13: Solve \(4 \cos \theta-3 \sec \theta=\tan \theta\).

Solution:
\(
\begin{aligned}
&\text { We have } 4 \cos \theta-3 \sec \theta=\tan \theta\\
&\begin{gathered}
\Rightarrow 4 \cos \theta-\frac{3}{\cos \theta}=\frac{\sin \theta}{\cos \theta} \\
\Rightarrow 4 \cos ^2 \theta-3=\sin \theta \\
\Rightarrow 4\left(1-\sin ^2 \theta\right)-3=\sin \theta \\
\Rightarrow 4 \sin ^2 \theta+\sin \theta-1=0 \\
\Rightarrow \sin \theta=\frac{-1 \pm \sqrt{1+16}}{8} \\
=\frac{-1 \pm \sqrt{17}}{8} \\
=\frac{-1+\sqrt{17}}{8} \text { or }=\frac{-1-\sqrt{17}}{8}
\end{gathered}
\end{aligned}
\)
Now, \(\sin \theta=\frac{-1+\sqrt{17}}{8}\)
\(\Rightarrow \sin \theta=\sin \alpha\), where \(\sin \alpha=\frac{-1+\sqrt{17}}{8}\)
\(\Rightarrow \theta=n \pi+(-1)^n \alpha\), where \(\sin \alpha=\frac{-1+\sqrt{17}}{8}\) and \(n \in Z\) and \(\sin \theta=\frac{-1-\sqrt{17}}{8}\).
\(\Rightarrow \sin \theta=\sin \beta\), where \(\sin \beta=\frac{-1-\sqrt{17}}{8}\)
\(\Rightarrow \theta=n \pi+(-1)^n \beta\), where \(\sin \beta=\frac{-1-\sqrt{17}}{8}\)

Example 14: Solve \(\sin ^3 \theta \cos \theta-\cos ^3 \theta \sin \theta=1 / 4\)

Solution:
\(
\begin{aligned}
& \sin ^3 \theta \cos \theta-\cos ^3 \theta \sin \theta=1 / 4 \\
& \Rightarrow 4 \sin \theta \cos \theta\left(\sin ^2 \theta-\cos ^2 \theta\right)=1 \\
& \Rightarrow 2 \sin 2 \theta(-\cos 2 \theta)=1 \\
& \Rightarrow-\sin 4 \theta=1 \\
& \Rightarrow \sin 4 \theta=-1 \\
& \Rightarrow 4 \theta=2 n \pi-\frac{\pi}{2} \\
& \Rightarrow \theta=(\pi / 2)+(-\pi / 8), n \in Z
\end{aligned}
\)

General Solution of Equation \(\cos \theta=\cos \alpha\)

\(
\begin{aligned}
&\text { Given, } \cos \theta=\cos \alpha\\
&\begin{aligned}
& \Rightarrow \quad \cos \alpha-\cos \theta=0 \\
& \Rightarrow \quad 2 \sin \frac{\alpha+\theta}{2} \sin \frac{\theta-\alpha}{2}=0 \\
& \Rightarrow \quad \sin \frac{\alpha+\theta}{2}=0 \text { or } \sin \frac{\theta-\alpha}{2}=0 \\
& \Rightarrow \quad \frac{\alpha+\theta}{2}=n \pi \text { or } \frac{\theta-\alpha}{2}=n \pi ; n \in Z \\
& \Rightarrow \quad \theta=2 n \pi-\alpha \text { or } \theta=2 n \pi+\alpha, n \in Z \\
& \quad=2 n \pi \pm \alpha, n \in Z
\end{aligned}
\end{aligned}
\)⇒cosα−cosθ=0⇒2sinα+θ2sinθ−α2=0⇒sinα+θ2=0 or sinθ−α2=0$$\begin{array}{rl}& \Rightarrow \cos \alpha -\cos \theta =0\\ & \Rightarrow 2\sin \frac{\alpha +\theta }{2}\sin \frac{\theta -\alpha }{2}=0\\ & \Rightarrow \sin \frac{\alpha +\theta }{2}=0\text{ or }\sin \frac{\theta -\alpha }{}\mathrm{}\end{array}$$

Note: For the general solution of the equation \(\sin \theta=k\), where \(-1 \leq k \leq 1\). We have \(\cos \theta=\cos \left(\cos ^{-1} k\right)\) \(\Rightarrow \theta=2 n \pi \pm\left(\cos ^{-1} k\right), n \in Z\).

Example 15: Solve \(\sqrt{3} \sec 2 \theta=2\).

Solution: We have \(\sqrt{3} \sec 2 \theta=2\)
\(
\begin{gathered}
\Rightarrow \quad \cos 2 \theta=\frac{\sqrt{3}}{2} \\
=\cos \frac{\pi}{6} \\
\Rightarrow \quad 2 \theta=2 n \pi \pm \frac{\pi}{6}, n \in Z \\
\Rightarrow \quad \theta=n \pi \pm \frac{\pi}{12}, n \in Z
\end{gathered}
\)

Example 16: Solve \(\sin 2 \theta+\cos \theta=0\).

Solution: We have \(\sin 2 \theta+\cos \theta=0\)We have \(\sin 2 \theta+\cos \theta=0\)
\(
\begin{aligned}
& \Rightarrow \cos \theta=-\sin 2 \theta \\
& \quad=\cos \left(\frac{\pi}{2}+2 \theta\right) \\
& \Rightarrow \theta=2 n \pi \pm\left(\frac{\pi}{2}+2 \theta\right) n \in Z
\end{aligned}
\)
Taking positive sign, we have.
\(
\begin{aligned}
\theta & =2 n \pi+\frac{\pi}{2}+2 \theta \\
& =2 n \pi-\frac{\pi}{2}, n \in Z
\end{aligned}
\)
Taking negative sign, we have
\(
\theta=2 n \pi-\left(\frac{\pi}{2}+2 \theta\right) \quad \Rightarrow \quad \theta=\frac{2 n \pi}{3}-\frac{\pi}{6}, n \in Z
\)

Example 17: Solve \(\cos \theta+\cos 3 \theta-2 \cos 2 \theta=0\).

Solution: We have \(\cos \theta+\cos 3 \theta-2 \cos 2 \theta=0\)
\(
\begin{aligned}
& \Rightarrow 2 \cos 2 \theta \cos \theta-2 \cos 2 \theta=0 \\
& \Rightarrow 2 \cos 2 \theta(\cos \theta-1)=0 \\
& \Rightarrow \cos 2 \theta=0 \text { or, } \cos \theta-1=0 \\
& \Rightarrow 2 \theta=(2 n+1) \frac{\pi}{2}, n \in Z \text { or } \theta=2 m \pi, m \in Z \\
& \Rightarrow \theta=(2 n+1) \frac{\pi}{4}, n \in Z \text { or } \theta=2 m \pi, m \in Z
\end{aligned}
\)

Example 18: Solve \(\sec 4 \theta-\sec 2 \theta=2\).

Solution:
\(
\begin{aligned}
& \frac{1}{\cos 4 \theta}-\frac{1}{\cos 2 \theta}=2 \\
& \Rightarrow \cos 2 \theta-\cos 4 \theta=2 \cos 2 \theta \cos 4 \theta=\cos 2 \theta+\cos 6 \theta \\
& \Rightarrow \cos 6 \theta+\cos 4 \theta=0 \\
& \Rightarrow 2 \cos 5 \theta \cos \theta=0 \\
& \Rightarrow \cos 5 \theta=0 \text { or } \cos \theta=0 \\
& \Rightarrow 5 \theta=(2 n+1) \frac{\pi}{2} \text { or } \theta=(2 n+1) \frac{\pi}{2}, n \in Z \\
& \Rightarrow \theta=\left(n+\frac{1}{2}\right) \frac{\pi}{5} \text { or } \theta=\left(n+\frac{1}{2}\right) \pi, n \in Z
\end{aligned}
\)

Example 19: Solve \(5 \cos 2 \theta+2 \cos ^2 \frac{\theta}{2}+1=0,-\pi<\theta<\pi\).

Solution:
\(
\begin{aligned}
&\text { Changing all the values in terms of } \cos \theta \text {, we get }\\
&\begin{aligned}
& 5\left(2 \cos ^2 \theta-1\right)+(1+\cos \theta)+1=0 \Rightarrow 10 \cos ^2 \theta+\cos \theta-3=0 \\
& \Rightarrow \quad(5 \cos \theta+3)(2 \cos \theta-1)=0 \\
& \Rightarrow \quad \theta=\frac{\pi}{3},-\frac{\pi}{3}, \cos ^{-1}\left(-\frac{3}{5}\right)=\pi-\cos ^{-1} \frac{3}{5} \text { and }-\pi+\cos ^{-1} \frac{3}{5} [\because-\pi<\theta<\pi]
\end{aligned}
\end{aligned}
\)

Example 20: Solve \(\cos x \cos 2 x \cos 3 x=1 / 4\).

Solution:
\(
\begin{aligned}
& \cos x \cos 2 x \cos 3 x=1 / 4 \\
& \Rightarrow 2(2 \cos x \cos 3 x) \cos 2 x=1 \\
& \Rightarrow 2(\cos 4 x+\cos 2 x) \cos 2 x=1 \\
& \Rightarrow 2\left(2 \cos ^2 2 x-1+\cos 2 x\right) \cos 2 x=1 \\
& \Rightarrow 4 \cos ^3 2 x+2 \cos ^2 2 x-2 \cos 2 x-1=0 \\
& \Rightarrow\left(2 \cos ^2 2 x-1\right)(2 \cos 2 x+1)=0 \\
& \Rightarrow \cos 4 x(2 \cos 2 x+1)=0 \\
& \Rightarrow \cos 4 x=0 \text { or } \cos 2 x=-1 / 2 \\
& \Rightarrow 4 x=(2 n+1) \frac{\pi}{2} \text { or } 2 x=2 m \pi \pm \frac{2 \pi}{3}, m, n \in Z \\
& \Rightarrow x=(2 n+1) \frac{\pi}{8} \text { or } x=m \pi \pm \frac{\pi}{3}
\end{aligned}
\)

General Solutions of the Equation \(\tan \theta=\tan \alpha\)

\(
\begin{aligned}
&\text { Given, } \tan \theta=\tan \alpha\\
&\begin{aligned}
& \Rightarrow \frac{\sin \theta}{\cos \theta}=\frac{\sin \alpha}{\cos \alpha} \\
& \Rightarrow \sin \theta \cos \alpha-\cos \theta \sin \alpha=0 \\
& \Rightarrow \sin (\theta-\alpha)=0 \\
& \Rightarrow \theta-\alpha=n \pi \\
& \Rightarrow \theta=n \pi+\alpha, \text { where } n \in Z
\end{aligned}
\end{aligned}
\)

Note: For the general solution of the equation \(\tan \theta=k\), where \(k \in R\). We have \(\tan \theta=\tan \left(\tan ^{-1} k\right)\) \(\Rightarrow \quad \theta=n \pi+\left(\tan ^{-1} k\right), n \in Z\)

Example 21: Solve \(\tan 3 \theta=-1\).

Solution:

\(
\begin{aligned}
\tan 3 \theta & =-1 \\
& =\tan \left(\frac{-\pi}{4}\right) \\
\Rightarrow \quad 3 \theta & =n \pi+\left(\frac{-\pi}{4}\right), n \in Z \\
\Rightarrow \quad \theta & =\frac{n \pi}{3}-\frac{\pi}{12}, n \in Z
\end{aligned}
\)

Example 22: Solve \(2 \tan \theta-\cot \theta=-1\).

Solution:

\(
\begin{aligned}
& 2 \tan \theta-\cot \theta=-1 \\
& \Rightarrow 2 \tan \theta-\frac{1}{\tan \theta}=-1 \\
& \Rightarrow 2 \tan ^2 \theta+\tan \theta-1=0 \\
& \Rightarrow(\tan \theta+1)(2 \tan \theta-1)=0 \\
& \Rightarrow \tan \theta=-1 \text { or } \tan \theta=\frac{1}{2} \\
& \Rightarrow \tan \theta=\tan \left(\frac{-\pi}{4}\right) \text { or } \tan \theta=\tan \left(\tan ^{-1} \frac{1}{2}\right) \\
& \Rightarrow \theta=n \pi+\left(\frac{-\pi}{4}\right) \text { or } \theta=m \pi+\alpha, \text { where } m, n \in Z \text { and } \tan \alpha=\frac{1}{2}
\end{aligned}
\)

Example 23: Solve \(\tan 5 \theta=\cot 2 \theta\).

Solution:
\(
\begin{aligned}
& \tan 5 \theta=\cot 2 \theta=\tan \left(\frac{\pi}{2}-2 \theta\right) \\
& \Rightarrow 5 \theta=n \pi+\frac{\pi}{2}-2 \theta
\end{aligned}
\)
\(
\begin{aligned}
& \Rightarrow \quad 7 \theta=n \pi+\frac{\pi}{2} \\
& \Rightarrow \quad \theta=\frac{n \pi}{7}+\frac{\pi}{14}, \text { where } n \in Z, \text { but } n \neq 3,10,17, \ldots \text { where } \tan 5 \theta \text { is not defined }
\end{aligned}
\)

Example 24: \(\tan \theta+\tan 2 \theta+\sqrt{3} \tan \theta \tan 2 \theta=\sqrt{3}\).

Solution:
\(
\begin{aligned}
& \tan \theta+\tan 2 \theta+\sqrt{3} \tan \theta \tan 2 \theta=\sqrt{3} \\
& \Rightarrow \quad \tan \theta+\tan 2 \theta=\sqrt{3}(1-\tan \theta \tan 2 \theta) \\
& \Rightarrow \quad \frac{\tan \theta+\tan 2 \theta}{1-\tan \theta \tan 2 \theta}=\sqrt{3} \\
& \Rightarrow \quad \tan 3 \theta=\sqrt{3} \\
& \quad=\tan \frac{\pi}{3} \\
& \Rightarrow \quad 3 \theta=n \pi+\frac{\pi}{3}, n \in Z \\
& \Rightarrow \theta=\frac{n \pi}{3}+\frac{\pi}{9}, n \in Z
\end{aligned}
\)

General Solutions of the Equation \(\sin ^2 \theta=\sin ^2 \alpha\) or \(\cos ^2 \theta=\cos ^2 \alpha\)

Here, both given equations are the same as \(\cos ^2 \theta=\cos ^2 \alpha\)
\(
\begin{aligned}
& \Rightarrow \quad\left(1-\sin ^2 \theta\right)-\left(1-\sin ^2 \alpha\right)=0 \\
& \Rightarrow \sin ^2 \theta=\sin ^2 \alpha \\
& \Rightarrow \sin (\theta+\alpha) \sin (\theta-\alpha)=0 \\
& \Rightarrow \sin (\theta+\alpha)=0 \text { or } \sin (\theta-\alpha)=0 \\
& \Rightarrow \theta+\alpha=n \pi \text { or } \theta-\alpha=n \pi, n \in Z \\
& \Rightarrow \theta=n \pi \pm \alpha, n \in Z
\end{aligned}
\)

General Solutions of the Equation \(\tan ^2 \theta=\tan ^2 \alpha\)

\(
\tan ^2 \theta=\tan ^2 \alpha \quad \Rightarrow \tan \theta= \pm \tan \alpha \quad \Rightarrow \tan \theta=\tan ( \pm \alpha) \quad \Rightarrow \quad \theta=n \pi \pm \alpha, n \in Z
\)

Example 25: Solve \(7 \cos ^2 \theta+3 \sin ^2 \theta=4\).

Solution:
\(
\begin{aligned}
&\text { We have } 7 \cos ^2 \theta+3 \sin ^2 \theta=4\\
&\Rightarrow 7\left(1-\sin ^2 \theta\right)+3 \sin ^2 \theta=4
\end{aligned}
\)
\(
\begin{aligned}
& \Rightarrow \quad 4 \sin ^2 \theta=3 \\
& \Rightarrow \quad \sin ^2 \theta=\frac{3}{4}=\left(\frac{\sqrt{3}}{2}\right)^2 \\
& \Rightarrow \quad \sin ^2 \theta=\sin ^2 \frac{\pi}{3} \\
& \Rightarrow \quad \theta=n \pi \pm \frac{\pi}{3}, n \in Z
\end{aligned}
\)

Example 26: Solve \(2 \sin ^2 x+\sin ^2 2 x=2\).

Solution: We have \(2 \sin ^2 x+\sin ^2 2 x=2\)
\(
\begin{aligned}
&\text { We have } 2 \sin ^2 x+\sin ^2 2 x=2\\
&\begin{aligned}
\Rightarrow & 2 \sin ^2 x+(2 \sin x \cos x)^2=2 \\
\Rightarrow & 2 \sin ^2 x \cos ^2 x+\sin ^2 x=1 \\
\Rightarrow & 2 \sin ^2 x \cos ^2 x-\left(1-\sin ^2 x\right)=0 \\
\Rightarrow & 2 \sin ^2 x \cos ^2 x-\cos ^2 x=0 \\
\Rightarrow & \cos ^2 x\left(2 \sin ^2 x-1\right)=0 \\
\Rightarrow & \cos ^2 x=0 \text { or } \sin ^2 x=\frac{1}{2} \\
\Rightarrow & x=2 n \pi+\frac{\pi}{2} \text { or } \sin ^2 x=\sin ^2 \frac{\pi}{4} \\
& =2 n \pi+\frac{\pi}{2} \text { or } x=m \pi \pm \frac{\pi}{4}, m \in Z, \text { where } m, n \in Z
\end{aligned}
\end{aligned}
\)

Example 27: Solve \(4 \cot 2 \theta=\cot ^2 \theta-\tan ^2 \theta\).

Solution:
\(
\begin{aligned}
& \frac{4}{\tan 2 \theta}=\frac{1}{\tan ^2 \theta}-\tan ^2 \theta \\
& \Rightarrow \frac{4\left(1-\tan ^2 \theta\right)}{2 \tan \theta}=\frac{1-\tan ^4 \theta}{\tan ^2 \theta}\left[\text { put } \tan 2 \theta=\frac{2 \tan \theta}{1-\tan ^2 \theta}\right] \\
& \Rightarrow\left(1-\tan ^2 \theta\right)\left[2 \tan \theta-\left(1+\tan ^2 \theta\right)\right]=0 \\
& \Rightarrow\left(1-\tan ^2 \theta\right)\left(\tan ^2 \theta-2 \tan \theta+1\right)=0 \\
& \Rightarrow\left(1-\tan ^2 \theta\right)(\tan \theta-1)^2=0 \\
& \Rightarrow \tan \theta= \pm 1 \\
& \Rightarrow \theta=n \pi \pm \frac{\pi}{4}, n \in Z
\end{aligned}
\)

Example 28: Find the most general solution of \(2^{1+|\cos x|+\cos ^2 x+|\cos x|^3+\cdots \infty}={4}\).

Solution:
\(
\begin{aligned}
&\text { We have } 2^{1+|\cos x|+\cos ^2 x+|\cos x|^3+\cdots \infty}=4\\
&\begin{aligned}
& \Rightarrow \quad 2^{1+|\cos x|+|\cos x|^2+|\cos x|^3+\cdots \infty}=4 \\
& \Rightarrow \quad 2^{\frac{1}{1-|\cos x|}}=2^2
\end{aligned}
\end{aligned}
\)
\(
\begin{aligned}
& \Rightarrow \frac{1}{1-|\cos x|}=2 \\
& \Rightarrow|\cos x|=\frac{1}{2} \text { or } \cos x= \pm \frac{1}{2} \\
& \Rightarrow x=n \pi \pm \frac{\pi}{3}, n \in Z
\end{aligned}
\)

Solutions of Equations of the Form \(a \cos \theta+b \sin \theta=c\)

To solve equation, let us convert the equation to the form \(\cos \theta=\cos \alpha\) or \(\sin \theta=\sin \alpha\), etc.
For this let us suppose that \(\left.\begin{array}{l}a=r \cos \phi \\ b=r \sin \phi\end{array}\right\} \Rightarrow\left\{\begin{array}{c}r=\sqrt{a^2+b^2} \\ \tan \phi=\frac{b}{a} \text { and. }\end{array}\right.\)
Substituting these values in the equation \(a \cos \theta+b \sin \theta=c\), we have
\(
\begin{aligned}
& r \cos \phi \cos \theta+r \sin \phi \sin \theta=c \\
& \Rightarrow \quad r \cos (\theta-\phi)=c \\
& \Rightarrow \quad \cos (\theta-\phi)=\frac{c}{r}=\frac{c}{\sqrt{a^2+b^2}}=\cos \beta \text { (suppose) } \\
& \Rightarrow \quad \theta-\phi=2 n \pi \pm \beta \\
& \Rightarrow \quad \theta=2 n \pi+\phi \pm \beta, n \in Z
\end{aligned}
\)
Here \(\phi\) and \(\beta\) are known as \(a, b\) and \(c\) are given.
Hence, we can solve the equation of this type by putting
\(
\begin{aligned}
& a=r \cos \phi \text { and } b=r \sin \phi, \text { provided }\left|\frac{c}{\sqrt{a^2+b^2}}\right| \leq 1 \quad[\because \cos \beta \text { lies between }-1 \text { and } 1] \\
& \text { or } \frac{|c|}{\sqrt{a^2+b^2}} \leq 1 \text { or }|c| \leq \sqrt{a^2+b^2}
\end{aligned}
\)

Working Rules for solving such equations

• First of all check whether \(|c| \leq \sqrt{a^2+b^2}\) or not.
• If \(|c|>\sqrt{a^2+b^2}\), then the given equation has no real solution.
• \(|\mathrm{f}| c \mid \leq \sqrt{a^2+b^2}\), then divide both sides of the equation by \(\sqrt{a^2+b^2}\).
• Take \(\cos \alpha=\frac{a}{\sqrt{a^2+b^2}}\) and \(\sin \alpha=\frac{b}{\sqrt{a^2+b^2}}\), then the given equation will become \(\cos (\theta-\alpha)=\cos \beta\), where \(\tan \alpha=\frac{b}{a}\) and \(\cos \beta=\frac{c}{\sqrt{a^2+b^2}}\).
  We can also take \(\sin \alpha=\frac{a}{\sqrt{a^2+b^2}}, \cos \alpha=\frac{b}{\sqrt{a^2+b^2}}\) and \(\sin \beta=\frac{c}{\sqrt{a^2+b^2}}\), then the given equation will reduce to the form \(\sin (\theta+\alpha)=\sin \beta\).

Example 29: Solve \(\sqrt{3} \cos \theta+\sin \theta=\sqrt{2}\).

Solution: We have \(\sqrt{3} \cos \theta+\sin \theta=\sqrt{2} \dots(i)\)
This is of the form \(a \cos \theta+b \sin \theta=c\), where \(a=\sqrt{3}, b=1\) and \(c=\sqrt{2}\)
Let \(\sqrt{3}=r \cos \alpha\) and \(1=r \sin \alpha\)
\(
\Rightarrow r=\sqrt{a^2+b^2}=\sqrt{(\sqrt{3})^2+1^2}=2 \text { and } \tan \alpha=\frac{1}{\sqrt{3}} \quad \Rightarrow \quad \alpha=\frac{\pi}{6}
\)
Substituting \(\sqrt{3}=r \cos \alpha\) and \(1=r \sin \alpha\) in Eq. (i), it reduces to \(r \cos \alpha \cos \theta+r \sin \theta=\sqrt{2}\)
\(
\begin{aligned}
\Rightarrow & r \cos (\theta-\alpha)=\sqrt{2} \\
\Rightarrow & 2 \cos \left(\theta-\frac{\pi}{6}\right)=\sqrt{2} \\
\Rightarrow & \cos \left(\theta-\frac{\pi}{6}\right)=\frac{1}{\sqrt{2}}=\cos \frac{\pi}{4} \\
\Rightarrow & \theta-\frac{\pi}{6}=2 n \pi \pm \frac{\pi}{4}, n \in Z \\
\Rightarrow & \theta=2 n \pi \pm \frac{\pi}{4}+\frac{\pi}{6}, n \in Z \\
& =2 n \pi+\frac{\pi}{4}+\frac{\pi}{6} \text { or, } \theta=2 n \pi-\frac{\pi}{4}+\frac{\pi}{6} \\
& =2 n \pi+\frac{5 \pi}{12} \text { or, } \theta=2 n \pi-\frac{\pi}{12}, \text { where } n \in Z
\end{aligned}
\)

Example 30: Solve \(\sqrt{3} \cos \theta-3 \sin \theta=4 \sin 2 \theta \cos 3 \theta\).

Solution: We have \(\sqrt{3} \cos \theta-3 \sin \theta=2(\sin 5 \theta-\sin \theta)\)
\(
\Rightarrow(\sqrt{3} / 2) \cos \theta-(1 / 2) \sin \theta=\sin 5 \theta
\)
\(
\begin{aligned}
& \Rightarrow \cos (\theta+\pi / 6)=\sin 5 \theta=\cos (\pi / 2-5 \theta) \\
& \Rightarrow \theta+\pi / 6=2 n \pi \pm(\pi / 2-5 \theta) \\
& \Rightarrow \theta=n \pi / 3+\pi / 18 \text { or } \theta=-n \pi / 2+\pi / 6, \forall n \in Z
\end{aligned}
\)

Example 31: Find the total number of integral values of \(n\) so that \(\sin x(\sin x+\cos x)=n\) has at least one solution.

Solution:
\(
\begin{aligned}
& \sin x(\sin x+\cos x)=n \\
& \Rightarrow \sin ^2 x+\sin x \cos x=n \\
& \Rightarrow \frac{1-\cos 2 x}{2}+\frac{\sin 2 x}{2}=n \\
& \Rightarrow \sin 2 x-\cos 2 x=2 n-1 \\
& \Rightarrow-\sqrt{2} \leq 2 n-1 \leq \sqrt{2} \\
& \Rightarrow \frac{1-\sqrt{2}}{2} \leq n \leq \frac{1+\sqrt{2}}{2} \\
& \Rightarrow n=0,1
\end{aligned}
\)

PROBLEMS BASED ON EXTREME VALUES OF FUNCTIONS

Example 32: If \(x, y \in|0,2 \pi|\), then find the total number of ordered pairs \((x, y)\) satisfying the equation \(\sin x \cos y=1\).

Solution: \(\sin x \cos y=1\)
\(
\Rightarrow \sin x=1, \cos y=1 \text { or } \sin x=-1, \cos y=-1
\)
If \(\sin x=1, \cos y=1 \quad \Rightarrow \quad x=\pi / 2, y=0,2 \pi\)
If \(\sin x=-1, \cos y=-1 \quad \Rightarrow \quad x=3 \pi / 2, y=\pi\)
Thus, the possible ordered pairs are \(\left(\frac{\pi}{2}, 0\right),\left(\frac{\pi}{2}, 2 \pi\right)\) and \(\left(\frac{3 \pi}{2}, \pi\right)\).

Example 33: If \(3 \sin x+4 \cos a x=7\) has at least one solution, then find the possible values of \(a\).

Solution: We have \(3 \sin x+4 \cos a x=7\) which is possible only when \(\sin x=1\) and \(\cos a x=1\)
\(
\begin{aligned}
& \Rightarrow \quad x=(4 n+1) \frac{\pi}{2} \text { and } a x=2 m \pi ; m, n \in Z \\
& \Rightarrow \quad(4 n+1) \frac{\pi}{2}=\frac{2 m \pi}{a} \\
& \Rightarrow \quad a=\frac{4 m}{4 n+1}
\end{aligned}
\)

Example 34: Solve \(\cos ^{50} x-\sin ^{50} x=1\).

Solution: \(\cos ^{50} x-\sin ^{50} x=1 \Rightarrow \cos ^{50} x=1+\sin ^{50} x\)
L.H.S. \(\leq 1\) and R.H.S. \(\geq 1\)
Hence, we must have \(\cos ^{50} x=1+\sin ^{50} x=1 \quad \Rightarrow \quad \sin x=0 \quad \Rightarrow \quad x=n \pi\)

Example 35: Solve \(\sin ^2 x+\cos ^2 y=2 \sec ^2 z\) for \(x, y\) and \(z\).

Solution:
\(
\text { L.H.S. }=\sin ^2 x+\cos ^2 y \leq 2 \quad\left[\because \sin ^2 x \leq \text { and } \cos ^2 y \leq 1\right]
\)
\(
\text { R.H.S. }=2 \sec ^2 z \geq 2
\)
Hence, L.H.S: \(=\) R.H.S. only when \(\sin ^2 x=1, \cos ^2 y=1\) and \(2 \sec ^2 z=2\)
\(
\begin{aligned}
& \Rightarrow \quad \cos ^2 x=0, \sin ^2 y=0, \cos ^2 z=1 \\
& \Rightarrow \quad \cos x=0, \sin y=0, \sin z=0
\end{aligned}
\)
\(x=(2 m+1) \frac{\pi}{2}, y=n \pi\) and \(z=t \pi\), where \(m, n\) and \(t\) are integers.

Example 36: Solve \(1+\sin x \sin ^2 \frac{x}{2}=0\).

Solution: 
\(
\begin{aligned}
& 1+\sin x \sin ^2 \frac{x}{2}=0 \\
& \Rightarrow 2+2 \sin x \sin ^2 \frac{x}{2}=0 \\
& \Rightarrow 2+\sin x(1-\cos x)=0 \\
& \Rightarrow 4+2 \sin x-\sin 2 x=0 \\
& \Rightarrow \sin 2 x=2 \sin x+4
\end{aligned}
\)
Above is not possible for any value of \(x\) as L.H.S. has maximum value 1 and R.H.S. has minimum value 2.
Hence, there is no solution.

Example 37: Solve \(\cos 4 \theta+\sin 5 \theta=2\).

Solution: The equation \(\cos 4 \theta+\sin 5 \theta=2\) is valid only when \(\cos 4 \theta=1\) and \(\sin 5 \theta=1\).
\(
\begin{aligned}
& \Rightarrow \quad 4 \theta=2 n \pi \text { and } 5 \theta=2 m \pi+\pi / 2, n, m \in Z \\
& \Rightarrow \quad \theta=\frac{2 n \pi}{4} \text { and } \theta=\frac{2 m \pi}{5}+\frac{\pi}{10}, n, m \in Z
\end{aligned}
\)
Putting \(n ; m=0, \pm 1, \pm 2, \ldots\), the common value in \([0,2 \pi]\) is \(\theta=\pi / 2\).
Therefore, the solution is \(\theta=2 k \pi+\pi / 2, k \in Z\).

INEQUALITIES

Trigonometric Inequations

To solve the trigonometric inequation of the type \(f(x) \leq a\), or \(f(x) \geq a\), where \(f(x)\) is some trigonometric ratio, the following steps should be taken:

• Draw the graph of \(f(x)\) in an interval length equal to the fundamental period of \(f(x)\).
• Draw the line \(y=a\).
• Take the portion of the graph for which the inequation is satisfied.
• To generalize, add \(n T(n \in I)\) and take union over the set of integers, where \(T\) is the fundamental period of \(f(x)\).

Example 38: Solve \(\sin x>-\frac{1}{2}\).

Solution: As the function \(\sin x\) has least positive period \(2 \pi\); therefore, it is sufficient to solve the inequality of the form \(\sin x>a, \sin x \geq a, \sin x<a\) and \(\sin x \leq a\) first on the interval of length \(2 \pi\). Then get the solution set by adding numbers of the form \(2 \pi n, n \in z\), to each of the solutions obtained on that interval.
Thus, let us solve this inequality on the interval \(\left[-\frac{\pi}{2}, \frac{3 \pi}{2}\right]\).

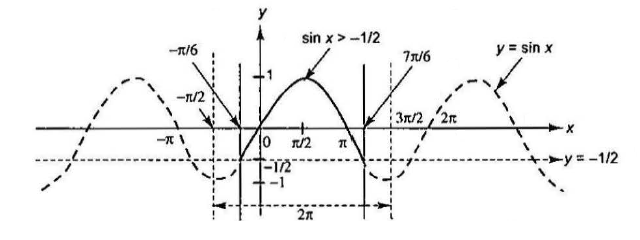
From the above Figure, \(\sin x>-\frac{1}{2}\), when \(-\frac{\pi}{6}<x<\frac{7 \pi}{6}\)
Thus, on generalizing, the above solution is \(2 n \pi-\frac{\pi}{6}<x<2 n \pi+\frac{7 \pi}{6}; n \in Z\).

Example 39: Solve \(2 \cos ^2 \theta+\sin \theta \leq 2\), where \(\pi / 2 \leq \theta \leq 3 \pi / 2\).

Solution:

\(
\begin{aligned}
&\begin{aligned}
& 2 \cos ^2 \theta+\sin \theta \leq 2 \\
& \Rightarrow \quad 2\left(1-\sin ^2 \theta\right)+\sin \theta \leq 2 \\
& \Rightarrow \quad-2 \sin ^2 \theta+\sin \theta \leq 0 \\
& \Rightarrow \quad 2 \sin ^2 \theta-\sin \theta \geq 0 \\
& \Rightarrow \quad \sin \theta(2 \sin \theta-1) \geq 0 \\
& \Rightarrow \quad \sin \theta(\sin \theta-1 / 2) \geq 0,
\end{aligned}\\
&\text { which is possible if } \sin \theta \leq 0 \text { or } \sin \theta \geq 1 / 2 \text {. }
\end{aligned}
\)

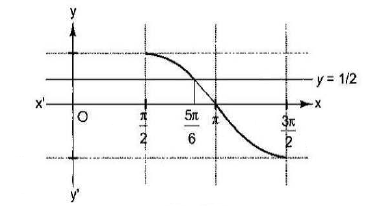
From the graph,
\(
\begin{aligned}
& \text { Now } \sin \theta \geq 1 / 2 \quad \Rightarrow \quad \pi / 2 \leq \theta \leq 5 \pi / 6 \\
& \text { and } \sin \theta \leq 0 \quad \Rightarrow \quad \pi \leq \theta \leq 3 \pi / 2
\end{aligned}
\)
Hence, the required values of \(\theta\) are given by
\(
\theta \in[\pi / 2,5 \pi / 6] \cup[\pi, 3 \pi / 2]
\)

Example 40: Solve \(\sin \theta+\sqrt{3} \cos \theta \geq 1,-\pi<\theta \leq \pi\).

Solution: The given inequation is
\(
\begin{aligned}
& \sin \theta+\sqrt{3} \cos \theta \geq 1,-\pi<\theta \leq \pi \\
& \Rightarrow \quad \frac{1}{2} \sin \theta+\frac{\sqrt{3}}{2} \cos \theta \geq \frac{1}{2}
\end{aligned}
\)

\(
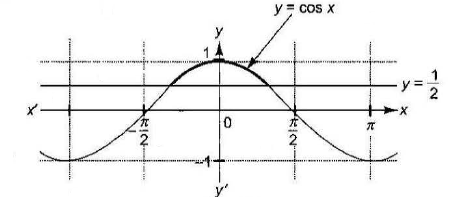
\Rightarrow \cos \left(\theta-\frac{\pi}{6}\right) \geq \frac{1}{2}=\cos \frac{\pi}{3} \quad \Rightarrow-\frac{\pi}{3} \leq \theta-\frac{\pi}{6} \leq \frac{\pi}{3} \quad \Rightarrow-\frac{\pi}{6} \leq \theta \leq \frac{\pi}{2}
\)

Example 44: Solve \(\cos 2 x>|\sin x|, x \in\left(-\frac{\pi}{2}, \pi\right)\).

Solution: Draw the graph of \(y=\cos 2 x\) and \(y=|\sin x|\)

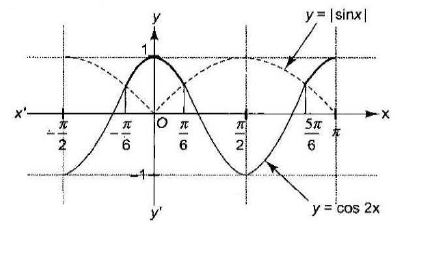
Let \(\cos 2 x=\sin x\)
\(
\Rightarrow 2 \sin ^2 x+\sin x-1=0 \Rightarrow \sin x=-1, \frac{1}{2}
\)
But \(\sin x \neq-1 \Rightarrow \sin x=\frac{1}{2}\)
Clearly from the graph, graphs of \(y=|\sin x|\) and \(y=\cos 2 x\) intersect at \(x= \pm \frac{\pi}{6}, \frac{5 \pi}{6}\).
Thus, the solution set is \(x \in\left(-\frac{\pi}{6}, \frac{\pi}{6}\right) \cup\left(\frac{5 \pi}{6}, \pi\right)\).

Example 45: Find the number of solutions of \(\sin x=\frac{x}{10}\).

Solution: Here, let \(f(x)=\sin x\) and \(g(x)=\frac{x}{10}\). Also, we know that \(-1 \leq \sin x \leq 1\).
\(
\Rightarrow-1 \leq \frac{x}{10} \quad \Rightarrow-10 \leq x \leq 10
\)
Thus, sketch both curves when \(x \in[-10,10]\).

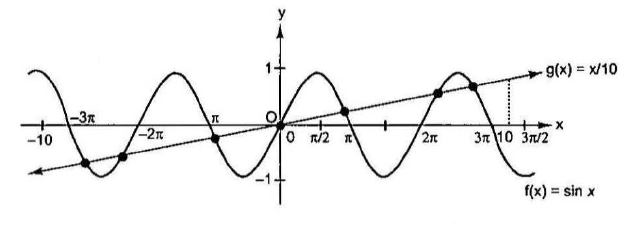
From the above, \(f(x)=\sin x\) and \(g(x)=x / 10\) intersect at seven points. So, the number of solutions is 7.

EXERCISES

Q1. Solve \(3 \tan 2 x-4 \tan 3 x=\tan ^2 3 x \tan 2 x\).

Solution:
\(
\begin{aligned}
&\text { We have } 3(\tan 2 x-\tan 3 x)=\tan 3 x(1+\tan 3 x \tan 2 x)\\
&\begin{aligned}
& \Rightarrow 3(\tan 2 x-\tan 3 x) /(1+\tan 3 x \tan 2 x)=\tan 3 x \\
& \Rightarrow 3 \tan (2 x-3 x)=\tan 3 x \\
& \Rightarrow 3 \tan x+\left(3 \tan x-\tan ^3 x\right) /\left(1-3 \tan ^2 x\right)=0 \\
& \Rightarrow \tan x\left[3\left(1-3 \tan ^2 x\right)+3-\tan ^2 x\right]=0 \\
& \Rightarrow \tan x\left(6-10 \tan ^2 x\right)=0 \\
& \Rightarrow \tan x=0 \text { or } \tan ^2 x=3 / 5 \\
& \text { If } \tan x=0 \quad \Rightarrow \quad x=n \pi, n \in Z \\
& \text { and if } \tan { }^2 x=3 / 5 \quad \Rightarrow \quad x=m \pi \pm \alpha=m \pi \pm \tan ^{-1} \sqrt{3 / 5}, m \in Z \\
& \text { Hence, } x=n \pi, m \pi \pm \tan ^{-1} \sqrt{3 / 5}, \forall m, n \in Z .
\end{aligned}
\end{aligned}
\)

Q2. For which values of \(a\), does the equation \(4 \sin (x+\pi / 3) \cos (x-\pi / 6)=a^2+\sqrt{3} \sin 2 x-\cos 2 x\) have solutions? Find the solutions for \(a=0\), if exist.

Solution: The given equation can be rewritten as \(2[\sin (2 x+\pi / 6)+\sin \pi / 2]=a^2+\sqrt{3} \cdot \sin 2 x-\cos 2 x\)
\(
\begin{aligned}
& \Rightarrow \cos 2 x=\left(a^2-2\right) / 2 \\
& \Rightarrow 2 \cos ^2 x=a^2 / 2 \text { or } \cos ^2 x=(a / 2)^2 \\
& \Rightarrow a^2 \leq 4 \text { or }-2 \leq a \leq 2
\end{aligned}
\)
For \(a=0\), the given equation is reduced to
\(
\cos x=0 \text {, i.e., } x=n \pi+(\pi / 2), n \in Z
\)

Q3. Solve \(\sin ^4(x / 3)+\cos ^4(x / 3)>1 / 2\).

Solution:
\(
\begin{aligned}
& \sin ^4(x / 3)+\cos ^4(x / 3)>1 / 2(n \in Z) \\
& \Rightarrow 1-2 \sin ^2(x / 3) \cos ^2(x / 3)>1 / 2 \\
& \Rightarrow 1-\frac{1}{2} \sin ^2(2 x / 3)>\frac{1}{2} . \\
& \Rightarrow \sin ^2(2 x / 3)<1
\end{aligned}
\)
which is always true except when \(\sin ^2(2 x / 3)=1\)
This means \(2 x / 3=n \pi \pm(\pi / 2)\) or \(x=(3 n \pi / 2) \pm(3 \pi / 4), n \in Z\)
Hence, the solution set of the inequality is \(R-\{x: x=(3 n \pi / 2) \pm(3 \pi / 4), n \in Z\}\).

Q4. Solve \(\sin x+\sin y=\sin (x+y)\) and \(|x|+|y|=1\).

Solution:
\(
\begin{aligned}
&\begin{aligned}
& \sin x+\sin y=\sin (x+y) \\
& \Rightarrow 2 \sin \frac{x+y}{2}\left[\cos \frac{x-y}{2}-\cos \frac{x+y}{2}\right]=0 \\
& \Rightarrow 4 \sin \frac{x+y}{2} \sin \frac{x}{2} \sin \frac{y}{2}=0
\end{aligned}\\
&\text { a. } \sin \frac{x+y}{2}=0 \quad \Rightarrow \quad x+y=2 n \pi, n \in Z \quad \Rightarrow \quad x+y=0(\because|x|+|y|=1 \Rightarrow-1 \leq x, y \leq 1)
\end{aligned}
\)
b. \(\sin \frac{x}{2}=0 \quad \Rightarrow \quad x=2 m \pi, m \in Z \quad \Rightarrow \quad x=0\)
c. \(\sin \frac{y}{2}=0 \quad \Rightarrow \quad y=2 p \pi, p \in Z \quad \Rightarrow \quad y=0\)

From \(|x|+|y|=1\)
If \(x=0\), then \(|y|=1 \quad \Rightarrow \quad y= \pm 1\)
If \(y=0\), then \(|x|=1 \quad \Rightarrow \quad x= \pm 1\)
If \(y=-x\), then \(|x|+|-x|=2 \quad \Rightarrow \quad x= \pm \frac{1}{2}\) and \(y=\mp \frac{1}{2}\)
Hence, solutions are \((0,1),(0,-1),(1,0),(-1,0),\left(\frac{1}{2},-\frac{1}{2}\right)\) and \(\left(-\frac{1}{2}, \frac{1}{2}\right)\).

Q5. Solve the equation \(\tan ^4 x+\tan ^4 y+2 \cot ^2 x \cot ^2 y=3+\sin ^2(x+y)\) for the values of \(x\) and \(y\).

Solution:
\(
\begin{aligned}
&\begin{aligned}
& \tan ^4 x+\tan ^4 y+2 \cot ^2 x \cot ^2 y=3+\sin ^2(x+y) \\
& \Rightarrow \tan ^4 x+\tan ^4 y+2 \cot ^2 x \cot ^2 y-2=1+\sin ^2(x+y) \\
& \Rightarrow\left(\tan ^2 x-\tan ^2 y\right)^2+2(\tan x \tan y-\cot x \cot y)^2=-1+\sin ^2(x+y)
\end{aligned}\\
&\text { Now L.H.S. } \geq 0 \text { and R.H.S. } \leq 0
\end{aligned}
\)
\(
\begin{aligned}
& \Rightarrow \text { L.H.S. }=\text { R.H.S. }=0 \\
& \Rightarrow \tan ^2 x=\tan ^2 y \text { and } \tan ^2 x \tan ^2 y=1 \text { and } \sin ^2(x+y)=0 \\
& \quad=\tan ^2 y=1 \text { and } x+y=n \pi, n \in Z \\
& \Rightarrow x=n \pi \pm \frac{\pi}{4}, n \in Z \text { and } y=n \pi \mp \frac{\pi}{4}, n \in Z .
\end{aligned}
\)

Q6. Find the smallest positive root of the equation \(\sqrt{\sin (1-x)}=\sqrt{\cos x}\).

Solution: The given equation is possible if \(\sin (1-x) \geq 0\) and \(\cos x \geq 0\). On squaring, we get \(\sin (1-x)=\cos x\)

\(
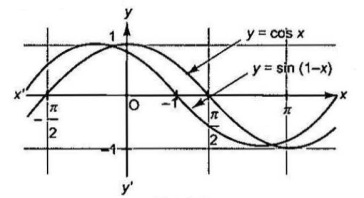
\begin{aligned}
&\begin{aligned}
& \Rightarrow \quad \cos \left(\frac{\pi}{2}-(1-x)\right)=\cos x \\
& \Rightarrow \quad \frac{\pi}{2}-1+x=2 n \pi \pm x, n \in Z \\
& \Rightarrow \quad x=\frac{2 n \pi-\frac{\pi}{2}+1}{2}, n \in Z
\end{aligned}\\
&\text { For } n=2, x=\frac{7 \pi}{4}+\frac{1}{2} \text { which is the smallest positive root of the given equation. }
\end{aligned}
\)

Q7. Solve the equation \(2 \sin x+\cos y=2\) for the values of \(x\) and \(y\).

Solution:
\(
\begin{aligned}
& 2 \sin x+\cos y=2 \\
& \Rightarrow \cos y=2(1-\sin x), \text { we have } \cos y \in[-1,1] \\
& \Rightarrow-\frac{1}{2} \leq 1-\sin x \leq \frac{1}{2} \quad \Rightarrow \quad \frac{1}{2} \leq \sin x \leq \frac{3}{2} \quad \Rightarrow \quad \frac{1}{2} \leq \sin x \leq 1
\end{aligned}
\)
\(
\begin{aligned}
& \text { Let } t=\sin x \quad \Rightarrow \quad x=\sin ^{-1}(t), t \in[1 / 2,1] \\
& \left.\Rightarrow \quad \cos y=2(1-t) \quad \Rightarrow \quad \begin{array}{l}
y=2 n_1 \pi \pm \cos ^{-1} 2(1-t) \\
\text { and } x=n_2 \pi+(-1)^{n_2} \sin ^{-1}(t)
\end{array}\right\} t \in[1 / 2,1]
\end{aligned}
\)

Q8. Prove that the equation \(2 \sin x=|x|+a\) has no solution for \(a \in\left(\frac{3 \sqrt{3}-\pi}{3}, \infty\right)\).

Solution:
\(\sin x=\frac{1}{2}|x|+\frac{a}{2}\) or \(2 \sin x=|x|+a\). Consider graphs of \(y=2 \sin x\) and \(y=|x|\).

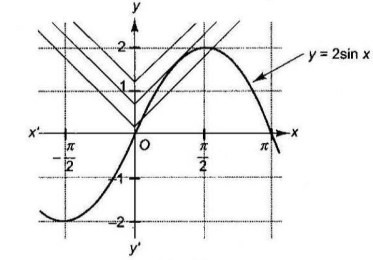
Equation \(2 \sin x=|x|+a\) will have a solution so long as the line \(y=|x|+a\) intersects or at least touches the curve, \(y=2 \sin x\). In this case, we must have \(d y / d x=2 \cos x=1=\) the slope of the line \(\Rightarrow x=\pi / 3\).
Hence, the solution exists if \(\frac{\pi}{3}+a>2 \sin \frac{\pi}{3} \Rightarrow a>\frac{3 \sqrt{3}-\pi}{3}\)

Q9. Solve \(\tan \left(\frac{\pi}{2} \cos \theta\right)=\cot \left(\frac{\pi}{2} \sin \theta\right)\).

Solution:
\(
\begin{aligned}
& \tan \left(\frac{\pi}{2} \cos \theta\right)=\cot \left(\frac{\pi}{2} \sin \theta\right)=\tan \left(\frac{\pi}{2}-\frac{\pi}{2} \sin \theta\right) \\
& \Rightarrow \quad \frac{\pi}{2} \cos \theta=n \pi+\frac{\pi}{2}-\frac{\pi}{2} \sin \theta, n \in Z \\
& \Rightarrow \quad \frac{\pi}{2}(\sin \theta+\cos \theta)=n \pi+\frac{\pi}{2}=\left(n+\frac{1}{2}\right) \pi \\
& \Rightarrow \quad \sin \theta+\cos \theta=(2 n+1) \\
& \Rightarrow \quad \sqrt{2} \sin \left(\theta+\frac{\pi}{4}\right)=(2 n+1) \\
& \Rightarrow \quad n=0,-1 \text { are the only possibilities } \\
& \text { So, } \sin \left(\theta+\frac{\pi}{4}\right)= \pm \frac{1}{\sqrt{2}}=\sin \left( \pm \frac{\pi}{4}\right) \\
& \Rightarrow \quad \theta+\frac{\pi}{4}=m \frac{\pi}{2}+\frac{\pi}{4}, m \in Z \\
& \Rightarrow \quad \theta=m \frac{\pi}{2}, m \in Z
\end{aligned}
\)
However, for the values of \(m=2 k, k \in Z\), the equation is not defined.
Hence, \(\theta=(2 k+1) \frac{\pi}{2}\), where \(k \in Z\).

Q10. Solve \(\sin x+\sin \left(\frac{\pi}{8} \sqrt{(1-\cos 2 x)^2+\sin ^2 2 x}\right)=0, x \in\left[\frac{5 \pi}{2}, \frac{7 \pi}{2}\right]\).

Solution:
\(
\begin{aligned}
& \sin x+\sin \left(\frac{\pi}{8} \sqrt{(1-\cos 2 x)^2+\sin ^2 2 x}\right)=0 \\
& \sin \left(\frac{\pi}{8} \sqrt{(1-\cos 2 x)^2+\sin ^2 2 x}\right)=\sin \frac{\pi}{8} \sqrt{2-2 \cos 2 x}=\sin \left(\frac{\pi}{4}|\sin x|\right) \\
& \text { Now } \sin x+\sin \left(\frac{\pi}{4}|\sin x|\right)=0 \dots(i)
\end{aligned}
\)
The equation has a solution only when \(\sin x \leq 0\).
The graph of \(f(x)=\sin x \leq 0\) is shown in Figure (a)

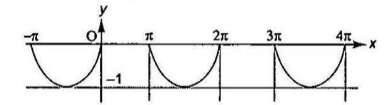
The graph \(y=\sin [\pi / 4|\sin x|]\) is as shown in Figure (b)

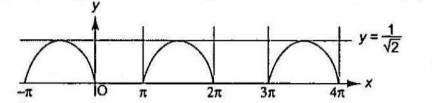
Hence, Eq. (i) has general solution \(x=n \pi, n \in Z\).

Q11. Solve \(\sin ^2 x+\frac{1}{4} \sin ^2 3 x=\sin x \sin ^2 3 x\).

Solution:
\(
\begin{aligned}
& \sin ^2 x+\frac{1}{4} \sin ^2 3 x=\sin x \sin ^2 3 x \\
& \Rightarrow \sin ^2 x-\sin x \sin ^2 3 x+\frac{1}{4} \sin ^2 3 x=0 \\
& \Rightarrow\left(\sin x-\frac{1}{2} \sin ^2 3 x\right)^2+\frac{1}{4} \sin ^2 3 x\left(1-\sin ^2 3 x\right)=0 \\
& \Rightarrow\left(\sin x-\frac{1}{2} \sin ^2 3 x\right)^2+\frac{1}{4} \sin ^2 3 x \cos ^2 3 x=0 \\
& \Rightarrow\left(\sin x-\frac{1}{2} \sin ^2 3 x\right)^2+\frac{1}{16} \sin ^2 6 x=0 \\
& \Rightarrow \sin x-\frac{1}{2} \sin ^2 3 x=0 \text { and } \sin 6 x=0 \\
& \Rightarrow 2 \sin x=\sin ^2 3 x \text { and } \sin 6 x=0 \quad \Rightarrow \text { From } \sin 6 x=0, x=k \pi / 6, k \in Z
\end{aligned}
\)
From here, we choose those values which satisfy the equation, \(2 \sin x=\sin ^2 3 x\)
Now \(\sin ^2 3\left(\frac{k \pi}{6}\right)=+\sin ^2 \frac{k \pi}{2}=\left\{\begin{array}{l}1, \text { if } k \text { is odd } \\ 0, \text { if } k \text { is even }\end{array}\right\}\)
\(
\begin{aligned}
& \Rightarrow \quad \sin x=0 \text { or } 1 / 2 \\
& \Rightarrow \quad x=n \pi \text { or } x=n \pi+\frac{\pi}{6}(-1)^n, n \in Z
\end{aligned}
\)