3.6 Entrance Corner: Trigonometric Ratios and Identities
MEASUREMENT OF ANGLES
Angles in Trigonometry
In trigonometry, the idea of angle is more general; it may be positive or negative and has any magnitude. Angles formed by anticlockwise rotation of the radius vector are taken as positive, whereas angles formed by clockwise rotation of the radius vector are taken as negative.
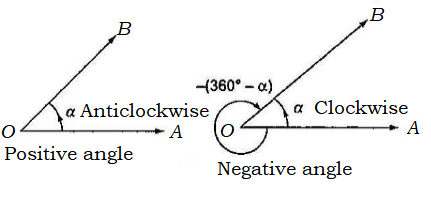
Angles Exceeding \(360^{\circ}\)
In geometry, we confine ourselves to angles from \(0^{\circ}\) to \(360^{\circ}\). But there may be problems in which rotation involves more than one revolution, for example, the rotation of a flywheel. In trigonometry, we generalise the concept of angle to angles greater than \(360^{\circ}\). This angle can be formed in the following way:
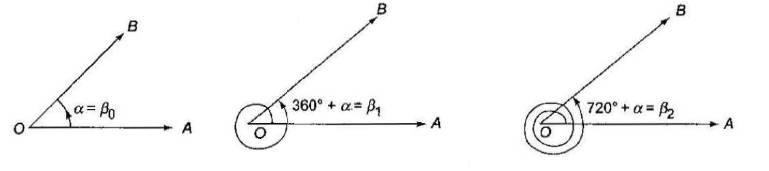
The revolving line (radius vector) starts from the initial position \(\overrightarrow{O A}\) and makes \(n\) complete revolutions in anticlockwise direction and also a further angle \(\alpha\) in the same direction. We then have a certain angle \(\beta_n\) given by \(\beta_n=360^{\circ} \times n+\alpha\), where \(0^{\circ}<\alpha<360^{\circ}\) and \(n\) is a positive integer or zero.
Thus, there are infinitely many \(\beta_n\) angles with initial side \(\overrightarrow{O A}\) and final side \(\overrightarrow{O B}\).
For example, \(\beta_0=\alpha, \beta_1=360^{\circ}+\alpha, \beta_2=720^{\circ}+\alpha\), etc.
Relation between Degree and Radian
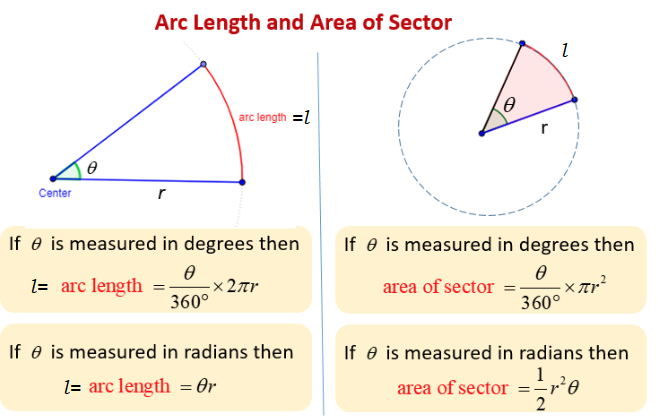
Radian is a constant angle. One radian is the angle subtended by an arc of a circle at the centre. It is equal to arc/radius. It is expressed as rad.
Let the arc (Arc is a portion of the circle) subtend angle \(\theta\) at the center
Then, Angle at center \(=\) Length of Arc/ Radius of circle
\(
\theta=l / r \text { (when } \theta \text { is in radians) }
\)
\(
l=\theta \times \frac{\pi}{180} \times r \quad \text { (when } \theta \text { is in degrees) }
\)
Important Points:
- \(1^{\circ}=60^{\prime}(60 \mathrm{~min}) \text { and } 1^{\prime}=60^{\prime \prime}(60 \mathrm{~sec})\)
- \(\text { Since } 180^{\circ}=\pi \mathrm{~rad} \text {. Therefore, } 1^{\circ}=\pi / 180 \mathrm{~rad} \text {. }\)
- We have \(\pi \mathrm{~rad}=180^{\circ}\)
\(
\begin{aligned}
& \Rightarrow \quad 1 \mathrm{~rad}=\frac{180^{\circ}}{\pi}=\left(\frac{180}{22} \times 7\right)^{\circ}=57^{\circ} 16^{\prime} 22^{\prime \prime} \text { (approx) } \\
& 180^{\circ}=\pi \mathrm{~rad} \Rightarrow 1^{\circ}=\frac{\pi}{180} \mathrm{~rad}=\left(\frac{22}{7 \times 180}\right) \mathrm{rad}=0.01746 \mathrm{rad}
\end{aligned}
\) - Sum of interior angles on convex polygon of \(n\) sides is \((n-2) \pi \mathrm{~rad}\) (A convex polygon with \(n\) sides can be divided into \(n-2\) triangles.)
Example 2.1: Express 1.2 rad in degree measure.
Answer:
\(
\begin{aligned}
&(1.2)^R=1.2 \times \frac{180}{\pi} \text { degrees }=1.2 \times \frac{180 \times 7}{22}\\
&\left[\because \pi=\frac{27}{7} \text { (approx) }\right]
\end{aligned}
\)
\(
=68.7272=68^{\circ}(.7272 \times 60)^{\prime}=68^{\circ}(43.63)^{\prime}=68^{\circ} 43^{\prime}(.63 \times 60)^{\prime \prime}=68^{\circ}\left(43^{\prime} 37.8^{\prime \prime}\right)
\)
Example 2.2: Find in degrees the angle subtended at the centre of a circle of diameter 50 cm by an arc of length 11 cm.
Answer: Here, \(r=25 \mathrm{~cm}\) and \(l=11 \mathrm{~cm}\).
\(\therefore \quad \theta=\left(\frac{l}{r}\right)^R \Rightarrow \theta=\left(\frac{11}{25}\right)^R=\left(\frac{11}{25} \times \frac{180}{\pi}\right)^0\)
\(
\begin{aligned}
& =\left(\frac{11}{25} \times \frac{180}{22} \times 7\right)^{\circ} \\
& =\left(\frac{126}{5}\right)^{\circ}=\left(25 \frac{1}{5}\right)^{\circ}=25^{\circ}\left(\frac{1}{5} \times 60\right)^{\circ}=25^{\circ} 12^{\prime}
\end{aligned}
\)
Example 2.3: If arcs of same length in two circles subtend angles of \(60^{\circ}\) and \(75^{\circ}\) at their centres, find the ratios of their radii.
Answer: Let \(r_1\) and \(r_2\) be the radii of the given circles and let their arcs of same length \(s\) subtend angles of \(60^{\circ}\) and \(75^{\circ}\) at their centres.
Now, \(60^R=\left(60 \times \frac{\pi}{180}\right)^R=\left(\frac{\pi}{3}\right)^R\) and \(75^{\circ}=\left(75 \times \frac{\pi}{180}\right)^R=\left(\frac{5 \pi}{12}\right)^R\)
\(\therefore \quad \frac{\pi}{3}=\frac{s}{r_1}\) and \(\frac{5 \pi}{12}=\frac{s}{r_2} \Rightarrow \frac{\pi}{3} r_1=s\) and \(\frac{5 \pi}{12} r_2=s \Rightarrow \frac{\pi}{3} r_1=\frac{5 \pi}{12} r_2 \Rightarrow 4 r_1=5 r_2 \Rightarrow r_1: r_2=5: 4\)
Hence, \(r_1: r_2=5: 4\).
Example 2.4: Assuming the distance of earth from the moon to be \(38,400 \mathrm{~km}\) and the angle subtended by the moon at the eye of a person on earth to be \(31^{\prime}\), find the diameter of the moon.
Answer:
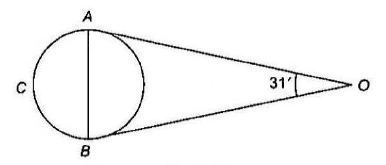
Let \(A B\) be the diameter of the moon and \(O\) be the observer. Given \(\angle A O B=31^{\prime}=\frac{31}{60} \times \frac{\pi}{180} \mathrm{rad}\)
Since the angle subtended by the moon is very small, its diameter will be approximately equal to the smalf arc of a circle whose centre is the eye of the observer and the radius is the distance of the earth from the moon. Also the moon subtends an angle of \(31^{\prime}\) at the centre of this circle.
\(
\begin{aligned}
& \Rightarrow \theta=\frac{l}{r}, \quad \text { therefore } \frac{31}{60} \times \frac{\pi}{180}=\frac{A B}{38400} \\
& \Rightarrow A B=\frac{31}{60} \times \frac{22}{7 \times 180} \times 38,400=3464 \frac{8}{63} \mathrm{~km}
\end{aligned}
\)
TRIGONOMETRIC FUNCTIONS
Trigonometric Functions of Acute Angles
An angle whose measure is greater than \(0^{\circ}\) but less than \(90^{\circ}\) is called an acute angle. Consider a right-angled triangle \(A B C\) with right angle at \(B\). The side opposite to the right angle is called the hypotenuse, the side opposite to angle \(A\) is called the perpendicular for angle \(A\), and the side opposite to the third angle is called the base for angle \(A\).
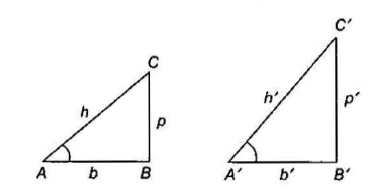
The ratio of any two sides of the triangle depends only on measure of angle \(A\), for if we take a larger and smaller right angle triangles as shown in Fig. above, we have \(\frac{h}{h^{\prime}}=\frac{b}{b^{\prime}}=\frac{p}{p^{\prime}}\) (as these triangles are similar).
Thus, the ratio of the lengths of any two sides of a triangle is completely determined by angle \(A\) alone and is independent of the size of the triangle. There are six possible ratios that can be formed from the three sides of a right-angled triangle. Each of them has been given a name as follows.
Definitions
- \(\sin A=\frac{p}{h}\)
- \(\cos A=\frac{b}{h}\)
- \(\tan A=\frac{p}{b}\)
- \(\cot A=\frac{b}{p}\)
- \(\sec A=\frac{h}{b}\)
- \(\operatorname{cosec} A=\frac{h}{p}\)
The abbreviations stand for sine, cosine, tangent, cotangent, secant, and cosecant of \(A\), respectively. These functions of angle \(A\) are called trigonometrical functions or trigonometrical ratios.
Example 2.5: The circumference of a circle circumscribing an equilateral triangle is \(24 \pi\) units. Find the area of the circle inscribed in the equilateral triangle.
Answer: \(2 \pi R=24 \pi\) ( \(R\) is the radius of circumcircle)
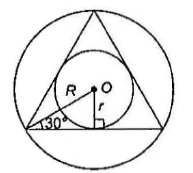
\(
\begin{aligned}
& R=12 \\
& \sin 30^{\circ}=\frac{r}{R}(r \text { is the radius of incircle) } \\
& r=\frac{12}{2}=6
\end{aligned}
\)
Therefore, area of incircle \(=\pi \pi^2=36 \pi\)
Example 2.6: In triangle \(A B C, B C=8, C A=6\) and \(A B=10\). A line dividing the triangle \(A B C\) into two regions of equal area is perpendicular to \(A B\) at the point \(X\). Then find the value of \(B X / \sqrt{2}\).
Answer: From the figure, \(2\left(\frac{x \times {y}}{2}\right)=\frac{8 \times 6}{2}=24\)
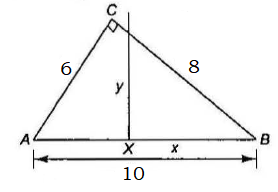
\(
\begin{aligned}
& x \times x \tan B=24 \\
& x^2 \times \frac{3}{4}=24 \\
& x^2=32 \Rightarrow x=4 \sqrt{2}
\end{aligned}
\)
\(
\mathbf{B X} / \sqrt{2} =4 \sqrt{2} / \sqrt{2} = 4
\)
Example 2.7:Let \(P Q\) and \(R S\) be tangents at the extremities of the diameter \(P R\) of a circle of radius \(r\). If \(P S\) and \(R Q\) intersect at a point \(X\) on the circumference of the circle, then prove that \(2 r\) \(=\sqrt{P Q \times R S}\)
Answer: From the figure, we have \(\frac{P Q}{P R}=\tan (\pi / 2-\theta)=\cot \theta\).
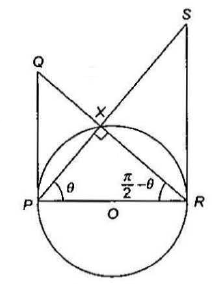
\(
\begin{aligned}
& \text { and } \frac{R S}{P R}=\tan \theta \\
& \Rightarrow \frac{P Q}{P R} \times \frac{R S}{P R}=1 \\
& \Rightarrow(P R)^2=P Q \times P S \\
& \Rightarrow(2 r)^2=P Q \times P S \\
& \Rightarrow 2 r=\sqrt{P Q \times P S}
\end{aligned}
\)
Example 2.8: Two circles of radii 4 cm and 1 cm touch each other externally and \(\theta\) is the angle contained by their direct common tangents. Then find \(\sin \theta\).
Answer:
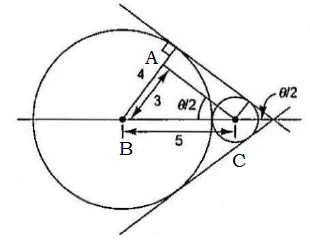
\(
\begin{aligned}
& A B=3 \mathrm{~cm} \\
& B C=5 \mathrm{~cm} \\
& \sin \theta / 2=\frac{A B}{B C} \\
& \sin \theta / 2=\frac{3}{5}
\end{aligned}
\)
\(
\begin{aligned}
\cos \theta / 2 & =\sqrt{1-\operatorname{sen}^2 \theta / 2} \\
& \Rightarrow \sqrt{1-\frac{9}{25}} \\
& \Rightarrow \sqrt{\frac{16}{25}}=4 / 5
\end{aligned}
\)
\(
\therefore \sin \theta=2 \times \frac{3}{5} \times \frac{4}{5}=\frac{24}{25}
\)
Example 2.9: If angle \(C\) of triangle \(A B C\) is \(90^{\circ}\), then prove that \(\tan A+\tan B=\frac{c^{2}}{a b}\) (where, \(a, b, c\) are sides opposite to angles \(A, B, C\) respectively)
Answer: Draw \(\triangle A B C\) with \(\angle C=90^{\circ}\).
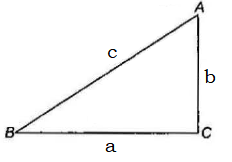
\(
\begin{aligned}
\tan A+\tan B & =\frac{a}{b}+\frac{b}{a} \\
& =\frac{a^2+b^2}{a b}=\frac{c^2}{a b}
\end{aligned}
\)
Example 2.10: In the following diagram \(\angle B A O=\tan ^{-1} 3\), then find the ratio \(B C: C A\)
Answer:
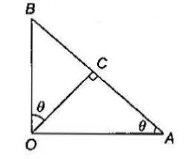
\(
\begin{aligned}
& \therefore \tan \theta=3 \\
& \therefore \frac{O C}{A C}=\tan \theta, \frac{O C}{B C}=\cot \theta \\
& \Rightarrow \frac{B C}{A C}=\frac{\tan \theta}{\cot \theta}=\tan ^2 \theta=9
\end{aligned}
\)
Trigonometric Functions of Any Angle
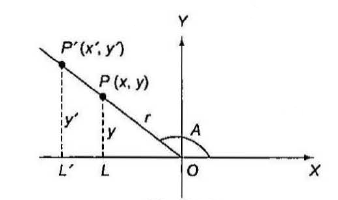
Let \(A\) bc a given angle with a specified initial ray. We introduce a rectangular coordinate system in the plane with the vertex of angle \(A\) as the origin and the initial ray of angle \(A\) as the positive ray of the \(x\)-axis (Figure above). We choose any point \(P\) on the terminal ray of angle \(A\). Let the coordinates of \(P\) be \((x, y)\) and its distance from the origin be \(r\), then we define
- \(\sin A=\frac{y}{r}\)
- \(\cos A=\frac{x}{r}\)
- \(\tan A=\frac{y}{x}\)
- \(\cot A=\frac{x}{y}\)
- \(\sec A=\frac{r}{x}\)
- \({cosec} A=\frac{r}{y}\)
These quantities are functions of angle \(A\) alone. They do not depend on the choice of point \(P\) and the terminal ray. If we choose a different point \(P^{\prime}\left(x^{\prime}, y^{\prime}\right)\) on the terminal ray of \(A\) at a distance \(r^{\prime}\) from the origin, it is clear that \(x^{\prime}\) and \(y^{\prime}\) will have the same sign as that of \(x\) and \(y\), respectively, because of similar triangles \(\triangle O P L\) and \(\triangle O P^{\prime} L^{\prime}\).
Also, any trigonometrical function of an angle \(A\) is equal to the same trigonometrical function of any angle \(360 n+A\), where \(n\) is any integer since all these angles will have the same terminal ray. For example, sin \(60^{\circ}=\sin 420^{\circ}=\sin \left(-300^{\circ}\right)\). After the coordinate system has been introduced, the plane is divided into four quadrants. An angle is said to be in that quadrant in which its terminal ray lies. For positive acute angles, this definition gives the same result as in the case of a right-angled triangle since both \(x\) and \(y\) are positive for any point in the first quadrant. Consequently, they are the length of the base and perpendicular of angle \(A\).
Graphs and Other Useful Data of Trigonometric Functions
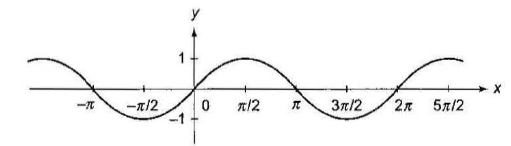
Case -1: \(f(x)=\sin x\)
\(
\begin{aligned}
& y=f(x)=\sin x \\
& \text { Domain } \rightarrow R, \text { Range } \rightarrow[-1,1] \\
& \text { Period } \rightarrow 2 \pi \\
& \sin ^2 x,|\sin x| \in[0,1] \\
& \sin x=0 \Rightarrow x=n \pi, n \in I \\
& \sin x=1 \Rightarrow x=(4 n+1) \pi / 2, n \in I \\
& \sin x=-1 \Rightarrow x=(4 n-1) \pi / 2, n \in I \\
& \sin x=\sin \alpha \Rightarrow x=n \pi+(-1)^n \alpha, n \in I \\
& \sin x \geq 0 \Rightarrow x \in \bigcup_{n \in I}[2 n \pi, \pi+2 n \pi]
\end{aligned}
\)
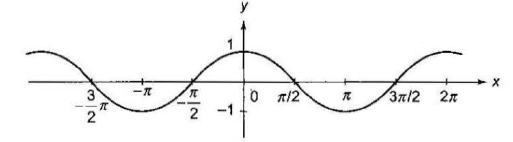
Case -2: \(f(x)=\cos x\)
\(
\begin{aligned}
& y=f(x)=\cos x \\
& \text { Domain } \rightarrow R, \text { Range } \rightarrow[-1,1] \\
& \text { Period } \rightarrow 2 \pi \\
& \cos ^2 x,|\cos x| \in[0,1] \\
& \cos x=0 \Rightarrow x=(2 n+1) \pi / 2, n \in I \\
& \cos x=1 \Rightarrow x=2 n \pi, n \in I \\
& \cos x=-1 \Rightarrow x=(2 n+1) \pi, n \in I \\
& \cos x=\cos \alpha \Rightarrow x=2 n \pi \pm \alpha, n \in I \\
& \cos x \geq 0 \Rightarrow x \in \bigcup_{n \in I}\left[2 n \pi-\frac{\pi}{2}, 2 n \pi+\pi / 2\right]
\end{aligned}
\)
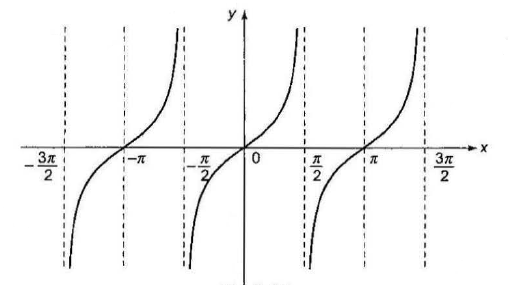
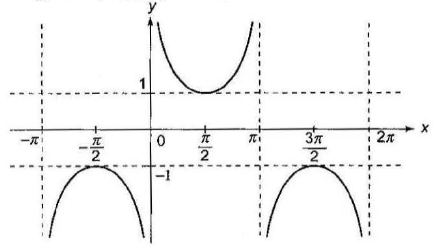
Case -3: \(f(x)=\tan x\)
\(
\begin{aligned}
& y=f(x)=\tan x \\
& \text { Domain } \rightarrow R \sim(2 n+1) \pi / 2, n \in I \\
& \text { Range } \rightarrow(-\infty, \infty) \\
& \text { Period } \rightarrow \pi \\
& \text { Discontinuous at } x=(2 n+1) \pi / 2, n \in I \\
& \tan ^2 x,|\tan x| \in[0, \infty) \\
& \tan x=0 \Rightarrow x=n \pi, n \in I \\
& \tan x=\tan \alpha \Rightarrow x=n \pi+\alpha, n \in I
\end{aligned}
\)
\(
y=f(x)=\cot x
\)
Domain \(\rightarrow R-n \pi, n \in I ;\) Range \(\rightarrow(-\infty, \infty)\); Period \(\rightarrow \pi\);
Discontinuous at \(x=n \pi, n \in I\)
\(\cot ^2 x,|\cot x| \in[0, \infty)\)
\(
\cot x=0 \Rightarrow x=(2 n+1) \pi / 2, n \in I
\)
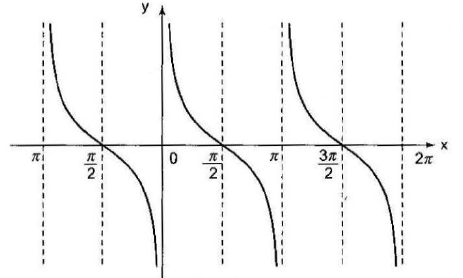
Case -5: \(f(x)=\sec x\)
\(
\begin{aligned}
& y=f(x)=\sec x \\
& \text { Domain } \rightarrow R \sim(2 n+1) \pi / 2, n \in I ; \text { Range } \rightarrow(-\infty,-1] \cup[1, \infty) \\
& \text { Period } \rightarrow 2 \pi, \sec ^2 x,|\sec x| \in[1, \infty)
\end{aligned}
\)
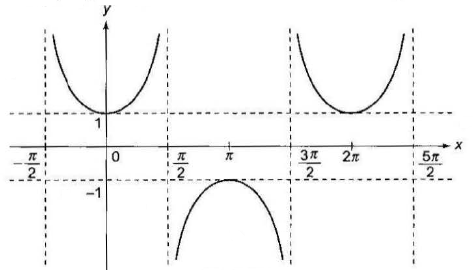
Case -6: \(f(x)=\operatorname{cosec} x\)
\(
\begin{aligned}
& y=f(x)=\operatorname{cosec} x \\
& \text { Domain } \rightarrow R \sim n \pi, n \in I ; \\
& \text { Range } \rightarrow(-\infty,-1] \cup[1, \infty) \\
& \text { Period } \rightarrow 2 \pi, \operatorname{cosec}^2 x,|\operatorname{cosec} x| \in[1, \infty)
\end{aligned}
\)
Signs of the Trigonometric Ratios or Functions
The signs of trigonometric functions depend on the quadrant in which the terminal side of the angle lies. We always take the length \(O P=r\) to be positive. Thus, \(\sin \theta=y / r\) has the \(\operatorname{sign}\) of \(y\) and \(\cos \theta=x / r\) has the sign of \(x\). The sign of \(\tan \theta\) depends on the signs of \(x\) and \(y\) and similarly the signs of other trigonometric ratios are determined by the signs of \(x\) and/or \(y\). Sign can also be determined by the graphs. Thus, we have the following:
\(
\begin{array}{|c|c|c|c|c|}
\hline \text { Function } & \begin{array}{c}
\text { 1st } \\
\text { quadrant }
\end{array} & \begin{array}{c}
\text { 2nd } \\
\text { quadrant }
\end{array} & \begin{array}{c}
\text { 3rd } \\
\text { quadrant }
\end{array} & \begin{array}{c}
\text { 4th } \\
\text { quadrant }
\end{array} \\
\hline \begin{array}{c}
\sin \theta \\
\operatorname{cosec} \theta
\end{array} & +\mathrm{ve} & +\mathrm{ve} & -\mathrm{ve} & -\mathrm{ve} \\
\hline \begin{array}{c}
\cos \theta \\
\sec \theta
\end{array} & +\mathrm{ve} & -\mathrm{ve} & -\mathrm{ve} & +\mathrm{ve} \\
\hline \begin{array}{c}
\tan \theta \\
\cot \theta
\end{array} & +\mathrm{ve} & -\mathrm{ve} & +\mathrm{ve} & -\mathrm{ve} \\
\hline
\end{array}
\)
Variations in the Values of Trigonometric Functions in Different Quadrants
\(\begin{array}{|l|l|l|l|l|}
\hline & 1^{\text {st }} \text { quadrant } & 2^{\text {nd }} \text { quadrant } & 3^{\text {rt }} \text { quadrant } & \text { 4 }^{\text {th }} \text { quadrant } \\
\hline \sin \theta & \uparrow \text { from } 0 \text { to } 1 & \downarrow \text { from } 1 \text { to } 0 & \downarrow \text { from } 0 \text { to }-1 & \uparrow \text { from }-1 \text { to } 0 \\
\hline \cos \theta & \downarrow \text { from } 1 \text { to } 0 & \downarrow \text { from } 0 \text { to-1 } & \uparrow \text { from }-1 \text { to } 0 & \uparrow \text { from } 0 \text { to } 1 \\
\hline \tan \theta & \uparrow \text { from } 0 \text { to } \infty & \uparrow \text { from }-\infty \text { to } 0 & \uparrow \text { from } 0 \text { to } \infty & \uparrow \text { from }-\infty \text { to } 0 \\
\hline \cot \theta & \downarrow \text { from } \infty \text { to } 0 & \downarrow \text { from } 0 \text { to }-\infty & \downarrow \text { from } \infty \text { to } 0 & \downarrow \text { from } 0 \text { to }-\infty \\
\hline \sec \theta & \uparrow \text { from } 1 \text { to } \infty & \uparrow \text { from }-\infty \text { to-1 } & \downarrow-1 \text { to }-\infty & \downarrow \text { from } \infty \text { to } 1 \\
\hline \operatorname{cosec} \theta & \downarrow \text { from } \infty \text { to } 1 & \uparrow \text { from } 1 \text { to } \infty & \uparrow \text { from }-\infty \text { to -1 } & \downarrow \text { from }-1 \text { to }-\infty \\
\hline
\end{array}
\)
Note: \(+\infty\) and \(-\infty\) are two symbols. These are not real numbers. When we say’ that tan \(\theta\) increases from 0 to \(\infty\) as \(\theta\) varies from 0 to \(\pi / 2\), it means that tan \(\theta\) increases in the interval \((0, \pi / 2)\) and it attains arbitrarily large positive values as \(\theta\) tends to \(\pi / 2\). Similarly, this happens for other trigonometrical functions as well.
\(\begin{aligned}
&\text { Trigonometric Ratios of Standard Angles }\\
&\begin{array}{|c|c|c|c|}
\hline \begin{array}{c}
\text { Angle }(\boldsymbol{\theta}) \rightarrow \\
\text { T-Ratio } \downarrow
\end{array} & \mathbf{3 0 ^ { \circ }} & \mathbf{4 5 ^ { \circ }} & \mathbf{6 0 ^ { \circ }} \\
\hline \sin \theta & 1 / 2 & 1 / \sqrt{2} & \sqrt{3} / 2 \\
\hline \cos \theta & \sqrt{3} / 2 & 1 / \sqrt{2} & 1 / 2 \\
\hline \tan \theta & 1 / \sqrt{3} & 1 & \sqrt{3} \\
\hline \operatorname{cosec} \theta & 2 & \sqrt{2} & 2 / \sqrt{3} \\
\hline \sec \theta & 2 / \sqrt{3} & \sqrt{2} & 2 \\
\hline \cot \theta & \sqrt{3} & 1 & 1 / \sqrt{3} \\
\hline
\end{array}
\end{aligned}
\)
Trigonometric Ratios of any Angle
\(
\begin{array}{ll}
\sin (-\theta)=-\sin \theta & \cos (-\theta)=\cos \theta \\
\sin \left(\frac{\pi}{2}-\theta\right)=\cos \theta & \cos \left(\frac{\pi}{2}-\theta\right)=\sin \theta \\
\tan (-\theta)=-\tan \theta & \cot (-\theta)=-\cot \theta \\
\tan \left(\frac{\pi}{2}-\theta\right)=\cot \theta & \cot \left(\frac{\pi}{2}-\theta\right)=\tan \theta
\end{array}
\)
\(
\begin{array}{ll}
\operatorname{cosec}(-\theta)=-\operatorname{cosec} \theta & \sec (-\theta)=\sec \theta \\
\sec \left(\frac{\pi}{2}-\theta\right)=\operatorname{cosec} \theta & \operatorname{cosec}\left(\frac{\pi}{2}-\theta\right)=\sec \theta \\
\sin \left(\frac{\pi}{2}+\theta\right)=\cos \theta & \cos \left(\frac{\pi}{2}+\theta\right)=-\sin \theta \\
\sin (\pi-\theta)=\sin \theta & \cos (\pi-\theta)=-\cos \theta
\end{array}
\)
\(
\begin{array}{ll}
\tan \left(\frac{\pi}{2}+\theta\right)=-\cot \theta & \cot \left(\frac{\pi}{2}+\theta\right)=-\tan \theta \\
\tan (\pi-\theta)=-\tan \theta & \cot (\pi-\theta)=-\cot \theta \\
\sec \left(\frac{\pi}{2}+\theta\right)=-\operatorname{cosec} \theta & \operatorname{cosec}\left(\frac{\pi}{2}+\theta\right)=\sec \theta \\
\sec (\pi-\theta)=-\sec \theta & \operatorname{cosec}(\pi-\theta)=\operatorname{cosec} \theta \\
\sin (\pi+\theta)=-\sin \theta & \cos (\pi+\theta)=-\cos \theta \\
\sin \left(\frac{3 \pi}{2}-\theta\right)=-\cos \theta & \cos \left(\frac{3 \pi}{2}-\theta\right)=-\sin \theta
\end{array}
\)
\(
\begin{array}{ll}
\tan (\pi+\theta)=\tan \theta & \cot (\pi+\theta)=\cot \theta \\
\tan \left(\frac{3 \pi}{2}-\theta\right)=\cot \theta & \cot \left(\frac{3 \pi}{2}-\theta\right)=\tan \theta \\
\sec (\pi+\theta)=-\sec \theta & \operatorname{cosec}(\pi+\theta)=-\operatorname{cosec} \theta \\
\sec \left(\frac{3 \pi}{2}-\theta\right)=-\operatorname{cosec} \theta & \operatorname{cosec}\left(\frac{3 \pi}{2}-\theta\right)=-\sec \theta \\
\sin \left(\frac{3 \pi}{2}+\theta\right)=-\cos \theta & \cos \left(\frac{3 \pi}{2}+\theta\right)=\sin \theta \\
\sin (2 \pi-\theta)=-\sin \theta & \cos (2 \pi-\theta)=\cos \theta \\
\tan \left(\frac{3 \pi}{2}+\theta\right)=-\cot \theta & \cot \left(\frac{3 \pi}{2}+\theta\right)=-\tan \theta
\end{array}
\)
\(
\begin{array}{ll}
\tan (2 \pi-\theta)=-\tan \theta & \cot (2 \pi-\theta)=-\cot \theta \\
\sec \left(\frac{3 \pi}{2}+\theta\right)=\operatorname{cosec} \theta & \operatorname{cosec}\left(\frac{3 \pi}{2}+\theta\right)=-\sec \theta \\
\sec (2 \pi-\theta)=\sec \theta & \operatorname{cosec}(2 \pi-\theta)=-\operatorname{cosec} \theta \\
\sin (2 \pi+\theta)=\sin \theta & \cos (2 \pi+\theta)=\cos \theta \\
\tan (2 \pi+\theta)=\tan \theta & \cot (2 \pi+\theta)=\cot \theta \\
\sec (2 \pi+\theta)=\sec \theta & \operatorname{cosec}(2 \pi+\theta)=\operatorname{cosec} \theta
\end{array}
\)
Transformation of the Graphs of Trigonometric Functions
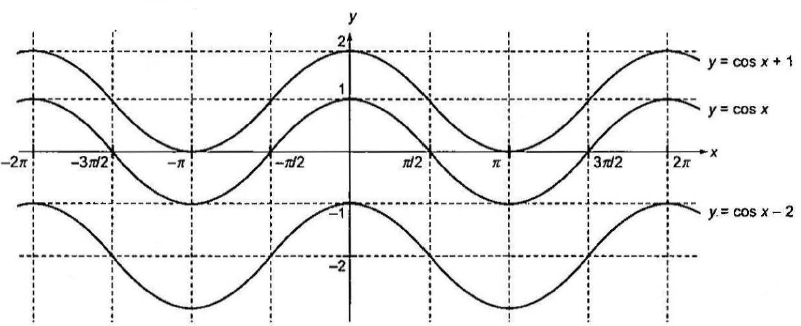
- To draw the graph of \(y=f(x+a) ;(a>0)\) from the graph of \(y=f(x)\), shift the graph of \(y=f(x), a\) units left along the \(x\)-axis.
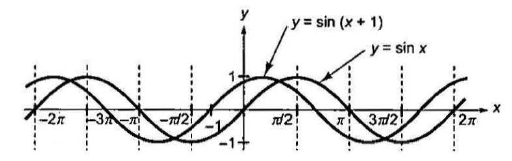
- To draw the graph of \(y=f(x-a) ;(a>0)\) from the graph of \(y=f(x)\), shift the graph of \(y=f(x), a\) units right along the \(x\)-axis.
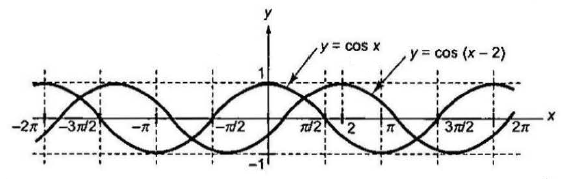
- To draw the graph of \(y=f(x)+a ;(a>0)\) from the graph of \(y=f(x)\), shift the graph of \(y=f(x), a\) units upward along the \(y\)-axis..
To draw the graph of \(y=f(x)-a ;(a>0)\) from the graph of \(y=f(x)\), shift the graph of \(y=f(x), a\) units downward along the \(y\)-axis.
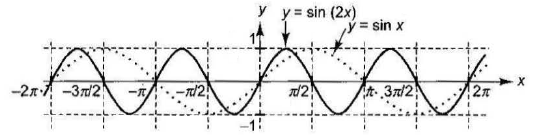
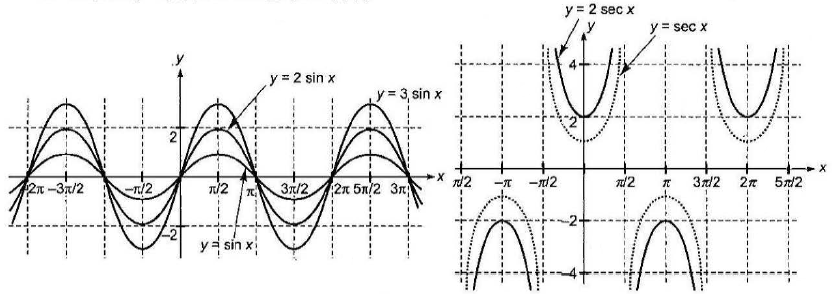
- If \(y=f(x)\) has period \(T\), then period of \(y=f(a x)\) is \(T /|a|\).
Period of \(y=\sin (2 x)\) is \(2 \pi / 2=\pi\)
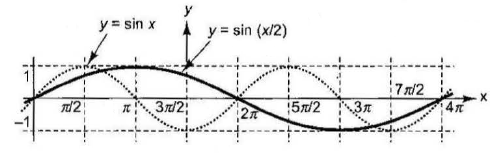
- Period of \(y=\sin (x / 2)\) is \(2 \pi /(1 / 2)=4 \pi\)
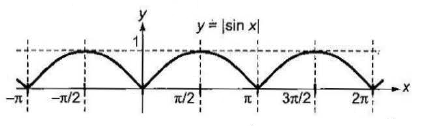
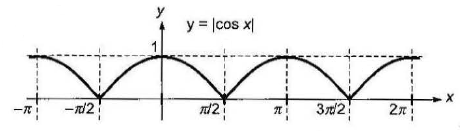
- Since \(y=|f(x)| \geq 0\), to draw the graph of \(y=|f(x)|\), take the mirror of the graph of \(y=f(x)\) in \(x\)-axis for \(f(x)<0\), retaining the graph for \(f(x)>0\). Here period of \(f(x)=|\sin x|\) is \(\pi\).
- Here period of \(f(x)=|\cos x|\) is \(\pi\)
- Graph of \(y=a f(x)\) from the graph of \(y f(x)\)
Example 2.11: If \(f(\theta)=4 \sin \theta+\cos ^2 \theta\), then what is maximum and minimum value of \(f(\theta)\)?
Solution:
\(
\begin{aligned}
f(\theta) & =4 \sin \theta+\cos ^2 \theta=4 \sin \theta+1-\sin ^2 \theta \\
& =5-\left(4-4 \sin \theta+\sin ^2 \theta\right)=5-(\sin \theta-2)^2
\end{aligned}
\)
Now maximum value of \(f(\theta)\) occurs when \((\sin \theta-2)^2\) is minimum.
Minimum value of \((\sin \theta-2)^2\) occurs when \(\sin \theta=1\), then maximum value of \(f(\theta)\) is \(5-(1-2)^2=4\).
Also minimum value of \(f(\theta)\) occurs when \((\sin \theta-2)^2\) is maximum.
Maximum value of \((\sin \theta-2)^2\) occurs when \(\sin \theta=-1\), then minimum value of \(f(\theta)\) is \(5-(-1-2)^2=-4\).
Example 2.12: Is the equation \(\sec ^2 \theta=\frac{4 x y}{(x+y)^2}\) possible for real values of \(x\) and \(y\)?
Solution: Given, \(\sec ^2 \theta=\frac{4 x y}{(x+y)^2}\)
Since \(\sec ^2 \theta \geq 1\), we get \(\frac{4 x y}{(x+y)^2} \geq 1\)
\(
\begin{aligned}
& \Rightarrow \quad(x+y)^2 \leq 4 x y \\
& \Rightarrow \quad(x+y)^2-4 x y \leq 0 \text { or }(x-y)^2 \leq 0
\end{aligned}
\)
But for real values of \(x\) and \(y,(x-y)^2 \geq 0\)
Since \((x-y)^2=0, x=y\). Also \(x+y \neq 0 \Rightarrow x \neq 0, y \neq 0\)
Therefore, the given equation \(\sec ^2 \theta=\frac{4 x y}{(x+y)^2}\) is possible for real values of \(x\) and \(y\) only when \(x=y(x \neq 0)\).
Example 2.13: Show that the equation \(\sin \theta=x+\frac{1}{x}\) is impossible if \(x\) is real.
Solution: Given, \(\sin \theta=x+\frac{1}{x}\)
\(
\therefore \quad \sin ^2 \theta=x^2+\frac{1}{x^2}+2 x \frac{1}{x}=x^2+\frac{1}{x^2}+2=\left(x-\frac{1}{x}\right)^2+4 \geq 4
\)
which is not possible since \(\sin \theta^2 \leq 1\).
Example 2.14: If \(\sin ^2 \theta_1+\sin ^2 \theta_2+\sin ^2 \theta_3=0\), then which of the following is not the possible value of \(\cos \theta_1\) \(+\cos \theta_2+\cos \theta_3\)
(a) 3 (b) -3 (c) -1 (d) -2
Solution:
\(
\begin{aligned}
& \sin ^2 \theta_1+\sin ^2 \theta_2+\sin ^2 \theta_3=0 \\
& \Rightarrow \sin ^2 \theta_1=\sin ^2 \theta_2=\sin ^2 \theta_3=0 \quad \Rightarrow \quad \cos ^2 \theta_1, \cos ^2 \theta_2, \cos ^2 \theta_3=1 \quad \Rightarrow \quad \cos \theta_1, \cos \theta_2, \cos \theta_3= \pm 1 \\
& \cos \theta_1+\cos \theta_2+\cos \theta_3 \text { can be }-3 \text { (when all are }-1 \text { ) } \\
& \text { or } 3 \quad \text { (when all are }+1 \text { ) } \\
& \text { or }-1 \quad \text { (when any two are }-1 \text { and one }+1 \text { ) } \\
& \text { or } 1 \quad \text { (when any two are }+1 \text { and one }-1 \text { ) } \\
& \text { but }-2 \text { is not a possible value. }
\end{aligned}
\)
Example 2.15: Find the range of \(f(x)=\frac{1}{4 \cos x-3}\).
Solution:
\(
\begin{aligned}
& -1 \leq \cos x \leq 1 \\
& \Rightarrow-4 \leq 4 \cos x \leq 4 \\
& \Rightarrow-7 \leq 4 \cos x-3 \leq 1
\end{aligned}
\)
\(
\begin{aligned}
& \Rightarrow-7 \leq 4 \cos x-3<0 \text { or } 0<4 \cos x-3 \leq 1 \quad(\because 4 \cos x-3 \neq 0) \\
& \Rightarrow-\frac{1}{7} \geq \frac{1}{4 \cos x-3}>-\infty \text { or } \infty>\frac{1}{4 \cos x-3} \geq 1 \\
& \Rightarrow \frac{1}{4 \cos x-3} \in\left(-\infty,-\frac{1}{7}\right] \cup[1, \infty)
\end{aligned}
\)
Example 2.16: Find the range of \(f(x)=\frac{1}{5 \sin x-6}\).
Solution:
\(
\begin{aligned}
& -1 \leq \sin x \leq 1 \\
& \Rightarrow-5 \leq 5 \sin x \leq 5 \\
& \Rightarrow-11 \leq 5 \sin x-6 \leq-1 \\
& \Rightarrow-1 \leq \frac{1}{5 \sin x-6} \leq-1 / 11 \\
& \Rightarrow \frac{1}{5 \sin x-6} \in[-1,-1 / 11]
\end{aligned}
\)
Example 2.17: Find the range of \(f(x)=\cos ^2 x+\sec ^2 x\)
Solution: We have
\(
\begin{aligned}
f(x) & =\cos ^2 x+\sec ^2 x \\
& =(\cos x-\sec x)^2+2 \cos x \sec x \\
& =2+(\cos x-\sec x)^2 \geq 2
\end{aligned}
\)
Example 2.18: Find the range of \(f(x)=\sin ^2 x-3 \sin x+2\)
Solution:
\(
\begin{aligned}
f(x)= & \sin ^2 x-3 \sin x+2 \\
= & (\sin x-3 / 2)^2+2-9 / 4 \\
= & (\sin x-3 / 2)^2-1 / 4 \\
& -1 \leq \sin x \leq 1 \\
\Rightarrow & -5 / 2 \leq \sin x-3 / 2 \leq-1 / 2 \\
\Rightarrow & 1 / 4 \leq(\sin x-3 / 2)^2 \leq 25 / 4 \\
\Rightarrow & 0 \leq(\sin x-3 / 2)^2-1 / 4 \leq 6
\end{aligned}
\)
Example 2.19: Find the range of \(f(x)=\sqrt{\sin ^2 x-6 \sin x+9}+3\).
Solution:
\(
\begin{aligned}
& \begin{aligned}
f(x) & =\sqrt{\sin ^2 x-6 \sin x+9}+3 \\
& =\sqrt{(\sin x-3)^2}+3 \\
& =|\sin x-3|+3
\end{aligned} \\
& \text { Now }-1 \leq \sin x \leq 1 \\
& \Rightarrow-4 \leq \sin x-3 \leq-2 \\
& \Rightarrow 2 \leq|\sin x-3| \leq 4 \\
& \Rightarrow 5 \leq|\sin x-3|+3 \leq 7
\end{aligned}
\)
Example 2.20: Find the range of \(f(x)=\operatorname{cosec}^2 x+25 \sec ^2 x\).
Solution:
\(
\begin{aligned}
f(x) & =\left(1+\cot ^2 x\right)+25\left(1+\tan ^2 x\right) \\
& =26+\cot ^2 x+25 \tan ^2 x \\
& =36+10+\left(\cot ^2 x+25 \tan ^2 x-2 \cot x 5 \tan x\right) \\
& =36+(\cot x-5 \tan x)^2 \geq 36
\end{aligned}
\)
Example 2.21: Find the value of \(x\) for which \(f(x)=\sqrt{\sin x-\cos x}\) is defined, \(x \in[0,2 \pi]\).
Solution: \(f(x)=\sqrt{\sin x-\cos x}\) is defined if \(\sin x \geq \cos x\)
Problems Based On Trigonometric Identities
Example 2.22: Show that \(2\left(\sin ^6 x+\cos ^6 x\right)-3\left(\sin ^4 x+\cos ^4 x\right)+1=0\).
Solution:
\(
\begin{aligned}
& 2\left(\sin ^6 x+\cos ^6 x\right)-3\left(\sin ^4 x+\cos ^4 x\right)+1 \\
= & 2\left[\left(\sin ^2 x\right)^3+\left(\cos ^2 x\right)^3\right]-3\left(\sin ^4 x+\cos ^4 x\right)+1=2\left[\left(\sin ^2 x+\cos ^2 x\right)^3-3 \sin ^2 x \cos ^2 x\left(\sin ^2 x+\cos ^2 x\right)\right] \\
& -3\left[\left(\sin ^2 x+\cos ^2 x\right)^2-2 \sin ^2 x \cos ^2 x\right]+1=2\left[1-3 \sin ^2 x \cos ^2 x\right]-3\left[1-2 \sin ^2 x \cos ^2 x\right]+1=0
\end{aligned}
\)
Example 2.23: If \(3 \sin \theta+5 \cos \theta=5\), then show that \(5 \sin \theta-3 \cos \theta= \pm 3\).
Solution: Given, \(3 \sin \theta+5 \cos \theta=5\)
Let \(5 \sin \theta-3 \cos \theta=x\)
By squaring and adding, we get
\(
\begin{aligned}
& \left(9 \sin ^2 \theta+25 \cos ^2 \theta+30 \sin \theta \cos \theta\right)+\left(25 \sin ^2 \theta+9 \cos ^2 \theta-30 \sin \theta \cos \theta\right)=25+x^2 \\
& \Rightarrow \quad 9\left(\sin ^2 \theta+\cos ^2 \theta\right)+25\left(\sin ^2 \theta+\cos ^2 \theta\right)=25+x^2 \\
& \Rightarrow \quad 34=25+x^2 \text { or } x^2=9
\end{aligned}
\)
\(
\Rightarrow \quad x= \pm 3
\)
Example 2.24: If \((\sec A+\tan A)(\sec B+\tan B)(\sec C+\tan C)=(\sec A-\tan A)(\sec B-\tan B)(\sec C-\tan C)\), prove that the value of each side is \(\pm 1\).
Solution:
\(
\begin{aligned}
& \text { Let }(\sec A+\tan A)(\sec B+\tan B)(\sec C+\tan C)=x \dots(i) \\
& (\sec A-\tan A)(\sec B-\tan B)(\sec C-\tan C)=x \dots(ii)
\end{aligned}
\)
Multiplying Eqs. (i) and (ii), we get.
\(
\begin{aligned}
& \left(\sec ^2 A-\tan ^2 A\right)\left(\sec ^2 B-\tan ^2 B\right)\left(\sec ^2 C-\tan ^2 C\right)=x^2 \\
& \text { or } x^2=1 \\
& \therefore x= \pm 1
\end{aligned}
\)
Hence, each side is equal to \(\pm 1\).
Example 2.25: If \(\tan \theta+\sec \theta=1.5\), find \(\sin \theta, \tan \theta\), and \(\sec \theta\).
Solution: Given, \(\sec \theta+\tan \theta=\frac{3}{2}\)
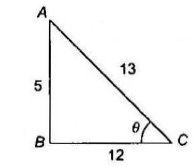
Now, \(\sec \theta-\tan \theta=\frac{1}{\sec \theta+\tan \theta}=\frac{2}{3}\)
Adding Eqs. (i) and (ii), we get \(2 \sec \theta=\frac{3}{2}+\frac{2}{3}=\frac{13}{6}\)
\(\therefore \sec \theta=\frac{13}{12}\)
\(\therefore \quad \tan \theta=\frac{5}{12}\)
and \(\sin \theta=\frac{5}{13}\)
Example 2.26: If \(x=\sec \theta-\tan \theta\) and \(y=\operatorname{cosec} \theta+\cot \theta\), then prove that \(x y+1=y-x\).
Solution:
\(
\begin{aligned}
x y+1 & =\frac{1-\sin \theta}{\cos \theta} \frac{1+\cos \theta}{\sin \theta}+1=\frac{1-\sin \theta+\cos \theta}{\sin \theta \cos \theta} \\
& =\frac{\left(\sin ^2 \theta+\cos ^2 \theta\right)}{\sin \theta \cos \theta}-\frac{(\sin \theta-\cos \theta)}{\sin \theta \cos \theta} \\
& =(\tan \theta+\cot \theta)-(\sec \theta-\operatorname{cosec} \theta) \\
& =(\operatorname{cosec} \theta+\cot \theta)-(\sec \theta-\tan \theta)=y-x
\end{aligned}
\)
Trigonometric Ratios Of Complementary and Supplementary Angles
\(
\begin{aligned}
& \sin (-\theta)=-\sin \theta \\
& \cos (-\theta)=\cos \theta
\end{aligned}
\)
\(
\begin{aligned}
&\sin \left(90^{\circ}-\theta\right)=\cos \theta\\
&\cos \left(90^{\circ}-\theta\right)=\sin \theta
\end{aligned}
\)
\(
\begin{aligned}
& \sin \left(90^{\circ}+\theta\right)=\cos \theta \\
& \cos \left(90^{\circ}+\theta\right)=-\sin \theta
\end{aligned}
\)
\(
\begin{aligned}
& \sin \left(180^{\circ}-\theta\right)=\sin \theta \\
& \cos \left(180^{\circ}-\theta\right)=-\cos \theta
\end{aligned}
\)
\(
\begin{aligned}
& \sin \left(180^{\circ}+\theta\right)=-\sin \theta \\
& \cos \left(180^{\circ}+\theta\right)=-\cos \theta
\end{aligned}
\)
Since the terminal sides of co-terminal angles coincide, hence their trigonometrical ratios are the same. Clearly, \(360^{\circ}-\theta\) and \(-\theta\) are coterminal angles.
Therefore, \(\sin \left(360^{\circ}-\theta\right)=\sin (-\theta)=-\sin \theta, \cos \left(360^{\circ}-\theta\right)=\cos (-\theta)=\cos \theta\), and \(\tan \left(360^{\circ}-\theta\right)=\tan (-\theta)\) \(=-\tan \theta\).
Similarly, \(\operatorname{cosec}\left(360^{\circ}-\theta\right)=-\operatorname{cosec} \theta, \sec \left(360^{\circ}-\theta\right)=\sec \theta\) and \(\cot \left(360^{\circ}-\theta\right)=-\cot \theta\).
Also \(\theta\) and \(360^{\circ}+\theta\) are co-terminal angles. Therefore, \(\sin \left(360^{\circ}+\theta\right)=\sin \theta, \cos \left(360^{\circ}+\theta\right)=\cos \theta, \tan \left(360^{\circ}\right.\) \(+\theta)=\tan \theta, \sec \left(360^{\circ}+\theta\right)=\sec \theta, \operatorname{cosec}\left(360^{\circ}+\theta\right)=\operatorname{cosec} \theta\) and \(\cot \left(360^{\circ}+\theta\right)=\cot \theta\).
In fact, for any positive integer \(n,\left(360^{\circ} \times n+\theta\right)\) is co-terminal to \(\theta\). Therefore, for any positive integer \(n\), we have \(\sin \left(360^{\circ} \times n+\theta\right)=\sin \theta, \cos \left(360^{\circ} \times n+\theta\right)=\cos \theta, \tan \left(360^{\circ} \times n+\theta\right)=\tan \theta, \operatorname{cosec}\left(360^{\circ} \times n+\theta\right)=\operatorname{cosec} \theta\), \(\sec \left(360^{\circ} \times n+\theta\right)=\sec \theta\) and \(\cot \left(360^{\circ} \times n+\theta\right)=\cot \theta\).
Example 2.27: Prove that \(\sin \left(-420^{\circ}\right)\left(\cos 390^{\circ}\right)+\cos \left(-660^{\circ}\right)\left(\sin 330^{\circ}\right)=-1\).
Solution:
\(
\begin{aligned}
\text { L.H.S. } & =\sin \left(-420^{\circ}\right)\left(\cos 390^{\circ}\right)+\cos \left(-660^{\circ}\right)\left(\sin 330^{\circ}\right) \\
& =-\sin 420^{\circ} \cos 390^{\circ}+\cos 660^{\circ} \sin 330^{\circ}
\end{aligned}
\)
\(
=-\sin 420^{\circ} \cos 390^{\circ}+\cos 660^{\circ} \sin 330^{\circ} \quad[\because \sin (-\theta)=-\sin \theta, \cos (-\theta)=\cos \theta]
\)
\(
\begin{aligned}
& =-\sin \left(90^{\circ} \times 4+60^{\circ}\right) \cos \left(90^{\circ} \times 4+30^{\circ}\right)+\cos \left(90^{\circ} \times 7+30^{\circ}\right) \sin \left(90^{\circ} \times 3+60^{\circ}\right) \\
& =-\left(\sin 60^{\circ}\right)\left(\cos 30^{\circ}\right)+\left(\sin 30^{\circ}\right)\left(-\cos 60^{\circ}\right) \\
& =-\frac{\sqrt{3}}{2} \times \frac{\sqrt{3}}{2}+\frac{1}{2}\left(-\frac{1}{2}\right)=-1=\text { R.H.S. }
\end{aligned}
\)
Example 2.28: Prove that \(\frac{\cos \left(90^{\circ}+\theta\right) \sec (-\theta) \tan \left(180^{\circ}-\theta\right)}{\sec \left(360^{\circ}-\theta\right) \sin \left(180^{\circ}+\theta\right) \cot \left(90^{\circ}-\theta\right)}=-1\).
Solution:
L.H.S \(=\frac{\cos \left(90^{\circ}+\theta\right) \sec (-\theta) \tan \left(180^{\circ}-\theta\right)}{\sec \left(360^{\circ}-\theta\right) \sin \left(180^{\circ}+\theta\right) \cot \left(90^{\circ}-\theta\right)}=\frac{(-\sin \theta)(\sec \theta)(-\tan \theta)}{(\sec \theta)(-\sin \theta)(\tan \theta)}=-1=\) R.H.S.
Example 2.29: If \(A, B, C, D\) are angles of a cyclic quadrilateral, then prove that
\(
\cos A+\cos B+\cos C+\cos D=0
\)
Solution: We know that the opposite angles of a cyclic quadrilateral are supplementary, i.e., \(A+C=\pi\) and \(B+D=\pi\).
\(
\begin{aligned}
& \therefore \quad A=\pi-C \text { and } B=\pi-D \\
& \Rightarrow \quad \cos A=\cos (\pi-C)=-\cos C \\
& \text { and } \cos B=\cos (\pi-D)=-\cos D \\
& \therefore \quad \cos A+\cos B+\cos C+\cos D=-\cos C-\cos D+\cos C+\cos D=0
\end{aligned}
\)
Example 2.30: Show that \(\tan 1^{\circ} \tan 2^{\circ} \ldots \tan 89^{\circ}=1\).
Solution:
\(
\begin{aligned}
\text { L.H.S. } & =\left(\tan 1^{\circ} \tan 89^{\circ}\right)\left(\tan 2^{\circ} \tan 88^{\circ}\right) \ldots\left(\tan 44^{\circ} \tan 46^{\circ}\right) \tan 45^{\circ} \\
& =\left[\tan 1^{\circ} \tan \left(90^{\circ}-1^{\circ}\right)\right]\left[\tan 2^{\circ} \tan \left(90^{\circ}-2^{\circ}\right)\right] \ldots\left[\tan 44^{\circ} \tan \left(90^{\circ}-44^{\circ}\right)\right] \tan 45^{\circ} \\
& =\left(\tan 1^{\circ} \cot 1^{\circ}\right)\left(\tan 2^{\circ} \cot 2^{\circ}\right) \ldots\left(\tan 44^{\circ} \cot 44^{\circ}\right) \tan 45^{\circ} \\
& =1 \quad\left[\because \tan \theta \cot \theta=1 \text { and } \tan 45^{\circ}=1\right]
\end{aligned}
\)
Example 2.31: Show that \(\sin ^2 5^{\circ}+\sin ^2 10^{\circ}+\sin ^2 15^{\circ}+\cdots+\sin ^2 90^{\circ}=9 \frac{1}{2}\).
Solution:
\(
\begin{aligned}
\text { L.H.S. } & =\left(\sin ^2 5^{\circ}+\sin ^2 85^{\circ}\right)+\left(\sin ^2 10^{\circ}+\sin ^2 80^{\circ}\right)+\cdots+\left(\sin ^2 40^{\circ}+\sin ^2 50^{\circ}\right)+\sin ^2 45^{\circ}+\sin ^2 90^{\circ} \\
& =\left(\sin ^2 5^{\circ}+\cos ^2 5^{\circ}\right)+\left(\sin ^2 10^{\circ}+\cos ^2 10^{\circ}\right)+\cdots+\left(\sin ^2 40^{\circ}+\cos ^2 40^{\circ}\right)+\sin ^2 45^{\circ}+\sin ^2 90^{\circ} \\
& =(1+1+1+1+1+1+1+1)+\left(\frac{1}{\sqrt{2}}\right)^2+1=9 \frac{1}{2}
\end{aligned}
\)
Example 2.32: Find the value of \(\cos ^2 \frac{\pi}{16}+\cos ^2 \frac{3 \pi}{16}+\cos ^2 \frac{5 \pi}{16}+\cos ^2 \frac{7 \pi}{16}\).
Solution:
\(
\begin{aligned}
\text { L.H.S. } & =\cos ^2 \frac{\pi}{16}+\cos ^2 \frac{3 \pi}{16}+\cos ^2\left(\frac{\pi}{2}-\frac{3 \pi}{16}\right)+\cos ^2\left(\frac{\pi}{2}-\frac{\pi}{16}\right) \\
& =\cos ^2 \frac{\pi}{16}+\cos ^2 \frac{3 \pi}{16}+\sin ^2 \frac{3 \pi}{16}+\sin ^2 \frac{\pi}{16} \\
& =\left(\cos ^2 \frac{\pi}{16}+\sin ^2 \frac{\pi}{16}\right)+\left(\cos ^2 \frac{3 \pi}{16}+\sin ^2 \frac{3 \pi}{16}\right) \\
& =1+1=2
\end{aligned}
\)
Example 2.33: If \(\sin \left(120^{\circ}-\alpha\right)=\sin \left(120^{\circ}-\beta\right), 0<\alpha, \beta<\pi\), then find the relation between \(\alpha\) and \(\beta\).
Solution:
\(
\begin{aligned}
& \text { If } \sin A=\sin B \text {, where } A=120^{\circ}-\alpha \text { and } B=120^{\circ}-\beta \\
& \Rightarrow A=B \text { or } A=\pi-B \text {, i.e., } A+B=\pi \\
& \Rightarrow 120^{\circ}-\alpha=120^{\circ}-\beta \text {, or } 120^{\circ}-\alpha+120^{\circ}-\beta=180^{\circ} \\
& \Rightarrow \alpha=\beta \text { or } \alpha+\beta=60^{\circ}
\end{aligned}
\)
Trigonometric Rations Of Compound Angles
Cosine of the Difference and Sum of Two Angles
1. \(\cos (A-B)=\cos A \cos B+\sin A \sin B\)
2. \(\cos (A+B)=\cos A \cos B-\sin A \sin B\)
for all angles \(A\) and \(B\).
Sine of the Difference and Sum of Two Angles
1. \(\sin (A-B)=\sin A \cos B-\cos A \sin B\)
2. \(\sin (A+B)=\sin A \cos B+\cos A \sin B\)
Tangent of the Difference and Sum of Two Angles
1. \(\tan (A+B)=\frac{\tan A+\tan B}{1-\tan A \tan B}\)
2. \(\tan (A-B)=\frac{\tan A-\tan B}{1+\tan A \tan B}\)
Similarly, it can be proved that
\(
\begin{aligned}
\cot (A+B) & =\frac{\cot A \cot B-1}{\cot B+\cot A} \\
\text { and } \cot (A-B) & =\frac{\cot A \cot B+1}{\cot B-\cot A}
\end{aligned}
\)
Some More Results
1. \(\sin (A+B) \sin (A-B)=\sin ^2 A-\sin ^2 B=\cos ^2 B-\cos ^2 A\)
2. \(\cos (A+B) \cos (A-B)=\cos ^2 A-\sin ^2 B=\cos ^2 B-\sin ^2 A\)
3. \(\sin (A+B+C)=\sin A \cos B \cos C+\cos A \sin B \cos C+\cos A \cos B \sin C-\sin A \sin B \sin C\)
4. \(\cos (A+B+C)=\cos A \cos B \cos C-\cos A \sin B \sin C-\sin A \cos B \sin C-\sin A \sin B \cos C\)
5. \(\tan (A+B+C)=\frac{\tan A+\tan B+\tan C-\tan A \tan B \tan C}{1-\tan A \tan B-\tan B \tan C-\tan C \tan A}\)
Example 2.34: Prove that \(\frac{\sin (B-C)}{\cos B \cos C}+\frac{\sin (C-A)}{\cos C \cos A}+\frac{\sin (A-B)}{\cos A \cos B}=0\).
Solution: First term of L.H.S. is
\(
\frac{\sin (B-C)}{\cos B \cos C}=\frac{\sin B \cos C-\cos B \sin C}{\cos B \cos C}=\frac{\sin B \cos C}{\cos B \cos C}-\frac{\cos B \sin C}{\cos B \cos C}=\tan B-\tan C
\)
Similarly, second term of L.H.S. \(=\tan C-\tan A\)
and, third term of L.H.S. \(=\tan A-\tan B\)
Now L.H.S. \(=(\tan B-\tan C)+(\tan C-\tan A)+(\tan A-\tan B)=0\).
Example 2.35: If \(\sin \alpha \sin \beta-\cos \alpha \cos \beta+1=0\), then prove that \(1+\cot \alpha \tan \beta=0\).
Solution: Given, \(3 \tan \theta \tan \varphi=1\) or \(\cot \theta \cot \varphi=3\)
or, \(\frac{\cos \theta \cos \varphi}{\sin \theta \sin \varphi}=\frac{3}{1}\)
By componendo and dividendo, we get
\(
\begin{aligned}
& \frac{\cos \theta \cos \varphi+\sin \theta \sin \varphi}{\cos \theta \cos \varphi-\sin \theta \sin \varphi}=\frac{3+1}{3-1} \\
& \Rightarrow \frac{\cos (\theta-\varphi)}{\cos (\theta+\varphi)}=2 \\
& \Rightarrow 2 \cos (\theta+\varphi)=\cos (\theta-\varphi)
\end{aligned}
\)
Example 2.36: If \(\sin (A-B)=\frac{1}{\sqrt{10}}, \cos (A+B)=\frac{2}{\sqrt{29}}\), find the value of \(\tan 2 A\) where \(A\) and \(B\) lie between 0 and \(\pi / 4\).
Solution: \(\tan 2 A=\tan [(A+B)+(A-B)]=\frac{\tan (A+B)+\tan (A-B)}{1-\tan (A+B) \tan (A-B)} \dots(i)\)
Given that, \(0<A<\frac{\pi}{4}\) and \(0<B<\frac{\pi}{4}\)
\(
\begin{aligned}
& \therefore \quad 0<A+B<\frac{\pi}{2} \\
& \text { Also, }-\frac{\pi}{4}<A-B<\frac{\pi}{4} \text { and } \sin (A-B)=\frac{1}{\sqrt{10}}=(+) \text { ve } \\
& \therefore \quad 0<A-B<\frac{\pi}{4} \\
& \text { Now, } \sin (A-B)=\frac{1}{\sqrt{10}} \\
& \Rightarrow \quad \tan (A-B)=\frac{1}{3} \dots(ii)
\end{aligned}
\)
\(
\begin{aligned}
&\begin{aligned}
\cos (A+B) & =\frac{2}{\sqrt{29}} \\
\Rightarrow \quad \tan (A+B) & =\frac{5}{2} \dots(iii)
\end{aligned}\\
&\text { From Eqs. (i), (ii) and (iii), we get }\\
&\tan 2 A=\frac{\frac{5}{2}+\frac{1}{3}}{1-\frac{5}{2} \times \frac{1}{3}}=\frac{17}{6} \times \frac{6}{1}=17
\end{aligned}
\)
Example 2.37: Prove that \(\frac{\cos 10^{\circ}+\sin 10^{\circ}}{\cos 10^{\circ}-\sin 10^{\circ}}=\tan 55^{\circ}\).
Solution:
\(
\frac{\cos 10^{\circ}+\sin 10^{\circ}}{\cos 10^{\circ}-\sin 10^{\circ}}=\frac{1+\tan 10^{\circ}}{1-\tan 10^{\circ}}=\frac{\tan 45^{\circ}+\tan 10^{\circ}}{1-\tan 45^{\circ} \tan 10^{\circ}}=\tan \left(45^{\circ}+10^{\circ}\right)=\tan 55^{\circ} \quad\left(\text { dividing by } \cos 10^{\circ}\right)
\)
Example 2.38: \(\text { Prove that } \tan 70^{\circ}=2 \tan 50^{\circ}+\tan 20^{\circ} \text {. }\)
Solution: \(\tan 70^{\circ}=\tan \left(50^{\circ}+20^{\circ}\right)=\frac{\tan 50^{\circ}+\tan 20^{\circ}}{1-\tan 50^{\circ} \tan20^{\circ}}\)
\(
\begin{aligned}
& \tan 70^{\circ}\left(1-\tan 50^{\circ} \tan 20^{\circ}\right)=\tan 50^{\circ}+\tan 20^{\circ} \\
& \tan 70^{\circ}-\tan 50^{\circ} \tan 20^{\circ} \tan 70^{\circ}=\tan 50^{\circ}+\tan 20^{\circ} \\
& \begin{aligned}
\tan 70^{\circ} & =\tan 70^{\circ} \tan 50^{\circ} \tan 20^{\circ}+\tan 50^{\circ}+\tan 20^{\circ} \\
& =\tan \left(90^{\circ}-20^{\circ}\right) \tan 50^{\circ} \tan 20^{\circ}+\tan 50^{\circ}+\tan 20^{\circ} \\
& =\cot 20^{\circ} \tan 50^{\circ} \tan 20^{\circ}+\tan 50^{\circ}+\tan 20^{\circ} \\
& =\tan 50^{\circ}+\tan 50^{\circ}+\tan 20^{\circ}=2 \tan 50^{\circ}+\tan 20^{\circ}
\end{aligned}
\end{aligned}
\)
Example 2.39: Let \(A, B, C\) be three angles such that \(A+B+C=\pi\). If \(\tan A \cdot \tan B=2\). Then find the value of \(\frac{\cos A \cos B}{\cos C}\).
Solution: Given \(\tan A \cdot \tan B=2\)
\(
\begin{aligned}
\text { Let } y & =\frac{\cos A \cos B}{\cos C}=-\frac{\cos A \cdot \cos B}{\cos (A+B)}=\frac{\cos A \cdot \cos B}{\sin A \sin B-\cos A \cos B} \\
& =\frac{1}{\tan A \tan B-1}=\frac{1}{2-1}=1
\end{aligned}
\)
Range of \(f(\theta)=a \cos \theta+b \sin \theta\)
\(
\begin{aligned}
& \text { Now } f(\theta)=a \cos \theta+b \sin \theta=r \sin \alpha \cos \theta+r \cos \alpha \sin \theta=r \sin (\theta+\alpha)=\sqrt{a^2+b^2} \sin \left(\theta+\tan ^{-1} \frac{a}{b}\right) \\
& \text { Now }-1 \leq \sin \left(\theta+\tan ^{-1} \frac{a}{b}\right) \leq 1 \\
& \Rightarrow-\sqrt{a^2+b^2} \leq \sqrt{a^2+b^2} \sin \left(\theta+\tan ^{-1} \frac{a}{b}\right) \leq \sqrt{a^2+b^2}
\end{aligned}
\)
Hence, range is \(\left[-\sqrt{a^2+b^2}, \sqrt{a^2+b^2}\right]\).
Example 2.40: Find the maximum value of \(\sqrt{3} \sin x+\cos x\) and \(x\) for which a maximum value occurs.
Solution:
\(
\begin{aligned}
&\sqrt{3} \sin x+\cos x=2\left(\frac{\sqrt{3}}{2} \sin x+\frac{1}{2} \cos x\right)=2 \sin (x+\pi / 6)\\
&\text { which is maximum when } x+\pi / 6=\pi / 2 \text { or } x=60^{\circ} \text { and has a maximum value } 2 \text {. }
\end{aligned}
\)
Example 2.41: Find the maximum and minimum values of \(\cos ^2 \theta-6 \sin \theta \cos \theta+3 \sin ^2 \theta+2\).
Solution: \(\cos ^2 \theta-6 \sin \theta \cos \theta+3 \sin ^2 \theta+2\)
\(
\begin{aligned}
& =\frac{1+\cos 2 \theta}{2}-3 \sin 2 \theta+3 \frac{(1-\cos 2 \theta)}{2}+2 \\
& =4-\cos 2 \theta-3 \sin 2 \theta \\
& \text { Now, }-\cos 2 \theta-3 \sin 2 \theta \in[-\sqrt{10}, \sqrt{10}] \\
& \Rightarrow 4-\cos 2 \theta-3 \sin 2 \theta \in[4-\sqrt{10}, 4+\sqrt{10}]
\end{aligned}
\)
TRANSFORMATION FORMULAE
Formulae to Transform the Product into Sum or Difference
We know that
\(
\begin{aligned}
& \sin A \cos B+\cos A \sin B=\sin (A+B) \\
& \sin A \cos B-\cos A \sin B=\sin (A-B) \\
& \cos A \cos B-\sin A \sin B=\cos (A+B) \\
& \cos A \cos B+\sin A \sin B=\cos (A-B)
\end{aligned}
\)
\(
2 \sin A \cos B=\sin (A+B)+\sin (A-B) .
\)
\(
2 \cos A \sin B=\sin (A+B)-\sin (A-B)
\)
\(
2 \cos A \cos B=\cos (A+B)+\cos (A-B)
\)
\(
2 \sin A \sin B=\cos (A-B)-\cos (A+B)
\)
Formulae to Transform the Sum or Difference into Product
Let \(A+B=C\) and \(A-B=D\). Then, \(A=\frac{C+D}{2}\) and \(B=\frac{C-D}{2}\)
\(
\begin{aligned}
& \sin C+\sin D=2 \sin \left(\frac{C+D}{2}\right) \cos \left(\frac{C-D}{2}\right) \\
& \sin C-\sin D=2 \sin \left(\frac{C-D}{2}\right) \cos \left(\frac{C+D}{2}\right) \\
& \cos C+\cos D=2 \cos \left(\frac{C+D}{2}\right) \cos \left(\frac{C-D}{2}\right)
\end{aligned}
\)
\(
\left.\begin{array}{l}
\cos D-\cos C=2 \sin \left(\frac{C+D}{2}\right) \sin \left(\frac{C-D}{2}\right) \\
\cos C-\cos D=-2 \sin \left(\frac{C+D}{2}\right) \sin \left(\frac{C-D}{2}\right) \\
\cos C-\cos D=2 \sin \left(\frac{C+D}{2}\right) \sin \left(\frac{D-C}{2}\right)
\end{array}\right\}
\)
These above formulae are used to convert the sum or difference of two sines or two cosines into the product of sines and cosines.
Example 2.42: Prove that \(\cos 55^{\circ}+\cos 65^{\circ}+\cos 175^{\circ}=0\).
Solution: \(\text { L.H.S. }=\cos 55^{\circ}+\cos 65^{\circ}+\cos 175^{\circ}\)
\(
=2 \cos \frac{55^{\circ}+65^{\circ}}{2} \cos \frac{55^{\circ}-65^{\circ}}{2}+\cos 175^{\circ} \left(\cos C+\cos D=2 \cos \left(\frac{C+D}{2}\right) \cos \left(\frac{C-D}{2}\right)\right)
\)
\(
=2 \cos 60^{\circ} \cos \left(-5^{\circ}\right)+\cos 175^{\circ}=2 \times \frac{1}{2} \cos 5^{\circ}+\cos \left(180^{\circ}-5^{\circ}\right)=\cos 5^{\circ}-\cos 5^{\circ}=0
\)
Example 2.43: Prove that \(\cos 18^{\circ}-\sin 18^{\circ}=\sqrt{2} \sin 27^{\circ}\).
Solution: L.H.S. \(=\cos 18^{\circ}-\sin 18^{\circ}=\cos 18^{\circ}-\sin \left(90^{\circ}-72^{\circ}\right)=\cos 18^{\circ}-\cos 72^{\circ}\)
\(\begin{aligned} & =2 \sin \frac{18^{\circ}+72^{\circ}}{2} \sin \frac{72^{\circ}-18^{\circ}}{2} \\ & =2 \sin 45^{\circ} \sin 27^{\circ}=2 \frac{1}{\sqrt{2}} \sin 27^{\circ}=\sqrt{2} \sin 27^{\circ}\end{aligned}\)
Example 2.44: Prove that \(\frac{\sin 5 A-\sin 3 A}{\cos 5 A+\cos 3 A}=\tan A\)
Solution:
\(
\text { L.H.S. }=\frac{\sin 5 A-\sin 3 A}{\cos 5 A+\cos 3 A}=\frac{2 \sin \left(\frac{5 A-3 A}{2}\right) \cos \left(\frac{5 A+3 A}{2}\right)}{2 \cos \left(\frac{5 A+3 A}{2}\right) \cos \left(\frac{5 A-3 A}{2}\right)}=\frac{2 \sin A \cos 4 A}{2 \cos 4 A \cos A}=\tan A
\)
\(\left(\sin C-\sin D=2 \sin \left(\frac{C-D}{2}\right) \cos \left(\frac{C+D}{2}\right)\right)\)
Example 2.45: Prove that \(\frac{\sin A+\sin 3 A}{\cos A+\cos 3 A}=\tan 2 A\)
Solution:
L.H.S. \(=\frac{\sin 3 A+\sin A}{\cos 3 A+\cos A}=\frac{2 \sin \left(\frac{3 A+A}{2}\right) \cos \left(\frac{3 A-A}{2}\right)}{2 \cos \left(\frac{3 A+A}{2}\right) \cos \left(\frac{3 A-A}{2}\right)}=\frac{\sin 2 A \cos A}{\cos 2 A \cos A}=\tan 2 A\)
\(\left(\sin C+\sin D=2 \sin \left(\frac{C+D}{2}\right) \cos \left(\frac{C-D}{2}\right)\right)\)
Example 2.46: Prove that \(\cos \alpha+\cos \beta+\cos \gamma+\cos (\alpha+\beta+\gamma)=4 \cos \frac{\alpha+\beta}{2} \cos \frac{\beta+\gamma}{2} \cos \frac{\gamma+\alpha}{2}\).
Solution: L.H.S. \(=\cos \alpha+\cos \beta+\cos \gamma+\cos (\alpha+\beta+\gamma)\)
\(
\begin{aligned}
& =(\cos \alpha+\cos \beta)+[\cos \gamma+\cos (\alpha+\beta+\gamma)] \\
& =2 \cos \left(\frac{\alpha+\beta}{2}\right) \cos \left(\frac{\alpha-\beta}{2}\right)+2 \cos \left(\frac{\alpha+\beta+\gamma+\gamma}{2}\right) \cos \left(\frac{\alpha+\beta+\gamma-\gamma}{2}\right) \\
& =2 \cos \left(\frac{\alpha+\beta}{2}\right) \cos \left(\frac{\alpha-\beta}{2}\right)+2 \cos \left(\frac{\alpha+\beta}{2}\right) \cos \left(\frac{\alpha+\beta+2 \gamma}{2}\right) \\
& =2 \cos \left(\frac{\alpha+\beta}{2}\right)\left\{\cos \left(\frac{\alpha-\beta}{2}\right)+\cos \left(\frac{\alpha+\beta+2 \gamma}{2}\right)\right\}
\end{aligned}
\)
\(
\begin{aligned}
& =2 \cos \left(\frac{\alpha+\beta}{2}\right)\left\{2 \cos \left(\frac{\frac{\alpha-\beta}{2}+\frac{\alpha+\beta+2 \gamma}{2}}{2}\right) \cos \left(\frac{\frac{\alpha+\beta+2 \gamma}{2}-\frac{\alpha-\beta}{2}}{2}\right)\right\} \\
& =2 \cos \left(\frac{\alpha+\beta}{2}\right)\left\{2 \cos \left(\frac{\alpha+\gamma}{2}\right) \cos \left(\frac{\beta+\gamma}{2}\right)\right\}=4 \cos \left(\frac{\alpha+\beta}{2}\right) \cos \left(\frac{\beta+\gamma}{2}\right) \cos \left(\frac{\gamma+\alpha}{2}\right)=\text { R.H.S. }
\end{aligned}
\)
Example 2.47: Prove that \(\frac{\sin A+\sin 2 A+\sin 4 A+\sin 5 A}{\cos A+\cos 2 A+\cos 4 A+\cos 5 A}=\tan 3 A\).
Solution:
\(
\begin{aligned}
& \frac{\sin A+\sin 2 A+\sin 4 A+\sin 5 A}{\cos A+\cos 2 A+\cos 4 A+\cos 5 A} \\
& =\frac{(\sin 5 A+\sin A)+(\sin 4 A+\sin 2 A)}{(\cos 5 A+\cos A)+(\cos 4 A+\cos 2 A)} \\
& =\frac{2 \sin 3 A \cos 2 A+2 \sin 3 A \cos A}{2 \cos 3 A \cos 2 A+2 \cos 3 A \cos A} \\
& =\frac{2 \sin 3 A(\cos 2 A+\cos A)}{2 \cos 3 A(\cos 2 A+\cos A)}=\tan 3 A
\end{aligned}
\)
Example 2.48: Prove that \(\left(\frac{\cos A+\cos B}{\sin A-\sin B}\right)^n+\left(\frac{\sin A+\sin B}{\cos A-\cos B}\right)^n=2 \cot ^n \frac{A-B}{2}\) or 0, accordingly as \(n\) is even or odd.
Solution:
\(
\text { L.H.S. }=\left(\frac{2 \cos \frac{A+B}{2} \cos \frac{A-B}{2}}{2 \cos \frac{A+B}{2} \sin \frac{A-B}{2}}\right)^n+\left(\frac{2 \sin \frac{A+B}{2} \cos \frac{A-B}{2}}{2 \sin \frac{A+B}{2} \sin \frac{B-A}{2}}\right)^n
\)
\(
=\left(\cot \frac{A-B}{2}\right)^n+\left(-\cot \frac{A-B}{2}\right)^n [\because \sin (-\theta)=-\sin \theta]
\)
\(
=\cot ^n \frac{A-B}{2}+(-1)^n \cot ^n \frac{A-B}{2}=\cot ^n \frac{A-B}{2}\left[1+(-1)^n\right]
\)
\(
=\left\{\begin{array}{l}
0, \text { if } n \text { is odd } \\
2 \cot ^n \frac{A-B}{2}, \text { if } n \text { is even. }
\end{array}\right.
\)
Example 2.49: Prove that \((\cos \alpha+\cos \beta)^2+(\sin \alpha+\sin \beta)^2=4 \cos ^2\left(\frac{\alpha-\beta}{2}\right)\).
Solution:
\(
\begin{aligned}
\text { L.H.S. } & =(\cos \alpha+\cos \beta)^2+(\sin \alpha+\sin \beta)^2 \\
& =\left\{2 \cos \left(\frac{\alpha+\beta}{2}\right) \cos \left(\frac{\alpha-\beta}{2}\right)\right\}^2+\left\{2 \sin \left(\frac{\alpha+\beta}{2}\right) \cos \left(\frac{\alpha-\beta}{2}\right)\right\}^2 \\
& =4 \cos ^2\left(\frac{\alpha-\beta}{2}\right)\left\{\cos ^2 \frac{\alpha+\beta}{2}+\sin ^2 \frac{\alpha+\beta}{-2}\right\}
\end{aligned}
\)
\(
\begin{aligned}
& =4 \cos ^2\left(\frac{\alpha-\beta}{2}\right) \quad\left[\because \cos ^2 \frac{\alpha+\beta}{2}+\sin ^2 \frac{\alpha+\beta}{2}=1\right] \\
& =\text { R.H.S. }
\end{aligned}
\)
Example 2.50: If \(\sec (\theta+\alpha)+\sec (\theta-\alpha)=2 \sec \theta\), then show that \(\cos ^2 \theta=1+\cos \alpha\).
Solution: \(\sec (\theta+\alpha)+\sec (\theta-\alpha)=2 \sec \theta\)
\(
\begin{aligned}
& \Rightarrow \frac{1}{\cos (\theta+\alpha)}+\frac{1}{\cos (\theta-\alpha)}=\frac{2}{\cos \theta} \\
& \Rightarrow \frac{\cos (\theta-\alpha)+\cos (\theta+\alpha)}{\cos (\theta+\alpha) \cos (\theta-\alpha)}=\frac{2}{\cos \theta} \\
& \Rightarrow \frac{2 \cos \theta \cos \alpha}{\cos ^2 \theta-\sin ^2 \alpha}=\frac{2}{\cos \theta} \\
& \Rightarrow \cos ^2 \theta \cos \alpha=\cos ^2 \theta-\sin ^2 \alpha \\
& \Rightarrow \sin ^2 \alpha=\cos ^2 \theta(1-\cos \alpha) \\
& \Rightarrow 1-\cos ^2 \alpha=\cos ^2 \theta(1-\cos \alpha) \quad \Rightarrow 1+\cos \alpha=\cos ^2 \theta
\end{aligned}
\)
Example 2.51: In quadrilateral \(A B C D\) if \(\sin \left(\frac{A+B}{2}\right) \cos \left(\frac{A-B}{2}\right)+\sin \left(\frac{C+D}{2}\right) \cos \left(\frac{C-D}{2}\right)=2\), then find the value of \(\sin \frac{A}{2} \sin \frac{B}{2} \sin \frac{C}{2} \sin \frac{D}{2}\).
Solution:
\(
\begin{aligned}
& \sin \left(\frac{A+B}{2}\right) \cos \left(\frac{A-B}{2}\right)+\sin \left(\frac{C+D}{2}\right) \cos \left(\frac{C-D}{2}\right)=2 \\
& \Rightarrow \frac{1}{2}[\sin A+\sin B+\sin C+\sin D]=2 \\
& \Rightarrow \sin A+\sin B+\sin C+\sin D=4 \\
& \Rightarrow A=B=C=D=90^{\circ} \\
& \Rightarrow \sin \frac{A}{2} \sin \frac{B}{2} \sin \frac{C}{2} \sin \frac{D}{2}=1 / 4
\end{aligned}
\)
TRIGONOMETRIC RATIOS OF MULTIPLES AND SUB-MULTIPLE ANGLES
Formulae for Multiple Angles
- \(\cos 2 A=\cos (A+A)=\cos ^2 A-\sin ^2 A=1-2 \sin ^2 A=2 \cos ^2 A-1\)
- \(\text { Also } \sin ^2 A=\frac{1}{2}(1-\cos 2 A), \cos ^2 A=\frac{1}{2}(1+\cos 2 A)\)
- \(\sin 2 A=\sin (A+A)=\sin A \cos A+\sin A \cos A=2 \sin A \cos A\)
- \(\tan 2 A=\tan (A+A)=\frac{\tan A+\tan A}{1-\tan A \tan A}=\frac{2 \tan A}{1-\tan ^2 A}\)
- \(\sin 3 A=\sin (2 A+A)\)
\(
\begin{aligned}
& =\sin 2 A \cos A+\cos 2 A \sin A=2 \sin A \cos A \cos A+\left(1-2 \sin ^2 A\right) \sin A \\
& =2 \sin A \cos ^2 A+\sin A-2 \sin ^3 A \\
& =2 \sin A\left(1-\sin ^2 A\right)+\sin A-2 \sin ^3 A \\
& =2 \sin A-2 \sin ^3 A+\sin A-2 \sin ^3 A \\
& =3 \sin A-4 \sin ^3 A
\end{aligned}
\) - \(\cos 3 A=\cos (2 A+A)\)
\(
\begin{aligned}
& =\cos 2 A \cos A-\sin 2 A \sin A=\left(2 \cos ^2 A-1\right) \cos A-2 \sin A \cos A \sin A \\
& =2 \cos ^3 A-\cos A-2 \cos A\left(1-\cos ^2 A\right) \\
& =2 \cos ^3 A-\cos A-2 \cos A+2 \cos ^3 A \\
& =4 \cos ^3 A-3 \cos A
\end{aligned}
\) - \(\sin 2 A \text { and } \cos 2 A \text { in terms of } \tan A\)
\(
\sin 2 A=2 \sin A \cos A=\frac{2 \sin A \cos A}{\cos ^2 A+\sin ^2 A}=\frac{2 \tan A}{1+\tan ^2 A} \text { [dividing numerator and denominator by } \cos ^2 A \text { ] }
\)
\(
\cos 2 A=\cos ^2 A-\sin ^2 A=\frac{\cos ^2 A-\sin ^2 A}{\cos ^2 A+\sin ^2 A}=\frac{1-\tan ^2 A}{1+\tan ^2 A} \text { [dividing numerator and denominator by } \cos ^2 A \text { ] }
\)
\(
\text { Also } \tan ^2 A=\frac{1-\cos 2 A}{1+\cos 2 A}
\) - In the formula of \(\tan (A+B+C)\), putting \(B=A\) and \(C=A\), we get
\(
\tan 3 A=\frac{3 \tan A-\tan ^3 A}{1-3 \tan ^2 A}
\)
Similarly, we can prove that \(\cot 3 A=\frac{\cot ^3 A-3 \cot A}{3 \cot ^2 A-1}\) - \(\tan \left(A_1+A_2+\cdots A_n\right)=\frac{S_1-S_3+S_5-S_7+\cdots}{1-S_2+S_4-S_6+\cdots}\),
where
\(S_1=\tan A_1+\tan A_2+\cdots+\tan A_n=\) Sum of the tangents of the separate angles, \(S_2=\tan A_1 \tan A_2+\tan A_1 \tan A_3+\ldots=\) Sum of the product of tangents taken two at a time, \(S_3=\tan A_1 \tan A_2 \tan A_3+\tan A_2 \tan A_3 \tan A_4+\ldots=\) Sum of the product of tangents taken three at a time, and so on.
If \(A_1=A_2=\ldots=A_n=A\), then we have
\(
S_1=n \tan A, S_2={ }^n C_2 \tan ^2 A, S_3={ }^n C_3 \tan ^3 A, \cdots
\)
Example 2.52: Prove that
a. \(\frac{\sin 2 \theta}{1+\cos 2 \theta}=\tan \theta\)
b. \(\frac{\sin 2 \theta}{1-\cos 2 \theta}=\cot \theta\)
c. \(\frac{1+\sin 2 \theta+\cos 2 \theta}{1+\sin 2 \theta-\cos 2 \theta}=\cot \theta\)
d \(\frac{1+\sin \theta-\cos \theta}{1+\sin \theta+\cos \theta}=\tan \theta / 2\)
e. \(\frac{\cos 2 \theta}{1+\sin 2 \theta}=\tan (\pi / 4-\theta)\)
f. \(\frac{\cos \theta}{1+\sin \theta}=\tan \left(\frac{\pi}{4}-\frac{\theta}{2}\right)\)
Solution:
a L.H.S. \(=\frac{\sin 2 \theta}{1+\cos 2 \theta}=\frac{2 \sin \theta \cos \theta}{2 \cos ^2 \theta}=\tan \theta=\) R.H.S.
b. L.H.S. \(=\frac{\sin 2 \theta}{1-\cos 2 \theta}=\frac{2 \sin \theta \cos \theta}{2 \sin ^2 \theta}=\cot \theta=\) R.H.S.
c. L.H.S. \(=\frac{1+\sin 2 \theta+\cos 2 \theta}{1+\sin 2 \theta-\cos 2 \theta}=\frac{(1+\cos 2 \theta)+\sin 2 \theta}{(1-\cos 2 \theta)+\sin 2 \theta}\)
\(
\begin{aligned}
& =\frac{2 \cos ^2 \theta+2 \sin \theta \cos \theta}{2 \sin ^2 \theta+2 \sin \theta \cos \theta} \\
& =\frac{2 \cos \theta(\cos \theta+\sin \theta)}{2 \sin \theta(\cos \theta+\sin \theta)}=\frac{\cos \theta}{\sin \theta}=\cot \theta=\text { R.H.S. }
\end{aligned}
\)
d L.H.S. \(=\frac{1+\sin \theta-\cos \theta}{1+\sin \theta+\cos \theta}=\frac{(1-\cos \theta)+\sin \theta}{(1+\cos \theta)+\sin \theta}\)
\(
\begin{aligned}
& =\frac{2 \sin ^2 \frac{\theta}{2}+2 \sin \frac{\theta}{2} \cos \frac{\theta}{2}}{2 \cos ^2 \frac{\theta}{2}+2 \sin \frac{\theta}{2} \cos \frac{\theta}{2}}=\frac{2 \sin \frac{\theta}{2}\left(\sin \frac{\theta}{2}+\cos \frac{\theta}{2}\right)}{2 \cos \frac{\theta}{2}\left(\sin \frac{\theta}{2}+\cos \frac{\theta}{2}\right)} \\
& =\tan \frac{\theta}{2}=\text { R.H.S. }
\end{aligned}
\)
e.
\(
\begin{aligned}
\text { L.H.S. } & =\frac{\cos 2 \theta}{1+\sin 2 \theta} \\
& =\frac{\sin \left(\frac{\pi}{2}-2 \theta\right)}{1+\cos \left(\frac{\pi}{2}-2 \theta\right)} \\
& =\frac{2 \sin \left(\frac{\pi}{4}-\theta\right) \cos \left(\frac{\pi}{4}-\theta\right)}{2 \cos ^2\left(\frac{\pi}{4}-\theta\right)} \\
& =\tan \left(\frac{\pi}{4}-\theta\right)=\text { R.H.S. }
\end{aligned}
\)
f. L.H.S. \(=\frac{\cos \theta}{1+\sin \theta}=\frac{\sin \left(\frac{\pi}{2}-\theta\right)}{1+\cos \left(\frac{\pi}{2}-\theta\right)}=\frac{2 \sin \left(\frac{\pi}{4}-\frac{\theta}{2}\right) \cos \left(\frac{\pi}{4}-\frac{\theta}{2}\right)}{2 \cos ^2\left(\frac{\pi}{4}-\frac{\theta}{2}\right)}=\tan \left(\frac{\pi}{4}-\frac{\theta}{2}\right)=\) R.H.S.
Example 2.53: Prove that \(\frac{1+\sin 2 \theta}{1-\sin 2 \theta}=\left(\frac{1+\tan \theta}{1-\tan \theta}\right)^2\).
Solution:
\(\begin{aligned} \text { L.H.S. } & =\frac{1+\sin 2 \theta}{1-\sin 2 \theta} \\ & =\frac{\sin ^2 \theta+\cos ^2 \theta+2 \sin \theta \cos \theta}{\sin ^2 \theta+\cos ^2 \theta-2 \sin \theta \cos \theta} \\ & =\left(\frac{\sin \theta+\cos \theta}{\sin \theta-\cos \theta}\right)^2=\left(\frac{1+\tan \theta}{1-\tan \theta}\right)^2\end{aligned}\)
\(
\text { (dividing numerator and denominator by } \cos \theta \text { ) }
\)
Example 2.54: If \(\alpha+\beta=90^{\circ}\), find the maximum value of \(\sin \alpha \sin \beta\).
Solution:
\(
\begin{aligned}
&\text { Let } y=\sin \alpha \sin \beta=\sin \alpha \sin \left(90^{\circ}-\alpha\right)=\sin \alpha \cos \alpha=\frac{1}{2} \sin 2 \alpha\\
&\text { which has the maximum value } 1 / 2 \text { when } \sin 2 \alpha=1 \text {. }
\end{aligned}
\)
Example 2.55: Prove that \(\frac{1-\tan ^2\left(\frac{\pi}{4}-A\right)}{1+\tan ^2\left(\frac{\pi}{4}-A\right)}=\sin 2 A\).
Solution:
\(
\frac{1-\tan ^2\left(\frac{\pi}{4}-A\right)}{1+\tan ^2\left(\frac{\pi}{4}-A\right)}=\frac{1-\tan ^2 \theta}{1+\tan ^2 \theta}\left(\text { where } \frac{\pi}{4}-A=\theta\right)=\cos 2 \theta=\cos \left(\frac{\pi}{2}-2 A\right)=\sin 2 A
\)
Example 2.56: Prove that \((\cos A-\cos B)^2+(\sin A-\sin B)^2=4 \sin ^2 \frac{A-B}{2}\).
Solution:
\(
\begin{aligned}
\text { L.H.S. } & =(\cos A-\cos B)^2+(\sin A-\sin B)^2 \\
& =\cos ^2 A+\cos ^2 B-2 \cos A \cos B+\sin ^2 A+\sin ^2 B-2 \sin A \sin B
\end{aligned}
\)
\(
\begin{aligned}
& =\left(\cos ^2 A+\sin ^2 A\right)+\left(\cos ^2 B+\sin ^2 B\right)-2(\cos A \cos B+\sin A \sin B) \\
& =2-2 \cos (A-B)=2(1-\cos (A-B))=4 \sin ^2 \frac{A-B}{2}
\end{aligned}
\)
Example 2.57: If \(\sin A=\frac{3}{5}\) and \(0^{\circ}<A<90^{\circ}\), find the values of \(\sin 2 A, \cos 2 A, \tan 2 A\), and \(\sin 4 A\).
Solution: Given \(\sin A=\frac{3}{5}\) and \(A\) is an acute angle.
\(
\therefore \quad \cos A=\frac{4}{5}
\)
\([\because A\) is acute \(]\)
and \(\tan A=\frac{3}{4}\)
Now, \(\sin 2 A=2 \sin A \cos A=2 \times \frac{3}{5} \times \frac{4}{5}=\frac{24}{25}\)
\(
\begin{aligned}
& \cos 2 A=1-2 \sin ^2 A=1-2 \times \frac{9}{25}=\frac{7}{25} \\
& \tan 2 A=\frac{2 \tan A}{1-\tan ^2 A}=\frac{2 \times \frac{3}{4}}{1-\left(\frac{3}{4}\right)^2}=\frac{\frac{6}{4}}{1-\frac{9}{16}}=\frac{\frac{6}{4}}{\frac{7}{16}}=\frac{6}{4} \times \frac{16}{7}=\frac{24}{7} \\
& \sin 4 A=2 \sin 2 A \cos 2 A=2 \times \frac{24}{25} \times \frac{7}{25}=\frac{336}{625} .
\end{aligned}
\)
Example 2.58: If \(\tan \alpha=\frac{1}{7}, \sin \beta=\frac{1}{\sqrt{10}}\), prove that \(\alpha+2 \beta=\frac{\pi}{4}\), where \(0<\alpha<\frac{\pi}{2}\) and \(0<\beta<\frac{\pi}{2}\).
Solution: \(\tan (\alpha+2 \beta)=\frac{\tan \alpha+\tan 2 \beta}{1-\tan \alpha \tan 2 \beta}=\frac{\frac{1}{7}+\tan 2 \beta}{1-\frac{1}{7} \tan 2 \beta} \dots(i)\)
\(
\text { Now, } \tan 2 \beta=\frac{2 \tan \beta}{1-\tan ^2 \beta}=\frac{2 \times \frac{1}{3}}{1-\frac{1}{9}}=\frac{3}{4}[\tan \beta>0 \text { as } 0<\beta<\pi / 2]
\)
Substituting the value of \(\tan 2 \beta\) in Eq. (i), we get
\(
\tan (\alpha+2 \beta)=\frac{\frac{1}{7}+\frac{3}{4}}{1-\frac{1}{7} \times \frac{3}{4}}=\frac{25}{25}=1
\)
Now, \(0<\alpha<\frac{\pi}{2}\) and \(0<\beta<\frac{\pi}{2}\)
\(
\begin{aligned}
& \therefore \quad 0<2 \beta<\pi, \text { but } \tan 2 \beta=\frac{3}{4}>0 \\
& \Rightarrow \quad 0<2 \beta<\frac{\pi}{2}
\end{aligned}
\)
Hence, \(0<\alpha+2 \beta<\pi\).
In the interval \((0, \pi), \tan \theta\) takes value 1 at \(\pi / 4\) only
\(
\therefore \quad \alpha+2 \beta=\frac{\pi}{4}
\)
Example 2.59: Show that \(\sqrt{2+\sqrt{2+\sqrt{2+2 \cos 8 \theta}}}=2 \cos \theta, \quad 0<\theta<\pi / 16\).
Solution: \(\text { L.H.S. }=\sqrt{2+\sqrt{2+\sqrt{2(1+\cos 8 \theta)}}}\)
\(
\begin{aligned}
&=\sqrt{2+\sqrt{2+\sqrt{2\left(2 \cos ^2 4 \theta\right)}}}\\
&\left[\because 1+\cos 8 \theta=2 \cos ^2 \frac{8 \theta}{2}\right]
\end{aligned}
\)
\(
\begin{aligned}
& =\sqrt{2+\sqrt{2+\sqrt{\left(4 \cos ^2 4 \theta\right)}}} \\
& =\sqrt{2+\sqrt{2+2 \cos 4 \theta}} \\
& =\sqrt{2+\sqrt{2(1+\cos 4 \theta)}} \\
& =\sqrt{2+\sqrt{2\left(2 \cos ^2 2 \theta\right)}} \left[\because 1+\cos 4 \theta=2 \cos ^2 2 \theta\right]
\end{aligned}
\)
\(
=\sqrt{2+2 \cos 2 \theta}=\sqrt{2(1+\cos 2 \theta)}=\sqrt{2\left(2 \cos ^2 \theta\right)}=2 \cos \theta=\text { R.H.S. }
\)
Example 2.60: Prove that \(\frac{\sec 8 \theta-1}{\sec 4 \theta-1}=\frac{\tan 8 \theta}{\tan 2 \theta}\).
Solution: L.H.S. \(=\frac{\sec 8 \theta-1}{\sec 4 \theta-1}=\frac{\frac{1}{\cos 8 \theta}-1}{\frac{1}{\cos 4 \theta}-1}=\frac{1-\cos 8 \theta}{\cos 8 \theta} \times \frac{\cos 4 \theta}{1-\cos 4 \theta}\)
\(
=\frac{2 \sin ^2 4 \theta}{\cos 8 \theta} \times \frac{\cos 4 \theta}{2 \sin ^2 2 \theta}
\)
\(
\left[\begin{array}{l}
\because 1-\cos 8 \theta=2 \sin ^2 \frac{8 \theta}{2}=2 \sin ^2 4 \theta \\
\text { and } 1-\cos 4 \theta=2 \sin ^2 \frac{4 \theta}{2}=2 \sin ^2 2 \theta
\end{array}\right]
\)
\(
\begin{aligned}
& =\frac{(2 \sin 4 \theta \cos 4 \theta)}{\cos 8 \theta} \times \frac{\sin 4 \theta}{2 \sin ^2 2 \theta} \\
& =\left(\frac{2 \sin 4 \theta \cos 4 \theta}{\cos 8 \theta}\right) \times\left(\frac{2 \sin 2 \theta \cos 2 \theta}{2 \sin ^2 2 \theta}\right) \\
& =\left(\frac{\sin 2(4 \theta)}{\cos 8 \theta}\right) \times\left(\frac{\cos 2 \theta}{\sin 2 \theta}\right)=\left(\frac{\sin 8 \theta}{\cos 8 \theta}\right) \times\left(\frac{\cos 2 \theta}{\sin 2 \theta}\right) \\
& =\tan 8 \theta \cot 2 \theta=\frac{\tan 8 \theta}{\tan 2 \theta}=\text { R.H.S. }
\end{aligned}
\)
Example 2.61: Show that \(\sqrt{3} \operatorname{cosec} 20^{\circ}-\sec 20^{\circ}=4\).
Solution: L.H.S. \(=\frac{\sqrt{3}}{\sin 20^{\circ}}-\frac{1}{\cos 20^{\circ}}=\frac{\sqrt{3} \cos 20^{\circ}-\sin 20^{\circ}}{\sin 20^{\circ} \cos 20^{\circ}}\)
\(
\begin{aligned}
& =\frac{2\left(\frac{\sqrt{3}}{2} \cos 20^{\circ}-\frac{1}{2} \sin 20^{\circ}\right)}{\sin 20^{\circ} \cos 20^{\circ}} \\
& =\frac{2\left(\sin 60^{\circ} \cos 20^{\circ}-\cos 60^{\circ} \sin 20^{\circ}\right)}{\sin 20^{\circ} \cos 20^{\circ}} \\
& =\frac{2 \sin \left(60^{\circ}-20^{\circ}\right)}{\sin 20^{\circ} \cos 20^{\circ}}=\frac{2 \sin 40^{\circ}}{\sin 20^{\circ} \cos 20^{\circ}} \\
& =\frac{4 \sin 40^{\circ}}{2 \sin 20^{\circ} \cos 20^{\circ}}=\frac{4 \sin 40^{\circ}}{\sin 40^{\circ}}=4
\end{aligned}
\)
Example 2.62: Prove that \(\left(1+\cos \frac{\pi}{8}\right)\left(1+\cos \frac{3 \pi}{8}\right)\left(1+\cos \frac{5 \pi}{8}\right)\left(1+\cos \frac{7 \pi}{8}\right)=\frac{1}{8}\).
Solution:
We have \(\cos \frac{7 \pi}{8}=\cos \left(\pi-\frac{\pi}{8}\right)=-\cos \frac{\pi}{8}\) and \(\cos \frac{5 \pi}{8}=\cos \left(\pi-\frac{3 \pi}{8}\right)=-\cos \frac{3 \pi}{8}\)
\(
\therefore \quad \text { L.H.S. }=\left(1+\cos \frac{\pi}{8}\right)\left(1+\cos \frac{3 \pi}{8}\right)\left(1-\cos \frac{3 \pi}{8}\right)\left(1-\cos \frac{\pi}{8}\right)
\)
\(
\begin{aligned}
& =\left(1-\cos ^2 \frac{\pi}{8}\right)\left(1-\cos ^2 \frac{3 \pi}{8}\right) \\
& =\sin ^2 \frac{\pi}{8} \sin ^2 \frac{3 \pi}{8} \\
& =\frac{1}{4}\left(2 \sin ^2 \frac{\pi}{8}\right)\left(2 \sin ^2 \frac{3 \pi}{8}\right) \\
& =\frac{1}{4}\left[\left(1-\cos \frac{\pi}{4}\right)\left(1-\cos \frac{3 \pi}{4}\right)\right] \left[\because 1-\cos \theta=2 \sin ^2 \frac{\theta}{2}\right]
\end{aligned}
\)
\(
=\frac{1}{4} \cdot\left[\left(1-\frac{1}{\sqrt{2}}\right)\left(1+\frac{1}{\sqrt{2}}\right)\right]=\frac{1}{4}\left(1-\frac{1}{2}\right)=\frac{1}{8}=\text { R.H.S. }
\)
Example 2.63: Prove that \(\cos ^4 \frac{\pi}{8}+\cos ^4 \frac{3 \pi}{8}+\cos ^4 \frac{5 \pi}{8}+\cos ^4 \frac{7 \pi}{8}=\frac{3}{2}\).
Solution:
We have \(\frac{7 \pi}{8}=\pi-\frac{\pi}{8}\) and \(\frac{5 \pi}{8}=\pi-\frac{3 \pi}{8}\)
\(
\begin{aligned}
& \Rightarrow \cos \frac{7 \pi}{8}=-\cos \frac{\pi}{8} \text { and } \cos \frac{5 \pi}{8}=-\cos \frac{3 \pi}{8} \\
& \Rightarrow \cos ^4 \frac{7 \pi}{8}=\cos ^4 \frac{\pi}{8} \text { and } \cos ^4 \frac{5 \pi}{8}=\cos ^4 \frac{3 \pi}{8} \\
& \therefore \text { L.H.S. }=2 \cos ^4 \frac{\pi}{8}+2 \cos ^4 \frac{3 \pi}{8}
\end{aligned}
\)
\(
\begin{aligned}
& =2\left[\left(\cos ^2 \frac{\pi}{8}\right)^2+\left(\cos ^2 \frac{3 \pi}{8}\right)^2\right] \\
& =2\left\{\frac{1+\cos \frac{\pi}{4}}{2}\right\}^2+\left\{\frac{1+\cos \frac{3 \pi}{4}}{2}\right\}^2 \left[\because \frac{1+\cos 2 \theta}{2}=\cos ^2 \theta\right]
\end{aligned}
\)
\(
\begin{aligned}
& =\frac{1}{2}\left\{\left(1+\cos \frac{\pi}{4}\right)^2+\left(1+\cos \frac{3 \pi}{4}\right)^2\right\}^2 \\
& =\frac{1}{2}\left\{\left(1+\frac{1}{\sqrt{2}}\right)^2+\left(1-\frac{1}{\sqrt{2}}\right)^2\right\} \\
& =\frac{1}{2}\left\{\left(1+\frac{1}{2}+\sqrt{2}\right)+\left(1+\frac{1}{2}-\sqrt{2}\right)\right\}=\frac{3}{2}=\text { R.H.S. }
\end{aligned}
\)
Example 2.64: If \(\pi<x<2 \pi\), prove that \(\frac{\sqrt{1+\cos x}+\sqrt{1-\cos x}}{\sqrt{1+\cos x}-\sqrt{1-\cos x}}=\cot \left(\frac{x}{2}+\frac{\pi}{4}\right)\).
Solution:
\(
\text { L.H.S. }=\frac{\sqrt{1+\cos x}+\sqrt{1-\cos x}}{\sqrt{1+\cos x}-\sqrt{1-\cos x}}=\frac{\sqrt{2 \cos ^2 \frac{x}{2}}+\sqrt{2 \sin ^2 \frac{x}{2}}}{\sqrt{2 \cos ^2 \frac{x}{2}}-\sqrt{2 \sin ^2 \frac{x}{2}}}
\)
\(
\begin{aligned}
& =\frac{\sqrt{2}\left|\cos \frac{x}{2}\right|+\sqrt{2}\left|\sin \frac{x}{2}\right|}{\sqrt{2}\left|\cos \frac{x}{2}\right|-\sqrt{2}\left|\sin \frac{x}{2}\right|} \\
& =\frac{\left|\cos \frac{x}{2}\right|+\left|\sin \frac{x}{2}\right|}{\left|\cos \frac{x}{2}\right|-\left|\sin \frac{x}{2}\right|} \\
& =\frac{-\cos \frac{x}{2}+\sin \frac{x}{2}}{-\cos \frac{x}{2}-\sin \frac{x}{2}} \left[\because \pi<x<2 \pi, \therefore \frac{\pi}{2}<\frac{x}{2}<\pi\right]
\end{aligned}
\)
\(
\begin{aligned}
&\Rightarrow \cos x / 2 \text { is negative and } \sin x / 2 \text { is positive. }\\
&=\frac{\cos \frac{x}{2}-\sin \frac{x}{2}}{\cos \frac{x}{2}+\sin \frac{x}{2}}=\frac{\cot \frac{x}{2}-1}{\cot \frac{x}{2}+1} \text { [dividing numerator and denominator by } \sin x / 2 \text { ] }
\end{aligned}
\)
\(
=\cot \left(\frac{x}{2}+\frac{\pi}{4}\right)=\text { R.H.S. }
\)
Example 2.65: If \(\sin \alpha+\sin \beta=a\) and \(\cos \alpha+\cos \beta=b\), prove that \(\tan \frac{a-\beta}{2}= \pm \sqrt{\frac{4-a^2-b^2}{a^2+b^2}}\).
Solution:
Given, \(\sin \alpha+\sin \beta=a \dots(i)\)
and \(\cos \alpha+\cos \beta=b \dots(ii)\)
\(
\begin{aligned}
& \text { Now }(\cos \alpha+\cos \beta)^2+(\sin \alpha+\sin \beta)^2=b^2+a^2 \\
& \Rightarrow \cos ^2 \alpha+\cos ^2 \beta+2 \cos \alpha \cos \beta+\sin ^2 \alpha+\sin ^2 \beta+2 \sin \alpha \sin \beta=b^2+a^2 \\
& \Rightarrow\left(\cos ^2 \alpha+\sin ^2 \alpha\right)+\left(\cos ^2 \beta+\sin ^2 \beta\right)+2(\cos \alpha \cos \beta+\sin \alpha \sin \beta)=a^2+b^2 \\
& \Rightarrow 2+2 \cos (\alpha-\beta)=a^2+b^2
\end{aligned}
\)
\(
\text { or } \cos (\alpha-\beta)=\frac{a^2+b^2-2}{2}
\)
\(
\begin{aligned}
&\text { Now, } \tan \frac{\alpha-\beta}{2}= \pm \sqrt{\frac{1-\cos (\alpha-\beta)}{1+\cos (\alpha-\beta)}}\\
&=4 \pm \sqrt{\frac{1-\frac{a^2+b^2-2}{2}}{1+\frac{a^2+b^2-2}{2}}}= \pm \sqrt{\frac{4-a^2-b^2}{a^2+b^2}}
\end{aligned}
\)
Example 2.66: If \(\tan \frac{\theta}{2}=\sqrt{\frac{a-b}{a+b}} \tan \frac{\varphi}{2}\), prove that \(\cos \alpha=\frac{a \cos \varphi+b}{a+b \cos \varphi}\).
Solution: Given, \(\tan \frac{\theta}{2}=\sqrt{\frac{a-b}{a+b}} \tan \frac{\varphi}{2} \dots(i)\)
\(
\begin{aligned}
&\text { Now, } \cos \theta=\frac{1-\tan ^2 \frac{\theta}{2}}{1+\tan ^2 \frac{\theta}{2}}=\frac{1-\frac{a-b}{a+b} \tan ^2 \frac{\varphi}{2}}{1+\frac{a-b}{a+b} \tan ^2 \frac{\varphi}{2}}\\
&=\frac{1-\frac{a-b}{a+b} \frac{\sin ^2 \frac{\varphi}{2}}{\cos ^2 \frac{\varphi}{2}}}{1+\frac{a-b}{a+b} \frac{\sin ^2 \frac{\varphi}{2}}{\cos ^2 \frac{\varphi}{2}}}
\end{aligned}
\)
\(
\begin{aligned}
& =\frac{(a+b) \cos ^2 \frac{\varphi}{2}-(a-b) \sin ^2 \frac{\varphi}{2}}{(a+b) \cos ^2 \frac{\varphi}{2}+(a-b) \sin ^2 \frac{\varphi}{2}} \\
& =\frac{a\left(\cos ^2 \frac{\varphi}{2}-\sin ^2 \frac{\varphi}{2}\right)+b\left(\cos ^2 \frac{\varphi}{2}+\sin ^2 \frac{\varphi}{2}\right)}{a\left(\cos ^2 \frac{\varphi}{2}+\sin ^2 \frac{\varphi}{2}\right)+b\left(\cos ^2 \frac{\varphi}{2}-\sin ^2 \frac{\varphi}{2}\right)} \\
& =\frac{a \cos \varphi+b}{a+b \cos \varphi}
\end{aligned}
\)
Example 2.67: If \(\cos \theta=\cos \alpha \cos \beta\), prove that \(\tan \frac{\theta+\alpha}{2} \tan \frac{\theta-\alpha}{2}=\tan ^2 \frac{\beta}{2}\).
Solution: Given, \(\cos \theta=\cos \alpha \cos \beta\), we have \(\cos \beta=\frac{\cos \theta}{\cos \alpha}\)
Now, \(\tan ^2 \frac{\beta}{2}=\frac{1-\cos \beta}{1+\cos \beta}=\frac{1-\frac{\cos \theta}{\cos \alpha}}{1+\frac{\cos \theta}{\cos \alpha}}\)
\(
\begin{aligned}
& =\frac{\cos \alpha-\cos \theta}{\cos \alpha+\cos \theta} \\
& =\frac{2 \sin \frac{\alpha+\theta}{2} \sin \frac{\theta-\alpha}{2}}{2 \cos \frac{\theta+\alpha}{2} \cos \frac{\theta-\alpha}{2}}=\tan \frac{\theta+\alpha}{2} \tan \frac{\theta-\alpha}{2}
\end{aligned}
\)
VALUES OF TRIGONOMETRIC RATIOS OF STANDARD ANGLES
Value of \(\sin 15^{\circ}, \cos 15^{\circ}, \sin 75^{\circ}, \cos 75^{\circ}, \tan 15^{\circ}, \tan 75^{\circ}\):
\(
\sin 15^{\circ}=\sin \left(45^{\circ}-30^{\circ}\right)=\sin 45^{\circ} \cos 30^{\circ}-\sin 30^{\circ} \cos 45^{\circ}=\frac{1}{\sqrt{2}} \frac{\sqrt{3}}{2}-\frac{1}{2} \frac{1}{\sqrt{2}}=\frac{\sqrt{3}-1}{2 \sqrt{2}}
\)
Also, \(\sin 15^{\circ}=\cos 75^{\circ}=-\cos 105^{\circ}\)
Similarly, we can prove that \(\cos 15^{\circ}=\frac{\sqrt{3}+1}{2 \sqrt{2}}\)
Also, \(\cos 15^{\circ}=\sin 75^{\circ}=\sin 105^{\circ}\)
\(
\tan 15^{\circ}=\tan \left(60^{\circ}-45^{\circ}\right)=\frac{\tan 60^{\circ}-\tan 45^{\circ}}{1+\tan 60^{\circ} \tan 45^{\circ}}=\frac{\sqrt{3}-1}{\sqrt{3}+1}=2-\sqrt{3}
\)
\(
\tan 75^{\circ}=\tan \left(60^{\circ}+45^{\circ}\right)=\frac{\tan 60^{\circ}+\tan 45^{\circ}}{1-\tan 60^{\circ} \tan 45^{\circ}}=\frac{\sqrt{3}+1}{\sqrt{3}-1}=2+\sqrt{3}
\)
Value of \(\sin 18^{\circ}, \cos 18^{\circ}\):
Let \(\theta=18^{\circ}\), then \(5 \theta=90^{\circ}\)
\(
\begin{aligned}
& \Rightarrow \quad 2 \theta+3 \theta=90^{\circ} \\
& \Rightarrow \quad 2 \theta=90^{\circ}-3 \theta \\
& \Rightarrow \quad \sin 2 \theta=\sin \left(90^{\circ}-3 \theta\right) \\
& \Rightarrow \quad \sin 2 \theta=\cos 3 \theta \\
& \Rightarrow \quad 2 \sin \theta \cos \theta=4 \cos ^3 \theta-3 \cos \theta \\
& \Rightarrow \quad 2 \sin \theta=4 \cos ^2 \theta-3 \text { [dividing by } \cos \theta \text { ] }\\
& \Rightarrow \quad 2 \sin \theta=4\left(1-\sin ^2 \theta\right)-3=1-4 \sin ^2 \theta \\
& \Rightarrow \quad 4 \sin ^2 \theta+2 \sin \theta-1=0 \\
& \Rightarrow \quad \sin \theta=\frac{-2 \pm \sqrt{4+16}}{8}=\frac{-2 \pm 2 \sqrt{5}}{8}=\frac{-1 \pm \sqrt{5}}{4} \\
& \because \quad \theta=18^{\circ}
\end{aligned}
\)
\(\therefore \sin \theta=\sin 18^{\circ}>0\), for \(18^{\circ}\) lies in the first quadrant.
\(
\therefore \quad \sin \theta \text {, i.e., } \sin 18^{\circ}=\frac{\sqrt{5}-1}{4}
\)
Value of \(\cos \mathbf{1 8}^{\boldsymbol{\circ}}\):
\(
\begin{aligned}
& \cos ^2 18^{\circ}=1-\sin ^2 18^{\circ}=1-\left(\frac{\sqrt{5}-1}{4}\right)^2=1-\frac{5+1-2 \sqrt{5}}{16}=\frac{10+2 \sqrt{5}}{16} \\
& \Rightarrow \cos 18^{\circ}=\frac{1}{4} \sqrt{10+2 \sqrt{5}} \left[\because \cos 18^{\circ}>0\right]
\end{aligned}
\)
Value of \(\cos 36^{\circ}, \sin 36^{\circ}\):
\(
\begin{aligned}
&\cos 36^{\circ}=1-2 \sin ^2 18^{\circ}=1-2\left(\frac{\sqrt{5}-1}{4}\right)^2=\frac{\sqrt{5}+1}{4}\\
&\text { Value of } \sin \mathbf{3 6}^{\circ} \text { : }\\
&\begin{aligned}
& \sin ^2 36^{\circ}=1-\cos ^2 36^{\circ}=1-\left(\frac{\sqrt{5}+1}{4}\right)^2=1-\frac{6+2 \sqrt{5}}{16}=\frac{16-6-2 \sqrt{5}}{16}=\frac{10-2 \sqrt{5}}{16} \\
& \therefore \sin 36^{\circ}=\frac{1}{4} \sqrt{10-2 \sqrt{5}} \left[\because \sin 36^{\circ}>0\right]
\end{aligned}
\end{aligned}
\)
Note:
\(
\begin{aligned}
& \sin 54^{\circ}=\sin \left(90^{\circ}-36^{\circ}\right)=\cos 36^{\circ}=\frac{\sqrt{5}+1}{4} \\
& \cos 54^{\circ}=\cos \left(90^{\circ}-36^{\circ}\right)=\sin 36^{\circ}=\frac{1}{4}(\sqrt{10-2 \sqrt{5}})
\end{aligned}
\)
Value of \(\tan 7 \frac{1^{\circ}}{2}, \cot 7 \frac{1}{2}^{\circ}\):
Let \(\theta=7 \frac{1}{2}^{\circ}\), then \(2 \theta=15^{\circ}\)
\(
\tan \theta=\frac{1-\cos 2 \theta}{\sin 2 \theta} \left[\because 1-\cos 2 \theta=2 \sin ^2 \theta \text { and } \sin 2 \theta=2 \sin \theta \cos \theta\right]
\)
\(
=\frac{1-\cos 15^{\circ}}{\sin 15^{\circ}}=\frac{1-\frac{\sqrt{3}+1}{2 \sqrt{2}}}{\frac{\sqrt{3}-1}{2 \sqrt{2}}}=\frac{2 \sqrt{2}-\sqrt{3}-1}{\sqrt{3}-1}=(\sqrt{3}-\sqrt{2})(\sqrt{2}-1)
\)
Value of \(\cot 82 \frac{1^{\circ}}{2}\):
\(
\cot 82 \frac{1}{2}^{\circ}=\cot \left(90^{\circ}-7 \frac{1}{2}^{\circ}\right)=\tan 7 \frac{1}{2}^{\circ}=(\sqrt{3}-\sqrt{2})(\sqrt{2}-1)
\)
Value of \(\cot 7 \frac{1}{2}^{\circ}\):
\(
\text { Let } \theta=7 \frac{1^{\circ}}{2} \text {, then } 2 \theta=15^{\circ}
\)
Now, \(\cot \theta=\frac{1+\cos 2 \theta}{\sin 2 \theta}=\frac{1+\cos 15^{\circ}}{\sin 15^{\circ}}=\frac{1+\frac{\sqrt{3}+1}{2 \sqrt{2}}}{\frac{\sqrt{3}-1}{2 \sqrt{2}}}=\frac{2 \sqrt{2}+\sqrt{3}+1}{\sqrt{3}-1}=(\sqrt{3}+\sqrt{2})(\sqrt{2}+1)\)
Value of \(\tan 82 \frac{1}{2}^{\circ}\):
\(
\tan 82 \frac{1^{\circ}}{2}=\tan \left(90^{\circ}-7 \frac{1}{2}^{\circ}\right)=\cot 7 \frac{1}{2}^{\circ}=(\sqrt{3}+\sqrt{2})(\sqrt{2}+1)
\)
Summary Table
\(
\begin{array}{|l|l|l|l|l|l|l|l|}
\hline & 7.5^{\circ} & 15^{\circ} & 18^{\circ} & 22.5^{\circ} & 36^{\circ} & 67.5^{\circ} & 75^{\circ} \\
\hline \sin & \frac{\sqrt{8-2 \sqrt{6}-2 \sqrt{2}}}{4} & \frac{\sqrt{3}-1}{2 \sqrt{2}} & \frac{\sqrt{5}-1}{4} & \frac{\sqrt{2-\sqrt{2}}}{2} & \frac{\sqrt{10-2 \sqrt{5}}}{4} & \frac{\sqrt{2+\sqrt{2}}}{2} & \frac{\sqrt{3}+1}{2 \sqrt{2}} \\
\hline \cos & \frac{\sqrt{8+2 \sqrt{6}+2 \sqrt{2}}}{4} & \frac{\sqrt{3}+1}{2 \sqrt{2}} & \frac{\sqrt{10+2 \sqrt{5}}}{4} & \frac{\sqrt{2+\sqrt{2}}}{2} & \frac{\sqrt{5}+1}{4} & \frac{\sqrt{2-\sqrt{2}}}{2} & \frac{\sqrt{3}-1}{2 \sqrt{2}} \\
\hline \tan & (\sqrt{3}-\sqrt{2})(\sqrt{2}-1) & 2-\sqrt{3} & \frac{\sqrt{10+2 \sqrt{5}}}{4} & \sqrt{2}-1 & \sqrt{5-2 \sqrt{5}} & \sqrt{2}+1 & 2+\sqrt{3} \\
\hline \cot & (\sqrt{3}+\sqrt{2})(\sqrt{2}+1) & 2+\sqrt{3} & \sqrt{(5+2 \sqrt{5}}) & \sqrt{2}+1 & \sqrt{\left(1+\frac{2}{\sqrt{5}}\right)} & \sqrt{2}-1 & 2-\sqrt{3} \\
\hline
\end{array}
\)
Example 2.68: Find the angle \(\theta\) whose cosine is equal to its tangent.
Solution:
\(
\begin{aligned}
& \text { Given, } \cos \theta=\tan \theta \quad \Rightarrow \quad \cos ^2 \theta=\sin \theta \\
& \Rightarrow \quad 1-\sin ^2 \theta=\sin \theta \text { or } \sin ^2 \theta+\sin \theta-1=0 \\
& \Rightarrow \quad \sin \theta=\frac{-1 \pm \sqrt{5}}{2}=2 \frac{\sqrt{5}-1}{4}=2 \sin 18^{\circ} \\
& \Rightarrow \quad \theta=\sin ^{-1}\left(2 \sin 18^{\circ}\right)
\end{aligned}
\)
Example 2.69: Find the value of \(\cos 12^{\circ}+\cos 84^{\circ}+\cos 156^{\circ}+\cos 132^{\circ}\).
Solution:
\(
\begin{aligned}
& \cos 12^{\circ}+\cos 84^{\circ}+\cos 156^{\circ}+\cos 132^{\circ} \\
& =\left(\cos 12^{\circ}+\cos 132^{\circ}\right)+\left(\cos 84^{\circ}+\cos 156^{\circ}\right) \\
& =2 \cos \left(\frac{12^{\circ}+132^{\circ}}{2}\right) \cos \left(\frac{132^{\circ}-12^{\circ}}{2}\right)+2 \cos \left(\frac{84^{\circ}+156^{\circ}}{2}\right) \cos \left(\frac{156^{\circ}-84^{\circ}}{2}\right) \\
& =2 \cos 72^{\circ} \cos 60^{\circ}+2 \cos 120^{\circ} \cos 36^{\circ} \\
& =2 \sin 18^{\circ} \cos 60^{\circ}+2 \cos 120^{\circ} \cos 36^{\circ} \\
& =2\left(\frac{\sqrt{5}-1}{4}\right) \frac{1}{2}+2\left(-\frac{1}{2}\right)\left(\frac{\sqrt{5}+1}{4}\right)=-\frac{1}{2}
\end{aligned}
\)
Example 2.70: Prove that \(\cos 36^{\circ} \cos 72^{\circ} \cos 108^{\circ} \cos 144^{\circ}=\frac{1}{16}\).
Solution:
\(
\begin{aligned}
& \cos 36^{\circ} \cos 72^{\circ} \cos 108^{\circ} \cos 144^{\circ} \\
& =\cos 36^{\circ} \sin 18^{\circ}\left(-\sin 18^{\circ}\right)\left(-\cos 36^{\circ}\right) \\
& =\cos ^2 36^{\circ} \sin ^2 18^{\circ}=\left(\frac{\sqrt{5}+1}{4}\right)^2\left(\frac{\sqrt{5}-1}{4}\right)^2 \\
& =\left[\left(\frac{\sqrt{5}+1}{4}\right)\left(\frac{\sqrt{5}-1}{4}\right)\right]^2=\frac{1}{16}
\end{aligned}
\)
SUM OF SINES OR COSINES OF \(N\) ANGLES IN A.P.
\(\sin \alpha+\sin (\alpha+\alpha \beta)+\sin (\alpha+2 \beta)+\cdots+\sin (\alpha+\overline{n-1} \beta)=\frac{\sin \frac{n \beta}{2}}{\sin \frac{\beta}{2}} \times \sin \left[\alpha+(n-1) \frac{\beta}{2}\right]\)
Proof: Let \(S=\sin \alpha+\sin (\alpha+\beta)+\sin (\alpha+2 \beta)+\cdots+\sin (\alpha+\overline{n-1} \beta)\)
Here angles are in A.P. and common difference of angles \(=\beta\)
Multiplying both sides by \(2 \sin \frac{\beta}{2}\), we get
\(
2 S \sin \frac{\beta}{2}=2 \sin \alpha \sin \frac{\beta}{2}+2 \sin (\alpha+\beta) \sin \frac{\beta}{2}+\cdots+2 \sin (\alpha+\overline{n-1} \beta) \sin \frac{\beta}{2} \dots(i)
\)
\(
\begin{aligned}
& \text { Now, } 2 \sin \alpha \sin \frac{\beta}{2}=\cos \left(\alpha-\frac{\beta}{2}\right)-\cos \left(\alpha+\frac{\beta}{2}\right) \\
& 2 \sin (\alpha+\beta) \sin \frac{\beta}{2}=\cos \left(\alpha+\frac{\beta}{2}\right)-\cos \left(\alpha+\frac{3 \beta}{2}\right) \\
& 2 \sin (\alpha+2 \beta) \sin \frac{\beta}{2}=\cos \left(\alpha+\frac{3 \beta}{2}\right)-\cos \left(\alpha+\frac{5 \beta}{2}\right) \\
& \vdots \\
\end{aligned}
\)
\(
\frac{2 \sin (\alpha+\overline{n-1} \beta) \sin \frac{\beta}{2}=\cos \left[\alpha+(2 n-3) \frac{\beta}{2}\right]-\cos \left[\alpha(2 n-1) \frac{\beta}{2}\right]}{\text { Adding, we get R.H.S. of .Eq. }(i)=\cos \left(\alpha-\frac{\beta}{2}\right)-\cos \left[\alpha+(2 n-1) \frac{\beta}{2}\right]} .
\)
\(
\begin{aligned}
& \text { or } 2 \sin \frac{\beta}{2} S=2 \sin \left[\alpha+(n-1) \frac{\beta}{2}\right] \sin \frac{n \beta}{2} \\
& \Rightarrow S=\frac{\sin \frac{n \beta}{2}}{\sin \frac{\beta}{2}} \sin \left[\alpha+(n-1) \frac{\beta}{2}\right]
\end{aligned}
\)
In the above result replacing \(\alpha\) by \(\pi / 2+\alpha\), we get
\(
\cos \alpha+\cos (\alpha+\beta)+\cos (\alpha+2 \beta)+\cdots+\cos (\alpha+\overline{n-1} \beta)=\frac{\sin \frac{n \beta}{2}}{\sin \frac{\beta}{2}} \cos \left[\alpha+(n-1) \frac{\beta}{2}\right]
\)
Example 2.71: Find the value of \(\cos \frac{2 \pi}{7}+\cos \frac{4 \pi}{7}+\cos \frac{6 \pi}{7}\).
Solution:
\(
\begin{aligned}
S & =\cos \frac{2 \pi}{7}+\cos \frac{4 \pi}{7}+\cos \frac{6 \pi}{7} \\
& =\frac{\sin \left(3 \frac{\pi}{7}\right)}{\sin \left(\frac{\pi}{7}\right)} \cos \left(\frac{\pi}{7}+\frac{3 \pi}{7}\right) \\
& =\frac{2 \sin \left(\frac{3 \pi}{7}\right) \cos \left(\frac{4 \pi}{7}\right)}{2 \sin \left(\frac{2 \pi}{7}\right)}=\frac{\sin \left(\frac{7 \pi}{7}\right)-\sin \left(\frac{\pi}{7}\right)}{2 \sin \left(\frac{2 \pi}{7}\right)}=-\frac{1}{2}
\end{aligned}
\)
Example 2.72: Prove that \(\sin \theta+\sin 3 \theta+\sin 5 \theta+\cdots+\sin (2 n-1) \theta=\frac{\sin ^2 n \theta}{\sin \theta}\).
Solution:
\(
\begin{aligned}
\sin \theta+\sin 3 \theta+\sin 5 \theta+\cdots+\sin (2 n-1) \theta & =\frac{\sin \left[n\left(\frac{2 \theta}{2}\right)\right]}{\sin \left(\frac{2 \theta}{2}\right)} \sin \left(\frac{\theta+(2 n-1) \theta}{2}\right) \\
& =\frac{\sin ^2 n \theta}{\sin \theta}
\end{aligned}
\)
CONDITIONAL IDENTITIES
Some Standard Identities in Triangle
Case-I: \(\tan A+\tan B+\tan C=\tan A \tan B \tan C\)
Proof:
In \(\triangle A B C\), we have \(A+B+C=\pi\)
\(
\begin{aligned}
& \Rightarrow A+B=\pi-C \\
& \Rightarrow \tan (A+B)=\tan (\pi-C) \\
& \Rightarrow \frac{\tan A+\tan B}{1-\tan A \tan B}=-\tan C \\
& \Rightarrow \tan A+\tan B=-\tan C+\tan A \tan B \tan C \\
& \Rightarrow \tan A+\tan B+\tan C=\tan A \tan B \tan C
\end{aligned}
\)
Case-II: \(\tan \frac{A}{2} \tan \frac{B}{2}+\tan \frac{C}{2} \tan \frac{B}{2}+\tan \frac{C}{2} \tan \frac{A}{2}=1\)
Proof:
Since \(A+B+C=\pi\), we have \(\frac{A}{2}+\frac{B}{2}=\frac{\pi}{2}-\frac{C}{2}\)
\(
\begin{aligned}
& \Rightarrow \tan \left(\frac{A}{2}+\frac{B}{2}\right)=\tan \left(\frac{\pi}{2}-\frac{C}{2}\right)=\cot \frac{C}{2} \\
& \Rightarrow \frac{\tan \frac{A}{2}+\tan \frac{B}{2}}{1-\tan \frac{A}{2} \tan \frac{B}{2}}=\frac{1}{\tan \frac{C}{2}} \\
& \Rightarrow \tan \frac{A}{2} \tan \frac{C}{2}+\tan \frac{B}{2} \tan \frac{C}{2}=1-\tan \frac{A}{2} \tan \frac{B}{2} \\
& \Rightarrow \tan \frac{A}{2} \tan \frac{B}{2}+\tan \frac{B}{2} \tan \frac{C}{2}+\tan \frac{C}{2} \tan \frac{A}{2}=1
\end{aligned}
\)
Case-III: \(\sin 2 A+\sin 2 B+\sin 2 C=4 \sin A \sin B \sin C\)
Proof:
\(
\begin{aligned}
(\sin 2 A+\sin 2 B)+\sin 2 C & =2 \sin (A+B) \cos (A-B)+\sin 2 C \\
& =2 \sin (\pi-C) \cos (A-B)+\sin 2 C \\
& =2 \sin C \cos (A-B)+2 \sin C \cos C \\
& =2 \sin C[\cos (A-B)+\cos C] \\
& =2 \sin C[\cos (A-B)+\cos \{\pi-(A+B)\}] \\
& =2 \sin C[\cos (A-B)-\cos (A+B)] \\
& =2 \sin C \times 2 \sin A \sin B=4 \sin A \sin B \sin C
\end{aligned}
\)
Case-IV: \(\cos 2 A+\cos 2 B+\cos 2 C=-1-4 \cos A \cos B \cos C\)
Proof:
\(
\begin{aligned}
& (\cos 2 A+\cos 2 B)+\cos 2 C \\
& =2 \cos (A+B) \cos (A-B)+2 \cos ^2 C-1 \\
& =2 \cos (\pi-C) \cos (A-B)+2 \cos ^2 C-1 \\
& =-2 \cos C \cos (A-B)+2 \cos ^2 C-1 \\
& =-2 \cos C[\cos (A-B)-\cos C]-1 \\
& =-2 \cos C[\cos (A-B)-\cos \{\pi-(A+B)\}]-1 \\
& =-2 \cos C[\cos (A-B)+\cos (A+B)]-1 \\
& =-1-4 \cos A \cos B \cos C
\end{aligned}
\)
Case-V: \(\cos A+\cos B+\cos C=1+4 \sin \frac{A}{2} \sin \frac{B}{2} \sin \frac{C}{2}\)
Proof:
\(
\begin{aligned}
& (\cos A+\cos B)+\cos C-1 \\
& =2 \cos \frac{A+B}{2} \cos \frac{A-B}{2}+\cos C-1 \\
& =2 \cos \left(\frac{\pi}{2}-\frac{C}{2}\right) \cos \frac{A-B}{2}+\cos C-1 \\
& =2 \sin \frac{C}{2} \cos \frac{A-B}{2}+1-2 \sin ^2 \frac{C}{2}-1 \\
& =2 \sin \frac{C}{2} \cos \frac{A-B}{2}-2 \sin ^2 \frac{C}{2} \\
& =2 \sin \frac{C}{2}\left[\cos \frac{A-B}{2}-\sin \frac{C}{2}\right] \\
& =2 \cos \frac{C}{2}\left[\cos \frac{A-B}{2}-\sin \left(\frac{\pi}{2}-\frac{A+B}{2}\right)\right] \\
& =2 \sin \frac{C}{2}\left[\cos \frac{A-B}{2}-\cos \frac{A+B}{2}\right] \\
& =2 \sin \frac{C}{2}\left(2 \sin \frac{A}{2} \sin \frac{B}{2}\right)=4 \sin \frac{A}{2} \sin \frac{B}{2} \sin \frac{C}{2}
\end{aligned}
\)
Case-VI: \(\sin A+\sin B+\sin C=4 \cos \frac{A}{2} \cos \frac{B}{2} \cos \frac{C}{2}\)
Proof:
\(
\begin{aligned}
& (\sin A+\sin B)+\sin C \\
& =2 \sin \frac{A+B}{2} \cos \frac{A-B}{2}+\sin C \\
& =2 \sin \left(\frac{\pi}{2}-\frac{C}{2}\right) \cos \frac{A-B}{2}+\sin C \\
& =2 \cos \frac{C}{2} \cos \frac{A-B}{2}+2 \sin \frac{C}{2} \cos \frac{C}{2} .
\end{aligned}
\)
\(
\begin{aligned}
& =2 \cos \frac{C}{2}\left[\cos \frac{A-B}{2}+\sin \frac{C}{2}\right] \\
& =2 \cos \frac{C}{2}\left[\cos \frac{A-B}{2}+\sin \left(\frac{\pi}{2}-\frac{A+B}{2}\right)\right] \\
& =2 \cos \frac{C}{2}\left[\cos \frac{A-B}{2}+\cos \frac{A+B}{2}\right] \\
& =4 \cos \frac{A}{2} \cos \frac{B}{2} \cos \frac{C}{2}
\end{aligned}
\)
\(
\begin{aligned}
&\text { Note: }\\
&\tan A+\tan B+\tan C=\tan A \tan B \tan C \text { is true for } A+B+C=n \pi \text {, where } n \in N \text {. }
\end{aligned}
\)
Example 2.73: If \(A+B+C=180^{\circ}\), prove that \(\cos ^2 A+\cos ^2 B+\cos ^2 C=1-2 \cos A \cos B \cos C\).
Solution:
\(
\begin{aligned}
\cos ^2 A+\cos ^2 B+\cos ^2 C & =\frac{1+\cos 2 A}{2}+\frac{1+\cos 2 B}{2}+\frac{1+\cos 2 C}{2} \\
& =\frac{1}{2}(\cos 2 A+\cos 2 B+\cos 2 C)+\frac{3}{2} \\
& =\frac{1}{2}(-1-4 \cos A \cos B \cos C)+\frac{3}{2} \\
& =1-2 \cos A \cos B \cos C .
\end{aligned}
\)
Example 2.74: Prove that in triangle \(A B C, \cos ^2 A+\cos ^2 B-\cos ^2 C=1-2 \sin A \sin B \cos C\).
Solution:
\(
\begin{aligned}
\cos ^2 A+\cos ^2 B-\cos ^2 C & =\cos ^2 A+\sin ^2 C-\sin ^2 B \\
& =\cos ^2 A+\sin (C+B) \sin (C-B) \\
& =1-\sin ^2 A+\sin A \sin (C-B) \\
& =1-\sin A[\sin A-\sin (C-B)] \\
& =1-\sin A[\sin (B+C)-\sin (C-B)] \\
& =1-2 \sin A \sin B \cos C
\end{aligned}
\)
Example 2.75: In triangle \(A B C\), prove that
\(
\sin (B+C-A)+\sin (C+A-B)+\sin (A+B-C)=4 \sin A \sin B \sin C .
\)
Solution:
\(\begin{aligned} \sin (B+C-A)+\sin (C+A-B)+\sin (A+B-C) & =\sin (\pi-2 A)+\sin (\pi-2 B)+\sin (\pi-2 C) \\ & =\sin 2 A+\sin 2 B+\sin 2 C=4 \sin A \sin B \sin C\end{aligned}\)
Example 2.76: If \(x+y+z=x y z\), prove that \(\frac{2 x}{1-x^2}+\frac{2 y}{1-y^2}+\frac{2 z}{1-z^2}=\frac{2 x}{1-x^2} \frac{2 y}{1-y^2} \frac{2 z}{1-z^2}\).
Solution: \(\text { Let } x=\tan A, y=\tan B, z=\tan C\)
Now \(x+y+z=x y z\)
\(\Rightarrow \tan A+\tan B+\tan C=\tan A \tan B \tan C\)
\(\Rightarrow A+B+C=n \pi\)
\(\Rightarrow 2 A+2 B+2 C=2 n \pi\)
\(\Rightarrow \tan 2 A+\tan 2 B+\tan 2 C=\tan 2 A \tan 2 B \tan 2 C\)
\(\Rightarrow \frac{2 \tan A}{1-\tan ^2 A}+\frac{2 \tan B}{1-\tan ^2 B}+\frac{2 \tan C}{1-\tan ^2 C}=\frac{2 \tan A}{1-\tan ^2 A} \frac{2 \tan B}{1-\tan ^2 B} \frac{2 \tan C}{1-\tan ^2 C}\)
\(\Rightarrow \frac{2 x}{1-x^2}+\frac{2 y}{1-y^2}+\frac{2 z}{1-z^2}=\frac{2 x}{1-x^2}+\frac{2 y}{1-y^2} \frac{2 z}{1-z^2}\)
Example 2.77: If \(A+B+C=\pi\), prove that \(\sin ^2 \frac{A}{2}+\sin ^2 \frac{B}{2}-\sin ^2 \frac{C}{2}=1-2 \cos \frac{A}{2} \cos \frac{B}{2} \sin \frac{C}{2}\).
Solution:
\(
\begin{aligned}
\sin ^2 \frac{A}{2}-\sin ^2 \frac{C}{2}+\sin ^2 \frac{B}{2} & =\sin \left(\frac{A+C}{2}\right) \sin \left(\frac{A-C}{2}\right)+1-\cos ^2 \frac{B}{2} \\
& =\cos \left(\frac{B}{2}\right) \sin \left(\frac{A-C}{2}\right)-\cos ^2 \frac{B}{2}+1 \\
& =\cos \left(\frac{B}{2}\right)\left[\sin \left(\frac{A-C}{2}\right)-\cos \frac{B}{2}\right]+1 \\
& =\cos \left(\frac{B}{2}\right)\left[\sin \left(\frac{A-C}{2}\right)-\sin \left(\frac{A+C}{2}\right)\right]+1 \\
& =1-2 \cos \frac{A}{2} \cos \frac{B}{2} \sin \frac{C}{2}
\end{aligned}
\)
Example 2.78: The product of the sines of the angles of a triangle is \(p\) and the product of their cosines is \(q\). Show that the tangents of the angles are the roots of the equation \(q x^2-p x^2+(1+q)\) \(x-p=0\).
Solution: From the question, \(\sin A \sin B \sin C=p\) and \(\cos A \cos B \cos C=q\)
\(\therefore \tan A \tan B \tan C=\frac{p}{q} \dots(i)\)
Also, \(\tan A+\tan B+\tan C=\tan A \tan B \tan C=\frac{p}{q} \dots(ii)\)
\(
\begin{aligned}
& \text { Now, } \tan A \tan B+\tan B \tan C+\tan C \tan A \\
& =\frac{\sin A \sin B \cos C+\sin B \sin C \cos A+\sin C \sin A \cos B}{\cos A \cos B \cos C} \\
& \left.=\frac{1}{2 q}\left[\left(\sin ^2 A+\sin ^2 B-\sin ^2 C\right)+\left(\sin ^2 B+\sin ^2 C \sin ^2 A\right)+\sin ^2 C+\sin ^2 A-\sin ^2 B\right)\right] \\
& \quad\left[\because A+B+C=\pi \text { and } 2 \sin A \sin B \cos C=\sin ^2 A+\sin ^2 B-\sin ^2 C\right]
\end{aligned}
\)
\(
=\frac{1}{2 q}\left[\sin ^2 A+\sin ^2 B+\sin ^2 C\right]=\frac{1}{4 q}[3-(\cos 2 A+\cos 2 B+\cos 2 C)]=\frac{1}{q}[1+\cos A \cos B \cos C]=\frac{1}{q}(1+q)
\)
The equation whose roots are \(\tan A, \tan B \tan C\) will be given by
\(
x^3-(\tan A+\tan B+\tan C) x^2+(\tan A \tan B+\tan B \tan C+\tan C \tan A) x-\tan A \tan B \tan C=0
\)
or \(x^3-\frac{p}{q} x^2+\frac{1+q}{q} x-\frac{p}{q}=0\), or \(q x^3-p x^2+(1+q) x-p=0\)
SOME IMPORTANT RESULTS AND THEIR APPLICATIONS
Case-I: \(\cos A \cos (60-A) \cos (60+A)=\frac{1}{4} \cos 3 A\)
Proof: We have
\(
\begin{aligned}
\text { L.H.S. } & =\cos A \cos (60-A) \cos (60+A) \\
& =\cos A\left(\cos ^2 60^{\circ}-\sin ^2 A\right) \\
& =\cos A\left(\frac{1}{4}-\sin ^2 A\right)=\cos A\left(\frac{1}{4}-\left(1-\cos ^2 A\right)\right)=\cos A\left(-\frac{3}{4}+\cos ^2 A\right) \\
& =\frac{1}{4} \cos A\left(-3+4 \cos ^2 A\right)=\frac{1}{4}\left(4 \cos ^3 A-3 \cos A\right) \\
& =\frac{1}{4} \cos 3 A=\text { R.H.S }
\end{aligned}
\)
Case-II: \(\sin A \sin (60-A) \sin (60+A)=\frac{1}{4} \sin 3 A\)
Proof: We have
\(
\begin{aligned}
\text { L.H.S. } & =\sin A \sin (60-A) \sin (60+A) \\
& =\sin A\left(\sin ^2 60^{\circ}-\sin ^2 A\right) \left[\because \sin (A+B) \sin (A-B)=\sin ^2 A-\sin ^2 B\right] \\
& =\sin A\left(\frac{3}{4}-\sin ^2 A\right)=\frac{1}{4} \sin A\left(3-4 \sin ^2 A\right) \\
& =\frac{1}{4}\left(3 \sin A-4 \sin ^3 A\right) \\
& =\frac{1}{4} \sin 3 A=\text { R.H.S }
\end{aligned}
\)
Case-III: \(\tan \alpha \tan \left(60^{\circ}-\alpha\right) \tan \left(60^{\circ}+\alpha\right)=\tan 3 \alpha\)
Proof:
\(
\begin{aligned}
& \tan \left(60^{\circ}-\alpha\right)=\frac{\sqrt{3}-\tan \alpha}{1+\sqrt{3} \tan \alpha} \\
& \tan \left(60^{\circ}+\alpha\right)=\frac{\sqrt{3}+\tan \alpha}{1-\sqrt{3} \tan \alpha}
\end{aligned}
\)
\(
\mathrm{LHS}=\tan \alpha \cdot \frac{(\sqrt{3}-\tan \alpha)(\sqrt{3}+\tan \alpha)}{(1+\sqrt{3} \tan \alpha)(1-\sqrt{3} \tan \alpha)}
\)
\(
\tan \alpha \cdot \frac{(\sqrt{3})^2-(\tan \alpha)^2}{(1)^2-(\sqrt{3} \tan \alpha)^2}
\)
\(
\frac{3 \tan \alpha-\tan ^3 \alpha}{1-3 \tan ^2 \alpha}
\)
\(
=\tan 3 \alpha
\)
Example 2.79: Prove that \(\cos 20^{\circ} \cos 40^{\circ} \cos 60^{\circ} \cos 80^{\circ}=\frac{1}{16}\).
Solution:
\(
\begin{aligned}
\cos 20^{\circ} \cos 40^{\circ} \cos 80^{\circ} \cos 60^{\circ} & =\cos 20^{\circ} \cos \left(60^{\circ}-20^{\circ}\right) \cos \left(60^{\circ}+20^{\circ}\right) \cos 60^{\circ} \\
& =\frac{1}{4} \cos \left(3 \times 20^{\circ}\right) \cos 60^{\circ}=\frac{1}{4} \cos ^2 60^{\circ}=\frac{1}{4} \times \frac{1}{4}=\frac{1}{16}
\end{aligned}
\)
Example 2.80: Prove that \(\sin 10^{\circ} \sin 30^{\circ} \sin 50^{\circ} \sin 70^{\circ}=\frac{1}{16}\).
Solution:
\(
\begin{aligned}
\sin 10^{\circ} \sin 30^{\circ} \sin 50^{\circ} \sin 70^{\circ} & =\sin 10^{\circ} \sin \left(60^{\circ}-10^{\circ}\right) \sin \left(60^{\circ}+10^{\circ}\right) \sin 30^{\circ} \\
& =\frac{1}{4} \sin \left(3 \times 10^{\circ}\right) \sin 30^{\circ}=\frac{1}{4} \sin ^2 30^{\circ}=\frac{1}{16}
\end{aligned}
\)
Example 2.81: Prove that \(\tan 20^{\circ} \tan 40^{\circ} \tan 80^{\circ}=\tan 60^{\circ}\).
Solution:
\(
\begin{aligned}
& \tan 20^{\circ} \tan 40^{\circ} \tan 80^{\circ} \\
& =\tan 20^{\circ} \tan \left(60^{\circ}-20^{\circ}\right) \tan \left(60^{\circ}+20^{\circ}\right)=\tan \left(3 \times 20^{\circ}\right)=\tan 60^{\circ}
\end{aligned}
\)
Case-IV: \(\cos A \cos 2 A \cos 2^2 A \cos 2^3 A \cdots \cos 2^{n-1} A=\frac{\sin 2^n A}{2^n \sin A}\)
Proof: \(\text { L.H.S. }=\cos A \cos 2 A \cos 2^2 A \cos 2^3 A \cdots \cos 2^{n-1} A\)
\(
\begin{aligned}
& =\frac{1}{2 \sin A}\left[(2 \sin A \cos A) \cos 2 A \cos 2^2 A \cos 2^3 A \cdots \cos 2^{n-1} A\right] \\
& =\frac{1}{2 \sin A}\left[\left(\sin 2 A \cos 2 A \cos 2^2 A \cos 2^3 A \cdots \cos 2^{n-1} A\right]\right. \\
& =\frac{1}{2^2 \sin A}\left[(2 \sin 2 A \cos 2 A) \cos 2^2 A \cos 2^3 A \cdots \cos 2^{n-1} A\right] \\
& =\frac{1}{2^2 \sin A}\left[\sin 2(2 A) \cdot \cos 2^2 A \cos 2^3 A \cdots \cos 2^{n-1} A\right] \\
& =\frac{1}{2^3 \sin A}\left[\left(2 \sin 2^2 A \cos 2^2 A\right) \cos 2^3 A \cdots \cos 2^{n-1} A\right]
\end{aligned}
\)
\(
\begin{aligned}
& =\frac{1}{2^3 \sin A}\left[\sin \left(2 \times 2^2 A\right) \cos 2^3 A \cdots \cos 2^{n-1} A\right] \\
& =\frac{1}{2^3 \sin A}\left[\left(\sin 2^3 A \cos 2^3 A \cos 2^4 A \cdots \cos 2^{n-1} A\right]\right. \\
& \cdots \\
& \cdots \\
& =\frac{1}{2^{n-1} \sin A}\left[\sin 2^{n-1} A \cos 2^{n-1} A\right] \\
& =\frac{1}{2^n \sin A}\left[2 \sin 2^{n-1} A \cos 2^{n-1} A\right] \\
& =\frac{1}{2^n \sin A} \sin \left(2 \times 2^{n-1} A\right) \\
& =\frac{1}{2^n \sin A} \sin 2^n A=\text { R.H.S. }
\end{aligned}
\)
Example 2.82: If \(\theta=\frac{\pi}{2^n+1}\), show that \(\cos \theta \cos 2 \theta ~2 \cos 2^2 \theta \cdots \cos 2^{n-1} \theta=\frac{1}{2^n}\).
Solution: In the above result, put \(\theta=\frac{\pi}{2^n+1}\)
\(
\begin{aligned}
\text { R.H.S. }=\frac{\sin 2^n \theta}{2^n \sin \theta}=\frac{\sin \left(\frac{\pi}{2^n+1}\right) 2^n}{2^n \sin \left(\frac{\pi}{2^n+1}\right)} & =\frac{\sin \left(\frac{2^n+1-1}{2^n+1}\right) \pi}{2^n \sin \left(\frac{\pi}{2^n+1}\right)} \\
& =\frac{\sin \left(\pi-\frac{\pi}{2^n+1}\right)}{2^n \sin \left(\frac{\pi}{2^n+1}\right)} \\
& =\frac{\sin \left(\frac{\pi}{2^n+1}\right)}{2^n \sin \left(\frac{\pi}{2^n+1}\right)} \\
& =\frac{1}{2^n}
\end{aligned}
\)
Example 2.83: Prove that \(\cos \frac{2 \pi}{15} \cos \frac{4 \pi}{15} \cos \frac{8 \pi}{15} \cos \frac{14 \pi}{15}=\frac{1}{16}\).
Solution: We have
\(
\text { L.H.S. }=\cos \frac{2 \pi}{15} \cos \frac{4 \pi}{15} \cos \frac{8 \pi}{15} \cos \left(\pi-\frac{\pi}{15}\right)
\)
\(
\begin{aligned}
& =\left(\cos \frac{2 \pi}{15} \cos \frac{4 \pi}{15} \cos \frac{8 \pi}{15}\right)\left(-\cos \frac{\pi}{15}\right) \\
& =-\cos \frac{\pi}{15} \cos \frac{2 \pi}{15} \cos \frac{4 \pi}{15} \cos \frac{8 \pi}{15} \\
& =-\cos A \cos 2 A \cos 2^2 A \cos 2^3 A, \text { where } A=\pi / 15 \\
& =-\left[\frac{\sin 2^4 A}{2^4 \sin A}\right]=-\frac{\sin 16 A}{2^4 \sin A} \\
& =-\frac{\sin (15 A+A)}{16 \sin A}=\frac{-\sin (\pi+A)}{16 \sin A} [\because 15 A=\pi]\\
& =\frac{\sin A}{16 \sin A}=\frac{1}{16}=\frac{1}{16}=\text { R.H.S. }
\end{aligned}
\)
Example 2.84: Prove that \(\sin 6^{\circ} \sin 42^{\circ} \sin 66^{\circ} \sin 78^{\circ}=\frac{1}{16}\).
Solution:
\(
\begin{aligned}
& \sin 6^{\circ} \sin 42^{\circ} \sin 66^{\circ} \sin 78^{\circ} \\
& =\sin 6^{\circ} \cos 48^{\circ} \cos 24^{\circ} \cos 12^{\circ} \\
& =\sin 6^{\circ} \frac{2^3 \sin 12^{\circ} \cos 12^{\circ} \cos 24^{\circ} \cos 48^{\circ}}{2^3 \sin 12^{\circ}} \\
& =\sin 6^{\circ} \frac{\sin 96^{\circ}}{2^3 \sin 12^{\circ}} \\
& =\frac{2 \sin 6^{\circ} \cos 6^{\circ}}{2^4 \sin 12^{\circ}}=\frac{\sin 12^{\circ}}{2^4 \sin 12^{\circ}}=\frac{1}{16}
\end{aligned}
\)
Example 2.85: In \(\triangle A B C, \tan A+\tan B+\tan C \geq 3 \sqrt{3}\), where \(A, B, C\) are acute angles.
Solution: In \(\triangle A B C\),
\(\tan A+\tan B+\tan C=\tan A \tan B \tan C\)
Also, \(\frac{\tan A+\tan B+\tan C}{3} \geq \sqrt[3]{\tan A \tan B \tan C} \text { [since A.M. } \geq \text { G.M.] }\)
\(
\begin{aligned}
& \Rightarrow \tan A \tan B \tan C \geq \sqrt[3]{\tan A \tan B \tan C} \\
& \Rightarrow \tan ^2 A \tan ^2 B \tan ^2 C \geq 27 \\
& \Rightarrow \tan A \tan B \tan C \geq 3 \sqrt{3} \text { [cubing both sides] }\\
& \Rightarrow \tan A+\tan B+\tan C \geq 3 \sqrt{3}
\end{aligned}
\)
Example 2.86: In \(\triangle A B C\), prove that \(\cos A+\cos B+\cos C \leq 3 / 2\).
Solution:
\(
\begin{aligned}
& \text { Let } \cos A+\cos B+\cos C=x \\
& \Rightarrow 2 \cos \left(\frac{A+B}{2}\right) \cos \left(\frac{A-B}{2}\right)+1-2 \sin ^2 \frac{C}{2}=x \\
& \Rightarrow 2 \sin \frac{C}{2} \cos \left(\frac{A-B}{2}\right)+1-2 \sin ^2 \frac{C}{2}=x \\
& \Rightarrow 2 \sin ^2 \frac{C}{2}-2 \sin \frac{C}{2} \cos \left(\frac{A-B}{2}\right)+x-1=0
\end{aligned}
\)
This is quadratic in \(\sin C / 2\), which is real. So, discriminant \(D \geq 0\).
\(
\begin{aligned}
& 4 \cos ^2\left(\frac{A-B}{2}\right)-4 \times 2(x-1) \geq 0 \\
& \Rightarrow 2(x-1) \leq \cos ^2\left(\frac{A-B}{2}\right) \\
& \Rightarrow 2(x-1) \leq 1 \\
& \Rightarrow x \leq 3 / 2
\end{aligned}
\)
Thus, \(\cos A+\cos B+\cos C \leq 3 / 2\)
Note: Since \(\cos A+\cos B+\cos C=1+4 \sin \frac{A}{2} \sin \frac{B}{2} \sin \frac{C}{2}\)
We have \(\sin \frac{A}{2} \sin \frac{B}{2} \sin \frac{C}{2} \leq \frac{1}{8}\).
Students are advised to remember this as a standard result.
Example 2.87: Find the least value of \(\sec A+\sec B+\sec C\) in an acute angle triangle.
Solution: In an acute angle triangle, \(\sec A, \sec B\) and \(\sec C\) are positive. Now A.M. \(\geq\) H.M.
\(
\Rightarrow \quad \frac{\sec A+\sec B+\sec C}{3} \geq \frac{3}{\cos A+\cos B+\cos C}
\)
But in \(\triangle A B C, \cos A+\cos B+\cos C \leq 3 / 2\)
\(
\begin{aligned}
& \Rightarrow \quad \frac{\sec A+\sec B+\sec C}{3} \geq 2 \\
& \Rightarrow \quad \sec A+\sec B+\sec C \geq 6
\end{aligned}
\)
EXERCISES
Q1. Are the set of angles \(\alpha\) and \(\beta\) given by \(\alpha=\left(2 n+\frac{1}{2}\right), \pi \pm A\) and \(\beta=m \pi+(-1)^m\left(\frac{\pi}{2}-A\right)[latex] same, where [latex]n, m \in I\)?
Solution: Let \(m=2 k\), i.e., \(m\) is even where \(k \in I\)
Now, \(\beta=2 k \pi+\frac{\pi}{2}-A=\left(2 k+\frac{1}{2}\right) \pi-A \dots(i)\)
If \(m=2 k+1\), i.e., \(m\) is odd, then
\(
\beta=(2 k+1) \pi-\left(\frac{\pi}{2}-A\right)=\left(2 k+\frac{1}{2}\right) \pi+A \dots(ii)
\)
From Eqs. (i) and (ii), \(\beta\) can be expressed as
\(
\beta=\left(2 k+\frac{1}{2}\right) \pi \pm A, k \in I
\)
which is same as \(\alpha\).
Q2. If \(A B C\) is a triangle and \(\tan \frac{A}{2}, \tan \frac{B}{2}, \tan \frac{C}{2}\) are in H.P., then find the minimum value of \(\cot B / 2\).
Solution:
\(
\begin{aligned}
& A+B+C=\pi \\
& \Rightarrow \frac{A}{2}+\frac{B}{2}=\frac{\pi}{2}-\frac{C}{2} \\
& \Rightarrow \cot \left(\frac{A}{2}+\frac{B}{2}\right)=\cot \left(\frac{\pi}{2}-\frac{C}{2}\right) \\
& \Rightarrow \frac{\cot \frac{A}{2} \cot \frac{B}{2}-1}{\cot \frac{A}{2}+\cot \frac{B}{2}}=\tan \frac{C}{2}=\frac{1}{\cot \frac{C}{2}} \\
& \Rightarrow \cot \frac{A}{2} \cot \frac{B}{2} \cot \frac{C}{2}=\cot \frac{A}{2}+\cot \frac{B}{2}+\cot \frac{C}{2} \dots(i)
\end{aligned}
\)
But \(\tan \frac{A}{2}, \tan \frac{B}{2}, \tan \frac{C}{2}\) are in H.P.
\(\therefore \cot \frac{A}{2}, \cot \frac{B}{2}, \cot \frac{C}{2}\) are in A.P.
So, \(\cot \frac{A}{2}+\cot \frac{C}{2}=2 \cot \frac{B}{2}\).
Hence, Eq. (i) becomes \(\cot \frac{A}{2} \cot \frac{B}{2} \cot \frac{C}{2}=3 \cot \frac{B}{2} \Rightarrow \cot \frac{A}{2} \cot \frac{C}{2}=3\)
\(\Rightarrow\) G.M. of \(\cot \frac{A}{2}\) and \(\cot \frac{C}{2}=\sqrt{\cot \frac{A}{2} \cot \frac{C}{2}}=\sqrt{3}\)
and A.M. of \(\cot \frac{A}{2}\) and \(\cot \frac{C}{2}=\frac{\cot \frac{A}{2}+\cot \frac{C}{2}}{2}=\cot \frac{B}{2}\)
But A.M. \(\geq\) G.M.
\(
\Rightarrow \quad \cot \frac{B}{2} \geq \sqrt{3}
\)
Therefore, the minimum value of \(\cot B / 2\) is \(\sqrt{3}\).
Q3. Find the sum of the series \(\operatorname{cosec} \theta+\operatorname{cosec} 2 \theta+\operatorname{cosec} 4 \theta+\cdots\) to \(n\) terms.
Solution:
\(
\begin{aligned}
& \operatorname{cosec} \theta=\frac{1}{\sin \theta} \\
& \quad=\frac{1}{\sin \theta} \frac{\sin \theta / 2}{\sin \theta / 2}=\frac{\sin \left(\theta-\frac{\theta}{2}\right)}{\sin \theta \sin \left(\frac{\theta}{2}\right)}=\frac{\sin \theta \cos \frac{\theta}{2}-\cos \theta \sin \frac{\theta}{2}}{\sin \theta \sin \frac{\theta}{2}} \\
& \therefore \operatorname{cosec} \theta=\cot \frac{\theta}{2}-\cot \theta \\
& \text { Similarly, } \operatorname{cosec} 2 \theta=\cot \theta-\cot 2 \theta \\
& \operatorname{cosec} 4 \theta=\cot 2 \theta-\cot 4 \theta \\
& \vdots \\
& \text { cosec } 2^{n-1} \theta=\cot 2^{n-2} \theta-\cot 2^{n-1} \theta \\
& \text { Therefore, sum }=\cot \frac{\theta}{2}-\cot 2^{n-1} \theta
\end{aligned}
\)
Q4. In \(\triangle A B C\), if \(\sin ^3 \theta=\sin (A-\theta) \sin (B-\theta) \sin (C-\theta)\), prove that \(\cot \theta=\cot A+\cot B+\cot C\).
Solution:
\(
\begin{aligned}
& \text { Let } \cot \theta=\cot A+\cot B+\cot C \\
& \Rightarrow \cot \theta-\cot A=\cot B+\cot C \\
& \Rightarrow \frac{\sin (A-\theta)}{\sin A \sin \theta}=\frac{\sin (B+C)}{\sin B \sin C} \\
& \Rightarrow \sin (A-\theta)=\frac{\sin ^2 A \sin \theta}{\sin B \sin C} \dots(i)
\end{aligned}
\)
Similarly, \(\sin (B-\theta)=\frac{\sin ^2 B \sin \theta}{\sin A \sin C} \dots(ii)\)
and \(\sin (C-\theta)=\frac{\sin ^2 C \sin \theta}{\sin A \sin B} \dots(iii)\)
By multiplying corresponding sides of Eqs. (i), (ii), and (iii), we have \(\sin ^3 \theta=\sin (A-\theta) \sin (B-\theta) \sin (C-\theta)\)
Q5. In triangle \(A B C\), prove that \(\sin \frac{A}{2}+\sin \frac{B}{2}+\sin \frac{C}{2} \leq \frac{3}{2}\). Hence, deduce that \(\cos \frac{\pi+A}{4} \cos \frac{\pi+B}{4} \cos \frac{\pi+C}{4} \leq \frac{1}{8}\).
Solution:
Let \(\sin \frac{A}{2}+\sin \frac{B}{2}+\sin \frac{C}{2}=k\)
or \(2 \sin \frac{A+B}{4} \cos \frac{A-B}{4}+\cos \frac{A+B}{2}=k\)
\(
\Rightarrow \quad 2 \sin ^2 \frac{A+B}{4}-2 \cos \frac{A-B}{4} \sin \frac{A+B}{4}+k-1=0
\)
\(
\begin{aligned}
& \text { Since } \sin \frac{A+B}{4} \text { is real, } 4 \cos ^2 \frac{A-B}{4}-8(k-1) \geq 0 \\
& \Rightarrow \quad 2(k-1) \leq \cos ^2 \frac{A-B}{4} \leq 1 \Rightarrow k \leq 3 / 2
\end{aligned}
\)
\(
\begin{aligned}
& \text { Hence, } 2 \sin \frac{A+B}{4}\left[\cos \frac{A-B}{4}-\sin \frac{\pi-C}{4}\right] \leq \frac{1}{2} \\
& \Rightarrow 2 \sin \frac{A+B}{4}\left[\cos \frac{A-B}{4}-\cos \frac{\pi+C}{4}\right] \leq \frac{1}{2} \\
& \Rightarrow 4 \sin \frac{A+B}{4} \sin \frac{\pi+C+A-B}{8} \sin \frac{\pi+C-A+B}{8} \leq \frac{1}{2} \\
& \Rightarrow 4 \sin \frac{\pi-C}{4} \sin \frac{\pi-B}{4} \sin \frac{\pi-A}{4} \leq \frac{1}{2} \Rightarrow \cos \frac{\pi+C}{4} \cos \frac{\pi+B}{4} \cos \frac{\pi+A}{4} \leq \frac{1}{8}
\end{aligned}
\)
Q6. If \(\frac{x}{\tan (\theta+\alpha)}=\frac{y}{\tan (\theta+\beta)}=\frac{z}{\tan (\theta+\gamma)}\), then show that \(\sum \frac{x+y}{x-y} \sin ^2(\alpha-\beta)=0\).
Solution:
Here \(\frac{x}{y}=\frac{\tan (\theta+\alpha)}{\tan (\theta+\beta)}\). By componendo and dividendo, we get
\(
\begin{array}{r}
\frac{x+y}{x-y}=\frac{\tan (\theta+\alpha)+\tan (\theta+\beta)}{\tan (\theta+\alpha)-\tan (\theta+\beta)}=\frac{\sin (2 \theta+\alpha+\beta)}{\sin (\alpha-\beta)} \\
\therefore \frac{x+y}{x-y} \sin ^2(\alpha-\beta)=\sin (2 \theta+\alpha+\beta) \sin (\alpha-\beta) \\
=\frac{1}{2}[\cos 2(\theta+\beta)-\cos 2(\theta+\alpha)] \dots(i)
\end{array}
\)
Similarly, \(\frac{y+z}{y-z} \sin ^2(\beta-\gamma)=\frac{1}{2}[\cos 2(\theta+\gamma)-\cos 2(\theta+\beta)] \dots(ii)\)
and \(\frac{z+x}{z-x} \sin ^2(\gamma-\alpha)=\frac{1}{2}[\cos 2(\theta+\alpha)-\cos 2(\theta+\gamma)] \dots(iii)\)
Adding Eqs. (i), (ii), and (iii), we get L.H.S. \(=0\).
Q7. If \(\tan 6 \theta=p / q\), find the value of \(\frac{1}{2}(p \operatorname{cosec} 2 \theta-q \sec 2 \theta)\) in terms of \(p\) and \(q\).
Solution:
\(
\begin{aligned}
&\text { Here, we have } \tan 6 \theta=p / q\\
&\begin{aligned}
& \Rightarrow \frac{\sin 6 \theta}{\cos 6 \theta}=\frac{p}{q} \quad \Rightarrow \frac{p}{\sin 6 \theta}=\frac{q}{\cos 6 \theta}=\frac{\sqrt{p^2+q^2}}{\sqrt{1}}=\sqrt{p^2+q^2}=k \text { (say) } \\
& \text { Now } y=\frac{1}{2}(p \operatorname{cosec} \theta-q \sec 2 \theta)=\frac{1}{2}\left(\frac{p}{\sin 2 \theta}-\frac{q}{\cos 2 \theta}\right) \\
& \Rightarrow y=\frac{1}{2}\left[\frac{p \cos 2 \theta-q \sin 2 \theta}{\sin 2 \theta \cos 2 \theta}\right] \\
& \qquad=\left[\frac{2 k \sin 6 \theta \cos 2 \theta-2 k \cos 6 \theta \sin 2 \theta}{4 \sin 2 \theta \cos 2 \theta}\right]=k \frac{\sin (6 \theta-2 \theta)}{\sin 4 \theta}=k=\sqrt{p^2+q^2}
\end{aligned}
\end{aligned}
\)
Q8. If \(0<\alpha<\pi / 2\) and \(\sin \alpha+\cos \alpha+\tan \alpha+\cot \alpha+\sec \alpha+\operatorname{cosec} \alpha=7\), then prove that \(\sin 2 \alpha\) is a root of the equation \(x^2-44 x-36=0\).
Solution:
\(
\begin{aligned}
& \sin \alpha+\cos \alpha+(\tan \alpha+\cot \alpha)+(\sec \alpha+\operatorname{cosec} \alpha)=7 \\
& \Rightarrow \quad(\sin \alpha+\cos \alpha)+\frac{1}{\sin \alpha \cos \alpha}+\frac{\sin \alpha+\cos \alpha}{\sin \alpha \cos \alpha}=7 \\
& \Rightarrow \quad(\sin \alpha+\cos \alpha)\left(1+\frac{1}{\sin \alpha \cos \alpha}\right)=7-\frac{1}{\sin \alpha \cos \alpha} \\
& \Rightarrow \quad(1+\sin 2 \alpha)\left(1+\frac{4}{\sin 2 \alpha}+\frac{4}{\sin ^2 2 \alpha}\right)=49-\frac{28}{\sin 2 \alpha}+\frac{4}{\sin ^2 2 \alpha}
\end{aligned}
\)
\(
\begin{aligned}
&\text { Let } \sin 2 \alpha=x\\
&\begin{aligned}
& \Rightarrow(1+x)\left(1+\frac{4}{x}+\frac{4}{x^2}\right)=49-\frac{28}{x}+\frac{4}{x^2} \quad \Rightarrow(1+x)\left(x^2+4 x+4\right)=49 x^2-28 x+4 \\
& \Rightarrow x^3-44 x^2-36 x=0 \\
& \Rightarrow x^2-44 x-36=0 .(\text { as } x=\sin 2 \alpha \neq 0)
\end{aligned}
\end{aligned}
\)
Q9. Prove that \(1+\cot \theta \leq \cot \frac{\theta}{2}\) for \(0<\theta<\pi\). Find \(\theta\) when the equality sign holds.
Solution:
We have
\(
\begin{aligned}
1+\cot \theta-\cot \frac{\theta}{2} & =1+\frac{\cot ^2 \frac{\theta}{2}-1}{2 \cot \frac{\theta}{2}}-\cot \frac{\theta}{2} \\
& =\frac{2 \cot \frac{\theta}{2}+\cot ^2 \frac{\theta}{2}-1-2 \cot ^2 \frac{\theta}{2}}{2 \cot \frac{\theta}{2}} \\
& =\frac{-\left(\cot \frac{\theta}{2}-1\right)^2}{2 \cot \frac{\theta}{2}} \leq 0 \text { for } 0<\theta<\pi
\end{aligned}
\)
\(
\begin{aligned}
&\Rightarrow \quad 1+\cot \theta \leq \cot \frac{\theta}{2}\\
&\text { Equality holds when } \cot \frac{\theta}{2}-1=0 \Rightarrow \theta=\frac{\pi}{2} \text {. }
\end{aligned}
\)
Q10. Show that \(2^{\sin x}+2^{\cos x} \geq 2^{1-1 / \sqrt{2}}\).
Solution:
\(
\begin{aligned}
&\text { Since A.M. of two positive quantities } \geq \text { their G.M., we have }\\
&\begin{aligned}
& \frac{2^{\sin x}+2^{\cos x}}{2} \geq \sqrt{2^{\sin x} 2^{\cos x}}=\sqrt{2^{\sin x+\cos x}}=\sqrt{2^{\sqrt{2} \sin \left(x+\frac{\pi}{4}\right)}} \geq \sqrt{2^{-\sqrt{2}}} \\
& \Rightarrow \quad 2^{\sin x}+2^{\cos x} \geq 2 \times 2^{\frac{-1}{\sqrt{2}}}=2^{1-\frac{1}{\sqrt{2}}}
\end{aligned}
\end{aligned}
\)
Q11. If \(A, B\) and \(C\) are the angles of a triangle, show that \(\tan ^2 \frac{A}{2}+\tan ^2 \frac{B}{2}+\tan ^2 \frac{C}{2} \geq 1\).
Solution:
\(
\begin{aligned}
&\text { We have } \frac{A}{2}+\frac{B}{2}+\frac{C}{2}=\frac{\pi}{2} \text {, so that }\\
&\begin{aligned}
& \tan \left(\frac{A}{2}+\frac{B}{2}\right)=\tan \left(\frac{\pi}{2}-\frac{C}{2}\right) \\
& \Rightarrow \frac{\tan \frac{A}{2}+\tan \frac{B}{2}}{1-\tan \frac{A}{2} \tan \frac{B}{2}}=\frac{1}{\tan \frac{C}{2}} \\
& \Rightarrow \tan \frac{A}{2} \tan \frac{B}{2}+\tan \frac{B}{2} \tan \frac{C}{2}+\tan \frac{C}{2} \tan \frac{A}{2}=1
\end{aligned}
\end{aligned}
\)
\(
\begin{aligned}
& \text { Now } \tan ^2 \frac{A}{2}+\tan ^2 \frac{B}{2}+\tan ^2 \frac{C}{2}-1 \\
& =\frac{1}{2}\left[\sum 2 \tan ^2 \frac{A}{2}-\sum 2 \tan \frac{A}{2} \tan \frac{B}{2}\right] \\
& =\frac{1}{2}\left[\left(\tan \frac{A}{2}-\tan \frac{B}{2}\right)^2+\left(\tan \frac{B}{2}-\tan \frac{C}{2}\right)^2+\left(\tan \frac{C}{2}-\tan \frac{A}{2}\right)^2\right] \geq 0
\end{aligned}
\)
Q12. Let \(A, B, C\) be three angles such that \(A=\pi / 4\) and \(\tan B \tan C=p\). Find all possible values of \(p\) such that \(A, B, C\) are the angles of a triangle.
Solution:
\(
\begin{aligned}
& A+B+C=\pi \\
& \Rightarrow B+C=\frac{3 \pi}{4} \Rightarrow 0<B, C<\frac{3 \pi}{4} \text { Also } \tan B \tan C=p \\
& \Rightarrow \frac{\sin B \sin C}{\cos B \cos C}=\frac{p}{1} \\
& \Rightarrow \frac{\cos B \cos C-\sin B \sin C}{\cos B \cos C+\sin B \sin C}=\frac{1-p}{1+p} \\
& \Rightarrow \frac{\cos (B+C)}{\cos (B-C)}=\frac{1-p}{1+p} \\
& \Rightarrow \frac{1+p}{\sqrt{2}(p-1)}=\cos (B-C) \dots(i)
\end{aligned}
\)
Since \(B\) or \(C\) can vary from 0 to \(3 \pi / 4\), we get
\(
0 \leq B-C<\frac{3 \pi}{4} \Rightarrow-\frac{1}{\sqrt{2}}<\cos (B-C) \leq 1 .
\)
Equation (i) will now lead to \(-\frac{1}{\sqrt{2}}<\frac{p+1}{\sqrt{2}(p-1)} \leq 1\)
For \(0<1+\frac{p+1}{p-1} \quad \Rightarrow \frac{2 p}{(p-1)}>0 \quad \Rightarrow p<0\) or \(p>1 \dots(ii)\)
\(
\begin{aligned}
&\begin{aligned}
& \text { Also } \frac{p+1-\sqrt{2}(p-1)}{\sqrt{2}(p-1)} \leq 0 \\
& \Rightarrow \frac{\left(p-(\sqrt{2}+1)^2\right)}{(p-1)} \geq 0 \\
& \Rightarrow p<1 \text { or } p \geq(\sqrt{2}+1)^2 \dots(iii)
\end{aligned}\\
&\text { Combining Eqs. (ii) and (iii), we get } p<0 \text { or } p \geq(\sqrt{2}+1)^2 \text {. }
\end{aligned}
\)
Q13. Eliminate \(x\) from the equations, \(\sin (a+x)=2 b\) and \(\sin (a-x)=2 c\).
Solution:
\(
\begin{aligned}
& \text { Adding } \sin (a+x)+\sin (a-x)=2(b+c) \\
& \Rightarrow 2 \sin a \cos x=2(b+c) \\
& \Rightarrow \cos x=\frac{b+c}{\sin a} \dots(i)
\end{aligned}
\)
\(
\begin{aligned}
&\text { Subtracting, we get }\\
&\begin{aligned}
& \sin (a+x)-\sin (a-x)=2(b-c) \\
& \Rightarrow 2 \cos a \sin x=2(b-c) \\
& \Rightarrow \sin x=\frac{b-c}{\cos a} \dots(ii)
\end{aligned}
\end{aligned}
\)
\(
\begin{aligned}
&\text { Squaring and adding Eq. (i) and Eq. (ii), we get }\\
&\frac{(b+c)^2}{\sin ^2 a}+\frac{(b-c)^2}{\cos ^2 a}=1
\end{aligned}
\)
Q14. If \(\tan \beta=\frac{n \sin \alpha \cos \alpha}{1-n \sin ^2 \alpha}\), prove that \(\tan (\alpha-\beta)=(1-n) \tan \alpha\).
Solution:
\(
\begin{aligned}
\tan \beta & =\frac{n \sin \alpha \cos \alpha}{1-n \sin ^2 \alpha} \\
& =\frac{\frac{n \sin \alpha \cos \alpha}{\cos ^2 \alpha}}{\frac{1}{\cos ^2 \alpha}-\frac{n \sin ^2 \alpha}{\cos ^2 \alpha}} \text { [dividing numerator and denominator by } \cos ^2 \alpha \text { ] }
\end{aligned}
\)
\(
=\frac{n \tan \alpha}{\sec ^2 \alpha-n \tan ^2 \alpha}=\frac{n \tan \alpha}{1+\tan ^2 \alpha-n \tan ^2 \alpha}=\frac{n \tan \alpha}{1+(1-n) \tan ^2 \alpha} \dots(i)
\)
\(
\text { Now, L.H.S. } \begin{aligned}
= & \tan (\alpha-\beta)=\frac{\tan \alpha-\tan \beta}{1+\tan \alpha \tan \beta} \\
= & \frac{\tan \alpha-\frac{n \tan \alpha}{1+(1-n) \tan ^2 \alpha}}{1+\tan \alpha \frac{n \tan \alpha}{1+(1-n) \tan ^2 \alpha}} \text { [From Eq. (i)] }
\end{aligned}
\)
\(
=\frac{\tan \alpha+(1-n) \tan ^3 \alpha-n \tan \alpha}{1+(1-n) \tan ^2 \alpha+n \tan ^2 \alpha}=\quad \frac{(1-n) \tan \alpha+(1-n) \tan ^3 \alpha}{1+\tan ^2 \alpha}=(1-n) \tan \alpha
\)
Q15. Show that \(\frac{\sin x}{\cos 3 x}+\frac{\sin 3 x}{\cos 9 x}+\frac{\cos 9 x}{\cos 27 x}=\frac{1}{2}[\tan 27 x-\tan x]\).
Solution: L.H.S. contains \(x, 3 x, 9 x\) and \(27 x\), whereas R.H.S contains \(27 x\) and \(x\) only. So, we will manipulate terms as shown below
\(
\begin{aligned}
\text { R.H.S. } & =\frac{1}{2}[\tan 27 x-\tan x] \\
& =\frac{1}{2}[(\tan 27 x-\tan 9 x)+(\tan 9 x-\tan 3 x)+(\tan 3 x-\tan x)] \\
& =\frac{1}{2}\left[\left(\frac{\sin 27 x}{\cos 27 x}-\frac{\sin 9 x}{\cos 9 x}\right)+\left(\frac{\sin 9 x}{\cos 9 x}-\frac{\sin 3 x}{\cos 3 x}\right)+\left(\frac{\sin 3 x}{\cos 3 x}-\frac{\sin x}{\cos x}\right)\right] \\
& =\frac{1}{2}\left[\frac{\sin (27 x-9 x)}{\cos 27 x \cos 9 x}+\frac{\sin (9 x-3 x)}{\cos 9 x \cos 3 x}+\frac{\sin (3 x-x)}{\cos 3 x \cos x}\right] \\
& =\frac{1}{2}\left[\frac{\sin 18 x}{\cos 27 x \cos 9 x}+\frac{\sin 6 x}{\cos 9 x \cos 3 x}+\frac{\sin 2 x}{\cos 3 x \cos x}\right]
\end{aligned}
\)
\(
\begin{aligned}
& =\frac{1}{2}\left[\frac{2 \sin 9 x \cos 9 x}{\cos 27 x \cos 9 x}+\frac{2 \sin 3 x \cos 3 x}{\cos 9 x \cos 3 x}+\frac{2 \sin x \cos x}{\cos 3 x \cos x}\right] \\
& =\frac{\sin 9 x}{\cos 27 x}+\frac{\sin 3 x}{\cos 9 x}+\frac{\sin x}{\cos 3 x}=\frac{\sin x}{\cos 3 x}+\frac{\sin 3 x}{\cos 9 x}+\frac{\sin 9 x}{\cos 27 x}=\text { L.H.S. }
\end{aligned}
\)
Q16. Prove that \(\frac{2 \cos 2^n \theta+1}{2 \cos \theta+1}=(2 \cos \theta-1)(2 \cos 2 \theta-1)\left(2 \cos 2^2 \theta-1\right) \cdots\left(2 \cos 2^{n-1} \theta-1\right)\).
Solution:
We have to prove \(\frac{2 \cos 2^n \theta+1}{2 \cos \theta+1}=(2 \cos \theta-1)(2 \cos 2 \theta-1)\left(2 \cos 2^2 \theta-1\right) \ldots\left(2 \cos 2^{n-1} \theta-1\right)\)
or \(2 \cos 2^n \theta+1=[(2 \cos \theta+1)(2 \cos \theta-1)](2 \cos 2 \theta-1)\left(2 \cos 2^2 \theta-1\right) \ldots\left(2 \cos 2^{n-1} \theta-1\right)\)
Now \([(2 \cos \theta+1)(2 \cos \theta-1)](2 \cos 2 \theta-1)\left(2 \cos 2^2 \theta-1\right) \ldots\left(2 \cos 2^{n-1} \theta-1\right)\)
\(=\left(4 \cos ^2 \theta-1\right)(2 \cos 2 \theta-1)\left(2 \cos 2^2 \theta-1 \ldots\left(2 \cos 2^{n-1} \theta-1\right)\right.\)
\(
=(2 \cos 2 \theta+1)(2 \cos 2 \theta-1)\left(2 \cos 2^2 \theta-1\right) \ldots\left(2 \cos 2^{n-1} \theta-1\right) \quad\left[\text { using } \cos 2 \theta=2 \cos ^2 \theta-1\right]
\)
\(
\begin{aligned}
& =\left(4 \cos ^2 2 \theta-1\right)\left(2 \cos 2^2 \theta-1\right) \ldots\left(2 \cos 2^{n-1} \theta-1\right) \\
& =\left(2 \cos ^2 \theta+1\right)\left(2 \cos 2^2 \theta-1\right) \ldots\left(2 \cos 2^{n-1} \theta-1\right) \\
& =\left(4 \cos ^2 2^2 \theta-1\right)\left(2 \cos 2^3 \theta-1\right) \ldots\left(2 \cos 2^{n-1} \theta-1\right) \\
& \vdots \\
& =\left(2 \cos 2^{n-1} \theta+1\right)\left(2 \cos 2^{n-1} \theta-1\right) \\
& =4 \cos ^2 2^{n-1} \theta-1 \\
& =2 \cos 2^n \theta+1
\end{aligned}
\)
Q17. Prove that \(\frac{\tan 2^n \theta}{\tan \theta}=(1+\sec 2 \theta)\left(1+\sec 2^2 \theta\right)\left(1+\sec 2^3 \theta\right) \cdots\left(1+\sec 2^n \theta\right)\).
Solution:
We have to prove that \(\frac{\tan 2^n \theta}{\tan \theta}=(1+\sec 2 \theta)\left(1+\sec 2^2 \theta\right)\left(1+\sec 2^3 \theta\right) \ldots\left(1+\sec 2^n \theta\right)\)
or \(\tan 2^n \theta=\tan \theta(1+\sec 2 \theta)\left(1+\sec 2^2 \theta\right)\left(1+\sec 2^3 \theta\right) \ldots\left(1+\sec 2^n \theta\right)\)
Now \(\tan \theta(1+\sec 2 \theta)\left(1+\sec 2^2 \theta\right)\left(1+\sec 2^3 \theta\right) \ldots\left(1+\sec 2^n \theta\right)\)
\(
\begin{aligned}
& =\tan \theta\left(\frac{1+\cos 2 \theta}{\cos 2 \theta}\right)\left(1+\sec 2^2 \theta\right)\left(1+\sec 2^3 \theta\right) \ldots\left(1+\sec 2^n \theta\right) \\
& =\frac{\sin \theta}{\cos \theta}\left(\frac{2 \cos 2 \theta}{\cos 2 \theta}\right)\left(1+\sec 2^2 \theta\right)\left(1+\sec 2^3 \theta\right) \ldots\left(1+\sec 2^n \theta\right) \\
& =(\tan 2 \theta)\left(1+\sec 2^2 \theta\right)\left(1+\sec 2^3 \theta\right) \ldots\left(1+\sec 2^n \theta\right) \\
& =(\tan 2 \theta)\left(\frac{1+\cos 2^2 \theta}{\cos 2^2 \theta}\right)\left(1+\sec 2^3 \theta\right) \ldots\left(1+\sec 2^n \theta\right) \\
& =(\tan 2 \theta)\left(\frac{2 \cos 2}{\cos 2^2 \theta}\right)\left(1+\sec 2^3 \theta\right) \ldots\left(1+\sec 2^n \theta\right) \\
& =\left(\tan 2^2 \theta\right)\left(1+\sec 2^3 \theta\right) \ldots\left(1+\sec 2^n \theta\right) \\
& \vdots \\
& =\tan 2^{n-1} \theta\left(1+\sec 2^n \theta\right) \\
& =\tan 2^{n-1} \theta\left(\frac{1+\cos 2^n \theta}{\cos 2^n \theta}\right) \\
& =\tan 2^{n-1} \theta\left(\frac{2 \cos 2^{n-1} \theta}{\cos 2^n \theta}\right) \\
& =\tan 2^n \theta
\end{aligned}
\)