3.3 Trigonometric Functions

What are Trigonometric Ratios?

The values of all trigonometric functions based on the ratio of sides of a right-angled triangle are known as trigonometric ratios. The trigonometric ratios of a right-angled triangle’s sides for any acute angles are known as that angle’s trigonometric ratios. Six different trigonometric ratios are used: Sine (Sin), Cosine (Cos), Tangent (Tan), Secant (Sec), Cosecant (Cosec), and Cotangent(Cot) are the six basic trigonometric ratios. These six trigonometric ratios can be defined using Fig 3.9 as:

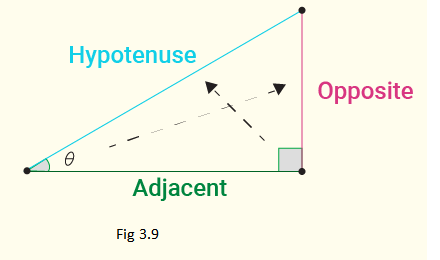
\(\begin{array}{|c|l|}
\hline \operatorname{Sin} \theta & \text { Opposite Side to } \theta / \text { Hypotenuse } \\
\hline \operatorname{Cos} \theta & \text { Adjacent Side to } \theta / \text { Hypotenuse } \\
\hline \operatorname{Tan} \theta & \text { Opposite Side/Adjacent Side \& } \operatorname{Sin} \theta / \operatorname{Cos} \theta \\
\hline \operatorname{Cot} \theta & \text { Adjacent Side/Opposite Side } \& 1 / \tan \theta \\
\hline \operatorname{Sec} \theta & \text { Hypotenuse/Adjacent Side \& } 1 / \cos \theta \\
\hline \operatorname{Cosec} \theta & \text { Hypotenuse/Opposite Side } \& 1 / \sin \theta \\
\hline
\end{array}\)

Trigonometric Functions

we have studied trigonometric ratios for acute angles as the ratio of sides of a right-angled triangle. We will now extend the definition of trigonometric ratios to any angle in terms of radian measure and study them as trigonometric functions.

Consider a unit circle with centre at origin of the coordinate axes. Let \(\mathrm{P}(a, b)\) be any point on the circle with angle \(\mathrm{AOP}=x\) radian, i.e., length of arc \(\mathrm{AP}=x(\mathrm{Fig} 3.10)\)

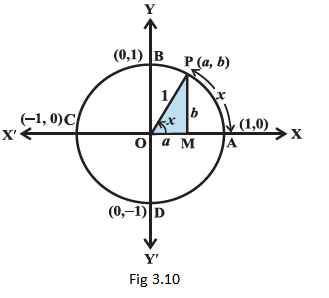
We define \(\cos x=a\) and \(\sin x=b\) Since \(\Delta \mathrm{OMP}\) is a right triangle, we have
\(\mathrm{OM}^{2}+\mathrm{MP}^{2}=\mathrm{OP}^{2} \text { or } a^{2}+b^{2}=1\) [Pythagoras’ Theorem]

Thus, for every point on the unit circle, we have
\(
a^{2}+b^{2}=1 \text { or } \cos ^{2} x+\sin ^{2} x=1
\)
Since one complete revolution subtends an angle of \(2 \pi\) radian at the centre of the circle, \(\angle \mathrm{AOB}=\frac{\pi}{2}\), \(\angle \mathrm{AOC}=\pi\) and \(\angle \mathrm{AOD}=\frac{3 \pi}{2}\). All angles which are integral multiples of \(\frac{\pi}{2}\) are called quadrantal angles. The coordinates of the points \(\mathrm{A}, \mathrm{B}, \mathrm{C}\) and \(\mathrm{D}\) are, respectively, \((1,0),(0,1),(-1,0)\) and \((0,-1)\). Therefore, for quadrantal angles, we have

\(\cos 0^{\circ}=1 \quad \sin 0^{\circ}=0\),
\(\cos \frac{\pi}{2}=0 \quad \sin \frac{\pi}{2}=1\)
\(\cos \pi=-1 \quad \sin \pi=0\)
\(\cos \frac{3 \pi}{2}=0 \quad \sin \frac{3 \pi}{2}=-1\)
\(\cos 2 \pi=1 \quad \sin 2 \pi=0\)
Now, if we take one complete revolution from the point \(P\), we again come back to same point \(\mathrm{P}\). Thus, we also observe that if \(x\) increases (or decreases) by any integral multiple of \(2 \pi\), the values of sine and cosine functions do not change. Thus,
\(
\sin (2 n \pi+x)=\sin x, n \in \mathbf{Z}, \cos (2 n \pi+x)=\cos x, n \in \mathbf{Z}
\)
Further, \(\sin x=0\), if \(x=0, \pm \pi, \pm 2 \pi, \pm 3 \pi, \ldots\), i.e., when \(x\) is an integral multiple of \(\pi\) and \(\cos x=0\), if \(x=\pm \frac{\pi}{2}, \pm \frac{3 \pi}{2}, \pm \frac{5 \pi}{2}, \ldots\) i.e., \(\cos x\) vanishes when \(x\) is an odd multiple of \(\frac{\pi}{2}\). Thus

\(\sin x=0\) implies \(x=n \pi\), where \(n\) is any integer

\(\cos x=0\) implies \(x=(2 n+1) \frac{\pi}{2}\), where \(n\) is any integer.

We now define other trigonometric functions in terms of sine and cosine functions:

\(\operatorname{cosec} x=\frac{1}{\sin x}, x \neq n \pi\), where \(n\) is any integer.

\(\sec x=\frac{1}{\cos x}, x \neq(2 n+1) \frac{\pi}{2}\), where \(n\) is any integer.

\(\tan x=\frac{\sin x}{\cos x}, x \neq(2 n+1) \frac{\pi}{2}\), where \(n\) is any integer.

\(\cot x=\frac{\cos x}{\sin x}, x \neq n \pi\), where \(n\) is any integer.

We have shown that for all real \(x, \sin ^{2} x+\cos ^{2} x=1\)
It follows that
\(
\begin{array}{ll}
1+\tan ^{2} x=\sec ^{2} x & \text { (why?) } \\
1+\cot ^{2} x=\operatorname{cosec}^{2} x & \text { (why?) }
\end{array}
\)
In earlier classes, we have discussed the values of trigonometric ratios for \(0^{\circ}\), \(30^{\circ}, 45^{\circ}, 60^{\circ}\) and \(90^{\circ}\). The values of trigonometric functions for these angles are same as that of trigonometric ratios studied in earlier classes. Thus, we have the following table:

Note: The values of \(\operatorname{cosec} x, \sec x\) and \(\cot x\) are the reciprocal of the values of \(\sin x\), \(\cos x\) and \(\tan x\), respectively.

Sign of trigonometric functions

Let \(\mathrm{P}(a, b)\) be a point on the unit circle with centre at the origin such that \(\angle \mathrm{AOP}=x\). If \(\angle \mathrm{AOQ}=-x\), then the coordinates of the point \(\mathrm{Q}\) will be \((a,-b)\) (Fig 3.11).

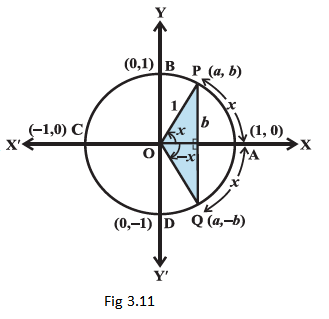
Therefore
\(
\cos (-x)=\cos x
\)
and \(\sin (-x)=-\sin x\)
Since for every point \(\mathrm{P}(a, b)\) on the unit circle, \(-1 \leq a \leq 1\) and
\(-1 \leq b \leq 1\), we have \(-1 \leq \cos x \leq 1\) and \(-1 \leq \sin x \leq 1\) for all \(x\). We have learnt in previous classes that in the first quadrant \(\left(0<x<\frac{\pi}{2}\right) a\) and \(b\) are both positive, in the second quadrant \(\left(\frac{\pi}{2}<x<\pi\right)\) \(a\) is negative and \(b\) is positive, in the third quadrant \(\left(\pi<x<\frac{3 \pi}{2}\right) a\) and \(b\) are both negative and in the fourth quadrant \(\left(\frac{3 \pi}{2}<x<2 \pi\right) a\) is positive and \(b\) is negative. Therefore, \(\sin x\) is positive for \(0<x<\pi\), and negative for \(\pi<x<2 \pi\). Similarly, \(\cos x\) is positive for \(0<x<\frac{\pi}{2}\), negative for \(\frac{\pi}{2}<x<\frac{3 \pi}{2}\) and also positive for \(\frac{3 \pi}{2}<x<2 \pi\). Likewise, we can find the signs of other trigonometric functions in different quadrants. In fact, we have the following table.

Domain and range of trigonometric functions From the definition of sine and cosine functions, we observe that they are defined for all real numbers. Further, we observe that for each real number \(x\),
\(
-1 \leq \sin x \leq 1 \text { and }-1 \leq \cos x \leq 1
\)
Thus, domain of \(y=\sin x\) and \(y=\cos x\) is the set of all real numbers and range is the interval \([-1,1]\), i.e., \(-1 \leq y \leq 1\).
Since \(\operatorname{cosec} x=\frac{1}{\sin x}\), the domain of \(y=\operatorname{cosec} x\) is the set \(\{x: x \in \mathbf{R}\) and \(x \neq n \pi, n \in \mathbf{Z}\}\) and range is the set \(\{y: y \in \mathbf{R}, y \geq 1\) or \(y \leq-1\}\). Similarly, the domain of \(y=\sec x\) is the set \(\left\{x: x \in \mathbf{R}\right.\) and \(\left.x \neq(2 n+1) \frac{\pi}{2}, n \in \mathbf{Z}\right\}\) and range is the set \(\{y: y \in \mathbf{R}, y \leq-1\) or \(y \geq 1\}\). The domain of \(y=\tan x\) is the set \(\{x: x \in \mathbf{R}\) and \(\left.x \neq(2 n+1) \frac{\pi}{2}, n \in \mathbf{Z}\right\}\) and range is the set of all real numbers. The domain of \(y=\cot x\) is the set \(\{x: x \in \mathbf{R}\) and \(x \neq n \pi, n \in \mathbf{Z}\}\) and the range is the set of all real numbers.

We further observe that in the first quadrant, as \(x\) increases from 0 to \(\frac{\pi}{2}, \sin x\) increases from 0 to 1 , as \(x\) increases from \(\frac{\pi}{2}\) to \(\pi\), \(\sin x\) decreases from 1 to 0 . In the third quadrant, as \(x\) increases from \(\pi\) to \(\frac{3 \pi}{2}\), \(\sin x\) decreases from 0 to \(-1\) and finally, in the fourth quadrant, \(\sin x\) increases from \(-1\) to 0 as \(x\) increases from \(\frac{3 \pi}{2}\) to \(2 \pi\). Similarly, we can discuss the behaviour of other trigonometric functions. In fact, we have the following table:

In the above table, the statement \(\tan x\) increases from 0 to \(\infty\) (infinity) for \(0<x<\frac{\pi}{2}\) simply means that \(\tan x\) increases as \(x\) increases for \(0<x<\frac{\pi}{2}\) and assumes arbitraily large positive values as \(x\) approaches to \(\frac{\pi}{2}\). Similarly, to say that \(\operatorname{cosec} x\) decreases from \(-1\) to \(-\infty\) (minus infinity) in the fourth quadrant means that \(\operatorname{cosec} x\) decreases for \(x \in\left(\frac{3 \pi}{2}, 2 \pi\right)\) and assumes arbitrarily large negative values as \(x\) approaches to \(2 \pi\). The symbols \(\infty\) and \(-\infty\) simply specify certain types of behaviour of functions and variables.

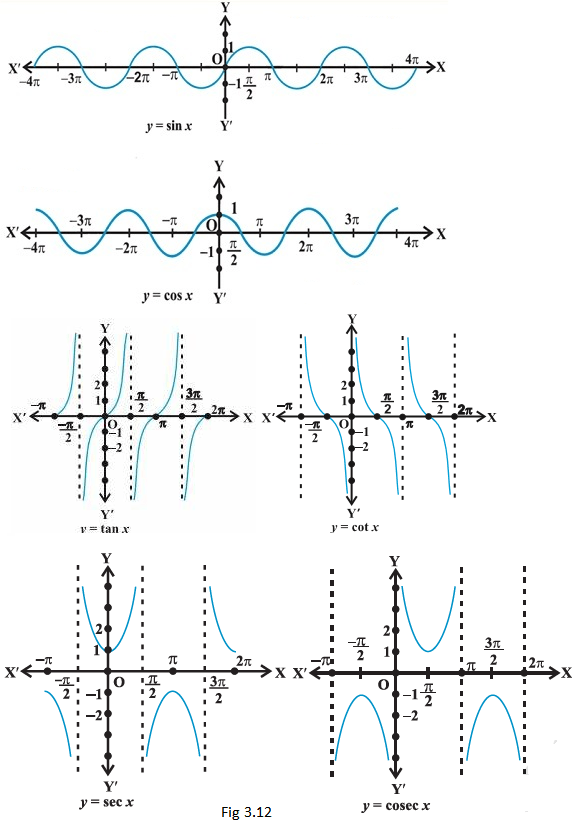
We have already seen that values of \(\sin x\) and \(\cos x\) repeats after an interval of \(2 \pi\). Hence, values of \(\operatorname{cosec} x\) and \(\sec x\) will also repeat after an interval of \(2 \pi\). We shall see in the next section that \(\tan (\pi+x)=\tan x\). Hence, values of \(\tan x\) will repeat after an interval of \(\pi\). Since \(\cot x\) is reciprocal of \(\tan x\), its values will also repeat after an interval of \(\pi\). Using this knowledge and behaviour of trigonometic functions, we can sketch the graph of these functions. The graph of these functions are given below.

Example 6: If \(\cos x=-\frac{3}{5}, x\) lies in the third quadrant, find the values of other five trigonometric functions.

Solution: Since \(\cos x=-\frac{3}{5}\), we have \(\sec x=-\frac{5}{3}\)
Now \(\quad \sin ^{2} x+\cos ^{2} x=1\), i.e., \(\sin ^{2} x=1-\cos ^{2} x\)
or
\(
\sin ^{2} x=1-\frac{9}{25}=\frac{16}{25}
\)
Hence \(\quad \sin x=\pm \frac{4}{5}\)
Since \(x\) lies in third quadrant, \(\sin x\) is negative. Therefore
\(\sin x=-\frac{4}{5}\)
which also gives
\(
\operatorname{cosec} x=-\frac{5}{4}
\)
Further, we have
\(\tan x=\frac{\sin x}{\cos x}=\frac{4}{3} \text { and } \cot x=\frac{\cos x}{\sin x}=\frac{3}{4} .\)

Example 7: If \(\cot x=-\frac{5}{12}, x\) lies in second quadrant, find the values of other five trigonometric functions.

Solution: Since \(\cot x=-\frac{5}{12}\), we have \(\tan x=-\frac{12}{5}\)
Now \(\quad \sec ^{2} x=1+\tan ^{2} x=1+\frac{144}{25}=\frac{169}{25}\)
Hence \(\quad \sec x=\pm \frac{13}{5}\)
Since \(x\) lies in second quadrant, \(\sec x\) will be negative. Therefore
\(\sec x=-\frac{13}{5}\)
which also gives
\(\cos x=-\frac{5}{13}\)
Further, we have
\(\sin x=\tan x \cos x=\left(-\frac{12}{5}\right) \times\left(-\frac{5}{13}\right)=\frac{12}{13}\)
and
\(\operatorname{cosec} x=\frac{1}{\sin x}=\frac{13}{12} .\)

Example 8: Find the value of \(\sin \frac{31 \pi}{3}\).

Solution: We know that values of \(\sin x\) repeats after an interval of \(2 \pi\). Therefore \(\sin \frac{31 \pi}{3}=\sin \left(10 \pi+\frac{\pi}{3}\right)=\sin \frac{\pi}{3}=\frac{\sqrt{3}}{2} \text {. }\)

Example 9: Find the value of \(\cos \left(-1710^{\circ}\right)\).

Solution: We know that values of \(\cos x\) repeats after an interval of \(2 \pi\) or \(360^{\circ}\). Therefore, \(\quad \cos \left(-1710^{\circ}\right)=\cos \left(-1710^{\circ}+5 \times 360^{\circ}\right)\)
\(=\cos \left(-1710^{\circ}+1800^{\circ}\right)=\cos 90^{\circ}=0\)