3.2 Angles

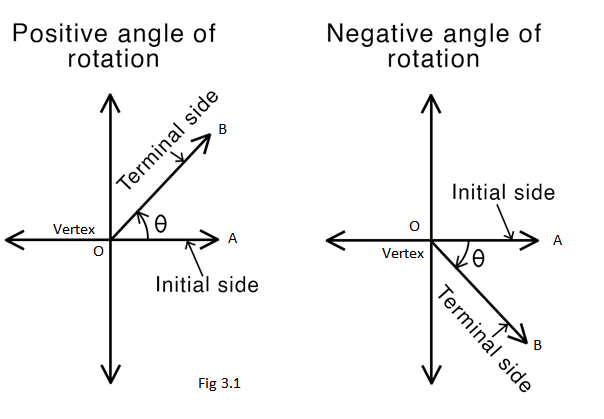
An angle is formed when two straight lines or rays meet at a common endpoint. Angle is a measure of rotation of a given ray about its initial point. The original ray is called the initial side and the final position of the ray after rotation is called the terminal side of the angle. The common point of contact is called the vertex of an angle. If the direction of rotation is anticlockwise, the angle is said to be positive and if the direction of rotation is clockwise, then the angle is negative (Fig 3.1). The Greek letter \(\theta\) (theta) is used in math as a variable to represent a measured angle.

The two most commonly used units of measurement of an angle are degree and radian. 

Degree measure

If a rotation from the initial side to terminal side is \(\left(\frac{1}{360}\right)^{\text {th }}\) of a revolution, the angle is said to have a measure of one degree, written as \(1^{\circ}\). A degree is divided into 60 minutes, and a minute is divided into 60 seconds. One-sixtieth of a degree is called a minute, written as \(1^{\prime}\), and one-sixtieth of a minute is called a second, written as \(1^{\prime \prime}\). Thus,
\(1^{\circ}=60^{\prime}, \quad 1^{\prime}=60^{\prime \prime}\)
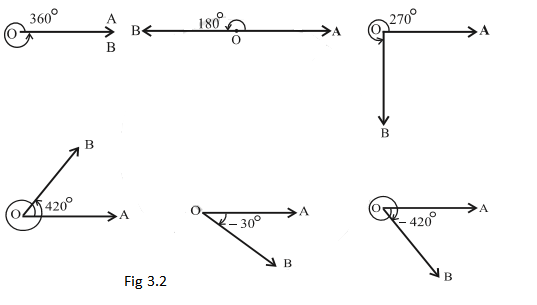
Some of the angles whose measures are \(360^{\circ}, 180^{\circ}, 270^{\circ}, 420^{\circ},-30^{\circ},-420^{\circ}\) are shown in Fig 3.2.

Radian Measure

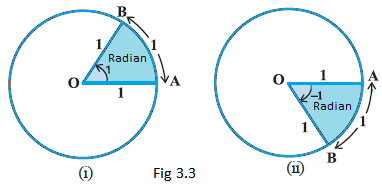
Radian is the angle made when we take the radius and wrap it round the circle. The angle subtended at the centre by an arc of length 1 unit in a unit circle (circle of radius 1 unit) is said to have a measure of 1 radian. In the Fig 3.3(i) and (ii), \(\mathrm{OA}\) is the initial side and \(\mathrm{OB}\) is the terminal side. The figures show the angles whose measures are 1 radian, \(-1\) radian.

We know that the circumference of a circle of radius 1 unit is \(2 \pi\). Thus, one complete revolution of the initial side subtends an angle of \(2 \pi\) radian.

Since in a circle of radius \(r\), an arc of length \(r\) subtends an angle whose measure is 1 radian, an \(\operatorname{arc}\) of length \(l\) will subtend an angle whose measure is \(\frac{l}{r}\) radian. Thus, if in a circle of radius \(r\), an arc of length \(l\) subtends an angle \(\theta\) radian at the centre, we have
\(\theta=\frac{l}{r} \text { or } l=r \theta \text {. }\)

The picture shown in Fig 3.4 illustrates the relationship between the radius, and the central angle in radians. The formula is \(l=r \theta\) where s represents the arc length, \(l=r \theta\) represents the central angle in radians and \(r\) is the length of the radius.

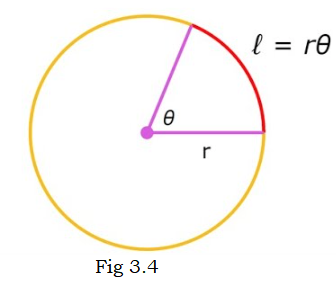
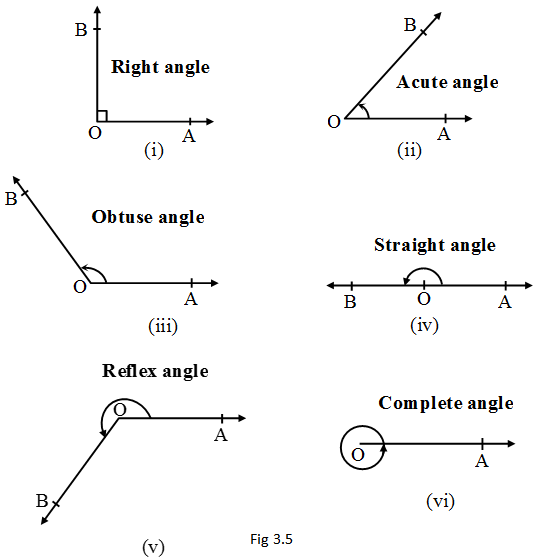
Angle Types

The figure below (Fig 3.5) illustrates these various angle types.

1. Right Angle – Exactly \(90^{\circ}\).
2. Acute Angle ranges from \(0^{\circ}\) to \(90^{\circ}\), and both are exclusive.
3. Obtuse Angle ranges from \(90^{\circ}\) to \(180^{\circ}\), and both are exclusive.
4. Straight Angle – Exactly \(180^{\circ}\).
5. Reflex Angle \(-180^{\circ}\) to \(360^{\circ}\), & both are exclusive.
6. Full Rotation (complete Angle)- Exactly \(360^{\circ}\)

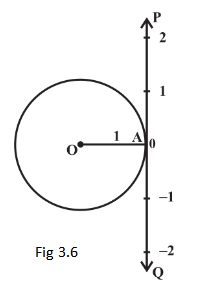
Relation between radian and real numbers

To establish the relationship between radian and real numbers, use the following steps:

• Consider the unit circle with centre \(O .\)
• Locate a point, say A on the circle.
• Consider the line segment OA as the initial side of an angle.
• From the initial side OA, the length of an arc of the circle will give the radian measure of the angle, which the arc will subtend at the centre of the circle.
• Draw the line PAQ, which is tangent to the circle with the point of contact A.
• Consider this line as a number line with real numbers such that the point A represents the real number zero (0), AP represents the positive real numbers, and AQ represents negative real numbers, as shown in Fig 3.6.

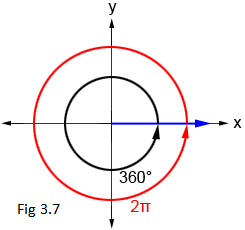
Relation between degree and radian

We can derive the relationship between degrees and radians based on one full rotation around a circle. One full rotation around a circle is equal to \(360^{\circ}\). The measure of a radian is equal to the length of the arc that subtends it divided by the radius, or
\(\theta=\frac{s}{r}\)
where \(\theta\) is the angle in radians, \(l\) is the arc length, and \(r\) is the radius of the circle. The circumference, c, of a circle is measured as
\(c=2 \pi r\)
where \(r\) is the radius. The length of the arc that subtends the central angle of a circle in the case of a full rotation is equal to the circumference of the circle. Thus, \(l=c=2 \pi r\). Substituting this into the equation for radian measure,
\(\theta=\frac{s}{r}=\frac{2 \pi r}{r}=2 \pi=360^{\circ}\)
In Fig 3.7, the blue ray indicates the terminal side of the angle whose initial side is the positive \(x\)-axis. The circular black arrow indicates the measure of a full rotation in degrees, and the angle measure in radians is shown in red.

Based on this, the relationship between radians and degrees is:
\(2 \pi\) radians \(=360^{\circ}\) \(\Rightarrow\) \(\pi\) radians \(=180^{\circ}\)
Therefore: 1 radian \(=\frac{180^{\circ}}{\pi}=57^{\circ} 16^{\prime}\) approximately.
Also \(1^{\circ}=\frac{\pi}{180}\) radian \(=0.01746\) radian approximately

Radian measure \(=\frac{\pi}{180} \times\) Degree measure

Degree measure \(=\frac{180}{\pi} \times\) Radian measure

The relation between degree measures and radian measure of some common angles are given in the following table:

Example 1: Convert \(40^{\circ} 20^{\prime}\) into radian measure.

Solution: We know that \(180^{\circ}=\pi\) radian.
Hence \(\quad 40^{\circ} 20^{\prime}=40 \frac{1}{3}\) degree \(=\frac{\pi}{180} \times \frac{121}{3}\) radian \(=\frac{121 \pi}{540}\) radian.

Example 2: Convert 6 radians into degree measure.

Solution: We know that \(\pi\) radian \(=180^{\circ}\).
\(
\begin{aligned}
\text { Hence } 6 \text { radians } &=\frac{180}{\pi} \times 6 \text { degree }=\frac{1080 \times 7}{22} \text { degree } \\
&=343 \frac{7}{11} \text { degree }=343^{\circ}+\frac{7 \times 60}{11} \text { minute }\left[\text { as } 1^{\circ}=60^{\prime}\right] \\
&=343^{\circ}+38^{\prime}+\frac{2}{11} \text { minute } \quad\left[\text { as } 1^{\prime}=60^{\prime \prime}\right] \\
&=343^{\circ}+38^{\prime}+10.9^{\prime \prime} \quad=343^{\circ} 38^{\prime} 11^{\prime \prime} \text { approximately. } \\
\text { Hence } \quad 6 \text { radians }=343^{\circ} 38^{\prime} 11^{\prime \prime} \text { approximately. }
\end{aligned}
\)

Example 3: Find the radius of the circle in which a central angle of \(60^{\circ}\) intercepts an arc of length \(37.4 \mathrm{~cm}\) (use \(\pi=\frac{22}{7}\) ).

Solution: Here \(l=37.4 \mathrm{~cm}\) and \(\theta=60^{\circ}=\frac{60 \pi}{180}\) radian \(=\frac{\pi}{3}\)
Hence, by \(r=\frac{l}{\theta}\), we have
\(r=\frac{37.4 \times 3}{\pi}=\frac{37.4 \times 3 \times 7}{22}=35.7 \mathrm{~cm}\)

Example 4: The minute hand of a watch is \(1.5 \mathrm{~cm}\) long. How far does its tip move in 40 minutes? (Use \(\pi=3.14\) ).

Solution: In 60 minutes, the minute hand of a watch completes one revolution. Therefore, in 40 minutes, the minute hand turns through \(\frac{2}{3}\) of a revolution. Therefore, \(\theta=\frac{2}{3} \times 360^{\circ}\) or \(\frac{4 \pi}{3}\) radian. Hence, the required distance travelled is given by
\(
l=r \theta=1.5 \times \frac{4 \pi}{3} \mathrm{~cm}=2 \pi \mathrm{cm}=2 \times 3.14 \mathrm{~cm}=6.28 \mathrm{~cm}
\)

Example 5: If the arcs of the same lengths in two circles subtend angles \(65^{\circ}\) and \(110^{\circ}\) at the centre, find the ratio of their radii.

Solution: Let \(r_{1}\) and \(r_{2}\) be the radii of the two circles. Given that
\(
\theta_{1}=65^{\circ}=\frac{\pi}{180} \times 65=\frac{13 \pi}{36} \text { radian }
\)
and \(\theta_{2}=110^{\circ}=\frac{\pi}{180} \times 110=\frac{22 \pi}{36}\) radian
Let \(l\) be the length of each of the arc. Then \(l=r_{1} \theta_{1}=r_{2} \theta_{2}\), which gives
\(
\frac{13 \pi}{36} \times r_{1}=\frac{22 \pi}{36} \times r_{2} \text {, i.e., } \frac{r_{1}}{r_{2}}=\frac{22}{13}
\)
Hence \(\quad r_{1}: r_{2}=22: 13\).

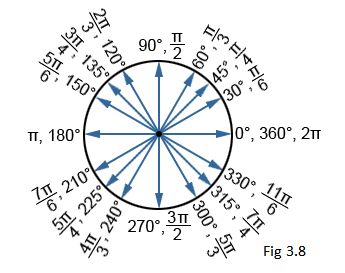
Commonly used angles in trigonometry

While the conversions above can be used to convert between any radian or degree measure, there are a number of angles in trigonometry that are so frequently used that it is worth memorizing their measures. These angles are shown in the circle below (Fig 3.8).