2.3 Relations
Relation is a connection between or among things. Every relation involves a minimum of two objects. Every relation has a pattern or property (like relation between mom and child, husband and wife, etc.).
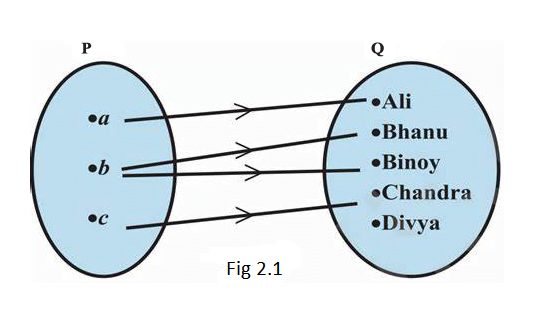
Consider the two sets \(\mathrm{P}=\{a, b, c\}\) and \(\mathrm{Q}=\{\mathrm{Ali}\), Bhanu, Binoy, Chandra, Divya \(\}\). The cartesian product of \(P\) and \(Q\) has 15 ordered pairs which can be listed as \(\mathrm{P} \times \mathrm{Q}=\{(a\), Ali \()\), \((a\), Bhanu \(),(a\), Binoy) \(, \ldots,(c\), Divya) \(\}\). \(\mathrm{P} \times \mathrm{Q}\) by introducing a relation \(\mathrm{R}\) between the first element \(x\) and the second element \(y\) of each ordered pair \((x, y)\) as
\(\mathrm{R}=\{(x, y): x\) is the first letter of the name \(y, x \in \mathrm{P}, y \in \mathrm{Q}\}\). Then \(\mathrm{R}=\{(a, \mathrm{Ali}),(b, \mathrm{Bhanu}),(b\), Binoy \(),(c\), Chandra) \(\}\)
A visual representation of this relation \(\mathrm{R}\) (called an arrow diagram) is shown in Fig 2.1.
- A relation \(R\) from a non-empty set \(A\) to a non-empty set \(B\) is a subset of the cartesian product \(\mathrm{A} \times \mathrm{B}\). The subset is derived by describing a relationship between the first element and the second element of the ordered pairs in \(\mathrm{A} \times \mathrm{B}\). The second element is called the image of the first element.
- The set of all first elements of the ordered pairs in a relation \(\mathrm{R}\) from a set A to a set \(\mathrm{B}\) is called the domain of the relation (Domain: set of all permissible inputs) \(\mathrm{R}\).
- The set of all second elements in a relation \(R\) from a set \(A\) to a set \(B\) is called the range of the relation (Range: set of all permissible outputs) \(\mathrm{R}\). The whole set \(\mathrm{B}\) is called the codomain of the relation R. Note that range \(\subset\) codomain (Codomain: set of all possible outputs).
Notes:
(i) A relation may be represented algebraically either by the Roster method or by the Set-builder method.
(ii) An arrow diagram is a visual representation of a relation.
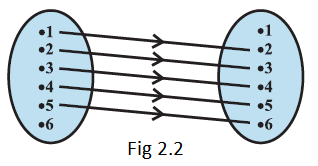
Example 7: Let \(\mathrm{A}=\{1,2,3,4,5,6\}\). Define a relation \(\mathrm{R}\) from \(\mathrm{A}\) to \(\mathrm{A}\) by \(\mathrm{R}=\{(x, y): y=x+1\}\)
(i) Depict this relation using an arrow diagram.
(ii) Write down the domain, codomain, and range of \(R\).
Solution:
(i) By the definition of the relation,
\(R=\{(1,2),(2,3),(3,4),(4,5),(5,6)\} \text {. }\)
The corresponding arrow diagram is shown in Fig 2.2.
(ii) We can see that the domain \(=\{1,2,3,4,5\), \(\}\)
Similarly, the range \(=\{2,3,4,5,6\}\) and the codomain \(=\{1,2,3,4,5,6\}\).
Example 8: Fig 2.3 shows a relation between the sets \(\mathrm{P}\) and \(\mathrm{Q}\). Write this relation (i) in set-builder form, (ii) in roster form. What is its domain and range?
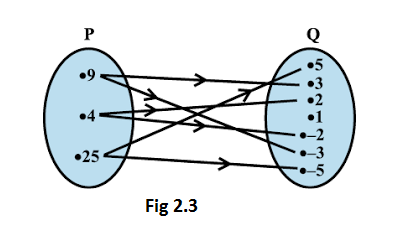
Solution: It is obvious that the relation \(R\) is ” \(x\) is the square of \(y\) “.
(i) In set-builder form, \(\mathrm{R}=\{(x, y): x\) is the square of \(y, x \in \mathrm{P}, y \in \mathbf{Q}\}\)
(ii) In roster form, \(R=\{(9,3)\),
\(
(9,-3),(4,2),(4,-2),(25,5),(25,-5)\}
\)
The domain of this relation is \(\{4,9,25\}\).
The range of this relation is \(\{-2,2,-3,3,-5,5\}\).
Note that the element 1 is not related to any element in set \(P\). The set \(\mathrm{Q}\) is the codomain of this relation.
Note: The total number of relations that can be defined from a set \(\mathrm{A}\) to a set \(\mathrm{B}\) is the number of possible subsets of \(\mathrm{A} \times \mathrm{B}\). If \(n(\mathrm{~A})=p\) and \(n(\mathrm{~B})=q\), then \(n(\mathrm{~A} \times \mathrm{B})=p q\) and the total number of relations is \(2^{p q}\).
Example 9: Let \(\mathrm{A}=\{1,2\}\) and \(\mathrm{B}=\{3,4\}\). Find the number of relations from \(\mathrm{A}\) to \(\mathrm{B}\).
Solution: We have,
\(
\mathrm{A} \times \mathrm{B}=\{(1,3),(1,4),(2,3),(2,4)\}
\)
Since \(n(\mathrm{~A} \times \mathrm{B})=4\), the number of subsets of \(\mathrm{A} \times \mathrm{B}\) is \(2^{4}\). Therefore, the number of relations from A into B will be \(2^{4}\).
Example 10:Let \(A=\{1,2,3, \ldots, 14\}\). Define a relation \(R\) from \(A\) to \(A\) by \(R=\{(x, y):(3 x-y=0\), where \(x, y \in A\}\). Write down its domain, codomain, and range.
Solution:
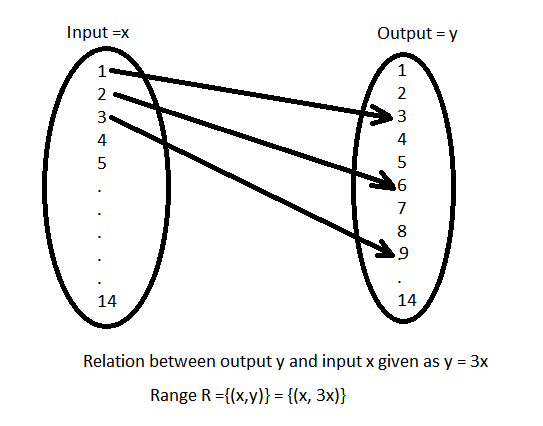
From the problem description we can write Range, \(R=\{(1,3),(2,6),(3,9),(4,12)\}\)
Domain (set of permissible inputs) \(\rightarrow \quad\{1,2,3,4\}\)
Range (set of permissible outputs) \(\rightarrow\{3,6,9,12\}\)
Codomain (set of total possible outputs) \(\rightarrow\{1,2,3, \ldots .14\}\)
How to calculate the number of relations?
It is the number of possible subsets of \(A \times B\). Let’s assume set A has 2 elements and set B has one element.
\(\begin{aligned}
&A=\{1, 2\}, \quad B=\{3\} \\
&n(A)=2, n(B)=1; \quad n(A \times B)=2 \times 1=2 \\
&\text { No. of subsets }=2^{2}
\end{aligned}\)
In general, we can write Number of relations = Number of possible subsets.
\(\begin{aligned}
&n(A)=p, n(B)=q; \quad n(A \times B)=pq \\
&\text { No. of subsets }=2^{pq}
\end{aligned}\)