16.4 Axiomatic Approach to Probability

Axiomatic approach is another way of describing probability of an event. In this approach some axioms or rules are depicted to assign probabilities.

Let S be the sample space of a random experiment. The probability \(P\) is a real valued function whose domain is the power set of \(S\) and range is the interval \([0,1]\) satisfying the following axioms
(i) For any event \(E, P(E) \geq 0\)
(ii) \(P ( S )=1\)
(iii) If \(E\) and \(F\) are mutually exclusive events, then \(P ( E \cup F )= P ( E )+ P ( F )\).

It follows from (iii) that \(P (\phi)=0\). To prove this, we take \(F =\phi\) and note that \(E\) and \(\phi\) are disjoint events. Therefore, from axiom (iii), we get
\(
P ( E \cup \phi)= P ( E )+ P (\phi) \text { or } \quad P ( E )= P ( E )+ P (\phi) \text { i.e. } P (\phi)=0 .
\)

Let \(S\) be a sample space containing outcomes \(\omega_1, \omega_2, \ldots, \omega_n\), i.e.,
\(
S =\left\{\omega_1, \omega_2, \ldots, \omega_n\right\}
\)

It follows from the axiomatic definition of probability that
(i) \(0 \leq P \left(\omega_i\right) \leq 1\) for each \(\omega_i \in S\)
(ii) \(P \left(\omega_1\right)+ P \left(\omega_2\right)+\ldots+ P \left(\omega_n\right)=1\)
(iii) For any event \(A , P ( A )=\sum^n P \left(\omega_i\right), \omega_i \in A\).

Note: It may be noted that the singleton \(\left\{\omega_i\right\}\) is called elementary event and for notational convenience, we write \(P \left(\omega_i\right)\) for \(P \left(\left\{\omega_i\right\}\right)\).

For example, in ‘a coin tossing’ experiment we can assign the number \(\frac{1}{2}\) to each of the outcomes \(H\) and \(T\) . i.e.
\(
P ( H )=\frac{1}{2} \text { and } P ( T )=\frac{1}{2} \dots(1)
\)
Clearly this assignment satisfies both the conditions i.e., each number is neither less than zero nor greater than 1 and
\(
P ( H )+ P ( T )=\frac{1}{2}+\frac{1}{2}=1
\)
Therefore, in this case we can say that probability of \(H =\frac{1}{2}\), and probability of \(T =\frac{1}{2}\)
If we take \(P ( H )=\frac{1}{4}\) and \(P ( T )=\frac{3}{4} \dots(2)\)
Does this assignment satisfy the conditions of axiomatic approach?
Yes, in this case, probability of \(H =\frac{1}{4}\) and probability of \(T =\frac{3}{4}\).
We find that both the assignments (1) and (2) are valid for probability of \(H\) and \(T\).

In fact, we can assign the numbers \(p\) and \((1-p)\) to both the outcomes such that \(0 \leq p \leq 1\) and \(P ( H )+ P ( T )=p+(1-p)=1\)

This assignment, too, satisfies both conditions of the axiomatic approach of probability. Hence, we can say that there are many ways (rather infinite) to assign probabilities to outcomes of an experiment.

Example 4: Let a sample space be \(S=\left\{\omega_1, \omega_2, \ldots, \omega_6\right\}\). Which of the following assignments of probabilities to each outcome are valid?
\(
\begin{array}{cccccc}
\text { Outcomes } \quad \omega_1 & \omega_2 & \omega_3 & \omega_4 & \omega_5 & \omega_6 \\
\text { (a) } \quad \quad \quad \quad \frac{1}{6} & \frac{1}{6} & \frac{1}{6} & \frac{1}{6} & \frac{1}{6} & \frac{1}{6} \\
\text { (b) } \quad \quad \quad \quad 1 & 0 & 0 & 0 & 0 & 0 \\
\text { (c) } \quad \quad \quad \quad \frac{1}{8} & \frac{2}{3} & \frac{1}{3} & \frac{1}{3} & -\frac{1}{4} & -\frac{1}{3} \\
\text { (d) } \quad \quad \quad \quad \frac{1}{12} & \frac{1}{12} & \frac{1}{6} & \frac{1}{6} & \frac{1}{6} & \frac{3}{2} \\
\text { (e) } \quad \quad \quad \quad 0.1 & 0.2 & 0.3 & 0.4 & 0.5 & 0.6
\end{array}
\)

Solution: (a) Condition (i): Each of the number \(p \left(\omega_i\right)\) is positive and less than one.
Condition (ii): Sum of probabilities
\(
=\frac{1}{6}+\frac{1}{6}+\frac{1}{6}+\frac{1}{6}+\frac{1}{6}+\frac{1}{6}=1
\)
Therefore, the assignment is valid
(b) Condition (i): Each of the number \(p\left(\omega_i\right)\) is either 0 or 1 .
Condition (ii) Sum of the probabilities \(=1+0+0+0+0+0=1\)
Therefore, the assignment is valid
(c) Condition (i) Two of the probabilities \(p\left(\omega_5\right)\) and \(p\left(\omega_6\right)\) are negative, the assignment is not valid
(d) Since \(p\left(\omega_6\right)=\frac{3}{2}>1\), the assignment is not valid
(e) Since, sum of probabilities \(=0.1+0.2+0.3+0.4+0.5+0.6=2.1\), the assignment is not valid.

Probability of an event

Let \(S\) be a sample space associated with the experiment ‘examining three consecutive pens produced by a machine and classified as Good (non-defective) and bad (defective)’. We may get \(0,1,2\) or 3 defective pens as result of this examination.
A sample space associated with this experiment is
\(
S =\{ BBB , BBG , BGB , GBB , BGG , GBG , GGB , GGG \},
\)
where B stands for a defective or bad pen and G for a non – defective or good pen.
Let the probabilities assigned to the outcomes be as follows
\(
\begin{array}{lcccccccc}
\text { Sample point: } & \text { BBB } & \text { BBG } & \text { BGB } & \text { GBB } & \text { BGG } & \text { GBG } & \text { GGB } & \text { GGG } \\
\text { Probability: } & \frac{1}{8} & \frac{1}{8} & \frac{1}{8} & \frac{1}{8} & \frac{1}{8} & \frac{1}{8} & \frac{1}{8} & \frac{1}{8}
\end{array}
\)

Let event A: there is exactly one defective pen and event B: there are atleast two defective pens.
Hence \(\quad A =\{ BGG , GBG , GGB \}[latex] and [latex]B =\{ BBG , BGB , GBB , BBB \}\)
Now
\(
\begin{aligned}
P ( A ) & =\sum P \left(\omega_i\right), \forall \omega_i \in A \\
& = P ( BGG )+ P ( GBG )+ P ( GGB )=\frac{1}{8}+\frac{1}{8}+\frac{1}{8}=\frac{3}{8}
\end{aligned}
\)
and
\(
\begin{aligned}
P ( B ) & =\sum P \left(\omega_i\right), \forall \omega_i \in B \\
& = P ( BBG )+ P ( BGB )+ P ( GBB )+ P ( BBB )=\frac{1}{8}+\frac{1}{8}+\frac{1}{8}+\frac{1}{8}=\frac{4}{8}=\frac{1}{2}
\end{aligned}
\)

Let us consider another experiment of “tossing a coin “twice”
The sample space of this experiment is \(S =\{ HH , HT , TH , TT \}\)
Let the following probabilities be assigned to the outcomes
\(
P ( HH )=\frac{1}{4}, P ( HT )=\frac{1}{7}, P ( TH )=\frac{2}{7}, P ( TT )=\frac{9}{28}
\)

Clearly this assignment satisfies the conditions of axiomatic approach. Now, let us find the probability of the event \(E\) : ‘Both the tosses yield the same result’.
Here \(\quad E =\{ HH , TT \}\)
Now \(\quad P ( E )=\Sigma P \left(w_i\right)\), for all \(w_i \in E\)
\(
= P ( HH )+ P ( TT )=\frac{1}{4}+\frac{9}{28}=\frac{4}{7}
\)

For the event \(F\): ‘exactly two heads’, we have \(F =\{ HH \}\)
and \(P ( F )= P ( HH )=\frac{1}{4}\)

Probabilities of equally likely outcomes

Let a sample space of an experiment be
\(
S=\left\{\omega_1, \omega_2, \ldots, \omega_n\right\}
\)
Let all the outcomes are equally likely to occur, i.e., the chance of occurrence of each simple event must be same.
i.e. \(P \left(\omega_i\right)=p\), for all \(\omega_i \in S\) where \(0 \leq p \leq 1\)

Since \(\sum_{i=1}^n P \left(\omega_i\right)=1\) i.e., \(p+p+\ldots+p(n\) times \()=1\)
\(\text { or } \quad n p=1\) i.e., \(p=\frac{1}{n}\)
Let \(S\) be a sample space and E be an event, such that \(n(S)=n\) and \(n( E )=m\). If each out come is equally likely, then it follows that
\(
P ( E )=\frac{m}{n}=\frac{\text { Number of outcomes favourable to } E }{\text { Total possible oultcomes }}
\)

Probability of the event ‘ \(A\) or \(B\) ‘

Let us now find the probability of event \(‘ A\) or \(B\)‘, i.e., \(P ( A \cup B )\)
Let \(A =\{ HHT , HTH , THH \}\) and \(B =\{ HTH , THH , HHH \}\) be two events associated with ‘tossing of a coin thrice’
Clearly \(\quad A \cup B =\{ HHT , HTH , THH , HHH \}\)
Now \(\quad P ( A \cup B )= P ( HHT )+ P ( HTH )+ P ( THH )+ P ( HHH )\)
If all the outcomes are equally likely, then
\(
P ( A \cup B )=\frac{1}{8}+\frac{1}{8}+\frac{1}{8}+\frac{1}{8}=\frac{4}{8}=\frac{1}{2}
\)
Also \(P ( A )= P ( HHT )+ P ( HTH )+ P ( THH )=\frac{3}{8}\)
and \(P ( B )= P ( HTH )+ P ( THH )+ P ( HHH )=\frac{3}{8}\)
Therefore
\(
P ( A )+ P ( B )=\frac{3}{8}+\frac{3}{8}=\frac{6}{8}
\)
It is clear that \(\quad P ( A \cup B ) \neq P ( A )+ P ( B )\)
The points \(\text { HTH and THH }\) are common to both \(A\) and \(B\). In the computation of \(P ( A )+ P ( B )\) the probabilities of points \(\text { HTH and THH }\) , i.e., the elements of \(A \cap B\) are included twice. Thus to get the probability \(P ( A \cup B )\) we have to subtract the probabilities of the sample points in \(A \cap B\) from \(P ( A )+ P ( B )\)
\(
P ( A \cup B )= P ( A )+ P ( B )- P ( A \cap B )
\)

Example 5: Prove that, \(P ( A \cup B )= P ( A )+ P ( B )- P ( A \cap B )\)

Solution: \(A \cup B = A \cup( B – A )\), where A and \(B – A\) are mutually exclusive, and \(B =( A \cap B ) \cup( B – A )\), where \(A \cap B\) and \(B – A\) are mutually exclusive. Using Axiom (iii) of probability, we get
\(
\begin{array}{ll}
& P ( A \cup B )= P ( A )+ P ( B – A ) \dots(1) \\
\text { and } & P ( B )= P ( A \cap B )+ P ( B – A ) \dots(2)
\end{array}
\)
Subtracting (2) from (1) gives
\(
\begin{aligned}
& P ( A \cup B )- P ( B )= P ( A )- P ( A \cap B ) \\
& \text { or } \quad P ( A \cup B )= P ( A )+ P ( B )- P ( A \cap B ) \\
&
\end{aligned}
\)
The above result can further be verified by observing the Venn Diagram shown below.

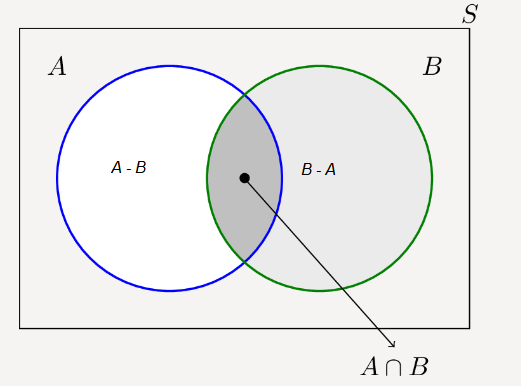
If A and B are disjoint sets, i.e., they are mutually exclusive events, then \(A \cap B =\phi\)
Therefore
\(
P ( A \cap B )= P (\phi)=0
\)
Thus, for mutually exclusive events A and B , we have
\(
P ( A \cup B )= P ( A )+ P ( B ),
\)
which is Axiom (iii) of probability.

Probability of event ‘not \(A\) ‘

Consider the event \(A=\{2,4,6,8\}\) associated with the experiment of drawing a card from a deck of ten cards numbered from 1 to 10 . Clearly the sample space is \(S=\{1,2,3, \ldots, 10\}\)
If all the outcomes \(1,2, \ldots, 10\) are considered to be equally likely, then the probability of each outcome is \(\frac{1}{10}\).
Now
\(
\begin{aligned}
P ( A ) & = P (2)+ P (4)+ P (6)+ P (8) \\
& =\frac{1}{10}+\frac{1}{10}+\frac{1}{10}+\frac{1}{10}=\frac{4}{10}=\frac{2}{5}
\end{aligned}
\)
Also event ‘not A’ \(= A ^{\prime}=\{1,3,5,7,9,10\}\)
Now \(\quad P \left( A ^{\prime}\right)= P (1)+ P (3)+ P (5)+ P (7)+ P (9)+ P (10)\)
\(
=\frac{6}{10}=\frac{3}{5}
\)
\(
\text { Thus, } \quad \quad P \left( A ^{\prime}\right)=\frac{3}{5}=1-\frac{2}{5}=1- P ( A )
\)
Also, we know that \(A ^{\prime}\) and A are mutually exclusive and exhaustive events i.e.,
\(
A \cap A ^{\prime}=\phi \text { and } A \cup A ^{\prime}= S
\)
\(
\begin{array}{ll}
\text { or } & P \left( A \cup A ^{\prime}\right)= P ( S ) \\
\text { Now } & P ( A )+ P \left( A ^{\prime}\right)=1,
\end{array}
\)
\(
\text { or } \quad P \left( A ^{\prime}\right)= P (\operatorname{not} A )=1- P ( A )
\)

Example 6: One card is drawn from a well shuffled deck of 52 cards. If each outcome is equally likely, calculate the probability that the card will be
(i) a diamond
(ii) not an ace
(iii) a black card (i.e., a club or, a spade)
(iv) not a diamond
(v) not a black card.

Solution:

(i) Let A be the event ‘the card drawn is a diamond’ Clearly the number of elements in set A is 13 .
Therefore, \(P ( A )=\frac{13}{52}=\frac{1}{4}\)
i.e. probability of a diamond card \(=\frac{1}{4}\)

(ii) We assume that the event ‘Card drawn is an ace’ is B
Therefore ‘Card drawn is not an ace’ should be B’.
We know that \(P \left( B ^{\prime}\right)=1- P ( B )=1-\frac{4}{52}=1-\frac{1}{13}=\frac{12}{13}\)

(iii) Let C denote the event ‘card drawn is black card’
Therefore, number of elements in the set \(C =26\)
i.e. \(P ( C )=\frac{26}{52}=\frac{1}{2}\)
Thus, probability of a black card \(=\frac{1}{2}\).

(iv) We assumed in (i) above that A is the event ‘card drawn is a diamond’, so the event ‘card drawn is not a diamond’ may be denoted as A’ or ‘not A’ Now \(P (\operatorname{not} A )=1- P ( A )=1-\frac{1}{4}=\frac{3}{4}\)

(v) The event ‘card drawn is not a black card’ may be denoted as \(C ^{\prime}\) or ‘not C ‘.
We know that \(P (\) not C \()=1- P ( C )=1-\frac{1}{2}=\frac{1}{2}\)
Therefore, probability of not a black card \(=\frac{1}{2}\)

Example 7: A bag contains 9 discs of which 4 are red, 3 are blue and 2 are yellow. The discs are similar in shape and size. A disc is drawn at random from the bag. Calculate the probability that it will be (i) red, (ii) yellow, (iii) blue, (iv) not blue, (v) either red or blue.

Solution: There are 9 dises in all so the total number of possible outcomes is 9 .
Let the events A, B, C be defined as
A: ‘the disc drawn is red’
B: ‘the disc drawn is yellow’
C: ‘the disc drawn is blue’.

(i) The number of red discs \(=4\), i.e., \(n(A)=4\)
Hence
\(
P ( A )=\frac{4}{9}
\)

(ii) The number of yellow discs \(=2\), i.e., \(n\) (B) \(=2\)
Therefore, \(\quad P ( B )=\frac{2}{9}\)

(iii) The number of blue discs \(=3\), i.e., \(n( C )=3\)
Therefore, \(\quad P ( C )=\frac{3}{9}=\frac{1}{3}\)

(iv) Clearly the event ‘not blue’ is ‘not C ‘. We know that \(P (\) not C \()=1- P ( C )\)
Therefore \(P (\operatorname{not} C )=1-\frac{1}{3}=\frac{2}{3}\)

(v) The event ‘either red or blue’ may be described by the set ‘A or C ‘
Since, A and C are mutually exclusive events, we have
\(
P ( A \text { or } C )= P ( A \cup C )= P ( A )+ P ( C )=\frac{4}{9}+\frac{1}{3}=\frac{7}{9}
\)

Example 8: Two students Anil and Ashima appeared in an examination. The probability that Anil will qualify the examination is 0.05 and that Ashima will qualify the examination is 0.10 . The probability that both will qualify the examination is 0.02 . Find the probability that
(a) Both Anil and Ashima will not qualify the examination.
(b) Atleast one of them will not qualify the examination and
(c) Only one of them will qualify the examination.

Solution: Let E and F denote the events that Anil and Ashima will qualify the examination, respectively. Given that
\(
P ( E )=0.05, P ( F )=0.10 \text { and } P ( E \cap F )=0.02 \text {. }
\)
Then
(a) The event ‘both Anil and Ashima will not qualify the examination’ may be expressed as \(E ^{\prime} \cap F ^{\prime}\).
Since, \(E ^{\prime}\) is ‘not \(E\) ‘, i.e., Anil will not qualify the examination and \(F\) ‘ is ‘not \(F\) ‘, i.e., Ashima will not qualify the examination.
Also \(\quad E^{\prime} \cap F^{\prime}=(E \cup F)^{\prime}(\) by Demorgan’s Law \()\)
Now \(\quad P ( E \cup F )= P ( E )+ P ( F )- P ( E \cap F )\)
or \(\quad P ( E \cup F )=0.05+0.10-0.02=0.13\)
Therefore \(P \left( E ^{\prime} \cap F ^{\prime}\right)= P ( E \cup F )^{\prime}=1- P ( E \cup F )=1-0.13=0.87\)

(b)
\(
\begin{aligned}
P \text { (atleast one of them will not qualify) } \\
=1- P (\text { both of them will qualify) } \\
=1-0.02=0.98
\end{aligned}
\)

(c) The event only one of them will qualify the examination is same as the event either (Anil will qualify, and Ashima will not qualify) or (Anil will not qualify and Ashima will qualify) i.e., \(E \cap F ^{\prime}\) or \(E ^{\prime} \cap F\), where \(E \cap F ^{\prime}\) and \(E ^{\prime} \cap F\) are mutually exclusive.
Therefore, P (only one of them will qualify) \(= P \left( E \cap F ^{\prime}\right.\) or \(\left.E ^{\prime} \cap F \right)\)
\(
\begin{aligned}
& = P \left( E \cap F ^{\prime}\right)+ P \left( E ^{\prime} \cap F \right)= P ( E )- P ( E \cap F )+ P ( F )- P ( E \cap F ) \\
& =0.05-0.02+0.10-0.02=0.11
\end{aligned}
\)

Example 9: A committee of two persons is selected from two men and two women. What is the probability that the committee will have (a) no man? (b) one man? (c) two men?

Solution: The total number of persons \(=2+2=4\). Out of these four person, two can be selected in \({ }^4 C _2\) ways.

(a) No men in the committee of two means there will be two women in the committee. Out of two women, two can be selected in \({ }^2 C _2=1\) way.
Therefore \(P (\) no man \()=\frac{{ }^2 C _2}{{ }^4 C _2}=\frac{1 \times 2 \times 1}{4 \times 3}=\frac{1}{6}\)

(b) One man in the committee means that there is one woman. One man out of 2 can be selected in \({ }^2 C _1\) ways and one woman out of 2 can be selected in \({ }^2 C _1\) ways.
Together they can be selected in \({ }^2 C _1 \times{ }^2 C _1\) ways.
Therefore \(P (\) One man \()=\frac{{ }^2 C _1 \times{ }^2 C _1}{{ }^4 C _2}=\frac{2 \times 2}{2 \times 3}=\frac{2}{3}\)

(c) Two men can be selected in \({ }^2 C _2\) way.
Hence \(P (\text { Two men })=\frac{{ }^2 C _2}{{ }^4 C _2}=\frac{1}{{ }^4 C _2}=\frac{1}{6}\)

Example 10: On her vacations Veena visits four cities (A, B, C and D) in a random order. What is the probability that she visits
(i) A before B?
(ii) A before B and B before C?
(iii) A first and B last?
(iv) A either first or second?
(v) A just before B?

Solution: The number of arrangements (orders) in which Veena can visit four cities A, B, C, or D is 4 ! i.e., 24.Therefore, \(n(S)=24\).
Since the number of elements in the sample space of the experiment is 24 all of these outcomes are considered to be equally likely. A sample space for the experiment is
\(
\begin{aligned}
S = & \{ ABCD , ABDC , ACBD , ACDB , ADBC , ADCB \\
& BACD , BADC , BDAC , BDCA , BCAD , BCDA \\
& CABD, CADB, CBDA, CBAD, CDAB, CDBA \\
& DABC, DACB, DBCA, DBAC, DCAB, DCBA\}
\end{aligned}
\)

(i) Let the event ‘she visits A before B ‘ be denoted by E
Therefore,
\(
\begin{aligned}
E = & \{ ABCD , CABD , DABC , ABDC , CADB , DACB \\
& ACBD , ACDB , ADBC , CDAB , DCAB , ADCB \}
\end{aligned}
\)
Thus \(\quad P ( E )=\frac{n( E )}{n(S)}=\frac{12}{24}=\frac{1}{2}\)

(ii) Let the event ‘Veena visits A before B and B before C’ be denoted by F.
Here \(\quad F=\{ ABCD , DABC , ABDC , ADBC \}\)
Therefore, \(P ( F )=\frac{n(F)}{n(S)}=\frac{4}{24}=\frac{1}{6}\)

(iii) Veena can visit city \(A\) first and city \(B\) last in any one of the following ways, i.e. \(ACDB, ADCB.\)
So, there are 2 ways.
\(\therefore\) Required probability \(=\frac{2}{24}=\frac{1}{12}\)

(iv) Number of ways Veena travels A either first or second =12
\(\therefore\) Probability of her traveling A either first or second
\(
=\frac{12}{24}=\frac{1}{2}
\)

(v) Number of ways Veena travels \(A\) just before \(B=6\)
\(\therefore\) Probability of her traveling A just before B \(=\frac{6}{24}=\frac{1}{4}\)

Example 11: Find the probability that when a hand of 7 cards is drawn from a well shuffled deck of 52 cards, it contains (i) all Kings (ii) 3 Kings (iii) atleast 3 Kings.

Solution: Total number of possible hands \(={ }^{52} C _7\)

(i) Number of hands with 4 Kings \(={ }^4 C _4 \times{ }^{48} C _3\) (other 3 cards must be chosen from the rest 48 cards)
Hence
\(
P (\text { a hand will have } 4 \text { Kings })=\frac{{ }^4 C _4 \times{ }^{48} C _3}{{ }^{52} C _7}=\frac{1}{7735}
\)

(ii) Number of hands with 3 Kings and 4 non-King cards \(={ }^4 C _3 \times{ }^{48} C _4\)
Therefore
\(
P(3 \text { Kings })=\frac{{ }^4 C_3 \times{ }^{48} C_4}{{ }^{52} C_7}=\frac{9}{1547}
\)

(iii)
\(
\begin{aligned}
P (\text { atleast } 3 \text { King }) & = P (3 \text { Kings or } 4 \text { Kings }) \\
& = P (3 \text { Kings })+ P (4 \text { Kings })
\end{aligned}
\)
\(=\frac{9}{1547}+\frac{1}{7735}=\frac{46}{7735}\)

Example 12: If \(A, B, C\) are three events associated with a random experiment, prove that
\(
\begin{aligned}
P ( A \cup B \cup C ) & = P ( A )+ P ( B )+ P ( C )- P ( A \cap B )- P ( A \cap C ) \\
& – P ( B \cap C )+ P ( A \cap B \cap C )
\end{aligned}
\)

Solution: 

\(
\begin{aligned}
\text { Consider } E & = B \cup C \text { so that } \\
P ( A \cup B \cup C ) & = P ( A \cup E ) \\
& = P ( A )+ P ( E )- P ( A \cap E ) \dots(1)
\end{aligned}
\)
Now
\(
\begin{aligned}
P ( E ) & = P ( B \cup C ) \\
& = P ( B )+ P ( C )- P ( B \cap C ) \dots(2)
\end{aligned}
\)
Also \(\quad A \cap E = A \cap( B \cup C )=( A \cap B ) \cup( A \cap C )\) [using distribution property of intersection of sets over the union]. Thus
\(
P ( A \cap E )= P ( A \cap B )+ P ( A \cap C )- P [( A \cap B ) \cap( A \cap C )]
\)
\(
= P ( A \cap B )+ P ( A \cap C )- P [ A \cap B \cap C ] \dots(3)
\)
Using (2) and (3) in (1), we get
\(
\begin{aligned}
P [ A \cup B \cup C ] & = P ( A )+ P ( B )+ P ( C )- P ( B \cap C ) \\
& – P ( A \cap B )- P ( A \cap C )+ P ( A \cap B \cap C )
\end{aligned}
\)

Example 13: In a relay race there are five teams \(A , B , C , D \text { and } E \text {. }\)
(a) What is the probability that \(A , B\) and C finish first, second and third, respectively.
(b) What is the probability that \(A , B\) and C are first three to finish (in any order) (Assume that all finishing orders are equally likely)

Solution: If we consider the sample space consisting of all finishing orders in the first three places, we will have \({ }^5 P _3\), i.e., \(\frac{5!}{(5-3)!}=5 \times 4 \times 3=60\) sample points, each with a probability of \(\frac{1}{60}\).

(a) \(A , B \text { and } C\) finish first, second and third, respectively. There is only one finishing order for this, i.e., \(ABC\).
Thus \(P \left( A , B\right.\) and C finish first, second and third respectively) \(=\frac{1}{60}\).

(b) \(A , B \text { and } C\) are the first three finishers. There will be 3! arrangements for \(A , B \text { and } C\) . Therefore, the sample points corresponding to this event will be 3! in number.

So \(\quad P(A, B\) and \(C\) are first three to finish \()=\frac{3!}{60}=\frac{6}{60}=\frac{1}{10}\)

Classical Definition of Probability

The probability of an event \(E\) to occur is the ratio of the number of cases in its favour to the total number of cases (equally likely).
\(
\therefore \quad P(E)=\frac{n(E)}{n(S)}=\frac{\text { Number of cases favourable to event } E }{\text { Total number of cases }}=\frac{\text { Number of outcomes favourable to E }}{\text { Total possible outcomes }}
\)

Range of Value of \(P(E)\)

Probability of occurrence of an event is a number lying between 0 and 1 .
Proof Let \(S\) be the sample space and \(E\) be an event. Then,
\(
\begin{aligned}
& E \subseteq S \dots(i) \\
& \phi \subseteq S \dots(ii)
\end{aligned}
\)

where \(\phi\) is a null set. From Eqs. (i) and (ii), we get
\(
\begin{aligned}
& \phi \subseteq S \supseteq E \Rightarrow n(\phi) \leq n(E) \leq n(S) \\
& \Rightarrow \quad 0 \leq \frac{n(E)}{n(S)} \leq 1 \quad[\because n(\phi)=0] \\
& \Rightarrow \quad 0 \leq P(E) \leq 1 \\
&
\end{aligned}
\)

Remark

1. For impossible event \(\phi ; P(\phi)=0\)

2. For sure event \(S, P(S)=1\)
Relationship between \(P(E)\) and \(P\left(E^{\prime}\right)\)
If \(E\) is any event and \(E^{\prime}\) be the complement of event \(E\), then
\(
P(E)+P\left(E^{\prime}\right)=1
\)

Proof: Let \(S\) be the sample space, then
\(
\begin{aligned}
E^{\prime} & =S-E \\
n\left(E^{\prime}\right) & =n(S)-n(E) \\
\frac{n\left(E^{\prime}\right)}{n(S)} & =1-\frac{n(E)}{n(S)} \\
P\left(E^{\prime}\right) & =1-P(E) \\
P(E)+P\left(E^{\prime}\right) & =1
\end{aligned}
\)

Odds in Favour and Odds Against the Event

Let \(S\) be the sample space. If \(a\) is the number of cases favourable to the event \(E, b\) is the number of cases favourable to the event \(E^{\prime}\), the odds in favour of \(E\) are defined by \(a: b\) and odds against of \(E\) are \(b: a\). i.e. odds in favour of event \(E\) is
\(
\begin{aligned}
\frac{a}{b}=\frac{n(E)}{n\left(E^{\prime}\right)} & =\frac{\frac{n(E)}{n(S)}}{\frac{n\left(E^{\prime}\right)}{n(S)}}=\frac{P(E)}{P\left(E^{\prime}\right)} \Rightarrow \frac{P\left(E^{\prime}\right)}{P(E)}=\frac{b}{a} \\
\frac{P\left(E^{\prime}\right)+P(E)}{P(E)} & =\frac{b+a}{a} \\
\frac{1}{P(E)} & =\frac{b+a}{a} \\
P(E) & =\frac{a}{a+b} \text { and } P\left(E^{\prime}\right)=\frac{b}{a+b}
\end{aligned}
\)

Remark

• We use the sign ‘ + ‘ for the operation ‘or’ and ‘ x ‘ for the operation ‘and’ in order to solve the problems on definition of probability.

Example 14: If three coins are tossed, represent the sample space and the event of getting atleast two heads, then find the number of elements in them.

Solution: Let \(S\) be the sample space and \(E\) be the event of occurrence of atleast two heads and let \(H\) denote the occurrence of head and \(T\) denote the occurrence of tail, when one coin is tossed.
\(
\begin{aligned}
& \text { Then, } \quad S=\{H, T\} \times\{H, T\} \times\{H, T\} \\
& S=\{(H, H, H),(H, H, T),(H, T, H),(T, H, H), \\
& (T, T, H),(T, H, T),(H, T, T),(T, T, T)\} \\
& \text { and } \quad E=\{(H, H, H),(H, H, T),(H, T, H),(T, H, H)\} \\
& \text { Also, } n(S)=8 \text { and } n(E)=4 \\
&
\end{aligned}
\)

Example 15: One ticket is drawn at random from a bag containing 24 tickets numbered 1 to 24. Represent the sample space and the event of drawing a ticket containing number which is a prime. Also, find the number of elements in them.

Solution: Let \(S\) be the sample space and \(E\) be the event of occurrence a prime number.
Then, \(\quad S=\{1,2,3,4,5, \ldots, 24\}\)
and \(\quad E=\{2,3,5,7,11,13,17,19,23\}\)
Also, \(\quad n(S)=24\) and \(n(E)=9\)

Example 16: Two dice are thrown simultaneously. What is the probability obtaining a total score less than 11?

Solution: Let \(S\) be the sample space and \(E\) be the event of obtaining a total less than 11 .
Then,\(S=\{1,2,3,4,5,6\} \times\{1,2,3,4,5,6\} \Rightarrow n(S)=6 \times 6=36\)
Let \(E^{\prime}\) be the event of obtaining a total score greater than or equal to 11 .
Also, \(\quad E^{\prime}=\{(5,6),(6,5),(6,6)\} ; \quad \therefore n\left(E^{\prime}\right)=3\)
Then, probability of obtaining a total score greater than or equal to 11 ,
\(
\begin{aligned}
& P\left(E^{\prime}\right)=\frac{n\left(E^{\prime}\right)}{n(S)}=\frac{3}{36}=\frac{1}{12} \\
& \therefore \quad P(E)=1-P\left(E^{\prime}\right)=1-\frac{1}{12}=\frac{11}{12} \\
&
\end{aligned}
\)
Hence, required probability is \(\frac{11}{12}\).

Example 17: If a leap-leap year is selected at random, then what is the chance it will contain 53 Sunday?

Solution: A leap-leap year has 367 days i.e., 52 complete week and three days more. These three days will be three consecutive days of a week. A leap-leap year will have 53 Sundays, if out of the three consecutive days of a week selected at random one is a Sunday.
Let be the sample space and \(E\) be the event that out of the three consecutive days of a week one is Sunday, then
\(S=\{\) Sunday, Monday, Tuesday), (Monday, Tuesday, Wednesday), (Tuesday, Wednesday, Thursday), (Wednesday, Thursday, Friday), (Thursday, Friday, Saturday), (Friday, Saturday, Sunday), (Saturday, Sunday, Monday) \(\} ; n(S)=7\)
and \(\quad E=\{\) (Sunday, Monday, Tuesday), (Friday, Saturday, Sunday), (Saturday, Sunday, Monday)\}
\(
\therefore \quad n(E)=3
\)
Now, required probability, \(P(E)=\frac{n(E)}{n(S)}=\frac{3}{7}\)

Example 18: From a pack of 52 playing cards, three cards are drawn at random. Find the probability of drawing a King, a Queen and a Knave.

Solution: Let \(S\) be the sample space and \(E\) be the event that out of the three cards drawn one is a King, one is a Queen and one is a Knave.
\(\therefore n(S)=\) Total number of selecting 3 cards out of 52 cards
\(
={ }^{52} C_3
\)
and \(n(E)=\) Number of selecting 3 cards out of one is King, one is Queen and one is Knave \(={ }^4 C_1 \cdot{ }^4 C_1 \cdot{ }^4 C_1=64\)
\(\therefore\) Required probability, \(P(E)=\frac{n(E)}{n(S)}=\frac{64}{{ }^{52} C_3}=\frac{\frac{64}{52 \cdot 51 \cdot 50}}{1 \cdot 2 \cdot 3}=\frac{16}{5525}\)

Example 19: A bag contains 8 red and 5 white balls. Three balls are drawn at random. Find the probability that
(i) all the three balls are white.
(ii) all the three balls are red.
(iii) one ball is red and two balls are white.

Solution: Let \(S\) be the sample space, \(E_1\) be the event of getting 3 white balls, \(E_2\) be the event of getting 3 red balls and \(E_3\) be the event of getting one red ball and two white balls.
\(\therefore n(S)=\) Number of ways of selecting 3 balls out of
\(
13(8+5)={ }^{13} C_3=\frac{13 \cdot 12 \cdot 11}{1 \cdot 2 \cdot 3}=286
\)

(i) \(n\left(E_1\right)=\) Number of ways of selecting 3 white balls out of 5
\(
\begin{aligned}
& \quad={ }^5 C_3={ }^5 C_2=\frac{5 \cdot 4}{1 \cdot 2}=10 \\
& \therefore P \text { (getting } 3 \text { white balls) }=\frac{n\left(E_1\right)}{n(S)}=\frac{10}{286}=\frac{5}{143}
\end{aligned}
\)

(ii) \(n\left(E_2\right)=\) Number of ways of selecting 3 red balls out of 8
\(
\begin{aligned}
&={ }^8 C_3=\frac{8 \cdot 7 \cdot 6}{1 \cdot 2 \cdot 3}=56 \\
& \therefore P \text { (getting } 3 \text { red balls) }=\frac{n\left(E_2\right)}{n(S)} \\
&=\frac{56}{286}=\frac{28}{143}
\end{aligned}
\)

(iii) \(n\left(E_3\right)=\) Number of ways of selecting 1 red ball out of 8 and 2 black balls out of \(5={ }^8 C_1 \cdot{ }^5 C_2=8 \cdot 10=80\)
\(\therefore P\) (getting 1 red and 2 black balls)
\(
=\frac{n\left(E_3\right)}{n(S)}=\frac{80}{286}=\frac{40}{143}
\)

Some Important Symbols, Conditional Probability

Some Important Symbols

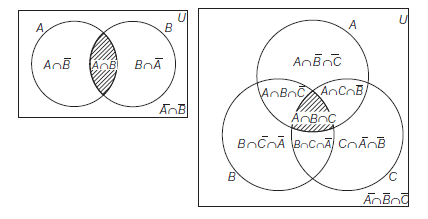
If \(A, B\) and \(C\) are any three events, then

• \(A \cap B\) or \(A B\) denotes the event of simultaneous occurrence of both the events \(A\) and \(B\).
• \(A \cup B\) or \(A+B\) denotes the event of occurrence of atleast one of the events \(A\) or \(B\).
• \(A-B\) denotes the occurrence of event \(A\) but not \(B\).
• \(\bar{A}\) denotes the not occurrence of event \(A\).
• \(A \cap \bar{B}\) denotes the occurrence of event \(A\) but not \(B\).
• \(\bar{A} \cap \bar{B}=(\overline{A \cup B})\) denotes the occurrence of neither \(A\) nor \(B\).
• \(A \cup B \cup C\) denotes the occurrence of atleast one event \(A, B\) or \(C\).
• \((A \cap \bar{B}) \cup(\bar{A} \cap B)\) denotes the occurrence of exactly one of \(A\) and \(B\).
• \(A \cap B \cap C\) denotes the occurrence of all three \(A, B\) and \(C\).
• \((A \cap B \cap \bar{C}) \cup(A \cap \bar{B} \cap C) \cup(\bar{A} \cap B \cap C)\) denotes the occurrence of exactly two of \(A, B\) and \(C\).

Remark
Remember with the help of figures.

Important Results

1. If \(A\) and \(B\) are arbitrary events, then
(a) \(P(A \cup B)=P(A)+P(B)-P(A \cap B)\)
Proof Let \(S\) be the sample space. Since, we know that
\(
\begin{aligned}
n(A \cup B) & =n(A)+n(B)-n(A \cap B) \\
\Rightarrow \quad \frac{n(A \cup B)}{n(S)} & =\frac{n(A)}{n(S)}+\frac{n(B)}{n(S)}-\frac{n(A \cap B)}{n(S)}
\end{aligned}
\)
\(
\Rightarrow P(A \cup B)=P(A)+P(B)-P(A \cap B)
\)

Remark

• If \(A\) and \(B\) are mutually exclusive events, then \(A \cap B=\phi\). Hence, \(P(A \cap B)=0\).
  \(
  \therefore P(A \cup B)=P(A)+P(B)
  \)

(b) \(P\) (exactly one of \(A, B\) occurs)
\(
\begin{aligned}
& =P(A \cap \bar{B})+P(\bar{A} \cap B) \\
& =P(A)-P(A \cap B)+P(B)-P(A \cap B) \\
& =P(A)+P(B)-2 P(A \cap B) \\
& =P(A \cup B)-P(A \cap B)
\end{aligned}
\)

(c) \(P\) (neither \(A\) nor \(B\) )
\(
=P(\bar{A} \cap \bar{B})=P(\overline{A \cup B})=1-P(A \cup B)
\)

Remark

• \(P(\bar{A} \cup \bar{B})=1-P(A \cap B)\)

2. If \(A, B\) and \(C\) are three events, then
(a)
\(
\begin{aligned}
P(A \cup B \cup C) & =P(A)+P(B)+P(C)-P(A \cap B) \\
– & P(B \cap C)-P(C \cap A)+P(A \cap B \cap C)
\end{aligned}
\)

Remark

If \(A, B\) and \(C\) are mutually exclusive events, then
\(
A \cap B=\phi, B \cap C=\phi, C \cap A=\phi, A \cap B \cap C=\phi
\)
\(
\begin{array}{ll}
\Rightarrow & P(A \cap B)=0, P(B \cap C)=0, P(C \cap A)=0, P(A \cap B \cap C)=0 \\
\therefore \quad & P(A \cup B \cup C)=P(A)+P(B)+P(C)
\end{array}
\)

General form of Addition Theorem of Probability
\(
\begin{aligned}
& P\left(A_1 \cup A_2 \cup \ldots \cup A_n\right)= \sum_{i=1}^n P\left(A_i\right)-\sum_{i<j} P\left(A_i \cap A_j\right) \\
&+\sum_{i<j<k} P\left(A_i \cap A_j \cap A_k\right)- \\
& \ldots+(-1)^{n-1} P\left(A_1 \cap A_2 \cap \ldots \cap A_n\right)
\end{aligned}
\)

Remark

If \(A_1, A_2, \ldots, A_n\) are mutually exclusive events, then
\(
\begin{aligned}
& \sum_{i<j} P\left(A_j \cap A_j\right)=0, \sum_{i<j<k} P\left(A_i \cap A_j \cap A_k\right)=0 \\
& \text { and } \\
& P\left(A_1 \cap A_2 \cap \ldots \cap A_n\right)=0 \\
& \therefore \quad P\left(A \cup A_2 \cup \ldots \cup A_n\right)=\sum_{i=1}^n P(A) \\
&
\end{aligned}
\)
\(
\begin{aligned}
& \text { (b) } P \text { (atleast two of } A, B, C \text { occur) } \\
& =P(A \cap B)+P(B \cap C)+P(C \cap A) \\
& -2 P(A \cap B \cap C)
\end{aligned}
\)
\(
\begin{aligned}
& \text { (c) } P \text { (exactly two of } A, B, C \text { occur) } \\
& =P(A \cap B)+P(B \cap C)+P(C \cap A) \\
& -3 P(A \cap B \cap C) \\
&
\end{aligned}
\)
(d) \(P\) (exactly one of \(A, B, C\) occur)
\(
\begin{array}{r}
=P(A)+P(B)+P(C)-2 P(A \cap B)-2 P(B \cap C) \\
-2 P(C \cap A)+3 P(A \cap B \cap C)
\end{array}
\)

3. (a) If \(A_1, A_2, \ldots, A_n\) are independent events, then
\(
P\left(A_1 \cap A_2 \cap \ldots \cap A_n\right)=P\left(A_1\right) P\left(A_2\right) \ldots P\left(A_n\right)
\)
(b) If \(A_1, A_2, \ldots, A_n\) are mutually exclusive events, then
\(
\begin{aligned}
& P\left(A_1 \cup A_2 \cup \ldots \cup A_n\right) \\
& \quad=P\left(A_1\right)+P\left(A_2\right)+\ldots+P\left(A_n\right)
\end{aligned}
\)
(c) If \(A_1, A_2, \ldots, A_n\) are exhaustive events, then
\(
P\left(A_1 \cup A_2 \cup \ldots \cup A_n\right)=1
\)
(d) If \(A_1, A_2, \ldots, A_n\) are mutually exclusive and exhaustive events, then
\(
\begin{aligned}
& P\left(A_1 \cup A_2 \cap \ldots \cap A_n\right) \\
&=P\left(A_1\right)+P\left(A_2\right)+\ldots+P\left(A_n\right)=1
\end{aligned}
\)

4. If \(A_1, A_2, \ldots, A_n\) are \(n\) events, then
(a) \(P\left(A_1 \cup A_2 \cup \ldots \cup A_n\right) \leq P\left(A_1\right)+P\left(A_2\right)+\ldots+P\left(A_n\right)\)
(b) \(P\left(A_1 \cap A_2 \cap \ldots \cap A_n\right) \geq 1-P\left(\bar{A}_1\right)-P\left(\bar{A}_2\right)-\) \(\ldots-P\left(\bar{A}_n\right)\)

Important Result

If \(E_1\) and \(E_2\) are independent events, then
(a) \(E_1\) and \(\bar{E}_2\) are independent events.
(b) \(\bar{E}_1\) and \(E_2\) are independent events.
(c) \(\bar{E}_1\) and \(\bar{E}_2\) are independent events.

Proof Given, \(E_1\) and \(E_2\) are independent events, then
\(
P\left(E_1 \cap E_2\right)=P\left(E_1\right) \cdot P\left(E_2\right)
\)
(a)
\(
\begin{aligned}
& P\left(E_1 \cap \bar{E}_2\right)=P\left(E_1\right)-P\left(E_1 \cap E_2\right) \\
&=P\left(E_1\right)-P\left(E_1\right) \cdot P\left(E_2\right) \\
&= P\left(E_1\right)\left[1-P\left(E_2\right)\right]=P\left(E_1\right) \cdot P\left(\bar{E}_2\right)
\end{aligned}
\)
So, \(E_1\) and \(\bar{E}_2\) are independent events.

(b) Same as in part (a).
\(
\text { (c) } \begin{aligned}
& P\left(\bar{E}_1 \cap \bar{E}_2\right)=P\left(\overline{E_1 \cup E_2}\right) \\
= & 1-P\left(E_1 \cup E_2\right)=1-\left[P\left(E_1\right)+P\left(E_2\right)-P\left(E_1 \cap E_2\right)\right] \\
= & 1-P\left(E_1\right)-P\left(E_2\right)+P\left(E_1\right) \cdot P\left(E_2\right) \\
= & P\left(\bar{E}_1\right)-P\left(E_2\right)\left[1-P\left(E_1\right)\right] \\
= & P\left(\bar{E}_1\right)-P\left(E_2\right) \cdot P\left(\bar{E}_1\right)=P\left(\bar{E}_1\right)\left[1-P\left(E_2\right)\right] \\
= & P\left(\bar{E}_1\right) P\left(\bar{E}_2\right)
\end{aligned}
\)

Remark

If \(E_1, E_2, \ldots, E_n\) are independent events, then \(P\left(E_1 \cup E_2 \cup \ldots \cup E_n\right)\)
\(
\begin{aligned}
& =1-P\left(E_1 \cup E_2 \cup \ldots \cup E_n\right)^{\prime}=1-P\left(E_1^{\prime} \cap E_2^{\prime} \cap \ldots \cap E_n^{\prime}\right) \\
& =1-P\left(E_1^{\prime}\right) \cdot P\left(E_2^{\prime}\right) \ldots P\left(E_n^{\prime}\right)
\end{aligned}
\)

Example 20: For a post, three persons A, B and C appear in the interview. The probability of A being selected is twice that of B and the probability of B being selected is thrice that of C. What are the individual probabilities of A, B and C being selected?

Solution: Let \(E_1, E_2\) and \(E_3\) be the events of selection of \(A, B\) and \(C\) respectively.
Let \(\quad P\left(E_3\right)=x\).
Then, \(P\left(E_2\right)=3 P\left(E_3\right)=3 x\) and \(P\left(E_1\right)=2 P\left(E_2\right)=6 x\)
Since, \(E_1, E_2\) and \(E_3\) are mutually exclusive and exhaustive events.
\(
\begin{aligned}
P\left(E_1 \cup E_2 \cup E_3\right) & =P\left(E_1\right)+P\left(E_2\right)+P\left(E_3\right)=1 \\
P\left(E_1\right)+P\left(E_2\right)+P\left(E_3\right) & =1 \\
6 x+3 x+x & =1 \\
x & =\frac{1}{10}
\end{aligned}
\)
Hence,
\(
\begin{aligned}
& P\left(E_1\right)=6 x=\frac{6}{10}=\frac{3}{5} \\
& P\left(E_2\right)=3 x=\frac{3}{10} \text { and } P\left(E_3\right)=x=\frac{1}{10}
\end{aligned}
\)

Example 21: If \(A\) and \(B\) are independent events, the probability that both \(A\) and \(B\) occur is \(\frac{1}{8}\) and the probability that none of them occurs is \(\frac{3}{8}\). Find the probability of the occurrence of \(A\).

Solution: We have,
\(
P(A \cap B)=\frac{1}{8} \Rightarrow P(A) P(B)=\frac{1}{8} \dots(i)
\)
\(
[\because A \text { and } B \text { are independent }]
\)
\(
\text { and } P(\bar{A} \cap \bar{B})=\frac{3}{8} \Rightarrow P(\bar{A}) P(\bar{B})=\frac{3}{8}
\)
\(
\begin{aligned}
& (1-P(A))(1-P(B))=\frac{3}{8} \\
& 1-P(A)-P(B)+\frac{1}{8}=\frac{3}{8} \text { [from Eq. (i)] }
\end{aligned}
\)
\(
P(A)+P(B)=\frac{3}{4} \dots(ii)
\)
The quadratic equation whose roots are \(P(A)\) and \(P(B)\) is
\(
\begin{aligned}
& x^2-[P(A)+P(B)] x+P(A) \cdot P(B)=0 \\
& \Rightarrow \quad x^2-\frac{3}{4} x+\frac{1}{8}=0 \text { [from Eqs. (i) and (ii)] }
\end{aligned}
\)
or \(\quad 8 x^2-6 x+1=0 \quad\) or \(\quad x=\frac{1}{2}, \frac{1}{4}\)
Hence, \(\quad P(A)=\frac{1}{2}\) or \(\frac{1}{4}\)

Example 22: \(A\) and \(B\) are two candidates seeking admission in IIT. The probability that \(A\) is selected is 0.5 and the probability that both \(A\) and \(B\) are selected is atmost 0.3 . Is it possible that the probability of \(B\) getting selected is 0.9 ?

Solution: Let \(E_1\) and \(E_2\) are the events of \(A\) and \(B\) selected, respectively.
\(
\begin{aligned}
& \text { Given, } P\left(E_1 \cap E_2\right) \leq 0.3 \text { and } P\left(E_1\right)=0.5 \\
& \text { Since, } P\left(E_1 \cup E_2\right)=P\left(E_1\right)+P\left(E_2\right)-P\left(E_1 \cap E_2\right) \\
& \because \quad P\left(E_1 \cup E_2\right) \leq 1 \\
& \therefore \quad P\left(E_1\right)+P\left(E_2\right)-P\left(E_1 \cap E_2\right) \leq 1 \\
& \Rightarrow \quad P\left(E_1\right)+P\left(E_2\right) \leq 1+P\left(E_1 \cap E_2\right) \\
& \Rightarrow \quad 0.5+P\left(E_2\right) \leq 1+0.3 \Rightarrow P\left(E_2\right) \leq 0.8 \\
& P\left(E_2\right) \neq 0.9 \\
&
\end{aligned}
\)

Example 23: Let \(A, B\) and \(C\) be three events. If the probability of occurring exactly one event out of \(A\) and \(B\) is \(1-a\), out of \(B\) and \(C\) is \(1-2 a\), out of \(C\) and \(A\) is \(1-a\) and that of occurring three events simultaneously is \(a^2\), then prove that the probability that atleast one out of \(A, B\) and \(C\) will occur is greater than \(\frac{1}{2}\).

Solution: Given,
\(
\begin{aligned}
& P(A)+P(B)-2 P(A \cap B)=1-a \dots(i) \\
& P(B)+P(C)-2 P(B \cap C)=1-2 a \dots(ii)
\end{aligned}
\)
\(
\text { and } \quad P(C)+P(A)-2 P(C \cap A)=1-a \dots(iii)
\)
\(
P(A \cap B \cap C)=a^2 \dots(iv)
\)
\(
\begin{aligned}
& \therefore P(A \cup B \cup C)=P(A)+P(B)+P(C)-P(A \cap B) \\
& -P(B \cap C)-P(C \cap A)+P(A \cap B \cap C) \\
& =\frac{1}{2}\{P(A)+P(B)-2 P(A \cap B)+P(B)+P(C)-2 P(B \cap C) \\
& +P(C)+P(A)-2 P(C \cap A)\}+P(A \cap B \cap C) \\
& =\frac{1}{2}\{1-a+1-2 a+1-a\}+a^2 \text { [from Eqs. (i), (ii), (iii) and (iv)] } \\
& =\frac{3}{2}-2 a+a^2=(a-1)^2+\frac{1}{2}>\frac{1}{2} \\
& {[\because a \neq 1]} \\
&
\end{aligned}
\)

Example 24: If \(A, B\) and \(C\) are three events, such that \(P(A)=0.3, P(B)=0.4, P(C)=0.8, P(A B)=0.08\), \(P(A C)=0.28, P(A B C)=0.09\). If \(P(A \cup B \cup C) \geq 0.75\), then show that \(P(B C)\) lies in the interval \(0.23 \leq x \leq 0.48\).

Solution: Let \(P(B C)=x\)
Since,
\(
\begin{aligned}
P(A \cup B \cup C)= & P(A)+P(B)+P(C)-P(A B) \\
& -P(B C)-P(C A)+P(A B C)
\end{aligned}
\)
\(
\begin{aligned}
& \therefore \quad=0.3+0.4+0.8-0.08-x-0.28+0.09=1.23-x \\
& \text { But given that, } P(A \cup B \cup C) \geq 0.75 \text { and } P(A \cup B \cup C) \leq 1 \\
& \therefore \quad 0.75 \leq 1.23-x \leq 1 \Rightarrow-0.75 \geq-1.23+x \geq-1 \\
& \text { or } \quad 1.23-0.75 \geq x \geq 1.23-1 \text { or } 0.23 \leq x \leq 0.48
\end{aligned}
\)

Example 25: If three integers are chosen at random from the set of first 20 natural numbers, the chance that their product is a multiple of 3, is?

Solution: \(n(S)=\) Total number of ways of selecting 3 integers from 20 natural numbers \(={ }^{20} C_3=1140\).
Their product is multiple of 3 means atleast one number is divisible by 3 . The number which are divisible by 3 are 3,6 , \(9,12,15\) and 16 .
\(\therefore n(E)=\) The number of ways of selecting atleast one of them multiple of 3
\(
\begin{aligned}
& ={ }^6 C_1 \times{ }^{14} C_2+{ }^6 C_2 \times{ }^{14} C_1 \times{ }^6 C_3=776 \\
& \therefore \text { Required probability }=\frac{n(E)}{n(S)} \\
& =\frac{776}{1140}=\frac{194}{285} \\
&
\end{aligned}
\)