15.5 Variance and Standard Deviation
Recall that while calculating mean deviation about mean or median, the absolute values of the deviations were taken. The absolute values were taken to give meaning to the mean deviation, otherwise the deviations may cancel among themselves.
Another way to overcome this difficulty which arose due to the signs of deviations, is to take squares of all the deviations. Obviously all these squares of deviations are non-negative. Let \(x_1, x_2, x_3, \ldots, x_n\) be \(n\) observations and \(\bar{x}\) be their mean. Then
\(
\left(x_1-\bar{x}\right)^2+\left(x_2-\bar{x}\right)^2+\ldots \ldots . .+\left(x_n-\bar{x}\right)^2=\sum_{i=1}^n\left(x_i-\bar{x}\right)^2 \text {. }
\)
If this sum is zero, then each \(\left(x_i-\bar{x}\right)\) has to be zero. This implies that there is no dispersion at all as all observations are equal to the mean \(\bar{x}\).
If \(\sum_{i=1}^n\left(x_i-\bar{x}\right)^2\) is small, this indicates that the observations \(x_1, x_2, x_3, \ldots, x_{ n }\) are close to the mean \(\bar{x}\) and therefore, there is a lower degree of dispersion. On the contrary, if this sum is large, there is a higher degree of dispersion of the observations from the mean \(\bar{x}\). Can we thus say that the sum \(\sum_{i=1}^n\left(x_i-\bar{x}\right)^2\) is a reasonable indicator of the degree of dispersion or scatter?
Let us take the set A of six observations \(5,15,25,35,45,55\). The mean of the observations is \(\bar{x}=30\). The sum of squares of deviations from \(\bar{x}\) for this set is
\(
\begin{aligned}
\sum_{i=1}^6\left(x_i-\bar{x}\right)^2 & =(5-30)^2+(15-30)^2+(25-30)^2+(35-30)^2+(45-30)^2+(55-30)^2 \\
& =625+225+25+25+225+625=1750
\end{aligned}
\)
Let us now take another set \(B\) of 31 observations \(15,16,17,18,19,20,21,22,23\), \(24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45\). The mean of these observations is \(\bar{y}=30\)
Note that both the sets A and B of observations have a mean of 30 .
Now, the sum of squares of deviations of observations for set \(B\) from the mean \(\bar{y}\) is given by
\(
\begin{aligned}
\sum_{i=1}^{31}\left(y_i-\bar{y}\right)^2 & =(15-30)^2+(16-30)^2+(17-30)^2+\ldots+(44-30)^2+(45-30)^2 \\
& =(-15)^2+(-14)^2+\ldots+(-1)^2+0^2+1^2+2^2+3^2+\ldots+14^2+15^2 \\
& =2\left[15^2+14^2+\ldots+1^2\right] \\
& =2 \times \frac{15 \times(15+1)(30+1)}{6}=5 \times 16 \times 31=2480
\end{aligned}
\)
(Because sum of squares of first \(n\) natural numbers \(=\frac{n(n+1)(2 n+1)}{6}\). Here \(n=15\) )
If \(\sum_{i=1}^n\left(x_i-\bar{x}\right)^2\) is simply our measure of dispersion or scatter about mean, we will tend to say that the set A of six observations has a lesser dispersion about the mean than the set \(B\) of 31 observations, even though the observations in set \(A\) are more scattered from the mean (the range of deviations being from -25 to 25 ) than in the set \(B\) (where the range of deviations is from -15 to 15 ).
This is also clear from the following diagrams.
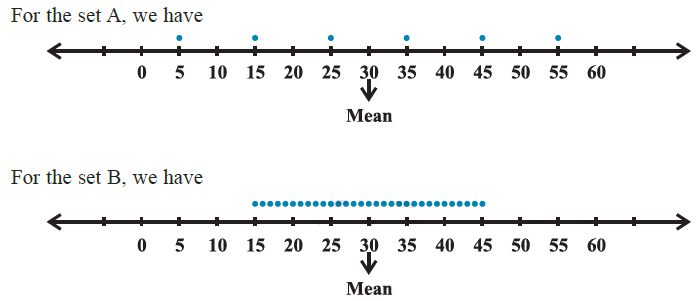
Thus, we can say that the sum of squares of deviations from the mean is not a proper measure of dispersion. To overcome this difficulty we take the mean of the squares of the deviations, i.e., we take \(\frac{1}{n} \sum_{i=1}^n\left(x_i-\bar{x}\right)^2\). In case of the set A, we have Mean \(=\frac{1}{6} \times 1750=291.67\) and in case of the set \(B\), it is \(\frac{1}{31} \times 2480=80\).
This indicates that the scatter or dispersion is more in set A than the scatter or dispersion in set \(B\), which confirms with the geometrical representation of the two sets.
Thus, we can take \(\frac{1}{n} \sum\left(x_i-\bar{x}\right)^2\) as a quantity which leads to a proper measure of dispersion. This number, i.e., mean of the squares of the deviations from mean is called the variance and is denoted by \(\sigma^2\) (read as sigma square). Therefore, the variance of \(n\) observations \(x_1, x_2, \ldots, x_n\) is given by
\(
\sigma^2=\frac{1}{n} \sum_{i=1}^n\left(x_i-\bar{x}\right)^2
\)
Standard Deviation
In the calculation of variance, we find that the units of individual observations \(x_{ i }\) and the unit of their mean \(\bar{x}\) are different from that of variance, since variance involves the sum of squares of \(\left(x_i-\bar{x}\right)\). For this reason, the proper measure of dispersion about the mean of a set of observations is expressed as positive square-root of the variance and is called standard deviation. Therefore, the standard deviation, usually denoted by \(\sigma\), is given by
\(
\sigma=\sqrt{\frac{1}{n} \sum_{i=1}^n\left(x_i-\bar{x}\right)^2} \dots(1)
\)
Let us take the following example to illustrate the calculation of variance and hence, standard deviation of ungrouped data.
Example 8: Find the variance of the following data:
\(
6,8,10,12,14,16,18,20,22,24
\)
Solution: From the given data we can form the following Table below. The mean is calculated by step-deviation method taking 14 as assumed mean. The number of observations is \(n=10\)
\(\begin{array}{|c|c|c|c|}
\hline x_i & d_i=\frac{x_i-14}{2} & \begin{array}{l}
\text { Deviations from mean } \\
\left(x_i-\bar{x}\right)
\end{array} & \left(x_i-\bar{x}\right) \\
\hline 6 & -4 & -9 & 81 \\
\hline 8 & -3 & -7 & 49 \\
\hline 10 & -2 & -5 & 25 \\
\hline 12 & -1 & -3 & 9 \\
\hline 14 & 0 & -1 & 1 \\
\hline 16 & 1 & 1 & 1 \\
\hline 18 & 2 & 3 & 9 \\
\hline 20 & 3 & 5 & 25 \\
\hline 22 & 4 & 7 & 49 \\
\hline 24 & 5 & 9 & 81 \\
\hline
\hline & 5 & & 330 \\
\hline
\end{array}
\)
Therefore \(\quad\) Mean \(\bar{x}=\) assumed mean \(+\frac{\sum_{i=1}^n d_i}{n} \times h=14+\frac{5}{10} \times 2=15\)
and \(\quad\) Variance \(\left(\sigma^2\right)=\frac{1}{n} \sum_{i=1}^{10}\left(x_i-\bar{x}\right)^2=\frac{1}{10} \times 330=33\)
Thus Standard deviation \((\sigma)=\sqrt{33}=5.74\)
Standard deviation of a discrete frequency distribution
Let the given discrete frequency distribution be
\(
\begin{array}{rlll}
x: & x_1, & x_2, & x_3, \ldots, x_n \\
& f: & f_1, & f_2, \quad f_3, \ldots, f_n
\end{array}
\)
In this case standard deviation \((\sigma)=\sqrt{\frac{1}{ N } \sum_{i=1}^n f_i\left(x_i-\bar{x}\right)^2} \dots(2)\)
where \(N =\sum_{i=1}^n f_i\).
Let us take up following example.
Example 9: Find the variance and standard deviation for the following data:
\(
\begin{array}{|c|c|c|c|c|c|c|c|}
\hline x_i & 4 & 8 & 11 & 17 & 20 & 24 & 32 \\
\hline f_i & 3 & 5 & 9 & 5 & 4 & 3 & 1 \\
\hline
\end{array}
\)
Solution: Presenting the data in tabular form (Table below), we get
\(
\begin{array}{|r|r|r|r|r|c|}
\hline x_i & f_i & f_i x_i & x_i-\bar{x} & \left(x_i-\bar{x}\right)^2 & f_i\left(x_i-\bar{x}\right)^2 \\
\hline 4 & 3 & 12 & -10 & 100 & 300 \\
8 & 5 & 40 & -6 & 36 & 180 \\
11 & 9 & 99 & -3 & 9 & 81 \\
17 & 5 & 85 & 3 & 9 & 45 \\
20 & 4 & 80 & 6 & 36 & 144 \\
24 & 3 & 72 & 10 & 100 & 300 \\
32 & 1 & 32 & 18 & 324 & 324 \\
\hline
& 30 & 420 & & & 1374 \\
\hline
\end{array}
\)
\(
N =30, \sum_{i=1}^7 f_i x_i=420, \sum_{i=1}^7 f_i\left(x_i-\bar{x}\right)^2=1374
\)
Therefore \(\bar{x}=\frac{\sum_{i=1}^7 f_i x_i}{ N }=\frac{1}{30} \times 420=14\)
\(
\text { Hence } \quad \text { variance }\left(\sigma^2\right)=\frac{1}{ N } \sum_{i=1}^7 f_i\left(x_i-\bar{x}\right)^2
\)
\(
=\frac{1}{30} \times 1374=45.8
\)
and Standard deviation \((\sigma)=\sqrt{45.8}=6.77\)
Standard deviation of a continuous frequency distribution
The given continuous frequency distribution can be represented as a discrete frequency distribution by replacing each class by its mid-point. Then, the standard deviation is calculated by the technique adopted in the case of a discrete frequency distribution.
If there is a frequency distribution of \(n\) classes each class defined by its mid-point \(x_i\) with frequency \(f_i\), the standard deviation will be obtained by the formula
\(
\sigma=\sqrt{\frac{1}{ N } \sum_{i=1}^n f_i\left(x_i-\bar{x}\right)^2} \text {, }
\)
where \(\bar{x}\) is the mean of the distribution and \(N =\sum_{i=1}^n f_i\).
Another formula for standard deviation
We know that Variance
\(
\begin{aligned}
\left(\sigma^2\right) & =\frac{1}{ N } \sum_{i=1}^n f_i\left(x_i-\bar{x}\right)^2=\frac{1}{ N } \sum_{i=1}^n f_i\left(x_i^2+\bar{x}^2-2 \bar{x} x_i\right) \\
& =\frac{1}{ N }\left[\sum_{i=1}^n f_i x_i^2+\sum_{i=1}^n \bar{x}^2 f_i-\sum_{i=1}^n 2 \bar{x} f_i x_i\right] \\
& =\frac{1}{ N }\left[\sum_{i=1}^n f_i x_i^2+\bar{x}^2 \sum_{i=1}^n f_i-2 \bar{x} \sum_{i=1}^n x_i f_i\right]
\end{aligned}
\)
\(
\begin{aligned}
& =\frac{1}{ N }{ }_{i=1}^n f_i x_i^2+\bar{x}^2 N -2 \bar{x} . N \bar{x} \quad\left[\text { Here } \frac{1}{ N } \sum_{i=1}^n x_i f_i=\bar{x} \text { or } \sum_{i=1}^n x_i f_i= N \bar{x}\right] \\
& =\frac{1}{ N } \sum_{i=1}^n f_i x_i^2+\bar{x}^2-2 \bar{x}^2=\frac{1}{ N } \sum_{i=1}^n f_i x_i^2-\bar{x}^2
\end{aligned}
\)
\(
\text { or } \quad \sigma^2=\frac{1}{ N } \sum_{i=1}^n f_i x_i^2-\left(\frac{\sum_{i=1}^n f_i x_i}{ N }\right)^2=\frac{1}{ N ^2}\left[ N \sum_{i=1}^n f_i x_i^2-\left(\sum_{i=1}^n f_i x_i\right)^2\right]
\)
Thus, standard deviation \((\sigma)=\frac{1}{ N } \sqrt{ N \sum_{i=1}^n f_i x_i^2-\left(\sum_{i=1}^n f_i x_i\right)^2} \dots(3)\)
Example 10: Calculate the mean, variance and standard deviation for the following distribution :
\(
\begin{array}{|l|c|c|c|c|c|c|c|}
\hline \text { Class } & 30-40 & 40-50 & 50-60 & 60-70 & 70-80 & 80-90 & 90-100 \\
\hline \text { Frequency } & 3 & 7 & 12 & 15 & 8 & 3 & 2 \\
\hline
\end{array}
\)
Solution: From the given data, we construct the following Table below.
\(
\begin{array}{|l|c|c|c|c|c|}
\hline \text { Class } & \begin{array}{c}
\text { Frequency } \\
\left(f_i\right)
\end{array} & \begin{array}{c}
\text { Mid-point } \\
\left(x_i\right)
\end{array} & f_i x_i & \left(x_i-\bar{x}\right)^2 & f_i\left(x_i-\bar{x}\right)^2 \\
\hline 30-40 & 3 & 35 & 105 & 729 & 2187 \\
40-50 & 7 & 45 & 315 & 289 & 2023 \\
50-60 & 12 & 55 & 660 & 49 & 588 \\
60-70 & 15 & 65 & 975 & 9 & 135 \\
70-80 & 8 & 75 & 600 & 169 & 1352 \\
80-90 & 3 & 85 & 255 & 529 & 1587 \\
90-100 & 2 & 95 & 190 & 1089 & 2178 \\
\hline
& 50 & & 3100 & & 10050 \\
\hline
\end{array}
\)
\(
\text { Thus } \quad \text { Mean } \bar{x}=\frac{1}{ N } \sum_{i=1}^7 f_i x_i=\frac{3100}{50}=62
\)
\(
\text { Variance } \begin{aligned}
\left(\sigma^2\right) & =\frac{1}{ N } \sum_{i=1}^7 f_i\left(x_i-\bar{x}\right)^2 \\
& =\frac{1}{50} \times 10050=201
\end{aligned}
\)
\(
\text { and } \quad \text { Standard deviation }(\sigma)=\sqrt{201}=14.18
\)
Example 11: Find the standard deviation for the following data :
\(
\begin{array}{|c|c|c|c|c|c|}
\hline x_i & 3 & 8 & 13 & 18 & 23 \\
\hline f_i & 7 & 10 & 15 & 10 & 6 \\
\hline
\end{array}
\)
Solution: Let us form the following Table below:
\(
\begin{array}{|r|r|r|r|r|}
\hline x_i & f_i & f_i x_i & x_i^2 & f_i x_i^2 \\
\hline 3 & 7 & 21 & 9 & 63 \\
8 & 10 & 80 & 64 & 640 \\
13 & 15 & 195 & 169 & 2535 \\
18 & 10 & 180 & 324 & 3240 \\
23 & 6 & 138 & 529 & 3174 \\
\hline & 48 & 614 & & 9652 \\
\hline
\end{array}
\)
Now, by formula (3), we have
\(
\begin{aligned}
\sigma & =\frac{1}{ N } \sqrt{ N \sum f_i x_i^2-\left(\sum f_i x_i\right)^2} \\
& =\frac{1}{48} \sqrt{48 \times 9652-(614)^2} \\
& =\frac{1}{48} \sqrt{463296-376996}
\end{aligned}
\)
\(
=\frac{1}{48} \times 293.77=6.12
\)
Therefore, \(\quad\) Standard deviation \((\sigma)=6.12\)
Shortcut method to find variance and standard deviation
Sometimes the values of \(x_{ i }\) in a discrete distribution or the mid points \(x_{ i }\) of different classes in a continuous distribution are large and so the calculation of mean and variance becomes tedious and time consuming. By using step-deviation method, it is possible to simplify the procedure.
Let the assumed mean be ‘A’ and the scale be reduced to \(\frac{1}{h}\) times ( \(h\) being the width of class-intervals). Let the step-deviations or the new values be \(y_i\).
Let the assumed mean be ‘A’ and the scale be reduced to \(\frac{1}{h}\) times ( \(h\) being the width of class-intervals). Let the step-deviations or the new values be \(y_i\).
\(
\text { i.e. } \quad y_i=\frac{x_i- A }{h} \text { or } x_i= A +h y_i \dots(1)
\)
We know that \(\bar{x}=\frac{\sum_{i=1}^n f_i x_i}{ N } \dots(2)\)
Replacing \(x_{ i }\) from (1) in (2), we get
\(
\begin{aligned}
\bar{x} & =\frac{\sum_{i=1}^n f_i\left( A +h y_i\right)}{ N } \\
& =\frac{1}{ N }\left(\sum_{i=1}^n f_i A +\sum_{i=1}^n h f_i y_i\right)=\frac{1}{ N }\left( A \sum_{i=1}^n f_i+h \sum_{i=1}^n f_i y_i\right) \\
& = A \cdot \frac{ N }{ N }+h \frac{\sum_{i=1}^n f_i y_i}{ N } \quad\left(\text { because } \sum_{i=1}^n f_i= N \right)
\end{aligned}
\)
Thus \(\quad \bar{x}= A +h \bar{y} \dots(3)\)
Now Variance of the variable \(x, \sigma_x^2=\frac{1}{ N } \sum_{i=1}^n f_i\left(x_i-\bar{x}\right)^2\)
\(
=\frac{1}{ N } \sum_{i=1}^n f_i\left( A +h y_i- A -h \bar{y}\right)^2 \quad \text { (Using (1) and (3)) }
\)
\(
\begin{aligned}
& =\frac{1}{ N } \sum_{i=1}^n f_i h^2\left(y_i-\bar{y}\right)^2 \\
& =\frac{h^2}{ N } \sum_{i=1}^n f_i\left(y_i-\bar{y}\right)^2=h^2 \times \text { variance of the variable } y_i
\end{aligned}
\)
\(
\begin{array}{ll}
\text { i.e. } & \sigma_x{ }^2=h^2 \sigma_y{ }^2 \\
\text { or } & \sigma_x=h \sigma_y \dots(4)
\end{array}
\)
From (3) and (4), we have
\(
\sigma_x=\frac{h}{ N } \sqrt{ N \sum_{i=1}^n f_i y_i^2-\left(\sum_{i=1}^n f_i y_i\right)^2} \dots(5)
\)
Example 12: Calculate mean, variance and standard deviation for the following distribution.
\(
\begin{array}{|l|c|c|c|c|c|c|c|}
\hline \text { Classes } & 30-40 & 40-50 & 50-60 & 60-70 & 70-80 & 80-90 & 90-100 \\
\hline \text { Frequency } & 3 & 7 & 12 & 15 & 8 & 3 & 2 \\
\hline
\end{array}
\)
Solution: Let the assumed mean \(A =65\). Here \(h=10\) We obtain the following Table below from the given data :
\(
\begin{array}{|l|c|c|c|c|c|c|}
\hline \text { Class } & \text { Frequency } & \text { Mid-point } & y_i=\frac{x_i-65}{10} & y_i^2 & f_i y_i & f_i y_i^2 \\
\hline & f_i & x_i & & & & \\
30-40 & 3 & 35 & -3 & 9 & -9 & 27 \\
40-50 & 7 & 45 & -2 & 4 & -14 & 28 \\
50-60 & 12 & 55 & -1 & 1 & -12 & 12 \\
60-70 & 15 & 65 & 0 & 0 & 0 & 0 \\
70-80 & 8 & 75 & 1 & 1 & 8 & 8 \\
80-90 & 3 & 85 & 2 & 4 & 6 & 12 \\
90-100 & 2 & 95 & 3 & 9 & 6 & 18 \\
\hline & N =50 & & & & -15 & 105 \\
\hline
\end{array}
\)
Therefore
\(
\bar{x}= A +\frac{\sum f_i y_i}{50} \times h=65-\frac{15}{50} \times 10=62
\)
Variance
\(
\begin{aligned}
\sigma^2 & =\frac{h^2}{ N ^2}\left[ N \Sigma f_i y_i^2-\left(\Sigma f_i y_i\right)^2\right] \\
& =\frac{(10)^2}{(50)^2}\left[50 \times 105-(-15)^2\right] \\
& =\frac{1}{25}[5250-225]=201
\end{aligned}
\)
and standard deviation \((\sigma)=\sqrt{201}=14.18\)
Example 13: The variance of 20 observations is 5 . If each observation is multiplied by 2 , find the new variance of the resulting observations.
Solution: Let the observations be \(x_1, x_2, \ldots, x_{20}\) and \(\bar{x}\) be their mean. Given that variance \(=5\) and \(n=20\). We know that
Variance \(\left(\sigma^2\right)=\frac{1}{n} \sum_{i=1}^{20}\left(x_i-\bar{x}\right)^2\), i.e., \(5=\frac{1}{20} \sum_{i=1}^{20}\left(x_i-\bar{x}\right)^2\)
\(
\text { or } \sum_{i=1}^{20}\left(x_i-\bar{x}\right)^2=100
\)
If each observation is multiplied by 2 , and the new resulting observations are \(y_{ i }\), then
\(
y_{ i }=2 x_{ i } \text { i.e., } x_{ i }=\frac{1}{2} y_i \dots(1)
\)
\(
\text { Therefore } \quad \bar{y}=\frac{1}{n} \sum_{i=1}^{20} y_i=\frac{1}{20} \sum_{i=1}^{20} 2 x_i=2 \cdot \frac{1}{20} \sum_{i=1}^{20} x_i
\)
i.e. \(\bar{y}=2 \bar{x} \quad \text { or } \quad \bar{x}=\frac{1}{2} \bar{y}\)
Substituting the values of \(x_i\) and \(\bar{x}\) in (1), we get
\(
\sum_{i=1}^{20}\left(\frac{1}{2} y_i-\frac{1}{2} \bar{y}\right)^2=100 \text {, i.e., } \sum_{i=1}^{20}\left(y_i-\bar{y}\right)^2=400
\)
Thus the variance of new observations \(=\frac{1}{20} \times 400=20=2^2 \times 5\)
Note: The reader may note that if each observation is multiplied by a constant \(k\), the variance of the resulting observations becomes \(k^2\) times the original variance.
Example 14: The mean of 5 observations is 4.4 and their variance is 8.24 . If three of the observations are 1,2 and 6 , find the other two observations.
Solution: Let the other two observations be \(x\) and \(y\).
Therefore, the series is \(1,2,6, x, y\).
Now \(\text { Mean } \bar{x}=4.4=\frac{1+2+6+x+y}{5}\)
or \(22=9+x+y\)
Therefore \(x+y=13 \dots(1)\)
\(
\text { Also } \quad \text { variance }=8.24=\frac{1}{n} \sum_{i=1}^5\left(x_i-\bar{x}\right)^2
\)
i.e. \(8.24=\frac{1}{5}\left[(3.4)^2+(2.4)^2+(1.6)^2+x^2+y^2-2 \times 4.4(x+y)+2 \times(4.4)^2\right]\)
or \(41.20=11.56+5.76+2.56+x^2+y^2-8.8 \times 13+38.72\)
Therefore \(\quad x^2+y^2=97 \dots(2)\)
But from (1), we have
\(
x^2+y^2+2 x y=169 \dots(3)
\)
From (2) and (3), we have
\(
2 x y=72 \dots(4)
\)
Subtracting (4) from (2), we get
\(
x^2+y^2-2 x y=97-72 \text { i.e. }(x-y)^2=25
\)
or \(x-y= \pm 5 \dots(5)\)
So, from (1) and (5), we get
\(
x=9, y=4 \text { when } x-y=5
\)
or \(\quad x=4, y=9\) when \(x-y=-5\)
Thus, the remaining observations are 4 and 9.
Example 15: If each of the observation \(x_1, x_2, \ldots, x_n\) is increased by ‘ \(a\) ‘, where \(a\) is a negative or positive number, show that the variance remains unchanged.
Solution: Let \(\bar{x}\) be the mean of \(x_1, x_2, \ldots, x_n\). Then the variance is given by
\(
\sigma_1^2=\frac{1}{n} \sum_{i=1}^n\left(x_i-\bar{x}\right)^2
\)
If ‘ \(a\) is added to each observation, the new observations will be
\(
y_i=x_{ i }+a \dots(1)
\)
Let the mean of the new observations be \(\bar{y}\). Then
\(
\begin{aligned}
\bar{y} & =\frac{1}{n} \sum_{i=1}^n y_i=\frac{1}{n} \sum_{i=1}^n\left(x_i+a\right) \\
& =\frac{1}{n}\left[\sum_{i=1}^n x_i+\sum_{i=1}^n a\right]=\frac{1}{n} \sum_{i=1}^n x_i+\frac{n a}{n}=\bar{x}+a
\end{aligned}
\)
i.e. \(\bar{y}=\bar{x}+a \dots(2)\)
Thus, the variance of the new observations
\(
\begin{aligned}
\sigma_2^2 & =\frac{1}{n} \sum_{i=1}^n\left(y_i-\bar{y}\right)^2=\frac{1}{n} \sum_{i=1}^n\left(x_i+a-\bar{x}-a\right)^2 \quad \text { [Using (1) and (2)] } \\
& =\frac{1}{n} \sum_{i=1}^n\left(x_i-\bar{x}\right)^2=\sigma_1^2
\end{aligned}
\)
Thus, the variance of the new observations is same as that of the original observations.
Note: We may note that adding (or subtracting) a positive number to (or from) each observation of a group does not affect the variance.
Example 16: The mean and standard deviation of 100 observations were calculated as 40 and 5.1 , respectively by a student who took by mistake 50 instead of 40 for one observation. What are the correct mean and standard deviation?
Solution: Given that number of observations \((n)=100\)
Incorrect mean \((\bar{x})=40\),
Incorrect standard deviation \((\sigma)=5.1\)
We know that \(\quad \bar{x}=\frac{1}{n} \sum_{i=1}^n x_i\)
i.e. \(40=\frac{1}{100} \sum_{i=1}^{100} x_i \quad \text { or } \quad \sum_{i=1}^{100} x_i=4000\)
\(
\begin{aligned}
& \text { i.e. } \quad \text { Incorrect sum of observations }=4000 \\
& \text { Thus the correct sum of observations }=\text { Incorrect sum }-50+40 \\
& =4000-50+40=3990 \\
&
\end{aligned}
\)
\(
\text { Hence } \quad \text { Correct mean }=\frac{\text { correct sum }}{100}=\frac{3990}{100}=39.9
\)
Also Standard deviation \(\sigma=\sqrt{\frac{1}{n} \sum_{i=1}^n x_i^2-\frac{1}{n^2}\left(\sum_{i=1}^n x_i\right)^2}\)
\(
=\sqrt{\frac{1}{n} \sum_{i=1}^n x_i^2-(\bar{x})^2}
\)
i.e. \(5.1=\sqrt{\frac{1}{100} \times \text { Incorrect } \sum_{i=1}^n x_i^2-(40)^2}\)
\(
\text { or } \quad 26.01=\frac{1}{100} \times \text { Incorrect } \sum_{i=1}^n x_i^2-1600
\)
Therefore \(\quad\) Incorrect \(\sum_{i=1}^n x_i^2=100(26.01+1600)=162601\)
Now
\(
\text { Correct } \begin{aligned}
\sum_{i=1}^n x_i^2 & =\text { Incorrect } \sum_{i=1}^n x_i^2-(50)^2+(40)^2 \\
& =162601-2500+1600=161701
\end{aligned}
\)
Therefore Correct standard deviation
\(
\begin{aligned}
& =\sqrt{\frac{\text { Correct } \sum x_i^2}{n}-(\text { Correct mean })^2} \\
& =\sqrt{\frac{161701}{100}-(39.9)^2} \\
& =\sqrt{1617.01-1592.01}=\sqrt{25}=5
\end{aligned}
\)