13.6 Entrance Corner (Limits)

CONCEPT OF LIMITS

Suppose \(f(x)\) is a real-valued function and \(c\) is a real number. The expression \(\lim _{x \rightarrow c} f(x)=L\) means that \(f(x)\) can be as close to \(L\) as desired by making \(x\) sufficiently close to \(c\). In such a case, we say that the limit of \(f\), as \(x\) approaches \(c\), is \(L\). Note that this statement is true even if \(f(c) \neq L\). Indeed, the function \(f(x)\) need not even be defined at \(c\). Two examples help illustrate this.

Example 1: Consider \(f(x)=\frac{x}{x^2+1}\) as \(x\) approaches 2 . In this case, \(f(x)\) is defined at 2, and it equals its limiting value 0.4.
\(
\begin{array}{|c|c|c|c|c|c|c|}
\hline f(1.9) & f(1.99) & f(1.999) & f(2) & f(2.001) & f(2.01) & \left.f(2.1)\right) \\
\hline 0.4121 & 0.4012 & 0.4001 & \Rightarrow \mathbf{0 . 4} \Leftarrow & 0.3998 & 0.3988 & 0.3882 \\
\hline
\end{array}
\)
As \(x\) approaches \(2, f(x)\) approaches 0.4 and hence we have \(\lim _{x \rightarrow 2} f(x)=0.4\). In the case where \(f(c)=\lim _{x \rightarrow c} f(x), f\) is said to be continuous at \(x=c\). But it is not always the case.

Example 2: Consider \(g(x)= \begin{cases}\frac{x}{x^2+1}, & \text { if } x \neq 2 \\ 0, & \text { if } x=2\end{cases}\)
This limit of \(g(x)\) as \(x\) approaches 2 is 0.4 (just as in \(f(x)\) ), but \(\lim _{x \rightarrow 2} g(x) \neq g(2): g\) is not continuous at \(x=2\). Or, consider the case where \(f(x)\) is undefined at \(x=c\).
\(f(x)=\frac{x-1}{\sqrt{x}-1}\), in this case as \(x\) approaches \(1, f(x)\) is undefined
\((0 / 0)\) at \(x=1\) but the limit equals 2.
\(
\begin{array}{|c|c|c|c|c|c|c|}
\hline f(0.9) & f(0.99) & f(0.999) & f(1.0) & f(1.001) & f(1.01) & f(1.1) \\
\hline 1.95 & 1.99 & 1999 & \text { undefined } & 2.001 & 2.010 & 2.10 \\
\hline
\end{array}
\)
Thus, \(f(x)\) can be made arbitrarily close to the limit of 2 just by making \(x\) sufficiently close to 1.

Formal Definition of Limit

Let \(f(x)\) be defined for all \(x \neq a\) over an open interval containing \(a\). Let \(L\) be a real number. Then
\(
\lim _{x \rightarrow a} f(x)=L
\)
if, for every \(\varepsilon>0\), there exists a \(\delta>0\), such that if \(0<|x-a|<\delta\), then \(|f(x)-L|<\varepsilon\).

Definition	Translation
1. For every \(\varepsilon>0\),	1. For every positive distance \(\varepsilon\) from \(L\),
2. there exists a \(\delta>0\),	2. There is a positive distance \(\delta\) from \(a\),
3. such that	3. such that
4. if \(0<|x-a|<\delta\), then \(|f(x)-L|<\varepsilon\).	4. if \(x\) is closer than \(\delta\) to \(a\) and \(x \neq a\), then \(f(x)\) is closer than \(\varepsilon\) to \(L\).

We can get a better handle on this definition by looking at the definition geometrically. Figure below shows possible values of \(\delta\) for various choices of \(\varepsilon>0\) for a given function \(f(x)\), a number \(a\), and a limit \(L\) at \(a\). Notice that as we choose smaller values of \(\varepsilon\) (the distance between the function and the limit), we can always find a \(\delta\) small enough so that if we have chosen an \(x\) value within \(\delta\) of \(a\), then the value of \(f(x)\) is within \(\varepsilon\) of the limit \(L\).

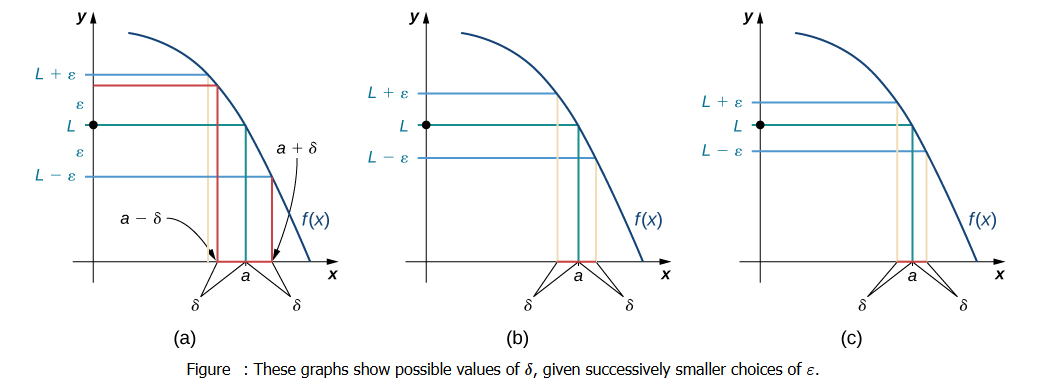
Left-Hand Limits

The left-hand limit of a function \(f(x)\) as \(x\) approaches a is denoted as:
\(
\lim _{x \rightarrow a^{-}} f(x)
\)
This means that x approaches a from the left (values smaller than a ).

The statement \(x \rightarrow a^{-}\)means that \(x\) is tending to a from the left hand side, i.e., \(x\) is a number less than a but very very close to \(a\). Therefore \(x \rightarrow a^{-}\)is equivalent to \(x=a-h\) where \(h>0\) such that \(h \rightarrow 0\). 

Thus, we have the following algorithms for finding left hand and right hand limits at \(x=a\).

ALGORITHM

• STEP-I: Write \(\lim _{x \rightarrow a^{-}} f(x)\)
• STEP-II: Put \(x=a-h\) and replace \(x \rightarrow a^{-}\)by \(h \rightarrow 0\) to obtain \(\lim _{h \rightarrow 0} f(a-h)\).
• STEP-III: Simplify \(\lim _{h \rightarrow 0} f(a-h)\) by using the formula for the given function.
• STEP-IV: The value obtain in step III is the LHL of \(f(x)\) at \(x=a\).

Example 1: Evaluate the left-hand limits of the function \(f(x)=\left\{\begin{array}{ll}\frac{|x-4|}{x-4}, & x \neq 4 \\ 0, & x=4\end{array}\right.\) at \(x=4\).

Solution:
\(
\begin{aligned}
& \text { L.H.L. of } f(x) \text { at } x=4 \\
& =\lim _{x \rightarrow 4^{-}} f(x) \\
& =\lim _{h \rightarrow 0} f(4-h) \\
& =\lim _{h \rightarrow 0} \frac{|4-h-4|}{4-h-4}=\lim _{h \rightarrow 0} \frac{|-h|}{-h} \\
& =\lim _{h \rightarrow 0} \frac{h}{-h}=\lim _{h \rightarrow 0}-1=-1 \\
\end{aligned}
\)

Right-Hand Limit

The right-hand limit of a function \(f(x)\) as \(x\) approaches a is denoted as:
\(
\lim _{x \rightarrow a^{+}} f(x)
\)
This means that x approaches a from the right (values larger than a ).

Similarly, for RHL \(x \rightarrow a^{+}\)is equivalent to \(x=a+h\) where \(h \rightarrow 0\).

To evaluate RHL of \(f(x)\) at \(x=a\) i.e., \(\lim f(x)\) we may use the \(x \rightarrow a^{+}\) following algorithm:

ALGORITHM

• STEP-I: Write \(\lim _{x \rightarrow a^{+}} f(x) .\)
• STEP-II: Put \(x=a+h\) and replace \(x \rightarrow a^{+}\)by \(h \rightarrow 0\) to obtain
  \(
  \lim _{h \rightarrow 0} f(a+h) .
  \)
• STEP-III: Simplify \(\lim _{h \rightarrow 0} f(a+h)\) by using the formula for the given function.
• STEP-IV: The value obtained in step III is the RHL of \(f(x)\) at \(x=a\).

Example 2: Evaluate the right-hand limits of the function \(f(x)=\left\{\begin{array}{ll}\frac{|x-4|}{x-4}, & x \neq 4 \\ 0, & x=4\end{array}\right.\) at \(x=4\).

Solution:
\(
\begin{aligned}
& \text { R.H.L. of } f(x) \text { at } x=4 \\
& =\lim _{x \rightarrow 4^{+}} f(x) \\
& =\lim _{h \rightarrow 0} f(4+h) \\
& =\lim _{h \rightarrow 0} \frac{|4+h-4|}{4+h-4} \\
& =\lim _{h \rightarrow 0} \frac{|h|}{h}=\lim _{h \rightarrow 0} \frac{h}{h}=\lim _{h \rightarrow 0} 1=1
\end{aligned}
\)

Existence of Limit

\(\lim _{x \rightarrow a} f(x)\) exists if \(\lim _{x \rightarrow a^{-}} f(x)\) and \(\lim _{x \rightarrow a^{+}} f(x)\) exists and both are equal.

Let’s consider an example for better understanding.
Consider the function: \(f(x)= \begin{cases}2 x+1 & \text { if } x<3 \\ x^2-4 & \text { if } x \geq 3\end{cases}\)
To find the one-sided limits at \(x=3 x=3 x=3\):
Left-hand limit: \(\lim _{x \rightarrow 3-} f(x)=2(3)+1=7\)
Right-hand limit: \(\lim _{x \rightarrow 3+} f(x)=3^2-4=5\)
Since the left-hand limit (7) and right-hand limit (5) are not equal, the limit does not exist at \(x=3\). However, the one-sided limits still exist separately.

Indeterminate Forms

If \(\lim _{x \rightarrow a} f(x)=\lim _{x \rightarrow a} g(x)=0\), then \(\lim _{x \rightarrow a} \frac{f(x)}{g(x)}\) takes the form \(\frac{0}{0}\) which seems to be undefined or meaningless. In fact, in many cases this limit exists and has a finite value. The determination of limit in such a case is traditionally referred to as the evaluation of the indeterminate form \(\frac{0}{0}\), though literally speaking nothing is indeterminate involved here. Sometimes \(\frac{0}{0}\) is referred to as undetermined form or illusory form.

Thus, \(\lim _{x \rightarrow a} \frac{f(x)}{g(x)}\) can take any real value or simply \(\lim _{x \rightarrow a} \frac{f(x)}{g(x)}\) cannot be determined by preliminary methods. Thus, this form is called indeterminate form.

Other Indeterminate Forms

• \(\frac{\infty_1}{\infty_2}=\frac{1 / \infty_2}{1 / \infty_1}=\frac{0}{0}\)
• \(0 \times \infty=\frac{0}{1 / \infty}=\frac{0}{0}\)
• \(y=0^0 \Rightarrow \log y=\log \left(0^0\right) \Rightarrow 0 \times \log (0)=0 \times \infty\)
• \(y=\infty^0 \Rightarrow \log y=\log \left(\infty^0\right) \Rightarrow 0 \times \log (\infty)=0 \times \infty\)
• \(y=1^{\infty} \Rightarrow \log y=\log \left(1^{\infty}\right) \Rightarrow \infty \times \log (1)=\infty \times 0\)
• \(\infty_1-\infty_2\) is also an indeterminate form as the \(\infty_1\) and \(\infty_2\) does not necessarily approach to the same infinity.

Example 3: Evaluate the left- and the right-hand limits of the function defined by \(f(x)=\left\{\begin{array}{l}1+x^2, \text { if } 0 \leq x<1 \\ 2-x, \text { if } x>1\end{array}\right.\) at \(x=1\). Also, show that \(\lim _{x \rightarrow 1} f(x)\) does not exist.

Solution:
\(
\begin{aligned}
& \text { L.H.L. of } f(x) \text { at } x=1 \\
& =\lim _{x \rightarrow 1^{-}} f(x)=\lim _{h \rightarrow 0} f(1-h) \\
& =\lim _{h \rightarrow 0}\left(1+(1-h)^2\right)=\lim _{h \rightarrow 0}\left(2-2 h+h^2\right)=2
\end{aligned}
\)
R.H.L. of \(f(x)\) at \(x=1\)
\(
\begin{aligned}
& =\lim _{x \rightarrow 1^{+}} f(x)=\lim _{h \rightarrow 0} f(1+h) \\
& =\lim _{h \rightarrow 0}[2-(1+h)]=\lim _{h \rightarrow 0}(1-h)=1
\end{aligned}
\)
Clearly, \(\lim _{x \rightarrow 1^{-}} f(x) \neq \lim _{x \rightarrow 1^{+}} f(x)\)
So, \(\lim _{x \rightarrow 1} f(x)\) does not exist.

Example 4: Let \(f(x)=\left\{\begin{array}{l}\cos x, \text { if } x \geq 0 \\ x+k, \text { if } x<0\end{array}\right.\). Find the value of constant \(k\), given that \(\lim _{x \rightarrow 0} f(x)\) exists.

Solution:
\(
\begin{aligned}
& \lim _{x \rightarrow 0} f(x) \text { exists } \\
& \Rightarrow \lim _{x \rightarrow 0^{-}} f(x)=\lim _{x \rightarrow 0^{+}} f(x) \\
& \Rightarrow \lim _{x \rightarrow 0} x+k=\lim _{x \rightarrow 0} \cos x \\
& \Rightarrow 0+k=\cos 0 \\
& \Rightarrow k=1 .
\end{aligned}
\)

Example 5: \(\lim _{x \rightarrow 0} \frac{e^{1 / x}-1}{e^{1 / x}+1} \text {, is }\)

Solution: Let \(\quad f(x)=\frac{e^{1 / x}-1}{e^{1 / x}+1}\). Then,
\(
=\lim _{x \rightarrow 0^{-}} f(x)=\lim _{h \rightarrow 0} f(0-h)=\lim _{h \rightarrow 0} \frac{e^{-1 / h}-1}{e^{-1 / h}+1}
\)
\(
=\lim _{h \rightarrow 0}\left(\frac{\frac{1}{e^{1 / h}}-1}{\frac{1}{e^{1 / h}}+1}\right)=-1 \quad\left[e^{1 / h} \rightarrow \infty \Rightarrow \frac{1}{e^{1 / h}} \rightarrow 0\right]
\)
and, [RHL of \(f(x)\) at \(x=0\) ]
\(
=\lim _{x \rightarrow 0^{+}} f(x)=\lim _{h \rightarrow 0} f(0+h)=\lim _{h \rightarrow 0} \frac{e^{1 / h}-1}{e^{1 / h}+1}
\)
\(
\begin{aligned}
&=\lim _{h \rightarrow 0}\left(\frac{1-\frac{1}{e^{1 / h}}}{1+e^{1 / h}}\right)\\
&\text { [Dividing } N r \text { and } D r \text { by } e^{1 / h} \text { ] }
\end{aligned}
\)
\(
=\frac{1-0}{1+0}=1
\)
Clearly, \(\lim _{x \rightarrow 0^{-}} f(x) \neq \lim _{x \rightarrow 0^{+}} f(x) .\)
Hence, \(\lim _{x \rightarrow 0} f(x)\) does not exist.

Example 6: Consider the following graph of the function \(y=f(x)\). Which of the following is/are correct?

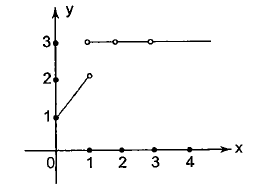
a. \(\lim _{x \rightarrow 1} f(x)\) does not exist
b. \(\lim _{x \rightarrow 2} f(x)\) does not exist
c. \(\lim _{x \rightarrow 3} f(x)=3\)
d. \(\lim _{x \rightarrow 1.99} f(x)\) exists

Solution: a. \(\lim _{x \rightarrow 1^{+}} f(x)=3\) and \(\lim _{x \rightarrow 1^{-}} f(x)=2\). Thus, \(\lim _{x \rightarrow 1} f(x)\) does not exist.
b. \(\lim _{x \rightarrow 2^{+}} f(x)=\lim _{x \rightarrow 2^{-}} f(x)=3\). Thus, \(\lim _{x \rightarrow 2} f(x)\) exist.
c. \(\lim _{x \rightarrow 3^{+}} f(x)=\lim _{x \rightarrow 3^{-}} f(x)=3\). Thus, \(\lim _{x \rightarrow 3} f(x)\) exist.
d. \(\lim _{x \rightarrow 1.99^{+}} f(x)=\lim _{x \rightarrow 1.99^{-}} f(x)=3\). Thus, \(\lim _{x \rightarrow 1.99} f(x)\) exist.

ALGEBRA OF LIMITS

Let \(\lim _{x \rightarrow a} f(x)=\ell\) and \(\lim _{x \rightarrow a} g(x)=m\). If \(\ell\) and \(m\) exist, then

• \(\lim _{x \rightarrow a}(f \pm g)(x)=\lim _{x \rightarrow a} f(x) \pm \lim _{x \rightarrow a} g(x)=\ell \pm m\)
• \(\lim _{x \rightarrow a}(f g)(x)=\lim _{x \rightarrow a} f(x) \lim _{x \rightarrow a} g(x)=\ell m\)
• \(\lim _{x \rightarrow a}\left(\frac{f}{g}\right)(x)=\frac{\lim _{x \rightarrow a} f(x)}{\lim _{x \rightarrow a} g(x)}=\frac{\ell}{m}\), provided \(m \neq 0\)
• \(\lim _{x \rightarrow a} k f(x)=k\). \(\lim _{x \rightarrow a} f(x)\), where \(k\) is constant
• \(\lim _{x \rightarrow a}|f(x)|=\left|\lim _{x \rightarrow a} f(x)\right|=|\ell|\)
• \(\lim _{x \rightarrow a}(f(x))^{g(x)}=\lim _{x \rightarrow a} f(x)^{\lim _{x \rightarrow a} g(x)}=\ell^m\)
• \(\lim _{x \rightarrow a} f \circ g(x)=f\left(\lim _{x \rightarrow a} g(x)\right)=f(m)\), only if \(f\) is continuous at \(g(x)=m\)
  In particular,
  a. \(\lim _{x \rightarrow a} \log f(x)=\log \left(\lim _{x \rightarrow a} f(x)\right)=\log \ell\)
  b. \(\lim _{x \rightarrow a} e^{f(x)}=e^{\lim _{x \rightarrow a} f(x)}=e^{\ell}\)
• If \(\lim _{x \rightarrow a} f(x)=+\infty\) or \(-\infty\), then \(\lim _{x \rightarrow a} \frac{1}{f(x)}=0\).
• If \(f(x) \leq g(x)\) for every \(x\) in the NBD of \(a\), then \(\lim _{x \rightarrow a} f(x) \leq \lim _{x \rightarrow a} g(x)\).

Example 7: Let \(f(x)=\left\{\begin{array}{l}x+1, x>0 \\ 2-x, x \leq 0\end{array}\right.\) and
\(
g(x)= \begin{cases}x+3, & x<1 \\ x^2-2 x-2, & 1 \leq x<2 \\ x-5, & x \geq 2\end{cases}
\)
find L.H.L. and R.H.L. of \(g(f(x))\) at \(x=0\) and hence find \(\lim _{x \rightarrow 0} g f(x)\).

Solution:
\(
\begin{aligned}
&\begin{aligned}
& \text { As } x \rightarrow 0^{-} \Rightarrow f(x) \rightarrow f\left(0^{-}\right)=2^{+} \\
& \Rightarrow \lim _{x \rightarrow 0^{-}} g(f(x))=g\left(2^{+}\right)=-3 \\
& \text { Also as } x \rightarrow 0^{+} \Rightarrow f(x) \rightarrow f\left(0^{+}\right)=1^{+} \\
& \Rightarrow \lim _{x \rightarrow 0^{+}} g(f(x))=g\left(1^{+}\right)=-3
\end{aligned}\\
&\text { Hence, } \lim _{x \rightarrow 0} g(f(x)) \text { exists and is equal to }-3\\
&\Rightarrow \lim _{x \rightarrow 0} g(f(x))=-3
\end{aligned}
\)

Sandwich Theorem for Evaluating Limits

If \(h(x) \leq g(x) \leq f(x)\) when \({x}\) is near \(a\), except possibly at \(a\), and \(\lim _{x \rightarrow a} f(x)=\lim _{x \rightarrow a} h(x)=L\), then \(\lim _{x \rightarrow a} g(x)=L\).

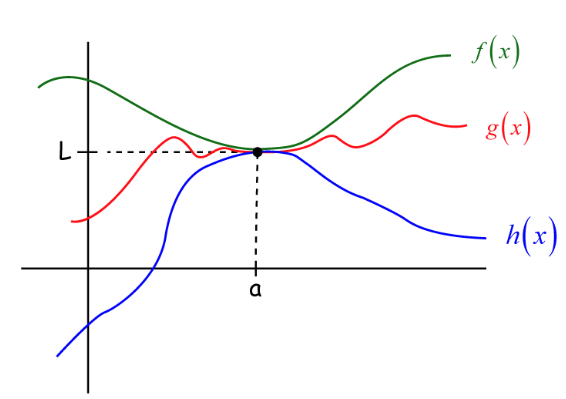
All this says is that if \(g(x)\) is squeezed between \(f(x)\) and \(h(x)\) near \(a\), and if \(f(x)\) and \(h(x)\) have the same limit \(L\) at \(a\), then \({g}({x})\) is trapped and will be forced to have the same limit \(L\) at \(a\) also. Below is an illustration of the sandwitch theorem.

\(
\begin{aligned}
&\text { Using the Squeeze Theorem, show that } \lim _{t \rightarrow 0}\left(t^2 \sin \frac{1}{t}\right)=0\\
&\begin{gathered}
-1 \leq \sin \frac{1}{t} \leq 1 \\
-t^2 \leq t^2 \sin \frac{1}{t} \leq t^2 \\
\lim _{t \rightarrow 0}\left(-t^2\right)=0 \text { and } \lim _{t \rightarrow 0}\left(t^2\right)=0 \\
\text { Therefore, } \lim _{t \rightarrow 0}\left(t^2 \sin \frac{1}{t}\right)=0
\end{gathered}
\end{aligned}
\)

Example 8: Evaluate \(\lim _{x \rightarrow \infty} \frac{x+7 \sin x}{-2 x+13}\) using sandwich theorem.

Solution: We know that \(-1 \leq \sin x \leq 1\) for all \(x\).
\(
\begin{aligned}
& \Rightarrow-7 \leq 7 \sin x \leq 7 \\
& \Rightarrow x-7 \leq x+7 \sin x \leq x+7
\end{aligned}
\)
Dividing throughout by \(-2 x+13\), we get
\(\frac{x-7}{-2 x+13} \geq \frac{x+7 \sin x}{-2 x+13} \geq \frac{x+7}{-2 x+13}\) for all \(x\) that are large.
Now,
\(
\begin{aligned}
& \lim _{x \rightarrow \infty} \frac{x-7}{-2 x+13}=\lim _{x \rightarrow \infty} \frac{1-\frac{7}{x}}{-2+\frac{13}{x}}=\frac{1-0}{-2+0}=-\frac{1}{2} \\
& \lim _{x \rightarrow \infty} \frac{x+7}{-2 x+13}=\lim _{x \rightarrow \infty} \frac{1+\frac{7}{x}}{-2+\frac{13}{x}}=\frac{1+0}{-2+0}=-\frac{1}{2}
\end{aligned}
\)

Example 9: If [.] denotes the greatest integer function, then find the value of \(\lim _{n \rightarrow \infty} \frac{[x]+[2 x]+\cdots+[n x]}{n^2}\).

Solution: For any integer \(k\), we have
\(k x-1<[k x] \leq k x\)
\(
\begin{aligned}
& \sum_{k=1}^n(k x-1)<\sum_{k=1}^n[k x] \leq \sum_{k=1}^n k x \\
& \frac{1}{n^2} \sum_{k=1}^n(k x-1)<\frac{1}{n^2} \sum_{k=1}^n[k x] \leq \frac{1}{n^2} \sum_{k=1}^n k x \\
& \frac{x}{n^2} \sum_{k=1}^n k-\frac{1}{n^2}<\frac{1}{n^2} \sum_{k=1}^n[k x] \leq \frac{x}{n^2} \sum_{k=1}^n k \\
& \frac{x}{2}\left(1+\frac{1}{n}\right)-\frac{1}{n^2}<\frac{1}{n^2} \sum_{k=1}^n[k x] \leq \frac{x}{2}\left(1+\frac{1}{n}\right)
\end{aligned}
\)
Now, \(\lim _{n \rightarrow \infty}\left\{\frac{x}{2}\left(1+\frac{1}{n}\right)-\frac{1}{n^2}\right\}=\frac{x}{2} \text { and, } \lim _{n \rightarrow \infty} \frac{x}{2}\left(1+\frac{1}{n}\right)=\frac{x}{2}\)
\(
\therefore \quad \lim _{n \rightarrow \infty} \frac{1}{n^2} \sum_{k=1}^n[k x]=\frac{x}{2} [\text { Using Sandwich Theorem }]
\)
\(
\text { i.e. } \quad \lim _{n \rightarrow \infty} \frac{[x]+[2 x]+[3 x]+\ldots+[n x]}{n^2}=\frac{x}{2}
\)

Example 10: Suppose that \(f\) is a function that \(2 x^2 \leq f(x) \leq x\left(x^2\right. +1)\) for all \(x\) that are near to 1 but not equal to 1. Show that this fact contains enough information for us to find \(\lim _{x \rightarrow 1} f(x)\). Also find this limit.

Solution: We see that \(\lim _{x \rightarrow 1} 2 x^2=2(1)^2=2\) and \(\lim _{x \rightarrow 1} x\left(x^2+1\right)=1\left(1^2+1\right)=2\)
This is enough for us to find \(\lim _{x \rightarrow 1} f(x)\).
Indeed, it follows from the Sandwich Theorem that \(\lim _{x \rightarrow 1} f(x)=2\).

Example 11: Evaluate \(\lim _{n \rightarrow \infty} \frac{1}{1+n^2}+\frac{2}{2+n^2}+\cdots+\frac{n}{n+n^2}\).

Solution: \(P_n=\frac{1}{1+n^2}+\frac{2}{2+n^2}+\cdots+\frac{n}{n+n^2}\)
\(
\begin{aligned}
&\text { Now, }\\
&\begin{aligned}
& P_n<\frac{1}{1+n^2}+\frac{2}{1+n^2}+\cdots+\frac{n}{1+n^2} \\
& =\frac{1}{1+n^2}(1+2+3+\cdots+n)
\end{aligned}
\end{aligned}
\)
\(
=\frac{n(n+1)}{2\left(1+n^2\right)}
\)
Also, \(\begin{aligned} P_n & >\frac{1}{n+n^2}+\frac{2}{n+n^2}+\frac{3}{n+n^2}+\cdots+\frac{n}{n+n^2} \\ & =\frac{n(n+1)}{2\left(n+n^2\right)}\end{aligned}\)
Thus, \(\frac{n(n+1)}{2\left(n+n^2\right)}<P_n<\frac{n(n+1)}{2\left(1+n^2\right)}\)
\(
\begin{aligned}
& \Rightarrow \lim _{n \rightarrow \infty} \frac{n(n+1)}{2\left(n+n^2\right)}<\lim _{n \rightarrow \infty} P_n<\lim _{n \rightarrow \infty} \frac{n(n+1)}{2\left(1+n^2\right)} \\
& \Rightarrow \lim _{n \rightarrow \infty} \frac{1\left(1+\frac{1}{n}\right)}{2\left(\frac{1}{n}+1\right)}<\lim _{n \rightarrow \infty} P_n<\lim _{n \rightarrow \infty} \frac{1\left(1+\frac{1}{n}\right)}{2\left(\frac{1}{n^2}+1\right)} \\
& \Rightarrow \frac{1}{2}<\lim _{n \rightarrow \infty} P_n<\frac{1}{2} \\
& \Rightarrow \lim _{n \rightarrow \infty} P_n=\frac{1}{2}
\end{aligned}
\)

Example 12: \(\lim _{x \rightarrow \infty} \frac{[x]}{x}\), where [.] represents greatest integer function.

Solution: When \(x\) becomes very large, \(x-1\) is very close to \(x\). The value of \([x]\) is also very close to \(x\).
For any real number x , we can write the inequality: \(x-1<[x] \leq x\)
\(
\frac{x-1}{x}<\frac{[x]}{x} \leq \frac{x}{x}
\)
\(
1-\frac{1}{x}<\frac{[x]}{x} \leq 1
\)
As \(x \rightarrow \infty\), the term \(\frac{1}{x}\) approaches 0.
Therefore, the left-hand limit \(1-\frac{1}{x}\) approaches \(1-0=1\).
The right-hand limit is simply 1.
Applying the Squeeze theorem, Since the expression \(\frac{[x]}{x}\) is squeezed between two functions that both approach 1 as \(x \rightarrow \infty\), the limit of \(\frac{[x]}{x}\) as \(x \rightarrow \infty\) must also be 1.
Therefore, \(\lim _{x \rightarrow \infty} \frac{[x]}{x}=1\).

Example 13: \(\lim _{x \rightarrow \infty} \cdot \frac{\log _e x}{x}\)

Solution: \(\text { Identify the limit: } L=\lim _{x \rightarrow \infty} \frac{\log x}{x} \text {. }\)
Apply L’Hôpital’s Rule: Take the derivative of the numerator and the denominator. The derivative of \(\log x\) is \(\frac{1}{x}\) and the derivative of \(x\) is 1.
Now the limit becomes: \(L=\lim _{x \rightarrow \infty} \frac{\frac{1}{2}}{1}=\lim _{x \rightarrow \infty} \frac{1}{x}\).
Evaluate the limit: As \(x\) approaches infinity, \(\frac{1}{x}\) approaches O . Therefore, \(L=0\).

USE OF EXPANSIONS IN EVALUATING LIMITS

Some Important Expansions

Sometimes, following expansions are useful in evaluating limits. Students are advised to learn these expansions.

• \(\log (1+x)=x-\frac{x^2}{2}+\frac{x^3}{3}-\frac{x^4}{4}+\frac{x^5}{5} \cdots(-1<x \leq 1)\)
• \(\log (1-x)=-x-\frac{x^2}{2}-\frac{x^3}{3}-\frac{x^4}{4}-\frac{x^5}{5} \cdots(-1<x \leq 1)\)
• \(e^x=1+x+\frac{x^2}{2!}+\frac{x^3}{3!}+\frac{x^4}{4!} \cdots\)
• \(e^{-x}=1-x+\frac{x^2}{2!}-\frac{x^3}{3!}+\frac{x^4}{4!} \cdots\)
• \(a^x=1+x\left(\log _e a\right)+\frac{x^2}{2!}\left(\log _e a\right)^2+\cdots\)
• \(\sin x=x-\frac{x^3}{3!}+\frac{x^5}{5!}-\frac{x^7}{7!} \ldots\)
• \(\cos x=1-\frac{x^2}{2!}+\frac{x^4}{4!}-\frac{x^6}{6!} \cdots\)
• \(\tan x=x+\frac{x^3}{3}+\frac{2}{15} x^5+\cdots\)

Example 14: Evaluate \(\lim _{x \rightarrow 0} \frac{\sin x-x}{x^3}\)

Solution: \(\lim _{x \rightarrow 0} \frac{\sin x-x}{x^3} \quad\left(\frac{0}{0} \text { form }\right)\)
\(
\begin{aligned}
& =\lim _{x \rightarrow 0} \frac{\left(x-\frac{x^3}{3!}+\frac{x^5}{5!}-\cdots\right)-x}{x^3} \\
& =\lim _{x \rightarrow 0}\left[-\frac{1}{3!}+\frac{x^2}{5!}-\cdots\right]=\frac{-1}{3!}=\frac{-1}{6}
\end{aligned}
\)

Example 15: Evaluate \(\lim _{x \rightarrow 0} \frac{5 \sin x-7 \sin 2 x+3 \sin 3 x}{x^2 \sin x}\).

Solution: \(\lim _{x \rightarrow 0} \frac{5 \sin x-7 \sin 2 x+3 \sin 3 x}{x^2 \sin x}\)
\(
=\lim _{x \rightarrow 0} \frac{5\left(x-\frac{x^3}{3!}+\cdots\right)-7\left(2 x-\frac{(2 x)^3}{3!}+\cdots\right)+3\left(3 x-\frac{(3 x)^3}{3!}+\cdots\right)}{x^2\left(x-\frac{x^3}{3!}+\cdots\right)}
\)
\(
\begin{aligned}
& =\lim _{x \rightarrow 0} \frac{-\frac{5 x^3}{3!}+\frac{56 x^3}{3!}-\frac{81 x^3}{3!}}{x^3\left(1-\frac{x^2}{3!}+\cdots\right)} \\
& =\frac{-5+56-81}{3!}=-5
\end{aligned}
\)

Example 16: Evaluate \(\lim _{x \rightarrow 0} \frac{(1+x)^{1 / x}-e+\frac{1}{2} e x}{x^2}\).

Solution:
\(
\begin{aligned}
(1+x)^{1 / x} & =e^{\frac{1}{x} \log (1+x)}=e^{\frac{1}{x}\left(x-\frac{x^2}{2}+\frac{x^3}{3}-\cdots\right)} \\
& =e^{1-\frac{x}{2}+\frac{x^2}{3}-\cdots}=e \cdot e^{-\frac{x}{2}+\frac{x^2}{3}-\cdots}
\end{aligned}
\)
\(
\begin{aligned}
& =e\left[1+\left(-\frac{x}{2}+\frac{x^2}{3}-\cdots\right)+\frac{1}{2!}\left(-\frac{x}{2}+\frac{x^2}{3} \cdots\right)^2+\cdots\right] \\
& =e\left[1-\frac{x}{2}+\frac{11}{24} x^2-\cdots\right]
\end{aligned}
\)
Hence, \(\lim _{x \rightarrow 0} \frac{(1+x)^{1 / x}-\dot{e}+\frac{1}{2} e x}{x^2}=\frac{11 e}{24}\)

Example 17: \(\lim _{x \rightarrow 0}\left(\frac{\sin x-x+\frac{x^3}{6}}{x^5}\right)\)

Solution: \(\lim _{x \rightarrow 0} \frac{\left(x-\frac{x^3}{3!}+\frac{x^5}{5!}-\frac{x^7}{7!}+\ldots\right)-x+\frac{x^3}{6}}{x^5}\)
\(
\begin{aligned}
& \lim _{x \rightarrow 0} \frac{x-\frac{x^3}{6}+\frac{x^5}{120}-\frac{x^7}{5040}+\ldots-x+\frac{x^3}{6}}{x^5} \\
& \lim _{x \rightarrow 0} \frac{\frac{x^5}{120}-\frac{x^7}{5040}+\ldots}{x^5}
\end{aligned}
\)
Divide each term in the numerator by \(x^5\) :
\(
\lim _{x \rightarrow 0}\left(\frac{1}{120}-\frac{x^2}{5040}+\ldots\right)
\)
As x approaches 0 , all terms with \(x\) in them will approach 0:
\(
\lim _{x \rightarrow 0}\left(\frac{1}{120}-\frac{x^2}{5040}+\ldots\right)=\frac{1}{120}
\)

Example 18: \(\lim _{x \rightarrow 0} \frac{\sin x+\log (1-x)}{x^2}\)

Solution:
\(
\lim _{x \rightarrow 0} \frac{\sin x+\log (1-x)}{x^2} \left[\frac{0}{0} \text { form }\right]
\)
Using L Hospital’s rule, we get
\(
\lim _{x \rightarrow 0} \frac{\cos x+\frac{1}{1-x}[0-1]}{2 x} \left[\frac{0}{0} \text { form }\right]
\)
Again Using L Hospital’s rule, we get
\(
\lim _{x \rightarrow 0} \frac{-\sin x-\frac{1}{(1-x^2)^2}}{2(x)}=-\frac{1}{2}
\)

Example 19: \(\lim _{x \rightarrow 0} \frac{e^x-1-x}{x^2}\)

Solution: \(e^x=1+x+\frac{x^2}{2!}+\frac{x^3}{3!}+\frac{x^4}{4!}+\ldots\)
\(
\lim _{x \rightarrow 0} \frac{\left(1+x+\frac{x^2}{2!}+\frac{x^3}{3!}+\ldots\right)-1-x}{x^2}
\)
Divide every term in the numerator by \({x}^2\) :
\(
\lim _{x \rightarrow 0}\left(\frac{1}{2!}+\frac{x}{3!}+\frac{x^2}{4!}+\ldots\right)
\)
Now, evaluate the limit by substituting \({x}={0}\) :
\(
\frac{1}{2!}+\frac{0}{3!}+\frac{0^2}{4!}+\ldots=\frac{1}{2}+0+0+\ldots=\frac{1}{2}
\)

EVALUATION OF ALGEBRAIC LIMITS

Direct Substitution Method

Consider the following limits: (i) \(\lim _{x \rightarrow a} f(x) \quad\) (ii) \(\lim _{x \rightarrow a} \frac{\Phi(x)}{\Psi(x)}\)
If \(f(a)\) and \(\frac{\Phi(a)}{\Psi(a)}\) exist and are fixed real numbers and
\(\Psi(a) \neq 0\) then we say that \(\lim _{x \rightarrow a} f(x)=f(a)\) and
\(
\lim _{x \rightarrow a} \frac{\Phi(x)}{\Psi(x)}=\frac{\Phi(a)}{\Psi(a)}
\)

In other words, if the direct substitution of the point to which the variable tends to, we obtain a fixed real number, then the number obtained is the limit of the function. In fact, if the point to which the variable tends to is a point in the domain of the function, then the value of the function at that point is its limit.

Following examples will illustrate the above method:
1. \(\lim _{x \rightarrow 1}\left(3 x^2+4 x+5\right)=3(1)^2+4(1)+5=12\)
2. \(\lim _{x \rightarrow 2} \frac{x^2-4}{x+3}=\frac{4-4}{2+3}=\frac{0}{5}=0\)

Factorization Method

Consider \(\lim _{x \rightarrow a} \frac{f(x)}{g(x)}\).
If by substituting \(x=a, \frac{f(x)}{g(x)}\) reduces to the form \(\frac{0}{0}\), then \((x-a)\) is a factor of both \(f(x)\) and \(g(x)\). So, we first factorize \(f(x)\) and \(g(x)\) and then cancel out the common factor to evaluate the limit. After cancelling out the common factor \((x-a)\), we again put \(x=a\) in the given expression and see whether we get a meaningful number or not. This process is repeated till we get a meaningful number.

Example 20: Evaluate \(\lim _{x \rightarrow 2} \frac{x^2-5 x+6}{x^2-4}\).

Solution: When \(x=2\), the expression \(\frac{x^2-5 x+6}{x^2-4}\) assumes the indeterminate form \(\frac{0}{0}\). Here, ( \(x-2\) ) is a common factor in numerator and denominator. Factorizing the numerator and denominator, we have
\(
\begin{aligned}
& \lim _{x \rightarrow 2} \frac{x^2-5 x+6}{x^2-4}=\lim _{x \rightarrow 2} \frac{(x-2)(x-3)}{(x+2)(x-2)} \\
= & \lim _{x \rightarrow 2} \frac{x-3}{x+2}=\frac{2-3}{2+2}=-\frac{1}{4}
\end{aligned}
\)

Example 21: Evaluate \(\lim _{x \rightarrow 1}\left(\frac{2}{1-x^2}+\frac{1}{x-1}\right)\)

Solution: We have
\(
\begin{gathered}
\lim _{x \rightarrow 1}\left(\frac{2}{1-x^2}+\frac{1}{x-1}\right)(\infty-\infty \text { form }) \\
=\lim _{x \rightarrow 1}\left(\frac{2}{1-x^2}-\frac{1}{1-x}\right)
\end{gathered}
\)
When \(x=1\), the expression \(\frac{2}{1-x^2}-\frac{1}{1-x}\) assumes the form \(\infty-\infty\), so we need some simplification to express it in the form \(\frac{0}{0}\).
Then,
\(
\lim _{x \rightarrow 1}\left(\frac{2}{1-x^2}-\frac{1}{1-x}\right)=\lim _{x \rightarrow 1} \frac{2-(1+x)}{1-x^2}=\lim _{x \rightarrow 1} \frac{1-x}{1-x^2}=\lim _{x \rightarrow 1} \frac{1}{1+x}=\frac{1}{2}
\)

Example 22: Evaluate \(\lim _{x \rightarrow 1} \frac{x^2+x \log _e x-\log _e x-1}{\left(x^2-1\right)}\)

Solution:
\(
\begin{aligned}
& \lim _{x \rightarrow 1} \frac{x^2+x \log _e x-\log _e x-1}{\left(x^2-1\right)}\left(\frac{0}{0} \text { form }\right) \\
& =\lim _{x \rightarrow 1} \frac{(x-1)\left(\log _e x+x+1\right)}{(x+1)(x-1)}\left(\frac{0}{0} \text { form }\right) \\
& =\lim _{x \rightarrow 1} \frac{\log _e x+x+1}{(x+1)}
\end{aligned}
\)
\(
=\frac{\log _e 1+1+1}{1+1}=\frac{0+2}{2}=1
\)

Example 23: Evaluate \(\lim _{x \rightarrow \frac{\pi}{4}} \frac{1-\sin 2 x}{1+\cos 4 x}\).

Solution:
\(
\begin{aligned}
& \lim _{x \rightarrow \frac{\pi}{4}} \frac{1-\sin 2 x}{1+\cos 4 x}\left(\frac{0}{0} \text { form }\right) \\
& =\lim _{x \rightarrow \frac{\pi}{4}} \frac{(\sin x-\cos x)^2}{2 \cos ^2 2 x}\left(\frac{0}{0} \text { form }\right) \\
& =\lim _{x \rightarrow \frac{\pi}{4}} \frac{(\sin x-\cos x)^2}{2\left(\cos ^2 x-\sin ^2 x\right)^2} \quad\left(\frac{0}{0} \text { form }\right) \\
& =\lim _{x \rightarrow \frac{\pi}{4}} \frac{1}{2(\cos x+\sin x)^2}=\frac{1}{4}
\end{aligned}
\)

Rationalization Method

This is particularly used when either the numerator or the denominator or both involved expressions consist of squares roots and on substituting the value of \(x\) the rational expression takes the form \(\frac{0}{0}, \frac{\infty}{\infty}\). Following examples illustrate the procedure.

Example 24: Evaluate \(\lim _{x \rightarrow 0} \frac{\sqrt{2+x}-\sqrt{2}}{x}\).

Solution: When \(x=0\), the expression \(\frac{\sqrt{2+x}-\sqrt{2}}{x}\) takes the form \(\frac{0}{0}\). Rationalizing the numerator, we have
\(
\begin{aligned}
& \lim _{x \rightarrow 0} \frac{\sqrt{2+x}-\sqrt{2}}{x} \\
& =\lim _{x \rightarrow 0} \frac{(\sqrt{2+x}-\sqrt{2})(\sqrt{2+x}+\sqrt{2})}{x(\sqrt{2+x}+\sqrt{2})} \\
& =\lim _{x \rightarrow 0} \frac{2+x-2}{x(\sqrt{2+x}+\sqrt{2})} \\
& =\lim _{x \rightarrow 0} \frac{1}{\sqrt{2+x}+\sqrt{2}}=\frac{1}{2 \sqrt{2}}
\end{aligned}
\)

Example 25: Evaluate \(\lim _{x \rightarrow a} \frac{\sqrt{a+2 x}-\sqrt{3 x}}{\sqrt{3 a+x}-2 \sqrt{x}}\).

Solution:
\(
\lim _{x \rightarrow a} \frac{\sqrt{a+2 x}-\sqrt{3 x}}{\sqrt{3 a+x}-2 \sqrt{x}} \quad\left(\text { form } \frac{0}{0}\right)
\)
\(
=\lim _{x \rightarrow a} \frac{(\sqrt{a+2 x}-\sqrt{3 x})(\sqrt{a+2 x}+\sqrt{3 x})}{(\sqrt{3 a+x}-2 \sqrt{x})(\sqrt{3 a+x}+2 \sqrt{x})} \frac{(\sqrt{3 a+x}+2 \sqrt{x})}{(\sqrt{a+2 x}+\sqrt{3 x})}\left(\text { form } \frac{0}{0}\right)
\)
\(
\begin{aligned}
& =\lim _{x \rightarrow a} \frac{(a+2 x-3 x)}{(3 a+x-4 x)} \frac{(\sqrt{3 a+x}+2 \sqrt{x})}{(\sqrt{a+2 x}+\sqrt{3 x})} \\
& =\lim _{x \rightarrow a} \frac{\sqrt{3 a+x}+2 \sqrt{x}}{3(\sqrt{a+2 x}+\sqrt{3 x})} \\
& =\frac{\sqrt{3 a+a}+2 \sqrt{a}}{3(\sqrt{a+2 a}+\sqrt{3 a})}=\frac{1}{3} \times \frac{4 \sqrt{a}}{2 \sqrt{3 a}}=\frac{2}{3 \sqrt{3}}
\end{aligned}
\)

Evaluation of Algebraic Limit Using Some Standard Results

Recall the binomial expansion for any rational power
\(
(1+x)^n=1+n x+\frac{n(n-1)}{2!} x^2+\frac{n(n-1)(n-2)}{3!} x^3 \ldots
\)
where \(|x|<1\)
When \(x\) is infinitely small (approaching to zero) such that we can ignore higher powers of \(x\), then we have \((1+x)^n=1+n x\) (approximately).

Following theorem will be used to evaluate some algebraic limits:

Theorem: If \(n \in Q\), then \(\lim _{x \rightarrow a} \frac{x^n-a^n}{x-a}=n a^{n-1}\)

Proof: We have \(\lim _{x \rightarrow a} \frac{x^n-a^n}{x-a}\)
\(
\begin{aligned}
& =\lim _{x \rightarrow a^{+}} \frac{x^n-a^n}{x-a} \\
& =\lim _{h \rightarrow 0} \frac{(a+h)^n-a^n}{a+h-a} \\
& =\lim _{h \rightarrow 0} \frac{a^n\left\{\left(1+\frac{h}{a}\right)^n-1\right\}}{h} \\
& =a^n \lim _{h \rightarrow 0} \frac{\left\{1+n \frac{h}{a}\right\}-1}{h} \quad\left[\text { when } x \rightarrow 0,(1+x)^n \rightarrow 1+n x\right] \\
& =a^n \frac{n}{a}=n a^{n-1}
\end{aligned}
\)

Example 26: Evaluate \(\lim _{x \rightarrow 2} \frac{x^{10}-1024}{x^5-32}\).

Solution:
\(
\begin{aligned}
& \lim _{x \rightarrow 2} \frac{x^{10}-1024}{x^5-32}=\lim _{x \rightarrow 2} \frac{x^{10}-2^{10}}{x^5-2^5}=\lim _{x \rightarrow 2} \frac{\frac{x^{10}-2^{10}}{x-2}}{\frac{x^5-2^5}{x-2}} \\
& =\frac{\lim _{x \rightarrow 2} \frac{x^{10}-2^{10}}{x-2}}{\lim _{x \rightarrow 2} \frac{x^5-2^5}{x-2}}=\frac{10 \times 2^{10-1}}{5 \times 2^{5-1}}=64
\end{aligned}
\)

Example 27: Evaluate \(\lim _{x \rightarrow a} \frac{(x+2)^{5 / 3}-(a+2)^{5 / 3}}{x-a}\).

Solution:
\(
\begin{aligned}
& \lim _{x \rightarrow a} \frac{(x+2)^{5 / 3}-(a+2)^{5 / 3}}{x-a} \\
& =\lim _{x \rightarrow a} \frac{(x+2)^{5 / 3}-(a+2)^{5 / 3}}{(x+2)-(a+2)} \\
& =\lim _{y \rightarrow b} \frac{y^{5 / 3}-b^{5 / 3}}{y-b}, \text { where } x+2=y \text { and } a+2=b \\
& =\frac{5}{3} b^{5 / 3-1}=\frac{5}{3} b^{2 / 3}=\frac{5}{3}(a+2)^{2 / 3}
\end{aligned}
\)

Example 28: If \(\lim _{x \rightarrow 2} \frac{x^n-2^n}{x-2}=80\) and \(n \in N\), then find the value of \(n\).

Solution: We have \(\lim _{x \rightarrow 2} \frac{x^n-2^n}{x-2}=80\)
\(
\begin{aligned}
& \Rightarrow n 2^{n-1}=80 \\
& \Rightarrow n 2^{n-1}=5 \times 2^{5-1} \\
& \Rightarrow n=5
\end{aligned}
\)

Example 29: Evaluate \(\lim _{x \rightarrow 2} \frac{\sqrt{(x+7)}-3 \sqrt{(2 x-3)}}{\sqrt[3]{(x+6)}-2 \sqrt[3]{(3 x-5)}}\).

Solution: We have \(L=\lim _{x \rightarrow 2} \frac{\sqrt{(x+7)}-3 \sqrt{(2 x-3)}}{\sqrt[3]{(x+6)}-2 \sqrt[3]{(3 x-5)}}\left(\frac{0}{0} \text { form }\right)\) 
Let \(x-2=t\) such that when \(x \rightarrow 2, t \rightarrow 0\).
Then \(L=\lim _{t \rightarrow 0} \frac{(t+9)^{\frac{1}{2}}-3(2 t+1)^{\frac{1}{2}}}{(t+8)^{\frac{1}{3}}-2(3 t+1)^{\frac{1}{3}}} \left(\frac{0}{0} \text { form }\right)\) 
\(
=\frac{3}{2} \lim _{t \rightarrow 0} \frac{\left(1+\frac{t}{9}\right)^{\frac{1}{2}}-(2 t+1)^{\frac{1}{2}}}{\left(1+\frac{t}{8}\right)^{\frac{1}{3}}-(3 t+1)^{\frac{1}{3}}} \left(\frac{0}{0} \text { form }\right)
\)
\(
=\frac{3}{2} \lim _{t \rightarrow 0} \frac{\frac{1}{2} \frac{t}{9}-(2 t) \frac{1}{2}}{\frac{t}{8} \frac{1}{3}-(3 t) \frac{1}{3}}=\frac{3}{2} \frac{\frac{1}{18}-1}{\frac{1}{24}-1}=\frac{34}{23}
\)

EVALUATION OF LIMITS WHEN VARIABLE TENDS TO \(\infty \mathrm{OR}-\infty\)

We know that \(\lim _{x \rightarrow+\infty} \frac{1}{x}=0\) and \(\lim _{x \rightarrow+\infty} \frac{1}{x^2}=0\).

To evaluate this type of limits we follow the following steps:

• STEP-I: Write down the given expression in form of a rational function, i.e., \(\frac{f(x)}{g(x)}\), if it is not so.
• STEP-II: If \(k\) is the highest power of \(x\) in numerator and denominator both, then divide each term in numerator and denominator by \(x^k\).
• STEP-III: Use the result \(\lim _{x \rightarrow \infty} \frac{1}{x^n}=0\), where \(n>0\).

Example 30: Evaluate \(\lim _{x \rightarrow \infty} \frac{a x^2+b x+c}{d x^2+e x+f}\).

Solution: Here the expression assumes the form \(\frac{\infty}{\infty}\). We notice that the highest power of \(x\) in both the numerator and denominator is 2 . So we divide each term in both the numerator and denominator by \(x^2\).
\(
\therefore \lim _{x \rightarrow \infty} \frac{a x^2+b x+c}{d x^2+e x+f}=\lim _{x \rightarrow \infty} \frac{a+\frac{b}{x}+\frac{c}{x^2}}{d+\frac{e}{x}+\frac{f}{x^2}}=\frac{a+0+0}{d+0+0}=\frac{a}{d}
\)

Example 31: Evaluate \(\lim _{x \rightarrow \infty} \frac{\sqrt{3 x^2-1}-\sqrt{2 x^2-1}}{4 x+3}\).

Solution: Dividing each term in the numerator and denominator by \(x\), we get
\(
\begin{aligned}
& \lim _{x \rightarrow \infty} \frac{\sqrt{3 x^2-1}-\sqrt{2 x^2-1}}{4 x+3} \\
= & \lim _{x \rightarrow \infty} \frac{\sqrt{3-1 / x^2}-\sqrt{2-1 / x^2}}{4+3 / x}=\frac{\sqrt{3}-\sqrt{2}}{4}
\end{aligned}
\)

Example 32: Evaluate \(\lim _{x \rightarrow \infty} \sqrt{x}(\sqrt{x+c}-\sqrt{x})\)

Solution: The given expression is in the form \(\infty-\infty\). So we first write it in the rational form \(\frac{f(x)}{g(x)}\).
We have \(\lim _{x \rightarrow \infty} \sqrt{x}(\sqrt{x+c}-\sqrt{x})\)
\(
\begin{aligned}
& =\lim _{x \rightarrow \infty} \frac{\sqrt{x}(\sqrt{x+c}-\sqrt{x})(\sqrt{x+c}+\sqrt{x})}{(\sqrt{x+c}+\sqrt{x})} \\
& =\lim _{x \rightarrow \infty} \frac{\sqrt{x}(x+c-x)}{\sqrt{x+c}+\sqrt{x}}=\lim _{x \rightarrow \infty} \frac{c \sqrt{x}}{\sqrt{x+c}+\sqrt{x}}\left(\text { form } \frac{\infty}{\infty}\right) \\
& =\lim _{x \rightarrow \infty} \frac{c}{\sqrt{1+\frac{c}{x}}+1} \quad\left[\text { Dividing } N^r \text { and } D^r \text { by } \sqrt{x}\right] \\
& =\frac{c}{\sqrt{1+0}+1}=\frac{c}{2}
\end{aligned}
\)

Example 33: Evaluate \(\lim _{x \rightarrow \infty} \frac{\sqrt{x^2+1}-\sqrt[3]{x^3+1}}{\sqrt[4]{x^4+1}-\sqrt[5]{x^4+1}}\).

Solution: We have \(\lim _{x \rightarrow \infty} \frac{\sqrt{x^2+1}-\sqrt[3]{x^3+1}}{\sqrt[4]{x^4+1}-\sqrt[5]{x^4+1}}\)
\(
=\lim _{x \rightarrow \infty} \frac{\sqrt{1+\frac{1}{x^2}}-\sqrt[3]{1+\frac{1}{x^3}}}{\sqrt[4]{1+\frac{1}{x^4}}-\sqrt[5]{\frac{1}{x}+\frac{1}{x^5}}}=\frac{1-1}{1-0}=0
\)

Example 34: Evaluate \(\lim _{x \rightarrow-\infty}\left(\sqrt{25 x^2-3 x}+5 x\right)\)

Solution:
\(
\begin{aligned}
&\text { We have } \lim _{x \rightarrow-\infty}\left(\sqrt{25 x^2-3 x}+5 x\right) \quad(\infty-\infty \text { form })\\
&\begin{aligned}
& =\lim _{y \rightarrow \infty}\left(\sqrt{25 y^2+3 y}-5 y\right), \text { where } y=-x \\
& =\lim _{y \rightarrow \infty} \frac{25 y^2+3 y-25 y^2}{\sqrt{25 y^2+3 y}+5 y} \\
& =\lim _{y \rightarrow \infty} \frac{3 y}{\sqrt{25 y^2+3 y}+5 y} \\
& =\lim _{y \rightarrow \infty} \frac{3}{\sqrt{25+\frac{3}{y}}+5}=\frac{3}{5+5}=\frac{3}{10}
\end{aligned}
\end{aligned}
\)

Example 35: \(\lim _{x \rightarrow 1} \frac{\sum_{k=1}^{100} x^k-100}{x-1}\)

Solution: We know \(\sum_{k=1}^{100} x^k-100=\left(x^1-1\right)+\left(x^2-1\right)+\ldots+\left(x^{100}-1\right)\)
\(
\lim _{x \rightarrow 1} \frac{(x-1)+\left(x^2-1\right)+\ldots+\left(x^{100}-1\right)}{x-1}
\)
By the limit sum law, we can split the limit of the sum:
\(
\lim _{x \rightarrow 1}\left[\frac{x-1}{x-1}+\frac{x^2-1}{x-1}+\ldots+\frac{x^{100}-1}{x-1}\right]
\)
Using the property \(\lim _{x \rightarrow a}(f(x)+g(x))=\lim _{x \rightarrow a} f(x)+\lim _{x \rightarrow a} g(x)\), we have:
\(
\sum_{k=1}^{100} \lim _{x \rightarrow 1} \frac{x^k-1}{x-1}
\)
Recall the limit formula \(\lim _{x \rightarrow a} \frac{x^n-a^n}{x-a}=n a^{n-1}\). Here, \(a=1\).
Thus, for each term, \(\lim _{x \rightarrow 1} \frac{x^k-1}{x-1}=k(1)^{k-1}=k\).
So the limit is:
\(
\sum_{k=1}^{100} k=1+2+3+\ldots+100=\frac{100(101)}{2}=5050
\)

EVALUATION OF TRIGONOMETRIC LIMITS

Some Important Trigonometric Limits to Remember

• \(\lim _{\theta \rightarrow 0} \frac{\sin \theta}{\theta}=1\) (where \(\theta\) is in radians)
• \(\lim _{\theta \rightarrow 0} \frac{\tan \theta}{\theta}=1\)
  We have
  \(
  \begin{aligned}
  \lim _{\theta \rightarrow 0} \frac{\tan \theta}{\theta}=\lim _{\theta \rightarrow 0} \frac{\sin \theta}{\theta} \frac{1}{\cos \theta} & =\lim _{\theta \rightarrow 0} \frac{\sin \theta}{\theta} \cdot \lim _{\theta \rightarrow 0} \frac{1}{\cos \theta} \\
  & =(1)(1)=1
  \end{aligned}
  \)
• \(\lim _{\theta \rightarrow a} \frac{\sin (\theta-a)}{\theta-a}=1\)
  We have \(\lim _{\theta \rightarrow a} \frac{\sin (\theta-a)}{\theta-a}=\lim _{h \rightarrow 0} \frac{\sin (a+h-a)}{(a+h-a)}\)
  \(
  =\lim _{h \rightarrow 0} \frac{\sin h}{h}=1
  \)
• \(\lim _{\theta \rightarrow a} \frac{\tan (\theta-a)}{\theta-a}=1\).
• \(\lim _{x \rightarrow 0} \frac{\sin ^{-1} x}{x}=1\)
• \(\lim _{x \rightarrow 0} \frac{\tan ^{-1} x}{x}=1\)

Example 36: Evaluate the following limits
a. \(\lim _{x \rightarrow 0} \frac{\sin 3 x}{x}\)
b. \(\lim _{x \rightarrow 0} \frac{\sin a x}{\sin b x}\)
c. \(\lim _{x \rightarrow 1} \frac{\sin (\log x)}{{ } \log x}\).

Solution:
a. We have \(\lim _{x \rightarrow 0} \frac{\sin 3 x}{x}\)
\(
=\lim _{x \rightarrow 0}\left(3 \frac{\sin 3 x}{3 x}\right)=3 \lim _{x \rightarrow 0} \frac{\sin 3 x}{3 x}=3(1)=3 \left[\because \lim _{x \rightarrow 0} \frac{\sin 3 x}{3 x}=1\right]
\)

b. We have
\(
\lim _{x \rightarrow 0} \frac{\sin a x}{\sin b x}=\lim _{x \rightarrow 0} \frac{\left(\frac{\sin a x}{a x}\right) a x}{\left(\frac{\sin b x}{b x}\right) b x}=\frac{a}{b} \frac{(1)}{(1)}=\frac{a}{b}
\)

c. Given \(L=\lim _{x \rightarrow 1} \frac{\sin (\log x)}{\log x}\)
Let \(\log x=t\) then
\(
\Rightarrow L=\lim _{t \rightarrow 0} \frac{\sin t}{t}=1
\)

Example 37: Evaluate \(\lim _{x \rightarrow 0} \frac{1}{x} \sin ^{-1}\left(\frac{2 x}{1+x^2}\right)\).

Solution: We know that \(\sin ^{-1}\left(\frac{2 x}{1+x^2}\right)=2 \tan ^{-1} x\), for \(-1 \leq x \leq 1\)
\(
\Rightarrow \lim _{x \rightarrow 0} \frac{1}{x} \sin ^{-1}\left(\frac{2 x}{1+x^2}\right)=\lim _{x \rightarrow 0} \frac{2 \tan ^{-1} x}{x}=2
\)

Example 38: Evaluate \(\lim _{x \rightarrow 0} \frac{1-\cos 2 x}{x^2}\).

Solution: We have \(\lim _{x \rightarrow 0} \frac{1-\cos 2 x}{x^2}\left(\frac{0}{0} \text { form }\right)\) 
\(
=\lim _{x \rightarrow 2} \frac{2 \sin ^2 x}{x^2}=2\left(\lim _{x \rightarrow 0} \frac{\sin x}{x}\right)^2=2
\)

Example 39: Evaluate \(\lim _{x \rightarrow 0} \frac{\tan x-\sin x}{x^3}\).

Solution: We have \(\lim _{x \rightarrow 0} \frac{\tan x-\sin x}{x^3}\left(\frac{0}{0} \text { form }\right)\) 
\(
\begin{aligned}
& =\lim _{x \rightarrow 0}\left(\frac{\sin x-\sin x \cos x}{x^3 \cos x}\right) \\
& =\lim _{x \rightarrow 0}\left\{\frac{\sin x(1-\cos x)}{x^3 \cos x}\right\}=\lim _{x \rightarrow 0}\left\{\frac{\sin x}{x} \frac{1-\cos x}{x^2} \frac{1}{\cos x}\right\} \\
& =\left\{\lim _{x \rightarrow 0} \frac{\sin x}{x}\right\}\left\{\lim _{x \rightarrow 0} \frac{2 \sin ^2 \frac{x}{2}}{\left(\frac{x}{2}\right)^2 \times 4}\right\} \lim _{x \rightarrow 0} \frac{1}{\cos x} \\
& =\left\{\lim _{x \rightarrow 0} \frac{\sin x}{x}\right\} \frac{1}{2}\left\{\lim _{x \rightarrow 0}\left(\frac{\sin \frac{x}{2}}{\frac{x}{2}}\right)^2\right\} \lim _{x \rightarrow 0} \frac{1}{\cos x}
\end{aligned}
\)
\(
=1 \times \frac{1}{2}(1)^2 \times \frac{1}{1}=\frac{1}{2}
\)

Example 40: Evaluate \(\lim _{x \rightarrow \frac{\pi}{2}} \frac{1+\cos 2 x}{(\pi-2 x)^2}\).

Solution: We have, \(\lim _{x \rightarrow \frac{\pi}{2}} \frac{1+\cos 2 x}{(\pi-2 x)^2}\left(\frac{0}{0} \text { form }\right)\) 
\(
\begin{aligned}
& =\lim _{h \rightarrow 0} \frac{1+\cos 2\left(\frac{\pi}{2}+h\right)}{\left[\pi-2\left(\frac{\pi}{2}+h\right)\right]^2} \\
& =\lim _{h \rightarrow 0} \frac{1+\cos (\pi+2 h)}{4 h^2} \\
& =\lim _{h \rightarrow 0} \frac{1-\cos 2 h}{4 h^2} \\
& =\lim _{h \rightarrow 0} \frac{2 \sin ^2 h}{4 h^2}=\frac{2}{4}\left(\lim _{h \rightarrow 0} \frac{\sin h}{h}\right)^2=\frac{1}{2}
\end{aligned}
\)

Example 41: Evaluate \(\lim _{x \rightarrow \infty} 2^{x-1} \tan \left(\frac{a}{2^x}\right)\).

Solution: We have \(\lim _{x \rightarrow \infty} 2^{x-1} \tan \left(\frac{a}{2^x}\right)\)
\(
\begin{aligned}
& =\lim _{x \rightarrow \infty} \frac{a}{2} \frac{\tan \left(\frac{a}{2^x}\right)}{\left(\frac{a}{2^x}\right)}\left(\frac{0}{0} \text { form }\right) \\
& =\frac{a}{2} \lim _{y \rightarrow 0} \frac{\tan y}{y}=\frac{a}{2}\left(\text { where } y=\frac{a}{2^x}\right)
\end{aligned}
\)

Example 42: Evaluate \(\lim _{x \rightarrow 2} \frac{x^2-x-2}{x^2-2 x-\sin (x-2)}\).

Solution:
\(
\begin{aligned}
& \lim _{x \rightarrow 2} \frac{x^2-x-2}{x^2-2 x-\sin (x-2)} \left(\frac{0}{0} \text { form }\right) \\
& =\lim _{x \rightarrow 2} \frac{(x-2)(x+1)}{x(x-2)-\sin (x-2)} \\
& =\lim _{x \rightarrow 2} \frac{(x+1)}{x-\frac{\sin (x-2)}{x-2}} \\
& =\frac{2+1}{2-1}=3
\end{aligned}
\)

Example 43: Evaluate \(\lim _{x \rightarrow \infty} x\left(\tan ^{-1} \frac{x+1}{x+4}-\frac{\pi}{4}\right)\).

Solution: We have \(\lim _{x \rightarrow \infty} x\left(\tan ^{-1} \frac{x+1}{x+4}-\frac{\pi}{4}\right)\)
\(
\begin{aligned}
& =\lim _{x \rightarrow \infty} x\left(\tan ^{-1} \frac{x+1}{x+4}-\tan ^{-1} 1\right) \\
& =\lim _{x \rightarrow \infty} x \tan ^{-1}\left(\frac{\frac{x+1}{x+4}-1}{1+\frac{x+1}{x+4}}\right)=\lim _{x \rightarrow \infty} x \tan ^{-1}\left(\frac{-3}{2 x+5}\right) \\
& =\lim _{x \rightarrow \infty}\left(\frac{\tan ^{-1}\left(\frac{-3}{2 x+5}\right)}{\frac{-3}{2 x+5}}\right)\left(\frac{-3 x}{2 x+5}\right) \\
& =\lim _{x \rightarrow \infty}\left(\frac{\tan ^{-1}\left(\frac{-3}{2 x+5}\right)}{\frac{-3}{2 x+5}}\right) \lim _{x \rightarrow \infty}\left(\frac{-3 x}{2 x+5}\right) \\
& =1 \times \lim _{x \rightarrow \infty}\left(\frac{-3}{2+\frac{5}{x}}\right)=1 \times-\left(\frac{3}{2}\right)=-\frac{3}{2}
\end{aligned}
\)

Example 44: Using \(\lim _{\theta \rightarrow 0} \frac{\sin \theta}{\theta}=1\), prove that the area of circle of radius \(\dot{R}\) is \(\pi R^2\).

Solution: Consider the regular polygon of \(n\) sides inscribed in a circle of radius \(R\) (Figure below).

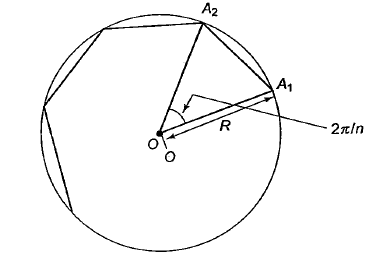
Area of polygon \(=n \times\left(\right.\) area of \(\left.\triangle O A_1 A_2\right)\)
\(
\begin{aligned}
& =n \times \frac{1}{2} O A_1 O A_2 \sin \left(\angle A_1 O A_2\right) \\
& =\frac{n}{2} R^2 \sin \left(\frac{2 \pi}{n}\right)
\end{aligned}
\)
Now circle is a regular polygon of infinite sides,
\(
\begin{aligned}
\text { Then the area of circle } & =\lim _{n \rightarrow \infty} \frac{n}{2} R^2 \sin \left(\frac{2 \pi}{n}\right) \\
& =\pi R^2 \lim _{n \rightarrow \infty} \frac{\sin \left(\frac{2 \pi}{n}\right)}{\frac{2 \pi}{n}} \\
& =\pi R^2
\end{aligned}
\)

EVALUATION OF EXPONENTIAL AND LOGARITHMIC LIMITS

In order to evaluate these types of limits, we use the following standard results:
Illustration-1: \(\lim _{x \rightarrow 0} \frac{a^x-1}{x}=\log _e a\)

Proof:
\(
\begin{aligned}
& \lim _{x \rightarrow 0} \frac{a^x-1}{x} \\
& =\lim _{x \rightarrow 0} \frac{\left(1+\frac{x(\log a)}{1!}+\frac{x^2(\log a)^2}{2!}+\cdots\right)-1}{x} \\
& =\lim _{x \rightarrow 0}\left(\frac{\log a}{1!}+\frac{x(\log a)^2}{2!}+\cdots\right) \\
& =\log _e a
\end{aligned}
\)

Illustration-2: \(\lim _{x \rightarrow 0} \frac{e^x-1}{x}=1\) 

Proof:
\(
e^x=1+x+\frac{x^2}{2!}+\frac{x^3}{3!}+\ldots
\)
\(
\lim _{x \rightarrow 0} \frac{\left(1+x+\frac{x^2}{2!}+\frac{x^3}{3!}+\ldots\right)-1}{x}
\)
\(
\lim _{x \rightarrow 0} \frac{x\left(1+\frac{x}{2!}+\frac{x^2}{3!}+\ldots\right)}{x}
\)
\(
\lim _{x \rightarrow 0}\left(1+\frac{x}{2!}+\frac{x^2}{3!}+\ldots\right)=1+\frac{0}{2!}+\frac{0^2}{3!}+\ldots=1
\)

Illustration-3: \(\lim _{x \rightarrow 0} \frac{\log (1+x)}{x}=1\)

Proof:
\(
\begin{aligned}
& \lim _{x \rightarrow 0} \frac{\log (1+x)}{x}=\lim _{x \rightarrow 0} \frac{x-\frac{x^2}{2}+\frac{x^3}{3}-\cdots}{x} \\
& =\lim _{x \rightarrow 0}\left(1-\frac{x}{2}+\frac{x^2}{3}-\cdots\right)=1
\end{aligned}
\)

Example 45: Evaluate \(\lim _{x \rightarrow 0} \frac{2^x-1}{\sqrt{1+x}-1}\)

Solution: We have \(\lim _{x \rightarrow 0} \frac{2^x-1}{\sqrt{1+x}-1} \left(\frac{0}{0} \text { form }\right)\)
\(
\begin{aligned}
& =\lim _{x \rightarrow 0} \frac{2^x-1}{\sqrt{1+x}-1} \frac{(\sqrt{1+x}+1)}{(\sqrt{1+x}+1)} \\
& =\lim _{x \rightarrow 0} \frac{2^x-1}{x} \lim _{x \rightarrow 0}(\sqrt{1+x}+1) \\
& =(\log 2) 2=\log 4
\end{aligned}
\)

Example 46: Evaluate \(\lim _{x \rightarrow 1} \frac{a^{x-1}-1}{\sin \pi x}\).

Solution: We have \(\lim _{x \rightarrow 1} \frac{a^{x-1}-1}{\sin \pi x} \left(\frac{0}{0} \text { form }\right)\)
\(
=\lim _{h \rightarrow 0} \frac{a^{1+h-1}-1}{\sin \pi(1+h)}=\lim _{h \rightarrow 0} \frac{a^h-1}{-\sin \pi h}
\)
\(
=\frac{-1}{\pi} \lim _{h \rightarrow 0}\left(\frac{a^h-1}{h}\right) \frac{\pi h}{\sin \pi h}=-\frac{1}{\pi} \log a
\)

Example 47: Evaluate \(\lim _{x \rightarrow 0} \frac{10^x-2^x-5^x+1}{x \tan x}\).

Solution: We have \(\lim _{x \rightarrow 0} \frac{10^x-2^x-5^x+1}{x \tan x}\left(\frac{0}{0} \text { form }\right)\)
\(
\begin{aligned}
& =\lim _{x \rightarrow 0} \frac{5^x \cdot 2^x-2^x-5^x+1}{x \tan x} \\
& =\lim _{x \rightarrow 0} \frac{\left(5^x-1\right)\left(2^x-1\right)}{x \tan x} \\
& =\lim _{x \rightarrow 0} \frac{5^x-1}{x} \frac{2^x-1}{x} \frac{x}{\tan x} \\
& =\lim _{x \rightarrow 0} \frac{5^x-1}{x} \lim _{x \rightarrow 0} \frac{2^x-1}{x} \lim _{x \rightarrow 0} \frac{x}{\tan x} \\
& =(\log 5)(\log 2)(1)=(\log 5)(\log 2)
\end{aligned}
\)

Example 48: Evaluate \(\lim _{x \rightarrow 0} \frac{3^{2 x}-2^{3 x}}{x}\).

Solution: We have \(\lim _{x \rightarrow 0} \frac{3^{2 x}-2^{3 x}}{x}\left(\frac{0}{0} \text { form }\right)\)
\(
\begin{aligned}
& =\lim _{x \rightarrow 0}\left\{\left(\frac{3^{2 x}-1}{x}\right)-\left(\frac{2^{3 x}-1}{x}\right)\right\} \\
& =\lim _{x \rightarrow 0}\left(\frac{3^{2 x}-1}{2 x} \cdot 2\right)-\lim _{x \rightarrow 0}\left(\frac{2^{3 x}-1}{3 x} \cdot 3\right) \\
& =2 \log 3-3 \log 2=\log 9-\log 8=\log \left(\frac{9}{8}\right)
\end{aligned}
\)

Example 49: Evaluate \(\lim _{x \rightarrow 2} \frac{x-2}{\log _a(x-1)}\)

Solution:
\(
\begin{aligned}
& \lim _{x \rightarrow 2} \frac{x-2}{\log _a(x-1)}\left(\frac{0}{0} \text { form }\right) \\
& =\lim _{x \rightarrow 2} \frac{x-2}{\log _a(1+(x-2))} \\
& =\lim _{h \rightarrow 0} \frac{h}{\log _a(1+h)}(\text { Substituting } x-2=h) \\
& =\log _e a
\end{aligned}
\)

Example 50: Evaluate \(\lim _{x \rightarrow a} \frac{\log x-\log a}{x-a}\)

Solution: Let \(x-a=h\), then if \(x \rightarrow a, h \rightarrow 0\)
\(
\begin{aligned}
& \Rightarrow \lim _{x \rightarrow a} \frac{\log x-\log a}{x-a}\left(\frac{0}{0} \text { form }\right) \\
& =\lim _{h \rightarrow 0} \frac{\log (a+h)-\log a}{h}
\end{aligned}
\)
\(
=\lim _{h \rightarrow 0} \frac{\log \left(1+\frac{h}{a}\right)}{\frac{h}{a} a}=\frac{1}{a}
\)

Example 51: Evaluate \(\lim _{x \rightarrow 0} \frac{\log (5+x)-\log (5-x)}{x}\).

Solution: We have \(\lim _{x \rightarrow 0} \frac{\log (5+x)-\log (5-x)}{x} \quad\left(\frac{0}{0} \text { form }\right)\)
\(
\begin{aligned}
& =\lim _{x \rightarrow 0} \frac{\log \left\{5\left(1+\frac{x}{5}\right)\right\}-\log \left\{5\left(1-\frac{x}{5}\right)\right\}}{x} \\
& =\lim _{x \rightarrow 0} \frac{\left\{\log 5+\log \left(1+\frac{x}{5}\right)\right\}-\left\{\log 5+\log \left(1-\frac{x}{5}\right)\right\}}{x} \\
& =\lim _{x \rightarrow 0} \frac{\log \left(1+\frac{x}{5}\right)-\log \left(1-\frac{x}{5}\right)}{x} \\
& =\lim _{x \rightarrow 0} \frac{1}{5} \frac{\log \left(1+\frac{x}{5}\right)}{x / 5}+\lim _{x \rightarrow 0} \frac{\log \left(1-\frac{x}{5}\right)}{-x / 5} \frac{1}{(-5)}=\frac{1}{5}+\frac{1}{5}=\frac{2}{5}
\end{aligned}
\)

Example 52: Let \(P_n=a^{P_{n-1}}-1, \forall n=2,3 \cdots\) and let \(P_1 =a^x-1\) where \(a \in R^{+}\), then evaluate \(\lim _{x \rightarrow 0} \frac{P_n}{x}\).

Solution: Clearly, if \(P_k \rightarrow 0 \Rightarrow P_{k+1} \rightarrow 0\)
Now, as \(x \rightarrow 0 \Rightarrow P_1 \rightarrow 0 \Rightarrow P_2, P_3, P_4, \cdots P_n \rightarrow 0\)
\(
\Rightarrow \lim _{x \rightarrow 0} \frac{P_n}{x}=\lim _{x \rightarrow 0} \frac{P_n}{P_{n-1}} \frac{P_{n-1}}{P_{n-2}} \ldots \frac{P_1}{x}
\)
Now, \(\lim _{x \rightarrow 0} \frac{P_k}{P_{k-1}}=\lim _{x \rightarrow 0} \frac{a^{P_{k-1}}-1}{P_{k-1}}=\ln a\)
\(
\Rightarrow \text { Required limit }=(\ln a)^n
\)

LIMITS OF THE FORM \(\lim _{x \rightarrow a}(f(x))^{g(x)}\)

Form: \(0^0, \infty^0\)

Let \(L=\lim _{x \rightarrow a}(f(x))^{g(x)}\)
\(
\log _e L=\log _e\left[\lim _{x \rightarrow a}(f(x))^{g(x)}\right]
\)
\(
\begin{aligned}
& =\lim _{x \rightarrow a}\left[\log _e(f(x))^{g(x)}\right] \\
& =\lim _{x \rightarrow a} g(x) \log _e[f(x)]
\end{aligned}
\)
\(
L=e^{\lim _{x \rightarrow a} g(x) \log _e f(x)}
\)

Example 53: \(\lim _{x \rightarrow \infty} x^{1 / x}\) equals to

Solution:
\(
\begin{aligned}
& \lim _{x \rightarrow \infty} x^{1 / x} \\
& =e^{\log _{x \rightarrow \infty} x^{1 / x}} \\
& =e^{\lim _{x \rightarrow \infty} \log x^{1 / x}} \\
& =e^{\lim _{x \rightarrow \infty} \frac{\log x}{x}} \\
& \left(\because x \text { increases faster than } \log _e x \text { when } x \rightarrow \infty\right) \\
& =e^0 \\
& =1
\end{aligned}
\)

Form: \(1^{\infty}\)

Illustration 1: \(\lim _{x \rightarrow 0}(1+x)^{\frac{1}{x}}=e \text { or } \lim _{x \rightarrow \infty}\left(1+\frac{1}{x}\right)^x=e\)

Proof:
\(
\lim _{x \rightarrow 0}(1+x)^{\frac{1}{x}}
\)
\(
\begin{aligned}
& =\lim _{x \rightarrow 0}\left(1+\frac{1}{x} x+\frac{\frac{1}{x}\left(\frac{1}{x}-1\right)}{2!} x^2+\frac{\frac{1}{x}\left(\frac{1}{x}-1\right)\left(\frac{1}{x}-2\right)}{3!} x^3+\cdots\right) \\
& =\lim _{x \rightarrow 0}\left(1+1+\frac{1(1-x)}{2!}+\frac{1(1-x)(1-2 x)}{3!}+\cdots\right)
\end{aligned}
\)
\(
=\left(1+1+\frac{1}{2!}+\frac{1}{3!}+\cdots\right)=e
\)

Illustration 2: 
\(
\begin{aligned}
& \begin{aligned}
L=\lim _{x \rightarrow a} f(x)^{g(x)} & \text { if } \lim _{x \rightarrow a} f(x)=1 \text { and } \lim _{x \rightarrow a} g(x)=\infty \\
\text { Then } L & =\lim _{x \rightarrow a} f(x)^{g(x)} \\
& =\lim _{x \rightarrow a}(1+(f(x)-1))^{\frac{1}{f(x)-1}(f(x)-1) \times g(x)} \\
& =\left[\lim _{x \rightarrow a}\left((1+(f(x)-1))^{\frac{1}{f(x)-1}}\right)\right]^{\lim _{x \rightarrow a}(f(x)-1) \times g(x)} \\
& =e^{\lim _{x \rightarrow a}(f(x)-1) \times g(x)}
\end{aligned}
\end{aligned}
\)

Example 54: Evaluate \(\lim _{x \rightarrow 0}(1+x)^{\operatorname{cosec} x}\)

Solution:
\(
\begin{aligned}
& \lim _{x \rightarrow 0}(1+x)^{\operatorname{cosec} x} \\
& =\lim _{x \rightarrow 0}\left[(1+x)^{\frac{1}{x}}\right]^{\frac{x}{\sin x}} \\
& =\left[\lim _{x \rightarrow 0}(1+x)^{\frac{1}{x}}\right]^{\lim _{x \rightarrow 0} \frac{x}{\sin x}}=e^1
\end{aligned}
\)

Example 55: Evaluate \(\lim _{x \rightarrow 0}(\cos x)^{\cot x}\).

Solution:
\(
\begin{aligned}
& \lim _{x \rightarrow 0}(\cos x)^{\cot x} \\
& =\lim _{x \rightarrow 0}\left[(1+(\cos x-1))^{\frac{1}{\cos x-1}}\right]^{\frac{\cos x-1}{\tan x}} \\
& =\left[\lim _{x \rightarrow 0}(1+(\cos x-1))^{\frac{1}{\cos x-1}}\right]^{\lim _{x \rightarrow 0} \frac{\cos x-1}{\tan x}} \\
& =e^{\lim _{x \rightarrow 0} \frac{\cos x-1}{\sin x} \cos x} \\
& =e^{\lim _{x \rightarrow 0} \frac{\cos x-1}{\sin ^2 x} \cos x \sin x} \\
& =e^{\lim _{x \rightarrow 0} \frac{\cos x-1}{1-\cos ^2 x} \cos x \sin x} \\
& =e^{\lim _{x \rightarrow 0} \frac{\sin x \cos x}{1+\cos x}}=e^0=1
\end{aligned}
\)

Example 56: Evaluate \(\lim _{x \rightarrow 0}\left(\frac{\sin x}{x}\right)^{\left(\frac{\sin x}{x-\sin x}\right)}\)

Solution: Since \(\lim _{x \rightarrow 0} \frac{\sin x}{x}=1\) and \(\lim _{x \rightarrow 0} \frac{\sin x}{x-\sin x}=\lim _{x \rightarrow 0} \frac{1}{\left(\frac{x}{\sin x}-1\right)}\)
\(
=\frac{1}{1-1}=\infty
\)
\(
\begin{aligned}
\Rightarrow \lim _{x \rightarrow 0}\left(\frac{\sin x}{x}\right)^{\left(\frac{\sin x}{x-\sin x}\right)} & =e^{\lim _{x \rightarrow 0}\left(\frac{\sin x}{x}-1\right)\left(\frac{\sin x}{(x-\sin x)}\right)} \\
& =e^{\lim _{x \rightarrow 0} \frac{-\sin x}{x}}=e^{-1}=\frac{1}{e}
\end{aligned}
\)

Example 57: Evaluate \(\lim _{x \rightarrow 0}\left(\frac{a^x+b^x+c^x}{3}\right)^{2 / x} ;(a, b, c>0)\).

Solution: We have \(\lim _{x \rightarrow 0}\left(\frac{a^x+b^x+c^x}{3}\right)^{2 / x}\)
\(
\begin{aligned}
& =e^{\lim _{x \rightarrow 0}\left(\frac{a^x+b^x+c^x}{3}-1\right) \frac{2}{x}} \\
& =e^{\frac{2}{3} \lim _{x \rightarrow 0}\left(\frac{a^x+b^x+c^x-3}{x}\right)} \\
& =e^{\frac{2}{3} \lim _{x \rightarrow 0}\left(\frac{a^x-1}{x}+\frac{b^x-1}{x}+\frac{c^x-1}{x}\right)} \\
& =e^{\frac{2}{3}\left\{\lim _{x \rightarrow 0} \frac{a^x-1}{x}+\lim _{x \rightarrow 0} \frac{b^x-1}{x}+\lim _{x \rightarrow 0} \frac{c^x-1}{x}\right\}}
\end{aligned}
\)
\(
=e^{(2 / 3)\{\ln a+\ln b+\ln c\}}=e^{(2 / 3) \ln (a b c)}=e^{\ln (a b c)^{2 / 3}}=(a b c)^{2 / 3}
\)

Example 58: The population of a country increases by \(2 \%\) every year. If it increases \(k\) times in a century, then prove that \([k]=7\), where \([\cdot]\) represents the greatest integer function.

Solution: If the initial number of inhabitant of a given country is \(A\), then after a year the total population will amount to \(A +\frac{A}{100} 2=\left(1+\frac{1}{50}\right) A\).
After two years, the population will amount to \(\left(1+\frac{1}{50}\right)^2 \mathrm{~A}\).
After 100 years, it will reach the total of \(\left(1+\frac{1}{50}\right)^{100} A\), i.e., it will have increased \(\left(\left(1+\frac{1}{50}\right)^{50}\right)^2\) times.
Taking into account that \(\lim _{n \rightarrow \infty}\left(1+\frac{1}{n}\right)^n=e\), we can
approximately consider that \(\left(1+\frac{1}{50}\right)^{50} \approx e\).
Hence after 100 years the population of the country will have increased \(e^2 \approx 7.39\) times.
Hence \([k]=[7.39]=7\).

L’HOPITAL’S RULE FOR EVALUATING LIMITS

It states that If \(\lim _{x \rightarrow a} \frac{f(x)}{g(x)}\) takes \(\frac{0}{0}\) or \(\frac{\infty}{\infty}\) form, then,
\(
\lim _{x \rightarrow a} \frac{f(x)}{g(x)}=\lim _{x \rightarrow a} \frac{f^{\prime}(x)}{g^{\prime}(x)}
\)
where \(f^{\prime}(x)=\frac{d f(x)}{d x}\) and \(g^{\prime}(x)=\frac{d g(x)}{d x}\).

Example 59: Let \(f(x)\) be a twice-differentiable function and \(f^{\prime \prime}(0)=2\), then evaluate
\(
\lim _{x \rightarrow 0} \frac{2 f(x)-3 f(2 x)+f(4 x)}{x^2}
\)

Solution: The given limit has \(\frac{0}{0}\) form.
Using L’ Hopital’s rule, we have
\(
\begin{aligned}
\text { Limit } & =\lim _{x \rightarrow 0} \frac{2 f^{\prime}(x)-6 f^{\prime}(2 x)+4 f^{\prime}(4 x)}{2 x}\left(\frac{0}{0} \text { form }\right) \\
& =\lim _{x \rightarrow 0} \frac{2 f^{\prime \prime}(x)-12 f^{\prime \prime}(2 x)+16 f^{\prime \prime}(4 x)}{2} \text { (using L’Hopital’s rule) }
\end{aligned}
\)
\(
=\frac{6 f^{\prime \prime}(0)}{2}=6
\)

Example 60: If the graph of the function \(y=f(x)\) has a unique tangent at the point \((a, 0)\) through which the graph passes, then evaluate
\(
\lim _{x \rightarrow a} \frac{\log _e\{1+6 f(x)\}}{3 f(x)} .
\)

Solution: From the question, \(f(a)=0\) and \(f(x)\) is differentiable at \(x=a\).
\(
\therefore \text { limit }=\lim _{x \rightarrow a} \frac{\frac{1}{1+6 f(x)} \times 6 f^{\prime}(x)}{3 f^{\prime}(x)}=2 \times \frac{1}{1+6 f(a)}=2
\)

Example 61: Evaluate \(\lim _{x \rightarrow 0} \log _{\tan ^2 x}\left(\tan ^2 2 x\right)\).

Solution: \(L=\lim _{x \rightarrow 0} \frac{\log \left(\tan ^2 2 x\right)}{\log \left(\tan ^2 x\right)} \quad\left(\frac{\infty}{\infty} \text { form }\right)\)
Using L’.Hopital’s rule,
We have \(L=\lim _{x \rightarrow 0} \frac{\left(\frac{1}{\tan ^2 2 x} 2 \tan 2 x \sec ^2 2 x\right) \times 2}{\frac{1}{\tan ^2 x} 2 \tan x \cdot \sec ^2 x}\)
\(
\begin{aligned}
=\lim _{x \rightarrow 0} \frac{2\left(\frac{1}{\sin 2 x \cos 2 x}\right)}{\left(\frac{1}{\sin x \cos x}\right)} & =\lim _{x \rightarrow 0} \frac{\left(\frac{1}{\sin 2 x \cos 2 x}\right)}{\left(\frac{1}{\sin 2 x}\right)} \\
& =\lim _{x \rightarrow 0} \frac{1}{\cos 2 x}=1
\end{aligned}
\)

Example 62: Evaluate \(\lim _{x \rightarrow 0^{+}} x^m(\log x)^n, m, n \in N\).

Solution: \(\lim _{x \rightarrow 0+} x^m(\log x)^n=\lim _{x \rightarrow 0^{+}} \frac{(\log x)^n}{x^{-m}} \cdot\left(\frac{\infty}{\infty} \text { form }\right)\)
\(
=\lim _{x \rightarrow 0+} \frac{n(\log x)^{(n-1)} \frac{1}{x}}{-m x^{-m-1}} \text { (using L’ Hopital’s rule) }
\)
\(
=\lim _{x \rightarrow 0+} \frac{n(\log x)^{n-1}}{-m x^{-m}} \quad\left(\frac{\infty}{\infty} \text { form }\right)
\)
\(
=\lim _{x \rightarrow 0+} \frac{n(n-1)(\log x)^{(n-2)} \frac{1}{x}}{(-m)^2 x^{-m-1}} \quad \text { (using L’ Hopital’s rule) }
\)
\(
\begin{aligned}
& =\lim _{x \rightarrow 0+} \frac{n(n-1)(\log x)^{n-2}}{m^2 x^{-m}}\left(\frac{\infty}{\infty} \text { form }\right) \\
& \ldots \\
& =\lim _{x \rightarrow 0+} \frac{n!}{(-m)^n x^{-m}}=0\left(\text { differentiating } N^r \text { and } D^r n \text { times }\right)
\end{aligned}
\)

Example 63: Evaluate \(\lim _{x \rightarrow 0} \frac{\sin ^{-1} x-\tan ^{-1} x}{x^3}\)

Solution: \(\lim _{x \rightarrow 0} \frac{\sin ^{-1} x-\tan ^{-1} x}{x^3}\)
\(
=\lim _{x \rightarrow 0} \frac{\left(1+x^2\right)-\sqrt{1-x^2}}{3 x^2 \sqrt{1-x^2}\left(1+x^2\right)} \quad \text { (using L’Hopital’s rule) }
\)
\(
=\lim _{x \rightarrow 0} \frac{\left(1+x^2\right)^2-\left(1-x^2\right)}{3 x^2 \sqrt{1-x^2}\left(1+x^2\right)} \times \frac{1}{\left(1+x^2\right)+\sqrt{1-x^2}} \text { (Rationalizing) }
\)
\(
\begin{aligned}
& =\lim _{x \rightarrow 0} \frac{x^4+3 x^2}{3 x^2 \sqrt{1-x^2}\left(1+x^2\right)} \times \frac{1}{\left(1+x^2\right)+\sqrt{1-x^2}} \\
& =\lim _{x \rightarrow 0} \frac{x^2+3}{3 \sqrt{1-x^2}\left(1+x^2\right)} \times \frac{1}{\left(1+x^2\right)+\sqrt{1-x^2}}=1 / 2
\end{aligned}
\)

Example 64: If \(\alpha_1, \alpha_2, \cdots, \alpha_n\) are the roots of equation \(x^n+\operatorname{nax} -b=0\), show that
\(
\left(\alpha_1-\alpha_2\right)\left(\alpha_1-\alpha_3\right) \cdots\left(\alpha_1-\alpha_n\right)=n\left(\alpha_1^{n-1}+a\right) .
\)

Solution: Since \(\alpha_1, \alpha_2, \cdots, \alpha_n\) are the roots of equation \(x^n+n a x-b=0\), we have \(x^n+\operatorname{nax}-b=\left(x-\alpha_1\right)\left(x-\alpha_2\right) \cdots\left(x-\alpha_n\right)\)
\(
\begin{aligned}
& \Rightarrow \frac{x^n+n a x-b}{x-\alpha_1}=\left(x-\alpha_2\right)\left(x-\alpha_3\right) \cdots\left(x-\alpha_n\right) \\
& \Rightarrow \lim _{x \rightarrow \alpha_1} \frac{x^n+n a x-b}{x-\alpha_1}=\lim _{x \rightarrow \alpha_1}\left[\left(x-\alpha_2\right)\left(x-\alpha_3\right) \cdots\left(x-\alpha_n\right)\right]
\end{aligned}
\)
\(
\begin{gathered}
\Rightarrow \lim _{x \rightarrow \alpha_1} \frac{n x^{n-1}+n a}{1}=\left(\alpha_1-\alpha_2\right)\left(\alpha_1-\alpha_3\right) \cdots\left(\alpha_1-\alpha_n\right) \\
\text { (using L’ Hopital’s rule on L.H.S.) } \\
\Rightarrow\left(\alpha_1-\alpha_2\right)\left(\alpha_1-\alpha_3\right) \cdots\left(\alpha_1-\alpha_n\right)=n \alpha_1^{n-1}+n a
\end{gathered}
\)

Finding unknowns When Limit is Given

Example 65: If \(L=\lim _{x \rightarrow 0} \frac{\sin 2 x+a \sin x}{x^3}\) be finite, then find the value of \(a\) and \(L\).

Solution: \(L=\lim _{x \rightarrow 0} \frac{\sin 2 x+a \sin x}{x^3}\)
\(
\begin{aligned}
& =\lim _{x \rightarrow 0} \frac{2 \sin x \cos x+a \sin x}{x^3} \\
& =\lim _{x \rightarrow 0} \frac{\sin x}{x} \frac{(2 \cos x+a)}{x^2} \\
& =\lim _{x \rightarrow 0} \frac{2 \cos x+a}{x^2}
\end{aligned}
\)
Now \(D^r\) tends to 0 when \(x \rightarrow 0\), then \(N^r\) also must tends to zero for which \(\lim _{x \rightarrow 0}(2 \cos x+a)=0 \Rightarrow a=-2\).
Now, \(L=\lim _{x \rightarrow 0} \frac{2 \cos x-2}{x^2}=-2 \lim _{x \rightarrow 0} \frac{2 \sin ^2 \frac{x}{2}}{x^2}=-1\).

Example 66: If \(\lim _{x \rightarrow 0} \frac{\cos 4 x+a \cos 2 x+b}{x^4}\) is finite, find \(a\) and \(b\) using expansion formula.

Solution: \(\lim _{x \rightarrow 0} \frac{\cos 4 x+a \cos 2 x+b}{x^4}=\) finite
Using expansion formula for \(\cos 4 x\) and \(\cos 2 x\), we get
\(
\Rightarrow \lim _{x \rightarrow 0} \frac{\left(1-\frac{(4 x)^2}{2!}+\frac{(4 x)^4}{4!}\right)+a\left(1-\frac{(2 x)^2}{2!}+\frac{(2 x)^4}{4!}\right)+b}{x^4}=\text { finite }
\)
\(
\begin{aligned}
& \Rightarrow \lim _{x \rightarrow 0} \frac{(1+a+b)+(-8-2 a) x^2+\left(\frac{32}{3}+\frac{2}{3} a\right) x^4+\cdots}{x^4} \\
& \Rightarrow 1+a+b=0, \text { and } \dots(1) \\
&-8-2 a=0 \dots(2)
\end{aligned}
\)
Solving equations (1) and (2) for \(a\) and \(b\), we ge \(a=-4\) and \(b=3\)
Also, \(L=\frac{32}{3}+\frac{2}{3} a=\frac{32-8}{3}=8\).

Example 67: Find the values of \(a\) and \(b\) in order that
\(
\left.\lim _{x \rightarrow 0} \frac{x(1+a \cos x)-b \sin x}{x^3}=1[\text { using L’ Hopital’s rule }]\right .
\)

Solution:
\(
\begin{aligned}
& \lim _{x \rightarrow 0} \frac{x(1+a \cos x)-b \sin x}{x^3}=1 \quad\left(\frac{0}{0} \text { form }\right) \\
& \Rightarrow \lim _{x \rightarrow 0} \frac{1(1+a \cos x)+x(-a \sin x)-b \cos x}{3 x^2}=1 [\text { using L’ Hopital’s rule }]
\end{aligned}
\)
Here numerator \(\rightarrow 1+a-b\) and denominator \(\rightarrow 0\) and limit is a finite number 1
\(
\therefore 1+a-b=0, \dots(1)
\)
[If \(1+a-b \neq 0\), then limit will not be finite.]
\(
\begin{aligned}
&\begin{aligned}
& \Rightarrow \lim _{x \rightarrow 0} \frac{1+a \cos x-a x \sin x-b \cos x}{3 x^2}=1\left(\frac{0}{0} \text { form }\right) \\
& \Rightarrow \lim _{x \rightarrow 0} \frac{0-a \sin x-a \sin x-a x \cos x+b \sin x}{6 x}=1\left(\frac{0}{0} \text { form }\right) \\
& \Rightarrow \lim _{x \rightarrow 0} \frac{-a \cos x-a \cos x-a \cos x+a x \sin x+b \cos x}{6}=1 \\
& \Rightarrow \frac{-3 a+b}{6}=1 \\
& \Rightarrow-3 a+b=6 \dots(2)
\end{aligned}\\
&\text { Solving equations (1) and (2), we get } a=-\frac{5}{2}, b=-\frac{3}{2} \text {. }
\end{aligned}
\)

MISCELLANEOUS SOLVED PROBLEMS

Q1: \(\lim _{n \rightarrow \infty}\left(4^n+5^n\right)^{1 / n}\) is equal to
a. 4
b. 5
c. \(e\)
d. None of these

Solution: (b) Given limit \(=\lim _{n \rightarrow \infty}\left(4^n+5^n\right)^{1 / n}\)
\(
\begin{aligned}
&=\lim _{n \rightarrow \infty} 5\left(1+\left(\frac{4}{5}\right)^n\right)^{1 / n}=5\\
&\left(\because\left(\frac{4}{5}\right)^n \rightarrow 0 \text { as } n \rightarrow \infty\right)
\end{aligned}
\)

Q2: \(\lim _{x \rightarrow \infty} \sqrt{\frac{x+\sin x}{x-\cos x}}\) is equal to
a. 0
b. 1
c. -1
d. None of these

Solution: (b)
\(
\begin{aligned}
&\lim _{x \rightarrow \infty} \sqrt{\left(\frac{x+\sin x}{x-\cos x}\right)}=\lim _{x \rightarrow \infty} \sqrt{\left(\frac{1+\frac{\sin x}{x}}{1-\frac{\cos x}{x}}\right)}=\lim _{x \rightarrow \infty} \sqrt{1}=1\\
&\left[\because \text { both } \lim _{x \rightarrow \infty} \frac{\sin x}{x} \text { and } \lim _{x \rightarrow \infty} \frac{\cos x}{x} \text { are equal to } 0\right]
\end{aligned}
\)

Q3: \(\lim _{n \rightarrow \infty} \frac{n^p \sin ^2(n!)}{n+1}, 0<p<1\), is equal to
a. 0
b. \(\infty\)
c. 1
d. None of these

Solution:
\(
\begin{aligned}
\lim _{n \rightarrow \infty} \frac{\sin ^2(n!)}{n^{1-p}\left(1+\frac{1}{n}\right)} & \\
& =\frac{\text { some number between } 0 \text { and } 1}{\infty}=0
\end{aligned}
\)

Q4: Let \(f(x)=\left\{\begin{array}{ll}\cos [x], & x \geq 0 \\ |x|+a, & x<0,\end{array}\right.\) then the value of \(a\), so that \(\lim _{x \rightarrow 0} f(x)\) exists, where \([x]\) denotes the greatest integer function \(\leq x\) is equal to
a. 0
b. -1
c. 2
d. 1

Solution:
\(
\begin{array}{rlrl}
\text { (d) } & \text { Since } & \lim _{x \rightarrow 0} f(x) \text { exists } \\
\Rightarrow & & \lim _{x \rightarrow 0^{-}} f(x) & =\lim _{x \rightarrow 0^{+}} f(x) \\
\Rightarrow & & \lim _{h \rightarrow 0} f(0-h) & =\lim _{h \rightarrow 0} f(0+h) \\
\Rightarrow & & \lim _{h \rightarrow 0}|0-h|+a & =\lim _{h \rightarrow 0} \cos [0+h] \\
\Rightarrow & & a & =\cos 0=1 \\
\therefore & & a & =1
\end{array}
\)

Q5: If \(3-\frac{x^2}{12} \leq f(x) \leq 3+\frac{x^3}{9}\) for all \(x \neq 0\), then the value of \(\lim _{x \rightarrow 0} f(x)\) is equal to
a. \(1 / 3\)
b. 3
c. -3
d. \(-1 / 3\)

Solution: (b) According to the question
\(
\begin{aligned}
& \lim _{x \rightarrow 0}\left(3-\frac{x^2}{12}\right) \leq \lim _{x \rightarrow 0} f(x) \leq \lim _{x \rightarrow 0}\left(3+\frac{x^3}{9}\right) \\
& \Rightarrow(3-0) \leq \lim _{x \rightarrow 0} f(x) \leq(3+0)
\end{aligned}
\)
Hence \(\lim _{x \rightarrow 0} f(x)=3\) (from sandwitch theorem).

Q6: \(\lim _{n \rightarrow \infty}\left[\sum_{r=1}^n \frac{1}{2^r}\right]\), where [.] denotes the greatest integer function, is equal to
a. 1
b. 0
c. Non-existent
d. None of these

Solution: (b) \(\sum_{r=1}^n \frac{1}{2^r}=\frac{\frac{1}{2}\left(1-\left(\frac{1}{2}\right)^n\right)}{\left(1-\frac{1}{2}\right)}=1-\left(\frac{1}{2}\right)^n\), which tends to 1 as \(n \rightarrow \infty\) (but in fact always remains less than 1). Thus, \(\lim _{n \rightarrow \infty}\left[\sum_{r=1}^n \frac{1}{2^r}\right]=0\).

Q7: \(\lim _{x \rightarrow 5 \pi / 4}[\sin x+\cos x]\), where [.] denotes the greatest integer function, is equal to
a. -2 .
b. -1
c. -3
d. None of these

Solution: (a) \(\sin x+\cos x=\sqrt{2} \sin \left(x+\frac{\pi}{4}\right)\)
For \(x \rightarrow \frac{5 \pi}{4}+0, \sqrt{2} \sin \left(x+\frac{\pi}{4}\right) \rightarrow-\sqrt{2}+0\)
and for \(x \rightarrow \frac{5 \pi}{4}-0\)
\(
\sqrt{2} \sin \left(x+\frac{\pi}{4}\right) \rightarrow-\sqrt{2}+0
\)
This given limit will be equal to -2.

Q8: \(\lim _{x \rightarrow 0} \frac{\sin [\cos x]}{1+[\cos x]}\), where [.] denotes the greatest integer function, is equal to
a. 1
b. 0
c. Does not exist
d. None of these

Solution:
\(
\begin{gathered}
\text { (b) L.H.L. }=\lim _{x \rightarrow 0^{-}} f(x)=\lim _{h \rightarrow 0} \frac{\sin [\cosh ]}{1+[\cosh ]}=\frac{\sin (0)}{1+0}=0 \\
\qquad(\because h>0 \Rightarrow \cosh <1) \\
\text { R.H.L. }=\lim _{x \rightarrow 0^{+}} f(x)=\lim _{h \rightarrow 0} \frac{\sin [\cosh ]}{1+[\cosh ]}=\frac{\sin (0)}{1+0}=0 \\
\therefore \lim _{x \rightarrow 0} \frac{\sin [\cos x]}{1+[\cos x]}=0
\end{gathered}
\)

Q9: \(\lim _{x \rightarrow 0}\left[\frac{\sin x}{x}\right]\), where [.] denotes the greatest integer function, is equal to
a. 1
b. 0
c: Does not exist
d None of these

Solution: (b) Since \(\left|\frac{\sin x}{x}\right|<1\)
\(\Rightarrow \frac{\sin x}{x}\) tends to 1 forms the values that are less than one as \(x \rightarrow 0\).
Thus, \(\lim _{x \rightarrow 0}\left[\frac{\sin x}{x}\right]=0\)

Q10: The value of \(\lim _{x \rightarrow \pi / 6} \frac{2-\sqrt{3} \cos x-\sin x}{(6 x-\pi)^2}\) is
a. \(1 / 12\)
b. \(1 / 24\)
c. \(1 / 36\)
d. \(1 / 48\)

Solution: (c) We have
\(
\begin{aligned}
& \lim _{x \rightarrow \frac{\pi}{6}} \frac{2-\sqrt{3} \cos x-\sin x}{(6 x-\pi)^2}=\lim _{h \rightarrow 0} \frac{2-\sqrt{3} \cos \left(\frac{\pi}{6}+h\right)-\sin \left(\frac{\pi}{6}+h\right)}{\left[6\left(\frac{\pi}{6}+h\right)-\pi\right]^2} \\
& =\lim _{h \rightarrow 0} \frac{2-\sqrt{3}\left(\cos \frac{\pi}{6} \cos h-\sin \frac{\pi}{6} \sin h\right)-\left(\sin \frac{\pi}{6} \cos h+\cos \frac{\pi}{6} \sin h\right)}{36 h^2} \\
& =\lim _{h \rightarrow 0} \frac{2-\frac{3}{2} \cos h+\frac{\sqrt{3}}{2} \sin h-\frac{1}{2} \cos h-\frac{\sqrt{3}}{2} \sin h}{36 h^2}
\end{aligned}
\)
\(
\begin{aligned}
& =\lim _{h \rightarrow 0} \frac{2(1-\cos h)}{36 h^2}=\frac{1}{18} \lim _{h \rightarrow 0} \frac{2 \sin ^2\left(\frac{h}{2}\right)}{h^2} \\
& =\frac{1}{9} \lim _{h \rightarrow 0}\left(\frac{\sin \left(\frac{h}{2}\right)}{\left(\frac{h}{2}\right)}\right)^2 \frac{1}{4}=\frac{1}{9}(1)^2 \times \frac{1}{4}=\frac{1}{36}
\end{aligned}
\)

Q11: The value of \(\lim _{x \rightarrow 0} \frac{\sqrt{2}-\sqrt{1+\cos x}}{\sin ^2 x}\) is
a. \(\frac{1}{2 \sqrt{2}}\)
b. \(\frac{1}{8 \sqrt{2}}\)
c. \(\frac{1}{4 \sqrt{2}}\)
d. \(-\frac{1}{4 \sqrt{2}}\)

Solution: (c) We have \(\lim _{x \rightarrow 0} \frac{\sqrt{2}-\sqrt{1+\cos x}}{\sin ^2 x}\)
\(
\begin{aligned}
& =\lim _{x \rightarrow 0} \frac{2-(1+\cos x)}{\sin ^2 x} \times \frac{1}{\sqrt{2}+\sqrt{1+\cos x}} \\
& =\lim _{x \rightarrow 0} \frac{1-\cos x}{(1+\cos x)(1-\cos x)} \times \lim _{x \rightarrow 0} \frac{1}{\sqrt{2}+\sqrt{1+\cos x}} \\
& =\lim _{x \rightarrow 0} \frac{1}{(1+\cos x)} \times \frac{1}{2 \sqrt{2}}=\frac{1}{4 \sqrt{2}}
\end{aligned}
\)

Q12: If \(a_1=1\) and \(a_{n+1}=\frac{4+3 a_n}{3+2 a_n}, n \geq 1\), and if \(\lim _{n \rightarrow \infty} a_n=n\), then the value of \(a\) is
a. \(\sqrt{2}\)
b. \(-\sqrt{2}\)
c. 2
d. None of these

Solution: (a) We have \(a_{n+1}=\frac{4+3 a_n}{3+2 a_n}\)
\(
\begin{aligned}
& \lim _{n \rightarrow \infty} a_{n+1}=\lim _{n \rightarrow \infty} \frac{4+3 a_n}{3+2 a_n} \\
& a=\frac{4+3 a}{3+2 a} \Rightarrow 2 a^2=4 \Rightarrow a=\sqrt{2}\left(\text { where } \lim _{n \rightarrow \infty} a_n=a\right) \\
& \left(a \neq-\sqrt{2} \text { because each } a_n>0\right)
\end{aligned}
\)

Q13: Evaluate \(\lim _{x \rightarrow 0} \frac{x-\sin x}{x^3}\) (do not use either L’Hopital’s rule or series expansion for \(\sin x\) ), hence evaluate
\(
\lim _{x \rightarrow 0} \frac{\sin x-x-x \cos x+x^2 \cot x}{x^5}
\)

Solution: \(L=\lim _{x \rightarrow 0} \frac{x-\sin x}{x^3}\)
Replace \(x\) by \(3 x\)
\(
\begin{aligned}
& \Rightarrow L=\lim _{x \rightarrow 0} \frac{3 x-\sin 3 x}{(3 x)^3} \\
& =\lim _{x \rightarrow 0} \frac{3 x-\left(3 \sin x-4 \sin ^3 x\right)}{(3 x)^3} \\
& =\lim _{x \rightarrow 0} \frac{3 x-3 \sin x}{(3 x)^3}+\lim _{x \rightarrow 0} \frac{4 \sin ^3 x}{(3 x)^3} \\
& =\frac{1}{9} \lim _{x \rightarrow 0} \frac{x-\sin x}{x^3}+\frac{4}{27} \lim _{x \rightarrow 0}\left(\frac{\sin x}{x}\right)^3
\end{aligned}
\)
\(
\begin{aligned}
& =\frac{1}{9} L+\frac{4}{27} \\
& \Rightarrow \frac{8}{9} L=\frac{4}{27} \\
& \Rightarrow L=\frac{1}{6} \\
& \text { Also } \lim _{x \rightarrow 0} \frac{\sin x-x-x \cos x+x^2 \cot x}{x^5} \\
& =\lim _{x \rightarrow 0} \frac{(\sin x-x)+x \cot x(x-\sin x)}{x^5} \\
& =\lim _{x \rightarrow 0} \frac{(\sin x-x)(1-x \cot x)}{x^5}
\end{aligned}
\)
\(
\begin{aligned}
& =\lim _{x \rightarrow 0} \frac{\sin x-x}{x^3} \times \frac{\tan x-x}{x^3} \times \frac{x}{\tan x} \\
& =\frac{-1}{6} \times \frac{1}{3} \times 1=\frac{-1}{18}(\text { Using expansions of } \sin x \text { and } \tan x)
\end{aligned}
\)

Q14: Evaluate \(\lim _{n \rightarrow \infty} \cos \left(\pi \sqrt{n^2+n}\right)\), when \(n\) is an integer.

Solution: \(L=\lim _{n \rightarrow \infty} \cos \left(\pi \sqrt{n^2+n}\right)\)
\(
\begin{aligned}
& =\lim _{n \rightarrow \infty} \pm \cos \left(n \pi-\pi \sqrt{n^2+n}\right) \\
& =\lim _{n \rightarrow \infty} \pm \cos \left(\pi\left(n-\sqrt{n^2+n}\right)\right) \\
& = \pm \lim _{n \rightarrow \infty} \cos \left(\frac{-n \pi}{n+\sqrt{n^2+n}}\right) \\
& = \pm \lim _{n \rightarrow \infty} \cos \left(\frac{n \pi}{n+n \sqrt{1+\frac{1}{n}}}\right) \\
& = \pm \lim _{n \rightarrow \infty} \cos \left(\frac{\pi}{1+\sqrt{1+\frac{1}{n}}}\right)
\end{aligned}
\)
\(
= \pm \cos \frac{\pi}{2} \rightarrow 0
\)

Q15: Let the variable \(x_n\) be determined by the following law of formation:
\(
\begin{aligned}
&\begin{aligned}
& x_0=\sqrt{a} \\
& x_1=\sqrt{a+\sqrt{a}} \\
& x_2=\sqrt{a+\sqrt{a+\sqrt{a}}} \\
& x_3=\sqrt{a+\sqrt{a+\sqrt{a+\sqrt{a}}}} \\
\vdots
\end{aligned}\\
&\text { Then, find the value of } \lim _{n \rightarrow \infty} x_n \text {. }
\end{aligned}
\)

Solution: We have \(x_n^2=a+x_{n-1}\)
\(
\Rightarrow L^2=a+L\left(\text { as at infinity } L=\lim _{n \rightarrow \infty} x_n » \lim _{n \rightarrow \infty} x_{n-1}\right)
\)
\(
\begin{aligned}
\Rightarrow & L^2-L-a=0 \\
\Rightarrow & L=\frac{1 \pm \sqrt{(1+4 a)}}{2} \\
\Rightarrow & L=\frac{1+\sqrt{(1+4 a)}}{2} \text { (as according to the question } a>0 \\
& \text { hence } \left.\frac{1-\sqrt{(1+4 a)}}{2}<0\right) .
\end{aligned}
\)

Q16: Evaluate \(\lim _{n \rightarrow \infty} \prod_{r=3}^n \frac{r^3-8}{r^3+8}\), where \(\prod\) represents the product of function.

Solution: Let \(P=\lim _{n \rightarrow \infty} \prod_{r=3}^n\left(\frac{r^3-8}{r^3+8}\right)\)
\(
\begin{aligned}
& =\lim _{n \rightarrow \infty} \prod_{r=3}^n\left(\frac{r-2}{r+2}\right)\left(\frac{r^2+2 r+4}{r^2-2 r+4}\right) \\
& =\lim _{n \rightarrow \infty} \prod_{r=3}^n\left(\frac{r-2}{r+2}\right) \prod_{r=3}^n\left(\frac{r^2+2 r+4}{r^2-2 r+4}\right) \\
& =\lim _{n \rightarrow \infty}\left\{\frac{1}{5} \frac{2}{6} \frac{3}{7} \frac{4}{8} \frac{5}{9} \cdots \frac{(n-5)}{(n-1)} \frac{(n-4)}{(n)} \frac{(n-3)}{(n+1)} \frac{(n-2)}{(n+2)}\right\} \times \\
& \left\{\frac{19}{7} \times \frac{28}{12} \times \frac{39}{19} \cdots \frac{\left(n^2-2 n+4\right)}{\left(n^2-6 n+12\right)} \times \frac{\left(n^2+3\right)}{\left(n^2-4 n+7\right)} \times \frac{\left(n^2+2 n+4\right)}{\left(n^2-2 n+4\right)}\right\} \\
& =\lim _{n \rightarrow \infty}\left\{\frac{1 \times 2 \times 3 \times 4}{(n-1) n(n+1)(n+2)} \times \frac{\left(n^2+3\right)\left(n^2+2 n+4\right)}{7 \times 12}\right\}
\end{aligned}
\)
\(
\begin{aligned}
& =\frac{2}{7} \lim _{n \rightarrow \infty}\left\{\frac{\left(n^2+3\right)\left(n^2+2 n+4\right)}{(n-1) n(n+1)(n-2)}\right\} \\
& =\frac{2}{7} \lim _{n \rightarrow \infty}\left\{\frac{\left(1+\frac{3}{n^2}\right)\left(1+\frac{2}{n}+\frac{4}{n^2}\right)}{\left(1-\frac{1}{n}\right) 1\left(1+\frac{1}{n}\right)\left(1+\frac{2}{n}\right)}\right\} \\
& =\frac{2}{7} \frac{(1+0)(1+0+0)}{(1-0) 1(1+0)(1+0)}=\frac{2}{7}
\end{aligned}
\)
\(
\text { Hence } P=\frac{2}{7}
\)

Q17: If \([x]\) denotes the greatest integer \(\leq x\), then evaluate \(\lim _{n \rightarrow \infty} \frac{1}{n^3}\left\{\left[1^2 x\right]+\left[2^2 x\right]+\left[3^2 x\right]+\cdots+\left[n^2 x\right]\right\}\)

Solution: \(\lim _{n \rightarrow \infty} \frac{1}{n^3}\left\{\left[1^2 x\right]+\left[2^2 x\right]+\left[3^2 x\right]+\cdots+\left[n^2 x\right]\right\}\)
\(
\begin{aligned}
& =\lim _{n \rightarrow \infty}\left\{\frac{\sum_{r=1}^n\left[r^2 x\right]}{n^3}\right\}=\lim _{n \rightarrow \infty}\left(\frac{\sum_{r=1}^n r^2 x-\left\{r^2 x\right\}}{n^3}\right) \\
& =\lim _{n \rightarrow \infty}\left(\frac{x \frac{n(n+1)(2 n+1)}{6}}{n^3}-\sum_{r=1}^n \frac{\left\{r^2 x\right\}}{n^3}\right) \\
& =x \frac{(1)(1)(2)}{6}-0=\frac{x}{3}
\end{aligned}
\)

Q18: Find the integral value of \(n\) for which the \(\lim _{x \rightarrow 0} \frac{\cos ^2 x-\cos x-e^x \cos x+e^x-\frac{x^3}{2}}{x^n}\) is a finite non-zero.

Solution:
\(
\begin{aligned}
& \cos x=1-\frac{x^2}{2!}+\frac{x^4}{4!}-\frac{x^6}{6!}+ \ldots\\
& e^x=1+x+\frac{x^2}{2!}+\frac{x^3}{3!}+\frac{x^4}{4!}+ \ldots
\end{aligned}
\)
\(
\begin{aligned}
& \cos ^2 x=\left(1-\frac{x^2}{2}+\frac{x^4}{24}-\ldots\right)^2=1-x^2+\frac{x^4}{3}-\ldots \\
& e^x \cos x=\left(1+x+\frac{x^2}{2}+\frac{x^3}{6}+\frac{x^4}{24}+\ldots\right)\left(1-\frac{x^2}{2}+\frac{x^4}{24}-\ldots\right)=1+x-\frac{x^3}{3}-\frac{x^4}{6}+\ldots
\end{aligned}
\)
Subsituting and simplifying we get
\(
\begin{gathered}
=\lim _{x \rightarrow 0} \frac{\left(-\frac{x^2}{2!}+\frac{x^4}{4!}-\frac{x^6}{6!}+\cdots\right)\left[\left(-x-x^2-\frac{x^3}{3!}-\frac{2 x^5}{5!}-\cdots\right)\right]-\frac{x^3}{2}}{x^n} \\
=\lim _{x \rightarrow 0} \frac{\left(\frac{x^3}{2}+\frac{x^4}{2}+\frac{x^5}{12}-\frac{x^5}{24}+\ldots\right)-\frac{x^3}{2}}{x^n}=\text { non-zero if } n=4
\end{gathered}
\)