13.3 Limits
Limits in maths are defined as the values that a function approaches the output for the given input values. Limits are all about approaching. Sometimes you can’t work something out directly, but you can see what it should be as you get closer and closer. Limits are important in calculus and mathematical analysis and are used to define integrals, derivatives, and continuity.
Limits Definition
Limits in maths are unique real numbers. Let us consider a real-valued function ” \(f\) ” and the real number ” \(\mathrm{a}\) “, the limit is normally defined
In general as \(x \rightarrow a, f(x) \rightarrow l\), then \(l\) is called limit of the function \(f(x)\) which is symbolically written as
\(\lim _{x \rightarrow a} f(x)=l\).
It is read as “the limit of \(f\) of \(x\), as \(x\) approaches \(a\) equals \(l\)“. The “lim” shows the limit, and fact that function \(f(x)\) approaches the limit \(l\) as \(x\) approaches \(a\) is described by the right arrow.
For Example; \(\lim _{x \rightarrow 10} \frac{x}{2}=5 \)
We know perfectly well that \(10 / 2=5\), but limits can still be used.
Limits and Functions
A function may approach two different limits. One where the variable approaches its limit through values larger than the limit and the other where the variable approaches its limit through values smaller than the limit. In such a case, the limit is not defined but the right-hand limits and left-hand limits exist.
Right-handed limit
We say
\(\lim _{x \rightarrow a^{+}} f(x)=L\)
provided we can make \(f(x)\) as close to \(L\) as we want for all \(x\) sufficiently close to \(a\) with \(x>a\) without actually letting \(x\) be \(a\).
Left-handed limit
We say
\(
\lim _{x \rightarrow a^{-}} f(x)=L
\)
provided we can make \(f(x)\) as close to \(L\) as we want for all \(x\) sufficiently close to \(a\) with \(x<a\) without actually letting \(x\) be \(a\).
How do you know Limit of a function exist?
A function’s limit exists at a point if and only if the left-hand limit and the right-hand limit at that point both exist and are equal to the same value.
\(\lim _{x \rightarrow a^{+}} f(x)=\lim _{x \rightarrow a^{-}} f(x)=\lim _{x \rightarrow a} f(x)=L
\)
How do you know Limit of a function exist?
A function’s limit exists at a point if and only if the left-hand limit and the right-hand limit at that point both exist and are equal to the same value.
\(\lim _{x \rightarrow a^{+}} f(x)=\lim _{x \rightarrow a^{-}} f(x)=\lim _{x \rightarrow a} f(x)=L
\)
So, when we are looking at limits it’s now important to pay very close attention to see whether we are doing a normal limit or one of the one-sided limits. Let’s now take a look at some of the problems from the last section and look at one-sided limits instead of the normal limit. Let’s look at a few examples.
Example 1: Estimate the value of the following limits.
\(
\lim _{t \rightarrow 0^{+}} h(t) \quad \text { and } \quad \lim _{t \rightarrow 0^{-}} h(t), \quad \text { where } \quad h(t)= \begin{cases}0 & \text { if } t<0 \\ 1 & \text { if } t \geq 0\end{cases}
\)
Solution:
Let’s draw the graph of the given function
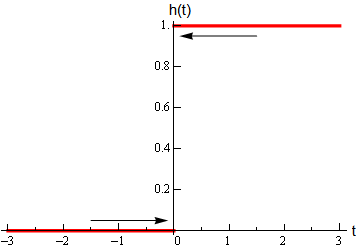
So, we can see that if we stay to the right of \(t=0\) (i.e. \(t>0\) ) then the function is moving in towards a value of 1 as we get closer and closer to \(t=0\), but staying to the right. We can therefore say that the right-handed limit is,
\(
\lim _{t \rightarrow 0^{+}} h(t)=1
\)
Likewise, if we stay to the left of \(t=0\) (i.e \(t<0\) ) the function is moving in towards a value of 0 as we get closer and closer to \(t=0\), but staying to the left. Therefore, the left-handed limit is,
\(
\lim _{t \rightarrow 0^{-}} h(t)=0
\)
In this example, we do get one-sided limits even though the normal limit itself doesn’t exist.
Example 2: Estimate the value of the following limits.
\(\lim _{x \rightarrow 1} \frac{x^2-1}{x-1}\)Solution:
\(
\lim _{x \rightarrow 1} \frac{x^2-1}{x-1}
\)
\(
\lim _{x \rightarrow 1} \frac{(x-1)(x+1)}{x-1}= \lim _{x \rightarrow 1} (x+1) =2
\)
Important Note:
Given a function \(f(x)\) if, \(\lim _{x \rightarrow a^{+}} f(x)=\lim _{x \rightarrow a^{-}} f(x)=L\)
then the normal limit will exist and \(\lim _{x \rightarrow a} f(x)=L\)
Likewise, if \(\lim _{x \rightarrow a} f(x)=L\)
then, \(\lim _{x \rightarrow a^{+}} f(x)=\lim _{x \rightarrow a^{-}} f(x)=L\)
This fact can be turned around to also say that if the two one-sided limits have different values, i.e.,
\(\lim _{x \rightarrow a^{+}} f(x) \neq \lim _{x \rightarrow a^{-}} f(x)\), then the normal limit will not exist.
This should make some sense. If the normal limit did exist then by the fact the two one-sided limits would have to exist and have the same value by the above fact. So, if the two one-sided limits have different values (or don’t even exist) then the normal limit simply can’t exist. Let’s look at the waveform below and find the limits and also determine if the normal limit exists in this case.
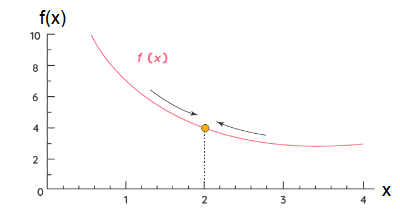
In the given waveform, we can calculate \(\lim _{x \rightarrow 2^{+}} f(x)=\lim _{x \rightarrow 2^{-}} f(x)=4\), therefore normal limit exist in this case. \(\lim _{x \rightarrow 2} f(x)=4\)
Example 3: Given the following graph, compute each of the following.
(a) \(f(-4)\)
(b) \(\lim _{x \rightarrow-4^{-}} f(x)\)
(c) \(\lim _{x \rightarrow-4^{+}} f(x)\)
(d) \(\lim _{x \rightarrow-4} f(x)\)
(e) \(f(1)\)
(f) \(\lim _{x \rightarrow 1^{-}} f(x)\)
(g) \(\lim _{x \rightarrow 1^{+}} f(x)\)
(h) \(\lim _{x \rightarrow 1} f(x)\)
(i) \(f(6)\)
(j) \(\lim _{x \rightarrow 6^{-}} f(x)\)
(k) \(\lim _{x \rightarrow 6^{+}} f(x)\)
(I) \(\lim _{x \rightarrow 6} f(x)\)
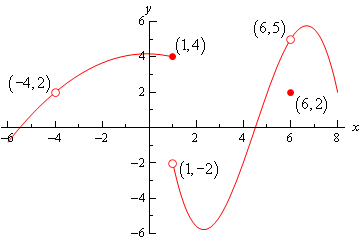
Solution:
(a) \(f(-4)\) doesn’t exist. There is no closed dot for this value of \(x\) and so the function doesn’t exist at this point.
(b) \(\lim _{x \rightarrow-4^{-}} f(x)=2\) The function is approaching a value of 2 as \(x\) moves in towards \(-4\) from the left.
(c) \(\lim _{x \rightarrow-4^{+}} f(x)=2\) The function is approaching a value of 2 as \(x\) moves in towards \(-4\) from the right.
(d) \(\lim _{x \rightarrow-4} f(x)=2\) We can do this one of two ways. Either we can use the fact here and notice that the two one-sided limits are the same and so the normal limit must exist and have the same value as the one-sided limits or just get the answer from the graph.
Also recall that a limit can exist at a point even if the function doesn’t exist at that point.
(e) \(f(1)=4\). The function will take on the \(y\) value where the closed dot is.
(f) \(\lim _{x \rightarrow 1^{-}} f(x)=4\) The function is approaching a value of 4 as \(x\) moves in towards 1 from the left.
(g) \(\lim _{x \rightarrow 1^{+}} f(x)=-2\) The function is approaching a value of \(-2\) as \(x\) moves in towards 1 from the right. Remember that the limit does not care about what the function is actually doing at the point, it only cares about what the function is doing around the point. In this case, always staying to the right of \(x=1\), the function is approaching a value of \(-2\) and so the limit is \(-2\). The limit is not 4 , as that is value of the function at the point and again the limit doesn’t care about that!
(h) \(\lim _{x \rightarrow 1} f(x)\) doesn’t exist. The two one-sided limits both exist, however they are different and so the normal limit doesn’t exist.
(i) \(f(6)=2\). The function will take on the \(y\) value where the closed dot is.
(j) \(\lim _{x \rightarrow 6^{-}} f(x)=5\) The function is approaching a value of 5 as \(x\) moves in towards 6 from the left.
(k) \(\lim _{x \rightarrow 6^{+}} f(x)=5\) The function is approaching a value of 5 as \(x\) moves in towards 6 from the right.
(I) \(\lim _{x \rightarrow 6} f(x)=5\) Again, we can use either the graph or the fact to get this.
Also, once more remember that the limit doesn’t care what is happening at the point and so it’s possible for the limit to have a different value than the function at a point. When dealing with limits we’ve always got to remember that limits simply do not care about what the function is doing at the point in question. Limits are only concerned with what the function is doing around the point.
Example 4: Consider the function
\(
f(x)= \begin{cases}1, & x \leq 0 \\ 2, & x>0\end{cases}
\)
Calculate \(\lim _{x \rightarrow 0} f(x)\) and \(\lim _{x \rightarrow 0^{+}} f(x)\)
Solution:
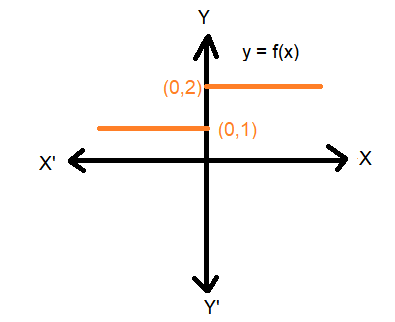
From the above graph it is clear that the value of \(f\) at 0 dictated by values of \(f(x)\) with \(x \leq 0\) equals 1, i.e., the left hand limit of \(f(x)\) at 0 is
\(
\lim _{x \rightarrow 0^{-}} f(x)=1 .
\)
Similarly, the value of \(f\) at 0 dictated by values of \(f(x)\) with \(x>0\) equals 2, i.e., the right hand limit of \(f(x)\) at 0 is
\(
\lim _{x \rightarrow 0^{+}} f(x)=2 .
\)
In this case, the right and left-hand limits are different, and hence we say that the limit of \(f(x)\) as \(x\) tends to zero does not exist (even though the function is defined at 0 ).
Example 5: Consider the constant function \(f(x)=3\). Find its limit at \(x=2\).
Solution:
\(\lim _{x \rightarrow 2^{-}} f(x)=\lim _{x \rightarrow 2^{+}} f(x)=\lim _{x \rightarrow 2} f(x)=3\)This function being the constant function takes the same value (3, in this case) everywhere, i.e., its value at points close to 2 is 3.
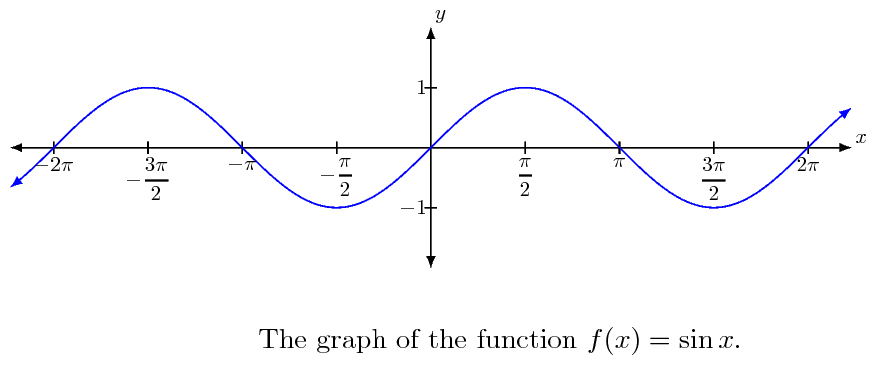
Example 6: Consider the function \(f(x)=\sin x\). Find the value of \(\lim _{x \rightarrow \frac{\pi}{2}} \sin x\), where the angle is measured in radians.
Solution:
We tabulate the (approximate) value of \(f(x)\) near \(\frac{\pi}{2}\) (Table below).
\begin{array}{|l|l|l|l|l|}
\hline x & \frac{\pi}{2}-0.1 & \frac{\pi}{2}-0.01 & \frac{\pi}{2}+0.01 & \frac{\pi}{2}+0.1 \\
\hline f(x) & 0.9950 & 0.9999 & 0.9999 & 0.9950 \\
\hline
\end{array}
\)
From this, we may deduce that
\(
\lim _{x \rightarrow \frac{\pi^{-}}{2}} f(x)=\lim _{x \rightarrow \frac{\pi^{+}}{2}} f(x)=\lim _{x \rightarrow \frac{\pi}{2}} f(x)=1 .
\)
Further, this is supported by the graph of \(f(x)=\sin x\).
Example 7: \(\text { Consider the function } f(x)=x+\cos x \text {. Find } \lim _{x \rightarrow 0} f(x) \text {. }\)
Solution: From the Table below, we may deduce that
\(
\lim _{x \rightarrow 0^{-}} f(x)=\lim _{x \rightarrow 0^{+}} f(x)=\lim _{x \rightarrow 0} f(x)=1
\)
In this case too, we observe that \(\lim _{x \rightarrow 0} f(x)=f(0)=1\).
Now, can you convince yourself that
\(\lim _{x \rightarrow 0}[x+\cos x]=\lim _{x \rightarrow 0} x+\lim _{x \rightarrow 0} \cos x\) is indeed true?
\begin{array}{|c|c|c|c|c|c|c|}
\hline x & -0.1 & -0.01 & -0.001 & 0.001 & 0.01 & 0.1 \\
\hline f(x) & 0.9850 & 0.98995 & 0.9989995 & 1.0009995 & 1.00995 & 1.0950 \\
\hline
\end{array}
\)
Example 8: \(\text { Consider the function } f(x)=\frac{1}{x^2} \text { for } x>0 \text {. Find } \lim _{x \rightarrow 0} f(x) \text {. }\)
Solution: From the table given below, we see that as \(x\) tends to \(0, f(x)\) becomes larger and larger. What we mean here is that the value of \(f(x)\) may be made larger than any given number.
\(\begin{array}{|l|l|l|l|l|}
\hline x & 1 & 0.1 & 0.01 & 10^{-n} \\
\hline f(x) & 1 & 100 & 10000 & 10^{2 n} \\
\hline
\end{array}
\)
Mathematically, we say \(\lim _{x \rightarrow 0} f(x)=+\infty\)
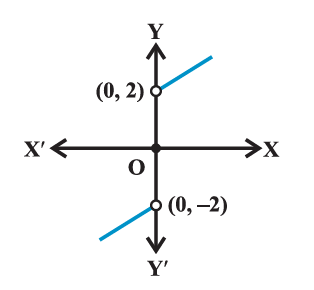
Example 9:
\(\begin{aligned}
&\text { We want to find } \lim _{x \rightarrow 0} f(x) \text {, where }\\
&f(x)= \begin{cases}x-2, & x<0 \\ 0, & x=0 \\ x+2, & x>0\end{cases}
\end{aligned}
\)
Solution: As usual we make a table of \(x\) near 0 with \(f(x)\). Observe that for negative values of \(x\) we need to evaluate \(x-2\) and for positive values, we need to evaluate \(x+2\).
\(
\begin{array}{|c|c|c|c|c|c|c|}
\hline x & -0.1 & -0.01 & -0.001 & 0.001 & 0.01 & 0.1 \\
\hline f(x) & -2.1 & -2.01 & -2.001 & 2.001 & 2.01 & 2.1 \\
\hline
\end{array}
\)
From the first three entries of the Table above, we deduce that the value of the function is decreasing to \(-2\) and hence.
\(
\lim _{x \rightarrow 0^{-}} f(x)=-2
\)
From the last three entries of the table, we deduce that the value of the function is increasing from 2 and hence
\(
\lim _{x \rightarrow 0^{+}} f(x)=2
\)
Since the|left and right-hand limits at 0 do not coincide, we say that the limit of the function at 0 does not exist.
Graph of this function is given in below. Here, we remark that the value of the function at \(x=0\) is well defined and is, indeed, equal to 0, but the limit of the function at \(x=0\) is not even defined.
Algebra of limits (Properties of Limits)
Algebra of limits of a function refers to addition, subtraction, multiplication, and division as long as the limits and functions under consideration are well defined.
Let \(f\) and \(g\) be two functions such that both \(\lim _{x \rightarrow a} f(x)\) and \(\lim _{x \rightarrow a} g(x)\) exist. Then
(i) Law of Addition: Limit of sum of two functions is sum of the limits of the functions, i.e.,
\(\lim _{x \rightarrow a}[f(x)+g(x)]=\lim _{x \rightarrow a} f(x)+\lim _{x \rightarrow a} g(x) .\)
(ii) Law of Subtraction: Limit of difference of two functions is difference of the limits of the functions, i.e.,
\(\lim _{x \rightarrow a}[f(x)-g(x)]=\lim _{x \rightarrow a} f(x)-\lim _{x \rightarrow a} g(x) .\)
(iii) Law of Multiplication: Limit of product of two functions is product of the limits of the functions, i.e.,
\(\lim _{x \rightarrow a}[f(x) \cdot g(x)]=\lim _{x \rightarrow a} f(x) . \lim _{x \rightarrow a} \mathrm{~g}(x) .\)
(iv) Law of Division: Limit of quotient of two functions is quotient of the limits of the functions (whenever the denominator is non zero), i.e.,
\(
\lim _{x \rightarrow a} \frac{f(x)}{g(x)}=\frac{\lim _{x \rightarrow a} f(x)}{\lim _{x \rightarrow a} g(x)}
\)
(v) Law of Constant: \(\lim _{x \rightarrow a} c=c\)
(vi) Law of Root:\(\lim _{x \rightarrow a} \sqrt[n]{f(x)}=\sqrt[n]{\lim _{x \rightarrow a} f(x)}\)
(vii) Law of Power: \(\lim _{x \rightarrow a}\left(f(x))^n=\left(\lim _{x \rightarrow a} f(x)\right)^n\right.\), where \(n\) is an integer.
Special Rules
\(1 .\) \(\lim _{x \rightarrow a} \frac{x^n-a^n}{x-a}=n a^{(n-1)}\) , for all real values of \(n\).
\(2 .\) \(\lim _{\theta \rightarrow 0} \frac{\sin \theta}{\theta}=1\)
\(3 .\) \(\lim _{\theta \rightarrow 0} \frac{\tan \theta}{\theta}=1\)
\(4 .\) \(\lim _{\theta \rightarrow 0} \frac{1-\cos \theta}{\theta}=0\)
\(5 .\) \(\lim _{\theta \rightarrow 0} \cos \theta=1\)
\(6 .\) \(\lim _{x \rightarrow 0} e^x=1\)
\(7 .\) \(\lim _{x \rightarrow 0} \frac{e^x-1}{x}=1\)
\(8 .\) \(\lim _{x \rightarrow \infty}\left(1+\frac{1}{x}\right)^x=e\)
Limits of Polynomials
A function \(f\) is said to be a polynomial function of degree \(n, f(x)=a_0+a_1 x+a_2 x^2+\ldots+a_n x^n\), where \(a_i s\) are real numbers such that \(a_n \neq 0\) for some natural number \(n\).
We know that \(\lim _{x \rightarrow a} x=a\). Hence
\(
\lim _{x \rightarrow a} x^2=\lim _{x \rightarrow a}(x \cdot x)=\lim _{x \rightarrow a} x \cdot \lim _{x \rightarrow a} x=a \cdot a=a^2
\)
An easy exercise in induction on \(n\) tells us that
\(
\lim _{x \rightarrow a} x^n=a^n
\)
Now, let \(f(x)=a_0+a_1 x+a_2 x^2+\ldots+a_n x^n\) be a polynomial function. Thinking of each of \(a_0, a_1 x, a_2 x^2, \ldots, a_n x^n\) as a function, we have
\begin{aligned}
\lim _{x \rightarrow a} f(x) & =\lim _{x \rightarrow a}\left[a_0+a_1 x+a_2 x^2+\ldots+a_n x^n\right] \\
& =\lim _{x \rightarrow a} a_0+\lim _{x \rightarrow a} a_1 x+\lim _{x \rightarrow a} a_2 x^2+\ldots+\lim _{x \rightarrow a} a_n x^n \\
& =a_0+a_1 \lim _{x \rightarrow a} x+a_2 \lim _{x \rightarrow a} x^2+\ldots+a_n \lim _{x \rightarrow a} x^n \\
& =a_0+a_1 a+a_2 a^2+\ldots+a_n a^n \\
& =f(a)
\end{aligned}
\)
Example 10: Find the limits:
(i) \(\lim _{x \rightarrow 1}\left[x^3-x^2+1\right]\)
(ii) \(\lim _{x \rightarrow 3}[x(x+1)]\)
(iii) \(\lim _{x \rightarrow-1}\left[1+x+x^2+\ldots+x^{10}\right]\).
Solution: The required limits are all limits of some polynomial functions. Hence the limits are the values of the function at the prescribed points. We have
(i) \(\lim _{x \rightarrow 1}\left[x^3-x^2+1\right]=1^3-1^2+1=1\)
(ii) \(\lim _{x \rightarrow 3}[x(x+1)]=3(3+1)=3(4)=12\)
(iii) \(\lim _{x \rightarrow-1}\left[1+x+x^2+\ldots+x^{10}\right]=1+(-1)+(-1)^2+\ldots+(-1)^{10}=1-1+1 \ldots+1=1\)
Limits of Rational Functions
Before we apply limits on rational functions, first, we must understand what rational functions are and how to write them.
A function \(\mathrm{f}\) is called a rational function, if
\(
f(x)=\frac{g(x)}{h(x)}
\)
, where \(g(x)\) and \(h(x)\) are polynomial functions such that \(h(x) \neq 0\).
The application of limit for \(f(x)\) as \(x\) tends to \(a\) is given as:
\(
\lim _{x \rightarrow a} f(x)=\lim _{x \rightarrow a} \frac{g(x)}{h(x)}=\frac{\lim _{x \rightarrow a} g(x)}{\lim _{x \rightarrow a} h(x)}=\frac{g(a)}{h(a)}
\)
If \(h(a)=0\), then we consider two cases to define the limit of the rational function \(g(x) / h(x)\).
Case 1: \(g(a) \neq 0\)
In this case, \(g(a) \neq 0\) and \(h(a)=0\) so the limit does not exist.
Case 2: \(g(a)=0\)
Here, we need to write the functions \(g(x)\) and \(h(x)\) as:
\(g(x)=(x-a)^k g_1(x)\), where \(k\) is the maximum of powers of \((x-a)\) in \(g(x)\)
\(h(x)=(x-a)^l h_1(x)\) as \(h(a)=0\)
Assume that \(\mathrm{k}>l\), then we have
\(
\lim _{x \rightarrow a} f(x)=\lim _{x \rightarrow a} \frac{g(x)}{h(x)}=\frac{\lim _{x \rightarrow a} g(x)}{\lim _{x \rightarrow a} h(x)}=\frac{\lim _{x \rightarrow a}(x-a)^k g_1(x)}{\lim _{x \rightarrow a}(x-a)^l h_1(x)}
\)
Now, by applying the limit,
\begin{aligned}
&=\frac{\lim _{x \rightarrow a}(x-a)^{(k-l)} g_1(x)}{\lim _{x \rightarrow a} h_1(x)}=\frac{0 . g_1(a)}{h_1(a)}=0\\
&\text { If } k<l \text {, the limit is not defined. }
\end{aligned}
\)
Thus, we need to evaluate the functions individually that are involved in the rational functions at the prescribed points at first. If this is of the form \(0 / 0\), then if possible, we have to rewrite the function such that we could cancel the factors which are causing the limit to be of the form \(0 / 0\).
Example 11:
Compute:
\(\lim _{x \rightarrow 2} \frac{x^2-100}{3 x+6}\)
Solution:
\(\lim _{x \rightarrow 2} \frac{x^2-100}{3 x+6}=\frac{\lim _{x \rightarrow 2}\left(x^2-100\right)}{\lim _{x \rightarrow 2}(3 x+6)}=\frac{(2)^2-100}{3(2)+6}=\frac{4-100}{6+6}=\frac{-96}{12}=-8\)
Similarly, we can compute the limits at specified points for a given rational function in different ways.
Example 12: Find the limits:
(i) \(\lim _{x \rightarrow 1}\left[x^3-x^2+1\right]\)
(ii) \(\lim _{x \rightarrow 3}[x(x+1)]\)
(iii) \(\lim _{x \rightarrow-1}\left[1+x+x^2+\ldots+x^{10}\right]\).
Solution: The required limits are all limits of some polynomial functions. Hence the limits are the values of the function at the prescribed points. We have
(i) \(\lim _{x \rightarrow 1}\left[x^3-x^2+1\right]=1^3-1^2+1=1\)
(ii) \(\lim _{x \rightarrow 3}[x(x+1)]=3(3+1)=3(4)=12\)
(iii) \(\lim _{x \rightarrow-1}\left[1+x+x^2+\ldots+x^{10}\right]=1+(-1)+(-1)^2+\ldots+(-1)^{10}\) \(=1-1+1 \ldots+1=1\).
Example 13: Find the limits:
(i) \(\lim _{x \rightarrow 1}\left[\frac{x^2+1}{x+100}\right]\)
(ii) \(\lim _{x \rightarrow 2}\left[\frac{x^3-4 x^2+4 x}{x^2-4}\right]\)
(iii) \(\lim _{x \rightarrow 2}\left[\frac{x^2-4}{x^3-4 x^2+4 x}\right]\)
(iv) \(\lim _{x \rightarrow 2}\left[\frac{x^3-2 x^2}{x^2-5 x+6}\right]\)
(v) \(\lim _{x \rightarrow 1}\left[\frac{x-2}{x^2-x}-\frac{1}{x^3-3 x^2+2 x}\right]\).
Solution: All the functions under consideration are rational functions. Hence, we first evaluate these functions at the prescribed points. If this is of the form \(\frac{0}{0}\), we try to rewrite the function cancelling the factors which are causing the limit to be of the form \(\frac{0}{0}\).
(i) We have \(\lim _{x \rightarrow 1} \frac{x^2+1}{x+100}=\frac{1^2+1}{1+100}=\frac{2}{101}\)
(ii) Evaluating the function at 2 , it is of the form \(\frac{0}{0}\).
\(
\begin{aligned}
&\text { Hence } \lim _{x \rightarrow 2} \frac{x^3-4 x^2+4 x}{x^2-4}=\lim _{x \rightarrow 2} \frac{x(x-2)^2}{(x+2)(x-2)}\\
&\begin{aligned}
& =\lim _{x \rightarrow 2} \frac{x(x-2)}{(x+2)} \quad \text { as } x \neq 2 \\
& =\frac{2(2-2)}{2+2}=\frac{0}{4}=0 .
\end{aligned}
\end{aligned}
\)
(iii) Evaluating the function at 2 , we get it of the form \(\frac{0}{0}\).
Hence \(\lim _{x \rightarrow 2} \frac{x^2-4}{x^3-4 x^2+4 x}=\lim _{x \rightarrow 2} \frac{(x+2)(x-2)}{x(x-2)^2}\)
\(
=\lim _{x \rightarrow 2} \frac{(x+2)}{x(x-2)}=\frac{2+2}{2(2-2)}=\frac{4}{0}
\)
Which is not defined.
(iv) Evaluating the function at 2 , we get it of the form \(\frac{0}{0}\).
Hence \(\quad \lim _{x \rightarrow 2} \frac{x^3-2 x^2}{x^2-5 x+6}=\lim _{x \rightarrow 2} \frac{x^2(x-2)}{(x-2)(x-3)}\)
\(
=\lim _{x \rightarrow 2} \frac{x^2}{(x-3)}=\frac{(2)^2}{2-3}=\frac{4}{-1}=-4 .
\)
(v) First, we rewrite the function as a rational function.
\(
\begin{aligned}
{\left[\frac{x-2}{x^2-x}-\frac{1}{x^3-3 x^2+2 x}\right] } & =\left[\frac{x-2}{x(x-1)}-\frac{1}{x\left(x^2-3 x+2\right)}\right] \\
& =\left[\frac{x-2}{x(x-1)}-\frac{1}{x(x-1)(x-2)}\right] \\
& =\left[\frac{x^2-4 x+4-1}{x(x-1)(x-2)}\right] \\
& =\frac{x^2-4 x+3}{x(x-1)(x-2)}
\end{aligned}
\)
Evaluating the function at 1 , we get it of the form \(\frac{0}{0}\).
\(
\text { Hence } \begin{aligned}
\lim _{x \rightarrow 1}\left[\frac{x^2-2}{x^2-x}-\frac{1}{x^3-3 x^2+2 x}\right] & =\lim _{x \rightarrow 1} \frac{x^2-4 x+3}{x(x-1)(x-2)} \\
& =\lim _{x \rightarrow 1} \frac{(x-3)(x-1)}{x(x-1)(x-2)} \\
& =\lim _{x \rightarrow 1} \frac{x-3}{x(x-2)}=\frac{1-3}{1(1-2)}=2 .
\end{aligned}
\)
We remark that we could cancel the term \((x-1)\) in the above evaluation because \(x \neq 1\).
Example 14: For any positive integer \(n\) prove that
\(\lim _{x \rightarrow a} \frac{x^n-a^n}{x-a}=n a^{n-1} .\)
Note: Remark The expression in the above theorem for the limit is true even if \(n\) is any rational number and \(a\) is positive.
Proof: Let’s Start from the geometric series
\(
1+\frac{x}{a}+\frac{x^2}{a^2}+\ldots+\frac{x^{n-1}}{a^{n-1}}=\frac{\frac{x^n}{a^n}-1}{\frac{x}{a}-1}
\)
Multiply through by \(a^{n-1}\), we get
\(x^n-a^n=(x-a)\left(x^{n-1}+x^{n-2} a+x^{n-3} a^2+\ldots+x a^{n-2}+a^{n-1}\right)\)Dividing \(\left(x^n-a^n\right)\) by \((x-a)\), we see that
\(
\begin{aligned}
&\text { Thus, }\\
&\begin{aligned}
\lim _{x \rightarrow a} \frac{x^n-a^n}{x-a} & =\lim _{x \rightarrow a}\left(x^{n-1}+x^{n-2} a+x^{n-3} a^2+\ldots+x a^{n-2}+a^{n-1}\right) \\
& =a^{n-1}+a a^{n-2}+\ldots+a^{n-2}(a)+a^{n-1} \\
& =a^{n-1}+a^{n-1}+\ldots+a^{n-1}+a^{n-1}(n \text { terms }) \\
& =n a^{n-1}
\end{aligned}
\end{aligned}
\)
Example 16: Evaluate the following limits.
(i) \(\lim _{x \rightarrow 1} \frac{x^{15}-1}{x^{10}-1}\)
(ii) \(\lim _{x \rightarrow 0} \frac{\sqrt{1+x}-1}{x}\)
Solution: (i) We have
\(
\begin{aligned}
\lim _{x \rightarrow 1} \frac{x^{15}-1}{x^{10}-1} & =\lim _{x \rightarrow 1}\left[\frac{x^{15}-1}{x-1} \div \frac{x^{10}-1}{x-1}\right] \\
& =\lim _{x \rightarrow 1}\left[\frac{x^{15}-1}{x-1}\right] \div \lim _{x \rightarrow 1}\left[\frac{x^{10}-1}{x-1}\right] \\
& =15(1)^{14} \div 10(1)^9 \text { (by the theorem above) } \\
& =15 \div 10=\frac{3}{2}
\end{aligned}
\)
(ii) Put \(y=1+x\), so that \(y \rightarrow 1\) as \(x \rightarrow 0\).
Then
\(
\begin{aligned}
\lim _{x \rightarrow 0} \frac{\sqrt{1+x}-1}{x} & =\lim _{y \rightarrow 1} \frac{\sqrt{y}-1}{y-1} \\
& =\lim _{y \rightarrow 1} \frac{y^{\frac{1}{2}}-1^{\frac{1}{2}}}{y-1} \\
& =\frac{1}{2}(1)^{\frac{1}{2}-1}(\text { by the remark above })=\frac{1}{2}
\end{aligned}
\)
Example 17: Evaluate \(\lim _{x \rightarrow 0}\left(x^x\right)\)
Solution: The limit of \(x^x\) as \(x\) approaches 0 is an indeterminate form of type \(0^0\). This limit is typically evaluated using L’Hôpital’s Rule after rewriting the expression.
Rewrite the expression: The expression \(x^x\) is rewritten using the exponential function as \(e^{x \ln (x)}\).
The limit of the exponent, \(\lim _{x \rightarrow 0} x \ln (x)\), is evaluated.
This is an indeterminate form of type \(0 \cdot(-\infty)\).
Change the form for L’Hôpital’s Rule: The expression \(x \ln (x)\) is rewritten as \(\frac{\ln (x)}{\frac{1}{x}}\) to apply L’Hôpital’s Rule, as it is now of the form \(\frac{-\infty}{\infty}\).
The derivatives of the numerator and denominator are taken.
The derivative of \(\ln (x)\) is \(\frac{1}{x}\), and the derivative of \(\frac{1}{x}\) is \(-\frac{1}{x^2}\).
Simplify and evaluate the limit of the exponent: The expression becomes
\(
\lim _{x \rightarrow 0} \frac{\frac{1}{x}}{-\frac{1}{x^2}}=\lim _{x \rightarrow 0}-\frac{x^2}{x}=\lim _{x \rightarrow 0}-x=0
\)
Substitute back into the original expression: Since \(\lim _{x \rightarrow 0} x \ln (x)=0\), the original limit becomes \(e^{\lim _{x \rightarrow 0} x \ln (x)}=e^0=1\).
Note: Exponential property: \(a^{bc}=(a^b)^c\)
Logarithmic Property: \(a^{\log_a (b)}=b \text { or } e^{\ln (b)}=b\)
Therefore, \(e^{x \ln (x)}=\left(e^{\ln (x)}\right)^x \quad [a^{bc}=(a^b)^c]\)
\(=x^x \quad [a^{\log_a (b)}=b]\)
\(x^x\)