12.4 Distance between Two Points

Distance Formula in 2-Dimension

We have studied about the distance between two points in two-dimensional coordinate system. If two points lie in the same coordinate plane, then it is straightforward to calculate the distance between them. We know that the distance \(d\) between two points \(\left(x_1, y_1\right)\) and \(\left(x_2, y_2\right)\) in the \(x y\)-coordinate plane is given by the formula
\(
d=\sqrt{\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2} .
\)

Let us now extend this study to three-dimensional system. 

Distance Formula in 3-Dimension

Let O be the origin, \(P \left(x_1, y_1, z_1\right)\) and \(Q \left(x_2, y_2, z_2\right)\) be two points referred to a system of rectangular axes \(OX , OY\) and \(OZ\). 

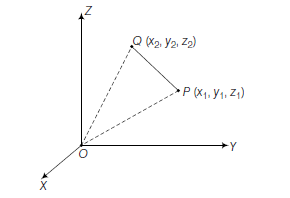
The, \(\quad OP =x_1 \hat{ i }+y_1 \hat{ j }+z_1 \hat{ k }\)
\(
OQ =x_2 \hat{ i }+y_2 \hat{ j }+z_2 \hat{ k }
\)
Now, \(PQ =\) Position vector of \(Q-\) Position vector of \(P\)
\(
\begin{aligned}
& = OQ – OP \\
& =\left(x_2 \hat{ i }+y_2 \hat{ j }+z_2 \hat{ k }\right)-\left(x_1 \hat{ i }+y_2 \hat{ j }+z_1 \hat{ k }\right) \\
& =\left(x_2-x_1\right) \hat{ i }+\left(y_2-y_1\right) \hat{ j }+\left(z_2-z_1\right) \hat{ k } \\
\therefore \quad P Q & =| PQ | \\
& =\sqrt{\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2+\left(z_2-z_1\right)^2}
\end{aligned}
\)
Hence, \(P Q=\sqrt{\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2+\left(z_2-z_1\right)^2}\)
Therefore, the distance between the points \(P\left(x_1, y_1, z_1\right)\) and \(Q\left(x_2, y_2, z_2\right)\) is given by
\(
P Q=\sqrt{\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2+\left(z_2-z_1\right)^2}
\)

Example 1: Find the distance between the points \(P (1,-3,4)\) and \(Q (-4,1,2)\).

Solution: The distance PQ between the points \(P (1,-3,4)\) and \(Q (-4,1,2)\) is
\(
\begin{aligned}
PQ & =\sqrt{(-4-1)^2+(1+3)^2+(2-4)^2} \\
& =\sqrt{25+16+4} \\
& =\sqrt{45}=3 \sqrt{5} \text { units }
\end{aligned}
\)

Example 2: Find the distance between points \(P_1=(3,-1,5)\) and \(P_2=(2,1,-1)\).

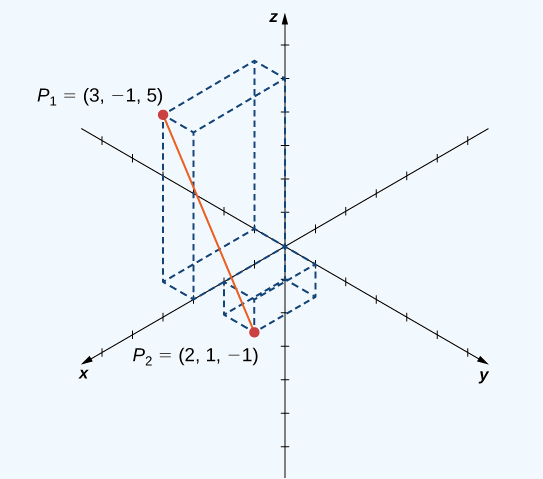
Solution:

\(
\begin{aligned}
d\left(P_1, P_2\right) & =\sqrt{\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2+\left(z_2-z_1\right)^2} \\
& =\sqrt{(2-3)^2+(1-(-1))^2+(-1-5)^2} \\
& =\sqrt{(-1)^2+2^2+(-6)^2} \\
& =\sqrt{41} .
\end{aligned}
\)

Example 3: Show that the points \(P (-2,3,5), Q (1,2,3)\) and \(R (7,0,-1)\) are collinear.

Solution: We know that points are said to be collinear if they lie on a line.
Now,
\(
\begin{array}{ll}
\text { Now, } & PQ =\sqrt{(1+2)^2+(2-3)^2+(3-5)^2}=\sqrt{9+1+4}=\sqrt{14} \\
& QR =\sqrt{(7-1)^2+(0-2)^2+(-1-3)^2}=\sqrt{36+4+16}=\sqrt{56}=2 \sqrt{14} \\
\text { and } & PR =\sqrt{(7+2)^2+(0-3)^2+(-1-5)^2}=\sqrt{81+9+36}=\sqrt{126}=3 \sqrt{14}
\end{array}
\)
Thus, \(PQ + QR = PR\). Hence, \(P , Q\) and \(R\) are collinear.

Example 4: Are the points A \((3,6,9), B (10,20,30)\) and \(C (25,-41,5)\), the vertices of a right angled triangle?

Solution: By the distance formula, we have
\(
\begin{aligned}
AB ^2 & =(10-3)^2+(20-6)^2+(30-9)^2 \\
& =49+196+441=686 \\
BC ^2 & =(25-10)^2+(-41-20)^2+(5-30)^2 \\
& =225+3721+625=4571
\end{aligned}
\)
\(
\begin{aligned}
CA ^2 & =(3-25)^2+(6+41)^2+(9-5)^2 \\
& =484+2209+16=2709
\end{aligned}
\)
We find that \(CA ^2+ AB ^2 \neq BC ^2\).
Hence, the triangle \(ABC\) is not a right angled triangle.

Example 5: Find the equation of set of points \(P\) such that \(PA ^2+ PB ^2=2 k^2\), where \(A\) and \(B\) are the points \((3,4,5)\) and \((-1,3,-7)\), respectively.

Solution: Let the coordinates of point \(P\) be \((x, y , z )\).
Here
\(
\begin{aligned}
& PA ^2=(x-3)^2+(y-4)^2+(z-5)^2 \\
& PB ^2=(x+1)^2+(y-3)^2+(z+7)^2
\end{aligned}
\)
By the given condition \(PA ^2+ PB ^2=2 k^2\), we have
\(
(x-3)^2+(y-4)^2+(z-5)^2+(x+1)^2+(y-3)^2+(z+7)^2=2 k^2
\)
i.e., \(\quad 2 x^2+2 y^2+2 z^2-4 x-14 y+4 z=2 k^2-109\).

Example 6: Show that the points \(A (1,2,3), B (-1,-2,-1), C (2,3,2)\) and \(D (4,7,6)\) are the vertices of a parallelogram \(ABCD\), but it is not a rectangle.

Solution: To show ABCD is a parallelogram we need to show opposite side are equal Note that.
\(
\begin{aligned}
& AB =\sqrt{(-1-1)^2+(-2-2)^2+(-1-3)^2}=\sqrt{4+16+16}=6 \\
& BC =\sqrt{(2+1)^2+(3+2)^2+(2+1)^2}=\sqrt{9+25+9}=\sqrt{43} \\
& CD =\sqrt{(4-2)^2+(7-3)^2+(6-2)^2}=\sqrt{4+16+16}=6 \\
& DA =\sqrt{(1-4)^2+(2-7)^2+(3-6)^2}=\sqrt{9+25+9}=\sqrt{43}
\end{aligned}
\)
Since \(AB = CD\) and \(BC = AD , ABCD\) is a parallelogram.
Now, it is required to prove that \(ABCD\) is not a rectangle. For this, we show that diagonals \(AC\) and \(BD\) are unequal. We have
\(
\begin{aligned}
& AC =\sqrt{(2-1)^2+(3-2)^2+(2-3)^2}=\sqrt{1+1+1}=\sqrt{3} \\
& BD =\sqrt{(4+1)^2+(7+2)^2+(6+1)^2}=\sqrt{25+81+49}=\sqrt{155} .
\end{aligned}
\)
Since \(A C \neq B D, A B C D\) is not a rectangle.

Note: We can also show that ABCD is a parallelogram, using the property that diagonals AC and BD bisect each other.

Example 7: Find the equation of the set of the points \(P\) such that its distances from the points \(A (3,4,-5)\) and \(B (-2,1,4)\) are equal.

Solution: If \(P (x, y, z)\) be any point such that \(PA = PB\).
Now \(\sqrt{(x-3)^2+(y-4)^2+(z+5)^2}=\sqrt{(x+2)^2+(y-1)^2+(z-4)^2}\)
or \((x-3)^2+(y-4)^2+(z+5)^2=(x+2)^2+(y-1)^2+(z-4)^2\)
or \(\quad 10 x+6 y-18 z-29=0\).

Example 8: The centroid of a triangle \(ABC\) is at the point \((1,1,1)\). If the coordinates of \(A\) and \(B\) are \((3,-5,7)\) and \((-1,7,-6)\), respectively, find the coordinates of the point C.

Solution: Let the coordinates of \(C\) be \((x, y, z)\) and the coordinates of the centroid \(G\) be \((1,1,1)\). Then
\(
\frac{x+3-1}{3}=1 \text {, i.e., } x=1 ; \frac{y-5+7}{3}=1 \text {, i.e., } y=1 ; \frac{z+7-6}{3}=1 \text {, i.e., } z=2 \text {. }
\)
Hence, coordinates of \(C\) are \((1,1,2)\).

Example 9: Prove by using distance formula that the points \(P(1,2,3), Q(-1,-1,-1)\) and \(R(3,5,7)\) are collinear.

Solution: We have,
\(
\begin{aligned}
P Q & =\sqrt{(-1-1)^2+(-1-2)^2+(-1-3)^2} \\
& =\sqrt{4+9+16}=\sqrt{29} \\
Q R & =\sqrt{(3+1)^2+(5+1)^2+(7+1)^2} \\
& =\sqrt{16+36+64} \\
& =\sqrt{116}=2 \sqrt{29}
\end{aligned}
\)
and
\(
\begin{aligned}
P R & =\sqrt{(3-1)^2+(5-2)^2+(7-3)^2} \\
& =\sqrt{4+9+16}=\sqrt{29}
\end{aligned}
\)
Since, \(\quad Q R=Q P+P R\)
Therefore, the given points are collinear.