11.3 Circle

Definition

A circle is the set of all points in a plane that are equidistant from a fixed point in the plane. The fixed point is called the centre of the circle and the distance from the centre to a point on the circle is called the radius of the circle (Fig 10.11).

\(
\text { i.e. } \quad O P_1=O P_2=O P_3=\text { constant distance }=\text { Radius }
\)

Equation of a Circle

The curve traced by the moving point is called its circumference. i.e. the equation of any circle is satisfied by co-ordinates of all points on its circumference.

Chord and Diameter

The line joining any two points on the circumference is called a chord. If any chord passing through its centre is called its diameter.

\(
A B=\text { Chord, } P Q=\text { Diameter }
\)
where, \(C\) is centre of the circle.

Equation of Circle in Different Forms

Case I: Centre-radius form

Let’s derive below the equation of the circle with a given centre and radius (Fig 10.12).

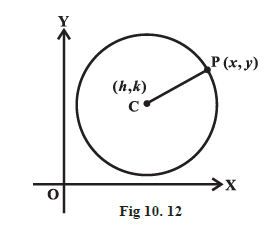
Given \(C (h, k)\) be the centre and \(r\) the radius of circle. Let \(P (x, y)\) be any point on the circle (Fig10.12). Then, by the definition, \(| CP |=r\). By the distance formula, we have
i.e.
\(
\begin{aligned}
& \sqrt{(x-h)^2+(y-k)^2}=r \\
& (x-h)^2+(y-k)^2=r^2
\end{aligned}
\)
This is the required equation of the circle with centre at \((h, k)\) and radius \(r\). This equation is known as the central form of the equation of a circle.

Remarks

• When, \(C(h, k)=C(0,0)\), then equation of circle becomes \(x^2+y^2=r^2\) which is known as standard form of the circle.

Some Particular Cases

The equation of a circle with centre at \((h, k)\) and radius equal to \(r\), is
\(
(x-h)^2+(y-k)^2=r^2 \dots(i)
\)

(i) When the centre of the circle coincides with the origin (Fig. below)

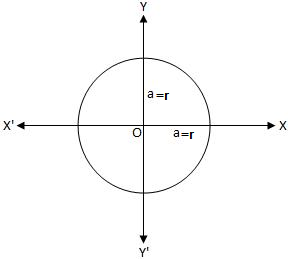
In this case, \(h=k=0\). Putting \(h=0, k=0\) in equation (i), we obtain \(x^2+y^2=r^2\) as the equation of the circle having centre at the origin and radius equal to \(a or r[latex].

(ii) When the circle passes through the origin (Fig. below)

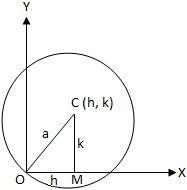
Let [latex]O\) be the origin and \(C(h, k)\) be the centre of the circle. Draw \(C M \perp O X\).
Using Pythagoras Theorem in \(\triangle O C M\), we obtain
\(
\begin{aligned}
O C^2 & =O M^2+C M^2 \\
\Rightarrow \quad a^2 & =h^2+k^2
\end{aligned}
\)
The equation of the circle (i) then becomes
\(
(x-h)^2+(y-k)^2=h^2+k^2 \text { or, } x^2+y^2-2 h x-2 k y=0 .
\)

(iii) When the circle touches \(x\)-axis (Fig. below)

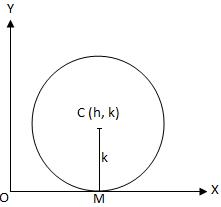
Let \(C(h, k)\) be the centre of the circle. Since the circle touches the \(x\)-axis. Therefore, \(a=k\) Hence, the equation of the circle is
\(
(x-h)^2+(y-a)^2=a^2 \text { or, } x^2+y^2-2 h x-2 a y+h^2=0
\)

(iv) When the circle touches y-axis (Fig. below)

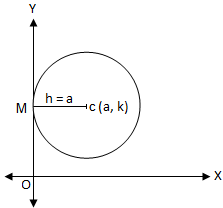
Let \(C(h, k)\) be the centre of the circle. Since the circle touches the \(y\)-axis. Therefore, \(h=a\) Hence, the equation of the circle is
\(
(x-a)^2+(y-k)^2=a^2 \text { or, } x^2+y^2-2 a x-2 k y+k^2=0 .
\)

(v) When the circle touches both the axes (Fig. below)

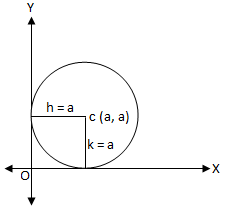
In this case we have, \(h=k=a\)
Hence, the equation of the circle is
\(
(x-a)^2+(y-a)^2=a^2 \text { or, } x^2+y^2-2 a x-2 a y+a^2=0 .
\)

(vi) When the circle passes through the origin and centre lies on \(x\)-axis (Fig. below)

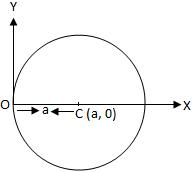
In this case, we have \(k=0\) and \(h=a\). Hence, the equation of the circle is
\(
(x-a)^2+(y-0)^2=a^2 \text { or, } x^2+y^2-2 a x=0 .
\)

(vii) When the circle passes through the origin and centre lies on y-axis (Fig. below)

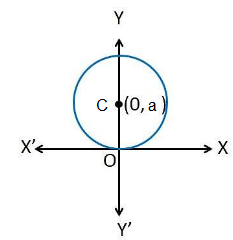
In this case, we have \(h=0\) and \(k=a\).
Hence, the equation of the circle is
\(
(x-0)^2+(y-a)^2=a^2 \text { or, } x^2+y^2-2 a y=0 .
\)

Example 1: Find the equation of the circle with centre \((-3,2)\) and radius 4.

Answer: Here \(h=-3, k=2\) and \(r=4\). Therefore, the equation of the required circle is
\(
(x+3)^2+(y-2)^2=16
\)

Example 2: Find the centre and the radius of the circle \(x^2+y^2+8 x+10 y-8=0\)

Answer: The given equation is
\(
\left(x^2+8 x\right)+\left(y^2+10 y\right)=8
\)
Now, completing the squares within the parenthesis, we get
i.e.
\(
\left(x^2+8 x+16\right)+\left(y^2+10 y+25\right)=8+16+25
\)
\(
(x+4)^2+(y+5)^2=49
\)
i.e.
\(
\{x-(-4)\}^2+\{y-(-5)\}^2=7^2
\)
Therefore, the given circle has centre at \((-4,-5)\) and radius 7.

Example 3: Find the equation of the circle which passes through the points \((2,-2)\), and \((3,4)\) and whose centre lies on the line \(x+y=2\).

Answer: Let the equation of the circle be \((x-h)^2+(y-k)^2=r^2\).
Since the circle passes through \((2,-2)\) and \((3,4)\), we have
\(
\begin{array}{ll}
& (2-h)^2+(-2-k)^2=r^2 \dots(1)\\
\text { and } & (3-h)^2+(4-k)^2=r^2 \dots(2)
\end{array}
\)
Also since the centre lies on the line \(x+y=2\), we have
\(
h+k=2 \dots(3)
\)
Solving the equations (1), (2) and (3), we get
\(
h=0.7, \quad k=1.3 \text { and } r^2=12.58
\)
Hence, the equation of the required circle is
\(
(x-0.7)^2+(y-1.3)^2=12.58 \text {. }
\)

Case II: Parametric form

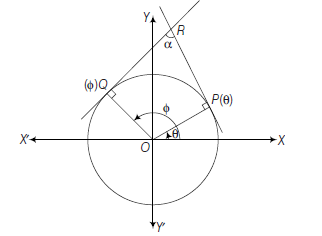
If the radius of a circle whose centre is at \(C(0,0)\) makes an angle \(\theta\) with the positive direction of \(X\)-axis, then \(\theta\) is called the parameter.
Let \(\quad C P=a\)
\(
\therefore \quad C M=x, P M=y \quad \Rightarrow x=a \cos \theta, y=a \sin \theta
\)

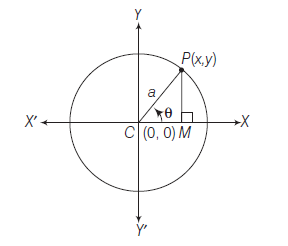
Hence, \((a \cos \theta, a \sin \theta)\) or ‘ \(\theta\) ‘ are the parametric coordinates of the circle \(x^2+y^2=a^2\) and \(x=a \cos \theta\) and \(y=a \sin \theta\) are called parametric equations of the circle \(x^2+y^2=a^2\) with parameters \(a\) and \(\theta\). \((0 \leq \theta<2 \pi)\).

Notes

• The parametric coordinates of any point on the circle \((x-h)^2+(y-k)^2=a^2\) are given by \((h+a \cos \theta, k+a \sin \theta)\) \((0 \leq \theta<2 \pi)\) and parametric equations of the circle \((x-h)^2+(y-k)^2=a^2\) are \(x=h+a \cos \theta \quad y=k+a \sin \theta\).
• Equation of the chord of the circle \(x^2+y^2=a^2\) joining \((a \cos \alpha, a \sin \alpha)\) and \((a \cos \beta, a \sin \beta)\) is
  \(
  x \cos \left(\frac{\alpha+\beta}{2}\right)+y \sin \left(\frac{\alpha+\beta}{2}\right)=a \cos \left(\frac{\alpha-\beta}{2}\right) .
  \)

Example 4: Find the parametric form of the equation of the circle \(x^2+y^2+p x+p y=0\)

Answer: Equation of the circle can be re-written in the form
\(
\left(x+\frac{p}{2}\right)^2+\left(y+\frac{p}{2}\right)^2=\frac{p^2}{2}
\)
Therefore, the parametric form of the equation of the given circle is
\(
\begin{aligned}
& x=-\frac{p}{2}+\frac{p}{\sqrt{2}} \cos \theta=\frac{p}{2}(-1+\sqrt{2} \cos \theta) \\
& y=-\frac{p}{2}+\frac{p}{\sqrt{2}} \sin \theta=\frac{p}{2}(-1+\sqrt{2} \sin \theta)
\end{aligned}
\)
where, \(0 \leq \theta<2 \pi\).

Example 5: If the parametric of form of a circle is given by
(a) \(x=-4+5 \cos \theta\) and \(y=-3+5 \sin \theta\)
(b) \(x=a \cos \alpha+b \sin \alpha\) and \(y=a \sin \alpha-b \cos \alpha\) find its cartesian form.

Answer: (a) The given equations are
\(
\begin{aligned}
& x=-4+5 \cos \theta \\
& y=-3+5 \sin \theta
\end{aligned}
\)
or \(\quad(x+4)=5 \cos \theta \dots(i)\)
and \(\quad(y+3)=5 \sin \theta \dots(ii)\)
Squaring and adding Eqs. (i) and (ii), then
\(
\begin{aligned}
(x+4)^2+(y+3)^2 & =5^2 \\
\text { or } \quad(x+4)^2+(y+3)^2 & =25
\end{aligned}
\)
(b) The given equations are
\(
\begin{aligned}
& x=a \cos \alpha+b \sin \alpha \dots(iii)\\
& y=a \sin \alpha-b \cos \alpha \dots(iv)
\end{aligned}
\)
Squaring and adding Eqs. (iii) and (iv), then
\(
\begin{aligned}
x^2+y^2 & =(a \cos \alpha+b \sin \alpha)^2+(a \sin \alpha-b \cos \alpha)^2 \\
\Rightarrow \quad x^2+y^2 & =a^2+b^2
\end{aligned}
\)

General Equation Of a Circle

Theorem: Prove that the equation \(x^2+y^2+2 g x+2 f y+c=0\) always represents a circle whose centre is \((-g,-f)\) and radius \(=\sqrt{g^2+f^2-c}\).

Proof: The given equation is \(x^2+y^2+2 g x+2 f y+c=0 \dots(i)\)
\(
\begin{aligned}
& \left(x^2+2 g x+g^2\right)+\left(y^2+2 f y+f^2\right)=g^2+f^2-c \\
& (x+g)^2+(y+f)^2=\left\{\sqrt{g^2+f^2-c}\right\}^2 \\
& \{x-(-g)\}^2+\{y-(-f)\}^2=\left\{\sqrt{g^2+f^2-c}\right\}^2
\end{aligned}
\)
This is of the form \((x-h)^2+(y-k)^2=a^2\) which represents a circle having centre at \((h, k)\) and radius equal to \(a\).
Hence, the given equation (i) represents a circle whose centre is at \((-g,-f)\) i.e. \(\left(-\frac{1}{2}\right.\) Coefficient of \(x,-\frac{1}{2}\) Coefficient of \(\left.y\right)\) and, Radius \(=\sqrt{g^2+f^2-c}=\sqrt{\left(\frac{1}{2} \text { Coeff. of } x\right)^2+\left(\frac{1}{2} \text { Coeff. of } y\right)^2-\text { Constant term }}\)

Notes

Rule for finding the centre and radius of a circle

• Make the coefficients of \(x^2\) and \(y^2\) equal to 1 and right hand side equal to zero.
• Then, coordinates of centre will be \((\alpha, \beta)\), where, \(\alpha=-\frac{1}{2}\) (coefficient of \(x\) ) and \(\beta=-\frac{1}{2}\) (coefficient of \(y\) )
• Radius \(=\sqrt{\alpha^2+\beta^2-(\text { constant term })}\)

Conditions for a circle A general equation of second degree

On comparing the general equation \(x^2+y^2+2 g x+2 f y+c=0\) of a circle with the general equation of second degree \(a x^2+2 h x y+b y^2+2 g x+2 f y+c=0\) in \(x, y\) represent a circle, if

• Coefficient of \(x^2=\) coefficient of \(y^2\) i.e. \(a=b\)
• Coefficient of \(x y\) is zero i.e.
  \(h=0\)

Nature of the circle

The equation \(x^2+y^2+2 g x+2 f y+c=0\) represents a circle of radius \(\sqrt{g^2+f^2-c}\).

• If \(g^2+f^2-c>0\), then the radius of the circle is real and hence the circle is also real.
• If \(g^2+f^2-c=0\), then the radius of the circle is zero. Such a circle is known as a point circle.
• If \(g^2+f^2-c<0\), then the radius \(\sqrt{g^2+f^2-c}\) of the circle is imaginary but the centre is real. Such a circle is called an imaginary circle as it is not possible to draw such a circle.

Concentric circle

• Two circles having the same centre \(C(h, k)\) but different radii \(r_1\) and \(r_2\) respectively are called concentric circles. Thus, the circles \((x-h)^2+(y-k)^2=r_1^2\) and \((x-h)^2+(y-k)^2=r_2^2, r_1 \neq r_2\) are concentric circles. Therefore, the equations of concentric circles differ only in constant terms.

Special features of the general equation \(x^2+y^2+2 g x+2 f y+c=0\) of the circle are:

• It is quadratic in both \(x\) and \(y\).
• Coefficient of \(x^2=\) Coefficient of \(y^2\).
• There is no term containing \(x y\) i.e., the coefficient of \(x y\) is zero.
• It contains three arbitrary constants viz. \(g, f\) and \(c\).

The equation \(a x^2+a y^2+2 g x+2 f y+c=0, a \neq 0\) also represents a circle.

• This equation can also be written as \(x^2+y^2+\frac{2 g}{a} x+\frac{2 f}{a} y+\frac{c}{a}=0\). The coordinates of the centre of the circle are \((-g / a,-f / a)\) and, radius \(=\sqrt{\frac{g^2}{a^2}+\frac{f^2}{a^2}-\frac{c}{a}}\).

 

Illustrative Examples

Type I: On Finding The Centre and Radius of a circle when its Equation is Given

The coordinates of the centre of the circle \(x^2+y^2+2 g x+2 f y+c=0\) are
\(\left(-\frac{1}{2}\right.\) Coefficient of \(x,-\frac{1}{2}\) Coefficient of \(y\) )
and, Radius \(=\sqrt{\left(\frac{1}{2} \text { Coefficient of } x\right)^2+\left(\frac{1}{2} \text { Coefficient of } y^2\right)^2-\text { Constant term }}\)

Example 6: Find the centre and radius of the circle \(x^2+y^2-6 x+4 y-12=0\).

Answer: The coordinates of the centre of the circle \(x^2+y^2-6 x+4 y-12=0\) are \(\left(-\frac{1}{2}\right.\) Coeff. of \(x,-\frac{1}{2}\) Coeff. of \(\left.y\right)\) i.e. \(\left(-\frac{1}{2} \times-6,-\frac{1}{2} \times 4\right)=(3,-2)\) and, \(\quad\) Radius \(=\sqrt{\left(-\frac{6}{2}\right)^2+\left(\frac{4}{2}\right)^2-(-12)}=\sqrt{9+4+12}=5\).

Example 7: Find the centre and radius of the circle given by the equation \(2 x^2+2 y^2+3 x+4 y+\frac{9}{8}=0\)

Answer: In the given equation the coefficients of \(x^2\) and \(y^2\) are not unity. So, we re-write the equation to make the coefficients of \(x^2\) and \(y^2\) unity.
We have, \(2 x^2+2 y^2+3 x+4 y+\frac{9}{8}=0 \Rightarrow x^2+y^2+\frac{3}{2} x+2 y+\frac{9}{16}=0\).
So, the coordinates of the centre are \((-3 / 4,-1)\) and, Radius \(=\sqrt{\left(\frac{3}{4}\right)^2+(1)^2-\frac{9}{16}}=1\).

Example 8: Prove that the radii of the circles \(x^2+y^2=1, x^2+y^2-2 x-6 y=6\) and \(x^2+y^2-4 x-12 y=9\) are in AP.

Answer: Given circles are \(\quad x^2+y^2=1\)
\(
x^2+y^2-2 x-6 y-6=0
\)
and
\(
x^2+y^2-4 x-12 y-9=0
\)
Let \(r_1, r_2\) and \(r_3\) be the radii of the circles Eqns. (i), (ii) and (iii), respectively.
Then,
\(
\begin{aligned}
& r_1=1 \\
& r_2=\sqrt{(-1)^2+(-3)^2+6}=4
\end{aligned}
\)
and
\(
r_3=\sqrt{(-2)^2+(-6)^2+9}=7
\)
Clearly, \(r_2-r_1=4-1=3=r_3-r_2\)
Hence, \(r_1, r_2, r_3\) are in AP.

Type II: On Finding The Equation Of a Circle Satisfying Given Conditions

Example 9: Find the equation of the circle whose centre is at the point \((4,5)\) and which passes through the centre of the circle \(x^2+y^2-6 x+4 y-12=0\).

Answer: The coordinates of the centre of the circle \(x^2+y^2-6 x+4 y-12=0\) are \(C_1(3,-2)\). Therefore, the required circle passes through the point \(C_1(3,-2)\) and has its centre at the point \(C(4,5)\). So, its radius is equal to
\(
C C_1=\sqrt{(4-3)^2+(5+2)^2}=\sqrt{50}
\)

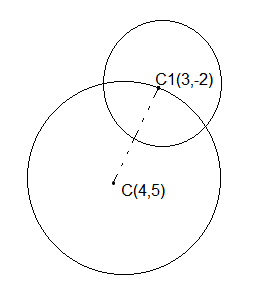
Hence, the equation of the required circle is
\(
(x-4)^2+(y-5)^2=(\sqrt{50})^2 \text { or, } x^2+y^2-8 x-10 y-9=0
\)

Example 10: Find the equation of the circle concentric with the circle \(2 x^2+2 y^2+8 x+10 y-39=0\) and having its area equal to \(16 \pi\) square units.

Answer: The equation of the given circle is
\(
2 x^2+2 y^2+8 x+10 y-39=0 \Rightarrow x^2+y^2+4 x+5 y-39 / 2=0 .
\)
The coordinates of its centre are \((-2,-5 / 2)\). The required circle is concentric with the above circle, therefore the coordinates its centre are \((-2,-5 / 2)\).
Let \(r\) be the radius of the required circle. Then, its area is \(\pi r^2\). But, it is given that its area is \(16 \pi\) sq. units.
\(
\therefore \quad \pi r^2=16 \pi \Rightarrow r=4
\)
Hence, the equation of the required circle is
\(
(x+2)^2+(y+5 / 2)^2=4^2 \text { or, } 4 x^2+4 y^2+16 x+20 y-23=0 .
\)

Example 11: Find the equation of the circle whose centre is the point of intersection of the lines \(2 x-3 y+4=0\) and \(3 x+4 y-5=0\) and passes through the origin.

Answer: The point of intersection of the lines \(2 x-3 y+4=0\) and \(3 x+4 y-5=0\) is \(\left(-\frac{1}{17}, \frac{22}{17}\right)\)
Therefore, the centre of the circle is at \(\left(-\frac{1}{17}, \frac{22}{17}\right)\).
Since, the origin lies on the circle, its distance from the centre of the circle is radius of the circle, therefore,
\(
r=\sqrt{\left(-\frac{1}{17}-0\right)^2+\left(\frac{22}{17}-0\right)^2}=\sqrt{\frac{485}{289}}
\)
\(\therefore\) The equation of the circle becomes
\(
\begin{aligned}
& \left(x+\frac{1}{17}\right)^2+\left(y-\frac{22}{17}\right)^2=\frac{485}{289} \\
& 17\left(x^2+y^2\right)+2 x-44 y=0
\end{aligned}
\)

Example 12: Find the equation of the circle concentric with the circle \(x^2+y^2-8 x+6 y-5=0\) and passing through the point \((-2,-7)\).

Answer: The given equation of circle is
\(
x^2+y^2-8 x+6 y-5=0
\)
Therefore, the centre of the circle is at \((4,-3)\). Since, the required circle is concentric with this circle, therefore, the centre of the required circle is also at \((4,-3)\). Since, the point \((-2,-7)\) lies on the circle, the distance of the centre from this point is the radius of the circle. Therefore, we get
\(
r=\sqrt{(4+2)^2+(-3+7)^2}=\sqrt{52}
\)
Hence, the equation of the circle becomes
\(
(x-4)^2+(y+3)^2=52
\)
or
\(
x^2+y^2-8 x+6 y-27=0
\)

Example 13: A circle has radius 3 units and its centre lies on the line \(y=x-1\). Find the equation of the circle if it passes through \((7,3)\).

Answer: Let the centre of the circle be \((h, k)\). Since, the centre lies on \(y=x-1\), we get
\(
k=h-1 \dots(i)
\)
Since, the circle passes through the point \((7,3)\), therefore the distance of the centre from this point is the radius \(r\) of the circle. We have,
\(
\begin{aligned}
& r=\sqrt{(h-7)^2+(k-3)^2} \\
& 3=\sqrt{(h-7)^2+(h-1-3)^2} \text { [from Eq. (i)] }\\
& (h-7)(h-4)=0 \\
& h=7 \text { and } h=4 \\
&
\end{aligned}
\)
\(\Rightarrow \quad 9=(h-7)^2+(h-4)^2\)
\(\Rightarrow \quad h^2-11 h+28=0\)
\(
h=7 \text { and } h=4
\)
For \(h=7\), we get \(k=6\) from Eq. (i) and for \(h=4\), we get \(k=3\), from Eq. (i).
Hence, there are two circles which satisfy the given conditions. They are
\(
(x-7)^2+(y-6)^2=9
\)
\(
\begin{aligned}
x^2+y^2-14 x-12 y+76 & =0 \\
(x-4)^2+(y-3)^2 & =9
\end{aligned}
\)
\(
(x-4)^2+(y-3)^2=9
\)
\(
x^2+y^2-8 x-6 y+16=0
\)

Example 14: Find the area of an equilateral triangle inscribed in the circle \(x^2+y^2+2 g x+2 f y+c=0 .\)

Answer: Given circle is
\(
x^2+y^2+2 g x+2 f y+c=0 \dots(i)
\)
Let \(O\) be the centre and \(A B C\) be an equilateral triangle inscribed in the circle Eq. (i).

\(
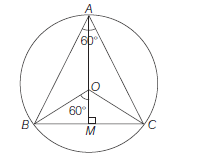
\begin{aligned}
O & \equiv(-g,-f) \\
O A & =O B=O C=\sqrt{g^2+f^2-c} \dots(ii)
\end{aligned}
\)
\(
\begin{aligned}
\text { In } \triangle B O M, \sin 60^{\circ} & =\frac{B M}{O B} \\
\Rightarrow \quad B M & =O B \sin 60^{\circ}=(O B) \frac{\sqrt{3}}{2}
\end{aligned}
\)
\(
\therefore \quad B C=2 B M=\sqrt{3}(O B) \dots(iii)
\)
\(
\begin{aligned}
\therefore \quad \text { Area of } \triangle A B C & =\frac{\sqrt{3}}{4}(B C)^2 \\
& =\frac{\sqrt{3}}{4} 3(O B)^2 \text { [from Eq. (iii)] }
\end{aligned}
\)
\(
=\frac{3 \sqrt{3}}{4}\left(g^2+f^2-c\right) \text { sq units. }
\)

Type III: On Finding Equation Of a Circle passing through three given points

Example 15: Find the equation of the circle that passes through the points \((1,0),(-1,0)\) and \((0,1)\)

Answer: Let the required circle be \(x^2+y^2+2 g x+2 f y+c=0 \dots(i)\)
It passes through \((1,0),(-1,0)\) and \((0,1)\). Therefore, on substituting the coordinates of three points successively in equation (i), we get
\(
1+2 g+c=0 \dots(ii)
\)
\(\quad 1-2 g+c=0 \dots(iii)\)
\(
1+2 f+c=0 \dots(iv)
\)
Subtracting (iii) from (ii), we get
\(
4 g=0 \Rightarrow g=0
\)
Putting \(g=0\) in (ii), we obtain \(c=-1\).
Now, putting \(c=-1\) in (iv), we get \(f=0\).
Substituting the values of \(g, f\) and \(c\) in equation (i), we obtain the equation of the required circle as \(x^2+y^2=1\).

Example 16: Find the equation of the circle which passes through the points \((5,-8),(2,-9)\) and \((2,1)\). Find also the coordinates of its centre and radius.

Answer: Let the required circle be
\(
x^2+y^2+2 g x+2 f y+c=0 \dots(i)
\)
It passes through the points \((5,-8),(2,-9)\) and \((2,1)\). Therefore,
\(
\begin{array}{r}
89+10 g-16 f+c=0 \dots(ii) \\
85+4 g-18 f+c=0 \dots(iii) \\
5+4 g+2 f+c=0 \dots(iv)
\end{array}
\)
Subtracting (iii) from (ii), we obtain
\(
4+6 g+2 f=0 \Rightarrow 2+3 g+f=0 \dots(v)
\)
Subtracting (iv) from (iii), we get
\(
80+0 g-20 f=0 \Rightarrow f=4
\)
Putting \(f=4\) in (v), we get \(g=-2\). Putting \(f=4, g=-2\) in (iv), we get
\(
5-8+8+c=0 \Rightarrow c=-5
\)
Substituting the values of \(g, f\) and \(c\) in equation (i), we obtain the equation of the required circle as
\(
x^2+y^2-4 x+8 y-5=0 .
\)
The coordinates of the centre are \((-g,-f)\) i.e \((2,-4)\).
and, Radius \(=\sqrt{g^2+f^2-c}=\sqrt{4+16+5}=5\).

Example 18: The straight line \(\frac{x}{a}+\frac{y}{b}=1\) cuts the coordinate axes at \(A\) and \(B\). Find the equation of the circle passing through \(O(0,0), A\) and \(B\).

Answer: The straight line \(\frac{x}{a}+\frac{y}{b}=1\) cuts the coordinate axes at \(A(a, 0)\) and \(B(0, b)\).
Let \(x^2+y^2+2 g x+2 f y+c=0 \dots(i)\)
be the circle passing through \(O, A\) and \(B\). Then,
\(
\begin{aligned}
& 0+0+c=0 \dots(ii) \\
& a^2+2 g a+c=0 \dots(iii) \\
& b^2+2 f b+c=0 \dots(iv) 
\end{aligned}
\)
Solving (ii), (iii) and (iv), we obtain
\(
g=-\frac{a}{2}, f=-\frac{b}{2} \text { and } c=0
\)
Substituting these values in (i), we obtain the equation of the required circle as
\(
x^2+y^2-a x-b y=0
\)

Example 19: Find the equation of the circle passing through \((1,0)\) and \((0,1)\) and having the smallest possible radius.

Answer: Let the equation of the required circle be
\(
x^2+y^2+2 g x+2 f y+c=0 \dots(i)
\)
This passes through the points \(A(1,0)\) and \(B(0,1)\).
\(
\therefore \quad 1+2 g+c=0 \text { and, } 1+2 f+c=0 \Rightarrow g=-\left(\frac{c+1}{2}\right) \text { and, } f=-\left(\frac{c+1}{2}\right)
\)
Let \(r\) be the radius of circle (i). Then,
\(
\begin{aligned}
r & =\sqrt{g^2+f^2-c} \\
\Rightarrow \quad r & =\sqrt{\left(\frac{c+1}{2}\right)^2+\left(\frac{c+1}{2}\right)^2-c} \Rightarrow r=\sqrt{\frac{c^2+1}{2}} \Rightarrow r^2=\frac{1}{2}\left(c^2+1\right)
\end{aligned}
\)
Now, \(\quad \frac{1}{2} c^2 \geq 0 \Rightarrow \frac{1}{2} c^2+\frac{1}{2} \geq \frac{1}{2} \Rightarrow r^2 \geq \frac{1}{2}\)
Thus, the minimum value of \(r^2\) is \(\frac{1}{2}\).
Also, \(\quad r^2=\frac{1}{2} \Rightarrow \frac{1}{2} c^2+\frac{1}{2}=\frac{1}{2} \Rightarrow c=0\)
So, \(r\) is minimum when \(c=0\) and in that case, the minimum value of \(r\) is \(\frac{1}{\sqrt{2}}\).
Putting \(c=0\) in \(g=-\frac{c+1}{2}\) and \(f=-\frac{c+1}{2}\), we get \(g=-\frac{1}{2}\) and \(f=-\frac{1}{2}\).
Substituting the values of \(g, f\) and \(c\) in (i), we get \(x^2+y^2-x-y=0\) as the equation of the required circle.

Type IV: On Concyclic Points

To prove that four given points are concyclic; find the equation of the circle passing through any of the three given points and show that the fourth point lies on it.

Example 20: Show that the points \((9,1),(7,9)(-2,12)\) and \((6,10)\) are concyclic.

Answer: Let the equation of the circle passing through \((9,1),(7,9)\) and \((-2,12)\) be
\(
x^2+y^2+2 g x+2 f y+c=0 \dots(i)
\)
Then,
\(
\begin{array}{r}
82+18 g+2 f+c=0 \dots(ii) \\
130+14 g+18 f+c=0 \dots(iii) \\
148-4 g+24 f+c=0 \dots(iv)
\end{array}
\)
Subtracting (ii) from (iii), we get
\(
48-4 g+16 f=0 \Rightarrow 12-g+4 f=0 \dots(v)
\)
Subtracting (iii) from (iv), we get
\(
18-18 g+6 f=0 \Rightarrow 3-3 g+f=0 \dots(vi)
\)
Solving (v) and (vi) as simultaneous linear equations in \(g\) and \(f\), we get: \(f=-3, g=0\).
Putting \(f=-3, g=0\) in (ii), we get
\(
82+0-6+c=0 \Rightarrow c=-76
\)
Substituting the values of \(g, f\) and \(c\) in (i), we get \(x^2+y^2-6 y-76=0\) as the equation of the circle passing through points \((9,1),(7,9)\) and \((-2,12)\).
Clearly, point \((6,10)\) satisfies this equation. Hence, the given points are concyclic.

Type V: On Finding The Equation of a Circle Satisfying three Given Conditions

Example 21: Find the equation of the circle which passes through the points \((1,-2)\) and \((4,-3)\) and has its centre on the line \(3 x+4 y=7\).

Answer: Let the equation of the required circle be
\(
x^2+y^2+2 g x+2 f y+c=0 \dots(i)
\)
It passes through \((1,-2)\) and \((4,-3)\).
\(
\therefore \quad 5+2 g-4 f+c=0 \dots(ii)
\)
and, \(\quad 25+8 g-6 f+c=0 \dots(iii)\)
The centre \((-g,-f)\) of (i) lies on \(3 x+4 y=7\).
\(
\therefore \quad-3 g-4 f=7 \dots(iv)
\)
Subtracting (ii) from (iii), we get
\(
20+6 g-2 f=0 \Rightarrow 10+3 g-f=0 \dots(v)
\)
Solving (iv) and (v) as simultaneous equations, we get
\(
g=-\frac{47}{15} \text { and } f=\frac{3}{5}
\)
Substituting the values of \(g\) and \(f\) in (ii), we get
\(
5-\frac{94}{15}-\frac{12}{5}+c=0 \Rightarrow c=\frac{55}{15}=\frac{11}{3}
\)
Substituting the values of \(g, f\) and \(c\) in (i) we obtain the required equation of the circle as
\(
x^2+y^2-\frac{94}{15} x+\frac{6}{5} y+\frac{11}{3}=0 \text { or, } 15\left(x^2+y^2\right)-94 x+18 y+33=0
\)

Example 22: Find the equation of the circle circumscribing the triangle formed by the lines \(x+y=6\), \(2 x+y=4\) and \(x+2 y=5\).

Answer: Let the equations of sides \(A B, B C\) and \(C A\) of \(\triangle A B C\) are respectively
\(x+y=6 \dots(i)\)
\(\quad 2 x+y=4 \dots(ii)\)
and \(x+2 y=5 \dots(iii)\)
Solving (i) and (iii), (i) and (ii); (ii) and (iii) we get the coordinates of \(A, B\) and \(C\). The coordinates \(A, B\) and \(C\) are \((7,-1),(-2,8)\) and \((1,2)\) respectively.
Let the equation of the circumcircle of \(\triangle A B C\) be
\(
x^2+y^2+2 g x+2 f y+c=0 \dots(iv)
\)
It passes through the points \(A(7,-1), B(-2,8)\) and \(C(1,2)\). Therefore,
\(
\begin{array}{r}
50+14 g-2 f+c=0 \dots(v) \\
68-4 g+16 f+c=0 \dots(vi) \\
5+2 g+4 f+c=0 \dots(vii)
\end{array}
\)
Subtracting (v) from (vi), we get
\(
18-18 g+18 f=0 \Rightarrow 1-g+f=0 \dots(viii)
\)
Subtracting (v) from (vii), we get: \(-45-12 g+6 f=0 \dots(ix)\)
Solving (viii) and (ix), we get: \(g=-17 / 2, f=-19 / 2\).
Putting the values of \(g\) and \(f\) in (v), we get \(c=50\).
Substituting the values of \(g, f\) and \(c\) in (iv), the equation of the required circumcircle is
\(
x^2+y^2-17 x-19 y+50=0
\)

Example 23: Find the radius of the circle \((x \cos \alpha+y \sin \alpha-a)^2+(x \sin \alpha-y \cos \alpha-b)^2=k^2\), if \(\alpha\) varies, the locus of its centre is again a circle. Also, find its centre and radius.

Answer: The given equation is
\(
\begin{aligned}
&(x \cos \alpha+y \sin \alpha-a)^2+(x \sin \alpha-y \cos \alpha-b)^2=k^2 \\
& \Rightarrow \quad x^2\left(\cos ^2 \alpha+\sin ^2 \alpha\right)+y^2\left(\sin ^2 \alpha+\cos ^2 \alpha\right)-2(a \cos \alpha+b \sin \alpha) x \\
&-2(a \sin \alpha-b \cos \alpha) y+a^2+b^2-k^2=0
\end{aligned}
\)
\(
\Rightarrow \quad x^2+y^2-2 x(a \cos \alpha+b \sin \alpha)-2 y(a \sin \alpha-b \cos \alpha)+a^2+b^2-k^2=0
\)
The coordinates of the centre of this circle are \((a \cos \alpha+b \sin \alpha, a \sin \alpha-b \cos \alpha)\). Let its radius be \(r\). Then,
\(
\begin{aligned}
r & =\sqrt{(a \cos \alpha+b \sin \alpha)^2+(a \sin \alpha-b \cos \alpha)^2-\left(a^2+b^2-k^2\right)} \\
\Rightarrow \quad r & =\sqrt{a^2\left(\cos ^2 \alpha+\sin ^2 \alpha\right)+b^2\left(\sin ^2 \alpha+\cos ^2 \alpha\right)-\left(a^2+b^2-k^2\right)} \\
\Rightarrow \quad r & =\sqrt{a^2+b^2-a^2-b^2+k^2}=k
\end{aligned}
\)
Let \((p, q)\) be the coordinates of the centre of the given circle. Then,
\(
p=a \cos \alpha+b \sin \alpha \text { and } q=a \sin \alpha-b \cos \alpha
\)
To find the locus of \((p, q)\) we have to eliminate \(\alpha\). Squaring and adding these two, we get
\(
\begin{array}{ll}
& p^2+q^2=(a \cos \alpha+b \sin \alpha)^2+(a \sin \alpha-b \cos \alpha)^2 \\
\Rightarrow & p^2+q^2=a^2\left(\cos ^2 \alpha+\sin ^2 \alpha\right)+b^2\left(\sin ^2 \alpha+\cos ^2 \alpha\right) \\
\Rightarrow & p^2+q^2=a^2+b^2
\end{array}
\)
Hence, the locus of \((p, q)\) is \(x^2+y^2=a^2+b^2\). This is a circle having centre at \((0,0)\) and radius equal to \(\sqrt{a^2+b^2}\).

Locus of the Mid-point of the Chords of the Circle that Subtends an Angle of \(2 \theta\) at its Centre

Let mid-point \(M\left(x_1, y_1\right)\) and centre, radius of circle are \((h, k), r\) respectively, then
\(
\cos \theta=\frac{C M}{r}=\frac{\sqrt{\left(x_1-h\right)^2+\left(y_1-k\right)^2}}{r}
\)

\(
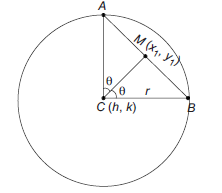
\therefore \text { Required locus is } \frac{(x-h)^2+(y-k)^2-r^2}{r^2}=-\sin ^2 \theta
\)

Remembering Method :
First make coefficient of \(x^2=\) coefficient of \(y^2=1\) and RHS of circle is zero, then \(\frac{\text { LHS of circle }}{\text { (radius) }^2}=-\sin ^2 \theta\)

Example 24: Find the locus of mid-points of the chords of the circle \(4 x^2+4 y^2-12 x+4 y+1=0\) that subtend an angle of \(\frac{2 \pi}{3}\) at its centre.

Answer: Here, \(2 \theta=\frac{2 \pi}{3} \Rightarrow \theta=\frac{\pi}{3}\)
Equation of circle can be written as
\(
x^2+y^2-3 x+y+\frac{1}{4}=0
\)
\(\therefore\) Required locus is
\(
\frac{x^2+y^2-3 x+y+\frac{1}{4}}{\left(\sqrt{\frac{9}{4}+\frac{1}{4}-\frac{1}{4}}\right)^2}=-\sin ^2\left(\frac{\pi}{3}\right)=-\frac{3}{4}
\)
\(
\Rightarrow \quad x^2+y^2-3 x+y+\frac{1}{4}=-\frac{27}{16}
\)
or \(16\left(x^2+y^2\right)-48 x+16 y+31=0\)

Diametric Form of a Circle

Theorem : The equation of the circle on the line segment joining \(\left(x_1, y_1\right)\) and \(\left(x_2, y_2\right)\) as diameter is
\(
\left(x-x_1\right)\left(x-x_2\right)+\left(y-y_1\right)\left(y-y_2\right)=0 .
\)

Proof: Let \(A\left(x_1, y_1\right)\) and \(B\left(x_2, y_2\right)\) be the end points of a diameter and let \(P(x, y)\) be any point on the circle.

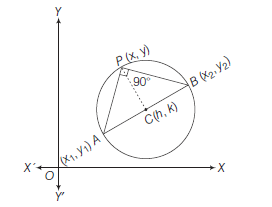
Now, Slope of \(A P=\frac{y-y_1}{x-x_1}\)
and Slope of \(B P=\frac{y-y_2}{x-x_2}\)
Since, \(\angle A P B=90^{\circ}\)
\(\therefore\) Slope of \(A P \times\) Slope of \(B P=-1\)
\(
\begin{array}{lc}
\Rightarrow & \frac{\left(y-y_1\right)}{\left(x-x_1\right)} \times \frac{\left(y-y_2\right)}{\left(x-x_2\right)}=-1 \\
\Rightarrow & \left(x-x_1\right)\left(x-x_2\right)+\left(y-y_1\right)\left(y-y_2\right)=0
\end{array}
\)

Remark

• The diameteric form of a circle can also be written as
  \(
  x^2+y^2-x\left(x_1+x_2\right)-y\left(y_1+y_2\right)+x_1 x_2+y_1 y_2=0
  \)
  or \(x^2+y^2-x\) (sum of abscissae) \(-y\) (sum of ordinates) + product of abscissae + product of ordinates \(=0\)
• If the coordinates of the end points of a diameter of a circle are given, we can also find the equation of the circle by finding the coordinates of the centre and radius. The centre is the mid-point of the diameter and radius is half of the length of the diameter.

Example 25: Find the equation of the circle, the coordinates of the end points of whose diameter are \((-1,2)\) and \((4,-3)\).

Answer: We know that the equation of the circle described on the line segment joining \(\left(x_1, y_1\right)\) and \(\left(x_2, y_2\right)\) as a diameter is \(\left(x-x_1\right)\left(x-x_2\right)+\left(y-y_1\right)\left(y-y_2\right)=0\).
Here, \(x_1=-1, x_2=4, y_1=2\) and \(y_2=-3\).
So, the equation of the required circle is
\(
(x+1)(x-4)+(y-2)(y+3)=0 \text { or, } x^2+y^2-3 x+y-10=0 .
\)

Example 26: Find the equation of the circle drawn on the intercept made by the line \(2 x+3 y=6\) between the coordinate axes as diameter.

Answer: The line \(2 x+3 y=6\) meets \(x\) and \(y\)-axes at \(A(3,0)\) and \(B(0,2)\) respectively. Taking \(A B\) as a diameter, the equation of the required circle is
\((x-3)(x-0)+(y-0)(y-2)=0\)
[Using: \(\left(x-x_1\right)\left(x-x_2\right)+\left(y-y_1\right)\left(y-y_2\right)=0\) ]
or, \(x^2+y^2-3 x-2 y=0\)

Example 27: Find the equations of the circles drawn on the diagonals of the rectangle as its diameter whose sides are \(x=6, x=-3, y=3\) and \(y=-1\).

Answer: Let the sides \(A B, B C, C D\) and \(D A\) of the rectangle \(A B C D\) be represented by the equations \(y=-1, x=6, y=3\) and \(x=-3\) respectively. Then, the coordinates of the vertices are \(A(-3,1), B(6,-1), C(6,3)\) and \(D(-3,3)\).

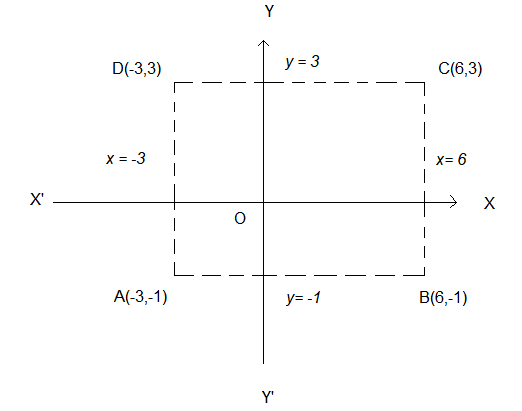
The equation of the circle with diagonal \(A C\) as diameter is
\(
(x+3)(x-6)+(y+1)(y-3)=0 \text { or, } x^2+y^2-3 x-2 y-21=0
\)
The equation of the circle with diagonal \(B D\) as diameter is
\(
(x-6)(x+3)+(y+1)(y-3)=0 \text { or, } x^2+y^2-3 x-2 y-21=0 .
\)

Example 28: If \(y=2 x\) is a chord of the circle \(x^2+y^2-10 x=0\), find the equation of a circle with this chord as diameter.

Answer: The points of intersection of the given chord and the given circle are obtained by solving \(y=2 x\) and \(x^2+y^2-10 x=0\) simultaneously. Putting \(y=2 x\) in \(x^2+y^2-10 x=0\), we get
\(
5 x^2-10 x=0 \Rightarrow 5 x(x-2)=0 \Rightarrow x=0,2 \text {. }
\)
Putting \(x=0\) and \(x=2\) respectively in \(y=2 x\), we get \(y=0\) and \(y=4\).
Thus, the coordinates of the points of intersection of the given line and the given circle are \(A(0,0)\) and \(B(2,4)\). The equation of the circle with chord \(A B\) as diameter is
\(
(x-0)(x-2)+(y-0)(y-4)=0 \text { or, } x^2+y^2-2 x-4 y=0 .
\)

Example 29: Find the equation of the circle the end points of whose diameter are the centres of the circles \(x^2+y^2+6 x-14 y=1\) and \(x^2+y^2-4 x+10 y=2\).

Answer: The centres of the given circles
\(
x^2+y^2+6 x-14 y-1=0
\)
and \(x^2+y^2-4 x+10 y-2=0\) are \((-3,7)\) and \((2,-5)\), respectively.
According to the question, the points \((-3,7)\) and \((2,-5)\) are the extremities of the diameter of required circle.
Hence, equation of circle is
\(
\begin{array}{rr}
& (x+3)(x-2)+(y-7)(y+5)=0 \\
\Rightarrow & x^2+y^2+x-2 y-41=0
\end{array}
\)

Example 30: The sides of a square are \(x=2, x=3, y=1\) and \(y=2\). Find the equation of the circle drawn on the diagonals of the square as its diameter.

Answer: Let \(A B C D\) be a square and equation of its sides \(A B, B C, C D\) and \(D A\) are \(y=1, x=3, y=2\), and \(x=2\), respectively.

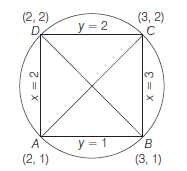
Then, \(A \equiv(2,1), B \equiv(3,1), C \equiv(3,2)\) and \(D \equiv(2,2)\)
Since, diagonals of squares are the diameters of the circle, then equation of circle is
\(
\begin{gathered}
(x-2)(x-3)+(y-1)(y-2)=0 \\
\Rightarrow \quad x^2+y^2-5 x-3 y+8=0 \text { (If } A C \text { as diameter). }
\end{gathered}
\)

Example 31: The abscissae of two points \(A\) and \(B\) are the roots of the equation \(x^2+2 a x-b^2=0\) and their ordinates are the roots of the equation \(x^2+2 p x-q^2=0\). Find the equation and the radius of the circle with \(A B\) as diameter.

Answer: Given equations are
\(
x^2+2 a x-b^2=0 \dots(i)
\)
and \(x^2+2 p x-q^2=0\)
Let the roots of the Eq. (i) be \(\alpha\) and \(\beta\) and those of Eq. (ii) be \(\gamma\) and \(\delta\). Then,
\(
\left.\begin{array}{r}
\alpha+\beta=-2 a \\
\alpha \beta=-b^2
\end{array}\right\}
\)
and
\(
\left.\begin{array}{rl}
\gamma+\delta & =-2 p \\
\gamma \delta & =-q^2
\end{array}\right\}
\)
Let \(A \equiv(\alpha, \gamma)\) and \(B \equiv(\beta, \delta)\).
Now, equation of circle whose diameter is \(A B\) will be
\(
\begin{aligned}
& (x-\alpha)(x-\beta)+(y-\gamma)(y-\delta)=0 \\
& \Rightarrow \quad x^2+y^2-(\alpha+\beta) x-(\gamma+\delta) y+\alpha \beta+\gamma \delta=0 \\
& \Rightarrow \quad x^2+y^2+2 a x+2 p y-b^2-q^2=0 \\
& \text { and radius} =\sqrt{\left(a^2+p^2+b^2+q^2\right)} \\
&
\end{aligned}
\)

Example 32: If the abscissae and the ordinates of two points \(A\) and \(B\) be the roots of \(a x^2+b x+c=0\) and \(a^{\prime} y^2+b^{\prime} y+c^{\prime}=0\) respectively, show that the equation of the circle described on \(A B\) as diameter is \(a a^{\prime}\left(x^2+y^2\right)+a^{\prime} b x+a b^{\prime} y+\left(c a^{\prime}+c^{\prime} a\right)=0\).

Answer: Let \(\left(x_1, y_1\right)\) and \(\left(x_2, y_2\right)\) be the coordinates of points \(A\) and \(B\) respectively. It is given that \(x_1, x_2\) are roots of \(a x^2+b x+c=0\) and \(y_1, y_2\) are roots of \(a^{\prime} y^2+b^{\prime} y+c^{\prime}=0\).
\(
\therefore \quad x_1+x_2=-\frac{b}{a}, x_1 x_2=\frac{c}{a}, y_1+y_2=-\frac{b^{\prime}}{a^{\prime}} \text { and } y_1 y_2=\frac{c^{\prime}}{a^{\prime}} \dots(i)
\)
The equation of the circle with \(A B\) as diameter is
\(
\begin{array}{ll}
& \left(x-x_1\right)\left(x-x_2\right)+\left(y-y_1\right)\left(y-y_2\right)=0 \\
\Rightarrow \quad & x^2+y^2-x\left(x_1+x_2\right)-y\left(y_1+y_2\right)+x_1 x_2+y_1 y_2=0 . \\
\Rightarrow \quad & x^2+y^2-x\left(-\frac{b}{a}\right)-\left(-\frac{b^{\prime}}{a^{\prime}}\right) y+\frac{c}{a}+\frac{c^{\prime}}{a^{\prime}}=0 \text { [Using (i)] }\\
\Rightarrow \quad & a a^{\prime}\left(x^2+y^2\right)+a^{\prime} b x+a b^{\prime} y+\left(c a^{\prime}+c^{\prime} a\right)=0
\end{array}
\)

Example 33: Find the equation of the circle on the straight line joining the points of intersection of \(a x^2+2 h x y+b y^2=0\) and \(l x+m y=1\) as diameter.

Answer: Suppose the line \(l x+m y=1\) intersects the lines given by \(a x^2+2 h x y+b y^2=0\) in \(A\) and \(B\). Let the coordinates of \(A\) and \(B\) are \(\left(x_1, y_1\right)\) and \(\left(x_2, y_2\right)\) respectively. Eliminating \(y\) between \(l x+m y=1\) and \(a x^2+2 h x y+b y^2=0\), we obtain
\(
x^2\left(a m^2-2 h l m+b l^2\right)-2 x(b l-h m)+b=0
\)
Clearly, \(x_1, x_2\) are roots of this equation.
\(
\therefore \quad x_1+x_2=\frac{2(b l-h m)}{a m^2-2 h l m+b l^2} \text { and, } x_1 x_2=\frac{b}{a m^2-2 h l m+b l^2}
\)
Now, eliminating \(x\) between \(l x+m y=1\) and \(a x^2+2 h x y+b y^2=0\), we get
\(
y^2\left(a m^2-2 h l m+b l^2\right)-2 y(a m-h l)+a=0 .
\)
Since \(y_1, y_2\) are roots of this equation.
\(
\therefore \quad y_1+y_2=\frac{2(a m-h l)}{a m^2-2 h l m+b l^2} \text { and, } y_1 y_2=\frac{a}{a m^2-2 h l m+b l^2}
\)
The equation of the circle with \(A B\) as diameter is
\(
\begin{aligned}
& \left(x-x_1\right)\left(x-x_2\right)+\left(y-y_1\right)\left(y-y_2\right)=0 \\
& \text { or, } x^2-x\left(x_1+x_2\right)+x_1 x_2+y^2-y\left(y_1+y_2\right)+y_1 y_2=0 \\
& \text { or, } x^2+y^2-\frac{2 x(b l-h m)}{a m^2-2 h l m+b l^2}-\frac{2 y(a m-h l)}{a m^2-2 h l m+b l^2}+\frac{b}{a m^2-2 h l m+b l^2}+\frac{a}{a m^2-2 h l m+b l^2}=0
\end{aligned}
\)
or, \(\left(x^2+y^2\right)\left(a m^2-2 h l m+b l^2\right)-2 x(b l-h m)-2 y(a m-h l)+(a+b)=0\). This is the required equation of the circle.

Example 34: On the line joining \((1,0)\) and \((3,0)\) an equilateral triangle is drawn, having its vertex in the first quadrant. Find the equation to the circles described on its sides as diameter.

Answer: Let \((1,0)\) and \((3,0)\) be the coordinates of the points \(A\) and \(B\) respectively. Then,
\(
A B=\sqrt{(1-3)^2+(0-0)^2}=2 .
\)
Let \(C\left(x_1, y_1\right)\) be the third vertex of the equilateral triangle \(A B C\). Then, \(A C=B C=2\)
Now, \(A C=\sqrt{\left(x_1-1\right)^2+\left(y_1-0\right)^2}, \quad B C=\sqrt{\left(x_1-3\right)^2+\left(y_1-0\right)^2}\)
\(
\begin{array}{ll}
\therefore & A C=B C \\
\Rightarrow & A C^2=B C^2 \\
\Rightarrow & \left(x_1-1\right)^2+y_1^2=\left(x_1-3\right)^2+y_1{ }^2 \Rightarrow 4 x_1=8 \Rightarrow x_1=2
\end{array}
\)
Again, \(A C=2\)
\(
\begin{array}{ll}
\Rightarrow & \sqrt{\left(x_1-1\right)^2+y_1^2}=2 \\
\Rightarrow & \left(x_1-1\right)^2+y_1^2=4 \\
\Rightarrow & (2-1)^2+y_1^2=4 \Rightarrow y_1= \pm \sqrt{3} \Rightarrow y_1=\sqrt{3} \left[\because x_1=2\right]
\end{array}
\)
So, the coordinates of \(C\) are \((2, \sqrt{3})\). \(\left[\because C\left(x_1, y_1\right)\right. \text { lies in first quadrant] }\)
The equation of the circle on \(A C\) as diameter is
\(
(x-1)(x-2)+(y-0)(y-\sqrt{3})=0 \text { or, } x^2+y^2-3 x-\sqrt{3} y+2=0 .
\)
Similarly, the equations of circles with \(A B\) and \(B C\) as diameters are
\(
(x-1)(x-3)+(y-0)(y-0)=0 \text { and, }(x-3)(x-2)+(y-0)(y-\sqrt{3})=0
\)
or, \(x^2+y^2-4 x+3=0\) and, \(x^2+y^2-5 x-\sqrt{3} y+6=0\) respectively.

Example 35: Find the equations to the circles which pass through the origin and cut off equal chords of length ‘ \(a\) ‘ from the straight lines \(y=x\) and \(y=-x\).

Answer: From Fig. below, we see that there will be four such circles which pass through the origin and cut off equal chords of length a from the straight lines \(y= \pm x\).

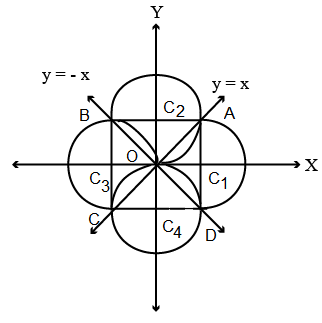
Since \(\angle A O B=\angle B O C=\angle C O D=\angle D O A=\pi / 2\). Therefore, \(A B, B C, C D\) and \(D A\) are diameters of the four circles.
Now, \(\angle X O A=\pi / 4\) and, \(O A=a\)
\(\therefore \quad A C_1=a \sin \frac{\pi}{4}=\frac{a}{\sqrt{2}}\) and, \(O C_1=a \cos \frac{\pi}{4}=\frac{a}{\sqrt{2}}\)
So, the coordinates of \(A\) are \((a / \sqrt{2}, a / \sqrt{2})\).
Similarly, the coordinates of \(B, C\) and \(D\) are \((-a / \sqrt{2}, a / \sqrt{2}),(-a / \sqrt{2},-a / \sqrt{2})\) and \((a / \sqrt{2},-a / \sqrt{2})\) respectively.
The equation of the circle with \(A D\) as diameter is
\(
\left(x-\frac{a}{\sqrt{2}}\right)\left(x-\frac{a}{\sqrt{2}}\right)+\left(y-\frac{a}{\sqrt{2}}\right)\left(y+\frac{a}{\sqrt{2}}\right)=0 \text { or, } x^2+y^2-\sqrt{2} a x=0 .
\)
Similarly, the equations of the required circles with \(B C, C D\) and \(A B\) as diameters are
\(
\begin{aligned}
& \left(x+\frac{a}{\sqrt{2}}\right)\left(x+\frac{a}{\sqrt{2}}\right)+\left(y-\frac{a}{\sqrt{2}}\right)\left(y+\frac{a}{\sqrt{2}}\right)=0 \text { or, } x^2+y^2+\sqrt{2} a x=0 \\
& \left(x+\frac{a}{\sqrt{2}}\right)\left(x-\frac{a}{\sqrt{2}}\right)+\left(y+\frac{a}{\sqrt{2}}\right)\left(y+\frac{a}{\sqrt{2}}\right)=0 \text { or, } x^2+y^2+\sqrt{2} a y=0
\end{aligned}
\)
and, \(\left(x-\frac{a}{\sqrt{2}}\right)\left(x+\frac{a}{\sqrt{2}}\right)+\left(y-\frac{a}{\sqrt{2}}\right)\left(y-\frac{a}{\sqrt{2}}\right)=0\) or, \(x^2+y^2-\sqrt{2} a y=0\) respectively.

Equation of Circle Passing Through Three Non-Collinear Points

Let the equation of circle be
\(
x^2+y^2+2 g x+2 f y+c=0 \dots(i)
\)
If three points \(\left(x_1, y_1\right),\left(x_2, y_2\right),\left(x_3, y_3\right)\) lie on the circle Eq. (i), their coordinates must satisfy its equation. Hence, solving equations
\(
\begin{aligned}
& x_1^2+y_1^2+2 g x_1+2 f y_1+c=0, \dots(ii) \\
& x_2^2+y_2^2+2 g x_2+2 f y_2+c=0, \dots(iii) \\
& x_3^2+y_3^2+2 g x_3+2 f y_3+c=0, \dots(iv)
\end{aligned}
\)
\(g, f, c\) are obtained from Eqs. (ii), (iii) and (iv). Then, to find the circle Eq. (i).

Aliter : Eliminate \(g, f, c\) from Eqs. (i), (ii), (iii) and (iv) with the help of determinant
\(
\left|\begin{array}{cccc}
x^2+y^2 & x & y & 1 \\
x_1^2+y_1^2 & x_1 & y_1 & 1 \\
x_2^2+y_2^2 & x_2 & y_2 & 1 \\
x_3^2+y_3^2 & x_3 & y_3 & 1
\end{array}\right|=0
\)
which is the required equation of circle Applying \(R_1 \rightarrow R_1-R_4, R_2 \rightarrow R_2-R_4\) and \(R_3 \rightarrow R_3-R_4\) then, we get
\(
\left|\begin{array}{llll}
x^2+y^2-x_3^2-y_3^2 & x-x_3 & y-y_3 & 0 \\
x_1^2+y_1^2-x_3^2-y_3^2 & x_1-x_3 & y_1-y_3 & 0 \\
x_2^2+y_2^2-x_3^2-y_3^2 & x_2-x_3 & y_2-y_3 & 0 \\
x_3^2+y_3^2 & x_3 & y_3 & 1
\end{array}\right|=0
\)
\(
\text { i.e. } \quad\left|\begin{array}{ccc}
x^2+y^2-x_3^2-y_3^2 & x-x_3 & y-y_3 \\
x_1^2+y_1^2-x_3^2-y_3^2 & x_1-x_3 & y_1-y_3 \\
x_2^2+y_2^2-x_3^2-y_3^2 & x_2-x_3 & y_2-y_3
\end{array}\right|=0
\)

Remarks

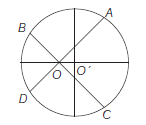
• Cyclic quadrilateral If all four vertices of a quadrilateral lie on a circle, then the quadrilateral is called a cyclic quadrilateral. The four vertices are said to be concyclic.
• Concyclic points If \(A, B, C, D\) are concyclic, then
  \(
  O A \cdot O D=O B \cdot O C
  \)
  where, \(O^{\prime}\) be the centre of the circle.

Example 36: Find the equation of the circle which passes through the points \((4,1),(6,5)\) and has its centre on the line \(4 x+y=16\).

Answer: Let the equation of circle be
\(
x^2+y^2+2 g x+2 f y+c=0 \dots(i)
\)
Since, the centre of Eq. (i) i.e. \((-g,-f)\) lies on \(4 x+y=16\)
then,\(-4 g-f=16\)
or \(4 g+f+16=0 \dots(ii)\)
Since, the points \((4,1)\) and \((6,5)\) lie on circle \(x^2+y^2+2 g x+2 f y+c=0\), we get the equations
\(
\begin{array}{r}
16+1+8 g+2 f+c=0 \\
17+8 g+2 f+c=0 \dots(iii)
\end{array}
\)
and
\(
\begin{aligned}
36+25+12 g+10 f+c & =0 \\
61+12 g+10 f+c & =0 \dots(iv)
\end{aligned}
\)
Subtracting Eq. (iii) from Eq. (iv), then
\(
44+4 g+8 f=0 \dots(v)
\)
Solving Eqs. (ii) and (v), we get
\(
f=-4 \text { and } g=-3
\)
Now, from Eq. (iii), \(17-24-8+c=0\)
\(
\Rightarrow \quad c=15
\)
Hence, the equation of circle becomes
\(
x^2+y^2-6 x-8 y+15=0
\)

Example 37: Show that the four points \((1,0),(2,-7),(8,1)\) and \((9,-6)\) are concyclic.

Answer: Since, the given four points are concyclic, we are to show that they lie on a circle. Let the general equation of circle is
\(
x^2+y^2+2 g x+2 f y+c=0 \dots(i)
\)
has three parameters, it is sufficient to obtain the equation of the circle passing through any three of these points. For concyclic, the fourth point should lie on this circle.
Let three points \(A(1,0), B(2,-7)\) and \(D(8,1)\) lie on Eq. (i), then
\(
1+0+2 g+0+c=0 \text { or } 1+2 g+c=0 \dots(ii)
\)

\(
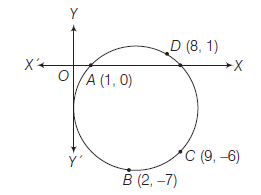
\begin{gathered}
(2)^2+(-7)^2+2 g(2)+2 f(-7)+c=0 \\
53+4 g-14 f+c=0 \dots(iii) \\
(8)^2+(1)^2+2 g(8)+2 f(1)+c=0 \\
65+16 g+2 f+c=0 \dots(iv)
\end{gathered}
\)
Now, subtracting Eq. (ii) from Eq. (iii), we get
\(
\begin{array}{r}
52+2 g-14 f=0 \\
26+g-7 f=0 \dots(v)
\end{array}
\)
and subtracting Eq. (iii) from Eq. (iv), we get
\(
\begin{array}{rlrl}
& & 12+12 g+16 f & =0 \\
\Rightarrow & 3+3 g+4 f =0 \dots(vi)
\end{array}
\)
Solving Eq. (v) and Eq. (vi), we get
\(
g=-5 \text { and } f=3
\)
From Eq. (ii), \(1-10+c=0\)
\(
\therefore \quad c=9
\)
Therefore, equation of circle passing through these points is
\(
x^2+y^2-10 x+6 y+9=0
\)
Substituting the fourth point in the equation of this circle, we get
\(
(9)^2+(-6)^2-10(9)+6(-6)+9=0
\)
Hence, the point \(C(9,-6)\) lies on the circle, that is, the four points are concyclic.

Intercepts Made on the Axes by a Circle

Let the circle \(x^2+y^2+2 g x+2 f y+c=0 \dots(i)\)
Length of intercepts on \(X\)-axis and \(Y\)-axis are
\(
|A B|=\left|x_2-x_1\right| \text { and }|C D|=\left|y_2-y_1\right| \text { respectively. }
\)

The circle intersects the \(X\)-axis, when \(y=0\) then
\(
x^2+2 g x+c=0
\)
Since, the circle intersects the \(X\)-axis at \(A\left(x_1, 0\right)\) and \(B\left(x_2, 0\right)\)
then,
\(
\begin{aligned}
& \begin{aligned}
x_1+x_2 & =-2 g, x_1 x_2=c \\
\therefore \quad|A B|=\left|x_2-x_1\right| & =\sqrt{\left(x_2+x_1\right)^2-4 x_1 x_2}
\end{aligned} \\
& =2 \sqrt{\left(g^2-c\right)} \\
&
\end{aligned}
\)
and the circle intersects the \(Y\)-axis, when \(x=0\), then
\(
y^2+2 f y+c=0
\)
Since, the circle intersects the \(Y\)-axis at \(C\left(0, y_1\right)\) and \(D\left(0, y_2\right)\)
then,
\(
\begin{aligned}
& y_1+y_2=-2 f, y_1 y_2=c \\
& \therefore \quad|C D|=\left|y_2-y_1\right|=\sqrt{\left(y_2+y_1\right)^2-4 y_2 y_1} \\
& =2 \sqrt{\left(f^2-c\right)} \\
&
\end{aligned}
\)

Remarks

• Intercepts are always positive.
• If circle touches \(X\)-axis, then \(|A B|=0\)
  \(
  \therefore \quad c=g^2
  \)
  and if circle touches \(Y\)-axis, then \(|C D|=0\)
  \(
  \therefore \quad c=f^2
  \)
• If circle touches both axes, then \(|A B|=0=|C D|\)
  \(
  \therefore \quad c=g^2=f^2
  \)

Example 38: Find the equation of the circle whose diameter is the line joining the points \((-4,3)\) and \((12,-1)\). Find also the intercept made by it on \(Y\)-axis.

Answer: Equation of circle having \((-4,3)\) and \((12,-1)\) as the ends of a diameter is
\(
\begin{array}{ll}
& (x+4)(x-12)+(y-3)(y+1)=0 \\
\Rightarrow & x^2+y^2-8 x-2 y-51=0 \dots(i)
\end{array}
\)
Comparing Eq. (i) with standard equation of circle
then,
\(
\begin{aligned}
& \quad x^2+y^2+2 g x+2 f y+c=0 \\
& \text { then, } \quad g=-4, f=-1, c=-51 \\
& \therefore \text { Intercept on Y-axis }=2 \sqrt{\left(f^2-c\right)}=2 \sqrt{(1+51)}=4 \sqrt{13} .
\end{aligned}
\)

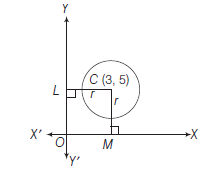
Example 39: Find the equation of the circle which touches the axis of \(y\) at a distance of 4 units from the origin and cuts the intercept of 6 units from the axis of \(x\).

Answer:

\(
\begin{array}{rlrl}
C M=N O & =4 \\
\text { In } \triangle P C M, (P C)^2 & =(3)^2+(4)^2 \\
P C & =5 \\
\text { radius of circle } & =5 \\
N C =5
\end{array}
\)
Centre of circle is \((5,4)\).

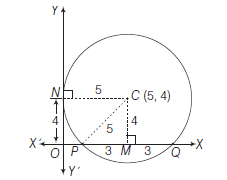
\(\therefore\) Equation of circle, if centre in I quadrant
\(
(x-5)^2+(y-4)^2=25
\)
If centre in II, III and IV quadrant, then equations are
\(
\begin{aligned}
(x+5)^2+(y-4)^2 & =25, \\
(x+5)^2+(y+4)^2 & =25 \\
\text { and } \quad(x-5)^2+(y+4)^2 & =25
\end{aligned}
\)
Hence, there are 4 circles which satisfy the given conditions. They are
\(
\begin{aligned}
(x \pm 5)^2+(y \pm 4)^2 & =25 \\
\text { or } \quad x^2+y^2 \pm 10 x \pm 8 y+16 & =0
\end{aligned}
\)

Example 40: Find the equation of the circle which passes through the origin and makes intercepts of length \(a\) and \(b\) on the \(X\) and \(Y\) axes, respectively.

Answer: Let the equation of the circle be
\(
x^2+y^2+2 g x+2 f y+c=0 \dots(i)
\)
Since, the circle passes through the origin, we get \(c=0\) and given the intercepts on \(X\) and \(Y\) axes are \(a\) and \(b\)
then, \(2 \sqrt{\left(g^2-c\right)}=a\)
or \(\quad 2 \sqrt{\left(g^2-0\right)}=a\)
\(
\begin{array}{ll}
\therefore & g= \pm a / 2 \\
\text { and } & 2 \sqrt{\left(f^2-c\right)}=b \\
\text { or } & 2 \sqrt{\left(f^2-0\right)}=b \\
\therefore & f= \pm b / 2
\end{array}
\)
Hence, the equation of circle from Eq. (i) becomes
\(
x^2+y^2 \pm a x \pm b y=0
\)

Example 41: Find the equation of the circle which touches the axes and whose centre lies on the line \(x-2 y=3\).

Answer: Since, the circle touches both the axes, let the radius of the circle by \(a\), then

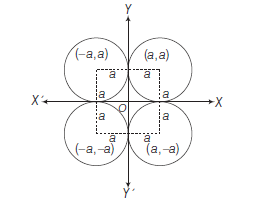
Case I: If centre \((a, a)\) but given centre lies on
\(
\begin{aligned}
& & x-2 y & =3 \\
& \therefore & a-2 a & =3 \\
& \therefore & a & =-3 \\
& & \text { Centre } & =(-3,-3)
\end{aligned}
\)
and \(\text { radius }=|-3|=3\)
\(\therefore\) Equation of circle is
\(
\begin{aligned}
(x+3)^2+(y+3)^2 & =3^2 \\
\text { and } \quad x^2+y^2+6 x+6 y+9 & =0
\end{aligned}
\)

Case II: If centre \((-a, a)\) but centre lies on \(x-2 y=3\)
\(
\begin{aligned}
& \therefore \quad-a-2 a=3 \\
& \therefore \quad a=-1
\end{aligned}
\)
then, \(\quad\) centre \(=(1,-1)\) and radius \(=|-1|=1\)
\(\therefore\) Equation of circle is \((x-1)^2+(y+1)^2=1\)
or \(\quad x^2+y^2-2 x+2 y+1=0\)

Case III:
\(
\begin{aligned}
& \text { If the centre }=(-a,-a) \\
& \text { but centre lies on } x-2 y=3 \\
& \therefore \quad-a+2 a=3 \\
& \therefore \quad a=3 \\
&
\end{aligned}
\)
\(
\text { then centre }(-3,-3) \text { and radius }=|3|=3
\)
\(\therefore\) Equation of circle is
\(
\begin{array}{r}
(x+3)^2+(y+3)^2=3^2 \\
\text { or } \quad x^2+y^2+6 x+6 y+9=0
\end{array}
\)

Case IV: If centre \(=(a,-a)\) but centre lies on \(x-2 y=3\)
\(
\begin{array}{rlrl}
\text { or } & a+2 a =3 \\
& \therefore & a =1
\end{array}
\)
then centre \(=(1,-1)\) and radius \(=1\)
\(\therefore\) Equation of circle is
\(
\begin{aligned}
(x-1)^2+(y+1)^2 & =1 \\
\text { or } \quad x^2+y^2-2 x+2 y+1 & =0
\end{aligned}
\)

Example 42: A circle of radius 2 lies in the first quadrant and touches both the axes of coordinates. Find the equation of the circle with centre at \((6,5)\) and touching the above circle externally.

Answer: Given, \(A C=2\) units
\(
\begin{aligned}
& \text { and } A \equiv(2,2), B \equiv(6,5) \\
& \text { then } A B=\sqrt{(2-6)^2+(2-5)^2} \\
& =\sqrt{16+9}=5 \\
&
\end{aligned}
\)

\(
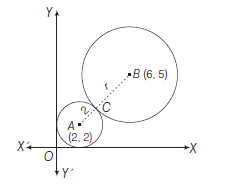
\begin{array}{rlrl}
\text { Since } & A C+C B & =A B \\
\therefore & 2+C B & =5 \\
& \therefore & C B & =3
\end{array}
\)
Hence, equation of required circle with centre at \((6,5)\) and radius 3 is
\(
\begin{array}{r}
(x-6)^2+(y-5)^2=3^2 \\
x^2+y^2-12 x-10 y+52=0
\end{array}
\)

Example 43: A circle of radius 5 units touches the coordinate axes in first quadrant. If the circle makes one complete roll on \(X\)-axis along the positive direction of \(X\)-axis, find its equation in the new position.

Answer: Let \(C\) be the centre of the circle in its initial position and \(D\) be its centre in the new position.

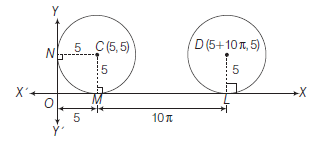
Since, the circle touches the coordinates axes in first quadrant and the radius of circle be 5 units.
\(
\begin{aligned}
& \therefore \text { Centre of circle is }(5,5) \\
& \text { Moving length of circle }=\text { circumference of the circle } \\
& \qquad=2 \pi r=2 \pi(5)=10 \pi
\end{aligned}
\)
Now, centre of circle in new position is \((5+10 \pi, 5)\) and radius is 5 units, therefore, its equation will be
\(
\begin{aligned}
& (x-5-10 \pi)^2+(y-5)^2=5^2 \\
& \text { or } \quad x^2+y^2-10(1+2 \pi) x-10 y+100 \pi^2+100 \pi+25=0
\end{aligned}
\)

Position of a Point with Respect to Circle

Theorem : A point \(\left(x_1, y_1\right)\) lies outside, on or inside a circle
\(
\begin{aligned}
& \qquad S \equiv x^2+y^2+2 g x+2 f y+c=0 \\
& \text { according as } \quad S_1>,=\text {, or }<0 \\
& \text { where, } S_1=x_1^2+y_1^2+2 g x_1+2 f y_1+c
\end{aligned}
\)

Proof: Let \(P\left(x_1, y_1\right)\) be the given point and let \(C\) be the centre of the circle
Then,
\(
\begin{array}{ll}
\text { Then, } & C \equiv(-g,-f) \\
\therefore & C P=\sqrt{\left(x_1+g\right)^2+\left(y_1+f\right)^2}
\end{array}
\)
If \(r\) be the radius of the circle, then
\(
r=\sqrt{\left(g^2+f^2-c\right)}
\)
The point \(P\) lies outside, on or inside the circle according as
\(
C P>,=\text {, or }<r
\)
\(
\Rightarrow \quad(C P)^2>,=\text {, or }<r^2
\)
\(
\Rightarrow \quad\left(x_1+g\right)^2+\left(y_1+f\right)^2>,=, \quad \text { or }<g^2+f^2-c
\)
\(
\Rightarrow \quad x_1^2+y_1^2+2 g x_1+2 f y_1+c>,=, \text { or }<0
\)
\(
\Rightarrow \quad S_1>,=, \quad \text { or }<0
\)
\(
\text { where, } S_1=x_1^2+y_1^2+2 g x_1+2 f y_1+c \text {. }
\)

Example 44: Discuss the position of the points \((1,2)\) and \((6,0)\) with respect to the circle
\(
x^2+y^2-4 x+2 y-11=0 .
\)

Answer: Let \(S \equiv x^2+y^2-4 x+2 y-11=0\) for the point \((1,2)\)
\(
\begin{aligned}
& S_1=1^2+2^2-4 \cdot 1+2 \cdot 2-11=-6 \\
& \therefore \quad S_1<0 \\
& \text { and for the point }(6,0) \\
& S_2=6^2+0-4 \cdot 6+2 \cdot 0-11 \\
& =36-24-11 \\
& =36-35=1 \\
& \therefore \quad S_2>0 \\
&
\end{aligned}
\)
Hence, the point \((1,2)\) lies inside the circle and the point \((6,0)\) lies outside the circle.

Example 45: The circle \(x^2+y^2-6 x-10 y+\lambda=0\) does not touch or intersect the coordinate axes and the point \((1,4)\) is inside the circle. Find the range of values of \(\lambda\).

Answer: Let \(S \equiv x^2+y^2-6 x-10 y+\lambda=0\)
\(\because\) Point \((1,4)\) is inside the circle, then \(S_1<0\)

\(
\begin{gathered}
1+16-6-40+\lambda<0 \\
\lambda<29 \dots(i)
\end{gathered}
\)
Centre and radius of the circle are \((3,5)\) and \(\sqrt{(34-\lambda)}\), respectively.
\(\because\) Circle does not touch or intersect the coordinate axes.
\(\therefore \quad 5>r\) and \(3>r\)
\(
\text { or } \quad 5>\sqrt{(34-\lambda)} \text { and } 3>\sqrt{(34-\lambda)}
\)
\(
\begin{array}{ll}
\Rightarrow & 25>34-\lambda \text { and } 9>34-\lambda \\
\Rightarrow & \lambda>9 \text { and } \lambda>25 \\
\therefore & \lambda>25 \dots(ii)
\end{array}
\)
Also,
\(
\begin{aligned}
34-\lambda & >0 \\
\end{aligned}
\)
\(
\therefore \quad \lambda<34 \dots(iii)
\)
From Eqns. (i), (ii) and (iii), we get \(25<\lambda<29\)

Maximum and Minimum Distance of a Point from the Circle

Let any point \(P\left(x_1, y_1\right)\) and circle
\(
S \equiv x^2+y^2+2 g x+2 f y+c=0 \dots(i)
\)
The centre and radius of the circle are
\(
C(-g,-f) \text { and } \sqrt{\left(g^2+f^2-c\right)} \text { respectively }
\)
Case I: If \(P\) inside the circle
In this case \(S_1<0\)
\(
\because \quad r=\sqrt{\left(g^2+f^2-c\right)}=C A=C B
\)

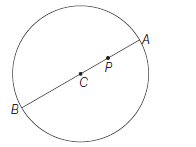
The minimum distance of \(P\) from circle \(=P A=C A-C P\) \(=r-C P\)
and the maximum distance of \(P\) from circle \(=P B\)
\(
=C B+C P=r+C P
\)

Case II: If \(P\) outside the circle
In this case \(S_1>0\) the minimum distance of \(P\) from circle
\(
=P A=C P-C A=C P-r
\)
and the maximum distance of \(P\) from the circle
\(
=P B=C P+C B=r+C P
\)

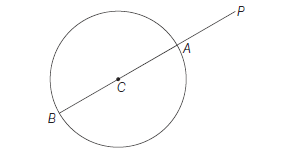
Case III: If \(P\) on the circle
In this case \(S_1=0\)
the minimum distance of \(P\) from the circle \(=0\)
and the maximum distance of \(P\) from the circle
\(
=P A=2 r
\)

Remark

• If point \(P\) inside or outside or on the circle and centre of circle at \(C\) and radius \(r\), then minimum distance of \(P\) from the circle \(=|C P-r|\) and maximum distance of \(P\) from the circle \(=C P+r\)

Example 46: Find the shortest and largest distance from the point \((2,-7)\) to the circle
\(
x^2+y^2-14 x-10 y-151=0
\)

Answer: Let \(S \equiv x^2+y^2-14 x-10 y-151=0\)
\(
\therefore \quad S_1=(2)^2+(-7)^2-14(2)-10(-7)-151=-56<0
\)

\(\therefore P(2,-7)\) inside the circle
radius of the circle, \(r=\sqrt{(-7)^2+(-5)^2+151}=15\)
\(\because\) Centre of circle \(C \equiv(7,5)\)
\(\therefore \quad C P=\sqrt{(7-2)^2+(5+7)^2}=13\)
\(\therefore\) Shortest distance \(=P A=r-C P=15-13=2\)
and Largest distance \(=P B=r+C P=15+13=28\)

Example 47: Find the points on the circle \(x^2+y^2-2 x+4 y-20=0\) which are farthest and nearest to the point \((-5,6)\).

Answer: The given circle is \(S \equiv x^2+y^2-2 x+4 y-20=0\)
Let \(\quad P \equiv(-5,6)\)

For the point \(P\)
\(
\begin{aligned}
S_1 & =25+36+10+24-20 \\
& =75>0
\end{aligned}
\)
\(\therefore\) Point \(P(-5,6)\) lies outside the circle.
The centre and radius of the circle are \((1,-2)\) and 5 , respectively.
\(
\because \quad C P=\sqrt{(1+5)^2+(-2-6)^2}=10
\)
Now, point \(A\) divides \(C P\) in the ratio
\(
\frac{A P}{A C}=\frac{C P-r}{r}=\frac{10-5}{5}=1
\)
\(\therefore A\) is mid-point of \(C P\).
\(\therefore \quad A \equiv\left(\frac{1-5}{2}, \frac{-2+6}{2}\right)\)
or \(\quad A \equiv(-2,2)\)
and \(C\) is the mid-point of \(A B\).
\(\therefore \quad B \equiv(2 \times 1-(-2), 2 \times-2-2)\)
or \(\quad B \equiv(4,-6)\)
Hence, point \(A(-2,2)\) is nearest to \(P\) and \(B(4,-6)\) is farthest from \(P\).

Intersection of a Line and a Circle

Let the equation of the circle be
\(
x^2+y^2=a^2 \dots(i)
\)
and the equation of the line be
\(
y=m x+c \dots(ii)
\)
From Eq. (i) and Eq. (ii)
\(
x^2+(m x+c)^2=a^2
\)
\(
\left(1+m^2\right) x^2+2 m c x+c^2-a^2=0 \dots(iii)
\)

Case I: When points of intersection are real and distinct, then Eq. (iii) has two distinct roots

\(
\begin{array}{lrl}
B^2-4 A C>0 \\
\text { or } & 4 m^2 c^2-4\left(1+m^2\right)\left(c^2-a^2\right)>0 \\
\text { or } & a^2>\frac{c^2}{1+m^2}
\end{array}
\)
or \(\quad a>\frac{|c|}{\sqrt{\left(1+m^2\right)}}=\) length of perpendicular
from \((0,0)\) to \(y=m x+c\)
\(\Rightarrow a>\) length of perpendicular from \((0,0)\) to \(y=m x+c\)
Thus, a line intersects a given circle at two distinct points if radius of circle is greater than the length of perpendicular from centre of the circle to the line.

Case II: When the points of intersection are coincident, then Eq. (iii) has two equal roots

\(
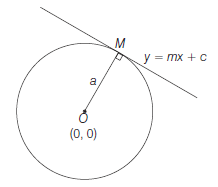
\begin{array}{lc}
\therefore & B^2-4 A C=0 \\
\Rightarrow & 4 m^2 c^2-4\left(1+m^2\right)\left(c^2-a^2\right)=0 \\
\therefore & a^2=\frac{c^2}{\left(1+m^2\right)} \\
\text { or } & a=\frac{|c|}{\sqrt{\left(1+m^2\right)}}
\end{array}
\)
\(a=\) length of the perpendicular from the point \((0,0)\) to
\(
y=m x+c
\)
Thus, a line touches the circle if radius of circle is equal to the length of perpendicular from centre of the circle to the line.

Case III: When the points of intersection are imaginary. In this case (iii) has imaginary roots

\(
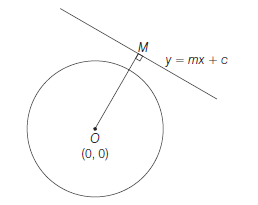
\begin{array}{ccc}
\therefore & B^2-4 A C<0 \\
& 4 m^2 c^2-4\left(1+m^2\right)\left(c^2-a^2\right)=0 \\
\therefore & a^2<\frac{c^2}{1+m^2}
\end{array}
\)
or \(a<\frac{|c|}{\sqrt{1+m^2}}=\) length of perpendicular from \((0,0)\) to \(y=m x+c\)
or \(a<\) length of perpendicular from \((0,0)\) to \(y=m x+c\) Thus, a line does not intersect a circle if the radius of circle is less than the length of perpendicular from centre of the circle to the line.

Example 48: Find the points of intersection of the line \(2 x+3 y=18\) and the circle \(x^2+y^2=25\).

Answer: We have, \(\quad 2 x+3 y=18 \dots(i)\)
and \(x^2+y^2=25 \dots(ii)\)
From Eq. (i), \(\quad y=\frac{18-2 x}{3}\)
Substituting in Eq. (ii), then \(x^2+\left(\frac{18-2 x}{3}\right)^2=25\)
Substituting in Eq. (ii), then \(x^2+\left(\frac{18-2 x}{3}\right)^2=25\)
\(
\begin{aligned}
& \Rightarrow \quad 9 x^2+4(9-x)^2=225 \\
& \Rightarrow \quad 9 x^2+4\left(81-18 x+x^2\right)=225 \\
& \Rightarrow \quad 13 x^2-72 x+324-225=0 \\
& \Rightarrow \quad 13 x^2-72 x+99=0 \\
& \Rightarrow \quad(x-3)(13 x-33)=0 \\
& \Rightarrow \quad x=3 \text { or } x=\frac{33}{13} \\
& \text { From Eq. (i), } \quad y=4 \text { or } y=\frac{56}{13} \\
&
\end{aligned}
\)
Hence, the points of intersection of the given line and the given circle are \((3,4)\) and \(\left(\frac{33}{13}, \frac{56}{13}\right)\).

Product of the Algebraical Distances \(P A\) and \(P B\) is Constant when from \(P, A\) Secant be Drawn to Cut the Circle in the Points \(A\) and \(B\)

If a straight line through \(P(\alpha, \beta)\) makes an angle \(\theta\) with the positive direction of \(X\)-axis, then its equation is
\(
\frac{x-\alpha}{\cos \theta}=\frac{y-\beta}{\sin \theta}=r
\)

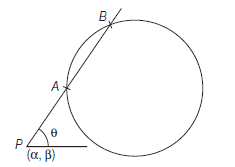
where, \(r\) is the algebraical distance of the point \((x, y)\) from the point \(P(\alpha, \beta)\).
\(
\therefore \quad(x, y)=(\alpha+r \cos \theta, \beta+r \sin \theta)
\)
If this point lies on the circle \(x^2+y^2+2 g x+2 f y+c=0\)
\(
\text { or } \quad(\alpha+r \cos \theta)^2+(\beta+r \sin \theta)^2+2 g(\alpha+r \cos \theta)+2 f(\beta+r \sin \theta)+c=0
\)
\(
\Rightarrow \quad r^2+2 r(\alpha \cos \theta+\beta \sin \theta+g \cos \theta+f \sin \theta)+\left(\alpha^2+\beta^2+2 g \alpha+2 f \beta+c\right)=0
\)
This is quadratic equation in \(r\), then \(P A\) and \(P B\) are the roots of this equation.
\(
\therefore \quad P A \cdot P B=\alpha^2+\beta^2+2 g \alpha+2 f \beta+c=\text { constant }
\)
Since, RHS is independent of \(\theta\).

Remark

• Secants are drawn from a given point \(A\) to cut a given circle at the pairs of points \(P_1, Q_1 ; P_2, Q_2 ; \ldots ; P_n, Q_n\), then
  \(
  A P_1 \cdot A Q_1=A P_2 \cdot A Q_2=\ldots=A P_n \cdot A Q_n
  \)

The Length of Intercept Cut-off from a Line by a Circle

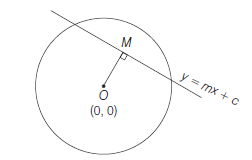
Theorem: The length of the intercept cut-off from the line \(y=m x+c\) by the circle \(x^2+y^2=a^2\) is
\(
2 \sqrt{\left\{\frac{a^2\left(1+m^2\right)-c^2}{\left(1+m^2\right)}\right\}}
\)

Proof: Draw \(O M\) perpendicular to \(P Q\)
Now, \(O M=\) length of perpendicular from \(O(0,0)\) to
\(
(y=m x+c)=\frac{|c|}{\sqrt{\left(1+m^2\right)}}
\)
and \(\quad O P=\) radius of the circle \(=a\)

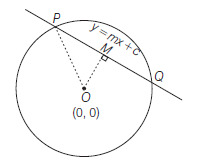
In \(\triangle O P M, \quad P M=\sqrt{(O P)^2-(O M)^2}\)
\(
\begin{aligned}
& =\sqrt{a^2-\frac{c^2}{\left(1+m^2\right)}}=\sqrt{\left\{\frac{a^2\left(1+m^2\right)-c^2}{1+m^2}\right\}} \\
\therefore \quad P Q & =2 P M=2 \sqrt{\left\{\frac{a^2\left(1+m^2\right)-c^2}{1+m^2}\right\}}
\end{aligned}
\)

Remarks

• If the line \(y=m x+c\) touches the circle \(x^2+y^2=a^2\), then intercepted length is zero
  \(
  \begin{aligned}
  & \text { i.e. } \quad P Q=0 \Rightarrow 2 \sqrt{\left\{\frac{a^2\left(1+m^2\right)-c^2}{1+m^2}\right\}}=0 \\
  & \therefore \quad c^2=a^2\left(1+m^2\right)
  \end{aligned}
  \)
  which is the required condition for tangency.
• If a line touches the circle, then length of perpendicular from the centre upon the line is equal to the radius of the circle.

Example 49: Find the length of the intercept on the straight line \(4 x-3 y-10=0\) by the circle \(x^2+y^2-2 x+4 y-20=0\).

Answer: Centre and radius of the circle \(x^2+y^2-2 x+4 y-20=0\) are \((1,-2)\) and \(\sqrt{1+4+20}=5\) respectively.

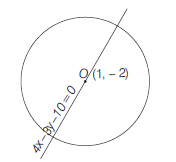
Let \(O M\) be the perpendicular from \(O\) on the line
\(
\text { then } \quad \begin{array}{ll}
4 x-3 y-10=0 \\
O M=\frac{|4 \times 1-3 \times(-2)-10|}{\sqrt{4^2+(-3)^2}}=0
\end{array}
\)
Hence, line \(4 x-3 y-10=0\) passes through the centre of the circle.
\(
\begin{aligned}
\text { Hence, intercepted length } & =\text { diameter of the circle } \\
& =2 \times 5=10
\end{aligned}
\)

Example 50: Find the coordinates of the middle point of the chord which the circle \(x^2+y^2+4 x-2 y-3=0\) cuts-off the line \(x-y+2=0\).

Answer: Centre and radius of the circle \(x^2+y^2+4 x-2 y-3=0\) are \((-2,1)\) and \(\sqrt{4+1+3}=2 \sqrt{2}\) respectively.

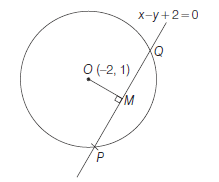
Draw perpendicular from \(O\) upon \(x-y+2=0\) is \(O M\).
Equation of \(O M\) which is perpendicular to \(x-y+2=0\) is \(x+y=\lambda\), it passes through \((-2,1)\)
Then,
\(
\begin{aligned}
& \text { Then, } & -2+1 & =\lambda \\
& \therefore & \lambda & =-1
\end{aligned}
\)
then equation of \(O M\) is \(x+y+1=0\)
Since, \(M\) is the mid-point of \(P Q\) which is point of intersection of \(x-y+2=0\) and \(x+y+1=0\), coordinates of \(M\) is \(\left(-\frac{3}{2}, \frac{1}{2}\right)\).

Example 51: For what value of \(\lambda\) will the line \(y=2 x+\lambda\) be a tangent to the circle \(x^2+y^2=5\)?

Answer: Comparing the given line with \(y=m x+c\), we get \(m=2, c=\lambda\) and given circle with \(x^2+y^2=a^2\) then \(a^2=5\)
\(\because\) Condition for tangency is
\(
\begin{array}{rlrl}
& & c^2 & =a^2\left(1+m^2\right) \\
& \lambda^2 & =5(1+4) \\
& \lambda^2 & =25 \\
\therefore & \lambda & = \pm 5
\end{array}
\)

Tangent to a Circle at a Given Point

Let \(P Q\) be a chord and \(A B\) be a secant passing through \(P\). Let \(P\) be the fixed point and move along the circle towards \(P\), then the secant \(P Q\) turns about \(P\). In the limit, when \(Q\) coincides with \(P\), then the secant \(A B\) becomes a tangent to the circle at the point \(P\).

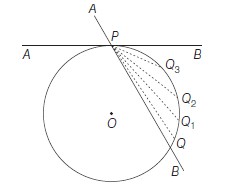
Different forms of the equations of tangents

Case 1: Point form

Theorem: The equation of tangent at the point \(P\left(x_1, y_1\right)\) to a circle
\(
\begin{gathered}
x^2+y^2+2 g x+2 f y+c=0 \text { is } \\
x x_1+y y_1+g\left(x+x_1\right)+f\left(y+y_1\right)+c=0
\end{gathered}
\)

Proof: Since, circle is \(x^2+y^2+2 g x+2 f y+c=0\) \(P\left(x_1, y_1\right)\) lie on the circle
\(
\therefore \quad x_1^2+y_1^2+2 g x_1+2 f y_1+c=0 \dots(i)
\)

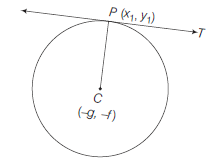
Its centre is \(C(-g,-f)\)
\(\therefore \quad\) Slope of \(C P=\frac{y_1-(-f)}{x_1-(-g)}=\frac{y_1+f}{x_1+g}\)
Since, tangent \(P T\) is perpendicular to \(C P\).
\(\therefore \quad\) Slope of tangent \(=-\left(\frac{x_1+g}{y_1+f}\right)\)
\(\therefore\) Equation of tangent at \(P\left(x_1, y_1\right)\) is
\(
\begin{gathered}
y-y_1=-\left(\frac{x_1+g}{y_1+f}\right)\left(x-x_1\right) \\
\Rightarrow \quad\left(y-y_1\right)\left(y_1+f\right)+\left(x_1+g\right)\left(x-x_1\right)=0 \\
\Rightarrow \quad x x_1+y y_1+g x+f y=x_1^2+y_1^2+g x_1+f y_1
\end{gathered}
\)
On adding \(g x_1+f y_1+c\) to both sides, we get
\(
\begin{array}{r}
x x_1+y y_1+g\left(x+x_1\right)+f\left(y+y_1\right)+c \\
=x_1^2+y_1^2+2 g x_1+2 f y_1+c=0 \text { [from Eq. (i)] }
\end{array}
\)
or \(\quad x x_1+y y_1+g\left(x+x_1\right)+f\left(y+y_1\right)+c=0\)
This is the required equation of the tangent \(P T\) to the circle at the point \(P\left(x_1, y_1\right)\).

Remarks

• For equation of tangent of circle at \(\left(x_1, y_1\right)\), substitute \(x x_1\) for \(x^2, y y_1\) for \(y^2, \frac{x+x_1}{2}\) for \(x, \frac{y+y_1}{2}\) for \(y\) and \(\frac{x y_1+x_1 y}{2}\) for \(x y\) and keep the constant as such.
• This method of tangent at \(\left(x_1, y_1\right)\) is applied only for any conics of second degree. i.e. equation of tangent of
  \(
  \begin{aligned}
  & a x^2+2 h x y+b y^2+2 g x+2 f y+c=0 \text { at }\left(x_1, y_1\right) \\
  & \text { is } a x x_1+h\left(x y_1+x_1 y\right)+b y y_1+g\left(x+x_1\right)+f\left(y+y_1\right)+c=0
  \end{aligned}
  \)

Example 52: Prove that the tangents to the circle \(x^2+y^2=25\) at \((3,4)\) and \((4,-3)\) are perpendicular to each other.

Answer: The equations of tangents to \(x^2+y^2=25\) at \((3,4)\) and \((4,-3)\) are
\(
\begin{aligned}
& 3 x+4 y=25 \dots(i)\\
& 4 x-3 y=25 \dots(ii)
\end{aligned}
\)
Now, slope of Eq. (i) \(=-\frac{3}{4}=m_1 \quad\) (say)
and slope of Eq. (ii) \(=\frac{4}{3}=m_2 \quad\) (say)
Clearly,
\(
m_1 m_2=-1
\)
Hence, Eq. (i) and Eq. (ii) are perpendicular to each other.

Example 53: Find the equation of tangent to the circle \(x^2+y^2-2 a x=0\) at the point \([a(1+\cos \alpha), a \sin \alpha]\).

Answer: The equation of tangent of \(x^2+y^2-2 a x=0\) at
\(
\begin{aligned}
& {[a(1+\cos \alpha), a \sin \alpha] \text { is }} \\
& x \cdot a(1+\cos \alpha)+y \cdot a \sin \alpha-a[x+a(1+\cos \alpha)]=0 \\
& \Rightarrow \quad a x \cos \alpha+a y \sin \alpha-a^2(1+\cos \alpha)=0 \\
& \text { or } \quad x \cos \alpha+y \sin \alpha=a(1+\cos \alpha)
\end{aligned}
\)

Example 54: Show that the circles
\(
\begin{aligned}
& x^2+y^2-4 x+6 y+8=0 \text { and } x^2+y^2-10 x \\
& -6 y+14=0 \text { touch at }(3,-1) .
\end{aligned}
\)

Answer: Equation of tangent at \((3,-1)\) of the circle
\(
\begin{aligned}
& x^2+y^2-4 x+6 y+8=0 \text { is } \\
& \quad 3 x+(-1) y-2(x+3)+3(y-1)+8=0 \\
& \text { or } \quad x+2 y-1=0 \dots(i)
\end{aligned}
\)
and equation of tangent at \((3,-1)\) of the circle
\(
\begin{aligned}
& x^2+y^2-10 x-6 y+14=0 \text { is } \\
& \quad 3 \cdot x+(-1) \cdot y-5(x+3)-3(y-1)+14=0
\end{aligned}
\)
\(
\begin{array}{r}
-2 x-4 y+2=0 \\
x+2 y-1=0 \dots(ii)
\end{array}
\)
which is the same as Eqn(i).
Hence, the given circles touch at \((3,-1)\).

Case 2: Parametric form

Theorem : The equation of tangent to the circle \(x^2+y^2=a^2\) at the point \((a \cos \theta, a \sin \theta)\) is \(x \cos \theta+y \sin \theta=a\)

Proof: The equation of tangent of \(x^2+y^2=a^2\) at \(\left(x_1, y_1\right)\) is \(x x_1+y y_1=a^2\) (using point form of the tangent)
\(
\begin{array}{ll}
\text { Putting } & x_1=a \cos \theta, y_1=a \sin \theta \\
\text { then, we get } & x \cos \theta+y \sin \theta=a
\end{array}
\)

• Corollary 1: Equation of chord joining \((a \cos \theta, a \sin \theta)\) and \((a \cos \phi, a \sin \phi)\) is
  \(
  x \cos \left(\frac{\theta+\phi}{2}\right)+y \sin \left(\frac{\theta+\phi}{2}\right)=a \cos \left(\frac{\theta-\phi}{2}\right)
  \)
• Corollary 2: Point of intersection of tangents at \((a \cos \theta, a \sin \theta)\) and \((a \cos \phi, a \sin \phi)\) is
  \(
  \left(\frac{a \cos \left(\frac{\theta+\phi}{2}\right)}{\cos \left(\frac{\theta-\phi}{2}\right)}, \frac{a \sin \left(\frac{\theta+\phi}{2}\right)}{\cos \left(\frac{\theta-\phi}{2}\right)}\right)
  \)

• Corollary 3: The angle between a pair of tangents from a point \(P\) to the circle \(x^2+y^2=a^2\) is \(\alpha\). Then, the locus of the point \(P\) is
  \(
  x^2+y^2=\frac{a^2}{\sin ^2\left(\frac{\alpha}{2}\right)}
  \)

   

       

• Proof:
  \(
  \begin{aligned}
  \phi-\theta+\alpha & =180^{\circ} \\
  \frac{\theta-\phi}{2} & =-\left(90^{\circ}-\frac{\alpha}{2}\right)
  \end{aligned}
  \)
  \(
  \text { or } \quad \cos \left(\frac{\theta-\phi}{2}\right)=\sin \left(\frac{\alpha}{2}\right)
  \)
  Now, point of intersection is
  \(
  \left(\frac{a \cos \left(\frac{\theta+\phi}{2}\right)}{\sin \left(\frac{\alpha}{2}\right)}, \frac{a \sin \left(\frac{\theta+\phi}{2}\right)}{\sin \left(\frac{\alpha}{2}\right)}\right)
  \)
  \(
  \text { Let } \quad x=\frac{a \cos \left(\frac{\theta+\phi}{2}\right)}{\sin \left(\frac{\alpha}{2}\right)} \text { and } y=\frac{a \sin \left(\frac{\theta+\phi}{2}\right)}{\sin \left(\frac{\alpha}{2}\right)}
  \)
  \(
  \therefore \quad x^2+y^2=\frac{a^2}{\sin ^2\left(\frac{\alpha}{2}\right)}
  \)

Remarks

• The angle between a pair of tangents from a point \(P\) to the circle \(x^2+y^2+2 g x+2 f y+c=0\) is \(2 \theta\) then the locus of \(P\) is \(x^2+y^2+2 g x+2 f y+c=\left(g^2+f^2-c\right) \cot ^2 \theta\)
• If angle between a pair of tangents from a point \(P\) to the circle \(x^2+y^2=a^2\) is \(\frac{\pi}{2}\), then the locus of \(P\) is
  \(
  x^2+y^2=2 a^2 \quad\left(\text { Here, } \alpha=\frac{\pi}{2}\right)
  \)
  which is director circle of \(x^2+y^2=a^2\).
  \((\because\) locus of point of intersection of perpendicular tangents is director circle)
• The equation of the tangent to the circle \((x-a)^2+(y-b)^2=r^2\) at the point \((a+r \cos \theta b+r \sin \theta)\) is \((x-a) \cos \theta+(y-b) \sin \theta=r\).

Example 55: The angle between a pair of tangents from a point \(P\) to the circle \(x^2+y^2=25\) is \(\frac{\pi}{3}\). Find the equation of the locus of the point \(P\).

Answer: Here, \(\alpha=\frac{\pi}{3}\)
\(\therefore\) Required locus is \(x^2+y^2=\frac{25}{\sin ^2\left(\frac{\pi}{6}\right)}=100\)

Example 56: The angle between a pair of tangents from a point \(P\) to the circle \(x^2+y^2-6 x-8 y+9=0\) is \(\frac{\pi}{3}\). Find the equation of the locus of the point \(P\).

Answer: Here, \(\quad 2 \theta=\frac{\pi}{3}\) or \(\theta=\frac{\pi}{6}\)
\(\therefore\) Required locus is
\(
\begin{aligned}
& x^2+y^2-6 x-8 y+9=(9+16-9) \cot ^2 \frac{\pi}{6} \\
& \text { or } \quad x^2+y^2-6 x-8 y+9=16 \times 3 \\
& \text { or } \quad x^2+y^2-6 x-8 y-39=0 \\
&
\end{aligned}
\)

Case 3: Slope Form

Theorem : The equation of a tangent of slope \(m\) to the circle \(x^2+y^2=a^2\) is \(y=m x \pm a \sqrt{\left(1+m^2\right)}\) and the coordinates of the point of contact are
\(
\left( \pm \frac{a m}{\sqrt{\left(1+m^2\right)}}, \mp \frac{a}{\sqrt{\left(1+m^2\right)}}\right)
\)

Proof : Let \(y=m x+c\) is the tangent of the circle \(x^2+y^2=a^2\).
\(\therefore\) Length of perpendicular from centre of circle \((0,0)\) on
\(
\begin{array}{r}
(y=m x+c)=\text { radius of circle } \\
\therefore \quad \frac{|c|}{\sqrt{\left(1+m^2\right)}}=a \Rightarrow c= \pm a \sqrt{\left(1+m^2\right)}
\end{array}
\)
On substituting this value of \(c\) in \(y=m x+c\), we get
\(
y=m x \pm a \sqrt{\left(1+m^2\right)} \dots(i)
\)
which are the required equations of tangents.
Also, let \(\left(x_1, y_1\right)\) be the point of contact, then equation of tangent at \(\left(x_1, y_1\right)\) to the circle \(x^2+y^2=a^2\) is
\(
x x_1+y y_1=a^2 \dots(ii)
\)
On comparing Eq. (i) and Eq. (ii), we get
\(
\frac{x_1}{m}=\frac{y_1}{-1}=\frac{a^2}{ \pm a \sqrt{\left(1+m^2\right)}}
\)
\(
\begin{aligned}
& \Rightarrow \quad \frac{x_1}{m}=-\frac{y_1}{1}= \pm \frac{a}{\sqrt{\left(1+m^2\right)}} \\
& \Rightarrow \quad x_1= \pm \frac{a m}{\sqrt{1+m^2}} \text { and } y_1=\mp \frac{a}{\sqrt{\left(1+m^2\right)}}
\end{aligned}
\)
Hence, \(\left(x_1, y_1\right)=\left( \pm \frac{a m}{\sqrt{\left(1+m^2\right)}}, \mp \frac{a}{\sqrt{\left(1+m^2\right)}}\right)\)

Corollary: It also follows that \(y=m x+c\) is a tangent to \(x^2+y^2=a^2\), if \(c^2=a^2\left(1+m^2\right)\) which is condition of tangency.

Remarks

• The reason why there are two equations \(y=m x \pm a \sqrt{1+m^2}\), there are two tangents, both are parallel and at the ends of diameter.
• The line \(a x+b y+c=0\) is tangent to the circle \(x^2+y^2=r^2\) if and only if \(c^2=r^2\left(a^2+b^2\right)\).
• If the line \(y=m x+c\) is the tangent to the circle \(x^2+y^2=r^2\), then point of contact is given by \(\left(-\frac{m r^2}{c}, \frac{r^2}{c}\right)\)
• If the line \(a x+b y+c=0\) is the tangent to the circle \(x^2+y^2=r^2\), then point of contact is given by \(\left(-\frac{a r^2}{c},-\frac{b r^2}{c}\right)\).
• The condition that the line \(l x+m y+n=0\) touches the circle \(x^2+y^2+2 g x+2 f y+c=0\) is \((/ g+m f-n)^2=\left(l^2+m^2\right)\left(g^2+f^2-c\right)\).
• Equation of tangent of the circle \(x^2+y^2+2 g x+2 f y+c=0\) in terms of slope is
  \(
  y+f=m(x+g) \pm \sqrt{\left(g^2+f^2-c\right)\left(1+m^2\right)}
  \)
• The equation of tangents of slope \(m\) to the circle \((x-a)^2+(y-b)^2=r^2\) are given by \((y-b)=m(x-a) \pm r \sqrt{\left(1+m^2\right)}\)
  and the coordinates of the points of contact are \(\left(a \pm \frac{m r}{\sqrt{\left(1+m^2\right)}}, b \mp \frac{r}{\sqrt{\left(1+m^2\right)}}\right)\)

Example 57: Find the equations of the tangents to the circle \(x^2+y^2=9\), which
(i) are parallel to the line \(3 x+4 y-5=0\)
(ii) are perpendicular to the line \(2 x+3 y+7=0\)
(iii) make an angle of \(60^{\circ}\) with the \(X\)-axis

Answer: (i) Slope of \(3 x+4 y-5=0\) is \(-\frac{3}{4}\)
Let \(m=-\frac{3}{4}\)
and equation of circle is \(x^2+y^2=9\)
\(\therefore\) Equations of tangents
\(
y=-\frac{3}{4} x \pm 3 \sqrt{\left(1+\left(-\frac{3}{4}\right)^2\right)}
\)
\(\Rightarrow \quad 4 y=-3 x \pm 15\) or \(3 x+4 y \pm 15=0\)
(ii) Slope of \(2 x+3 y+7=0\) is \(-\frac{2}{3}\)
\(\therefore\) Slope of perpendicular to \(2 x+3 y+7=0\) is \(\frac{3}{2}=m\) (say)
and given circle is \(x^2+y^2=9\)
\(\therefore\) Equations of tangents perpendicular to \(2 x+3 y+7=0\) is
\(
\begin{array}{rlrl}
y & =\frac{3}{2} x \pm 3 \sqrt{1+\left(\frac{3}{2}\right)^2} \\
\Rightarrow 2 y & =3 x \pm 3 \sqrt{13} \\
& \text { or } 3 x & -2 y \pm 3 \sqrt{13}=0
\end{array}
\)
(iii) Since, tangent make an angle \(60^{\circ}\) with the \(X\)-axis
\(
\therefore \quad m=\tan 60^{\circ}=\sqrt{3}
\)
and given circle \(\quad x^2+y^2=9\)
\(\therefore\) Equation of tangents \(y=\sqrt{3} x \pm 3 \sqrt{1+(\sqrt{3})^2}\)
\(
\sqrt{3} x-y \pm 6=0
\)

Example 58: Prove that the line \(l x+m y+n=0\) touches the circle \((x-a)^2+(y-b)^2=r^2\) if \((a l+b m+n)^2=r^2\left(I^2+m^2\right)\).

Answer: If the line \(l x+m y+n=0\) touches the circle \((x-a)^2+(y-b)^2=r^2\), then length of the perpendicular from the centre \(=\) radius
\(
\begin{aligned}
& \frac{|l a+m b+n|}{\sqrt{\left(l^2+m^2\right)}}=r \\
\Rightarrow \quad(l a+m b+n)^2 & =r^2\left(l^2+m^2\right)
\end{aligned}
\)

Example 59: Show that the line \(3 x-4 y=1\) touches the circle \(x^2+y^2-2 x+4 y+1=0\). Find the coordinates of the point of contact.

Answer: The centre and radius of the circle
\(
x^2+y^2-2 x+4 y+1=0 \operatorname{are}(1,-2)
\)
and \(\sqrt{(-1)+(2)^2-1}=2\) respectively.
Since, length of perpendicular from centre \((1,-2)\) on \(3 x-4 y=1\) is
\(
\begin{array}{r}
\frac{|3 \times 1-4 \times(-2)-1|}{\sqrt{(3)^2+(-4)^2}}=\frac{10}{5} \\
=2=\text { radius of the circle }
\end{array}
\)
Hence, \(3 x-4 y=1\) touches the circle
\(
x^2+y^2-2 x+4 y+1=0
\)
For second part : Since, perpendicular line to tangent always passes through the centre of the circle, perpendicular line to
\(
\begin{aligned}
& 3 x-4 y=1 \dots(i)\\
\text { is } & 4 x+3 y=\lambda \dots(ii)
\end{aligned}
\)
which passes through \((1,-2)\), then
\(
\begin{aligned}
4-6 & =\lambda \\
\lambda & =-2
\end{aligned}
\)
\(
\text { From Eq. (ii), } \quad 4 x+3 y=-2
\)
Solving Eq. (i) and Eq. (iii), we get the point of contact i.e. \(x=-\frac{1}{5}\) and \(y=-\frac{2}{5}\)
Hence, point of contact is \(\left(-\frac{1}{5},-\frac{2}{5}\right)\)

Example 60: If \(\mid x+m y=1\) touches the circle \(x^2+y^2=a^2\), prove that the point \((l, m)\) lies on the circle \(x^2+y^2=a^{-2}\).

Answer: Since, \(l x+m y=1\) touches the circle \(x^2+y^2=a^2\).
Then, length of perpendicular from \((0,0)\) on \(l x+m y=1\) is equal to radius
then, \(\frac{|-1|}{\sqrt{l^2+m^2}}=a\) or \(l^2+m^2=a^{-2}\)
Hence, locus of \((l, m)\) is \(x^2+y^2=a^{-2}\)

Example 61: Show that the line \((x-2) \cos \theta+(y-2) \sin \theta=1\) touches a circle for all values of \(\theta\). Find the circle.

Answer: Given line is \((x-2) \cos \theta+(y-2) \sin \theta\)
\(
1=\cos ^2 \theta+\sin ^2 \theta
\)
On comparing
\(
\begin{aligned}
& x-2=\cos \theta \dots(i)\\
\text { and } & y-2=\sin \theta \dots(ii)
\end{aligned}
\)
Squaring and adding Eq. (i) and Eq. (ii), then
\(
\begin{array}{lc}
& (x-2)^2+(y-2)^2=\cos ^2 \theta+\sin ^2 \theta \\
\Rightarrow & (x-2)^2+(y-2)^2=1 \\
\text { or } & x^2+y^2-4 x-4 y+7=0
\end{array}
\)

Normal to a Circle at a Given Point

The normal of a circle at any point is a straight line which is perpendicular to the tangent at the point and always passes through the centre of the circle.

Different form of the Equation of Normals

Case 1: Point form 

Theorem : The equation of normal at the point \(P\left(x_1, y_1\right)\) to the circle \(x^2+y^2+2 g x+2 f y+c=0\) is
\(
\frac{x-x_1}{x_1+g}=\frac{y-y_1}{y_1+f}
\)
Proof :
Equation of the given circle is
\(
x^2+y^2+2 g x+2 f y+c=0 \dots(i)
\)
Its centre \(C\) is \((-g,-f)\)

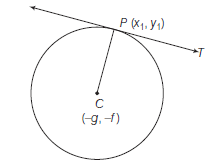
Let \(P\left(x_1, y_1\right)\) be the given point.
\(\because\) Normal of the circle at \(P\left(x_1, y_1\right)\) passes through centre \(C(-g,-f)\) of the circle.
Then, equation of normal \(C P\) passes through the points \(C(-g,-f)\) and \(P\left(x_1, y_1\right)\) is
\(
\begin{aligned}
y-y_1 & =\frac{\left(y_1+f\right)}{\left(x_1+g\right)}\left(x-x_1\right) \\
\text { or } \quad \frac{x-x_1}{x_1+g} & =\frac{y-y_1}{y_1+f}
\end{aligned}
\)
This is the required equation of normal at \(P\left(x_1, y_1\right)\) of the given circle.

Remark

• Easy method to find normal at \(\left(x_1, y_1\right)\) of second degree conics
  \(
  a x^2+2 h x y+b y^2+2 g x+2 f y+c=0 \dots(i)
  \)
  then, according to determinant \(\left|\begin{array}{lll}a & h & g \\ h & b & f \\ g & f & c\end{array}\right|\)
  write first two rows as \(a x_1+h y_1+g\) and \(h x_1+b y_1+f\) Then, normal at \(\left(x_1, y_1\right)\) of conic (i)
  \(
  \frac{x-x_1}{a x_1+h y_1+g}=\frac{y-y_1}{h x_1+b y_1+f}
  \)
• Corollary 1: Equation of normal of \(x^2+y^2=a^2\) at \(\left(x_1, y_1\right)\) is
  \(
  \frac{x-x_1}{1 \cdot x_1+0+0}=\frac{y-y_1}{0+1 \cdot y_1+0}
  \)
  (Here, \(g, f=0\) and \(a=b=1\) )
  \(
  \begin{array}{ll}
  \Rightarrow & \frac{x-x_1}{x_1}=\frac{y-y_1}{y_1} \\
  \text { or } & \frac{x}{x_1}=\frac{y}{y_1}
  \end{array}
  \)
• Corollary 2 : Equation of normal of
  \(x^2+y^2+2 g x+2 f y+c=0\) at \(\left(x_1, y_1\right)\) is
  \(\frac{x-x_1}{x_1+g}=\frac{y-y_1}{y_1+f}\)
  (Here, \(a=b=1\) and \(h=0\) )
• Normal always passes through the centre of the circle. Just write the equation of the line joining \(\left(x_1, y_1\right)\) and the centre of the circle.
• The equation s of the normals show that they pass through the centre i.e. the normals are the radii which we know from Euclidean geometry.

Example 62: Find the equation of the normal to the circle \(x^2+y^2=2 x\), which is parallel to the line \(x+2 y=3\)

Answer: Equation of normal at \(\left(x_1, y_1\right)\) of \(x^2+y^2-2 x=0\) is
\(
\begin{aligned}
& \frac{x-x_1}{x_1-1}=\frac{y-y_1}{y_1-0} \\
& \text { Slope }=\frac{y_1}{x_1-1}=m_1 \text { (say) }
\end{aligned}
\)
Since normal is parallel to \(x+2 y=3\)
\(\therefore \quad\) Slope \(=-\frac{1}{2}=m_2 \text { (say) }\)
but given \(m_1=m_2\)
\(
\frac{y_1}{x_1-1}=-\frac{1}{2} \text { or } x_1+2 y_1-1=0
\)
\(\therefore\) Locus of \(\left(x_1, y_1\right)\) is \(x+2 y-1=0\)

Example 63: Find the equation of the normal to the circle \(x^2+y^2-5 x+2 y-48=0\) at the point \((5,6)\).

Answer: Equation of the normal at \((5,6)\) is
\(
\begin{aligned}
& \frac{x-5}{5-\frac{5}{2}}=\frac{y-6}{6+1} \Rightarrow \frac{x-5}{\frac{5}{2}}=\frac{y-6}{7} \Rightarrow \frac{2 x-10}{5}=\frac{y-6}{7} \\
& \Rightarrow \quad 14 x-70=5 y-30 \\
& \therefore \quad 14 x-5 y-40=0
\end{aligned}
\)

Case 2: Parametric form

Since, parametric coordinates of circle \(x^2+y^2=a^2\) is \((a \cos \theta, a \sin \theta\) ).
\(\therefore\) Equation of normal at \((a \cos \theta, a \sin \theta)\) is
\(
\frac{x}{a \cos \theta}=\frac{y}{a \sin \theta}
\)
\(
\text { or } \frac{x}{\cos \theta}=\frac{y}{\sin \theta} \text { or } y=x \tan \theta
\)
\(
\text { or } y=m x \text {, where } m=\tan \theta
\)
which is slope form of normal.

Tangent from a Point to the Circle

Theorem : From a given point two tangents can be drawn to a circle which are real, coincident or imaginary according as the given point lies outside, on or inside the circle.

Proof : If circle is
\(
x^2+y^2=a^2 \dots(i)
\)
any tangent to the circle Eq. (i) is
\(
y=m x+a \sqrt{\left(1+m^2\right)} \dots(ii)
\)
If outside point is \(\left(x_1, y_1\right)\)
then, \(y_1=m x_1+a \sqrt{1+m^2}\)
\(
\left(y_1-m x_1\right)^2=a^2\left(1+m^2\right)
\)
\(\quad y_1^2+m^2 x_1^2-2 m x_1 y_1=a^2+a^2 m^2\)
\(
\Rightarrow \quad m^2\left(x_1^2-a^2\right)-2 m x_1 y_1+y_1^2-a^2=0 \dots(iii)
\)
which is quadratic in \(m\) which gives two values of \(m\). (real coincident or imaginary) corresponding to any value of \(x_1\) and \(y_1\).

Example 64: Find the equations of the tangents to the circle \(x^2+y^2=16\) drawn from the point \((1,4)\).

Answer: Given circle is
\(
x^2+y^2=16 \dots(i)
\)
Any tangent of Eq. (i) in terms of slope is
\(
y=m x+4 \sqrt{\left(1+m^2\right)} \dots(ii)
\)
which passes through \((1,4)\)
then, \(4=m+4 \sqrt{\left(1+m^2\right)}\)
\(
\begin{array}{rlrl}
\Rightarrow & & (4-m)^2 & =16\left(1+m^2\right) \\
\Rightarrow & 15 m^2+8 m & =0 \\
& \therefore & m & =0,-\frac{8}{15}
\end{array}
\)
From Eq. (ii), equations of tangents drawn from \((1,4)\) are
\(
\begin{aligned}
y & =4 \\
\text { and } y & =-\frac{8}{15} x+4 \sqrt{\left(1+\frac{64}{225}\right)}
\end{aligned}
\)
or \(8 x+15 y=68\) respectively.

Example 65: The angle between a pair of tangents from a point \(P\) to the circle \(x^2+y^2+4 x-6 y+9 \sin ^2 \alpha\) \(+13 \cos ^2 \alpha=0[latex] is [latex]2 \alpha\). Find the equation of the locus of the point \(P\).

Answer: Let coordinates of \(P\) be \(\left(x_1, y_1\right)\) and given circle is
\(
\begin{array}{cc}
& x^2+y^2+4 x-6 y+9 \sin ^2 \alpha+13 \cos ^2 \alpha=0 \\
\text { or } & (x+2)^2+(y-3)^2-4-9+9 \sin ^2 \alpha+13 \cos ^2 \alpha=0 \\
\Rightarrow & (x+2)^2+(y-3)^2+9 \sin ^2 \alpha-13\left(1-\cos ^2 \alpha\right)=0 \\
\Rightarrow & (x+2)^2+(y-3)^2=4 \sin ^2 \alpha
\end{array}
\)
\(\therefore\) Centre and radius are \((-2,3)\) and \(2 \sin \alpha\), respectively.

Distance between \(P\left(x_1, y_1\right)\) and centre of circle \(C(-2,3)\) is
\(
C P=\sqrt{\left(x_1+2\right)^2+\left(y_1-3\right)^2}
\)
In \(\triangle P C T, \sin \alpha=\frac{C T}{C P}=\frac{2 \sin \alpha}{\sqrt{\left(x_1+2\right)^2+\left(y_1-3\right)^2}}\)
\(
\sqrt{\left(x_1+2\right)^2+\left(y_1-3\right)^2}=2
\)
\(
\left(x_1+2\right)^2+\left(y_1-3\right)^2=4
\)
The required locus of \(P\left(x_1, y_1\right)\) is
\(
(x+2)^2+(y-3)^2=4
\)

Length of the Tangent from a Point to a Circle

Theorem : The length of tangent from the point \(P\left(x_1, y_1\right)\) to the circle \(x^2+y^2+2 g x+2 f y+c=0\) is
\(
\sqrt{\left(x_1^2+y_1^2+2 g x_1+2 f y_1+c\right)}=\sqrt{S_1}
\)

Proof : Let \(P T\) and \(P T^{\prime}\) be two tangents from the given point \(P\left(x_1, y_1\right)\) to the circle \(x^2+y^2+2 g x+2 f y+c=0\).
Then, the centre and radius are \(C(-g,-f)\) and \(\left.\sqrt{\left(g^2+f^2-c\right.}\right)\left(=C T=C T^{\prime}\right)\) respectively.

In \(\triangle P C T\),
\(
\begin{aligned}
P T & =\sqrt{(P C)^2-(C T)^2} \\
& =\sqrt{\left(x_1+g\right)^2+\left(y_1+f\right)^2-g^2-f^2+c} \\
& =\sqrt{\left(x_1^2+y_1^2+2 g x_1+2 f y_1+c\right)}=\sqrt{S_1}=P T^{\prime}
\end{aligned}
\)
where, \(S_1=x_1^2+y_1^2+2 g x_1+2 f y_1+c\)

Remarks

• To find length of tangent
  let
  \(
  \begin{aligned}
  & S=x^2+y^2+2 g x+2 f y+c \\
  \text { then, } & S_1=x_1^2+y_1^2+2 g x_1+2 f y_1+c
  \end{aligned}
  \)
  where, \(P\left(x_1, y_1\right)\)
  \(\therefore\) length of tangent \(=\sqrt{S_1}\)
• For \(S\) first write the equation of circle in general form i.e. coefficient of \(x^2=\) coefficient of \(y^2=1\) and making RHS of circle is zero, then let LHS by \(S\).

Example 66: Find the length of tangents drawn from the point \((3,-4)\) to the circle
\(
2 x^2+2 y^2-7 x-9 y-13=0 \text {. }
\)

Answer: The equation of the given circle is
\(
2 x^2+2 y^2-7 x-9 y-13=0
\)
Re-writing the given equation of the circle i.e. \(x^2+y^2-\frac{7}{2} x-\frac{9}{2} y-\frac{13}{2}=0\)
\(
\begin{aligned}
& \text { Let } \quad S=x^2+y^2-\frac{7}{2} x-\frac{9}{2} y-\frac{13}{2} \\
& \begin{array}{l}
\therefore \quad S_1=(3)^2+(-4)^2-\frac{7}{2} \times 3-\frac{9}{2} \times(-4)-\frac{13}{2} \\
\quad=25-\frac{21}{2}+18-\frac{13}{2}=43-17=26
\end{array} \\
& \therefore \text { Length of tangent }=\sqrt{S_1}=\sqrt{26}
\end{aligned}
\)

Example 67: If the length of tangent from \((f, g)\) to the circle \(x^2+y^2=6\) be twice the length of the tangent from \((f, g)\) to circle \(x^2+y^2+3 x+3 y=0\), then find the value of \(f^2+g^2+4 f+4 g\).

Answer: According to the question
\(
\begin{array}{llrl}
\sqrt{\left(g^2+f^2-6\right)} =2 \sqrt{\left(f^2+g^2+3 f+3 g\right)} \\
\text { On squaring } g^2+f^2-6=4 f^2+4 g^2+12 f+12 g \\
\text { or } 3 f^2+3 g^2+12 f+12 g+6 =0 \\
\text { or } f^2+g^2+4 f+4 g+2 =0 \\
\text { or } f^2+g^2+4 f+4 g =-2
\end{array}
\)

Example 68: Show that the area of the triangle formed by tangents from the point \((4,3)\) to the circle \(x^2+y^2=9\) and the line segment joining their points of contact is \(7 \frac{17}{25}\) square units in length.

Answer:

\(
\begin{array}{ll}
\text { Since, } P Q=P R=\sqrt{4^2+3^2-9}=4 \text { units } \\
\therefore \angle C P Q=\angle C P R=\alpha \\
\therefore P C=\sqrt{(4-0)^2+(3-0)^2}=5 \text { units }
\end{array}
\)

\(
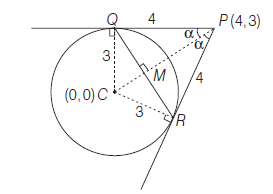
\begin{aligned}
& \therefore \text { In } \triangle P Q C, \quad \tan \alpha=\frac{3}{4} \text {, } \\
& \therefore \quad \sin \alpha=\frac{3}{5} \\
& \text { and } \quad \cos \alpha=\frac{4}{5} \\
& \text { In } \triangle P M Q, \quad \cos \alpha=\frac{P M}{4}=\frac{4}{5} \\
& \therefore \quad P M=\frac{16}{5} \\
& \text { and } \quad \sin \alpha=\frac{Q M}{4}=\frac{3}{5} \\
&
\end{aligned}
\)
\(
\begin{aligned}
& \therefore \quad Q M=\frac{12}{5} \\
& \therefore \quad \text { Area of } \triangle P Q R=\frac{1}{2} \cdot Q R \cdot P M \\
& =\frac{1}{2}(2 Q M) \cdot P M=(Q M)(P M) \\
& =\left(\frac{12}{5}\right)\left(\frac{16}{5}\right)=\frac{192}{25} \\
& =7 \frac{17}{25} \text { sq units } \\
&
\end{aligned}
\)

Power of a Point With Respect to a Circle

Theorem : The power of a point \(P\left(x_1, y_1\right)\) with respect to the circle
\(
x^2+y^2+2 g x+2 f y+c=0 \text { is } S_1
\)
where, \(S_1=x_1^2+y_1^2+2 g x_1+2 f y_1+c\)

Proof : Let \(P\left(x_1, y_1\right)\) be a point outside the circle and \(P A B\) and PCD drawn two secants. The power of \(P\left(x_1, y_1\right)\) with respect to

\(
S \equiv x^2+y^2+2 g x+2 f y+c=0
\)
is equal to \(P A \cdot P B\) which is
\(
x_1^2+y_1^2+2 g x_1+2 f y_1+c=S_1
\)
\(\therefore\) Power remains constant for the circle
i.e. independent of \(A\) and \(B\).
\(\therefore P A \cdot P B=P C \cdot P D=(P T)^2=S_1=\left(\sqrt{S_1}\right)^2\)
\(\therefore P A \cdot P B=\left(\sqrt{S_1}\right)^2=\) square of the length of tangent.

Remark

• If \(P\) outside, inside or on the circle, then \(P A \cdot P B\) is + ve, – ve or zero, respectively.

Example 69: Find the power of point \((2,4)\) with respect to the circle \(x^2+y^2-6 x+4 y-8=0\)

Answer: The power of the point \((2,4)\) with respect to the circle
\(
\begin{aligned}
& x^2+y^2-6 x+4 y-8=0 \text { is }\left(\sqrt{S_1}\right)^2 \text { or } S_1 \\
& \therefore \quad S_1=(2)^2+(4)^2-6 \times 2+4 \times 4-8 \\
& =4+16-12+16-8=16 \\
&
\end{aligned}
\)
where, \(S=x^2+y^2-6 x+4 y-8\)
\(\left[\because(2,4)\right.\) is outside from the circle \(\left.x^2+y^2-6 x+4 y-8=0\right]\)

Chord of Contact

From any external point, two tangents can be drawn to a given circle. The chord joining the points of contact of the two tangents is called the chord of contact of tangents.
Theorem : The equation of the chord of contact of tangents drawn from a point \(\left(x_1, y_1\right)\) to the circle \(x^2+y^2=a^2\) is \(x x_1+y y_1=a^2\).

Proof: Let \(T\left(x^{\prime}, y^{\prime}\right)\) and \(T^{\prime}\left(x^{\prime \prime}, y^{\prime \prime}\right)\) be the points of contact of tangents drawn from \(P\left(x_1, y_1\right)\) to \(x^2+y^2=a^2\).

Then, equations of tangents \(P T\) and \(P T^{\prime}\) are
\(
x x^{\prime}+y y^{\prime}=a^2 \text { and } x x^{\prime \prime}+y y^{\prime \prime}=a^2 \text { respectively. }
\)
Since, both tangents pass through \(P\left(x_1, y_1\right)\), then
\(
x_1 x^{\prime}+y_1 y^{\prime}=a^2
\)
\(
x_1 x^{\prime \prime}+y_1 y^{\prime \prime}=a^2
\)
\(\because\) Points \(T\left(x^{\prime}, y^{\prime}\right)\) and \(T^{\prime}\left(x^{\prime \prime}, y^{\prime \prime}\right)\) lie on
\(
x x_1+y y_1=a^2
\)
\(\therefore\) Equation of chord of contact \(T T^{\prime}\) is \(x x_1+y y_1=a^2\)

• Corollary 1 : If \(R\) is the radius of the circle and \(L\) is the length of the tangent from \(P\left(x_1, y_1\right)\) on \(S=0\).
  Here, \(L=\sqrt{S_1}\), then
  (a) Length of chord of contact \(T T^{\prime}=\frac{2 L R}{\sqrt{\left(R^2+L^2\right)}}\)
  (b) Area of triangle formed by the pair of tangents and its chord of contact \(=\frac{R L^3}{R^2+L^2}\)
  (c) Angle between the pair of tangents from \(P\left(x_1, y_1\right)\)
  \(
  =\tan ^{-1}\left(\frac{2 R L}{L^2-R^2}\right)
  \)
• Corollary 2 : Equation of the circle circumscribing the triangle \(P T T^{\prime}\) is
  \(
  \left(x-x_1\right)(x+g)+\left(y-y_1\right)(y+f)=0,
  \)
  where, \(O(-g,-f)\) is the centre of the circle
  \(
  x^2+y^2+2 g x+2 f x+c=0
  \)

i.e. Required circle always passes through the centre of the given circle (Here, \(O P\) is the diameter of the required circle).

Example 70: If the pair of tangents are drawn from the point \((4,5)\) to the circle \(x^2+y^2-4 x-2 y-11=0\), then,
(i) Find the length of chord of contact.
(ii) Find the area of the triangle formed by a pair of tangents and their chord of contact.
(iii) Find the angle between the pair of tangents.

Answer: Here, \(P \equiv(4,5)\),
\(
\begin{aligned}
R & =\sqrt{\left((2)^2+(1)^2+11\right)}=4 \\
\text { and } L & =\sqrt{S_1}=\sqrt{\left((4)^2+(5)^2-4 \times 4-2 \times 5-11\right)}=2
\end{aligned}
\)
and \(L=\sqrt{S_1}=\sqrt{\left((4)^2+(5)^2-4 \times 4-2 \times 5-11\right)}=2\)
(i) Length of chord of contact
\(
=\frac{2 L R}{\sqrt{\left(R^2+L^2\right)}}=\frac{2 \times 2 \times 4}{\sqrt{(4)^2+(2)^2}}=\frac{8}{\sqrt{5}} \text { unit }
\)
(ii) Area of triangle \(=\frac{R L^3}{R^2+L^2}=\frac{4 \times 8}{16+4}=\frac{8}{5}\) sq units
(iii) Angle between the pair of tangents
\(
\begin{aligned}
& =\pi+\tan ^{-1}\left(\frac{2 \times 4 \times 2}{2^2-4^2}\right) \\
& =\pi-\tan ^{-1}\left(\frac{4}{3}\right) \quad(\because L<R)
\end{aligned}
\)

Example 71: Tangents \(P Q, P R\) are drawn to the circle \(x^2+y^2=36\) from the point \(P(-8,2)\) touching the circle at \(Q, R\) respectively. Find the equation of the circumcircle of \(\triangle P Q R\).

Answer: Here, \(P \equiv(-8,2)\) and \(O \equiv(0,0)\)
\(\therefore\) Equation of the required circle is
\(
(x-(-8))(x-0)+(y-2)(y-0)=0
\)
or \(\quad x^2+y^2+8 x-2 y=0 \quad(\because O P\) is the diameter \()\)

Example 72: The chord of contact of tangents drawn from a point on the circle \(x^2+y^2=a^2\) to the circle \(x^2+y^2=b^2\) touches the circle \(x^2+y^2=c^2\). Show that \(a, b, c\) are in GP.

Answer: Let \(P(a \cos \theta, a \sin \theta)\) be a point on the circle
\(
x^2+y^2=a^2 \text {. }
\)
Then, equation of chord of contact of tangents drawn from \(P(a \cos \theta, a \sin \theta)\) to the circle \(x^2+y^2=b^2\) is

\(
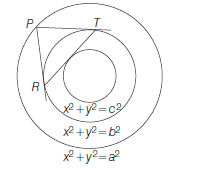
a x \cos \theta+a y \sin \theta=b^2 \dots(i)
\)
This touches the circle \(x^2+y^2=c^2 \dots(ii)\)
\(\therefore\) Length of perpendicular from \((0,0)\) to Eq. (i) = radius of Eq. (ii)
\(
\begin{aligned}
& \therefore \quad \frac{\left|0+0-b^2\right|}{\sqrt{\left(a^2 \cos ^2 \theta+a^2 \sin ^2 \theta\right)}}=c \\
& \text { or } \\
& b^2=a c \\
&
\end{aligned}
\)
\(\Rightarrow a, b, c\) are in GP.

Chord Bisected at a Given Point

Theorem : The equation of the chord of the circle \(x^2+y^2=a^2\) bisected at the point \(\left(x_1, y_1\right)\) is given by
\(
\begin{aligned}
x x_1+y y_1-a^2 & =x_1^2+y_1^2-a^2 \\
T & =S_1
\end{aligned}
\)

Proof : Let any chord \(A B\) of the circle \(x^2+y^2=a^2\) be bisected at \(D\left(x_1, y_1\right)\).
If centre of circle is represented by \(C\)

then, \(\quad\) slope of \(D C=\frac{0-y_1}{0-x_1}=\frac{y_1}{x_1}\)
\(\therefore\) Slope of the chord \(A B\) is \(-\frac{x_1}{y_1}\)
then, equation of \(A B\) is \(y-y_1=-\frac{x_1}{y_1}\left(x-x_1\right)\)
\(
y y_1-y_1^2=-x x_1+x_1^2
\)
\(
x x_1+y y_1=x_1^2+y_1^2
\)
\(
x x_1+y y_1-a^2=x_1^2+y_1^2-a^2 \text { or } T=S_1
\)

Remarks

• The equation of chord of the circle \(x^2+y^2+2 g x+2 f y+c=0\), which is bisected at \(\left(x_1, y_1\right)\); is \(T=S_1\)
  where, \(T=x x_1+y y_1+g\left(x+x_1\right)+f\left(y+y_1\right)+c\)
  and \(S_1=x_1^2+y_1^2+2 g x_1+2 f y_1+c\)
• The chord bisected at point \(\left(x_1, y_1\right)\) is the farthest from the centre among all the chords passing through the point \(\left(x_1, y_1\right)\). Also, for such chord, the length of the chord is minimum.

Example 73: Find the equation of the chord of \(x^2+y^2-6 x+10 y-9=0\) which is bisected at \((-2,4)\).

Answer: The equation of the required chord is
\(
\begin{aligned}
& -2 x+4 y-3(x-2)+5(y+4)-9 \\
& =4+16+12+40-9 \\
& \Rightarrow \quad-5 x+9 y-46=0 \\
& \text { or } \quad 5 x-9 y+46=0 \\
&
\end{aligned}
\)

Example 74: Find the equation of the chord of the circle \(x^2+y^2=r^2\) passing through the point \((2,3)\) farthest from the centre.

Answer: Let \(P \equiv(2,3)\) be the given point and \(M\) be the middle point of chord of circle \(x^2+y^2=r^2\) through \(P\).

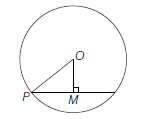
Then, \((O M)^2=(O P)^2-(P M)^2\)
If \(O M\) maximum, then \(P M\) is minimum. i.e. \(P\) coincides with \(M\), which is middle point of the chord. Hence, the equation of the chord is
\(
T=S_1
\)
i.e. \(2 x+3 y-r^2=2^2+3^2-r^2\)
\(
2 x+3 y=13
\)

Example 75: Find the locus of middle points of chords of the circle \(x^2+y^2=a^2\), which subtend right angle at the point \((c, 0)\).

Answer: Let \(N(h, k)\) be the middle point of any chord \(A B\), which subtend a right angle at \(P(c, 0)\).
Since, \(\angle A P B=90^{\circ}\)
\(\therefore \quad N A=N B=N P\)

(since distance of the vertices from middle point of the hypotenuse are equal)
\(
\text { or } \quad(N A)^2=(N B)^2=(h-c)^2+(k-0)^2 \dots(i)
\)
\(
\begin{aligned}
& \text { But also } \quad \angle B N O=90^{\circ} \\
& \therefore \quad(O B)^2=(O N)^2+(N B)^2 \\
& \Rightarrow \quad-(N B)^2=(O N)^2-(O B)^2 \\
& \Rightarrow-\left[(h-c)^2+(k-0)^2\right]=\left(h^2+k^2\right)-a^2 \\
& \text { or } \quad 2\left(h^2+k^2\right)-2 c h+c^2-a^2=0 \\
&
\end{aligned}
\)
\(\therefore\) Locus of \(N(h, k)\) is
\(
2\left(x^2+y^2\right)-2 c x+c^2-a^2=0
\)

Pair of Tangents

Theorem : The combined equation of the pair of tangents drawn from a point \(P\left(x_1, y_1\right)\) to the circle \(x^2+y^2=a^2\) is
\(
\left(x^2+y^2-a^2\right)\left(x_1^2+y_1^2-a^2\right)=\left(x x_1+y y_1-a^2\right)^2
\)
\(
S S_1=T^2
\)
where, \(S=x^2+y^2-a^2, S_1=x_1^2+y_1^2-a^2\)
and \(T=x x_1+y y_1-a^2\)

Proof : The given circle is \(x^2+y^2=a^2\)
Its centre and radius are \(C(0,0)\) and \(a\) respectively . Given external point be \(P\left(x_1, y_1\right)\).
From point \(P\left(x_1, y_1\right)\) two tangents \(P T\) and \(P R\) be drawn to the circle, touching circle at \(T\) and \(R\) respectively.

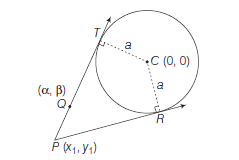
Let \(Q(\alpha, \beta)\) on \(P T\), then equation of \(P Q\) is
\(
\begin{aligned}
& y-y_1=\frac{\beta-y_1}{\alpha-x_1}\left(x-x_1\right) \\
& \text { or } \quad y\left(\alpha-x_1\right)-x\left(\beta-y_1\right)-\alpha y_1+\beta x_1=0
\end{aligned}
\)
Length of perpendicular from \(C(0,0)\) on \(P T=a\) (radius)
\(
\begin{aligned}
& \Rightarrow \quad \frac{\left|\beta x_1-\alpha y_1\right|}{\sqrt{\left(\alpha-x_1\right)^2+\left(\beta-y_1\right)^2}}=a \\
& \text { or } \\
& \left(\beta x_1-\alpha y_1\right)^2=a^2\left\{\left(\alpha-x_1\right)^2+\left(\beta-y_1\right)^2\right\} \\
&
\end{aligned}
\)
\(\therefore\) Locus of \(Q(\alpha, \beta)\) is
\(
\begin{gathered}
\left(y x_1-x y_1\right)^2=a^2\left\{\left(x-x_1\right)^2+\left(y-y_1\right)^2\right\} \\
\Rightarrow \quad y^2 x_1^2+x^2 y_1^2-2 x y x_1 y_1=a^2 \\
\left\{x^2+x_1^2-2 x x_1+y^2+y_1^2-2 y y_1\right\} \\
\Rightarrow y^2\left(x_1^2-a^2\right)+x^2\left(y_1^2-a^2\right)-a^2\left(x_1^2+y_1^2\right) \\
=2 x y x_1 y_1-2 a^2 x x_1-2 a^2 y y_1
\end{gathered}
\)
On adding both sides, \(\left(x^2 x_1^2+y^2 y_1^2+a^4\right)\), then
\(
\begin{aligned}
y^2\left(x_1^2\right. & \left.+y_1^2-a^2\right)+x^2\left(x_1^2+y_1^2-a^2\right)-a^2\left(x_1^2+y_1^2-a^2\right) \\
& =\left(x x_1+y y_1-a^2\right)^2
\end{aligned}
\)
\(
\Rightarrow\left(x^2+y^2-a^2\right)\left(x_1^2+y_1^2-a^2\right)=\left(x x_1+y y_1-a^2\right)^2
\)
This is the required equation of pair of tangents drawn from \(\left(x_1, y_1\right)\) to circle \(x^2+y^2=a^2\).

Corollary: The angle between the two tangents from \(\left(x_1, y_1\right)\) to the circle \(x^2+y^2=a^2\) is \(2 \tan ^{-1}\left(\frac{a}{\sqrt{S_1}}\right)\), where \(S_1=x_1^2+y_1^2-a^2\).

Remarks

• Equation of pair of tangents in notation form is \(S S_1=T^2\)
  where,
  \(
  \begin{aligned}
  & S \equiv x^2+y^2-a^2 \\
  & S_1 \equiv x_1^2+y_1^2-a^2, T \equiv x x_1+y y_1-a^2
  \end{aligned}
  \)
• When circle is \(x^2+y^2+2 g x+2 f y+c=0\) and tangents are drawn from \(\left(x_1, y_1\right)\), then pair of tangents is
  \(
  \begin{aligned}
  & \left(x^2+y^2+2 g x+2 f y+c\right)\left(x_1^2+y_1^2+2 g x_1+2 f y_1+c\right) \\
  & =\left[x x_1+y y_1+g\left(x+x_1\right)+f\left(y+y_1\right)+c\right]^2 \\
  \text { where, } & S \equiv x^2+y^2+2 g x+2 f y+c_1 \\
  & S_1 \equiv x_1^2+y_1^2+2 g x_1+2 f y_1+c \text {, } \\
  \text { and } & T \equiv x x_1+y y_1+g\left(x+x_1\right)+f\left(y+y_1\right)+c \\
  &
  \end{aligned}
  \)

Advised for Students

Students are advised that, if they do not want to use the formula \(\left(S S_1=T^2\right)\), then use the following method :
Let \(y-y_1=m\left(x-x_1\right)\) be any line through \(P\left(x_1, y_1\right)\).
Then, use condition of tangency \(p=r\) i.e.
Length of perpendicular from the centre of circle or this line \(=\) radius of the circle.
Gives the values of \(m\). In such away, we can find the equations of tangents from \(P\).

Example 76: Find the equations of the tangents from the point \(A(3,2)\) to the circle
\(
x^2+y^2+4 x+6 y+8=0
\)

Answer: Combined equation of the pair of tangents drawn from
\(A(3,2)\) to the given circle \(x^2+y^2+4 x+6 y+8=0\) can be written in the usual notation.
\(
\begin{aligned}
& T^2=S S_1 \text { namely } \\
& \Rightarrow[3 x+2 y+2(x+3)+3(y+2)+8]^2 \\
& =\left[x^2+y^2+4 x+6 y+8\right][9+4+12+12+8] \\
& \Rightarrow \quad(5 x+5 y+20)^2=45\left(x^2+y^2+4 x+6 y+8\right) \\
& \Rightarrow \quad 5(x+y+4)^2=9\left(x^2+y^2+4 x+6 y+8\right) \\
& \Rightarrow \quad 5\left(x^2+y^2+2 x y+8 x+8 y+16\right) \\
& =9\left(x^2+y^2+4 x+6 y+8\right) \\
& \Rightarrow \quad 4 x^2+4 y^2-10 x y-4 x+14 y-8=0 \\
& \text { or } \quad 2 x^2+2 y^2-5 x y-2 x+7 y-4=0 \\
& \text { or } \quad(2 x-y-4)(x-2 y+1)=0 \\
&
\end{aligned}
\)
Hence, the required tangents to the circle from \(A(3,2)\) are
\(
2 x-y-4=0 \text { and } x-2 y+1=0
\)

Alternate: Let \(S \equiv x^2+y^2+4 x+6 y+8=0\)
Centre \(C(-2,-3)\) and radius \(=\sqrt{5}\)
Let the slope of a tangent from \(A\) to ‘ \(S=0\) ‘ be \(m\), then equation of tangent is
\(
\begin{aligned}
& \quad y-2=m(x-3) \\
& \text { or } \quad m x-y+2-3 m=0 \dots(i)\\
& \text { Length of perpendicular from } C(-2,-3) \text { on Eq. (i) } \\
& \quad=\text { radius of circle. }
\end{aligned}
\)

\(
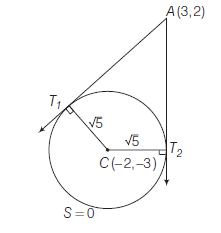
\begin{array}{lc}
\Rightarrow & \frac{|-2 m+3+2-3 m|}{\sqrt{\left(m^2+1\right)}}=\sqrt{5} \\
\text { or } & (5 m-5)^2=5\left(m^2+1\right) \\
\Rightarrow & 25 m^2-50 m+25=5 m^2+5 \\
\Rightarrow & 20 m^2-50 m+20=0 \\
\text { or } & 2 m^2-5 m+2=0 \\
\text { or } & (2 m-1)(m-2)=0 \\
\therefore & m=\frac{1}{2} \text { or } m=2
\end{array}
\)
Substituting these values of \(m\) in Eq. (i), we get the equations of two tangents are \(x-2 y+1=0\) and \(2 x-y-4=0\).

Director Circle

Director circle : The locus of the point of intersection of two perpendicular tangents to a given circle is known as its director circle.
Theorem : The equation of the director circle of the circle \(x^2+y^2=a^2\) is
\(
x^2+y^2=2 a^2
\)

Proof: The equation of any tangent to the circle
\(
\begin{aligned}
& x^2+y^2=a^2 \\
& \text { is } \quad y=m x+a \sqrt{\left(1+m^2\right)} \dots(i)
\end{aligned}
\)
Let \(P(h, k)\) be the point of intersection of tangents, then \(P(h, k)\) lies on Eq. (i)
\(
\begin{aligned}
& \therefore \quad k=m h+a \sqrt{\left(1+m^2\right)} \\
& \text { or } \\
& (k-m h)^2=a^2\left(1+m^2\right) q \\
&
\end{aligned}
\)
\(
m^2\left(h^2-a^2\right)-2 m k h+k^2-a^2=0
\)
This is quadratic equation in \(m\), let two roots are \(m_1\) and \(m_2\).
But tangents are perpendiculars, then

\(
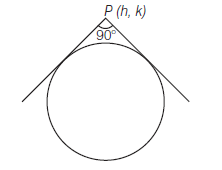
\begin{aligned}
m_1 m_2 & =-1 \\
\Rightarrow \quad \frac{k^2-a^2}{h^2-a^2} & =-1 \text { or } k^2-a^2=-h^2+a^2
\end{aligned}
\)
\(
h^2+k^2=2 a^2
\)
Hence, locus of \(P(h, k)\) is \(x^2+y^2=2 a^2\)

Alternate: The combined equation of the pair of tangents drawn from \((h, k)\) to \(x^2+y^2=a^2\) is
\(
S S_1=T^2
\)
where,
\(
\begin{aligned}
S & =x^2+y^2-a^2 \\
S_1 & =h^2+k^2-a^2
\end{aligned}
\)
and \(\quad T=h x+k y-a^2\)
\(
\therefore \quad\left(x^2+y^2-a^2\right)\left(h^2+k^2-a^2\right)=\left(h x+k y-a^2\right)^2
\)
This equation will represent a pair of perpendicular lines if, coefficient of \(x^2+\) coefficient of \(y^2=0\)
\(
\begin{array}{ll}
\Rightarrow & h^2+k^2-a^2-h^2+h^2+k^2-a^2-k^2=0 \\
\Rightarrow & h^2+k^2-2 a^2=0 \text { or } h^2+k^2=2 a^2
\end{array}
\)
Hence, the locus of \((h, k)\) is \(x^2+y^2=2 a^2\)

Remarks

• The equation of the director circle of the circle
  \(
  (x-h)^2+(y-k)^2=a^2 \text { is }(x-h)^2+(y-k)^2=2 a^2
  \)
• The equation of the director circle of the circle \(x^2+y^2+2 g x+2 f y+c=0\) is \(x^2+y^2+2 g x+2 f y+c=g^2+f^2-c\)
  3. If two tangents are drawn from a point on the director circle to the circle, then angle between tangents is \(90^{\circ}\).

Example 77: If two tangents are drawn from a point on the circle \(x^2+y^2=50\) to the circle \(x^2+y^2=25\), then find the angle between the tangents.

Answer: \(\because x^2+y^2=50\) is the director circle of \(x^2+y^2=25\)
Hence, angle between tangents \(=90^{\circ}\)

ExamDiameter of a Circle

The locus of the middle points of a system of parallel chords of a circle is called a diameter of the circle.
Let the circle be \(x^2+y^2=a^2\) and equation of parallel chord is
\(
y=m x+c
\)

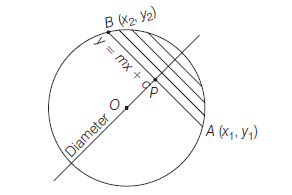
Let \(P(h, k)\) be the middle point of the chord \(y=m x+c\). Since, \(P\) is the mid-point of \(A\left(x_1 y_1\right)\) and \(B\left(x_2, y_2\right)\), then
\(
\frac{x_1+x_2}{2}=h \text { and } \frac{y_1+y_2}{2}=k
\)
\(
\text { or } \quad x_1+x_2=2 h \text { and } y_1+y_2=2 k \dots(i)
\)
\(
\begin{array}{rlrl}
\because & P(h, k) \text { lie on } y =m x+c \\
& \text { then, } k =m h+c
\end{array}
\)
or \(k-m h=c \dots(ii)\)
Substituting \(y=m x+c\) in \(x^2+y^2=a^2\)
then, \(\quad x^2+(m x+c)^2=a^2\)
or \(\left(1+m^2\right) x^2+2 m c x+c^2-a^2=0 \dots(iii)\)
Let \(x_1, x_2\) are roots of Eq. (iii), then
\(
\begin{gathered}
x_1+x_2=-\frac{2 m c}{1+m^2} \\
\Rightarrow \quad 2 h=-\frac{2 m}{\left(1+m^2\right)}(k-m h) \quad \text { [from Eq. (i) and Eq. (ii)] } \\
\Rightarrow \quad h+m^2 h=-m k+m^2 h \Rightarrow h+m k=0
\end{gathered}
\)
Hence, locus of \((h, k)\) is \(x+m y=0\)

Remark

• The diameter of circle always passes through the centre of the circle and perpendicular to the parallel chords.
  Let circle is \(x^2+y^2=a^2\) and parallel chord be \(y=m x+c\), then equation of line \(\perp\) to \(y=m x+c\) is
  \(
  m y+x+\lambda=0 \dots(i)
  \)
  which passes through origin (centre)
  then, \(\quad 0+0+\lambda=0 \quad \therefore \quad \lambda=0\)
  Then, equation of diameter from Eq. (i) is \(x+m y=0\).

Example 78: Find the equation of the diameter of the circle \(x^2+y^2+2 g x+2 f y+c=0\) which corresponds to the chord \(a x+b y+d=0\).

Answer: The diameter of circle passes through the centre of the circle and perpendicular to the chord \(a x+b y+d=0\) is
\(
b x-a y+\lambda=0 \dots(i)
\)
which passes through centre of circle i.e. \((-g,-f)\)
Then, \(\quad-b g+a f+\lambda=0\)
\(
\therefore \quad \lambda=b g-a f
\)
From Eq. (i), the equation of the diameter is
\(
b x-a y+b g-a f=0
\)

Two Circles Touching Each Other

Case-I: When two circles touch each other externally

Then, distance between their centres \(=\) sum of their radii i.e. \(\left|C_1 C_2\right|=r_1+r_2\)
In such cases, the point of contact \(P\) divides the line joining \(C_1\) and \(C_2\) internally in the ratio \(r_1: r_2\)

\(
\begin{aligned}
& \Rightarrow \quad \frac{C_1 P}{C_2 P}=\frac{r_1}{r_2} \\
& \text { If } \quad C_1 \equiv\left(x_1, y_1\right) \text { and } C_2 \equiv\left(x_2, y_2\right) \\
& \text { then, coordinate of } P \text { is }\left(\frac{r_1 x_2+r_2 x_1}{r_1+r_2}, \frac{r_1 y_2+r_2 y_1}{r_1+r_2}\right)
\end{aligned}
\)

Case II: When two Circles Touch each other Internally

Then, distance between their centres =Difference of their radii
i.e. \(\quad\left|C_1 C_2\right|=\left|r_1-r_2\right|\)
In such cases, the point of contact \(P\) divides the line joining \(C_1\) and \(C_2\) externally in the ratio \(r_1: r_2\)

\(\Rightarrow \quad \frac{C_1 P}{C_2 P}=\frac{r_1}{r_2}\)
If \(\quad C_1 \equiv\left(x_1, y_1\right)\) and \(C_2 \equiv\left(x_2, y_2\right)\)
then, coordinates of \(P\) is \(\left(\frac{r_1 x_2-r_2 x_1}{r_1-r_2}, \frac{r_1 y_2-r_2 y_1}{r_1-r_2}\right)\)

Example 79: Examine if the two circles \(x^2+y^2-2 x-4 y=0\) and \(x^2+y^2-8 y-4=0\) touch each other externally or internally.

Answer: Given circles are
\(
\text { and } \quad \begin{aligned}
& x^2+y^2-2 x-4 y=0 \dots(i) \\
\text { and } & x^2+y^2-8 y-4=0 \dots(ii)
\end{aligned}
\)
Let centres and radii of circles Eqs. (i) and (ii) are represented by \(C_1, r_1\) and \(C_2, r_2\), respectively.
\(
\begin{array}{ll}
\therefore C_1 \equiv(1,2), r_1=\sqrt{(1+4)} \text { or } r_1=\sqrt{5} \\
\text { and } C_2 \equiv(0,4), r_2=\sqrt{0+16+4} \text { or } r_2=2 \sqrt{5} \\
\text { Now, } C_1 C_2=\sqrt{(1-0)^2+(2-4)^2} \\
C_1 C_2=\sqrt{5}=r_2-r_1
\end{array}
\)
Hence, the two circles touch each other internally.

Example 80: Prove that the circles \(x^2+y^2+2 a x+c^2=0\) and \(x^2+y^2+2 b y+c^2=0\) touch each other, if \(\frac{1}{a^2}+\frac{1}{b^2}=\frac{1}{c^2}\).

Answer: Given circles are
\(
\begin{aligned}
& x^2+y^2+2 a x+c^2=0 \dots(i) \\
\text { and } & x^2+y^2+2 b y+c^2=0 \dots(ii)
\end{aligned}
\)
Let \(C_1\) and \(C_2\) be the centres of circles Eqs. (i) and (ii), respectively and \(r_1\) and \(r_2\) be their radii, then
\(
\begin{aligned}
& C_1=(-a, 0), C_2=(0,-b), \\
& r_1=\sqrt{\left(a^2-c^2\right)}, r_2=\sqrt{\left(b^2-c^2\right)}
\end{aligned}
\)
Here, we do not find the two circles touch each other internally or externally.
For touch, \(\left|C_1 C_2\right|=\left|r_1 \pm r_2\right|\)
\(
\text { or } \quad \sqrt{\left(a^2+b^2\right)}=\left|\sqrt{\left(a^2-c^2\right)} \pm \sqrt{\left(b^2-c^2\right)}\right|
\)
On squaring
\(
\begin{aligned}
a^2+b^2 & =a^2-c^2+b^2-c^2 \pm 2 \sqrt{\left(a^2-c^2\right)} \sqrt{\left(b^2-c^2\right)} \\
c^2 & = \pm \sqrt{a^2 b^2-c^2\left(a^2+b^2\right)+c^4}
\end{aligned}
\)
Again, squaring,
\(
c^4=a^2 b^2-c^2\left(a^2+b^2\right)+c^4
\)
or \(\quad c^2\left(a^2+b^2\right)=a^2 b^2\) or \(\frac{1}{a^2}+\frac{1}{b^2}=\frac{1}{c^2}\)

Common Tangents to Two Circles

Different Cases of Intersection of Two Circles:

Let the two circles be
\(
\begin{aligned}
\left(x-x_1\right)^2+\left(y-y_1\right)^2 & =r_1^2 \dots(i) \\
\text { and } \quad\left(x-x_2\right)^2+\left(y-y_2\right)^2 & =r_2^2 \dots(ii)
\end{aligned}
\)
with centres \(C_1\left(x_1, y_1\right)\) and \(C_2\left(x_2, y_2\right)\) and radii \(r_1\) and \(r_2\) respectively. Then following cases may arise

Case I: When \(\left|C_1 C_2\right|>r_1+r_2\) i.e. the distance between the centres is greater than the sum of their radii.

\(
\begin{array}{rlrl}
\because  C_1 & \equiv\left(x_1, y_1\right), C_2 \equiv\left(x_2, y_2\right) \\
\therefore  D & \equiv\left(\frac{r_1 x_2-r_2 x_1}{r_1-r_2}, \frac{r_1 y_2-r_2 y_1}{r_1-r_2}\right) \equiv(\alpha, \beta) \text { (say) } \\
\text { and }  T  \equiv\left(\frac{r_1 x_2+r_2 x_1}{r_1+r_2}, \frac{r_1 y_2+r_2 y_1}{r_1+r_2}\right) \\
\equiv(\gamma, \delta) \text { (say) }
\end{array}
\)

How to find direct common tangents

Let equation of common tangent through \(D(\alpha, \beta)\) is
\(
y-\beta=m(x-\alpha) \dots(i)
[latex]
Now, length of [latex]\perp\) from \(C_1\) or \(C_2\) on Eq. (i) \(=r_1\) or \(r_2\)
Then, we get two values of \(m\).
Substituting the values of \(m\) in Eq. (i), we get two direct common tangents.

How to find transverse common tangents

Let equation of common tangent through \(T(\gamma, \delta)\) is
\(
y-\delta=M(x-\gamma) \dots(ii)
\)
Now, length of \(\perp\) from \(C_1\) or \(C_2\) on Eq. (i) \(=r_1\) or \(r_2\) then, we get two values of \(M\).
Substituting the values of \(M\) in Eq. (i), we get two transverse common tangents.

Remark

• In this case circles neither cut nor touch i.e. Number of solutions of two circles is zero.

Case II: When \(\left|C_1 C_2\right|=r_1+r_2\)
i.e. the distance between the centres is equal to the sum of their radii.
In this case two direct common tangents are real and distinct while the transverse tangents are coincident.

How to find transverse common tangent

\(\because\) Equation of circles are
\(
S_1 \equiv\left(x-x_1\right)^2+\left(y-y_1\right)^2-r_1^2=0
\)
and \(S_2 \equiv\left(x-x_2\right)^2+\left(y-y_2\right)^2-r_2^2=0\)
then, equation of common tangent is
\(
S_1-S_2=0
\)
which is same as equation of common chord.

Remark

• In this case circles touch at one point i.e. Number of solutions of two circles is one.

Case III : When \(\left|r_1-r_2\right|<\left|C_1 C_2\right|<r_1+r_2\)
i.e. the distance between the centres is less than sum of their radii and greater than difference of their radii.
In this case two direct common tangents are real and distinct while the transverse tangents are imaginary.

Remark

• In this case circles cuts at two points i.e. Number of solutions of two circles is two.

Case IV: When \(\left|C_1 C_2\right|=\left|r_1-r_2\right|\), i.e. the distance between the centres is equal to the difference of their radii.

In this case two tangents are real and coincident while the other two tangents are imaginary.
If circles are represented by \(S_1=0\) and \(S_2=0[latex], then equation of common tangent is [latex]S_1-S_2=0\).

Remark

• If circles touch each other externally, i.e. \(\left|C C_2\right|=r_1+r_2\), then equation of tangent at the point of contact is
  \(
  S_1-S_2=0
  \)

In this case circles touch at one point.
i.e. Number of solutions of two circles is one.

Case V: When \(\left|C_1 C_2\right|<\left|r_1-r_2\right|\), i.e. the distance between the centres is less than the difference of their radii.

In this case, all the four common tangents are imaginary.

Remark

In this case circles neither cut nor touch each other i.e. Number of solution of two circles is zero.

Common Tangents to two Circles

If two circles with centres \(C_1\) and \(C_2\) and their radii are \(r_1\) and \(r_2\), then

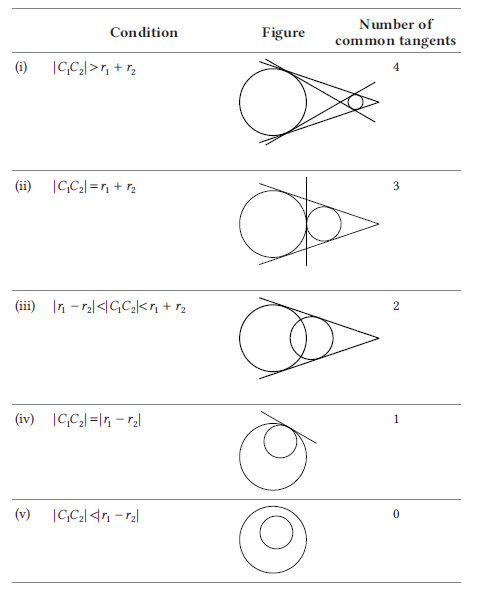
Length of External Common Tangent and Internal Common Tangent to Two Circles

Length of external common tangent \(L_{e x}=\sqrt{d^2-\left(r_1-r_2\right)^2}\) and length of internal common tangent

\(
\left.L_{\text {in }}=\sqrt{d^2-\left(r_1+r_2\right)^2} \text { (Applicable only when } d>r_1+r_2\right)
\)
where, \(d\) is the distance between the centres of two circles and \(r_1, r_2\) are the radii of two circles, when \(\left|C_1 C_2\right|=d\).

Angle between Direct Common Tangents (DCT) and Transverse Common Tangents (TCT)

Case I: If \(d>r_1+r_2\), then
Angle between DCT \(=2 \sin ^{-1}\left(\frac{\left|r_1-r_2\right|}{d}\right)\)
And angle between TCT \(=2 \sin ^{-1}\left(\frac{r_1+r_2}{d}\right)\)

Case II : If \(d=r_1+r_2\), then
angle between DCT \(=2 \sin ^{-1}\left(\frac{\left|r_1-r_2\right|}{r_1+r_2}\right)\)
and angle between TCT \(=\pi\)

Case III : If \(\left|r_1-r_2\right|<d<r_1+r_2\), then
angle between DCT \(=2 \sin ^{-1}\left(\frac{\left|r_1-r_2\right|}{d}\right)\)
Here, transverse common tangents are not possible.

Case IV : If \(d=\left|r_1-r_2\right|\)
Angle between DCT \(=\pi\)
Here, transverse common tangents are not possible.

Case V : If \(d<\left|r_1-r_2\right|\)
Here, tangents are not possible.

Example 81: Find the number of common tangents to the circles \(x^2+y^2-8 x+2 y+8=0\) and \(x^2+y^2-2 x-6 y-15=0\).

Answer: For \(x^2+y^2-8 x+2 y+8=0\)
\(
C_1 \equiv(4,-1), r_1=\sqrt{(16+1-8)}=3
\)
and for \(x^2+y^2-2 x-6 y-15=0\)
\(
C_2 \equiv(1,3), r_2=\sqrt{(1+9+15)}=5
\)
Now, \(\left|C_1 C_2\right|=\) Distance between centres
\(
=\sqrt{(4-1)^2+(-1-3)^2}=5
\)
\(
\begin{aligned}
& r_1+r_2=3+5=8 \\
& \left|r_1-r_2\right|=|3-5|=2
\end{aligned}
\)
\(
\left|r_1-r_2\right|<\left|C_1 C_2\right|<r_1+r_2
\)
Hence, the two circles intersect at two distinct points. Therefore, two tangents can be drawn.

Example 82: Find the lengths of external and internal common tangents and also find the angle between external common tangents and internal common tangents of the circles \(x^2+y^2+2 x-8 y+13=0\) and \(x^2+y^2-8 x-2 y+8=0\).

Answer: The given circles are \(x^2+y^2+2 x-8 y+13=0\)
\(
\begin{array}{lrl}
\Rightarrow & (x+1)^2+(y-4)^2 & =2^2 \dots(i) \\
\text { and } & x^2+y^2-8 x-2 y+8 & =0 \\
\Rightarrow & (x-4)^2+(y-1)^2 & =3^2 \dots(ii)
\end{array}
\)
Centres and radii of circles Eqs. (i) and (ii) are \(C_1(-1,4)\), \(r_1=2\) and \(C_2(4,1), r_2=3\) respectively.
\(
\begin{array}{ll}
\therefore & \left|C_1 C_2\right|=d=\sqrt{(25+9)}=\sqrt{34} \\
\Rightarrow & d>r_1+r_2
\end{array}
\)
Hence, the circles do not intersect to each other.
\(
\begin{array}{ll}
\therefore & L_{e x}=\sqrt{d^2-\left(r_1-r_2\right)^2}=\sqrt{34-1}=\sqrt{33} \\
\text { and } & L_{i n}=\sqrt{d^2-\left(r_1+r_2\right)^2}=\sqrt{(34-25)}=3
\end{array}
\)
Angle between external common tangents
\(
=2 \sin ^{-1}\left(\frac{\left|r_1-r_2\right|}{d}\right)=2 \sin ^{-1}\left(\frac{1}{\sqrt{33}}\right)
\)
and angle between internal common tangent
\(
=2 \sin ^{-1}\left(\frac{r_1+r_2}{d}\right)=2 \sin ^{-1}\left(\frac{5}{\sqrt{33}}\right)
\)

Common Chord of Two Circles

The chord joining the points of intersection of two given circles is called their common chord.

Theorem : The equation of common chord of two circles
\(
S \equiv x^2+y^2+2 g x+2 f y+c=0
\)
\(
\begin{array}{lc}
\text { and } & S^{\prime} \equiv x^2+y^2+2 g^{\prime} x+2 f^{\prime} y+c^{\prime}=0 \\
\text { is } & 2 x\left(g-g^{\prime}\right)+2 y\left(f-f^{\prime}\right)+c-c^{\prime}=0 \\
\text { i.e. } & S-S^{\prime}=0
\end{array}
\)

Proof: 

\(\because S=0\) and \(S^{\prime}=0\)
be two intersecting circles.
Then, \(S-S^{\prime}=0\) or
\(
2 x\left(g-g^{\prime}\right)+2 y\left(f-f^{\prime}\right)+c-c^{\prime}=0
\)
is a first degree equation in \(x\) and \(y\).
So, it represent a straight line. Also, this equation satisfied by the intersecting points of two given circles \(S=0\) and \(S^{\prime}=0\).
Hence, \(S-S^{\prime}=0\) represents the common chord of circles \(S=0\) and \(S^{\prime}=0\)

Length of common chord :
\(
\text { We have, } \quad \begin{aligned}
P Q & =2(P M) \quad(\because M \text { is mid-point of } P Q) \\
& =2 \sqrt{\left\{\left(C_1 P\right)^2-\left(C_1 M\right)^2\right\}}
\end{aligned}
\)
where, \(C_1 P=\) radius of the circle \((S=0)\)
and \(C_1 M=\) length of perpendicular from \(C_1\) on common chord \(P Q\).

• Corollary 1 : The common chord \(P Q\) of two circles becomes of the maximum length when it is a diameter of the smaller one between them.
• Corollary 2: Circle on the common chord a diameter, then centre of the circle passing through \(P\) and \(Q\) lie on the common chord of two circles i.e.
  \(
  S-S^{\prime}=0
  \)
• Corollary 3 : If the length of common chord is zero, then the two circles touch each other and the common chord becomes the common tangent to the two circles at the common point of contact.

Example 83: Prove that the length of the common chord of the two circles :
\(
(x-a)^2+(y-b)^2=c^2
\)
and \((x-b)^2+(y-a)^2=c^2\) is \(\sqrt{4 c^2-2(a-b)^2}\).
Find also the condition when the given circles touch.

Answer: The equation of circles are
\(
\begin{aligned}
& S_1 \equiv(x-a)^2+(y-b)^2-c^2=0 \dots(i) \\
\text { and } & S_2 \equiv(x-b)^2+(y-a)^2-c^2=0 \dots(ii)
\end{aligned}
\)
\(
\begin{aligned}
& \qquad S_1 \equiv(x-a)^2+(y-b)^2-c^2=0 \\
& \text { and } \quad S_2 \equiv(x-b)^2+(y-a)^2-c^2=0 \\
& \text { then equation of common chord is } \quad S_1-S_2=0 \\
& \Rightarrow \quad(x-a)^2-(x-b)^2+(y-b)^2-(y-a)^2=0
\end{aligned}
\)
\(
\begin{gathered}
(2 x-a-b)(-a+b)+(2 y-b-a)(-b+a)=0 \\
2 x-a-b-2 y+b+a=0 \\
x-y=0
\end{gathered}
\)

Now, \(C_1 M=\) Length of perpendicular from \(C_1(a, b)\) on
\(
P Q(x-y=0)=\frac{|a-b|}{\sqrt{2}}
\)
and \(\quad C_1 P=\) radius of the circle Eq. (i) \(=c\)
\(
\begin{aligned}
\therefore \text { In } \triangle P C_1 M, \quad P M & =\sqrt{\left(P C_1\right)^2-\left(C_1 M\right)^2} \\
& =\sqrt{c^2-\frac{(a-b)^2}{2}} \\
\therefore \quad P Q & =2 P M=2 \sqrt{c^2-\frac{(a-b)^2}{2}} \\
& =\sqrt{4 c^2-2(a-b)^2}
\end{aligned}
\)
Also, when the circles touch, then chord \(P Q\) becomes the tangent and \(P Q=0\).
\(\therefore\) The condition of tangency is \(4 c^2-2(a-b)^2=0\).
i.e.\(2 c^2=(a-b)^2\)

Family of Circles

• The equation of the family of circles passing through the point of intersection of two given circles \(S=0\) and \(S^{\prime}=0\) is given as
  \(
  S+\lambda S^{\prime}=0 \quad \text { (where, } \lambda \text { is a parameter, } \lambda \neq-1 \text { ) }
  \)

• The equation of the family of circles passing through the point of intersection of circle \(S=0\) and a line \(L=0\) is given as
  \(
  S+\lambda L=0 \quad \text { (where, } \lambda \text { is a parameter) }
  \)

• The equation of the family of circles touching the circle \(S=0\) and the line \(L=0\) at their point of contact \(P\) is
  \(
  S+\lambda L=0
  \)
  (where, \(\lambda\) is a parameter)

• The equation of a family of circles passing through two given points \(P\left(x_1, y_1\right)\) and \(Q\left(x_2, y_2\right)\) can be written in the form
  \(
  \begin{gathered}
  \left(x-x_1\right)\left(x-x_2\right)+\left(y-y_1\right)\left(y-y_2\right) \\
  +\lambda\left|\begin{array}{lll}
  x & y & 1 \\
  x_1 & y_1 & 1 \\
  x_2 & y_2 & 1
  \end{array}\right|=0 \text { (where, } \lambda \text { is a parameter) }
  \end{gathered}
  \)

 

• The equation of family of circles which touch \(y-y_1=m\left(x-x_1\right)\) at \(\left(x_1, y_1\right)\) for any finite \(m\) is
  \(
  \left(x-x_1\right)^2+\left(y-y_1\right)^2+\lambda\left\{\left(y-y_1\right)-m\left(x-x_1\right)\right\}=0
  \)
  and if \(m\) is infinite, the family of circles is
  \(
  \left(x-x_1\right)^2+\left(y-y_1\right)^2+\lambda\left(x-x_1\right)=0 \text { (where, } \lambda \text { is a parameter) }
  \)

• Equation of the circles given in diagram are
  \(
  \begin{aligned}
  & \left(x-x_1\right)\left(x-x_2\right)+\left(y-y_1\right)\left(y-y_2\right) \\
  & \pm \cot \theta\left\{\left(x-x_1\right)\left(y-y_2\right)-\left(x-x_2\right)\left(y-y_1\right)\right\}=0
  \end{aligned}
  \)

Example 84: Find the equation of the circle passing through \((1,1)\) and the points of intersection of the circles \(x^2+y^2+13 x-3 y=0\) and \(2 x^2+2 y^2+4 x-7 y-25=0\).

Answer: The given circles are
\(
x^2+y^2+13 x-3 y=0 \dots(i)
\)
and \(2 x^2+2 y^2+4 x-7 y-25=0\)
or \(x^2+y^2+2 x-\frac{7}{2} y-\frac{25}{2}=0 \dots(ii)\)
Equation of any circle passing through the point of intersection of the circles Eqs. (i) and (ii) is
\(
\left(x^2+y^2+13 x-3 y\right)+\lambda\left(x^2+y^2+2 x-\frac{7}{2} y-\frac{25}{2}\right)=0 \dots(iii)
\)
Its passes through \((1,1)\), then
\(
\begin{aligned}
& (1+1+13-3)+\lambda\left(1+1+2-\frac{7}{2}-\frac{25}{2}\right)=0 \\
& \Rightarrow \quad 12+\lambda(-12)=0 \therefore \lambda=1
\end{aligned}
\)
Substituting the value of \(\lambda\) in Eq. (iii), the required equation is
\(
\begin{aligned}
& x^2+y^2+13 x-3 y+x^2+y^2+2 x-\frac{7}{2} y-\frac{25}{2}=0 \\
\Rightarrow \quad & 2 x^2+2 y^2+15 x-\frac{13}{2} y-\frac{25}{2}=0 \\
\Rightarrow \quad & 4 x^2+4 y^2+30 x-13 y-25=0
\end{aligned}
\)

Example 85: Find the equation of the circle passing through the point of intersection of the circles
\(
x^2+y^2-6 x+2 y+4=0, x^2+y^2+2 x-4 y-6=0
\)
and with its centre on the line \(y=x\).

Answer: Equation of any circle through the points of intersection of given circles is
\(
\begin{aligned}
& \left(x^2+y^2-6 x+2 y+4\right)+\lambda\left(x^2+y^2+2 x-4 y-6\right)=0 \\
& \Rightarrow \quad x^2(1+\lambda)+y^2(1+\lambda)-2 x(3-\lambda)+2 y(1-2 \lambda)+(4-6 \lambda)=0
\end{aligned}
\)
\(
\text { or } x^2+y^2-\frac{2 x(3-\lambda)}{(1+\lambda)}+\frac{2 y(1-2 \lambda)}{(1+\lambda)}+\frac{(4-6 \lambda)}{(1+\lambda)}=0 \dots(i)
\)
Its centre \(\left\{\frac{3-\lambda}{1+\lambda}, \frac{2 \lambda-1}{1+\lambda}\right\}\) lies on the line \(y=x\)
then
\(
\begin{aligned}
& \frac{2 \lambda-1}{1+\lambda}=\frac{3-\lambda}{1+\lambda} \Rightarrow \lambda \neq-1 \\
& \therefore \quad 2 \lambda-1=3-\lambda \text { or } 3 \lambda=4 \\
& \therefore \quad \lambda=4 / 3 \\
&
\end{aligned}
\)
\(\therefore\) Substituting the value of \(\lambda=4 / 3\) in Eq. (i), we get the required equation is
\(
7 x^2+7 y^2-10 x-10 y-12=0
\)

Example 86: Find the equation of the circle passing through the points of intersection of the circles \(x^2+y^2-2 x-4 y-4=0\) and \(x^2+y^2-10 x-12 y+40=0\) and whose radius is 4.

Answer: Equation of the any circle through the points of intersection of given circles is
\(
\begin{aligned}
& \left(x^2+y^2-2 x-4 y-4\right) \\
& +\lambda\left(x^2+y^2-10 x-12 y+40\right)=0 \\
& \Rightarrow \quad x^2(1+\lambda)+y^2(1+\lambda)-2 x(1+5 \lambda) \\
& -2 y(2+6 \lambda)-4+40 \lambda=0 \\
& \text { or } \quad x^2+y^2-2 x \frac{(1+5 \lambda)}{(1+\lambda)}-2 y \frac{(2+6 \lambda)}{(1+\lambda)}+\frac{(40 \lambda-4)}{(1+\lambda)}=0 \dots(i) \\
&
\end{aligned}
\)
Its radius
\(
\sqrt{\left(\frac{1+5 \lambda}{1+\lambda}\right)^2+\left(\frac{2+6 \lambda}{1+\lambda}\right)^2-\left(\frac{40 \lambda-4}{1+\lambda}\right)}=4 \text { (given) }
\)
\(
\begin{array}{lc}
\Rightarrow & \frac{(1+5 \lambda)^2+(2+6 \lambda)^2-(40 \lambda-4)(1+\lambda)}{(1+\lambda)^2}=16 \\
\Rightarrow & 5 \lambda^2-34 \lambda-7=0 \\
\text { or } & (\lambda-7)(5 \lambda+1)=0 \\
\therefore & \lambda=7 \text { or } \lambda=-\frac{1}{5}
\end{array}
\)
Substituting the values of \(\lambda\) in Eq. (i), the required circles are
\(
2 x^2+2 y^2-18 x-22 y+69=0
\)
and \(x^2+y^2-2 y-15=0\)

Example 87: Find the equation of the circle passing through points of intersection of the circle \(x^2+y^2-2 x-4 y+4=0\) and the line \(x+2 y=4\) which touches the line \(x+2 y=0\).

Answer: Equation of any circle through points of intersection of the given circle and the line is
\(
\left(x^2+y^2-2 x-4 y+4\right)+\lambda(x+2 y-4)=0
\)
\(
\text { or } \quad x^2+y^2+(\lambda-2) x+(2 \lambda-4) y+4(1-\lambda)=0 \dots(i)
\)
It will touch the line \(x+2 y=0\), then solution of Eq. (i) and \(x=-2 y\) be unique.
Hence, the roots of the equation
\(
(-2 y)^2+y^2+(\lambda-2)(-2 y)+(2 \lambda-4) y+4(1-\lambda)=0
\)
or \(5 y^2+4(1-\lambda)=0\)
must be equal.
Then, \(0-4 \cdot 5 \cdot 4(1-\lambda)=0\) or \(1-\lambda=0\) or \(\lambda=1\)
From Eq. (i), the required circle is \(x^2+y^2-x-2 y=0\)

Example 88: Find the circle whose diameter is the common chord of the circles \(x^2+y^2+2 x+3 y+1=0\) and \(x^2+y^2+4 x+3 y+2=0\).

Answer: Given circles are
\(
\begin{aligned}
S & \equiv x^2+y^2+2 x+3 y+1=0 \\
\text { and } \quad S^{\prime} & \equiv x^2+y^2+4 x+3 y+2=0
\end{aligned}
\)
Hence, their common chord is \(S-S^{\prime}=0\)
\(
\Rightarrow \quad-2 x-1=0 \text { or } 2 x+1=0 \dots(i)
\)
Now, the required circle must pass through the point of intersection of \(S\) and \(S^{\prime}\).
Hence, its equation is \(\quad S+\lambda S^{\prime}=0\)
\(
\Rightarrow \quad\left(x^2+y^2+2 x+3 y+1\right)+\lambda\left(x^2+y^2+4 x+3 y+2\right)=0
\)
\(
\begin{aligned}
& \Rightarrow \quad x^2(1+\lambda)+y^2(1+\lambda)+2 x(1+2 \lambda) \\
& +3 y(1+\lambda)+(1+2 \lambda)=0 \\
& \text { or } \quad x^2+y^2+2 x \frac{(1+2 \lambda)}{(1+\lambda)}+3 y+\frac{(1+2 \lambda)}{(1+\lambda)}=0 \dots(ii) \\
&
\end{aligned}
\)
Its centre is \(\left(-\frac{1+2 \lambda}{1+\lambda},-\frac{3}{2}\right)\)
But from Eq. (i), \(2 x+1=0\) is a diameter of this circle.
Hence, its centre must lie on this line
\(
\begin{aligned}
& \therefore \quad-2\left(\frac{1+2 \lambda}{1+\lambda}\right)+1=0 \\
& \Rightarrow \quad-2-4 \lambda+1+\lambda=0 \\
& \Rightarrow \quad-1-3 \lambda=0 \\
& \therefore \quad \lambda=-\frac{1}{3} \\
&
\end{aligned}
\)
Hence, from Eq. (ii), the required circle is
\(
2 x^2+2 y^2+2 x+6 y+1=0
\)

Angle of Intersection of Two Circles

Let the two circles
\(
S \equiv x^2+y^2+2 g x+2 f y+c=0
\)
and \(S^{\prime} \equiv x^2+y^2+2 g_1 x+2 f_1 y+c_1=0\)
intersect each other at the points \(P[latex] and [latex]Q\).The angle \(\theta\) between two circles \(S=0\) and \(S^{\prime}=0\) is defined as the angle between the tangents to the two circles at the point of intersection.

\(C_1\) and \(C_2\) are the centres of circles
\(S=0\) and \(S^{\prime}=0\), then
\(C_1 \equiv(-g,-f) \quad\) and \(\quad C_2 \equiv\left(-g_1,-f_1\right)\)
and radii of circles \(S=0\) and \(S^{\prime}=0\) are
\(
r_1=\sqrt{\left(g^2+f^2-c\right)} \text { and } r_2=\sqrt{\left(g_1^2+f_1^2-c_1\right)}
\)
Let
\(
\begin{aligned}
d & =\left|C_1 C_2\right|=\text { Distance between their centres } \\
& =\sqrt{\left(-g+g_1\right)^2+\left(-f+f_1\right)^2} \\
& =\sqrt{\left(g^2+f^2+g_1^2+f_1^2-2 g g_1-2 f f_1\right)}
\end{aligned}
\)
\(
\text { Now, in } \Delta C_1 P C_2, \cos \alpha=\left(\frac{r_1^2+r_2^2-d^2}{2 r_1 r_2}\right)\left(\begin{array}{c}
\because \alpha+\theta+90^{\circ}+90^{\circ} \\
=360^{\circ}
\end{array}\right)
\)
\(
\text { or } \quad \cos \left(180^{\circ}-\theta\right)=\left(\frac{r_1^2+r_2^2-d^2}{2 r_1 r_2}\right) \quad\left(\therefore \alpha=180^{\circ}-\theta\right)
\)
\(
\therefore \quad \cos \theta=\left|\frac{r_1^2+r_2^2-d^2}{2 r_1 r_2}\right| \dots(i)
\)

Orthogonal Intersection of Circles

If the angle between the circles is \(90^{\circ}[latex], i.e. [latex]\theta=90^{\circ}\), then the circles are said to be orthogonal circles or we say that the circles cut each other orthogonally.
\(
\begin{aligned}
& \text { Then, from Eq. (i), } 0=\frac{r_1^2+r_2^2-d^2}{2 r_1 r_2} \\
& \begin{array}{r}
\text { or } \quad r_1^2+r_2^2-d^2=0 \text { or } r_1^2+r_2^2=d^2 \\
\Rightarrow \quad g^2+f^2-c+g_1^2+f_1^2-c_1=g^2+f^2+g_1^2 \\
+f_1^2-2 g g_1-2 f f_1
\end{array}
\end{aligned}
\)
\(
2 g g_1+2 f f_1=c+c_1
\)

Remark

Equation of a circle cutting the three circles \(x^2+y^2+2 g_i x+2 f_i y+c_i=0(i=1,2,3)\) orthogonally is
\(
\left|\begin{array}{cccr}
x^2+y^2 & x & y & 1 \\
-c_1 & g_1 & f_1 & -1 \\
-c_2 & g_2 & f_2 & -1 \\
-c_3 & g_3 & f_3 & -1
\end{array}\right|
\)

Example 89: Find the angle between the circles
\(
s: x^2+y^2-4 x+6 y+11=0
\)
and \(S^{\prime}: x^2+y^2-2 x+8 y+13=0\)

Answer: Centres and radii of circles \(S\) and \(S^{\prime}\) are
\(
C_1(2,-3), r_1=\sqrt{2}, C_2(1,-4), r_2=2 .
\)
Distance between centres, \(d=\left|C_1 C_2\right|\)
\(
=\sqrt{(2-1)^2+(-3+4)^2}=\sqrt{2}
\)
If angle between the circles is \(\theta\), then
\(
\begin{aligned}
\cos \theta & =\left|\frac{r_1^2+r_2^2-d^2}{2 r_1 r_2}\right| \\
\cos \theta & =\left|\frac{2+4-2}{2 \cdot \sqrt{2} \cdot 2}\right|=\frac{1}{\sqrt{2}} \\
\therefore \quad \theta & =45^{\circ}
\end{aligned}
\)

Example 90: Show that the circles
\(x^2+y^2-6 x+4 y+4=0\) and
\(x^2+y^2+x+4 y+1=0\) cut orthogonally.

Answer: Comparing the given circles by general equation of circles
\(
x^2+y^2+2 g x+2 f y+c=0
\)
\(
\text { and } \quad x^2+y^2+2 g_1 x+2 f_1 y+c_1=0
\)
then, \(g=-3, f=2, c=4\)
and \(g_1=\frac{1}{2}, f_1=2, c_1=1\)
Then, given circles cut orthogonally, if
\(
\begin{array}{ll}
& 2 gg _1+2 ff _1=c+c_1 \\
\text { We have, } & 2 \times(-3) \times \frac{1}{2}+2 \times 2 \times 2=4+1 \\
\Rightarrow & -3+8=5 \text { or } 5=5 .
\end{array}
\)
Hence, the given circles cut each other orthogonally.

Example 91: Find the equation of the circle which cuts the circle \(x^2+y^2+5 x+7 y-4=0\) orthogonally, has its centre on the line \(x=2\) and passes through the point \((4,-1)\)

Answer: Let the required circle be
\(
x^2+y^2+2 g x+2 f y+c=0 \dots(i)
\)
Since, \((4,-1)\) lie on Eq. (i), then
\(
17+8 g-2 f+c=0 \dots(ii)
\)
Centre of Eq. (i) is \((-g,-f)\)
Since, centre lie on \(x=2\) then \(-g=2\)
\(
\therefore \quad g=-2 \dots(iii)
\)
\(
\text { From Eq. (ii), } 1-2 f+c=0 \dots(iv)
\)
and given circle is
\(
x^2+y^2+5 x+7 y-4=0 \dots(v)
\)
Given the circles Eqs. (i) and (v) cut each other orthogonally,
\(
\therefore \quad 2 g \times \frac{5}{2}+2 f \times \frac{7}{2}=c-4
\)
\(
\begin{aligned}
& 5 g+7 f=c-4 \\
& -10+7 f=c-4 \text { [from Eq. (iii)] }\\
& -6+7 f-c=0 \dots(vi)
\end{aligned}
\)
Solving Eqs. (iv) and (vi), we get
\(
f=1 \text { and } c=1
\)
Substituting the values of \(g, f, c\) in Eq. (i), we get
\(
x^2+y^2-4 x+2 y+1=0
\)

Example 92: Find the equations of the two circles which intersect the circles \(x^2+y^2-6 y+1=0\) and \(x^2+y^2-4 y+1=0\) orthogonally and touch the line \(3 x+4 y+5=0\).

Answer: Let the required circle be
\(
x^2+y^2+2 g x+2 f y+c=0 \dots(i)
\)
\(
\text { and given circles are } x^2+y^2-6 y+1=0 \dots(ii)
\)
and \(x^2+y^2-4 y+1=0 \dots(iii)\)
Since, Eq. (i) cuts Eq. (ii) and Eq. (iii) orthogonally
\(
\begin{aligned}
\therefore & & 2 g \times 0+2 f \times(-3) & =c+1 \\
\text { or } & & -6 f & =c+1 \dots(iv)
\end{aligned}
\)
and \(\quad 2 g \times 0+2 f \times(-2)=c+1\)
or \(\quad-4 f=c+1 \dots(v)\)
Solving, Eqs. (iv) and (v), we get
\(
\begin{aligned}
& \qquad f=0 \quad \text { and } \quad c=-1 \\
& \text { From Eq. (i), } \quad x^2+y^2+2 g x-1=0 \dots(vi)
\end{aligned}
\)
centre and radius of Eq. (vi) are \((-g, 0)\) and \(\sqrt{\left(g^2+1\right)}\), respectively.
Since, \(3 x+4 y+5=0\) is tangent of Eq. (vi), then length of perpendicular from \((-g, 0)\) to this line \(=\) radius of circle
\(
\begin{aligned}
& \frac{|-3 g+0+5|}{\sqrt{(9+16)}}=\sqrt{\left(g^2+1\right)} \\
& |-3 g+5|=5 \sqrt{\left(g^2+1\right)} \\
& (-3 g+5)^2=25\left(g^2+1\right) \\
& 9 g^2+25-30 g=25 g^2+25 \\
& 16 g^2+30 g=0 \\
& g=0 \text { and } g=-\frac{15}{8} \\
&
\end{aligned}
\)
Equations of circles are from Eq. (vi),
\(
\begin{aligned}
& x^2+y^2-1=0 \quad \text { and } \quad x^2+y^2-\frac{15}{4} x-1=0 \\
& \text { or } \quad x^2+y^2-1=0 \text { and } 4 x^2+4 y^2-15 x-4=0
\end{aligned}
\)

Example 93: Prove that the two circles, which pass through \((0, a)\) and \((0,-a)\) and touch the line \(y=m x+c\), will cut orthogonally, if \(c^2=a^2\left(2+m^2\right)\)

Answer: Let the equation of the circles be
\(
x^2+y^2+2 g x+2 f y+d=0 \dots(i)
\)
Since, these circles pass through \((0, a)\) and \((0,-a)\), then
\(
a^2+2 f a+d=0 \dots(ii)
\)
and \(a^2-2 f a+d=0 \dots(iii)\)
Solving, Eq. (ii) and Eq. (iii), we get \(f=0\) and \(d=-a^2\). Substituting these values of \(f\) and \(d\) in Eq. (i), we obtain
\(
x^2+y^2+2 g x-a^2=0 \dots(iv)
\)
Now, \(y=m x+c\) touch this circle, therefore, length of the perpendicular from the centre \(=\) radius
\(
\begin{aligned}
& \frac{|-m g-0+c|}{\sqrt{1+m^2}}=\sqrt{\left(g^2+a^2\right)} \\
& (c-m g)^2=\left(1+m^2\right)\left(g^2+a^2\right)
\end{aligned}
\)
\(
g^2+2 m c g+a^2\left(1+m^2\right)-c^2=0
\)
Let \(g_1, g_2\) are the roots of this equation
\(
\therefore \quad g_1 g_2=a^2\left(1+m^2\right)-c^2 \dots(v)
\)
Now, the equations of the two circles represented by Eq. (iv) are
\(
\begin{aligned}
& x^2+y^2+2 g_1 x-a^2=0 \\
& x^2+y^2+2 g_2 x-a^2=0 .
\end{aligned}
\)
These two circles will be cuts orthogonal, if
\(
2 g_1 g_2+0=-a^2-a^2
\)
\(
g_1 g_2=-a^2 \dots(vi)
\)
From Eqs. (v) and (vi),
\(
\begin{aligned}
-a^2 & =a^2\left(1+m^2\right)-c^2 \\
c^2 & =a^2\left(2+m^2\right)
\end{aligned}
\)
which is the required condition.

Example 94: Find the equation of the circle which cuts orthogonally each of the three circles given below
\(
x^2+y^2-2 x+3 y-7=0, x^2+y^2+5 x-5 y+9=0
\)
and \(x^2+y^2+7 x-9 x+29=0\).

Answer: Let the required circle be
\(
x^2+y^2+2 g x+2 f y+c=0 \dots(i)
\)
Since, it is orthogonal to three given circles respectively, therefore
\(
2 g \times(-1)+2 f \times \frac{3}{2}=c-7
\)
\(
\begin{gathered}
-2 g+3 f=c-7 \dots(ii) \\
2 g \times \frac{5}{2}+2 f \times\left(-\frac{5}{2}\right)=c+9 \\
5 g-5 f=c+9 \dots(iii)
\end{gathered}
\)
\(
\text { and } \quad 2 g \times \frac{7}{2}+2 f \times\left(-\frac{9}{2}\right)=c+29
\)
\(
7 g-9 f=c+29 \dots(iv)
\)
Subtracting, Eq. (ii) from Eq. (iii),
\(
7 g-8 f=16 \dots(v)
\)
and subtracting Eq. (iii) from Eq. (iv),
\(
2 g-4 f=20 \dots(vi)
\)
Solving Eq. (v) and Eq. (vi), we get
\(
g=-8 \text { and } f=-9
\)
Putting the values of \(g\) and \(f\) in Eq. (iii)
\(
\begin{array}{ll}
& -40+45=c+9 \\
\Rightarrow & 5=c+9
\end{array}
\)
\(
c=-4
\)
Substituting the values of \(g, f, c\) in Eq. (i), then required circle is
\(
x^2+y^2-16 x-18 y-4=0
\)

Radical Axis

The radical axis of two circles is the locus of a point which moves such that the lengths of the tangents drawn from it to the two circles are equal.
Consider,
\(
\begin{aligned}
S & \equiv x^2+y^2+2 g x+2 f y+c=0 \\
S^{\prime} & \equiv x^2+y^2+2 g_1 x+2 f_1 y+c_1=0
\end{aligned}
\)
Let \(P\left(x_1, y_1\right)\) be a point such that
\(
\begin{gathered}
|P A|=|P B| \\
\Rightarrow \quad \sqrt{\left(x_1^2+y_1^2+2 g x_1+2 f y_1+c\right)} \\
=\sqrt{\left(x_1^2+y_1^2+2 g_1 x_1+2 f_1 y_1+c_1\right)}
\end{gathered}
\)
\(
\begin{aligned}
& \text { On squaring, } \quad x_1^2+y_1^2+2 g x_1+2 f y_1+c \\
& =x_1^2+y_1^2+2 g_1 x_1+2 f_1 y_1+c_1 \\
& \Rightarrow \quad 2\left(g-g_1\right) x_1+2\left(f-f_1\right) y_1+c-c_1=0
\end{aligned}
\)
\(\therefore\) Locus of \(P\left(x_1, y_1\right)\) is
\(
2\left(g-g_1\right) x+2\left(f-f_1\right) y+c-c_1=0
\)
which is the required equation of radical axis of the given circles. Clearly this is a straight line.

Some Properties of the Radical Axis

• The radical axis and common chord are identical.
• The radical axis is perpendicular to the straight line which joins the centres of the circles.
• The radical axis bisects common tangents of two circles.
• The radical axis of three circles taken in pairs are concurrent.
• The locus of the centre of a circle cutting two given circles orthogonally is the radical axis of the two circles.

Remark

• Radical axis need not always pass through the mid-point of the line joining the centres of the two circles.

Example 95: If two circles \(x^2+y^2+2 g x+2 f y=0\) and \(x^2+y^2+2 g^{\prime} x+2 f^{\prime} y=0\) touch each other, then prove that \(f^{\prime} g=f g^{\prime}\).

Answer: If two circles touch each other, then their radical axis is their common tangent.
\(\therefore\) Radical axis of two circles is
\(
\left(x^2+y^2+2 g x+2 f y\right)-\left(x^2+y^2+2 g^{\prime} x+2 f^{\prime} y\right)=0
\)
\(
\begin{aligned}
& 2 x\left(g-g^{\prime}\right)+2 y\left(f-f^{\prime}\right)=0 \\
& x\left(g-g^{\prime}\right)+y\left(f-f^{\prime}\right)=0 \dots(i)
\end{aligned}
\)
If this touches the circle \(x^2+y^2+2 g x+2 f y=0\), then the length of perpendicular from its centre \((-g,-f)\) to (i) \(=\) radius \(\sqrt{\left(g^2+f^2\right)}\) of the circle
\(
\text { i.e. } \frac{\left|-g\left(g-g^{\prime}\right)-f\left(f-f^{\prime}\right)\right|}{\sqrt{\left(g-g^{\prime}\right)^2+\left(f-f^{\prime}\right)^2}}=\sqrt{g^2+f^2}
\)
\(
\begin{aligned}
& \left\{\left(-\left(g^2+f^2\right)+g g^{\prime}+f f^{\prime}\right)\right\}^2 \\
& \quad=\left(g^2+f^2\right)\left\{\left(g-g^{\prime}\right)^2+\left(f+f^{\prime}\right)^2\right\}
\end{aligned}
\)
\(
\begin{aligned}
& \left(g^2+f^2\right)^2+\left(g g^{\prime}+f f^{\prime}\right)^2-2\left(g^2+f^2\right)\left(g g^{\prime}+f f^{\prime}\right) \\
& \quad=\left(g^2+f^2\right)\left\{\left(g^2+f^2\right)+\left(g^{\prime 2}+f^{\prime 2}\right)-2\left(g g^{\prime}+f f^{\prime}\right)\right\}
\end{aligned}
\)
\(
\left(g g^{\prime}+f f^{\prime}\right)^2=\left(g^2+f^2\right)\left(g^{\prime 2}+f^{\prime 2}\right)
\)
\(
\text { On simplifying, } \quad 2 g g^{\prime} f f^{\prime}=g^2 f^{\prime 2}+f^2 g^{\prime 2}
\)
\(
\begin{aligned}
\left(g f^{\prime}-g^{\prime} f\right)^2 & =0 \\
g f^{\prime} & =g^{\prime} f
\end{aligned}
\)

Radical Centre

The radical axes of three circles, taken in pairs, meet in a point, which is called their radical centre. Let the three circles be
\(
\begin{aligned}
& S_1=0 \dots(i) \\
& S_2=0 \dots(ii) \\
& S_3=0 \dots(iii)
\end{aligned}
\)

Let \(O L, O M\) and \(O N\) be radical axes of the pair sets of circles
\(
\left\{S_1=0, S_2=0\right\},\left\{S_3=0, S_1=0\right\}
\)
and \(\left\{S_2=0, S_3=0\right\} \text { respectively. }\)
Equations of \(O L, O M\) and \(O N\) are respectively
\(
\begin{aligned}
& S_1-S_2=0 \dots(iv) \\
& S_3-S_1=0 \dots(v) \\
& S_2-S_3=0 \dots(vi)
\end{aligned}
\)
Let the straight lines Eqs. (iv) and (v) i.e. \(O L\) and \(O M\) meet in \(O\). The equation of any straight line passing through \(O\) is
\(
\left(S_1-S_2\right)+\lambda\left(S_3-S_1\right)=0
\)
where \(\lambda\) is any constant.
For \(\lambda=1\) this equation becomes
\(
S_2-S_3=0
\)
which is, by Eq. (vi), equation of \(O N\).
Thus, the third radical axis also passes through the point where the Eqs. (iv) and (v) meet. In the above figure \(O[latex] is the radical centre.

Properties of Radical Centre

• Coordinates of radical centre can be found by solving the equations
  [latex]
  S_1=S_2=S_3=0
  \)
• The radical centre of three circles described on the sides of a triangle as diameters is the orthocentre of the triangle :

Draw perpendicular from \(A\) on \(B C\).
\(
\therefore \quad \angle A D B=\angle A D C=\pi / 2
\)
Therefore, the circles whose diameters are \(A B\) and \(A C\) passes through \(D\) and \(A\). Hence, \(A D\) is their radical axis. Similarly, the radical axis of the circles on \(A B\) and \(B C\) as diameters is the perpendicular line from \(B\) on \(C A\) and radical axis of the circles on \(B C\) and \(C A\) as diameters is the perpendicular line from \(C\) on \(A B\). Hence, the radial axis of three circles meet in a point. This point \(I\) is radical centre but here radical centre is the point of intersection of altitudes i.e. \(A D, B E\) and \(C F\). Hence, radical centre = orthocentre.

• The radical centre of three given circles will be the centre of a fourth circle which cuts all the three circles orthogonally and the radius of the fourth circle is the length of tangent drawn from radical centre of the three given circles to any of these circles. Let the fourth circle be \((x-h)^2+(y-k)^2=r^2\), where \((h, k)\) is centre of this circle and \(r\) be the radius. The centre of circle is the radical centre of the given circles and \(r\) is the length of tangent from \((h, k)\) to any of the given three circles.

Example 96: Find the radical centre of circles \(x^2+y^2+3 x+2 y+1=0, x^2+y^2-x+6 y+5=0\) and \(x^2+y^2+5 x-8 y+15=0\). Also, find the equation of the circle cutting them orthogonally.

Answer: Given circles are
\(
\begin{aligned}
& S_1 \equiv x^2+y^2+3 x+2 y+1=0 \\
& S_2 \equiv x^2+y^2-x+6 y+5=0 \\
& S_3 \equiv x^2+y^2+5 x-8 y+15=0
\end{aligned}
\)
Equations of two radical axes are
\(
\begin{aligned}
& S_1-S_2 \equiv 4 x-4 y-4=0 \text { or } x-y-1=0 \\
& \text { and } \quad S_2-S_3 \equiv-6 x+14 y-10=0 \text { or } 3 x-7 x+5=0 \\
&
\end{aligned}
\)
Solving them the radical centre is \((3,2)\) also, if \(r\) is the length of the tangent drawn from the radical centre \((3,2)\) to any one of the given circles, say \(S_1\), we have
\(
r=\sqrt{S_1}=\sqrt{3^2+2^2+3 \cdot 3+2 \cdot 2+1}=\sqrt{27}
\)
Hence, \((3,2)\) is the centre and \(\sqrt{27}\) is the radius of the circle intersecting them orthogonally.
\(\therefore\) Its equation is
\(
(x-3)^2+(y-2)^2=r^2=27 \text { or } x^2+y^2-6 x-4 y-14=0
\)

Example 97: Find the radical centre of three circles described on the three sides \(4 x-7 y+10=0\), \(x+y-5=0\) and \(7 x+4 y-15=0\) of a triangle as diameters.

Answer: Since, the radical centre of three circles described on the sides of a triangle as diameters is the orthocentre of the triangle.
\(\therefore \quad\) Radical centre \(=\) orthocentre
Given sides are
\(
\begin{aligned}
& 4 x-7 y+10=0 \dots(i) \\
& x+y-5=0 \dots(ii) \\
& 7 x+4 y-15=0 \dots(iii)
\end{aligned}
\)
Since, lines Eqs. (i) and (iii) are perpendiculars the point of intersection of Eqs. (i) and (iii) is (1, 2), the orthocentre of the triangle. Hence, radical centre is \((1,2)\).

Co-axial System of Circles

A system (or a family) of circles, every pair of which have the same radical axis, are called co-axial circles.

• The equation of a system of co-axial circles, when the equation of the radical axis and of one circle of the system are

\(
\begin{aligned}
& P \equiv l x+m y+n=0 \\
\text { and } \quad S & \equiv x^2+y^2+2 g x+2 f y+c=0
\end{aligned}
\)
respectively, is
\(S+\lambda P=0(\lambda\) is an arbitrary constant \()\)

• The equation of a co-axial system of circles, where the equation of any two circles of the system are

\(
\begin{aligned}
& S_1 \equiv x^2+y^2+2 g_1 x+2 f_1 y+c_1=0 \\
& \text { and } \quad S_2 \equiv x^2+y^2+2 g_2 x+2 f_2 y+c_2=0
\end{aligned}
\)
respectively is
\(
\begin{array}{lrr}
S_1+\lambda\left(S_1-S_2\right)=0 & (\lambda \neq-1) \\
\text { or } \quad S_2+\lambda_1\left(S_1-S_2\right)=0 & \left(\lambda_1 \neq-1\right) \\
\text { Other form } S_1+\lambda S_2=0 & (\lambda \neq-1)
\end{array}
\)

• The equation of a system of co-axial circles in the simplest form is
  \(
  x^2+y^2+2 g x+c=0
  \)
  where, \(g\) is variable and \(c\), a constant.
  The common radical axis is the \(Y\)-axis (since centre on \(X\)-axis) and the equation of a system of other co-axial circles in the simplest form is
  \(
  x^2+y^2+2 f y+c=0
  \)
  where, \(f\) is variable and \(c\), a constant (since centre on \(Y\)-axis). The common radical axis is the \(X\)-axis.

Example 98: Find the equation of the system of circles co-axial with the circles
\(
x^2+y^2+4 x+2 y+1=0
\)
and \(x^2+y^2-2 x+6 y-6=0\)
Also, find the equation of that particular circle whose centre lies on the radical axis.

Answer: Given circles are
\(
\begin{aligned}
& S_1 \equiv x^2+y^2+4 x+2 y+1=0 \\
\text { and } & S_2 \equiv x^2+y^2-2 x+6 y-6=0
\end{aligned}
\)
\(\therefore\) Radical axis is \(S_1-S_2=0\)
i.e. \(\quad 6 x-4 y+7=0 \dots(i)\)
Now, system of co-axial circle is
\(
\begin{array}{ll}
& S_1+\lambda\left(S_1-S_2\right)=0 \\
\Rightarrow & \left(x^2+y^2+4 x+2 y+1\right)+\lambda(6 x-4 y+7)=0
\end{array}
\)
\(
x^2+y^2+2 x(2+3 \lambda)+2 y(1-2 \lambda)+1+7 \lambda=0 \quad \ldots \text { (ii) }
\)
Its centre \([-(2+3 \lambda),-(1-2 \lambda)]\) lies on Eq. (i)
\(
\therefore \quad 6 \times-(2+3 \lambda)-4 \times-(1-2 \lambda)+7=0
\)
\(
\begin{aligned}
& -12-18 \lambda+4-8 \lambda+7=0 \\
& -26 \lambda-1=0
\end{aligned}
\)
\(
\therefore \quad \lambda=-\frac{1}{26}
\)
Substituting the value of \(\lambda\) in Eq. (ii), the equation of circle is
\(
\begin{aligned}
& x^2+y^2+2 x\left(2-\frac{3}{26}\right)+2 y\left(1+\frac{2}{26}\right)+1-\frac{7}{26}=0 \\
\Rightarrow \quad & 26\left(x^2+y^2\right)+98 x+56 y+9=0
\end{aligned}
\)

Limiting Point

Limiting points of system of co-axial circles are the centres of the point circles belonging to the family (Circles whose radii are zero are called point circles).

• Limiting points of the co-axial system
  Let the circle is
  \(
  x^2+y^2+2 g x+c=0 \dots(i)
  \)
  where, \(g\) is variable and \(c\) is constant.
  \(\therefore\) Centre and the radius of Eq. (i) are \((-g, 0)\) and \(\sqrt{\left(g^2-c\right)}\), respectively. Let
  \(
  \begin{array}{rlrl}
  & \sqrt{g^2-c} & =0 \\
  \therefore \quad g & = \pm \sqrt{c}
  \end{array}
  \)
  Thus, we get the two limiting points of the given co-axial system as
  \(
  (\sqrt{c}, 0) \text { and }(-\sqrt{c}, 0)
  \)
  Clearly the above limiting points are real and distinct, real and coincident or imaginary according as \(c>,=,<0\)
• System of co-axial circles whose two limiting point are given :
  Let \((\alpha, \beta)\) and \((\gamma, \delta)\) be the two given limiting points. Then, the corresponding point circles with zero radii are
  \(
  \begin{aligned}
  & (x-\alpha)^2+(y-\beta)^2=0 \\
  & (x-\gamma)^2+(y-\delta)^2=0
  \end{aligned}
  \)
  \(
  \begin{aligned}
  x^2+y^2-2 \alpha x-2 \beta y+\alpha^2+\beta^2 & =0 \\
  x^2+y^2-2 \gamma x-2 \delta y+\gamma^2+\delta^2 & =0
  \end{aligned}
  \)
  The equation of co-axial system is
  \(
  \begin{aligned}
  & \left(x^2+y^2-2 \alpha x-2 \beta y+\alpha^2+\beta^2\right) \\
  & +\lambda\left(x^2+y^2-2 \gamma x-2 \delta y+\gamma^2+\delta^2\right)=0
  \end{aligned}
  \)
  where, \(\lambda \neq-1\) is a variable parameter.
  \(
  \begin{aligned}
  & \Rightarrow x^2(1+\lambda)+y^2(1+\lambda)-2 x(\alpha+\gamma \lambda) \\
  & -2 y(\beta+\delta \lambda)+\left(\alpha^2+\beta^2\right)+\lambda\left(\gamma^2+\delta^2\right)=0 \\
  & \text { or } \quad x^2+y^2-\frac{2(\alpha+\gamma \lambda)}{(1+\lambda)} x-2 \frac{(\beta+\delta \lambda)}{(1+\lambda)} y \\
  & \qquad+\frac{\left(\alpha^2+\beta^2\right)+\lambda\left(\gamma^2+\delta^2\right)}{(1+\lambda)}=0
  \end{aligned}
  \)
  Centre of this circle is \(\left(\frac{(\alpha+\gamma \lambda)}{(1+\lambda)}, \frac{(\beta+\delta \lambda)}{(1+\lambda)}\right) \dots(i)\)
  For limiting point,
  Radius
  \(
  =\sqrt{\frac{(\alpha+\gamma \lambda)^2}{(1+\lambda)^2}+\frac{(\beta+\delta \lambda)^2}{(1+\lambda)^2}-\frac{\left(\alpha^2+\beta^2\right)+\lambda\left(\gamma^2+\delta^2\right)}{(1+\lambda)}}=0
  \)
  After solving, find \(\lambda\). Substituting value of \(\lambda\) in Eq. (i), we get the limiting point of co-axial system.

Example 99: Find the coordinates of the limiting points of the system of circles determined by the two circles
\(
x^2+y^2+5 x+y+4=0 \text { and } x^2+y^2+10 x-4 y-1=0
\)

Answer: The given circles are
\(
\begin{aligned}
& S_1 \equiv x^2+y^2+5 x+y+4=0 \\
& S_2 \equiv x^2+y^2+10 x-4 y-1=0
\end{aligned}
\)
\(\therefore\) Equation of the co-axial system of circles is \(S_1+\lambda S_2=0\)
\(
\begin{aligned}
\left(x^2+y^2+5 x+y\right. & +4) \\
& +\lambda\left(x^2+y^2+10 x-4 y-1\right)=0
\end{aligned}
\)
\(
\begin{aligned}
x^2(1+\lambda)+y^2(1+\lambda) & +5 x(1+2 \lambda) \\
& +y(1-4 \lambda)+(4-\lambda)=0
\end{aligned}
\)
\(
\text { or } \quad x^2+y^2+\frac{5(1+2 \lambda)}{(1+\lambda)} x+\frac{(1-4 \lambda)}{(1+\lambda)} y+\frac{(4-\lambda)}{(1+\lambda)}=0
\)
The centre of this circles is
\(
\left(\frac{-5(1+2 \lambda)}{2(1+\lambda)},-\frac{(1-4 \lambda)}{2(1+\lambda)}\right) \dots(i)
\)
\(
\text { Radius }=\sqrt{\frac{25(1+2 \lambda)^2}{4(1+\lambda)^2}+\frac{(1-4 \lambda)^2}{4(1+\lambda)^2}-\frac{(4-\lambda)}{(1+\lambda)}}=0
\)
\(
\begin{gathered}
25(1+2 \lambda)^2+(1-4 \lambda)^2-4(4-\lambda)(1+\lambda)=0 \\
25\left(4 \lambda^2+4 \lambda+1\right)+\left(16 \lambda^2-8 \lambda+1\right)-4\left(-\lambda^2+3 \lambda+4\right)=0 \\
120 \lambda^2+80 \lambda+10=0 \text { or } 12 \lambda^2+8 \lambda+1=0 \\
(6 \lambda+1)(2 \lambda+1)=0 \\
\lambda=-\frac{1}{6} \text { and }-\frac{1}{2}
\end{gathered}
\)
Substituting these values of \(\lambda\) in Eq. (i), we get the points \((-2,-1)\) and \((0,-3)\) which are the required limiting points.

Example 100: Find the radical axis of co-axial system of circles whose limiting points are \((-1,2)\) and \((2,3)\).

Answer: Equations of circles with limiting points are \((-1,2)\) and \((2,3)\) are
\(
\begin{aligned}
& (x+1)^2+(y-2)^2=0 \\
& x^2+y^2+2 x-4 y+5=0 \dots(i) \\
& (x-2)^2+(y-3)^2=0 \\
& x^2+y^2-4 x-6 y+13=0 \dots(ii)
\end{aligned}
\)
respectively.
\(\therefore \quad\) Radical axis of circles Eqs. (i) and (ii) is
\(
\begin{aligned}
\left(x^2+y^2+\right. & 2 x-4 y+5) \\
& -\left(x^2+y^2-4 x-6 y+13\right)=0 \\
6 x+2 y-8 & =0 \\
3 x+y-4 & =0
\end{aligned}
\)

Example 101: Find the equation of the circle which passes through the origin and belongs to the co-axial of circles whose limiting points are \((1,2)\) and \((4,3)\).

Answer: Equations of circles whose limiting points are \((1,2)\) and \((4,3)\) are
\(
\begin{gathered}
(x-1)^2+(y-2)^2=0 \\
x^2+y^2-2 x-4 y+5=0 \dots(i) \\
(x-4)^2+(y-3)^2=0 \\
x^2+y^2-8 x-6 y+25=0 \dots(ii)
\end{gathered}
\)
Therefore, the corresponding system of co-axial circles is
\(
\begin{aligned}
& \left(x^2+y^2-2 x-4 y+5\right) \\
& \quad+\lambda\left(x^2+y^2-8 x-6 y+25\right)=0 \dots(iii)
\end{aligned}
\)
It passes through origin, then
\(
\begin{aligned}
& & 5+25 \lambda & =0 \\
& \therefore & \lambda & =-\frac{1}{5}
\end{aligned}
\)
Substituting the value of \(\lambda\) in Eq. (iii), the required circle is
\(
\begin{aligned}
& 5\left(x^2+y^2-2 x-4 y+5\right) \\
&-\left(x^2+y^2-8 x-6 y+25\right)=0
\end{aligned}
\)
\(
\begin{aligned}
& 4 x^2+4 y^2-2 x-14 y=0 \\
& 2 x^2+2 y^2-x-7 y=0
\end{aligned}
\)

Image of the Circle by the Line Mirror

Let the circle be \(x^2+y^2+2 g x+2 f y+c=0\) and line mirror is \(l x+m y+n=0\) in this condition, radius of circle remains unchanged but centres changes. Let the centre of imaged circle be \(\left(x_1, y_1\right)\).
Then, \(\quad \frac{x_1-(-g)}{l}=\frac{y_1-(-f)}{m}=\frac{-2(-l g-m f+c)}{\left(l^2+m^2\right)}\)
we get, \(x_1=\frac{\left(l^2 g-m^2 g+2 m l f-2 n l\right)}{\left(l^2+m^2\right)}\)
and \(\quad y_1=\frac{\left(m^2 f-l^2 f+2 m l g-2 m n\right)}{\left(l^2+m^2\right)}\)

\(\therefore\) Required imaged circle is \(\left(x-x_1\right)^2+\left(y-y_1\right)^2=r^2\)
where, \(r=\sqrt{\left(g^2+f^2-c\right)}\)

Example 102: Find the equation of the image of the circle \(x^2+y^2+16 x-24 y+183=0\) by the line mirror \(4 x+7 y+13=0\).

Answer: The given circle and line are
\(
\begin{array}{r}
x^2+y^2+16 x-24 y+183=0 \dots(i) \\
4 x+7 y+13=0 \dots(ii)
\end{array}
\)
Centre and radius of circle Eq. (i) are \((-8,12)\) and 5 , respectively. Let the centre of the imaged circle be \(\left(x_1, y_1\right)\).
Hence, \(\left(x_1, y_1\right)\) be the image of the point \((-8,12)\) with respect to the line \(4 x+7 y+13=0\), then
\(
\begin{aligned}
& \frac{x_1-(-8)}{4}=\frac{y_1-12}{7} \\
& =\frac{-2(4(-8)+7(12)+13)}{\left(4^2+7^2\right)} \\
& \frac{x_1+8}{4}=\frac{y_1-12}{7}=-2
\end{aligned}
\)
\(
\therefore x_1=-16, y_1=-2
\)
\(\therefore\) Equation of the imaged circle is \((x+16)^2+(y+2)^2=5^2\)
or \(x^2+y^2+32 x+4 y+235=0\)