11.2 Sections of a Cone

A conic section (or simply a conic) is a curve obtained by intersecting the surface of a right circular cone with a flat plane. Depending on the angle at which the plane cuts the cone, four distinct types of curves are formed: the circle, ellipse, parabola, and hyperbola.

Types of Conic Sections:

The shape of the curve is determined by the angle of the plane relative to the axis of the cone:
Circle: Formed when the plane cuts perpendicular to the axis of the cone.
Ellipse: Formed when the plane cuts at a slight angle, creating a closed loop.
Parabola: Formed when the plane is parallel to the side (generating line) of the cone.
Hyperbola: Formed when the plane cuts both halves (nappes) of a double cone, resulting in two separate, symmetrical curves.

The Focus-Directrix Definition:

While conics are defined by slicing a cone, they are also defined algebraically as the set of all points \(P\) in a plane such that the ratio of the distance from \(P\) to a fixed point (the focus) to the distance from \(P\) to a fixed line (the directrix) is constant.

This constant ratio is called the eccentricity (\(e\)):
Circle: \(e=0\)
Ellipse: \(0<e<1\)
Parabola: \(e=1\)
Hyperbola: \(e>1\)

General Equation:

In coordinate geometry, every conic section can be represented by a second-degree polynomial equation in two variables (\(x\) and \(y\)):
\(
A x^2+B x y+C y^2+D x+E y+F=0
\)
The values of the constants \(A, B\), and \(C\) determine which type of conic the equation represents.
For example, if \(B^2-4 A C<0\), it is an ellipse; if \(B^2-4 A C=0\), it is a parabola; and if \(B^2-4 A C>0\), it is a hyperbola.

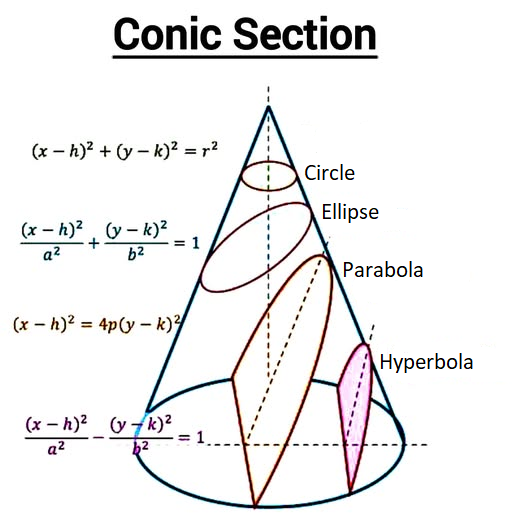
Explanation: How Conic Sections are formed?

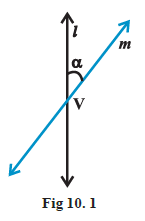
Let \(l\) be a fixed vertical line and \(m\) be another line intersecting it at a fixed point \(V\) and inclined to it an angle \(\alpha\) (Fig10.1).

Suppose we rotate the line \(m\) around the line \(l\) in such a way that the angle \(\alpha\) remains constant. Then the surface generated is a double-napped right circular hollow cone herein after referred as cone and extending indefinitely far in both directions (Fig10.2).

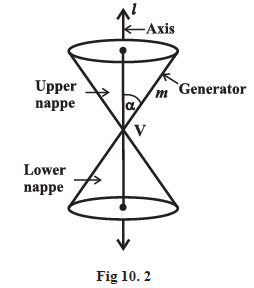
The point \(V\) is called the vertex; the line \(l\) is the axis of the cone. The rotating line \(m\) is called a generator of the cone. The vertex separates the cone into two parts called nappes.

If we take the intersection of a plane with a cone, the section so obtained is called a conic section. Thus, conic sections are the curves obtained by intersecting a right circular cone by a plane.

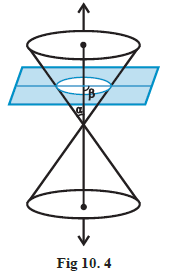
We obtain different kinds of conic sections depending on the position of the intersecting plane with respect to the cone and by the angle made by it with the vertical axis of the cone. Let \(\beta\) be the angle made by the intersecting plane with the vertical axis of the cone (Fig10.3).

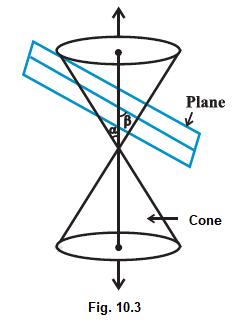
The intersection of the plane with the cone can take place either at the vertex of the cone or at any other part of the nappe either below or above the vertex.

Circle, ellipse, parabola and hyperbola When the plane cuts the nappe (other than the vertex) of the cone, we have the following situations:

Case-I: When \(\beta=90^{\circ}\), the section is a circle (Fig10.4).

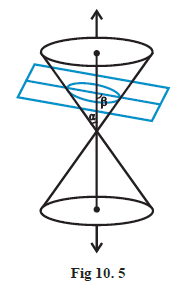
Case II: When \(\alpha<\beta<90^{\circ}\), the section is an ellipse (Fig10.5).

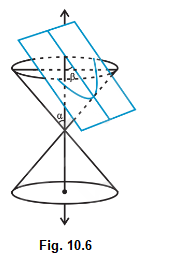
Case III: When \(\beta=\alpha\); the section is a parabola (Fig10.6).

(In each of the above three situations, the plane cuts entirely across one nappe of the cone).

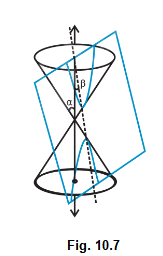
Case iv:  When \(0 \leq \beta<\alpha\); the plane cuts through both the nappes and the curves of intersection is a hyperbola (Fig10.7).

Degenerated conic sections

When the plane cuts at the vertex of the cone, we have the following different cases:
Case I: When \(\alpha<\beta \leq 90^{\circ}\), then the section is a point (Fig10.8).

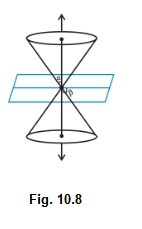
Case II: When \(\beta=\alpha\), the plane contains a generator of the cone and the section is a straight line (Fig10.9). It is the degenerated case of a parabola.

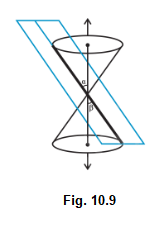
Case III: When \(0 \leq \beta<\alpha\), the section is a pair of intersecting straight lines (Fig10.10). It is the degenerated case of a hyperbola.

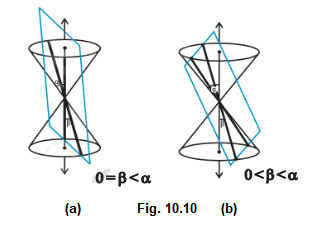
In the following sections, we shall obtain the equations of each of these conic sections in standard form by defining them based on geometric properties.