11.10 Entrance Corner (Parabola)

A parabola is the locus of a point moving in a plane such that its distance from a fixed point (focus) is equal to its distance from a fixed line (directrix). Hence it is a conic section with eccentricity \(\mathrm{e}=1\).

\(
\begin{aligned}
& \frac{P S}{P M}=e=1 \\
& \Rightarrow P S=P M
\end{aligned}
\)

Standard equation of a parabola

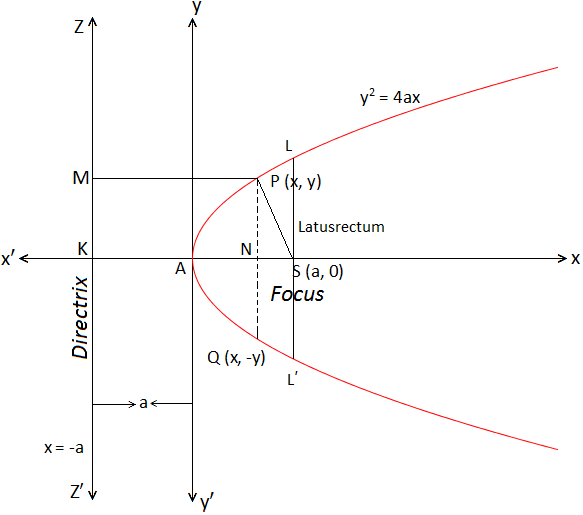
Let \(S\) be the focus and the straight line \(Z Z^{\prime}\), the directrix of the required parabola. Let \(S K\) be the straight line through \(S\) perpendicular to the directrix, bisect \(S K\) at \(A\) and \(K\) being the point of intersection with the directrix.
Then \(\mathrm{AS}=\mathrm{AK}\)
Distance of \(A\) from the focus \(=\) Distance of \(A\) from the directrix
A lies on the parabola
Let \(S K=2 a\), where, \(a>0\).
Then \(A S=A K=a\).
If this line SK intersects the parabola at A then SK is the axis and A is the vertex of the parabola. Draw the straight line AY through A perpendicular to the axis. Now, we choose the origin of co-ordinates at \(A\) and \(x\) and \(y\)-axis along \(A S\) and \(A Y\) respectively.
Let \(P(x, y)\) be any point on the required parabola. Join SP and draw PM and PN perpendicular to the directrix \(Z Z^{\prime}\) and \(x\)-axis. Then,
\(
\begin{aligned}
&{PM}={NK}={AN}+{AK}={x}+{a}\\
&\text { Now, } \mathrm{P} \text { lies on the parabola } \Rightarrow \mathrm{SP}=\mathrm{PM}
\end{aligned}
\)

Consider the focus of the parabola as \(S(a, 0)\) and directrix be \(x+a=0\), and axis as \(x\)-axis.

Now according to the definition of the parabola, for any point on the parabola, we must have
\(
\begin{array}{rlrl}
& S P=P M \\
\Rightarrow & \sqrt{(x-a)^2+(y-0)^2}=A N+A K=x+a \\
\Rightarrow & (x-a)^2+y^2=(a+x)^2 \\
\Rightarrow & y^2=(a+x)^2-(x-a)^2 \\
\Rightarrow & y^2=4 a x
\end{array}
\)
This is the equation of the parabola in its standard form.
Note: The parabola has two real foci situated on its axis one of which is the focus S and the other lies at infinity. The corresponding directrix is also at infinity.
The focus of the parabola \(y^2=4 a x\) is at \((a, 0)\), the directrix is \(x=-a\). The axis is a line passing through the focus and perpendicular to the directrix.

Remarks

If the vertex of a parabola is at the point \(A(h, k)\) and its latus-rectum is of length \(4 a\), then its equation is

• \((y-k)^2=4 a(x-h)\), if its axis is parallel to \(OX\) i.e. parabola opens rightward
• \((y-k)^2=-4 a(x-h)\), if its axis is parallel to \(O X^{\prime}\) i.e. opens leftward.
• \((x-h)^2=4 a(y-k)\), if its axis is parallel to \(O Y\) i.e. it opens upward.
• \((x-h)^2=-4 a(y-k)\), if its axis is parallel to \(O Y^{\prime}\) i.e. it opens downward.
• The general equation of a parabola whose axis is parallel to \(x\)-axis is \(x=a y^2+b y+c\) and the general equation of a parabola whose axis is parallel to \(y\)-axis is \(y=a x^2+b x+c\).

Vertex of Parabola (0 , 0):

In Figure above, \(x\)-axis i.e., \(y=0\) is the axis of the parabola \(y^2=4 a x\). The axis meets the curve \(y^2=4 a x\) at \(A\), the origin. At point \(A\) \(x=0\) so \(y^2=4 a \times 0=0\), hence \(y=0\). So the coordinates of the vertex are \((0,0)\). Clearly, the vertex \(A\) is the mid-way between the focus and the directrix i.e., the vertex is equidistant from the focus and the directrix.

Tangent at vertex \(x=0\): 

If the tangent at the vertex is the line (Point \(A\)) \(x=0\) (which is the \(y\)-axis), it tells us two very specific things about the orientation of your parabola:
It is a Horizontal Parabola: Since the tangent line is vertical, the parabola must open either to the left or to the right.
The Axis of Symmetry is Horizontal: The axis of symmetry is always perpendicular to the tangent at the vertex. Therefore, the axis of symmetry is the line \(y=0\) (the \(x\)-axis).

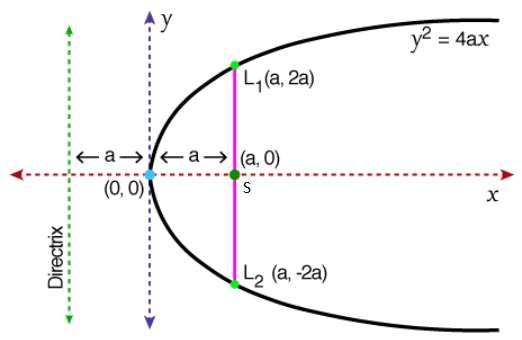
Latus Rectum of Parabola (\(L_1L_2\)):

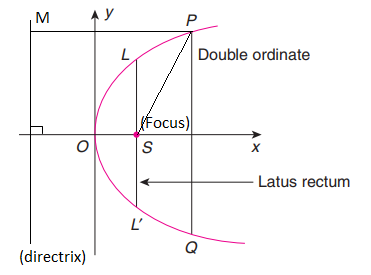
The latus rectum in a parabola is the chord passing through its focus and perpendicular to its axis. It is also the focal chord parallel to the directrix. A parabola has only one latus rectum.

Equation of latus rectum:

The latus rectum always passes through the focus which is located at \(x=a\). Therefore the equation of Latus Rectum: \(x=a\) a vertical line passing through the focus.

Extremities of latus rectum:

We can find by plugging \(x=a\) into the parabola equation \(y^2=4 a x\)
\(
y^2=4 a(a) \Longrightarrow y= \pm 2 a
\)
Therefore Extremities (Endpoints) are: \((a, 2 a)\) and \((a,-2 a)\)

Length of latus rectum:

This is the total distance between \((a, 2 a)\) and \((a,-2 a)\) which is \(4 a\).

Focal Distance of Any Point

The distance of \(P(x, y)\) from the focus \(S\) is called the focal distance of the point \(P\).
Now,
\(
\begin{aligned}
S P & =\sqrt{(x-a)^2+(y-0)^2} \\
\Rightarrow \quad S P & =\sqrt{(x-a)^2+y^2}
\end{aligned}
\)
\(
\Rightarrow \quad S P=\sqrt{(x-a)^2+4 a x} \quad\left[\begin{array}{r}
\because P(x, y) \text { lies on the parabola } \\
\therefore y^2=4 a x
\end{array}\right]
\)
\(
\begin{aligned}
&\Rightarrow \quad S P=\sqrt{(x+a)^2}=a+x\\
&\text { Hence, } a+x \text { is the focal distance of the point } P(x, y) \text {. }
\end{aligned}
\)

Focal Chord

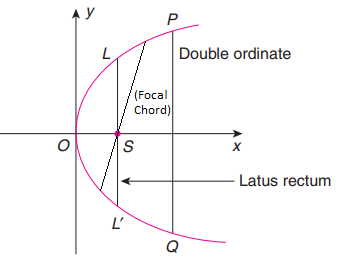
A focal chord is any line segment that passes through the focus and has both its endpoints on the parabola.

Double Ordinate

Let \(P\) be any point on the parabola \(y^2=4 a x\). A chord passing through \(P\) perpendicular to the axis of the parabola is called the double ordinate through the point \(P\).

Parametric Form Of \(y^2=4 a x\):

The parabola \(y^2=4 a x\) is a lot of times specified not in the standard \(x-y\) form of but instead in a parametric form, i.e., in terms of a parameter, say \(t\).
The equation \(y^2=4 a x\) can be equivalently written in parametric form
\(
x=a t^2, y=2 a t
\)
This is easily verifiable by substitution. Thus, for any value of \(t\), the point \(\left(a t^2, 2 a t\right)\) will always lie on the parabola \(y^2=4 a x\) Different values of referred to as simply the point give rise to different points on the parabola.
The point \(\left(a t^2, 2 a t\right)\) is many times referred to as simply the point \(t\).

Derive Parametric form Of \(y^2=4 a x\):
Let’s derive it for the standard horizontal parabola: \(y^2=4 a x\).
Step 1: The Strategy: Proportional Substitution
To turn \(y^2=4 a x\) into a single-variable form, we want to choose a value for \(y\) that makes \(x\) easy to solve for without involving square roots.
We define the parameter \(t\) based on the ratio of \(y\) to \(2 a\) :
\(
t=\frac{y}{2 a}
\)
Step 2: Solving for \(y\)
By simply rearranging the definition above, we get our first parametric equation:
\(
y=2 a t
\)
Step 3: Solving for \(x\)
Now, we substitute this expression for \(y\) back into the standard parabola equation \(\left(y^2=4 a x\right)\) to find the corresponding \(x\) :
Start with the equation: \((2 a t)^2=4 a x\)
Expand the left side: \(4 a^2 t^2=4 a x\)
Divide both sides by \(4 a\) : \(\frac{4 a^2 t^2}{4 a}=x\)
Simplify: \(x=a t^2\)
Step 4: Verification
To ensure this is correct, we “plug and chise” back into the original equation:
Left Hand Side \(\left(y^2\right):(2 a t)^2=4 a^2 t^2\)
Right Hand Side \((4 a x): 4 a\left(a t^2\right)=4 a^2 t^2\)
Since \(L H S=R H S\), the coordinates \(\left(a t^2, 2 a t\right)\) are guaranteed to lie on the parabola for any value of \(t\).

Summary Table of Derivations
Depending on the orientation of the parabola, the substitution changes slightly:
\(
\begin{array}{llll}
\text { Standard Form } & \text { Substitution Used } & \text { Parametric } x & \text { Parametric } y \\
y^2=4 a x & y=2 a t & x=a t^2 & y=2 a t \\
x^2=4 a y & x=2 a t & x=2 a t & y=a t^2 \\
y^2=-4 a x & y=2 a t & x=-a t^2 & y=2 a t
\end{array}
\)

Example 1: From a point \(t\) on \(y^2=4 a x\) a focal chord is drawn. Find the other end-point of this chord.

Solution: Let the other end-point be the point \(t_1\). Thus, the co-ordinates of the two ends of the chord are \(\left(a t^2, 2 a t\right)\) and \(\left(a t_1^2, 2 a t_1\right)\).

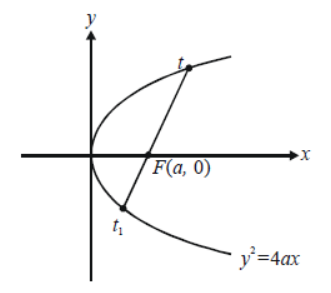
The equation of this chord is therefore
\(
\frac{y-2 a t}{x-a t^2}=\frac{2 a t-2 a t_1}{a t^2-a t_1^2} \dots(1)
\)
Since this chord is a focal chord, the coordinates of \(F\), i.e. ( \(a, 0\) ) must satisfy (1)
\(
\begin{array}{ll}
\Rightarrow & \frac{-2 a t}{a-a t^2}=\frac{2 a\left(t-t_1\right)}{a\left(t^2-t_1^2\right)} \\
\Rightarrow & \frac{-t}{1-t^2}=\frac{1}{t+t_1} \\
\Rightarrow & -t^2-t t_1=1-t^2 \\
\Rightarrow & t t_1=-1
\end{array}
\)
This very widely used result simply states that the product of the two end-points \(t\) and \(t_1\) of any focal chord will be -1.

Example 2: If \((2,-8)\) is at an end of a focal chord of the parabola \(y^2=32 x\), then find the other end of the chord.

Solution: To solve this, we can use the properties of the parametric coordinates of a parabola. This is often the fastest way to handle focal chord problems.
Step 1: Identify the Parabola Parameters
The given equation is \(y^2=32 x\). Comparing this to the standard form \(y^2=4 a x\) :
\(4 a=32\)
\(a=8\)
Any point on this parabola can be represented in parametric form as \(\left(a t^2, 2 a t\right)\), which in this case is \(\left(8 t^2, 16 t\right)\).
Step 2: Find the Parameter \(t_1\) for the Given End
The first end of the focal chord is \((2,-8)\). We set the \(y\)-coordinate equal to the parametric \(y\) :
\(
\begin{gathered}
16 t_1=-8 \\
t_1=-\frac{8}{16}=-\frac{1}{2}
\end{gathered}
\)
(We can verify this with \(x\) : \(8 t_1^2=8(-1 / 2)^2=8(1 / 4)=2\), which matches the given \(x\) coordinate.)
Step 3: Use the Focal Chord Property
For any focal chord of a parabola, if the endpoints have parameters \(t_1\) and \(t_2\), they satisfy the following property:
\(
t_1 \cdot t_2=-1
\)
Now, substitute \(t_1=-1 / 2\) to find \(t_2\) :
\(
\begin{gathered}
\left(-\frac{1}{2}\right) \cdot t_2=-1 \\
t_2=2
\end{gathered}
\)
Step 4: Calculate the Other End
Now we substitute \(t_2=2\) back into the parametric coordinates \(\left(8 t^2, 16 t\right)\) :
\(x\)-coordinate: \(8(2)^2=8 \times 4=32\)
\(y\)-coordinate: \(16(2)=32\)
The other end of the focal chord is \((32,32)\).

0ther Standard Forms of Parabola

We observe that there are three other standard forms of parabola viz. \(y^2=-4 a x, x^2=4 a y\) and \(x^2=-4 a y\) depending upon the choice of the axes. Thus, in all there are four standard forms. The shapes of the curves in these four standard forms and their corresponding results are as follows:

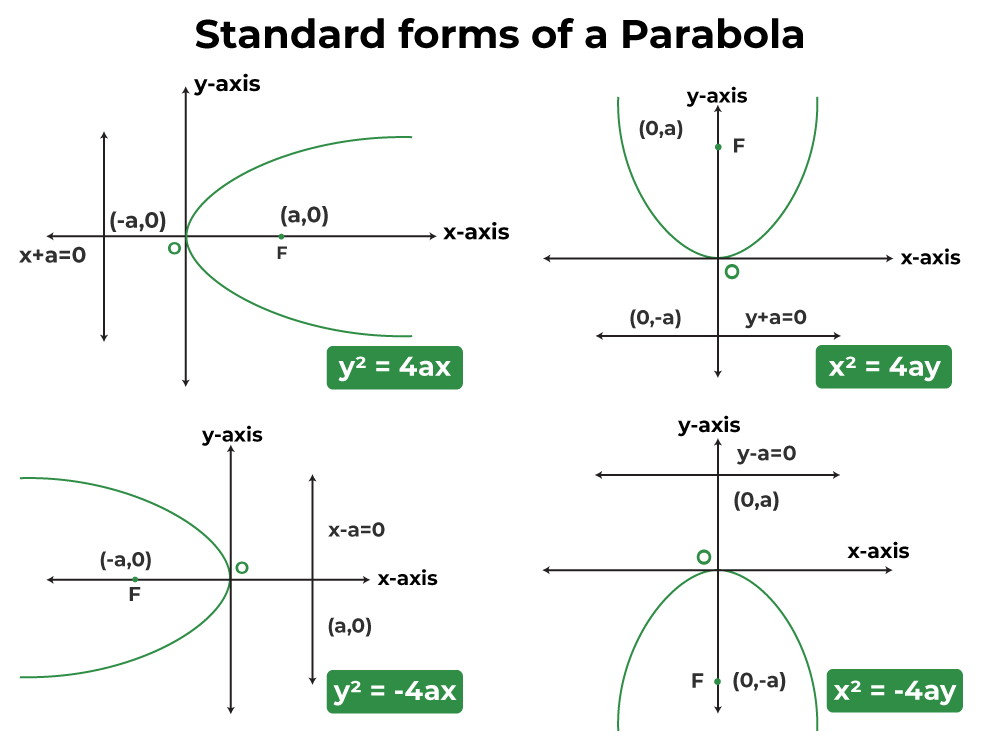
Table below shows the various parameters of a parabola.
\(
\begin{array}{|l|l|l|l|l|}
\hline \text { Standard form } & y^2=4 a x & y^2=-4 a x & x^2=4 a y & x^2=-4 a y \\
\hline \text { Coordinates of vertex } & (0,0) & (0,0) & (0,0) & (0,0) \\
\hline \text { Coordinates of focus } & (a, 0) & (-a, 0) & (0, a) & (0,-a) \\
\hline \text { Equation of the directrix } & x=-a & x=a & y=-a & y=a \\
\hline \text { Equation of the axis } & y=0 & y=0 & x=0 & x=0 \\
\hline \text { Length of the Latusrectum } & 4 a & 4 a & 4 a & 4 a \\
\hline \begin{array}{l}
\text { Focal distance of a point } \\
P(x, y)
\end{array} & x+a & a-x & y+a & a-y \\
\hline
\end{array}
\)

Example 3: If the parabola \(y^2=4ax\) passes through \((3,2)\), then the length of its latusrectum, is
(a) \(2 / 3\)
(b) \(4 / 3\)
(c) \(1 / 3\)
(d) 4

Solution: (b) Step 1: Understanding the Equation
The given equation is \(y^2=4 a x\). In any parabola of this form:
The coefficient of \(x\) (which is \(4 a\)) is defined as the length of the latus rectum.
The latus rectum is the chord passing through the focus perpendicular to the axis of symmetry.
Step 2: Substituting the Point
Since the parabola passes through the point ( 3,2 ), this point must satisfy the equation. We substitute \(x=3\) and \(y=2\) into \(y^2=4 a x\) :
\(
\begin{gathered}
(2)^2=4 a(3) \\
4=12 a
\end{gathered}
\)
Step 3: Calculating the Length
We are looking for the length of the latus rectum, which is \({4}{a}\). We can solve for \({4}{a}\) directly from the step above:
\(
\begin{gathered}
4=(4 a) \times 3 \\
\frac{4}{3}=4 a
\end{gathered}
\)
The length of the latus rectum is \(4 / 3\).

Example 4: Find the equation of a parabola
i. having its vertex at \(A(1,0)\) and focus at \(S(3,0)\)
ii. having its focus at \(S(2,0)\) and one extremity of its latus rectum as \((2,2)\)
iii. having focus at \((0,-3)\) and its directrix is \(y=3\)

Solution: (i) Vertex \(A(1,0)\) and Focus \(S(3,0)\)
Identify the Orientation: Since the \(y\)-coordinates of the vertex and focus are the same (\(y=0\)), the axis of symmetry is horizontal. The focus is to the right of the vertex, so the parabola opens to the right.
Find \(a\) : The distance between the vertex and the focus is \(a\).
\(a=3-1=2\)
Apply the Equation: The standard form for a right-opening parabola with vertex (\(h, k\)) is \((y-k)^2=4 a(x-h)\).
Substitute \(h=1, k=0\), and \(a=2\) :
\((y-0)^2=4(2)(x-1)\)
\(y^2=8(x-1)\) or \(y^2=8 x-8\)
(ii) Focus \(S(2,0)\) and extremity of latus rectum \((2,2)\)
Identify the Orientation: The latus rectum is a vertical line passing through \((2,0)\) and \((2,2)\). Since the latus rectum is vertical, the axis of symmetry must be horizontal.
Find the Latus Rectum Length: The distance from the focus ( 2,0 ) to one extremity \((2,2)\) is half the length of the latus rectum.
Half-length \(=2-0=2\)
Total length of latus rectum \((4 a)=2 \times 2=4\).
Therefore, \(4 a=4\), which means \(a=1\).
Find the Vertex: Since the parabola opens toward the focus and \(a=1\), the vertex must be 1 unit to the left of the focus \((2,0)\).
\(\operatorname{Vertex}(h, k)=(2-1,0)=(1,0)\).
Apply the Equation: \((y-k)^2=4 a(x-h)\)
\((y-0)^2=4(1)(x-1)\)
\(y^2=4(x-1)\) or \(y^2=4 x-4\)
(iii) Focus \((0,-3)\) and Directrix \(y=3\)

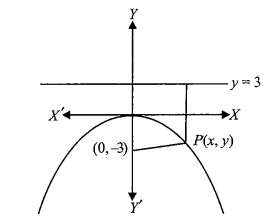
Identify the Orientation: The focus is on the \(y\)-axis and the directrix is a horizontal line (\(y=3\)). Since the focus is below the directrix, the parabola opens downward.
Let \(P(x, y)\) be any point on the parabola.
Then by definition \(\sqrt{(x-0)^2+(y+3)^2}=y-3\)
\(
\Rightarrow \quad x^2=-12 y
\)

Example 5: Find the coordinates of a point on the parabola \(y^2=8 x\) whose focal distance is 4.

Solution: Step 1: Identify the Parabola Parameters
The given equation is \(y^2=8 x\). Comparing this to the standard form \(y^2=4 a x\) :
\(4 a=8\)
\(a=2\)
For this parabola, the focus is at \(S(2,0)\) and the directrix is the line \(x=-2\).
Step 2: Understanding Focal Distance
The focal distance of any point \(P(x, y)\) on a parabola is the distance from the point to the focus \(S\). By the definition of a parabola (the distance from the focus equals the distance from the directrix), the focal distance is also equal to the distance of the point \(P\) from the directrix \(x=-a\).
For \(y^2=4 a x\), the focal distance formula is:
\(
\text { Focal Distance }=x+a
\)
Step 3: Solve for \(x\)
We are given that the focal distance is 4. Using the formula \(x+a=4\) :
\(x+2=4\)
\(x=2\)
Step 4: Find the \(y\)-coordinates
Now, substitute \(x=2\) back into the original parabola equation \(y^2=8 x\) to find the corresponding \(y\) values:
\(y^2=8(2)\)
\(y^2=16\)
\(y= \pm 4\)
The coordinates of the points on the parabola whose focal distance is 4 are: \((2,4)\) and \((2,-4)\)

Example 6: If the vertex of a parabola is the point \((-3,0)\) and the directrix is the line \(x+5=0\), then find its equation.

Solution: Step 1: Identify the Orientation
Vertex (V): \((-3,0)\)
Directrix: \(x+5=0\), which simplifies to \(x=-5\).
The directrix is a vertical line. Since the vertex lies to the right of the directrix (\(-3>-5\)), the parabola must open to the right. This means the axis of symmetry is horizontal (\(y=0\)).
Step 2: Find the value of \(a\)
The parameter \(a\) is the distance between the vertex and the directrix (or the vertex and the focus).
Distance \(a=\left|x_{\text {vertex }}-x_{\text {directrix }}\right|\)
\(a=|-3-(-5)|\)
\(a=2\)
Step 3: Formulate the Equation
For a parabola opening to the right with vertex (\(h, k\)), the standard equation is:
\(
(y-k)^2=4 a(x-h)
\)
Substitute the values:
\(h=-3\)
\(k=0\)
\(a=2\)
\(
\begin{gathered}
(y-0)^2=4(2)(x-(-3)) \\
y^2=8(x+3)
\end{gathered}
\)
Final Expanded Form:
\(
y^2=8 x+24
\)

Example 7: The equation of the parabola whose focus is the point \((0,0)\) and the tangent at the vertex is \(x-y+1=0\), is [JEE (Orissa) 2002]
(a) \(x^2+y^2-2 x y-4 x+4 y-4=0\)
(b) \(x^2+y^2-2 x y+4 x-4 y-4=0\)
(c) \(x^2+y^2+2 x y-4 x+4 y-4=0\)
(d) \(x^2+y^2+2 x y-4 x-4 y+4=0\)

Solution: (c) To solve this, we use the property that the distance of any point \(P(x, y)\) from the focus is equal to its distance from the directrix.
Step 1: Find the Vertex and Directrix
Focus \((S):(0,0)\)
Tangent at Vertex (TV): \(x-y+1=0\)
The axis of symmetry is perpendicular to the tangent at the vertex and passes through the focus. However, we can use a simpler geometric relationship: the vertex (\(V\)) is the foot of the perpendicular from the focus to the tangent at the vertex.
The distance from the focus \((0,0)\) to the Tangent at Vertex is \(a\) :
\(
a=\frac{|0-0+1|}{\sqrt{1^2+(-1)^2}}=\frac{1}{\sqrt{2}}
\)
Since the vertex is exactly halfway between the focus and the directrix, the directrix is a line parallel to the tangent at the vertex, but twice as far from the focus.
Equation of Tangent at Vertex: \(x-y+1=0\)
Equation of Directrix: \(x-y+k=0\)
Since the distance from the focus \((0,0)\) to the directrix must be \(2 a=\sqrt{2}\) :
\(
\frac{|0-0+k|}{\sqrt{2}}=\sqrt{2} \Longrightarrow|k|=2
\)
Because the tangent at the vertex (\(k=1\)) lies between the focus (\(k=0\)) and the directrix, \(k\) must be 2. Directrix Equation: \(x-y+2=0\)
Step 2: Use the Parabola Definition ( \(S P=P M\) )

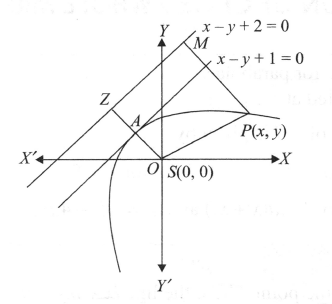
Let \(P(x, y)\) be any point on the parabola. The distance from \(S(0,0)\) to \(P\) equals the perpendicular distance from \(P\) to the directrix \(x-y+2=0\).
\(
\sqrt{x^2+y^2}=\frac{|x-y+2|}{\sqrt{1^2+(-1)^2}}
\)
Square both sides:
\(
\begin{gathered}
x^2+y^2=\frac{(x-y+2)^2}{2} \\
2\left(x^2+y^2\right)=(x-y)^2+2(x-y)(2)+4 \\
2 x^2+2 y^2=x^2+y^2-2 x y+4 x-4 y+4
\end{gathered}
\)
Rearrange all terms to one side:
\(
\begin{gathered}
\left(2 x^2-x^2\right)+\left(2 y^2-y^2\right)+2 x y-4 x+4 y-4=0 \\
x^2+y^2+2 x y-4 x+4 y-4=0
\end{gathered}
\)

Position of a Point With Respect to a Parabola \(y^2=4 a x\)

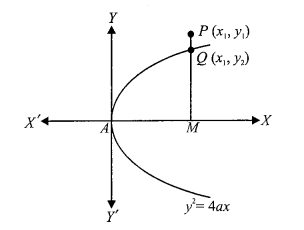
Let \(P\left(x_1, y_1\right)\) be a point in the plane (in 1st or 4th quadrant) From \(P\) draw \(P M \perp A X\), meeting the parabola \(y^2=4 a x\) at \(Q\). Then the coordinates of \(Q\) be \(\left(x_1, y_2\right)\). Since \(Q\) lies on the parabola, we have \(y_2^2=4 a x_1\)
Now, point \(\left(x_1, y_1\right)\) will be outside, on or inside the parabola \(y^2=4 a x\) according to
\(
\begin{gathered}
P M>,=\text { or }<Q M \\
P M^2>,=\text { or }<Q M^2
\end{gathered}
\)
\(
\begin{aligned}
& y_1^2>,=\text { or }<y_2^2 \\
& y_1^2>,=\text { or }<4 a x_1
\end{aligned}
\)
For \(P\) lying in 3rd or 4th quadrant, \(y_1^2-4 a x_1>0\left(\because x_1<0\right)\)

Example 8: The equation of a parabola is \({y}^2={4}{x}\). \(P(1,3)\) and \(Q(1,1)\) are two points in the \(x y\) plane. Then, for the parabola
a. \(P\) and \(Q\) are exterior points
b. \(P\) is an interior point while \(Q\) is an exterior point
c. \(P\) and \(Q\) are interior points
d. \(P\) is an exterior point while \(Q\) is an interior point

Solution: (d) To determine the position of points \(P\) and \(Q\) relative to the parabola \(y^2=4 x\), we use the Power of the Point \(\left(S_1\right)\).
Step 1: Define the Parabola Function
For the parabola \(y^2=4 x\), we define the function \(S\) as:
\(
S_1=y^2-4 x
\)
Recall the rules for the sign of \(S_1\) :
If \(S_1>0\), the point is exterior (outside).
If \(S_1<0\), the point is interior (inside).
If \(S_1=0\), the point is on the parabola.
Step 2: Test Point \(P(1,3)\)
Substitute \(x=1\) and \(y=3\) into the function:
\(
\begin{aligned}
& S_1=(3)^2-4(1) \\
& S_1=9-4=5
\end{aligned}
\)
Since \(S_1>0\), point \(P\) is an exterior point.
Step 3: Test Point \(Q(1,1)\)
Substitute \(x=1\) and \(y=1\) into the function:
\(
\begin{aligned}
& S_1=(1)^2-4(1) \\
& S_1=1-4=-3
\end{aligned}
\)
Since \(S_1<0\), point \(Q\) is an interior point.
Conclusion
\(P\) is an exterior point.
\(Q\) is an interior point.
Looking at the options provided, the correct match is (d).

Example 9: The point \((a, 2 a)\) is an interior point of the region bounded by the parabola \(y^2=16 x\) and the double ordinate through the focus. Then find the values of \(a\).

Solution: Step 1: Identify the Boundaries of the Region

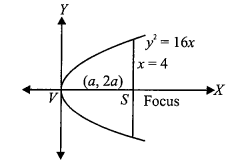
The parabola is given by \(y^2=16 x\). Comparing this to the standard form \(y^2=4 a x\), we find \(4 a=16\), which gives \(a=4\). The focus of this parabola is at \((a, 0)=(4,0)\). The double ordinate through the focus is the vertical line passing through the focus, which is \(x=4\). The region is thus bounded by the curve \(y^2=16 x\) and the line \(x=4\)
Step 2: Apply Interior Conditions for the Parabola
For a point \(\left(x_1, y_1\right)\) to lie inside a parabola \(y^2-4 a x=0\), the expression \(y_1^2-4 a x_1\) must be less than zero. Substituting the point (\(a, 2 a\)) into the parabola’s equation:
\(
\begin{gathered}
(2 a)^2-16(a)<0 \\
4 a^2-16 a<0 \\
4 a(a-4)<0
\end{gathered}
\)
Dividing by 4 , we get \(a(a-4)<0\). This inequality holds when \(a\) is between the roots of the quadratic:
\(
0<a<4
\)
Step 3: Apply the Boundary Condition for the Double Ordinate
The region is bounded by the line \(x=4\). Since the parabola opens to the right and is bounded by this line, any interior point must satisfy the condition \(x<4\). For the point (\(a, 2 a\)), this implies:
\(
a<4
\)
Combining the results from Step \(2(0<a<4)\) and Step \(3(a<4)\), the intersection of these conditions is \(0<a<4\).
The values of \(a\) are in the interval \((0,4)\), or expressed as \(0<a<4\).

Equation of Parabola When Vertex is (\(h, k\)) and Axis is Parallel to \(x\)-Axis

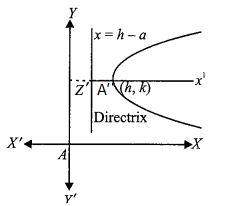
The parabola
\(
y^2=4 a x \dots(i)
\)
can be written as
\(
(y-0)^2=4 a(x-0)
\)
The vertex of this parabola is \(A(0,0)\).
Now when origin is shifted to \(A^{\prime}(h, k)\) without changing the direction of axes, its equation becomes
\(
(y-k)^2=4 a(x-h) \dots(ii)
\)
This is called general form of the parabola Eq. (i) and axis \(A^{\prime} X^{\prime} \| A X\) with its vertex at \(A^{\prime}(h, k)\). Its focus is at \((a+h, k)\) and length of latus rectum \(=4 a\).
The equation of the directrix is
\(
x=h-a
\)
\(
x+a-h=0
\)

Example 10: Find the equation of the parabola with vertex (\(2,-3\)) and focus (\(5,-3\)).

Solution: Identify \(h\) and \(k: h=2, k=-3\).
Find \(a\) : The distance between the vertex \((2,-3)\) and focus \((5,-3)\) is \(a=5-2=3\).
Plug into the formula:
\(
\begin{gathered}
(y-(-3))^2=4(3)(x-2) \\
(y+3)^2=12(x-2)
\end{gathered}
\)

Equation of Parabola When Vertex is \((h, k)\) and Axis is Parallel to \(y\)-Axis

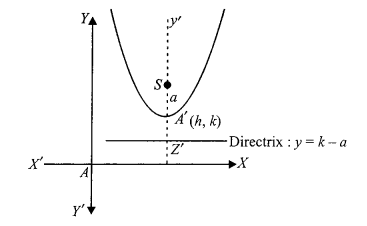
The equation of parabola with vertex \((h, k)\) is
\(
(x-h)^2=4 a(y-k)
\)
Its focus is at \((h, a+k)\) and length of latus rectum \(=4 a\).
The equation of the directrix is
\(
y=k-a
\)
\(
y+a-k=0
\)

Example 11: Find the equation of a parabola with vertex \((1,2)\) and focus \((1,5)\).

Solution: Identify \(h\) and \(k: h=1, k=2\).
Find \(a\) : The change is in the \(y\)-direction. \(a=5-2=3\).
Plug into the formula:
\(
\begin{gathered}
(x-1)^2=4(3)(y-2) \\
(x-1)^2=12(y-2)
\end{gathered}
\)

Parabolic Curve

The equations \(y=A x^2+B x+C\) and \(x=A y^2+B y+C(A \neq 0)\) represent parabola and are called parabolic curve.
Now,
\(
\begin{aligned}
y & =A x^2+B x+C \\
& =A\left\{x^2+\frac{B}{A} x+\frac{C}{A}\right\} \\
& =A\left\{\left(x+\frac{B}{2 A}\right)^2-\frac{B^2}{4 A^2}+\frac{C}{A}\right\} \\
& =A\left\{\left(x+\frac{B}{2 A}\right)^2-\frac{\left(B^2-4 A C\right)}{4 A^2}\right\} \\
\left(x+\frac{B}{2 A}\right)^2 & =\frac{1}{A}\left(y+\frac{B^2-4 A C}{4 A}\right)
\end{aligned}
\)
Comparing it with \((x-h)^2=4 a(y-k)\) it represents a parabola with vertex at \((h, k) \equiv\left(-\frac{B}{2 A},-\frac{B^2-4 A C}{4 A}\right)\), axis parallel to \(y\)-axis, latus rectum \(=\frac{1}{|A|}\) and the curve opening upwards and downwards depending upon the sign of \(A\) (for \(A>0\) curve opens upward, for \(A<0\) curve opens downward).
Similarly, \(x=A y^2+B y+C\) can be simplified to
\(
\left(y+\frac{B}{2 A}\right)^2=\frac{1}{A}\left(x+\frac{B^2-4 A C}{4 A}\right)
\)
Comparing it with \((y-k)^2=4 a(x-h)\) it represents a parabola with vertex at \((h, k) \equiv\left(-\frac{B^2-4 A C}{4 A},-\frac{B}{2 A}\right)\) axis parallel to \(x\)-axis and latus rectum \(=\frac{1}{|A|}\) and the curve opening left and right according to \(A<0\) and \(A>0\) respectively.

Note: Parametric form of the parabola \((y-k)^2=4 a(x-h)\) is \(x=h+a t^2\) and \(y=k+2 a t\).

Example 12: \(y^2+2 y-x+5=0\) represents a parabola. Find its vertex, equation of axis, equation of latus rectum, coordinates of the focus, equation of the directrix, extremities of the latus rectum and the length of the latus rectum.

Solution: To solve this, we first need to convert the general equation into the standard form \((y-k)^2= 4 a(x-h)\) by completing the square for the \(y\) terms.

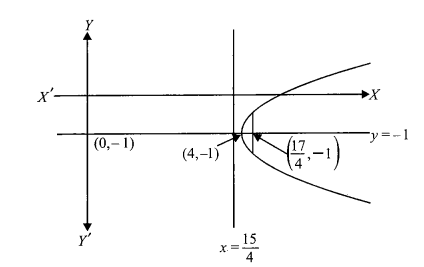
Step 1: Convert to Standard Form
Given equation: \(y^2+2 y-x+5=0\)
Keep the \(y\) terms on one side and move everything else to the right:
\(
y^2+2 y=x-5
\)
Complete the square for \(y^2+2 y\) by adding \(\left(\frac{2}{2}\right)^2=1\) to both sides:
\(
\begin{gathered}
y^2+2 y+1=x-5+1 \\
(y+1)^2=x-4
\end{gathered}
\)
Write it in the form \((y-k)^2=4 a(x-h)\) :
\(
(y-(-1))^2=1 \cdot(x-4)
\)
Step 2: Identify the Parameters
Comparing \((y+1)^2=1(x-4)\) with the standard form:
Vertex \((h, k):(4,-1)\)
\(4 a=1 \Longrightarrow a=\frac{1}{4}\)
Direction: Since \(a\) is positive and the \(y\) term is squared, the parabola opens to the right.
Step 3: Calculate the Properties
Using the value \(a=\frac{1}{4}, h=4\), and \(k=-1\) :
\(
\begin{array}{lll}
\text { Property } & \text { Formula / Logic } & \text { Result } \\
\text { Vertex } & (h, k) & (4,-1) \\
\text { Length of Latus Rectum } & L & 4 a \\
\text { Equation of Axis } & y=k & y=-1 \\
\text { Coordinates of Focus } & (h+a, k)=\left(4+\frac{1}{4},-1\right) & \left(\frac{17}{4},-1\right) \\
\text { Equation of Directrix } & x=h-a=4-\frac{1}{4} & x=\frac{15}{4} \text { or } 4 x-15=0 \\
\text { Equation of Latus Rectum } & x=h+a & x=\frac{17}{4} \text { or } 4 x-17=0 \\
\text { Extremities of Latus Rectum } & (h+a, k \pm 2 a)=\left(\frac{17}{4},-1 \pm \frac{1}{2}\right) & \left(\frac{17}{4},-\frac{1}{2}\right) \text { and }\left(\frac{17}{4},-\frac{3}{2}\right)
\end{array}
\)

Example 13: Find the equation of parabola which has axis parallel to \(y\)-axis and which passes through points \((0,2),(-1,0)\) and \((1,6)\).

Solution: General equation of such parabola is
\(
y=A x^2+B x+C
\)
It passes through points \((0,2),(-1,0)\) and \((1,6)\). Then we have,
\(
\begin{aligned}
C & =2 \dots(i) \\
A-B+C & =0 \dots(ii) \\
A+B+C & =6 \dots(iii)
\end{aligned}
\)
Solving (i), (ii) and (iii) we get \(C=2, A=1\) and \(B=3\).
Hence equation of parabola is
\(
y=x^2+3 x+2
\)

Example 14: The parametric equation of a parabola is \(x=t^2+1, y=2 t+1\). Then find the equation of directrix.

Solution: To find the equation of the directrix from the parametric equations, we first need to convert them into the standard Cartesian form \((y-k)^2=4 a(x-h)\).
Step 1: Eliminate the Parameter \(t\)
We have:
\(x=t^2+1 \Longrightarrow t^2=x-1\)
\(y=2 t+1 \Longrightarrow 2 t=y-1 \Longrightarrow t=\frac{y-1}{2}\)
Now, substitute the value of \(t\) from the second equation into the first:
\(
\begin{aligned}
& x-1=\left(\frac{y-1}{2}\right)^2 \\
& x-1=\frac{(y-1)^2}{4}
\end{aligned}
\)
Step 2: Standard Form
Rearranging the equation gives us:
\(
(y-1)^2=4(x-1)
\)
Step 3: Identify the Parameter
Comparing this to the standard form \((y-k)^2=4 a(x-h)\) :
Vertex \((h, k):(1,1)\)
\(4 a=4 \Longrightarrow a=1\)
Since the \(y\) term is squared and \(a\) is positive, this is a horizontal parabola opening to the right.
Step 4: Find the Equation of the Directrix
For a parabola opening to the right with vertex (\(h, k\)), the directrix is a vertical line located \(a\) units to the left of the vertex.
Formula: \(x=h-a\)
Calculation: \(x=1-1\)
Result: \(x=0\)
\(
\begin{array}{ll}
\text { Vertex } & (1,1) \\
\text { Focal Length }(a) & 1 \\
\text { Focus } & (2,1) \\
\text { Directrix } & x=0 \text { (the } \mathbf{y} \text {-axis) }
\end{array}
\)

Example 15: Find the points on the parabola \(y^2-2 y-4 x =0\) whose focal length is 6.

Solution: To find the points on the parabola \(y^2-2 y-4 x=0\) with a focal length (focal distance) of 6 , we first need to convert the equation into standard form to identify the vertex and the focal parameter \(a\).
Step 1: Convert to Standard Form
We complete the square for the \(y\) terms:
\(y^2-2 y=4 x\)
Add \(\left(\frac{-2}{2}\right)^2=1\) to both sides:
\(
\begin{aligned}
& y^2-2 y+1=4 x+1 \\
& (y-1)^2=4(x+1 / 4)
\end{aligned}
\)
Comparing this to \((y-k)^2=4 a(x-h)\) :
Vertex \((h, k)\) : \((-1 / 4,1)\)
\(4 a=4 \Longrightarrow a=1\)
Step 2: Use the Focal Distance Formula
For a parabola opening to the right, the focal distance of a point \(P(x, y)\) is given by the distance from the point to the directrix, which simplifies to:
\(
\text { Focal Distance }=(x-h)+a
\)
Given that the focal distance is 6 :
\(
6=(x-(-1 / 4))+1
\)
\(
x=\frac{19}{4}
\)
Step 3: Find the \(y\)-coordinates
Substitute \(x=\frac{19}{4}\) into the simplified equation \((y-1)^2=4 x+1\) :
\(
(y-1)^2=4\left(\frac{19}{4}\right)+1
\)
\(
y=1 \pm 2 \sqrt{5}
\)
The coordinates of the points are: \(\left(\frac{19}{4}, 1+2 \sqrt{5}\right)\) and \(\left(\frac{19}{4}, 1-2 \sqrt{5}\right)\)
\(
\begin{array}{ll}
\text { Standard Form } & (y-1)^2=4(x+1 / 4) \\
\text { Focal Parameter }(a) & 1 \\
x \text {-coordinate } & 19 / 4 \\
y \text {-coordinates } & 1 \pm 2 \sqrt{5}
\end{array}
\)

Example 16: If the length of chord of circle \(x^2+y^2=4\) and \(y^2=4(x-h)\) is maximum, then find the value of \(h\).

Solution: To find the value of \(h\) that maximizes the length of the common chord, we need to analyze the intersection of the circle and the parabola.

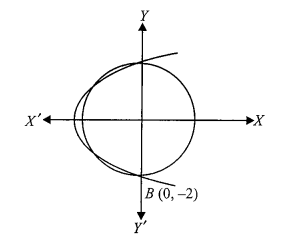
Step 1: Identify the Curves
Circle: \(x^2+y^2=4\)
Center: \((0,0)\), Radius: 2.
Parabola: \(y^2=4(x-h)\)
Vertex: (\(h, 0\)), opens to the right.
Step 2: Find the Intersection (Common Chord)
The common chord is a vertical line formed by the intersection points of the two curves. To find where they meet, we substitute the parabola’s equation (\(y^2=4 x-4 h\)) into the circle’s equation:
\(
\begin{gathered}
x^2+(4 x-4 h)=4 \\
x^2+4 x-4 h-4=0
\end{gathered}
\)
Using the quadratic formula to solve for \(x\) :
\(
x=\frac{-4 \pm \sqrt{16-4(1)(-4 h-4)}}{2}
\)
\(
x=\frac{-4 \pm \sqrt{16+16 h+16}}{2}=\frac{-4 \pm \sqrt{32+16 h}}{2}=-2 \pm 2 \sqrt{2+h}
\)
Since the parabola \(y^2=4(x-h)\) only exists for \(x \geq h\), we typically look for the intersection point where \(x\) is positive or within the circle’s bounds.
STep 3: Maximize the Chord Length
The length of a vertical chord in a circle \(x^2+y^2=r^2\) is \(L=2 y\). The length is maximum when the chord is the diameter of the circle.
For the common chord to be a diameter:
The chord must pass through the center of the circle \((0,0)\).
Therefore, the \(x\)-coordinate of the intersection must be \(x=0\).
Substitute \(x=0\) into our intersection quadratic:
\(
0^2+4(0)-4 h-4=0
\)
\(
h=-1
\)
Step 4: Verification
If \(h=-1\), the parabola is \(y^2=4(x+1)\). At \(x=0\) (the \(y\)-axis), \(y^2=4(1) \Longrightarrow y= \pm 2\). The points of intersection are \((0,2)\) and \((0,-2)\). These are the endpoints of the vertical diameter of the circle \(x^2+y^2=4\). Since the diameter is the longest possible chord in a circle, the length is maximized.

General Equation of a Parabola

Let \(S(a, b)\) be the focus and \(l x+m y+n=0\) is the equation of the directrix.
Let \(P(x, y)\) be any point on the parabola.

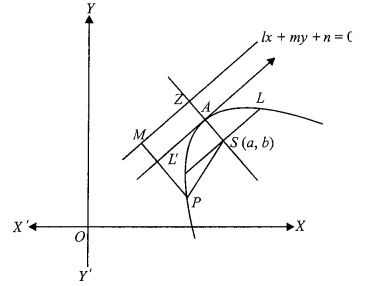
By definition,
\(
\begin{gathered}
S P=P M \\
\Rightarrow \quad \sqrt{(x-a)^2+(y-b)^2}=\frac{|l x+m y+n|}{\sqrt{\left(l^2+m^2\right)}} \\
\Rightarrow \quad(x-a)^2+(y-b)^2=\frac{(l x+m y+n)^2}{\left(l^2+m^2\right)} \\
\Rightarrow \quad m^2 x^2+l^2 y^2-2 l m x y+x \text { term }+y \text { term }+ \text { constant }=0
\end{gathered}
\)
This is of the form \((m x-l y)^2+2 g x+2 f y+c=0\)
This equation is the general equation of parabola.

Recognition of Conics

The equation of conics represented by the general equation of second degree
\(
a x^2+2 h x y+b y^2+2 g x+2 f y+c=0 \dots(i)
\)
can be recognized easily by the condition given in the tabular form. For this, first we have to find \(\Delta=a b c+2 f g h-a f^2-b g^2 -c h^2\). When \(\Delta \neq 0\), Eq. (i) represents the non-degenerate conic whose nature is given in the following table:
\(
\begin{array}{|l|l|}
\hline \begin{array}{l}
\hline \text { Condition } & \text { Nature of conics } \\
\hline \Delta \neq 0, h=0, a=b & \text { A circle } \\
\Delta \neq 0, a b-h^2=0(\because \text { 2nd degree } \\
\text { terms form a perfect square })
\end{array} & \text { A parabola } \\
\hline \Delta \neq 0, a b-h^2>0 & \text { An ellipse or empty set } \\
\hline \Delta \neq 0, a b-h^2<0 & \text { A hyperbola } \\
\hline \Delta \neq 0, a b-h^2<0 \text { and } a+b=0 & \text { A rectangular hyperbola } \\
\hline
\end{array}
\)

Example 17: Find the value of \(\lambda\) if equation \(9 x^2+4 y^2+ 2 \lambda x y+4 x-2 y+3=0\) represents parabola.

Solution: Comparing this equation with \(a x^2+b y^2+2 h x y+2 g x+ 2 f y+c=0\) we have \(a=9, b=4, c=3, h=\lambda, g=2, f=-\) 1.
If the equation \(9 x^2+4 y^2+2 \lambda x y+4 x-2 y+3=0\) represents the parabola then its second degree terms must form the perfect square.
\(
\begin{aligned}
& \Rightarrow \lambda^2=36\left(\text { using } h^2-a b=0\right) \\
& \Rightarrow \lambda= \pm 6
\end{aligned}
\)
Also for these values of \(\lambda, \Delta \neq 0\).

Explanation: The Algebraic Reason: The Perfect Square
In the general equation \(a x^2+2 h x y+b y^2+2 g x+2 f y+c=0\), the terms \(a x^2+ 2 h x y+b y^2\) determine the “shape” of the conic at infinity.
For a parabola, these terms must be expressible as a square of a linear expression, such as \((\alpha x+\beta y)^2\). Let’s expand that:
\(
(\alpha x+\beta y)^2=\alpha^2 x^2+2 \alpha \beta x y+\beta^2 y^2
\)
Comparing this to \(a x^2+2 h x y+b y^2\) :
\(a=\alpha^2\)
\(b=\beta^2\)
\(h=\alpha \beta\)
Now, look what happens when we calculate \(h^2\) :
\(
h^2=(\alpha \beta)^2=\alpha^2 \beta^2
\)
Since \(a=\alpha^2\) and \(b=\beta^2\), it follows that:
\(
h^2=a b
\)

Example 18: Find the equation to the parabola whose focus is \(S(-1,1)\) and directrix is \(4 x+3 y-24=0\). Also find its axis, the vertex, the length and the equation of the latus rectum.

Solution: Let \(P(x, y)\) be any point on the parabola. Since the distance of \(P\) from the focus is equal to its distance from the directrix, i.e., \(P S=P Q\) or \(P S^2=P Q^2\)
\(
\begin{aligned}
& \text { or } \quad(x+1)^2+(y-1)^2=\left[\frac{(4 x+3 y-24)}{5}\right]^2 \\
& \text { i.e., } 9 x^2+16 y^2-24 x y+242 x+94 y-526=0 \dots(i)
\end{aligned}
\)
This is the required equation of the parabola.

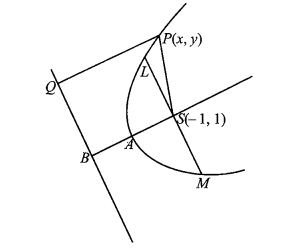
The axis is a line through \(S(-1,1)\) and ⟂ to the directrix \(4 x+3 y-24=0\). Thus the equation of the axis is
\(
3(x+1)-4(y-1)=0 \text { or } 3 x-4 y+7=0 \dots(ii)
\)
The axis and the directrix intersect at \(B\). Solving them, we get \(B(3,4)\).
The vertex \(A\) is the midpoint of \(S(-1,1)\) and \(B(3,4)\)
Thus vertex \(A\) is \(\left(1, \frac{5}{2}\right) \dots(iii)\)
Also
\(
A S=\sqrt{\left[2^2+\left(\frac{3}{2}\right)^2\right]}=\frac{5}{2}
\)
Hence length of the latus rectum \(=4 A S=10 \dots(iv)\)
Now, latus rectum is a straight line through the focus \(S\) and parallel to the directrix.
Hence its equation is \(4 x+3 y+1=0\)

Example 19: Circles are drawn with diameter being any focal chord of the parabola \(y^2-4 x-y-4=0\) will always touch a fixed line, find its equation.

Solution: A fundamental property of parabolas states that any circle drawn with a focal chord as its diameter will always touch the directrix of that parabola. To find the equation of this fixed line, we must find the equation of the directrix for the given parabola \(y^2-4 x-y-4=0\).
Step 1: Rewrite in standard form
Convert the given equation into the standard form of a parabola \((y-k)^2=4 a(x-h)\) by completing the square for the \(y\) terms:
\(
\begin{gathered}
y^2-y=4 x+4 \\
\left(y-\frac{1}{2}\right)^2-\frac{1}{4}=4 x+4
\end{gathered}
\)
\(
\left(y-\frac{1}{2}\right)^2=4\left(x+\frac{17}{16}\right)
\)
Step 2: Identify parabola parameters
Comparing this to the standard form \((y-k)^2=4 a(x-h)\), we identify:
\(a=1\)
\(h=-\frac{17}{16}\)
\(k=\frac{1}{2}\)
Step 3: Determine the directrix equation
The directrix of a right-opening parabola is given by the formula \(x=h-a\) :
\(
\begin{aligned}
& x=-\frac{17}{16}-1 \\
& x=-\frac{17+16}{16}
\end{aligned}
\)
\(
x=-\frac{33}{16}
\)
Multiplying by 16 to clear the fraction, we get \(16 x=-33\).
The fixed line is the directrix of the parabola, and its equation is \(\mathbf{1 6 x + 3 3 = 0}\)

Intersection of a Line and a Parabola

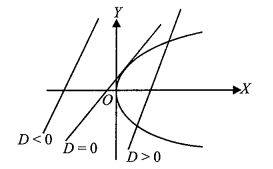
To understand the intersection of a line and a parabola, we typically use the standard horizontal parabola \(y^2=4 a x\) and a line in slope-intercept form \(y=m x+c\).
Step 1: The Algebraic Approach
To find the intersection points, we substitute the equation of the line into the equation of the parabola:
\(
\begin{gathered}
(m x+c)^2=4 a x \\
m^2 x^2+2 m c x+c^2=4 a x \\
m^2 x^2+(2 m c-4 a) x+c^2=0
\end{gathered}
\)
This results in a quadratic equation in terms of \(x\). The nature of the roots of this quadratic (using the discriminant \(D=B^2-4 A C\) ) tells us how the line and parabola interact.
Step 2: Three Possible Scenarios
The relationship between the line and the parabola depends on the value of the discriminant:
\(
\begin{array}{lll}
\text { Condition } & \text { Discriminant }(D) & \text { Interaction } \\
c>a / m & D>0 & \text { The line is a Secant (intersects at two distinct points). } \\
c=a / m & D=0 & \text { The line is a Tangent (touches at exactly one point). } \\
c<a / m & D<0 & \text { The line does not intersect the parabola. }
\end{array}
\)
Step 3: The Condition of Tangency
The most important result in this topic is the condition for a line \(y=m x+c\) to be a tangent to the parabola \(y^2=4 a x\) :
\(
c=\frac{a}{m}
\)
If this condition is met, the point of contact is given by:
\(
\left(\frac{a}{m^2}, \frac{2 a}{m}\right)
\)
Step 4: Intersection with Vertical Parabolas
If the parabola is vertical (\(x^2=4 a y\)) and the line is \(y=m x+c\), the substitution yields a quadratic in \(x\) :
\(
\begin{gathered}
x^2=4 a(m x+c) \\
x^2-4 a m x-4 a c=0
\end{gathered}
\)
In this case, the condition for tangency becomes:
\(
c=-a m^2
\)

Example 20: If the line \(x+y-1=0\) touches the parabola \(y^2=k x\), then the value of \(k\), is
(a) 4
(b) -4
(c) 2
(d) -2

Solution: (b) To solve this, we use the condition of tangency for a parabola.
Step 1: Identify the Parameters
First, let’s put the line and the parabola into their standard forms:
Parabola: \(y^2=k x\)
Comparing this to \(y^2=4 a x\), we find that \(4 a=k\), so \(a=k / 4\).
Line: \(x+y-1=0\)
Rearranging into \(y=m x+c\) form: \(y=-x+1\).
Here, \(m=-1\) and \(c=1\).
Step 2: Apply the Condition of Tangency
For the line \(y=m x+c\) to touch the parabola \(y^2=4 a x\), the constant \(c\) must satisfy:
\(
c=\frac{a}{m}
\)
Substituting our values into this formula:
\(
1=\frac{k / 4}{-1}
\)
Step 3: Solve for \(k\)
\(
\begin{aligned}
& 1=-\frac{k}{4} \\
& k=-4
\end{aligned}
\)

Equation of Tangent

Equation of Tangent at Point \(P\left(x_1, y_1\right)\) to Parabola \(y^2=4 a x\)

To find the equation of the tangent at a specific point \(P\left(x_1, y_1\right)\) on the parabola \(y^2=4 a x\), we can use the method of differentiation or the “Substitution Method” (\(T=0\)).
Step 1: Derivation using Differentiation
For the parabola \(y^2=4 a x\), we differentiate both sides with respect to \(x\) :
\(
\begin{gathered}
2 y \frac{d y}{d x}=4 a \\
\frac{d y}{d x}=\frac{4 a}{2 y}=\frac{2 a}{y}
\end{gathered}
\)
The slope of the tangent at the point \(\left(x_1, y_1\right)\) is:
\(
m=\left[\frac{d y}{d x}\right]_{\left(x_1, y_1\right)}=\frac{2 a}{y_1}
\)
Using the point-slope form of a line, \(y-y_1=m\left(x-x_1\right)\) :
\(
\begin{gathered}
y-y_1=\frac{2 a}{y_1}\left(x-x_1\right) \\
y y_1-y_1^2=2 a x-2 a x_1
\end{gathered}
\)
Since \(\left(x_1, y_1\right)\) lies on the parabola, we know \(y_1^2=4 a x_1\). Substituting this into the equation:
\(
\begin{gathered}
y y_1-4 a x_1=2 a x-2 a x_1 \\
y y_1=2 a x+2 a x_1 \\
y y_1=2 a\left(x+x_1\right) \dots(i)
\end{gathered}
\)
Step 2: The \(T=0\) Shortcut (Transformation Table)
In coordinate geometry, the equation of a tangent at a point (\(x_1, y_1\)) can be written directly by replacing terms in the original curve equation:
\(
\begin{array}{ll}
\text { Original Term } & \text { Replace with Tangent Term } \\
y^2 & y y_1 \\
x^2 & x x_1 \\
2 x & x+x_1 \\
2 y & y+y_1
\end{array}
\)
Substitution Method: Applying this to \(y^2=4 a(x)\) :
\(y^2 \rightarrow y y_1\)
\(4 a x\) is \(2 a(2 x)\), so \(2 x \rightarrow x+x_1\)
Result: \(y y_1=2 a\left(x+x_1\right)\)

Tangents for Other Parabola Forms

Using the same transformation logic, here are the equations for the other standard orientations:
\(
\begin{aligned}
&\text { Parabola Form Tangent at }\left(x_1, y_1\right)\\
&\begin{array}{ll}
y^2=4 a x & y y_1=2 a\left(x+x_1\right) \\
x^2=4 a y & x x_1=2 a\left(y+y_1\right) \\
y^2=-4 a x & y y_1=-2 a\left(x+x_1\right) \\
x^2=-4 a y & x x_1=-2 a\left(y+y_1\right)
\end{array}
\end{aligned}
\)

Example 21: Find the equation of the tangent to \(y^2=12 x\) at the point \((3,6)\).

Solution: Identify \(\mathbf{4} \boldsymbol{a}=\mathbf{1 2}\), so \(\mathbf{2 a}=\mathbf{6}\).
Use \(y y_1=2 a\left(x+x_1\right)\) :
\(y(6)=6(x+3)\)
\(6 y=6 x+18\)
\(y=x+3\)

Equation of Tangent at Point \(P(t)\) or \(P\left(a t^2, 2 a t\right)\)

In Eq. (i) replace \(y_1\) by \(2 a t\) and \(x_1\) by \(a t^2\)
we have
\(
2 a t y=2 a\left(x+a t^2\right) \text { or } t y=x+a t^2 \dots(ii)
\)

Equation of Tangent if Slope of Tangent is \(m\)

In Eq. (ii), slope of tangent \(m=\frac{1}{t}\)
In Eq. (ii) replacing \(t\) by \(\frac{1}{m}\) we have \(y=m x+\frac{a}{m}\) which is equation of tangent in terms of slope.

This is tangent at point \(\left(\frac{a}{m^2}, \frac{2 a}{m}\right)\)
If line \(y=m x+c\) touches parabola \(y^2=4 a x\) we must have \(c=\frac{a}{m}\) (comparing equation with \(y=m x+\frac{a}{m}\))

Note:
Equation of tangent to the parabola \((y-k)^2=4 a(x-h)\) having slope \(m\) is \(y-k=m(x-h)+\frac{a}{m}\).
Equation of tangent at point \(p(t)\) on different parabolas:

\(
\begin{array}{|c|c|c|}
\hline \begin{array}{c}
\text { Equations of } \\
\text { parabola }
\end{array} & \begin{array}{c}
\text { Parametric co- } \\
\text { ordinates } t
\end{array} & \text { Tangent at } \boldsymbol{P}(t) \\
\hline y^2=4 a x & \left(a t^2, 2 a t\right) & t y=x+a t^2 \\
\hline y^2=-4 a x & \left(-a t^2, 2 a t\right) & t y=-x+a t^2 \\
\hline x^2=4 a y & \left(2 a t, a t^2\right) & t x=y+a t^2 \\
\hline x^2=-4 a y & \left(2 a t,-a t^2\right) & t x=-y+a t^2 \\
\hline
\end{array}
\) \(
\begin{array}{|c|c|c|c|}
\hline \begin{array}{c}
\text { Equation } \\
\text { of } \\
\text { parabola }
\end{array} & \begin{array}{c}
\text { Point of } \\
\text { contact in } \\
\text { terms of } \\
\text { slope }(m)
\end{array} & \begin{array}{c}
\text { Equation } \\
\text { of tangent } \\
\text { in terms of } \\
\text { slope }(m)
\end{array} & \begin{array}{c}
\text { Condition } \\
\text { of tangency } \\
\text { for line } \\
y=m x+c \\
\end{array} \\
\hline y^2=4 a x & \left(\frac{a}{m^2}, \frac{2 a}{m}\right) & y=m x+\frac{a}{m} & c=\frac{a}{m} \\
\hline y^2=-4 a x & \left(-\frac{a}{m^2},-\frac{2 a}{m}\right) & y=m x-\frac{a}{m} & c=-\frac{a}{m} \\
\hline x^2=4 a y & \left(2 a m, a m^2\right) & \begin{array}{c} \\
y=m x- \\
a m^2 \\
\end{array} & c=-a m^2 \\
\hline x^2=-4 a y & \begin{array}{c}
(-2 a m,- \\
\left.a m^2\right)
\end{array} & \begin{array}{c}
y=m x+ \\
a m^2
\end{array} & c=a m^2 \\
\hline
\end{array}
\)

Example 22: Find equation of the tangent to the parabola \(y^2=8 x\) having slope 2 and also find the point of contact.

Solution: Equation of the tangent to \(y^2=4 a x\) having slope \(m\) is \(y=m x+\frac{a}{m}\).
Hence, for the given parabola, equation of the tangent is \(y=2 x+\frac{2}{2}\) or \(y=2 x+1\) and point of contact is
\(
\left(\frac{a}{m^2}, \frac{2 a}{m}\right) \equiv\left(\frac{2}{2^2}, \frac{2(2)}{2}\right) \equiv\left(\frac{1}{2}, 2\right) .
\)

Pair of Tangents from Point (\(x_1, y_1\))

Let \(T(h, k)\) be any point on the pair of tangents \(P Q\) or \(P R\) drawn from any external point \(P\left(x_1, y_1\right)\) to the parabola \(y^2=\mathbf{4} a x\).

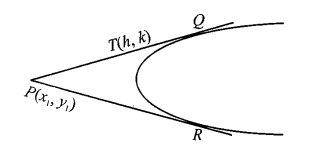
Equation of \(P T\) is
\(
\begin{aligned}
y-y_1 & =\frac{k-y_1}{h-x_1}\left(x-x_1\right) \\
y & =\left(\frac{k-y_1}{h-x_1}\right) x+\left(\frac{h y_1-k x_1}{h-x_1}\right)
\end{aligned}
\)
which is tangent to the parabola \(y^2=4 a x\)
\(
\begin{array}{ll}
\therefore & c=\frac{a}{m} \\
\text { or } & c m=a
\end{array}
\)
or \(\quad\left(\frac{h y_1-k x_1}{h-x_1}\right)\left(\frac{k-y_1}{h-x_1}\right)=a\)
\(
\text { or } \quad\left(k-y_1\right)\left(h y_1-k x_1\right)=a\left(h-x_1\right)^2
\)
∴ Locus of \((h, k)\), equation of pair of tangents is
\(
\left(y-y_1\right)\left(x y_1-x_1 y\right)=a\left(x-x_1\right)^2
\)
or \(\left(y^2-4 a x\right)\left(y_1^2-4 a x_1\right)=\left\{\left(y y_1-2 a\left(x+x_1\right)\right\}^2\right.\)
\(
S S_1=T^2,
\)
Where \(S=y^2-4 a x, S_1=y_1^2-4 a x_1\) and \(T=y y_1-2 a\left(x+x_1\right)\)

Example 23: If the line \(y=3 x+c\) touches the parabola \(y^2=12 x\) at point \(P\), then find the equation of the tangent at point \(Q\) where \(P Q\) is a focal chord.

Solution: Step 1: Find the point of tangency \(P\)
For the parabola \(y^2=12 x\), we have \(4 a=12\), which means \(a=3\). The line is \(y=3 x+c\), so the slope \(m=3\).
For a line to be tangent to \(y^2=4 a x\), the condition is \(c=\frac{a}{m}\).
\(
c=\frac{3}{3}=1
\)
The point of tangency \(P\left(x_1, y_1\right)\) is given by the formula:
\(
P=\left(\frac{a}{m^2}, \frac{2 a}{m}\right)=\left(\frac{3}{3^2}, \frac{2(3)}{3}\right)=\left(\frac{1}{3}, 2\right)
\)
Step 2: Find the coordinates of \(Q\)
Since \(P Q\) is a focal chord, we can use the parametric relationship. Let the parameter of \(P\) be \(t_1\). Using \(y=2 a t_1\) :
\(
2=2(3) t_1 \Longrightarrow 6 t_1=2 \Longrightarrow t_1=\frac{1}{3}
\)
For a focal chord, the relationship between the parameters of the endpoints is \(t_1 t_2=-1\).
\(
\left(\frac{1}{3}\right) t_2=-1 \Longrightarrow t_2=-3
\)
Now, find the coordinates of \(Q\left(x_2, y_2\right)\) using \(t_2=-3\) :
\(x_2=a t_2^2=3(-3)^2=27\)
\(y_2=2 a t_2=2(3)(-3)=-18\) So, \(Q=(27,-18)\).
Step 3: Equation of the tangent at \(Q\)
We use the \(T=0\) formula \(\left(y y_1=2 a\left(x+x_1\right)\right)\) at the point \((27,-18)\) :
\(
\begin{gathered}
y(-18)=2(3)(x+27) \\
-18 y=6(x+27)
\end{gathered}
\)
Divide both sides by 6 :
\(
\begin{gathered}
-3 y=x+27 \\
x+3 y+27=0
\end{gathered}
\)

Example 24: Find the equation of tangent to parabola \(y =x^2-2 x+3\) at point \((2,3)\).

Solution: Since the equation of parabola is not in the standard form, we use calculus method to find the equation of tangent.
\(
y=x^2-2 x+3
\)
Differentiating, w.r.t. \(x[latex], we have [latex]\frac{d y}{d x}=2 x-2\)
We want to find tangent at point \((2,3)\)
Then \(\left(\frac{d y}{d x}\right)_{(2,3)}=2(2)-2=2\)
Hence using point slope form equation of tangent is \(y-3=2(x-2)\) or \(y=2 x-1\)

Example 25: Find the equation of tangent to parabola \(\boldsymbol{x}=\boldsymbol{y}^{\mathbf{2}}+\mathbf{3} \boldsymbol{y}+\mathbf{2}\) having slope 1.

Solution: \(\boldsymbol{x}=y^2+3 y+2\)
Differentiating both sides w.r.t. x , we have
\(
\begin{aligned}
& 1=2 y \frac{d y}{d x}+3 \frac{d y}{d x} \\
& \Rightarrow \frac{d y}{d x}=\frac{1}{2 y+3}
\end{aligned}
\)
Now slope of tangent is 1
\(
\Rightarrow \quad \frac{d y}{d x}=\frac{1}{2 y+3}=1
\)
\(\Rightarrow y=-1\), which is the ordinate of the point on the curve where slope of tangent is 1 .
Putting \(y=-1\), in equation of parabola we get \(x=0\)
Hence using point-slope form we have \(y-(-1)=1(x-0)\) or \(x-y-1=0\)

Example 26: Find the equation of tangents drawn to parabola \(y=x^2-3 x+2\) from the point \((1,-1)\).

Solution: Tangents are drawn to the parabola from the point \((1,-1)\).
Now equation of line from \((1,-1)\) having slope \(m\) is \(y-(-1)=m(x-1)\)
or \(m x-y-m-1=0\) or \(y=m x-m-1\)
Since this line touches the parabola, when we solve line and parabola and the resulting quadratic will have equal roots
Solving we have \(m x-m-1=x^2-3 x+2\)
\(
x^2-(3+m) x+3+m=0
\)
This equation has equal roots
\(
\begin{aligned}
\Rightarrow & & (m+3)^2-4(m+3) & =0 \\
\Rightarrow & & m & =-3 \text { or } m=1
\end{aligned}
\)
Hence equation of tangents are \(y+1=-3(x-1)\) and \(y+1=x-1\)
or \(3 x+y-2=0\) and \(x-y-2=0\)

Example 27: Find the shortest distance between the line \(y=x-2\) and the parabola \(y=x^2+3 x+2\).

Solution: Let \(P\left(x_1, y_1\right)\) be a point closest to the line \(y=x-2\)
then \(\left.\frac{d y}{d x}\right|_{\left(x_1, y_1\right)}=\) slope of given line

\(
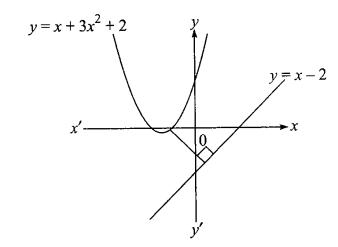
2 x_1+3=1 \Rightarrow x_1=-1 \Rightarrow y_1=0
\)
Hence point \((-1,0)\) is the closest and its perpendicular distance from the line \(y=x-2\) will be the shortest dis-
\(
\text { tance ⇒ Shortest distance }=\frac{3}{\sqrt{2}}
\)

Example 28: Find the equation of common tangent of \(y^2=4 a x\) and \(x^2=4 a y\).

Solution: 

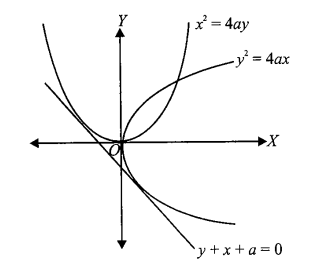
To find the common tangent of the two parabolas \(y^2=4 a x\) and \(x^2=4 a y\), we use the condition of tangency for both curves and solve for the unknown parameters.
Step 1: General Tangent to the First Parabola
For the parabola \(y^2=4 a x\), any tangent with slope \(m\) can be written in the form:
\(
y=m x+\frac{a}{m} \dots(i)
\)
Step 2: Condition for Tangency with the Second Parabola
The second parabola is \(x^2=4 a y\). For a line \(y=m x+c\) to be a tangent to a vertical parabola of the form \(x^2=4 a y\), the condition of tangency is:
\(
c=-a m^2
\)
In our line equation \((i)\), the constant term \(c\) is \(\frac{a}{m}\). Substituting this into the tangency condition:
\(
\frac{a}{m}=-a m^2
\)
Step 3: Solve for \(m\)
Assuming \(a \neq 0\), we can divide both sides by \(a\) :
\(
\begin{gathered}
\frac{1}{m}=-m^2 \\
1=-m^3 \\
m^3=-1
\end{gathered}
\)
Taking the real cube root:
\(
m=-1
\)
Now, substitute \(m=-1\) back into the tangent equation \((i)\) :
\(
\begin{gathered}
y=(-1) x+\frac{a}{-1} \\
y=-x-a
\end{gathered}
\)
Rearranging into standard form:
\(
x+y+a=0
\)

Example 29: A tangent to the parabola \(y^2=8 x\) makes an angle of \(45^{\circ}\) with the straight line \(y=3 x+5\). Then find one of the points of contact.

Solution: To find the point of contact, we need to determine the slope of the tangent and then use the standard coordinates for the point of contact.
Step 1: Identify Parabola Parameters
For the parabola \(y^2=8 x\) :
\(4 a=8 \Longrightarrow a=2\).
The standard point of contact for a tangent with slope \(m\) is \(\left(\frac{a}{m^2}, \frac{2 a}{m}\right)\).
Step 2: Find the Slope of the Tangent (\(m\))
The tangent makes an angle of \(45^{\circ}\) with the line \(L: y=3 x+5\).
Slope of given line \(\left(m_1\right)=3\).
Angle \((\theta)=45^{\circ}\).
Let the slope of the tangent be \(m\).
Using the angle formula between two lines:
\(
\begin{gathered}
\tan \theta=\left|\frac{m-m_1}{1+m m_1}\right| \\
\tan 45^{\circ}=\left|\frac{m-3}{1+3 m}\right| \\
1=\left|\frac{m-3}{1+3 m}\right|
\end{gathered}
\)
This gives us two possible cases:
Case 1:
\(
\frac{m-3}{1+3 m}=1 \Longrightarrow m-3=1+3 m \Longrightarrow-2 m=4 \Longrightarrow m=-2
\)
Case 2:
\(
\frac{m-3}{1+3 m}=-1 \Longrightarrow m-3=-1-3 m \Longrightarrow 4 m=2 \Longrightarrow m=\frac{1}{2}
\)
Step 3: Calculate Points of Contact
Now we substitute \(a=2\) and our slopes into the point of contact formula \(\left(\frac{2}{m^2}, \frac{4}{m}\right)\).
For \(m=-2\) :
\(
P_1=\left(\frac{2}{(-2)^2}, \frac{4}{-2}\right)=\left(\frac{2}{4},-2\right)=\left(\frac{1}{2},-2\right)
\)
For \(m=\frac{1}{2}\) :
\(
P_2=\left(\frac{2}{(1 / 2)^2}, \frac{4}{1 / 2}\right)=\left(\frac{2}{1 / 4}, 8\right)=(8,8)
\)
One of the points of contact is \((1 / 2,-2)\) or \((8,8)\).

Example 30: Two tangents are drawn from the point \((-2,-1)\) to the parabola \(y^2=4 x\). If \(\alpha\) is the angle between these tangents, then find the value of \(\tan \alpha\).

Solution: Step 1: Identify the Parameters

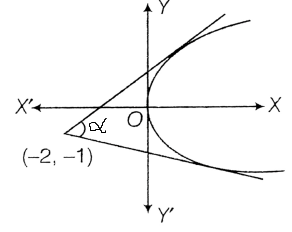
For the parabola \(y^2=4 x\) :
\(\cdot 4 a=4 \Longrightarrow a=1\).
The external point is \(\left(x_1, y_1\right)=(-2,-1)\).
Step 2: The Quadratic in Slope ( \(m\) )
Any tangent to \(y^2=4 a x\) with slope \(m\) has the equation \(y=m x+\frac{a}{m}\). Since the tangents pass through \((-2,-1)\), we substitute these coordinates:
\(
-1=m(-2)+\frac{1}{m}
\)
\(
2 m^2-m-1=0
\)
We solve the quadratic equation \(2 m^2-m-1=0\) using the quadratic formula or factoring:
\(
(2 m+1)(m-1)=0
\)
The slopes of the two tangents are:
\(m_1=1\)
\(m_2=-1 / 2\)
Step 4: Calculate \(\tan \alpha\)
The formula for the angle \(\alpha\) between two lines with slopes \(m_1\) and \(m_2\) is:
\(
\tan \alpha=\left|\frac{m_1-m_2}{1+m_1 m_2}\right|
\)
\(
\tan \alpha=\left|\frac{1-(-1 / 2)}{1+(1)(-1 / 2)}\right|=3
\)

Faster: You can also use the direct formula for the angle between tangents from \(\left(x_1, y_1\right)\) to \(y^2=4 a x\) :
\(
\tan \alpha=\left|\frac{\sqrt{y_1^2-4 a x_1}}{x_1+a}\right|
\)
Substituting the values:
\(
\tan \alpha=\left|\frac{\sqrt{(-1)^2-4(1)(-2)}}{-2+1}\right|=\left|\frac{\sqrt{1+8}}{-1}\right|=\left|\frac{3}{-1}\right|=3
\)

Example 31: The angle between the tangents drawn from the point \((1,4)\) to the parabola \(y^2=4 x\), is [IIT (S) 2004]
(a) \(\pi / 6\)
(b) \(\pi / 4\)
(c) \(\pi / 3\)
(d) \(\pi / 2\)

Solution: (c) Using the formula \(\tan \theta=\left|\frac{\sqrt{y_1^2-4 a x_1}}{x_1+a}\right|\) :
\(
\tan \theta=\left|\frac{\sqrt{4^2-4(1)(1)}}{1+1}\right|=\frac{\sqrt{16-4}}{2}=\frac{\sqrt{12}}{2}=\frac{2 \sqrt{3}}{2}=\sqrt{3}
\)
This confirms \(\theta=60^{\circ}\) or \(\pi / 3\).

Equation of Normal

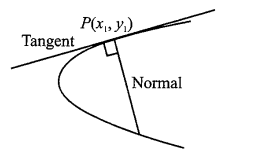
Differentiating \(y^2=4 a x\) with respect to \(x\), we have \(\frac{d y}{d x}=\frac{2 a}{y}\)
The slope of the tangent at \(\left(x_1, y_1\right)=\frac{2 a}{y_1}\)
Since the normal at \(\left(x_1, y_1\right)\) is perpendicular to the tangent at \(\left(x_1, y_1\right)\)
∴ Slope of normal at \(\left(x_1, y_1\right)=-\frac{y_1}{2 a}\)
Hence, the equation of the normal at \(\left(x_1, y_1\right)\) is
\(
y-y_1=-\frac{y_1}{2 a}\left(x-x_1\right) \dots(i)
\)

Parametric Form

Replacing \(x_1\) by \(a t^2\) and \(y_1\) by \(2 a t\), then Eq. (i) becomes \(y-2 a t=-t\left(x-a t^2\right)\) or \(y=-t x+2 a t+a t^3\)
The equations of normals of all standard parabolas are as follows:

\(
\begin{array}{|c|c|c|}
\hline \begin{array}{c}
\text { Equations of } \\
\text { parabola }
\end{array} & \begin{array}{c}
\text { Parametric } \\
\text { coordinates } t
\end{array} & \text { Normals at } t \\
\hline y^2=4 a x & \left(a t^2, 2 a t\right) & y+t x=2 a t+a t^3 \\
\hline y^2=-4 a x & \left(-a t^2, 2 a t\right) & y-t x=2 a t+a t^3 \\
\hline x^2=4 a y & \left(2 a t, a t^2\right) & x+t y=2 a t+a t^3 \\
\hline x^2=-4 a y & \left(2 a t,-a t^2\right) & x-t y=2 a t+a t^3 \\
\hline
\end{array}
\)

Slope Form

The equation of normal to the parabola \(y^2=4 a x\) at \(\left(a t^2, 2 a t\right)\) is
\(
y=-t x+2 a t+a t^3 \dots(i)
\)
Since \(m\) is the slope of the normal, then \(m=-t\)
Then equation of normal is
\(
y=m x-2 a m-a m^3 \dots(ii)
\)
Thus \(y=m x-2 a m-a m^3\) is a normal to the parabola \(y^2=\mathbf{4} a x\) where \(m\) is the slope of the normal.
The coordinates of the foot of normal are \(\left(a m^2,-2 a m\right)\).
\(
\begin{array}{ll}
\text { Comparing (ii) with } & y=m x+c \\
\therefore & c=-2 a m-a m^3
\end{array}
\)
which is the condition when \(y=m x+c\) is the normal of \(y^2=\mathbf{4} a x\).
Equation of normal for all parabolas in terms of \(m\).

\(
\begin{array}{|l|l|l|l|}
\hline \begin{array}{c}
\text { Equations } \\
\text { of parabolas }
\end{array} & \begin{array}{c}
\text { Point of con- } \\
\text { tact in terms } \\
\text { of slope }(m)
\end{array} & \begin{array}{l}
\text { Equations of } \\
\text { normals in terms } \\
\text { of slope }(m)
\end{array} & \begin{array}{c}
\text { Condition } \\
\text { for line } y \\
=m x+c \text { is } \\
\text { normal }
\end{array} \\
\hline y^2=4 a x & \left(a m^2,-2 a m\right) & \begin{array}{l}
y=m x-2 a m \\
-a m^3
\end{array} & \begin{array}{l}
c=-2 a m \\
-a m^3
\end{array} \\
\hline y^2=-4 a x & \left(-a m^2, 2 a m\right) & \begin{array}{l}
y=m x+2 a m \\
+a m^3
\end{array} & \begin{array}{l}
c=2 a m+ \\
a m^3
\end{array} \\
\hline x^2=4 a y & \left(-\frac{2 a}{m}, \frac{a}{m^2}\right) & \begin{array}{l}
y=m x+2 a \\
+\frac{a}{m^2}
\end{array} & \begin{array}{l}
c=2 a \\
+\frac{a}{m^2}
\end{array} \\
\hline x^2=-4 a y & \left(\frac{2 a}{m},-\frac{a}{m^2}\right) & \begin{array}{l}
y=m x- \\
2 a-\frac{a}{m^2}
\end{array} & \begin{array}{l}
c=-2 a \\
-\frac{a}{m^2}
\end{array} \\
\hline
\end{array}
\)

Example 32: Find the equations of normals to the parabola \(y^2=4 a x\) at the ends of the latus rectum.

Solution: Differentiating \(y^2=4 a x\) w.r.t. \(x\), we have \(\frac{d y}{d x}=\frac{2 a}{y}\)
Hence, slope of normal at point \(P(a, 2 a)\) is \(-\frac{2 a}{2 a}=-1\)
Slope of normal at point \(Q(a,-2 a)\) is \(-\frac{-2 a}{2 a}=1\)
Hence, equation of normal at point \(P\) and \(Q\) are \(x+y-3 a=0\) and \(x-y-3 a=0\).

Example 33: If \(y=x+2\) is normal to parabola \(y^2=4 a x\), then find the value of \(a\).

Solution: Normal to parabola \(y^2=4 a x\) having slope \(m\) is \(y=m x- 2 a m-a m^3\)
Given normal is \(y=x+2 \Rightarrow m=1\) and \(-2 a m-a m^3=2\)
\(
\begin{array}{rlrl}
\Rightarrow & -2 a(1)-a(1)^3 & =1 \\
\Rightarrow & a & =-1 / 3
\end{array}
\)

Example 34: Find the equation of normal to the parabola \(y=x^2-x-1\) which has equal intercept on axis.
Also find the point where this normal meets the curve again.

Solution: Normal has equal intercept on axis, then its slope is -1.
Now differentiating \(y=x^2-x-1\) w.r.t. \(x\) both sides we have \(\frac{d y}{d x}=2 x-1\), which is the slope of the tangent to the parabola at any point on the parabola.
Now Slope of normal to curve at any point is
\(
m=-\frac{d x}{d y}=\frac{1}{1-2 x}
\)
Then we want slope of normal as \(-1 \Rightarrow \frac{1}{1-2 x}=-1\)
\(
\begin{aligned}
& \Rightarrow x=1 \\
& \Rightarrow y=-1\left(\text { from } y=x^2-x-1\right)
\end{aligned}
\)
Hence from point – slope form equation of normal is
\(
y-(-1)=-1(x-1) \text { or } x+y=0
\)
Solving this equation of normal with the equation of parabola.
\(
-x=x^2-x-1 \text { or } x^2=1 \text { or } x= \pm 1
\)
Hence normal meets parabola again at point whose abscissa is -1 /, for which ordinate is 1.
Thus normal meets parabola again at \((1,-1)\).

Example 35: Find the minimum distance between the curves \(y^2=4 x\) and \(x^2+y^2-12 x+31=0\).

Solution: Centre and radius of the given circle is \(P(6,0)\) and \(\sqrt{5}\), respectively.
Now the shortest distance always occurs along common normal.

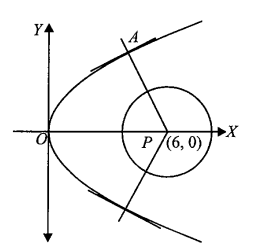
Differentiating \(y^2=4 x\) with respect to \(x\), we get
\(
\frac{d y}{d x}=\frac{2}{y}
\)
Then the slope of normal at point \(A\left(y_1^2 / 4, y_1\right)\) is \(\frac{y_1}{2}\).
Also from definition, the slope of \(A P\) is given by
\(
\begin{aligned}
\frac{y_1-0}{\frac{y_1^2}{4}-6} & =-\frac{y_1}{2} \\
y_1 & =0 \text { or } y_1= \pm 4
\end{aligned}
\)
Hence, the points are \(O(0,0), A(4,4), C(4,-4)\).
The shortest distance is \(A P-\sqrt{5}=\sqrt{20}-\sqrt{5}=\sqrt{5}\).