10.4 General Equation of a Line

In earlier classes, we have studied general equation of first degree in two variables, $\mathrm{Ax}+\mathrm{B} y+\mathrm{C}=0$, where $\mathrm{A}, \mathrm{B}$ and $\mathrm{C}$ are real constants such that $\mathrm{A}$ and $\mathrm{B}$ are not zero simultaneously. Graph of the equation $\mathrm{A} x+\mathrm{B} y+\mathrm{C}=0$ is always a straight line. Therefore, any equation of the form $\mathrm{Ax}+\mathrm{B} y+\mathrm{C}=0$, where $\mathrm{A}$ and $\mathrm{B}$ are not zero simultaneously is called general linear equation or general equation of a line.

Different forms of $\mathrm{Ax}+\mathrm{B} y+C=0$ The general equation of a line can be reduced into various forms of the equation of a line, by the following procedures:

Case-I: Slope-intercept form 

If $\mathrm{B} \neq 0$, then $\mathrm{Ax}+\mathrm{B} y+\mathrm{C}=0$ can be written as
$y=-\frac{\mathrm{A}}{\mathrm{B}} x-\frac{\mathrm{C}}{\mathrm{B}} \text { (Assuming } B \neq 0 \text { ) } \dots(1)$
Comparing it with $y=m x+c$
we get slope $(m)=-\frac{A}{B}=-\frac{\text { coefficient of } x}{\text { coefficient of } y}$
and $\quad y$ intercept $(c)=-\frac{C}{B}=-\frac{\text { constant term }}{\text { coefficient of } y}$
We know that Equation (1) is the slope-intercept form of the equation of a line whose slope is $-\frac{\mathrm{A}}{\mathrm{B}}$, and $y$-intercept is $-\frac{\mathrm{C}}{\mathrm{B}}$.
If $\mathrm{B}=0$, then $x=-\frac{\mathrm{C}}{\mathrm{A}}$, which is a vertical line whose slope is undefined and $x$-intercept is $-\frac{\mathrm{C}}{\mathrm{A}}$.

Corollary 1 : Find angle between the lines $A_1 x+B_1 y+C_1=0$ and $A_2 x+B_2 y+C_2=0$.
Slope of the line
$A_1 x+B_1 y+C_1=0 \text { is }-\frac{A_1}{B_1}=m_1 \text { (say) }$
and slope of the line
$A_2 x+B_2 y+C_2=0 \text { is }-\frac{A_2}{B_2}=m_2 \text { (say) }$
If $\theta$ is the angle between the two lines, then
$\begin{aligned} \tan \theta & =\left|\frac{m_1-m_2}{1+m_1 m_2}\right|=\left\lvert\, \frac{\left.\left(-\frac{A_1}{B_1}\right)-\left(-\frac{A_2}{B_2}\right) \right\rvert\,}{\left.1+\left(-\frac{A_1}{B_1}\right)\left(-\frac{A_2}{B_2}\right) \right\rvert\,}\right. \\ & =\left|\frac{A_1 B_2-A_2 B_1}{A_1 A_2+B_1 B_2}\right| \\ \therefore \quad \theta & =\tan ^{-1}\left|\frac{A_1 B_2-A_2 B_1}{A_1 A_2+B_1 B_2}\right| \end{aligned}$

Corollary 2 : Find the condition of (i) parallelism (ii) perpendicularity of the lines
$\quad \begin{array}{l} A_1 x+B_1 y+C_1=0 \\ A_2 x+B_2 y+C_2=0 \end{array}$
(i) If the two lines are parallel, $\theta=0^{\circ}$
$\begin{array}{ll} \therefore & \tan \theta=\tan 0^{\circ}=0 \\ \Rightarrow & \left|\frac{A_1 B_2-A_2 B_1 \mid}{A_1 A_2+B_1 B_2}\right|=0 \\ \Rightarrow & A_1 B_2-A_2 B_1=0 \end{array}$
$\frac{A_1}{A_2}=\frac{B_1}{B_2} \quad \text { (Remember) }$
which is required condition of parallelism.
(ii) If the two lines are perpendicular, $\theta=90^{\circ}$
$\begin{array}{ll} \therefore & \tan \theta=\tan 90^{\circ}=\infty \\ \Rightarrow & \left|\frac{A_1 B_2-A_2 B_1}{A_1 A_2+B_1 B_2}\right|=\infty \end{array}$
$\Rightarrow \quad A_1 A_2+B_1 B_2=0 \text { (Remember) }$
which is required condition of perpendicularity.

Note: If two lines are coincident, then
$\frac{A_1}{A_2}=\frac{B_1}{B_2}=\frac{C_1}{C_2} \text { (Remember) }$

Example 1: Reduce $x+\sqrt{3} y+4=0$ to the slope-intercept form and find its slope and $y$-intercept.

Answer: Given equation is $x+\sqrt{3} y+4=0$
$\begin{aligned} \Rightarrow & & \sqrt{3} y & =-x-4 \\ \Rightarrow & & y & =\left(-\frac{1}{\sqrt{3}}\right) x+\left(-\frac{4}{\sqrt{3}}\right) \end{aligned}$
which is in the slope-intercept form $y=m x+c$
Where slope $(m)=-\frac{1}{\sqrt{3}}$ and $y$-intercept $(c)=-\frac{4}{\sqrt{3}}$

Case-II: Intercept form 

Given equation is $A x+B y+C=0$
$\begin{aligned} A x+B y & =-C \\ \frac{A}{-C} x+\frac{B}{-C} y & =1 \quad(\text { Assuming } C \neq 0) \end{aligned}$
$\left.\frac{x}{(-C / A)}+\frac{y}{(-C / B)}=1 \text { (Assuming } A \neq 0, B \neq 0\right) \dots(2)$
Comparing with $\frac{x}{a}+\frac{y}{b}=1$
we get, $x$-intercept $(a)=-\frac{C}{A}=-\frac{\text { constant term }}{\text { coefficient of } x}$
and $\quad y$-intercept $(b)=-\frac{C}{B}=-\frac{\text { constant term }}{\text { coefficient of } y}$

Example 2: Reduce $x+\sqrt{3} y+4=0$ to the Intercept form and find its intercepts on the axes.

Answer: Given equation is
$\begin{aligned} x+\sqrt{3} y+4 & =0 \\ x+\sqrt{3} y & =-4 \\ \frac{x}{-4}+\frac{\sqrt{3} y}{-4} & =1 \\ \frac{x}{-4}+\frac{y}{-4 / \sqrt{3}} & =1 \end{aligned}$
which is in the intercept form $\frac{x}{a}+\frac{y}{b}=1$ where $x$-intercept $(a)=-4$ and $y$-intercept $(b)=-\frac{4}{\sqrt{3}}$

Case-III: Normal Form

Let $x \cos \omega+y \sin \omega=p$ be the normal form of the line represented by the equation $\mathrm{A} x+\mathrm{B} y+\mathrm{C}=0$ or $\mathrm{A} x+\mathrm{B} y=-\mathrm{C}$. Thus, both the equations are same and therefore,
$\frac{A}{\cos \omega}=\frac{B}{\sin \omega}=-\frac{C}{p}$
which gives $\cos \omega=-\frac{\mathrm{A} p}{\mathrm{C}} \text { and } \sin \omega=-\frac{\mathrm{B} p}{\mathrm{C}}$
Now
$\sin ^2 \omega+\cos ^2 \omega=\left(-\frac{\mathrm{A} p}{\mathrm{C}}\right)^2+\left(-\frac{\mathrm{B} p}{\mathrm{C}}\right)^2=1$
or
$p^2=\frac{\mathrm{C}^2}{\mathrm{~A}^2+\mathrm{B}^2} \quad \text { or } \quad p= \pm \frac{\mathrm{C}}{\sqrt{\mathrm{A}^2+\mathrm{B}^2}}$
Therefore
$\cos \omega= \pm \frac{A}{\sqrt{A^2+B^2}} \text { and } \sin \omega= \pm \frac{B}{\sqrt{A^2+B^2}}$
Thus, the normal form of the equation $\mathrm{Ax}+\mathrm{B} y+\mathrm{C}=0$ is
$x \cos \omega+y \sin \omega=p,$
where $\cos \omega= \pm \frac{\mathrm{A}}{\sqrt{\mathrm{A}^2+\mathrm{B}^2}}, \sin \omega= \pm \frac{\mathrm{B}}{\sqrt{\mathrm{A}^2+\mathrm{B}^2}}$ and $p= \pm \frac{\mathrm{C}}{\sqrt{\mathrm{A}^2+\mathrm{B}^2}}$.
Proper choice of signs is made so that $p$ should be positive.

Example 3: Reduce $x+\sqrt{3} y+4=0$ to the Normal form and find the values of $p$ and $\alpha$.

Answer: Given equation is $x+\sqrt{3} y+4=0$
$\begin{aligned} \Rightarrow & & x+\sqrt{3} y & =-4 \\ \Rightarrow & & -x-\sqrt{3} y & =4 \quad \text { (RHS made positive) } \end{aligned}$
Dividing both sides by $\sqrt{(-1)^2+(-\sqrt{3})^2}=2$, we get
$\left(-\frac{1}{2}\right) x+\left(-\frac{\sqrt{3}}{2}\right) y=2$
Which is the normal form $x \cos \alpha+y \sin \alpha=p$.
where, $\quad \cos \alpha=-\frac{1}{2}=-\cos 60^{\circ}=\cos \left(180^{\circ}-60^{\circ}\right)$
$\begin{array}{l} \text { or } \cos \left(180^{\circ}+60^{\circ}\right) \\ \therefore \alpha=120^{\circ} \text { or } 240^{\circ} \\ \text { and } \sin \alpha=-\frac{\sqrt{3}}{2}=-\sin 60^{\circ}=\sin \left(180^{\circ}+60^{\circ}\right) \\ \text { or } \sin \left(360^{\circ}-60^{\circ}\right) \\ \therefore \alpha=240^{\circ} \text { or } 300^{\circ} \\ \text { Hence, } \alpha=240^{\circ}, p=2 \end{array}$
$\therefore$ Required normal form is
$x \cos 240^{\circ}+y \sin 240^{\circ}=2$

Example 4: Equation of a line is $3 x-4 y+10=0$. Find its (i) slope, (ii) $x$ – and $y$-intercepts.

Answer: (i) Given equation $3 x-4 y+10=0$ can be written as
$y=\frac{3}{4} x+\frac{5}{2} \dots(1)$
Comparing (1) with $y=m x+c$, we have slope of the given line as $m=\frac{3}{4}$.
(ii) Equation $3 x-4 y+10=0$ can be written as
$3 x-4 y=-10$ or $\frac{x}{-\frac{10}{3}}+\frac{y}{\frac{5}{2}}=1 \dots(2)$
Comparing (2) with $\frac{x}{a}+\frac{y}{b}=1$, we have $x$-intercept as $a=-\frac{10}{3}$ and $y$-intercept as $b=\frac{5}{2}$.

Example 5: Reduce the equation $\sqrt{3} x+y-8=0$ into normal form. Find the values of $p$ and $\omega$.

Answer: Given equation is
$\sqrt{3} x+y-8=0 \dots(1)$
Dividing (1) by $\sqrt{(\sqrt{3})^2+(1)^2}=2$, we get
$\frac{\sqrt{3}}{2} x+\frac{1}{2} y=4 \text { or } \cos 30^{\circ} x+\sin 30^{\circ} y=4 \dots(2)$
Comparing (2) with $x \cos \omega+y \sin \omega=p$, we get $p=4$ and $\omega=30^{\circ}$.

Example 6: Find the angle between the lines $y-\sqrt{3} x-5=0$ and $\sqrt{3} y-x+6=0$.

Answer: Given lines are
$y-\sqrt{3} x-5=0 \text { or } y=\sqrt{3} x+5 \dots(1)$
and $\sqrt{3} y-x+6=0$ or $y=\frac{1}{\sqrt{3}} x-2 \sqrt{3} \dots(2)$
Slope of line (1) is $m_1=\sqrt{3}$ and slope of line (2) is $m_2=\frac{1}{\sqrt{3}}$.
The acute angle (say) $\theta$ between two lines is given by
$\tan \theta=\left|\frac{m_2-m_1}{1+m_1 m_2}\right| \dots(3)$
Putting the values of $m_1$ and $m_2$ in (3), we get
$\tan \theta=\left|\frac{\frac{1}{\sqrt{3}}-\sqrt{3}}{1+\sqrt{3} \times \frac{1}{\sqrt{3}}}\right|=\left|\frac{1-3}{2 \sqrt{3}}\right|=\frac{1}{\sqrt{3}}$
which gives $\theta=30^{\circ}$. Hence, angle between two lines is either $30^{\circ}$ or $180^{\circ}-30^{\circ}=150^{\circ}$.

Example 7: Show that two lines $a_1 x+b_1 y+c_1=0$ and $a_2 x+b_2 y+c_2=0$, where $b_1, b_2 \neq 0$ are: (i) Parallel if $\frac{a_1}{b_1}=\frac{a_2}{b_2}$, and (ii) Perpendicular if $a_1 a_2+b_1 b_2=0$.

Answer: Given lines can be written as
$\begin{array}{l} y=-\frac{a_1}{b_1} x-\frac{c_1}{b_1} \dots(1) \\ \text { and } y=-\frac{a_2}{b_2} x-\frac{c_2}{b_2} \dots(2) \end{array}$
Slopes of the lines (1) and (2) are $m_1=-\frac{a_1}{b_1}$ and $m_2=-\frac{a_2}{b_2}$, respectively. Now
(i) Lines are parallel, if $m_1=m_2$, which gives
$-\frac{a_1}{b_1}=-\frac{a_2}{b_2} \text { or } \frac{a_1}{b_1}=\frac{a_2}{b_2} .$
(ii) Lines are perpendicular, if $m_1 \cdot m_2=-1$, which gives
$\frac{a_1}{b_1} \cdot \frac{a_2}{b_2}=-1 \text { or } a_1 a_2+b_1 b_2=0$

Example 8: Find the equation of a line perpendicular to the line $x-2 y+3=0$ and passing through the point $(1,-2)$.

Answer: Given line $x-2 y+3=0$ can be written as
$y=\frac{1}{2} x+\frac{3}{2} \dots(1)$
Slope of the line (1) is $m_1=\frac{1}{2}$. Therefore, slope of the line perpendicular to line (1) is
$m_2=-\frac{1}{m_1}=-2$
Equation of the line with slope -2 and passing through the point $(1,-2)$ is
$y-(-2)=-2(x-1) \text { or } y=-2 x \text {, }$
which is the required equation.

Example 9: Find the measure of the angle of intersection of the lines whose equations are $3 x+4 y+7=0$ and $4 x-3 y+5=0$.

Answer: Given lines are $3 x+4 y+7=0,4 x-3 y+5=0$. Comparing
the given lines with $A_1 x+B_1 y+C_1=0, A_2 x+B_2 y+C_2=0$
respectively, we get
$\begin{array}{c} A_1=3, B_1=4 \text { and } A_2=4, B_2=-3 \\ \because \quad A_1 A_2+B_1 B_2=3 \times 4+4(-3)=0 \end{array}$
Hence, the given lines are perpendicular.

Example 10: Find the angle between the lines
$\begin{array}{l} \left(a^2-a b\right) y=\left(a b+b^2\right) x+b^3 \\ \text { and }\left(a b+a^2\right) y=\left(a b-b^2\right) x+a^3 \\ \text { where } a>b>0 \text {. } \\ \end{array}$

Answer: The given equations of lines can be written as
$\begin{aligned} \left(a b+b^2\right) x-\left(a^2-a b\right) y+b^3 & =0 \dots(i) \\ \text { and } \quad\left(a b-b^2\right) x-\left(a b+a^2\right) y+a^3 & =0 \dots(ii) \end{aligned}$
Comparing the given lines (i) and (ii) with the lines
$A_1 x+B_1 y+C_1=0 \text { and } A_2 x+B_2 y+C_2=0$
respectively, we get
$\begin{aligned} A_1 & =a b+b^2, B_1=-\left(a^2-a b\right) \\ \text { and } \quad A_2 & =a b-b^2, B_2=-\left(a b+a^2\right) \end{aligned}$
Let $\theta$ be the acute angle between the lines, then
$\tan \theta=\left|\frac{A_1 B_2-A_2 B_1}{A_1 A_2+B_1 B_2}\right|$
$\begin{aligned} \tan \theta & =\left|\frac{\left(a b+b^2\right) \times\left(-\left(a b+a^2\right)\right)-\left(a b-b^2\right) \times\left(-\left(a^2-a b\right)\right)}{\left(a b+b^2\right)\left(a b-b^2\right)+\left(a^2-a b\right)\left(a b+a^2\right)}\right| \\ & =\left|\frac{-\left\{a^2 b^2+a^3 b+a b^3+a^2 b^2-a^3 b+a^2 b^2+a^2 b^2-b^3 a\right\}}{\left(a^2 b^2-b^4+a^4-a^2 b^2\right)}\right| \\ & =\left|\frac{-4 a^2 b^2}{a^4-b^4}\right|=\frac{4 a^2 b^2}{a^4-b^4} \\ \therefore \theta & =\tan ^{-1}\left(\frac{4 a^2 b^2}{a^4-b^4}\right) \end{aligned}$

Example 11: Two equal sides of an isosceles triangle are given by the equations $7 x-y+3=0$ and $x+y-3=0$ and its third side passes through the point $(1,-10)$. Determine the equation of the third side.

Answer: Given equations
$\begin{array}{r} 7 x-y+3=0 \dots(i)\\ x+y-3=0 \dots(ii) \end{array}$
represents two equal sides $A B$ and $A C$ of an isosceles
triangle $A B C$. Since its third side passes through $D(1,-10)$ then its equation is
$y+10=m(x-1) \dots(iii)$
$\because \quad A B=A C$
Let $\angle A B C=\angle A C B=\theta$
then $\quad \angle A C E=\pi-\theta$

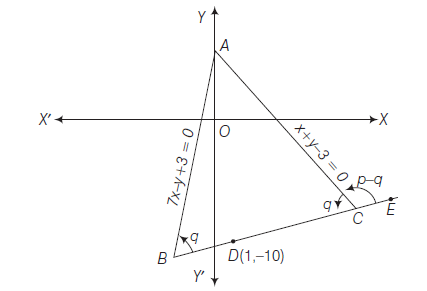
From Eqs. (i) and (ii), slopes of $A B$ and $A C$ are
$m_1=7 \text { and } m_2=-1$
respectively.
$\therefore \quad \tan \theta=\frac{7-m}{1+7 m}$
and $\tan (\pi-\theta)=\frac{-1-m}{1+(-1) m}=-\left(\frac{1+m}{1-m}\right)$
$\Rightarrow \quad-\tan \theta=-\left(\frac{1+m}{1-m}\right) \Rightarrow \tan \theta=\left(\frac{1+m}{1-m}\right)$
$\therefore \quad \frac{7-m}{1+7 m}=\frac{1+m}{1-m}$
$\Rightarrow \quad(7-m)(1-m)=(1+7 m)(1+m)$
$\Rightarrow \quad 6 m^2+16 m-6=0$
or $\quad 3 m^2+8 m-3=0$ or $(3 m-1)(m+3)=0$
$\Rightarrow \quad m=\frac{1}{3},-3$
Hence from Eq. (iii), the third side $B C$ has two equations
$y+10=\frac{1}{3}(x-1) \text { and } y+10=-3(x-1)$
or $\quad x-3 y-31=0$ and $3 x+y+7=0$