10.2 Slope of a Line

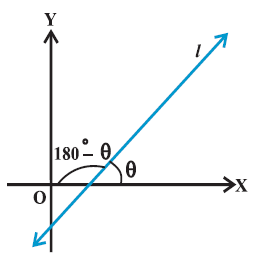
A line in a coordinate plane forms two angles with the $x$-axis, which are supplementary. The angle (say) $\theta$ made by the line $l$ with positive direction of $x$-axis and measured anti-clockwise is called the inclination of the line. Obviously $0^{\circ} \leq \theta \leq 180^{\circ}$ (Fig above).

Important Points to Remember

• When two lines are parallel, they have the same inclination.
• The inclination of a line which is parallel to $X$-axis or coinciding with $X$-axis is $0^{\circ}$.
• The inclination of a vertical line (parallel to or coinciding with $y$-axis) is $90^{\circ}$.
• The angle of inclination of the line lies between $0^{\circ}$ and $180^{\circ}$ i.e. $0<\theta \leq \pi$ and $\theta \neq \frac{\pi}{2}$.

Slope (Gradient) of a line when coordinates of any two points on the line are given

We know that a line is completely determined when we are given two points on it. Hence, we proceed to find the slope of a line in terms of the coordinates of two points on the line. Let $\mathrm{P}\left(x_1, y_1\right)$ and $\mathrm{Q}\left(x_2, y_2\right)$ be two points on non-vertical line $l$ whose inclination is $\theta$. Obviously, $x_1 \neq x_2$, otherwise the line will become perpendicular to $x$-axis and its slope will not be defined. The inclination of the line $l$ may be acute or obtuse. Let us take these two cases.

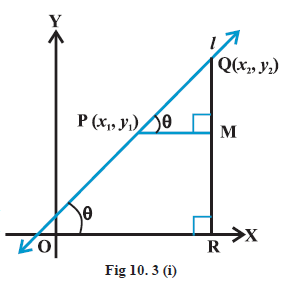
Draw perpendicular $\mathrm{QR}$ to $x$-axis and PM perpendicular to RQ as shown in Figs. 10.3 (i) and (ii).

Case-I: When angle $\theta$ is acute: Any angle that measures greater than $0^{\circ}$ and less than $90^{\circ}$ is called an acute angle.

In Fig 10.3 (i), $\angle \mathrm{MPQ}=\theta \dots(1)$.
Therefore, slope of line $l=m=\tan \theta$.
But in $\triangle \mathrm{MPQ}$, we have $\tan \theta=\frac{\mathrm{MQ}}{\mathrm{MP}}=\frac{y_2-y_1}{x_2-x_1} \dots(2)$.
From equations (1) and (2), we have
$m=\tan \theta=\frac{y_2-y_1}{x_2-x_1}$

Case II: When angle $\theta$ is obtuse: An obtuse angle is an angle which is greater than $90^{\circ}$ and less than $180^{\circ}$.

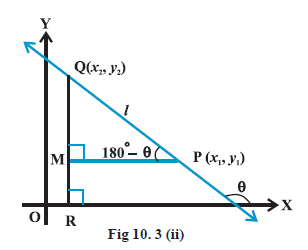
In Fig 10.3 (ii), we have $\angle \mathrm{MPQ}=180^{\circ}-\theta$.
Therefore, $\theta=180^{\circ}-\angle \mathrm{MPQ}$.
Now, slope of the line $l$
$\begin{aligned} m & =\tan \theta \\ & =\tan \left(180^{\circ}-\angle \mathrm{MPQ}\right)=-\tan \angle \mathrm{MPQ} \\ & =-\frac{\mathrm{MQ}}{\mathrm{MP}}=-\frac{y_2-y_1}{x_1-x_2}=\frac{y_2-y_1}{x_2-x_1} . \end{aligned}$
Consequently, we see that in both the cases the slope $m$ of the line through the points $\left(x_1, y_1\right)$ and $\left(x_2, y_2\right)$ is given by $m=\frac{y_2-y_1}{x_2-x_1}$.

Important Points to Remember

• If $\theta$ is the inclination of a line $l$, then $\tan \theta$ is called the slope or gradient of the line $l$.
• The slope of a line whose inclination is $90^{\circ}$ is not defined. If $x_1=x_2$, then $\tan \theta=\infty$ or $\theta=\frac{\pi}{2}$ i.e. $m$ is not defined or the line is perpendicular to $X$-axis.
• The slope of a line is denoted by $m$. Thus, $m=\tan \theta, \theta \neq 90^{\circ}$.
• It may be observed that the slope of $x$-axis is zero and slope of $y$-axis is not defined.

Example 1: Find the slope of the lines:
(a) Passing through the points $(3,-2)$ and $(-1,4)$,
(b) Making inclination of $60^{\circ}$ with the positive direction of $x$-axis.

Answer: 

(a) The slope of the line through $(3,-2)$ and $(-1,4)$ is
$m=\frac{4-(-2)}{-1-3}=\frac{6}{-4}=-\frac{3}{2} \text {. }$
(b) Here inclination of the line $\alpha=60^{\circ}$. Therefore, slope of the line is
$m=\tan 60^{\circ}=\sqrt{3} .$

Example 2: Determine $\lambda$, so that 2 is the slope of the line through $(2,5)$ and $(\lambda, 3)$.

Answer: Slope of the line joining $(2,5)$ and $(\lambda, 3)$
$\begin{aligned} & =\frac{3-5}{\lambda-2} =\frac{-2}{\lambda-2}=2 \\ \Rightarrow & -2 =2 \lambda-4 \\ \Rightarrow & 2 \lambda =2 \\ \therefore & \lambda =1 \end{aligned}$

Conditions for parallelism in terms of their slopes In a coordinate plane

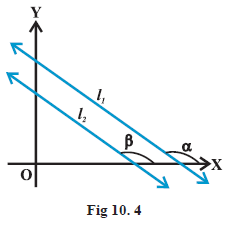
Suppose that non-vertical lines $l_1$ and $l_2$ have slopes $m_1$ and $m_2$, respectively. Let their inclinations be $\alpha$ and $\beta$, respectively.
If the line $l_1$ is parallel to $l_2$ (Fig 10.4), then their inclinations are equal, i.e.,
$\alpha=\beta \text {, and hence, } \tan \alpha=\tan \beta$
Therefore $m_1=m_2$, i.e., their slopes are equal.
Conversely, if the slope of two lines $l_1$ and $l_2$ (Fig 10.4) is same, i.e.,
Then
$m_1=m_2 \text {. }$
By the property of tangent function (between $0^{\circ}$ and $180^{\circ}$ ), $\alpha=\beta$.
Therefore, the lines are parallel.

Note: Hence, two non vertical lines $l_1$ and $l_2$ are parallel if and only if their slopes are equal.

Example 3: Show that the line joining the points $(2,-3)$ and $(-5,1)$ is parallel to the line joining $(7,-1)$ and $(0,3)$.

Answer: Slope of the line joining the points $(2,-3)$ and $(-5,1)$ is
$m_1=\frac{1-(-3)}{-5-2}=-\frac{4}{7}$
and slope of the line joining the points $(7,-1)$ and $(0,3)$ is
$m_2=\frac{3-(-1)}{0-7}=\frac{-4}{7}$
Here, $\quad m_1=m_2$
Hence, lines are parallel.

Conditions for perpendicularity in terms of their slopes In a coordinate plane

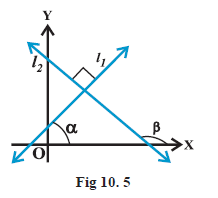
If the lines $l_1$ and $l_2$ are perpendicular (Fig 10.5), then $\beta=\alpha+90^{\circ}$. Therefore, $\tan \beta=\tan \left(\alpha+90^{\circ}\right)$
$=-\cot \alpha=-\frac{1}{\tan \alpha}$
i.e., $\quad m_2=-\frac{1}{m_1}$ or $\quad m_1 m_2=-1$
Conversely, if $m_1 m_2=-1$, i.e., $\tan \alpha \tan \beta=-1$.
Then $\tan \alpha=-\cot \beta=\tan \left(\beta+90^{\circ}\right)$ or $\tan \left(\beta-90^{\circ}\right)$
Therefore, $\alpha$ and $\beta$ differ by $90^{\circ}$.
Thus, lines $l_1$ and $l_2$ are perpendicular to each other.

Note: Hence, two non-vertical lines are perpendicular to each other if and only if their slopes are negative reciprocals of each other,
i.e.,
$m_2=-\frac{1}{m_1} \text { or, } m_1 m_2=-1$

Example 4: Find the equation of the line perpendicular to
$y=-2 x+3$
and passing through the point $(-3,9)$.

Answer: The slope of the given line is -2 . Then the slope of the perpendicular to the given line is
$m=-\frac{1}{-2}=\frac{1}{2} \text {. }$
Now, we have the slope of the perpendicular and a point on the line, so the equation of the perpendicular line is
$\begin{aligned} y-9 & =\frac{1}{2}(x-(-3)) \\ y-9 & =\frac{x}{2}+\frac{3}{2} \\ y & =\frac{x}{2}+\frac{21}{2} \end{aligned}$

Example 5: Line through the points $(-2,6)$ and $(4,8)$ is perpendicular to the line through the points $(8,12)$ and $(x, 24)$. Find the value of $x$.

Answer: Slope of the line through the points $(-2,6)$ and $(4,8)$ is
$m_1=\frac{8-6}{4-(-2)}=\frac{2}{6}=\frac{1}{3}$
Slope of the line through the points $(8,12)$ and $(x, 24)$ is
$m_2=\frac{24-12}{x-8}=\frac{12}{x-8}$
Since two lines are perpendicular, $m_1 m_2=-1$, which gives
$\frac{1}{3} \times \frac{12}{x-8}=-1 \text { or } x=4 \text {. }$

Angle between two lines

When we think about more than one line in a plane, then we find that these lines are either intersecting or parallel. Here we will discuss the angle between two lines in terms of their slopes.

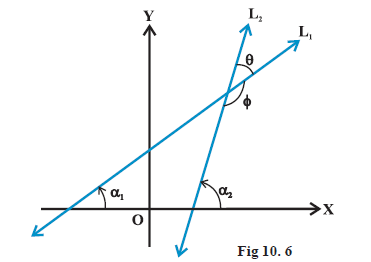
Let $\mathrm{L}_1$ and $\mathrm{L}_2$ be two non-vertical lines with slopes $m_1$ and $m_2$, respectively. If $\alpha_1$ and $\alpha_2$ are the inclinations of lines $L_1$ and $L_2$, respectively. Then
$m_1=\tan \alpha_1 \text { and } m_2=\tan \alpha_2 .$
We know that when two lines intersect each other, they make two pairs of vertically opposite angles such that sum of any two adjacent angles is $180^{\circ}$. Let $\theta$ and $\phi$ be the adjacent angles between the lines $\mathrm{L}_1$ and $\mathrm{L}_2$ (Fig10.6). Then
$\theta=\alpha_2-\alpha_1 \text { and } \alpha_1, \alpha_2 \neq 90^{\circ} \text {. }$
Therefore $\tan \theta=\tan \left(\alpha_2-\alpha_1\right)=\frac{\tan \alpha_2-\tan \alpha_1}{1+\tan \alpha_1 \tan \alpha_2}=\frac{m_2-m_1}{1+m_1 m_2} \quad\left(\right.$ as $1+m_1 m_2 \neq 0$ ) and $\phi=180^{\circ}-\theta$ so that
$\tan \phi=\tan \left(180^{\circ}-\theta\right)=-\tan \theta=-\frac{m_2-m_1}{1+m_1 m_2} \text {, as } 1+m_1 m_2 \neq 0$

Now, there arise two cases:

Case I: If $\frac{m_2-m_1}{1+m_1 m_2}$ is positive, then $\tan \theta$ will be positive and $\tan \phi$ will be negative, which means $\theta$ will be acute and $\phi$ will be obtuse.

Case II: If $\frac{m_2-m_1}{1+m_1 m_2}$ is negative, then $\tan \theta$ will be negative and $\tan \phi$ will be positive, which means that $\theta$ will be obtuse and $\phi$ will be acute.

Thus, the acute angle (say $\theta$ ) between lines $\mathrm{L}_1$ and $\mathrm{L}_2$ with slopes $m_1$ and $m_2$, respectively, is given by
$\tan \theta=\left|\frac{m_2-m_1}{1+m_1 m_2}\right| \text {, as } 1+m_1 m_2 \neq 0 \dots(1)$
The obtuse angle (say $\phi$ ) can be found by using $\phi=180^{\circ}-\theta$.

Example 6: If the angle between two lines is $\frac{\pi}{4}$ and slope of one of the lines is $\frac{1}{2}$, find the slope of the other line.

Answer: We know that the acute angle $\theta$ between two lines with slopes $m_1$ and $m_2$ is given by
$\tan \theta=\left|\frac{m_2-m_1}{1+m_1 m_2}\right| \dots(1)$
Let $m_1=\frac{1}{2}, m_2=m$ and $\theta=\frac{\pi}{4}$.
Now, putting these values in (1), we get
$\tan \frac{\pi}{4}=\left|\frac{m-\frac{1}{2}}{1+\frac{1}{2} m}\right| \text { or } 1=\left|\frac{m-\frac{1}{2}}{1+\frac{1}{2} m}\right| \text {, }$
which gives $\quad \frac{m-\frac{1}{2}}{1+\frac{1}{2} m}=1$ or $\frac{m-\frac{1}{2}}{1+\frac{1}{2} m}=-1$.
Therefore $m=3$ or $m=-\frac{1}{3}$.

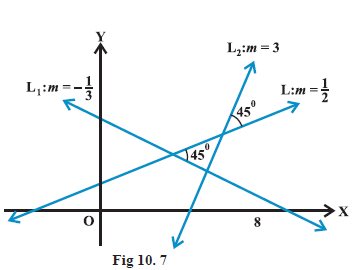
Hence, slope of the other line is 3 or $-\frac{1}{3}$. Fig 10.7 explains the reason of two answers.

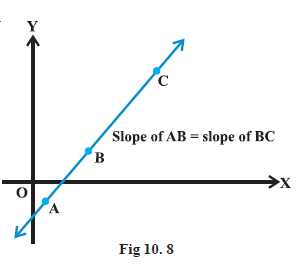
Collinearity of three points

We know that slopes of two parallel lines are equal. If two lines having the same slope pass through a common point, then two lines will coincide. Hence, if A, B and C are three points in the $\mathrm{XY}$-plane, then they will lie on a line, i.e., three points are collinear (Fig 10.8) if and only if slope of $A B=$ slope of $B C$.

Example 7: Find whether the points
$(-a,-b),[-(s+1) a,-(s+1) b] \text { and }[(t-1) a,(t-1) b]$
are collinear?

Answer: Let $A \equiv(-a,-b), B \equiv[-(s+1) a,-(s+1) b]$ and
$C \equiv((t-1) a,(t-1) b)$
Then, slope of $A B=\frac{-(s+1) b+b}{-(s+1) a+a}=\frac{b}{a}$
and slope of $B C=\frac{(t-1) b+(s+1) b}{(t-1) a+(s+1) a}=\frac{b}{a}$
Hence, given points are collinear.

Example 8: For what value of $k$ the points $(k, 2-2 k),(-k+1,2 k)$ and $(-4-k, 6-2 k)$ are collinear?

Answer: Let $A \equiv(k, 2-2 k), B \equiv(-k+1,2 k)$ and $C \equiv(-4-k, 6-2 k)$ are collinear, then
Slope of $A B=$ Slope of $A C$
$\begin{array}{l} \Rightarrow \quad \frac{2 k-(2-2 k)}{-k+1-k}=\frac{6-2 k-(2-2 k)}{-4-k-k} \\ \Rightarrow \quad \frac{4 k-2}{-2 k+1}=\frac{4}{-4-2 k} \quad\left(k \neq \frac{1}{2}(\because \text { Denominator } \neq 0)\right) \\ \Rightarrow \quad(4 k-2)(-4-2 k)=4(-2 k+1) \\ \Rightarrow \quad(2 k-1)(-2-k)-(-2 k+1)=0 \\ \Rightarrow \quad(2 k-1)(-2-k+1)=0 \\ \therefore \quad k \neq \frac{1}{2}, \quad \therefore \quad k=-1 \end{array}$

Example 9: Find the angle between the lines joining the points $(0,0),(2,3)$ and $(2,-2),(3,5)$.

Answer: Let the given points be $A \equiv(0,0), B \equiv(2,3), C \equiv(2,-2)$ and $D \equiv(3,5)$. Let $m_1$ and $m_2$ be the slopes of the lines $A B$ and $C D$ respectively.
$\therefore \quad m_1=\frac{3-0}{2-0}=\frac{3}{2} \text { and } m_2=\frac{5-(-2)}{3-2}=7$
Let $\theta$ be the acute angle between the lines
$\begin{array}{l} \therefore \quad \tan \theta=\left|\frac{m_1-m_2}{\mid 1+m_1 m_2}\right|=\left|\frac{\frac{3}{2}-7}{1+\left(\frac{3}{2}\right) \cdot 7}\right| \\ =\left|\frac{-11}{23}\right|=\frac{11}{23} \\ \therefore \quad \theta=\tan ^{-1}\left(\frac{11}{23}\right) \\ \end{array}$

Example 10: Without using pythagoras theorem, show that the points $A(-1,3), B(0,5)$ and $C(3,1)$ are the vertices of a right angled triangle.

Answer: In $\triangle A B C$, we have
Slope of side $A B=\frac{5-3}{0-(-1)}=2=m_1 \text { (say) }$
Slope of side $B C=\frac{1-5}{3-0}=-\frac{4}{3}=m_2 \text { (say) }$
and Slope of side $C A=\frac{3-1}{-1-3}=-\frac{1}{2}=m_3 \text { (say) }$
Clearly,
$m_1 m_3=2 \times\left(-\frac{1}{2}\right)=-1$
$\therefore A B$ and $C A$ are perpendicular to each other i.e.
$\angle B A C=90^{\circ}$
Hence, the given points are the vertices of a right angled triangle.

Example 11: Show that the triangle which has one of the angles as $60^{\circ}$, can not have all vertices with integral coordinates.

Answer: Let $A B C$ be a triangle whose vertices are $A\left(x_1, y_1\right), B\left(x_2, y_2\right)$ and $C\left(x_3, y_3\right)$. Assume $x_1, x_2, x_3, y_1, y_2, y_3$ all are integers.
Let $\angle B A C=60^{\circ}$
Slope of $A C=\frac{y_3-y_1}{x_3-x_1}=\mid m_1 \text { (say) }$
and Slope of $A B=\frac{y_2-y_1}{x_2-x_1}=m_2 \text { (say) }$

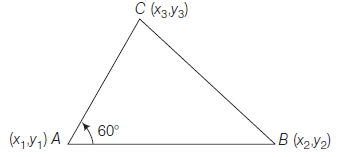
Here, $m_1$ and $m_2$ are rational numbers $\left(\because x_1, x_2, x_3, y_1, y_2, y_3\right.$ are integers)
$\begin{array}{l} \therefore \quad \tan (\angle B A C)=\frac{m_1-m_2}{1+m_1 m_2} \\ =\text { Rational } \quad\left(\because m_1 \text { and } m_2 \text { are rational }\right) \\ \text { But } \tan (\angle B A C)=\tan 60^{\circ}=\sqrt{3}=\text { Irrational } \end{array}$
$\because$ Rational number $\neq$ Irrational number
Which is contradiction so our assumption that the vertices are integers is wrong. Hence, the triangle having one angle of $60^{\circ}$ can not have all vertices with integral coordinates.

Example 12: Three points $\mathrm{P}(h, k), \mathrm{Q}\left(x_1, y_1\right)$ and $\mathrm{R}\left(x_2, y_2\right)$ lie on a line. Show that
$\left(h-x_1\right)\left(y_2-y_1\right)=\left(k-y_1\right)\left(x_2-x_1\right) .$

Answer: Since points P, Q and R are collinear, we have
Slope of $\mathrm{PQ}=$ Slope of $\mathrm{QR}$, i.e., $\frac{y_1-k}{x_1-h}=\frac{y_2-y_1}{x_2-x_1}$
or $\quad \frac{k-y_1}{h-x_1}=\frac{y_2-y_1}{x_2-x_1}$,
or $\quad\left(h-x_1\right)\left(y_2-y_1\right)=\left(k-y_1\right)\left(x_2-x_1\right)$.

Example 13: In Fig 10.9, time and distance graph of a linear motion is given. Two positions of time and distance are recorded as, when $\mathrm{T}=0, \mathrm{D}=2$ and when $\mathrm{T}=3, \mathrm{D}=8$. Using the concept of slope, find law of motion, i.e., how distance depends upon time.

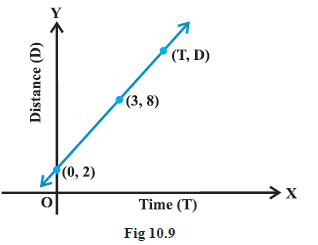
Answer: Let ( $T, D)$ be any point on the line, where $\mathrm{D}$ denotes the distance at time $\mathrm{T}$. Therefore, points $(0,2),(3,8)$ and (T, D) are collinear so that
$\begin{array}{l} \frac{8-2}{3-0}=\frac{\mathrm{D}-8}{\mathrm{~T}-3} \text { or } \quad 6(\mathrm{~T}-3)=3(\mathrm{D}-8) \\ \text { or } \quad \mathrm{D}=2(\mathrm{~T}+1), \end{array}$
which is the required relation.