1.14 NCERT Exemplar Q & A

Short Answer Type

Q1. Write the following sets in the roaster from
(i) \(\mathrm{A}=\{x: x \in \mathbf{R}, 2 x+11=15\}\)
(ii) \(\mathrm{B}=\left\{x \mid x^2=x, x \in \mathbf{R}\right\}\)
(iii) \(\mathrm{C}=\{x \mid x\) is a positive factor of a prime number \(p\}\)

Solution: (i) Given that: \(A=\{x: x \in R, 2 x+11=15\}\)
\(
\begin{aligned}
& \therefore 2 \mathrm{x}+11=15 \\
& \Rightarrow 2 \mathrm{x}=15-11 \\
& \Rightarrow 2 \mathrm{x}=4 \\
& \Rightarrow \mathrm{x}=2
\end{aligned}
\)
Hence, \(A=\{2\}\)
(ii) Given that: \(B=\left\{x \mid x^2=x, x \in R\right\}\)
\(
\begin{aligned}
& \therefore \mathrm{x}^2=\mathrm{x} \\
& \Rightarrow \mathrm{x}^2-\mathrm{x}=0 \\
& \Rightarrow \mathrm{x}(\mathrm{x}-1)=0 \\
& \therefore \mathrm{x}=0, \mathrm{x}=1
\end{aligned}
\)
Hence, \(B=\{0,1\}\)
(iii) Given that: \(\mathrm{C}=\{\mathrm{x} \mid \mathrm{x}\) is a positive factor of a prime number P\(\}\)
So, the positive factors of prime number P are 1 and P.
Hence, \(\mathrm{C}=\{1, \mathrm{P}\}\)

Q2. Write the following sets in the roaster form:
(i) \(\mathrm{D}=\left\{t \mid t^3=t, t \in \mathrm{R}\right\}\)
(ii) \(\mathrm{E}=\left\{w \left\lvert\, \frac{w-2}{w+3}=3\right., w \in \mathbf{R}\right\}\)
(iii) \(\mathrm{F}=\left\{x \mid x^4-5 x^2+6=0, x \in \mathbf{R}\right\}\)

Solution: (i) Given: \(D=\left\{t \mid t^3=t, t \in R\right\}\)
To find: Roster form of the given set
\(
\begin{aligned}
& \mathrm{t}^3=\mathrm{t} \\
& \Rightarrow \mathrm{t}^3-\mathrm{t}=0 \\
& \Rightarrow \mathrm{t}\left(\mathrm{t}^2-1\right)=0 \\
& \Rightarrow \mathrm{t}(\mathrm{t}-1)(\mathrm{t}+1)=0 \\
& \Rightarrow \mathrm{t}=0,-1 \text { or } 1 \\
& \text { So, } \mathrm{D}=\{-1,0,1\}
\end{aligned}
\)
(ii) Given: \(E=\left\{w \left\lvert\, \frac{w-2}{w+3}=3\right., w \in R\right\}\)
To find: Roster form of the given set
\(
\begin{aligned}
& \frac{w-2}{w+3}=3 \\
& \Rightarrow \mathrm{w}-2=3(\mathrm{w}+3) \\
& \Rightarrow \mathrm{w}-2=3 \mathrm{w}+9 \\
& \Rightarrow 3 \mathrm{w}-\mathrm{w}=-9-2 \\
& \Rightarrow 2 \mathrm{w}=-11 \\
& \Rightarrow \mathrm{w}=-\frac{11}{2} \\
& \text { So, } \mathrm{E}=\left\{-\frac{11}{2}\right\}
\end{aligned}
\)
(iii) Given: \(F=\left\{x \mid x^4-5 x^2+6=0, x \in R\right\}\)
To find: Roster form of the given set
\(
\begin{aligned}
& \mathrm{x}^4-5 \mathrm{x}^2+6=0 \\
& \Rightarrow \mathrm{x}^4-3 \mathrm{x}^2-2 \mathrm{x}^2+6=0 \\
& \Rightarrow \mathrm{x}^2\left(\mathrm{x}^2-3\right)-2\left(\mathrm{x}^2-3\right)=0 \\
& \Rightarrow\left(\mathrm{x}^2-3\right)\left(\mathrm{x}^2-2\right)=0 \\
& \Rightarrow \mathrm{x}^2=3 \text { or } 2 \\
& \Rightarrow \mathrm{x}= \pm \sqrt{3} \text { or } \pm \sqrt{2} \\
& \Rightarrow \mathrm{x}=\sqrt{3},-\sqrt{3}, \sqrt{2} \text { or }-\sqrt{2} \\
& \text { So, } \mathrm{F}=\{-\sqrt{3},-\sqrt{2}, \sqrt{2}, \sqrt{3}\}
\end{aligned}
\)

Q3. If \(\mathrm{Y}=\left\{x \mid x\right.\) is a positive factor of the number \(2^{p-1}\left(2^p-1\right)\), where \(2^p-1\) is a prime number }. Write Y in the roaster form.

Solution: You are finding the set \(Y\) containing all positive factors of \(2^{p-1}\left(2^p-1\right)\), where \(2^p-1\) is a prime number.
What’s given in the problem
The set Y is defined as \(\left\{x \mid x\right.\) is a positive factor of the number \(\left.2^{p-1}\left(2^p-1\right)\right\}\).
The term \(2^p-1\) is a prime number.
How to solve
List all factors of the given number by considering its prime factorization.
Identify the prime factors of the given number.
The given number is \(N=2^{p-1}\left(2^p-1\right)\).
Since \(2^p-1\) is a prime number, the prime factors are 2 and \(\left(2^p-1\right)\).
The factors of \(2^{p-1}\) are \(2^0, 2^1, 2^2, \ldots, 2^{p-1}\).
The factors of \(\left(2^p-1\right)\) are 1 and \(\left(2^p-1\right)\) because it is prime.
The positive factors of \(N\) are the products of these factors.
\(
\mathrm{Y}=\left\{1,2,2^2, \ldots, 2^{p-1},\left(2^p-1\right), 2\left(2^p-1\right), 2^2\left(2^p-1\right), \ldots, 2^{p-1}\left(2^p-1\right)\right\}
\)
The set Y in roster form is
\(
\mathrm{Y}=\left\{1,2,2^2, \ldots, 2^{p-1},\left(2^p-1\right), 2\left(2^p-1\right), 2^2\left(2^p-1\right), \ldots, 2^{p-1}\left(2^p-1\right)\right\}
\)

Q4. State which of the following statements are true and which are false. Justify your answer.
(i) \(35 \in\{x \mid x\) has exactly four positive factors \(\}\).
(ii) \(128 \in\{y \mid\) the sum of all the positive factors of \(y\) is \(2 y\}\)
(iii) \(3 \notin\left\{x \mid x^4-5 x^3+2 x^2-112 x+6=0\right\}\)
(iv) \(496 \notin\{y \mid\) the sum of all the positive factors of \(y\) is \(2 y\}\).

Solution: (i) Given that: \(35 \in\{x \mid x\) has exactly four positive factors \(\}\)
\(\therefore\) Factors of 35 are \(1,5,7,35\)
Hence, the statement ( \(i\) ) is ‘True’.
(ii) Given that: \(128 \in\{y \mid\) the sum of all positive factors of \(y\) is \(2 y\}\)
\(\therefore\) Factors of 128 are \(1,2,4,8,16,32,64\) and 128.
Sum of all the factors \(=1+2+4+8+16+32+64+128\)
\(
=255 \neq 2 \times 128
\)
Hence, the given statement is ‘False.’
(iii) Given that: \(3 \notin\left\{x \mid x^4-5 x^3+2 x^2-112 x+6=0\right\}\)
\(
\therefore \quad x^4-5 x^3+2 x^2-112 x+6=0
\)
Now for \(x=3\), we have
\(
\begin{aligned}
& (3)^4-5(3)^3+2(3)^2-112(3)+6 \\
& \Rightarrow 81-135+18-336+6 \Rightarrow-366 \neq 0
\end{aligned}
\)
Hence, statement (iii) is ‘True’.
(iv) Given that:
\(496 \notin\{y \mid\) the sum of all the positive factors of \(y\) is \(2 y\}\)
\(\therefore\) The positive factors of 496 are \(1,2,4,8,16,31,62,124,248\) and 496
\(\therefore\) The sum of all the positive factors of 496
\(
=1+2+4+8+16+31+62+124+248+496=992=2 \times 496
\)
Hence, the given statement is ‘False’.

Q5. Given \(\mathrm{L}=\{1,2,3,4\}, \mathrm{M}=\{3,4,5,6\}\) and \(\mathrm{N}=\{1,3,5\}\)
Verify that \(\mathrm{L}-(\mathrm{M} \cup \mathrm{N})=(\mathrm{L}-\mathrm{M}) \cap(\mathrm{L}-\mathrm{N})\)

Solution: Given that: \(\mathrm{L}=\{1,2,3,4\}, \mathrm{M}=\{3,4,5,6\}\) and \(\mathrm{N}=\{1,3,5\}\)
To verify that \(\mathrm{L}-(\mathrm{M} \cup \mathrm{N})=(\mathrm{L}-\mathrm{M}) \cap(\mathrm{L}-\mathrm{N})\)
\(
\begin{aligned}
\text { L.H.S. }=\mathrm{L}-(\mathrm{M} \cup \mathrm{~N}) & =\{1,2,3,4\}-\{\{3,4,5,6\} \cup\{1,3,5\}\} \\
& =\{1,2,3,4\}-\{1,3,4,5,6\}=\{2\} \\
\text { R.H.S. }=(\mathrm{L}-\mathrm{M}) \cap(\mathrm{L}-\mathrm{N}) & \\
(\mathrm{L}-\mathrm{M}) & =\{1,2,3,4\}-\{3,4,5,6\}=\{1,2\} \\
(\mathrm{L}-\mathrm{N}) & =\{1,2,3,4\}-\{1,3,5\}=\{2,4\} \\
\therefore \quad(\mathrm{L}-\mathrm{M}) \cap(\mathrm{L}-\mathrm{N}) & =\{1,2\} \cap\{2,4\}=\{2\} \\
\text { L.H.S. } & =\text { R.H.S. }
\end{aligned}
\)
Hence, verified.

Q6. If \(A\) and \(B\) are subsets of the universal set \(U\), then show that
(i) \(A \subset A \cup B\)
(ii) \(\mathrm{A} \subset \mathrm{B} \Leftrightarrow \mathrm{A} \cup \mathrm{B}=\mathrm{B}\)
(iii) \((A \cap B) \subset A\)

Solution: (i) Given that: \(\mathrm{A} \subset \mathrm{U}\) and \(\mathrm{B} \subset \mathrm{U}\)
Let \(x \in \mathrm{~A}\) or \(x \in \mathrm{~B}\)
\(\Rightarrow x \in \mathrm{~A} \cup \mathrm{~B}\)
Hence, \(A \subset(A \cup B)\)
(ii) If \(\mathrm{A} \subset \mathrm{B}\)
Then let \(x \in \mathrm{~A} \cup \mathrm{~B}\)
\(\Rightarrow x \in \mathrm{~A}\) or \(x \in \mathrm{~B}\)
\(\Rightarrow \quad \mathrm{A} \cup \mathrm{B} \subset \mathrm{B} \dots(1)\)
But \(B \subset A \cup B \dots(2)\)
From eqn. (1) and (2), we get
\(A \cup B=B\)
Let \(y \in A \Rightarrow y \in(A \cup B) \Rightarrow y \in B\)
\(\Rightarrow y \in \mathrm{~B} \Leftrightarrow \mathrm{~A} \cup \mathrm{~B}=\mathrm{B}\)
(iii) Let \(x \in A \cap B\)
\(\Rightarrow x \in \mathrm{~A}\) and \(x \in \mathrm{~B} \Rightarrow x \in \mathrm{~A}\)
So \(A \cap B \subset A\).

Q7. Given that \(\mathrm{N}=\{1,2,3, \ldots, 100\}\). Then write
(i) the subset of N whose elements are even numbers.
(ii) the subset of N whose elements are perfect square numbers.

Solution: We are given that: \(\mathrm{N}=\{1,2,3,4,5, \ldots, 100\}\)
(i) Required subset whose elements are even
\(
=\{2,4,6,8, \ldots, 100\}
\)
(ii) Required subset whose elements are perfect squares
\(
=\{1,4,9,16,25,36, \ldots, 100\}
\)

Q8. If \(X=\{1,2,3\}\), if \(n\) represents any member of \(X\), write the following sets containing all numbers represented by
(i) \(4 n\)
(ii) \(n+6\)
(iii) \(\frac{n}{2}\)
(iv) \(n-1\)

Solution: Given that: \(X=\{1,2,3\}\)
(i) \(\{4 n \mid n \in \mathrm{X}\}=\{4,8,12\}\)
(ii) \(\{n+6 \mid n \in X\}=\{7,8,9\}\)
(iii) \(\left\{\left.\frac{n}{2} \right\rvert\, n \in \mathrm{X}\right\}=\left\{\frac{1}{2}, 1, \frac{3}{2}\right\}\)
(iv) \(\{(n-1) \mid n \in X\}=\{0,1,2\}\)

Q9. If \(\mathrm{Y}=\{1,2,3, \ldots 10\}\), and \(a\) represents any element of Y, write the following sets, containing all the elements satisfying the given conditions.
(i) \(a \in \mathrm{Y}\) but \(a^2 \notin \mathrm{Y}\)
(ii) \(a+1=6, a \in \mathrm{Y}\)
(iii) \(a\) is less than 6 and \(a \in \mathrm{Y}\)

Solution: Given that: \(\mathrm{Y}=\{1,2,3, \ldots, 10\}\)
(i) \(\left\{a \in Y\right.\) but \(\left.a^2 \notin Y\right\}=\{4,5,6,7,8,9,10\}\)
(ii) \(\{a+1=6, a \in \mathrm{Y}\}=\{5\}\)
(iii) \(\{a<6\) and \(a \in \mathrm{Y}\}=\{1,2,3,4,5\}\)

Q10. \(A, B\) and \(C\) are subsets of Universal Set \(U\). If \(A=\{2,4,6,8,12,20\}\) \(B=\{3,6,9,12,15\}, C=\{5,10,15,20\}\) and \(U\) is the set of all whole numbers, draw a Venn diagram showing the relation of \(\mathrm{U}, \mathrm{A}, \mathrm{B}\) and \(\mathrm{C}\)

Solution: Given that: \(\mathrm{A}, \mathrm{B}\) and C are the subsets of a universal set U.

\(
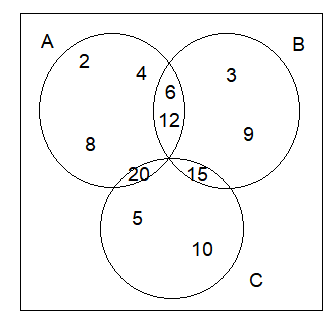
\begin{aligned}
\text { Where } A & =\{2,4,6,8,12,20\} \\
B & =\{3,6,9,12,15\} \\
\text { and } & C=\{5,10,15,20\}
\end{aligned}
\)

Q11. Let U be the set of all boys and girls in a school, G be the set of all girls in the school, B be the set of all boys in the school, and S be the set of all students in the school who take swimming. Some, but not all, students in the school take swimming. Draw a Venn diagram showing one of the possible interrelationships among sets \(\mathrm{U}, \mathrm{G}, \mathrm{B}\) and S.

Solution: Given that:
U = Set of universal
G = Set of girls
B = Set of boys
S = Set of all students who take swimming.

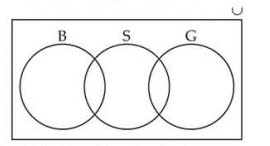
Q12. For all sets \(\mathrm{A}, \mathrm{B}\) and C , show that \((\mathrm{A}-\mathrm{B}) \cap(\mathrm{C}-\mathrm{B})=\mathrm{A}-(\mathrm{B} \cup \mathrm{C})\) 

Solution: To prove \((A-B) \cap(A-C)=A-(B \cup C)\)
L.H.S. Let \(x \in(\mathrm{~A}-\mathrm{B}) \cap(\mathrm{A}-\mathrm{C})\)
\(\Rightarrow x \in(\mathrm{~A}-\mathrm{B})\) and \(x \in(\mathrm{~A}-\mathrm{C})\)
\(\Rightarrow(x \in \mathrm{~A}\) and \(x \notin \mathrm{~B})\) and \((x \in \mathrm{~A}\) and \(x \notin \mathrm{C})\)
\(\Rightarrow x \in \mathrm{~A}\) and \((x \notin \mathrm{~B}\) and \(x \notin \mathrm{C})\)
\(\Rightarrow x \in \mathrm{~A}-(\mathrm{B} \cup \mathrm{C})\)
So \((A-B) \cap(A-C) \subset A-(B \cup C) \dots(i)\)
R.H.S. Let \(y \in A-(B \cup C)\)
\(\Rightarrow y \in A\) and \(y \notin(B \cup C)\)
\(\Rightarrow y \in A\) and \((y \notin B\) and \(y \notin C)\)
\(\Rightarrow(y \in A\) and \(y \notin B)\) and \((y \in A\) and \(y \notin C)\)
\(\Rightarrow y \in(\mathrm{~A}-\mathrm{B})\) and \(y \in(\mathrm{~A}-\mathrm{C})\)
So \(A-(B \cup C) \subset(A-B) \cap(A-C) \dots(ii)\)
From eqn. (i) and (ii), we get
\(
A-(B \cup C)=(A-B) \cap(A-C)
\)

Q13. For all sets A and \(\mathrm{B},(\mathrm{A}-\mathrm{B}) \cup(\mathrm{A} \cap \mathrm{B})=\mathrm{A}\), True or False?

Solution: 

\(
\begin{aligned}
&\begin{aligned}
\text { L.H.S. }=(A-B) & \cup(A \cap B) \\
= & {[(A-B) \cup A] \cap[(A-B) \cup B] } \\
= & A \cap(A \cup B)=A=\text { R.H.S. }
\end{aligned}\\
&\text { Hence, the given statement is ‘True’. }
\end{aligned}
\)

Q14. For all sets \(\mathrm{A}, \mathrm{B}\) and \(\mathrm{C}, \mathrm{A}-(\mathrm{B}-\mathrm{C})=(\mathrm{A}-\mathrm{B})-\mathrm{C}\), True or False?

Solution: Let us solve the given statement by the following Venn diagram.

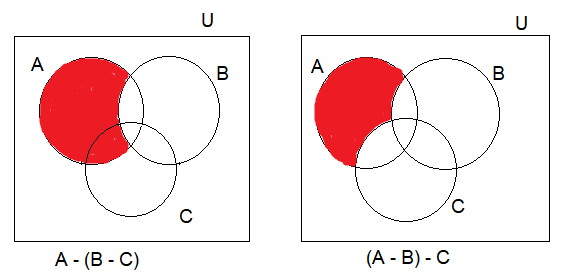
Clearly, from the above diagram, we calculate that
\(
A-(B-C) \neq(A-B)-C
\)
Hence, the given statement is not ‘True’.

Q15. For all sets \(\mathrm{A}, \mathrm{B}\) and C , if \(\mathrm{A} \subset \mathrm{B}\), then \(\mathrm{A} \cap \mathrm{C} \subset \mathrm{B} \cap \mathrm{C}\), True or False?

Solution: Let \(x \in \mathrm{~A} \cap \mathrm{C}\)
\(\Rightarrow x \in \mathrm{~A}\) and \(x \in \mathrm{C}\)
\(\Rightarrow x \in \mathrm{~B}\) and \(x \in \mathrm{C}\)
\(\Rightarrow x \in(\mathrm{~B} \cap \mathrm{C}) \Rightarrow(\mathrm{A} \cap \mathrm{C}) \subset(\mathrm{B} \cap \mathrm{C})\)
Hence, the given statement is ‘True’.

Q16. For all sets \(A, B\) and \(C\), if \(A \subset B\), then \(A \cup C \subset B \cup C\), True or False?

Solution: Let \(x \in \mathrm{~A} \cup \mathrm{C}\)
\(\Rightarrow x \in \mathrm{~A}\) or \(x \in \mathrm{C}\)
\(\Rightarrow x \in \mathrm{~B}\) or \(x \in \mathrm{C}\) \([\because A \subset B]\)
\(\Rightarrow x \in(\mathrm{~B} \cup \mathrm{C}) \Rightarrow(\mathrm{A} \cup \mathrm{C}) \subset(\mathrm{B} \cup \mathrm{C})\)
Hence, the given statement is ‘True’.

Q17. For all sets \(\mathrm{A}, \mathrm{B}\) and C , if \(\mathrm{A} \subset \mathrm{C}\) and \(\mathrm{B} \subset \mathrm{C}\), then \(\mathrm{A} \cup \mathrm{B} \subset \mathrm{C}\), True or False?

Solution: Let \(x \in A \cup B\)
\(\Rightarrow x \in \mathrm{~A}\) or \(x \in \mathrm{~B}\)
\(\Rightarrow x \in \mathrm{C}\) or \(x \in \mathrm{C}\) \([\because A \subset C\) and \(B \subset C]\)
\(\Rightarrow x \in \mathrm{C} \Rightarrow \mathrm{A} \cup \mathrm{B} \subset \mathrm{C}\)
Hence, the given statement is ‘True’.

Q18. Prove that for all sets A and \(\mathrm{B}, \mathrm{A} \cup(\mathrm{B}-\mathrm{A})=\mathrm{A} \cup \mathrm{B}\)

Solution: \(\text { L.H.S. }=A \cup(B-A)=A \cup\left(B \cap A^{\prime}\right) \quad\left[\because A-B=A \cap B^{\prime}\right]\)
\(
=(A \cup B) \cap\left(A \cup A^{\prime}\right)
\)
\(
=\mathrm{A} \cup \mathrm{~B} \cap \mathrm{U} \left[\because \mathrm{A} \cup \mathrm{~A}^{\prime}=\mathrm{U}\right]
\)
\(
=A \cup B=R . H . S . \quad[\because A \cup U=A]
\)
Hence, the given statement is proved.

Q19. Prove that for all sets A and \(\mathrm{B}, \mathrm{A}-(\mathrm{A}-\mathrm{B})=\mathrm{A} \cap \mathrm{B}\)

Solution: \(\text { L.H.S. }=A-(A-B)=A-\left(A \cap B^{\prime}\right) \left[\because A-B=A \cap B^{\prime}\right]\)
\(
=A \cap\left(A \cap B^{\prime}\right)^{\prime}=A \cap\left[A^{\prime} \cup\left(B^{\prime}\right)^{\prime}\right]\left[\because(A \cap B)^{\prime}=A^{\prime} \cup B^{\prime}\right]
\)
\(
=A \cap\left[A^{\prime} \cup B\right] \quad\left[\because\left(A^{\prime}\right)^{\prime}=A\right]
\)
\(
\begin{aligned}
& =\left(A \cap A^{\prime}\right) \cup(A \cap B)=\phi \cup(A \cap B) \\
& =A \cap B=R . H . S .
\end{aligned}
\)
L.H.S. = R.H.S. Hence proved.

Q20. Prove that for all sets A and \(\mathrm{B}, \mathrm{A}-(\mathrm{A} \cap \mathrm{B})=\mathrm{A}-\mathrm{B}\)

Solution:

\(
\begin{aligned}
\text { L.H.S. }=A-(A \cap B) & =A \cap(A \cap B)^{\prime} \\
& =A \cap\left(A^{\prime} \cup B^{\prime}\right)=\left(A \cap A^{\prime}\right) \cup\left(A \cap B^{\prime}\right) \\
& =\phi \cup(A-B) \quad\left[\because A-B=A \cap B^{\prime}\right] \\
& =A-B=\text { R.H.S. } \\
\text { L.H.S. }= & \text { R.H.S. Hence proved. }
\end{aligned}
\)

Q21. Prove that for all sets A and \(\mathrm{B},(\mathrm{A} \cup \mathrm{B})-\mathrm{B}=\mathrm{A}-\mathrm{B}\)

Solution: 

\(
\begin{aligned}
\text { L.H.S. }(A \cup B)-B & =(A \cup B) \cap B^{\prime} & {\left[\because A-B=A \cap B^{\prime}\right] } \\
& =\left(A \cap B^{\prime}\right) \cup\left(B \cap B^{\prime}\right) & {\left[\because A \cap A^{\prime}=\phi\right] } \\
& =(A-B) \cup \phi & \\
& =A-B \text { R.H.S. } & \\
\text { L.H.S. } & =\text { R.H.S. Hence proved. } &
\end{aligned}
\)

Q22. Let \(\mathrm{T}=\left\{x \left\lvert\, \frac{x+5}{x-7}-5=\frac{4 x-40}{13-x}\right.\right\}\). Is T an empty set? Justify your answer.

Solution: \(\text { Given that: } \mathrm{T}=\left\{x \left\lvert\, \frac{x+5}{x-7}-5=\frac{4 x-40}{13-x}\right.\right\}\)
\(
\begin{aligned}
\frac{x+5}{x-7}-5 & =\frac{4 x-40}{13-x} \\
\frac{x+5}{x-7}-\frac{4 x-40}{13-x} & =5
\end{aligned}
\)
\(
\begin{aligned}
\frac{(x+5)(13-x)-(x-7)(4 x-40)}{(x-7)(13-x)} & =5 \\
\frac{13 x-x^2+65-5 x-4 x^2+40 x+28 x-280}{13 x-x^2-91+7 x} & =5 \\
-5 x^2+76 x-215 & =5\left(13 x-x^2+7 x-91\right) \\
-5 x^2+86 x-215 & =65 x-5 x^2+35 x-455 \\
76 x-100 x & =-455+215 \Rightarrow-24 x=-240 \\
x & =\frac{240}{24}=10 \\
T & =10
\end{aligned}
\)
Hence, T is not an empty set.

Long Answer Type

Q23. Let \(\mathrm{A}, \mathrm{B}\) and C be sets. Then show that \(A \cap(B \cup C)=(A \cap B) \cup(A \cap C)\)

Solution: Let \(x \in A \cap(B \cup C)\)
\(\Rightarrow x \in \mathrm{~A}\) and \(x \in(\mathrm{~B} \cup \mathrm{C})\)
\(\Rightarrow x \in \mathrm{~A}\) and \((x \in \mathrm{~B}\) or \(x \in \mathrm{C})\)
\(\Rightarrow(x \in \mathrm{~A}\) and \(x \in \mathrm{~B})\) or \((x \in \mathrm{~A}\) and \(x \in \mathrm{C})\)
\(\Rightarrow(x \in \mathrm{~A} \cap \mathrm{~B})\) or \((x \in \mathrm{~A} \cap \mathrm{C})\)
\(\Rightarrow x \in(\mathrm{~A} \cap \mathrm{~B}) \cup(\mathrm{A} \cap \mathrm{C}) \dots(i)\)
Now let \(y \in(A \cap B) \cup(A \cap C)\)
\(\Rightarrow y \in(\mathrm{~A} \cap \mathrm{~B})\) or \(y \in(\mathrm{~A} \cap \mathrm{C})\)
\(\Rightarrow(y \in A[latex] and [latex]y \in B)\) or \((y \in A[latex] and [latex]y \in C)\)
\(\Rightarrow y \in \mathrm{~A}\) and \((y \in \mathrm{~B}\) or \(y \in \mathrm{C})\)
\(
\begin{aligned}
& \Rightarrow y \in A \text { and } y \subset(B \cup C) \\
& \Rightarrow y \in A \cap(B \cup C) \dots(ii)\\
& \text { From eqn. }(i) \text { and }(i i) \text { we get } \\
& A \cap(B \cup C)=(A \cap B) \cup(A \cap C) \\
& \text { L.H.S. }=\text { R.H.S. Hence proved. }
\end{aligned}
\)

Q24. Out of 100 students, 15 passed in English, 12 passed in Mathematics, 8 in Science, 6 in English and Mathematics, 7 in Mathematics and Science, 4 in English and Science, 4 in all the three. Find how many passed
(i) in English and Mathematics but not in Science
(ii) in Mathematics and Science but not in English
(iii) in Mathematics only
(iv) in more than one subject only

Solution: Let the number of students passed in Mathematics M, E be in English and \(S\) be in Science. Then \(n(\mathrm{U})=100, n(\mathrm{M})=12\), \(n(\mathrm{E})=15, n(\mathrm{~S})=8, n(\mathrm{E} \cap \mathrm{M})=6\), \(n(\mathrm{M} \cap \mathrm{S})=7, n(\mathrm{E} \cap \mathrm{S})=4\) and \(n(\mathrm{E} \cap \mathrm{M} \cap \mathrm{S})=4\)
Let us draw a Venn diagram. According to the Venn diagram, we get

\(
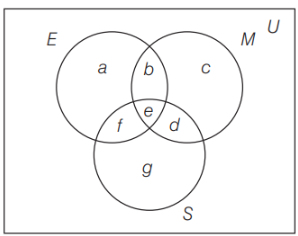
\begin{aligned}
a+b+d+e & =15 \dots(i) \\
b+c+e+f & =12 \dots(ii) \\
d+e+f+g & =8 \dots(iii) \\
n(\mathrm{E} \cap \mathrm{M}) & =6 \quad \therefore b+e=6 \dots(iv) \\
n(\mathrm{M} \cap \mathrm{~S}) & =7 \quad \therefore e+f=7 \dots(v) \\
n(\mathrm{E} \cap \mathrm{~S}) & =4 \quad \therefore d+e=4 \dots(vi) \\
n(\mathrm{E} \cap \mathrm{M} \cap \mathrm{~S}) & =4 \quad \therefore e=4 \dots(vii)
\end{aligned}
\)
From eqn. (iv) and (vii) we get \(b+4=6 \quad \therefore b=2\)
From eqn. (v) and (vii) we get \(4+f=7 \quad \therefore f=3\)
From eqn. (vi) and (vii) we get \(d+4=4 \quad \therefore d=0\)
From eqn. (i) we get
\(
a+b+d+e=15 \Rightarrow a+2+0+4=15 \Rightarrow a=9
\)
From eqn. (ii) \(b+c+e+f=12 \Rightarrow 2+c+4+3=12 \Rightarrow c=3\)
From eqn. (iii) \(d+e+f+g=8 \Rightarrow 0+4+3+g=8 \Rightarrow g=1\)
(i) Number of students who passed in English and Mathematics but not in Science, \(b=2\).
(ii) Number of students who passed in Mathematics and Science but not in English, \(f=3\).
(iii) Number of students who passed in Mathematics only, \(c=3\).
(iv) Number of students who passed in more than one subject \(=b+e+d+f=2+4+0+3=9\).

Q25. In a class of 60 students, 25 students play cricket and 20 students play tennis, and 10 students play both the games. Find the number of students who play neither?

Solution: Total number of students \(=60 \Rightarrow n(\mathrm{U})=60\)
Number of students who play cricket \(=25 \Rightarrow n(\mathrm{C})=25\)
Number of students who play tennis \(=20 \Rightarrow n(\mathrm{~T})=20\)
Number of students who play both the games \(=10 \Rightarrow n(\mathrm{C} \cap \mathrm{T})=10\)
\(
\begin{aligned}
\therefore \quad n(\mathrm{C} \cup \mathrm{~T}) & =n(\mathrm{C})+n(\mathrm{~T})-n(\mathrm{C} \cap \mathrm{~T}) \\
& =25+20-10=35
\end{aligned}
\)
The number of students who play neither
\(
\begin{aligned}
& =n(\mathrm{U})-n(\mathrm{C} \cup \mathrm{~T}) \\
& =60-35=25
\end{aligned}
\)

Q26. In a survey of 200 students of a school, it was found that 120 study Mathematics, 90 study Physics and 70 study Chemistry, 40 study Mathematics and Physics, 30 study Physics and Chemistry, 50 study Chemistry and Mathematics and 20 none of these subjects. Find the number of students who study all the three subjects.

Solution: Total number of student \(=200 \Rightarrow n(\mathrm{U})=200\)
Number of students who study Mathematics \(=120 \Rightarrow n(\mathrm{M})=120\)
Number of students who study Physics \(=90 \Rightarrow n(\mathrm{P})=90\)
Number of students who study Chemistry \(=70 \Rightarrow n(\mathrm{C})=70\)
Number of students who study Mathematics and Physics
\(
=40 \Rightarrow n(\mathrm{M} \cap \mathrm{P})=40
\)
Number of students who study Physics and Chemistry
\(
=30 \Rightarrow n(\mathrm{P} \cap \mathrm{C})=30
\)
Number of students who study Chemistry and Mathematics
\(
=50 \Rightarrow n(\mathrm{C} \cap \mathrm{M})=50
\)
\(
\begin{aligned}
&\text { Number of students who study none of the subjects }=20\\
&\begin{aligned}
\Rightarrow \quad n\left(\mathrm{M}^{\prime} \cap \mathrm{P}^{\prime} \cap \mathrm{C}^{\prime}\right) & =20 \\
\therefore n(\mathrm{U})-n\left(\mathrm{M}^{\prime} \cap \mathrm{P}^{\prime} \cap \mathrm{C}^{\prime}\right) & =n(\mathrm{M} \cup \mathrm{P} \cup \mathrm{C})=200-20=180 \\
\text { Now } \quad n(\mathrm{M} \cup \mathrm{P} \cup \mathrm{C}) & =n(\mathrm{M})+n(\mathrm{P})+n(\mathrm{C})-n(\mathrm{M} \cap \mathrm{P})-n(\mathrm{P} \cap \mathrm{C}) \\
& -n(\mathrm{M} \cap \mathrm{C})+n(\mathrm{M} \cap \mathrm{P} \cap \mathrm{C})
\end{aligned}
\end{aligned}
\)
\(
\begin{aligned}
180 & =120+90+70-40-30-50+n(\mathrm{M} \cap \mathrm{P} \cap \mathrm{C}) \\
180-160 & =n(\mathrm{M} \cap \mathrm{P} \cap \mathrm{C}) \\
n(\mathrm{M} \cap \mathrm{P} \cap \mathrm{C}) & =20
\end{aligned}
\)
Hence, the number of students who study all the three subjects \(=20\).

Q27. In a town of 10,000 families it was found that \(40 \%\) families buy newspaper \(A\), \(20 \%\) families buy newspaper B, \(10 \%\) families buy newspaper C, \(5 \%\) families buy A and B, \(3 \%\) buy B and C and \(4 \%\) buy A and C. If \(2 \%\) families buy all the three newspapers. Find
(a) The number of families which buy newspaper A only.
(b) The number of families which buy none of \(\mathrm{A}, \mathrm{B}\) and \(\mathrm{C}\)

Solution: Total number of families \(=10000 \Rightarrow n(\mathrm{U})=10000\)
Number of families who buy newspaper \(\mathrm{A}=40 \% \Rightarrow n(\mathrm{~A})=40 \%\)
Number of families who buy newspaper \(\mathrm{B}=20 \% \Rightarrow n(\mathrm{~B})=20 \%\)
Number of families who buy newspaper \(\mathrm{C}=10 \% \Rightarrow n(\mathrm{C})=10 \%\)
Number of families who buy newspapers A and B \(=5 \%\)
\(
\Rightarrow n(A \cap B)=5 \%
\)
Number of families who buy newspapers B and C=3%
\(
\Rightarrow n(\mathrm{~B} \cap \mathrm{C})=3 \%
\)
Number of families who buy newspapers A and \(\mathrm{C}=4 \%\)
\(
\Rightarrow n(A \cap C)=4 \%
\)
Number of families who buy all the three newspapers \(=2 \%\)
\(
\Rightarrow n(\mathrm{~A} \cap \mathrm{~B} \cap \mathrm{C})=2 \%
\)
(i) Number of families who buy newspaper A only
\(
\begin{aligned}
& =n(\mathrm{~A})-n(\mathrm{~A} \cap \mathrm{~B})-n(\mathrm{~A} \cap \mathrm{C})+n(\mathrm{~A} \cap \mathrm{~B} \cap \mathrm{C}) \\
& =\frac{40}{100}-\frac{5}{100}-\frac{4}{100}+\frac{2}{100}=\frac{33}{100} \\
& =10000 \times \frac{33}{100}=3300 \text { families }
\end{aligned}
\)
(ii) Number of families who buy none of \(\mathrm{A}, \mathrm{B}\) and C
Newspaper in percent \((\%)=n(\mathrm{U})-n(\mathrm{~A} \cup \mathrm{~B} \cup \mathrm{C})\)
\(
\begin{array}{lr}
\Rightarrow n(\mathrm{U})-[n(\mathrm{~A})+n(\mathrm{~B})+n(\mathrm{C})-n(\mathrm{~A} \cap \mathrm{~B})-n(\mathrm{~B} \cap \mathrm{C})-n(\mathrm{~A} \cap \mathrm{C}) & \\
\Rightarrow & +n(\mathrm{~A} \cap \mathrm{~B} \cap \mathrm{C})] \\
\Rightarrow(100-(40+20+10-5-3-4+2)] \% &
\end{array}
\)
\(\therefore\) Number of families, who buy none of \(\mathrm{A}, \mathrm{B}\) and C newspaper out of 10000 families are
\(
=10000 \times \frac{40}{100}=4000 \text { families }
\)

Q28. In a group of 50 students, the number of students studying French, English, and Sanskrit were found to be as follows:
French = 17, English = 13, Sanskrit = 15
French and English = 09, English and Sanskrit = 4
French and Sanskrit = 5, English, French and Sanskrit = 3. Find the number of students who study
(i) French only
(v) French and Sanskrit but not English
(ii) English only
(vi) French and English but not Sanskrit
(iii) Sanskrit only
(vii) at least one of the three languages
(iv) English and Sanskrit
(viii) none of the three languages but not French

Solution: Let us use Venn diagram method.

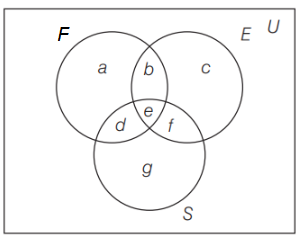
Total number of students \(=50 \Rightarrow n(\mathrm{U})=50\)
Number of students who study French \(=17 \Rightarrow n(\mathrm{~F})=17\)
Number of students who study English \(=13 \Rightarrow n(\mathrm{E})=13\)
Number of students who study Sanskrit \(=15 \Rightarrow n(\mathrm{~S})=15\)
Number of students who study French and English \(=9\)
\(
\Rightarrow n(\mathrm{~F} \cap \mathrm{E})=9
\)
Number of students who study English and Sanskrit = 4
\(
\Rightarrow n(\mathrm{E} \cap \mathrm{~S})=4
\)
Number of students who study
French and Sanskrit = 5
\(
\Rightarrow n(\mathrm{~F} \cap \mathrm{~S})=5
\)
Number of students who study French, English and Sanskrit = 3
\(
\Rightarrow n(\mathrm{~F} \cap \mathrm{E} \cap \mathrm{~S})=3
\)
\(
\begin{aligned}
n(\mathrm{~F}) & =17 \\
a+b+d+e & =17 \dots(i) \\
n(\mathrm{E}) & =13 \\
b+c+e+f & =13 \dots(ii)\\
n(\mathrm{~S}) & =15 \\
d+e+f+g & =15 \dots(iii)
\end{aligned}
\)
\(
\begin{aligned}
n(\mathrm{~F} \cap \mathrm{E}) & =9 \quad \therefore b+e=9 \dots(iv) \\
n(\mathrm{E} \cap \mathrm{~S}) & =4 \quad \therefore e+f=4 \dots(v) \\
n(\mathrm{~F} \cap \mathrm{~S}) & =5 \quad \therefore d+e=5 \dots(vi) \\
n(\mathrm{E} \cap \mathrm{~F} \cap \mathrm{~S}) & =3 \quad \therefore e=3 \dots(vii)
\end{aligned}
\)
\(
\begin{array}{ll}
\text { From }(i v) & b+3=9 \Rightarrow b=9-3=6 \\
\text { From }(v) & 3+f=4 \Rightarrow f=4-3=1 \\
\text { From }(\mathrm{vi}) & d+3=5 \Rightarrow d=5-3=2
\end{array}
\)
Now from eqn. (i) \(a+6+2+3=17 \Rightarrow a=17-11 \Rightarrow a=6\)
Now from eqn. (ii) \(6+c+3+1=13 \Rightarrow c=13-10 \Rightarrow c=3\)
From eqn. (iii) \(\quad 2+3+1+g=15 \Rightarrow g=15-6 \Rightarrow g=9\)
(i) Number of students who study French only, \(a=6\)
(ii) Number of students who study English only, \(c=3\)
(iii) Number of students who study Sanskrit only, \(g=9\)
(iv) Number of students who study English and Sanskrit but not French, \(f=1\)
(v) Number of students who study French and Sanskrit but not English, \(d=2\)
(vi) Number of students who study French and English but not Sanskrit, \(b=6\)
(vii) Number of students who study at least one of the three languages
\(
\begin{aligned}
& =a+b+c+d+e+f+g \\
& =6+6+3+2+3+1+9=30
\end{aligned}
\)
(viii) Number of students who study none of the three language
\(
=50-30=20
\)