1.10 Operations on Set

Sets are treated as mathematical objects. Similar to numbers, we can perform certain mathematical operations on sets. To visualize set operations, we will use Venn diagrams. In a Venn diagram, a rectangle shows the universal set, and all other sets are usually represented by circles within the rectangle. The shaded region represents the result of the operation. The operations on sets are classified into the following types:

• Union of sets
• Intersection of sets
• Difference of sets
• Symmetric difference of sets
• Complement of sets

Union of sets

Let \(\mathrm{A}\) and \(\mathrm{B}\) be any two sets. The union of \(\mathrm{A}\) and \(\mathrm{B}\) is the set which consists of all the elements of \(\mathrm{A}\) and all the elements of \(\mathrm{B}\), the common elements being taken only once. The symbol ‘ \(\cup\) ‘ is used to denote the union. Symbolically, we write \(\mathrm{A} \cup \mathrm{B}\) and usually read as ‘ \(A\) union \(B\) ‘.

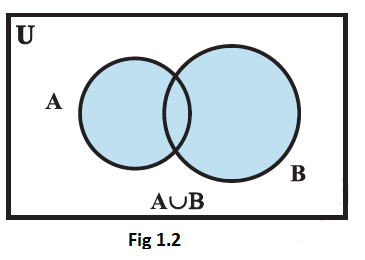
The union of two sets can be represented by a Venn diagram as shown in Fig. 1.2. The shaded portion in Fig \(1.2\) represents \(\mathrm{A} \cup \mathrm{B}\).

The union of two sets \(\mathrm{A}\) and \(\mathrm{B}\) is the set \(\mathrm{C}\) which consists of all those elements which are either in \(\mathrm{A}\) or in \(\mathrm{B}\) (including those which are in both). In symbols, we write. \(\mathrm{A} \cup \mathrm{B}=\{x: x \in \mathrm{A}\) or \(x \in \mathrm{B}\}\)

Example 1: Let \(\mathrm{A}=\{2,4,6,8\}\) and \(\mathrm{B}=\{6,8,10,12\}\). Find \(\mathrm{A} \cup \mathrm{B}\).

Solution: We have \(\mathrm{A} \cup \mathrm{B}=\{2,4,6,8,10,12\}\)
Note that the common elements 6 and 8 have been taken only once while writing \(A \cup B\).

Example 2: Let \(\mathrm{A}=\{a, e, i, o, u\}\) and \(\mathrm{B}=\{a, i, u\}\). Show that \(\mathrm{A} \cup \mathrm{B}=\mathrm{A}\)

Solution: We have, \(\mathrm{A} \cup \mathrm{B}=\{a, e, i, o, u\}=\mathrm{A}\).
This example illustrates that union of sets \(\mathrm{A}\) and its subset \(\mathrm{B}\) is the set \(\mathrm{A}\) itself, i.e., if \(\mathrm{B} \subset \mathrm{A}\), then \(\mathrm{A} \cup \mathrm{B}=\mathrm{A}\).

Example 3: Let \(\mathrm{X}=\{\) Ram, Geeta, Akbar \(\}\) be the set of students of Class XI, who are in school hockey team. Let \(\mathrm{Y}=\{\) Geeta, David, Ashok \(\}\) be the set of students from Class XI who are in the school football team. Find \(\mathrm{X} \cup \mathrm{Y}\) and interpret the set.

Solution: We have, \(X \cup Y=\{\) Ram, Geeta, Akbar, David, Ashok \(\}\). This is the set of students from Class XI who are in the hockey team or the football team, or both.

Some Properties of the Operation of Union

(i) \(\mathrm{A} \cup \mathrm{B}=\mathrm{B} \cup \mathrm{A}\) (Commutative law)
(ii) \((\mathrm{A} \cup \mathrm{B}) \cup \mathrm{C}=\mathrm{A} \cup(\mathrm{B} \cup \mathrm{C})\) (Associative law )
(iii) \(\mathrm{A} \cup \phi=\mathrm{A} \quad\) (Law of identity element, \(\phi\) is the identity of \(\cup\) )
(iv) \(\mathrm{A} \cup \mathrm{A}=\mathrm{A} \quad\) (Idempotent law)
(v) \(\mathrm{U} \cup \mathrm{A}=\mathrm{U} \quad(\) Law of \(\mathrm{U})\)
(vi) If \(x \notin \mathrm{A} \cup \mathrm{B}\), then certainly \(x \notin \mathrm{A}\) and \(x \notin \mathrm{B}\).
(vii) If \(\mathrm{A} \subseteq \mathrm{B}\), then \(\mathrm{A} \cup \mathrm{B}=\mathrm{B}\).
(viii) \(A \subseteq \mathrm{A} \cup \mathrm{B}\) and \(\mathrm{B} \subseteq \mathrm{A} \cup \mathrm{B}\)

Union and the word ‘or’

The word ‘or’ tells us that there is a union of two sets.
For example,
{singers} \(\cup\{\) instrumentalists \(\} \equiv\{\) people who sing or play an instrument}
\(\{\) vowels} \(\cup\{\) letters in word ARMED \(\} \equiv\{\) letters that are vowels or are in word ARMED}

Union and the word ‘at least’

The word ‘at least’ tells us that there is a union of two sets.
Let sets \(A, B\) and \(C\) be the sets of students who play cricket, football and hockey, respectively.
Then set \(A \cup B\) is the set of students who play at least one of the sports cricket and football.
Similarly, \(B \cup C\) is the set of students who play at least one of the sports football and hockey.
Also, \(A \cup B \cup C\) is the set of students who play at least one of the sports, cricket, football and hockey.

Intersection of sets

The intersection of sets \(\mathrm{A}\) and \(\mathrm{B}\) is the set of all elements which are common to both \(\mathrm{A}\) and \(\mathrm{B}\). The symbol ‘ \(\cap\) ‘ is used to denote the intersection. The intersection of two sets \(\mathrm{A}\) and \(\mathrm{B}\) is the set of all those elements which belong to both \(\mathrm{A}\) and \(\mathrm{B}\). Symbolically, we write \(\mathrm{A} \cap \mathrm{B}=\{x: x \in \mathrm{A}\) and \(x \in \mathrm{B}\}\).

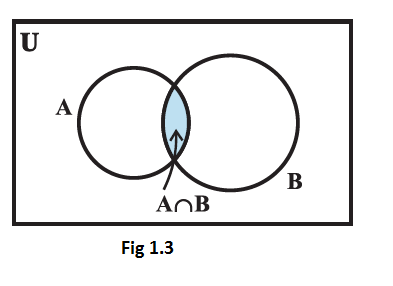
The shaded portion in Fig. 1.3 indicates the intersection of \(\mathrm{A}\) and \(\mathrm{B}\).

Disjoint Sets

If \(\mathrm{A}\) and \(\mathrm{B}\) are two sets such that \(\mathrm{A} \cap \mathrm{B}=\phi\), then \(\mathrm{A}\) and \(\mathrm{B}\) are called disjoint sets.

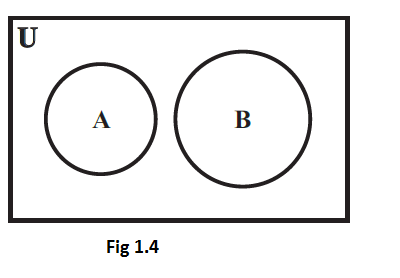
For example, let \(\mathrm{A}=\{2,4,6,8\}\) and \(\mathrm{B}=\{1,3,5,7\}\). Then \(\mathrm{A}\) and \(\mathrm{B}\) are disjoint sets, because there are no elements which are common to \(\mathrm{A}\) and \(\mathrm{B}\). The disjoint sets can be represented by means of Venn diagram as shown in the Fig 1.4. In the above diagram, \(A\) and \(B\) are disjoint sets.

Some Properties of the Operation of Intersection

(i) \(\mathrm{A} \cap \mathrm{B}=\mathrm{B} \cap \mathrm{A} \quad\) (Commutative law).
(ii) \((\mathrm{A} \cap \mathrm{B}) \cap \mathrm{C}=\mathrm{A} \cap(\mathrm{B} \cap \mathrm{C})\) (Associative law).
(iii) \(\phi \cap \mathrm{A}=\phi, \mathrm{U} \cap \mathrm{A}=\mathrm{A} \quad\) (Law of \(\phi\) and \(\mathrm{U}\) ).
(iv) \(\mathrm{A} \cap \mathrm{A}=\mathrm{A} \quad\) (Idempotent law)
(v) \(\mathrm{A} \cap(\mathrm{B} \cup \mathrm{C})=(\mathrm{A} \cap \mathrm{B}) \cup(\mathrm{A} \cap \mathrm{C})\) (Distributive law ) i. e., \(\cap\) distributes over \(\cup\)
(vi) \(x \notin A\) and \(x \notin B \Leftrightarrow x \notin A \cap B\)
If \(x \notin\left(A_1 \cap A_2 \cap A_3 \cap \ldots\right)\) then \(x\) is not the element of at least one of the sets.
(vii) If \(A \subseteq B\) then \(A \cap B=A\).
(viii) \(A \cap B \subseteq A\) and \(A \cap B \subseteq B\)
(ix) \((A \cup B) \cap A=A\) and \((A \cup B) \cap B=B\)
(x) \((A \cap B) \cup A=A\) and \((A \cap B) \cup B=B\)
(xi) \(A \cup(B \cap C)=(A \cup B) \cap(A \cup C) \text { (Distributive law) }\)
(xii) \(A \cap(B \cup C)=(A \cap B) \cup(A \cap C) \text { (Distributive law) }\)

Intersection and the word ‘and’

The word ‘and’ tells us that there is an intersection of two sets. For example,
{singers} \(\cap\) {instrumentalists} \(\equiv\) {people who sing and play an instrument}
{vowels} \(\cap\) {letters of word EXAMINATION} \(\equiv\) {letters that are vowels and are in word EXAMINATION}

Intersection and the word ‘both

The word ‘both’ tells us that there is an intersection of two sets.
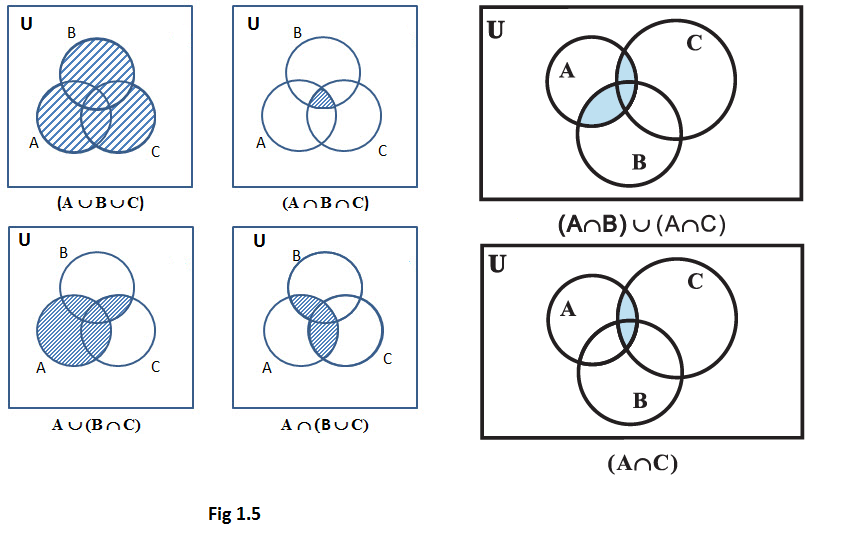
Let sets \(A, B\) and \(C\) be the sets of students who play cricket, football and hockey, respectively.
Then set \(A \cap B\) is the set of students who play both the sports cricket and football.
Similarly, \(B \cap C\) is the set of students who play both the sports football and hockey.
Also, \(A \cap B \cap C\) is the set of students who play all the sports cricket, football and hockey.

This can be seen easily from the following Venn diagrams shown in Fig. 1.5 below.

Example 4: Let \(A=\{1,2,3,4,5,6,7,8,9,10\}\) and \(\mathrm{B}=\{2,3,5,7\}\). Find \(\mathrm{A} \cap \mathrm{B}\) and hence show that \(\mathrm{A} \cap \mathrm{B}=\mathrm{B}\).

Solution: We have \(\mathrm{A} \cap \mathrm{B}=\{2,3,5,7\}=\mathrm{B}\). We note that \(\mathrm{B} \subset \mathrm{A}\) and that \(\mathrm{A} \cap \mathrm{B}=\mathrm{B}\).

Difference of sets

The difference of two sets \(\mathrm{A}\) and \(\mathrm{B}\), denoted by \(\mathrm{A}-\mathrm{B}\) is defined as set of elements which belong to \(\mathrm{A}\) but not to \(\mathrm{B}\). We write
\(
\begin{aligned}
&\mathrm{A}-\mathrm{B}=\{x: x \in \mathrm{A} \text { and } x \notin \mathrm{B}\} \\
&\mathrm{B}-\mathrm{A}=\{x: x \in \mathrm{B} \text { and } x \notin \mathrm{A}\}
\end{aligned}
\)

For example,
(i) Consider sets, \(A=\{1,3,5,6,7\}\) and \(B=\{2,3,4,5\}\).
Here, elements 3 and 5 are common in sets \(A\) and \(B\).
So, \(A-B=\{1,6,7\}\) and \(B-A=\{2,4\}\)
(ii) Consider sets \(A=\{1,2,3\}\) and \(B=\{5,6,7,8\}\).
We observe that there is no element common between sets \(A\) and \(B\).
So. \(A-B=\{1,2,3\}=A\) and \(B-A=\{5,6,7,8\}=B\)
(iii) Consider sets \(A=\{1,2,3\}\) and \(B=\{1,2,3,4,5,6\}\).
We observe that all the elements of set \(A\) are in set \(B\). i.e., set \(A\) is subset of set \(B\).
So. \(A-B=\phi\) and \(B-A=\{4,5,6\}\)

The difference of two sets \(\mathrm{A}\) and \(\mathrm{B}\) can be represented by Venn diagram as shown in Fig 1.6. The shaded portion represents the difference of the two sets \(A\) and \(B\).

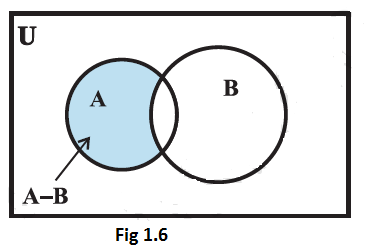
Properties of the difference of sets

• If \(A \cap B=\phi\) (i.e., sets \(A\) and \(B\) have no common elements), then \(A-B=A\) and \(B-A=B\).
• If \(A \subseteq B\), then \(A-B=\phi\).
• \(x\) is not the element of set \(A-B\) if \(x \in A\) and \(x \in B\).
• \(A-B \neq B-A\)

Difference and the word ‘only’

Consider \(A=\) set of students who play cricket
and \(B=\) set of students who play football.
Now, \(A-B=\) set of students who play cricket but not football
\(=\) set of students who play cricket only
Similarly, \(B-A=\) set of students who play football only

Example 5:
Let \(\mathrm{A}=\{1,2,3,4,5,6\}, \mathrm{B}=\{2,4,6,8\}\). Find \(\mathrm{A}-\mathrm{B}\) and \(\mathrm{B}-\mathrm{A}\).

Solution: We have, \(\mathrm{A}-\mathrm{B}=\{1,3,5\}\), since the elements \(1,3,5\) belong to \(\mathrm{A}\) but not to \(\mathrm{B}\) and \(\mathrm{B}-\mathrm{A}=\{8\}\), since the element 8 belongs to \(\mathrm{B}\) and not to \(\mathrm{A}\). We note that \(\mathrm{A}-\mathrm{B} \neq \mathrm{B}-\mathrm{A}\).

Symmetric difference of sets

The symmetric difference of the two sets A and B is the set that contains the elements of A and the elements of B, but not the elements of their intersection. The notation used to represent this is \(\oplus\), or \(\Delta\).

Definition: The symmetric difference of \(\mathbf{A}\) and \(\mathbf{B}\), denoted by \(A \oplus B\) is the set \((A-B) \cup(B-A)\). Thus

\(
 \begin{aligned}
A \Delta B & =(A-B) \cup(B-A) \\
& =(x: x \notin A \cap B) \\
& =(A \cup B)-(A \cap B)
\end{aligned}
\)

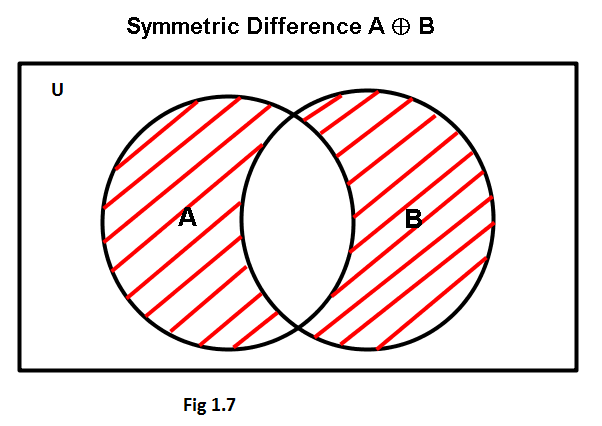
Example 6:
\(\begin{aligned}
U &=\{0,1,2,3,4,5,6,7,8,9,10\} \\
A &=\{1,2,3,4,5\} \quad B=\{4,5,6,7,8\}
\end{aligned}\)
What is \(A \oplus B?\)

Solution:

\(A \oplus B\) = \((A-B) \cup(B-A)\) = \(\{1,2,3\}\) \( \cup \) \(\{6,7,8\}\)= \(\{1,2,3,6,7,8\}\)