Sample Quiz
These 10 sample quiz questions are taken from JEE 2021 Physics paper (Section-B)
Quiz Summary
0 of 10 Questions completed
Questions:
Information
You have already completed the quiz before. Hence you can not start it again.
Quiz is loading…
You must sign in or sign up to start the quiz.
You must first complete the following:
Results
Results
0 of 10 Questions answered correctly
Your time:
Time has elapsed
You have reached 0 of 0 point(s), (0)
Earned Point(s): 0 of 0, (0)
0 Essay(s) Pending (Possible Point(s): 0)
Categories
- Not categorized 0%
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- Current
- Review
- Answered
- Correct
- Incorrect
-
Question 1 of 10
1. Question
Two waves are simultaneously passing through a string and their equations are:
\(\mathrm{y}_{1}=\mathrm{A}_{1} \sin \mathrm{k}(\mathrm{x}-\mathrm{vt}), \mathrm{y}_{2}=\mathrm{A}_{2} \sin \mathrm{k}\left(\mathrm{x}-\mathrm{vt}+\mathrm{x}_{0}\right)\). Given amplitudes \(\mathrm{A}_{1}=12 \mathrm{~mm}\) and \(\mathrm{A}_{2}=5 \mathrm{~mm}\), \(\mathrm{x}_{0}=3.5 \mathrm{~cm}\) and wave number \(\mathrm{k}=6.28 \mathrm{~cm}^{-1}\). The amplitude of resulting wave will be ………. \(\mathrm{mm}\).CorrectIncorrect -
Question 2 of 10
2. Question
A source of light is placed in front of a screen. The intensity of light on the screen is I. Two Polaroids P1 and P2 are so placed in between the source of light and the screen that the intensity of light on the screen is I/2. P2 should be rotated by an angle of ………..(degrees) so that the intensity of light on the screen becomes \(\frac{3 \mathrm{I}}{8}\)
CorrectIncorrect -
Question 3 of 10
3. Question
If the maximum value of accelerating potential provided by a ratio frequency oscillator is 12 kV. The number of revolution made by a proton in a cyclotron to achieve one-sixth of the speed of light is …………
CorrectIncorrectHint
\(
\mathrm{V}=12 \mathrm{kV}
\)
Number of revolution \(=\mathrm{n}\)
\(
\begin{aligned}
&\mathrm{n}\left[2 \times \mathrm{q}_{\mathrm{P}} \times \mathrm{V}\right]=\frac{1}{2} \mathrm{~m}_{\mathrm{P}} \times \mathrm{v}_{\mathrm{P}}^{2} \\
&\mathrm{n}\left[2 \times 1.6 \times 10^{-19} \times 12 \times 10^{3}\right. \\
&=\frac{1}{2} \times 1.67 \times 10^{-27} \times\left[\frac{3 \times 10^{8}}{6}\right]^{2} \\
&\mathrm{n}\left(38.4 \times 10^{-16}\right)=0.2087 \times 10^{-11} \\
&\mathrm{n}=543.4
\end{aligned}
\)
Ans. 543 -
Question 4 of 10
4. Question
The acceleration due to gravity is found up to an accuracy of 4% on a planet. The energy supplied to a simple pendulum to known mass ‘m’ to undertake oscillations of time period T is being estimated. If the time period is measured to an accuracy of 3%, the accuracy to which E is known as ……….%
CorrectIncorrectHint
\(\begin{aligned}
&\mathrm{T}=2 \pi \sqrt{\frac{\ell}{\mathrm{g}}} \Rightarrow \ell=\frac{\mathrm{T}^{2} \mathrm{~g}}{4 \pi^{2}} \\
&\mathrm{E}=\mathrm{mg} \ell \frac{\theta^{2}}{2}=\mathrm{mg}^{2} \frac{\mathrm{T}^{2} \theta^{2}}{8 \pi^{2}} \\
&\frac{\mathrm{dE}}{\mathrm{E}}=2\left(\frac{\mathrm{dg}}{\mathrm{g}}+\frac{\mathrm{dT}}{\mathrm{T}}\right) \\
&=2(4+3)=14 \%
\end{aligned}\) -
Question 5 of 10
5. Question
A circular coil of radius \(8.0 \mathrm{~cm}\) and 20 turns is rotated about its vertical diameter with an angular speed of \(50 \mathrm{rad} \mathrm{} \mathrm{s}^{-1}\) in a uniform horizontal magnetic field of \(3.0 \times 10^{-2} \mathrm{~T}\). The maximum emf induced the coil will be \(\ldots \ldots \ldots \times 10^{-2}\) volt (rounded off to the nearest integer)
CorrectIncorrectHint
Maximum emf \(\varepsilon=\mathrm{N} \omega \mathrm{AB}\)
\(
\begin{aligned}
&\mathrm{N}=20, \omega=50, \mathrm{~B}=3 \times 10^{-2} \mathrm{~T} \\
&\varepsilon=20 \times 50 \times \pi \times(0.08)^{2} \times 3 \times 10^{-2}=60.28 \times 10^{-2}
\end{aligned}
\)
Rounded off to nearest integer =60
Ans. 60 -
Question 6 of 10
6. Question
Two simple harmonic motions are represented by the equations
\(x_{1}=5 \sin \left(2 \pi t+\frac{\pi}{4}\right) \text { and } x_{2}=5 \sqrt{2}(\sin 2 \pi t+\cos 2 \pi t)\)
The amplitude of the second motion is ………….. times the amplitude in the first motion.
CorrectIncorrectHint
\(
\begin{aligned}
&\mathrm{x}_{2}=5 \sqrt{2}\left(\frac{1}{\sqrt{2}} \sin 2 \pi \mathrm{t}+\frac{1}{\sqrt{2}} \cos 2 \pi \mathrm{t}\right) \sqrt{2} \\
&=10 \sin \left(2 \pi \mathrm{t}+\frac{\pi}{4}\right) \\
&\therefore \frac{\mathrm{A}_{2}}{\mathrm{~A}_{1}}=\frac{10}{5}=2
\end{aligned}
\)
Ans. 2 -
Question 7 of 10
7. Question
A coil in the shape of an equilateral triangle of side \(10 \mathrm{~cm}\) lies in a vertical plane between the pole pieces of a permanent magnet producing a horizontal magnetic field \(20 \mathrm{mT}\). The torque acting on the coil when a current of \(0.2 \mathrm{~A}\) is passed through it and its plane becomes parallel to the magnetic field will be \(\sqrt{x} \times 10^{-5} \mathrm{Nm}\). The value of \(\mathrm{x}\) is
CorrectIncorrect -
Question 8 of 10
8. Question
For the given circuit, the power across Zener diode is ………… mW
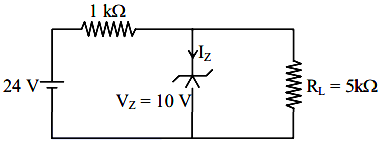CorrectIncorrectHint
\(
\begin{aligned}
&\mathrm{i}=\frac{10 \mathrm{~V}}{5 \mathrm{k} \Omega}=2 \mathrm{~mA} \\
&\mathrm{I}=\frac{14 \mathrm{~V}}{1 \mathrm{k} \Omega}=14 \mathrm{~mA} \\
&\therefore \mathrm{I}_{\mathrm{z}}=12 \mathrm{~mA} \\
&\therefore \mathrm{P}=\mathrm{I}_{z} \mathrm{~V}_{\mathrm{z}}=120 \mathrm{~mW}
\end{aligned}
\)
Ans. 120 -
Question 9 of 10
9. Question
An object is placed at a distance of 12 cm from a convex lens. A convex mirror of focal length of 15 cm is placed on other side of the lens at 8 cm as shown in the figure. The image of the object coincides with the object.
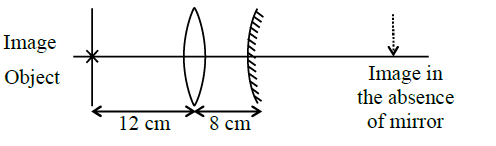
When the convex mirror is removed, a real and inverted image is formed at a position. The distance of the image from the object will be ……..(cm)
CorrectIncorrect -
Question 10 of 10
10. Question
The coefficient of static friction between two blocks is 0.5 and the table is smooth. The maximum horizontal force that can be applied to move the blocks together is …….N.
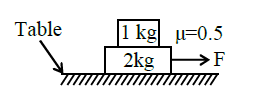CorrectIncorrect