Quiz Level-3
Quiz Summary
0 of 40 Questions completed
Questions:
Information
You have already completed the quiz before. Hence you can not start it again.
Quiz is loading…
You must sign in or sign up to start the quiz.
You must first complete the following:
Results
Results
0 of 40 Questions answered correctly
Your time:
Time has elapsed
You have reached 0 of 0 point(s), (0)
Earned Point(s): 0 of 0, (0)
0 Essay(s) Pending (Possible Point(s): 0)
Categories
- Not categorized 0%
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- Current
- Review
- Answered
- Correct
- Incorrect
-
Question 1 of 40
1. Question
Twenty percent of the paintings in a gallery are not originals. A collector buys a painting. He has probability 0.10 of buying a fake for an original but never rejects an original as a fake, What is the (conditional) probability the painting he purchases is an original?
CorrectIncorrectHint
Let \(B=\) the event the collector buys, and \(G=\) the event the painting is original. Assume \(P(B \mid G)=1\) and \(P\left(B \mid G^c\right)=0.1\). If \(P(G)=0.8\), then
\(
P(G \mid B)=\frac{P(G B)}{P(B)}=\frac{P(B \mid G) P(G)}{P(B \mid G) P(G)+P\left(B \mid G^c\right) P\left(G^c\right)}=\frac{0.8}{0.8+0.1 \cdot 0.2}=\frac{40}{41}
\) -
Question 2 of 40
2. Question
Five percent of the units of a certain type of equipment brought in for service have a common defect. Experience shows that 93 percent of the units with this defect exhibit a certain behavioral characteristic, while only two percent of the units which do not have this defect exhibit that characteristic. A unit is examined and found to have the characteristic symptom. What is the conditional probability that the unit has the defect, given this behavior?
CorrectIncorrectHint
Let \(D=\) the event the unit is defective and \(C=\) the event it has the characteristic. Then \(P(D)=0.05, P(C \mid D)=0.93\), and \(P\left(C \mid D^c\right)=0.02\).
\(
P(D \mid C)=\frac{P(C \mid D) P(D)}{P(C \mid D) P(D)+P\left(C \mid D^c\right) P\left(D^c\right)}=\frac{0.93 \cdot 0.05}{0.93 \cdot 0.05+0.02 \cdot 0.95}=\frac{93}{131}
\) -
Question 3 of 40
3. Question
A shipment of 1000 electronic units is received. There is an equally likely probability that there are 0,1,2, or 3 defective units in the lot. If one is selected at random and found to be good, what is the probability of no defective units in the lot?
CorrectIncorrectHint
Let \(D_k=\) the event of \(k\) defective and \(G\) be the event a good one is chosen.
\(
\begin{aligned}
& P\left(D_0 \mid G\right)=\frac{P\left(G \mid D_0\right) P\left(D_0\right)}{P\left(G \mid D_0\right) P\left(D_0\right)+P\left(G \mid D_1\right) P\left(D_1\right)+P\left(G \mid D_2\right) P\left(D_2\right)+P\left(G \mid D_3\right) P\left(D_3\right)} \\
& =\frac{1 \cdot 1 / 4}{(1 / 4)(1+999 / 1000+998 / 1000+997 / 1000)}=\frac{1000}{3994} \\
&
\end{aligned}
\) -
Question 4 of 40
4. Question
In a survey, 85 percent of the employees say they favor a certain company policy. Previous experience indicates that 20 percent of those who do not favor the policy say that they do, out of fear of reprisal. What is the probability that an employee picked at random really does favor the company policy? It is reasonable to assume that all who favor say so.
CorrectIncorrectHint
\(
\begin{aligned}
&P(S)=0.85, P\left(S \mid F^c\right)=0.20 \text {. Also, reasonable to assume } P(S \mid F)=1 \text {. }\\
&P(S)=P(S \mid F) P(F)+P\left(S \mid F^c\right)[1-P(F)] \text { implies } P(F)=\frac{P(S)-P\left(S \mid F^c\right)}{1-P\left(S \mid F^c\right)}=\frac{13}{16}
\end{aligned}
\) -
Question 5 of 40
5. Question
At a certain stage in a trial, the judge feels the odds are two to one the defendent is guilty. It is determined that the defendent is left handed. An investigator convinces the judge this is six times more likely if the defendent is guilty than if he were not. What is the likelihood, given this evidence, that the defendent is guilty?
CorrectIncorrectHint
Let \(G=\) event the defendent is guilty, \(L=\) the event the defendent is left handed. Prior odds: \(P(G) / P\left(G^c\right)=2\). Result of testimony: \(P(L \mid G) / P\left(L \mid G^c\right)=6\).
\(
\begin{gathered}
\frac{P(G \mid L)}{P\left(G^c \mid L\right)}=\frac{P(G)}{P\left(G^c\right)} \cdot \frac{P(L \mid G)}{P\left(L \mid G^c\right)}=2 \cdot 6=12 \\
P(G \mid L)=12 / 13
\end{gathered}
\) -
Question 6 of 40
6. Question
Four persons are to be selected from a group of 12 people, 7 of whom are women. What is the probability that the first and third selected are women?
CorrectIncorrectHint
\(
P\left(W_1 W_3\right)=P\left(W_1 W_2 W_3\right)+P\left(W_1 W_2^c W_3\right)=\frac{7}{12} \cdot \frac{6}{11} \cdot \frac{5}{10}+\frac{7}{12} \cdot \frac{5}{11} \cdot \frac{6}{10}=\frac{7}{22}
\) -
Question 7 of 40
7. Question
In a certain population, the probability a woman lives to at least seventy years is \(0.70\) and is \(0.55\) that she will live to at least eighty years. If a woman is seventy years old, what is the conditional probability she will survive to eighty years? Note that if \(A \subset B\) then \(P(A B)=P(A)\)
CorrectIncorrectHint
Let \(A=\) event she lives to seventy and \(B=\) event she lives to eighty. Since \(B \subset A\), \(P(B \mid A)=P(A B) / P(A)=P(B) / P(A)=55 / 70\)
-
Question 8 of 40
8. Question
What is the probability of the occurrence of a number that is odd or less than 5 when a fair die is rolled.
CorrectIncorrectHint
Let the event of the occurrence of a number that is odd be ‘ \(\mathrm{A}\) ‘ and the event of the occurrence of a number that is less than 5 be ‘ \(B\) ‘. We need to find \(P(A\) or \(B)\).
\(P(A)=3 / 6\) (odd numbers \(=1,3\) and 5 )
\(P(B)=4 / 6\) (numbers less than \(5=1,2,3\) and 4 )
\(P(A\) and \(B)=2 / 6\) (numbers that are both odd and less than \(5=1\) and 3 )
Now, \(P(A\) or \(B) \quad=P(A)+P(B)-P(A\) and \(B)\)
\(
=3 / 6+4 / 6-2 / 6
\)
\(
P(A \text { or } B)=5 / 6
\) -
Question 9 of 40
9. Question
A box contains 4 chocobars and 4 ice creams. Tom eats 3 of them one after another. What is the probability of sequentially choosing 2 chocobars and 1 icecream?
CorrectIncorrectHint
Probability of choosing 1 chocobar \(=4 / 8=1 / 2\)
After taking out 1 chocobar, the total number is 7.
Probability of choosing 2 nd chocobar \(=3 / 7\)
Probability of choosing 1 icecream out of a total of \(6=4 / 6=2 / 3\)
So the final probability of choosing 2 chocobars and 1 icecream \(=1 / 2 \times 3 / 7 \times 2 / 3=1 / 7\) -
Question 10 of 40
10. Question
In a class, \(40 \%\) of the students study math and science. \(60 \%\) of the students study math. What is the probability of a student studying science given he/she is already studying math?
CorrectIncorrectHint
\(P(M\) and \(S)=0.40\)
\(
P(M)=0.60
\)
\(
P(S \mid M)=P(M \text { and } S) / P(S)=0.40 / 0.60=2 / 3=0.67
\) -
Question 11 of 40
11. Question
There exist 60 novels and 20 books of poetry on a shelf. A person named A chooses a book at random and leaves with it. After a short period of time, person B chooses another random book. Find the probability that the book selected by person B is a novel.
CorrectIncorrectHint
\(P(\) that the book selected by person \(B\) is a novel \()=(60 / 80)(59 / 79)+(20 / 80)(60 / 79)\)
\(
=237 / 316
\) -
Question 12 of 40
12. Question
What is the probability of selecting three red cards in a row with replacement from a standard deck of 52 cards?
CorrectIncorrectHint
There are 52 cards and the total red cards =26, so the probability of drawing a red card 26/52=1/2. If you draw 3 red cards in a row without replacement probability \( 1/2 \times 1/2 \times 1/2=1/8\)
-
Question 13 of 40
13. Question
What is the probability of selecting two cards from different suits with replacement? Assume you are using a standard deck of cards(52 cards).
CorrectIncorrectHint
Your first selection can be any card from the deck = 52/52 =1
The probability that the second card will be from a different suit is (52-13)/52=3/4
-
Question 14 of 40
14. Question
What is the probability that the top two cards of a shuffled deck are both face cards? (Kings, Queens, and Jacks are all face cards.) Assume you are using a standard deck of 52 cards.
CorrectIncorrectHint
There are 3 face cards in each suit of 13 cards. So the total number of face cards =12.
The probability that the top card is a face card is 12/52. If the top card is face card the probability that the second card is a face card is 11/51. The probability that both are face cards is \(12/52 \times 11/51=11/221\)
-
Question 15 of 40
15. Question
What is the probability that the top four cards of a shuffled deck are all of the same suit? Assume a standard deck of 52 cards.
CorrectIncorrectHint
The first card can be of any suit. Probability = 52/52.
The next 3 cards must be of the same suit as the first. So the probability = \(52/52 \times 12/51 \times 11/50 \times 10/49 = 44/4165\)
-
Question 16 of 40
16. Question
What is the probability that the top card in a shuffled deck is a red Ace, and the second card is a spade? Assume a standard deck of 52 cards.
CorrectIncorrectHint
There are 2 red aces in a 52-card deck. If the top card is a red ace, 13 of the remaining 51 cards are spades. So the probability = [/latex]2/52 \times 13/51=1/102[/latex]
-
Question 17 of 40
17. Question
What is the probability that the top card in a shuffled deck is an Ace (of any color), and the second card is a spade? The Ace may be the Ace of spades. Assume a standard deck of 52 cards.
CorrectIncorrectHint
There are two cases to consider.
Case-1: The first card can be any ace of spades or an ace from another suit. If the ace is the ace of spades, the probability is:
\(1/52 \times 12/51=12/(52 \times 51)\)
Case-2: If the top card is the ace of another suit the probability =\(3/52 \times 13/51=39/(52 \times 51)\)
Added together the probability = \(51/(52 \times 51)=1/52\)
-
Question 18 of 40
18. Question
What is the probability that the top two cards in a shuffled deck are an Ace (of any suit) and a spade? The Ace of spades cannot be used to satisfy both requirements. Assume a standard deck of 52 cards.
CorrectIncorrectHint
If the ace is the ace of spades, the probability is: \(2 \times 1/52 \times 12/51 = 24/(52 \times 51)\)
If the ace is of another suit the probability is: \(2 \times 3/52 \times 13/51 = 78/(52 \times 51)\)
Added together we get: \(102/(52 \times 51) = 2/52 = 1/26\)
-
Question 19 of 40
19. Question
What is the probability that the top two cards in a shuffled deck are consecutive cards of the same suit? (The Ace can be high or low). Assume a standard deck of 52 cards.
CorrectIncorrectHint
There are 13 pairs of consecutive cards in each suit for a total of 52 pairs of consecutive cards. There are
\({ }^{52} C_2=(52 \times 51)/2\) combinations that could be the top two cards of a shuffled deck: \(52/[(52 \times 51)/2]=2/51\)
-
Question 20 of 40
20. Question
For a lottery drawing, a set of balls numbered 1 through 9 is placed in each of three bins. One ball is selected from each bin. What is the probability that all three digits drawn will be odd?
CorrectIncorrectHint
The probability of drawing an odd digit (1 through 9) = 5/9. We multiply 3 times to get 125/729/
-
Question 21 of 40
21. Question
For a randomly selected phone number, what is the probability that the last three digits are all the same?
CorrectIncorrectHint
There are \(10^3 = 1000\) possible combinations of three digits for the last 3 digits of a phone number(000 through 999). Only 10 have the same three digits (111, 222 etc.). So the probability is 10/1000 = 1/100.
-
Question 22 of 40
22. Question
What is the probability of rolling each of the numbers 1 through 6 in any order in six rolls of a standard die?
CorrectIncorrectHint
There are \(6^6=46,656\) rolls. The first roll can be any of the 6 digits, after which there are only 5 available rolls, and then 4,3,2, and 1. There are 6! ways to roll a 1-6 in any order. So the probability = 6!/46656 = 5/324.
-
Question 23 of 40
23. Question
A dot is added to each face of two standard dice. What is the probability of rolling an 8 with the modified pair of dice?
CorrectIncorrectHint
The modified die will have faces with 2,3,4,5,6, and 7 dots. There will still be 36 possible rolls with a pair of modified dice. Of these 36 rolls, 5 will show an 8 (2,6), (3,5), (4,4), (5,3),(6,2). So the probability of rolling an 8 =5/36.
-
Question 24 of 40
24. Question
For three randomly selected positive integers, what is the probability that the sum of the units digits is even?
CorrectIncorrectHint
The units digit of each integer can be odd or even, with equal probability. For the sum of the three units digits to be even, we can have either 2 odd digits and 1 even digit: \(\{O, O, E\},\{O, O, E\}\), or \(\{O, O, E\}\), or we can have 3 even digits: \(\{\mathrm{E}, \mathrm{E}, \mathrm{E}\}\). There are \(2^3=8\) possibilities (think of this as counting coin flips, where each flip determines whether the units digit is odd or even), which makes the probability that the sum is even \(4 / 8=1 / 2\).
-
Question 25 of 40
25. Question
Six students are randomly seated in the first row of a classroom. What is the probability that from left to right they are in order from oldest to youngest?
CorrectIncorrectHint
There are \(6 !=720\) ways to arrange 6 students in order, and only one of these ways seats the students from oldest to youngest, so the probability is \(1 / 720\).
-
Question 26 of 40
26. Question
Each spinner below is divided into four equal sectors. Each is spun once, and the product of the spins is calculated. What is the probability that the product is positive?
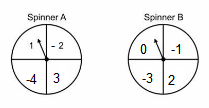 CorrectIncorrect
CorrectIncorrectHint
The product will be positive if the two spins are either both positive or both negative.
\(
P(\text { both positive })=\frac{1}{2} \cdot \frac{1}{4}=\frac{1}{8}
\)
\(
P(\text { both negative })=\frac{1}{2} \cdot \frac{1}{2}=\frac{1}{4}
\)
Add these together to get a probability of \(\mathbf{3} / \mathbf{8}\). -
Question 27 of 40
27. Question
Three fair dice are rolled. What is the probability that exactly two of the rolls show a 1?
CorrectIncorrectHint
First, we find the probability of rolling
\(
\frac{1}{6} \cdot \frac{1}{6} \cdot \frac{5}{6}=\frac{5}{216} \text {. }
\)
Second, we find the number of ways to arrange the \(1-1-X\). The probability of rolling \(1-1-X\) is the same as the probability of rolling \(1-X-1\) or \(X-1-1\) (consider each of the three dice as distinguishable in some way, like being different colors or rolled in order). We triple the probability to get:
\(
\frac{5}{216} \cdot 3=\frac{15}{216}=\frac{5}{72}
\) -
Question 28 of 40
28. Question
Lisa shakes her piggy bank which contains 5 quarters and 5 nickels until 5 coins fall out. Assuming nickels and quarters fall out with equal probability, what is the probability that the sum of the change that has fallen out is \($0.85\)?
CorrectIncorrectHint
The only way for five Nickels \((N)\) and Quarters \((Q)\) to add up to \($0.85\) is with three Quarters and two Nickels. Begin by computing \(P(Q Q Q N N)\) :
\(
\frac{5}{10} \cdot \frac{4}{9} \cdot \frac{3}{8} \cdot \frac{5}{7} \cdot \frac{4}{6}=\frac{5}{126}
\)
However, there are \(5 \mathrm{C}_2=10\) ways to arrange \(Q Q Q N N\), each has an equal probability of occurring:
\(
\frac{5}{126} \cdot 10=\frac{50}{126}=\frac{25}{63} \text {. }
\) -
Question 29 of 40
29. Question
Hriday attempts five free throws at practice. If Hriday has a \(40 \%\) chance of making each free throw, what is the probability that he will make exactly three of the five shots?
CorrectIncorrectHint
Let \(O\) represent a made free-throw and \(X\) represent a miss. The probability of making a free throw is \(2 / 5\), so the probability of a miss is \(3 / 5\). The probability \(P(O O O X X)\) of making the first three and missing the last two is:
\(\frac{2}{5} \cdot \frac{2}{5} \cdot \frac{2}{5} \cdot \frac{3}{5} \cdot \frac{3}{5}\) and there are \(\left(\begin{array}{l}5 \\ 2\end{array}\right)=\frac{5 \cdot 4}{2}\) ways to arrange the missed shots (for example, OOXOX and XOOOX). Multiplying gives us:
\(
\frac{2}{5} \cdot \frac{2}{5} \cdot \frac{2}{5} \cdot \frac{3}{5} \cdot \frac{3}{5} \cdot \frac{5 \cdot 4}{2}=\frac{144}{625}
\) -
Question 30 of 40
30. Question
A homeroom has 7 boys and 5 girls. The homeroom teacher randomly selects two representatives to serve on student council. What is the probability that the teacher selects one boy and one girl?
CorrectIncorrectHint
There are \({ }^{12} \mathrm{C}_2=66\) ways to select 2 representatives. With 7 boys and 5 girls there are 7 choices for the boy and 5 for the girl, or \(7 \cdot 5=35\) different pairs, making the probability \(35 / 66\). Alternatively, we find the probability of selecting boy then a girl and add it to the probability of selecting a girl then a boy: \(P(\) Boy, Girl \()=(7 / 12)(5 / 11)=35 / 132\) and \(P(\) Girl, Boy \()=(5 / 12)(7 / 11)=35 / 132\), so \(P(\) Boy, Girl or Girl, Boy) \(=35 / 132+35 / 132=35 / 66\)
-
Question 31 of 40
31. Question
Jeremy has found a way to flip a coin so that tails lands face up twice as often as heads. What is the probability of Jeremy flipping more tails than heads in three coin flips using this method?
CorrectIncorrectHint
The probability of flipping tails on a single toss is \(2 / 3\). The probability of flipping three tails in a row is \((2 / 3)^3\) \(=8 / 27\). There are three ways to flip two tails and a heads (TTH, THT, and HTT). The probability of each is \((1 / 3)(2 / 3)^2=4 / 27\). Multiply this by three to get \(12 / 27\). The probability of flipping more tails than heads is the combined probability of flipping two or three tails on three tosses. \(8 / 27+12 / 27=20 / 27\).
-
Question 32 of 40
32. Question
The school cafeteria has chocolate chip cookies and oatmeal cookies for dessert. What is the probability that exactly 3 of the next 5 students in line will select chocolate chip cookies if everyone selects a cookie, and students prefer chocolate to oatmeal 2 to 1?
CorrectIncorrectHint
A student will select a chocolate chip cookie with a probability of \(2 / 3\). Using \(C\) for chocolate chip and \(O\) for oatmeal, the probability that the first three students will choose chocolate chip followed by two students selecting oatmeal is:
\(P(\) CCCOO \()=\left(\frac{2}{3}\right)^3\left(\frac{1}{3}\right)^2=\frac{8}{243}\), but there are \(5 \mathrm{C}_2=10\) ways to arrange \(\mathrm{CCCOO}\), making the probability \(80 / 243\). -
Question 33 of 40
33. Question
If the probability of rain on any given day in February is \(40 \%\), what is the probability that for a given week in February, there will be exactly three rainy days? Express your answer to the nearest percent.
CorrectIncorrectHint
The probability of rain expressed as a fraction is \(2 / 5\) (and the probability that it will not rain is \(3 / 5\) ), so the probability of three rainy days in a week is \(\left(\frac{2}{5}\right)^3 \cdot\left(\frac{3}{5}\right)^t=\frac{647}{78,125}\). We must multiply this by the number of ways to arrange these three rainy days in a 7-day week: \(7 C 3=35\), so \(35 \cdot \frac{647}{78,125} \approx 29 \%\).
-
Question 34 of 40
34. Question
A drawer contains 7 blue socks and 5 black socks. Four socks are randomly selected from the drawer. What is the probability that a pair of blue socks and a pair of black socks can be made from the 4 socks drawn?
CorrectIncorrectHint
The probability of selecting two blue socks black socks is found by:
\(\frac{7}{12} \cdot \frac{6}{11} \cdot \frac{5}{10} \cdot \frac{4}{9}=\frac{7}{99}\), and there are \({ }^4 \mathrm{C} 2=6\) ways to arrange the order of two black and two blue socks. Multiplying, we get a probability of:
\(
6 \cdot \frac{7}{99}=\frac{14}{33} \text {. }
\)
Alternatively, there are \(12 \mathrm{C} 4=495\) ways to choose 4 socks from a set of 12 . There are \({ }^7 \mathrm{C}_2=21\) ways to choose two of the blue socks and \({ }^5 \mathrm{C}_2=10\) ways to choose two black socks, which makes \(21 \cdot 10=210\) ways to choose 2 blue and two black socks from the drawer. \(210 / 495=14 / 33\). -
Question 35 of 40
35. Question
In six rolls of a standard die, what is the probability that the same number will be rolled exactly five times?
CorrectIncorrectHint
There are \(6^6\) possible outcomes for six rolls of a standard die. Consider \(OOOOOX\) as a representation of five of the same digit and one different digit. There are 6 ways to arrange \(00000 X\), six numbers to select for the \(O\), and five numbers to select for the \(X\). This gives us: \(\frac{6 \cdot 6 \cdot 5}{6^6}=\frac{5}{6^4}=\frac{5}{1,296}\).
-
Question 36 of 40
36. Question
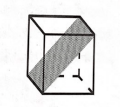
Four of the vertices of a cube are selected at random. What is the probability that all four selected points will be coplanar?
CorrectIncorrectHint
There are \({ }^8 C_4=70\) ways to select 4 of the 8 vertices of a cube. For all four points to be on the same plane, they can all be on the same face (6 ways), or on one of 6 diagonal planes slicing through the cube (one is shown). \(12 / 70=6 / 35\).
-
Question 37 of 40
37. Question
When you drop a piece of buttered toast, your mother suggests that it will land buttered-side down twice as often as buttered-side up. If this is true, what is the probability that at least one out of three dropped slices of toast will land buttered-side up?
CorrectIncorrectHint
The toast will land buttered-side down \(2 / 3\) of the time. At least one piece will land buttered-side up as long as all three pieces do not land buttered-side down. The probability that all three will land buttered-side down is \((2 / 3)^3=8 / 27\). Subtract this from 1 to get \(19 / 27\)
-
Question 38 of 40
38. Question
Three of the vertices of a cube are connected to form a triangle. What is the probability that all three vertices are on the same face of the cube?
CorrectIncorrectHint
There are 8 vertices of a cube, which means there are \({ }^8 C_3=56\) ways to connect three of the vertices to form a triangle. There are \({ }^4 C_3=4\) possible triangles on each of 6 faces for a total of 24 out of 56 triangles: \(24 / 56=3 / 7\).
-
Question 39 of 40
39. Question
The weatherman has predicted a \(30 \%\) chance of snow for each of the next three days. Your younger brother shows off his addition skills, suggesting that there is a \(90 \%\) chance of snow. What is the actual probability that it will snow on at least one of the next three days? Express your answer as a percent rounded to the tenth.
CorrectIncorrectHint
There is a \(70 \%\) chance that it will not snow on each of the next three days. The probability that it will not snow at all is \((0.7)^3=0.343\) or \(34.3 \%\). This leaves a probability that it will snow at least once:
\(
1-0.343=0.657=\mathbf{6 5 . 7 \%} \text {. }
\) -
Question 40 of 40
40. Question
3 digits are selected from the set \(\{2,3,4,5,6,7,8\}\) without replacement. What is the probability that the sum of the three digits is prime?
CorrectIncorrectHint
There are \({ }^7 C_3=35\) possible combinations. We are looking for combinations whose sum is prime. The smallest possible sum is 9 and the largest possible sum is 21 . Primes between 9 and 21 are \(11,13,17\), and 19 . Look for ways to get each:
\(
\begin{aligned}
& 11=2+4+5=2+3+6 \text { ( } 2 \text { ways)} \\
& 13=2+5+6=2+4+7=2+3+8=3+4+6 \text { ( } 4 \text { ways) } \\
& 17=2+7+8=3+6+8=4+6+7=4+5+8 \text { ( } 4 \text { ways) } \\
& 19=4+7+8=5+6+8 \text { ( } 2 \text { ways) }
\end{aligned}
\)
This gives us a total of 12 out of 35 sums that are prime, or a probability of \(12 / 35\).