Quiz Level-2
Quiz Summary
0 of 33 Questions completed
Questions:
Information
You have already completed the quiz before. Hence you can not start it again.
Quiz is loading…
You must sign in or sign up to start the quiz.
You must first complete the following:
Results
Results
0 of 33 Questions answered correctly
Your time:
Time has elapsed
You have reached 0 of 0 point(s), (0)
Earned Point(s): 0 of 0, (0)
0 Essay(s) Pending (Possible Point(s): 0)
Categories
- Not categorized 0%
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- Current
- Review
- Answered
- Correct
- Incorrect
-
Question 1 of 33
1. Question
A group of friends decide to go out to the movies. Fred and Tom are bringing dates, while their 2 friends are going alone. When the friends arrive at the movie theater, they find a row of six seats so they can all sit together.
If Fred and Tom must sit next to their dates, how many different ways can the group sit down?
CorrectIncorrectHint
Think of the seats as an arrangement of people in a line. Fred and Tom must sit next to their dates, so you can treat the pair as a single object. The only difference is that we must then multiply by 2, since we can switch the order in which they sit down at will (either Fred or his date can sit on the left).
So instead of dealing with 6 objects, we now simply work with 4. An arrangement of 4 objects, can be made in 4 x 3 x 2=24 different ways. You can choose any of 4 objects to be in the first spot. Once that spot is taken, you move onto the next of four spots. You place any of the remaining three there, giving you 3 more choices (or multiplying by 3). You do the same thing 2 more times to end up with 24 possibilities.
Finally, you have to take into account switching the positions of Fred/Tom and their respective dates. Since there are two pairs, you multiply by 2 twice. This gives you
24 x 2 x 2=96 different arrangements.
-
Question 2 of 33
2. Question
For a certain lunch special, customers must order a salad, an entree, and a dessert. If there are three different salads, four different entrees, and two different desserts available, then how many different lunch specials are possible?
CorrectIncorrectHint
Customers must choose a salad, an entree, and a dessert. There are three different salads, four entrees, and two desserts.
The simplest way of determining the number of combinations is by multiplying the number of options for each part of the meal. In other words, we can find the product of 3, 4, and 2, which would give us 24.
-
Question 3 of 33
3. Question
There are five pictures but only four display cases. The display cases are unique. How many different arrangements of pictures in display cases can be created?
CorrectIncorrectHint
There are five possible choices for the first space. For the second there are four possible, three for the third, and two for the fourth. 5 x 4 x 3 x 2 = 120 possible arrangements.
-
Question 4 of 33
4. Question
Ernie has 4 shirts, 7 ties, and 3 pants. How many different possible outfits can Ernie make?
CorrectIncorrectHint
The purpose of this question is to understand how to calculate a number of combinations. All different combinations of clothing articles are equally possible. Since all combinations are possible, the numbers of articles of clothing are all multiplied together, 4(shirts)x7(ties)x3(pants)=84, yielding 84 different possible outfits.
-
Question 5 of 33
5. Question
Ghani has six clean shirts and four pairs of pants to choose from. How many possible combinations of outfits can she make with these items?
CorrectIncorrectHint
If she has six shirts and four pairs of pants, then the total number of options she has can be found by multiplication.
6 x 4=24
To double-check, you can create a tree diagram, listing the possible combinations.
-
Question 6 of 33
6. Question
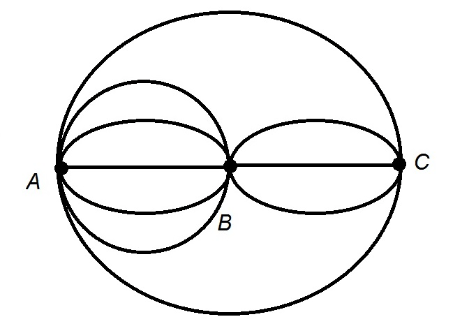
How many ways can a route be drawn that goes from Point A, to Point B, to Point C, then point A again, in that order?
 CorrectIncorrect
CorrectIncorrectHint
The multiplication principle can be applied here. There are 5 ways to get directly from Point A to Point B, 3 ways to get directly from Point B to Point C, and 2 ways to get directly from Point C to Point A. Multiply:
5×3×2=30 possible routes.
-
Question 7 of 33
7. Question
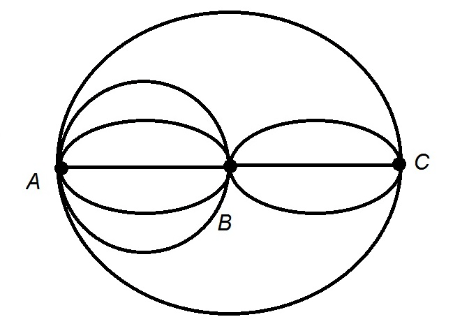
How many ways can a route be drawn that goes from Point A, through Point B, to Point C, then back through Point B, and back to Point A? Any path between points can be taken twice.
 CorrectIncorrect
CorrectIncorrectHint
The multiplication principle can be applied here. There are 5 ways to get from Point A to Point B, 3 ways to get from Point B to Point C, 3 ways to get from Point C to Point B, and 5 ways to get from Point B to Point A. Multiply:
5×3×3×5=225 possible routes.
-
Question 8 of 33
8. Question
How many ways can a route be drawn that goes from Point A, through Point B, to Point C, then back through Point B, and back to Point A, so that no path is taken twice?
 CorrectIncorrect
CorrectIncorrectHint
The multiplication principle can be applied here. There are 5 ways to get from Point A to Point B, and 3 ways to get from Point B to Point C. Since traveling the same path twice is not allowed, there are 2 ways left to get from Point C to Point B, and 4 ways left to get from Point B to Point A.
Multiply:
5×3×2×4=120
There are 120 possible routes.
-
Question 9 of 33
9. Question
There are seven unique placemats around a circular table. How many different orders of placemats are possible?
CorrectIncorrectHint
Since the table is circular, you need to find the total number of orders and divide this number by 7.
The total number of different orders that the placemats could be set in is 7! (7 factorial).
7!/7 = 6! = 720
Note that had this been a linear, and not circular, arrangement there would be no need to divide by 7. But in a circular arrangement, there are no “ends” so you must divide by N! by N to account for the circular arrangement.
-
Question 10 of 33
10. Question
If a team of 7 basketball players win a game and each high-five each other once after a game, how many high-fives take place?
CorrectIncorrectHint
To start, the first player makes 6 high-fives. The second player needs to make only 5 new high-fives because he doesn’t need to re high-five the first player. The third player needs to only make 4 high-fives and so on.
This adds up to 6 + 5 + 4 + 3 + 2 + 1 = 21
-
Question 11 of 33
11. Question
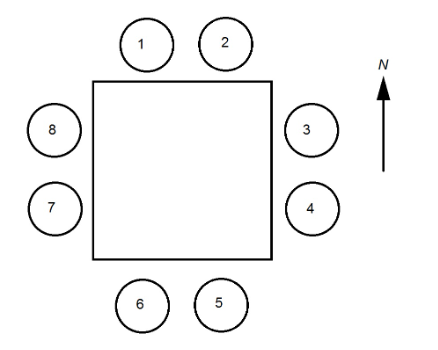
Mr. and Mrs. Jones have invited three other married couples to a dinner party; the eight are to be seated at the table shown above. It is desired that each husband sit directly across from his wife -for example, a husband at Seat 1, his wife at Seat 6. How many ways can the eight persons be seated to fit this specification?
 CorrectIncorrect
CorrectIncorrectHint
There are four pairs of seats directly across from each other: 1-6, 2-5, 3-8, 4-7.
There are four married couples to be placed in these four pairs of seats; since order is relevant, these are permutations. The number of ways to seat these couples is equal to the number of orderings, or permutations, of four elements from a set of four:
\(
P(4,4)=\frac{4 !}{(4-4)) !}=\frac{4 !}{0 !}=\frac{4 !}{1}=4 !
\)
which is equal to
\(
4 !=1 \times 2 \times 3 \times 4=24
\)
Within each pairing, there are two ways for the husband to select one seat and the wife to select the other, and there are four such pairings, so, applying the multiplication principle, the number of arrangements is
\(
24 \times 2 \times 2 \times 2 \times 2=384
\) -
Question 12 of 33
12. Question
Mr. and Mrs. Williams have invited three other married couples to a dinner party; the eight are to be seated at the table shown above. Since Mr. and Mrs. Williams need to be close to the kitchen so that they can serve the meal, it is desired that they sit at Seats 1 and 8, although it does not matter which one sits in which seat. There are no other restrictions. How many ways can the eight persons be seated to fit this specification?
 CorrectIncorrect
CorrectIncorrectHint
Since Seats 1 and 8 will be occupied by the Williamses, there are two ways to fill these seats – Mr. Williams in Seat 1 and Mrs. Williams in Seat 8 , and the opposite case.
The remaining six persons will be seated in the other six seats; since order is material here, this is a number of permutations. The number of permutations of six elements from a set of six is
\(
P(6,6)=\frac{6 !}{(6-6) !}=\frac{6 !}{0 !}=\frac{6 !}{1}=6 ! \text {, }
\)
which is equal to
\(
6 !=1 \times 2 \times 3 \times 4 \times 5 \times 6=720 .
\)
By the multiplication principle, the number of seating arrangements is
\(
2 \times 720=1,440 .
\) -
Question 13 of 33
13. Question
Yvonne wants to invite seven of her twenty classmates to her birthday party. She and her classmates will all be seated at the above table. Which of the following expressions gives the number of ways she can select seven classmates and seat them, and herself, at the table?
 CorrectIncorrect
CorrectIncorrectHint
One way to look at this is as follows:
Yvonne can sit at any one of the eight seats—eight ways to make this decision.
Yvonne can fill the remaining seven seats with seven out of twenty classmates. Since order is important, this is a permutation of seven elements chosen from a set of twenty; there are P(20,7) ways to make this decision.
By the multiplication principle, there are 8⋅P(20,7) ways Yvonne can invite seven classmates and seat them and herself at the table.
-
Question 14 of 33
14. Question
There are 7 consonants and 4 vowels. Find the number of words that can be made out of 3 consonants and 2 vowels.
CorrectIncorrectHint
Total consonants \(=7\)
Total vowels \(=4\)
Number of methods of choosing 3 consonants from 7 consonants \(={ }^7 \mathrm{C}_3\), Number of methods of choosing 2 vowels from 4 vowels \(={ }^4 \mathrm{C}_2\), Number of methods of choosing 3 consonants from 7 consonants and 2 vowels from 4 vowels \(={ }^7 \mathrm{C}_3 \times{ }^4 \mathrm{C}_2\)
\(=\left(\frac{7 \times 6 \times 5}{3 \times 2 \times 1}\right) \times\left(\frac{4 \times 3}{2 \times 1}\right)\)
\(=210\)
There exist, 210 groups, where each set has a total 5 letters ( 3 consonants and 2 vowels). Number of ways of presenting 5 letters \(=5\) ! \(=5 \times 4 \times 3 \times 2 \times 1=120\)
The required number of ways
\(=210 \times 120\)
\(=25200\) -
Question 15 of 33
15. Question
To form a committee, it requires 5 men and 6 women. There are 8 men and 10 women in total. Find the number of ways of forming the required committee.
CorrectIncorrectHint
There are 8 men and 10 women in total.
To form a committee, it requires 5 men and 6 women.
Number of ways
\(
\begin{aligned}
& ={ }^8 \mathrm{C}_5 \times{ }^{10} \mathrm{C}_6 \\
& ={ }^8 \mathrm{C}_3 \times{ }^{10} \mathrm{C}_4\left[\because{ }^{\mathrm{n}} \mathrm{C}_{\mathrm{r}}={ }^{\mathrm{n}} \mathrm{C}_{(\mathrm{n}-\mathrm{r})}\right] \\
& =[(8 \times 7 \times 6) /(3 \times 2 \times 1)] \times[(10 \times 9 \times 8 \times 7) /(4 \times 3 \times 2 \times 1)] \\
& =56 \times 210 \\
& =11760
\end{aligned}
\) -
Question 16 of 33
16. Question
There are 2 white coloured balls, 3 black coloured balls, 4 red coloured balls. Find the number of ways of drawing 3 balls such that at least 1 black ball is present in the draw from the bag.
CorrectIncorrectHint
There are 2 white coloured balls, 3 black coloured balls, 4 red coloured balls.
3 balls need to be drawn such that at least 1 black ball is present in the draw from the bag.
There exist 3 cases.
Case 1: Choosing 3 black balls.
Case 2: Choosing 2 black balls and one non-black ball.
Case 3: Choosing 1 black ball and 2 non-black balls.
Number of methods of selecting 3 black balls
\(={ }^3 \mathrm{C}_3\)
Number of ways to select 2 black balls and 1 non-black ball \(={ }^3 \mathrm{C}_2 \times{ }^6 \mathrm{C}_1\)
Number of ways to select 1 black ball and 2 non-black balls \(={ }^3 \mathrm{C}_1 \times{ }^6 \mathrm{C}_2\)
Total number of ways
\(={ }^3 C_3+{ }^3 C_2 \times{ }^6 C_1+{ }^3 C_1 \times{ }^6 C_2\)
\(={ }^3 C_3+{ }^3 C_1 \times{ }^6 C_1+{ }^3 C_1 \times{ }^6 C_2\left[\because{ }^n C_r={ }^n C_{(n-r)}\right]\)
\(=1+(3 \times 6)+[3 \times(6 \times 5) /(2 \times 1)]\)
\(=1+18+45\)
\(=64\) -
Question 17 of 33
17. Question
There are 6 boys and 4 girls. 4 need to be selected. Find the number of ways of selecting such that at least one boy should be selected.
CorrectIncorrectHint
There are 6 boys and 4 girls. 4 need to be chosen such that at least one boy should be selected.
There can be four options.
Selecting 4 boys.
Number of ways \(={ }^6 \mathrm{C}_4\)
Selecting 3 boys and 1 girl.
Number of ways \(={ }^6 \mathrm{C}_3 \times{ }^4 \mathrm{C}_1\)
Selecting 2 boys and 2 girls.
Number of ways \(={ }^6 \mathrm{C}_2 \times{ }^4 \mathrm{C}_2\)
Selecting 1 boy and 3 girls.
Number of ways \(={ }^6 \mathrm{C}_1 \times{ }^4 \mathrm{C}_3\)
Total number of ways
\(
\begin{aligned}
& ={ }^6 \mathrm{C}_4+{ }^6 \mathrm{C}_3 \times{ }^4 \mathrm{C}_1+{ }^6 \mathrm{C}_2 \times{ }^4 \mathrm{C}_2+{ }^6 \mathrm{C}_1 \times{ }^4 \mathrm{C}_3 \\
& ={ }^6 \mathrm{C}_2+{ }^6 \mathrm{C}_3 \times{ }^4 \mathrm{C}_1+{ }^6 \mathrm{C}_2 \times{ }^4 \mathrm{C}_2+{ }^6 \mathrm{C}_1 \times{ }^4 \mathrm{C}_1 \quad\left[\because{ }^{\mathrm{n}} \mathrm{C}_{\mathrm{r}}={ }^{\mathrm{n}} \mathrm{C}_{(\mathrm{n}-\mathrm{r})}\right] \\
& =\frac{6 \times 5}{2 \times 1}+\frac{6 \times 5 \times 4}{3 \times 2 \times 1} \times 4+\frac{6 \times 5}{2 \times 1} \times \frac{4 \times 3}{2 \times 1}+6 \times 4 \\
& =15+80+90+24 \\
& =209
\end{aligned}
\) -
Question 18 of 33
18. Question
Eight people are asked to select a leadership team of three members. How many different leadership teams are possible?
CorrectIncorrectHint
\({ }^8 \mathrm{C}_3=56\)
-
Question 19 of 33
19. Question
There are six scrabble letters left in the bad at the end of the game (AUGRX and Z). If you reach in and grab two letters, how many different pairs of letters are possible?
CorrectIncorrectHint
\({ }^6 \mathrm{C}_2=30/2=15\)
-
Question 20 of 33
20. Question
Jim wants to offer 3 sodas at his snack stand. He has a list of 8 sodas to choose from. How many combinations of 3 sodas are possible?
CorrectIncorrectHint
\({ }^8 \mathrm{C}_3=8!/(5!. 3!)=56\)
-
Question 21 of 33
21. Question
Rakesh has won a contest at the fair and gets to choose four different prizes from a set of nine. How many combinations of four prizes can he choose from a set of nine?
CorrectIncorrectHint
\({ }^9 \mathrm{C}_4=9!/(5! . 4!) =126\)
-
Question 22 of 33
22. Question
Out of 5 men and 3 women, a committee of three members is to be formed so that it has 1 woman and 2 men. In how many different ways can it be done?
CorrectIncorrectHint
\(
\text { Required number of ways }=\left({ }^3 C_1 \times{ }^5 C_2\right)=3 \times \frac{5 \times 4}{2 \times 1}=30
\) -
Question 23 of 33
23. Question
Out of 5 women and 4 men, a committee of three members is to be formed in such a way that at least one member is a woman. In how many different ways can it be done?
CorrectIncorrectHint
\(
\begin{aligned}
& \text { Required number of ways }=\left({ }^5 C_1 \times{ }^4 C_2\right)+\left({ }^5 C_2 \times{ }^4 C_1\right)+ \\
& \left({ }^5 C_3\right) \\
& =\left(5 \times \frac{4 \times 3}{2 \times 1}\right)+\left(\frac{5 \times 4}{2 \times 1} \times 4\right)+\left(\frac{5 \times 4 \times 3}{3 \times 2 \times 1}\right) \\
& =(30+40+10)=80
\end{aligned}
\) -
Question 24 of 33
24. Question
A committee of 5 members is to be formed out of 3 trainees, 4 professors and 6 research associates. In how many different ways can this be done, if the committee should have 4 professors and 1 research associate or all 3 trainees and 2 professors?
CorrectIncorrectHint
Required number of ways \(=\left({ }^4 C_4 \times{ }^6 C_1\right)+\left({ }^3 C_3 \times{ }^4 C_2\right)\)
\(
=(1+6)+\left(1+\frac{4 \times 3}{2}\right)=(7+7)=14
\) -
Question 25 of 33
25. Question
A committee of 5 members is to be formed out of 3 trainees, 4 professors and 6 research associates. In how many different ways can this be done if the committee should have 2 trainees and 3 research associates?
CorrectIncorrectHint
Required number of ways \(=\left({ }^3 C_2 \times{ }^6 C_3\right)=\left({ }^3 C_1 \times{ }^6 C_3\right)\)
\(
=\left(3 \times \frac{6 \times 5 \times 4}{3 \times 2 \times 1}\right)=60 \text {. }
\) -
Question 26 of 33
26. Question
In how many ways can a committee of 4 people be chosen out of 8 people?
CorrectIncorrectHint
\(
\text { Required number of ways }={ }^8 C_4=\frac{8 \times 7 \times 6 \times 5}{4 \times 3 \times 2 \times 1}=70
\) -
Question 27 of 33
27. Question
A committee of 5 members is to be formed by selecting out of 4 men and 5 women. In how many different ways the committee can be formed if it should have 2 men and 3 women?
CorrectIncorrectHint
Required number of ways \(=\left({ }^4 C_2 \times{ }^5 C_3\right)=\left({ }^4 C_2 \times{ }^5 C_2\right)\)
\(
=\left(\frac{4 \times 3}{2 \times 1} \times \frac{5 \times 4}{2 \times 1}\right)=60 \text {. }
\) -
Question 28 of 33
28. Question
A committee of 5 members is to be formed by selecting out of 4 men and 5 women. In how many different ways the committee can be formed if it should have at least 1 man?
CorrectIncorrectHint
The committee should have
( 1 man, 4 women) or ( 2 men, 3 women) or ( 3 men, 2 women) or (4 men, 1 woman).
Required number of ways \(=\left({ }^4 C_1 \times{ }^5 C_4\right)+\left({ }^4 C_2 \times{ }^5 C_3\right)+\)
\(\left({ }^4 C_3 \times{ }^5 C_2\right)+\left({ }^4 C_6 \times{ }^5 C_1\right)\)
\(=\left({ }^4 C_1 \times{ }^5 C_1\right)+\left({ }^4 C_2 \times{ }^5 C_2\right)+\left({ }^4 C_1 \times{ }^5 C_2\right)+\left({ }^4 C_4 \times{ }^5 C_1\right)\)
\(=(4 \times 5)+\left(\frac{4 \times 3}{2 \times 1} \times \frac{5 \times 4}{2 \times 1}\right)+\left(4 \times \frac{5 \times 4}{2 \times 1}\right)+(1 \times 5)\)
\(=(20+60+40+5)=125\). -
Question 29 of 33
29. Question
In how many ways a committee consisting of 5 men and 6 women can be formed from 8 men and 10 women?
CorrectIncorrectHint
Required number of ways \(=\left({ }^8 C_5 \times{ }^{10} C_6\right)+\left({ }^8 C_3 \times{ }^{10} C_4\right)\)
\(
\begin{aligned}
& =\frac{8 \times 7 \times 6}{{3 !}} \times \frac{10 \times 9 \times 8 \times 7}{{4 !}} \\
& =\frac{8 \times 7 \times 6}{6} \times \frac{10 \times 9 \times 8 \times 7}{4 \times 3 \times 2 \times 1}=11760 .
\end{aligned}
\) -
Question 30 of 33
30. Question
A select group of 4 is to be formed from 8 men and 6 women in such a way that the group must have at least 1 woman. In how many different ways can it be done?
CorrectIncorrectHint
Required number of ways
\(
\begin{aligned}
= & \left({ }^6 C_1 \times{ }^8 C_3\right)+\left({ }^6 C_2 \times{ }^8 C_2\right)+\left({ }^6 C_3 \times{ }^8 C_1\right)+\left({ }^6 C_4 \times{ }^8 C_0\right) \\
& =\left\{6 \times \frac{8 \times 7 \times 6}{{3 !}}\right\}+\left(\frac{6 \times 5}{2 \times 1} \times \frac{8 \times 7}{2 \times 1}\right) \\
& \quad+\left(\frac{6 \times 5 \times 4}{3 !} \times 8\right)+\left({ }^6 C_2 \times 1\right) \\
= & \left\{6 \times \frac{8 \times 7 \times 6}{3 \times 2 \times 1}\right\}+420+\left(\frac{6 \times 5 \times 4}{6} \times 8\right)+\left(\frac{6 \times 5}{2 \times 1} \times 1\right) \\
= & (336+420+160+15)=931 .
\end{aligned}
\) -
Question 31 of 33
31. Question
From a group of 7 men and 6 women, 5 persons are to be selected to form a committee so that at least 3 men are there on the committee. In how many ways can it be done?
CorrectIncorrectHint
Required number of ways
\(
\begin{aligned}
& =\left({ }^7 C_3 \times{ }^6 C_2\right)+\left({ }^7 C_4 \times{ }^6 C_1\right)+\left({ }^7 C_5 \times{ }^6 C_0\right) \\
& =\left\{\frac{7 \times 6 \times 5}{3 !} \times \frac{6 \times 5}{2 !}\right\}+\left({ }^7 C_3 \times{ }^6 C_1\right)+\left({ }^7 C_2 \times 1\right) \\
& =\left(\frac{7 \times 6 \times 5}{6} \times \frac{6 \times 5}{2 \times 1}\right)+\left(\frac{7 \times 6 \times 5}{3 \times 2 \times 1} \times 6\right)+\left(\frac{7 \times 6}{2 \times 1} \times 1\right) \\
& =(525+210+21)=756 .
\end{aligned}
\) -
Question 32 of 33
32. Question
A box contains 2 white, 3 black, and 4 red balls. In how many ways can 3 balls be drawn from the box, if at least 1 black ball is to be included in the draw?
CorrectIncorrectHint
We may have ( 1 black and 2 non-black) or ( 2 black and 1 non-black) or ( 3 black).
Required no. of ways \(=\left({ }^3 C_1 \times{ }^6 C_2\right)+\left({ }^3 C_2 \times{ }^6 C_1\right)+\left({ }^3 C_3\right)\) \(=\left(3 \times \frac{6 \times 5}{2 \times 1}\right)+\left(\frac{3 \times 2}{2 \times 1} \times 6\right)+1=(45+18+1)=64\). -
Question 33 of 33
33. Question
In how many ways can a group of 5 men and 2 women be made out of a total of 7 men and 3 women?
CorrectIncorrectHint
Required no. of ways
\(
=\left({ }^7 C_5 \times{ }^3 C_2\right)=\left({ }^7 C_2 \times{ }^3 C_1\right)=\frac{7 \times 6}{2 \times 1} \times 3=63 .
\)