Quiz Level-1
Quiz Summary
0 of 50 Questions completed
Questions:
Information
You have already completed the quiz before. Hence you can not start it again.
Quiz is loading…
You must sign in or sign up to start the quiz.
You must first complete the following:
Results
Results
0 of 50 Questions answered correctly
Your time:
Time has elapsed
You have reached 0 of 0 point(s), (0)
Earned Point(s): 0 of 0, (0)
0 Essay(s) Pending (Possible Point(s): 0)
Categories
- Not categorized 0%
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- Current
- Review
- Answered
- Correct
- Incorrect
-
Question 1 of 50
1. Question
A dog takes 4 leaps for every 5 leaps of a hare but 3 leaps of a dog are equal to 4 leaps of the hare. Compare their speeds. (M.B.A., 2007)
CorrectIncorrectHint
Let the distance covered in 1 leap of the dog be \(x\) and that covered in 1 leap of the hare be \(y\).
Then, \(3 x=4 y \Rightarrow x=\frac{4}{3} y \Rightarrow 4 x=\frac{16}{3} y\).
\(\therefore \quad\) Ratio of speeds of dog and hare
\(=\) Ratio of distances covered by them in the same time
\(
=4 x: 5 y=\frac{16}{3} y: 5 y=\frac{16}{3}: 5=16: 15 \text {. }
\) -
Question 2 of 50
2. Question
While covering a distance of \(24 \mathrm{~km}\), a man noticed that after walking for 1 hour and 40 minutes, the distance covered by him was \(\frac{5}{7}\) of the remaining distance. What was his speed in metres per second?
CorrectIncorrectHint
Let the speed be \(x \mathrm{~km} / \mathrm{hr}\).
Then, distance covered in \(1 \mathrm{hr} .40 \mathrm{~min}\). i.e., \(1 \frac{2}{3} \mathrm{hrs}=\frac{5 x}{3} \mathrm{~km}\).
Remaining distance \(=\left(24-\frac{5 x}{3}\right) \mathrm{km}\).
\(
\begin{aligned}
\therefore \quad \frac{5 x}{3}=\frac{5}{7}\left(24-\frac{5 x}{3}\right) & \Leftrightarrow \frac{5 x}{3}=\frac{5}{7}\left(\frac{72-5 x}{3}\right) \Leftrightarrow 7 x=72-5 x \\
& \Leftrightarrow 12 x=72 \Leftrightarrow x=6 .
\end{aligned}
\)
Hence, speed \(=6 \mathrm{~km} / \mathrm{hr}=\left(6 \times \frac{5}{18}\right) \mathrm{m} / \mathrm{sec}=\frac{5}{3} \mathrm{~m} / \mathrm{sec}=1 \frac{2}{3} \mathrm{~m} / \mathrm{sec}\) -
Question 3 of 50
3. Question
A trip to a destination is made in the following way:900 km by train at an average speed of \(60 \mathrm{~km} / \mathrm{hr}\), \(3000 \mathrm{~km}\) by plane at an average speed of \(500 \mathrm{~km} / \mathrm{hr}, 400 \mathrm{~km}\) by boat at an average speed of \(25 \mathrm{~km} / \mathrm{hr}, 15\) \(\mathrm{km}\) by taxi at an average speed of \(45 \mathrm{~km} / \mathrm{hr}\). What is the average speed for the entire journey? (I.A.S., 2008)
CorrectIncorrectHint
Total distance travelled \(=(900+3000+400+15) \mathrm{km}=4315 \mathrm{~km}\).
\(
\begin{aligned}
\text { Total time taken } & =\left(\frac{900}{60}+\frac{3000}{500}+\frac{400}{25}+\frac{15}{45}\right) \mathrm{hr} \\
& =\left(15+6+16+\frac{1}{3}\right) \mathrm{hr}=37 \frac{1}{3} \mathrm{hr}=\frac{112}{3} \mathrm{hr} .
\end{aligned}
\)
\(\therefore \quad\) Average speed for the whole journey
\(
=\left(4315 \times \frac{3}{112}\right) \mathrm{km} / \mathrm{hr}=115 \frac{65}{112} \mathrm{~km} / \mathrm{hr}
\) -
Question 4 of 50
4. Question
Peter can cover a certain distance in 1 hr. 24 min. by covering two-third of the distance at 4 kmph and the rest at 5 kmph. Find the total distance.
CorrectIncorrectHint
\(
\frac{\frac{2}{3} x}{4}+\frac{\frac{1}{3} x}{5}=\frac{7}{5} \Leftrightarrow \frac{x}{6}+\frac{x}{15}=\frac{7}{5} \Leftrightarrow 7 x=42 \Leftrightarrow x=6 .
\)
Total distance \(=6 \mathrm{~km}\). -
Question 5 of 50
5. Question
One-third of a certain journey was covered at the speed of \(20 \mathrm{~km} / \mathrm{hr}\), one-fourth at \(30 \mathrm{~km} / \mathrm{hr}\) and the rest at the speed of \(50 \mathrm{~km} / \mathrm{hr}\). Find the average speed per hour for the whole journey. (A.A.O. Exam., 2009)
CorrectIncorrectHint
Let the total distance be \(x \mathrm{~km}\). Then,
Distance covered at \(20 \mathrm{~km} / \mathrm{hr}=\frac{x}{3} \mathrm{~km} ;\) Distance covered at \(30 \mathrm{~km} / \mathrm{hr}=\frac{x}{4} \mathrm{~km}\);
Distance covered at \(50 \mathrm{~km} / \mathrm{hr}=\left[x-\left(\frac{x}{3}+\frac{x}{4}\right)\right] \mathrm{km}=\frac{5 x}{12} \mathrm{~km}\)
Total time taken \(=\left[\frac{(x / 3)}{20}+\frac{(x / 4)}{30}+\frac{(5 x / 12)}{50}\right]\) hrs
\(
=\left(\frac{x}{60}+\frac{x}{120}+\frac{x}{120}\right) \mathrm{hrs}=\frac{4 x}{120} \mathrm{hrs}=\frac{x}{30} \mathrm{hrs} \text {. }
\)
\(\therefore \quad\) Average speed for the whole journey \(=\left(x \times \frac{30}{x}\right) \mathrm{km} / \mathrm{hr}=30 \mathrm{~km} / \mathrm{hr}\). -
Question 6 of 50
6. Question
A man travelled from the village to the post-office at the rate of \(25 \mathrm{kmph}\) and walked back at the rate of \(4 \mathrm{kmph}\). If the whole journey took 5 hours 48 minutes, find the distance of the post-office from the village.
CorrectIncorrectHint
Average speed \(=\left(\frac{2 x y}{x+y}\right) \mathrm{km} / \mathrm{hr}=\left(\frac{2 \times 25 \times 4}{25+4}\right) \mathrm{km} / \mathrm{hr}=\frac{200}{29} \mathrm{~km} / \mathrm{hr}\).
Distance travelled in 5 hours 48 minutes, i.e., \(5 \frac{4}{5} \mathrm{hrs}=\left(\frac{200}{29} \times \frac{29}{5}\right) \mathrm{km}=40 \mathrm{~km}\).
\(\therefore \quad\) Distance of the post-office from the village \(=\left(\frac{40}{2}\right)=20 \mathrm{~km}\). -
Question 7 of 50
7. Question
An aeroplane flies along the four sides of a square at the speeds of \(100,200,300\) and \(400 \mathrm{~km} / \mathrm{hr}\). Find the average speed of the plane around the field. (P.C.S., 2009)
CorrectIncorrectHint
Let each side of the square be \(x \mathrm{~km}\) and let the average speed of the plane around the field be \(y \mathrm{~km} / \mathrm{hr}\). Then, \(\frac{x}{100}+\frac{x}{200}+\frac{x}{300}+\frac{x}{400}=\frac{4 x}{y} \Leftrightarrow \frac{25 x}{1200}=\frac{4 x}{y} \Leftrightarrow y=\left(\frac{1200 \times 4}{25}\right)=192\).
\(\therefore \quad\) Average speed \(=192 \mathrm{~km} / \mathrm{hr}\) -
Question 8 of 50
8. Question
A fast train takes 3 hours less than a slow train for a journey of \(600 \mathrm{~km}\). If the speed of the slow train is \(10 \mathrm{~km} / \mathrm{hr}\) less than that of the fast train, then find the speeds of the two trains. (M.A.T., 2006)
CorrectIncorrectHint
Let the speed of the fast train be \(x \mathrm{~km} / \mathrm{hr}\).
The, speed of the slow train \(=(x-10) \mathrm{km} / \mathrm{hr}\).
\(
\begin{aligned}
\therefore \quad & \frac{600}{(x-10)}-\frac{600}{x}=3 \Leftrightarrow 600 x-600(x-10)=3 x(x-10) \\
& \Leftrightarrow x^2-10 x-2000=0 \Leftrightarrow x^2-50 x+40 x-2000=0 \\
& \Leftrightarrow x(x-50)+40(x-50)=0 \Leftrightarrow(x-50)(x+40)=0 \Leftrightarrow x=50 .
\end{aligned}
\)
Hence, speed of fast train \(=50 \mathrm{~km} / \mathrm{hr}\) and speed of slow train \(=40 \mathrm{~km} / \mathrm{hr}\). -
Question 9 of 50
9. Question
By walking at \(\frac{3}{4}\) of his usual speed, a man reaches his office 20 minutes later than his usual time. Find the usual time taken by him to reach his office. (S.S.C., 2010)
CorrectIncorrectHint
New speed \(=\frac{3}{4}\) of usual speed.
\(\therefore \quad\) New time taken \(=\frac{4}{3}\) of usual time.
So, \(\left(\frac{4}{3}\right.\) of the usual time \()-\) (usual time) \(=20 \mathrm{~min}\)
\(\Rightarrow \quad \frac{1}{3}\) of the usual time \(=20 \mathrm{~min} \Rightarrow\) Usual time \(=60 \mathrm{~min}=1 \mathrm{hr}\). -
Question 10 of 50
10. Question
A person reaches his destination 40 minutes late if his speed is \(3 \mathrm{~km} / \mathrm{hr}\), and reaches 30 minutes before time if his speed is \(4 \mathrm{~km} / \mathrm{hr}\). Find the distance of his destination from his starting point. (S.S.C., 2007)
CorrectIncorrectHint
Let the required distance be \(x \mathrm{~km}\).
Difference in the times taken at two speeds \(=70 \mathrm{~min}=\frac{7}{6} \mathrm{hr}\).
\(
\therefore \quad \frac{x}{3}-\frac{x}{4}=\frac{7}{6} \Leftrightarrow 4 x-3 x=14 \Leftrightarrow x=14 \text {. }
\)
Hence, the required distance is \(14 \mathrm{~km}\). -
Question 11 of 50
11. Question
A carriage driving in a fog passed a man who was walking at the rate of 3 kmph in the same direction. He could see the carriage for 4 minutes and it was visible to him upto a distance of 100 m. What was the speed of the carriage?
CorrectIncorrectHint
Let the speed of the carriage be \(x \mathrm{kmph}\). Then, relative speed \(=(x-3) \mathrm{kmph}\).
Distance covered in \(4 \mathrm{~min}\) i.e., \(\frac{1}{15} \mathrm{hr}\) at relative speed \(=100 \mathrm{~m}=\frac{1}{10} \mathrm{~km}\).
\(
\therefore \quad(x-3)=\frac{1}{10} \times 15=\frac{3}{2} \Leftrightarrow x=3+\frac{3}{2}=\frac{9}{2}=4 \frac{1}{2} \text {. }
\)
Hence, speed of the carriage \(=4 \frac{1}{2} \mathrm{kmph}\). -
Question 12 of 50
12. Question
A train after travelling \(150 \mathrm{~km}\) meets with an accident and then proceeds at \(\frac{3}{5}\) of its former speed and arrives at its destination 8 hours late. Had the accident occurred \(360 \mathrm{~km}\) further, it would have reached the destination 4 hours late. What is the total distance travelled by the train? (M.A.T., 2007)
CorrectIncorrectHint
Let the original speed of the train be \(x \mathrm{~km} / \mathrm{hr}\).
Then, \(\frac{360}{\left(\frac{3}{5} x\right)}-\frac{360}{x}=4 \Leftrightarrow \frac{600}{x}-\frac{360}{x}=4 \Leftrightarrow \frac{240}{x}=4 \Leftrightarrow x=60\).
Let the total distance travelled by the train be \(y \mathrm{~km}\).
Then, \(\left[\frac{150}{60}+\frac{(y-150)}{\left(\frac{3}{5} \times 60\right)}\right]-\frac{y}{60}=8 \Leftrightarrow \frac{5}{2}+\frac{(y-150)}{36}-\frac{y}{60}=8 \Leftrightarrow 2 x=1740 \Leftrightarrow x=870\).
Hence, required distance \(=870 \mathrm{~km}\). -
Question 13 of 50
13. Question
A ship \(77 \mathrm{~km}\) from the shore, springs a leak which admits \(2 \frac{1}{4}\) tonnes of water in \(5 \frac{1}{2}\) minutes. 92 tonnes of water would sink it. But the pumps can throw out 12 tonnes of water per hour. Find the average rate of sailing so that the ship may just reach the shore as it begins to sink.
CorrectIncorrectHint
Quantity of water let in by the leak in \(1 \mathrm{~min}\)
\(
=\frac{\left(2 \frac{1}{4}\right)}{\left(5 \frac{1}{2}\right)} \text { tonnes }=\left(\frac{9}{4} \times \frac{2}{11}\right) \text { tonnes }=\frac{9}{22} \text { tonnes. }
\)
Quantity of water thrown out by the pumps in \(1 \mathrm{~min}=\left(\frac{12}{60}\right)\) tonnes \(=\frac{1}{5}\) tonnes.
Net quantity of water filled in the ship in \(1 \mathrm{~min}=\left(\frac{9}{22}-\frac{1}{5}\right)\) tonnes \(=\frac{23}{110}\) tonnes.
\(\frac{23}{110}\) tonnes water is filled in \(1 \mathrm{~min}\).
92 tonnes water is filled in \(\left(\frac{110}{23} \times 92\right) \mathrm{min}=440 \mathrm{~min}=\frac{22}{3} \mathrm{hrs}\).
\(
\text { Hence, required speed }=\frac{77}{(22 / 3)} \mathrm{km} / \mathrm{hr}=\left(77 \times \frac{3}{22}\right) \mathrm{km} / \mathrm{hr}=10.5 \mathrm{~km} / \mathrm{hr} \text {. }
\) -
Question 14 of 50
14. Question
Excluding the stoppages, the speed of a bus is \(64 \mathrm{~km} / \mathrm{hr}\) and including the stoppages, the speed of the bus is \(48 \mathrm{~km} / \mathrm{hr}\). For how many minutes does the bus stop per hour? (Bank P.O., 2009)
CorrectIncorrectHint
Due to stoppage, the bus covers \((64-48)=16 \mathrm{~km}\) less per hour.
Time taken to cover \(16 \mathrm{~km}=\left(\frac{16}{64} \times 60\right) \mathrm{min}=15 \mathrm{~min}\).
Hence, stoppage time per hour \(=15 \mathrm{~min}\). -
Question 15 of 50
15. Question
An aeroplane started 30 minutes later than the scheduled time from a place \(1500 \mathrm{~km}\) away from its destination. To reach the destination at the scheduled time the pilot had to increase the speed by \(250 \mathrm{~km} / \mathrm{hr}\). What was the speed of the aeroplane per hour during the journey? (P.C.S., 2006)
CorrectIncorrectHint
Let the original speed of the aeroplane be \(x \mathrm{~km} / \mathrm{hr}\).
\(
\begin{aligned}
& \therefore \quad \frac{1500}{x}-\frac{1500}{(x+250)}=\frac{1}{2} \Leftrightarrow 3000(x+250)-3000 x=x(x+250) \\
& \Leftrightarrow x^2+250 x-750000=0 \\
& \Leftrightarrow x^2+1000 x-750 x-750000=0 \\
& \Leftrightarrow x(x+1000)-750(x+1000)=0 \\
& \Leftrightarrow(x+1000)(x-750)=0 \Leftrightarrow x=750 .
\end{aligned}
\)
Hence, speed of the aeroplane during the journey \(=(750+250) \mathrm{km} / \mathrm{hr}=1000 \mathrm{~km} / \mathrm{hr}\). -
Question 16 of 50
16. Question
Two boys \(A\) and \(B\) start at the same time to ride from Delhi to Meerut, \(60 \mathrm{~km}\) away. A travels \(4 \mathrm{~km}\) an hour slower than B. B reaches Meerut and at once turns back meeting A 12, km from Meerut. Find A’s speed. (M.B.A., 2011)
CorrectIncorrectHint
Let \(A^{\prime}\) s speed \(=x \mathrm{~km} / \mathrm{hr}\). Then, \(B^{\prime}\) s speed \(=(x+4) \mathrm{km} / \mathrm{hr}\).
Clearly, time taken by \(B\) to cover \((60+12)\), i.e., \(72 \mathrm{~km}=\) time taken by \(A\) to cover \((60-12)\) i.e., \(48 \mathrm{~km}\) \(\therefore \quad \frac{72}{x+4}=\frac{48}{x} \Leftrightarrow 72 x=48 x+192 \Leftrightarrow 24 x=192 \Leftrightarrow x=8\).
Hence, \(A^{\prime}\) s speed \(=8 \mathrm{~km} / \mathrm{hr}\). -
Question 17 of 50
17. Question
A man covers a certain distance on a toy train. Had the train moved \(4 \mathrm{~km} / \mathrm{hr}\) faster, it would have taken 30 minutes less. If it moved \(2 \mathrm{~km} / \mathrm{hr}\) slower, it would have taken 20 minutes more. Find the distance. (M.A.T., 2010)
CorrectIncorrectHint
Let the distance be \(x \mathrm{~km}\) and initial speed be \(y \mathrm{~km} / \mathrm{hr}\).
Then, \(\frac{x}{y}-\frac{x}{y+4}=\frac{30}{60}=\frac{1}{2} \Leftrightarrow \frac{4 x}{y(y+4)}=2 \Leftrightarrow 8 x=y^2+4 y \Leftrightarrow x=\frac{y^2+4 y}{8} \dots(i)\)
And, \(\frac{x}{y-2}-\frac{x}{y}=\frac{20}{60}=\frac{1}{3} \Leftrightarrow \frac{2 x}{y(y-2)}=\frac{1}{3} \Leftrightarrow 6 x=y^2-2 y \Leftrightarrow x=\frac{y^2-2 y}{6} \dots(ii)\)
From \((i)\) and \((i i)\), we have :
\(
\frac{y^2+4 y}{8}=\frac{y^2-2 y}{6} \Leftrightarrow 6 y^2+24 y=8 y^2-16 y \Leftrightarrow 2 y^2=40 y \Leftrightarrow 2 y=40 \Leftrightarrow y=20
\)
Putting \(y=20\) in \((i)\), we get : \(x=60\).
Hence, required distance \(=60 \mathrm{~km}\). -
Question 18 of 50
18. Question
A and B are two stations 390 km apart. A train starts from A at 10 a.m. and travels towards B at 65 kmph. Another train starts from B at 11 a.m. and travels towards A at 35 kmph. At what time do they meet? (M.B.A., 2007)
CorrectIncorrectHint
Suppose they meet \(x\) hours after 10 a.m. Then,
(Distance moved by first in \(x\) hrs) + [Distance moved by second in \((x-1)\) hrs \(]=390\)
\(
\therefore 65 x+35(x-1)=390 \Rightarrow 100 x=425 \Rightarrow x=4 \frac{1}{4} .
\)
So, they meet 4 hrs. \(15 \mathrm{~min}\). after 10 a.m., i.e., at 2.15 p.m. -
Question 19 of 50
19. Question
A goods train leaves a station at a certain time and at a fixed speed. After 6 hours, an express train leaves the same station and moves in the same direction at a uniform speed of 90 kmph. This train catches up the goods train in 4 hours. Find the speed of the goods train.
CorrectIncorrectHint
Let the speed of the goods train be \(x \mathrm{kmph}\).
Distance covered by goods train in 10 hours = Distance covered by express train in 4 hours \(\therefore \quad 10 x=4 \times 90\) or \(x=36\).
So, speed of goods train \(=36 \mathrm{kmph}\). -
Question 20 of 50
20. Question
A thief is spotted by a policeman from a distance of 100 metres. When the policeman starts the chase, the thief also starts running. If the speed of the thief be 8 km / hr and that of the policeman 10 km / hr, how far the thief will have run before he is overtaken?
CorrectIncorrectHint
Relative speed of the policeman \(=(10-8) \mathrm{km} / \mathrm{hr}=2 \mathrm{~km} / \mathrm{hr}\).
Time taken by policeman to cover \(100 \mathrm{~m}=\left(\frac{100}{1000} \times \frac{1}{2}\right) \mathrm{hr}=\frac{1}{20} \mathrm{hr}\).
In \(\frac{1}{20} \mathrm{hrs}\), the thief covers a distance of \(\left(8 \times \frac{1}{20}\right) \mathrm{km}=\frac{2}{5} \mathrm{~km}=400 \mathrm{~m}\). -
Question 21 of 50
21. Question
Two places A and B are 80 km apart from each other on a highway. A car starts from A and another from B at the same time. If they move in the same direction they meet each other in 8 hours. If they move in opposite directions towards each other, they meet in 1 hour 20 minutes. Determine the speeds of the cars. (S.S.C., 2006)
CorrectIncorrectHint
Let their speeds be \(x \mathrm{kmph}\) and \(y \mathrm{kmph}\) respectively.
Then, \(\frac{80}{x-y}=8 \Rightarrow x-y=10 \dots(i)\)
And, \(\frac{80}{x+y}=1 \frac{1}{3}=\frac{4}{3} \Rightarrow x+y=60 \dots(ii)\)
Adding (i) and (ii), we get : \(2 x=70\) or \(x=35\).
Putting \(x=35\) in \((i)\), we get : \(y=25\).
Hence, the speeds of the two cars are \(35 \mathrm{kmph}\) and \(25 \mathrm{kmph}\). -
Question 22 of 50
22. Question
A man takes 6 hours 30 min in going by a cycle and coming back by scooter. He would have lost 2 hours and 10 min by going on cycle both ways. How long would it take him to go by scooter both ways? (M.A.T. 2006)
CorrectIncorrectHint
Let the distance be \(x \mathrm{~km}\). Then,
(Time taken to cover \(x \mathrm{~km}\) by cycle) + (Time taken to cover \(x \mathrm{~km}\) by scooter) \(=6 \mathrm{hr} 30\) min
\(\Rightarrow\) (Time taken to cover \(2 x \mathrm{~km}\) by cycle) + (Time taken to cover \(2 x \mathrm{~km}\) by scooter) \(=13 \mathrm{hrs}\)
But, time taken to cover \(2 x \mathrm{~km}\) by cycle \(=8 \mathrm{hr} 40\) min.
\(\therefore\) Time taken to cover \(2 x \mathrm{~km}\) by scooter \(=13 \mathrm{hrs}-8 \mathrm{hr} 40 \mathrm{~min}=4 \mathrm{hr} 20 \mathrm{~min}\).
Hence, required time \(=4\) hr \(20 \mathrm{~min}\) -
Question 23 of 50
23. Question
Sneha is picked up by her father by car from college every day. The college gets over at 4 p.m. daily. One day, the college got over an hour earlier than usual. Sneha started walking towards her house. Her father, unaware of this fact, leaves his house as usual, meets his daughter on the way, picks her up and they reach the house 15 minutes earlier than usual. What is the ratio of the father’s driving speed to Sneha’s walking speed?
CorrectIncorrectHint
Since 15 minutes are saved, it means that Sneha’s father drives from the meeting point to the college and back to the meeting point in \(15 \mathrm{~min}\). i.e. he can drive from the meeting point to the college in \(\left(\frac{15}{2}\right)=7.5 \mathrm{~min}\).
But he reaches the college daily at 4 p.m. So Sneha and her father meet on the way at \(3: 52 \frac{1}{2} \mathrm{p} . \mathrm{m}\). Thus, Sneha walked for \(52.5 \mathrm{~min}\) and covered the same distance as covered by her father in \(7.5 \mathrm{~min}\). Since speed varies inversely as time taken to cover a distance, we have:
\(\frac{\text { Father’s driving speed }}{\text { Sneha’s walking speed }}=\frac{52.5}{7.5}=\frac{7}{1}\).
Hence, the required ratio \(=7: 1\). -
Question 24 of 50
24. Question
\(
\text { A speed of } 30.6 \mathrm{~km} / \mathrm{hr} \text { is the same as (R.R.B., 2008) }
\)CorrectIncorrectHint
\(
30.6 \mathrm{~km} / \mathrm{hr}=\left(30.6 \times \frac{5}{18}\right) \mathrm{m} / \mathrm{sec}=\frac{153}{18} \mathrm{~m} / \mathrm{sec}=8.5 \mathrm{~m} / \mathrm{sec}
\) -
Question 25 of 50
25. Question
A man riding his bicycle covers 150 metres in 25 seconds. What is his speed in km per hour? (S.S.C., 2005)
CorrectIncorrectHint
\(
\begin{aligned}
\text { Speed } & =\left(\frac{150}{25}\right) \mathrm{m} / \mathrm{sec}=6 \mathrm{~m} / \mathrm{sec} \\
& =\left(6 \times \frac{18}{5}\right) \mathrm{km} / \mathrm{hr}=\left(\frac{108}{5}\right) \mathrm{km} / \mathrm{hr}=21.6 \mathrm{~km} / \mathrm{hr}
\end{aligned}
\) -
Question 26 of 50
26. Question
A bus covers a distance of \(2924 \mathrm{~km}\) in 43 hours. What is the speed of the bus? (Bank Recruitment, 2008)
CorrectIncorrectHint
\(
\text { Speed }=\left(\frac{2924}{43}\right) \mathrm{km} / \mathrm{hr}=68 \mathrm{~km} / \mathrm{hr}
\) -
Question 27 of 50
27. Question
A is travelling at 72 km per hour on a highway while B is travelling at a speed of 25 metres per second. What is the difference in their speeds in metres per second? (Campus Recruitment, 2010)
CorrectIncorrectHint
\(
\begin{aligned}
& A^{\prime} \text { s speed }=72 \mathrm{~km} / \mathrm{hr}=\left(72 \times \frac{5}{18}\right) \mathrm{m} / \mathrm{sec}=20 \mathrm{~m} / \mathrm{sec} \\
& B^{\prime} \text { s speed }=25 \mathrm{~m} / \mathrm{sec} \\
& \text { Difference }=(25-20) \mathrm{m} / \mathrm{sec}=5 \mathrm{~m} / \mathrm{sec}
\end{aligned}
\) -
Question 28 of 50
28. Question
motorist travelled between two towns, which are \(65 \mathrm{~km}\) apart, in 2 hours and 10 minutes. Find the speed in metres per minute. (R.R.B., 2006)
CorrectIncorrectHint
Distance covered \(=65 \mathrm{~km}=65000 \mathrm{~m}\).
Time taken \(=2 \mathrm{hrs} 10 \mathrm{~min}\)
\(=[(2 \times 60)+10] \mathrm{min}=130 \mathrm{~min}\).
\(\therefore\) Speed \(=\left(\frac{65000}{130}\right) \mathrm{m} / \mathrm{min}=500 \mathrm{~m} / \mathrm{min}\). -
Question 29 of 50
29. Question
In track meets both 100 yards and 100 metres are used as distances. By how many metres is 100 metres longer than 100 yards?
CorrectIncorrectHint
\(
\begin{aligned}
& 1 \text { yard }=0.9144 \mathrm{~m} \Rightarrow 100 \text { yards }=(100 \times 0.9144) \mathrm{m}=91.44 \mathrm{~m} \\
& \therefore \text { Required difference }=(100-91.44) \mathrm{m}=8.56 \mathrm{~m} .
\end{aligned}
\) -
Question 30 of 50
30. Question
A man covered a distance of \(180 \mathrm{~km}\) in 4 hours on a bike. How much distance will be cover on a bicycle in 8 hours if he rides the bicycle at one-sixth the speed of the bike? (Bank Recruitment, 2010)
CorrectIncorrectHint
Speed of the bike \(=\left(\frac{180}{4}\right) \mathrm{km} / \mathrm{hr}=45 \mathrm{~km} / \mathrm{hr}\)
Speed of the bicycle \(=\left(\frac{1}{6} \times 45\right) \mathrm{km} / \mathrm{hr}=7.5 \mathrm{~km} / \mathrm{hr}\).
\(\therefore\) Required distance \(=(7.5 \times 8) \mathrm{km}=60 \mathrm{~km}\). -
Question 31 of 50
31. Question
The ratio of the speeds of a car, a train and \(a\) bus is \(5: 9: 4\). The average speed of the car, the bus and the train is \(72 \mathrm{~km} / \mathrm{hr}\). What is the average speed of the car and the train together? (Bank P.O., 2010)
CorrectIncorrectHint
Let the speeds of the car, train and bus be \(5 x, 9 x\) and \(4 x\) \(\mathrm{km} / \mathrm{hr}\) respectively.
Then, \(\frac{5 x+9 x+4 x}{3}=72 \Leftrightarrow 6 x=72 \Leftrightarrow x=12\).
\(\therefore\) Speed of the car \(=60 \mathrm{~km} / \mathrm{hr}\);
speed of the train \(=108 \mathrm{~km} / \mathrm{hr}\).
Average speed of car and train
\(
=\left(\frac{60+108}{2}\right) \mathrm{km} / \mathrm{hr}=84 \mathrm{~km} / \mathrm{hr} .
\) -
Question 32 of 50
32. Question
Car A travels at the speed of \(65 \mathrm{~km} / \mathrm{hr}\) and reaches its destination in 8 hours. Car B travels at the speed of \(70 \mathrm{~km} / \mathrm{hr}\) and reaches its destination in 4 hours. What is the ratio of the distance covered by car A and car B respectively? (Bank P.O., 2010)
CorrectIncorrectHint
\(
\text { Required ratio }=(65 \times 8):(70 \times 4)=520: 280=13: 7 .
\) -
Question 33 of 50
33. Question
The average speed of a bus is one-third of the speed of a train. The train covers \(1125 \mathrm{~km}\) in 15 hours. How much distance will the bus cover in 36 minutes? (Bank Recruitment, 2010)
CorrectIncorrectHint
None of theseSpeed of the train \(=\left(\frac{1125}{15}\right) \mathrm{km} / \mathrm{hr}=75 \mathrm{~km} / \mathrm{hr}\).
Speed of the bus \(=\left(\frac{1}{3} \times 75\right) \mathrm{km} / \mathrm{hr}=25 \mathrm{~km} / \mathrm{hr}\).
Distance covered by the bus in \(60 \mathrm{~min}=25 \mathrm{~km}\).
Distance covered by the bus in \(36 \mathrm{~min}\)
\(
=\left(\frac{25}{60} \times 36\right) \mathrm{km}=15 \mathrm{~km}
\) -
Question 34 of 50
34. Question
The mileage of a motorbike \(A\) and a motorbike \(B\) is \(42 \mathrm{~km}\) per litre and \(52 \mathrm{~km}\) per litre respectively. Motorbike \(A\) covered \(294 \mathrm{~km}\) and motorbike \(B\) covered \(208 \mathrm{~km}\). If the cost of 1 litre of petrol is \(₹ 48\), how much amount would be spent on petrol to cover the total distance by both the motor bikes together? (Bank P.O., 2010)
CorrectIncorrectHint
Quantity of petrol consumed by both the motorbikes
\(
\begin{aligned}
& =\left(\frac{294}{42}+\frac{208}{52}\right) \text { litres }=11 \text { litres. } \\
& \therefore \text { Total amount spent on petrol }=\text { Rs }(48 \times 11)=₹ 528 .
\end{aligned}
\) -
Question 35 of 50
35. Question
A train leaves Delhi at 4.10 P.M. and reaches Aligarh at 7.25 P.M. The average speed of the train is 40 \(\mathrm{km} / \mathrm{hr}\). What is the distance from Delhi to Aligarh? (R.R.B., 2006)
CorrectIncorrectHint
Time taken \(=3 \mathrm{hrs} 15 \mathrm{~min}=3 \frac{1}{4} \mathrm{hrs}=\frac{13}{4} \mathrm{hrs}\).
\(
\therefore \text { Required distance }=\left(40 \times \frac{13}{4}\right) \mathrm{km}=130 \mathrm{~km}
\) -
Question 36 of 50
36. Question
\(A\) is 10 miles west of \(B\). C is 30 miles north of \(B. D\) is 20 miles east of \(C\). What is the distance from \(A\) to \(D\)? (M.B.A., 2006)
CorrectIncorrectHint
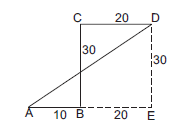
Required distance
\(
\begin{aligned}
& =A D \quad \sqrt{(A E)^2+(D E)^2} \\
& =\sqrt{(30)^2+(30)^2} \\
& =\sqrt{900+900}=\sqrt{1800} \\
& =30 \sqrt{2} \text { miles. }
\end{aligned}
\) -
Question 37 of 50
37. Question
A plane flying north at \(500 \mathrm{mph}\) passes over a city at 12 noon. A plane flying east at the same altitude passes over the same city at \(12: 30 \mathrm{P} M\). The plane is flying east at \(400 \mathrm{mph}\). To the nearest hundred miles, how far apart are the two planes at 2 P.M.?
CorrectIncorrectHint

Distance covered by the first plane till 2 P.M., i.e., in 2 hrs \(=(500 \times 2)\) miles \(=1000\) miles.
Distance covered by the second plane till 2 P.M., i.e., in
\(
\begin{aligned}
& 1 \frac{1}{2} \text { hrs }=\left(400 \times \frac{3}{2}\right) \text { miles }=600 \text { miles. } \\
& \therefore \text { Required distance } \\
& \qquad=A B=\sqrt{(1000)^2+(600)^2} \\
& \quad=\sqrt{1000000+360000}
\end{aligned}
\)
\(
\begin{aligned}
& =\sqrt{1360000} \text { miles }=200 \sqrt{34} \text { miles } \\
& =1166 \text { miles } \approx 1200 \text { miles. }
\end{aligned}
\) -
Question 38 of 50
38. Question
A train travels at the speed of \(65 \mathrm{~km} / \mathrm{hr}\) and halts at 8 junctions for a certain time. It covers a distance of \(1300 \mathrm{~km}\) in 1 day (24 hours). How long does the train stop at each junction, if it halts for the same period of time at all the junctions? (Bank P.O., 2006)
CorrectIncorrectHint
Time taken to cover \(1300 \mathrm{~km}=\left(\frac{1300}{65}\right) \mathrm{hrs}=20 \mathrm{hrs}\). Halt time \(=(24-20) \mathrm{hrs}=4 \mathrm{hrs}\).
Halting time at each junction \(=\left(\frac{4 \times 60}{8}\right) \mathrm{min}=30 \mathrm{~min}\). -
Question 39 of 50
39. Question
Jane travelled \(\frac{4}{7}\) as many miles on foot as by water and \(\frac{2}{5}\) as many miles on horseback as by water. If she covered a total of 3036 miles, how many miles did she travel on foot? (SNAP, 2005)
CorrectIncorrectHint
Suppose Jane travelled \(x\) miles by water, \(\left(\frac{4 x}{7}\right)\) miles on foot and \(\left(\frac{2 x}{5}\right)\) miles on horseback.
Then, \(x+\frac{4 x}{7}+\frac{2 x}{5}=3036 \Leftrightarrow \frac{69 x}{35}=3036\)
\(
\Leftrightarrow x=\left(\frac{3036 \times 35}{69}\right)=1540 .
\)
\(\therefore\) Distance travelled on foot \(=\left(\frac{4}{7} \times 1540\right)\) miles \(=880\) miles. -
Question 40 of 50
40. Question
A star is \(8.1 \times 10^{13} \mathrm{~km}\) away from the earth. Suppose light travels at the speed of \(3.0 \times 10^5 \mathrm{~km}\) per second. How long will it take the light from the star to reach the earth? (R.R.B., 2005)
CorrectIncorrectHint
\(
\begin{aligned}
\text { Required time } & =\left(\frac{8.1 \times 10^{13}}{3.0 \times 10^5}\right) \text { seconds }=2.7 \times 10^8 \mathrm{sec} \\
& =\left(\frac{2.7 \times 10^8}{60 \times 60}\right) \mathrm{hrs}=7.5 \times 10^4 \mathrm{hrs} .
\end{aligned}
\) -
Question 41 of 50
41. Question
Akash leaves home for school which is \(12 \mathrm{~km}\) from his house. After the school, he goes to his club which is \(7 \mathrm{~km}\) from his school. If his house, school and club all fall in a line, then what is the minimum distance he has to travel to get back home?
CorrectIncorrectHint
For the distance to be minimum, the club must lie between Akash’s home and school.
Hence, required distance \(=(12-7) \mathrm{km}=5 \mathrm{~km}\).
-
Question 42 of 50
42. Question
A train covers a distance of \(193 \frac{1}{3} \mathrm{~km}\) in \(4 \frac{1}{4}\) hours with one stoppage of 10 minutes, two of 5 minutes and one of 3 minutes on the way. The average speed of the train is
CorrectIncorrectHint
Actual time taken for the journey
\(
\begin{aligned}
& =4 \text { hrs } 15 \mathrm{~min}-(10+2 \times 5+3) \mathrm{min} \\
& =4 \mathrm{hrs} 15 \mathrm{~min}-23 \mathrm{~min}=3 \mathrm{hrs} 52 \mathrm{~min}=3 \frac{26}{30} \mathrm{hrs}=\frac{116}{30} \mathrm{hrs} . \\
& \therefore \text { Average speed }=\left(\frac{580}{3} \times \frac{30}{116}\right) \mathrm{km} / \mathrm{hr}=50 \mathrm{~km} / \mathrm{hr} .
\end{aligned}
\) -
Question 43 of 50
43. Question
Deepa rides her bike at an average speed of 30 \(\mathrm{km} / \mathrm{hr}\) and reaches her destination in 6 hours. Hema covers the same distance in 4 hours. If Deepa increases her average speed by \(10 \mathrm{~km}\) / \(\mathrm{hr}\) and Hema increases her average speed by \(5 \mathrm{~km} / \mathrm{hr}\), what would be the difference in their time taken to reach the destination?
CorrectIncorrectHint
Deepa’s original speed \(=30 \mathrm{~km} / \mathrm{hr}\).
Deepa’s new speed \(=(30+10) \mathrm{km} / \mathrm{hr}=40 \mathrm{~km} / \mathrm{hr}\).
Distance \(=(30 \times 6) \mathrm{km}=180 \mathrm{~km}\).
Hema’s original speed \(=\left(\frac{180}{4}\right) \mathrm{km} / \mathrm{hr}=45 \mathrm{~km} / \mathrm{hr}\).
Hema’s new speed \(=(45+5) \mathrm{km} / \mathrm{hr}=50 \mathrm{~km} / \mathrm{hr}\).
Difference in time
\(
=\left(\frac{180}{40}-\frac{180}{50}\right) \mathrm{hrs}=\frac{9}{10} \mathrm{hrs}=\left(\frac{9}{10} \times 60\right) \mathrm{min}=54 \mathrm{~min} .
\) -
Question 44 of 50
44. Question
A monkey climbing up a pole ascends 6 metres and slips 3 metres in alternate minutes. If the pole is 60 metres high, how long will it take the monkey to reach the top? (Campus Recruitment, 2010)
CorrectIncorrectHint
Net height ascended in \(2 \mathrm{~min}=(6-3) \mathrm{m}=3 \mathrm{~m}\).
Net height ascended in \(36 \mathrm{~min}=\left(\frac{3}{2} \times 36\right) \mathrm{m}=54 \mathrm{~m}\).
In the 37 th \(\mathrm{min}\), the monkey ascends \(6 \mathrm{~m}\) and reaches the top.
Hence, total time taken \(=37\) minutes. -
Question 45 of 50
45. Question
An aeroplane flies twice as fast as a train which covers 60 miles in 80 minutes. What distance will the aeroplane cover in 20 minutes? (E.S.I.C., 2006)
CorrectIncorrectHint
Time taken to cover 60 miles \(=80 \mathrm{~min}=\frac{4}{3} \mathrm{hrs}\).
\(\therefore\) Speed of the train \(=\left(60 \times \frac{3}{4}\right) \mathrm{mph}=45 \mathrm{mph}\).
Speed of the aeroplane \(=(2 \times 45) \mathrm{mph}=90 \mathrm{mph}\).
Distance covered by the aeroplane in \(60 \mathrm{~min}=90\) miles.
Distance covered by the aeroplane in \(20 \mathrm{~min}\)
\(
=\left(\frac{90}{60} \times 20\right) \text { miles }=30 \text { miles. }
\) -
Question 46 of 50
46. Question
A boy is running at a speed of \(p kmph\) to cover a distance of \(1 km\). But, due to the slippery ground, his speed is reduced by \(q kmph (p>q)\). If he takes \(r\) hours to cover the distance, then (M.B.A., 2006)
CorrectIncorrectHint
\(
\text { Speed }=\frac{\text { Distance }}{\text { Time }} \Rightarrow p-q=\frac{1}{r} \text {. }
\) -
Question 47 of 50
47. Question
Ravi can walk a certain distance in 40 days when he rests 9 hours a day. How long will he take to walk twice the distance, twice as fast and rest twice as long each day? (A.A.O. Exam, 2010)
CorrectIncorrectHint
100 daysLet the required number of days be \(x\).
More distance, More days required (Direct Proportion)
More speed, Less days required (Indirect Proportion)
More resting hours, More days required (Direct Proportion)
\(\left.\begin{array}{ll}\text { Distance } & 1: 2 \\ \text { Speed } & 2: 1 \\ \text { Resting hours } & 9: 18\end{array}\right\}:: 40: x\)
\(
\begin{aligned}
& \therefore \quad 1 \times 2 \times 9 \times x= \\
& 2 \times 1 \times 18 \times 40 \Leftrightarrow x=\frac{2 \times 18 \times 40}{2 \times 9}=80 .
\end{aligned}
\) -
Question 48 of 50
48. Question
A car is driven at the speed of \(100 \mathrm{~km} / \mathrm{hr}\) and stops for 10 minutes at the end of every \(150 \mathrm{~km}\). To cover a distance of \(1000 \mathrm{~km}\), it will take
CorrectIncorrectHint
Time taken to cover \(150 \mathrm{~km}=(1 \mathrm{hr} 30 \mathrm{~min}+10 \mathrm{~min})\)
\(
=1 \mathrm{hr} 40 \mathrm{~min}=1 \frac{2}{3} \mathrm{hr}=\frac{5}{3} \mathrm{hr} \text {. }
\)
Time taken to cover \((150 \times 6)\) i.e., \(900 \mathrm{~km}\)
\(
=\left(\frac{5}{3} \times 6\right) \text { hrs. }=10 \mathrm{hrs} \text {. }
\)
Remaining \(100 \mathrm{~km}\) is covered in 1 hour.
Total time taken \(=(10+1)\) hrs \(=11\) hrs. -
Question 49 of 50
49. Question
A man takes 50 minutes to cover a certain distance at a speed of \(6 \mathrm{~km} / \mathrm{hr}\). If he walks with a speed of \(10 \mathrm{~km} / \mathrm{hr}\), he covers the same distance in
CorrectIncorrectHint
\(
\begin{aligned}
& \text { Distance }=\text { Speed } \times \text { Time }=\left(6 \times \frac{50}{60}\right) \mathrm{km}=5 \mathrm{~km} . \\
& \therefore \text { Required time }=\frac{\text { Distance }}{\text { Speed }}=\left(\frac{5}{10}\right) \mathrm{hrs}=\frac{1}{2} \mathrm{hr}=30 \mathrm{~min} \text {. }
\end{aligned}
\) -
Question 50 of 50
50. Question
A truck covers a distance of 550 metres in 1 minute whereas a bus covers a distance of \(33 \mathrm{kms}\) in 45 minutes. The ratio of their speeds is
CorrectIncorrectHint
\(
\text { Ratio of speeds }=\left(\frac{550}{60} \times \frac{18}{5}\right):\left(\frac{33}{45} \times 60\right)=33: 44=3: 4 \text {. }
\)