Quiz
Quiz Summary
0 of 40 Questions completed
Questions:
Information
You have already completed the quiz before. Hence you can not start it again.
Quiz is loading…
You must sign in or sign up to start the quiz.
You must first complete the following:
Results
Results
0 of 40 Questions answered correctly
Your time:
Time has elapsed
You have reached 0 of 0 point(s), (0)
Earned Point(s): 0 of 0, (0)
0 Essay(s) Pending (Possible Point(s): 0)
Categories
- Not categorized 0%
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- Current
- Review
- Answered
- Correct
- Incorrect
-
Question 1 of 40
1. Question
A vector is not changed if
CorrectIncorrect -
Question 2 of 40
2. Question
Which of the sets given below may represent the magnitudes of three vectors adding to zero?
CorrectIncorrect -
Question 3 of 40
3. Question
The resultant of \(\vec{A}\) and \(\vec{B}\) makes an angle \(\alpha\) with \(\vec{A}\) and \(\beta\) with \(\vec{B}\),
CorrectIncorrect -
Question 4 of 40
4. Question
The component of a vector is
CorrectIncorrect -
Question 5 of 40
5. Question
A vector \(\vec{A}\) points vertically upward and \(\vec{B}\) points towards north. The vector product \(\vec{A} \times \vec{B}\) is
CorrectIncorrect -
Question 6 of 40
6. Question
The radius of a circle is stated as \(2.12 \mathrm{~cm}\). Its area should be written as
CorrectIncorrect -
Question 7 of 40
7. Question
A situation may be described by using different sets of coordinate axes having different orientations. Which of the following do not depend on the orientation of the axes?
CorrectIncorrect -
Question 8 of 40
8. Question
Let \(\vec{C}=\vec{A}+\vec{B}\)
CorrectIncorrect -
Question 9 of 40
9. Question
Let the angle between two nonzero vectors \(\vec{A}\) and \(\vec{B}\) be \(120^{\circ}\) and its resultant be \(\vec{C}\).
CorrectIncorrect -
Question 10 of 40
10. Question
The x-component of the resultant of several vectors
CorrectIncorrect -
Question 11 of 40
11. Question
The magnitude of the vector product of two vectors \(|\vec{A}|\) and \(|\vec{B}|\) may be
CorrectIncorrect -
Question 12 of 40
12. Question
\(
\text { Given } \vec{u}=8 \vec{i}-\vec{j}+3 \vec{k} \text { and } \vec{v}=7 \vec{j}-4 \vec{k} \text { compute the following. }
\)
\(12 \vec{u}+\vec{v}\)CorrectIncorrectHint
\(
12 \vec{u}+\vec{v}=12(8 \vec{i}-\vec{j}+3 \vec{k})+(7 \vec{j}-4 \vec{k})=(96 \vec{i}-12 \vec{j}+36 \vec{k})+(7 \vec{j}-4 \vec{k})=96 \vec{i}-5 \vec{j}+32 \vec{k}
\) -
Question 13 of 40
13. Question
\(
\text { Find a unit vector that points in the same direction as } \vec{q}=\vec{i}+3 \vec{j}+9 \vec{k} \text {. }
\)CorrectIncorrectHint
Of course, the first step here really should be to check and see if we are lucky enough to actually have a unit vector already. It’s unlikely we do have a unit vector but you never know until you check!
\(
\mid\vec{q}\mid=\sqrt{(1)^2+(3)^2+(9)^2}=\sqrt{91}
\)
Okay, as we pretty much had already guessed, this isn’t a unit vector (its magnitude isn’t one!) but we can use this to help find the answer.
Hide Step 27
Recall that all we need to do to turn any vector into a unit vector is divide the vector by its magnitude. Doing that for this vector gives,
\(
\vec{u}=\frac{\vec{q}}{\mid\vec{q}\mid}=\frac{1}{\sqrt{91}}(\vec{i}+3 \vec{j}+9 \vec{k})=\frac{1}{\sqrt{91}} \vec{i}+\frac{3}{\sqrt{91}} \vec{j}+\frac{9}{\sqrt{91}} \vec{k}
\)
As a quick check, not really required of course, we can compute a quick magnitude to verify that we do in fact have a unit vector.
\(
\mid\vec{u}\mid=\sqrt{\left(\frac{1}{\sqrt{91}}\right)^2+\left(\frac{3}{\sqrt{91}}\right)^2+\left(\frac{9}{\sqrt{91}}\right)^2}=\sqrt{\frac{91}{91}}=1
\)
So, we do have a unit vector -
Question 14 of 40
14. Question
\(
\text { Find a vector that points in the same direction as } \vec{c}=\langle-1,4\rangle \text { with a magnitude of } 10 \text {. }
\)CorrectIncorrectHint
First, let’s check to see what the magnitude of this vector is.
\(
\mid\vec{c}\mid=\sqrt{(-1)^2+(4)^2}=\sqrt{17}
\)
The unit vector is,
\(
\vec{u}=\frac{\vec{c}}{\mid\vec{c}\mid}=\frac{1}{\sqrt{17}}\langle-1,4\rangle=\left\langle-\frac{1}{\sqrt{17}}, \frac{4}{\sqrt{17}}\right\rangle
\)We know that scalar multiplication can change the magnitude of a vector. We’ve got a vector with magnitude of one that points in the correct direction. To convert this into a vector with magnitude of 10 all we need to do is multiply this new unit vector by 10 to get,
\(
\vec{v}=10 \vec{u}=10\left\langle-\frac{1}{\sqrt{17}}, \frac{4}{\sqrt{17}}\right\rangle=\left\langle-\frac{10}{\sqrt{17}}, \frac{40}{\sqrt{17}}\right\rangle
\)
Now, let’s verify that this does what we want it to do with a quick magnitude computation.
\(
\mid\vec{v}\mid=\sqrt{\left(-\frac{10}{\sqrt{17}}\right)^2+\left(\frac{40}{\sqrt{17}}\right)^2}=\sqrt{\frac{1700}{17}}=\sqrt{100}=10
\)
So, we do have a vector with magnitude 10 as predicted. -
Question 15 of 40
15. Question
\(
\text { Determine if } \vec{a}=\langle 3,-5,1\rangle \text { and } \vec{b}=\langle 6,-2,2\rangle \text { are parallel vectors. }
\)CorrectIncorrectHint
Recall that two vectors are parallel if they are scalar multiples of each other. In other words, these two vectors will be scalar multiples if we can find a number \(k\) such that,
\(
\vec{a}=k \vec{b}
\)Let’s just take a look at the first component from each vector. It is obvious that \(6=2(3)\). So, to convert the first components we’d need to multiply \(\vec{a}\) by 2 . However, if we did that we’d get,
\(
2 \vec{a}=\langle 6,-10,2\rangle \neq \vec{b}
\)
This is clearly not \(\vec{b}\). The first component is correct and the third component is correct but the second isn’t correct. Therefore, there is no single number, \(k\), that we can use to convert \(\vec{a}\) into \(\vec{b}\) through scalar multiplication.
This in turn means that \(\vec{a}\) and \(\vec{b}\) cannot possibly be parallel. -
Question 16 of 40
16. Question
\(
\text { Determine the dot product, } \vec{a} \cdot \vec{b} \text { if } \vec{a}=\langle 0,4,-2\rangle \text { and } \vec{b}=2 \vec{i}-\vec{j}+7 \vec{k}
\)CorrectIncorrectHint
\(
\vec{a} \cdot \vec{b}=(0)(2)+(4)(-1)+(-2)(7)=-18
\) -
Question 17 of 40
17. Question
\(
\text { Determine the dot product, } \vec{a} \cdot \vec{b} \text { if }\mid\vec{a}\mid=5,\mid\vec{b}\mid=\frac{3}{7} \text { and the angle between the two vectors is } \theta=\frac{\pi}{12} \text {. }
\)CorrectIncorrectHint
\(
\vec{a} \cdot \vec{b}=(5)\left(\frac{3}{7}\right) \cos \left(\frac{\pi}{12}\right)=2.0698
\) -
Question 18 of 40
18. Question
\(
\text { Determine the angle between } \vec{v}=\langle 1,2,3,4\rangle \text { and } \vec{w}=\langle 0,-1,4,-2\rangle
\)CorrectIncorrectHint
All we really need to do is rewrite the formula from the geometric interpretation of the dot product as,
\(
\cos \theta=\frac{\vec{v} \cdot \vec{w}}{\mid\vec{v}\mid\mid\vec{w}\mid}
\)
This will allow us to quickly determine the angle between the two vectors.
We’ll first need the following quantities (we’ll leave it to you to verify the arithmetic involved in these computations….).
\(
\vec{v} \cdot \vec{w}=2 \quad\mid\vec{v}\mid=\sqrt{30} \quad\mid\vec{w}\mid=\sqrt{21}
\)
The angle between the vectors is then,
\(
\cos \theta=\frac{2}{\sqrt{30} \sqrt{21}}=0.07968 \quad \Rightarrow \quad \theta=\cos ^{-1}(0.07968)=1.49103 \text { radians }
\) -
Question 19 of 40
19. Question
\(
\text { Determine if } \vec{q}=\langle 4,-2,7\rangle \text { and } \vec{p}=-3 \vec{i}+\vec{j}+2 \vec{k} \text { are parallel, orthogonal or neither. }
\)CorrectIncorrectHint
Based on a quick inspection of the components we can see that the first and second components of the two vectors have opposite signs and the third doesn’t. This means there is no possible way for these two vectors to be scalar multiples since there is no number that will change the sign on the first two components and leave the sign of the third component unchanged.
Therefore, we can quickly see that the two vectors are not parallel.
Let’s do a quick dot product on the two vectors next.
\(
\vec{q} \cdot \vec{p}=0
\)
Okay, the dot product is zero and we know from the notes that this in turn means that the two vectors must be orthogonal.
On a side note an alternate method for working this problem is to find the angle between the two vectors and using that to determine the answer.
Depending on which method you find easiest either will get you the correct answer. -
Question 20 of 40
20. Question
\(
\text { Determine if } \vec{a}=\langle 3,10\rangle \text { and } \vec{b}=\langle 4,-1\rangle \text { are parallel, orthogonal or neither. }
\)CorrectIncorrectHint
Based on a quick inspection of the components we can see that the first components of the vectors have the same sign and the second have opposite signs. This means there is no possible way for these two vectors to be scalar multiples since there is no number that will change the sign on the second components and leave the sign of the first component unchanged.
Therefore, we can quickly see that the two vectors are not parallel.Let’s do a quick dot product on the two vectors next.
\(
\vec{a} \cdot \vec{b}=2
\)
Okay, the dot product is not zero and we know from the notes that this in turn means that the two vectors are not orthogonal.
The answer to the problem is therefore the two vectors are neither parallel or orthogonal. -
Question 21 of 40
21. Question
\(
\text { Determine if } \vec{w}=\vec{i}+4 \vec{j}-2 \vec{k} \text { and } \vec{v}=-3 \vec{i}-12 \vec{j}+6 \vec{k} \text { are parallel, orthogonal or neither. }
\)CorrectIncorrectHint
Based on a quick inspection is seems (hopefully) fairly clear that we have,
\(
\vec{v}=-3 \vec{w}
\)
Therefore, the two vectors are parallel. -
Question 22 of 40
22. Question
\(
\text { Given } \vec{a}=\langle-8,2\rangle \text { and } \vec{b}=\langle-1,-7\rangle \text { compute } \operatorname{proj}_\vec{a} \vec{b} \text {. }
\)CorrectIncorrectHint
All we really need to do here is use the formula from the notes. That will need the following quantities.
\(
\vec{a} \cdot \vec{b}=-6 \quad\mid\vec{a}\mid^2=68
\)
The projection is then,
\(
\operatorname{proj}_\vec{a} \vec{b}=\frac{-6}{68}\langle-8,2\rangle=\left\langle\frac{12}{17},-\frac{3}{17}\right\rangle
\) -
Question 23 of 40
23. Question
\(
\text { Given } \vec{u}=7 \vec{i}-\vec{j}+\vec{k} \text { and } \vec{w}=-2 \vec{i}+5 \vec{j}-6 \vec{k} \text { compute } \operatorname{proj}_\vec{w} \vec{u} \text {. }
\)CorrectIncorrectHint
All we really need to do here is use the formula from the notes. That will need the following quantities.
\(
\vec{u} \cdot \vec{w}=-25 \quad\mid\vec{w}\mid^2=65
\)
The projection is then,
\(
\operatorname{proj}_{\vec{w}} \vec{u}=\frac{-25}{65}(-2 \vec{i}+5 \vec{j}-6 \vec{k})=\frac{10}{13} \vec{i}-\frac{25}{13} \vec{j}+\frac{30}{13} \vec{k}
\) -
Question 24 of 40
24. Question
\(
\text { Determine the direction cosines and direction angles for } \vec{r}=\left\langle-3,-\frac{1}{4}, 1\right\rangle \text {. }
\)CorrectIncorrectHint
All we really need to do here is use the formulas from the notes. That will need the following quantity.
\(
\mid\vec{r}\mid=\sqrt{\frac{161}{16}}=\frac{\sqrt{161}}{4}
\)
The direction cosines and angles are then,
\(
\begin{aligned}
& \cos \alpha=\frac{-3}{\sqrt{161} / 4}=-\frac{12}{\sqrt{161}} \quad \Rightarrow \quad \alpha=\cos ^{-1}\left(-\frac{12}{\sqrt{161}}\right)=2.8106 \text { radians } \\
& \cos \beta=\frac{-1 / 4}{\sqrt{161} / 4}=-\frac{1}{\sqrt{161}} \quad \Rightarrow \quad \beta=\cos ^{-1}\left(-\frac{1}{\sqrt{161}}\right)=1.6497 \text { radians } \\
& \cos \gamma=\frac{1}{\sqrt{161} / 4}=\frac{4}{\sqrt{161}} \quad \Rightarrow \quad \gamma=\cos ^{-1}\left(\frac{4}{\sqrt{161}}\right)=1.2501 \text { radians } \\
&
\end{aligned}
\) -
Question 25 of 40
25. Question
\(
\text { If } \vec{w}=\langle 3,-1,5\rangle \text { and } \vec{v}=\langle 0,4,-2\rangle \text { compute } \vec{v} \times \vec{w}
\)CorrectIncorrectHint
\(
\vec{w} \times \vec{v}=\left|\begin{array}{ccc}
\vec{i} & \vec{j} & \vec{k} \\
0 & 4 & -2 \\
3 & -1 & 5
\end{array}\right| \quad \begin{array}{cc}
\vec{i} & \vec{j} \\
0 & 4 \\
3 & -1
\end{array}
\)\(
=20 \vec{i}-6 \vec{j}+0 \vec{k}-0 \vec{j}-2 \vec{i}-12 \vec{k}=18 \vec{i}-6 \vec{j}-12 \vec{k}
\) -
Question 26 of 40
26. Question
\(
\text { Find a vector that is orthogonal to the plane containing the points } P=(3,0,1), Q=(4,-2,1) \text { and } R=(5,3,-1) \text {. }
\)CorrectIncorrectHint
We first need two vectors that are both parallel to the plane. Using the points that we are given (all in the plane) we can quickly get quite a few vectors that are parallel to the plane. We’ll use the following two vectors.
\(
\overrightarrow{P Q}=\langle 1,-2,0\rangle \quad \overrightarrow{P R}=\langle 2,3,-2\rangle
\)Now we know that the cross product of any two vectors will be orthogonal to the two original vectors. Since the two vectors from Step 1 are parallel to the plane (they actually lie in the plane in this case!) we know that the cross product must then also be orthogonal, or normal, to the plane.
So, using the “trick” we used in the notes the cross product is,\(
\overrightarrow{P Q} \times \overrightarrow{P R}=\left|\begin{array}{ccc}
\vec{i} & \vec{j} & \vec{k} \\
1 & -2 & 0 \\
2 & 3 & -2
\end{array}\right| \quad \begin{array}{cc}
\vec{i} & \vec{j} \\
1 & -2 \\
2 & 3
\end{array}
\)\(
=4 \vec{i}+0 \vec{j}+3 \vec{k}-(-2 \vec{j})-0 \vec{i}-(-4 \vec{k})=4 \vec{i}+2 \vec{j}+7 \vec{k}
\) -
Question 27 of 40
27. Question
\(
\text { Are the vectors } \vec{u}=\langle 1,2,-4\rangle, \vec{v}=\langle-5,3,-7\rangle \text { and } \vec{w}=\langle-1,4,2\rangle \text { are in the same plane? }
\)CorrectIncorrectHint
\(
\begin{aligned}
\vec{u} \cdot(\vec{v} \times \vec{w}) & =\left|\begin{array}{ccc}
1 & 2 & -4 \\
-5 & 3 & -7 \\
-1 & 4 & 2
\end{array}\right| \begin{array}{cl}
1 & 2 \\
-5 & 3 \\
-1 & 4
\end{array} \\
& =6+14+80-(-20)-(-28)-12=136
\end{aligned}
\)
Okay, since this is not zero we know that they are not in the same plane. -
Question 28 of 40
28. Question
Find the angle and the magnitude of a resultant vector.
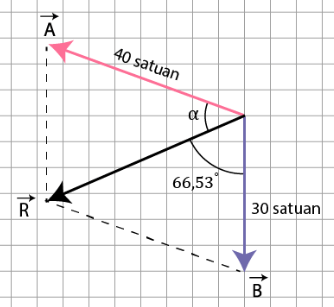 CorrectIncorrect
CorrectIncorrectHint
Take a deep look to the picture, we have to find \(\alpha\) first. The method is below.
\(
\begin{aligned}
\frac{A}{\sin \beta} & =\frac{B}{\sin \alpha} \\
\frac{40}{\sin 66.53^{\circ}} & =\frac{30}{\sin \alpha} \\
\sin \alpha & =0.687 \\
\alpha & =\sin ^{-1} 0.687 \\
& \approx 43.47^{\circ}
\end{aligned}
\)
Once we know \(\alpha\), we can calculate \(\theta\).
\(
\begin{aligned}
\theta & =\alpha+\beta \\
& =43.47^{\circ}+66.53^{\circ} \\
& =110^{\circ}
\end{aligned}
\)
Since we already know \(\theta\) we can finally calculate the magnitude of \(\vec{R}\).
\(
\begin{aligned}
R & =\sqrt{A^2+B^2+2 A B \cos \theta} \\
& =\sqrt{40^2+30^2+2(40)(30) \cos 110^{\circ}} \\
& \approx 40.98 \text { units }
\end{aligned}
\)
Based on the above calculation, we get \(\alpha=43.47^{\circ}\) and \(|R|=40.98\) units(satuan) -
Question 29 of 40
29. Question
Given
\(\vec{A}=4 \hat{i}+5 \hat{j}\)
\(\vec{B}=9 \hat{i}-7 \hat{j}\)
\(\vec{C}=-3 \hat{i}+2 \hat{j}\)
Find the resultant of \(\vec{A}-\vec{B}+\vec{C}\). Determine the resultant magnitude.CorrectIncorrectHint
First, we operate using \(\hat{i}\) and \(\hat{j}\) notation.
\(
\begin{aligned}
\vec{R} & =\vec{A}-\vec{B}+\vec{C} \\
& =(4 \hat{i}+5 \hat{j})-(9 \hat{i}-7 \hat{j})+(-3 \hat{i}+2 \hat{j}) \\
& =(4-9-3) \hat{i}+(5+7+2) \hat{j} \\
& =-8 \hat{i}+14 \hat{j}
\end{aligned}
\)
Then we can calculate the resultant magnitude as follows.
\(
\begin{aligned}
R & =\sqrt{-8^2+14^2} \\
& =16.12 \text { units }
\end{aligned}
\)
Based on our calculation, the resultant length of the \(\vec{A}-\vec{B}+\vec{C}\) is \(16.12\) units. -
Question 30 of 40
30. Question
Calculate the resultant of 3 vectors which 2 of them are symmetric.
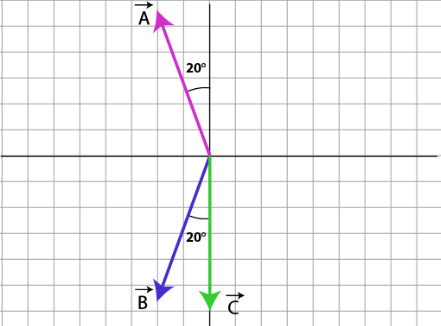 CorrectIncorrect
CorrectIncorrectHint
Take a more deep look at \(\vec{A}\) and \(\vec{B}\). The y-components of the two vectors have the same magnitude but opposite directions, so they cancel each other out. So the resultant of \(\vec{A}+\vec{B}\) is simply an addition of the x-component of the two vectors and points to the left.
\(|A+B|\) is the resultant magnitude of the \(\vec{A}+\vec{B}\) which we can calculate as follows.
\(
\begin{aligned}
|A+B| & =A_x+B_x \\
& =A \sin 20+B \sin 20 \\
& =30 \sin 20+30 \sin 20 \\
& \approx 20.521 \text { units }
\end{aligned}
\)
Next, we can calculate the magnitude of the resultant vector.
\(
\begin{aligned}
R & =\sqrt{|A+B|^2+C^2} \\
& =\sqrt{20.521^2+30^2} \\
& =36.35 \text { units }
\end{aligned}
\)
Based on the calculation we have done, the resultant magnitude of the addition of the three vectors is \(\mathbf{3 6 . 3 5}\) units. -
Question 31 of 40
31. Question
An object experiences 2 forces as shown above. Determine the direction \((\theta)\) and the magnitude of the object’s acceleration.
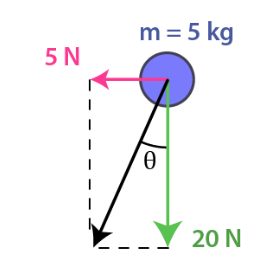 CorrectIncorrect
CorrectIncorrectHint
We can calculate the resultant force first.
\(
\begin{aligned}
& F_R=\sqrt{{F_1}^2+{F_2}^2} \\
& =\sqrt{20^2+5^2} \\
& =\sqrt{425} \\
& =5 \sqrt{17} \mathrm{~N} \\
&
\end{aligned}
\)
Then using Newton’s law formula \(F_R=m a\) we can find the acceleration of the object.
\(
\begin{aligned}
a & =\frac{F}{m} \\
& =\frac{5 \sqrt{17}}{5} \\
& =\sqrt{17} \mathrm{~m} / \mathrm{s}^2
\end{aligned}
\)
The direction of the object’s acceleration is the same as the direction of the resultant force and can be calculated as follows.
\(
\begin{aligned}
\theta & =\tan ^{-1} \frac{\text { opposite }}{\text { adjacent }} \\
& =\tan ^{-1} \frac{5}{20} \\
& \approx 14^{\circ}
\end{aligned}
\)
So the object’s acceleration is \(\sqrt{17} \mathrm{~m} / \mathrm{s}^2\) with direction about \(-14^{\circ}\) from the negative \(y\)-axis. -
Question 32 of 40
32. Question
An object is under the influence of many forces as shown above. If the object remains at rest, determine the magnitude of \(F_2\) and \(\mathrm{N}\) (normal force).
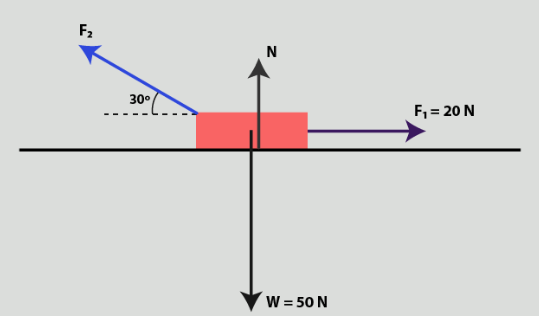 CorrectIncorrect
CorrectIncorrectHint
An object is said to be at rest if it satisfies two conditions.
The first condition is that the force to the right is equal to the force to the left. Look at the second slide of the image above. In this case, the force to the right is \(F_1[latex] while the force to the left is [latex]F_{2 x}[latex]. So to fulfill the first condition we must write as follows.
[latex]
F_{2 x}=F_1=20 \text { Newton }
\)
Since we already know \(F_{2 x}\), we can find \(F_2\). The method is below.
\(
\begin{aligned}
F_{2 x} & =F_2 \cos 30^{\circ} \\
F_2 & =\frac{F_{2 x}}{\cos 30^{\circ}} \\
& =\frac{20}{\cos 30^{\circ}} \\
& =\frac{40}{3} \sqrt{3} \text { Newton }
\end{aligned}
\)
The second condition is the upward force must be equal to the downward force. Slide the image above and see. In this case, there are 2 upward forces, namely \(F_{2 y}\) and N(normal force). While there is one downward force, namely \(w\) (weight). To fulfill the condition that the upward force equals the downward force, we must write the following mathematical equation.
\(
N+F_{2 y}=W
\)
We can operate equation above further
\(
\begin{aligned}
N+F_{2 y} & =W \\
N+F_2 \sin 30 & =50 \\
N+\frac{40}{3} \sqrt{3} \times \frac{1}{2} & =50 \\
N & =50-\frac{40}{6} \sqrt{3} \\
& =38.45 \text { Newton }
\end{aligned}
\)
So \(F_2=\frac{40}{3} \sqrt{3}\) Newtons and \(N=38.45\) Newton. -
Question 33 of 40
33. Question
Sabrina walked 75 meters to the east. Then she turned 30 degrees to the left and walked 25 meters. Determine the magnitude of Sabrina’s displacement vector.
CorrectIncorrectHint
Slide the image above to see the resultant vector. The resultant vector magnitude calculation is as follows.
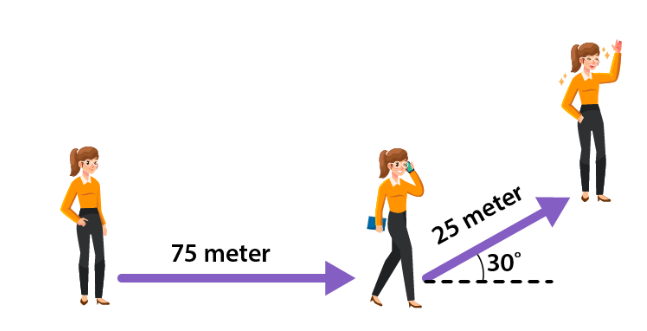
\(
\begin{aligned}
R & =\sqrt{A^2+B^2+2 A B \cos \theta} \\
& =\sqrt{75^2+25^2+2(75)(25) \cos 30^{\circ}} \\
& =97.46 \text { meter }
\end{aligned}
\) -
Question 34 of 40
34. Question
Look at the image above. \(\vec{A}\) has magnitude of 45 units. At the same time, \(\vec{B}\) is 30 units in magnitude. Determine the magnitude of \(\vec{A}-\vec{B}\).
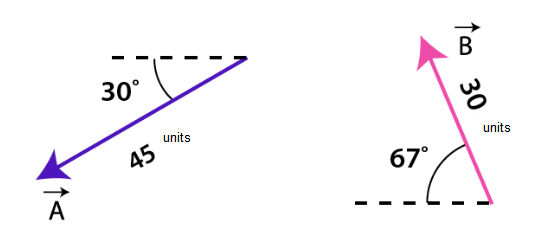 CorrectIncorrect
CorrectIncorrectHint
First we have to realize that the angle between \(\vec{A}\) and \(\vec{B}\) is \(\theta=30^{\circ}+\) \(67^{\circ}=97^{\circ}\). Then we can calculate the magnitude.
\(
\begin{aligned}
R & =\sqrt{A^2+B^2-2 A B \cos \theta} \\
& =\sqrt{45^2+30^2-2(45)(30) \cos 97^{\circ}} \\
& \approx 57 \text { unit }
\end{aligned}
\)
So, the magnitude of \(\vec{A}-\vec{B}\) is about 57 units. -
Question 35 of 40
35. Question
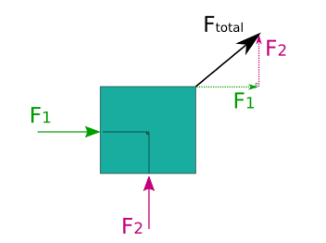
Two friends are pushing a box. The two forces they apply are perpendicular to each other. One of the friends is applying a force of 3 Newtons \(\left(F_1\right)\) in the eastern direction, while the other is applying a force of 4 Newtons \(\left(F_2\right)\) in the northern direction. Determine the resultant vector for the total force that is being applied to the box.
CorrectIncorrectHint
Two forces, \(F_1\) and \(F_2\), are perpendicular to each other, which means that the magnitude of \(F_{\text {total }}\) is equal to the hypotenuse of the triangle formed by these vectors.
\(
\begin{aligned}
& F_{\text {total }}=\sqrt{F_1{ }^2+F_2{ }^2} \\
& F_{\text {total }}=\sqrt{3^2+4^2}=5 \text { Newtons }
\end{aligned}
\)
-
Question 36 of 40
36. Question
A ball is thrown with an initial velocity of 70 feet per second., at an angle of \(35^{\circ}\) with the horizontal. Find the vertical and horizontal components of the velocity.
CorrectIncorrectHint
Let \(v\) represent the velocity and use the given information to write \(\mathrm{v}\) in unit vector form:
\(
\mathrm{v}=70\left(\cos \left(35^{\circ}\right)\right) i+70\left(\sin \left(35^{\circ}\right)\right) j
\)
Simplify the scalars, we get:
\(
\mathrm{v} \approx 57.34 i+40.15 j
\)
Since the scalars are the horizontal and vertical components of \(v\),
Therefore, the horizontal component is \(57.34\) feet per second and the vertical component is \(40.15\) feet per second. -
Question 37 of 40
37. Question
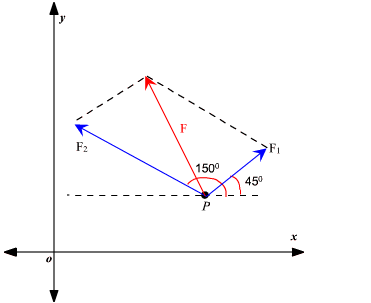
Two forces \(\mathrm{F}_1\) and \(\mathrm{F}_2\) with magnitudes 20 and \(30 \mathrm{lb}\), respectively, act on an object at a point \(\mathrm{P}\) as shown. Find the resultant forces acting at \(\mathrm{P}\)
 CorrectIncorrect
CorrectIncorrectHint
First we write \(\mathrm{F}_1\) and \(\mathrm{F}_2\) in component form:
\(
\mathrm{v} \approx 57.34 i+40.15 j
\)
Simplify the scalars, we get:
\(
\begin{aligned}
& \mathrm{F}_1=\left(20 \cos \left(45^{\circ}\right)\right) i+\left(20 \sin \left(45^{\circ}\right)\right) j \\
& =20\left(\frac{\sqrt{2}}{2}\right) i+20\left(\frac{\sqrt{2}}{2}\right) j \\
& =10 \sqrt{2} i+10 \sqrt{2} j \\
& \mathrm{~F}_2=\left(30 \cos \left(150^{\circ}\right)\right) i+\left(30 \sin \left(150^{\circ}\right)\right) j \\
& =30\left(-\frac{\sqrt{3}}{2}\right) i+30\left(\frac{1}{2}\right) j \\
& =-15 \sqrt{3} i+15 j
\end{aligned}
\)
So, the resultant force \(\mathrm{F}\) is
\(
\begin{aligned}
& \mathrm{F}=\mathrm{F}_1+\mathrm{F}_2 \\
& =(10 \sqrt{2} i+10 \sqrt{2} j)+(-15 \sqrt{3} i+15 j) \\
& =(10 \sqrt{2}-15 \sqrt{3}) i+(10 \sqrt{2}+15) j \\
& \approx-12 i+29 j
\end{aligned}
\) -
Question 38 of 40
38. Question
\(
\text { A force is given by the vector } \mathrm{F}=\langle 2,3\rangle \text { and moves an object from the point }(1,3) \text { to the point }(5,9) \text {. Find the work done. }
\)CorrectIncorrectHint
First we find the Displacement.
The displacement vector is
\(
\mathrm{D}=\langle 5-1,9-3\rangle=\langle 4,6\rangle
\)
By using the formula, the work done is
\(
\mathrm{W}=\mathrm{F} \cdot \mathrm{D}=\langle 2,3\rangle \cdot\langle 4,6\rangle=26
\)
If the unit of force is pounds and the distance is measured in feet, then the work done is \(26 \mathrm{ft}-\mathrm{lb}\). -
Question 39 of 40
39. Question
A person walks \(57.0 \mathrm{~m}\) at \(47.0^{\circ}\) north of east, turns and walks \(72.0 \mathrm{~m}\) at \(15.0^{\circ}\) south of east, and then turns and walks \(24.0 \mathrm{~m} 30.0^{\circ}\) west of north. How far and at what angle is the person’s final position from his/her initial position?
CorrectIncorrectHint
For vector problems, we first draw a neat sketch of the vectors and the vector operation of interest. Here we are adding three vectors.
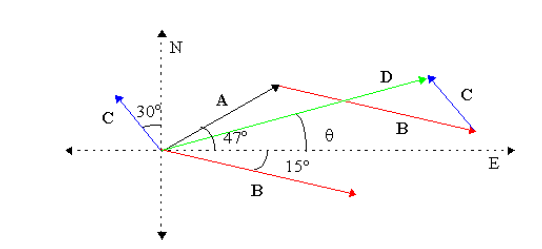
Then to solve the problem numerically, we break the vectors into their components.
\(
\mathbf{A}=i\left[57 \cos \left(47^{\circ}\right)\right]+j\left[57 \sin \left(47^{\circ}\right)\right]=i[38.8739]+j[41.6872]
\)
\(
\begin{aligned}
& \mathrm{B}=i\left[72 \cos \left(15^{\circ}\right)\right]+j\left[-72 \sin \left(15^{\circ}\right)\right]=i[69.5467]+j[-18.6350] \\
& \mathrm{C}=i\left[-24 \sin \left(30^{\circ}\right)\right]+j\left[24 \cos \left(30^{\circ}\right)\right]=i[-12]+j[20.7846]
\end{aligned}
\)
Next we add them to get the components of vector \(\mathbf{D}\).
\(
\mathrm{D}=i[38.8739+69.5467+-12]+j[41.6872+-18.6350+20.7846]=i[96.4206]+j[43.8368]
\)
Then we convert to polar coordinate form. Using Pythagoras’ Theorem, \(D=\left[(96.4206)^2+(43.8368)^2\right]^{1 / 2}=105.92 \mathrm{~m}\) The angle \(\theta=\) \(\arctan \left(\mid \mathrm{D}_{\mathrm{y}} / \mathrm{D}_{\mathrm{x}}\mid\right)=\arctan (43.8368 / 96.4206)=24.45^{\circ}\). Thus the person’s displacement is \(106 \mathrm{~m}\) at \(24.4^{\circ}\) north of east. -
Question 40 of 40
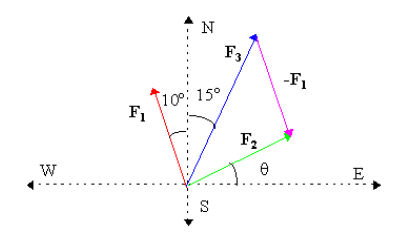
40. Question
Forces are vector quantities. Two forces \(\mathbf{F}_1\) and \(\mathbf{F}_2\) act on a body such the total force \(\mathbf{F}_3\) has a magnitude of \(150 \mathrm{~N}\) at \(15.0^{\circ}\) east of north. If \(F_1\) has magnitude \(100 \mathrm{~N}\) at \(10.0^{\circ}\) west of north, what is the magnitude and direction of \(F_2\)?
CorrectIncorrectHint
We are looking for \(\mathbf{F}_2=\mathbf{F}_3-\mathbf{F}_1\), a vector subtraction. For vector problems, we first draw a neat sketch of the vectors and the vector operation of interest.
Then to solve the problem numerically, we break the vectors into their components:
\(
\begin{aligned}
& \mathbf{F}_1=i\left[150 \sin \left(15^{\circ}\right)\right]+j\left[150 \cos \left(15^{\circ}\right)\right]=i[38.823]+j[144.889] \\
& \mathbf{F}_3=i\left[-100 \sin \left(10^{\circ}\right)\right]+j\left[100 \cos \left(10^{\circ}\right)\right]=i[-17.365]+j[98.481]
\end{aligned}
\)
We subtract the components to get the components of vector \(\mathbf{F}_2\).
\(
\mathbf{F}_2=i[38.823-(-17.365)]+j[144.889-98.481]=i[56.188]+j[46.408]
\)
Then we convert to polar coordinate form Using Pythagoras’ Theorem, \(F_2=\left[(56.188)^2+(46.408)^2\right]^{1 / 2}=72.875 \mathrm{~N}\). The angle \(\theta=\) \(\arctan \left(\mid \mathrm{F}_{2 \mathrm{y}} / \mathrm{F}_{2 \mathrm{x}}\mid\right)=\arctan (46.408 / 56.188)=39.55^{\circ}\). Thus the other force is \(72.9 \mathrm{~N}\) at \(39.6^{\circ}\) north of east.