Quiz
Quiz Summary
0 of 70 Questions completed
Questions:
Information
You have already completed the quiz before. Hence you can not start it again.
Quiz is loading…
You must sign in or sign up to start the quiz.
You must first complete the following:
Results
Results
0 of 70 Questions answered correctly
Your time:
Time has elapsed
You have reached 0 of 0 point(s), (0)
Earned Point(s): 0 of 0, (0)
0 Essay(s) Pending (Possible Point(s): 0)
Categories
- Not categorized 0%
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- Current
- Review
- Answered
- Correct
- Incorrect
-
Question 1 of 70
1. Question
What is the value of 7!?
CorrectIncorrectHint
\(
\text { The value of } 7 \text { ! is } 5040 \text {, i.e. } 7 \text { ! }=7 \times 6 \times 5 \times 4 \times 3 \times 2 \times 1=5040 \text {. }
\) -
Question 2 of 70
2. Question
How many positions are there to store three books on the shelf?
CorrectIncorrectHint
\(
3 ! =3 \cdot 2 \cdot 1=6
\) -
Question 3 of 70
3. Question
In how many ways can 10 shuttle vans line up at the airport?
CorrectIncorrectHint
\(
10 !=3628800
\) -
Question 4 of 70
4. Question
In how many different ways can the letters of the word DISPLAY be arranged?
CorrectIncorrectHint
The given word contains 7 letters, all different. \(\therefore\) Required number of ways \(=7 !\)
\(
=(7 \times 6 \times 5 \times 4 \times 3 \times 2 \times 1)=5040 \text {. }
\) -
Question 5 of 70
5. Question
In how many different ways can the letters of the word RIDDLED be arranged?
CorrectIncorrectHint
The given word contains 7 letters of which \(D\) is taken 3 times. \(\therefore\) Required number of ways \(=\frac{7 !}{3 !}=\frac{7 \times 6 \times 5 \times 4 \times {3 !}}{3 !}\) \(\quad=(7 \times 6 \times 5 \times 4)=840\).
-
Question 6 of 70
6. Question
In how many different ways can the letters of the word CREATE be arranged?
CorrectIncorrectHint
The given word contains 6 letters of which E is taken 2 times.
\(
\frac{6 !}{{2 !}}=\frac{6 \times 5 \times 4 \times 3 \times {2 !}}{2 !}=360 .
\) -
Question 7 of 70
7. Question
In how many different ways can the letters of the word JUDGE be arranged in such a way that the vowels always come together?
CorrectIncorrectHint
The given word contains 5 different letters.
Keeping the vowels UE together, we suppose them as 1 letter.
Then, we have to arrange the letters JDG(UE).
Now, 4 letters can be arranged in \({4 !}=24\) ways.
The vowels (UE) can be arranged among themselves in 2 ways.
\(\therefore\) Required number of ways \(=(24 \times 2)=48\). -
Question 8 of 70
8. Question
In how many different ways can the letters of the word AUCTION be arranged in such a way that the vowels always come together?
CorrectIncorrectHint
The given word contains 7 different letters. Keeping the vowels (AUIO) together, we take them as 1 letter.
Then, we have to arrange the letters CTN(AUIO).
\(\text { Now, } 4 \text { letters can be arranged in } {4 !}=24 \text { ways. }\)
The vowels (AUIO) can be arranged among themselves in 4 ! = 24 ways.
∴ Required number of ways = (24 × 24) = 576. -
Question 9 of 70
9. Question
In how many different ways can the letters of the word EXTRA be arranged so that the vowels are never together?
CorrectIncorrectHint
Taking the vowels (EA) as one letter, the given word has the letters XTR (EA), i.e., 4 letters.
These letters can be arranged in \({4 !}=24\) ways.
The letters \(E A\) may be arranged amongst themselves in 2 ways.
The number of arrangements having vowels together \(=(24 \times 2)=48\) ways.
Total arrangements of all letters \(={5 !}=(5 \times 4 \times 3 \times 2 \times 1)=120\).
Number of arrangements not having vowels together \(=(120-48)=72\) -
Question 10 of 70
10. Question
In an examination, there are three multiple-choice questions and each question has 4 choices. The number of ways in which a student can fail to get all answers correct is
CorrectIncorrectHint
Number of ways of attempting 1st, 2nd, \(3^{\text {rd }}\) questions are each. Total number of ways \(=4^3=4 \times 4 \times 4=64\)
Number of ways, getting all correct answers \(=1^3=1\)
\(\therefore\) Number of ways of not getting all answers correct
\(=64-1=63\) -
Question 11 of 70
11. Question
There are six teachers. Out of them two are primary teachers and two are secondary teachers. They are to stand in a row, so as the primary teachers, middle teachers and secondary teachers are always in a set. The number of ways in which they can do so, is
CorrectIncorrectHint
There are 2 primary teachers.
They can stand in a row in = 2! = 2 × 1 ways = 2 ways
Two middle teachers.
They can stand in a row in = 2! = 2 × 1 = 2 ways
There are two secondary teachers.
They can stand in a row in = 2! = 2 × 1 = 2 ways
These three sets can be arranged in 3! ways = 3 × 2 × 1 = 6 ways
Hence, the required number of ways = 2 × 2 × 2 × 6 = 48 ways -
Question 12 of 70
12. Question
In how many ways is it possible for 15 students to arrange themselves among 15 seats in the front row of an auditorium?
CorrectIncorrectHint
Number of persons available to sit in the first chair = 15
Number of persons available to sit in the second chair = 14
It keeps going in this way,
So, the total number of ways to sit 15 students = 15!
-
Question 13 of 70
13. Question
There are 8 greyhounds in a race. How many different orders of finish (first place through the eighth place) are possible?
CorrectIncorrectHint
Number of greyhounds will take the 1st position = 8
The number of greyhounds will take the 2nd position = 7
Continuing in this way, we get
8 ! = 8 x 7 x 6 x 5 x 4 x 3 x 2 x 1
= 40320 -
Question 14 of 70
14. Question
There are ten candidates for a job. The search committee will choose four of them, and rank the chosen four from strongest to weakest. How many different outcomes are possible?
CorrectIncorrectHint
Total number of candidates = 10
To choose the first strongest candidate, there are 10 options. To choose the second strongest candidate, there are 9 options available. To choose the third strongest candidate, there are 8 options available. To choose the fourth strongest candidate, there are 7 options available, So, we get
= 10 x 9 x 8 x 7
= 5040
So, the total number of ways to select 4 candidates, we have 5040 ways. -
Question 15 of 70
15. Question
There are 8 horses in a race. If all we are concerned with are the first, second, and third place finishers (the trifecta), how many different orders of finish are possible?
CorrectIncorrectHint
Total number of horses = 8
Number of persons who are having the chance to reach the first position = 8
Number of persons who are having the chance to reach the second position = 7
Number of persons who are having the chance to reach the third position = 6
= 8 x 7 x 6
= 336
So, the total number of ways is 336. -
Question 16 of 70
16. Question
Suppose we are going to use the symbols {a, b, c, d, e, f, g, h} to form a 5-character “password” having no repeated characters. How many different passwords are possible?
CorrectIncorrectHint
Given set = {a, b, c, d, e, f, g, h}
Total number of distinct characters = 8
The number of options to fix the 1st letter of the password = 8
The number of options to fix the 2nd letter of the password = 7
The number of options to fix the 3rd letter of the password = 6
The number of options to fix the 4th letter of the password = 5
The number of options to fix the 3rd letter of the password = 4
= 8 x 7 x 6 x 5 x 4
= 6720
So, the total number of ways = 6720. -
Question 17 of 70
17. Question
There are six greyhounds in a race:
Spot, Fido, Bowser, Mack, Tuffy, William.
We are concerned about who finishes first, second and third. How many different \(1^{\text {st }}, 2^{\text {nd }}, 3^{\text {rd }}\) orders of finish are possible?CorrectIncorrectHint
Number of greyhounds = 6
Number of greyhounds to fill the 1st position = 6
Number of greyhounds to fill the 2nd position = 5
Number of greyhounds to fill the 3rd position = 4
= 6 x 5 x 4
= 120 -
Question 18 of 70
18. Question
Homer, Gomer, Plato, Euclid, Socrates, Aristotle, Homerina, and Gomerina form the board of directors of the Lawyer and Poodle Admirers Club. They will choose from amongst themselves a Chairperson, Secretary, and Treasurer.
No person will hold more than one position. How many different outcomes are possible?
CorrectIncorrectHint
Number of persons = 8
Number of persons who occupies the position of Chairperson = 8
Number of persons who occupies the position of Secretary = 7
Number of persons who occupies the position of Treasurer = 6
The total number of outcomes = 8 x 7 x 6 = 336 -
Question 19 of 70
19. Question
How many arrangements are there of the letters from ABACUS in which the A’ s are together?
CorrectIncorrectHint
Total number of letters in the given word = 6
Excluding two A’s, we have B, C, U and S. We consider 4 + 1 = 5 units.
Total number of ways = 5!
= 5 x 4 x 3 x 2 x 1
= 120 -
Question 20 of 70
20. Question
How many arrangements are there of the letters of the word SCROOGE?
In how many of these are the O’ s together?
CorrectIncorrectHint
Total number of letters in the given word \(=7\)
To arrange those 7 letters, we have 7 ! ways. Here 2 terms cannot be separated.
\(
\begin{gathered}
\text { Total number of ways }=7 ! / 2 ! \\
=(7 \times 6 \times 5 \times 4 \times 3 \times 2 \times 1) /(2 \times 1) \\
=2520
\end{gathered}
\) -
Question 21 of 70
21. Question
How many arrangements of the letters of the word REMAND are possible if:
a) there are no restrictions?
b) they begin with RE?
c) they do not begin with RE?
CorrectIncorrectHint
Given word : REMAND
Number of letters in the word \(=6\)a) Without restrictions:
Number of ways, that letters can be arranged \(=6\) !b) they begin with RE?
\(
R E _ _ _ _
\)
Number of words to be arranged \(=4\)
Number of ways available \(=4\) !c) they do not begin with RE?
Number of words can be created, that doesn’t start with RE
\(
\begin{gathered}
=6 !-4 ! \\
=4 !(6 \times 5-1) \\
=4 ! \times 29 = 696
\end{gathered}
\) -
Question 22 of 70
22. Question
In how many ways can 5 boys and 4 girls be arranged on a bench if
a) there are no restrictions?
b) boys and girls alternate?
CorrectIncorrectHint
a) Without restriction :
Number of boys = 5, number of girls = 4
Total number of members = 5 + 4
= 9
Without restrictions, we have = 9! ways.b) Boys and girls to be seated in alternate positions.
= 5! x 4! ways -
Question 23 of 70
23. Question
There are 7 horses in a race.
a) In how many different orders can the horses finish?
b) How many trifectas (1st, 2nd and 3rd) are possible?
CorrectIncorrectHint
a) Number of available options = 7 x 6 x 5 x 4 x 3 x 2 x 1
= 5040b) Number of ways to choose 1st, 2nd and 3rd position :
= 7 x 6 x 5
= 210 -
Question 24 of 70
24. Question
How many different possibilities of settling friends A B C D E F on six seats if A wants to sit next to C?
CorrectIncorrectHint
\(
n=2 \cdot 5 !=240
\)Explanation: Let the 6 persons be \(A, B, C, D, E\), and \(F\).
If two persons ( \(A\) and \(C\)) sitting beside each other, then let’s club them into one unit, K
We have
\(B, D, E, F, K(\) total 5)
Now we have 5 ! ways = 120
Now \(\mathrm{K}\) can be arranged in 2! ways.
Number of ways
\(
\begin{aligned}
& =5 ! \times 2 ! \\
& =120 \times 2 \\
& =240
\end{aligned}
\) -
Question 25 of 70
25. Question
Peter, Jano, Alice, and Rebecca went to a classical music concert. How many different ways can they sit in the four free seats if Rebecca wants to sit with John?
CorrectIncorrectHint
\(
n=2 \cdot 3 !=12
\)Explanation: The two-person seating together consider as 1, so there are total 3! = 6 possible ways. The two-person seating together there are 2! ways. Therefore the total number of ways to seat = 3! x 2! = 12 ways.
-
Question 26 of 70
26. Question
In Fourland, they only have four letters F, O, U, and R, and every word has exactly four letters. No letter may be repeated in any word. Write all the words that can be written with them.
CorrectIncorrectHint
Total possible number of words \(4!=4 \cdot 3 \cdot 2 \cdot 1=24\)
-
Question 27 of 70
27. Question
5 friends went to the cinema. How many possible ways can they sit in a row if one of them wants to sit in the middle and the remaining place does not matter?
CorrectIncorrectHint
As one position already fixed, we have \(n=(5-1) !=24\) ways.
-
Question 28 of 70
28. Question
The gardener is to plant 6 ornamental trees. There are 8 different types of trees available. Two trees, A and B, will be planted on the left edge. How many ways can a gardener do this if all the saplings planted are to be different?
CorrectIncorrectHint
\(
n=(8-2) \cdot(8-2-1) \cdot(8-2-2) \cdot(8-2-3)=360
\) -
Question 29 of 70
29. Question
There are 4 classrooms on the ground floor of the school building, which are numbered 1,2,3,4. First-year students A, B, C, and D will be placed in these classrooms. Write all possible class arrangements and their number.
CorrectIncorrectHint
\(
n=4 \cdot 3 \cdot 2 \cdot 1=24
\) -
Question 30 of 70
30. Question
In the computer game, you need to collect 5 objects in the room: a sword, a ring, a picture, a key, and a coin. It depends on the order in which we collect the individual objects. If the order is wrong, we will lose a life. How many are all in order?
CorrectIncorrectHint
\(n=5 !=120\)
-
Question 31 of 70
31. Question
How many possible ways are to shuffle 7 playing cards?
CorrectIncorrectHint
\(
n=7 !=5040
\) -
Question 32 of 70
32. Question
Solve the equation: x!: \(5=1008\)
The solution to the equation is a natural number.CorrectIncorrectHint
\(
\begin{aligned}
& x !: 5=1008 \\
& x !=5040 \\
& x=7
\end{aligned}
\) -
Question 33 of 70
33. Question
How many ways can ten cars park side by side in a parking lot?
CorrectIncorrectHint
\(n=10 !=3628800\)
-
Question 34 of 70
34. Question
How many different four-letter words can we create from the letters of the word JAMA?
CorrectIncorrectHint
\(n=\frac{4 !}{2 !}=12\)
-
Question 35 of 70
35. Question
\(
\text { Determine the value of } x \text { in this equation: } x ! \times 4=x^3 \cdot x \text { is a natural number. }
\)CorrectIncorrectHint
\(
\begin{aligned}
& 2^3=8 \\
& 8 / 4=2 \\
& x=2
\end{aligned}
\) -
Question 36 of 70
36. Question
Petra borrowed four books from the library at the beginning of the summer holidays. How many orders in which she could gradually read them?
CorrectIncorrectHint
\(
n=4 !=24
\) -
Question 37 of 70
37. Question
How many ways can we thread four red, five blue, and six yellow beads onto a thread?
CorrectIncorrectHint
\(
n=\frac{(4+5+6) !}{4 ! \cdot 5 ! \cdot 6 !}=630630
\) -
Question 38 of 70
38. Question
How many ways can six athletes be placed on the podium at the Olympics? Depend on the color of the medal.
CorrectIncorrectHint
\(
n=6 \cdot 5 \cdot 4=120
\) -
Question 39 of 70
39. Question
6 heroes galloping on 6 horses behind. How many ways can we sort them behind?
CorrectIncorrectHint
\(
\begin{aligned}
& n=6 \\
& x=n !=6 !=720
\end{aligned}
\) -
Question 40 of 70
40. Question
Marian obtained two different marks in one day. How many ways these marks can he get?
CorrectIncorrectHint
\(
n=2 \cdot 1=2
\) -
Question 41 of 70
41. Question
We have eight compartments where we put three indistinguishable balls and two distinguishable ones. How many options do we have?
CorrectIncorrectHint
\(
n=\frac{8 \cdot 7 \cdot 6 \cdot 5 \cdot 4}{3 !}=1120
\) -
Question 42 of 70
42. Question
Willie got birthday 6 color pens in different colors. How many ways can he give them side by side in pencil?
CorrectIncorrectHint
\(
n=6 !=720
\) -
Question 43 of 70
43. Question
In elections, candidates 10 political parties. Calculate how many possible ways the elections can finish if two parties do not get the same number of votes?
CorrectIncorrectHint
\(
n=10 !=3628800
\) -
Question 44 of 70
44. Question
We have two identical blue balls and two identical red balls. We arrange them in a row in all ways. How many different arrangements are there?
CorrectIncorrectHint
\(
n=\frac{(2+2) !}{2 ! \cdot 2 !}=6
\) -
Question 45 of 70
45. Question
I have 7 cups: 1 2 3 4 5 6 7. How many opportunities for standings cups are there if 1 and 2 are always neighborhood?
CorrectIncorrectHint
\(
n=2 \cdot(7-1) !=1440
\)Note: Consider 1 and 2 as one having 2 ways and the rest 6!(7-1)!.
-
Question 46 of 70
46. Question
The class has 19 students. How can students be accommodated in the hostel, where available 3× 2-bed, 3× 3-bed and 1× 4-bed rooms? (Each room has its unique number)
CorrectIncorrectHint
\(
n=\frac{19 !}{2 ! \cdot 2 ! \cdot 2 ! \cdot 3 ! \cdot 3 ! \cdot 3 ! \cdot 4 !}=2933186256000
\) -
Question 47 of 70
47. Question
Sixteen teams will compete in the hockey tournament. How many ways can a gold, silver, and bronze medal be awarded?
CorrectIncorrectHint
\(
n=16 \cdot 15 \cdot 14=3360
\) -
Question 48 of 70
48. Question
How many different ways can sit 8 boys and 3 girls in line if girls want to sit on the edge?
CorrectIncorrectHint
\(
n=3 \cdot(8+3-2) ! \cdot(3-1)=2177280
\) -
Question 49 of 70
49. Question
How many ways can we build eight indistinguishable towers on an 8 × 8 board, so they don’t endanger each other?
CorrectIncorrectHint
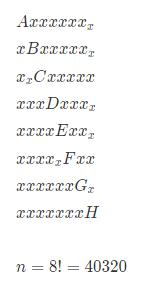
-
Question 50 of 70
50. Question
How many ways can you store seven different books side-by-side when a math book has to be on the edge of the shelf?
CorrectIncorrectHint
\(
n=2 \cdot 6 !=1440
\) -
Question 51 of 70
51. Question
How many ways can we assemble five wagons when sand is in three wagons and cement in two?
CorrectIncorrectHint
\(
n=\frac{5 !}{3 ! \cdot 2 !}=10
\) -
Question 52 of 70
52. Question
There are 11 products in the box, of which just four are defective. How many ways can we choose five products so that at least four are not faulty?
CorrectIncorrectHint
\(
n=(11-4) \cdot(11-4-1) \cdot(11-4-2) \cdot(11-4-3) \cdot(11-4) / 5 !=49
\) -
Question 53 of 70
53. Question
The arranger is to display three identical beige, two identical green, and one black coat in the shop window. How many ways can it do that?
CorrectIncorrectHint
\(
n=\frac{(3+2+1) !}{3 ! \cdot 2 ! \cdot 1 !}=60
\) -
Question 54 of 70
54. Question
You have four reindeer, and you want to have 3 fly your sleigh. You always have your reindeer fly in a single-file line. How many different ways can you arrange your reindeer?
CorrectIncorrectHint
\(
n=4 \cdot 3 \cdot 2=24
\) -
Question 55 of 70
55. Question
Six boys and six girls (among them Emil, Félix, Gertrude, and Hanka) want to dance. The number of ways they can make six (mixed) couples if Emil does not want to dance with Gertrude and Hanka wants to dance with Felix is?
CorrectIncorrectHint
\(
n=1 \cdot 4 \cdot 4 \cdot 3 \cdot 2 \cdot 1=96
\) -
Question 56 of 70
56. Question
How many ways can 9 participants be rewarded with the first, second, and third prizes in a sports competition?
CorrectIncorrectHint
\(
n=9 \cdot 8 \cdot 7=504
\) -
Question 57 of 70
57. Question
Janka wants to organize 4 English and 3 Slovak books on the shelf so that first English and then Slovak books are arranged. How many ways can it do that?
CorrectIncorrectHint
\(
n=(4 \cdot 3 \cdot 2 \cdot 1) \cdot(3 \cdot 2 \cdot 1)=144
\) -
Question 58 of 70
58. Question
Classmates Anka, Bea, Villa, and Danka can sit next to each other on the bus. How many ways can they sit down?
CorrectIncorrectHint
\(
n=4 !=24
\) -
Question 59 of 70
59. Question
I have four sweaters, two are white, one red and one green. How many ways can you sort it out?
CorrectIncorrectHint
\(
n=\frac{4 \cdot 3 \cdot 2 \cdot 1}{2 \cdot 1}=12
\) -
Question 60 of 70
60. Question
A class has 20 students. The classroom consists of 20 desks, with four desks in each of 5 different rows. Amy, Bob, Chloe, and David are all friends and would like to sit in the same row. How many possible seating arrangements are there such that Amy, Bob, Chloe, and David are all in the same row?
CorrectIncorrectHint
\(
n=5 \cdot 4 !=120
\) -
Question 61 of 70
61. Question
Find the number of possible different arrangements of the letters of the word OPTICAL such that the vowels would always be together.
CorrectIncorrectHint
\(
\begin{aligned}
& O I A \\
& \text { PTCL } \\
& n_1=(4+1) !=120 \\
& n_2=3 !=6 \\
& n=n_1 \cdot n_2=120 \cdot 6=720
\end{aligned}
\)Explanation:
the word OPTICAL has three vowels and 4 consonants. Since all the three vowels are to be together, mark as one symbol X This with the 4 consonants become 5 which can be permuted in \(5 !=120\) ways. The three vowels in \(\mathrm{X}\) can be permuted among themselves in \(3 !=6\) ways.
The total number of arrangements of the letters of the word OPTICAL so that all the vowels are always together is \(120 \times 6=720\). -
Question 62 of 70
62. Question
Eva, Lucia, Barbora, Ivana, and Slávka are good friends, so they always want to sit at one long table next to each other in biology class. How many ways can they sit if Slavka is left-handed and, therefore, always wants to sit on the left side of the table?
CorrectIncorrectHint
\(
n=4 \cdot 3 \cdot 2 \cdot 1=24
\) -
Question 63 of 70
63. Question
How many different flags can be made from green, white, blue, red, orange, yellow, and purple materials, so each flag consists of three different colors?
CorrectIncorrectHint
\(
\begin{aligned}
& n=4 \\
& x=n(n-1)(n-2) \\
& x=4 \cdot 3 \cdot 2=24
\end{aligned}
\) -
Question 64 of 70
64. Question
The Mabini Book Store (MBS) is reducing the prices of Mathematics books for promotion. The store has 6 Algebra books, 6 Geometry books, and 5 Statistics books to be arranged on a shelf. Books of the same kind are to be placed beside each other. How many ways can these books be arranged on a shelf?
CorrectIncorrectHint
\(
\begin{aligned}
& a=6 \\
& b=6 \\
& c=5 \\
& n_1=a !=6 !=720 \\
& n_2=b !=6 !=720 \\
& n_3=c !=5 !=120 \\
& n=3 ! \cdot n_1 \cdot n_2 \cdot n_3=3 ! \cdot 720 \cdot 720 \cdot 120=373248000=3.732 \cdot 10^8
\end{aligned}
\)Explanation:
Andrea, first, calculate how many ways to arrange each type of book individually. Each algebra book has 6! ways of being arranged. Each geometry book has 6! ways of being arranged. Each statistics book has 5! ways of being arranged. Now, there are three groups of books, so there are 3! ways of arranging them on the shelf. 6! x 6! x 5! x 3! = 373248000
-
Question 65 of 70
65. Question
There are five girls and seven boys in the group. They sit in a row next to each other. How many options if no two girls sit next to each other?
CorrectIncorrectHint
This problem is identical to saying if you have 7 boys in a row, how many ways are there to place 5 girls in that row without having two girls next to each other? you would have 8 locations to choose from.
B B B B B B B
+ B + B + B + B + B + B + B +Here you have 8 places to arrange the girls and 5 girls. This is the same as 8 choose 5 which equals 56.
Then for each of those 56 arrangements, you can look at every possible arrangement of individual girls, the number of which is 5!
Lastly for each of those unique placements of girls, and unique orders of girls, you can take the unique order of boys which would be 7!
In my calculation, the total should be 56 x 5! x 7! = 33868800
-
Question 66 of 70
66. Question
How many 6-digit telephone numbers can be compiled from the digits 0,1,2,..,8,9 that no digit is repeated?
CorrectIncorrectHint
\(
n=10 \cdot 9 \cdot 8 \cdot 7 \cdot 6 \cdot 5=151200
\) -
Question 67 of 70
67. Question
How many words can we make from all letters of the word BRATISLAVA?
CorrectIncorrectHint
BRATISLAVA
Number of A: 3
\(
n=\frac{10 !}{3 !}=604800
\) -
Question 68 of 70
68. Question
Determine the number of arrangements of these six elements: a, a, a, b, b, c.
CorrectIncorrectHint
\(
n=\frac{6 !}{3 ! \cdot 2 !}=60
\) -
Question 69 of 70
69. Question
How many characters can we create from two commas and four dots?
CorrectIncorrectHint
\(
n=\frac{6 !}{2 ! \cdot 4 !}=15
\) -
Question 70 of 70
70. Question
How many ways can the letters F, A, I, and R be arranged?
CorrectIncorrectHint
\(
n=4 !=24
\)