Quiz
Quiz Summary
0 of 15 Questions completed
Questions:
Information
You have already completed the quiz before. Hence you can not start it again.
Quiz is loading…
You must sign in or sign up to start the quiz.
You must first complete the following:
Results
Results
0 of 15 Questions answered correctly
Your time:
Time has elapsed
You have reached 0 of 0 point(s), (0)
Earned Point(s): 0 of 0, (0)
0 Essay(s) Pending (Possible Point(s): 0)
Categories
- Not categorized 0%
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- Current
- Review
- Answered
- Correct
- Incorrect
-
Question 1 of 15
1. Question
\(
\text { Simplify: } \frac{12 !}{11 !}+\frac{10 !}{9 !}+\frac{8 !}{7 !}+\frac{6 !}{5 !}+\frac{4 !}{3 !}+\frac{2 !}{1 !}
\)CorrectIncorrectHint
\(\frac{12 !}{11 !}+\frac{10 !}{9 !}+\frac{8 !}{7 !}+\frac{6 !}{5 !}+\frac{4 !}{3 !}+\frac{2 !}{1 !}\) simplifies to \(12+10+8+6\) \(+4+2=\mathbf{4 2}\)
-
Question 2 of 15
2. Question
\(
\text { How many positive integers are factors of (7!)? }
\)CorrectIncorrectHint
\(
7 !=7 \cdot 6 \cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1=7 \cdot 2 \cdot 3 \cdot 5 \cdot 2 \cdot 2 \cdot 3 \cdot 2=
\)
\(2^4 \cdot 3^2 \cdot 5 \cdot 7\), which has \(5 \cdot 3 \cdot 2 \cdot 2=60\) factors. -
Question 3 of 15
3. Question
\(
\text { Find the sum of the factors of (7!). }
\)CorrectIncorrectHint
\(7 !=7 \cdot 6 \cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1=2^4 \cdot 3^2 \cdot 5 \cdot 7\), so the factor sum is \((1+2+4+8+16)(1+3+9)(1+5)(1+7)\), or \((31)(13)(6)(8)=\mathbf{1 9 , 3 4 4}\)
-
Question 4 of 15
4. Question
\(
\text { What is the LCM of } 6 ! \text { and } 600 ?
\)CorrectIncorrectHint
\(
\begin{aligned}
& 6 !=6 \cdot 5 \cdot 4 \cdot 3 \cdot 2=2^4 \cdot 3^2 \cdot 5 \\
& 600=2^3 \cdot 3 \cdot 5^2 \\
& \operatorname{LCM}=\mathbf{3 , 6 0 0}
\end{aligned}
\)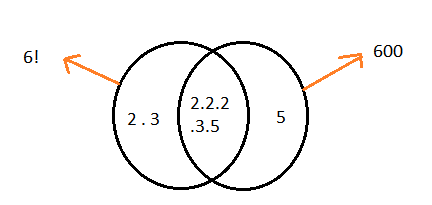
-
Question 5 of 15
5. Question
\(
\text { What is the largest prime factor of (100!)? }
\)CorrectIncorrectHint
\(100 !=100 \cdot 99 \cdot 98 \cdot 97 \cdot 96 \cdot 95 \cdot \ldots \cdot 3 \cdot 2 \cdot 1\). There is no way to create a larger prime factor by multiplication, so 97 is the greatest prime factor of \(100 !\).
-
Question 6 of 15
6. Question
\(
\text { Find the largest power of } 6 \text { that divides (18!). }
\)CorrectIncorrectHint
We are looking for multiples of 3 (there are 6 in 18 !) and multiples of \(3^2=9\) (there are 2 ). This gives us 8 threes in the prime factorization of 18 ! which, when paired with 8 twos, gives us 8 sixes or \(6^8\).
-
Question 7 of 15
7. Question
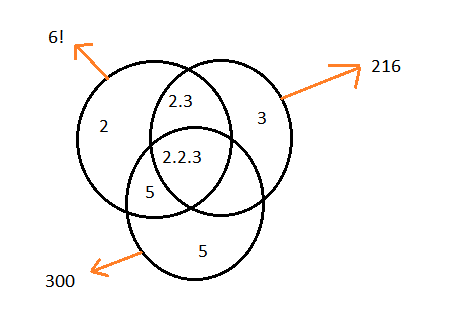
\(
\text { What is the LCM of } 6 !, 216 \text {, and } 300 ?
\)CorrectIncorrectHint
\(
\begin{aligned}
& 6 !=2^4 \cdot 3^2 \cdot 5 \\
& 216=2^3 \cdot 3^3 \\
& 300=2^2 \cdot 3 \cdot 5^2 \\
& \text { LCM }=\mathbf{1 0}, \mathbf{8 0 0}
\end{aligned}
\)
-
Question 8 of 15
8. Question
In the prime factorization of 2,500 !, what is the power of \(7 ?\)
CorrectIncorrectHint
For this problem I will introduce a function called the floor value. The floor value of a number, indicated by \(\lfloor x\rfloor\) represents the greatest integer value of \(x\) and basically means round down.
For example: \(\lfloor 9.8\rfloor=9\) and \(\lfloor 73 / 11\rfloor=6\).
To find the power of 7 in 2,500 ! we add \(\left\lfloor\frac{2,500}{7}\right\rfloor+\left\lfloor\frac{2,500}{7^2}\right\rfloor+\left\lfloor\frac{2,500}{7^3}\right\rfloor+\left\lfloor\frac{2,500}{7^4}\right\rfloor\). \(\left\lfloor\frac{2,500}{7}\right\rfloor=357\), which means there are 357 multiples of 7 in 2,500! Each contributes a 7 to the prime factorization of 2,500! Continuing, there are 51 multiples of \(7^2\), and each contributes an additional 7. There are 7 multiples of \(7^3\) and 1 multiple of \(7^4\). This gives us a total of \(357+51+7+1=416\) sevens in the prime factorization of 2,500!, making \(416\left(7^{416}\right)\) the power of 7 in \(2500 !\) -
Question 9 of 15
9. Question
Find the smallest positive integer value of \(n\) for which \(2^{15}\) divides ( \(n !\) !).
CorrectIncorrectHint
We are looking for a number \(n\) for which \(n\) ! includes fifteen 2 ‘s in its prime factorization. This one is small enough that we can get the answer quickly simply by counting up by 2 ‘s and adding the powers contributed by each: \(2,4\left(2^2\right), 6,8\left(2^3\right), 10,12\left(3 \cdot 2^2\right), 14,16\left(2^4\right)\). We are up to fifteen 2 ‘s, which means that \(2^{15}\) divides \(\mathbf{1 6}\) ! (but will not divide 15 !).
-
Question 10 of 15
10. Question
Find the smallest positive integer value of \(n\) for which \(3^{15}\) divides \((n !)\).
CorrectIncorrectHint
We are looking for a number \(n\) for which \(n\) ! includes fifteen 3 ‘s in its prime factorization. This one is small enough that we can get the answer quickly simply by counting up by threes and adding the number of 3 ‘s contributed by each until we get to fifteen 3’s: \(3,6,9\left(3^2\right), 12,15,18\left(2 \cdot 3^2\right), 21,24,27\left(3^3\right), 30,33\).
Counting the 3 ‘s above gives us 15. This means that \(3^{15}\) divides 33! (but will not divide 32 !). -
Question 11 of 15
11. Question
When 125 ! is written as an integer, how many zeros does it end with?
CorrectIncorrectHint
The number of zeros at the end of a number is determined by the number of times 10 is a factor, so we are looking to pair up as many 2’s and 5’s in the prime factorization as possible. There are many more 2’s than 5’s, so we will concentrate on counting 5 ‘s. Every number that is divisible by 5 will contribute at least one 5 . From \(1(5)=5\) to \(25(5)=125\) there are 25 multiples of 5 . Additionally, multiples of 25 contribute two 5 ‘s. There are 5 multiples of 25 . This gives us an additional five 5’s. Finally, 125 contributes three 5’s (we have already counted it twice, so we add just one more 5). This gives us a total of \(25+5+1=31\) fives. This means that 125 ! has \(5^{31}\) in its prime factorization. Pairing each five with a 2 , we see that \(10^{31}\) divides 125 !, and 125 ! therefore ends in \(\mathbf{3 1}\) zeros.
-
Question 12 of 15
12. Question
\(
\text { Find the largest integer } n \text { where } n^2 \text { is a factor of (10!). }
\)CorrectIncorrectHint
The prime factorization of 10 ! is \(2^8 \cdot 3^4 \cdot 5^2 \cdot 7\). Notice that \(\left(2^4 \cdot 3^2 \cdot 5\right)^2\) is a factor of 10 !, so \(2^4 \cdot 3^2 \cdot 5=720\) is the largest \(n\) where \(n^2\) is a factor of (10!).
-
Question 13 of 15
13. Question
\(
\text { Find the largest prime factor of }(17 !+18 !) \text {. }
\)CorrectIncorrectHint
\(17 !+18 !=17 !(1+18)=19 \cdot 17 !\), making 19 the largest prime factor of \(17 !+18 !\).
-
Question 14 of 15
14. Question
If \(n\) ! ends in exactly 100 zeros, what is the greatest possible value of \(n\) ?
CorrectIncorrectHint
For \(n\) ! to end in exactly 100 zeros, it must have exactly one-hundred 5’s in its prime factorization (when paired with a 2, these 5’s contribute a factor of 10 , adding a zero to the end of the number). We first look for multiples of 5 : 5 ! has one 5,10 ! has two, etc. 500 ! has 100 multiples of 5 , however, multiples of 25 contributes two 5’s and multiples of 125 contribute three 5’s. 500! includes 20 multiples of 25 and 4 multiples of 125 , so 500 ! ends in \(100+40+4\) \(=144\) zeros. Some quick guess-and-check working backwards and we find that 400 ! ends in \(80+16+3\) \(=99\) zeros, so 405 ! ends in \(81+16+3=100\) zeros, but we can go as high as 409 ! without adding another 5 , so \(n=409\) is our answer.
-
Question 15 of 15
15. Question
In a non-leap year, the number of minutes in February is equal to \(n !\), what is \(n\) ?
CorrectIncorrectHint
The number of minutes in February is \(60 \cdot 24 \cdot 28\). We work our way up starting at \(2 \cdot 3 \cdot 4 \ldots\) until we have the same factors at \(8 !=2 \cdot 3 \cdot 4 \cdot 5 \cdot 6 \cdot 7 \cdot 8 . n=8\).