Quiz
Summary
- Limit of a function may be a finite or an infinite number.
- If \(\lim _{x \rightarrow a} f(x)=\infty\), it just implies that the function \(f(x)\) tends to assume extremely large positive values in the vicinity of \(x=\) a i.e. \(\lim _{x \rightarrow 0} 1 /|x|=\infty\).
- A function is said to be indeterminate at any point if it acquires one of the following values at that particular point:
\(0 / 0,0 \times \infty, \infty / \infty, \infty-\infty, 0^0, 1^{\infty}, {\infty}^0 \text {. }\) - The 0/0 form is the standard indeterminate form.
- The point ‘ \(\infty\) ‘ cannot be plotted on the paper. It is just a symbol and not a number.
Infinity ( \({ }^{\infty}\) ) does not obey the laws of elementary algebra.- \(\infty+\infty=\infty\)
- \(\infty \times \infty=\infty\)
- \((a / \infty)=0,\), if \(a\) is finite
- \((a / 0)\) is not defined if \(a \neq 0\).
- \(a b=0\) if either \(a=0\) or \(b=0\) and both’ \(a\) ‘ and ‘ \(b\) ‘ are finite.
- The limit may exist at a point \(x=a\) even if the function is not defined at that point.
- Left Hand Limit & Right Hand Limit of a Function:
Left hand limit \((L H L)=\operatorname{Lim}_{x \rightarrow a^{-}} f(x)=\operatorname{Lim}_{h \rightarrow 0} f(a-h), h>0\).
Right hand \(\operatorname{limit}(R H L)=\operatorname{Lim}_{x \rightarrow a^{+}} f(x)=\operatorname{Lim}_{h \rightarrow 0} f(a+h), h>0\).
Limit of a function \(f(x)\) is said to exist as \(x \rightarrow\) a when \(\operatorname{Lim}_{x \rightarrow a^{-}} f(x)=\operatorname{Lim}_{x \rightarrow a^{-}} f(x)=\) Finite and fixed quantity. - If a function \(f\) is defined at a point ‘\(a\)‘ i.e. \(f(a)\) exists even then it is not necessary that the limit at ‘ \(a\) ‘ should exist. Moreover, even if the limit exists it need not be equal to \(f(a)\).
- Fundamental Results on Limits:
Suppose \(\lim _{x \rightarrow a} f(x)=\alpha\) andlim \({ }_{x \rightarrow a} g(x)=\beta\) then we can define the following rules:- \(\lim _{x \rightarrow a}[f(x)+g(x)]=\lim _{x \rightarrow a} f(x)+g(x)=\alpha+\beta\)
- \(\lim _{x \rightarrow a}[f(x)-g(x)]=\lim _{x \rightarrow a} f(x)-\lim _{x \rightarrow a} g(x)=\alpha-\beta\)
- \(\lim _{x \rightarrow a}[f(x)-g(x)]=\lim _{x \rightarrow a} f(x) \lim _{x \rightarrow a} g(x)=\alpha \cdot \beta\)
- \(\quad \lim _{x \rightarrow a}\left[\frac{f(x)}{g(x)}\right]=\frac{\lim _{x \rightarrow a} f(x)}{\lim _{x \rightarrow a} g(x)}=\frac{\alpha}{\beta}\) (provide \(\beta \neq 0\) )
- The above rules are applicable only when both the limits i.e. \(\lim f(x)\) and \(g(x)\) exist separately. In addition to above rules, we have two more rules:
\(\lim _{x \rightarrow a} k f(x)=k \lim _{x \rightarrow a} f(x)\), where \(k\) is a constant
\(\lim _{x \rightarrow a} f[g(x)]=f\left[\lim _{x \rightarrow a} g(x)\right]=f(m)\), provided \(f\) is continuous at \(g(x)=m\). - Some standard limits which should be remembered include:
- If \(p(x)\) is a polynomial, \(\lim _{x \rightarrow a} p(x)=p(a)\)
- \(\lim _{x \rightarrow 0} \frac{\sin x}{x}=\lim _{x \rightarrow 0} \frac{\tan x}{x}=\lim _{x \rightarrow 0} \cos x=1\) (where ‘ \(x\) ‘ is in radians)
- \(\lim _{x \rightarrow 0}(1+x)^{1 / x}=e=\operatorname{Lim}_{x \rightarrow \infty}\left(1+\frac{1}{x}\right)^x\)
- \(\lim _{x \rightarrow \infty}\left(1+\frac{1}{x}\right)^x=0\)
- \(\lim _{x \rightarrow 0} \frac{\ln (1+x)}{x}=1\)
- \(\lim _{x \rightarrow 0} \frac{(1+x)^n-1}{x}=n\)
- \(\lim _{x \rightarrow 0} \frac{a^x-1}{x}=\ln (a), a \in R^{+}\)
- \(\lim _{x \rightarrow 0} \frac{\ln (a+x)}{x}=1/a\)
- \(\lim _{x \rightarrow 0} \frac{e^x-1}{x}=1\)
- \(\lim _{x \rightarrow a} \frac{x^n-a^n}{(x-a)}=n \cdot a^{n-1}\)
- \(\lim _{x \rightarrow 0} \frac{(1+x)^m-1}{x}=m\)
- \(\lim _{x \rightarrow \infty}\left(1+\frac{a}{x}\right)^x=e^a\)
- \(\lim _{x \rightarrow a} \frac{x^m a^m}{x^n-a^x}=\frac{m}{n} a^{m-n}\)
- \(\lim _{x \rightarrow 0} \frac{\sin ^{-1} x}{x}=1=\lim _{x \rightarrow 0} \frac{\tan ^{-1} x}{x}\)
- \( \lim _{x \rightarrow+\infty} \ln x=+\infty\)
- \(\lim _{x \rightarrow 0} \ln x=-\infty\)
- \(\lim _{x \rightarrow 0} x \ln x=0\)
- \(\lim _{x \rightarrow 0} x^n \ln x=0\)
- \(\lim _{x \rightarrow+\infty} \frac{\ln x}{x}=0\)
- \(\lim _{x \rightarrow+\infty} \frac{\ln x}{x^n}=0\)
- \(\lim _{x \rightarrow \infty}\left(1+\frac{1}{x}\right)^x=e=\lim _{y \rightarrow 0}(1+y)^{1 / y} \text { where } e=2.71828\)
- \(\lim _{x \rightarrow 0} \frac{\log _a(1+x)}{x}=\log _a e \text { where } a>0 \text { and } a \neq 1\)
- If \(\lim _{x \rightarrow a} f(x)=\alpha>0\) and \(\lim _{x \rightarrow a} g(x)=\beta\) (finite number), then \(\lim _{x \rightarrow a}(f(x))^{g(x)}=\alpha^\beta\).
- Following are some of the frequently used series expansions:
- \(\sin x=x-\frac{x^3}{3!}+\frac{x^5}{5!}-\frac{x^7}{7!}+\ldots \ldots \ldots \ldots .\).
- \(\cos x=1-\frac{x^2}{2!}+\frac{x^4}{4!}-\frac{x^5}{6!}+\ldots \ldots \ldots \ldots .\).
- \(\tan x=x+\frac{x^3}{3!}+\frac{2 x^5}{15!}+\ldots \ldots \ldots \ldots \cdot\)
- \(e ^{ x }=1+x+\frac{x^2}{2!}+\frac{x^3}{3!}+\ldots \ldots \ldots \ldots\)
- \(a ^{ x }=1+(\operatorname{Ina}) x+(\operatorname{Ina})^2 \frac{x^2}{2!}+\ldots \ldots \ldots \ldots, a \in R ^{+}\)
- \((1+x)^n=1+n x+\) \(\frac{n(n-1)}{2!} x^2+\frac{n(n-1)(n-2)}{3!} x^3+\ldots \ldots, n \in R .<1, n\) is any real number
- \(\ln (1+ x )= x -\frac{ x ^2}{2}+\frac{x^3}{3}+\ldots \ldots \ldots \ldots . . . . . \text { for } -1<x \leq 1\)
- \(\tan ^{-1} x=x-\frac{x^3}{3}+\frac{x^5}{5}-\frac{x^7}{7}+\ldots, x \in R\)
- \(\sin ^{-1} x=x+\frac{1^2}{3!} x^3+\frac{1^2 \cdot 3^2}{5!} x^5+\frac{1^2 \cdot 3^2 \cdot 5^2}{7!} x^7+\ldots, x \in[-1,1]\)
- The term infinite limit means that when \(x\) tends to a particular value ‘\(a\)‘, then the limit of the function tends to infinity i.e. \(\lim _{x \rightarrow a} f(x)=\infty\).
- In questions which involve the evaluation if limit at infinity, the function \(f(x)\) should first be changed to \(g(1 / x)\) and then we can evaluate the value at \(\infty\).
- If while calculating limits, infinite limit is encountered i.e. a zero is obtained in the denominator as \(x \rightarrow a\), then there can be two cases:
- The term ( \(x-a\) ) gets cancelled from the numerator and denominator both.
- If it does not get cancelled, then the value of the limit is put as infinity.
- Such limits are termed as improper limits i.e. \(\lim _{x \rightarrow \infty} 1 / x^2=\infty\).
- Let \(f(x), g(x)\) and \(h(x)\) be there real numbers having a common domain \(D\) such that \(h(x) \leq f(x) \leq\) \(g(x) \forall x \in D\). If \(\lim _{x \rightarrow a} h(x)=\lim _{x \rightarrow a} g(x)=l\), then \(\lim _{x \rightarrow a} f(x)=l\). This is known as Sandwich Theorem.
- L’Hospital’s Rule: \(\lim _{x \rightarrow a} \frac{f(x)}{g(x)}=\lim _{x \rightarrow a} \frac{f^{\prime}(x)}{g^{\prime}(x)}\)
- If the sequence of partial sums is a convergent sequence (i.e. its limit exists and is finite) then the series is also called convergent and in this case if \(\lim _{n \rightarrow \infty} s_n=s\) then, \(\sum_{i=1}^{\infty} a_i=s\).
- If the sequence of partial sums is a divergent sequence (i.e. its limit doesn’t exist or is plus or minus infinity) then the series is also called divergent.
Quiz Summary
0 of 135 Questions completed
Questions:
Information
You have already completed the quiz before. Hence you can not start it again.
Quiz is loading…
You must sign in or sign up to start the quiz.
You must first complete the following:
Results
Results
0 of 135 Questions answered correctly
Your time:
Time has elapsed
You have reached 0 of 0 point(s), (0)
Earned Point(s): 0 of 0, (0)
0 Essay(s) Pending (Possible Point(s): 0)
Categories
- Not categorized 0%
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
- 94
- 95
- 96
- 97
- 98
- 99
- 100
- 101
- 102
- 103
- 104
- 105
- 106
- 107
- 108
- 109
- 110
- 111
- 112
- 113
- 114
- 115
- 116
- 117
- 118
- 119
- 120
- 121
- 122
- 123
- 124
- 125
- 126
- 127
- 128
- 129
- 130
- 131
- 132
- 133
- 134
- 135
- Current
- Review
- Answered
- Correct
- Incorrect
-
Question 1 of 135
1. Question
Find \(\lim _{x \rightarrow-1}\left[1+x+x^2+\ldots+x^{10}\right]\)
CorrectIncorrectHint
\(
\begin{aligned}
& \lim _{x \rightarrow-1}\left[1+x+x^2+\ldots+x^{10}\right]=1+(-1)+(-1)^2+\ldots+(-1)^{10} \\
&=1-1+1 \ldots+1=1 .
\end{aligned}
\) -
Question 2 of 135
2. Question
Find \(\lim _{x \rightarrow 1}\left[\frac{x^2+1}{x+100}\right]\)
CorrectIncorrectHint
\(
\text { We have } \lim _{x \rightarrow 1} \frac{x^2+1}{x+100}=\frac{1^2+1}{1+100}=\frac{2}{101}
\) -
Question 3 of 135
3. Question
Evaluate \(\lim _{x \rightarrow 2}\left[\frac{x^2-4}{x^3-4 x^2+4 x}\right]\)
CorrectIncorrectHint
Evaluating the function at 2, we get it of the form \(\frac{0}{0}\).
Hence \(\lim _{x \rightarrow 2} \frac{x^2-4}{x^3-4 x^2+4 x}=\lim _{x \rightarrow 2} \frac{(x+2)(x-2)}{x(x-2)^2}\)
\(
=\lim _{x \rightarrow 2} \frac{(x+2)}{x(x-2)}=\frac{2+2}{2(2-2)}=\frac{4}{0}
\)
which is not defined. -
Question 4 of 135
4. Question
Evaluate\(\lim _{x \rightarrow 0} \frac{\sqrt{1+x}-1}{x}\)
CorrectIncorrectHint
Put \(y=1+x\), so that \(y \rightarrow 1\) as \(x \rightarrow 0\).
Then
\(
\begin{aligned}
\lim _{x \rightarrow 0} \frac{\sqrt{1+x}-1}{x} & =\lim _{y \rightarrow 1} \frac{\sqrt{y}-1}{y-1} \\
& =\lim _{y \rightarrow 1} \frac{y^{\frac{1}{2}}-1^{\frac{1}{2}}}{y-1} \\
& =\frac{1}{2}(1)^{\frac{1}{2}-1} \text { (by the remark above) }=\frac{1}{2}
\end{aligned}
\) -
Question 5 of 135
5. Question
Evaluate \(\lim _{x \rightarrow 0} \frac{\sin x}{x}\)
CorrectIncorrectHint
\(\lim _{x \rightarrow 0} {\sin x}\approx{x}\)
Therefore \(
\lim _{x \rightarrow 0} \frac{\sin x}{x}\approx x/x=1
\) -
Question 6 of 135
6. Question
Evaluate \(\lim _{x \rightarrow 0} \frac{1-\cos x}{x}\)
CorrectIncorrectHint
\(
\begin{aligned}
\lim _{x \rightarrow 0} \frac{1-\cos x}{x}= & \lim _{x \rightarrow 0} \frac{2 \sin ^2\left(\frac{x}{2}\right)}{x}=\lim _{x \rightarrow 0} \frac{\sin \left(\frac{x}{2}\right)}{\frac{x}{2}} \cdot \sin \left(\frac{x}{2}\right) \\
= & \lim _{x \rightarrow 0} \frac{\sin \left(\frac{x}{2}\right)}{\frac{x}{2}} \cdot \lim _{x \rightarrow 0} \sin \left(\frac{x}{2}\right)=1.0=0
\end{aligned}
\) -
Question 7 of 135
7. Question
Evaluate \(\lim _{x \rightarrow 0} \frac{\sin 4 x}{\sin 2 x}\)
CorrectIncorrectHint
\(
\begin{aligned}
\lim _{x \rightarrow 0} \frac{\sin 4 x}{\sin 2 x} & =\lim _{x \rightarrow 0}\left[\frac{\sin 4 x}{4 x} \cdot \frac{2 x}{\sin 2 x} \cdot 2\right] \\
& =2 \cdot \lim _{x \rightarrow 0}\left[\frac{\sin 4 x}{4 x}\right] \div\left[\frac{\sin 2 x}{2 x}\right] \\
& =2 \cdot \lim _{4 x \rightarrow 0}\left[\frac{\sin 4 x}{4 x}\right] \div \lim _{2 x \rightarrow 0}\left[\frac{\sin 2 x}{2 x}\right] \\
& =2.1 .1=2(\text { as } x \rightarrow 0,4 x \rightarrow 0 \text { and } 2 x \rightarrow 0)
\end{aligned}
\) -
Question 8 of 135
8. Question
Evaluate \(\lim _{x \rightarrow 0} \frac{\tan x}{x}\)
CorrectIncorrectHint
\(
\lim _{x \rightarrow 0} \frac{\tan x}{x}=\lim _{x \rightarrow 0} \frac{\sin x}{x \cos x}=\lim _{x \rightarrow 0} \frac{\sin x}{x} \cdot \lim _{x \rightarrow 0} \frac{1}{\cos x}=1.1=1
\) -
Question 9 of 135
9. Question
\(
\text { Find the derivative of the function } f(x)=2 x^2+3 x-5 \text { at } x=-1 \text {. }
\)CorrectIncorrectHint
\(
\begin{aligned}
f^{\prime}(-1) & =\lim _{h \rightarrow 0} \frac{f(-1+h)-f(-1)}{h} \\
& =\lim _{h \rightarrow 0} \frac{\left[2(-1+h)^2+3(-1+h)-5\right]-\left[2(-1)^2+3(-1)-5\right]}{h} \\
& =\lim _{h \rightarrow 0} \frac{2 h^2-h}{h}=\lim _{h \rightarrow 0}(2 h-1)=2(0)-1=-1
\end{aligned}
\) -
Question 10 of 135
10. Question
\(
\text { Find the derivative of } f(x)=1+x+x^2+x^3+\ldots+x^{50} \text { at } x=1 \text {. }
\)CorrectIncorrectHint
A direct application of the above Theorem 6 tells that the derivative of the above function is \(1+2 x+3 x^2+\ldots+50 x^{49}\). At \(x=1\) the value of this function equals
\(
1+2(1)+3(1)^2+\ldots+50(1)^{49}=1+2+3+\ldots+50=\frac{(50)(51)}{2}=1275
\) -
Question 11 of 135
11. Question
\(
\text { Compute the derivative of } f(x)=\sin ^2 x \text {. }
\)CorrectIncorrectHint
\(
\begin{aligned}
\frac{d f(x)}{d x} & =\frac{d}{d x}(\sin x \sin x) \\
& =(\sin x)^{\prime} \sin x+\sin x(\sin x)^{\prime} \\
& =(\cos x) \sin x+\sin x(\cos x) \\
& =2 \sin x \cos x=\sin 2 x
\end{aligned}
\) -
Question 12 of 135
12. Question
Compute \(\lim _{x \rightarrow 0} \frac{\sin (2+x)-\sin (2-x)}{x}\)
CorrectIncorrectHint
\(
\lim _{x \rightarrow 0} \frac{\sin (2+x) \sin (2-x)}{x}
\)
\(
\begin{aligned}
& =\lim _{x \rightarrow 0} \frac{2 \cos \frac{(2+x+2-x)}{2} \sin \frac{2+x-2+x}{2}}{x} \\
& =\lim _{x \rightarrow 0} \frac{2 \cos 2 \sin x}{x} \\
& =2 \cos 2 \lim _{x \rightarrow 0} \frac{\sin x}{x} \\
& =2 \cos 2(1) \\
& \text { (As, } \left.\lim _{x \rightarrow 0} \frac{\sin x}{x}=1\right)
\end{aligned}
\)
Hence, \(\lim _{x \rightarrow 0} \frac{\sin (2+x)-\sin (2-x)}{x}=2 \cos 2\) -
Question 13 of 135
13. Question
Compute \(\lim _{x \rightarrow 0} \frac{\cos (2 x)-1}{\cos x-1}\)
CorrectIncorrectHint
\(
\lim _{x \rightarrow 0} \frac{\cos (2 x)-1}{\cos x-1}=\frac{0}{0}
\)
(Recall the trigonometry identity \(\cos (2 x)=2 \cos ^2 x-1\) )
\(
\begin{aligned}
& =\lim _{x \rightarrow 0} \frac{\left(2 \cos ^2 x-1\right)-1}{\cos x-1} \\
& =\lim _{x \rightarrow 0} \frac{2 \cos ^2 x-2}{\cos x-1} \\
& =\lim _{x \rightarrow 0} \frac{2\left(\cos ^2 x-1\right)}{\cos x-1}
\end{aligned}
\)
(The numerator is the difference of squares. Factor it.)
\(
=\lim _{x \rightarrow 0} \frac{2(\cos x-1)(\cos x+1)}{\cos x-1}
\)
(Divide out the factors \(\cos x-1\), the factors which are causing the indeterminate form \(\frac{0}{0}\). Now the limit can be computed.)
\(
\begin{gathered}
=\lim _{x \rightarrow 0} 2(\cos x+1) \\
=2(\cos 0+1) \\
=4 .
\end{gathered}
\) -
Question 14 of 135
14. Question
Compute \(
\lim _{x \rightarrow \frac{\pi}{2}} \frac{\tan 2 x}{x-\frac{\pi}{2}}
\)CorrectIncorrectHint
\(
\lim _{x \rightarrow \frac{\pi}{2}} \frac{\tan 2 x}{x-\frac{\pi}{2}}=\frac{0}{0}
\)
(Make the replacement \(h=x-\frac{\pi}{2}\) so that \(x=h+\frac{\pi}{2}\). Note that as \(x\) approaches \(\frac{\pi}{2}, h\) approaches 0 .)
\(
=\lim _{h \rightarrow 0} \frac{\tan (2 h+\pi)}{h}
\)
(Recall the well-known, but seldom-used, trigonometry identity \(\tan (A+B)=\frac{\tan A+\tan B}{1-\tan A \tan B}\).)
\(
\begin{gathered}
=\lim _{h \rightarrow 0} \frac{1}{h} \frac{\tan 2 h+\tan \pi}{1-\tan 2 h \tan \pi} \\
=\lim _{h \rightarrow 0} \frac{1}{h} \frac{\tan 2 h+\{0\}}{1-\tan 2 h\{0\}} \\
=\lim _{h \rightarrow 0} \frac{1}{h} \tan 2 h \\
=\lim _{h \rightarrow 0} \frac{1}{h} \frac{\sin 2 h}{\cos 2 h}
\end{gathered}
\)
(Recall the well-known trigonometry identity \(\sin 2 h=2 \sin h \cos h\). )
\(
\begin{aligned}
& =\lim _{h \rightarrow 0} \frac{1}{h} \frac{2 \sin h \cos h}{\cos 2 h} \\
& =\lim _{h \rightarrow 0} \frac{\sin h}{h} \frac{2 \cos h}{\cos 2 h}
\end{aligned}
\)
(Recall that \(\lim _{h \rightarrow 0} \frac{\sin h}{h}=1\).)
\(
\begin{aligned}
& =\{1\} \frac{2 \cos 0}{\cos 0} \\
& =\{1\} \frac{2\{1\}}{\{1\}}=2
\end{aligned}
\) -
Question 15 of 135
15. Question
\(
\text { What is the value of } \lim _{y \rightarrow \infty} \frac{2}{y} \text { ? }
\)CorrectIncorrectHint
Any number divided by infinity gives us 0.
Here, since the number 2 is divided by \(y\), as \(y\) approaches infinity, we get 0. -
Question 16 of 135
16. Question
\(
\text { What is the value of } \lim _{x \rightarrow \infty} \frac{x^2-9}{x^2-3 x+2} ?
\)CorrectIncorrectHint
Since it is of the form \(\frac{\infty}{\infty}\), we use L’Hospital’s rule and differentiate the numerator and denominator
\(
\mathrm{L}=\lim _{x \rightarrow \infty} \frac{x^2-9}{x^2-3 x+2}
\)
On differentiating once, we get \(\lim _{x \rightarrow \infty} \frac{2 x}{2 x}\)
Which is equal to, \(\lim _{x \rightarrow \infty} 1=1\). -
Question 17 of 135
17. Question
\(
\text { What is the value of } \lim _{y \rightarrow 4} f(y) \text { ? It is given that } f(y)=y^2+6 y(y \geq 2) \text { and } f(y)=0(y<2) \text {. }
\)CorrectIncorrectHint
Explanation: \(\lim _{y \rightarrow 4} f(y)=y^2+6 y\)
\(
\begin{aligned}
& f(4)=4^2+6(4) \\
& f(4)=16+24 \\
& f(4)=40
\end{aligned}
\) -
Question 18 of 135
18. Question
\(
\text { What is the value of the limit } f(x)=\frac{x^2+\sqrt{2 x}}{x^2-4 x} \text { if } x \text { approaches infinity? }
\)CorrectIncorrectHint
Divide both numerator and denominator by \(x^2\) and they apply the limit. You will get ratio of 1/1=1.
-
Question 19 of 135
19. Question
Let
\(
f(x)=\left\{\begin{array}{ll}
x+2, & \text { if } x<0 \\
3 x-7, & \text { if } x \geq 0
\end{array},\right.
\)
then
\(
\lim _{x \rightarrow 0^{+}} f(x)=?
\)CorrectIncorrectHint
\(
\begin{aligned}
\lim _{x \rightarrow 0^{+}} f(x) & =\lim _{x \rightarrow 0^{+}}(3 x-7) \\
& =0-7 \\
& =-7
\end{aligned}
\) -
Question 20 of 135
20. Question
Let
\(
f(x)= \begin{cases}x+2, & \text { if } x<0 \\ 3 x-7, & \text { if } x \geq 0\end{cases}
\)
then
\(
\lim _{x \rightarrow 0^{-}} f(x)=?
\)CorrectIncorrectHint
\(
\begin{aligned}
\lim _{x \rightarrow 0^{-}} f(x) & =\lim _{x \rightarrow 0^{-}}(x+2) \\
& =0+2 \\
& =2
\end{aligned}
\) -
Question 21 of 135
21. Question
Let
\(
f(x)=\left\{\begin{array}{cl}
x+2, & \text { if } x<0 \\
3 x-7, & \text { if } x \geq 0
\end{array},\right.
\)
then
\(
\lim _{x \rightarrow 0} f(x)=?
\)CorrectIncorrectHint
\(\lim _{x \rightarrow 0} f(x)\) does not exist
since
\(
\lim _{x \rightarrow 0^{+}} f(x) \neq \lim _{x \rightarrow 0^{-}} f(x) .
\)
Recall from the previous two questions that
\(
\lim _{x \rightarrow 0^{-}} f(x)=2
\)
and
\(
\lim _{x \rightarrow 0^{+}} f(x)=-7 .
\) -
Question 22 of 135
22. Question
\(
\lim _{x \rightarrow a} 17=?
\)CorrectIncorrectHint
\(
\lim _{x \rightarrow a} 17=17
\) -
Question 23 of 135
23. Question
\(
\lim _{x \rightarrow-7} \sqrt{x+4}=?
\)CorrectIncorrectHint
\(
\begin{aligned}
\lim _{x \rightarrow-7} \sqrt{x+4} & =\sqrt{-7+4} \\
& =\sqrt{-3} \\
& =i \sqrt{3},
\end{aligned}
\)
where \(i=\sqrt{-1}\) is called the “imaginary number.” -
Question 24 of 135
24. Question
\(
\text { Let } a_n=2+1 / n \text {. Then } \lim _{n \rightarrow \infty} a_n=\text { ? }
\)CorrectIncorrectHint
\(
\begin{aligned}
\lim _{n \rightarrow \infty} a_n & =\lim _{n \rightarrow \infty}\left(2+\frac{1}{n}\right) \\
& =\lim _{n \rightarrow \infty} 2+\lim _{n \rightarrow \infty} \frac{1}{n} \\
& =2+0 \\
& =2 .
\end{aligned}
\) -
Question 25 of 135
25. Question
\(
\lim _{x \rightarrow-\infty} \frac{5 x^3+4 x+7}{25-2 x^3}=?
\)CorrectIncorrectHint
First, divide both the numerator and denominator by \(x^3\) and let \(h=\frac{-1}{x}\). This allows us to rewrite the limit as
\(
\begin{aligned}
\lim _{x \rightarrow-\infty} \frac{5 x^3+4 x+7}{25-2 x^3} & =\lim _{h \rightarrow 0^{+}} \frac{5+4 h^2-7 h^3}{-25 h^3-2} \\
& =\frac{-5}{2} .
\end{aligned}
\) -
Question 26 of 135
26. Question
\(
\lim _{x \rightarrow \infty} \frac{e^x}{x^2+4}=?
\)CorrectIncorrectHint
Since
\(
\frac{\lim _{x \rightarrow \infty} e^x}{\lim _{x \rightarrow \infty}\left(x^2+4\right)}=\frac{\infty}{\infty},
\)
we apply l’Hôpital’s rule, which gives us
\(
\begin{aligned}
\lim _{x \rightarrow \infty} \frac{e^x}{x^2+4} & =\lim _{x \rightarrow \infty} \frac{\left(e^x\right)^{\prime}}{\left(x^2+4\right)^{\prime}} \\
& =\lim _{x \rightarrow \infty} \frac{e^x}{2 x} .
\end{aligned}
\)
Since
\(
\frac{\lim _{x \rightarrow \infty} e^x}{\lim _{x \rightarrow \infty} 2 x}=\frac{\infty}{\infty},
\)
we apply l’Hôpital’s rule a second time:
\(
\begin{aligned}
\lim _{x \rightarrow \infty} \frac{e^x}{2 x} & =\lim _{x \rightarrow \infty} \frac{\left(e^x\right)^{\prime}}{(2 x)^{\prime}} \\
& =\lim _{x \rightarrow \infty} \frac{e^x}{2} \\
& =\frac{\infty}{2} \\
& =\infty
\end{aligned}
\) -
Question 27 of 135
27. Question
\(
\text { Find } \lim _{x \rightarrow-\infty} \frac{3 x-2}{e^{x^2}} \text {. }
\)CorrectIncorrectHint
We have
\(
\begin{aligned}
\lim _{x \rightarrow-\infty} \frac{3 x-2}{e^{x^2}}\left(\frac{-\infty}{\infty}\right) = \lim _{x \rightarrow-\infty} \frac{3}{e^{x^2(2 x)}} \quad\left(\frac{3}{\text { large neg. }}\right) \\
& =0 .
\end{aligned}
\) -
Question 28 of 135
28. Question
\(
\text { Find } \lim _{x \rightarrow 0} \frac{e^x-1-x-x^2 / 2}{x^3}
\)CorrectIncorrectHint
\(
\begin{aligned}
\lim _{x \rightarrow 0} \frac{e^x-1-x-x^2 / 2}{x^3}\left(\frac{0}{0}\right) {=} \lim _{x \rightarrow 0} \frac{e^x-1-x}{3 x^2}\left(\frac{0}{0}\right) \\
{=} \lim _{x \rightarrow 0} \frac{e^x-1}{6 x}\left(\frac{0}{0}\right) \\
{=} \lim _{x \rightarrow 0} \frac{e^x}{6}=\frac{e^0}{6}=\frac{1}{6} .
\end{aligned}
\) -
Question 29 of 135
29. Question
\(
\text { Find } \lim _{x \rightarrow \infty} x e^{-x} \text {. }
\)CorrectIncorrectHint
\(
\begin{aligned}
\lim _{x \rightarrow \infty} x e^{-x} & =\lim _{x \rightarrow \infty} \frac{x}{e^x}\left(\frac{\infty}{\infty}\right) \\
{=} \lim _{x \rightarrow \infty} \frac{1}{e^x} \quad\left(\frac{1}{\text { large pos. }}\right) \\
& =0 .
\end{aligned}
\) -
Question 30 of 135
30. Question
\(
\text { Find } \lim _{x \rightarrow 0^{+}}(\cot 2 x)(\sin 6 x) \text {. }
\)CorrectIncorrectHint
First
\(
\begin{aligned}
\lim _{x \rightarrow 0^{+}} \cot 2 x & =\lim _{x \rightarrow 0^{+}} \frac{\cos 2 x}{\sin 2 x} \quad\left(\frac{\text { about } 1}{\text { small pos. }}\right) \\
& =\infty .
\end{aligned}
\)
Therefore, the given limit is indeterminate of type \(\infty \cdot 0\). We rewrite as a fraction and then use l’Hôpital’s rule:
\(
\begin{aligned}
\lim _{x \rightarrow 0^{+}}(\cot 2 x)(\sin 6 x) & =\lim _{x \rightarrow 0^{+}} \frac{\sin 6 x}{\tan 2 x}\left(\frac{0}{0}\right) \\
{=} \lim _{x \rightarrow 0^{+}} \frac{6 \cos 6 x}{2 \sec ^2 2 x} \\
& =\frac{6}{2}=3 .
\end{aligned}
\) -
Question 31 of 135
31. Question
\(
\text { Find } \lim _{x \rightarrow \frac{\pi}{2}^{-}}(\tan x-\sec x) \text {. }
\)CorrectIncorrectHint
As observed above, this limit is indeterminate of type \(\infty-\infty\). We combine the terms and then use l’Hôpital’s rule:
\(
\begin{aligned}
\lim _{x \rightarrow \frac{\pi}{2}^{-}}(\tan x-\sec x) & =\lim _{x \rightarrow \frac{\pi}{2}^{-}}\left(\frac{\sin x}{\cos x}-\frac{1}{\cos x}\right) \\
& =\lim _{x \rightarrow \frac{\pi}{2}^{-}} \frac{\sin x-1}{\cos x}\left(\frac{0}{0}\right) \\
{=} \lim _{x \rightarrow \frac{\pi}{2}^{-}} \frac{\cos x}{-\sin x} \\
& =\frac{0}{-1}=0 .
\end{aligned}
\) -
Question 32 of 135
32. Question
\(
\text { Find } \lim _{x \rightarrow 1^{+}}\left(\frac{x}{x-1}-\frac{1}{\ln x}\right) \text {. }
\)CorrectIncorrectHint
\(
\text { The limit is indeterminate of type } \infty-\infty \text {. We combine the terms and then use }
\)
l’Hoppital’s rule:
\(
\begin{aligned}
\lim _{x \rightarrow 1^{+}}\left(\frac{x}{x-1}-\frac{1}{\ln x}\right) & =\lim _{x \rightarrow 1^{+}} \frac{x \ln x-x+1}{(x-1) \ln x}\left(\frac{0}{0}\right) \\
{=} \lim _{x \rightarrow 1^{+}} \frac{\ln x+x(1 / x)-1}{\ln x+(x-1)(1 / x)} \\
& =\lim _{x \rightarrow 1^{+}} \frac{\ln x}{\ln x+1-1 / x}\left(\frac{0}{0}\right) \\
& =\lim _{x \rightarrow 1^{+}} \frac{1 / x}{1 / x+1 / x^2} \\
& =\frac{1}{2} .
\end{aligned}
\) -
Question 33 of 135
33. Question
\(
\text { Find } \lim _{x \rightarrow \infty} x^{1 / x} \text {. }
\)CorrectIncorrectHint
As was noted above, this limit is of indeterminate type \(\infty^{\circ}\). We first find the limit of the natural logarithm of the given expression:
\(
\begin{aligned}
\lim _{x \rightarrow \infty} \ln x^{1 / x} & =\lim _{x \rightarrow \infty}(1 / x) \ln x \quad(0 \cdot \infty) \\
& =\lim _{x \rightarrow \infty} \frac{\ln x}{x} \quad\left(\frac{\infty}{\infty}\right) \\
{=} \lim _{x \rightarrow \infty} \frac{1 / x}{1} \\
& =0 .
\end{aligned}
\)
Therefore,
\(
\lim _{x \rightarrow \infty} x^{1 / x}=\lim _{x \rightarrow \infty} e^{\ln x^{1 / x}}=e^0=1,
\)
where we have used the inverse property of logarithms \(y=e^{\ln y}\) and then the previous computation. -
Question 34 of 135
34. Question
Find \(\lim _{x \rightarrow 0}(\tan x)^x\)
CorrectIncorrectHint
As was noted above, this limit is indeterminate of type \(0^0\). We first find the limit of the natural logarithm of the given expression:
\(
\begin{aligned}
\lim _{x \rightarrow 0^{+}} \ln (\tan x)^x & =\lim _{x \rightarrow 0^{+}} x \ln \tan x \\
& =\lim _{x \rightarrow 0^{+}} \frac{\ln \tan x}{x^{-1}}\left(\frac{-\infty}{\infty}\right) \\
{=} \lim _{x \rightarrow 0^{+}} \frac{\cot x \sec ^2 x}{-x^{-2}} \\
& =\lim _{x \rightarrow 0^{+}} \frac{-x^2}{\sin x \cos x}\left(\frac{0}{0}\right) \\
{=} \lim _{x \rightarrow 0^{+}} \frac{-2 x}{\cos ^2 x-\sin ^2 x} \\
& =\frac{0}{1}=0 .
\end{aligned}
\)
Therefore,
\(
\lim _{x \rightarrow 0^{+}}(\tan x)^x=\lim _{x \rightarrow 0^{+}} e^{\ln (\tan x)^x}=e^0=1 .
\) -
Question 35 of 135
35. Question
\(
\text { Find } \lim _{x \rightarrow \infty}\left(1+\frac{1}{x}\right)^x
\)CorrectIncorrectHint
As was noted above, this limit is indeterminate of type \(1^{\infty}\). We first find the limit of the natural logarithm of the given expression:
\(
\begin{aligned}
\lim _{x \rightarrow \infty} \ln \left(1+\frac{1}{x}\right)^x & =\lim _{x \rightarrow \infty} x \ln \left(1+\frac{1}{x}\right) \\
& =\lim _{x \rightarrow \infty} \frac{\ln (1+1 / x)}{x^{-1}}\left(\frac{0}{0}\right) \\
& {=} \lim _{x \rightarrow \infty} \frac{\frac{1}{1+1 / x}\left(-x^{-2}\right)}{-x^{-2}} \\
& =\lim _{x \rightarrow \infty} \frac{1}{1+1 / x}=1 .
\end{aligned}
\)
Therefore,
\(
\lim _{x \rightarrow \infty}\left(1+\frac{1}{x}\right)^x=\lim _{x \rightarrow \infty} e^{\ln \left(1+\frac{1}{x}\right)^x}=e^1=e .
\) -
Question 36 of 135
36. Question
The domain of the function \(f(x)=\sqrt{x^2-3 x+2}+\frac{1}{\sqrt{3+2 x-x^2}}\) is
CorrectIncorrectHint
We have
\(
\begin{aligned}
\sqrt{x^2-3 x+2} \text { is real } & \Leftrightarrow x^2-3 x+2 \geq 0 \\
& \Leftrightarrow(x-1)(x-2) \geq 0 \\
& \Leftrightarrow x \leq 1 \quad \text { or } \quad x \geq 2 \dots(i)
\end{aligned}
\)
Again
\(
\begin{aligned}
\frac{1}{\sqrt{3+2 x-x^2}} \text { is defined } & \Leftrightarrow 3+2 x-x^2>0 \\
& \Leftrightarrow-(x+1)(x-3)>0 \\
& \Leftrightarrow(x+1)(x-3)<0 \\
& \Leftrightarrow-1<x<3 \dots(ii)
\end{aligned}
\)
From Eqs. (i) and (ii), it follows that \(f(x)\) is defined for \(x \in(-1,1] \cup[2,3)\). -
Question 37 of 135
37. Question
The graph in Fig. below represents a function whose domain is
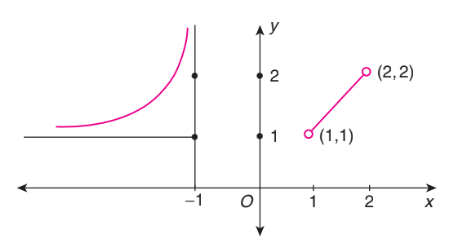 CorrectIncorrect
CorrectIncorrectHint
The given graph is represented by the function
\(
f(x)= \begin{cases}\frac{1}{x+1}+1 & \text { for } x<-1 \\ x & \text { for } 1<x<2\end{cases}
\) -
Question 38 of 135
38. Question
If \(f(x)=x^2+\lambda x+1\) for all real \(x\) and \(f\) is an even function, then the value of \(\lambda\) is
CorrectIncorrectHint
Since \(f\) is even, we have \(f(1)=f(-1)\). Therefore \(2+\lambda=2-\lambda\), which implies that \(\lambda=0\).
-
Question 39 of 135
39. Question
Let \(C_1\) be the graph of the curve represented by the equation \(x^2-13 x+4 y=1\). If \(C_2\) is the new curve obtained when \(C_1\) is reflected in the origin, then the equation of \(C_2\) is
CorrectIncorrectHint
Since \(C_2\) is the reflection of \(C_1\) in the origin, we have
\(
\begin{aligned}
(x, y) \in C_1 & \Leftrightarrow(-x,-y) \in C_2 \\
& \Leftrightarrow(-x)^2-13(-x)+4(-y)=1 \\
& \Leftrightarrow x^2+13 x-4 y=1
\end{aligned}
\) -
Question 40 of 135
40. Question
Let \(f(x)=x-3\) and
\(
g(x)= \begin{cases}\frac{x^2-9}{x+3} & \text { if } x \neq-3 \\ k & \text { if } x=-3\end{cases}
\)
If \(f(x)=g(x)\) for all real \(x\), then the value of \(k\) isCorrectIncorrectHint
Clearly
\(
g(x)=\frac{x^2-9}{x+3}=x-3=f(x)
\)
for \(x \neq-3\) and \(f(-3)=-6\). Hence \(k=-6\). -
Question 41 of 135
41. Question
The domain of the function \(f(x)=\sqrt{|x-1|-1}\) is
CorrectIncorrectHint
We have
\(
\begin{aligned}
|x-1| \geq 1 & \Leftrightarrow x-1 \leq-1 \quad \text { or } \quad x-1 \geq 1 \\
& \Leftrightarrow x \leq 0 \quad \text { or } \quad x \geq 2
\end{aligned}
\) -
Question 42 of 135
42. Question
If [.] denotes the greatest integer function, then the domain of the function
\(f(x)=\frac{1}{\sqrt{[|x|-1] \mid-5}}\) isCorrectIncorrectHint
We have that
\(
\begin{aligned}
f(x) \text { is defined } & \Leftrightarrow|[|x|-1]|-5>0 \\
& \Leftrightarrow[|x|-1]<-5 \text { or } \quad[|x|-1]>5 \\
& \Leftrightarrow|x|-1<-5 \text { or }|x|-1 \geq 6
\end{aligned}
\)
\(
\begin{aligned}
& \Leftrightarrow|x|<-4 \quad \text { or } \quad|x| \geq 7 \\
& \Leftrightarrow x \leq-7 \quad \text { or } \quad x \geq 7 \\
& \Leftrightarrow x \in(-\infty,-7] \cup[7, \infty)
\end{aligned}
\) -
Question 43 of 135
43. Question
The domain of the function \(\operatorname{Cos}^{-1}\left(\frac{|x|-3}{2}\right)+\frac{1}{\log _{10}(4-x)}\) is
CorrectIncorrectHint
\(\operatorname{Cos}^{-1}[(|x|-3) / 2]\) is defined for
\(
\begin{aligned}
& -1 \leq \frac{|x|-3}{2} \leq 1 \\
\Rightarrow & -2 \leq|x|-3 \leq 2 \\
\Rightarrow & 1 \leq|x| \leq 5
\end{aligned}
\)
Therefore
\(
x \in[-5,-1] \cup[1,5] \dots(i)
\)
Again \(1 / \log _{10}(4-x)\) is defined for \(x<4\) and \(x \neq 3\). That is
\(
x \in(-\infty, 3) \cup(3,4) \dots(ii)
\)
Therefore, from Eqs. (i) and (ii), the domain of the given function is
\(
[-5,-1] \cup[1,3) \cup(3,4)
\) -
Question 44 of 135
44. Question
The domain of the function \(e^{\operatorname{Sin}^{-1} x}+\frac{1}{[x]}+\frac{1}{\sqrt{x+1}}\) is
CorrectIncorrectHint
We have
\(
\operatorname{Sin}^{-1} x \text { is defined for }-1 \leq x \leq 1 \dots(i)
\)
Now \(1 /[x]\) is defined when \([x] \neq 0\), that is
\(
x \notin[0,1) \dots(ii)
\)
Also \(1 / \sqrt{x+1}\) is defined only when \(x+1>0\), that is
\(
x>-1 \dots(iii)
\)
From Eqs. (i) – (ii), the domain of the given function is \((-1,0) \cup\{1\}\). -
Question 45 of 135
45. Question
The domain of the function
\(
e^x+\operatorname{Sin}^{-1}\left(\frac{x}{2}-1\right)+\log (\sqrt{x-[x]})
\)
where \([x]\) is the integral part of \(x\) isCorrectIncorrectHint
1. \(e^x\) is defined for all \(x\) (real or complex). In this context \(x\) is real.
2. \(\sin ^{-1}[(x / 2)-1]\) is defined for \(-1 \leq(x / 2)-1 \leq 1\), that is, \(0 \leq x \leq 4\).
3. \(x \geq[x] \Rightarrow \sqrt{x-[x]}\) is defined for all real \(x\). Therefore, \(\log (\sqrt{x-[x]})\) is defined when \(x\) is not an integer, because \(x=[x]\) when \(x\) is an integer.Therefore from the above, the domain of the given function is \((0,4)-\{1,2,3\}\).
-
Question 46 of 135
46. Question
The domain of the function \(f(x)=\sqrt{\log _{10} \frac{\left(3 x-x^2\right)}{2}}\) is
CorrectIncorrectHint
\(\log _{10}\left[\left(3 x-x^2\right) / 2\right]\) is defined only when
\(
\begin{aligned}
& \frac{3 x-x^2}{2}>0 \\
\Rightarrow & x^2-3 x<0 \\
\Rightarrow & 0<x<3 \dots(i)
\end{aligned}
\)
Now \(\sqrt{\log _{10}\left[\left(3 x-x^2\right) / 2\right]}\) is defined when
\(
\begin{aligned}
& \frac{3 x-x^2}{2} \geq 1 \\
\Rightarrow & x^2-3 x+2 \leq 0 \\
\Rightarrow & (x-1)(x-2) \leq 0 \\
\Rightarrow & 1 \leq x \leq 2 \dots(ii)
\end{aligned}
\)
From Eqs. (i) and (ii), the domain of \(f(x)\) is \([1,2]\). -
Question 47 of 135
47. Question
Let \(f: R \rightarrow R\) be a function such that \(f(x+y)=\) \(f(x)+f(y)\) for all \(x, y\) belonging to \(R\). If \(m[latex] and [latex]n\) are integers, then \(f(m / n)\) is equal to
CorrectIncorrectHint
Clearly \(f(0)=f(0+0)=f(0)+f(0)\) implies \(f(0)=0\). Also
\(
0=f(0)=f(x-x)=f(x+(-x))=f(x)+f(-x)
\)
Therefore
\(
f(-x)=-f(x) \dots(i)
\)
Case I: Suppose \(x\) is a positive integer. Now
\(
\begin{gathered}
f(2)=f(1+1)=f(1)+f(1)=2 f(1) \\
f(3)=f(2+1)=f(2)+f(1)=2 f(1)+f(1)=3 f(1)
\end{gathered}
\)
Therefore, by induction,
\(
f(x)=x f(1) \dots(ii)
\)
Case II: Suppose \(x\) is a negative integer, say \(x=-y\) where \(y\) is a positive integer. Now from Eqs. (i) and (ii) we have
\(
f(x)=f(-y)=-f(y)=-y f(1)=x f(1)
\)
Case III: Suppose \(m\) and \(n\) are integers and \(x=m / n\) and \(n\) is positive. Now
\(
\begin{aligned}
m f(1) & =f(m)[\text { By cases }(1) \text { and }(2)] \\
& =f(n x) \\
& =f(x+x+\cdots+n \text { times }) \\
& =f(x)+f(x)+\cdots \text { upto } n \text { times } \\
& =n f(x)
\end{aligned}
\)
Therefore
\(
f(x)=\left(\frac{m}{n}\right) f(1)
\)
Hence, \(f(x)=x f(1)\) for all rational numbers \(x\).Note: In the above problem, if \(f\) is also continuous, then \(f(x)=x f(1)\) for all real \(x\) which we discuss later.
-
Question 48 of 135
48. Question
If \([x]\) denotes the integer part of \(x\), then the domain of the function \(f(x)=\frac{e^{-x}}{1+[x]}\) is
CorrectIncorrectHint
\(f(x)\) is defined when \(1+[x] \neq 0\).
\(
\begin{aligned}
1+[x]=0 & \Leftrightarrow[x]=-1 \\
& \Leftrightarrow-1 \leq x<0 \\
& \Leftrightarrow x \in[-1,0)
\end{aligned}
\) -
Question 49 of 135
49. Question
The domain of the function \(f(x)=\frac{x|x-3|}{\left(x^2-x-6\right)|x|}, x \in R\) is
CorrectIncorrectHint
The given function can be written as
\(
f(x)=\frac{x|x-3|}{(x-3)(x+2)|x|}
\)
Therefore, \(f\) is defined for \(x \neq-2,0,3\). -
Question 50 of 135
50. Question
Domain of the function \(f(x)=2 \operatorname{Sin}^{-1} \sqrt{1-x}+\operatorname{Sin}^{-1}[2 \sqrt{x(1-x)}]\) is
CorrectIncorrectHint
\(1-x \geq 0\) and \(x(1-x) \geq 0\) when \(0 \leq x \leq 1\). In this case, \(0 \leq 2 \sqrt{(1-x) x} \leq 1\).
-
Question 51 of 135
51. Question
Let \(f: R \rightarrow R -\{3\}\) be a function such that for some \(p>0\),
\(
f(x+p)=\frac{f(x)-5}{f(x)-3}
\)
for all \(x \in R\). Then, period of \(f\) isCorrectIncorrectHint
3 does not belong to the range of \(f\) implies 2 also cannot belong to range of \(f\) because, if \(f(x)=2\) for some \(x \in R\). Then
\(
f(x+p)=\frac{2-5}{2-3}=3
\)
which is not in the range of \(f\). Hence 2 and 3 are not in the range of \(f\). If \(f(x+2 p)=f(x)\), this implies
\(
\begin{aligned}
f(x) & =f(x+p+p) \\
& =\frac{f(x+p)-5}{f(x+p)-3} \\
& =\frac{\frac{f(x)-5}{f(x)-3}-5}{\frac{f(x)-5}{f(x)-3}-3}
\end{aligned}
\)
\(
=\frac{-4 f(x)+10}{-2 f(x)+4}=\frac{2 f(x)-5}{f(x)-2}
\)
so that \([f(x)-2]^2=-1\) which is absurd. Therefore, \(2 p\) is not a period. Again
\(
\begin{aligned}
f(x+3 p) & =\frac{2 f(x+p)-5}{f(x+p)-2} \\
& =\frac{3 f(x)-5}{f(x)-1} \neq f(x)
\end{aligned}
\)
Now
\(
\begin{aligned}
f(x+4 p) & =f(x+3 p+p) \\
& =\frac{f(x+3 p)-5}{f(x+3 p)-3} \\
& =\frac{\frac{3 f(x)-5}{f(x)-1}-5}{\frac{3 f(x)-5}{f(x)-1}-3} \\
& =\frac{-2 f(x)}{-2}=f(x)
\end{aligned}
\)
Therefore \(4 p\) is a period. -
Question 52 of 135
52. Question
Let \(f: R \rightarrow R\) be a function such that
\(
f(x+y)+f(x-y)=2 f(x) f(y)
\)
for all \(x, y \in R\) and \(f(\alpha)=-1\) for some \(\alpha \in R\). Then period of \(f\) isCorrectIncorrectHint
Given that
\(
f(x+y)+f(x-y)=2 f(x) f(y) \forall x, y \in R
\)
Substituting \(x=0\) and \(y=0\), we have
\(
f(0)=(f(0))^2 \Rightarrow f(0)=0 \quad \text { or } 1
\)
If \(f(0)=0\), then
\(
f(x+0)+f(x-0)=2 f(x) f(0)
\)
and hence \(f(x)=0\) for all \(x \in R\) which contradicts the fact that \(f(\alpha)=-1\). Therefore
\(
f(0)=1
\)
Now, replacing \(x\) with \(x+2 \alpha\) and \(y\) with \(x-2 \alpha\) in the given relation, we have
\(
f(2 x)+f(4 \alpha)=2 f(x+2 \alpha) f(x-2 \alpha) \dots(1)
\)
Also in the given relation, if we put \(y=x\), then we have
\(
f(2 x)+f(0)=2 f(x) f(x)
\)
Therefore
\(
f(2 x)=2[f(x)]^2-1 \dots(2)
\)
In Eq. (2), if we replace \(x\) with \(2 \alpha\), then
\(
f(4 \alpha)=2[f(2 \alpha)]^2-1 \dots(3)
\)
But
\(
\begin{aligned}
x=y=\alpha & \Rightarrow f(2 \alpha)+f(0)=2[f(\alpha)]^2 \\
& \Rightarrow f(2 \alpha)=2[f(\alpha)]^2-1 \\
& =2(1)-1 \quad[\because f(\alpha)=-1] \\
& =1 \dots(4)
\end{aligned}
\)
From Eqs. (3) and (4) we have
\(
f(4 \alpha)=1 \dots(5)
\)
From Eqs. (1), (2) and (5), we get that
\(
f(x+2 \alpha) f(x-2 \alpha)=(f(x))^2 \dots(6)
\)
Similarly if we put \(y=2 \alpha\) in the given relation, we have
\(
f(x+2 \alpha)+f(x-2 \alpha)=2 f(x) \dots(7)
\)
From Eqs. (6) and (7), we have
\(
f(x-2 \alpha)=f(x+2 \alpha)=f(x)
\)
Therefore \(2 \alpha\) is a period of \(f(x)\). -
Question 53 of 135
53. Question
Let \(f: R \rightarrow R\) be a function satisfying the relation
\(
f(x+1)=\frac{1}{2}+\sqrt{f(x)-(f(x))^2}
\)
for all \(x \in R\). Then period of \(f(x)\) isCorrectIncorrectHint
Observe that \(f(x) \geq 1 / 2\) for all \(x \in R\). Now
\(
\begin{aligned}
& =\frac{1}{2}+\sqrt{\frac{1}{4}-f(x)+[f(x)]^2} \\
&
\end{aligned}
\)
\(
\begin{aligned}
& =\frac{1}{2}+\left|\frac{1}{2}-f(x)\right| \\
& =\frac{1}{2}-\frac{1}{2}+f(x) \quad\left(\because f(x) \geq \frac{1}{2} \forall x\right) \\
& =f(x)
\end{aligned}
\)
Therefore, 2 is period of \(f(x)\). -
Question 54 of 135
54. Question
The period of the function \(f(x)=\operatorname{Tan}^{-1}(\tan x)\) is
CorrectIncorrectHint
\(\quad f(x+\pi)=\operatorname{Tan}^{-1}(\tan (\pi+x))=\operatorname{Tan}^{-1}(\tan x)=f(x)\)
This implies \(\pi\) is the least period of \(f(x)\). -
Question 55 of 135
55. Question
The period of \(f(x)=2 \cos \left(\frac{x-\pi}{3}\right)\) is
CorrectIncorrectHint
Period of \(a \cos (a x+b)\) is \(2 \pi\) when \(a\) is an integer and the period of \(\cos (k x)=2 \pi / k\) when \(k>0\) integer. Therefore, period of \(f(x)\) is \(6 \pi\).
-
Question 56 of 135
56. Question
Which of the following graphs represents \(y=2|x-2|-|x+1|+x ?\)
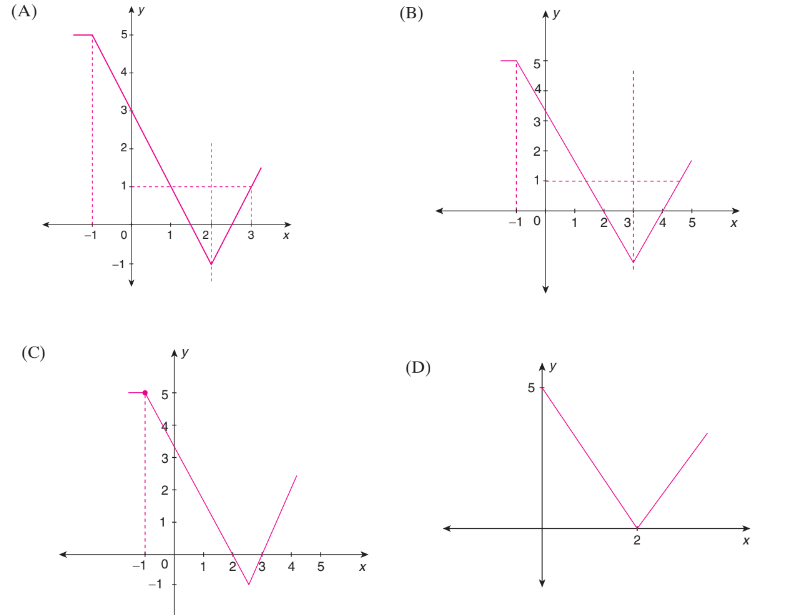 CorrectIncorrect
CorrectIncorrectHint
It can be seen that
\(
f(x)= \begin{cases}5 & \text { if } x \leq-1 \\ 3-2 x & \text { if }-1 \leq x \leq 2 \\ 2 x-5 & \text { if } x \geq 2\end{cases}
\) -
Question 57 of 135
57. Question
The graph in Fig. below is represented by which of the following function?
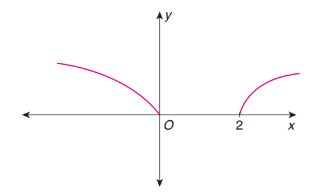 CorrectIncorrect
CorrectIncorrectHint
The domain of \(f(x)=\sqrt{|x-1|-1}\) is \((-\infty, 0] \cup\) \([2, \infty)\) because \(|x-1| \geq 1\). Now
\(
x \leq 0 \Rightarrow f(x)=\sqrt{|x-1|-1}=\sqrt{-x}
\)
So the graph must be upper half the parabola \(y^2=-x\) with vertex at origin. Again
\(
x \geq 2 \Rightarrow y=\sqrt{x-2} \Rightarrow y^2=x-2
\)
which represents parabola in the upper half of the \(x\)-axis with vertex at \((2,0)\). -
Question 58 of 135
58. Question
\(\lim _{x \rightarrow 3+0} f(x)\) of the graph of the function given in Fig. below is
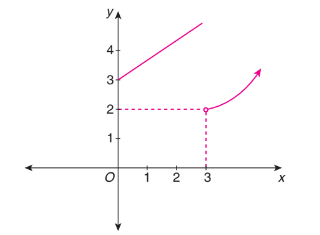 CorrectIncorrect
CorrectIncorrectHint
As per the graph, \(\lim _{x \rightarrow 3+0} f(x)=2\)
-
Question 59 of 135
59. Question
If \(f(x)=3 x^2-x\), then
\(
\lim _{h \rightarrow 0} \frac{f(x+h)-f(x)}{h}=
\)CorrectIncorrectHint
We have
\(
\lim _{h \rightarrow 0} \frac{f(x+h)-f(x)}{h}=\lim _{h \rightarrow 0} \frac{\left[3(x+h)^2-(x+h)\right]-\left(3 x^2-x\right)}{h}
\)
\(
\begin{aligned}
& =\lim _{h \rightarrow 0} \frac{6 x h+3 h^2-h}{h} \\
& =\lim _{h \rightarrow 0}[6 x+3 h-1]=6 x-1
\end{aligned}
\) -
Question 60 of 135
60. Question
Let
\(
f(x)= \begin{cases}x & \text { if } 0 \leq x \leq 1 \\ 2 x-1 & \text { if } 1 \leq x \leq 2 x\end{cases}
\)
Then \(\lim _{x \rightarrow 1} f(x)\) is equal toCorrectIncorrectHint
We have
\(
\begin{aligned}
\lim _{x \rightarrow 1-0} f(x) & =\lim _{h \rightarrow 0} f(1-h)=\lim _{h \rightarrow 0}(1-h)=1 \\
\lim _{x \rightarrow 1+0} f(x) & =\lim _{h \rightarrow 0} f(1+h)=\lim _{h \rightarrow 0}[2(1+h)-1] \\
& =\lim _{h \rightarrow 0}(2+2 h-1)=1
\end{aligned}
\)
Therefore
\(
\begin{aligned}
& \lim _{x \rightarrow 1-0} f(x)=\lim _{x \rightarrow 1+0} f(x)=1 \\
\Rightarrow & \lim _{x \rightarrow 1} f(x)=1
\end{aligned}
\) -
Question 61 of 135
61. Question
Let
\(
f(x)= \begin{cases}x-1 & \text { if } x \leq 1 \\ 2 x-1 & \text { if } 1<x<2 \\ x+1 & \text { if } x \geq 2\end{cases}
\)
Then \(\lim _{x \rightarrow 1} f(x)\)CorrectIncorrectHint
\(
\begin{aligned}
& \lim _{x \rightarrow 1-0} f(x)=\lim _{h \rightarrow 0} f(1-h)=\lim _{h \rightarrow 0}[(1-h)-1]=0 \\
& \lim _{x \rightarrow 1+0} f(x)=\lim _{h \rightarrow 0} f(1+h)=\lim _{h \rightarrow 0}[2(1+h)-1]=1 \\
& \lim _{x \rightarrow 1-0} f(x) \neq \lim _{x \rightarrow 1+0} f(x) \Rightarrow \lim _{x \rightarrow 1} f(x) \text { does not exist }
\end{aligned}
\) -
Question 62 of 135
62. Question
Let \(f(x)=x[x]\), where \([x]\) denotes integral part of \(x\).
If \(a\) is not an integer, then
\(
\lim _{h \rightarrow 0} \frac{f(a+h)-f(a)}{h}=
\)CorrectIncorrectHint
We have
\(
\begin{aligned}
& \lim _{h \rightarrow 0} \frac{f(a+h)-f(a)}{h}=\lim _{h \rightarrow 0} \frac{(a+h)[a+h]-a[a]}{h} \\
& =\lim _{h \rightarrow 0} \frac{(a+h)[a]-a[a]}{h} \quad(\because a \text { is not an integer, } \\
& {[a+h]=[a] \text { for small values of } h \text { ) }} \\
& =\lim _{h \rightarrow 0}[a]=[a] \\
&
\end{aligned}
\) -
Question 63 of 135
63. Question
Let
\(
f(x)= \begin{cases}\frac{\sin \left(x^2\right)}{x} & \text { if } x \neq 0 \\ 1 & \text { if } x=0\end{cases}
\)
Then \(\lim _{x \rightarrow 0} f(x)\) isCorrectIncorrectHint
We have
\(
\begin{aligned}
\lim _{x \rightarrow 0} f(x) & =\lim _{x \rightarrow 0} x\left(\frac{\sin x^2}{x^2}\right) \\
& =0 \times 1 \quad \text { (By Theorem 1.27) } \\
& =0
\end{aligned}
\) -
Question 64 of 135
64. Question
\(\lim _{x \rightarrow 0} \frac{(1+x)^{1 / 2}-1}{(1+x)^{1 / 3}-1}\) is equal to
CorrectIncorrectHint
\(
\begin{aligned}
f(x) & =\frac{(1+x)^{1 / 2}-1}{(1+x)^{1 / 3}-1} \\
& =\left(\frac{(1+x)^{1 / 2}-1}{1+x-1}\right) \div \frac{(1+x)^{1 / 3}-1}{1+x-1} \\
& =\frac{y^{1 / 2}-1}{y-1} \div \frac{y^{1 / 3}-1}{y-1}
\end{aligned}
\)
where \(y=1+x\). Now \(y \rightarrow 1\) as \(x \rightarrow 0\). Therefore
\(
\begin{aligned}
\lim _{x \rightarrow 0} f(x) & =\lim _{y \rightarrow 1}\left[\left(\frac{y^{1 / 2}-1}{y-1}\right) \div\left(\frac{y^{1 / 3}-1}{y-1}\right)\right] \\
& =\lim _{y \rightarrow 1}\left(\frac{y^{1 / 2}-1}{y-1}\right) \div \lim _{y \rightarrow 1}\left(\frac{y^{1 / 3}-1}{y-1}\right) \\
& =\frac{1}{2} \div \frac{1}{3} \quad \text { (By Theorem 1.26) } \\
& =\frac{3}{2}
\end{aligned}
\) -
Question 65 of 135
65. Question
\(\lim _{x \rightarrow 0} \frac{\sin (a+x)-\sin (a-x)}{x}\) equals
CorrectIncorrectHint
Let
\(
\begin{aligned}
f(x) & =\frac{\sin (a+x)-\sin (a-x)}{x} \\
& =\frac{2 \cos a \sin x}{x} \\
& =(2 \cos a)\left(\frac{\sin x}{x}\right)
\end{aligned}
\)
Therefore
\(
\begin{aligned}
\lim _{x \rightarrow 0} f(x) & =\lim _{x \rightarrow 0}(2 \cos a)\left(\frac{\sin x}{x}\right) \\
& =(2 \cos a) \lim _{x \rightarrow a}\left(\frac{\sin x}{x}\right) \quad \text { (By Corollary 1.2) } \\
& =(2 \cos a) \times 1 \\
& =2 \cos a
\end{aligned}
\) -
Question 66 of 135
66. Question
\(\lim _{x \rightarrow a}\left(\frac{\tan x-\tan a}{x-a}\right)\) is
CorrectIncorrectHint
We have
\(
\begin{aligned}
f(x) & =\frac{\tan x-\tan a}{x-a} \\
& =\frac{\sin x \cos a-\cos x \sin a}{(x-a) \cos x \cos a} \\
& =\left(\frac{\sin (x-a)}{x-a}\right) \frac{1}{\cos x \cos a}
\end{aligned}
\)
Therefore
\(
\begin{aligned}
\lim _{x \rightarrow a} f(x) & =\lim _{x \rightarrow a}\left(\frac{\sin (x-a)}{x-a}\right) \times \lim _{x \rightarrow a}\left(\frac{1}{\cos x \cos a}\right) \\
& =1 \times \frac{1}{\cos a \cos a} \\
& =\sec ^2 a
\end{aligned}
\) -
Question 67 of 135
67. Question
\(\lim _{x \rightarrow 0} \frac{\sin 2 x}{x \cos x}\) is equal to
CorrectIncorrectHint
We have
\(
\begin{aligned}
\lim _{x \rightarrow 0} \frac{\sin 2 x}{x \cos x} & =\lim _{x \rightarrow 0} 2\left(\frac{\sin 2 x}{2 x}\right)\left(\frac{1}{\cos x}\right) \\
& =2 \times 1 \times \frac{1}{1} \\
& =2
\end{aligned}
\) -
Question 68 of 135
68. Question
Let \(f(x)=\sin x / x\) for \(x \neq 0\) and [.] denote the greatest integer function. Then \(\lim _{x \rightarrow 0}[f(x)]\) is
CorrectIncorrectHint
Let \(0<\delta<1\).
\(
0<\frac{\sin x}{x}<1 \quad \forall x \in(-\delta, \delta)
\)
Therefore
\(
\left[\frac{\sin x}{x}\right]=0 \quad \forall x \in(-\delta, \delta)
\)
Hence \(\lim _{x \rightarrow 0}[f(x)]=0\). -
Question 69 of 135
69. Question
\(\lim _{x \rightarrow \infty} \sqrt{\frac{x+\sin x}{x-\cos x}}\) is equal to
CorrectIncorrectHint
We have
\(
\frac{x+\sin x}{x-\cos x}=\frac{1+\frac{\sin x}{x}}{1-\frac{\cos x}{x}}
\)
Put \(y=1 / x\) so that \(y \rightarrow 0\) as \(x \rightarrow \infty\). Now
\(
y \sin \frac{1}{y} \rightarrow 0 \text { and } y \cos \frac{1}{y} \rightarrow 0
\)
as \(y \rightarrow 0\), Therefore
\(
\lim _{x \rightarrow \infty} f(x)=\sqrt{\frac{1}{1}}=1
\) -
Question 70 of 135
70. Question
Let
\(
f(x)=\frac{2-\sqrt{3} \cos x-\sin x}{(6 x-\pi)^2}
\)
for \(x \neq \pi / 6\). Then \(\lim _{x \rightarrow \pi / 6} f(x)\) isCorrectIncorrectHint
Put \(y=6 x-\pi\) so that \(y \rightarrow 0\) as \(x \rightarrow \pi / 6\). Also \(x=(\pi+y) / 6\). Therefore
\(
\begin{aligned}
f(x) & =\frac{2-\sqrt{3} \cos \left(\frac{\pi}{6}+\frac{y}{6}\right)-\sin \left(\frac{\pi}{6}+\frac{y}{6}\right)}{y^2} \\
& =\frac{2-\sqrt{3}\left[\frac{\sqrt{3}}{2} \cos \frac{y}{6}-\frac{1}{2} \sin \frac{y}{6}\right]-\left[\frac{1}{2} \cos \frac{y}{6}+\frac{\sqrt{3}}{2} \sin \frac{y}{6}\right]}{y^2} \\
& =\frac{2-2 \cos (y / 6)}{y^2} \\
& =\frac{4 \sin ^2(y / 12)}{y^2} \\
& =4\left[\frac{\sin (y / 12)}{y / 12}\right]^2 \times \frac{1}{144} \\
& =\frac{1}{36}\left(\frac{\sin \theta}{\theta}\right)^2
\end{aligned}
\)
where \(\theta=y / 12 \rightarrow 0\) as \(y \rightarrow 0\). Therefore
\(
\begin{aligned}
\lim _{x \rightarrow 0} f(x) & =\frac{1}{36} \lim _{\theta \rightarrow 0}\left(\frac{\sin \theta}{\theta}\right)^2 \\
& =\frac{1}{36} \times 1^2=\frac{1}{36}
\end{aligned}
\) -
Question 71 of 135
71. Question
\(\lim _{x \rightarrow 0} \frac{\sqrt{2}-\sqrt{1+\cos x}}{\sin ^2 x}\) is equal to
CorrectIncorrectHint
We have
\(
\begin{aligned}
\frac{\sqrt{2}-\sqrt{1+\cos x}}{\sin ^2 x} & =\frac{2-(1+\cos x)}{\sin ^2 x} \times \frac{1}{\sqrt{2}+\sqrt{1+\cos x}} \\
& =\left(\frac{2 \sin ^2 \frac{x}{2}}{4 \sin ^2 \frac{x}{2} \cos ^2 \frac{x}{2}}\right) \frac{1}{\sqrt{2}+\sqrt{1+\cos x}} \\
& =\frac{1}{2 \cos ^2 \frac{x}{2}} \times \frac{1}{\sqrt{2}+\sqrt{1+\cos x}}
\end{aligned}
\)
Therefore
\(
\lim _{x \rightarrow 0} \frac{\sqrt{2}-\sqrt{1+\cos x}}{\sin ^2 x}=\frac{1}{2} \times \frac{1}{\sqrt{2}+\sqrt{1+1}}=\frac{1}{4 \sqrt{2}}
\) -
Question 72 of 135
72. Question
\(\lim _{x \rightarrow 0} \frac{\sin \left(\pi \cos ^2 x\right)}{x^2}\) is equal to
CorrectIncorrectHint
We have
\(
\begin{aligned}
\lim _{x \rightarrow 0} \frac{\sin \left(\pi \cos ^2 x\right)}{x^2} & =\lim _{x \rightarrow 0} \frac{\sin \left(\pi\left(1-\sin ^2 x\right)\right)}{x^2} \\
& =\lim _{x \rightarrow 0} \frac{\sin \left(\pi-\pi \sin ^2 x\right)}{x^2} \\
& =\lim _{x \rightarrow 0} \frac{\sin \left(\pi \sin ^2 x\right)}{x^2} \\
& =\lim _{x \rightarrow 0} \pi \cdot \frac{\sin \left(\pi \sin ^2 x\right)}{\left(\pi \sin ^2 x\right)} \cdot \frac{\sin ^2 x}{x^2} \\
& =\pi \lim _{x \rightarrow 0}\left(\frac{\sin \left(\pi \sin ^2 x\right)}{\pi \sin ^2 x}\right) \cdot \lim _{x \rightarrow 0}\left(\frac{\sin x}{x}\right)^2 \\
& =\pi \times 1 \times 1=\pi
\end{aligned}
\) -
Question 73 of 135
73. Question
Let
\(
f(x)= \begin{cases}\frac{\sin [x]}{[x]} & \text { if }[x] \neq 0 \\ 0 & \text { if }[x]=0\end{cases}
\)
where \([x]\) is the integral part of \(x\). Then \(\lim _{x \rightarrow 0} f(x)\) equalsCorrectIncorrectHint
Observe that \([x]=0 \Leftrightarrow 0<x<1\). Therefore if \(0<\delta<1\), then
\(
f(x)= \begin{cases}0 & \text { if } 0<x<\delta \\ \frac{\sin (-1)}{(-1)}=\sin 1 & \text { if }-\delta<x<0\end{cases}
\)
So
\(
\lim _{x \rightarrow 0+0} f(x)=0 \text { and } \lim _{x \rightarrow 0-0} f(x)=\sin 1
\)
Hence \(\lim _{x \rightarrow 0} f(x)\) does not exist. -
Question 74 of 135
74. Question
\(\lim _{x \rightarrow 1} \frac{\sqrt{1-\cos 2(x-1)}}{x-1}\)
CorrectIncorrectHint
We have
\(
\frac{\sqrt{1-\cos 2(x-1)}}{x-1}=\sqrt{2} \frac{|\sin (x-1)|}{x-1}
\)
Therefore
\(
\begin{aligned}
\lim _{x \rightarrow 1-0} \frac{\sqrt{1-\cos 2(x-1)}}{x-1} & =\lim _{h \rightarrow 0} \frac{\sqrt{2}|\sin (1-h-1)|}{(1-h)-1} \\
& =\lim _{h \rightarrow 0} \sqrt{2}\left(\frac{-\sinh }{h}\right)=-\sqrt{2} \\
\lim _{x \rightarrow 1+0} \frac{\sqrt{1-\cos 2(x-1)}}{x-1} & =\sqrt{2} \lim _{h \rightarrow 0} \frac{|\sin (1+h-1)|}{1+h-1} \\
& =\sqrt{2} \lim _{h \rightarrow 0}\left(\frac{\sin h}{h}\right) \\
& =\sqrt{2}
\end{aligned}
\)
Left limit \(\neq\) Right limit -
Question 75 of 135
75. Question
\(\lim _{x \rightarrow 0} \frac{x \tan 2 x-2 x \tan x}{(1-\cos 2 x)^2}\) equals
CorrectIncorrectHint
Let
\(
\begin{aligned}
f(x) & =\frac{x \tan 2 x-2 x \tan x}{(1-\cos 2 x)^2} \\
& =\frac{2 x \tan x\left(\frac{1}{1-\tan ^2 x}-1\right)}{4 \sin ^4 x} \\
& =\frac{x \tan ^3 x}{2 \sin ^4 x} \times \frac{1}{1-\tan ^2 x} \\
& =\frac{x \sin ^3 x}{2 \cos ^3 x \sin ^4 x} \times \frac{\cos ^2 x}{\cos 2 x} \\
& =\frac{1}{2}\left(\frac{x}{\sin x}\right) \frac{1}{\cos x \cos 2 x}
\end{aligned}
\)
So
\(
\lim _{x \rightarrow 0} f(x)=\frac{1}{2}(1) \times \frac{1}{1}=\frac{1}{2}
\) -
Question 76 of 135
76. Question
Let \(f: R ^{+} \rightarrow R ^{+}\)be a function satisfying the relation \(f(x \cdot f(y))=f(x y)+x\) for all \(x, y \in R ^{+}\). Then
\(
\lim _{x \rightarrow 0}\left(\frac{f(x)^{1 / 3}-1}{f(x)^{1 / 2}-1}\right)=
\)CorrectIncorrectHint
Given relation is
\(
f(x \cdot f(y))=f(x y)+x \dots(1)
\)
Interchanging \(x\) and \(y\) in Eq. (1), we have
\(
f(y \cdot f(x))=f(y x)+y \dots(2)
\)
Again replacing \(x\) with \(f(x)\) in Eq. (1) we get
\(
f(f(x) \cdot f(y))=f(y \cdot f(x))+f(x) \dots(3)
\)
Therefore, Eqs. (1)-(3) imply
\(
f(f(x) \cdot f(y))=f(x y)+y+f(x) \dots(4)
\)
Again interchanging \(x\) and \(y\) in Eq. (4), we have
\(
f(f(y) \cdot f(x))=f(y x)+x+f(y) \dots(5)
\)
Equations (4) and (5) imply
\(
\begin{aligned}
& f(x y)+y+f(x)=f(y x)+x+f(y) \dots(6) \\
\Rightarrow & f(x)-x=f(y)-y \forall x, y \in R ^{+}
\end{aligned}
\)
Suppose
\(
f(x)-x=f(y)-y=\lambda
\)
Substituting \(f(x)=\lambda+x\) in Eq. (1), we have
\(
\begin{aligned}
& x \cdot f(y)+\lambda=(x y+\lambda)+x \\
\Rightarrow & x \cdot f(y)=x y+x
\end{aligned}
\)
Therefore
\(
\begin{aligned}
& x(y+\lambda)=x y+x \quad[\because f(y)=\lambda+y] \\
\Rightarrow & \lambda x=x \\
\Rightarrow & \lambda=1 \quad(\because x>0)
\end{aligned}
\)
So \(f(x)=x+\lambda=x+1\)
Hence
\(
\begin{aligned}
\lim _{x \rightarrow 0} \frac{(f(x))^{1 / 3}-1}{(f(x))^{1 / 2}-1} & =\lim _{x \rightarrow 0} \frac{(1+x)^{1 / 3}-1}{(1+x)^{1 / 2}-1} \\
& =\lim _{x \rightarrow 0}\left(\frac{(1+x)^{1 / 3}-1}{1+x-1}\right) \cdot\left(\frac{1+x-1}{(1+x)^{1 / 2}-1}\right) \\
& =\frac{1 / 3}{1 / 2}=\frac{2}{3}
\end{aligned}
\) -
Question 77 of 135
77. Question
Let
\(
f(x)= \begin{cases}\sin x & \text { if } x \neq n \pi, n \neq 0, \pm 1, \pm 2, \ldots \\ 2 & \text { otherwise }\end{cases}
\)
and \(g(x)= \begin{cases}x^2+1, & x \neq 0,2 \\ 4, & x=0 \\ 5, & x=2\end{cases}\)
Then \(\lim _{x \rightarrow 0} g(f(x))\) isCorrectIncorrectHint
If \(0<\delta<1\), then \(f(x)=\sin x\) for \(x \in(-\delta, \delta)\), \(x \neq 0\). Therefore
\(
\lim _{x \rightarrow 0} g(f(x))=\lim _{x \rightarrow 0} g(\sin x)=\lim _{x \rightarrow 0}\left(\sin ^2 x+1\right)=1
\) -
Question 78 of 135
78. Question
\(\lim _{x \rightarrow 1}(1-x) \tan \frac{\pi x}{2}=\)
CorrectIncorrectHint
Put \(1-x=\theta\) so that \(\theta \rightarrow 0\) as \(x \rightarrow 1\). Therefore
\(
\begin{aligned}
\lim _{x \rightarrow 1}(1-x) \tan \frac{\pi x}{2} & =\lim _{\theta \rightarrow 0} \theta \tan \frac{\pi}{2}(1-\theta) \\
& =\lim _{\theta \rightarrow 0} \theta \cot \left(\frac{\pi \theta}{2}\right) \\
& =\lim _{\theta \rightarrow 0} \frac{\theta \cos \left(\frac{\pi}{2} \theta\right)}{\sin \left(\frac{\pi}{2} \theta\right)} \\
& =\lim _{\theta \rightarrow 0} \frac{2}{\pi} \cdot\left(\frac{\frac{\pi}{2} \theta}{\sin \left(\frac{\pi}{2} \theta\right)}\right) \cos \left(\frac{\pi}{2} \theta\right) \\
& =\frac{2}{\pi} \times 1 \times 1=\frac{2}{\pi}
\end{aligned}
\) -
Question 79 of 135
79. Question
Let
\(
f(x)= \begin{cases}|x-3| & \text { if } x \geq 1 \\ \frac{x^2}{4}-\frac{3 x}{2}+\frac{13}{4} & \text { if } x<1\end{cases}
\)
Then \(\lim _{x \rightarrow 1} f(x)\) is equal toCorrectIncorrectHint
We have
\(
\begin{gathered}
\lim _{x \rightarrow 1-0} f(x)=\lim _{h \rightarrow 0}\left[\frac{(1-h)^2}{4}-\frac{3}{2}(1-h)+\frac{13}{4}\right]=\frac{1}{4}-\frac{3}{2}+\frac{13}{4}=2 \\
\lim _{x \rightarrow 1+0} f(x)=\lim _{h \rightarrow 0}|1+h-3|=2
\end{gathered}
\)
Therefore
\(
\lim _{x \rightarrow 1} f(x)=2
\) -
Question 80 of 135
80. Question
Let \(f(x)=\operatorname{Min}\left\{x, x^2\right\}\). Then
\(
\lim _{h \rightarrow 0} \frac{f(1+h)-f(1)}{h}=
\)CorrectIncorrectHint
We can see that (Fig. below)
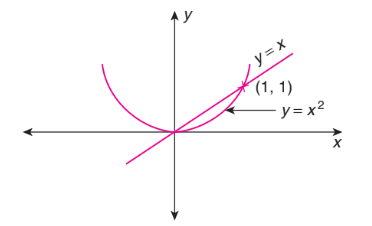
\(
f(x)= \begin{cases}x & \text { if } x \leq 0 \\ x^2 & \text { if } 0<x \leq 1 \\ x & \text { if } x>1\end{cases}
\)
Now
\(
\begin{aligned}
\lim _{h \rightarrow 0-0} \frac{f(1+h)-f(1)}{-h} & =\lim _{h \rightarrow 0} \frac{(1-h)^2-1}{-h} \\
& =\lim _{h \rightarrow 0} \frac{-2 h+h^2}{-h}=2
\end{aligned}
\)
Now
\(
\lim _{h \rightarrow 0+0} \frac{f(1+h)-f(1)}{h}=\lim _{h \rightarrow 0} \frac{(1+0+h)-1}{0+h}=\lim _{h \rightarrow 0}\left(\frac{h}{h}\right)=1
\)
Therefore the required limit does not exist. -
Question 81 of 135
81. Question
\(\lim _{x \rightarrow 0} \frac{\tan x-\sin x}{x^3}=\)
CorrectIncorrectHint
We have
\(
\begin{aligned}
\lim _{x \rightarrow 0} \frac{\tan x-\sin x}{x^3} & =\lim _{x \rightarrow 0} \frac{\sin x(1-\cos x)}{x^3 \cos x} \\
& =\lim _{x \rightarrow 0} \frac{\left(2 \sin \frac{x}{2} \cos \frac{x}{2}\right)\left(2 \sin ^2 \frac{x}{2}\right)}{x^3 \cos x} \\
& =\lim _{x \rightarrow 0} 4\left(\frac{\sin \frac{x}{2}}{\left(\frac{x}{2}\right)}\right) \cdot\left(\frac{\cos \frac{x}{2}}{8 \cos x}\right) \\
& =\frac{1}{2} \times 1^3 \times 1=\frac{1}{2}
\end{aligned}
\) -
Question 82 of 135
82. Question
\(\lim _{x \rightarrow-1} \frac{x+1}{(17+x)^{1 / 4}-2}=\)
CorrectIncorrectHint
Let
\(
f(x)=\frac{x+1}{(17+x)^{1 / 4}-2}
\)
Put \((17+x)^{1 / 4}=y\) so that \(y \rightarrow 2\) as \(x \rightarrow-1\). Therefore
\(
f(x)=\frac{y^4-16}{y-2}=\frac{y^4-2^4}{y-2}
\)
So
\(
\lim _{x \rightarrow-1} f(x)=\lim _{y \rightarrow 2}\left(\frac{y^4-2^4}{y-2}\right)=4 \times 2^3=32
\) -
Question 83 of 135
83. Question
\(\lim _{x \rightarrow-1} \frac{1+\sqrt[n]{x}}{1+\sqrt[m]{x}}\) ( \(m, n\) are odd positive integers) is
CorrectIncorrectHint
Put \(x=z^{m n}\) so that \(x \rightarrow-1 \Rightarrow z \rightarrow-1\) and \(x^{1 / n}=z^m, x^{1 / m}=z^n\). Therefore
\(
\begin{aligned}
& \lim _{x \rightarrow-1} \frac{1+\sqrt[n]{x}}{1+\sqrt[m]{x}}=\lim _{z-1} \frac{z^m+1}{z^n+1} \\
&=\lim _{z \rightarrow-1}\left(\frac{z^m-(-1)^m}{z+1} \cdot \frac{z+1}{z^n-(-1)^n}\right) \\
&(\because m, n \text { are odd }) \\
&=m(-1)^{m-1} \cdot \frac{1}{n(-1)^{n-1}} \\
&=\frac{m}{n}(\because m, n \text { are odd })
\end{aligned}
\) -
Question 84 of 135
84. Question
\(\lim _{x \rightarrow \frac{\pi}{6}}\left(\frac{2 \sin ^2 x+\sin x-1}{2 \sin ^2 x-3 \sin x+1}\right)=\)
CorrectIncorrectHint
Given limit is
\(
\lim _{x \rightarrow \frac{\pi}{6}} \frac{(2 \sin x-1)(\sin x+1)}{(2 \sin x-1)(\sin x-1)}=\lim _{x \rightarrow \frac{\pi}{6}}\left(\frac{\sin x+1}{\sin x-1}\right)
\)
\(
=\frac{(1 / 2)+1}{(1 / 2)-1}=-3
\) -
Question 85 of 135
85. Question
\(\lim _{x \rightarrow 0} \frac{1-\cos m x}{1-\cos n x}=\)
CorrectIncorrectHint
We have
\(
\begin{aligned}
\lim _{x \rightarrow 0}\left(\frac{1-\cos m x}{1-\cos n x}\right) & =\lim _{x \rightarrow 0} \frac{2 \sin ^2\left(\frac{m x}{2}\right)}{2 \sin ^2\left(\frac{n x}{2}\right)} \\
& =\lim _{x \rightarrow 0}\left(\frac{\sin \left(\frac{m x}{2}\right)}{m x / 2} \cdot \frac{m x}{2}\right)^2\left(\frac{n x / 2}{\sin \left(\frac{n x}{2}\right)} \cdot \frac{1}{n x / 2}\right) \\
& =\lim _{x \rightarrow 0}\left(\frac{\sin \frac{m x}{2}}{\frac{m x}{2}}\right)^2 \cdot \lim _{x \rightarrow 0}\left(\frac{\frac{n x}{2}}{\sin \frac{n x}{2}}\right)^2 \cdot \frac{m^2}{n^2} \\
& =1^2 \times 1^2 \times \frac{m^2}{n^2}=\frac{m^2}{n^2}
\end{aligned}
\) -
Question 86 of 135
86. Question
\(\lim _{x \rightarrow 0}\left(\frac{\operatorname{Sin}^{-1} x}{x}\right)=\)
CorrectIncorrectHint
Put \(\theta=\operatorname{Sin}^{-1} x\) so that \(\theta \rightarrow 0\) as \(x \rightarrow 0\) and \(x=\sin \theta\). Therefore
\(
\lim _{x \rightarrow 0}\left(\frac{\operatorname{Sin}^{-1} x}{x}\right)=\lim _{\theta \rightarrow 0}\left(\frac{\theta}{\sin \theta}\right)=1
\) -
Question 87 of 135
87. Question
\(\lim _{x \rightarrow 1}\left(\frac{1+\cos \pi x}{\tan ^2 \pi x}\right)=\)
CorrectIncorrectHint
Let
\(
f(x)=\frac{1+\cos \pi x}{\tan ^2 \pi x}=\frac{(1+\cos \pi x) \cos ^2 \pi x}{\sin ^2 \pi x}
\)
\(
=\frac{(1+\cos \pi x) \cos ^2 \pi x}{1-\cos ^2 \pi x}=\frac{\cos ^2 \pi x}{1-\cos \pi x}
\)
Therefore
\(
\begin{aligned}
\lim _{x \rightarrow 1} f(x) & =\lim _{x \rightarrow 1} \frac{\cos ^2 \pi x}{1-\cos \pi x} \\
& =\frac{\cos ^2(\pi)}{1-\cos \pi} \\
& =\frac{(-1)^2}{1-(-1)}=\frac{1}{2}
\end{aligned}
\) -
Question 88 of 135
88. Question
\(\lim _{x \rightarrow 1}\left(\frac{x^{-1 / 3}-1}{x^{-2 / 3}-1}\right)=\)
CorrectIncorrectHint
We have
\(
\frac{x^{-1 / 3}-1}{x^{-2 / 3}-1}=\frac{x^{-1 / 3}-1}{x-1} \cdot \frac{x-1}{x^{-2 / 3}-1}
\)
Therefore
\(
\begin{aligned}
\lim _{x \rightarrow 1}\left(\frac{x^{-1 / 3}-1}{x^{-2 / 3}-1}\right) & =\lim _{x \rightarrow 1}\left(\frac{x^{-1 / 3}-1}{x-1}\right) \cdot \lim _{x \rightarrow 1}\left(\frac{x-1}{x^{-2 / 3}-1}\right) \\
& =\frac{-\frac{1}{3}(1)^{(-1 / 3)-1}}{-\frac{2}{3}(1)^{(-2 / 3)-1}}=\frac{1}{2}
\end{aligned}
\) -
Question 89 of 135
89. Question
\(\lim _{x \rightarrow \frac{\pi}{2}}(\sec x-\tan x)=\)
CorrectIncorrectHint
We have
\(
\begin{aligned}
\lim _{x \rightarrow \frac{\pi}{2}}(\sec x-\tan x) & =\lim _{x \rightarrow \frac{\pi}{2}}\left(\frac{1-\sin x}{\cos x}\right) \\
& =\lim _{x \rightarrow \frac{\pi}{2}} \frac{1-\cos \left(\frac{\pi}{2}-x\right)}{\sin \left(\frac{\pi}{2}-x\right)} \\
& =\lim _{x \rightarrow \frac{\pi}{2}} \frac{2 \sin ^2\left(\frac{\pi}{4}-\frac{x}{2}\right)}{2 \sin \left(\frac{\pi}{4}-\frac{x}{2}\right) \cos \left(\frac{\pi}{4}-\frac{x}{2}\right)}
\end{aligned}
\)
\(
\begin{gathered}
=\lim _{x \rightarrow \frac{\pi}{2}} \frac{\sin \left(\frac{\pi}{4}-\frac{x}{2}\right)}{\cos \left(\frac{\pi}{4}-\frac{x}{2}\right)} \\
=\frac{\sin \left(\frac{\pi}{4}-\frac{\pi}{4}\right)}{\cos \left(\frac{\pi}{4}-\frac{\pi}{4}\right)}=0
\end{gathered}
\)
Alternate:
\(
\begin{aligned}
\lim _{x \rightarrow \frac{\pi}{2}}(\sec x-\tan x) & =\lim _{x \rightarrow \frac{\pi}{2}}\left(\frac{1-\sin x}{\cos x}\right) \\
& =\lim _{x \rightarrow \frac{\pi}{2}} \frac{1-\sin x}{\sqrt{1-\sin ^2 x}} \\
& =\lim _{x \rightarrow \frac{\pi}{2}} \sqrt{\frac{1-\sin x}{1+\sin x}} \\
& =\sqrt{\frac{1-1}{1+1}}=0
\end{aligned}
\) -
Question 90 of 135
90. Question
If
\(
f(x)=\frac{(2 x-3)(\sqrt{x}-1)}{2 x^2+x-3}
\)
then \(\lim _{x \rightarrow 1} f(x)\) is equal toCorrectIncorrectHint
\(f(x)\) is defined in a deleted neighbourhood 1.
Also
\(
f(x)=\frac{(2 x-3)(\sqrt{x}-1)}{(2 x+3)(x-1)}=\frac{(2 x-3)}{(2 x+3)(\sqrt{x}+1)}
\)
Therefore
\(
\lim _{x \rightarrow 1} f(x)=\frac{2-3}{(2+3)(1+1)}=-\frac{1}{10}
\) -
Question 91 of 135
91. Question
Let
\(
g(x)=\frac{\tan ^3 x-\tan x}{\cos [x+(\pi / 4)]}
\)
Then \(\lim _{x \rightarrow \frac{\pi}{4}} g(x)\) isCorrectIncorrectHint
\(g(x)\) is defined in \(a\) neighbourhood of \(\pi / 4\) except at \(\pi / 4\). Now,
\(
\begin{aligned}
g(x) & =\frac{\tan x(\tan x+1)(\tan x-1)}{(1 / \sqrt{2})(\cos x-\sin x)} \\
& =\frac{\sqrt{2} \tan x(\tan x+1)(\sin x-\cos x)}{\cos x(\cos x-\sin x)} \\
& =\frac{-\sqrt{2} \tan x(\tan x+1)}{\cos x}
\end{aligned}
\)
Therefore
\(
\lim _{x \rightarrow \frac{\pi}{4}} g(x)=\frac{-\sqrt{2}(1)(1+1)}{1 / \sqrt{2}}=-2(2)=-4
\) -
Question 92 of 135
92. Question
\(\lim _{x \rightarrow+\infty} x\left(\sqrt{x^2+1}-x\right)=\)
CorrectIncorrectHint
We have
\(
\begin{aligned}
\lim _{x \rightarrow+\infty} x\left(\sqrt{x^2+1}-x\right) & =\lim _{x \rightarrow+\infty} \frac{x\left(x^2+1-x^2\right)}{\sqrt{x^2+1}+x} \\
& =\lim _{x \rightarrow+\infty} \frac{1}{\sqrt{1+\frac{1}{x^2}}+1} \\
& =\frac{1}{1+1}=\frac{1}{2}
\end{aligned}
\) -
Question 93 of 135
93. Question
\(\lim _{x \rightarrow-\infty}\left(\sqrt{2 x^2-3}-5 x\right)\) is
CorrectIncorrectHint
We have
\(
\begin{aligned}
\lim _{x \rightarrow-\infty}\left(\sqrt{2 x^2-3}-5 x\right) & =\lim _{x \rightarrow-\infty}\left(\frac{2 x^2-3-25 x^2}{\sqrt{2 x^2-3}+5 x}\right) \\
& =-\lim _{x \rightarrow-\infty}\left(\frac{23 x^2+3}{\sqrt{2 x^2-3}+5 x}\right) \\
& =-\lim _{x \rightarrow-\infty}\left(\frac{23 x+\frac{3}{x}}{\sqrt{2-\frac{3}{x^2}+5 x}}\right)
\end{aligned}
\)
\(
=\frac{-(-\infty)}{\sqrt{2}+5}=+\infty
\) -
Question 94 of 135
94. Question
\(\lim _{x \rightarrow \frac{\pi}{2}} \frac{\cos x}{(1-\sin x)^{2 / 3}}=\)
CorrectIncorrectHint
Let
\(
f(x)=\frac{\cos x}{(1-\sin x)^{2 / 3}}
\)
Put \(\theta=(\pi / 2)-x\) so that \(\theta \rightarrow 0\) as \(x \rightarrow \pi / 2\). Now
\(
\begin{aligned}
f(x) & =\frac{\cos \left(\frac{\pi}{2}-\theta\right)}{\left(1-\sin \left(\frac{\pi}{2}-\theta\right)\right)^{2 / 3}} \\
& =\frac{\sin \theta}{(1-\cos \theta)^{2 / 3}} \\
& =\frac{2 \sin \left(\frac{\theta}{2}\right) \cos \left(\frac{\theta}{2}\right)}{2^{2 / 3} \cdot \sin ^{4 / 3}\left(\frac{\theta}{2}\right)} \\
& =\frac{2^{1 / 3} \cos \theta}{\sin ^{1 / 3}\left(\frac{\theta}{2}\right)} \rightarrow \infty \quad \text { as } \theta \rightarrow 0
\end{aligned}
\) -
Question 95 of 135
95. Question
Let \(f(x)=x^3\left\{\sqrt{x^2+\sqrt{x^4+1}}-x \sqrt{2}\right\}\). Then \(\lim _{x \rightarrow \infty} f(x)\) is equal to
CorrectIncorrectHint
We have
\(
\begin{aligned}
f(x) & =\frac{x^3\left\{x^2+\sqrt{x^4+1}-2 x^2\right\}}{\sqrt{x^2+\sqrt{x^4+1}}+x \sqrt{2}} \\
& =\frac{x^3\left\{\sqrt{x^4+1}-x^2\right\}}{\sqrt{x^2+\sqrt{x^4+1}}+x \sqrt{2}} \\
& =\frac{x^3\left(x^4+1-x^4\right)}{\left[\sqrt{x^2+\sqrt{x^4+1}}+x \sqrt{2}\right]\left[\sqrt{x^4+1}+x^2\right]} \\
& =\frac{x^3}{\left[\sqrt{x^2 \sqrt{x^4+1}}+x \sqrt{2}\right]\left[\sqrt{x^4+1}+x^2\right]} \\
& =\frac{1}{\left[\sqrt{1+\sqrt{1+\frac{1}{x^4}}}+\sqrt{2}\right]\left[\sqrt{1+\frac{1}{x^4}}+1\right]}
\end{aligned}
\)
\(
\begin{aligned}
& =\frac{1}{(\sqrt{1+\sqrt{1}}+\sqrt{2})(\sqrt{1}+1)} \\
& =\frac{1}{2 \sqrt{2}(2)}=\frac{1}{4 \sqrt{2}}
\end{aligned}
\) -
Question 96 of 135
96. Question
\(\lim _{x \rightarrow 0}\left[\frac{1}{x} \operatorname{Sin}^{-1}\left(\frac{2 x}{1+x^2}\right)\right]=\)
CorrectIncorrectHint
In a neighbourhood of zero,
\(
\operatorname{Sin}^{-1}\left(\frac{2 x}{1+x^2}\right)=2 \operatorname{Tan}^{-1} x
\)
Therefore
\(
\begin{aligned}
\lim _{x \rightarrow 0}\left(\frac{1}{x} \operatorname{Sin}^{-1} x\right) & =\lim _{x \rightarrow 0}\left(\frac{2 \operatorname{Tan}^{-1} x}{x}\right) \\
& =2 \lim _{\theta \rightarrow 0}\left(\frac{\theta}{\tan \theta}\right) \text { where } \theta=\operatorname{Tan}^{-1} x \\
& =2 \times 1=2
\end{aligned}
\) -
Question 97 of 135
97. Question
\(\lim _{x \rightarrow+\infty}\left[2^{x-1} \tan \left(\frac{3}{2^x}\right)\right]=\)
CorrectIncorrectHint
We have
\(
\begin{aligned}
\lim _{x \rightarrow+\infty}\left(2^{x-1} \tan \left(\frac{3}{2^x}\right)\right) & =\lim _{x \rightarrow+\infty}\left(\frac{1}{2} \frac{\tan \left(\frac{3}{2^x}\right)}{3 / 2^x} \cdot 3\right) \\
& =\frac{3}{2} \lim _{\theta \rightarrow 0}\left(\frac{\tan \theta}{\theta}\right) \quad\left(\text { where } \theta=\frac{3}{2^x}\right) \\
& =\frac{3}{2} \times 1=\frac{3}{2}
\end{aligned}
\) -
Question 98 of 135
98. Question
\(\lim _{x \rightarrow 0} \frac{a^{\tan x}-a^{\sin x}}{\tan x-\sin x}\) is equal to \((a>0)\)
CorrectIncorrectHint
We have
\(
\begin{gathered}
\lim _{x \rightarrow 0} \frac{a^{\tan x}-a^{\sin x}}{\tan x-\sin x}=\lim _{x \rightarrow 0} a^{\sin x}\left(\frac{a^{\tan x-\sin x}-1}{\tan x-\sin x}\right) \\
=\lim _{x \rightarrow 0}\left(a^{\sin x}\right) \times \lim _{t \rightarrow 0}\left(\frac{a^t-1}{t}\right) \quad(\text { where } t=\tan x-\sin x) \\
=a^0 \times \log _e a=\log _e a
\end{gathered}
\) -
Question 99 of 135
99. Question
\(\lim _{x \rightarrow 0}\left(\frac{\log (6+x)-\log (6-x)}{x}\right)=\)
CorrectIncorrectHint
We have
\(
\begin{aligned}
\lim _{x \rightarrow 0}\left(\frac{\log (6+x)-\log (6-x)}{x}\right)= & \lim _{x \rightarrow 0} \frac{\frac{1}{6} \log \left(1+\frac{x}{6}\right)}{x / 6} \\
& +\lim _{x \rightarrow 0} \frac{\frac{1}{6} \log \left(1-\frac{x}{6}\right)}{-x / 6} \\
& =\frac{1}{6} \times 1+\frac{1}{6} \times 1=\frac{1}{3}
\end{aligned}
\) -
Question 100 of 135
100. Question
\(\lim _{x \rightarrow 0} \frac{12^x-3^x-4^x+1}{\sqrt{2 \cos x+7}-3}=\)
CorrectIncorrectHint
The given limit can be written as
\(
\begin{aligned}
& \lim _{x \rightarrow 0} \frac{\left(3^x-1\right)\left(4^x-1\right)(\sqrt{2 \cos x+7}+3)}{2 \cos x-2} \\
& =\lim _{x \rightarrow 0} \frac{\left(\frac{3^x-1}{x}\right)\left(\frac{4^x-1}{x}\right)(\sqrt{2 \cos x+7}+3) x^2}{-4 \sin ^2 \frac{x}{2}} \\
& =\lim _{x \rightarrow 0} \frac{\left(\frac{3^x-1}{x}\right)\left(\frac{4^x-1}{x}\right)(\sqrt{2 \cos x+7}+3)}{-[\sin (x / 2) /(x / 2)]^2} \\
& =-\log _e 3 \times \log _e 4 \times 6
\end{aligned}
\) -
Question 101 of 135
101. Question
\(\lim _{x \rightarrow 0}\left(\frac{1-2^x-5^x+10^x}{x \sin x}\right)=\)
CorrectIncorrectHint
We have
\(
\begin{aligned}
\text { Given limit } & =\lim _{x \rightarrow 0} \frac{\left(5^x-1\right)\left(2^x-1\right)}{x \sin x} \\
& =\lim _{x \rightarrow 0}\left(\frac{5^x-1}{x}\right)\left(\frac{2^x-1}{x}\right)\left(\frac{x}{\sin x}\right) \\
& =\log _e 5 \cdot \log _e 2 \cdot 1 \\
& =\log _e 5 \cdot \log _e 2
\end{aligned}
\) -
Question 102 of 135
102. Question
If \(G(x)=-\sqrt{25-x^2}\), then
\(
\lim _{x \rightarrow 1}\left(\frac{G(x)-G(1)}{x-1}\right)=
\)CorrectIncorrectHint
We have
\(
\frac{G(x)-G(1)}{x-1}=-\frac{\sqrt{25-x^2}-(-\sqrt{24})}{x-1}
\)
\(
\begin{aligned}
& =-\frac{\left[\sqrt{25-x^2}-\sqrt{24}\right]}{x-1} \\
& =-\frac{\left[25-x^2-24\right]}{x-1}-\frac{1}{\left(\sqrt{25-x^2}+\sqrt{24}\right)} \\
& =\frac{x+1}{\sqrt{25-x^2}+\sqrt{24}}
\end{aligned}
\)
Therefore
\(
\lim _{x \rightarrow 1}\left(\frac{G(x)-G(1)}{x-1}\right)=\frac{1+1}{\sqrt{24}+\sqrt{24}}=\frac{1}{\sqrt{24}}=\frac{1}{2 \sqrt{6}}
\) -
Question 103 of 135
103. Question
\(\lim _{x \rightarrow \infty}\left(\frac{x+6}{x+1}\right)^{x+4}=\)
CorrectIncorrectHint
We have
\(
\begin{aligned}
\left(\frac{x+6}{x+1}\right)^{x+4} & =\frac{\left(1+\frac{6}{x}\right)^x}{\left(1+\frac{1}{x}\right)^x} \cdot\left(\frac{1+\frac{6}{x}}{1+\frac{1}{x}}\right)^4 \\
& =\frac{\left[\left(1+\frac{6}{x}\right)^{x / 6}\right]^6}{\left(1+\frac{1}{x}\right)^x} \cdot\left(\frac{1+\frac{6}{x}}{1+\frac{1}{x}}\right)^4
\end{aligned}
\)
Therefore
\(
\lim _{x \rightarrow \infty}\left(\frac{x+6}{x+1}\right)^{x+4}=\frac{e^6}{e} \cdot\left(\frac{1+0}{1+0}\right)=e^5
\) -
Question 104 of 135
104. Question
\(\lim _{x \rightarrow 0}\left(\frac{1+6 x^2}{1+3 x^2}\right)^{1 / x^2}=\)
CorrectIncorrectHint
We have
\(
\left(\frac{1+6 x^2}{1+3 x^2}\right)^{1 / x^2}=\frac{\left[\left(1+6 x^2\right)^{1 / 6 x^2}\right]^6}{\left[\left(1+3 x^2\right)^{1 / 3 x^2}\right]^3}
\)
\(
\lim _{x \rightarrow 0}\left(\frac{1+6 x^2}{1+3 x^2}\right)^{1 / x^2}=\frac{e^6}{e^3}=e^3
\) -
Question 105 of 135
105. Question
\(\lim _{x \rightarrow 0}\left\{\tan \left(\frac{\pi}{4}+x\right)\right\}^{1 / x}=\)
CorrectIncorrectHint
Let
\(
\begin{aligned}
f(x) & =\left[\tan \left(\frac{\pi}{4}+x\right)\right]^{1 / x} \\
& =\left(\frac{1+\tan x}{1-\tan x}\right)^{1 / x} \\
& =\frac{\left[(1+\tan x)^{1 / \tan x}\right]^{\tan x / x}}{\left[(1-\tan x)^{-1 / \tan x}\right]^{-\tan x / x}}
\end{aligned}
\)
\(
\lim _{x \rightarrow 0} f(x)=\frac{e^1}{e^{-1}}=e^2
\) -
Question 106 of 135
106. Question
\(\lim _{x \rightarrow 0}(\cos x)^{\cot x}=\)
CorrectIncorrectHint
We have
\(
(\cos x)^{\cot x}=\left[(1+\cos x-1)^{1 /(\cos x-1)}\right]^{(\cos x-1) \tan x}
\)
Take
\(
f(x)=[1+(\cos x-1)]^{1 /(\cos x-1)} \text { and } g(x)=\frac{\cos x-1}{\tan x}
\)
We know that [by part (1) of Important Formulae]
\(
\lim _{x \rightarrow 0} f(x)=e
\)
Now,
\(
g(x)=\frac{-2 \sin ^2 \frac{x}{2} \cos x}{\sin x}=-\frac{\sin \frac{x}{2} \cos x}{\cos \frac{x}{2}} \rightarrow 0 \text { as } x \rightarrow 0
\)
Therefore, by part (7) of Important Formulae
\(
\lim _{x \rightarrow 0}(f(x))^{g(x)}=e^0=1
\) -
Question 107 of 135
107. Question
\(\lim _{x \rightarrow \frac{\pi}{2}} \frac{(1-\sin x)\left(8 x^3-\pi^3\right) \cos x}{(\pi-2 x)^4}=\)
CorrectIncorrectHint
Let
\(
\begin{aligned}
f(x) & =\frac{(1-\sin x)\left(8 x^3-\pi^3\right) \cos x}{(\pi-2 x)^4} \\
& =\frac{(1-\sin x) \cos x(2 x-\pi)\left(4 x^2+2 \pi x+\pi^2\right)}{(2 x-\pi)^4} \\
& =\frac{(1-\sin x) \cos x\left(4 x^2+2 \pi x+\pi^2\right)}{(2 x-\pi)^3}
\end{aligned}
\)
Therefore
\(
\lim _{x \rightarrow \frac{\pi}{2}} f(x)=\lim _{x \rightarrow \frac{\pi}{2}} \frac{(1-\sin x) \cos x}{(2 x-\pi)^3} \cdot\left(3 \pi^2\right) \dots(1)
\)
Put \(2 x-\pi=y\) so that \(y \rightarrow 0\) as \(x \rightarrow \pi / 2\). Therefore now
\(
\begin{aligned}
\frac{(1-\sin x) \cos x}{(2 x-\pi)^3} & =\frac{\left[1-\sin \left(\frac{\pi+y}{2}\right)\right] \cos \left(\frac{\pi+y}{2}\right)}{y^3} \\
& =\frac{\left(1-\cos \frac{y}{2}\right)\left(-\sin \frac{y}{2}\right)}{y^3} \\
& =-\left(\frac{2 \sin ^2 \frac{y}{4}}{y^2}\right)\left(\frac{\sin \frac{y}{2}}{y}\right) \\
& =-2\left(\frac{\sin ^2 \frac{y}{4}}{y / 4}\right)^2 \cdot \frac{1}{16} \cdot\left(\frac{\sin \frac{y}{2}}{y / 2}\right) \cdot \frac{1}{2} \\
& =-\frac{1}{16}\left(\frac{\sin \frac{y}{4}}{y / 4}\right)^2\left(\frac{\sin \frac{y}{2}}{y / 2}\right) \dots(2)
\end{aligned}
\)
Therefore from Eqs. (1) and (2)
\(
\lim _{x \rightarrow 0} f(y)=\frac{-3 \pi^2}{16} \times 1 \times 1
\) -
Question 108 of 135
108. Question
\(\lim _{x \rightarrow 1}\left(2-\frac{1}{x}\right)^{\tan (\pi / 2 x)}=\)
CorrectIncorrectHint
Suppose
\(
f(x)=\left(2-\frac{1}{x}\right)^{\tan (\pi x / 2)}=\left(1+\left(1-\frac{1}{x}\right)\right)^{\tan (\pi x / 2)}
\)
Put \(y=1-(1 / x)\) so that \(y \rightarrow 0\) as \(x \rightarrow 1\). Therefore
\(
\begin{aligned}
f(x) & =(1+y)^{\tan (\pi / 2)(1-y)} \\
& =(1+y)^{\cot (\pi y / 2)} \\
& =\left[(1+y)^{1 / y}\right]^{y \cot (\pi y / 2)} \\
& =\left[(1+y)^{1 / y}\right]^{[(\pi y / 2) / \tan (\pi y / 2)] \times(2 / \pi)}
\end{aligned}
\)
\(
\text { Given limit }=e^{1 \times 2 / \pi}=e^{2 / \pi}
\) -
Question 109 of 135
109. Question
If
\(
\lim _{x \rightarrow 0} \frac{a e^x-b}{x}=2
\)
then \((a, b)\) is equal toCorrectIncorrectHint
We have
\(
\lim _{x \rightarrow 0} \frac{a e^x-b}{x}=2
\)
Since the denominator \(x \rightarrow 0\) as \(x \rightarrow 0\)
\(
\lim _{x \rightarrow 0}\left(a e^x-b\right)=0
\)
which implies that \(a-b=0\).
\(
2=\lim _{x \rightarrow 0}\left(\frac{a e^x-a}{x}\right)=\lim _{x \rightarrow 0} a\left(\frac{e^x-1}{x}\right)=a
\)
Hence
\(
a=2=b
\) -
Question 110 of 135
110. Question
If \(\lim _{x \rightarrow 0}\left(1+a x+b x^2\right)^{1 / x}=e^3\), then
CorrectIncorrect -
Question 111 of 135
111. Question
If
\(
\lim _{x \rightarrow \infty}\left(\frac{x^2+1}{x+1}-a x-b\right)=0
\)
then \((a, b)\) value isCorrectIncorrectHint
Let
\(
\begin{aligned}
f(x) & =\frac{x^2+1}{x+1}-a x-b \\
& =\frac{\left(x^2+1\right)-(x+1)(a x+b)}{x+1} \\
& =\frac{(1-a) x^2-(a+b) x+1-b}{x+1}
\end{aligned}
\)
Put \(y=1 / x\) so that \(y \rightarrow 0\) as \(x \rightarrow \infty\). Therefore
\(
f(x)=f\left(\frac{1}{y}\right)=\frac{(1-a)-(a+b) y+(1-b) y^2}{y(1+y)}
\)
Now,
\(
\begin{aligned}
& \lim _{x \rightarrow \infty} f(x)=0 \\
\Rightarrow & \lim _{y \rightarrow 0} \frac{(1-a)-(a+b) y+(1-b) y^2}{y(y+1)}=0
\end{aligned}
\)
Since the denominator tends to zero as \(y \rightarrow 0\), the numerator must tend to zero as \(y \rightarrow 0\). Therefore
\(
\begin{gathered}
1-a=0 \quad \text { or } \quad a=1 \\
0=\lim _{y \rightarrow 0} \frac{[-(a+b)+(1-b) y]}{y+1}=-(a+b) \\
a=-b
\end{gathered}
\)
Hence \((a, b)=(1,-1)\). -
Question 112 of 135
112. Question
\(\lim _{x \rightarrow \infty} \frac{x^3 \sin (1 / x)+2 x^2}{1+3 x^2}=\)
CorrectIncorrectHint
We have
\(
\begin{aligned}
\lim _{x \rightarrow \infty} \frac{x^3 \sin \frac{1}{x}+2 x^2}{1+3 x^2} & =\lim _{x \rightarrow \infty} \frac{x \sin \frac{1}{x}+2}{\frac{1}{x^2}+3} \\
& =\frac{1+2}{0+3}\left[\because \lim _{x \rightarrow \infty}\left(x \sin \frac{1}{x}\right)=1\right] \\
& =\frac{3}{3}=1
\end{aligned}
\) -
Question 113 of 135
113. Question
If \(n\) is a fixed positive integer then
\(
\lim _{x \rightarrow \frac{\pi}{2}}\left(1^{\sec ^2 x}+2^{\sec ^2 x}+3^{\sec ^2 x}+\cdots+n^{\sec ^2 x}\right)^{\cos ^2 x}=
\)CorrectIncorrectHint
It is known that \(K^{\sec ^2 x} \leq n^{\sec ^2 x}\) for \(K=1,2\), \(3, \ldots, n\). Therefore
\(
\left(1^{\sec ^2 x}+2^{\sec ^2 x}+\cdots+n^{\sec ^2 x}\right)^{\cos ^2 x} \leq\left(n \cdot n^{\sec ^2 x}\right)^{\cos ^2 x}=n \cdot n^{\cos ^2 x}
\)
Again
\(
\left(1^{\sec ^2 x}+2^{\sec ^2 x}+\cdots+n^{\sec ^2 x}\right)^{\cos ^2 x} \geq\left(n^{\sec ^2 x}\right)^{\cos ^2 x}=n
\)
Therefore
\(
\begin{aligned}
n & =\lim _{x \rightarrow \frac{\pi}{2}}(n) \leq \lim _{x \rightarrow \frac{\pi}{2}}\left(1^{\sec ^2 x}+2^{\sec ^2 x}+\cdots+n^{\sec ^2 x}\right)^{\cos ^2 x} \\
& \leq \lim _{x \rightarrow \frac{\pi}{2}}\left(n \cdot n^{\cos ^2 x}\right)=n
\end{aligned}
\)
By squeezing theorem, we have
\(
\lim _{x \rightarrow \frac{\pi}{2}}\left(1^{\sec ^2 x}+2^{\sec ^2 x}+\cdots+n^{\sec ^2 x}\right)^{\cos ^2 x}=n
\)Try it out:
\(
\lim _{x \rightarrow 0}\left(1^{\operatorname{cosec}^2 x}+2^{\operatorname{cosec}^2 x}+\cdots+n^{\operatorname{cosec}^2 x}\right)^{\sin ^2 x}=n
\) -
Question 114 of 135
114. Question
Let \(x_n=\frac{1+2+3+\cdots+n}{n^2}\)
for \(n=1,2,3, \ldots\). Then the value of \(\lim _{n \rightarrow \infty} x_n\) isCorrectIncorrectHint
We have
\(
x_n=\frac{n(n+1)}{2 n^2}=\frac{1}{2}\left(1+\frac{1}{n}\right) \rightarrow \frac{1}{2} \quad \text { as } n \rightarrow \infty
\) -
Question 115 of 135
115. Question
If \(y_n=\frac{1^2+2^2+3^2+\cdots+n^2}{n^3}\) then \(\lim _{n \rightarrow \infty} y_n\) is equal to
CorrectIncorrectHint
We have
\(
\begin{aligned}
& \quad y_n=\frac{n(n+1)(2 n+1)}{6 n^3}=\frac{1}{6}(1)\left(1+\frac{1}{n}\right)\left(2+\frac{1}{n}\right) \rightarrow \frac{2}{6}=\frac{1}{3} \\
& \text { as } n \rightarrow \infty .
\end{aligned}
\) -
Question 116 of 135
116. Question
Let \(z_n=\frac{1^3+2^3+3^3+\cdots+n^3}{n^4}\) Then \(\lim _{n \rightarrow \infty} z_n\) is
CorrectIncorrectHint
We have
\(
z_n=\frac{n^2(n+1)^2}{4 n^4}=\frac{1}{4}\left(1+\frac{1}{n}\right)^2 \rightarrow \frac{1}{4} \quad \text { as } n \rightarrow \infty
\) -
Question 117 of 135
117. Question
Let \(x\) be a real number and [.] denote the integral part function. Then
\(
\lim _{n \rightarrow \infty} \frac{[1 x]+[2 x]+[3 x]+\cdots+[n x]}{n^2}=
\)CorrectIncorrectHint
By the definition of the integral part
\(
\begin{gathered}
x-1<[x] \leq x \\
2 x-1<[2 x] \leq 2 x \\
3 x-1<[3 x] \leq 3 x \\
\cdots \cdots \cdots \cdots \\
\cdots \cdots \cdots \cdots \\
n x-1<[n x] \leq n x
\end{gathered}
\)
Adding all the inequalities we have
\(
\begin{aligned}
x(1+2+3+\cdots+n)-n & <[1 x]+[2 x]+\cdots+[n x] \\
& \leq x(1+2+\cdots+n) \\
\frac{x}{2} n(n+1)-n<[1 x]+[2 x]+\cdots+[n x] & \leq \frac{x n(n+1)}{2}
\end{aligned}
\)
Dividing throughout by \(n^2\), we get
\(
\frac{x}{2}\left(1+\frac{1}{n}\right)-\frac{1}{n}<\frac{[1 x]+[2 x]+\cdots+[n x]}{n^2} \leq \frac{x}{2}\left(1+\frac{1}{n}\right)
\)
Taking limit as \(n \rightarrow \infty\) and using squeezing theorem we have
\(
\lim _{n \rightarrow \infty} \frac{[1 x]+[2 x]+\cdots+[n x]}{n^2}=\frac{x}{2}
\)Note: Try it out On similar lines (i.e., by using the concept of \([x])\) we can show that
1. \(\lim _{n \rightarrow \infty} \frac{\left[1^2 x\right]+\left[2^2 x\right]+\cdots+\left[n^2 x\right]}{n^3}=\frac{x}{3}\)
2. \(\lim _{n \rightarrow \infty} \frac{\left[1^3 x\right]+\left[2^3 x\right]+\cdots+\left[n^3 x\right]}{n^4}=\frac{x}{4}\) -
Question 118 of 135
118. Question
Let \(x\) be a real number and
\(
a_n=\frac{1}{n^2}\{[x+1]+[2 x+2]+[3 x+3]+\cdots+[n x+n]\}
\)
then \(\lim _{x \rightarrow \infty} a_n\) is equal to (where [latex]\cdot[/latex] denotes integral part)CorrectIncorrectHint
We know that \([x+y]=[x]+[y]\) if one of \(x\) or \(y\) is an integer. Therefore
\(
\begin{gathered}
{[x+1]=[x]+1} \\
{[2 x+2]=[2 x]+2} \\
{[3 x+2]=[3 x]+3} \\
\cdots \cdots \cdots \cdots \cdots \cdots \\
\cdots \cdots \cdots \cdots \cdots \cdots \\
{[n x+n]=[n x]+n}
\end{gathered}
\)
Adding all the equations and dividing by \(n^2\), we get
\(
\begin{aligned}
\lim _{n \rightarrow \infty} a_n & =\lim _{n \rightarrow \infty} \frac{1}{n^2}\left\{[x]+[2 x]+\cdots+[n x]+\frac{1}{2} n(n+1)\right\} \\
& =\lim _{n \rightarrow \infty} \frac{[x]+[2 x]+\cdots+[n x]}{n^2}+\lim _{n \rightarrow \infty} \frac{n(n+1)}{2 n^2} \\
& =\frac{x}{2}+\frac{1}{2} \quad \text { (by Problem 98) }
\end{aligned}
\) -
Question 119 of 135
119. Question
Let
\(
x_1=1 \quad \text { and } \quad x_{n+1}=\frac{4+3 x_n}{3+2 x_n} \text { for } n \geq 1
\)
If \(\lim _{n \rightarrow \infty} x_n\) exists finitely, then the limit is equal toCorrectIncorrectHint
We have
\(
\begin{aligned}
& x_1=1, x_2=\frac{4+3}{3+2}=\frac{7}{5} \\
& x_3=\frac{4+3 x_2}{3+2 x_2}=\frac{4+3\left(\frac{7}{5}\right)}{3+2\left(\frac{7}{5}\right)}=\frac{41}{29}>x_2
\end{aligned}
\)
We can easily verify that \(x_n<x_{n+1}\) and hence \(\left\{x_n\right\}\) is strictly increasing sequence of positive terms. Let \(\lim _{n \rightarrow \infty} x_n=l\). Therefore
\(
\begin{aligned}
l & =\lim _{n \rightarrow \infty} x_{n+1} \\
& =\lim _{n \rightarrow \infty}\left(\frac{4+3 x_n}{3+2 x_n}\right) \\
& =\frac{4+3 \lim _{n \rightarrow \infty} x_n}{3+2 \lim _{n \rightarrow \infty} x_n}
\end{aligned}
\)
\(
=\frac{4+3 l}{3+2 l}
\)
Hence \(3 l+2 l^2=4+3 l\)
\(
l^2=2 \Rightarrow l=\sqrt{2} \quad\left(\because x_n>0 \quad \forall n\right)
\) -
Question 120 of 135
120. Question
Let \(x_0=0, x_1=1\) and \(x_{n+1}=x_n+\sqrt{1+x_n^2}\) for \(n \geq 1\). Then
\(
\lim _{n \rightarrow \infty}\left(\frac{x_n}{2^{n-1}}\right)=
\)CorrectIncorrectHint
\(\left\{x_n\right\}\) is an increasing sequence. Define
\(
\theta_n=\operatorname{Cot}^{-1}\left(x_n\right) \text { or } x_n=\cot \theta_n
\)
Now
\(
x_0=0=\cot \frac{\pi}{2}, x_1=1=\cot \frac{\pi}{2^2}
\)
and in general
\(
\begin{aligned}
x_{n+1} & =\cot \theta_n+\operatorname{cosec} \theta_n \\
& =\frac{1+\cos \theta_n}{\sin \theta_n} \\
& =\cot \left(\frac{\theta_n}{2}\right) \\
& =\cot \left(\frac{\pi}{4 \times 2^n}\right) \\
\left(\because x_p=1=\cot \left(\frac{\pi}{4}\right),\right. & \left.x_2=\cot \left(\frac{\pi}{8}\right)=\cot \left(\frac{\pi}{4 \times 2}\right), \text { etc. }\right)
\end{aligned}
\)
Therefore
\(
\begin{aligned}
\frac{x_n}{2^{n-1}} & =\frac{\cot \left(\frac{\pi}{4 \times 2^{n-1}}\right)}{2^{n-1}} \\
& =\frac{1}{2^{n-1} \tan \left(\frac{\pi}{4 \times 2^{n-1}}\right)}
\end{aligned}
\)
\(
\begin{aligned}
& =\frac{1}{\frac{\tan \left(\frac{\pi}{4 \times 2^{n-1}}\right)}{\left(\frac{\pi}{4 \times 2^{n-1}}\right)} \cdot \frac{\pi}{4}} \\
& =\frac{4}{\pi} \frac{1}{\left(\frac{\tan x}{x}\right)}
\end{aligned}
\)
where \(x=\frac{\pi}{4 \times 2^{n-1}} \rightarrow 0\) as \(n \rightarrow \infty\). Therefore
\(
\lim _{n \rightarrow \infty} x_n=\frac{4}{\pi} \cdot 1=\frac{4}{\pi}
\) -
Question 121 of 135
121. Question
Let \(a_0=1, a_1=2\) and
\(
n(n+1) a_{n+1}=n(n-1) a_n-(n-2) a_{n-1}
\)
for \(n \geq 1\). Then \(\lim _{n \rightarrow \infty} a_n\) isCorrectIncorrectHint
From the given relation we have
\(
\begin{aligned}
& 1 \cdot 2 \cdot a_2=0-(1-2) a_0=1 \\
& \Rightarrow a_2=\frac{1}{2}=\frac{1}{2!}
\end{aligned}
\)
\(
\text { and } \quad 6 \cdot a_3=2 a_2-0 \cdot a_1=2\left(\frac{1}{2}\right)=1
\)
\(
\Rightarrow a_3=\frac{1}{6}=\frac{1}{3!}
\)
Assume that \(a_k=1 / {k}\) for all \(k=2,3, \ldots, m\). Now
\(
\begin{aligned}
m(m+1) \cdot a_{m+1} & =m(m-1) a_m-(m-2) a_{m-1} \\
& =\frac{m(m-1)}{{m!}}-\frac{m-2}{(m-1)!} \\
& =\frac{1}{(m-2)!}-\frac{m-2}{(m-1)!} \\
& =\frac{(m-1)-(m-2)}{(m-1)!}=\frac{1}{(m-1)!}
\end{aligned}
\)
Therefore
\(
a_{m+1}=\frac{1}{m(m+1)(m-1)!}=\frac{1}{(m+1)!}
\)
Hence by complete induction, \(a_k=1 / k\) for \(k \geq 2\).
Therefore
\(
\lim _{n \rightarrow \infty} a_n=\lim _{n \rightarrow \infty}\left(\frac{1}{{n!}}\right)=0
\) -
Question 122 of 135
122. Question
Let \(x>1\) and for each positive integer \(n\), define
\(
\begin{aligned}
s_n(x)= & \frac{x}{x+1}+\frac{x^2}{(x+1)\left(x^2+1\right)}+\frac{x^4}{(x+1)\left(x^2+1\right)\left(x^4+1\right)}+ \\
& \cdots+\frac{x^{2^{n-1}}}{(x+1)\left(x^2+1\right) \cdots\left(x^{2^{n-1}}+1\right)}
\end{aligned}
\)
Then \(\lim _{n \rightarrow \infty} s_n(x)\) is equal toCorrectIncorrectHint
We have
\(
\begin{aligned}
\frac{s_n(x)}{x-1}= & \frac{x}{x^2-1}+\frac{x^2}{x^4-1}+\frac{x^4}{x^{16}-1}+\cdots+\frac{x^{2^{n-1}}}{x^{2^n}-1} \\
= & \left(\frac{1}{x-1}-\frac{1}{x^2-1}\right)+\left(\frac{1}{x^2-1}-\frac{1}{x^4-1}\right)+\cdots \\
& +\left(\frac{1}{x^{2^{n-1}}-1}-\frac{1}{x^{2^n}-1}\right) \\
= & \frac{1}{x-1}-\frac{1}{x^{2^n}-1}
\end{aligned}
\)
Therefore
\(
s_n(x)=1-\frac{x-1}{x^{2^n}-1}
\)
Since \(x>1\), we have \(\lim _{n \rightarrow \infty}\left(x^{2^n}-1\right)=+\infty\) so that
\(
\frac{1}{x^{2^n}-1} \rightarrow 0 \quad \text { as } n \rightarrow \infty
\)
Therefore
\(
\lim _{n \rightarrow \infty} s_n(x)=1-0=1
\) -
Question 123 of 135
123. Question
The sequence \(\left\{a_n\right\}\) is defined as \(a_1=1\) and \(a_n=\) \(n\left(a_{n-1}+1\right)\) for \(n \geq 2\). If
\(
P_n=\left(1+\frac{1}{a_1}\right)\left(1+\frac{1}{a_2}\right) \cdots\left(1+\frac{1}{a_n}\right)
\)
then \(\lim _{n \rightarrow \infty} P_n\) equalsCorrectIncorrectHint
We have
\(
\begin{aligned}
P_n & =\left(\frac{a_1+1}{a_1}\right)\left(\frac{a_2+1}{a_2}\right) \cdots\left(\frac{a_n+1}{a_n}\right) \\
& =\left(\frac{a_2}{2 a_1}\right)\left(\frac{a_3}{3 a_2}\right) \cdots\left(\frac{a_n+1}{(n+1) a_n}\right)\left(\because \frac{a_k}{k}=a_{k-1}+1 \text { for } k \geq 2\right)
\end{aligned}
\)
\(
=\frac{a_{n+1}}{(n+1)!} \dots(1)
\)
Now
\(
\begin{aligned}
& \frac{a_n+1}{(n+1)!}=\frac{(n+1)\left(a_n+1\right)}{(n+1)!} \\
\Rightarrow & \frac{a_n+1}{(n+1)!}-\frac{a_n}{{n!}}=\frac{1}{{n!}}
\end{aligned}
\)
Therefore
\(
\begin{aligned}
& \frac{a_2}{2!}-\frac{a_1}{1!}=\frac{1}{1!} \\
& \frac{a_3}{{3!}}-\frac{a_2}{2!}=\frac{1}{{2!}} \\
& \frac{a_{n+1}}{(n+1)!}-\frac{a_n}{n!}=\frac{1}{n!} \\
&
\end{aligned}
\)
Adding all the above equations we get
\(
\frac{a_{n+1}}{(n+1)!}-\frac{a_1}{1!}=\frac{1}{1!}+\frac{1}{2!}+\cdots+\frac{1}{n!}
\)
From Eq. (1) we have
\(
P_n=1+\frac{1}{1!}+\frac{1}{2!}+ \dots + \frac{1}{n!} \left(\therefore a_1=1\right)
\)
But the number \(e\) is the sum of the infinite series \(\sum_{n=0}^{\infty} \frac{1}{n!}\) (this is to be assumed). Note that \(\sum a_n\) is defined as the limit of the sequence of the partial sums \(\left\{s_n\right\}\) where \(s_n=a_1+a_2+\cdots+a_n\). Thus
\(
\lim _{n \rightarrow \infty} P_n=e
\) -
Question 124 of 135
124. Question
Suppose \(x\) is real. Define
\(
f(x)=\frac{x}{2}+1
\)
\(
\begin{aligned}
& f^{(2)}(x)=f(f(x)) \\
& f^{(3)}(x)=f\left(f^{(2)}(x)\right)
\end{aligned}
\)
and in general
\(
f^{n+1}(x)=f\left(f^{(n)}(x)\right)
\)
for \(n \geq 1\) where
\(
f^{(1)}(x)=f(x)=\frac{x}{2}+1
\)
Then \(\lim _{n \rightarrow \infty} f^{(n)}(x)\) is equal toCorrectIncorrectHint
We have
\(
\begin{gathered}
f^{(2)}(x)=f\left(f^{(1)}(x)\right)=f(f(x))=\frac{f(x)}{2}+1=\frac{x}{2^2}+\frac{1}{2}+1 \\
f^{(3)}(x)=f\left(f^{(2)}(x)\right)=\frac{1}{2}\left(\frac{x}{2^2}+\frac{1}{2}+1\right)+1=\frac{x}{2^3}+\frac{1}{2^2}+\frac{1}{2}+1
\end{gathered}
\)
By induction we can see that
\(
\begin{aligned}
f^{(n)}(x) & =\frac{x}{2^n}+\frac{1}{2^{n-1}}+\frac{1}{2^{n-2}}+\cdots+\frac{1}{2}+1 \\
& =\frac{x}{2^n}+\frac{1-\frac{1}{2^n}}{1-\frac{1}{2}} \\
& =\frac{x}{2^n}+2-\frac{1}{2^{n-1}}
\end{aligned}
\)
Now
\(
\lim _{n \rightarrow \infty} \frac{1}{2^n}=0 \Rightarrow \lim _{n \rightarrow \infty} f^{(n)}(x)=0+2-0=2
\) -
Question 125 of 135
125. Question
Define \(a_n=n^2+20\) for \(n=1,2,3, \ldots\). Let \(d_n\) be the greatest common divisor of \(a_n\) and \(a_{n+1}\) and \(d\) be the least common multiple of \(d_n\) for \(n=1,2,3, \ldots\). Then the infinite sum of the series \(d+\frac{d}{4}+\frac{d}{4^2}+\frac{d}{4^3}+\cdots\) is
CorrectIncorrectHint
We have
\(
a_{n+1}-a_n=2 n+1
\)
This implies \(d_n\) divides \(2 n+1\) for all \(n=1,2,3, \ldots\). Now
\(
3 a_n+a_{n+1}=4 n^2+2 n+81=2 n(2 n+1)+81
\)
This implies \(d_n\) divides 81 and 81 will be the L.C.M. of \(d_n\) for \(n=1,2,3, \ldots\) so that \(d=81\). Now
\(
\begin{aligned}
d+\frac{d}{4}+\frac{d}{4^2}+\cdots \infty & =\frac{d}{1-\frac{1}{4}} \\
& =(81) \frac{4}{3}=108
\end{aligned}
\) -
Question 126 of 135
126. Question
\(\lim _{n \rightarrow \infty}\left(1+\frac{1}{n^2+\cos n}\right)^{n^2+n}\) is equal to
CorrectIncorrectHint
\(
\text { Put } m=n^2+\cos n \text { so that } m \rightarrow \infty=\text { as } n \rightarrow \infty \text {. }
\)
Now
\(
\begin{aligned}
\frac{n^2+n}{m} & =\frac{n^2+n}{n^2+\cos n} \\
& =\frac{1+\frac{1}{n}}{1+\frac{\cos n}{n^2}} \rightarrow 1 \text { as } n \rightarrow \infty
\end{aligned}
\)
because
\(
\lim _{n \rightarrow \infty} \frac{1}{n}=0 \text { and } \lim _{n \rightarrow \infty} \frac{\cos n}{n^2}=0
\)
Therefore
\(
\lim _{n \rightarrow \infty}\left(1+\frac{1}{n^2+\cos n}\right)^{n^2+n}=\lim _{n \rightarrow \infty}\left[\left(1+\frac{1}{m}\right)^m\right]^{\left(n^2+n\right) / m}=e
\) -
Question 127 of 135
127. Question
Let \(x_n=2+\sqrt{2+\sqrt{2+\cdots+\sqrt{2}}}\) ( \(n\) square roots). Then \(\lim _{n \rightarrow \infty} x_n\) is equal to
CorrectIncorrectHint
We have \(x_n=2+\sqrt{x_{n-1}}\). Suppose \(\lim _{n \rightarrow \infty}=l\). Then
\(
\begin{aligned}
& l=2+\sqrt{l} \\
\Rightarrow & l^2-5 l+4=0 \\
\Rightarrow & (l-1)(l-4)=0
\end{aligned}
\)
\(
\Rightarrow l=1 \text { or } 4
\)
But \(x_n>2\) and \(\left\{x_n\right\}\) is an increasing sequence and hence \(l\) \(\neq 1\). Thus \(l=4\). -
Question 128 of 135
128. Question
\(\lim _{n \rightarrow \infty}\left[2 \log (3 n)-\log \left(n^2+1\right)\right]\) is equal to
CorrectIncorrectHint
The given limit is
\(
\begin{aligned}
\lim _{n \rightarrow \infty}\left[\log \left(9 n^2\right)-\log \left(n^2+1\right)\right] & =\lim _{n \rightarrow \infty} \log \frac{9 n^2}{n^2+1} \\
& =\lim _{n \rightarrow \infty} \log \left(\frac{9}{1+\frac{1}{n^2}}\right) \\
& =\log \left(\frac{9}{1+0}\right) \\
& =\log 9=2 \log 3
\end{aligned}
\) -
Question 129 of 135
129. Question
\(\lim _{n \rightarrow \infty}\left(1+\frac{1}{n^2}\right)^{\frac{8 n^3}{\pi} \sin \left(\frac{\pi}{2 n}\right)}\) is equal to
CorrectIncorrectHint
We have
Given limit \(=\lim _{n \rightarrow \infty}\left[\left(1+\frac{1}{n^2}\right)^{n^2}\right]^{\frac{4\left(\sin \frac{\pi}{2 n}\right)}{\pi / 2 n}}=e^{4 \times 1}=e^4\) -
Question 130 of 135
130. Question
If \(\sum_{n=1}^{\infty} \frac{1}{n^2}=\frac{\pi^2}{6}\), then \(\sum_{n=1}^{\infty} \frac{1}{(2 n-1)^2}\) is
CorrectIncorrectHint
We have
\(
\begin{aligned}
\sum_{n=1}^{\infty} \frac{1}{(2 n-1)^2} & =\sum_{n=1}^{\infty} \frac{1}{n^2}-\sum_{n=1}^{\infty} \frac{1}{(2 n)^2} \\
& =\frac{\pi^2}{6}-\frac{1}{4} \sum_{n=1}^{\infty} \frac{1}{n^2} \\
& =\frac{\pi^2}{6}-\frac{\pi^2}{24}=\frac{\pi^2}{8}
\end{aligned}
\) -
Question 131 of 135
131. Question
If
\(
\alpha=\lim _{n \rightarrow \infty}\left(\frac{1^2+2^2+\cdots+n^2}{n^3}\right)
\)
and
\(
\beta=\lim _{n \rightarrow \infty}\left[\frac{\left(1^3-1^2\right)+\left(2^3-2^2\right)+\left(3^3-3^2\right)+\cdots+\left(n^3-n^2\right)}{n^4}\right]
\)
ThenCorrectIncorrectHint
We have
\(
\begin{aligned}
\alpha & =\lim _{n \rightarrow \infty} \frac{n(n+1)(2 n+1)}{6 n^3}=\frac{2}{6}=\frac{1}{3} \\
\beta & =\lim _{n \rightarrow \infty}\left(\frac{1^3+2^3+3^3+\cdots+n^3}{n^4}\right)-\lim _{n \rightarrow \infty} \frac{1^2+2^2+3^2+\cdots+n^2}{n^4} \\
& =\lim _{n \rightarrow \infty} \frac{n^2(n+1)^2}{4 n^4}-\lim _{n \rightarrow \infty} \frac{n(n+1)(2 n+1)}{6 n^4} \\
& =\frac{1}{4}-0
\end{aligned}
\)
Therefore \(3 \alpha=4 \beta\). -
Question 132 of 135
132. Question
\(\lim _{n \rightarrow \infty} \frac{1}{n} \sum_{K=0}^{n-1} \cos \left(\frac{K \pi}{2 n}\right)\) is
CorrectIncorrectHint
First we show that
\(
\begin{aligned}
& \cos \alpha+\cos (\alpha+\beta)+\cos (\alpha+2 \beta)+\cdots+\cos (\alpha+(n-1) \beta) \\
& =\frac{\cos \frac{(\alpha+\alpha+(n-1) \beta)}{2} \sin \left(\frac{n \beta}{2}\right)}{\sin \frac{\beta}{2}}
\end{aligned}
\)
Let
\(
s=\cos \alpha+\cos (\alpha+\beta)+\cos (\alpha+2 \beta)+\cdots+\cos (\alpha+(n-1) \beta)
\)
Multiply both sides with \(2 \sin (\beta / 2)\). Therefore
\(
\begin{aligned}
s\left(2 \sin \frac{\beta}{2}\right)= & 2 \cos \alpha \sin \frac{\beta}{2}+2 \cos (\alpha+\beta) \sin \frac{\beta}{2} \\
& +\cdots+2 \cos (\alpha+(n-1) \beta) \sin \frac{\beta}{2} \\
= & {\left[\sin \left(\alpha+\frac{\beta}{2}\right)-\sin \left(\alpha-\frac{\beta}{2}\right)\right] }
\end{aligned}
\)
\(
\begin{aligned}
& +\left[\sin \left(\alpha+\beta+\frac{\beta}{2}\right)-\sin \left(\alpha+\beta-\frac{\beta}{2}\right)\right] \\
& +\cdots+\left[\begin{array}{l}
\sin \left(\alpha+(n-1) \beta+\frac{\beta}{2}\right) \\
-\sin \left(\alpha+(n-1) \beta-\frac{\beta}{2}\right)
\end{array}\right] \\
= & \sin \left(\alpha+(2 n-1) \frac{\beta}{2}\right)-\sin \left(\alpha-\frac{\beta}{2}\right) \\
= & 2 \cos \frac{\left(\alpha+(2 n-1) \frac{\beta}{2}+\alpha-\frac{\beta}{2}\right)}{2} \sin \frac{n \beta}{2}
\end{aligned}
\)
Therefore
\(
s=\frac{\cos \left(\frac{\alpha+\alpha+(n-1) \beta}{2}\right) \sin \left(\frac{n \beta}{2}\right)}{\sin \frac{\beta}{2}}
\)
In the given problem, \(\alpha=0\) and \(\beta=\pi / 2 n\). Therefore
\(
s_n=\cos 0+\cos \frac{\pi}{2 n}+\cos \frac{\pi}{2 n}+\cdots+\cos \left(\frac{(n-1) \pi}{2 n}\right)
\)
\(
\begin{aligned}
& =\frac{\cos \left(\frac{0+\frac{(n-1) \pi}{2 n}}{2}\right) \sin \left(n \frac{\pi}{4 n}\right)}{\sin \left(\frac{\pi}{4 n}\right)} \\
& =\frac{\cos (n-1) \frac{\pi}{4 n} \cdot \sin \frac{\pi}{4}}{\sin \left(\frac{\pi}{4 n}\right)} \\
& =\frac{\frac{1}{\sqrt{2}} \cos \left(\frac{\pi}{4}-\frac{\pi}{4 n}\right)}{\sin \left(\frac{\pi}{4 n}\right)}
\end{aligned}
\)
Therefore
\(
\begin{aligned}
\lim _{n \rightarrow \infty}\left(\frac{1}{n} \sum_{r=1}^{n-1} \cos \left(\frac{r \pi}{2 n}\right)\right) & =\frac{1}{\sqrt{2}} \lim _{n \rightarrow \infty}\left(\frac{\cos \left(\frac{\pi}{4}-\frac{\pi}{4 n}\right)}{\frac{\left(\sin \frac{\pi}{4 n}\right)}{\left(\frac{\pi}{4 n}\right)} \cdot \frac{4}{\pi}}\right) \\
& =\frac{\frac{1}{\sqrt{2}} \cdot \cos \left(\frac{\pi}{4}\right)}{1} \cdot \frac{4}{\pi}=\frac{2}{\pi}
\end{aligned}
\) -
Question 133 of 135
133. Question
Let
\(
P_n=\frac{2^3-1}{2^3+1} \cdot \frac{3^3-1}{3^3+1}+\cdots+\frac{n^3-1}{n^3+1} ; n=2,3,4, \ldots .
\)
Then \(\lim _{n \rightarrow \infty} P_n\) is equal toCorrectIncorrectHint
We have
\(
\begin{aligned}
\frac{k^3-1}{k^3+1} & =\frac{(k-1)\left(k^2+k+1\right)}{(k+1)\left(k^2-k+1\right)} \\
& =\left(\frac{k-1}{k+1}\right)\left(\frac{k^2+k+1}{(k-1)^2+(k-1)+1}\right)
\end{aligned}
\)
for \(k=2,3, \ldots, n\). Therefore
\(
\begin{aligned}
P_n & =\left(\frac{2-1}{2+1} \cdot \frac{3-1}{3+1} \cdot \frac{4-1}{4+1} \cdots \frac{n-2}{n} \cdot \frac{n-1}{n+1}\right) \\
& \left(\frac{7}{3} \cdot \frac{13}{7} \cdot \frac{21}{13} \cdots \frac{n^2+n+1}{(n-1)^2+(n-1)+1}\right) \\
& =\left(\frac{1}{3} \cdot \frac{2}{4} \cdot \frac{3}{5} \cdots \frac{n-2}{n} \cdot \frac{n-1}{n+1}\right)\left(\frac{7}{3} \cdot \frac{13}{7} \cdot \frac{21}{13} \cdots \frac{n^2+n+1}{(n-1)^2+(n-1)+1}\right) \\
& =\left(\frac{2}{n(n+1)}\right)\left(\frac{n^2+n+1}{3}\right) \\
& =\frac{2}{3}\left[1+\frac{1}{n(n+1)}\right]
\end{aligned}
\)
Therefore
\(
\lim _{n \rightarrow \infty} P_n=\frac{2}{3}(1+0)=\frac{2}{3}
\) -
Question 134 of 135
134. Question
If \(a_n\) and \(b_n\) are positive integers and \(a_n+\sqrt{2} b_n\) \(=(2+\sqrt{2})^n\), then
\(
\lim _{n \rightarrow \infty}\left(\frac{a_n}{b_n}\right)=
\)CorrectIncorrectHint
We have
\(
\begin{aligned}
a_n+\sqrt{2} b_n & =(2+\sqrt{2})^n \\
\Rightarrow a_n-\sqrt{2} b_n & =(2-\sqrt{2})^n
\end{aligned}
\)
Therefore
and
\(
\begin{aligned}
& a_n=\frac{1}{2}\left[(2+\sqrt{2})^n+(2-\sqrt{2})^n\right] \\
& b_n=\frac{\left[(2+\sqrt{2})^n-(2-\sqrt{2})^n\right]}{2 \sqrt{2}}
\end{aligned}
\)
Therefore
\(
\begin{aligned}
\frac{a_n}{b_n} & =\sqrt{2}\left[\frac{(2+\sqrt{2})^n+(2-\sqrt{2})^n}{(2+\sqrt{2})^n-(2-\sqrt{2})^n}\right] \\
& =\sqrt{2} \frac{\left[1+\left(\frac{2-\sqrt{2}}{2+\sqrt{2}}\right)^n\right]}{\left[1-\left(\frac{2-\sqrt{2}}{2+\sqrt{2}}\right)^n\right]}
\end{aligned}
\)
Hence
\(
\begin{aligned}
\lim _{n \rightarrow \infty}\left(\frac{a_n}{b_n}\right) & =\sqrt{2}\left(\frac{1+0}{1-0}\right) \quad\left(\because \frac{2-\sqrt{2}}{2+\sqrt{2}}<1\right) \\
& =\sqrt{2}
\end{aligned}
\) -
Question 135 of 135
135. Question
If
\(
\lim _{x \rightarrow 0}\left[1+x \log \left(1+b^2\right)\right]^{(1 / x)}=2 b \sin ^2 \theta, b>0
\)
and \(\theta \in(-\pi, \pi]\) then the value of \(\theta\) isCorrectIncorrectHint
Let
\(
\begin{aligned}
f(x) & =\left[1+x \log \left(1+b^2\right)\right]^{1 / x} \\
& =\left\{\left[1+x \log \left(1+b^2\right)\right]^{\frac{1}{x \log \left(1+b^2\right)}}\right\}^{\log \left(1+b^2\right)}
\end{aligned}
\)
Therefore
\(
\begin{aligned}
& \lim _{x \rightarrow 0} f(x)=e^{\log \left(1+b^2\right)}=1+b^2 \\
\Rightarrow & 1+b^2=2 b \sin ^2 \theta \\
\Rightarrow & 2 b \sin ^2 \theta=1+b^2 \geq 2 b(\therefore b>0) \\
\Leftrightarrow & b=1 \text { and } \sin ^2 \theta=1
\end{aligned}
\)
Therefore
\(
\theta= \pm \frac{\pi}{2}
\)