Past JEE PYQs (Integer type)
Overview
- An expression consisting of two terms, connected by + or – sign is called a binomial expression. For example, \(x+a, 2 x-3 y, \frac{1}{x}-\frac{1}{x^3}, 7 x-\frac{4}{5 y}\), etc., are all binomial expressions.
Binomial theorem
If \(a\) and \(b\) are real numbers and \(n\) is a positive integer, then \((a+b)^n={ }^n C _0 a^n+{ }^n C _1 a^{n-1} b^1+{ }^n C _2 a^{n-2} b^2+\ldots\)
\(
\ldots+{ }^n C _r a^{n-r} b^r+\ldots+{ }^n C _n b^n \text {, where }{ }^n C _r=\frac{{n!}}{{r!} {(n-r)}!} \text { for } 0 \leq r \leq n
\)
The general term or \((r+1)^{ th }\) term in the expansion is given by
\(
T _{r+1}={ }^n C _r a^{n-r} b^r
\)
Some important observations
- The total number of terms in the binomial expansion of \((a+b)^n\) is \(n+1\), i.e. one more than the exponent \(n\).
- In the expansion, the first term is raised to the power of the binomial and in each subsequent terms the power of \(a\) reduces by one with simultaneous increase in the power of \(b\) by one, till power of \(b\) becomes equal to the power of binomial, i.e., the power of \(a\) is \(n\) in the first term, ( \(n-1)\) in the second term and so on ending with zero in the last term. At the same time power of \(b\) is 0 in the first term, 1 in the second term and 2 in the third term and so on, ending with \(n\) in the last term.
- In any term the sum of the indices (exponents) of ‘ \(a\) ‘ and ‘ \(b\) ‘ is equal to \(n\) (i.e., the power of the binomial).
- The coefficients in the expansion follow a certain pattern known as pascal’s triangle.
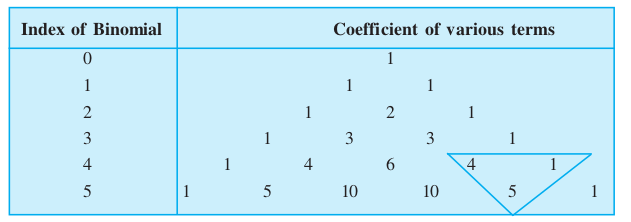
Each coefficient of any row is obtained by adding two coefficients in the preceding row, one on the immediate left and the other on the immediate right and each row is bounded by 1 on both sides.
The \((r+1)^{ \text {th} }\) term or general term is given by
\(
T _{r+1}={ }^n C _r a^{n-r} b^r
\)
Some particular cases
If \(n\) is a positive integer, then
\(
\begin{aligned}
& (a+b)^n={ }^n C _0 a^n b^0+{ }^n C _1 a^n b^1+{ }^n C _2 a^{n-2} b^2+\ldots+{ }^n C _r a^{n-r} b^r+\ldots+ { }^n C _n a^0 b^n \dots(1)
\end{aligned}
\)
In particular
- Replacing \(b\) by \(-b\) in (1), we get
\(
\begin{aligned}
& (a-b)^n={ }^n C _0 a^n b^0-{ }^n C _1 a^{n-1} b^1+{ }^n C _2 a^{n-2} b^2+\ldots+(-1)^r{ }^n C _r a^{n-r} b^r+\ldots+ \\
& (-1)^n{ }^n C _n a^0 b^n \dots(2)
\end{aligned}
\) - Adding (1) and (2), we get
\(
\begin{aligned}
(a+b)^n+(a-b)^n & =2\left[{ }^n C _0 a^n b^0+{ }^n C _2 a^{n-2} b^2+{ }^n C _4 a^{n-4} b^4+\ldots\right] \\
& =2[\text { terms at odd places }]
\end{aligned}
\) - Subtracting (2) from (1), we get
\(
\begin{aligned}
(a+b)^n-(a-b)^n & =2\left[{ }^n C _1 a^{n-1} b^1+{ }^n C _3 a^{n-3} b^3+\ldots\right] \\
& =2[\text { sum of terms at even places }]
\end{aligned}
\) - Replacing \(a\) by 1 and \(b\) by \(x\) in (1), we get
\(
(1+x)^n={ }^n C _0 x^0+{ }^n C _1 x+{ }^n C _2 x^2+\ldots+{ }^n C _r x^r+\ldots+{ }^n C _{n-1} x^{n-1}+{ }^n C _n x^n
\)
i.e. \(\quad(1+x)^n=\sum_{r=0}^n{ }^n C _r x^r\) - Replacing \(a\) by 1 and \(b\) by \(-x\) in … (1), we get
\(
(1-x)^n={ }^n C _0 x^0-{ }^n C _1 x+{ }^n C _2 x^2 \ldots+{ }^n C _{n-1}(-1)^{n-1} x^{n-1}+{ }^n C _n(-1)^n x^n
\)
i.e., \(\quad(1-x)^n=\sum_{r=0}^n(-1)^r{ }^n C _r x^r\)
The \(p~{\text {th }}\) term from the end
The \(p~{\text {th }}\) term from the end in the expansion of \((a+b)^n\) is \((n-p+2)^{\text {th }}\) term from the beginning.
Middle terms
The middle term depends upon the value of \(n\).
- If \(n\) is even: then the total number of terms in the expansion of \((a+b)^n\) is \(n+1\) (odd). Hence, there is only one middle term, i.e., \(\left(\frac{n}{2}+1\right)^{\text {th }}\) term is the middle term.
- If \(n\) is odd: then the total number of terms in the expansion of \((a+b)^n\) is \(n+1\) (even). So there are two middle terms i.e., \(\left(\frac{n+1}{2}\right)^{ th }\) and \(\left(\frac{n+3}{2}\right)^{\text {th }}\) are two middle terms.
Binomial coefficient
In the Binomial expression, we have
\(
(a+b)^n={ }^n C _0 a^n+{ }^n C _1 a^{n-1} b+{ }^n C _2 a^{n-2} b^2+\ldots+{ }^n C _n b^n \dots(1)
\)
The coefficients \({ }^n C _0,{ }^n C _1,{ }^n C _2, \ldots,{ }^n C _n\) are known as binomial or combinatorial coefficients.
Putting \(a=b=1\) in (1), we get
\(
{ }^n C _0+{ }^n C _1+{ }^n C _2+\ldots+{ }^n C _n=2^n
\)
Thus the sum of all the binomial coefficients is equal to \(2^n\).
Again, putting \(a=1\) and \(b=-1\) in (1), we get
\(
{ }^n C _0+{ }^n C _2+{ }^n C _4+\ldots={ }^n C _1+{ }^n C _3+{ }^n C _5+\ldots
\)
Thus, the sum of all the odd binomial coefficients is equal to the sum of all the even binomial coefficients and each is equal to \(\frac{2^n}{2}=2^{n-1}\).
\(
{ }^n C _0+{ }^n C _2+{ }^n C _4+\ldots={ }^n C _1+{ }^n C _3+{ }^n C _5+\ldots=2^{n-1}
\)
Quiz Summary
0 of 8 Questions completed
Questions:
Information
You have already completed the quiz before. Hence you can not start it again.
Quiz is loading…
You must sign in or sign up to start the quiz.
You must first complete the following:
Results
Results
0 of 8 Questions answered correctly
Your time:
Time has elapsed
You have reached 0 of 0 point(s), (0)
Earned Point(s): 0 of 0, (0)
0 Essay(s) Pending (Possible Point(s): 0)
Categories
- Not categorized 0%
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- Current
- Review
- Answered
- Correct
- Incorrect
-
Question 1 of 8
1. Question
The product of the last two digits of \((1919)^{1919}\) is [JEE Main 2025 (Online) 8th April Evening Shift]
CorrectIncorrectHint
(b) Using the Binomial Theorem: The expression is expanded using the binomial theorem for \((1920-1)^{1919}\). All terms except the last two contain a factor of \(1920^2\) (or higher powers), which is a multiple of \(100\left(1920^2=3,686,400\right)\). Any term that is a multiple of 100 does not affect the last two digits of the final number. These terms are represented collectively as \(100 \lambda\).
\(
(1919)^{1919}=100 \lambda+{ }^{1919} \mathrm{C}_{1918}(1920)^1-{ }^{1919} \mathrm{C}_{1919}
\)
Simplifying the Remaining Terms: The expression simplifies to the last two terms:
\(
100 \lambda+1919 \times 1920-1
\)
Calculating the Relevant Value: The value of the non- \(100 \lambda\) part is calculated:
\(
1919 \times 1920-1=3,684,480-1=3,684,479
\)
Finding the Last Two Digits: The full number is therefore \(100 \lambda+3,684,479\). Since \(100 \lambda\) ends in two zeros, the last two digits of the entire expression are determined solely by the last two digits of \(3,684,479\), which are 79.
The Final Product: The text concludes: “Number having last two digit 79 : Product of last two digit 63”. This final step refers to multiplying the two digits themselves:
Product of last two digits \(=7 \times 9=63\)
Explanation: Rewrite the number
\(
1919^{1919}=(1920-1)^{1919}
\)
Apply the binomial theorem
\(
(1920-1)^{1919}=\sum_{k=0}^{1919}\binom{1919}{k}(1920)^{1919-k}(-1)^k
\)
\(
=\binom{1919}{0} 1920^{1919}-\binom{1919}{1} 1920^{1918}+\binom{1919}{2} 1920^{1917}-\cdots-\binom{1919}{1919}
\)
Observe which terms affect the last two digits
Since
\(
1920=100 \times 19+20
\)
any term containing \(1920^2\) or higher powers is divisible by 100.
So these terms do not affect the last two digits.
Hence, only the last two terms matter:
\(
\binom{1919}{1918} 1920-\binom{1919}{1919}
\)
Simplify the remaining terms
\(
\binom{1919}{1918}=1919
\)
So we get:
\(
1919 \cdot 1920-1
\)
Find the last two digits (For example:\(3479=100 \cdot 34+79\), which gives Last two digits = 79)
Reduce modulo 100:
\(
\begin{gathered}
1919 \cdot 1920 \equiv 19 \cdot 20=380 \equiv 80(\bmod 100) \\
80-1=79
\end{gathered}
\)
So, the last two digits of \(1919^{1919}\) are 79.
Find the product of the last two digits
\(
7 \times 9=63
\) -
Question 2 of 8
2. Question
The sum of the series \(2 \times 1 \times{ }^{20} \mathrm{C}_4-3 \times 2 \times{ }^{20} \mathrm{C}_5+4 \times 3 \times{ }^{20} \mathrm{C}_6-5 \times 4 \times{ }^{20} \mathrm{C}_7+\cdots \cdots+18 \times 17 \times{ }^{20} \mathrm{C}_{20}\), is equal to ____. [JEE Main 2025 (Online) 7th April Evening Shift]
CorrectIncorrectHint
(a) Step 1: Start with the binomial expansion
\(
(1-x)^{20}=\binom{20}{0}-\binom{20}{1} x+\binom{20}{2} x^2-\binom{20}{3} x^3+\cdots+(-1)^{20}\binom{20}{20} x^{20}
\)
Step 2: Divide by \(\boldsymbol{x}^{\mathbf{2}}\)
\(
\frac{(1-x)^{20}}{x^2}=\frac{\binom{20}{0}}{x^2}-\frac{\binom{20}{1}}{x}+\binom{20}{2}-\binom{20}{3} x+\binom{20}{4} x^2-\cdots+\binom{20}{20} x^{18}
\)
Step 3: Differentiate twice
Differentiate term-by-term:
First derivative
\(
\frac{d}{d x}\left(\frac{(1-x)^{20}}{x^2}\right)=-2\binom{20}{0} x^{-3}+\binom{20}{1} x^{-2}-\binom{20}{3}+2\binom{20}{4} x-\cdots
\)
Second derivative
\(
\frac{d^2}{d x^2}\left(\frac{(1-x)^{20}}{x^2}\right)=6\binom{20}{0} x^{-4}-2\binom{20}{1} x^{-3}+2\binom{20}{4}-6\binom{20}{5} x+\cdots
\)
Step 4: Substitute \(x=1\)
At \(x=1\) :
\(
=6\binom{20}{0}-2\binom{20}{1}+2\binom{20}{4}-6\binom{20}{5}+12\binom{20}{6}-\cdots+18 \cdot 17\binom{20}{20}
\)
This matches exactly the given series:
\(
2 \cdot 1\binom{20}{4}-3 \cdot 2\binom{20}{5}+4 \cdot 3\binom{20}{6}-\cdots+18 \cdot 17\binom{20}{20}
\)
Let this required sum be \(A\).
So we have:
\(
\text { Value at } x=1=6-2\binom{20}{1}+A
\)
Step 5: Evaluate the LHS directly
\(
\frac{(1-x)^{20}}{x^2} \Rightarrow \frac{d^2}{d x^2}\left(\frac{(1-x)^{20}}{x^2}\right)
\)
Substitute \(x=1\) :
\(
(1-1)^{20}=0 \Rightarrow \text { value }=0
\)
Thus,
\(
\begin{gathered}
6-2(20)+A=0 \\
6-40+A=0 \\
A=34
\end{gathered}
\) -
Question 3 of 8
3. Question
Let \(\left(1+x+x^2\right)^{10}=a_0+a_1 x+a_2 x^2+\ldots+a_{20} x^{20}\). If \(\left(a_1+a_3+a_5+\ldots+a_{19}\right)-11 a_2=121 k\), then \(k\) is equal to ____. [JEE Main 2025 (Online) 3rd April Evening Shift]
CorrectIncorrectHint
(b) Step 1: Find the value of \(\left(a_1+a_3+a_5+\ldots+a_{19}\right)\)
Let \(P(x)=\left(1+x+x^2\right)^{10}=a_0+a_1 x+a_2 x^2+\ldots+a_{20} x^{20}\).
Substitute \(x=1\) into the equation:
\(
P(1)=(1+1+1)^{10}=3^{10}=a_0+a_1+a_2+\ldots+a_{20}
\)
Substitute \(x=-1\) into the equation:
\(
P(-1)=\left(1-1+(-1)^2\right)^{10}=(1)^{10}=1=a_0-a_1+a_2-a_3+\ldots+a_{20}
\)
Subtract the second equation from the first to get the sum of odd coefficients:
\(
\begin{gathered}
P(1)-P(-1)=3^{10}-1=2\left(a_1+a_3+a_5+\ldots+a_{19}\right) \\
a_1+a_3+a_5+\ldots+a_{19}=\frac{3^{10}-1}{2}
\end{gathered}
\)
Step 2: Find the value of \(a_2\)
The coefficient of \(x^2, a_2\), can be found by considering the general term of the trinomial expansion or by using the binomial theorem repeatedly.
The coefficient \(a_2\) is 55.
Step 3: Solve for \(\boldsymbol{k}\)
Substitute the values into the given equation:
\(
\begin{gathered}
\left(a_1+a_3+a_5+\ldots+a_{19}\right)-11 a_2=121 k \\
\frac{3^{10}-1}{2}-11 \times 55=121 k
\end{gathered}
\)
\(
\begin{gathered}
\frac{59049-1}{2}-605=121 k \\
\frac{59048}{2}-605=121 k \\
29524-605=121 k \\
28919=121 k \\
k=\frac{28919}{121} \\
k=239
\end{gathered}
\) -
Question 4 of 8
4. Question
If \(\alpha=1+\sum_{r=1}^6(-3)^{r-1} \quad{ }^{12} \mathrm{C}_{2 r-1}\), then the distance of the point \((12, \sqrt{3})\) from the line \(\alpha x-\sqrt{3} y+1=0\) is ____. [JEE Main 2025 (Online) 28th January Morning Shift]
CorrectIncorrectHint
(d) Step 1: Evaluate
\(
\alpha=1+\sum_{r=1}^6(-3)^{r-1}\binom{12}{2 r-1}
\)
Key trick (odd-term binomial identity)
Consider:
\(
(1+x)^{12}-(1-x)^{12}=2\left[\binom{12}{1} x+\binom{12}{3} x^3+\cdots+\binom{12}{11} x^{11}\right]
\)
Divide by \(2 x\) :
\(
\frac{(1+x)^{12}-(1-x)^{12}}{2 x}=\sum_{r=1}^6\binom{12}{2 r-1} x^{2 r-2}
\)
Now substitute \(x^2=3 \Rightarrow x=\sqrt{3}\) :
\(
\sum_{r=1}^6\binom{12}{2 r-1} 3^{r-1}=\frac{(1+\sqrt{3})^{12}-(1-\sqrt{3})^{12}}{2 \sqrt{3}}
\)
But our sum has \((-3)^{r-1}\), so put \(x=i \sqrt{3}\) :
\(
\sum_{r=1}^6\binom{12}{2 r-1}(-3)^{r-1}=\frac{(1+i \sqrt{3})^{12}-(1-i \sqrt{3})^{12}}{2 i \sqrt{3}}
\)
Step 2: Simplify the expression
\(
1+i \sqrt{3}=2 e^{i \pi / 3}
\)
So,
\(
\begin{gathered}
(1+i \sqrt{3})^{12}=2^{12} e^{i 4 \pi}=4096 \\
(1-i \sqrt{3})^{12}=4096
\end{gathered}
\)
Hence,
\(
\sum_{r=1}^6(-3)^{r-1}\binom{12}{2 r-1}=\frac{4096-4096}{2 i \sqrt{3}}=0
\)
Therefore:
\(
\alpha=1
\)
Substitute the value of \(\alpha=1\) into the line equation \(\alpha x-\sqrt{3} y+1=0\) to get:
\(
\alpha x-\sqrt{3} y+1=0 \Rightarrow x-\sqrt{3} y+1=0
\)
Step 3: Calculate the distance
The distance \(\boldsymbol{d}\) from a point ( \(\boldsymbol{x}_{\mathbf{0}}, \boldsymbol{y}_{\mathbf{0}}\) ) to the line \(\boldsymbol{A} \boldsymbol{x}+\boldsymbol{B} \boldsymbol{y}+\boldsymbol{C}=\mathbf{0}\) is given by the formula:
\(
d=\frac{\left|A x_0+B y_0+C\right|}{\sqrt{A^2+B^2}}
\)
For our point \((12, \sqrt{3})\) and line \(x-\sqrt{3} y+1=0(A=1, B=-\sqrt{3}, C=1)\), the distance is:
\(
\begin{gathered}
d=\frac{|1(12)+(-\sqrt{3})(\sqrt{3})+1|}{\sqrt{1^2+(-\sqrt{3})^2}} \\
d=\frac{|12-3+1|}{\sqrt{1+3}} \\
d=\frac{|10|}{\sqrt{4}} \\
d=\frac{10}{2}=5
\end{gathered}
\)
The distance of the point \((12, \sqrt{3})\) from the line \(\alpha x-\sqrt{3} y+1=0\) is 5 units. -
Question 5 of 8
5. Question
The sum of all rational terms in the expansion of \(\left(1+2^{1 / 3}+3^{1 / 2}\right)^6\) is equal to _____. [JEE Main 2025 (Online) 23rd January Morning Shift]
CorrectIncorrectHint
(c) The general term in the expansion of \(\left(1+2^{1 / 3}+3^{1 / 2}\right)^6\) is given by the multinomial theorem as:
\(
T_{p, q, r}=\frac{6!}{p!q!r!}(1)^p\left(2^{1 / 3}\right)^q\left(3^{1 / 2}\right)^r=\frac{6!}{p!q!r!} 2^{q / 3} 3^{r / 2}
\)
where \(p+q+r=6\), and \(p, q, r\) are non-negative integers. For the term to be rational, the exponents of 2 and 3 must be integers. Thus, \(q\) must be a multiple of \(3(q \in\{0,3,6\})\) and \(r\) must be a multiple of \(2(r \in\{0,2,4,6\})\).
Step 2: List all valid combinations of exponents
We list the possible combinations of \((p, q, r)\) that satisfy \(p+q+r=6\) and the rationality conditions:
If \(q=0, r=0 \Longrightarrow p=6\). Combination: \((6,0,0)\).
If \(q=0, r=2 \Longrightarrow p=4\). Combination: \((4,0,2)\).
If \(q=0, r=4 \Longrightarrow p=2\). Combination: \((2,0,4)\).
If \(q=0, r=6 \Longrightarrow p=0\). Combination: \((0,0,6)\).
If \(q=3, r=0 \Longrightarrow p=3\). Combination: \((3,3,0)\).
If \(q=3, r=2 \Longrightarrow p=1\). Combination: \((1,3,2)\).
If \(q=6, r=0 \Longrightarrow p=0\). Combination: \((0,6,0)\). Other combinations violate \(p \geq 0\) or \(p+q+r=6\).
Step 3: Calculate the value of each rational term
We calculate the value for each valid combination:
\((6,0,0): \frac{6!}{6!0!0!} 2^0 3^0=1 \times 1=1\).
\((4,0,2): \frac{6!}{4!0!2!} 2^0 3^1=15 \times 3=45\).
\((2,0,4): \frac{6!}{2!0!4!} 2^0 3^2=15 \times 9=135\).
\((0,0,6): \frac{6!}{0!0!6!} 2^0 3^3=1 \times 27=27\).
\((3,3,0): \frac{6!}{3!3!0!} 2^1 3^0=20 \times 2=40\).
\((1,3,2): \frac{6!}{1!3!2!} 2^1 3^1=60 \times 6=360\).
\((0,6,0): \frac{6!}{0!6!0!} 2^2 3^0=1 \times 4=4\).
Step 4: Sum all the rational terms
The sum of all rational terms is the sum of the values calculated above:
\(
\text { Sum }=1+45+135+27+40+360+4=612
\) -
Question 6 of 8
6. Question
If \(\sum_{r=1}^{30} \frac{r^2\left({ }^{30} C_r\right)^2}{{ }^{30} C_{r-1}}=\alpha \times 2^{29}\), then \(\alpha\) is equal to ____. [JEE Main 2025 (Online) 22nd January Evening Shift]
CorrectIncorrectHint
(a) Given
\(
\sum_{r=1}^{30} \frac{r^2\left(\binom{30}{r}\right)^2}{\binom{30}{r-1}}=\alpha \times 2^{29}
\)
Step 1: Simplify the general term
Use the identity:
\(
\frac{\binom{30}{r}}{\binom{30}{r-1}}=\frac{31-r}{r}
\)
So,
\(
\frac{r^2\left(\binom{30}{r}\right)^2}{\binom{30}{r-1}}=r^2\binom{30}{r} \cdot \frac{31-r}{r}=r(31-r)\binom{30}{r}
\)
Hence the sum becomes:
\(
\sum_{r=1}^{30} r(31-r)\binom{30}{r}
\)
Step 2: Split the sum
\(
r(31-r)=31 r-r^2
\)
So,
\(
\sum_{r=1}^{30} r(31-r)\binom{30}{r}=31 \sum r\binom{30}{r}-\sum r^2\binom{30}{r}
\)
Step 3: Use standard binomial sums
For \(n=30\) :
\(
\begin{gathered}
\sum r\binom{30}{r}=30 \cdot 2^{29} \\
\sum r^2\binom{30}{r}=30 \cdot 31 \cdot 2^{28}
\end{gathered}
\)
Step 4: Substitute
\(
\begin{gathered}
=31\left(30 \cdot 2^{29}\right)-\left(30 \cdot 31 \cdot 2^{28}\right) \\
=30 \cdot 31 \cdot 2^{28}(2-1) \\
=30 \cdot 31 \cdot 2^{28}
\end{gathered}
\)
Rewrite in terms of \(2^{29}\) :
\(
\begin{gathered}
30 \cdot 31 \cdot 2^{28}=\frac{30 \cdot 31}{2} \cdot 2^{29} \\
=465 \cdot 2^{29}
\end{gathered}
\)
Step 5: Identify \(\alpha\)
\(
\alpha=465
\) -
Question 7 of 8
7. Question
If \(\sum_{r=0}^5 \frac{{ }^{11} C_{2 r+1}}{2 r+2}=\frac{\mathrm{m}}{\mathrm{n}}, \operatorname{gcd}(\mathrm{m}, \mathrm{n})=1\), then \(\mathrm{m}-\mathrm{n}\) is equal to ____. [JEE Main 2025 (Online) 22nd January Morning Shift]
CorrectIncorrectHint
(b) We evaluate
\(
S=\sum_{r=0}^5 \frac{\binom{11}{2 r+1}}{2 r+2}
\)
Step 1: Rewrite the denominator
\(
\frac{1}{2 r+2}=\int_0^1 x^{2 r+1} d x
\)
So,
\(
S=\sum_{r=0}^5\binom{11}{2 r+1} \int_0^1 x^{2 r+1} d x=\int_0^1 \sum_{r=0}^5\binom{11}{2 r+1} x^{2 r+1} d x
\)
Step 2: Recognize the odd-power binomial sum
\(
(1+x)^{11}-(1-x)^{11}=2 \sum_{r=0}^5\binom{11}{2 r+1} x^{2 r+1}
\)
Hence,
\(
\sum_{r=0}^5\binom{11}{2 r+1} x^{2 r+1}=\frac{(1+x)^{11}-(1-x)^{11}}{2}
\)
Step 3: Substitute into the integral
\(
S=\frac{1}{2} \int_0^1\left[(1+x)^{11}-(1-x)^{11}\right] d x
\)
Step 4: Integrate
\(
\begin{gathered}
\int_0^1(1+x)^{11} d x=\left[\frac{(1+x)^{12}}{12}\right]_0^1=\frac{2^{12}-1}{12} \\
\int_0^1(1-x)^{11} d x=\left[-\frac{(1-x)^{12}}{12}\right]_0^1=\frac{1}{12}
\end{gathered}
\)
So,
\(
\begin{gathered}
S=\frac{1}{2}\left(\frac{2^{12}-1}{12}-\frac{1}{12}\right)=\frac{2^{12}-2}{24} \\
S=\frac{4094}{24}=\frac{2047}{12}
\end{gathered}
\)
Step 5: Compute \(m-n\)
\(
\begin{gathered}
m=2047, \quad n=12, \quad \operatorname{gcd}(2047,12)=1 \\
m-n=2047-12=2035
\end{gathered}
\) -
Question 8 of 8
8. Question
The remainder when \(428^{2024}\) is divided by 21 is ____. [JEE Main 2024 (Online) 9th April Morning Shift]
CorrectIncorrectHint
(d) Step 1: Simplify the base modulo 21
First, we find the remainder of the base, 428 , when divided by 21 . We calculate \(428 \div 21:\)
\(
428=20 \times 21+8
\)
This means \(428 \equiv 8(\bmod 21)\).
Step 2: Use the property of modular exponentiation
The problem simplifies to finding the remainder of \(8^{2024}\) when divided by 21. We look for a pattern in the powers of 8 modulo 21:
\(
\begin{gathered}
8^1 \equiv 8 \quad(\bmod 21) \\
8^2 \equiv 64 \equiv 1 \quad(\bmod 21)
\end{gathered}
\)
Since \(8^2 \equiv 1(\bmod 21)\), we can rewrite the exponent 2024 as an even number:
\(
8^{2024}=\left(8^2\right)^{1012}
\)
Substituting the modular equivalence, the expression becomes:
\(
\begin{aligned}
\left(8^2\right)^{1012} & \equiv 1^{1012} \quad(\bmod 21) \\
1^{1012} & \equiv 1 \quad(\bmod 21)
\end{aligned}
\)Alternate:
We find the remainder of
\(
428^{2024}(\bmod 21)
\)
Step 1: Reduce the base modulo 21
\(
428 \equiv 428-21 \times 20=428-420=8 \quad(\bmod 21)
\)
So,
\(
428^{2024} \equiv 8^{2024}(\bmod 21)
\)
Since
\(
21=3 \times 7
\)
we compute modulo 3 and 7 separately.
Modulo 3
\(
\begin{gathered}
8 \equiv 2 \quad(\bmod 3) \\
2^{2024} \equiv(-1)^{2024} \equiv 1 \quad(\bmod 3)
\end{gathered}
\)
Modulo 7
\(
\begin{gathered}
8 \equiv 1 \quad(\bmod 7) \\
1^{2024} \equiv 1 \quad(\bmod 7)
\end{gathered}
\)
Step 2: Combine results
We need a number \(x[latex] such that:
[latex]
\begin{aligned}
& x \equiv 1 \quad(\bmod 3) \\
& x \equiv 1 \quad(\bmod 7)
\end{aligned}
\)
The common solution is:
\(
x \equiv 1 \quad(\bmod 21)
\)