Past JEE PYQs (Integer Type)

Hint

(d) Step 1: Analyze the root \(\boldsymbol{\alpha}\) and the expression \(\boldsymbol{T}_{\boldsymbol{k}}\)
The equation \(x^2+x+1=0\) has roots that are the complex cube roots of unity, \(\omega\) and \(\omega^2\). Let \(\alpha=\omega\). The expression inside the summation is
\(
T_k=\left(\alpha^k+\frac{1}{\alpha^k}\right)^2=\left(\omega^k+\omega^{2 k}\right)^2 .
\)
Step 2: Evaluate \(\boldsymbol{T}_{\boldsymbol{k}}\) for small \(\boldsymbol{k}\)
Using the property \(\omega^3=1\) and \(1+\omega+\omega^2=0\), we evaluate the terms:
For \(k=1, T_1=\left(\omega+\omega^2\right)^2=(-1)^2=1\).
For \(k=2, T_2=\left(\omega^2+\omega^4\right)^2=\left(\omega^2+\omega\right)^2=(-1)^2=1\).
For \(k=3, T_3=\left(\omega^3+\omega^6\right)^2=(1+1)^2=4\).
The values of \(T_k\) repeat in a cycle of \(3:(1,1,4)\).
Step 3: Find the sum and determine \(\boldsymbol{n}\)
The sum for one cycle is \(1+1+4=6\). The cumulative sum is required to be 20.
The sums for multiple cycles:
\(
\begin{aligned}
& k=1 \text { to } 3: \text { sum }=6 . \\
& k=1 \text { to } 6: \text { sum }=12 . \\
& k=1 \text { to } 9: \text { sum }=18 .
\end{aligned}
\)
To reach 20, we add the next terms: \(T_{10}=T_1=1\) (sum becomes 19), \(T_{11}=T_2=1\) (sum becomes 20).
Thus, \(n=11\).

Hint

(b) Step 1: Interpret the sets
\(A\) is a circle with center \(2+i\) and radius 3 :
\(
|z-(2+i)|=3
\)
\(B\) is a line. Let \(z=x+i y\). Then
\(
z-i z=x+i y-i(x+i y)=x+i y-i x-i^2 y=x+i y-i x+y
\)
Because \(i^2=-1\) :
\(
z-i z=x+i y-i x+y=(x+y)+i(y-x)
\)
Take real part:
\(
\operatorname{Re}(z-i z)=x+y=2
\)
So \(B\) is the line:
\(
x+y=2
\)
Step 2: Circle equation in \(x, y\)
\(
\begin{gathered}
|z-(2+i)|=3 \Longrightarrow|(x-2)+i(y-1)|=3 \\
(x-2)^2+(y-1)^2=9
\end{gathered}
\)
Step 3: Solve circle and line system
Line: \(x+y=2 \Longrightarrow y=2-x\)
Substitute into circle:
\(
(x-2)^2+((2-x)-1)^2=9
\)
Simplify second term:
\(
(2-x-1)^2=(1-x)^2
\)
Equation:
\(
\begin{gathered}
(x-2)^2+(1-x)^2=9 \\
\left(x^2-4 x+4\right)+\left(x^2-2 x+1\right)=9 \\
2 x^2-6 x+5=9 \\
2 x^2-6 x+5-9=0 \Longrightarrow 2 x^2-6 x-4=0
\end{gathered}
\)
Divide by 2 :
\(
x^2-3 x-2=0
\)
Factor:
\(
x^2-3 x-2=0 \Longrightarrow x=\frac{3 \pm \sqrt{9+8}}{2}=\frac{3 \pm \sqrt{17}}{2}
\)
Corresponding \(y=2-x\) :
\(
y=2-\frac{3 \pm \sqrt{17}}{2}=\frac{4-3 \pm \sqrt{17}}{2}=\frac{1 \mp \sqrt{17}}{2}
\)
So points:
\(
z_1=\frac{3+\sqrt{17}}{2}+i \frac{1-\sqrt{17}}{2}, \quad z_2=\frac{3-\sqrt{17}}{2}+i \frac{1+\sqrt{17}}{2}
\)
Step 4: Compute \(\left|z_1\right|^2+\left|z_2\right|^2\)
\(
|z|^2=x^2+y^2
\)
For \(z_1\) :
\(
x_1^2+y_1^2=\left(\frac{3+\sqrt{17}}{2}\right)^2+\left(\frac{1-\sqrt{17}}{2}\right)^2
\)
Compute:
\(x_1^2=\frac{(3+\sqrt{17})^2}{4}=\frac{9+6 \sqrt{17}+17}{4}=\frac{26+6 \sqrt{17}}{4}=\frac{13+3 \sqrt{17}}{2}\)
\(y_1^2=\frac{(1-\sqrt{17})^2}{4}=\frac{1-2 \sqrt{17}+17}{4}=\frac{18-2 \sqrt{17}}{4}=\frac{9-\sqrt{17}}{2}\)
\(
\left|z_1\right|^2=\frac{13+3 \sqrt{17}}{2}+\frac{9-\sqrt{17}}{2}=\frac{22+2 \sqrt{17}}{2}=11+\sqrt{17}
\)
For \(z_2\) :
\(
\begin{gathered}
x_2^2=\left(\frac{3-\sqrt{17}}{2}\right)^2=\frac{9-6 \sqrt{17}+17}{4}=\frac{26-6 \sqrt{17}}{4}=\frac{13-3 \sqrt{17}}{2} \\
y_2^2=\left(\frac{1+\sqrt{17}}{2}\right)^2=\frac{1+2 \sqrt{17}+17}{4}=\frac{18+2 \sqrt{17}}{4}=\frac{9+\sqrt{17}}{2} \\
\left|z_2\right|^2=\frac{13-3 \sqrt{17}}{2}+\frac{9+\sqrt{17}}{2}=\frac{22-2 \sqrt{17}}{2}=11-\sqrt{17}
\end{gathered}
\)
Step 5: Sum
\(
\left|z_1\right|^2+\left|z_2\right|^2=(11+\sqrt{17})+(11-\sqrt{17})=22
\)

Hint

(b) Step 1: Analyze the first condition
The condition \(\left|\frac{\mathrm{z}-\mathrm{a}}{\mathrm{z}+\mathrm{b}}\right|=1\) implies \(|\mathrm{z}-\mathrm{a}|=|\mathrm{z}+\mathrm{b}|\). Squaring both sides and simplifying yields the relationship between the real part of \(\mathbf{z}\) and the integers \(\boldsymbol{a}\) and \(\boldsymbol{b}\) :
\(
\operatorname{Re}(\mathrm{z})=\frac{\mathrm{a}-\mathrm{b}}{2}
\)
Step 2: Analyze the second condition
The condition involving the determinant of the matrix is:
\(
\left|\begin{array}{ccc}
z+1 & \omega & \omega^2 \\
\omega & z+\omega^2 & 1 \\
\omega^2 & 1 & z+\omega
\end{array}\right|=1
\)
Using properties of the roots of \(x^2+x+1=0\left(\omega^3=1,1+\omega+\omega^2=0\right)\) and determinant operations, the equation simplifies to \(z^3=1\). The solutions for \(z\) are the cube roots of unity: \(z=1, z=\omega\), and \(z=\omega^2\).
Step 3: Determine valid pairs (a, b)
The possible values for \(\operatorname{Re}(\mathrm{z})\) are \(\operatorname{Re}(1)=1\) and \(\operatorname{Re}(\omega)=\operatorname{Re}\left(\omega^2\right)=-\frac{1}{2}\).
We check integer pairs \((\mathrm{a}, \mathrm{b}) \in[-3,3]\) for these two cases, ensuring \(\mathrm{a}+\mathrm{b} \neq 0\).
For \(\operatorname{Re}(z)=1 \Longrightarrow a-b=2\), the valid pairs are ( \(-1,-3\) ), ( \(0,-2[latex] ), ( 2,0 ), and ( 3,1 ) (4 pairs). The pair [latex](1,-1)\) is excluded because \(\mathrm{a}+\mathrm{b}=0\).
For \(\operatorname{Re}(z)=-\frac{1}{2} \Longrightarrow a-b=-1 \Longrightarrow b=a+1\), the valid pairs are \((-3,-2)\), \((-2,-1),(-1,0),(0,1),(1,2)\), and \((2,3)\) (6 pairs). All these pairs satisfy the condition \(\mathrm{a}+\mathrm{b} \neq 0\).
Step 4: Calculate the total number of pairs
The total number of valid ordered pairs is the sum of pairs from both cases: \(4+6=10\)

Hint

(c) The sequence \(P_n=\alpha^n-\beta^n\) follows the linear recurrence relation \(P_n=a P_{n-1}+b P_{n-2}\) , where \(\alpha\) and \(\beta\) are the roots of \(x^2-a x-b=0\). We use the given values to find \(a\) and b.
Using \(P_5=a P_4+b P_3\) :
\(11 \sqrt{7} i=a(-3 \sqrt{7} i)+b(-5 \sqrt{7} i)\)
\(11=-3 a-5 b \dots(1)\)
Using \(P_6=a P_5+b P_4\) :
\(45 \sqrt{7} i=a(11 \sqrt{7} i)+b(-3 \sqrt{7} i)\)
\(45=11 a-3 b \dots(2)\)
Solving these two equations simultaneously yields \(a=3\) and \(b=-4\).
Let \(Q_n=\alpha^n+\beta^n\), which also satisfies the recurrence relation \(Q_n=a Q_{n-1}+b Q_{n-2}\).
We need to find \(Q_4=\alpha^4+\beta^4\).
\(Q_0=\alpha^0+\beta^0=1+1=2\).
\(Q_1=\alpha^1+\beta^1=a=3\).
\(Q_2=a Q_1+b Q_0=3(3)+(-4)(2)=9-8=1\).
\(Q_3=a Q_2+b Q_1=3(1)+(-4)(3)=3-12=-9\).
\(Q_4=a Q_3+b Q_2=3(-9)+(-4)(1)=-27-4=-31\).
Thus, \(\alpha^4+\beta^4=-31\), and \(\left|\alpha^4+\beta^4\right|=|-31|=31\).

Hint

(d) The conditions define a set of integer points in the complex plane:
\(|z-1| \leq 1 \Longrightarrow(a-1)^2+b^2 \leq 1\). This inequality is satisfied by the integer points \((0,0),(1,0),(2,0),(1,1)\), and \((1,-1)\).
\(|z-5| \leq|z-5 i| \Longrightarrow \sqrt{(a-5)^2+b^2} \leq \sqrt{a^2+(b-5)^2}\). This simplifies to \(a \geq b\)
The integer points that satisfy both conditions are:
( 0,0 ) (where \(a=0, b=0 ; 0 \geq 0\) is true)
( 1,0 ) (where \(a=1, b=0 ; 1 \geq 0\) is true)
( 2,0 ) (where \(a=2, b=0 ; 2 \geq 0\) is true)
(1,1) (where \(a=1, b=1 ; 1 \geq 1\) is true)
\((1,-1)\) (where \(a=1, b=-1 ; 1 \geq-1\) is true)
The sum of the squares of the moduli \(\left(|z|^2=a^2+b^2\right)\) for these points is:
\(|(0,0)|^2=0^2+0^2=0\)
\(|(1,0)|^2=1^2+0^2=1\)
\(|(2,0)|^2=2^2+0^2=4\)
\(|(1,1)|^2=1^2+1^2=2\)
\(|(1,-1)|^2=1^2+(-1)^2=2\)
The total sum is \(0+1+4+2+2=9\).

Hint

(d) The solution involves the geometric interpretation of complex numbers in the Argand plane.
1. Set P: \(\left|z-z_0\right| \leq r\) represents a closed disk with center \(z_0\) and radius \(r\).
2. Set Q: \(z(1+i)+\bar{z}(1-i) \leq-8\). By substituting \(z=x+i y\), this inequality simplifies to define a half-plane bounded by a straight line.
3. Intersection \(P \cap Q\) : This is the geometric intersection of the disk and the half-plane, which forms a segment of a circle.
4. Extremum of \(\left|z-z_A\right|\) : This represents the maximum or minimum distance from a point \(z\) in the region \(P \cap Q\) to a fixed point \(z_A\). These extrema will occur at the boundary points of the region \(P \cap Q\).
Step-by-Step Solution:
Step 1: Characterize the sets P and Q geometrically.
For set \(\mathrm{P}:|z+2-3 i| \leq 1\). This inequality describes a closed disk with center \(C_p=-2+3 i\) (coordinates \((-2,3)\) ) and radius \(r=1\).
For set Q : Let \(z=x+i y\). The inequality is \((x+i y)(1+i)+(x-i y)(1-i) \leq-8\).
\(
\begin{gathered}
(x-y+i(x+y))+(x-y-i(x+y)) \leq-8 \\
2(x-y) \leq-8 \Longrightarrow x-y \leq-4 \Longrightarrow y \geq x+4
\end{gathered}
\)
This represents a half-plane on and above the line \(L: y=x+4\).
Step 2: Analyze the intersection region \(P \cap Q\).
We need to find the points in the disk \((x+2)^2+(y-3)^2 \leq 1\) that also satisfy \(y \geq x+4\). Let’s check the distance from the disk’s center \(C_p(-2,3)\) to the line \(x-y+4=0\).
\(
d=\frac{|(-2)-(3)+4|}{\sqrt{1^2+(-1)^2}}=\frac{|-1|}{\sqrt{2}}=\frac{1}{\sqrt{2}}
\)
Since the distance \(d=1 / \sqrt{2}<r=1\), the line intersects the circle. The region \(P \cap Q\) is a segment of the disk.
Step 3: Identify the points \(z_1\) and \(z_2\) for maximum and minimum distance from \(A=3-2 i\).
We need to find the points in \(P \cap Q\) that are farthest from and closest to the point \(A(3,-2)\). Let the point corresponding to \(z\) be \(Z(x, y)\).
The point \(z_1\) (maximum distance) will be the point on the circle’s boundary \(|z+2-3 i|=1\) that is furthest from A, provided it lies in the region Q. This point lies on the line passing through A and \(C_p\). The vector from A to \(C_p\) is \(\vec{v}=C_p-A=(-2-3)+i(3-(-2))=-5+5 i\). The unit vector is \(\hat{u}=\frac{-1+i}{\sqrt{2}}\).
\(
z_1=C_p+r \cdot \hat{u}=(-2+3 i)+1 \cdot\left(\frac{-1+i}{\sqrt{2}}\right)=\left(-2-\frac{1}{\sqrt{2}}\right)+i\left(3+\frac{1}{\sqrt{2}}\right)
\)
Let’s check if \(z_1\) is in Q. For \(z_1=x+i y\), we check if \(y \geq x+4\).
\(
3+\frac{1}{\sqrt{2}} \geq\left(-2-\frac{1}{\sqrt{2}}\right)+4 \Longrightarrow 3+\frac{1}{\sqrt{2}} \geq 2-\frac{1}{\sqrt{2}} \Longrightarrow 1 \geq-\frac{2}{\sqrt{2}}
\)
This is true, so \(z_1\) is in the region \(P \cap Q\).
The point \(z_2\) (minimum distance) will be the point in \(P \cap Q\) closest to A. The point on the circle closest to A is \(C_p-r \hat{u}\), but this point does not satisfy \(y \geq x+4\). Therefore, the minimum distance must be to a point on the line segment boundary of the region, which is the chord \(y= x+4\). The closest point on this line to A is the perpendicular projection of A onto the line. Let this point be M.
The line is \(x-y+4=0\). The projection M is \(\left(x_M, y_M\right)\). Let’s find its coordinates. The projection of \((3,-2)\) on \(x-y+4=0\) is \(\frac{x_M-3}{1}=\frac{y_M-(-2)}{-1}=-\frac{3-(-2)+4}{1^2+(-1)^2}=-\frac{9}{2} . x_M=3- 9 / 2=-3 / 2 . y_M=-2+9 / 2=5 / 2\). This point \(M(-1.5,2.5)\) lies on the chord, so \(z_2= -3 / 2+i(5 / 2)\).
Final Computation & Result:
Step 4: Calculate \(\left|z_1\right|^2\) and \(\left|z_2\right|^2\).
\(
\begin{gathered}
\left|z_1\right|^2=\left(-2-\frac{1}{\sqrt{2}}\right)^2+\left(3+\frac{1}{\sqrt{2}}\right)^2 \\
=\left(4+\frac{4}{\sqrt{2}}+\frac{1}{2}\right)+\left(9+\frac{6}{\sqrt{2}}+\frac{1}{2}\right) \\
=14+\frac{10}{\sqrt{2}}=14+5 \sqrt{2}
\end{gathered}
\)
And for \(z_2\) :
\(
\left|z_2\right|^2=\left(-\frac{3}{2}\right)^2+\left(\frac{5}{2}\right)^2=\frac{9}{4}+\frac{25}{4}=\frac{34}{4}=\frac{17}{2}
\)
Step 5: Compute the final expression.
\(
\begin{gathered}
\left|z_1\right|^2+2\left|z_2\right|^2=(14+5 \sqrt{2})+2\left(\frac{17}{2}\right) \\
=14+5 \sqrt{2}+17=31+5 \sqrt{2}
\end{gathered}
\)
Comparing this with \(\alpha+\beta \sqrt{2}\), we have \(\alpha=31\) and \(\beta=5\).
\(
\alpha+\beta=31+5=36
\)
The value of \(\alpha+\beta\) is \(\mathbf{3 6}\).

Hint

(a) Step 1: Find \(\alpha\)
We have:
\(
|1-i|^x=2^x
\)
Compute \(|1-i|\) :
\(
|1-i|=\sqrt{1^2+(-1)^2}=\sqrt{2}
\)
So the equation becomes:
\(
(\sqrt{2})^x=2^x
\)
But \(2^x=(\sqrt{2})^{2 x}\), so we get:
\(
(\sqrt{2})^x=(\sqrt{2})^{2 x} \Longrightarrow x=0
\)
So, there is exactly one solution, hence:
\(
\alpha=1
\)
Step 2: Simplify \(z\) and find \(\beta\)
We are given:
\(
z=\frac{\pi}{4}(1+i)^4\left[\frac{1-\sqrt{\pi} i}{\sqrt{\pi}+i}+\frac{\sqrt{\pi}-i}{1+\sqrt{\pi} i}\right]
\)
Step 2a: Simplify \((1+i)^4\)
\(
\begin{gathered}
(1+i)^2=1+2 i+i^2=2 i \\
(1+i)^4=\left((1+i)^2\right)^2=(2 i)^2=-4
\end{gathered}
\)
So:
\(
z=\frac{\pi}{4}(-4)\left[\frac{1-\sqrt{\pi} i}{\sqrt{\pi}+i}+\frac{\sqrt{\pi}-i}{1+\sqrt{\pi} i}\right]=-\pi\left[\frac{1-\sqrt{\pi} i}{\sqrt{\pi}+i}+\frac{\sqrt{\pi}-i}{1+\sqrt{\pi} i}\right]
\)
Step 2b: Simplify each fraction
1. \(\frac{1-\sqrt{\pi} i}{\sqrt{\pi}+i}\)
Multiply numerator and denominator by the conjugate of the denominator: \(\sqrt{\pi}-i\)
\(
\frac{(1-\sqrt{\pi} i)(\sqrt{\pi}-i)}{(\sqrt{\pi}+i)(\sqrt{\pi}-i)}=\frac{(1)(\sqrt{\pi}-i)-\sqrt{\pi} i(\sqrt{\pi}-i)}{\pi+1}
\)
Denominator: \((\sqrt{\pi}+i)(\sqrt{\pi}-i)=\pi+1\)
Numerator:
(1) \((\sqrt{\pi}-i)-(\sqrt{\pi} i)(\sqrt{\pi}-i)=\sqrt{\pi}-i-\left(\pi i-\sqrt{\pi} i^2\right)=\sqrt{\pi}-i-(\pi i+\sqrt{\pi})=-i-\pi i=-(1+\pi) i\)
So the first fraction:
\(
\frac{-(1+\pi) i}{\pi+1}=-i
\)
Wait, double-check numerator:
\(
\begin{aligned}
& (1-\sqrt{\pi} i)(\sqrt{\pi}-i)=1 \cdot \sqrt{\pi}-1 \cdot i-\sqrt{\pi} i \cdot \sqrt{\pi}+\sqrt{\pi} i \cdot i=\sqrt{\pi}-i-\pi i+\sqrt{\pi} i^2=\sqrt{\pi}-i- \\
& \pi i-\sqrt{\pi}=-i-\pi i=-(1+\pi) i \checkmark \text { Correct. }
\end{aligned}
\)
Denominator \(=\pi+1\). So fraction \(=-i \checkmark\) Perfect.
2. Similarly, \(\frac{\sqrt{\pi}-i}{1+\sqrt{\pi i}}\)
Multiply numerator and denominator by \(1-\sqrt{\pi} i\) :
\(
\frac{(\sqrt{\pi}-i)(1-\sqrt{\pi} i)}{1+\pi}
\)
Numerator: \(\sqrt{\pi} \cdot 1-\sqrt{\pi} \cdot \sqrt{\pi} i-i \cdot 1+(-i)(-\sqrt{\pi} i)=\sqrt{\pi}-\pi i-i+\sqrt{\pi} i^2=\sqrt{\pi}-\pi i-i- \sqrt{\pi}=-(\pi+1) i\)
Denominator \(=1+\pi\)
So fraction \(=-i \checkmark\) Same.
Step 2c: Sum of fractions
\(
\frac{1-\sqrt{\pi} i}{\sqrt{\pi}+i}+\frac{\sqrt{\pi}-i}{1+\sqrt{\pi} i}=-i+(-i)=-2 i
\)
Step 2d: Multiply by \(-\pi\)
\(
z=-\pi \cdot(-2 i)=2 \pi i
\)
Step 2e: Compute \(|z|\) and \(\arg (z)\)
\(|z|=|2 \pi i|=2 \pi\)
\(\arg (z)=\arg (2 \pi i)=\frac{\pi}{2}\) (positive imaginary axis)
Hence:
\(
\beta=\frac{|z|}{\arg (z)}=\frac{2 \pi}{\pi / 2}=4
\)
So \(\beta=4\)
Step 3: Distance from point \((\alpha, \beta)=(1,4)\) to line \(4 x-3 y=7\)
Distance formula from point \(\left(x_0, y_0\right)\) to line \(A x+B y+C=0\) :
\(
d=\frac{\left|A x_0+B y_0+C\right|}{\sqrt{A^2+B^2}}
\)
Line \(4 x-3 y=7 \Longrightarrow 4 x-3 y-7=0\)
\(A=4, B=-3, C=-7\)
Point \((1,4)\)
\(
d=\frac{|4(1)-3(4)-7|}{\sqrt{4^2+(-3)^2}}=\frac{|4-12-7|}{\sqrt{16+9}}=\frac{|-15|}{5}=3
\)

Hint

(a) The roots of the equation \(x^2-\sqrt{6} x+3=0\) are \(\alpha=\frac{\sqrt{6}+i \sqrt{6}}{2}\) and \(\beta=\frac{\sqrt{6}-i \sqrt{6}}{2}\). These can be written in polar form as:
\(\alpha=\sqrt{3} e^{i \pi / 4}\)
\(\beta=\sqrt{3} e^{-i \pi / 4}\)
The expression \(\frac{\alpha^{99}}{\beta}+\alpha^{98}\) simplifies to:
\(\alpha^{98}\left(\frac{\alpha}{\beta}+1\right)\)
\(\alpha^{98}\left(\frac{\alpha+\beta}{\beta}\right)\)
Substituting the polar forms, the value becomes \(3^{49}(-1+i)\).
Comparing this to the given expression \(3^n(a+i b)\) :
\(n=49\)
\(a=-1\)
\(b=1\)
Both \(a[latex] and [latex]b\) are integers not divisible by 3, satisfying the given condition.
Thus, \(n+a+b=49+(-1)+1=49\).

Hint

(c) Find \(\alpha+\beta\) and \(\alpha \beta\)
For a quadratic \(x^2-x+2=0\) :
\(
\alpha+\beta=1, \quad \alpha \beta=2
\)
\(
\begin{aligned}
& \alpha^6+\alpha^4+\beta^4-5 \alpha^2 \\
& =\alpha^4(\alpha-2)+\alpha^4-5 \alpha^2+(\beta-2)^2 \\
& =\alpha^5-\alpha^4-5 \alpha^2+\beta^2-4 \beta+4 \\
& =\alpha^3(\alpha-2)-\alpha^4-5 \alpha^2+\beta-2-4 \beta+4 \\
& =-2 \alpha^3-5 \alpha^2-3 \beta+2 \\
& =-2 \alpha(\alpha-2)-5 \alpha^2-3 \beta+2 \\
& =-7 \alpha^2+4 \alpha-3 \beta+2 \\
& =-7(\alpha-2)+4 \alpha-3 \beta+2 \\
& =-3 \alpha-3 \beta+16=-3(1)+16=13
\end{aligned}
\)

Hint

(c) Step 1: Formulate the equations
The given conditions are used to form two equations based on the definition of a circle in the complex plane, \(\left|z-z_0\right|^2=r^2\).
\(
\begin{aligned}
& \left|\alpha-z_0\right|^2=4 \\
& \left|\frac{1}{\bar{\alpha}}-z_0\right|^2=16
\end{aligned}
\)
Expanding the modulus squared for the first equation using \(|w|^2=w \bar{w}\) :
\(
\left(\alpha-z_0\right)\left(\bar{\alpha}-\bar{z}_0\right)=4 \Longrightarrow|\alpha|^2-\left(\alpha \bar{z}_0+\bar{\alpha} z_0\right)+\left|z_0\right|^2=4
\)
Step 2: Expand the second equation
Expanding the modulus squared for the second equation:
\(
\left(\frac{1}{\bar{\alpha}}-z_0\right)\left(\frac{1}{\alpha}-\bar{z}_0\right)=16 \Longrightarrow \frac{1}{|\alpha|^2}-\frac{\left(\alpha \bar{z}_0+\bar{\alpha} z_0\right)}{|\alpha|^2}+\left|z_0\right|^2=16
\)
Multiplying the entire equation by \(|\alpha|^2\) to simplify:
\(
1-\left(\alpha \bar{z}_0+\bar{\alpha} z_0\right)+|\alpha|^2\left|z_0\right|^2=16|\alpha|^2
\)
Step 3: Solve the system
Let \(A=|\alpha|^2\) and \(B=\alpha \bar{z}_0+\bar{\alpha} z_0\).
From the first equation, \(B=A+\left|z_0\right|^2-4\).
From the second equation, \(B=1+A\left|z_0\right|^2-16 A\).
Equating the expressions for \(\boldsymbol{B}\) :
\(
A+\left|z_0\right|^2-4=1+A\left|z_0\right|^2-16 A
\)
Substituting the value of \(\left|z_0\right|^2=|1+i|^2=1^2+1^2=2\) :
\(
A+2-4=1+2 A-16 A \Longrightarrow A-2=1-14 A
\)
Solving for \(\boldsymbol{A}\) :
\(
15 A=3 \Longrightarrow A=\frac{1}{5}
\)
Step 4: Calculate the final value
The problem requires the value of \(100|\alpha|^2\), which is \(100 A\).
\(
100 \mathrm{~A}=100 \times \frac{1}{5}=20
\)

Hint

(c) Step 1: Simplify \((1+\alpha)^7\)
We are given that \(\alpha\) satisfies the equation \(\alpha^2+\alpha+1=0\). This implies \(\alpha^3=1\) and \(1+\alpha+\alpha^2=0\), so \(1+\alpha=-\alpha^2\).
Using this identity, we simplify the expression \((1+\alpha)^7\) :
\(
(1+\alpha)^7=\left(-\alpha^2\right)^7=-\left(\alpha^2\right)^7=-\alpha^{14}
\)
We know \(\alpha^3=1\), so \(\alpha^{14}=\alpha^{12} \cdot \alpha^2=\left(\alpha^3\right)^4 \cdot \alpha^2=1^4 \cdot \alpha^2=\alpha^2\).
Thus, \((1+\alpha)^7=-\alpha^2\).
Step 2: Express in the form \(A+B \alpha+C \alpha^2\)
The equation is \((1+\alpha)^7=A+B \alpha+C \alpha^2\).
Substituting our result:
\(
-\alpha^2=A+B \alpha+C \alpha^2
\)
We use the relationship \(\alpha^2=-1-\alpha\) to express everything in terms of 1 and \(\alpha\).
\(
-\left(-\alpha^2\right)=1+\alpha
\)
So, the equation becomes:
\(
1+\alpha=A+B \alpha+C \alpha^2
\)
Substitute \(\alpha^2=-1-\alpha\) on the right side:
\(
\begin{aligned}
& 1+\alpha=A+B \alpha+C(-1-\alpha) \\
& 1+\alpha=(A-C)+(B-C) \alpha
\end{aligned}
\)
Step 3: Determine the relationship between \(A, B\), and \(C\)
Comparing the coefficients of 1 and \(\alpha\) (assuming \(A, B, C\) are real), we get:
\(
\begin{aligned}
& A-C=1 \Longrightarrow A=C+1 \\
& B-C=1 \Longrightarrow B=C+1
\end{aligned}
\)
Thus, \(\boldsymbol{A}=\boldsymbol{B}=\boldsymbol{C}+1\). The non-negativity conditions \(\boldsymbol{A}, \boldsymbol{B}, \boldsymbol{C} \geq 0\) mean \(\boldsymbol{C}+1 \geq 0\) and \(C \geq 0\), which is consistent.
Step 4: Calculate the final value
We need to find the value of \(5(3 A-2 B-C)\).
Substitute \(A=C+1\) and \(B=C+1\) into the expression:
\(
\begin{gathered}
5(3 A-2 B-C)=5(3(C+1)-2(C+1)-C) \\
5(3 A-2 B-C)=5(3 C+3-2 C-2-C) \\
5(3 A-2 B-C)=5((3 C-2 C-C)+(3-2)) \\
5(3 A-2 B-C)=5(0 \times C+1)=5
\end{gathered}
\)

Hint

(c) 

\(
\Re(w)=x^2+y^2+k_1 x-k_2 y+\lambda=0
\)
Comparing with a circle:
\(
(x-h)^2+(y-k)^2=1
\)
gives
\(
h=-\frac{k_1}{2}, \quad k=\frac{k_2}{2} .
\)
You correctly set:
\(
(h, k)=(1,2),
\)
because the circle touches:
the \(y\)-axis \(\rightarrow h=1\)
the line \(y=1 \rightarrow\) center height \(=2\).
Thus:
\(
k_1=-2, \quad k_2=4 .
\)
\(
\lambda=-h^2-k^2+1=-\left(1^2+2^2\right)+1=-4
\)
Imaginary part
\(
\Im(w)=k_1 y+k_2 x+\lambda=-2 y+4 x-4=0
\)
Divide by 2 :
\(
2 x-y-2=0
\)
Your version had +2 ; the correct equation is:
\(
y=2 x-2
\)
Distance from center to the line
Line: \(2 x-y-2=0\).
Center: \((1,2)\).
Use the distance formula:
\(
d=\frac{|2(1)-2-2|}{\sqrt{2^2+(-1)^2}}=\frac{|-2|}{\sqrt{5}}=\frac{2}{\sqrt{5}} .
\)
Matches your value:
\(
d=\frac{2}{\sqrt{5}}
\)
For a circle of radius 1, chord distance \(d\) :
\(
\text { half chord length }=\sqrt{1^2-d^2}=\sqrt{1-\frac{4}{5}}=\sqrt{\frac{1}{5}}=\frac{1}{\sqrt{5}} \text {. }
\)
Full chord length:
\(
A B=2 \cdot \frac{1}{\sqrt{5}}=\frac{2}{\sqrt{5}} .
\)
Thus:
\(
A B^2=\frac{4}{5}
\)
Required value
\(
30(A B)^2=30 \cdot \frac{4}{5}=24 \text {. }
\)

Hint

(b) We are tasked with solving the given expression:
\(
z^2+8 i z-15 \text { and } z^2-3 i z-2 \in \mathbb{R}
\)
Step 1: Simplify the condition
Rewrite the given condition:
Let: \(1+\frac{11 i z-13}{z^2-3 i z-2} \in \mathbb{R} . Z=\alpha-\frac{13}{11} i\).
Step 2: Imaginary part condition
The imaginary part of the denominator must satisfy:
\(z^2-3 i z-2\) is imaginary. Substitute \(z=x+i y\) :
\(
\begin{aligned}
& z^2=x^2-y^2+2 x y i, \quad-3 i z=-3(x+i y) i=-3 y i+3 x, \\
& \text { so: } z^2-3 i z-2=\left(x^2-y^2+3 x-2\right)+(2 x y-3 y) i .
\end{aligned}
\)
For the expression to be purely imaginary:
\(
\operatorname{Re}\left(z^2-3 i z-2\right)=0 \Longrightarrow x^2-y^2+3 x-2=0 .
\)
Step 3: Solve the real part equation
Rewriting:
Factorize:
Step 4: Solve for \(z\)
Let:
where: \(x^2=y^2-3 y+2 . x^2=(y-1)(y-2) . z=\alpha-\frac{13}{11} i, x=\alpha, \quad y=-\frac{13}{11}\).
Substitute \(x=\alpha\) and \(y=-\frac{13}{11}\) into \(x^2=(y-1)(y-2)\) :
\(
\alpha^2=-\frac{13}{11}-1-\frac{13}{11}-2
\)
Step 5: Calculate \(242 \alpha^2\)
Substitute \(\alpha^2=\frac{24 \times 35}{121}\) :
\(
\begin{aligned}
& \alpha^2=-\frac{24}{11}-\frac{35}{11}, \alpha^2=\frac{24 \times 35}{121} . \\
& 242 \alpha^2=242 \cdot \frac{24 \times 35}{121} .
\end{aligned}
\)
Final Answer: \(242 \alpha^2=1680\).

Hint

(b) Step 1: Simplify the equation to standard circle form
The given equation is \(|z-\alpha|^2+|z-\beta|^2=2 \lambda\). Expanding the moduli in terms of \(z, \alpha\), and \(\beta\) yields the equation of a circle. The standard form \(\left|z-z_0\right|^2=R^2\) is reached by algebraic manipulation:
\(
\left|z-\frac{\alpha+\beta}{2}\right|^2=\lambda-\frac{|\alpha-\beta|^2}{4}
\)
The radius squared \(\left(R^2\right)\) is \(\lambda-\frac{|\alpha-\beta|^2}{4}\).
Step 2: Equate the derived radius with the given radius
The problem states the radius of the circle is \(\sqrt{\lambda-1}\). Therefore, the radius squared is \(R^2=(\sqrt{\lambda-1})^2=\lambda-1\).
Equating the two expressions for \(R^2\) :
\(
\begin{aligned}
\lambda-1 & =\lambda-\frac{|\alpha-\beta|^2}{4} \\
-1 & =-\frac{|\alpha-\beta|^2}{4} \\
4 & =|\alpha-\beta|^2
\end{aligned}
\)
Taking the square root of both sides (and noting the modulus is non-negative):
\(
|\alpha-\beta|=2
\)

Hint

(c) Given values
\(
z=1+i, \quad \bar{z}=1-i
\)
The expression:
\(
z_1=\frac{1+i \bar{z}}{\bar{z}(1-z)+\frac{1}{z}}
\)
Multiply numerator and denominator by \(z\) :
\(
z_1=\frac{z(1+i \bar{z})}{|z|^2(1-z)+1}
\)
Since:
\(
|z|^2=(1)^2+(1)^2=2
\)
Compute numerator
\(
1+i \bar{z}=1+i(1-i) .
\)
Compute inside:
\(
1-i \longrightarrow i(1-i)=i-i^2=i+1=1+i
\)
Thus:
\(
1+i \bar{z}=1+(1+i)=2+i .
\)
Now multiply by \(z=1+i\) :
\(
z(2+i)=(1+i)(2+i)=2+i+2 i+i^2=2+3 i-1=1+3 i
\)
So the numerator is:
\(
1+3 i
\)
\(
|z|^2(1-z)+1=2(1-(1+i))+1=2(-i)+1=1-2 i
\)
Thus:
\(
z_1=\frac{1+3 i}{1-2 i}
\)
Multiply numerator and denominator by \(1+2 i\) :
Denominator:
\(
(1-2 i)(1+2 i)=1+4=5
\)
Numerator:
\(
(1+3 i)(1+2 i)=1+2 i+3 i+6 i^2=1+5 i-6=-5+5 i
\)
So:
\(
z_1=\frac{-5+5 i}{5}=-1+i
\)
Thus:
\(
z_1=-1+i
\)
For:
\(
z_1=-1+i,
\)
the point lies in Quadrant II, so:
\(
\arg z_1=\frac{3 \pi}{4}
\)
\(
\frac{12}{\pi} \arg \left(z_1\right)=\frac{12}{\pi} \cdot \frac{3 \pi}{4}=9 .
\)

Hint

(b) Given, \(\alpha=8-14 i\)
Let \(z=x+i y\)
\(
\alpha z=(8-14 i)(x+i y)=(8 x+14 y)+i(-14 x+8 y)
\)
Now, \(z+\bar{z}=2 x\) and \(z-\bar{z}=2 i y\)
For \(A, \quad \frac{2 i(-14 x+8 y)}{i(4 x y-112)}=1\)
\(
\Rightarrow(x-4)(y+7)=0 \Rightarrow x=4 \text { or } y=-7
\)
For \(B, \quad x^2+(y+3)^2=16\)
When \(x=4\), then \(y=-3\); when \(y=-7\), then \(x=0\)
\(
\therefore A \cap B=\{4-3 i, \quad 0-7 i\}
\)
So, \(\Sigma_{z \in A \cap B}(\operatorname{Re} z-\operatorname{Im} z)=4-(-3)+(0-(-7))=7+7=14\)

Hint

(c) Step 1: Solve the first equation for \(z\)
The problem statement as presented appears to have a slight transcription error. Based on search results for the exact problem from the JEE Main 2022 exam, the equation is likely \(z^2=\bar{z} \cdot 2^{1-|z|}\). Assuming this is the intended equation, we can find the value of \(z\).
Take the modulus on both sides of the equation:
\(
\begin{aligned}
& \left|z^2\right|=\left|\bar{z} \cdot 2^{1-|z|}\right| \\
& |z|^2=|\bar{z}| \cdot\left|2^{1-|z|}\right|
\end{aligned}
\)
Since \(|\bar{z}|=|z|\) and \(2^{1-|z|}\) is a positive real number, we have:
\(
|z|^2=|z| \cdot 2^{1-|z|}
\)
As \(b \neq 0\), we know \(z \neq 0\), so we can divide by \(|z|\) :
\(
|z|=2^{1-|z|}
\)
Let \(r=|z|\). Then \(r=2^{1-r}\). Taking logarithm base 2 on both sides, we have \(\log _2 r=1-r\), or \(r+\log _2 r=1\). The only real solution to this equation is \(r=1\). Thus, \(|z|=1\).
Substitute \(|\mathrm{z}|=1\) back into the original equation:
\(
z^2=\bar{z} \cdot 2^{1-1} \Longrightarrow z^2=\bar{z}
\)
We also know that for a complex number with \(|z|=1, \bar{z}=\frac{1}{z}\). So, the equation becomes:
\(
z^2=\frac{1}{z} \Longrightarrow z^3=1
\)
The solutions to \(z^3=1\) are the cubic roots of unity: \(z=1, \omega, \omega^2\), where \(\omega=e^{i 2 \pi / 3}=-\frac{1}{2}+i \frac{\sqrt{3}}{2}\) and \(\omega^2=e^{i 4 \pi / 3}=-\frac{1}{2}-i \frac{\sqrt{3}}{2}\).
Since the problem states \(b \neq 0\), we must have \(z=\omega\) or \(z=\omega^2\). Let’s take \(z=\omega\) for the next steps, the result for \(n[latex] will be the same for [latex]z=\omega^2\).
Step 2: Solve the second equation for the least value of \(\boldsymbol{n}\)
We need to find the least \(n \in \mathbb{N}\) such that \(z^n=(z+1)^n\).
This can be rewritten as \(\left(\frac{z+1}{z}\right)^n=1\), which simplifies to \(\left(1+\frac{1}{z}\right)^n=1\).
Substitute \(z=\omega\) into the expression:
\(
1+\frac{1}{z}=1+\frac{1}{\omega}=1+\omega^2
\)
We know that \(1+\omega+\omega^2=0\), so \(1+\omega^2=-\omega\).
The condition becomes \((-\omega)^n=1\), or \((-1)^n \omega^n=1\).
Step 3: Find the least integer \(\boldsymbol{n}\)
We need to find the least natural number \(n\) such that \((-1)^n \omega^n=1\). This requires both \((-1)^n\) to be 1 (so \(n\) must be even) and \(\omega^n\) to be 1. For \(\omega^n=1\), the least natural number \(n\) is 3 (as \(\omega\) is a cubic root of unity). The least common multiple of 2 and 3 is 6.
For \(n=6\), we have \((-1)^6 \omega^6=1^6 \cdot\left(e^{i 2 \pi / 3}\right)^6=1 \cdot e^{i 4 \pi}=1\). This is the least natural number \(n\) that satisfies the condition.
The least value of \(n \in \mathbb{N}\), such that \(z^n=(z+1)^n\), is equal to 6.

Hint

(a) The set \(S[latex] contains the following solutions:
[latex]z_1=0\), where \(\operatorname{Re}\left(z_1\right)=0, \operatorname{Im}\left(z_1\right)=0\)
\(z_2=-1\), where \(\operatorname{Re}\left(z_2\right)=-1, \operatorname{Im}\left(z_2\right)=0\)
\(z_3=\frac{1}{2}+i \frac{\sqrt{3}}{2}\), where \(\operatorname{Re}\left(z_3\right)=\frac{1}{2}, \operatorname{Im}\left(z_3\right)=\frac{\sqrt{3}}{2}\)
\(z_4=\frac{1}{2}-i \frac{\sqrt{3}}{2}\), where \(\operatorname{Re}\left(z_4\right)=\frac{1}{2}, \operatorname{Im}\left(z_4\right)=-\frac{\sqrt{3}}{2}\)
The sum of ( \(\operatorname{Re}(z)+\operatorname{Im}(z)\) ) for all \(z \in S\) is:
\(
(0+0)+(-1+0)+\left(\frac{1}{2}+\frac{\sqrt{3}}{2}\right)+\left(\frac{1}{2}-\frac{\sqrt{3}}{2}\right)=0-1+\frac{1}{2}+\frac{\sqrt{3}}{2}+\frac{1}{2}-\frac{\sqrt{3}}{2}=0
\)

Hint

(d) The set \(\boldsymbol{S}\) is defined by the intersection of a disk and a half-plane:
\(|z-2| \leq 1\) describes a closed disk with center \(C(2,0)\) and radius \(r=1\).
\(z(1+i)+\bar{z}(1-i) \leq 2\) simplifies to \(x-y \leq 1\) (or \(x-y-1 \leq 0\) ) for \(z=x+i y\)
The points \(z_1\) and \(z_2\) that minimize and maximize \(|z-4 i|\) (distance from point \(A(0,4)\) ) lie on the boundary of the region \(S\).
\(z_1\) (minimum distance) is the point on the circle closest to \(A\). This point lies on the line segment connecting the center of the circle \(C(2,0)\) and \(A(0,4)\) extended to the circle boundary, within \(S\). The coordinates of \(z_1\) are found to be \((2-1 / \sqrt{5}, 2 / \sqrt{5})\). Then \(\left|z_1\right|^2=5-4 / \sqrt{5}\).
\(z_2\) (maximum distance) is one of the points on the boundary farthest from \(A\). The intersection points of the line \(x-y=1\) and the circle \((x-2)^2+y^2=1\) are candidates. One such point is found to be \((1,0)\left(\right.\) so \(\left.\mathbf{z}_2=1\right)\). Then \(\left|z_2\right|^2=1^2+0^2=1\).
Substituting these values into the given equation:
\(
5\left(\left|z_1\right|^2+\left|z_2\right|^2\right)=5\left(\left(5-\frac{4}{\sqrt{5}}\right)+1\right)=5\left(6-\frac{4 \sqrt{5}}{5}\right)=30-4 \sqrt{5}
\)
Comparing this with \(\alpha+\beta \sqrt{5}\), we get \(\alpha=30\) and \(\beta=-4\).
Therefore, \(\alpha+\beta=30+(-4)=26\).

Hint

(b) Step 1: Rearrange the equation and separate into real and imaginary components
The given equation is \(\bar{z}=i z^2+z^2-z\), which can be rearranged as \(\bar{z}+z=(i+1) z^2\). Using the property that \(\bar{z}+z=2 \operatorname{Re}(z)\), and substituting \(z=x+i y\), we get \(2 x=(i+1)(x+i y)^2\). Expanding this equation and equating the real and imaginary parts yields a system of equations:
\(
\begin{gathered}
2 x=x^2-y^2-2 x y \\
0=x^2-y^2+2 x y
\end{gathered}
\)
Step 2: Solve the system of equations for all solutions
From the second equation, \(x^2-y^2=-2 x y\). Substituting this into the first equation gives \(2 x=-2 x y-2 x y\), which simplifies to \(2 x=-4 x y\), or \(2 x(1+2 y)=0\). This leads to two cases:
Case 1: \(x=0\). Substituting into \(x^2-y^2=-2 x y\) gives \(0-y^2=0\), so \(y=0\). This solution is \(\mathrm{z}_0=0\).
Case 2: \(1+2 y=0\), which means \(y=-1 / 2\). Substituting into \(x^2-y^2=-2 x y\) gives \(x^2-(-1 / 2)^2=-2 x(-1 / 2)\), or \(x^2-1 / 4=x\). Solving the quadratic equation \(4 x^2-4 x-1=0\) using the quadratic formula \(x=\frac{-b \pm \sqrt{b^2-4 a c}}{2 a}\) gives \(x=\frac{4 \pm \sqrt{16+16}}{8}=\frac{4 \pm 4 \sqrt{2}}{8}=\frac{1 \pm \sqrt{2}}{2}\).
This yields two more solutions: \(z_1=\frac{1+\sqrt{2}}{2}-\frac{1}{2} i\) and \(z_2=\frac{1-\sqrt{2}}{2}-\frac{1}{2} i\).
Step 3: Calculate the sum of squares of moduli
We calculate the square of the modulus \(|z|^2=x^2+y^2\) for each solution:
\(\left|z_0\right|^2=0^2+0^2=0\).
\(\left|z_1\right|^2=\left(\frac{1+\sqrt{2}}{2}\right)^2+\left(-\frac{1}{2}\right)^2=\frac{1+2 \sqrt{2}+2}{4}+\frac{1}{4}=\frac{4+2 \sqrt{2}}{4}=\frac{2+\sqrt{2}}{2}\).
\(\left|z_2\right|^2=\left(\frac{1-\sqrt{2}}{2}\right)^2+\left(-\frac{1}{2}\right)^2=\frac{1-2 \sqrt{2}+2}{4}+\frac{1}{4}=\frac{4-2 \sqrt{2}}{4}=\frac{2-\sqrt{2}}{2}\)
The sum of these squares is:
\(
S=\left|z_0\right|^2+\left|z_1\right|^2+\left|z_2\right|^2=0+\frac{2+\sqrt{2}}{2}+\frac{2-\sqrt{2}}{2}=\frac{4}{2}=2
\)

Hint

(d) Step 1: Rewrite the condition
Let \(z=a+i b\). Then
\(
|z-(3-2 i)|=|(a+i b)-(3-2 i)|=\mid(a-3)+i(b+2) \| .
\)
The modulus is
\(
|(a-3)+i(b+2)|=\sqrt{(a-3)^2+(b+2)^2} .
\)
So the inequality becomes
\(
1<\sqrt{(a-3)^2+(b+2)^2}<4 .
\)
Squaring both sides:
\(
1^2<(a-3)^2+(b+2)^2<4^2 \Longrightarrow 1<(a-3)^2+(b+2)^2<16 .
\)
This is the set of integer lattice points inside an annulus centered at \((3,-2)\) with inner radius 1 and outer radius 4.
Step 2: Consider integer solutions
We are looking for integers \(a, b\) such that
\(
(a-3)^2+(b+2)^2=r^2
\)
with \(2 \leq r^2 \leq 15\) (because strictly greater than 1 and strictly less than 16 ).
So \(r^2 \in\{2,3,4,5,6,7,8,9,10,11,12,13,14,15\}\).
Step 3: Find lattice points for each possible \(r^2\)
Let \(x=a-3\) and \(y=b+2\). Then \(x, y \in \mathbb{Z}\) and
\(
x^2+y^2=r^2, \quad r^2=2,3, \ldots, 15
\)
We list integer solutions for \(x^2+y^2=n\) for each \(n\) in the range:
1. \(x^2+y^2=2\) : solutions \(( \pm 1, \pm 1) \rightarrow 4\) points
2. \(x^2+y^2=3\) : solutions \(( \pm 1, \pm \sqrt{2}) \rightarrow\) not integers \(\rightarrow 0\) points
3. \(x^2+y^2=4\) : solutions \(( \pm 2,0),(0, \pm 2) \rightarrow 4\) points
4. \(x^2+y^2=5\) : solutions \(( \pm 1, \pm 2),( \pm 2, \pm 1) \rightarrow 8\) points
5. \(x^2+y^2=6\) : no integer solutions \(\rightarrow 0\)
6. \(x^2+y^2=7\) : no integer solutions \(\rightarrow 0\)
7. \(x^2+y^2=8\) : solutions \(( \pm 2, \pm 2) \rightarrow 4\) points
8. \(x^2+y^2=9\) : solutions \(( \pm 3,0),(0, \pm 3) \rightarrow 4\) points
9. \(x^2+y^2=10\) : solutions \(( \pm 1, \pm 3),( \pm 3, \pm 1) \rightarrow 8\) points
10. \(x^2+y^2=11\) : no integer solutions \(\rightarrow 0\)
11. \(x^2+y^2=12\) : solutions \(( \pm 2, \pm 2 \sqrt{2}) \rightarrow\) not integers \(\rightarrow 0\)
12. \(x^2+y^2=13\) : solutions \(( \pm 2, \pm 3),( \pm 3, \pm 2) \rightarrow 8\) points
13. \(x^2+y^2=14\) : no integer solutions \(\rightarrow 0\)
14. \(x^2+y^2=15\) : no integer solutions \(\rightarrow 0\)
Step 4: Total number of points
Add them up:
\(
4+0+4+8+0+0+4+4+8+0+0+8+0+0=40
\)
So there are 40 elements in the set.

Hint

(b) The roots of the equation \(z^2+z+1=0\) are complex cube roots of unity, \(\omega\) and \(\omega^2\). A key property of these roots is \(z^3=1\) and \(1+z+z^2=0\). Also, \(1 / z=z^2\) and \(1 / z^2=z\)
The expression inside the modulus simplifies as follows:
\(
\left(z^n+(-1)^n \frac{1}{z^n}\right)^2=\left(z^n+\frac{(-1)^n}{z^n}\right)^2=z^{2 n}+\frac{(-1)^{2 n}}{z^{2 n}}+2 \cdot z^n \cdot \frac{(-1)^n}{z^n}=z^{2 n}+\frac{1}{z^{2 n}}+2(-1)^n
\)
The sum can be broken into three parts:
\(\sum_{n=1}^{15} z^{2 n}\)
\(\sum_{n=1}^{15} \frac{1}{z^{2 n}}=\sum_{n=1}^{15} z^{-2 n}\)
\(\sum_{n=1}^{15} 2(-1)^n\)
Using the property that the sum of the \(k\)-th powers of the \(n\)-th roots of unity is 0 if \(k\) is not a multiple of \(n\) (and \(n\) otherwise, with \(n=3\) here):
\(\sum_{n=1}^{15} z^{2 n}=\sum_{n=1}^{15}\left(z^2\right)^n=5 \times\left(z^2+z^4+z^6\right)=5 \times\left(z^2+z+1\right)=5 \times 0=0\). (Or simply, \(2 \times 15=30\), which is a multiple of 3, so sum of powers from 1 to 15 is 0 )
\(\sum_{n=1}^{15} z^{-2 n}=0\) by the same logic.
\(\sum_{n=1}^{15} 2(-1)^n=2 \sum_{n=1}^{15}(-1)^n=2 \times(-1+1-1+1 \ldots-1)=2 \times(-1)=-2\).
The entire sum is \(0+0-2=-2\).
The modulus is \(|-2|=2\).

Hint

(d) The set \(S\) is the region within or on the boundary of the circle centered at \((3,0)\) with a radius of 1, and also restricted to the half-plane where \(\boldsymbol{x} \leq 3\).
The point in \(\boldsymbol{S}\) closest to \(\mathbf{4} \boldsymbol{i}\) (the point \((0,4)\) in the complex plane) is on the boundary of the circle, specifically the point \((\alpha, \beta)=\left(\frac{12}{5}, \frac{4}{5}\right)\).
The calculation is as follows:
The point is \(\alpha+i \beta=\frac{12}{5}+i \frac{4}{5}\), so \(\alpha=\frac{12}{5}\) and \(\beta=\frac{4}{5}\).
\(\alpha+\beta=\frac{12}{5}+\frac{4}{5}=\frac{16}{5}\).
\(25(\alpha+\beta)=25 \times \frac{16}{5}=5 \times 16=80\).

Hint

(c) Step 1: Geometric interpretation
Let \(z=x+i y\). Then the condition
\(
|z-(2+2 i)| \leq 1
\)
means that \(z\) lies inside or on the circle of radius 1 centered at \((2,2)\) in the complex plane.
We want to maximize
\(
|3 i z+6|=|3 i(x+i y)+6|=|3 i x-3 y+6|=|(-3 y+6)+i(3 x)| .
\)
So in the \(X Y\)-plane, the complex number is
\(
u+i v=(-3 y+6)+i(3 x),
\)
and we want to maximize its modulus:
\(
|3 i z+6|=\sqrt{(3 x)^2+(-3 y+6)^2}=\sqrt{9 x^2+9(y-2)^2}=3 \sqrt{x^2+(y-2)^2} .
\)
Step 2: Reduce the problem
We need to maximize
\(
3 \sqrt{x^2+(y-2)^2} \text { subject to }(x-2)^2+(y-2)^2 \leq 1 .
\)
Geometrically: we want the point on or inside the circle \((x-2)^2+(y-2)^2 \leq 1\) that is farthest from the point \((0,2)\) (because \(\sqrt{x^2+(y-2)^2}\) is the distance from \((0,2)\) ).
Step 3: Find the farthest point
The circle is centered at \(C=(2,2)\) with radius \(r=1\).
Distance from the point \(P=(0,2)\) to the circle center \(C=(2,2)\) is \(|C-P|= \sqrt{(2-0)^2+(2-2)^2}=2\).
The maximum distance from \(P\) to the circle is along the line connecting \(P\) and \(C\), moving away from P by the radius:
\(
d_{\max }=|C-P|+r=2+1=3
\)
The point on the circle along this line is
\(
x=2+\frac{2}{2} \cdot 1=3 ? \quad \text { check carefully. }
\)
Direction vector from \(P=(0,2)\) to \(C=(2,2)\) is \(\vec{d}=(2,0)\). Unit vector: \(\hat{d}=(1,0)\).
Farthest point from \(P\) along this line (on the circle) is
\(
C+r \hat{d}=(2,2)+1 \cdot(1,0)=(3,2) .
\)
Step 4: Maximum modulus
Distance from \(P=(0,2)\) to \((3,2)\) is \(\sqrt{(3-0)^2+(2-2)^2}=3\).
Then
\(
|3 i z+6|_{\max }=3 \cdot 3=9 .
\)
Step 5: Answer \(a+b\)
The point where maximum occurs: \(z=x+i y=3+2 i \rightarrow a=3, b=2\)
\(
a+b=3+2=5
\)

Hint

(a)

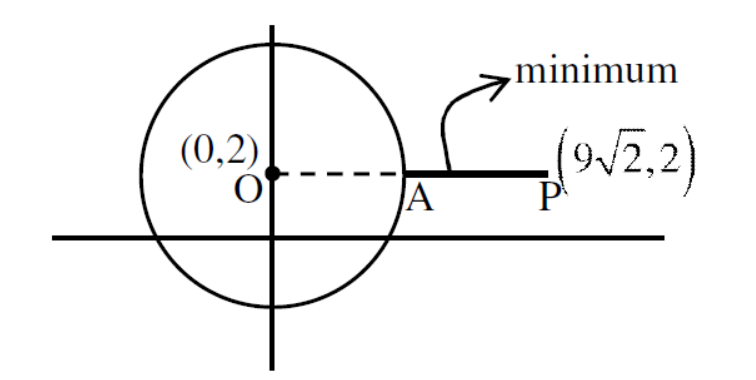
Step 1: Determine the locus of point z
The given condition is \(\arg \left(\frac{z-2}{z+2}\right)=\frac{\pi}{4}\). By substituting \(z=x+i y\) into the expression \(\frac{z-2}{z+2}\) and simplifying, we get:
\(
\frac{z-2}{z+2}=\frac{x^2+y^2-4+i(4 y)}{(x+2)^2+y^2}
\)
The argument condition \(\tan (\theta)=1\) implies the real and imaginary parts are equal and positive:
\(
\frac{4 y}{x^2+y^2-4}=1 \Longrightarrow x^2+y^2-4 y-4=0 \Longrightarrow x^2+(y-2)^2=8
\)
The locus of \(z\) is a circular arc of a circle centered at \(C(0,2)\) with a radius \(R=\sqrt{8}=2 \sqrt{2}\). The condition for the argument to be exactly \(\pi / 4\) restricts the locus to the arc where the real part is positive, which corresponds to \(x^2+y^2>4\) and \(y>0\)
Step 2: Identify the point to minimize distance from and its location relative to the locus
The quantity to minimize is \(|z-P|^2\) where \(P\) is the point \(9 \sqrt{2}+2 i\), corresponding to coordinates \((9 \sqrt{2}, 2)\). The center of the circle \(C\) has coordinates \((0,2)\).
The distance \(d\) between the center \(C\) and point \(P\) is calculated as:
\(
d=|C P|=\sqrt{(9 \sqrt{2}-0)^2+(2-2)^2}=9 \sqrt{2}
\)
Since \(d=9 \sqrt{2}\) and the radius \(R=2 \sqrt{2}\), we have \(d>R\), meaning the point \(P\) lies outside the circle.
Step 3: Calculate the minimum distance
The minimum distance from a point \(\mathbf{z}\) on the circle to an external point \(P\) occurs along the line segment connecting the center \(C\) to \(P\). The minimum distance value is \(d-R\).
\(
d-R=9 \sqrt{2}-2 \sqrt{2}=7 \sqrt{2}
\)
The minimum value of the squared distance is \((d-R)^2\).
\(
(7 \sqrt{2})^2=49 \times 2=98
\)
The point \(z[latex] on the circle that minimizes the distance is [latex](2 \sqrt{2}, 2)\), which satisfies the arc conditions.

Hint

(c) Step 1: Identify the locus of points satisfying the given condition
The equation \(|z-3|=\operatorname{Re}(z)\) defines a locus of points in the complex plane. Let \(z=x+i y\). Substituting this into the equation, we get \(|x+i y-3|=x\), which expands to \(\sqrt{(x-3)^2+y^2}=x\). Squaring both sides yields \((x-3)^2+y^2=x^2\), which simplifies to \(x^2-6 x+9+y^2=x^2\), or \(y^2=6 x-9\). This is the equation of a parabola. Thus, both \(z_1\) and \(z_2\) lie on the parabola \(y^2=6 x-9\).
Step 2: Use the argument condition to relate the coordinates The condition arg \(\left(z_1-z_2\right)=\frac{\pi}{4}\) implies that the slope of the line segment connecting \(z_1=x_1+i y_1\) and \(z_2=x_2+i y_2\) is \(\tan \left(\frac{\pi}{4}\right)=1\). The slope is given by \(\frac{y_1-y_2}{x_1-x_2}=1\), which means \(y_1-y_2=x_1-x_2\).
Step 3: Solve for the required value
We have the equations \(y_1^2=6 x_1-9\) and \(y_2^2=6 x_2-9\). Subtracting the second from the first gives \(y_1^2-y_2^2=6 x_1-6 x_2=6\left(x_1-x_2\right)\). Using the relation from Step 2, \(x_1-x_2=y_1-y_2\), we can write:
\(
\begin{gathered}
y_1^2-y_2^2=6\left(y_1-y_2\right) \\
\left(y_1-y_2\right)\left(y_1+y_2\right)=6\left(y_1-y_2\right)
\end{gathered}
\)
Assuming \(z_1 \neq z_2\), we have \(y_1 \neq y_2\), so we can divide by ( \(y_1-y_2\) ) to get \(y_1+y_2=6\). The imaginary part of \(z_1+z_2\) is \(\operatorname{Im}\left(z_1+z_2\right)=y_1+y_2\).

Hint

(b) Step 1: Write \(1-i\) in polar form
We have:
\(
1-i=\sqrt{2} e^{-i \pi / 4}
\)
Check:
\(|1-i|=\sqrt{1^2+(-1)^2}=\sqrt{2}\)
Argument \(\theta=\arctan (-1 / 1)=-\pi / 4\)
Step 2: Write \(2 i\) in polar form
\(
2 i=2 e^{i \pi / 2} .
\)
Step 3: Express the fraction in polar form
\(
\frac{(2 i)^n}{(1-i)^{n-2}}=\frac{\left(2 e^{i \pi / 2}\right)^n}{\left(\sqrt{2} e^{-i \pi / 4}\right)^{n-2}} .
\)
Simplify numerator and denominator:
\(
\left(2 e^{i \pi / 2}\right)^n=2^n e^{i n \pi / 2}, \quad\left(\sqrt{2} e^{-i \pi / 4}\right)^{n-2}=2^{(n-2) / 2} e^{-i(n-2) \pi / 4}=2^{(n-2) / 2} e^{-i(n-2) \pi / 4} .
\)
So the fraction becomes:
\(
\frac{2^n e^{i n \pi / 2}}{2^{(n-2) / 2} e^{-i(n-2) \pi / 4}}=2^{n-(n-2) / 2} \cdot e^{i(n \pi / 2+(n-2) \pi / 4)} .
\)
Simplify exponent of 2:
\(
n-\frac{n-2}{2}=n-\frac{n}{2}+1=\frac{n}{2}+1
\)
So magnitude part: \(2^{n / 2+1}\).
Step 4: Simplify exponent of \(e^{i \theta}\)
\(
n \frac{\pi}{2}+(n-2) \frac{\pi}{4}=\frac{2 n \pi}{4}+\frac{(n-2) \pi}{4}=\frac{3 n-2}{4} \pi
\)
So fraction:
\(
\frac{(2 i)^n}{(1-i)^{n-2}}=2^{n / 2+1} \cdot e^{i(3 n-2) \pi / 4}
\)
Step 5: Condition for being a positive integer
A positive integer has zero argument: \(e^{i(3 n-2) \pi / 4}=1\)
So the exponent must be a multiple of \(2 \pi\) :
\(
\frac{3 n-2}{4} \pi=2 k \pi, \quad k \in \mathbb{Z} .
\)
Divide both sides by \(\pi\) :
\(
\frac{3 n-2}{4}=2 k \Longrightarrow 3 n-2=8 k \Longrightarrow 3 n=8 k+2 \Longrightarrow n=\frac{8 k+2}{3} .
\)
We want least positive integer \(n\).
Try \(k=1: n=\frac{8+2}{3}=10 / 3 \times\) not integer
\(k=2: n=\frac{16+2}{3}=18 / 3=6\) integer

Hint

(a) Step 1: Analyze the complex number
The given complex number is \(z=\frac{1-i \sqrt{3}}{2}\). Its polar form can be determined by finding its magnitude and argument. The magnitude is \(|z|=\sqrt{\left(\frac{1}{2}\right)^2+\left(-\frac{\sqrt{3}}{2}\right)^2}=1\). The argument is \(\theta=-\frac{\pi}{3}\). Thus, \(z=e^{-i \pi / 3}\).
Step 2: Simplify the general term of the series
For any integer \(k\), the term in the series is \(\left(z^k+\frac{1}{z^k}\right)^3\). Since \(|z|=1\), we have \(\frac{1}{z}=\bar{z}\) and \(\frac{1}{z^k}=\bar{z}^k\). Therefore, \(z^k+\frac{1}{z^k}=z^k+\bar{z}^k=2 \operatorname{Re}\left(z^k\right)=2 \cos \left(\frac{k \pi}{3}\right)\). The \(k\)-th term becomes \(\left(2 \cos \left(\frac{k \pi}{3}\right)\right)^3=8 \cos ^3\left(\frac{k \pi}{3}\right)\). Using the trigonometric identity \(\cos (3 \theta)=4 \cos ^3(\theta)-3 \cos (\theta)\), we can rewrite this as \(8 \cos ^3\left(\frac{k \pi}{3}\right)=2 \cos (k \pi)+6 \cos \left(\frac{k \pi}{3}\right)=2(-1)^k+6 \cos \left(\frac{k \pi}{3}\right)\).
Step 3: Sum the series terms
The total expression is \(21+\sum_{k=1}^{21}\left(z^k+\frac{1}{z^k}\right)^3=21+\sum_{k=1}^{21}\left(2(-1)^k+6 \cos \left(\frac{k \pi}{3}\right)\right)\). We split the summation into two parts:
\(
\begin{gathered}
\sum_{k=1}^{21} 2(-1)^k=2(-1+1-1+1-\ldots-1)=2(-1)=-2 \\
\sum_{k=1}^{21} 6 \cos \left(\frac{k \pi}{3}\right)=6 \sum_{k=1}^{21} \cos \left(\frac{k \pi}{3}\right)
\end{gathered}
\)
Using the summation formula for cosines, \(\sum_{k=1}^n \cos (k x)=\frac{\sin (n x / 2) \cos ((n+1) x / 2)}{\sin (x / 2)}\), with \(n=21\) and \(x=\pi / 3\), the sum is:
\(
\frac{\sin (21 \pi / 6) \cos (22 \pi / 6)}{\sin (\pi / 6)}=\frac{\sin (7 \pi / 2) \cos (11 \pi / 3)}{\sin (\pi / 6)}=\frac{(-1)(1 / 2)}{(1 / 2)}=-1
\)
The second part of the sum is \(6 \times(-1)=-6\). The total sum of the series part is \(-2+(-6)=-8\).
The final value of the entire expression is \(21+(-8)=13\).

Hint

(a) Step 1: Rationalize the complex number
To find the real part of \(\mathbf{z}\), multiply the numerator and denominator by the conjugate of the denominator:
\(
z=\frac{3+2 i \cos \theta}{1-3 i \cos \theta} \times \frac{1+3 i \cos \theta}{1+3 i \cos \theta}
\)
The expression expands to:
\(
z=\frac{3+9 i \cos \theta+2 i \cos \theta+6 i^2 \cos ^2 \theta}{1+9 \cos ^2 \theta}
\)
Simplifying the expression and separating the real and imaginary parts:
\(
z=\frac{3-6 \cos ^2 \theta}{1+9 \cos ^2 \theta}+i \frac{11 \cos \theta}{1+9 \cos ^2 \theta}
\)
Step 2: Determine the value of \(\theta\)
The real part of \(\mathbf{z}\) is given as zero. Setting the real part of the simplified expression to zero:
\(
\frac{3-6 \cos ^2 \theta}{1+9 \cos ^2 \theta}=0
\)
This implies that the numerator must be zero:
\(
\begin{gathered}
3-6 \cos ^2 \theta=0 \\
6 \cos ^2 \theta=3 \\
\cos ^2 \theta=\frac{1}{2} \\
\cos \theta= \pm \frac{1}{\sqrt{2}}
\end{gathered}
\)
Given the condition \(\theta \in\left(0, \frac{\pi}{2}\right)\), \(\cos \theta\) must be positive, so \(\cos \theta=\frac{1}{\sqrt{2}}\), which means
\(
\theta=\frac{\pi}{4} .
\)
\(
\begin{aligned}
&\text { Substitute } \theta=\frac{\pi}{4} \text { into the given expression } \sin ^2(3 \theta)+\cos ^2(\theta) \text { : }\\
&\begin{gathered}
\sin ^2\left(3 \times \frac{\pi}{4}\right)+\cos ^2\left(\frac{\pi}{4}\right) \\
\sin ^2\left(\frac{3 \pi}{4}\right)+\cos ^2\left(\frac{\pi}{4}\right) \\
\left(\frac{1}{\sqrt{2}}\right)^2+\left(\frac{1}{\sqrt{2}}\right)^2 \\
\frac{1}{2}+\frac{1}{2}=1
\end{gathered}
\end{aligned}
\)

Hint

(a) Circle Center: The equation of the circle, \(\operatorname{Re}\left(z^2\right)+2(\operatorname{Im}(z))^2+2 \operatorname{Re}(z)=0\), translates to \(x^2+y^2+2 x=0\) or \((x+1)^2+y^2=1\). The center of the circle is \((-1,0)\).
Parabola Vertex: The equation of the parabola, \(x^2-6 x-y+13=0\), can be rewritten in vertex form as \(y=(x-3)^2+4\). The vertex is \((3,4)\).
Line Equation: The line passes through the points \((-1,0)\) and \((3,4)\). The slope is \(m=\frac{4-0}{3-(-1)}=\frac{4}{4}=1\). Using the point-slope form with \((-1,0)\), the line equation is \(y-0=1(x-(-1))\), which simplifies to \(y=x+1\).
Y-intercept: The \(y\)-intercept is the value of \(y\) when \(x=0\). Substituting \(x=0\) into the line equation gives \(y=0+1=1\). The \(y\)-intercept is 1.

Hint

(b) The condition \(\left(\begin{array}{ll}0 & i \\ 1 & 0\end{array}\right)^n\left(\begin{array}{ll}a & b \\ c & d\end{array}\right)=\left(\begin{array}{ll}a & b \\ c & d\end{array}\right)\) for all real \(a, b, c, d\) implies that the matrix \(\boldsymbol{M}^n\) must be the identity matrix, \(\boldsymbol{I}=\left(\begin{array}{ll}1 & 0 \\ 0 & 1\end{array}\right)\).
Let \(\boldsymbol{M}=\left(\begin{array}{ll}0 & i \\ 1 & 0\end{array}\right)\). We calculate the powers of \(\boldsymbol{M}\) :
\(M^1=M=\left(\begin{array}{ll}0 & i \\ 1 & 0\end{array}\right)\)
\(M^2=M \times M=\left(\begin{array}{ll}0 & i \\ 1 & 0\end{array}\right)\left(\begin{array}{ll}0 & i \\ 1 & 0\end{array}\right)=\left(\begin{array}{ll}0 \cdot 0+i \cdot 1 & 0 \cdot i+i \cdot 0 \\ 1 \cdot 0+0 \cdot 1 & 1 \cdot i+0 \cdot 0\end{array}\right)=\left(\begin{array}{ll}i & 0 \\ 0 & i\end{array}\right)=i I\)
\(M^3=M^2 \times M=i I \times M=i M=\left(\begin{array}{ll}0 & -1 \\ i & 0\end{array}\right)\)
\(M^4=M^2 \times M^2=(i I) \times(i I)=i^2 I^2=-I=\left(\begin{array}{ll}-1 & 0 \\ 0 & -1\end{array}\right)\)
\(M^5=M^4 \times M=-I \times M=-M=\left(\begin{array}{cc}0 & -i \\ -1 & 0\end{array}\right)\)
\(M^6=M^4 \times M^2=-I \times i I=-i I=\left(\begin{array}{cc}-i & 0 \\ 0 & -i\end{array}\right)\)
\(M^7=M^6 \times M=-i I \times M=-i M=\left(\begin{array}{cc}0 & 1 \\ -i & 0\end{array}\right)\)
\(M^8=M^4 \times M^4=(-I) \times(-I)=I^2=I=\left(\begin{array}{ll}1 & 0 \\ 0 & 1\end{array}\right)\)
The smallest positive integer \(n\) for which \(\boldsymbol{M}^{\boldsymbol{n}}=\boldsymbol{I}\) is \(\boldsymbol{n}=8\). The set \(S\) consists of all positive integer multiples of 8 : \(S=\{8,16,24,32,40,48,56,64,72,80,88,96,104, \ldots\}\)
The “2-digit” numbers in the set \(\boldsymbol{S}\) are the elements between 10 and 99, inclusive. These numbers are the multiples of 8 within that range:
\(
16,24,32,40,48,56,64,72,80,88,96.
\)
Counting these numbers, we find there are 11 such values. There are 90 two-digit natural numbers in total, ranging from 10 to 99.
The number of 2-digit numbers in the set \(S\) is \(\mathbf{1 1}\).

Hint

(c) Step 1: Use the condition for an equilateral triangle
The roots \(\mathbf{z}_1, \mathbf{z}_2\) and the origin \(O\) form an equilateral triangle if they satisfy the condition \(z_1^2+z_2^2+O^2=z_1 z_2+z_2 O+O z_1\), which simplifies to \(z_1^2+z_2^2=z_1 z_2\).
Step 2: Relate the condition to the coefficients of the equation
The condition from Step 1 can be rewritten using the identity \(\left(z_1+z_2\right)^2-2 z_1 z_2=z_1 z_2\), which simplifies to \(\left(z_1+z_2\right)^2=3 z_1 z_2\). From the given equation \(z^2+a z+12=0\), we know the sum of the roots is \(z_1+z_2=-a\) and the product of the roots is \(z_1 z_2=12\).
Step 3: Solve for \(|a|\)
Substitute the sum and product of the roots into the simplified condition:
\(
\begin{gathered}
(-a)^2=3(12) \\
a^2=36
\end{gathered}
\)
Taking the square root of both sides gives \(a= \pm 6\). The value of \(|a|\) is calculated as:
\(
|a|=| \pm 6|=6
\)

Hint

(b) Step 1: Determine the locus of \(z\)
The given condition is \(\left|\frac{z+i}{z-3 i}\right|=1\), which simplifies to \(|z+i|=|z-3 i|\). By letting \(z=x+i y\), the condition becomes:
\(
\sqrt{x^2+(y+1)^2}=\sqrt{x^2+(y-3)^2}
\)
Squaring both sides and simplifying the equation yields \(y=1\). Thus, the locus of \(z\) is the line \(z=x+i\) where \(x \in \mathbf{R}\).
Step 2: Minimize the real part of \(\omega\)
The expression for \(\omega\) is \(\omega=z \bar{z}-2 z+2\). Substituting \(z=x+i\) and \(\bar{z}=x-i\), we get:
\(
\begin{gathered}
\omega=(x+i)(x-i)-2(x+i)+2 \\
\omega=\left(x^2+1\right)-2 x-2 i+2 \\
\omega=\left(x^2-2 x+3\right)-2 i
\end{gathered}
\)
The real part of \(\omega\) is \(\operatorname{Re}(\omega)=x^2-2 x+3\). This quadratic function has a minimum value at \(x=-\frac{b}{2 a}=-\frac{-2}{2(1)}=1\). The specific value of \(\omega\) for this \(x\) is
\(
\omega=1^2-2(1)+3-2 i=2-2 i .
\)
Step 3: Find the minimum \(n\) for which \(\omega^n\) is real
To determine when \(\omega^n\) is real, we express \(\omega=2-2 i\) in polar form. The magnitude is \(|\omega|=\sqrt{2^2+(-2)^2}=\sqrt{8}=2 \sqrt{2}\), and the argument is \(\theta=-\frac{\pi}{4}\).
Using De Moivre’s theorem, \(\omega^n=(2 \sqrt{2})^n\left(\cos \left(-\frac{n \pi}{4}\right)+i \sin \left(-\frac{n \pi}{4}\right)\right)\).
For \(\omega^n\) to be real, the imaginary part must be zero: \(\sin \left(-\frac{n \pi}{4}\right)=0\), which means \(\frac{n \pi}{4}=k \pi\) for some integer \(k\).
This condition requires \(n\) to be a multiple of \(4(n=4 k)\). The minimum natural number \(n \in \mathrm{~N}\) is 4 (when \(k=1\) ).
The minimum value of \(\mathbf{n} \in \mathbf{N}\) for which \(\omega^{\mathbf{n}}\) is real, is equal to 4.

Hint

(c) The first inequality \(|z+5| \leq 4\) defines a closed disk centered at ( \(-5,0\) ) with a radius of 4 in the complex plane.
The second inequality \(z(1+i)+\bar{z}(1-i) \geq-10\) simplifies to \(x-y \geq-5\) in Cartesian coordinates ( \(z=x+i y\) ).
The region satisfying both conditions is a segment of the disk bounded by the line \(x-y=-5\).
The quantity \(|z+1|^2\) represents the squared distance of \(z\) from the point \(Q(-1,0)\).
The maximum distance occurs at a boundary point \(\boldsymbol{P}\) on the circle that is furthest from \(Q\). This point \(P\) is found to be \((-5-2 \sqrt{2},-2 \sqrt{2})\).
The maximum value of \(|z+1|^2\) is \(32+16 \sqrt{2}\).
Comparing this to the given form \(\alpha+\beta \sqrt{2}\), we have \(\alpha=32\) and \(\beta=16\).
The value of \((\alpha+\beta)\) is \(32+16=48\).

Hint

(c) Step 1: Calculate the value of k
We convert the complex numbers to polar form using \(r e^{i \theta}\).
For the first term’s numerator: \((-1+i \sqrt{3})=2 e^{i \frac{2 x}{3}}\). The denominator is \((1-i)=\sqrt{2} e^{-i \frac{x}{4}}\).
\(
\frac{(-1+i \sqrt{3})^{21}}{(1-i)^{24}}=\frac{\left(2 e^{i \frac{2 \pi}{3}}\right)^{21}}{\left(\sqrt{2} e^{-i \frac{\pi}{4}}\right)^{24}}=\frac{2^{21} e^{i 14 \pi}}{2^{12} e^{-i 6 \pi}}=2^9 e^{i 20 \pi}=2^9=512
\)
For the second term’s numerator: \((1+i \sqrt{3})=2 e^{i \frac{x}{3}}\). The denominator is \((1+i)=\sqrt{2} e^{i \frac{\pi}{4}}\).
\(
\frac{(1+i \sqrt{3})^{21}}{(1+i)^{24}}=\frac{\left(2 e^{i \frac{\pi}{3}}\right)^{21}}{\left(\sqrt{2} e^{i \frac{\pi}{4}}\right)^{24}}=\frac{2^{21} e^{i 7 \pi}}{2^{12} e^{i 6 \pi}}=2^9 e^{i \pi}=2^9(-1)=-512
\)
Thus, \(k=512+(-512)=0\).
Step 2: Determine \(\mathbf{n}\)
We need to find \(n=[|k|]\), where \([|k|]\) is the greatest integral part of \(|k|\).
\(
\begin{gathered}
|k|=|0|=0 \\
n=[0]=0
\end{gathered}
\)
Step 3: Evaluate the summation
We need to calculate the value of \(\sum_5^{n+5}(j+5)^2-\sum_{j=0}^{n+5}(j+5)\).
Substitute \(n=0: \sum_{j=0}^5(j+5)^2-\sum_{j=0}^5(j+5)\).
This can be written as \(\sum_{j=0}^5\left((j+5)^2-(j+5)\right)=\sum_{j=0}^5(j+5)(j+4)\).
Expanding the summation:
\(
\begin{aligned}
& (5)(4)+(6)(5)+(7)(6)+(8)(7)+(9)(8)+(10)(9) \\
& =20+30+42+56+72+90=310
\end{aligned}
\)

Hint

(b) Step 1: Separate the equation into real and imaginary parts
Let the complex number be \(z=x+i y\), where \(x, y\) are real numbers and \(i=\sqrt{-1}\). The given equation is:
\(
z+\alpha|z-1|+2 i=0
\)
Substituting \(z=x+i y\) :
\(
\begin{gathered}
(x+i y)+\alpha|(x+i y)-1|+2 i=0 \\
(x+i y)+\alpha|(x-1)+i y|+2 i=0 \\
\left(x+\alpha \sqrt{(x-1)^2+y^2}\right)+i(y+2)=0
\end{gathered}
\)
For this equation to hold, both the real and imaginary parts must be zero.
Step 2: Solve for y
The imaginary part gives:
\(
y+2=0 \Longrightarrow y=-2
\)
Step 3: Substitute y into the real part and solve for \(\alpha\)
The real part gives:
\(
x+\alpha \sqrt{(x-1)^2+y^2}=0
\)
Substitute \(y=-2\) :
\(
\begin{gathered}
x+\alpha \sqrt{(x-1)^2+(-2)^2}=0 \\
x+\alpha \sqrt{(x-1)^2+4}=0 \\
\alpha \sqrt{x^2-2 x+1+4}=-x \\
\alpha \sqrt{x^2-2 x+5}=-x
\end{gathered}
\)
For a solution to exist for \(\alpha \in \mathbb{R}\), we must have \(-x \geq 0\), which means \(x \leq 0\). Squaring both sides (valid as both sides are non-negative for \(x \leq 0\) ):
\(
\begin{gathered}
\alpha^2\left(x^2-2 x+5\right)=x^2 \\
\alpha^2 x^2-2 x \alpha^2+5 \alpha^2=x^2 \\
\left(\alpha^2-1\right) x^2-2 \alpha^2 x+5 \alpha^2=0
\end{gathered}
\)
This is a quadratic equation in \(\boldsymbol{x}\). Since \(\boldsymbol{x}\) must be a real number for a valid solution \(\boldsymbol{z}\), the discriminant of this quadratic equation must be greater than or equal to zero ( \(D \geq 0\) ).
Step 4: Apply the discriminant condition to find the range of \(\alpha\) The discriminant \(D\) for the quadratic equation \(A x^2+B x+C=0\) is \(B^2-4 A C\). Here, \(A=\alpha^2-1, B=-2 \alpha^2, C=5 \alpha^2\).
\(
\begin{gathered}
D=\left(-2 \alpha^2\right)^2-4\left(\alpha^2-1\right)\left(5 \alpha^2\right) \geq 0 \\
4 \alpha^4-20 \alpha^2\left(\alpha^2-1\right) \geq 0 \\
4 \alpha^4-20 \alpha^4+20 \alpha^2 \geq 0 \\
-16 \alpha^4+20 \alpha^2 \geq 0
\end{gathered}
\)
Divide by 4:
\(
-4 \alpha^4+5 \alpha^2 \geq 0
\)
Multiply by -1 (reversing the inequality sign):
\(
4 \alpha^4-5 \alpha^2 \leq 0
\)
Factor out \(\boldsymbol{\alpha}^{\mathbf{2}}\) :
\(
\alpha^2\left(4 \alpha^2-5\right) \leq 0
\)
This inequality holds if \(4 \alpha^2-5 \leq 0\) (since \(\alpha^2 \geq 0\) ).
\(
\begin{gathered}
4 \alpha^2 \leq 5 \\
\alpha^2 \leq \frac{5}{4} \\
-\sqrt{\frac{5}{4}} \leq \alpha \leq \sqrt{\frac{5}{4}} \\
-\frac{\sqrt{5}}{2} \leq \alpha \leq \frac{\sqrt{5}}{2}
\end{gathered}
\)
\(
\text { The range of } \alpha \text { is }\left[-\frac{\sqrt{5}}{2}, \frac{\sqrt{5}}{2}\right] \text {. }
\)
Step 5: Identify \(p\) and q, and calculate the final value
The least value is \(p=-\frac{\sqrt{5}}{2}\), and the largest value is \(q=\frac{\sqrt{5}}{2}\).
We need to find the value of \(4\left(p^2+q^2\right)\).
\(
\begin{gathered}
4\left(p^2+q^2\right)=4\left(\left(-\frac{\sqrt{5}}{2}\right)^2+\left(\frac{\sqrt{5}}{2}\right)^2\right) \\
4\left(p^2+q^2\right)=4\left(\frac{5}{4}+\frac{5}{4}\right) \\
4\left(p^2+q^2\right)=4\left(\frac{10}{4}\right) \\
4\left(p^2+q^2\right)=10
\end{gathered}
\)

Hint

(d) Step 1: Simplify the complex expression
The given expression in the equations is \(\left(\frac{1+i}{1-i}\right)\). We simplify this fraction by multiplying the numerator and denominator by the conjugate of the denominator:
\(
z=\frac{1+i}{1-i} \times \frac{1+i}{1+i}=\frac{(1+i)^2}{1^2-i^2}=\frac{1+2 i+i^2}{1-(-1)}=\frac{1+2 i-1}{2}=\frac{2 i}{2}=i
\)
The equations become \(i^{\frac{m}{2}}=1\) and \(i^{\frac{n}{3}}=1\).
Step 2: Determine the least values of \(m\) and \(n\)
For \(i^k\) to equal 1, the exponent \(k\) must be an integer multiple of 4 , i.e., \(k=4 j\) for some integer j.
For the first condition, we have \(\frac{m}{2}=4 j\), which means \(m=8 j\). The least natural number (positive integer) value for \(m\) is obtained when \(j=1\), so \(m_{\text {least }}=8\).
For the second condition, we have \(\frac{n}{3}=4 I\), which means \(n=12 I\). The least natural number value for \(n\) is obtained when \(l=1\), so \(n_{\text {least }}=12\).
Step 3: Calculate the greatest common divisor
We need to find the greatest common divisor (GCD) of the least values of \(m\) and \(n\), which are 8 and 12 , respectively.
The divisors of 8 are 1, 2, 4, 8.
The divisors of 12 are 1, 2, 3, 4, 6, 12.
The greatest common divisor is 4.
The greatest common divisor of the least values of \(m\) and \(n\) is 4.