Past JEE Main Entrance Papers

Hint

Let’s denote the outcomes of the three rolls as \(X_1, X_2\), and \(X_3\), where \(X_i\) represents the number obtained in the \(i^{\text {th }}\) roll. We are looking for the probability that:
\(
X_2>X_1 \text { and } X_3>X_2
\)
The total number of outcomes when rolling a dice three times is:
\(
6^3=216
\)
Let’s count the favorable outcomes. For each satisfying outcome, we must ensure that both inequalities are adhered to. Consider the possible sequences where every subsequent roll’s number is higher than the previous roll’s number. These sequences are:
\(
\begin{aligned}
& (1,2,3) \\
& (1,2,4) \\
& (1,2,5) \\
& (1,2,6) \\
& (1,3,4) \\
& (1,3,5) \\
& (1,3,6) \\
& (1,4,5) \\
& (1,4,6) \\
& (1,5,6) \\
& (2,3,4) \\
& (2,3,5) \\
& (2,3,6) \\
& (2,4,5) \\
& (2,4,6) \\
& (2,5,6) \\
& (3,4,5) \\
& (3,4,6) \\
& (3,5,6) \\
& (4,5,6)
\end{aligned}
\)
Clearly, there are 20 such favorable outcomes. Hence, the probability is given by:
Number of favorable outcomes
\(
\frac{\text { Number of favorable outcomes }}{\text { Total number of outcomes }}=\frac{20}{216}=\frac{5}{54}
\)

Alternate:

Let \(x _1, x _2, x _3\) be the numbers on \(1^{\text {st }}, 2^{\text {nd }} \& 3^{\text {rd }}\) throw respectively.
Given: \(x _1< x _2< x _3\)
\(\therefore\) Favorable cases \(={ }^6 C _3\)
Total cases \(=6^3=216\)
Prob \(=\frac{{ }^6 C _3}{216} \Rightarrow \frac{20}{216}=\frac{5}{54}\)

Hint

To solve this problem, we use Bayes’ theorem. Let’s define the events:
\(X\) : Selecting bag \(X\)
\(Y\) : Selecting bag \(Y\)
\(Z\) : Selecting bag \(Z\)
\(A\) : Drawing a one-rupee coin
We are given that a bag is selected at random, so the probabilities for choosing any of the bags are:
\(
P(X)=P(Y)=P(Z)=\frac{1}{3}
\)
Next, we need the probability of drawing a one-rupee coin from each bag:
From bag \(X: P(A \mid X)=\frac{5}{5+4}=\frac{5}{9}\)
From bag \(Y: P(A \mid Y)=\frac{4}{4+5}=\frac{4}{9}\)
From bag \(Z: P(A \mid Z)=\frac{3}{3+6}=\frac{3}{9}=\frac{1}{3}\)
We need to find the probability that the coin came from bag \(Y\) given that a one-rupee coin was drawn, i.e., we need \(P(Y \mid A)\). Using Bayes’ theorem:
\(
P(Y \mid A)=\frac{P(A \mid Y) \cdot P(Y)}{P(A)}
\)
To find \(P(A)\), the total probability of drawing a one-rupee coin can be calculated as follows:
\(
P(A)=P(A \mid X) \cdot P(X)+P(A \mid Y) \cdot P(Y)+P(A \mid Z) \cdot P(Z)
\)
Substituting the values:
\(
P(A)=\left(\frac{5}{9} \cdot \frac{1}{3}\right)+\left(\frac{4}{9} \cdot \frac{1}{3}\right)+\left(\frac{1}{3} \cdot \frac{1}{3}\right)
\)
Calculating the above, we get:
\(
P(A)=\frac{5}{27}+\frac{4}{27}+\frac{1}{9}
\)
Note that \(\frac{1}{9}=\frac{3}{27}\), so:
\(
P(A)=\frac{5}{27}+\frac{4}{27}+\frac{3}{27}=\frac{12}{27}=\frac{4}{9}
\)
Now, substituting back into Bayes’ theorem:
\(
P(Y \mid A)=\frac{\left(\frac{4}{9}\right) \cdot\left(\frac{1}{3}\right)}{\frac{4}{9}}=\frac{4}{9} \cdot \frac{1}{3} \cdot \frac{9}{4}=\frac{1}{3}
\)

Hint

Take two numbers as \(a\) and \(b\)
\(
a+b=24
\)
For product to be maximum
\(
\begin{aligned}
\frac{a+b}{2} & \geq \sqrt{a b} \\
144 & >a b
\end{aligned}
\)
Maximum product is 144
Now, \(a b \geq \frac{3}{4} \cdot 144=108\)
Sample space \(=\{(23,1),(22,2), \ldots\}\)
Integer points on line in shaded region
\(
\begin{aligned}
& \{(6,18),(7,17),(8,16), \ldots(18,6)\} \\
& P(E)=\frac{n(E)}{n(S)}=\frac{13}{23}=\frac{m}{n} \Rightarrow n-m=10
\end{aligned}
\)

Hint

We have 3 letters and 5 addresses, where 3 letters are posted to exactly 2 addresses. First, we will select 2 addresses in \({ }^5 C_2\) ways.
Now, 3 letters can be posted to exactly 2 addresses in 6 ways.
\(
\begin{aligned}
\therefore \text { Probability }=\frac{{ }^5 C_2 \times 6}{5^3} & \\
& =\frac{60}{125}=\frac{12}{25}
\end{aligned}
\)

Alternate:

\(
\begin{aligned}
& \text { Total method }=5^3 \\
& \text { Favorable }={ }^5 C _2\left(2^3-2\right)=60 \\
& \text { Probability }=\frac{60}{125}=\frac{12}{25}
\end{aligned}
\)

Hint

\(
\begin{aligned}
&\begin{aligned}
& P(\text { standard automobile from } A)=\frac{6}{10} \times \frac{8}{10}=\frac{12}{25} \\
& P(\text { standard automobile from } B)=\frac{4}{10} \times \frac{9}{10}=\frac{9}{25} \\
& \text { Required Probability } \frac{\frac{9}{25}}{\frac{12}{25}+\frac{9}{25}} \\
& P=\frac{9}{21}=\frac{3}{7}
\end{aligned}\\
&\text { So, } 126 P=126 \times \frac{3}{7}=54
\end{aligned}
\)

aLTERNATE:

\(
\begin{array}{|l|c|c|}
\hline & \text { A } & \text { B } \\
\hline \text { Manufactured } & 60 \% & 40 \% \\
\hline \text { Standard quality } & 80 \% & 90 \% \\
\hline
\end{array}
\)
\(P (\) Manufactured at \(B /\) found standard quality \()=\) ?
A: Found S.Q
B : Manufacture B
C: Manufacture A
\(
\begin{aligned}
& P\left(E_1\right)=\frac{40}{100} \\
& P \left( E _2\right)=\frac{60}{100} \\
& P \left( A / E _1\right)=\frac{90}{100} \\
& P \left( A / E _2\right)=\frac{80}{100}
\end{aligned}
\)
\(
\begin{aligned}
& \because P \left( E _1 / A \right)=\frac{ P \left( A / E _1\right) P \left( E _1\right)}{ P \left( A / E _1\right) P \left( E _1\right)+ P \left( A / E _2\right) P \left( E _2\right)}=\frac{3}{7} \\
& \therefore 126 P =54
\end{aligned}
\)

Hint

Equation is \(a x^2+b x+c=0\)
D \(>0\) [for roots to be real & distinct]
\(
\Rightarrow b^2-4 a c>0
\)
For \(b<2\) no value of \(a \& c\) are possible
For \(b=3 \Rightarrow a c<\frac{9}{4}\)
\((a, c) \in\{(1,1),(1,2),(2,1)\} \Rightarrow 3\) cases
For \(b=4 \Rightarrow a c<4\)
\(
(a, c) \in\{(1,1),(1,2),(2,1),(3,1),(1,3)\} \Rightarrow 5 \text { cases }
\)
For \(b=5 \Rightarrow a c<\frac{25}{4}\)
\(
\begin{aligned}
& (a, c) \in\{(1,1),(1,2),(2,1),(3,1),(1,3),(2,2) \\
& (4,1),(1,4),(3,2),(2,3),(5,1),(1,5),(1,6) \\
& (6,1)\}=14 \text { cases }
\end{aligned}
\)
For \(b=6 \Rightarrow a c<9\)
\((a, c) \in\{(1,1),(1,2),(2,1),(3,1),(1,3),(2,2)\),
\((4,1),(1,4),(3,2),(2,3),(5,1),(1,5),(1,6)\),
\((6,1),(2,4),(4,2)\}=16\) cases
Total cases \(=3+5+14+16=38\) cases
\(\Rightarrow\) Probability, \(p =\frac{38}{216}\)
\(
\Rightarrow 216 p=38
\)

Hint

Given quadratic equation is
\(
a x^2+b x+c=0 \text { where } a, b, c \in\{1,2,3, \ldots, 8\}
\)
For repeated roots,
\(
\begin{array}{r}
b^2-4 a c=0 \\
\Rightarrow b^2=4 a c
\end{array}
\)
\(\Rightarrow a c\) must be a perfect square
\(
(a, c) \in\{(1,1),(1,4),(2,2),(2,8),(3,3),(4,1),(4,4),(5,5),(6,6),(7,7),(8,2),(8,8)\}
\)
Corresponding \(b\) must lie in set \(\{1,2,3, \ldots 8\}\)
\(
\begin{aligned}
& (a, b, c) \in\{(1,2,1),(1,2,4),(2,4,2),(2,8,8) \\
& (3,6,3),(4,4,1),(4,8,4),(8,8,2)\} \\
& \therefore \text { probability }=\frac{8}{8^3} \\
& =\frac{1}{64}
\end{aligned}
\)

Alternate:

Hint

\(
\begin{array}{|c|c|c|c|c|c|}
\hline X & 0 & 2 & 4 & 6 & 8 \\
\hline P(X) & a & 2 a & a+b & 2 b & 3 b \\
\hline
\end{array}
\)
\(
\begin{aligned}
& \text { Mean }=\sum x_i P\left(x_i\right) \\
& \frac{46}{9}=4 a+4 a+4 b+12 b+24 b \\
& \frac{46}{9}=8 a+40 b \\
& \frac{23}{9}=4 a+20 b \\
& 36 a+180 b=23 \dots(1)
\end{aligned}
\)
Sum of probability is 1
\(
\Rightarrow 4 a+6 b=1 \dots(2)
\)
Solving (1) and (2)
\(
\begin{aligned}
a & =\frac{1}{12}, b=\frac{1}{9} \\
\sigma^2 & =\sum x_i^2 P\left(x_i\right)-\left(\sum x_i P\left(x_i\right)\right)^2 \\
& =4 \times 2 a+16(a+b)+36(2 b)+64(3 b)-\left(\frac{46}{9}\right)^2 \\
& =8(a+2(a+b)+9 b+24 b)-\left(\frac{46}{9}\right)^2 \\
& =8(3 a+35 b)-\left(\frac{46}{9}\right)^2 \\
& =8\left(\frac{3}{12}+\frac{35}{9}\right)-\left(\frac{46}{9}\right)^2 \\
& =8\left(\frac{149}{36}\right)-\left(\frac{46}{9}\right)^2=\frac{566}{81}
\end{aligned}
\)

Hint

Let’s denote the events as follows:
Let \(A_1, A_2\), and \(A_3\) be the events that urns \(A , B\), and C are chosen, respectively.
Let \(B\) be the event that a black ball is drawn.
We need to find the probability that the chosen urn is A given that a black ball is drawn, which is \(P\left(A_1 \mid B\right)\).

Using Bayes’ theorem, we have :
\(
P\left(A_1 \mid B\right)=\frac{P\left(B \mid A_1\right) P\left(A_1\right)}{P(B)}
\)
First, we calculate each term individually :
1. The probability of choosing any urn, since they are chosen at random :
\(
P\left(A_1\right)=P\left(A_2\right)=P\left(A_3\right)=\frac{1}{3}
\)
2. The probability of drawing a black ball from each urn :
Urn A: \(P\left(B \mid A_1\right)=\frac{5}{12}\)
Urn B: \(P\left(B \mid A_2\right)=\frac{7}{12}\)
Urn C: \(P\left(B \mid A_3\right)=\frac{6}{12}=\frac{1}{2}\)
3. The total probability of drawing a black ball, \(P(B)\) :
\(
\begin{aligned}
& P(B)=P\left(B \mid A_1\right) P\left(A_1\right)+P\left(B \mid A_2\right) P\left(A_2\right)+P\left(B \mid A_3\right) P\left(A_3\right) \\
& P(B)=\frac{5}{12} \cdot \frac{1}{3}+\frac{7}{12} \cdot \frac{1}{3}+\frac{1}{2} \cdot \frac{1}{3} \\
& P(B)=\frac{5}{36}+\frac{7}{36}+\frac{6}{36} \\
& P(B)=\frac{18}{36}=\frac{1}{2}
\end{aligned}
\)
Now, substitute these into Bayes’ theorem :
\(
\begin{aligned}
& P\left(A_1 \mid B\right)=\frac{P\left(B \mid A_1\right) P\left(A_1\right)}{P(B)} \\
& P\left(A_1 \mid B\right)=\frac{\frac{5}{12} \cdot \frac{1}{3}}{\frac{1}{2}} \\
& P\left(A_1 \mid B\right)=\frac{\frac{5}{36}}{\frac{1}{2}} \\
& P\left(A_1 \mid B\right)=\frac{5}{18}
\end{aligned}
\)

Hint

We are given that the probability of Ajay not appearing in the JEE exam is \(p=\frac{2}{7}\), and the probability that both Ajay and Vijay will appear in the exam is \(q=\frac{1}{5}\).
We are asked to find the probability that Ajay will appear in the exam and Vijay will not. Let’s denote this probability as r .
To find \(r\), we need to use the concept of complementary events. The probability that Ajay will appear in the exam is the complement of the probability that he will not appear. So,
\(
P(\text { Ajay appears })=1-P(\text { Ajay does not appear })=1- p =1-\frac{2}{7}=\frac{5}{7} \text {. }
\)
The event that both Ajay and Vijay appear in the exam is independent of the event that only Ajay appears (and Vijay does not). Therefore, we can express the probability that only Ajay will appear (and Vijay will not) as the difference of Ajay appearing minus both Ajay and Vijay appearing, because the probability of both appearing (q) is included in the probability of Ajay appearing:
\(
r =P(\text { Ajay appears })-P(\text { Both Ajay and Vijay appear })=\frac{5}{7}-\frac{1}{5} \text {. }
\)
To subtract these two fractions, we need a common denominator, which would be 35 in this case. So,
\(
r=\frac{5}{7} \cdot \frac{5}{5}-\frac{1}{5} \cdot \frac{7}{7}=\frac{25}{35}-\frac{7}{35}=\frac{25-7}{35}=\frac{18}{35}
\)

Alternate:

\(
\begin{aligned}
& P (\overline{ A })=\frac{2}{7}= p \\
& P ( A \cap V )=\frac{1}{5}= q \\
& P ( A )=\frac{5}{7} \\
& P ( A \cap \overline{ V })=\frac{18}{35}
\end{aligned}
\)

Hint

\(n(s)=\) there are 5 possible sample space.
\(
P\left(\frac{A_1}{E}\right)=\frac{P\left(A_1\right) P\left(\frac{E}{A_1}\right)}{P\left(A_1\right) P\left(\frac{E}{A_1}\right)+P\left(A_2\right) P\left(\frac{E}{A_2}\right)+\ldots \ldots}
\)
\(
\begin{aligned}
& P (4 W 4 B / 2 W 2 B)= \\
& \frac{P(4 W 4 B) \times P(2 W 2 B / 4 W 4 B)}{P(2 W 6 B) \times P(2 W 2 B / 2 W 6 B)+P(3 W 5 B) \times P(2 W 2 B / 3 W 5 B)+\ldots \ldots \ldots \ldots+P(6 W 2 B) \times P(2 W 2 B / 6 W 2 B)}
\end{aligned}
\)
\(
\begin{aligned}
& =\frac{\frac{1}{5} \times \frac{{ }^4 C _2 \times{ }^4 C _2}{{ }^8 C _4}}{\frac{1}{5} \times \frac{{ }^2 C _2 \times{ }^6 C _2}{{ }^8 C _4}+\frac{1}{5} \times \frac{{ }^3 C _2 \times{ }^5 C _2}{{ }^8 C _4}+\ldots+\frac{1}{5} \times \frac{{ }^6 C _2 \times{ }^2 C _2}{{ }^8 C _4}} \\
& =\frac{2}{7}
\end{aligned}
\)

Hint

To solve this problem, we need to first determine the probability of getting a head \(( H )\) and the probability of getting a tail \(( T )\).
Since a head is twice as likely to occur as a tail, we can denote the probability of getting a tail as \(P(T)=p\) and the probability of getting a head as \(P(H)=2 p\).
These probabilities must sum to 1 because those are the only two possible outcomes for each coin toss :
\(
\begin{aligned}
& P(H)+P(T)=1 \\
& 2 p+p=1 \\
& 3 p=1 \\
& p=\frac{1}{3}
\end{aligned}
\)
Therefore, the probability of getting a tail \(( T )\) is \(P(T)=\frac{1}{3}\) and the probability of getting a head \(( H )\) is \(P(H)=2 \times \frac{1}{3}=\frac{2}{3}\).
Now to find the probability of getting two tails and one head, we need to consider the different sequences in which this can occur. There are three unique sequences: TTH, THT, and HTT.
The probability of each sequence is found by multiplying the probabilities of each individual event since each coin toss is independent:
\(
\begin{aligned}
& P(T T H)=P(T) \times P(T) \times P(H)=\left(\frac{1}{3}\right)^2 \times \frac{2}{3}=\frac{1}{9} \times \frac{2}{3}=\frac{2}{27} \\
& P(T H T)=P(T) \times P(H) \times P(T)=\frac{1}{3} \times \frac{2}{3} \times \frac{1}{3}=\frac{2}{27} \\
& P(H T T)=P(H) \times P(T) \times P(T)=\frac{2}{3} \times\left(\frac{1}{3}\right)^2=\frac{2}{27}
\end{aligned}
\)
The overall probability of getting two tails and one head in any order is the sum of these individual probabilities :
\(
P(2 T 1 H)=P(T T H)+P(T H T)+P(H T T)=\frac{2}{27}+\frac{2}{27}+\frac{2}{27}=\frac{6}{27}
\)
Simplifying this expression gives us: \(P(2 T 1 H)=\frac{6}{27}=\frac{2}{9}\)

Alternate:

Let probability of tail is \(\frac{1}{3}\)
\(\Rightarrow\) Probability of getting head \(=\frac{2}{3}\)
\(\therefore\) Probability of getting 2 tails and 1 head
\(
\begin{aligned}
& =\left(\frac{1}{3} \times \frac{2}{3} \times \frac{1}{3}\right) \times 3 \\
& =\frac{2}{27} \times 3 \\
& =\frac{2}{9}
\end{aligned}
\)

Hint

3 bad apples, 15 good apples.
Let X be no of bad apples
Then \(P ( X =0)=\frac{{ }^{15} C _2}{{ }^{18} C _2}=\frac{105}{153}\)
\(P ( X =1)=\frac{{ }^3 C _1 \times{ }^{15} C _1}{{ }^{18} C _2}=\frac{45}{153}\)
\(P ( X =2)=\frac{{ }^3 C _2}{{ }^{18} C _2}=\frac{3}{153}\)
\(E ( X )=0 \times \frac{105}{153}+1 \times \frac{45}{153}+2 \times \frac{3}{153}=\frac{51}{153}\)
\(=\frac{1}{3}\)
\(\operatorname{Var}( X )= E \left( X ^2\right)-( E ( X ))^2\)
\(=0 \times \frac{105}{153}+1 \times \frac{45}{153}+4 \times \frac{3}{153}-\left(\frac{1}{3}\right)^2\)
\(=\frac{57}{153}-\frac{1}{9}=\frac{40}{153}\)

Hint

Probability of drawing first red and then white
\(
\begin{aligned}
& =\frac{10}{75} \times \frac{30}{75} \\
& =\frac{4}{75}
\end{aligned}
\)

Alternate:

To solve this problem, we need to calculate the probability of two independent events occurring in succession: the first marble drawn is red, and the second marble drawn is white. Since the drawing is with replacement, the number of marbles of each color remains the same for both draws.
The total number of marbles in the box is the sum of red, white, blue, and orange marbles:
\(
\text { Total } \text { marbles }=10(\text { red })+30(\text { white })+20(\text { blue })+15(\text { orange })=75 .
\)
The probability of drawing a red marble in the first draw is the number of red marbles divided by the total number of marbles:
\(
P(\text { First is red })=\frac{10}{75} \text {. }
\)
Since the marble is replaced, the probability of drawing a white marble in the second draw remains as the number of white marbles divided by the total number of marbles:
\(
P(\text { Second is white })=\frac{30}{75} \text {. }
\)
The probability of both independent events occurring in succession (drawing a red marble first and then a white marble) is the product of their individual probabilities:
\(
P(\text { First is red and second is white })=P(\text { First is red }) \times P(\text { Second is white })=\frac{10}{75} \times \frac{30}{75}
\)
Now, let’s calculate this probability:
\(
P(\text { First is red and second is white })=\frac{10 \times 30}{75 \times 75}=\frac{300}{5625}=\frac{4}{75} \text {. }
\)

Hint

\(E _1: A\) is selected
\(E _2: B\) is selected
\(E :\) white ball is drawn
\(
\begin{aligned}
& P \left( E _1 / E \right)= \\
& \frac{P(E) \cdot P\left(E / E_1\right)}{P\left(E_1\right) \cdot P\left(E / E_1\right)+P\left(E_2\right) \cdot P\left(E / E_2\right)}=\frac{\frac{1}{2} \times \frac{3}{10}}{\frac{1}{2} \times \frac{3}{10}+\frac{1}{2} \times \frac{3}{5}} \\
& =\frac{3}{3+6}=\frac{1}{3}
\end{aligned}
\)

Hint

If \(x=0, y=6,7,8,9,10\)
If \(x=1, y=7,8,9,10\)
If \(x=2, y=8,9,10\)
If \(x=3, y=9,10\)
If \(x=4, y=10\)
If \(x=5, y=\) no possible value
Total possible ways \(=(5+4+3+2+1) \times 2\)
\(=30\)
Required probability \(=\frac{30}{11 \times 11}=\frac{30}{121}\)

Hint

Given set \(=\{1,2,3, \ldots \ldots . .50\}\)
\(P ( A )=\) Probability that number is multiple of 4
\(P ( B )=\) Probability that number is multiple of 6
\(P ( C )=\) Probability that number is multiple of 7
Now,
\(
P ( A )=\frac{12}{50}, P ( B )=\frac{8}{50}, P ( C )=\frac{7}{50}
\)
again
\(
\begin{aligned}
& P ( A \cap B )=\frac{4}{50}, P ( B \cap C )=\frac{1}{50}, P ( A \cap C )=\frac{1}{50} \\
& P ( A \cap B \cap C )=0
\end{aligned}
\)
Thus
\(
\begin{aligned}
& P(A \cup B \cup C)=\frac{12}{50}+\frac{8}{50}+\frac{7}{50}-\frac{4}{50}-\frac{1}{50}-\frac{1}{50}+0 \\
& \quad=\frac{21}{50}
\end{aligned}
\)

Hint

Required probability \(=\)
\(
\begin{aligned}
& \frac{5}{6} \times \frac{1}{6}+\left(\frac{5}{6}\right)^3 \times \frac{1}{6}+\left(\frac{5}{6}\right)^5 \times \frac{1}{6}+\ldots \\
& =\frac{1}{6} \times \frac{\frac{5}{6}}{1-\frac{25}{36}}=\frac{5}{11}
\end{aligned}
\)

Alternate:

The probability that a fair die will land on 2 in an even number of throws can be understood by considering the die’s first roll and subsequent pairs of rolls. The chance of not rolling a 2 on the first roll is \(5 / 6\), and the probability of not rolling a 2 on two consecutive rolls is \((5 / 6)^2\). We want to find the sum of probabilities that 2 appears for the first time on the second, fourth, sixth, etc., roll. The probability of 2 appearing on the second roll is \((5 / 6) \times(1 / 6)\). To find the total probability for all even rolls, we use the geometric series formula for infinite series.
Total probability for even rolls: \((5 / 6) \times(1 / 6) /\left(1-(5 / 6)^2\right)=(5 / 6) \times(1 / 6) /(11 / 36)=\) 5/11

Hint

\(
\begin{aligned}
& P=\frac{{ }^6 C _4}{{ }^{15} C _4} \cdot \frac{{ }^9 C _4}{{ }^{11} C _4} \\
& =\frac{15 \times 24}{15 \cdot 14 \cdot 13 \cdot 12} \times \frac{9 \cdot 8 \cdot 7 \cdot 6 \times 24}{24 \cdot 11 \cdot 10 \cdot 9 \cdot 8} \\
& =\frac{1}{13 \cdot 7} \times \frac{7 \cdot 6}{10 \cdot 11} \\
& =\frac{6}{13 \cdot 10 \cdot 11} \\
& =\frac{3}{13 \cdot 5 \cdot 11} \\
& =\frac{3}{715}
\end{aligned}
\)

Hint

\(
\begin{array}{|ll|}
\hline 6 & W \\
4 & R \\
\hline
\end{array}
\)
\(
\begin{aligned}
& \frac{1}{6} \times\left[\frac{{ }^6 C _1}{{ }^{10} C _1}+\frac{{ }^6 C _2}{{ }^{10} C _2}+\frac{{ }^6 C _3}{{ }^{10} C _3}+\frac{{ }^6 C _4}{{ }^{10} C _4}+\frac{{ }^6 C _5}{{ }^{10} C _5}+\frac{{ }^6 C _6}{{ }^{10} C _6}\right] \\
& =\frac{1}{6}\left(\frac{126+70+35+15+5+1}{210}\right)=\frac{42}{210}=\frac{1}{5} \\
&
\end{aligned}
\)

Alternate:

Let \(X\) be the number rolled on the die, and let \(W\) be the event that all balls drawn are white. We want to find the probability \(P(W)\), which can be calculated using the law of total probability as follows :
\(
P(W)=\sum_{x=1}^6 P(W \mid X=x) P(X=x)
\)
The probability of rolling any number from 1 to 6 on the die is equal, so \(P(X=x)=\frac{1}{6}\) for all \(x \in\{1,2,3,4,5,6\}\).
Now let’s calculate the conditional probabilities \(P(W \mid X=x)\) for each possible value of \(x\) :
1. \(P(W \mid X=1)=\frac{{ }^6 C_1}{{ }^{10} C_1}=\frac{6}{10}=\frac{3}{5}\), since there are 6 white balls out of a total of 10 balls.
2. \(P(W \mid X=2)=\frac{{ }^6 C_2}{{ }^{10} C_2}=\frac{15}{45}=\frac{1}{3}\), since there are 15 ways to choose 2 white balls out of 6 , and 45 ways to choose 2 balls out of 10 .
4. \(P(W \mid X=4)=\frac{{ }^6 C_4}{{ }^{10} C_4}=\frac{15}{210}=\frac{1}{14}\), since there are 15 ways to choose 4 white balls out of 6 , and 210 ways to choose 4 balls out of 10 .
5. \(P(W \mid X=5)=\frac{{ }^6 C_5}{{ }^{10} C_5}=\frac{6}{252}=\frac{1}{42}\), since there are 6 ways to choose 5 white balls out of 6 , and 252 ways to choose 5 balls out of 10 .
6. \(P(W \mid X=6)=\frac{{ }^6 C_6}{{ }^{10} C_6}=\frac{1}{210}\), since there are 1 ways to choose 6 white balls out of 6 , and 210 ways to choose 6 balls out of 10 .
Using the law of total probability, we have :
\(
\begin{aligned}
& P(W)=\frac{1}{6}(P(W \mid X=1)+P(W \mid X=2)+P(W \mid X=3)+P(W \mid X=4)+P(W \mid X=5)+P(W \mid X=6)) \\
& P(W)=\frac{1}{6}\left(\frac{3}{5}+\frac{1}{3}+\frac{1}{6}+\frac{1}{14}+\frac{1}{42}+\frac{1}{210}\right)
\end{aligned}
\)
To simplify this expression, find a common denominator :
\(
P(W)=\frac{1}{6}\left(\frac{126}{210}+\frac{70}{210}+\frac{35}{210}+\frac{15}{210}+\frac{5}{210}+\frac{1}{210}\right)
\)
Add the fractions :
\(
P(W)=\frac{1}{6}\left(\frac{126+70+35+15+5+1}{210}\right)=\frac{42}{210}=\frac{1}{5}
\)

Hint

The given probabilities for getting a head \(( H )\) and a tail \(( T )\) are as follows:
\(
P(H)=\frac{3}{4}, \quad P(T)=\frac{1}{4}
\)
The random variable \(X\) can take the values 1,2 , or 3 . These correspond to the following events:
\(X =1\) : A head is obtained on the first toss. This happens with probability
\(
P(H)=\frac{3}{4}
\)
\(X =2\) : A tail is obtained on the first toss and a head on the second. This happens with probability \(P(T) P(H)=\frac{1}{4} \times \frac{3}{4}\).
\(X = 3\) : Either two tails and then a head are obtained, or three tails are obtained. This happens with probability
\(
P(T) P(T) P(H)+P(T) P(T) P(T)=\left(\frac{1}{4}\right)^2 \times \frac{3}{4}+\left(\frac{1}{4}\right)^3
\)
Now, we calculate the mean (expected value) of \(X\) :
\(
\begin{aligned}
E(X) & =1 \cdot P(X=1)+2 \cdot P(X=2)+3 \cdot P(X=3) \\
& =1 \cdot \frac{3}{4}+2 \cdot\left(\frac{1}{4} \times \frac{3}{4}\right)+3 \cdot\left[\left(\frac{1}{4}\right)^2 \times \frac{3}{4}+\left(\frac{1}{4}\right)^3\right] \\
& =\frac{3}{4}+\frac{3}{8}+3 \cdot\left(\frac{1}{64}+\frac{3}{64}\right) \\
& =\frac{3}{4}+\frac{3}{8}+\frac{3}{16} \\
& =3 \cdot\left(\frac{7}{16}\right) \\
& =\frac{21}{16} .
\end{aligned}
\)

Hint

\(
\begin{array}{|c|l|c|}
\hline \alpha-\beta & \text { Case } & P \\
\hline 5 & (6,1) & 1 / 36 \\
\hline 4 & (6,2)(5,1) & 2 / 36 \\
\hline 3 & (6,3)(5,2)(4,1) & 3 / 36 \\
\hline 2 & (6,4)(5,3)(4,3)(3,1) & 4 / 36 \\
\hline 1 & (6,5)(5,4)(4,3)(3,2)(2,1) & 5 / 36 \\
\hline 0 & (6,6)(5,5) \ldots \ldots(1,1) & 6 / 36 \\
\hline-1 & —– & 5 / 36 \\
\hline-2 & —– & 4 / 36 \\
\hline-3 & —– & 3 / 36 \\
\hline-4 & (2,6)(1,5) & 2 / 36 \\
\hline-5 & (1,6) & 1 / 36 \\
\hline
\end{array}
\)
\(
E\left[X^2\right]=\sum_{i=-5}^5\left(x_i\right)^2 P\left(x_i\right)
\)
Substituting the values from table :
\(
E\left[X^2\right]=2\left[\frac{25}{36}+\frac{32}{36}+\frac{27}{36}+\frac{16}{36}+\frac{5}{36}\right]=\frac{105}{18}=\frac{35}{6}
\)
Next, we calculate the expected value of the differences. The expected value is calculated as the sum of the products of each outcome and its corresponding probability. Given that the table is symmetric around 0 , the expected value is 0 .
\(
E[X]=\sum_{i=-5}^5 x_i P\left(x_i\right)=0
\)
Now, we can calculate the variance, which is the expected value of the squared differences minus the square of the expected value of the differences:
\(
\operatorname{Var}[X]=E\left[X^2\right]-(E[X])^2=\frac{35}{6}-0^2=\frac{35}{6}
\)
Here, \(p=35\) and \(q=6\), and they are co-prime.
The positive divisors of 35 are 1, 5, 7, and 35 . The sum of these divisors is \(1+5+7+35=48\)

Hint

We have, \(S=\left\{M=\left[a_{i j}\right], a_{i j} \in\{0,1,2\}, 1 \leq i, j \leq 2\right\}\)
Let \(M=\left[\begin{array}{ll}a & b \\ c & d\end{array}\right]\), where \(a, b, c, d \in\{0,1,2\}\)
\(
n(s)=3^4=81
\)
If \(A\) is invertible, then \(|A| \neq 0\)
Now, if \(|A|=0\), then \(|M|=0\)
\(
\therefore a d-b c=0 \text { or } a d=b c
\)
Case I: When \(a d=b c=0\), then
There are five ways when \(a d=0\) i.e.,
\(
(a, d)=(0,0),(0,1),(0,2),(1,0),(2,0)
\)
Similarly, there are again five ways, when \(b c=0\)
\(\therefore\) There are total \(5 \times 5=25\) ways, when \(a d=b c=0\)
Case II: When \(a d=b c=1\)
There is only one way, when \(a d=b c=1\)
i.e. \(\quad a=b=c=d=1\)
Case III: When \(a d=b c=2\)
There are two ways, when \(a d=2\), i.e.
\(
(a, d)=(1,2) \text { or }(2,1)
\)
Similarly, there are two ways
when \(b c=2\) i.e., \((b, c)=(1,2)\) or \((2,1)\)
Case IV: When \(a d-b c=4\)
There is only way, when \(a d=b c=4\)
i.e., \(a=b=c=d=2\)
\(\therefore\) Total number of ways, when
\((\bar{A})=\frac{31}{81}|A|=0[latex] is [latex]25+1+4+1=31\)
Hence, \(P(A)=1-P(\bar{A})=1-\frac{31}{81}=\frac{50}{81}\)

Hint

\(N\) denote the sum of the numbers obtained when two dice are rolled.
Such that \(2^N<N\) !
i.e., \(4 \leq N \leq 12\) i.e., \(N \in\{4,5,6, \ldots 12\}\)
Now, \(P(N=2)+P(N=3)=\frac{1}{36}+\frac{2}{36}=\frac{3}{36}=\frac{1}{12}\)
So, required probability \(=1-\frac{1}{12}=\frac{11}{12}=\frac{m}{n}\)
\(
4 m-3 n=4 \times 11-3 \times 12=44-36=8
\)

Hint

As, we know that sum of all the probabilities \(=1\)
So, \(\sum_{x=1}^{\infty} P ( X =x)=1\)
\(
\Rightarrow k\left[1+2 \cdot 3^{-1}+3 \cdot 3^{-2}+\ldots \infty\right]=1
\)
Let \(S=1+\frac{2}{3}+\frac{3}{3^2}+\ldots+\infty\)
\(
\Rightarrow \frac{S}{3}=0+\frac{1}{3}+\frac{2}{3^2}+\frac{3}{3^3}+\ldots+\infty
\)
On subtracting, we get
\(
\begin{aligned}
& \frac{2 S}{3}=1+\frac{1}{3}+\frac{1}{3^2}+\ldots+\infty \\
& \Rightarrow \frac{2 S}{3}=\frac{1}{1-\frac{1}{3}}=\frac{1}{\frac{2}{3}} \\
& \Rightarrow \frac{2 S}{3}=\frac{3}{2} \\
& \Rightarrow S=\frac{9}{4}
\end{aligned}
\)
So, \(k \times \frac{9}{4}=1 \Rightarrow k=\frac{4}{9}\)
Now, \(P ( X \geq 2)=1- P ( X <2)\)
\(
\begin{aligned}
& =1- P ( X =0)- P ( X =1) \\
& =1-\frac{4}{9}(1)-\frac{4}{9} \times \frac{2}{3} \\
& =1-\frac{4}{9}-\frac{8}{27}=\frac{27-12-8}{27}=\frac{7}{27}
\end{aligned}
\)

Hint

Given : \(P(A)=\frac{20}{100}=\frac{2}{10}\)
\(
\begin{aligned}
& P(B)=\frac{30}{100}=\frac{3}{10} \\
& P(C)=\frac{50}{100}=\frac{5}{10}
\end{aligned}
\)
Let \(E \rightarrow\) Event that the bolt is defective.
\(
\begin{aligned}
& \text { So, } P(E / A)=\frac{3}{100} \\
& P\left(\frac{E}{B}\right)=\frac{4}{100}, P\left(\frac{E}{C}\right)=\frac{2}{100} \\
& \text { So, } P ( C / E ) \\
& =\frac{P\left(\frac{E}{C}\right) \times P(C)}{P\left(\frac{E}{A}\right) \times P(A)+P\left(\frac{E}{B}\right) \times P(B)+P\left(\frac{E}{C}\right) \times P(C)} \\
& =\frac{\frac{5}{10} \times \frac{2}{100}}{\frac{3}{100} \times \frac{2}{10}+\frac{4}{100} \times \frac{3}{10}+\frac{2}{100} \times \frac{5}{10}} \\
& =\frac{10}{6+12+10}=\frac{10}{28}=\frac{5}{14}
\end{aligned}
\)

Hint

Total number of outcomes \(=6 \times 6 \times 6=216\)
Number of outcomes getting different numbers on the three dice are \({ }^6 P_3=\frac{6!}{3!}=120\)
\(\therefore\) Required probability \(=\frac{120}{216}=\frac{5}{9}\)
\(\therefore p=5\) and \(q=9\)
\(
\therefore q-p=9-5=4
\)

Hint

\(
\begin{aligned}
& A=\{(1,2),(1,3),(1,4),(1,5),(1,6),(2,3),(2,4),(2,5),(2,6),(3,4),(3,5),(3,6),(4,5),(4,6),(5,6)\} \\
& n(A)=15 \\
& B=\{(2,1),(2,3),(2,5),(4,1),(4,3),(4,5),(6,1),(6,3),(6,5)\} \\
& n(B)=9 \\
& C=\{(1,2),(1,4),(1,6),(3,2),(3,4),(3,6),(5,2),(5,4),(5,6)\} \\
& n(C)=9 \\
& (4,5) \in A \text { and }(4,5) \in B \\
& \therefore A \text { and } B \text { are not exclusive events } \\
& \quad n((A \cup B) \cap C)=n(A \cap C)+n(B \cap C)-n(A \cap B \cap C) \\
& =3+3-0 \\
& =6
\end{aligned}
\)
Option (d) is correct.
\(
\begin{aligned}
& n(B)=\frac{9}{36}, n(C)=\frac{9}{36}, n(B \cap C)=0 \\
& \Rightarrow n(B) \cdot n(C) \neq n(B \cap C)
\end{aligned}
\)
\(\therefore B\) and \(C\) are not independent.

Hint

Let \(E_i \rightarrow\) Bag have at least \(i\) black balls
\(E \rightarrow 2\) balls are drawn & both black
\(
\begin{aligned}
& \therefore P\left(\frac{E_5 \text { or } E_6}{E}\right)=\frac{P\left(\frac{E}{E_5}\right)+P\left(\frac{E}{E_6}\right)}{\sum_{i=1}^6 P\left(\frac{E}{E_i}\right)} \\
& =\frac{\frac{{ }^5 C_2}{{ }^6 C_2}+\frac{{ }^6 C_2}{{ }^6 C_2}}{0+\frac{{ }^2 C_2}{{ }^6 C_2}+\frac{{ }^3 C_2}{{ }^6 C_2}+\frac{{ }^4 C_2}{{ }^6 C_2}+\frac{{ }^5 C_2}{{ }^6 C_2}+\frac{{ }^6 C_2}{{ }^6 C_2}} \\
& =\frac{10+15}{1+3+6+10+15}=\frac{25}{35}=\frac{5}{7} \\
&
\end{aligned}
\)

Hint

\(
\begin{aligned}
& { }^5 C_0 \times 3^5=243 \\
& { }^5 C_2 \times 2^2 \times 3^3=1080 \\
& { }^5 C_4 \times 2^4 .3=240 \\
& \therefore \text { required probability } \\
& =\frac{243+1080+240}{6 \times 6 \times 6 \times 6 \times 6}=\frac{521}{2592}
\end{aligned}
\)

Hint

\(
\begin{aligned}
& P\left(w_1\right)+\frac{P\left(w_1\right)}{2}+\frac{P\left(w_1\right)}{2^2}+\ldots \ldots=1 \\
& \therefore P\left(w_1\right)=\frac{1}{2}
\end{aligned}
\)
Hence, \(P\left(w_n\right)=\frac{1}{2^n}\)
Every number except \(1,2,3,4,6\) is representable in the form \(2 k+3 l\) where \(k, l \in N\).
\(
\begin{aligned}
& \therefore P(B)=1-P\left(w_1\right)-P\left(w_2\right)-P\left(w_3\right)-P\left(w_4\right)-P\left(w_6\right) \\
& =\frac{3}{64}
\end{aligned}
\)

Hint

Required probability \(=1-\frac{D_{(15)}+{ }^{15} C_1 \cdot D_{(14)}+{ }^{15} C_2 D_{(13)}}{15!}\)
Taking \(D _{(15)}[latex] as [latex]\frac{15!}{e}\)
\(D _{(14)}\) as \(\frac{14!}{e}\)
\(D _{(13)}\) as \(\frac{13!}{e}\)
We get, Required probability \(=1-\left(\frac{\frac{15!}{e}+15 \cdot \frac{144}{e}+\frac{15 \times 14}{2} \times \frac{13!}{e}}{15!}\right)\)
\(
=1-\left(\frac{1}{e}+\frac{1}{e}+\frac{1}{2 e}\right)=1-\frac{5}{2 e} \approx .08
\)

Hint

\(
\begin{aligned}
& n-2, \sqrt{3 n}, n+2 \rightarrow \text { G.P. } \\
& 3 n=n^2-4 \\
& \Rightarrow n^2-3 n-4=0 \\
& \Rightarrow n=4,-1 \text { (rejected) } \\
& P(S=4)=\frac{3}{36}=\frac{1}{12}=\frac{4}{48} \\
& \therefore k=4
\end{aligned}
\)

Hint

\(
\begin{aligned}
& x+y=66 \\
& \frac{x+y}{2} \geq \sqrt{x y} \\
& \Rightarrow 33 \geq \sqrt{x y} \\
& \Rightarrow x y \leq 1089 \\
& \therefore M=1089 \\
& S: x(66-x) \geq \frac{5}{9} \cdot 1089 \\
& 66 x-x^2 \geq 605 \\
& \Rightarrow x^2-66 x+605 \leq 0 \\
& \Rightarrow(x-55)(x-11) \leq 0 ; 11 \leq x \leq 55 \\
& \text { Therefore } S=\{11,12,13 \ldots 55\} \\
&
\end{aligned}
\)
\(
\Rightarrow n(S)=45
\)
Elements of \(S\) which are multiple of 3 are
\(
\begin{aligned}
& 12+(n-1) 3=54 \Rightarrow 3(n-1)=42 \Rightarrow n=15 \\
& n(A)=15 \\
& \Rightarrow P(A)=\frac{15}{45}=\frac{1}{3}
\end{aligned}
\)

Hint

For unique solution \(\Delta \neq 0\)
\(
\begin{aligned}
& \text { i.e. }\left|\begin{array}{ccc}
1 & 1 & 1 \\
2 & N & 2 \\
3 & 3 & N
\end{array}\right| \neq 0 \\
& \Rightarrow\left(N^2-6\right)-(2 N-6)+(6-3 N) \neq 0 \\
& \Rightarrow N^2-5 N+6 \neq 0 \\
& \therefore N \neq 2 \text { and } N \neq 3
\end{aligned}
\)
\(\therefore\) Probability of not getting 2 or 3 in a throw of dice \(=\frac{2}{3}\)
As given \(\frac{2}{3}=\frac{k}{6} \Rightarrow k=4\)
\(\therefore\) Required value \(=1+4+5+6+4=20\)

Hint

\(\Omega=\) sample space
\(A =\) be an event
\(\Omega=\) A wire of length 1 which starts at point 0 and ends at point 1 on the coordinate axis \(=[0,1]\)
A \(=\left\{\frac{1}{2}\right\}=\) Selecting a point on the wire which is at \(\left\{\frac{1}{2}\right\}\) or 0.5
As wire is an 1-D object so from geometrical probability
\(
P(A)=\frac{\text { Favourable Length }}{\text { Total Length }}
\)
Here total length of wire \(=1\) unit and point has zero length so point \(A\) at \(\left\{\frac{1}{2}\right\}\) or 0.5 has length \(=0\).
\(\therefore\) Favorable length \(=0\)
\(\therefore P ( A )=0\) but \(A \neq \phi\)
Now \(\overline{ A }=[0,1]-\left\{\frac{1}{2}\right\}\)
So, length of \(\bar{A}=\) Length of entire wire – Length of point \(A=1\)
\(
\therefore P (\overline{ A })=1 \text { but } \overline{ A } \neq \Omega
\)
Then both statements are false.

Note:

Geometrical probability :
1. For 1-D object, \(P(A)=\frac{\text { Favourable Length }}{\text { Total Length }}\)
2. For 2-D object, \(P(A)=\frac{\text { Favourable Area }}{\text { Total Area }}\)
3. For 2-D object, \(P(A)=\frac{\text { Favourable volume }}{\text { Total volume }}\)

Hint

Let \(E \rightarrow\) Ball drawn from Bag II is black.
\(E_R \rightarrow\) Bag I to Bag II red ball transferred.
\(E_B \rightarrow\) Bag I to Bag II black ball transferred.
\(E_w \rightarrow\) Bag I to Bag II white ball transferred.
\(
P\left(E_R / E\right)=\frac{P\left(E / E_R\right) \cdot P\left(E_R\right)}{P\left(E / E_R\right) P\left(E_R\right)+P\left(E / E_B\right) P\left(E_B\right)+P\left(E / E_W\right) P\left(E_W\right)}
\)
Here,
\(
P\left(E_R\right)=3 / 10, \quad P\left(E_B\right)=4 / 10, \quad P\left(E_W\right)=3 / 10
\)
and
\(
\begin{aligned}
& P\left(E / E_R\right)=5 / 10, \quad P\left(E / E_B\right)=6 / 10, \quad P\left(E / E_W\right)=5 / 10 \\
& \therefore \quad P\left(E_R / E\right)=\frac{15 / 100}{15 / 100+24 / 100+15 / 100} \\
& =\frac{15}{54}=\frac{5}{18}
\end{aligned}
\)

Hint

\(
\begin{aligned}
& S=\{1,2,3, \ldots \ldots \ldots .2022\} \\
& \operatorname{HCF}( n , 2022)=1 \\
& \Rightarrow n \text { and } 2022 \text { have no common factor } \\
& \text { Total elements }=2022 \\
& 2022=2 \times 3 \times 337
\end{aligned}
\)
M : numbers divisible by 2 .
\(
\{2,4,6, \ldots \ldots . ., 2022\} \quad n(M)=1011
\)
N : numbers divisible by 3 .
\(
\{3,6,9, \ldots \ldots \ldots, 2022\} \quad n(N)=674
\)
L : numbers divisible by 6 .
\(
\begin{aligned}
& \{6,12,18, \ldots \ldots . .2022\} \quad n(L)=337 \\
& n(M \cup N)=n(M)+n(N)-n(L) \\
& =1011+674-337 \\
& =1348
\end{aligned}
\)
\(0=\) Number divisible by 337 but not in \(M \cup N\)
\(
\{337,1685\}
\)
Number divisible by 2, 3 or 337
\(
\begin{aligned}
& =1348+2=1350 \\
& \text { Required probability }=\frac{2022-1350}{2022} \\
& =\frac{672}{2022} \\
& =\frac{112}{337}
\end{aligned}
\)

Hint

\(
\begin{aligned}
&\begin{aligned}
& P(A / B)=\frac{1}{7} \Rightarrow \frac{P(A \cap B)}{P(B)}=\frac{1}{7} \\
& \Rightarrow P(B)=\frac{7}{9} \\
& P(B / A)=\frac{2}{5} \Rightarrow \frac{P(A \cap B)}{P(A)}=\frac{2}{5} \\
& P(A)=\frac{5}{2} \cdot \frac{1}{9}=\frac{5}{18} \\
& S 2: P\left(A^{\prime} \cap B^{\prime}\right)=\frac{1}{18}
\end{aligned}\\
&S 1 \text { : and } P\left(A^{\prime} \cup B\right)=\frac{1}{9}+\frac{6}{9}+\frac{1}{18}=\frac{5}{6} \text {. }
\end{aligned}
\)

Hint

\(
\begin{aligned}
& P(\text { Female })=\frac{60}{100}=\frac{3}{5} \\
& P(\text { Male })=\frac{2}{5} \\
& P(\text { Female/Qualified })=\frac{40}{60}=\frac{2}{3} \\
& P(\text { Male/qualified })=\frac{20}{60}=\frac{1}{3}
\end{aligned}
\)

Hint

Let \(P (\) a prime number \()=\alpha\)
\(P (\) a composite number \()=\beta\)
and \(P(1)=\gamma\)
\(\because 3 \alpha=6 \beta=2 \gamma=k\) (say)
and \(3 \alpha+2 \beta+\gamma=1\)
\(
\Rightarrow k+\frac{k}{3}+\frac{k}{2}=1 \Rightarrow k=\frac{6}{11}
\)
Mean \(=n p[latex] where [latex]n=2\)
and \(p=\) probability of getting perfect square
\(
=P(1)+P(4)=\frac{k}{2}+\frac{k}{6}=\frac{4}{11}
\)
So, mean \(=2 \cdot\left(\frac{4}{11}\right)=\frac{8}{11}\)

Hint

Among the 5 digit numbers,
First number divisible by 7 is 10003 and last is 99995 .
\(
\begin{aligned}
& \Rightarrow \text { Number of numbers divisible by } 7 . \\
& =\frac{99995-10003}{7}+1 \\
& =12857
\end{aligned}
\)
First number divisible by 35 is 10010 and last is 99995.
\(
\begin{aligned}
& \Rightarrow \text { Number of numbers divisible by } 35 \\
& =\frac{99995-10010}{35}+1 \\
& =2572
\end{aligned}
\)
Hence number of number divisible by 7 but not by 5
\(
\begin{aligned}
& =12857-2572 \\
& =10285
\end{aligned}
\)
\(
\begin{aligned}
& 9 P .=\frac{10285}{90000} \times 9 \\
& =1.0285
\end{aligned}
\)

Hint

\(
\begin{aligned}
& 0 \leq \frac{2+3 P}{6} \leq 1 \Rightarrow P \in\left[-\frac{2}{3}, \frac{4}{3}\right] \\
& 0 \leq \frac{2-P}{8} \leq 1 \Rightarrow P \in[-6,2] \\
& 0 \leq \frac{1-P}{2} \leq 1 \Rightarrow P \in[-1,1] \\
& 0<P\left(E_1\right)+P\left(E_2\right)+P\left(E_3\right) \leq 1 \\
& 0<\frac{13}{12}-\frac{P}{8} \leq 1 \\
& P \in\left[\frac{2}{3}, \frac{26}{3}\right]
\end{aligned}
\)
Taking intersection of all
\(
\begin{aligned}
& P \in\left[\frac{2}{3}, 1\right) \\
& P_1+P_2=\frac{5}{3}
\end{aligned}
\)

Hint

\(
\begin{aligned}
& P(A)=\frac{1}{3}, P(B)=\frac{1}{5} \text { and } P(A \cup B)=\frac{1}{2} \\
& \therefore P(A \cap B)=\frac{1}{3}+\frac{1}{5}-\frac{1}{2}=\frac{1}{30}
\end{aligned}
\)
Now, \(P\left(A \mid B^{\prime}\right)+P\left(B \mid A^{\prime}\right)=\frac{P\left(A \cap B^{\prime}\right)}{P\left(B^{\prime}\right)}+\frac{P\left(B \cap A^{\prime}\right)}{P\left(A^{\prime}\right)}\)
\(
=\frac{\frac{9}{30}}{\frac{4}{5}}+\frac{\frac{5}{30}}{\frac{2}{3}}=\frac{5}{8}
\)

Hint

For \(x^2+\alpha x+\beta>0 \forall x \in R\) to hold, we should have \(\alpha^2-4 \beta<0\)
If \(\alpha=1, \beta\) can be \(1,2,3,4,5,6\) i.e., 6 choices
If \(\alpha=2, \beta\) can be \(2,3,4,5,6\) i.e., 5 choices
If \(\alpha=3, \beta\) can be \(3,4,5,6\) i.e., 4 choices
If \(\alpha=4, \beta\) can be 5 or 6 i.e., 2 choices
If \(\alpha=6\), No possible value for \(\beta\) i.e., 0 choices
Hence total favourable outcomes
\(
\begin{aligned}
& =6+5+4+2+0+0 \\
& =17
\end{aligned}
\)
Total possible choices for \(\alpha\) and \(\beta=6 \times 6=36\)
Required probability \(=\frac{17}{36}\)

Hint

Total number of relations \(=2^{2^2}=2^4=16\)
Relations that are symmetric as well as transitive are
\(
\phi,\{(x, x)\},\{(y, y)\},\{(x, x),(x, y),(y, y),(y, x)\},\{(x, x),(y, y)\}
\)
\(\therefore\) favourable cases \(=5\)
\(
\therefore \quad P_r=\frac{5}{16}
\)

Hint

Let M be a \(2 \times 2\) matrix such that \(M =\left[\begin{array}{cc}m & n \\ o & p\end{array}\right]\) and For M to be a singular matrix, \(| M |=0\)
\(
\Rightarrow mp – on =0
\)

Case 1: All four elements are equal
\(
\begin{aligned}
& m = n = o = p \\
& \Rightarrow mp – on =0
\end{aligned}
\)
So, number of matrices possible \(=10\)

Case 2: When two prime numbers are used
\(\Rightarrow\) Either \(m = n\) and \(o = p\) or \(m = o\) and \(n = p\)
So, number of matrices possible \(={ }^{10} C _2 \times 2!\times 2!\)
\(
\begin{aligned}
& \Rightarrow \frac{10 \times 9}{2} \times 2 \times 2 \\
& =180
\end{aligned}
\)
So, number of matrices possible \(=10+180=190\)
And total number of matrices that can be formed \(=10 \times 10 \times 10 \times 10=10^4\)
So, required probability \(=\frac{190}{10^4}=\frac{19}{10^3}\)

Hint

Number of one-one function from \(\{a, b, c, d\}\) to set \(\{1,2,3,4,5\}\) is \({ }^5 P_4=120 n(s)\).
The required possible set of value (f(a), \(f(b), f(c), f(d)\) ) such that \(f(a)+2 f(b)-f(c)=f(d)\) are \((5,3,2,1),(5,1,2,3),(4,1,3,5),(3,1,4,5),(5,4,3,2)\) and \((3,4,5,2)\)
\(
\therefore n(E)=6
\)
\(\therefore\) Required probability \(=\frac{n(E)}{n(S)}=\frac{6}{120}=\frac{1}{20}\)

Hint

At least two digits are odd
= exactly two digits are odd + exactly there 3 digits are odd
For exactly three digits are odd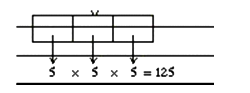

For exactly two digits odd :
If 0 is used then : \(2 \times 5 \times 5=50\)
If 0 is not used then: \({ }^3 C _1 \times 4 \times 5 \times 5=300\)
Required Probability \(=475 / 900\)
\(=19 / 36\)

Hint

\(
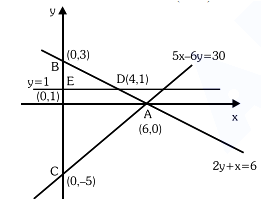
\text { Required probability = ar(ADEC)/ar(ABC) }
\)
\(
\begin{aligned}
& =1-\frac{\operatorname{ar}( BDE )}{\operatorname{ar}( ABC )} \\
& =1-\frac{\frac{1}{2} \times 2 \times 4}{\frac{1}{2} \times 8 \times 6}=1-\frac{1}{6}=\frac{5}{6}
\end{aligned}
\)

Alternate:

\(
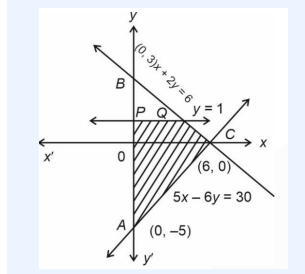
\begin{aligned}
& =\frac{\text { Area of Region } P Q C A P}{\text { Area of Region } A B C A} \\
& =\frac{\frac{1}{2} \times 8 \times 6-\frac{1}{2} \times 2 \times 4}{\frac{1}{2} \times 8 \times 6} \\
& =\frac{5}{6}
\end{aligned}
\)

Hint

No. of ways to select and arrange \(x _1, x _2, x _3, x _4, x _5\) from \(1,2,3 \ldots \ldots . .18\)
\(
n ( s )={ }^{18} C _5
\)
\(
\begin{array}{ccccc}
x_1 & \left(x_2\right) & x_3 & \left(x_4\right) & x_5 \\
& 7 & & 11 &
\end{array}
\)
\(
\begin{aligned}
& n ( E )={ }^6 C _1 \times{ }^3 C _1 \times{ }^7 C _1 \\
& P(E)=\frac{6 \times 3 \times 7}{{ }^{18} C_5} \\
& \frac{1}{17 \times 4}=\frac{1}{68}
\end{aligned}
\)

Hint

There are only two ways to get sum 48 , which are \((32,8,8)\) and \((16,16,16)\)
So, required probability
\(
\begin{aligned}
& =3\left(\frac{2}{32} \cdot \frac{1}{8} \cdot \frac{1}{8}\right)+\left(\frac{1}{16} \cdot \frac{1}{16} \cdot \frac{1}{16}\right) \\
& =\frac{3}{2^{10}}+\frac{1}{2^{12}} \\
& =\frac{13}{2^{12}}
\end{aligned}
\)

Hint

\(
\begin{aligned}
& P\left(\frac{E_1}{E_2}\right)=\frac{1}{2} \Rightarrow \frac{P\left(E_1 \cap E_2\right)}{P\left(E_2\right)}=\frac{1}{2} \\
& P\left(\frac{E_2}{E_1}\right)=\frac{3}{4} \Rightarrow \frac{P\left(E_2 \cap E_1\right)}{P\left(E_1\right)}=\frac{3}{4} \\
& P\left(E_1 \cap E_2\right)=\frac{1}{8} \\
& P\left(E_2\right)=\frac{1}{4}, P\left(E_1\right)=\frac{1}{6}
\end{aligned}
\)
\(
\begin{aligned}
& \text { (A) } P\left(E_1 \cap E_2\right)=\frac{1}{8} \text { and } P\left(E_1\right) \cdot P\left(E_2\right)=\frac{1}{24} \\
& \Rightarrow P\left(E_1 \cap E_2\right) \neq P\left(E_1\right) \cdot P\left(E_2\right)
\end{aligned}
\)
\(
\begin{aligned}
& \text { (B) } P\left(E_1^{\prime} \cap E_2^{\prime}\right)=1-P\left(E_1 \cup E_2\right) \\
& =1-\left[\frac{1}{4}+\frac{1}{6}-\frac{1}{8}\right]=\frac{17}{24} \\
& P\left(E_1^{\prime}\right)=\frac{3}{4} \Rightarrow P\left(E_1^{\prime}\right) P\left(E_2\right)=\frac{3}{24} \\
& \Rightarrow P\left(E_1^{\prime} \cap E_2^{\prime}\right) \neq P\left(E_1^{\prime}\right) \cdot P\left(E_2\right)
\end{aligned}
\)
(C) \(P\left(E_1 \cap E_2^{\prime}\right)=P\left(E_1\right)-P\left(E_1 \cap E_2\right)\)
\(
=\frac{1}{6}-\frac{1}{8}=\frac{1}{24}
\)
\(
\begin{aligned}
& P\left(E_1\right) \cdot P\left(E_2\right)=\frac{1}{24} \\
& \Rightarrow P\left(E_1 \cap E_2^{\prime}\right)=P\left(E_1\right) \cdot P\left(E_2\right) \\
& \text { (D) } P\left(E_1^{\prime} \cap E_2\right)=P\left(E_2\right)-P\left(E_1 \cap E_2\right) \\
& =\frac{1}{4}-\frac{1}{8}=\frac{1}{8} \\
& P\left(E_1\right) P\left(E_2\right)=\frac{1}{24} \\
& \Rightarrow P\left(E_1^{\prime} \cap E_2\right) \neq P\left(E_1\right) \cdot P\left(E_2\right)
\end{aligned}
\)

Hint

\(\because x\) is a random variable
\(
\begin{aligned}
& \therefore k+2 k+4 k+6 k+8 k=1 \\
& \therefore k=\frac{1}{21}
\end{aligned}
\)
Now, \(P(1<x<4 \mid x \leq 2)=\frac{4 k}{7 k}=\frac{4}{7}\)

Hint

\(
\begin{aligned}
& P(1 R \text { and } 1 B)=P(A) \cdot P\left(\frac{1 R 1 B}{A}\right)+P(B) \cdot P\left(\frac{1 R 1 B}{B}\right) \\
& =\frac{1}{2} \cdot \frac{{ }^3 C_1 \cdot{ }^1 C_1}{{ }^6 C_2}+\frac{1}{2} \cdot \frac{{ }^2 C_1 \cdot{ }^3 C_1}{{ }^{n+5} C_2} \\
& P\left(\frac{1 R 1 B}{A}\right)=\frac{\frac{1}{2} \cdot \frac{3}{15}}{\frac{1}{2} \cdot \frac{3}{15}+\frac{1}{2} \cdot \frac{6 \cdot 2}{(n+5)(n+4)}}=\frac{6}{11} \\
& \Rightarrow \frac{\frac{1}{10}}{\frac{1}{10}+\frac{6}{(n+5)(n+4)}}=\frac{6}{11} \\
& \Rightarrow \frac{11}{10}=\frac{6}{10}+\frac{36}{(n+5)(n+4)} \\
& \Rightarrow \frac{5}{10 \times 36}=\frac{1}{(n+5)(n+4)} \\
& \Rightarrow n^2+9 n-52=0 \\
& \Rightarrow n=4 \text { is only possible value }
\end{aligned}
\)

Hint

Total ways of choosing square \(={ }^{64} C_2\)
\(
=\frac{64 \times 63}{2 \times 1}=32 \times 63
\)
ways of choosing two squares having common side \(=2(7 \times 8)=112\)
\(
\text { Required probability }=\frac{112}{32 \times 63}=\frac{16}{32 \times 9}=\frac{1}{18} .
\)

Hint

\(g(3)=2 g(1)\) can be defined in 3 ways
number of onto functions in this condition \(=3 \times 4\) !
Total number of onto functions \(=6\) !
Required probability \(=\frac{3 \times 4!}{6!}=\frac{1}{10}\)

Hint

Probability of obtaining total sum 7 = probability of getting opposite faces.
Probability of getting opposite faces
\(
\begin{aligned}
& =2\left[\left(\frac{1}{6}-x\right)\left(\frac{1}{6}+x\right)+\frac{1}{6} \times \frac{1}{6}+\frac{1}{6} \times \frac{1}{6}\right] \\
& \Rightarrow 2\left[\left(\frac{1}{6}-x\right)\left(\frac{1}{6}+x\right)+\frac{1}{6} \times \frac{1}{6}+\frac{1}{6} \times \frac{1}{6}\right]=\frac{13}{96} \text { (given) } \\
& \Rightarrow x=\frac{1}{8}
\end{aligned}
\)

Hint

\(
\begin{aligned}
&\begin{aligned}
& P(x \geq 5 \mid x>2)=\frac{P(x \geq 5)}{P(x>2)} \\
& =\frac{\left(\frac{5}{6}\right)^4 \cdot \frac{1}{6}+\left(\frac{5}{6}\right)^5 \cdot \frac{1}{6}+\ldots \ldots+\infty}{\left(\frac{5}{6}\right)^2 \cdot \frac{1}{6}+\left(\frac{5}{6}\right)^3 \cdot \frac{1}{6}+\ldots \ldots+\infty}
\end{aligned}\\
&=\frac{\frac{\left(\frac{5}{6}\right)^4 \cdot \frac{1}{5}}{1-\frac{5}{6}}}{\frac{\left(\frac{5}{6}\right)^2 \cdot \frac{1}{6}}{1-\frac{5}{6}}}=\left(\frac{5}{6}\right)^2=\frac{25}{36}
\end{aligned}
\)

Hint

\(
D \neq 0 \Rightarrow\left|\begin{array}{lll}
1 & 1 & 1 \\
1 & 2 & 3 \\
1 & 3 & \lambda
\end{array}\right| \neq 0 \Rightarrow \lambda \neq 5
\)
For no solution \(D =0 \Rightarrow \lambda=5\)
\(
\begin{aligned}
& D_1=\left|\begin{array}{lll}
1 & 1 & 5 \\
1 & 2 & \mu \\
1 & 3 & 1
\end{array}\right| \neq 0 \Rightarrow \mu \neq 3 \\
& p=\frac{5}{6} \\
& q=\frac{1}{6} \times \frac{5}{6}=\frac{5}{36}
\end{aligned}
\)

Hint

\(
\begin{aligned}
& P (\text { Exactly one of } A \text { or } B ) \\
& =P(A \cap \bar{B})+(\bar{A} \cap B)=\frac{5}{9} \\
& =P(A) P(\bar{B})+P(\bar{A}) P(B)=\frac{5}{9} \\
& \Rightarrow P(A)(1-P(B))+(1-P(A)) P(B)=\frac{5}{9} \\
& \Rightarrow p(1-2 p)+(1-p) 2 p=\frac{5}{9} \\
& \Rightarrow 36 p^2-27 p+5=0 \\
& \Rightarrow p=\frac{1}{3} \text { or } \frac{5}{12} \\
& p_{\max }=\frac{5}{12}
\end{aligned}
\)

Hint

Total number of cases \(={ }^{90} C_1=90\)
Now, \(2^n-2=(3-1)^n-2\)
\(
\begin{aligned}
& { }^n C_0 3^n-{ }^n C_1 \cdot 3^{n-1}+\ldots+(-1)^{n-1} \cdot{ }^n C_{n-1} 3+(-1)^n \cdot{ }^n C_n-2 \\
& =3\left(3^{n-1}-n 3^{n-2}+\ldots+(-1)^{n-1} \cdot n\right)+(-1)^n-2
\end{aligned}
\)
\(\left(2^n-2\right)\) is multiply of 3 only when \(n\) is odd
\(
\text { Required Probability }=\frac{45}{90}=\frac{1}{2}
\)

Hint

\(
\begin{aligned}
& \text { Mean }=\sum X_i P_i=\sum_{r=0}^{\infty} r \cdot \frac{1}{3^r}=\frac{3}{4} \\
& P ( X \text { is even })=\frac{1}{3^2}+\frac{1}{3^4}+\ldots \infty \\
& =\frac{\frac{1}{9}}{1-\frac{1}{9}}=\frac{1 / 9}{8 / 9}=\frac{1}{8}
\end{aligned}
\)

Hint

\(
\begin{aligned}
& \text { Required probability }=\frac{{ }^9 C_3 \cdot 3^6}{4^9} \\
& =\frac{{ }^9 C_3}{27} \cdot\left(\frac{3}{4}\right)^9 \\
& =\frac{28}{9} \cdot\left(\frac{3}{4}\right)^9 \Rightarrow k=\frac{28}{9}
\end{aligned}
\)
Which satisfies \(|x-3|<1\)

Hint

\(
\begin{aligned}
& A=\left|\begin{array}{ll}
a & b \\
c & d
\end{array}\right| \\
& | A |= ad – bc
\end{aligned}
\)
Total case \(=6^4\)
For non-singular matrix \(|A| \neq 0 \Rightarrow a d-b c \neq 0\)
\(
\Rightarrow ad \neq bc
\)
And \(a, b, c, d\) are all different numbers in the set \(\{1,2,3,4,5,6\}\)
Now for \(ad = bc\)
\(
\text { (i) } 6 \times 1=2 \times 3
\)
Total 8 Cases:
\(
\begin{aligned}
& a=6, b=3, c=4, d=2 \\
& \text { or } a=2, b=3, c=4, d=6 \\
\vdots
\end{aligned}
\)
\(
\text { (ii) } 6 \times 2=3 \times 4
\)
Total 8 Cases:
\(
\begin{aligned}
& a=6, b=3, c=4, d=2 \\
& \text { or } a=2, b=3, c=4, d=6 \\
\vdots
\end{aligned}
\)
favourable cases
\(
={ }^6 C_4 \times 4!-16
\)
required probability
\(
=\frac{{ }^6 C_4 \times 4!-16}{6^4}=\frac{43}{162}
\)

Hint

\(
\begin{aligned}
& P(\bar{A} \cap B)+P(A \cap \bar{B})=1-k \\
& P(\bar{A} \cap C)+P(A \cap \bar{C})=1-2 k \\
& P(\bar{B} \cap C)+P(B \cap \bar{C})=1-k \\
& P(A \cap B \cap C)=k^2
\end{aligned}
\)
\(
\begin{aligned}
& P(A)+P(B)-2 P(A \cap B)=1-k \ldots . . \text { (i) } \\
& P(B)+P(C)-2 P(B \cap C)=1-k \ldots . . \text { (ii) } \\
& P(C)+P(A)-2 P(A \cap C)=1-2 k \ldots . .\text { (iii) }
\end{aligned}
\)
\(
\begin{aligned}
& (\text { i })+(\text { ii })+(\text { iii }) \\
& P(A)+P(B)+P(C)-P(A \cap B)-P(B \cap C)-P(C \cap A)=\frac{-4 k+3}{2}
\end{aligned}
\)
So,
\(
\begin{aligned}
& P(A \cup B \cup C)=\frac{-4 k+3}{2}+k^2 \\
& P(A \cup B \cup C)=\frac{2 k^2-4 k+3}{2} \\
& =\frac{2(k-1)^2+1}{2} \\
& P(A \cup B \cup C)>\frac{1}{2}
\end{aligned}
\)

Hint

\(
\begin{aligned}
& \text { Since } x^2+2(a+4) x-5 a+64>0, \text { we have discriminant(D) }<0 \\
& \Rightarrow 4(a+4)^2-4(64-5 a)<0 \\
& \Rightarrow a^2+8 a+16-64+5 a<0 \\
& \Rightarrow a^2+13 a-48<0 \\
& \Rightarrow a^2+16 a-3 a-48<0 \\
& \Rightarrow(a+16)(a-3)<0 \\
& a \in(-16,3) \\
& \text { in set }[-5,30] \text { total integers } 36 \\
& \text { favourable integers } 8 \\
& \text { Required probability is } \frac{8}{36}=\frac{2}{9}
\end{aligned}
\)

Hint

Letters: AA II NN ET OX M
Total possible words
\(
\Rightarrow n(S)=\frac{11!}{(2!)^3}
\)
Now when \(M\) is at \(4 t h\) position
\(
\begin{aligned}
& \Rightarrow n(E)=\frac{10!}{(2!)^3} \\
& P( M \text { is at } 4 \text { th position })=\frac{n(E)}{n(S)} \\
& \Rightarrow=\frac{1}{11}
\end{aligned}
\)

Hint

\(
\begin{aligned}
& P (0 \text { at even place })=\frac{1}{2} \\
& P (0 \text { at odd place })=\frac{1}{3} \\
& P (1 \text { at even place })=\frac{1}{2} \\
& P (1 \text { at odd place })=\frac{2}{3} \\
& P (10 \text { is followed by 01 }) \\
& =\left(\frac{2}{3} \times \frac{1}{2} \times \frac{1}{3} \times \frac{1}{2}\right)+\left(\frac{1}{2} \times \frac{1}{3} \times \frac{1}{2} \times \frac{2}{3}\right) \\
& =\frac{1}{18}+\frac{1}{18} \\
& =\frac{1}{9}
\end{aligned}
\)

Hint

\(
n(S)=36
\)
possible ordered pair :
\(
\begin{aligned}
& (1,1),(1,2),(1,3),(1,5),(1,7) \\
& (2,1),(2,2),(2,3),(2,5) \\
& (3,1),(3,2),(3,3),(3,5) \\
& (5,1),(5,2),(5,3) \\
& (7,1)
\end{aligned}
\)
Number of favourable outcomes \(=17\)
Probability \(=\frac{17}{36}\)

Hint

We have, \(0,1,2,3,4,5,6\) using which 6 -digit number without repetition is to be formed.
We know that 0 cannot be used in the first place, So the possibility of filling the first place is by 6 remaining digits, now we have five more numbers and zero, so there is 6 possible ways of filling the second place, similarly for third place, its is 5 , for fourth place it is 4 , for fifth place it is 3 , for sixth place it is 2 .
Therefore sample space is \(6 \times 6 \times 5 \times 4 \times 3 \times 2=4320\)
\(A=6\)-digit integers divisible by three without repetition.
Condition for a number divisible by 3 is a sum of the digits in the number is divisible by 3
\((0,1,2,3,4,5),(0,1,2,4,5,6),(1,2,3,4,5,6)\) these are the sets with the possibility of forming a number divisible by 3 .
Therefore the total such number formed are:
\(
=(5 \times 5 \times 4 \times 3 \times 2 \times 1)+(5 \times 5 \times 4 \times 3 \times 2 \times 1)+(6 \times 5 \times 4 \times 3 \times 2 \times 1)
\)
[Refer the above explanation]
\(
\begin{aligned}
& =600+600+720 \\
& =1920
\end{aligned}
\)
Therefore, \(P(A)=\frac{1920}{4320}=\frac{4}{9}\)

Hint

Consider the events,
\(E _1=\) missing card is spade
\(E _2=\) missing card is not a spade
A = Two spade cards are drawn
\(
\begin{aligned}
& P\left(E_1\right)=\frac{1}{4} \\
& P\left(E_2\right)=\frac{3}{4} \\
& P\left(\frac{A}{E_1}\right)=\frac{{ }^{12} C_2}{{ }^{51} C_2} \\
& P\left(\frac{A}{E_2}\right)=\frac{{ }^{13} C_2}{{ }^{51} C_2}
\end{aligned}
\)
\(
\begin{aligned}
&\begin{aligned}
& P\left(\frac{E_2}{A}\right)=\frac{P\left(\frac{A}{E_2}\right) \cdot P\left(E_2\right)}{P\left(\frac{A}{E_1}\right) \cdot P\left(E_1\right)+P\left(\frac{A}{E_2}\right) \cdot P\left(E_2\right)}
\end{aligned}\\
&P\left(\frac{E_2}{A}\right)=\frac{P\left(\frac{A}{E_2}\right) \cdot P\left(E_2\right)}{P\left(\frac{A}{E_1}\right) \cdot P\left(E_1\right)+P\left(\frac{A}{E_2}\right) \cdot P\left(E_2\right)}\\
&\begin{aligned}
& =\frac{39}{50}
\end{aligned}\\
&=\frac{39}{50}
\end{aligned}
\)

Hint

Number of ways in which the seven digited number formed is
\(
n ( s )=\frac{7!}{2!3!2!}
\)
Number of ways in which the seven digited number is divisible by 2 is
\(
n(E)=\frac{6!}{2!2!2!}
\)
Hence required probability is
\(
\begin{aligned}
& P(E)=\frac{n(E)}{n(S)} \\
& =\frac{6!}{7!} \times \frac{2!3!2!}{2!2!2!}=\frac{3}{7}
\end{aligned}
\)

Hint

\(
\begin{aligned}
& n ( s )= n (\text { when } 7 \text { appears on thousands place }) \\
& + n (7 \text { does not appear on thousands place }) \\
& =9 \times 9 \times 9+8 \times 9 \times 9 \times 3 \\
& =33 \times 9 \times 9 \\
& n ( E )= n \text { (last digit } 7 \& 7 \text { appears once) } \\
& + n (\text { last digit } 2 \text { when } 7 \text { appears once }) \\
& =8 \times 9 \times 9+(3 \times 9 \times 9-2 \times 9) \\
& \therefore P(E)=\frac{8 \times 9 \times 9+9 \times 25}{33 \times 9 \times 9}=\frac{97}{297}
\end{aligned}
\)

Alternate:

Total cases
\(
={ }^4 C_1 \times 9 \times 9 \times 9-{ }^3 C_1 \times 9 \times 9
\)
(as 4 digit number having 0 at thousands place have to be excluded)
For a number to have remainder 2 when divided by 5 it’s unit digit should be 2 or 7
Case 1: when unit digit is 2
Number of four digit number \(={ }^3 C_1 \times 9 \times 9-{ }^2 C_1 \times 9\)
Case 2 : when unit digit is 7
Number of four digit number \(=8 \times 9 \times 9\)
So, total number favorable cases \(=3 \times 9^2-2 \times 9+8 \times 9^2\)
\(\therefore\) required Probability \(=\frac{(3 \times 9 \times 9)-(2 \times 9)+(8 \times 9 \times 9)}{\left(4 \times 9^3\right)-\left(3 \times 9^2\right)}\)
\(
=\frac{97}{297}
\)

Hint

Consider following events
A: Person chosen is a smoker and non vegetarian.
B : Person chosen in a smoker and vegetarian.
C : Person chosen is a non-smoker and vegetarian.
E : Person chosen has a chest disorder
Given
\(
\begin{aligned}
&\begin{aligned}
& P(A)=\frac{160}{400} \\
& P(B)=\frac{100}{400} \\
& P(C)=\frac{140}{400} \\
& P\left(\frac{E}{A}\right)=\frac{35}{100} \\
& P\left(\frac{E}{B}\right)=\frac{20}{100} \\
& P\left(\frac{E}{C}\right)=\frac{10}{100}
\end{aligned}\\
&\text { To find }\\
&\begin{aligned}
& P\left(\frac{A}{E}\right)=\frac{P(A) P\left(\frac{E}{A}\right)}{P(A) \cdot P\left(\frac{E}{A}\right)+P(B) \cdot P\left(\frac{E}{B}\right)+P(C) \cdot P\left(\frac{E}{C}\right)} \\
& =\frac{\frac{160}{40} \times \frac{35}{100}}{\frac{160}{400} \times \frac{35}{100} \times \frac{100}{400} \times \frac{20}{200}+\frac{140}{400} \times \frac{10}{100}} \\
& =\frac{28}{45}
\end{aligned}
\end{aligned}
\)

Hint

Probability of not getting intercepted \(=\frac{2}{3}\)
When it is not intercepted, probability of missile hitting target \(=\frac{3}{4}\)
\(\therefore\) So when such 3 missiles launched then P (all 3 hitting the target)
\(
\begin{aligned}
& =\left(\frac{2}{3} \times \frac{3}{4}\right) \times\left(\frac{2}{3} \times \frac{3}{4}\right) \times\left(\frac{2}{3} \times \frac{3}{4}\right) \\
& =\frac{1}{8}
\end{aligned}
\)

Hint

\(
\begin{aligned}
& a x^2+b x+c=0 \\
& a, b, c \in\{1,2,3,4,5,6\} \\
& n(s)=6 \times 6 \times 6=216
\end{aligned}
\)
For equal roots, \(D=0 \Rightarrow b^2=4 a c\)
\(
\Rightarrow ac =\frac{b^2}{4}
\)
Favourable case :
If \(b=2, a c=1 \Rightarrow a=1, c=1\)
\(
\begin{aligned}
& \text { If } b=4, a c=4: \\
& a=1, c=4 \\
& a=4, c=1 \\
& a=2, c=2
\end{aligned}
\)
If \(b=6, a c=9 \Rightarrow a=3, c=3\)
\(\therefore\) Favorable cases \(=5\)
\(\therefore\) Required probability \(=\frac{5}{216}\)

Hint

Given, set \(P=\{1,2,3,4,5\}\)

Let the two subsets be \(A[latex] and [latex]B\)

Then, \(n ( A \cap B )=2\) (as given in question)

We can choose two elements from set P in \({ }^5 C _2\) ways.

After choosing two common elements for set \(A\) and \(B\), each of remaining three elements from set \(P\) have three choice (1) It can go to set \(A\) (2) It can go to set \(B\) (3) It don’t go to any sets it stays at set \(P\).
\(\therefore\) Total ways for the three elements \(=3 \times 3 \times 3=3^3\)
\(\therefore\) Required probability \(=\frac{{ }^5 C_2 \times 3^3}{\left(2^5\right)\left(2^5\right)}=\frac{{ }^5 C_2 \times 3^3}{4^5}=\frac{10 \times 27}{2^{10}}=\frac{135}{2^9}\)

Hint

\(
\begin{aligned}
& P ( A \cup B )= P ( A )+ P ( B )- P ( A \cup B ) \\
& \Rightarrow 0.8=0.6+0.4- P ( A \cap B ) \\
& \Rightarrow P ( A \cap B )=0.2 \\
& P ( A \cup B \cup C )= P ( A )+ P ( B )+ P ( C )- P ( A \cap B )- P ( B \cap C )- P ( C \cap A )+ P ( A \cap B \cap C ) \\
& \Rightarrow \alpha=0.6+0.4+0.5-0.2-\beta-0.3+0.2 \\
& \Rightarrow \alpha+\beta=1.2 \\
& \Rightarrow \alpha=1.2-\beta \\
& \text { Given, } 0.85 \leq \alpha \leq 0.95 \\
& \Rightarrow 0.85 \leq 1.2-\beta \leq 0.95 \\
& \Rightarrow 0.25 \leq \beta \leq 0.35
\end{aligned}
\)

Hint

Calculating the probability of selecting three random numbers that are in A.P
Given, there are 11consecutive natural numbers
Case-1:
\(E, O, E, O, E, O, E, O, E, O, E\) (Here, \(O\) stands for odd and \(E\)
stands for even)
For the numbers to be in A.P: \(2 b=a+c\) (It should be even)
\(\Rightarrow\) Both \(a\) and \(c\) should be either even or odd.
In the above case, there are 6 even numbers and 5 odd numbers.
Therefore, the probability will be:
\(
P =\frac{{ }^6 C _2+{ }^5 C _2}{{ }^{11} C _3}=\frac{5}{33}
\)
Case-2:
\(
O, E, O, E, O, E, O, E, O, E, O
\)
In this case, there are 5 even numbers and 6odd numbers.
Hence, the probability will be:
\(
P =\frac{{ }^5 C _2+{ }^6 C _2}{{ }^{11} C _3}=\frac{5}{33}
\)
Therefore, the Total probability :
\(
\begin{aligned}
& =\left(\frac{1}{2}\right) \times\left(\frac{5}{33}\right)+\left(\frac{1}{2}\right) \times\left(\frac{5}{33}\right) \\
& =\frac{5}{33}
\end{aligned}
\)

Hint

\(
P ( A )=\frac{5}{36}, P ( B )=\frac{1}{6}
\)
Sum total \(6=\{(1,5)(2,4)(3,3)(4,2)(5,1)\}\)
\(
P(6)=\frac{5}{36}
\)
Sum total \(7=\{(1,6)(2,5)(3,4)(4,3)(5,2)(6,1)\}\)
\(
P(7)=\frac{6}{36}=\frac{1}{6}
\)
Game ends and \(A\) wins if \(A\) throws 6 in \(1^{\text {st }}\) throw or \(A\) don’t throw 6 in \(1^{\text {st }}\) throw, \(B\) don’t throw 7 in \(1^{\text {st }}\) throw and then \(A\) throw 6 in his \(2^{\text {nd }}\) chance and so on.
\(
P ( A \text { wins })= W + FFW + FFFFW + \dots
\)
\(
\begin{aligned}
& =\frac{5}{36}+\left(\frac{31}{36}\right)\left(\frac{30}{36}\right)\left(\frac{5}{36}\right)+\ldots . . \infty \\
& =\frac{\frac{5}{36}}{1-\left(\frac{31}{36}\right)\left(\frac{30}{36}\right)} \\
& =\frac{5 \times 36}{36 \times 36-31 \times 30} \\
& =\frac{30}{61}
\end{aligned}
\)

Hint

Flrst Case: Choose two non-zero digits \({ }^9 C _2\)
Now, number of 5-digit numbers containing both digits \(=2^5-2\)
Second Case: Choose one non-zero & one zero as digit \({ }^9 C _1\).
Number of 5-digit numbers containg one non zero and one zero both \(=\left(2^4-1\right.\)) Required prob.
\(
\begin{aligned}
& =\frac{\left({ }^9 C _2 \times\left(2^5-2\right)+{ }^9 C _1 \times\left(2^4-1\right)\right)}{9 \times 10^4} \\
& =\frac{36 \times(32-2)+9 \times(16-1)}{9 \times 10^4} \\
& =\frac{4 \times 30+15}{10^4} \\
& =\frac{135}{10^4}
\end{aligned}
\)

Hint

Let A is the event for getting score a multiple of 4 .
So, \(A=\{(1,3),(3,1),(2,2),(2,6),(6,2),(3,5),(5,3),(4,4),(6,6)\}=09\)
\(
n(A)=9
\)
B : Score of 4 has appeared at least once.
\(
B=\{(4,4)\}
\)
So, Required probability \(=\frac{1}{9}\)

Hint

Given \(E_1, E_2, E_3\) are pairwise indepedent events

\(
\text { so } P\left(E_1 \cap E_2\right)=P\left(E_1\right) \cdot P\left(E_2\right)
\)

and \(P\left(E_2 \cap E_3\right)=P\left(E_2\right) \cdot P\left(E_3\right)\)
and \(P\left(E_3 \cap E_1\right)=P\left(E_3\right) \cdot P\left(E_1\right)\)
and \(P\left(E_1 \cap E_2 \cap E_3\right)=0\)
\(
\begin{aligned}
&\text { Now } P\left(\frac{E_2^C \cap E_3^C}{E_1}\right)\\
&\begin{aligned}
& =\frac{P\left[E_1 \cap\left(E_2^C \cap E_3^C\right)\right]}{P\left(E_1\right)} \\
& =\frac{P\left(E_1\right)-\left[P\left(E_1 \cap E_2\right)+P\left(E_1 \cap E_3\right)-P\left(E_1 \cap E_2 \cap E_3\right)\right]}{P\left(E_1\right)} \\
& =\frac{P\left(E_1\right)-P\left(E_1\right) \cdot P\left(E_2\right)-P\left(E_1\right) \cdot P\left(E_3\right)-0}{P\left(E_1\right)} \\
& =1-P\left(E_2\right)-P\left(E_3\right) \\
& =1-P\left(E_3\right)-P\left(E_2\right) \\
& =P\left(E_3^C\right)-P\left(E_2\right)
\end{aligned}
\end{aligned}
\)

Hint

Let \(B_1\) be the event where Box-I is selected.
And \(B_2\) be the event where Box-II is selected.
\(
P\left(B_1\right)=P\left(B_2\right)=\frac{1}{2}
\)
Let E be the event where selected card is non prime.
For \(B _1\) : Prime numbers: \(\{2,3,5,7,11,13,17,19,23,29\}\)
For \(B _2\) : Prime numbers: \(\{31,37,41,43,47\}\)
\(
\begin{aligned}
& P ( E )= P \left( B _1\right) \times P\left(\frac{E}{B_1}\right)+ P \left( B _2\right) \times P\left(\frac{E}{B_2}\right) \\
& =\frac{1}{2} \times \frac{20}{30}+\frac{1}{2} \times \frac{15}{20}
\end{aligned}
\)
Required probability :
\(
\begin{aligned}
& P\left(\frac{B_1}{E}\right)=\frac{P\left(B_2\right) \cdot P\left(\frac{E}{B_1}\right)}{P(E)} \\
& =\frac{\frac{1}{2} \times \frac{20}{30}}{\frac{1}{2} \times \frac{20}{30}+\frac{1}{2} \frac{15}{20}} \\
& =\frac{\frac{2}{3}}{\frac{2}{3}+\frac{3}{4}} \\
& =\frac{8}{17}
\end{aligned}
\)

Hint

\(
\begin{aligned}
& \sum_{i=1}^5 P(X)=1 \\
& \Rightarrow K ^2+2 K+ K +2 K+5 K^2=1 \\
& \Rightarrow 6 K^2+5 K-1=0 \\
& \Rightarrow(6 K-1)( K +1)=0 \\
& \Rightarrow K =\frac{1}{6} \text { and } K =-1(\text { rejected }) \\
& \therefore P ( X >2) \\
& = K +2 K+5 K^2 \\
& =\frac{1}{6}+\frac{2}{6}+\frac{5}{36} \\
& =\frac{23}{36}
\end{aligned}
\)

Hint

Total ways of distribution \(=4^{10}=2^{20}\)
Number of ways selecting two boxes out of four \(={ }^4 C _2\)
Then number of ways selecting 5 balls out of \(10={ }^{10} C _5\)
Then no of ways of distributing 5 balls into two groups of 2 balls and 3 balls = \({ }^5 C _3 \cdot 2\) !
Then number of ways to distributing remaining balls into two boxes \(=2^5\)
Number of ways placing exactly 2 and 3 balls in two of these boxes
\(
\begin{aligned}
& ={ }^4 C _2 \times{ }^{10} C _5 \times{ }^5 C _3 \cdot 2!\times 2^5 \\
& =\frac{6.252 .10 .2 .2^5}{2^{20}} \\
& =\frac{945}{2^{10}}
\end{aligned}
\)

Hint

Number of ways 3 consecutive heads can appers
(1) \(HHHT _{-}\)
(2) \(\_\)THHH
(3) THHHT
\(\therefore\) Probablity of getting 3 consecutive heads
\(
=\frac{2}{32}+\frac{2}{32}+\frac{1}{32}=\frac{5}{32}
\)
Number of ways 4 consecutive heads can appers
(1) HHHHT
(2) THHHH
\(\therefore[latex] Probablity of getting 4 consecutive heads
[latex]
=\frac{1}{32}+\frac{1}{32}=\frac{2}{32}
\)
Number of ways 5 consecutive heads can appers
(1) HHHHH
\(\therefore\) Probablity of getting 5 consecutive heads
\(
=\frac{1}{32}
\)
Now Probablity of getting 0,1 , and 2 consecutive heads
\(
=1-\left(\frac{5}{32}+\frac{2}{32}+\frac{1}{32}\right)=\frac{24}{32}
\)
Now, Expectation
\(
\begin{aligned}
& =(-1) \times \frac{24}{32}+3 \times \frac{5}{32}+4 \times \frac{2}{32}+5 \times \frac{1}{32} \\
& =\frac{1}{8}
\end{aligned}
\)

Hint

When two dice are thrown then sample space will \(\{(1,1),(2,2)\) \(\dots[latex] [latex](6,6)\}\) contain total 36 elements number of cases.

Then the expectation will be \(\frac{6}{36} \times 15 \times \frac{4}{36} \times 12-\frac{26}{36} \times 6\)
\(
\frac{90+48-156}{36}=-\frac{1}{2}=\frac{1}{2} \text { loss }
\)

Hint

Choosing three vertices of a regular hexagon alternately, only two equilateral triangles are possible,
i.e., \(A_1, A_3, A_5\) and \(A_2, A_4, A_6\) Hence, required probability \(==\frac{2}{{ }^6 C_3}=\frac{2}{20}=\frac{1}{10}\)

Hint

Given that a fair coin is tossed such that we get at least one head.
Probability of getting head we a fair coin is tossed \(=\frac{1}{2}\)
Now, let n be the required minimum numbers of coins tossed to get at least one head.
Probability of getting at least one head \(=1-\) (probability of getting no head in n tossed).
Probability of getting at least one head \(=1-\left(\frac{1}{2}\right)^n\)
Also, given that the probability of getting at least one head is more than \(99 \%\)
This implies that, Probability of getting at least one head \(>\frac{99}{100}\)

\(
\begin{aligned}
& \Rightarrow 1-\left(\frac{1}{2}\right)^n>\frac{99}{100} \\
& \Rightarrow 1-\frac{99}{100}>\left(\frac{1}{2}\right)^n
\end{aligned}
\)
By cross multiplication, we get
\(
\begin{aligned}
& \Rightarrow \frac{100-99}{100}>\left(\frac{1}{2}\right)^n \\
& \Rightarrow \frac{1}{100}>\left(\frac{1}{2}\right)^n \\
& \Rightarrow \frac{1}{100}>\frac{1}{2^n} \\
& \Rightarrow 2^n>100
\end{aligned}
\)
Implies, \(n =7\)

Hint

A= At least two girls
\(B=\) All girls

\(
\begin{aligned}
& P\left(\frac{B}{A}\right)=\frac{P(B \cap A)}{P(A)} \\
& \Rightarrow \frac{P(B)}{P(A)}=\frac{\left(\frac{1}{4}\right)^2}{1-{ }^4 C_0\left(\frac{1}{2}\right)^4-{ }^4 C_1\left(\frac{1}{2}\right)^4} \\
& \Rightarrow \frac{1}{16-1-4}=\frac{1}{11}
\end{aligned}
\)

Hint

Let four persons are \(A, B, C\) and \(D\).
Probablity of hitting a target by them,
\(
\begin{aligned}
& P(A)=\frac{1}{2} \\
& P(B)=\frac{1}{3} \\
& P(C)=\frac{1}{4} \\
& P(D)=\frac{1}{8}
\end{aligned}
\)
Probablity of hitting target atleast once \(=1\) – Probablity of not hitting by anybody
\(
\begin{aligned}
& P (\text { Hit })=1-P(\bar{A} \cap \bar{B} \cap \bar{C} \cap \bar{D}) \\
& =1-P(\bar{A}) \cdot P(\bar{B}) \cdot P(\bar{C}) \cdot P(\bar{D}) \\
& =1-\frac{1}{2} \cdot \frac{2}{3} \cdot \frac{3}{4} \cdot \frac{7}{8} \\
& =\frac{25}{32}
\end{aligned}
\)

Hint

Probablity of getting head \(P(H)=\frac{1}{2}\)
Probablity of getting tail \(P(T)=1-\frac{1}{2}=\frac{1}{2}\)
Probability of observing at least one head out of \(n\) tosses
\(=1\) – Probability of observing no head occurs out of \(n\) tosses
\(
=1-\left(\frac{1}{2}\right)^n
\)
According to the question,
\(
\begin{aligned}
& 1-\left(\frac{1}{2}\right)^n \geq \frac{90}{100} \\
& \Rightarrow\left(\frac{1}{2}\right)^n \leq \frac{1}{10} \\
& \Rightarrow 2^n \geq 10
\end{aligned}
\)
As \(2^3=8\)
\(
2^4=16
\)
\(\therefore\) Minimum value of \(n =4\)

Hint

\(
P\left(\frac{A}{B}\right)=\frac{P(A \cap B)}{P(B)}
\)
As \(A \subset B\),
then \(P ( A \cap B )= P ( A )\)
\(
\therefore P\left(\frac{A}{B}\right)=\frac{P(A)}{P(B)}
\)
As \(P ( B ) \leq 1\)
\(
\therefore \frac{P(A)}{P(B)} \geq P ( A )
\)

Hint

Step 1: calculate the probability of success and failure of the experiment.
Let \(X\) be a random variable i.e. the amount of rupees gain/loss in the game.
Let success, p is getting 5 or 6 on a throw.
Probability \((5\) or 6\()=\frac{1}{6}+\frac{1}{6}=\frac{2}{6}\)
\(\Rightarrow\) Success,\(p=\frac{1}{3}\)
Let failure, \(q\) is getting other than 5 or 6 on a throw.
Probability (other than 5 or 6\()=\frac{4}{6}\)
\(\Rightarrow[latex] Failure, [latex]q=\frac{2}{3}\)
Maximum numbers of throws \(=3\).
Step 2: Consider the following cases:
Case 1: Getting 5 or 6 in first throw.
\(\Rightarrow\) person win amount of 100 rupees,
\(
\because X=100
\)
\(
\begin{aligned}
P(X & =100)=\text { Success in first throw } \\
=p & =\frac{1}{3}
\end{aligned}
\)
Case 2: Getting 5 or 6 in the second throw, that means in the first throw there was a number other than 5 or 6 .
\(\Rightarrow\) person lose amount of 50 rupees in first throw and then win 100 rupees in second throw
\(
\because X=-50+100=50
\)
\(
\begin{aligned}
& P(X=50)=\text { Failure in first throw } \times \text { Success in second throw } \\
& =q \times p \\
& =\frac{2}{3} \times \frac{1}{3}=\frac{2}{9}
\end{aligned}
\)
Case 3 : Getting 5 or 6 in the third throw, that means in the first and second throw there were numbers other than 5 or 6 .
\(\Rightarrow[latex] person lose twice amount of 50 rupees in first and second throw and then win 100 rupees in third throw
[latex]
\because X=-50-50+100=0
\)
\(P(X=0)=\) Failure in first throw \(\times\) Failure in second throw
\(\times\) Success in third throw
\(
\begin{aligned}
& =q \times q \times p \\
& =\frac{2}{3} \times \frac{2}{3} \times \frac{1}{3}=\frac{4}{27}
\end{aligned}
\)
Case 4: Not getting 5 or 6 consecutively in first, second and third throws.
\(\Rightarrow[latex] person lose three times the amount of 50 rupees in first, second and third throw
[latex]
\because X=-50-50-50=-150
\)
\(
\begin{gathered}
P(X=-150)=\text { Failure in first throw } \times \text { Failure in second throw } \\
\times \text { Failure in third throw } \\
\quad=q \times q \times q \\
=\frac{2}{3} \times \frac{2}{3} \times \frac{2}{3}=\frac{8}{27}
\end{gathered}
\)
Thus the Probability Distribution of the given question.
\(
\begin{array}{|l|l|l|l|l|}
\hline X \text { or } x_i & 100 & 50 & 0 & -150 \\
\hline P(X) \text { or } p_i & \frac{1}{3} & \frac{2}{9} & \frac{4}{27} & \frac{8}{27} \\
\hline
\end{array}
\)
\(
\begin{aligned}
& \text { Expected value, } E(X)=\sum_{i=1}^n x_i p_i \\
& =100 \times \frac{1}{3}+50 \times \frac{2}{9}+0 \times \frac{4}{27}+(-150) \times \frac{8}{27} \\
& =\frac{100}{3}+\frac{100}{9}-\frac{1200}{27} \\
& =\frac{900+300-1200}{27} \\
& =\frac{0}{27} \\
& =0
\end{aligned}
\)

Hint

We are given that
Total number of students in class \(=60\)
\(
U=60
\)
Let use denote NCC by A and NSS by B
Number of students who opted for NCC \(=40\)
\(
P(A)=40
\)
Number of students who opted for NSS \(=30\)
\(
P(B)=30
\)
Number of students who opted for both NCC and NSS \(=20\)
\(
P(A \cap B)=20
\)
Then the number of students who opted for either NCC or NSS is given by \(P(A \cup B)\)
Then we can draw a Venn diagram depicting the number of students who opted for A, B and both A and B . Here U is the universal set which depicts the total number of students in class.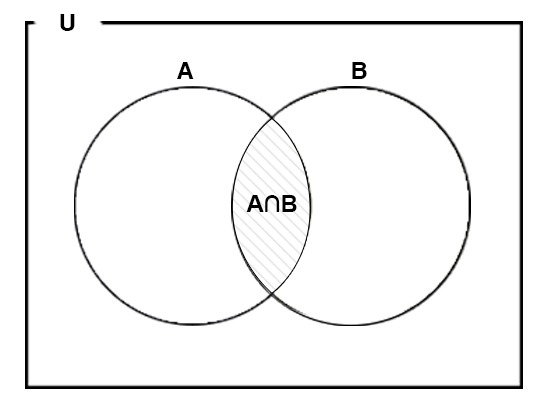

We use the formula \(P(A \cup B)=P(A)+P(B)-P(A \cap B)\) to find the value of union of \(A\) and \(B\).
Substitute the value of \(P(A)=40, P(B)=30\) and \(P(A \cap B)=20\) in the formula
\(
\Rightarrow P(A \cup B)=40+30-20
\)
Add the terms in RHS
\(
\Rightarrow P(A \cup B)=70-20
\)
Calculate the difference
\(
\Rightarrow P(A \cup B)=50
\)
Now we have the number of students which have opted either A or B or both A and B .
Therefore, the number of students who have opted for neither A nor B is given by subtracting the number of students which have opted A or B from the total number of students in the class.
\(\Rightarrow\) Number of students who opted for neither NCC nor NSS \(=U-P(A \cup B)\)

Substituting the value of \(U=60, P(A \cup B)=50\)
\(\Rightarrow\) Number of students who opted for neither NCC nor NSS \(=60-50\)
\(\Rightarrow\) Number of students who opted for neither NCC nor NSS \(=10\)
Now we know Probability of an event is given by dividing the number of favorable outcomes by the total number of outcomes.

Here the number of favorable outcomes is 10 and the total number of outcomes is 60 .
\(\Rightarrow\) Probability \(=\frac{10}{60}\)
Cancel same factors from numerator and denominator
\(\Rightarrow\) Probability \(=\frac{1}{6}\)

Hint

We are given that a fair die is rolled until two fours are obtained in succession.
Now we know that the numbers which appear on a dice are given by 1,2,3,4,5 and 6 .
Now the probability of getting a 4 while throwing a fair dice is given by
\(
\frac{1}{6}
\)
Now the number of digits other than 4 which appears on the dice is equals to
\(
6-1=5
\)
Therefore the probability of getting a non number not equal to 4 is given by
\(
\frac{5}{6}
\)
Now in order to determine the probability that the experiment will end in the fifth throw of the die. That is a die is rolled 5 times and it is fixed in each that that number 4 occurs on the fourth and fifth throw of the dice.
For this we have three possible cases.
In case 1, we can have that any number other than 4 occurs in the first three throws and then we get two fours successively in the fourth and fifth throw.
We will now calculate the probability of the event that can occur in case 1 using the fact that Therefore the probability of getting a 4 is given by \(\frac{1}{6}\) and the probability of getting a non number not equal to 4 is given by \(\frac{5}{6}\).
We have
\(
\frac{5}{6} \times \frac{5}{6} \times \frac{5}{6} \times \frac{1}{6} \times \frac{1}{6}=\frac{125}{6^5}
\)

In case 2, we can have a non four in the first throw, a four in the second throw, again a non four in the third throw and then we get two fours successively in the fourth and fifth throw.
We will now calculate the probability of the event that can occur in case 1 using the fact that Therefore the probability of getting a 4 is given by \(\frac{1}{6}\) and the probability of getting a non number not equal to 4 is given by \(\frac{5}{6}\).
We have
\(
\frac{5}{6} \times \frac{1}{6} \times \frac{5}{6} \times \frac{1}{6} \times \frac{1}{6}=\frac{25}{6^5}
\)
In case 3, we can have a four on the first throw, two non fours in the second and third throw and we get two fours successively in the fourth and fifth throw.
We will now calculate the probability of the event that can occur in case 1 using the fact that Therefore the probability of getting a 4 is given by \(\frac{1}{6}\) and the probability of getting a non number not equal to 4 is given by \(\frac{5}{6}\).
We have
\(
\frac{1}{6} \times \frac{5}{6} \times \frac{5}{6} \times \frac{1}{6} \times \frac{1}{6}=\frac{25}{6^5}
\)
Now we will add all the probabilities of all the three cases to get the probability that the experiment will end in the fifth throw of the die.
Therefore we have
\(
\frac{125}{6^5}+\frac{25}{6^5}+\frac{25}{6^5}=\frac{175}{6^5}
\)
Hence the probability that the experiment will end in the fifth throw of the die is equal to \(\frac{175}{6^5}\)

Hint

We can solve this problem by counting the number of “nice” subsets in the set \(S =\) \(\{1,2, \ldots, 20\}\), and then dividing that number by the total number of possible subsets of \(S\).
The sum of all elements in \(S\) is :
\(
1+2+\ldots+20=\frac{20 \times 21}{2}=210
\)
Since a “nice” subset must sum to 203, the elements not in the subset must sum to \(210-203=7\).
Now we need to find the ways to make the sum of 7 using the elements of \(S\). The combinations are :
1. 7
2. \(1+6\)
3. \(2+5\)
4. \(3+4\)
5. \(1+2+4\)
6. \(1+3+3\) (This doesn’t work since 3 is repeated)
7. \(2+2+3\) (This doesn’t work since 2 is repeated)
So, there are 5 “nice” subsets.
Since the set S has 20 elements, there are \(2^{20}\) possible subsets (including the empty set and the set itself). The probability of randomly choosing a “nice” subset is therefore:
\(
P=\frac{5}{2^{20}}
\)

Hint

Since sum of two numbers is even so either both are odd or both are even. Hence number of elements in reduced samples space \(={ }^5 C _2+{ }^6 C _2\)

So, required probability \(=\frac{{ }^5 C_2}{{ }^5 C_2+{ }^6 C_2}=\frac{2}{5}\)

Hint

Let \(P(H)\) be the probability of getting a head and \(P(T)\) is getting a tail.
We know that for an unbiased coin probability of getting a head and probability of getting a tail are equal to \(\frac{1}{2}\).
Therefore, \(P(H)=P(T)=\frac{1}{2}\).
Now, let \(E_1\) be the event of getting a sum of 7 or 8 when a pair of dice is thrown.
So, the total number of outcomes for event \(E_1=6 \times 6=36\).
We know that, when two dices are rolled the possible outcomes are
\(
\begin{aligned}
& (1,1),(1,2),(1,3),(1,4),(1,5),(1,6) \\
& (2,1),(2,2),(3,3),(4,4),(5,5),(6,6) \\
& (3,1),(3,2),(3,3),(3,4),(3,5),(3,6) \\
& (4,1),(4,2),(4,3),(4,4),(4,5),(4,6) \\
& (5,1),(5,2),(5,3),(5,4),(5,5),(5,6) \\
& (6,1),(6,2),(6,3),(6,4),(6,5),(6,6)
\end{aligned}
\)
Out of these outcomes, the possibilities of getting a sum of 7 or 8 on the two dice are
\(
(1,6),(2,5),(2,6),(3,4),(3,5),(4,3),(4,4),(5,2),(5,3),(6,1),(6,2)
\)
So, the number of possible outcomes for event \(E_1=11\)
We know that the probability of an event \(E\) is given by
\(
P(E)=\frac{\text { Number of favorable outcomes }}{\text { Total number of outcomes }}
\)
Thus, \(P\left(E_1\right)=\frac{11}{36}\)
Let \(E_2\) be the event of getting 7 or 8 when a card is picked from \(1,2,3, \ldots \ldots \ldots, 9\)
So, the total number of outcomes for \(E_2=9\)
The possibilities of getting 7 or 8 from cards are 7 and 8 numbered cards only.
So, the number of possible outcomes for event \(E_2=2\)
Now, the probability of that the noted number is either 7 or 8 \(=P\left(\left(H \cap E_1\right)\right.[latex] or [latex]\left.\left(T \cap E_2\right)\right)\)
\(
\begin{aligned}
&=P\left(H \cap E_1\right)+P\left(T \cap E_2\right)\left[\because\left\{H, E_1\right\} \text { and }\left\{T, E_2\right\}\right. \text { are mutually exclusive events] }
\end{aligned}
\)
\(
=P(H) \cdot P\left(E_1\right)+P(T) \cdot P\left(E_2\right)\left[\because\left\{H, E_1\right\} \text { and }\left\{T, E_2\right\} \text { are sets of independent events }\right]
\)
\(
\begin{gathered}
=\frac{1}{2} \times \frac{11}{36}+\frac{1}{2} \times \frac{2}{9} \\
=\frac{11}{72}+\frac{2}{18} \\
=\frac{11+8}{72}=\frac{19}{72}
\end{gathered}
\)
Hence, the probability that the noted number is either 7 or 8 is \(\frac{19}{72}\)

Hint

Let,
\(E _1\) : Event of drawing a red ball and replacing a green ball in the bag.
\(E _2\) : Event of drawing a green ball and placing a red ball in the bag.
E: Event of drawing a red ball in the second draw.
It is given that an urn contains 5 red and 2 green balls.
Thus, total outcomes \(=\) Total number of ballscontain in an urn
\(
\begin{gathered}
=5+2 \\
=7
\end{gathered}
\)
It is known that the probability is the ratio of the number of favorable outcomes to the total outcomes.
Now, we have to find the probability of events.
Probability of event \(E _1: P \left( E _1\right)=\frac{5}{7}\)
Probability of event \(E _2: P \left( E _2\right)=\frac{2}{7}\)
Probability of event \(\frac{ E }{ E _1}: P \left(\frac{ E }{ E _1}\right)=\frac{4}{7}\)
Probability of event \(\frac{ E }{ E _2}: P \left(\frac{ E }{ E _2}\right)=\frac{6}{7}\)
Thus, the probability of event of drawing a red ball in second draw is
\(
P(E)=P\left(E_1\right) \times P\left(\frac{E}{E_1}\right)+P\left(E_2\right) \times P\left(\frac{E}{E_2}\right)
\)
Substitute \(\frac{5}{7}\) for \(P \left( E _1\right), \frac{4}{7}\) for \(P \left(\frac{ E }{ E _1}\right), \frac{2}{7}[latex] for [latex]P \left( E _2\right)\) and \(\frac{6}{7}\) for \(P \left(\frac{ E }{ E _2}\right)\) in the above expression.
\(
\begin{aligned}
& P(E)=\frac{5}{7} \times \frac{4}{7}+\frac{2}{7} \times \frac{6}{7} \\
& P(E)=\frac{32}{49}
\end{aligned}
\)

Hint

Here, \(P(\bar{A} \cap \bar{B} \mid C)=\frac{P(\bar{A} \cap \bar{B} \cap C)}{P(C)}\)
\(
\begin{aligned}
& =\frac{P[(\overline{A \cup B}) \cap C]}{P(C)} \\
& =\frac{P[C-(A \cup B)]}{P(C)} \\
& =\frac{P(C)-P(A \cap C)-P(B \cap C)+P(A \cap B \cap C)}{P(C)} \\
& =\frac{P(C)-P(A \cap C)-P(B \cap C)}{P(C)}(\because P(A \cap B \cap C)=0) \\
& =\frac{P(C)-P(A) \cdot P(C)-P(B) \cdot P(C)}{P(C)}
\end{aligned}
\)
\([\because A , B\) and C are independent events]
\(
\begin{aligned}
& =1- P ( A )- P ( B ) \\
& =P(\bar{A})- P ( B ) \text { or } P(\bar{B})- P ( A )
\end{aligned}
\)

Hint

We are given that two different families \(A\) and \(B\) are blessed with equal number of children.
Let \(x\) be the children in both the families A and B .
We are given that gets more than one ticket and 3 tickets to be distributed amongst the children of these families.
So, we get
Total number of ways that the ticket is being distributed to two families \(={ }^{2 x} C_3\)
Total number of ways that the ticket is being distributed to one of the two families B only
\(
={ }^x C_3
\)
We are given that the probability that all the ticket go to the children of the family B is \(\frac{1}{12}\).
So, we have
\(
\frac{{ }^x C_3}{{ }^{2 x} C_3}=\frac{1}{12}
\)
By cross- multiplying, we get
\(
\begin{aligned}
& \Rightarrow 12^x C_3={ }^{2 x} C_3 \\
& \Rightarrow \frac{12 x(x-1)(x-2)}{1 \cdot 2 \cdot 3}=\frac{2 x(2 x-1)(2 x-2)}{1 \cdot 2 \cdot 3}
\end{aligned}
\)
By cancelling the terms, we get
\(
\begin{aligned}
& \Rightarrow \frac{12 x(x-1)(x-2)}{6}=\frac{2 x(2 x-1)(2 x-2)}{6} \\
& \Rightarrow 6 x(x-1)(x-2)=2 x(2 x-1)(x-1) \\
& \Rightarrow 6(x-1)(x-2)=2(2 x-1)(x-1)
\end{aligned}
\)
By rewriting the equation, we get
\(
\begin{aligned}
& \Rightarrow 6(x-1)(x-2)-2(2 x-1)(x-1)=0 \\
& \Rightarrow(x-1)(6 x-12-4 x+2)=0
\end{aligned}
\)
By simplifying the equation, we get
\(
\begin{aligned}
& \Rightarrow(x-1)(2 x-10)=0 \\
& \Rightarrow x-1=0 ; 2 x-10=0
\end{aligned}
\)
When \(x-1=0 \Rightarrow x=1\) which is not possible to give 3 tickets for a child. When \(2 x-10=0 \Rightarrow x=\frac{10}{2}=5\)
Thus, the number of children is 5.

Hint

We are given a bag containing 4 red balls and 6 black balls. A ball is drawn at random from the bag, its color is observed and this ball along with two additional balls of the same color are returned to the bag.
From the above, we can see that there can be two possible cases in this situation, the first case involves drawing a red ball and the second case involves drawing a black ball.
Finding out the probability of drawing the second ball as a red ball when the first ball drawn is black, we get,
\(
\Rightarrow \frac{4}{4+8}=\frac{1}{3}
\)
Finding out the probability of drawing the second ball as a red ball when the first ball drawn is red, we get,
\(
\Rightarrow \frac{4+2}{6+6}=\frac{1}{2}
\)
From the above, the probability of the second ball being red can be given as follows,
Probability of first ball being black \(\times\) Probability of second ball being red when the first ball is black + probability of first ball being red \(\times\) Probability of second ball being red when the first ball is red.
\(
\Rightarrow \frac{6}{10} \times \frac{1}{3}+\frac{4}{10} \times \frac{1}{2}
\)
Simplifying the above expression, we get,
\(
\Rightarrow \frac{6}{30}+\frac{4}{20}
\)
Cancelling out the common factors, we get,
\(
\Rightarrow \frac{2}{5}
\)
\(
\text { Therefore, the probability of drawing a red ball is } \frac{2}{5} \text {. }
\)

Hint

\(X\) wins, when the outcome is one of the following set of outcomes:
\(H, T T H, T T T T H, \ldots \ldots \ldots \ldots\)
Since subsequent tosses are independent, the probability that \(X\) wins is
\(
\Rightarrow P(H)+P(T T H)+P(T T T T H)+\ldots \ldots \ldots \ldots \ldots \ldots
\)
As the probability of showing heads is \(p\), we have
\(
\begin{aligned}
& \Rightarrow p+(1-p) \frac{1}{2} p+(1-p)^2 \frac{1}{2^2} p+\ldots \ldots \ldots \ldots \ldots \ldots \ldots \\
& \quad \Rightarrow p\left[1+\left(\frac{1-p}{2}\right)+\left(\frac{1-p}{2}\right)^2+\ldots \ldots \ldots \ldots\right]
\end{aligned}
\)
As the terms are in infinity G.P the sum of the terms are given by \(S_{\infty}=\frac{a}{1-r}\) where \(a\) is the first term and \(r\) is the common ratio of the infinity series.
\(
\begin{aligned}
& \Rightarrow p\left[\frac{1}{1-\left(\frac{1-p}{2}\right)}\right] \\
& \Rightarrow \frac{p}{1-\frac{1-p}{2}}=\frac{2 p}{1+p} \dots(1)
\end{aligned}
\)
So, the probability of \(X\) wins are \(\frac{2 p}{1+p}\).
Similarly, \(Y\) wins if the outcome is one of the following:
\(T H, T T T H, T T T T T H, \ldots\)
We know that the sum of probabilities of showing head and showing tail is equal to 1 .
So, the probability of showing tile is \(1-p\), we have
\(
\Rightarrow P(H)+P(T T H)+P(T T T T T H)+ \ldots
\)
\(
\Rightarrow \frac{1-p}{2}+\frac{(1-p)^2}{4}+\frac{(1-p)^3}{8}+\ldots
\)
\(
\Rightarrow\left(\frac{1-p}{2}\right)\left[1+\frac{1-p}{2}+\left(\frac{1-p}{2}\right)^2+\ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots\right]
\)
As the terms are in infinity G.P the sum of the terms are given by \(S_{\infty}=\frac{a}{1-r}\) where \(a\) is the first term and \(r\) is the common ratio of the infinity series.
\(
\begin{gathered}
\Rightarrow\left(\frac{1-p}{2}\right)\left[\frac{1}{1-\left(\frac{1-p}{2}\right)}\right] \\
\Rightarrow \frac{\frac{1-p}{2}}{1-\left(\frac{1-p}{2}\right)}=\frac{1-p}{1+p}
\end{gathered}
\)
So, the probability of \(Y\) wins are \(\frac{1-p}{1+p} \ldots(2)\)
We know that
Probability of \(X\) wins \(=\) Probability of \(Y\) wins
\(
\begin{gathered}
\Rightarrow \frac{2 p}{1+p}=\frac{1-p}{1+p} \\
\Rightarrow 2 p=1-p \\
\Rightarrow 2 p+p=1 \\
\Rightarrow 3 p=1 \\
\therefore p=\frac{1}{3}
\end{gathered}
\)
Thus, the value of \(p\) is \(\frac{1}{3}\).

Hint

Probability of drawing a white ball and then a red ball from bag \(B[latex] is given by [latex]\frac{{ }^4 C_1 \times{ }^2 C_1}{{ }^9 C_2}=\frac{2}{9}\)
Probability of drawing a white ball and then a red ball from bag A is given by \(\frac{{ }^2 C_1 \times{ }^3 C_1}{{ }^7 C_2}=\frac{2}{7}\)
Hence, the probability of drawing a white ball and then a red ball from bag \(B=\frac{\frac{2}{9}}{\frac{2}{7}+\frac{2}{9}}=\frac{2 \times 7}{18+14}=\frac{7}{16}\)

Alternate:

P(E) : Probability of choosing 1 red ball and 1 white ball.
P(Box A) : Probability of choosing box A.
P(Box B) : Probability of choosing box B.
Hence the required probabiity will be,
\(
P\left(\frac{Box ~B}{E}\right)=\frac{P(Box ~B) \times P\left(\frac{E}{Box ~B}\right)}{P(Box ~A) \times P\left(\frac{E}{Box ~A}\right)+P(Box ~B) \times P\left(\frac{E}{Box ~B}\right)}
\)
\(
=\frac{\frac{1}{2} \times \frac{{ }^4 C _1 \times{ }^2 C _1}{{ }^9 C _2}}{\frac{1}{2} \times \frac{{ }^2 C _1 \times{ }^3 C _1}{{ }^7 C _2}+\frac{1}{2} \times \frac{{ }^4 C _1 \times{ }^2 C _1}{{ }^9 C _2}}
\)
\(
=\frac{\frac{1}{9}}{\frac{1}{7}+\frac{1}{9}}
\)
\(
=\frac{7}{16}
\)