Past JEE Main Entrance Papers
Quiz Summary
0 of 177 Questions completed
Questions:
Information
You have already completed the quiz before. Hence you can not start it again.
Quiz is loading…
You must sign in or sign up to start the quiz.
You must first complete the following:
Results
Results
0 of 177 Questions answered correctly
Your time:
Time has elapsed
You have reached 0 of 0 point(s), (0)
Earned Point(s): 0 of 0, (0)
0 Essay(s) Pending (Possible Point(s): 0)
Categories
- Not categorized 0%
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
- 94
- 95
- 96
- 97
- 98
- 99
- 100
- 101
- 102
- 103
- 104
- 105
- 106
- 107
- 108
- 109
- 110
- 111
- 112
- 113
- 114
- 115
- 116
- 117
- 118
- 119
- 120
- 121
- 122
- 123
- 124
- 125
- 126
- 127
- 128
- 129
- 130
- 131
- 132
- 133
- 134
- 135
- 136
- 137
- 138
- 139
- 140
- 141
- 142
- 143
- 144
- 145
- 146
- 147
- 148
- 149
- 150
- 151
- 152
- 153
- 154
- 155
- 156
- 157
- 158
- 159
- 160
- 161
- 162
- 163
- 164
- 165
- 166
- 167
- 168
- 169
- 170
- 171
- 172
- 173
- 174
- 175
- 176
- 177
- Current
- Review
- Answered
- Correct
- Incorrect
-
Question 1 of 177
1. Question
Let \(ABC\) be an isosceles triangle in which \(A\) is at \((-1,0), \angle A =\frac{2 \pi}{3}, AB = AC\) and \(B\) is on the positive \(x\)-axis. If \(B C=4 \sqrt{3}\) and the line \(B C\) intersects the line \(y=x+3\) at \((\alpha, \beta)\), then \(\frac{\beta^4}{\alpha^2}\) is ____. [JEE Main 2024]
CorrectIncorrectHint
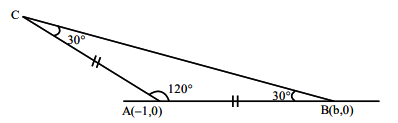
\(
\begin{array}{l}
\frac{\mathrm{c}}{\sin 30^{\circ}}=\frac{4 \sqrt{3}}{\sin 120^{\circ}} \quad \text { [By sine rule] } \\
2 \mathrm{c}=8 \Rightarrow \mathrm{c}=4 \\
\mathrm{AB}=|(\mathrm{b}+1)|=4 \\
\mathrm{~b}=3, \mathrm{~m}_{\mathrm{AB}}=0 \\
\mathrm{~m}_{\mathrm{BC}}=\frac{-1}{\sqrt{3}} \\
\mathrm{BC}:-\mathrm{y}=\frac{-1}{\sqrt{3}}(\mathrm{x}-3) \\
\sqrt{3} \mathrm{y}+\mathrm{x}=3
\end{array}
\)
Point of intersection: \(y=x+3, \sqrt{3} y+x=3\)
\(
\begin{array}{l}
(\sqrt{3+1}) y=6 \\
y=\frac{6}{\sqrt{3}+1} \\
x=\frac{6}{\sqrt{3}+1}-3 \\
=\frac{6-3 \sqrt{3}-3}{\sqrt{3}+1} \\
=3 \frac{(1-\sqrt{3})}{(1+\sqrt{3})} \\
=\frac{-6}{(1+\sqrt{3})^2} \\
\frac{\beta^4}{\alpha^2}=36
\end{array}
\) -
Question 2 of 177
2. Question
The portion of the line \(4 x+5 y=20\) in the first quadrant is trisected by the lines \(\mathrm{L}_1\) and \(\mathrm{L}_2\) passing through the origin. The tangent of an angle between the lines \(\mathrm{L}_1\) and \(\mathrm{L}_2\) is : [JEE Main 2024]
CorrectIncorrectHint
Co-ordinates of \(\mathrm{A}=\left(\frac{5}{3}, \frac{8}{3}\right)\)
Co-ordinates of \(\mathrm{B}=\left(\frac{10}{3}, \frac{4}{3}\right)\)
Slope of \(\mathrm{OA}=\mathrm{m}_1=\frac{8}{5}\)
Slope of \(\mathrm{OB}=\mathrm{m}_2=\frac{2}{5}\)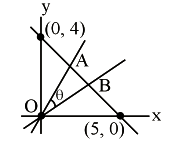
\(
\begin{array}{l}
\tan \theta=\left|\frac{\mathrm{m}_1-\mathrm{m}_2}{1+\mathrm{m}_1 \mathrm{~m}_2}\right| \\
\tan \theta=\frac{\frac{6}{5}}{1+\frac{16}{25}}=\frac{30}{41} \\
\tan \theta=\frac{30}{41}
\end{array}
\) -
Question 3 of 177
3. Question
Let \(\mathrm{R}\) be the interior region between the lines \(3 x-y+1=0\) and \(x+2 y-5=0\) containing the origin. The set of all values of \(a\), for which the points \(\left(a^2, a+1\right)\) lie in \(R\), is: [JEE Main 2024]
CorrectIncorrectHint
\(
\begin{array}{l}
\mathrm{P}\left(\mathrm{a}^2, \mathrm{a}+1\right) \\
\mathrm{L}_1=3 \mathrm{x}-\mathrm{y}+1=0
\end{array}
\)
Origin and \(\mathrm{P}\) lies same side w.r.t. \(\mathrm{L}_1\)
\(
\begin{array}{l}
\Rightarrow \mathrm{L}_1(0) \cdot \mathrm{L}_1(\mathrm{P})>0 \\
\therefore 3\left(\mathrm{a}^2\right)-(\mathrm{a}+1)+1>0
\end{array}
\)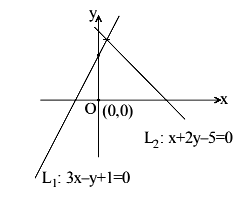
\(
\begin{array}{l}
\Rightarrow 3 \mathrm{a}^2-\mathrm{a}>0 \\
\mathrm{a} \in(-\infty, 0) \cup\left(\frac{1}{3}, \infty\right) \quad \ldots(1)
\end{array}
\)
Let \(\mathrm{L}_2: \mathrm{x}+2 \mathrm{y}-5=0\)
Origin and \(\mathrm{P}\) lies same side w.r.t. \(\mathrm{L}_2\)
\(
\begin{array}{l}
\Rightarrow \mathrm{L}_2(0) \cdot \mathrm{L}_2(\mathrm{P})>0 \\
\Rightarrow \mathrm{a}^2+2(\mathrm{a}+1)-5<0 \\
\Rightarrow \mathrm{a}^2+2 \mathrm{a}-3<0 \\
\Rightarrow(\mathrm{a}+3)(\mathrm{a}-1)<0 \\
\therefore \mathrm{a} \in(-3,1) \quad \ldots(2)
\end{array}
\)
Intersection of (1) and (2)
\(
\mathrm{a} \in(-3,0) \cup\left(\frac{1}{3}, 1\right)
\) -
Question 4 of 177
4. Question
Let \(A\) and \(B\) be two finite sets with \(m\) and \(n\) elements respectively. The total number of subsets of the set \(A\) is 56 more than the total number of subsets of \(B\). Then the distance of the point \(P(m, n)\) from the point \(\mathrm{Q}(-2,-3)\) is [JEE Main 2024]
CorrectIncorrectHint
\(
\begin{array}{l}
2^{\mathrm{m}}-2^{\mathrm{n}}=56 \\
2^{\mathrm{n}}\left(2^{\mathrm{m}-\mathrm{n}}-1\right)=2^3 \times 7 \\
2^{\mathrm{n}}=2^3 \text { and } 2^{\mathrm{m}-\mathrm{n}}-1=7 \\
\Rightarrow \mathrm{n}=3 \text { and } 2^{\mathrm{m}-\mathrm{n}}=8 \\
\Rightarrow \mathrm{n}=3 \text { and } \mathrm{m}-\mathrm{n}=3 \\
\Rightarrow \mathrm{n}=3 \text { and } \mathrm{m}=6 \\
\mathrm{P}(6,3) \text { and } \mathrm{Q}(-2,-3) \\
\mathrm{PQ}=\sqrt{8^2+6^2}=\sqrt{100}=10
\end{array}
\) -
Question 5 of 177
5. Question
If the sum of squares of all real values of \(\alpha\), for which the lines \(2 x-y+3=0,6 x+3 y+1=0\) and \(\alpha x+2 y-2=0\) do not form a triangle is \(p\), then the greatest integer less than or equal to \(p\) is [JEE Main 2024]
CorrectIncorrectHint
\(
\begin{array}{l}
2 x-y+3=0 \\
6 x+3 y+1=0 \\
\alpha x+2 y-2=0
\end{array}
\)
Will not form a \(\Delta\) if \(\alpha x+2 y-2=0\) is concurrent with \(2 x-y+3=0\) and \(6 x+3 y+1=0\) or parallel to either of them so
Case-1: Concurrent lines
\(
\left|\begin{array}{ccc}
2 & -1 & 3 \\
6 & 3 & 1 \\
\alpha & 2 & -2
\end{array}\right|=0 \Rightarrow \alpha=\frac{4}{5}
\)
Case-2 : Parallel lines
\(
\begin{array}{l}
-\frac{\alpha}{2}=\frac{-6}{3} \text { or }-\frac{\alpha}{2}=2 \\
\Rightarrow \alpha=4 \text { or } \alpha=-4 \\
P=16+16+\frac{16}{25} \\
{[P]=\left[32+\frac{16}{25}\right]=32}
\end{array}
\) -
Question 6 of 177
6. Question
In a \(\triangle A B C\), suppose \(y=x\) is the equation of the bisector of the angle \(\mathrm{B}\) and the equation of the side \(A C\) is \(2 x-y=2\). If \(2 A B=B C\) and the point \(A\) and B are respectively \((4,6)\) and \((\alpha, \beta)\), then \(\alpha+2 \beta\) is equal to [JEE Main 2024]
CorrectIncorrectHint
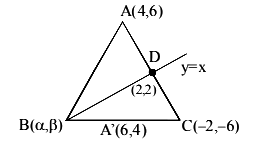
\(
\begin{array}{l}
\mathrm{AD}: \mathrm{DC}=1: 2 \\
\frac{4-\alpha}{6-\alpha}=\frac{10}{8} \\
\alpha=\beta \\
\alpha=14 \text { and } \beta=14
\end{array}
\)\(
\alpha+2 \beta=42
\) -
Question 7 of 177
7. Question
Let \(\left(5, \frac{a}{4}\right)\), be the circumcenter of a triangle with vertices \(A(a,-2), B(a, 6)\) and \(C\left(\frac{a}{4},-2\right)\). Let \(\alpha\) denote the circumradius, \(\beta\) denote the area and \(\gamma\) denote the perimeter of the triangle. Then \(\alpha+\beta+\gamma\) is [JEE Main 2024]
CorrectIncorrectHint
\(
\begin{array}{l}
A(a,-2), B(a, 6), C\left(\frac{a}{4},-2\right), O\left(5, \frac{a}{4}\right) \\
A O=B O \\
{AO}^2={BO}^2 \\
(a-5)^2+\left(\frac{a}{4}+2\right)^2=(a-5)^2+\left(\frac{a}{4}-6\right)^2 \\
a=8 \\
A B=8, A C=6, B C=10 \\
\alpha=5, \beta=24, \gamma=24
\end{array}
\)\(
\alpha+\beta+\gamma=53
\) -
Question 8 of 177
8. Question
The distance of the point \((2,3)\) from the line \(2 x-3 y+28=0\), measured parallel to the line \(\sqrt{3} x-y+1=0\), is equal to [JEE Main 2024]
CorrectIncorrectHint
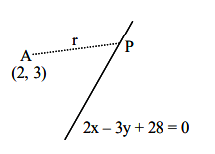
Writing \(P\) in terms of parametric co-ordinates \(2+r\)
\(
\begin{array}{l}
\cos \theta, 3+r \sin \theta \text { as } \tan \theta=\sqrt{3} \\
P\left(2+\frac{r}{2}, 3+\frac{\sqrt{3} r}{2}\right)
\end{array}
\)
\(P\) must satisfy \(2 x-3 y+28=0\)
So, \(2\left(2+\frac{r}{2}\right)-3\left(3+\frac{\sqrt{3} r}{2}\right)+28=0\)
We find \(r=4+6 \sqrt{3}\) -
Question 9 of 177
9. Question
Let \(A\) be the point of intersection of the lines \(3 x+2 y=14,5 x-y=6\) and \(B\) be the point of intersection of the lines \(4 x+3 y=8,6 x+y=5\). The distance of the point \(P(5,-2)\) from the line \(A B\) is [JEE Main 2024]
CorrectIncorrectHint
Solving lines \(\mathrm{L}_1(3 \mathrm{x}+2 \mathrm{y}=14)\) and \(\mathrm{L}_2(5 \mathrm{x}-\mathrm{y}=6)\) to get \(\mathrm{A}(2,4)\) and solving lines \(\mathrm{L}_3(4 \mathrm{x}+3 \mathrm{y}=8)\) and \(L_4(6 x+y=5)\) to get \(B\left(\frac{1}{2}, 2\right)\).
Finding Eqn. of \(A B: 4 x-3 y+4=0\)
Calculate distance PM
\(
\Rightarrow\left|\frac{4(5)-3(-2)+4}{5}\right|=6
\) -
Question 10 of 177
10. Question
A line passing through the point \(\mathrm{A}(9,0)\) makes an angle of \(30^{\circ}\) with the positive direction of \(x\)-axis. If this line is rotated about \(\mathrm{A}\) through an angle of \(15^{\circ}\) in the clockwise direction, then its equation in the new position is [JEE Main 2024]
CorrectIncorrectHint
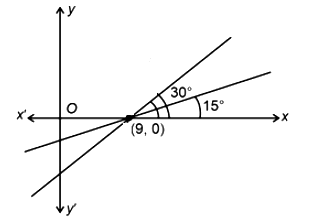
\(
\mathrm{Eq}^{\mathrm{n}}: y-0=\tan 15^{\circ}(x-9) \Rightarrow y=(2-\sqrt{3})(x-9)
\)
\(
\frac{y}{\sqrt{3}-2}+x=9
\) -
Question 11 of 177
11. Question
If \(x^2-y^2+2 h x y+2 g x+2 f y+c=0\) is the locus of a point, which moves such that it is always equidistant from the lines \(\mathrm{x}+2 \mathrm{y}+7=0\) and \(2 \mathrm{x}-\mathrm{y}+8=0\), then the value of \(\mathrm{g}+\mathrm{c}+\mathrm{h}-\mathrm{f}\) equals [JEE Main 2024]
CorrectIncorrectHint
Locus of point \(P(x, y)\) whose distance from Gives \(X+2 y+7=0 \& 2 x-y+8=0\) are equal is
\(
\frac{x+2 y+7}{\sqrt{5}}= \pm \frac{2 x-y+8}{\sqrt{5}} \Rightarrow (x+2 y+7)^2-(2 x-y+8)^2=0
\)
Combined equation of lines
\(
\begin{array}{l}
(x-3 y+1)(3 x+y+15)=0 \\
3 x^2-3 y^2-8 x y+18 x-44 y+15=0 \\
x^2-y^2-\frac{8}{3} x y+6 x-\frac{44}{3} y+5=0 \\
x^2-y^2+2 h x y+2 g x +2 f y+c=0 \\
h=\frac{4}{3}, g=3, f=-\frac{22}{3}, c=5 \\
g+c+h-f=3+5-\frac{4}{3}+\frac{22}{3}=8+6=14
\end{array}
\) -
Question 12 of 177
12. Question
Let \(\alpha, \beta, \gamma, \delta \in \mathbf{Z}\) and let \(\mathrm{A}(\alpha, \beta), \mathrm{B}(1,0), \mathrm{C}(\gamma, \delta)\) and \(D(1,2)\) be the vertices of a parallelogram \(A B C D\). If \(A B=\sqrt{10}\) and the points \(A\) and \(C\) lie on the line \(3 y=2 x+1\), then \(2(\alpha+\beta+\gamma+\delta)\) is equal to [JEE Main 2024]
CorrectIncorrectHint
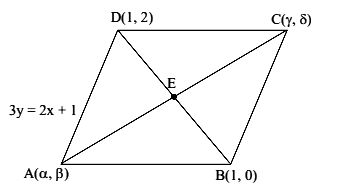
Let \(\mathrm{E}\) is mid point of diagonals
\(
\begin{array}{ll}
\frac{\alpha+\gamma}{2}=\frac{1+1}{2} & \& \frac{\beta+\delta}{2}=\frac{2+0}{2} \\
\alpha+\gamma=2 & \beta+\delta=2 \\
2(\alpha+\beta+\gamma+\delta)=2(2+2)=8 &
\end{array}
\) -
Question 13 of 177
13. Question
Let \(A(a, b), B(3,4)\) and \((-6,-8)\) respectively denote the centroid, circumcentre and orthocentre of a triangle. Then, the distance of the point \(P(2 a+3,7 b+5)\) from the line \(2 x+3 y-4=0\) measured parallel to the line \(x-2 y-1=0\) is [JEE Main 2024]
CorrectIncorrectHint
To solve this problem, we need to find the distance of the point \(P(2 a+3,7 b\) \(+5)\) from the line \(2 x+3 y-4=0\) measured parallel to the line \(x-2 y-1=0\).
First, let’s review the information given:
1. A (a, b), B \((3,4)\), and \(C(-6,-8)\) are the centroid, circumcentre, and orthocentre of a triangle, respectively.
2. Point \(P\) has coordinates \((2 a+3,7 b+5)\).Now, we need to ensure the format and distance parallel to the given line equation, \(x-2 y-1=0\).
1. Define point \(P: P(2 a+3,7 b+5)\)
2. Find \(a\) and \(b\) : – The centroid (A) of a triangle with vertices at coordinates ( \(x_1, y_1 ), ( x_2,y_2 ), and ( x_3,y_3\) ) can be found using:
\(
A=\left(\frac{x_1+x_2+x_3}{3}, \frac{y_1+y_2+y_3}{3}\right)
\)
Similarly, we can find the coordinates \(a\) and \(b\) in the context of centroid, orthocentre, and circumcentre from points \(B\) and \(C\).
3. Calculate the distance from point \(P\) to the line \(2 x+3 y-4=0\) measured parallel to \(x-2 y-1=0\) :
Use the distance formula between a point \((x_1, y_1)\) and a line
\(
\begin{aligned}
& A x+B y+C=0 \\
& \text { Distance }=\frac{|A x 1+B y 1+C|}{\sqrt{A^2+B^2}}
\end{aligned}
\)
Let’s denote the normal distance formula:
\(
\begin{aligned}
& d=\frac{|2(2 a+3)+3(7 b+5)-4|}{\sqrt{2^2+3^2}} \\
& d=\frac{|4 a+6+21 b+15-4|}{\sqrt{13}}
\end{aligned}
\)
Thus:
Simplified distance:
\(
d=\frac{|4 a+21 b+17|}{\sqrt{13}}
\)
From given multiple choices and trigonometric approximation to distance, the answer is most likely matching option closest calculated trigonometric distance as: \(\frac{17 \sqrt{5}}{7}\) -
Question 14 of 177
14. Question
Let \(A(-2,-1), B(1,0), C(\alpha, \beta)\) and \(D(\gamma, \delta)\) be the vertices of a parallelogram \(A B C D\). If the point \(C\) lies on \(2 x-y=5\) and the point \(D\) lies on \(3 x-2 y=6\), then the value of \(|\alpha+\beta+\gamma+\delta|\) is equal to [JEE Main 2024]
CorrectIncorrectHint
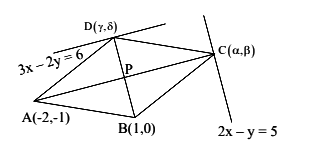
\(
\begin{array}{l}
\mathrm{P} \equiv\left(\frac{\alpha-2}{2}, \frac{\beta-1}{2}\right) \equiv\left(\frac{\gamma+1}{2}, \frac{\delta}{2}\right) \\
\frac{\alpha-2}{2}=\frac{\gamma+1}{2} \text { and } \frac{\beta-1}{2}=\frac{\delta}{2} \\
\Rightarrow \alpha-\gamma=3 \quad \ldots(1) \\
\beta-\delta=1 \quad \ldots(2)
\end{array}
\)
Also, \((\gamma, \delta)\) lies on \(3 \mathrm{x}-2 \mathrm{y}=6\)
\(
3 \gamma-2 \delta=6 \quad \ldots(3)
\)
and \((\alpha, \beta)\) lies on \(2 x-y=5\)
\(
\Rightarrow 2 \alpha-\beta=5 \quad \ldots .(4)
\)
Solving (1), (2), (3), (4)
\(
\begin{array}{l}
\alpha=-3, \beta=-11, \gamma=-6, \delta=-12 \\
|\alpha+\beta+\gamma+\delta|=32
\end{array}
\) -
Question 15 of 177
15. Question
Let \(\mathrm{PQR}\) be a triangle. The points \(\mathrm{A}, \mathrm{B}\) and \(\mathrm{C}\) are on the sides QR, RP and PQ respectively such that \(\frac{\mathrm{QA}}{\mathrm{AR}}=\frac{\mathrm{RB}}{\mathrm{BP}}=\frac{\mathrm{PC}}{\mathrm{CQ}}=\frac{1}{2}\). Then \(\frac{\operatorname{Area}(\triangle \mathrm{PQR})}{\operatorname{Area}(\triangle \mathrm{ABC})}\) is equal to [JEE Main 2023]
CorrectIncorrectHint
Let the position vector of \(P, Q, R\) be \(\overrightarrow{0}, \vec{a}, \vec{b}\)
\(\Rightarrow\) Position vector of \(A=\frac{2 \vec{a}+\vec{b}}{3}\),
Position vector of \(B=\frac{2 \vec{b}}{3}\) and
Position vector of \(C=\frac{\vec{a}}{3}\)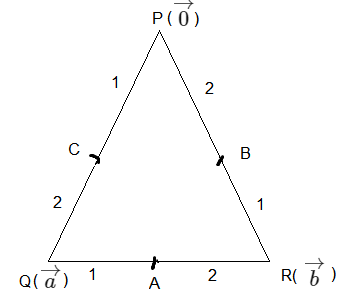
\(
\begin{array}{l}
\therefore \overrightarrow{A B}=\frac{2 \vec{b}}{3}-\left(\frac{2 \vec{a}+\vec{b}}{3}\right)=\frac{\vec{b}}{3}-\frac{2 \vec{a}}{3}=\frac{\vec{b}-2 \vec{a}}{3} \\
\overrightarrow{C A}=\frac{2 \vec{a}+\vec{b}}{3}-\frac{\vec{a}}{3}=\frac{\vec{a}+\vec{b}}{3}
\end{array}
\)
Area of \(\triangle P Q R=\frac{1}{2}|\overrightarrow{P Q} \times \overrightarrow{P R}|=\frac{1}{2}|\vec{a} \times \vec{b}|\)
Area of \(\triangle A B C=\frac{1}{2}|\overrightarrow{C A} \times \overrightarrow{A B}|\)
\(
=\frac{1}{2}\left|\left(\frac{\vec{a}+\vec{b}}{3}\right) \times\left(\frac{\vec{b}-2 \vec{a}}{3}\right)\right|=\frac{1}{2}\left|\frac{\vec{a} \times \vec{b}}{3}\right|
\)
\(\therefore \frac{\text { Area }(\triangle P Q R)}{\text { Area }(\triangle A B C)}=\frac{\frac{1}{2}|\vec{a} \times \vec{b}|}{\frac{1}{2}\left|\frac{\vec{a} \times \vec{b}}{3}\right|}=3\) sq. units -
Question 16 of 177
16. Question
The equations of the sides \(\mathrm{AB}, \mathrm{BC}\) and \(\mathrm{CA}\) of a triangle \(A B C\) are: \(2 x+y=0, x+p y=21 a,(a \neq 0)\) and \(x-y=3\) respectively. Let \(P(2, a)\) be the centroid of \(\triangle \mathrm{ABC}\). Then \((\mathrm{BC})^2\) is equal to [JEE Main 2023]
CorrectIncorrectHint
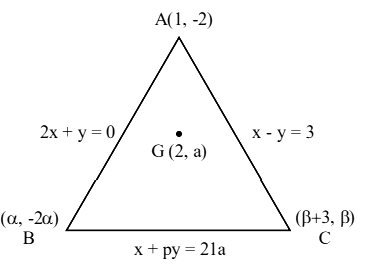
\(
\begin{array}{ll}
\text { Assume } \mathrm{B}(\alpha,-2 \alpha) & \text { and } \mathrm{C}(\beta+3, \beta) \\
\frac{\alpha+\beta+3+1}{3}=2 & \text { also } \frac{-2 \alpha-2+\beta}{3}=\mathrm{a} \\
\Rightarrow \alpha+\beta=2 & -2 \alpha-2+\beta=3 \mathrm{a} \\
\Rightarrow \beta=2-\alpha & -2 \alpha-\not 2+\not 2-\alpha=3 \mathrm{a} \Rightarrow \alpha=-\mathrm{a}
\end{array}
\)
Now both \(B\) and \(C\) lies as given line
\(
\begin{array}{l}
\alpha-p \cdot 2 \alpha=21 a \\
\alpha(1-2 p)=21 a \\
-a(1-2 p)=21 a \Rightarrow p=11 \\
\beta+3+p \beta=21 a \\
\beta+3+11 \beta=21 a \\
21 \alpha+12 \beta+3=0
\end{array}
\)
Also \(\beta=2-\alpha\)
\(
\begin{array}{l}
21 \alpha+12(2-\alpha)+3=0 \\
21 \alpha+24-12 \alpha+3=0 \\
9 \alpha+27=0 \\
\alpha=-3, \beta=5
\end{array}
\)
So \(\mathrm{BC}=\sqrt{122}\) and \((\mathrm{BC})^2=122\) -
Question 17 of 177
17. Question
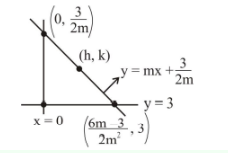
The equations of two sides of a variable triangle are \(x=0\) and \(y=3\), and its third side is a tangent to the parabola \(y^2=6 x\). The locus of its circumcentre is : [JEE Main 2023]
CorrectIncorrectHint
\(
\begin{array}{l}
y^2=6 x & y^2=4 a x \\
\Rightarrow 4 a=6 \Rightarrow a=\frac{3}{2}
\end{array}
\)
\(
\begin{array}{l}
y=m x+\frac{3}{2 m} ;(m \neq 0) \\
h=\frac{6 m-3}{4 m^2}, k=\frac{6 m+3}{4 m}, \text { Now eliminating } m \text { and we get } \\
\Rightarrow 3 h=2\left(-2 k^2+9 k-9\right) \\
\Rightarrow 4 y^2-18 y+3 x+18=0
\end{array}
\) -
Question 18 of 177
18. Question
A triangle is formed by \(\mathrm{X}\) – axis, \(\mathrm{Y}\) – axis and the line \(3 x+4 y=60\). Then the number of points \(P(a, b)\) which lie strictly inside the triangle, where a is an integer and \(b\) is a multiple of \(a\), is [JEE Main 2023]
CorrectIncorrectHint
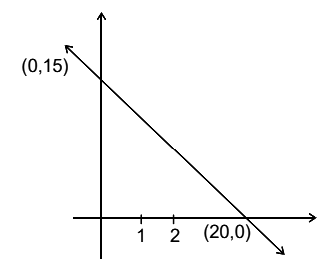
\(
\text { If } x=1, y=\frac{57}{4}=14.25
\)
\((1,1)(1,2) \ldots(1,14) \quad \Rightarrow 14\) pts.
If \(x=2, y=\frac{27}{2}=13.5\)
\((2,2)(2,4) \ldots(2,12) \quad \Rightarrow 6\) pts.
If \(x=3, y=\frac{51}{4}=12.75\)
\((3,3)(3,6)(3,9)(3,12) \Rightarrow 4\) pts.
If \(x=4, y=12\)
\((4,4)(4,8) \quad \Rightarrow 2\) pts.
If \(x=5 . y=\frac{45}{4}=11.25\)
\((5,5),(5,10) \quad \Rightarrow 2\) pts.
If \(x=6, y=\frac{21}{2}=10.5\)
\(
\Rightarrow 1 \mathrm{pt} \text {. }
\)
If \(x=7, y=\frac{39}{4}=9.75\)
\((7,7) \quad \Rightarrow 1 \mathrm{pt}\).
If \(x=8, y=9\)
\((8,8) \quad \Rightarrow 1 \mathrm{pt}\).
If \(x=9 y=\frac{33}{4}=8.25 \Rightarrow\) no pt.
Total \(=31\) pts. -
Question 19 of 177
19. Question
A light ray emits from the origin making an angle \(30^{\circ}\) with the positive \(\mathrm{x}\)-axis. After getting reflected by the line \(x+y=1\), if this ray intersects \(x\)-axis at \(\mathrm{Q}\), then the abscissa of \(\mathrm{Q}\) is [JEE Main 2023]
CorrectIncorrectHint
Slope of reflected ray \(=\tan 60^{\circ}=\sqrt{3}\)
Line \(y=\frac{x}{\sqrt{3}}\) intersect \(y+x=1\) at \(\left(\frac{\sqrt{3}}{\sqrt{3}+1}, \frac{1}{\sqrt{3}+1}\right)\)
Equation of reflected ray is
\(
y-\frac{1}{\sqrt{3}+1}=\sqrt{3}\left(x-\frac{\sqrt{3}}{\sqrt{3}+1}\right)
\)
Put \(y=0 \Rightarrow x=\frac{2}{3+\sqrt{3}}\) -
Question 20 of 177
20. Question
Let \(\mathrm{B}\) and \(\mathrm{C}\) be the two points on the line \(\mathrm{y}+\mathrm{x}=0\) such that \(B\) and \(C\) are symmetric with respect to the origin. Suppose \(A\) is a point on \(y-2 x=2\) such that \(\triangle \mathrm{ABC}\) is an equilateral triangle. Then, the area of the \(\triangle \mathrm{ABC}\) is [JEE Main 2023]
CorrectIncorrectHint
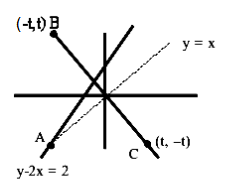
At A \(x=y\)
\(
\begin{array}{l}
Y-2 x=2 \\
(-2,-2)
\end{array}
\)
Height from line \(\mathrm{x}+\mathrm{y}=0\)
\(
\mathrm{h}=\frac{4}{\sqrt{2}}
\)
Area of \(\Delta=\frac{\sqrt{3}}{4} \frac{h^2}{\sin ^2 60}=\frac{8}{\sqrt{3}}\) -
Question 21 of 177
21. Question
A triangle is formed by the tangents at the point \((2,2)\) on the curves \(y^2=2 x\) and \(x^2+y^2=4 x\), and the line \(x+y+2=0\). If \(r\) is the radius of its circumcircle, then \(\mathrm{r}^2\) is equal to [JEE Main 2023]
CorrectIncorrectHint
A triangle is formed by the tangents at the point \((2,2)\) on the curves \(y^2=2 x\) and \(x^2+\) \(y^2=4 x\), and the line \(x+y+2=0\). If \(r\) is the radius of its circumcircle, then \(r^2\) is equal to 10 .
\(
S_1: y^2=2 x \quad S_2: x^2+y^2=4 x
\)
\(\mathrm{P}(2,2)\) is common point on \(\mathrm{S}_1 \& \mathrm{~S}_2\)
\(T_1\) is tangent to \(S_1\) at \(P \quad \Rightarrow T_1: y \cdot 2=x+2\)
\(
\Rightarrow T_1: x-2 y+2=0
\)
\(\mathrm{T}_2\) is tangent to \(\mathrm{S}_2\) at \(\mathrm{P}\)
\(
\begin{array}{c}
\Rightarrow \mathrm{T}_2: \mathrm{x} \cdot 2+\mathrm{y} \cdot 2=2(\mathrm{x}+2) \\
\Rightarrow \mathrm{T}_2: \mathrm{y}=2
\end{array}
\)
& \(\mathrm{~L}_3: \mathrm{x}+\mathrm{y}+2=0\) is third line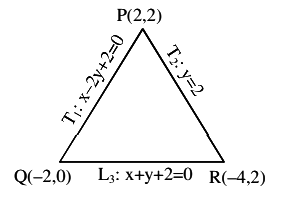
\(
\begin{array}{l}
P Q=a=\sqrt{20} \\
Q R=b=\sqrt{8} \\
R P=c=6 \\
\text { Area }(\Delta P Q R)=\Delta=\frac{1}{2} \times 6 \times 2=6 \\
\therefore r=\frac{a b c}{4 \Delta}=\frac{\sqrt{160}}{4}=\sqrt{10} \Rightarrow r^2=10
\end{array}
\) -
Question 22 of 177
22. Question
A straight line cuts off the intercepts \(\mathrm{OA}=\mathrm{a}\) and \(\mathrm{OB}=\mathrm{b}\) on the positive directions of \(\mathrm{x}\)-axis and \(\mathrm{y}-\) axis respectively. If the perpendicular from origin \(\mathrm{O}\) to this line makes an angle of \(\frac{\pi}{6}\) with positive direction of \(y\)-axis and the area of \(\triangle O A B\) is \(\frac{98}{3} \sqrt{3}\), then \(\mathrm{a}^2-\mathrm{b}^2\) is equal to: [JEE Main 2023]
CorrectIncorrectHint
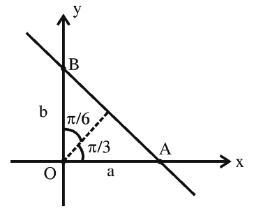
Equation of straight line : \(\frac{x}{a}+\frac{y}{b}=1\)
Or \(\mathrm{x} \cos \frac{\pi}{3}+\mathrm{y} \sin \frac{\pi}{3}=\mathrm{p}\)
\(
\begin{array}{l}
\frac{\mathrm{x}}{2}+\frac{\mathrm{y} \sqrt{3}}{2}=\mathrm{p} \\
\frac{\mathrm{x}}{2 \mathrm{p}}+\frac{\mathrm{y}}{\frac{2 \mathrm{p}}{\sqrt{3}}}=1
\end{array}
\)
Comparing both : \(\mathrm{a}=2 \mathrm{p}, \mathrm{b}=\frac{2 \mathrm{p}}{\sqrt{3}}\)
Now area of \(\triangle \mathrm{OAB}=\frac{1}{2} \cdot \mathrm{ab}=\frac{98}{3} \cdot \sqrt{3}\)
\(
\begin{array}{l}
\frac{1}{2} \cdot 2 \mathrm{p} \cdot \frac{2 \mathrm{p}}{\sqrt{3}}=\frac{98}{3} \cdot \sqrt{3} \\
\mathrm{p}^2=49 \\
\mathrm{a}^2-\mathrm{b}^2=4 \mathrm{p}^2-\frac{4 \mathrm{p}^2}{3}=\frac{2}{3} 4 \mathrm{p}^2 \\
=\frac{8}{3} \cdot 49=\frac{392}{3}
\end{array}
\) -
Question 23 of 177
23. Question
If the orthocentre of the triangle, whose vertices are \((1,2),(2,3)\) and \((3,1)\) is \((\alpha, \beta)\), then the quadratic equation whose roots are \(\alpha+4 \beta\) and \(4 \alpha+\beta\), is [JEE Main 2023]
CorrectIncorrectHint
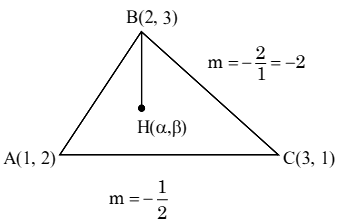
Here \(\mathrm{m}_{\mathrm{BH}} \times \mathrm{m}_{\mathrm{AC}}=-1\)
\(
\begin{array}{l}
\left(\frac{\beta-3}{\alpha-2}\right)\left(\frac{1}{-2}\right)=-1 \\
\beta-3=2 \alpha-4 \\
\beta=2 \alpha-1 \\
m_{A H} \times m_{B C}=-1
\end{array}
\)
\(
\begin{array}{l}
\left(\frac{\beta-2}{\alpha-1}\right)(-2)=-1 \\
2 \beta-4=\alpha-1 \\
2(2 \alpha-1)=\alpha+3 \\
3 \alpha=5
\end{array}
\)
\(
\begin{array}{l}
\alpha=\frac{5}{3}, \beta=\frac{7}{3} \Rightarrow \mathrm{H}\left(\frac{5}{3}, \frac{7}{3}\right) \\
\alpha+4 \beta=\frac{5}{3}+\frac{28}{3}=\frac{33}{3}=11 \\
\beta+4 \alpha=\frac{7}{3}+\frac{20}{3}=\frac{27}{3}=9 \\
\mathrm{x}^2-20 \mathrm{x}+99=0
\end{array}
\) -
Question 24 of 177
24. Question
The combined equation of the two lines \(a x+b y+c=0\) and \(a^{\prime} x+b^{\prime} y+c^{\prime}=0\) can be written as \((a x+b y+c)\left(a^{\prime} x+b^{\prime} y+c^{\prime}\right)=0\). The equation of the angle bisectors of the lines represented by the equation \(2 x^2+x y-3 y^2=0\) is [JEE Main 2023]
CorrectIncorrectHint
Equation of the pair of angle bisector for the homogenous equation \(\mathrm{ax}^2+2 \mathrm{hxy}+\mathrm{by}^2=0\) is given as
\(
\frac{x^2-y^2}{a-b}=\frac{x y}{h}
\)
Here \(\mathrm{a}=2, \mathrm{~h}=1 / 2\) & \(\mathrm{b}=-3\)
Equation will become
\(
\begin{array}{l}
\frac{x^2-y^2}{2-(-3)}=\frac{x y}{1 / 2} \\
x^2-y^2=10 x y \\
x^2-y^2-10 x y=0
\end{array}
\) -
Question 25 of 177
25. Question
The straight lines \(l_1\) and \(l_2\) pass through the origin and trisect the line segment of the line \(L: 9 x+5 y=45\) between the axes. If \(m_1\) and \(m_2\) are the slopes of the lines \(l_1\) and \(l_2\), then the point of intersection of the line \(y=\left(m_1+m_2\right) x\) with \(L\) lies on [JEE Main 2023 (06 Apr Shift 1)]
CorrectIncorrectHint
The straight lines \(l_1\) and \(l_2\) pass through the origin and trisect the line segment of the line \(L: 9 x+5 y=45\) between the axes, And \(m_1\) and \(m_2\) are the slopes of the lines \(l_1\) and \(l_2\), Now on plotting the diagram we get,
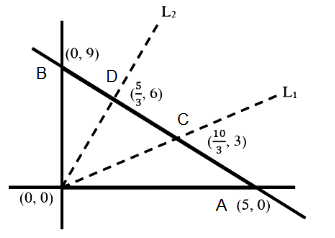
Given equation of line, \(L: 9 x+5 y=45\)
\(
\Rightarrow \frac{x}{5}+\frac{y}{9}=1
\)
Now using the section formula between point \(A(5,0) \& B(0,9)\) we get the value of point \(C \& D\) \(\Rightarrow C \equiv\left(\frac{10}{3}, 3\right)\) and \(D \equiv\left(\frac{5}{3}, 6\right)\)
Now finding the slope \(m_1 \& m_2\) we get,
\(
m_1=\frac{3-0}{\frac{10}{3}-0}=\frac{9}{10} \& m_2=\frac{6 \times 3}{5}=\frac{18}{5}
\)
So, equation of line \(y=\left(m_1+m_2\right) x\) will be,
\(
y=\left(\frac{9}{10}+\frac{36}{10}\right) x=\frac{9}{2} x
\)
So, intersection point with \(L\) will be,
\(
7 y=45 \Rightarrow y=\frac{45}{7}, x=\frac{10}{7}
\)
Hence, \(y-x=\frac{45-10}{7}=5\) -
Question 26 of 177
26. Question
Let \(A(0,1), B(1,1)\) and \(C(1,0)\) be the mid-points of the sides of a triangle with incentre at the point \(D\). If the focus of the parabola \(y^2=4 a x\) passing through \(D\) is \((\alpha+\beta \sqrt{2}, 0)\), where \(\alpha\) and \(\beta\) are rational numbers, then \(\frac{\alpha}{\beta^2}\) is equal to [JEE Main 2023 (08 Apr Shift 2)]
CorrectIncorrectHint
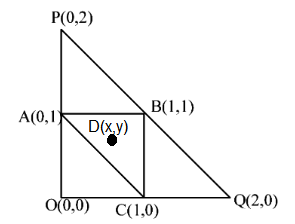
Given,
\(A(0,1), B(1,1)\) and \(C(1,0)\) be the mid-points of the sides of a triangle with incentre at the point \(D\), Now finding the vertices of the triangle by using midpoint formula and plotting the diagram we get, Now finding the incentre of the above triangle using the formula,
\(
I \equiv\left(\frac{a x_1+b x_2+c x_3}{a+b+c}, \frac{a y_1+b y_2+c y_3}{a+b+c}\right)
\)
We get, Incentre \(D=\left(\frac{4}{4+2 \sqrt{2}}, \frac{4}{4+2 \sqrt{2}}\right)\)
Now given parabola \(y^2=4 a x\) passes through the incentre \(D\) we get,
\(
\begin{array}{l}
\left(\frac{4}{4+2 \sqrt{2}}\right)^2=4 a\left(\frac{4}{4+2 \sqrt{2}}\right) \\
\Rightarrow a=\frac{1}{4+2 \sqrt{2}}
\end{array}
\)
Now we know that focus of parabola is given by, focus \((a, 0)\)
Hence, focus will be \(\left(\frac{1}{4+2 \sqrt{2}}, 0\right)=\left(\frac{4-2 \sqrt{2}}{8}, 0\right)\)
Now comparing with \((\alpha+\beta \sqrt{2}, 0)\) we get,
\(
\alpha=\frac{4}{8}=\frac{1}{2}, \beta=-\frac{1}{4}
\)
Hence, \(\frac{\alpha}{\beta^2}=\frac{\frac{1}{2}}{\left(\frac{-1}{4}\right)^2}=\frac{16}{2}=8\) -
Question 27 of 177
27. Question
The area of the quadrilateral \(A B C D\) with vertices \(A(2,1,1), B(1,2,5), C(-2,-3,5)\) and \(D(1,-6,-7)\) is equal to [JEE Main 2023 (08 Apr Shift 2)]
CorrectIncorrectHint
Given,
The quadrilateral \(A B C D\) with vertices \(A(2,1,1), B(1,2,5), C(-2,-3,5)\) and \(D(1,-6,-7)\) Now finding, \(\overrightarrow{A B}=-\hat{i}+\hat{j}+4 \hat{k}\) and \(\overrightarrow{A D}=-\hat{i}-7 \hat{j}-8 \hat{k}\)
And plotting the diagram we get,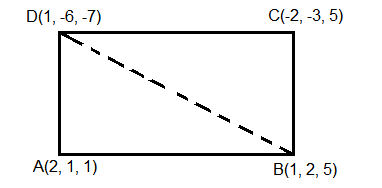
Now we know that,
Area of \(\triangle A B D\) is given by,
\(
\begin{array}{l}
=\frac{1}{2}\left|\begin{array}{ccc}
\hat{i} & \hat{j} & \hat{k} \\
-1 & 1 & 4 \\
-1 & -7 & 8
\end{array}\right| \\
=|10 \hat{i}-6 \hat{j}+4 \hat{k}|=2 \sqrt{38}
\end{array}
\)
Now finding, \(\overrightarrow{C B}=3 \hat{i}+5 \hat{j}\) and \(\overrightarrow{C D}=3 \hat{i}-3 \hat{j}-12 \hat{k}\)
So, Area of \(\triangle C B D=\frac{1}{2}\left|\begin{array}{ccc}\hat{i} & \hat{j} & \hat{k} \\ 3 & -3 & -12 \\ 3 & 5 & 0\end{array}\right|\)
\(
\begin{array}{l}
=|6(5 \hat{i}-3 \hat{j}-2 \hat{k})| \\
=6 \sqrt{38}
\end{array}
\)
\(\therefore\) Area of quadrilateral \(A B C D=8 \sqrt{38}\) square units -
Question 28 of 177
28. Question
A line segment \(A B\) of length \(\lambda\) moves such that the points \(A\) and \(B\) remain on the periphery of a circle of radius \(\lambda\). Then the locus of the point, that divides the line segment \(A B\) in the ratio \(2: 3\), is a circle of radius [JEE Main 2023 (10 Apr Shift 1)]
CorrectIncorrectHint
Given,
A line segment \(A B\) of length \(\lambda\) moves such that the points \(A\) and \(B\) remain on the periphery of a circle of radius \(\lambda\), Now taking the points on the circle of radius \(\lambda\) as \(B\left(\lambda \cos \theta_1, \lambda \sin \theta_1\right) \& A\left(\lambda \cos \theta_2 \lambda \sin \theta_2\right)\) and taking the point \(P(h, k)\) which divides the line segment in \(A B\) of length \(\lambda\) in \(2: 3\)
Now plotting the diagram we get,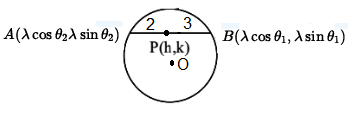
Now, let \(O\) be the origin and radius of circle is \(\lambda\) and \(A B=\lambda\) and using distance formula we get,
\(
\begin{array}{l}
A B=\lambda=\sqrt{\left(\lambda \cos \theta_1-\lambda \cos \theta_2\right)^2+\left(\lambda \sin \theta_1-\lambda \sin \theta_2\right)^2} \\
\Rightarrow 1=2-2 \cos \left(\theta_1-\theta_2\right) \\
\Rightarrow \cos \left(\theta_1-\theta_2\right)=\frac{1}{2}
\end{array}
\)
Now using section formula we get,
\(
h=\frac{2 \lambda \cos \theta_1+3 \lambda \cos \theta_2}{5} \text { and } k=\frac{2 \lambda \sin \theta_1+3 \lambda \sin \theta_2}{5}
\)
Now squaring and adding above two value we get,
\(
\begin{array}{l}
h^2+k^2=\frac{\lambda^2}{25}\left[4+9+12\left(\cos \left(\theta_1-\theta_2\right)\right)\right] \\
\Rightarrow h^2+k^2=\frac{\lambda^2}{25} \cdot 19
\end{array}
\)
Hence, Radius \(=\frac{\lambda}{5} \sqrt{19}\) -
Question 29 of 177
29. Question
Let \(A\) be the point \((1,2)\) and \(B\) be any point on the curve \(x^2+y^2=16\). If the centre of the locus of the point \(P\), which divides the line segment \(A B\) in the ratio \(3: 2\) is the point \(C(\alpha, \beta)\), then the length of the line segment \(A C\) is [JEE Main 2023 (10 Apr Shift 2)]
CorrectIncorrectHint
Given,
\(A\) be the point \((1,2)\) and \(B\) be any point on the curve \(x^2+y^2=16\),
And the centre of the locus of the point \(P\), which divides the line segment \(A B\) in the ratio \(3: 2\) is the point \(C(\alpha, \beta)\),
Now let the point on the circle \(x^2+y^2=16\) be \(B(4 \cos \theta, 4 \sin \theta)\)
Now using section formula in \(A(1,2)\) and \(B(4 \cos \theta, 4 \sin \theta)\) we get,
\(
\begin{array}{l}
P\left(\frac{12 \cos \theta+2}{5}, \frac{12 \sin \theta+4}{5}\right) \equiv(h, k) \\
\Rightarrow \cos \theta=\frac{5 h-2}{12} \& \sin \theta=\frac{5 k-4}{12}
\end{array}
\)
Now squaring and adding we get,
\(
\begin{array}{l}
\left(\frac{5 h-2}{12}\right)^2+\left(\frac{5 k-4}{12}\right)^2=1 \\
\Rightarrow\left(h-\frac{2}{5}\right)^2+\left(k-\frac{4}{5}\right)^2=\left(\frac{12}{5}\right)^2
\end{array}
\)
So, the centre of the locus is \(C\left(\frac{2}{5}, \frac{4}{5}\right)\)
Hence, by distance formula we get, \(A C=\sqrt{\left(\frac{3}{5}\right)^2+\left(\frac{6}{5}\right)^2}=\frac{3 \sqrt{5}}{5}\) -
Question 30 of 177
30. Question
Let the equations of two adjacent sides of a parallelogram \(A B C D\) be \(2 x-3 y=-23\) and \(5 x+4 y=23\). If the equation of its one diagonal \(A C\) is \(3 x+7 y=23\) and the distance of \(A\) from the other diagonal is \(d\), then \(50 d^2\) is equal to [JEE Main 2023 (10 Apr Shift 2)]
CorrectIncorrectHint
Given,
The equations of two adjacent sides of a parallelogram \(A B C D\) be \(2 x-3 y=-23\) and \(5 x+4 y=23\),
So, \(A B \equiv 2 x-3 y=-23\) and \(B C \equiv 5 x+4 y=23\)
Also given, \(A C \equiv 3 x+7 y=23\)
Solving the above lines we get, \(A(-4,5), B(-1,7), C(3,2)\)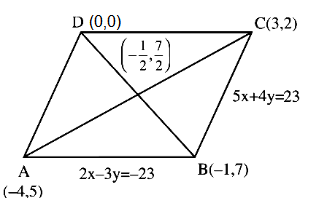
We know that,
Diagonal of parallelogram have same midpoint,
So \(A C\) and \(B D\) have same mid-point and let point \(D\) be \((x, y)\),
So midpoint formula we get,
\(
\frac{x-1}{2}=\frac{-4+3}{2} \Rightarrow x=0 \text { and } \frac{y+7}{2}=\frac{2+5}{2} \Rightarrow y=0
\)
Hence, point \(D\) is \((0,0)\)
Now Equation of \(B D\) will be \(7 x+y=0\)
Now finding the distance of \(A(-4,5)\) from \(7 x+y=0\) we get,
\(
d=\left|\frac{7(-4)+5}{\sqrt{7^2+1^2}}\right|=\frac{23}{\sqrt{50}}
\)
Hence, \(50 d^2=23^2=529\) -
Question 31 of 177
31. Question
Let \(\mathrm{R}\) be a rectangle given by the lines \(x=0, x=2, y=0\) and \(y=5\). Let \(\mathrm{A}(\alpha, 0)\) and \(\mathrm{B}(0, \beta), \alpha \in[0,2]\) and \(\beta \in[0,5]\), be such that the line segment \(A B\) divides the area of the rectangle \(R\) in the ratio \(4: 1\). Then, the mid-point of \(A B\) lies on a [JEE Main 2023 (11 Apr Shift 1)]
CorrectIncorrectHint
Given,
\(\mathrm{R}\) be a rectangle given by the lines \(x=0, x=2, y=0\) and \(y=5\) And point \(\mathrm{A}(\alpha, 0)\) and \(\mathrm{B}(0, \beta), \alpha \in[0,2]\) and \(\beta \in[0,5]\),
Now plotting the diagram we get,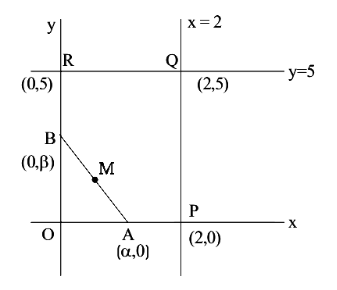
Now given that line segment \(A B\) divides the ratio of area in \(4: 1\), we get
\(
\begin{array}{l}
\frac{10-\frac{1}{2} \alpha \beta}{\frac{1}{2} \alpha \beta}=\frac{4}{1} \\
\Rightarrow 20-\alpha \beta=4 \alpha \beta \\
\Rightarrow \alpha \beta=4 \ldots \ldots(1)
\end{array}
\)
Now using midpoint formula we get,
\(
h=\frac{\alpha}{2} \& \beta=\frac{k}{2}
\)
Now using equation (1) we get,
\(
\Rightarrow 4 h k=4
\)
\(\Rightarrow x y=1\) which is a equation of rectangular hyperbola. -
Question 32 of 177
32. Question
If the line \(l_1: 3 y-2 x=3\) is the angular bisector of the lines \(l_2: x-y+1=0\) and \(l_3: \alpha x+\beta y+17=0\), then \(\alpha^2+\beta^2-\alpha-\beta\) is equal to [JEE Main 2023 (11 Apr Shift 2)]
CorrectIncorrectHint
Given,
\(L_1: 3 y-2 x=3\) is angular bisector of \(L_2: x-y+1=0\) and \(L_3: \alpha x+\beta y+17=0\) Now finding point of intersection of \(L_1 \& L_2\) we get, \((0,1)\)
And point will lie on \(L_3\), so \(\alpha \times 0+\beta \times 1+17=0\)
\(
\Rightarrow \beta=-17
\)
Any point, say \(\left(\frac{-3}{2}, 0\right)\) on \(L_1\) should be equidistant from lines \(L_2 \& L_3\)
Now using the formula of distance of a point from the line we get,
\(
\Rightarrow\left|\frac{\frac{-3}{2}-0+1}{\sqrt{1^2+1^2}}\right|=\left|\frac{\frac{-3 \alpha}{2}+0+17}{\sqrt{\alpha^2+(-17)^2}}\right|
\)
\(
\Rightarrow(\alpha-7)(\alpha-17)=0
\)
Now, for \(\alpha=17, L_2 \& L_3\) coincides
So, \(\alpha=7\)
Now putting the value of \(\alpha \& \beta\) in given expression we get,
\(
\alpha^2+\beta^2-\alpha-\beta=(-17)^2+7^2-7+17=348
\) -
Question 33 of 177
33. Question
If the point \(\left(\alpha, \frac{7 \sqrt{3}}{3}\right)\) lies on the curve traced by the mid-points of the line segments of the lines \(x \cos \theta+y \sin \theta=7, \theta \in\left(0, \frac{\pi}{2}\right)\) between the co-ordinates axes, then \(\alpha\) is equal to [JEE Main 2023 (12 Apr Shift 1)]
CorrectIncorrectHint
The straight line is shown below with the intercepts.
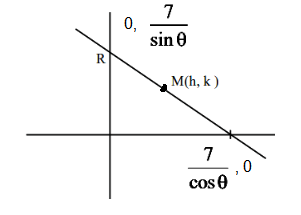
\(
\begin{array}{l}
M\left(\frac{7}{2 \cos \theta}, \frac{7}{2 \sin \theta}\right) \equiv(h, k) \\
\therefore \cos \theta=\frac{7}{2 h} \quad \sin \theta=\frac{7}{2 k} \\
\because \theta \in\left(0, \frac{\pi}{2}\right) \\
\Rightarrow \frac{49}{4 h^2}+\frac{49}{4 k^2}=1 \quad \therefore x \text { and } y \text { are positive } \\
\therefore \text { Locus }=\frac{1}{x^2}+\frac{1}{y^2}=\frac{4}{49}
\end{array}
\)
Now \(\left(\alpha, \frac{7 \sqrt{3}}{3}\right)\) lies on curve
\(
\begin{array}{l}
\Rightarrow \frac{1}{\alpha^2}+\frac{9}{147}=\frac{4}{49} \\
\frac{1}{\alpha^2}=\frac{1}{49} \\
\therefore \alpha= \pm 7 \\
\therefore \alpha=7
\end{array}
\)
Hence this is the required option. -
Question 34 of 177
34. Question
Let \((\alpha, \beta)\) be the centroid of the triangle formed by the lines \(15 x-y=82,6 x-5 y=-4\) and \(9 x+4 y=17\). Then \(\alpha+2 \beta\) and \(2 \alpha-\beta\) are the roots of the equation [JEE Main 2023 (13 Apr Shift 2)]
CorrectIncorrectHint
The given set of equations are:
\(
\begin{array}{l}
15 x-y=82 \\
6 x-5 y=-4 \\
9 x+4 y=17
\end{array}
\)
Now on solving the above equation by taking two at a time and plotting the diagram we get,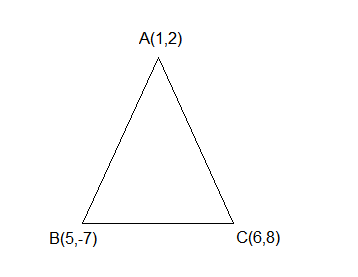
\(
(\alpha, \beta) \equiv\left(\frac{1+5+6}{3}, \frac{2-7+8}{3}\right) \equiv(4,1)
\)Hence, \(\alpha+2 \beta=6\) and \(2 \alpha-\beta=7\)
The required equation is \((x-6)(x-7)=0\)
Equation \(x^2-13 x+42=0\)
Hence this is the required option. -
Question 35 of 177
35. Question
If \((\alpha, \beta)\) is the orthocenter of the triangle \(A B C\) with vertices \(A(3,-7), B(-1,2)\) and \(C(4,5)\), then \(9 \alpha-6 \beta+60\) is equal to [JEE Main 2023 (15 Apr Shift 1)]
CorrectIncorrectHint
The required diagram will be:
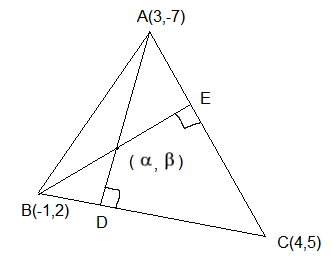
\(
\begin{array}{l}
\text { Equation of } A D: y+7=\frac{-5}{3}(x-3) \\
\Rightarrow 3 y+21=-5 x+15 \\
\Rightarrow 5 x+3 y+6=0 \ldots \ldots(\mathrm{i}) \\
\text { Equation of } B E: y-2=\frac{-1}{12}(x+1) \\
\Rightarrow 12 y-24=-x-1 \\
\Rightarrow x=23-12 y \ldots(i i)
\end{array}
\)
by (ii) \(115-60 y+3 y+6=0\)
\(
\begin{array}{l}
\Rightarrow 57 y=121 \\
y=\frac{121}{57}, x=23-12 \times \frac{121}{57} \\
\therefore 9 \alpha-6 \beta+60=9 \times 23-108 \times \frac{121}{57}-6 \times \frac{121}{57}+60 \\
=207-242+60=25
\end{array}
\)
Hence this is the required option. -
Question 36 of 177
36. Question
Let \(\mathrm{A}\left(\frac{3}{\sqrt{\mathrm{a}}}, \sqrt{\mathrm{a}}\right) \mathrm{a}>0\), be a fixed point in the \(x y\)-plane. The image of \(A\) in \(y\)-axis be \(B\) and the image of \(B\) in \(x\)-axis be \(C\). If \(D(3 \cos \theta, a \sin \theta)\) is a point in the fourth quadrant such that the maximum area of \(\triangle \mathrm{ACD}\) is 12 square units, then a is equal to [JEE Main 2022 June]
CorrectIncorrectHint
\(
\begin{array}{l}
\mathrm{A}=\left(\frac{3}{\sqrt{\mathrm{a}}}, \sqrt{\mathrm{a}}\right) \\
\mathrm{B}=\left(\frac{-3}{\sqrt{\mathrm{a}}}, \sqrt{\mathrm{a}}\right) \\
\mathrm{C}=\left(-\frac{3}{\sqrt{\mathrm{a}}},-\sqrt{\mathrm{a}}\right)
\end{array}
\)
Area of \(\triangle \mathrm{ACD}\)
\(
=\frac{1}{2}\left|\begin{array}{cc}
\frac{3}{\sqrt{a}} & \sqrt{a} \\
-\frac{3}{\sqrt{a}} & -\sqrt{a} \\
3 \cos \theta & a \sin \theta \\
\frac{3}{\sqrt{a}} & \sqrt{a}
\end{array}\right|
\)
\(
\begin{array}{l}
=\frac{1}{2} 6 \sqrt{\mathrm{a}}(\cos \theta-\sin \theta) \\
=3 \sqrt{\mathrm{a}}(\cos \theta-\sin \theta)
\end{array}
\)
max values of function is \(3 \sqrt{\mathrm{a}} \sqrt{2}\)
\(
\begin{array}{l}
3 \sqrt{a} \sqrt{2}=12 \\
2 a=16 \\
a=8
\end{array}
\) -
Question 37 of 177
37. Question
Let the area of the triangle with vertices \(A(1, \alpha)\), \(\mathrm{B}(\alpha, 0)\) and \(\mathrm{C}(0, \alpha)\) be 4 sq. units. If the point \((\alpha,-\alpha),(-\alpha, \alpha)\) and \(\left(\alpha^2, \beta\right)\) are collinear, then \(\beta\) is equal to [JEE Main 2022 June]
CorrectIncorrectHint
\(
\frac{1}{2}\left|\begin{array}{lll}
\alpha & 0 & 1 \\
1 & \alpha & 1 \\
0 & \alpha & 1
\end{array}\right|= \pm 4
\)
\(
\alpha= \pm 8
\)Now given points \((8,-8),(-8,8),(64, \beta)\)
\(
\text { OR }(-8,8),(8,-8),(64, \beta)
\)
are collinear \(\Rightarrow\) Slope \(=-1\).
\(
\beta=-64
\) -
Question 38 of 177
38. Question
Let \(R\) be the point \((3,7)\) and let \(P\) and \(Q\) be two points on the line \(x+y=5\) such that \(P Q R\) is an equilateral triangle. Then the area of \(\triangle \mathrm{PQR}\) is : [JEE Main 2022 June]
CorrectIncorrectHint
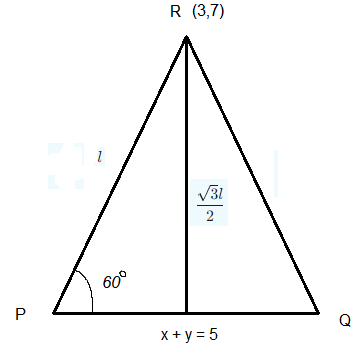
Altitude of equilateral triangle,
\(
\begin{array}{l}
\frac{\sqrt{3} l}{2}=\frac{5}{\sqrt{2}} \\
l=\frac{5 \sqrt{2}}{\sqrt{3}}
\end{array}
\)Area of triangle
\(
=\frac{\sqrt{3}}{4} l^2=\frac{\sqrt{3}}{4} \cdot \frac{50}{3}=\frac{25}{2 \sqrt{3}}
\) -
Question 39 of 177
39. Question
In an isosceles triangle \(A B C\), the vertex \(A\) is \((6,1)\) and the equation of the base \(\mathrm{BC}\) is \(2 \mathrm{x}+\mathrm{y}=4\). Let the point \(B\) lie on the line \(x+3 y=7\). If \((\alpha, \beta)\) is the centroid \(\triangle A B C\), then \(15(\alpha+\beta)\) is equal to : [JEE Main 2022 June]
CorrectIncorrectHint
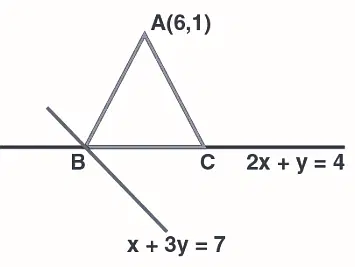
\(
\begin{array}{l}
2 x+y=4 \dots(1) \\
2 x+6 y=14 \dots(2)
\end{array}
\)
On solving eq(1) and eq(2)
\(
\begin{array}{l}
y=2, x=3 \\
B(1,2) \text { and } C(k, 4-2 k) \\
\text { Hence, } A B^2=A C^2 \\
52+(-1)^2=(6-k)^2+(-3+2 k)^2 \\
\Rightarrow 5 k^2-24 k+19=0 \\
(5 k-19)(k-1)=0 \\
\Rightarrow k=\frac{19}{5} \\
C\left(\frac{19}{5},-\frac{18}{5}\right) \Rightarrow \text { Centroid }(\alpha, \beta) \\
\alpha=\frac{6+1+\frac{19}{5}}{3} \\
\alpha=\frac{18}{5} \\
\beta=\frac{1+2-\frac{18}{5}}{3} \\
\beta=-\frac{1}{5}
\end{array}
\)
Now \(15(\alpha+\beta)=15\left(\frac{18}{5}+\left(-\frac{1}{5}\right)\right)\)
\(
\begin{array}{l}
=15 \times \frac{17}{5} \\
=51
\end{array}
\) -
Question 40 of 177
40. Question
A rectangle \(\mathrm{R}\) with end points of the one of its dies as \((1,2)\) and \((3,6)\) is inscribed in a circle. If the equation of a diameter of the circle is \(2 x-y+4=\) 0 , then the area of \(\mathrm{R}\) is [JEE Main 2022 June]
CorrectIncorrectHint
Equation of line \(A B\)
\(
\mathrm{y}=2 \mathrm{x}
\)Slope of \(A B=2\)
Slope of given diameter \(=2\)
So the diameter is parallel to \(\mathrm{AB}\)
Distance between diameter and line \(A B\)
\(
=\left(\frac{4}{\sqrt{2^2+12}}\right)=\frac{4}{\sqrt{5}}
\)Thus BC \(=2 \times \frac{4}{\sqrt{5}}=\frac{8}{\sqrt{5}}\)
\(
\begin{array}{l}
\qquad \mathrm{AB}=\sqrt{(1-3)^2+(2-6)^2}=\sqrt{20}=2 \sqrt{5} \\
\text { Area }=\mathrm{AB} \times \mathrm{BC}=\frac{8}{\sqrt{5}} \times 2 \sqrt{5}=16
\end{array}
\) -
Question 41 of 177
41. Question
A ray of light passing through the point \(\mathrm{P}(2,3)\) reflects on the \(\mathrm{x}\)-axis at point \(\mathrm{A}\) and the reflected ray passes through the point \(Q(5,4)\). Let \(R\) be the point that divides the line segment AQ internally into the ratio \(2: 1\). Let the co-ordinates of the foot of the perpendicular \(\mathrm{M}\) from \(\mathrm{R}\) on the bisector of the angle PAQ be \((\alpha, \beta)\). Then, the value of \(7 \alpha+3 \beta\) is equal to [JEE Main 2022 June]
CorrectIncorrectHint
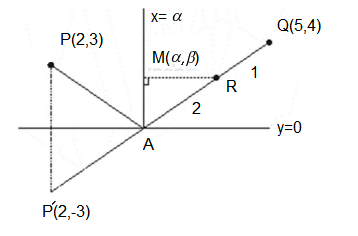
By observation we see that \(\mathrm{A}(\alpha, 0)\).
And \(\beta=\mathrm{y}\)-cordinate of \(\mathrm{R}\)
\(
=\frac{2 \times 4+1 \times 0}{2+1}=\frac{8}{3} \dots(1)
\)
Now \(P^{\prime}\) is image of \(P\) in \(y=0\) which will be \(\mathrm{P}^{\prime}(2,-3)\)
Equation of \(P^{\prime} Q\) is \((y+3)=\frac{4+3}{5-2}(x-2)\)
i.e. \(3 y+9=7 x-14\)
\(\mathrm{A} \equiv\left(\frac{23}{7}, 0\right)\) by solving with \(\mathrm{y}=0\)
\(
\therefore \alpha=\frac{23}{7} \dots(2)
\)
\(
\begin{array}{l}
\text { By (1), (2) } \\
\qquad 7 \alpha+3 \beta=23+8=31
\end{array}
\) -
Question 42 of 177
42. Question
Let a triangle be bounded by the lines \(\mathrm{L}_1: 2 \mathrm{x}+5 \mathrm{y}=10\); \(L_2:-4 x+3 y=12\) and the line \(L_3\), which passes through the point \(\mathrm{P}(2,3)\), intersect \(\mathrm{L}_2\) at \(\mathrm{A}\) and \(\mathrm{L}_1\) at B. If the point \(\mathrm{P}\) divides the line-segment \(\mathrm{AB}\), internally in the ratio \(1: 3\), then the area of the triangle is equal to [JEE Main 2022 June]
CorrectIncorrectHint
Points \(A\) lies on \(\mathrm{L}_2\)
\(
\mathrm{A}\left(\alpha, 4+\frac{4}{3} \alpha\right)
\)
Points B lies on \(\mathrm{L}_1\)
\(
\mathrm{B}\left(\beta, 2-\frac{2}{5} \beta\right)
\)
Points \(\mathrm{P}\) divides \(\mathrm{AB}\) internally in the ratio \(1: 3\)
\(
\begin{array}{l}
\Rightarrow \mathrm{P}(2,3)=\mathrm{P}\left(\frac{3 \alpha+\beta}{4}, \frac{3\left(4+\frac{4}{3} \alpha\right)+1\left(2-\frac{2}{5} \beta\right)}{4}\right) \\
\Rightarrow \alpha=\frac{3}{13}, \beta=\frac{95}{13}
\end{array}
\)
Point \(\mathrm{A}\left(\frac{3}{13}, \frac{56}{13}\right), \mathrm{B}\left(\frac{95}{13},-\frac{12}{13}\right)\)
Vertex \(\mathrm{C}\) of triangle is the point of intersection \(\mathrm{L}_1 \& \mathrm{~L}_2\)
\(
\Rightarrow \mathrm{C}\left(-\frac{15}{13}, \frac{32}{13}\right)
\)
\(
\begin{array}{l}
\text { area } \triangle \mathrm{ABC}=\frac{1}{2}\left\|\begin{array}{ccc}
\frac{3}{13} & \frac{56}{13} & 1 \\
\frac{95}{13} & -\frac{12}{13} & 1 \\
-\frac{15}{13} & \frac{32}{13} & 1
\end{array}\right\| \\
=\frac{1}{2 \times 13^3}\left\|\begin{array}{ccc}
3 & 56 & 13 \\
95 & -12 & 13 \\
-15 & 32 & 13
\end{array}\right\| \\
\text { area } \triangle \mathrm{ABC}=\frac{132}{13} \text { sq. units. }
\end{array}
\) -
Question 43 of 177
43. Question
The distance between the two points \(A\) and \(A^{\prime}\) which lie on \(\mathrm{y}=2\) such that both the line segments \(A B\) and \(A^{\prime} B\) (where \(B\) is the point \((2,3)\) ) subtend angle \(\frac{\pi}{4}\) at the origin, is equal to : [JEE Main 2022 June]
CorrectIncorrectHint
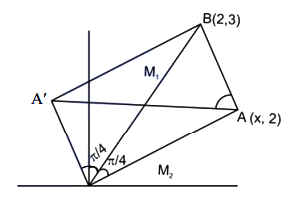
\(
\begin{array}{l}
\mathrm{M}_1=3 / 2 \quad \mathrm{M}_2=2 / \mathrm{x} \\
\tan \pi / 4=\left|\frac{3 / 2-2 / \mathrm{x}}{1+6 / 2 \mathrm{x}}\right|=1 \\
\Rightarrow \mathrm{x}_1=10, \quad \mathrm{x}_2=-2 / 5 \\
\Rightarrow \mathrm{AA}^{\prime}=52 / 5
\end{array}
\) -
Question 44 of 177
44. Question
The distance of the origin from the centroid of the triangle whose two sides have the equations \(x-2 y+1=0\) and \(2 x-y-1=0\) and whose orthocenter is \(\left(\frac{7}{3}, \frac{7}{3}\right)\) is: [JEE Main 2022 June]
CorrectIncorrectHint
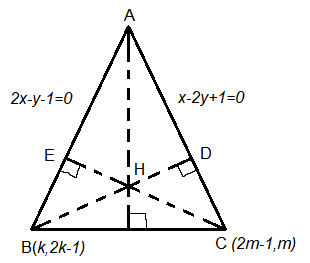
\(
\begin{array}{l}
\because B D \perp A C \\
\therefore \quad(m)_{B D}(m)_{A C}=-1 \\
\Rightarrow\left(\frac{1}{2}\right)\left(\frac{\frac{7}{3}-2 k+1}{\frac{7}{3}-k}\right)=-1
\end{array}
\)
\(
\begin{aligned}
k & =2 \\
\text { Also, }(m)_{C E}(m)_{A B} & =-1 \\
m & =2
\end{aligned}
\)
\(
\therefore A(1,1), B(2,3), C(3,2)
\)
So, coordinates of centroid is
\(
\begin{aligned}
G & =\left(\frac{1+2+3}{3}, \frac{1+3+2}{3}\right)=(2,2) \\
\therefore \quad O G & =\sqrt{2^2+2^2}=2 \sqrt{2}
\end{aligned}
\) -
Question 45 of 177
45. Question
A line, with the slope greater than one, passes through the point \(\mathrm{A}(4,3)\) and intersects the line \(\mathrm{x}-\) \(y-2=0\) at the point \(B\). If the length of the line segment \(A B\) is \(\frac{\sqrt{29}}{3}\), then \(B\) also lies on the line : [JEE Main 2022 July]
CorrectIncorrectHint
Let \(\mathrm{B}\left(\mathrm{x}_1, \mathrm{x}_1-2\right)\)
\(
\sqrt{\left(\mathrm{x}_1-4\right)^2+\left(\mathrm{x}_1-2-3\right)^2}=\frac{\sqrt{29}}{3}
\)
Squaring on both side
\(
\begin{array}{lll}
18 x_1^2-162 x_1+340 & =0 \\
x_1=\frac{51}{9} & \text { or } & x_1=\frac{10}{3} \\
y_1=\frac{33}{9} & \text { or } & y_1=\frac{4}{3}
\end{array}
\)
Option (c) will satisfy \(\left(\frac{10}{3}, \frac{4}{3}\right)\) -
Question 46 of 177
46. Question
Let the point \(\mathrm{P}(\alpha, \beta)\) be at a unit distance from each of the two lines \(L_1: 3 x-4 y+12=0\), and \(\mathrm{L}_2: 8 \mathrm{x}+6 \mathrm{y}+11=0\). If \(\mathrm{P}\) lies below \(\mathrm{L}_1\) and above \(L_2\), then \(100(\alpha+\beta)\) is equal to [JEE Main 2022 July]
CorrectIncorrectHint
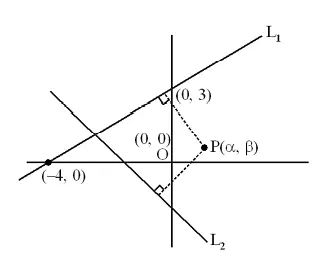
By observing origin and \(P\) lies in same region.
\(
\begin{array}{l}
L_1(0,0)>0 ; L_1(\alpha, \beta)>0 \Rightarrow 3 \alpha-4 \beta+12>01=\left|\frac{3 \alpha-4 \beta+12}{5}\right| \\
3 \alpha-4 \beta+12=5 \ldots \ldots(1)
\end{array}
\)
Similarly for \(L_2\)
\(
\begin{array}{l}
L_2(0,0)>0 ; L_2(\alpha, \beta)>0 \\
1=\left|\frac{8 \alpha+6 \beta+11}{10}\right| \Rightarrow 8 \alpha+6 \beta+11=10 \ldots \ldots .(2)
\end{array}
\)
Solving (1) and (2)
\(
\begin{array}{l}
\alpha=-\frac{23}{25} ; \beta=\frac{106}{100} \\
100(\alpha+\beta)=100\left(\frac{-92}{100}+\frac{106}{100}\right)=14
\end{array}
\) -
Question 47 of 177
47. Question
A point \(\mathrm{P}\) moves so that the sum of squares of its distances from the points \((1,2)\) and \((-2,1)\) is 14 . Let \(f(x, y)=0\) be the locus of \(P\), which intersects the \(\mathrm{x}\)-axis at the points \(\mathrm{A}, \mathrm{B}\) and the \(\mathrm{y}\)-axis at the point \(C, D\). Then the area of the quadrilateral \(A C B D\) is equal to [JEE Main 2022 July]
CorrectIncorrectHint
\(
\begin{array}{l}
(x-1)^2+(y-2)^2+(x+2)^2+(y-1)^2=14 \\
\Rightarrow x^2+y^2+x-3 y-2=0 \\
\text { Put } x=0 \\
\Rightarrow y^2-3 y-2=0 \\
\Rightarrow y=\frac{3 \pm \sqrt{17}}{2}
\end{array}
\)
Put \(y=0\)
\(
\begin{array}{l}
\Rightarrow \mathrm{x}^2+\mathrm{x}-2=0 \\
(\mathrm{x}+2)(\mathrm{x}-1)=0 \\
\therefore \mathrm{A}(-2,0), \mathrm{B}(1,0), \mathrm{C}\left(0, \frac{3+\sqrt{17}}{2}\right), \mathrm{D}\left(0, \frac{3-\sqrt{17}}{2}\right) \\
\text { Area }=\frac{1}{2} \cdot 3 \cdot \sqrt{17}=\frac{3 \sqrt{17}}{2}
\end{array}
\) -
Question 48 of 177
48. Question
The equations of the sides \(\mathrm{AB}, \mathrm{BC}\) and \(\mathrm{CA}\) of a triangle \(A B C\) are \(2 x+y=0, x+p y=15 a\) and \(x-y=3\) respectively. If its orthocentre is \((2, a)\), \(-\frac{1}{2}<\mathrm{a}<2\), then \(\mathrm{p}\) is equal to [JEE Main 2022 July]
CorrectIncorrectHint
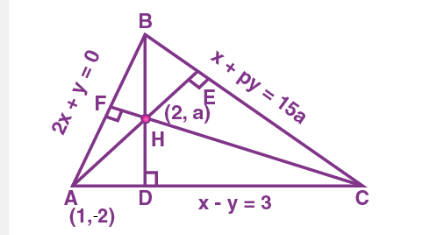
Coordinates of \(\mathrm{A}(1,-2), \mathrm{B}\left(\frac{15 \mathrm{a}}{1-2 \mathrm{p}}, \frac{-30 \mathrm{a}}{1-2 \mathrm{p}}\right)\) and orthocentre \(\mathrm{H}(2, \mathrm{a})\)
Slope of \(\mathrm{AH}=\frac{a+2}{1}\)
Slope of BC \(=-\frac{1}{p}\)
\(
\text { Slope of } \mathrm{AH}=\mathrm{p}
\)
\(
a+2=p \dots(1)
\)
Slope of BH \(=-1\)
\(
31 a-2 a b=15 a+4 p-2 \dots(2)
\)
From (1) and (2)
\(
a=1 \& p=3
\) -
Question 49 of 177
49. Question
Let \(A(1,1), B(-4,3), C(-2,-5)\) be vertices of a triangle \(\mathrm{ABC}, \mathrm{P}\) be a point on side \(\mathrm{BC}\), and \(\Delta_1\) and \(\Delta_2\) be the areas of triangle \(\mathrm{APB}\) and \(\mathrm{ABC}\). Respectively.
If \(\Delta_1: \Delta_2=4: 7\), then the area enclosed by the lines \(\mathrm{AP}, \mathrm{AC}\) and the \(\mathrm{x}\)-axis is [JEE Main 2022 July]CorrectIncorrectHint
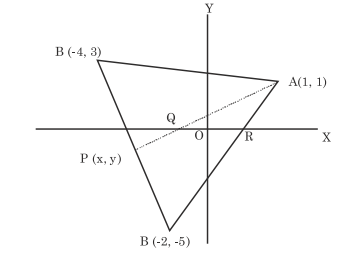
Given \(\Delta_1=\frac{1}{2}\left|\begin{array}{lll}x & y & 1 \\ 1 & 1 & 1 \\ -4 & 3 & 1\end{array}\right|\)
\(\& \Delta_2=\frac{1}{2}\left|\begin{array}{ccc}1 & 1 & 1 \\ -4 & 3 & 1 \\ -2 & -5 & 1\end{array}\right|\)
Given \(\frac{\Delta_1}{\Delta_2}=\frac{4}{7} \Rightarrow \frac{-2 x-5 y+7}{36}=\frac{4}{7}\)
\(
\Rightarrow 14 x+35 y=-95 \dots(1)
\)Equation of \(\mathrm{BC}\) is \(4 \mathrm{x}+\mathrm{y}=-13 \dots(2)\)
Solve equation (1) & (2)
Point \(P\left(\frac{-20}{7}, \frac{-11}{7}\right)\)
Here point \(Q\left(\frac{-1}{2}, 0\right) \& R\left(\frac{1}{2}, 0\right)\)
So Area of triangle \(\mathrm{AQR}=\frac{1}{2} \times 1 \times 1=\frac{1}{2}\) -
Question 50 of 177
50. Question
The equations of the sides \(\mathrm{AB}, \mathrm{BC}\) and \(\mathrm{CA}\) of a triangle \(\mathrm{ABC}\) are \(2 \mathrm{x}+\mathrm{y}=0, \mathrm{x}+\mathrm{py}=39\) and \(x-y=3\) respectively and \(P(2,3)\) is its circumcentre. Then which of the following is NOT true: [JEE Main 2022 July]
CorrectIncorrectHint
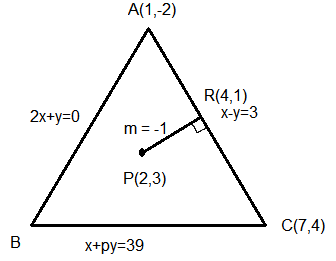
Equation of line
\(R P\) is \(x+y=5\)
By solving \(x-y=3\)
and \(x+y=5\), we get \(R(4,1)\)
The point \(R\) is mid point of \(A\) and \(C\).
So, point \(C\) is \((7,4)\).
Since line \(B C\) passes through point \(C(7,4)\). So, it must satisfy the equation of line \(B C\).
\(
\Rightarrow 7+4 p=39 \Rightarrow p=8
\)
Coordinates of point \(B\) are \(\left(\frac{-39}{15}, \frac{78}{15}\right)\)
\(
\text { Area of } \triangle A B C=\frac{1}{2}\left|\begin{array}{lll}
1 & -2 & 1 \\
7 & 4 & 1 \\
\frac{-39}{15} & \frac{78}{15} & 1
\end{array}\right|=32.4
\) -
Question 51 of 177
51. Question
For \(t \in(0,2 \pi)\), if \(\mathrm{ABC}\) is an equilateral triangle with vertices \(\mathrm{A}(\sin t,-\) cost \(), \mathrm{B}(\cos t\), sint \()\) and \(\mathrm{C}(\mathrm{a}, \mathrm{b})\) such that its orthocentre lies on a circle with centre \(\left(1, \frac{1}{3}\right)\), then \(\left(a^2-b^2\right)\) is equal to: [JEE Main 2022 July]
CorrectIncorrectHint
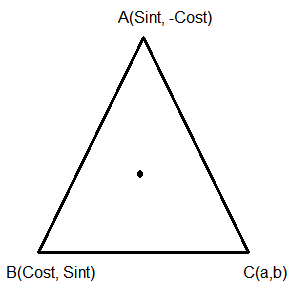
Let \(P(h, k)\) be the orthocentre of \(\triangle \mathrm{ABC}\)
Then
\(
h=\frac{\sin t+\cos t+a}{3}, k=\frac{-\cos t+\sin t+b}{3}
\)
(Orthocentre coincide with centroid)
\(
\begin{array}{l}
\therefore(3 h-a)^2+(3 k-b)^2=2 \\
\therefore\left(h-\frac{a}{3}\right)^2+\left(k-\frac{b}{3}\right)^2=\frac{2}{9}
\end{array}
\)
\(\because\) Orthocentre lies on circle with centre \(\left(1, \frac{1}{3}\right)\)
\(
\begin{array}{l}
\therefore a=3, b=1 \\
\therefore a^2-b^2=8
\end{array}
\) -
Question 52 of 177
52. Question
Let the circumcentre of a triangle with vertices \(\mathrm{A}(\mathrm{a}, 3), \mathrm{B}(\mathrm{b}, 5)\) and \(\mathrm{C}(\mathrm{a}, \mathrm{b}), \mathrm{ab}>0\) be \(\mathrm{P}(1,1)\). If the line \(\mathrm{AP}\) intersects the line \(\mathrm{BC}\) at the point \(\mathrm{Q}\left(\mathrm{k}_1, \mathrm{k}_2\right)\), then \(\mathrm{k}_1+\mathrm{k}_2\) is equal to : [JEE Main 2022 July]
CorrectIncorrectHint
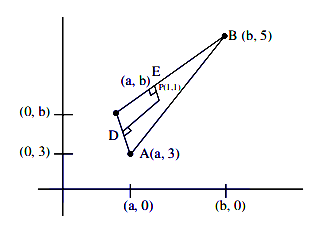
\(
\begin{array}{l}
\mathrm{m}_{\mathrm{AC}} \longrightarrow \infty \\
\mathrm{m}_{\mathrm{PD}}=0 \\
\mathrm{D}\left(\frac{\mathrm{a}+\mathrm{a}}{2}, \frac{\mathrm{b}+3}{2}\right)
\end{array}
\)
\(
\begin{array}{l}
\mathrm{m}_{\mathrm{PD}}=0 \\
\frac{\mathrm{b}+3}{2}-1=0; \mathrm{~b}+3-2=0; \mathrm{~b}=-1
\end{array}
\)
\(
\begin{array}{l}
\mathrm{E}\left(\frac{\mathrm{b}+\mathrm{a}}{2}, \frac{5+\mathrm{b}}{2}\right)=\left(\frac{\mathrm{af}}{2}, 2\right) \\
\mathrm{m}_{\mathrm{CB}} \cdot \mathrm{m}_{\mathrm{EP}}=-1
\end{array}
\)
\(
\left(\frac{5-b}{b-a}\right)=\left(\frac{2-1}{\frac{a-1}{2}-1}\right)=-1
\)
\(
\begin{array}{l}
(a-5)(a+3)=0 \\
a=5 \text { or } a=-3; \text { Given } a b>0 \\
a(-1)>0
\end{array}
\)
\(
\begin{array}{l}
a<0 \\
a=-3 \text { Accept }
\end{array}
\)
AP line \(A(-3,3), \mathrm{P}(1,1)\)
\(
\begin{array}{l}
y-1=\left(\frac{3-1}{-3-1}\right)(x-1) ; -2 y+2=x-1
\end{array}
\)
\(
x+2 y=3 \dots(1)
\)
\(
\begin{array}{l}
\text { Line BC B }(-1,5), \quad C(-3,-1) \\
(y-5)=\frac{6}{2}(x+1) \\
y-5=3 x+3; y=3 x+8 \dots(2)
\end{array}
\)
\(
\text { Solving (1) & (2) }
\)
\(
x+y=\frac{-13+17}{7}=\frac{4}{7}
\) -
Question 53 of 177
53. Question
Let \(\mathrm{m}_1, \mathrm{~m}_2\) be the slopes of two adjacent sides of a square of side a such that \(\mathrm{a}^2+11 \mathrm{a}+3\left(\mathrm{~m}_1^2+\mathrm{m}_2^2\right)=220\). If one vertex of the square is \((10(\cos \alpha-\sin \alpha), 10(\sin \alpha+\cos \alpha))\), where \(\alpha \in\left(0, \frac{\pi}{2}\right)\) and the equation of one diagonal is \((\cos \alpha-\sin \alpha) \mathrm{x}+(\sin \alpha+\cos \alpha) \mathrm{y}=10\), then 72 \(\left(\sin ^4 \alpha+\cos ^4 \alpha\right)+a^2-3 a+13\) is equal to: [JEE Main 2022 July]
CorrectIncorrectHint
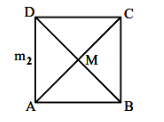
\(
\begin{array}{l}
m_1 m_2=-1 \\
a^2+11 a+3\left(m_1^2+\frac{1}{m_1^2}\right)=220
\end{array}
\)
Eq. of \(A C\)
\(
\begin{array}{l}
\mathrm{AC}=(\cos \alpha-\sin \alpha)x+(\sin \alpha+\cos \alpha) y=10 \\
\mathrm{BD}=(\sin \alpha-\cos \alpha) x+(\sin \alpha-\cos \alpha) y=0
\end{array}
\)
So, the point of intersection of the diagonal will be
\(
(5(\cos \alpha-\sin \alpha), 5(\cos \alpha+\sin \alpha)) \text {. }
\)
Therefore, the vertex opposite to the given vertex is \((0,0)\).
So, the diagonal length \(=10 \sqrt{2}\)
Side length \((a)=10\)
It is given that
\(
\begin{array}{l}
a^2+11 a+3\left(m_1^2+m_2^2\right)=220 \\
m_1^2+m_2^2=\frac{220-100-110}{3}=\frac{10}{3} \\
\text { and } m_1 m_2=-1
\end{array}
\)
Slopes of the sides are \(\tan \alpha\) and \(-\cot \alpha\)
\(
\begin{array}{l}
\tan ^2 \alpha=3 \text { or } \frac{1}{3} \\
72\left(\sin ^4 \alpha+\cos ^4 \alpha\right)+a^2-3 a+13 \\
=72 \cdot \frac{\tan ^4 \alpha+1}{\left(1+\tan ^2 \alpha\right)^2}+a^2-3 a+13=128
\end{array}
\) -
Question 54 of 177
54. Question
Let \(\mathrm{A}(\alpha,-2), \mathrm{B}(\alpha, 6)\) and \(\mathrm{C}\left(\frac{\alpha}{4},-2\right)\) be vertices of a \(\triangle \mathrm{ABC}\). If \(\left(5, \frac{\alpha}{4}\right)\) is the circumcentre of \(\triangle \mathrm{ABC}\), then which of the following is NOT correct about \(\triangle \mathrm{ABC}\) : [JEE Main 2022 July]
CorrectIncorrectHint
\(\mathrm{A}(\alpha,-2): \mathrm{B}(\alpha, 6): \mathrm{C}\left(\frac{\alpha}{4},-2\right)\)
since \(A C\) is perpendicular to \(A B\).
So, \(\triangle \mathrm{ABC}\) is right angled at \(\mathrm{A}\).
\(
\begin{array}{l}
\text { Circumcentre }=\text { mid point of } \mathrm{BC} .=\left(\frac{5 \alpha}{8}, 2\right) \\
\therefore \frac{5 \alpha}{8}=5 \& \frac{\alpha}{4}=2 \\
\alpha=8
\end{array}
\)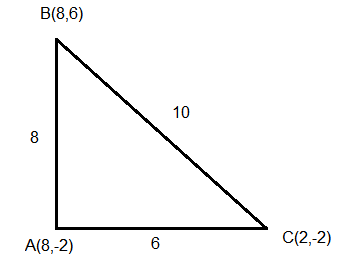
\(
\text { Area }=\frac{1}{2}(6)(8)=24
\)Perimeter \(=24\)
Circumradius \(=5\)
Inradius \(=\frac{\Delta}{\mathrm{s}}=\frac{24}{12}=2\) -
Question 55 of 177
55. Question
A man is walking on a straight line. The arithmetic mean of the reciprocals of the intercepts of this line on the coordinate axes is \(\frac{1}{4}\). Three stones \(A, B\) and \(C\) are placed at the points \((1,1),(2,2)\) and \((4,4)\) respectively. Then which of these stones is/are on the path of the man? [JEE Main 2021 Feb]
CorrectIncorrectHint
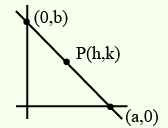
\(
\begin{array}{l}
\frac{x}{a}+\frac{y}{b}=1 \\
\frac{h}{a}+\frac{k}{b}=1 \ldots(1) \\
\text { and } \frac{\frac{1}{a}+\frac{1}{b}}{2}=\frac{1}{4} \\
\therefore \frac{1}{a}+\frac{1}{b}=\frac{1}{2} \ldots(2)
\end{array}
\)
From (1) and (2)
Line passes through fixed point \(B(2,2)\) -
Question 56 of 177
56. Question
Let a point \(P\) be such that its distance from the point \((5,0)\) is thrice the distance of \(P\) from the point \((-5,0)\). If the locus of the point \(P\) is a circle of radius \(r\), then \(4 r^2\) is equal to (Round off to the nearest integer) [JEE Main 2021 Feb]
CorrectIncorrectHint
Considering the points according to the given data:
\(
P(h, k), A(5,0) \text { and } B(-5,0)
\)
Given, \(P A=3 P B\)
Distance between the points \(P(h, k) \& A(5,0)\) is:
\(
P A=\sqrt{(h-5)^2+k^2}
\)
Similarly, the distance between the points \(P(h, k) \& B(-5,0)\)
\(
P B=\sqrt{(h+5)^2+k^2}
\)
Given
\(
\begin{array}{l}
P A=3 P B\\
P A^2=9 P B^2
\end{array}
\)
Euqating both sides we get,
\(
\begin{aligned}
(h-5)^2+k^2 & =9\left[(h+5)^2+k^2\right] \\
8 h^2+8 k^2+100 h+200 & =0 \\
x^2+y^2+\frac{25}{2} x+25 & =0
\end{aligned}
\)
Therefore, the locus of point \(P\) is \(x^2+y^2+\frac{25}{2} x+25=0 \ldots \ldots(i)\)
Finding the radius of the circle:
We know that a circle of the form \(x^2+y^2+2 g x+2 f y+c=0\) has a center \((-g,-f)\) and radius \(\sqrt{g^2+f^2-c}\).
Therefore, from equation \((i)\) we have,
\(
\begin{array}{l}
g=\frac{25}{4}, f=0 \& c=25 \\
\text { Thus, Centre }=(-g,-f)=\left(-\frac{25}{4}, 0\right)
\end{array}
\)
\(
r=\sqrt{\left(\frac{25}{4}\right)^2-25}
\)
\(
4 r^2=56.25
\) -
Question 57 of 177
57. Question
The image of the point \((3,5)\) in the line \(x-y+1=0\), lies on : [JEE Main 2021 Feb]
CorrectIncorrectHint
Step 1.Find the image of the point
We know that if \(B\left(x, y\right)\) is the image of a point \(P(p, q)\) with respect to a line
\(a x+b y+c=0\) then
\(
\frac{x-p}{a}=\frac{y-q}{b}=\frac{-2(a p+b q+c)}{a^2+b^2}
\)
Image of the point \((3,5)\) in the line \(x-y+1=0\), is
\(
\begin{array}{l}
\frac{x-3}{1}=\frac{y-5}{-1}=\frac{-2(3-5+1)}{2}=1 \\
\therefore x=4, y=4
\end{array}
\)
Step2: Finding answer
Image of the point \((3,5)\) is \((4,4)\)
If the image lies on the circle \((x-2)^2+(y-4)^2=4\), then the image must satisfy the equation of the circle
Since,
\(
\begin{array}{l}
(4-2)^2+(4-4)^2 \\
=2^2+0 \\
=4
\end{array}
\) -
Question 58 of 177
58. Question
The intersection of three lines \(x-y=0, x+2 y=3\) and \(2 x+y=6\) is a: [JEE Main 2021 Feb]
CorrectIncorrectHint
Given equations of the straight lines are as follows,
\(
\begin{array}{l}
x-y=0 \dots(i) \\
x+2 y=3 \dots(ii) \\
2 x+y=6 \dots(iii)
\end{array}
\)
Step 1: Solving Equation (ii) – Equation (i).
\(
\begin{array}{l}
(x+2 y)-(x-y)=3-0 \Rightarrow 3 y=3 \Rightarrow y=1
\end{array}
\)
Substitute \(y\) with 1 in equation (i).
\(
\begin{array}{l}
x-y=0 \Rightarrow \quad x-1=0 \Rightarrow \quad x=1
\end{array}
\)
Thus, the point is \(A(1,1)\).
Step 2: Solve the equation (iii) -equation (ii).
Equation (iii) \(\times 2-\) Equation (ii).
\(
\begin{array}{l}
2 \times(2 x+y)-(x+2 y)=(2 \times 6)-3 \\
\quad \Rightarrow 3 x=9 \Rightarrow x=3
\end{array}
\)
Substitute \(x\) with 3 in equation (ii).
\(
\begin{array}{l}
x+2 y=3 \Rightarrow 3+2 y=3 \Rightarrow \quad y=0
\end{array}
\)
Thus, the point is \(B(3,0)\).
Step 3: Solve the equation (iii) -equation \((i)\)
Equation (iii) + Equation (i).
\(
\begin{array}{l}
(2 x+y)+(x-y)=6+0 \Rightarrow 3 x=6 \\
\Rightarrow x=2
\end{array}
\)
Substitute \(x\) with 2 in equation (i).
\(
\begin{array}{l}
x-y=0 \\
\Rightarrow 2-y=0 \Rightarrow \quad y=2
\end{array}
\)
Thus, the point is \(C(2,2)\).
Step 4: Check which type of triangle formed.
Apply the distance formula, \(\sqrt{\left(\mathbf{x}_1-\mathbf{x}_2\right)^2+\left(\mathbf{y}_1-\mathbf{y}_2\right)^2}\). \(A B=\sqrt{(1-3)^2+(1-0)^2}\) units \(=\sqrt{4+1}\) units \(=\sqrt{5}\) units. \(B C=\sqrt{(3-2)^2+(0-2)^2}\) units \(=\sqrt{1+4}\) units \(=\sqrt{5}\) units. \(C A=\sqrt{(2-1)^2+(2-1)^2}\) units \(=\sqrt{1+1}\) units \(=\sqrt{2}\) units.
So, the given triangle has \(A B=B C \neq C A\), thus the triangle is an isosceles triangle. -
Question 59 of 177
59. Question
If the locus of the mid-point of the line segment from the point \((3,2)\) to a point on the circle, \(x^2+y^2=1\) is a circle of the radius \(r\), then \(r\) is equal to : [JEE Main 2021 Feb]
CorrectIncorrectHint
Step 1: Derive a relation between the general point on the given circle and the mid-point.
In the question, an equation of the circle \(x^2+y^2=1\) and a point \((3,2)\) is given.
We know that the standard equation of a circle is given by \(\left(x-x_1\right)^2+\left(y-y_1\right)^2=r^2\), where \((x, y)\) is the general point on the circle, the centre of the circle is at \(\left(x_1, y_1\right)\) and \(r\) is the radius of the circle.
Assume that, the mid-point of the line segment from the point \((3,2)\) to a point on the circle, \(x^2+y^2=1\) is \((h, k)\).
So, \(\left(\frac{x+3}{2}, \frac{y+2}{2}\right)=(h, k)\)
Now, compute \(x\) and \(y\) is terms of \(h\) and \(k\) respectively.
Therefore,
\(
\begin{array}{l}
\frac{x+3}{2}=h \\
\Rightarrow \quad x=2 h-3
\end{array}
\)
\(
\begin{array}{l}
\frac{y+2}{2}=k \\
\Rightarrow \quad y=2 k-2
\end{array}
\)
Therefore, \((x, y)=(2 h-3,2 k-2)\).
Step 2: Derive an equation for the locus of the mid-point.
Since, \((x, y)\) lies on the given circle. So, it satisfy the given equation of the circle.
So,
\(
\begin{aligned}
& (2 h-3)^2+(2 k-2)^2=1 \\
\Rightarrow & \frac{(2 h-3)^2}{4}+\frac{(2 k-2)^2}{4}=\frac{1}{4} \\
\Rightarrow \quad & \left(h-\frac{3}{2}\right)^2+(k-1)^2=\left(\frac{1}{2}\right)^2
\end{aligned}
\)
Which represents the locus of the mid-point of the line segment from the point \((3,2)\) to a point on the circle, \(x^2+y^2=1\).
Since, the radius of the locus of the mid-point of the line segment from the point \((3,2)\) to a point on the circle, \(x^2+y^2=1\) is \(\frac{1}{2}\).
Therefore, the value of \(r\) is \(\frac{1}{2}\). -
Question 60 of 177
60. Question
Let \(\mathrm{A}(-1,1), \mathrm{B}(3,4)\) and \(\mathrm{C}(2,0)\) be given three points. \(\mathrm{A}\) line \(y=m x, m>0\), intersects lines \(\mathrm{AC}\) and \(\mathrm{BC}\) at point \(\mathrm{P}\) and \(\mathrm{Q}\) respectively. Let \(\mathrm{A}_1\) and \(\mathrm{A}_2\) be the areas of \(\triangle \mathrm{ABC}\) and \(\triangle \mathrm{PQC}\) respectively, such that \(A_1=3 A_2\), then the value of \(m\) is equal to : [JEE Main 2021 March]
CorrectIncorrectHint
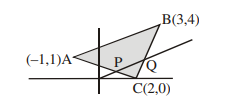
\(
\begin{array}{l}
\mathrm{P} \equiv\left(\mathrm{x}_1, \mathrm{mx}_1\right) \\
\mathrm{Q} \equiv\left(\mathrm{x}_2, \mathrm{mx}_2\right) \\
A_1=\frac{1}{2}\left|\begin{array}{ccc}
3 & 4 & 1 \\
2 & 0 & 1 \\
-1 & 1 & 1
\end{array}\right|=\frac{13}{2} \\
A_2=\frac{1}{2}\left|\begin{array}{ccc}
x_1 & m x_1 & 1 \\
x_2 & m x_2 & 1 \\
2 & 0 & 1
\end{array}\right| \\
\mathrm{A}_2=\frac{1}{2}\left|2\left(\mathrm{mx}_1-\mathrm{mx}_2\right)\right|=\mathrm{m}\left|\mathrm{x}_1-\mathrm{x}_2\right| \\
A_1=3 A_2 \Rightarrow \frac{13}{2}=3 m\left|x_1-x_2\right|
\end{array}
\)
\(
\begin{array}{l}
A C: x+3 y=2 \\
B C: y=4 x-8 \\
P: x+3 y=2 \& y=m x \Rightarrow x_1=\frac{2}{1+3 m} \\
Q: y=4 x-8 \& y=m x \Rightarrow x_2=\frac{8}{4-m} \\
\left|x_1-x_2\right|=\left|\frac{2}{1+3 m}-\frac{8}{4-m}\right| \\
=\left|\frac{-26 m}{(1+3 m)(4-m)}\right|=\frac{26 m}{(3 m+1)|m-4|} \\
=\frac{26 m}{(3 m+1)(4-m)} \\
\left|x_1-x_2\right|=\frac{13}{6 m} \\
\frac{26 m}{(3 m+1)(4-m)}=\frac{13}{6 m}
\end{array}
\)
\(
\begin{array}{l}
\Rightarrow 12 \mathrm{~m}^2=-(3 \mathrm{~m}+1)(\mathrm{m}-4) \\
\Rightarrow 12 \mathrm{~m}^2=-\left(3 \mathrm{~m}^2-11 \mathrm{~m}-4\right) \\
\Rightarrow 15 \mathrm{~m}^2-11 \mathrm{~m}-4=0 \\
\Rightarrow 15 \mathrm{~m}^2-15 \mathrm{~m}+4 \mathrm{~m}-4=0 \\
\Rightarrow(15 \mathrm{~m}+4)(\mathrm{m}-1)=0 \\
\Rightarrow \mathrm{m}=1
\end{array}
\) -
Question 61 of 177
61. Question
In a triangle \(P Q R\), the co-ordinates of the points \(P\) and \(Q\) are \((-2,4)\) and \((4,-2)\) respectively. If the equation of the perpendicular bisector of \(\mathrm{PR}\) is \(2 x-y+2=0\), then the centre of the circumcircle of the \(\triangle \mathrm{PQR}\) is: [JEE Main 2021 March]
CorrectIncorrectHint
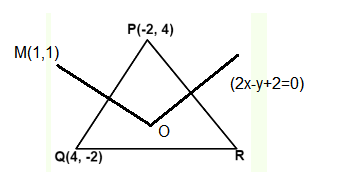
Perpendicular bisector of \(\mathrm{PR}\) is
\(
2 x-y+2=0 \dots(i)
\)Mid-points of \(P Q\) is \(M \equiv(1,1)\)
Equation of perpendicular bisector of \(P Q\) is
\(
\begin{array}{l}
y-1=-\left(\frac{4+2}{-2-4}\right)(x-1) \\
\Rightarrow x=y \dots(ii)
\end{array}
\)
Solving eqn (i) and eqn (ii), therefore, circumcentre is point of intersection of the two perpendicular bisectors i.e., \((-2,-2)\) -
Question 62 of 177
62. Question
Let the tangent to the circle \(x^2+y^2=25\) at the point \(R(3,4)\) meet \(x\)-axis and \(y\)-axis at point \(P\) and \(Q\), respectively. If \(r\) is the radius of the circle passing through the origin \(\mathrm{O}\) and having centre at the incentre of the triangle \(\mathrm{OPQ}\), then \(\mathrm{r}^2\) is equal to [JEE Main 2021 March]
CorrectIncorrectHint
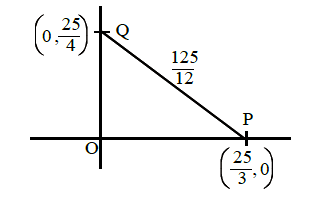
Tangent to circle \(3 x+4 y=25\)
\(
\begin{aligned}
\mathrm{OP}+\mathrm{OQ} & +\mathrm{OR}=25 \\
\text { Incentre } & =\left(\frac{\frac{25}{4} \times \frac{25}{3}}{25}, \frac{\frac{25}{4} \times \frac{25}{3}}{25}\right) \\
& =\left(\frac{25}{12}, \frac{25}{12}\right)
\end{aligned}
\)
\(
\therefore \mathrm{r}^2=2\left(\frac{25}{12}\right)^2=2 \times \frac{625}{144}=\frac{625}{72}
\) -
Question 63 of 177
63. Question
Let \(\tan \alpha, \tan \beta\) and \(\tan \gamma ; \alpha, \beta \neq[2 n-1] \pi / 2, n \in N\) be the slopes of three-line segments \(O A, O B\) and \(O C\), respectively, where \(O\) is the origin. If the circumcentre of the \(\triangle A B C\) coincides with the origin and its orthocentre lies on the \(y-a x i s\), then the value of \(\left[\frac{\cos 3 \alpha+\cos 3 \beta+\cos 3 \gamma}{\cos \alpha \cdot \cos \beta \cdot \cos \gamma}\right]^2\) is equal to [JEE Main 2021 March]
CorrectIncorrectHint
Since orthocentre and circumcentre both lies on y-axis.
\(\Rightarrow\) Centroid also lies on \(y\)-axis.
\(
\begin{array}{l}
\Rightarrow \sum \cos \alpha=0 \\
\cos \alpha+\cos \beta+\cos \gamma=0 \\
\Rightarrow \cos ^3 \alpha+\cos ^3 \beta+\cos ^3 \gamma=3 \cos \alpha \cos \beta \cos \gamma \\
\therefore \frac{\cos 3 \alpha+\cos 3 \beta+\cos 3 \gamma}{\cos \alpha \cos \beta \cos \gamma} \\
=\frac{4\left(\cos ^3 \alpha+\cos ^3 \beta+\cos ^3 \gamma\right)-3(\cos \alpha+\cos \beta+\cos \gamma)}{\cos \alpha \cos \beta \cos \gamma}=12
\end{array}
\)
then, \(\left(\frac{\cos 3 \alpha+\cos 3 \beta+\cos 3 \gamma}{\cos \alpha \cos \beta \cos \gamma}\right)^2=144\) -
Question 64 of 177
64. Question
The number of integral values of \(m\) so that the abscissa of point of intersection of lines \(3 x+4 y=9\) and \(y=m x+1\) is also an integer, is :[JEE Main 2021 March]
CorrectIncorrectHint
Given equation of the lines are \(3 x+4 y=9\) and \(y=m x+1\)
\(
\begin{array}{l}
\therefore \quad 3 x+4 y=9 \\
\Rightarrow 3 x+4(m x+1)=9 \\
\Rightarrow \quad x(3+4 m)=9-4 \\
\Rightarrow \quad x=\frac{5}{3+4 m} \\
\end{array}
\)
Clearly \(x\) will attain integer values when \(3+4 m=5,-5,1,-1\)
\(
\Rightarrow \mathrm{m}=\frac{1}{2},-2,-\frac{1}{2},-1
\)
so, number of integral values of \(m\) is 2. -
Question 65 of 177
65. Question
The equation of one of the straight lines which passes through the point \((1,3)\) and makes an angles \(\tan ^{-1}(\sqrt{2})\) with the straight line, \(y+1=3 \sqrt{2} x\) is [JEE Main 2021 March]
CorrectIncorrectHint
\(
\begin{array}{l}
y=m x+c \\
3=m+c \\
\sqrt{2}=\left|\frac{m-3 \sqrt{2}}{1+3 \sqrt{2} m}\right| \\
=6 m+\sqrt{2}=m-3 \sqrt{2}
\end{array}
\)
\(
\begin{array}{l}
=\sin =-4 \sqrt{2} \rightarrow \mathrm{m}=\frac{-4 \sqrt{2}}{5} \\
=6 m-\sqrt{2}=m-3 \sqrt{2} \\
=7 \mathrm{~m}-2 \sqrt{2} \rightarrow \mathrm{m}=\frac{2 \sqrt{2}}{7}
\end{array}
\)
According to options take \(\mathrm{m}=\frac{-4 \sqrt{2}}{5}\)
So \(y=\frac{-4 \sqrt{2} x}{5}+\frac{3+4 \sqrt{2}}{5}\)
\(
4 \sqrt{2} \mathrm{x}+5 \mathrm{y}-(15+4 \sqrt{2})=0
\) -
Question 66 of 177
66. Question
Let the centroid of an equilateral triangle \(\mathrm{ABC}\) be at the origin. Let one of the sides of the equilateral triangle be along the straight line \(\mathrm{x}+\mathrm{y}=3\). If \(\mathrm{R}\) and \(\mathrm{r}\) be the radius of circumcircle and incircle respectively of \(\triangle \mathrm{ABC}\), then \((\mathrm{R}+\mathrm{r})\) is equal to: [JEE Main 2021 March]
CorrectIncorrectHint
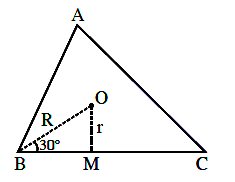
\(
\begin{array}{l}
r=O M=\frac{3}{\sqrt{2}} \\
\& \sin 30^{\circ}=\frac{1}{2}=\frac{r}{R} \Rightarrow R=\frac{6}{\sqrt{2}} \\
\therefore r+R=\frac{9}{\sqrt{2}}
\end{array}
\) -
Question 67 of 177
67. Question
Consider a triangle having vertices \(\mathrm{A}(-2,3), \mathrm{B}(1,9)\) and \(C(3,8)\). If a line \(L\) passing through the circum-centre of triangle \(\mathrm{ABC}\), bisects line \(\mathrm{BC}\), and intersects \(\mathrm{y}\)-axis at point \(\left(0, \frac{\alpha}{2}\right)\), then the value of real number \(\alpha\) is [JEE Main 2021 July]
CorrectIncorrectHint
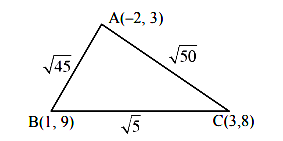
\(
\begin{array}{l}
(\sqrt{50})^2=(\sqrt{45})^2+(\sqrt{5})^2 \\
\angle \mathrm{B}=90^{\circ}
\end{array}
\)
Circum-center \(=\left(\frac{1}{2}, \frac{11}{2}\right)\)
Mid point of \(\mathrm{BC}=\left(2, \frac{17}{2}\right)\)
Line : \(\left(y-\frac{11}{2}\right)=2\left(x-\frac{1}{2}\right) \Rightarrow y=2 x+\frac{9}{2}\)
Passing though \(\left(0, \frac{\alpha}{2}\right)\)
\(
\frac{\alpha}{2}=\frac{9}{2} \Rightarrow \alpha=9
\) -
Question 68 of 177
68. Question
Let \(P\) and \(Q\) be two distinct points on a circle which has center at \(C(2,3)\) and which passes through origin \(O\).
If \(O C\) is perpendicular to both the line segments \(C P\) and \(C Q\), then the set \(\{P, Q\}\) is equal to [JEE Main 2021 July]CorrectIncorrectHint
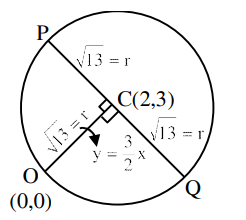
\(
\tan \theta=-\frac{2}{3}
\)
Using symmetric from of line
\(
\begin{array}{l}
P, Q:(2 \pm \sqrt{13} \cos \theta, 3 \pm \sqrt{13} \sin \theta) \\
\left(2 \pm \sqrt{13} \cdot\left(-\frac{3}{\sqrt{13}}\right), 3 \pm \sqrt{13}\left(\frac{2}{\sqrt{13}}\right)\right) \\
(-1,5) \&(5,1)
\end{array}
\) -
Question 69 of 177
69. Question
The point \(P(a, b)\) undergoes the following three transformations successively:
(a) reflection about the line \(\mathbf{y}=\mathbf{x}\).
(b) translation through 2 units along the positive direction of \(\mathbf{x}\)-axis.
(c) rotation through angle \(\frac{\pi}{4}\) about the origin in the anti-clockwise direction.
If the co-ordinates of the final position of the point \(P\) are \(\left(-\frac{1}{\sqrt{2}}, \frac{7}{\sqrt{2}}\right)\), then the value of \(2 a+b\) is equal to : [JEE Main 2021 July]CorrectIncorrectHint
Image of \(\mathrm{A}(\mathrm{a}, \mathrm{b})\) along \(\mathrm{y}=\mathrm{x}\) is \(\mathrm{B}(\mathrm{b}, \mathrm{a})\).
Translating it 2 units it becomes \(\mathrm{C}(\mathrm{b}+2, \mathrm{a})\).Now, applying rotation theorem
\(
\begin{array}{l}
-\frac{1}{\sqrt{2}}+\frac{7}{\sqrt{2}} i=((b+2)+a i)\left(\cos \frac{\pi}{4}+i \sin \frac{\pi}{4}\right) \\
-\frac{1}{\sqrt{2}}+\frac{7}{\sqrt{2}} i=\left(\frac{b+2}{\sqrt{2}}-\frac{a}{\sqrt{2}}\right)+i\left(\frac{b+2}{\sqrt{2}}+\frac{a}{\sqrt{2}}\right) \\
\Rightarrow \mathrm{b}-\mathrm{a}+2=-1 \ldots \ldots \text { (i) }
\end{array}
\)
and \(b+2+a=7 \dots(ii)\)
\(
\Rightarrow a=4 ; b=1
\)
\(
\Rightarrow 2 \mathrm{a}+\mathrm{b}=9
\) -
Question 70 of 177
70. Question
Two sides of a parallelogram are along the lines \(4 x+5 y=0\) and \(7 x+2 y=0\). If the equation of one of the diagonals of the parallelogram is \(11 x+7 y=9\), then other diagonal passes through the point:[JEE Main 2021 July]
CorrectIncorrectHint
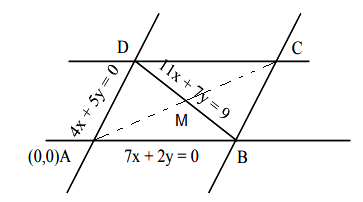
The sides are \(4 x+5 y=0 \dots(1)\)
and \(7 \mathrm{x}+2 \mathrm{y}=0 \dots(2)\)Equation of the diagonal,
\(
11 x+7 y=9 \dots(3)
\)
Solving (1) and (3) co-ordinates of D are (5/3, -4/3)
Solving (2) and (3) co-ordinates of B are \((-2 / 3,7 / 3)\)
diagonals of parallelogram intersect at middle
let middle point of \(M=B, D\)
\(
\Rightarrow\left(\frac{\frac{5}{3}-\frac{2}{3}}{2}, \frac{\frac{-4}{3}+\frac{7}{3}}{2}\right)=\left(\frac{1}{2}, \frac{1}{2}\right)
\)
equation of diagonal \(\mathrm{AC}\)
\(
\begin{array}{l}
\Rightarrow(y-0)=\frac{\frac{1}{\alpha}-0}{\frac{1}{\alpha}-0}(x-0)\\
y=x
\end{array}
\)
dlagonal AC passes through \((2,2)\). -
Question 71 of 177
71. Question
Let the points of intersections of the lines \(x-y+1=0, x-2 y+3=0\) and \(2 x-5 y+11=0\) are the mid points of the sides of a triangle \(\mathrm{ABC}\). Then the area of the triangle \(\mathrm{ABC}\) is. [JEE Main 2021 August]
CorrectIncorrectHint
Intersection point of give lines are \((1,2),(7,5),(2,3)\)
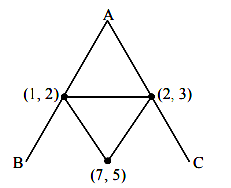
\(
\begin{array}{l}
\Delta=\frac{1}{2}\left|\begin{array}{lll}
1 & 2 & 1 \\
7 & 5 & 1 \\
2 & 3 & 1
\end{array}\right| \\
=\frac{1}{2}[1(5-3)-2(7-2)+1(21-10)] \\
=\frac{1}{2}[2-10+11] \\
\Delta \mathrm{DEF}=\frac{1}{2}(3)=\frac{3}{2} \\
\Delta \mathrm{ABC}=4 \Delta \mathrm{DEF}=4\left(\frac{3}{2}\right)=6
\end{array}
\) -
Question 72 of 177
72. Question
Let \(\mathrm{A}\) be the set of all points \((\alpha, \beta)\) such that the area of triangle formed by the points \((5,6),(3,2)\) and \((\alpha, \beta)\) is 12 square units. Then the least possible length of a line segment joining the origin to a point in \(\mathrm{A}\), is : [JEE Main 2021 August]
CorrectIncorrectHint
\(
\frac{1}{2}\left|\begin{array}{lll}
5 & 6 & 1 \\
3 & 2 & 1 \\
\alpha & \beta & 1
\end{array}\right|=12
\)
\(
\begin{array}{l}
4 \alpha-2 \beta= \pm 24+8 \\
\Rightarrow 4 \alpha-2 \beta=+24+8 \Rightarrow 2 \alpha-\beta=16 \\
2 x-y-16=0 \ldots(1) \\
\Rightarrow 4 \alpha-2 \beta=-24+8 \Rightarrow 2 \alpha-\beta=-8 \\
2 x-y+8=0 \ldots(2)
\end{array}
\)
perpendicular distance of (1) from \((0,0)\)
\(
\left|\frac{0-0-16}{\sqrt{5}}\right|=\frac{16}{\sqrt{5}}
\)
perpendicular distance of \((2)\) from \((0,0)\) is
\(
\left|\frac{0-0+8}{\sqrt{5}}\right|=\frac{8}{\sqrt{5}}
\)
Required length \(=\) minimum perpendicular distance from origin
\(
=\min \left\{\frac{16}{\sqrt{5}}, \frac{8}{\sqrt{5}}\right\}=\frac{8}{\sqrt{5}}
\) -
Question 73 of 177
73. Question
If \(\mathrm{p}\) and \(\mathrm{q}\) are the lengths of the perpendiculars from the origin on the lines, \(x \operatorname{cosec} \alpha-y \sec \alpha=\mathrm{k} \cot 2 \alpha\) and \(x \sin \alpha+y \cos \alpha=k \sin 2 \alpha\) respectively, then \(\mathrm{k}^2\) is equal to: [JEE Main 2021]
CorrectIncorrectHint
Let \(L_1=x \operatorname{cosec} \alpha-y \sec \alpha=k \cot 2 \alpha\).
Then \(\frac{x}{\sin \alpha}-\frac{y}{\cos \alpha}=\frac{k \cos 2 \alpha}{\sin 2 \alpha}\)
\(\Rightarrow x \cos \alpha-y \sin \alpha=\frac{k}{2} \cos 2 \alpha\)
Perpendicular distance from \((0,0)\) is
\(
\begin{array}{l}
\mathrm{p}=\left|\frac{0-0-\frac{k}{2} \cos 2 \alpha}{\sqrt{\cos ^2 \alpha+\sin ^2 \alpha}}\right| \\
\Rightarrow \mathrm{p}=\left|\frac{k}{2} \cos 2 \alpha\right|
\end{array}
\)
\(
\Rightarrow 2 p=|k \cos 2 \alpha| \ldots \text { (i) }
\)
\(
\mathrm{L}_2=\mathrm{x} \sin \alpha+\mathrm{y} \cos \alpha=\mathrm{k} \sin 2 \alpha
\)
Perpendicular distance from \((0,0)\) is
\(
\begin{array}{l}
\mathrm{q}=\left|\frac{0+0-k \sin 2 \alpha}{\sqrt{\sin ^2 \alpha+\cos ^2 \alpha}}\right| \\
\Rightarrow \mathrm{q}=|\mathrm{k} \sin 2 \alpha| \ldots \text { (ii) }
\end{array}
\)
Hence \(4 p^2+q^2=k^3 \ldots(\) From (i) and (ii)) -
Question 74 of 177
74. Question
Let \(A(a, 0), B(b, 2 b+1)\) and \(C(0, b), b \neq 0, b b \neq 1\), be points such that the area of triangle \(A B C\) is 1 sq. unit, then the sum of all possible values of \(a\) is : [JEE Main 2021 August]
CorrectIncorrectHint
\(
\frac{1}{2}\left|\begin{array}{ccc}
a & 0 & 1 \\
b & 2 b+1 & 1 \\
0 & b & 1
\end{array}\right|=1
\)
\(
\begin{array}{l}
\Rightarrow\left|\begin{array}{ccc}
\mathrm{a} & 0 & 1 \\
\mathrm{~b} & 2 \mathrm{~b}+1 & 1 \\
0 & \mathrm{~b} & 1
\end{array}\right|= \pm 2 \\
\Rightarrow a(2 b+1-b)-0+1\left(b^2-0\right)= \pm 2 \\
\Rightarrow \mathrm{a}=\frac{ \pm 2-\mathrm{b}^2}{\mathrm{~b}+1} \\
\therefore \mathrm{a}=\frac{2-\mathrm{b}^2}{\mathrm{~b}+1} \text { and } \mathrm{a}=\frac{-2-\mathrm{b}^2}{\mathrm{~b}+1}
\end{array}
\)
sum of possible values of ‘ \(a\) ‘ is
\(
=\frac{-2 b^2}{a+1} \text { Ans. }
\) -
Question 75 of 177
75. Question
Let \(A\) be a fixed point \((0,6)\) and \(B\) be a moving point \((2 t, 0)\). Let \(\mathrm{M}\) be the mid-point of \(\mathrm{AB}\) and the perpendicular bisector of \(\mathrm{AB}\) meets the \(y\)-axis at \(C\). The locus of the mid-point \(\mathrm{P}\) of \(\mathrm{MC}\) is : [JEE Main 2021 August]
CorrectIncorrectHint
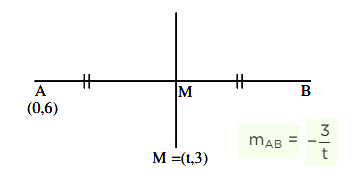
Let \(A(0,6)\) and \(B(2 t, 0)\)
Then, mid point of \(A B\) is \(M=(t, 3)\) and slope of \(A B\) is
\(
m_{A B}=\frac{-6}{2 t}=-\frac{3}{t}
\)Perpendicular bisector of \(A B\) is
\(
(y-3)=\frac{t}{3}(x-t)
\)
So, \(C=\left(0,3-\frac{t^2}{3}\right)\)
Let \(\mathrm{P}\) be \((\mathrm{h}, \mathrm{k})\)
\(
\begin{array}{l}
\mathrm{h}=\frac{\mathrm{t}}{2} ; \mathrm{k}=\left(3-\frac{\mathrm{t}^2}{6}\right) \\
\Rightarrow \mathrm{k}=3-\frac{4 \mathrm{~h}^2}{6} \Rightarrow 2 \mathrm{x}^2+3 \mathrm{y}-9=0
\end{array}
\) -
Question 76 of 177
76. Question
Let \(\mathrm{ABC}\) be a triangle with \(\mathrm{A}(-3,1)\) and \(\angle \mathrm{ACB}=\theta, 0<\theta<\frac{\pi}{2}\). If the equation of the median through \(\mathrm{B}\) is \(2 \mathrm{x}+\mathrm{y}-3=0\) and the equation of angle bisector of \(\mathrm{C}\) is \(7 \mathrm{x}-4 \mathrm{y}-1=0\), then \(\tan \theta\) is equal to: [JEE Main 2021 August]
CorrectIncorrectHint
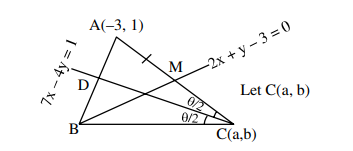
\(
\therefore \quad M\left(\frac{a-3}{2}, \frac{b+1}{2}\right) \text { lies on } 2 x+y-3=0
\)
\(
\Rightarrow 2 \mathrm{a}+\mathrm{b}=11 \dots(i)
\)
\(\because\) C lies on \(7 x-4 y=1\)
\(
\Rightarrow 7 \mathrm{a}-4 \mathrm{~b}=1 \dots(ii)
\)
\(\therefore\) by (i) and (ii) : \(\mathrm{a}=3, \mathrm{~b}=5\)
\(
\begin{array}{l}
\Rightarrow \mathrm{C}(3,5) \\
\therefore \mathrm{m}_{A C}=2 / 3
\end{array}
\)
Also, \(\mathrm{m}_{\mathrm{CD}}=7 / 4\)
\(
\begin{array}{l}
\Rightarrow \tan \frac{\theta}{2}=\left|\frac{\frac{2}{3}-\frac{4}{4}}{1+\frac{14}{12}}\right| \Rightarrow \tan \frac{\theta}{2}=\frac{1}{2} \\
\Rightarrow \tan \theta=\frac{2 \cdot \frac{1}{2}}{1-\frac{1}{4}}=\frac{4}{3}
\end{array}
\) -
Question 77 of 177
77. Question
Let \(A(1,0), B(6,2)\) and \(C\left(\frac{3}{2}, 6\right)\) be the vertices of a triangle \(A B C\). If \(P\) is a point inside the triangle \(A B C\) such that the triangles \(A P C, A P B\) and \(B P C\) have equal areas, then the length of the line segment \(P Q\), where \(Q\) is the point \(\left(-\frac{7}{6},-\frac{1}{3}\right)\), is [JEE Main 2020 Jan]
CorrectIncorrectHint
\(
\begin{array}{l}
P \text { is the centroid which is } \equiv\left(\frac{1+6+\frac{3}{2}}{3}, \frac{0+2+6}{3}\right) \\
P \equiv\left(\frac{17}{6}, \frac{8}{3}\right) \\
Q \equiv\left(-\frac{7}{6},-\frac{1}{3}\right) \\
\therefore P Q=\sqrt{(4)^2+(3)^2}=5
\end{array}
\) -
Question 78 of 177
78. Question
The locus of the mid-point of the perpendiculars drawn from points on the line, \(x=2 y\) to the line \(x=y\) is: [JEE Main 2020 Jan]
CorrectIncorrectHint
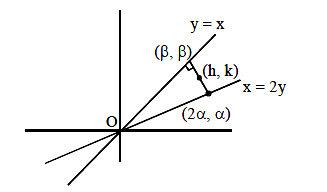
\(
\begin{array}{l}
\text { slope of } P Q=\frac{k-\alpha}{h-2 \alpha}=-1 \\
\Rightarrow k-\alpha=-h+2 \alpha \\
\Rightarrow \alpha=\frac{h+k}{3} \quad \ldots \text { (1) }
\end{array}
\)
Also \(2 h=2 \alpha+\beta\)
\(
2 k=\alpha+\beta
\)
\(
\begin{array}{l}
\Rightarrow 2 h=\alpha+2 k \\
\Rightarrow \alpha=2 h-2 k \dots(2)
\end{array}
\)
from (1) and (2)
\(
\begin{array}{l}
\frac{h+k}{3}=2(h-k) \\
\text { so locus } 6 x-6 y=x+y \Rightarrow 5 x=7 y
\end{array}
\) -
Question 79 of 177
79. Question
Let two points be \(A(1,-1)\) and \(B(0,2)\). If a point \(P\left(x^{\prime}, y^{\prime}\right)\) be such that the area of \(\triangle P A B=5\) square. units and it lies on the line, \(3 x+y-4 \lambda=0\), then a value of \(\lambda\) is : [JEE Main 2020 Jan]
CorrectIncorrectHint
\(
D=\frac{1}{2}\left|\begin{array}{ccc}
0 & 2 & 1 \\
1 & -1 & 1 \\
x^{\prime} & y^{\prime} & 1
\end{array}\right|
\)
\(
\begin{array}{l}
-2\left(1-x^{\prime}\right)+\left(y^{\prime}+x^{\prime}\right)= \pm 10 \\
-2+2 x^{\prime}+y^{\prime}+x^{\prime}= \pm 10 \\
3 x^{\prime}+y^{\prime}=12 \text { or } 3 x^{\prime}+y^{\prime}=-8 \\
\lambda=3,-2
\end{array}
\) -
Question 80 of 177
80. Question
The length of the perpendicular from the origin on the normal to the curve, \(x^2+2 x y-3 y^2=0\) at the point \((2,2)\) is [JEE Main 2020 Jan]
CorrectIncorrectHint
\(
\begin{array}{l}
x^2+2 x y-3 y^2=0 \\
x^2+3 x y-x y-3 y^2=0 \\
(x-y)(x+3 y)=0 \\
x-y=0 \quad x+3 y=0 \\
(2,2) \text { satisfy } x-y=0 \\
\text { Normal } \\
x+y=\lambda \\
\lambda=4 \\
\text { Hence } x+y=0
\end{array}
\)
perpendicular distance from origin \(=\left|\frac{0+0-4}{\sqrt{2}}\right|=2 \sqrt{2}\) -
Question 81 of 177
81. Question
\(A(3,-1), B(1,3), C(2,4)\) are vertices of \(\triangle A B C\) if \(D\) is centroid of \(\triangle A B C\) and \(P\) is point of intersection of lines \(x+3 y-1=0\) and \(3 x-y+1=0\) then which of the following points lies on line joining \(D\) and \(P\) [JEE Main 2020 Jan]
CorrectIncorrectHint
\(
\text { Centroid of } \Delta=(2,2)
\)
line passing through intersection of \(x+3 y-1=0\) and \(3 x-y+1=0\), be given by \((x+3 y-1)+\lambda(3 x-y+1)=0\)
If passes through \((2,2)\) \(\Rightarrow 7+5 \lambda=0 \Rightarrow \lambda=-7 / 5\)
\(\therefore\) Required line is \(8 x-11 y+6=0\)
\(\because(-9,-6)\) satisfies this equation. -
Question 82 of 177
82. Question
The set of all possible values of \(\theta\) in the interval \((0, \pi)\) for which the points \((1,2)\) and \((\sin \theta, \cos \theta)\) lie on the same side of the line \(x+y=1\) is : [JEE Main 2020 Sept]
CorrectIncorrectHint
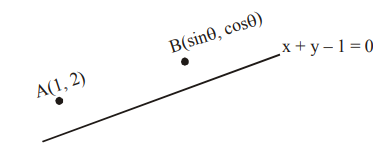
Given that both points \((1,2) \&(\sin \theta, \cos \theta)\) lie on same side of the line \(x+y-1=0\)
\(
\begin{array}{l}
\text { Let } f(x, y)=x+y-1 \\
\because \quad f(1,2) \cdot f(\sin \theta, \cos \theta)>0 \\
\Rightarrow \quad 2[\sin \theta+\cos \theta-1]>0 \\
\Rightarrow \quad \sin \theta+\cos \theta>1 \\
\Rightarrow \quad \sin \left(\theta+\frac{\pi}{4}\right)>\frac{1}{\sqrt{2}} \\
\Rightarrow \quad \theta+\frac{\pi}{4} \in\left(\frac{\pi}{4}, \frac{3 \pi}{4}\right) \\
\Rightarrow \quad \theta \in\left(0, \frac{\pi}{2}\right)
\end{array}
\) -
Question 83 of 177
83. Question
If a \(\triangle \mathrm{ABC}\) has vertices \(\mathrm{A}(-1,7), \mathrm{B}(-7,1)\) and \(\mathrm{C}(5,-5)\), then its orthocentre has coordinates [JEE Main 2020 Sept]
CorrectIncorrectHint
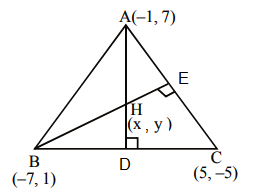
Let \(H(x, y)\) be ortho center of the triangle and let \(A D\) and \(B E\) be lines passing through the orthocenter.
Thus
\(
\begin{aligned}
& m_{A H} \cdot m_{B C}=-1 \\
\Rightarrow & \left(\frac{y-7}{x+1}\right)\left(\frac{-5-1}{5+7}\right)=-1 \\
\Rightarrow & 2 x-y+9=0 \ldots \ldots \ldots(i)
\end{aligned}
\)
and
\(
\begin{array}{c}
m_{B H} \cdot m_{A C}=-1 \\
\Rightarrow\left(\frac{y-1}{x+7}\right)\left(\frac{7-5}{-1-5}\right)=-1 \\
\Rightarrow \quad x-2 y+9=0 \ldots \ldots(i i)
\end{array}
\)
Solving equations (i) and (ii) we get
\(
(x, y)=(-3,3)
\) -
Question 84 of 177
84. Question
A triangle \(A B C\) lying in the first quadrant has two vertices as \(\mathrm{A}(1,2)\) and \(\mathrm{B}(3,1)\). If \(\angle \mathrm{BAC}=\) \(90^{\circ}\), and \(\operatorname{ar}(\triangle \mathrm{ABC})=5 \sqrt{5}\) sq. units, then the abscissa of the vertex \(C\) is : [JEE Main 2020 Sept]
CorrectIncorrectHint
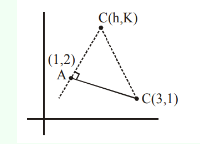
\(
\begin{array}{l}
\left(\frac{K-2}{h-1}\right)\left(\frac{1-2}{3-1}\right)=-1 \\
\Rightarrow K=2 h \ldots(1) \\
\sqrt{5}|h-1|=10 \\
\because[\Delta A B C]=5 \sqrt{5} \\
\Rightarrow \frac{1}{2}(\sqrt{5}) \sqrt{(h-1)^2+(K-2)^2}=5 \sqrt{5} \ldots \text { (2) } \\
\Rightarrow h=2 \sqrt{5}+1(h>0)
\end{array}
\) -
Question 85 of 177
85. Question
If the perpendicular bisector of the line segment joining the points \(P(1,4)\) and \(Q(k, 3)\) has \(y\) intercept equal to -4 , then a value of \(k\) is: [JEE Main 2020 Sept]
CorrectIncorrectHint
Mid point of line segment \(\mathrm{PQ}\) is \(\left(\frac{\mathrm{k}+1}{2}, \frac{7}{2}\right)\)
Slope of PQ is \(\frac{1}{1-\mathrm{k}}\)
So equation of perpendicular bisector of \(P Q\) is
\(
y-\frac{7}{2}=(k-1)\left[x-\frac{k+1}{2}\right]
\)
\(\therefore\) Line passes through \((0,-4)\); then
\(
-\frac{15}{2}=-\frac{\left(k^2-1\right)}{2} \Rightarrow k= \pm 4
\) -
Question 86 of 177
86. Question
If the line, \(2 x-y+3=0\) is at a distance \(\frac{1}{\sqrt{5}}\) and \(\frac{2}{\sqrt{5}}\) from the lines \(4 x-2 y+\alpha=0\) and \(6 x-3 y+\beta=0\), respectively, then the sum of all possible values of \(\alpha\) and \(\beta\) is [JEE Main 2020 Sept]
CorrectIncorrectHint
\(
\begin{array}{l}
L_1: 2 x-y+3=0 \\
L_1: 4 x-2 y+\alpha=0 \\
L_1: 6 x-3 y+\beta=0
\end{array}
\)
Distance between \(L_1\) and \(L_2\)
\(
\begin{array}{l}
\left|\frac{\alpha-6}{2 \sqrt{5}}\right|=\frac{1}{\sqrt{5}} \Rightarrow|\alpha-6|=2 \\
\Rightarrow \alpha=4,8
\end{array}
\)
Distance between \(L_1\) and \(L_3\left|\frac{\beta-9}{3 \sqrt{5}}\right|=\frac{2}{\sqrt{5}} \Rightarrow|\beta-9|=6\)
\(
\Rightarrow \beta=15,3
\)
Sum of all values \(=4+8+15+3=30\) -
Question 87 of 177
87. Question
A ray of light coming from the point \((2,2 \sqrt{3})\) is incident at an angle \(30^{\circ}\) on the line \(x=1\) at the point \(\mathrm{A}\). The ray gets reflected on the line \(x=1\) and meets \(\mathrm{x}\)-axis at the point \(\mathrm{B}\). Then, the line \(\mathrm{AB}\) passes through the point: [JEE Main 2020 Sept]
CorrectIncorrectHint
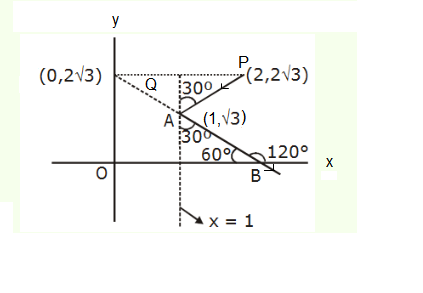
Equation of incident line AP is
\(
\begin{array}{c}
y-2 \sqrt{3}=\sqrt{3}(x-2) \\
\sqrt{3} x-y=0
\end{array}
\)Image of \(P\) w.r.t. line \(x=1\)
is point \(Q=(0,2 \sqrt{3})\)
Equation of reflected Ray \(A B\) :
\(
\begin{array}{l}
y-\sqrt{3}=\frac{2 \sqrt{3}-\sqrt{3}}{0-1}(x-1) \\
\sqrt{3} x+y=2 \sqrt{3}
\end{array}
\)
\(\therefore\) Point \((3,-\sqrt{3})\) lies on line \(A B\) -
Question 88 of 177
88. Question
Let \(L\) denote the line in the \(x y\)-plane with \(x\) and \(y\) intercepts as 3 and 1 respectively. Then the image of the point \((-1,-4)\) in this line is : [JEE Main 2020 Sept]
CorrectIncorrectHint
\(
\begin{array}{l}
\text { Line is } \frac{x}{3}+y=1 \\
x+3 y-3=0
\end{array}
\)Let image be \((\alpha, \beta)\)
Hence, \(\frac{\alpha+1}{1}=\frac{\beta+y}{3}=-\frac{2(-1-12-3)}{10}\)
\(
\begin{array}{l}
\alpha+1=\frac{\beta+4}{3}=\frac{16}{5} \\
\Rightarrow \alpha=\frac{11}{5}, \beta=\frac{28}{5}
\end{array}
\) -
Question 89 of 177
89. Question
Consider the set of all lines \(\mathrm{p} x+\mathrm{q} y+\mathrm{r}=0\) such that \(3 p+2 q+4 r=0\). Which one of the following statements is true? [JEE Main 2019 Jan]
CorrectIncorrectHint
Given, the equation of the set of lines is,
\(
p x+q y+r=0 \dots(i)
\)
such that
\(
3 p+2 q+4 r=0 \dots(ii)
\)
Dividing (ii) by 4 and subtrating from (i)
\(
\Rightarrow\left(x-\frac{3}{4}\right) p+\left(y-\frac{1}{2}\right) q=0
\)
The lines pass through the point \(\left(\frac{3}{4}, \frac{1}{2}\right)\).
Hence, the lines are concurrent at the point \(\left(\frac{3}{4}, \frac{1}{2}\right)\). -
Question 90 of 177
90. Question
Let \(S\) be the set of all triangles in the \(x y\)-plane, each having one vertex at the origin and the other two vertices lie on coordinate axes with integral coordinates. If each triangle in \(\mathrm{S}\) has area 50 sq. units, then the number of elements in the set \(\mathrm{S}\) is: [JEE Main 2019 Jan]
CorrectIncorrectHint
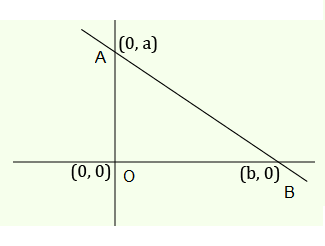
One of the possible \(\triangle O A B\) is \(A(a, 0)\) and \(B(0, b)\). Area of \(\triangle O A B=\frac{1}{2}|a b|\).
\(
\begin{aligned}
\therefore \quad & |a b|=100 \\
& |a||b|=100
\end{aligned}
\)
So the possible pairs \((|a|,|b|)\) are \((1,100),(100,1),(2,50),(50,2),(4,25),(25,4)\),
\(
(5,20),(20,5),(10,10)
\)No. of possible pairs \(=9\)
As we know, one pair can draw 4 triangles,
so the total number of possible triangles \(=9 \times 4=36\) -
Question 91 of 177
91. Question
Let the equations of two sides of a triangle be \(3 x-2 y+6=0\) and \(4 x+5 y-20=0\). If the orthocentre of this triangle is at \((1,1)\), then the equation of its third side is: [JEE Main 2019 Jan]
CorrectIncorrectHint
Let equation of side \(A B: 3 x-2 y+6=0 \dots(1)\)
and equation of side \(B C\) : \(4 x+5 y-20=0 \dots(2)\)
\(\mathrm{O}\) is the orthocentre.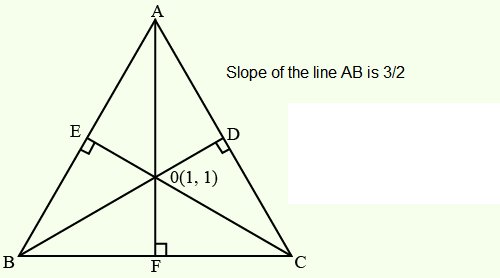
Line \(C E\) is perpendicular to \(A B\)
So, slope of line CE is \(-\frac{2}{3}\)
\(\therefore\) Equation of line \(C E\) is
\(
\begin{array}{l}
(y-1)=-\frac{2}{3}(x-1) \\
\Rightarrow 2 x+3 y-5=0 \dots(3)
\end{array}
\)
From Equations (2) and (3), we obtain ordinate C,
\(
x=\frac{35}{2}, y=-10
\)
Now, slope of line \(B C\) is \(-\frac{4}{5}\)
\(\therefore\) Slope of line AF is \(\frac{5}{4}\)
Thus, Equation of line \(A F\) is
\(
\begin{array}{l}
y-1=\frac{5}{4}(x-1) \\
\Rightarrow 5 x-4 y-1=0 \dots(4)
\end{array}
\)
From Equations (1) and (4), we obtain ordinate A, \(x=-13, y=-\frac{66}{4}\)
\(
\therefore \text { Equation of } A B \text { is } \frac{y+10}{x-\frac{35}{2}}=\frac{-10+\frac{66}{4}}{\frac{35}{2}+13}
\)
\(
26 x-122 y-1675=0
\) -
Question 92 of 177
92. Question
If the lines \(x=a y+\mathrm{b}, z=c y+\mathrm{d}\) and \(x=\mathrm{a}^{\prime} z+\mathrm{b}^{\prime}\), \(y=\mathrm{c}^{\prime} z+\mathrm{d}^{\prime}\) are perpendicular, then: [JEE Main 2019 Jan]
CorrectIncorrectHint
Consider the lines
\(
\begin{array}{l}
x=a y+b, z=c y+d \\
\Rightarrow \frac{x-b}{a}=\frac{y}{1}=\frac{z-d}{c} \\
\therefore \vec{b}_1=a \hat{i}+\hat{j}+c \hat{k}
\end{array}
\)
Now,
\(
\begin{array}{l}
x=a^{\prime} z+b^{\prime}, y=c^{\prime} z+d^{\prime} \\
\Rightarrow \frac{x-b^{\prime}}{a^{\prime}}=\frac{y-d^{\prime}}{c^{\prime}}=\frac{z}{1} \\
\therefore \vec{b}_2=a^{\prime} \hat{i}+c^{\prime} \hat{j}+\hat{k}
\end{array}
\)
The two lines are perpendicular.
\(
\begin{array}{l}
\text { So, } \vec{b}_1 \cdot \vec{b}_2=0 \\
\Rightarrow a a^{\prime}+c^{\prime}+c=0
\end{array}
\) -
Question 93 of 177
93. Question
A point \(\mathrm{P}\) moves on the line \(2 x-3 y+4=0\). If \(\mathrm{Q}(1,4)\) and \(R(3,-2)\) are fixed points, then the locus of the centroid of \(\triangle \mathrm{PQR}\) is a line: [JEE Main 2019 Jan]
CorrectIncorrectHint
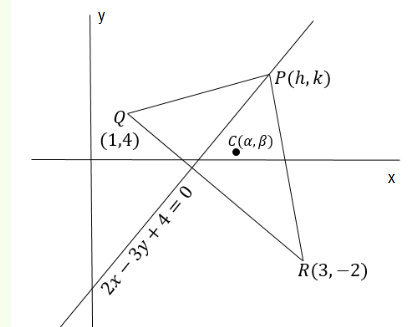
Let the centroid of the \(\triangle P Q R\) is \(C(\alpha, \beta)\)
\(
\begin{array}{l}
\therefore a=\frac{h+1+3}{3} \Rightarrow h=3 a-4 \\
\beta=\frac{4+\mathrm{k}-2}{3} \Rightarrow k=3 \beta-2
\end{array}
\)
\(P(h, k)\) passes through the line \(2 x-3 y+4=0\)
\(
\begin{array}{l}
\therefore 2(3 a-4)-3(3 \beta-2)+4=0 \\
\Rightarrow 6 a-9 \beta+2=0
\end{array}
\)
Hence, the locus is \(6 x-9 y+2=0\)
\(
\therefore \text { slope }=\frac{6}{9}=\frac{2}{3}
\) -
Question 94 of 177
94. Question
If the line \(3 x+4 y-24=0\) intersects the \(x\)-axis at the point \(\mathrm{A}\) and the \(y\)-axis at the point \(\mathrm{B}\), then the incentre of the triangle \(O A B\), where \(O\) is the origin, is: [JEE Main 2019 Jan]
CorrectIncorrectHint
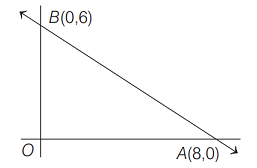
Given equation of line is
\(
3 x+4 y-24=0
\)
For intersection with \(X\)-axis put \(y=0\)
\(
\Rightarrow 3 x-24=0 \Rightarrow x=8
\)For intersection with \(Y\)-axis, put \(x=0\)
\(
\Rightarrow \quad 4 y-24=0 \Rightarrow y=6
\)
Let \(A B=c=\sqrt{(8^2+6^2)}=10\)
\(O B=a=6\) and \(O A=b=8\)
Also, let incentre is \((h, k)\), then
\(
\begin{array}{l}
h=\frac{a x_1+b x_2+c x_3}{a+b+c} \\
=\frac{6 \times 8+8 \times 0+10 \times 0}{6+8+10}=\frac{48}{24}=2 \\
\text { and } k=\frac{a y_1+b y_2+c y_3}{a+b+c} \\
\left(\text { here, } y_1=0, y_2=6, y_3=0\right) \\
=\frac{6 \times 0+8 \times 6+10 \times 0}{6+8+10}=\frac{48}{24}=2 \\
\therefore \text { incentre is }(2,2)
\end{array}
\) -
Question 95 of 177
95. Question
Two sides of a parallelogram are along the lines, \(x+y=3\) and \(x-y+3=0\). If its diagonals intersect at \((2,4)\), then one of its vertex is: [JEE Main 2019 Jan]
CorrectIncorrectHint
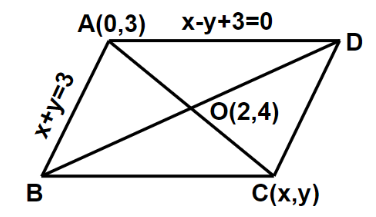
Let the point \(C\) is \((x, y)\)
\(
\begin{array}{l}
x+y=3 \quad \cdots(1) \\
\text { and } x-y+3=0 \quad \cdots(2)
\end{array}
\)
The point of intersection from the equation (1) and (2) is point \(A:(0,3)\) So, if point \(C\) is \((x, y)\) then, \(\frac{x+0}{2}=2 \Rightarrow x=4\) and \(\frac{y+3}{2}=4 \Rightarrow y=5\)
As line \(B C\) and \(A D\) are parrallel
\(\therefore\) slope of line \(B C=1\)
\(\therefore\) equation of \(\mathrm{BC}\) is
\(
\begin{array}{l}
y-5=1(x-4) \\
\Rightarrow x-y+1=0 \dots(3)
\end{array}
\)
As line \(C D\) and \(A B\) are parrallel
\(\therefore\) slope of line \(C D=-1\)
\(\therefore\) equation of \(C D\) is
\(
\begin{array}{l}
y-5=-1(x-4) \\
\Rightarrow x+y=9 \dots(4)
\end{array}
\)
\(
\text { Hence, from (1) and ( } 3 \text { ), point } B \text { is }(1,2) \text { and from ( } 2 \text { ) and (4), point } D \text { is }(3,6 \text { ). }
\) -
Question 96 of 177
96. Question
Two vertices of a triangle are \((0,2)\) and \((4,3)\). If its orthocentre is at the origin, then its third vertex lies in which quadrant? [JEE Main 2019 Jan]
CorrectIncorrectHint
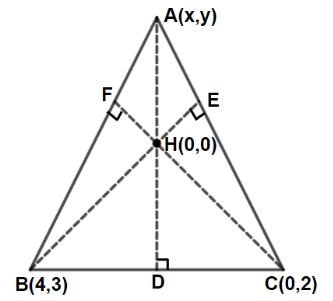
\(
\begin{array}{l}
m_{A D} \cdot m_{B C}=-1 \Rightarrow m_{A H} \cdot m_{B C}=-1 \\
\Rightarrow\left(\frac{y-0}{x-0}\right) \cdot\left(\frac{3-2}{4-0}\right)=-1 \\
\Rightarrow 4 x+y=0 \quad \cdots(1)
\end{array}
\)Now,
\(
\begin{array}{l}
m_{B E} \cdot m_{A C}=-1 \Rightarrow m_{B H} \cdot m_{A C}=-1 \\
\Rightarrow\left(\frac{3-0}{4-0}\right) \cdot\left(\frac{y-2}{x-0}\right)=-1 \\
\Rightarrow 4 x+3 y=6 \quad \cdots(2)
\end{array}
\)
from the equations (1) and (2), we get \(x=-\frac{3}{4}, y=3\)
Hence, Point \((x, y)\) lies in second quadrant. -
Question 97 of 177
97. Question
The straight line \(x+2 y=1\) meets the coordinate axes at \(A\) and B. A circle is drawn through A, B and the origin. Then the sum of perpendicular distances from \(A\) and \(B\) on the tangent to the circle at the origin is : [JEE Main 2019 Jan]
CorrectIncorrectHint
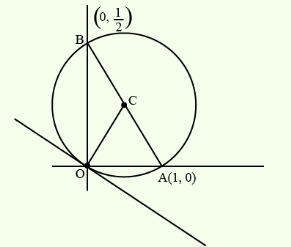
(1)Given line \(A B\) is \(x+2 y=1\)
Slope of line \(A B\)
\(
=-\frac{1}{2}
\)Coordinates of \(A\) and \(B\) are
\(
A=(1,0), B=\left(0, \frac{1}{2}\right)
\)
Co-ordinates of \(\mathrm{C}\)
\(
=\left(\frac{1+0}{2}, \frac{0+\frac{1}{2}}{2}\right)=\left(\frac{1}{2}, \frac{1}{4}\right)
\)Slope of OC
\(
=\frac{0-\frac{1}{4}}{0-\frac{1}{2}}=\frac{1}{2}
\)
\(\therefore\) Slope of tangent \(=-2\)
So, the equation of tangent is
\(
2 \mathrm{x}+\mathrm{y}=0
\)Sum of distance from \(A(1,0)\) and \(B\left(0, \frac{1}{2}\right)\) of tangent
\(
\begin{array}{l}
=\left|\frac{2}{\sqrt{2^2+1^2}}\right|+\left|\frac{\frac{1}{2}}{\sqrt{2^2+1^2}}\right| \\
=\frac{2}{\sqrt{5}}+\frac{\frac{1}{2}}{\sqrt{5}}=\frac{5}{2 \sqrt{5}}=\frac{\sqrt{5}}{2}
\end{array}
\) -
Question 98 of 177
98. Question
If in a parallelogram \(\mathrm{ABDC}\), the coordinates of \(\mathrm{A}, \mathrm{B}\) and \(\mathrm{C}\) are respectively \((1,2),(3,4)\) and \((2,5)\), then the equation of the diagonal \(\mathrm{AD}\) is : [JEE Main 2019 Jan]
CorrectIncorrectHint
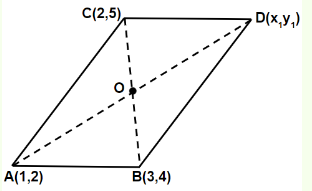
Diagonals of a parallelogram bisect each other.
\(
\begin{array}{l}
\therefore\left(\frac{x_1+1}{2}, \frac{y_1+2}{2}\right)=\left(\frac{3+2}{2}, \frac{5+4}{2}\right) \\
\Rightarrow \frac{x_1+1}{2}=\frac{5}{2} \Rightarrow x_1=4 \\
\text { and } \frac{y_1+2}{2}=\frac{9}{2} \Rightarrow y_1=7
\end{array}
\)
\(\therefore\) Coordinates of \(D\) is \((4,7)\)
\(\therefore\) Equation of \(A D\) is
\(
\frac{y-2}{x-1}=\frac{7-2}{4-1}
\)
\(
\Rightarrow \frac{y-2}{x-1}=\frac{5}{3}
\)
\(
\begin{array}{l}
\Rightarrow 3 y-6=5 x-5 \\
\Rightarrow 5 x-3 y+1=0
\end{array}
\) -
Question 99 of 177
99. Question
A tetrahedron has vertices \(\mathrm{P}(1,2,1), {Q}(2,1,3), {R}(-1,1,2)\) and \(O(0,0,0)\). The angle between the faces OPQ and \(P Q R\) is: [JEE Main 2019 Jan]
CorrectIncorrectHint
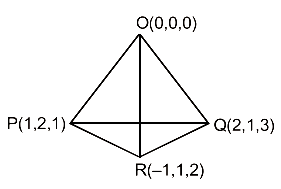
Let \(\vec{v}_1\) and \(\vec{v}_2\) be the vectors perpendicular to the plane \(O P Q\) and \(P Q R\) respectively,
\(
\begin{array}{l}
\vec{v}_1=\overrightarrow{P Q} \times \overrightarrow{O Q}=\left|\begin{array}{lll}
\hat{i} & \hat{j} & \hat{k} \\
1 & 2 & 1 \\
2 & 1 & 3
\end{array}\right| \\
=5 \hat{i}-\hat{j}-3 \hat{k}
\end{array}
\)
\(
\begin{array}{l}
\vec{v}_2=\overrightarrow{P Q} \times \overrightarrow{P R}=\left|\begin{array}{ccc}
\hat{i} & \hat{j} & \hat{k} \\
1 & -1 & 2 \\
-2 & -1 & 1
\end{array}\right| \\
=\hat{i}-5 \hat{j}-3 \hat{k}
\end{array}
\)
\(
\begin{array}{l}
\because \quad \cos \theta=\frac{\vec{v}_1 \cdot \vec{v}_2}{\left|\vec{v}_1\right|\left|\vec{v}_2\right|}=\frac{5+5+9}{25+1+9}=\frac{19}{35} \\
\therefore \quad \theta=\cos ^{-1}\left(\frac{19}{35}\right)
\end{array}
\) -
Question 100 of 177
100. Question
If the straight line, \(2 x-3 y+17=0\) is perpendicular to the line passing through the points \((7,17)\) and \((15, \beta)\), then \(\beta\) equals : [JEE Main 2019 Jan]
CorrectIncorrectHint
Slope of straight line. \(2 x-3 y+17=0\) is \(m_1=\frac{2}{3}\)
Let slope of line passing through \((7,17)\) and \((15, \beta)\) be \(m_2\).
\(
\Rightarrow m_2=\frac{\beta-17}{15-7}
\)Since, both the lines are perpendicular
\(
\begin{array}{l}
\text { So, } m_1 \cdot m_2=-1 \\
\Rightarrow \frac{2}{3} \cdot \frac{\beta-17}{8}=-1 \\
\Rightarrow \beta-17=-12 \\
\Rightarrow \beta=5
\end{array}
\) -
Question 101 of 177
101. Question
If a straight line passing through the point \(P(-3,4)\) is such that its intercepted portion between the coordinate axes is bisected at \(\mathrm{P}\), then its equation is : [JEE Main 2019 Jan]
CorrectIncorrectHint
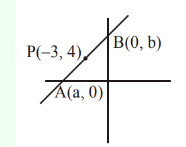
Let the line be \(\frac{x}{a}+\frac{y}{b}=1\)
\(
\begin{array}{l}
(-3,4)=\left(\frac{a}{2}, \frac{b}{2}\right) \\
a=-6, b=8
\end{array}
\)
equation of line is \(4 x-3 y+24=0\) -
Question 102 of 177
102. Question
A point on the straight line, \(3 x+5 y=15\) which is equidistant from the coordinate axes will lie only in : [JEE Main 2019 April]
CorrectIncorrectHint
A point which is equidistant from both the axes lies on either \(y=x\) and \(y=-x\).
Since, point lies on the line \(3 x+5 y=15\)
Then the required point
\(
\begin{array}{l}
3 x+5 y=15 \\
x+y=0 \\
\hline x=-\frac{15}{2}
\end{array}
\)
\(
y=\frac{15}{2} \Rightarrow(x, y)=\left(-\frac{15}{2}, \frac{15}{2}\right)\left\{2^{\text {nd }} \text { quadrant }\right\}
\)
or
\(
\begin{array}{c}
3 x+5 y=15 \\
x-y=0 \\
\hline x=\frac{15}{8}
\end{array}
\)
\(
y=\frac{15}{8} \Rightarrow(x, y)=\left(\frac{15}{8}, \frac{15}{8}\right)\left\{1^{\text {st }} \text { quadrant }\right\}
\)
Hence, the required point lies in \(1^{\text {st }}\) and \(2^{\text {nd }}\) quadrant. -
Question 103 of 177
103. Question
Let \(\mathrm{O}(0,0)\) and \(\mathrm{A}(0,1)\) be two fixed points. Then the locus of a point \(P\) such that the perimeter of \(\triangle A O P\) is 4 , is : [JEE Main 2019 April]
CorrectIncorrectHint
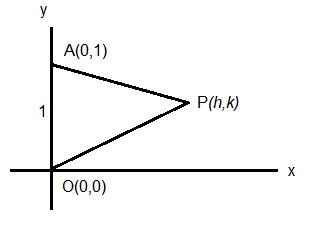
\(
O A+A P+O P=4
\)
Let point \(P(h, k)\)
\(
\begin{array}{l}
\because \\
\text { So, } O P+A P=3 \quad O A=1 \\
\Rightarrow \sqrt{h^2+k^2}+\sqrt{h^2+(k-1)^2}=3
\end{array}
\)
\(
\begin{array}{l}
\Rightarrow h^2+(k-1)^2=9+h^2+k^2-6 \sqrt{h^2+k^2} \\
\Rightarrow 6 \sqrt{h^2+k^2}=2 k+8 \\
\Rightarrow 9 h^2+8 k^2-8 k-16=0
\end{array}
\)
Hence, locus of point \(P\) is
\(
9 x^2+8 y^2-8 y-16=0
\) -
Question 104 of 177
104. Question
Suppose that the points \((h, k),(1,2)\) and \((-3,4)\) lie on the line \(\mathrm{L}_1\). If a line \(\mathrm{L}_2\) passing through the points \((h, k)\) and \((4,3)\) is perpendicular on \(\mathrm{L}_1\), then \(\frac{k}{h}\) equals : [JEE Main 2019 April]
CorrectIncorrectHint
\((h, k),(1,2)\) and \((-3,4)\) are collinear
\(
\begin{array}{l}
\therefore\left|\begin{array}{lll}
h & k & 1 \\
1 & 2 & 1 \\
-3 & 4 & 1
\end{array}\right|=0 \Rightarrow-2 h-4 k+10=0 \\
\Rightarrow h+2 k=5 \dots(i) \\
\text { Now, } m_{L_1}=\frac{4-2}{-3-1}=-\frac{1}{2} \Rightarrow m_{L_2}=2 \quad\left[\because L_1 \perp L_2\right]
\end{array}
\)By the given points \((h, k)\) and \((4,3)\),
\(
\begin{array}{l}
m_{L_2}=\frac{k-3}{h-4} \Rightarrow \frac{k-3}{h-4}=2 \Rightarrow k-3=2 h-8 \\
2 h-k=5 \dots(ii)
\end{array}
\)From (i) and (ii)
\(
h=3, k=1 \Rightarrow \frac{k}{h}=\frac{1}{3}
\) -
Question 105 of 177
105. Question
Slope of a line passing through \(\mathrm{P}(2,3)\) and intersecting the line \(x+y=7\) at a distance of 4 units from \(P\), is: [JEE Main 2019 April]
CorrectIncorrectHint
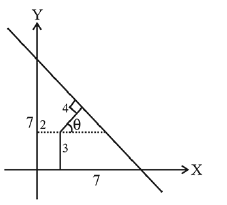
Since point at 4 units from \(P(2,3)\) will be \(\mathrm{A}(4 \cos \theta+2,4 \sin (\theta+3)\) and this point will satisfy the equation of line \(x+y=7\)
\(
\Rightarrow \cos \theta+\sin \theta=\frac{1}{2}
\)On squaring
\(
\begin{array}{l}
\Rightarrow \sin 2 \theta-\frac{3}{4} \Rightarrow \frac{2 \tan \theta}{1+\tan ^2 \theta}=-\frac{3}{4} \\
\Rightarrow 3 \tan ^2 \theta+8 \tan \theta+3=0 \\
\Rightarrow \tan \theta=\frac{-8 \pm 2 \sqrt{7}}{6} \quad \text { (ignoring – ve sign) } \\
\Rightarrow \tan \theta=\frac{-8+2 \sqrt{7}}{6}=\frac{1-\sqrt{7}}{1+\sqrt{7}}
\end{array}
\) -
Question 106 of 177
106. Question
If the two lines \(x+(a-1) y=1\) and \(2 x+a^2 y=1(a \in \mathbf{R}-\{0,1\})\) are perpendicular, then the distance of their point of intersection from the origin is: [JEE Main 2019 April]
CorrectIncorrectHint
\(\because\) two lines are perpendicular \(\Rightarrow m_1 m_2=-1\)
\(
\begin{array}{l}
\Rightarrow\left(\frac{-1}{a-1}\right)\left(\frac{-2}{a^2}\right)=-1 \\
\Rightarrow 2=a^2(1-a) \Rightarrow a^3-a^2+2=0 \\
\Rightarrow(a+1)\left(a^2+2 a+2\right)=0 \Rightarrow a=-1
\end{array}
\)Hence equations of lines are \(x-2 y=1\) and \(2 x+y=1\)
\(\therefore\) intersection point is \(\left(\frac{3}{5}, \frac{-1}{5}\right)\)
Now, distance from origin \(=\sqrt{\frac{9}{25}+\frac{1}{25}}=\sqrt{\frac{10}{25}}=\sqrt{\frac{2}{5}}\) -
Question 107 of 177
107. Question
A rectangle is inscribed in a circle with a diameter lying along the line \(3 y=x+7\). If the two adjacent vertices of the rectangle are \((-8,5)\) and \((6,5)\), then the area of the rectangle (in sq. units) is: [JEE Main 2019 April]
CorrectIncorrectHint
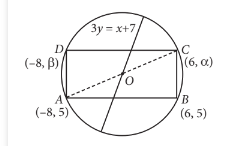
Let the vertices of the rectangle are \(\mathrm{A}(-8,5), \mathrm{B}(6,5), \mathrm{C}(6, \alpha)\) and \(\mathrm{D}(-8, \beta)\). So, coordinates of mid point of diameter \(\mathrm{AC}\) are \(\left(\frac{-8+6}{2}, \frac{\alpha+5}{2}\right)=\left(-1, \frac{\alpha+5}{2}\right)\)
It lies on the line, \(3 y=x+7\)
\(
\begin{array}{l}
\Rightarrow 3\left(\frac{\alpha+5}{2}\right)=-1+7 \\
\Rightarrow \alpha+5=\frac{6 \times 2}{3} \Rightarrow \alpha=-1 \\
\text { Now, } \mathrm{AB}=\sqrt{(-8-6)^2+0}=14 \\
\mathrm{BC}=\sqrt{0+(5+1)^2}=6
\end{array}
\)Sides of rectangle are 14 and 6 .
Hence, area of rectangle \(=14 \times 6=84\) sq. units. -
Question 108 of 177
108. Question
Lines are drawn parallel to the line \(4 x-3 y+2=0\), at a distance \(\frac{3}{5}\) from the origin. Then which one of the following points lies on any of these lines ? [JEE Main 2019 April]
CorrectIncorrectHint
Equation of line parallel to the line
\(
4 x-3 y+2=0 \text { is } 4 x-3 y+\lambda=0 \dots(1)
\)Distance of line from the origin is
\(
\begin{array}{l}
\left|\frac{4(0)-3(0)+\mid \lambda}{\sqrt{4^2+(-3)^3}}\right|=\frac{3}{5} \\
\Rightarrow \lambda= \pm 3
\end{array}
\)
putting the value of \(\lambda\) in equation (1)
\(\therefore\) the required lines are \(4 x-3 y+3=0\) and \(4 x-3 y-3=0\)
Point \(\left(-\frac{1}{4}, \frac{2}{3}\right)\) satisfies the line \(4 x-3 y+3=0\) -
Question 109 of 177
109. Question
The equation \(y=\sin x \sin (x+2)-\sin ^2(x+1)\) represents a straight line lying in : [JEE Main 2019 April]
CorrectIncorrectHint
Consider the equation,
\(
\begin{array}{l}
y=\sin x \cdot \sin (x+2)-\sin ^2(x+1) \\
=\frac{1}{2} \cos (-2)-\frac{\cos (2 x+2)}{2}-\left[\frac{1-\cos (2 x+2)}{2}\right] \\
=\frac{(\cos 2)-1}{2}=-\sin ^2 1
\end{array}
\)
\(
\text { By the graph } y \text { lies in III and IV quadrant. }
\) -
Question 110 of 177
110. Question
A triangle has a vertex at \((1,2)\) and the mid points of the two sides through it are \((-1,1)\) and \((2,3)\). Then the centroid of this triangle is : [JEE Main 2019 April]
CorrectIncorrectHint
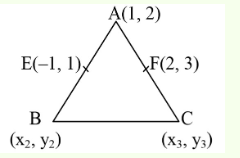
As \(E\) is the midpoint of \(A B\), we get
\(
\begin{array}{l}
\frac{\mathrm{x}_2+1}{2}=-1, \quad \frac{\mathrm{y}_2+2}{2}=1 \\
\Rightarrow \mathrm{x}_2=-3, \mathrm{y}_2=0
\end{array}
\)Point \(B\) is \((-3,0)\)
Similarly, point \(C\) is \((3,4)\)
So, centroid of the triangle is
\(
\left(\frac{1-3+3}{3}, \frac{2+0+4}{3}\right)=\left(\frac{1}{3}, 2\right)
\) -
Question 111 of 177
111. Question
A straight line \(\mathrm{L}\) at a distance of 4 units from the origin makes positive intercepts on the coordinate axes and the perpendicular from the origin to this line makes an angle of \(60^{\circ}\) with the line \(x+y=0\). Then an equation of the line \(\mathrm{L}\) is: [JEE Main 2019 April]
CorrectIncorrectHint
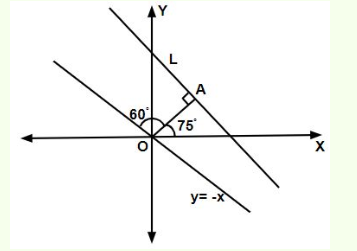
Given \(O A=p=4\)
\(x+y=0\) makes an angle of \(135^{\circ}\) with the positive \(x\)-axis because \(\tan \theta=\) slope of line \(x+y=0 \Rightarrow y=-x\) comparing with \(y=m x\), we get slope \(m=-1\)
\(
\begin{array}{l}
\Rightarrow \tan \theta_1=-1 \\
\Rightarrow \tan \theta_1=\tan 135^{\circ} \\
\therefore \theta_1=135^{\circ}
\end{array}
\)Thus, line OA makes an angle of \(135-60=75^{\circ}\) with the \(x\)-axis.
Equation of the line \(L\) in perpendicular form is \(x \cos \theta+y \sin \theta=p\)
\(
\begin{array}{l}
\Rightarrow \mathrm{x} \cos 75^{\circ}+\mathrm{y} \sin 75^{\circ}=\mathrm{p} \\
\Rightarrow {x}\left(\frac{\sqrt{3}-1}{2 \sqrt{2}}\right)+{y}\left(\frac{\sqrt{3}+1}{2 \sqrt{2}}\right)=4
\end{array}
\)
\(\therefore x(\sqrt{3}-1)+y(\sqrt{3}+1)=8 \sqrt{2}\) is the required equation. -
Question 112 of 177
112. Question
A straight line through a fixed point \((2,3)\) intersects the coordinate axes at distinct points \(\mathrm{P}\) and \(\mathrm{Q}\). If \(\mathrm{O}\) is the origin and the rectangle OPRQ is completed, then the locus of \(R\) is : [JEE Main 2018]
CorrectIncorrectHint
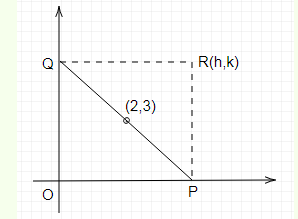
Finding the locus of \(R\)
The general equation of straight line through point is \(\frac{x}{h}+\frac{y}{k}=1\)
where \(h\) is the \(x\)-intercept and \(k\) is the \(y\)-intercept.
The line passes through \((2,3)\), so we get
\(
\begin{aligned}
\Rightarrow & \frac{2}{h}+\frac{3}{k}=1 \\
& 2 k+3 h=h k
\end{aligned}
\)Now substitute \(h\) as \(x\) and \(k\) as \(y\), we get the locus of \(R\) as
\(
\Rightarrow 3 x+2 y=x y
\) -
Question 113 of 177
113. Question
The sides of a rhombus \(A B C D\) are parallel to the lines, \(x-y+2=0\) and \(7 x-y+3=\) 0 . If the diagonals of the rhombus intersect \(P(1,2)\) and the vertex \(A\) (different from the origin) is on the \(y\)-axis, then the coordinate of \(A\) is : [JEE Main 2018 April]
CorrectIncorrectHint
From the given data, we plot the graph below.
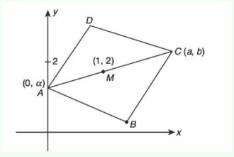
Now, midpoint of \(A C\) is
\(
\begin{array}{l}
\frac{a+0}{2}=1 \Rightarrow a=2 \\
\frac{b+\alpha}{2}=2 \Rightarrow b+\alpha=4
\end{array}
\)Sides of rhombus are parallel to the lines \(x-y+2=0\) and \(7 x-y+3=0\).
Equation of parallel lines to diagonals
\(
\frac{x-y+2}{\sqrt{2}} \pm \frac{7 x-y+3}{5 \sqrt{2}} \Rightarrow 2 x+4 y-7=0 \text { and } 12 x-6 y+13=0
\)So, slope \(=\frac{-1}{2}\) and \(2=\) slope of \(A C\)
Therefore, \(\frac{2-\alpha}{1-0}=\frac{-1}{2}\) or \(2 \Rightarrow 2-\alpha=-\frac{1}{2}\) or \(2 \Rightarrow \alpha=\frac{5}{2}\) or 0
Therefore, ordinate of \(A\) is \(\frac{5}{2}\). -
Question 114 of 177
114. Question
The foot of the perpendicular drawn from the origin, on the line, \(3 x+y=\lambda(\lambda \neq 0)\) is \(P\). If the line meets \(x\)-axis at \(A\) and \(y\)-axis at \(B\), then the ratio \(B P: P A\) is : [JEE Main 2018 April]
CorrectIncorrectHint
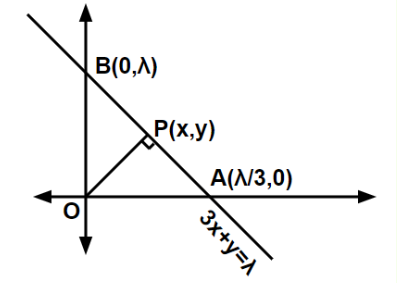
Let the equation of line is
\(
3 x+y=\lambda \quad \ldots \text { (1) }
\)
\(
\begin{array}{l}
\text { slope of } A B=-3 \\
\therefore \text { slope of } O P=\frac{1}{3}
\end{array}
\)
Equation of OP is
\(
\begin{array}{l}
y-0=\frac{1}{3}(x-0) \\
\Rightarrow x=3 y
\end{array}
\)
Put in equation (1)
\(
\begin{array}{l}
\Rightarrow 9 y+y=\lambda \\
\Rightarrow y=\frac{\lambda}{10}
\end{array}
\)
Suppose \(P\) divides \(A B\) into \(m\) : \(n\)
\(
\begin{array}{l}
\therefore \frac{3 \lambda}{10}=\frac{m \cdot 0+n \cdot \frac{\lambda}{3}}{m+n} \\
\Rightarrow \frac{m}{n}=\frac{1}{9}
\end{array}
\)
Hence, \(B P: A P=n: m=9: 1\) -
Question 115 of 177
115. Question
In a triangle \(A B C\), coordinates of \(A\) are \((1,2)\) and the equations of the medians through \(B\) and \(C\) are respectively, \(x+y=5\) and \(x=4\). Then area of \(\triangle A B C\) (in sq. units) is: [JEE Main April 15]
CorrectIncorrectHint
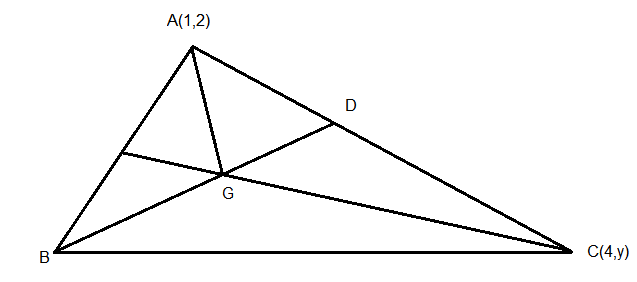
Median through \(\mathrm{C}\) is \(\mathrm{x}=4\)
So the coordinate of \(C\) is 4 . Let \(C=(4, y)\), then the midpoint of \(A(1,2)\) and \(C(4, y)\) is \(D\) which lies on the median through \(B\).
\(
\therefore \quad \mathrm{D}=\left(\frac{1+4}{2}, \frac{2+y}{2}\right)
\)
Now, \(\frac{1+4+2+y}{2}=5 \Rightarrow \mathrm{y}=3\).
So, \(C \equiv(4,3)\).
The centroid of the triangle is the intersection of the medians, Here the medians \(x=4\) and \(x+4\) and \(x+y=5\) intersect at \(G(4,1)\).
The area of triangle \(\triangle \mathrm{ABC}=3 \times \Delta \mathrm{AGC}\)
\(
=3 \times \frac{1}{2}[1(1-3)+4(3-2)+4(2-1)]=9
\) -
Question 116 of 177
116. Question
A square, of each side 2 , lies above the \(x\)-axis and has one vertex at the origin. If one of the sides passing through the origin makes an angle \(30^{\circ}\) with the positive direction of the \(x\)-axis, then the sum of the \(x\)-coordinates of the vertices of the square is : [JEE April 9, 2017]
CorrectIncorrectHint
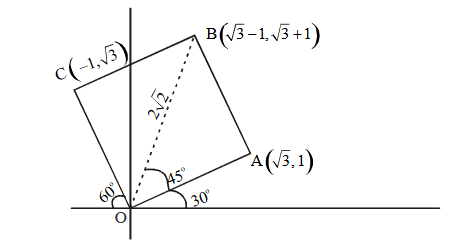
A coordinates \(\Rightarrow\left(2 \cos 30^{\circ}, 2 \sin 30^{\circ}\right)\)
\(\mathrm{C}\) coordinates \(\Rightarrow\left(-2 \cos 60^{\circ}, 2 \sin 60^{\circ}\right)\)
B coordinates \(\Rightarrow\left(2 \sqrt{2} \cos 75^{\circ}, 2 \sqrt{2} \sin 75^{\circ}\right)\)
O coordinates \(\Rightarrow (0,0)\)
Sum at \(x\) coordinates \(=2 \cos 30^{\circ}-2 \cos 60^{\circ}+2 \sqrt{2} \cos 75^{\circ}\)
\(
\begin{array}{l}
=2\left(\frac{\sqrt{3}}{2}\right)-2\left(\frac{1}{2}\right)+2 \sqrt{2}\left(\frac{\sqrt{3}-1}{2 \sqrt{2}}\right) \\
=\sqrt{3}-1+\sqrt{3}-1=2 \sqrt{3}-2
\end{array}
\) -
Question 117 of 177
117. Question
A ray of light is incident along a line which meets another line, \(7 x-y+1=0\), at the point \((0,1)\). The ray is then reflected from this point along the line, \(y+2 x=1\). Then the equation of the line of incidence of the ray of light is: [JEE April 10, 2016]
CorrectIncorrectHint
Let slope of incident ray be \(m\).
\(\therefore\) angle of incidence \(=\) angle of reflection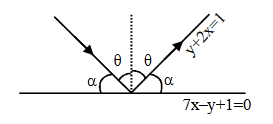
\(
\therefore \quad\left|\frac{m-7}{1+7 m}\right|=\left|\frac{-2-7}{1-14}\right|=\frac{9}{13}
\)
\(
\begin{array}{l}
\Rightarrow \frac{m-7}{1+7 m}=\frac{9}{13} \text { or } \frac{m-7}{1+7 m}=-\frac{9}{13} \\
\Rightarrow 13 m-91=9+63 m \text { or } 13 m-91=-9-63 m \\
\Rightarrow 50 m=-100 \text { or } 76 m=82 \\
\Rightarrow \quad m=-\frac{1}{2} \quad \text { or } \quad m=\frac{41}{38}
\end{array}
\)
\(
y-1=-\frac{1}{2}(x-0) \quad \text { or } \quad y-1=\frac{41}{38}(x-0)
\)
\(
\begin{array}{l}
\text { i.e } x+2 y-2=0 \quad \text { or } \quad 38 y-38-41 x=0 \\
41 x-38 y+38=0
\end{array}
\) -
Question 118 of 177
118. Question
Let \(L\) be the line passing through the point \(P(1,2)\) such that its intercepted segment between the co-ordinate axes is bisected at \(P\). If \(L_1\) is the line perpendicular to \(L\) and passing through the point \((-2,1)\), then the point of intersection of \(\mathrm{L}\) and \(\mathrm{L}_1\) is: [JEE April 10, 2015]
CorrectIncorrectHint
Equation of line \(L\)
\(
\begin{array}{l}
\frac{x}{2}+\frac{y}{4}=1 \dots(1) \\
2 x+y=4
\end{array}
\)
For line
\(
x-2 y=-4 \dots(2)
\)
solving equation (1) and (2); we get point of intersection
\(
\left(4 / 5, \frac{12}{5}\right)
\) -
Question 119 of 177
119. Question
The points \(\left(0, \frac{8}{3}\right),(1,3)\) and \((82,30)\) : [JEE April 10, 2015]
CorrectIncorrectHint
\(
\mathrm{A}\left(0, \frac{8}{3}\right), \mathrm{B}(1,3), \mathrm{C}(89,30)
\)Slope of \(A B=\frac{1}{3}\)
Slope of \(B C=\frac{1}{3}\)
So, the points lies on the same line. -
Question 120 of 177
120. Question
The \(x\)-coordinate of the incentre of the triangle that has the coordinates of mid points of its sides as \((0,1)(1,1)\) and \((1,0)\) is :[JEE 2013]
CorrectIncorrectHint
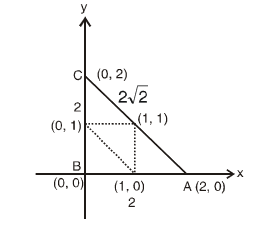
From the figure, we have
\(
\begin{array}{l}
a=2, b=2 \sqrt{2}, c=2 \\
x_1=0, x_2=0, x_3=2
\end{array}
\)
Now, \(x\)-co-ordinate of incentre is given as
\(
\begin{array}{l}
\frac{a x_1+b x_2+c x_3}{a+b+c} \\
\Rightarrow x \text {-coordinate of incentre } \\
=\frac{2 \times 0+2 \sqrt{2} \cdot 0+2.2}{2+2+2 \sqrt{2}} \\
=\frac{2}{2+\sqrt{2}}=2-\sqrt{2}
\end{array}
\) -
Question 121 of 177
121. Question
A light ray emerging from the point source placed at \(P(1,3)\) is reflected at a point \(Q\) in the axis of \(x\). If the reflected ray passes through the point \(R(6,7)\), then the abscissa of \(Q\) is: [JEE April 9, 2013]
CorrectIncorrectHint
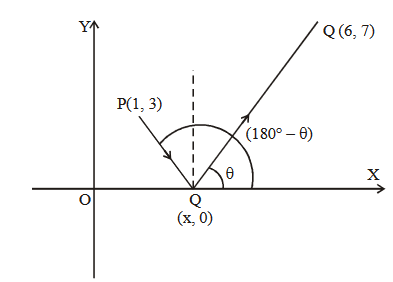
Let abcissa of \(\mathrm{Q}=x\)
\(
\begin{array}{l}
\therefore \quad \mathrm{Q}=(x, 0) \\
\tan \theta=\frac{0-7}{x-6}, \tan \left(180^{\circ}-\theta\right)=\frac{0-3}{x-1}
\end{array}
\)Now, \(\tan \left(180^{\circ}-\theta\right)=-\tan \theta\)
\(
\therefore \frac{-3}{x-1}=\frac{-7}{x-6} \Rightarrow x=\frac{5}{2}
\) -
Question 122 of 177
122. Question
Let \(A(h, k), B(1,1)\) and \(C(2,1)\) be the vertices of a right angled triangle with \(\mathrm{AC}\) as its hypotenuse. If the area of the triangle is 1 square unit, then the set of values which ‘ \(\mathrm{k}\) ‘ can take is given by [JEE 2007]
CorrectIncorrectHint
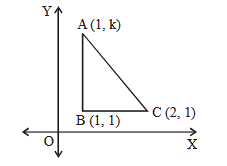
Given : The vertices of a right angled triangle \(\mathrm{A}(1, \mathrm{k})\), \(\mathrm{B}(1,1)\) and \(\mathrm{C}(2,1)\) and Area of \(\triangle A B C=1\) square unit
We know that, area of right angled triangle
\(
\begin{array}{l}
=\frac{1}{2} \times \mathrm{BC} \times \mathrm{AB}=1=\frac{1}{2}(1)|(\mathrm{k}-1)| \\
\Rightarrow \pm(k-1)=2 \Rightarrow \mathrm{k}=-1,3
\end{array}
\) -
Question 123 of 177
123. Question
If a vertex of a triangle is \((1,1)\) and the mid points of two sides through this vertex are \((-1,2)\) and \((3,2)\) then the centroid of the triangle is [JEE 2005]
CorrectIncorrectHint
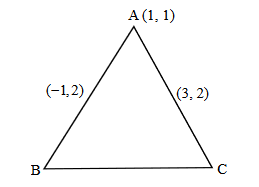
Vertex of triangle is \((1,1)\) and midpoint of sides through this vertex is \((-1,2)\) and \((3,2)\)
\(\Rightarrow\) vertex \(B\) and \(C\) come out to be \((-3,3)\) and \((5,3)\)
\(\therefore\) Centroid is \(\frac{1-3+5}{3}, \frac{1+3+5}{3}\)
\(
\Rightarrow\left(1, \frac{7}{3}\right)
\) -
Question 124 of 177
124. Question
If the equation of the locus of a point equidistant from the point \(\left(a_1, b_1\right)\) and \(\left(a_2, b_2\right)\) is \(\left(a_1-b_2\right) x+\left(a_1-b_2\right) y+c=0\), then the value of ‘ \(c\) ‘ is [JEE 2003]
CorrectIncorrectHint
\(
\begin{array}{l}
\left(x-a_1\right)^2+\left(y-b_1\right)^2=\left(x-a_2\right)^2+\left(y-b_2\right)^2 \\
\left(a_1-a_2\right) x+\left(b_1-b_2\right) y \\
\quad+\frac{1}{2}\left(a_2{ }^2+b_2{ }^2-a_1{ }^2-b_1{ }^2\right)=0 \\
c=\frac{1}{2}\left(a_2{ }^2+b_2{ }^2-a_1{ }^2-b_1{ }^2\right)
\end{array}
\) -
Question 125 of 177
125. Question
Locus of centroid of the triangle whose vertices are \((a \cos t, a \sin t),(b \sin t,-b \cos t)\) and \((1,0)\), where \(t\) is a parameter, is [JEE 2003]
CorrectIncorrectHint
\(
\begin{array}{l}
x=\frac{a \cos t+b \sin t+1}{3} \\
\Rightarrow a \cos t+b \sin t=3 x-1 \\
y=\frac{a \sin t-b \cos t}{3} \\
\Rightarrow a \sin t-b \cos t=3 y
\end{array}
\)Squaring and adding,
\(
(3 x-1)^2+(3 y)^2=a^2+b^2
\) -
Question 126 of 177
126. Question
A triangle with vertices \((4,0),(-1,-1),(3,5)\) is [JEE 2002]
CorrectIncorrectHint
\(
\begin{array}{l}
A B=\sqrt{(4+1)^2+(0+1)^2}=\sqrt{26} ; \\
B C=\sqrt{(3+1)^2+(5+1)^2}=\sqrt{52} \\
C A=\sqrt{(4-3)^2+(0-5)^2}=\sqrt{26}
\end{array}
\)In isosceles triangle side \(A B=C A\)
For right angled triangle, \(B C^2=A B^2+A C^2\)
So, here \(B C=\sqrt{52}\) or \(B C^2=52\)
or \(\quad(\sqrt{26})^2+(\sqrt{26})^2=52\)
So, the given triangle is right angled and also isosceles. -
Question 127 of 177
127. Question
Two sides of a rhombus are along the lines, \(x-y+1=0\) and \(7 x-y-5=0\). If its diagonals intersect at \((-1,-2)\), then which one of the following is a vertex of this rhombus? [JEE 2016]
CorrectIncorrectHint
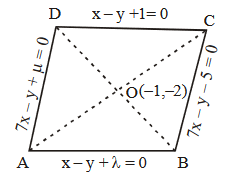
Let other two sides of rhombus are
\(
\mathrm{x}-\mathrm{y}+\lambda=0
\)
and \(7 x-y+\mu=0\)
then \(O\) is equidistant from \(A B\) and \(D C\) and from \(A D\) and \(B C\)
\(
\begin{array}{l}
\therefore|-1+2+1|=|-1+2+\lambda| \Rightarrow \lambda=-3 \\
\text { and }|-7+2-5|=|-7+2+\mu| \Rightarrow \mu=15
\end{array}
\)
\(\therefore\) Other two sides are \(x-y-3=0\) and \(7 x-y+15=0\)
On solving the equations of sides pairwise, we get
the vertices as \(\left(\frac{1}{3}, \frac{-8}{3}\right),(1,2),\left(\frac{-7}{3}, \frac{-4}{3}\right),(-3,-6)\) -
Question 128 of 177
128. Question
A straight line through origin \(O\) meets the lines \(3 y=10-4 x\) and \(8 x+6 y+5=0\) at points \(A\) and \(B\) respectively. Then \(O\) divides the segment \(A B\) in the ratio :[JEE April 10, 2016]
CorrectIncorrectHint
Length of \(\perp\) to \(4 x+3 y=10\) from origin \((0,0)\)
\(
P_1=\frac{10}{5}=2
\)Length of \(\perp\) to \(8 x+6 y+5=0\) from origin \((0,0)\)
\(
P_2=\frac{5}{10}=\frac{1}{2}
\)Lines are parallel to each other \(\Rightarrow\) ratio will be \(4: 1\) or \(1: 4\)
-
Question 129 of 177
129. Question
If a variable line drawn through the intersection of the lines \(\frac{x}{3}+\frac{y}{4}=1\) and \(\frac{x}{4}+\frac{y}{3}=1\), meets the coordinate axes at \(A\) and \(B,(A \neq B)\), then the locus of the midpoint of \(A B\) is : [JEE April 9, 2016]
CorrectIncorrectHint
\(
\begin{array}{l}
L_1: 4 x+3 y-12=0 \\
L_2: 3 x+4 y-12=0 \\
L_1+\lambda L_2=0 \\
(4 x+3 y-12)+\lambda(3 x+4 y-12)=0 \\
x(4+3 \lambda)+y(3+4 \lambda)-12(1+\lambda)=0 \\
\text { Point A }\left(\frac{12(1+\lambda)}{4+3 \lambda}, 0\right)
\end{array}
\)
\(
\begin{array}{l}
\text { Point B }\left(0, \frac{12(1+\lambda)}{3+4 \lambda}\right) \\
\text { mid point } \Rightarrow h=\frac{6(1+\lambda)}{4+3 \lambda} \dots(i) \\
\quad k=\frac{6(1+\lambda)}{3+4 \lambda} \dots(ii)
\end{array}
\)
Eliminate \(\lambda\) from (i) and (ii), then
\(
\begin{array}{l}
6(h+k)=7 h k \\
6(x+y)=7 x y
\end{array}
\) -
Question 130 of 177
130. Question
The point \((2,1)\) is translated parallel to the line \(L: x-y=4\) by \(2 \sqrt{3}\) units. If the new points \(Q\) lies in the third quadrant, then the equation of the line passing through \(Q\) and perpendicular to \(\mathrm{L}\) is : [JEE April 9, 2016]
CorrectIncorrectHint
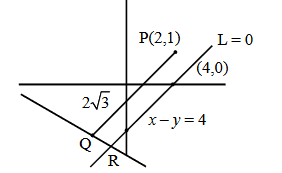
\(
x-y=4
\)
To find equation of \(R\)
slope of \(L=0\) is 1
slope of \(\mathrm{QR}=-1\)
Let \(\mathrm{QR}\) is \(y=m x+c\)
\(
\begin{array}{l}
y=-x+c \\
x+y-c=0
\end{array}
\)
distance of \(Q R\) from \((2,1)\) is \(2 \sqrt{3}\)
\(
2 \sqrt{3}=\frac{|2+1-c|}{\sqrt{2}}
\)
\(
\begin{array}{l}
2 \sqrt{6}=|3-c| \\
c-3= \pm 2 \sqrt{6} c=3 \pm 2 \sqrt{6} \\
\text { Line can be } x+y=3 \pm 2 \sqrt{6} \\
x+y=3-2 \sqrt{6}
\end{array}
\) -
Question 131 of 177
131. Question
A straight line \(L\) through the point \((3,-2)\) is inclined at an angle of \(60^{\circ}\) to the line \(\sqrt{3} x+y=1\). If \(L\) also intersects the \(x\)-axis, then the equation of \(L\) is : [JEE April 11, 2015]
CorrectIncorrectHint
Given eqn of line is \(y+\sqrt{3} x-1=0\)
\(
\begin{array}{l}
\Rightarrow \mathrm{y}=-\sqrt{3} \mathrm{x}+1 \\
\Rightarrow \text { (slope) } \mathrm{m}_2=-\sqrt{3}
\end{array}
\)Let the other slope be \(m_1\)
\(
\begin{array}{l}
\therefore \tan 60^{\circ}=\left|\frac{\mathrm{m}_1-(-\sqrt{3})}{1+\left(-\sqrt{3} \mathrm{~m}_1\right)}\right| \\
\Rightarrow \mathrm{m}_1=0, \mathrm{~m}_2=\sqrt{3}
\end{array}
\)Since line \(L\) is passing through \((3,-2)\)
\(
\begin{array}{l}
\therefore \mathrm{y}-(-2)=+\sqrt{3}(\mathrm{x}-3) \\
\Rightarrow \mathrm{y}+2=\sqrt{3}(\mathrm{x}-3) \\
\mathrm{y}-\sqrt{3} \mathrm{x}+2+3 \sqrt{3}=0
\end{array}
\) -
Question 132 of 177
132. Question
The circumcentre of a triangle lies at the origin and its centroid is the mid point of the line segment joining the points \(\left(a^2+1, a^2+1\right)\) and \((2 a,-2 a), a \neq 0\). Then for any \(a\), the orthocentre of this triangle lies on the line: [JEE April 19, 2014]
CorrectIncorrectHint
\(
\begin{array}{l}
\text { Circumcentre }=(0,0) \\
\text { Centroid }=\left(\frac{(a+1)^2}{2}, \frac{(a-1)^2}{2}\right)
\end{array}
\)
We know the circumcentre \((\mathrm{O})\),
Centroid \((\mathrm{G})\) and orthocentre \((\mathrm{H})\) of a triangle lie on the line joining the \(\mathrm{O}\) and \(\mathrm{G}\).Also, \(\frac{\mathrm{HG}}{\mathrm{GO}}=\frac{2}{1}\)
\(\Rightarrow\) Coordinate of orthocentre \(=\frac{3(a+1)^2}{2}, \frac{3(a-1)^2}{2}\)
Now, these coordinates satisfies eqn given in option (d)
Hence, required eqn of line is
\(
(a-1)^2 x-(a+1)^2 y=0
\) -
Question 133 of 177
133. Question
If a line intercepted between the coordinate axes is trisected at a point \(A(4,3)\), which is nearer to \(x\)-axis, then its equation is: [JEE April 12, 2014]
CorrectIncorrectHint
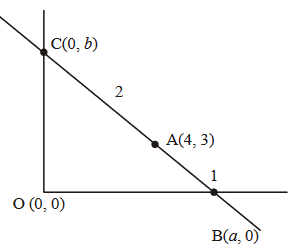
A divides \(C B\) in \(2: 1\)
\(
\Rightarrow 4=\left(\frac{1 \times 0+2 \times a}{1+2}\right)=\frac{2 a}{3}
\)
\(\Rightarrow a=6 \Rightarrow\) coordinate of \(\mathrm{B}\) is \(\mathrm{B}(6,0)\)
\(
3=\left(\frac{1 \times b+2 \times 0}{1+2}\right)=\frac{b}{3}
\)
\(
\Rightarrow b=9 \text { and } C(0,9)
\)Slope of line passing through \((6,0),(0,9)\) slope, \(m=\frac{9}{-6}=-\frac{3}{2}\)
Equation of line \(y-0=\frac{-3}{2}(x-6)\)
\(
\begin{array}{l}
2 y=-3 x+18 \\
3 x+2 y=18
\end{array}
\) -
Question 134 of 177
134. Question
Given three points \(P, Q, R\) with \(P(5,3)\) and \(R\) lies on the \(x\)-axis. If equation of \(R Q\) is \(x-2 y=2\) and \(P Q\) is parallel to the \(x\)-axis, then the centroid of \(\triangle P Q R\) lies on the line: [JEE April 9, 2014]
CorrectIncorrectHint
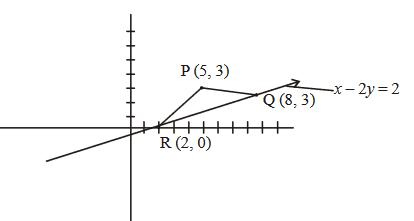
Equation of RQ is \(x-2 y=2 \dots(1)\)
at \(y=0, x=2[\mathrm{R}(2,0)]\)
as \(\mathrm{PQ}\) is parallel to \(x, y\)-coordinates of \(\mathrm{Q}\) is also 3
Putting value of \(y\) in equation (1), we get
\(\mathrm{Q}(8,3)\)
Centroid of \(\triangle \mathrm{PQR}=\left(\frac{8+5+2}{3}, \frac{3+3}{3}\right)=(5,2)\)
Only \((2 x-5 y=0)\) satisfy the given co-ordinates. -
Question 135 of 177
135. Question
A ray of light along \(x+\sqrt{3} y=\sqrt{3}\) gets reflected upon reaching \(x\)-axis, the equation of the reflected ray is [JEE 2013]
CorrectIncorrectHint
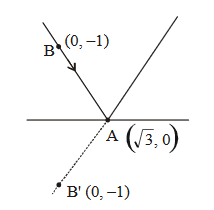
Suppose \(\mathrm{B}(0,1)\) be any point on given line and coordinate of \(A\) is \((\sqrt{3}, 0)\). So, equation of
Reflected Ray is \(\frac{-1-0}{0-\sqrt{3}}=\frac{y-0}{x-\sqrt{3}}\) \(\Rightarrow \sqrt{3} y=x-\sqrt{3}\) -
Question 136 of 177
136. Question
Let \(A(-3,2)\) and \(B(-2,1)\) be the vertices of a triangle \(A B C\). If the centroid of this triangle lies on the line \(3 x+4 y+2=0\), then the vertex \(C\) lies on the line : [JEE April 25, 2013]
CorrectIncorrectHint
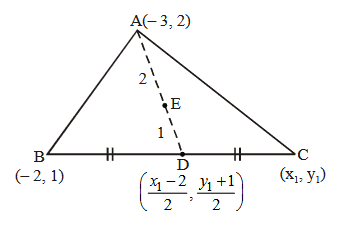
Let \(\mathrm{C}=\left(x_1, y_1\right)\)
Centroid, \(\mathrm{E}=\left(\frac{x_1-5}{3}, \frac{y_1+3}{3}\right)\)
Since centroid lies on the line \(3 x+4 y+2=0\)
\(
\therefore \quad 3\left(\frac{x_1-5}{3}\right)+4\left(\frac{y_1+3}{3}\right)+2=0
\)
\(
\Rightarrow 3 x_1+4 y_1+3=0
\)
Hence vertex \(\left(x_1, y_1\right)\) lies on the line
\(
3 x+4 y+3=0
\) -
Question 137 of 177
137. Question
If the extremities of the base of an isosceles triangle are the points \((2 a, 0)\) and \((0, a)\) and the equation of one of the sides is \(x=2 a\), then the area of the triangle, in square units, is : [JEE April 23, 2013]
CorrectIncorrectHint
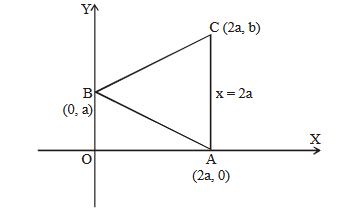
Let \(y\)-coordinate of \(\mathrm{C}=b\)
\(
\therefore \mathrm{C}=(2 a, b)
\)
\(
\begin{array}{l}
\mathrm{AB}=\sqrt{4 a^2+a^2}=\sqrt{5} a \\
\text { Now, } \mathrm{AC}=\mathrm{BC} \Rightarrow b=\sqrt{4 a^2+(b-a)^2} \\
\Rightarrow b^2=4 a^2+b^2+a^2-2 a b \\
\Rightarrow 2 a b=5 a^2 \Rightarrow b=\frac{5 a}{2} \\
\therefore \mathrm{C}=\left(2 a, \frac{5 a}{2}\right)
\end{array}
\)
Hence area of the triangle
\(
\begin{array}{l}
=\frac{1}{2}\left|\begin{array}{ccc}
2 a & 0 & 1 \\
0 & a & 1 \\
2 a & \frac{5 a}{2} & 1
\end{array}\right|=\frac{1}{2}\left|\begin{array}{ccc}
2 a & 0 & 1 \\
0 & a & 1 \\
0 & \frac{5 a}{2} & 0
\end{array}\right| \\
=\frac{1}{2} \times 2 a\left(-\frac{5 a}{2}\right)=-\frac{5 a^2}{2}
\end{array}
\)
Since area is always +ve, hence area
\(
=\frac{5 a^2}{2} \text { sq. unit }
\) -
Question 138 of 177
138. Question
If the \(x\)-intercept of some line \(L\) is double as that of the line, \(3 x+4 y=12\) and the \(y\)-intercept of \(L\) is half as that of the same line, then the slope of \(L\) is : [JEE April 22, 2013]
CorrectIncorrectHint
Given line \(3 x+4 y=12\) can be rewritten as
\(
\frac{3 x}{12}+\frac{4 y}{12}=1 \Rightarrow \frac{x}{4}+\frac{y}{3}=1
\)
\(\Rightarrow x\)-intercept \(=4\) and \(y\)-intercept \(=3\)
Let the required line be
\(\mathrm{L}: \frac{x}{a}+\frac{y}{b}=1\) where
\(a=x\)-intercept and \(b=y\)-intercept
According to the question
\(a=4 \times 2=8\) and \(b=3 / 2\)
\(\therefore\) Required line is \(\frac{x}{8}+\frac{2 y}{3}=1\)
\(\Rightarrow 3 x+16 y=24\)
\(\Rightarrow y=\frac{-3}{16} x+\frac{24}{16}\)Hence, required slope \(=\frac{-3}{16}\).
-
Question 139 of 177
139. Question
If the line \(2 x+y=k\) passes through the point which divides the line segment joining the points \((1,1)\) and \((2,4)\) in the ratio \(3: 2\), then \(k\) equals: [JEE 2012]
CorrectIncorrectHint
Let the joining points be \(A(1,1)\) and \(B(2,4)\).
Let point \(C\) divides line \(A B\) in the ratio \(3: 2\).
So, by section formula we have
\(
C=\left(\frac{3 \times 2+2 \times 1}{3+2}, \frac{3 \times 4+2 \times 1}{3+2}\right)=\left(\frac{8}{5}, \frac{14}{5}\right)
\)Since Line \(2 x+y=k\) passes through \(C\left(\frac{8}{5}, \frac{14}{5}\right)\)
\(\therefore C\) satisfies the equation \(2 x+y=k\).
\(\Rightarrow \frac{2+8}{5}+\frac{14}{5}=k \Rightarrow k=6\) -
Question 140 of 177
140. Question
The line parallel to \(x\)-axis and passing through the point of intersection of lines \(a x+2 b y+3 b=0\) and \(b x-2 a y-3 a=0\), where \((a, b) \neq(0,0)\) is [JEE May 26, 2012]
CorrectIncorrectHint
Given lines are
\(
a x+2 b y+3 b=0 \text { and } b x-2 a y-3 a=0
\)Since, required line is \(\|\) to \(x\)-axis
\(
\therefore x=0
\)We put \(x=0\) in given equation, we get
\(
2 b y=-3 b \Rightarrow y=-\frac{3}{2}
\)This shows that the required line is below \(x\)-axis at a distance of \(\frac{3}{2}\) from it.
-
Question 141 of 177
141. Question
If the point \((1, a)\) lies between the straight lines \(x+y=1\) and \(2(x+y)=3\) then a lies in interval [JEE May 12, 2012]
CorrectIncorrectHint
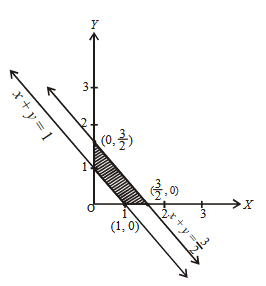
Since, \((1, a)\) lies between \(x+y=1\) and \(2(x+y)=3\)
\(\therefore\) Put \(x=1\) in \(2(x+y)=3\).
We get the range of \(y\). Thus, \(2(1+y)=3 \Rightarrow y=\frac{3}{2}-1=\frac{1}{2}\)
Thus ‘ \(a\) ‘lies in \(\left(0, \frac{1}{2}\right)\) -
Question 142 of 177
142. Question
If the straight lines \(x+3 y=4,3 x+y=4\) and \(x+y=0\) form a triangle, then the triangle is [JEE May 7, 2012]
CorrectIncorrectHint
Let equation of \(A B: x+3 y=4\)
Let equation of \(B C: 3 x+y=4\)
Let equation of \(C A: x+y=0\)
Now, By solving these equations we get \(A=(-2,2), B=(1,1)\) and \(C=(2,-2)\)
Now, \(A B=\sqrt{9+1}=\sqrt{10}\),
\(
B C=\sqrt{1+9}=\sqrt{10}
\)
and \(C A=\sqrt{16+16}=\sqrt{32}\)
Since, length of \(A B\) and \(B C\) are same therefore triangle is isosceles. -
Question 143 of 177
143. Question
If \(A(2,-3)\) and \(B(-2,1)\) are two vertices of a triangle and third vertex moves on the line \(2 x+3 y=9\), then the locus of the centroid of the triangle is: [JEE 2011RS]
CorrectIncorrectHint
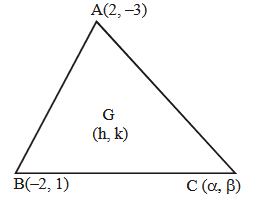
\(
\begin{array}{l}
\alpha=3 h \\
\beta-2=3 k \\
\beta=3 k+2
\end{array}
\)Third vertex \((\alpha, \beta)\) lies on the line
\(
\begin{array}{l}
2 x+3 y=9 \\
2 \alpha+3 \beta=9 \\
2(3 h)+3(3 k+2)=9 \\
2 h+3 k=1 \\
2 x+3 y=1
\end{array}
\) -
Question 144 of 177
144. Question
If \(\left(a, a^2\right)\) falls inside the angle made by the lines \(y=\frac{x}{2}\), \(x>0\) and \(y=3 x, x>0\), then a belong to [JEE 2006]
CorrectIncorrectHint
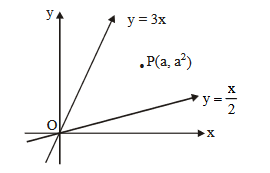
Clearly for point \(P\),
\(
a^2-3 a<0 \text { and } a^2-\frac{a}{2}>0 \Rightarrow \frac{1}{2}<a<3
\) -
Question 145 of 177
145. Question
A straight line through the point \(\mathrm{A}(3,4)\) is such that its intercept between the axes is bisected at A. Its equation is [JEE 2006]
CorrectIncorrectHint
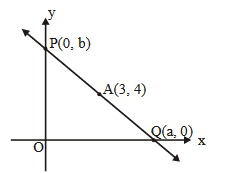
\(\because A\) is the mid point of \(P Q\), therefore
\(
\frac{a+0}{2}=3, \frac{0+b}{2}=4 \Rightarrow a=6, b=8
\)
\(\therefore\) Equation of line is \(\frac{x}{6}+\frac{y}{8}=1\) or \(4 x+3 y=24\) -
Question 146 of 177
146. Question
The line parallel to the \(x\)-axis and passing through the intersection of the lines \(a x+2 b y+3 b=0\) and \(b x-2 a y-3 a=0\), where \((a, b) \neq(0,0)\) is [JEE 2005]
CorrectIncorrectHint
The line passing through the intersection of lines \(a x+2 b y=3 b=0\) and \(b x-2 a y-3 a=0\) is
\(
\begin{array}{l}
a x+2 b y+3 b+\lambda(b x-2 a y-3 a)=0 \\
\Rightarrow(a+b \lambda) x+(2 b-2 a \lambda) y+3 b-3 \lambda a=0
\end{array}
\)As this line is parallel to \(x\)-axis.
\(
\begin{array}{l}
\therefore a+b \lambda=0 \Rightarrow \lambda=-a / b \\
\Rightarrow a x+2 b y+3 b-\frac{a}{b}(b x-2 a y-3 a)=0 \\
\Rightarrow a x+2 b y+3 b-a x+\frac{2 a^2}{b} y+\frac{3 a^2}{b}=0 \\
y\left(2 b+\frac{2 a^2}{b}\right)+3 b+\frac{3 a^2}{b}=0 \\
y\left(\frac{2 b^2+2 a^2}{b}\right)=-\left(\frac{3 b^2+3 a^2}{b}\right) \\
y=\frac{-3\left(a^2+b^2\right)}{2\left(b^2+a^2\right)}=\frac{-3}{2}
\end{array}
\)So it is \(3 / 2\) units below \(x\)-axis.
-
Question 147 of 177
147. Question
The equation of the straight line passing through the point \((4,3)\) and making intercepts on the co-ordinate axes whose sum is -1 is [JEE 2004]
CorrectIncorrectHint
Let the required line be \(\frac{x}{a}+\frac{y}{b}=1 \dots(1)\)
then \(a+b=-1 \dots(2)\)
(1) passes through \((4,3), \Rightarrow \frac{4}{a}+\frac{3}{b}=1\)
\(
\Rightarrow 4 b+3 a=a b \dots(3)
\)Eliminating \(b\) from (2) and (3), we get
\(
a^2-4=0 \Rightarrow a= \pm 2 \Rightarrow b=-3 \text { or } 1
\)
\(\therefore\) Equations of straight lines are
\(
\frac{x}{2}+\frac{y}{-3}=1 \text { or } \frac{x}{-2}+\frac{y}{1}=1
\) -
Question 148 of 177
148. Question
Let \(A(2,-3)\) and \(B(-2,3)\) be vertices of a triangle \(A B C\). If the centroid of this triangle moves on the line \(2 x+3 y=1\), then the locus of the vertex \(C\) is the line [JEE 2004]
CorrectIncorrectHint
Let the vertex \(C\) be \((h, k)\),
then the centroid of \(\triangle A B C\) is \(\left(\frac{2-2+h}{3}, \frac{-3+1+k}{3}\right)\)
or \(\left(\frac{h}{3}, \frac{-2+k}{3}\right)\).
It lies on \(2 \mathrm{x}+3 \mathrm{y}=1\)
\(\Rightarrow \frac{2 h}{3}-2+k=1 \Rightarrow 2 h+3 k=9\)
\(\Rightarrow\) Locus of \(C\) is \(2 x+3 y=9\) -
Question 149 of 177
149. Question
Locus of mid point of the portion between the axes of \(x \cos \alpha+y \sin \alpha=p\) where \(p\) is constant is [JEE 2002]
CorrectIncorrectHint
Equation of \(A B\) is
\(
x \cos \alpha+y \sin \alpha=p
\)
\(
\begin{array}{l}
\Rightarrow \frac{x \cos \alpha}{p}+\frac{y \sin \alpha}{p}=1 ; \\
\Rightarrow \frac{x}{p / \cos \alpha}+\frac{y}{p / \sin \alpha}=1
\end{array}
\)So co-ordinates of \(A\) and \(B\) are
\(
\left(\frac{p}{\cos \alpha}, 0\right) \text { and }\left(0, \frac{p}{\sin \alpha}\right) \text {; }
\)So coordinates of midpoint of \(A B\) are
\(
\begin{array}{l}
\left(\frac{p}{2 \cos \alpha}, \frac{p}{2 \sin \alpha}\right)=\left(x_1, y_1\right)(\text { let }) ; \\
x_1=\frac{p}{2 \cos \alpha} \& y_1=\frac{p}{2 \sin \alpha} ; \\
\Rightarrow \cos \alpha=p / 2 x_1 \text { and } \sin \alpha=p / 2 y_1 ; \\
\cos ^2 \alpha+\sin ^2 \alpha=1 \Rightarrow \frac{p^2}{4}\left(\frac{1}{x_1^2}+\frac{1}{y_1^2}\right)=1
\end{array}
\)Locus of \(\left(x_1, y_1\right)\) is \(\frac{1}{x^2}+\frac{1}{y^2}=\frac{4}{p^2}\).
-
Question 150 of 177
150. Question
Let a, \(b, c\) and \(d\) be non-zero numbers. If the point of intersection of the lines \(4 a x+2 a y+c=0\) and \(5 b x+2 b y+d=0\) lies in the fourth quadrant and is equidistant from the two axes then [JEE 2014]
CorrectIncorrectHint
Given lines are
\(
\begin{array}{l}
4 a x+2 a y+c=0 \\
5 b x+2 b y+d=0
\end{array}
\)The point of intersection will be
\(
\begin{array}{l}
\frac{x}{2 a d-2 b c}=\frac{-y}{4 a d-5 b c}=\frac{1}{8 a b-10 a b} \\
\Rightarrow \quad x=\frac{2(a d-b c)}{-2 a b}=\frac{b c-a d}{a b} \\
\Rightarrow \quad y=\frac{5 b c-4 a d}{-2 a b}=\frac{4 a d-5 b c}{2 a b}
\end{array}
\)
\(\because \quad\) Point of intersection is in fourth quadrant so \(x\) is positive and \(y\) is negative.
Also distance from axes is same
So \(x=-y\) ( \(\because\) distance from \(x\)-axis is \(-y\) as \(y\) is negative)
\(
\frac{b c-a d}{a b}=\frac{5 b c-4 a d}{2 a b} \Rightarrow 3 b c-2 a d=0
\) -
Question 151 of 177
151. Question
Let \(P S\) be the median of the triangle vertices \(P(2,2), Q(6,-1)\) and \(R(7,3)\). The equation of the line passing through \((1,-1)\) and parallel to \(P S\) is: [JEE 2014]
CorrectIncorrectHint
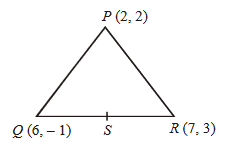
Let \(P, Q, R\), be the vertices of \(\triangle P Q R\)
Since \(P S\) is the median
\(S\) is mid-point of \(Q R\)
So, \(S=\left(\frac{7+6}{2}, \frac{3-1}{2}\right)=\left(\frac{13}{2}, 1\right)\)Now, slope of \(P S=\frac{2-1}{2-\frac{13}{2}}=-\frac{2}{9}\)
Since, required line is parallel to PS therefore
slope of required line \(=\) slope of PS
Now, eqn of line passing through \((1,-1)\) and having slope \(-\frac{2}{9}\) is
\(
\begin{array}{l}
y-(-1)=-\frac{2}{9}(x-1) \\
9 y+9=-2 x+2 \Rightarrow 2 x+9 y+7=0
\end{array}
\) -
Question 152 of 177
152. Question
If a line \(L\) is perpendicular to the line \(5 x-y=1\), and the area of the triangle formed by the line \(\mathrm{L}\) and the coordinate axes is 5 , then the distance of line \(L\) from the line \(x+5 y=0\) is: [JEE April 19, 2014]
CorrectIncorrectHint
Let equation of line \(\mathrm{L}\), perpendicular to \(5 x-y=1\) be \(x+5 y=c\)
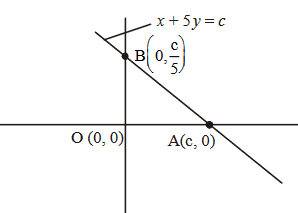
Given that area of \(\triangle \mathrm{AOB}\) is 5. We know
\(
\left\{\text { area, } A=\frac{1}{2}\left[x_1\left(y_2-y_3\right)+x_2\left(y_3-y_1\right)+x_3\left(y_1-y_2\right)\right]\right\}
\)
\(
\Rightarrow 5=\frac{1}{2}\left[c\left(\frac{c}{5}\right)\right]
\)
\(
\left(\begin{array}{l}
\because\left(x_1, y_1\right)=(10,0),\left(x_3, y_3\right)=\left(0, \frac{c}{5}\right) \\
\left(x_2, y_2\right)=(c, 0)
\end{array}\right)
\)
\(
\Rightarrow c= \pm \sqrt{50}
\)
\(\therefore\) Equation of line \(\mathrm{L}\) is \(x+5 y= \pm \sqrt{50}\) Distance between \(\mathrm{L}\) and line \(x+5 y=0\) is
\(
\mathrm{d}=\left|\frac{ \pm \sqrt{50}-0}{\sqrt{1^2+5^2}}\right|=\frac{\sqrt{50}}{\sqrt{26}}=\frac{5}{\sqrt{13}}
\) -
Question 153 of 177
153. Question
If the three distinct lines \(x+2 a y+a=0, x+3 b y+b=0\) and \(x+4 a y+a=0\) are concurrent, then the point \((a, b)\) lies on \(a\) : [JEE April 12, 2014]
CorrectIncorrectHint
\(
\begin{array}{l}
x+2 a y+a=0 \dots(1) \\
x+3 b y+b=0 \dots(2) \\
x+4 a y+a=0 \dots(3)
\end{array}
\)Subtracting equation (3) from (1)
\(
\begin{array}{l}
-2 a y=0 \\
a y=0 \Rightarrow y=0
\end{array}
\)Putting value of \(y\) in equation (1), we get
\(
\begin{array}{l}
x+0+a=0 \\
x=-a
\end{array}
\)Putting value of \(x\) and \(y\) in equation (2), we get
\(
\begin{array}{l}
-a+b=0 \\
a=b
\end{array}
\)Thus, \((a, b)\) lies on a straight line
-
Question 154 of 177
154. Question
The base of an equilateral triangle is along the line given by \(3 x+4 y=9\). If a vertex of the triangle is \((1,2)\), then the length of a side of the triangle is: [JEE April 11, 2014]
CorrectIncorrectHint
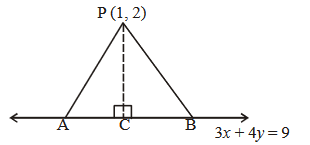
Shortest distance of a point \(\left(x_1, y_1\right)\) from line
\(
a x+b y=c \text { is } d=\left|\frac{a x_1+b y_1-c}{\sqrt{a^2+b^2}}\right|
\)Now shortest distance of \(\mathrm{P}(1,2)\) from \(3 x+4 y=9\) is
\(
\mathrm{PC}=d=\left|\frac{3(1)+4(2)-9}{\sqrt{3^2+4^2}}\right|=\frac{2}{5}
\)Given that \(\triangle \mathrm{APB}\) is an equilateral triangle
Let ‘ \(a\) ‘ be its side
then \(\mathrm{PB}=a, \mathrm{CB}=\frac{a}{2}\)
Now, In \(\triangle \mathrm{PCB},(\mathrm{PB})^2=(\mathrm{PC})^2+(\mathrm{CB})^2\)
(By Pythagoras theoream)
\(
\begin{array}{l}
a^2=\left(\frac{2}{5}\right)^2+\frac{a^2}{4} \\
a^2-\frac{a^4}{4}=\frac{4}{25} \Rightarrow \frac{3 a^2}{4}=\frac{4}{25} \\
a^2=\frac{16}{75} \Rightarrow a=\sqrt{\frac{16}{75}}=\frac{4}{5 \sqrt{3}} \times \frac{\sqrt{3}}{\sqrt{3}}=\frac{4 \sqrt{3}}{15}
\end{array}
\)
\(\therefore\) Length of Equilateral triangle \((a)=\frac{4 \sqrt{3}}{15}\) -
Question 155 of 177
155. Question
If the image of point \(\mathrm{P}(2,3)\) in a line \(\mathrm{L}\) is \(\mathrm{Q}(4,5)\), then the image of point \(R(0,0)\) in the same line is: [JEE April 25, 2013]
CorrectIncorrectHint
Mid-point of \(\mathrm{P}(2,3)\) and \(\mathrm{Q}(4,5)=(3,4)\)
Slope of \(\mathrm{PQ}=1\)
Slope of the line \(L=-1\)
Mid-point \((3,4)\) lies on the line L.
Equation of line \(\mathrm{L}\),
\(
y-4=-1(x-3) \Rightarrow x+y-7=0 \dots(i)
\)Let image of point \(\mathrm{R}(0,0)\) be \(\mathrm{S}\left(x_1, y_1\right)\)
Mid-point of RS \(=\left(\frac{x_1}{2}, \frac{y_1}{2}\right)\)
Mid-point \(\left(\frac{x_1}{2}, \frac{y_1}{2}\right)\) lies on the line(i)
\(
x_1+y_1=14 \dots(ii)
\)Slope of RS \(=\frac{y_1}{x_1}\)
Since RS \(\perp\) line L
\(
\begin{array}{l}
\frac{y_1}{x_1} \times(-1)=-1 \\
x_1=y_1 \dots(iii)
\end{array}
\)From (ii) and (iii),
\(
x_1=y_1=7
\)Hence the image of \(R=(7,7)\)
-
Question 156 of 177
156. Question
Let \(\theta_1\) be the angle between two lines \(2 x+3 y+c_1=0\) and \(-x+5 y+c_2=0\) and \(\theta_2\) be the angle between two lines \(2 x+3 y+c_1=0\) and \(-x+5 y+c_3=0\), where \(c_1, c_2, c_3\) are any real numbers:
Statement-1: If \(c_2\) and \(c_3\) are proportional, then \(\theta_1=\theta_2\).
Statement-2: \(\theta_1=\theta_2\) for all \(c_2\) and \(c_3\). [JEE April 23, 2013]CorrectIncorrectHint
Two lines \(-x+5 y+c_2=0\) and \(-x+5 y+c_3=0\) are parallel to each other. Hence statement-1 is true, statement-2 is true and statement-2 is the correct explanation of statement-1.
-
Question 157 of 177
157. Question
If the three lines \(x-3 y=p, a x+2 y=q\) and \(a x+y=r\) form a right-angled triangle then : [JEE April 9, 2013]
CorrectIncorrectHint
Since three lines \(x-3 y=p\),
\(a x+2 y=q\) and \(a x+y=r\)
form a right angled triangle
\(\therefore\) product of slopes of any two lines \(=-1\)
Suppose \(\mathrm{ax}+2 \mathrm{y}=\mathrm{q}\) and \(\mathrm{x}-3 \mathrm{y}=\mathrm{p}\) are \(\perp\) to each other.
\(
\therefore \frac{-a}{2} \times \frac{1}{3}=-1 \Rightarrow a=6
\)Now, consider option one by one
\(a=6\) satisfies only option (a)
\(\therefore\) Required answer is \(a^2-9 a+18=0\) -
Question 158 of 177
158. Question
Consider the straight lines
\(
\begin{array}{l}
L_1: x-y=1 \\
L_2: x+y=1 \\
L_3: 2 x+2 y=5 \\
L_4: 2 x-2 y=7
\end{array}
\)
The correct statement is [JEE May 26, 2012]CorrectIncorrectHint
Consider the lines
\(
\begin{array}{l}
L_1: x-y=1 \\
L_2: x+y=1 \\
L_3: 2 x+2 y=5 \\
L_4: 2 x-2 y=7
\end{array}
\)
\(L_1 \perp L_2\) is correct statement
( \(\because\) Product of their slopes \(=-1\) )
\(L_1 \perp L_3\) is also correct statement
\((\because\) Product of their slopes \(=-1)\)
Now, \(L_2: x+y=1\)
\(
\begin{array}{l}
L_4: 2 x-2 y=7 \\
\Rightarrow 2 x-2(1-x)=7 \\
\Rightarrow 2 x-2+2 x=7
\end{array}
\)
\(\Rightarrow x=\frac{9}{4}\) and \(y=\frac{-5}{4}\)
Hence, \(L_2\) intersects \(L_4\). -
Question 159 of 177
159. Question
If \(a, b, c \in \mathrm{R}\) and 1 is a root of equation \(a x^2+b x+c=0\), then the curve \(y=4 a x^2+3 b x+2 c, a \neq 0\) intersect \(x\)-axis at [Online May 26, 2012]
CorrectIncorrectHint
Given \(a x^2+b x+c=0\)
\(
\Rightarrow a x^2=-b x-\mathrm{c}
\)Now, consider
\(
\begin{aligned}
y & =4 a x^2+3 b x+2 c \\
& =4[-b x-c]+3 b x+2 c \\
& =-4 b x-4 c+3 b x+2 c \\
& =-b x-2 c
\end{aligned}
\)Since, this curve intersects \(x\)-axis
\(
\begin{array}{l}
\therefore \text { put } y=0, \text { we get } \\
-b x-2 c=0 \Rightarrow-b x=2 c \\
\Rightarrow x=\frac{-2 c}{b}
\end{array}
\)Thus, given curve intersects \(x\)-axis at exactly one point.
-
Question 160 of 177
160. Question
Let \(L\) be the line \(y=2 x\), in the two dimensional plane. [Online May 19, 2012]
Statement 1: The image of the point \((0,1)\) in \(L\) is the point
\(
\left(\frac{4}{5}, \frac{3}{5}\right)
\)
Statement 2: The points \((0,1)\) and \(\left(\frac{4}{5}, \frac{3}{5}\right)\) lie on opposite sides of the line \(\mathrm{L}\) and are at equal distance from it.CorrectIncorrectHint
Statement – 1
Let \(P^{\prime}\left(x_1, y_1\right)\) be the image of \((0,1)\) with respect to the line \(2 x-y=0\) then
\(
\begin{array}{l}
\frac{x_1}{2}=\frac{y_1-1}{-1}=\frac{-4(0)+2(1)}{5} \\
\Rightarrow x_1=\frac{4}{5}, y_1=\frac{3}{5}
\end{array}
\)Thus, statement-1 is true.
Also, statement-2 is true and correct explanation for statement-1. -
Question 161 of 177
161. Question
If two vertices of a triangle are \((5,-1)\) and \((-2,3)\) and its orthocentre is at \((0,0)\), then the third vertex is [JEE May 12, 2012]
CorrectIncorrectHint
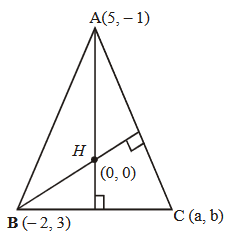
Let the third vertex of \(\triangle A B C\) be \((a, b)\).
Orthocentre \(=H(0,0)\)
Let \(A(5,-1)\) and \(B(-2,3)\) be other two vertices of \(\triangle A B C\).
Now, \((\) Slope of \(A H) \times(\) Slope of \(B C)=-1\)
\(
\begin{array}{l}
\Rightarrow\left(\frac{-1-0}{5-0}\right)\left(\frac{b-3}{a+2}\right)=-1 \\
\Rightarrow b-3=5(a+2) \dots(1)
\end{array}
\)Similarly,
(Slope of \(B H) \times(\) Slope of \(A C)=-1\)
\(
\begin{array}{l}
\Rightarrow-\left(\frac{3}{2}\right) \times\left(\frac{b+1}{a-5}\right)=-1 \\
\Rightarrow 3 b+3=2 a-10 \\
\Rightarrow 3 b-2 a+13=0 \dots(2)
\end{array}
\)On solving equation (1) and (2) we get \(a=-4, b=-7\)
Hence, third vertex is \((-4,-7)\). -
Question 162 of 177
162. Question
If two vertical poles \(20 \mathrm{~m}\) and \(80 \mathrm{~m}\) high stand apart on a horizontal plane, then the height (in \(\mathrm{m}\) ) of the point of intersection of the lines joining the top of each pole to the foot of other is [JEE May 7, 2012]
CorrectIncorrectHint
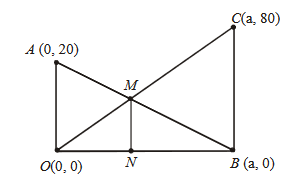
We put one pole at origin.
\(B C=80 \mathrm{~m}, O A=20 \mathrm{~m}\)
Line \(O C\) and \(A B\) intersect at \(M\).
To find: Length of \(M N\).
Eqn of \(O C: y=\left(\frac{80-0}{a-0}\right) x\)
\(
\Rightarrow y=\frac{80}{a} x \dots(1)
\)Eqn of \(A B: y=\left(\frac{20-0}{0-a}\right)(x-a)\)
\(
\Rightarrow y=\frac{-20}{a}(x-a) \dots(2)
\)At \(M:(1)=(2)\)
\(
\begin{array}{l}
\Rightarrow \quad \frac{80}{a} x=\frac{-20}{a}(x-a) \\
\Rightarrow \quad \frac{80}{a} x=\frac{-20}{a} x+20 \Rightarrow x=\frac{a}{5} \\
\therefore y=\frac{80}{a} \times \frac{a}{5}=16
\end{array}
\) -
Question 163 of 177
163. Question
The point of intersection of the lines \(\left(a^3+3\right) x+a y+a-3=0\) and \(\left(a^5+2\right) x+(a+2) y+2 a+3=0\) (a real) lies on the y-axis for [JEE May 7, 2012]
CorrectIncorrectHint
Given equation of lines are
\(
\begin{array}{l}
\left(a^3+3\right) x+a y+a-3=0 \text { and } \\
\left(a^5+2\right) x+(a+2) y+2 a+3=0 \text { (a real) }
\end{array}
\)Since point of intersection of lines lies on \(\mathrm{y}\)-axis.
\(\therefore\) Put \(x=0\) in each equation, we get
\(
\begin{array}{l}
a \mathrm{y}+a-3=0 \text { and } \\
(a+2) y+2 a+3=0
\end{array}
\)
On solving these we get
\(
\begin{array}{l}
(a+2)(a-3)-a(2 a+3)=0 \\
\Rightarrow a^2-a-6-2 a^2-3 a=0 \\
\Rightarrow-a^2-4 a-6=0 \Rightarrow a^2+4 a+6=0
\end{array}
\)
\(
\Rightarrow \quad a=\frac{-4 \pm \sqrt{16-24}}{2}=\frac{-4 \pm \sqrt{-8}}{2} \text { (not real) }
\)
This shows that the point of intersection of the lines lies on the \(y\)-axis for no value of ‘ \(a\) ‘. -
Question 164 of 177
164. Question
The lines \(x+y=|a|\) and \(a x-y=1\) intersect each other in the first quadrant. Then the set of all possible values of \(a\) in the interval : [JEE 2011]
CorrectIncorrectHint
\(x+y=|a|\) and \(a x-y=1\)
Case I: If \(a>0\)
\(
\begin{array}{l}
x+y=a \dots(1) \\
a x-y=1 \dots(2)
\end{array}
\)
On adding equation (1) and (2), we get
\(
\begin{array}{l}
x(1+a)=1+a \Rightarrow x=1 \\
y=a-1
\end{array}
\)
It is in first quadrant
\(
\begin{array}{ll}
\text { so } \quad a-1 \geq 0 \\
\Rightarrow & a \geq 1 \\
\Rightarrow & a \in[1, \infty)
\end{array}
\)
Case II : If \(a<0\)
\(
\begin{array}{l}
x+y=-a \dots(3) \\
a x-y=1 \dots(4)
\end{array}
\)
On adding equation (3) and (4), we get
\(
\begin{array}{l}
x(1+a)=1-a \\
x=\frac{1-a}{1+a}>0 \Rightarrow \frac{a-1}{a+1}<0
\end{array}
\)
Since \(a-1<0\)
\(
\begin{array}{l}
\therefore \quad a+1>0 \\
\Rightarrow \quad a>-1 \dots(5)
\end{array}
\)
\(
\begin{array}{l}
y=-a-\frac{1-a}{1+a}>0=\frac{-a-a^2-1+a}{1+a}>0 \\
\Rightarrow-\left(\frac{a^2+1}{a+1}\right)>0 \Rightarrow \frac{a^2+1}{a+1}<0
\end{array}
\)
\(
\begin{array}{l}
\text { Since } a^2+1>0 \\
\therefore \quad a+1<0 \\
\Rightarrow \quad a<-1 \dots(6)
\end{array}
\)
From (5) and (6), \(a \in \phi\)
Hence Case-II is not possible.
So, correct answer is \(a \in[1, \infty)\) -
Question 165 of 177
165. Question
The lines \(L_1: y-x=0\) and \(L_2: 2 x+y=0\) intersect the line \(L_3: y+2=0\) at \(P\) and \(Q\) respectively. The bisector of the acute angle between \(L_1\) and \(L_2\) intersects \(L_3\) at \(R\). [JEE 2011]
Statement-1: The ratio \(P R: R Q\) equals \(2 \sqrt{2}: \sqrt{5}\)
Statement-2: In any triangle, bisector of an angle divides the triangle into two similar triangles.CorrectIncorrectHint
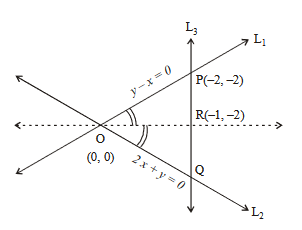
\(
\begin{array}{l}
L_1: y-x=0 \\
L_2: 2 x+y=0 \\
L_3: y+2=0
\end{array}
\)On solving the equation of line \(L_1\) and \(L_2\) we get their point of intersection \((0,0)\) i.e., origin \(\mathrm{O}\).
On solving the equation of line \(L_1\) and \(L_3\), we get \(P=(-2,-2)\).
Similarly, we get \(Q=(-1,-2)\)
We know that bisector of an angle of a triangle, divide the opposite side the triangle in the ratio of the sides including the angle [Angle Bisector Theorem of a Triangle]
\(
\therefore \frac{P R}{R Q}=\frac{O P}{O Q}=\frac{\sqrt{(-2)^2+(-2)^2}}{\sqrt{(-1)^2+(-2)^2}}=\frac{2 \sqrt{2}}{\sqrt{5}}
\) -
Question 166 of 177
166. Question
The lines \(p\left(p^2+1\right) x-y+q=0\) and \(\left(p^2+1\right)^2 x+\left(p^2+1\right) y+2 q=0\) are perpendicular to a common line for: [JEE 2009]
CorrectIncorrectHint
If the lines \(p\left(p^2+1\right) x-y+q=0\)
and \(\left(p^2+1\right)^2 x+\left(p^2+1\right) y+2 q=0\)
are perpendicular to a common line then these lines must be parallel to each other,
\(
\begin{aligned}
m_1=m_2 & \Rightarrow-\frac{p\left(p^2+1\right)}{-1}=-\frac{\left(p^2+1\right)^2}{p^2+1} \\
& \Rightarrow\left(p^2+1\right)(p+1)=0 \\
& \Rightarrow p=-1
\end{aligned}
\)
\(\therefore p\) can have exactly one value. -
Question 167 of 177
167. Question
The shortest distance between the line \(\mathrm{y}-\mathrm{x}=1\) and the curve \(x=y^2\) is : [JEE 2009]
CorrectIncorrectHint
Let \(\left(a^2, a\right)\) be the point of shortest distance on \(x=y^2\)
Then distance between \(\left(a^2, a\right)\) and line \(x-y+1=0\) is given by
\(
D=\frac{a^2-a+1}{\sqrt{2}}=\frac{1}{\sqrt{2}}\left[\left(a-\frac{1}{2}\right)^2+\frac{3}{4}\right]
\)
It is min when \(\mathrm{a}=\frac{1}{2}\) and \(\mathrm{D}_{\min }\)
\(=\frac{3}{4 \sqrt{2}}=\frac{3 \sqrt{2}}{8}\) -
Question 168 of 177
168. Question
The perpendicular bisector of the line segment joining \(\mathrm{P}(1,4)\) and \(\mathrm{Q}(\mathrm{k}, 3)\) has \(\mathrm{y}\)-intercept -4 . Then a possible value of \(k\) is [JEE 2008]
CorrectIncorrectHint
Slope of \(P Q=\frac{3-4}{k-1}=\frac{-1}{k-1}\)
\(\therefore\) Slope of perpendicular bisector of \(\mathrm{PQ}=(\mathrm{k}-1)\)
Also mid point of PQ \(\left(\frac{k+1}{2}, \frac{7}{2}\right)\).
\(\therefore\) Equation of perpendicular bisector is
\(
\begin{aligned}
& y-\frac{7}{2}=(k-1)\left(x-\frac{k+1}{2}\right) \\
\Rightarrow \quad & 2 \mathrm{y}-7=2(\mathrm{k}-1) \mathrm{x}-\left(\mathrm{k}^2-1\right) \\
\Rightarrow \quad & 2(\mathrm{k}-1) \mathrm{x}-2 \mathrm{y}+\left(8-\mathrm{k}^2\right)=0 \\
\therefore \quad & \mathrm{y} \text {-intercept }=-\frac{8-k^2}{-2}=-4 \\
\Rightarrow \quad & 8-\mathrm{k}^2=-8 \text { or } \mathrm{k}^2=16 \Rightarrow \mathrm{k}= \pm 4
\end{aligned}
\) -
Question 169 of 177
169. Question
Let \(P=(-1,0), Q=(0,0)\) and \(R=(3,3 \sqrt{3})\) be three point. The equation of the bisector of the angle \(P Q R\) is [JEE 2007]
CorrectIncorrectHint
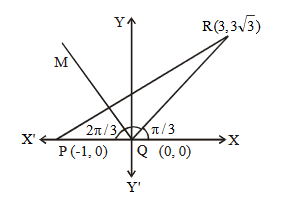
Given : The coordinates of points \(P, Q, R\) are \((-1,0)\), \((0,0),(3,3 \sqrt{3})\) respectively.
\(
\begin{array}{l}
\text { Slope of } \mathrm{QR}=\frac{y_2-y_1}{x_2-x_1}=\frac{3 \sqrt{3}}{3} \\
\Rightarrow \quad \tan \theta=\sqrt{3} \Rightarrow \theta=\frac{\pi}{3} \\
\Rightarrow \quad \angle R Q X=\frac{\pi}{3}
\end{array}
\)
\(
\therefore \quad \angle R Q P=\pi-\frac{\pi}{3}=\frac{2 \pi}{3}
\)
Let \(\mathrm{QM}\) bisects the \(\angle P Q R\),
\(\therefore \quad\) Slope of the line \(\mathrm{QM}=\tan \frac{2 \pi}{3}=-\sqrt{3}\)
\(\therefore \quad\) Equation of line \(\mathrm{QM}\) is \((\mathrm{y}-0)=-\sqrt{3}(\mathrm{x}-0)\)
\(\Rightarrow \mathrm{y}=-\sqrt{3} \mathrm{x} \Rightarrow \sqrt{3} \mathrm{x}+\mathrm{y}=0\) -
Question 170 of 177
170. Question
If \(x_1, x_2, x_3\) and \(y_1, y_2, y_3\) are both in G.P. with the same common ratio, then the points \(\left(x_1, y_1\right),\left(x_2, y_2\right)\) and \(\left(x_3, y_3\right)\) [JEE 2003]
CorrectIncorrectHint
Taking co-ordinates as
\(
\left(\frac{x}{r}, \frac{y}{r}\right) ;(x, y) \&(x r, y r) \text {. }
\)Then slope of line joining
\(
\left(\frac{x}{r}, \frac{y}{r}\right),(x, y)=\frac{y\left(1-\frac{1}{r}\right)}{x\left(1-\frac{1}{r}\right)}=\frac{y}{x}
\)
and slope of line joining \((x, y)\) and \((x r, y r)\)
\(
\begin{array}{l}
=\frac{y(r-1)}{x(r-1)}=\frac{y}{x} \\
\therefore m_1=m_2
\end{array}
\)
\(\Rightarrow\) Points lie on the straight line. -
Question 171 of 177
171. Question
A square of side a lies above the \(x\)-axis and has one vertex at the origin. The side passing through the origin makes an angle \(\alpha\left(0<\alpha<\frac{\pi}{4}\right)\) with the positive direction of \(x\)-axis. The equation of its diagonal not passing through the origin is [JEE 2003]
CorrectIncorrectHint
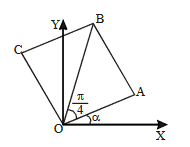
Co-ordinates of \(A=(a \cos \alpha, a \sin \alpha)\) Equation of \(\mathrm{OB}\),
\(
\begin{array}{l}
\mathrm{y}=\tan \left(\frac{\pi}{4}+\alpha\right) \mathrm{x} \\
\mathrm{CA} \perp^{\mathrm{r}} \text { to } \mathrm{OB}
\end{array}
\)
\(
\therefore \text { slope of } \mathrm{CA}=-\cot \left(\frac{\pi}{4}+\alpha\right)
\)
Equation of \(\mathrm{CA}\)
\(
y-a \sin \alpha=-\cot \left(\frac{\pi}{4}+\alpha\right)(x-a \cos \alpha)
\)
\(
\begin{array}{l}
\Rightarrow(\mathrm{y}-\mathrm{a} \sin \alpha)\left(\tan \left(\frac{\pi}{4}+\alpha\right)\right)=(\mathrm{a} \cos \alpha-\mathrm{x}) \\
\Rightarrow(\mathrm{y}-\mathrm{a} \sin \alpha)\left(\frac{\tan \frac{\pi}{4}+\tan \alpha}{1-\tan \frac{\pi}{4} \tan \alpha}\right)(\mathrm{a} \cos \alpha-\mathrm{x})
\end{array}
\)
\(
\begin{array}{l}
\Rightarrow(y-a \sin \alpha)(1+\tan \alpha)=(a \cos \alpha-x)(1-\tan \alpha) \\
\Rightarrow(y-a \sin \alpha)(\cos \alpha+\sin \alpha)=(a \cos \alpha-x)(\cos \alpha-\sin \alpha) \\
\Rightarrow y(\cos +\sin \alpha)-a \sin \alpha \cos \alpha-a \sin ^2 \alpha
\end{array}
\)
\(
=a \cos ^2 \alpha-a \cos \alpha \sin \alpha-x(\cos \alpha-\sin \alpha)
\)
\(
\begin{array}{l}
\Rightarrow \mathrm{y}(\cos \alpha+\sin \alpha)+\mathrm{x}(\cos \alpha-\sin \alpha)=\mathrm{a} \\
y(\sin \alpha+\cos \alpha)+x(\cos \alpha-\sin \alpha)=a .
\end{array}
\) -
Question 172 of 177
172. Question
If one of the lines of \(m y^2+\left(1-m^2\right) x y-m x^2=0\) is a bisector of the angle between the lines \(x y=0\), then \(m\) is [JEE 2007]
CorrectIncorrectHint
Equation of bisectors of lines, \(x y=0\) are \(y= \pm x\)
Put \(y= \pm x\) in the given equation
\(
m y^2+\left(1-m^2\right) x y-m x^2=0
\)
\(
\begin{array}{l}
m x^2+\left(1-m^2\right) x^2-m x^2=0 \\
1-m^2=0 \Rightarrow m= \pm 1
\end{array}
\) -
Question 173 of 177
173. Question
If one of the lines given by \(6 x^2-x y+4 c y^2=0\) is \(3 x+4 y=0\), then c equals [JEE 2004]
CorrectIncorrectHint
\(3 x+4 y=0\) is one of the lines of the pair \(6 x^2-x y+4 c y^2=0, \quad\) Put \(y=-\frac{3}{4} x\),
we get \(6 x^2+\frac{3}{4} x^2+4 c\left(-\frac{3}{4} x\right)^2=0\)
\(\Rightarrow 6+\frac{3}{4}+\frac{9 c}{4}=0 \Rightarrow c=-3\) -
Question 174 of 177
174. Question
If the sum of the slopes of the lines given by \(x^2-2 c x y-7 y^2=0\) is four times their product \(c\) has the value [JEE 2004]
CorrectIncorrectHint
Let the lines be \(y=m_1 x\) and \(y=m_2 x\) then \(m_1+m_2=-\frac{2 c}{7}\) and \(m_1 m_2=-\frac{1}{7}\)
Given \(m_1+m_2=4 m_1 m_2\)
\(
\Rightarrow \frac{2 c}{7}=-\frac{4}{7} \Rightarrow c=2
\) -
Question 175 of 177
175. Question
If the pair of straight lines \(x^2-2 p x y-y^2=0\) and \(x^2-2 q x y-y^2=0\) be such that each pair bisects the angle between the other pair, then [JEE 2003]
CorrectIncorrectHint
Equation of bisectors of second pair of straight lines is,
\(
q x^2+2 x y-q y^2=0 \dots(1)
\)
It must be identical to the first pair
\(
x^2-2 p x y-y^2=0 \dots(2)
\)
from (1) and (2)
\(
\frac{q}{1}=\frac{2}{-2 p}=\frac{-q}{-1} \Rightarrow p q=-1
\) -
Question 176 of 177
176. Question
The pair of lines represented by
\(
3 a x^2+5 x y+\left(a^2-2\right) y^2=0
\)
are perpendicular to each other for [JEE 2002]CorrectIncorrectHint
\(
\begin{array}{l}
3 a+a^2-2=0 \Rightarrow a^2+3 a-2=0 \\
\Rightarrow a=\frac{-3 \pm \sqrt{9+8}}{2}=\frac{-3 \pm \sqrt{17}}{2}
\end{array}
\) -
Question 177 of 177
177. Question
If the pair of lines \(a x^2+2 h x y+b y^2+2 g x+2 f y+c=0\) intersect on the \(y\)-axis then [JEE 2002]
CorrectIncorrectHint
Put \(x=0\) in the given equation
\(
\Rightarrow b y^2+2 f y+c=0 \text {. }
\)For unique point of intersection \(f^2-b c=0\)
\(
\Rightarrow a f^2-a b c=0 \text {. }
\)Since \(a b c+2 f g h-a f^2-b g^2-c h^2=0\)
\(
\Rightarrow 2 f g h-b g^2-c h^2=0
\)