Past JEE Main Entrance Papers
Quiz Summary
0 of 269 Questions completed
Questions:
Information
You have already completed the quiz before. Hence you can not start it again.
Quiz is loading…
You must sign in or sign up to start the quiz.
You must first complete the following:
Results
Results
0 of 269 Questions answered correctly
Your time:
Time has elapsed
You have reached 0 of 0 point(s), (0)
Earned Point(s): 0 of 0, (0)
0 Essay(s) Pending (Possible Point(s): 0)
Categories
- Not categorized 0%
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
- 94
- 95
- 96
- 97
- 98
- 99
- 100
- 101
- 102
- 103
- 104
- 105
- 106
- 107
- 108
- 109
- 110
- 111
- 112
- 113
- 114
- 115
- 116
- 117
- 118
- 119
- 120
- 121
- 122
- 123
- 124
- 125
- 126
- 127
- 128
- 129
- 130
- 131
- 132
- 133
- 134
- 135
- 136
- 137
- 138
- 139
- 140
- 141
- 142
- 143
- 144
- 145
- 146
- 147
- 148
- 149
- 150
- 151
- 152
- 153
- 154
- 155
- 156
- 157
- 158
- 159
- 160
- 161
- 162
- 163
- 164
- 165
- 166
- 167
- 168
- 169
- 170
- 171
- 172
- 173
- 174
- 175
- 176
- 177
- 178
- 179
- 180
- 181
- 182
- 183
- 184
- 185
- 186
- 187
- 188
- 189
- 190
- 191
- 192
- 193
- 194
- 195
- 196
- 197
- 198
- 199
- 200
- 201
- 202
- 203
- 204
- 205
- 206
- 207
- 208
- 209
- 210
- 211
- 212
- 213
- 214
- 215
- 216
- 217
- 218
- 219
- 220
- 221
- 222
- 223
- 224
- 225
- 226
- 227
- 228
- 229
- 230
- 231
- 232
- 233
- 234
- 235
- 236
- 237
- 238
- 239
- 240
- 241
- 242
- 243
- 244
- 245
- 246
- 247
- 248
- 249
- 250
- 251
- 252
- 253
- 254
- 255
- 256
- 257
- 258
- 259
- 260
- 261
- 262
- 263
- 264
- 265
- 266
- 267
- 268
- 269
- Current
- Review
- Answered
- Correct
- Incorrect
-
Question 1 of 269
1. Question
Let \(C: x^2+y^2=4\) and \(C^{\prime}: x^2+y^2-4 \lambda x+9=0\) be two circles. If the set of all values of \(\lambda\) so that the circles \(C\) and \(C ^{\prime}\) intersect at two distinct points, is \(R -[a, b]\), then the point \((8 a+12,16 b-20)\) lies on the curve : [JEE Main 2024 Feb Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& x^2+y^2=4 \\
& C (0,0) \quad r_1=2 \\
& C^{\prime}(2 \lambda, 0) \quad r_2=\sqrt{4 \lambda^2-9} \\
& \left|r_1-r_2\right|<C C^{\prime}<\left|r_1+r_2\right| \\
& \left|2-\sqrt{4 \lambda^2-9}\right|<|2 \lambda|<2+\sqrt{4 \lambda^2-9} \\
& 4+4 \lambda^2-9-4 \sqrt{4 \lambda^2-9}<4 \lambda^2
\end{aligned}
\)
True \(\lambda \in R \ldots .\). (1)
\(
\begin{aligned}
& 4 \lambda^2<4+4 \lambda^2-9+4 \sqrt{4 \lambda^2-9} \\
& 5<4 \sqrt{4 \lambda^2-9} \text { and } \quad \lambda^2 \geq \frac{9}{4} \\
& \frac{25}{16}<4 \lambda^2-9 \quad \lambda \in\left(-\infty,-\frac{3}{2}\right] \cup\left[\frac{3}{2}, \infty\right) \\
& \frac{169}{64}<\lambda^2 \\
& \lambda \in\left(-\infty,-\frac{13}{8}\right) \cup\left(\frac{13}{8}, \infty\right) \dots(2)
\end{aligned}
\)
from (1) and (2)
\(
\lambda \in\left(-\infty,-\frac{13}{8}\right) \cup\left(\frac{13}{8}, \infty\right) \Rightarrow R -\left[-\frac{13}{8}, \frac{13}{8}\right]
\)
as per question \(a=-\frac{13}{8}\) and \(b=\frac{13}{8}\)
\(\therefore \quad\) required point is \((-1,6)\) with satisfies option (4) -
Question 2 of 269
2. Question
Let the line \(L : \sqrt{2} x + y =\alpha\) pass through the point of the intersection \(P\) (in the first quadrant) of the circle \(x^2+y^2=3\) and the parabola \(x^2=2 y\). Let the line \(L\) touch two circles \(C_1\) and \(C_2\) of equal radius \(2 \sqrt{3}\). If the centres \(Q_1\) and \(Q_2\) of the circles \(C_1\) and \(C_2\) lie on the \(y\)-axis, then the square of the area of the triangle \(P Q_1 Q_2\) is equal to [JEE Main 2024 Feb Shift 1]
CorrectIncorrectHint
\(
\begin{array}{r}
x^2+y^2=3 \text { and } x^2=2 y \\
y^2+2 y-3=0 \Rightarrow(y+3)(y-1)=0 \\
y=-3 \text { or } y=1 \\
y =1 x =\sqrt{2} \Rightarrow P(\sqrt{2}, 1)
\end{array}
\)
\(p\) lies on the line
\(
\begin{aligned}
& \sqrt{2} x+y=\alpha \\
& \sqrt{2}(\sqrt{2})+1=\alpha \\
& \alpha=3
\end{aligned}
\)
For circle \(C _1\)
\(Q _1\) lies on \(y\) axis
Let \(Q _1(0, \alpha)\) coordinates
\(
R _1=2 \sqrt{3} \text { (Given }
\)
Line \(L\) act as tangent
Apply \(P = r\) (condition of tangency)
\(
\begin{aligned}
& \Rightarrow\left|\frac{\alpha-3}{\sqrt{3}}\right|=2 \sqrt{3} \\
& \Rightarrow|\alpha-3|=6 \\
& \alpha-3=6 \quad \text { or } \quad \alpha-3=-6 \\
& \Rightarrow \alpha=9 \quad \alpha=-3
\end{aligned}
\)
\(
\begin{aligned}
& \triangle P Q_1 Q_2=\frac{1}{2}\left|\begin{array}{ccc}
\sqrt{2} & 1 & 1 \\
0 & 9 & 1 \\
0 & -3 & 1
\end{array}\right| \\
& =\frac{1}{2}(\sqrt{2}(12))=6 \sqrt{2} \\
& \left(\Delta P Q_1 Q_2\right)^2=72
\end{aligned}
\) -
Question 3 of 269
3. Question
Let the locus of the mid points of the chords of circle \(x^2+(y-1)^2=1\) drawn from the origin intersect the line \(x+y=1\) at \(P\) and \(Q\). Then, the length of \(P Q\) is : [JEE Main 2024 Feb Shift 1]
CorrectIncorrectHint
Eq. of chord whose mid point is \((h, k)\)
\(
\begin{aligned}
& T=S_1 \\
& x h+y k-(y+k)=h^2+k^2-2 k \\
& x h+y k-y=h^2+k^2-k
\end{aligned}
\)
It passes through \((0,0)\)
\(
\therefore h^2+k^2-k=0
\)
Locus: \(x^2+y^2-y=0\)
Locus intersect \(x+y=1\) at \(P\) and \(Q\)
\(
\begin{aligned}
& \therefore y^2-y+(1-y)^2=0 \\
& 2 y^2-3 y+1=0 \\
& (y-1)(2 y-1)=0 \\
& y=1 \text { or } y=\frac{1}{2} \\
& x=0 \text { or } x=\frac{1}{2} \\
& P (0,1) \text { and } Q \left(\frac{1}{2}, \frac{1}{2}\right) \\
& PQ =\sqrt{\frac{1}{4}+\frac{1}{4}}=\frac{1}{\sqrt{2}}
\end{aligned}
\) -
Question 4 of 269
4. Question
Four distinct points \((2 k, 3 k),(1,0),(0,1)\) and \((0,0)\) lie on a circle for \(k\) equal to : [JEE Main 2024 Jan Shift 1]
CorrectIncorrectHint
The equation of the circle through \((1,0),(0,1)\) and \((0,0)\) is
\(
\begin{aligned}
& ( x -1)( x )+( y -1)( y )=0 \\
& x^2+y^2-x-y=0 \ldots( i )
\end{aligned}
\)
\(
\begin{aligned}
& \text { Satisfy }(2 k, 3 k) \text { in (i) } \\
& (2 k)^2+(3 k)^2-2 k-3 k=0 \\
& 13 k^2-5 k=0 \\
& k =0, k =\frac{5}{13} \\
& \text { hence } k =\frac{5}{13}
\end{aligned}
\) -
Question 5 of 269
5. Question
Consider a circle \((x-\alpha)^2+(y-\beta)^2=50\), where \(\alpha, \beta>0\). If the circle touches the line \(y+x=0\) at the point \(P\), whose distance from the origin is \(4 \sqrt{2}\), then \((\alpha+\beta)^2\) is equal to [JEE Main Jan Shift 2]
CorrectIncorrectHint
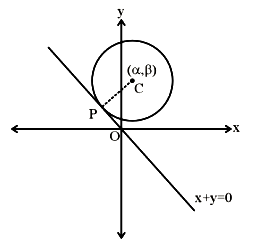
\(
\begin{aligned}
& S:(x-\alpha)^2+(y-\beta)^2=50 \\
& CP = r \\
& \left|\frac{\alpha+\beta}{\sqrt{2}}\right|=5 \sqrt{2} \\
& \Rightarrow(\alpha+\beta)^2=100
\end{aligned}
\) -
Question 6 of 269
6. Question
Equation of two diameters of a circle are \(2 x-3 y=5\) and \(3 x-4 y=7\). The line joining the points \(\left(-\frac{22}{7},-4\right)\) and \(\left(-\frac{1}{7}, 3\right)\) intersects the circle at only one point \(P(\alpha, \beta)\). Then \(17 \beta-\alpha\) is equal to [JEE Main 2024 Jan Shift 1]
CorrectIncorrectHint
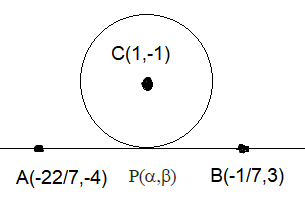
Centre of circle is \((1,-1)\)
Equation of \(A B\) is \(7 x-3 y+10=0 \dots(i)\)
Equation of \(CP\) is \(3 x +7 y +4=0 \ldots\) (ii)
Solving (i) and (ii)
\(
\alpha=\frac{-41}{29}, \beta=\frac{1}{29} \quad \therefore 17 \beta-\alpha=2
\) -
Question 7 of 269
7. Question
If the circles \((x+1)^2+(y+2)^2=r^2 \quad\) and \(x^2+y^2-4 x-4 y+4=0\) intersect at exactly two distinct points, then [JEE Main 2024 Shift 1]
CorrectIncorrectHint
If two circles intersect at two distinct points
\(
\begin{aligned}
& \Rightarrow\left| r _1- r _2\right|< C _1 C _2< r _1+ r _2 \\
& |r-2|<\sqrt{9+16}<r+2 \\
& |r-2|<5 \text { and } r+2>5 \\
& -5< r -2<5 \quad r >3 \ldots \ldots .(1)
\end{aligned}
\)
\(
-3<r<7 \dots(2)
\)
From (1) and (2)
\(
3< r <7
\) -
Question 8 of 269
8. Question
Consider two circles \(C_1: x^2+y^2=25\) and \(C_2:(x-\alpha)^2+y^2=16\), where \(\alpha \in(5,9)\). Let the angle between the two radii (one to each circle) drawn from one of the intersection points of \(C _1\) and \(C _2\) be \(\sin ^{-1}\left(\frac{\sqrt{63}}{8}\right)\). If the length of common chord of \(C_1\) and \(C_2\) is \(\beta\), then the value of \((\alpha \beta)^2\) equals [JEE Main 2024 Jan Shift 2]
CorrectIncorrectHint
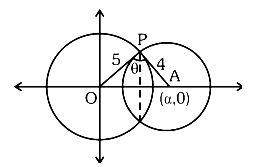
\(
\begin{aligned}
& C_1: x^2+y^2=25, C_2:(x-\alpha)^2+y^2=16 \\
& 5<\alpha<9
\end{aligned}
\)
\(
\begin{aligned}
& \theta=\sin ^{-1}\left(\frac{\sqrt{63}}{8}\right) \\
& \sin \theta=\frac{\sqrt{63}}{8} \\
& \text { Area of } \triangle OAP =\frac{1}{2} \times \alpha\left(\frac{\beta}{2}\right)=\frac{1}{2} \times 5 \times 4 \sin \theta \\
& \Rightarrow \alpha \beta=40 \times \frac{\sqrt{63}}{8} \\
& \alpha \beta=5 \times \sqrt{63} \\
& (\alpha \beta)^2=25 \times 63=1575
\end{aligned}
\) -
Question 9 of 269
9. Question
If one of the diameters of the circle \(x^2+y^2-10 x+4 y+13=0\) is a chord of another circle \(C\), whose center is the point of intersection of the lines \(2 x+3 y=12\) and \(3 x-2 y=5\), then the radius of the circle \(C\) is [JEE Main 2024 Jan Shift 2]
CorrectIncorrectHint
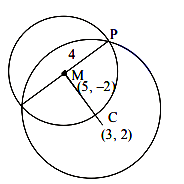
\(
\begin{aligned}
& 2 x+3 y=12 \\
& 3 x-2 y=5 \\
& 13 x=39 \\
& x=3, y=2
\end{aligned}
\)
Center of given circle is \((5,-2)\)
Radius \(\sqrt{25+4-13}=4\)
\(
\begin{aligned}
& \therefore C M=\sqrt{4+16}=5 \sqrt{2} \\
& \therefore C P=\sqrt{16+20}=6
\end{aligned}
\) -
Question 10 of 269
10. Question
Let a variable line passing through the centre of the circle \(x^2+y^2-16 x-4 y=0\), meet the positive coordinate axes at the point \(A\) and \(B\). Then the minimum value of \(O A+O B\), where \(O\) is the origin, is equal to [JEE Main 2024 Jan Shift 2]
CorrectIncorrectHint
\(
\begin{aligned}
& (y-2)=m(x-8) \\
& \Rightarrow x \text {-intercept } \\
& \Rightarrow\left(\frac{-2}{m}+8\right) \\
& \Rightarrow y \text {-intercept } \\
& \Rightarrow(-8 m +2) \\
& \Rightarrow OA + OB =\frac{-2}{ m }+8-8 m +2 \\
& f ^{\prime}( m )=\frac{2}{ m ^2}-8=0 \\
& \Rightarrow m ^2=\frac{1}{4} \\
& \Rightarrow m =\frac{-1}{2} \\
& \Rightarrow f \left(\frac{-1}{2}\right)=18 \\
& \Rightarrow \text { Minimum }=18
\end{aligned}
\) -
Question 11 of 269
11. Question
Let \(P\) be a point on the ellipse \(\frac{x^2}{9}+\frac{y^2}{4}=1\). Let the line passing through \(P\) and parallel to \(y\)-axis meet the circle \(x^2+y^2=9\) at point \(Q\) such that \(P\) and \(Q\) are on the same side of the \(x\)-axis. Then, the eccentricity of the locus of the point \(R\) on \(P Q\) such that \(P R: R Q=4: 3\) as \(P\) moves on the ellipse, is : [JEE Main 2024 Feb Shift 2]
CorrectIncorrectHint
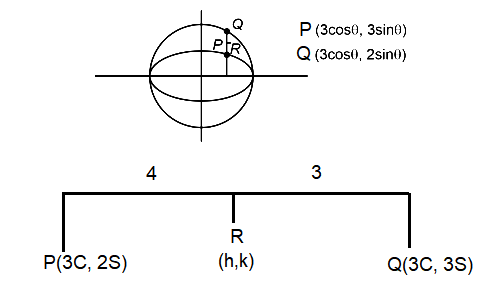
\(
\begin{aligned}
& h =3 \cos \theta \\
& k =\frac{18}{7} \sin \theta \\
& \therefore \text { locus }=\frac{ x ^2}{9}+\frac{49 y ^2}{324}=1 \\
& e =\sqrt{1-\frac{324}{49 \times 9}}=\frac{\sqrt{117}}{21}=\frac{\sqrt{13}}{7}
\end{aligned}
\) -
Question 12 of 269
12. Question
The length of the chord of the ellipse \(\frac{x^2}{25}+\frac{y^2}{16}=1\), whose mid point is \(\left(1, \frac{2}{5}\right)\), is equal to: [JEE Main 2024 Jan Shift 1]
CorrectIncorrectHint
Equation of chord with given middle point.
\(
\begin{aligned}
& T = S _1 \\
& \frac{x}{25}+\frac{y}{40}=\frac{1}{25}+\frac{1}{100} \\
& \frac{8 x+5 y}{200}=\frac{8+2}{200} \\
& y=\frac{10-8 x}{5} \ldots( i ) \\
& \frac{x^2}{25}+\frac{(10-8 x)^2}{400}=1 \quad \text { (put in original equation) } \\
& \frac{16 x^2+100+64 x^2-160 x}{400}=1 \\
& 4 x^2-8 x-15=0 \\
& x=\frac{8 \pm \sqrt{304}}{8} \\
& x_1=\frac{8+\sqrt{304}}{8} ; x_2=\frac{8-\sqrt{304}}{8}
\end{aligned}
\)
\(
\begin{aligned}
& \text { Similarly, } y=\frac{10-18 \pm \sqrt{304}}{5}=\frac{2 \pm \sqrt{304}}{5} \\
& y _1=\frac{2-\sqrt{304}}{5} ; y _2=\frac{2+\sqrt{304}}{5}
\end{aligned}
\)
\(
\begin{aligned}
& \text { Distance }=\sqrt{\left( x _1- x _2\right)^2+\left( y _1- y _2\right)^2} \\
& =\sqrt{\frac{4 \times 304}{64}+\frac{4 \times 304}{25}}=\frac{\sqrt{1691}}{5}
\end{aligned}
\) -
Question 13 of 269
13. Question
If the points of intersection of two distinct conics \(x^2+y^2=4 b\) and \(\frac{x^2}{16}+\frac{y^2}{b^2}=1\) lie on the curve \(y^2=3 x^2\), then \(3 \sqrt{3}\) times the area of the rectangle formed by the intersection points is ________
CorrectIncorrectHint
Putting \(y^2=3 x^2\) in both the conics
We get \(x^2=b\) and \(\frac{b}{16}+\frac{3}{b}=1\)
\(\Rightarrow b =4,12 \quad( b =4\) is rejected because curves coincide \()\)
\(
\therefore b =12
\)
Hence points of intersection are
\(
( \pm \sqrt{12}, \pm 6) \Rightarrow \text { area of rectangle }=432
\) -
Question 14 of 269
14. Question
If the length of the minor axis of ellipse is equal to half of the distance between the foci, then the eccentricity of the ellipse is : [JEE Main 2014 Jan Shift 1]
CorrectIncorrectHint
\(
\begin{aligned}
& 2 b = ae \\
& \frac{ b }{ a }=\frac{ e }{2} \\
& e =\sqrt{1-\frac{ e ^2}{4}} \\
& e =\frac{2}{\sqrt{5}}
\end{aligned}
\) -
Question 15 of 269
15. Question
Let \(A (\alpha, 0)\) and \(B (0, \beta)\) be the points on the line \(5 x+7 y=50\). Let the point \(P\) divide the line segment \(A B\) internally in the ratio \(7: 3\). Let \(3 x-25=0\) be a directrix of the ellipse \(E: \frac{x^2}{a^2}+\frac{y^2}{b^2}=1\) and the corresponding focus be \(S\). If from \(S\), the perpendicular on the \(x\)-axis passes through \(P\), then the length of the latus rectum of \(E\) is equal to [JEE Main 2024 Jan Shift 2]
CorrectIncorrectHint
\(
\left.\begin{array}{l}
A=(10,0) \\
B=\left(0, \frac{50}{7}\right)
\end{array}\right\} P=(3,5)
\)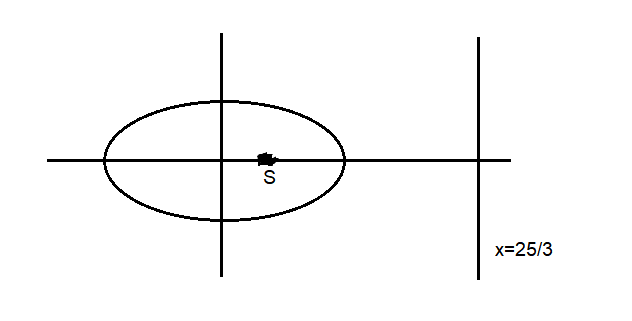
\(
\begin{gathered}
ae =3 \\
\frac{ a }{ e }=\frac{25}{3} \\
a =5 \\
b =4
\end{gathered}
\)
Length of \(L R=\frac{2 b^2}{a}=\frac{32}{5}\) -
Question 16 of 269
16. Question
Let \(P\) be a parabola with vertex \((2,3)\) and directrix \(2 x+y=6\). Let an ellipse \(E: \frac{x^2}{a^2}+\frac{y^2}{b^2}=1, a>b\) of eccentricity \(\frac{1}{\sqrt{2}}\) pass through the focus of the parabola \(P\). Then the square of the length of the latus rectum of \(E\), is [JEE Main 2024 Jan Shift 2]
CorrectIncorrectHint
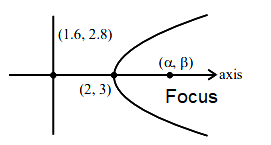
\(
\begin{aligned}
& \text { Slope of axis }=\frac{1}{2} \\
& y-3=\frac{1}{2}(x-2) \\
& \Rightarrow 2 y-6=x-2 \\
& \Rightarrow 2 y-x-4=0 \\
& 2 x+y-6=0 \\
& 4 x+2 y-12=0 \\
& \alpha+1.6=4 \Rightarrow \alpha=2.4 \\
& \beta+2.8=6 \Rightarrow \beta=3.2
\end{aligned}
\)
Ellipse passes through \((2.4,3.2)\)
\(
\Rightarrow \frac{\left(\frac{24}{10}\right)^2}{a^2}+\frac{\left(\frac{32}{10}\right)^2}{b^2}=1
\)
Also \(1-\frac{ b ^2}{ a ^2}=\frac{1}{2}=\frac{ b ^2}{ a ^2}=\frac{1}{2}\)
\(
\Rightarrow a^2=2 b^2
\)
Put in (1) \(\Rightarrow b^2=\frac{328}{25}\)
\(
\Rightarrow\left(\frac{2 b^2}{a}\right)^2=\frac{4 b^2}{a^2} \times b^2=4 \times \frac{1}{2} \times \frac{328}{25}=\frac{656}{25}
\) -
Question 17 of 269
17. Question
For \(0<\theta<\pi / 2\), if the eccentricity of the hyperbola \(x^2-y^2 \operatorname{cosec}^2 \theta=5\) is \(\sqrt{7}\) times eccentricity of the ellipse \(x^2 \operatorname{cosec}^2 \theta+y^2=5\), then the value of \(\theta\) is : [JEE Main 2024 Feb Shift 1]
CorrectIncorrectHint
\(
\begin{aligned}
& e_h=\sqrt{1+\sin ^2 \theta} \\
& e_c=\sqrt{1-\sin ^2 \theta} \\
& e_h=\sqrt{7} e_c \\
& 1+\sin ^2 \theta=7\left(1-\sin ^2 \theta\right) \\
& \sin ^2 \theta=\frac{6}{8}=\frac{3}{4} \\
& \sin \theta=\frac{\sqrt{3}}{2} \\
& \theta=\frac{\pi}{3}
\end{aligned}
\) -
Question 18 of 269
18. Question
Let \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1, a>b\) be an ellipse, whose eccentricity is \(\frac{1}{\sqrt{2}}\) and the length of the latus rectum is \(\sqrt{ 1 4 }\). Then the square of the eccentricity of \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\) is : [JEE Main 2024 Feb Shift 1]
CorrectIncorrectHint
\(
\begin{aligned}
& e=\frac{1}{\sqrt{2}}=\sqrt{1-\frac{b^2}{a^2}} \Rightarrow \frac{1}{2}=1-\frac{b^2}{a^2} \\
& \frac{2 b^2}{a}=14 \\
& e_H=\sqrt{1+\frac{b^2}{a^2}}=\sqrt{1+\frac{1}{2}}=\sqrt{\frac{3}{2}} \\
& \left(e_H\right)^2=\frac{3}{2}
\end{aligned}
\) -
Question 19 of 269
19. Question
Let \(e_1\) be the eccentricity of the hyperbola \(\frac{x^2}{16}-\frac{y^2}{9}=1\) and \(e_2\) be the eccentricity of the ellipse \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1, a>b\), which passes through the foci of the hyperbola. If \(e _1 e _2=1\), then the length of the chord of the ellipse parallel to the \(x\)-axis and passing through \((0,2)\) is : [JEE Main 2024 Jan Shift 2]
CorrectIncorrectHint
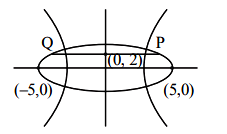
\(
\begin{aligned}
& H: \frac{x^2}{16}-\frac{y^2}{9}=1 \\
& e_1=\frac{5}{4} \\
& \therefore e_1 e_2=1 \Rightarrow e_2=\frac{4}{5}
\end{aligned}
\)
Also, ellipse is passing through \(( \pm 5,0)\)
\(
\begin{aligned}
& \therefore a=5 \text { and } b=3 \\
& E: \frac{x^2}{25}+\frac{y^2}{9}=1
\end{aligned}
\)
End point of chord are \(\left( \pm \frac{5 \sqrt{5}}{3}, 2\right)\)
\(
\therefore L _{ PQ }=\frac{10 \sqrt{5}}{3}
\) -
Question 20 of 269
20. Question
Let the latus rectum of the hyperbola \(\frac{x^2}{9}-\frac{y^2}{b^2}=1\) subtend an angle of \(\frac{\pi}{3}\) at the centre of the hyperbola. If \(b^2\) is equal to \(\frac{l}{ m }(1+\sqrt{ n })\), where \(l\) and \(m\) are co-prime numbers, then \(l^2+ m ^2+ n ^2\) is equal to ____. [JEE Main 2024 Jan Shift 1]
CorrectIncorrectHint
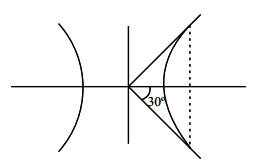
LR subtends \(60^{\circ}\) at centre
\(
\begin{aligned}
& \Rightarrow \tan 30^{\circ}=\frac{b^2 / a}{a e}=\frac{b^2}{a^2 e}=\frac{1}{\sqrt{3}} \\
& \Rightarrow e =\frac{\sqrt{3} b ^2}{9}
\end{aligned}
\)
Also, \(e ^2=1+\frac{ b ^2}{9} \Rightarrow 1+\frac{ b ^2}{9}=\frac{3 b ^4}{81}\)
\(
\begin{aligned}
& \Rightarrow b^4=3 b^2+27 \\
& \Rightarrow b^4-3 b^2-27=0 \\
& \Rightarrow b^2=\frac{3}{2}(1+\sqrt{13})
\end{aligned}
\)
\(
\begin{aligned}
& \Rightarrow 1=3, m=2, n=13 \\
& \Rightarrow l^2+m^2+n^2=182
\end{aligned}
\) -
Question 21 of 269
21. Question
Let \(P\) be a point on the hyperbola \(H : \frac{x^2}{9}-\frac{y^2}{4}=1\), in the first quadrant such that the area of triangle formed by \(P\) and the two foci of \(H\) is \(2 \sqrt{13}\). Then, the square of the distance of \(P\) from the origin is [JEE Main 2024 Jan Shift 2]
CorrectIncorrectHint
\(
\begin{aligned}
& \frac{x^2}{9}-\frac{y^2}{4}=1 \\
& a^2=9, b^2=4 \\
& b^2=a^2\left(e^2-1\right) \Rightarrow e^2=1+\frac{b^2}{a^2} \\
& e^2=1+\frac{4}{9}=\frac{13}{9} \\
& e=\frac{\sqrt{13}}{3} \Rightarrow s_1 s_2=2 a e=2 \times 3 \times \sqrt{\frac{13}{3}}=2 \sqrt{13}
\end{aligned}
\)
\(
\begin{aligned}
& \text { Area of } \Delta PS _1 S _2=\frac{1}{2} \times \beta \times s _1 S _2=2 \sqrt{13} \\
& \Rightarrow \frac{1}{2} \times \beta \times(2 \sqrt{13})=2 \sqrt{13} \Rightarrow \beta=2 \\
& \frac{\alpha^2}{9}-\frac{\beta^2}{4}=1 \Rightarrow \frac{\alpha^2}{9}-1=1 \Rightarrow \alpha^2=18 \Rightarrow \alpha=3 \sqrt{2} \\
& \text { Distance of } P \text { from origin }=\sqrt{\alpha^2+\beta^2} \\
& =\sqrt{18+4}=\sqrt{22}
\end{aligned}
\) -
Question 22 of 269
22. Question
If the foci of a hyperbola are same as that of the ellipse \(\frac{x^2}{9}+\frac{y^2}{25}=1\) and the eccentricity of the hyperbola is \(\frac{15}{8}\) times the eccentricity of the ellipse, then the smaller focal distance of the point \(\left(\sqrt{2}, \frac{14}{3} \sqrt{\frac{2}{5}}\right)\) on the hyperbola, is equal to [JEE Main 2024 Jan Shift 1]
CorrectIncorrectHint
\(
\begin{aligned}
& \frac{x^2}{9}+\frac{y^2}{25}=1 \\
& a=3, b=5 \\
& e=\sqrt{1-\frac{9}{25}}=\frac{4}{5} \therefore \text { foci }=(0, \pm b e)=(0, \pm 4) \\
& \therefore e_H=\frac{4}{5} \times \frac{15}{8}=\frac{3}{2}
\end{aligned}
\)
Let equation hyperbola
\(
\begin{aligned}
& \frac{ x ^2}{ A ^2}-\frac{ y ^2}{ B ^2}=-1 \\
& \therefore B \cdot e _{ H }=4 \quad \therefore B =\frac{8}{3} \\
& \therefore A ^2= B ^2\left( e _{ H }^2-1\right)=\frac{64}{9}\left(\frac{9}{4}-1\right) \therefore A ^2=\frac{80}{9} \\
& \therefore \frac{ x ^2}{\frac{80}{9}}-\frac{ y ^2}{\frac{64}{9}}=-1 \\
& \text { Directrix : } y= \pm \frac{B}{e_{ H }}= \pm \frac{16}{9} \\
& PS = e \cdot PM =\frac{3}{2}\left|\frac{14}{3} \cdot \sqrt{\frac{2}{5}}-\frac{16}{9}\right| \\
& =7 \sqrt{\frac{2}{5}}-\frac{8}{3} \\
&
\end{aligned}
\) -
Question 23 of 269
23. Question
Let the foci and length of the latus rectum of an ellipse \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1, a>b\) be \(( \pm 5,0)\) and \(\sqrt{50}\), respectively. Then, the square of the eccentricity of the hyperbola \(\frac{x^2}{b^2}-\frac{y^2}{a^2 b^2}=1\) equals [JEE Main 2024 Jan Shift 1]
CorrectIncorrectHint
\(
\begin{aligned}
& \text { focii } \equiv( \pm 5,0) ; \frac{2 b^2}{a}=\sqrt{50} \\
& a=5 \quad b^2=\frac{5 \sqrt{2} a}{2} \\
& b^2=a^2\left(1-e^2\right)=\frac{5 \sqrt{2} a}{2} \\
& \Rightarrow a \left(1- e ^2\right)=\frac{5 \sqrt{2}}{2} \\
& \Rightarrow \frac{5}{ e }\left(1- e ^2\right)=\frac{5 \sqrt{2}}{2} \\
& \Rightarrow \sqrt{2}-\sqrt{2} e ^2= e \\
& \Rightarrow \sqrt{2} e ^2+ e -\sqrt{2}=0 \\
& \Rightarrow \sqrt{2} e ^2+2 e – e -\sqrt{2}=0 \\
& \Rightarrow \sqrt{2} e ( e +\sqrt{2})-1(1+\sqrt{2})=0 \\
& \Rightarrow( e +\sqrt{2})(\sqrt{2} e -1)=0 \\
& \therefore e \neq-\sqrt{2} ; e =\frac{1}{\sqrt{2}} \\
& \frac{ x ^2}{ b ^2}-\frac{ y ^2}{ a ^2 b ^2}=1 \quad a =5 \sqrt{2} \\
& b =5 \\
& a^2 b^2=b^2\left(e_1^2-1\right) \Rightarrow e_1^2=51
\end{aligned}
\) -
Question 24 of 269
24. Question
If the shortest distance of the parabola \(y^2=4 x\) from the centre of the circle \(x^2+y^2-4 x-16 y+64=0\) is \(d\), then \(d^2\) is equal to : [JEE Main 2024 Jan Shift 1]
CorrectIncorrectHint
Equation of normal to parabola
\(
y=m x-2 m-m^3
\)
this normal passing through center of circle \((2,8)\)
\(
\begin{aligned}
& 8=2 m-2 m-m^3 \\
& m=-2
\end{aligned}
\)
So point \(P\) on parabola \(\Rightarrow\left( am ^2,-2 am \right)=(4,4)\)
And \(C =(2,8)\)
\(
\begin{aligned}
& PC =\sqrt{4+16}=\sqrt{20} \\
& d ^2=20
\end{aligned}
\) -
Question 25 of 269
25. Question
Let \(P (\alpha, \beta)\) be a point on the parabola \(y ^2=4 x\). If \(P\) also lies on the chord of the parabola \(x^2=8 y\) whose mid point is \(\left(1, \frac{5}{4}\right)\). Then \((\alpha-28)(\beta-8)\) is equal to ____ [JEE Main 2024 Jan Shift 2]
CorrectIncorrectHint
Parabola is \(x^2=8 y\)
Chord with mid point \(\left( x _1, y _1\right)\) is \(T = S _1\)
\(
\begin{aligned}
& \therefore xx _1-4\left( y + y _1\right)= x _1^2-8 y _1 \\
& \therefore\left( x _1, y _1\right)=\left(1, \frac{5}{4}\right) \\
& \Rightarrow x -4\left( y +\frac{5}{4}\right)=1-8 \times \frac{5}{4}=-9 \\
& \therefore x -4 y +4=0 \ldots(i)
\end{aligned}
\)
\((\alpha, \beta)\) lies on (i) & also on \(y^2=4 x\)
\(
\begin{aligned}
& \therefore \alpha-4 \beta+4=0 \ldots(i i) \\
& \& \beta^2=4 \alpha \ldots \text { (iii) }
\end{aligned}
\)
Solving (ii) & (iii)
\(
\begin{aligned}
& \beta^2=4(4 \beta-4) \Rightarrow \beta^2-16 \beta+16=0 \\
& \therefore \beta=8 \pm 4 \sqrt{3} \text { and } \alpha=4 \beta-4=28 \pm 16 \sqrt{3} \\
& \therefore(\alpha, \quad \beta) \quad=\quad(28+16 \sqrt{3}, 8+4 \sqrt{3}) \quad \& \\
& (28-16 \sqrt{3}, 8-4 \sqrt{3}) \\
& \therefore(\alpha-28)(\beta-8)=( \pm 16 \sqrt{3})( \pm 4 \sqrt{3}) \\
& =192
\end{aligned}
\) -
Question 26 of 269
26. Question
The maximum area of a triangle whose one vertex is at \((0,0)\) and the other two vertices lie on the curve \(y=-2 x^2+54\) at points \((x, y)\) and \((-x, y)\) where \(y>0\) is : [JEE Main 2024 Jan Shift 1]
CorrectIncorrectHint
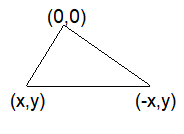
\(
\begin{aligned}
& =\frac{1}{2}\left|\begin{array}{ccc}
0 & 0 & 1 \\
x & y & 1 \\
– x & y & 1
\end{array}\right| \\
& \Rightarrow\left|\frac{1}{2}( xy + xy )\right|=| xy | \\
& \text { Area }(\Delta)=| xy |=\left| x \left(-2 x ^2+54\right)\right| \\
& \frac{ d (\Delta)}{ dx }=\left|\left(-6 x ^2+54\right)\right| \Rightarrow \frac{ d \Delta}{ dx }=0 \text { at } x =3 \\
& \text { Area }=3(-2 \times 9+54)=108
\end{aligned}
\) -
Question 27 of 269
27. Question
A circle passes through \((0,0)\) and \((1,0)\) and touches the circle \(x^2+y^2=9\). Then the locus of the centre of the circle is [JEE Main 2024 April Shift 1]
CorrectIncorrectHint
Circle will touch internally.
\(
\begin{aligned}
& C_1 C_2=\left|r_1-r_2\right| \\
& \sqrt{h^2+k^2}=3-\sqrt{h^2+k^2} \\
& \Rightarrow 2 \sqrt{h^2+k^2}=3 \\
& \Rightarrow x^2+y^2=\frac{9}{4}
\end{aligned}
\) -
Question 28 of 269
28. Question
If \(y^2=4 x\) and \(x^2+y^2=5\), then the area of smaller part of the circle cut by parabola is [JEE Main 2024 April Shift 1]
CorrectIncorrectHint
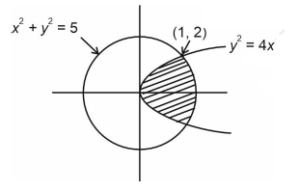
\(
\begin{aligned}
& \text { Area }=2\left[\int_0^1 2 \sqrt{x} d x+\int_1^{\sqrt{5}} \sqrt{5-x^2} d x\right] \\
& =2\left[\left(\frac{4}{3} x^{\frac{3}{2}}\right)_0^1+\left(\frac{x}{2} \sqrt{5-x^2}+\frac{5}{2} \sin ^{-1}\left(\frac{x}{\sqrt{5}}\right)\right)_1^{\sqrt{5}}\right] \\
& =2\left[\frac{4}{3}+\frac{5 \pi}{4}-1-\frac{5}{2} \sin ^{-1}\left(\frac{1}{\sqrt{5}}\right)\right] \\
& =\left(\frac{2}{3}+\frac{5 \pi}{2}-5 \sin ^{-1} \frac{1}{\sqrt{5}}\right) \text { sq. unit }
\end{aligned}
\) -
Question 29 of 269
29. Question
If \(\frac{y d y}{d x}+3=\frac{2 d y}{d x}\) is a parabola passing through \((1,0)\). Then, the vertices of the parabola satisfy the equation [JEE Main 2024 April Shift 1]
CorrectIncorrectHint
\(
\begin{aligned}
& y d y+3 d x=2 d y \\
& \Rightarrow \quad \frac{y^2}{2}+3 x=2 y+\left.c\right|_{(1,0)} \\
& \Rightarrow \quad c=3 \\
& \therefore \quad(y-2)^2=-6\left(x-\frac{5}{3}\right) \\
& \therefore \text { Vertex }=\left(\frac{5}{3}, 2\right)
\end{aligned}
\) -
Question 30 of 269
30. Question
If \(f(x)=x^2-8, g(x)=\frac{x}{x-9}\) and \(a=f(g(10))\) and \(b=g(f(3))\) and \(e\) and \(I\) be eccentricity and length of latus rectum of conic \(\frac{x^2}{|a|}+\frac{y^2}{|b|}=1\), then \(\left(92 I^2+\right.\) \(46 e ^2\) ) is [JEE Main 2024 April Shift 1]
CorrectIncorrectHint
\(
\begin{aligned}
& f(x)=x^2-8 \\
& g(x)=\frac{x}{x-9} \\
& \Rightarrow f(g(10))=f(10)=a=92
\end{aligned}
\)
\(
\begin{aligned}
& g(f(3))=g(1)=b=-\frac{1}{8} \\
& \Rightarrow \text { conic : } \\
& \frac{x^2}{92}+\frac{y^2}{1 / 8}=1 \\
& I( L \cdot R )=\frac{2(1 / 8)}{\sqrt{92}}=\frac{1}{4 \sqrt{92}} \Rightarrow I^2=\frac{1}{16(92)} \\
& e^2=1-\frac{1 / 8}{92}=\frac{92 \times 8-1}{92 \times 8} \\
& \Rightarrow 92 I^2+46 e^2=\frac{1}{16}+\frac{735}{16} \\
& =\frac{736}{16}=46
\end{aligned}
\) -
Question 31 of 269
31. Question
Find the area bounded by ellipse \(x^2+3 y^2=18\) below the line \(y=x\) is (in first quadrant) [JEE Main 2024 April Shift 2]
CorrectIncorrectHint
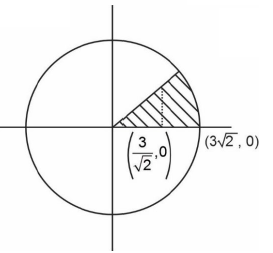
\(
\begin{aligned}
& \text { Area }=\int_0^{\frac{3}{\sqrt{2}}} x d x+\int_{\frac{3}{\sqrt{2}}}^{3 \sqrt{2}} \sqrt{\frac{18-x^2}{3}} d x \\
& =\frac{1}{2}\left(x^2\right)_0^{\frac{3}{\sqrt{2}}}+\frac{1}{\sqrt{3}}\left[\frac{x}{2} \sqrt{18-x^2}+9 \sin ^{-1}\left(\frac{x}{3 \sqrt{2}}\right)\right]_{\frac{3}{\sqrt{2}}}^{3 \sqrt{2}}
\end{aligned}
\)
\(
\begin{aligned}
& =\frac{1}{2}\left(\frac{9}{2}\right)+\frac{1}{\sqrt{3}}\left[9 \sin ^{-1}(1)-\frac{3}{2 \sqrt{2}} \frac{3 \sqrt{3}}{\sqrt{2}}-9 \sin ^{-1}\left(\frac{1}{2}\right)\right] \\
& =\frac{9}{4}+\frac{1}{\sqrt{3}}\left(\frac{9 \pi}{2}-\frac{9 \sqrt{3}}{4}-\frac{9 \pi}{6}\right) \\
& =\sqrt{3} \pi
\end{aligned}
\) -
Question 32 of 269
32. Question
If the length of focal chord of \(y^2=12 x\) is 15 and if the distance of the focal chord from origin is \(P\) then \(10 P^2\) is equal to [JEE Main 2024 April Shift 1]
CorrectIncorrectHint
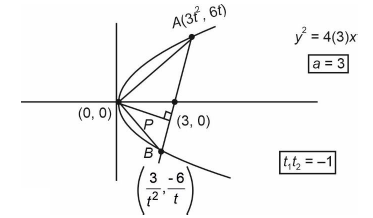
\(
\begin{aligned}
& \Rightarrow A B=15 \\
& \left(3 t^2-\frac{3}{t^2}\right)^2+\left(6 t+\frac{6}{t}\right)^2=225 \\
& \Rightarrow 9\left(t^2-\frac{1}{t^2}\right)^2+36\left(t+\frac{1}{t}\right)^2=225 \\
& \Rightarrow 9\left(t+\frac{1}{t}\right)^2\left[\left(t-\frac{1}{t}\right)^2+4\right]=225 \\
& \Rightarrow 9\left(t+\frac{1}{t}\right)^2\left(t+\frac{1}{t}\right)^2=225 \\
& \Rightarrow t+\frac{1}{t}=\left(\frac{225}{9}\right)^{1 / 4}=(25)^{1 / 4}=\sqrt{5} \\
& \text { Equation of } A B \equiv(y-0)=\frac{2}{\left(t-\frac{1}{t}\right)}(x-3) \Rightarrow\left|t-\frac{1}{t}\right|=1 \\
& \Rightarrow y=2 x-6 \Rightarrow y-2 x+6=0 \\
& \text { Distance from origin } \Rightarrow P=\frac{6}{\sqrt{5}} \Rightarrow 10 P^2=\frac{10 \times 36}{5} \\
& =72
\end{aligned}
\) -
Question 33 of 269
33. Question
A line \(L_1\) having equation \(y=x+3\). A square is inscribed in a circle \(x^2+y^2-10 x-6 y+30=0\) such that one side of square is parallel to \(L_1\). Find \(\sum_{i=1}^4\left(x_i^2+y_i^2\right)\) where \(\left(x_i, y_i\right) i \in\{1,2,3,4\}\) are the vertices of square. [JEE Main 2024 April Shift 1]
CorrectIncorrectHint
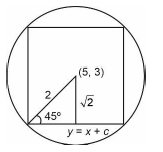
Distance of \((5,3)\) to the line \(y=x+c\) is \(\sqrt{2}\)
\(
\begin{aligned}
& \Rightarrow \frac{|3-5-c|}{\sqrt{2}}=\sqrt{2} \\
& |c+2|=2 \\
& \Rightarrow c=0 \\
& \quad c=-4
\end{aligned}
\)
So, the lines are \(y=x\) and \(y=x-4\)
Now, solving these lines with the circle
\(
\begin{aligned}
& y=x \text { and } x^2+y^2-10 x-6 y+30=0 \\
& 2 x^2-16 x+30=0 \\
& x^2-8 x+15=0 \\
& x=3, y=3 \\
& x=5, y=5 \\
& y=x-4 \text { and } x^2+y^2-10 x-6 y+30=0 \\
& 2 x^2-24 x+70=0 \\
& x^2-12 x+35=0 \\
& x=5, y=1 \\
& x=7, y=3 \\
& \sum_{i=1}^4 x_i^2+y_i^2=9+9+25+25+25+1+49+9=152
\end{aligned}
\) -
Question 34 of 269
34. Question
The locus of \(P\) such that the ratio of distance \(P\) from \(A(3,1)\) and \(B(1,2)\) is \(5: 4\) is [JEE Main 2024 April Shift 2]
CorrectIncorrectHint
Take point \(P(x, y)\)
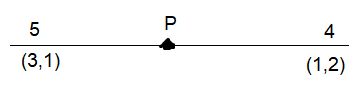
\(
\begin{aligned}
& x=\frac{5+12}{9}, y=\frac{10+4}{9} \\
& P=\left(\frac{17}{9}, \frac{14}{9}\right) \text { (internally) }
\end{aligned}
\)
for externally division.
\(
\begin{aligned}
& x=-\frac{7}{9}, y=\frac{6}{9} \\
& P^{\prime}=\left(\frac{-7}{9}, \frac{6}{9}\right)
\end{aligned}
\)
Locus of \(P\) is the circle whose diameter is \(P P^{\prime}\)
\(
\begin{aligned}
& \left(x-\frac{-17}{9}\right)\left(x+\frac{7}{9}\right)+\left(y-\frac{14}{9}\right)\left(y-\frac{6}{9}\right)=0 \\
& (9 x-17)(9 x+7)+(9 y-14)(9 y-6)=0 \\
& \text { So } 81 x^2-90 x+81 y^2-180 y=35
\end{aligned}
\) -
Question 35 of 269
35. Question
If \(\left|\frac{z_1-2 z_2}{\frac{1}{2}-\bar{z}_1 z_2}\right|=2\) then [JEE Main 2024 April Shift 2]
CorrectIncorrectHint
\(
\begin{aligned}
& \left|z_1-2 z_2\right|=\left|1-2 \bar{z}_1 z_2\right| \\
& \Rightarrow \quad\left(z_1-2 z_2\right)\left(\bar{z}_1-2 \bar{z}_2\right)=\left(1-2 \bar{z}_1 z_2\right)\left(1-2 z_1 \bar{z}_2\right)
\end{aligned}
\)
\(
\Rightarrow\left|z_1\right|^2+4\left|z_2\right|^2-2 z_1 \bar{z}_2-2 \bar{z}_1 z_2
\)
\(
=1-2 z_1 \bar{z}_2-2 \bar{z}_1 z_2+4\left|z_1\right|^2\left|z_2\right|^2
\)
\(
\begin{aligned}
\Rightarrow & \left|z_1\right|^2+4\left|z_2\right|^2-4\left|z_1\right|^2\left|z_2\right|^2-1=0 \\
& \left(\left|z_1\right|^2-1\right)\left(4\left|z_2\right|^2-1\right)=0 \\
\Rightarrow & \left|z_1\right|=1 \text { and }\left|z_2\right|=\frac{1}{2}
\end{aligned}
\) -
Question 36 of 269
36. Question
If the orthocentre of triangle formed by \((8,3),(5,1)\) and \((h, k)\) is \((6,1)\), then \((h, k)\) lie on [JEE Main 2024 April Shift 2]
CorrectIncorrectHint
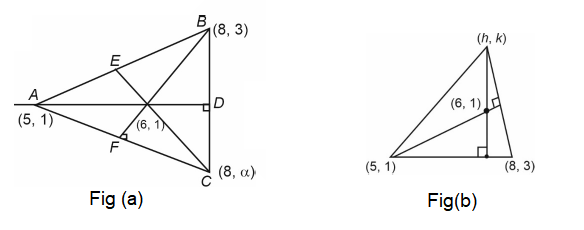
\(
\begin{aligned}
& \text { Slope of BF }=1 \\
& \Rightarrow \text { Slope of } A C \equiv\left(\frac{\alpha-1}{8-5}\right)=-1 \\
& \Rightarrow \alpha-1=-3 \\
& \Rightarrow \alpha=-2
\end{aligned}
\)From Fig(b)
\((h, k)\) lie on \((y-1)=\frac{-3}{2}(x-6)\)
\(
\begin{aligned}
2 y-2+3 x-18 & =0 \\
2 y+3 x & =20
\end{aligned}
\)
\((h, k)\) lies on circumcircle eg. of circumcircle is \(x^2+y^2=68\) -
Question 37 of 269
37. Question
A parabola \(y ^2=12 x\) has a chord \(PQ\) with mid-point \((4,1)\) then equation of \(P Q\) passes through [JEE Main 2024 April Shift 2]
CorrectIncorrectHint
Chord with the given middle point is given by \(\Rightarrow\)
\(
\begin{aligned}
T= & S_1 \\
\Rightarrow & y y_1-6\left(x+x_1\right)=y_1^2-12 x_1\left(\left(x_1, y_1\right) \equiv(4,1)\right) \\
& y-6(x+4)=1-48 \\
\Rightarrow & y-6 x+23=0
\end{aligned}
\)
\(\left(\frac{1}{2},-20\right)\) is correct answer. -
Question 38 of 269
38. Question
For a hyperbola \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1, C_1\) is a circle touching hyperbola having centre at origin and \(C_2\) is circle centred at four and touching hyperbola at vertices, if area of \(C_1=36 \pi\) and area of \(C_2=4 \pi\). Find \(a^2+b^2=\) ? [JEE Main 2024 April Shift 2]
CorrectIncorrectHint
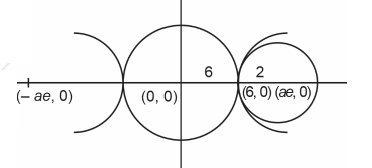
Radius of \(C_1=6\)
Radius of \(C_2=2\)
\(
\begin{aligned}
& 2 a e=16 \\
& a e=8 \\
& b^2=a^2 e^2-a^2 \\
& \Rightarrow b^2+a^2=64
\end{aligned}
\) -
Question 39 of 269
39. Question
Find area bounded by \(y^2 \leq 2 x\) and \(y \geq 4 x-1\) [JEE Main 2024 April Shift 2]
CorrectIncorrectHint
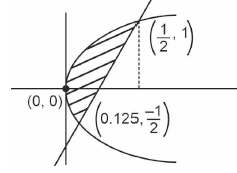
\(
\begin{aligned}
& \text { Area }=\int_{-1 / 2}^1\left(\frac{y+1}{4}-\frac{y^2}{2}\right) d y \\
& =\left[\frac{y^2}{8}+\frac{y}{4}-\frac{y^3}{6}\right]_{-1 / 2}^1 \\
& =\left(\frac{1}{8}+\frac{1}{4}-\frac{1}{6}\right)-\left(\frac{1}{32}-\frac{1}{8}+\frac{1}{48}\right) \\
& =\frac{5}{24}-\left(\frac{3-12+2}{96}\right) \\
& =\frac{5}{24}+\frac{7}{96} \\
& =\frac{27}{96}=\frac{9}{32}
\end{aligned}
\) -
Question 40 of 269
40. Question
The radius of a circle is \(\sqrt{10} \cdot x+y=4\) is the line intersecting the circle at \(P \& Q\). A chord \(M N\) is of length \(2 m\) having slope -1 . Find perpendicular distance between the two chords \(P Q\) and \(M N\). [JEE Main 2024 April Shift 2]
CorrectIncorrectHint
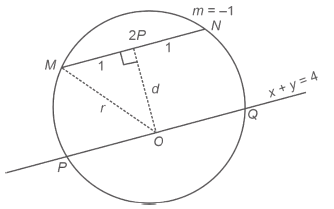
Radius of circle \(=\sqrt{10}\)
\(
\begin{aligned}
& \ln \triangle M P O, \\
& \sqrt{1^2+d^2}=r \\
& 1+d^2=10[\because r=\sqrt{10}] \\
& d^2=9 \\
& d= \pm 3
\end{aligned}
\)
Since, distance is positive, distance between chord is 3 . -
Question 41 of 269
41. Question
A line \(L\) is perpendicular to \(y=2 x+10\) such that it touches the parabola \(y^2=4(x-9)\). Then the distance between point of contact and origin is equal to [JEE Main 2024 April Shift 2]
CorrectIncorrectHint
L: \(2 y+x=c\)
\(
y^2=4(x-9)
\)
Now
\(
\begin{aligned}
& \left(\frac{c-x}{2}\right)^2=4(x-9) \\
& x^2-2(c+8) x+c^2+144=0 \\
& D=0 \\
& \Rightarrow c=5 \\
& \therefore L: 2 y+x=5
\end{aligned}
\)
Parabola and \(L\) meets at \((13,-4)\)
Now, distance \(=\sqrt{185}\) -
Question 42 of 269
42. Question
Let \(f(x)=x^2-5 x\) and \(g(x)=7 x-x^2\). Then the area between curves equals to [JEE Main 2024 April Shift 1]
CorrectIncorrectHint
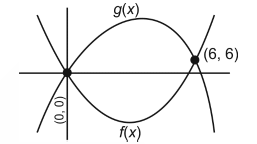
Given \(f(x)=x^2-5 x \dots(1)\)
\(g(x)=7 x-x^2 \dots(2)\)
Intersection of (1) and (2)
\(
\begin{aligned}
& x^2-5 x=7 x-x^2 \\
& 2 x^2-12 x=0 \\
& 2\left(x^2-6 x\right)=0 \\
& 2 x(x-6)=0 \\
& x=0, x=6 \\
& \therefore A=\int_0^6(g(x)-f(x)) d x \\
& =\int_0^6\left(7 x-x^2-\left(x^2-5 x\right)\right) d x \\
& =\int_0^6\left(7 x-x^2-x^2+5 x\right) d x \\
& =\int_0^6\left(12 x-2 x^2\right) d x \\
& =12\left(\frac{6^2}{2}\right)-\frac{2}{3}(6)^3 \\
& =216-144 \\
& =72 \text { sq. units }
\end{aligned}
\) -
Question 43 of 269
43. Question
Two lines passing through \((2,3)\) parallel to coordinate axes. A circle of unit radius touches both the lines and lie on the origin side. Then the shortest distance of point \((5,5)\) from the circle is [JEE Main 2024 April Shift 2]
CorrectIncorrectHint
\(\Rightarrow\) Centre \(\equiv(1,2)\)
\(\Rightarrow\) Equation of circle is \((x-1)^2+(y-2)^2=1\)
\(
\begin{aligned}
& P C=5 \\
& C B=1 \\
& \Rightarrow P B \text { = shortest distance }=4
\end{aligned}
\) -
Question 44 of 269
44. Question
Let \(2 x+3 y-k=0\) is a curve which intersects axis at points \(A\) and \(B\). A circle is drawn through \(A\) and \(B\) as diameter has equation \(x^2+y^2-3 x-2 y=0\). If the latus rectum of ellipse \(x^2+9 y^2=k^2\) is \(l\) then \(3 l\) is equal to [JEE Main 2024 April Shift 2]
CorrectIncorrectHint
Equation of circle with \(A B\) as diameter
\(
\begin{aligned}
& \left(x-\frac{k}{2}\right) x+y\left(y-\frac{k}{3}\right)=0 \\
& \Rightarrow x^2+y^2-\frac{k x}{2}-\frac{k y}{3}=0
\end{aligned}
\)
Comparing, \(k=6\)
Latus rectum of ellipse
\(
\begin{aligned}
& x^2+9 y^2=k^2=6^2 \\
& \Rightarrow \frac{x^2}{6^2}+\frac{y^2}{2^2}=1 \quad \Rightarrow \text { L.R. }=\frac{2 b^2}{a}=\frac{2(4)}{6} \\
& =\frac{4}{3}
\end{aligned}
\) -
Question 45 of 269
45. Question
A circle \(x^2+y^2=8\) and a parabola \(y^2=2 x\) are given. Find area bounded by these two curves in first quadrant which lie inside the circle and outside the parabola. [JEE Main 2024 April Shift 2]
CorrectIncorrectHint
\(
\begin{aligned}
& \text { Area }=\int_0^2\left(\sqrt{8-x^2}-\sqrt{2 x}\right) d x \\
& =\left[\frac{x}{2} \sqrt{8-x^2}+\frac{8}{2} \sin ^{-1}\left(\frac{x}{2 \sqrt{2}}\right)\right]_0^2-\sqrt{2} \times \frac{2}{3}\left[x^{3 / 2}\right]_0^2 \\
& =2+4 \sin ^{-1}\left(\frac{1}{\sqrt{2}}\right)-\frac{2 \sqrt{2}}{3}(2 \sqrt{2}) \\
& =\left(\pi-\frac{2}{3}\right) \text { sq. units. }
\end{aligned}
\) -
Question 46 of 269
46. Question
A triangle is drawn inside bounded region of \(y^2=2 x\) and \(x=24\). Then maximum area of triangle is [JEE Main 2024 April Shift 2]
CorrectIncorrectHint
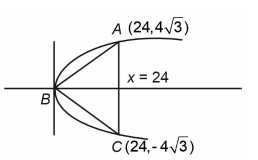
Base is constant i.e., \(A C=8 \sqrt{3}\)
Area of \(\triangle A B C\) will be maximum when height is maximum
\(\therefore B\) is \((0,0)\)
\(\therefore(\text { Area) })_{\max }==\frac{1}{2} \times 24 \times 8 \sqrt{3}=96 \sqrt{3}\) -
Question 47 of 269
47. Question
A ray of light coming from \((3,1)\) incident on \(2 x+y\) \(=6\) and deflected ray passing through \((7,2)\). If equation of incident ray is \(a x+b y+1=0\), then \(a^2+b^2+3 a b=\) [JEE Main 2024 April Shift 2]
CorrectIncorrectHint
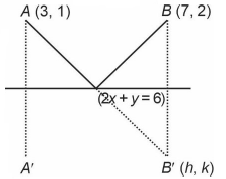
\(
\begin{aligned}
& \frac{h-7}{2}=\frac{k-2}{1}=-2 \frac{(14+2-6)}{5}=-4 \\
& \therefore \quad h=-1, k=-2 \\
& \therefore \quad B^{\prime}(-1,-2) \\
& \therefore \quad A B^{\prime} \equiv \frac{4}{5} y-\frac{3}{5} x+1=0 \\
& a=\frac{4}{5}, b=\frac{-3}{5} \\
& a^2+b^2+3 a b=\frac{16}{25}+\frac{9}{25}-\frac{36}{25}=\frac{-11}{25}
\end{aligned}
\) -
Question 48 of 269
48. Question
If \(C_1=(x-\alpha)^2+(y-\beta)^2=r_1^2\), \(C_2:(x-6)^2+\left(y-\frac{15}{2}\right)^2=r_2^2\) touches each other at \((6,6)\). If line joining centres of \(C_1\) and \(C_2\) is divided by \((6,6)\) in \(2: 1\) internally, then \((\alpha+\beta)+\) \(4\left(r_1^2+r_2^2\right)\) is equal to [JEE Main 2024 April Shift 1]
CorrectIncorrectHint
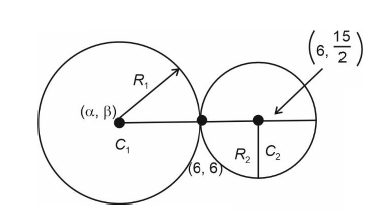
\(
\begin{aligned}
& \frac{\alpha+2.6}{3}=6, \frac{\beta+\frac{2.15}{2}}{3}=6 \\
& \Rightarrow \alpha=6, \beta=3 \\
& \Rightarrow \text { Also, } \frac{R_1}{R_2}=\frac{2}{1} \\
& R_2=\sqrt{(6-6)^2+\left(6-\frac{15}{2}\right)^2}=\frac{3}{2} \\
& \Rightarrow R_1=2 R_2=3 \\
& \Rightarrow \alpha+\beta+4\left(r_1^2+r_2^2\right)=6+3+4\left(3^2+\frac{9}{4}\right) \\
& =54
\end{aligned}
\) -
Question 49 of 269
49. Question
The locus of the mid points of the chords of the circle \(C:(x-4)^2+(y-5)^2=4\) which subtend an angle \(\theta_i\) at the centre of the circle \(C_1\), is a circle of radius \(r_1\). If \(\theta_1=\frac{\pi}{3}, \theta_3=\frac{2 \pi}{3}\) and \(r_1^2=r_2^2+r_3^2\), then \(\theta_2\) is equal to [JEE Main 2023 Jan Shift 2]
CorrectIncorrectHint
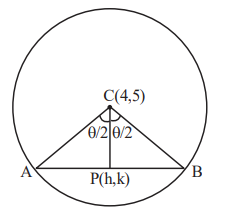
In \(\triangle CPB\)
\(
\begin{aligned}
& \cos \frac{\theta}{2}=\frac{P C}{2} \Rightarrow P C=2 \cos \frac{\theta}{2} \\
& \Rightarrow(h-4)^2+(k-5)^2=4 \cos ^2 \frac{\theta}{2} \\
& \text { Now }(x-4)^2+(y-5)^2=\left(2 \cos \frac{\theta}{2}\right)^2 \\
& \Rightarrow r_1=2 \cos \frac{\pi}{6}=\sqrt{3} \\
& r_2=2 \cos \frac{\theta_2}{2} \\
& r_3=2 \cos \frac{\pi}{3}=1 \\
& \Rightarrow r_1^2=r_2^2+r_3^2 \\
& \Rightarrow 3=4 \cos ^2 \frac{\theta_2}{2}+1 \\
& \Rightarrow 4 \cos ^2 \frac{\theta_2}{2}=2 \\
& \Rightarrow \cos ^2 \frac{\theta_2}{2}=\frac{1}{2} \\
& \Rightarrow \theta_2=\frac{\pi}{2}
\end{aligned}
\) -
Question 50 of 269
50. Question
The points of intersection of the line \(a x+b y=0\), \((a \neq b)\) and the circle \(x^2+y^2-2 x=0\) are \(A(\alpha, 0)\) and \(B(1, \beta)\). The image of the circle with \(A B\) as a diameter in the line \(x+y+2=0\) is : [JEE Main 2023 Jan Shift 1]
CorrectIncorrectHint
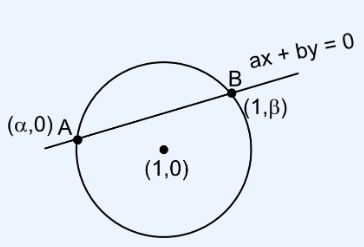
As \(A\) and \(B\) satisfy both line and circle we have \(\alpha=0 \Rightarrow A(0,0)\) and \(\beta=1\) i.e. \(B(1,1)\)
Centre of circle as \(A B\) diameter is \(\left(\frac{1}{2}, \frac{1}{2}\right)\) and radius \(=\frac{1}{\sqrt{2}}\)
\(\therefore\) For image of \(\left(\frac{1}{2} ; \frac{1}{2}\right)\) in \(x+y+z\) we get \(\frac{x-\frac{1}{2}}{1}=\frac{y-\frac{1}{2}}{1}=\frac{-2(3)}{2}\)
\(\Rightarrow\) Image \(\left(-\frac{5}{2},-\frac{5}{2}\right)\)
\(\therefore\) Equation of required circle
\(
\begin{aligned}
& \left(x+\frac{5}{2}\right)^2+\left(y+\frac{5}{2}\right)^2=\frac{1}{2} \\
& \Rightarrow x^2+y^2+5 x+5 y+\frac{50}{4}-\frac{1}{2}=0 \\
& \Rightarrow x^2+y^2+5 x+5 y+12=0
\end{aligned}
\) -
Question 51 of 269
51. Question
Points \(P(-3,2), Q(9,10)\) and \(R(\alpha, 4)\) lie on a circle \(C\) with PR as its diameter. The tangents to \(C\) at the points \(Q\) and \(R\) intersect at the point \(S\). If \(S\) lies on the line \(2 x-k y=1\), then \(k\) is equal to ____. [JEE Main 2023 Jan Shift 2]
CorrectIncorrectHint
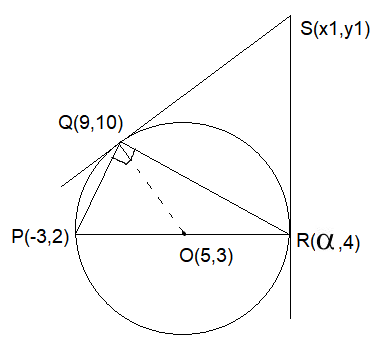
\(
\begin{aligned}
& m _{ PQ } \cdot m _{ QR }=-1 \\
& \Rightarrow \frac{10-2}{9+3} \times \frac{10-4}{9-\alpha}=-1 \Rightarrow \alpha=13 \\
& m _{ OP } \cdot m _{ QS }=-1 \Rightarrow m _{ QS }=-\frac{4}{7}
\end{aligned}
\)
Equation of \(QS\)
\(
\begin{aligned}
& y-10=-\frac{4}{7}(x-9) \\
& \Rightarrow 4 x+7 y=106 \ldots .(1) \\
& m_{O R} \cdot m_{R S}=-1 \Rightarrow m_{R S}=-8
\end{aligned}
\)
Equation of \(R S\)
\(
y-4=-8(x-13)
\)
\(
\Rightarrow 8 x+y=108 \ldots .(2)
\)
Solving eq. (1) & (2)
\(
x_1=\frac{25}{2} y_1=8
\)
\(
S\left(x_1, y_1 \right. \text { lies on ) } 2x-ky =1
\)
\(
25-8 k=1
\)
\(
\Rightarrow 8 k =24 \Rightarrow k = 3.
\) -
Question 52 of 269
52. Question
Let the tangents at the points \(A (4,-11)\) and \(B (8,-5)\) on the circle \(x^2+y^2-3 x+10 y-15=0\), intersect at the point \(C\). Then the radius of the circle, whose centre is \(C\) and the line joining \(A\) and \(B\) is its tangent, is equal to [JEE Main 2023 Jan Shift 1]
CorrectIncorrectHint
Equation of tangent at \(A(4,-11)\) on circle is
\(
\begin{aligned}
& \Rightarrow 4 x-11 y-3\left(\frac{x+4}{2}\right)+10\left(\frac{y-11}{2}\right)-15=0 \\
& \Rightarrow 5 x-12 y-152=0 \ldots . .(1)
\end{aligned}
\)
Equation of tangent at \(B (8,-5)\) on circle is
\(
\begin{aligned}
& \Rightarrow 8 x-5 y-3\left(\frac{x+8}{2}\right)+10\left(\frac{y-5}{2}\right)-15=0 \\
& \Rightarrow 13 x-104=0 \Rightarrow x=8 \\
& \text { put in }(1) \Rightarrow y=\frac{28}{3} \\
& r=\left|\frac{3.8+\frac{2.28}{3}-34}{\sqrt{13}}\right|=\frac{2 \sqrt{13}}{3}
\end{aligned}
\) -
Question 53 of 269
53. Question
A circle with centre \((2,3)\) and radius 4 intersects the line \(x + y =3\) at the points \(P\) and \(Q\). If the tangents at \(P\) and \(Q\) intersect at the point \(S (\alpha, \beta)\), then \(4 \alpha-7 \beta\) is equal to ____. [JEE Main 2023 Jan Shift 2]
CorrectIncorrectHint
The given line is polar or \(P (2, \beta)\) w.r.t. given circle
\(
x^2+y^2-4 x-6 y-3=0
\)
Chord or contact
\(
\begin{aligned}
& \alpha x+\beta y-2(x+\alpha)-3(y+\beta)-3=0 \\
& \Rightarrow(\alpha-2) x+(\beta-3) y-(2 \alpha+3 \beta+3)=0 \dots(i)
\end{aligned}
\)
\(\because\) But the equation of chord of contact is given
\(
\text { as : } x+y-3=0 \dots(ii)
\)
comparing the coefficients
\(
\frac{\alpha-2}{1}=\frac{\beta-3}{1}=-\left(\frac{2 \alpha+3 \beta+3}{-3}\right)
\)
On solving \(\alpha=-6\)
\(
\beta=-5
\)
Now \(4 \alpha-7 \beta=11\) -
Question 54 of 269
54. Question
Let \(y=x+2,4 y=3 x+6\) and \(3 y=4 x+1\) be three tangent lines to the circle \((x-h)^2+(y-k)^2=r^2\). Then \(h+k\) is equal to : [JEE Main 2023 Jan Shift 1]
CorrectIncorrectHint
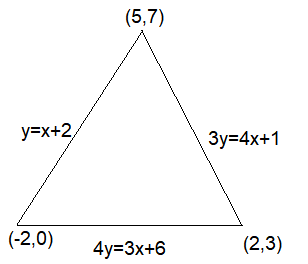
\(
\begin{aligned}
& (h, k)=\left(\frac{5.5+5(-2)+14 \sqrt{2}}{10+7 \sqrt{2}}, \frac{35+21 \sqrt{2}}{10+7 \sqrt{2}}\right) \\
& h+k=\frac{50+35 \sqrt{2}}{10+7 \sqrt{2}}=5
\end{aligned}
\) -
Question 55 of 269
55. Question
Let \(P\left(a_1, b_1\right)\) and \(Q\left(a_2, b_2\right)\) be two distinct points on a circle with center \(C(\sqrt{2}, \sqrt{3})\). Let \(O\) be the origin and \(OC\) be perpendicular to both \(CP\) and \(CQ\). If the area of the triangle \(OCP\) is \(\frac{\sqrt{35}}{2}\), then \(a_1^2+a_2^2+b_1^2+b_2^2\) is equal to ____. [JEE Main 2023 Jan Shift 2]
CorrectIncorrectHint
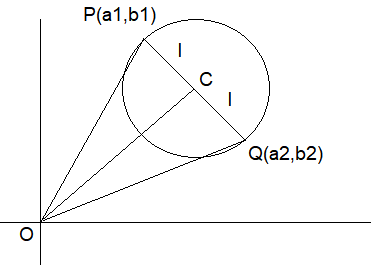
\(O C \perp C P\) and \(O C \perp C Q\)
\(\Rightarrow P C Q\) is a straight line
\(
O C=\sqrt{(\sqrt{2})^2+(\sqrt{3})^2}=\sqrt{5}
\)
Let \(C P=C Q=I\)
\(
\begin{aligned}
& {[O C P]=\frac{1}{2} \times O C \times I=\frac{\sqrt{35}}{2}} \\
& I=\sqrt{7} \\
& O P=O Q=\sqrt{(O C)^2+I^2}=\sqrt{5+7}=\sqrt{12} \\
& a_1^2+a_2^2+b_1^2+b_2^2=\left(a_1^2+b_2^2\right)+\left(a_2^2+b_2^2\right) \\
& O P^2+O Q^2=12+12=24
\end{aligned}
\) -
Question 56 of 269
56. Question
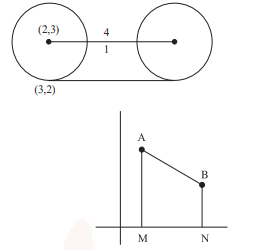
Let a circle \(C_1\) be obtained on rolling the circle \(x^2+y^2-4 x-6 y+11=0\) upwards 4 units on the tangent \(T\) to it at the point \((3,2)\). Let \(C _2\) be the image of \(C_1\) in \(T\). Let \(A\) and \(B\) be the centers of circles \(C _1\) and \(C _2\) respectively, and \(M\) and \(N\) be respectively the feet of perpendiculars drawn from \(A\) and \(B\) on the \(x\)-axis. Then the area of the trapezium AMNB is : [JEE Main 2023 Jan Shift 1]
CorrectIncorrectHint
\(
\begin{aligned}
& C =(2,3), r =\sqrt{2} \\
& \text { Centre of } G = A =2+4 \frac{1}{\sqrt{2}}, \\
& 3+\frac{4}{\sqrt{2}}=(2+2 \sqrt{2}, 3+2 \sqrt{2}) \\
& A (2+2 \sqrt{2}, 3+2 \sqrt{2}) \\
& B (4+2 \sqrt{2}, 1+2 \sqrt{2}) \\
& \frac{ x -(2+2 \sqrt{2})}{1}=\frac{ y -(3+2 \sqrt{2})}{-1}=2 \\
& \therefore \text { area of trapezium: } \\
& \frac{1}{2}(4+4 \sqrt{2}) 2=4(1+\sqrt{2})
\end{aligned}
\)
-
Question 57 of 269
57. Question
The set of all values of \(a ^2\) for which the line \(x + y =0\) bisects two distinct chords drawn from a point \(P \left(\frac{1+ a }{2}, \frac{1- a }{2}\right) \quad\) on the circle \(2 x^2+2 y^2-(1+a) x-(1-a) y=0\) is equal to: [JEE Main 2023 Jan Shift 2]
CorrectIncorrectHint
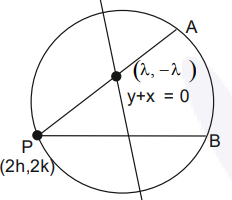
\(
\begin{aligned}
& x^2+y^2-\frac{(1+a) x}{2}-\frac{(1-a) y}{2}=0 \\
& \text { Centre }\left(\frac{1+a}{4}, \frac{1-a}{4}\right) \Rightarrow(h, k) \\
& P\left(\frac{1+a}{2}, \frac{1-a}{2}\right) \Rightarrow(2 h, 2 k)
\end{aligned}
\)
Equation of chord \(\Rightarrow T = S _1\)
\(
\begin{aligned}
& \Rightarrow( x – y ) \lambda-\frac{2 h ( x +\lambda)}{2}-\frac{(2 k )( y -\lambda)}{2} \\
& =2 \lambda^2-2 h (\lambda)+2 k \lambda
\end{aligned}
\)
Now, \(\lambda(2 h , 2 k )\) satisfies the chord
\(
\begin{aligned}
& \therefore(2 h -2 k ) \lambda- h ( x +\lambda)- k ( y -\lambda) \\
& \Rightarrow 2 \lambda^2+4 k \lambda-4 h \lambda+ h \lambda- k \lambda+ hx + ky =0 \\
& \Rightarrow 2 \lambda^2+\lambda(3 k -3 h )+ ky + hx =0 \\
& \Rightarrow D >0 \\
& \Rightarrow 9( k – h )^2-8( ky + hx )>0 \\
& \Rightarrow 9( k – h )^2-8\left(2 k ^2+2 h ^2\right)>0 \\
& \Rightarrow-7 k ^2-7 h ^2-18 kh >0 \\
& \Rightarrow 7 k ^2+7 h ^2+18 kh <0 \\
& \Rightarrow 7\left(\frac{1- a }{4}\right)^2+7\left(\frac{1+ a }{4}\right)^2+18\left(\frac{1- a ^2}{16}\right)<0
\end{aligned}
\)
\(
\begin{aligned}
& \Rightarrow 7\left[\frac{2\left(1+a^2\right)}{16}\right]+\frac{18\left(1-a^2\right)}{16}<0, \quad a^2=t \\
& \Rightarrow \frac{7}{8}(1+t)+\frac{18(1-t)}{16}<0 \\
& \Rightarrow \frac{14+14 t+18-18 t}{16}<0 \\
& \Rightarrow 4 t>32 \\
& t>8 \quad a^2>8
\end{aligned}
\) -
Question 58 of 269
58. Question
Let a tangent to the Curve \(9 x^2+16 y^2=144\) intersect the coordinate axes at the points A and B. Then, the minimum length of the line segment \(A B\) is [JEE Main 2024 Jan Shift 1]
CorrectIncorrectHint
Equation of tangent at point \(P(4 \cos \theta, 3 \sin \theta)\) is \(\frac{ x \cos \theta}{4}+\frac{ y \sin \theta}{3}=1\)
So \(A\) is \((4 \sec \theta, 0)\) and point \(B\) is \((0,3 \operatorname{cosec} \theta)\)
\(
\begin{aligned}
& \text { Length } A B =\sqrt{16 \sec ^2 \theta+9 \operatorname{cosec}^2 \theta} \\
& =\sqrt{25+16 \tan ^2 \theta+9 \cot ^2 \theta} \geq 7
\end{aligned}
\) -
Question 59 of 269
59. Question
Let \(C\) be the largest circle centred at \((2,0)\) and inscribed in the ellipse \(=\frac{x^2}{36}+\frac{y^2}{16}=1\). If \((1, \alpha)\) lies on \(C\), then \(10 \alpha^2\) is equal to ____. [JEE Main 2023 Jan Shift 1]
CorrectIncorrectHint
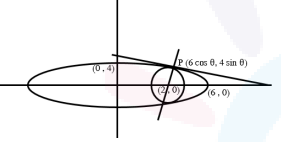
Equation of normal of ellipse \(\frac{x^2}{36}+\frac{y^2}{16}=1\) at any point \(P (6 \cos \theta, 4 \sin \theta)\) is
\(3 \sec \theta x-2 \operatorname{cosec} \theta y=10\) this normal is also the normal of the circle passing through the point \((2,0)\) So,
\(6 \sec \theta=10\) or \(\sin \theta=0\) (Not possible)
\(\cos \theta=\frac{3}{5}\) and \(\sin \theta=\frac{4}{5}\) so point \(P =\left(\frac{18}{5}, \frac{16}{5}\right)\)
So the largest radius of circle
\(
r=\frac{\sqrt{320}}{5}
\)
So the equation of circle \((x-2)^2+y^2=\frac{64}{5}\)
Passing it through \((1, \alpha)\)
Then \(\alpha^2=\frac{59}{5}\)
\(
10 \alpha^2=118
\) -
Question 60 of 269
60. Question
If the tangent at a point \(P\) on the parabola \(y ^2=3 x\) is parallel to the line \(x+2 y=1\) and the tangents at the points \(Q\) and \(R\) on the ellipse \(\frac{x^2}{4}+\frac{y^2}{1}=1\) are perpendicular to the line \(x-y=2\), then the area of the triangle \(PQR\) is: [JEE Main 2023 Jan Shift 2]
CorrectIncorrectHint
\(
y^2=3 x
\)
Tangent \(P \left( x _1, y _1\right)\) is parallel to \(x +2 y =1\)
Then slope at \(P =-\frac{1}{2}\)
\(
\begin{aligned}
& 2 y \frac{d y}{d x}=3 \\
& \Rightarrow \frac{d y}{d x}=\frac{3}{2 y}=-\frac{1}{2} \\
& \Rightarrow y_1=-3
\end{aligned}
\)
Coordinates of \(P (3,-3)\)
Similarly \(Q\left(\frac{4}{\sqrt{3}}, \frac{1}{\sqrt{5}}\right), R\left(-\frac{4}{\sqrt{5}}, \frac{-1}{\sqrt{5}}\right)\)
Area of \(\triangle PQR\)
\(
\begin{aligned}
& =\frac{1}{2}\left|\begin{array}{ccc}
3 & -3 & 1 \\
\frac{4}{\sqrt{5}} & \frac{1}{\sqrt{5}} & 1 \\
-\frac{4}{\sqrt{5}} & -\frac{1}{\sqrt{5}} & 1
\end{array}\right| \\
& =\frac{1}{2}\left[3\left(\frac{2}{\sqrt{5}}\right)+3\left(\frac{8}{\sqrt{5}}\right)+0\right]=\frac{30}{2 \sqrt{5}}=3 \sqrt{5}
\end{aligned}
\) -
Question 61 of 269
61. Question
If the maximum distance of normal to the ellipse \(\frac{x^2}{4}+\frac{y^2}{b^2}=1, b<2\), from the origin is 1 , then the eccentricity of the ellipse is: [JEE Main 2023 Jan Shift 1]
CorrectIncorrectHint
Equation of normal is
\(
2 x \sec \theta-b y \operatorname{cosec} \theta=4-b^2
\)
Distance from \((0,0)=\frac{4-b^2}{\sqrt{4 \sec ^2 \theta+b^2 \operatorname{cosec}^2 \theta}}\)
Distance is maximum if
\(
\begin{aligned}
& 4 \sec ^2 \theta+b^2 \operatorname{cosec}^2 \theta \text { is minimum } \\
& \Rightarrow \tan ^2 \theta=\frac{b}{2} \\
& \Rightarrow \frac{4-b^2}{\sqrt{4 \cdot \frac{b+2}{2}+b^2 \cdot \frac{b+2}{b}}}=1 \\
& \Rightarrow 4-b^2=b+2 \Rightarrow b=1 \Rightarrow e=\frac{\sqrt{3}}{2}
\end{aligned}
\) -
Question 62 of 269
62. Question
The line \(x=8\) is the directrix of the ellipse \(E: \frac{x^2}{a^2}+\frac{y^2}{b^2}=1\) with the corresponding focus \((2,0)\). If the tangent to \(E\) at the point \(P\) in the first quadrant passes through the point \((0,4 \sqrt{3})\) and intersects the \(x\)-axis at \(Q\), then \((3 P Q)^2\) is equal to ____. [JEE Main 2023 Feb Shift 2]
CorrectIncorrectHint
\(
\begin{aligned}
& \frac{a}{e}=8 \ldots \ldots . .(1) \quad a e=2 \dots(ii) \\
& 8 e=\frac{2}{e} \\
& e^2=\frac{1}{4} \Rightarrow e=\frac{1}{2} \\
& a=4 \\
& b^2=a^2\left(1-e^2\right) \\
& =16\left(\frac{3}{4}\right)=12 \\
& \frac{x \cos \theta}{4}+\frac{y \sin \theta}{2 \sqrt{3}}=1 \\
& \sin \theta=\frac{1}{2} \\
& \theta=30^{\circ} \\
& P(2 \sqrt{3}, \sqrt{3}) \\
& Q\left(\frac{8}{\sqrt{3}}, 0\right) \\
& (3 P Q)^2=39
\end{aligned}
\) -
Question 63 of 269
63. Question
Let a tangent to the curve \(y^2=24 x\) meet the curve \(xy =2\) at the points \(A\) and \(B\). Then the mid points of such line segments \(AB\) lie on a parabola with the [JEE Main 2023 Jan Shift 1]
CorrectIncorrectHint
\(
\begin{aligned}
& y^2=24 x \\
& a=6 \\
& x y=2 \\
& A B \equiv t y=x+6 t^2 \dots(1) \\
& A B \equiv T=S_1 \\
& k x+h y=2 h k \dots(2)
\end{aligned}
\)
From (1) and (2)
\(
\begin{aligned}
& \frac{ k }{1}=\frac{ h }{- t }=\frac{2 hk }{-6 t ^2} \\
& \Rightarrow \text { then locus is } y^2=-3 x
\end{aligned}
\)
Therefore directrix is \(4 x=3\) -
Question 64 of 269
64. Question
For some \(a, b, c \in N\), let \(f(x)=a x-3\) and
\(
g(x)=x^b+c, x \in R . \text { If }(\text { fog })^{-1}(x)=\left(\frac{x-7}{2}\right)^{1 / 3}
\)
\(
\text { then }(f o g)( ac )+( gof )( b ) \text { is equal to }
\)CorrectIncorrectHint
Let \(f o g(x)=h(x)\)
\(
\begin{aligned}
& \Rightarrow h^{-1}(x)=\left(\frac{x-7}{2}\right)^{\frac{1}{3}} \\
& \Rightarrow h(x)=f o g(x)=2 x^3+7
\end{aligned}
\)
\(
\begin{aligned}
& f o g(x)=a\left(x^b+c\right)-3 \\
& \Rightarrow a=2, b=3, c=5 \\
& \Rightarrow f o g(a c)=f o g(10)=2007 \\
& g\left(f(x)=(2 x-3)^3+5\right. \\
& \Rightarrow \operatorname{gof}(b)=\operatorname{gof}(3)=32 \\
& \Rightarrow \operatorname{sum}=2039
\end{aligned}
\) -
Question 65 of 269
65. Question
Let \(T\) and \(C\) respectively be the transverse and conjugate axes of the hyperbola \(16 x^2-\) \(y^2+64 x+4 y+44=0\). Then the area of the region above the parabola \(x^2=y+4\), below the transverse axis \(T\) and on the right of the conjugate axis \(C\) is: [JEE Main 2023 Jan Shift 2]
CorrectIncorrectHint
\(
\begin{aligned}
& 16\left(x^2+4 x\right)-\left(y^2-4 y\right)+44=0 \\
& 16(x+2)^2-64-(y-2)^2+4+44=0 \\
& 16(x+2)^2-(y-2)^2=16 \\
& \frac{(x+2)^2}{1}-\frac{(y-2)^2}{16}=1
\end{aligned}
\)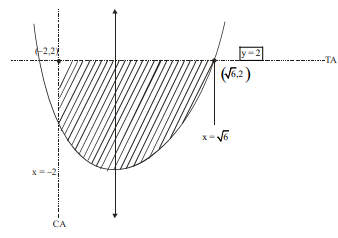
\(
\begin{aligned}
& A=\int_{-2}^{\sqrt{6}}\left(2-\left(x^2-4\right)\right) d x \\
& A=\int_{-2}^{\sqrt{6}}\left(6-x^2\right) d x=\left(6 x-\frac{x^3}{3}\right)_{-2}^{\sqrt{6}}
\end{aligned}
\)
\(
\begin{aligned}
& A=\left(6 \sqrt{6}-\frac{6 \sqrt{6}}{3}\right)-\left(-12+\frac{8}{3}\right) \\
& A=\frac{12 \sqrt{6}}{3}+\frac{28}{3} \\
& A=4 \sqrt{6}+\frac{28}{3}
\end{aligned}
\) -
Question 66 of 269
66. Question
Let \(H\) be the hyperbola, whose foci are \((1 \pm \sqrt{2}, 0)\) and eccentricity is \(\sqrt{2}\). Then the length of its latus rectum is ____. [JEE Main 2023 Jan Shift 2]
CorrectIncorrectHint
\(
\begin{aligned}
& 2 ae =|(1+\sqrt{2})-(1+\sqrt{2})|=2 \sqrt{2} \\
& ae =\sqrt{2} \\
& a =1 \\
& \Rightarrow b =1 \quad \because e =\sqrt{2} \Rightarrow \text { Hyperbola is rectangular } \\
& \Rightarrow L \cdot R =\frac{2 b ^2}{ a }=2
\end{aligned}
\) -
Question 67 of 269
67. Question
Let \(P \left( x _0, y _0\right)\) be the point on the hyperbola \(3 x ^2-4 y ^2\) \(=36\), which is nearest to the line \(3 x+2 y=1\). Then \(\sqrt{2}\left( y _0- x _0\right)\) is equal to : [JEE Main 2023 Feb Shift 1]
CorrectIncorrectHint
\(
\begin{aligned}
& 3 x^2-4 y^2=36 , 3 x+2 y=1\\
& m=-\frac{3}{2} \\
& m=+\frac{\sec \theta 3}{\sqrt{12} \cdot \tan \theta} \\
& \Rightarrow \frac{3}{\sqrt{12}} \times \frac{1}{\sin \theta}=\frac{-3}{2} \\
& \sin \theta=-\frac{1}{\sqrt{3}} \\
& (\sqrt{12} \cdot \sec \theta, 3 \tan \theta) \\
& \left(\sqrt{12} \cdot \frac{\sqrt{3}}{\sqrt{2}},-3 \times \frac{1}{\sqrt{2}}\right) \Rightarrow\left(\frac{6}{\sqrt{2}}, \frac{-3}{\sqrt{2}}\right)
\end{aligned}
\)\(
\sqrt{2}\left( y _0- x _0\right) =-9
\) -
Question 68 of 269
68. Question
The equations of the sides \(A B\) and \(A C\) of a triangle \(ABC\) are
\(
(\lambda+1) x+\lambda y=4 \text { and } \lambda x+(1-\lambda) y+\lambda=0
\)
respectively. Its vertex \(A\) is on the \(y\)-axis and its orthocentre is \((1,2)\). The length of the tangent from the point \(C\) to the part of the parabola \(y^2=6 x\) in the first quadrant is [JEE Main 2023 Jan Shift 2]CorrectIncorrectHint
\(
\begin{aligned}
& AB :(\lambda+1) x +\lambda y =4 \\
& AC : \lambda x +(1-\lambda) y +\lambda=0
\end{aligned}
\)
Vertex \(A\) is on \(y\)-axis \(\Rightarrow x=0\)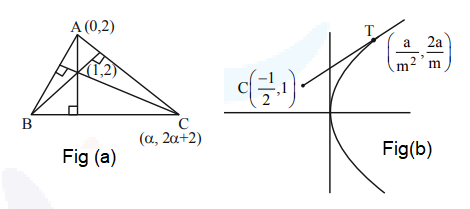
\(
\begin{aligned}
& \text { So } y=\frac{4}{\lambda}, y=\frac{\lambda}{\lambda-1} \\
& \Rightarrow \frac{4}{\lambda}=\frac{\lambda}{\lambda-1} \\
& \Rightarrow \lambda=2
\end{aligned}
\)
\(
\begin{aligned}
& AB : 3 x +2 y =4 \\
& AC : 2 x – y +2=0 \\
& \Rightarrow A (0,2) \text { Let } C (\alpha, 2 \alpha+2)
\end{aligned}
\)
Now (Slope of Altitude through C) \(\left(-\frac{3}{2}\right)=-1\)
\(
\left(\frac{2 \alpha}{\alpha-1}\right)\left(-\frac{3}{2}\right)=-1 \Rightarrow \alpha=-\frac{1}{2}
\)
So \(C \left(-\frac{1}{2}, 1\right)\)
Let Equation(Fig(b)) of tangent be \(y=m x+\frac{3}{2 m}\)
\(
\begin{aligned}
& m ^2+2 m -3=0 \\
& \Rightarrow m =1,-3
\end{aligned}
\)
So tangent which touches in first quadrant at \(T\) is
\(
\begin{aligned}
& T \equiv\left(\frac{ a }{ m ^2}, \frac{2 a }{ m }\right) \\
& \equiv\left(\frac{3}{2}, 3\right) \\
& \Rightarrow CT =\sqrt{4+4}=2 \sqrt{2}
\end{aligned}
\) -
Question 69 of 269
69. Question
The urns A, B and C contain 4 red, 6 black; 5 red, 5 black and \(\lambda\) red, 4 black balls respectively. One of the urns is selected at random and a ball is drawn. If the ball drawn is red and the probability that it is drawn from urn \(C\) is 0.4 then the square of the length of the side of the largest equilateral triangle, inscribed in the parabola \(y ^2=\lambda x\) with one vertex at the vertex of the parabola is [JEE Main 2023 Jan Shift 2]
CorrectIncorrectHint
\(
\begin{array}{lcl}
\text { Urn A } & \text { Urn B } & \text { Urn C } \\
\end{array}
\)
\(
\begin{array}{llcccc}
\text { Red } & \text { Black } & \text { Red } & \text { Black } & \text { Red } & \text { Black } \\
4 & 6 & 5 & 5 & \lambda & 4
\end{array}
\)
\(
\begin{aligned}
& P\left(\frac{C}{R}\right)=\frac{P(C) P\left(\frac{R}{C}\right)}{P(A) P\left(\frac{R}{A}\right)+P(B) P\left(\frac{R}{B}\right)+P(C) P\left(\frac{R}{C}\right)} \\
& 0.4=\frac{\frac{1}{3} \times \frac{\lambda}{(\lambda+4)}}{\frac{1}{3} \times \frac{4}{10}+\frac{1}{3} \times \frac{5}{10}+\frac{1}{3} \frac{\lambda}{(\lambda+4)}} \\
& \Rightarrow \lambda=6
\end{aligned}
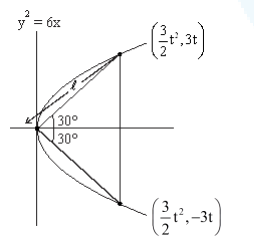
\)
\(
\begin{aligned}
& \tan 30^{\circ}=\frac{3 t}{{3/2t^2} } \\
& \frac{1}{\sqrt{3}}=\frac{2}{t} \\
& t=2 \sqrt{3}
\end{aligned}
\)
\(
\begin{aligned}
& \left(\frac{3}{2} t ^2, 3 t \right)=(18,6 \sqrt{3}) \\
& \ell^2=18^2+(6 \sqrt{3})^2 \\
& =324+108 \\
& =432
\end{aligned}
\) -
Question 70 of 269
70. Question
The distance of the point \((6,-2 \sqrt{2})\) from the common tangent \(y = mx + c , m >0\), of the curves \(x=2 y^2\) and \(x=1+y^2\) is [JEE Main 2023 Jan Shift 1]
CorrectIncorrectHint
\(
y^2=\frac{x}{2}, T: y=m x+\frac{1}{8 m}
\)
For tangent to \(y^2+1=x\)
\(
\begin{aligned}
& \Rightarrow\left( mx +\frac{1}{8 m }\right)^2+1= x \\
& D =0 \Rightarrow m =\frac{1}{2 \sqrt{2}} \\
& \therefore T : x -2 \sqrt{2} y +1=0 \\
& d =\left|\frac{6+8+1}{\sqrt{9}}\right|=5
\end{aligned}
\) -
Question 71 of 269
71. Question
If \(P ( h , k )\) be point on the parabola \(x=4 y^2\), which is nearest to the point \(Q(0,33)\), then the distance of \(P\) from the directrix of the parabola \(y^2=4(x+y)\) is equal to: [JEE Main 2023 Jan Shift 1]
CorrectIncorrectHint
Equation of normal
\(
\begin{aligned}
& y=-t x+2 a t+a t^3 \\
& y=-t x+\frac{2}{16} t+\frac{1}{16} t^3
\end{aligned}
\)
It passes through \((0,33)\)
\(
\begin{aligned}
& 33=\frac{t}{8}+\frac{t^3}{16} \\
& t ^3+2 t -528=0 \\
& ( t -8)\left( t ^2+8 t +66\right)=0 \\
& t =8 \\
& P \left( at ^2, 2 at \right)=\left(\frac{1}{16} \times 64,2 \times \frac{1}{16} \times 8\right)=(4,1)
\end{aligned}
\)
Parabola :
\(
\begin{aligned}
& y^2=4(x+y) \\
& \Rightarrow y^2-4 y=4 x \\
& \Rightarrow(y-2)^2=4(x+1)
\end{aligned}
\)
Equation of directix :
\(
\begin{aligned}
& x+1=-1 \\
& x=-2
\end{aligned}
\)
Distance of point \(=6\) -
Question 72 of 269
72. Question
Let \(A\) be a point on the \(x\)-axis. Common tangents are drawn from \(A\) to the curves \(x^2+y^2=8\) and \(y^2=16x\). If one of these tangents touches the two curves at \(Q\) and \(R\), then \((Q R)^2\) is equal to [JEE Main 2023 Jan Shift 2]
CorrectIncorrectHint
\(
\begin{aligned}
& y= mx +\frac{4}{ m } \\
& \frac{\left|\frac{4}{ m }\right|}{\sqrt{1+ m ^2}}=2 \sqrt{2} \therefore m = \pm 1 \\
& y = \pm x \pm 4 \text {. Point of contact on parabola }
\end{aligned}
\)
Let \(m =1,\left(\frac{ a }{ m ^2}, \frac{2 a }{ m }\right)\)
\(R (4,8)\)
Point of contact on circle \(Q (-2,2)\)
\(
\therefore( QR )^2=36+36=72
\) -
Question 73 of 269
73. Question
Let \(S\) be the set of all \(a \in N\) such that the area of the triangle formed by the tangent at the point \(P ( b , c ), b , c \in N\), on the parabola \(y ^2=2 ax\) and the lines \(x=b, y=0\) is 16 unit \(^2\), then \(\sum_{a \in S} a\) is equal to [JEE Main 2023 Jan Shift 2]
CorrectIncorrectHint
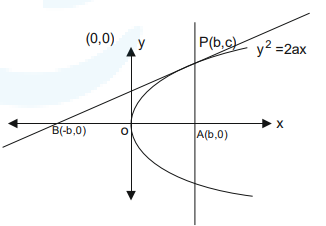
\(
\text { As } P ( b , c ) \text { lies on parabola so } c ^2=2 ab \dots(1)
\)
Now equation of tangent to parabola \(y^2=2 a x\) in point form is
\(
y y_1=2 a \frac{\left(x+x_1\right)}{2},\left(x_1, y_1\right)=(b, c)
\)
\(
\Rightarrow y c=a(x+b)
\)
\(
\text { For point } B \text {, put } y=0 \text {, now } x=-b
\)
So, area of \(\triangle PBA , \frac{1}{2} \times AB \times AP =16\)
\(
\begin{aligned}
& \Rightarrow \frac{1}{2} \times 2 b \times c =16 \\
& \Rightarrow bc =16
\end{aligned}
\)
As \(b\) and \(c\) are natural number so possible values of (b, c) are \((1,16),(2,8),(4,4),(8,2)\) and \((16,1)\)
Now from equation (1) \(a=\frac{c^2}{2 b}\) and \(a \in N\), so values of \((b, c)\) are \((1,16),(2,8)\) and \((4,4)\) now values of are 128,16 and 2. Hence sum of values of a is 146. -
Question 74 of 269
74. Question
If the \(x\)-intercept of a focal chord of the parabola \(y^2=8 x+4 y+4\) is 3 , then the length of this chord is equal to ____. [JEE Main 2023 Feb Shift 2]
CorrectIncorrectHint
\(
\begin{aligned}
& y^2=8 x+4 y+4 \\
& (y-2)^2=8(x+1) \\
& y^2=4 a x \\
& a=2, X=x+1, Y=y-2
\end{aligned}
\)
focus \((1,2)\)
\(
y-2=m(x-1)
\)
Put \((3,0)\) in the above line
\(
m =-1
\)
Length of focal chord \(=16\) -
Question 75 of 269
75. Question
A circle passing through the point \(P(\alpha, \beta)\) in the first quadrant touches the two coordinate axes at the points \(A\) and \(B\). The point \(P\) is above the line \(A B\). The point \(Q\) on the line segment \(A B\) is the foot of perpendicular from \(P\) on \(A B\). If \(P Q\) is equal to 11 units, then the value of \(\alpha \beta\) is ____. [2023 (06 Apr Shift 1)]
CorrectIncorrectHint
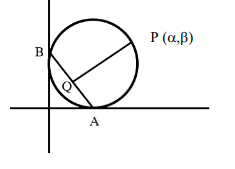
Let equation of circle is \((x-a)^2+(y-a)^2=a^2\) which is passing through \(P(\alpha, \beta)\)
then \((\alpha-a)^2+(\beta-a)^2=a^2\)
\(
\alpha^2+\beta^2-2 \alpha a-2 \beta a+a^2=0
\)
Here equation of \(AB\) is \(x+y=a\)
Let \(Q \left(\alpha^{\prime}, \beta^{\prime}\right)\) be foot of perpendicular of \(P\) on \(AB\)
\(
\frac{\alpha^{\prime}-\alpha}{1}=\frac{\beta^{\prime}-\beta}{1}=\frac{-(\alpha+\beta-a)}{2}
\)
\(
\begin{aligned}
& PQ ^2=\left(\alpha^{\prime}-\alpha\right)+\left(\beta^{\prime}-\beta\right)=\frac{1}{4}(\alpha+\beta-a)^2+\frac{1}{4}(\alpha+\beta-a)^2 \\
& 121=\frac{1}{2}(\alpha+\beta-a)^2 \\
& 242=\alpha^2+\beta^2-2 \alpha a-2 \beta a+a^2+2 \alpha \beta \\
& 242=2 \alpha \beta \\
& \Rightarrow \alpha \beta=121
\end{aligned}
\) -
Question 76 of 269
76. Question
If the tangents at the points \(P\) and \(Q\) on the circle \(x^2+y^2-2 x+y=5\) meet at the point \(R\left(\frac{9}{4}, 2\right)\), then the area of the triangle \(P Q R\) is [2023 (06 Apr Shift 2)]
CorrectIncorrectHint
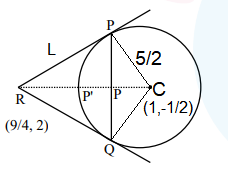
Given, The tangents at the points \(P\) and \(Q\) on the circle \(x^2+y^2-2 x+y=5\) meet at the point \(R\left(\frac{9}{4}, 2\right)\), Now plotting the diagram of the above data we have,
Now we know that,
Length of tangent is given by, \(P R=Q R=\sqrt{S_1}\)
So, \(L=\sqrt{S_1}=\sqrt{\left(\frac{9}{4}\right)^2+(2)^2-2 \times \frac{9}{4}+2-5} \Rightarrow L=\frac{5}{4}\)
Now distance between \(C R\) will be, \(C R=\sqrt{\left(\frac{9}{4}-1\right)^2+\left(2+\frac{1}{2}\right)^2}=\sqrt{\frac{25}{16}+\frac{25}{4}}=\sqrt{\frac{125}{16}}=\frac{5 \sqrt{5}}{4}\)
Now finding \(P Q\) by equating area, we get
\(
\begin{aligned}
& \frac{1}{2} \times \frac{5}{2} \times L=\frac{1}{2} \times \frac{P Q}{2} \times C R \\
& \Rightarrow \frac{1}{2} \times \frac{5}{2} \times \frac{5}{4}=\frac{1}{2} \times \frac{P Q}{2} \times \frac{5 \sqrt{5}}{4} \\
& \Rightarrow P Q=\sqrt{5}
\end{aligned}
\)
Now finding area of triangle \(P Q R\) by heron’s formula,
\(
s=\frac{2 \sqrt{5}+5}{4}
\)
So, area will be \(\Delta=\sqrt{s(s-a)(s-b)(s-c)}\)
\(
\begin{aligned}
& \Rightarrow \Delta=\sqrt{\frac{2 \sqrt{5}+5}{4}\left(\frac{2 \sqrt{5}+5}{4}-\frac{5}{4}\right)\left(\frac{2 \sqrt{5}+5}{4}-\frac{5}{4}\right)\left(\frac{2 \sqrt{5}+5}{4}-\sqrt{5}\right)} \\
& \Rightarrow \Delta=\sqrt{\frac{2 \sqrt{5}+5}{4}\left(\frac{2 \sqrt{5}}{4}\right)\left(\frac{2 \sqrt{5}}{4}\right)\left(\frac{5-2 \sqrt{5}}{4}\right)} \\
& \Rightarrow \Delta=\sqrt{\left(\frac{5}{4}\right)\left(\frac{25-20}{16}\right)}=\frac{5}{8}
\end{aligned}
\) -
Question 77 of 269
77. Question
Consider a circle \(C_1: x^2+y^2-4 x-2 y=\alpha-5\). Let its mirror image in the line \(y=2 x+1\) be another circle \(C_2: 5 x^2+5 y^2-10 f x-10 g y+36=0\). Let \(r\) be the radius of \(C_2\). Then \(\alpha+r\) is equal to ____. [2023 (08 Apr Shift 1)]
CorrectIncorrectHint
Given,
\(
C_1: x^2+y^2-4 x-2 y+(5-\alpha)=0
\)
So, its centre will be, \(O_1=(2,1)\) and radius \(=\sqrt{\alpha}\)
And \(C_2: 5 x^2+5 y^2-10 f x-10 g y+36=0\)
\(
\Rightarrow C_2: x^2+y^2-2 f x-2 g y+\frac{36}{5}=0
\)
So, Centre \(O_2=(f, g)\) and radius \(r=\sqrt{f^2+g^2-\frac{36}{5}}\)
Also given \(O_2\) is reflection of \(O_1\) in \(2 x-y+1=0\), so image formula we get,
\(
\begin{aligned}
& \Rightarrow \frac{f-2}{2}=\frac{g-1}{-1}=-2 \cdot\left(\frac{2 \times 2-1+1}{2^2+1^2}\right) \\
& \Rightarrow f=\frac{-6}{5} \text { and } g=\frac{13}{5}
\end{aligned}
\)
So, radius \(r=\sqrt{\left(\frac{-6}{5}\right)^2+\left(\frac{13}{5}\right)^2-\frac{36}{5}}=\frac{\sqrt{25}}{5}=1\)
\(\Rightarrow r=1\) and \(\alpha=1\) as they both are same radius circle,
Hence, \(r+\alpha=2\). -
Question 78 of 269
78. Question
Let \(O\) be the origin and \(O P\) and \(O Q\) be the tangents to the circle \(x^2+y^2-6 x+4 y+8=0\) at the points \(P\) and \(Q\) on it. If the circumcircle of the triangle \(O P Q\) passes through the point \(\left(\alpha, \frac{1}{2}\right)\), then a value of \(\alpha\) is [2023 (08 Apr Shift 2)]
CorrectIncorrectHint
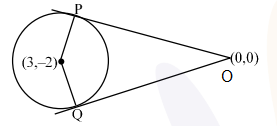
The given information can be represented in the form of the diagram below.
Since angle in a semicircle is a right angle.
Hence, the other circle will be passing through the centre of the first circle.
The two ends of diameter of the circle is \(O(0,0)\) and \(C(3,-2)\).
Hence, the required equation of circle is \((x-0)(x-3)+(y-0)(y-(-2))=0\)
\(
\Rightarrow x^2+y^2-3 x+2 y=0
\)
Put \(\left(\alpha, \frac{1}{2}\right)\) in the above equation \(\Rightarrow \alpha^2+\frac{1}{4}-3 \alpha+1=0\)
\(
\begin{aligned}
& \Rightarrow \alpha^2-3 \alpha+\frac{5}{4}=0 \\
& \Rightarrow 4 \alpha^2-12 \alpha+5=0 \\
& \Rightarrow 4 \alpha^2-10 \alpha-2 \alpha+5=0 \\
& \Rightarrow 2 \alpha(2 \alpha-5)-1(2 \alpha-5)=0 \Rightarrow \alpha=\frac{1}{2}, \frac{5}{2}
\end{aligned}
\)
Therefore this is the correct option. -
Question 79 of 269
79. Question
If the radius of the largest circle with centre \((2,0)\) inscribed in the ellipse \(x^2+4 y^2=36\) is \(r\), then \(12 r^2\) is equal to [2023 (11 Apr Shift 2)]
CorrectIncorrectHint
Given equation of ellipse is \(\frac{x^2}{36}+\frac{y^2}{9}=1\)
It is of the form \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\)
With \(a=6, b=3\).
The centre of the circle is \(C(2,0)\).
Let \(P(a \cos \theta, b \sin \theta)\) be the common point for ellipse and circle.
\(
P \equiv(6 \cos \theta, 3 \sin \theta)
\)
Equation of normal to the ellipse will be \(\frac{a x}{\cos \theta}-\frac{b y}{\sin \theta}=a^2-b^2\).
\(
\Rightarrow 6 x \sec \theta-3 y \operatorname{cosec} \theta=36-9
\)
But the normal through \(P\) passes through the centre of the circle \(C(2,0)\).
\(
\begin{aligned}
& \Rightarrow 6(2) \sec \theta-3(0) \operatorname{cosec} \theta=27 \\
& \Rightarrow \sec \theta=\frac{27}{12} \\
& \Rightarrow \cos \theta=\frac{4}{9} \text { and } \sin \theta=\frac{\sqrt{65}}{9} \\
& P \equiv\left(6 \times \frac{4}{9}, 3 \times \frac{\sqrt{65}}{9}\right) \\
& P \equiv\left(\frac{8}{3}, \frac{\sqrt{65}}{3}\right)
\end{aligned}
\)
Now \(C P=r=\sqrt{\left(2-\frac{8}{3}\right)^2+\left(0-\frac{\sqrt{65}}{3}\right)^2}\)
\(
\begin{aligned}
& \Rightarrow r^2=\frac{69}{9} \\
& \Rightarrow 12 r^2=12 \times \frac{69}{9}=92
\end{aligned}
\)
Therefore, the required answer is 92. -
Question 80 of 269
80. Question
Two circles in the first quadrant of radii \(r_1\) and \(r_2\) touch the coordinate axes. Each of them cuts off an intercept of 2 units with the line \(x+y=2\). Then \(r_1^2+r_2^2-r_1 r_2\) is equal to _____. [2023 (12 Apr Shift 1)]
CorrectIncorrectHint
Assuming a circle of radius \(r\) which touches both the axis is given by, \((x-r)^2+(y-r)^2=r^2\) Now given line \(x+y=2\) makes the intercept 2 the circle, so plotting the diagram we get,
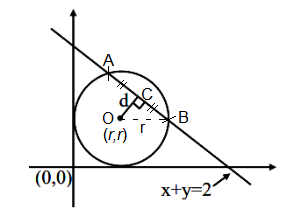
Where \(d=OC\) perpendicular distance of centre from line \(x+y=2\)
Now from diagram,
\(
A C=B C=1, O C=\sqrt{r^2-1}
\)
Now using the formula of perpendicular distance of point from the line we get,
\(
\begin{aligned}
& O C=\left|\frac{2 r-2}{\sqrt{2}}\right|=\sqrt{r^2-1} \\
& \Rightarrow 2(r-1)^2=r^2-1 \\
& \Rightarrow r^2-4 r+3=0 \\
& \Rightarrow r_1=1, r_2=3
\end{aligned}
\)
Hence, \(r_1^2+r_2^2-r_1 r_2=1+9-3=7\) -
Question 81 of 269
81. Question
Let the tangent and normal at the point \((3 \sqrt{3}, 1)\) on the ellipse \(\frac{x^2}{36}+\frac{y^2}{4}=1\) meet the \(y\)-axis at the points \(A\) and \(B\) respectively. Let the circle \(C\) be drawn taking \(A B\) as a diameter and the line \(x=2 \sqrt{5}\) intersect \(C\) at the points \(P\) and \(Q\). If the tangents at the points \(P\) and \(Q\) on the circle intersect at the point ( \(\alpha, \beta\) ), then \(\alpha^2-\beta^2\) is equal to [2023 (13 Apr Shift 1)]
CorrectIncorrectHint
Given that \(\frac{x^2}{36}+\frac{y^2}{4}=1\)
Observe that \((3 \sqrt{3}, 1)\) lies on the given ellipse.
Equation of tangent to the ellipse at the given point is \(T: \frac{3 \sqrt{3} x}{36}+\frac{y}{4}=1\)
\(
\Rightarrow \frac{\sqrt{3} x}{12}+\frac{y}{4}=1
\)
Equation of normal passing through same point will be \(N: \frac{x-3 \sqrt{3}}{\frac{3 \sqrt{3}}{36}}=\frac{y-1}{\frac{1}{4}}\)
\(
\begin{aligned}
& \Rightarrow \frac{12 x-36 \sqrt{3}}{\sqrt{3}}=4 y-4 \\
& \Rightarrow 3 x-9 \sqrt{3}=\sqrt{3} y-\sqrt{3} \\
& \Rightarrow 3 x-\sqrt{3} y=8 \sqrt{3}
\end{aligned}
\)
Now tangent and normal intersects the \(y\)-axis at \(A\) and \(B\) respectively.
\(
A(0,4) \quad B(0,-8)
\)
Equation of circle with \(A B\) as diameter will be
\(
\begin{aligned}
& \left(x-x_1\right)\left(x-x_2\right)+\left(y-y_1\right)\left(y-y_2\right)=0 \\
& \Rightarrow x^2+(y-4)(y+8)=0
\end{aligned}
\)
Line \(x=2 \sqrt{5}\) intersects the circle.
\(
\begin{aligned}
& \Rightarrow 20+y^2+4 y-32=0 \\
& \Rightarrow y^2+4 y-12=0 \\
& \Rightarrow(y+6)(y-2)=0
\end{aligned}
\)
Hence \(P(2 \sqrt{5},-6) Q(2 \sqrt{5}, 2)\)
Now let us find the equation of tangents to the circle at \(P, Q\).
\(
\begin{aligned}
& \Rightarrow T_1: x x_1+y y_1+2 y+2 y_1-32=0 \\
& \Rightarrow T_1: 2 \sqrt{5} x-6 y+2 y-12-32=0 \\
& \Rightarrow 2 \sqrt{5} x-4 y=44
\end{aligned}
\)
\(
\begin{aligned}
& \Rightarrow T_1: \sqrt{5} x-2 y=22 \ldots \ldots \ldots \text { (i) } \\
& \Rightarrow T_2: 2 \sqrt{5} x+2 y+2 y+4-32=0 \\
& \Rightarrow 2 \sqrt{5} x+4 y=28 \\
& \Rightarrow T_2: \sqrt{5} x+2 y=14 \ldots \ldots \ldots \text { (ii) }
\end{aligned}
\)
From (i) and (ii)
\(
\begin{aligned}
& \alpha=\frac{18}{\sqrt{5}} \beta=-2 \\
& \Rightarrow \alpha^2-\beta^2=\frac{304}{5}
\end{aligned}
\)
Hence this is the required option. -
Question 82 of 269
82. Question
Let the centre of a circle \(C\) be \(\alpha, \beta\) and its radius \(r<8\). Let \(3 x+4 y=24\) and \(3 x-4 y=32\) be two tangents and \(4 x+3 y=1\) be a normal to \(C\). Then \((\alpha-\beta+r)\) is equal to [2023 (13 Apr Shift 2)]
CorrectIncorrectHint
Given,
The centre of a circle \(C\) be \(\alpha, \beta\) and its radius \(r<8\), And \(3 x+4 y=24\) and \(3 x-4 y=32\) be two tangents
So, the distance from centre will be radius,
\(
\left|\frac{3 \alpha+4 \beta-24}{5}\right|=\left|\frac{3 \alpha-4 \beta-32}{5}\right|
\)
Taking + sign we get,
\(
\begin{aligned}
& \Rightarrow 3 \alpha+4 \beta-24=3 \alpha-4 \beta-32 \\
& \Rightarrow 8 \beta=-8 \Rightarrow \beta=-1
\end{aligned}
\)
And taking – sign we get,
\(
\begin{aligned}
& 3 \alpha+4 \beta-24=-3 \alpha+4 \beta+32 \\
& \Rightarrow 6 \alpha=56 \Rightarrow \alpha=\frac{56}{6}
\end{aligned}
\)
And \(4 x+3 y=1\) be a normal to \(C\)
So, \((\alpha, \beta)\) lies on \(4 x+3 y=1\)
\(
\Rightarrow 4 \alpha+3 \beta=1
\)
So, \(\alpha=1\) when \(\beta=-1\) and \(\beta=\frac{1}{3}\left(1-4 \times \frac{28}{3}\right)=\frac{-109}{9}\), if \(\alpha=\frac{28}{3}\)
Hence, radius will be,
\(
r=\left|\frac{3-4-24}{5}\right|=5<8 \text { if }(\alpha, \beta)=(1,-1)
\)
And if \((\alpha, \beta)=\left(\frac{28}{3}, \frac{-109}{9}\right)\) then \(r>8\), so neglected.
\(
\begin{aligned}
& \therefore r=5, \alpha=1, \beta=-1 \\
& \therefore \alpha-\beta+r=7
\end{aligned}
\) -
Question 83 of 269
83. Question
The number of common tangents, to the circles \(x^2+y^2-18 x-15 y+131=0\) and \(x^2+y^2-6 x-6 y-7=0\), is [2023 (15 Apr Shift 1)]
CorrectIncorrectHint
If \(S \equiv x^2+y^2+2 g x+2 f y+c=0\).
\(C \equiv(-g,-f)\) and \(r=\sqrt{g^2+f^2-c}\).
The given circles are \(x^2+y^2-18 x-15 y+131=0\)
\(
\Rightarrow C_1\left(9, \frac{15}{2}\right), r_1=\sqrt{81+\frac{225}{4}-131}=\frac{5}{2}
\)
and \(x^2+y^2-6 x-6 y-7=0\)
\(\Rightarrow C_2(3,3), r_2=\sqrt{9+9+7}=5\)
\(\Rightarrow d=C_1 C_2=\sqrt{(9-3)^2+\left(\frac{15}{2}-3\right)^2}=\sqrt{36+\frac{81}{4}}=\frac{15}{2}\)
\(\Rightarrow r_1+r_2=\frac{5}{2}+5=\frac{15}{2}\)
\(\Rightarrow C_1 C_2=r_1+r_2\)
\(\therefore\) Circles touch each other externally, 3 common tangents.
Hence this is the correct option. -
Question 84 of 269
84. Question
Let the eccentricity of an ellipse \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\) is reciprocal to that of the hyperbola \(2 x^2-2 y^2=1\). If the ellipse intersects the hyperbola at right angles, then square of length of the latus-rectum of the ellipse is _____. [2023 (06 Apr Shift 2)]
CorrectIncorrectHint
\(
\begin{aligned}
& E: \frac{x^2}{a^2}+\frac{y^2}{b^2}=1 \rightarrow e \\
& H: x^2-y^2=\frac{1}{2} \Rightarrow e^{\prime}=\sqrt{2} \\
& e=\frac{1}{\sqrt{2}} \\
& \because e^2=\frac{1}{2} \\
& 1-\frac{b^2}{a^2}=\frac{1}{2} \Rightarrow \frac{b^2}{a^2}=\frac{1}{2} \\
& a^2=2 b^2
\end{aligned}
\)
\(E \& H\) are at right angle
they are confocal
Focus of Hyperbola = focus of ellipse
\(
\begin{aligned}
& \left( \pm \frac{1}{\sqrt{2}} \cdot \sqrt{2}, 0\right)=\left( \pm \frac{a}{\sqrt{2}}, 0\right) \\
& a=\sqrt{2} \\
& \because a^2=2 b^2 \Rightarrow b^2=1 \\
& \text { Length of } L R=\frac{2 b^2}{a}=\frac{2(1)}{\sqrt{2}} \\
& =\sqrt{2}
\end{aligned}
\)
Square of \(L R=2\) -
Question 85 of 269
85. Question
Let the ellipse \(E: x^2+9 y^2=9\) intersect the positive \(x\) – and \(y\)-axes at the points \(A\) and \(B\) respectively. Let the major axis of \(E\) be a diameter of the circle \(C\). Let the line passing through \(A\) and \(B\) meet the circle \(C\) at the point \(P\). If the area of the triangle with vertices \(A, P\) and the origin \(O\) is \(\frac{m}{n}\), where \(m\) and \(n\) are coprime, then \(m-n\) is equal to [2023 (10 Apr Shift 1)]
CorrectIncorrectHint
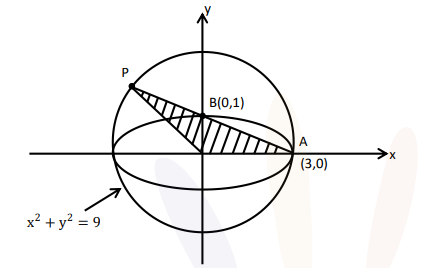
Equation of line \(AB\) or \(AP\) is
\(
\begin{aligned}
& \frac{x}{3}+\frac{y}{1}=1 \\
& x+3 y=3 \\
& x=(3-3 y)
\end{aligned}
\)
Intersection point of line AP & circle is \(P \left( x _0, y _0\right)\)
\(
\begin{aligned}
& x^2+y^2=9 \Rightarrow(3-3 y)^2+y^2=9 \\
& \Rightarrow 3^2\left(1+y^2-2 y\right)+y^2=9 \\
& \Rightarrow 5 y^2-9 y=0 \Rightarrow y(5 y-9)=0 \\
& \Rightarrow y=9 / 5
\end{aligned}
\)
\(
\begin{aligned}
& \text { Hence } x=3(1-y)=3\left(1-\frac{9}{5}\right)=3\left(\frac{-4}{5}\right) \\
& x=\frac{-12}{5} \\
& P\left(x_0, y_0\right)=\left(\frac{-12}{5}, \frac{9}{5}\right)
\end{aligned}
\)
Area of \(\triangle AOP\) is \(=\frac{1}{2} \times OA \times\) height
Height \(=9 / 5, O A=3\)
\(
=\frac{1}{2} \times 3 \times \frac{9}{5}=\frac{27}{10}=\frac{ m }{ n }
\)
Compare both side \(m =27, n =10 \Rightarrow m – n =17\) -
Question 86 of 269
86. Question
Let a circle of radius 4 be concentric to the ellipse \(15 x^2+19 y^2=285\). Then the common tangents are inclined to the minor axis of the ellipse at the angle [2023 (10 Apr Shift 2)]
CorrectIncorrectHint
Given,
\(
\begin{aligned}
& 15 x^2+19 y^2=285 \\
& \Rightarrow \frac{x^2}{19}+\frac{y^2}{15}=1
\end{aligned}
\)
Now plotting the diagram with given circle of radius 4 we get,
Now, let the equation of tangent of ellipse be \(y=m x \pm \sqrt{19 m^2+15}\left\{\right.\) as \(\left.c^2=a^2 m^2+b^2\right\}\) If it is tangent to circle \(x^2+y^2=16\) then using the formula, \(c^2=r^2\left(1+m^2\right)\) we get,
\(
\begin{aligned}
& \frac{\sqrt{19 m^2+15}}{\sqrt{1+m^2}}=4 \\
& \Rightarrow 19 m^2+15=16+16 m^2 \\
& \Rightarrow 3 m^2=1 \\
& \Rightarrow m= \pm \frac{1}{\sqrt{3}} \\
& \Rightarrow \theta=30^{\circ} \text { with } x \text {-axis, }
\end{aligned}
\)
Hence, Angle made by tangent with minor axis i.e., with \(y\) axis is \(\frac{\pi}{3}\) -
Question 87 of 269
87. Question
Consider ellipses \(E_k: k x^2+k^2 y^2=1, k=1,2, \ldots, 20\). Let \(C_k\) be the circle which touches the four chords joining the end points (one on minor axis and another on major axis) of the ellipse \(E_k\). If \(r_k\) is the radius of the circle \(C_k\), then the value of \(\sum_{k=1}^{20} \frac{1}{r_k^2}\) is [2023 (11 Apr Shift 1)]
CorrectIncorrectHint
Given,
\(
\begin{aligned}
& E_k: k x^2+k^2 y^2=1 \\
& \Rightarrow E_k: \frac{x^2}{\left(\frac{1}{\sqrt{k}}\right)^2}+\frac{y^2}{\left(\frac{1}{k}\right)^2}=1
\end{aligned}
\)
Now equation of the chord joining the points \(\left(\frac{1}{\sqrt{k}}, 0\right) \&\left(0, \frac{1}{k}\right)\) will be,
\(
\begin{aligned}
& L_k: \frac{x}{\left(\frac{1}{\sqrt{k}}\right)}+\frac{y}{\left(\frac{1}{k}\right)}=1 \\
& \Rightarrow \sqrt{k} x+k y-1=0
\end{aligned}
\)
Now \(r_k=\) Perpendicular distance of \(L_k\) from \((0,0)\) we get,
\(
\begin{aligned}
& r_k=\left|\frac{-1}{\sqrt{k+k^2}}\right| \\
& \Rightarrow r_k^2=\frac{1}{k+k^2}
\end{aligned}
\)
Now putting the value of \(r_k^2\) in \(\sum_{k=1}^{20} \frac{1}{r_k^2}\) we get,
\(
\begin{aligned}
& \sum_{k=1}^{20} \frac{1}{r_k^2}=\sum_{k=1}^{20} k+k^2=\frac{20 \times 21}{2}+\frac{20 \times 21 \times 41}{6} \\
& =210+2870=3080
\end{aligned}
\) -
Question 88 of 269
88. Question
Let \(P\left(\frac{2 \sqrt{3}}{\sqrt{7}}, \frac{6}{\sqrt{7}}\right), Q, R\) and \(S\) be four points on the ellipse \(9 x^2+4 y^2=36\). Let \(P Q\) and \(R S\) be mutually perpendicular and pass through the origin. If \(\frac{1}{(P Q)^2}+\frac{1}{(R S)^2}=\frac{p}{q}\), where \(p\) and \(q\) are coprime, then \(p+q\) is equal to [2023 (12 Apr Shift 1)]
CorrectIncorrectHint
Given, \(P\left(\frac{2 \sqrt{3}}{\sqrt{7}}, \frac{6}{\sqrt{7}}\right), Q, R\) and \(S\) be four points on the ellipse \(\frac{x^2}{4}+\frac{y^2}{9}=1\)
Now, \(O P=r_1=\sqrt{\left(\frac{2 \sqrt{3}}{\sqrt{7}}\right)^2+\left(\frac{6}{\sqrt{7}}\right)^2}=\sqrt{\frac{48}{7}}\) where \(O\) is origin,
Let \(P\) be \(\left(r_1 \cos \theta, r_1 \sin \theta\right)\)
\(P\) lies on ellipse, so we get,
\(
\begin{aligned}
& \frac{r_1{ }^2 \cos ^2 \theta}{4}+\frac{r_1^2 \sin ^2 \theta}{9}=1 \\
& \Rightarrow \frac{\cos ^2 \theta}{4}+\frac{\sin ^2 \theta}{9}=\frac{7}{48}
\end{aligned}
\)
Let \(R\) be \(\left(-r_2 \sin \theta, r_2 \cos \theta\right)\) as \(P Q \& R S\) are perpendicular and pass through origin,
So, \(\frac{r_2{ }^2 \sin ^2 \theta}{4}+\frac{r_2{ }^2 \cos ^2 \theta}{9}=1\)
\(
\Rightarrow \frac{\sin ^2 \theta}{4}+\frac{\cos ^2 \theta}{9}=\frac{1}{r_2^2} \ldots
\)
Now adding equation (i) & (ii) we get,
\(
\frac{1}{r_2{ }^2}=\frac{1}{4}+\frac{1}{9}-\frac{7}{48}=\frac{31}{144}
\)
Now solving,
\(
\begin{aligned}
& \frac{1}{P Q^2}+\frac{1}{R S^2}=\frac{1}{4}\left(\frac{1}{O P^2}+\frac{1}{O R^2}\right) \\
& \Rightarrow \frac{1}{P Q^2}+\frac{1}{R S^2}=\frac{1}{4}\left(\frac{1}{r_1^2}+\frac{1}{r_2^2}\right) \\
& \Rightarrow \frac{1}{P Q^2}+\frac{1}{R S^2}=\frac{1}{4}\left(\frac{7}{48}+\frac{31}{144}\right)=\frac{13}{144}=\frac{p}{m} \\
& \therefore p+m=157
\end{aligned}
\) -
Question 89 of 269
89. Question
Let an ellipse with centre \((1,0)\) and latus rectum of length \(\frac{1}{2}\) have its major axis allong \(x\)-axis. If its minor axis subtends an angle \(60^{\circ}\) at the foci, then the square of the sum of the lengths of its minor and major axes is equal to ____. [JEE Main 2023 April 15th Shift 1]
CorrectIncorrectHint
\(
\begin{aligned}
& \text { L.R. }=\frac{2 b^2}{a}=\frac{1}{2} \\
& 4 b^2=a \dots(i) \\
& \text { Ellipse } \frac{(x-1)^2}{a^2}+\frac{y^2}{b^2}=1 \\
& m_{B_1 F_1}=\frac{1}{\sqrt{3}} \\
& \frac{b}{a}=\frac{1}{\sqrt{3}} \\
& 3 b^2=a^2 e^2=a^2-b^2 \\
& 4 b^2=a^2 \dots(ii) \\
& \text { From }(i) \text { and (ii) } \\
& a=a^2 \\
& \therefore a=1 \\
& b^2=\frac{1}{4} \\
& ((2 a)+(2 b))^2=9
\end{aligned}
\) -
Question 90 of 269
90. Question
Let \(H_n: \frac{x^2}{1+n}-\frac{y^2}{3+n}=1, n \in N\). Let \(k\) be the smallest even value of \(n\) such that the eccentricity of \(H_k\) is a rational number. If \(l\) is the length of the latus rectum of \(H_k\), then \(21 l\) is equal to [2023 (11 Apr Shift 1)]
CorrectIncorrectHint
Given, Equation of hyperbola,
\(
H_n: \frac{x^2}{1+n}-\frac{y^2}{3+n}=1, n \in N
\)
Now using the eccentricity formula we get,
\(
\begin{aligned}
& e^2=1+\frac{3+n}{1+n} \\
& \Rightarrow e^2=\frac{2 n+4}{n+1}=\frac{2(n+2)}{n+1}
\end{aligned}
\)
Now check when \((n+1)=9,25,49, \ldots \ldots\) is perfect square and then at the same time \(2(n+2)\) should also be perfect square,
So checking for \(n=8 \rightarrow e^2=\frac{20}{9}\)
\(
\begin{aligned}
& n=24 \rightarrow e^2=\frac{52}{25} \\
& n=48 \rightarrow e^2=\frac{100}{49} \Rightarrow e=\frac{10}{7}
\end{aligned}
\)
Hence, for \(n=48\) both \(n+1 \& 2(n+2)\) are perfect square,
Now we know that,
Length of latusrectum is given by \(l=\frac{2 b^2}{a}=\frac{2(n+3)}{\sqrt{n+1}}=\frac{2 \times 51}{7}\)
Hence, \(21 l=\frac{42 \times 51}{7}=306\) -
Question 91 of 269
91. Question
Let the tangent to the parabola \(y^2=12 x\) at the point \((3, \alpha)\) be perpendicular to the line \(2 x+2 y=3\). Then the square of distance of the point \((6,-4)\) from the normal to the hyperbola \(\alpha^2 x^2-9 y^2=9 \alpha^2\) at its point \((\alpha-1, \alpha+2)\) is equal to ____. [2023 (11 Apr Shift 2)]
CorrectIncorrectHint
Given, The tangent to the parabola \(y^2=12 x\) at the point \((3, \alpha)\) be perpendicular to the line \(2 x+2 y=3\)
So, Slope of tangent \(=1=\frac{6}{\alpha} \Rightarrow \alpha=6\)
So, equation of hyperbola will be,
\(
\begin{aligned}
& 36 x^2-9 y^2=324 \\
& \Rightarrow \frac{x^2}{9}-\frac{y^2}{36}=1
\end{aligned}
\)
Now equation of tangent at \((5,8)\) will be,
\(
\begin{aligned}
& \frac{5 x}{9}-\frac{8 y}{36}=1 \\
& \Rightarrow 5 x-2 y=9
\end{aligned}
\)
So, slope of normal \(=\frac{-2}{5}\)
Now finding, equation of normal \(y-8=\frac{-2}{5}(x-5)\)
\(
\begin{aligned}
& \Rightarrow 5 y-40=-2 x+10 \\
& \Rightarrow 5 y+2 x=50
\end{aligned}
\)
Now finding, distance from \((6,-4)\), we get,
\(
\begin{aligned}
& =\left|\frac{12-20-50}{\sqrt{29}}\right|=\frac{58}{\sqrt{29}} \\
& =2 \sqrt{29}
\end{aligned}
\)
Hence, \((2 \sqrt{29})^2=116\) -
Question 92 of 269
92. Question
Let \(m_1\) and \(m_2\) be the slopes of the tangents drawn from the point \(P(4,1)\) to the hyperbola \(H: \frac{y^2}{25}-\frac{x^2}{16}=1\) If \(Q\) is the point from which the tangents drawn to \(H\) have slopes \(\left|m_1\right|\) and \(\left|m_2\right|\) and they make positive intercepts \(\alpha\) and \(\beta\) on the \(x\)-axis, then \(\frac{(P Q)^2}{\alpha \beta}\) is equal to ____. [2023 (13 Apr Shift 1)]
CorrectIncorrectHint
Given that \(H: \frac{y^2}{25}-\frac{x^2}{16}=1\)
Equation of tangent to the hyperbola is: \(y=m x+\sqrt{25-16 m^2}\)
Passes through \((4,1)\)
\(
\begin{aligned}
& \Rightarrow y=m x+\sqrt{25-16 m^2} \\
& \Rightarrow 1=4 m+\sqrt{25-16 m^2} \\
& \Rightarrow 4 m^2-m-3 \\
& \Rightarrow m_1=1, m_2=\frac{-3}{4} \\
& \Rightarrow\left|m_1\right|=1,\left|m_2\right|=\frac{3}{4}
\end{aligned}
\)
Equation of tangents with slopes \(1 \& \frac{3}{4}\)
\(
\begin{aligned}
& \Rightarrow y=x-3 \ldots \ldots .( i ) \\
& \Rightarrow y=\frac{3}{4} x-4 \ldots \ldots \text { (ii) } \\
& \text { (i) & (ii) } \Rightarrow Q \equiv(-4,-7) \\
& P \equiv(4,1) \\
& \Rightarrow(P Q)^2=8^2+8^2=128
\end{aligned}
\)
On converting \((i)\) and \((i i)\) in intercept form we get,
\(
\begin{aligned}
& \text { (i) } \Rightarrow \alpha=3,( ii ) \Rightarrow \beta=\frac{16}{3} \\
& \Rightarrow \frac{(P Q)^2}{\alpha \beta}=\frac{128}{3 \times \frac{16}{3}}=8
\end{aligned}
\)
Hence this is the required option. -
Question 93 of 269
93. Question
The foci of a hyperbola are \(( \pm 2,0)\) and its eccentricity is \(\frac{3}{2}\). A tangent, perpendicular to the line \(2 x+3 y=6\), is drawn at a point in the first quadrant on the hyperbola. If the intercepts made by the tangent on the \(x\)-and \(y\)-axes are \(a\) and \(b\) respectively, then \(|6 a|+|5 b|\) is equal to [2023 (13 Apr Shift 2)]
CorrectIncorrectHint
The given equation of hyperbola is \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1, a e=2, e=\frac{3}{2}\)
\(
\begin{aligned}
& \Rightarrow a=\frac{4}{3} \\
& \Rightarrow b^2=a^2 e^2-a^2=4-\frac{16}{9}=\frac{20}{9}
\end{aligned}
\)
The tangent is perpendicular to \(2 x+3 y=6\).
Slope of tangent is \(m=\frac{-1}{\frac{-2}{3}}=\frac{3}{2}\)
Equation of tangent is \(y=m x-\sqrt{a^2 m^2-b^2}\)
\(
\Rightarrow y=\frac{3}{2} x-\sqrt{\frac{16}{9} \times \frac{9}{4}-\frac{20}{9}}
\)
\(\left(\because\right.\) Tangent is in \(1^{\text {st }}\) quadrant \(\left.\Rightarrow C<0\right)\)
\(
\Rightarrow y=\frac{3}{2} x-\frac{4}{3}
\)
Converting the equation into intercept form:
\(
\begin{aligned}
& \Rightarrow \frac{x}{\left(\frac{8}{9}\right)}+\frac{y}{\left(-\frac{4}{3}\right)}=1 \\
& \Rightarrow|6 a|+|5 b|=\left|\frac{6 \times 8}{9}\right|+\left|\frac{5 \times(-4)}{3}\right|=12
\end{aligned}
\)
Hence this is the required option. -
Question 94 of 269
94. Question
Let \(R\) be the focus of the parabola \(y^2=20 x\) and the line \(y=m x+c\) intersect the parabola at two points \(P\) and \(Q\). Let the points \(G(10,10)\) be the centroid of the triangle \(P Q R\). If \(c-m=6\), then \(P Q^2\) is [2023 (08 Apr Shift 1)]
CorrectIncorrectHint
\(
y^2=20 x, y=m x+ c
\)
Put value of \(x\)
\(
\begin{aligned}
& y^2=20\left(\frac{y-c}{m}\right) \\
& \Rightarrow y^2-\frac{20}{m} y+\frac{20}{m} c=0 \ldots \ldots(i)
\end{aligned}
\)
Since, centroid \(=(10,10)\)
So, \(\frac{y_1+y_2+0}{3}=10\)
\(
\Rightarrow y_1+y_2=30
\)
From (i), Sum of roots \(=\frac{20}{m}=30 \Rightarrow m=\frac{2}{3}\)
Also, \(c-m=6 \Rightarrow c=6+\frac{2}{3}=\frac{20}{3}\)
Now, the equation is :
\(
\begin{aligned}
& y^2-\frac{20}{2} \times 3 y+\frac{20}{2} \times 3 \times \frac{20}{3}=0 \\
& \Rightarrow y^2-30 y+200=0 \\
& \Rightarrow y^2-20 y-10 y+200=0 \\
& \Rightarrow(y-20)(y-10)=0 \\
& \Rightarrow y=10,20 \Rightarrow x=5, x=20 \\
& \therefore P \equiv(5,10), Q \equiv(20,20) \\
& \text { So, }(P Q)^2=(20-5)^2+(20-10)^2 \\
& =225+100=325
\end{aligned}
\) -
Question 95 of 269
95. Question
The ordinates of the points \(P\) and \(Q\) on the parabola with focus \((3,0)\) and directrix \(x=-3\) are in the ratio \(3: 1\). If \(R(\alpha, \beta)\) is the point of intersection of the tangents to the parabola at \(P\) and \(Q\), then \(\frac{\beta^2}{\alpha}\) is equal to [2023 (08 Apr Shift 2)]
CorrectIncorrectHint
Given, Focus \((3,0)\), Directrix, \(x=-3\)
So, the equation of parabola will be, \(y^2=12 x\)
Now taking the parametric point \(\left(3 t^2, 6 t\right)\)
Now we know that \(R(\alpha, \beta)\) will be the aithematic mean of ordinate and geometric mean of abscissa will be,
Hence, \(\beta=\frac{6\left(t_1+t_2\right)}{2}\) and \(\alpha=\sqrt{3 t_1{ }^2 \times 3 t_2{ }^2}=3 t_1 t_2\)
So, putting the value in \(\frac{\beta^2}{\alpha}, \Rightarrow \frac{\beta^2}{\alpha}=\frac{9\left(t_1+t_2\right)^2}{3 t_1 t_2}=\frac{9\left(4 t_2\right)^2}{3 \times 3 t_2{ }^2}=16\left(\because \frac{6 t_1}{6 t_2}=3\right.\), given \()\) -
Question 96 of 269
96. Question
Let a common tangent to the curves \(y^2=4 x\) and \((x-4)^2+y^2=16\) touch the curves at the points \(P\) and \(Q\). Then \((P Q)^2\) is equal to ____. [2023 (10 Apr Shift 1)]
CorrectIncorrectHint
Given, Common tangent to the curves \(y^2=4 x\) and \((x-4)^2+y^2=16\) touch the curves at the points \(P\) and \(Q\) Let, the equation of tangent be, \(y=m x+\frac{a}{m}\), where \(a=1\) is focus and \(m\) is slope,
So, equation of tangent to parabola will be, \(y=m x+\frac{1}{m}\)
Also line is tangent to circle, So, using perpendicular distance formula from centre \((4,0)\) to tangent which will be radius \(r=4\), we get,
\(
\begin{aligned}
& \left|\frac{4 m+\frac{1}{m}}{m^2+1}\right|=4 \\
& \Rightarrow 16 m^2+\frac{1}{m^2}+8=16 m^2+16 \\
& \Rightarrow m^2=\frac{1}{8} \\
& \Rightarrow m= \pm \frac{1}{2 \sqrt{2}}
\end{aligned}
\)
Now if \(m=\frac{1}{2 \sqrt{2}}\) then \(P=\left(\frac{a}{m^2}, \frac{2 a}{m}\right)=(8,4 \sqrt{2})\)
Now equation of tangent will be, \(x-2 \sqrt{2} y+8=0\)
And \(Q\) will be foot of perpendicular from \((4,0)\) on tangent \(x-2 \sqrt{2} y+8=0\),
So, using foot of perpendicular formula we get,
\(
\begin{aligned}
& \frac{x-4}{1}=\frac{y-0}{-2 \sqrt{2}}=-\frac{4-0+8}{1^2+(2 \sqrt{2})^2} \\
& \Rightarrow(x, y)=\left(\frac{8}{3}, \frac{8 \sqrt{2}}{3}\right)
\end{aligned}
\)
Hence, by distance formula we get,
\(
\begin{aligned}
& (P Q)^2=\left(\frac{16}{3}\right)^2+\left(\frac{4 \sqrt{2}}{3}\right)^2 \\
& \Rightarrow(P Q)^2=\frac{256+32}{9}=32
\end{aligned}
\) -
Question 97 of 269
97. Question
Let \(P Q\) be a focal chord of the parabola \(y^2=36 x\) of length 100 , making an acute angle with the positive \(x\)-axis. Let the ordinate of \(P\) be positive and \(M\) be the point on the line segment \(P Q\) such that \(P M: M Q=3: 1\). Then which of the following points does NOT lie on the line passing through \(M\) and perpendicular to the line \(P Q\) ? [2023 (13 Apr Shift 1)]
CorrectIncorrectHint
We have been given the length of focal chord \(P Q=100\).
Length of focal chord at \((t)=a\left(t+\frac{1}{t}\right)^2=100\)
Where \(a=9\)
\(
\begin{aligned}
& t+\frac{1}{t}= \pm \frac{10}{3} \\
& \therefore t=3, \frac{1}{3},-3, \frac{-1}{3}
\end{aligned}
\)
Since ordinate of \(P\) is + ve
\(
\therefore t=3 \text { or } \frac{1}{3}
\)
\(
\Rightarrow P(81,54) \& Q(1,-6)
\)
( \(t=3\) as slope of \(P Q\) is positive)
\(
\therefore M(21,9)
\)
Required line: \(y-9=\frac{-80}{60}(x-21)\)
\(
\Rightarrow 4 x+3 y=111
\)
\((-3,43)\) does not lie on line.
Hence this is the correct option. -
Question 98 of 269
98. Question
Let a circle \(C :( x – h )^2+( y – k )^2= r ^2, k >0\), touch the \(x\)-axis at \((1,0)\). If the line \(x + y =0\) intersects the circle \(C\) at \(P\) and \(Q\) such that the length of the chord \(P Q\) is 2, then the value of \(h+k+r\) is equal to ___. [JEE Main 2022 25th June Shift 2]
CorrectIncorrectHint
\(
\begin{aligned}
& k=r \\
& h=1
\end{aligned}
\)
Circle touches xaxis at \((1,0)\)
\(\Rightarrow\) radius \(=r=k \Rightarrow\) perpendicular distance from \((1, r)\) to the line \(x+y=0\) is \(\frac{r+1}{\sqrt{2}}\)
\(
OP = r , PR =1
\)
\(
\Rightarrow OR =\frac{ r +1}{\sqrt{2}}
\)
\(
\begin{gathered}
\Rightarrow r^2=1+\frac{(r+1)^2}{2} \\
2 r^2=2+r^2+1+2 r \\
r^2-2 r-3=0 \\
(r-3)(r+1)=0 \\
r=3,-1
\end{gathered}
\)
\(
\text { The value of } h+k+r \text { is equal to } 1+3+3=7 \text {. }
\) -
Question 99 of 269
99. Question
Let a circle \(C\) touch the lines \(L _1: 4 x -3 y + K _1\) \(=0\) and \(L_2: 4 x-3 y+K_2=0, K_1, K_2 \in R\). If a line passing through the centre of the circle \(C\) intersects \(L_1\) at \((-1,2)\) and \(L_2\) at \((3,-6)\), then the equation of the circle \(C\) is [JEE Main 2022 25th June Shift 1]
CorrectIncorrectHint
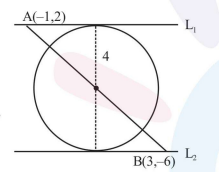
\(
\begin{aligned}
& L _1: 4 x -3 y + K _1=0 \\
& L _2: 4 x -3 y + K _2=0 \\
& \text { now } \\
& -4-6+ K _1=0 \Rightarrow K _1=10 \\
& 12+18+ K _2=0 \Rightarrow K _2=-30
\end{aligned}
\)
\(\Rightarrow\) Tangent to the circle are
\(
\begin{aligned}
& 4 x-3 y+10=0 \\
& 4 x-3 y-30=0
\end{aligned}
\)
Length of diameter \(2 r=\frac{|10+30|}{5}=8\)
\(
\Rightarrow r =4
\)
Now centre is mid point of \(A \& B\)
\(
x =1, y =-2
\)
Equation of circle
\(
(x-1)^2+(y+2)^2=16
\) -
Question 100 of 269
100. Question
Let the abscissae of the two points \(P\) and \(Q\) be the roots of \(2 x^2-r x+p=0\) and the ordinates of \(P\) and \(Q\) be the roots of \(x^2-s x-q=0\). If the equation of the circle described on \(PQ\) as diameter is \(2\left(x^2+y^2\right)-11 x-14 y-22=0\), then \(2 r+s-2 q+p\) is equal to [JEE Main 2022 25th June Shift 1]
CorrectIncorrectHint
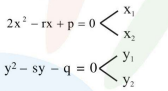
Equation of the circle with \(PQ\) as diameter is
\(
2\left(x^2+y^2\right)-r x-2 s y+p-2 q=0
\)
on comparing with the given equation
\(
\begin{aligned}
& r =11, s =7 \\
& p -2 q =-22 \\
& \therefore 2 r + s -2 q + p =22+7-22=7
\end{aligned}
\) -
Question 101 of 269
101. Question
A circle touches both the \(y\)-axis and the line \(x+y=0\). Then the locus of its center is [JEE Main 2022 25th June Shift 2]
CorrectIncorrectHint
Let \((h, k)\) is centre of circle
\(
\begin{aligned}
& \left|\frac{h-k}{\sqrt{2}}\right|=|h| \\
& k^2-h^2+2 h k=0
\end{aligned}
\)
\(\therefore\) Equation of locus is \(y^2-x^2+2 x y=0\)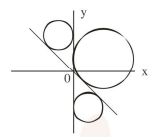
-
Question 102 of 269
102. Question
Let \(C\) be a circle passing through the points \(A (2,-1)\) and \(B (3,4)\). The line segment \(AB\) is not a diameter of \(C\). If \(r\) is the radius of \(C\) and its centre lies on the circle \((x-5)^2+(y-1)^2=\frac{13}{2}\), then \(r^2\) is equal to : [JEE Main 2022 26th June Shift 1]
CorrectIncorrectHint
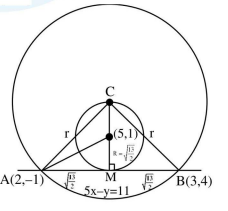
\(
\begin{aligned}
& AB =\sqrt{ } 26 \\
& r ^2= CM ^2+ AM ^2 \\
& =\left(2 \times \sqrt{\frac{13}{2}}\right)^2+\left(\sqrt{\frac{13}{2}}\right)^2 \\
& r ^2=\frac{65}{2}
\end{aligned}
\) -
Question 103 of 269
103. Question
The set of values of \(k\) for which the circle C : \(4 x^2+4 y^2-12 x+8 y+k=0\) lies inside the fourth quadrant and the point \(\left(1,-\frac{1}{3}\right)\) lies on or inside the circle \(C\) is : [JEE Main 2022 27th June Shift 2]
CorrectIncorrectHint
\(
\begin{aligned}
& \text { C }: 4 x^2+4 y^2-12 x+8 y+k=0 \\
& \Rightarrow x^2+y^2-3 x+2 y+\left(\frac{k}{4}\right)=0 \\
& \text { Centre }\left(\frac{3}{2},-1\right) ; r=\sqrt{\frac{13-k}{2}} \Rightarrow k \leq 13 \ldots (1)
\end{aligned}
\)
(i) Point \(\left(1, \frac{-1}{3}\right)\) lies on or inside circle \(C\)
\(
\Rightarrow S _1 \leq 0 \Rightarrow k \leq \frac{92}{9}
\)
(ii) \(C\) lies in \(4^{\text {th }}\) quadrant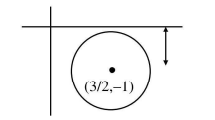
\(
\begin{aligned}
& r<1 \\
& \Rightarrow \frac{\sqrt{13-k}}{2}<1 \\
& \Rightarrow k<9 \ldots .(3)
\end{aligned}
\)
Hence \((1) \cap(2) \cap(3) \Rightarrow k \in\left(9, \frac{92}{9}\right]\) -
Question 104 of 269
104. Question
Let a circle \(C\) of radius 5 lie below the \(x\)-axis. The line \(L _1=4 x+3 y-2\) passes through the centre \(P\) of the circle \(C\) and intersects the line \(L _2: 3 x -4 y -11=0\) at \(Q\). The line \(L _2\) touches \(C\) at the point \(Q\). Then the distance of \(P\) from the line \(5 x-12 y+51=0\) is [JEE Main 2022 27th June Shift 2]
CorrectIncorrectHint
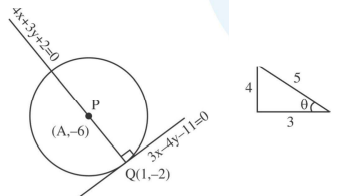
\(
\begin{aligned}
& 4 x+3 y+2=0 \\
& 3 x-4 y-11=0
\end{aligned}
\)
\(
\begin{aligned}
& \frac{x}{-25}=\frac{y}{50}=\frac{1}{-25} \\
& \frac{x-1}{\cos \theta}=\frac{y+2}{\sin \theta}= \pm 5 \\
& y=-2+5\left(-\frac{4}{5}\right)=-6 \\
& x=1+5\left(\frac{3}{5}\right)=4
\end{aligned}
\)
Req. distance
\(
\begin{aligned}
& \left|\frac{5(4)-12(-6)+51}{13}\right| \\
& =\left|\frac{20+72+51}{13}\right| \\
& =\frac{143}{13}=11
\end{aligned}
\) -
Question 105 of 269
105. Question
If the tangents drawn at the point \(O (0,0)\) and \(P (1+\sqrt{5}, 2)\) on the circle \(x^2+y^2-2 x-4 y=0\) intersect at the point \(Q\), then the area of the triangle \(OPQ\) is equal to [JEE Main 2022 28th June Shift 1]
CorrectIncorrectHint
Tangent at \(O\)
\(
\begin{aligned}
& -(x+0)-2(y+0)=0 \\
& \Rightarrow x+2 y=0
\end{aligned}
\)
Tangent at \(P\)
\(
x(1+\sqrt{5})+y \cdot 2-(x+1+\sqrt{5})-2(y+2)=0
\)
Put \(x=-2 y\)
\(
\begin{aligned}
& -2 y(1+\sqrt{5})+2 y+2 y-1-\sqrt{5}-2 y-4=0 \\
& -2 \sqrt{5} y=5+\sqrt{5} \Rightarrow y=\left(\frac{\sqrt{5}+1}{2}\right)
\end{aligned}
\)
\(
Q\left(\sqrt{5}+1,-\frac{\sqrt{5}+1}{2}\right)
\)
Length of tangent \(O Q=\frac{5+\sqrt{5}}{2}\)
\(
\begin{aligned}
& \text { Area }=\frac{ RL ^3}{ R ^2+ L ^2} \\
& R =\sqrt{5} \\
& =\frac{\sqrt{5} \times\left(\frac{5+\sqrt{5}}{2}\right)^3}{5+\left(\frac{5+\sqrt{5}}{2}\right)^2} \\
& =\frac{\sqrt{5}}{2} \times \frac{4 \times(125+75+75 \sqrt{5}+5 \sqrt{5})}{(20+25+10 \sqrt{5}+5)} \\
& =\frac{5+3 \sqrt{5}}{2}
\end{aligned}
\) -
Question 106 of 269
106. Question
Let the lines \(y+2 x=\sqrt{ } 11+7 \sqrt{7} \quad\) and \(2 y + x =2 \sqrt{11}+6 \sqrt{7}\) be normal to a circle \(C:(x-h)^2+(y-k)^2=r^2\). If the line \(\sqrt{11} y-3 x=\frac{5 \sqrt{77}}{3}+11\) is tangent to the circle C, then the value of \((5 h-8 k)^2+5 r^2\) is equal to ____. [JEE Main 2022 28th June Shift 1]
CorrectIncorrectHint
Normal are
\(
\begin{aligned}
& y+2 x=\sqrt{11}+7 \sqrt{7} \\
& 2 y+x=2 \sqrt{11}+6 \sqrt{7}
\end{aligned}
\)
Center of the circle is point of intersection of normals i.e.
\(
\left(\frac{8 \sqrt{7}}{3}, \sqrt{11}+\frac{5 \sqrt{7}}{3}\right)
\)
Tangent is \(\sqrt{11} y-3 x=\frac{5 \sqrt{77}}{3}+11\)
Radius will be \(\perp\) distance of tangent from center i.e. \(4 \sqrt{\frac{7}{5}}\)
Now \((5 h-8 k)^2+5 r^2=816\) -
Question 107 of 269
107. Question
If one of the diameters of the circle \(x^2+y^2-2 \sqrt{2} x\) \(-6 \sqrt{2} y+14=0\) is a chord of the circle \((x-2 \sqrt{2})^2\) \(+(y-2 \sqrt{2})^2=r^2\), then the value of \(r^2\) is equal to [JEE Main 2022 28th June Shift 2]
CorrectIncorrectHint
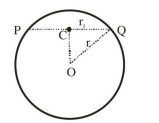
\(PQ\) is diameter of circle
\(
\begin{aligned}
& S: x^2+y^2-2 \sqrt{2} x-6 \sqrt{2} y+14=0 \\
& C(\sqrt{2}, 3 \sqrt{2}), O(2 \sqrt{2}, 2 \sqrt{2}) \\
& r_1=\sqrt{6} \\
& S_1:(x-2 \sqrt{2})^2+(y-2 \sqrt{2})^2=r^2
\end{aligned}
\)
Now in \(\triangle OCQ\)
\(
\begin{aligned}
& | OC |^2+| CQ |^2=| OQ |^2 \\
& 4+6= r ^2 \\
& r ^2=10
\end{aligned}
\) -
Question 108 of 269
108. Question
Let the tangent to the circle \(C_1: x^2+y^2=2\) at the point \(M(-1,1)\) intersect the circle \(C_2\) : \((x-3)^2+(y-2)^2=5\), at two distinct points A and \(B\). If the tangents to \(C_2\) at the points \(A\) and \(B\) intersect at \(N\), then the area of the triangle ANB is equal to : [JEE Main 2022 29th June Shift 1]
CorrectIncorrectHint
\(
OP =\left|\frac{2-3+2}{\sqrt{2}}\right|
\)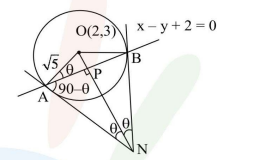
\(
\begin{aligned}
& OP =\frac{3}{\sqrt{2}} \\
& AP =\sqrt{ OA ^2- OP ^2} \\
& =\frac{1}{\sqrt{2}} \\
& \tan \theta=3 \\
& \therefore \sin \theta=\frac{3}{\sqrt{10}}=\frac{ AP }{ AN } \\
& \Rightarrow AN =\frac{\sqrt{5}}{3}= BN \\
& \text { Area of } \triangle ANB =\frac{1}{2} \cdot\left( AN ^2\right) \sin 2 \theta=\frac{1}{6}
\end{aligned}
\) -
Question 109 of 269
109. Question
Let a triangle \(A B C\) be inscribed in the circle \(x ^2-\) \(\sqrt{2}(x+y)+y^2=0\) such that \(\angle B A C=\frac{\pi}{2}\). If the length of side \(A B\) is \(\sqrt{2}\), then the area of the \(\triangle ABC\) is equal to: [JEE Main 2022 29th June Shift 2]
CorrectIncorrectHint
Radius of given circle is 1 .
\(
\begin{aligned}
& BC =\text { diameter }=2 , AB =\sqrt{2} \\
& AC =\sqrt{ BC ^2- AB ^2}=\sqrt{2} \\
& \triangle ABC =\frac{1}{2} AB \cdot AC =1
\end{aligned}
\) -
Question 110 of 269
110. Question
Let the maximum area of the triangle that can be inscribed in the ellipse \(\frac{x^2}{a^2}+\frac{y^2}{4}=1, a>2\), having one of its vertices at one end of the major axis of the ellipse and one of its sides parallel to the \(y\)-axis, be \(6 \sqrt{3}\). Then the eccentricity of the ellipse is : [JEE Main 2022 25th June Shift 2]
CorrectIncorrectHint
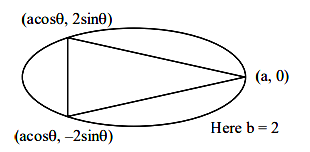
\(
\begin{aligned}
& A =\frac{1}{2} a (1-\cos \theta)(4 \sin \theta) \\
& A =2 a (1-\cos \theta) \sin \theta \\
& \frac{ dA }{ d \theta}=2 a \left(\sin ^2 \theta+\cos \theta-\cos ^2 \theta\right) \\
& \frac{ dA }{ d \theta}=0 \Rightarrow 1+\cos \theta-2 \cos ^2 \theta=0 \\
& \cos \theta=1 \text { (Reject) }
\end{aligned}
\)
or
\(
\begin{aligned}
& \cos \theta=\frac{-1}{2} \Rightarrow \theta=\frac{2 \pi}{3} \\
& \frac{ d ^2 A }{ d \theta^2}=2 a \left(2 \sin ^2 \theta-\sin \theta\right) \\
& \frac{ d ^2 A }{ d \theta^2}<0 \text { for } \theta=\frac{2 \pi}{3}
\end{aligned}
\)
Now, \(A_{\max }=\frac{3 \sqrt{3}}{2} a=6 \sqrt{3}\)
\(
a=4
\)
Now, \(e=\sqrt{\frac{a^2-b^2}{a^2}}=\frac{\sqrt{3}}{2}\) -
Question 111 of 269
111. Question
The line \(y=x+1\) meets the ellipse \(\frac{x^2}{4}+\frac{y^2}{2}=1\) at two points \(P\) and \(Q\). If \(r\) is the radius of the circle with \(PQ\) as diameter then ( \(3 r )^2\) is equal to [JEE Main 2022 25th June Shift 2]
CorrectIncorrectHint
Ellipse \(x^2+2 y^2=4\)
Line \(y=x+1\)
Point of intersection
\(
\begin{aligned}
& x^2+2(x+1)^2=4 \\
& 3 x^2+4 x-2=0 \\
& \left|x_1-x_2\right|=\frac{\sqrt{40}}{3} \\
& A B=2 r=\left|x_1-x_2\right| \sqrt{1+m^2}
\end{aligned}
\)
\(m\) is slope of given line
\(
\begin{aligned}
& AB =\frac{\sqrt{40}}{3} \sqrt{1+1} \\
& 2 r =\frac{\sqrt{80}}{3} \Rightarrow r =\frac{\sqrt{80}}{6} \\
& (3 r )^2=\left(3 \times \frac{\sqrt{80}}{6}\right)^2=\frac{80}{4}=20
\end{aligned}
\)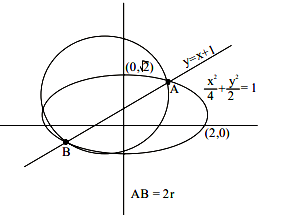
-
Question 112 of 269
112. Question
Let the common tangents to the curves \(4\left(x^2+y^2\right)=\) 9 and \(y^2=4 x\) intersect at the point \(Q\). Let an ellipse, centered at the origin \(O\), has lengths of semi-minor and semi-major axes equal to \(O Q\) and 6 , respectively. If e and \(l\) respectively denote the eccentricity and the length of the latus rectum of this ellipse, then \(\frac{l}{ e ^2}\) is equal to ____. [JEE Main 2022 26th June Shift 1]
CorrectIncorrectHint
\(
x^2+y^2=\frac{9}{4} \quad y=4 x
\)
Equation tangent in slope form
\(
\begin{aligned}
& y=m x+\frac{3}{2} \sqrt{\left(1+m^2\right)} \dots(1) \\
& y=m x+\frac{1}{m} \dots(2)\\
& \text { compare (1) & (2) } \\
& \pm \frac{3}{2} \sqrt{\left(1+m^2\right)}=\frac{1}{m^2} \\
& 9 m^2\left(1+m^2\right)=4 \\
& 9 m^4+9 m^2-4=0 \\
& 9 m^4+12 m^2-3 m^2-4=0 \\
& 3 m^2\left(3 m^2+4\right)-\left(3 m^2+4\right)=0 \\
& m^2=-\frac{4}{3}(\text { Rejected ) } \\
& m^2=\frac{1}{3} \Rightarrow m= \pm \frac{1}{\sqrt{3}}
\end{aligned}
\)
Equation of common tangent
\(
y=\frac{1}{\sqrt{3}} x+\sqrt{3}
\)
on \(X\) axis \(y=0\)
\(
\begin{aligned}
& O Q=-3 \\
& b=|O Q|=3 \\
& a=6 \\
& b^2=a^2\left(1-e^2\right) \\
& \Rightarrow e^2=1-\frac{9}{36}=\frac{3}{4}
\end{aligned}
\)
\(
\begin{aligned}
& l=\frac{2 b^2}{a}=\frac{2 \times 9}{6}=3 \\
& \frac{l}{e^2}=\frac{3}{3 / 4}=4
\end{aligned}
\) -
Question 113 of 269
113. Question
If \(m\) is the slope of a common tangent to the curves \(\frac{x^2}{16}+\frac{y^2}{9}=1\) and \(x^2+y^2=12\), then \(12 m^2\) is equal to : [JEE Main 2022 26th June Shift 2]
CorrectIncorrectHint
\(
\frac{x^2}{16}+\frac{y^2}{9}=1
\)
equation of tangent to the ellipse is
\(
\begin{aligned}
& y=m x \pm \sqrt{a^2 m^2+b^2} \\
& y=m x \pm \sqrt{16 m^2+9} \dots(i) \\
& x^2+y^2=12
\end{aligned}
\)
equation of tangent to the circle is
\(
y = mx \pm \sqrt{12} \sqrt{1+ m ^2} \dots(ii)
\)
for common tangent equate eq. (i) and (ii)
\(
\begin{aligned}
& \Rightarrow 16 m ^2+9=12\left(1+ m ^2\right) \\
& 16 m ^2-12 m ^2=3 \\
& 4 m ^2=3 \\
& 12 m ^2=9
\end{aligned}
\) -
Question 114 of 269
114. Question
The locus of the mid point of the line segment joining the point \((4,3)\) and the points on the ellipse \(x^2+2 y^2=4\) is an ellipse with eccentricity : [JEE Main 2022 26th June Shift 2]
CorrectIncorrectHint
\(
\frac{x^2}{4}+\frac{y^2}{2}=1
\)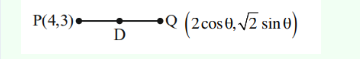
Coordinate of \(D\) is
\(
\begin{aligned}
& \left(\frac{2 \cos \theta+4}{2}, \frac{\sqrt{2} \sin \theta+3}{2}\right) \equiv(h, k) \\
& \frac{2 h-4}{2}=\cos \theta \ldots \text { (i) } \\
& \frac{2 k-3}{\sqrt{2}}=\sin \theta \ldots \text { (ii) }
\end{aligned}
\)
\((i)^2+(i i)^2\), then we get
\(
\begin{aligned}
& \left(\frac{2 h-4}{2}\right)^2+\left(\frac{2 k-3}{\sqrt{2}}\right)^2=1 \\
& \Rightarrow \frac{(x-2)^2}{1}+\frac{\left(y-\frac{3}{2}\right)^2}{\left(\frac{1}{2}\right)}=1
\end{aligned}
\)
\(\therefore\) Required eccentricity is
\(
e=\sqrt{1-\frac{1}{2}}=\frac{1}{\sqrt{2}}
\) -
Question 115 of 269
115. Question
Let the eccentricity of an ellipse \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1, a>b\), be \(\frac{1}{4}\). If this ellipse passes through the point \(\left(-4 \sqrt{\frac{2}{5}}, 3\right)\), then \(a ^2+ b ^2\) is equal to : [JEE Main 27th 2022 June Shift 1]
CorrectIncorrectHint
\(
\begin{aligned}
& \frac{x^2}{a^2}+\frac{y^2}{b^2}=1, a > b \\
& e^2=1-\frac{b^2}{a^2} \\
& \frac{1}{16}=1-\frac{b^2}{a^2} \\
& \frac{b^2}{a^2}=1-\frac{1}{16}=\frac{15}{16} \Rightarrow b^2=\frac{15}{16} a^2 \\
& \frac{x^2}{a^2}+\frac{y^2}{b^2}=1
\end{aligned}
\)
\(
\begin{aligned}
& \frac{16 \times \frac{2}{5}}{a^2}+\frac{9}{b^2}=1 \\
& \frac{32}{5 a^2}+\frac{9}{b^2}=1 \\
& \frac{32}{5 a^2}+\frac{9}{\frac{15}{16} a^2}=1 \\
& \frac{80}{5 a^2}=1 \\
& 16= a ^2 \\
& b ^2=15
\end{aligned}
\)
\(a ^2+ b ^2=16+15=31\) -
Question 116 of 269
116. Question
Let PQ be a focal chord of the parabola \(y^2=4 x\) such that it subtends an angle of \(\frac{\pi}{2}\) at the point (3, \(0)\). Let the line segment \(P Q\) be also a focal chord of the ellipse \(E: \frac{x^2}{a^2}+\frac{y^2}{b^2}=1, a^2>b^2\). If \(e\) is the eccentricity of the ellipse E, then the value of \(\frac{1}{e^2}\) is equal to : [JEE main 2022 29th June Shift 1]
CorrectIncorrectHint
\(P Q\) is focal chord
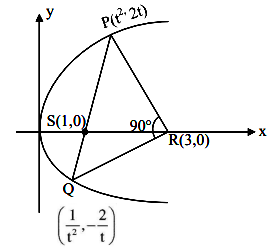
\(
\begin{aligned}
& m_{P R} \cdot m_{P Q}=-1 \\
& \frac{2 t}{t^2-3} \times \frac{-2 / t}{\frac{1}{t^2}-3}=-1 \\
& \left(t^2-1\right)^2=0 \\
& \Rightarrow t=1
\end{aligned}
\)
\(\Rightarrow P \& Q\) must be end point of latus rectum: \(P(1,2) \& Q(1,-2)\)
\(
\therefore \frac{2 b^2}{a}=4 \& ae =1
\)
\(\because\) We know that \(b ^2= a ^2\left(1- e ^2\right)\)
\(
\begin{aligned}
& \therefore a =1+\sqrt{2} \\
& \because e ^2=1-\frac{ b ^2}{ a ^2} \\
& \therefore e ^2=3-2 \sqrt{2} \\
& \frac{1}{ e ^2}=3+2 \sqrt{2}
\end{aligned}
\) -
Question 117 of 269
117. Question
Let \(\lambda x-2 y=\mu\) be a tangent to the hyperbola \(a^2 x^2-y^2=b^2\). Then \(\left(\frac{\lambda}{a}\right)^2-\left(\frac{\mu}{b}\right)^2\) is equal to: [JEE Main 2022 24 June Shift 1]
CorrectIncorrectHint
\(\lambda x-2 y=\mu\) is a tangent to the curve \(a^2 x^2-y^2=b^2\) then
\(
\begin{aligned}
& a^2 x^2-\left(\frac{\lambda x-\mu}{2}\right)^2=b^2 \\
& \left(4 a^2-\lambda^2\right) x^2+2 \lambda \mu x-\mu^2-4 b^2=0
\end{aligned}
\)
Disc. \(=0\)
\(4 \lambda^2 \mu^2+4\left(4 a^2-\lambda^2\right)\left(\mu^2+4 b^2\right)=0\)
\(4 \lambda^2 b^2-4 a^2 \mu^2=16 a^2 b^2\)
\(
\frac{\lambda^2}{a^2}-\frac{\mu^2}{b^2}=4
\) -
Question 118 of 269
118. Question
Let the hyperbola \(H : \frac{ x ^2}{ a ^2}- y ^2=1\) and the ellipse E : \(3 x^2+4 y^2=12\) be such that the length of latus rectum of \(H\) is equal to the length of latus rectum of \(E\). If \(e_H\) and \(e_E\) are the eccentricities of \(H\) and \(E\) respectively, then the value of \(12\left( e _{ H }^2+ e _{ E }^2\right)\) is equal to ____. [JEE Main 2022 24th June Shift 2]
CorrectIncorrectHint
\(
\frac{x^2}{a^2}-\frac{y^2}{1}=1, \quad \frac{x^2}{4}+\frac{y^2}{3}=1
\)
\(
\begin{aligned}
& e _{ H }=\sqrt{1+\frac{1}{ a ^2}}, \quad e _{ E }=\sqrt{1-\frac{3}{4}}=\frac{1}{2} \\
& \ell . R .=\frac{2}{ a }, \quad \ell R =\frac{2 \times 3}{2}=3 \\
& \frac{2}{ a }=3 \\
& a =\frac{2}{3}
\end{aligned}
\)
\(
\begin{aligned}
& e _{ H }=\sqrt{1+\frac{9}{4}}=\frac{\sqrt{13}}{2} \\
& 12\left( e _{ H }^2+ e _{ E }^2\right)=12\left(\frac{13}{4}+\frac{1}{4}\right) \\
& =\frac{12 \times 14}{4}=42
\end{aligned}
\) -
Question 119 of 269
119. Question
Let the eccentricity of the hyperbola \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\) be \(\frac{5}{4}\). If the equation of the normal at the point \(\left(\frac{8}{\sqrt{5}}, \frac{12}{5}\right)\) on the hyperbola is \(8 \sqrt{5} x+\beta y=\lambda\), then \(\lambda-\beta\) is equal to [JEE Main 2022 25th June Shift 2]
CorrectIncorrectHint
\(
e ^2=1+\frac{ b ^2}{ a ^2}=\frac{25}{16} \Rightarrow \frac{ b ^2}{ a ^2}=\frac{9}{16} \dots(1)
\)
\(A\left(\frac{8}{\sqrt{5}}, \frac{12}{5}\right)\) satisfies \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\)
\(
\Rightarrow \frac{64}{5 a^2}-\frac{144}{25 b^2}=1 \dots(2)
\)
Solving (1) & (2) \(b =\frac{6}{5}, \quad a =\frac{8}{5}\)
Normal at \(A\) is \(\frac{\sqrt{5} a^2 x}{8}+\frac{5 b^2 y}{12}=a^2+b^2\)
Comparing it \(8 \sqrt{5} x+\beta y=\lambda\)
Gives \(\lambda=100, \beta=15\)
\(
\lambda-\beta=85
\) -
Question 120 of 269
120. Question
The normal to the hyperbola \(\frac{x^2}{a^2}-\frac{y^2}{9}=1\) at the point \((8,3 \sqrt{3})\) on it passes through the point : [JEE Main 2022 26th June Shift 2]
CorrectIncorrectHint
\(\frac{x^2}{a^2}-\frac{y^2}{9}=1:(8,3 \sqrt{3})\) lie on Hyperbola then
\(
\frac{64}{a^2}-\frac{27}{9}=1 \Rightarrow a^2=\frac{64}{4}=16
\)
equation of normal at \((8,3 \sqrt{3})\) :
\(
\begin{aligned}
& \frac{16 x}{8}+\frac{9 y}{3 \sqrt{3}}=16+9 \\
& 2 x+\sqrt{3} y=25 \dots(i)
\end{aligned}
\)
Only option c satisfies the equation(i). -
Question 121 of 269
121. Question
Let a line \(L _1\) be tangent to the hyperbola \(\frac{x^2}{16}-\frac{y^2}{4}=1\) and let \(L _2\) be the line passing through the origin and perpendicular to \(L_1\). If the locus of the point of intersection of \(L_1\) and \(L_2\) is \(\left(x^2+y^2\right)^2=\) \(\alpha x^2+\beta y^2\), then \(\alpha+\beta\) is equal to _____. [JEE Main 2022 26th June Shift 2]
CorrectIncorrectHint
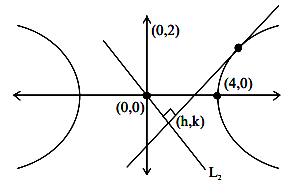
\(
\begin{aligned}
& \frac{ xsec \theta}{4}-\frac{ y \tan \theta}{2}=1 \\
& m _1=\frac{\sec \theta \times 2}{4(\tan \theta)}=\frac{\sec \theta}{2 \tan \theta} \\
& m _2=\frac{ k }{ h } \\
& m _1 m _2=-1
\end{aligned}
\)
\(
\begin{aligned}
& \frac{ k \cdot \sec \theta}{ h \cdot 2 \tan \theta}=-1 \\
& \frac{ k }{2 h \sin \theta}=-1 \\
& \sin \theta=\frac{- k }{2 h } \quad \cos \theta=\frac{\sqrt{4 h^2-k^2}}{2 h}
\end{aligned}
\)
also
\(
\begin{aligned}
& \frac{ h \sec \theta}{4}-\frac{ k \tan \theta}{2}=1 \\
& \frac{ h }{4} \frac{2 h }{\sqrt{4 h ^2- k ^2}}-\frac{ k }{2}\left(\frac{- k }{\sqrt{4 h ^2- k ^2}}\right)=1 \\
& h ^2+ k ^2=2 \sqrt{4 h ^2- k ^2} \\
& \left( x ^2+ y ^2\right)^2=4\left(4 x ^2- y ^2\right) \\
& \left( x ^2+ y ^2\right)^2=16 x ^2-4 y ^2 \\
& \alpha=16, \beta=-4
\end{aligned}
\)
\(
\alpha+\beta=16-4=12
\) -
Question 122 of 269
122. Question
Let the eccentricity of the hyperbola \(H : \frac{ x ^2}{ a ^2}-\frac{ y ^2}{ b ^2}=1\) be \(\sqrt{\frac{5}{2}}\) and length of its latus rectum be \(6 \sqrt{2}\), If \(y=2 x+c\) is a tangent to the hyperbola \(H\), then the value of \(c ^2\) is equal to ____. [JEE Main 2022 28th June Shift 1]
CorrectIncorrectHint
\(
\begin{aligned}
& y=m x \pm \sqrt{a^2 m^2-b^2} \\
& m=2, c^2=a^2 m^2-b^2 \\
& c^2=4 a^2-b^2 \\
& e^2=1+\frac{b^2}{a^2}
\end{aligned}
\)
\(
\begin{aligned}
& \frac{5}{2}=1+\frac{b^2}{a^2} \\
& \frac{3}{2}=\frac{b^2}{a^2} \Rightarrow b^2=\frac{3 a^2}{2} \\
& \frac{2 b^2}{a}=6 \sqrt{2} \\
& \frac{2}{a} \times \frac{3 a^2}{2}=6 \sqrt{2} \\
& 3 a=6 \sqrt{2} \\
& a=2 \sqrt{2} \\
& b^2=\frac{3}{2} \times 8=12 \\
& b=2 \sqrt{3} \\
& \therefore c^2=4 \times 8-12 \\
& c^2=20
\end{aligned}
\) -
Question 123 of 269
123. Question
Let \(a >0, b >0\). Let \(e\) and \(\ell\) respectively be the eccentricity and length of the latus rectum of the hyperbola \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\). Let \(e^{\prime}\) and \(\ell^{\prime}\) respectively the eccentricity and length of the latus rectum of its conjugate hyperbola. If \(e ^2=\frac{11}{14} \ell\) and \(\left( e ^{\prime}\right)^2=\frac{11}{8} \ell^{\prime}\), then the value of \(77 a+44 b\) is equal to [JEE Main 2022 28th June Shift 2]
CorrectIncorrectHint
\(
\begin{aligned}
& e =\sqrt{1+\frac{ b ^2}{ a ^2}}, \ell=\frac{2 b ^2}{ a } \\
& \text { Given } e ^2=\frac{11}{14} \ell \\
& 1+\frac{ b ^2}{ a ^2}=\frac{11}{14} \cdot \frac{2 b ^2}{ a } \\
& \frac{ a ^2+ b ^2}{ a ^2}=\frac{11}{7} \cdot \frac{ b ^2}{ a } \dots(1)
\end{aligned}
\)
\(
\begin{aligned}
& \text { Also } e ^{\prime}=\sqrt{1+\frac{ a ^2}{ b ^2}}, \ell^{\prime}=\frac{2 a ^2}{ b } \\
& \text { Given }\left( e ^{\prime}\right)^2=\frac{11}{8} \ell^{\prime} \\
& 1+\frac{ a ^2}{ b ^2}=\frac{11}{8} \cdot \frac{2 a ^2}{ b } \\
& \frac{ a ^2+ b ^2}{ b ^2}=\frac{11}{4} \cdot \frac{ a ^2}{ b } \dots(2)
\end{aligned}
\)
\(
\begin{aligned}
& \text { New }(1) \div(2) \\
& \frac{ b ^2}{ a ^2}=\frac{4}{7} \cdot \frac{ b ^3}{ a ^3} \\
& \therefore 7 a =4 b \dots(3)
\end{aligned}
\)
From (2)
\(
\begin{aligned}
& \frac{\frac{16 b^2}{49}+b^2}{b^2}=\frac{11}{4} \cdot \frac{16 b^2}{49 b} \\
& \frac{65}{49}=\frac{11}{4} \cdot \frac{16}{49} \cdot b \\
& \therefore b=\frac{4 \times 65}{11 \times 16} \dots(4)
\end{aligned}
\)
We have to find value of
\(
\begin{aligned}
& 77 a+44 b \\
& 11(7 a+4 b)=11(4 b+4 b)=11 \times 8 b \\
& \therefore \text { Value of } 11 \times 8 b=11 \times 8 \times \frac{4 \times 65}{16 \times 11}=130
\end{aligned}
\) -
Question 124 of 269
124. Question
Let \(H : \frac{ x ^2}{ a ^2}-\frac{y^2}{ b ^2}=1, a >0, b >0\), be a hyperbola such that the sum of lengths of the transverse and the conjugate axes is \(4(2 \sqrt{2}+\sqrt{14})\). If the eccentricity \(H\) is \(\frac{\sqrt{11}}{2}\), then value of \(a ^2+b^2\) is equal to ____. [JEE Main 2022 29th June Shift 1]
CorrectIncorrectHint
\(
\frac{x^2}{a^2}-\frac{y^2}{b^2}=1
\)
Given \(e^2=1+\frac{b^2}{a^2} \Rightarrow \frac{11}{4}=1+\frac{b^2}{a^2} \Rightarrow b^2=\frac{7}{4} a^2\)
\(\therefore \frac{x^2}{(a)^2}-\frac{y^2}{\left(\frac{\sqrt{7}}{2} a\right)^2}=1\) Now given
\(
\begin{aligned}
& 2 a+2 \cdot \frac{\sqrt{7} a}{2}=4(2 \sqrt{2}+\sqrt{14}) \\
& a(2+\sqrt{7})=4 \sqrt{2}(2+\sqrt{7}) \\
& a=4 \sqrt{2} \Rightarrow a^2=32 \\
& b^2=\frac{7}{4} \times 16 \times 2=56
\end{aligned}
\)
\(a ^2+b^2=32+56=88\) -
Question 125 of 269
125. Question
Let \(x^2+y^2+A x+B y+C=0\) be a circle passing through \((0,6)\) and touching the parabola \(y=x^2\) at \((2,4)\). Then \(A + C\) is equal to ____. [JEE Main 2022 24th June Shift 1]
CorrectIncorrectHint
\(x ^2+ y ^2+ Ax + By + C =0\) is passing through \((0,6)\)
\(
\Rightarrow 6 B+C=-36
\)
The tangent of the parabola \(y=x^2\) at \((2,4)\) is
\(
4 x-y-4=0 \dots(1)
\)
The tangent of circle \(x^2+y^2+A x+B y+C=0\) at \((2,4)\) is
\(
(4+A) x+(8+B) y+2 A+4 B+2 C=0 \dots(2)
\)
From Equation (1) and (2)
\(
\frac{4+ A }{4}=\frac{8+ B }{-1}=\frac{2 A +4 B +2 C }{-4}
\)
\(
A +4 B =-36 \dots(3)
\)
\(
3 A +4 B +2 C =-4 \dots(4)
\)
From equation (3) and (4)
\(
A+C=16
\) -
Question 126 of 269
126. Question
If two tangents drawn from a point \((\alpha, \beta)\) lying on the ellipse \(25 x^2+4 y^2=1\) to the parabola \(y^2=4 x\) are such that the slope of one tangent is four times the other, then the value of \((10 \alpha+5)^2+\left(16 \beta^2+50\right)^2\) equals ____. [JEE Main 2022 24th June Shift 1]
CorrectIncorrectHint
\(
\alpha=\frac{1}{5} \cos \theta, \beta=\frac{1}{2} \sin \theta
\)
Equation of tangent to \(y^2=4 x\)
\(
y=m x+\frac{1}{m}
\)
It passes through \((\alpha, \beta)\)
\(
\begin{aligned}
& \frac{1}{2} \sin \theta= m \frac{1}{5} \cos \theta+\frac{1}{ m } \\
& m ^2\left(\frac{\cos \theta}{5}\right)- m \left(\frac{1}{2} \sin \theta\right)+1=0
\end{aligned}
\)
It has two roots \(m_1\) and \(m_2\) where \(m_1=4 m_2\)
\(
m _1+ m _2=\frac{\frac{1}{2} \sin \theta}{\frac{\cos \theta}{5}}
\)
\(
m _1 m _2=\frac{5}{\cos \theta}
\)
After eliminating \(m _1\) and \(m _2\)
\(
\begin{aligned}
& \cos \theta=\frac{-5 \pm \sqrt{29}}{2} \\
& \alpha=\frac{-5 \pm \sqrt{29}}{10} \Rightarrow 10 \alpha+5= \pm \sqrt{29} \\
& \beta^2=\frac{1}{4} \sin ^2 \theta \Rightarrow 16 \beta^2=-50 \pm 10 \sqrt{29} \\
& (10 \alpha+5)^2+\left(16 \beta^2+50\right)^2=2929
\end{aligned}
\) -
Question 127 of 269
127. Question
A particle is moving in the \(x y\)-plane along a curve C passing through the point \((3,3)\). The tangent to the curve \(C\) at the point \(P\) meets the \(x\)-axis at \(Q\). If the \(y\)-axis bisects the segment \(P Q\), then \(C\) is a parabola with [JEE Main 2022 24th June Shift 2]
CorrectIncorrectHint
Let Point \(P(x, y)\)
\(
\begin{aligned}
& Y-y=y^{\prime}(X-x) \\
& Y=0 \Rightarrow X=x-\frac{y}{y^{\prime}} \\
& Q\left(x-\frac{y}{y^{\prime}}, 0\right)
\end{aligned}
\)
Mid Point of PQ lies on y axis
\(
\begin{aligned}
& x-\frac{y}{y^{\prime}}+x=0 \\
& y^{\prime}=\frac{y}{2 \cdot x} \Rightarrow 2 \frac{d y}{y}=\frac{d x}{x}
\end{aligned}
\)
\(
\begin{aligned}
& 2 \ell ny =\ell nx +\ell nk \\
& y ^2= kx
\end{aligned}
\)
It passes through \((3,3) \Rightarrow k=3\)
curve \(c \Rightarrow y^2=3 x\)
Length of L.R. \(=3\)
Focus \(=\left(\frac{3}{4}, 0\right)\) -
Question 128 of 269
128. Question
Let \(P_1\) be a parabola with vertex \((3,2)\) and focus \((4,4)\) and \(P _2\) be its mirror image with respect to the line \(x+2 y=6\). Then the directrix of \(P_2\) is \(x+2 y=\) ____. [JEE Main 2022 24th June Shift 2]
CorrectIncorrectHint
\(P_1\) : Directrix:
\(
\begin{aligned}
& x+2 y=k \\
& x+2 y-k=0 \\
& \left|\frac{3+4-K}{\sqrt{5}}\right|=\sqrt{5}
\end{aligned}
\)
\(
\begin{aligned}
& |7-k|=5 \\
& 7-k=5,7-k=-5
\end{aligned}
\)
\(
k =2 \quad \text { Accepted }
\)
\(
k =12 \quad \text { Rejected Passes through focus }
\)
\(
\left.\begin{array}{l}
D_1=x+2 y=2 \\
\ell=x+2 y=6
\end{array}\right] \Rightarrow d
\)
\(
\left.\begin{array}{l}
\ell=x+2 y=6 \\
D_2=x+2 y=C
\end{array}\right] \Rightarrow d
\)
\(
\Rightarrow c =10
\) -
Question 129 of 269
129. Question
If \(y = m _1 x + c _1\) and \(y = m _2 x + c _2, m _1 \neq m _2\) are two common tangents of circle \(x^2+y^2=2\) and parabola \(y^2=x\), then the value of \(8\left|m_1 m_2\right|\) is equal to [JEE Main 2022 25th June Shift 1]
CorrectIncorrectHint
\(
\begin{aligned}
& C_1: x^2+y^2=2 \\
& C_2: y^2=x
\end{aligned}
\)
Let tangent to parabola be \(y=m x+\frac{1}{4 m}\).
It is also a tangent of circle so distance from centre of circle \((0,0)\) will be \(\sqrt{2}\).
\(
\left|\frac{\frac{1}{4 m }}{\sqrt{1+ m ^2}}\right|=\sqrt{2} \Rightarrow 1=32 m ^2+32 m ^4
\)
by solving
\(
\begin{aligned}
& m ^2=\frac{3 \sqrt{2}-4}{8}, m ^2=\frac{-3 \sqrt{2}-4}{8} \text { (rejected) } \\
& m = \pm \sqrt{\frac{3 \sqrt{2}-4}{8}}
\end{aligned}
\)
\(
\text { so, } 8\left| m _1 m _2\right|=3 \sqrt{2}-4
\) -
Question 130 of 269
130. Question
Let \(x=2 t, y=\frac{t}{3}\) be a conic. Let \(S\) be the focus and \(B\) be the point on the axis of the conic such that \(SA \perp BA\), where \(A\) is any point on the conic. If \(k\) is the ordinate of the centroid of \(\triangle SAB\), then \(\lim _{t \rightarrow 1} k\) is equal to [JEE Main 2022 25th June Shift 1]
CorrectIncorrectHint
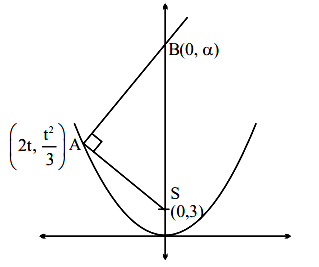
parabola \(x^2=12 y\)
\(
\begin{aligned}
& SA \perp SB \\
& \text { so, } m _{ AS } \cdot m _{ AB }=-1 \\
& \frac{\left(3-\frac{ t ^2}{3}\right)}{(0-2 t )} \cdot \frac{\left(\alpha-\frac{ t ^2}{3}\right)}{(0-2 t )}=-1
\end{aligned}
\)
by solving
\(
3 \alpha=\frac{27 t ^2+ t ^4}{ t ^2-9}
\)
ordinate of centriod of \(\triangle SAB\)
\(
\begin{aligned}
& = K =\frac{\alpha+\frac{ t ^2}{3}+3}{3} \\
& k =\frac{9+3 \alpha+ t ^2}{9} \\
& \lim _{ t \rightarrow 1} k \\
& =\lim _{ t \rightarrow 1} \frac{1}{9}\left(9+ t ^2+\frac{27 t ^2+ t ^4}{\left( t ^2-9\right)}\right) \\
& =\frac{13}{18}
\end{aligned}
\) -
Question 131 of 269
131. Question
If the line \(y=4+k x, k>0\), is the tangent to the parabola \(y = x – x ^2\) at the point \(P\) and \(V\) is the vertex of the parabola, then the slope of the line through \(P\) and \(V\) is : [JEE Main 2022 25th June Shift 2]
CorrectIncorrectHint
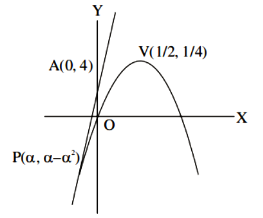
Slope of tangent at \(P=\) Slope of line AP
\(
\left.y^{\prime}\right|_P=1-2 \alpha=\frac{\alpha-\alpha^2-4}{\alpha-0}
\)
Solving \(\alpha=-2 \Rightarrow P(-2,-6)\),
vertex of the parabola \(=\left(\frac{1}{2}, \frac{1}{4}\right)\)
Slope of \(PV =\frac{5}{2}\) -
Question 132 of 269
132. Question
Let the normal at the point \(P\) on the parabola \(y ^2=\) 6x pass through the point \((5,-8)\). If the tangent at \(P\) to the parabola intersects its directrix at the point \(Q\), then the ordinate of the point \(Q\) is : [JEE Main 2022 26th June Shift 1]
CorrectIncorrectHint
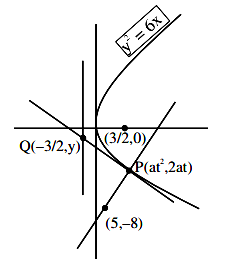
Equation of normal : \(y=-t x+2 a t+a t^3(a=3 / 2)\)
since passing through \((5,-8)\), we get \(t=-2\)
Co-ordinate of \(Q :(6,-6)\)
Equation of tangent at \(Q: x+2 y+6=0\)
Put \(x=-3 / 2\) to get \(R(-3 / 2,-9 / 4)\) -
Question 133 of 269
133. Question
A circle of radius 2 unit passes through the vertex and the focus of the parabola \(y^2=2 x\) and touches the parabola \(y=\left(x-\frac{1}{4}\right)^2+\alpha\), where \(\alpha>0\). Then \((4 \alpha-8)^2\) is equal to _____. [JEE Main 2022 27th June Shift 1]
CorrectIncorrectHint
Vertex and focus of parabola \(y^2=2 x\) are \(V (0,0)\) and \(S\left(\frac{1}{2}, 0\right)\) resp.
Let equation of circle be
\(
(x-h)^2+(y-k)^2=4
\)
\(\because\) Circle passes through \((0,0)\)
\(
\Rightarrow h^2+k^2=4 \dots(1)
\)
\(\because\) Circle passes through \(\left(\frac{1}{2}, 0\right)\)
\(
\begin{aligned}
& \left(\frac{1}{2}-h\right)^2+k^2=4 \\
& \Rightarrow h^2+k^2-h=\frac{15}{4} \dots(2)
\end{aligned}
\)
On solving (1) and (2)
\(
\begin{aligned}
& 4-h=\frac{15}{4} \\
& h=4-\frac{15}{4}=\frac{1}{4} \\
& k=+\frac{\sqrt{63}}{4}
\end{aligned}
\)
\(k=-\frac{\sqrt{63}}{4}\) is rejected as circle with centre
\(\left(\frac{1}{4},-\frac{\sqrt{63}}{4}\right)\) can’t touch given parabola.
Equation of circle is
\(
\left(x-\frac{1}{4}\right)^2+\left(k-\frac{\sqrt{63}}{4}\right)^2=4
\)
From figure
\(
\begin{aligned}
& \alpha=2+\frac{\sqrt{63}}{4}=\frac{8+\sqrt{63}}{4} \\
& 4 \alpha-8=\sqrt{63} \\
& (4 \alpha-8)^2=63
\end{aligned}
\) -
Question 134 of 269
134. Question
If the equation of the parabola, whose vertex is at \((5,4)\) and the directrix is \(3 x+y-29=0\), is \(x^2+a y^2+b x y+c x+d y+k=0\) then \(a+b+c+d+k\) is equal to [JEE Main 2022 27th June Shift 2]
CorrectIncorrectHint
vertex \((5,4) \&\) directrix at \(3 x+y-29=0\)
Thus, foot of perpendicular from vertex to directrix
Thus, by calculating, focus will be \((2,3)\).
Now, equation of parabola
\(
\begin{aligned}
& \sqrt{(x-2)^2+(y-3)^2}=\left|\frac{3 x+y-29}{\sqrt{9+1}}\right| \\
& 10\left[x^2+4-4 x+y^2+9-6 y\right] \\
= & 9 x^2+y^2+841+6 x y-174 x-58 y \\
& x^2+9 y^2-6 x y+134 x-2 y-711=0
\end{aligned}
\)
Comparing with
\(
\begin{aligned}
& x^2+a y^2+b x y+c x+d y+k=0 \\
& a=9, b=-6, c=134, d=-2, k=-711 \\
& \therefore a+b+c+d+k=-576
\end{aligned}
\) -
Question 135 of 269
135. Question
If vertex of a parabola is \((2,-1)\) and the equation of its directrix is \(4 x-3 y=21\), then the length of its latus rectum is [JEE Main 2022 28th June Shift 2]
CorrectIncorrectHint
\(
\begin{aligned}
& \quad 4 x-3 y=21 \\
& a=\frac{|8+3-21|}{5}=\frac{10}{5}=2 \\
& \therefore \text { latus rectum }=4 a=8
\end{aligned}
\) -
Question 136 of 269
136. Question
Let \(P : y ^2=4 a x , a>0\) be a parabola with focus S.Let the tangents to the parabola \(P\) make an angle of \(\frac{\pi}{4}\) with the line \(y=3 x+5\) touch the parabola \(P\) at A and B. Then the value of \(a\) for which A,B and \(S\) are collinear is: [JEE Main 2022 29th June Shift 2]
CorrectIncorrectHint
Lines making angle \(\frac{\pi}{4}\) with \(y=3 x+5\)
\(
\tan \frac{\pi}{4}=\frac{m-3}{1+3 m} \Rightarrow 1+3 m= \pm(m-3) 1+3 m=m-3 \Rightarrow m=-21+3 m=-m+2 \Rightarrow m=\frac{1}{2}
\)
Which are perpendicular to each-other so, A, S, B are collinear for all \(a>0\).
-
Question 137 of 269
137. Question
Let \(r_1\) and \(r_2\) be the radii of the largest and smallest circles, respectively, which pass through the point \((-4,1)\) and having their centres on the circumference of the circle \(x^2+y^2+2 x+4 y-4=0\) If \(\frac{r_1}{r_2}=a+b \sqrt{2}\), then \(a+b\) is equal to : [JEE Main 2021 20th July Shift 2]
CorrectIncorrectHint
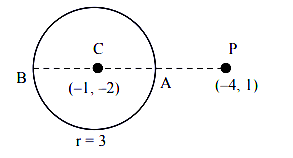
Centre of smallest circle is A
Centre of largest circle is B
\(
\begin{aligned}
& r _2=|C P-C A|=3 \sqrt{2}-3 \\
& r_1=C P+C B=3 \sqrt{2}+3 \\
& \frac{r_1}{r_2}=\frac{3 \sqrt{2}+3}{3 \sqrt{2}-3}=\frac{(3 \sqrt{2}+3)^2}{9} \\
& =(\sqrt{2}+1)^2=3+2 \sqrt{2} \\
& a =3, b = 2
\end{aligned}
\)
\(
a+b=2+3=5
\) -
Question 138 of 269
138. Question
Let the circle \(S: 36 x^2+36 y^2-108 x+120 y+C=0\) be such that it neither intersects nor touches the co-ordinate axes. If the point of intersection of the lines, \(x-2 y=4\) and \(2 x-y=5\) lies inside the circle \(S\), then : [JEE Main 2021 22nd July Shift 1]
CorrectIncorrectHint
\(
\begin{aligned}
& \text { S: } 36 x^2+36 y^2-108 x+120 y+C=0 \\
& \Rightarrow x^2+y^2-3 x+\frac{10}{3} y+\frac{C}{36}=0 \\
& \text { Centre } \equiv(-g,-f) \equiv\left(\frac{3}{2}, \frac{-10}{6}\right) \\
& \text { radius }=r=\sqrt{\frac{9}{4}+\frac{100}{36}-\frac{C}{36}}
\end{aligned}
\)
\(
\begin{aligned}
& \text { Now} \Rightarrow r<\frac{3}{2} \\
& \Rightarrow \frac{9}{4}+\frac{100}{36}-\frac{C}{36}<\frac{9}{4} \\
& \Rightarrow C>100 \dots(1)
\end{aligned}
\)
Now point of intersection of \(x-2 y=4\) and \(2 x-y=5\) is \((2,-1)\), which lies inside the circle \(S\).
\(
\begin{aligned}
& \therefore S (2,-1)<0 \\
& \Rightarrow(2)^2+(-1)^2-3(2)+\frac{10}{3}(-1)+\frac{ C }{36}<0 \\
& \Rightarrow 4+1-6-\frac{10}{3}+\frac{ C }{36}<0
\end{aligned}
\)
\(
C <156 \dots(2)
\)
From 1 & 2, \(100< C <156\) -
Question 139 of 269
139. Question
Two tangents are drawn from the point \(P (-1,1)\) to the circle \(x^2+y^2-2 x-6 y+6=0\). If these tangents touch the circle at points \(A\) and \(B\), and if \(D\) is a point on the circle such that length of the segments \(A B\) and \(A D\) are equal, then the area of the triangle \(A B D\) is equal to: [JEE Main 2021 27th July Shift 1]
CorrectIncorrectHint
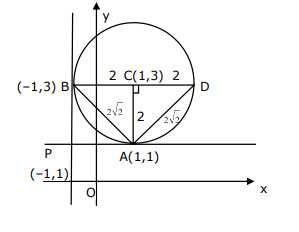
\(
\begin{aligned}
& \triangle A B D=\frac{1}{2} \times 2 \times 4 \\
& =4
\end{aligned}
\) -
Question 140 of 269
140. Question
\(
\begin{aligned}
& \text { Let } A=\left\{( x , y ) \in R \times R \mid 2 x ^2+2 y ^2-2 x -2 y =1\right\} \\
& B =\left\{( x , y ) \in R \times R \mid 4 x ^2+4 y ^2-16 y +7=0\right\} \text { and } \\
& C =\left\{( x , y ) \in R \times R \mid x ^2+ y ^2-4 x -2 y +5 \leq r ^2\right\}
\end{aligned}
\)
Then the minimum value of \(| r |\) such that \(A \cup B \subseteq C\) is equal to [JEE Main 2021 27th July Shift 1]CorrectIncorrectHint
\(
\begin{aligned}
& S_1: x^2+y^2-x-y-\frac{1}{2}=0 ; C_1\left(\frac{1}{2}, \frac{1}{2}\right) \\
& r_1=\sqrt{\frac{1}{4}+\frac{1}{4}+\frac{1}{2}}=1 \\
& S_2: x^2+y^2-4 y+\frac{7}{4}=0 ; C_2:(0,2) \\
& r_2=\sqrt{4-\frac{7}{4}}=\frac{3}{2} \\
& S_3: x^2+y^2-4 x-2 y+5-r^2=0 \\
& C_3:(2,1) \\
& r_3=\sqrt{4+1-5+r^2}=|r|
\end{aligned}
\)
\(
C_1 C_3=\sqrt{\frac{5}{2}}
\)
\(
\begin{aligned}
& \left.\sqrt{\frac{5}{2}} \leq|r-1| \Rightarrow \begin{array}{r}
r \leq 1+\sqrt{\frac{5}{2}} \\
r \geq \frac{3}{2}+\sqrt{5}
\end{array}\right\} \\
& \left.\begin{array}{l}
C_2 C_3=\sqrt{5} \leq\left|r-\frac{3}{2}\right| \\
r-\frac{3}{2} \geq \sqrt{5} \\
r-\frac{3}{2} \leq-\sqrt{5}
\end{array}\right\}
\end{aligned}
\) -
Question 141 of 269
141. Question
Consider a circle \(C\) which touches the \(y\)-axis at \((0,6)\) and cuts off an intercept \(6 \sqrt{5}\) on the \(x\)-axis. Then the radius of the circle \(C\) is equal to : [JEE Main 2021 27th July Shift 2]
CorrectIncorrectHint
\(
\begin{aligned}
& r=\sqrt{6^2+(3 \sqrt{5})^2} \\
& =\sqrt{36+45}=9
\end{aligned}
\) -
Question 142 of 269
142. Question
Let \(T\) be the tangent to the ellipse \(E : x ^2+4 y ^2=5\) at the point \(P (1,1)\). If the area of the region bounded by the tangent \(T\), ellipse \(E\), lines \(x =1\) and \(x =\sqrt{5}\) is \(\alpha \sqrt{5}+\beta+\gamma \cos ^{-1}\left(\frac{1}{\sqrt{5}}\right)\), then \(|\alpha+\beta+\gamma|\) is equal to ____. [JEE Main 2021 20th July Shift 1]
CorrectIncorrectHint
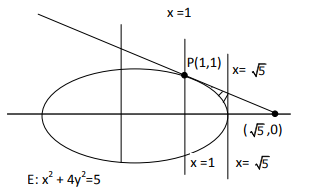
Tangent at \(P: x+4 y=5\)
\(
\begin{aligned}
& \text { Required Area }=\int_1^{\sqrt{5}}\left(\frac{5-x}{4}-\frac{\sqrt{5-x^2}}{2}\right) d x \\
& =\left[\frac{5 x}{4}-\frac{x^2}{8}-\frac{x}{4} \sqrt{5-x^2}-\frac{5}{2} \sin ^{-1} \frac{x}{\sqrt{5}}\right]_1^{\sqrt{5}} \\
& =\frac{5}{4} \sqrt{5}-\frac{5}{4}-\frac{5}{4} \cos ^{-1}\left(\frac{1}{\sqrt{5}}\right)
\end{aligned}
\)
It we assume \(\alpha, \beta, \gamma, \in Q\) (Not given in question) then \(\alpha=\frac{5}{4}, \beta=-\frac{5}{4} \& \gamma=-\frac{5}{4}\)
\(
|\alpha+\beta+\gamma|=1.25
\) -
Question 143 of 269
143. Question
Let \(E_1: \frac{x^2}{a^2}+\frac{y^2}{b^2}=1, a>b\). Let \(E_2\) be another ellipse such that it touches the end points of major axis of \(E_1\) and the foci of \(E_2\) are the end points of minor axis of \(E _1\). If \(E _1\) and \(E _2\) have same eccentricities, then its value is: [JEE Main 2021 22nd July Shift 1]
CorrectIncorrectHint
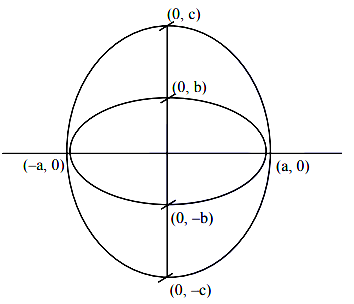
\(
e ^2=1-\frac{ b ^2}{ a ^2}
\)
\(
\begin{aligned}
& e ^2=1-\frac{ a ^2}{ c ^2} \\
& \Rightarrow \frac{ b ^2}{ a ^2}=\frac{ a ^2}{ c ^2} \\
& \Rightarrow c ^2=\frac{ a ^4}{ b ^2} \Rightarrow c =\frac{ a ^2}{ b } \\
& \text { Also } b = ce \\
& \Rightarrow c=\frac{b}{e} \\
& \frac{b}{e}=\frac{a^2}{b} \\
& \Rightarrow e=\frac{b^2}{a^2}=1-e^2 \\
& \Rightarrow e^2+e-1=0 \\
& \Rightarrow e=\frac{-1+\sqrt{5}}{2}
\end{aligned}
\) -
Question 144 of 269
144. Question
Let an ellipse \(E: \frac{ x ^2}{ a ^2}+\frac{ y ^2}{ b ^2}=1, a ^2> b ^2\), passes through \(\left(\sqrt{\frac{3}{2}}, 1\right)\) and has eccentricity \(\frac{1}{\sqrt{3}}\). If a circle, centered at focus \(F (\alpha, 0), \alpha>0\), of \(E\) and radius \(\frac{2}{\sqrt{3}}\), intersects \(E\) at two points \(P\) and \(Q\), then \(PQ ^2\) is equal to : [JEE Main 2021 25th July Shift 1]
CorrectIncorrectHint
\(
\begin{aligned}
& \frac{3}{2 a^2}+\frac{1}{b^2}=1 \text { and } 1-\frac{b^2}{a^2}=\frac{1}{3} \\
& \Rightarrow a^2=3 b^2=3 \\
& \Rightarrow \frac{x^2}{3}+\frac{y^2}{2}=1 \ldots \text { (i) }
\end{aligned}
\)
Its focus is \((1,0)\)
Now, eqn of circle is
\(
(x-1)^2+y^2=\frac{4}{3} \dots(ii)
\)
Solving (i) and (ii) we get \(y= \pm \frac{2}{\sqrt{3}}, x=1\)
\(
\Rightarrow P Q^2=\left(\frac{4}{\sqrt{3}}\right)^2=\frac{16}{3}
\) -
Question 145 of 269
145. Question
If a tangent to the ellipse \(x^2+4 y^2=4\) meets the tangents at the extremities of its major axis at \(B\) and \(C\), then the circle with \(BC\) as diameter passes through the point: [JEE Main 2021 25th July Shift 2]
CorrectIncorrectHint
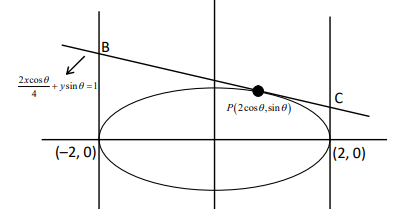
\(\frac{x^2}{4}+\frac{y^2}{1}=1 \Rightarrow a=2 \& b=1\), Let \(P(2 \cos \theta, \sin \theta)\)
Equation of tangent at \(P\) is \((\cos \theta) x+2 \sin \theta y=2\)
\(B\left(-2, \frac{1+\cos \theta}{\sin \theta}\right)\),
\(C \left(2, \frac{1-\cos \theta}{\sin \theta}\right)\)
\(B\left(-2, \cot \frac{\theta}{2}\right)\),
\(C\left(2, \tan \frac{\theta}{2}\right)\)
Equation of circle is
\(
\begin{aligned}
& (x+2)(x-2)+\left(y-\cot \frac{\theta}{2}\right)\left(y-\tan \frac{\theta}{2}\right)=0 \\
& x^2-4+y^2-\left(\tan \frac{\theta}{2}+\cot \frac{\theta}{2}\right) y+1=0 \ldots(1)
\end{aligned}
\)
so, \((\sqrt{3}, 0)\) satisfying equation (1) -
Question 146 of 269
146. Question
A ray of light through \((2,1)\) is reflected at a point \(P\) on the \(y\)-axis and then passes through the point \((5,3)\). If this reflected ray is the directrix of an ellipse with eccentricity \(\frac{1}{3}\) and the distance of the nearer focus from this directrix is \(\frac{8}{\sqrt{53}}\), then the equation of the other directrix can be: [JEE Main 2021 27th July Shift 1]
CorrectIncorrectHint
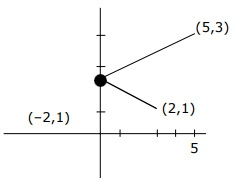
Equation of reflected Ray \(y-1=\frac{2}{7}(x+2)\)
\(
\begin{aligned}
& 7 y-7=2 x+4 \\
& 2 x-7 y+11=0
\end{aligned}
\)
Let the equation of other directrix is
\(
2 x-7 y+\lambda
\)
Distance of directrix from Focub \(\frac{a}{e}-a e=\frac{8}{\sqrt{53}}\)
\(
3 a-\frac{a}{3}=\frac{8}{\sqrt{53}} \text { or } a=\frac{3}{\sqrt{53}}
\)
Distance from other focus \(\frac{ a }{ e }+ ae\)
\(
3 a+\frac{a}{3}=\frac{10 a}{3}=\frac{10}{3} \times \frac{3}{\sqrt{53}}=\frac{10}{\sqrt{53}}
\)
Distance between two directrix \(=\frac{2 a }{ e }\)
\(
=2 \times 3 \times \frac{3}{\sqrt{53}}=\frac{18}{\sqrt{53}}
\)
\(
\begin{aligned}
& \left|\frac{\lambda-11}{\sqrt{53}}\right|=\frac{18}{\sqrt{53}} \\
& \lambda-11=18 \text { or }-18 \\
& \lambda=29 \text { or }-7 \\
& 2 x-7 y-7=0 \text { or } 2 x-7 y+29=0
\end{aligned}
\) -
Question 147 of 269
147. Question
Let \(E\) be an ellipse whose axes are parallel to the co-ordinates axes, having its center at \((3,-4)\), one focus at \((4,-4)\) and one vertex at \((5,-4)\). If \(mx – y =4, m >0\) is a tangent to the ellipse \(E\), then the value of \(5 m ^2\) is equal to [JEE Main 2021 27th July Shift 2]
CorrectIncorrectHint
\(A(5,-4)\)
Hence, \(a =2 \& ae =1\)
\(\Rightarrow e =\frac{1}{2}\)
\(\Rightarrow b^2=3\).
So, \(E: \frac{(x-3)^2}{4}+\frac{(y+4)^2}{3}=1\)
Intersecting with given tangent.
\(
\frac{x^2-6 x+9}{4}+\frac{m^2 x^2}{3}=1
\)
Now, \(D =0\) (as it is tangent)
So, \(5 m^2=3\). -
Question 148 of 269
148. Question
Let a line \(L : 2 x + y = k , k >0\) be a tangent to the hyperbola \(x^2-y^2=3\). If \(L\) is also a tangent to the parabola \(y ^2=\alpha x\), then \(\alpha\) is equal to: [JEE Main 2021 22nd July Shift 1]
CorrectIncorrectHint
Tangent to hyperbola of
Slope \(m =-2\) (given)
\(
\begin{aligned}
& y=-2 x \pm \sqrt{3(3)} \\
& \left( y = mx \pm \sqrt{ x ^2 m ^2- b ^2}\right) \\
& \Rightarrow y+2 x= \pm 3 \Rightarrow 2 x+y=3 \quad(k>0)
\end{aligned}
\)
For parabola \(y ^2=\alpha x\)
\(
\begin{aligned}
& y=m x+\frac{\alpha}{4 m} \\
& \Rightarrow y=-2 x+\frac{\alpha}{-8} \\
& \Rightarrow \frac{\alpha}{-8}=3 \\
& \Rightarrow=-24 .
\end{aligned}
\) -
Question 149 of 269
149. Question
The locus of the centroid of the triangle formed by any point \(P\) on the hyperbola \(16 x^2-9 y^2+32 x+36 y-164=0\), and its foci is : [JEE Main 2021 25th July Shift 1]
CorrectIncorrectHint
Given hyperbola is \(16(x+1)^2-9(y-2)^2=164+16-36=144\)
\(
\Rightarrow \frac{(x+1)^2}{9}-\frac{(y-2)^2}{16}=1
\)
Eccentricity, \(e =\sqrt{1+\frac{16}{9}}=\frac{5}{3}\)
\(\Rightarrow\) foci are \((4,2)\) and \((-6,2)\)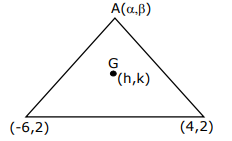
Let the centroic be ( \(h, k\) ) \(\& A (\alpha, \beta)\) be point on hyperbola
\(
\begin{aligned}
& \text { So } h =\frac{\alpha-6+4}{3}, k =\frac{\beta+2+2}{3} \\
& \Rightarrow \alpha=3 h +2, \beta=3 k -4
\end{aligned}
\)
\((\alpha, \beta)\) lies on hyperbola so
\(
\begin{aligned}
& 16(3 h+2+1)^2-9(3 k-4-2)^2=144 \\
& \Rightarrow 144(h+1)^2-81(k-2)^2=144 \\
& \Rightarrow 16\left(h^2+2 h+1\right)-9\left(k^2-4 k+4\right)=16 \\
& \Rightarrow 16 x^2-9 y^2+32 x+36 y-36=0
\end{aligned}
\) -
Question 150 of 269
150. Question
Let the tangent to the parabola \(S: y^2=2 x\) at the point \(P (2,2)\) meet the \(x\)-axis at \(Q\) and normal at it meet the parabola \(S\) at the point \(R\). Then the area (in sq. units) of the triangle PQR is equal to: [JEE Main 2021 20th July Shift 1]
CorrectIncorrectHint
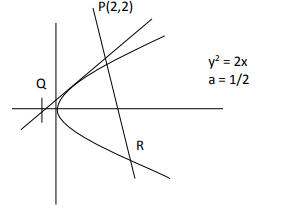
\(
\begin{aligned}
& \text { Tangent at } P: y(2)=2(1 / 2)(x+2) \\
& \Rightarrow 2 y=x+2 \\
& \therefore \quad Q=(-2,0) \\
& \text { Normal at } P: y-2=-\frac{(2)}{2.1 / 2}(x-2) \\
& \Rightarrow y-2=-2(x-2) \\
& \Rightarrow y=6-2 x
\end{aligned}
\)
Normal at \(P: y-2=-\frac{(2)}{2.1 / 2}(x-2)\)
\(\therefore\) Solving with \(y^2=2 x \Rightarrow R\left(\frac{9}{2}-3\right)\)
\(
\begin{aligned}
& \therefore \operatorname{Ar}(\Delta P Q R)=\frac{1}{2}\left|\begin{array}{ccc}
2 & 2 & 1 \\
-2 & 1 & 1 \\
\frac{9}{2} & 3- & 1
\end{array}\right| \\
& =\frac{25}{2} \text { sq.units }
\end{aligned}
\) -
Question 151 of 269
151. Question
Let \(y=m x+c, m>0\) be the focal chord of \(y^2=-64 x\), which is tangent to \((x+10)^2+y^2=4\) Then, the value of \(4 \sqrt{2}( m + c )\) is equal to ____. [JEE Main 2021 20th July Shift 1]
CorrectIncorrectHint
\(
\begin{aligned}
& y^2=-64 x \\
& \text { focus : }(-16,0) \\
& y = mx + c \text { is focal chord } \\
& \Rightarrow c =16 m \\
& y=m x+c \text { is tangent to }(x+10)^2+y^2=4
\end{aligned}
\)
\(
\begin{aligned}
& \Rightarrow y = m ( x +10) \pm 2 \sqrt{1+ m ^2} \\
& \Rightarrow c =10 m \pm 2 \sqrt{1+ m ^2}
\end{aligned}
\)
\(
\begin{aligned}
& \Rightarrow 16 m =10 m \pm 2 \sqrt{1+ m ^2} \\
& \Rightarrow 6 m =2 \sqrt{1+ m ^2} \quad( m >0) \\
& \Rightarrow 9 m ^2=1+ m ^2 \\
& \Rightarrow m =\frac{1}{2 \sqrt{2}} \& c =\frac{8}{\sqrt{2}} \\
& 4 \sqrt{2}( m + c )=4 \sqrt{2}\left(\frac{17}{2 \sqrt{2}}\right)=34
\end{aligned}
\) -
Question 152 of 269
152. Question
Let \(P\) be a variable point on the parabola \(y =4 x ^2+1\). Then, the locus of the mid-point of the point \(P\) and the foot of the perpendicular drawn from the point \(P\) to the line \(y = x\) is : [JEE Main 2021 20th July Shift 2]
CorrectIncorrectHint
\(
\begin{aligned}
& \frac{ K – C }{ h – C }=-1 \\
& C =\frac{ h + K }{2} \quad P(x, y)\\
& R =\left(\frac{ x + C }{2}, \frac{ y + C }{2}\right)
\end{aligned}
\)
\(
\begin{aligned}
& R =\left(\frac{ x }{2}+\frac{ h }{4}+\frac{ K }{4}, \frac{ y }{2}+\frac{ h }{4}+\frac{ k }{4}\right) \\
& \therefore x =\frac{3 h }{2}-\frac{ K }{2}, y=\frac{3 K }{2}-\frac{ h }{2}, \text { put in } \\
& Y=4 x ^2+1 \\
& \left(\frac{3 K – h }{2}\right)=4\left(\frac{3 h – k }{2}\right)^2+1
\end{aligned}
\) -
Question 153 of 269
153. Question
If the point on the curve \(y ^2=6 x\), nearest to the point \(\left(3, \frac{3}{2}\right)\) is \((\alpha, \beta)\), then \(2(\alpha+\beta)\) is equal to [JEE Main 2021 20th July Shift 2]
CorrectIncorrectHint
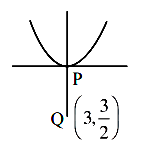
\(
P \equiv\left(\frac{3}{2} t^2, 3 t\right)
\)
Normal at point \(P: \quad t x + y =3 t +\frac{3}{2} t ^3\)
Passes through \(\left(3, \frac{3}{2}\right)\)
\(
\begin{aligned}
& \Rightarrow 3 t +\frac{3}{2}=3 t +\frac{3}{2} t ^3 \\
& P \equiv\left(\frac{3}{2}, 3\right)=(\alpha, \beta) \\
& \Rightarrow t ^3=1 \Rightarrow t =1 \\
& 2(\alpha+\beta)=2\left(\frac{3}{2}+3\right)=9
\end{aligned}
\) -
Question 154 of 269
154. Question
Let a parabola \(P\) be such that its vertex and focus lie on the positive \(x\)-axis at a distance 2 and 4 units from the origin, respectively. If tangents are drawn from \(O(0,0)\) to the parabola \(P\) which meet \(P\) at \(S\) and \(R\), then the area (in sq. units) of \(\Delta S O R\) is equal to [JEE Main 2021 25th July Shift 1]
CorrectIncorrectHint
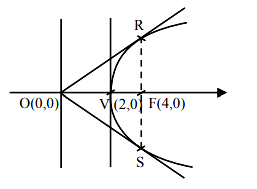
Clearly RS is latus-rectum
\(\because VF =2= a\)
\(\because R S=4 a=8\)
Now \(O F=2 a =4\)
\(\Rightarrow\) Area of triangle ORS \(=16\) -
Question 155 of 269
155. Question
Let \(B\) be the centre of the circle \(x^2+y^2-2 x+4 y+1=0\). Let the tangents at two points \(P\) and \(Q\) on the circle intersect at the point \(A(3,1)\). Then \(8 \cdot\left(\frac{\operatorname{area} \Delta APQ }{\operatorname{area} \Delta BPQ }\right)\) is equal to [JEE Main 2021 31st Aug Shift 2]
CorrectIncorrectHint
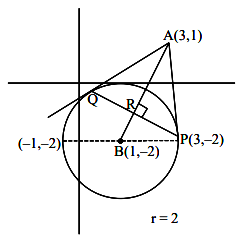
\(
\begin{aligned}
& \tan \theta=\frac{3}{2} \\
& \frac{\text { Area } \triangle APQ }{\text { Area } \triangle BPQ }=\frac{ AR }{ RB }=\frac{3 \sin \theta}{2 \cos \theta}=\frac{9}{4} \\
& 8\left(\frac{\text { Area } \triangle APQ }{\text { Area } \triangle BPQ }\right)=18
\end{aligned}
\) -
Question 156 of 269
156. Question
An angle of intersection of the curves, \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\) and \(x^2+y^2=a b, a>b\), is: [JEE Main 2021 Aug Shift 2]
CorrectIncorrectHint
Let point of intersection be \(\left(x_1, y_1\right)\)
\(
\begin{aligned}
& x_1^2+y_1^2-a b=0 \text { and } \\
& b^2 x_1^2+a^2 y_1^2-a^2 b^2=0
\end{aligned}
\)
We get
\(
\begin{aligned}
& x_1^2=\frac{a^2 b}{a+b}, y_1^2=\frac{a b^2}{a+b} \\
& \Rightarrow x_1=a \sqrt{\frac{b}{a+b}}, y_1=b \sqrt{\frac{a}{a+b}} \dots(1)
\end{aligned}
\)
Tangent to ellipse: \(\frac{x x_1}{a^2}+\frac{y y_1}{b^2}=1\)
Slope \(=m_1=-\frac{b^2 x_1}{a^2 y_1}\)
Tangent to circle: \(x x_1+y y_1=a b\)
Slope \(=m_2=-\frac{x_1}{y_1}\)
Let angle between both curves be \(\theta\)
\(
\begin{aligned}
& \tan \theta=\left|\frac{m_1-m_2}{1+m_1 m_2}\right| \\
& =\left|\frac{\frac{-b^2 x_1}{a^2 y_1}+\frac{x_1}{y_1}}{1+\frac{b^2 x_1}{a^2 y_1} \cdot \frac{x_1}{y_1}}\right| \\
& =\frac{x_1 y_1\left(a^2-b^2\right)}{b^2 x_1^2+a^2 y_1^2} \\
& =\frac{x_1 y_1\left(a^2-b^2\right)}{\frac{a^2 b^2}{a b}} \\
& =\frac{a b \sqrt{a b}}{a+b} \cdot \frac{\left(a^2-b^2\right)}{a^2 b^2} \text { using (1) } \\
& \Rightarrow \tan \theta=\frac{a-b}{\sqrt{a b}}
\end{aligned}
\) -
Question 157 of 269
157. Question
If the variable line \(3 x+4 y=\alpha\) lies between the two circles \((x-1)^2+(y-1)^2=1\) and \((x-9)^2+(y-1)^2=4\) without intercepting a chord on either circle, then the sum of all the integral values of \(\alpha\) is [JEE Main 2021 Aug Shift 1]
CorrectIncorrectHint
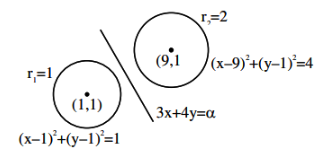
Both centres should lie on either side of the line as well as line can be tangent to circle.
\(
\begin{aligned}
& (3+4-\alpha) \cdot(27+4-\alpha)<0 \\
& (7-\alpha) \cdot(31-\alpha)<0 \\
& \Rightarrow \alpha \in(7,31) \ldots(1)
\end{aligned}
\)
\(d_1=\) distance of \((1,1)\) from line
\(d _2=\) distance of \((9,1)\) from line
\(
\begin{aligned}
& d_1=\text { distance of }(1,1) \text { from line } \\
& d_2=\text { distance of }(9,1) \text { from line } \\
& d_1 \geq r_1 \Rightarrow \frac{|7-\alpha|}{5} 1 \\
& \Rightarrow \alpha \in(-\infty, 2] \cup[12, \infty) \ldots(2) \\
& d_2 \geq r_2 \Rightarrow \frac{|31-\alpha|}{5} \geq 2 \\
& \Rightarrow \alpha \in(-\infty, 21] \cup[41, \infty) \ldots(3) \\
& \text { (1) } \cap(2) \cap(3) \Rightarrow \alpha \in[12,21] \\
& \text { Sum of integers }=165
\end{aligned}
\) -
Question 158 of 269
158. Question
Two circles each of radius 5 units touch each other at the point \((1,2)\). If the equation of their common tangent is \(4 x +3 y =10\), and \(C _1(\alpha, \beta)\) and \(C _2(\gamma, \delta), C _1 \neq C _2\) are their centres, then \(|(\alpha+\beta)(\gamma+\delta)|\) is equal to [JEE Main 2021 27th Aug Shift 2]
CorrectIncorrectHint
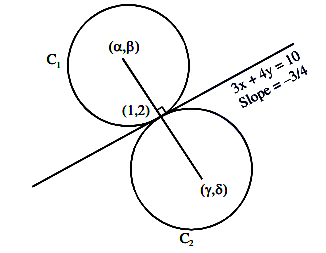
Slope of line joining centres of circles \(=\frac{4}{3}=\tan \theta\)
\(
\Rightarrow \cos \theta=\frac{3}{5}, \sin \theta=\frac{4}{5}
\)
Now using parametric form
\(
\frac{x-1}{\cos \theta}=\frac{y-2}{\sin \theta}= \pm 5
\)
\(
\begin{aligned}
& (x, y)=(1+5 \cos \theta, 2+5 \sin \theta) \\
& (\alpha, \beta)=(4,6)
\end{aligned}
\)
\(
\begin{aligned}
& ( x , y )=(\gamma, \delta)=(1-5 \cos \theta, 2-5 \sin \theta) \\
& (\gamma, s )=(-2,-2)
\end{aligned}
\)
\(
\Rightarrow|(\alpha+\beta)(\gamma+\delta)|=|10 x -4|=40
\) -
Question 159 of 269
159. Question
Let the equation \(x^2+y^2+p x+(1-p) y+5=0\) represent circles of varying radius \(r \in(0,5]\). Then the number of elements in the set \(S=\left\{q: q=p^2\right.\) and \(q\) is an integer \(\}\) is [JEE Main 2021 27th Aug Shift 1]
CorrectIncorrectHint
\(
r=\sqrt{\frac{p^2}{4}+\frac{(1-p)^2}{4}-5}=\frac{\sqrt{2 p^2-2 p-19}}{2}
\)
Since, \(r \in(0,5]\)
So, \(0<2 p ^2-2 p -19 \leq 100\)
\(\Rightarrow p \in\left[\frac{1-\sqrt{239}}{2}, \frac{1-\sqrt{39}}{2}\right) \cup\left(\frac{1+\sqrt{39}}{2}, \frac{1+\sqrt{239}}{2}\right]\) so, number of integral values of \(p ^2\) is 61. -
Question 160 of 269
160. Question
A circle \(C\) touches the line \(x=2 y\) at the point \((2,1)\) and intersects the circle \(C_1: x^2+y^2+2 y-5=0\) at two points \(P\) and \(Q\) such that \(P Q\) is a diameter of \(C _1\). Then the diameter of \(C\) is : [JEE Main 2021 26th Aug Shift 2]
CorrectIncorrectHint
\(
\begin{aligned}
& (x-2)^2+(y-1)^2+\lambda(x-2 y)=0 \\
& C: x^2+y^2+x(\lambda-4)+y(-2-2 \lambda)+5=0 \\
& C_1: x^2+y^2+2 y-5=0
\end{aligned}
\)
\(
\begin{aligned}
& S _1- S _2=0(\text { Equation of } PQ ) \\
& (\lambda-4) x-(2 \lambda+4) y+10=0 \text { Passes through }(0,-1) \\
& \Rightarrow \lambda=-7 \\
& C: x^2+y^2-11 x+12 y+5=0 \\
& =\frac{\sqrt{245}}{4} \\
& \text { Diameter }=7 \sqrt{5}
\end{aligned}
\) -
Question 161 of 269
161. Question
The locus of a point, which moves such that the sum of squares of its distances from the points \((0,0),(1,0),(0,1)(1,1)\) is 18 units, is a circle of diameter \(d\). Then \(d ^2\) is equal to [JEE Main 2021 26th Aug Shift 1]
CorrectIncorrectHint
\(
\begin{aligned}
& \text { Let } P ( x , y ) \\
& x^2+y^2+x^2+(y-1)^2+(x-1)^2+y^2+(x-1)^2+(y-1)^2 \\
& \Rightarrow 4\left(x^2+y^2\right)-4 y-4 x=14 \\
& \Rightarrow x^2+y^2-x-y-\frac{7}{2}=0 \\
& d =2 \sqrt{\frac{1}{4}+\frac{1}{4}+\frac{7}{2}} \\
& \Rightarrow d ^2=16
\end{aligned}
\) -
Question 162 of 269
162. Question
If a line along a chord of the circle \(4 x^2+4 y^2+120 x+675=0\), passes through the point \((-30,0)\) and is tangent to the parabola \(y^2=30 x\), then the length of this chord is: [JEE Main 2021 26th Aug Shift 1]
CorrectIncorrectHint
\(
\begin{aligned}
& \text { Equation of tangent to } y^2=30 x \\
& \begin{array}{l}
y=m x+\frac{30}{4 m} \\
\text { Pass thru }(-30,0): a \\
=-30 m+\frac{30}{4 m} \Rightarrow m^2=1 / 4 \\
\Rightarrow m=\frac{1}{2} \text { or } m=-\frac{1}{2} \\
\text { At } m=\frac{1}{2}: y=\frac{x}{2}+15 \\
\Rightarrow x-2 y+30=0
\end{array}
\end{aligned}
\)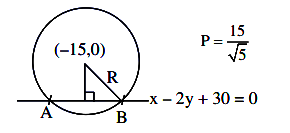
\(
\begin{aligned}
& \ell_{ AB }=2 \sqrt{ R ^2- P ^2}=2 \sqrt{\frac{225}{4}-\frac{225}{5}} \\
& \Rightarrow \ell_{ AB }=30 \cdot \sqrt{\frac{1}{20}}=\frac{15}{\sqrt{5}}=3 \sqrt{5}
\end{aligned}
\) -
Question 163 of 269
163. Question
The locus of mid-points of the line segments joining \((-3,-5)\) and the points on the ellipse \(\frac{x^2}{4}+\frac{y^2}{9}=1\) is: [JEE Main 2021 31st Aug Shift 2]
CorrectIncorrectHint
\(
\begin{aligned}
& \text { General point on } \frac{ x ^2}{4}+\frac{ y ^2}{9}=1 \text { is } A (2 \cos \theta, 3 \sin \theta) \\
& \text { given } B (-3,-5) \\
& \text { midpoint } C \left(\frac{2 \cos \theta-3}{2}, \frac{3 \sin \theta-5}{2}\right) \\
& h =\frac{2 \cos \theta-3}{2} ; k =\frac{3 \sin \theta-5}{2} \\
& \Rightarrow\left(\frac{2 h +3}{2}\right)^2+\left(\frac{2 k +5}{3}\right)^2=1 \\
& \Rightarrow 36 x ^2+16 y ^2+108 x +80 y +145=0
\end{aligned}
\) -
Question 164 of 269
164. Question
The line \(12 x \cos \theta+5 y \sin \theta=60\) is tangent to which of the following curves? [JEE Main 2021 31st Aug Shift 1]
CorrectIncorrectHint
\(
\begin{aligned}
& 12 x \cos \theta+5 y \sin \theta=60 \\
& \frac{x \cos \theta}{5}+\frac{y \sin \theta}{12}=1
\end{aligned}
\)
is tangent to \(\frac{x^2}{25}+\frac{y^2}{144}=1\)
\(
144 x^2+25 y^2=3600
\) -
Question 165 of 269
165. Question
If the minimum area of the triangle formed by a tangent to the ellipse \(\frac{x^2}{b^2}+\frac{y^2}{4 a^2}=1\) and the co-ordinate axis is \(kab\), then \(k\) is equal to [JEE Main 2021 27th Aug Shift 1]
CorrectIncorrectHint
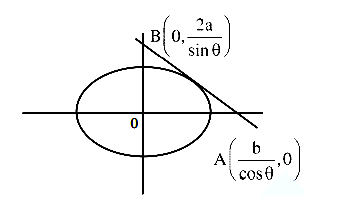
Tangent
\(
\frac{x \cos \theta}{b}+\frac{y \sin \theta}{2 a}=1
\)
\(
\begin{aligned}
& \text { So, area }(\triangle OAB )=\frac{1}{2} \times \frac{ b }{\cos \theta} \times \frac{2 a }{\sin \theta} \\
& =\frac{2 ab }{\sin 2 \theta} \geq 2 ab \\
& \Rightarrow k =2
\end{aligned}
\) -
Question 166 of 269
166. Question
If \(x^2+9 y^2-4 x+3=0, x, y \in R\), then \(x\) and \(y\) respectively lie in the intervals: [JEE Main 2021 27th Aug Shift 1]
CorrectIncorrectHint
\(
\begin{aligned}
& x^2+9 y^2-4 x+3=0 \\
& \left(x^2-4 x\right)+\left(9 y^2\right)+3=0 \\
& \left(x^2-4 x+4\right)+\left(9 y^2\right)+3-4=0 \\
& (x-2)^2+(3 y)^2=1 \\
& \frac{(x-2)^2}{(1)^2}+\frac{y^2}{\left(\frac{1}{3}\right)^2}=1 \text { (equation of an ellipse). }
\end{aligned}
\)
As it is equation of an ellipse, \(x \& y\) can vary inside the ellipse.
So, \(x-2 \in[-1,1]\) and \(y \in\left[-\frac{1}{3}, \frac{1}{3}\right]\)
\(
x \in[1,3] y \in\left[-\frac{1}{3}, \frac{1}{3}\right]
\) -
Question 167 of 269
167. Question
On the ellipse \(\frac{x^2}{8}+\frac{y^2}{4}=1\) let \(P\) be a point in the second quadrant such that the tangent at \(P\) to the ellipse is perpendicular to the line \(x+2 y=0\). Let \(S\) and \(S ^{\prime}\) be the foci of the ellipse and e be its eccentricity. If \(A\) is the area of the triangle \(SP S ^{\prime}\) then, the value of \(\left(5-e^2\right) . A\) is : [JEE Main 2021 26th Aug Shift 1]
CorrectIncorrectHint
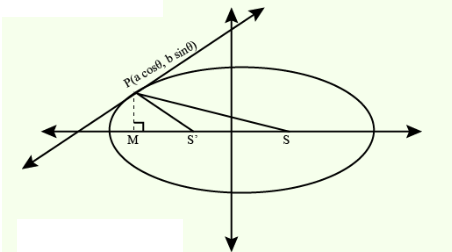
Slope of line \(=-\frac{1}{2}\)
Slope of tangent \(=2\)
Equation of tangent
\(
\begin{aligned}
& \frac{x}{2 \sqrt{2}} \cos \theta+\frac{y}{2} \sin \theta=1 \\
& \text { Slope }=-\frac{\cos \theta}{\sqrt{2} \sin \theta}=2 \\
& \tan \theta=\frac{-1}{2 \sqrt{2}} \Rightarrow \cos \theta=\frac{-2 \sqrt{2}}{3}, \sin \theta=\frac{1}{3} \\
& P(2 \sqrt{2} \cos \theta, 2 \sin \theta) \equiv\left(\frac{-8}{3}, \frac{2}{3}\right)
\end{aligned}
\)
\(
\begin{aligned}
& P M=\frac{2}{3} \\
& A=\frac{1}{2} \times S S^{\prime} \times P M \\
& =\frac{1}{2} \times 2 a e \times \frac{2}{3} \\
& =\sqrt{a^2-b^2} \times \frac{2}{3} \\
& =\sqrt{8-4} \times \frac{2}{3} \\
& =\frac{4}{3} \\
& e=\sqrt{1-\frac{4}{8}}=\frac{1}{\sqrt{2}} \\
& \therefore\left(5-e^2\right) \cdot A=\left(5-\left(\frac{1}{\sqrt{2}}\right)^2\right) \times \frac{4}{3}=6
\end{aligned}
\) -
Question 168 of 269
168. Question
Let \(A (\sec \theta, 2 \tan \theta)\) and \(B (\sec \phi, 2 \tan \phi)\), where \(\theta+\phi=\pi / 2\), be two points on the hyperbola \(2 x ^2- y ^2=2\). If \((\alpha, \beta)\) is the point of the intersection of the normals to the hyperbola at \(A\) and \(B\), then \((2 \beta)^2\) is equal to. [JEE Main 2021 27th Aug Shift 2]
CorrectIncorrectHint
Point \(A(\sec \theta, 2 \tan \theta)\) lies on the hyperbola \(2 x^2-y^2=2\).
\(
\begin{aligned}
& \Rightarrow 2 \sec ^2 \theta-4 \tan ^2 \theta=2 \\
& \Rightarrow 2+2 \tan ^2 \theta-4 \tan ^2 \theta=2 \\
& \Rightarrow \tan ^2 \theta=0 \\
& \Rightarrow \theta=\pi n, n \in Z
\end{aligned}
\)
Similarly, point \(B(\sec \phi, 2 \tan \phi)\) lies on the hyperbola \(2 x^2-y^2=2\).
\(
\Rightarrow \phi=\pi n, \quad n \in Z
\)
But in question, it is given that \(\theta+\phi=\frac{\pi}{2}\), which is not possible. Hence, it is a Bonus question. -
Question 169 of 269
169. Question
The locus of the mid points of the chords of the hyperbola \(x^2-y^2=4\), which touch the parabola \(y ^2=8 x\), is : [JEE Main 2021 26th Aug Shift 2]
CorrectIncorrectHint
\(
\begin{aligned}
& T=S_1 \\
& x h-y k=h^2-k^2 \\
& y=\frac{x h}{k}-\frac{\left(h^2-k^2\right)}{k}
\end{aligned}
\)
this touches \(y^2=8 x\) then \(c=\frac{a}{m}\)
\(
\begin{aligned}
& \left(\frac{ k ^2- h ^2}{ k }\right)=\frac{2 k }{ h } \\
& 2 y^2=x\left(y^2-x^2\right) \\
& y^2(x-2)=x^3
\end{aligned}
\) -
Question 170 of 269
170. Question
The point \(P (-2 \sqrt{6}, \sqrt{3})\) lies on the hyperbola \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\) having eccentricity \(\frac{\sqrt{5}}{2}\). If the tangent and normal at \(P\) to the hyperbola intersect its conjugate axis at the point \(Q\) and \(R\) respectively, then \(QR\) is equal to : [JEE Main 2021 26th Aug Shift 2]
CorrectIncorrectHint
\(
\begin{aligned}
& P (-2 \sqrt{6}, \sqrt{3}) \text { lies on hyperbola } \\
& \Rightarrow \frac{24}{a^2}-\frac{3}{b^2}=1 \ldots \ldots \ldots \text { (i) } \\
& e=\frac{\sqrt{5}}{2} \Rightarrow b^2=a^2\left(\frac{5}{4}-1\right) \Rightarrow 4 b^2=a^2 \\
& \text { Put in (i) } \Rightarrow \frac{6}{ b ^2}-\frac{3}{ b ^2}=1 \Rightarrow b =\sqrt{3} \\
& \Rightarrow a =\sqrt{12} \\
& \frac{x^2}{12}-\frac{y^2}{3}=1
\end{aligned}
\)
Tangent at \(P\):
\(
\frac{-x}{\sqrt{6}}-\frac{y}{\sqrt{3}}=1 \Rightarrow Q(0, \sqrt{3})
\)
Slope of \(T=-\frac{1}{\sqrt{2}}\)
Normal at \(P\):
\(
\begin{aligned}
& y-\sqrt{3}=\sqrt{2}(x+2 \sqrt{6}) \\
& \Rightarrow R=(0,5 \sqrt{3}) \\
& Q R=6 \sqrt{3}
\end{aligned}
\) -
Question 171 of 269
171. Question
Consider the parabola with vertex \(\left(\frac{1}{2}, \frac{3}{4}\right)\) and the directrix \(y =\frac{1}{2}\). Let \(P\) be the point where the parabola meets the line \(x=-\frac{1}{2}\). If the normal to the parabola at \(P\) intersects the parabola again at the point \(Q\), then \((P Q)^2\) is equal to : [JEE Main 2021 01 Sept Shift 2]
CorrectIncorrectHint
The equation of parabola is
\(
\begin{aligned}
& \left(x-\frac{1}{2}\right)^2=\left(y-\frac{3}{4}\right) \\
& \therefore y=x^2-x+1 \\
& \therefore \text { Point } P=\left(-\frac{1}{2}, \frac{7}{4}\right) \\
& \therefore \frac{d y}{d x}=2 x-1
\end{aligned}
\)
Slope of normal at \(x=-\frac{1}{2}\) is \(\frac{1}{2}\).
Equation of normal is : \(y-\frac{7}{4}=\frac{1}{2}\left(x+\frac{1}{2}\right)\)
\(
\begin{aligned}
& \therefore 2 x -4 y +8=0 \\
& \therefore x -2 y +4=0
\end{aligned}
\)
\(\therefore\) Coordinate of \(Q=(2,3)\)
\(
\therefore P Q^2=\left(2+\frac{1}{2}\right)^2+\left(3-\frac{7}{4}\right)^2=\frac{125}{16}
\) -
Question 172 of 269
172. Question
A tangent line \(L\) is drawn at the point \((2,-4)\) on the parabola \(y^2=8 x\). If the line \(L\) is also tangent to the circle \(x^2+y^2=a\), then ‘ \(a\) ‘ is equal to [JEE Main 2021 31st Aug Shift 2]
CorrectIncorrectHint
\(
\begin{aligned}
& \text { tangent of } y^2=8 x \text { is } y=m x+\frac{2}{m} \\
& P (2,-4) \Rightarrow-4=2 m +\frac{2}{ m } \\
& \Rightarrow m +\frac{1}{ m }=-2 \Rightarrow m =-1 \\
& \therefore \text { tangent is } y =- x -2 \\
& \Rightarrow x+y+2=0 \ldots(1)
\end{aligned}
\)
(1) is also tangent to \(x^2+y^2=a\)
\(
\begin{aligned}
& \text { So } \frac{2}{\sqrt{2}}=\sqrt{a} \Rightarrow \sqrt{a}=\sqrt{2} \\
& \Rightarrow a=2
\end{aligned}
\) -
Question 173 of 269
173. Question
The length of the latus rectum of a parabola, whose vertex and focus are on the positive \(x\)-axis at a distance \(R\) and \(S(>R)\) respectively from the origin, is: [JEE Main 2021 31st Aug Shift 1]
CorrectIncorrectHint
\(
V \rightarrow \text { Vertex }
\)
\(F \rightarrow\) focus
\(
VF = S – R
\)
So latus rectum \(=4(S-R)\) -
Question 174 of 269
174. Question
If two tangents drawn from a point \(P\) to the parabola \(y ^2=16( x -3)\) are at right angles, then the locus of point \(P\) is : [JEE Main 2021 27th Aug Shift 2]
CorrectIncorrectHint
Locus is directrix of parabola
\(
x-3+4=0 \Rightarrow x+1=0
\) -
Question 175 of 269
175. Question
A tangent and a normal are drawn at the point \(P (2,-4)\) on the parabola \(y ^2=8 x\), which meet the directrix of the parabola at the points \(A\) and \(B\) respectively. If \(Q(a, b)\) is a point such that \(A Q B P\) is a square, then \(2 a+b\) is equal to : [JEE Main 2021 27th Aug Shift 1]
CorrectIncorrectHint
For the parabola \(y^2=8 x\),
Directrix is \(x=-2\)
Slope of tangent at point \(P(2,-4)\) is \(\frac{d y}{d x}=\frac{8}{-8}=-1\)
\(\therefore\) equation of tangent at \(P (2,-4)\) is
\(
\begin{aligned}
& y+4=-1(x-2) \\
& \Rightarrow x+y+2=0
\end{aligned}
\)
Now, for \(x =-2 \Rightarrow y =0\)
\(
\therefore A \equiv(-2,0)
\)
Also, normal at \(P(2,-4)\) is
\(
\begin{aligned}
& y+4=1(x-2) \\
& \Rightarrow x-y=6 \\
& \text { For } x=-2 \Rightarrow y=-8 \\
& \therefore B \equiv(-2,-8)
\end{aligned}
\)
Now, since \(A Q B P\) is a square, therefore mid point of \(Q P\) is the same as the mid point of \(A B\). So, on equating the \(x-\) coordinate, we have
\(
\begin{aligned}
& \frac{a+2}{2}=\frac{(-2)+(-2)}{2} \\
& \Rightarrow a=-6
\end{aligned}
\)
Similarly, for \(y\)-coordinate, we have
\(
\begin{aligned}
& \frac{b+(-4)}{2}=\frac{0+(-8)}{2} \\
& \Rightarrow b=-4 \\
& \therefore 2 a+b=-16
\end{aligned}
\) -
Question 176 of 269
176. Question
Let the tangents drawn from the origin to the circle, \(x^2+y^2-8 x-4 y+16=0\) touch it at the point \(A\) and \(B\). The \((A B)^2\) is equal to: [JEE Main 2020 7th Jan Shift 2]
CorrectIncorrectHint
\(
\begin{aligned}
& L=\sqrt{S_1}=\sqrt{16}=4 \\
& R=\sqrt{16+4-16}=2
\end{aligned}
\)
Length of Chord of contact \(=\frac{2 L R}{\sqrt{L^2+R^2}}=\frac{2 \times 4 \times 2}{\sqrt{16+4}}=\frac{16}{\sqrt{20}}\)
square of length of chord of contact \(=\frac{64}{5}\) -
Question 177 of 269
177. Question
If a line, \(y=m x+c\) is a tangent to the circle, \((x-3)^2+y^2=1\) and it is perpendicular to a line \(L_1\), where \(L_1\) is the tangent to the circle, \(x^2+y^2=1\) at the point \(\left(\frac{1}{\sqrt{2}}, \frac{1}{\sqrt{2}}\right)\); [JEE Main 2020 8th Jan Shift2]
CorrectIncorrectHint
Slope of tangent to \(x^2+y^2=1\) at \(\left(\frac{1}{\sqrt{2}}, \frac{1}{\sqrt{2}}\right)\)
\(
\begin{aligned}
& x^2+y^2=1 \\
& 2 x+2 y y^{\prime}=0 \\
& y^{\prime}=-\frac{x}{y}=-1
\end{aligned}
\)
\(y=m x+c\) is tangent of \(x^2+y^2=1\)
so \(m=1\)
\(
y=x+c
\)
now distance of \((3,0)\) from \(y=x+c\) is
\(
\begin{aligned}
& \left|\frac{c+3}{\sqrt{2}}\right|=1 \\
& c^2+6 c+9=2 \\
& c^2+6 c+7=0
\end{aligned}
\) -
Question 178 of 269
178. Question
If a circle touches \(y\)-axis at \((0,4)\) and passes through \((2,0)\) then which of the following can-not be the tangent to the circle [JEE Main 2020 9th Jan Shift 1]
CorrectIncorrectHint
(d) We know that,
\(
\begin{aligned}
& A M=r-2 \\
& A C=r
\end{aligned}
\)
Now, \(A C^2=C M^2+A M^2\)
\(
\begin{aligned}
& \Rightarrow r^2=16+(r-2)^2 \\
& \Rightarrow r^2=16+r^2-4 r+4 \\
& \Rightarrow r=5
\end{aligned}
\)
Therefore, the centre is \((5,4)\)
Distance from centre to the tangent is equal to radius.
For \(4 x-3 y+17=0\),
\(
\frac{|20-12+17|}{5}=5
\)
For \(3 x+4 y-6=0\),
\(
\frac{|15+16-6|}{5}=5
\)
For \(4 x+3 y-8=0\),
\(
\frac{|20+12-8|}{5} \neq 5
\)
For \(3 x-4 y-24=0\),
\(
\frac{|15-16-24|}{5}=5
\) -
Question 179 of 269
179. Question
If the curves, \(x^2-6 x+y^2+8=0\) and \(x^2-8 y+y^2+16-k=0,(k>0)\) touch each other at a point, then the largest value of \(k\) is [JEE Main 2020 9th Jan Shift 2]
CorrectIncorrectHint
Two circles touches each other if \(C_1 C_2\left|r_1 \pm r_2\right|\) Distance between \(C_2(3,0)\) and \(C_1(0,4)\) is either
\(
\begin{aligned}
& \sqrt{k}+1 \text { or }|\sqrt{k}-1| \quad\left(C_1 C_2=5\right) \\
& \Rightarrow \quad \sqrt{k}+1=5 \text { or }|\sqrt{k}-1|=5 \\
& \Rightarrow k=16 \text { or } k=36 \\
& \Rightarrow \text { maximum value of } k \text { is } 36
\end{aligned}
\) -
Question 180 of 269
180. Question
The number of integral values of \(k\) for which the line, \(3 x+4 y=k\) intersects the circle, \(x^2+y^2-2 x-4 y+4=0\) at two distinct points is [JEE Main 2020 2nd Sept Shift 1]
CorrectIncorrectHint
A equation of line \(3 x+4 y=k\) and a equation \(x^2+y^2-2 x-4 y+4=0\) of a circle is given.
Rewrite the equation of the circle as follows:
\(
\begin{array}{cc}
x^2+y^2-2 x-4 y+4+1-1=0 \\
\Rightarrow & (x-1)^2+(y-2)^2=1
\end{array}
\)
Therefore, the centre of the given circle is \((1,2)\) and the radius is 1 .
Rewrite the equation of line as follows:
\(
3 x+4 y-k=0
\)
So, if the line intersects the circle at two distinct points then distance of centre from the line \(<\) radius
\(
\begin{aligned}
& \frac{|3(1)+4(2)-k|}{\sqrt{3^2+4^2}}<1 \text {. } \\
& \frac{|3+8-k|}{\sqrt{3^2+4^2}}<1 \\
& \Rightarrow \quad \frac{|11-k|}{5}<1 \\
& \Rightarrow \quad|11-k|<5 \\
& \Rightarrow-5<k-11<5 \\
& \Rightarrow 6<k<16 \\
&
\end{aligned}
\)
\(
\therefore \quad k=7,8, \ldots \ldots .15
\)
i.e. 9 values of \(k\) -
Question 181 of 269
181. Question
The diameter of the circle, whose centre lies on the line \(x+y=2\) in the first quadrant and which touches both the lines \(x=3\) and \(y=2\), is [JEE Main 2020 3rd Sept Shift 1]
CorrectIncorrectHint
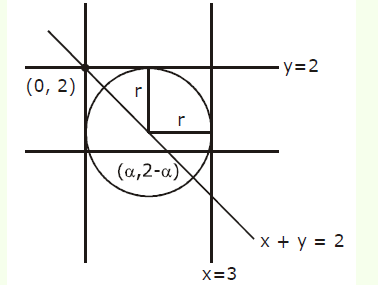
Let the \(x\)-coordinate of centre of circle is \(a\) and radius \(r\).
\(\because\) centre lies on the \(x + y =2\) and in \(1^{\text {st }}\) quadrant.
\(\Rightarrow a+y=2 \Rightarrow y=2-a\)
\(\therefore\) centre of circle \(=(a, 2-a)\)
where \(a>0\) and \(2-a>0\)
\(
\Rightarrow 0<a<2
\)
\(\because\) circle touches \(x =3\) and \(y =2\)
\(
\begin{aligned}
& \Rightarrow|3-a|=|2-(2-a)|=r \\
& \Rightarrow|a|=|a-3| \Rightarrow a^2=(a-3)^2 \\
& \Rightarrow a=\frac{3}{2} \\
& \therefore r=a=\frac{3}{2} \\
& \Rightarrow \text { Diameter }(2 r)=2 a=3
\end{aligned}
\) -
Question 182 of 269
182. Question
The circle passing through the intersection of the circles, \(x^2+y^2-6 x=0\) and \(x^2+y^2-4 y=0\) having its centre on the line, \(2 x-3 y+12=0\), also passes through the point: [JEE Main 2020 4th Sept Shift 2]
CorrectIncorrectHint
Let circle be \(S_1+\lambda S_2=0\)
\(
\begin{aligned}
& x^2+y^2-6 x+\lambda\left(x^2+y^2-4 y\right)=0 \\
& \Rightarrow(1+\lambda) x^2+(1+\lambda) y^2-6 x-4 \lambda y=0 \\
& \text { Centre } \equiv\left(\frac{3}{1+\lambda}, \frac{2 \lambda}{\lambda+1}\right)
\end{aligned}
\)
Centre lies on \(2 x-3 y+12=0\) then
\(
\begin{aligned}
& \frac{6}{\lambda+1}-\frac{6 \lambda}{\lambda+1}+12=0 \\
& \Rightarrow \lambda=-3 \\
& C \equiv-2 x^2-2 y^2-6 x+12 y=0
\end{aligned}
\)
\(
x^2+y^2+3 x-6 y=0
\)
It passes through \((-3,6)\) -
Question 183 of 269
183. Question
Let \(PQ\) be a diameter of the circle \(x^2+y^2=9\). If \(\alpha\) and \(\beta\) are the lengths of the perpendiculars from \(P\) and \(Q\) on the straight line, \(x+y=2\) respectively, then the maximum value of \(\alpha \beta\) is [JEE Main 2020 4th Sept Shift 2]
CorrectIncorrectHint
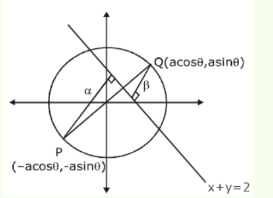
\(
\begin{aligned}
& \text { Let } Q(3 \cos \theta, 3 \sin \theta) \\
& P(-3 \cos \theta,-3 \sin \theta) \\
& \alpha=\left|\frac{3 \cos \theta+3 \sin \theta-2}{\sqrt{2}}\right| \\
& \beta=\left|\frac{-3 \cos \theta-3 \sin \theta-2 \mid}{\sqrt{2}}\right| \\
& \alpha \beta=\left\lvert\, \frac{(3 \cos \theta+3 \sin \theta)^2-4}{2}\right. \\
& =\left|\frac{5+9 \sin 2 \theta}{2}\right| \\
& \left.\alpha \beta\right|_{\max }=\frac{5+9}{2}=7(\text { when } \sin 2 \theta=1)
\end{aligned}
\) -
Question 184 of 269
184. Question
If the length of the chord of the circle, \(x^2+y^2=r^2(r>0)\) along the line, \(y-2 x=3\) is \(r\) then \(r^2\) is equal to: [JEE Main 2020 5 Sept Shift 2]
CorrectIncorrectHint
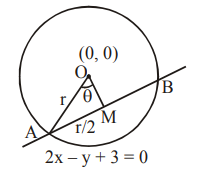
Let chord
\(
AB = r
\)
\(\because \triangle AOM\) is right angled triangle
\(\therefore OM =\frac{ r \sqrt{3}}{2}=\) perpendicular distance of line
\(AB\) from \((0,0)\)
\(
\begin{aligned}
& \frac{ r \sqrt{3}}{2}=\left|\frac{3}{\sqrt{5}}\right| \\
& r ^2=\frac{12}{5}
\end{aligned}
\) -
Question 185 of 269
185. Question
The centre of the circle passing through the point \((0,1)\) and touching the parabola \(y=x^2\) at the point \((2,4)\) is : [JEE Main 2020 6th Sept Shift 2]
CorrectIncorrectHint
Circle passes through \(A(0,1)\) and \(B(2,4)\). So its centre is the point of intersection of perpendicular bisector of \(AB\) and normal to the parabola at \((2,4)\).
Perpendicular bisector of \(AB\);
\(
y-\frac{5}{2}=-\frac{2}{3}(x-1) \Rightarrow 4 x+6 y=19
\)
Normal to the parabola at \((2,4)\),
\(
y-4=-\frac{1}{4}(x-2) \Rightarrow x+4 y=18
\)
Centre of the circle is \(\left(-\frac{16}{5}, \frac{53}{10}\right)\) -
Question 186 of 269
186. Question
If distance between the foci of an ellipse is 6 and distance between its directrices is 12 , then length of its latus rectum is [JEE Main 2020 7th Jan Shift 1]
CorrectIncorrectHint
\(
\begin{aligned}
& 2 a e=6 \text { and } \frac{2 a}{e}=12 \\
& \Rightarrow a e=3 \text { and } \frac{a}{e}=6 \\
& \Rightarrow a^2=18 \\
& \Rightarrow b^2=a^2-a^2 e^2=18-9=9 \\
& \Rightarrow \text { L.R. }=\frac{2 b^2}{a}=\frac{2 \times 9}{3 \sqrt{2}}=3 \sqrt{2}
\end{aligned}
\) -
Question 187 of 269
187. Question
If \(3 x+4 y=12 \sqrt{2}\) is a tangent to the ellipse \(\frac{x^2}{a^2}+\frac{y^2}{9}=1\) for some \(a \in R\), then the distance between the foci of the ellipse is: [JEE Main 2020 7th Jan Shift 2]
CorrectIncorrectHint
\(
\begin{aligned}
& 3 x+4 y=12 \sqrt{2} \\
& \Rightarrow \quad 4 y=-3 x+12 \sqrt{2} \\
& \Rightarrow y=-\frac{3}{4} x+3 \sqrt{2}
\end{aligned}
\)
condition of tangency \(c^2=a^2 m^2+b^2\)
\(
\begin{aligned}
& 18=a^2 \cdot \frac{9}{16}+9 \\
& a^2 \cdot \frac{9}{16}=9 \\
& a^2=16 \\
& 1 a=4 \\
& e=\sqrt{1-\frac{b^2}{a^2}}=\sqrt{1-\frac{9}{16}}=\frac{\sqrt{7}}{4} \\
& \therefore \quad a e=\frac{\sqrt{7}}{4} \cdot 4=\sqrt{7}
\end{aligned}
\)
\(\therefore\) focus are \(( \pm \sqrt{7}, 0)\)
\(\therefore \quad\) distance between foci \(=2 \sqrt{7}\) -
Question 188 of 269
188. Question
Let the line \(y=m x\) and the ellipse \(2 x^2+y^2=1\) intersect at a point \(P\) in the first quadrant. If the normal to this ellipse at \(P\) meets the co-ordinate axes at \(\left(-\frac{1}{3 \sqrt{2}}, 0\right)\) and \((0, \beta)\), then \(\beta\) is equal to [JEE Main 2020 8th Jan Shift 1]
CorrectIncorrectHint
Let \(P\) be \(\left(x_1, y_1\right)\)
Equation of normal at \(P\) is \(\frac{x}{2 x_1}-\frac{y}{y_1}=-\frac{1}{2}\)
It passes through \(\left(-\frac{1}{3 \sqrt{2}}, 0\right) \Rightarrow \frac{-1}{6 \sqrt{2} x_1}=-\frac{1}{2}\)
\(\Rightarrow x_1=\frac{1}{3 \sqrt{2}}\)
So \(y_1=\frac{2 \sqrt{2}}{3}\) (as \(P\) lies in \({\text {1 st }}\) quadrant \()\)
So \(\beta=\frac{y_1}{2}=\frac{\sqrt{2}}{3}\) -
Question 189 of 269
189. Question
If \(e_1\) and \(e_2\) are eccentricities of the ellipse \(\frac{x^2}{18}+\frac{y^2}{4}=1\) and the hyperbola \(\frac{x^2}{9}-\frac{y^2}{4}=1\) respectively and if the point \(\left(e_1, e_2\right)\) lies on ellipse \(15 x^2+3 y^2=k\). Then find value of \(k\) [JEE Main 2020 9th Jan Shift 1]
CorrectIncorrectHint
\(
\begin{aligned}
& e_1=\sqrt{1-\frac{4}{18}}=\sqrt{\frac{7}{9}}=\frac{\sqrt{7}}{3} \\
& e_2=\sqrt{1+\frac{4}{9}}=\sqrt{\frac{13}{9}}=\frac{\sqrt{13}}{3} \\
& 15 e_1^2+3 e_2^2=k \Rightarrow k=15\left(\frac{7}{9}\right)+3\left(\frac{13}{9}\right) \\
& \therefore k=16
\end{aligned}
\) -
Question 190 of 269
190. Question
The length of the minor axis (along \(y\)-axis) of an ellipse in the standard form is \(\frac{4}{\sqrt{3}}\). If this ellipse touches the line, \(x+6 y=8\); then its eccentricity is : [JEE Main 2020 9th Jan Shift 2]
CorrectIncorrectHint
Let \(m\) be the slope, the length of major axis \(2 a\), length of minor axis \(2 b\) and \(e\) the eccentricity.
\(
\begin{array}{rlrl}
\text { Minor axis } & =\frac{4}{\sqrt{3}} \\
\Rightarrow & 2 b & =\frac{4}{\sqrt{3}} \\
\Rightarrow & b & =\frac{2}{\sqrt{3}}
\end{array}
\)
Equation of the tangent \(\Rightarrow y=m x \pm \sqrt{a^2 m^2+b^2}\)
Comparing with \(y=-\frac{x}{6}+\frac{4}{3}\)
We get \(m=-\frac{1}{6}\) and \(\sqrt{a^2 m^2+b^2}=\frac{4}{3}\)
So, \(a^2 m^2+b^2=\frac{16}{9}\)
\(\Rightarrow \frac{a^2}{36}+\frac{4}{3}=\frac{16}{9}\)
\(\Rightarrow \quad \frac{a^2}{36}=\frac{16}{9}-\frac{4}{3}\)
\(\Rightarrow \quad \frac{a^2}{36}=\frac{4}{9}\)
\(\Rightarrow \quad a^2=16\)
\(\therefore e=\sqrt{1-\frac{b^2}{a^2}}=\sqrt{1-\frac{4}{3 \times 16}}=\sqrt{\frac{11}{12}}=\frac{1}{2} \sqrt{\frac{11}{3}}\) -
Question 191 of 269
191. Question
Let \(e_1\) and \(e_2\) be the eccentricities of the ellipse, \(\frac{x^2}{25}+\frac{y^2}{b^2}=1(b<5)\) and the hyperbola, \(\frac{x^2}{16}-\frac{y^2}{b^2}=1\) respectively satisfying \(e_1 e_2=1\). If \(\alpha\) and \(\beta\) are the distances between the foci of the ellipse and the foci of the hyperbola respectively, then the ordered pair \((\alpha, \beta)\) is equal to : [JEE Main 2020 3rd Sept Shift 2]
CorrectIncorrectHint
Equation of ellipse: \(\frac{x^2}{25}+\frac{y^2}{b^2}=1\)
\(
e_1=\sqrt{1-\frac{b^2}{25}}
\)
Equation of hyperbola : \(\frac{x^2}{16}-\frac{y^2}{b^2}=1\) then \(e_2=\sqrt{1+\frac{b^2}{16}}\)
\(
\begin{aligned}
& \because e_1 \cdot e_2=1 \\
& \left(\frac{25-b^2}{25}\right)\left(\frac{16+b^2}{16}\right)=1 \\
& \Rightarrow b ^2\left( b ^2-9\right)=0 \\
& \Rightarrow \quad b=3 \\
& e_1=\frac{4}{5} \text { and } e_2=\frac{5}{4}
\end{aligned}
\)
\(\therefore\) Distance between focii of ellipse \(=\alpha=8\)
Distance between focii of hyperbola \(=\beta=10\) -
Question 192 of 269
192. Question
Let \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b)\) be a given ellipse, length of whose latus rectum is 10 . If its eccentricity is the maximum value of the function, \(\phi(t)=\frac{5}{12}+t-t^2\), then \(a^2+b^2\) is equal to : [JEE Main 2020 4th Sept Shift 1]
CorrectIncorrectHint
\(\because\) Ellipse \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1,(a>b)\)
Given \(\frac{2 b^2}{a}=10 \Rightarrow b^2=5 a\)
Now \(\phi(t)=\frac{5}{12}+t-t^2\)
\(\phi^{\prime}( t )=1-2 t =0 \Rightarrow t =\frac{1}{2}\)
\(\phi^{\prime \prime}(t)=-2<0 \Rightarrow\) maximum
\(\Rightarrow \phi(t)_{\max }=\frac{5}{12}+\frac{1}{2}-\frac{1}{4}=\frac{8}{12}=\frac{2}{3}=e(\) given \()\)
Now \(b^2=a^2\left(1-e^2\right)\)
\(
\begin{aligned}
& 5 a=a^2\left(1-\frac{4}{9}\right) \\
& 5 a=\frac{5 a^2}{9} \Rightarrow a^2-9 a=0 \\
& \Rightarrow a=9 \Rightarrow a^2=81 \Rightarrow b^2=45 \\
& \Rightarrow a^2+b^2=81+45=126
\end{aligned}
\) -
Question 193 of 269
193. Question
Let \(x=4\) be a directrix to an ellipse whose centre is at the origin and its eccentricity is \(\frac{1}{2}\) If \(P(1, \beta), \beta>0\) is a point on this ellipse, then the equation of the normal to it at \(P\) is [JEE Main 2020 4th Sept Shift 2]
CorrectIncorrectHint
Given \(x=4\)
\(
\begin{aligned}
& \Rightarrow \quad \pm \frac{a}{e}=4 \\
& \Rightarrow \quad a=4 e \\
& \Rightarrow \quad a=4 \times \frac{1}{2}=2 \\
& \Rightarrow \quad a=2
\end{aligned}
\)
Now, \(b^2=a^2\left(1-e^2\right)\)
\(
\Rightarrow \quad b^2=4\left(1-\frac{1}{4}\right)=4 \times \frac{3}{4}=3
\)
So, equation \(\frac{x^2}{4}+\frac{y^2}{3}=1\)
\(
\Rightarrow 3 x^2+4 y^2=12 \dots(i)
\)
Now \(P (1, \beta)\) lies on it
\(
\begin{aligned}
& \Rightarrow 3+4 \beta^2=12 \\
& \Rightarrow 4 \beta^2=9 \\
& \Rightarrow \beta=\frac{3}{2}
\end{aligned}
\)
So, \(P\left(1, \frac{3}{2}\right)\)
Now differentiating (i)
\(
\begin{aligned}
& 6 x+8 y \frac{d y}{d x}=0 \\
& \Rightarrow \frac{d y}{d x}=\frac{-3 x}{4 y}
\end{aligned}
\)
\(
\left.\Rightarrow \frac{d y}{d x}\right]\left(1, \frac{3}{2}\right)=-\frac{1}{2}
\)
So, slope of normal \(=2\)
So, equation of normal: \(y-\frac{3}{2}=2(x-1)\)
\(
\begin{aligned}
& \Rightarrow \quad 2 y-3=4 x-4 \\
& \Rightarrow \quad 4 x-2 y=1
\end{aligned}
\) -
Question 194 of 269
194. Question
If the co-ordinates of two points \(A\) and \(B\) are \((\sqrt{7}, 0)\) and \((-\sqrt{7}, 0)\) respectively and \(P\) is any point on the conic, \(9 x^2+16 y^2=144\), then \(PA + PB\) is equal to : [JEE Main 2020 5th Sept Shift 1]
CorrectIncorrectHint
\(
E: \frac{x^2}{16}+\frac{y^2}{9}=1
\)
\(( \pm \sqrt{7}, 0)\) are the foci of given ellipse. So for any point \(P\) on \(i t ; P A+P B=2 a\)
\(
\Rightarrow P A+P B=2(4)=8
\) -
Question 195 of 269
195. Question
If the point \(P\) on the curve, \(4 x^2+5 y^2=20\) is farthest from the point \(Q(0,-4)\), then \(P Q^2\) is equal to : [JEE Main 2020 5th Sept Shift 1]
CorrectIncorrectHint
Curve is \(C \equiv \frac{ x ^2}{5}+\frac{ y ^2}{4}=1\)
Let a point on curve be \((\sqrt{5} \cos \theta, 2 \sin \theta)\)
\(
\begin{gathered}
P Q^2=(\sqrt{5} \cos \theta)^2+(-4-2 \sin \theta)^2 \\
=5 \cos ^2 \theta+4 \sin ^2 \theta+16+16 \sin \theta \\
\Rightarrow P Q^2=21+16 \sin \theta-\sin ^2 \theta \\
=21+64-(\sin \theta-8)^2 \\
=85-(\sin \theta-8)^2
\end{gathered}
\)
For \(P Q^2\) to be maximum \(\sin \theta=1\)
\(
P Q_{\max }^2=85-49=36
\) -
Question 196 of 269
196. Question
Which of the following points lies on the locus of the foot of perpendicular drawn upon any tangent to the ellipse, \(\frac{x^2}{4}+\frac{y^2}{2}=1\) from any of its foci? [JEE Main 2020 6th Sept Shift 1]
CorrectIncorrectHint
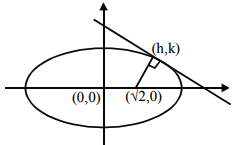
Let foot of perpendicular is \((h, k)\)
\(\frac{x^2}{4}+\frac{y^2}{2}=1\) (Given)
\(a =2, b =\sqrt{2}, e =\sqrt{1-\frac{2}{4}}=\frac{1}{\sqrt{2}}\)
\(\therefore\) Focus \(( ae , 0)=(\sqrt{2}, 0)\)
Equation of tangent
\(
\begin{aligned}
& y=m x+\sqrt{a^2 m^2+b^2} \\
& y=m x+\sqrt{4 m^2+2}
\end{aligned}
\)
Passes throguh (h,k)
\(
( k – mh )^2=4 m ^2+2 \dots(1)
\)
line perpendicular to tangent will have slope
\(
\begin{aligned}
& -\frac{1}{m} \\
& y-0=-\frac{1}{m}(x-\sqrt{2}) \\
& m y=-x+\sqrt{2} \\
& (h+m k)^2=2 \ldots(2)
\end{aligned}
\)
Add equation (1) and (2)
\(
\begin{aligned}
& k^2\left(1+m^2\right)+h^2\left(1+m^2\right)=4\left(1+m^2\right) \\
& h^2+k^2=4
\end{aligned}
\)
\(
x^2+y^2=4 \text { (Auxilary circle) }
\)
\(\therefore(-1, \sqrt{3})\) lies on the locus. -
Question 197 of 269
197. Question
If the normal at an end of a latus rectum of an ellipse passes through an extremity of the minor axis, then the eccentricity e of the ellipse satisfies: [JEE Main 2020 6th Sept Shift 2]
CorrectIncorrectHint
Normal to the ellipse \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\) at \(\left(a e_1 \frac{b^2}{a}\right)\) is \(x-e y=\frac{e\left(a^2-b^2\right)}{a}\)
\(\because(0,-b)\) lies on it, so
\(
\begin{aligned}
& be =\frac{e\left(a^2-b^2\right)}{a} \\
& \Rightarrow \quad a b=a^2 e^2 \\
& \Rightarrow \quad b=a e^2 \Rightarrow \frac{b^2}{a^2}=e^4 \\
& 1-e^2=e^4 \Rightarrow e^4+e^2-1=0
\end{aligned}
\) -
Question 198 of 269
198. Question
If a hyperbola passes through the point \(P(10,16)\) and it has vertices at \(( \pm 6,0)\), then the equation of the normal to it at \(P\) is : [JEE Main 2020 8th Jan Shift 2]
CorrectIncorrectHint
Vertex is at \(( \pm 6,0)\)
\(\therefore \quad a=6\)
Let the hyperbola is \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\)
Putting point \(P(10,16)\) on the hyperbola
\(
\frac{100}{36}-\frac{256}{b^2}=1 \Rightarrow b^2=144
\)
\(\therefore\) hyperbola is \(\frac{x^2}{36}-\frac{y^2}{144}=1\)
\(\therefore\) equation of normal is \(\frac{a^2 x}{x_1}+\frac{b^2 y}{y_1}=a^2+b^2\)
\(\therefore\) putting we get \(2 x+5 y=100\) -
Question 199 of 269
199. Question
A line parallel to the straight line \(2 x-y=0\) is tangent to the hyperbola \(\frac{x^2}{4}-\frac{y^2}{2}=1\) at the point \(\left(x_1, y_1\right) \cdot\) Then \(x_1^2+5 y_1^2\) is equal to : [JEE Main 2020 2nd Sept Shift 1]
CorrectIncorrectHint
Hyperbola: \(\frac{x^2}{4}-\frac{y^2}{2}=1\)
So, let the point on it be \((2 \sec \theta, \sqrt{2} \tan \theta)=\left(x_1, y_1\right)\)
So, equation of tangent \(=\frac{2 \times \sec \theta}{4}-\frac{\sqrt{2} y \tan \theta}{2}=1\)
\(\Rightarrow\) slope \(=\frac{1}{\sqrt{2} \sin \theta}\)
Which will be equal to the slope of given line \(2 x-y=0\)
\(
\begin{aligned}
& \Rightarrow \frac{1}{\sqrt{2} \sin \theta}=2 \Rightarrow \sin \theta=\frac{1}{2 \sqrt{2}} \\
& \Rightarrow \cos ^2 \theta=1-\sin ^2 \theta=1-\frac{1}{8}=\frac{7}{8} \\
& \Rightarrow \sec ^2 \theta=\frac{8}{7} \\
& \Rightarrow \tan ^2 \theta=\frac{8}{7}-1=\frac{1}{7}
\end{aligned}
\)
Now, \(x_1^2+5 y_1^2=4 \sec ^2 \theta+10 \tan ^2 \theta\)
\(
=4 \times \frac{8}{7}+10 \times \frac{1}{7}=\frac{42}{7}=6
\) -
Question 200 of 269
200. Question
For some \(\theta \in\left(0, \frac{\pi}{2}\right)\), if the eccentricity of the hyperbola, \(x^2-y^2 \sec ^2 \theta=10\) is \(\sqrt{5}\) times the eccentricity of the ellipse, \(x^2 \sec ^2 \theta+y^2=5\), then the length of the latus rectum of the ellipse, is : [JEE Main 2020 2nd Sept Shift 2]
CorrectIncorrectHint
\(
\begin{aligned}
& E: \frac{x^2}{\cos ^2 \theta}+\frac{y^2}{1}=5 \Rightarrow e_e=\sqrt{1-\frac{\cos ^2 \theta}{1}}=\sin \theta \\
& H: \frac{x^2}{1}-\frac{y^2}{\cos ^2 \theta}=10 \Rightarrow e_H=\sqrt{1+\cos ^2 \theta}
\end{aligned}
\)
\(
\because e_H=\sqrt{5} e_e \Rightarrow 1+\cos ^2 \theta=5 \sin ^2 \theta \Rightarrow \sin \theta=\frac{1}{\sqrt{3}}
\)
Length of latus rectum of ellipse \(=\frac{2 a^2}{b}\)
\(
\begin{aligned}
& =\frac{2\left(5 \cos ^2 \theta\right)}{\sqrt{5}} \\
& =2 \sqrt{5}\left(\frac{2}{3}\right)=\frac{4 \sqrt{5}}{3}
\end{aligned}
\) -
Question 201 of 269
201. Question
A hyperbola having the transverse axis of length \(\sqrt{2}\) has the same foci as that of the ellipse of \(3 x^2+4 y^2=12\), then this hyperbola does not pass through which of the following points? [JEE Main 2020 3rd Sept Shift 1]
CorrectIncorrectHint
Here ellipse : \(3 x^2+4 y^2=12\)
\(
\begin{aligned}
& \Rightarrow \frac{x^2}{4}+\frac{y^2}{3}=1 \\
& \Rightarrow b ^2= a ^2\left(1- e ^2\right) \\
& \Rightarrow e=\frac{1}{2} \\
& \text { Foci }=( \pm 1,0)
\end{aligned}
\)
Now for Hyperbola –
\(
2 a=\sqrt{2} \Rightarrow a=\frac{1}{\sqrt{2}} \& a e=1 \Rightarrow e=\sqrt{2} \Rightarrow b=\frac{1}{\sqrt{2}}
\)
So equation of hyperbola: \(\frac{x^2}{\frac{1}{2}}-\frac{y^2}{\frac{1}{2}}=1\)
\(
\Rightarrow \quad x^2-y^2=\frac{1}{2}
\)
So option (2) does not satisfy it. -
Question 202 of 269
202. Question
Let \(P(3,3)\) be a point on the hyperbola, \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\). If the normal to it at \(P\) intersects the \(x\)-axis at \((9,0)\) and \(e\) is its eccentricity, then the ordered pair \(\left(a^2, e^2\right)\) is equal to: [JEE Main 2020 4th Sept Shift 1]
CorrectIncorrectHint
\(\because\) equation of hyperbola is : \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\)
\(\because \quad\) it passes through \((3,3): \frac{1}{a^2}-\frac{1}{b^2}=\frac{1}{9} \ldots(1)\) equation of normal at point \((3,3)\) is :
\(
\frac{x-3}{\frac{1}{a^2} \cdot 3}=\frac{y-3}{-\frac{1}{b^2} \cdot 3}
\)
\(\therefore\) It passes through \((9,0): \frac{6}{\frac{1}{a^2}}=\frac{-3}{b^2}\)
\(
\therefore \frac{1}{b^2}=\frac{1}{2 a^2} \dots(2)
\)
From equation (1) and equation (2)
\(
a^2=\frac{9}{2}, b^2=9
\)
\(\therefore \quad\) Eccentricity \(=e\), then \(e^2=1+\frac{b^2}{a^2}=3\)
\(
\therefore\left(a^2, e^2\right)=\left(\frac{9}{2}, 3\right)
\) -
Question 203 of 269
203. Question
If the line \(y=m x+c\) is a common tangent to the hyperbola \(\frac{x^2}{100}-\frac{y^2}{64}=1\) and the circle \(x^2+y^2=36\), then which one of the following is true? [JEE Main 2020 5th Sept Shift 2]
CorrectIncorrectHint
General tangent to hyperbola in slope form is
\(
y=m x \pm \sqrt{100 m^2-64}
\)
and that of cirlce is
\(
y=m x \pm 6 \sqrt{1+m^2}
\)
For common tangent
\(
\begin{aligned}
& 36\left(1+m^2\right)=100 m^2-64 \\
& 100=64 m^2 \\
& \Rightarrow \quad m^2=\frac{100}{64} \\
& \therefore \quad c^2=36\left(1+\frac{100}{64}\right)=\frac{164 \times 36}{64}=\frac{369}{4} \\
& \Rightarrow 4 c^2=369
\end{aligned}
\) -
Question 204 of 269
204. Question
If \(y=m x+4\) is a tangent to both the parabolas \(y^2=4 x\) and \(x^2=2 b y\). Then value of \(b\) is [JEE Main 2020 7th Jan Shift 1]
CorrectIncorrectHint
\(
y=m x+4 \dots(i)
\)
\(
y^2=4 x \text { tangent } y=m x+\frac{a}{m} \Rightarrow y=m x+\frac{1}{m} \dots(ii)
\)
from (i) and (ii)
\(
4=\frac{1}{m} \Rightarrow m=\frac{1}{4}
\)
So line \(y=\frac{1}{4} x+4\) is also tangent to parabola
\(
\begin{aligned}
& x^2=2 b y, \text { so solve } \\
& x^2=2 b\left(\frac{x+16}{4}\right) \\
& \Rightarrow 2 x^2-b x-16 b=0 \Rightarrow D=0 \\
& \Rightarrow b^2-4 \times 2 \times(-16 b)=0 \\
& \Rightarrow b^2+32 \times 4 b=0 \\
& b=-128, b=0 \text { (not possible) }
\end{aligned}
\) -
Question 205 of 269
205. Question
The locus of a point which divides the line segment joining the point \((0,-1)\) and a point on the parabola, \(x^2=4 y\), internally in the ratio \(1: 2\), is : [JEE Main 2020 8th Jan Shift 1]
CorrectIncorrectHint
Let point \(P\) be \(\left(2 t, t^2\right)\) and \(Q\) be \((h, k)\).
\(
h=\frac{2 t}{3}, k=\frac{-2+t^2}{3}
\)
Hence locus is \(3 k+2=\left(\frac{3 h}{2}\right)^2\)
\(
\Rightarrow 9 x^2=12 y+8
\) -
Question 206 of 269
206. Question
Let a line \(y=m x(m>0)\) intersect the parabola, \(y^2=x\) at a point \(P\), other than the origin. Let the tangent to it at \(P\) meet the \(x\)-axis at the point \(Q\). If area \((\Delta O P Q)=4\) sq. units, then \(m\) is equal to [JEE Main 2020 8th Jan Shift 2]
CorrectIncorrectHint
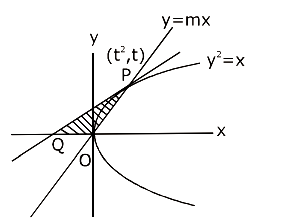
let \(p\left(t^2, t\right)\)
Tangent at \(P\left(t^2, t\right)\)
\(
\begin{aligned}
& t y=\frac{x+t^2}{2} \\
& 2 t y=x+t^2 \rightarrow \text { equation of tangent } \\
& Q \equiv\left(-t^2, 0\right) \\
& O(0,0) \\
& \Delta(O P Q)=4
\end{aligned}
\)
\(
\frac{1}{2}\left|\begin{array}{ccc}
0 & 0 & 1 \\
t^2 & t & 1 \\
-t^2 & 0 & 1
\end{array}\right|=4
\)
\(
\begin{aligned}
& \left|t^3\right|=8 \\
& t=2 \\
& \therefore 4 y=x+4 \text { is tangent } \therefore P \text { is }(4,2) \\
& y=m x \Rightarrow 2=4 m \Rightarrow m=\frac{1}{2} \Rightarrow 0.5
\end{aligned}
\) -
Question 207 of 269
207. Question
If one end of a focal chord \(A B\) of the parabola \(y^2=8 x\) is at \(A\left(\frac{1}{2},-2\right)\), then the equation of the tangent to it at \(B\) is : [JEE Main 2020 9th Jan Shift 2]
CorrectIncorrectHint
Let \(\left(\frac{1}{2},-2\right)\) is \(\left(2 t^2, 4 t\right) \Rightarrow t=\frac{-1}{2}\)
Parameter of other end of focal chord is 2
\(\Rightarrow\) point is \((8,8)\)
\(\Rightarrow\) equation of tangent is \(8 y-4(x+8)=0\)
\(\Rightarrow 2 y-x=8\) -
Question 208 of 269
208. Question
Let \(P(h, \quad k)\) be a point on the curve \(y=x^2+7 x+2\), nearest to the line, \(y=3 x-3\) Then the equation of the normal to the curve at \(P\) is : [JEE Main 2020 2nd Sept Shift 1]
CorrectIncorrectHint
\(
\begin{aligned}
& \because y=x^2+7 x+2 \\
& \therefore \frac{d y}{d x}=2 x+7
\end{aligned}
\)
Slope of tangent parallel to line \(y=3 x-3\)
\(
\begin{aligned}
& \therefore 2 x+7=3 \\
& \therefore x=-2
\end{aligned}
\)
\(\therefore\) Point on curve \(=(-2,-8)\)
Equation of normal at point \((-2,-8)\)
\(
\begin{aligned}
& y+8=-\frac{1}{3}(x+2) \\
& x+3 y+26=0
\end{aligned}
\) -
Question 209 of 269
209. Question
The area (in sq. units) of an equilateral triangle inscribed in the parabola \(y^2=8 x\), with one of its vertices on the vertex of this parabola, is : [JEE Main 2020 2nd Sept Shift 2]
CorrectIncorrectHint
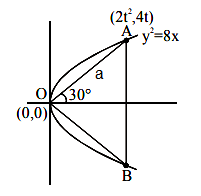
The graph of the given problem is as shown:
Let \(A B O\) is an equilateral triangle with side equal to ‘ \(a\) ‘.
Now, a component of \(O A\) along positive \(x\)-axis is \(a \cos \left(30^{\circ}\right)\)
Also, a component of \(O A\) along positive \(y\)-axis is \(a \sin \left(30^{\circ}\right)\)
Hence, the coordinates of a point \(A\) are,
\(A\left(a \cos \left(30^{\circ}\right), a \sin \left(30^{\circ}\right)\right)\) which lies on the parabola.
Now \(y^2=8 x\)
Put \(y=a \sin \left(30^{\circ}\right)\) and \(x=a \cos \left(30^{\circ}\right)\) in a parabolic equation we get,
Now \(y^2=8 x\)
Put \(y=a \sin \left(30^{\circ}\right)\) and \(x=a \cos \left(30^{\circ}\right)\) in a parabolic equation we get,
\(
\begin{aligned}
& \Rightarrow\left(a \sin \left(30^{\circ}\right)\right)^2=8 \times\left(a \cos \left(30^{\circ}\right)\right) \\
& \Rightarrow \quad a^2 \times\left(\frac{1}{2}\right)^2=8 \times a \times\left(\frac{\sqrt{3}}{2}\right) \quad\left[\because \sin \left(30^{\circ}\right)=\frac{1}{2}, \quad \cos \left(30^{\circ}\right)=\frac{\sqrt{3}}{2}\right] \\
& \Rightarrow \quad \frac{a}{4}=4 \times \sqrt{3} \\
& \Rightarrow \quad a=16 \sqrt{3} \\
&
\end{aligned}
\)
Now area of an equilateral triangle is equal to
\(
\begin{aligned}
\operatorname{Ar}(\triangle) & =\frac{\sqrt{3}}{4} a^2 \\
& =\frac{\sqrt{3}}{} \times(16 \sqrt{3})^2 \\
& =\frac{\sqrt{3}}{4} \times 768 \\
& =192 \sqrt{3}
\end{aligned}
\) -
Question 210 of 269
210. Question
Let \(P\) be a point on the parabola, \(y^2=12 x\) and \(N\) be the foot of the perpendicular drawn from \(P\) on the axis of the parabola. A line is now drawn through the mid-point \(M\) of \(P N\), parallel to its axis which meets the parabola at \(Q\). If the \(y\)-intercept of the line \(N Q\) is \(\frac{4}{3}\), then : [JEE Main 2020 3rd Sept Shift 1]
CorrectIncorrectHint
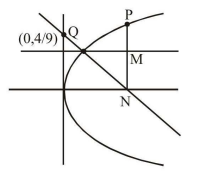
Let \(P=\left(3 t^2, 6 t\right) ; N=\left(3 t^2, 0\right)\)
\(
M =\left(3 t ^2, 3 t \right)
\)
Equation of MQ : \(y=3 t\)
\(
\therefore \quad Q=\left(\frac{3}{4} t^2, 3 t\right)
\)
Equation of \(NQ\)
\(
\begin{gathered}
y=\frac{3 t}{\left(\frac{3}{4} t^2-3 t^2\right)}\left(x-3 t^2\right) \\
y \text {-intercept of } N Q=4 t=\frac{4}{3} \Rightarrow t=\frac{1}{3} \\
\therefore \quad M Q=\frac{9}{4} t^2=\frac{1}{4} \\
P N=6 t=2
\end{gathered}
\) -
Question 211 of 269
211. Question
Let the latus ractum of the parabola \(y^2=4 x\) be the common chord to the circles \(C_1\) and \(C_2\) each of them having radius \(2 \sqrt{5}\). Then, the distance between the centres of the circles \(C_1\) and \(C _2\) is : [JEE Main 2020 4th Sept Shift 2]
CorrectIncorrectHint
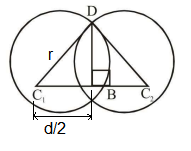
Length of latus rectum =4
\(
\begin{aligned}
& D B=2 \\
& C_1 B=\sqrt{\left(C_1 D\right)^2-(D B)^2}=4 \\
& C_1 C_2=8
\end{aligned}
\)Alternate:
\(
\begin{aligned}
& \text { Length of common chord }=2 \sqrt{r^2-\left(\frac{d}{2}\right)^2}=4 \\
& \Rightarrow r^2-\frac{d^2}{4}=4 \quad(\text { given } r=2 \sqrt{5}) \\
& \Rightarrow \frac{d^2}{4}=16 \\
& \Rightarrow d=8
\end{aligned}
\) -
Question 212 of 269
212. Question
The area (in sq. units) of the largest rectangle \(ABCD\) whose vertices \(A\) and \(B\) lie on the \(x\)-axis and vertices \(C\) and \(D\) lie on the parabola, \(y=x^2-1\) below the \(x\)-axis, is : [JEE Main 2020 4th Sept Shift 2]
CorrectIncorrectHint

Area of rectangle \(A B C D\)
\(
\begin{aligned}
& A=\left|2 t \cdot\left(t^2-1\right)\right| \\
& A=\left|2 t^3-2 t\right| \\
& \therefore \quad \frac{ dA }{ dt }=\left|6 t ^2-2\right|
\end{aligned}
\)
For maximum area \(\frac{ dA }{ dt }=0 \Rightarrow t = \pm \frac{1}{\sqrt{3}}\)
\(
\therefore \quad \text { Maximum area }=\left|\frac{2}{3 \sqrt{3}}-\frac{2}{\sqrt{3}}\right|=\frac{4}{3 \sqrt{3}}
\) -
Question 213 of 269
213. Question
If the common tangent to the parabolas, \(y^2=4 x\) and \(x^2=4 y\) also touches the circle, \(x^2+y^2=c^2\), then \(c\) is equal to: [JEE Main 2020 5th Sept Shift 1]
CorrectIncorrectHint
Step 1: Find the equation of the common tangent
Any tangent to \(y ^2=4 x\) is \(y = mx +\frac{1}{ m }\), tangent to \(x ^2=4 y\) with slope \(m\) is
\(
\begin{aligned}
x & =\left(\frac{1}{m}\right) y+m \text { or } y=m x-m^2 \\
\frac{1}{ m } & =- m ^2 \\
m ^3 & =-1 \\
m & =-1
\end{aligned}
\)
Substituting the value of \(m\) in equation \(y = mx +\frac{1}{ m }\) we get the equation of common tangent as:
\(
x+y=-1
\)Step 2: Find value of \(c\)
As the line \(x+y=-1\) touches the circle \(x^2+y^2=c^2\) it means that the radius is equal to the distance between the center and the tangent.
\(
\begin{aligned}
& \Rightarrow|c|=-\frac{1}{\sqrt{2}} \\
& \Rightarrow c= \pm \frac{1}{\sqrt{2}}
\end{aligned}
\)
Hence, the \(c\) is equal to \(\pm \frac{1}{\sqrt{2}}\). -
Question 214 of 269
214. Question
If the lines \(x+y=a\) and \(x-y=b\) touch the curve \(y=x^2-3 x+2\) at the points where the curve intersects the \(x\)-axis, then \(\frac{a}{b}\) is equal to [JEE Main 2020 5th Sept Shift 2]
CorrectIncorrectHint
\(y=(x-1)(x-2)\), this curve intersects the \(x\)-axis at A \((1,0)\) and \(B (2,0)\)
\(\therefore \frac{d y}{d x}=2 x-3 ; \frac{d y}{d x(x=1)}=-1\) and \(\frac{d y}{d x(x=2)}=1\)
Equation of tangent at \(A (1,0)\);
\(
\begin{aligned}
& y=-1(x-1) \\
& \Rightarrow x+y=1
\end{aligned}
\)
and equation of tangent at \(B(2,0)\)
\(
y=1(x-2)
\)
\(
\begin{aligned}
& \Rightarrow \quad x-y=2 \\
& \text { So } a=1 \text { and } b=2 \\
& \Rightarrow \frac{a}{b}=0.5
\end{aligned}
\) -
Question 215 of 269
215. Question
Let \(L_1\) be a tangent to the parabola \(y^2=4(x+1)\) and \(L_2\) be a tangent to the parabola \(y^2=8(x+2)\) such that \(L_1\) and \(L_2\) intersect at right angles. Then \(L_1\) and \(L_2\) meet on the straight line: [JEE Main 2020 6th Sept Shift 1]
CorrectIncorrectHint
\(
y^2=4(x+1)
\)
equation of tangent \(y=m(x+1)+\frac{1}{m}\)
\(
\begin{aligned}
& y=m x+m+\frac{1}{m} \\
& y^2=8(x+2)
\end{aligned}
\)
equation of tangent \(y=m^{\prime}(x+2)+\frac{2}{m^{\prime}}\)
\(
y=m^{\prime} x+2\left(m^{\prime}+\frac{1}{m^{\prime}}\right)
\)
since lines intersect at right angles
\(\therefore m m^{\prime}=-1\)
Now \(y=m x+m+\frac{1}{m} \dots(1)\)
\(
\begin{aligned}
& y=m^{\prime} x+2\left(m^{\prime}+\frac{1}{m^{\prime}}\right) \\
& y=-\frac{1}{m} x+2\left(-\frac{1}{m}-m\right) \\
& y=-\frac{1}{m} x-2\left(m+\frac{1}{m}\right) \dots(2)
\end{aligned}
\)
From equation (1) and (2)
\(
\begin{aligned}
& m x+m+\frac{1}{m}=-\frac{1}{m} x-2\left(m+\frac{1}{m}\right) \\
& \left(m+\frac{1}{m}\right) x+3\left(m+\frac{1}{m}\right)=0 \\
& \therefore x+3=0
\end{aligned}
\) -
Question 216 of 269
216. Question
Equation of a common tangent to the circle, \(x^2+y^2-6 x=0\) and the parabola, \(y^2=4 x\), is : [JEE Main 2019 9th Jan Morning]
CorrectIncorrectHint
(2) Since, the equation of tangent to parabola \(y^2=4 x\) is
\(
y=m x+\frac{1}{m} \dots(1)
\)
The line (1) is also the tangent to circle
\(
x^2+y^2-6 x=0
\)
Then centre of circle \(=(3,0)\)
radius of circle \(=3\)
The perpendicular distance from centre to tangent is equal to the radius of circle
\(
\begin{aligned}
& \therefore \quad \frac{\left|3 m+\frac{1}{m}\right|}{\sqrt{1+m^2}}=3 \Rightarrow\left(3 m+\frac{1}{m}\right)^2=9\left(1+m^2\right) \\
& \Rightarrow \quad m= \pm \frac{1}{\sqrt{3}} \\
&
\end{aligned}
\)
Then, from equation (1): \(y= \pm \frac{1}{\sqrt{3}} x \pm \sqrt{3}\) -
Question 217 of 269
217. Question
Three circles of radii \(a, b, c(a<b<c)\) touch each other externally. If they have \(x\)-axis as a common tangent, then: [JEE Main 2019 9th Jan Morning]
CorrectIncorrectHint
\(
\begin{aligned}
& A M^2=A C^2-M C^2 \\
= & (a+c)^2-(a-c)^2=4 a c \\
\Rightarrow & A M^2=X Y^2=4 a c \\
\Rightarrow & X Y=2 \sqrt{a c}
\end{aligned}
\)
Similarly, \(Y Z=2 \sqrt{b a}\) and \(X Z=2 \sqrt{b c}\)
Then, \(\quad X Z=X Y+Y Z\)
\(
\begin{aligned}
& \Rightarrow \quad 2 \sqrt{b c}=2 \sqrt{a c}+2 \sqrt{b a} \\
& \Rightarrow \quad \frac{1}{\sqrt{a}}=\frac{1}{\sqrt{b}}+\frac{1}{\sqrt{c}}
\end{aligned}
\) -
Question 218 of 269
218. Question
If the circles \(x^2+y^2-16 x-20 y+164=r^2\) and \((x-4)^2+(y-7)^2=36\) intersect at two distinct points, then: [JEE Main 2019 9th Jan Evening]
CorrectIncorrectHint
(d) Consider the equation of circles as,
\(
x^2+y^2-16 x-20 y+164=r^2
\)
i.e. \((x-8)^2+(y-10)^2=r^2 \dots(1)\)
and \((x-4)^2+(y-7)^2=36 \dots(2)\)
Both the circles intersect each other at two distinct points.
Distance between centres
\(
\begin{array}{ll}
& =\sqrt{(8-4)^2+(10-7)^2}=5 \\
\therefore \quad & |r-6|<5<|r+6| \\
\therefore \quad & \text { If }|r-6|<5 \Rightarrow r \in(1,11) \dots(3)
\end{array}
\)
and \(|r+6|>5 \Rightarrow r \in(-\infty,-11) \cup(-1, \infty) \dots(4)\)
From (3) and (4),
\(
r \in(1,11)
\) -
Question 219 of 269
219. Question
If a circle \(C\) passing through the point \((4,0)\) touches the circle \(x^2+y^2+4 x-6 y=12\) externally at the point \((1,-1)\), then the radius of \(C\) is: [JEE Main 2019 10th Jan Morning]
CorrectIncorrectHint
The equation of circle \(x^2+y^2+4 x-6 y=12\) can be written as \((x+2)^2+(y-3)^2=25\)
Let \(P=(1,-1) \& Q=(4,0)\)
Equation of tangent at \(P(1,-1)\) to the given circle :
\(
\begin{aligned}
& x(1)+y(-1)+2(x+1)-3(y-1)-12=0 \\
& 3 x-4 y-7=0 \dots(1)
\end{aligned}
\)
The required circle is tangent to \((1)\) at \((1,-1)\).
\(
\therefore(x-1)^2+(y+1)^2+\lambda(3 x-4 y-7)=0 \dots(2)
\)
Equation (2) passes through \(Q(4,0)\)
\(
\begin{aligned}
& \Rightarrow 3^2+1^2+\lambda(12-7)=0 \Rightarrow 5 \lambda+10=0 \\
& \Rightarrow \lambda=-2
\end{aligned}
\)
Equation (2) becomes \(x^2+y^2-8 x+10 y+16=0\)
\(
\text { radius }=\sqrt{(-4)^2+(5)^2-16}=5
\) -
Question 220 of 269
220. Question
If the area of an equilateral triangle inscribed in the circle, \(x^2+y^2+10 x+12 y+c=0\) is \(27 \sqrt{3}\) sq. units then \(c\) is equal to: [JEE Main 2019 10th Jan Evening]
CorrectIncorrectHint
Let the sides of equilateral \(\Delta\) inscribed in the circle be a, then
\(
\begin{aligned}
& \cos 30^{\circ}=\frac{a}{2 r} \\
& \frac{\sqrt{3}}{2}=\frac{a}{2 r} \\
& a=\sqrt{3} r
\end{aligned}
\)
Then, area of the equilateral triangle \(=\frac{\sqrt{3}}{4} a^2\)
\(
\begin{aligned}
& =\frac{\sqrt{3}}{4}(\sqrt{3} r)^2 \\
& =\frac{3 \sqrt{3}}{4} r^2
\end{aligned}
\)
But it is given that area of equilateral triangle \(=27 \sqrt{3}\)
Then, \(27 \sqrt{3}=\frac{3 \sqrt{3}}{4} r^2\)
\(
\begin{aligned}
& r^2=36 \\
& \Rightarrow \quad r=6 \\
& \text { But }\left(-\frac{1}{2} \text { coeff. of } x\right)^2+\left(-\frac{1}{2} \text { coeff. of } y\right)^2 – \text { constant term }=r^2
\end{aligned}
\)
\(
\begin{aligned}
& (-5)^2+(-6)^2-c=36 \\
& c=25
\end{aligned}
\) -
Question 221 of 269
221. Question
A square is inscribed in the circle \(x^2+y^2-6 x+8 y-103=0\) with its sides parallel to the coordinate axes. Then the distance of the vertex of this square which is nearest to the origin is : [JEE Main 2019 11th Jan Morning]
CorrectIncorrectHint
The equation of circle is,
\(
\begin{aligned}
& x^2+y^2-6 x+8 y-103=0 \\
& (x-3)^2+(y+4)^2=(8 \sqrt{2})^2 \\
& C(3,-4), r=8 \sqrt{2}
\end{aligned}
\)
Length of side of square \(=\sqrt{2} r=16\)
\(
\begin{aligned}
\Rightarrow \quad & P(-5,4), Q(-5,-12) \\
& R(11,-12), S(11,4) \\
\Rightarrow \quad & \text { Required distance }=O P \\
& =\sqrt{(-5-0)^2+(-4-0)^2}=\sqrt{25+16}=\sqrt{41}
\end{aligned}
\) -
Question 222 of 269
222. Question
Two circles with equal radii are intersecting at the points \((0\), \(1)\) and \((0,-1)\). The tangent at the point \((0,1)\) to one of the circles passes through the centre of the other circle. Then the distance between the centres of these circles is : [JEE Main 2019 11th Jan Morning]
CorrectIncorrectHint
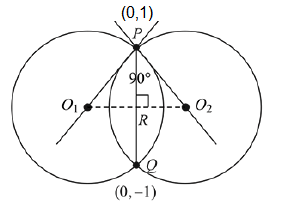
\(\because\) Two circles of equal radii intersect each other orthogonally. Then \(R\) is mid point of \(P Q\).
and
\(
\begin{aligned}
& P R=O_1 R=O_2 R \\
& P R=\frac{1}{2} \sqrt{(0-0)^2+(1+1)^2}=1
\end{aligned}
\)
\(\therefore\) Distance between centres \(=1+1=2\). -
Question 223 of 269
223. Question
A circle cuts a chord of length 4a on the \(x\)-axis and passes through a point on the \(y\)-axis, distant \(2 b\) from the origin. Then the locus of the centre of this circle, is : [JEE Main 2019 11th Jan Evening]
CorrectIncorrectHint
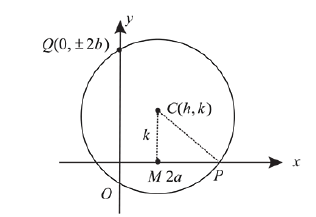
Let centre be \(C(h, k)\)
\(
\begin{gathered}
C Q=C P=r \\
\Rightarrow \quad C Q^2=C P^2 \\
(h-0)^2+(k \pm 0)^2=C M^2+M P^2 \\
h^2+(k \pm 2 b)^2=k^2+4 a^2 \\
h^2+k^2+4 b^2 \pm 4 b k=k^2+4 a^2
\end{gathered}
\)
Then, the locus of centre \(C(h, k)\)
\(
x^2+4 b^2 \pm 4 b y=4 a^2
\)
Hence, the above locus of the centre of circle is a parabola. -
Question 224 of 269
224. Question
Let \(C_1\) and \(C_2\) be the centres of the circles \(x^2+y^2-2 x-2 y-2=\) 0 and \(x^2+y^2-6 x-6 y+14=0\) respectively. If \(P\) and \(Q\) are the points of intersection of these circles then, the area (in sq. units) of the quadrilateral \(PC _1 QC _2\) is : [JEE Main 2019 12th Jan Morning]
CorrectIncorrectHint
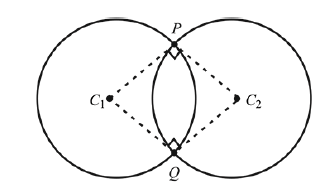
\(
\begin{aligned}
& 2 g_1 g_2+2 f_1 f_2=2(-1)(-3)+2(-1)(-3)=12 \\
& c_1+c_2=14-2=12
\end{aligned}
\)
Since, \(2 g_1 g_2+2 f_1 f_2=c_1+c_2\)
Hence, circles intersect orthogonally
\(\therefore \quad\) Area of the quadrilateral \(PC _1 QC _1\)
\(
\begin{aligned}
= & 2\left(\frac{1}{2}\left(C_1 P\right)\left(C_2 P\right)\right) \\
& =2 \times \frac{1}{2} r_1 r_2=(2)(2)=4 \text { sq, units }
\end{aligned}
\) -
Question 225 of 269
225. Question
If a variable line, \(3 x+4 y-\lambda=0\) is such that the two circles \(x^2+y^2-2 x-2 y+1=0\) and \(x^2+y^2-18 x-2 y+78=0\) are on its opposite sides, then the set of all values of \(\lambda\) is the interval : [JEE Main 2019 12th Jan Morning]
CorrectIncorrectHint
Condition 1: The centre of the two circles are \((1,1)\) and \((9,1)\). The circles are on opposite sides of the line \(3 x+4 y-\lambda=0\).
Put \(x=1, y=1\) in the equation of line,
\(
\begin{aligned}
& 3(1)+4(1)-\lambda=0 \\
& 7-\lambda=0
\end{aligned}
\)
Now, put \(x=9, y=1\) in the equation of line,
\(
\begin{aligned}
& 3(9)+4(1)-\lambda=0 \\
& \text { Then, }(7-\lambda)(27+4-\lambda)<0 \\
& \Rightarrow \quad(\lambda-7)(\lambda-31)<0 \\
& \quad \lambda \in(7,31) \ldots(1)
\end{aligned}
\)
Condition 2: Perpendicular distance from centre on line \(\geq\) radius of circle.
For \(x^2+y^2-2 x-2 y=1\),
\(
\begin{aligned}
& \Rightarrow \quad \frac{|3+4-\lambda|}{5} \geq 1 \\
& \Rightarrow \quad|\lambda-7| \geq 5 \\
& \Rightarrow \quad \lambda \geq 12 \text { or } \lambda \Rightarrow 2 \ldots \text { (2) }
\end{aligned}
\)
For \(x^2+y^2-18 x-2 y+78=0\)
\(
\begin{aligned}
& \frac{|27+4-\lambda|}{5} \geq 2 \\
\Rightarrow \quad & \lambda \geq 41 \text { or } \lambda \leq 21 \ldots \text { (3) }
\end{aligned}
\)
Intersection of (1), (2) and (3) gives \(\lambda \in[12,21]\). -
Question 226 of 269
226. Question
If a circle of radius \(R\) passes through the origin \(O\) and intersects the coordinate axes at \(A\) and \(B\), then the locus of the foot of perpendicular from \(O\) on \(A B\) is : [JEE Main 2019 12th Jan Evening]
CorrectIncorrectHint
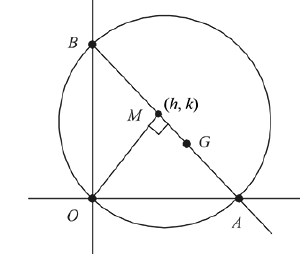
As \(\angle A O B=90^{\circ}\)
Let \(A B\) diameter and \(M(h, k)\) be foot of perpendicular, then
\(
M_{A B}=\frac{-h}{k}
\)
Then, equation of \(A B\)
\(
\begin{aligned}
& (y-k)=\frac{-h}{k}(x-h) \\
& \Rightarrow \quad h x+k y=h^2+k^2 \\
&
\end{aligned}
\)
Then, \(A\left(\frac{h^2+k^2}{h}, 0\right)\) and \(B\left(0, \frac{h^2+k^2}{k}\right)\)
\(\because A B\) is the diameter, then
\(
\begin{aligned}
& A B=2 R \\
& \Rightarrow \quad A B^2=4 R^2
\end{aligned}
\)
\(
\Rightarrow \quad\left(\frac{h^2+k^2}{h}\right)^2+\left(\frac{h^2+k^2}{k}\right)=4 R^2
\)
Hence, required locus is \(\left(x^2+y^2\right)^3=4 R^2 x^2 y^2\) -
Question 227 of 269
227. Question
The sum of the squares of the lengths of the chords intercepted on the circle, \(x^2+y^2=16\), by the lines, \(x+y=n\), \(n \in N\), where \(N\) is the set of all natural numbers, is : [JEE Main 2019 8th April Morning]
CorrectIncorrectHint
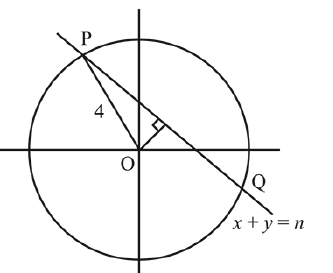
Let the chord \(x+y=n\) cuts the circle \(x^2+y^2=16\) at \(P\) and \(Q\) Length of perpendicular from \(O\) on \(P Q\)
\(
=\left|\frac{0+0-n}{\sqrt{1^2+1^2}}\right|=\frac{n}{\sqrt{2}}
\)
Then, length of chord \(P Q=2 \sqrt{4^2-\left(\frac{n}{\sqrt{2}}\right)^2}\)
\(
=2 \sqrt{16-\frac{n^2}{2}}
\)
Thus only possible values of \(n\) are \(1,2,3,4,5\). Hence, the sum of squares of lengths of chords
\(
\begin{aligned}
& =\sum_{n=1}^5 4\left(16-\frac{n^2}{2}\right) \\
& =64 \times 5-2 . \frac{5 \times 6 \times 11}{6}=210
\end{aligned}
\) -
Question 228 of 269
228. Question
The tangent and the normal lines at the point \((\sqrt{3}, 1)\) to the circle \(x^2+y^2=4\) and the \(x\)-axis form a triangle. The area of this triangle (in square units) is : [JEE Main 2019 8th April Evening]
CorrectIncorrectHint
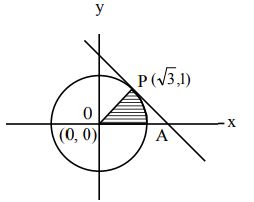
Equation of tangent to circle at point \((\sqrt{3}, 1)\) is \(\sqrt{3} x+y=4\)
point \(A\left(\frac{4}{\sqrt{3}}, 0\right)\)
Area of \(\triangle OPA =\frac{1}{2} \times \frac{4}{\sqrt{3}} \times 1=\frac{2}{\sqrt{3}}\) -
Question 229 of 269
229. Question
If a tangent to the circle \(x^2+y^2=1\) intersects the coordinate axes at distinct points \(P\) and \(Q\), then the locus of the midpoint of \(P Q\) is: [JEE Main 2019 9th April Morning]
CorrectIncorrectHint
Let any tangent to circle \(x^2+y^2=1\) is \(x \cos \theta+y \sin \theta=1\)
Since, \(P\) and \(Q\) are the point of intersection on the coordinate axes.
Then \(P \equiv\left(\frac{1}{\cos \theta}, 0\right) \& Q \equiv\left(0, \frac{1}{\sin \theta}\right)\)
\(\therefore\) mid-point of \(PQ\) be \(M \equiv\left(\frac{1}{2 \cos \theta}, \frac{1}{2 \sin \theta}\right) \equiv(h, k)\)
\(\Rightarrow \cos \theta=\frac{1}{2 h} \dots(1)\)
\(\sin \theta=\frac{1}{2 k} \dots(2)\)
Now squaring and adding equation (1) and (2)
\(
\begin{aligned}
& \frac{1}{h^2}+\frac{1}{k^2}=4 \\
& \Rightarrow h^2+k^2=4 h^2 k^2
\end{aligned}
\)
\(\therefore\) locus of \(M\) is: \(x^2+y^2=4 x^2 y^2\) -
Question 230 of 269
230. Question
The common tangent to the circles \(x^2+y^2=4\) and \(x^2+y^2+6 x+8 y-24=0\) also passes through the point: [JEE Main 2019 9th April Evening]
CorrectIncorrectHint
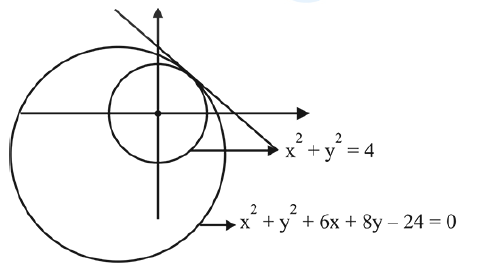
By the diagram, \(d_{c_1 c_2}=\left|r_1-r_2\right|\)
Equation of common tangent is,
\(
\begin{aligned}
& S_1-S_2=0 \\
& 6 x+8 y-20=0 \Rightarrow 3 x+4 y-10=0
\end{aligned}
\)
Hence \((6,-2)\) lies on it. -
Question 231 of 269
231. Question
If the circles \(x^2+y^2+5 K x+2 y+K=0\) and \(2\left(x^2+y^2\right)+2 K x+3 y-1=0,(K \in R )\), intersect at the points \(P\) and \(Q\), then the line \(4 x+5 y-K=0\) passes through \(P\) and \(Q\), for : [JEE Main 2019 10th April Morning]
CorrectIncorrectHint
\(
\begin{aligned}
& S _1 \equiv x^2+y^2+5 K x+2 y+K=0 \\
& S _2 \equiv x^2+y^2+K x+\frac{3}{2} y-\frac{1}{2}=0
\end{aligned}
\)
Equation of common chord is \(S _1- S _2=0\)
\(
\Rightarrow 4 K x+\frac{y}{2}+K+\frac{1}{2}=0 \dots(1)
\)
Equation of the line passing through the intersection points \(P \& Q\) is,
\(
4 x+5 y-K=0 \dots(2)
\)
Comparing (1) and (2),
\(
\frac{4 K}{4}=\frac{1}{10}=\frac{2 K+1}{-2 K} \dots(3)
\)
\(\Rightarrow K=\frac{1}{10}\) and \(-2 K=20 K+10\)
\(\Rightarrow 22 K=-10 \Rightarrow K=\frac{-5}{11}\)
\(\because K=\frac{1}{10}\) or \(\frac{-5}{11}\) is not satisfying equation (3)
\(\therefore\) No value of \(K\) exists. -
Question 232 of 269
232. Question
The line \(x=y\) touches a circle at the point \((1,1)\). If the circle also passes through the point \((1,-3)\), then its radius is: [JEE Main 2019 10th April Morning]
CorrectIncorrectHint
Equation of circle which touches the line \(y=x\) at \((1,1)\) is, \((x-1)^2+(y-1)^2+\lambda(y-x)=0\)
This circle passes through \((1,-3)\)
\(
\begin{aligned}
& \therefore 0+16+\lambda(-3-1)=0 \\
& \Rightarrow 16+\lambda(-4)=0 \Rightarrow \lambda=4
\end{aligned}
\)
Hence, equation of circle will be,
\(
\begin{aligned}
& (x-1)^2+(y-1)^2+4 y-4 x=0 \\
& \Rightarrow x^2+y^2-6 x+2 y+2=0 \\
& \therefore \text { Radius }=\sqrt{9+1-2}=2 \sqrt{2}
\end{aligned}
\) -
Question 233 of 269
233. Question
The locus of the centres of the circles, which touch the circle, \(x^2+y^2=1\) externally, also touch the \(y\)-axis and lie in the first quadrant, is: [JEE Main 2019 10th April Evening]
CorrectIncorrectHint
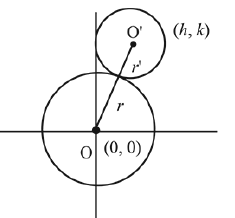
Let centre of required circle is \((h, k)\)
\(
\begin{aligned}
& \therefore OO ^{\prime}=r+r^{\prime} \text { [By the diagram] } \\
& \Rightarrow \sqrt{h^2+k^2}=1+h \\
& \Rightarrow h^2+k^2=1+h^2+2 h \\
& \Rightarrow k^2=1+2 h
\end{aligned}
\)
\(\therefore\) locus is \(y=\sqrt{1+2 x}\), \(x \geq 0\) -
Question 234 of 269
234. Question
If the angle of intersection at a point where the two circles with radii \(5 cm\) and \(12 cm\) intersect is \(90^{\circ}\), then the length (in \(cm\) ) of their common chord is : [JEE Main 2019 12th April Morning]
CorrectIncorrectHint
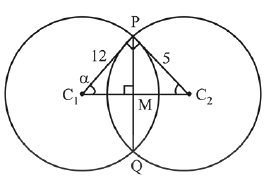
According to the diagram,
In \(\triangle P C_1 C_2, \tan \alpha=\frac{5}{12} \Rightarrow \sin \alpha=\frac{5}{13}\)
In \(\triangle P C_1 M, \sin \alpha=\frac{P M}{12} \Rightarrow \frac{5}{13}=\frac{P M}{12} \Rightarrow P M=\frac{60}{13}\)
Hence, length of common chord \((P Q)=\frac{120}{13}\) -
Question 235 of 269
235. Question
A circle touching the \(x\)-axis at \((3,0)\) and making an intercept of length 8 on the \(y\)-axis passes through the point : [JEE Main 2019 12th April Evening]
CorrectIncorrectHint
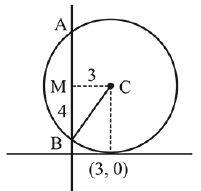
Let centre of circle is \(C\) and circle cuts the \(y\)-axis at \(B\) and \(A\). Let mid-point of chord \(B A\) is \(M\).
\(
\begin{aligned}
& C B=\sqrt{M C^2+M B^2} \\
& \sqrt{3^2+4^2}=5=\text { radius of circle } \\
& \therefore \text { equation of circle is, } \\
& (x-3)^2+(y-5)^2=5^2
\end{aligned}
\)
\((3,10)\) satisfies this equation.
Although there will be another circle satisfying the same conditions that will lie below the \(x\)-axis having equation \((x-3)^2+(y-5)^2=5^2\) -
Question 236 of 269
236. Question
If tangents are drawn to the ellipse \(x^2+2 y^2=2\) at all points on the ellipse other than its four vertices then the mid points of the tangents intercepted between the coordinate axes lie on the curve : [JEE Main 2019 11th Jan Morning]
CorrectIncorrectHint
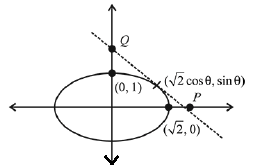
Given the equation of ellipse,
\(
\frac{x^2}{(\sqrt{2})^2}+y^2=1
\)
\(
\begin{aligned}
& \frac{\sqrt{2} \cos \theta x}{2}+y \sin \theta=1 \\
& P\left(\frac{\sqrt{2}}{\cos \theta}, 0\right) \text { and } Q\left(0, \frac{1}{\sin \theta}\right)
\end{aligned}
\)
Let mid point be \((h, k)\)
\(
\Rightarrow h=\frac{1}{\sqrt{2} \cos \theta}, k=\frac{1}{2 \sin \theta}
\)
As \(\cos ^2 \theta+\sin ^2 \theta=1\)
\(
\therefore \quad \frac{1}{2 h^2}+\frac{1}{4 k^2}=1
\)
Locus is \(\frac{1}{2 x^2}+\frac{1}{4 y^2}=1\) -
Question 237 of 269
237. Question
Let the length of the latus rectum of an ellipse with its major axis along \(x\)-axis and centre at the origin, be 8 . If the distance between the foci of this ellipse is equal to the length of its minor axis, then which one of the following points lies on it? [JEE Main 2019 11th Jan Evening]
CorrectIncorrectHint
Let the ellipse be \(\frac{x^2}{a^2} + \frac{y^2}{b^2}=1\)
Then, \(\frac{2 b^2}{a}=8,2 a e=b^2\) and \(b^2=a^2\left(1-e^2\right)\)
\(
\Rightarrow \quad a=8, b^2=32
\)
Then, the equation of the ellipse
\(
\frac{x^2}{64}+\frac{y^2}{32}=1
\)
Hence, the point \((4 \sqrt{3}, 2 \sqrt{2})\) lies on the ellipse. -
Question 238 of 269
238. Question
Let \(S\) and \(S^{\prime}\) be the foci of an ellipse and \(B\) be any one of the extremities of its minor axis. If \(\Delta S ^{\prime} BS\) is a right angled triangle with right angle at \(B\) and area \(\left(\Delta S^{\prime} B S\right)=8\) sq. units, then the length of a latus rectum of the ellipse is : [JEE Main 2019 12th Jan Evening]
CorrectIncorrectHint
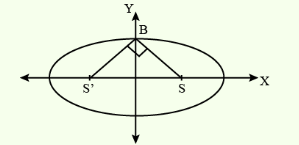
\(
\text { where } S \equiv(a e, 0), S^{\prime} \equiv(-a e, 0) \text { and } B \equiv(0, b)
\)\(\because \Delta S^{\prime} B S\) is right angled triangle, then
\((\) Slope of \(B S) \times\left(\right.\) Slope of \(\left.B S^{\prime}\right)=-1\)
\(
\begin{aligned}
\frac{b}{-a e} \times \frac{b}{a e} & =-1 \\
b^2 & =a^2 e^2 \dots(1)
\end{aligned}
\)
Since, area of \(\triangle S^{\prime} B S=8\)
\(
\begin{aligned}
\Rightarrow \quad \frac{1}{2} \cdot 2 a e \cdot b & =8 \\
b^2 & =8 \dots(2)
\end{aligned}
\)
From \(eq ^{ n }(1)\)
\(
\begin{aligned}
& \qquad a^2 e^2=8 \\
& \text { Also, } \quad e^2=1-\frac{b^2}{a^2}
\end{aligned}
\)
\(
\begin{aligned}
& \Rightarrow a^2 e^2=a^2-b^2 \\
& \Rightarrow 8=a^2-8 \\
& \Rightarrow a^2=16
\end{aligned}
\)
Hence, required length of latus rectum \(=\frac{2 b^2}{a}=\frac{2(8)}{4}\) \(=4\) units -
Question 239 of 269
239. Question
If the tangents on the ellipse \(4 x^2+y^2=8\) at the points \((1,2)\) and \((a, b)\) are perpendicular to each other, then \(a^2\) is equal to : [JEE Main 2019 8th April Morning]
CorrectIncorrectHint
Since \((a, b)\) touches the given ellipse \(4 x^2+y^2=8\) \(\therefore 4 a^2+b^2=8 \dots(1)\)
Equation of tangent on the ellipse at the point \(A(1,2)\) is:
\(
4 x+2 y=8 \Rightarrow 2 x+y=4 \Rightarrow y=-2 x+4
\)
But, also equation of tangent at \(P(a, b)\) is:
\(
4 a x+b y=8 \Rightarrow y=\frac{-4 a}{b}+\frac{8}{b} \text {. }
\)
Since, tangents are perpendicular to each other.
\(
\begin{aligned}
& \Rightarrow \frac{-4 a}{b}=\frac{-1}{2} \\
& \Rightarrow b=8 a \dots(2)
\end{aligned}
\)
from (1) & (2) we get:
\(
\Rightarrow a= \pm \frac{2}{\sqrt{34}} \Rightarrow a^2=\frac{2}{17}
\) -
Question 240 of 269
240. Question
In an ellipse, with centre at the origin, if the difference of the lengths of major axis and minor axis is 10 and one of the foci is at \((0,5 \sqrt{3})\), then the length of its latus rectum is: [JEE Main 2019 8th April Evening]
CorrectIncorrectHint
Given that focus is \((0,5 \sqrt{3}) \Rightarrow|b|>|a|\)
Let \(b>a>0\) and foci is \((0, \pm b e)\)
\(
\begin{aligned}
& \because a^2=b^2-b^2 e^2 \Rightarrow b^2 e^2=b^2-a^2 \\
& b e=\sqrt{b^2-a^2} \Rightarrow b^2-a^2=75 \dots(i)
\end{aligned}
\)
\(
\because 2 b-2 a=10 \Rightarrow b-a=5 \dots(ii)
\)
From (i) and (ii)
\(
b+a=15 \dots(iii)
\)
On solving (ii) and (iii), we get
\(
\Rightarrow b=10, a=5
\)
Now, length of latus rectum \(=\frac{2 a^2}{b}=\frac{50}{10}=5\) -
Question 241 of 269
241. Question
If the line \(x-2 y=12\) is tangent to the ellipse \(\frac{x^2}{ a ^2}+\frac{y^2}{ b ^2}=1\) at the point \(\left(3, \frac{-9}{2}\right)\), then the length of the latus rectum of the ellipse is : [JEE Main 2019 10th April Morning]
CorrectIncorrectHint
Equation of tangent to \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\) at \(\left(3,-\frac{9}{2}\right)\) is, \(\frac{3 x}{a^2}-\frac{9 y}{2 b^2}=1\)
But given equation of tangent is, \(x-2 y=12\)
\(\therefore \frac{3}{a^2}=\frac{-9}{2 b^2 \cdot(-2)}=\frac{1}{12}\) (On comparing)
\(\Rightarrow a^2=3 \times 12\) and \(b^2=\frac{9 \times 12}{4}\)
\(\Rightarrow a=6\) and \(b=3 \sqrt{3}\)
Therefore, latus rectum \(=\frac{2 b^2}{a}=\frac{2 \times 27}{6}=9\) -
Question 242 of 269
242. Question
The tangent and normal to the ellipse \(3 x^2+5 y^2=32\) at the point \(P(2,2)\) meet the \(x\)-axis at \(Q\) and \(R\), respectively. Then the area (in sq. units) of the triangle \(P Q R\) is : [JEE Main 2019 10th April Evening]
CorrectIncorrectHint
Given, Equation of ellipse \(\Rightarrow 3 x^2+5 y^2=32\)
Diffrentiating both sides
\(
\begin{aligned}
& 6 x+10 y y^{\prime}=0 \\
& y^{\prime}=\frac{-3 x}{5 y} \\
& y_{(2,2)}^{\prime}=-\frac{3}{5}
\end{aligned}
\)
Equation of tangent at \((2,2)\) is,
\(
\begin{aligned}
& (y-2)=-\frac{3}{5}(x-2) \\
& \Rightarrow 3 x+5 y=16 \\
& Q=\left(\frac{16}{3}, 0\right)
\end{aligned}
\)
Equation of normal at \((2,2)\) is,
\(
\begin{aligned}
& (y-2)=\frac{5}{3}(x-2) \\
& \Rightarrow 5 x-3 y=4 \\
& R=\left(\frac{4}{5}, 0\right) \\
& Q R=\sqrt{\left(\frac{16}{3}-\frac{4}{5}\right)^2}=\sqrt{\left(\frac{68}{15}\right)^2}=\frac{68}{15} \text { and height }=2 \\
& \therefore \text { Area }=\frac{1}{2} \times(Q R) \times 2=Q R=\frac{68}{15} \\
&
\end{aligned}
\) -
Question 243 of 269
243. Question
If the normal to the ellipse \(3 x^2+4 y^2=12\) at a point \(P\) on it is parallel to the line, \(2 x+y=4\) and the tangent to the ellipse at \(P\) passes through \(Q(4,4)\) then \(P Q\) is equal to : [JEE Main 2019 12th April Morning]
CorrectIncorrectHint
Slope of tangent on the line \(2 x+y=4\) at point \(P\) is \(\frac{1}{2}\). Given ellipse is,
\(
3 x^2+4 y^2=12 \Rightarrow \frac{x^2}{2^2}+\frac{y^2}{(\sqrt{3})^2}=1
\)
Let point \(P(2 \cos \theta, \sqrt{3} \sin \theta)\)
\(\therefore\) equation of tangent on the ellipse, at \(P\) is,
\(
\frac{x}{2} \cos \theta+\frac{y}{\sqrt{3}} \sin \theta=1
\)
\(\Rightarrow m_T=-\frac{\sqrt{3}}{2} \cot \theta\)
\(\because\) both the tangents are parallel \(\Rightarrow-\frac{\sqrt{3}}{2} \cot \theta=\frac{1}{2}\)
\(\Rightarrow \tan \theta=-\sqrt{3} \Rightarrow \theta=\pi-\frac{\pi}{3}\) or \(\theta=2 \pi-\frac{\pi}{3}\)
Case-1: \(\theta=\frac{2 \pi}{3}\), then point \(P\left(-1, \frac{3}{2}\right)\) and \(P Q=\frac{5 \sqrt{5}}{2}\)
Case-2: \(\theta=\frac{5 \pi}{3}\), then tangent does not pass through \(Q(4,4)\). -
Question 244 of 269
244. Question
An ellipse, with foci at \((0,2)\) and \((0,-2)\) and minor axis of length 4, passes through which of the following points? [JEE Main 2019 12th April Evening]
CorrectIncorrectHint
Let the equation of ellipse :
\(
\frac{x^2}{a^2}+\frac{y^2}{b^2}=1
\)
Given that length of minor axis is 4 i.e. \(a=4\).
Also given be \(=2\)
\(\because \quad a^2=b^2\left(1-e^2\right) \Rightarrow 4=b^2-4 \Rightarrow b=2 \sqrt{2}\)
Hence, equation of ellipse will be \(\frac{x^2}{4}+\frac{y^2}{8}=1\)
\(\because(\sqrt{2}, 2)\) satisfies this equation.
\(\therefore\) ellipse passes through \((\sqrt{2}, 2)\). -
Question 245 of 269
245. Question
Let \(0<\theta<\frac{\pi}{2}\). If the eccentricity of the hyperbola \(\frac{x^2}{\cos ^2 \theta}-\frac{y^2}{\sin ^2 \theta}=1\) is greater than 2 , then the length of its latus rectum lies in the interval: [JEE Main 2019 9th Jan Morning]
CorrectIncorrectHint
\(\because a^2=\cos ^2 \theta, b^2=\sin ^2 \theta\)
and \(e>2 \Rightarrow e^2>4 \Rightarrow 1+b^2 / a^2>4\)
\(
\begin{aligned}
& \Rightarrow 1+\tan ^2 \theta>4 \\
& \Rightarrow \sec ^2 \theta>4 \Rightarrow \theta \in\left(\frac{\pi}{3}, \frac{\pi}{2}\right)
\end{aligned}
\)
Latus rectum,
\(
\begin{aligned}
& L R=\frac{2 b^2}{a}=\frac{2 \sin ^2 \theta}{\cos \theta}=2(\sec \theta-\cos \theta) \\
\Rightarrow \quad & \frac{d(L R)}{d \theta}=2(\sec \theta \tan \theta+\sin \theta)>0 \forall \theta \in\left(\frac{\pi}{3}, \frac{\pi}{2}\right) \\
\therefore \quad & \min (L R)=2\left(\sec \frac{\pi}{3}-\cos \frac{\pi}{3}\right)=2\left(2-\frac{1}{2}\right)=3
\end{aligned}
\)
\(\max (L R)\) tends to infinity as \(\theta \rightarrow \frac{\pi}{2}\)
Hence, length of latus rectum lies in the interval \((3, \infty)\) -
Question 246 of 269
246. Question
A hyperbola has its centre at the origin, passes through the point \((4,2)\) and has transverse axis of length 4 along the \(x\)-axis. Then the eccentricity of the hyperbola is : [JEE Main 2019 9th Jan Evening]
CorrectIncorrectHint
Consider equation of hyperbola
\(
\frac{x^2}{2^2}-\frac{y^2}{b^2}=1
\)
\(\because(4,2)\) lies on hyperbola
\(\therefore \frac{16}{4}-\frac{4}{b^2}=1\)
\(\therefore b^2=\frac{4}{3}\)
Since, eccentricity \(=\sqrt{1+\frac{b^2}{a^2}}\)
Hence, eccentricity \(=\sqrt{1+\frac{\frac{4}{3}}{4}}=\sqrt{1+\frac{1}{3}}=\frac{2}{\sqrt{3}}\) -
Question 247 of 269
247. Question
The equation of a tangent to the hyperbola \(4 x^2-5 y^2=20\) parallel to the line \(x-y=2\) is: [JEE Main 2019 10th Jan Morning]
CorrectIncorrectHint
Given, the equation of line,
\(
x-y=2 \Rightarrow y=x-2
\)
\(\therefore\) its slope \(=m=1\)
Equation of hyperbola is:
\(
\Rightarrow a^2=5, b^2=4
\)
The equation of tangent to the hyperbola is,
\(
\begin{aligned}
y=m x & \pm \sqrt{a^2 m^2-b^2} \\
& =x \pm \sqrt{5-4}
\end{aligned}
\)
\(
\Rightarrow y=x \pm 1
\) -
Question 248 of 269
248. Question
Let
\(
S =\left\{(x, y) \in R ^2: \frac{y^2}{1+ r }-\frac{x^2}{1- r }=1\right\},
\)
where \(r \neq \pm 1\) Then \(S\) represents: [JEE Main 10th Jan Evening]CorrectIncorrectHint
Since, \(r \neq \pm 1\), then there are two cases, when \(r>1\)
\(
\frac{x^2}{r-1}+\frac{y^2}{r+1}=1 \text { (Ellipse) }
\)
Then,
\(
\begin{aligned}
& (r-1)=(r+1)\left(1-e^2\right) \Rightarrow 1-e^2=\frac{(r-1)}{(r+1)} \\
\Rightarrow & e^2=1-\frac{(r-1)}{(r+1)}=\frac{2}{(r+1)} \\
\Rightarrow & e=\sqrt{\frac{2}{(r+1)}}
\end{aligned}
\)
When \(0<r<1\), then
\(
\frac{x^2}{1-r}-\frac{y^2}{1+r}=-1 \quad \text { (Hyperbola) }
\)
Then,
\(
\begin{aligned}
& (1-r)=(1+r)\left(e^2-1\right) \Rightarrow e^2=1+\frac{(r-1)}{(r+1)}=\frac{2 r}{(r+1)} \\
\Rightarrow & e=\sqrt{\frac{2 r}{r+1}}
\end{aligned}
\) -
Question 249 of 269
249. Question
Equation of a common tangent to the parabola \(y^2=4 x\) and the hyperbola \(x y=2\) is : [JEE Main 2019 11th Jan Evening]
CorrectIncorrectHint
Equation of a tangent to parabola \(y^2=4 x\) is:
\(
y=m x+\frac{1}{m}
\)
This line is a tangent to \(x y=2\)
\(
\begin{aligned}
& \therefore \quad x\left(m x+\frac{1}{m}\right)=2 \\
& \Rightarrow \quad m x^2+\frac{1}{m} x-2=0
\end{aligned}
\)
\(\because\) Tangent is common for parabola and hyperbola.
\(
\begin{gathered}
\therefore \quad D=\left(\frac{1}{m}\right)^2-4 \cdot m \cdot(-2)=0 \\
\frac{1}{m^2}+8 m=0 \\
1+8 m^3=0 \\
m^3=-\frac{1}{8} \\
m=-\frac{1}{2}
\end{gathered}
\)
\(\therefore\) Equation of common tangent: \(y=-\frac{1}{2} x-2\)
\(
\begin{aligned}
& \Rightarrow \quad 2 y=-x-4 \\
& \Rightarrow \quad x+2 y+4=0
\end{aligned}
\) -
Question 250 of 269
250. Question
If a hyperbola has length of its conjugate axis equal to 5 and the distance between its foci is 13 , then the eccentricity of the hyperbola is : [JEE Main 2019 11th Jan Evening]
CorrectIncorrectHint
\(\therefore\) Conjugate axis \(=5\)
\(
\therefore \quad 2 b=5
\)
Distance between foci \(=13\)
\(
2 a e=13
\)
Then, \(b^2=a^2\left(e^2-1\right)\)
\(
\begin{aligned}
& \Rightarrow \quad a^2=36 \\
& \therefore \quad a=6 \\
& a e=\frac{13}{2} \Rightarrow e=\frac{13}{12}
\end{aligned}
\) -
Question 251 of 269
251. Question
If the vertices of a hyperbola be at \((-2,0)\) and \((2,0)\) and one of its foci be at \((-3,0)\), then which one of the following points does not lie on this hyperbola? [JEE Main 2019 12th Jan Morning]
CorrectIncorrectHint
Let the points are,
\(
A(2,0), A^{\prime}(-2,0) \text { and } S(-3,0)
\)
\(\Rightarrow \quad\) Centre of hyperbola is \(O(0,0)\)
\(
A A^{\prime}=2 a \Rightarrow 4=2 a \Rightarrow a=2
\)
\(\because \quad\) Distance between the centre and foci is ae.
\(\therefore \quad O S=a e \Rightarrow 3=2 e \Rightarrow e=\frac{3}{2}\)
\(\Rightarrow \quad b^2=a^2\left(e^2-1\right)=a^2 e^2-a^2=9-4=5\)
\(\Rightarrow\) Equation of hyperbola is \(\frac{x^2}{4}-\frac{y^2}{5}=1 \dots(1)\)
\(\because \quad(6,552)\) does not satisfy eq \((1)\).
\(\therefore \quad(6,5 \sqrt{2})\) does not lie on this hyperbola. -
Question 252 of 269
252. Question
If the eccentricity of the standard hyperbola passing through the point \((4,6)\) is 2 , then the equation of the tangent to the hyperbola at \((4,6)\) is : [JEE Main 8th April Evening]
CorrectIncorrectHint
Let equation of hyperbola be
\(
\frac{x^2}{a^2}-\frac{y^2}{b^2}=1 \dots(i)
\)
\(
\begin{aligned}
& \because e=\sqrt{1+\frac{b^2}{a^2}} \Rightarrow b^2=a^2\left(e^2-1\right) \\
& e=2 \Rightarrow b^2=3 a^2 \dots(ii)
\end{aligned}
\)
Equation (i) passes through \((4,6)\),
\(
\therefore \frac{16}{a^2}-\frac{36}{b^2}=1 \dots(iii)
\)
On solving (i) and (ii), we get
\(
a^2=4, b^2=12
\)
Now equation of hyperbola is \(\frac{x^2}{4}-\frac{y^2}{12}=1\)
Now equation of tangent to the hyperbola at \((4,6)\) is
\(
\frac{4 x}{4}-\frac{6 y}{12}=1 \Rightarrow x-\frac{y}{2}=1 \Rightarrow 2 x-y=2
\) -
Question 253 of 269
253. Question
If the line \(y = mx +7 \sqrt{3}\) is normal to the hyperbola \(\frac{x^2}{24}-\frac{y^2}{18}=1\), then a value of \(m\) is : [JEE Main 2019 9th April Morning]
CorrectIncorrectHint
Since, \(lx + my + n =0\) is a normal to \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\), then \(\frac{a^2}{l^2}-\frac{b^2}{m^2}=\frac{\left(a^2+b^2\right)^2}{n^2}\)
but it is given that \(m x-y+7 \sqrt{3}\) is normal to hyperbola \(\frac{x^2}{24}-\frac{y^2}{18}=1\)
then \(\frac{24}{m^2}-\frac{18}{(-1)^2}=\frac{(24+18)^2}{(7 \sqrt{3})^2} \Rightarrow m=\frac{2}{\sqrt{5}}\) -
Question 254 of 269
254. Question
If a directrix of a hyperbola centred at the origin and passing through the point \((4,-2 \sqrt{3})\) is \(5 x=4 \sqrt{5}\) and its eccentricity is e, then : [JEE Main 2019 10th April Morning]
CorrectIncorrectHint
\(\because\) directrix of a hyperbola is,
\(
5 x=4 \sqrt{5} \Rightarrow x=\frac{4}{\sqrt{5}} \Rightarrow \frac{ a }{ e }=\frac{4}{\sqrt{5}}
\)
Now, hyperbola \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\) passes through \((4,-2 \sqrt{3})\)
\(
\begin{aligned}
& \therefore \frac{16}{a^2}-\frac{12}{a^2 e^2-a^2}=1 \\
& \Rightarrow \frac{4}{a^2}\left[\frac{4}{1}-\frac{3}{ e ^2-1}\right]=1 \Rightarrow 4 e ^2-4-3=\left( e ^2-1\right)\left(\frac{ a ^2}{4}\right) \\
& \Rightarrow 4\left(4 e ^2-7\right)=\left( e ^2-1\right)\left(\frac{4 e }{\sqrt{5}}\right)^2 \\
& \Rightarrow 4 e ^4-24 e ^2+35=0
\end{aligned}
\) -
Question 255 of 269
255. Question
If \(5 x+9=0\) is the directrix of the hyperbola \(16 x^2-9 y^2=144\), then its corresponding focus is : [JEE Main 2019 10th April Evening]
CorrectIncorrectHint
\(16 x^2-9 y^2=144 \Rightarrow \frac{x^2}{9}-\frac{y^2}{16}=1\)
Then focus is \(S ^{\prime}(-a e, 0)\)
\(
a =3, b =4 \Rightarrow e^2=1+\frac{16}{9}=\frac{25}{9} \quad\left[\because e=\sqrt{1+\frac{b^2}{a^2}}\right]
\)
\(\therefore\) the focus \(S^{\prime} \equiv\left(3-\times \frac{5}{3}, 0\right) \equiv(-5,0)\) -
Question 256 of 269
256. Question
Axis of a parabola lies along \(x\)-axis. If its vertex and focus are at distance 2 and 4 respectively from the origin, on the positive \(x\)-axis then which of the following points does not lie on it? [JEE Main 2019 9th Jan Morning]
CorrectIncorrectHint
Since, vertex and focus of given parabola is \((2,0)\) and \((4,0)\) respectively
Then, equation of parabola is
\(
\begin{aligned}
(y-0)^2 & =4 \times 2(x-2) \\
\Rightarrow y^2 & =8 x-16
\end{aligned}
\)
Hence, the point \((8,6)\) does not lie on given parabola. -
Question 257 of 269
257. Question
If \(\theta\) denotes the acute angle between the curves, \(y=10-x^2\) and \(y=2+x^2\) at a point of their intersection, then \(|\tan \theta|\) is equal to: [JEE Main 2019 9th Jan Morning]
CorrectIncorrectHint
Since, the equation of curves are
\(
\begin{aligned}
& y=10-x^2 \dots(1) \\
& y=2+x^2 \dots(2)
\end{aligned}
\)
Adding eqn (1) and (2), we get
\(
2 y=12 \Rightarrow y=6
\)
Then, from eqn (1)
\(
x= \pm 2
\)
Differentiate equation (1) with respect to \(x\)
\(
\frac{d y}{d x}=-2 x \Rightarrow\left(\frac{d y}{d x}\right)_{(2,6)}=-4 \text { and }\left(\frac{d y}{d x}\right)_{(-2,6)}=4
\)
Differentiate equation (2) with respect to \(x\)
\(
\frac{d y}{d x}=2 x \Rightarrow\left(\frac{d y}{d x}\right)_{(2,6)}=4 \text { and }\left(\frac{d y}{d x}\right)_{(-2,6)}=-4
\)
At \((2,6) \tan \theta=\left(\frac{(-4)-(4)}{1+(-4) \times(4)}\right)=\frac{-8}{15}\)
At \((-2,6), \tan \theta=\frac{(4)-(-4)}{1+(4)(-4)}=\frac{8}{-15}\)
\(
\therefore|\tan \theta|=\frac{8}{15}
\) -
Question 258 of 269
258. Question
Two cards are drawn successively with replacement from a well-shuffled deck of 52 cards. Let \(X\) denote the random variable of number of aces obtained in the two drawn cards. Then \(P ( X =1)+ P ( X =2)\) equals: [JEE Main 2019 9th Jan Morning]
CorrectIncorrectHint
\(X=\) number of aces drawn
\(
\begin{aligned}
\therefore \quad & P(X=1)+P(X=2) \\
& =\left\{\frac{4}{52} \times \frac{48}{52}+\frac{48}{52} \times \frac{4}{52}\right\}+\left\{\frac{4}{52} \times \frac{4}{52}\right\} \\
& =\frac{24}{169}+\frac{1}{169}=\frac{25}{169}
\end{aligned}
\) -
Question 259 of 269
259. Question
Let \(A(4,-4)\) and \(B(9,6)\) be points on the parabola, \(y^2=4 x\). Let \(C\) be chosen on the \(\operatorname{arc} AOB\) of the parabola, where \(O\) is the origin, such that the area of \(\triangle A C B\) is maximum. Then, the area (in sq. units) of \(\triangle A C B\), is: [JEE Main 2019 9th Jan Morning]
CorrectIncorrectHint
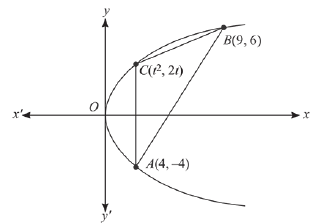
Let the coordinates of \(C\) is \(\left(t^2, 2 t\right)\).
Since, area of \(\triangle A C B\)
\(
\begin{aligned}
& =\frac{1}{2}\left|\begin{array}{ccc}
t^2 & 2 t & 1 \\
9 & 6 & 1 \\
4 & -4 & 1
\end{array}\right| \\
& =\frac{1}{2}\left|t^2(6+4)-2 t(9-4)+1(-36-24)\right| \\
& =\frac{1}{2}\left|10 t^2-10 t-60\right| \\
& =5\left|t^2-t-6\right| \\
& \left.=5\left|\left(t-\frac{1}{2}\right)^2-\frac{25}{4}\right| \quad \text { [Here, } t \in(0,3)\right]
\end{aligned}
\)
For maximum area, \(t=\frac{1}{2}\)
Hence, maximum area \(=\frac{125}{4}=31 \frac{1}{4}\) sq. units -
Question 260 of 269
260. Question
If the parabolas \(y^2=4 b (x- c )\) and \(y^2=8 ax\) have \(a\) common normal, then which one of the following is a valid choice for the ordered triad \((a, b, c)\) ? [JEE Main 2019 10th Jan Morning]
CorrectIncorrectHint
Normal to \(y^2=8 a x\) is
\(
y=m x-4 a m-2 a m^3 \dots(1)
\)
and normal to \(y^2=4 b(x-c)\) with slope \(m\) is
\(
y=m(x-c)-2 b m-b m^3 \dots(2)
\)
Since, both parabolas have a common normal.
\(
\begin{aligned}
& \therefore 4 a m+2 a m^3=c m+2 b m+b m^3 \\
& \Rightarrow 4 a+2 a m^2=c+2 b+b m^2 \text { or } m=0 \\
& \Rightarrow 4 a-c-2 b=(b-2 a) m^2
\end{aligned}
\)
or ( \(X\)-axis is common normal always)
Since, \(x\)-axis is a common normal. Hence all the options are correct for \(m=0\). -
Question 261 of 269
261. Question
The length of the chord of the parabola \(x^2=4 y\) having equation \(x-\sqrt{2} y+4 \sqrt{2}=0\) is: [JEE Main 2019 10th Jan Evening]
CorrectIncorrectHint
Let intersection points be \(P\left(x_1, y_1\right)\) and \(Q\left(x_2, y_2\right)\)
The given equations
\(
\begin{aligned}
& x^2=4 y \dots(1) \\
& x-\sqrt{2} y+4 \sqrt{2}=0 \dots(2)
\end{aligned}
\)
Use eqn (1) in eqn (2)
\(
\begin{aligned}
& x-\sqrt{2} \frac{x^2}{4}+4 \sqrt{2}=0 \\
& \sqrt{2} x^2-4 x-16 \sqrt{2}=0 \\
& x_1+x_2=2 \sqrt{2}, x_1 x_2=-16,\left(x_1-x_2\right)^2=8+64=72
\end{aligned}
\)
Since, points \(P\) and \(Q\) both satisfy the equations (2), then
\(
\begin{aligned}
& x_1-\sqrt{2} y_1+4 \sqrt{2}=0 \\
& x_1-\sqrt{2} y_2+4 \sqrt{2}=0 \\
& \left(x_2-x_1\right)=\sqrt{2}\left(y_2-y_1\right) \Rightarrow\left(x_2-x_1\right)^2=2\left(y_2-y_1\right)^2
\end{aligned}
\)
\(
\begin{aligned}
\Rightarrow \quad & P Q=\sqrt{\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2} \\
& =\sqrt{\left(x_2-x_1\right)^2+\frac{\left(x_2-y_1\right)^2}{2}} \\
& =\left|x_2-x_1\right| \cdot \frac{\sqrt{3}}{\sqrt{2}}=6 \sqrt{2} \times \frac{\sqrt{3}}{\sqrt{2}}=6 \sqrt{3}
\end{aligned}
\)
Hence, length of chord \(=6 \sqrt{3}\). -
Question 262 of 269
262. Question
If the area of the triangle whose one vertex is at the vertex of the parabola, \(y^2+4\left(x- a ^2\right)=0\) and the other two vertices are the points of intersection of the parabola and \(y\)-axis, is \(250 sq\). units, then a value of ‘ \(a\) ‘ is : [JEE Main 2019 11th Jan Evening]
CorrectIncorrectHint
\(
y^2=-4\left(x-a^2\right)
\)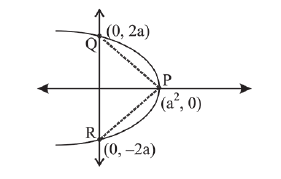
\(
\begin{aligned}
\text { Area } & =\frac{1}{2}(4 a)\left(a^2\right) \\
& =2 a^3
\end{aligned}
\)
Since \(2 a^3=250\)
\(
\Rightarrow \quad a=5
\) -
Question 263 of 269
263. Question
The equation of a tangent to the parabola, \(x^2=8 y\), which makes an angle \(\theta\) with the positive direction of \(x\)-axis, is : [JEE Main 2019 12th Jan Evening]
CorrectIncorrectHint
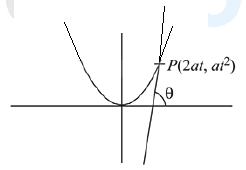
\(
x^2=8 y
\)
Then, equation of tangent at \(P\)
\(
\begin{aligned}
& t x=y+a t^2 \\
& \Rightarrow y=t x-a t^2 \\
& \text { Then, slope } \quad t=\tan \theta \\
& \text { Now, } y=\tan \theta x-2 \tan ^2 \theta \\
& \Rightarrow \cot \theta y=x-2 \tan \theta \\
& x=y \cot \theta+2 \tan \theta \\
&
\end{aligned}
\) -
Question 264 of 269
264. Question
The tangent to the parabola \(y^2=4 x\) at the point where it intersects the circle \(x^2+y^2=5\) in the first quadrant, passes through the point : [JEE Main 2019 8th April Evening]
CorrectIncorrectHint
To find intersection point of \(x^2+y^2=5\) and \(y^2=4 x\), substitute \(y^2=4 x\) in \(x^2+y^2=5\), we get
\(
\begin{aligned}
& x^2+4 x-5=0 \Rightarrow x^2+5 x-x-5=0 \\
& \Rightarrow x(x+5)-1(x+5)=0 \\
& \therefore x=1,-5
\end{aligned}
\)
Intersection point in \(1^{\text {st }}\) quadrant be \((1,2)\).
Now, equation of tangent to \(y^2=4 x\) at \((1,2)\) is
\(
\begin{aligned}
& y \times 2=2(x+1) \quad \Rightarrow y=x+1 \\
& \Rightarrow x-y+1=0 \dots(i)
\end{aligned}
\)
Hence, \(\left(\frac{3}{4}, \frac{7}{4}\right)\) lies on (i) -
Question 265 of 269
265. Question
If one end of a focal chord of the parabola, \(y^2=16 x\) is at \((1,4)\), then the length of this focal chord is: [JEE Main 2019 9th April Morning]
CorrectIncorrectHint
\(
\begin{aligned}
& \because y^2=16 x \\
& \Rightarrow a=4
\end{aligned}
\)
One end of focal of the parabola is at \((1,4)\)
\(\because y\) – coordinate of focal chord is \(2 a t\)
\(\therefore 2 a t=4\)
\(
\Rightarrow t=\frac{1}{2}
\)
Hence, the required length of focal chord
\(
=a\left(t+\frac{1}{t}\right)^2=4 \times\left(2+\frac{1}{2}\right)^2=25
\) -
Question 266 of 269
266. Question
The area (in sq. units) of the smaller of the two circles that touch the parabola, \(y^2=4 x\) at the point \((1,2)\) and the \(x\)-axis is: [JEE Main 2019 9th April Evening]
CorrectIncorrectHint
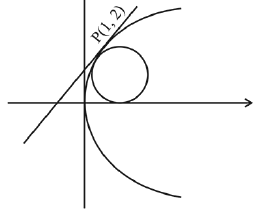
The circle and parabola will have common tangent at \(P\) \((1,2)\).
So, equation of tangent to parabola is,
\(
y \times(2)=\frac{4(x+1)}{2} \Rightarrow 2 y=2 x+2 \Rightarrow y=x+1
\)
Let equation of circle (by family of circles) is
\(
\begin{aligned}
& \left(x-x_1\right)^2+\left(y-y_1\right)^2+\lambda T =0 \\
& \Rightarrow c \equiv(x-1)^2+(y-2)^2+\lambda(x-y+1)=0
\end{aligned}
\)
\(\because\) circles touches \(x\)-axis.
\(\therefore y\)-coordinate of centre \(=\) radius
\(
\begin{aligned}
& \Rightarrow c=x^2+y^2+(\lambda-2) x+(-\lambda-4) y+(\lambda+5)=0 \\
& \frac{\lambda+4}{2}=\sqrt{\left(\frac{\lambda-2}{2}\right)^2+\left(\frac{-\lambda-4}{2}\right)^2-(\lambda+5)} \\
& \Rightarrow \frac{\lambda^2-4 \lambda+4}{4}=\lambda+5 \Rightarrow \lambda^2-4 \lambda+4=4 \lambda+20 \\
& \Rightarrow \lambda^2-8 \lambda-16=0 \Rightarrow \lambda=4 \pm 4 \sqrt{2}
\end{aligned}
\)
\(\Rightarrow \lambda=4-4 \sqrt{2}(\because \lambda=4+4 \sqrt{2}\) forms bigger circle \()\)
Hence, centre of circle \((2 \sqrt{2}-2,4-2 \sqrt{2})\) and radius
\(
\begin{aligned}
& =4-2 \sqrt{2} \\
& \therefore \text { area }=\pi(4-2 \sqrt{2})^2=8 \pi(3-2 \sqrt{2})
\end{aligned}
\) -
Question 267 of 269
267. Question
If the tangent to the parabola \(y^2=x\) at a point \((\alpha, \beta),(\beta>0)\) is also a tangent to the ellipse, \(x^2+2 y^2=1\), then \(\alpha\) is equal to: [JEE Main 2019 9th April Evening]
CorrectIncorrectHint
Let tangent to parabola at point \(\left(\frac{1}{4 m^2},-\frac{1}{2 m}\right)\) is
\(
y=m x+\frac{1}{4 m}
\)
and tangent to ellipse is, \(y=m x \pm \sqrt{m^2+\frac{1}{2}}\)
Now, condition for common tangency,
\(
\begin{aligned}
& \frac{1}{4 m}= \pm \sqrt{m^2+\frac{1}{2}} \Rightarrow \frac{1}{16 m^2}=m^2+\frac{1}{2} \\
& \Rightarrow 16 m^4+8 m^2-1=0 \Rightarrow m^2=\frac{-8 \pm \sqrt{64+64}}{2(16)} \\
& =\frac{-8 \pm 8 \sqrt{2}}{2(16)}=\frac{\sqrt{2}-1}{4} \\
& \alpha=\frac{1}{4 m^2}=\frac{1}{4 \frac{\sqrt{2}-1}{4}}=\sqrt{2}+1
\end{aligned}
\) -
Question 268 of 269
268. Question
If the line \(a x+y=c\), touches both the curves \(x^2+y^2=1\) and \(y^2=4 \sqrt{2} x\), then \(|c|\) is equal to [JEE Main 2019 10th April Evening]
CorrectIncorrectHint
Equation of tangent on \(y^2=4 \sqrt{2} x\) is \(y t=x+\sqrt{2} t^2\) This is also tangent on circle
\(
\therefore\left|\frac{\sqrt{2} t^2}{\sqrt{1+t^2}}=1\right| \Rightarrow 2 t^4=1+t^2 \Rightarrow t^2=1
\)
Hence, equation is \(\pm y=x+\sqrt{2} \Rightarrow| c |=\sqrt{2}\) -
Question 269 of 269
269. Question
Let \(P\) be the point of intersection of the common tangents to the parabola \(y^2=12 x\) and hyperbola \(8 x^2-y^2=8\). If \(S\) and \(S ^{\prime}\) denote the foci of the hyperbola where \(S\) lies on the positive \(x\)-axis then \(P\) divides \(SS ^{\prime}\) in a ratio : [JEE Main 2019 12th April Morning]
CorrectIncorrectHint
Equation of tangent to \(y^2=12 x\) is \(y=m x+\frac{3}{m}\)
Equation of tangent to
\(
\frac{x^2}{1}-\frac{y^2}{8}=1 \text { is } y=m x \pm \sqrt{m^2-8}
\)
\(\because\) parabola and hyperbola have common tangent.
\(
\therefore \frac{3}{m}= \pm \sqrt{m^2-8} \Rightarrow \frac{9}{m^2}=m^2-8
\)
Put \(m^2=u\)
\(
\begin{aligned}
& u^2-8 u-9=0 \Rightarrow u^2-9 u+u-9=0 \\
\Rightarrow & (u+1)(u-9)=0 \\
\because & u=m^2 \geq 0 \Rightarrow u=m^2=9 \Rightarrow m= \pm 3 \\
\therefore \quad & \text { equation of tangent is } y=3 x+1
\end{aligned}
\)
or \(y=-3 x-1\)
\(\therefore\) intersection point is \(P\left(-\frac{1}{3}, 0\right)\).
\(
\begin{aligned}
& e=\sqrt{1+\frac{b^2}{a^2}} \Rightarrow e=\sqrt{1+\frac{8}{1}} \Rightarrow e=3 \\
& \therefore \text { foci }( \pm 3,0)
\end{aligned}
\)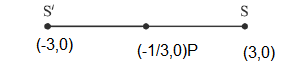
\(
\frac{S P}{S P^{\prime}}=\frac{3+\frac{1}{3}}{3-\frac{1}{3}}=\frac{10}{8}=\frac{5}{4}
\)