Past JEE Main Entrance Paper Set-I
Overview
By a sequence, we mean an arrangement of numbers in a definite order according to some rule. We denote the terms of a sequence by \(a_1, a_2, a_3, \ldots\), etc., the subscript denotes the position of the term.
In view of the above a sequence in the set \(X\) can be regarded as a mapping or a function \(f: N \rightarrow X\) defined by
\(
f(n)=t_n \forall n \in N .
\)
Domain of \(f\) is a set of natural numbers or some subset of it denoting the position of term. If its range denoting the value of terms is a subset of \(R\) real numbers then it is called a real sequence. A sequence is either finite or infinite depending upon the number of terms in a sequence. We should not expect that its terms will be necessarily given by a specific formula. However, we expect a theoretical scheme or rule for generating the terms.
Let \(a_1, a_2, a_3, \ldots\), be the sequence, then, the expression \(a_1+a_2+a_3+\ldots\) is called the series associated with given sequence. The series is finite or infinite according as the given sequence is finite or infinite.
Remark
- When the series is used, it refers to the indicated sum not to the sum itself. Sequence following certain patterns are more often called progressions. In progressions, we note that each term except the first progresses in a definite manner.
Arithmetic progression (A.P.)
A. P. is a sequence in which each term except the first is obtained by adding a fixed number (positive or negative) to the preceding term. Thus any sequence \(a_1, a_2, a_3 \ldots a_n, \ldots\) is called an arithmetic progression if \(a_{n+1}=a_n+d, n \in N\), where \(d\) is called the common difference of the A.P., usually we denote the first term of an A.P by \(a\) and the last term by \(l\)
The general term or the \(n ^{\text {th }}\) term of the A.P. is given by
\(
\begin{aligned}
& a_n=a+(n-1) d \\
& a_n=l-(n-1) d
\end{aligned}
\)
The \(\operatorname{sum} S _n\) of the first \(n\) terms of an A.P. is given by \(S _n=\frac{n}{2}[2 a+(n-1) d]=\frac{n}{2}(a+l)\), where \(l=a+(n-1) d\) is the last terms of the A.P., and the general term is given by \(a_n= S _n- S _{n-1}\) The arithmetic mean for any \(n\) positive numbers \(a_1, a_2, a_3, \ldots a_n\) is given by
\(
\text { A.M. }=\frac{a_1+a_2+\ldots+a_n}{n}
\)
If \(a, A\) and \(b\) are in A.P., then A is called the arithmetic mean of numbers \(a\) and \(b\) and
\(
A =\frac{a+b}{2}
\)
If the terms of an A.P. are increased, decreased, multiplied or divided by the same constant, they still remain in A.P.
If \(a_1, a_2, a_3 \ldots\) are in A.P. with common difference \(d\), then
- \(a_1 \pm k, a_2 \pm k, a_3 \pm k, \ldots\) are also in A.P with common difference \(d\).
- \(a_1 k, a_2 k, a_3 k, \ldots\) are also in A.P with common difference \(d k(k \neq 0)\).
and \(\frac{a_1}{k}, \frac{a_2}{k}, \frac{a_3}{k} \ldots\) are also in A.P. with common difference \(\frac{d}{k}(k \neq 0)\).
If \(a_1, a_2, a_3 \ldots\) and \(b_1, b_2, b_3 \ldots\) are two A.P., then
- \(a_1 \pm b_1, a_2 \pm b_2, a_3 \pm b_3, \ldots\) are also in A.P.
- \(a_1 b_1, a_2 b_2, a_3 b_3, \ldots\) and \(\frac{a_1}{b_1}, \frac{a_2}{b_2}, \frac{a_3}{b_3}, \ldots\) are not in A.P.
If \(a_1, a_2, a_3 \ldots\) and \(a_n\) are in A.Ps, then
- \(a_1+a_n=a_2+a_{n-1}=a_3+a_{n-2}=\ldots\)
- \(a_r=\frac{a_{r-k}+a_{r+k}}{2} \forall k, 0 \leq k \leq n-r\)
- If \(n^{\text {th }}\) term of any sequence is linear expression in \(n\), then the sequence is an A.P.
- If sum of \(n\) terms of any sequence is a quadratic expression in \(n\), then sequence is an A.P.
A Geometric progression (G.P.)
G. P. is a sequence in which each term except the first is obtained by multiplying the previous term by a non-zero constant called the common ratio. Let us consider a G.P. with first non-zero term \(a\) and common ratio \(r\), i.e.,
\(
a, a r, a r^2, \ldots, a r^{n-1}, \ldots
\)
Here, common ratio \(r=\frac{a r^{n-1}}{a r^{n-2}}\)
The general term or \(n^{\text {th }}\) term of G.P. is given by \(a_n=a r^{n-1}\).
Last term \(l\) of a G.P. is same as the \(n^{\text {mim }}\) term and is given by \(l=a r^{n-1}\).
and the \(n^{\text {th }}\) term from the last is given by \(a_n=\frac{l}{r^{n-1}}\)
The sum \(S _n\) of the first \(n\) terms is given by
\(
\begin{array}{ll}
S _n=\frac{a\left(r^n-1\right)}{r-1}, & \text { if } r \neq 1 \\
S _n=n a & \text { if } r=1
\end{array}
\)
If \(a, G\), and \(b\) are in G.P., then \(G\) is called the geometric mean of the numbers \(a\) and \(b\) and is given by
\(
G =\sqrt{a b}
\)
- If the terms of a G.P. are multiplied or divided by the same non-zero constant \((k \neq 0)\), they still remain in G.P.
If \(a_1, a_2, a_3, \ldots\), are in GP., then \(a_1 k, a_2 k, a_3 k, \ldots\) and \(\frac{a_1}{k}, \frac{a_2}{k}, \frac{a_3}{k}, \ldots\) are also in GP. with same common ratio, in particularly if \(a_1, a_2, a_3, \ldots\) are in GP., then
\(\frac{1}{a_1}, \frac{1}{a_2}, \frac{1}{a_3}, \ldots\) are also in G.P. - If \(a_1, a_2, a_3, \ldots\) and \(b_1, b_2, b_3, \ldots\) are two G.P.s, then \(a_1 b_1, a_2 b_2, a_3 b_3, \ldots\) and \(\frac{a_1}{b_1}, \frac{a_2}{b_2}, \frac{a_3}{b_3}, \ldots\) are also in G.P.
- If \(a_1, a_2, a_3, \ldots\) are in A.P. \(\left(a_i>0 \forall i\right)\), then \(x^{a_1}, x^{a_2}, x^{a_3}, \ldots\), are in G.P. \((\forall x>0)\)
- If \(a_1, a_2, a_3, \ldots, a_n\) are in G.P., then \(a_1 a_n=a_2 a_{n-1}=a_3 a_{n-2}=\ldots\)
Important results on the sum of special sequences
- Sum of the first \(n\) natural numbers:
\(
\sum n=1+2+3+\ldots+n=\frac{n(n+1)}{2}
\) - Sum of the squares of first \(n\) natural numbers.
\(
\sum n^2=1^2+2^2+3^2+\ldots+n^2=\frac{n(n+1)(2 n+1)}{6}
\) - Sum of cubes of first \(n\) natural numbers:
\(
\sum n^3=1^3+2^3+3^3+\ldots+n^3=\left[\frac{n(n+1)}{2}\right]^2
\)
Quiz Summary
0 of 213 Questions completed
Questions:
Information
You have already completed the quiz before. Hence you can not start it again.
Quiz is loading…
You must sign in or sign up to start the quiz.
You must first complete the following:
Results
Results
0 of 213 Questions answered correctly
Your time:
Time has elapsed
You have reached 0 of 0 point(s), (0)
Earned Point(s): 0 of 0, (0)
0 Essay(s) Pending (Possible Point(s): 0)
Categories
- Not categorized 0%
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
- 94
- 95
- 96
- 97
- 98
- 99
- 100
- 101
- 102
- 103
- 104
- 105
- 106
- 107
- 108
- 109
- 110
- 111
- 112
- 113
- 114
- 115
- 116
- 117
- 118
- 119
- 120
- 121
- 122
- 123
- 124
- 125
- 126
- 127
- 128
- 129
- 130
- 131
- 132
- 133
- 134
- 135
- 136
- 137
- 138
- 139
- 140
- 141
- 142
- 143
- 144
- 145
- 146
- 147
- 148
- 149
- 150
- 151
- 152
- 153
- 154
- 155
- 156
- 157
- 158
- 159
- 160
- 161
- 162
- 163
- 164
- 165
- 166
- 167
- 168
- 169
- 170
- 171
- 172
- 173
- 174
- 175
- 176
- 177
- 178
- 179
- 180
- 181
- 182
- 183
- 184
- 185
- 186
- 187
- 188
- 189
- 190
- 191
- 192
- 193
- 194
- 195
- 196
- 197
- 198
- 199
- 200
- 201
- 202
- 203
- 204
- 205
- 206
- 207
- 208
- 209
- 210
- 211
- 212
- 213
- Current
- Review
- Answered
- Correct
- Incorrect
-
Question 1 of 213
1. Question
If \(\left(\frac{1}{\alpha+1}+\frac{1}{\alpha+2}+\ldots \ldots+\frac{1}{\alpha+1012}\right)-\left(\frac{1}{2 \cdot 1}+\frac{1}{4 \cdot 3}+\frac{1}{6 \cdot 5}+\ldots \ldots+\frac{1}{2024 \cdot 2023}\right)= \) , then \(\alpha\) is equal to _______. [JEE Main 2024 (Online) 9th April Evening Shift]
CorrectIncorrectHint
(d)
\(
\begin{aligned}
& \frac{1}{\alpha+1}+\frac{1}{\alpha+2}+\ldots+\frac{1}{\alpha+2012}- \\
& \left(\frac{1}{2 \times 1}+\frac{1}{4 \times 3}+\ldots+\frac{1}{2024} \cdot \frac{1}{2023}\right)=\frac{1}{2024} \\
& \sum_{r=1}^{1012} \frac{1}{2 r(2 r-1)}=\sum_{r=1}^{1012}\left(\frac{1}{2 r-1}-\frac{1}{2 r}\right) \\
& \quad=\left(1-\frac{1}{2}\right)+\left(\frac{1}{3}-\frac{1}{4}\right)+\ldots+\left(\frac{1}{2023}-\frac{1}{2024}\right)
\end{aligned}
\)
\(
\begin{aligned}
& =\left(1+\frac{1}{3}+\frac{1}{5}+\ldots+\frac{1}{2023}\right) \\
& -\left(\frac{1}{2}+\frac{1}{4}+\frac{1}{6}+\ldots+\frac{1}{2024}\right) \\
& =\left(1+\frac{1}{3}+\ldots+\frac{1}{2023}\right)-\frac{1}{2}\left(1+\frac{1}{2}+\frac{1}{3}+\ldots+\frac{1}{1012}\right) \\
& =\left(1+\frac{1}{2}+\frac{1}{3}+\ldots+\frac{1}{2023}\right)-\frac{1}{2}\left(1+\frac{1}{2}+\ldots+\frac{1}{1011}\right) \\
& \frac{-1}{2}\left(1+\frac{1}{2}+\ldots+\frac{1}{1012}\right) \\
& =\frac{1}{1012}+\frac{1}{1013}+\ldots+\frac{1}{2023}-\frac{1}{2024} \\
& \Rightarrow \alpha+1012=2023 \\
& \Rightarrow \alpha=1011
\end{aligned}
\) -
Question 2 of 213
2. Question
An arithmetic progression is written in the following way
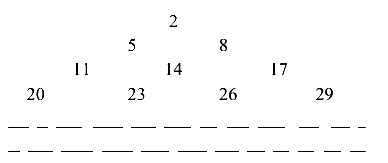
The sum of all the terms of the \(10^{\text {th }}\) row is ____. [JEE Main 2024 (Online) 8th April Evening Shift]
CorrectIncorrectHint
First term is each row form pattern \(2, \quad 5, \quad 11, \quad 20\) and the difference between consecutive numbers forms an A. P. (3, 6, 9)
\(
\begin{aligned}
& \Rightarrow T_n=a n^2+b n+c \\
& \Rightarrow T_1=a+b+c=2 \\
& \Rightarrow T_2=4 a+2 b+c=5 \\
& \Rightarrow T_3=9 a+3 b+c=11 \\
& \Rightarrow 3 a+b=3 \\
& 5 a+b=6 \\
& \Rightarrow 2 a=3 \Rightarrow a=\frac{3}{2}, \quad b=\frac{-3}{2} \Rightarrow c=2 \\
& \Rightarrow T_n=\frac{3}{2} n^2-\frac{3(n)}{2}+2 \Rightarrow \frac{3 n^2-3 n+4}{2} \\
& T_{10}=\frac{3 \times 100-3 \times 10+4}{2}=\frac{274}{2}=137
\end{aligned}
\)
Terms in \(10^{\text {th }}\) row is 10 with 3 differences
\(
\begin{aligned}
& \Rightarrow 137,140,143 \ldots \\
& \Rightarrow \quad S_{10}=\frac{10}{2}(2 \times 137+(10-1) \times 3) \\
& =5(274+27)=5 \times 301=1505
\end{aligned}
\) -
Question 3 of 213
3. Question
Let the positive integers be written in the form
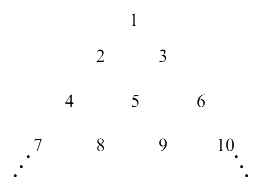
If the \(k ^{\text {th }}\) row contains exactly \(k\) numbers for every natural number \(k\), then the row in which the number 5310 will be, is _____. [JEE Main 2024 (Online) 8th April Morning Shift]
CorrectIncorrectHint
Let 5310 lies in \(k ^{\text {th }}\) row
\(\Rightarrow\) First element of \(k^{\text {th }}\) row is \(\frac{(k-1) k}{2}+1\)
Last element of \(k^{\text {th }}\) row is \(\frac{k(k+1)}{2}\)
\(
\begin{aligned}
& \Rightarrow \frac{(k-1) k}{2}+1 \leq 5310 \leq \frac{k(k+1)}{2} \\
& \Rightarrow k=103
\end{aligned}
\) -
Question 4 of 213
4. Question
Let \(\alpha=\sum_{r=0}^n\left(4 r^2+2 r+1\right)^n C_r\) and \(\beta=\left(\sum_{r=0}^n \frac{{ }^n C_r}{r+1}\right)+\frac{1}{n+1}\). If \(140<\frac{2 \alpha}{\beta}<281\), then the value of \(n\) is _____. [JEE Main 2024 (Online) 8th April Morning Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& \alpha=\sum_{r=0}^n\left(4 r^2+2 r+1\right)^n C_r \\
& =4 \sum_{r=0}^n r^{2} \cdot{ }^n C_r+2 \sum_{r=0}^n r \cdot{ }^n C_r+\sum_{r=0}^n{ }^n C_r \\
& =4 n(n+1) 2^{n-2}+2 \cdot n \cdot 2^{n-1}+2^n \\
& =2^n(n(n+1)+n+1)=2^n(n+1)^2 \\
& \beta=\sum_{r=0}^n\left(\frac{{ }^n C_r}{r+1}\right)+\left(\frac{1}{n+1}\right) \\
& (1+x)^n=\sum_{r=0}^n{ }^n C_r x^r \\
& \int_0^1(1+x)^n d x=\left.\sum_{r=0}^n \frac{{ }^n C_r x^{r+1}}{r+1}\right|_0 ^1=\sum_{r=0} \frac{{ }^n C_r}{r+1} \\
& \left.\frac{(1+x)^{n+1}}{n+1}\right|_0 ^1=\frac{2^{n+1} -1}{n+1} \\
& \Rightarrow \beta=\frac{2^{n+1}-1+1}{(n+1)}=\frac{2^{n+1}}{n+1} \\
& \Rightarrow \frac{2 \alpha}{\beta}=\frac{2^{n+1}{(n+1)}^2}{\left(\frac{2^{n+1}}{n+1}\right)}=(n+1)^3 \in(140,281) \\
& \Rightarrow(n+1)^3=216 \\
& \Rightarrow n+1=6 \Rightarrow n=5 \\
&
\end{aligned}
\) -
Question 5 of 213
5. Question
If \(S (x)=(1+x)+2(1+x)^2+3(1+x)^3+\cdots+60(1+x)^{60}, x \neq 0\), and \((60)^2 S (60)= a ( b )^{ b }+ b\), where \(a, b \in N\), then \((a+b)\) equal to ____. [JEE Main 2024 (Online) 6th April Evening Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& S(x)=(1+x)+2(1+x)^2+3(1+x)^3+\ldots .+60(1+x)^{60} \\
& (1+x) S(x) \quad=1(1+x)^2+2(1+x)^3+\ldots .+59(1+x)^{60}+60(1+x)^{61} \\
\hline \\
& S(x)[1-1-x]=\left[(1+x)+(1+x)^2+\ldots+(1+x)^{60}\right]-60(1+x)^{61} \\
&
\end{aligned}
\)
\(
\begin{aligned}
& (-x)(S(x))=\frac{(1+x)\left[(1+x)^{60}-1\right]}{(1+x-1)}-60(1+x)^{61} \\
& (-x) S(x)=\frac{(1+x)\left[(1+x)^{60}-1\right]}{x}-60(1+x)^{61} \\
& x S(x)=60(1+x)^{61}-\frac{(1+x)\left[(1+x)^{60}-1\right]}{x}
\end{aligned}
\)
Multiplying \(x\) on both side,
\(
x^2 S(x)=60 x(1+x)^{61}-(1+x)\left[(1+x)^{60}-1\right]
\)
Putting \(x=60\)
\(
\begin{aligned}
& (60)^2 S(60)=60 \times 60(61)^{61}-(61)\left[61^{60}-1\right] \\
& =60 \times 60(61)^{61}-(61) \cdot 61^{60}+61 \\
& =(61)^{61}[60 \times 60-1]+61 \\
& =(3600-1) \cdot 61^{61}+61 \\
& a=3600-1, \quad b=61 \Rightarrow a+b=3660
\end{aligned}
\) -
Question 6 of 213
6. Question
Let the first term of a series be \(T_1=6\) and its \(r^{\text {th }}\) term \(T_r=3 T_{r-1}+6^r, r=2,3\), \(n\). If the sum of the first \(n\) terms of this series is \(\frac{1}{5}\left(n^2-12 n+39\right)\left(4 \cdot 6^n-5 \cdot 3^n+1\right)\), then \(n\) is equal to ____. [JEE Main 2024 (Online) 6th April Morning Shift]
CorrectIncorrectHint
\(
T_r=3 T_{r-1}+6^r
\)
\(\Rightarrow\) solving homogenous part
\(
T_r=3 T_{r-1}
\)
\(\Rightarrow x=3\) is the root
\(
\therefore T_r=a .3^r
\)
Solving for particular part
\(
\begin{aligned}
& T_r=b .6^r \\
& b .6^r=3 b 6^{r-1}+6^r \\
& \Rightarrow 6 b=3 b+6 \\
& \Rightarrow 3 b=6 \\
& \Rightarrow b=2 \\
& T_r=a^n+a^p \\
& T_r=a 3^{b r}+2.6^r \dots(i) \\
& T_r=3 T_{r-1}+6^r
\end{aligned}
\)
Putting \(r=2\)
\(
T_2=18+36=54 \dots(ii)
\)
Using equation (i) and (ii)
\(
\begin{aligned}
& 54=9 a+72 \Rightarrow-18=9 a \Rightarrow a=-2 \\
& \therefore T_r=2 \cdot 6^r-2 \cdot 3^r=2\left(6^r-3^r\right) \\
& \sum_{r=1}^n T_r=2 \sum 6^r-2 \sum 3^r \\
& =2 \cdot 6 \frac{\left(6^n-1\right)}{5}-2 \cdot 3 \frac{\left(3^n-1\right)}{2} \\
& =\frac{3}{5}\left(4 \cdot 6^n-5 \cdot 3^n+1\right) \\
& \therefore n^2-12 n+39=3 \\
& n^2-12 n+36=0 \\
& (n-6)^2=0 \\
& \therefore n=6
\end{aligned}
\) -
Question 7 of 213
7. Question
If \(1+\frac{\sqrt{3}-\sqrt{2}}{2 \sqrt{3}}+\frac{5-2 \sqrt{6}}{18}+\frac{9 \sqrt{3}-11 \sqrt{2}}{36 \sqrt{3}}+\frac{49-20 \sqrt{6}}{180}+\ldots\) upto \(\infty=2+\left(\sqrt{\frac{b}{a}}+1\right) \log _e\left(\frac{a}{b}\right)\), where \(a\) and \(b\) are integers with \(\operatorname{gcd}(a, b)=1\), then \(11 a +18 b\) is equal to ____. [JEE Main 2024 (Online) 5th April Evening Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& S=1+\frac{\sqrt{3}-\sqrt{2}}{2 \sqrt{3}}+\frac{5-2 \sqrt{6}}{18}+\frac{9 \sqrt{3}-11 \sqrt{2}}{36 \sqrt{3}}+\ldots \infty \\
& =1+\frac{(1-\sqrt{2} / \sqrt{3})}{2}+\frac{(1-\sqrt{2} / \sqrt{3})^2}{6}+\frac{(1-\sqrt{2} / \sqrt{3})^3}{12}+\ldots \infty
\end{aligned}
\)
let \(1-\frac{\sqrt{2}}{\sqrt{3}}=a\)
\(
\begin{aligned}
& S=1+\frac{a}{2}+\frac{a^2}{6}+\frac{a^3}{12}+\ldots \\
& =1+\left(1-\frac{1}{2}\right) a+\left(\frac{1}{2}-\frac{1}{3}\right) a^2+\left(\frac{1}{3}-\frac{1}{4}\right) a^3+\ldots \\
& =1+\left(a+\frac{a^2}{2}+\frac{a^3}{3} \ldots \infty\right)+\frac{1}{a}\left(\frac{-a^2}{2}-\frac{a^3}{3}-\frac{a^4}{4} \ldots \infty\right) \\
& =-\ln (1-a)+\frac{1}{a}\left(-a-\frac{a^2}{2}-\frac{a^3}{3} \ldots \infty\right)+2 \\
& =-\ln (1-a)+\frac{1}{a} \ln (1-a)+2 \\
& =2+\left(\frac{1}{a}-1\right) \ln (1-a)
\end{aligned}
\)
\(
\begin{aligned}
& =2+\left(\frac{\sqrt{3}}{\sqrt{3}-\sqrt{2}}-1\right) \ln \left(1-1+\sqrt{\frac{2}{3}}\right) \\
& =2+(\frac{\sqrt{2}}{\sqrt{3}-\sqrt{2}}) \times \ln \sqrt{\frac{2}{3}} \\
& =2+\left(\frac{\sqrt{6}+2}{1} \cdot \frac{1}{2} \ln \frac{2}{3}\right) \\
& \therefore 2+\left(\sqrt{\frac{3}{2}}+1\right) \ln \frac{2}{3} \\
& \therefore 11 a+18 b=76
\end{aligned}
\) -
Question 8 of 213
8. Question
Let \(a_1, a_2, a_3, \ldots\) be in an arithmetic progression of positive terms.
Let \(A_k=a_1^2-a_2^2+a_3^2-a_4^2+\ldots+a_{2 k-1}^2-a_{2 k}^2\).
If \(A _3=-153, A _5=-435\) and \(a _1^2+ a _2^2+ a _3^2=66\), then \(a _{17}- A _7\) is equal to ____. [JEE Main 2024 (Online) 5th April Morning Shift]CorrectIncorrectHint
Let \(a_n=a+(n-1) d \forall n \in N\)
\(
\begin{aligned}
& A_k=\left(a_1^2-a_2^2\right)+\left(a_3^2-a_4^2\right)+\ldots a_{2 k-1}^2-a_{2 k}^2 \\
&=(-d)\left(a_1+a_2+\ldots+a_{2 k}\right) \\
& A_k=(-d k)(2 a+(2 k-1) d) \\
& \Rightarrow A_3=(-3 d)(2 a+5 d)=-153 \\
& \Rightarrow d(2 a+5 d)=51 \quad \ldots \text { (i) } \\
& A_5=(-5 d)(2 a+9 d)=-435 \\
& \Rightarrow d(2 a+9 d)=87 \\
& \Rightarrow 4 d^2=36 \Rightarrow d= \pm 3(d=3 \text { positive terms }) \\
& \Rightarrow 3(2 a+27)=87 \\
& \Rightarrow 2 a=29-27 \\
& \Rightarrow a=1 \\
& a_{17}-A_7=(a+16 d)-(-7 d)(2+13 d) \\
&=49+7 \times 3(2+39) \\
&=49+21 \times 41=910
\end{aligned}
\) -
Question 9 of 213
9. Question
If three successive terms of a G.P. with common ratio \(r(r>1)\) are the lengths of the sides of a triangle and \([r]\) denotes the greatest integer less than or equal to \(r\), then \(3[r]+[-r]\) is equal to ____. [JEE Main 2024 (Online) 1st February Evening Shift]
CorrectIncorrectHint
To solve this problem, let’s first denote the three successive terms of a geometric progression (G.P.) with common ratio \(r\) as \(a, a r\), and \(a r^2\), where \(a\) is the first term and \(r>1\). These three terms represent the lengths of the sides of a triangle.
According to the triangle inequality theorem, the sum of the lengths of any two sides of a triangle must be greater than the length of the third side. Therefore, for the three terms to form a triangle, the following inequalities must hold:
1) \(a+a r>a r^2\)
2) \(a+a r^2>a r\)
3) \(a r+a r^2>a\)
Given that \(r>1\), inequalities 2 and 3 will always hold because:
\(
a r<a r^2 \text { and } a<a r
\)
indicating that both \(a+a r^2\) and \(a r+a r^2\) will be greater than \(a r\) and \(a\) respectively. Therefore, we only need to check the first inequality to ensure that the three terms can form a triangle:
\(
a+a r>a r^2
\)
Simplifying the right side by factoring \(r\) :
\(
1>r(r-1)
\)
Given that \(r>1\), the quantity \((r-1)\) is positive; hence, \(r(r-1)\) is also positive. This means the actual value for \(r\) to satisfy the inequality is within the interval \((1, \sqrt{2})\) because \(r(r-1)\) increases with increasing \(r\), and it would be 1 when \(r=\sqrt{2}\). It should be greater than 1 , and less than \(\sqrt{2}\) such that \(r^2-r\) stays below 1 .
Now let’s consider the expressions \([r]\) and \([-r]\). The symbol \([x]\) denotes the greatest integer less than or equal to \(x\) (also known as the floor function).
Since \(1<r<\sqrt{2},[r]=1\), because 1 is the greatest integer less than \(r\) within that interval.
For \([-r]\), we need the greatest integer less than or equal to \(-r\). Since \(-r\) is negative and less than -1 (because \(r>1\) ), \([-r]=-2\), as this is the greatest integer that does not exceed the negative value of \(r\) (which lies between \(-\sqrt{2}\) and -1 ).
Now we can substitute these values into the expression:
\(
3[r]+[-r]=3 \cdot 1+(-2)=3-2=1
\)
Therefore \(3[r]+[-r]\) is equal to 1 . -
Question 10 of 213
10. Question
Let \(3,7,11,15, \ldots, 403\) and \(2,5,8,11, \ldots, 404\) be two arithmetic progressions. Then the sum, of the common terms in them, is equal to ______. [JEE Main 2024 (Online) 1st February Morning Shift]
CorrectIncorrectHint
To find the common terms in the two given arithmetic progressions (AP), we need to first identify the common difference for each sequence and then find the sequence that represents their overlap by employing the concept of least common multiple (LCM).
The first AP is:
\(
3,7,11,15, \ldots, 403
\)
The common difference \(\left(d_1\right)\) for the first AP can be calculated by subtracting the first term from the second term:
\(
d_1=7-3=4
\)
The second AP is:
\(
2,5,8,11, \ldots, 404
\)
The common difference \(\left(d_2\right)\) for the second AP is:
\(
d_2=5-2=3
\)
To find the terms common to both sequences, we need to find a term that appears in both sequences. Any common term must be of the form \(3+4 k\) and \(2+3 l\) for some integers \(k\) and \(l\). We want to find when these two forms will give us the same number, so we set them equal to each other:
\(
3+4 k=2+3 l
\)
Rearranging the terms gives us:
\(
4 k-3 l=2-3
\)
This simplifies to:
\(
4 k-3 l=-1 \ldots \ldots(1)
\)
The solutions to equation (1) will give us the common terms. Notice this is a Diophantine equation (A Diophantine equation is a polynomial equation, usually with two or more variables,) and has an infinite number of solutions. Let’s find one such solution. We can see that:
\(
k=1 \text { yields } 4(1)-3 l=-1 \Longrightarrow 4-3 l=-1 \Longrightarrow 3 l=5 \Longrightarrow l=5/3
\)
This is not an integer solution for \(l\), so \(k=1\) does not work. Trying \(k=2\) gives:
\(
4(2)-3 l=-1 \Longrightarrow 8-3 l=-1 \Longrightarrow 3 l=9 \Longrightarrow l=3
\)
Now we’ve found integers \(k=2\) and \(l=3\) that satisfy the equation. The corresponding term in both sequences would be:
\(
3+4(2)=3+8=11 \text { and } 2+3(3)=2+9=11
\)
Since 11 is a common term, we can assert that every common term in both APs will be of the form \(11+m(4 \times 3)\), where \(m\) is a non-negative integer, and \(4 \times 3=12\) is the LCM of the common differences of the two APs. Thus, the general form for the common terms would be:
\(
11+12 m
\)
Now we are to find all terms that are common up to 403 in the first sequence and up to 404 in the second sequence. Because the first sequence doesn’t exceed 403 , we’ll use this as our limit:
\(
11+12 m \leq 403
\)
To find the largest possible integer value for \(m\), we solve the inequality:
\(
\begin{aligned}
& 12 m \leq 403-11 \\
& 12 m \leq 392 \\
& m \leq 32 \frac{2}{3}
\end{aligned}
\)
Since \(m\) has to be an integer, the largest possible value for \(m\) is 32 . Therefore, the common terms are generated by \(m=0,1,2, \ldots, 32\). There are \(32+1=33\) terms in total.
We will now sum these up. The sum of an AP is given by the formula:
\(
S=\frac{n}{2}\left(a_1+a_n\right)
\)
Where \(S\) is the sum, \(n\) is the number of terms, \(a_1\) is the first term, and \(a_n\) is the last term. Using the formula:
\(
\begin{aligned}
& S=\frac{33}{2}(11+(11+12 \times 32)) \\
& S=\frac{33}{2}(11+11+384) \\
& S=\frac{33}{2}(11+11+384)
\end{aligned}
\)
\(
\begin{aligned}
& S=\frac{33}{2}(406) \\
& S=33 \times 203 \\
& S=6699
\end{aligned}
\)
Therefore, the sum of the common terms in the two arithmetic progressions is 6699. -
Question 11 of 213
11. Question
Let \(S_n\) be the sum to \(n\)-terms of an arithmetic progression \(3,7,11\), If \(40<\left(\frac{6}{n(n+1)} \sum_{k=1}^n S_k\right)<42\), then \(n\) equals _____. [JEE Main 2024 (Online) 30th January Evening Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& S _{ n }=3+7+11+\ldots \ldots n \text { terms } \\
& =\frac{ n }{2}(6+( n -1) 4)=3 n +2 n ^2-2 n \\
& =2 n ^2+ n \\
& \sum_{ k =1}^{ n } S _{ k }=2 \sum_{ k =1}^{ n } K ^2+\sum_{ k =1}^{ n } K \\
& =2 \cdot \frac{ n ( n +1)(2 n +1)}{6}+\frac{ n ( n +1)}{2} \\
& = n ( n +1)\left[\frac{2 n +1}{3}+\frac{1}{2}\right] \\
& =\frac{ n ( n +1)(4 n +5)}{6} \\
& \Rightarrow 40<\frac{6}{ n ( n +1)} \sum_{k=1}^n S_{ k }<42 \\
& 40<4 n +5<42 \\
& 35<4 n<37 \\
& n =9
\end{aligned}
\) -
Question 12 of 213
12. Question
Let \(\alpha=1^2+4^2+8^2+13^2+19^2+26^2+\ldots\) upto 10 terms and \(\beta=\sum_{n=1}^{10} n^4\). If \(4 \alpha-\beta=55 k+40\), then \(k\) is equal to _____. [JEE Main 2024 (Online) 30th January Morning Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& \alpha=1^2+4^2+8^2 \ldots \\
& \quad t_n=a^2+b n+c \\
& 1=a+b+c \\
& 4=4 a+2 b+c \\
& 8=9 a+3 b+c
\end{aligned}
\)
On solving we get, \(a =\frac{1}{2}, b =\frac{3}{2}, c =-1\)
\(
\begin{aligned}
& \alpha=\sum_{n=1}^{10}\left(\frac{n^2}{2}+\frac{3 n}{2}-1\right)^2 \\
& 4 \alpha=\sum_{n=1}^{10}\left(n^2+3 n-2\right)^2, \beta=\sum_{n=1}^{10} n^4 \\
& 4 \alpha-\beta=\sum_{n=1}^{10}\left(6 n^3+5 n^2-12 n+4\right)=55(353)+40
\end{aligned}
\) -
Question 13 of 213
13. Question
If \(8=3+\frac{1}{4}(3+p)+\frac{1}{4^2}(3+2 p)+\frac{1}{4^3}(3+3 p)+\cdots \cdots \infty\), then the value of \(p\) is ____. [JEE Main 2024 (Online) 27th January Morning Shift]
CorrectIncorrectHint
\(
8=\frac{3}{1-\frac{1}{4}}+\frac{p \cdot \frac{1}{4}}{\left(1-\frac{1}{4}\right)^2}
\)
(sum of infinite terms of A.G.P \(=\frac{a}{1-r}+\frac{d r}{(1-r)^2}\) )
\(
\Rightarrow \frac{4 p}{9}=4 \Rightarrow p=9
\) -
Question 14 of 213
14. Question
If the sum of the series
\(
\begin{aligned}
& \left(\frac{1}{2}-\frac{1}{3}\right)+\left(\frac{1}{2^2}-\frac{1}{2 \cdot 3}+\frac{1}{3^2}\right)+\left(\frac{1}{2^3}-\frac{1}{2^{2 \cdot 3}}+\frac{1}{2 \cdot 3^2}-\frac{1}{3^3}\right)+ \\
& \left(\frac{1}{2^4}-\frac{1}{2^{3 \cdot 3}}+\frac{1}{2^2 \cdot 3^2}-\frac{1}{2 \cdot 3^3}+\frac{1}{3^4}\right)+\ldots
\end{aligned}
\)
is \(\frac{\alpha}{\beta}\), where \(\alpha\) and \(\beta\) are co-prime, then \(\alpha+3 \beta\) is equal to [JEE Main 2023 (Online) 15th April Morning Shift]CorrectIncorrectHint
We can rewrite the given series as follows :
\(
S=\left(\frac{1}{2}-\frac{1}{3}\right)+\left(\frac{1}{4}-\frac{1}{6}+\frac{1}{9}\right)+\left(\frac{1}{8}-\frac{1}{12}+\frac{1}{18}-\frac{1}{27}\right)+\left(\frac{1}{16}-\frac{1}{24}+\frac{1}{36}-\frac{1}{54}+\frac{1}{81}\right)+\ldots
\)
The first few terms of the series are :
\(
S=\left(\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\ldots\right)-\left(\frac{1}{3}+\frac{1}{6}+\frac{1}{12}+\frac{1}{24}+\ldots\right)+\left(\frac{1}{9}+\frac{1}{18}+\frac{1}{36}+\ldots\right)-\left(\frac{1}{27}+\frac{1}{54}+\ldots\right)+\ldots
\)
We can now see that each group of terms forms a geometric series with a common ratio of \(\frac{1}{2}\) :
\(
S=\frac{\frac{1}{2}}{1-\frac{1}{2}}-\frac{\frac{1}{3}}{1-\frac{1}{2}}+\frac{\frac{1}{9}}{1-\frac{1}{2}}-\frac{\frac{1}{27}}{1-\frac{1}{2}}+\ldots
\)
The series can be rewritten as :
\(
S=2\left(\frac{1}{2}-\frac{1}{3}+\frac{1}{9}-\frac{1}{27}+\ldots\right)
\)
Now, we can simplify and rewrite the series inside the parentheses as:
\(
S=2\left[\frac{1}{2}+\left(-\frac{1}{3}+\frac{1}{9}-\frac{1}{27}+\ldots\right)\right]
\)
The series inside the parentheses is an infinite geometric series with the first term \(a=-\frac{1}{3}\) and the common ratio \(r=-\frac{1}{3}\) :
\(
\begin{aligned}
& S=2\left(\frac{1}{2}+\frac{a}{1-r}\right)=2\left(\frac{1}{2}+\frac{-\frac{1}{3}}{1+\frac{1}{3}}\right)=2\left(\frac{1}{2}+\frac{-\frac{1}{3}}{\frac{4}{3}}\right) \\
& =2\left(\frac{1}{2}-\frac{1}{3} \times \frac{3}{4}\right) \\
& =2\left(\frac{1}{2}-\frac{1}{4}\right)=2\left(\frac{1}{4}\right)=\frac{1}{2}
\end{aligned}
\)
Thus, the sum of the series is \(\frac{1}{2}\), and \(\alpha=1\) and \(\beta=2\) are co-prime.
Therefore, \(\alpha+3 \beta=1+6=7\) -
Question 15 of 213
15. Question
The sum to 20 terms of the series \(2 \cdot 2^2-3^2+2 \cdot 4^2-5^2+2 \cdot 6^2-\ldots \ldots\) is equal to ______. [JEE Main 2023 (Online) 13th April Morning Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& \sum_{r=1}^{10}\left(2 \cdot(2 r)^2-(2 r+1)^2\right) \\
& =\sum_{r=1}^{10}\left(8 r^2-4 r^2-4 r-1\right) \\
& =\sum_{r=1}^{10}\left(4 r^2-4 r-1\right) \\
& =\frac{4 \cdot 10 \cdot 11 \cdot 21}{6}-4 \frac{10 \cdot 11}{2}-10 \\
& =44 \cdot 35-220-10 \\
& =1540-230=1310
\end{aligned}
\) -
Question 16 of 213
16. Question
For \(k \in N\), if the sum of the series \(1+\frac{4}{k}+\frac{8}{k^2}+\frac{13}{k^3}+\frac{19}{k^4}+\ldots\) is 10 , then the value of \(k\) is _____. [JEE Main 2023 (Online) 11th April Evening Shift]
CorrectIncorrectHint
From the given series :
\(
10=1+\frac{4}{k}+\frac{8}{k^2}+\frac{13}{k^3}+\frac{19}{k^4}+\ldots
\)
We isolate the 1 to get :
\(
9=\frac{4}{k}+\frac{8}{k^2}+\frac{13}{k^3}+\frac{19}{k^4}+\ldots(1)
\)
Divide each term in the equation by \(k\) :
\(
\frac{9}{k}=\frac{4}{k^2}+\frac{8}{k^3}+\frac{13}{k^4}+\ldots(2)
\)
Subtracting the second equation from the first, we obtain :
\(
9\left(1-\frac{1}{k}\right)=\frac{4}{k}+\frac{4}{k^2}+\frac{5}{k^3}+\frac{6}{k^4}+\ldots
\)
This is equivalent to :
\(
S=9\left(1-\frac{1}{k}\right)=\frac{4}{k}+\frac{4}{k^2}+\frac{5}{k^3}+\frac{6}{k^4}+\ldots(3)
\)
Divide both sides by \(k\) again, we get : \(\frac{S}{k}=\frac{4}{k^2}+\frac{4}{k^3}+\frac{5}{k^4}+\ldots(4)\)
Subtracting equation (4) from (3), we have :
\(
\left(1-\frac{1}{k}\right) S=\frac{4}{k}+\frac{1}{k^3}+\frac{1}{k^4}+\ldots
\)
In this equation, you’ve treated the infinite series on the right-hand side as a geometric series with a ratio of \(1 / k\), so the sum of this series can be expressed as \(\frac{1 / k^3}{1-1 / k}\).
Therefore, we get :
\(
9\left(1-\frac{1}{k}\right)^2=\frac{4}{k}+\frac{1 / k^3}{1-1 / k}
\)
Now, simplifying this equation, we get :
\(
\begin{aligned}
& 9(k-1)^2=4 k^2-4 k+1 \\
& \Rightarrow 9\left(k^2-2 k+1\right)=4 k^2-4 k+1 \\
& \Rightarrow 9 k^2-18 k+9=4 k^2-4 k+1 \\
& \Rightarrow 9 k^2-4 k^2-18 k+4 k+9-1=0 \\
& \Rightarrow 5 k^2-14 k+8=0
\end{aligned}
\)
This is a standard form quadratic equation, \(a x^2+b x+c=0\), where \(a=5, b=-14\), and \(c=8\).
The solutions can be found using the quadratic formula, \(k=\frac{-b \pm \sqrt{b^2-4 a c}}{2 a}\).
Substituting the values for \(a, b\), and \(c\), we have :
\(
\begin{aligned}
& \Rightarrow k=\frac{14 \pm \sqrt{(-14)^2-4 \times 5 \times 8}}{2 \times 5} \\
& \Rightarrow k=\frac{14 \pm \sqrt{196-160}}{10} \\
& \Rightarrow k=\frac{14 \pm \sqrt{36}}{10} \\
& \Rightarrow k=\frac{14 \pm 6}{10}
\end{aligned}
\)
So, the solutions are \(k=2\) or \(k=0.8\). However, since the question mentions \(k \in N\), i.e., \(k\) is a natural number, the only valid solution is \(k=2\). -
Question 17 of 213
17. Question
Let \(S=109+\frac{108}{5}+\frac{107}{5^2}+\ldots+\frac{2}{5^{107}}+\frac{1}{5^{108}}\). Then the value of \(\left(16 S-(25)^{-54}\right)\) is equal to ____. [JEE Main 2023 (Online) 11th April Morning Shift]
CorrectIncorrectHint
We have, \(S=109+\frac{108}{5}+\frac{107}{5^2}+\ldots+\frac{2}{5^{107}}+\frac{1}{5^{108}} \dots(i)\)
\(\frac{S}{5}=\frac{109}{5}+\frac{108}{5^2}+\frac{107}{5^3}+\ldots+\frac{2}{5^{108}}+\frac{1}{5^{109}} \dots(ii)\)
On subtracting Eq. (ii) from Eq. (i), we get
\(
\begin{aligned}
& \frac{4 S}{5}=109-\frac{1}{5}-\frac{1}{5^2}-\ldots .-\frac{1}{5^{108}}-\frac{1}{5^{109}} \\
& \frac{4 S}{5}=109-\left[\frac{1}{5}+\frac{1}{5^2}+\ldots+\frac{1}{5^{108}}+\frac{1}{5^{109}}\right]
\end{aligned}
\)
This form a GP with \(r=\frac{1}{5}\)
\(
\begin{aligned}
& \frac{4 S}{5}=109-\frac{1}{5}\left[\frac{1-\frac{1}{5^{109}}}{1-\frac{1}{5}}\right] \\
& =109-\frac{1}{4}\left[1-\frac{1}{5^{109}}\right] \\
& =109-\frac{1}{4}+\frac{1}{4} \times \frac{1}{5^{109}} \\
& \therefore 4 S=\frac{5}{4}\left[435+\frac{1}{5^{1009}}\right] \\
& \Rightarrow 16 S=2175+\frac{1}{5^{108}} \\
& 16 S-(25)^{-54}=2175 \\
&
\end{aligned}
\) -
Question 18 of 213
18. Question
Suppose \(a_1, a_2, 2, a_3, a_4\) be in an arithmetico-geometric progression. If the common ratio of the corresponding geometric progression is 2 and the sum of all 5 terms of the arithmetico-geometric progression is \(\frac{49}{2}\), then \(a_4\) is equal to [JEE Main 2023 (Online) 10th April Evening Shift]
CorrectIncorrectHint
Since, common ratio of A.G.P. is 2 therefore A.G.P. can be taken as
\(
\begin{aligned}
& \frac{(a-2 d)}{4}, \frac{(c-d)}{2}, a, 2(a+d), 4(a+2 d) \\
& \text { or } a_1, a_2, 2, a_3, a_4 \text { (Given) } \\
& \Rightarrow a=2
\end{aligned}
\)
also sum of thes A.G.P. is \(\frac{49}{2}\)
\(
\begin{aligned}
& \Rightarrow \frac{2-2 d}{4}+\frac{2-d}{2}+2+2(2+d)+4(2+2 d)=\frac{49}{2} \\
& \Rightarrow \frac{1}{4}[2-2 d+4-2 d+8+16+8 d+32+32 d]=\frac{49}{2} \\
& \Rightarrow 36 d+62=98 \\
& \Rightarrow 36 d=36 \Rightarrow d=1
\end{aligned}
\)
Hence, \(a_4=4(a+2 d)=4(2+2 \times 1)=16\) -
Question 19 of 213
19. Question
The sum of all those terms, of the arithmetic progression \(3,8,13, \ldots ., 373\), which are not divisible by 3 , is equal to _____. [JEE Main 2023 (Online) 10th April Morning Shift]
CorrectIncorrectHint
\(
\begin{aligned}
&\begin{aligned}
& \text { A.P }: 3,8,13 \ldots 373 \\
& T_n=a+(n-1) d \\
& 373=3+(n-1) 5 \\
& \Rightarrow \mathrm{n}=\frac{370}{5} \\
& \Rightarrow n=75 \\
& \text { Now Sum }=\frac{\mathrm{n}}{2}[\mathrm{a}+1] \\
& =\frac{75}{2}[3+373]=14100
\end{aligned}\\
&\text { Now numbers divisible by } 3 \text { are }\\
&\begin{aligned}
& 3,18,33 \ldots \ldots 363 \\
& 363=3+(\mathrm{k}-1) 15 \\
& \Rightarrow \mathrm{k}-1=\frac{360}{15}=24 \Rightarrow \mathrm{k}=25 \\
& \text { Now, sum }=\frac{25}{2}(3+363)=4575 \\
& \therefore \text { req. sum }=14100-4575 \\
& =9525
\end{aligned}
\end{aligned}
\) -
Question 20 of 213
20. Question
Let \(0<z<y<x\) be three real numbers such that \(\frac{1}{x}, \frac{1}{y}, \frac{1}{z}\) are in an arithmetic progression and \(x, \sqrt{2} y, z\) are in a geometric progression. If \(x y+y z+z x=\frac{3}{\sqrt{2}} x y z\), then \(3(x+y+z)^2\) is equal to ____. [JEE Main 2023 (Online) 8th April Evening Shift]
CorrectIncorrectHint
\(\because \frac{1}{x}, \frac{1}{y}, \frac{1}{z}\) are in A.P.
\(\Rightarrow \frac{1}{x}+\frac{1}{z}=\frac{2}{y} \dots(i)\)
and \(x, \sqrt{2} y, z\) are in G.P.
\(\Rightarrow 2 y^2=x z \dots(ii)\)
\(
\begin{aligned}
& \text { from (i), } \frac{2}{y}=\frac{x+z}{x z}=\frac{x+z}{2 y^2} \\
& \Rightarrow 4 y=x+z \\
& \text { Also, } x y+y z+z x=\frac{3}{\sqrt{2}} x y z \\
& y(4 y)+x z=\frac{3}{\sqrt{2}}\left(2 y^2\right) y \\
& \Rightarrow 4 y^2+2 y^2=3 \sqrt{2} y^3 \\
& \Rightarrow 6 y^2=3 \sqrt{2} y^3 \Rightarrow y=\sqrt{2} \\
& \therefore 3(x+y+z)^2=3(5 y)^2=3(5 \sqrt{2})^2 \\
& =150
\end{aligned}
\) -
Question 21 of 213
21. Question
If \((20)^{19}+2(21)(20)^{18}+3(21)^2(20)^{17}+\ldots+20(21)^{19}=k(20)^{19} \text {, }\) then \(k\) is equal to ____. [JEE Main 2023 (Online) 6th April Evening Shift]
CorrectIncorrectHint
\(
(20)^{19}+2(21)(20)^{18}+3(21)^2(20)^{17}+\ldots \ldots+20(21)^{19}=k(20)^{19}
\)
\(
\Rightarrow(20)^{19}\left[1+2\left(\frac{21}{20}\right)+3\left(\frac{21}{20}\right)^2+\ldots+20\left(\frac{21}{20}\right)^{19}\right]=k(20)^{19}
\)
\(
\Rightarrow k=1+2\left(\frac{21}{20}\right)+3\left(\frac{21}{20}\right)^2+\ldots+20\left(\frac{21}{20}\right)^{19} \dots(i)
\)
Now,
\(
k\left(\frac{21}{20}\right)=\left(\frac{21}{20}\right)+2\left(\frac{21}{20}\right)^2+3\left(\frac{21}{20}\right)^3+\ldots+20\left(\frac{21}{20}\right)^{20} \dots(ii)
\)
On subtracting Equation (ii) from Equation (i), we get
\(
\begin{aligned}
& k\left(\frac{-1}{20}\right)=1+\frac{21}{20}+\left(\frac{21}{20}\right)^2+\ldots \ldots+\left(\frac{21}{20}\right)^{19}-20\left(\frac{21}{20}\right)^{20} \\
& \Rightarrow k\left(\frac{-1}{20}\right)=\frac{1\left(\left(\frac{21}{20}\right)^{20}-1\right)}{\frac{21}{20}-1}-20\left(\frac{21}{20}\right)^{20} \\
& \Rightarrow k\left(\frac{-1}{20}\right)=20\left(\left(\frac{21}{20}\right)^{20}-1\right)-20\left(\frac{21}{20}\right)^{20} \\
& =20\left(\frac{21}{20}\right)^{20}-20-20\left(\frac{21}{20}\right)^{20} \\
& \Rightarrow k\left(\frac{-1}{20}\right)=-20 \\
& \Rightarrow k=400
\end{aligned}
\) -
Question 22 of 213
22. Question
The sum of the common terms of the following three arithmetic progressions.
\(3,7,11,15, \ldots, 399\),
\(2,5,8,11, \ldots, 359\) and
\(2,7,12,17, \ldots, 197\),
is equal to _____. [JEE Main 2023 (Online) 1st February Evening Shift]CorrectIncorrectHint
\(
\begin{array}{ll}
3,7,11,15, \ldots \ldots \ldots \ldots 399: & d _1=4 \\
2,5,8,11, \ldots \ldots \ldots \ldots, 359: & d _2=3 \\
2,7,12,17, \ldots \ldots, 197: & d _3=5
\end{array}
\)
\(
\operatorname{LCM}\left( d _1, d _2, d _3\right)=60
\)
Common terms are \(47,107,167\)
\(
\text { Sum }=321
\) -
Question 23 of 213
23. Question
Let \(a_1=8, a_2, a_3, \ldots, a_n\) be an A.P. If the sum of its first four terms is 50 and the sum of its last four terms is 170 , then the product of its middle two terms is ____. [JEE Main 2023 (Online) 1st February Morning Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& a_1+a_2+a_3+a_4=50 \\
& \Rightarrow 32+6 d=50 \\
& \Rightarrow d=3 \\
& \text { and, } a_{n-3}+a_{n-2}+a_{n-1}+a_n=170 \\
& \Rightarrow 32+(4 n-10) \cdot 3=170 \\
& \Rightarrow n =14 \\
& a_7=26, a_8=29 \\
& \Rightarrow a_7 \cdot a_8=754
\end{aligned}
\) -
Question 24 of 213
24. Question
The sum \(1^2-2 \cdot 3^2+3 \cdot 5^2-4 \cdot 7^2+5 \cdot 9^2-\ldots+15 \cdot 29^2\) is ___. [JEE Main 2023 (Online) 31st January Evening Shift]
CorrectIncorrectHint
\(
S=1^2-2.3^2+3.5^2-4.7^2+\ldots \ldots+15.29^2
\)
Separating odd placed and even placed terms we get
\(
\begin{aligned}
& S =\left(1.1^2+3.5^2+\ldots .15 \cdot(29)^2\right)-\left(2.3^2+4.7^2\right. \\
& +\ldots+14 \cdot(27)^2 \\
& =\sum_{r=1}^8(2 r-1)(4 r-3)^2-\sum_{r=1}^7 2 r(4 r-1)^2 \\
& =\sum_{r=1}^8\left(32 r^3-64 r^2+42 r-9\right)-2 \sum_{r=1}^7 (16 r^3-8 r^2+r ) \\
& =32 \times 36^2-64 \times 204+1512-72 \\
& -2\left(16 \times 28^2-1120+28\right) \\
& =6592
\end{aligned}
\) -
Question 25 of 213
25. Question
Let \(a_1, a_2, \ldots, a_n\) be in A.P. If \(a_5=2 a_7\) and \(a_{11}=18\), then \(12\left(\frac{1}{\sqrt{a_{10}}+\sqrt{a_{11}}}+\frac{1}{\sqrt{a_{11}}+\sqrt{a_{12}}}+\ldots+\frac{1}{\sqrt{a_{17}}+\sqrt{a_{18}}}\right)\) is equal to ___. [JEE Main 2023 (Online) 31st January Morning Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& a_{11}=18 \\
& a+10 d=18 \dots(i) \\
& a_5=2 a_7 \\
& a+4 d=2(a+6 d) \\
& a=-8 d \dots(ii)
\end{aligned}
\)
\(
\text { (i) and (ii) } \Rightarrow a=-72, d=9 \text {. }
\)
On rationalising the denominator, given expression
\(
\begin{aligned}
& =12\left[\frac{\sqrt{a_{10}}-\sqrt{a_{11}}}{-d}+\frac{\sqrt{a_{11}}-\sqrt{a_{12}}}{-d}+\ldots+\frac{\sqrt{a_{17}}-\sqrt{a_{18}}}{-d}\right] \\
& =12\left[\frac{\sqrt{a_{10}}-\sqrt{a_{18}}}{-d}\right] \\
& =12\left[\frac{\sqrt{a_{11}-d}-\sqrt{a_{11}+7 d}}{-d}\right] \\
& =12\left[\frac{\sqrt{18-9}-\sqrt{18+63}}{-9}\right]=12 \times \frac{2}{3}=8
\end{aligned}
\) -
Question 26 of 213
26. Question
The \(8^{\text {th }}\) common term of the series
\(
\begin{aligned}
& S_1=3+7+11+15+19+\ldots \\
& S_2=1+6+11+16+21+\ldots
\end{aligned}
\)
is: [JEE Main 2023 (Online) 30th January Evening Shift]CorrectIncorrectHint
First common term is 11
Common difference of series of common terms is \(\operatorname{LCM}(4,5)=20\)
\(
\begin{aligned}
& a_8=a+7 d \\
& =11+7 \times 20=151
\end{aligned}
\) -
Question 27 of 213
27. Question
Let \(\sum_{n=0}^{\infty} \frac{ n ^3((2 n )!)+(2 n -1)( n !)}{( n !)((2 n )!)}= ae +\frac{ b }{ e }+ c\), where \(a , b , c \in Z\) and \(e=\sum_{ n =0}^{\infty} \frac{1}{ n !}\) Then \(a ^2- b + c\) is equal to ____. [JEE Main 2023 (Online) 30th January Morning Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& \sum_{n=0}^{\infty} \frac{n^3(2 n!)+(2 n-1)(n!)}{n!\cdot(2 n)!} \\
& =\sum_{n=0}^{\infty} (\frac{n^3}{n!}+\frac{2 n-1}{2 n!}) \\
& =\sum_{n=0}^{\infty} \frac{3}{(n-2)!}+\frac{1}{(n-3)!}+\frac{1}{(n-1)!}+\frac{1}{(2 n-1)!}-\frac{1}{(2 n)!} \\
& =3 e+e+e-\frac{1}{e} \\
& =5 e-\frac{1}{e} \\
& \therefore a=5, b=-1, c=0 \\
& \therefore a^2-b+c=26
\end{aligned}
\) -
Question 28 of 213
28. Question
Let \(a_1=b_1=1\) and \(a_n=a_{n-1}+(n-1), b_n=b_{n-1}+a_{n-1}, \forall n \geq 2\). If \(S=\sum_{n=1}^{10} \frac{b_n}{2^n}\) and \(T=\sum_{n=1}^8 \frac{n}{2^{n-1}}\), then \(2^7(2 S-T)\) is equal to ___. [JEE Main 2023 (Online) 29th January Evening Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& \because a_n=a_{n-1}+(n-1) \text { and } a_1=b_1=1 \\
& b_n=b_{n-1}+a_{n-1} \\
& \therefore b_{n+1}=2 b_n-b_{n-1}+n-1
\end{aligned}
\)
\(
\begin{array}{|c|c|c|}
\hline n & b_n & b_n-n \\
\hline 1 & 1 & 0 \\
\hline 2 & 2 & 0 \\
\hline 3 & 4 & 1 \\
\hline 4 & 8 & 4 \\
\hline 5 & 15 & 10 \\
\hline 6 & 26 & 20 \\
\hline 7 & 42 & 35 \\
\hline 8 & 64 & 56 \\
\hline 9 & 93 & 84 \\
\hline 10 & 130 & 120 \\
\hline
\end{array}
\)
\(
\begin{aligned}
& \therefore 2 S-T=\left(\sum_{n=1}^8 \frac{b_n-n}{2^{n-1}}\right)+\frac{b_9}{2^8}+\frac{b_{10}}{2^9} \\
& =\frac{461}{128} \\
& \therefore 2^7(2 S-T)=461
\end{aligned}
\) -
Question 29 of 213
29. Question
Let \(\left\{a_k\right\}\) and \(\left\{b_k\right\}, k \in N\), be two G.P.s with common ratios \(r_1\) and \(r_2\) respectively such that \(a_1=b_1=4\) and \(r_1<r_2\). Let \(c_k=a_k+b_k, k \in N\). If \(c_2=5\) and \(c_3=\frac{13}{4}\) then \(\sum_{k=1}^{\infty} c_k-\left(12 a_6+8 b_4\right)\) is equal to ____. [JEE Main 2023 (Online) 29th January Evening Shift]
CorrectIncorrectHint
\(\left\{a_k\right\}\) be a G.P. with \(a_1=4, r=r_1\)
and
\(\left\{b_k\right\}\) be G.P. with \(b_1=4, r=r_2\left(r_1<r_2\right)\)
Now
\(
\begin{aligned}
& C_k=a_k+b_k \\
& c_1=4+4=8 \text { and } c_2=5 \\
& a_2+b_2=5 \\
& \therefore r_1+r_2=\frac{5}{4} \\
& \text { and } c_3=\frac{13}{4} \Rightarrow r_4^2+r_2^2=\frac{13}{16} \\
& \therefore \frac{25}{16}-2 r_1 r_2=\frac{13}{16} \Rightarrow 2 r_1 r_2=\frac{3}{4} \\
& \therefore r_2-r_1=\sqrt{\frac{25}{16}-\frac{3}{2}}=\frac{1}{4} \\
& \therefore r_2=\frac{3}{4}, r_1=\frac{1}{2} \\
& \therefore a_6=4 \times \frac{1}{2^5}=\frac{1}{8}, b_4=4 \times \frac{27}{64}=\frac{27}{16} \\
& \text { and } \sum_{K=1}^{\infty} C_K=4\left[\frac{1}{1-\frac{1}{2}}+\frac{1}{1-\frac{3}{4}}\right]=24 \\
& \therefore \sum_{K=1}^{\infty} C_K-\left(12 a_6+8 b_4\right)=09
\end{aligned}
\) -
Question 30 of 213
30. Question
Let \(a_1, a_2, a_3, \ldots\) be a \(G P\) of increasing positive numbers. If the product of fourth and sixth terms is 9 and the sum of fifth and seventh terms is 24 , then \(a_1 a_9+a_2 a_4 a_9+a_5+a_7\) is equal to ___. [JEE Main 2023 (Online) 29th January Morning Shift]
CorrectIncorrectHint
Let \(r\) be the common ratio of the G.P
\(
\begin{aligned}
& \therefore a_1 r^3 \times a_1 r^5=9 \\
& a_1^2 r^8=9 \Rightarrow a_1 r^4=3
\end{aligned}
\)
and
\(
\begin{gathered}
a_1\left(r^4+r^6\right)=24 \\
\Rightarrow 3\left(1+r^2\right)=24 \\
\therefore r^2=7 \text { and } a_1=\frac{3}{49}
\end{gathered}
\)
Now
\(
\begin{aligned}
& a_1 a_9+a_2 a_4 a_9+a_5+a_7 \\
& =a_1^2 r^8+a_1^3 r^{12}+24 \\
& =24+\frac{9}{7^4} \times 7^4+\frac{27}{7^6} \cdot 7^6=60
\end{aligned}
\) -
Question 31 of 213
31. Question
For the two positive numbers \(a, b\), if \(a, b\) and \(\frac{1}{18}\) are in a geometric progression, while \(\frac{1}{a}, 10\) and \(\frac{1}{b}\) are in an arithmetic progression, then \(16 a+12 b\) is equal to ____. [JEE Main 2023 (Online) 25th January Evening Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& a , b , \frac{1}{18} \rightarrow GP \\
& \frac{ a }{18}= b ^2 \quad \ldots(i)
\end{aligned}
\)
\(
\begin{aligned}
& \frac{1}{ a }, 10, \frac{1}{ b } \rightarrow AP \\
& \frac{1}{ a }+\frac{1}{ b }=20
\end{aligned}
\)
\(\Rightarrow a + b =20 ab\), from eq. (i) ; we get
\(
\begin{aligned}
& \Rightarrow 18 b ^2+ b =360 b ^3 \\
& \Rightarrow 360 b ^2-18 b -1=0 \quad\{\because b \neq 0\} \\
& \Rightarrow b =\frac{18 \pm \sqrt{324+1440}}{720} \\
& \Rightarrow b=\frac{18+\sqrt{1764}}{720} \quad\{\because b >0\} \\
& \Rightarrow b=\frac{1}{12} \\
& \Rightarrow a =18 \times \frac{1}{144}=\frac{1}{8}
\end{aligned}
\)
Now, \(16 a+12 b=16 \times \frac{1}{8}+12 \times \frac{1}{12}=3\) -
Question 32 of 213
32. Question
If \(\frac{1^3+2^3+3^3+\ldots \text { up to } n \text { terms }}{1 \cdot 3+2 \cdot 5+3 \cdot 7+\ldots \text { up to } n \text { terms }} =\frac{9}{5} \text {, then the value of } n \text { is }\) [JEE Main 2023 (Online) 24th January Evening Shift]
CorrectIncorrectHint
Given \(\frac{1^3+2^3+3^3+\ldots \text { up to } \quad n \text { terms }}{1.3+2.5+3.7+\ldots \text { up to } \quad n \text { terms }}=\frac{9}{5}\)
Now, Let \(S=1.3+2.5+3.7+\ldots\)
\(T_n=n \cdot(2 n+1)\)
\(\therefore S=\frac{2 n(n+1)(2 n+1)}{6}+\frac{n(n+1)}{2}\)
\(\Rightarrow \frac{\left(\frac{n(n+1)}{2}\right)^2}{n(n+1)\left[\frac{2 n+1}{3}+\frac{1}{2}\right]}=\frac{9}{5}\)
\(\Rightarrow 5 n^2-19 n-30=0\)
\(\Rightarrow(5 n+6)(n-5)=0\)
\(\therefore n=5\) -
Question 33 of 213
33. Question
The \(4^{\text {th }}\) term of GP is 500 and its common ratio is \(\frac{1}{m}, m \in N\). Let \(S_n\) denote the sum of the first \(n\) terms of this GP. If \(S _6> S _5+1\) and \(S _7< S _6+\frac{1}{2}\), then the number of possible values of \(m\) is ____. [JEE Main 2023 (Online) 24th January Morning Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& T_4=500 \\
& a r^3=500 \Rightarrow a=\frac{500}{r^3}
\end{aligned}
\)
Now,
\(
\begin{aligned}
& S_6>S_5+1 \\
& \frac{a\left(1-r^6\right)}{1-r}-\frac{a\left(1-r^5\right)}{1-r}>1 \\
& a r^5>1
\end{aligned}
\)
Now, \(r=\frac{1}{m}\) and \(a=\frac{500}{r^3}\)
\(
\begin{aligned}
& \Rightarrow \quad m^2<500 \\
& \because m>0 \Rightarrow m \in(0,10 \sqrt{5}) \\
& S_7<S_6+\frac{1}{2} \\
& \frac{a\left(1-r^6\right)}{1-r}<\frac{a\left(1-r^6\right)}{1-r}+\frac{1}{2} \\
& a r^6<\frac{1}{2} \\
& \because r=\frac{1}{m} \text { and } a=\frac{500}{r^5} \\
& \frac{1}{m^3}<\frac{1}{1000} \\
& \Rightarrow m \in(10, \infty) \\
&
\end{aligned}
\)
Possible values of \(m\) is \(\{11,12, \ldots .22\}\)
\(
\because m \in N
\)
Total 12 values -
Question 34 of 213
34. Question
Let \(a_1, a_2, a_3, \ldots\) be an A.P. If \(\sum_{r=1}^{\infty} \frac{a_r}{2^r}=4\), then \(4 a_2\) is equal to ___. [JEE Main 2022 (Online) 29th July Morning Shift]
CorrectIncorrectHint
Given
\(
\begin{aligned}
& S=\frac{a_1}{2}+\frac{a_2}{2^2}+\frac{a_3}{2^3}+\frac{a_4}{2^4}+\ldots \ldots \infty \\
& \frac{\frac{1}{2} S=\frac{a_1}{2^2}+\frac{a_2}{2^3}+\ldots \ldots \ldots \infty}{\frac{S}{2}=\frac{a_1}{2}+\frac{\left(a_2+a_1\right)}{2^2}+\frac{\left(a_3+a_2\right)}{2^3}+\ldots \ldots \infty} \\
& \Rightarrow \frac{S}{2}=\frac{a_1}{2}+\frac{d}{2} \\
& \Rightarrow a_1+d=a_2=4 \Rightarrow 4 a_2=16
\end{aligned}
\) -
Question 35 of 213
35. Question
If \(\frac{1}{2 \times 3 \times 4}+\frac{1}{3 \times 4 \times 5}+\frac{1}{4 \times 5 \times 6}+\ldots+\frac{1}{100 \times 101 \times 102}=\frac{ k }{101}\), then \(34 k\) is equal to ___. [JEE Main 2022 (Online) 29th July Morning Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& S=\frac{1}{2 \times 3 \times 4}+\frac{1}{3 \times 4 \times 5}+\frac{1}{4 \times 5 \times 6}+\ldots+\frac{1}{100 \times 101 \times 102} \\
& =\frac{1}{(3-1) .1}\left[\frac{1}{2 \times 3}-\frac{1}{101 \times 102}\right] \\
& =\frac{1}{2}\left(\frac{1}{6}-\frac{1}{101 \times 102}\right) \\
& =\frac{143}{102 \times 101}=\frac{k}{101} \\
& \therefore 34 k=286
\end{aligned}
\) -
Question 36 of 213
36. Question
\(\frac{6}{3^{12}}+\frac{10}{3^{11}}+\frac{20}{3^{10}}+\frac{40}{3^9}+\ldots+\frac{10240}{3}=2^n \cdot m\), where \(m\) is odd, then \(m . n\) is equal to ____ [JEE Main 2022 (Online) 28th July Evening Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& \frac{1}{3^{12}}+5\left(\frac{2^0}{3^{12}}+\frac{2^1}{3^{11}}+\frac{2^2}{3^{10}}+\ldots \ldots+\frac{2^{11}}{3}\right)=2^n \cdot m \\
& \Rightarrow \frac{1}{3^{12}}+5\left(\frac{1}{3^{12}} \frac{\left((6)^2-1\right)}{(6-1)}\right)=2^n \cdot m \\
& \Rightarrow \frac{1}{3^{12}}+\frac{5}{5}\left(\frac{1}{3^{12}} \cdot 2^{12} \cdot 3^{12}-\frac{1}{3^{12}}\right)=2^n \cdot m \\
& \Rightarrow \frac{1}{3^{12}}+2^{12}-\frac{1}{3^{12}}=2^n \cdot m \\
& \Rightarrow 2^n \cdot m=2^{12} \\
& \Rightarrow m=1 \text { and } n=12 \\
& m \cdot n=12
\end{aligned}
\) -
Question 37 of 213
37. Question
\(
\frac{2^3-1^3}{1 \times 7}+\frac{4^3-3^3+2^3-1^3}{2 \times 11}+\frac{6^3-5^3+4^3-3^3+2^3-1^3}{3 \times 15}+\cdots+\frac{30^3-29^3+28^3-27^3+\ldots+2^3-1^3}{15 \times 63}
\)
is equal to ____. [JEE Main 2022 (Online) 27th July Evening Shift]CorrectIncorrectHint
\(
\begin{aligned}
& T_n=\frac{\sum_{k=1}^n\left[(2 k)^3-(2 k-1)^3\right]}{n(4 n+3)} \\
& =\frac{\sum_{k=1}^n 4 k^2+(2 k-1)^2+2 k(2 k-1)}{n(4 n+3)} \\
& =\frac{\sum_{k=1}^n\left(12 k^2-6 k+1\right)}{n(4 n+3)} \\
& =\frac{2 n\left(2 n^2+3 n+1\right)-3 n^2-3 n+n}{n(4 n+3)} \\
& =\frac{n^2(4 n+3)}{n(4 n+3)}=n \\
& \therefore T_n=n \\
& S_n=\sum_{n=1}^{15} T_n=\frac{15 \times 16}{2}=120
\end{aligned}
\) -
Question 38 of 213
38. Question
If \(\sum_{k=1}^{10} \frac{k}{k^4+k^2+1}=\frac{m}{n}\), where \(m\) and \(n\) are co-prime, then \(m+n\) is equal to ____. [JEE Main 2022 (Online) 26th July Evening Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& \sum_{k=1}^{10} \frac{k}{k^4+k^2+1} \\
& =\frac{1}{2}\left[\sum_{k=1}^{10}\left(\frac{1}{k^2-k+1}-\frac{1}{k^2+k+1}\right)\right. \\
& =\frac{1}{2}\left[1-\frac{1}{3}+\frac{1}{3}-\frac{1}{7}+\frac{1}{7}-\frac{1}{13}+\ldots+\frac{1}{91}-\frac{1}{111}\right] \\
& =\frac{1}{2}\left[1-\frac{1}{111}\right]=\frac{110}{2.111}=\frac{55}{111}=\frac{m}{n} \\
& \therefore m+n=55+111=166
\end{aligned}
\) -
Question 39 of 213
39. Question
Different A.P.’s are constructed with the first term 100 , the last term 199 , and integral common differences. The sum of the common differences of all such A.P.’s having at least 3 terms and at most 33 terms is ____. [JEE Main 2022 (Online) 26th July Evening Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& d_1=\frac{199-100}{2} \notin I \\
& d_2=\frac{199-100}{3}=33 \\
& d_3=\frac{199-100}{4} \notin I \\
& d_n=\frac{199-100}{i+1} \in I \\
& d_i=33+11,9 \\
& \text { Sum of CD’s }=33+11+9 \\
& =53
\end{aligned}
\) -
Question 40 of 213
40. Question
The series of positive multiples of 3 is divided into sets : \(\{3\},\{6,9,12\},\{15,18,21,24,27\}, \ldots\) Then the sum of the elements in the \(11^{\text {th }}\) set is equal to ____. [JEE Main 2022 (Online) 26th July Morning Shift]
CorrectIncorrectHint
Given series
\(
\{3 \times 1\},\{3 \times 2,3 \times 3,3 \times 4\},\{3 \times 5,3 \times 6,3 \times 7,3 \times 8,3 \times 9\}, \ldots .
\)
\(\text{ 1-term } \quad \quad \text { 3-terms } \quad \quad \quad \text { 5-terms }\)
\(\therefore 11^{\text {th }}\) set will have \(1+(10) 2=21\) term
Also upto \(10^{\text {th }}\) set total \(3 \times k\) type terms will be
\(
1+3+5+\ldots \ldots+19=100-\text { term }
\)
\(
\begin{aligned}
& \therefore \text { Set } 11=\{3 \times 101,3 \times 102, \ldots \ldots 3 \times 121\} \\
& \therefore \text { Sum of elements }=3 \times(101+102+\ldots+121) \\
& =\frac{3 \times 222 \times 21}{2}=6993
\end{aligned}
\) -
Question 41 of 213
41. Question
Let \(a, b\) be two non-zero real numbers. If \(p\) and \(r\) are the roots of the equation \(x^2-8 a x+2 a =0\) and \(q\) and \(s\) are the roots of the equation \(x^2+12 b x+6 b =0\), such that \(\frac{1}{ p }, \frac{1}{ q }, \frac{1}{ r }, \frac{1}{ s }\) are in A.P., then \(a ^{-1}- b ^{-1}\) is equal to ____. [JEE Main 2022 (Online) 25th July Morning Shift]
CorrectIncorrectHint
\(\because\) Roots of \(2 a x^2-8 a x+1=0\) are \(\frac{1}{p}\) and \(\frac{1}{r}\) and roots of \(6 b x^2+12 b x+1=0\) are \(\frac{1}{q}\) and \(\frac{1}{s}\).
Let \(\frac{1}{p}, \frac{1}{q}, \frac{1}{r}, \frac{1}{s}\) as \(\alpha-3 \beta, \alpha-\beta, \alpha+\beta, \alpha+3 \beta\)
So sum of roots \(2 \alpha-2 \beta=4\) and \(2 \alpha+2 \beta=-2\)
Clearly \(\alpha=\frac{1}{2}\) and \(\beta=-\frac{3}{2}\)
Now product of roots, \(\frac{1}{p} \cdot \frac{1}{r}=\frac{1}{2 a}=-5 \Rightarrow \frac{1}{a}=-10\) and \(\frac{1}{q} \cdot \frac{1}{x}=\frac{1}{6 b}=-8 \Rightarrow \frac{1}{b}=-48\)
So, \(\frac{1}{a}-\frac{1}{b}=38\) -
Question 42 of 213
42. Question
Let \(a_1=b_1=1, a_n=a_{n-1}+2\) and \(b_n=a_n+b_{n-1}\) for every natural number \(n \geqslant 2\). Then \(\sum_{n=1}^{15} a_n . b_n\) is equal to ____. [JEE Main 2022 (Online) 25th July Morning Shift]
CorrectIncorrectHint
Given,
\(
\begin{aligned}
& a_n=a_{n-1}+2 \\
& \Rightarrow a_n-a_{n-1}=2
\end{aligned}
\)
\(\therefore\) In this series between any two consecutives terms difference is 2 . So this is an A.P. with common difference 2 .
Also given \(a_1=1\)
\(\therefore\) Series is \(=1,3,5,7 \ldots\)
\(
\therefore a_n=1+(n-1) 2=2 n-1
\)
Also \(b_n=a_n+b_{n-1}\)
When \(n=2\) then
\(
\begin{aligned}
& b_2-b_1=a_2=3 \\
& \Rightarrow b_2-1=3 \text { [Given } b_1=1 \text { ] } \\
& \Rightarrow b_2=4
\end{aligned}
\)
When \(n=3\) then
\(
\begin{aligned}
& b_3-b_2=a_3 \\
& \Rightarrow b_3-4=5 \\
& \Rightarrow b_3=9
\end{aligned}
\)
\(\therefore\) Series is \(=1,4,9 \ldots\)
\(=1^2, 2^2, 3^2 \ldots\) \(n^2\)
\(
\therefore b_n=n^2
\)
\(
\begin{aligned}
& \text { Now, } \sum_{n=1}^{15}\left(a_n \cdot b_n\right) \\
& =\sum_{n=1}^{15}\left[(2 n-1) n^2\right] \\
& =\sum_{n=1}^{15} 2 n^3-\sum_{n=1}^{15} n^2 \\
& =2\left(1^3+2^3+\ldots 15^3\right)-\left(1^2+2^2+\ldots 15^2\right) \\
& =2 \times\left(\frac{15 \times 16}{2}\right)^2-\left(\frac{15(16) \times 31}{6}\right) \\
& =27560
\end{aligned}
\) -
Question 43 of 213
43. Question
Let for \(f(x)=a_0 x^2+a_1 x+a_2, f^{\prime}(0)=1\) and \(f^{\prime}(1)=0\). If \(a _0, a _1, a _2\) are in an arithmetico-geometric progression, whose corresponding A.P. has common difference 1 and corresponding G.P. has common ratio 2 , then \(f(4)\) is equal to ____. [JEE Main 2022 (Online) 30th June Morning Shift]
CorrectIncorrectHint
Given,
\(
\begin{aligned}
& f(x)=a_0 x^2+a_1 x+a_2 \\
& f^{\prime}(0)=1 \\
& f^{\prime}(1)=0
\end{aligned}
\)
\(a_0, a_1, a_2\) are in A. G. P
Common difference of \(A P=1\)
Common ratio of \(G P=2\)
A.P terms \(=a, a+1, a+2\)
G.P terms \(=y, r y, r^2 y\)
\(\therefore\) AGP terms \(=a y,(a+1) r y,(a+2) r^2 y\)
\(
\begin{aligned}
& \therefore a_0=a y \\
& a_1=(a+1) r y=(a+1) 2 y \\
& a_2=(a+2) r^2 y=(a+2) 4 y
\end{aligned}
\)
Now, \(f^{\prime}(x)=2 x a_0+a_1\)
\(
\therefore f^{\prime}(0)=a_1=1
\)
\(
\begin{aligned}
& \text { and } f^{\prime}(1)=2 a_0+a_1=0 \\
& \Rightarrow 2 a_0+1=0 \\
& \Rightarrow a_0=-\frac{1}{2} \\
& \therefore a y=-\frac{1}{2} \\
& \text { and }(a+1) 2 y=1 \\
& \Rightarrow 2 a y+2 y=1 \\
& \Rightarrow 2 \times\left(-\frac{1}{2}\right)+2 y=1 \\
& \Rightarrow 2 y=+2 \\
& \Rightarrow y=+1 \\
& \therefore a=-\frac{1}{2} \\
& \therefore a_2=(a+2) 4 y \\
& =\left(-\frac{1}{2}+2\right) \times 4.1 \\
& =6 \\
& \therefore f(x)=-\frac{1}{2} x^2+x+6 \\
& \therefore f(4)=-\frac{1}{2}(4)^2+4+6 \\
& =-8+10 \\
& =2
\end{aligned}
\) -
Question 44 of 213
44. Question
Let \(3,6,9,12 \ldots\), upto 78 terms and \(5,9,13,17 \ldots\), upto 59 terms be two series. Then, the sum of the terms common to both the series is equal to ____. [JEE Main 2022 (Online) 29th June Evening Shift]
CorrectIncorrectHint
1st AP:
\(3,6,9,12 \ldots\), upto 78 terms
\(
\begin{aligned}
& t _{78}=3+(78-1) 3 \\
& =3+77 \times 3 \\
& =234
\end{aligned}
\)
2nd AP :
\(5,9,13,17, \ldots .\). upto 59 terms
\(
\begin{aligned}
& t _{59}=5+(59-1) 4 \\
& =5+58 \times 4 \\
& =237
\end{aligned}
\)
Common term’s AP :
First term \(=9\)
Common difference of first \(AP =3\)
And common difference of second AP \(=4\)
\(\therefore\) Common difference of common terms
\(
A P=\operatorname{LCM}(3,4)=12
\)
\(\therefore\) New AP \(=9,21,33, \ldots \ldots\).
\(
\begin{aligned}
& t _{ n }=9+( n -1) 12 \leq 234 \\
& \Rightarrow n \leq \frac{237}{12} \\
& \Rightarrow n=19 \\
& \therefore S_{19}=\frac{19}{2}[2.9+(19-1) 12] \\
& =19(9+108) \\
& =2223
\end{aligned}
\) -
Question 45 of 213
45. Question
Let for \(n=1,2, \ldots . ., 50, S_n\) be the sum of the infinite geometric progression whose first term is \(n ^2\) and whose common ratio is \(\frac{1}{(n+1)^2}\). Then the value of \(\frac{1}{26}+\sum_{n=1}^{50}\left(S_n+\frac{2}{n+1}-n-1\right) \text { is equal to } \) ___. [JEE Main 2022 (Online) 28th June Evening Shift]
CorrectIncorrectHint
\(
S_n=\frac{n^2}{1-\frac{1}{(n+1)^2}}=\frac{n(n+1)^2}{n+2}=\left(n^2+1\right)-\frac{2}{n+2}
\)
Now \(\frac{1}{26}+\sum_{n=1}^{50}\left(S_n+\frac{2}{n+1}-n-1\right)\)
\(
\begin{aligned}
& =\frac{1}{26}+\sum_{n=1}^{50}\left\{\left(n^2-n\right)+2\left(\frac{1}{n+1}-\frac{1}{n+2}\right)\right\} \\
& =\frac{1}{26}+\frac{50 \times 51 \times 101}{6}-\frac{50 \times 51}{2}+2\left(\frac{1}{2}-\frac{1}{52}\right) \\
& =1+25 \times 17(101-3) \\
& =41651
\end{aligned}
\) -
Question 46 of 213
46. Question
If \(a_1(>0), a_2, a_3, a_4, a_5\) are in a G.P., \(a_2+a_4=2 a_3+1\) and \(3 a_2+a_3=2 a_4\), then \(a_2+\) \(a_4+2 a_5\) is equal to ____. [JEE Main 2022 (Online) 26th June Evening Shift]
CorrectIncorrectHint
\(
\text { Let G.P. be } a_1=a, a_2=a r, a_3=a r^2 \ldots
\)
\(
\begin{aligned}
& \because 3 a_2+a_3=2 a_4 \\
& \Rightarrow 3 a r+a r^2=2 a r^3 \\
& \Rightarrow 2 a r^2-r-3=0 \\
& \therefore r=-1 \text { or } \frac{3}{2}
\end{aligned}
\)
\(\because a_1= a >0\) then \(r \neq-1\)
Now, \(a _2+ a _4=2 a _3+1\)
\(
\begin{aligned}
& a r+a r^3=2 a r^2+1 \\
& a\left(\frac{3}{2}+\frac{27}{8}-\frac{9}{2}\right)=1 \\
& \therefore a=\frac{8}{3}
\end{aligned}
\)
\(
\begin{aligned}
& \therefore a_2+a_4+2 a_5=a\left(r+r^3+2 r^4\right) \\
& =\frac{8}{3}\left(\frac{3}{2}+\frac{27}{8}+\frac{81}{8}\right)=40
\end{aligned}
\) -
Question 47 of 213
47. Question
Let \(A =\left\{1, a _1, a _2 \ldots \ldots . . a _{18}, 77\right\}\) be a set of integers with \(1< a _1< a _2<\ldots \ldots . .< a _{18}<77\). Let the set \(A+A=\{x+y: x, y \in A\}\) contain exactly 39 elements. Then, the value of \(a_1+a_2+\ldots . . .+a_{18} \text { is equal to }\) _____. [JEE Main 2022 (Online) 28th June Morning Shift]
CorrectIncorrectHint
If we write the elements of \(A+A\), we can certainly find 39 distinct elements as
\(
\begin{aligned}
& 1+1,1+a_1, 1+a_2, \ldots 1 \\
& +a_{18}, 1+77, a_1+77, a_2+77, \ldots \ldots a_{18}+77,77+77
\end{aligned}
\)It means all other sums are already present in these 39 values, which is only possible in case when all numbers are in A.P.
Let the common difference be ‘ \(d\) ‘.
\(
77=1+19 d \Rightarrow d=4
\)
So, \(\sum_{i=1}^{18} a_1=\frac{18}{2}\left[2 a_1+17 d\right]=9[10+68]=702\) -
Question 48 of 213
48. Question
If the sum of the first ten terms of the series
\(
\frac{1}{5}+\frac{2}{65}+\frac{3}{325}+\frac{4}{1025}+\frac{5}{2501}+\ldots
\)
is \(\frac{m}{n}\), where \(m\) and \(n\) are co-prime numbers, then \(m + n\) is equal to ___. [JEE Main 2022 (Online) 27th June Morning Shift]CorrectIncorrectHint
\(
\begin{aligned}
& T_r=\frac{r}{\left(2 r^2\right)^2+1} \\
& =\frac{r}{\left(2 r^2+1\right)^2-(2 r)^2} \\
& =\frac{1}{4} \frac{4 r}{\left(2 r^2+2 r+1\right)\left(2 r^2-2 r+1\right)} \\
& S_{10}=\frac{1}{4} \sum_{r=1}^{10}\left(\frac{1}{\left(2 r^2-2 r+1\right)}-\frac{1}{\left(2 r^2+2 r+1\right)}\right) \\
& =\frac{1}{4}\left[1-\frac{1}{5}+\frac{1}{5}-\frac{1}{13}+\ldots+\frac{1}{181}-\frac{1}{221}\right] \\
& \Rightarrow S_{10}=\frac{1}{4} \cdot \frac{220}{221}=\frac{55}{221}=\frac{m}{n} \\
& \therefore m+n=276
\end{aligned}
\) -
Question 49 of 213
49. Question
For a natural number \(n\), let \(\alpha_n=19^n-12^n\). Then, the value of \(\frac{31 \alpha_9-\alpha_{10}}{57 \alpha_8}\) is ___. [JEE Main 2022 (Online) 25th June Morning Shift]
CorrectIncorrectHint
\(
\alpha_n=19^n-12^n
\)
Let equation of roots \(12 \& 19\) i.e.
\(
\begin{aligned}
& x^2-31 x+228=0 \\
& \Rightarrow(31-x)=\frac{228}{x} \text { (where } x \text { can be } 19 \text { or } 12 \text { ) }
\end{aligned}
\)
\(
\begin{aligned}
& \therefore \frac{31 \alpha_9-\alpha_{10}}{57 \alpha_8}=\frac{31\left(19^9-12^9\right)-\left(19^{10}-12^{10}\right)}{57\left(19^8-12^8\right)} \\
& =\frac{19^9(31-19)-12^9(31-12)}{57\left(19^8-12^8\right)} \\
& =\frac{228\left(19^8-12^8\right)}{57\left(19^8-12^8\right)}=4 .
\end{aligned}
\) -
Question 50 of 213
50. Question
The greatest integer less than or equal to the sum of first 100 terms of the sequence \(\frac{1}{3}, \frac{5}{9}, \frac{19}{27}, \frac{65}{81}, \ldots \ldots\). is equal to ____. [JEE Main 2022 (Online) 25th June Morning Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& S=\frac{1}{3}+\frac{5}{9}+\frac{19}{27}+\frac{65}{81}+\ldots . \\
& =\sum_{r=1}^{100}\left(\frac{3^r-2^r}{3^r}\right) \\
& =100-\frac{2}{3} \frac{\left(1-\left(\frac{2}{3}\right)^{100}\right)}{1 / 3} \\
& =98+2\left(\frac{2}{3}\right)^{100} \\
& \therefore[S]=98
\end{aligned}
\) -
Question 51 of 213
51. Question
The number of 4 -digit numbers which are neither multiple of 7 nor multiple of 3 is ____. [JEE Main 2021 (Online) 31st August Evening Shift]
CorrectIncorrectHint
\(A=4\)-digit numbers divisible by 3
\(
A=1002,1005, \ldots . ., 9999
\)
\(
\begin{aligned}
& 9999=1002+(n-1) 3 \\
& \Rightarrow(n-1) 3=8997 \Rightarrow n=3000
\end{aligned}
\)
\(B=4\)-digit numbers divisible by 7
\(B=1001,1008, \ldots \ldots ., 9996\)
\(
\begin{aligned}
& \Rightarrow 9996=1001+( n -1) 7 \\
& \Rightarrow n =1286
\end{aligned}
\)
\(A \cap B=1008,1029, \ldots . ., 9996\)
\(
\begin{aligned}
& 9996=1008+(n-1) 21 \\
& \Rightarrow n=429
\end{aligned}
\)
So, no divisible by either 3 or 7
\(
=3000+1286-429=3857
\)
total 4-digits numbers \(=9000\)
required numbers \(=9000-3857=5143\) -
Question 52 of 213
52. Question
If \(S=\frac{7}{5}+\frac{9}{5^2}+\frac{13}{5^3}+\frac{19}{5^4}+\ldots\), then \(160 S\) is equal to ___. [JEE Main 2021 (Online) 31st August Evening Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& S=\frac{7}{5}+\frac{9}{5^2}+\frac{13}{5^3}+\frac{19}{5^4}+\ldots \\
& \frac{1}{5} S=\frac{7}{5}+\frac{9}{5^3}+\frac{13}{5^4}+\ldots
\end{aligned}
\)
On subtracting
\(
\begin{aligned}
& \frac{4}{5} S=\frac{7}{5}+\frac{2}{5^2}+\frac{4}{5^3}+\frac{6}{5^4}+\ldots \\
& S=\frac{7}{14}+\frac{1}{10}\left(1+\frac{2}{5}+\frac{3}{5^2}+\ldots\right) \\
& S=\frac{7}{4}+\frac{1}{10}\left(1-\frac{1}{5}\right)^{-2} \\
& =\frac{7}{4}+\frac{1}{10} \times \frac{25}{16}=\frac{61}{32} \\
& \Rightarrow 160 S=5 \times 61=305
\end{aligned}
\) -
Question 53 of 213
53. Question
The sum of all 3 -digit numbers less than or equal to 500 , that are formed without using the digit ” 1 ” and they all are multiple of 11 , is ____. [JEE Main 2021 (Online) 26th August Evening Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& 209,220,231, \ldots \ldots \ldots, 495 \\
& \text { Sum }=\frac{27}{2}(209+495)=9504
\end{aligned}
\)
Number containing 1 at unit place
\(
\begin{array}{lll}
\underline{2} & \underline{3} & \underline{1} \\
\underline{3} & \underline{4} & \underline{1} \\
\underline{4} & \underline{5} & \underline{1}
\end{array}
\)
Number containing 1 at \(10^{\text {th }}\) place
\(
\begin{array}{lll}
\underline{3} & \underline{1} & \underline{9} \\
\underline{4} & \underline{1} & \underline{8}
\end{array}
\)
Required \(=9504-(231+341+451+319+418)\)
\(
=7744
\) -
Question 54 of 213
54. Question
Let \(a_1, a_2, \ldots . . ., a_{10}\) be an AP with common difference -3 and \(b_1, b_2, \ldots . . . ., b_{10}\) be a GP with common ratio 2 . Let \(c_k=a_k+b_k, k=1,2, \ldots \ldots ., 10\). If \(c_2=12\) and \(c_3=13\), then \(\sum_{k=1}^{10} c_k\) is equal to ___. [JEE Main 2021 (Online) 26th August Evening Shift]
CorrectIncorrectHint
\(a_1, a_2, a_3, \ldots, a_{10}\) are in AP common difference \(=-3\)
\(b_1, b_2, b_3, \ldots, b_{10}\) are in GP common ratio \(=2\)
Since, \(c_k=a_k+b_k, k=1,2,3 \ldots \ldots, 10\)
\(
\begin{aligned}
& \therefore c_2=a_2+b_2=12 \\
& c_3=a_3+b_3=13
\end{aligned}
\)
Now, \(C _3- C _2=1\)
\(
\begin{aligned}
& \Rightarrow \quad\left(a_3-a_2\right)+\left(b_3-b_2\right) \neq 1 \Rightarrow-3+\left(2 b_2-b_2\right) \neq 1 \\
& \Rightarrow \quad b_2=4 \\
& \therefore \quad a_2=8
\end{aligned}
\)
So, \(AP\) is \(11,8,5, \ldots\).
\(
\begin{aligned}
& \text { Now, } \sum_{k=1}^{10} C_k=\sum_{k=1}^{10} a_k+\sum_{k=1}^{10} b_k \\
& =\left(\frac{10}{2}\right)[22+9(-3)]+2\left(\frac{2^{10}-1}{2-1}\right) \\
& =5(22-27)+2(1023)=2046-25 \\
& =2021
\end{aligned}
\) -
Question 55 of 213
55. Question
If \(\log _3 2, \log _3\left(2^x-5\right), \log _3\left(2^x-\frac{7}{2}\right)\) are in an arithmetic progression, then the value of \(x\) is equal to ____. [JEE Main 2021 (Online) 27th July Morning Shift]
CorrectIncorrectHint
\(
\begin{aligned}
&\begin{aligned}
& 2 \log _3\left(2^x-5\right)=\log _2+\log _3\left(2^x-\frac{7}{2}\right) \\
& \text { Let } 2^x=t \\
& \log _3(t-5)^2=\log _3 2\left(t-\frac{7}{2}\right) \\
& (t-5)^2=2 t-7 \\
& t^2-12 t+32=0 \\
& (t-4)(t-8)=0 \\
& \Rightarrow 2^x=4 \text { or } 2^x=8 \\
& x=2 \text { (Rejected) }
\end{aligned}\\
&\text { Or } x=3
\end{aligned}
\) -
Question 56 of 213
56. Question
If the value of
\(
\left(1+\frac{2}{3}+\frac{6}{3^2}+\frac{10}{3^3}+\ldots \text { upto } \infty\right)^{\log _{(0.25)}\left(\frac{1}{3}+\frac{1}{3^2}+\frac{1}{3^3}+\ldots . \text { upto } \infty\right)}
\)
is \(l\), then \(l^2\) is equal to ____. [JEE Main 2021 (Online) 25th July Morning Shift]CorrectIncorrectHint
\(
l=(\underbrace{1+\frac{2}{3}+\frac{6}{3^2}+\frac{10}{3^3}}_S+\ldots)^{\log _{0.25}\left(\frac{1}{3}+\frac{1}{3^2}+\ldots\right)}
\)
\(
\begin{aligned}
& S=1+\frac{2}{3}+\frac{6}{3^2}+\frac{10}{3^3}+\ldots \\
& \frac{S}{3}=\frac{1}{3}+\frac{2}{3^2}+\frac{6}{3^3}+\ldots \ldots \frac{2 x}{3}=1+\frac{1}{3}+\frac{4}{3^2}+\frac{4}{3^3}+\ldots \\
& \frac{2 S}{3}=\frac{4}{3}+\frac{4}{3^2}+\frac{4}{3^3}+\ldots \ldots \\
& S=\frac{3}{2}\left(\frac{4 / 3}{1-1 / 3}\right)=3
\end{aligned}
\)
Now, \(l=(3)^{\log _{0.25}\left(\frac{1 / 3}{1-1 / 3}\right)}\)
\(
l=3^{\log _{((1 / 4))}\left(\frac{1}{2}\right)}=3^{1 / 2}=\sqrt{3}
\)
\(
\Rightarrow l^2=3
\) -
Question 57 of 213
57. Question
The sum of all the elements in the set \(\{n \in\{1,2, \ldots ., 100\} \mid\) H.C.F. of \(n\) and 2040 is \(1\}\) is equal to _____. [JEE Main 2021 (Online) 22th July Evening Shift]
CorrectIncorrectHint
\(
2040=2^3 \times 3 \times 5 \times 17
\)
\(n\) should not be multiple of \(2,3,5\) and 17 .
\(
\begin{aligned}
& \text { Sum of all } n=(1+3+5+\ldots . .+99)-(3+9+15+21+\ldots . .+99)-(5+25+35 \\
& +55+65+85+95)-(17) \\
& =2500-\frac{17}{2}(3+99)-365-17 \\
& 2500-867-365-17 \\
& =1251
\end{aligned}
\) -
Question 58 of 213
58. Question
For \(k \in N\), let \(\frac{1}{\alpha(\alpha+1)(\alpha+2) \ldots \ldots . . .(\alpha+20)}=\sum_{K=0}^{20} \frac{A_k}{\alpha+k}\), where \(\alpha>0\). Then the value of \(100\left(\frac{A_{14}+A_{15}}{A_{13}}\right)^2\) is equal to ____. [JEE Main 2021 (Online) 20th July Evening Shift]
CorrectIncorrectHint
\(
\frac{1}{\alpha(\alpha+1)(\alpha+2) \ldots \ldots \ldots .(\alpha+20)}=\sum_{K=0}^{20} \frac{A_k}{\alpha+k}
\)
\(
A_{14}=\frac{1}{(-14)(-13) \ldots \ldots .(-1)(1) \ldots \ldots . .(6)}=\frac{1}{14!6!}
\)
\(
A_{15}=\frac{1}{(-15)(-14) \ldots \ldots .(-1)(1) \ldots \ldots . .(5)}=\frac{-1}{15!.5!}
\)
\(
A_{13}=\frac{1}{(-13) \ldots \ldots .(-1)(1) \ldots \ldots . .(7)}=\frac{-1}{13!.7!}
\)
\(
\begin{aligned}
& \frac{A_{14}}{A_{13}}=\frac{1}{14!.6!} \times-13!\times 7!=\frac{-7}{14}=-\frac{1}{2} \\
& \frac{A_{15}}{A_{13}}=\frac{-1}{15!\times 5!} \times-13!\times 7!=\frac{42}{15 \times 14}=\frac{1}{5} \\
& 100\left(\frac{A_{14}}{A_{13}}+\frac{A_{15}}{A_{13}}\right)^2=100\left(-\frac{1}{2}+\frac{1}{5}\right)^2=9
\end{aligned}
\) -
Question 59 of 213
59. Question
Let \(\left\{a_n\right\}_{n=1}^{\infty}\) be a sequence such that \(a _1=1, a _2=1\) and \(a_{n+2}=2 a_{n+1}+a_n\) for all \(n \geq 1\). Then the value of \(47 \sum_{n=1}^{\infty} \frac{a_n}{2^{3 n}}\) is equal to ____. [JEE Main 2021 (Online) 20th July Evening Shift]
CorrectIncorrectHint
\(
a_{n+2}=2 a_{n+1}+a_n \text {, let } \sum_{n=1}^{\infty} \frac{a_n}{8^n}=P
\)
Divide by \(8^n\) we get
\(
\begin{aligned}
& \frac{a_{n+2}}{8^n}=\frac{2 a_{n+1}}{8^n}+\frac{a_n}{8^n} \\
& \Rightarrow 64 \frac{a_{n+2}}{8^{n+2}}=\frac{16 a_{n+1}}{8^{n+1}}+\frac{a_n}{8^n}
\end{aligned}
\)
\(
\begin{aligned}
& 64 \sum_{n=1}^{\infty} \frac{a_{n+2}}{8^{n+2}}=16 \sum_{n=1}^{\infty} \frac{a_{n+1}}{8^{n+1}}+\sum_{n=1}^{\infty} \frac{a_n}{8^n} \\
& 64\left(P-\frac{a_1}{8}-\frac{a_2}{8^2}\right)=16\left(P-\frac{a_1}{8}\right)+P \\
& \Rightarrow 64\left(P-\frac{1}{8}-\frac{1}{64}\right)=16\left(P-\frac{1}{8}\right)+P \\
& 64 P-8-1=16 P-2+P \\
& 47 P=7
\end{aligned}
\) -
Question 60 of 213
60. Question
\(S_n(x)=\log _a 1 / 2 X+\log _a {1 / 3} X+\log _a {1 / 6} X+\log _a {1 / 11} X X+\log _a {1 / 18} X+\log _a {1 / 27} X+\ldots \ldots\) up to n-term, where \(a>1\). If \(S_{24}(x)=1093\) and \(S_{12}(2 x)=265\), then value of \(a\) is equal to ____. [JEE Main 2021 (Online) 16th March Evening Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& S_n(x)=\log _a x^2+\log _a x^3+\log _a x^6+\log _a x^{11} \\
& S_n(x)=2 \log _a x+3 \log _a x+6 \log _a x+11 \log _a x+\ldots \ldots \\
& S_n(x)=\log _a x(2+3+6+11+\ldots \ldots) \\
& S_r=2+3+6+11
\end{aligned}
\)
\(
\begin{aligned}
& S_r=2+3+6+11 \\
& \therefore T_n=2+(1+3+5+\ldots \ldots+(n-1))
\end{aligned}
\)
\(
\begin{aligned}
& =2+\frac{n-1}{2}[2.1+(n-2) 2] \\
& =2+(n-1)[1+(n-2)] \\
& =n^2-2 n+3
\end{aligned}
\)
General term \(T_r=r^2-2 r+3\)
\(
\begin{aligned}
& S_n(x)=\sum_{r=1}^n \log _a x\left(r^2-2 r+3\right) \\
& S_{24}(x)=\sum_{r=1}^{24} \log _a x\left(r^2-2 r+3\right) \\
& S_{24}(x)=\log _a x \sum_{r=1}^{24}\left(r^2-2 r+3\right) \\
& 1093=4372 \log _a x
\end{aligned}
\)
\(
\begin{aligned}
& \log _a x=\frac{1}{4} \\
& x=a^{1 / 4} \ldots . .( i ) \\
& S_{12}(2 x)=\log _a(2 x) \sum_{r=1}^{12}\left(r^2-2 r+3\right) \\
& 265=530 \log _a(2 x) \\
& \log _a(2 x)=\frac{1}{2} \\
& 2 x=a^{1 / 2} \ldots \text { (ii) }
\end{aligned}
\)
From (i) and (ii), we get
\(
\begin{aligned}
& 2 a^{\frac{1}{4}}=a^{\frac{1}{2}} \\
& \Rightarrow\left(2 a^{\frac{1}{4}}\right)^4=\left(a^{\frac{1}{2}}\right)^4 \\
& \Rightarrow 16 a=a^2 \\
& \Rightarrow a=16
\end{aligned}
\) -
Question 61 of 213
61. Question
Let \(\frac{1}{16}\), \(a\) and \(b\) be in G.P. and \(\frac{1}{a}, \frac{1}{b}, 6\) be in A.P., where \(a, b>0\). Then \(72(a+b)\) is equal to _____. [JEE Main 2021 (Online) 16th March Evening Shift]
CorrectIncorrectHint
\(a^2=\frac{b}{16}\) and \(\frac{2}{b}=\frac{1}{a}+6\)
Solving, we get \(a=\frac{1}{12}\) or \(a=-\frac{1}{4}\) [rejected]
if \(a=\frac{1}{12} \Rightarrow b=\frac{1}{9}\)
\(
\therefore 72(a+b)=72\left(\frac{1}{12}+\frac{1}{9}\right)=14
\) -
Question 62 of 213
62. Question
Consider an arithmetic series and a geometric series having four initial terms from the set \(\{11,8,21,16,26,32,4\}\). If the last terms of these series are the maximum possible four digit numbers, then the number of common terms in these two series is equal to ____. [JEE Main 2021 (Online) 16th March Morning Shift]
CorrectIncorrectHint
A.P. from the set will be \(11,16,21,26 \ldots .\).
G.P. from the set will be \(4,8,16,32,64,128,256,512,1024,2048,4096,8192 \ldots .\).So common terms are \(16,256,4096\).
-
Question 63 of 213
63. Question
The total number of 4-digit numbers whose greatest common divisor with 18 is 3 , is _____. [JEE Main 2021 (Online) 26th February Evening Shift]
CorrectIncorrectHint
Let \(N\) be the four digit number
\(
\operatorname{gcd}( N , 18)=3
\)Hence \(N\) is an odd integer which is divisible by 3 but not by 9 .
4 digit odd multiples of 3
1005,1011, \(\ldots\) \(9999 \rightarrow 1500\)
4 digit odd multiples of 9
1017,1035, \(\ldots\) \(9999 \rightarrow 500\)Hence number of such \(N =1000\)
-
Question 64 of 213
64. Question
If the arithmetic mean and geometric mean of the \(p^{\text {th }}\) and \(q^{\text {th }}\) terms of the sequence \(-16,8,-4,2, \ldots .\). . satisfy the equation \(4 x^2-9 x+5=0\), then \(p+q\) is equal to _____. [JEE Main 2021 (Online) 26th February Evening Shift]
CorrectIncorrectHint
Given, \(4 x^2-9 x+5=0\)
\(
\begin{aligned}
& \Rightarrow(x-1)(4 x-5)=0 \\
& \Rightarrow \text { A. M. }=\frac{5}{4}, \text { G. M. }=1 \text { (As A. M. } \geq \text { G. M) }
\end{aligned}
\)
Again, for the series
\(
-16,8,-4,2 \ldots
\)
\(
\begin{aligned}
& p^{t h} \text { term } t_p=-16\left(\frac{-1}{2}\right)^{p-1} \\
& q^{\text {th }} \text { term } t_p=16\left(\frac{-1}{2}\right)^{q-1} \\
& \text { Now, A. M. }=\frac{t_p+t_q}{2}=\frac{5}{4} \& \text { G. M. }=\sqrt{t_p t_q}=1 \\
& \Rightarrow 16^2\left(-\frac{1}{2}\right)^{p+q-2}=1 \\
& \Rightarrow(-2)^8=(-2)^{(p+q-2)} \\
& \Rightarrow p+q=10
\end{aligned}
\) -
Question 65 of 213
65. Question
Let \(A_1, A_2, A_3, \ldots . .\). be squares such that for each \(n \geq 1\), the length of the side of \(A_n\) equals the length of diagonal of \(A_{n+1}\). If the length of \(A_1\) is \(12 cm\), then the smallest value of \(n\) for which area of \(A_n\) is less than one, is ____. [JEE Main 2021 (Online) 25th February Morning Shift]
CorrectIncorrectHint
Let the terms are \(a, a r, a r^2, a r^3\)
\(
\begin{aligned}
& a+a r+a r^2+a r^3=\frac{65}{12} \dots(1)\\
& \frac{1}{a}+\frac{1}{a r}+\frac{1}{a r^2}+\frac{1}{a r^3}=\frac{65}{18} \\
& \frac{1}{a}\left(\frac{r^3+r^2+r+1}{r^3}\right)=\frac{65}{18} \ldots \ldots \ldots(2)
\end{aligned}
\)
Doing \(\frac{(1)}{(2)}\),
\(
a^2 r^3=\frac{18}{12}=\frac{3}{2}
\)
Also given, \(a^3 r^3=1 \Rightarrow a\left(\frac{3}{2}\right)=1 \Rightarrow a=\frac{2}{3}\)
\(
\begin{aligned}
& \frac{4}{9} r^3=\frac{3}{2} \Rightarrow r^3=\frac{3^3}{2^3} \Rightarrow r=\frac{3}{2} \\
& \alpha=a r^2=\frac{2}{3} \cdot\left(\frac{3}{2}\right)^2=\frac{3}{2} \\
& 2 \alpha=3
\end{aligned}
\) -
Question 66 of 213
66. Question
If \(m\) arithmetic means (A.Ms) and three geometric means (G.Ms) are inserted between 3 and 243 such that \(4^{\text {th }}\) A.M. is equal to \(2^{\text {nd }}\) G.M., then \(m\) is equal to ____. [JEE Main 2020 (Online) 3rd September Evening Slot]
CorrectIncorrectHint
Given \(m\) arithmetic means (A.Ms) present between 3 and 243
\(\therefore\) Common difference, \(d=\frac{b-a}{m+1}=\frac{240}{m+1}\)
\(\therefore\) 4th A.M. \(= a +4 d\)
\(
=3+4 \times \frac{240}{m+1}
\)
Also there are 3 G.M between 3 and 243
\(\therefore\) Common ratio \(( r )=\left(\frac{b}{a}\right)^{\frac{1}{n+1}}\)
where \(n =\) number of G.M inserted.
\(
\therefore r=\left(\frac{243}{3}\right)^{\frac{1}{3+1}}=3
\)
Given,
\(
\begin{aligned}
& 4^{\text {th }} A . M=2^{\text {nd }} G . M \\
& \Rightarrow 3+4 \times \frac{240}{m+1}=3(3)^2 \\
& \Rightarrow \frac{960}{m+1}=24 \\
& \Rightarrow m=39
\end{aligned}
\) -
Question 67 of 213
67. Question
The value of \((0.16)^{\log _{2.5}\left(\frac{1}{3}+\frac{1}{3^2}+\ldots . \text { to } \infty\right)}\) is equal to ____. [JEE Main 2020 (Online) 3rd September Morning Slot]
CorrectIncorrectHint
Given, \((0.16)^{\log _{2.5}\left(\frac{1}{3}+\frac{1}{3^2}+\ldots . \text { to } \infty\right)}\)
As sum of GP upto infinity \(=\frac{a}{1-r}\)
\(
\therefore \frac{1}{3}+\frac{1}{3^2}+\frac{1}{3^3}+\ldots \infty=\frac{\frac{1}{3}}{1-\frac{1}{3}}=\frac{1}{2}
\)
\(
\begin{aligned}
& \therefore(0.16)^{\log _{2.5}\left(\frac{1}{3}+\frac{1}{3^2}+\ldots . \text { to } \infty\right)} \\
& =(0.16)^{\log _{2.5}\left(\frac{1}{2}\right)} \\
& =\left(\frac{16}{100}\right)^{\log _{2.5}\left(\frac{1}{2}\right)} \\
& =\left(\frac{4}{10}\right)^{2\log _{2.5}\left(\frac{1}{2}\right)} \\
& =\left[\left(\frac{10}{4}\right)^{-2}\right]^{\log _{2.5}\left(\frac{1}{2}\right)} \\
& =\left[(2.5)^{-2}\right]^{\log _{2.5}\left(\frac{1}{2}\right)} \\
& =(2.5)^{-2 \log _{2.5}\left(\frac{1}{2}\right)} \\
& =\left(\frac{1}{2}\right)^{-2}=4 \\
&
\end{aligned}
\) -
Question 68 of 213
68. Question
The number of terms common to the two A.P’s \(3,7,11, \ldots . ., 407\) and \(2,9,16, \ldots .\). , 709 is _____. [JEE Main 2020 (Online) 9th January Evening Slot]
CorrectIncorrectHint
First A.P. is \(3,7,11,15,19,23, \ldots . .407\)
\(
d _1=4
\)
Second A.P. is \(2,9,16,23, \ldots . .709\)
\(
d_2=7
\)
First common term \(=23\)Common difference of new A.P using the common terms of the two given A.P’s is \(d =\) L.C.M. \((4,7)=28\)
Last term \(\leq 407\)
\(
\begin{aligned}
& \Rightarrow 23+(n-1)(28) \leq 407 \\
& \Rightarrow n \leq 14.7 \\
& \therefore n=14
\end{aligned}
\) -
Question 69 of 213
69. Question
The sum, \(\sum_{n=1}^7 \frac{n(n+1)(2 n+1)}{4}\) is equal to _____. [JEE Main 2020 (Online) 8th January Evening Slot]
CorrectIncorrectHint
\(
\begin{aligned}
& \sum_{n=1}^7 \frac{n(n+1)(2 n+1)}{4} \\
& =\frac{1}{4} \sum_{n=1}^7\left(2 n^3+3 n^2+n\right) \\
& =\frac{1}{2} \sum_{n=1}^7 n^3+\frac{3}{4} \sum_{n=1}^7 n^2+\frac{1}{4} \sum_{n=1}^7 n \\
& =\frac{1}{2}\left(\frac{7(7+1)}{2}\right)^2+\frac{3}{4}\left(\frac{7(7+1)(14+1)}{6}\right)+\frac{1}{4} \frac{7(8)}{2} \\
& =(49)(8)+(15 \times 7)+(7) \\
& =392+105+7=504
\end{aligned}
\) -
Question 70 of 213
70. Question
The sum \(\sum_{k=1}^{20}(1+2+3+\ldots+k)\) is : [JEE Main 2020 (Online) 8th January Morning Slot]
CorrectIncorrectHint
\(
\begin{aligned}
& \sum_{k=1}^{20}(1+2+3+\ldots+k) \\
& =\sum_{k=1}^{20} \frac{k(k+1)}{2} \\
& =\sum_{k=1}^{20} \frac{k^2}{2}+\sum_{k=1}^{20} \frac{k}{2} \\
& =\frac{1}{2} \times \frac{20 \times 21 \times 41}{6}+\frac{1}{2} \times \frac{20 \times 21}{2} \\
& =1540
\end{aligned}
\) -
Question 71 of 213
71. Question
Let \(a, a r, a r^2, \ldots\) be an infinite G.P. If \(\sum_{n=0}^{\infty} a r^n=57\) and \(\sum_{n=0}^{\infty} a^3 r^{3 n}=9747\), then \(a+18 r\) is equal to [JEE Main 2024 (Online) 9th April Evening Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& \sum_{n=0}^{\infty} a r^n=57 \quad \Rightarrow \frac{a}{1-r}=57 \dots(i) \\
& \sum_{n=0}^{\infty} a^3 r^{3 n}=9747 \quad \Rightarrow \frac{a^3}{1-r^3}=9747 \dots(ii) \\
& \frac{\left(1-r^3\right)}{(1-r)^3}=\frac{(57)^3}{9747}=19 \\
& \Rightarrow \quad \frac{(1-r)\left(1+r+r^2\right)}{(1-r)^3}=19 \\
& \Rightarrow \quad 18 r^2-39 r+18=0 \\
& \Rightarrow \quad r=\frac{2}{3}, \frac{3}{2} \text { (rejected) } \\
& \therefore \quad a=19 \\
& \quad a+18 r \\
& \quad=19+12=31
\end{aligned}
\) -
Question 72 of 213
72. Question
If the sum of the series \(\frac{1}{1 \cdot(1+ d )}+\frac{1}{(1+ d )(1+2 d )}+\ldots+\frac{1}{(1+9 d )(1+10 d )}\) is equal to 5 , then \(50 d\) is equal to : [JEE Main 2024 (Online) 9th April Morning Shift]
CorrectIncorrectHint
\(
\frac{1}{1 \cdot(1+d)}+\frac{1}{(1+d)(1+2 d)}+\ldots+\frac{1}{(1+9 d)(1+10 d)}=5
\)
Multiply and divide by \(d\)
\(
\begin{aligned}
& \frac{1}{d}\left[\frac{d}{1 \times(1+d)}+\frac{d}{(1+d)(1+2 d)}+\ldots+\frac{d}{(1+9 d)(1+10 d)}\right]=5 \\
& \frac{1}{d}\left[\left(1-\frac{1}{1+d}\right)+\left(\frac{1}{1+d}-\frac{1}{1+2 d}\right)+\ldots+\left(\frac{1}{1+9 d}-\frac{1}{1+10 d}\right)\right]=5 \\
& \frac{1}{d}\left[1-\frac{1}{1+10 d}\right]=5 \\
& \frac{1}{d}\left[\frac{1+10 d-1}{1+10 d}\right]=5 \\
& \frac{10}{1+10 d}=5 \\
& 1+10 d=2 \\
& d=\frac{1}{10} \\
& 50 d=50 \times \frac{1}{10}=5
\end{aligned}
\) -
Question 73 of 213
73. Question
In an increasing geometric progression of positive terms, the sum of the second and sixth terms is \(\frac{70}{3}\) and the product of the third and fifth terms is 49 . Then the sum of the \(4^{\text {th }}, 6^{\text {th }}\) and \(8^{\text {th }}\) terms is equal to: [JEE Main 2024 (Online) 8th April Evening Shift]
CorrectIncorrectHint
Let’s denote the first term of the geometric progression by \(a\) and the common ratio by \(r\). The terms of the geometric progression can be written as follows:
First term: \(a\)
Second term: \(a r\)
Third term: \(\left(a r^2\right)\)
Fourth term: \(\left(a r^3\right)\)
Fifth term: \(\left(a r^4\right)\)
Sixth term: \(\left(a r^5\right)\)
Eighth term: \(\left(a r^7\right)\)
We are given two key pieces of information:
1. The sum of the second and sixth terms is \(\frac{70}{3}\) :
\(
a r+a r^5=\frac{70}{3}
\)
2. The product of the third and fifth terms is 49 :
\(
\begin{aligned}
& \left(a r^2\right) \cdot\left(a r^4\right)=49 \\
& a^2 r^6=49 \\
& a^2=\frac{49}{r^6} \\
& a=\frac{7}{r^3}
\end{aligned}
\)
Substituting \(a=\frac{7}{r^3}\) into the first equation:
\(
\begin{aligned}
& \frac{7}{r^3} \cdot r+\frac{7}{r^3} \cdot r^5=\frac{70}{3} \\
& \frac{7 r}{r^3}+\frac{7 r^5}{r^3}=\frac{70}{3} \\
& \frac{7}{r^2}+\frac{7 r^2}{1}=\frac{70}{3}
\end{aligned}
\)
Let \(x=r^2\). Then:
\(
\frac{7}{x}+7 x=\frac{70}{3}
\)
Multiply through by \(3 x\) to clear the denominator:
\(
21+21 x^2=70 x
\)
Rearrange into a standard quadratic equation:
\(
21 x^2-70 x+21=0
\)
Divide by 7 to simplify:
\(
3 x^2-10 x+3=0
\)
Solve this quadratic equation using the quadratic formula:
\(
x=\frac{-b \pm \sqrt{b^2-4 a c}}{2 a}
\)
Where \(a=3, b=-10\), and \(c=3\). Thus:
\(
\begin{aligned}
& x=\frac{10 \pm \sqrt{100-36}}{6} \\
& x=\frac{10 \pm \sqrt{64}}{6} \\
& x=\frac{10 \pm 8}{6} \\
& x=3 \text { or } x=\frac{1}{3}
\end{aligned}
\)
Since \(x=r^2\) and \(r\) is positive, we get \(r=\sqrt{3}\) or \(r=\frac{1}{\sqrt{3}}\). We need to choose the value that results in positive, increasing terms:
If \(r=\sqrt{3}\) :
\(
a=\frac{7}{r^3}=\frac{7}{(\sqrt{3})^3}=\frac{7}{3 \sqrt{3}}=\frac{7}{3} \cdot \frac{1}{\sqrt{3}}=\frac{7 \sqrt{3}}{9}
\)
Now we can determine the sum of the 4 th, 6 th, and 8th terms:
The 4th term is: \(a r^3=\frac{7 \sqrt{3}}{9} \cdot 3 \sqrt{3}=7\)
The 6 th term is: \(a r^5=\frac{7 \sqrt{3}}{9} \cdot 9 \sqrt{3}=21\)
The 8th term is: \(a r^7=\frac{7 \sqrt{3}}{9} \cdot 27(\sqrt{3})=49\)
Adding these together:
\(
(4 t h+6 \text { th }+8 \text { thterms })=7+21+63=91
\)
Therefore, the sum of the 4 th, 6th, and 8th terms is 91 . -
Question 74 of 213
74. Question
Let \(A B C\) be an equilateral triangle. A new triangle is formed by joining the middle points of all sides of the triangle \(A B C\) and the same process is repeated infinitely many times. If \(P\) is the sum of perimeters and \(Q\) is be the sum of areas of all the triangles formed in this process, then : [JEE Main 2024 (Online) 6th April Evening Shift]
CorrectIncorrectHint
\(\triangle A B C\) is an equilateral triangle having side \(=a\) unit
Now, perimeter \(=\) sum of all sides \(=3 a\)
\(
\text { Area }=\frac{\sqrt{3}}{4} a^2
\)
Now, \(\ln \triangle D E F, D E=\frac{a}{2}=E F=D F\)
Perimeter \(=3 \times \frac{a}{2}=\frac{3 a}{2}\)
Area \(=\frac{\sqrt{3}}{4} \times\left(\frac{a}{2}\right)^2=\frac{\sqrt{3} a^2}{16}\)
Now, \(P=3 a+\frac{3 a}{2}+\frac{3 a}{4}+\cdots\)
\(
\begin{aligned}
& Q=\frac{\sqrt{3}}{4} a^2+\frac{\sqrt{3}}{16} a^2+\frac{\sqrt{3}}{64} a^2+\cdots \\
& P=\frac{3 a}{1-\frac{1}{2}}=3 a \times 2 \Rightarrow P=6 a \dots(i) \\
& Q=\frac{\frac{\sqrt{3}}{4} a^2}{1-\frac{1}{4}}=\frac{4}{3} \times \frac{\sqrt{3}}{4} a^2 \quad Q=\frac{\sqrt{3}}{3} a^2 \dots(ii)
\end{aligned}
\)
From equation (i) & (ii)
\(
\begin{aligned}
& P=6 a \\
& Q=\frac{\sqrt{3}}{3} a^2 \\
& Q=\frac{\sqrt{3}}{3} \times \frac{P^2}{36} \\
& P^2=36 \sqrt{3} Q
\end{aligned}
\) -
Question 75 of 213
75. Question
A software company sets up \(m\) number of computer systems to finish an assignment in 17 days. If 4 computer systems crashed on the start of the second day, 4 more computer systems crashed on the start of the third day and so on, then it took 8 more days to finish the assignment. The value of \(m\) is equal to: [JEE Main 2024 (Online) 6th April Evening Shift]
CorrectIncorrectHint
To determine the value of \(m\), we need to formulate the problem using some basic concepts of arithmetic progression and work. Let’s first understand the nature of the problem:
Initially, there are \(m\) computers, and it is estimated that with these \(m\) computers, the assignment can be completed in 17 days.
However, due to the crash of 4 computers every day starting from the second day onward, the total time taken extends by 8 days, making it 25 days in total.
To begin with, let’s define the total work ( \(W\) ) in terms of the number of computers and days:
The total work \(( W )\) is given by:
The amount of work completed each day with \(m\) computers for 17 days:
\(
W=17 m
\)
When computers crash, the number of working computers each day forms an arithmetic sequence. On the first day, there are \(m\) computers. On the second day, there are \(m -4\) computers, on the third day, there are \(m -8\) computers, and so on. We need to sum this series until 25 days are completed.
This can be formulated as:
Total work done over 25 days with decrement in the number of computers:
\(
W=m+(m-4)+(m-8)+\ldots+[m-4 \times(n-1)]
\)
where \(n\) is the number of days. Here, \(n=25\).
Notice that we form an arithmetic series where the first term (a) is \(m\) and the common difference (d) is -4 . The sum of the first \(n\) terms of an arithmetic series is:
\(
S_n=\frac{n}{2}[2 a+(n-1) d]
\)
Plugging in the values:
\(
\begin{aligned}
& S_{25}=\frac{25}{2}[2 m+(25-1)(-4)] \\
& S_{25}=\frac{25}{2}[2 m-96] \\
& S_{25}=\frac{25}{2}[2 m-96]=25(m-48)
\end{aligned}
\)
This work should be equivalent to the work calculated earlier, so:
\(
17 m=25(m-48)
\)
Solving for \(m\) :
\(
\begin{aligned}
& 17 m=25 m-1200 \\
& 8 m=1200 \\
& m=150
\end{aligned}
\) -
Question 76 of 213
76. Question
For \(x \geqslant 0\), the least value of \(K\), for which \(4^{1+x}+4^{1-x}, \frac{ K }{2}, 16^x+16^{-x}\) are three consecutive terms of an A.P., is equal to : [JEE Main 2024 (Online) 5th April Evening Shift]
CorrectIncorrectHint
To determine the least value of \(K\) for which the terms \(4^{1+x}+4^{1-x}, \frac{ K }{2}, 16^x+16^{-x}\) form an arithmetic progression (A.P.), we need to establish the relationship among these terms in an A.P.
For three numbers to be in an arithmetic progression, the middle term must be the average of the other two terms. Therefore, we can write:
\(
\frac{4^{1+x}+4^{1-x}+16^x+16^{-x}}{2}=\frac{K}{2}
\)
First, simplify each term individually:
1. Consider \(4^{1+x}+4^{1-x}\) :
\(
4^{1+x}=4 \cdot 4^x=4 \cdot\left(2^2\right)^x=4 \cdot 2^{2 x}=4 \cdot 2^{2 x}
\)
and \(4^{1-x}=4 \cdot 4^{-x}=4 \cdot\left(2^2\right)^{-x}=4 \cdot 2^{-2 x}=4 \cdot 2^{-2 x}\)
Thus,
\(
4^{1+x}+4^{1-x}=4 \cdot 2^{2 x}+4 \cdot 2^{-2 x}=4\left(2^{2 x}+2^{-2 x}\right)
\)
2. Consider \(16^x+16^{-x}\) :
\(
16^x=\left(2^4\right)^x=2^{4 x}
\)
and \(16^{-x}=\left(2^4\right)^{-x}=2^{-4 x}\)
Thus,
\(
16^x+16^{-x}=2^{4 x}+2^{-4 x}
\)
3. Combine the terms and set up the equation:
\(
\frac{4\left(2^{2 x}+2^{-2 x}\right)+2^{4 x}+2^{-4 x}}{2}=\frac{K}{2}
\)
Multiply both sides by 2 :
\(
4\left(2^{2 x}+2^{-2 x}\right)+2^{4 x}+2^{-4 x}=K
\)
To find the least value of \(K\), let’s assume \(x=0\) (since \(x\) can range over non-negative values):
For \(x=0\) :
\(
4\left(2^{2 \cdot 0}+2^{-2 \cdot 0}\right)+2^{4 \cdot 0}+2^{-4 \cdot 0}
\)
This simplifies to:
\(
\begin{aligned}
& 4\left(2^0+2^0\right)+2^0+2^0 \\
& =4(1+1)+1+1 \\
& =4 \cdot 2+1+1 \\
& =8+1+1 \\
& =10
\end{aligned}
\)
Therefore, the least value of \(K\) that ensures the values form an arithmetic progression is 10 . -
Question 77 of 213
77. Question
If \(\frac{1}{\sqrt{1}+\sqrt{2}}+\frac{1}{\sqrt{2}+\sqrt{3}}+\ldots+\frac{1}{\sqrt{99}+\sqrt{100}}=m\) and \(\frac{1}{1 \cdot 2}+\frac{1}{2 \cdot 3}+\ldots+\frac{1}{99 \cdot 100}= n\), then the point \(( m , n )\) lies on the line [JEE Main 2024 (Online) 5th April Morning Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& \frac{1}{\sqrt{1}+\sqrt{2}}+\frac{1}{\sqrt{2}+\sqrt{3}}+\ldots+\frac{1}{\sqrt{99}+\sqrt{100}}=m \\
& \text { and } \frac{1}{1 \cdot 2}+\frac{1}{2 \cdot 3}+\ldots+\frac{1}{99 \cdot 100}=n \\
& \frac{1}{\sqrt{1}+\sqrt{2}}+\frac{1}{\sqrt{2}+\sqrt{3}}+\ldots+\frac{1}{\sqrt{99}+\sqrt{100}} \\
& =\frac{1}{\sqrt{1}+\sqrt{2}} \times \frac{\sqrt{2}-\sqrt{1}}{\sqrt{2}-\sqrt{1}}+\frac{1}{\sqrt{3}+\sqrt{2}} \times \frac{\sqrt{3}-\sqrt{2}}{\sqrt{3}-\sqrt{2}} \\
& \quad+\ldots+\frac{1}{\sqrt{99}+\sqrt{100}} \times \frac{\sqrt{100}-\sqrt{99}}{\sqrt{100}-\sqrt{99}} \\
& =\sqrt{2}-\sqrt{1}+\sqrt{3}-\sqrt{2}+\ldots+\sqrt{100}-\sqrt{99} \\
& =\sqrt{100}-\sqrt{1} \\
& =10-1 \\
& \Rightarrow m=9
\end{aligned}
\)
and \(\frac{1}{1 \cdot 2}+\frac{1}{2 \cdot 3}+\ldots+\frac{1}{99 \cdot 100}=n\)
\(
\begin{aligned}
& \frac{2-1}{1 \times 2}+\frac{3-2}{2 \times 3}+\ldots+\frac{100-99}{100 \times 99}=n \\
& \Rightarrow 1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\ldots+\frac{1}{99}-\frac{1}{100}=n \\
& \Rightarrow n=1-\frac{1}{100} \\
& \Rightarrow n=\frac{99}{100} \\
& (m, n)=\left(9, \frac{99}{100}\right)
\end{aligned}
\)
Satisfies the line \(11 x-100 y=0\) -
Question 78 of 213
78. Question
The value of \(\frac{1 \times 2^2+2 \times 3^2+\ldots+100 \times(101)^2}{1^2 \times 2+2^2 \times 3+\ldots+100^2 \times 101}\) is [JEE Main 2024 (Online) 4th April Evening Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& \frac{1 \times 2^2+2 \times 3^2+\ldots+100 \times(101)^2}{1^2 \times 2+2^2 \times 3+\ldots+100^2 \times 101} \\
& \Rightarrow \frac{\sum_{n=1}^{100} n(n+1)^2}{\sum_{n=1}^{100} n^2(n+1)} \\
& \Rightarrow \frac{\sum_{n=1}^{100} n^3+2 n^2+n}{\sum_{n=1}^{100} n^3+n^2}
\end{aligned}
\)
\(
\begin{aligned}
& =\frac{\left(\frac{100(101)}{2}\right)^2+\frac{2 \cdot 100(101)(201)}{6}+\frac{100(101)}{2}}{\left(\frac{100(101)}{2}\right)^2+\frac{100(101)(201)}{6}} \\
& =\frac{300(101)+4(201)+6}{300(101)+2(201)}=\frac{5185}{5117}=\frac{305}{301}
\end{aligned}
\) -
Question 79 of 213
79. Question
Let three real numbers \(a, b, c\) be in arithmetic progression and \(a+1, b, c+3\) be in geometric progression. If \(a>10\) and the arithmetic mean of \(a, b\) and \(c\) is 8 , then the cube of the geometric mean of \(a, b\) and \(c\) is [JEE Main 2024 (Online) 4th April Evening Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& 2 b=a+c \dots(1) \\
& b^2=(a+1)(c+3) \dots(2) \\
& \frac{a+b+c}{3}=8 \dots(3) \\
& \Rightarrow \frac{3 b}{3}=8 \\
& \quad b=8 \\
& \Rightarrow \quad a c+3 a+c+3=64 \\
& 3 a+c+a c=61 \dots(4) \\
& a+c=16 \\
& c=16-a
\end{aligned}
\)
from equation (4)
\(
\begin{aligned}
& 3 a+16-a+a(16-a)=61 \\
& \Rightarrow \quad(a-15)(a-3)=0 \\
& \quad a=15(a>10) \\
& \Rightarrow \quad a=15, b=8, c=1 \\
& \left((a \cdot b \cdot c)^{\frac{1}{3}}\right)^3=15 \times 8 \times 1=120
\end{aligned}
\) -
Question 80 of 213
80. Question
Let the first three terms \(2, p\) and \(q\), with \(q \neq 2\), of a G.P. be respectively the \(7^{\text {th }}, 8^{\text {th }}\) and \(13^{\text {th }}\) terms of an A.P. If the \(5^{\text {th }}\) term of the G.P. is the \(n^{\text {th }}\) term of the A.P., then \(n\) is equal to: [EE Main 2024 (Online) 4th April Morning Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& \text { Let } p=2 r, q=2 r^2 \\
& T_7=2, T_8=2 r, T_{13}=2 r^2 \\
& d=2 r-2=2(r-1) \\
& 2 r^2=T_7+6 d=2+6(2)(r-1)=12 r-10 \\
& \Rightarrow r^2-6 r+5=0 \\
& \Rightarrow(r-1)(r-5)=0 \\
& \therefore r=1,5 \\
& r=1 \text { (rejected) as } q \neq 2 \\
& \therefore r=5 \\
& 5^{\text {th }} \text { term of G.P }=2 . r^4=2.5^4 \\
& \text { Let } 1^{\text {st }} \text { term of A.P be} a, d=8 \\
& 2=a+(6)(8) \Rightarrow a=-46 \\
& n ^{\text {th }} \text { term of A.P }=-46+(n-1) 8=8 n-54 \\
& 2.5^4=8 n-54 \\
& \Rightarrow 1250+54=8 n \\
& \Rightarrow n=\frac{1304}{8}=163
\end{aligned}
\) -
Question 81 of 213
81. Question
Let \(S_n\) denote the sum of the first \(n\) terms of an arithmetic progression. If \(S_{10}=390\) and the ratio of the tenth and the fifth terms is \(15: 7\), then \(S_{15}-S_5\) is equal to : [JEE Main 2024 (Online) 1st February Evening Shift]
CorrectIncorrectHint
To solve this problem, we will start by using the properties of an arithmetic progression (AP).
The sum of the first \(n\) terms of an AP can be calculated using the formula: \(S_n=\frac{n}{2}(2 a+(n-1) d)\) where \(S_n\) is the sum of the first \(n\) terms, \(a\) is the first term, and \(d\) is the common difference between the terms.
Given the information: \(S_{10}=390\)
We can plug \(n=10\) into the sum formula to get:
\(
\begin{aligned}
& S_{10}=\frac{10}{2}(2 a+(10-1) d) \\
& 390=5(2 a+9 d) \\
& 390=10 a+45 d \\
& 78=2 a+9 d \quad \ldots \ldots \ldots .(1)
\end{aligned}
\)
Next, we’re given the ratio of the tenth term \(\left(T_{10}\right)\) to the fifth term \(\left(T_5\right): \frac{T_{10}}{T_5}=\frac{15}{7}\)
The \(n\)th term of an AP is given by:
\(
T_n=a+(n-1) d
\)
So, for the tenth term: \(T_{10}=a+(10-1) d=a+9 d\)
And for the fifth term:
\(
T_5=a+(5-1) d=a+4 d
\)
Now we can write the ratio as:
\(
\begin{aligned}
& \frac{a+9 d}{a+4 d}=\frac{15}{7} \\
& 7(a+9 d)=15(a+4 d) \\
& 7 a+63 d=15 a+60 d \\
& 63 d-60 d=15 a-7 a \\
& 3 d=8 a \quad \ldots \ldots \ldots(2)
\end{aligned}
\)
Now we have two equations (1) and (2):
\(
\begin{aligned}
& 78=2 a+9 d \\
& 3 d=8 a
\end{aligned}
\)
We can solve these equations simultaneously.
From equation (2):
\(
d=\frac{8}{3} a
\)
Plugging this back into (1):
\(
\begin{aligned}
& 78=2 a+9\left(\frac{8}{3} a\right) \\
& 78=2 a+24 a \\
& 78=26 a \\
& a=3
\end{aligned}
\)
Now we can find \(d\) :
\(
\begin{aligned}
& d=\frac{8}{3} a \\
& d=\frac{8}{3} \times 3 \\
& d=8
\end{aligned}
\)
Now we can find \(S_{15}\) and \(S_5\) using the formula for the sum of an AP.
For \(S_{15}\) :
\(
\begin{aligned}
& S_{15}=\frac{15}{2}(2 \cdot 3+(15-1) \cdot 8) \\
& S_{15}=\frac{15}{2}(6+14 \cdot 8) \\
& S_{15}=\frac{15}{2}(6+112) \\
& S_{15}=\frac{15}{2} \cdot 118 \\
& S_{15}=15 \cdot 59 \\
& S_{15}=885
\end{aligned}
\)
For \(S_5\) :
\(
\begin{aligned}
& S_5=\frac{5}{2}(2 \cdot 3+(5-1) \cdot 8) \\
& S_5=\frac{5}{2}(6+4 \cdot 8) \\
& S_5=\frac{5}{2}(6+32) \\
& S_5=\frac{5}{2} \cdot 38 \\
& S_5=5 \cdot 19 \\
& S_5=95
\end{aligned}
\)
The difference \(S_{15}-S_5\) is:
\(
\begin{aligned}
& S_{15}-S_5=885-95 \\
& S_{15}-S_5=790
\end{aligned}
\) -
Question 82 of 213
82. Question
Let \(3, a, b, c\) be in A.P. and \(3, a-1, b+1, c+9\) be in G.P. Then, the arithmetic mean of \(a, b\) and \(c\) is : [JEE Main 2024 (Online) 1st February Morning Shift]
CorrectIncorrectHint
Since \(3, a, b, c\) are in arithmetic progression (A.P.), the common difference can be calculated using the term \(a\) (the second term) as follows:
\(
d=a-3
\)
The nth term of an A.P. is given by the formula:
\(
T_n=a+(n-1) d
\)
So, using this formula, we can express \(b\) and \(c\) in terms of \(a\) and \(d\) :
\(
\begin{aligned}
& b=a+d \\
& c=a+2 d
\end{aligned}
\)
Substituting \(d=a-3\) into these expressions:
\(
\begin{aligned}
& b=a+(a-3) \\
& c=a+2(a-3)
\end{aligned}
\)
Therefore:
\(
\begin{aligned}
& b=2 a-3 \\
& c=3 a-6
\end{aligned}
\)
Now, let’s consider that \(3, a-1, b+1, c+9\) are in geometric progression (G.P.). For terms in a G.P., the ratio (common ratio, r) between consecutive terms is constant. So:
\(
\frac{a-1}{3}=\frac{b+1}{a-1}=\frac{c+9}{b+1}
\)
Now, we will establish the relation between the terms using the property of G.P.:
\(
\begin{aligned}
& \frac{a-1}{3}=\frac{b+1}{a-1} \\
& (a-1)^2=3(b+1) \\
& a^2-2 a+1=3 b+3
\end{aligned}
\)
Substituting \(b=2 a-3\), we get:
\(
\begin{aligned}
& a^2-2 a+1=3(2 a-3)+3 \\
& a^2-2 a+1=6 a-9+3 \\
& a^2-8 a+7=0
\end{aligned}
\)
Solving this quadratic equation:
\(
(a-7)(a-1)=0
\)
Hence, \(a=7\) or \(a=1\). However, if \(a=1\), the terms \(3, a-1, b+1, c+9\) cannot form a G.P. as it would involve division by zero. Therefore, \(a=7\). We use this value to find \(b\) and \(c\) :
\(
\begin{aligned}
& b=2 a-3=2(7)-3=14-3=11 \\
& c=3 a-6=3(7)-6=21-6=15
\end{aligned}
\)
Now we can find the arithmetic mean \((A)\) of \(a, b\), and \(c\) :
\(
\begin{aligned}
& A=\frac{a+b+c}{3} \\
& A=\frac{7+11+15}{3} \\
& A=\frac{33}{3} \\
& A=11
\end{aligned}
\)
Hence, the arithmetic mean of \(a, b\), and \(c\) is 11 , which corresponds to Option D. -
Question 83 of 213
83. Question
Let \(2^{\text {nd }}, 8^{\text {th }}\) and \(44^{\text {th }}\) terms of a non-constant A. P. be respectively the \(1^{\text {st }}, 2^{\text {nd }}\) and \(3^{\text {rd }}\) terms of a G. P. If the first term of the A. P. is 1 , then the sum of its first 20 terms is equal to [JEE Main 2024 (Online) 31st January Evening Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& 1+d, \quad 1+7 d, 1+43 d \text { are in GP } \\
& (1+7 d)^2=(1+d)(1+43 d) \\
& 1+49 d^2+14 d=1+44 d+43 d^2 \\
& 6 d^2-30 d=0 \\
& d=5 \\
& S_{20}=\frac{20}{2}[2 \times 1+(20-1) \times 5] \\
& \quad=10[2+95] \\
& \quad=970
\end{aligned}
\) -
Question 84 of 213
84. Question
For \(0<c<b<a\), let \((a+b-2 c) x^2+(b+c-2 a) x+(c+a-2 b)=0\) and \(\alpha \neq 1\) be one of its root. Then, among the two statements
(I) If \(\alpha \in(-1,0)\), then \(b\) cannot be the geometric mean of \(a\) and \(c\)
(II) If \(\alpha \in(0,1)\), then \(b\) may be the geometric mean of \(a\) and \(c\) [JEE Main 2024 (Online) 31st January Morning Shift]CorrectIncorrectHint
\(
\begin{aligned}
& f(x)=(a+b-2 c) x^2+(b+c-2 a) x+(c+a-2 b) \\
& f(x)=a+b-2 c+b+c-2 a+c+a-2 b=0 \\
& f(1)=0 \\
& \therefore \alpha \cdot 1=\frac{c+a-2 b}{a+b-2 c} \\
& \alpha=\frac{c+a-2 b}{a+b-2 c} \\
& \text { If, }-1<\alpha<0 \\
& -1<\frac{c+a-2 b}{a+b-2 c}<0 \\
& b+c<2 a \text { and } b>\frac{a+c}{2}
\end{aligned}
\)
therefore, \(b\) cannot be G.M. between \(a\) and \(c\).
\(
\begin{aligned}
& \text { If, } 0<\alpha<1 \\
& 0<\frac{c+a-2 b}{a+b-2 c}<1 \\
& b>c \text { and } b<\frac{a+c}{2}
\end{aligned}
\)
Therefore, \(b\) may be the G.M. between \(a\) and \(c\). -
Question 85 of 213
85. Question
The sum of the series \(\frac{1}{1-3 \cdot 1^2+1^4}+\frac{2}{1-3 \cdot 2^2+2^4}+\frac{3}{1-3 \cdot 3^2+3^4}+\ldots\) up to 10 terms is [JEE Main 2024 (Online) 31st January Morning Shift]
CorrectIncorrectHint
General term of the sequence,
\(
\begin{aligned}
& T _{ r }=\frac{ r }{1-3 r ^2+ r ^4} \\
& T _{ r }=\frac{ r }{ r ^4-2 r ^2+1- r ^2} \\
& T _{ r }=\frac{ r }{\left( r ^2-1\right)^2- r ^2} \\
& T _{ r }=\frac{ r }{\left( r ^2- r -1\right)\left( r ^2+ r -1\right)} \\
& T _{ r }=\frac{\frac{1}{2}\left[\left( r ^2+ r -1\right)-\left( r ^2- r -1\right)\right]}{\left( r ^2- r -1\right)\left( r ^2+ r -1\right)} \\
&=\frac{1}{2}\left[\frac{1}{ r ^2- r -1}-\frac{1}{ r ^2+ r -1}\right]
\end{aligned}
\)
Sum of 10 terms,
\(
\sum_{ r =1}^{10} T _{ r }=\frac{1}{2}\left[\frac{1}{-1}-\frac{1}{109}\right]=\frac{-55}{109}
\) -
Question 86 of 213
86. Question
Let \(a\) and \(b\) be be two distinct positive real numbers. Let \(11^{\text {th }}\) term of a GP, whose first term is \(a\) and third term is \(b\), is equal to \(p^{\text {th }}\) term of another GP, whose first term is \(a\) and fifth term is \(b\). Then \(p\) is equal to [JEE Main 2024 (Online) 30th January Evening Shift]
CorrectIncorrectHint
The problem involves finding a relation between terms of two different geometric progressions (GPs) which share common first terms but have different terms equated to the same value. We solve this by setting up equations based on the given conditions for each GP and comparing the terms specified to be equal.
For the first GP, with first term \(a\) and third term \(b\) :
The third term is given by \(t_3=a r^2=b\), leading to \(r^2=\frac{b}{a}\).
The eleventh term is \(t_{11}=a r^{10}=a\left(\frac{b}{a}\right)^5\).
For the second GP, with first term \(a\) and fifth term \(b\) :
The fifth term is \(T_5=a r^4=b\), yielding \(r^4=\frac{b}{a}\) and \(r=\left(\frac{b}{a}\right)^{1 / 4}\). The \(p^{\text {th }}\) term is thus \(T_p=a r^{p-1}=a\left(\frac{b}{a}\right)^{\frac{p-1}{4}}\).Equating the eleventh term of the first GP to the \(p ^{\text {th }}\) term of the second GP gives: \(a\left(\frac{b}{a}\right)^5=a\left(\frac{b}{a}\right)^{\frac{p-1}{4}}\).
Simplifying, we find that \(5=\frac{p-1}{4}\), leading to \(p=21\), which is the solution. -
Question 87 of 213
87. Question
Let \(S_n\) denote the sum of first \(n\) terms of an arithmetic progression. If \(S_{20}=790\) and \(S_{10}=145\), then \(S _{15}- S _5\) is : [JEE Main 2024 (Online) 30th January Morning Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& S _{20}=\frac{20}{2}[2 a +19 d ]=790 \\
& 2 a +19 d =79 \\
& S _{10}=\frac{10}{2}[2 a +9 d ]=145 \\
& 2 a +9 d =29
\end{aligned}
\)
From (1) and (2) \(a=-8, d=5\)
\(
\begin{aligned}
& S_{15}-S_5=\frac{15}{2}[2 a+14 d]-\frac{5}{2}[2 a+4 d] \\
& =\frac{15}{2}[-16+70]-\frac{5}{2}[-16+20] \\
& =405-10 \\
& =395
\end{aligned}
\) -
Question 88 of 213
88. Question
If \(\log _e a , \log _e b , \log _e c\) are in an A.P. and \(\log _e a -\log _e 2 b , \log _e 2 b -\log _e 3 c , \log _e 3 c -\log _e\) a are also in an A.P, then \(a: b: c\) is equal to [JEE Main 2024 (Online) 29th January Evening Shift]
CorrectIncorrectHint
\(\log _e a, \log _e b, \log _e c\) are in A.P.
\(
\therefore b ^2= ac \ldots . . \text { (i) }
\)
Also
\(\log _e\left(\frac{a}{2 b}\right), \log _e\left(\frac{2 b}{3 c}\right), \log _e\left(\frac{3 c}{a}\right)\) are in A.P.
\(
\begin{aligned}
& \left(\frac{2 b}{3 c}\right)^2=\frac{a}{2 b} \times \frac{3 c}{a} \\
& \frac{b}{c}=\frac{3}{2}
\end{aligned}
\)
Putting in eq. (i) \(b^2=a \times \frac{2 b}{3}\)
\(
\begin{aligned}
& \frac{a}{b}=\frac{3}{2} \\
& a: b: c=9: 6: 4
\end{aligned}
\) -
Question 89 of 213
89. Question
If each term of a geometric progression \(a_1, a_2, a_3, \ldots\) with \(a_1=\frac{1}{8}\) and \(a_2 \neq a_1\), is the arithmetic mean of the next two terms and \(S_n=a_1+a_2+\ldots \ldots+a_n\), then \(S_{20}-S_{18}\) is equal to [JEE Main 2024 (Online) 29th January Evening Shift]
CorrectIncorrectHint
Let \(r\) th term of the GP be \(a^{n-1}\). Given,
\(
\begin{aligned}
& 2 a_r=a_{r+1}+a_{r+2} \\
& 2 a r^{n-1}=a r^n+a r^{n+1} \\
& \frac{2}{r}=1+r \\
& r^2+r-2=0
\end{aligned}
\)
Hence, we get, \(r=-2\) (as \(r \neq 1)\)
So, \(S _{20}- S _{18}=\) (Sum upto 20 terms) – (Sum upto 18 terms) \(= T _{19}+ T _{20}\)
\(
T _{19}+ T _{20}=\operatorname{ar}^{18}(1+ r )
\)
Putting the values \(a =\frac{1}{8}\) and \(r =-2\);
we get \(T_{19}+T_{20}=-2^{15}\) -
Question 90 of 213
90. Question
If in a G.P. of 64 terms, the sum of all the terms is 7 times the sum of the odd terms of the G.P, then the common ratio of the G.P. is equal to [JEE Main 2024 (Online) 29th January Morning Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& a+a r+a r^2+a r^3+\ldots+a r^{63} \\
& =7\left(a+a r^2+a r^4 \ldots+a r^{62}\right) \\
& \Rightarrow \frac{a\left(1-r^{64}\right)}{1-r}=\frac{7 a\left(1-r^{64}\right)}{1-r^2} \\
& r=6
\end{aligned}
\) -
Question 91 of 213
91. Question
In an A.P., the sixth term \(a_6=2\). If the product \(a_1 a_4 a_5\) is the greatest, then the common difference of the A.P. is equal to [JEE Main 2024 (Online) 29th January Morning Shift]
CorrectIncorrectHint
Step 1: Find the required product of terms of A.P.
Let \(a\) be the first term and \(d\) be the common difference of the AP.
Given 6 th term \(=2\)
\(
\begin{aligned}
\Rightarrow & a+5 d=2 \\
\Rightarrow & a=2-5 d
\end{aligned}
\)
Let the product of \(a_1 a_4 a_5\) is \(P\)
\(
\begin{aligned}
P & =a(a+3 d)(a+4 d) \\
& =(2-5 d)(2-5 d+3 d)(2-5 d+4 d) \\
& =(2-5 d)(2-2 d)(2-d) \\
& =2(1-d)(2-d)(2-5 d) \\
\therefore & P=2\left(-5 d^3+17 d^2-16 d+4\right)
\end{aligned}
\)
Step 2: Find the minimum value of the above product.
For minimum value of \(P, P ^{\prime}(d)=0\)
Differentiate \(P\) w.r.t. \(d\), we get
\(
\begin{aligned}
& P ^{\prime}(d)=2\left(-15 d^2+34 d-16\right) \\
& \therefore 2\left(-15 d^2+34 d-16\right)=0 \\
& \Rightarrow \quad\left(-15 d^2+34 d-16\right)=0 \\
& \Rightarrow \quad(3 d-2)(5 d-8)=0 \\
& \Rightarrow \quad d=\frac{2}{3} \text { or } d=\frac{8}{5} \\
&
\end{aligned}
\)
Again differentiate w.r.t. \(d\), we get
\(
P ^{\prime \prime}(d)=2(-30 d+34)
\)
Now at \(d=\frac{2}{3}\)
\(
P ^{\prime \prime}(d)=28 \text { [ positive ] }
\)
and at \(d=\frac{8}{5}\)
\(
P ^{\prime \prime}(d)=-28[\text { negative }]
\)
We get minimum value when \(P ^{\prime \prime}(d)>0\).
So \(d=\frac{2}{3}\) gives the least value. -
Question 92 of 213
92. Question
The \(20^{\text {th }}\) term from the end of the progression \(20,19 \frac{1}{4}, 18 \frac{1}{2}, 17 \frac{3}{4}, \ldots,-129 \frac{1}{4}\) is : [JEE Main 2024 (Online) 27th January Evening Shift]
CorrectIncorrectHint
\(
20,19 \frac{1}{4}, 18 \frac{1}{2}, 17 \frac{3}{4}, \ldots \ldots,-129 \frac{1}{4}
\)
This is A.P. with common difference
\(
\begin{aligned}
& d_1=-1+\frac{1}{4}=-\frac{3}{4} \\
& -129 \frac{1}{4}, \ldots \ldots \ldots \ldots \ldots 19 \frac{1}{4}, 20
\end{aligned}
\)
This is also A.P. \(a =-129 \frac{1}{4}\) and \(d =\frac{3}{4}\)
Required term \(=\)
\(
\begin{aligned}
& -129 \frac{1}{4}+(20-1)\left(\frac{3}{4}\right) \\
& =-129-\frac{1}{4}+15-\frac{3}{4}=-115
\end{aligned}
\) -
Question 93 of 213
93. Question
The number of common terms in the progressions \(4,9,14,19, \ldots \ldots\), up to \(25^{\text {th }}\) term and \(3,6,9,12, \ldots \ldots\), up to \(37^{\text {th }}\) term is : [JEE Main 2024 (Online) 27th January Morning Shift]
CorrectIncorrectHint
\(4,9,14,19, \ldots\), up to \(25^{\text {th }}\) term
\(
T _{25}=4+(25-1) 5=4+120=124
\)
\(3,6,9,12, \ldots\), up to \(37^{\text {th }}\) term
\(
T _{37}=3+(37-1) 3=3+108=111
\)
Common difference of \(I ^{\text {st }}\) series \(d _1=5\)
Common difference of \(II ^{\text {nd }}\) series \(d _2=3\)
First common term \(=9\), and their common difference \(=15\left( LCM\right.\) of \(d _1\) and \(\left.d _2\right)\) then common terms are \(9,24,39,54,69,84,99\) -
Question 94 of 213
94. Question
Let \(A_1\) and \(A_2\) be two arithmetic means and \(G_1, G_2, G_3\) be three geometric means of two distinct positive numbers. Then \(G_1^4+G_2^4+G_3^4+G_1^2 G_3^2\) is equal to : [JEE Main 2023 (Online) 15th April Morning Shift]
CorrectIncorrectHint
Now, we have the following relations :
Arithmetic progression :
Since \(A_1\) and \(A_2\) are arithmetic means between \(a\) and \(b\), we can say that \(a, A_1, A_2\), and \(b\) are in an arithmetic progression. This means there are three equal intervals between \(a\) and \(b\), which are represented by the common difference \(d\).
To find the value of \(d\), we can use the following equation:
\(
b-a=3 d
\)
From this equation, we can find the value of \(d\) :
\(
\begin{aligned}
& d=\frac{b-a}{3} \\
& A_1=a+\frac{b-a}{3}=\frac{2 a+b}{3} \\
& A_2=\frac{a+2 b}{3} \\
& A_1+A_2=a+b
\end{aligned}
\)
Geometric progression :
\(a, G_1, G_2, G_3, b\) are in G.P.
\(r=\left(\frac{b}{a}\right)^{\frac{1}{4}}\)
\(G_1=\left(a^3 b\right)^{\frac{1}{4}}\)
\(G_2=\left(a^2 b^2\right)^{\frac{1}{4}}\)
\(G_3=\left(a b^3\right)^{\frac{1}{4}}\)
We have the expression :
\(
G_1^4+G_2^4+G_3^4+G_1^2 G_3^2=a^3 b+a^2 b^2+a b^3+\left(a^3 b\right)^{\frac{1}{2}} \cdot\left(a b^3\right)^{\frac{1}{2}}
\)
Simplify the expression :
\(
a^3 b+a^2 b^2+a b^3+a b\left(a^2 b^2\right)
\)
Factor out \(a b\) :
\(
a b\left(a^2+a b+b^2+a^2 b^2\right)
\)
Combine the terms :
\(
a b\left(a^2+2 a b+b^2\right)
\)
Rewrite the expression using the sum of squares :
\(
a b(a+b)^2
\)
Now, recall that \(A_1+A_2=a+b\). Substitute this into the expression:
\(
G_1 \cdot G_3 \cdot\left(A_1+A_2\right)^2
\) -
Question 95 of 213
95. Question
Let \(a_1, a_2, a_3, \ldots\). be a G.P. of increasing positive numbers. Let the sum of its \(6^{\text {th }}\) and \(8^{\text {th }}\) terms be 2 and the product of its \(3^{\text {rd }}\) and \(5^{\text {th }}\) terms be \(\frac{1}{9}\). Then \(6\left(a_2+a_4\right)\left(a_4+a_6\right)\) is equal to [JEE Main 2023 (Online) 13th April Evening Shift]
CorrectIncorrectHint
Given the conditions :
\(
\begin{aligned}
& a_6+a_8=2 \Rightarrow a r^5+a r^7=2 \\
& a_3 \cdot a_5=\frac{1}{9} \Rightarrow a^2 \cdot r^2 \cdot r^4=\frac{1}{9} \Rightarrow a r^3=\frac{1}{3}
\end{aligned}
\)
From this, we can form the equation \(\frac{r^2}{3}+\frac{r^4}{3}=2\), which simplifies to \(r^4+r^2=6\).
This can be factored to give \(\left(r^2-2\right)\left(r^2+3\right)=0\), yielding \(r^2=2\) (since \(r^2\) cannot be -3 for real \(r)\).
So, we have \(r=\sqrt{2}\).
Substituting \(r=\sqrt{2}\) into the equation \(a r=\frac{1}{6}\), we get \(a=\frac{1}{6 \sqrt{2}}\).
Now, we find the value of \(6\left(a_2+a_4\right)\left(a_4+a_6\right)\) :
\(
\begin{aligned}
& 6\left(a_2+a_4\right)\left(a_4+a_6\right)=6\left(a r+a r^3\right)\left(a r^3+a r^5\right) \\
& =6\left(\frac{1}{6 \sqrt{2}}+\frac{1}{3 \sqrt{2}}\right)\left(\frac{1}{3 \sqrt{2}}+\frac{2}{3 \sqrt{2}}\right) \\
& =6 \cdot \frac{1}{2} \cdot 1=3
\end{aligned}
\) -
Question 96 of 213
96. Question
Let \(s_1, s_2, s_3, \ldots, s_{10}\) respectively be the sum to 12 terms of 10 A.P. \(s\) whose first terms are \(1,2,3, \ldots 10\) and the common differences are \(1,3,5, \ldots \ldots, 19\) respectively. Then \(\sum_{i=1}^{10} s_i\) is equal to : [JEE Main 2023 (Online) 13th April Morning Shift]
CorrectIncorrectHint
We have 10 arithmetic progressions (A.P.s) with the first terms \(a_i\) and the common differences \(d_i\), where \(i=1,2, \ldots, 10\).
The first terms are \(a_i=i\) and the common differences are \(d_i=2 i-1\).
Now, we need to find the sum of the first 12 terms for each A.P. The formula for the sum of the first \(n\) terms of an A.P. is:
\(
S_n=n\left(\frac{2 a+(n-1) d}{2}\right)
\)In this case, we need to find the sum of the first 12 terms for each A.P., so we have:
\(
S_{12}=12\left(\frac{2 a+11 d}{2}\right)
\)
Now, we can compute the sum \(s_i\) for each A.P.:
\(
s_i=12\left(\frac{2 i+11(2 i-1)}{2}\right)=6(2 i+22 i-11)=6(24 i-11)
\)
Finally, we need to find the sum of all \(s_i\) for \(i=1,2, \ldots, 10\) :
\(
\sum_{i=1}^{10} s_i=6 \sum_{i=1}^{10}(24 i-11)=6\left(24 \sum_{i=1}^{10} i-11 \sum_{i=1}^{10} 1\right)
\)
The sum of the first 10 integers is \(\sum_{i=1}^{10} i=\frac{10(10+1)}{2}=55\), so we have:
\(
\sum_{i=1}^{10} s_i=6(24 \cdot 55-11 \cdot 10)=6(1320-110)=6 \cdot 1210=7260
\)
Thus, the sum \(\sum_{i=1}^{10} s_i\) is equal to 7260 . -
Question 97 of 213
97. Question
Let \(<a_{ n }>\) be a sequence such that \(a_1+a_2+\ldots+a_n=\frac{n^2+3 n}{(n+1)(n+2)}\). If \(28 \sum_{k=1}^{10} \frac{1}{a_k}=p_1 p_2 p_3 \ldots p_m\), where \(p _1, p _2, \ldots, p _{ m }\) are the first \(m\) prime numbers, then \(m\) is equal to [JEE Main 2023 (Online) 12th April Morning Shift]
CorrectIncorrectHint
Given the sum of the first \(n\) terms, \(S_n=\frac{n^2+3 n}{(n+1)(n+2)}\), we can find the \(n ^{\text {th }}\) term \(a_n\) as the difference between the sum of the first \(n\) terms and the sum of the first \(n-1\) terms :
So, \(a_n=S_n-S_{n-1}\)
Solving, we get :
\(
a_n=\frac{n^2+3 n}{(n+1)(n+2)}-\frac{(n-1)^2+3(n-1)}{n(n+1)}
\)
Simplifying further, we find :
\(
a_n=\frac{4}{n(n+1)(n+2)}
\)Then, we find the reciprocal of \(a_n\) :
\(
\frac{1}{a_n}=\frac{n(n+1)(n+2)}{4}
\)
Now, we sum this over the first 10 terms :
\(
\sum_{k=1}^{10} \frac{1}{a_k}=\sum_{k=1}^{10} \frac{k(k+1)(k+2)}{4}
\)
Evaluating the sum :
\(
\sum_{k=1}^{10} \frac{1}{a_k}=\frac{1}{16}\left[\sum_{k=1}^{10} k(k+1)(k+2)(k+3)-(k-1) k(k+1)(k+2)\right]
\)
This can be rewritten as the sum of differences :
\(
\sum_{k=1}^{10} \frac{1}{a_k}=\frac{1}{16}[(1 \cdot 2 \cdot 3 \cdot 4-0)+(2 \cdot 3 \cdot 4 \cdot 5-1 \cdot 2 \cdot 3 \cdot 4)+\cdots+(10 \cdot 11 \cdot 12 \cdot 13-9 \cdot 10 \cdot 11 \cdot 12)]
\)
\(
\sum_{k=1}^{10} \frac{1}{a_k}=\frac{1}{16}(10 \cdot 11 \cdot 12 \cdot 13-0)=\frac{1}{16} \cdot 17160
\)
Now, given the condition that :
\(
28 \sum_{k=1}^{10} \frac{1}{a_k}=p_1 p_2 p_3 \ldots p_m
\)
Substituting the sum we’ve calculated:
\(28 \cdot \frac{1}{16} \cdot 17160=p_1 p_2 p_3 \ldots p_m\)
This simplifies to :
\(
30030=p_1 p_2 p_3 \ldots p_m
\)
The prime factorization of 30030 is \(2 \cdot 3 \cdot 5 \cdot 7 \cdot 11 \cdot 13\), which consists of 6 primes.
Therefore, \(m\) is equal to 6 . -
Question 98 of 213
98. Question
Let \(a, b, c\) and \(d\) be positive real numbers such that \(a+b+c+d=11\). If the maximum value of \(a^5 b^3 c^2 d\) is \(3750 \beta\), then the value of \(\beta\) is [JEE Main 2023 (Online) 11th April Evening Shift]
CorrectIncorrectHint
Given that \(a+b+c+d=11\) and the maximum value of \(a^5 b^3 c^2 d\) is \(3750 \beta\), you assumed the numbers to be \(\frac{a}{5}, \frac{a}{5}, \frac{a}{5}, \frac{a}{5}, \frac{a}{5}, \frac{b}{3}, \frac{b}{3}, \frac{b}{3}, \frac{c}{2}, \frac{c}{2}, d\).
Applying the AM-GM inequality:
\(
\frac{\frac{a}{5}+\frac{a}{5}+\frac{a}{5}+\frac{a}{5}+\frac{a}{5}+\frac{b}{3}+\frac{b}{3}+\frac{b}{3}+\frac{c}{2}+\frac{c}{2}+d}{11} \geq\left(\frac{\left(a^5 b^3 c^2 d\right)}{5^5 3^3 2^2 1}\right)^{\frac{1}{11}}
\)
Since \(a+b+c+d=11\), we have:
\(
1 \geq\left(\frac{\left(a^5 b^3 c^2 d\right)}{5^5 3^3 2^2 1}\right)^{\frac{1}{11}}
\)
Now, raising both sides to the power of 11 :
\(
1^{11} \geq \frac{a^5 b^3 c^2 d}{5^5 3^3 2^2 1}
\)From the given information, we know that \(a^5 b^3 c^2 d \geq 3750 \beta\) :
\(
5^5 3^3 2^2 \geq 3750 \beta
\)
Now, we can solve for \(\beta\) :
\(
\beta \leq \frac{1}{3750} \cdot 5^5 3^3 2^2
\)
Since we are looking for the maximum value of \(\beta\), we take the equality case:
\(
\beta=\frac{1}{3750} \cdot 5^5 3^3 2^2
\)
Calculating the value, we find that:
\(
\beta=90
\)
So, the value of \(\beta\) is 90 . -
Question 99 of 213
99. Question
Let \(x_1, x_2, \ldots, x_{100}\) be in an arithmetic progression, with \(x_1=2\) and their mean equal to 200 . If \(y_i=i\left(x_i-i\right), 1 \leq i \leq 100\), then the mean of \(y_1, y_2, \ldots, y_{100}\) is : [JEE Main 2023 (Online) 11th April Morning Shift]
CorrectIncorrectHint
We have, mean of \(x_1, x_2 \ldots \ldots x_{100}=200\)
Where, \(x_1, x_2 \ldots x_{100}\) are in AP with first term as 2 .
\(
\begin{aligned}
& \text { Mean }=200 \\
& =\frac{\sum_{i=1}^{100} x_i}{100}=200 \\
& \frac{100}{2} \times[2 \times 2+99 d]=20000 \\
& \Rightarrow 4+99 d=400 \\
& \Rightarrow 99 d=396 \\
& d=4
\end{aligned}
\)
Also,
\(
\begin{aligned}
y_i & =i\left(x_i-i\right) \\
& =i[2+(i-1) 4-i] \\
& =i[3 i-2] \\
& =3 i^2-2 i
\end{aligned}
\)
\(
\begin{aligned}
\text { Required mean } & =\frac{\sum_{i=1}^{100} y_i}{100} \\
& =\frac{1}{100}\left[\sum_{i=1}^{100}\left(3 i^2-2 i\right)\right] \\
& =\frac{1}{100}\left[\frac{3 \times 100 \times 101 \times 201}{6}-2 \times \frac{100 \times 101}{2}\right] \\
& =\frac{20301}{2}-101 \\
& =10049.50
\end{aligned}
\) -
Question 100 of 213
100. Question
If \(S _n=4+11+21+34+50+\ldots\) to \(n\) terms, then \(\frac{1}{60}\left( S _{29}- S _9\right)\) is equal to : [JEE Main 2023 (Online) 10th April Evening Shift]
CorrectIncorrectHint
\(
\begin{aligned}
&S _n=4+11+21+24+50+\ldots+ T _n\\
&\begin{aligned}
& S _n=4+11+21+34++ T _{n-1}+ T _n \\
& -\quad-\quad-\quad-\quad- \quad-\quad-\quad- \\
& \hline 0=4+7+10+13+16+\ldots\left( T _n- T _{n-2}\right)- T _n
\end{aligned}
\end{aligned}
\)
\(
\begin{aligned}
& \Rightarrow T _n=4+7+10+13+16+\ldots \text { to } n \text { terms } \\
& \Rightarrow T _n=\frac{n}{2}[2 \times 4+(n-1) 3] \\
& T _n=\frac{3}{2} n^2+\frac{5}{2} n
\end{aligned}
\)
So \(S _n=\Sigma T _n=\frac{3}{2} \Sigma n^2+\frac{5}{2} \Sigma n\)
\(
\begin{aligned}
& \Rightarrow S _n=\frac{3}{2} \times \frac{n(n+1)(2 n+1)}{6}+\frac{5}{2} \times \frac{n(n+1)}{2} \\
& \Rightarrow S_n=\frac{n(n+1)}{4}(2 n+1+5)=\frac{n(n+1)(n+3)}{2}
\end{aligned}
\)Hence, \(\frac{1}{60}\left(S_{29}-S_9\right)=\frac{1}{60} \times \frac{1}{2}(29 \times 30 \times 32-9 \times 10 \times 12)\)
\(
=223
\) -
Question 101 of 213
101. Question
Let the first term \(\alpha\) and the common ratio \(r\) of a geometric progression be positive integers. If the sum of squares of its first three terms is 33033 , then the sum of these three terms is equal to [JEE Main 2023 (Online) 10th April Morning Shift]
CorrectIncorrectHint
Given that the first term \(a\) and common ratio \(r\) of a geometric progression be positive integer. So, their 1 st three terms are \(a, a r, a r^2\)
According to the question, \(a^2+a^2 r^2+a^2 r^4=33033\)
\(
\begin{aligned}
& \Rightarrow a^2\left(1+r^2+r^4\right)=3 \times 7 \times 11 \times 11 \times 13 \\
& =3 \times 7 \times 13 \times 11^2 \\
& \therefore \quad a^2=11^2 \\
& \Rightarrow \quad a=11 \\
&
\end{aligned}
\)
and \(1+r^2+r^4=273\)
\(
\begin{aligned}
& \Rightarrow r^2+r^4=272 \\
& \Rightarrow r^4+r^2-272=0 \\
& \Rightarrow\left(r^2+17\right)\left(r^2-16\right)=0
\end{aligned}
\)
\(
\begin{aligned}
& \Rightarrow r^2=-17(\text { not possible) } \\
& \Rightarrow r^2-16=0 \\
& \Rightarrow r= \pm 4 \\
& \Rightarrow r=4(\because r>0)
\end{aligned}
\)
So, sum of these first three terms is \(a+a r+a r^2=11+44+176=231\) -
Question 102 of 213
102. Question
Let \(a _{ n }\) be the \(n ^{\text {th }}\) term of the series \(5+8+14+23+35+50+\ldots\) and \(S _{ n }=\sum_{k=1}^n a_k\). Then \(S _{30}-a_{40}\) is equal to : [JEE Main 2023 (Online) 8th April Evening Shift]
CorrectIncorrectHint
Let \(S _n=5+8+14+23+\ldots+a_n\) and \(S _n=0+5+8+14+\ldots .+a_n\)
On subtracting, we get
\(
\begin{aligned}
& 0=5+3+6 \ldots-a_n \\
& \Rightarrow a_n=5+3+6+9+\ldots(n-1) \text { terms } \\
& =5+\left[\frac{(n-1)}{2}(6+(n-2) 3)\right] \\
& =5+\left[\frac{(n-1)}{2}(6+3 n-6)\right] \\
& =5+\frac{(n-1)(3 n)}{2} \\
& =\frac{10+3 n^2-3 n}{2}
\end{aligned}
\)
\(
\begin{aligned}
& \text { So, } a_{40}=\frac{3(40)^2-3(40)+10}{2} \\
& =\frac{4800-120+10}{2}=2345 \\
& \text { Now, } S_n=\sum_{k=1}^n a_k \\
& \Rightarrow S_{30}=\frac{3 \sum_{n=1}^{30} n^2-3 \sum_{n=1}^{30} n+10 \sum_{n=1}^{30} 1}{2} \\
& =\frac{3 \times(30)(30+1)(60+1)}{12}-\frac{3 \times 30 \times 31}{4}+\frac{10 \times 30}{2} \\
& =\frac{28365-1395+300}{2}=\frac{27270}{2} \\
& =13635 \\
& \therefore S_{30}-a_{40}=13635-2345=11290
\end{aligned}
\) -
Question 103 of 213
103. Question
Let \(S_K=\frac{1+2+\ldots+K}{K}\) and \(\sum_{j=1}^n S_j^2=\frac{n}{A}\left(B n^2+C n+D\right)\), where \(A, B, C, D \in N\) and \(A\) has least value. Then [JEE Main 2023 (Online) 8th April Morning Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& \because S_k=\frac{1+2+\ldots+k}{k} \\
& =\frac{k(k+1)}{2 k}=\frac{k+1}{2} \\
& \Rightarrow S_k^2=\left(\frac{k+1}{2}\right)^2=\frac{k^2+1+2 k}{4} \\
& \Rightarrow \sum_{j=1}^n S_j^2=\frac{1}{4}\left[\sum_{j=1}^n k^2+\sum_{j=1}^n 1+2 \sum_{j=1}^n k\right] \\
& =\frac{1}{4}\left[\frac{n(n+1)(2 n+1)}{6}+n+\frac{2 n(n+1)}{2}\right] \\
& =\frac{n}{4}\left[\frac{(n+1)(2 n+1)}{6}+1+n+1\right] \\
& =\frac{n}{24}\left[2 n^2+3 n+1+6+6 n+6\right] \\
& =\frac{n}{24}\left[2 n^2+9 n+13\right]
\end{aligned}
\)
On comparing, we get
\(
A =24, B =2, C =9, D =13
\)
(A) \(A+B+C+D=48\), which is not divisible by 5 .
(B) \(A + C + D =46\), which is divisible by 2.
(C) \(A+B=26\)
\(
\begin{aligned}
& 5( D – C )=5(13-9)=20 \\
& \therefore 26 \neq 20
\end{aligned}
\)
(D) \(A+B=24+2=26\), divisible by 13 . -
Question 104 of 213
104. Question
If \(\operatorname{gcd}( m , n )=1\) and \(1^2-2^2+3^2-4^2+\ldots \ldots+(2021)^2-(2022)^2+(2023)^2=1012 m^2 n\) then \(m^2-n^2\) is equal to : [JEE Main 2023 (Online) 6th April Evening Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& \text { Given } \operatorname{gcd}(m, n)=1 \text { and } \\
& \Rightarrow 1^2-2^2+3^2-4^2+\ldots .+(2021)^2-(2022)^2+(2023)^2 \\
& =1012 m^2 n \\
& \Rightarrow 1^2-2^2+3^2-4^2+\ldots .+(2021)^2-(2022)^2+(2023)^2 \\
& =1012 m^2 n \\
& \Rightarrow(1-2)(1+2)+(3-4)(3+4)+\ldots .(2021-2022) \\
& (2021+2022)+(2023)^2=(1012) m^2 n \\
& \Rightarrow(-1)(1+2)+(-1)(3+4)+\ldots .+ \\
& (-1)(2021+2022)+\left(2023^2\right)=(1012) m^2 n \\
& \Rightarrow(-1)[1+2+3+4+\ldots+2022]+(2023)^2=1012 m^2 n \\
& \Rightarrow(-1)\left[\frac{(2022) \cdot(2022+1)}{2}\right]+(2023)^2=(1012) m^2 n \\
& \Rightarrow(-1)\left[\frac{(2022)(2023)}{2}\right]+(2023)^2=(1012) m^2 n \\
&
\end{aligned}
\)
\(
\begin{aligned}
& \Rightarrow(2023)[2023-1011]=(1012) m^2 n \\
& \Rightarrow m^2 n=2023 \\
& \Rightarrow m^2 n=289 \times 7 \\
& \Rightarrow m^2=289 \text { and } n=7 \\
& \Rightarrow m=17 \text { and } n=7(\text { such that } \operatorname{gcd}(m, n)=1) \\
& \therefore m^2-n^2=289-49=240
\end{aligned}
\) -
Question 105 of 213
105. Question
The sum of the first 20 terms of the series \(5+11+19+29+41+\ldots\) is : [JEE Main 2023 (Online) 6th April Morning Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& S _n=5+11+19+29+41+\ldots+ T _n \\
& S _n=\quad 5+11+19+29+\ldots .+ T _{n-1}+ T _n \\
& \hline 0=5+6+8+10+12+\ldots \ldots T _n
\end{aligned}
\)
\(
\begin{aligned}
& 0=5+\frac{n-1}{2}[2 \times 6+(n-2)(2)]-T_n \\
& \Rightarrow T_n=5+(n-1)(n+4) \\
& \Rightarrow T_n=5+n^2+3 n-4 \\
& \Rightarrow T_n=n^2+3 n+1 \\
& \Sigma T_n=\Sigma n^2+3 \Sigma n+\Sigma 1 \\
& \Rightarrow \quad S_n=\frac{n(n+1)(2 n+1)}{6}+\frac{3 n(n+1)}{2}+n
\end{aligned}
\)
When, \(n=20\)
Then,
\(
\begin{aligned}
S_{20} & =\frac{20 \times 21 \times 41}{6}+\frac{3 \times 20 \times 21}{2}+20 \\
& =2870+630+20=3520
\end{aligned}
\) -
Question 106 of 213
106. Question
The sum \(\sum_{n=1}^{\infty} \frac{2 n^2+3 n+4}{(2 n)!}\) is equal to : [JEE Main 2023 (Online) 1st February Evening Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& \sum_{n=1}^{\infty} \frac{2 n^2+3 n+4}{(2 n)!} \\
& =\frac{1}{2} \sum_{n=1}^{\infty} \frac{2 n(2 n-1)+8 n+8}{(2 n)!} \\
& =\frac{1}{2} \sum_{n=1}^{\infty} \frac{1}{(2 n-2)!}+2 \sum_{n=1}^{\infty} \frac{1}{(2 n-1)!}+4 \sum_{n=1}^{\infty} \frac{1}{(2 n)!}
\end{aligned}
\)
\(
\begin{aligned}
& e=1+1+\frac{1}{2!}+\frac{1}{3!}+\frac{1}{4!}+\ldots \\
& e^{-1}=1-1+\frac{1}{2!}-\frac{1}{3!}+\frac{1}{4!}+\ldots \\
& \left( e +\frac{1}{ e }\right)=2\left(1+\frac{1}{2!}+\frac{1}{4!}+\ldots \ldots\right) \\
& e-\frac{1}{e}=\left(1+\frac{1}{3!}+\frac{1}{5!}+\ldots \ldots\right)
\end{aligned}
\)
Now
\(
\begin{aligned}
& \frac{1}{2}\left(\sum_{n=1}^{\infty} \frac{1}{(2 n-2)!}\right)+2 \sum_{n=1}^{\infty} \frac{1}{(2 n-1)!}+4 \sum_{n=1}^{\infty} \frac{1}{(2 n)!} \\
& =\frac{1}{2}\left[\frac{e+\frac{1}{ e }}{2}\right]+2\left[\frac{ e -\frac{1}{ e }}{2}\right]+4\left[\frac{ e +\frac{1}{ e }-2}{2}\right] \\
& =\frac{\left( e +\frac{1}{ e }\right)}{4}+e-\frac{1}{ e }+2 e +\frac{2}{ e }-4 \\
& =\frac{13}{4} e+\frac{5}{4 e}-4
\end{aligned}
\) -
Question 107 of 213
107. Question
The sum of 10 terms of the series \(\frac{1}{1+1^2+1^4}+\frac{2}{1+2^2+2^4}+\frac{3}{1+3^2+3^4}+\ldots\) is [JEE Main 2023 (Online) 1st February Morning Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& T_n=\frac{n}{1+n^2+n^4} \\
& =\frac{n}{\left( n ^2- n +1\right)\left( n ^2+ n +1\right)} \\
& =\frac{1}{2}\left[\frac{\left( n ^2+ n +1\right)-\left( n ^2- n +1\right)}{\left( n ^2- n +1\right)\left( n ^2+ n +1\right)}\right] \\
& \Rightarrow T _{ n }=\frac{1}{2}\left[\frac{1}{\left( n ^2- n +1\right)}-\frac{1}{\left( n ^2+ n +1\right)}\right] \\
& S _{ n }=\sum_{n=1}^{10} T_n \\
& =\frac{1}{2} \sum\left(\frac{1}{n^2-n+1}-\frac{1}{n^2+n+1}\right) \\
& =\frac{1}{2}\left[\left(\frac{1}{1}-\frac{1}{3}\right)+\left(\frac{1}{3}-\frac{1}{7}\right)+\left(\frac{1}{7}-\frac{1}{13}\right)\right. \left.\ldots \ldots \ldots \ldots \ldots \ldots \ldots .+\left(\frac{1}{91}-\frac{1}{111}\right)\right]\\
&
\end{aligned}
\)
\(
\therefore S=\frac{1}{2}\left(1-\frac{1}{111}\right)=\frac{55}{111}
\) -
Question 108 of 213
108. Question
Let \(a_1, a_2, a_3, \ldots\) be an A.P. If \(a_7=3\), the product \(a_1 a_4\) is minimum and the sum of its first \(n\) terms is zero, then \(n!-4 a_{n(n+2)}\) is equal to : [JEE Main 2023 (Online) 31st January Evening Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& a_7=3 \Rightarrow a+6 d=3 \Rightarrow a=3-6 d \\
& a_1 \cdot a_4=a(a+3 d) \\
& \Rightarrow(3-6 d)(3-6 d+3 d) \\
& \Rightarrow 3(1-2 d) 3(1-d) \\
& \Rightarrow 9\left(2 d^2-3 d+1\right) \\
& \text { Let } f(d)=2 d^2-3 d+1 \\
& f^{\prime}(d)=4 d-3 \Rightarrow d=\frac{3}{4} \\
& \therefore a=3-6 \cdot \frac{3}{4}=3-\frac{9}{2}=-\frac{3}{2}
\end{aligned}
\)
\(
\begin{aligned}
& S_n=0 \\
& \frac{n}{2}(29+(n-1) d)=0 \\
& \Rightarrow 2 \cdot\left(-\frac{3}{2}\right)+(n-1)\left(\frac{3}{4}\right)=0 \\
& \Rightarrow \quad 3=\frac{3}{4}(n-1) \\
& \Rightarrow n=5
\end{aligned}
\)Now, \(n!-4 \cdot a_{n(n+2)}\)
\(
\begin{aligned}
& =5!-4 \cdot a_{35} \\
& =120-4\left(-\frac{3}{2}+34 \cdot \frac{3}{4}\right) \\
& =120-(-6+102) \\
& =120-(96) \\
& =24
\end{aligned}
\) -
Question 109 of 213
109. Question
If the sum and product of four positive consecutive terms of a G.P., are 126 and 1296, respectively, then the sum of common ratios of all such GPs is [JEE Main 2023 (Online) 31st January Morning Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& a , ar , ar ^2, ar ^3( a , r >0) \\
& a^4 r^6=1296 \\
& a^2 r^3=36 \\
& a=\frac{6}{r^{3 / 2}} \\
& a+a r+a r^2+a r^3=126 \\
& \frac{1}{ r ^{3 / 2}}+\frac{ r }{ r ^{3 / 2}}+\frac{ r ^2}{ r ^{3 / 2}}+\frac{ r ^3}{ r ^{3 / 2}}=\frac{126}{6}=21 \\
& \left(r^{-3 / 2}+r^{3 / 2}\right)+\left(r^{1 / 2}+r^{-1 / 2}\right)=21 \\
& r ^{1 / 2}+ r ^{-1 / 2}= A \\
& r ^{-3 / 2}+ r ^{3 / 2}+3 A = A ^3 \\
& A ^3-3 A + A =21 \\
& A ^3-2 A =21
\end{aligned}
\)
\(
\begin{aligned}
& A=3 \\
& \sqrt{ r }+\frac{1}{\sqrt{ r }}=3 \\
& r +1=3 \sqrt{ r } \\
& r^2+2 r+1=9 r \\
& r^2-7 r+1=0 \\
& \Rightarrow r_1+r_2=7
\end{aligned}
\) -
Question 110 of 213
110. Question
Let \(a, b, c>1, a^3, b^3\) and \(c^3\) be in A.P., and \(\log _a b, \log _c a\) and \(\log _b c\) be in G.P. If the sum of first 20 terms of an A.P., whose first term is \(\frac{a+4 b+c}{3}\) and the common difference is \(\frac{a-8 b+c}{10}\) is -444 , then \(a b c\) is equal to : [JEE Main 2023 (Online) 30th January Evening Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& 2 b^3=a^3+c^3 \\
& \left(\frac{\log a}{\log c}\right)^2=\left(\frac{\log b}{\log a}\right)\left(\frac{\log c}{\log b}\right) \\
& \Rightarrow(\log a)^3=(\log c)^3 \\
& \Rightarrow \log a=\log c \\
& \Rightarrow a=c \\
& \Rightarrow a=b=c \\
& T_1=2 a, d=-\frac{3 a}{5} \\
& S_{20}=-444 \\
& \Rightarrow \frac{20}{2}\left(2(2 a)+(19)\left(-\frac{3 a}{5}\right)\right)=-444 \\
& \Rightarrow 10 \frac{(20 a-57 a)}{5}=-444 \\
& \Rightarrow 37 a=222 \\
& \Rightarrow a=6 \\
& \Rightarrow a b c=(6)^3=216
\end{aligned}
\) -
Question 111 of 213
111. Question
If \(a_n=\frac{-2}{4 n^2-16 n+15}\), then \(a_1+a_2+\ldots+a_{25}\) is equal to : [JEE Main 2023 (Online) 30th January Morning Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& \sum_{i=1}^{25} a_i=\sum \frac{-2}{4 n^2-16 n+15}=\sum \frac{-2}{(2 n-5)(2 n-3)} \\
& =\sum_{i=1}^{25}\left(\frac{1}{2 n-3}-\frac{1}{2 n-5}\right) \\
& =\left[\left(\frac{1}{-1}-\frac{1}{-3}\right)+\left(\frac{1}{1}-\frac{1}{-1}\right)+\left(\frac{1}{3}-\frac{1}{1}\right) \ldots \ldots\right. \\
& =\frac{1}{2(25)-3}+\frac{1}{3}=\frac{50}{141}
\end{aligned}
\) -
Question 112 of 213
112. Question
For three positive integers \(p , q , r , x^{p q^2}=y^{q r}=z^{p^2 r}\) and \(r = pq +1\) such that \(3,3 \log _y x, 3\) \(\log _z y, 7 \log _x z\) are in A.P. with common difference \(\frac{1}{2}\). Then r-p-q is equal to [JEE Main 2023 (Online) 24th January Morning Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& x^{p q^2}=y^{q r}=z^{p^2 r} \\
& 3 \log _y x=\frac{7}{2}, 3 \log _z y=4,7 \log _x z=\frac{9}{2} \\
& \Rightarrow x=y^{\frac{7}{6}}, y=z^{\frac{4}{3}}, z=x^{\frac{9}{14}} \\
& y^{\frac{7}{6} p q^2}=y^{q r}=y^{\frac{3}{4}} p^2 r \\
& \Rightarrow \frac{7}{6} p q^2=q r=\frac{3}{4} p^2 r \\
& \therefore 7 p q=6 r, 4 q=3 p^2 \\
& r=p q+1 \\
& r=\frac{6 r}{7}+1 \Rightarrow r=7 \\
& p q=6 \\
& p\left(\frac{3 p^2}{4}\right)=6 \\
& p=2, q=3 \\
& r-p-q=7-5=2
\end{aligned}
\) -
Question 113 of 213
113. Question
Let \(\left\{a_n\right\}_{n=0}^{\infty}\) be a sequence such that \(a_0=a_1=0\) and
\(
a_{n+2}=3 a_{n+1}-2 a_n+1, \forall n \geq 0 \text {. }
\)
Then \(a_{25} a_{23}-2 a_{25} a_{22}-2 a_{23} a_{24}+4 a_{22} a_{24}\) is equal to [JEE Main 2022 (Online) 29th July Evening Shift]CorrectIncorrectHint
Given,
\(
\begin{aligned}
& a_0=a_1=0 \\
& \text { and } a_{n+2}=3 a_{n+1}-2 a_n+1 \\
& \text { For } n=0, a_2=3 a_1-2 a_0+1 \\
& =3 \cdot 0-2 \cdot 0+1 \\
& =1 \\
& \text { For } n=1, a_3=3 a_2-2 a_1+1 \\
& =3 \cdot 1-2 \cdot 0+1 \\
& =4
\end{aligned}
\)
For \(n=2, a_4=3 a_3-2 a_2+1\)
\(
\begin{aligned}
& =3.4-2.1+1 \\
& =11
\end{aligned}
\)
For \(n=3, a_5=3 a_4-2 a_3+1\)
\(
\begin{aligned}
& =3.11-2.4+1 \\
& =26
\end{aligned}
\)
For \(n=4, a_6=3 a_5-2 a_4+1\)
\(
\begin{aligned}
& =3.26-2.11+1 \\
& =57
\end{aligned}
\)
\(
\begin{aligned}
& \therefore S_n=1+4+11+26+57+\ldots+t_n \\
& S_n=1+4+11+26+\ldots+t_{n-1}+t_n
\end{aligned}
\)
\(
\begin{aligned}
& 0=1+3+7+15+31+\ldots \ldots-t_n \\
& \Rightarrow t_n=1+3+7+15+31+\ldots
\end{aligned}
\)
Now, find the sum of the series,
\(
t_n=1+3+7+15+31+\ldots .+x_{n-1}+x_n \ldots .(1)
\)
\(
t_n=1+3+7+15+\ldots \ldots+x_{n-1}+x_n \ldots \ldots (2)
\)
Subtracting (2) from (1), we get
\(
\begin{aligned}
& 0=1+2+4+8+16+\ldots+x_n \\
& \Rightarrow x_n=1+2+4+8+16+\ldots \ldots+n \text { terms } \\
& =\frac{1\left(2^n-1\right)}{2-1} \\
& =2^n-1
\end{aligned}
\)
\(
\begin{aligned}
& \therefore t_n=\sum_{n=1}^n x_n \\
& =\sum_{n=1}^n\left(2^n-1\right) \\
& =\sum_{n=1}^n 2^n-\sum_{n=1}^n 1 \\
& =\frac{2\left(2^n-1\right)}{2-1}-n \\
& =2^{n+1}-2-n \\
& t_1=2^2-2-1=1=a_2 \\
& t_2=2^3-2-2=4=a_3 \\
& t_3=2^4-2-3=11=a_4 \\
& \therefore a_{22}=t_{21}=2^{22}-2-21=2^{22}-23 \\
& a_{23}=t_{22}=2^{23}-2-22=2^{23}-24 \\
& a_{24}=t_{23}=2^{24}-2-23=2^{24}-25 \\
& a_{25}=t_{24}=2^{25}-2-24=2^{25}-26
\end{aligned}
\)
Now,
\(
\begin{aligned}
& a_{25} a_{23}-2 a_{25} a_{22}-2 a_{23} a_{24}+4 a_{22} a_{24} \\
& =a_{25}\left(a_{23}-2 a_{22}\right)-2 a_{24}\left(a_{23}-2 a_{22}\right) \\
& =\left(a_{23}-2 a_{22}\right)\left(a_{25}-2 a_{24}\right) \\
& =\left[\left(2^{23}-24\right)-2\left(2^{22}-23\right)\right]\left[\left(2^{25}-26\right)-2\left(2^{24}-25\right)\right] \\
& =\left[\left(2^{23}-24-2^{23}+46\right)\right]\left[\left(2^{25}-26-2^{25}+50\right)\right] \\
& =(22)(24) \\
& =528
\end{aligned}
\) -
Question 114 of 213
114. Question
Consider the sequence \(a_1, a_2, a_3, \ldots\) such that \(a_1=1, a_2=2\) and \(a_{n+2}=\frac{2}{a_{n+1}}+a_n\) for \(n =1,2,3, \ldots\) If \(\left(\frac{a_1+\frac{1}{a_2}}{a_3}\right) \cdot\left(\frac{a_2+\frac{1}{a_3}}{a_4}\right) \cdot\left(\frac{a_3+\frac{1}{a_4}}{a_5}\right) \ldots\left(\frac{a_{30}+\frac{1}{a_{31}}}{a_{32}}\right)=2^\alpha\left({ }^{61} C_{31}\right)\), then \(\alpha\) is equal to : [JEE Main 2022 (Online) 28th July Morning Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& a_{n+2}=\frac{2}{a_{n+1}}+a_n \\
& \Rightarrow a_n a_{n+1}+1=a_{n+1} a_{n+2}-1 \\
& \Rightarrow a_{n+2} a_{n+1}-a_n \cdot a_{n+1}=2
\end{aligned}
\)
For
\(
\begin{array}{ll}
n=1 & a_3 a_2-a_1 a_2=2 \\
n=2 & a_4 a_3-a_3 a_2=2 \\
n=3 & a_5 a_4-a_4 a_3=2
\end{array}
\)
\(\vdots\)
\(
n=n \quad \frac{a_{n+2} a_{n+1}-a_n a_{n+1}=2}{a_{n+2} a_{n+1}=2 n+a_1 a_2}
\)
Now, \(
\frac{\left(a_1 a_2+1\right)}{a_2 a_3} \cdot \frac{\left(a_2 a_3+1\right)}{a_3 a_4} \cdot \frac{\left(a_3 a_4+1\right)}{a_4 a_5} \ldots \ldots \cdot \frac{\left(a_{30} a_{31}+1\right)}{a_{31} a_{32}}
\)
\(
\begin{aligned}
& =\frac{3}{4} \cdot \frac{5}{6} \cdot \frac{7}{8} \cdot \ldots \cdot \frac{61}{62} \\
& =2^{-60}\left({ }^{61} C_{31}\right)
\end{aligned}
\) -
Question 115 of 213
115. Question
Let the sum of an infinite G.P., whose first term is a and the common ratio is \(r\), be 5 . Let the sum of its first five terms be \(\frac{98}{25}\). Then the sum of the first 21 terms of an AP, whose first term is \(10 ar , n ^{\text {th }}\) term is \(a _{ n }\) and the common difference is \(10 ar ^2\), is equal to: [JEE Main 2022 (Online) 27th July Evening Shift]
CorrectIncorrectHint
Let first term of G.P. be a and common ratio is \(r\)
Then, \(\frac{a}{1-r}=5\)
\(
\begin{aligned}
& a \frac{\left(r^5-1\right)}{(r-1)}=\frac{98}{25} \Rightarrow 1-r^5=\frac{98}{125} \\
& \therefore r^5=\frac{27}{125}, r=\left(\frac{3}{5}\right)^{\frac{3}{5}} \\
& \therefore \text { Then, } S_{21}=\frac{21}{2}\left[2 \times 10 a r+20 \times 10 a r^2\right] \\
& =21\left[10 a r+10.10 a r^2\right] \\
& =21 a_{11}
\end{aligned}
\) -
Question 116 of 213
116. Question
Suppose \(a_1, a_2, \ldots, a_n\)… be an arithmetic progression of natural numbers. If the ratio of the sum of first five terms to the sum of first nine terms of the progression is \(5: 17\) and , \(110<a_{15}<120\), then the sum of the first ten terms of the progression is equal to [JEE Main 2022 (Online) 27th July Morning Shift]
CorrectIncorrectHint
\(\because a _1, a _2, \ldots . a _{ n }\) be an A.P of natural numbers and
\(
\begin{aligned}
& \frac{S_5}{S_9}=\frac{5}{17} \Rightarrow \frac{\frac{5}{2}\left[2 a_1+4 d\right]}{\frac{9}{2}\left[2 a_1+8 d\right]}=\frac{5}{17} \\
& \Rightarrow 34 a_1+68 d=18 a_1+72 d \\
& \Rightarrow 16 a_1=4 d \\
& \therefore d=4 a_1
\end{aligned}
\)
And \(110<a_{15}<120\)
\(
\begin{aligned}
& \therefore 110<a_1+14 d<120 \Rightarrow 110<57 a_1<120 \\
& \therefore a_1=2\left(\because a_i \in N\right) \\
& d=8 \\
& \therefore S_{10}=5[4+9 \times 8]=380
\end{aligned}
\) -
Question 117 of 213
117. Question
Consider two G.Ps. \(2,2^2, 2^3\) \(\qquad\) and \(4,4^2, 4^3, \ldots\). of 60 and \(n\) terms respectively. If the geometric mean of all the \(60+ n\) terms is \((2)^{\frac{225}{8}}\), then \(\sum_{k=1}^n k(n-k)\) is equal to : [JEE Main 2022 (Online) 26th July Morning Shift]
CorrectIncorrectHint
Given G.P’s \(2,2^2, 2^3, \ldots .60\) terms
\(4,4^2, \ldots . n\) terms
Now, G.M \(=2^{\frac{225}{8}}\)
\(
\begin{aligned}
& \left(2.2^2 \ldots 4.4^2 \ldots\right)^{\frac{1}{60+n}}=2^{\frac{225}{8}} \\
& \left(2^{\frac{n^2+n+1830}{60+n}}\right)=2^{\frac{225}{8}} \\
& \Rightarrow \frac{n^2+n+1830}{60+n}=\frac{225}{8} \\
& \Rightarrow 8 n^2-217 n+1140=0 \\
& n=\frac{57}{8}, 20, \text { so } n=20 \\
& \therefore \sum_{k=1}^{20} k(20-k)=20 \times \frac{20 \times 21}{2}-\frac{20 \times 21 \times 41}{6} \\
& =\frac{20 \times 21}{2}\left[20-\frac{41}{3}\right]=1330
\end{aligned}
\) -
Question 118 of 213
118. Question
The sum \(\sum_{n=1}^{21} \frac{3}{(4 n-1)(4 n+3)}\) is equal to [JEE Main 2022 (Online) 25th July Evening Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& \sum_{n=1}^{21} \frac{3}{(4 n-1)(4 n+3)}=\frac{3}{4} \sum_{n=1}^{21} \frac{1}{4 n-1}-\frac{1}{4 n+3} \\
& =\frac{3}{4}\left[\left(\frac{1}{3}-\frac{1}{7}\right)+\left(\frac{1}{7}-\frac{1}{11}\right)+\ldots+\left(\frac{1}{83}-\frac{1}{87}\right)\right] \\
& =\frac{3}{4}\left[\frac{1}{3}-\frac{1}{87}\right]=\frac{3}{4} \frac{84}{3.87}=\frac{7}{29}
\end{aligned}
\) -
Question 119 of 213
119. Question
The value of \(1+\frac{1}{1+2}+\frac{1}{1+2+3}+\ldots .+\frac{1}{1+2+3+\ldots . .+11}\) is equal to: [JEE Main 2022 (Online) 30th June Morning Shift]
CorrectIncorrectHint
Given,
\(
1+\frac{1}{1+2}+\frac{1}{1+2+3}+\ldots+\frac{1}{1+2+3+\ldots .+11}
\)
General term,
\(
T_n=\frac{1}{1+2+3+\ldots .+n}
\)
\(
\begin{aligned}
& =\frac{1}{\frac{n(n+1)}{2}} \\
& =\frac{2}{n(n+1)} \\
& =2\left[\frac{n+1-n}{n(n+1)}\right] \\
& =2\left[\frac{1}{n}-\frac{1}{n+1}\right] \\
& t_1=2\left[\frac{1}{1}-\frac{1}{2}\right] \\
& t_2=2\left[\frac{1}{2}-\frac{1}{3}\right] \\
& t_3=2\left[\frac{1}{3}-\frac{1}{4}\right]
\end{aligned}
\)
\(\vdots\)
\(
\begin{aligned}
& t_n=2\left[\frac{1}{n}-\frac{1}{n+1}\right] \\
& \therefore S_n=t_1+t_2+t_3+\ldots+t_n \\
& =2\left[\frac{1}{1}-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+\ldots+\frac{1}{n}-\frac{1}{n+1}\right] \\
& =2\left[1-\frac{1}{n+1}\right] \\
& =2\left[\frac{n+1-1}{n+1}\right] \\
& =\frac{2 n}{n+1} \\
& \therefore S_{11}=\frac{2 \times 11}{11+1}=\frac{22}{12}=\frac{11}{6}
\end{aligned}
\) -
Question 120 of 213
120. Question
The sum of the infinite series \(1+\frac{5}{6}+\frac{12}{6^2}+\frac{22}{6^3}+\frac{35}{6^4}+\frac{51}{6^5}+\frac{70}{6^6}+\ldots\) is equal to : [JEE Main 2022 (Online) 29th June Evening Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& S=1+\frac{5}{6}+\frac{12}{6^2}+\frac{22}{6^3}+\ldots \ldots (1)\\
& \frac{1}{6} S=\frac{1}{6}+\frac{5}{6^2}+\frac{12}{6^3}+\ldots \ldots(2)
\end{aligned}
\)
\(
S-\frac{1}{6} S=1+\frac{4}{6}+\frac{7}{6^2}+\frac{10}{6^3}+\ldots \ldots \ldots
\)
\(
\Rightarrow \frac{5 S}{6}=1+\frac{4}{6}+\frac{7}{6^2}+\frac{10}{6^3}+\ldots \ldots .(3)
\)
Now, multiplying both sides by \(\frac{1}{6}\), we get
\(
\Rightarrow \frac{5 S}{36}=\frac{1}{6}+\frac{4}{6^2}+\frac{7}{6^3}+\frac{10}{6^4}+ \ldots(4)
\)
Subtract equation (4) from equation (3), we get
\(
\begin{aligned}
& \frac{25}{36} S=1+\frac{3}{6}+\frac{3}{6^2}+\frac{3}{6^3}+\ldots . . \\
& \Rightarrow \frac{25 S}{36}=1+\frac{\frac{3}{5}}{1-\frac{1}{6}} \\
& =1+\frac{3}{6} \times \frac{6}{5} \\
& =1+\frac{3}{5}=\frac{8}{5} \\
& \Rightarrow S=\frac{8}{5} \times \frac{36}{25}=\frac{288}{125}
\end{aligned}
\) -
Question 121 of 213
121. Question
Let \(\left\{a_n\right\}_{n=0}^{\infty}\) be a sequence such that \(a_0=a_1=0\) and \(a_{n+2}=2 a_{n+1}-a_n+1\) for all \(n \geq 0\). Then, \(\sum_{n=2}^{\infty} \frac{a_n}{7^n}\) is equal to: [JEE Main 2022 (Online) 29th June Morning Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& a_{n+2}=2 a_{n+1}-a_n+1 \& a_0=a_1=0 \\
& a_2=2 a_1-a_0+1=1 \\
& a_3=2 a_2-a_1+1=3 \\
& a_4=2 a_3-a_2+1=6 \\
& a_5=2 a_4-a_3+1=10 \\
& \sum_{n=2}^{\infty} \frac{a_n}{7^n}=\frac{a_2}{7^2}+\frac{a_3}{7^3}+\frac{a_4}{7^4}+\ldots \\
& s=\frac{1}{7^2}+\frac{3}{7^3}+\frac{6}{7^4}+\frac{10}{7^5}+\ldots
\end{aligned}
\)
\(
\frac{\frac{1}{7} s=\frac{1}{7^3}+\frac{3}{7^4}+\frac{6}{7^5}+\ldots}{\frac{6 s}{7}=\frac{1}{7^2}+\frac{2}{7^3}+\frac{3}{7^4}+\ldots}
\)
\(
\frac{\frac{68}{49}=\quad \frac{1}{7^3}+\frac{2}{7^4}+\ldots}{\frac{368}{49}=\frac{1}{7^2}+\frac{1}{7^3}+\frac{1}{7^4}+\ldots}
\)
\(
\begin{aligned}
& \frac{36 s}{49}=\frac{\frac{1}{7^2}}{1-\frac{1}{7}} \\
& \frac{36 s}{49}=\frac{7}{49 \times 6} \\
& s=\frac{7}{216}
\end{aligned}
\) -
Question 122 of 213
122. Question
If \(n\) arithmetic means are inserted between a and 100 such that the ratio of the first mean to the last mean is \(1: 7\) and \(a+n=33\), then the value of \(n\) is : [JEE Main 2022 (Online) 28th June Evening Shift]
CorrectIncorrectHint
\(a , A _1, A _2\). \(\ldots\) \(A_n, 100\)
Let \(d\) be the common difference of above A.P. then
\(
\frac{a+d}{100-d}=\frac{1}{7}
\)
\(
\Rightarrow 7 a+8 d=100 \ldots \ldots . \text { (i) }
\)
and \(a+n=33 \ldots .\). (ii)
\(
\begin{aligned}
& \text { and } 100=a+(n+1) d \\
& \Rightarrow 100=a+(34-a) \frac{(100-7 a)}{8} \\
& \Rightarrow 800=8 a+7 a^2-338 a+3400 \\
& \Rightarrow 7 a^2-330 a+2600=0 \\
& \Rightarrow a=10, \frac{260}{7}, \text { but } a \neq \frac{260}{7} \\
& \therefore n=23
\end{aligned}
\) -
Question 123 of 213
123. Question
Let \(A_1, A_2, A_3, \ldots . .\). be an increasing geometric progression of positive real numbers. If \(A_1 A_3 A_5 A_7=\frac{1}{1296}\) and \(A_2+A_4=\frac{7}{36}\), then the value of \(A_6+A_8+A_{10}\) is equal to [JEE Main 2022 (Online) 28th June Morning Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& \frac{A_4}{r^3} \cdot \frac{A_4}{r} \cdot A_4 r \cdot A_4 r^3=\frac{1}{1296} \\
& A_4=\frac{1}{6} \\
& A_2=\frac{7}{36}-\frac{1}{6}=\frac{1}{36}
\end{aligned}
\)
So \(A_6+A_8+A_{10}=1+6+36=43\) -
Question 124 of 213
124. Question
Let \(S=2+\frac{6}{7}+\frac{12}{7^2}+\frac{20}{7^3}+\frac{30}{7^4}+\ldots\). Then \(4 S\) is equal to [JEE Main 2022 (Online) 27th June Evening Shift]
CorrectIncorrectHint
\(
S=2+\frac{6}{7}+\frac{12}{7^2}+\frac{20}{7^3}+\frac{30}{7^4}+\ldots \ldots \ldots \ldots \text { (i) }
\)
\(
\frac{1}{7} S=\frac{2}{7}+\frac{6}{7^2}+\frac{12}{7^3}+\frac{20}{7^4}+\ldots \ldots \ldots \text { (ii) }
\)
(i) – (ii)
\(
\frac{6}{7} S=2+\frac{4}{7}+\frac{6}{7^2}+\frac{8}{7^3}+\ldots \ldots \ldots \ldots(iii)
\)
\(
\frac{6}{7^2} S=\frac{2}{7}+\frac{4}{7^2}+\frac{6}{7^3}+ \ldots(iv)
\)
(iii) – (iv)
\(
\left(\frac{6}{7}\right)^2 S=2+\frac{2}{7}+\frac{2}{7^2}+\frac{2}{7^3}+\ldots \ldots
\)
\(
\begin{aligned}
& =2\left[\frac{1}{1-\frac{1}{7}}\right]=2\left(\frac{7}{6}\right) \\
& \therefore 4 S=8\left(\frac{7}{6}\right)^3=\left(\frac{7}{3}\right)^3
\end{aligned}
\) -
Question 125 of 213
125. Question
If \(a_1, a_2, a_3\) \(\ldots\) and \(b_1, b_2, b_3\) \(\ldots\) are A.P., and \(a_1=2, a_{10}=3, a_1 b_1=1=a_{10} b_{10}\), then \(a_4 b_4\) is equal to [JEE Main 2022 (Online) 27th June Evening Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& a_1, a_2, a_3 \ldots . \text { are in A.P. (Let common difference is } d_1 \text { ) } \\
& b_1, b_2, b_3 \ldots \text { are in A.P. (Let common difference is } d_2 \text { ) } \\
& \text { and } a_1=2, a_{10}=3, a_1 b_1=1=a_{10} b_{10} \\
& \because a_1 b_1=1 \\
& \therefore b_1=\frac{1}{2} \\
& a_{10} b_{10}=1 \\
& \therefore b_{10}=\frac{1}{3} \\
& \text { Now, } a_{10}=a_1+9 d_1 \Rightarrow d_1=\frac{1}{9} \\
& b_{10}=b_1+9 d_2 \Rightarrow d_2=\frac{1}{9}\left[\frac{1}{3}-\frac{1}{2}\right]=-\frac{1}{54} \\
& \text { Now, } a_4=2+\frac{3}{9}=\frac{7}{3} \\
& b_4=\frac{1}{2}-\frac{3}{54}=\frac{4}{9} \\
& \therefore a_4 b_4=\frac{28}{27}
\end{aligned}
\) -
Question 126 of 213
126. Question
\(x=\sum_{n=0}^{\infty} a^n, y=\sum_{n=0}^{\infty} b^n, z=\sum_{n=0}^{\infty} c^n\), where \(a , b , c\) are in A.P. and \(| a |<1,| b |<1,| c |<\) \(1, a b c \neq 0\), then : [JEE Main 2022 (Online) 27th June Morning Shift]
CorrectIncorrectHint
\(
x=\sum_{n=0}^{\infty} a^n=\frac{1}{1-a} ; y=\sum_{n=0}^{\infty} b^n=\frac{1}{1-b} ; z=\sum_{n=0}^{\infty} c^n=\frac{1}{1-c}
\)
Now,
\(
\begin{aligned}
& a, b, c \rightarrow A P \\
& 1-a, 1-b, 1-c \rightarrow A P \\
& \frac{1}{1-a}, \frac{1}{1-b}, \frac{1}{1-c} \rightarrow H P \\
& x, y, z \rightarrow H P \\
& \therefore \frac{1}{x}, \frac{1}{y}, \frac{1}{z} \rightarrow A P
\end{aligned}
\) -
Question 127 of 213
127. Question
If \(A=\sum_{n=1}^{\infty} \frac{1}{\left(3+(-1)^n\right)^n}\) and \(B=\sum_{n=1}^{\infty} \frac{(-1)^n}{\left(3+(-1)^n\right)^n}\), then \(\frac{A}{B}\) is equal to : [JEE Main 2022 (Online) 26th June Evening Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& A=\sum_{n=1}^{\infty} \frac{1}{\left(3+(-1)^n\right)^n} \text { and } B=\sum_{n=1}^{\infty} \frac{(-1)^n}{\left(3+(-1)^n\right)^n} \\
& A=\frac{1}{2}+\frac{1}{4^2}+\frac{1}{2^3}+\frac{1}{4^4}+\ldots . . . \\
& B=\frac{-1}{2}+\frac{1}{4^2}-\frac{1}{2^3}+\frac{1}{4^4}+\ldots . . . \\
& A=\frac{\frac{1}{2}}{1-\frac{1}{4}}+\frac{\frac{1}{16}}{1-\frac{1}{16}}, B=\frac{-\frac{1}{2}}{1-\frac{1}{4}}+\frac{\frac{1}{16}}{1-\frac{1}{16}} \\
& A=\frac{11}{15}, B=\frac{-9}{15} \\
& \therefore \frac{A}{B}=\frac{-11}{9} \\
&
\end{aligned}
\) -
Question 128 of 213
128. Question
The sum \(1+2 \cdot 3+3 \cdot 3^2+\) \(\ldots\) \(+10 \cdot 3^9\) is equal to : [JEE Main 2022 (Online) 25th June Evening Shift]
CorrectIncorrectHint
\(
\text { Let } S=1 \cdot 3^0+2 \cdot 3^1+3 \cdot 3^2+\ldots \ldots+10 \cdot 3^9 \dots(1)
\)
\(
3 S=1.3^1+2.3^2+\ldots \ldots \ldots+10.3^{10} \dots(2)
\)
Eqn. (1) – Eqn. (2)
\(
\begin{aligned}
& -2 S=\left(1 \cdot 3^0+1 \cdot 3^1+1 \cdot 3^2+\ldots \ldots+1 \cdot 3^9\right)-10 \cdot 3^{10} \\
& \Rightarrow S=\frac{1}{2}\left[10 \cdot 3^{10}-\frac{3^{10}-1}{3-1}\right] \\
& \Rightarrow S=\frac{19 \cdot 3^{10}+1}{4}
\end{aligned}
\) -
Question 129 of 213
129. Question
Let \(x, y>0\). If \(x^3 y^2=2^{15}\), then the least value of \(3 x+2 y\) is [JEE Main 2022 (Online) 24th June Evening Shift]
CorrectIncorrectHint
\(
x, y>0 \text { and } x^3 y^2=2^{15}
\)
Now, \(3 x+2 y=(x+x+x)+(y+y)\)
So, by A.M \(\geq\) G.M inequality
\(
\begin{aligned}
& \frac{3 x+2 y}{5} \geq \sqrt[5]{x^3 \cdot y^2} \\
& \therefore 3 x+2 y \geq 5 \sqrt[5]{2^{15}} \geq 40
\end{aligned}
\)
\(\therefore\) Least value of \(3 x+4 y=40\) -
Question 130 of 213
130. Question
If \(\left\{a_i\right\}_{i=1}^n\), where \(n\) is an even integer, is an arithmetic progression with common difference 1 , and \(\sum_{i=1}^n a_i=192, \sum_{i=1}^{n / 2} a_{2 i}=120\), then \(n\) is equal to : [JEE Main 2022 (Online) 24th June Morning Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& \sum_{i=1}^n a_i=192 \\
& \Rightarrow a_1+a_2+a_3+\ldots . .+a_n=192 \\
& \Rightarrow \frac{n}{2}\left[a_1+a_n\right]=192 \\
& \Rightarrow a_1+a_n=\frac{384}{n} \ldots . .(1)
\end{aligned}
\)
Now, \(\sum_{i=1}^{\frac{n}{2}} a_{2 i}=120\)
\(
\Rightarrow a_2+a_4+a_6+\ldots . .+a_n=120
\)
Here total \(\frac{n}{2}\) terms present.
\(
\begin{aligned}
& \therefore \frac{\frac{n}{2}}{2}\left[a_2+a_n\right]=120 \\
& \Rightarrow \frac{n}{4}\left[a_1+1+a_n\right]=120 \\
& \Rightarrow a_1+a_n+1=\frac{480}{n} \ldots . .(2)
\end{aligned}
\)
Subtracting (1) from (2), we get
\(
\begin{aligned}
& 1=\frac{480}{n}-\frac{384}{n} \\
& \Rightarrow 1=\frac{96}{n} \\
& \Rightarrow n=96
\end{aligned}
\) -
Question 131 of 213
131. Question
Let \(S_n=1 \cdot(n-1)+2 \cdot(n-2)+3 \cdot(n-3)+\ldots . .+(n-1) \cdot 1, n \geq 4\). The sum \(\sum_{n=4}^{\infty}\left(\frac{2 S_n}{n!}-\frac{1}{(n-2)!}\right)\) is equal to : [JEE Main 2021 (Online) 1st September Evening Shift]
CorrectIncorrectHint
Let \(T_r=r(n-r)\)
\(
\begin{aligned}
& T _{ r }= nr – r ^2 \\
& \Rightarrow S_n=\sum_{r=1}^n T_r=\sum_{r=1}^n\left(n r-r^2\right) \\
& S_n=\frac{n \cdot(n)(n+1)}{2}-\frac{n(n+1)(2 n+1)}{6} \\
& S_n=\frac{n(n-1)(n+1)}{6}
\end{aligned}
\)Now, \(\sum_{n=4}^{\infty}\left(\frac{2 S_n}{n!}-\frac{1}{(n-2)!}\right)\)
\(
\begin{aligned}
& =\sum_{r=4}^{\infty}\left(2 \cdot \frac{n(n-1)(n+1)}{6 \cdot n(n-1)(n-2)!}-\frac{1}{(n-2)!}\right) \\
& =\sum_{r=4}^{\infty}\left(\frac{1}{3}\left(\frac{n-2+3}{(n-2)!}\right)-\frac{1}{(n-2)!}\right) \\
& =\sum_{r=4}^{\infty} \frac{1}{3} \cdot \frac{1}{(n-3)!}=\frac{1}{3}(e-1)
\end{aligned}
\) -
Question 132 of 213
132. Question
Let \(a _1, a _2\), \(\ldots\) \(a_{21}\) be an AP such that \(\sum_{n=1}^{20} \frac{1}{a_n a_{n+1}}=\frac{4}{9}\). If the sum of this AP is 189 , then \(a_6 a_{16}\) is equal to : [JEE Main 2021 (Online) 1st September Evening Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& \sum_{n=1}^{20} \frac{1}{a_n a_{n+1}}=\sum_{n=1}^{20} \frac{1}{a_n\left(a_n+d\right)} \\
& =\frac{1}{d} \sum_{n=1}^{20}\left(\frac{1}{a_n}-\frac{1}{a_n+d}\right) \\
& \Rightarrow \frac{1}{d}\left(\frac{1}{a_1}-\frac{1}{a_{21}}\right)=\frac{4}{9} \text { (Given) } \\
& \Rightarrow \frac{1}{d}\left(\frac{a_{21}-a_1}{a_1 a_{21}}\right)=\frac{4}{9} \\
& \Rightarrow \frac{1}{d}\left(\frac{a_1+20 d-a_1}{a_1 a_2}\right)=\frac{4}{9} \Rightarrow a_1 a_2=45 \ldots(1)
\end{aligned}
\)
Now sum of first 21 terms \(=\frac{21}{2}\left(2 a_1+20 d\right)=189\)
\(
\Rightarrow a_1+10 d=9 \dots(2)
\)
For equation (1) & (2) we get
\(
a_1=3 \& d=\frac{3}{5}
\)
or \(a_1=15 \& d=-\frac{3}{5}\)
So, \(a_6 \cdot a_{16}=\left(a_1+5 d\right)\left(a_1+15 d\right)\)
\(
\Rightarrow a _6 a _{16}=72
\) -
Question 133 of 213
133. Question
Let \(a _1, a _2, a _3, \ldots .\). be an A.P. If \(\frac{a_1+a_2+\ldots .+a_{10}}{a_1+a_2+\ldots .+a_p}=\frac{100}{p^2}, p \neq 10\), then \(\frac{a_{11}}{a_{10}}\) is equal to : [JEE Main 2021 (Online) 31st August Evening Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& \frac{\frac{10}{2}\left(2 a_1+9 d\right)}{\frac{p}{2}\left(2 a_1+(p-1) d\right)}=\frac{100}{p^2} \\
& \left(2 a_1+9 d\right) p=10\left(2 a_1+(p-1) d\right) \\
& 9 d p=20 a_1-2 p a_1+10 d(p-1) \\
& 9 p=(20-2 p) \frac{a_1}{d}+10(p-1) \\
& \frac{a_1}{d}=\frac{(10-p)}{2(10-p)}=\frac{1}{2} \\
& \therefore \frac{a_{11}}{a_{10}}=\frac{a_1+10 d}{a_1+9 d}=\frac{\frac{1}{2}+10}{\frac{1}{2}+9}=\frac{21}{19}
\end{aligned}
\) -
Question 134 of 213
134. Question
The sum of 10 terms of the series \(\frac{3}{1^2 \times 2^2}+\frac{5}{2^2 \times 3^2}+\frac{7}{3^2 \times 4^2}+\ldots\) is : [JEE Main 2021 (Online) 31st August Morning Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& S=\frac{2^2-1^2}{1^2 \times 2^2}+\frac{3^2-2^2}{2^2 \times 3^2}+\frac{4^2-3^2}{3^2 \times 4^2}+\ldots \\
& =\left[\frac{1}{1^2}-\frac{1}{2^2}\right]+\left[\frac{1}{2^2}-\frac{1}{3^2}\right]+\left[\frac{1}{3^2}-\frac{1}{4^2}\right]+\ldots+\left[\frac{1}{10^2}-\frac{1}{11^2}\right] \\
& =1-\frac{1}{121} \\
& =\frac{120}{121}
\end{aligned}
\) -
Question 135 of 213
135. Question
Three numbers are in an increasing geometric progression with common ratio r. If the middle number is doubled, then the new numbers are in an arithmetic progression with common difference \(d\). If the fourth term of \(G P\) is \(3 r^2\), then \(r^2-d\) is equal to : [JEE Main 2021 (Online) 31st August Morning Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& \text { Let numbers be } \frac{a}{r}, a , ar \rightarrow \text { G.P. } \\
& \frac{a}{r}, 2 a , ar \rightarrow \text { A.P. } \Rightarrow 4 a =\frac{a}{r}+ ar \Rightarrow r +\frac{1}{r}=4 \\
& r =2 \pm \sqrt{3} \\
& 4^{\text {th }} \text { form of G.P. }=3 r ^2 \Rightarrow ar ^2=3 r ^2 \Rightarrow a =3 \\
& r =2+\sqrt{3}, a =3, d =2 a -\frac{a}{r}=3 \sqrt{3} \\
& r ^2- d =(2+\sqrt{3})^2-3 \sqrt{3} \\
& =7+4 \sqrt{3}-3 \sqrt{3} \\
& =7+\sqrt{3}
\end{aligned}
\) -
Question 136 of 213
136. Question
If \(0< x <1\) and \(y=\frac{1}{2} x^2+\frac{2}{3} x^3+\frac{3}{4} x^4+\ldots\), then the value of \(e ^{1+ y }\) at \(x=\frac{1}{2}\) is : [JEE Main 2021 (Online) 27th August Evening Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& y=\left(1-\frac{1}{2}\right) x^2+\left(1-\frac{1}{3}\right) x^3+\ldots \\
& =\left(x^2+x^3+x^4+\ldots \ldots\right)-\left(\frac{x^2}{2}+\frac{x^3}{3}+\frac{x^4}{4}+\ldots\right) \\
& =\frac{x^2}{1-x}+x-\left(x+\frac{x^2}{2}+\frac{x^3}{3}+\ldots\right) \\
& =\frac{x}{1-x}+\ln (1-x) \\
& x=\frac{1}{2} \Rightarrow y=1-\ln 2 \\
& e^{1+y}=e^{1+1-\ln 2} \\
& =e^{2-\ln 2}=\frac{e^2}{2}
\end{aligned}
\) -
Question 137 of 213
137. Question
If \(0< x <1\), then \(\frac{3}{2} x^2+\frac{5}{3} x^3+\frac{7}{4} x^4+\ldots\), is equal to : [JEE Main 2021 (Online) 27th August Morning Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& \text { Let } t=\frac{3}{2} x^2+\frac{5}{3} x^3+\frac{7}{4} x^4+\ldots \ldots \infty \\
& =\left(2-\frac{1}{2}\right) x^2+\left(2-\frac{1}{3}\right) x^3+\left(2-\frac{1}{4}\right) x^4+\ldots \ldots \infty \\
& =2\left(x^2+x^3+x^4+\ldots \ldots \infty\right)-\left(\frac{x^2}{2}+\frac{x^3}{3}+\frac{x^4}{4}+\ldots \ldots \infty\right) \\
& =\frac{2 x^2}{1-x}-(\ln (1-x)-x) \\
& \Rightarrow t=\frac{2 x^2}{1-x}+x-\ln (1-x) \\
& \Rightarrow t=\frac{x(1+x)}{1-x}-\ln (1-x)
\end{aligned}
\) -
Question 138 of 213
138. Question
If for \(x, y \in R, x>0, y=\log _{10} x+\log _{10} x^{1 / 3}+\log _{10} x^{1 / 9}+\) \(\ldots\) upto \(\infty\) terms and \(\frac{2+4+6+\ldots .+2 y}{3+6+9+\ldots .+3 y}=\frac{4}{\log _{10} x}\), then the ordered pair \((x, y)\) is equal to : [JEE Main 2021 (Online) 27th August Morning Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& \frac{2(1+2+3+\ldots .+y)}{3(1+2+3+\ldots .+y)}=\frac{4}{\log _{10} x} \\
& \Rightarrow \log _{10} x=6 \Rightarrow x=10^6
\end{aligned}
\)
Now,
\(
\begin{aligned}
& y=\left(\log _{10} x\right)+\left(\log _{10} x^{\frac{1}{3}}\right)+\left(\log _{10} x^{\frac{1}{9}}\right)+\ldots \infty \\
& =\left(1+\frac{1}{3}+\frac{1}{9}+\ldots \infty\right) \log _{10} x \\
& =\left(\frac{1}{1-\frac{1}{3}}\right) \log _{10} x=9
\end{aligned}
\)
So, \((x, y)=\left(10^6, 9\right)\) -
Question 139 of 213
139. Question
The sum of the series \(\frac{1}{x+1}+\frac{2}{x^2+1}+\frac{2^2}{x^4+1}+\ldots \ldots+\frac{2^{100}}{x^{2^{100}}+1}\) when \(x =2\) is : [JEE Main 2021 (Online) 26th August Morning Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& S=\frac{1}{x+1}+\frac{2}{x^2+1}+\frac{2^2}{x^4+1}+\ldots \ldots+\frac{2^{100}}{x^{210}}+1 \\
& S+\frac{1}{1-x}=\frac{1}{1-x}+\frac{1}{x+1}+\ldots \ldots=\frac{2}{1-x^2}+\frac{2}{1+x^2}+\ldots
\end{aligned}
\)
\(
\begin{aligned}
& S+\frac{1}{1-x}=\frac{2^{101}}{1-x^{400}} \\
& S=1-\frac{2^{101}}{2^{400}-1}
\end{aligned}
\) -
Question 140 of 213
140. Question
If the sum of an infinite GP a, \(a r, ar ^2, ar ^3\), \(\ldots\) is 15 and the sum of the squares of its each term is 150 , then the sum of \(a r^2, a r^4, a r^6\), \(\ldots\) is : [JEE Main 2021 (Online) 26th August Morning Shift]
CorrectIncorrectHint
Sum of infinite terms :
\(
\frac{a}{1-r}=15 \ldots .(i)
\)
Series formed by square of terms:
\(
\begin{aligned}
& a^2, a^2 r^2, a^2 r^4, a^2 r^6 \ldots \ldots . \\
& \text { Sum }=\frac{a^2}{1-r^2}=150 \\
& \Rightarrow \frac{a}{1-r} \cdot \frac{a}{1+r}=150 \Rightarrow 15 \cdot \frac{a}{1+r}=150
\end{aligned}
\)
\(
\Rightarrow \frac{a}{1+r}=10 \ldots \ldots \text { (ii) }
\)
by (i) and (ii), \(a=12 ; r=\frac{1}{5}\)
Now, series : \(a r^2, a r^4, a r^6\)
\(
\text { Sum }=\frac{a r^2}{1-r^2}=\frac{12 \cdot\left(\frac{1}{25}\right)}{1-\frac{1}{25}}=\frac{1}{2}
\) -
Question 141 of 213
141. Question
Let \(S_n\) be the sum of the first \(n\) terms of an arithmetic progression. If \(S_{3 n}=3 S_{2 n}\), then the value of \(\frac{S_{4 n}}{S_{2 n}}\) is: [JEE Main 2021 (Online) 25th July Morning Shift]
CorrectIncorrectHint
Let a be first term and \(d\) be common diff. of this A.P.
Given, \(S _{3 n }=3 S _{2 n }\)
\(
\begin{aligned}
& \Rightarrow \frac{3 n}{2}[2 a+(3 n-1) d]=3 \frac{2 n}{2}[2 a+(2 n-1) d] \\
& \Rightarrow 2 a+(3 n-1) d=4 a+(4 n-2) d \\
& \Rightarrow 2 a+(n-1) d=0
\end{aligned}
\)
\(
\text { NoW, } \frac{S_{4 n}}{S_{2 n}}=\frac{\frac{4 n}{2}[2 a+(4 n-1) d]}{\frac{2 n}{2}[2 a+(2 n-1) d]}=\frac{2\lceil\underbrace{2 a+(n-1) d}_{=0}+3 n d]}{\lceil\underbrace{2 a+(n-1) d}_{=0}+n d\rceil}
\)
\(
=\frac{6 n d}{n d}=6
\) -
Question 142 of 213
142. Question
Let \(S_n\) denote the sum of first \(n\)-terms of an arithmetic progression. If \(S_{10}=530, S_5=\) 140 , then \(S_{20}-S_6\) is equal to: [JEE Main 2021 (Online) 22th July Evening Shift]
CorrectIncorrectHint
Let first term of A.P. be \(a\) and common difference is \(d\).
\(
\begin{aligned}
& \therefore S_{10}=\frac{10}{2}\{2 a+9 d\}=530 \\
& \therefore 2 a+9 d=106 \ldots . \text { (i) }
\end{aligned}
\)
\(
\begin{aligned}
& S_5=\frac{5}{2}\{2 a+4 d\}=140 \\
& a+2 d=28 \ldots \ldots \text { (ii) }
\end{aligned}
\)
From equation (i) and (ii), \(a=8, d=10\)
\(
\begin{aligned}
& \therefore S_{20}-S_6=\frac{20}{2}\{2 \times 8+19 \times 10\}-\frac{6}{2}\{2 \times 8+5 \times 10\} \\
& =2060-198 \\
& =1862
\end{aligned}
\) -
Question 143 of 213
143. Question
If sum of the first 21 terms of the series \(\log _{9^{1 / 2}} x+\log _{9^{1 / 3}} x+\log _{9^{1 / 4}} x+\ldots \ldots\), where \(x>0\) is 504 , then \(x\) is equal to [JEE Main 2021 (Online) 20th July Evening Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& s=2 \log _9 x+3 \log _9 x+\ldots \ldots .+22 \log _9 x \\
& s=\log _9 x(2+3+\ldots \ldots+22) \\
& s=\log _9 x\left\{\frac{21}{2}(2+22)\right\}
\end{aligned}
\)Given, \(252 \log _9 x=504\)
\(
\Rightarrow \log _9 x=2 \Rightarrow x=81
\) -
Question 144 of 213
144. Question
Let \(S_1\) be the sum of first \(2 n\) terms of an arithmetic progression. Let \(S_2\) be the sum of first \(4 n\) terms of the same arithmetic progression. If \(\left(S_2-S_1\right)\) is 1000 , then the sum of the first \(6 n\) terms of the arithmetic progression is equal to : [JEE Main 2021 (Online) 18th March Evening Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& S_1=\frac{2 n}{2}[2 a+(2 n-1) d] \\
& S_2=\frac{4 n}{2}[2 a+(4 n-1) d]
\end{aligned}
\)
(where \(a = T _1\) and \(d\) is common difference)
\(
\begin{aligned}
& S_2-S_1 \Rightarrow 2 n[2 a+(4 n-1) d]-n[2 a+(2 n-1) d]=1000 \\
& \Rightarrow n[2 a+d(8 n-2-2 n+1)]=1000 \\
& \Rightarrow n[2 a+(6 n-1) d]=1000 \\
& S_6=\frac{6 n}{2}[2 a+(6 n-1) d]=3\left(S_2-S_1\right)=3000
\end{aligned}
\) -
Question 145 of 213
145. Question
If \(\alpha, \beta\) are natural numbers such that \(100^\alpha-199 \beta=(100)(100)+(99)(101)+(98)(102)+\ldots . .+(1)(199)\), then the slope of the line passing through \((\alpha, \beta)\) and origin is : [JEE Main 2021 (Online) 18th March Morning Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& \text { RHS }=\sum_{r=0}^{99}(100-r)(100+r) \\
& =(100)^3-\frac{99 \times 100 \times 199}{6}=(100)^3-(1650) 199 \\
& \text { LHS }=(100)^\alpha-(199)^\beta \\
& \text { So, } \alpha=3, \beta=1650 \\
& \text { Slope }=\tan \theta=\frac{\beta}{\alpha} \\
& \Rightarrow \tan \theta=550
\end{aligned}
\) -
Question 146 of 213
146. Question
\(\frac{1}{3^2-1}+\frac{1}{5^2-1}+\frac{1}{7^2-1}+\ldots+\frac{1}{(201)^2-1}\) is equal to [JEE Main 2021 (Online) 18th March Morning Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& S=\sum_{r=1}^{100} \frac{1}{(2 n+1)^2-1} \\
& =\sum_{r=1}^{100} \frac{1}{(2 n+1+1)(2 n+1-1)} \\
& =\sum_{r=1}^{100} \frac{1}{2 n(2 n+2)} \\
& =\frac{1}{4} \sum_{r=1}^{100} \frac{1}{n(n+1)} \\
& =\frac{1}{4} \sum_{r=1}^{100} \frac{(n+1)-n}{n(n+1)} \\
& =\frac{1}{4} \sum_{r=1}^{100}\left(\frac{1}{n}-\frac{1}{n+1}\right) \\
& S=\frac{1}{4}\left(\left(1-\frac{1}{2}\right)+\left(\frac{1}{2}-\frac{1}{3}\right)+\left(\frac{1}{3}-\frac{1}{4}\right)+\ldots \ldots+\left(\frac{1}{100}-\frac{1}{101}\right)\right) \\
& \therefore S=\frac{1}{4}\left[\frac{100}{101}\right]=\frac{25}{101}
\end{aligned}
\) -
Question 147 of 213
147. Question
The sum of the series \(\sum_{n=1}^{\infty} \frac{n^2+6 n+10}{(2 n+1)!}\) is equal to : [JEE Main 2021 (Online) 26th February Evening Shift]
CorrectIncorrectHint
\(
\sum_{n=1}^{\infty} \frac{n^2+6 n+10}{(2 n+1)!}
\)
Put \(2 n+1=r\), where \(r=3,5,7\), \(\ldots\)
\(
\begin{aligned}
& \Rightarrow n=\frac{r-1}{2} \\
& \frac{n^2+6 n+10}{(2 n+1)!}=\frac{\left(\frac{r-1}{2}\right)^2+3 r-3+10}{r!} \\
& =\frac{r^2+10 r+29}{4 r!}=\frac{r(r-1)+11 r+29}{4 r!}
\end{aligned}
\)
Now, \(\sum_{r=3,5,7} \frac{r(r-1)+11 r+29}{4 r!}\)
\(
=\frac{1}{4} \sum_{r=3,5,7, \ldots \ldots . .}\left(\frac{1}{(r-2)!}+\frac{11}{(r-1)!}+\frac{29}{r!}\right)
\)
\(
\begin{aligned}
& =\frac{1}{4}\left\{\left(\frac{1}{1!}+\frac{1}{3!}+\frac{1}{5!}+\ldots \ldots\right)+11\left(\frac{1}{2!}+\frac{1}{4!}+\frac{1}{6!}+\ldots \ldots\right)+29\left(\frac{1}{3!}+\frac{1}{5!}+\frac{1}{7!}+\ldots \ldots\right)\right\} \\
& =\frac{1}{4}\left\{\frac{e-\frac{1}{e}}{2}+11\left(\frac{e+\frac{1}{e}-2}{2}\right)+29\left(\frac{e-\frac{1}{e}-2}{2}\right)\right\} \\
& =\frac{1}{8}\left\{e-\frac{1}{e}+11 e+\frac{11}{e}-22+29 e-\frac{29}{e}-58\right\} \\
& =\frac{1}{8}\left\{41 e-\frac{19}{e}-80\right\}
\end{aligned}
\) -
Question 148 of 213
148. Question
The sum of the infinite series \(1+\frac{2}{3}+\frac{7}{3^2}+\frac{12}{3^3}+\frac{17}{3^4}+\frac{22}{3^5}+\ldots \ldots\) is equal to : [JEE Main 2021 (Online) 26th February Morning Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& S=1+\frac{2}{3}+\frac{7}{3^2}+\frac{12}{3^3}+\frac{17}{3^4}+\ldots \\
& \frac{S}{3}=\frac{1}{3}+\frac{2}{3^2}+\frac{7}{3^3}+\frac{12}{3^4}+\ldots \\
& 2 S=1+\frac{1}{3}+\frac{5}{3^2}+\frac{5}{3^3}+\frac{5}{3^4}+\ldots .+ \text { up to infinite terms } \\
& \frac{2 S}{3}=\frac{4}{3}+\frac{5}{3}\left\{\frac{1 / 3}{1-\frac{1}{3}}\right\}=\frac{5}{6}+\frac{4}{3}=\frac{13}{6} \\
& \Rightarrow S=\frac{13}{4}
\end{aligned}
\) -
Question 149 of 213
149. Question
In an increasing geometric series, the sum of the second and the sixth term is \(\frac{25}{2}\) and the product of the third and fifth term is 25 . Then, the sum of \(4^{\text {th }}, 6^{\text {th }}\) and \(8^{\text {th }}\) terms is equal to: [JEE Main 2021 (Online) 26th February Morning Shift]
CorrectIncorrectHint
\(a , ar , ar ^2, \ldots\).
\(
\begin{aligned}
& T_2+T_6=\frac{25}{2} \Rightarrow \operatorname{ar}\left(1+r^4\right)=\frac{25}{2} \\
& a^2 r^2\left(1+r^4\right)^2=\frac{625}{4} \ldots .(1)
\end{aligned}
\)
\(
\begin{aligned}
& T_3 . T_5=25 \Rightarrow\left(a r^2\right)\left(a r^4\right)=25 \\
& a^2 r^6=25 \ldots \ldots(2)
\end{aligned}
\)
On dividing (1) by (2)
\(
\begin{aligned}
& \frac{\left(1+r^4\right)^2}{r^4}=\frac{25}{4} \\
& 4 r^8-14 r^4+4=0 \\
& \left(4 r^4-1\right)\left(r^4-4\right)=0 \\
& r^4=\frac{1}{4}, 4 \Rightarrow r^4=4 \text { (an increasing geometric series) } \\
& a^2 r^6=25 \Rightarrow\left(a r^3\right)^2=25 \\
& T_4+T_6+T_8=a r^3+a r^5+a r^7 \\
& =a r^3\left(1+r^2+r^4\right) \\
& =5(1+2+4)=35
\end{aligned}
\) -
Question 150 of 213
150. Question
The minimum value of \(f(x)=a^{a^x}+a^{1-a^x}\), where a, \(x \in R\) and \(a>0\), is equal to : [JEE Main 2021 (Online) 25th February Evening Shift]
CorrectIncorrectHint
We know, \(A M \geq G M\)
\(
\begin{aligned}
& \therefore \frac{a^{a^x}+\frac{a}{a^x}}{2} \geq\left(a^{a^x} \cdot \frac{a}{a^{a^x}}\right)^{1 / 2} \\
& \Rightarrow a^{a^x}+a^{1-a^x} \geq 2 \sqrt{a}
\end{aligned}
\) -
Question 151 of 213
151. Question
If \(0<\theta, \phi<\frac{\pi}{2}, x=\sum_{n=0}^{\infty} \cos ^{2 n} \theta, y=\sum_{n=0}^{\infty} \sin ^{2 n} \phi\) and \(z=\sum_{n=0}^{\infty} \cos ^{2 n} \theta \cdot \sin ^{2 n} \phi\) then : [JEE Main 2021 (Online) 25th February Morning Shift]
CorrectIncorrectHint
\(
x=1+\cos ^2 \theta+\ldots \ldots \ldots \infty
\)
\(
x=\frac{1}{1-\cos ^2 \theta}=\frac{1}{\sin ^2 \theta} \dots(1)
\)
\(
\begin{aligned}
& y=1+\sin ^2 \phi+\ldots \ldots \ldots \infty \\
& y=\frac{1}{1-\sin ^2 \phi}=\frac{1}{\cos ^2 \phi} \ldots \ldots \text { (2) }
\end{aligned}
\)
\(
\begin{aligned}
& z=\frac{1}{1-\cos ^2 \theta \cdot \sin ^2 \phi}=\frac{1}{1-\left(1-\frac{1}{x}\right)\left(1-\frac{1}{y}\right)}=\frac{x y}{x y-(x-1)(y-1)} \\
& \Rightarrow x z+y z-z=x y \\
& \Rightarrow x y+z=(x+y) z
\end{aligned}
\) -
Question 152 of 213
152. Question
The common difference of the A.P. \(b _1, b _2, \ldots, b _{ m }\) is 2 more than the common difference of A.P. \(a_1, a_2, \ldots, a_n\). If \(a_{40}=-159, a_{100}=-399\) and \(b_{100}=a_{70}\), then \(b_1\) is equal to : [JEE Main 2020 (Online) 6th September Evening Slot]
CorrectIncorrectHint
Let common difference of series \(a_1, a_2, a_3, \ldots, a_n\) be \(d\).
\(
\because a_{40}=a_1+39 d==-159 \dots(i)
\)
and \(a_{100}=a_1+99 d=-399 \dots(ii)\)
From eqn. (ii) and (i) \(d =-4\) and \(a _1=-3\).
The common difference of the A.P. \(b _1, b _2, \ldots, b _{ m }\) is 2 more than the common difference of A.P. \(a_1, a_2, \ldots, a_n\).
\(\therefore\) Common difference of \(b _1, b _2, b _3, \ldots\), be (-2).
\(
\begin{aligned}
& \because b_{100}=a_{70} \\
& \therefore b_1+99(-2)=(-3)+69(-4) \\
& \therefore b_1=198-279 \\
& \therefore b_1=-81
\end{aligned}
\) -
Question 153 of 213
153. Question
Let \(a, b, c, d\) and \(p\) be any non zero distinct real numbers such that \(\left(a^2+b^2+c^2\right) p^2-2(a b+b c+c d) p+\left(b^2+c^2+d^2\right)=0\). Then : [JEE Main 2020 (Online) 6th September Morning Slot]
CorrectIncorrectHint
\(
\begin{aligned}
& \left(a^2+b^2+c^2\right) p^2-2(a b+b c+c d) p+\left(b^2+c^2+d^2\right)=0 \\
& \Rightarrow\left(a^2 p^2+2 a b p+b^2\right)+\left(b^2 p^2+2 b c p+c^2\right)+\left(c^2 p^2+2 c d p+d^2\right)=0 \\
& \Rightarrow(a b+b)^2+(b p+c)^2+(c p+d)^2=0
\end{aligned}
\)Note: If sum of two or more positive quantity is zero then they are all zero.
\(\therefore a p+b=0\) and \(b p+c=0\) and \(c p+d=0\)
\(
p =-\frac{b}{a}=-\frac{c}{b}=-\frac{d}{c}
\)
or \(\frac{b}{a}=\frac{c}{b}=\frac{d}{c}\)
\(\therefore a , b , c , d\) are in G.P. -
Question 154 of 213
154. Question
If the sum of the second, third and fourth terms of a positive term G.P. is 3 and the sum of its sixth, seventh and eighth terms is 243 , then the sum of the first 50 terms of this G.P. is : [JEE Main 2020 (Online) 5th September Evening Slot]
CorrectIncorrectHint
\(
\begin{aligned}
& \text { Let first term }=a>0 \\
& \text { Common ratio }=r>0 \\
& a r+a r^2+a r^3=3 \ldots . \text { (i) } \\
& a r^5+a r^6+a r^7=243 \ldots . \text { (ii) } \\
& \Rightarrow r^4\left(a r+a r^2+a r^3\right)=243 \\
& \Rightarrow r^4(3)=243 \\
& \Rightarrow r=3 \quad r>0 \\
& \text { from (i) } \\
& 3 a+9 a+27 a=3 \\
& \Rightarrow a=\frac{1}{13} \\
& \therefore S_{50}=\frac{a\left(r^{50}-1\right)}{(r-1)} \\
& =\frac{1}{26}\left(3^{50}-1\right)
\end{aligned}
\) -
Question 155 of 213
155. Question
If the sum of the first 20 terms of the series \(\log _{\left(7^{1 / 2}\right)} x+\log _{\left(7^{1 / 3}\right)} x+\log _{\left(7^{1 / 4}\right)} x+\ldots\) is 460 , then \(x\) is equal to : [JEE Main 2020 (Online) 5th September Evening Slot]
CorrectIncorrectHint
\(
\begin{aligned}
& 460=\log _7 x \cdot(2+3+4+\ldots . .+20+21) \\
& \Rightarrow 460=\log _7 x \cdot\left(\frac{21 \times 22}{2}-1\right) \\
& \Rightarrow 460=230 \cdot \log _7 x \\
& \Rightarrow \log _7 x=2 \\
& \Rightarrow x=49
\end{aligned}
\) -
Question 156 of 213
156. Question
If \(2^{10}+2^9 \cdot 3^1+2^8 \cdot 3^2+\ldots . .+2 \cdot 3^9+3^{10}=S-2^{11}\), then \(S\) is equal to : [JEE Main 2020 (Online) 5th September Morning Slot]
CorrectIncorrectHint
\(
\text { Let } S_1=2^{10}+2^9 \cdot 3^1+2^8 \cdot 3^2+\ldots . .+2 \cdot 3^9+3^{10} \dots(1)
\)
Also \(\frac{3 S_1}{2}=2^9 \cdot 3^1+2^8 \cdot 3^2+\ldots . .+2 \cdot 3^9+3^{10}+\frac{3^{11}}{2} \dots(2)\)
Performing (1) – (2), we get
\(
\begin{aligned}
& -\frac{S_1}{2}=2^{10}-\frac{3^{11}}{2} \\
& \Rightarrow S_1=3^{11}-2^{11}
\end{aligned}
\)
According to question,
\(
\begin{aligned}
& 3^{11}-2^{11}=S-2^{11} \\
& \Rightarrow S=3^{11}
\end{aligned}
\) -
Question 157 of 213
157. Question
If \(3^{2 \sin 2 \alpha-1}, 14\) and \(3^{4-2 \sin 2 \alpha}\) are the first three terms of an A.P. for some \(\alpha\), then the sixth terms of this A.P. is: [JEE Main 2020 (Online) 5th September Morning Slot]
CorrectIncorrectHint
Given that
\(
3^{4-\sin 2 \alpha}+3^{2 \sin 2 \alpha-1}=28
\)
Let \(3^{2 \sin 2 \alpha}= t\)
\(
\begin{aligned}
& \Rightarrow \frac{81}{t}+\frac{t}{3}=28 \\
& \Rightarrow t=81,3
\end{aligned}
\)
\(
\begin{aligned}
& \therefore 3^{2 \sin 2 \alpha}=3^1, 3^4 \\
& \sin 2 \alpha=\frac{1}{2}, 2 \text { (rejected) }
\end{aligned}
\)
First term \(a =3^{2 \sin 2 \alpha-1}=3^0\)
\(
\Rightarrow a =1
\)
Given Second term \(=14\)
\(\therefore\) Common difference \(d=13\)
\(
\begin{aligned}
& T_6=a+5 d \\
& T_6=1+5 \times 13 \\
& T_6=66
\end{aligned}
\) -
Question 158 of 213
158. Question
The minimum value of \(2^{\sin x}+2^{\cos x}\) is : [JEE Main 2020 (Online) 4th September Evening Slot]
CorrectIncorrectHint
Using \(AM \geq GM\)
\(
\begin{aligned}
& \Rightarrow \frac{2^{\sin x}+2^{\cos x}}{2} \geq \sqrt{2^{\sin x} \cdot 2^{\cos x}} \\
& \Rightarrow 2^{\sin x}+2^{\cos x} \geq 2^{1+\left(\frac{\sin x \cos x}{2}\right)} \\
& \Rightarrow \min \left(2^{\sin x}+2^{\cos x}\right)=2^{1-\frac{1}{\sqrt{2}}}
\end{aligned}
\)
As we know range of \(\sin x+\cos x\) is :
\(
-\sqrt{2} \leq \sin x+\cos x \leq \sqrt{2} \text {. }
\)
So Minimum value of \(\sin x+\cos x=-\sqrt{2}\) -
Question 159 of 213
159. Question
Let \(a_1, a_2, \ldots\), an be a given A.P. whose common difference is an integer and \(S_n=a_1+a_2+\ldots .+a_n\). If \(a_1=1, a_n=300\) and \(15 \leq n \leq 50\), then the ordered pair \(\left(S_{n-4}, a_{n-4}\right)\) is equal to: [JEE Main 2020 (Online) 4th September Evening Slot]
CorrectIncorrectHint
\(
\begin{aligned}
& a_n=a_1+(n-1) d \\
& \Rightarrow 300=1+(n-1) d \\
& \Rightarrow(n-1) d=299=13 \times 23 \\
& \text { since, } n \in[15,50] \\
& \therefore n =24 \text { and } d =13 \\
& a_{n-4}=a_{20}=1+19 \times 13=248 \\
& \Rightarrow a_{n-4}=248 \\
& S_{n-4}=\frac{20}{2}\{1+248\}=2490
\end{aligned}
\) -
Question 160 of 213
160. Question
\(\text { If } 1+\left(1-2^2 \cdot 1\right)+\left(1-4^2 \cdot 3\right)+\left(1-6^2 \cdot 5\right)+\ldots . .+\left(1-20^2 .19\right)=\alpha-220 \beta, \text { then an ordered pair }(\alpha, \beta) \text { is equal to: }\) [JEE Main 2020 (Online) 4th September Morning Slot]
CorrectIncorrectHint
\(
\begin{aligned}
& 1+\left(1-2^2 .1\right)+\left(1-4^2 .3\right)+\left(1-6^2 .5\right)+\ldots\left(1-20^2 .19\right) \\
& S=1+\sum_{r=1}^{10}\left[1-(2 r)^2(2 r-1)\right]=1+\sum_{r=1}^{10}\left(1-8 r^3+4 r^2\right)==1+10-\sum_{r=1}^{10}\left(8 r^3-4 r^2\right)
\end{aligned}
\)
\(
\begin{aligned}
& =11-8\left(\frac{10 \times 11}{2}\right)^2+4 \times\left(\frac{10 \times 11 \times 21}{6}\right) \\
& =11-2 \times(110)^2+4 \times 55 \times 7 \\
& =11-220(110-7) \\
& =11-220 \times 103=\alpha-220 \beta \\
& \Rightarrow \alpha=11, \beta=103
\end{aligned}
\) -
Question 161 of 213
161. Question
If the sum of the series
\(
20+19 \frac{3}{5}+19 \frac{1}{5}+18 \frac{4}{5}+\ldots
\)
upto nth term is 488 and the \(n ^{\text {th }}\) term is negative, then : [JEE Main 2020 (Online) 3rd September Evening Slot]CorrectIncorrectHint
\(
\begin{aligned}
& S=\frac{100}{5}+\frac{98}{5}+\frac{96}{5}+\frac{94}{5}+\ldots n \\
& S_n=\frac{n}{2}\left(2 \times \frac{100}{5}+(n-1)\left(\frac{-2}{5}\right)\right)=188 \\
& \Rightarrow n(100-n+1)=488 \times 5 \\
& \Rightarrow n^2-101 n+488 \times 5=0 \\
& \Rightarrow n=61,40
\end{aligned}
\)
For negative term \(n=61\)
\(
\begin{aligned}
& T_n=a+(n-1) d=\frac{100}{5}-\frac{2}{5} \times 60 \\
& =20-24=-4
\end{aligned}
\) -
Question 162 of 213
162. Question
If the first term of an A.P. is 3 and the sum of its first 25 terms is equal to the sum of its next 15 terms, then the common difference of this A.P. is : [JEE Main 2020 (Online) 3rd September Morning Slot]
CorrectIncorrectHint
First 25 terms \(=a, a+d, \ldots \ldots ., a+24 d\)
Next 15 terms \(=a+25 d, a+26 d, \ldots . . ., a+39 d\)
\(
\therefore \frac{25}{2}[2 a+24 d]=\frac{15}{2}[2(a+25 d)+14 d]
\)
\(
\begin{aligned}
& \Rightarrow 50 a+600 d=15[2 a+50 d+14 d] \\
& \Rightarrow 20 a+600 d=960 d \\
& \Rightarrow 60=360 d \\
& \Rightarrow d=\frac{1}{6}
\end{aligned}
\) -
Question 163 of 213
163. Question
If the sum of first 11 terms of an A.P., \(a_1, a_2, a_3, \ldots\) is \(0(a \neq 0)\), then the sum of the A.P., \(a_1, a_3, a_5, \ldots . ., a_{23}\) is \(k a_1\), where \(k\) is equal to : [JEE Main 2020 (Online) 2nd September Evening Slot]
CorrectIncorrectHint
Let common difference be \(d\).
\(
\begin{aligned}
& \because a_1+a_2+a_3+\ldots+a_{11}=0 \\
& \therefore \frac{11}{2}\left[2 a_1+10 d\right]=0 \\
& \Rightarrow a_1+5 d=0 \\
& \Rightarrow d=-\frac{a_1}{5} \ldots . .(1)
\end{aligned}
\)
\(
\begin{aligned}
& \text { Now } a_1+a_3+a_5+\ldots+a_{23} \\
& =\left(a_1+a_{23}\right) \times \frac{12}{2} \\
& =\left(a_1+a_1+22 d\right) \times 6 \\
& =\left[2 a_1+22\left(-\frac{a_1}{5}\right)\right] \times 6 \\
& =-\frac{72}{2} a_1 \\
& \therefore k=-\frac{72}{2}
\end{aligned}
\) -
Question 164 of 213
164. Question
Let \(S\) be the sum of the first 9 terms of the series :
\(
\begin{aligned}
& \{ x + k a\}+\left\{ x ^2+( k +2) a\right\}+\left\{ x ^3+( k +4) a\right\} \\
& +\left\{ x ^4+( k +6) a\right\}+\ldots . \text { where } a \neq 0 \text { and } x \neq 1 .
\end{aligned}
\)
If \(S =\frac{x^{10}-x+45 a(x-1)}{x-1}\), then \(k\) is equal to : [JEE Main 2020 (Online) 2nd September Evening Slot]CorrectIncorrectHint
\(
\begin{aligned}
& S =\{ x + k a\}+\left\{ x ^2+( k +2) a\right\}+\left\{ x ^3+( k +4) a\right\} \\
& +\left\{ x ^4+( k +6) a\right\}+\ldots \\
& S=\left(x+x^2+x^3+\ldots 9 \text { terms }\right)+ \\
& a(k+(k+2)+(k+4)+(k+6)+\ldots .9 \text { terms }) \\
& S=\frac{x\left(x^9-1\right)}{(x-1)}+a\left[\frac{9}{2}[2 k+(9-1) 2]\right] \\
& S=\frac{x^{10}-x}{x-1}+9 a(k+8) \\
& S=\frac{x^{10}-x+9 a(k+8)(x-1)}{x-1} \\
& S=\frac{x^{10}-x+9(k+8) a(x-1)}{x-1}
\end{aligned}
\)
Compare with given sum, then we get
\(
\begin{aligned}
& 9(k+8)=45 \\
& \Rightarrow(k+8)=5 \\
& \Rightarrow k=-3
\end{aligned}
\) -
Question 165 of 213
165. Question
If \(|x|<1,|y|<1\) and \(x \neq y\), then the sum to infinity of the following series
\(
(x+y)+\left(x^2+x y+y^2\right)+\left(x^3+x^2 y+x y^2+y^3\right)+\ldots
\) [JEE Main 2020 (Online) 2nd September Morning Slot]CorrectIncorrectHint
\(
(x+y)+\left(x^2+x y+y^2\right)+\left(x^3+x^2 y+x y^2+y^3\right)+\ldots
\)By multiplying and dividing \(x-y\) :
\(
\begin{aligned}
& \frac{\left(x^2-y^2\right)+\left(x^3-y^3\right)+\left(x^4-y^4\right)+\ldots}{x-y} \\
& =\frac{\left(x^2+x^3+x^4+\ldots\right)-\left(y^2+y^3+y^4+\ldots\right)}{x-y} \\
& =\frac{\frac{x^2}{1-x}-\frac{y^2}{1-y}}{x-y} \\
& =\frac{\left(x^2-y^2\right)-x y(x-y)}{(1-x)(1-y)(x-y)} \\
& =\frac{x+y-x y}{(1-x)(1-y)}
\end{aligned}
\) -
Question 166 of 213
166. Question
The sum of the first three terms of a G.P. is \(S\) and their product is 27 . Then all such \(S\) lie in : [JEE Main 2020 (Online) 2nd September Morning Slot]
CorrectIncorrectHint
Let three terms of G.P. are \(\frac{a}{r}, a\), ar
\(
\therefore a\left(\frac{1}{r}+1+r\right)= S \text {. } \dots(1)
\)
and \(a^3=27\)
\(
\Rightarrow a=3
\)
\(
\begin{aligned}
& \therefore 3\left(\frac{1}{r}+1+r\right)= S \\
& \Rightarrow \frac{1}{r}+r=\frac{S}{3}-1 \\
& \Rightarrow As \frac{1}{r}+r \geq 2 \text { or } \frac{1}{r}+r \leq-2 \\
& \therefore \frac{S}{3}-1 \geq 2 \text { or } \frac{S}{3}-1 \leq-2 \\
& \Rightarrow \frac{S}{3} \geq 3 \text { or } \frac{S}{3} \leq-1 \\
& \Rightarrow S \geq 9 \text { or } S \leq-3 \\
& \therefore S \in(-\propto,-3] \cup[9, \infty)
\end{aligned}
\) -
Question 167 of 213
167. Question
Let \(a_n\) be the \(n ^{\text {th }}\) term of a G.P. of positive terms.
\(
\sum_{n=1}^{100} a_{2 n+1}=200 \text { and } \sum_{n=1}^{100} a_{2 n}=100 \text {, }
\)
then \(\sum_{n=1}^{200} a_n\) is equal to : [JEE Main 2020 (Online) 9th January Evening Slot]CorrectIncorrectHint
\(
\begin{aligned}
& \sum_{n=1}^{100} a_{2 n+1}=200 \\
& \Rightarrow a _3+ a _5+ a _7+\ldots .+ a _{201}=200 \\
& \Rightarrow a r^2 \frac{\left(r^{200}-1\right)}{\left(r^2-1\right)}=200 \ldots .(1)
\end{aligned}
\)
\(
\begin{aligned}
& \sum_{n=1}^{100} a_{2 n}=100 \\
& \Rightarrow a _2+ a _4+ a _6+\ldots+ a _{200}=100 \\
& \Rightarrow \operatorname{ar} \frac{\left(r^{200}-1\right)}{\left(r^2-1\right)}=100 \ldots .(2)
\end{aligned}
\)
dividing (1) by (2)
we get, \(r=2\)
adding both (1) and (2), we get
\(
\begin{aligned}
& a _2+ a _3+ a _4+ a _5+\ldots . .+ a _{201}=300 \\
& \Rightarrow r \left( a _1+ a _2+\ldots . .+ a _{200}\right)=300 \\
& \Rightarrow a _1+ a _2+\ldots . .+ a _{200}=\frac{300}{r} \\
& \Rightarrow \sum_{n=1}^{200} a_n=\frac{300}{2}=150
\end{aligned}
\) -
Question 168 of 213
168. Question
The product \(2^{\frac{1}{4}} \cdot 4^{\frac{1}{16}} \cdot 8^{\frac{1}{48}} \cdot 16^{\frac{1}{128}} \ldots\) to \(\infty\) is equal to : [JEE Main 2020 (Online) 9th January Morning Slot]
CorrectIncorrectHint
\(
\begin{aligned}
& 2^{\frac{1}{4}} \cdot 4^{\frac{1}{16}} \cdot 8^{\frac{1}{48}} \cdot 16^{\frac{1}{128}} \ldots \\
& =2^{\frac{1}{4}+\frac{2}{16}+\frac{3}{48}+\ldots \infty} \\
& =2^{\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\ldots \infty} \\
& =2^{\left(\frac{\frac{1}{4}}{1-\frac{1}{2}}\right)} \\
& =2^{\frac{1}{2}}
\end{aligned}
\) -
Question 169 of 213
169. Question
If the \(10^{\text {th }}\) term of an A.P. is \(\frac{1}{20}\) and its \(20^{\text {th }}\) term is \(\frac{1}{10}\), then the sum of its first 200 terms is [JEE Main 2020 (Online) 8th January Evening Slot]
CorrectIncorrectHint
\(
\begin{aligned}
& T_{10}=a+9 d=\frac{1}{20} \ldots .(1) \\
& T_{20}=a+19 d=\frac{1}{10} \ldots . .(2) \\
& \text { Equation (2) – (1) }
\end{aligned}
\)
\(
\begin{aligned}
& 10 d=\frac{1}{10}-\frac{1}{20} \\
& \Rightarrow d=\frac{1}{200} \\
& a+\frac{9}{200}=\frac{1}{20} \\
& \Rightarrow a=\frac{1}{200} \\
& S_{200}=\frac{200}{2}\left[\frac{2}{200}+(200-1) \times \frac{1}{200}\right] \\
& =100\left[\frac{2}{200}+\frac{199}{200}\right] \\
& =\frac{201}{2}=100 \frac{1}{2}
\end{aligned}
\) -
Question 170 of 213
170. Question
Let \(f: R \rightarrow R\) be such that for all \(x \in R\) \(\left(2^{1+x}+2^{1-x}\right), f(x)\) and \(\left(3^x+3^{-x}\right)\) are in A.P., then the minimum value of \(f(x)\) is [JEE Main 2020 (Online) 8th January Morning Slot]
CorrectIncorrectHint
\(2^{1-x}+2^{1+x}, f(x), 3^x+3^{-x}\) are in A.P.
\(
\begin{aligned}
\therefore f(x) & =\frac{3^x+3^{-x}+2^{1+x}+2^{1-x}}{2} \\
& =\frac{3^x+3^{-x}}{2}+\frac{2^{1+x}+2^{1-x}}{2}
\end{aligned}
\)
Applying A. M. \(\geq\) G. M. inequality, we get
\(
\begin{aligned}
& \frac{\left(3^x+3^{-x}\right)}{2} \geq \sqrt{3^x \cdot 3^{-x}} \\
& \Rightarrow \frac{\left(3^x+3^{-x}\right)}{2} \geq 1 \quad \ldots(1)
\end{aligned}
\)
\(
\begin{aligned}
& \frac{2^{1+x}+2^{1-x}}{2} \geq \sqrt{2^{1+x} \cdot 2^{1-x}} \\
& \Rightarrow \frac{2^{1+x}+2^{1-x}}{2} \geq 2 \quad \ldots \text { (2) }
\end{aligned}
\)Adding (1) and (2), we get
\(
f(x) \geq 1+2=3
\)
Also, \(f (0)=3\)
Thus, the minimum value of \(f(x)\) is 3 . -
Question 171 of 213
171. Question
Let \(a_1, a_2, a_3\) \(\ldots\) be a G.P. such that \(a_1<0, a_1+a_2=4\) and \(a_3+a_4=16\). If \(\sum_{i=1}^9 a_i=4 \lambda\), then \(\lambda\) is equal to: [JEE Main 2020 (Online) 7th January Evening Slot]
CorrectIncorrectHint
\(
\begin{aligned}
& a_1+a_2=4 \\
& \Rightarrow a_1+a_1 r =4 \ldots(1) \\
& a_3+a_4=16 \\
& \Rightarrow a_1 r ^2+a_1 r ^3=16 \ldots(2)
\end{aligned}
\)
Doing (1) \(\div\) (2), we get
\(
r= \pm 2
\)
If \(r=2\), then \(a_1=\frac{4}{3}\)
If \(r=-2\), then \(a_1=-4\)
Given \(a_1<0\)
\(
\begin{aligned}
& \therefore a _1=-4 \\
& \therefore \sum_{i=1}^9 a_i=\frac{a\left(r^9-1\right)}{r-1}=4 \lambda \\
& \Rightarrow \frac{-4\left((-2)^9-1\right)}{-2-1}=4 \lambda \\
& \Rightarrow \lambda=-171
\end{aligned}
\) -
Question 172 of 213
172. Question
If the sum of the first 40 terms of the series, \(3+4+8+9+13+14+18+19+\ldots .\). is (102)m, then \(m\) is equal to : [JEE Main 2020 (Online) 7th January Evening Slot]
CorrectIncorrectHint
\(3+4+8+9+13+14+\ldots . . .\). upto 40 terms
\(\Rightarrow 7+17+27+\ldots . . . .20\) terms
\(S=\frac{20}{2}[2 \times 7+19 \times 10]\)
\(=102 \times 20=102 m\)
\(\therefore m =20\) -
Question 173 of 213
173. Question
Five numbers are in A.P. whose sum is 25 and product is 2520 . If one of these five numbers is \(-\frac{1}{2}\), then the greatest number amongst them is: [JEE Main 2020 (Online) 7th January Morning Slot]
CorrectIncorrectHint
Let the A.P is
\(
\begin{aligned}
& a-2 d, a-d, a, a+d, a+2 d \\
& \because \text { sum }=25 \\
& \Rightarrow 5 a=25 \Rightarrow a=5
\end{aligned}
\)
Also given,
\(
\begin{aligned}
& \text { product }\left(a^2-4 d^2\right)\left(a^2-d^2\right) \cdot a=2520 \\
& \Rightarrow\left(25-4 d^2\right)\left(25-d^2\right) 5=2520 \\
& \Rightarrow 4 d^4-121 d^2-4 d^2+121=0 \\
& \Rightarrow\left(d^2-1\right)\left(4 d^2-121\right)=0 \\
& \Rightarrow d= \pm 1, d= \pm \frac{11}{2}
\end{aligned}
\)When \(d= \pm 1\) we can’t get any fraction term like \(-\frac{1}{2}\).
\(
\therefore d= \pm \frac{11}{2}
\)
And when \(d =\frac{11}{2}\)
we get largest term \(=5+2 d=5+11=16\) -
Question 174 of 213
174. Question
If \(a_1, a_2, a_3, \ldots .\). are in A.P. such that \(a_1+a_7+a_{16}=40\), then the sum of the first 15 terms of this A.P. is : [JEE Main 2019 (Online) 12th April Evening Slot]
CorrectIncorrectHint
\(
\begin{aligned}
& a_1+a_7+a_{16}=40 \\
& a_1+\left(a_1+6 d\right)+\left(a_1+15 d\right)=40 \\
& \Rightarrow 3 a_1+21 d=40
\end{aligned}
\)
\(
\begin{aligned}
& \Rightarrow a_1+7 d=\frac{40}{3} \\
& \Rightarrow a_1+a_2 \ldots \ldots+a_{15}=\frac{15}{2}\left[a_1+a_{15}\right] \\
& \Rightarrow \frac{15}{2}\left[a_1+a_1+14 d\right] \Rightarrow 15\left(a_1+7 d\right)=15 \times \frac{40}{3}=200
\end{aligned}
\) -
Question 175 of 213
175. Question
For \(x \varepsilon R\), let \([ x ]\) denote the greatest integer \(\leq x\), then the sum of the series \(\left[-\frac{1}{3}\right]+\left[-\frac{1}{3}-\frac{1}{100}\right]+\left[-\frac{1}{3}-\frac{2}{100}\right]+\ldots+\left[-\frac{1}{3}-\frac{99}{100}\right]\) is : [JEE Main 2019 (Online) 12th April Morning Slot]
CorrectIncorrectHint
\(
\left[\frac{-1}{3}\right]+\left[\frac{-1}{3}-\frac{1}{100}\right]+\left[\frac{-1}{3}-\frac{2}{100}\right]+\ldots \ldots .+\left[\frac{-1}{3}-\frac{99}{100}\right]
\)
\(
\begin{aligned}
& \Rightarrow(-1-1-1-\ldots .67 \text { times })+(-2-2-2-\ldots .33 \text { times }) \\
& \Rightarrow-133
\end{aligned}
\) -
Question 176 of 213
176. Question
Let \(S_n\) denote the sum of the first \(n\) terms of an A.P. If \(S_4=16\) and \(S_6=-48\), then \(S_{10}\) is equal to: [JEE Main 2019 (Online) 12th April Morning Slot]
CorrectIncorrectHint
\(
\begin{aligned}
& S _4=\frac{4}{2}(2 a+3 d)=16 \\
& \Rightarrow 2 a+3 d=8 \\
& S _4=\frac{6}{2}(2 a+5 d)=-48 \\
& \Rightarrow 2 a+5 d=-16
\end{aligned}
\)
\(\therefore d =-12\) and \(a =22\), Now \(S _{10}=\frac{10}{2}(44-108)=-320\) -
Question 177 of 213
177. Question
The sum \(1+\frac{1^3+2^3}{1+2}+\frac{1^3+2^3+3^3}{1+2+3}+\ldots \ldots+\frac{1^3+2^3+3^3+\ldots+15^3}{1+2+3+\ldots+15}-\frac{1}{2}(1+2+3+\ldots+15)\) is equal to : [JEE Main 2019 (Online) 10th April Evening Slot]
CorrectIncorrectHint
\(
\begin{aligned}
& \text { Sum }=\sum_{n=1}^{15} \frac{1^3+2^3+\ldots .+n^3}{1+2+\ldots .+n}-\frac{1}{2} \frac{15 \times 16}{2} \\
& =\sum_{n=1}^{15} \frac{n(n+1)}{2}-60 \\
& =\frac{1}{2} \sum_{n=1}^{15} n^2+\frac{1}{2} \sum_{n=1}^{15} n-60 \\
& =\frac{1}{2} \times \frac{15 \times 16 \times 31}{6}+\frac{1}{2} \times \frac{15 \times 16}{2}-60 \\
& =620
\end{aligned}
\) -
Question 178 of 213
178. Question
Let \(a\), \(b\) and \(c\) be in G.P. with common ratio \(r\), where \(a \neq 0\) and \(0< r \leq \frac{1}{2}\). If \(3 a, 7 b\) and \(15 c\) are the first three terms of an A.P., then the \(4^{\text {th }}\) term of this A.P. is : [JEE Main 2019 (Online) 10th April Evening Slot]
CorrectIncorrectHint
\(a = a , b =\) ar and \(c = ar ^2\)
\(3 a, 7 b, 15 c \rightarrow\) A.P.
\(14 b=3 a+15 c\)
\(14(a r)=3 a+15\left(a r^2\right)\)
\(15 r^2-14 r+3=0\)
\(
\begin{aligned}
& \Rightarrow r=\frac{1}{3}, \frac{3}{5}(\text { rejected }) \\
& \text { Common difference }=7 b -3 a \\
& =7 ar -3 a \\
& \Rightarrow \frac{7 a}{3}-3 a=-\frac{2}{3} a \\
& 4^{\text {th }} \text { term is } \Rightarrow 15 c-\frac{2}{3} a=\frac{15}{9} a-\frac{2}{3} a=a
\end{aligned}
\) -
Question 179 of 213
179. Question
Let \(a_1, a_2, a_3, \ldots . .\). be an A.P. with \(a_6=2\). Then the common difference of this A.P., which maximises the product \(a_1 a_4 a_5\), is : [JEE Main 2019 (Online) 10th April Evening Slot]
CorrectIncorrectHint
first term \(= a\), Common difference \(= d\)
\(
\begin{aligned}
& \therefore a+5 d=2 \\
& a_1 \cdot a_4 \cdot a_5=a(a+3 d)(a+4 d)
\end{aligned}
\)
\(
\begin{aligned}
& f(d)=(2-5 d)(2-2 d)(2-d) \\
& \Rightarrow f^{\prime}(d)=0 \Rightarrow d=\frac{2}{3}, \frac{8}{5} \\
& \Rightarrow f^{\prime \prime}(d)<0 \text { at } d=\frac{8}{5} \\
& \Rightarrow d=\frac{8}{5}
\end{aligned}
\) -
Question 180 of 213
180. Question
The sum \(\frac{3 \times 1^3}{1^3}+\frac{5 \times\left(1^3+2^3\right)}{1^2+2^2}+\frac{7 \times\left(1^3+2^3+3^3\right)}{1^2+2^2+3^2}+\ldots\) upto 10 terms is: [JEE Main 2019 (Online) 10th April Morning Slot]
CorrectIncorrectHint
\(
\begin{aligned}
& T_r=\frac{(2 r+1)\left(1^3+2^3+3^3+\ldots . .+r^3\right)}{1^2+2^2+3^2+\ldots . .+r^2} \\
& T_r=(2 r+1)\left(\frac{r(r+1)}{2}\right)^2 \times \frac{6}{r(r+1)(2 r+1)} \\
& T_r=\frac{3 r(r+1)}{2} \\
& \text { Now, } S=\sum_{r=1}^{10} T_r=\frac{3}{2} \sum_{r=1}^{10}\left(r^2+r\right) \\
& \Rightarrow \frac{3}{2}\left\{\frac{10 \times(10+1)(2 \times 10+1)}{6}+\frac{10 \times 11}{2}\right\} \\
& \Rightarrow \frac{3}{2}\left\{\frac{10 \times 11 \times 21}{6}+5 \times 11\right\} \\
& \Rightarrow \frac{3}{2} \times 5 \times 11 \times 8=660
\end{aligned}
\) -
Question 181 of 213
181. Question
If \(a_1, a_2, a_3\), \(\ldots\) \(a_n\) are in A.P. and \(a_1+a_4+a_7+\) \(\ldots\) \(+a_{16}=114\), then \(a_1+a_6+\) \(a_{11}+a_{16}\) is equal to: [JEE Main 2019 (Online) 10th April Morning Slot]
CorrectIncorrectHint
\(
\begin{aligned}
& 3\left(a_1+a_{16}\right)=114 \\
& a_1+a_{16}=38
\end{aligned}
\)
Now \(a_1+a_6+a_{11}+a_{16}=2\left(a_1+a_{16}\right)\)
\(
=2 \times 38=76
\) -
Question 182 of 213
182. Question
Some identical balls are arranged in rows to form an equilateral triangle. The first row consists of one ball, the second row consists of two balls and so on. If 99 more identical balls are added to the total number of balls used in forming the equilateral triangle, then all these balls can be arranged in a square whose each side contains exactly 2 balls less than the number of balls each side of the triangle contains. Then the number of balls used to form the equilateral triangle is : [JEE Main 2019 (Online) 9th April Evening Slot]
CorrectIncorrectHint
As triangle is equilateral so each side of triangle has n-balls.
At the top of the triangle there is 1 ball then next line has 2 balls. Similarly last line has \(n\) balls.
\(\therefore\) Total no of balls used to create this triangle
\(
\begin{aligned}
& =1+2+3+\ldots \ldots \ldots \ldots . n \\
& =\frac{n(n+1)}{2}
\end{aligned}
\)
Here Number of balls in each side of square is \(=(n-2)\)
\(\therefore\) Total no of balls used to create this square
\(
=(n-2)^2
\)
According to the question,
\(
\begin{aligned}
& \frac{n(n+1)}{2}+99=(n-2)^2 \\
& \Rightarrow n^2-9 n-190=0 \\
& \Rightarrow(n-19)(n+10)=0 \\
& \therefore n=19
\end{aligned}
\)
So total balls used to form triangle
\(
=\frac{n(n+1)}{2}=\frac{19(20)}{2}=190
\) -
Question 183 of 213
183. Question
If the sum and product of the first three term in an A.P. are 33 and 1155 , respectively, then a value of its \(11^{\text {th }}\) term is : [JEE Main 2019 (Online) 9th April Evening Slot]
CorrectIncorrectHint
Let the three terms are \(a-d, a, a+d\)
Given \(a-d+a+a+d=33\)
\(
\begin{aligned}
& \Rightarrow 3 a =33 \\
& \Rightarrow a =11
\end{aligned}
\)
Also given,
\(
\begin{aligned}
& (a-d) a(a+d)=1155 \\
& \Rightarrow\left(a^2-d^2\right) a=1155 \\
& \Rightarrow\left(11^2-d^2\right) 11=1155 \\
& \Rightarrow\left(11^2-d^2\right)=105 \\
& \Rightarrow d= \pm 4
\end{aligned}
\)
When \(d=4\) and \(a=11\) then series is
\(7,11,15, \ldots\)
\(
\therefore T_{11}=a+10 d=7+10 \times 4=47
\)
When \(d=-4\) and \(a=11\) then series is
\(
\begin{aligned}
& 15,11,7, \ldots \\
& \therefore T_{11}=a+10 d=15+10 \times-4=-25
\end{aligned}
\) -
Question 184 of 213
184. Question
The sum of the series \(1+2 \times 3+3 \times 5+4 \times 7+\ldots\). upto 11 th term is : [JEE Main 2019 (Online) 9th April Evening Slot]
CorrectIncorrectHint
\(S=1+2 \times 3+3 \times 5+4 \times 7+\ldots\). upto 11th term
General term \(T_n=n(2 n-1)\)
\(
\begin{aligned}
& \therefore S _{ n }=\sum T_n \\
& \Rightarrow S _{ n }=\sum\left(2 n^2-n\right) \\
& \Rightarrow S _{ n }=2 \sum n^2-\sum n \\
& \Rightarrow S _{ n }=2\left(\frac{n(n+1)(2 n+1)}{6}\right)-\frac{n(n+1)}{2} \\
& \therefore S _{11}=2\left(\frac{11(12)(23)}{6}\right)-\frac{11(12)}{2} \\
& \Rightarrow S _{11}=946
\end{aligned}
\) -
Question 185 of 213
185. Question
Let the sum of the first \(n\) terms of a non-constant A.P., \(a_1, a_2, a_3, \ldots .\). be \(50 n+\frac{n(n-7)}{2} A\), where \(A\) is a constant. If \(d\) is the common difference of this A.P., then the ordered pair \(\left( d , a _{50}\right)\) is equal to [JEE Main 2019 (Online) 9th April Morning Slot]
CorrectIncorrectHint
\(
S _{ n }=50 n+\frac{n(n-7)}{2} A
\)
We know, \(n ^{\text {th }}\) term
\(
\begin{aligned}
& T _{ n }= S _{ n }- S _{ n -1} \\
& =50 n+\frac{n(n-7)}{2} A-50(n-1)-\frac{(n-1)(n-8)}{2} A \\
& =50+\frac{A}{2}\left[n^2-7 n-n^2+9 n-8\right] \\
& =50+ A ( n -4)
\end{aligned}
\)
We also know, common difference
\(
\begin{aligned}
& d=T_n-T_{n-1} \\
& =50+A(n-4)-50-A(n-5) \\
& =A
\end{aligned}
\)
And \(T_{50}=50+A(50-4)\)
\(
\begin{aligned}
& =50+46 A \\
& \therefore\left(d, a_{50}\right)=(A, 50+46 A)
\end{aligned}
\) -
Question 186 of 213
186. Question
The sum \(\sum_{k=1}^{20} k \frac{1}{2^k}\) is equal to [JEE Main 2019 (Online) 8th April Evening Slot]
CorrectIncorrectHint
Let \(S=\sum_{k=1}^{20} k \frac{1}{2^k}\)
\(
\Rightarrow S=\frac{1}{2}+\frac{2}{2^2}+\frac{3}{2^3}+\frac{4}{2^4}+\ldots \ldots .+\frac{20}{2^{20}} \dots(1)
\)
This is an Arithmetic Geometric Sequence. Here numerator is in A.P and denominator is in G.P.
To solve Arithmetic Geometric Sequence, we multiply the series \(S\) with the common ratio of G.P. Here common ratio of G.P is \(\frac{1}{2}\).By multiplying (1) with \(\frac{1}{2}\) we get,
\(
\frac{S}{2}=\frac{1}{2^2}+\frac{2}{2^3}+\frac{3}{2^4}+\frac{4}{2^5}+\ldots \ldots .+\frac{19}{2^{20}}+\frac{20}{2^{21}} \ldots . \text { (2) }
\)
Subtract (2) from (1),
\(
\begin{aligned}
& S -\frac{S}{2}=\frac{1}{2}+\frac{1}{2^2}+\frac{1}{2^3}+\frac{1}{2^4}+\ldots \ldots .+\frac{1}{2^{20}}-\frac{20}{2^{21}} \\
& \Rightarrow \frac{S}{2}=\frac{\frac{1}{2}\left(1-\frac{1}{2^{20}}\right)}{1-\frac{1}{2}}-\frac{20}{2^{21}} \\
& \Rightarrow S =2\left(1-\frac{1}{2^{20}}\right)-\frac{20}{2^{20}} \\
& \Rightarrow S =2-\frac{2}{2^{20}}-\frac{20}{2^{20}} \\
& \Rightarrow S =2-\frac{22}{2^{20}} \\
& \Rightarrow S =2-\frac{11}{2^{19}}
\end{aligned}
\) -
Question 187 of 213
187. Question
If three distinct numbers \(a, b, c\) are in G.P. and the equations \(a x^2+2 b x+c=0\) and \(d x^2\) \(+2 e x+f=0\) have a common root, then which one of the following statements is correct? [JEE Main 2019 (Online) 8th April Evening Slot]
CorrectIncorrectHint
Given, \(a, b, c\) are in G.P.
\(
\therefore b^2= ac
\)
In this equation \(a x^2+2 b x+c=0\),
Discriminant, \(D=4 b^2-4 a c\)
\(
\begin{aligned}
& =4 a c-4 a c \\
& =0
\end{aligned}
\)Discriminant \(=0\) means roots of the equation are equal.
Let both the roots of the equation \(=\alpha\)
\(
\begin{aligned}
& \therefore 2 \alpha=-\frac{2 b}{a} \\
& \Rightarrow \alpha=-\frac{b}{a}
\end{aligned}
\)
As both the equations \(a x^2+2 b x+c=0\) and \(d x^2+2 e x+f=0\) have a common root, so \(-\frac{b}{a}\) is also root of the equation \(dx ^2+2 ex +f=0\).
\(\therefore-\frac{b}{a}\) satisfy the equation \(dx ^2+2 ex + f =0\).
\(
\begin{aligned}
& \therefore d\left(-\frac{b}{a}\right)^2+2 e\left(-\frac{b}{a}\right)+f=0 \\
& \Rightarrow d b^2-2 a e b+f a^2=0 \\
& \Rightarrow d a c-2 a e b+f a^2=0 \\
& \Rightarrow d c-2 e b+f a=0 \\
& \Rightarrow \frac{d c}{a c}-\frac{2 e b}{a c}+\frac{f a}{a c}=0 \\
& \Rightarrow \frac{d c}{a c}-\frac{2 e b}{b^2}+\frac{f a}{a c}=0 \\
& \Rightarrow \frac{d}{a}-\frac{2 e}{b}+\frac{f}{c}=0 \\
& \Rightarrow \frac{2 e}{b}=\frac{d}{a}+\frac{f}{c} \\
& \therefore \frac{d}{a}, \frac{e}{b}, \frac{f}{c} \text { are in A.P. }
\end{aligned}
\) -
Question 188 of 213
188. Question
The sum of all natural numbers ‘ \(n\) ‘ such that \(100< n <200\) and H.C.F. \((91, n )>1\) is : [JEE Main 2019 (Online) 8th April Morning Slot]
CorrectIncorrectHint
\(
\because 91=13 \times 7
\)
So the required numbers are either divisible by 7 or 13 .
\(S_A=\) sum of numbers between 100 and 200 which are divisible by 7 .
\(
\begin{aligned}
& \Rightarrow S_A=105+112+\ldots . .+196 \\
& S_A=\frac{14}{2}[105+196]=2107
\end{aligned}
\)
\(S _{ B }=\) Sum of numbers between 100 and 200 which are divisible by 13 .
\(
\begin{aligned}
& S_B=104+117+\ldots \ldots . .+195 \\
& S_B=\frac{8}{2}[104+195]=1196
\end{aligned}
\)
\(S _{ C }=\) Sum of numbers between 100 and 200 which are divisible by 7 and 13 .
\(
S_C=182
\)
Sum of numbers divisible by 7 or \(13=\) Sum of no. divisible by \(7+\) sum of the no. divisible by 13 – Sum of the numbers divisible by 7 and 13
\(
\begin{aligned}
& =2107+1196-182 \\
& =3121
\end{aligned}
\) -
Question 189 of 213
189. Question
If the sum of the first 15 terms of the series \(\left(\frac{3}{4}\right)^3+\left(1 \frac{1}{2}\right)^3+\left(2 \frac{1}{4}\right)^3+3^3+\left(3 \frac{3}{4}\right)^3+\ldots\) is equal to \(225 k\), then \(k\) is equal to : [JEE Main 2019 (Online) 12th January Evening Slot]
CorrectIncorrectHint
\(
\begin{aligned}
& S =\left(\frac{3}{4}\right)^3+\left(\frac{6}{4}\right)^3+\left(\frac{9}{4}\right)^3+\left(\frac{12}{4}\right)^3+\ldots \ldots .15 \text { term } \\
& =\frac{27}{64} \sum_{r=1}^{15} r^3 \\
& =\frac{27}{64}\left[\frac{15(15+1)}{2}\right]^2 \\
& =225 K \text { (Given in question) } \\
& K =27
\end{aligned}
\) -
Question 190 of 213
190. Question
If \(\sin ^4 \alpha+4 \cos ^4 \beta+2=4 \sqrt{2} \sin \alpha \cos \beta ; \alpha, \beta \in[0, \pi]\), then \(\cos (\alpha+\beta)-\cos (\alpha-\beta)\) is equal to : [JEE Main 2019 (Online) 12th January Evening Slot]
CorrectIncorrectHint
\(
\begin{aligned}
& \text { A.M. } \geq \text { G.M. } \\
& \frac{\sin ^4 \alpha+4 \cos ^4 \beta+1+1}{4} \geq\left(\sin ^4 \alpha \cdot 4 \cos ^4 \beta \cdot 1 \cdot 1\right)^{\frac{1}{4}}
\end{aligned}
\)
\(
\begin{aligned}
& \sin ^4 \alpha+4 \cos ^2 \beta+2 \geq 4 \sqrt{2} \sin \alpha \cos \beta \\
& \text { Given that } \sin ^4 \alpha+4 \cos ^4 \beta+2=4 \sqrt{2} \sin \alpha \cos \beta \\
& \Rightarrow \text { A.M. }=\text { G.M. } \Rightarrow \sin ^4 \alpha=1=4 \cos ^4 \beta \\
& \sin \alpha=1, \cos \beta= \pm \frac{1}{\sqrt{2}} \\
& \Rightarrow \sin \beta=\frac{1}{\sqrt{2}} \text { as } \beta \in[0, \pi] \\
& \cos (\alpha+\beta)-\cos (\alpha-\beta)=-2 \sin \alpha \beta \\
& =-\sqrt{2}
\end{aligned}
\) -
Question 191 of 213
191. Question
If \({ }^n C_4,{ }^n C_5\) and \({ }^n C_6\) are in A.P., then \(n\) can be: [JEE Main 2019 (Online) 12th January Evening Slot]
CorrectIncorrectHint
2. \({ }^n C_5={ }^n C_4+{ }^n C_6\)
2. \(\frac{n!}{5! (n-5)!}=\frac{n!}{4! (n-4)!}+\frac{n!}{6! (n-6)!}\)
\(
\frac{2}{5} \cdot \frac{1}{n-5}=\frac{1}{(n-4)(n-5)}+\frac{1}{30}
\)
\(n=14\) satisfying equation. -
Question 192 of 213
192. Question
Let \(S_{ k }=\frac{1+2+3+\ldots .+k}{k}\). If \(S_1^2+S_2^2+\ldots \ldots+S_{10}^2=\frac{5}{12} A \text {, then } A \text { is equal to : }\) [JEE Main 2019 (Online) 12th January Morning Slot]
CorrectIncorrectHint
\(
\begin{aligned}
& S _{ k }=\frac{K+1}{2} \\
& \sum S_k^2=\frac{5}{12} A \\
& \sum_{K=1}^{10}\left(\frac{K+1}{2}\right)^2=\frac{2^2+3^2+–+11^2}{4}=\frac{5}{12} A \\
& \frac{11 \times 12 \times 23}{6}-1=\frac{5}{3} A \\
& 505=\frac{5}{3} A , \quad A =303
\end{aligned}
\) -
Question 193 of 213
193. Question
The product of three consecutive terms of a G.P. is 512 . If 4 is added to each of the first and the second of these terms, the three terms now form an A.P. Then the sum of the original three terms of the given G.P. is : [JEE Main 2019 (Online) 12th January Morning Slot]
CorrectIncorrectHint
Let terms are \(\frac{a}{r}, a, a r \rightarrow G . P\)
\(
\begin{aligned}
& \therefore a^3=512 \Rightarrow a =8 \\
& \frac{8}{r}+4,12,8 r \rightarrow A . P . \\
& 24=\frac{8}{r}+4+8 r \\
& r=2, r=\frac{1}{2} \\
& r=2(4,8,16) \\
& r=\frac{1}{2}(16,8,4) \\
& \text { Sum }=28
\end{aligned}
\) -
Question 194 of 213
194. Question
If \(19^{\text {th }}\) term of a non-zero A.P. is zero, then its \(\left(49^{\text {th }}\right.\) term \():\left(29^{\text {th }}\right.\) term \()\) is : [JEE Main 2019 (Online) 11th January Evening Slot]
CorrectIncorrectHint
\(
\begin{aligned}
& a+18 d=0 \\
& \frac{a+48 d}{a+28 d}=\frac{-18 d+48 d}{-18 d+28 d}=\frac{3}{1}
\end{aligned}
\) -
Question 195 of 213
195. Question
Let \(x , y\) be positive real numbers and \(m , n\) positive integers. The maximum value of the expression \(\frac{x^m y^n}{\left(1+x^{2 m}\right)\left(1+y^{2 n}\right)}\) is : [JEE Main 2019 (Online) 11th January Evening Slot]
CorrectIncorrectHint
Let \(T=\frac{x^m y^n}{\left(1+x^{2 m}\right)\left(1+y^{2 n}\right)}\)
\(
\Rightarrow T=\frac{1}{\left(x^{-m}+x^m\right)\left(y^{-n}+y^n\right)}
\)Using AM-GM inequality,
\(
\begin{aligned}
& x^{-m}+x^m \geq 2 \\
& \text { and } y^{-n}+y^n \geq 2 \\
& \therefore\left(x^{-m}+x^m\right)\left(y^{-m}+y^m\right) \geq 4 \\
& \frac{1}{\left(x^{-m}+x^m\right)\left(y^{-m}+y^m\right)} \leq \frac{1}{4}
\end{aligned}
\)At \(x=0, T=\frac{1}{4}\)
\(\therefore\) Maximum value \(=\frac{1}{4}\) -
Question 196 of 213
196. Question
The sum of an infinite geometric series with positive terms is 3 and the sum of the cubes of its terms is \(\frac{27}{19}\). Then the common ratio of this series is : [JEE Main 2019 (Online) 11th January Morning Slot]
CorrectIncorrectHint
\(
\frac{a}{1-r}=3 \quad \ldots \ldots(1)
\)
\(
\begin{aligned}
& \frac{a^3}{1-r^3}=\frac{27}{19} \Rightarrow \frac{27(1-r)^3}{1-r^3}=\frac{27}{19} \\
& \Rightarrow 6 r^2-13 r+6=0 \\
& \Rightarrow r=\frac{2}{3} \\
& \text { as }|r|<1
\end{aligned}
\) -
Question 197 of 213
197. Question
Let \(a _1, a _2, \ldots \ldots, a _{10}\) be a G.P. If \(\frac{a_3}{a_1}=25\), then \(\frac{a_9}{a_5}\) equals [JEE Main 2019 (Online) 11th January Morning Slot]
CorrectIncorrectHint
\(a_1, a_2, \ldots \ldots, a_{10}\) are in G.P.,
Let the common ratio be \(r\)
\(
\begin{aligned}
& \frac{a_3}{a_1}=25 \Rightarrow \frac{a_1 r^2}{a_1}=25 \Rightarrow r^2=25 \\
& \frac{a_9}{a_5}=\frac{a_1 r^8}{a_1 r^4}=r^4=5^4
\end{aligned}
\) -
Question 198 of 213
198. Question
\(\text { Let } a_1, a_2, a_3, \ldots . . a_{10} \text { be in G.P. with } a_i>0 \text { for } i=1,2, \ldots . ., 10 \text { and } S \text { be the set of pairs ( } r \text {, }k ), r , k \in N \text { (the set of natural numbers) for which }\)
\(
\left|\begin{array}{lll}
\log _e a_1{ }^r a_2{ }^k & \log _e a_2{ }^r a_3{ }^k & \log _e a_3{ }^r a_4{ }^k \\
\log _e a_4{ }^r a_5{ }^k & \log _e a_5{ }^r a_6{ }^k & \log _e a_6{ }^r a_7{ }^k \\
\log _e a_7{ }^r a_8{ }^k & \log _e a_8{ }^r a_9{ }^k & \log _e a_9 a_{10} a_{10}
\end{array}\right|=0 .
\)
Then the number of elements in \(S\), is [JEE Main 2019 (Online) 10th January Evening Slot]CorrectIncorrectHint
\(
\left|\begin{array}{lll}
\log _e a_1^r a_2^k & \log _e a_2^r a_3^k & \log _e a_3^r a_4^k \\
\log _e a_4^r a_5^k & \log _e a_5^\pi a_6^k & \log _e a_6^r a_7^k \\
\log _e a_7^r a_8^k & \log _e a_8^\pi a_9^k & \log _e a_9^r a_{10}^k
\end{array}\right|=0
\)
\(
\text { On applying, } C _2 \rightarrow C _2- C _1 \text { and } C _3 \rightarrow C _3- C _1 \text {, }
\)
\(
\left|\begin{array}{ccc}
\log _e a_1^r a_2^k & \log _e a_2^r a_3^k-\log _e a_1^r a_2^k & \log _e a_3^r a_4^k-\log _e a_1^r a_2^k \\
\log _e a_4^r a_5^k & \log _e a_5^r a_6^k-\log _e a_4^r a_5^k & \log _e a_6^r a_7^k-\log _e a_4^r a_5^k \\
\log _e a_7^r a_8^k & \log _e a_8^r a_9^k-\log _e a_7^r a_8^k & \log _e a_9^r a_{10}^k-\log _e a_7^r a_8^k
\end{array}\right|=0
\)
\(
\because\left[\log _e m-\log _e n=\log _e\left(\frac{m}{n}\right)\right]
\)
\(
\left|\begin{array}{lll}
\log _e a_1^r a_2^k & \log _e\left(\frac{a_2^r a_3^k}{a_1^r a_2^k}\right) & \log _e\left(\frac{a_3^r a_4^k}{a_1^r a_2^k}\right) \\
\log _e a_4^r a_5^k & \log _e\left(\frac{a_5^r a_6^k}{a_4^r a_5^k}\right) & \log _e\left(\frac{a_6^r a_7^k}{a_4^r a_5^k}\right) \\
\log _e a_7^r a_8^k & \log _e\left(\frac{a_8^r a_9^k}{a_7^r a_8^k}\right) & \log _e\left(\frac{a_9^r a_{10}^k}{a_7^r a_8^k}\right)
\end{array}\right|=0
\)
\(a_1, a_2, a_3, \ldots . ., a_{10}\) are in GP, therefore, we can put, \(a_1=a ; a_2=a R ; a_3=a R^2 ; \ldots . a_{10}=\) \(aR ^9\)
\(
\left|\begin{array}{ccc}
\log _e a^{r+k} R^k & \log _e\left(\frac{a^{r+k} R^{r+2 k}}{a^{r+k} R^k}\right) & \log _e\left(\frac{a^{r+k} R^{2 r+3 k}}{a^{r+k} R^k}\right) \\
\log _e a^{r+k} R^{3 r+4 k} & \log _e\left(\frac{a^{r+k} R^{4 r+5 k}}{a^{r+k} R^{3 r+4 k}}\right) & \log _e\left(\frac{a^{r+k} R^{5 r 6 k}}{a^{r+k} R^{3 r+4 k}}\right) \\
\log _e a^{r+k} R^{6 r+7 k} & \log _e\left(\frac{a^{r+k} R^{7 r+8 k}}{a^{r+k} R^{6 r+7 k}}\right) & \log _e\left(\frac{a^{r+k} R^{8 r+9 k}}{a^{r+k} R^{6 r+7 k}}\right)
\end{array}\right|=0
\)
\(
\left|\begin{array}{ccc}
\log _e\left(a^{r+k} R^k\right) & \log _e R^{r+k} & \log _e R^{2 r+2 k} \\
\log _e a^{r+k} R^{3 r+4 k} & \log _e R^{r+k} & \log _e R^{2 r+2 k} \\
\log _e a^{r+k} R^{6 r+7 k} & \log _e R^{r+k} & \log _e R^{2 r+2 k}
\end{array}\right|=0
\)
\(
\left[\begin{array}{c}
\log m^n=n \log m \\
\log _e R^{2 r+2 k}=\log _e R^{2(r+k)}=2 \log _e R^{r+k}
\end{array}\right]
\)
\(
\left|\begin{array}{ccc}
\log _e\left(a^{r+k} R^k\right) & \log _e R^{r+k} & 2 \log _e R^{r+k} \\
\log _e\left(a^{r+k} R^{3 r+4 k}\right) & \log _e R^{r+k} & 2 \log _e R^{r+k} \\
\log _e\left(a^{r+k} R^{6 r+7 k}\right) & \log _e R^{r+k} & 2 \log _e R^{r+k}
\end{array}\right|=0
\)
Now, column \(C _2\) and \(C _3\) are proportional.
So, value of determinant will be zero for any value of \((r, k), r, k \in N\).
Thus, Set ‘S’ has infinitely many elements. -
Question 199 of 213
199. Question
The sum of all two digit positive numbers which when divided by 7 yield 2 or 5 as remainder is [JEE Main 2019 (Online) 10th January Morning Slot]
CorrectIncorrectHint
\(
\begin{aligned}
& \sum_{r=2}^{13}(7 r+2)=7 . \frac{2+13}{2} \times 6+2 \times 12 \\
& =7 \times 90+24=654 \\
& \sum_{r=1}^{13}(7 r+5)=7\left(\frac{1+13}{2}\right) \times 13+5 \times 13=702 \\
& \text { Total }=654+702=1356
\end{aligned}
\) -
Question 200 of 213
200. Question
The sum of the following series \(1+6+\frac{9\left(1^2+2^2+3^2\right)}{7}+\frac{12\left(1^2+2^2+3^2+4^2\right)}{9}+\frac{15\left(1^2+2^2+\ldots+5^2\right)}{11}+\ldots \text {. up to } 15 \text { terms, is : }\) [JEE Main 2019 (Online) 9th January Evening Slot]
CorrectIncorrectHint
\(
1+6+\frac{9\left(1^2+2^2+3^2\right)}{7}+\frac{12\left(1^2+2^2+3^2+4^2\right)}{9}+\frac{15\left(1^2+2^2+\ldots+5^2\right)}{11}+\ldots .15
\)
\(
=\frac{3\left(1^2\right)}{3}+\frac{6\left(1^2+2^2\right)}{5}+\frac{9\left(1^2+2^2+3^2\right)}{7}+\frac{12}{9}\left(1^2+2^2+3^2+4^2\right)+\ldots \ldots
\)
\(
\begin{aligned}
& T_r=\frac{3 r}{2 r+1}\left(1^2+2^2+\ldots+r^2\right) \\
& T_r=\frac{3 r}{2 r+1} \frac{r(r+1)(2 r+1)}{6}=\frac{1}{2} r^2(r+1)
\end{aligned}
\)
\(
\begin{aligned}
& \text { Sum of } n \text { terms }=\sum_{r=1}^n T_r=\frac{1}{2} \sum_{r=1}^n\left(r^3+r^2\right) \\
& =\frac{1}{2}\left[\frac{n^2(n+1)^2}{4}+\frac{n(n+1)(2 n+1)}{6}\right]
\end{aligned}
\)
Sum upto 15 terms \(\Rightarrow\) then put \(n=15\)
\(
=\frac{1}{2}\left(\frac{(15 \times 16)^2}{4}+\frac{15 \times 16 \times 31}{6}\right)=7820
\) -
Question 201 of 213
201. Question
Let \(a, b\) and \(c\) be the \(7^{\text {th }}, 11^{\text {th }}\) and \(13^{\text {th }}\) terms respectively of a non-constant A.P. If these are also three consecutive terms of a G.P., then \(\frac{a}{c}\) equal to : [JEE Main 2019 (Online) 9th January Evening Slot]
CorrectIncorrectHint
\(
T_7=A+6 d=a ; T_{11}=A+10 d=b ; T_{13}=A+12 d=c
\)
Now \(a, b, c\) are in G.P.
\(
\begin{aligned}
& \therefore b ^2= ac \\
& \Rightarrow( A +10 d )^2=( A +6 d )( A +12 d ) \\
& \Rightarrow A ^2+100 d ^2+20 Ad = A ^2+18 Ad +72 d ^2 \\
& \Rightarrow A +14 d =0, A =-14 d \\
& \frac{a}{c}=\frac{A+6 d}{A+12 d}=\frac{-8 d}{-2 d}=4
\end{aligned}
\) -
Question 202 of 213
202. Question
If \(a, b, c\) be three distinct real numbers in G.P. and \(a+b+c=x b\), then \(x\) cannot be [JEE Main 2019 (Online) 9th January Morning Slot]
CorrectIncorrectHint
\(
\begin{aligned}
& a, b, c \text { are in G.P. } \\
& \text { So, } b=a r \\
& \text { and } c=a r^2 \\
& \text { given } a+b+c=x b \\
& \Rightarrow a+b r+a r^2=x(a r) \\
& \Rightarrow 1+r+r^2=x r \\
& \Rightarrow x=1+r+\frac{1}{r} \\
& \text { let sum of } r+\frac{1}{r}=M \\
& \therefore r^2+1=M r \\
& \Rightarrow r^2-M r+1=0
\end{aligned}
\)
this quadratic equation will have
real solution when discriminant is \(\geq 0\)
\(
\begin{aligned}
& \therefore b^2-4 a c \geq 0 \\
& M^2-4.1 .1 \geq 0 \\
& \Rightarrow M^2 \geq 4
\end{aligned}
\)
\(
\begin{aligned}
& M \geq 2 \text { or } M \leq-2 \\
& \therefore M \in(-\propto,-2] \cup[2, \propto)
\end{aligned}
\)
As \(x =1+ r +\frac{1}{r}\)
\(
\begin{aligned}
& =1+ M \\
& \therefore x \in(-\propto,-1] \cup[3, \propto)
\end{aligned}
\)
\(
\therefore x \text { can’t be } 0,1,2 \text {. }
\) -
Question 203 of 213
203. Question
Let \(a _1, a _2, \ldots ., a _{30}\) be an A.P., \(S =\sum_{i=1}^{30} a _i\) and \(T =\sum_{i=1}^{15} a _{(2 i-1)}\). If \(a _5=27\) and \(S -2 T =75\), then \(a _{10}\) is equal to: [JEE Main 2019 (Online) 9th January Morning Slot]
CorrectIncorrectHint
Let the common difference \(= d\)
\(
\begin{aligned}
& S =\sum_{i=1}^{30} a_i \\
& =a_1+a_2+\ldots \ldots+a_{30} \\
& \therefore S =\frac{30}{2}\left[a_1+a_{30}\right] \\
& =15\left[a_1+a_1+29 d \right] \\
& =15\left(2 a_1+29 d \right) \\
& T =\sum_{i=1}^{15} a_{(2 i-1)} \\
& =a_1+a_3+\ldots \ldots+a_{29} \\
& =\frac{15}{2}\left[a_1+a_{29}\right] \\
& =\frac{15}{2}\left[a_1+a_1+28 d\right] \\
& =\frac{15}{2}\left[2 a_1+28 d\right] \\
& =15\left(a_1+14 d \right)
\end{aligned}
\)
Given,
\(
\begin{aligned}
& S-2 T=75 \\
& \Rightarrow 15\left(2 a_1+29 d \right)-2 \times 15\left(a_1+14 d \right)=75 \\
& \Rightarrow 30 a_1+15 \times 29 d -30 a_1-420 d =75 \\
& \Rightarrow 435 d -420 d =75 \\
& \Rightarrow 15 d =75 \\
& \Rightarrow d=5
\end{aligned}
\)
Given that,
\(
\begin{aligned}
& a_5=27 \\
& \Rightarrow a_1+4 d =27 \\
& \Rightarrow a_1+20=27 \\
& \Rightarrow a_1=7 \\
& \therefore a_{10}=a_1+9 d \\
& =7+45 \\
& =52
\end{aligned}
\) -
Question 204 of 213
204. Question
Let \(\sum_{k=1}^{10} f(a+k)=16\left(2^{10}-1\right)\), where the function \(f\) satisfies \(f(x+y)=f(x) f(y)\) for all natural numbers \(x, y\) and \(f(1)=2\). Then the natural number ‘ \(a\) ‘ is: [Set II, April 2019]
CorrectIncorrectHint
\(
\begin{aligned}
& \because f(x+y)=f(x) \cdot f(y) \\
& \Rightarrow \text { Let } f(x)=t^x \\
& f(1)=2 \\
& \therefore t^{\prime}=2 \\
& \Rightarrow f(x)=2^x
\end{aligned}
\)Since, \(\sum_{k=1}^{10} f(a+k)=16\left(2^{10}-1\right)\)
Then, \(\sum_{k=1}^{10} 2^{a+k}=16\left(2^{10}-1\right)\)
\(
\begin{aligned}
& \Rightarrow 2^a \sum_{k=1}^{10} 2^k=16\left(2^{10}-1\right) \\
& \Rightarrow 2^a \times \frac{\left(\left(2^{10}\right)-1\right) \times 2}{(2-1)}=16 \times\left(2^{10}-1\right) \Rightarrow 2.2^a=16 \\
& \Rightarrow a =3
\end{aligned}
\) -
Question 205 of 213
205. Question
The sum of all values of \(\theta \in\left(0, \frac{\pi}{2}\right)\) satisfying \(\sin ^2 2 \theta+\cos ^4 2 \theta=\frac{3}{4}\) is: [Set II, Jan 2019]
CorrectIncorrectHint
\(
\begin{aligned}
& \text { (c) } \sin ^2 2 \theta+\cos ^4 2 \theta=\frac{3}{4} \\
& \Rightarrow \quad 1-\cos ^2 2 \theta+\cos ^4 2 \theta=\frac{3}{4} \\
& \Rightarrow \quad \cos ^2 2 \theta\left(1-\cos ^2 2 \theta\right)=\frac{1}{4} \dots(1)
\end{aligned}
\)
\(
\begin{aligned}
& \because \quad \text { G.M. } \leq \text { A.M. } \\
& \therefore \quad\left(\cos ^2 2 \theta\right)\left(1-\cos ^2 2 \theta\right) \leq\left(\frac{\cos ^2 2 \theta+\left(1-\cos ^2 2 \theta\right.}{2}\right)^2=\frac{1}{4} \dots(2)
\end{aligned}
\)
So, from equation (1) and (2) we get.
G.M. = A.M.
It is possible only if,
\(
\cos ^2 2 \theta=1-\cos ^2 2 \theta
\)
\(
\begin{aligned}
& \cos ^2 2 \theta=\frac{1}{2} \Rightarrow \cos 2 \theta= \pm \frac{1}{\sqrt{2}} \\
& \theta=\frac{\pi}{8}, \frac{3 \pi}{8} \quad \therefore \text { Sum }=\frac{\pi}{8}+\frac{3 \pi}{8}=\frac{\pi}{2}
\end{aligned}
\) -
Question 206 of 213
206. Question
The sum of the first 20 terms of the series \(1+\frac{3}{2}+\frac{7}{4}+\frac{15}{8}+\frac{31}{16}+\ldots\), is : [JEE Main 2018 (Online) 16th April Morning Slot]
CorrectIncorrectHint
The general term of the given series \(=\frac{2 \times 2^r-1}{2^r}\), where \(r \geq 0\)
\(
\therefore \text { req. sum }=1+\sum_{r=1}^{19} \frac{2 \times 2^r-1}{2^r}
\)
Now, \(\sum_{r=1}^{19}\left(\frac{2 \times 2^r-1}{2^r}\right)=\sum_{r=1}^{19}\left(2-\frac{1}{2^r}\right)\)
\(
\begin{aligned}
& =2(19)-\frac{\frac{1}{2}\left(1-\left(\frac{1}{2}\right)^{19}\right)}{1-\frac{1}{2}}=38+\frac{\left(\frac{1}{2}\right)^{19}-1}{1} \\
& =38+\left(\frac{1}{2}\right)^{19}-1=37+\left(\frac{1}{2}\right)^{19} \\
& \therefore \text { req. sum }=1+37+\left(\frac{1}{2}\right)^{19}=38+\left(\frac{1}{2}\right)^{19}
\end{aligned}
\)Alternate:
\(
\begin{aligned}
& 1+\frac{3}{2}+\frac{7}{4}+\frac{15}{8}+\frac{31}{16}+\ldots \\
& =(2-1)+\left(2-\frac{1}{2}\right)+\left(2-\frac{1}{4}\right)+\left(2-\frac{1}{8}\right)+\ldots .+20 \text { terms } \\
& =(2+2+\ldots .20 \text { terms })-\left(1+\frac{1}{2}+\frac{1}{4}+\ldots .20 \text { terms }\right) \\
& =2 \times 20-\left(\frac{1-\left(\frac{1}{2}\right)^{20}}{1-\frac{1}{2}}\right) \\
& =40-2+2\left(\frac{1}{2}\right)^{20} \\
& =38+\frac{1}{2^{19}}
\end{aligned}
\) -
Question 207 of 213
207. Question
Let \(\frac{1}{x_1}, \frac{1}{x_2}, \frac{1}{x_3}, \ldots .,\left(x_i \neq 0\right.\) for \(\left.i=1,2, \ldots ., n\right)\) be in A.P. such that \(x_1=4\) and \(x_{21}=20\). If \(n\) is the least positive integer for which \(x_n>50\), then \(\sum_{i=1}^n\left(\frac{1}{x_i}\right)\) is equal to. [JEE Main 2018 (Online) 16th April Morning Slot]
CorrectIncorrectHint
\(\because \frac{1}{x_1}, \frac{1}{x_2}, \frac{1}{x_3}, \ldots \ldots, \frac{1}{x_n}\) are in A.P
\(
x_1=4 \text { and } x_{21}=20
\)
Let ‘ \(d\) ‘ be the common difference of this A.P
\(
\begin{aligned}
& \therefore \text { its } 21^{\text {st }} \text { term }=\frac{1}{x_{21}}=\frac{1}{x_1}+[(21-1) \times d] \\
& \Rightarrow d=\frac{1}{20} \times\left(\frac{1}{20}-\frac{1}{4}\right) \Rightarrow d=-\frac{1}{100}
\end{aligned}
\)
Also \(x_n>50\) (given).
\(
\begin{aligned}
& \therefore \frac{1}{x_n}=\frac{1}{x_1}+[(n-1) \times d] \\
& \Rightarrow x_n=\frac{x_1}{1+(n-1) \times d \times x_1} \\
& \therefore \frac{x_1}{1+(n-1) \times d \times x_1}>50 \\
& \Rightarrow \frac{4}{1+(n-1) \times\left(-\frac{1}{100}\right) \times 4}>50 \\
& \Rightarrow 1+(n-1) \times\left(-\frac{1}{100}\right) \times 4<\frac{4}{50} \\
& \Rightarrow-\frac{1}{100}(n-1)<-\frac{23}{100} \\
& \Rightarrow n-1>23 \Rightarrow n>24
\end{aligned}
\)
Therefore, \(n=25\).
\(
\Rightarrow \sum_{i=1}^{25} \frac{1}{x_i}=\frac{25}{2}\left[\left(2 \times \frac{1}{4}\right)+(25-1) \times\left(-\frac{1}{100}\right)\right]=\frac{13}{4}
\) -
Question 208 of 213
208. Question
Let \(A\) be the sum of the first 20 terms and \(B\) be the sum of the first 40 terms of the series
\(
1^2+2 \cdot 2^2+3^2+2.4^2+5^2+2.6^2+\ldots
\)
If \(B-2 A=100 \lambda\), then \(\lambda\) is equal to : [JEE Main 2018 (Offline)]CorrectIncorrectHint
Sum of square of first \(n\) odd terms
\(
1^2+3^2+5^2+\ldots \ldots+n^2=\frac{n(2 n-1)(2 n+1)}{3}
\)
Given,
\(
1^2+2.2^2+3^2+2.4^2+5^2+2.6^2+\ldots \ldots
\)
Given,
\(
1^2+2.2^2+3^2+2.4^2+5^2+2.6^2+\ldots \ldots
\)
\(A=\) Sum of first 20 terms
\(
\therefore A=1^2+2.2^2+3^2+24^2+5^2+2.6^2+\ldots \ldots 20 \text { terms }
\)
Arrange those terms this way,
\(A=\left[1^2+3^2+5^2+\ldots .10\right.\) terms \(]+\left[2.2^2+2.4^2+2.6^2+\ldots .10\right.\) terms \(]\)
\(A=\left[1^2+3^2+5^2+\ldots 10\right.\) terms \(]+2 \cdot{ }^2\left[1^2+2^2+3^2+\ldots 10\right.\) terms \(]\)
\(
\begin{aligned}
& A=\frac{10 \times(2.10-1)(2.10+1)}{3}+2.2^2\left[\frac{10 \times 11 \times 21}{6}\right] \\
& A=\frac{10 \times 19 \times 21}{3}+8 \times \frac{10 \times 11 \times 21}{6} \\
& A=70 \times 19+70 \times 44 \\
& A=70 \times 63
\end{aligned}
\)
\(B=\) Sum of first 40 terms
Arrange those terms this way.
\(
\begin{aligned}
& B=\left[1^2+3^2+5^2+\ldots 20 \text { terms }\right]+\left[2.2^2+2.4^2+\ldots 20 \text { terms }\right] \\
& B=\left[1^2+3^2+5^2+\ldots 20 \text { terms }\right]+2.2^2\left[1^2+2^2+\ldots 20 \text { terms }\right] \\
& B=\frac{20 \times 39 \times 41}{3}+8 \times \frac{20 \times 21 \times 41}{6} \\
& B=260 \times 41+560 \times 41 \\
& B=41 \times 820 \\
& \therefore B-2 A=41 \times 820-2 \times 70 \times 63=24800
\end{aligned}
\)
Given that \(B-2 A=100 \lambda\)
\(
\begin{aligned}
& \therefore 100 \lambda=24800 \\
& \Rightarrow \lambda=248
\end{aligned}
\) -
Question 209 of 213
209. Question
Let \(a_1, a_2, a_3, \ldots, a_{49}\) be in A.P. such that \(\sum_{k=0}^{12} a_{4 k+1}=416\) and \(a_9+a_{43}=66\). If \(a_1^2+a_2^2+\ldots+a_{17}^2=140 m\), then \(m\) is equal to: [JEE Main 2018 (Offline)]
CorrectIncorrectHint
\(
a_1, a_2, a_3 \ldots a_{43} \text { are in AP }
\)
So, \(a_2=a_1+d\)
\(
a_3=a_1+2 d
\)
\(\vdots\)
\(
a_{49}=a_1+48 d
\)
Now given, \(a_9+a_{43}=66\)
\(
\begin{aligned}
& \Rightarrow \quad a_1+8 d+a_1+42 d=66 \\
& \Rightarrow \quad 2 a_1+50 d=66
\end{aligned}
\)
\(
\Rightarrow a_1+25 d=33 \ldots .(1)
\)
\(
\begin{aligned}
& \sum_{k=0}^{12} a_{4 k+1}=416 \\
& \Rightarrow a_1+a_5+a_9+a_{13}+\ldots .13 \text { items }=416
\end{aligned}
\)
\(
\begin{aligned}
& \Rightarrow \quad a_1+a_1+4 d+a_1+8 d+\ldots . a_1+48 d=416 \\
& \Rightarrow \quad 13 a_1+4 d+8 d+12 d+\ldots .48 d=416 \\
& \Rightarrow \quad 13 a_1+4(1+2+3+\ldots+12) d=416 \\
& \Rightarrow \quad 13 a_1+4 \times \frac{12 \times 13}{2} \times d=416 \\
& \Rightarrow \quad 13 a_1+24 \times 13 d=416
\end{aligned}
\)
\(
\Rightarrow a_1+24 d=32 \ldots \text { (2) }
\)
Solving (1) and (2) we get,
\(
d=1
\)
and \(a_1=8\)
\(
\begin{aligned}
& \therefore a_1=8 \\
& a_2=8+1=9 \\
& a_3=8+2=10
\end{aligned}
\)
\(\vdots\)
\(
a_{17}=8+16=24
\)
Now, \(a_1^2+a_2^2+\ldots \ldots+a_{17}^2=140 m\)
\(
\begin{aligned}
& \Rightarrow a_1^2+a_2^2+\ldots \ldots+a_{17}^2=140 m \\
& \Rightarrow 8^2+9^2+10^2+\ldots \ldots(24)^2=140 m
\end{aligned}
\)
We can write above series like this,
\(
\begin{aligned}
& \Rightarrow \quad\left(1^2+2^2+\ldots+24^2\right)-\left(1^2+2^2+\ldots .+7^2\right)=140 m \\
& \Rightarrow \frac{24(25)(49)}{6}-\frac{7 \times 8 \times 15}{6}=140 m \\
& \Rightarrow \quad 490-140=140 m \\
& \Rightarrow 4760=140 m \\
& \Rightarrow \quad m =34
\end{aligned}
\) -
Question 210 of 213
210. Question
If \(a, b, c\) are in A.P. and \(a^2, b^2, c^2\) are in G.P. such that \(a<b<c\) and \(a+b+c=\frac{3}{4}\), then the value of \(a\) is : [JEE Main 2018 (Online) 15th April Evening Slot]
CorrectIncorrectHint
\(\because a, b, c\) are in A.P. then
\(
a+c=2 b
\)
also it is given that,
\(
\begin{aligned}
& a+b+c=\frac{3}{4} \dots(1) \\
& \Rightarrow 2 b+b=\frac{3}{4} \Rightarrow b=\frac{1}{4} \dots(2)
\end{aligned}
\)
Again it is given that, \(a^2, b^2, c^2\) are in G.P. then
\(
\left(b^2\right)^2=a^2 c^2 \Rightarrow a c= \pm \frac{1}{16} \dots(3)
\)
From (1), (2) and (3), we get;
\(
a \pm \frac{1}{16 a}=\frac{1}{2} \Rightarrow 16 a^2-8 a \pm 1=0
\)Case I: \(16 a^2-8 a+1=0\)
\(\Rightarrow a=\frac{1}{4}\) (not possible as \(a<b\) )Case II: \(16 a^2-8 a-1=0 \Rightarrow a=\frac{8 \pm \sqrt{128}}{32}\)
\(
\begin{aligned}
& \Rightarrow a=\frac{1}{4} \pm \frac{1}{2 \sqrt{2}} \\
& \therefore a=\frac{1}{4}-\frac{1}{2 \sqrt{2}} \quad(\because a<b)
\end{aligned}
\) -
Question 211 of 213
211. Question
Let \(A_n=\left(\frac{3}{4}\right)-\left(\frac{3}{4}\right)^2+\left(\frac{3}{4}\right)^3-\ldots+(-1)^{n-1}\left(\frac{3}{4}\right)^n\) and \(B_n=1-A_n\). Then, the least odd natural number \(p\), so that \(B_n>A_n\), for all \(n \geq p\) is [Online April 15, 2018]
CorrectIncorrectHint
\(
A_n=\left(\frac{3}{4}\right)-\left(\frac{3}{4}\right)^2+\left(\frac{3}{4}\right)^3-\ldots+(-1)^{n-1}\left(\frac{3}{4}\right)^n
\)
Which is a G.P. with \(a=\frac{3}{4}, r=\frac{-3}{4}\) and number of
\(
\begin{aligned}
& \text { terms }=n \\
& \therefore A_n=\frac{\frac{3}{4} \times\left(1-\left(\frac{-3}{4}\right)^n\right)}{1-\left(\frac{-3}{4}\right)}=\frac{\frac{3}{4} \times\left(1-\left(\frac{-3}{4}\right)^n\right)}{\frac{7}{4}} \\
& \Rightarrow A_n=\frac{3}{7}\left[1-\left(\frac{-3}{4}\right)^n\right] \dots(1)
\end{aligned}
\)
As, \(B_n=1-A_n\)
For least odd natural number \(p\), such that \(B_n>A_n\)
\(
\Rightarrow 1-A_n>A_n \Rightarrow 1>2 \times A_n \Rightarrow A_n<\frac{1}{2}
\)
From eqn. (1), we get
\(
\begin{aligned}
& \frac{3}{7} \times\left[1-\left(\frac{-3}{4}\right)^n\right]<\frac{1}{2} \Rightarrow 1-\left(\frac{-3}{4}\right)^n<\frac{7}{6} \\
& \Rightarrow 1-\frac{7}{6}<\left(\frac{-3}{4}\right)^n \Rightarrow \frac{-1}{6}<\left(\frac{-3}{4}\right)^n
\end{aligned}
\)
As \(n\) is odd, then \(\left(\frac{-3}{4}\right)^n=-\frac{3^n}{4^n}\)
So \(\frac{-1}{6}<-\left(\frac{3}{4}\right)^n \Rightarrow \frac{1}{6}>\left(\frac{3}{4}\right)^n\)
\(
\log \left(\frac{1}{6}\right)=n \log \left(\frac{3}{4}\right) \Rightarrow 6.228<n
\)
Hence, \(n\) should be 7. -
Question 212 of 213
212. Question
If \(x_1, x_2, \ldots ., x_n\) and \(\frac{1}{h_1}, \frac{1}{h^2}, \ldots . \frac{1}{h_n}\) are two A.P’s such that \(x_3=h_2=8\) and \(x_8=h_7=20\), then \(x_5 \cdot h_{10}\) equals. [Online April 15, 2018]
CorrectIncorrectHint
Suppose \(d _1\) is the common difference of the A.P.
\(x_1, x_2, \ldots . x_n\) then
\(
\begin{aligned}
& \because x_8-x_3=5 d_1=12 \Rightarrow d_1=\frac{12}{5}=2.4 \\
& \Rightarrow x_5=x_3+2 d_1=8+2 \times \frac{12}{5}=12.8
\end{aligned}
\)
Suppose \(d _2\) is the common difference of the A.P \(\frac{1}{h_1}, \frac{1}{h_2}, \ldots \ldots \frac{1}{h_n}\) then
\(
\begin{aligned}
& 5 d_2=\frac{1}{20}-\frac{1}{8}=\frac{-3}{40} \Rightarrow d_2=\frac{-3}{200} \\
& \because \frac{1}{h_{10}}=\frac{1}{h_7}+3 d_2=\frac{1}{200} \Rightarrow h_{10}=200 \\
& \Rightarrow x_5 \cdot h_{10}=12.8 \times 200=2560
\end{aligned}
\) -
Question 213 of 213
213. Question
If \(b\) is the first term of an infinite G. P whose sum is five, then \(b\) lies in the interval. [Online April 15, 2018]
CorrectIncorrectHint
Sum of infinite G.P,
\(
\begin{aligned}
& S=\frac{b}{1-r} \text { where }|r|<1 \\
& \Rightarrow 5=\frac{b}{1-r} \\
& \Rightarrow 1-r=\frac{b}{5} \\
& \Rightarrow b=5(1-r) \\
& \text { as }|r|<1 \\
& \therefore-1<r<1 \\
& \Rightarrow 1>-r>-1 \\
& \Rightarrow 2>1-r>0 \\
& \Rightarrow 10>5(1-r)>0 \\
& \Rightarrow 10>b>0
\end{aligned}
\)
\(\therefore\) interval of \(b=(0,10)\)Alternate:
First term \(=b\) and common ratio \(= r\)
For infinite series, Sum \(=\frac{b}{1-r}=5\)
\(
\Rightarrow b=5(1- r )
\)
So, interval of \(b=(0,10)\) as, \(-1< r <1\) for infinite G.P.