Past JEE Main Entrance Paper
Overview
Fundamental principle of counting
Multiplication principle (Fundamental Principle of Counting)
Suppose an event \(E\) can occur in \(m\) different ways and associated with each way of occurring of \(E\), another event \(F\) can occur in \(n\) different ways, then the total number of occurrence of the two events in the given order is \(m \times n\).
Addition principle
If an event \(E\) can occur in \(m\) ways and another event \(F\) can occur in \(n\) ways, and suppose that both can not occur together, then \(E\) or \(F\) can occur in \(m+n\) ways.
Permutations
A permutation is an arrangement of objects in a definite order.
Permutation of \(n\) different objects
The number of permutations of \(n\) objects taken all at a time, denoted by the symbol \({ }^n P _n\), is given by
\(
{ }^n P _n=n!
\)
where \(n!=n(n-1)(n-2) \ldots 3.2 .1\), read as factorial \(n\), or \(n\) factorial.
The number of permutations of \(n\) objects taken \(r\) at a time, where \(0<r \leq n\), denoted by \({ }^n P _r\), is given by
\(
{ }^n P _r=\frac{n!}{(n-r)!}
\)
\(
\text { We assume that } 0!=1
\)
When repetition of objects is allowed
The number of permutations of \(n\) things taken all at a time, when repetition of objects is allowed is \(n^n\).
The number of permutations of \(n\) objects, taken \(r\) at a time, when repetition of objects is allowed, is \(n^r\).
Permutations when the objects are not distinct
The number of permutations of \(n\) objects of which \(p_1\) are of one kind, \(p_2\) are of second kind, …, \(p_k\) are of \(k^{\text {th }}\) kind and the rest if any, are of different kinds is \(\frac{n!}{p_{1}!p_{2}!\ldots p_{k}!}\)
Combinations
On many occasions we are not interested in arranging but only in selecting \(r\) objects from given \(n\) objects. A combination is a selection of some or all of a number of different objects where the order of selection is immaterial. The number of selections of \(r\) objects from the given \(n\) objects is denoted by \({ }^n C _r\), and is given by
\(
{ }^n C _r=\frac{n!}{r!(n-r)!}
\)
Remarks
- Use permutations if a problem calls for the number of arrangements of objects and different orders are to be counted.
- Use combinations if a problem calls for the number of ways of selecting objects and the order of selection is not to be counted.
Some important results
Let \(n\) and \(r\) be positive integers such that \(r \leq n\). Then
- \({ }^n C _r={ }^n C _{n-r}\)
- \({ }^n C _r+{ }^n C _{r-1}={ }^{n+1} C _r\)
- \(n^{n-1} C _{r-1}=(n-r+1)^n C _{r-1}\)
Quiz Summary
0 of 205 Questions completed
Questions:
Information
You have already completed the quiz before. Hence you can not start it again.
Quiz is loading…
You must sign in or sign up to start the quiz.
You must first complete the following:
Results
Results
0 of 205 Questions answered correctly
Your time:
Time has elapsed
You have reached 0 of 0 point(s), (0)
Earned Point(s): 0 of 0, (0)
0 Essay(s) Pending (Possible Point(s): 0)
Categories
- Not categorized 0%
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
- 94
- 95
- 96
- 97
- 98
- 99
- 100
- 101
- 102
- 103
- 104
- 105
- 106
- 107
- 108
- 109
- 110
- 111
- 112
- 113
- 114
- 115
- 116
- 117
- 118
- 119
- 120
- 121
- 122
- 123
- 124
- 125
- 126
- 127
- 128
- 129
- 130
- 131
- 132
- 133
- 134
- 135
- 136
- 137
- 138
- 139
- 140
- 141
- 142
- 143
- 144
- 145
- 146
- 147
- 148
- 149
- 150
- 151
- 152
- 153
- 154
- 155
- 156
- 157
- 158
- 159
- 160
- 161
- 162
- 163
- 164
- 165
- 166
- 167
- 168
- 169
- 170
- 171
- 172
- 173
- 174
- 175
- 176
- 177
- 178
- 179
- 180
- 181
- 182
- 183
- 184
- 185
- 186
- 187
- 188
- 189
- 190
- 191
- 192
- 193
- 194
- 195
- 196
- 197
- 198
- 199
- 200
- 201
- 202
- 203
- 204
- 205
- Current
- Review
- Answered
- Correct
- Incorrect
-
Question 1 of 205
1. Question
Two families with three members each and one family with four members are to be seated in a row. In how many ways can they be seated so that the same family members are not separated? [Main Sep. 06, 2020 (I)]
CorrectIncorrectHint
(b) Number of arrangement
\(
=(3 ! \times 3 ! \times 4 !) \times 3 !=(3 !)^3 4 !
\) -
Question 2 of 205
2. Question
The value of \(\left(2 \cdot{ }^1 P_0-3 \cdot{ }^2 P_1+4 \cdot{ }^3 P_2-\ldots\right.\) up to \(51^{\text {th }}\) term \()+(1 !-2 !+\) \(3 !-\ldots\) up to \(51^{\text {th }}\) term) is equal to : [Main Sep. 03, 2020 (I)]
CorrectIncorrectHint
(c) We know, \((r+1) \cdot{ }^r P_{r-1}=(r+1) \cdot \frac{r !}{1 !}=(r+1)\) !
So, \(\left(2 \cdot{ }^1 P_0-3 \cdot{ }^2 P_1+\ldots . .51\right.\) terms \()+\)
\(
\begin{aligned}
&\quad(1 !-2 !+3 !-\ldots \text { upto } 51 \text { terms }) \\
&=[2 !-3 !+4 !-\ldots+52 !]+[1 !-2 !+3 !-\ldots+51 !] \\
&=52 !+1 !=52 !+1
\end{aligned}
\) -
Question 3 of 205
3. Question
If the number of five-digit numbers with distinct digits and 2 at the \(10^{\text {th }}\) place is \(336 \mathrm{k}\), then \(\mathrm{k}\) is equal to: [Main Jan. 9, 2020 (I)]
CorrectIncorrectHint
(d) Number of five digit numbers with 2 at \(10^{\text {th }}\) place \(=8 \times 8 \times 7 \times 6=2688\)
It is given that, number of five digit number with 2 at \(10^{\text {th }}\) place \(=336 \mathrm{k}\)
\(
\therefore \quad 336 k=2688 \Rightarrow k=8
\) -
Question 4 of 205
4. Question
Total number of 6-digit numbers in which only and all the five digits \(1,3,5,7\) and 9 appear, is: [Main Jan. 7, 2020 (I)]
CorrectIncorrectHint
(d) Five digits numbers be \(1,3,5,7,9\) For selection of one digit, we have \({ }^5 C_1\) choice. And six digits can be arrange in \(\frac{6 !}{2 !}\) ways. Hence, total such numbers \(=\frac{5.6 !}{2 !}=\frac{5}{2} \cdot 6 !\)
-
Question 5 of 205
5. Question
The number of 6 digit numbers that can be formed using the digits 0 , \(1,2,5,7\) and 9 which are divisible by 11 and no digit is repeated, is: [Main April 10, 2019(I)]
CorrectIncorrectHint
Let the six digit number be abcdef for this number to be divisible by \(11, \mid(a+c+e)-\) \((b+d+f) \mid\) must be multiple of 11
possibility is \(a+c+e=b+d+f=12\)
Case : \(1\{a, c, e\}=\{7,5,0\}\)
\(\&\{b, d, f\}=\{9,2,1\}\)
So, number of numbers \(=2 \times 2 ! \times 3 !=24\)
Case : \(2\{a, c, e\}=\{9,2,1\}\)
\(\&\{b, d, f\}=\{7,5,0\}\)
So, number of numbers \(=3 ! \times 3 !=36\)
\(\Rightarrow\) total \(24+36\)
\(=60\) -
Question 6 of 205
6. Question
The number of four-digit numbers strictly greater than 4321 that can be formed using the digits \(0,1,2,3,4,5\) (repetition of digits is allowed) is: [Main April 08, 2019 (II)]
CorrectIncorrectHint
The numbers greater than 4321 must have 4 or 5 in the thousand’s place.
Case 1: Let us fix first place as 4
4 _ _ _
The second place can be filled in 2 ways \((4,5)\), third and fourth place can be filled in 6 ways.
Number of such four-digit numbers \(=2 \times 6 \times 6=72\)
Case 2: Let us fix first place as 4 and second place as 3
43 _ _
The third place can be filled in 3 ways \((3,4,5)\) and the fourth place can be filled in 6 ways.
Number of such four-digit numbers \(=3 \times 6=18\)
Case 3: Let us fix first place as 4 , second place as 3 and third place as 2 432 _
The fourth place can be filled in 4 ways \((2,3,4,5)\)
Number of such four-digit numbers \(=4\)
Case 4: Let us fix first place as 5
5 _ _ _
Number of such four-digit numbers \(=6 \times 6 \times 6=216\)
So, total number \(=72+18+4+216=310\) -
Question 7 of 205
7. Question
Consider three boxes, each containing 10 balls labelled \(1,2, \ldots, 10\). Suppose one ball is randomly drawn from each of the boxes. Denote by \(\mathrm{n}_{\mathrm{i}}\), the label of the ball drawn from the \(i^{\text {th }}\) box, \((i=1,2,3)\). Then, the number of ways in which the balls can be chosen such that \(\mathrm{n}_1<\mathrm{n}_2\) \(<\mathrm{n}_3\) is: [Main Jan. 12, 2019 (I)]
CorrectIncorrectHint
\(
n=10
\)
Select any three distinct numbers by \({ }^{10} \mathrm{C}_3\), then assign the biggest number to \(n_1\), the second biggest to \(n_2\) and smallest to \(n_3\)
\(\therefore\) required number of ways in which the balls can be chosen \(={ }^{10} \mathrm{C}_3\)
\(
\begin{aligned}
&=\frac{10 !}{3 ! 7 !} \\
&=\frac{10 \times 9 \times 8}{3 \times 2} \\
&=120
\end{aligned}
\) -
Question 8 of 205
8. Question
The number of numbers between 2,000 and 5,000 that can be formed with the digits \(0,1,2,3,4\), (repetition of digits is not allowed) and are multiple of 3 is? [Main Online April 16, 2018]
CorrectIncorrectHint
(a) The thousands place can only be filled with 2,3 or 4 , since the number is greater than 2000 .
For the remaining 3 places, we have pick out digits such that the resultant number is divisible by 3 .
If the sum of digits of the number is divisible by 3 , then the number itself is divisible by 3 .
Case 1: If we take 2 at thousands place.
The remaining digits can be filled as:
0,1 and 3 as \(2+1+0+3=6\) is divisible by 3 .
0,3 and 4 as \(2+3+0+4=9\) is divisible by 3 .
In both the above combinations the remaining three digits can be arranged in 3! ways.
\(\therefore\) Total number of numbers in this case \(=2 \times 3 !=12\).
Case 2: If we take 3 at thousands place. The remaining digits can be filled as:
0,1 and 2 as \(3+1+0+2=6\) is divisible by 3 .
0,2 and 4 as \(3+2+0+4=9\) is divisible by 3 .
In both the above combinations, the remaining three digits can be arranged in 3 ! ways. Total number of numbers in this case \(=2 \times 3 !=12\).
Case 3: If we take 4 at thousands place.
The remaining digits can be filled as:
0,2 and 3 as \(4+2+0+3=9\) is divisible by 3 .
In the above combination, the remaining three digits can be arranged in 3! ways.
\(\therefore\) Total number of numbers in this case \(=3 !=6\).
\(\therefore\) Total number of numbers between 2000 and 5000 divisible by 3 are \(12+12+6=30\). -
Question 9 of 205
9. Question
The number of ways in which 5 boys and 3 girls can be seated on a round table if a particular boy \(\mathrm{B}_1\) and a particular girl \(\mathrm{G}_1\) never sit adjacent to each other, is: [Main Online April 9, 2017]
CorrectIncorrectHint
The number of ways of arranging 5 boys and 3 girls, i.e. 8 people on a round table would be 7 !
We subtract the number of ways of arranging those people when \(B_1\) and \(G_1\) are always together to get the required answer.
When \(B_1\) and \(G_1\) are together, we get 4 boys \(+2\) girls \(+1\left(B_1+G_1\right)\) i.e. 7 people and since \(B_1+G_1\) can be permuted in 2 ways, these can be arranged in 6 ! \(\times 2\) ways.
Subtracting, we have \(7 !-6 ! \times 2=6 !(7-2)\)
\(=5 \times 6\) ! ways in total.Alternate:
(a) 4 boys and 2 girls in circle
\(
\Rightarrow 5 ! \times \frac{6 !}{4 ! 2 !} \times 2 ! \Rightarrow 5 \times 6 !
\) -
Question 10 of 205
10. Question
If all the words (with or without meaning) having five letters, formed using the letters of the word SMALL and arranged as in a dictionary; then the position of the word SMALL is: [Main 2016]
CorrectIncorrectHint
Position of SMALL in a dictionary:
Let us fix A in the first position.
Then, \(\mathrm{A}\)
At the 4 places we want to arrange L,L,M and \(S\) which can be done in \(\frac{4 !}{2 !}=12\) ways. (since 2 Ls are there)
Let us fix L in the first position.
Then, \(\mathrm{L}\)
At the 4 places we want to arrange L,A,M and \(S\) which can be done in \(4 !=24\) ways.
Let us fix \(M\) in the first position.
Then, \(\mathrm{M}\)
At the 4 places we want to arrange L,L,A and \(S\) which can be done in \(\frac{4 !}{2 !}=12\) ways. (since 2 Ls are there)
Let us fix \(\mathrm{S}\) in the first position and \(\mathrm{A}\) in second position.
Then, SA
At the 3 places we want to arrange \(L, L\) and \(M\) which can be done in \(\frac{3 !}{2 !}=3\) ways.
Let us fix \(\mathrm{S}\) in the first position and \(\mathrm{L}\) in second position.
Then, S L
At the 3 places we want to arrange L,A and \(M\) which can be done in \(3 !=6\) ways.
Let us fix \(\mathrm{M}\) in second position.
Then, S M
There arranging in alphabetical order, the next word is
SMALL
Position \(=12+24+12+3+6+1=58^{\text {th }}\) -
Question 11 of 205
11. Question
If the four-letter words (need not be meaningful) are to be formed using the letters from the word “MEDITERRANEAN” such that the first letter is \(R\) and the fourth letter is \(E\), then the total number of all such words is : [Main Online April 9, 2016]
CorrectIncorrectHint
(b) M, EEE, D. I, T, RR, AA, NN \(\mathrm{R}–\mathrm{E}\)
Two empty places can be filled with identical letters[EE, AA, NN] \(\Rightarrow 3\) ways
Two empty places, can be filled with distinct letters[M, E, D, I, T, R, A, N] \(\Rightarrow{ }^8 \mathrm{P}_2\)
\(\therefore \quad\) Number of words \(3+{ }^8 \mathrm{P}_2=59\)Alternate:
First letter is R and Fourth letter is \(\mathrm{E}\).
So now we have 11 letters left with \(2 \mathrm{E}, 2 \mathrm{~A}, 1 \mathrm{M}, 1 \mathrm{D}, 1 \mathrm{I}, 1 \mathrm{~T}, 1 \mathrm{R}\) and \(2 \mathrm{~N}\) And with this we have to form a two-letter word.
There will be 2 cases when both these two letters of the middle will be the same. And this will be when they both are either EE, AA or NN.
Now when middle two letters are not same. So we have to form a 2letter word with 8letters without repetition .
Number of such words will be \(8 \times 7=56\)
Hence, the total number of such four-letter words with \(\mathrm{R}\) as the first letter and \(\mathrm{E}\) as the last letter will be \(56+3=59\). -
Question 12 of 205
12. Question
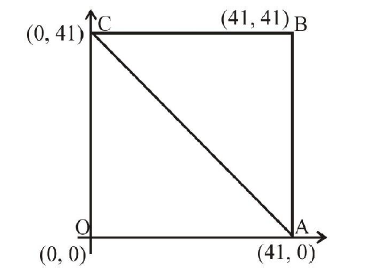
The number of points, having both co-ordinates as integers, that lie in the interior of the triangle with vertices \((0,0),(0,41)\) and \((41,0)\) is: [Main 2015]
CorrectIncorrectHint
(b) Total number of integral points inside the square \(\mathrm{OABC}=40 \times\) \(40=1600\)
No. of integral points on AC
\(
\begin{aligned}
=& \text { No. of integral points on } \mathrm{OB} \\
=& 40[\text { namely }(1,1),(2,2) \ldots(40,40)] \\
& \quad \therefore \quad \text { No. of integral points inside the } \triangle O A C \\
=& \frac{1600-40}{2}=780
\end{aligned}
\)
-
Question 13 of 205
13. Question
The number of integers greater than 6,000 that can be formed, using the digits \(3,5,6,7\) and 8 , without repetition, is: [Main 2015]
CorrectIncorrectHint
(d) Four digits number can be arranged in \(3 \times 4\) ! ways. Five digits number can be arranged in 5! ways. Number of integers \(=3 \times 4 !+5 !=192\).
-
Question 14 of 205
14. Question
The number of ways of selecting 15 teams from 15 men and 15 women, such that each team consists of a man and a woman, is: [Main Online April 10, 2015]
CorrectIncorrectHint
(d) Number of ways of selecting a man and a woman for a team from 15 men and 15 women \(=15 \times 15=(15)^2\)
Number of ways of selecting a man and a woman for next team out of the remaining 14 men and 14 women.
\(
=14 \times 14=(14)^2
\)
Similarly for other teams
Hence required number of ways
\(
=(15)^2+(14)^2+\ldots .+(1)^2=\frac{15 \times 16 \times 31}{6}=1240
\) -
Question 15 of 205
15. Question
The sum of the digits in the unit’s place of all the 4-digit numbers formed by using the numbers \(3,4,5\) and 6 , without repetition, is: [Main Online April 9, 2014]
CorrectIncorrectHint
(b) With 3 at unit place, total possible four digit number (without repetition) will be \(3 !=6\)
With 4 at unit place, total possible four digit numbers will be \(3 !=6\)
With 5 at unit place, total possible four digit numbers will be \(3 !=6\)
With 6 at unit place, total possible four digit numbers will be \(3 !=6\)
Sum of unit digits of all possible numbers
\(
\begin{aligned}
&=6 \times 3+6 \times 4+6 \times 5+6 \times 6 \\
&=6[3+4+5+6]=6[18]=108
\end{aligned}
\) -
Question 16 of 205
16. Question
Six cards and six envelopes are numbered 1, 2, 3, 4, 5, 6 and cards are to be placed in envelopes so that each envelope contains exactly one card and no card is placed in the envelope bearing the same number and moreover the card numbered 1 is always placed in envelope numbered 2. Then the number of ways it can be done is [ADV 2014]
CorrectIncorrectHint
(c) Card numbered 1 is always placed in envelope numbered 2 , we can consider two cases :
Case I: Card numbered 2 is placed in envelope numbered 1.
Then it is dearrangement of 4 objects, which can be done in \(4 !\left(1-\frac{1}{1 !}+\frac{1}{2 !}-\frac{1}{3 !}+\frac{1}{4 !}\right)=9\) ways
Case II: Card numbered 2 is not placed in envelope numbered 1.
Then it is dearrangement of 5 objects, which can be done in \(5 !\left(1-\frac{1}{1 !}+\frac{1}{2 !}-\frac{1}{3 !}+\frac{1}{4 !}-\frac{1}{5 !}\right)=44\) ways
\(\therefore \quad\) Total ways \(=44+9=53\)Alternate:
(Number of derrangements of \(6=6 !\left(1-\frac{1}{1 !}+\frac{1}{2 !}-\frac{1}{3 !}+\frac{1}{4 !}-\frac{1}{5 !}+\frac{1}{6 !}\right)\)
\(
=360-120+30-6+1
\)
\(=265\)
Out of these derrangements, there are five ways in which card numbered 1 is going wrong.
So, when it is going in envelope numbered 2 is,
\(
=\frac{265}{5}=53 \text { ways. }
\) -
Question 17 of 205
17. Question
5 – digit numbers are to be formed using \(2,3,5,7,9\) without repeating the digits. If \(p\) be the number of such numbers that exceed 20000 and \(q\) be the number of those that lie between 30000 and 90000, then \(p: q\) is: [Main Online April 25, 2013]
CorrectIncorrectHint
(d) Any number 5 -digit formed by \(2,3,5,7,9\), exceeds 20000 .
Therefore, \(p=5!=120\)
A number will lie between 30000 and 90000 if it begins with 3,5 or 7 \(\therefore q=(3)(4!)\). Thus \(p: q=5: 3\) -
Question 18 of 205
18. Question
The number of seven-digit integers, with sum of the digits equal to 10 and formed by using the digits 1,2 and 3 only, is [2009]
CorrectIncorrectHint
(c) We have to form 7 digit numbers, using the digits 1,2 and 3 only, such that the sum of the digits in a number \(=10\).
This can be done by taking \(2,2,2,1,1,1\), 1, or by taking \(2,3,1,1,1,1,1\).
\(
\therefore \text { Number of ways }=\frac{7 !}{3 ! 4 !}+\frac{7 !}{5 !}=77
\)Alternate:
Case-1:
\(1,1,1,1,1,2,3\)
Number of ways \(=\frac{7 !}{5 !}=42\) [Since, 1 repeat five times \(]\)
Case- 2 :
\(1,1,1,1,2,2,2\)
Number of ways \(=\frac{7 !}{4 ! \times 3 !}=35\) [Since, 4 repeat four times and 2 repeat three times ]
Total number of ways \(=42+35=77\) -
Question 19 of 205
19. Question
The letters of the word COCHIN are permuted and all the permutations are arranged in an alphabetical order as in an English dictionary. The number of words that appear before the word COCHIN is [2007-3 marks]
CorrectIncorrectHint
The given word is \(\mathrm{COCHIN}\)
So, we have two times \(C\) appearing in the word.
Fixing position these \(C\) we have number of letters for permutation \(=4\)
Therefore, the number of words, having two letter of \(C\) in first and second
places \(=4 !\)
Similarly,
The number of words starting with letter \(\mathrm{CH}=4\) !
The number of words starting with letter \(C I=4\) !
The number of words starting with letter \(C N=4\) !
Therefore,
The total number of words that appear before the word ‘COCHIN’
\(
\begin{aligned}
&=4 !+4 !+4 !+4 ! \\
&=(4 \times 3 \times 2 \times 1)+(4 \times 3 \times 2 \times 1)+(4 \times 3 \times 2 \times 1)+(4 \times 3 \times 2 \times 1) \\
&=24+24+24+24 \\
&=96
\end{aligned}
\)Alternate:
(c) The letter of word \(C O C H I N\) in alphabetic order are \(C, C, H, I, N\), 0.
Fixing first and second letter as \(C, C\), rest 4 can be arranged in \(4 !\) ways. Similarly the words starting with each of \(C H, C I, C N\) are 4 ! Then fixing first two letters as \(C O\) and next four places when filled in alphabetic order with remaining 4 letters give the word COCHIN.
\(\therefore \quad\) Numbers of words coming before COCHIN \(=4 \times 4 !=4 \times 24=96\) -
Question 20 of 205
20. Question
If the LCM of \(p, q\) is \(r^2 t^4 s^2\), where \(r, s, t\) are prime numbers and \(p, q\) are the positive integers then the number of ordered pair \((p, q)\) is [2006-3 M,-1]
CorrectIncorrectHint
Step 1: Find the number of ways of choosing exponents of \(r\).
The LCM of \(p, q\) is \(r^2 t^4 s^2\), it means \(r^2, t^4, s^2\) must be among the prime factors of \(p, q\).
Now, if \(r^2\) is a factor of \(p\), then \(q\) has \(r^x\), where \(x=(0,1)\)
So, the number of ways of choosing exponents of \(r\) will be 2 .
Similarly, if \(r^2\) is a factor of \(q\), then \(p\) has \(r^x\), where \(x=(0,1)\)
So, the number of ways of choosing exponents of \(r\) will again be 2.
But if \(r^2\) is a factor of both \(p, q\), then the number of ways of choosing exponents of \(r\) will be 1 .
So, the exponents of \(r\) can be chosen in \(2+2+1=5\) ways.Step 2: Find the number of ways of choosing exponents of \(t\).
If \(t^4\) is a factor of \(p\), then \(q\) has \(t^x\), where \(x=(0,1,2,3)\)
So, the number of ways of choosing exponents of \(t\) will be 4 .
Similarly, if \(t^4\) is a factor of \(q\), then \(p\) has \(t^x\), where \(x=(0,1,2,3)\)
So, the number of ways of choosing exponents of \(t\) will again be 4 .
But if \(t^4\) is a factor of both \(p, q\), then the number of ways of choosing exponents of \(t\) will be 1 .
So, the exponents of \(t\) can be chosen in \(4+4+1=9\) ways.Step 3: Find the number of ways of choosing exponents of \(s\).
If \(s^2\) is a factor of \(p\), then \(q\) has \(s^x\), where \(x=(0,1)\)
So, the number of ways of choosing exponents of \(s\) will be 2 .
Similarly, if \(s^2\) is a factor of \(q\), then \(p\) has \(s^x\), where \(x=(0,1)\)
So, the number of ways of choosing exponents of \(s\) will again be 2 .
But if \(s^2\) is a factor of both \(p, q\), then the number of ways of choosing exponents of \(s\) will be 1 .
So, the exponents of \(s\) can be chosen in \(2+2+1=5\) ways.Step 4: Find the number of ordered pair \((p, q)\).
The number of ordered pair \((p, q)\) is \(5 \times 9 \times 5=225\) -
Question 21 of 205
21. Question
The number of arrangements of the letters of the word BANANA in which the two N’s do not appear adjacently is [2002S]
CorrectIncorrectHint
(a) Total number of ways of arranging the letters of the word BANANA is \(\frac{6 !}{2 ! 3 !}=60\). Number of words in which 2 N’s come together is \(\frac{5 !}{3 !}=20\)
\(\therefore\) the required number \(=60-20=40\) -
Question 22 of 205
22. Question
How many different nine-digit numbers can be formed from the number 223355888 by rearranging its digits so that the odd digits occupy even positions? [2000S]
CorrectIncorrectHint
(c) \(X-X-X-X-X\). The four digits \(3,3,5,5\) can be arranged at (-) places in \(\frac{4 !}{2 ! 2 !}=6\) ways
The five digits \(2,2,8,8,8\) can be arranged at (X) places in \(\frac{5 !}{2 ! 3 !}=10\) ways
\(\therefore\) Total number of arrangements \(=6 \times 10=60\) ways -
Question 23 of 205
23. Question
A five-digit number divisible by 3 is to be formed using the numerals \(0,1,2,3,4\) and 5, without repetition. The total number of ways this can be done is [1989 – 2 Marks]
CorrectIncorrectHint
(a) We know that a number is divisible by 3 if the sum of its digits is divisibly by 3.
Now out of \(0,1,2,3,4,5\) if we take \(1,2,3,4,5\) or \(0,1,2,4,5\) then the 5 digit numbers will be divisible by 3 .
Case I: Number of 5-digit numbers formed using the digits 1, 2, 3, 4, \(5=\) \(5 !=120\)
Case II : Taking \(0,1,2,4,5\) if we make 5 digit number then 1st place can be filled in 4 ways ( 0 can not come at I place)
2nd place can be filled in 4 ways
3 rd place can be filled in 3 ways
4th place can be filled in 2 ways
5 th place can be filled in 1 way
\(\therefore \quad\) Total numbers \(=4 \times 4 !=96\)
Thus total numbers divisible by 3 are \(=120+96=216\) -
Question 24 of 205
24. Question
Ten different letters of an alphabet are given. Words with five letters are formed from these given letters. Then the number of words which have at least one letter repeated are [1982 – 2 Marks]
CorrectIncorrectHint
(a) Total number of words that can be formed using 5 letters out of 10 given different letters
\(
\begin{aligned}
&=10 \times 10 \times 10 \times 10 \times 10 \text { (as letters can repeat) } \\
&=1,00,000
\end{aligned}
\)
Number of words that can be formed using 5 different letters out of 10 different letters
\(={ }^{10} P_5\) (none can repeat)
\(
=\frac{10 !}{5 !}=30,240
\)
\(\therefore \quad\) Number of words in which at least one letter is repeated
\(=\) total words-words with none of the letters repeated
\(=1,00,000-30,240 \quad=69,760\) -
Question 25 of 205
25. Question
Five persons A, B, C, D and E are seated in a circular arrangement. If each of them is given a hat of one of the three colours red, blue and green, then the number of ways of distributing the hats such that the persons seated in adjacent seats get different coloured hats is ___ [ADV. 2019]
CorrectIncorrectHint
maximum number of hats used of same are 2 .They can not be 3 otherwise atleast 2 hats of same colour are consecutive
Now,Let hats used are R, R, G, G, B
(which can be selected in 3 ways .it can be RGGBB or RRGBB also )
Now numbers of ways of distributing blue hat (single one) in 5 Person equal to 5 let blue hat goes to person \(A\).
Now either position \(B\) and \(D\) are filled by green hats and \(C\) and \(E\) are filled by reds hats or \(\mathrm{B}\) and \(\mathrm{D}\) are filled by Red hats and \(\mathrm{C}\) and \(\mathrm{E}\) are filled by green hats \(\Rightarrow 2\) ways are possible
Hence total number of ways \(=3 \times 5 \times 2=30\) ways -
Question 26 of 205
26. Question
The number of 5-digit numbers which are divisible by 4, with digits from the set \(\{1,2,3,4,5\}\) and the repetition of digits is allowed, is ____.[Adv. 2018]
CorrectIncorrectHint
A number is divisible by 4 if last two digits of that number is divisible by 4 The 2 digits numbers which are divisible by 4 from the given set \(\{1,2,3,4,5\}\) are \(12,24,32,44\) or 52
So, if a number ends with \(12,24,32,44\) or 52 , then it is divisible by 4.
Also each of the first 3 digits can be any of {1,2,3,4,5}
Therefore 5 options for each of the first 3 digits and total 5 options for the last 2 digits.
First 3 digits can be arranged in \(5^3\) ways
So, the total number of 5-digit numbers that are divisible by 4 without repetition is
\(
5^3 \times 5=625
\) -
Question 27 of 205
27. Question
Let \(n_1<n_2<n_3<n_4<n_5\) be positive integers such that \(n_1+n_2+n_3+n_4\) \(+n_5=20\). Then the number of such distinct arrangements \(\left(n_1, n_2, n_3\right.\), \(n_4, n_5\) ) is [Adv. 2014]
CorrectIncorrectHint
(7) \(\because n_1, n_2, n_3, n_4\) and \(n_5\) are positive integers such that \(n_1<n_2<n_3<\) \(n_4<n_5\)
Then for \(n_1+n_2+n_3+n_4+n_5=20\)
If \(n_1, n_2, n_3, n_4\) take minimum values \(1,2,3,4\) respectively then \(n_5\) will be maximum 10 .
\(\therefore\) Corresponding to \(n_5=10\), there is only one solution \(n_1=1, n_2=2, n_3=3, n_4=4\).
Corresponding to \(n_5=9\), we can have, only solution \(n_1=1, n_2=2, n_3=3, n_4=5\) i.e., one solution
Corresponding to \(n_5=8\), we can have, only solution
\(
n_1=1, n_2=2, n_3=3, n_4=6
\)
or \(n_1=1, n_2=2, n_3=4, n_4=5\)
i.e., 2 solution
For \(n_5=7\), we can have
\(
n_1=1, n_2=2, n_3=4, n_4=6
\)
or \(n_1=1, n_2=3, n_3=4, n_4=5\)
i.e. 2 solutions
For \(n_5=6\), we can have
\(
n_1=2, n_2=3, n_3=4, n_4=5
\)
i.e., one solution
Thus there can be 7 solutions. -
Question 28 of 205
28. Question
If the letters of the word ‘MOTHER’ be permuted and all the words so formed (with or without meaning) be listed as in a dictionary, then the position of the word ‘MOTHER’ is [Main Sep. 02, 2020 (I)]
CorrectIncorrectHint
To find rank of MOTHER
Total words starting from \(E=5 !=120\)
Total words starting from \(\mathrm{H}=5 !=120\)
Number of words starting from \(\mathrm{ME}=4 !=24\)
Number of words starting from \(\mathrm{MH}=4 !=24\)
Number of words starting from \(\mathrm{MOE}=3 !=6\)
Number of words starting from \(\mathrm{MOH}=3 !=6\)
Number of words starting from \(\mathrm{MOR}=3 !=6\)
Number of words starting from MOTE \(=2 !=2\)
Next word \(=\) MOTHER
\(\operatorname{Rank}=120+120+24+24+6+6+6+2+1\) \(=309\) -
Question 29 of 205
29. Question
In a hotel, four rooms are available. Six persons are to be accommodated in these four rooms in such a way that each of these rooms contains at least one person and at most two persons. Then the number of all possible ways in which this can be done is [Adv. 2020]
CorrectIncorrectHint
(1080) Groups can be possible in only \(2,2,1,1\) way. Number of ways of dividing persons in group
\(
=\frac{6 !}{(2 !)^2(1 !)^2(2 !)^2}
\)
Number of ways after arranging rooms \(=\frac{6 !}{(2 !)^4} \cdot 4 !=1080\) -
Question 30 of 205
30. Question
There are four balls of different colours and four boxes of colours, same as those of the balls. The number of ways in which the balls, one each in a box, could be placed such that a ball does not go to a box of its own colour is [1988-2 Marks]
CorrectIncorrectHint
We know that number of dearrangements of \(n\) objects
\(
=n !\left[1-\frac{1}{1 !}+\frac{1}{2 !}-\frac{1}{3 !}+\frac{1}{4 !}-\ldots . \frac{1}{n !}\right]
\)
\(\therefore \quad\) No. of ways of putting all the 4 balls into boxes of different colour
\(
\begin{aligned}
&=4 !\left[1-\frac{1}{1 !}+\frac{1}{2 !}-\frac{1}{3 !}+\frac{1}{4 !}\right]=4 !\left(\frac{1}{2}-\frac{1}{6}+\frac{1}{24}\right) \\
&=24\left(\frac{12-4+1}{24}\right)=9
\end{aligned}
\) -
Question 31 of 205
31. Question
In a certain test, \(a_i\) students gave wrong answers to at least i questions, where \(i=1,2, \ldots, k\). No student gave more than \(k\) wrong answers. The total number of wrong answers given is [1982 – 2 Marks]
CorrectIncorrectHint
Number of students who gave wrong answers to exactly one question \(=a_1-a_2, \quad\) Two questions \(=a_2-a_3\) Three questions \(=a_3-a_4, k-1\) question \(=a_{k-1}-a_k, k_{\text {question }}=a_{\mathrm{k}}\)
\(\therefore\) Total number of wrong answers
\(
\begin{aligned}
&=1\left(a_1-a_2\right)+2\left(a_2-a_3\right)+3\left(a_3-a_4\right)+\ldots .(k-1) \\
&\left(a_{k-1}-a_k\right)+k a_1 \\
&=a_1+a_2+a_3+\ldots . a_k
\end{aligned}
\) -
Question 32 of 205
32. Question
An n-digit number is a positive number with exactly \(\mathrm{n}\) digits. Nine hundred distinct \(\mathrm{n}\) – digit numbers are to be formed using only the three digits 2,5 and 7. The smallest value of \(\mathrm{n}\) for which this is possible is [1998 – 2 Marks]
CorrectIncorrectHint
(b) Distinct \(n\) digit numbers which can be formed using digits 2,5 and 7 are \(3^n\).
We have to find \(n\) so that \(3^n \geq 900 \Rightarrow 3^{n-2} \geq 100\)
\(\Rightarrow n-2 \geq 5 \Rightarrow n \geq 7\). So the least value of \(n\) is 7 -
Question 33 of 205
33. Question
In a high school, a committee has to be formed from a group of 6 boys \(M_1, M_2, M_3, M_4, M_5, M_6\) and 5 girls \(G_1, G_2, G_3, G_4, G_5\).
(i) Let \(\alpha_1\) be the total number of ways in which the committee can be formed such that the committee has 5 members, having exactly 3 boys and 2 girls.
(ii) Let \(\alpha_2\) be the total number of ways in which the committee can be formed such that the committee has at least 2 members, and having an equal number of boys and girls.
(iii) Let \(\alpha_3\) be the total number of ways in which the committee can be formed such that the committee has 5 members, at least 2 of them being girls.
(iv) Let \(\alpha_4\) be the total number of ways in which the committee can be formed such that the committee has 4 members, having at least 2 girls such that both \(M_1\) and \(G_1\) are NOT in the committee together.\(
\begin{aligned}
&\begin{array}{|c|c|}
\hline \text { LIST – I } & \text { LIST – II } \\
\hline \text { P. The value of } \alpha_1 \text { is } & 1.136 \\
\hline \text { Q. The value of } \alpha_2 \text { is } & 2.189 \\
\hline \text { R. The value of } \alpha_3 \text { is } & 3.192 \\
\hline \text { S. The value of } \alpha_4 \text { is } & 4.200 \\
\hline & 5.381 \\
\hline & 6.461 \\
\hline
\end{array}\\
&\text { The correct option is }
\end{aligned}
\)CorrectIncorrectHint
(c) Given 6 boys \(M_1, M_2, M_3, M_4, M_5, M_6\) and 5 girls \(G_1, G_2, G_3, G_4\), \(G_5\)
(i) \(\alpha_1 \rightarrow\) Total number of ways of selecting 3 boys and 2 girls from 6 boys and 5 girls
i.e., \({ }^6 \mathrm{C}_3 \times{ }^5 \mathrm{C}_2=20 \times 10=200\)
\(\therefore \quad \alpha_1=200\)
(ii) \(\alpha_2 \rightarrow\) Total number of ways selecting at least 2 member and having equal number of boys and girls
\(
\begin{aligned}
&\text { i.e., } \begin{aligned}
{ }^6 \mathrm{C}_1^5 \mathrm{C}_1+{ }^6 \mathrm{C}_2^5 \mathrm{C}_2+{ }^6 \mathrm{C}_3^5 \mathrm{C}_3+{ }^6 \mathrm{C}_4^5 \mathrm{C}_4+{ }^6 \mathrm{C}_5{ }^5 \mathrm{C}_5 \\
&=30+150+200+75+6=461
\end{aligned} \\
&\Rightarrow \alpha_2=461
\end{aligned}
\)
(iii) \(\alpha_3 \rightarrow\) Total number of ways of selecting 5 members in which at least 2 of them girls
\(
\begin{aligned}
&\text { i.e., }{ }^5 \mathrm{C}_2{ }^6 \mathrm{C}_3+{ }^5 \mathrm{C}_3{ }^6 \mathrm{C}_2+{ }^5 \mathrm{C}_4{ }^6 \mathrm{C}_1+{ }^5 \mathrm{C}_5{ }^6 \mathrm{C}_0 \\
&=200+150+30+1=381 \\
&\Rightarrow a_3=381
\end{aligned}
\)
(iv) \(\alpha_4 \rightarrow\) Total number of ways for selecting 4 members in which at least two girls such that \(M_1\) and \(G_1\) are not included together.
\(G_1\) is included \(\rightarrow{ }^4 \mathrm{C}_1 \cdot{ }^5 \mathrm{C}_2+{ }^4 \mathrm{C}_2 \cdot{ }^5 \mathrm{C}_1+{ }^4 \mathrm{C}_3\)
\(
=40+30+4=74
\)
\(M_1\) is included \(\rightarrow{ }^4 \mathrm{C}_2 \cdot{ }^5 \mathrm{C}_1+{ }^4 \mathrm{C}_3=30+4=34\)
\(G_1\) and \(M_1\) both are not included
\(
\begin{gathered}
1+20+60=81 \quad{ }^4 \mathrm{C}_4+{ }^4 \mathrm{C}_3 \cdot{ }^5 \mathrm{C}_1+{ }^4 \mathrm{C}_2 \cdot{ }^5 \mathrm{C}_2 \\
\therefore \quad \text { Total number }=74+34+81=189 \\
\alpha_4=189
\end{gathered}
\)
Now, \(P \rightarrow 4 ; Q \rightarrow 6 ; R \rightarrow 5 ; S \rightarrow 2\) -
Question 34 of 205
34. Question
Consider all possible permutations of the letters of the word ENDEANOEL. Match the Statements / Expressions in Column I with the Statements / Expressions in Column II and indicate your answer by darkening the appropriate bubbles in the \(4 \times 4\) matrix given in the ORS. [2008]
\(
\begin{array}{|l|l|}
\hline \text { column I } & \begin{array}{l}
\text { column II }
\end{array} \\
\hline \begin{array}{l}
\text { (A) The number of permutations containing the word ENDEA, is }
\end{array} & \text { (p) } 5 \text { ! } \\
\hline \begin{array}{l}
\text { (B) The number of permutations in which the letter E occurs in the first and the } \\
\text { last positions, is }
\end{array} & \text { (q) } 2 \times 5 \text { ! } \\
\hline \begin{array}{l}
\text { (C) The number of permutations in which none of the letters D, L, N occurs in the } \\
\text { last five positions, is }
\end{array} & \text { (r) } 7 \times 5 \text { ! } \\
\hline \begin{array}{l}
\text { (D) The number of permutations in which the letters A, E, O occur only in odd } \\
\text { positions, is }
\end{array} & \text { (s) } 21 \times 5 \text { ! } \\
\hline
\end{array}
\)CorrectIncorrectHint
(A) For the permutations containing the word ENDEA we consider ‘ENDEA’ as single letter. Then we have total ENDEA, N, O, E, L i.e. 5 letters which can be arranged in 5! ways.
\(
\therefore(\mathrm{A}) \rightarrow(\mathrm{p})
\)
(B) If \(\mathrm{E}\) occupies the first and last position, the middle 7 positions can be filled by \(\mathrm{N}, \mathrm{D}, \mathrm{E}, \mathrm{A}, \mathrm{N}, \mathrm{O}, \mathrm{L}\). in \(\frac{7 !}{2 !}=7 \times 6 \times 5 \times 4 \times 3=21 \times 120=21 \times 5 !\) ways. \(\therefore(\mathrm{B}) \rightarrow(\mathrm{s})\)
(C) If none of the letters D, L, N occur in the last five positions then we should arrange D, L, N, N at first four positions and rest five i.e. \(\mathrm{E}, \mathrm{E}, \mathrm{E}, \mathrm{A}, \mathrm{O}\) at last five positions. This can be done in
\(
\begin{aligned}
&\frac{4 !}{2 !} \times \frac{5 !}{3 !}=4 \times 3 \times \frac{5 !}{3 \times 2}=2 \times 5 \text { ! ways } \\
&\therefore \quad(C) \rightarrow \text { (q) }
\end{aligned}
\)
(D) As per question A, E, E, E, O can be arranged at 1st, 3rd, 5th, 7th and 9th positions and rest \(\mathrm{D}, \mathrm{L}, \mathrm{N}, \mathrm{N}\) at rest 4 positions. This can be done in
\(
\frac{5 !}{3 !} \times \frac{4 !}{2 !} \text { ways }=2 \times 5 \text { ! ways } \quad \therefore \quad \text { (D) } \rightarrow \text { (q) }
\) -
Question 35 of 205
35. Question
If total number of runs scored in \(n\) matches is \(\left(\frac{n+1}{4}\right)\left(2^{n+1}-n-2\right)\) where \(n>1\), and the runs scored in the \(\mathrm{k}^{\text {th }}\) match are given by \(\mathrm{k} .2^{n+1-}\) \({ }^k\), where \(1 \leq k \leq n\). Find \(n\). [2005 – 2 Marks]
CorrectIncorrectHint
Given: Runs scored in \(k^{\text {th }}\) match \(=k \cdot 2^{n+1-k}, 1 \leq k \leq n\) and runs scored in \(\mathrm{n}\) matches \(=\frac{n+1}{4}\left(2^{n+1}-n-2\right)\)
\(
\begin{array}{cl}
\therefore & \sum_{k=1}^n k \cdot 2^{n+1-k}=\frac{n+1}{4}\left(2^{n+1}-n-2\right) \\
\Rightarrow & 2^{\mathrm{n}+1}\left[\sum_{k=1}^n \frac{k}{2^k}\right]=\frac{n+1}{4}\left(2^{n+1}-n-2\right) \\
\Rightarrow & 2^{n+1}\left[\frac{1}{2}+\frac{2}{2^2}+\frac{3}{2^3}+\ldots+\frac{n}{2^n}\right] \\
& =\frac{n+1}{4}\left(2^{n+1}-n-2\right) \dots(i)
\end{array}
\)
Let \(S=\frac{1}{2}+\frac{2}{2^2}+\frac{3}{2^3}+\ldots .+\frac{n}{2^n} \dots(ii)\)
\(
\therefore \quad \frac{1}{2} S=\frac{1}{2^2}+\frac{2}{2^3}+\ldots .+\frac{n-1}{2^n}+\frac{n}{2^{n+1}} \dots(iii)
\)
On subtracting eq. (iii), from (ii), we get i.e., \(\frac{1}{2} S=\frac{1}{2}+\frac{1}{2^2}+\frac{1}{2^3} .+\ldots+\frac{1}{2^n}-\frac{n}{2^{n+1}}\)
\(
\begin{aligned}
&\Rightarrow \frac{1}{2} S=\frac{\frac{1}{2}\left(1-\frac{1}{2^n}\right)}{1-\frac{1}{2}}-\frac{n}{2^{n+1}} \\
&\Rightarrow S=2\left[1-\frac{1}{2^n}-\frac{n}{2^{n+1}}\right] \dots(iv)
\end{aligned}
\)
From equation (i) and (iv),
\(
\begin{aligned}
2.2^{\mathrm{n}+1} & {\left[1-\frac{1}{2^n}-\frac{n}{2^{n+1}}\right]=\frac{n+1}{4}\left[2^{n+1}-n-2\right] } \\
& \Rightarrow 2 .\left[2^{n+1}-2-n\right]=\frac{n+1}{4}\left[2^{n+1}-2-n\right] \\
& \Rightarrow \frac{n+1}{4}=2 \Rightarrow n=7
\end{aligned}
\) -
Question 36 of 205
36. Question
Given by permutation or otherwise \(\frac{\left(n^2\right) !}{(n !)^n}\) is an integer \(\left(n \in I^{+}\right)\). Is this true or false? [2004 – 2 Marks]
CorrectIncorrectHint
Let there be \(n\) sets of different objects each set containing \(n\) identical objects [eg (1, 1, \(1 \ldots 1\) ( \(n\) times) ), \((2,2,2 \ldots, 2\) \((n\) times \()) \ldots(n, n, n \ldots n(n\) times \())]\)
Then the number of ways in which these \(n \times n=n^2\) objects can be arranged
\(
\text { in a row }=\frac{\left(n^2\right) !}{n ! n ! \ldots n !}=\frac{\left(n^2\right) !}{(n !)^n}
\)
But these number of ways should be a natural number.
Hence \(\frac{\left(n^2\right) !}{(n !)^n}\) is an integer. \(\left(n \in I^{+}\right)\) -
Question 37 of 205
37. Question
\(\mathrm{m}\) men and \(\mathrm{n}\) women are to be seated in a row so that no two women sit together. If \(m>n\), Given the number of ways in which they can be seated is \(\frac{m !(m+1) !}{(m-n+1) !}\). Is this true or false? [1983 – 2 Marks]
CorrectIncorrectHint
Since, \(\mathrm{m}\) men can be seated in \(\mathrm{m}\) ! ways creating \((m+1)\) places for ladies to sit.
\(\therefore \quad n\) ladies out of \((m+1)\) places \((\) as \(n<m)\) can be seated in \({ }^{m+1} P_n\) ways
\(
\begin{aligned}
&\therefore \quad \text { Total ways }=m ! \times{ }^{m+1} P_n \\
&\quad=m ! \times \frac{(m+1) !}{(m+1-n) !}=\frac{(m+1) ! m !}{(m-n+1) !}
\end{aligned}
\) -
Question 38 of 205
38. Question
There are 3 sections in a question paper and each section contains 5 questions. A candidate has to answer a total of 5 questions, choosing at least one question from each section. Then the number of ways, in which the candidate can choose the questions, is: [Main Sep. 05, 2020 (II)]
CorrectIncorrectHint
Given: There are three sections containing 4,5 and 6 questions respectively.
Now, from each question, 3 questions should be answered.
Therefore total number of ways, for the selection of question can be done
\(
(1,1,3)+(1,2,2)+(1,3,1)+(2,1,2)+(2,2,1)+(3,1,1)
\)
\(\therefore\) Total number of selection of 5 questions
\(
\begin{gathered}
=3 \times{ }^5 C_1 \times{ }^5 C_1 \times{ }^5 C_3+3 \times{ }^5 C_1 \times{ }^5 C_2 \times{ }^5 C_2 \\
=3 \times 5 \times 5 \times 10+3 \times 5 \times 10 \times 10=750+1500=2250
\end{gathered}
\) -
Question 39 of 205
39. Question
Let \(n>2\) be an integer. Suppose that there are \(n\) Metro stations in a city located along a circular path. Each pair of stations is connected by a straight track only. Further, each pair of nearest stations is connected by blue line, whereas all remaining pairs of stations are connected by red line. If the number of red lines is 99 times the number of blue lines, then the value of \(n\) is: [Main Sep. 02, 2020 (II)]
CorrectIncorrectHint
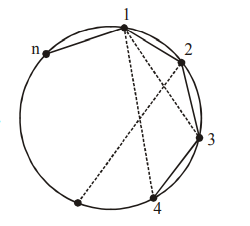
It is given that, there are metro stations located in a city along a circular path. Each pair of the nearest station is connected by a blue line whereas all remaining are connected by a red line.
Also the number of red lines is equal to 99 times the number of blue lines Therefore we have,
Number of blue lines \(=\) Number of sides \(=n\)
Number of red lines \(=\) number of diagonals \(={ }^n C_2-n\)
\(
\begin{aligned}
&{ }^n C_2-n=99 n \Rightarrow \frac{n(n-1)}{2}-n=99 n \\
&\frac{(n-1)}{2}-1=99 \Rightarrow n=201
\end{aligned}
\) -
Question 40 of 205
40. Question
If \(a, b\) and \(c\) are the greatest values of \({ }^{19} C_p,{ }^{20} C_q\) and \({ }^{21} C_r\) respectively, then: [Main Jan. 8, 2020 (I)]
CorrectIncorrectHint
Step 1: Expressing the given data:
Given that \(a, b\) and \(c\) are the greatest values of \({ }^{19} C_p,{ }^{20} C_q,{ }^{21} C{ }_r\).
We know that
\({ }^n C_r\) is maximum when \(r= \begin{cases}\frac{n}{2} & , n \text { is even } \\ \frac{n-1}{2} \text { or } \frac{n+1}{2} & , n \text { is odd }\end{cases}\)
Therefore, \(\max \left({ }^{19} C_p\right)=\left({ }^{19} C_9\right)=a\)
\(
\begin{aligned}
&\max \left({ }^{20} C_q\right)={ }^{20} C_{10}=b \\
&\max \left({ }^{21} C_r\right)={ }^{21} C_{11}=c
\end{aligned}
\)
Step 2: Find the relation :
\(
\begin{aligned}
&\therefore \frac{a}{{ }^{19} C_9}=\frac{b}{\frac{20}{10} \times{ }^{19} C_9}=\frac{c}{\frac{21}{11} \times \frac{20}{10} \times{ }^{19} C_9} \\
&\Rightarrow \quad \frac{a}{1}=\frac{b}{2}=\frac{c}{\frac{42}{11}} \\
&\Rightarrow \frac{a}{11}=\frac{b}{22}=\frac{c}{42}
\end{aligned}
\) -
Question 41 of 205
41. Question
The number of ordered pairs \((r, k)\) for which \(6 .{ }^{35} C_r=\left(k^2-3\right) \cdot{ }^{36} C_{r+1}\), where \(k\) is an integer, is: [Main Jan. 7, 2020 (II)]
CorrectIncorrectHint
Using \({ }^{36} \mathrm{C}_{r+1}=\frac{36}{r+1} \times{ }^{35} \mathrm{C}_r\), we get
\(
\begin{aligned}
&\frac{36}{r+1} \times{ }^{35} C_r \times\left(k^2-3\right)={ }^{35} C_r \times 6 \\
&\Rightarrow k^2-3=\frac{r+1}{6} \\
&\Rightarrow k^2=\frac{r+1}{6}+3 \\
&k \in I
\end{aligned}
\)
\(r \rightarrow\) Non-negative integer \(0 \leq \mathrm{r} \leq 35\)
\(
\begin{aligned}
&r=5 \Rightarrow k=\pm 2 \\
&r=35 \Rightarrow k=\pm 3
\end{aligned}
\)
\(\therefore\) No. of ordered pairs \((r, k)=4\)
Therefore, the required ordered pairs are \((5,-2),(5,2),(35,-3)\) and \((35,3)\). Therefore, The total number of required ordered pairs \((r, k)\) is 4. -
Question 42 of 205
42. Question
The number of ways of choosing 10 objects out of 31 objects of which 10 are identical and the remaining 21 are distinct is: [Main April 12, 2019(I)]
CorrectIncorrectHint
Given that there are 31 Objects in which 10 are identical and 21 are distinct
The number of ways of choosing 0 identical and 10 distinct \(=1 \times{ }^{21} \mathrm{C}_{10}\)
The number of ways of choosing 1 identical and 9 distinct \(=1 \times{ }^{21} \mathrm{C}_9\)
The number of ways of choosing 2 identical and 8 distinct \(=1 \times{ }^{21} \mathrm{C}_8\)
The number of ways of choosing 3 identical and 7 distinct \(=1 \times{ }^{21} C_7\)
The number of ways of choosing 4 identical and 6 distinct \(=1 \times{ }^{21} \mathrm{C}_6\)
The number of ways of choosing 5 identical and 5 distinct \(=1 \times{ }^{21} \mathrm{C}_5\)
The number of ways of choosing 6 identical and 4 distinct \(=1 \times{ }^{21} \mathrm{C}_4\)
The number of ways of choosing 7 identical and 3 distinct \(=1 \times{ }^{21} C_3\)
The number of ways of choosing 8 identical and 2 distinct \(=1 \times{ }^{21} C_2\)
The number of ways of choosing 9 identical and 1 distinct \(=1 \times{ }^{21} C_1\)
The number of ways of choosing 10 identical and 0 distinct= \(1 \times{ }^{21} \mathrm{C}_0\)
So, total number of ways in which we can choose 10 objects is
\(
\begin{aligned}
&{ }^{21} \mathrm{C}_{10}+{ }^{21} \mathrm{C}_9+{ }^{21} \mathrm{C}_8+\cdots+{ }^{21} \mathrm{C}_0=\mathrm{x} \text { (Let) } \dots(i)\\
&\because{ }^{\mathrm{n}} \mathrm{C}_{\mathrm{r}}={ }^{\mathrm{n}} \mathrm{C}_{\mathrm{n}-\mathrm{r}} \\
&{ }^{21} \mathrm{C}_{11}+{ }^{21} \mathrm{C}_{12}+{ }^{21} \mathrm{C}_{13}+\cdots+{ }^{21} \mathrm{C}_{21}=\mathrm{x} \dots(ii)
\end{aligned}
\)
On adding both Equation (i) and (ii), we get
\(
\begin{aligned}
&2 x={ }^{21} C_0+{ }^{21} C_1+{ }^{21} C_2+\cdots+{ }^{21} C_{21} \\
&\therefore 2 x=2^{21} \Rightarrow x=2^{20}
\end{aligned}
\) -
Question 43 of 205
43. Question
Suppose that 20 pillars of the same height have been erected along the boundary of a circular stadium. If the top of each pillar has been connected by beams with the top of all its non-adjacent pillars, then the total number of beams is : [Main April 10, 2019 (II)]
CorrectIncorrectHint
It is given that, there are 20 pillars of the same height have been erected along the boundary of a circular stadium.
Now, the top of each pillar has been connected by beams with the top of all its non adjacent pillars, then total number of beams = number of diagonals of 20 – sided polygon.
\(\because{ }^{20} C_2\) is selection of any two vertices of 20 – sided polygon which included the sides as well.
So, required number of total beams \(={ }^{20} C_2-20\)
[ \(\because\) the number of diagonals in a \(n\) – sided closed polygon \(={ }^n C_2-n\) ] \(=\frac{20 \times 19}{2}-20\)
\(=190-20=170\) -
Question 44 of 205
44. Question
A committee of 11 members is to be formed from 8 males and 5 females. If \(\mathrm{m}\) is the number of ways the committee is formed with at least 6 males and \(\mathrm{n}\) is the number of ways the committee is formed with at least 3 females, then: [Main April 9, 2019 (I)]
CorrectIncorrectHint
Given: ( 8 males, 5 females)
Committee to be selected = 11 members
\(\mathrm{m}=\) no. of ways the committee is formed with at least 6 males.
\(
\begin{aligned}
&\Rightarrow(6 M, 5 F) \text { or }(7 M, 4 F) \text { or }(8 M, 3 F) \\
&={ }^8 C_6 \times{ }^5 C_5+{ }^8 C_7 \times{ }^5 C_4+{ }^8 C_8 \times{ }^5 C_3=78
\end{aligned}
\)
\(n=\) no. of ways the committee is formed with atleast 3 female
\(
\begin{aligned}
&\Rightarrow(8 \mathrm{M}, 3 \mathrm{~F}) \text { or }(7 \mathrm{M}, 4 \mathrm{~F}) \text { or }(6 \mathrm{M}, 5 \mathrm{~F}) \\
&={ }^8 \mathrm{C}_8 \times{ }^5 \mathrm{C}_3+{ }^8 \mathrm{C}_7 \times{ }^5 \mathrm{C}_4+{ }^8 \mathrm{C}_6 \times{ }^5 \mathrm{C}_5 \\
&=10+40+28=78 \\
&\Rightarrow \mathrm{m}=\mathrm{n}=78
\end{aligned}
\) -
Question 45 of 205
45. Question
There are m men and two women participating in a chess tournament. Each participant plays two games with every other participant. If the number of games played by the men between themselves exceeds the number of games played between the men and the women by 84, then the value of m is [Main Jan. 12, 2019(II)]
CorrectIncorrectHint
Number of games played by men among themselves \(=2 \times{ }^m \mathrm{C}_2=\mathrm{m}(\mathrm{m}-1)\)
Number of games played between men and women
\(
=2 \times{ }^m \mathrm{C}_1 \times{ }^2 \mathrm{C}_1=4 \mathrm{~m}
\)
\(
\begin{aligned}
&\therefore m(m-1)-4 m=84 \\
&\Rightarrow m^2-5 m-84=0 \\
&\Rightarrow m=12 \text { or }-7 \text { (Not possible) }
\end{aligned}
\)
Hence, \(m=12\) -
Question 46 of 205
46. Question
Consider a class of 5 girls and 7 boys. The number of different teams consisting of 2 girls and 3 boys that can be formed from this class, if there are two specific boys \(\mathrm{A}\) and \(\mathrm{B}\), who refuse to be the members of the same team, is: [Main Jan. 9, 2019 (I)]
CorrectIncorrectHint
Given :Girls- 5 and boys- 7
Team members:Girls- 2 and boys- 3
Total number of ways \(={ }^5 \mathrm{C}_2 \cdot{ }^7 \mathrm{C}_3\)
consider when \(\mathrm{A}\) and \(\mathrm{B}\) are always included \(={ }^5 \mathrm{C}_1{ }^5 \mathrm{C}_2\) as only 1 boy and 2 girls are to be selected
Require number of ways
\(=\) Total number of ways \(–\) When \(\mathrm{A}\) and \(\mathrm{B}\) are always included.
\(={ }^5 \mathrm{C}_2 \cdot{ }^7 \mathrm{C}_3-{ }^5 \mathrm{C}_1{ }^5 \mathrm{C}_2=300\). -
Question 47 of 205
47. Question
The number of four-letter words that can be formed using the letters of the word BARRACK is [Main Online April 15, 2018]
CorrectIncorrectHint
Case (i): The first letter out of 5 can be chosen in 5 ways. The second letter can be chosen out of the remaining 4 in 4 ways. Again, the third letter can be chosen out of the remaining 3 in 3 ways, and lastly the fourth letter can be chosen out of the remaining 2 in 2 ways. Hence, the total arrangements of 4 lettered words with no repetition is \(5 \times 4 \times 3 \times 2=120\)
Case (ii): If two letters are \(\mathrm{R}\) and other two different letters are chosen from \(\mathrm{B}, \mathrm{A}, \mathrm{C}, \mathrm{K}\),
then the number of words \(={ }^4 \mathrm{C}_2 \times \frac{4 !}{2 !}=72\)
If two letters are A and other two different letters are chosen from B, R, C, K
then the number of words \(={ }^4 \mathrm{C}_2 \times \frac{4 !}{2 !}=72\)Case (iii) : Similarly, when 2 letters are different and 2 letters are both \(\mathbf{R}\), the total arrangement is also 72 .
Case (iv) : Here, 2 letters are both \(\mathbf{R}\) and remaining 2 letters are both \(\mathbf{A}\) and hence, the total arrangement is \(4 ! / (2 ! \times 2 !)=6\)
So, the total number of 4 lettered words is \(120+72+72+6=270\) -
Question 48 of 205
48. Question
From 6 different novels and 3 different dictionaries, 4 novels and 1 dictionary are to be selected and arranged in a row on a shelf so that the dictionary is always in the middle. The number of such arrangements is: [Main 2018]
CorrectIncorrectHint
Out of 6 novels, 4 novels can be selected in \({ }^6 \mathrm{C}_4\) ways.
Also out of 3 dictionaries, 1 dictionary can be selected in \({ }^3 C_1\) ways.
Since the dictionary is fixed in the middle, we only have to arrange 4 novels which can be done in 4 ! ways.
Then the number of ways \(={ }^6 \mathrm{C}_4 \cdot{ }^3 \mathrm{C}_1 \cdot 4\) !
\(
=15 \times 3 \times 24=1080
\) -
Question 49 of 205
49. Question
A man X has 7 friends, 4 of them are ladies and 3 are men. His wife \(\mathrm{Y}\) also has 7 friends, 3 of them are ladies and 4 are men. Assume \(\mathrm{X}\) and \(\mathrm{Y}\) have no common friends. Then the total number of ways in which \(\mathrm{X}\) and \(\mathrm{Y}\) together can throw a party inviting 3 ladies and 3 men so that 3 friends of each of \(X\) and \(Y\) are in this party, is: [Main 2017]
CorrectIncorrectHint
Given, \(\mathrm{X}\) has 7 friends, 4 of them are ladies and 3 are men while \(\mathrm{Y}\) has 7 friends, 3 of them ladies and 4 are men.
Possible cases for \(\mathrm{X}\) are
(1) 3 ladies, 0 man
(2) 2 ladies, 1 man
(3) 1 lady, 2 men
(4) 0 ladies, 3 men
Possible cases for \(\mathrm{Y}\) are
(1) 0 ladies, 3 men
(2) 1 lady, 2 men
(3) 2 ladies, 1 man
(4) 3 ladies, 0 manTotal number of required ways
\(
\begin{aligned}
&={ }^3 \mathrm{C}_3 \times{ }^4 \mathrm{C}_0 \times{ }^4 \mathrm{C}_0 \times{ }^3 \mathrm{C}_3+{ }^3 \mathrm{C}_2 \times{ }^4 \mathrm{C}_1 \times{ }^4 \mathrm{C}_1 \times{ }^3 \mathrm{C}_2+{ }^3 \mathrm{C}_1 \times{ }^4 \mathrm{C}_2 \times{ }^4 \mathrm{C}_2 \times{ }^3 \mathrm{C}_1+ \\
&{ }^3 \mathrm{C}_0 \times{ }^4 \mathrm{C}_3 \times{ }^4 \mathrm{C}_3 \times{ }^3 \mathrm{C}_0 \\
&=1+144+324+16=485
\end{aligned}
\) -
Question 50 of 205
50. Question
The value of \(\sum_{\mathrm{r}=1}^{15} \mathrm{r}^2\left(\frac{{ }^{15} \mathrm{C}_{\mathrm{r}}}{{ }^{15} \mathrm{C}_{\mathrm{r}-1}}\right)\) is equal to: [Main Online April 9, 2016]
CorrectIncorrectHint
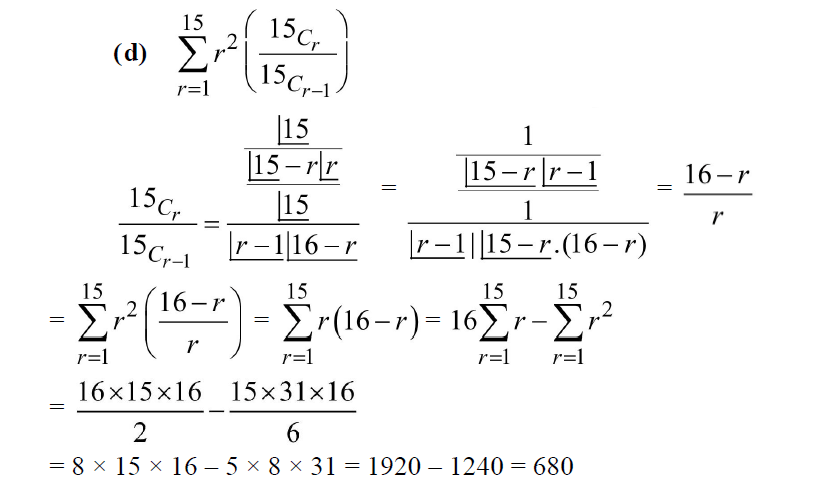
-
Question 51 of 205
51. Question
A debate club consists of 6 girls and 4 boys. A team of 4 members is to be selected from this club including the selection of a captain (from among these 4 members) for the team. If the team has to include at most one boy, then the number of ways of selecting the team is [Adv. 2016]
CorrectIncorrectHint
The club consists of 6 girls and 4 boys. If a team of 4 members is to be selected which consists at most 1 boy (including 1 captain), then the number of ways of selecting the team is obtained as follows:
\(
{ }^4 \mathrm{C}_1\left({ }^4 \mathrm{C}_1 \cdot{ }^6 \mathrm{C}_3+{ }^6 \mathrm{C}_4\right)=4(80+15)=380 \text { ways }
\) -
Question 52 of 205
52. Question
Let \(\mathrm{A}\) and \(\mathrm{B}\) be two sets containing four and two elements respectively. Then the number of subsets of the set \(\mathrm{A} \times \mathrm{B}\), each having at least three elements is: [Main 2015]
CorrectIncorrectHint
(c) Given
\(
n(\mathrm{~A})=4, n(\mathrm{~B})=2, n(\mathrm{~A} \times \mathrm{B})=8
\)
Required number of subsets
\(
\begin{aligned}
&={ }^8 \mathrm{C}_3+{ }^8 \mathrm{C}_4+\ldots .+{ }^8 \mathrm{C}_8=2^8-{ }^8 \mathrm{C}_0-{ }^8 \mathrm{C}_1-{ }^8 \mathrm{C}_2 \\
&=256-1-8-28=219
\end{aligned}
\) -
Question 53 of 205
53. Question
If in a regular polygon the number of diagonals is 54, then the number of sides of this polygon is [Main online April 11, 2015]
CorrectIncorrectHint
(a) Number of diagonal \(=54\)
\(
\begin{aligned}
&\Rightarrow \frac{\mathrm{n}(\mathrm{n}-3)}{2}=54 \\
&\Rightarrow \mathrm{n}^2-3 \mathrm{n}-108=0 \Rightarrow \mathrm{n}^2-12 \mathrm{n}+9 \mathrm{n}-108=0 \\
&\Rightarrow \mathrm{n}(\mathrm{n}-12)+9(\mathrm{n}-12)=0 \\
&\quad \Rightarrow \mathrm{n}=12,-9 \Rightarrow \mathrm{n}=12(\mathrm{n} \neq-9)
\end{aligned}
\) -
Question 54 of 205
54. Question
Let \(\mathrm{A}\) and \(\mathrm{B}\) two sets containing 2 elements and 4 elements respectively. The number of subsets of \(\mathrm{A} \times \mathrm{B}\) having 3 or more elements is [Main 2013]
CorrectIncorrectHint
(c) Given
\(
n(\mathrm{~A})=2, n(\mathrm{~B})=4, n(\mathrm{~A} \times \mathrm{B})=8
\)
Required number of subsets \(=\)
\(
\begin{aligned}
&{ }^8 \mathrm{C}_3+{ }^8 \mathrm{C}_4+\ldots .+{ }^8 \mathrm{C}_8=2^8-{ }^8 \mathrm{C}_0-{ }^8 \mathrm{C}_1-{ }^8 \mathrm{C}_2 \\
&=256-1-8-28=219
\end{aligned}
\) -
Question 55 of 205
55. Question
Let \(T_n\) be the number of all possible triangles formed by joining vertices of an \(n\)-sided regular polygon. If \(\mathrm{T}_{n+1}-\mathrm{T}_n=10\), then the value of \(n\) is: [Main 2013]
CorrectIncorrectHint
(b) We know,
\(
\begin{aligned}
&\mathrm{T}_n={ }^n \mathrm{C}_3, \mathrm{~T}_{n+1}={ }^{n+1} \mathrm{C}_3 \\
&\begin{array}{l}
\mathrm{ATQ}, \\
\mathrm{T}_{n+1}-\mathrm{T}_n={ }^{n+1} \mathrm{C}_3-{ }^n \mathrm{C}_3=10 \\
\Rightarrow \quad{ }^n \mathrm{C}_2=10 \quad \Rightarrow \quad n=5 .
\end{array}
\end{aligned}
\) -
Question 56 of 205
56. Question
On the sides \(\mathrm{AB}, \mathrm{BC}, \mathrm{CA}\) of a \(\angle \mathrm{ABC}, 3,4,5\) distinct points (excluding vertices \(\mathrm{A}, \mathrm{B}, \mathrm{C}\) ) are respectively chosen. The number of triangles that can be constructed using these chosen points as vertices are: [Main Online April 23, 2013]
CorrectIncorrectHint
(b) Required number of triangles
\(
={ }^{12} \mathrm{C}_3-\left({ }^3 \mathrm{C}_3+{ }^4 \mathrm{C}_3+{ }^5 \mathrm{C}_3\right)=205
\) -
Question 57 of 205
57. Question
The total number of ways in which 5 balls of different colours can be distributed among 3 persons so that each person gets at least one ball is [2012]
CorrectIncorrectHint
(b) Each person gets at least one ball.
3 Persons can have 5 balls as follow.
\(
\begin{array}{|c|c|c|}
\hline \text { Person } & \text { No. of balls } & \text { No. of balls } \\
\hline \text { I } & 1 & 1 \\
\hline \text { II } & 1 & 2 \\
\hline \text { III } & 3 & 2 \\
\hline
\end{array}
\)
The number of ways to distribute balls \(1,1,3\) in first to three persons
\(
={ }^5 \mathrm{C}_1 \times{ }^4 \mathrm{C}_1 \times{ }^3 \mathrm{C}_3
\)
Also 3 , persons having 1,1 and 3 balls can be arranged in \(\frac{3 !}{2 !}\) ways.
\(\therefore \quad\) Total no. of ways to distribute 1, 1, 3 balls to the three persons \(={ }^5 \mathrm{C}_1 \times{ }^4 \mathrm{C}_1 \times{ }^3 \mathrm{C}_3 \times \frac{3 !}{2 !}=60\)
Similarly, total no. of ways to distribute 1, 2, 2 balls to three persons \(={ }^5 \mathrm{C}_1 \times{ }^4 \mathrm{C}_2 \times{ }^2 \mathrm{C}_2 \times \frac{3 !}{2 !}=90\)
\(\therefore \quad\) The required number of ways \(=60+90=150\) -
Question 58 of 205
58. Question
A rectangle with sides of length \((2 m-1)\) and \((2 n-1)\) units is divided into squares of unit length by drawing parallel lines as shown in the diagram, then the number of rectangles possible with odd side lengths is [2005S]
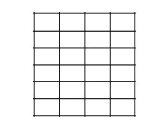 CorrectIncorrect
CorrectIncorrectHint
If we see the blocks in terms of lines then there are \(2 \mathrm{~m}\) vertical lines and \(2 n\) horizontal lines. To form the required rectangle, we must select two horizontal lines, one even numbered (out of 2,4, \(.2 n\) ) and one odd numbered (out of \(1,3 \ldots . .2 n-1\) ) and similarly two vertical lines.
The number of rectangles
\(
={ }^m C_1 \cdot{ }^m C_1 \cdot{ }^n C_1 \cdot{ }^n C_1=m^2 n^2
\) -
Question 59 of 205
59. Question
Let \(T_n\) denote the number of triangles which can be formed using the vertices of a regular polygon of \(n\) sides. If \(T_{n+1}-T_n=21\), then \(n\) equals [2001S]
CorrectIncorrectHint
\(
\begin{aligned}
& T_n={ }^n C_3 ; T_{n+1}={ }^{n+1} C_3 \\
& \text { Now, } T_{n+1}-T_n=21 \Rightarrow{ }^{n+1} C_3-{ }^n C_3=21 \\
\Rightarrow & \frac{(n+1) n(n-1)}{3.2 .1}-\frac{n(n-1)(n-2)}{3.2 .1}=21 \\
\Rightarrow & n(n-1)(n+1-n+2)=126 \\
\Rightarrow & n(n-1)=42 \Rightarrow n(n-1)=7 \times 6, \quad \therefore n=7
\end{aligned}
\) -
Question 60 of 205
60. Question
Eight chairs are numbered 1 to 8. Two women and three men wish to occupy one chair each. First, the women choose the chairs from amongst the chairs marked 1 to 4; and then the men select the chairs from amongst the remaining. The number of possible arrangements is [1982 – 2 Marks]
CorrectIncorrectHint
Two women can choose two chairs out of \(1,2,3,4\), in \({ }^4 C_2\) ways and can arrange themselves in 2! ways. Three men can choose 3
chairs out of 6 remaining chairs in \({ }^6 C_3\) ways and can arrange themselves in 3 ! ways
\(\therefore \quad\) Total number of possible arrangements are \({ }^4 C_2 \times 2 ! \times{ }^6 C_3 \times 3 !={ }^4 P_2 \times{ }^6 P_3\)Alternate:
First the 2 women can select any chair of the 4 chairs numbered 1 to 4 in \({ }^4 P_2\) ways
Then there will be \(8-2=6\) chairs remaining, the 3 men can select any chair of the 6 chairs in \({ }^6 \mathrm{P}_3\) ways
So, total number of ways \(={ }^4 \mathrm{P}_2 \times{ }^6 \mathrm{P}_3\) ways -
Question 61 of 205
61. Question
The value of the expression \({ }^{47} C_4+\sum_{j=1}^5{ }^{52-j} C_3\) is equal to [1982 – 2 Marks]
CorrectIncorrectHint
\(
\begin{aligned}
&\text { (c) }{ }^{47} C_4+\sum_{j=1}^5{ }^{52-j} C_3 \\
&={ }^{47} C_4+{ }^{51} C_3+{ }^{50} C_3+{ }^{49} C_3+{ }^{48} C_3+{ }^{47} C_3 \\
&={ }^{51} C_3+{ }^{50} C_3+{ }^{49} C_3+{ }^{48} C_3+\left({ }^{47} C_3+{ }^{47} C_4\right) \\
&={ }^{51} C_3+{ }^{50} C_3+{ }^{49} C_3+\left({ }^{48} C_3+{ }^{48} C_4\right) \\
&\quad\left[\mathrm{U} \operatorname{sing}{ }^n C_r+{ }^n C_{r+1}={ }^{n+1} C_{r+1}\right] \\
&={ }^{51} C_3+{ }^{50} C_3+\left({ }^{49} C_3+{ }^{49} C_4\right) \\
&={ }^{51} C_3+\left({ }^{50} C_3+{ }^{50} C_4\right)={ }^{51} C_3+{ }^{51} C_4={ }^{52} C_4
\end{aligned}
\) -
Question 62 of 205
62. Question
\({ }^n C_{r-1}=36,{ }^n C_r=84\) and \({ }^n C_{r+1}=126\), then \(r\) is: [1979]
CorrectIncorrectHint
(c) \({ }^n C_{r-1}=36,{ }^n C_r=84,{ }^n C_{r+1}=126\)
We know that
\(
\begin{aligned}
\frac{{ }^n C_{r-1}}{{ }^n C_r}=\frac{r}{n-r+1} \quad \Rightarrow \frac{36}{84}=\frac{r}{n-r+1} \\
\Rightarrow \frac{r}{n-r+1}=\frac{3}{7} \Rightarrow 3 n-10 r+3=0 \dots(i)\\
\text { Also, } \frac{{ }^n C_r}{{ }^n C_{r+1}}=\frac{r+1}{n-r}=\frac{84}{126}=\frac{2}{3} \\
\Rightarrow 2 n-5 r-3=0 \dots(ii)
\end{aligned}
\)
On solving (i) and (ii), we get \(n=9\) and \(r=3\). -
Question 63 of 205
63. Question
Let \(|X|\) denote the number of elements in a set \(X\) Let \(S=\{1,2,3,4\), \(5,6\}\) be a sample space, where each element is equally likely to occur. If \(\mathrm{A}\) and \(\mathrm{B}\) are independent events associated with \(\mathrm{S}\), then the number of ordered pairs \((A, B)\) such that \(1 \leq|B|<|A|\), equals [Adv. 2019]
CorrectIncorrectHint
Let \(n(A)=a, n(B)=b, n(A \cap B)=c\)
\(
\therefore \quad 1 \leq \mathrm{b}<\mathrm{a}
\)
Also given that \(\mathrm{A}\) and \(\mathrm{B}\) are independent events
\(
\therefore \mathrm{P}(\mathrm{A} \cap \mathrm{B})=\mathrm{P}(\mathrm{A}) \mathrm{P}(\mathrm{B})
\)
\(
\begin{aligned}
&\Rightarrow \frac{\mathrm{n}(\mathrm{A} \cap \mathrm{B})}{\mathrm{n}(\mathrm{S})}=\frac{\mathrm{n}(\mathrm{A})}{\mathrm{n}(\mathrm{S})} \times \frac{\mathrm{n}(\mathrm{B})}{\mathrm{n}(\mathrm{S})} \\
&\Rightarrow \frac{\mathrm{c}}{6}=\frac{\mathrm{a}}{6} \times \frac{\mathrm{b}}{6} \Rightarrow \mathrm{ab}=6 \mathrm{c}
\end{aligned}
\)
If \(a=6\) then \(b=c=5,4,3,2,1 \quad(b<a)\)
There is only one way to select all 6 elements of set A. Number of ways of selecting \(5,4,3,2\) or 1 elements in \(\mathrm{B}\) and \(\mathrm{A} \cap \mathrm{B}\) are
\(
{ }^6 \mathrm{C}_5+{ }^6 \mathrm{C}_4+{ }^6 \mathrm{C}_3+{ }^6 \mathrm{C}_2+{ }^6 \mathrm{C}_1=2^6-2=62
\)
If \(a=5\) then \(b=\frac{6 c}{5}\), which is not possible because if c \(=5\) then \(b=6\), while \(\mathrm{b}<\mathrm{a}\).If \(a=4\) then \(b=\frac{6 c}{4}=\frac{3 c}{2}\), which is possible because if \(c=2\) then \(b=3\)
2 elements in \(\mathrm{A} \cap \mathrm{B}\) can be selected in \({ }^6 \mathrm{C}_2\) ways.
2 additional elements in \(\mathrm{A}\) can be selected in \({ }^4 \mathrm{C}_2\) ways.
1 additional element in \(\mathrm{B}\) can be selected in \({ }^2 \mathrm{C}_1\) ways.
\(\therefore\) No. of ways for \(\mathrm{a}=4, \mathrm{~b}=3, \mathrm{c}=2\) are
\(
{ }^6 \mathrm{C}_1 \times{ }^4 \mathrm{C}_1 \times{ }^2 \mathrm{C}_1=15 \times 6 \times 2=180
\)
If \(\mathrm{a}=3\) then \(\mathrm{b}=2 \mathrm{c} \Rightarrow \mathrm{c}=1, \mathrm{~b}=2\)
which can be done in \({ }^6 \mathrm{C}_1 \times{ }^5 \mathrm{C}_1+{ }^4 \mathrm{C}_2=6 \times 5 \times 6=180\) ways.
If \(a=2\) then \(b=3 c\) which is not possible
\(\therefore\) Total number of required ways \(=62+180+180=422\). -
Question 64 of 205
64. Question
Words of length 10 are formed using the letters A, B, C, D, E, F, G, H, \(\mathrm{I}, \mathrm{J}\). Let \(\mathrm{x}\) be the number of such words where no letter is repeated, and let \(y\) be the number of such words where exactly one letter is repeated twice and no other letter is repeated. Then, \(\frac{y}{9 x}\) \(=\) [Adv. 2017]
CorrectIncorrectHint
\(\mathrm{x}=10\) ! and \(\mathrm{y}={ }^{10} \mathrm{C}_1 \times{ }^9 \mathrm{C}_8 \times \frac{10 !}{2 !}=10 \times 9 \times \frac{10 !}{2 !}\)
\(
\therefore \quad \frac{y}{9 x}=\frac{10 \times 9 \times \frac{10 !}{2}}{9 \times 10 !}=5
\) -
Question 65 of 205
65. Question
Let \(n\) be the number of ways in which 5 boys and 5 girls can stand in a queue in such a way that all the girls stand consecutively in the queue. Let \(\mathrm{m}\) be the number of ways in which 5 boys and 5 girls can stand in a queue in such a way that exactly four girls stand consecutively in the queue. Then the value of \(\frac{m}{n}\) is [Adv. 2015]
CorrectIncorrectHint
Here, \(-B_1 -B_2 -B_3 -B_4 -B_5\)
Out of 5 girls, 4 girls are together and 1 girl is separate. Now,
no of ways to select 2 positions out of 6 positions between boys \(={ }^6 \mathrm{C}_2 \dots(i)\)
4 girls are to be selected out of \(5={ }^5 \mathrm{C}_4\) ways …(ii)
Now, 2 groups of girls can be arranged in 2! ways. …(iii)
Also, the group of 4 girls and 5 boys is arranged in \(4 ! \times 5\) !ways
Now, total number of ways \(={ }^6 \mathrm{C}_2 \times{ }^5 \mathrm{C}_4 \times 2 ! \times 4 ! \times 5\) ! [from Eqs. (i), (ii), (iii) and (iv)]
\(\therefore \mathrm{m}={ }^6 \mathrm{C}_2 \times{ }^5 \mathrm{C}_4 \times 2 ! \times 4 ! \times 5\) !
And \(\mathrm{n}=5\) ! \(\times 6\) !
\(
\Rightarrow \frac{m}{n}=\frac{{ }^6 C_2 \times{ }^5 C_4 \times 2 ! \times 4 ! \times 5 !}{6 ! \times 5 !}=\frac{15 \times 5 \times 2 \times 4 !}{6 \times 5 \times 4 !}=5
\) -
Question 66 of 205
66. Question
Let \(n \geq 2\) be an integer. Take \(n\) distinct points on a circle and join each pair of points by a line segment. Colour the line segment joining every pair of adjacent points by blue and the rest by red. If the number of red and blue line segments are equal, then the value of \(\)n\(\) is [Adv. 2014]
CorrectIncorrectHint
Number of adjacent lines \(=n\)
Number of non adjacent lines \(={ }^n C_2-n\)
\(
\begin{aligned}
&\therefore{ }^{\mathrm{n}} \mathrm{C}_2-n=n \Rightarrow \frac{n(n-1)}{2}-2 n=0 \\
&\Rightarrow n^2-5 n=0 \Rightarrow n=0 \text { or } 5 \text { But } n \geq 2 \Rightarrow n=5
\end{aligned}
\) -
Question 67 of 205
67. Question
Consider the set of eight vectors \(V=\{a \hat{i}+b \hat{j}+c \hat{k}: a, b, c \in\{-1,1\}\}\). Three non-coplanar vectors can be chosen from \(\mathrm{V}\) in \(2^{\mathrm{p}}\) ways. Then \(\mathrm{p}\) is [Adv. 2013]
CorrectIncorrectHint
Given 8 vectors are
\((1,1,1),(-1,-1,-1) ;(-1,1,1),(1,-1,-1) ;(1,-1,1),(-1,1,-1) ;(1,1,-1)\), \((-1,-1,1)\)
These are 4 diagonals of a cube and their opposites.
For 3 non coplanar vectors first we select 3 groups of diagonals and its opposite in \({ }^4 C_3\) ways.
Then one vector from each group can be selected in \(2 \times 2 \times 2\) ways.
\(\therefore \quad\) Total ways \(={ }^4 \mathrm{C}_3 \times 2 \times 2 \times 2=32=2^5 \therefore p=5\) -
Question 68 of 205
68. Question
The number of words (with or without meaning) that can be formed from all the letters of the word “LETTER” in which vowels never come together is ______. [Main Sep. 06, 2020 (II)]
CorrectIncorrectHint
For vowels not together
Number of ways to arrange \(\mathrm{L}, \mathrm{T}, \mathrm{T}, \mathrm{R}=\frac{4 !}{2 !}\)
Then put both \(\mathrm{E}\) in 5 gaps formed in \({ }^5 C_2\) ways.
\(
\therefore \text { No. of ways }=\frac{4 !}{2 !} \cdot{ }^5 C_2=120
\) -
Question 69 of 205
69. Question
The number of words, with or without meaning, that can be formed by taking 4 letters at a time from the letters of the word ‘SYLLABUS’ such that two letters are distinct and two letters are alike, is ______. [Main Sep. 05, 2020 (I)]
CorrectIncorrectHint
\(S \rightarrow 2, L \rightarrow 2, A, B, Y, U\).
\(\therefore\) Required number of ways \(={ }^2 C_1 \times{ }^5 C_2 \times \frac{4 !}{2 !}=240\). -
Question 70 of 205
70. Question
A test consists of 6 multiple-choice questions, each having 4 alternative answers of which only one is correct. The number of ways, in which a candidate answers all six questions such that exactly four of the answers are correct, is __________. [Main Sep. 04, 2020 (II)]
CorrectIncorrectHint
Number of ways to select four questions from six questions \(={ }^6 C_4\)
And number of ways to answer these questions correctly \(=1 \times 1 \times 1 \times 1=1\)
And the number of ways to answer remain two questions wrongly \(=3 \times 3=9\)
\(
\begin{aligned}
&\therefore \text { Required number of ways }={ }^6 C_4 \times 1 \times 9 \\
&=\frac{6 !}{2 ! 4 !} \times 9 \\
&=\frac{6 \times 5}{2} \times 9=135
\end{aligned}
\) -
Question 71 of 205
71. Question
The total number of 3 -digit numbers, whose sum of digits is 10 , is [Main Sep. 03, 2020 (II)]
CorrectIncorrectHint
Let \(x y z\) be the three digit number
\(
\begin{array}{ll}
x+y+z=10, x \leq 1, y \geq 0, z \geq 0 \\
x-1=t \Rightarrow x=1+t & x-1 \geq 0, t \geq 0 \\
t+y+z=10-1=9 & 0 \leq t, z, z \leq 9
\end{array}
\)
\(\therefore\) Total number of non-negative integral solution
\(
={ }^{9+3-1} C_{3-1}={ }^{11} C_2=\frac{11 \cdot 10}{2}=55
\)
But for \(t=9, x=10\), so required number of integers \(=55-1=54\). -
Question 72 of 205
72. Question
If \(\mathrm{C}_{\mathrm{r}} \equiv{ }^{25} \mathrm{C}_{\mathrm{r}}\) and \(\mathrm{C}_0+5 \cdot \mathrm{C}_1+9 \cdot \mathrm{C}_2+\ldots+(101) \cdot \mathrm{C}_{25}=2^{25} \cdot k\), then \(k\) is equal to [Main Jan. 9, 2020 (II)]
CorrectIncorrectHint
\(
\begin{aligned}
\sum_{r=0}^{25}(4 r+1){ }^{25} C_r=4 \sum_{r=0}^{25} r \cdot{ }^{25} C_r+\sum_{r=0}^{25}{ }^{25} C_r \\
=4 \sum_{r=1}^{25} r \times \frac{25}{r}{ }^{24} C_{r-1}+2^{25}=100 \sum_{r=1}^{25}{ }^{24} C_{r-1}+2^{25} \\
=100.2^{24}+2^{25}=2^{25}(50+1)=51.2^{25}
\end{aligned}
\)
Hence, by comparison \(k=51\) -
Question 73 of 205
73. Question
An urn contains 5 red marbles, 4 black marbles and 3 white marbles. Then the number of ways in which 4 marbles can be drawn so that at the most three of them are red is [Main Jan. 8, 2020 (I)]
CorrectIncorrectHint
Total marbles are 5 red, 4 black and 3 white. 4 marbles are drawn, atmost 3 of them are red. Case are:
3R and 1 other \(\rightarrow^5 \mathrm{C}_3 \times{ }^7 \mathrm{C}_1=70\)
2Rand 2 other \(\rightarrow{ }^5 \mathrm{C}_2 \times{ }^7 \mathrm{C}_2=210\)
1R and 3 other \(\rightarrow{ }^5 \mathrm{C}_1 \times{ }^7 \mathrm{C}_3=175\)
Zero \(\mathrm{R}\) and 4 other \(\rightarrow^5 \mathrm{C}_0 \times{ }^7 \mathrm{C}_4=35\)
Total \(=490\) -
Question 74 of 205
74. Question
The number of 4 letter words (with or without meaning) that can be formed from the eleven letters of the word ‘EXAMINATION’ is _____. [Main Jan. 8, 2020 (II)]
CorrectIncorrectHint
Word “EXAMINATION” consists of 2A, 2I, 2N, E, X, M, T, O
Case I: All different letters are selected
Number of words formed: \({ }^8 \mathrm{C}_4 \times 4 !=1680\)Case II: 2 letters are the same and 2 are different
Number of words formed \(={ }^3 \mathrm{C}_1 \times{ }^7 \mathrm{C}_2 \times \frac{4 !}{2 !}=756\)Case III: 2 pairs of letters are the same
Number of words formed \(={ }^3 \mathrm{C}_2 \times \frac{4 !}{2 ! \times 2 !}=18\)
Total number of words formed \(=1680+756+18=2454\) -
Question 75 of 205
75. Question
An engineer is required to visit a factory for exactly four days during the first 15 days of every month and it is mandatory that no two visits take place on consecutive days. Then the number of all possible ways in which such visits to the factory can be made by the engineer during 1-15 June 2021 is [Adv. 2020]
CorrectIncorrectHint
We know that total number of ways of selection of \(r\) days out of \(n\) days such that no two of them are consecutive \(=n-r+{ }^{1} C_r\).
\(\therefore\) Selection of 4days out of 15 days such that no two of them are consecutive \(={ }^{15-4+1} C_4={ }^{12} C_4\)
\(
=\frac{12 \times 11 \times 10 \times 9}{4 \times 3 \times 2}=11 \times 5 \times 9=495
\) -
Question 76 of 205
76. Question
Total number of ways in which six ‘ \(+\) ‘ and four ‘ \(-\) ‘ signs can be arranged in a line such that no two ‘-‘ signs occur together is [1988 – 2 Marks]
CorrectIncorrectHint
Among \(6^{\prime}+’\) there are 7 intervals
\(
\mathrm{X}+\mathrm{X}+\mathrm{X}+\mathrm{X}+\mathrm{X}+\mathrm{X}+\mathrm{X}
\)
Number of ways of filling 7 gaps by \(4^{\prime}-^{\prime}={ }^7 \mathrm{C}_4=35\)
\(\therefore\) Required ways \(=35\) -
Question 77 of 205
77. Question
The side \(A B, B C\) and \(C A\) of a triangle \(A B C\) have 3,4 and 5 interior points respectively on them. The number of triangles that can be constructed using these interior points as vertices is \(\text { [1984 – } 2 \text { Marks] }\)
CorrectIncorrectHint
We have in all 12 point. Since 3 points are used to form a triangle, therefore the total number of triangles including the triangles formed by collinear points on \(\mathrm{AB}, \mathrm{BC}\), and \(\mathrm{CA}\) is \({ }^{12} \mathrm{C}_3=220\). But this includes the following: The number of triangles formed by 3 points on \(\mathrm{AB}={ }^3 \mathrm{C}_3=1\)
The number of triangles formed by 4 points on \(B C={ }^4 C_3=4\).
The number of triangles formed by 5 points on \(\mathrm{CA}={ }^5 \mathrm{C}_3=10\).
Hence, the required number of triangles
\(
=220-(10+4+1)=205 \text {. }
\) -
Question 78 of 205
78. Question
The product of any \(r\) consecutive natural numbers is always divisible by \(r !\). \(\text { [1985 – } 1 \text { Mark] }\)
CorrectIncorrectHint
\(
\begin{aligned}
&\text { (True) Consider, } \frac{(n+1)(n+2) \ldots(n+r)}{r !} \\
&=\frac{1.2 .3 \ldots(n-1) n(n+1)(n+2) \ldots(n+r)}{1.2 .3 \ldots n . r !} \\
&=\frac{(n+r) !}{n ! r !}={ }^{\mathrm{n}+\mathrm{r}} \mathrm{C}_{\mathrm{r}}=\text { An integral value } \\
&
\end{aligned}
\)
Thus given statement is true. -
Question 79 of 205
79. Question
For nonnegative integers \(s\) and \(r\), let
\(
\left(\begin{array}{c}
s \\
r
\end{array}\right)=\left\{\begin{array}{cc}
\frac{s !}{r !(s-r) !} & \text { if } r \leq s \\
0 & \text { if } r>s
\end{array}\right.
\)
For positive integers \(m\) and \(n\), let
\(
g(m, n)=\sum_{p=0}^{m+n} \frac{f(m, n, p)}{\left(\begin{array}{c}
n+p \\
p
\end{array}\right)}
\)
where for any nonnegative integer \(p\),
\(
f(m, n, p)=\sum_{i=0}^p\left(\begin{array}{c}
m \\
i
\end{array}\right)\left(\begin{array}{c}
n+i \\
p
\end{array}\right)\left(\begin{array}{c}
p+n \\
p-i
\end{array}\right) .
\)
Then which of the following statements is/are TRUE? [Adv. 2020]CorrectIncorrectHint
-
Question 80 of 205
80. Question
Let \(a_n\) denote the number of all \(n\)-digit positive integers formed by the digits 0,1 or both such that no consecutive digits in them are 0 . Let \(b_n=\) the number of such \(n\)-digit integers ending with digit 1 and \(c_n=\) the number of such \(n\)-digit integers ending with digit 0. [2012]
\(
\text { The value of } b_6 \text { is }
\)CorrectIncorrectHint
(b) \(\because a_n=\) number of all \(n\) digit \(+\) ve integers formed by the digits 0,1 or both such that no consecutive digits in them are 0 . and \(b_n=\) number of such \(n\) digit integers ending with 1
\(c_n=\) number of such \(n\) digit integers ending with 0
Clearly, \(a_n=b_n+c_n\left(\because a_n\right.\) can end with 0 or 1\()\)
Also \(b_n=a_{n-1}\)
and \(c_n=a_{n-2}[\because\) if last digit is 0 , second last has to be 1]
\(\therefore\) We get \(a_n=a_{n-1}+a_{n-2}, n \geq 3\)
Also \(a_1=1, a_2=2\),
Now by this recurring formula, we get
\(
\begin{aligned}
&a_3=a_2+a_1=3 \\
&a_4=a_3+a_2=3+2=5 \\
&a_5=a_4+a_3=5+3=8
\end{aligned}
\)
Also \(b_6=a_5=8\) -
Question 81 of 205
81. Question
Let \(a_n\) denote the number of all \(n\)-digit positive integers formed by the digits 0,1 or both such that no consecutive digits in them are 0 . Let \(b_n=\) the number of such \(n\)-digit integers ending with digit 1 and \(c_n=\) the number of such \(n\)-digit integers ending with digit 0. [2012]
Which of the following is correct?
CorrectIncorrectHint
(a) By recurring formula, \(a_{17}=a_{16}+a_{15}\) is correct
Also \(c_{17} \neq c_{16}+c_{15}\)
\(
\begin{aligned}
&\Rightarrow a_{15} \neq a_{14}+a_{13} \quad\left(\because c_n=a_{n-2}\right) \\
&\therefore \text { Incorrect }
\end{aligned}
\)
Similarly, other parts are also incorrect. -
Question 82 of 205
82. Question
A committee of 12 is to be formed from 9 women and 8 men. In how many ways this can be done if at least five women have to be included in a committee? In how many of these committees [1994- 4 Marks]
(a) The women are in majority?
(b) The men are in majority?CorrectIncorrectHint
Given that, there are 9 women and 8 men, a committee of 12 is to be formed including at least 5 women.
This can be done in \(=(5\) women and 7 men \()+(6\) women and 6 men \()+(7\) women and 5 men \()+\) ( 8 women and 4 men \()+(9\) women and 3 men) ways
Total number of ways of forming committee
\(
\begin{aligned}
&=\left({ }^9 C_5 \cdot{ }^8 C_7\right)+\left({ }^9 C_6 \cdot{ }^8 C_6\right)+\left({ }^9 C_7 \cdot{ }^8 C_5\right)+\left({ }^9 C_8 \cdot{ }^8 C_4\right) \\
&+\left({ }^9 C_9 \cdot{ }^8 C_3\right) \\
&=1008+2352+2016+630+56=6062 \\
&
\end{aligned}
\)
(i) The women are in majority \(=2016+630+56=2702\)
(ii) The men are in majority \(=1008\) ways. -
Question 83 of 205
83. Question
Eighteen guests have to be seated, half on each side of a long table. Four particular guests desire to sit on one particular side and three others on the other side. Determine the number of ways in which the sitting arrangements can be made. [1991-4 Marks]
CorrectIncorrectHint
Out of 18 guests, 9 to be seated on side \(A\) and rest 9 on side \(B\). Now out of 18 guests, 4 particular guests desire to sit on one particular side say side \(A\) and other 3 on other side \(B\). Out of rest \(18-4-3=11\) guests we can select 5 more for side \(A\) and rest 6 can be seated on side \(B\). Selection of 5 out of 11 can be done in \({ }^{11} C_5\) ways and 9 guests on each side of the table can be seated in \(9 ! \times 9\) ! ways. Thus there are total \({ }^{11} C_5 \times 9\) ! \(\times 9\) ! arrangements.
-
Question 84 of 205
84. Question
A box contains two white balls, three black balls and four red balls. In how many ways can three balls be drawn from the box if at least one black ball is to be included in the draw? [1986 – 2½ Marks]
CorrectIncorrectHint
Number of ways of drawing at least one black ball \(=1\) black and 2 other or 2 black and 1 other or 3 black \(={ }^3 C_1 \times{ }^6 C_2+{ }^3 C_2 \times{ }^6 C_1+{ }^3 C_3=3 \times 15+3 \times 6+1\) \(=45+18+1=64\)
-
Question 85 of 205
85. Question
7 relatives of a man comprises 4 ladies and 3 gentlemen; his wife has also 7 relatives; 3 of them are ladies and 4 gentlemen. In how many ways can they invite a dinner party of 3 ladies and 3 gentlemen so that there are 3 of man’s relatives and 3 of the wife’s relatives? [1985 – 5 Marks]
CorrectIncorrectHint
The possible cases are:
Case I : A man invites (3 ladies) and woman invites (3 gentlemen)
\(
{ }^4 \mathrm{C}_3{ }^4 \mathrm{C}_3=16
\)Case II : A man invites (2 ladies,1 gentleman) and woman invites (2 gentleman, 1 lady)
\(
\left({ }^4 \mathrm{C}_2{ }^3 \mathrm{C}_1\right)\left({ }^3 \mathrm{C}_1{ }^4 \mathrm{C}_2\right)=324
\)Case III : A man invites (1 lady, 2 gentlemen) and woman invites (2 ladies, 1 gentleman)
\(
\Rightarrow\left({ }^4 \mathrm{C}_1{ }^3 \mathrm{C}_2\right)\left({ }^3 \mathrm{C}_2{ }^4 \mathrm{C}_1\right)=144
\)Case IV : A man invites ( 3 gentlemen) and woman invites (3 ladies)
\(
{ }^3 \mathrm{C}_3{ }^3 \mathrm{C}_3=1
\)
Total number of ways
\(
=16+324+144+1=485
\) -
Question 86 of 205
86. Question
Five balls of different colours are to be placed in three boxes of different size. Each box can hold all five balls. In how many different ways can we place the balls so that no box remains empty? [1981 – 4 Marks]
CorrectIncorrectHint
The various possibilities to put 5 different balls in 3 different size boxes, when no box remains empty: The balls can be 1,1 and 3 in different or \(2,2,1\).
Case I: To put 1, 1 and 3 balls in different boxes. Selection of 1,1 and 3 balls out of 5 balls can be done in \({ }^5 C_1 \times{ }^4 C_1 \times{ }^3 C_3\) ways and then \(1,1,3\) can permute (as different size boxes) in 3 ! ways.
\(\therefore\) No. of ways
\(={ }^5 C_1 \times{ }^4 C_1 \times{ }^3 C_3 \times 3 !=5 \times 4 \times 1 \times 6=120\)Case II: To put 2, 2 and 1 ball in different boxes. Selection of 2,2 and 1 balls out of 5 balls can be done in \({ }^5 C_2 \times{ }^3 C_2 \times{ }^1 C_1\) ways
And then 2, 2, 1 can permute (different boxes) in 3 ! Ways
\(\therefore\) No. of ways
\({ }^5 C_1 \times{ }^3 C_2 \times{ }^1 C_1 \times 3 !=10 \times 3 \times 1 \times 6=180\)
Combining case I and II, total number of required ways are \(=120+180=300\). -
Question 87 of 205
87. Question
Six X’s have to be placed in the squares of the figure below in such a way that each row contains at least one \(\mathrm{X}\). In how many different ways can this be done? [1978]
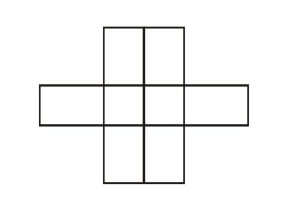 CorrectIncorrect
CorrectIncorrectHint
As all the X’s are identical, the question is of selection of 6 squares from 8 squares, so that no row remains empty. Here \(R_1\) has 2 squares, \(R_2\) has 4 squares, and \(\mathrm{R}_3\) has 2 squares. The selection scheme is as follows:
\(
\begin{array}{|c|c|c|}
\hline \mathrm{R}_1 & \mathrm{R}_2 & \mathrm{R}_3 \\
\hline 1 & 4 & 1 \\
\hline 1 & 3 & 2 \\
\hline 2 & 3 & 1 \\
\hline 2 & 2 & 2 \\
\hline
\end{array}
\)
Therefore, number of selection is
\(
\begin{aligned}
&{ }^2 \mathrm{C}_1 \times{ }^4 \mathrm{C}_4 \times{ }^2 \mathrm{C}_1+{ }^2 \mathrm{C}_1 \times{ }^4 \mathrm{C}_3 \times{ }^2 \mathrm{C}_2+{ }^2 \mathrm{C}_2 \times{ }^4 \mathrm{C}_3 \times{ }^2 \mathrm{C}_1+{ }^2 \mathrm{C}_2 \times{ }^4 \mathrm{C}_2 \times{ }^2 \mathrm{C}_2=4+8+8+6=26 \\
\end{aligned}
\) -
Question 88 of 205
88. Question
The number of integers, between 100 and 1000 having the sum of their digits equals to 14 , is _____. [JEE Main 2024 (Online) 9th April Evening Shift]
CorrectIncorrectHint
Number in this range will be 3 -digit number.
\(N=\overline{a b c}\) such that \(a+b+c=14\)
Also, \(a \geq 1, \quad a, b, c \in\{0,1,2, \ldots 9\}\)
Case I:
All 3-digit same
\(\Rightarrow 3 a=14\) not possibleCase II:
Exactly 2 digit same:
\(
\begin{aligned}
& \Rightarrow 2 a+c=14 \\
& (a, c) \in\{(3,8),(4,6),(5,4),(6,2),(7,0)\} \\
& \Rightarrow\left(\frac{3!}{2!}\right) \text { ways } \Rightarrow 5 \times 3-1 \\
& =15-1=14
\end{aligned}
\)Case III:
All digits are distinct
\(
a+b+c=14
\)
without losing generality \(a>b>c\)
\(
\begin{aligned}
& (a, b, c) \in\left\{\begin{array}{l}
(9,5,0),(9,4,1),(9,3,2) \\
(8,6,0),(8,5,1),(8,4,2) \\
(7,6,1),(7,5,2),(7,4,3) \\
(6,5,3)
\end{array}\right. \\
& \Rightarrow 8 \times 3!+2(3!-2!)=48+8=56 \\
& =0+14+56=70 \\
&
\end{aligned}
\) -
Question 89 of 205
89. Question
The number of 3 -digit numbers, formed using the digits \(2,3,4,5\) and 7 , when the repetition of digits is not allowed, and which are not divisible by 3 , is equal to [JEE Main 2024 (Online) 8th April Morning Shift]
CorrectIncorrectHint
To solve this problem, we need to find the number of 3-digit numbers formed using the digits \(2,3,4,5\), and 7 , with no repetition of digits allowed, and these numbers should not be divisible by 3 . Let’s break down the solution step-by-step:
1. Calculating the total number of 3 -digit numbers without repetition:The number of ways to form a 3-digit number from 5 unique digits \((2,3,4,5,7)\) without repetition can be calculated using permutations:
The total number of permutations for choosing 3 digits out of 5 and arranging them is given by:
\(
5 P 3=\frac{5!}{(5-3)!}=\frac{5 \times 4 \times 3 \times 2 \times 1}{2 \times 1}=5 \times 4 \times 3=60
\)
So, there are 60 possible 3-digit numbers that can be formed from the digits 2, 3, 4, 5 , and 7 without repetition.2. Finding the 3 -digit numbers divisible by 3 :
A number is divisible by 3 if the sum of its digits is divisible by 3 . Let’s consider the sums of every combination of these three digits to find out which sums are divisible by 3 :
Possible sums of combinations:
\(
\begin{aligned}
& 2+3+4=9 \text { (divisible by } 3 \text { ) } \\
& 2+4+7=13 \\
& 2+5+7=14 \\
& 2+3+5=10 \\
& 2+3+7=12 \text { (divisible by } 3 \text { ) } \\
& 3+4+5=12 \text { (divisible by } 3 \text { ) } \\
& 3+4+7=14 \\
& 3+5+7=15 \text { (divisible by } 3 \text { ) } \\
& 4+5+7=16
\end{aligned}
\)
The combinations whose sums are divisible by 3 are:
\(
\begin{aligned}
& 2,3,4 \\
& 2,3,7 \\
& 3,4,5 \\
& 3,5,7
\end{aligned}
\)
Since the sum of the digits is divisible by 3 for these combinations, any permutation of these sets will yield a number divisible by 3 :
The number of 3 -digit numbers that can be formed from each set of 3 digits is:
\(
3!=6
\)
So, the total number of 3-digit numbers divisible by 3 is:
4 sets \(\times 6\) permutations per set \(=24\)3. Calculating the 3 -digit numbers not divisible by 3 :
To find the 3-digit numbers not divisible by 3 , we subtract the number of those divisible by 3 from the total number of 3 -digit numbers:
\(
60-24=36
\)
Therefore, the number of 3-digit numbers that can be formed using the digits 2,3, 4,5 , and 7 without repetition, and which are not divisible by 3 , is equal to 36 . -
Question 90 of 205
90. Question
The number of ways of getting a sum 16 on throwing a dice four times is ___ [JEE Main 2024 (Online) 5th April Morning Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& \text { Number of ways }=\text { coefficient of } x^{16} \text { in }\left(x+x^2+\ldots+x^6\right)^4 \\
& =\text { coefficient of } x^{16} \text { in }\left(1-x^6\right)^4(1-x)^{-4} \\
& =\text { coefficient of } x^{16} \text { in }\left(1-4 x^6+6 x^{12} \ldots\right)(1-x)^{-4} \\
& ={ }^{15} C_3-4 \cdot{ }^9 C_3+6=125
\end{aligned}
\) -
Question 91 of 205
91. Question
There are 4 men and 5 women in Group A, and 5 men and 4 women in Group B. If 4 persons are selected from each group, then the number of ways of selecting 4 men and 4 women is _____. [JEE Main 2024 (Online) 4th April Evening Shift]
CorrectIncorrectHint
\(
\begin{array}{|l|l|l|}
\hline \text { Group A } & \text { Group B } & \text { Ways } \\
\hline 4 m & 4 w & { }^4 C_4 \cdot{ }^4 C_4=1 \\
3 m+1 w & 1 m+3 w & { }^4 C_1 \cdot{ }^5 C_1 \cdot{ }^5 C_1^4 C_3 \quad=400 \\
2 m+2 w & 2 m+2 w & { }^4 C_2 \cdot{ }^5 C_2{ }^5 C_2{ }^4 C_2 \quad=3600 \\
1 m+3 w & 3 m+w & { }^4 C_1{ }^5 C_3{ }^5 C_3{ }^4 C_1 \quad=1600 \\
4 w & 4 m & { }^5 C_4{ }^5 C_4 \quad=25 \\
\hline
\end{array}
\)\(
\begin{aligned}
\text { Total ways } & =1+400+3600+1600+25 \\
& =5626
\end{aligned}
\) -
Question 92 of 205
92. Question
The number of elements in the set \(S =\{(x, y, z): x, y, z \in Z , x+2 y+3 z=42, x, y, z \geqslant 0\} \text { equals }\) [JEE Main 2024 (Online) 1st February Morning Shift]
CorrectIncorrectHint
\(
\begin{array}{ll}
x+2 y+3 z=42 \\
x, y, z \geq 0 \\
\text { as } & \\
z=0 & x+2 y=42 \Rightarrow 22 \text { cases } \\
z=1 & x+2 y=39 \Rightarrow 20 \text { cases } \\
z=2 & x+2 y=36 \Rightarrow 19 \text { cases } \\
z=3 & x+2 y=33 \Rightarrow 17 \text { cases } \\
z=4 & x+2 y=30 \Rightarrow 16 \text { cases } \\
z=5 & x+2 y=27 \Rightarrow 14 \text { cases } \\
z=6 & x+2 y=24 \Rightarrow 13 \text { cases } \\
z=7 & x+2 y=21 \Rightarrow 11 \text { cases }
\end{array}
\)
\(
\begin{aligned}
& z=8 \quad x+2 y=18 \Rightarrow 10 \text { cases } \\
& z=9 \quad x+2 y=15 \Rightarrow 8 \text { cases } \\
& z=10 x+2 y=12 \Rightarrow 7 \text { cases } \\
& z=11 x+2 y=9 \Rightarrow 5 \text { cases } \\
& z=12 x+2 y=6 \Rightarrow 4 \text { cases } \\
& z=13 x+2 y=3 \Rightarrow 2 \text { cases } \\
& z=14 x+2 y=0 \Rightarrow 1 \text { case } \\
& \text { Total }=169 \\
&
\end{aligned}
\) -
Question 93 of 205
93. Question
The total number of words (with or without meaning) that can be formed out of the letters of the word ‘DISTRIBUTION’ taken four at a time, is equal to _____. [JEE Main 2024 (Online) 31st January Morning Shift]
CorrectIncorrectHint
We have III, TT, D, S, R, B, U, O, N
Number of words with selection \(( a , a , a , b )\)
\(
={ }^8 C _1 \times \frac{4!}{3!}=32
\)
Number of words with selection \(( a , a , b , b )\)
\(
=\frac{4!}{2!2!}=6
\)
Number of words with selection \(( a , a , b , c )\)
\(
={ }^2 C _1 \times{ }^8 C _2 \times \frac{4!}{2!}=672
\)
Number of words with selection \(( a , b , c , d )\)
\(
\begin{aligned}
& ={ }^9 C _4 \times 4!=3024 \\
& \therefore \text { Total }=3024+672+6+32 \\
& =3734
\end{aligned}
\) -
Question 94 of 205
94. Question
In an examination of Mathematics paper, there are 20 questions of equal marks and the question paper is divided into three sections : \(A, B\) and \(C\). A student is required to attempt total 15 questions taking at least 4 questions from each section. If section \(A\) has 8 questions, section \(B\) has 6 questions and section \(C\) has 6 questions, then the total number of ways a student can select 15 questions is ______. [JEE Main 2024 (Online) 30th January Evening Shift]
CorrectIncorrectHint
The problem involves choosing 15 questions out of a total of 20 available questions, with the constraint that at least 4 questions must be chosen from each of the three sections A, B, and C. To evaluate the total number of ways a student can select these questions, we need to consider every possible combination of questions from sections \(A, B\), and \(C\) that sum up to 15 questions while respecting the constraints.
Section \(A\) has 8 questions, Section \(B\) and \(C\) each have 6 questions. The student must choose at least 4 questions from each section, which satisfies the minimum requirement. However, since the student is to attempt a total of 15 questions, there are several combinations to consider, as outlined below:
Choosing 4 questions from \(A , 5\) from \(B\), and 6 from \(C\)
Choosing 4 questions from \(A, 6\) from \(B\), and 5 from \(C\)
Choosing 7 questions from \(A, 4\) from \(B\), and 4 from \(C\)
Choosing 6 questions from \(A , 5\) from \(B\), and 4 from \(C\)
Choosing 6 questions from \(A , 4\) from \(B\), and 5 from \(C\)
Choosing 5 questions from \(A , 5\) from \(B\), and 5 from \(C\)
Choosing 5 questions from \(A, 6\) from \(B\), and 4 from \(C\)
Choosing 5 questions from \(A , 4\) from \(B\), and 6 from \(C\)
\(
\begin{array}{|c|c|c|c|c|}
\hline A & B & C & \Rightarrow & \begin{array}{c}
\text { No. of } \\
\text { question }
\end{array} \\
\hline 4 & 5 & 6 & \rightarrow & { }^8 C_4{ }^6 C_5{ }^6 C_6 \\
\hline 4 & 6 & 5 & \rightarrow & { }^8 C_4{ }^6 C_6{ }^6 C_5 \\
\hline 7 & 4 & 4 & \rightarrow & { }^8 C_7{ }^6 C_4{ }^6 C_4 \\
\hline 6 & 5 & 4 & \rightarrow & { }^8 C_6{ }^6 C_5{ }^6 C_4 \\
\hline 6 & 4 & 5 & \rightarrow & { }^8 C_6{ }^6 C_4{ }^6 C_5 \\
\hline 5 & 5 & 5 & \rightarrow & { }^8 C_5{ }^6 C_5{ }^6 C_5 \\
\hline 5 & 6 & 4 & \rightarrow & { }^8 C_5{ }^6 C_6{ }^6 C_4 \\
\hline 5 & 4 & 6 & \rightarrow & { }^8 C_5{ }^6 C_4{ }^6 C_6 \\
\hline
\end{array}
\)
Total ways of select \(=11376\) -
Question 95 of 205
95. Question
All the letters of the word “GTWENTY” are written in all possible ways with or without meaning and these words are written as in a dictionary. The serial number of the word “GTWENTY” is _____. [JEE Main 2024 (Online) 29th January Morning Shift]
CorrectIncorrectHint
Words starting with \(E =360\)
Words starting with \(GE =60\)
Words starting with \(GN =60\)
Words starting with \(GTE =24\)
Words starting with \(GTN =24\)
Words starting with GTT \(=24\)
GTWENTY \(=1\)
Total \(=553\) -
Question 96 of 205
96. Question
The number of ways five alphabets can be chosen from the alphabets of the word MATHEMATICS, where the chosen alphabets are not necessarily distinct, is equal to: [JEE Main 2024 (Online) 8th April Evening Shift]
CorrectIncorrectHint
The word MATHEMATICS has
\(2 M\)
\(2 A\)
\(2 T\)
\(H, E, I, C, S\)Case-I:
2 Alike 2 Alike 1 Diff
\({ }^3 C_2 \times{ }^6 C_1=18\)Case-II:
2 Alike +3 Diff
\({ }^3 C_1 \times{ }^7 C_3=105\)Case-III:
All different
\({ }^8 C_5=56\)
Total ways \(=179\) -
Question 97 of 205
97. Question
Let \([t]\) be the greatest integer less than or equal to \(t\). Let \(A\) be the set of all prime factors of 2310 and \(f: A \rightarrow Z\) be the function \(f(x)=\left[\log _2\left(x^2+\left[\frac{x^3}{5}\right]\right)\right]\). The number of one-to-one functions from \(A\) to the range of \(f\) is [JEE Main 2024 (Online) 8th April Morning Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& N =2310=231 \times 10 \\
& =3 \times 11 \times 7 \times 2 \times 5 \\
& A =\{2,3,5,7,11\} \\
& f(x)=\left[\log _2\left(x^2+\left[\frac{x^3}{5}\right]\right)\right] \\
& f (2)=\left[\log _2(5)\right]=2 \\
& f(3)=\left[\log _2(14)\right]=3 \\
& f(5)=\left[\log _2(25+25)\right]=5 \\
& f(7)=\left[\log _2(117)\right]=6 \\
& f(11)=\left[\log _2 387\right]=8
\end{aligned}
\)
\(
\text { Range of } f : B =\{2,3,5,6,8\}
\)
No. of one-one functions \(=5!=120\) -
Question 98 of 205
98. Question
If all the words with or without meaning made using all the letters of the word “NAGPUR” are arranged as in a dictionary, then the word at \(315^{\text {th }}\) position in this arrangement is : [JEE Main 2024 (Online) 6th April Evening Shift]
CorrectIncorrectHint
Word at \(315^{\text {th }}\) position
\(
\begin{aligned}
& \text { A….. }=5!=120 \\
& \text { G…… }=5!=120 \\
& \text { NA…. }=4!=24 \\
& \text { NG…. }=4!=24 \\
& \text { NP…. }=4!=24
\end{aligned}
\)
….. Till 312 words
\(
\begin{aligned}
& 313^{\text {th }} \text { word }=\text { NRAGPU } \\
& 314^{\text {th }} \text { word }=\text { NRAGUP } \\
& 315^{\text {th }} \text { word }=\text { NRAPGU }
\end{aligned}
\) -
Question 99 of 205
99. Question
Let \(0 \leq r \leq n\). If \({ }^{n+1} C_{r+1}:{ }^n C_r:{ }^{n-1} C_{r-1}=55: 35: 21\), then \(2 n+5 r\) is equal to : [JEE Main 2024 (Online) 6th April Evening Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& \frac{n+1}{r+1} \times{ }^n C_r:{ }^n C_r: \frac{r}{n}{ }^n C_r=55: 35: 21 \\
& \Rightarrow \frac{n+1}{r+1}=\frac{55}{35} \text { and } \frac{n}{r}=\frac{35}{21}
\end{aligned}
\)
\(
\begin{gathered}
\Rightarrow 7 n-11 r=4 \dots(1)\\
3 n-5 r=0 \dots(2)
\end{gathered}
\)
Solving (1) and (2)
\(
\begin{aligned}
& r=6 \text { and } n=10 \\
& \Rightarrow 2 n+5 r=20+30=50
\end{aligned}
\) -
Question 100 of 205
100. Question
The number of triangles whose vertices are at the vertices of a regular octagon but none of whose sides is a side of the octagon is [JEE Main 2024 (Online) 6th April Morning Shift]
CorrectIncorrectHint
Number of all possible triangles
\(=\) Number of selections of 3 points from 8 vertices
\(
={ }^8 C_3=56
\)
Number of triangle with one side common with octagon \(=8 \times 4=32\)
(Consider side \(A_1 A_2\). Since two points \(A_3, A_8\) are adjacent, 3 rd point should be chosen from remaining 4 points).
Number of triangles having two sides common with octagon: All such triangles have three consecutive vertices, viz., \(A_1 A_2 A_3, A_2 A_3 A_4 . \cdots A_8 A_1 A_2\).
Number of such triangles \(=8\)
\(\therefore\) Number of triangles with no side common
\(
=56-32-8=16 \text {. }
\) -
Question 101 of 205
101. Question
Let the set \(S=\{2,4,8,16, \ldots, 512\}\) be partitioned into 3 sets \(A, B, C\) with equal number of elements such that \(A \cup B \cup C = S\) and \(A \cap B = B \cap C = A \cap C =\phi\). The maximum number of such possible partitions of \(S\) is equal to: [JEE Main 2024 (Online) 5th April Evening Shift]
CorrectIncorrectHint
Given set \(S=\left\{2^1, 2^2, \ldots 2^9\right\}\) which consist of 9 elements.
Maximum number of possible partitions (in set \(A, B\) and \(C\) )
\(
={ }^9 C_3 \cdot{ }^6 C_3 \cdot{ }^3 C_3=1680
\)Alternate:
\(
\begin{aligned}
& \left\{2,2^2, 2^3 \ldots \ldots 2^9\right\} \\
& \Rightarrow \frac{9!}{3!3!3!3!} \times 3!=\frac{9 \times 8 \times 7 \times 6 \times 5 \times 4}{6 \times 6} \\
& =1680
\end{aligned}
\) -
Question 102 of 205
102. Question
60 words can be made using all the letters of the word \(BHBJO\), with or without meaning. If these words are written as in a dictionary, then the \(50^{\text {th }}\) word is: [JEE Main 2024 (Online) 5th April Evening Shift]
CorrectIncorrectHint
B,H,J,O
B. . . 4!=24
H. . . \(\frac{4!}{2!}=12\)
J. . . \(\frac{4!}{2!}=12\)O B B H J \(\rightarrow 49{\text {th }}\)
O B B J H \(\rightarrow 50^{\text {th }}\) rank -
Question 103 of 205
103. Question
There are 5 points \(P_1, P_2, P_3, P_4, P_5\) on the side \(A B\), excluding \(A\) and \(B\), of a triangle \(A B C\). Similarly there are 6 points \(P _6, P _7, \ldots, P _{11}\) on the side \(BC\) and 7 points \(P _{12}, P _{13}, \ldots, P _{18}\) on the side \(CA\) of the triangle. The number of triangles, that can be formed using the points \(P _1, P _2, \ldots, P _{18}\) as vertices, is: [JEE Main 2024 (Online) 4th April Morning Shift]
CorrectIncorrectHint
Number of points on side \(A B=5\)
Number of points on side \(B C=6\)
Number of points on side \(A C=7\)
Number of ways selecting three points from side
\(
A B={ }^5 C_3
\)
Number of ways selecting three points from side
\(
B C={ }^6 C_3
\)
Number of ways selecting three points from side
\(
A C={ }^7 C_3
\)
Total number of triangle possible formed using the points \(P_1 P_2 \ldots P_{18}\)
\(
\begin{aligned}
& ={ }^{18} C_3-{ }^5 C_3-{ }^6 C_3-{ }^7 C_3 \\
& =816-10-20-35 \\
& =751
\end{aligned}
\) -
Question 104 of 205
104. Question
If \(n\) is the number of ways five different employees can sit into four indistinguishable offices where any office may have any number of persons including zero, then \(n\) is equal to : [JEE Main 2024 (Online) 1st February Morning Shift]
CorrectIncorrectHint
Total ways to partition 5 into 4 parts are :
\((5,0,0,0) \Rightarrow 1\) way
\((4,1,0,0) \Rightarrow \frac{5!}{4!}=5\) ways
\((3,2,0,0) \Rightarrow \frac{5!}{3!2!}=10\) ways
\((2,2,0,1) \Rightarrow \frac{5!}{2!2!2!}=15\) ways
\((2,1,1,1) \Rightarrow \frac{5!}{2!(1!)^3 3!}=10\) ways
\((3,1,1,0) \Rightarrow \frac{5!}{3!2!}=10\) ways
Total \(\Rightarrow 1+5+10+15+10+10=51\) ways -
Question 105 of 205
105. Question
The number of ways in which 21 identical apples can be distributed among three children such that each child gets at least 2 apples, is [JEE Main 2024 (Online) 31st January Evening Shift]
CorrectIncorrectHint
After giving 2 apples to each child 15 apples left now 15 apples can be distributed in \({ }^{15+3-1} C _2={ }^{17} C _2\) ways
\(
\begin{aligned}
& =\frac{17 \times 16}{2} \\
& =136
\end{aligned}
\)Explanation:
First, since each child must get at least 2 apples, let’s give 2 apples to each child right away. That accounts for 6 apples ( 2 apples for each of the 3 children). Now, we have \(21-6=15\) apples left to distribute freely among the three children.
The “stars and bars” technique involves representing the apples as stars (*) and the divisions between children as bars (|). For example, if we had 5 apples to distribute among three children, one possible distribution could be represented as \(* *|*| * *\). This means the first child gets 2 apples, the second child gets 1 apple, and the third child gets 2 apples.
In our case, we need to distribute 15 apples (stars) among the three children with 2 bars to create the partitions. We arrange 15 stars and 2 bars in a row, where the arrangement of stars and bars corresponds to a distribution of the apples.
The total number of objects we’re arranging is 15 apples +2 bars \(=17\) objects. We need to choose 2 positions out of these 17 to place the bars. The remaining positions will be occupied by the stars (apples).
The number of ways to choose 2 positions out of 17 for the bars is given by the binomial coefficient:
\(
\text { Number of ways }=\binom{17}{2}=\frac{17!}{2!(17-2)!}=\frac{17 \times 16}{2 \times 1}=136
\) -
Question 106 of 205
106. Question
If for some \(m, n ;{ }^6 C_m+2\left({ }^6 C_{m+1}\right)+{ }^6 C_{m+2}>{ }^8 C_3\) and \({ }^{n-1} P_3:{ }^n P_4=1: 8\), then \({ }^n P_{m+1}+{ }^{n+1} C_m\) is equal to [JEE Main 2024 (Online) 31st January Evening Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& { }^6 C _{ m }+2\left({ }^6 C _{ m +1}\right)+{ }^6 C _{ m +2}>{ }^8 C _3 \\
& { }^7 C _{ m +1}+{ }^7 C _{ m +2}>{ }^8 C _3 \\
& { }^8 C _{ m +2}>{ }^8 C _3 \\
& \therefore m =2 \\
& \text { And }{ }^{ n -1} P _3:{ }^n P _4=1: 8 \\
& \frac{( n -1)( n -2)( n -3)}{ n ( n -1)( n -2)( n -3)}=\frac{1}{8} \\
& \therefore n =8 \\
& \therefore{ }^{ n } P _{ m +1}+{ }^{ n +1} C _{ m }={ }^8 P _3+{ }^9 C _2 \\
& =8 \times 7 \times 6+\frac{9 \times 8}{2} \\
& =372
\end{aligned}
\) -
Question 107 of 205
107. Question
Number of ways of arranging 8 identical books into 4 identical shelves where any number of shelves may remain empty is equal to [JEE Main 2024 (Online) 29th January Evening Shift]
CorrectIncorrectHint
3 Shelf empty: \((8,0,0,0) \rightarrow 1\) way
2 shelf empty: \(\left.\begin{array}{c}(7,1,0,0) \\ (6,2,0,0) \\ (5,3,0,0) \\ (4,4,0,0)\end{array}\right] \rightarrow 4\) ways
\(
\left.1 \text { shelf empty: } \begin{array}{rr}
(6,1,1,0) & (3,3,2,0) \\
(4,2,1,0) & (4,2,2,0)
\end{array}\right] \rightarrow 5 \text { ways }
\)
\(
\left.0 \text { Shelf empty : } \begin{array}{ll}
(1,2,3,2) & (5,1,1,1) \\
(2,2,2,2) & \\
(4,3,2,1,1) &
\end{array}\right] \rightarrow 5 \text { ways }
\)
\(
\text { Total }=15 \text { ways }
\) -
Question 108 of 205
108. Question
Let \(\alpha=\frac{(4!)!}{(4!)^{3!}}\) and \(\beta=\frac{(5!)!}{(5!)^{4!}}\). Then : [JEE Main 2024 (Online) 27th January Evening Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& \alpha=\frac{(4!)!}{(4!)^{3!}}, \beta=\frac{(5!)!}{(5!)^{4!}} \\
& \alpha=\frac{(24)!}{(4!)^6}, \beta=\frac{(120)!}{(5!)^{24}}
\end{aligned}
\)
Let 24 distinct objects are divided into 6 groups of 4 objects in each group.
No. of ways of formation of group \(=\frac{24!}{(4!)^6 .6!} \in N\)
Similarly,
Let 120 distinct objects are divided into 24 groups of 5 objects in each group.
No. of ways of formation of groups
\(
=\frac{(120)!}{(5!)^{24} \cdot 24!} \in N
\) -
Question 109 of 205
109. Question
A person forgets his 4-digit ATM pin code. But he remembers that in the code all the digits are different, the greatest digit is 7 and the sum of the first two digits is equal to the sum of the last two digits. Then the maximum number of trials necessary to obtain the correct code is ____. [JEE Main 2023 (Online) 15th April Morning Shift]
CorrectIncorrectHint
Sum of first two digits
Sum of last two digits \(=\alpha\)
Case-I : \(\alpha=7\)
\(2 \times 12=24\) ways.
-
Question 110 of 205
110. Question
Total numbers of 3-digit numbers that are divisible by 6 and can be formed by using the digits 1,2,3,4,5 with repetition, is _____. [JEE Main 2023 (Online) 13th April Evening Shift]
CorrectIncorrectHint
A number is divisible by 6 if it is divisible by both 2 and 3 . A number is divisible by 2 if its last digit is even, which means it must be either 2 or 4 from the given digits. A number is divisible by 3 if the sum of its digits is divisible by 3.
\(
\begin{aligned}
& (2,1,3),(2,3,4),(2,5,5),(2,2,5),(2,2,2) \\
& (4,1,1),(4,4,1),(4,4,4),(4,3,5) \\
& 2,1,3 \Rightarrow 312,132 \\
& 2,3,4 \Rightarrow 342,432,234,324 \\
& 2,5,5 \Rightarrow 552 \\
& 2,2,5 \Rightarrow 252,522 \\
& 2,2,2 \Rightarrow 222 \\
& 4,1,1 \Rightarrow 114 \\
& 4,4,1 \Rightarrow 414,144 \\
& 4,4,4 \Rightarrow 444 \\
& 4,3,5 \Rightarrow 354,534 \\
& \text { Total } 16 \text { numbers. }
\end{aligned}
\) -
Question 111 of 205
111. Question
The number of seven digit positive integers formed using the digits 1,2,3 and 4 only and sum of the digits equal to 12 is _____. [JEE Main 2023 (Online) 13th April Evening Shift]
CorrectIncorrectHint
\(x_1+x_2+x_3+\ldots x_7=12\). This equation represents the number of ways to distribute 12 identical items (the sum of the digits) into 7 distinct boxes (the seven digits of the number), where each box can contain one of the numbers \(1,2,3\), or 4 .
Number of solutions
\(
\begin{aligned}
& =\text { Coefficient of } x^{12} \text { in }\left(x^1+x^2+x^3+x^4\right)^7 \\
& =\text { Coefficient of } x^5 \text { in }\left(1+x+x^2+x^3\right)^7 \\
& =\text { Coefficient of } x^5 \text { in }\left(1-x^4\right)^7(1-x)^{-7} \\
& =\text { Coefficient of } x^5 \text { in }\left(1-7 x^4\right)(1-x)^{-7} \\
& =\text { Coefficient of } x^5 \text { in }\left(1-7 x^4\right) \sum_{r=0}^{\infty}{ }^{7+r-1} C_r \cdot x^r \\
& ={ }^{11} C_5-7 \times{ }^7 C_1 \\
& =462-49=413
\end{aligned}
\) -
Question 112 of 205
112. Question
Let the digits \(a, b, c\) be in A. P. Nine-digit numbers are to be formed using each of these three digits thrice such that three consecutive digits are in A.P. at least once. How many such numbers can be formed? [JEE Main 2023 (Online) 12th April Morning Shift]
CorrectIncorrectHint
The problem involves forming nine-digit numbers from three digits \(a, b, c\) which are in Arithmetic Progression (AP), used three times each, such that at least once, three consecutive digits are in AP.
We have the two possible sequences for the AP :
\(
\begin{aligned}
& a, b, c \\
& c, b, a
\end{aligned}
\)
This shows the flexibility in ordering the three digits that are in AP in our nine-digit number.
The next step is to choose the location of this sequence of three numbers within our nine-digit number.
Since there are nine places in our number and our sequence takes up three places, we have seven different starting points for our sequence : it can start at the first place, the second place, and so on, up to the seventh place.
Therefore, the number of ways to select 3 consecutive places out of the 9 places for the AP sequence is 7 .
However, we also have to account for the fact that our sequence can be in one of two orders ( \(a , b , c\) or \(c , b , a\) ). So, we multiply the number of starting points by 2 to get \({ }^7 C_1 \times 2=14\) ways to arrange the sequence within our nine-digit number.
The remaining 6 digits (two ‘a’, two ‘b’, two ‘c”) can be arranged in \(\frac{6!}{2!2!2!}\) ways.
Therefore, the total number of such nine-digit numbers is \({ }^7 C_1 \times 2 \times \frac{6!}{2!2!2!}=1260\) -
Question 113 of 205
113. Question
In an examination, 5 students have been allotted their seats as per their roll numbers. The number of ways, in which none of the students sits on the allotted seat, is ____. [JEE Main 2023 (Online) 11th April Morning Shift]
CorrectIncorrectHint
This problem can be solved using the concept of derangements, which is a permutation of objects where no object appears in its original position. In this case, we have 5 students who should not sit in their allotted seats.
The formula for calculating the number of derangements (also known as subfactorials) is :
\(
D(n)=n!\left[\frac{1}{0!}-\frac{1}{1!}+\frac{1}{2!}-\frac{1}{3!}+\frac{1}{4!}-\ldots \ldots .+(-1)^n \frac{1}{n!}\right]
\)
Where \(n\) is the number of students, in this case, 5 .
Using the formula, let’s calculate the derangements for 5 students :
\(
\begin{aligned}
& D(5)=5!\left(\frac{1}{0!}-\frac{1}{1!}+\frac{1}{2!}-\frac{1}{3!}+\frac{1}{4!}-\frac{1}{5!}\right) \\
& D(5)=120\left(1-1+\frac{1}{2}-\frac{1}{6}+\frac{1}{24}-\frac{1}{120}\right) \\
& D(5)=120\left(0+\frac{1}{2}-\frac{1}{6}+\frac{1}{24}-\frac{1}{120}\right) \\
& D(5)=120\left(\frac{1}{2}-\frac{1}{6}+\frac{1}{24}-\frac{1}{120}\right) \\
& D(5)=120\left(\frac{60}{120}-\frac{20}{120}+\frac{5}{120}-\frac{1}{120}\right) \\
& D(5)=120\left(\frac{44}{120}\right) \\
& D(5)=44
\end{aligned}
\) -
Question 114 of 205
114. Question
The sum of all the four-digit numbers that can be formed using all the digits 2, 1, 2, 3 is equal to _____. [JEE Main 2023 (Online) 10th April Evening Shift]
CorrectIncorrectHint
We have, four digits are \(2,1,2,3\).
Total numbers when 1 is at unit digit \(=\frac{3!}{2!}=3\)
Total number when 2 is at unit digit \(=3!=6\)
Total numbers when 3 is at unit digit \(=\frac{3!}{2!}=3\)
Sum of digits at unit place \(=3 \times 1+6 \times 2+3 \times 3=24\)
\(\therefore\) Required sum \(=24 \times 1000+24 \times 100+24 \times 10+24 \times 1\)
\(=24 \times 1111=26664\) -
Question 115 of 205
115. Question
The number of permutations, of the digits 1, 2, 3, …, 7 without repetition, which neither contain the string 153 nor the string 2467, is ______. [JEE Main 2023 (Online) 10th April Morning Shift]
CorrectIncorrectHint
Given that digits are \(1,2,3,4,5,6,7\)
Total permutations \(=7!\)
Let \(p=\) Number which containing string 153
\(q=\) Number which containing string 2467
\(
\begin{aligned}
& \therefore n(p)=5!\times 1 \\
& \Rightarrow n(q)=4!\times 1 \\
& \Rightarrow n(p \cap q)=2! \\
& \therefore n(p \cup q)=n(p)+n(q)-n(p \cap q) \\
& =5!+4!-2!=120+24-2=142
\end{aligned}
\)
\(\therefore n\) (neither string 143 nor string 2467)
\(
=7!-142=5040-142=4898
\) -
Question 116 of 205
116. Question
Some couples participated in a mixed doubles badminton tournament. If the number of matches played, so that no couple played in a match, is 840, then the total number of persons, who participated in the tournament, is _____. [JEE Main 2023 (Online) 10th April Morning Shift]
CorrectIncorrectHint
Let, \(n\) be the total number of couples who participated in the tournament.
According to the question, \(2 \times{ }^n C_2 \times{ }^{n-2} C_2=840\)
\(
\begin{aligned}
& \Rightarrow{ }^n C_2 \times{ }^{n-2} C_2=420 \\
& \Rightarrow \frac{n!}{2!(n-2)!} \times \frac{(n-2)!}{(n-4)!2!}=420 \\
& \Rightarrow \frac{n(n-1)(n-2)(n-3)}{4}=420
\end{aligned}
\)
Put \(n=8\) satisfied the equation.
So, \(n=8\)
Hence, total number of players who participated in the tournament \(=2 \times 8=16\) -
Question 117 of 205
117. Question
The number of 4 -letter words, with or without meaning, each consisting of 2 vowels and 2 consonants, which can be formed from the letters of the word UNIVERSE without repetition is _____. [JEE Main 2023 (Online) 6th April Evening Shift]
CorrectIncorrectHint
Given, word is UNIVERSE
Here, vowels are E, I, U and consonants are N, R, S, V
\(\therefore\) Required number of 4 -letters words, with or without meaning,
each consisting of 2 vowels and 2 consonants
\(
\begin{aligned}
& ={ }^3 C_2 \times{ }^4 C_2 \times 4! \\
& ={ }^3 C_1 \times{ }^4 C_2 \times 24 \\
& =3 \times 6 \times 24=432
\end{aligned}
\) -
Question 118 of 205
118. Question
The number of ways of giving 20 distinct oranges to 3 children such that each child gets at least one orange is ______. [JEE Main 2023 (Online) 6th April Morning Shift]
CorrectIncorrectHint
Total – (one child receive no orange + two child receive no orange)
\(
\begin{aligned}
& =3^{20}-\left({ }^3 C_1\left(2^{20}-2\right)+{ }^3 C_2 1^{20}\right) \\
& =3483638676
\end{aligned}
\)Alternate:
Total ways without any restrictions :
There are \(3^{20}\) ways to distribute the oranges to the 3 children.
Number of ways one child receives no orange :
Choose 1 child out of the 3 to not receive any orange in \({ }^3 C_1=3\) ways. Distribute 20 oranges to the remaining 2 children in \(2^{20}\) ways. However, we’ve included the scenarios where the 2 children each get all the oranges. So, we subtract the 2 ways where one of the two remaining children gets all the oranges. \({ }^3 C_1\left(2^{20}-2\right)\)
Number of ways two children receive no orange :
Choose 2 children out of the 3 to not receive any oranges in \({ }^3 C_2=3\) ways. The third child will receive all 20 oranges in \(1^{20}=1\) way. \({ }^3 C_2 \times 1^{20}=3\)
Number of ways
\(
\begin{aligned}
& =\text { Total }-(\text { One child receive no orange }+ \text { two child receive no orange }) \\
& =3^{20}-\left({ }^3 C_1\left(2^{20}-2\right)+{ }^3 C_2 1^{20}\right) \\
& =3483638676
\end{aligned}
\) -
Question 119 of 205
119. Question
Number of integral solutions to the equation \(x+y+z=21\), where \(x \geq 1, y \geq 3, z \geq 4\), is equal to _____. [JEE Main 2023 (Online) 1st February Evening Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& x+y+z=21 \\
& \because \quad x \geq 1, y \geq 3, y \geq 4 \\
& \therefore \quad x_1+y_1+z_1=13 \\
& \text { Number of solutions }={ }^{13+3-1} C_{3-1} \\
& ={ }^{15} C_2=\frac{15 \times 14}{2}=7 \times 15 \\
& =105
\end{aligned}
\) -
Question 120 of 205
120. Question
The total number of six digit numbers, formed using the digits 4, 5, 9 only and divisible by 6, is _______. [JEE Main 2023 (Online) 1st February Evening Shift]
CorrectIncorrectHint
A number will be divisible by 6 iff the digit at the unit place of the number is divisible by 2 and sum of all digits of the number is divisible by 3 .
Units, place must be occupied by 4 and hence, at least one 4 must be there.
\(
\begin{aligned}
&\text { Possible combination of } 4,5,9 \text { are as follows : }\\
&\begin{array}{|l|l|l|l|}
\hline 4 & 5 & 9 & \begin{array}{l}
\text { Total number } \\
\text { of Number }
\end{array} \\
\hline 1 & 1 & 4 & \frac{5!}{4!}=5 \\
\hline 1 & 4 & 1 & \frac{5!}{4!}=5 \\
\hline 2 & 2 & 2 & \frac{5!}{2!2!}=30 \\
\hline 3 & 0 & 3 & \frac{5!}{2!3!}=10 \\
\hline 3 & 3 & 0 & \frac{5!}{2!3!}=10 \\
\hline 4 & 1 & 1 & \frac{5!}{3!}=20 \\
\hline 6 & 0 & 0 & \frac{5!}{5!}=1 \\
\hline
\end{array}
\end{aligned}
\)
\(
\text { Total }=5+5+30+10+10+20+1=81 \text {. }
\) -
Question 121 of 205
121. Question
The number of 3-digit numbers, that are divisible by either 2 or 3 but not divisible by 7, is _____. [JEE Main 2023 (Online) 1st February Morning Shift]
CorrectIncorrectHint
3 digit numbers divisible by either 2 or 3
\(P = n (\) divisible by 2\()+ n (\) divisible by 3\()- n (\) divisible by 6\()\)
\(P=450+300-150\)
\(P =600\)
\(Q = n (\) divisible by 14\()+ n (\) divisible by 21\()- n (\) divisible by 42\()\)
\(
=64+43-21=86
\)
3 digit number divisible by either 2 or 3
But not divisible by 7 so \(P – Q =600-86=514\)Alternate:
\(
\begin{aligned}
& n (2)=450, n (3)=300, n (7)=128, n (2 \cap 7)=64 \\
& n (3 \cap 7)=43, n (2 \cap 3)=150, n (2 \cap 3 \cap 7)=21 \\
& \text { Total numbers }=450+300-150-(64+43-21) \\
& =514
\end{aligned}
\)Explanation:
\(
\begin{aligned}
& A=\text { Numbers divisible by } 2 \\
& B=\text { Numbers divisible by } 3 \\
& C=\text { Numbers divisible by } 7 \\
& n(A \cup B)=n(A)+n(B)-n(A \cap B) \\
& =n(2)+n(3)-n(6) \\
& n(A)=n(2)=100,102 \ldots, 998=450 \\
& n(B)=n(3)=102,105, \ldots, 999=30 \\
& n(A \cap B)=n(6)=102,108, \ldots, 996=150 \\
& n(2 \text { or } 3)=450+300-150=600
\end{aligned}
\)
\(
\begin{aligned}
& n( A \cap C)=n(14)=112,126, \ldots, 994=64 \\
& n(A \cap B \cap C)=n(42)=126,168, \ldots, 966=21 \\
& n(B \cap C)=n(21)=105,126, \ldots \ldots, 987,=43 \\
& n(2 \text { or } 3 \text { not by } 7)=600-[64+43-21] =514
\end{aligned}
\) -
Question 122 of 205
122. Question
The number of words, with or without meaning, that can be formed using all the letters of the word ASSASSINATION so that the vowels occur together, is ____. [JEE Main 2023 (Online) 1st February Morning Shift]
CorrectIncorrectHint
Vowels : A,A,A,I,I,O
Consonants : S,S,S,S,N,N,T
\(\therefore\) Total number of ways in which vowels come together
\(
=\frac{8!}{4!2!} \times \frac{6!}{3!2!}=50400
\) -
Question 123 of 205
123. Question
Let \(A =\left[ a _{i j}\right], a _{i j} \in Z \cap[0,4], 1 \leq i, j \leq 2\).
The number of matrices A such that the sum of all entries is a prime number \(p \in(2,13)\) is ____. [JEE Main 2023 (Online) 31st January Evening Shift]CorrectIncorrectHint
\(
A=\left[\begin{array}{ll}
a_{11} & a_{12} \\
a_{13} & a_{14}
\end{array}\right]
\)
Such that \(\Sigma a_{i i}=3,5,7\) or 11
Then for sum 3 , the possible entries are \((0,0,0,3),(0,0,1,2),(0,1,1,1)\).
Then total number of possible matrices \(=4+12+4=20\)
For sum 5 the possible entries are \((0,0,1,4),(0,0,2,3),(0,1,2,2),(0,1,1,3)\) and \((1,1,1,2)\).
\(\therefore\) Total possible matrices \(=12+12+12+12+4=52\)
For sum 7 the possible entries are \((0,0,3,4)\),
\((0,2,2,3),(0,1,2,4),(0,1,3,3),(1,2,2,2),(1,1,2,3)\) and \((1,1,1,4)\).
\(\therefore\) Total possible matrices \(=80\)
For sum 11 the possible entries are \((0,3,4,4)\), \((1,2,4,4),(2,3,3,3),(2,2,3,4)\).
\(\therefore\) Total number of matrices \(=52\)
\(\therefore\) Total required matrices \(=20+52+80+52=204\) -
Question 124 of 205
124. Question
If \({ }^{2 n+1} P _{n-1}:{ }^{2 n-1} P _n=11: 21\), then \(n^2+n+15\) is equal to : [JEE Main 2023 (Online) 31st January Evening Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& \frac{\frac{(2 n+1)!}{(n+2)!}}{\frac{(2 n-1)!}{(n-1)!}}=\frac{11}{21} \\
& \frac{(2 n+1) 2 n}{(n+2)(n+1) n}=\frac{11}{21} \\
& 84 n+42=11\left(n^2+3 n+2\right) \\
& 11 n^2-51 n-20=0 \\
& (n-5)(11 n+4)=0 \\
& n=5, \frac{-4}{11} \text { (Rejected) } \\
& n^2+n+15=45 \\
\end{aligned}
\) -
Question 125 of 205
125. Question
Let 5 digit numbers be constructed using the digits \(0,2,3,4,7,9\) with repetition allowed, and are arranged in ascending order with serial numbers. Then the serial number of the number 42923 is _____. [JEE Main 2023 (Online) 31st January Morning Shift]
CorrectIncorrectHint
2 – – – – \(\rightarrow 6^4=1296\)
3 – – – – \(\rightarrow 6^4=1296\)
4 0 – – – \(\rightarrow 6^3=216\)\(
\left.\begin{array}{lllll}
4 & 2 & – & – & – \\
4 & 3 & – & – & – \\
4 & 4 & – & – & –
\end{array}\right\} \rightarrow 5 \times 6^2=180
\)
\(
\begin{array}{llllllc}
4 & 2 & 9 & 0 & – & \rightarrow & 6 \\
4 & 2 & 9 & 2 & 0 & \rightarrow & 1 \\
4 & 2 & 9 & 2 & 2 & \rightarrow & 1 \\
4 & 2 & 9 & 2 & 3 & \rightarrow & 1 \\
\hline
& & & & & & & & 2997
\end{array}
\) -
Question 126 of 205
126. Question
Number of 4-digit numbers that are less than or equal to 2800 and either divisible by 3 or by 11 , is equal to ______. [JEE Main 2023 (Online) 31st January Morning Shift]
CorrectIncorrectHint
Numbers which are divisible by 3 (4 digit) and less than or equal to 2800
\(
=\frac{2799-1002}{3}+1=600
\)
Numbers which are divisible by 11 ( 4 digit) and less than or equal to 2800
\(
=\frac{2794-1001}{11}+1=164
\)
Numbers which are divisible by 33 ( 4 digit) and less than or equal to 2800
\(
=\frac{2772-1023}{33}+1=54
\)
\(\therefore\) Total numbers \(=600+164-54=710\) -
Question 127 of 205
127. Question
The number of seven digits odd numbers, that can be formed using all the seven digits \(1,2,2,2,3,3,5\) is _______. [JEE Main 2023 (Online) 30th January Evening Shift]
CorrectIncorrectHint
The number of seven digits odd numbers, that can be formed using all the seven digits \(1,2,2,2,3,3,5\) is 240 .
Digits are \(1,2,2,2,3,3,5\)
If unit digit 5 , then total numbers \(=\frac{6!}{3!2!}\)
If unit digit 3 , then total numbers \(=\frac{6!}{3!}\)
If unit digit 1 , then total numbers \(=\frac{6!}{3!2!}\)
\(\therefore\) total numbers \(=60+60+120=240\) -
Question 128 of 205
128. Question
Number of 4-digit numbers (the repetition of digits is allowed) which are made using the digits 1, 2, 3 and 5, and are divisible by 15, is equal to ______. [JEE Main 2023 (Online) 30th January Morning Shift]
CorrectIncorrectHint
\(
\begin{aligned}
&\text { The unit digit of the } 4 \text { digit number will be } 5 \text {. }\\
&\begin{array}{|c|c|c|c|}
\hline x & y & z & 5 \\
\hline
\end{array}
\end{aligned}
\)
Now, the sum \((x+y+z)\) should be of the \((3 p+1)\).
Therefore, the possible cases are
\(
(x, y, z)=(1,1,5),(1,1,2),(2,2,3),(2,3,5),(3,3,1) \text { and }(5,5,3) \text {. }
\)
So, total arrangements are
For \((1,1,5) \rightarrow \frac{3!}{2!}=3\);
For \((1,1,2) \rightarrow \frac{3!}{2!}=3\);
For \((2,2,3) \rightarrow \frac{3!}{2!}=3\);
For \((2,3,5) \rightarrow 3!=6\);
For \((3,3,1) \rightarrow \frac{3!}{2!}=3\);
For \((5,5,3) \rightarrow \frac{3!}{2!}=3\);
So, total number of arrangements \(=3+3+3+6+3+3=21\) -
Question 129 of 205
129. Question
The total number of 4-digit numbers whose greatest common divisor with 54 is 2, is ______. [JEE Main 2023 (Online) 29th January Evening Shift]
CorrectIncorrectHint
\(\operatorname{gcd}(a, 54)=2\) when a is a 4 digit no.
And \(54=3 \times 3 \times 3 \times 2\)
So, \(a=\) all even no. of 4 digits – Even multiple of 3 (4 digits)
\(
\begin{aligned}
& =4500-1500 \\
& =3000
\end{aligned}
\) -
Question 130 of 205
130. Question
If all the six digit numbers \(x_1 x_2 x_3 x_4 x_5 x_6\) with \(0<x_1<x_2<x_3<x_4<x_5<x_6\) are arranged in the increasing order, then the sum of the digits in the \(72^{\text {th }}\) number is _____. [JEE Main 2023 (Online) 29th January Morning Shift]
CorrectIncorrectHint
\(
1 \ldots \ldots \ldots \ldots \rightarrow{ }^8 C_5=56
\)
\(
23 \ldots \ldots \ldots \ldots \ldots \rightarrow{ }^6 C_4=\frac{15}{71}
\)
\(
\begin{aligned}
& 72^{\text {th }} \text { number }=245678 \\
& \text { Sum }=32
\end{aligned}
\) -
Question 131 of 205
131. Question
Five digit numbers are formed using the digits 1, 2, 3, 5, 7 with repetitions and are written in descending order with serial numbers. For example, the number 77777 has serial number 1. Then the serial number of 35337 is ______. [JEE Main 2023 (Online) 29th January Morning Shift]
CorrectIncorrectHint
No of 5 digit numbers starting with digit 1
\(
=5 \times 5 \times 5 \times 5=625
\)
No of 5 digit numbers starting with digit 2
\(
=5 \times 5 \times 5 \times 5=625
\)
No of 5 digit numbers starting with 31
\(
=5 \times 5 \times 5=125
\)
No of 5 digit numbers starting with 32
\(
=5 \times 5 \times 5=125
\)
No of 5 digit numbers starting with 33
\(
=5 \times 5 \times 5=125
\)
No of 5 digit numbers starting with 351
\(=5 \times 5=25\)No of 5 digit numbers starting with 352
\(
=5 \times 5=25
\)
No of 5 digit numbers starting with 3531
\(
=5
\)
No of 5 digit numbers starting with 3532
\(
=5
\)
Before 35337 will be 4 numbers,
So rank of 35337 will be 1690
So, in descending order serial number will be
\(
3125-1690+1=1436
\) -
Question 132 of 205
132. Question
A triangle is formed by \(X\)-axis, \(Y\)-axis and the line \(3 x+4 y=60\). Then the number of points \(P(a, b)\) which lie strictly inside the triangle, where \(a\) is an integer and \(b\) is a multiple of \(a\), is —–. [JEE Main 2023 (Online) 25th January Evening Shift]
CorrectIncorrectHint
\(
\text { If } x=1, y=\frac{57}{4}=14.25
\)
\((1,1)(1,2)-(1,14) \Rightarrow 14\) pts.
If \(x=2, y=\frac{27}{2}=13.5\)
\((2,2)(2,4) \ldots(2,12) \quad \Rightarrow 6\) pts.
If \(x=3, y=\frac{51}{4}=12.75\)
\((3,3)(3,6)-(3,12) \Rightarrow 4\) pts.
If \(x=4, y=12\)
\((4,4)(4,8) \quad \Rightarrow 2\) pts.
If \(x=5 . y=\frac{45}{4}=11.25\)
\((5,5),(5,10) \Rightarrow 2\) pts.
If \(x=6, y=\frac{21}{2}=10.5\)
\(
(6,6) \Rightarrow 1 pt
\)
If \(x=7, y=\frac{39}{4}=9.75\)
\(
(7,7) \Rightarrow 1 \text { pt. }
\)
If \(x=8, y=9\)
\(
(8,8) \quad \Rightarrow 1 pt \text {. }
\)
If \(x=9 y=\frac{33}{4}=8.25 \Rightarrow\) no pt.
Total = 31 pts. -
Question 133 of 205
133. Question
Suppose Anil’s mother wants to give 5 whole fruits to Anil from a basket of 7 red apples, 5 white apples and 8 oranges. If in the selected 5 fruits, at least 2 oranges, at least one red apple and at least one white apple must be given, then the number of ways, Anil’s mother can offer 5 fruits to Anil is _____. [JEE Main 2023 (Online) 25th January Evening Shift]
CorrectIncorrectHint
Total 8 oranges, 5 white apple and 7 red apple. 5 fruits needs to be selected.
Case I: 3 orange +1 red apple +1 white apple
\(
={ }^8 C_3 \times{ }^7 C_1 \times{ }^5 C_1=1960
\)Case II : 2 oranges +2 red apples +1 white apple.
\(
={ }^8 C_2 \times{ }^7 C_2 \times{ }^5 C_1=2940
\)Case III : 2 oranges +1 red apples +2 white apple.
\(
\begin{aligned}
& ={ }^8 C_2 \times{ }^7 C_1 \times{ }^5 C_2 \\
& =1960 \\
\text { Total } & =1960+2940+1960 \\
& =6860
\end{aligned}
\) -
Question 134 of 205
134. Question
Let \(x\) and \(y\) be distinct integers where \(1 \leq x \leq 25\) and \(1 \leq y \leq 25\). Then, the number of ways of choosing \(x\) and \(y\), such that \(x+y\) is divisible by 5 , is ____. [JEE Main 2023 (Online) 25th January Morning Shift]
CorrectIncorrectHint
Let \(x+y=5 \lambda\)
Possible cases are
\(
\begin{array}{llc}
x & y & \text { Number of ways } \\
5 \lambda(5,10,15,20,25) & 5 \lambda(5,10,15,20,25) & 20 \\
5 \lambda+1(1,6,11,16,21) & 5 \lambda+4(4,9,14,19,24) & 25 \\
5 \lambda+2(2,7,12,17,22) & 5 \lambda+3(3,8,13,18,23) & 25 \\
5 \lambda+3(3,8,13,18,23) & 5 \lambda+2(2,7,12,17,22) & 25 \\
5 \lambda+4(4,9,14,19,24) & 5 \lambda+1(1,6,11,16,21) & 25
\end{array}
\)
Total number of ways \(=20+25+25+25+25=120\)Note : In first case total number of ways \(=20\) as in the question given that the chosen \(x\) and \(y\) are distinct integers each time. So when you choose \(x\) as 5 then you can’t choose \(y\) as 5 . Possible values of \(y\) are \((10,15,20,25)\). So, here four possible pairs of \(( x , y )\) possible \(\{(5,10),(5,15),(5,20),(5,25)\}\).
Similarly, four possible pairs of \((x, y)\) possible each time when \(x=10,15,20\) and 25.
\(\therefore\) Total number of ways in the first case \(=5 \times 4=20\). -
Question 135 of 205
135. Question
A boy needs to select five courses from 12 available courses, out of which 5 courses are language courses. If he can choose at most two language courses, then the number of ways he can choose five courses is ________. [JEE Main 2023 (Online) 24th January Morning Shift]
CorrectIncorrectHint
Among 12 courses, 5 courses are of language.
\(\therefore\) Remaining 7 are different courses.
Now, number of ways to select 5 courses where at most 2 language courses present.
\(
\begin{array}{|c|c|c|c|}
\hline & \text { Language } & \text { Different } & \text { Number of ways } \\
\hline \text { Case 1 } & 0 & 5 & { }^5 C_0 \times{ }^7 C_5 \\
\hline \text { Case 2 } & 1 & 4 & { }^5 C_1 \times{ }^7 C_4 \\
\hline \text { Case 3 } & 2 & 3 & { }^5 C_2 \times{ }^7 C_3 \\
\hline
\end{array}
\)
\(
\begin{aligned}
& \therefore \text { Total number of ways } \\
& ={ }^5 C_0 \times{ }^7 C_5+{ }^5 C_1 \times{ }^7 C_4+{ }^5 C_2 \times{ }^7 C_3 \\
& =546
\end{aligned}
\) -
Question 136 of 205
136. Question
The number of 9 digit numbers, that can be formed using all the digits of the number 123412341 so that the even digits occupy only even places, is _______. [JEE Main 2023 (Online) 24th January Morning Shift]
CorrectIncorrectHint
Here, even digits are 2 and 4 .
Number of digit “2” presents \(=2\)
Number of digit “4” presents \(=2\)
\(\therefore\) Total even digits \(=4\)
\(\therefore\) Total 4 even places presents.
Number of ways to put those 4 digits in those 4 places \(=\frac{{ }^4 C_4 \times 4!}{2!2!}=\frac{4!}{2!2!}\)
Now, remaining 5 digits (three 1 and two 3 ) can be put in those 5 places in \(=\frac{{ }^5 C_5 \times 5!}{3!2!}=\frac{5!}{3!2!}\) ways.
\(\therefore\) Total possible 9 digit numbers
\(
=\frac{4!}{2!2!} \times \frac{5!}{3!2!}=60
\) -
Question 137 of 205
137. Question
The total number of three-digit numbers, divisible by 3 , which can be formed using the digits \(1,3,5,8\), if repetition of digits is allowed, is : [JEE Main 2023 (Online) 15th April Morning Shift]
CorrectIncorrectHint
The number of three-digit numbers divisible by 3 by considering the possible sums of digits that are divisible by 3 . Your approach is as follows:
1. Sum of digits is \(3:(1,1,1)\) – 1 possible number
2. Sum of digits is 9 : \((1,3,5)\) and \((3,3,3)\)Let’s consider the cases separately :
a. Sum of digits is 9 : \((1,3,5)\) For this case, we can arrange the digits in 3 ! ways : \(135,153,315,351,513\), and 531 .
b. Sum of digits is 9 : \((3,3,3)\) For this case, since all the digits are the same, there is only 1 possible number: 333 .Now, the total number of possible numbers when the sum of digits is 9 is :
\(
3!+1=6+1=7
\)
3. Sum of digits is 12 : \((1,3,8)-3\) ! possible numbers
4. Sum of digits is \(15:(5,5,5)\) – 1 possible number
5. Sum of digits is \(18:(5,5,8)-\frac{3!}{2!}\) possible numbers (since 5 is repeated)
6. Sum of digits is \(21:(5,8,8)-\frac{3!}{2!}\) possible numbers (since 8 is repeated)
7. Sum of digits is \(24:(8,8,8)\) – 1 possible numberAdding up the possible numbers for each case, we get:
\(
1+7+3!+1+\frac{3!}{2!}+\frac{3!}{2!}+1=1+7+6+1+3+3+1=22
\)
So, there are a total of 22 three-digit numbers divisible by 3 that can be formed using the digits \(\)1,3,5,8\(\) with repetition allowed. -
Question 138 of 205
138. Question
All words, with or without meaning, are made using all the letters of the word MONDAY. These words are written as in a dictionary with serial numbers. The serial number of the word MONDAY is : [JEE Main 2023 (Online) 13th April Evening Shift]
CorrectIncorrectHint
The letters of “MONDAY” arranged in alphabetical order are: \(A , D , M , N , O , Y\).
Fix A as the first letter, we can arrange the remaining 5 letters in 5 ! ways \(=120\) ways.
Fix \(D\) as the first letter, we can arrange the remaining 5 letters in 5 ! ways \(=120\) ways.
So far, we have 120 (for A) +120 (for D) \(=240\) words.
Now, let’s proceed with words starting with M:
Fix MA as the first two letters, we can arrange the remaining 4 letters in 4 ! ways = 24 ways.
Fix MD as the first two letters, we can arrange the remaining 4 letters in 4 ! ways = 24 ways.
Fix MN as the first two letters, we can arrange the remaining 4 letters in 4 ! ways = 24 ways.Now, we have 240 (for A and D) +24 (for MA) +24 (for MD) +24 (for MN) \(=312\) words.
After MN, we consider words that start with MO:
Fix MOA as the first three letters, we can arrange the remaining 3 letters in 3 ! ways \(=6\) ways.
Fix MOD as the first three letters, we can arrange the remaining 3 letters in 3 ! ways \(=6\) ways.Adding these to the total, we have 312 (previous total) +6 (for MOA) +6 (for MOD) \(=324\) words.
Next, we consider words that start with ‘MON’. The word ‘MONDAY’ comes after ‘MONAD’ in dictionary order, so:
Fix ‘MONA’ as the first four letters. The remaining 2 letters (‘D’ and ‘Y’) can be arranged in 2 ! ways, which gives us 2 more words: ‘MONADY’ and ‘MONAYD’.
So, we have 324 (previous total) +2 (for ‘MONADY’ and ‘MONAYD’) \(=326\) words.
Finally, we have the word ‘MONDAY’ itself, which is the 327 th word. -
Question 139 of 205
139. Question
The number of five digit numbers, greater than 40000 and divisible by 5 , which can be formed using the digits \(0,1,3,5,7\) and 9 without repetition, is equal to : [JEE Main 2023 (Online) 12th April Morning Shift]
CorrectIncorrectHint
Since the five-digit number must be greater than 40000 , the only options for the first digit are 5,7 , or 9 . That leaves 3 remaining choices for the first digit.
Since the number has to be divisible by 5 , the last digit must be 0 or 5 . If the first digit is 5 , the last digit can only be 0 , since digits cannot be repeated. If the first digit is 7 or 9 , the last digit can be 0 or 5 , so there are 2 choices.
Five possible configurations for the first and last digits :
\(-5 x x x 0\)
\(-7 x x x 0\)
\(-7 x x x 5\)
\(-9 x x x 0\)
\(-9 x x x 5\)
For each of these configurations, there are three places in the middle that can be filled with the remaining 4 unused digits.
Since repetition isn’t allowed, there are 4 options for the second digit, 3 for the third, and 2 for the fourth, which can be represented as \({ }^4 P_3\), or permutations of 4 items taken 3 at a time. This is equal to \(4 \times 3 \times 2=24\).So, for each of the 5 configurations, there are 24 ways to arrange the middle three digits. Therefore, the total number of five-digit numbers that meet the criteria is 5 \(\times 24=120\).
-
Question 140 of 205
140. Question
If the letters of the word MATHS are permuted and all possible words so formed are arranged as in a dictionary with serial numbers, then the serial number of the word THAMS is : [JEE Main 2023 (Online) 11th April Evening Shift]
CorrectIncorrectHint
To solve this problem, we start by finding the number of permutations before we reach a word that begins with \(T\).
We have 5 letters in the word MATHS. If we fix the first letter, there are \(4!(=4 \times 3 \times 2\) \(\times 1=24\) ) ways to arrange the remaining letters.
The letters before T in alphabetical order are A, H, M, and S. For each of these 4 letters, there are 4 ! ways to arrange the rest of the word, giving \(4 \times 4\) ! \(=96\) words that come before any words starting with \(T\).
Then, in the section of words that start with ‘ \(T\) ‘, we start with ‘TA’. There are 3 remaining letters after ‘TA’, hence the permutations for words that start with ‘TA’ are \((5-2)!=3!=6\).
So, the total permutations for all words that come before ‘TH’ is \(96+6=102\).
Now, we need to count the words that come before ‘THAMS’. After ‘TH’, the letters left are ‘AMS’. Arranged in dictionary order, they would be ‘AMS’, ‘ASM’, ‘MAS’, ‘MSA’, ‘SAM’, ‘SMA’. So, ‘THAMS’ is the first word in the ‘TH’ category, so it is the \(103^{\text {rd }}\) word overall when counting from the beginning. -
Question 141 of 205
141. Question
The number of triplets \((x, y , z )\), where \(x, y , z\) are distinct non negative integers satisfying \(x+y+z=15\), is : [JEE Main 2023 (Online) 11th April Morning Shift]
CorrectIncorrectHint
We have, \(x+y+z=15\)
\(
\begin{aligned}
\text { Total number of solution } & ={ }^{15+3-1} C_{3-1} \\
& ={ }^{17} C_2=\frac{17 \times 16}{1 \times 2}=136
\end{aligned}
\)Now, we need to exclude the solutions where two of \((x, y, z)\) are the same.
1) For the case \(x=y \neq z\) :
\(
2 x+z=15
\)
The solutions are :
\(
\begin{aligned}
& x=0, z=15 \\
& x=1, z=13 \\
& x=2, z=11 \\
& x=3, z=9 \\
& x=4, z=7 \\
& x=5, z=5 \text { (Not valid as all are the same) } \\
& x=6, z=3 \\
& x=7, z=1
\end{aligned}
\)
Out of these, 7 are valid.
Similarly, for the cases \(y=z \neq x\) and \(z=x \neq y\), there will be 7 valid solutions for each, so a total of \(7 \times 3=21\) solutions where two of the variables are equal.
Thus, the number of triplets where all are distinct is :
\(
136-21=115
\)
There is one solution in which \(x = y = z\)
Required answer \(=136-21-1=114\) -
Question 142 of 205
142. Question
Eight persons are to be transported from city \(A\) to city \(B\) in three cars of different makes. If each car can accommodate at most three persons, then the number of ways, in which they can be transported, is : [JEE Main 2023 (Online) 10th April Evening Shift]
CorrectIncorrectHint
Let \(C_1, C_2\) and \(C_3\) be the three cars in which 8 person are to be transported from city \(A\) to city \(B\).
\(
\begin{array}{ccc}
C_1 & C_2 & C_3 \\
\downarrow & \downarrow & \downarrow \\
3 & 3 & 2
\end{array}
\)
Let the number of persons transported in cars \(C_1, C_2\) and \(C_3\) are 3,3 and 2 respectively.There are total \(\frac{8!}{3!3!2!2!}\) group
\(
\therefore \text { They can travel } \frac{8!}{3!3!2!2!} \times 3 \text { ! ways or } 1680 \text { ways }
\) -
Question 143 of 205
143. Question
If the number of words, with or without meaning, which can be made using all the letters of the word MATHEMATICS in which \(C\) and \(S\) do not come together, is \((6!) k\) , then \(k\) is equal to : [JEE Main 2023 (Online) 8th April Evening Shift]
CorrectIncorrectHint
Total number of words \(=\frac{11!}{2!2!2!}\)
Number of words in which \(C\) and \(S\) are together
\(
=\frac{10!}{2!2!2!} \times 2!
\)
So, required number of words
\(
\begin{aligned}
& =\frac{11!}{2!2!2!}-\frac{10!}{2!2!} \\
& =\frac{11 \times 10!}{2!2!2!}-\frac{10!}{2!2!} \\
& =\frac{10!}{2!2!}\left[\frac{11}{2}-1\right]=\frac{10!}{2!2!} \times \frac{9}{2} \\
& =5670 \times 6! \\
& \Rightarrow k(6!)=5670 \times 6! \\
& \Rightarrow k=5670
\end{aligned}
\) -
Question 144 of 205
144. Question
The number of arrangements of the letters of the word “INDEPENDENCE” in which all the vowels always occur together is : [JEE Main 2023 (Online) 8th April Morning Shift]
CorrectIncorrectHint
In the given word,
vowels are : I, E, E, E, EConsonants are : N, D, P, N, D, N, C
So, number of words \(=\frac{8!}{3!2!} \times \frac{5!}{4!}\)
\(
=\frac{8 \times 7 \times 6 \times 5 \times 4}{2} \times 5=16800
\)
Concept :Out of \(n\) objects, if \(r\) things are same, so number of ways \(=\frac{n!}{r!}\)
-
Question 145 of 205
145. Question
The number of ways, in which 5 girls and 7 boys can be seated at a round table so that no two girls sit together, is : [JEE Main 2023 (Online) 8th April Morning Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& 6!\times^7 C_5 \times 5! \\
& \Rightarrow 720 \times 21 \times 120 \\
& \Rightarrow 2 \times 360 \times 7 \times 3 \times 120 \\
& \Rightarrow 126 \times(5!)^2
\end{aligned}
\)Alternate:
We have,
Number of girls \(=5\)
Number of boys \(=7\)
So, number of ways of arranging boys
around the table \(=6\) ! and 5 girls can be arranged in 7 gaps in \({ }^7 P_5\) ways.
\(\therefore\) Required no. of ways \(=6!\times{ }^7 P _5=126 \times(5!)^2\) -
Question 146 of 205
146. Question
Let the number of elements in sets \(A\) and \(B\) be five and two respectively. Then the number of subsets of \(A \times B\) each having at least 3 and at most 6 elements is: [JEE Main 2023 (Online) 8th April Morning Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& \text { Since, } n( A )=5, n( B )=2 \\
& \Rightarrow n( A \times B )=n( A ) \times n( B ) \\
& =5 \times 2=10
\end{aligned}
\)So, number of subsets having 3 elements \(={ }^{10} C _3\)
Number of subsets having 4 elements \(={ }^{10} C _4\)
Number of subsets having 5 elements \(={ }^{10} C _5\)
Number of subsets having 6 elements \(={ }^{10} C _6\)
\(\therefore\) No. of subsets \(={ }^{10} C _3+{ }^{10} C _4+{ }^{10} C _5+{ }^{10} C _6\)
\(
=120+210+252+210=792
\) -
Question 147 of 205
147. Question
All the letters of the word PUBLIC are written in all possible orders and these words are written as in a dictionary with serial numbers. Then the serial number of the word PUBLIC is :[JEE Main 2023 (Online) 6th April Evening Shift]
CorrectIncorrectHint
Given word is PUBLIC.
Alphabetical order of letters is BCILPU. So, number of words start with letter.
\(
\text { B }—-\text { is } 5!=120
\)
\(
\begin{aligned}
& \text { C—- is } 5!=120 \\
& \text { I—- is } 5!=120
\end{aligned}
\)
\(L —–\) is \(5!=120\)
\(PB —-\) is \(4!=24\)
\(PC —-\) is \(4!=24\)
\(
\begin{aligned}
& PI —-\text { is } 4!=24 \\
& PL —- \text { is } 4!=24
\end{aligned}
\)
PUBC — is \(2!=2\)PUBI – is \(2!=2\)
PUBLC – is \(1!=1\)
PUBLIC is \(0!=1\)
\(\therefore\) Serial number of the word PUBLIC
\(
=4 \times 120+4 \times 24+2 \times 2+2 \times 1=582
\) -
Question 148 of 205
148. Question
The value of \(\frac{1}{1!50!}+\frac{1}{3!48!}+\frac{1}{5!46!}+\ldots .+\frac{1}{49!2!}+\frac{1}{51!1!}\) is : [JEE Main 2023 (Online) 1st February Morning Shift]
CorrectIncorrectHint
\(
\begin{aligned}
S & =\frac{1}{1!50!}+\frac{1}{3!48!}+\frac{1}{5!46!}+\ldots \ldots+\frac{1}{49!2!}+\frac{1}{51!1!} \\
& =\frac{1}{51!}\left(\frac{51!}{1!50!}+\frac{51!}{3!48!}+\frac{51!}{5!46!}+\ldots \ldots+\frac{51!}{49!2!}+\frac{51!}{51!0!}\right)
\end{aligned}
\)
\(
\begin{aligned}
& =\frac{1}{51!}\left({ }^{51} C_{50}+{ }^{51} C_{48}+{ }^{51} C_{46}+\ldots \ldots .+{ }^{51} C_2+{ }^{51} C_0\right) \\
& \because{ }^n C_0+{ }^n C_2+{ }^n C_4+\ldots \ldots=2^{n-1} \\
& \therefore S=\frac{2^{50}}{51!}
\end{aligned}
\) -
Question 149 of 205
149. Question
The number of ways of selecting two numbers \(a\) and \(b, a \in\{2,4,6, \ldots, 100\}\) and \(b \in\{1,3,5, \ldots \ldots, 99\}\) such that 2 is the remainder when \(a+b\) is divided by 23 is : [JEE Main 2023 (Online) 30th January Evening Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& a+b=23 \lambda+2 \\
& \lambda=0,1,2, \ldots ., \text { but } \lambda \text { cannot be even as } a+b \text { is odd } \\
& \lambda=1(a, b) \rightarrow 12 \text { pairs } \\
& \lambda=3(a, b) \rightarrow 35 \text { pairs } \\
& \lambda=5(a, b) \rightarrow 42 \text { pairs } \\
& \lambda=7(a, b) \rightarrow 19 \text { pairs } \\
& \lambda=9(a, b) \rightarrow 0 \text { pairs }
\end{aligned}
\)
.
.
.
\(
\text { Total }=12+35+42+19=108
\) -
Question 150 of 205
150. Question
The letters of the word OUGHT are written in all possible ways and these words are arranged as in a dictionary, in a series. Then the serial number of the word TOUGH is : [JEE Main 2023 (Online) 29th January Evening Shift]
CorrectIncorrectHint
Lets arrange the letters of OUGHT in alphabetical order.
\(
G , H , O , T , U
\)
\(
\begin{aligned}
& G —-\rightarrow 4! \\
& H —-\rightarrow 4! \\
& O —-\rightarrow 4! \\
& TG —\rightarrow 3! \\
& \text { Т H }—\rightarrow 3! \\
& \text { T O G }–\rightarrow 2! \\
& \text { T O H }–\rightarrow 2! \\
& \text { T O U G H } \rightarrow 1! \\
& \hline \text { Total }=89
\end{aligned}
\) -
Question 151 of 205
151. Question
The number of 3 digit numbers, that are divisible by either 3 or 4 but not divisible by 48, is : [JEE Main 2023 (Online) 29th January Evening Shift]
CorrectIncorrectHint
Number divisible by \(3=300\)
Number divisible by \(4=225\)
Number divisible by \(12=75\)
Number divisible by \(48=18\)
Total required number \(=300+225-75-18=432\) -
Question 152 of 205
152. Question
The number of numbers, strictly between 5000 and 10000 can be formed using the digits 1, 3, 5, 7, 9 without repetition, is : [JEE Main 2023 (Online) 25th January Evening Shift]
CorrectIncorrectHint
Numbers between 5000 & 10000
Using digits \(1,3,5,7,9\)
\(
\text { Total Numbers }=3 \times 4 \times 3 \times 2=72
\) -
Question 153 of 205
153. Question
\(\sum_{k=0}^6{ }^{51-k} C_3\) is equal to : [JEE Main 2023 (Online) 25th January Evening Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& \sum_{ k =0}^6{ }^{51- k } C _3 \\
& ={ }^{51} C _3+{ }^{50} C _3+{ }^{49} C _3+\ldots+{ }^{45} C _3 \\
& ={ }^{45} C _3+{ }^{46} C _3+\ldots \ldots+{ }^{51} C _3 \\
& ={ }^{45} C _4+{ }^{45} C _3+{ }^{46} C _3+\ldots \ldots+{ }^{51} C _3-{ }^{45} C _4 \\
& \left({ }^{ n } C _{ r }+{ }^{ n } C _{ r -1}={ }^{ n +1} C _{ r }\right) \\
& ={ }^{52} C _4-{ }^{45} C _4
\end{aligned}
\) -
Question 154 of 205
154. Question
The number of integers, greater than 7000 that can be formed, using the digits 3, 5, 6, 7, 8 without repetition is : [JEE Main 2023 (Online) 24th January Evening Shift]
CorrectIncorrectHint
Four digit numbers greater than \(7000=2 \times 4 \times 3 \times 2=48\)
Five digit number \(=5!=120\)
Total number greater than \(7000=120+48=168\)
-
Question 155 of 205
155. Question
The number of square matrices of order 5 with entries from the set \(\{0,1\}\), such that the sum of all the elements in each row is 1 and the sum of all the elements in each column is also 1 , is : [JEE Main 2023 (Online) 24th January Evening Shift]
CorrectIncorrectHint
\(\because\) In every row and every column there would be exactly one 1 and four zeroes.
Number of matrices \(={ }^5 C_1 \cdot{ }^4 C_1 \cdot{ }^3 C_1 \cdot{ }^2 C_1 \cdot{ }^1 C_1=120\)
-
Question 156 of 205
156. Question
The number of natural numbers lying between 1012 and 23421 that can be formed using the digits \(2,3,4,5,6\) (repetition of digits is not allowed) and divisible by 55 is ______. [JEE Main 2022 (Online) 29th July Evening Shift]
CorrectIncorrectHint
Case-I:
When number is 4-digit number \((\overline{a b c d})\) here \(d\) is fixed as 5
So, \((a, b, c)\) can be \((6,4,3),(3,4,6),(2,3,6),(6,3,2),(3,2,4)\) or \((4,2,3)\)
\(\Rightarrow 6\) numbersCase-II: No number possible
-
Question 157 of 205
157. Question
The number of matrices of order \(3 \times 3\), whose entries are either 0 or 1 and the sum of all the entries is a prime number, is _____. [JEE Main 2022 (Online) 29th July Morning Shift]
CorrectIncorrectHint
In a \(3 \times 3\) order matrix there are 9 entries.
These nine entries are zero or one.
The sum of positive prime entries are \(2,3,5\) or 7 .
\(
\begin{aligned}
& \text { Total possible matrices }=\frac{9!}{2!\cdot 7!}+\frac{9!}{3!\cdot 6!}+\frac{9!}{5!\cdot 4!}+\frac{9!}{7!\cdot 2!} \\
& =34+84+126+36 \\
& =282
\end{aligned}
\) -
Question 158 of 205
158. Question
A class contains \(b\) boys and \(g\) girls. If the number of ways of selecting 3 boys and 2 girls from the class is 168 , then \(b +3 g\) is equal to ____. [JEE Main 2022 (Online) 28th July Evening Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& { }^b C_3 \cdot{ }^g C_2=168 \\
& \Rightarrow \frac{b(b-1)(b-2)}{6} \cdot \frac{g(g-1)}{2}=168 \\
& \Rightarrow b(b-1)(b-2) \quad g(g-1)=2^5 \cdot 3^2 \cdot 7 \\
& \Rightarrow b(b-1)(b-2) \quad g(g-1)=6 \cdot 7 \cdot 8 \cdot 3 \cdot 2 \\
& \therefore b=8 \text { and } g=3 \\
& \therefore b+3 g=17
\end{aligned}
\) -
Question 159 of 205
159. Question
Let \(S\) be the set of all passwords which are six to eight characters long, where each character is either an alphabet from \(\{A, B, C, D, E\}\) or a number from \(\{1,2,3,4,5\}\) with the repetition of characters allowed. If the number of passwords in \(S\) whose at least one character is a number from \(\{1,2,3,4,5\}\) is \(\alpha \times 5^6\), then \(\alpha\) is equal to ____. [JEE Main 2022 (Online) 28th July Morning Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& \text { If password is } 6 \text { character long, then } \\
& \text { Total number of ways having atleast one number }=10^6-5^6 \\
& \text { Similarly, if } 7 \text { character long }=10^7-5^7 \\
& \text { and if } 8 \text {-character long }=10^8-5^8 \\
& \text { Number of password }=\left(10^6+10^7+10^8\right)-\left(5^6+5^7+5^8\right) \\
& =5^6\left(2^6+5.2^7+25.2^8-1-5-25\right) \\
& =5^6(64+640+6400-31) \\
& =7073 \times 5^6 \\
& \therefore \alpha=7073 .
\end{aligned}
\) -
Question 160 of 205
160. Question
Numbers are to be formed between 1000 and 3000 , which are divisible by 4 , using the digits \(1,2,3,4,5\) and 6 without repetition of digits. Then the total number of such numbers is ____. [JEE Main 2022 (Online) 26th July Evening Shift]
CorrectIncorrectHint
Here \(1^{\text {st }}\) digit is 1 or 2 only
Case-I:
If first digit is 1
Then last two digits can be \(24,32,36,52,56,64\)
Case – II:
If first digit is 2 then last two digit can be \(16,36,56,64\)
\(
\text { Total ways }=12+18=30 \text { ways }
\) -
Question 161 of 205
161. Question
The number of 5-digit natural numbers, such that the product of their digits is 36 , is ____. [JEE Main 2022 (Online) 26th July Morning Shift]
CorrectIncorrectHint
Factors of \(36=2^2 \cdot 3^2 \cdot 1\)
Five-digit combinations can be
\(
\begin{aligned}
& (1,2,2,3,3)(1,4,3,3,1),(1,9,2,2,1) \\
& (1,4,9,11)(1,2,3,6,1)(1,6,6,1,1)
\end{aligned}
\)
i.e., total numbers
\(
\begin{aligned}
& \frac{5!}{2!2!}+\frac{5!}{2!2!}+\frac{5!}{2!2!}+\frac{5!}{3!}+\frac{5!}{2!}+\frac{5!}{3!2!} \\
& =(30 \times 3)+20+60+10=180
\end{aligned}
\) -
Question 162 of 205
162. Question
The letters of the word ‘MANKIND’ are written in all possible orders and arranged in serial order as in an English dictionary. Then the serial number of the word ‘MANKIND’ is _____. [JEE Main 2022 (Online) 25th July Morning Shift]
CorrectIncorrectHint
\(
\begin{array}{|l|l|l|l|l|l|l|}
\hline M & A & N & K & I & N & D \\
\hline
\end{array}
\)
Alphabetical order of the given word is
A,D,I,K,M,N,N
\(
\frac{4 \times 6!}{2!}+(5!\times 0)+\frac{4!\times 3}{2!}+(3!\times 2)+(2!\times 1)+(1!\times 1)+(0!\times 0)+1=1492
\)Explanation:
Arranging the letters alphabetically, we get
ADIKMNN
When the word starts with any of the letters \(A / D / I / K\), the number of possibilities = \(\frac{6!}{2!} \times 4=1440\)
Now when the word starts with MA, then the number of possibilities \(=\frac{4!}{2!} \times 3=36\)
Now when the word starts with MAN, then the number of possibilities \(=3!\times 2=12\)
Now when the word starts with MANK, then the number of possibilities \(=4\)
Hence, rank of the work MANKIND is 1492 -
Question 163 of 205
163. Question
The number of 6 -digit numbers made by using the digits \(1,2,3,4,5,6,7\), without repetition and which are multiple of 15 is ____. [JEE Main 2022 (Online) 30th June Morning Shift]
CorrectIncorrectHint
A number is multiple of 15 when the number is divisible by 5 and sum of digits of the number is divisible by 3 .
\(
\begin{array}{|l|l|l|l|l|l|}
\hline & & & & & 5 \\
\hline
\end{array}
\)
Among \(1,2,3,4,5,6,7\) unit place is filled with 5 so it is multiple of 5 .
Now to make it divisible by 3 , take remaining 5 digits such a way that sum becomes divisible by 3 .
Remaining 5 digits can be
(1) \(1,2,3,4,6\)Here sum \(=1+2+3+4+6+5=21\) (divisible by 3 )
This 5 digits can be filled in those 5 placed without repetition in \(5 \times 4 \times 3 \times 2 \times 1\) \(=51=120\) ways(2) \(2,3,4,6,7\)
Here sum \(=2+3+4+6+7+5=27\) (divisible by 3 )
\(\therefore\) Number of ways \(=51=120\)(3) \(1,2,3,6,7\)
Here sum \(=1+2+3+6+7+5=24\) (divisible by 3 )
\(\therefore\) Number of ways \(=51=120\)
\(\therefore\) Total possible 6 digit numbers divisible by 15
\(
=120+120+120=360
\) -
Question 164 of 205
164. Question
The total number of four digit numbers such that each of first three digits is divisible by the last digit, is equal to ______. [JEE Main 2022 (Online) 29th June Evening Shift]
CorrectIncorrectHint
If unit digit is 1 then \(\rightarrow 9 \times 10 \times 10=900\) numbers
If unit digit is 2 then \(\rightarrow 4 \times 5 \times 5=100\) numbers
If unit digit is 3 then \(\rightarrow 3 \times 4 \times 4=48\) numbers
If unit digit is 4 then \(\rightarrow 2 \times 3 \times 3=18\) numbers
If unit digit is 5 then \(\rightarrow 1 \times 2 \times 2=4\) numbers
If unit digit is 6 then \(\rightarrow 1 \times 2 \times 2=4\) numbers
For \(7,8,9 \rightarrow 4+4+4=12\) Numbers
Total \(=1086\) Numbers
-
Question 165 of 205
165. Question
Let \(b_1 b_2 b_3 b_4\) be a 4-element permutation with \(b_i \in\{1,2,3, \ldots \ldots . ., 100\}\) for \(1 \leq i \leq 4\) and \(b_i \neq b_j\) for \(i \neq j\), such that either \(b_1, b_2, b_3\) are consecutive integers or \(b_2, b_3, b_4\) are consecutive integers. Then the number of such permutations \(b_1 b_2 b_3 b_4\) is equal to ____. [JEE Main 2022 (Online) 29th June Morning Shift]
CorrectIncorrectHint
There are 98 sets of three consecutive integer and 97 sets of four consecutive integers.
Using the principle of inclusion and exclusion,
Number of permutations of \(b_1 b_2 b_3 b_4=\) Number of permutations when \(b_1 b_2 b_3\) are consecutive + Number of permutations when \(b_2 b_3 b_4\) are consecutive – Number of permutations when \(b_1 b_2 b_3 b_4\) are consecutive
\(
=97 \times 98+97 \times 98-97=97 \times 195=18915 \text {. }
\) -
Question 166 of 205
166. Question
Let \(A\) be a matrix of order \(2 \times 2\), whose entries are from the set \(\{0,1,2,3,4,5\}\). If the sum of all the entries of \(A\) is a prime number \(p, 2<p<8\), then the number of such matrices \(A\) is ____. [JEE Main 2022 (Online) 27th June Evening Shift]
CorrectIncorrectHint
\(\because\) Sum of all entries of matrix A must be prime \(p\) such that \(2<p<8\) then sum of entries may be 3,5 or 7 .
If sum is 3 then possible entries are \((0,0,0,3),(0,0,1,2)\) or \((0,1,1,1)\).
\(\therefore\) Total number of matrices \(=4+4+12=20\)
If sum of 5 then possible entries are \((0,0,0,5),(0,0,1,4),(0,0,2,3),(0,1,1,3),(0,1,2,2)\) and \((1,1,1,2)\).
\(\therefore\) Total number of matrices \(=4+12+12+12+12+4=56\)
If sum is 7 then possible entries are
\(
(0,0,2,5),(0,0,3,4),(0,1,1,5),(0,3,3,1),(0,2,2,3),(1,1,1,4),(1,2,2,2),(1,1,2 \text {, }
\)
\(3)\) and \((0,1,2,4)\).
Total number of matrices with sum \(7=104\)
\(\therefore\) Total number of required matrices
\(
\begin{aligned}
& =20+56+104 \\
& =180
\end{aligned}
\) -
Question 167 of 205
167. Question
The number of ways, 16 identical cubes, of which 11 are blue and rest are red, can be placed in a row so that between any two red cubes there should be at least 2 blue cubes, is _____.[JEE Main 2022 (Online) 27th June Morning Shift]
CorrectIncorrectHint
First we arrange 5 red cubes in a row and assume \(x_1, x_2, x_3, x_4, x_5\) and \(x_6\) number of blue cubes between them
\(
\begin{array}{rrrrrr}
\square & \square & \square & \square & \square \\
x_1 & x_2 & x_3 & x_4 & x_5 & x_6
\end{array}
\)
Here, \(x_1+x_2+x_3+x_4+x_5+x_6=11\) and \(x_2, x_3, x_4, x_5 \geq 2\)
So \(x_1+x_2+x_3+x_4+x_5+x_6=3\)No. of solutions \(={ }^8 C_5=56\)
-
Question 168 of 205
168. Question
The total number of 3-digit numbers, whose greatest common divisor with 36 is 2, is _____. [JEE Main 2022 (Online) 26th June Evening Shift]
CorrectIncorrectHint
\(
\because x \in[100,999], x \in N
\)Then \(\frac{x}{2} \in[50,499], \frac{x}{2} \in N\)
Number whose G.C.D. with 18 is 1 in this range have the required condition. There are 6 such number from \(18 \times 3\) to \(18 \times 4\). Similarly from \(18 \times 4\) to \(18 \times 5 \ldots . . ., 26\) \(\times 18\) to \(27 \times 18\)
\(\therefore\) Total numbers \(=24 \times 6+6=150\)
The extra numbers are \(53,487,491,493,497\) and 499 . -
Question 169 of 205
169. Question
There are ten boys \(B _1, B _2\), \(\qquad\) \(B_{10}\) and five girls \(G_1, G_2\), \(\qquad\) \(G _5\) in a class. Then the number of ways of forming a group consisting of three boys and three girls, if both \(B_1\) and \(B_2\) together should not be the members of a group, is ______. [JEE Main 2022 (Online) 26th June Morning Shift]
CorrectIncorrectHint
Number of ways when \(B _1\) and \(B _2\) are not together
\(=\) Total number of ways of selecting 3 boys \(-B_1\) and \(B_2\) are together
\(
\begin{aligned}
& ={ }^{10} C _3-{ }^8 C _1 \\
& =\frac{10.9 \cdot 8}{1.2 \cdot 3}-8 \\
& =112
\end{aligned}
\)Number of ways to select 3 girls \(={ }^5 C _3=10\)
\(\therefore\) Total number of ways \(=112 \times 10=1120\) -
Question 170 of 205
170. Question
The total number of three-digit numbers, with one digit repeated exactly two times, is _______. [JEE Main 2022 (Online) 25th June Evening Shift]
CorrectIncorrectHint
Case-1 : All digits are non-zero
\(
{ }^9 C_2 \text {. 2. } \frac{3!}{2}=216
\)
Case-2 : One digit is 0
\(
\begin{aligned}
& 0,0, x \Rightarrow{ }^9 C_1 \cdot 1=9 \\
& 0, x, x \Rightarrow{ }^9 C_1 \cdot 2=18 \\
& \text { Total }=216+27=243
\end{aligned}
\) -
Question 171 of 205
171. Question
The number of 3-digit odd numbers, whose sum of digits is a multiple of 7, is ____.[JEE Main 2022 (Online) 25th June Morning Shift]
CorrectIncorrectHint
For odd number unit place shall be \(1,3,5,7\) or 9 .
\(\therefore xy 1, xy 3, xy 5, xy 7, xy 9\) are the type of numbers. numbers.If \(x y 1\) then \(x+y=6,13,20 \ldots\) Cases are required
i.e., \(6+6+0+\ldots=12\) waysIf \(x y 3\) then
\(x+y=4,11,18, \ldots\) Cases are required
i.e., \(4+8+1+0 \ldots=13\) waysSimilarly for \(x y 5\), we have \(x+y=2,9,16, \ldots\)
i.e., \(2+9+3=14\) ways
for \(x y\) we have
\(
x+y=0,7,14, \ldots
\)
i.e., \(0+7+5=12\) waysAnd for \(x\) y we have
\(
x+y=5,12,19 \ldots
\)
i.e., \(5+7+0 \ldots=12\) ways
\(\therefore\) Total 63 ways -
Question 172 of 205
172. Question
Let \(A\) be a \(3 \times 3\) matrix having entries from the set \(\{-1,0,1\}\). The number of all such matrices A having sum of all the entries equal to 5 , is _____. [JEE Main 2022 (Online) 25th June Morning Shift]
CorrectIncorrectHint
CASE I:
\(1 \rightarrow 7\) times and \(-1 \rightarrow 2\) times number of possible marrix \(=\frac{9!}{7!2!}=36\)
Case-II:
\(1 \rightarrow 6\) times,
\(-1 \rightarrow 1\) times
and \(0 \rightarrow 2\) times
number of possible marrix \(=\frac{9!}{6!2!}=252\)
Case-III:
\(1 \rightarrow 5\) times,
and \(0 \rightarrow 4\) times
number of possible marrix \(=\frac{9!}{5!4!}=126\)Hence total number of all such matrix \(A=414\)
-
Question 173 of 205
173. Question
The number of 7-digit numbers which are multiples of 11 and are formed using all the digits \(1,2,3,4,5,7\) and 9 is _____. [JEE Main 2022 (Online) 24th June Evening Shift]
CorrectIncorrectHint
Digits are \(1,2,3,4,5,7,9\)
Multiple of \(11 \rightarrow\) Difference of sum at even and odd place is divisible by 11 .
Let number of the form abcdefg
\(
\begin{aligned}
& \therefore(a+c+e+g)-(b+d+f)=11 x \\
& a+b+c+d+e+f=31 \\
& \therefore \text { either } a+c+e+g=21 \text { or } 10 \\
& \therefore b+d+f=10 \text { or } 21
\end{aligned}
\)
Case-1
\(
\begin{aligned}
& a+c+e+g=21 \\
& b+d+f=10 \\
& (b, d, f) \in\{(1,2,7)(2,3,5)(1,4,5)\} \\
& (a, c, e, g) \in\{(1,4,7,9),(3,4,5,9),(2,3,7,9)\}
\end{aligned}
\)Case-2
\(
\begin{aligned}
& a + c + e + g =10 \\
& b + d + f =21 \\
& ( a , b , e , g ) \in\{1,2,3,4)\} \\
& ( b , d , f ) \&\{(5,7,9)\}
\end{aligned}
\)
\(\therefore\) Total number in case \(2=3!\times 4!=144\)
\(
\therefore \text { Total numbers }=144+432=576
\) -
Question 174 of 205
174. Question
In an examination, there are 5 multiple choice questions with 3 choices, out of which exactly one is correct. There are 3 marks for each correct answer, -2 marks for each wrong answer and 0 mark if the question is not attempted. Then, the number of ways a student appearing in the examination gets 5 marks is _____.[JEE Main 2022 (Online) 24th June Morning Shift]
CorrectIncorrectHint
Let student marks \(x\) correct answers and \(y\) incorrect. So
\(
3 x-2 y=5 \text { and } x+y \leq 5 \text { where } x, y \in W
\)
Only possible solution is \((x, y)=(3,2)\)
Students can mark correct answers by only one choice but for an incorrect answer, there are two choices. So total number of ways of scoring 5 marks \(={ }^5 C_3(1)^3 \cdot(2)^2=40\) -
Question 175 of 205
175. Question
The number of ways to distribute 30 identical candies among four children \(C _1, C _2\) \(C _3\) and \(C _4\) so that \(C _2\) receives at least 4 and at most 7 candies, \(C _3\) receives at least 2 and at most 6 candies, is equal to : [JEE Main 2022 (Online) 28th June Evening Shift]
CorrectIncorrectHint
By multinomial theorem, no. of ways to distribute 30 identical candies among four children \(C _1, C _2\) and \(C _3, C _4\)
\(
=\text { Coefficient of } x^{30} \text { in }\left(x^4+x^5+\ldots .+x^7\right)\left(x^2+x^3+\ldots .+x^6\right)\left(1+x+x^2 \ldots .\right)^2
\)
\(
\begin{aligned}
& =\text { Coefficient of } x^{24} \text { in } \frac{\left(1-x^4\right)}{1-x} \frac{\left(1-x^5\right)}{1-x} \frac{\left(1-x^{31}\right)^2}{(1-x)^2} \\
& =\text { Coefficient of } x^{24} \text { in }\left(1-x^4-x^5+x^9\right)(1-x)^{-4} \\
& ={ }^{27} C_{24}-{ }^{23} C_{20}-{ }^{22} C_{19}+{ }^{18} C_{15}=430
\end{aligned}
\) -
Question 176 of 205
176. Question
The total number of 5-digit numbers, formed by using the digits 1, 2, 3, 5, 6, 7 without repetition, which are multiple of 6, is : [JEE Main 2022 (Online) 28th June Morning Shift]
CorrectIncorrectHint
To make a no. divisible by 3 we can use the digits \(1,2,5,6,7\) or \(1,2,3,5,7\).
Using \(1,2,5,6,7\), number of even numbers is \(=4 \times 3 \times 2 \times 1 \times 2=48\)
Using \(1,2,3,5,7\), number of even numbers is \(=4 \times 3 \times 2 \times 1 \times 1=24\)
Required answer is 72 .
-
Question 177 of 205
177. Question
Let \(P_1, P_2, \ldots . ., P_{15}\) be 15 points on a circle. The number of distinct triangles formed by points \(P_i, P_j, P_k\) such that \(i+j+k \neq 15\), is : [JEE Main 2021 (Online) 1st September Evening Shift]
CorrectIncorrectHint
Total Number of Triangles \(={ }^{15} C_3\) \(i+j+k=15\) (Given)
\(
\begin{aligned}
&5 \text { Cases } \quad \quad 4 \text { Cases } \quad \quad 3 \text { Cases } \quad 1 \text { Cases }\\
&\begin{array}{c|c|cc|c|cc|c|cc|c|c}
i & j & k & i & j & k & i & j & k & i & j & k \\
\hline 1 & 2 & 12 & 2 & 3 & 10 & 3 & 4 & 8 & 4 & 5 & 6 \\
1 & 3 & 11 & 2 & 4 & 9 & 3 & 5 & 7 & & & \\
1 & 4 & 10 & 2 & 5 & 8 & & & & & & \\
1 & 5 & 9 & 2 & 6 & 7 & & & & & \\
1 & 6 & 8 & & & & & & & &
\end{array}
\end{aligned}
\)
Number of Possible triangles using the vertices \(P_i, P_j\),
\(P_k\) such that \(i+j+k \neq 15\) is equal to \({ }^{15} C_3-12=443\) -
Question 178 of 205
178. Question
If \({ }^n P_r={ }^n P_{r+1}\) and \({ }^n C_r={ }^n C_{r-1}\), then the value of \(r\) is equal to : [JEE Main 2021 (Online) 25th July Evening Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& { }^n P_r={ }^n P_{r+1} \Rightarrow \frac{n!}{(n-r)!}=\frac{n!}{(n-r-1)!} \\
& \Rightarrow(n-r)=1 \ldots . .(1) \\
& \Rightarrow \frac{n!}{r!(n-r)!}=\frac{n!}{(r-1)!(n-r+1)!} \\
& \Rightarrow \frac{1}{r(n-r)!}=\frac{1}{(n-r+1)(n-r)!}
\end{aligned}
\)
\(
\begin{aligned}
& \Rightarrow n-r+1=r \\
& \Rightarrow n+1=2 r \ldots (2)
\end{aligned}
\)
From (1) and (2), \(2 r-1-r=1 \Rightarrow r=2\) -
Question 179 of 205
179. Question
The sum of all the 4-digit distinct numbers that can be formed with the digits 1, 2, 2 and 3 is : [JEE Main 2021 (Online) 18th March Morning Shift]
CorrectIncorrectHint
The 4 -digit distinct numbers that can be formed with the digits \(1,2,2\) and 3 is 1223, 1232, 1322, 3122, 3212, 3221, 2132, 2312, 2213, 2231, 2321, 2123
The sum of the 4 -digit distinct numbers is \(=26664\)
Alternatively,
Digits are \(1,2,2\) and 3
Total number of distinct numbers \({ }^4 P _2=\frac{4!}{(4-2)!}=12\)
Total number when
1. 1 at unit place is 3
2. 2 at unit place is 6
3. 3 at unit place is 3
So, for different number \(1\) is at unit, tenth hundred and thousand place \(3\) times each
Therefore, \(3 \cdot 1 \cdot\left(1+10+10^2+10^3\right)\)
Similarly for different number 2 is at unit, tenth hundred and thousand place 6 times each
Therefore \(6 \cdot 2 \cdot\left(1+10+10^2+10^3\right)\)
Similarly for different number 3 is at unit, tenth hundred and thousand place 3 times each
Therefore \(3 \cdot 3 \cdot\left(1+10+10^2+10^3\right)\)
So the sum of the number is
\(
\begin{aligned}
& =(1 \cdot 3+2 \cdot 6+3 \cdot 3)\left(10^3+10^2+10+1\right) \\
& =(24) \cdot(1111) \\
& =26664
\end{aligned}
\) -
Question 180 of 205
180. Question
If the sides \(A B, B C\) and \(C A\) of a triangle \(A B C\) have 3,5 and 6 interior points respectively, then the total number of triangles that can be constructed using these points as vertices, is equal to : [JEE Main 2021 (Online) 17th March Evening Shift]
CorrectIncorrectHint
Total Number of triangles formed
\(
\begin{aligned}
& ={ }^{14}{C_3}-{ }^3{C_3}-{ }^5{C_3}-{ }^6{C_3} \\
& =333
\end{aligned}
\)Alternate:
Permutation :
We can construct a triangle by choosing any one point of all three sides. We can also construct a triangle by choosing one point from one side and remaining two points from either sides.
Number of ways of choosing 1 points out of 3 points from the side \(A B={ }^3 C_1\)
Number of ways of choosing 1 points out of 5 points from the side \(B C={ }^5 C_1\)
Number of ways of choosing 1points out of 6 points from the side \(A C={ }^6 C_1\)
Number of ways of choosing 2 points out of 6 points from the side \(A C={ }^6 C _2\)
Number of ways of choosing 2 points out of 5 points from the side \(B C={ }^5 C _2\)
Number of ways of choosing 2 points out of 3 points from the side \(A B={ }^3 C _2\)
Therefore total number of triangles will be,
\(
\begin{aligned}
& ={ }^3 C_1 \times{ }^5 C_1 \times{ }^6 C_1+{ }^3 C_1 \times{ }^5 C_2+{ }^5 C_1 \times{ }^3 C_2+{ }^3 C_1 \times{ }^6 C_2+{ }^6 C_1 \times \\
& { }^3 C_2+{ }^5 C _1 \times{ }^6 C _2+{ }^6 C _1 \times{ }^5 C _2 \\
& =90+30+15+45+18+75+60 \\
& =333
\end{aligned}
\) -
Question 181 of 205
181. Question
Team ‘A’ consists of 7 boys and \(n\) girls and Team ‘B’ has 4 boys and 6 girls. If a total of 52 single matches can be arranged between these two teams when a boy plays against a boy and a girl plays against a girl, then \(n\) is equal to : [JEE Main 2021 (Online) 17th March Morning Shift]
CorrectIncorrectHint
Total matches between boys of both team \(={ }^7 C_1 \times{ }^4 C_1=28\)
Total matches between girls of both team \(={ }^n C_1{ }^6 C_1=6 n\)
Now, \(28+6 n=52\)
\(
\Rightarrow n =4
\) -
Question 182 of 205
182. Question
Consider a rectangle \(ABCD\) having \(5,7,6,9\) points in the interior of the line segments \(AB , CD , BC , DA\) respectively. Let \(\alpha\) be the number of triangles having these points from different sides as vertices and \(\beta\) be the number of quadrilaterals having these points from different sides as vertices. Then \((\beta-\alpha)\) is equal to : [JEE Main 2021 (Online) 16th March Evening Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& \alpha={ }^6 C_1{ }^7 C_1{ }^9 C_1+{ }^5 C_1{ }^7 C_1{ }^9 C_1+{ }^5 C_1{ }^6 C_1{ }^9 C_1+{ }^5 C_1{ }^6 C_1{ }^7 C_1 \\
& =378+315+270+210=1173 \\
& \beta={ }^5 C_1{ }^6 C_1{ }^7 C_1{ }^9 C_1=1890 \\
& \therefore \beta-\alpha=1890-1173=717
\end{aligned}
\) -
Question 183 of 205
183. Question
A natural number has prime factorization given by \(n =2^{x}3^{y}5^{z}\), where \(y\) and \(z\) are such that \(y+z=5\) and \(y^{-1}+z^{-1}=\frac{5}{6}, y>z\). Then the number of odd divisions of \(n\), including 1 , is : [JEE Main 2021 (Online) 26th February Evening Shift]
CorrectIncorrectHint
Calculate the number of odd divisors of \(n\) :
Given \(n=2^x 3^y 5^z, y+z=5, \frac{1}{y}+\frac{1}{z}=\frac{5}{6}\) and \(y z=6\)
Also,
\(
\begin{aligned}
(y-z)^2 & =(y+z)^2-4 y z \\
& =25-24 \\
& = \pm 1
\end{aligned}
\)
\(
\begin{aligned}
& y+z=5 \quad \ldots \ldots(1) \\
& y-z= \pm 1 \quad \ldots \ldots .(2) \\
&
\end{aligned}
\)
By solving these equations we get \(y=3\) or \(2 \quad, z=2\) or 3
To calculate the odd divisors of \(n, x\) must be 0.
\(
n=2^0 3^3 5^2 \text { or } n=2^0 3^2 5^3
\)
Total odd divisors must be \((3+1)(2+1)=12\) -
Question 184 of 205
184. Question
The number of seven digit integers with sum of the digits equal to 10 and formed by using the digits 1, 2 and 3 only is : [JEE Main 2021 (Online) 26th February Morning Shift]
CorrectIncorrectHint
(I) First possibility is \(1,1,1,1,1,2,3\)
\(
\text { required number }=\frac{7!}{5!}=7 \times 6=42
\)
(II) Second possibility is 1, 1, 1, 1, 2, 2, 2
required number \(=\frac{7!}{4!3!}=\frac{7 \times 6 \times 5}{6}=35\)
\(
\text { Total }=42+35=77
\) -
Question 185 of 205
185. Question
The total number of positive integral solutions \((x, y, z)\) such that \(x y z=24\) is : [JEE Main 2021 (Online) 25th February Morning Shift]
CorrectIncorrectHint
x. y. \(z=24\)
x. \(y . z=2^3 .3^1\)Three 2 has to be distributed among \(x , y\) and \(z\)
Each may receive none, one or two
\(\therefore\) Number of ways \(={ }^{3+3-1} C_{3-1}={ }^5 C_2\) ways
Similarly one 3 has to be distributed among \(x, y\) and \(z\)
\(\therefore\) Number of ways \(={ }^{1+3-1} C_{3-1}={ }^3 C_2\) waysTotal ways \(={ }^5 C_2 \cdot{ }^3 C_2=30\)
-
Question 186 of 205
186. Question
A scientific committee is to be formed from 6 Indians and 8 foreigners, which includes at least 2 Indians and double the number of foreigners as Indians. Then the number of ways, the committee can be formed, is : [JEE Main 2021 (Online) 24th February Morning Shift]
CorrectIncorrectHint
Given,
Number of Indians \(=6\)
Number of foreigners \(=8\)
Committee of at least 2 Indians and double number of foreigners is to be formed.
Hence, the required cases are
\(
\begin{aligned}
& (2 I , 4 F )+(3 I , 6 F )+(4 I , 8 F ) \\
& ={ }^6 C_2 \times{ }^8 C_4+{ }^6 C_3 \times{ }^8 C_6+{ }^6 C_4 \times{ }^8 C_8 \\
& =(15 \times 70)+(20 \times 28)+(15 \times 1) \\
& =1050+560+15=1625
\end{aligned}
\) -
Question 187 of 205
187. Question
All the arrangements, with or without meaning, of the word FARMER are written excluding any word that has two \(R\) appearing together. The arrangements are listed serially in the alphabetic order as in the English dictionary. Then the serial number of the word FARMER in this list is ____. [JEE Main 2021 (Online) 1st September Evening Shift]
CorrectIncorrectHint
First find all possible words and then subtract words from each case that have both \(R\) together.
FARMER (6)
\(
A, E, F, M, R, R
\)
\(
\begin{array}{|l|l|l|l|l|l|}
\hline \text { A } & & & & & \\
\hline \text { E } & & & & & \\
\hline \text { F } & \text { A } & \text { E } & & & \\
\hline \text { F } & \text { A } & \text { M } & & & \\
\hline \text { F } & \text { A } & \text { R } & \text { E } \\
\hline \text { F } & \text { A } & \text { R } & \text { M } & \text { E } & \text { R } \\
\hline
\end{array}
\)
\(
\text { A……… } \Rightarrow \frac{5!}{2!}-4!\quad=36
\)
\(
\text { E…….. } \Rightarrow \frac{5!}{2!}-4!\quad=36
\)
\(
\text { FAE……. } \Rightarrow \frac{3!}{2!}-2=1
\)
\(
\text { FAM……. } \Rightarrow \frac{3!}{2!}-2=1
\)
\(
\begin{array}{lll}
\text { FARE …. } & \Rightarrow 2! & =2 \\
\text { FARMER } & \Rightarrow 1 & =1
\end{array}
\)
Total = 77 -
Question 188 of 205
188. Question
The number of six letter words (with or without meaning), formed using all the letters of the word ‘VOWELS’, so that all the consonants never come together, is _____. [JEE Main 2021 (Online) 31st August Morning Shift]
CorrectIncorrectHint
Total possible words \(=6!=720\)
When 4 consonants are together ( \(V , W , L , S\) ) such cases \(=3!\cdot 4!=144\)
All consonants should not be together
\(
\begin{aligned}
& =\text { Total }- \text { All consonants together, } \\
& =6!-3!4!=576
\end{aligned}
\) -
Question 189 of 205
189. Question
Let \(S=\{1,2,3,4,5,6,9\}\). Then the number of elements in the set \(T=\{A \subseteq S: A \neq \phi\) and the sum of all the elements of \(A\) is not a multiple of 3\(\}\) is ____. [JEE Main 2021 (Online) 27th August Evening Shift]
CorrectIncorrectHint
3 n type \(\rightarrow 3,6,9=P\)
\(3 n-1\) type \(\rightarrow 2,5=Q\)
\(3 n-2\) type \(\rightarrow 1,4=R\)
number of subset of \(S\) containing one element which are not divisible by \(3={ }^2 C _1+{ }^2\) \(C _1=4\)
number of subset of \(S\) containing two numbers whose some is not divisible by 3
\(
={ }^3 C _1 \times{ }^2 C _1+{ }^3 C _1 \times{ }^2 C _1+{ }^2 C _2+{ }^2 C _2=14
\)
number of subsets containing 3 elements whose sum is not divisible by 3
\(
={ }^3 C _2 \times{ }^4 C _1+\left({ }^2 C _2 \times{ }^2 C _1\right) 2+{ }^3 C _1\left({ }^2 C _2+{ }^2 C _2\right)=22
\)
number of subsets containing 4 elements whose sum is not divisible by 3
\(
\begin{aligned}
& ={ }^3 C _3 \times{ }^4 C _1+{ }^3 C _2\left({ }^2 C _2+{ }^2 C _2\right)+\left({ }^3 C _1{ }^2 C _1 \times{ }^2 C _2\right) 2 \\
& =4+6+12=22
\end{aligned}
\)
number of subsets of \(S\) containing 5 elements whose sum is not divisible by 3 .
\(
={ }^3 C _3\left({ }^2 C _2+{ }^2 C _2\right)+\left({ }^3 C _2{ }^2 C _1 \times{ }^2 C _2\right) \times 2=2+12=14
\)
number of subsets of \(S\) containing 6 elements whose sum is not divisible by \(3=4\)
\(\Rightarrow\) Total subsets of Set A whose sum of digits is not divisible by \(3=4+14+22+\) \(22+14+4=80\). -
Question 190 of 205
190. Question
A number is called a palindrome if it reads the same backward as well as forward. For example 285582 is a six digit palindrome. The number of six digit palindromes, which are divisible by 55 , is _____. [JEE Main 2021 (Online) 27th August Morning Shift]
CorrectIncorrectHint
\(5 a b b a 5\)
For divisible by 55 it shall be divisible by 11 and 5 both, for divisibility by 5 unit digit shall be 0 or 5 but as the number is six digit palindrome unit digit is 5 .
A number is divisible by 11 if the difference between sum of the digits in the odd places and the sum of the digits in the even places is a multiple of 11 or zero.
Sum of the digits in the even place \(=a+b+5\)
Sum of the digits in the odd places \(=a+b+5\)
Difference between the two sums \(=(a+b+5)-(a+b+5)=0\)
0 is divisible by 11 .Hence, 5 abba5 is divisible by 11 .
So, required number \(=10 \times 10=100\) -
Question 191 of 205
191. Question
If \({ }^1 P_1+2 \cdot{ }^2 P_2+3 .{ }^3 P_3+\ldots+15 \cdot{ }^{15} P_{15}={ }^q P_r-s, 0 \leq s \leq 1\), then \({ }^{q+s} C_{r-s}\) is equal to ____. [JEE Main 2021 (Online) 26th August Morning Shift]
CorrectIncorrectHint
\(
{ }^1 P_1+2 .{ }^2 P_2+3 .{ }^3 P_3+\ldots+15 .{ }^{15} P_{15}
\)
\(
\begin{aligned}
& =1!+2 \cdot 2!+3 \cdot 3!+\ldots .15 \times 15! \\
& =\sum_{r=1}^{15}(r+1)!-(r)!
\end{aligned}
\)
\(
\begin{aligned}
& =16!-1 \\
& ={ }^{16} P_{16}-1 \\
& \Rightarrow q = r =16, s =1 \\
& { }^{q+s} C_{r-s}={ }^{17} C_{15}=136
\end{aligned}
\) -
Question 192 of 205
192. Question
The number of three-digit even numbers, formed by the digits 0, 1, 3, 4, 6, 7 if the repetition of digits is not allowed, is _______. [JEE Main 2021 (Online) 26th August Morning Shift]
CorrectIncorrectHint
(i) When ‘0’ is at unit place
\(
\begin{array}{rlll}
\text { Case-ı } & \bar{\downarrow} & \bar{\downarrow} & \bar{\downarrow} \\
& 4 & 5 & 1(0)
\end{array} \quad \Rightarrow 4 \times 5 \times 1=20
\)
Number of numbers \(=20\)
(ii) When 4 or 6 are at unit place
\(
\begin{array}{rlll}
\text { Case-II } & \bar{\downarrow} & \bar{\downarrow} & \bar{\downarrow} \\
& 4 & 4 & 2(4,6)
\end{array}=4 \times 4 \times 2=32
\)
Total three digit even number \(=20+32=52\) -
Question 193 of 205
193. Question
Let \(n\) be a non-negative integer. Then the number of divisors of the form ” \(4 n+1\) ” of the number \((10)^{10} \cdot(11)^{11} \cdot(13)^{13}\) is equal to ____. [JEE Main 2021 (Online) 27th July Evening Shift]
CorrectIncorrectHint
\(
N=2^{10} \times 5^{10} \times 11^{11} \times 13^{13}
\)
Now, power of 2 must be zero,
power of 5 can be anything,
power of 13 can be anything
But, power of 11 should be even.
So, required number of divisors is
\(
1 \times 11 \times 14 \times 6=924
\) -
Question 194 of 205
194. Question
There are 5 students in class 10,6 students in class 11 and 8 students in class 12 . If the number of ways, in which 10 students can be selected from them so as to include at least 2 students from each class and at most 5 students from the total 11 students of class 10 and 11 is \(100 k\), then \(k\) is equal to ____. [JEE Main 2021 (Online) 25th July Morning Shift]
CorrectIncorrectHint
Class \(10^{\text {th }} 11^{\text {th }} 12^{\text {th }}\)
Total student \(5 \quad 6 \quad 8\)
Number of selection \(2 \quad 3 \quad 5 \Rightarrow{ }^5 C_2 \times{ }^6 C_3 \times{ }^8 C_5\)
Number of selection \(2 \quad 2 \quad 6 \Rightarrow{ }^5 C_2 \times{ }^6 C_2 \times{ }^8 C_6\)
Number of selection \(3 \quad 2 \quad 5 \Rightarrow{ }^5 C_3 \times{ }^6 C_2 \times{ }^8 C_5\)
\(\Rightarrow\) Total number of ways \(=23800\)
According to question \(100 K =23800\)
\(
\Rightarrow K =238
\) -
Question 195 of 205
195. Question
If the digits are not allowed to repeat in any number formed by using the digits 0, 2, 4, 6, 8, then the number of all numbers greater than 10,000 is equal to _______. [JEE Main 2021 (Online) 22th July Evening Shift]
CorrectIncorrectHint
\(
\begin{array}{|l|l|l|l|l|}
\hline 2,4,6,8 & & & & \\
\hline 4 & 4 & 3 & 2 & 1 \\
\end{array}
\)
\(
=4 \times 4 \times 3 \times 2=96
\) -
Question 196 of 205
196. Question
There are 15 players in a cricket team, out of which 6 are bowlers, 7 are batsman and 2 are wicketkeepers. The number of ways, a team of 11 players be selected from them so as to include at least 4 bowlers, 5 batsman and 1 wicketkeeper, is ____. [JEE Main 2021 (Online) 20th July Morning Shift]
CorrectIncorrectHint
15 : Players
6: Bowlers
7: Batsman
2: Wicket keepersTotal number of ways for :
at least 4 bowler, 5 batsman & 1 wicket keeper
\(
\begin{aligned}
& ={ }^6 C_4\left({ }^7 C_6 \times{ }^2 C_1+{ }^7 C_5 \times{ }^2 C_2\right)+{ }^6 C_5 \times{ }^7 C_5 \times{ }^2 C_1 \\
& =777
\end{aligned}
\) -
Question 197 of 205
197. Question
If \(\sum_{r=1}^{10} r!\left(r^3+6 r^2+2 r+5\right)=\alpha(11!)\), then the value of \(\alpha\) is equal to ____. [JEE Main 2021 (Online) 18th March Evening Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& \sum_{r=1}^{10} r![(r+1)(r+2)(r+3)-9(r+1)+8] \\
& =\sum_{r=1}^{10}[\{(r+3)!-(r+1)!\}-8\{(r+1)!-r!\}] \\
& =(13!+12!-2!-3!)-8(11!-1) \\
& =(12 \cdot 13+12-8) \cdot 11!-8+8=(160)(11!)
\end{aligned}
\)
Therefore, \(\alpha=160\) -
Question 198 of 205
198. Question
The number of times the digit 3 will be written when listing the integers from 1 to 1000 is : [JEE Main 2021 (Online) 18th March Morning Shift]
CorrectIncorrectHint
In single digit numbers \(=1\)
In double digit numbers \(=10+9=19\)
In triple digit numbers \(=100+90+90=280\)
Total \(=300\) times
-
Question 199 of 205
199. Question
The missing value in the following figure is [JEE Main 2021 (Online) 18th March Morning Shift]
 CorrectIncorrect
CorrectIncorrectHint
\(
\begin{aligned}
& x=(2-1)^{1!}=1 \\
& w=(12-8)^{4!}=4^{24} \\
& z=(7-4)^{3!}=3^6
\end{aligned}
\)
hence \(y=(5-3)^{2!}=2^2\)Alternate:
\(
\begin{aligned}
& \text { Inside number }=(\text { difference }) ^{\text { (difference })!} \\
& =(\text { Greater number – Smaller number) })^{\text {(Greater number – Smaller number)! }}
\end{aligned}
\)
\(
\begin{aligned}
& \text { i.e. } 1=(2-1)^{(2-1)!} \\
& 4^{24}=(12-8)^{(12-8)!} \\
& 3^6=(7-4)^{(7-4)!} \\
& \therefore \text { Required number }=2^{2!}=2^{2 \times 1}=4
\end{aligned}
\) -
Question 200 of 205
200. Question
The total number of numbers, lying between 100 and 1000 that can be formed with the digits \(1,2,3,4,5\), if the repetition of digits is not allowed and numbers are divisible by either 3 or 5 , is ____. [JEE Main 2021 (Online) 25th February Morning Shift]
CorrectIncorrectHint
The numbers are lying between 100 and 1000 then each number is of three digits.
The possible combination of 3 digits numbers are
\(
1,2,3 ; 1,2,4 ; 1,2,5 ; 1,3,4 ; 1,3,5 ; 1,4,5 ; 2,3,4 ; 2,3,5 ; 2,4,5 \text {; and } 3,4,5 \text {. }
\)The possible combination of numbers which are divisible by 3 are \(1,2,3 ; 3,4,5 ; 1,3\), 5 and \(2,3,4\).
(If sum of digits of a number is divisible by 3 then the number is divisible by 3 )
\(\therefore\) Total number of numbers \(=4 \times 3!=24\)The possible combination of numbers divisible by 5 are \(1,2,5 ; 2,3,5 ; 3,4,5 ; 1,3,5\); \(1,4,5\) and \(2,4,5\).
(If the last digit of a number is 0 or 5 then the number is divisible by 5 )
\(\therefore\) Total number of numbers \(=6 \times 2!=12\)The possible combination of number divisible by both 3 and 5 are \(1,3,5\) and \(3,4,5\).
\(\therefore\) Total number of numbers \(=2 \times 2!=4\)
\(\therefore\) Total required number \(=24+12-4=32\) -
Question 201 of 205
201. Question
The students \(S _1, S _2, \ldots . ., S _{10}\) are to be divided into 3 groups \(A , B\) and \(C\) such that each group has at least one student and the group \(C\) has at most 3 students. Then the total number of possibilities of forming such groups is ____. [JEE Main 2021 (Online) 24th February Evening Shift]
CorrectIncorrectHint
If group \(C\) has one student then number of groups
\(
={ }^{10} C _1\left[2^9-2\right]=5100
\)
If group \(C\) has two students then number of groups
\(
={ }^{10} C _2\left[2^8-2\right]=11430
\)If group \(C\) has three students then number of groups
\(
={ }^{10} C_3 \times\left[2^7-2\right]=15120
\)
So total groups \(=31650\) -
Question 202 of 205
202. Question
There are 12 points in a plane, no three of which are in the same straight line, except 5 points which are collinear. Then the total number of triangles that can be formed with the vertices at any three of these 12 points is [JEE Main 2025 (Online) 8th April Evening Shift]
CorrectIncorrectHint
(b) Step 1: Calculate Total Possible Combinations
First, we calculate the total number of combinations of choosing 3 points out of 12, assuming no points are collinear, using the combination formula \(C(n, r)=\frac{n!}{r!(n-r)!}\)
\(
C(12,3)=\frac{12!}{3!(12-3)!}=\frac{12 \times 11 \times 10}{3 \times 2 \times 1}=220
\)
Step 2: Calculate Invalid Combinations (from Collinear Points)
The 5 collinear points cannot form a triangle among themselves. We calculate the number of invalid combinations of choosing 3 points from these 5 collinear points.
\(
C(5,3)=\frac{5!}{3!(5-3)!}=\frac{5 \times 4}{2 \times 1}=10
\)
Step 3: Subtract Invalid from Total Combinations
The actual number of valid triangles is the total possible combinations minus the invalid combinations formed by the collinear points.
\(
\text { Total Triangles }=C(12,3)-C(5,3)=220-10=210
\) -
Question 203 of 205
203. Question
From a group of 7 batsmen and 6 bowlers, 10 players are to be chosen for a team, which should include atleast 4 batsmen and atleast 4 bowlers. One batsmen and one bowler who are captain and vice-captain respectively of the team should be included. Then the total number of ways such a selection can be made, is [JEE Main 2025 (Online) 7th April Morning Shift]
CorrectIncorrectHint
(c) Step 1: Select the captain and vice-captain
One batsman must be selected as captain, which can be done in \(\binom{7}{1}=7\) ways from the available 7 batsmen. One bowler must be selected as vice-captain, which can be done in \(\binom{6}{1}=6\) ways from the available 6 bowlers.
These two players are automatically included in the 10-player team.
Number of players remaining to be chosen is \(10-2=8\).
Number of batsmen remaining to be chosen is \(7-1=6\).
Number of bowlers remaining to be chosen is \(6-1=5\).
Step 2: Determine possible combinations of remaining players
The final team must have at least 4 batsmen and at least 4 bowlers.
The number of selected batsmen must be \(B \geq 4\) and the number of selected bowlers must be \(W \geq 4\), with \(B+W=10\).
Since one batsman and one bowler are already selected (captain and vice-captain), we need to select \(b\) more batsmen from the remaining 6 and \(w\) more bowlers from the remaining 5, such that the total number of batsmen is \(1+b \geq 4 \Longrightarrow b \geq 3\) and total bowlers is \(1+w \geq 4 \Longrightarrow w \geq 3\).
Also, the total number of additional players to select is \(b+w=8\).
Possible cases for \((b, w)\) are:
Case 1: \(b=3, w=5\) (Total batsmen \(=4\), total bowlers \(=6\) )
Case 2: \(b=4, w=4\) (Total batsmen = 5, total bowlers = 5)
Case 3: \(b=5, w=3\) (Total batsmen = 6, total bowlers = 4)
We need to check the remaining players pool: 6 batsmen and 5 bowlers available for these additional selections.
All three cases are possible.
Step 3: Calculate ways for each case and sum up
The number of ways to choose the remaining players for each case is:
Case 1: \(\binom{6}{3} \times\binom{ 5}{5}=\frac{6!}{3!3!} \times 1=20 \times 1=20\) ways.
Case 2: \(\binom{6}{4} \times\binom{ 5}{4}=\frac{6!}{4!2!} \times \frac{5!}{4!1!}=15 \times 5=75\) ways.
Case 3: \(\binom{6}{5} \times\binom{ 5}{3}=\frac{6!}{5!1!} \times \frac{5!}{3!2!}=6 \times 10=60\) ways.
The total number of ways to form the team after fixing the captain and vice-captain is the sum of ways for these cases: \(20+75+60=155\).Note:
\(
\begin{array}{|c|c|c|}
\hline \text { Batsman } & \text { Bowler } & \text { Number of ways } \\
\hline 3 & 5 & { }^6 C_3 \cdot{ }^5 C_5=20 \\
\hline 4 & 4 & { }^6 C_4 \cdot{ }^5 C_4=75 \\
\hline 5 & 3 & { }^6 C_5 \cdot{ }^5 C_3=60 \\
\hline
\end{array}
\) -
Question 204 of 205
204. Question
Line \(L_1\) of slope 2 and line \(L_2\) of slope \(\frac{1}{2}\) intersect at the origin O. In the first quadrant, \(\mathrm{P}_1, P_2, \ldots, P_{12}\) are 12 points on line \(L_1\) and \(Q_1, Q_2, \ldots, Q_9\) are 9 points on line \(L_2\). Then the total number of triangles, that can be formed having vertices at three of the 22 points \(\mathrm{O}, \mathrm{P}_1, \mathrm{P}_2, \ldots, \mathrm{P}_{12}, \mathrm{Q}_1, \mathrm{Q}_2, \ldots, \mathrm{Q}_9\), is: [JEE Main 2025 (Online) 3rd April Evening Shift]
CorrectIncorrectHint
(c) Step 1: Calculate Total Possible Combinations
The total number of points available is the sum of points on line \(L_1\), points on line \(L_2\), and the origin, which is \(12+9+1=22\) points. The total number of ways to pick any 3 points from these 22 is calculated using the combination formula \(\binom{n}{k}=\frac{n!}{k!(n-k)!}\) :
\(
\binom{22}{3}=\frac{22 \times 21 \times 20}{3 \times 2 \times 1}=1540
\)
Step 2: Subtract Collinear Combinations on \(\mathbf{L}_{\mathbf{1}}\)
Points chosen from the same line do not form a triangle. There are \(12+1=13\) points on line \(L_1\) (including the origin). The number of ways to choose 3 points from \(L_1\) is:
\(
\binom{13}{3}=\frac{13 \times 12 \times 11}{3 \times 2 \times 1}=286
\)
Step 3: Subtract Collinear Combinations on \(\mathbf{L}_{\mathbf{2}}\)
There are \(9+1=10\) points on line \(L_2\) (including the origin). The number of ways to choose 3 points from \(L_2\) is:
\(
\binom{10}{3}=\frac{10 \times 9 \times 8}{3 \times 2 \times 1}=120
\)
Step 4: Determine the Total Number of Triangles
The total number of triangles is the total number of 3-point combinations minus the combinations that are collinear:
\(
\text { Total Triangles }=1540-286-120=1134
\) -
Question 205 of 205
205. Question
The number of ways, in which the letters A, B, C, D, E can be placed in the 8 boxes of the figure below so that no row remains empty and at most one letter can be placed in a box, is : [JEE Main 2025 (Online) 2nd April Evening Shift]
 CorrectIncorrect
CorrectIncorrectHint
(d) We have 5 letters \(A, B, C, D, E\).
The following table shows the numbers of ways to fill 5 boxes so that no row remains empty.
\(
\begin{array}{|c|c|c|c|}
\hline \text { Row-I } & \text { Row-II } & \text { Row-III } & \text { Number of ways } \\
\hline 3 & 1 & 1 & { }^3 C_3 \cdot{ }^3 C_1 \cdot{ }^2 C_1=6 \\
\hline 2 & 2 & 1 & { }^3 C_2 \cdot{ }^3 C_2 \cdot{ }^2 C_1=18 \\
\hline 1 & 3 & 1 & { }^3 C_1 \cdot{ }^3 C_3 \cdot{ }^2 C_1=6 \\
\hline 2 & 1 & 2 & { }^3 C_2 \cdot{ }^3 C_1 \cdot{ }^2 C_2=9 \\
\hline 1 & 2 & 2 & { }^3 C_1 \cdot{ }^3 C_2 \cdot{ }^2 C_2=9 \\
\hline
\end{array}
\)
Number of ways to fill boxes \(=6+18+6+9+9=48\)
Now, these 5 letters can be arranged in 5! ways
∴ Total number of ways \(48 \times 5!=5760\).