Past JEE Main Entrance Paper
Overview
Cartesian products of sets
Definition : Given two non-empty sets A and B, the set of all ordered pairs \((x, y)\), where \(x \in A\) and \(y \in B\) is called Cartesian product of \(A\) and \(B\); symbolically, we write
\(
A \times B =\{(x, y) \mid x \in A \text { and } y \in B \}
\)
\(
\begin{array}{ll}
\text { If } & A =\{1,2,3\} \text { and } B =\{4,5\}, \text { then } \\
& A \times B =\{(1,4),(2,4),(3,4),(1,5),(2,5),(3,5)\} \\
\text { and } & B \times A =\{(4,1),(4,2),(4,3),(5,1),(5,2),(5,3)\}
\end{array}
\)
- Two ordered pairs are equal, if and only if the corresponding first elements are equal and the second elements are also equal, i.e. \((x, y)=(u, v)\) if and only if \(x=\) \(u, y=v\).
- If \(n( A )=p\) and \(n( B )=q\), then \(n( A \times B )=p \times q\).
- \(A \times A \times A =\{(a, b, c): a, b, c \in A \}\). Here \((a, b, c)\) is called an ordered triplet.
Relations
A Relation \(R\) from a non-empty set \(A\) to a non empty set \(B\) is a subset of the Cartesian product set \(A \times B\). The subset is derived by describing a relationship between the first element and the second element of the ordered pairs in \(A \times B\).
The set of all first elements in a relation \(R\), is called the domain of the relation \(R\), and the set of all second elements called images, is called the range of \(R\).
For example, the set \(R =\left\{(1,2),(-2,3),\left(\frac{1}{2}, 3\right)\right\}\) is a relation; the domain of \(R=\left\{1,-2, \frac{1}{2}\right\}\) and the range of \(R=\{2,3\}\).
- A relation may be represented either by the Roster form or by the set builder form, or by an arrow diagram which is a visual representation of a relation.
- If \(n( A )=p, n( B )=q\); then the \(n( A \times B )=p q\) and the total number of possible relations from the set \(A\) to set \(B =2^{p q}\).
Functions
A relation \(f\) from a set \(A\) to a set \(B\) is said to be function if every element of set \(A\) has one and only one image in set \(B\). In other words, a function \(f\) is a relation such that no two pairs in the relation has the same first element.
The notation \(f: X \rightarrow Y\) means that \(f\) is a function from \(X\) to \(Y \text { where } X\) is called the domain of \(f\) and \(Y\) is called the co-domain of \(f\). Given an element \(x \in X\), there is a unique element \(y\) in \(Y\) that is related to \(x\). The unique element \(y\) to which \(f\) relates \(x\) is denoted by \(f(x)\) and is called \(f\) of \(x\), or the value of \(f\) at \(x\), or the image of \(x\) under \(f\).
The set of all values of \(f(x)\) taken together is called the range of \(f\) or image of \(X\) under \(f\). Symbolically.
\(
\text { range of } f=\{y \in Y \mid y=f(x) \text {, for some } x \text { in } X \}
\)
Definition : A function which has either \(R\) or one of its subsets as its range, is called a real valued function. Further, if its domain is also either \(R\) or a subset of \(R\), it is called a real function.
Some specific types of functions
Identity function:
The function \(f: R \rightarrow R\) defined by \(y=f(x)=x\) for each \(x \in R\) is called the identity function.
Domain of \(f= R\)
Range of \(f= R\)
Constant function:
The function \(f: R \rightarrow R\) defined by \(y=f(x)= C , x \in R\), where \(C\) is a constant \(\in R\), is a constant function.
\(
\begin{aligned}
& \text { Domain of } f= R \\
& \text { Range of } f=\{ C \}
\end{aligned}
\)
Polynomial function:
A function \(f: R \rightarrow R\) is said to be polynomial function if for each \(x\) in \(R , y=f(x)=a_0+a_1 x+a_2 x^2+\ldots+a_n x^n\), where \(n\) is a non-negative integer and \(a_0, a_1, a_2, \ldots, a_n \in R\).
The functions defined by \(f(x)=x^3-x^2+2\), and \(g(x)=x^4+\sqrt{2} x\) are some examples of polynomial functions, whereas the function \(h\) defined by \(h(x)=x^{\frac{2}{3}}+2 x\) is not a polynomial function because power of \(x\) is not a whole number.
Rational function:
These are the real functions of the type \(\frac{f(x)}{g(x)}\), where \(f(x)\) and \(g(x)\) are polynomial functions of \(x\) defined in a domain, where \(g(x) \neq 0\). For example \(f: R -\{-2\} \rightarrow R\) defined by \(f(x)=\frac{x+1}{x+2}, \forall x \in R -\{-2\}\) is a rational function.
The Modulus function:
The real function \(f: R \rightarrow R\) defined by \(f(x)=|x|=\)
\(
\left\{\begin{array}{l}
x, x \geq 0 \\
-x, x<0
\end{array}\right.
\)
\(\forall x \in R\) is called the modulus function.
Domain of \(f= R\)
Range of \(f= R ^{+} \cup\{0\}\)
Signum function:
The real function \(f: R \rightarrow R\) defined by
\(
f(x)=\left\{\begin{array}{c}
\frac{|x|}{x}, x \neq 0 \\
0, x=0
\end{array}=\left\{\begin{array}{rll}
1, & \text { if } & x>0 \\
0, & \text { if } & x=0 \\
-1, & \text { if } & x<0
\end{array}\right.\right.
\)
is called the signum function. Domain of \(f= R\), Range of \(f=\{1,0,-1\}\)
Greatest integer function:
The real function \(f: R \rightarrow R\) defined by \(f(x)=[x], x \in R\) assumes the value of the greatest integer less than or equal to \(x\), is called the greatest integer function.
Thus
\(
\begin{aligned}
f(x)= & {[x]=-1 \text { for }-1 \leq x<0 } \\
f(x)= & {[x]=0 \text { for } 0 \leq x<1 } \\
& {[x]=1 \text { for } 1 \leq x<2 } \\
& {[x]=2 \text { for } 2 \leq x<3 \text { and so on } }
\end{aligned}
\)
Algebra of real functions
Addition of two real functions:
Let \(f: X \rightarrow R\) and \(g: X \rightarrow R\) be any two real functions, where \(X \in R\). Then we define \((f+g): X \rightarrow R\) by \((f+g)(x)=f(x)+g(x)\), for all \(x \in X\).
Subtraction of a real function from another
Let \(f: X \rightarrow R\) and \(g: X \rightarrow R\) be any two real functions, where \(X \subseteq R\). Then, we define \((f-g): X \rightarrow R\) by \((f-g)(x)=f(x)-g(x)\), for all \(x \in X\).
Multiplication by a Scalar
Let \(f: X \rightarrow R\) be a real function and \(\alpha\) be any scalar belonging to \(R\). Then the product \(\alpha f\) is function from \(X\) to \(R\) defined by \((\alpha f)(x)=\alpha f(x), x \in X\).
Multiplication of two real functions
Let \(f: X \rightarrow R\) and \(g: x \rightarrow R\) be any two real functions, where \(X \subseteq R\). Then product of these two functions i.e. \(f g: X \rightarrow R\) is defined by \((f g)(x)=f(x) g(x) \forall x \in X\).
Quotient of two real function
Let \(f\) and \(g\) be two real functions defined from \(X \rightarrow R\). The quotient of \(f\) by \(g\) denoted by \(\frac{f}{g}\) is a function defined from \(X \rightarrow R\) as \(\left(\frac{f}{g}\right)(x)=\frac{f(x)}{g(x)}\), provided \(g(x) \neq 0, x \in X\)
Note: Domain of sum function \(f+g\), difference function \(f-g\) and product
function \(f g\).
\(=\left\{x: x \in D _f \cap D _g\right\}\)
where \(D _f=\) Domain of function \(f\)
\(D _g=\) Domain of function \(g\)
Domain of quotient function \(\frac{f}{g}\)
\(=\left\{x: x \in D _f \cap D _g\right.\) and \(\left.g(x) \neq 0\right\}\)
Quiz Summary
0 of 73 Questions completed
Questions:
Information
You have already completed the quiz before. Hence you can not start it again.
Quiz is loading…
You must sign in or sign up to start the quiz.
You must first complete the following:
Results
Results
0 of 73 Questions answered correctly
Your time:
Time has elapsed
You have reached 0 of 0 point(s), (0)
Earned Point(s): 0 of 0, (0)
0 Essay(s) Pending (Possible Point(s): 0)
Categories
- Not categorized 0%
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- Current
- Review
- Answered
- Correct
- Incorrect
-
Question 1 of 73
1. Question
Let \(R_{1}\) and \(R_{2}\) be two relations defined as follows : \(R_{1}=\left\{(a, b) \in \mathbf{R}^{2}: a^{2}+b^{2} \in Q\right\}\) and \(R_{2}=\left\{(a, b) \in \mathbf{R}^{2}: a^{2}+b^{2} \notin Q\right\}\), where \(Q\) is the set of all rational numbers. Then :
[Main Sep. 03, 2020 (II)]CorrectIncorrectHint
(a) For \(R_{1}\) let \(a=1+\sqrt{2}, b=1-\sqrt{2}, c=8^{1 / 4}\) \(a R_{\mathrm{l}} b \Rightarrow a^{2}+b^{2}=(1+\sqrt{2})^{2}+(1-\sqrt{2})^{2}=6 \in Q\) \(b R_{1} c \Rightarrow b^{2}+c^{2}=(1-\sqrt{2})^{2}+\left(8^{1 / 4}\right)^{2}=3 \in Q\) \(a R_{1} c \Rightarrow a^{2}+c^{2}=(1+\sqrt{2})^{2}+\left(8^{1 / 4}\right)^{2}=3+4 \sqrt{2} \notin Q\) \(\therefore R_{1}\) is not transitive.
For \(R_{2}\) let \(a=1+\sqrt{2}, b=\sqrt{2}, c=1-\sqrt{2}\)
\(
\begin{aligned}
&a R_{2} b \Rightarrow a^{2}+b^{2}=(1+\sqrt{2})^{2}+(\sqrt{2})^{2}=5+2 \sqrt{2} \notin Q \\
&b R_{2} c \Rightarrow b^{2}+c^{2}=(\sqrt{2})^{2}+(1-\sqrt{2})^{2}=5-2 \sqrt{2} \notin Q \\
&a R_{2} c \Rightarrow a^{2}+c^{2}=(1+\sqrt{2})^{2}+(1-\sqrt{2})^{2}=6 \in Q
\end{aligned}
\)
\(\therefore R_{2}\) is not transitive. -
Question 2 of 73
2. Question
The domain of the function \(f(x)=\sin ^{-1}\left(\frac{|x|+5}{x^{2}+1}\right)\) is \((-\infty,-a] \cup[a, \infty]\). Then \(a\) is equal to: [Main Sep. 02, 2020(I)]
CorrectIncorrectHint
\(
\begin{aligned}
&\text { (c) } \because f(x)=\sin ^{-1}\left(\frac{|x|+5}{x^{2}+1}\right)\\
&\therefore-1 \leq \frac{|x|+5}{x^{2}+1} \leq 1\\
&\Rightarrow|x|+5 \leq x^{2}+1\\
&\left[\because x^{2}+1 \neq 0\right]\\
&\Rightarrow x^{2}-|x|-4 \geq 0\\
&\Rightarrow\left(|x|-\frac{1-\sqrt{17}}{2}\right)\left(|x|-\frac{1+\sqrt{17}}{2}\right) \geq 0\\
&\Rightarrow x \in\left(-\infty,-\frac{1+\sqrt{17}}{2}\right) \cup\left[\frac{1+\sqrt{17}}{2}, \infty\right)
\end{aligned}
\)\(
\therefore a=\frac{1+\sqrt{17}}{2}
\) -
Question 3 of 73
3. Question
If \(R=\left\{(x, y): x, y \in \mathbf{Z}, x^{2}+3 y^{2} \leq 8\right\}\) is a relation on the set of integers \(\mathbf{Z}\), then the domain of \(R^{-1}\) is: [Main Sep. 02, 2020 (I)]
CorrectIncorrectHint
(d) Since, \(R=\left\{(x, y): x, y \in \mathbf{Z}, x^{2}+3 y^{2} \leq 8\right\}\)
\(\therefore R=\{(1,1),(2,1),(1,-1),(0,1),(1,0)\}\) \(\Rightarrow D_{R^{-1}}=\{-1,0,1\}\) -
Question 4 of 73
4. Question
The domain of the definition of the function \(f(x)=\frac{1}{4-x^{2}}+\log _{10}\left(x^{3}-x\right)\) is: [Main April. 09, 2019 (II)]
CorrectIncorrectHint
(c) To determine domain, denominator \(\neq 0\) and \(x^{3}-x>0\)
i.e., \(4-x^{2} \neq 0 \Rightarrow x \neq \pm 2\)…(i)
and \(x(x-1)(x+1)>0\)
\(x \in(-1,0) \cup(1, \infty)\)…(ii)
Hence domain is intersection of (i) & (ii).
i.e., \(x \in(-1,0) \cup(1,2) \cup(2, \infty)\) -
Question 5 of 73
5. Question
Let \(f: R \rightarrow R\) be defined by \(f(x)=\frac{x}{1+x^{2}}, x \in R\). Then the range of \(f\) is: [Main Jan. 11, 2019 (I)]
CorrectIncorrectHint
(a) \(f(0)=0 \& f(x)\) is odd.
Further, if \(\mathrm{x}>0\) then
\(
f(x)=\frac{1}{x+\frac{1}{x}} \in\left(0, \frac{1}{2}\right]
\)
\(x<0\) then
\(
f(x)=\frac{1}{x+\frac{1}{x}} \in\left[-\frac{1}{2}, 0\right)
\)
Hence, \(\mathrm{f}(\mathrm{x}) \in\left[-\frac{1}{2}, \frac{1}{2}\right]\) -
Question 6 of 73
6. Question
Range of the function \(f(x)=\frac{x^{2}+x+2}{x^{2}+x+1} ; x \in R\) is [2003S]
CorrectIncorrectHint
(c) \(\mathrm{f}\)(x)
\(=\frac{x^{2}+x+2}{x^{2}+x+1}=\frac{\left(x^{2}+x+1\right)+1}{x^{2}+x+1}\)
\(=1+\frac{1}{\left(x+\frac{1}{2}\right)^{2}+\frac{3}{4}}\)
We can see here that as \(x \rightarrow \infty, f(x) \rightarrow 1\) which is the minimum value of \(f(x)\). i.e. \(f_{\min }=1\). Also \(f(x)\) is maximum when \(\left(x+\frac{1}{2}\right)^{2}+\frac{3}{4}\) is minimum which is so when \(x=-1 / 2\)
\(
\therefore f_{\max }=1+\frac{1}{3 / 4}=7 / 3, \quad \therefore R_{f}=(1,7 / 3]
\) -
Question 7 of 73
7. Question
Let the function \(f:[0,1] \rightarrow \mathbb{R}\) be defined by
\(
f(x)=\frac{4^{x}}{4^{x}+2} .
\)
Then the value of
\(
f\left(\frac{1}{40}\right)+f\left(\frac{2}{40}\right)+f\left(\frac{3}{40}\right)+\ldots+f\left(\frac{39}{40}\right)-f\left(\frac{1}{2}\right)\)is ___ [Adv. 2020]CorrectIncorrectHint
Since, \(f(x)+f(1-x)=\frac{4^{x}}{4^{x}+2}+\frac{4^{1-x}}{4^{1-x}+2}\)
\(
\begin{aligned}
&=\frac{4^{x}}{4^{x}+2}+\frac{4 / 4^{x}}{\frac{4}{4^{x}}+2}=\frac{4^{x}}{4^{x}+2}+\frac{2}{2+4^{x}}=1 \\
&\therefore f\left(\frac{1}{40}\right)+f\left(\frac{2}{40}\right)+\ldots+f\left(\frac{39}{40}\right)-f\left(\frac{1}{2}\right) \\
&=\left[f\left(\frac{1}{40}\right)+f\left(\frac{39}{40}\right)\right]+\left[f\left(\frac{2}{40}\right)+f\left(\frac{38}{40}\right)\right] \\
&=(1+1+\ldots . .19 \text { times })+f\left(\frac{1}{2}\right)-f\left(\frac{1}{2}\right) \\
&=19
\end{aligned}
\) -
Question 8 of 73
8. Question
Let \([t]\) denote the greatest integer \(\leq t\). Then the equation in \(x,[x]^{2}+\) \(2[x+2]-7=0\) has: [Main Sep. 04, 2020 (I)]
CorrectIncorrectHint
(d) The given equation
\(
\begin{aligned}
&{[x]^{2}+2[x]+4-7=0} \\
&\Rightarrow[x]^{2}+2[x]-3=0 \Rightarrow[x]^{2}+3[x]-[x]-3=0 \\
&\Rightarrow([x]+3)([x]-1)=0 \Rightarrow[x]=1 \text { or }-3 \\
&\Rightarrow x \in[-3,-2) \cup[1,2)
\end{aligned}
\)
\(\therefore\) The equation has infinitely many solutions. -
Question 9 of 73
9. Question
Let \(f(x)\) be a quadratic polynomial such that \(f(-1)+f(2)=0\). If one of the roots of \(f(x)=0\) is 3 , then its other root lies in : [Main Sep. 02, 2020 (II)]
CorrectIncorrectHint
\(
\text { (a) Let } f(x)=a x^{2}+b x+c
\)Given: \(f(-1)+f(2)=0\)
\(a-b+c+4 a+2 b+c=0\)
\(\Rightarrow 5 a+b+2 c=0\)…(i)
and \(f(3)=0 \Rightarrow 9 a+3 b+c=0\)…(ii)
From equations (i) and (ii),
\(
\frac{a}{1-6}=\frac{b}{18-5}=\frac{c}{15-9} \Rightarrow \frac{a}{-5}=\frac{b}{13}=\frac{c}{6}
\)
Product of roots, \(\alpha \beta=\frac{c}{a}=\frac{-6}{5}\) and \(\alpha=3\)
\(
\Rightarrow \beta=\frac{-2}{5} \in(-1,0)
\) -
Question 10 of 73
10. Question
Let \(f(1,3) \longrightarrow R\) be a function defined by \(f(x)=\frac{x[x]}{1+x^{2}}\), where \([x]\) denotes the greatest integer \(\leq x\). Then the range of \(f\) is: [Main Jan. 8, 2020 (II)]
CorrectIncorrectHint
\(
\begin{aligned}
&\text { (b) } f(x) \begin{cases}\frac{x}{x^{2}+1} ; & x \in(1,2) \\
\frac{2 x}{x^{2}+1} ; & x \in[2,3)\end{cases} \\
&f^{\prime}(x) \begin{cases}\frac{1-x^{2}}{1+x^{2}} ; & x \in(1,2) \\
\frac{1-2 x^{2}}{1+x^{2}} ; & x \in[2,3)\end{cases}
\end{aligned}
\)
\(\therefore f(x)\) is a decreasing function
\(
\therefore \quad y \in\left(\frac{2}{5}, \frac{1}{2}\right) \cup\left(\frac{6}{10}, \frac{4}{5}\right] \Rightarrow y \in\left(\frac{2}{5}, \frac{1}{2}\right) \cup\left(\frac{3}{5}, \frac{4}{5}\right]
\) -
Question 11 of 73
11. Question
If \(f(x)=\log _{e}\left(\frac{1-x}{1+x}\right),|x|<1\), then \(f\left(\frac{2 x}{1+x^{2}}\right)\) is equal to: [Main April 8,2019(I)]
CorrectIncorrectHint
(a) \(f(x)=\log \left(\frac{1-x}{1+x}\right),|x|<1\)
\(
\begin{aligned}
& f\left(\frac{2 x}{1+x^{2}}\right)=\log \left(\frac{1-\frac{2 x}{1+x^{2}}}{1+\frac{2 x}{1+x^{2}}}\right) \\
=& \log \left(\frac{1+x^{2}-2 x}{1+x^{2}+2 x}\right)=\log \left(\frac{1-x}{1+x}\right)^{2}=2 \log \left(\frac{1-x}{1+x}\right)=2 f(x)
\end{aligned}
\) -
Question 12 of 73
12. Question
Let \(f(x)=a^{x}(a>0)\) be written as \(f(x)=f_{1}(x)+f_{2}(x)\), where \(f_{1}(x)\) is an even function and \(f_{2}(x)\) is an odd function. Then \(f_{1}(x+y)+f_{1}(x-y)\) equals: [Main April. 08, 2019 (II)]
CorrectIncorrectHint
(a) Given function can be written as
\(
f(x)=a^{x}=\left(\frac{a^{x}+a^{-x}}{2}\right)+\left(\frac{a^{x}-a^{-x}}{2}\right)
\)
where \(f_{1}(x)=\frac{a^{x}+a^{-x}}{2}\) is even function
\(
\begin{aligned}
& f_{2}(x)=\frac{a^{x}-a^{-x}}{2} \text { is odd function } \\
\Rightarrow f_{1}(x+y)+f_{1}(x-y) \\
=&\left(\frac{a^{x+y}+a^{-x-y}}{2}\right)+\left(\frac{a^{x-y}+a^{-x+y}}{2}\right) \\
=& \frac{1}{2}\left[a^{x}\left(a^{y}+a^{-y}\right)+a^{-x}\left(a^{y}+a^{-y}\right)\right] \\
=& \frac{\left(a^{x}+a^{-x}\right)\left(a^{y}+a^{-y}\right)}{2}=2 f_{1}(x) \cdot f_{1}(y)
\end{aligned}
\) -
Question 13 of 73
13. Question
Let \(f(n)=\left[\frac{1}{3}+\frac{3 n}{100}\right] n\), where \([\mathrm{n}]\) denotes the greatest integer less than or equal to \(n\). Then \(\sum_{n=1}^{56} f(n)\) is equal to: [Main Online April 19, 2014]
CorrectIncorrectHint
(d) Let \(f(n)=\left[\frac{1}{3}+\frac{3 n}{100}\right] n\)
where \([n]\) is greatest integer function, \(=\left[0.33+\frac{3 n}{100}\right] n\)For \(n=1,2, \ldots, 22\), we get \(f(n)=0\)
and for \(n=23,24, \ldots, 55\), we get \(f(n)=1 \times n\)
For \(n=56, f(n)=2 \times n\)
\(
\begin{aligned}
&\text { So, } \sum_{n=1}^{56} f(n)=1(23)+1(24)+\ldots+1(55)+2(56) \\
&=(23+24+\ldots+55)+112 \\
&=\frac{33}{2}[46+32]+112=\frac{33}{2}(78)+112=1399
\end{aligned}
\) -
Question 14 of 73
14. Question
\(
\text { The value of } 6+\log _{3 / 2}\left(\frac{1}{3 \sqrt{2}}\right.
\sqrt{4-\frac{1}{3 \sqrt{2}} \sqrt{\left.4-\frac{1}{3 \sqrt{2}} \sqrt{4-\frac{1}{3 \sqrt{2}}} \ldots\right)}} \text { is ? } \) [2012]CorrectIncorrectHint
(b)
\(
\text { (4) Let } x=\frac{1}{3 \sqrt{2}} \sqrt{4-\frac{1}{3 \sqrt{2}} \sqrt{4-\frac{1}{3 \sqrt{2}} \sqrt{4-\frac{1}{3 \sqrt{2}}}}} \ldots \ldots
\)\(
\begin{aligned}
&\Rightarrow \quad x=\frac{1}{3 \sqrt{2}} \sqrt{4-x} \\
&\Rightarrow \quad 3 \sqrt{2} x=\sqrt{4-x} \\
&\Rightarrow \quad 18 x^{2}=4-x \\
&\Rightarrow \quad 18 x^{2}+x-4=0 \\
&\Rightarrow \quad(9 x-4)(2 x+1)=0 \\
&\Rightarrow \quad x=\frac{4}{9} \text { or } x=-\frac{1}{2}
\end{aligned}
\)
(Not possible because log is not define for-ve value)
\(
\begin{aligned}
&\therefore \quad 6+\log _{\frac{3}{2}}\left(\frac{4}{9}\right)=6+\log _{\frac{3}{2}}\left(\frac{3}{2}\right)^{-2} \\
&=6-2=4
\end{aligned}
\) -
Question 15 of 73
15. Question
Let \(N\) denote the set of all natural numbers. Define two binary relations on \(N\) as \(R_1=\{(x, y) \in N \times N: 2 x+y=10\}\) and \(R_2=\{(x, y) \in N \times N: x+2 y=10\}\). Then [Online April 16, 2018]
CorrectIncorrectHint
(c) Here,
\(
\begin{aligned}
& R_1=\{(x, y) \in N \times N: 2 x+y=10\} \text { and } \\
& R_2=\{(x, y) \in N \times N: x+2 y=10\} \\
& \text { For } R_1 ; 2 x+y=10 \text { and } x, y \in N
\end{aligned}
\)
So, possible values for \(x\) and \(y\) are:
\(
\begin{aligned}
& x=1, y=8 \text { i.e. }(1,8) ; \\
& x=2, y=6 \text { i.e. }(2,6) ; \\
& x=3, y=4 \text { i.e. }(3,4) \text { and } \\
& x=4, y=2 \text { i.e. }(4,2) . \\
& R_1=\{(1,8),(2,6),(3,4),(4,2)\}
\end{aligned}
\)
Therefore, Range of \(R_1\) is \(\{2,4,6,8\}\)
\(R_1\) is not symmetric
Also, \(R_1\) is not transitive because \((3,4),(4,2) \in R_1\) but
\(
(3,2) \notin R_1
\)
Thus, options A, \(B\) and \(D\) are incorrect.
For \(R_2 ; x+2 y=10\) and \(x, y \in N\)
So, possible values for \(x\) and \(y\) are:
\(
x=8, y=1 \text { i.e. }(8,1) \text {; }
\)
\(x=6, y=2\) i.e. \((6,2)\);
\(x=4, y=3\) i.e. \((4,3)\) and
\(
\begin{aligned}
& x=2, y=4 \text { i.e. }(2,4) \\
& R_2=\{(8,1),(6,2),(4,3),(2,4)\}
\end{aligned}
\)
Therefore, Range of \(R_2\) is \(\{1,2,3,4\}\)
\(R_2\) is not symmetric and transitive. -
Question 16 of 73
16. Question
Consider the following two binary relations on the set \(A=\{a, b, c\}: R_1=\{( c , a)(b, b),( a , c),(c, c),(b, c),(a, a)\}\) and \(R_2=\{(a, b),(b, a),(c, c),(c, a),(a, a),(b, b),(a, c)\). Then [Online April 15, 2018]
CorrectIncorrectHint
(a) Both \(R_1\) and \(R_2\) are symmetric as
For any \((x, y) \in R_1\), we have \((y, x) \in R_1\) and similarly for \(R_2\)
Now, for \(R_2,(b, a) \in R_2,(a, c) \in R_2\) but \((b, c) \notin R_2\).
Similarly, for \(R_1,(b, c) \in R_1,(c, a) \in R_1\) but \((b, a) \notin R_1\).
Therefore, neither \(R_1\) nor \(R_2\) is transitive. -
Question 17 of 73
17. Question
The range of the function \(f(x)=\frac{x}{1+|x|}, x \in R\), is [Online May 7, 2012]
CorrectIncorrectHint
(b) \(f(x)=\frac{x}{1+|x|}, x \in R\)
If \(x>0,|x|=x \Rightarrow f(x)=\frac{x}{1+x}\)
which is not defined for \(x=-1\)
If \(x<0,|x|=-x \Rightarrow f(x)=\frac{x}{1-x}\)
which is not defined for \(x=1\)
Thus \(f(x)\) defined for all values of \(R\) except 1 and -1
Hence, range \(=(-1,1)\). -
Question 18 of 73
18. Question
The domain of the function \(f(x)=\frac{1}{\sqrt{|x|-x}}\) is [JEE Main 2011]
CorrectIncorrectHint
(b) \(f(x)=\frac{1}{\sqrt{|x|-x}}\), define if \(|x|-x>0\)
\(
\Rightarrow|x|>x, \Rightarrow x<0
\)
Hence domain of \(f(x)\) is \((-\infty, 0)\) -
Question 19 of 73
19. Question
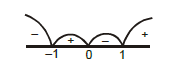
Domain of definition of the function \(f(x)=\frac{3}{4-x^2}+\log _{10}\left(x^3-x\right)\), is [JEE 2003]
CorrectIncorrectHint
\(
\text { (a) } \begin{aligned}
& f(x)=\frac{3}{4-x^2}+\log _{10}\left(x^3-x\right) \\
& 4-x^2 \neq 0 ; x^3-x>0 ; \\
& x \neq \pm \sqrt{4} \text { and }-1<x<0 \text { or } 1<x<\infty
\end{aligned}
\)
\(
\begin{aligned}
& \therefore D=(-1,0) \cup(1, \infty)-\{\sqrt{4}\} \\
& D=(-1,0) \cup(1,2) \cup(2, \infty) .
\end{aligned}
\) -
Question 20 of 73
20. Question
A real valued function \(f(x)\) satisfies the functional equation
\(
f(x-y)=f(x) f(y)-f(a-x) f(a+y)
\)
where a is a given constant and \(f(0)=1\), \(f(2 a-x)\) is equal to [JEE 2005]CorrectIncorrectHint
(a)
\(
\begin{aligned}
& f(2 a-x)=f(a-(x-a)) \\
& =f(a) f(x-a)-f(0) f(x)=f(a) f(x-a)-f(x) \\
& =-f(x) \\
& {\left[\because x=0, y=0, f(0)=f^2(0)-f^2(a)\right.} \\
& \Rightarrow f^2(a)=0 \Rightarrow f(a)=0 \\
& \Rightarrow f(2 a-x)=-f(x)
\end{aligned}
\) -
Question 21 of 73
21. Question
Let \(f\) be an odd function defined on the set of real numbers such that for \(x \geq 0\),
\(
f(x)=3 \sin x+4 \cos x \text {. }
\)
Then \(f(x)\) at \(x=-\frac{11 \pi}{6}\) is equal to: [JEE Main 2014]CorrectIncorrectHint
(c) Given \(f\) be an odd function
\(
f(x)=3 \sin x+4 \cos x
\)
Now,
\(
\begin{aligned}
& f\left(\frac{-11 \pi}{6}\right)=3 \sin \left(\frac{-11 \pi}{6}\right)+4 \cos \left(\frac{-11 \pi}{6}\right) \\
& f\left(\frac{-11 \pi}{6}\right)=3 \sin \left(-2 \pi+\frac{\pi}{6}\right)+4 \cos \left(-2 \pi+\frac{\pi}{6}\right) \\
& f\left(\frac{-11 \pi}{6}\right)=3 \sin \left\{-\left(2 \pi-\frac{\pi}{6}\right)\right\}+4 \cos \left\{-\left(2 \pi-\frac{\pi}{6}\right)\right\}
\end{aligned}
\)
\(
\left\{\text { For odd functions } \begin{array}{l}
\sin (-\theta)=-\sin \theta \\
\text { and } \cos (-\theta)=-\cos \theta
\end{array}\right\}
\)
\(
\begin{aligned}
& \therefore f\left(\frac{-11 \pi}{6}\right)=-3 \sin \left(2 \pi-\frac{\pi}{6}\right)-4 \cos \left(2 \pi-\frac{\pi}{6}\right) \\
& \Rightarrow f\left(\frac{-11 \pi}{6}\right)=+3 \sin \left(\frac{\pi}{6}\right)-4 \cos \frac{\pi}{6} \\
& \Rightarrow f\left(\frac{-11 \pi}{6}\right)=3 \times \frac{1}{2}-4 \times \frac{\sqrt{3}}{2} \\
& \text { or } f\left(\frac{-11 \pi}{6}\right)=\frac{3}{2}-2 \sqrt{3}
\end{aligned}
\) -
Question 22 of 73
22. Question
The graph of the function \(y=f(x)\) is symmetrical about the line \(x=2\), then [JEE 2004]
CorrectIncorrectHint
(b) Let us consider a graph symm. with respect to line \(x=2\) as shown in the figure.
From the figure \(f\left(x_1\right)=f\left(x_2\right)\), where \(x_1=2-x\) and \(x_2=2+x\) \(\therefore f(2-x)=f(2+x)\)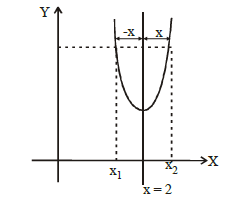
-
Question 23 of 73
23. Question
If \(f: R \rightarrow R\) satisfies \(f(x+y)=f(x)+f(y)\), for all \(x\), \(y \in R\) and \(f(1)=7\), then \(\sum_{r=1}^n f(r)\) is [JEE 2003]
CorrectIncorrectHint
(a) \(\quad f(x+y)=f(x)+f(y)\).
Function should be \(f(x)=m x\)
\(
\begin{aligned}
& f(1)=7 ; \quad \therefore m=7, f(x)=7 x \\
& \sum_{r=1}^n f(r)=7 \sum_1^n r=\frac{7 n(n+1)}{2}
\end{aligned}
\) -
Question 24 of 73
24. Question
The function \(f: R \rightarrow\left[-\frac{1}{2}, \frac{1}{2}\right]\) defined as \(f(x)=\frac{x}{1+x^2}\), is : [JEE Main 2017]
CorrectIncorrectHint
(d) we have \(f : R \rightarrow\left[-\frac{1}{2}, \frac{1}{2}\right]\),
\(
\begin{aligned}
f ( x ) & =\frac{x}{1+x^2} \forall x \in R \\
\Rightarrow f ^{\prime}( x ) & =\frac{\left(1+ x ^2\right) \cdot 1- x \cdot 2 x }{\left(1+ x ^2\right)^2}=\frac{-( x +1)( x -1)}{\left(1+ x ^2\right)^2}
\end{aligned}
\)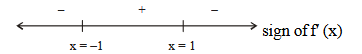
\(\Rightarrow f ^{\prime}( x )\) changes sign in different intervals.
\(\therefore\) Not injective
Now \(y=\frac{x}{1+x^2}\)
\(\Rightarrow y+y x^2=x\)
\(\Rightarrow y x^2-x+y=0\)
For \(y \neq 0, D=1-4 y^2 \geq 0\)
\(\Rightarrow y \in\left[\frac{-1}{2}, \frac{1}{2}\right]-\{0\}\)
For \(y=0 \Rightarrow x=0\)
\(\therefore\) Range is \(\left[\frac{-1}{2}, \frac{1}{2}\right]\)
\(\Rightarrow\) Surjective but not injective -
Question 25 of 73
25. Question
The function \(f: N \rightarrow N\) defined by \(f ( x )= x -5\left[\frac{ x }{5}\right]\), where \(N\) is set of natural numbers and \([x]\) denotes the greatest integer less than or equal to \(x\), is : [Online April 9, 2017]
CorrectIncorrectHint
(d)
\(\left.\begin{array}{l}f(1)=1-5[1 / 5]=1 \\ f(6)=6-5[6 / 5]=1\end{array}\right\} \rightarrow\) Many one \(f(10)=10-5(2)=0\) which is not in co-domain. Therefore, \(f\) is neither 0ne-one nor onto.
-
Question 26 of 73
26. Question
Let \(A =\left\{x_1, x_2, \ldots \ldots ., x_7\right\}\) and \(B =\left\{y_1, y_2, y_3\right\}\) be two sets containing seven and three distinct elements respectively. Then the total number of functions \(f : A \rightarrow B\) that are onto, if there exist exactly three elements \(x\) in A such that \(f (x)=y_2\), is equal to (Online April 11, 2015)
CorrectIncorrectHint
(a) Number of onto function such that exactly three elements in \(x \in A\) such that \(f ( x )=\frac{1}{2}\) is equal to \(={ }^7 C _3\), \(\left\{2^4-2\right\}=14 \cdot{ }^7 C _3\)
-
Question 27 of 73
27. Question
Let \(f: R \rightarrow R\) be defined by \(f(x)=\frac{|x|-1}{|x|+1}\) then \(f\) is: [Online April 19, 2014]
CorrectIncorrectHint
(d) \(P =\left\{(a, b): \sec ^2 a-\tan ^2 b=1\right\}\)
For reflexive :
\(\sec ^2 a-\tan ^2 a=1\) (true \(\forall a\) )
For symmetric :
\(
\sec ^2 b-\tan ^2 a=1
\)
LHS
\(
\begin{aligned}
& 1+\tan ^2 b-\left(\sec ^2 a-1\right)=1+\tan ^2 b-\sec ^2 a+1 \\
& =-\left(\sec ^2 a-\tan ^2 b\right)+2
\end{aligned}
\)
\(
=-1+2=1
\)
So, Relation is symmetric
For transitive :
\(
\begin{aligned}
& \text { if } \sec ^2 a-\tan ^2 b=1 \text { and } \sec ^2 b-\tan ^2 c=1 \\
& \sec ^2 a-\tan ^2 c=\left(1+\tan ^2 b\right)-\left(\sec ^2 b-1\right) \\
& =-\sec ^2 b+\tan ^2 b+2 \\
& =-1+2=1
\end{aligned}
\)
So, Relation is transitive.
Hence, Relation \(P\) is an equivalence relation -
Question 28 of 73
28. Question
Let \(P\) be the relation defined on the set of all real numbers such that
\(P=\left\{(a, b): \sec ^2 a-\tan ^2 b=1\right\} \text {. Then } P \text { is: }\) [Online April 9, 2014]CorrectIncorrectHint
(c) \(\quad f(x)=\frac{|x|-1}{|x|+1}\)
for one-one function if \(f\left(x_1\right)=f\left(x_2\right)\) then \(x_1\) must be equal to \(x_2\)
Let \(f\left(x_1\right)=f\left(x_2\right)\)
\(
\begin{aligned}
& \quad \frac{\left|x_1\right|-1}{\left|x_1\right|+1}=\frac{\left|x_2\right|-1}{\left|x_2\right|+1} \\
& \left|x_1\right|\left|x_2\right|+\left|x_1\right|-\left|x_2\right|-1=\left|x_1\right|\left|x_2\right|-\left|x_1\right|+\left|x_2\right|-1 \\
& \Rightarrow\left|x_1\right|-\left|x_2\right|=\left|x_2\right|-\left|x_1\right| \\
& 2\left|x_1\right|=2\left|x_2\right| \\
& \left|x_1\right|=\left|x_2\right| \\
& x_1=x_2, x_1=-x_2
\end{aligned}
\)
here \(x_1\) has two values therefore function is many one function.
For onto : \(f(x)=\frac{|x|-1}{|x|+1}\)
for every value of \(f(x)\) there is a value of \(x\) in domain set.
If \(f(x)\) is negative then \(x=0\)
for all positive value of \(f(x)\), domain contain atleast one element. Hence \(f(x)\) is onto function. -
Question 29 of 73
29. Question
Let \(R =\left\{(x, y): x, y \in N\right.\) and \(\left.x^2-4 x y+3 y^2=0\right\}\), where \(N\) is the set of all natural numbers. Then the relation \(R\) is : [Online April 23, 2013]
CorrectIncorrectHint
(d) \(R =\left\{(x, y): x, y \in N\right.\) and \(\left.x^2-4 x y+3 y^2=0\right\}\)
Now, \(x^2-4 x y+3 y^2=0\)
\(\Rightarrow(x-y)(x-3 y)=0\)
\(\therefore x=y\) or \(x=3 y\)
\(\therefore \quad R =\{(1,1),(3,1),(2,2),(6,2),(3,3)\),
\((9,3), \ldots \ldots\).
Since \((1,1),(2,2),(3,3), \ldots \ldots\) are present in the relation, therefore \(R\) is reflexive.
Since \((3,1)\) is an element of \(R\) but \((1,3)\) is not the element of \(R\), therefore \(R\) is not symmetric
Here \((3,1) \in R\) and \((1,1) \in R \Rightarrow(3,1) \in R\)
\((6,2) \in R\) and \((2,2) \in R \Rightarrow(6,2) \in R\)
For all such \((a, b) \in R\) and \((b, c) \in R\) \(\Rightarrow(a, c) \in R\)
Hence \(R\) is transitive. -
Question 30 of 73
30. Question
Let \(R=\{(3,3)(5,5),(9,9),(12,12),(5,12),(3,9),(3,12),(3,5)\}\) be a relation on the set \(A=\{3,5,9,12\}\). Then, \(R\) is : [Online April 22, 2013]
CorrectIncorrectHint
(d) Let \(R =\{(3,3),(5,5),(9,9),(12,12),(5,12),(3,9),(3,12)\), \((3,5)\}\) be a relation on set
\(
A=\{3,5,9,12\}
\)
Clearly, every element of \(A\) is related to itself. Therefore, it is a reflexive.
Now, \(R\) is not symmetry because 3 is related to 5 but 5 is not related to 3 .
Also \(R\) is transitive relation because it satisfies the property that if \(a R b\) and \(b R c\) then \(a R c\). -
Question 31 of 73
31. Question
Let \(A=\{1,2,3,4\}\) and \(R: A \rightarrow A\) be the relation defined by \(R=\{(1,1),(2,3),(3,4),(4,2)\}\). The correct statement is : [Online April 9, 2013]
CorrectIncorrectHint
(c) Domain \(=\{1,2,3,4\}\)
Range \(=\{1,2,3,4\}\)
\(\therefore \quad\) Domain \(=\) Range
Hence the relation \(R\) is onto function. -
Question 32 of 73
32. Question
If \(P(S)\) denotes the set of all subsets of a given set \(S\), then the number of one-to-one functions from the set \(S=\{1,2,3\}\) to the set \(P(S)\) is [Online May 19, 2012]
CorrectIncorrectHint
(c) Let \(S=\{1,2,3\} \Rightarrow n(S)=3\)
Now, \(P(S)=\) set of all subsets of \(S\) total no. of subsets \(=2^3=8\)
\(
\therefore n[P(S)]=8
\)
Now, number of one-to-one functions from \(S \rightarrow P\left(S^{\prime}\right)\) is
\(
{ }^8 P_3=\frac{8!}{5!}=8 \times 7 \times 6=336 .
\) -
Question 33 of 73
33. Question
If \(A=\left\{x \in z^{+}: x<10\right.\) and \(x\) is a multiple of 3 or 4\(\}\), where \(z^{+}\) is the set of positive integers, then the total number of symmetric relations on \(A\) is [Online May 12, 2012]
CorrectIncorrectHint
(b) A relation on a set \(A\) is said to be symmetric if \((a, b) \in A \Rightarrow(b, a) \in A, \forall a, b \in A\)
Here \(A=\{3,4,6,8,9\}\)
Number of order pairs of \(A \times A=5 \times 5=25\)
Divide 25 order pairs of \(A \times A\) in 3 parts as follows :
Part \(-A:(3,3),(4,4),(6,6),(8,8),(9,9)\)
Part \(-B:(3,4),(3,6),(3,8),(3,9),(4,6)\), \((4,8),(4,9),(6,8),(6,9),(8,9)\)
Part \(-C:(4,3),(6,3),(8,3),(9,3),(6,4),(8,4),(9,4)\), \((8,6),(9,6),(9,8)\)
In part \(-A\), both components of each order pair are same.
In part \(-B\), both components are different but not two such order pairs are present in which first component of one order pair is the second component of another order pair and vice-versa.
In part- \(C\), only reverse of the order pairs of part \(-B\) are present i.e., if \((a, b)\) is present in part \(-B\), then \(( b , a )\) will be present in part \(-C\)
For example \((3,4)\) is present in part \(-B\) and \((4,3)\) present in part \(-C\).
Number of order pair in \(A, B\) and \(C\) are 5, 10 and 10 respectively.
In any symmetric relation on set \(A\), if any order pair of part \(-B\) is present then its reverse order pair of part \(-C\) will must be also present.
Hence number of symmetric relation on set \(A\) is equal to the number of all relations on a set \(D\), which contains all the order pairs of part \(-A\) and part- \(B\).
Now \(n(D)=n(A)+n(B)=5+10=15\)
Hence number of all relations on set \(D=(2)^{15}\)
\(\Rightarrow\) Number of symmetric relations on set \(D=(2)^{15}\) -
Question 34 of 73
34. Question
Let \(R\) be the set of real numbers. [JEE Main 2011]
Statement-1: \(A=\{(x, y) \in R \times R: y-x\) is an integer \(\}\) is an equivalence relation on \(R\).
Statement-2: \(B=\{(x, y) \in R \times R: x=\alpha y\) for some rational number \(\alpha\}\) is an equivalence relation on \(R\).CorrectIncorrectHint
(a) Let for statement 1: \(x R y=x-y \in I\). As \(x R x\) is an integer and \(y R x\) as well as \(x R z\) (for \(x R y\) and \(y R z\) ) is also an integer.
Hence equivalence.
Similarly as \(x=\alpha y\) hence \(\alpha=1\) for reflexive and \(\frac{1}{\alpha}\) being a rational for symmetric for some non zero \(\alpha\) and product of rationals also being rational \(\Rightarrow\) equivalence But not symmetric because of \(\alpha=0\) case Both relations are equivalence but not the correct explanation. -
Question 35 of 73
35. Question
Consider the following relations:
\(R =\{(x, y) \mid x, y\) are real numbers and \(x=w y\) for some rational number \(w\}\)
\(S=\left\{\left.\left(\frac{m}{n}, \frac{p}{q}\right) \right\rvert\, m, n, p\right.\) and \(q\) are integers such that \(n, q \neq 0\)
and \(q m=p n\}\). Then [JEE 2010]CorrectIncorrectHint
(b)
\(S\) is an equivalence relation but \(R\) is not an equivalence relation
Step 1. Check the relation \(R\) :
\(R=\{(x, y) \mid x, y\) are real numbers and \(x=w y\) for some rational number \(w\}\);
We have \((x, x) \in R\) for \(w=1\) implying that \(R\) is reflexive. For \(a \neq 0,(a, 0) \notin R\) for any \(w\) but \((0, a) \in R\). Thus \(R\) is not symmetric i.e. \(x R y\) need not implies \(y R x\). Thus, \(R\) is not an equivalence relation
Step2. Check the relation S:
\(S=\left\{\left(\frac{m}{n}, \frac{p}{q}\right)\right\}: m, n, p\) and \(q\) are integers such that \(n, q \neq 0\) and \(\left.q m=p n\right\}\). As \(\left(\frac{m}{n}, \frac{m}{n}\right) \in S\) since \(m n=m n, S\) is reflexive.
\(
\left(\frac{m}{n}, \frac{p}{q}\right) \in S \Rightarrow q m=p n .
\)
But this can be written as \(n p=m q\), giving \(\left(\frac{p}{q}, \frac{m}{n}\right) \in S\). Thus \(S\) is symmetric.
Again \(\left(\frac{m}{n}, \frac{p}{q}\right) \in S,\left(\frac{p}{q}, \frac{a}{b}\right) \in S\)
means \(q m=p n\) and \(b q=a q\).
Thus \(\left(\frac{m}{n}, \frac{a}{b}\right) \in S\)
This means \(S\) is transitive. -
Question 36 of 73
36. Question
Let \(R\) be the real line. Consider the following subsets of the plane \(R \times R\) :
\(S=\{(x, y): y=x+1\) and \(0<x<2\}\)
\(T=\{(x, y): x-y\) is an integer \(\}\),
Which one of the following is true? [JEE 2008]CorrectIncorrectHint
(d) Given \(S=\{(x, y): y=x+1\) and \(0<x<2\}\)
\(\because x \neq x+1\) for any \(x \in(0,2)\)
\(\Rightarrow(x, x) \notin S\)
\(\therefore S\) is not reflexive.
Hence \(S\) in not an equivalence relation.
Also \(T=\{(x, y): x-y\) is an integer \(\}\)
\(\because x-x=0\) is an integer \(\forall x \in R\)
\(\therefore T\) is reflexive.
If \(x-y\) is an integer then \(y-x\) is also an integer
\(\therefore T\) is symmetric
If \(x-y\) is an integer and \(y-z\) is an integer then \((x-y)+(y-z)=x-z\) is also an integer.
\(\therefore T\) is transitive -
Question 37 of 73
37. Question
Let \(W\) denote the words in the English dictionary. Define the relation \(R\) by \(R=\{(x, y) \in W \times W \mid\) the words \(x\) and \(y\) have at least one letter in common. \(\}\) Then \(R\) is [JEE 2006]
CorrectIncorrectHint
(b) Clearly \((x, x) \in R \forall x \in W\). So \(R\) is reflexive.
Let \((x, y) \in R\), then \((y, x) \in R\) as \(x\) and \(y\) have at least one letter in common. So, \(R\) is symmetric.
But \(R\) is not transitive for example
Let \(x=\) INDIA, \(y=\) BOMBAY and \(z=\) JOKER
then \((x, y) \in R(A\) is common) and \((y, z) \in R \quad(O\) is common) but \((x, z) \notin R\). (as no letter is common) -
Question 38 of 73
38. Question
Let \(R=\{(3,3),(6,6),(9,9),(12,12),(6,12),(3,9)\), \((3,12),(3,6)\}\) be a relation on the set \(A=\{3,6,9,12\}\). The relation is [JEE 2005]
CorrectIncorrectHint
\(
\begin{aligned}
& \text { (a) Reflexive and transitive only. } \\
& \text { e.g. }(3,3),(6,6),(9,9),(12,12) \text { [Reflexive] } \\
& (3,6),(6,12),(3,12)[\text { Transitive }] . \\
& (3,6) \in R \text { but }(6,3) \notin R[\text { non symmetric }]
\end{aligned}
\) -
Question 39 of 73
39. Question
Let \(f:(-1,1) \rightarrow B\), be a function defined by \(f(x)=\tan ^{-1} \frac{2 x}{1-x^2}\), then \(f\) is both one – one and onto when \(B\) is the interval [JEE 2005]
CorrectIncorrectHint
(d) Given \(f(x)=\tan ^{-1}\left(\frac{2 x}{1-x^2}\right)=2 \tan ^{-1} x\) for \(x \in(-1,1)\)
If \(x \in(-1,1) \Rightarrow \tan ^{-1} x \in\left(\frac{-\pi}{4}, \frac{\pi}{4}\right)\)
\(
\Rightarrow 2 \tan ^{-1} x \in\left(\frac{-\pi}{2}, \frac{\pi}{2}\right)
\)
Clearly, range of \(f(x)=\left(-\frac{\pi}{2}, \frac{\pi}{2}\right)\)
For \(f\) to be onto, codomain \(=\) range
\(\therefore\) Co-domain of function \(=B=\left(-\frac{\pi}{2}, \frac{\pi}{2}\right)\). -
Question 40 of 73
40. Question
Let \(R=\{(1,3),(4,2),(2,4),(2,3),(3,1)\}\) be a relation on the set \(A=\{1,2,3,4\}\).. The relation \(R\) is [JEE 2004]
CorrectIncorrectHint
(c) \(\because(1,1) \notin R \Rightarrow R\) is not reflexive \((2,3) \in R\) but \((3,2) \notin R\)
\(\therefore R\) is not symmetric -
Question 41 of 73
41. Question
If \(f: R \rightarrow S\), defined by \(f(x)=\sin x-\sqrt{3} \cos x+1\), is onto, then the interval of \(S\) is [JEE 2004]
CorrectIncorrectHint
(a) \(f(x)\) is onto \(\quad \therefore S=\) range of \(f(x)\)
\(
\begin{aligned}
& \text { Now } f(x)=\sin x-\sqrt{3} \cos x+1 \\
& =2 \sin \left(x-\frac{\pi}{3}\right)+1 \\
& \because-1 \leq \sin \left(x-\frac{\pi}{3}\right) \leq 1 \\
& -1 \leq 2 \sin \left(x-\frac{\pi}{3}\right)+1 \leq 3 \\
& \therefore f(x) \in[-1,3]=S
\end{aligned}
\)Alternate Solution:
We know that
\(
\begin{aligned}
& -\sqrt{a^2+b^2} \leq a \sin \theta+b \cos \theta \leq \sqrt{a^2+b^2} \\
& \therefore-2 \leq \sin x-\sqrt{3} \cos x \leq 2 \\
& \Rightarrow-1 \leq \sin x-\sqrt{3} \cos x+1 \leq 3 \\
& \therefore f(x) \in[-1,3]
\end{aligned}
\) -
Question 42 of 73
42. Question
A function \(f\) from the set of natural numbers to integers defined by [JEE 2003]
\(
f(n)=\left\{\begin{array}{l}
\frac{n-1}{2}, \text { when } n \text { is odd } \\
-\frac{n}{2}, \text { when } n \text { is even }
\end{array}\right. \text { is }
\)CorrectIncorrectHint
(d) We have \(f: N \rightarrow I\)
If \(x\) and \(y\) are two even natural numbers, then \(f(x)=f(y) \Rightarrow \frac{-x}{2}=\frac{-y}{2} \Rightarrow x=y\)
Again if \(x\) and \(y\) are two odd natural numbers then
\(
f(x)=f(y) \Rightarrow \frac{x-1}{2}=\frac{y-1}{2} \Rightarrow x=y
\)
\(\therefore f\) is onto.
Also each negative integer is an image of even natural number and each positive integer is an image of odd natural number.
\(\therefore f\) is onto.
Hence \(f\) is one one and onto both. -
Question 43 of 73
43. Question
Let \(f(x)=2^{10} \cdot x+1\) and \(g(x)=3^{10} \cdot x-1\). If \((f \circ g)(x)=x\), then \(x\) is equal to: [Online April 8, 2017]
CorrectIncorrectHint
\(
\begin{array}{ll}
\text { (d) } & f(g(x))=x \\
\Rightarrow & f\left(3^{10} x-1\right)=2^{10}\left(3^{10} \cdot x-1\right)+1=x \\
\Rightarrow & 2^{10}\left(3^{10} x-1\right)+1=x \\
\Rightarrow & x\left(6^{10}-1\right)=2^{10}-1 \\
\Rightarrow & x=\frac{2^{10}-1}{6^{10}-1}=\frac{1-2^{-10}}{3^{10}-2^{-10}}
\end{array}
\) -
Question 44 of 73
44. Question
For \(x \in R, x \neq 0\), let \(f_0(x)=\frac{1}{1-x}\) and \(f_{n+1}(x)=f_0\left(f_n(x)\right)\), \(n=0,1,2, \ldots\). Then the value of \(f_{100}(3)+f_1\left(\frac{2}{3}\right)+f_2\left(\frac{3}{2}\right)\) is equal to : [Online April 9, 2016]
CorrectIncorrectHint
\(
\begin{aligned}
& f_1(x)=f_{0+1}(x)=f_0\left(f_0(x)\right)=\frac{1}{1-\frac{1}{1-x}}=\frac{x-1}{x} \\
& f_2(x)=f_{1+1}(x)=f_0\left(f_1(x)\right)=\frac{1}{1-\frac{x-1}{x}}=x \\
& f_3(x)=f_{2+1}(x)=f_0\left(f_2(x)\right)=f_0(x)=\frac{1}{1-x} \\
& f_4(x)=f_{3+1}(x)=f_0\left(f_3(x)\right)=\frac{x-1}{x}
\end{aligned}
\)
\(
\begin{aligned}
\therefore f_0=f_3=f_6=\ldots \ldots \ldots . & =\frac{1}{1-x} \\
f_1=f_4=f_7=\ldots \ldots \ldots . & =\frac{x-1}{x} \\
f_2=f_5=f_8=\ldots \ldots \ldots . . & =x
\end{aligned}
\)
\(
f_{100}(3)=\frac{3-1}{3}=\frac{2}{3} f_1\left(\frac{2}{3}\right)=\frac{\frac{2}{3}-1}{\frac{2}{3}}=-\frac{1}{2}
\)
\(
\begin{aligned}
& f_2\left(\frac{3}{2}\right)=\frac{3}{2} \\
\therefore \quad & f_{100}(3)+f_1\left(\frac{2}{3}\right)+f_2\left(\frac{3}{2}\right)=\frac{5}{3}
\end{aligned}
\) -
Question 45 of 73
45. Question
If \(g\) is the inverse of a function \(f\) and \(f^{\prime}(x)=\frac{1}{1+x^5}\), then \(g^{\prime}(x)\) is equal to: [JEE Main 2014]
CorrectIncorrectHint
(b) Since \(f(x)\) and \(g(x)\) are inverse of each other
\(
\begin{aligned}
& \therefore g^{\prime}(f(x))=\frac{1}{f^{\prime}(x)} \\
& \Rightarrow g^{\prime}(f(x))=1+x^5 \quad\left(\because f^{\prime}(x)=\frac{1}{1+x^5}\right)
\end{aligned}
\)
\(
\begin{aligned}
& \text { Here } x=g(y) \\
& \therefore \quad g^{\prime}(y)=1+[g(y)]^5 \\
& \Rightarrow g^{\prime}(x)=1+(g(x))^5
\end{aligned}
\) -
Question 46 of 73
46. Question
Let \(A\) and \(B\) be non empty sets in \(R\) and \(f: A \rightarrow B\) is a bijective function. [Online May 26, 2012]
Statement 1: \(f\) is an onto function.
Statement 2: There exists a function \(g: B \rightarrow A\) such that fog \(=I_B\).CorrectIncorrectHint
(d) Let \(A\) and \(B\) be non-empty sets in \(R\).
Let \(f: A \rightarrow B\) is bijective function.
Clearly statement – 1 is true which says that \(f\) is an onto function.
Statement – 2 is also true statement but it is not the correct explanation for statement-1 -
Question 47 of 73
47. Question
Let \(f\) be a function defined by
\(
f(x)=(x-1)^2+1(x \geq 1) \text {. }
\)
Statement -1 : The set \(\left\{x: f(x)=f^{-1}(x)\right\}=\{1,2\}\).
Statement-2: \(f\) is a bijection and \(f^{-1}(x)=1+\sqrt{x-1}, x \geq 1\). [JEE 2011]CorrectIncorrectHint
(a) \(f(x)=(x-1)^2+1, x \geq 1\)
Since \(f\) is a bijective function
\(
\begin{aligned}
& \therefore \quad f:[1, \infty) \rightarrow[1, \infty) \\
& \Rightarrow \quad y=(x-1)^2+1 \Rightarrow(x-1)^2=y-1 \\
& \Rightarrow x=1 \pm \sqrt{y-1} \Rightarrow f^{-1}(y)=1 \pm \sqrt{y-1} \\
& \Rightarrow f^{-1}(x)=1+\sqrt{x-1}\{\therefore x \geq 1\}
\end{aligned}
\)
Hence statement-2 is correct
Now \(f(x)=f^{-1}(x)\)
\(
\begin{aligned}
& \Rightarrow f(x)=x \Rightarrow(x-1)^2+1=x \\
& \Rightarrow x^2-3 x+2=0 \Rightarrow x=1,2
\end{aligned}
\)
Hence statement-1 is correct -
Question 48 of 73
48. Question
Let \(f(x)=(x+1)^2-1, x \geq-1\)
Statement -1 : \(\text { The set }\{\mathbf{x}: \mathbf{f}(\mathbf{x})=\mathbf{f}^{-1}(\mathbf{x})\}=\{0,-1\} \text {. }\)
Statement-2 : \(f\) is a bijection. [JEE 2009]CorrectIncorrectHint
(b) Given that \(f(x)=(x+1)^2-1, x \geq-1\)
Clearly \(D _{ f }=[-1, \infty)\) but co-domain is not given.
Therefore \(f(x)\) need not be necessarily onto.
But if \(f(x)\) is onto then as \(f(x)\) is one one also, \((x+1)\) being something \(+ ve\),
\(f^{-1}(x)\) will exist where
\(
\begin{aligned}
& (x+1)^2-1=y \\
& \Rightarrow x+1=\sqrt{y+1}
\end{aligned}
\)
(+ve square root as \(x+1 \geq 0\) )
\(
\begin{aligned}
& \Rightarrow x=-1+\sqrt{y+1} \\
& \Rightarrow f^{-1}(x)=\sqrt{x+1}-1
\end{aligned}
\)
Then \(f(x)=f^{-1}(x)\)
\(
\begin{aligned}
& \Rightarrow(x+1)^2-1=\sqrt{x+1}-1 \\
& \Rightarrow(x+1)^2=\sqrt{x+1} \Rightarrow(x+1)^4=(x+1) \\
& \Rightarrow(x+1)\left[(x+1)^3-1\right]=0 \Rightarrow x=-1,0
\end{aligned}
\)
\(\therefore\) The statement- 1 is correct but statement- 2 is false. -
Question 49 of 73
49. Question
Let \(f: N \rightarrow Y\) be a function defined as \(f(x)=4 x+3\) where \(Y=\{y\) \(\in N: y=4 x+3\) for some \(x \in N\}\). Show that \(f\) is invertible and its inverse is [JEE 2008]
CorrectIncorrectHint
(d) Clearly \(f\) is one one and onto, so invertible
Also \(f( x )=4 x+3=y\)
\(
\Rightarrow x=\frac{y-3}{4} \quad \therefore g(y)=\frac{y-3}{4}
\) -
Question 50 of 73
50. Question
Let \(A=\{1,2,3, \ldots 20\}\). Let \(R_1\) and \(R_2\) two relation on \(A\) such that
\(R _1=\{( a , b ): b\) is divisible by \(a \}\)
\(R _2=\{( a , b ): a\) is an integral multiple of \(b \}\).
Then, number of elements in \(R_1-R_2\) is equal to [JEE Main 2024 1st Feb Shift 1]CorrectIncorrectHint
(c)
\(
n\left(R_1\right)=20+10+6+5+4+3+2+2+2+2+\underbrace{1+\ldots+1}_{10 \text { times }}
\)
\(
\begin{aligned}
& n \left( R _1\right)=66 \\
& R _1 \cap R _2=\{(1,1),(2,2), \ldots(20,20)\}
\end{aligned}
\)
\(
\begin{aligned}
& n \left( R _1 \cap R _2\right)=20 \\
& n \left( R _1- R _2\right)= n \left( R _1\right)- n \left( R _1 \cap R _2\right) \\
& = n \left( R _1\right)-20 \\
& =66-20 \\
& n \left( R _1- R _2\right)=46 \text { Pair }
\end{aligned}
\) -
Question 51 of 73
51. Question
Consider the relations \(R_1\) and \(R_2\) defined as \(a R_1 b \Leftrightarrow a^2+b^2=1\) for all \(a, b, \in R\) and \((a, b) R_2(c, d)\) \(\Leftrightarrow a+d=b+c\) for all \((a, b),(c, d) \in N \times N\). Then [JEE Main 2024 1st Feb Shift 2]
CorrectIncorrectHint
\(
\begin{aligned}
& a R_1 b \Leftrightarrow a^2+b^2=1 ; a, b \in R \\
& (a, b) R_2(c, d) \Leftrightarrow a+d=b+c ;(a, b),(c, d) \in N
\end{aligned}
\)
for \(R_1:\) Not reflexive symmetric not transitive
for \(R_2: R_2\) is reflexive, symmetric and transitive Hence only \(R_2\) is equivalence relation. -
Question 52 of 73
52. Question
Let \(S=\{1,2,3, \ldots, 10\}\). Suppose \(M\) is the set of all the subsets of \(S\), then the relation \(R =\{( A , B ): A \cap B \neq \phi ; A , B \in M \}\) is : [JEE Main 2024 27th Jan Shift 1]
CorrectIncorrectHint
Let \(S=\{1,2,3, \ldots, 10\}\)
\(
R =\{( A , B ): A \cap B \neq \phi ; A , B \in M \}
\)
For Reflexive,
\(M\) is subset of ‘ \(S^{\prime}\)
So \(\phi \in M\)
for \(\phi \cap \phi=\phi\)
\(\Rightarrow\) but relation is \(A \cap B \neq \phi\)
So it is not reflexive.
For symmetric,
\(
\begin{array}{ll}
\text { ARB } & A \cap B \neq \phi, \\
\Rightarrow BRA & \Rightarrow B \cap A \neq \phi,
\end{array}
\)
So it is symmetric.
For transitive,
\(
\begin{gathered}
\text { If } A=\{(1,2),(2,3)\} \\
B=\{(2,3),(3,4)\} \\
C=\{(3,4),(5,6)\}
\end{gathered}
\)
ARB & BRC but A does not relate to C
So it not transitive -
Question 53 of 73
53. Question
Let \(R\) be a relation on \(Z \times Z\) defined by \((a, b) R(c, d)\) if and only if ad \(-b c\) is divisible by 5 . Then \(R\) is [JEE Main 2024 29th Jan Shift 1]
CorrectIncorrectHint
\(( a , b ) R ( a , b )\) as \(ab – ab =0\)
Therefore reflexive
Let \((a, b) R(c, d) \Rightarrow a d-b c\) is divisible by \(5 \Rightarrow bc –\) ad is divisible by \(5 \Rightarrow( c , d ) R ( a , b )\)
Therefore symmetric
Relation not transitive as \((3,1) R (10,5)\) and
\((10,5) R (1,1)\) but \((3,1)\) is not related to \((1,1)\) -
Question 54 of 73
54. Question
If \(R\) is the smallest equivalence relation on the set \(\{1,2,3,4\}\) such that \(\{(1,2),(1,3)\} \subset R\), then the number of elements in \(R\) is [JEE Main 2024 29th Jan Shift 2]
CorrectIncorrectHint
Given set \(\{1,2,3,4\}\)
Minimum order pairs are
\(
\begin{aligned}
& (1,1),(2,2),(3,3),(4,4),(3,1),(2,1),(2,3),(3,2), \\
& (1,3),(1,2)
\end{aligned}
\)
Thus no. of elements \(=10\) -
Question 55 of 73
55. Question
A group of 40 students appeared in an examination of 3 subjects – Mathematics, Physics & Chemistry. It was found that all students passed in at least one of the subjects, 20 students passed in Mathematics, 25 students passed in Physics, 16 students passed in Chemistry, at most 11 students passed in both Mathematics and Physics, at most 15 students passed in both Physics and Chemistry, at most 15 students passed in both Mathematics and Chemistry. The maximum number of students passed in all the three subjects is [JEE Main 2024 30th Jan Shift 1]
CorrectIncorrectHint
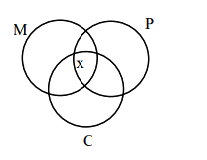
\(11-x \geq 0\) (Maths and Physics)
\(
x \leq 11
\)
\(x=11\) does not satisfy the data.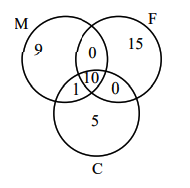
For \(x=10\)
Hence maximum number of students passed in all the three subjects is 10. -
Question 56 of 73
56. Question
The number of symmetric relations defined on the set \(\{1,2,3,4\}\) which are not reflexive is [JEE Main 2024 30th Jan Shift 2]
CorrectIncorrectHint
Total number of relation both symmetric and reflexive \(=2^{\frac{n^2-n}{2}}\)
Total number of symmetric relation \(=2^{\left(\frac{n^2+n}{2}\right)}\)
\(\Rightarrow\) Then number of symmetric relation which are not reflexive
\(
\begin{aligned}
\Rightarrow & 2^{\frac{n(n+1)}{2}}-2^{\frac{n(n-1)}{2}} \\
\Rightarrow & 2^{10}-2^6 \\
\Rightarrow & 1024-64 \\
& =960
\end{aligned}
\) -
Question 57 of 73
57. Question
Let \(A=\{1,2,3,4\}\) and \(R=\{(1,2),(2,3),(1,4)\}\) be a relation on \(A\). Let \(S\) be the equivalence relation on \(A\) such that \(R \subset S\) and the number of elements in \(S\) is \(n\). Then, the minimum value of \(n\) is [JEE Main 2024 31st Jan Shift 1]
CorrectIncorrectHint
\(
\begin{aligned}
& A=\{1,2,3,4\} \\
& R=\{(1,2)(2,3)(1,4)\}
\end{aligned}
\)
For equivalence relation, relation must be reflexive, symmetric & transitive
\(
\begin{aligned}
& R=\{(1,1)(2,2)(3,3)(4,4)(1,2)(2,1)(2,3) \\
& (3,2)(1,4)(4,1)(1,3)(3,1)(2,4)(4,2)(4,3)(3,4)\}
\end{aligned}
\)
All elements are included
\(\therefore\) Answer is 16. -
Question 58 of 73
58. Question
Let \(A=\{1,2,3, \ldots \ldots \ldots 100\}\). Let \(R\) be a relation on \(A\) defined by \((x, y) \in R\) if and only if \(2 x=3 y\). Let \(R_1\) be a symmetric relation on \(A\) such that \(R \subset R _1\) and the number of elements in \(R _1\) is \(n\). Then, the minimum value of \(n\) is [JEE Main 2024 31st Jan Shift 2]
CorrectIncorrectHint
\(
\begin{aligned}
& A =\{1,2,3 \ldots 100\} \\
& R \Rightarrow 2 x=3 y \Rightarrow y=\frac{2 x}{3} \\
& R =\{(3,2),(6,4),(9,6) \ldots(99,66)\} \\
& n ( R )=33 \\
& R \subset R _1
\end{aligned}
\)
Now
\(
\begin{aligned}
& R _1=\{(3,2),(6,4),(9,6) \ldots(99,66) \\
&(2,3),(4,6),(6,9) \ldots(66,99)\}
\end{aligned}
\)
\(\Rightarrow\) minimum number of elements in \(R _1=66\) -
Question 59 of 73
59. Question
The relation \(R =\{( a , b ): \operatorname{gcd}( a , b )=1,2 a \neq b , a , b \in Z \}\) is: [JEE Main 2023 24th Jan Shift 1]
CorrectIncorrectHint
Reflexive : \((a, a) \Rightarrow \operatorname{gcd}\) of \((a, a)=1\)
Which is not true for every \(a \in Z\).
Symmetric:
Take \(a =2, b =1 \Rightarrow \operatorname{gcd}(2,1)=1\)
Also \(2 a =4 \neq b\)
Now when \(a =1, b =2 \Rightarrow \operatorname{gcd}(1,2)=1\)
Also now \(2 a =2= b\)
Hence \(a=2 b\)
\(\Rightarrow R\) is not Symmetric
Transitive:
Let \(a =14, b =19, c =21\)
\(\operatorname{gcd}(a, b)=1\)
\(\operatorname{gcd}(b, c)=1\)
\(\operatorname{gcd}(a, c)=7\)
Hence not transitive
\(\Rightarrow R\) is neither symmetric nor transitive. -
Question 60 of 73
60. Question
The minimum number of elements that must be added to the relation \(R =\{( a , b ),( b , c ),( b , d )\}\) on the set \(\{ a , b , c , d \}\) so that it is an equivalence relation, is [JEE Main 2023 24th Jan Shift 2]
CorrectIncorrectHint
(d) Given \(R =\{( a , b ),( b , c ),( b , d )\}\)
In order to make it equivalence relation as per given set, \(R\) must be
\(
\begin{aligned}
& \{(a, a),(b, b),(c, c),(d, d),(a, b),(b, a),(b, c),(c, b), \\
& (b, d),(d, b),(a, c),(a, d),(c, d),(d, c),(c, a),(d, a)\}
\end{aligned}
\)
Three already given so 13 more to be added. -
Question 61 of 73
61. Question
Let \(R\) be a relation defined on \(N\) as a \(R\) b is \(2 a+3 b\) is a multiple of \(5, a, b \in N\). Then \(R\) is [JEE Main 2023 29th Jan Shift 2]
CorrectIncorrectHint
(d) \(a R a \Rightarrow 5 a\) is multiple it 5
So reflexive
\(a R b \Rightarrow 2 a +3 b =5 \alpha\),
Now b R a
\(
2 b+3 a=2 b+\left(\frac{5 \alpha-3 b}{2}\right) \cdot 3
\)
\(
\begin{aligned}
& =\frac{15}{2} \alpha-\frac{5}{2} b=\frac{5}{2}(3 \alpha-b) \\
& =\frac{5}{2}(2 a+2 b-2 \alpha) \\
& =5(a+b-\alpha)
\end{aligned}
\)
Hence symmetric
\(aRb \quad \Rightarrow 2 a +3 b =5 \alpha\).
\(bRc \quad \Rightarrow 2 b +3 c =5 \beta\)
\(
\begin{aligned}
& \text { Now } \quad 2 a+5 b+3 c=5(\alpha+\beta) \\
& \Rightarrow 2 a+5 b+3 c=5(\alpha+\beta) \\
& \Rightarrow 2 a+3 c=5(\alpha+\beta-b) \\
& \Rightarrow a R c
\end{aligned}
\)
Hence relation is equivalence relation. -
Question 62 of 73
62. Question
The minimum number of elements that must be added to the relation \(R =\{( a , b ),( b , c )\}\) on the set \(\{ a , b , c \}\) so that it becomes symmetric and transitive is: [JEE Main 2023 30th Jan Shift 1]
CorrectIncorrectHint
For Symmetric \((a, b),(b, c) \in R\)
\(
\Rightarrow(b, a),(c, b) \in R
\)
For Transitive \((a, b),(b, c) \in R\)
\(
\Rightarrow(a, c) \in R
\)
Now
1. Symmetric
\(
\therefore(a, c) \in R \Rightarrow(c, a) \in R
\)
2. Transitive
\(
\begin{aligned}
& \therefore(a, b),(b, a) \in R \\
& \Rightarrow(a, a) \in R \&(b, c),(c, b) \in R \\
& \Rightarrow(b, b) \&(c, c) \in R
\end{aligned}
\)
\(\therefore\) Elements to be added
\(
\left\{\begin{array}{r}
(b, a),(c, b),(a, c),(c, a) \\
,(a, a),(b, b),(c, c)
\end{array}\right\}
\)
Number of elements to be added \(=7\) -
Question 63 of 73
63. Question
Let \(R\) be a relation on \(N \times N\) defined by ( \(a , b ) R\) \((c, d)\) if and only if \(ad ( b – c )= bc ( a – d )\). Then \(R\) is [JEE Main 2023 31st Jan Shift 1]
CorrectIncorrectHint
\((a, b) R(c, d) \Rightarrow a d(b-c)=b c(a-d)\)
Symmetric:
\(( c , d ) R ( a , b ) \Rightarrow cb ( d – a )= da ( c – b ) \Rightarrow \text { Symmetric }\)Reflexive:
\(
(a, b) R(a, b) \Rightarrow a b(b-a) \neq b a(a-b) \Rightarrow \text { Not reflexive }
\)
Transitive: \((2,3) R (3,2)\) and \((3,2) R (5,30)\)
but \(((2,3),(5,30)) \notin R \Rightarrow\) Not transitive -
Question 64 of 73
64. Question
Among the relations
\(
S=\left\{(a, b): a, b \in R -\{0\}, 2+\frac{a}{b}>0\right\}
\)
And \(T=\left\{(a, b): a, b \in R , a^2-b^2 \in Z\right\}\). [JEE Main 2023 31st Jan Shift 2]CorrectIncorrectHint
For relation \(T = a ^2- b ^2=- I\)
Then, (b, a) on relation \(R\)
\(
\Rightarrow b ^2- a ^2=- I
\)
\(\therefore T\) is symmetric
\(
\begin{aligned}
& S=\left\{(a, b): a, b \in R-\{0\}, 2+\frac{a}{b}>0\right\} \\
& 2+\frac{a}{b}>0 \Rightarrow \frac{a}{b}>-2, \Rightarrow \frac{b}{a}<\frac{-1}{2}
\end{aligned}
\)
If \((b, a) \in S\) then
\(2+\frac{ b }{ a }\) not necessarily positive
\(\therefore S\) is not symmetric -
Question 65 of 73
65. Question
Let \(R\) be a relation on
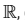 given by \(R=\{(a, b): 3 a-3 b+\sqrt{7}\) is an irrational number \(\}\). Then \(R\) is [JEE Main 2023 1st Feb Shift 1]CorrectIncorrect
given by \(R=\{(a, b): 3 a-3 b+\sqrt{7}\) is an irrational number \(\}\). Then \(R\) is [JEE Main 2023 1st Feb Shift 1]CorrectIncorrectHint
Check for reflexivity:
As \(3(a-a)+\sqrt{7}=\sqrt{7}\) which belongs to relation so relation is reflexive
Check for symmetric:
Take \(a =\frac{\sqrt{7}}{3}, b=0\)
Now \((a, b) \in R\) but \((b, a) \notin R\)
As \(3(b-a)+\sqrt{7}=0\) which is rational so relation is not symmetric.
Check for Transitivity:
Take (a, b) as \(\left(\frac{\sqrt{7}}{3}, 1\right)\)
\(\&( b , c )\) as \(\left(1, \frac{2 \sqrt{7}}{3}\right)\)
So now \(( a , b ) \in R~ \&( b , c ) \in R\) but \(( a , c ) \notin R\) which means relation is not transitive -
Question 66 of 73
66. Question
Let \(P ( S )\) denote the power set of \(S =\{1,2,3, \ldots, 10\}\). Define the relations \(R_1\) and \(R_2\) on \(P(S)\) as \(A R_1 B\) if \(\left(A \cap B^c\right) \cup\left(B \cap A^c\right)=\varnothing\) and \(A R_2 B\) if \(A \cup B^c=\) \(B \cup A ^{ c }, \forall A , B \in P ( S )\). Then : [JEE Main 2023 1st Feb Shift 2]
CorrectIncorrectHint
\(
\begin{aligned}
& S =\{1,2,3, \ldots \ldots 10\} \\
& P ( S )=\text { power set of } S \\
& AR _1 B \Rightarrow\left( A \cap B ^{ c }\right) \cup\left( A ^{ c } \cap B \right)=\phi
\end{aligned}
\)
\(R_1\) is reflexive, symmetric
For transitive
\(
\begin{aligned}
& \left( A \cap B ^{ c }\right) \cup\left( A ^{ c } \cap B \right)=\phi ;\{ a \}=\phi=\{ b \} A = B \\
& \Rightarrow A =\phi= B \text { or } A = B \\
& \left( B \cap C ^{ c }\right) \cup\left( B ^{ c } \cap C \right)=\phi \therefore B = C \text { or } B =\phi= C \\
& \therefore A = C \text { equivalence. }
\end{aligned}
\)
\(
R _2 \equiv A \cup B ^{ c }= A ^{ c } \cup B
\)
\(R _2 \rightarrow\) Reflexive, symmetric for transitive
\(
\begin{aligned}
& A \cup B ^{ c }= A ^{ c } \cup B \Rightarrow\{ a , c , d \}=\{ b , c , d \} \\
& \{ a \}=\{ b \} \therefore A = B \\
& B \cup C ^{ c }= B ^{ c } \cup C \Rightarrow B = C \\
& \therefore A = C \quad \therefore A \cup C ^{ c }= A ^{ c } \cup C \therefore \text { Equivalence }
\end{aligned}
\) -
Question 67 of 73
67. Question
Let \(A=\{x \in R:|x+1|<2\}\) and \(B=\{x \in R:|x-1| \geq 2\}\). Then which one of the following statements is NOT true? [JEE Main 2022 25th June Shift 2]
CorrectIncorrectHint
\(
\begin{aligned}
& A: x \in(-3,1) \quad B: x \in(-\infty,-1] \cup[3, \infty) \\
& B-A=(-\infty,-3] \cup[3, \infty)=R-(-3,3)
\end{aligned}
\) -
Question 68 of 73
68. Question
Let \(A=\{n \in N\) : H.C.F. \((n, 45)=1\}\) and
Let \(B=\{2 k: k \in\{1,2, \ldots, 100\}\}\). Then the sum of all the elements of \(A \cap B\) is [JEE Main 2022 26th June Shift 1]CorrectIncorrectHint
Sum of elements in \(A \cap B\)
\(
\begin{aligned}
= & \underbrace{(2+4+6+\ldots+200)}_{\text {Multiple of } 2}-\underbrace{(6+12+\ldots+198)}_{\text {Multiple of } 2 \& 3 \text { i.e. } 6} \\
& -\underbrace{(10+20+\ldots+200)}_{\text {Multiple of } 5 \& 2 \text { i.e. } 10}+\underbrace{(30+60+\ldots+180)}_{\text {Multiple of } 2.5 \text { & 3 i.e. } 30} \\
= & 5264
\end{aligned}
\) -
Question 69 of 73
69. Question
Let \(R_1\) and \(R_2\) be relations on the set \(\{1,2, \ldots, 50\}\) such that \(R _1=\left\{\left( p , p ^{ n }\right): p\right.\) is a prime and \(n \geq 0\) is an integer \(\}\) and \(R _2=\left\{\left( p , p ^{ n }\right): p\right.\) is a prime and \(n =0\) or 1\(\}\). Then, the number of elements in \(R _1- R _2\) is [JEE Main 2022 28th June Shift 1]
CorrectIncorrectHint
Here, \(p, p^n \in\{1,2, \ldots 50\}\)
Now \(p\) can take values
\(2,3,5,7,11,13,17,23,29,31,37,41,43\) and 47.
we can calculate no. of elements in \(R\), as
\(
\begin{aligned}
& \left(2,2^{\circ}\right),\left(2,2^1\right) . .\left(2,2^5\right) \\
& \left(3,3^{\circ}\right), \ldots\left(3,3^3\right) \\
& \left(5,5^{\circ}\right), \ldots\left(5,5^2\right) \\
& \left(7,7^{\circ}\right), \ldots\left(7,7^2\right) \\
& \left(11,11^{\circ}\right), \ldots\left(11,11^1\right)
\end{aligned}
\)
And rest for all other two elements each
\(
\therefore n\left(R_1\right)=6+4+3+3+(2 \times 10)=36
\)
Similarly for \(R_2\)
\(
\begin{aligned}
& \left(2,2^{\circ}\right),\left(2,2^1\right) \\
& \left(47,47^{\circ}\right),\left(47,47^1\right) \\
& \therefore n\left(R_2\right)=2 \times 14=28 \\
& \therefore n\left(R_1\right)-n\left(R_2\right)=36-28=8
\end{aligned}
\) -
Question 70 of 73
70. Question
Let \(R _1=\{( a , b ) \in N \times N :| a – b | \leq 13\}\) and \(R _2=\{( a , b ) \in N \times N :| a – b | \neq 13\}\). Then \(N :\) [JEE Main 2022 28th June Shift 2]
CorrectIncorrectHint
\(
R_1=\{(a, b) \in N \times N:|a-b| \leq 13\}
\)\(
R_2=\{(a, b) \in N \times N:|a-b| \neq 13\}
\)
For \(R _1\) :
(i) Reflexive relation
\(
(a, a) \in N \times N:|a-a| \leq 13
\)
(ii) Symmetric relation
\(
(a, b) \in R_1,(b, a) \in R_1:|b-a| \leq 13
\)
(iii) Transitive relation
\(
\begin{aligned}
& (a, b) \in R_1,(b, c) \in R_1,(a, c) \in R_1: \\
& (1,3) \in R_{1 .}(3,16) \in R_1 \text { but }(1,16) \notin R_1
\end{aligned}
\)
For \(R _2\) :
(i) Reflexive relation
\(
(a, a) \in N \times N:|a-a| \neq 13
\)
(ii) Symmetric relation
\(
(b, a) \in N \times N:|b-a| \neq 13
\)
(iii) Transitive relation
\(
\begin{aligned}
& (a, b) \in R_2,(b, c) \in R_2,(a, c) \in R_2 \\
& (1,3) \in R_{2,}(3,14) \in R_2 \text { but }(1,14) \notin R_2
\end{aligned}
\) -
Question 71 of 73
71. Question
Let \(a\) set \(A=A_1 \cup A_2 \cup \ldots \cup A_k\), where \(A_i \cap A_j=\phi\) for \(i \neq j 1 \leq i, j \leq k\). Define the relation \(R\) from \(A\) to \(A\) by \(R=\left\{(x, y): y \in A_i\right.\) if and only if \(\left.x \in A_i, 1 \leq i \leq k\right\}\). Then, \(R\) is : [JEE Main 2022 29th June Shift 1]
CorrectIncorrectHint
(d)
\(
R=\left\{(x, y): y \in A_i, \text { iff } x \in A_i 1 \leq i \geq k\right\}
\)
(1) Reflexive
\(
( a , a ) \Rightarrow a \in A_i \text { iff } a \in A_i
\)
(2) Symmetric
\(( a , b ) \Rightarrow a \in A_i\) iff \(b \in A_i\)
(b, a) \(\in R\) as \(b \in A_i\) iff \(a \in A_i\)
(3) Transitive
\(
\begin{aligned}
& ( a , b ) \in R \&( b , c ) \in R . \\
& \Rightarrow a \in A_i \text { iff } b \in A_i \& b \in A_i \text { iff } c \in A_i \\
& \Rightarrow a \in A_i \text { iff } c \in A_i \\
& \Rightarrow( a , c ) \in R . \\
& \Rightarrow \text { Relation is equivalence. }
\end{aligned}
\) -
Question 72 of 73
72. Question
The probability that a relation \(R\) from \(\{ x , y \}\) to \(\{ x , y \}\) is both symmetric and transitive, is equal to: [JEE Main 2022 29th June Shift 2]
CorrectIncorrectHint
(a) Total no. of relations \(=2^{2 \times 2}=16\)
Fav. relation \(=\phi,\{( x , x )\},\{( y , y )\},\{( x , x )( y , y )\},\)
\(
\{(x, x),(y, y),(x, y)(y, x)\}
\)
Prob. \(=\frac{5}{16}\) -
Question 73 of 73
73. Question
Define a relation \(R\) over a class of \(n \times n\) real matrices \(A\) and \(B\) as “ARB iff there exists a non-singular matrix \(P\) such that \(PAP ^{-1}= B ^{\prime \prime}\). Then which of the following is true? [JEE Main 2021 18th March Shift 2]
CorrectIncorrectHint
(c) A and \(B\) are matrices of \(n \times n\) order & ARB iff there exists a non singular matrix \(P (\operatorname{det}( P ) \neq 0)\) such that \(\operatorname{PAP}^{-1}= B\)
For reflexive \(ARA \Rightarrow PAP ^{-1}= A \dots(1)\) must be true
\(
\text { for } P = I , Eq .(1) \text { is true so ‘ } R \text { ‘ is reflexive; For symmetric } ARB \Leftrightarrow PAP ^{-1}= B \quad \ldots(1) \text { is true }
\)
\(
\text { for BRA iff } PBP ^{-1}= A \dots(2) \text { must be true } \because PAP ^{-1}= B
\)
\(
\begin{aligned}
& P ^{-1} PAP ^{-1}= P ^{-1} B \\
& IAP ^{-1} P = P ^{-1} BP \\
& A=P^{-1} B P \dots(3)
\end{aligned}
\)
from (2) & (3) \( PBP ^{-1}= P ^{-1} BP\)
can be true some \(P = P ^{-1} \Rightarrow P ^2= I (\operatorname{det}( P ) \neq 0)\)
So ‘ \(R\) ‘ is symmetric For transitive
\(ARB \Leftrightarrow PAP ^{-1}= B \ldots\) is true
\(BRC \Leftrightarrow PBP ^{-1}= C \ldots\) is true
now \(\operatorname{PPAP}^{-1} P ^{-1}= C\)
\(
P ^2 A \left( P ^2\right)^{-1}= C \Rightarrow ARC
\)
So ‘ \(R\) ‘ is transitive relation
\(\Rightarrow\) Hence \(R\) is equivalence